Теги: storia matematica i geni della matematica rba storia della matematica numeri naturali
ISBN: 2531-890X
Год: 2018
Текст
Diofanto
GENI
della
MATEMATICA
Il precursore
del linguaggio aritmetico
Diofanto
RBA
JOAN GÓMEZIURGELLÉS è professore titolare dell’Università Politecnica
della Catalogna, dottore in Pedagogia e divulgatore scientifico.
I geni della matematica
Pubblicazione periodica settimanale
Anno I - Numero 44 - Milano, 22 marzo 2018
Edita da RBA Italia
Via Gustavo Fara, 35 - 20124 Milano
Direttore generale: Andrea Ferdeghini
Responsabile editoriale: Anna Franchini
Responsabile marketing: Tiziana Mandameli
Direttore responsabile: Stefano Mammini
© 2016 Joan Gómez i Urgellés per il testo
© 2016 RBA Coleccionables, S.A.U.
© 2017 RBA Italia S.r.l. per la presente edizione
Impaginazione e adattamento: Lesteia, Milano
Traduzione: Vittoria Rinaldi
Copertina: Lorenç Marti
Progetto pagine interne: Luz de la Mora
Infografica: Joan Pejoan
Crediti fotografici: Alamy: 117; Archivo RBA: 21, 27, 43, 47, 7las, 71 ad, 83, 89,
99as, 125a, 144, 151as, 151ad; Klaus Bamer: 61; Daverdis: 99b; Didier Descouens:
71b; 123rtf: 23a, 23b, 151b; Shutterstock: 125b; Twice25: 99ad.
Registrazione presso il Tribunale di Milano n. 286 del 24/11/2016
Iscrizione al ROC n. 16647 in data 1/03/2008
ISSN 2531-890X
Distributore per l’Italia: Press-di Distribuzione
Stampa e Multimedia S.r.l. - 20090 Segrate (MI)
PI. Spa Sped, in abb. post. DL 353/2003 legge del 27/04/04 n. 46 art. 1
Stampato nel 2017 presso LIBERDUPLEX
Tutti i diritti riservati. Nessuna parte di questa pubblicazione
può essere riprodotta o diffusa senza il consenso dell’editore.
Sommario
INTRODUZIONE 7
CAPITOLO 1 Sulle orme di Diofanto: la matematica
nel mondo antico 15
CAPITOLO 2 Un approccio a\\Aritmetica 39
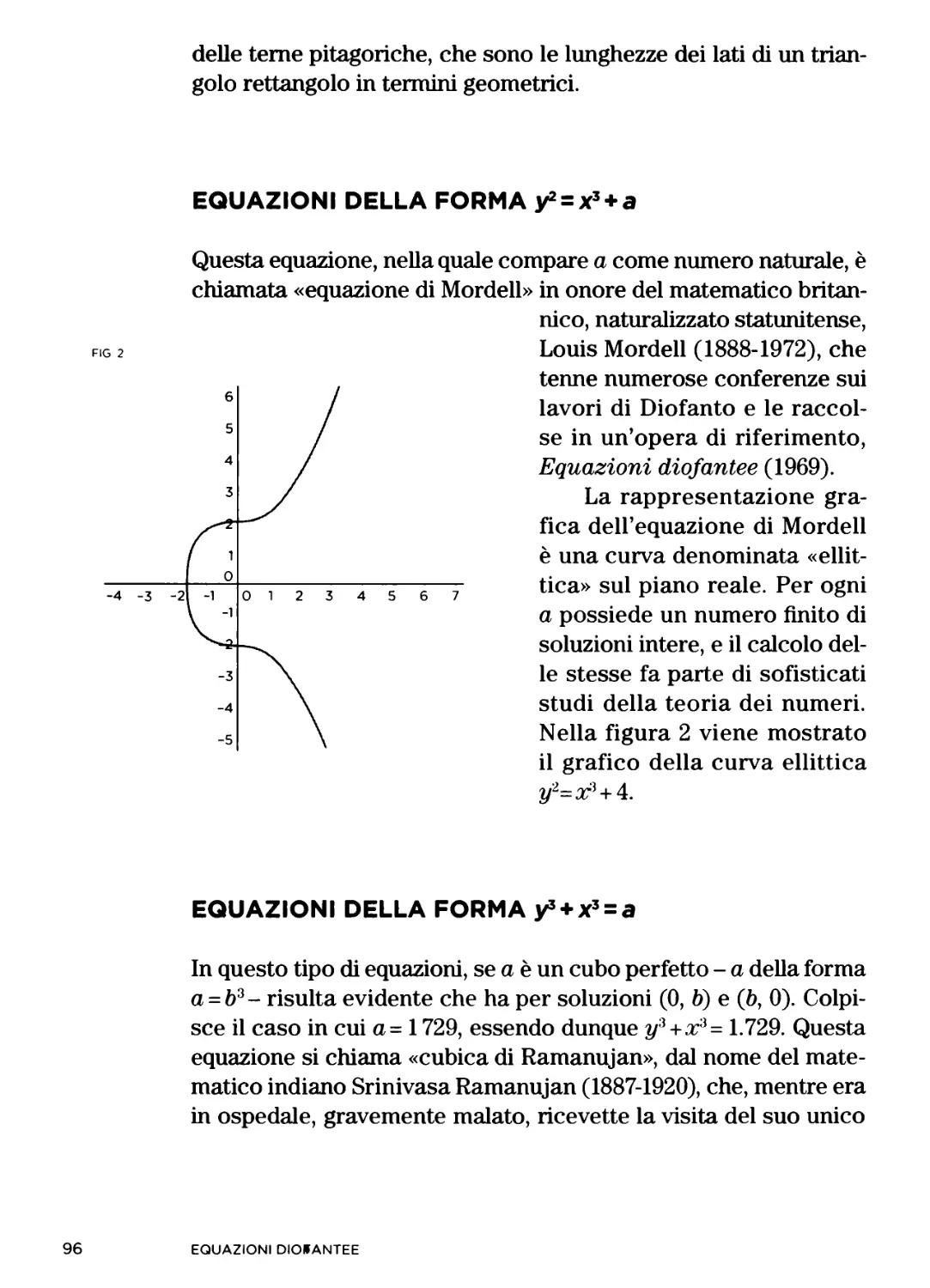
CAPITOLO 3 Equazioni diofantee 73
CAPITOLO 4 Problemi e soluzioni áe\YAritmetica 103
CAPITOLO 5 II lascito di Diofanto e la sua validità
nel xxi secolo 141
LETTURE CONSIGLIATE 155
INDICE 157
Introduzione
Diofanto è stato un personaggio enigmatico, della cui esistenza si
sa praticamente nulla, al di là del fatto che scrisse in greco, che
visse nel m secolo d.C. e che sviluppò le sue capacità matematiche
ad Alessandria. Non è un caso che questa città egiziana, fondata
da Alessandro Magno ed ellenizzata dai suoi successori, durante
l’Antichità si ergesse a capitale mondiale della conoscenza: il suo
celebre museo e la biblioteca, di una magnificenza quasi leggenda¬
ria, diedero un notevole impulso alle scienze e alle arti, e accolsero
i migliori eruditi dell’epoca, tra i quali anche alcuni dei più grandi
matematici della Grecia classica. Tra di loro si distinse partico¬
larmente Diofanto, il protagonista indiscusso di questa biografia.
La città egiziana, pertanto, farà da sfondo alla nostra storia, e in
particolare sarà il filo conduttore del primo capitolo. Si tratta di
un’equazione molto semplice e rivelatrice: non è possibile com¬
prendere Diofanto senza Alessandria, e Alessandria non può essere
del tutto compresa senza Diofanto.
La storiografia, con non poche difficoltà, è riuscita a delimitare
il periodo temporale compreso tra la nascita e la morte di Diofanto.
In realtà, si ritiene sia morto ottuagenario, che si sposò e che ebbe
un figlio, che purtroppo morì prima di lui. Tuttavia, nessuno di
questi dati, abilmente ottenuti mediante lo studio approfondito di
alcuni indizi nascosti, offre una certezza assoluta. Non si sa nulla
circa il suo aspetto fisico, sebbene sia probabile che portasse la
7
barba, e non si hanno neppure indicazioni circa la sua personalità.
Sebbene sappiamo che scriveva in greco, si ignora qualsiasi altro
aspetto della sua formazione intellettuale, perché fu citato in ma¬
niera vaga ed erratica negli scritti dei suoi contemporanei. E ciono¬
nostante, il lascito accademico di Diofanto ha lasciato un’impronta
decisiva per secoli. La ragione risiede nel fatto che fu l’autore di
un’opera fondamentale per la storia universale della matematica:
l’Aritmetica. Con essa, Diofanto ha rivoluzionato il sapere dell’e¬
poca, soprattutto per quanto riguarda la simbologia e la scrittura,
l’interpretazione dei concetti stabiliti e l’euristica nella risoluzione
di problemi, elementi che sono giunti fino ai giorni nostri.
Ad Alessandria, le scienze, e in particolare la matematica, fe¬
cero passi da gigante, dando luogo a un’esplosione del sapere, in
cui Diofanto ebbe un ruolo da protagonista. L’autore delXAritmetica
guidò il pensiero matematico dell’epoca, dato che non solo consolidò
il passaggio dalla tradizione all’innovazione, dalla geometria fino al
linguaggio simbolico, ma intuì anche la regola alla base dei segni dei
numeri negativi. Nel 275 d.C. si imbattè accidentalmente in radici di
numeri negativi, e si ritrovò ad avere a che fare con i numeri imma¬
ginari. In realtà, espose un problema dei triangoli nella cui soluzione
fa la sua timida comparsa la radice quadrata di -1. Non conoscendo
un numero qualsiasi che elevato al quadrato fosse uguale a quella
cifra, ritenne che il problema non avesse soluzione.
A differenza dei suoi contemporanei, Diofanto si distinse per
la metodologia usata per affrontare i problemi matematici, me¬
diante strumenti caratterizzati da una grande dose di creatività.
Senza dubbio, la cosa più sorprendente della sua opera fu il lin¬
guaggio matematico, assolutamente nuovo, ma anche la sua au¬
dacia nell’esporre e nel risolvere i problemi: senza l’ausilio della
geometria. Questo ramo della matematica fu per molti decenni al
centro dell’attenzione degli specialisti greci, soprattutto da quando
Euclide aveva pubblicato la sua opera principale, gli Elementi.
Perciò, uno dei meriti di Diofanto fu di cambiare questo scenario
di egemonia, spostando il dominio del linguaggio geometrico a
favore di quello algebrico. Prima de\Y Aritmetica, i «quadrati» e
i «cubi» erano considerati oggetti geometrici. Cioè, un quadrato
rappresentava la misura di una superficie, e un cubo la misura di un
8
INTRODUZIONE
volume. Risultava inconcepibile «sommare» un quadrato e un cubo.
Avrebbe significato sommare aree con volumi! Per gli antichi Greci,
l’operazione di addizione era definita solo da grandezze omogenee,
cioè i segmenti si sommavano con segmenti, le aree con le aree, e
non era quindi possibile sommare un segmento con un’area. La som¬
ma era considerata come un’operazione geometrica, e non come la
somma aritmetica di numeri corrispondenti. Si può affermare, con
questo, che Diofanto abbia «spogliato» la geometria.
Sebbene possa sembrare che i problemi dell’Aritmetica siano
mascherati da un linguaggio apparentemente geometrico, poiché
si chiede di trovare un triangolo, un quadrato ecc, in realtà non è
così. Diofanto considerò gli oggetti propri della matematica greca
come numeri naturali, e i loro rapporti (a differenza di Euclide, e
per la prima volta nella storia) come quelli che oggi sono cono¬
sciuti come «numeri razionali». Grazie a due tratti differenziali, il
linguaggio utilizzato e l’introduzione della simbologia, Diofanto ha
rappresentato un prima e un dopo nella scrittura dei testi mate¬
matici. La matematica greca, fino ad allora, non aveva avuto alcun
tipo di simbolismo speciale. Era una matematica «retorica», dove
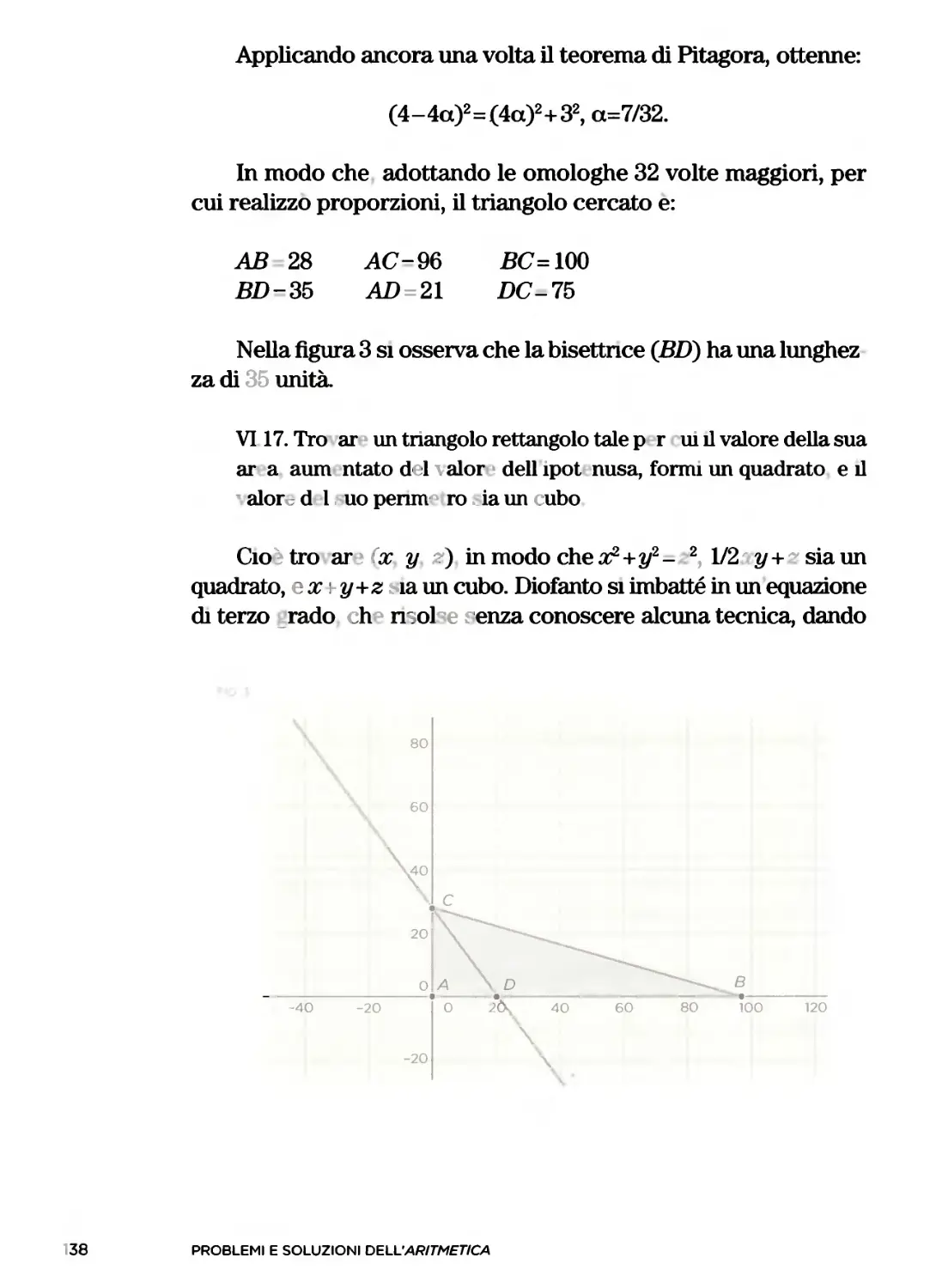
i problemi e le loro soluzioni erano decritti mediante il linguaggio
naturale, senza includere alcun simbolo, neppure nelle operazioni.
Diofanto introdusse quella che successivamente sarebbe divenu¬
ta nota come «notazione sincopata». Questa, a dispetto dei suoi
notevoli vantaggi algebrici, andò perduta immediatamente dopo
Diofanto. Sarebbe stato necessario attendere fino al Rinascimento,
dalla fine del xv secolo al xvn secolo, per recuperare, lentamente e
faticosamente, la nuova notazione algebrica. Il processo sarebbe
culminato nel 1637 con l’azione decisiva di Cartesio, che fissò la
notazione matematica attuale.
La maestria di Diofanto, pertanto, impregna tutta la storia del¬
la matematica. Il suo lascito, che è ancora oggi valido, diede origine
a diversi dibattiti circa la risoluzione di problemi e alle metodolo¬
gie, creando così altri problemi la cui soluzione richiese secoli per
essere trovata. Bachet de Méziriac, François Viète, Cartesio, Pierre
de Fermat, Joseph-Louis de Lagrange, Eulero..., l’elenco dei grandi
matematici che in ogni epoca hanno affrontato le sfide dell'Arit-
metica e si sono dedicati anima e corpo a trovare i loro metodi
INTRODUZIONE
9
generali di risoluzione risulta tanto esteso quanto sorprendente.
Non è un caso che l’ottavo problema del Libro II de\YAritmetica,
che chiede di scomporre un quadrato dato in due quadrati, abbia
ispirato in Fermat un teorema che ha richiesto oltre tre secoli per
essere risolto. Si tratta di alcuni problemi che, in onore dell’insigne
e singolare matematico alessandrino, sono ancora oggi noti come
«equazioni diofantee».
Non è necessario ricordare che sotto questo nome sono com¬
prese le equazioni indeterminate, che in generale possiedono un
numero infinito di soluzioni. Non è neppure necessario ricordare
che un’equazione indeterminata lineare (o di primo grado) ha la
forma ax + by + cz +... = n, prendendo a, b, c,n... come numeri in¬
teri e come incognite x, y, z... In maniera analoga, un esempio di
una equazione indeterminata non lineare è del tipo ax2 + by2 = c,
oppure del tipo ax + bx2 + cy] + dxy +... = 0, con a, b, c, d numeri
naturali. Le incognite sono di grado uno nell’equazione lineare,
cioè l’esponente è uno; da parte loro, le equazioni non lineari pos¬
siedono almeno un’incognita con esponente maggiore di uno. Per
capire l’opera di Diofanto è necessaria la comprensione di queste
equazioni, che acquisiscono una grande importanza in certi campi
dell’insegnamento e della ricerca matematica.
Una caratteristica dell 'Aritmetica è che non propone alcun te¬
orema, né alcuna definizione. I problemi qui presentati sono stati
debitamente selezionati, commentati ed esposti con le soluzioni
corrispondenti, sebbene in alcuni casi sia stato omesso il processo
di risoluzione per il suo elevato grado di difficoltà. In questo senso,
basti segnalare che la lista dei problemi matematici proposta da Da¬
vid Hilbert nel 1900 incluse anche una complessa sfida legata alle
equazioni diofantee. Il lettore più audace, tuttavia, può affrontare la
sfida e cercare di risolvere i problemi che sono stati scelti. Da parte
sua, il lettore meno abile comprenderà senza ostacoli la bellezza che
racchiudono gli stessi. L’obiettivo è che tutto ciò che viene affrontato
in queste pagine riveli le abilità mostrate da Diofanto e, a sua volta,
faccia conoscere l’euristica plasmata nei problemi dell'Aritmetica.
Gli scritti di Diofanto hanno attraversato una serie di vicissitu¬
dini storiche che, in alcuni casi, ne hanno comportato la scomparsa.
Così avvenne, per esempio, con i Porismi. Fortunatamente, 1 Aritme¬
10
INTRODUZIONE
tica e un trattato sui numeri poligonali furono riscattati dall’oblio in
Occidente, grazie a scoperte che possono solo essere definite felici,
e a varie brillanti traduzioni, come l’edizione canonica di Bachet de
Méziriac, arricchita da commenti e contributi matematici. Entrambi
i lavori hanno dimostrato che Diofanto è stato un pioniere nell’intro-
durre processi algebrici per la risoluzione di equazioni non lineari
indeterminate, e anche nell’uso di notazioni algebriche concrete ed
estese. Queste innovazioni hanno rappresentato un grande progres¬
so rispetto agli stili verbali dei suoi predecessori, e di molti dei suoi
successori. Si deve insistere, pertanto, sul fatto che il suo lascito non
si limita a che le equazioni diofantee abbiano fornito diverse appli¬
cazioni pratiche, come il loro utilizzo nella dittologia e nei moderni
sistemi di sicurezza (transazioni bancarie, carte di credito). La cosa
davvero essenziale è che antepose la risoluzione di problemi alle
considerazioni teoriche, e che la sua opera costituì, in definitiva, l’em¬
brione di un ramo attuale della matematica: la «teoria dei numeri».
In queste pagine verranno offerte al lettore alcune informazio¬
ni sulla vita di Diofanto e sulle principali nozioni delle sue opere,
con i problemi e le soluzioni pertinenti. Tutto ciò verrà mostrato
all’intemo di una visione della matematica che, sebbene trovi il suo
contesto nel mondo antico, verrà qui spiegata con un linguaggio
moderno, sempre in maniera semplice e divulgativa, senza trascu¬
rare nulla. Il lettore viaggerà attraverso una delle epoche d’oro
del sapere e conoscerà i suoi grandi protagonisti, da Archimede
a Euclide fino alla sfortunata Ipazia di Alessandria, passando per
Apollonio di Perga, Erone, Teone e tanti altri. Inoltre, potrà scopri¬
re come attraverso grandi opere di riferimento, come XAntologia
Palatina., sia possibile calcolare quanti anni visse Diofanto, quando
gli crebbe la barba e quando si sposò.
Il presente testo riunisce e presenta una grande quantità di
informazioni sparpagliate sull’opera di Diofanto, così come le prin¬
cipali ricerche che si sono sviluppate sulla sua vita. Il proposito è
di dare una visione globale e rigorosa. Perciò, il libro è strutturato
in cinque capitoli e parte con una panoramica generale sulla ma¬
tematica nel mondo ellenico classico, in un percorso che va dal m
secolo a.C. fino al m secolo d.C. Il secondo capitolo rappresenta un
approccio all Aritmetica, con le sue notevoli e proficue influenze
INTRODUZIONE
11
su altri matematici e sulla sua proiezione nelle scoperte matema¬
tiche successive. Quanto al terzo capitolo, l’elemento protagonista
è uno solo: le equazioni diofantee. In seguito, verranno presentati
i contenuti e gli esercizi di gran parte dell’Aritmetica e, infine,
si darà spazio alle applicazioni attuali del lascito matematico di
Diofanto e al testo che scrisse sui numeri poligonali, di indubbio
interesse. Questo libro presenta, dunque, un percorso strutturato
in diverse tappe, con aneddoti sul mondo della matematica. Inol¬
tre, le sue pagine si soffermano su alcuni aspetti epistemologici e
trasversali, che invitano a scoprire, in maniera piacevole, alcuni
concetti della conoscenza matematica. Diofanto sarà l’anfitrione
e la guida di una visione rivoluzionaria della matematica, dall’An¬
tichità fino al presente, con particolare attenzione ai contributi
di Bachet de Méziriac, Cartesio, Fermat e tanti altri matematici
di indiscusso valore. In realtà, tutti loro contribuirono a rendere
grande la figura di un saggio del m secolo d.C., che visse ad Ales¬
sandria, scrisse in greco, si dedicò alla permanente ricerca del
sapere e, con un talento e un’audacia degni di ammirazione, elevò
la matematica di un ulteriore gradino nella sua eterna corsa verso
la perfezione: Diofanto.
12
INTRODUZIONE
200-217 Periodo fissato dalla storiografia 1625 Albert Girard pubblica in parte i Libri V
per la nascita di Diofanto. e VI dell'Aritmetica in francese.
233-250 Data approssimativa in cui si sposò.
Si ritiene avesse trentatré anni.
238-255 Data approssimativa della nascita
di suo figlio. Aveva trentotto anni.
250 Anno stimato della pubblicazione della
sua opera maestra, l'Aritmetica, in greco.
275 Anno stimato del primo contatto di
Diofanto con i numeri immaginari.
280-297 Data stimata della morte del figlio.
284-298 Data approssimativa della morte
di Diofanto, a ottantaquattro anni.
870 Qusta ben Luqa traduce e commenta
l'Aritmetica in lingua araba.
1464 Johann Müller Regiomontano trova una
traduzione in arabo dell'Aritmetica.
1556 Joachim Liebhard scopre resistenza di un
manoscritto di Diofanto in Vaticano.
1657 Fermat sfida i matematici inglesi a trovare
il metodo generale di risoluzione di
un’equazione diofantea concreta.
1769 Lagrange ottiene un algoritmo completo
per un’equazione diofantea concreta. Un
anno dopo, dimostra il teorema
dei quattro quadrati.
1685 Muore John Peli, che diede il nome a un
tipo di equazione diofantea il cui metodo
di risoluzione generale, tuttavia, era stato
ottenuto da William Brouncker.
1885 Paul Tannery cura un’edizione
dell’opera completa di Diofanto.
1900 David Hilbert propone di trovare
un algoritmo universale che risolva
qualsiasi equazione diofantea.
1920 Muore Srinivasa Ramanqjan, che diede il
nome a un tipo di equazione cubica.
1926 Sono pubblicati in francese l'Aritmetica
e il testo Numeri poligonali.
1570 Rafael Bombelli traduce l'Aritmetica in
latino, ma viene pubblicata solo in parte. 1969 Louis Mordell pubblica Equazioni
diofantee.
1575 Guilielmus Xylander pubblica la prima
edizione completa in latino dell 'Aritmetica. 1970 Yurü Matyasevich dimostra che non
esiste un algoritmo universale per
1621 Bachet de Méziriac pubblica l’edizione verificare se un’equazione diofantea
canonica dell Aritmetica, che ispirerà polinomica con coefficienti interi dati
Pierre de Fermat e altri matematici. ammette o no soluzioni intere.
INTRODUZIONE
13
CAPITOLO 1
Sulle orme di Diofanto:
la matematica
nel mondo antico
La storia di Diofanto fu indissolubilmente
legata al Museo e alla Biblioteca di Alessandria, la grande
capitale del sapere ellenistico per undici secoli.
Lì si raccolse un’élite intellettuale che condusse
la matematica a livelli molto elevati, dove Diofanto
si erse come il grande rinnovatore. Sebbene si conservino
solo due delle sue opere, YAritmetica e Numeri poligonali,
entrambe riflettono il ruolo decisivo che esercitò
sulla matematica del m secolo d.C.
Qualsiasi tentativo di ricostruire la vita di Diofanto incappa nell’o¬
stacolo rappresentato dalle pochissime informazioni disponibili.
Sebbene esista un problema matematico il cui risultato rivela che
morì alla veneranda età di ottantaquattro anni, e sebbene le ricer¬
che di alcuni prestigiosi accademici abbiano concluso che visse
nel in secolo d.C., purtroppo non si conosce con esattezza il suo
anno di nascita, né la data della sua morte. Secondo alcune opere,
sembra sia venuto al mondo tra il 200 e il 217 d.C. e che sia morto
verso il 284-298 d.C., ma non vi sono certezze al riguardo. In realtà,
lo storico francese Paul Tannery (1843-1904), forse il maggiore
studioso dell’opera di Diofanto, afferma che, sostanzialmente, non
esiste alcuna certezza sulla sua vita. Nonostante questa lacuna
storiografica, che rende molto difficile tracciare una biografia
completa, si conosce un dato fondamentale della vita di Diofanto:
che i suoi giorni trascorsero nella città egiziana di Alessandria, la
grande capitale del pensiero scientifico ellenico. Tra il ni e il n se¬
colo a.C., nel Museo di Alessandria lavorarono personaggi illustri
come Euclide, Apollonio di Perga ed Eratostene. Successivamente,
l’istituzione accolse, tra il i e il ni secolo d.C., scienziati del calibro
di Erone di Alessandria, Claudio Tolomeo e lo stesso Diofanto.
L’informazione che Diofanto sia vissuto fino a ottantaquattro
anni si può ricavare da un curioso epitaffio, cioè un’iscrizione se¬
polcrale con fini descrittivi o di lode al defunto. Tale epitaffio fu
SULLE ORME DI DIOFANTO: LA MATEMATICA NEL MONDO ANTICO
17
scritto in forma di problema matematico ed è presente nell’opera
Antologia Palatina. Come si vedrà più avanti, la sua soluzione per¬
mette di verificare questioni davvero sorprendenti, come per esempio
a quale età gli spuntò la barba, quando si sposò e se ebbe figli. Quanto
al dato che sia vissuto nel m secolo d.C., si trova una conferma nelle
ricerche del già citato Paul Tannery, che si concentrò sul problema
30 del Libro V delVAritmetica. Questo problema, che fornisce dati
su una questione classica e che ancora oggi è di grande interesse (il
prezzo del vino e la sua qualità), suggerì allo storico francese una
ipotesi: se i dati di quell’enunciato erano reali, si deve ritenere che
Diofanto sia vissuto intorno alla seconda metà del m secolo d.C., e
che pertanto fu contemporaneo di Pappo di Alessandria, autore di
una preziosa raccolta, la Collezione matematica, e che inoltre sia
vissuto un secolo prima di Teone di Alessandria e di sua figlia Ipazia.
Come mi segnalasti, rispettato Dionisio, il tuo interesse per
imparare a risolvere i problemi che si possono porre a proposito
dei numeri mi ha suggerito di scrivere una guida metodica
che ti serva a tale scopo, a partire, come mi chiedi, dai principi
più basilari che rappresentano la natura essenziale dei numeri
e la loro potenzialità.
— Diofanto.
Sebbene esistano pochi elementi per delimitare le date in cui
si svolse la vita di Diofanto, due fonti storiche circoscrivono la sua
esistenza a un arco temporale di cinquecento anni. Questa delimi¬
tazione fa riferimento, da una parte, a un’opera che viene attribuita
a Diofanto, Numeri poligonali, dove viene citato un matematico
che visse nel m secolo d.C., Ipsicle di Alessandria; e dall’altra parte
al fatto che Teone di Alessandria, già nel iv secolo d.C., abbia citato
Diofanto all’interno di un suo commento all 'Almagesto di Claudio
Tolomeo. Questa congiunzione situa Diofanto nel m secolo d.C.,
proprio come dedusse Paul Tannery. Si deve accettare, dunque,
che Diofanto visse in questo secolo e che la sua opera è stretta-
mente legata al Museo di Alessandria.
18
SULLE ORME DI DIOFANTO' LA MATEMATICA NEL MONDO ANTICO
ALESSANDRIA, CAPITALE DEL SAPERE
Alessandria, situata nel delta del fiume Nilo, nel nord dell’Egitto, fu
un’enclave ellenica in Africa, fondata nel 331 a.C. dal conquistatore
macedone Alessandro Magno (356-323 a.C.), da cui proviene il suo
toponimo. Successivamente, nel 46 a.C., cadde nelle mani di un
altro grande conquistatore, Giulio Cesare (100-44 a.C.), che la fece
entrare nell’orbita romana. Oggi è la seconda città più importante
dell’Egitto, dopo II Cairo, e ospita il principale porto del Paese.
Tuttavia, la sua fama e la sua reputazione risalgono all’Antichità,
quando si erse a capitale dell’ambiente ellenico e, per estensione,
a principale centro culturale del mondo. Il prestigio di Alessandria
derivò dallo straordinario patrimonio del suo celebre museo e della
sua biblioteca, così come dal grande numero di eruditi e scienziati
che ospitò per numerosi secoli. Gli sforzi dell’élite intellettuale
alessandrina diedero come frutto lo sviluppo di conoscenze molto
specializzate e avanzate in diversi rami della scienza: astronomia,
geografìa, matematica, fisica, ingegneria, medicina ecc. Questo fe¬
nomeno si verificò anche in altre città di influenza ellenistica, ma
in maniera molto più limitata.
Alessandria era attraversata da viali di 30 metri di larghezza,
e nel suo porto si innalzava un gigantesco faro, che con un’altez¬
za stimata tra i 115 e i 150 metri fu una delle sette meraviglie del
mondo antico. Precisamente, la parola «faro» proviene dal latino
pharus, toponimo dell’isola di Pharo o Faro, situata nella baia di
Alessandria. Lì si ergeva la torre costruita tra il 300 e il 280 a.C. da
Sostrato di Cnido, uno dei discepoli di Euclide, e sulla cui cima era
tenuto costantemente acceso un falò visibile a 55 chilometri, quale
riferimento per annunciare ai marinai che si stavano avvicinando
al porto. Vale la pena soffermarsi un po’ sulla descrizione del faro,
poiché rappresentò un modello di costruzione per la sua struttura
e i suoi elementi geometrici. Su una base quadrangolare, si ergeva
la snella torre ortogonale di circa 100 metri di altezza, in cima alla
quale era posta la sorgente di luce. La torre era divisa in tre cor¬
pi: il primo era un tronco di piramide, su cui si ergeva un prisma
ottagonale; su di esso poggiava un cilindro di altezza sempre più
piccola, e nella parte superiore, sostenuto da otto colonne, un cono
SULLE ORME DI DIOFANTO' LA MATEMATICA NEL MONDO ANTICO
19
che finiva la costruzione. Sfortunatamente, un terremoto distrusse
i resti del faro nel 1373 e le sue rovine sono state cercate invano.
Fu, senza dubbio, una delle maggiori produzioni tecniche dell’An¬
tichità, e un altro dei grandi motivi di orgoglio di Alessandria.
Sul piano culturale, la caduta della Grecia nelle mani del re Fi¬
lippo II di Macedonia (382-336 aC.) fu di ostacolo a che la creatività
dei Greci venisse sviluppata sul suo territorio, il che spiega come
il campo della ricerca si spostasse in Egitto alla fine del iv secolo
a.C. In questo senso si deve sottolineare la ricerca matematica,
un campo nel quale i contributi ellenici furono immensi. Come si
sa, Filippo II fu il padre di Alessandro Magno, che oltre alla fon¬
dazione di Alessandria promosse anche la creazione del museo,
un antecedente della moderna università. Nonostante la sua breve
vita, Alessandro Magno, al quale nella sua gioventù aveva fatto
da tutore Aristotele, non esitò a promuovere il rispetto per altre
culture, mentre proponeva la propria cultura ellenica. In realtà, e
senza esagerare, si può affermare che il Museo di Alessandria fu
il primo centro scientifico e umanistico della storia. L’impronta
civilizzatrice di Alessandro Magno e il suo sforzo intercultura¬
le si percepisce anche nella cosiddetta Scuola di Alessandria o
scuola neoplatonica di Alessandria, una corrente di pensiero che
sarebbe stata sostenuta durante il m secolo d.C. dal filosofo ales¬
sandrino Ammonio Sacca (175-242 d.C.), e che ebbe contributi da
una serie di personaggi del mondo intellettuale. Questi pensatori,
fino alla fine del v secolo d.C., cercarono di fondere la filosofia
greca con quella orientale.
Oltre alla maestosità del suo faro e al prestigio del suo mu¬
seo, l’enclave più famosa di Alessandria fu, senza dubbio, la sua
splendida biblioteca, che era annessa al museo. Questo bastione
del sapere fu fondato da Tolomeo I Sotere (367-283 a.C.), uno dei
generali (o Diadochi) di Alessandro Magno e il fondatore della
dinastia tolemaica (o lagide). La biblioteca era composta da dieci
sale di studio, ognuna di esse dedicata a una differente discipli¬
na. Un gran numero di poeti e filosofi, che superò il centinaio nel
periodo di massimo splendore, si occupò del suo mantenimento
con una dedizione assoluta. La Biblioteca di Alessandria custodi¬
va una enorme quantità di rotoli - come erano denominati i libri
20
SULLE ORME DI DIOFANTO. LA MATEMATICA NEL MONDO ANTICO
LA NUOVA BIBLIOTECA ALESSANDRINA
La nuova Biblioteca Alessandrina è stata inaugurata il 16 ottobre 2002 ad
Alessandria, con il patrocinio dell’ünesco e un proposito molto ambizioso:
ricordare la leggendaria biblioteca originale. A tal fine, sono stati dati i mezzi
necessari affinché possa operare come un gigantesco tempio moderno del
sapere. Così, occupa un’area di 85.000 m2 e custodisce un patrimonio di 8
milioni di libri, circa 100.000 manoscritti antichi e circa 10.000 libri molto rari,
oltre a una grande quantità di materiale su supporto elettronico e audiovisivo
e molti database.
Oggi la nuova Biblio¬
teca Alessandrina
ospita un centro per
conferenze, un museo
delle scienze, un pla¬
netario, un centro di
studi e il Centro di
Calligrafia.
Il rivestimento esterno
della nuova Biblioteca
Alessandrina rimanda
al disco solare che
il dio Ra porta in testa.
all’epoca - dal valore incalcolabile, un patrimonio che gli storici
stimano in circa 900.000 esemplari. Fu la più grande biblioteca
della storia, superiore anche a quella di Pergamo, in Asia Minore,
della quale si racconta che conservasse 500.000 rotoli all’epoca
di Giulio Cesare. Bisogna citare una pratica che contribuì in ma¬
niera considerevole alla crescita dei volumi della Biblioteca di
Alessandria: la confisca di rotoli dai vascelli visitatori. Quando su
una nave che entrava in porto veniva individuato qualche testo,
veniva copiato e aggiunto alla biblioteca; fatto questo, l’originale
veniva restituito al suo proprietario.
La biblioteca ricevette un primo duro colpo nel 272 d.C., anno
in cui l’imperatore romano Aureliano fece incendiare e saccheggia¬
re la città nel corso della sua campagna contro la regina Zenobia
SULLE ORME DI DIOFANTO: LA MATEMATICA NEL MONDO ANTICO
21
di Paimira. Successivamente, l’attività della biblioteca risentì ne¬
gativamente della proclamazione del cristianesimo come religione
ufficiale dell’Impero romano (380 d.C.) e delle rivolte antipagane
della fine del iv secolo d.C. e degli inizi del v secolo d.C. I cristiani,
perseguitati da lungo tempo, misero in discussione il sapere che
non proveniva dalle Sacre Scritture. Convenientemente aizzati da
personalità ecclesiastiche, alcuni fanatici si diedero ai tumulti, fino
a quando le autorità imposero la convivenza. Questa disposizione
facilitò il fatto che, alla fine, l’élite intellettuale cristiana si unisse
ai lavori della biblioteca, con notevole profitto. Sfortunatamente,
la Biblioteca di Alessandria subì la sua distruzione totale nel vii
secolo d.C. Sebbene l’istituzione riuscisse a superare le ostilità
generate dalle dispute per la successione in epoca bizantina, do¬
vette soccombere alla conquista della città da parte dell’imperatore
persiano Cosroe (614 d.C.), e il suo patrimonio fu poi distrutto con
l’invasione araba (640 d.C.), che islamizzò definitivamente il Paese.
In definitiva, il Museo di Alessandria, con la sua biblioteca an¬
nessa come emblema, operò per secoli come un vero e proprio
tempio del sapere e attirò nella città egiziana numerosi intellettuali
e scienziati di tutti gli ambiti della conoscenza. Provenivano dal
cuore della Grecia, dalle colonie greche e dalle parti più remote del
mondo conosciuto, e furono i precursori di Diofanto. I membri del
museo erano esenti da imposte e percepivano un salario, purché
realizzassero lavori di ricerca e li presentassero tramite esposizioni
orali. Tra il 300 e il 100 a.C. le produzioni accademiche sviluppate
in questa istituzione, e in particolare quelle che riguardarono la
matematica, dimostrarono una qualità eccezionale, al punto che
possono essere confrontate solo con le produzioni e lo sviluppo
scientifico raggiunti tra il 1600 e il 1850 per opera di giganti come
Keplero (Johannes Kepler, 1571-1630), Isaac Newton (1642-1727)
e Cari Friedrich Gauss (1777-1855).
Il Museo di Alessandria ricevette inestimabili contributi da
alcuni degli scienziati più illustri e famosi dell’Antichità. Così, nel
iv secolo a.C., fu il turno del matematico e astronomo Eudosso di
Cnido e del matematico Euclide. Nel m secolo a.C., il testimone fu
raccolto dal fisico, astronomo e matematico Archimede (287-212
a.C. ca.), dall’astronomo Eratostene (276-194 a.C. ca.) e dal geo-
22
SULLE ORME DI DIOFANTO LA MATEMATICA NEL MONDO ANTICO
FOTO IN ALTO
La fortezza di
Qaitbay, sull’isola
di Pharo, è stata
costruita intorno
al 1480 con i resti
del faro di
Alessandria e
occupa lo stesso
sito in cui sorgeva.
FOTO IN BASSO
Rovine del tempio
di Amon, nell’oasi
di Siwa, dove
Alessandro Magno
ufficializzò la sua
conquista
dell’Egitto grazie
alla sua
designazione a
figlio del dio
Amon.
SULLE ORME DI DIOFANTO: LA MATEMATICA NEL MONDO ANTICO
23
metra Apollonio di Perga (262-190 a.C. ca.). In quanto al n secolo
a.C., brillarono di luce propria l’astronomo e geografo Ipparco e
l’astronomo, chimico e matematico Claudio Tolomeo (100-170 a.C.
ca.). Più tardi, nel i secolo a.C. il museo poté contare sulle abilità
matematiche di Erone di Alessandria. Senza sminuire il periodo
immediatamente successivo, l’istituzione sperimentò una certa ri¬
nascita nel secolo iv d.C., un secolo che ebbe inizio con il sapere
del geometra Pappo di Alessandria e terminò con i lavori del mate¬
matico Teone, padre della filosofa, astronoma e matematica Ipazia
(m. 415 d.C.); quest’ultima è di vitale importanza per conoscere
l’opera di Diofanto.
In definitiva, le produzioni e il lascito intellettuale di questi
protagonisti della scienza greca illustrano a chiare lettere il sape¬
re matematico raggiunto nell’Antichità, per cui vale la pena sof¬
fermarsi sui loro contributi. In effetti, tutti loro hanno gettato le
fondamenta della matematica moderna.
LA NASCITA DELLA GEOMETRIA EUCLIDEA
Il primo di questi protagonisti è Eudosso di Cnido, che lavorò
con i numeri e arrivò a trattare le quantità continue. In questo
senso, la sua teoria della proporzionalità aprì le porte alle sco¬
perte dei matematici rinascimentali italiani del xvi secolo. La
tecnica utilizzata da Eudosso, di carattere visuale e intuitivo, è
nota come «metodo di esaustione», strumento che Archimede
usò meravigliosamente nei suoi lavori e che, inoltre, rappresen¬
tò l’embrione dell’attuale calcolo integrale per calcolare aree e
volumi. Questo metodo acquisì ricchezza nel suo rigore e nel
formalismo matematico per mano di Isaac Newton (1642-1727)
e Gottfried Wilhelm Leibniz (1646-1716). Tuttavia, Eudosso ri¬
scosse maggiore fama come astronomo, ideando la sfera celeste,
sostenendo un modello cosmologico geocentrico e cercando di
comprendere il movimento dei pianeti.
Un peso maggiore nella storia lo ebbe un altro dotto ellenico
del iv-iii secolo a.C., Euclide, noto come «il padre della geome¬
24
SULLE ORME DI DIOFANTO. LA MATEMATICA NEL MONDO ANTICO
tria». Euclide scrisse, approssimativamente intorno al 300 a.C.,
un’opera di capitale importanza per la matematica: gli Elementi,
un testo il cui contenuto è strettamente teorico, con teoremi e
numerose immagini geometriche, ad accompagnare le dimostra¬
zioni dei risultati. Tutto si basa su alcune piccole ipotesi chia¬
mate postulati o assiomi - verità accettate senza giustificazione
come base di un ragionamento successivo -, da cui derivano i
risultati esposti nel testo.
I primi quattro libri degli Elementi sono relativi alla geome¬
tria piana e comprendono le proprietà più elementari di linee e
angoli, oltre allo studio di triangoli, uguaglianza di aree e il teore¬
ma di Pitagora - Libro I, proposizione 47 -, che venne introdotto
come proprietà di aree. Il quinto libro presenta la teoria delle
proporzioni a partire da un punto di vista geometrico, cosa che
nel sesto libro viene applicata alla somiglianza di figure piane.
Di questo Libro VI bisogna sottolineare che contiene anche un
teorema con il primo problema di ottimizzazione che è arrivato
fino ad oggi, dove viene proposto il calcolo di una grandezza
massima:
Data una lunghezza, trovare il rettangolo di area massima il cui
perimetro è la lunghezza data.
Euclide dimostrò che, di tutti i rettangoli aventi un dato pe¬
rimetro, il quadrato ha area massima. Questo problema avrebbe
guadagnato grande popolarità grazie alla matematica italiana
Emma Castelnuovo (1913-2014). Da parte loro, i Libri da VII a IX
degli Elementi affrontano la teoria dei numeri, principalmente la
divisibilità dei numeri interi, la somma delle serie geometriche
e alcune proprietà dei numeri primi. Nelle loro pagine vengono
introdotti sia il popolare «algoritmo di Euclide» per trovare il
massimo comune divisore di un insieme di numeri, sia il teorema
di Euclide, relativo all’esistenza di un numero infinito di primi.
Più esattamente, l’algoritmo di Euclide sarebbe stato utilizza¬
to molto tempo per la risoluzione delle cosiddette «equazioni
diofantee», uno dei contributi per i quali Diofanto si sarebbe
guadagnato un posto d’onore nella storia.
SULLE ORME DI DIOFANTO: LA MATEMATICA NEL MONDO ANTICO
25
Probabilmente il Libro X degli Elementi è il meno divulga¬
tivo, poiché include una classificazione geometrica dei «numeri
irrazionali quadratici». Per non immergerci in spiegazioni, si può
riassumere che quando un numero intero positivo non è un qua¬
drato perfetto, la sua radice quadrata viene denominata numero
irrazionale quadratico. Per esempio, il 2 non è un quadrato perfet¬
to, per cui si tratta di un numero irrazionale quadratico.
ERONE SI IMBATTE NEI NUMERI COMPLESSI
La parabola della Biblioteca di Alessandria si prolungò fino a dopo
la nascita di Cristo e sopravvisse all’irruzione dell’Impero romano in
territorio egiziano nel i secolo d.C., poiché non vi è alcuna base sto¬
riografica solida ad accreditare l’incendio della stessa per mano degli
eserciti di Cesare, né la sua attività fu in alcun modo fermata Di fatto,
fino al v secolo d.C. accolse diversi personaggi che, per essere stati i
precursori dei lavori di Diofanto, per il citarlo a posteriori o, semplice-
mente, per aver arricchito il sapere matematico dell’epoca, meritano
un trattamento speciale. Si tratta di Erone, Pappo, Teone e Ipazia.
Il primo è il poliedrico Erone di Alessandria, che si ritiene
sia nato in Egitto e la cui vita personale e accademica si svolse in
questa città nel i secolo d.C. Autore di tredici opere su meccani¬
ca, matematica e fisica, inventò diversi strumenti meccanici per
uso pratico, tra i quali la macchina a vapore girevole. In ambito
matematico emerse nei campi della geometria e della geodesia.
Ideò anche un metodo di approssimazione alle radici quadrate e
cubiche dei numeri le cui radici non sono numeri interi. Ciono¬
nostante, il suo lavoro più celebre fu il contributo geometrico al
calcolo di aree di triangoli in funzione delle misure dei loro lati: la
cosiddetta «formula di Erone». Questa permette di calcolare l’area
di un triangolo a partire dalla lunghezza dei lati e rappresentò un
metodo approssimato per trovare la radice quadrata di un numero
che viene ancora oggi utilizzato dai computer.
La formula è presente nel primo dei tre libri della Metrica, che
insieme alla Meccanica rappresenta il principale lascito di Erone.
26
SULLE ORME DI DIOFANTO' LA MATEMATICA NEL MONDO ANTICO
EUCLIDE
Si sa ben poco in relazione alla vita di Euclide, al di là del fatto che il matema¬
tico visse tra il iv e il m secolo a.C, durante il regno di Tolomeo I Sotere, e che
fondò una scuola ad Alessandria. Probabilmente si formò ad Atene, nella scuo¬
la di Platone. L’importanza del suo lascito si basa su un fatto importante: fu
l’autore degli Elementi, l’esemplare completo più antico che si conservi della
storia della matematica. In realtà, si tratta del libro più pubblicato dopo la
Bibbia, dato che dal 1482 ha superato il migliaio di edizioni, tanto per la ricer¬
ca matematica quanto per fini educativi - prima di questa data, si utilizzava
solo per l’insegnamento della matematica -. L’assoluta validità degli Elemen¬
ti di Euclide ha avuto fine nel 1794, quando sono stati sostituiti come opera di
riferimento dagli Elementi di geometria di Adrien-Marie Legendre (1752-1833).
Questo famoso matematico francese introdusse nella meccanica concetti
come la funzione che porta il suo nome e la prima dimostrazione del metodo
«dei minimi quadrati» - oltre a essere stato il primo a dedicare un’opera alla
teoria dei numeri e a dimostrare la legge della reciprocità quadratica -, per
cui il suo riuscire a scalzare l’opera seminale di Euclide risultò indiscutibile. A
parte qualche altro testo di importanza minore, Euclide scrisse anche l’opera
Dati, che si configura come un insieme di esercizi sulla geometria, oltre a
quattro libri sulle sezioni coniche. A ogni modo, la quasi totale assenza di in¬
formazioni e documenti sulla sua vita risulta compensata daM’enorme influen¬
za che gli Elementi avrebbero avuto nei secoli, determinando il sentiero se¬
guito da uno dei rami più belli della matematica: la geometria.
*
Particolare della
Scuola di Atene,
di Raffaello, in
cui Euclide è
intento a
tracciare figure
geometriche con
un compasso.
SULLE ORME DI DIOFANTO: LA MATEMATICA NEL MONDO ANTICO
27
Nella Metrica sono presentati i differenti metodi per trovare le aree
di triangoli, quadrilateri, poligoni regolari da tre a dodici lati, cerchi
ed ellissi, così come il volume di cilindri, coni e sfere; il tutto tramite
procedimenti rigorosi e calcoli approssimati.
È necessario sottolineare il fatto che Erone incappò nei nu¬
meri complessi, cioè numeri che derivano da radici quadrate
di numeri negativi. Una breve classificazione dell’insieme dei
numeri e delle loro tipologie - naturali, razionali ecc - ci aiuterà
a comprenderli. L’insieme dei numeri «naturali» o «interi positi¬
vi», denotato con N, contiene i numeri 0, 1, 2, 3, 4 ..., senza alcun
decimale, mentre i loro opposti sono denominati come «interi
negativi» (-1, -2, -3,...). L’unione dei numeri naturali e negativi
prende il nome di «interi» e riceve come denotazione Z. Quelli
che possono essere espressi in forma di frazioni vengono detti
«razionali» - che sono denotati con la lettera Q - , dove quelli
«irrazionali», denotati con la lettera I, sono quelli che non pos¬
sono essere scritti in forma di frazione: per esempio, il numero
e (2,71 ...) e il numero n (3,14 ...). Infine, l’insieme di tutti que¬
sti numeri prende il nome di «reali», denotato con la lettera R.
Lo schema a fondo pagina renderà più chiara la distribuzione
dell’insieme dei numeri e le loro tipologie.
Infine, si deve far notare che l’equazione 3# = 2 non ha solu¬
zione nell’insieme dei numeri interi, poiché il valore dell’indeter¬
minata x che verifica l’uguaglianza non è un valore intero, ma il
numero razionale x - 2/3. Con questo è possibile affermare che ha
una soluzione razionale non intera.
Reali
(R)
Razionali
(Q)
Irrazionali
(I)
Interi
(Z)
1 fi
Naturali (N) —0; 1; — ;7Õ
Cè
16
Interi negativi -> -1; —— V9
Frazionari -> 5,23; — ; 0,54;——
2 2
» ji = 3,141592654...; e = 2,718281...;
= =1,618033988...; 72=1,414213...
28
SULLE ORME DI DIOFANTO: LA MATEMATICA NEL MONDO ANTICO
Erone documentò la sua esperienza con i numeri complessi
in un piccolo testo: Stereometria, nel quale compare l’espressione
V81-144. Successivamente, Diofanto, nella sua Aritmetica, si im¬
battè in radici di numeri negativi quando si trattò di calcolare i lati
di un triangolo rettangolo di perimetro 12 e area 7. Questo lo portò
a dover affrontare l’equazione 6:r2-43:r+84 = 0, nella cui soluzione
sono presenti radici di numeri negativi. Giunti a questo punto, si
rende necessario mostrare un’applicazione della formula di Erone.
Per esempio, consideriamo un triangolo i cui lati misurino a, b, c.
La formula di Erone entra in gioco per calcolare l’area di un trian¬
golo nel caso in cui si conosca solo la misura dei suoi lati. In essa,
se a, b, c sono le misure dei lati del triangolo, e il semiperimetro,
o metà del perimetro, è denotato con s, allora:
a + b + c
e l’area viene determinata da:
A = yfs(s^aXs^bXs^c).
Qualsiasi poligono semplice può essere suddiviso in triangoli
che hanno al massimo un lato comune o un vertice comune, me¬
diante diagonali che partono da un unico vertice appropriato. Il
processo prende il nome di «triangolazione». Questa suddivisione
e l’applicazione della formula di Erone per l’area di un triangolo
permettono di calcolare l’area della regione piana delimitata dal
poligono semplice, semplicemente misurando le lunghezze. In ciò è
possibile osservare la rilevanza e l’importanza della formula. Come
esempio del calcolo dell’area di un triangolo si può esporre come
determinare l’area di un terreno triangolare, i cui lati misurano 70,
60 e 45 metri. In base alla formula di Erone, il semiperimetro è:
70 + 60 + 45
2
= 87,5m.
Quindi si applica la formula e si ottiene che l’area è:
A = ^87,5 • (87,5 - 70) • (87,5 - 60) • (87,5 - 45) = 1337,78m2.
SULLE ORME DI DIOFANTO: LA MATEMATICA NEL MONDO ANTICO
29
Diofanto, da parte sua, costruì un triangolo con una corda sulla
quale aveva realizzato dodici nodi equidistanti. I lati misuravano 3,
4 e 5 unità. Il triangolo era rettangolo e soddisfaceva il teorema di
Pitagora: 32 + 42 = 52. Essendo un triangolo rettangolo, risulta faci¬
le dimostrare che l’area è di 6 unità. Con la stessa corda cercò di
costruire un altro triangolo rettangolo in modo tale che la sua area
fosse di 7 unità e la somma dei suoi lati desse come risultato 12. La
sua impostazione fu la seguente. Un cateto misura#, l’area sarebbe
7 e l’altro cateto 14/#. Così, per il teorema di Pitagora, si ha che:
e operando, ö#2-43#+ 84 = 0, la cui soluzione Diofanto espresse:
43 ±71677-1
12
Diofanto non conosceva alcun numero che elevato al quadrato
fosse uguale a -1, per cui mise da parte il problema, che sarebbe
stato risolto solo dopo secoli e che è considerato l’embrione dei
numeri immaginari. Uno dei primi a riconoscere quanto fosse utile
il fatto che i numeri negativi avessero radici quadrate fu il mate¬
matico italiano Rafael Bombelli (1526-1572), che diede inizio alla
formalizzazione della teoria dei numeri immaginari o complessi.
Alla metà del xvi secolo, un altro matematico italiano, Gerolamo
Cardano (1501-1576), si occupò di equazioni con soluzioni che in¬
cludevano radici quadrate di numeri negativi. Per esempio, suggerì
che il numero reale 40 può essere espresso:
Tuttavia, la somma dei suoi lati doveva essere 12, cioè:
# + — + h = 12.
#
Risolvendo in e sostituendo, si ha:
(5+ 7-15)-(5-7^15).
30
SULLE ORME DI DIOFANTO LA MATEMATICA NEL MONDO ANTICO
Nel 1777, il matematico svizzero Eulero (Leonhard Euler, 1707-
1783) assegnò alla radice quadrata di -1 la lettera i o unità imma¬
ginaria. In seguito, Gauss diede una interpretazione geometrica
dell’unità immaginaria e nel 1799 dimostrò il teorema fondamen¬
tale dell’algebra, che afferma che ogni polinomio con coefficienti
complessi ha almeno una soluzione complessa. In questo modo fu
possibile aggirare l’ostacolo nel quale si era imbattuto Diofanto,
sebbene ciò fosse avvenuto quindici secoli dopo.
DA PAPPO DI ALESSANDRIA A IPAZIA
Desta sorpresa il fatto che Pappo di Alessandria, che visse nel iv
secolo d.C. ed era considerato come uno degli ultimi matematici
della scuola alessandrina, non abbia mai citato Diofanto. Oltre ad
alcuni commenti agli Elementi di Euclide e alYAlmagesto di Tolo¬
meo, Pappo scrisse un’opera essenziale: la Collezione matematica
(340 d.C.). Composta da otto libri, dei quali tuttavia sono andati
perduti il primo e parte del secondo, questa raccolta del sapere non
solo presenta un panorama storico della matematica classica, ma
include anche commenti sui lavori di diversi scienziati (Euclide,
Archimede, Apollonio), oltre ad alcune dimostrazioni alternative e
nuovi risultati geometrici.
Un altro matematico e astronomo greco posteriore a Diofanto,
e che neppure da lui fu citato, fu Teone di Alessandria, che visse
nel iv secolo d.C. nella città egiziana. Insegnante di matematica e
astronomia, fu l’ultimo direttore del Museo di Alessandria. Il suo
principale contributo fu di arricchire i lavori di Euclide e Tolomeo.
In quanto al primo, realizzò una revisione dell’Ottica e, in partico¬
lare, degli Elementi, in una versione che eliminava le difficoltà e
che da allora sarebbe divenuta il punto di riferimento.
In questo lavoro, insieme all’edizione moderna, poté conta¬
re sulla collaborazione di un personaggio che risulta essenziale
per tracciare una biografia completa di Diofanto: sua figlia, Ipazia
di Alessandria. Fu infatti la principale sostenitrice dell’opera di
Diofanto nell’Antichità. Non solo diede notizia dell’esistenza dello
SULLE ORME DI DIOFANTO: LA MATEMATICA NEL MONDO ANTICO
31
stesso Diofanto, ma scrisse anche interessanti commenti sull’A-
ritmetica e trasmise in maniera instancabile i suoi contenuti a
numerosi studenti provenienti da tutti gli angoli del mondo. Ipazia
approfondì le tecniche matematiche che erano state sviluppate da
Diofanto, come le soluzioni dei problemi indeterminati di vari tipi
e il simbolismo che questi aveva ideato. I suoi commenti sul trat¬
tato di algebra diofantea con equazioni di primo e secondo grado
inclusero alcune soluzioni alternative, cosa che rappresenta una
dimostrazione del suo talento matematico.
Sebbene diversi accademici abbiano espresso dubbi sul fatto
che alcuni problemi siano di paternità esclusiva dello stesso Dio¬
fanto, il celebre storico britannico Thomas Little Heath (1861-1940)
non esitò invece ad attribuirli a Ipazia, sebbene dal punto di vista
cronologico appartenessero a periodi di tempo differenti.
AVVICINARSI ALL’OPERA DI DIOFANTO
La carenza di dati biografici su Diofanto è compensata dal fatto
che sia giunta fino a noi la parte più fondamentale della sua opera
matematica, nella quale dimostrò che utilizzando i numeri era pos¬
sibile dedurre regole esenti da pregiudizi geometrici. In effetti, ri¬
nunciò al numero come misura, come grandezza, mettendo da parte
la concettualizzazione pitagorica ed euclidea. Inoltre, ruppe molti
dei canoni seguiti da anni dalla scuola di Alessandria, mostrando un
concetto di numero che non ubbidiva alla norma ellenica né si inse¬
riva nella cultura esistente, la cui pietra angolare era rappresentata
da un’opera di geometria, gli Elementi di Euclide. Con Diofanto,
il numero avrebbe adottato il ruolo «deU’indeterminato». Fu lui il
primo a prendere in considerazione i numeri razionali - solamente
quelli positivi - come numeri autentici, e in tal senso è necessario
osservare che il pieno riconoscimento dei numeri razionali, con la
loro indipendenza, sarebbe avvenuto solo nel xvn secolo.
Gli accademici dell’epoca si mostrarono restii ad accettare
il concetto di numero come un’interpretazione simbolica e come
un concetto distinto da quello classico. Diofanto non interpretò il
32
SULLE ORME DI DIOFANTO. LA MATEMATICA NEL MONDO ANTICO
quadrato e il cubo come oggetti geometrici di aree e volumi, bensì
come numeri. In questo modo riuscì a liberarsi dalle limitazioni
dimensionali della geometria, dove era possibile moltiplicare solo
tre grandezze, dato che tre sono le dimensioni dello spazio. Dio-
fanto ammise senza alcun problema prodotti e potenze fino a sei
fattori e i loro inversi.
Un altro degli aspetti innovativi dell’opera di Diofanto fu
l’introduzione della prima notazione simbolica propriamente
matematica. La matematica greca non aveva avuto alcun tipo
di simbolismo speciale: si trattava di una matematica «retori¬
ca», che usava unicamente il linguaggio verbale. Diofanto reagì
contro questa tendenza egemonica e introdusse un simbolismo
adattato al calcolo algebrico e molto flessibile. Questa nota¬
zione ricevette il nome di «sincopata», dato che trascriveva
il linguaggio verbale in quello simbolico. A dispetto dei suoi
indubbi vantaggi algebrici, sarebbe andata perduta subito dopo
Diofanto, e neppure la matematica araba l’avrebbe recuperata.
Solo durante il Rinascimento, dalla fine del xv secolo fino al
xvii secolo, si sarebbe tornati a introdurre la nuova notazione
algebrica, che sarebbe culminata nel 1637 grazie a Cartesio
(René Descartes, 1596-1650), e che è ancora oggi in uso.
In sintesi, l’introduzione del simbolismo, il cui protagonismo
relegava il numero in quanto grandezza in secondo piano, fu ne¬
cessaria per la creazione dell’algebra. La questione ci permette di
sottolineare che l’algebra nacque in Grecia per mano di Diofanto.
Per questo si è soliti attribuirgli il titolo di «padre dell’algebra»,
nonostante la qualifica formale sarebbe da attribuire al matematico
e astronomo arabo Al-Khwarizmi (780-850 ca.), autore di Al-kitab
al-mujtasarfi hisab al-jabr wa al-muqabala o Libro concreto del
calcolo delValgebra e della muqabala, cioè della restaurazione e
dell’opposizione. L’opera, scritta a Baghdad intorno all’825, mo¬
stra la prima formula generale per risolvere equazioni di primo
e secondo grado. Il mondo arabo medievale avrebbe conosciuto
l’Aritmetica di Diofanto poco dopo.
Oggi, il nome di Diofanto è in genere associato alle equazioni
indeterminate lineari e non lineari, e alla soluzione delle stesse. Gli
scritti disponibili permettono di sapere che Diofanto fu il primo a
SULLE ORME DI DIOFANTO' LA MATEMATICA NEL MONDO ANTICO
33
usare processi algebrici sistematici per la soluzione di equazioni
non lineari indeterminate. Inoltre, fu il primo a introdurre notazio¬
ni algebriche concrete ed estese, che non solo furono un grande
progresso rispetto ai suoi predecessori, ma anche ad alcuni suoi
successori.
«Diofanto non fu, come è stato spesso chiamato, il padre dell’algebra.
Ciononostante, la sua sorprendente, sebbene non sistematica,
raccolta di problemi indeterminati è un risultato singolare, che non
fu del tutto riconosciuto e che sarebbe stato sviluppato molto più
tardi in maniera più ampia.»
— Kurt Vogel (1888-1985), storico della matematica tedesco.
Il ritrovamento del testo dell 'Aritmetica attraverso fonti bi¬
zantine aiutò la rinascita della matematica nell’Europa occidentale
e stimolò gli studi di molti matematici. In realtà, segnò un prima
e un dopo per quanto riguardava matematica: l’opera di Diofanto,
per esempio, inspirò indiscutibilmente Fermat, molti dei cui lavori
sono conosciuti attraverso le note da lui realizzate su una copia di
questo libro, e anche François Viète (1540-1603), che ebbe Diofan¬
to come riferimento. A livello scientifico, pertanto, era possibile
definire Diofanto come l’uomo della transizione, il matematico che
riuscì a portare questa scienza dalla geometria all’algebra; o più
concretamente, a una maniera assolutamente nuova di costruire
l’algebra, che non si basava sulla geometria, come fece Euclide,
bensì sull’aritmetica.
Si tratta dell’unico matematico greco che non fu un geometra,
bensì un aritmetico puro. Parlare di Diofanto è parlare di inno¬
vazione, di un’autentica rivoluzione nel modo di pensare e agire
matematicamente. Sebbene si faccia riferimento a Diofanto come
a un precursore dell’algebra, in contrapposizione alle idee geome¬
triche che imperavano nell’antica Grecia, fu in realtà più vincolato
con l’aritmetica dei Paesi orientali che con quella dei Paesi greci.
Inoltre, considerò che il pensiero geometrico era ermetico e fece
un totale rinnovo contestuale dei concetti.
34
SULLE ORME DI DIOFANTO: LA MATEMATICA NEL MONDO ANTICO
OPERE CONSERVATE E OPERE PERDUTE
Di Diofanto ci sono pervenute solamente due opere: l'Aritmetica
e Numeri poligonali. Di entrambe verrà esposto dettagliatamente
il contenuto nel corso di queste pagine. Un altro dei suoi lavori,
Porismi, è andato irrimediabilmente perduto, e alcuni autori gli
attribuiscono la paternità di Preliminari agli elementi geome¬
trici, tradizionalmente attribuita a Erone di Alessandria. Rispetto
a Porismi, Diofanto si riferiva all’opera come a una raccolta di
lemmi (proprietà), che sono appunto chiamati porismi o pori-
smata. Alcuni studiosi ritengono che in realtà si trattasse di una
sezione dell'Aritmetica che è andata perduta. Ciononostante, si
conoscono tre dei suoi lemmi o proprietà grazie a Diofanto, che li
incluse nell'Aritmetica. Uno di essi afferma che la differenza dei
cubi di due numeri razionali è uguale alla somma dei cubi di altri
due numeri razionali (si deve ricordare che «razionale» significa
che può essere espresso nella forma di una frazione). Cioè, dati a
e b, con a>b, esistono c ed, tutti positivi e razionali per cui:
a3-ft3 = c3 + d3
Per esempio:
203-173= 143 + 73.
A titolo di curiosità, bisogna sottolineare il linguaggio utilizza¬
to da Diofanto nelle sue opere, dove parla di «numeri dati» in ma¬
niera generale e utilizza «numeri concreti» nella soluzione, come si
osserverà nel capitolo dove vengono presentati i problemi risolti.
Inoltre, dove oggi si esprimerebbe
(6n+12)/(n2-3),
il matematico alessandrino lo dovette scrivere a parole:
Un numero per un fattore di sei aumentato di dodici, che viene divi¬
so per la differenza tra il quadrato del numero meno tre.
SULLE ORME DI DIOFANTO: LA MATEMATICA NEL MONDO ANTICO
35
UN EPIGRAMMA RIVELATORE
L’unica traccia plausibile della vita e della morte di Diofanto si trova
aU’intemo delYAntologia Palatina, una raccolta di circa 3.700 poemi
greci composti da oltre trecento autori, che riflette la cultura greca
dal iv secolo d.C. fino alla fine dell’epoca bizantina, e che ha dato
vita a diverse versioni nel corso della storia. L’opera deriva dalla
prima antologia scritta in greco che si conosca, nella quale il poeta
e filosofo Meleagro di Gadara riunì, nel i secolo a.C., i poemi da lui
scritti e quelli di altri quarantasei poeti. L'Antologia Palatina deve
il suo nome al ritrovamento, nel 1606, nella biblioteca del Palatina¬
to di Heidelberg (in Germania) di una collezione completa basata
sull’edizione definitiva dell’opera, realizzata nel 917 da Costantino
Cefala, che fu protopapa (o arciprete) a Costantinopoli.
Fino ad allora, si conosceva solo la versione rivista nel 1301
dal monaco greco Massimo Pianude (1260-1330 ca.), pubblicata
per la prima volta nel 1494. Il principale contributo di Cefala fu
di arricchire l’opera con epigrammi, una serie di componimenti
poetici brevi che è caratterizzato da brevità e icasticità, di carat¬
tere encomiastico e dedicatorio, o anche funerario, che vengono
solitamente incisi su materiali come la pietra, che si tratti di una
statua o di una tomba. In quest’ultimo caso, prendono il nome
di «epitaffi» - dal latino epitaphium, che a sua volta deriva dal
greco epi, che significa «sopra», e taphos, «tomba» - e descrivono
fatti legati all’individuo che giace nella sepoltura. Nel mondo el¬
lenico, gli epitaffi solitamente venivano scritti in versi e, secondo
quanto riportato da Platone, dovevano essere brevi per essere
certi che venissero letti. Invece, l’epitaffio di Diofanto è lungo e
rende omaggio alla sua passione e al suo talento per la matema¬
tica, poiché è stato scritto sotto forma di problema.
L’edizione canonica áe\YAntologia Palatina consiste in quin¬
dici libri, dei quali in questo contesto si presta particolare atten¬
zione all’epigramma 24 del Libro XIV, che corrisponde all’epitaffio
di Diofanto, così come fu riportato dal grammatico e aritmetico
bizantino Metrodoro verso il 500 d.C. L’epigramma è una sfida ma¬
tematica e la sua soluzione offre dati preziosi sulla vita e la morte
del matematico alessandrino. Tradotto dal latino il testo recita:
36
SULLE ORME DI DIOFANTO' LA MATEMATICA NEL MONDO ANTICO
Passante, questa è la tomba di Diofanto: sarà lui stesso, per mezzo
dell’arte aritmetica, a dare la misura della sua vita. La sua fanciullezza
fu un sesto della sua vita; durante la dodicesima parte della sua vita la
barba coprì le sue guance; dopo un settimo accese la fiaccola nuziale,
e dopo cinque anni ebbe un figlio. D fanciullo tanto amato visse solo la
metà degli anni del padre. Quattro anni ancora, mitigando il proprio
dolore con la scienza dei numeri, visse Diofanto, fino a raggiungere il
termine della sua vita.
Il lettore può fermare qui la sua lettura e cercare di risolvere il
problema da solo, cosa che non comporta una eccessiva difficoltà.
A ogni modo, si riporta una tabella con la soluzione dell’enigma
esposto, per la quale si utilizza la notazione attuale. Quindi, si de¬
nomina x il totale degli anni vissuti da Diofanto e si mostra la
traduzione dal linguaggio verbale a quello algebrico:
Linguaggio verbale
Linguaggio algebrico
Passante, questa è la tomba di Diofanto: sara lui
stesso, per mezzo dell’arte aritmetica, a dare la
misura della sua vita
X
La sua fanciullezza fu un sesto della sua vita
x/6
Durante la dodicesima parte della sua vita la
barba coprì le sue guance
x/12
Dopo ancora una settima parte accese la fiaccola
nuziale
x/7
Dopo cinque anni ebbe un figlio
5
Il fanciullo tanto amato visse solo la metà degli
anni del padre
x/2
Quattro anni ancora, mitigando il proprio dolore
con la scienza dei numeri, visse Diofanto
4
La traduzione dal linguaggio verbale a quello algebrico suggerisce
di porre questa equazione di primo grado, la cui soluzione è #=84.
x x
— + —
6 12
+
x r x
— + 5 + —
7 2
+ 4 = x.
Esiste anche un ragionamento più semplice che conduce alla
soluzione corretta. Basta pensare che si parla di un dodicesimo del¬
SULLE ORME DI DIOFANTO: LA MATEMATICA NEL MONDO ANTICO
37
la sua età e di un settimo della stessa, per cui questa deve essere
un multiplo di 7 e 12, cioè 84. Questa era infatti la sua età, perché
altri multipli di 84 vanno ben oltre la vita di un uomo. Certamente,
l’epigramma di Diofanto fornisce dati sorprendenti: non solo rivela
che morì a ottantaquattro anni, ma anche che fu considerato un
bambino fino ai quattordici, che a ventuno gli spuntò la barba, si
sposò a trentatré anni ed ebbe un figlio a trentotto, che purtroppo
morì quando lui aveva ottant’anni.
38
SULLE ORME DI DIOFANTO LA MATEMATICA NEL MONDO ANTICO
CAPITOLO 2
Un approccio
all 'Aritmetica
L'Aritmetica di Diofanto è una delle opere matematiche
più influenti dell’Antichità. Il suo impatto andò oltre
l’epoca classica e costituì un riferimento per diversi
secoli. Bachet de Méziriac, Pierre de Fermat ed Eulero,
tra gli altri grandi matematici, rimasero affascinati
dal sistema di numerazione, dai simboli e dai segni
utilizzati da Diofanto, e crearono metodi generali
per la soluzione di molti problemi.
L’aritmetica è il più antico ed elementare ramo della matematica, e
viene utilizzato in tutto il mondo, sia per portare a termine incomben¬
ze nella vita di tutti i giorni, come contare, oppure per eseguire i più
avanzati calcoli scientifici. La sua origine risale all’antica Grecia e ha
le sue radici nel termine arithmos, che significa «numero», sebbene
lo stesso Diofanto identificasse il vocabolo arithmos come sinonimo
di quella che oggi chiamiamo «incognita». L’aritmetica, in sintesi,
studia alcune operazioni con i numeri e le loro proprietà elementari;
in particolare, quelle che sono note come «le quattro operazioni»,
cioè, la somma, la sottrazione, la moltiplicazione e la divisione. A un
livello superiore, il concetto di «aritmetica» si usa, nelle sue nume¬
rose varianti, nell’ambito della teoria dei numeri, come avviene per
esempio con l’aritmetica modulare.
Come ramo della matematica, l’aritmetica dà il titolo a uno dei
trattati più importanti della Grecia classica e, senza alcun dubbio,
l’opera più importante di Diofanto: VAritmetica. Il contesto storico
della sua creazione, come è stato spiegato, fu Alessandria, vero e
proprio punto di riferimento intellettuale della conoscenza grazie
al fatto di essere un luogo di incontro multiculturale. Il museo e la
biblioteca della città egiziana rappresentarono lo spazio favorevole
per la nascita della figura del matematico professionista. Fu quindi
in questo ambiente privilegiato che Diofanto concepì e plasmò
le sue ricerche matematiche, che oltre d\YAritmetica avrebbero
UN APPROCCIO ALL'ARITMETICA
41
dato come frutto il testo Numeri poligonali, nel quale presentò il
concetto di «numero poligonale» e dimostrò una serie di risultati.
Bisogna segnalare che, a differenza dell'Aritmetica, il testo di Nu¬
meri poligonali non è prettamente un libro di esercizi. Secondo
gli antichi, Diofanto avrebbe inoltre scritto un libro di Porismi e
un trattato relativo alle frazioni conosciuto come Moriastica, che
purtroppo è da considerare perduto.
L’eredità accademica di Diofanto, presentata in maniera ma¬
gistrale nell'Aritmetica, ebbe una enorme importanza lungo il
percorso verso le attuali conoscenze dell’algebra. A grandi linee,
questo ramo della matematica studia la combinazione di elementi
di strutture astratte mediante numeri, lettere e segni con un dop¬
pio obiettivo: fare riferimento a operazioni aritmetiche multiple e
poter essere interpretati come un altro tipo di numeri o quantità
per le espressioni che comportano una certa complessità. Senza
dubbio, i propulsori dell’algebra trassero un notevole vantaggio
dalle conclusioni di Diofanto, sebbene non si tratti dell’unica area
di conoscenza nella quale si lavora con le cosiddette «equazioni
diofantee», delle quale si parlerà più avanti.
L’impostazione numerica che Diofanto applicò alle equazioni
può essere considerata come un’eredità pitagorica. In ogni caso,
risultò un elemento chiave all’interno dell'Aritmetica, poiché con
questo metodo ottenne ciò che sembrava impossibile all’epoca, e
perfino molto tempo dopo: fornire una collezione di problemi ri¬
solti senza ricorrere alla rappresentazione geometrica. Con questo,
Diofanto uscì dal sentiero tracciato da Euclide, che usava costan¬
temente questo strumento matematico. La rappresentazione geo¬
metrica trae vantaggio dallo studio delle proprietà delle figure sul
piano o nello spazio e permette di rappresentare gli elementi con
«disegni», in modo tale che gli oggetti matematici risultino «più
visuali». A tal fine, utilizza i cosiddetti «sistemi formali», così come
nozioni quali «rette», «semirette», «curve» e «punti», tra gli altri
elementi suscettibili di essere disegnati. Tuttavia, Diofanto volle
superare le limitazioni che erano caratteristiche della geometria
e, con una manifesta abilità nel calcolo (e non poca audacia), lo
rivoluzionò completamente. I suoi lavori usarono sistematicamen¬
te i simboli per indicare potenze, uguaglianze o numeri negativi,
42
UN APPROCCIO ALL’ARITMETICA
LA DEDICA A DIONISIO
Lo storico francese Paul Tannery (1843-1904),
un celebre specialista in scienza e tecnica, rea¬
lizzò un’esaustiva analisi dell’Aritmetica, in cui
non dimenticò di indagare sull’identità del mi¬
sterioso personaggio al quale è dedicata gran
parte della stessa: Dionisio. Questa dedica è
presente nel preambolo e fu scritta in questi
termini da Diofanto: «Poiché so, molto ono¬
revole Dionisio, che vuoi imparare a risolvere
problemi numerici, ho intrapreso il compito
di esporre la natura e il potere dei numeri,
partendo dai fondamenti sui quali si basano
questi problemi. Questo può sembrare, a pri¬
ma vista, molto difficile, perché non è ancora
conosciuto in assoluto. I principianti sono in¬
clini a scoraggiarsi facilmente. Ma a te sarà
facile capire il tema grazie al tuo entusiasmo
e alle mie spiegazioni, poiché il desiderio unito
all’insegnamento conduce rapidamente alla conoscenza». La cosa certa è che
il nome di Dionisio era abbastanza comune in Grecia, perché così si chiamava il
dio della vendemmia e del vino, figlio di Zeus e procuratore dell’estasi rituale. Il
culto a questa divinità fu molto diffuso in tutta l'Ellade e, successivamente, tro¬
vò un equivalente nella mitologia romana: Bacco. Ciononostante, Paul Tannery
riuscì a superare questa difficoltà e fece indagini sulla premessa che si dovesse
trattare di un personaggio importante dell’epoca. Alla fine, le sue conclusioni
indicarono che il destinatario dell’opera di Diofanto doveva essere san Dionisio
(o Dionigi) di Alessandria (200-265 ca.), uomo di grande cultura convertitosi al
cristianesimo, che fu designato vescovo della città verso il 247-248 d.C. e che
sopravvisse alle persecuzioni degli imperatori romani Decio e Valeriano. Questa
deduzione condusse Tannery a stimare, allo stesso modo, che Diofanto fosse
cristiano, come tanti altri greci alessandrini. Va detto che il culto cristiano non
fu tollerato nell’Impero romano fino alla proclamazione dell’Editto di Milano,
nel 313 d.C., da parte dell’imperatore Costantino I il Grande.
Icona bizantina con l’immagine di
san Dionisio di Alessandria.
cosa che avrebbe esercitato una notevole influenza su numerosi
matematici posteriori, come Viète, Cartesio, Fermat ed Eulero.
Tutti loro rimasero stregati dall’edizione canonica dell 'Aritmetica
realizzata nel 1621 dal matematico francese Claude Gaspard Ba-
chet de Méziriac (1581-1638).
UN APPROCCIO ALL'ARITMETICA
43
LE VICISSITUDINI DI UN CAPOLAVORO
VAritmetica sarebbe rimasta per secoli avvolta nell’oscurità per
l’Occidente. Inizialmente, l’opera era composta da tredici libri, dei
quali se ne sono conservati solo sei, per un totale di 189 problemi.
I rimanenti libri sono andati perduti già in epoca antica, e si ignora
1’esistenza di una qualsiasi traduzione. A linee generali, i sei volumi
conservatisi contengono un trattato sulle equazioni e i sistemi di
equazioni determinati e indeterminati - con una o diverse soluzioni
rispettivamente -, nei quali Diofanto cercò, in maniera sistematica,
la soluzione in numeri interi e, in qualche caso, razionali. Si deve
sottolineare che non si informò mai sulle idee generali, ma che
si accontentava nel trovare soluzioni corrette. Questa preferenza
spiega il fatto che non avesse trovato tutte le soluzioni delle equa¬
zioni indeterminate e che si fosse limitato a dare una sola solu¬
zione. La restrizione risulta più comprensibile se si tiene presente
che il suo proposito era risolvere un problema, e non un’unica
equazione. Il paradosso consiste nel fatto che Diofanto risolveva
equazioni durante tale processo. La questione spiega perché YA-
ritmetica divenne un grande trattato di algebra, poiché si liberò
del peso geometrico stabilito dai suoi predecessori.
Sebbene l’edizione più estesa áe\YAritmetica si basi sulla sua
versione originale in lingua greca, esiste anche un’edizione araba, di
minore diffusione. Databile all’870, rappresentò la prima traduzione
conosciuta e commentata del testo di Diofanto e consiste in sette
libri, dove sono principalmente trattate le equazioni di secondo
grado e cubiche. Si ignora a partire da quale copia greca sia stata
realizzata la sua traduzione, e se questa contenesse i tredici libri
menzionati da Diofanto. L’autore di questa edizione fu Qusta ben
Luqa al-Ba’albakki (820-912). I quattro libri di fonte araba aggiunse¬
ro 101 problemi ai 189 che erano contenuti nei sei libri greci dell’A-
ritmetica. Questi, conservati in copie manoscritte, furono trasmessi
dagli eruditi bizantini, che li numerarono dall’I al VI. Tuttavia, non
sarebbero stati conosciuti in Europa fino alla metà del xv secolo,
quando un appassionato cercatore di antichi testi di matematica,
10 scienziato tedesco Johann Müller Regiomontano (1436-1476),
11 localizzò a Venezia, nel 1464. Un altro erudito tedesco, Joachim
44
UN APPROCCIO ALL'ARITMETICA
Liebhard o Joachim Camerarius (1500-1574), nel 1556 diede una
notizia sensazionale: 1’esistenza in Vaticano di un manoscritto di
Diofanto. A dispetto di questi ritrovamenti, l'Aritmetica sarebbe
stata tradotta in latino solo nel 1570, grazie al matematico italiano
Rafael Bombelli (1526-1572). Questi decise di pubblicarla in cinque
volumi, ma videro la luce solo i primi tre, sotto il titolo di L’Algebra,
opera di Rafael Bombelli da Bologna, divisa in tre libri con la
quale ciascuno da sé potrà venire in perfetta cognitione della
teoria dell’Aritmetica (1572).
«Nessuno ha ancora tradotto dal greco al latino i tredici
libri di Diofanto, nei quali giace nascosto
il fior fiore della matematica.»
— Johann Müller Regiomontano.
Maggiore fortuna ebbe la traduzione latina del filologo tedesco
Guilielmus Xylander (1532-1576), realizzata nel 1575 a partire da
alcuni manoscritti dell’Università di Wittenberg. L’edizione, che
poteva vantare l’aggiunta di un frammento del manoscritto di Dio¬
fanto sui numeri poligonali, attirò l’attenzione verso la teoria dei
numeri. Nel 1577 apparve un’altra opera in latino, De arte magna
seu de occulta parte numerorum quae et algebra et almucabala
vulgo dicitur (1577), del matematico francese Guillaume Gosselin
(m. 1590), che divulgò i metodi di Diofanto e fece conoscere l’opera
di Xylander. Nel 1625, il matematico francese Albert Girard (1595-
1632) pubblicò parte dei volumi quinto e sesto in lingua francese.
A ogni modo, è necessario insistere sul fatto che l’edizione più
completa dell’Aritmetica è quella di Bachet de Méziriac, la cui ver¬
sione commentata contiene, oltre al testo greco e alla corrispon¬
dente traduzione latina, diversi contributi di grande interesse, come
alcune traduzioni dall’Antologia Palatina. Si dà il caso che Pierre de
Fermat possedeva una copia di questa traduzione e che fece alcune
annotazioni ai suoi margini; tra esse, e senza alcuna dimostrazione,
vi è anche il celebre ultimo teorema di Fermat. Nel 1642, Bachet de
Méziriac pubblicò una versione più estesa dell ’Aritmetica e incluse
anche trucchi e curiosità aritmetiche. L’influenza di Diofanto sui suoi
UN APPROCCIO ALL'ARITMETICA
45
lavori era di lunga data, perché Fermat già aveva pubblicato un’opera
considerata come il primo testo di matematica «ricreativa»: Problemi
piacevoli e deliziosi che si possono porre con i numeri (1612). Il
libro contiene un problema classico, di chiara ispirazione diofantea,
il cui enunciato affermava: «Un mercante aveva un peso di 40 chi¬
logrammi che cadde a terra e si ruppe, dividendosi in quattro parti
disuguali. Portò questi pezzi a una bilancia e dimostrò che ognuno
aveva un peso equivalente a un numero intero di chilogrammi. Os¬
servò che con essi poteva pesare oggetti il cui peso fosse un numero
intero qualsiasi di chilogrammi tra 1 e 40. Quanti chilogrammi pesano
ognuno di essi?». Bachet de Méziriac diede come soluzione 1,3, 9 e
27, rispettivamente. Si noti che queste cifre sono potenze di 3 e danno
come somma 40. Infine, si deve segnalare la brillante edizione delle
opere di Diofanto realizzata da Paul Tannery nel 1885.
VARITMETICA: SEI LIBRI E 189 PROBLEMI
L'Aritmetica non è un testo di teoria, bensì una raccolta di pro¬
blemi che ammettono una o molteplici soluzioni razionali, e dove
vengono sempre risolti casi particolari. Talvolta, vengono incluse
anche le condizioni affinché si possano avere le soluzioni, cosa
che ricorda l’attuale teoria dei numeri. La struttura dell’opera è
semplice, perché le definizioni, i problemi e le proposte si diffe¬
renziano chiaramente. L'Aritmetica non si divide in un insieme
di articoli o riflessioni, e non è stata neppure scritte secondo
il metodo degli Elementi, con definizioni e assiomi iniziali per
dimostrare le proposte posteriori. Si tratta, semplicemente, di
una raccolta di 189 problemi senza un criterio o un ordine appa¬
rente, suddivisi in sei libri. Ognuno di essi è accompagnato dalla
sua soluzione e in alcuni casi ne viene presentata più di una,
suggellando il fatto che non sia strettamente un’opera teorica.
Tutti gli enunciati dei problemi sono scritti in maniera ge¬
nerale, cioè senza specificare un valore concreto per i numeri.
Perciò, vi sono molte espressioni del tipo «dati due numeri», «se
due quadrati» ecc. Un esempio di quanto detto è l’enunciato del
46
UN APPROCCIO ALL'ARITMETICA
IL PROBLEMA DEL VINO
Vi è un solo enunciato con numeri
concreti in tutta VAritmetica. Si tratta
del problema 30 del Libro V, che
esprime quanto segue nella sua tradu¬
zione letterale: «Una persona si imbar¬
cò con i suoi domestici, affinché po¬
tessero essergli utili. Mescolò alcune
misure di vino, alcune da 8 dracme e
altre da 5, e pagò per tutto un nume¬
ro quadrato che, aumentato nel nu¬
mero di unità che ti saranno indicate,
60, farà sì che si ottenga un altro qua¬
drato la cui radice è il numero totale
delle misure. Verifica quante vi erano
da 8 e quante da 5 dracme». Questo
problema, contestualizzato nella vita
quotidiana dell’epoca, fu preso come
riferimento da Paul Tannery per situa¬
re cronologicamente Diofanto, poiché
faceva riferimento a prezzi di vini di
bassa qualità e al periodo del mondo
greco-romano durante il quale furono
in vigore. Infine, Diofanto pose il
n2 + 60 = (x+y)2, e diede come soluzioni
Statua romana in marmo raffigurante Dionisio
come incarnazione antropomorfa del vino,
databile al 150-200 d.C.
problema come 8x + 5y-n2, con
x = 59/12 e y= 79/12.
problema quattordicesimo del Libro II, che chiede di «scomporre
un numero dato in due parti e trovare un quadrato che aggiunto a
ognuna di queste due parti formi un quadrato». L’unica eccezione
è costituita dal problema 30 del Libro V in greco, perché include
numeri concreti. Si tratta proprio del problema del prezzo del
vino che fornì l’indizio a Paul Tannery per situare cronologica¬
mente Diofanto.
VAritmetica è, pertanto, una raccolta di sfide che ispirò
numerose indagini durante i secoli. Per esempio, François Viète,
uno dei pionieri dell’algebra attuale, si ispirò a lei per scrivere
In artem analycitem isagoge (1591). Come lui stesso commen¬
tò nel primo capitolo di quest’opera, non esitò a introdurre nel
UN APPROCCIO ALL'ARITMETICA
47
testo un sistema di notazione che, nello stile di Diofanto, usava
lettere nelle formule algebriche. Viète non solo fu uno dei primi
a rappresentare i parametri di un’equazione mediante lettere,
ma stabilì anche regole per l’estrazione di radici e strutturò la
trigonometria così come la si conosce ancora oggi.
Nessuno mette in discussione, pertanto, l’originalità dell’A-
ritmetica nel risolvere problemi e la sua influenza sulla ricerca
posteriore di nuovi rami della matematica. Uno dei risultati più
rappresentativi di questa «ispirazione» fu l’ultimo teorema di
Fermat, sostanzialmente la scomposizione di un quadrato come
somma di due quadrati.
Si sa che Diofanto cercò soluzioni razionali positive di quelle
che in seguito sarebbero state chiamate «equazioni diofantee»,
e non esclusivamente intere. In realtà, fu Fermat colui che real¬
mente iniziò lo studio delle soluzioni esclusivamente intere di
queste equazioni. Inoltre, Diofanto arrivò a conoscere metodi
generali per trovare soluzioni razionali di queste equazioni, date
una o varie soluzioni iniziali. Per tutto questo, non deve mera¬
vigliare il fatto che, spesso, VAritmetica è considerata un testo
esclusivamente di algebra.
UN APPUNTO SULLE EQUAZIONI DIOFANTEE
E LA NOTAZIONE PROPRIA
Prima di proseguire, si rende necessario un breve appunto su
che cosa siano le equazioni diofantee e quale notazione utilizzò
Diofanto nella sua opera. In onore di Diofanto, le equazioni con
coefficienti interi le cui soluzioni sono anch’esse intere vengono
chiamate equazioni diofantee e, talvolta, «diofantine», voce però
in disuso. Una equazione diofantea è un’equazione algebrica - per
esempio, 3xy2-2y + x = 5 - nella quale compaiono diverse variabili
le cui soluzioni sono numeri interi. Cioè risolvere un’equazione
diofantea consiste nel determinare quali numeri interi la compiono.
Diofanto si dedicò, tra gli altri temi, allo studio di queste equazioni,
e ammise perfino soluzioni razionali per alcuni casi. In questo sen-
48
UN APPROCCIO ALL’ARITMETICA
so, sono di particolare interesse le equazioni lineari - cioè di grado
1 - di due variabili -xey- che hanno coefficienti interi. Risolvere
un’equazione diofantea significa trovare i valori delle variabili che
verificano l’equazione. Un esempio sarebbe trovare le soluzioni di:
3(Xr+ Ì2y= 1.200.
Un paio di valori interi che verificano l’equazione lineare
dell’esempio sono x = 24 e y = 40. Nel prossimo capitolo verranno
illustrati diversi tipi di equazioni diofantee e alcuni algoritmi di
risoluzione, che ci aiuteranno a comprenderle.
Dopo la dedica a Dionisio, Y Aritmetica inizia introducendo
alcune definizioni che oggi risultano in realtà abbastanza ovvie:
quadrati, cubi, incognite, costanti, frazioni, moltiplicazioni, equa¬
zioni ecc. A tale scopo utilizzò una notazione propria che non cor¬
risponde a quella attuale. Nella prefazione del libro, per esempio,
appare sotto il titolo di «definizione I» un appunto su quadrati, cubi
e termini affini. Così, i quadrati - in greco, Texpaycbvcov - sono il
risultato della moltiplicazione di un numero, che denomina «lato»
- jiXeupá - del quadrato, per se stesso. Scritto secondo i termini
odierni, se si chiama a il lato, il suo quadrato è a • a = a2. Questo
viene esteso ai casi seguenti:
— I cubi o KÚßcov, risultanti dal moltiplicare i quadrati con il
loro lato corrispondente, cioè a2 • a = a3.
— I quadrati-quadrati o òuvapoòuvápecov, risultanti dal mol¬
tiplicare i quadrati per se stessi, a2 • a2 = a4.
— I quadrato-cubi o òuvapoKÚßcov, derivanti dal moltiplicare
un quadrato per il cubo dello stesso lato del quadrato, cioè
a2 • a3 = a5.
— I cubo-cubi o KußoKÚßcov, prodotti di cubi moltiplicati per
se stessi, cioè a3 • a3 = a6.
Diofanto non disponeva di una notazione speciale per questi
numeri. Per esempio, il quadrato di 5 oggi si scrive come 52. Tut¬
tavia, Diofanto affermava che 25 era un numero quadrato, ovvero
scriveva che il quadrato era 25 e il suo lato era 5.
UN APPROCCIO ALL'ARITMETICA
49
Il matematico alessandrino ricorse a enunciati generali e
astratti nell’Aritmetica, ma al momento di effettuare i calcoli per
risolvere i problemi usò numeri concreti, abilmente scelti. Nono¬
stante tutto, la strada che seguì fu rigorosamente scientifica. In
questo senso, può risultare un esercizio interessante per il lettore
trovare la generalità negli enunciati di Diofanto, usando le solu¬
zioni numeriche da lui proposte.
UN CONTENUTO BRILLANTE E ISPIRATORE
Il Libro I dell'Aritmetica è composto da 25 problemi di equazioni
di primo grado (21 determinati e quattro indeterminati) e da 14 di
equazioni di secondo grado (13 determinati e uno indeterminati).
I problemi indeterminati sono quelli che possiedono molte solu¬
zioni, mentre quelli determinati sono quelli che hanno un’unica
soluzione. Diofanto si occupò in questa fase iniziale di spiegare i
principi di base dei numeri, degli arithmos (numeri incogniti) e
di alcune delle loro potenze (sia dei numeri sia degli arithmos).
Descrisse anche il modo di sommare, sottrarre, moltiplicare e divi¬
dere i numeri che aveva definito, e spiegò come si doveva operare
con numeri della forma x" e con frazioni, includendo quelle il cui
numeratore è 1 e il denominatore è un numero del tipo xn.
«Accade che i problemi aritmetici, nella loro maggior parte, abbiano
a che fare con addizione, sottrazione, moltiplicazione o divisione di
numeri di questi tipi, tra loro stessi oppure tra qualsiasi di essi e i
lati di qualunque altro di essi. Tali sono i problemi che si potranno
risolvere percorrendo la via che mostreremo.»
— Diofanto.
Solitamente, Diofanto ricorreva a numeri concreti e nella ri¬
soluzione ragionava con casi particolari. Per esempio, suggerì di
scomporre il numero 5 in due numeri interi che, sommati, davano
50
UN APPROCCIO ALL'ARITMETICA
il numero 5, e che, sottratti, davano 1. In questo caso, il lettore può
dimostrare che i numeri sono 3 e 2. Se vengono sommati, si ottiene
il 5, mentre se si sottrae il 3 dal 2, si ottiene 1. Secondo il linguag¬
gio algebrico attuale verrebbe esposto come un sistema semplice di
equazioni lineari. Così, se due numeri cercati fossero denotati come
x e y, basterebbe esporre:
x + y = 5 e x-y - 1.
Da parte sua, il Libro II è composto da 35 problemi, dei quali
30 sono indeterminati. Tra essi si distingue il problema ottavo, che
avrebbe sedotto Fermat tramite questo enunciato:
II. 8. Scomporre un quadrato in due quadrati.
n Libro n è conosciuto attraverso diversi aneddoti che hanno per
protagonista Fermat, che saranno esposti più avanti, e attraverso il
problema ottavo, che diede origine all’ultimo teorema di Fermat, di
grande risonanza nella storia della matematica
Quanto al Libro III, comprende 21 problemi, tra cui attira l’at¬
tenzione il numero III. 19, per la cui soluzione Diofanto ricorse alla
geometria. Il suo enunciato è il seguente:
III. 19. Trovare quattro numeri tali per cui il quadrato della somma
dei quattro, aumentato o diminuito in ciascuno di essi, formi un
quadrato.
Maggiore importanza acquisisce il Libro IV, che raccoglie 40
problemi, in gran parte sui cubi. Quasi tutti includono potenze
di tre nei loro calcoli e fanno riferimento ai cosiddetti «numeri
cubici». Poiché i Greci ignoravano la formula per risolvere un’e¬
quazione cubica, l’abilità e i sistemi di Diofanto condussero alla
soluzione di alcuni casi particolari.
Nell’introduzione del Libro IV sono presenti i metodi di «restau¬
razione» e «riduzione» per risolvere problemi. Per restaurazione si
intende un metodo utilizzato per la soluzione di equazioni che con¬
siste, secondo i termini attuali, nel sommare a entrambi i membri
UN APPROCCIO ALL'ARITMETICA
51
dell’uguaglianza quello che si sta sottraendo, e per riduzione invece
l’azione di eliminare i termini uguali in entrambi i membri dell’ugua¬
glianza Questi metodi ricordano quelli che sarebbero stati utilizzati
da Al-Khwarizmi, che li chiamò al-jábr (sommare a entrambi i lati di
una equazione una medesima espressione) e al-muqabala (eliminare
quello che appare uguale in due espressioni equivalenti). Così, il meto¬
do di restaurazione può essere esemplificato nella seguente maniera
#-7 = 9,
e aggiungendo 7 a entrambi i lati,
risulta allora
#—7+7 — 9 + 7,
# = 16.
In quanto alla riduzione o al-muqabala, se si considera:
# + 6 = 11,
e si «toglie 6», cioè si aggiunge -6 a entrambi i lati, risulta
per cui si ha:
# + 6-6= 11-6,
# = 5.
Si osservi che in un certo modo si conosceva lo zero, sebbene
non in maniera esplicita, poiché quello che in realtà si faceva era:
# + 6=11,
e allora
cioè:
# + 6-6= 11-6,
# + 0 = 5.
Questi metodi per risolvere i problemi erano già presenti nei
libri greci e arabi, ma Diofanto li enunciò di nuovo e li integrò
52
UN APPROCCIO ALL'ARITMETICA
con queste parole, nelle quali per «calcolo» si deve intendere la
conseguenza della restaurazione e della riduzione, e per «specie»
i diversi tipi di potenze dell’incognita.
Il calcolo ci conduce a una sola delle specie di cui abbiamo descrit¬
to la moltiplicazione di alcune per altre e la divisione di alcune per
altre ancora uguale a un’altra specie; sarà necessario dividerlo tutto
per la specie meno elevata di quelle tra entrambi i membri al fine di
ottenere una sola specie uguale a un numero.
Una situazione di moltiplicazione e divisione «tra specie» vie¬
ne illustrata nel seguente esempio:
(3 • a)2 = 9 • a2.
Poiché si tratta di un quadrato, la definizione proposta da Dio-
fanto sostiene che è il risultato del moltiplicare il lato, cioè
(3a) • (3a),
da cui risulta un’altra specie, che è 9a2.
Nel linguaggio odierno, si combinerebbero potenze di primo
grado, moltiplicando per ottenere una potenza di secondo grado.
Così, da a3 =7a2 si ottiene a = 7. In questo caso, Diofanto, per giun¬
gere alla soluzione in cui una sola specie è uguale a un numero,
realizzò qualcosa di simile all’operazione
3 „ 2 a3 7a2
aJ=7a2 e —r = —5-,
a a
per concludere infine che a = 7.
Pertanto, il matematico alessandrino combinò in questo caso
potenze - divisione - di grado superiore a zero per giungere a una
espressione di grado zero - un numero-. In quanto al Libro V, di
enorme interesse, Diofanto risolse un totale di 30 problemi, 28 dei
quali sono relativi a equazioni di secondo e terzo grado. Per esem¬
pio, nei problemi V.28 e V.29 sono presenti equazioni biquadratiche
che rimandano a equazioni di secondo grado. Come si è già detto,
UN APPROCCIO ALL'ARITMETICA
53
il problema V.30 che tratta del mescolare vini di prezzi differenti,
fu l’unico dove incluse numeri concreti. A titolo di curiosità, la
versione araba di questo libro varia sensibilmente, poiché plasma
come problemi settimo e ottavo esattamente i problemi che figu¬
rano come primo e secondo nel Libro IV in greco.
In altri ordini, gli enunciati delle equazioni quadratiche di que¬
sto Libro V espongono problemi come, per esempio, «scrivere 13
come la somma di due quadrati ognuno maggiore di 6». La solu¬
zione che viene data da Diofanto è la seguente:
66049 66564
10201 6 10201'
Un altro esercizio consiste nello «scrivere 10 come la somma
di tre quadrati maggiori di 3». Diofanto trovò i tre quadrati in:
1745 041 1651225 1658944
505521 ’ 505521 ’ 505521 '
Infine, il Libro VI, e l’ultimo nella versione e greca, propone e
risolve 24 problemi sui triangoli rettangoli. Tutti i problemi inclu¬
dono calcoli con cubi. Di essi, dieci cercano di trovare un cubo
e un quadrato; otto si propongono di trovare due quadrati; tre,
di trovare tre quadrati, e solo in uno si cerca di trovare un cubo.
Diofanto realizzò il calcolo di radici quadrate nei problemi VI.3,
VI.9 e VI. 10. Il Libro VI avrebbe ispirato al matematico francese
Bernard Frénicle de Bessy (1604-1675 ca.) la stesura del Traité
des triangles rectangles en nombres, dans lequel plusieurs belles
propriétés de ces triangles sont démontrées par de nouveaux
principes (1676). Frénicle ebbe un punto di riferimento in Diofan¬
to, la cui opera studiò a fondo prima di concentrarsi sullo studio
della teoria dei numeri. Spinto dal suo entusiasmo per YAritme¬
tica, Frénicle propose al suo amico, il matematico e astronomo
olandese Christiaan Huygens (1629-1695), di risolvere il seguente
sistema di equazioni diofantee:
x2 + y2 = z2, v2 = u2 + v2, x-y = u-v.
54
UN APPROCCIO ALL'ARITMETICA
La sua complessità era tale che neppure Huygens riuscì a ot¬
tenerla. In realtà, nessuno nel xvii e xvm secolo vi sarebbe riuscito.
Bisognò aspettare fino al 1880 per conoscere finalmente la sua
soluzione, che fu ottenuta con grande merito dal matematico fran¬
cese Jean-François-Théophile Pépin (1826-1904).
Come nota, si deve ricordare che la versione araba dell’Aritme¬
tica annovera un settimo libro, che raccoglie 18 problemi di diversa
tipologia. A grandi linee, sono incluse espressioni con potenze di
9, 6, 4, 3, 2 e 1. Per esempio, il problema VII.2 cerca di trovare tre
cubi che siano allo stesso tempo dei quadrati, e nel problema VII.5
le incognite sono una potenza di 9, un cubo e un quadrato. Da parte
sua, il problema VII.3 chiede di trovare una quarta potenza e un
cubo, e in molti altri problemi le quantità sconosciute sono una
potenza di 6 - cubo-cubo - insieme a quadrati - potenze di grado
2 - e lati - potenze di grado 1-. Infine, i problemi VII. 17 e VII. 18
chiedono di trovare, in progressione geometrica, tre e quattro qua¬
drati, rispettivamente.
In definitiva, i sei libri della fonte greca dell ’Aritmetica forma¬
no una raccolta di 189 problemi e i quattro libri di fonte araba ne
propongono altri 101. Ognuno di essi ammette una o più soluzioni,
sempre con soluzione positiva e razionale.
DIOFANTO E I NUMERI NEGATIVI
Il testo dell ’Aritmetica comprende la soluzione di molti problemi
che rimandano a equazioni lineari e quadratiche, ma prende in
considerazione solo soluzioni positive intere o, al massimo, ra¬
zionali. Diofanto ritenne infatti inutili le equazioni che portavano
a soluzioni negative o a radici quadrate irrazionali - un «nume¬
ro irrazionale» è un numero reale che non è razionale, cioè che
non può essere scritto come il quoziente di due numeri interi; per
esempio, n, e, V2 In questo senso, per Diofanto risultava quindi
assurda un’equazione come 4 = 4x + 20, dal momento che portava
a una risposta priva di senso. In altre parole, come potrebbe un
problema portare a una soluzione di -4?
UN APPROCCIO ALL'ARITMETICA
55
Il matematico alessandrino si accontentava di una soluzione
intera o, al massimo, razionale. In altri ordini, Diofanto considerò
tre tipi di equazioni quadratiche:
ax2 + bx = c, ax2 = bx + c, ax2 + c = bx.
Oggi si osserva che tutte loro sono equivalenti e costitu¬
iscono un solo caso, mentre per il matematico alessandrino
esistevano tre casi. La spiegazione è semplice: Diofanto non
aveva alcuna nozione dello zero. Per questo motivo evitò i coef¬
ficienti negativi e considerò i numeri dati a, b, c come tutti po¬
sitivi in ognuno dei tre casi menzionati. Le tre equazioni che
propose risultano, così, casi particolari della tradizionale equa¬
zione di secondo grado che, nel linguaggio odierno, ha la forma:
Ax2 + Bx+C=0.
Tuttavia, esistono molti altri tipi di problemi che furono in¬
vece presi in considerazione da Diofanto e che non conducevano
necessariamente a numeri negativi. Come si vedrà più avanti, il
matematico alessandrino risolse sistemi di equazioni non lineari.
Per esempio, il sistema di equazioni
y + z=ì0,yz = 9,
per il quale ragionò nel modo seguente. Come prima cosa intro¬
dusse una nuova variabile: x. Quindi, abilmente, definì 2x = y-z.
Pertanto, risulta come
y + z=10,y-z = 2x,
e con questo otteneva, sommando le equazioni,
2 y= 10 + 2x.
Cioè si ha y = 5 + x. Quindi, sottraendo, dà z = 5-x. Per cui,
riassumendo:
56
UN APPROCCIO ALL'ARITMETICA
Q = yz = {ß+x) (ß-x) = 25-of,
da dove si ha che
e, di conseguenza,
16,
x=4,
il che porta alla soluzione
y = 9, 2=1.
Come è possibile osservare nella figura 1, se prendiamo come
assi y, z sarà possibile dimostrare che le soluzioni intere sono i
punti A(9,l) e B(l,9).
FIG 1
UN APPROCCIO ALL'ARITMETICA
57
LA GRANDE SFIDA DI FERMAT
Il matematico francese Pierre de Fermat, uno dei pionieri del
calcolo infinitesimale, arricchì l’opera di Diofanto nell’ambito
relativo allo studio dei numeri interi e delle sue proprietà. Il
suo principale contributo alla scienza partì, precisamente, dal
problema ottavo del Libro II di Diofanto. Si tratta del risultato
conosciuto come ultimo teorema di Fermat, che lui stesso an¬
notò ai margini del suo esemplare dell'Aritmetica, nell’edizio¬
ne canonica di Bachet de Méziriac. Lì stabilì, senza dimostrazione
alcuna, che non esiste soluzione con numeri interi non nulli - né
x = 0, né y = 0, né z = 0 - per l’equazione xn + y" = z" se n è un intero
più grande di due. Fermat era solito scrivere le soluzioni ai problemi
sul margine dei libri. In realtà, inserì 48 osservazioni nelle traduzioni
originali in greco e in latino di Bachet de Méziriac. Sul margine di
una pagina del suo esemplare dell'Aritmetica scrisse:
È impossibile scrivere un cubo come somma di due cubi o una
quarta potenza come somma di due quarte potenze o, in generale,
nessun numero che sia una potenza maggiore di due può essere
scritto come somma di due potenze dello stesso valore. Ho sco¬
perto una dimostrazione notevole di questo fatto, ma purtroppo
questo margine è troppo stretto per contenerla.
Il che, traducendo nel linguaggio simbolico, sostiene che non
vi sono soluzioni intere per n>2, dove n è un numero naturale,
nell’equazione:
xìl + yn = zn.
Questo teorema, ipotizzato da Fermat nel 1637, non venne
divulgato fino al 1670, quando suo figlio Samuel presentò l’edizio¬
ne delle sue opere complete. Inoltre, non poté essere dimostrato
per tre secoli, per cui divenne uno dei problemi più popolari della
matematica e la sua soluzione è legata al nome di grandi perso¬
naggi di questa scienza. Lo stesso Fermat lo dimostrò per il caso
di n = 4 usando il metodo della discesa infinita: se si trovano tre
58
UN APPROCCIO ALL'ARITMETICA
valori interi positivi di x, y, z che soddisfino l’equazione, è possibile
trovare anche altri numeri interi positivi minori che la soddisfino,
arrivando a un assurdo. Nel 1739, Eulero utilizzò lo stesso metodo
per dimostrare il caso di n = 3.
Quasi un secolo dopo, sarebbero state pubblicate altre solu¬
zioni parziali. Nel 1825 il matematico francese Adrien-Marie Legen¬
dre (1752-1833) e fanalista tedesco Peter Gustav Lejeune Dirichlet
(1805-1859) dimostrarono, in maniera indipendente l’uno dall’altro,
il caso di n = 5, basandosi su precedenti idee della matematica fran¬
cese Sophie Germain (1776-1831). Sette anni dopo, Dirichlet ebbe
di nuovo successo affrontando il caso n = 14. Più tardi, nel 1845, i
suoi colleghi Gabriel Lamé (1795-1870) e Victor-Amédée Lebesgue
(1791-1875) riuscirono a dimostrarlo per n = 7, ma la questione
poi si arenò. A ottenere un notevole progresso in questa sfida fu il
tedesco Emst Kummer (1810-1893), con la cosiddetta «teoria dei
numeri algebrici». Kummer si servì della radice ennesima dell’unità
E = e'Zni/u che permette di scomporre zn-yn in fattori lineari, per
scrivere l’equazione di Fermat in questo modo:
xn = {z-y) Çz-ey) (.z-èzy)... (z-en-ly),
cioè l’ennesima potenza del numero intero x deve essere scompo¬
sta in fattori formati dai numeri interi y e z.
Tuttavia, la cosa certa è che si era giunti al xx secolo e nessuno
aveva dimostrato interamente l’ultimo teorema di Fermat, cosa che
fece sorgere un dubbio: e se la dimostrazione dello stesso Fermat,
rimasta sconosciuta perché il margine del libro di Diofanto era
«troppo stretto per contenerla», fosse stata sbagliata?
Era difficile pensare che un genio come Fermat si fosse sba¬
gliato, ma anche i più grandi matematici, esseri umani in fin dei
conti, commettono errori. L’incertezza fece sì che il matematico
tedesco Paul Wolfskehl (1856-1906) lasciasse alla sua morte una
ricompensa di 100.000 marchi per chi fosse riuscito a dimostrare
integralmente l’ultimo teorema di Fermat, oppure adducesse un
esempio del fatto che fosse errato. Se il primo compito esigeva
profonde conoscenze nella teoria dei numeri, neppure il secondo
era facile.
UN APPROCCIO ALL'ARITMETICA
59
La frustrazione fu la nota predominante dei tanti matematici
che provarono, fallendo, a risolvere il teorema. Questa dispera¬
zione è testimoniata dal commento scritto da uno sconosciuto sul
margine di un manoscritto conservato nella Biblioteca Nazionale
di Madrid in merito al problema che diede origine all’ultimo teo¬
rema di Fermat: «Che la tua anima, Diofanto, sia con Satana per
la difficoltà degli altri teoremi e soprattutto per quella di questo».
Nel 1954, con i computer, è stato verificato il teorema per tutti gli
esponenti minori di 10.000. Finalmente, il matematico britannico
Andrew Wiles (Cambridge, 1953) entusiasmò la comunità matema¬
tica nel 1995 ottenendo «l’impossibile»: dimostrare integralmente
l’ultimo teorema di Fermat. Wiles ci riuscì tramite strumenti ma¬
tematici basati sulla teoria dei numeri e sull’aritmetica modulare.
Inutile dire che ebbe un grande trionfo e, in più, si aggiudicò la
ricompensa offerta 87 anni prima da Paul Wolfskehl. Ebbe così
fine una «gara matematica» durata oltre tre secoli. E tutto questo
ebbe origine da un problema di Diofanto.
Di seguito, per illustrare la soluzione del caso particolare di n=2,
si mostrano come esempi i valori x=3, y=4 e z=5, che verificano che:
32 + 42 = 52.-
Un’altra tema sarebbe x = 6, y = 8, z = 10, dove si osserva che:
62 + 82= IO2.
Queste teme numeriche, che sono soluzioni di oc2 + y2 = z2, sono
chiamate «teme pitagoriche» e sono definite come una sequenza
di tre numeri naturali x, y, z che verificano che x2 + y2 = z2. Il nome
deriva dal teorema di Pitagora, che afferma che in un triangolo ret¬
tangolo con cateti di lunghezza x e y, la cui lunghezza di ipotenusa
è indicata da z, si verifica questa equazione. A partire da una tema
pitagorica a, b, c-à2 + b2 = c2- anche qualsiasi multiplo di questi lo
è. In questo modo, se k è un numero reale, si ha che anche ka, kb,
kc forma una tema pitagorica, poiché si verifica (ka)2 + (kb)2 = (kc)2.
A titolo di curiosità, non esiste alcuna terna pitagorica i cui tre
numeri siano dispari.
60
UN APPROCCIO ALL'ARITMETICA
ANDREW WILES
Il matematico britannico Andrew John Wiles nacque il 11 di aprile di 1953 a
Cambridge (Inghilterra). Lui stesso descrisse la sua passione per il lascito ma¬
tematico di Fermat, e particolarmente per il suo ultimo teorema, con queste
parole: «Non c’è un altro problema che possa rappresentare lo stesso per me.
Fu l’illusione della mia infanzia. Niente può rimpiazzarlo. L’ho risolto. Cercherò
di risolvere altri problemi, ne sono sicuro. Alcuni saranno molto difficili e avrò
ancora una volta una sensazione di realizzazione, ma non c’è nessun proble¬
ma matematico che possa attirarmi come lo fece quello di Fermat». Nel 1993,
Wiles approfittò di un ciclo di tre conferenze presso l’Istituto Isaac Newton,
all’Università di Cambridge, per dare l’annuncio della sua dimostrazione. Tutta¬
via, il titolo delle sue conferenze fu deliberatamente poco specifico. Al termine
del primo dei tre giorni di sessioni, si sparse
la voce di ciò che avrebbe annunciato. La
sua ultima dissertazione trascorse, dun¬
que, in mezzo all’attesa generale. In essa,
Wiles non solo spiegò che cosa aveva ot¬
tenuto, ma anche come, per terminare la
sua brillante esposizione in maniera molto
modesta, propria dei più grandi matemati¬
ci: «E questo dimostra l’ultimo teorema di
Fermat. Credo che lo lascerò qui». Quella
che seguì fu un’ovazione. Nel 1995, Wiles
completò la dimostrazione correggendo
una lacuna della stessa. Infine, nel 2016 fu
premiato con il premio Abel.
Andrew Wiles nel 1995, anno in cui ha dimostrato
integralmente l’ultimo teorema di Fermat.
IL LINGUAGGIO SINCOPATO DI DIOFANTO
Gli storici normalmente fanno riferimento a Diofanto come al pa¬
dre degli algebristi moderni, perché gli è attribuita l’introduzione del
calcolo algebrico nella matematica e l’uso sistematico di simboli e
caratteri speciali per indicare potenze e uguaglianze. La notazione
matematica comprende i simboli e i caratteri usati per scrivere equa¬
zioni matematiche e formule. A livello generale, la notazione mate¬
matica comprende numeri arabi, lettere romane, greche ed ebraiche,
UN APPROCCIO ALL'ARITMETICA
61
alfabeti di diverse lingue e di diverse epoche, oltre a una serie di
simboli inventati dai vari matematici durante gli ultimi secoli. Lo svi¬
luppo della notazione matematica per l’algebra può essere suddivisa
in tre tappe. La prima corrisponde all’algebra retorica, sviluppata in
gran parte dai matematici islamici di epoca medievale, dove tutti i
calcoli venivano realizzato utilizzando parole, senza includere alcun
simbolo, neppure quello delle operazioni, e inoltre i problemi erano
particolari e non vi erano metodi generali di risoluzione. La seconda
è quella dell’algebra sincopata, utilizzata da Diofanto, dove le ope¬
razioni utilizzate e le quantità erano rappresentate frequentemente
da abbreviazioni simboliche. Questa tappa rappresentò la fase di
passaggio dal linguaggio verbale a quello simbolico. Infine, l’algebra
simbolica, un sistema completo di notazione e sostituzione di tutti
i retorici. Usata dai matematici di India ed Europa a partire dalla
metà del xvii secolo, oggi è il linguaggio più avanzato dell’algebra ed
è caratterizzata dalla proliferazione della simbologia. Diofanto fece
un passo fondamentale dall’algebra verbale all’algebra simbolica e,
in generale, si può affermare che usò un «linguaggio sincopato». Poi¬
ché in alcune occasioni utilizzò simbologia, e perfino abbreviazioni
di parole che divennero simboli, non vi è dubbio che rappresentò
la transizione dal linguaggio verbale a quello simbolico. Tuttavia,
bisogna puntualizzare che ricorse anche al linguaggio naturale in
gran parte della sua opera, allontanandolo quindi dalla concezione
più stretta dell’algebra simbolica. Per meglio comprendere ciò, si
può esporre un problema espresso con il linguaggio verbale attuale
per poi trattarlo secondo l’ottica di Diofanto e dimostrare quindi se
utilizzò o meno il linguaggio sincopato. Così, sia 80 il numero che si
desidera scomporre in due parti tali per cui la maggiore sia il triplo
della minore e la ecceda, inoltre, di 4 unità. Se x rappresenta la parte
maggiore e la parte minore è rappresentata con y, allora si avrà:
con soluzione
x+y = 80,
x = 3y + A.
Ebbene, per Diofanto il problema avrà la seguente impostazio¬
ne: se la parte minore è un arithmos (una incognita), quella mag-
62
UN APPROCCIO ALL'ARITMETICA
giore sarà 3 arithmos più 4 unità. Cioè secondo lo stile di Diofanto
una incognita verrà denominata con il simbolo ç. In questo modo,
molto simile alla maniera attuale, si avrebbe:
con soluzione
2/ = Ç
a; = 3ç + 4.
Questa combinazione di linguaggio verbale e simbolico in un
medesimo problema è ciò che caratterizza il linguaggio sincopato.
SIMBOLI NUMERICI
Il sistema di simboli per i numeri utilizzato da Diofanto fu quello
della numerazione ionica, che utilizzava 24 lettere dell’alfabeto
greco classico, insieme alle tre lettere Digamma (6; nell’uso
moderno e medievale, il numerale viene tuttavia scritto nella
forma grafica di una ç), Qoppa (90) e Sampi (900), per arrivare
in questo modo a un totale di 27 lettere. Queste sono illustrate
nella seguente tabella.
Unità
Decine
Centinaia
a
A
Alfa
1
1
1
Iota
IO
P
P
Rho
100
ß
B
Beta
2
K
K
Kappa
20
a
2
Sigma
200
Y
r
Gamma
3
k
A
Lambda
30
T
T
Tau
300
ò
A
Delta
4
F
M
Mi
40
V
Y
Ypsilon
400
8
E
Epsilon
5
V
N
Ni
50
<!>
Phi
500
5
F
Digamma
6
?
2
XI
60
X
X
Chi
600
ç
Z
Zeta
7
o
0
Omicron
70
V
¥
Psi
700
11
H
Età
8
Jl
n
Pi
80
a»
Q
Omega
800
Ö
0
Theta
9
h
9
Qoppa
90
>
Sampi
900
UN APPROCCIO ALL'ARITMETICA
63
Bisogna precisare che le lettere che venivano utilizzate per
scrivere testi erano anche utilizzate per rappresentare numeri.
Per differenziarle, si scriveva una lettera che rappresentava un
numero con una linea orizzontale sopra di essa. In questo modo, ß
indicava il numero 2 (ß = 2), ã = 1, y = 3, e così via. Se la scrittura
contestuale non induceva a confusione, si ometteva la linea nella
parte superiore del carattere per indicare che si trattava di un
valore numerico. Queste lettere si dividono in tre classi:
— La prima di esse, che è possibile osservare nella prima co¬
lonna della tabella, sono le unità. Rappresentano i numeri
dalli al 9, simbolizzati dalle prime otto lettere dell’alfabeto
greco classico, insieme alla lettera Digamma, che simbo¬
lizza il numero 6.
— La seconda colonna presenta le decine. Rappresentano i
numeri dal 10 al 90, simbolizzati dalle successive otto lette¬
re dell’alfabeto greco classico, insieme alla lettera Qoppa,
che rappresenta il numero 90.
— La terza colonna è quella delle centinaia, dal 100 al 900,
rappresentate dalle ultime lettere dell’alfabeto greco clas¬
sico più la lettera Sampi, che rappresenta il numero 900.
Il sistema di notazione dei numeri era realizzato con il ricorso
all’alfabeto. Così, a era uguale a 1; i era uguale a 10; p era uguale
a 100... Se si scriveva pia, in effetti si stava scrivendo il numero
111. La notazione abc significa a + b + c, per cui pia rappresenta:
pia = p +1 + a = 100+ 10 + 1 = 111.
I numeri dall’11 al 19 erano scritti in base alla seguente tabella:
ia
n
ie
15
Tß
12
LÇ
16
ìy
13
£
17
iô
14
Tri
18
Te
19
64
UN APPROCCIO ALL'ARITMETICA
Questo metodo può essere utilizzato in maniera analoga per
le centinaia, e anche per i numeri 1.000, 2.000, 3.000, ..., 9.000. Un
buon esempio è stato proposto dallo storico e matematico svizzero
Florian Cgjori (1859-1930), che nel suo testo A History of Mathe¬
matical Notations (1928) li ha rappresentati come viene illustrato
nella seguente tabella.
«
,P
,Y
ô
,ç
£
*1
0
1.000
2.000
3.000
4.000
5.000
6.000
7.000
8.000
9.000
Il numero 10.000 inizialmente è stato denotato da Diofanto
con la lettera M - l’iniziale della parola Mopioi, che sta per dieci¬
mila - insieme a una piccola lettera a nella parte superiore. Fece
lo stesso con il numero 20.000 con una M e la lettera ß nella parte
superiore - si ricordi che ß è il simbolo del 2 - e così di seguito,
così come viene mostrato nella seguente tabella.
a
ß
Y
ô
e
la
iß
xÇö
M
M
M
M
M
M
M
M
10.000
20.000
30.000
40.000
50.000
110.000
120.000
6.690.000
Si è proceduto nello stesso modo per rappresentare le altre
decine di migliaia: per esempio, la lettera M con una piccola lettera
Y nella parte superiore è stata inizialmente usata per rappresentare
il numero 30.000. In seguito, si utilizzò anche la notazione «a » per
indicare 10.000 - la lettera greca con un punto -, «ß » per indicare
20.000, e così via.
In questo modo, 20.074 era rappresentato come
20.074 = 2 • 10.000 + 70 +4 = ß • + o + ô = ß • o ô.
Un altro esempio della notazione usata da Diofanto sarebbe:
a-oa = a- + o + a= l-10.000 + 200 + 1 = 10.201.
UN APPROCCIO ALL'ARITMETICA
65
SIMBOLOGIA PER POTENZE
La simbologia per potenze è stata un altro contributo importante
di Diofanto nel campo della notazione. Sebbene i simboli da lui
utilizzati non siano quelli attuali, introdusse novità come l’impiego
di un simbolo unico per la variabile sconosciuta.
Per questo, nel Libro I dell 'Aritmetica scrisse che «dopo averti
spiegato le diverse denominazioni dei numeri, passo a esporre le
loro moltiplicazioni. Ti sembreranno facili».
Più avanti, Diofanto aggiunse: «in questo modo, il numero mol¬
tiplicato per il numero dà il quadrato». Con questa affermazione
ha stabilito che a • a = a2. In maniera simile, proseguì presentando
potenze di numeri e affermò:
Tu sai che i numeri sono un insieme di unità e che si estendono
fino all’inflnito. Tra essi figurano i quadrati, che si ottengono mol¬
tiplicando un numero per se stesso, che si chiama lato del qua¬
drato, e i cubi, che risultano dal moltiplicare i quadrati per i loro
lati; quindi vi sono i biquadrati, che sono i prodotti dei quadrati
per se stessi; i quadrato-cubi, che si ottengono moltiplicando i
quadrati per i cubi aventi lo stesso lato dei quadrati, e, infine, i
cubo-cubi, formati dai cubi moltiplicati per se stessi.
I commenti riportati da Diofanto possono essere genera¬
lizzati non solo con numeri, ma anche con incognite, cioè le
variabili numeriche sconosciute che Diofanto ha chiamato ari-
thmos. La simbologia da lui utilizzata nel caso delle potenze di
arithmos è riportata in questa tabella.
Nome
Notazione di Diofanto
Notazione attuale
Quadrato
AY
X2
Cubo
IO
X3
Quadrato-quadrato
AY A
X4
Quadrato-cubo
AIO
X5
Cubo-cubo
K'K
X6
66
UN APPROCCIO ALL'ARITMETICA
L’incognita da sola e che non è riportata in maniera individuale
nella tabella precedente, cioè Yarithmos, è stata denotata da Dio-
fanto con ç. Secondo la notazione odierna, l’incognita è solitamente
rappresentata con la lettera x.
In base a questo criterio, «Yarithmos moltiplicato per il suo
arithmos» sarebbe «Yarithmos al quadrato»; «Yarithmos per il
quadrato» equivarrebbe al cubo ecc.
Allo stesso modo, tradotto secondo il linguaggio attuale, «l’a-
rithmos per il suo arithmos è il suo quadrato» sarebbe x •x=ocz.
V«arithmos per il quadrato è il cubo» sarebbe x -a? = x\ Il «qua¬
drato-quadrato», x2-x2 = x4. Il «quadrato-cubo», oc2-x1 = af>. Il «cu¬
bo-cubo», x'-x^x6 ecc.
Alla luce di tutto ciò, si osserva che sarebbe possibile stabilire
le uguaglianze del tipo
ry*2, /y»4 /y*Ò ry*ì ry*') _
X * X ” «A/ j X * X — X y • • • ^ •••
Da ciò è possibile dedurre che Diofanto abbia utilizzato, con
la formulazione odierna, il risultato:
a" • am = a"+w.
In rapporto alla simbologia utilizzata ne\YAritmetica, il ma¬
tematico alessandrino si rivolse nuovamente a Dionisio per fargli
sapere, tra le altre questioni, che i numeri sono un insieme di unità;
che comprendono i quadrati, i cubi, i biquadrati - quadrato-quadra¬
to -, i quadrato-cubi e i cubo-cubi, e che si estendono all’infinito.
Di seguito, spiegò al suo interlocutore quanto segue:
Si è convenuto sul fatto che, invece di indicarli in forma abbrevia¬
ta, ciascuno di questi numeri costituisca un elemento della teoria
aritmetica, così viene chiamata potenza il quadrato e il suo simbolo
distintivo è una A con l’esponente Y, in modo tale che la potenza sia
rappresentata come AY. Il simbolo distintivo del cubo è una K con
l’indice Y, e viene quindi rappresentato con KY. Quella del biqua¬
drato è AY A. Quella del quadrato-cubo AKY. E quella del cubo-cubo
KYK. Il numero che non ha nessuna di queste caratteristiche, ma
UN APPROCCIO ALL'ARITMETICA
67
che costituisce un sistema indeterminato di unità, è chiamato ari-
thmos, e il suo simbolo distintivo è una ç.
Per indicare l’inverso áeWarithmos, Diofanto utilizzò la no¬
menclatura di arithmoston\ per indicare l’inverso del quadrato
áeWarithmos utilizzò dunamoston, e così di seguito. Queste ar¬
gomentazioni sono illustrate nella seguente tabella:
arithmoston
dunamoston
cuboston
dunamodunamoston
dunamocuboston
cubocuboston
1/x
1/x2
1/x3
1/x4
1/x5
1/x6
Diofanto affermò inoltre che «ogni numero moltiplicato per
una frazione che abbia per denominatore lo stesso numero è l’u¬
nità». Cioè:
a• l/a = l.
Circa questa espressione, Diofanto affermò che «qualsiasi spe¬
cie moltiplicata per l’unità dà la stessa specie». Da questo com¬
mento e dall’uguaglianza precedente emerge che Diofanto era al
corrente del fatto che l’elemento neutro della moltiplicazione era
l’unità, cioè:
a - ì = a.
Allo stesso modo, un’attenta lettura áeWAritmetica rivela inol¬
tre che Diofanto non passò dalla sesta potenza, e che conosceva
la seguente proprietà.
11 1
a b ab
Inoltre, se espresso con la simbologia attuale, Diofanto in pra¬
tica utilizzò proprietà del tipo:
11 1 11 1
— 2 ’ 2 ~
XXX XXX
68
UN APPROCCIO ALL'ARITMETICA
Va segnalato che i matematici greci classici respingevano
tutti i prodotti che presentassero più di tre fattori, poiché per
loro non avevano alcun significato geometrico. In questo modo,
«X al quadrato» veniva interpretato come l’area di un quadrato
di lato X; da parte sua, «X al cubo» rappresentava il volume di
un cubo la cui lunghezza di ogni di ogni lato era di X unità. No¬
nostante queste limitazioni, Diofanto prese in considerazione
potenze maggiori di due.
Di seguito sarà illustrato come Diofanto scriveva un problema
e la sua soluzione. Si tratta del problema 28 del Libro I dell 'Arit¬
metica, che chiede di trovare due numeri tali per cui la somma dei
loro quadrati sia 208 e che sommati tra loro diano 20. L’enunciato
di Diofanto è il seguente:
1.28. Trovare due numeri per cui la loro somma e la somma dei loro
quadrati siano numeri dati.
Simbologia di Diofanto
Traduzione
K
ari
1 numeri sono: 20 e 208
ek0.
çãp“T
p-’upçä
Il numero maggiore e quello minore
sono dati da: x + 10; 10-x
TEXp.
A'ãçKp”p
ATp°pi|)Ç K
Elevandoli al quadrato si ottiene:
x2 + 20x + 100; x2-20x-100
(TÚV0.
A'ßp”õ i"
p‘’õri
Sommandoli e uguagliando il
numero maggiore 2x2 + 200 = 208
á<J).
AYß i”
Sottraendo 2x2 = 8
pep.
AYã i°
p"5
x2 = 4
çã iH
p‘-ß
CN
II
Di conseguenza, i numeri sono x+ 10= 12 e 10-;r = 8.
La scrittura, la notazione e la simbologia utilizzate da Diofanto
erano già state sviluppate da Archimede nel m secolo a.C. e da Eu-
tocio di Ascalona nel vi secolo d.C. A partire dalla simbologia usata,
si ritiene che Diofanto sia stato il primo matematico greco a ricono¬
scere le frazioni come numeri, usando diversi modi per presentare
una frazione. Ha rappresentato la frazione 1/4 indistintamente in tre
UN APPROCCIO ALL'ARITMETICA
69
maniere: ô”, ôT e ôx. Si deve ricordare che ò rappresenta il numero 4.
Un altro esempio è la rappresentazione della frazione 1/2 come ßT,
poiché ß corrisponde al numero 2. Se il numeratore no era l’unità
utilizzata abitualmente, la rappresentazione era del tipo «(numerato¬
re) denominatore». In questo modo, Diofanto rappresentava la frazio¬
ne 15/4 come isô. D’altra parte, non utilizzò nessun simbolo speciale
per i numeri negativi, nonostante avesse scritto nella definizione IX
del Libro I dell'Aritmetica che «il prodotto di ciò che manca per ciò
che manca è positivo, quello di ciò che manca per la cosa positiva è
mancante». In altre parole, meno moltiplicato per meno è più, e meno
per più è meno. Sebbene non abbia mai specificato tutte le proprietà
dei numeri con i quali lavorava, la sua opera mette in evidenza l’uso
dell’elemento neutro della moltiplicazione, la proprietà distributiva
della moltiplicazione rispetto all’addizione, le operazioni con potenze
di base uguale ed esponente diverso, le operazioni con frazioni e, in
maniera implicita, la regola dei segni, tra le altre proprietà.
L’INCOGNITO IN UNA ESPRESSIONE
Sebbene Diofanto abbia utilizzato il simbolo ç per indicare l’inco¬
gnita, con il passare dei secoli sarebbe stato sostituito da x. Ma
perché proprio x? L’uso di lettere quali simboli di numeri risale
ad Aristotele, che utilizzava una o due lettere maiuscole per indi¬
care numeri. Successivamente, Leonardo Pisano (1175-1235 ca.),
meglio noto come Fibonacci, rappresentò i dati con lettere minu¬
scole nel suo Liber abaci (1202). Nel xvi secolo si ebbero alcuni
progressi: Cardano ricorse alle lettere a e b per indicare numeri
noti, Xylander utilizzò la lettera N (che stava per numerus) e
Viète fu il primo a usare lettere per rappresentare incognite in
equazioni algebriche. Infine, il merito di aver introdotto la x per
indicare «l’incognita in una espressione» spetta a Cartesio (René
Descartes, 1596-1650). Nelle parole di Florian Cajori:
L’uso di z, y o x per rappresentare incognite si deve a Cartesio, e in
particolare alla sua opera Geometria (1637). Senza spiegazioni, intro-
70
UN APPROCCIO ALL'ARITMETICA
FOTO IN ALTO
A SINISTRA
Nel xvii secolo,
Cartesio scelse la
x come incognita
di una equazione
e pose fine
all’arithmos, creato
molti secoli prima
da Diofanto.
FOTO IN ALTO
A DESTRA
Bachet de
Méziriac creò
i metodi di
risoluzione
generale dei
numerosi problemi
áe\VAritmetica.
FOTO IN BASSO
Monumento a
Fermat, pioniere
nello studio
di soluzioni
esclusivamente
intere per
le equazioni
diofantee.
UN APPROCCIO ALL'ARITMETICA
71
duce l’utilizzo delle prime lettere dell’alfabeto per esprimere quantità
note e l’utilizzo delle ultime lettere dell’alfabeto per esprimere inco¬
gnite. Per indicare le coordinate utilizza solo xey. Nelle equazioni,
nel terzo volume della Geometria, la x ha una maggiore rilevanza.
L’utilizzo della lettera x creò un problema alla tipografia che
aveva l’incarico di stampare la Geometria e la sua appendice, il Di¬
scorso sul metodo, poiché mentre si stava preparando il testo per la
stampa le ultime lettere dell’alfabeto iniziarono a scarseggiare. Lo
stampatore chiese quindi a Cartesio se sarebbe stato un problema
che x, y o z comparissero indistintamente in ogni equazione del
libro, e il filosofo e matematico francese disse che non importava.
Lo stampatore scelse la x per la maggior parte delle variabili scono¬
sciute, poiché la y e la z erano maggiormente utilizzate in francese.
In merito alla notazione, Cartesio aveva raccolto il simboli¬
smo di Diofanto e lo aveva notevolmente arricchito: la prova è il
fatto che la sua notazione è ancora oggi utilizzata. Comunque, il
matematico scozzese Eric Tempie Bell (1883-1960), autore di The
Development Of Mathematics (1940), ha segnalato che ancora
più delle soluzioni algebriche ottenute da Diofanto è il fatto che
avesse iniziato a operare tramite simboli, un fatto «ancora più
notevole se si pensa che la sua annotazione algebrica, paragona¬
ta con quella attuale o con quella del xvn secolo, quando Cartesio
la perfezionò dal punto di vista pratico, era quasi altrettanto
complessa della logica greca». Infine, Bell ha sottolineato il me¬
rito di Diofanto con queste parole:
L’essere riuscito a ottenere tali risultati con la tecnica disponibile
all’epoca ne fa, senza alcun dubbio, uno dei più grandi algebristi.
72
UN APPROCCIO ALL'ARITMETICA
CAPITOLO 3
Equazioni diofantee
I matematici alessandrini affrontarono le equazioni
lineari indeterminate a partire dal m secolo a.C. Diofanto
fu il primo a formalizzarle e a strutturarle, ma i suoi
metodi generali di risoluzione avrebbero richiesto
il successivo intervento di Pierre de Fermat ed Eulero,
tra gli altri. Oggi, le equazioni diofantee sono una delle
aree più belle e complesse della matematica.
Prima di addentrarci nei problemi, nelle equazioni e nelle soluzioni
presenti nell 'Aritmetica, è necessario soffermarsi su uno dei con¬
tributi matematici che è maggiormente associato al protagonista
di questa biografia: le equazioni diofantee. Nel capitolo successivo
saranno dettagliatamente descritti gli enunciati, gli sviluppi e le
conclusioni dell’opera principale di Diofanto, per cui in questo
capitolo saranno trattati solo alcuni casi particolari, per il loro
interesse storico e le loro applicazioni nella teoria dei numeri, che
è la disciplina incaricata di studiarli.
È giunto quindi il momento di addentrarci nelle equazioni
diofantee più note, come quella presente nell’ultimo teorema di
Fermat. Saranno spiegati anche i diversi metodi di risoluzione
dell’equazione lineare a due incognite, e verranno dati alcuni
esempi per chiarire meglio l’argomento. Inoltre, verrà dato un
riassunto dei concetti che sono utilizzati per risolverli e saran¬
no presentate alcune applicazioni delle equazioni diofantee. Il
proposito è di affrontarle con semplicità e con un linguaggio
semplice, affinché siano di facile comprensione anche per i let¬
tori meno esperti.
A tale proposito, si può partire da una situazione della realtà
quotidiana, che richiede di essere risolta mediante una semplice
equazione diofantea. Per esempio, l’organizzazione di un evento
pubblico all’intemo di un complesso, per cui è necessario siste-
EQUAZIONI DIOFANTEE
75
mare in base a determinati criteri una certa quantità di tavoli.
Per l’esercizio, avremo che i tavoli hanno tra i 5 e 3 i tre metri di
lunghezza. Il vincolo è il fatto che lo spazio in cui andranno inse¬
riti dispone di 240 metri utili, e che i tavoli devono essere l’uno
di seguito all’altro. Quanti tavoli di 3 metri e quanti di 5 metri
sarà possibile collocare? Il primo passo sarà quello di assegnare le
incognite. Se se esprime con x la quantità di tavoli di 3 metri e con
y la quantità di tavoli di 5 metri, si ha il rapporto:
3#+52/= 240.
Nel linguaggio formale, il modello matematico dell’espressio¬
ne presuppone una equazione diofantea che chiede di trovare valo¬
ri di x e y che soddisfino l’uguaglianza. Un semplice ragionamento
ci permette di scrivere:
240 - 3x
A interessarci qui sono le soluzioni naturali. In questo modo,
se x prendesse il valore l,si avrebbe per y il valore 47,40. Questo
risultato non sarebbe soddisfacente, poiché stiamo cercando so¬
luzioni intere positive. Di fatto, con il semplice metodo di «trial-
and-error» (o dei tentativi ripetuti), una calcolatrice indicherebbe
rapidamente le possibili soluzioni considerando diversi valori na¬
turali di x convenientemente scelti per selezionare i valori natura¬
li di 2/. Un altro metodo di risoluzione sarebbe quello di realizzare
la tabella con un programma informatico semplice che verifichi
che 3x + 52/ = 240, dove 240 sono i metri disponibili, e scegliere
solamente le coppie xey intere positive che confermano l’ugua¬
glianza. In questo caso, i valori di x presi di 5 in 5 che vanno dal 5
fino al 75 soddisfano l’equazione, dando un valore positivo a y. A
seconda delle necessità e della tipologia e dimensione dei tavoli,
è possibile scegliere diverse combinazioni tra i risultati ottenuti.
In questo modo, l’espressione 3x + 5y = 240 è un tipo di equa¬
zione diofantea le cui soluzioni esigono di prendere valori interi o, in
maniera più ampia, valori razionali. Tuttavia, qual è il suo metodo
di risoluzione generale? La risposta non è semplice. Diofanto ave-
76
EQUAZIONI DIOFANTEE
va già dato alcune soluzioni nel m secolo d.C., ma la teoria delle
equazioni diofantee, con il passare del tempo, fu annoverata tra le
aree più difficili della matematica. In merito, Gauss affermò che
«la matematica è la regina delle scienze, e l’aritmetica è la regina
della matematica».
ANTECEDENTI IN INDIA
Malgrado le equazioni diofantee prendano il proprio nome da Dio-
fanto, va detto che questo tipo di equazioni era già presente in pro¬
blemi geometrici e algebrici da molti secoli, sebbene i suoi metodi
di risoluzione non siano stati formalizzati se non dopo l’importante
contributo del matematico alessandrino. Le equazioni diofantee af¬
fondano le loro radici in una regione geografica molto distante dal
territorio greco: l’India L’interesse dei matematici indiani per trovare
soluzioni intere rimanda all’epoca dei Vedas («conoscenza», in san¬
scrito), i quattro testi più antichi più antichi della letteratura indiana
Questi libri religiosi furono composti tra il 1600 e il 700 aC. e rappre¬
sentarono le basi della religione vedica, precedente all’induismo, dal
quale alla fine sarebbe stata scalzata. L’ultimo di essi, YAtarva-veda,
contiene un’appendice di testi scritti da diversi autori, daU’viii secolo
fino al vi secolo a.C., che ha valore matematico: gli Shulba Sutra. In
essi viene esposto, per la prima volta, l’uso geometrico delle equa¬
zioni diofantee.
Baudhayana, uno degli autori presenti negli Shulba Sutra, nel
secolo vii a.C. trovò soluzioni formate da numeri interi positivi a
un insieme di equazioni diofantee simultanee (sistema di equa¬
zioni), perfino con più di quattro incognite. Un altro matematico
che contribuì ai testi degli Shulba Sutra fu Apastamba, che nel
vi secolo a.C. utilizzò equazioni diofantee simultanee con più di
cinque incognite. Apastamba scrisse inoltre in merito alla corretta
costruzione di altari e alle loro forme, per cui si interessò, tra altri
temi, alla conversione di spazi circolari in quadrati aventi la stessa
superficie e alla costruzione di quadrati sulla diagonale di un altro
quadrato. Ciononostante, lo stile aforistico degli Shulba Sutra for-
EQUAZIONI DIOFANTEE
77
nisce solo formule per realizzare determinate costruzioni, e non
spiega quindi il procedimento tramite il quale sono state ottenute:
non comprendono quella che oggi chiamiamo «dimostrazione».
Da ciò si deduce che Baudhayana e Apastamba ottennero i dati
effettuando misurazioni, quindi in maniera empirica e senza usare
alcuna formula teorica. In ogni caso, Apastamba mostrò comunque
ragionamenti paragonabili a una dimostrazione.
In questa opera originaria furono aggiunte regole per la co¬
struzione di angoli retti, cosa che probabilmente era un requisito
necessario per costruire altari che fossero perfettamente quadrati,
come richiesto dai rituali mistici. I matematici indiani ottennero
la soluzione desiderata per mezzo di teme di archi. Di altri grandi
matematici indiani del periodo, come Aryabhata (476-550 a.C.) e
Brahmagupta (598-665 ca.) si parlerà invece più avanti.
TIPI DI EQUAZIONI DIOFANTEE
A partire dal m secolo a.C., l’aritmetica fu una delle discipline
di studio favorite dai matematici greci di Alessandria, che co¬
noscevano il concetto di equazione diofantea per alcuni casi
particolari. Fu in questo contesto che sorse la figura del primo
matematico ellenistico che studiò a fondo queste espressioni,
che le formalizzò e le strutturò: Diofanto.
Diofanto andò oltre l’impostazione che i matematici indiani
svilupparono in altre epoche e in altri luoghi. In questo senso, stu¬
diò a fondo un metodo che permettesse di trovare soluzioni intere
per le equazioni lineari indeterminate, quelle in cui mancano i dati
necessari per trovare un insieme unico di numeri interi che veri¬
fichino l’equazione (per esempio, x + y = 5). Diofanto scoprì che
molte equazioni indeterminate possono essere ridotte a una forma
in cui determinate categorie di soluzioni sono conosciute perfino
attraverso una soluzione che non lo è. Si sa per certo, inoltre, che
utilizzò i numeri negativi, e gli è attribuita la regola empirica di
«meno per meno dà più, e meno per più dà meno», che ancora oggi
viene comunemente applicata nell’algebra e nell’aritmetica Inoltre,
78
EQUAZIONI DIOFANTEE
bisogna sottolineare che la notazione algebrica di Diofanto ha un
grande valore per la storia della matematica, e che sarebbe stata
utilizzata per oltre un millennio. In realtà, sarebbe stata sostituita
solo nel xvii secolo, quando venne adottata la notazione proposta
da Viète, che è quella che si utilizza ancora oggi, e Cartesio intro¬
dusse il carattere x per indicare l’incognita.
Il simbolismo greco, approssimativamente fino al m secolo d.C.,
a parte l’uso di cifre, si limitava a denotare le quantità usando le
lettere dell’alfabeto. Non possedeva formule algebriche, e
nessuna classe di algoritmo. Solamente con l’alessandrino
Diofanto compaiono alcuni simboli algebrici.
— Carl Boyer, storico e matematico statunitense.
Sulle equazioni diofantee di ordine 2 e superiori è stata re¬
alizzata una moltitudine di studi. Il primo di essi è relativo alla
soluzione dell’equazione quadratica diofantea
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0,
dove A, B, C, D, E, F sono numeri interi.
Nel 1769, Joseph-Louis de Lagrange (1736-1813), un famoso
matematico, fisico e astronomo francese di origine italiana, trovò
un algoritmo completo per questa equazione. Un anno dopo, La-
grange dimostrò il risultato già enunciato da Diofanto e noto come
«teorema dei quattro quadrati»:
Ogni numero intero positivo può essere espresso come somma di
quattro quadrati di numeri interi.
Di seguito sono mostrati alcuni esempi che verificano il teorema
5= 22 + l2 + 02 + 02,
18 = 32 + 32 + 02 + 02,
348 = 182 + 42 + 22 + 22,
8 764 = 702 + 622 + 42 + 22.
EQUAZIONI DIOFANTEE
79
Tuttavia, questo teorema non si verifica necessariamente in una
unica forma Per esempio, il 252 ha dodici diverse scomposizioni come
somma di quadrati, delle quali ne sono riportate alcune:
252 = l2 + 72 + 92 + 112,
252 = 22 + 42 + 62 + 142,
252 = 22 + 22 + IO2 + 122,
252 = 12 + l2 + 92+ 132,
252 = 12+ 12 + 52+ 152,
252 = 42 + 62 + IO2 + IO2,
252 = 62 + 62 + 62 +122.
EQUAZIONE DI PELL
Il secondo studio che esamineremo sulle equazioni diofantee di
grado 2 e superiori è relativo alla cosiddetta «equazione di Peli»,
un caso speciale dell’equazione quadratica diofantea della forma
a?-dy2 = n dove de un intero positivo che non è un quadrato perfetto,
e n è un intero diverso da zero. Un quadrato perfetto è un numero
intero che è il quadrato di un altro numero naturale - una potenza
di esponente 2 Per esempio, 9 è un quadrato perfetto, perché può
essere scritto come 3 • 3, cioè 32.
Questo tipo di equazioni fu studiato verso il 400 a.C. dai ma¬
tematici greci e indiani, che all’inizio riversarono il loro interesse
verso l’equazione con n = 2. Trattandosi di un’equazione diofantea,
l’obiettivo era di trovare le sue soluzioni intere. In alcuni lavori
di Archimede sono state presentate alcune soluzione per il caso
d = 3. Ciononostante, le equazioni diofantee furono studiate più
approfonditamente dai matematici indiani, i primi a cercare siste¬
maticamente metodi per la determinazione di soluzioni intere. Nel
499 d.C., Aryabhata fece la prima descrizione esplicita della solu¬
zione intera generale dell’equazione diofantea lineare ax-dy = c,
che compare nella sua opera Aryabhatiya. L’algoritmo kuttaka
- letteralmente, «polverizzare» o «rompere in piccoli pezzi»— è
uno dei suoi contributi più significativi alla matematica pura,
80
EQUAZIONI DIOFANTEE
poiché permette di trovare le soluzioni intere di un sistema di
equazioni diofantee lineari, un problema che trova importanti
applicazioni in astronomia, e che inoltre facilita la soluzione
generale dell’equazione generale indeterminata. Il metodo di
Aryabhata ha a che fare con un algoritmo ricorsivo per scrivere
i fattori originali in numeri più piccoli. Questo algoritmo fu cre¬
ato durante il primo terzo del vii secolo da un altro matematico e
astronomo indiano, Bhaskara, e oggi costituisce il metodo stan¬
dard per risolvere equazioni diofantee di primo grado. Da parte
sua, il matematico e astronomo indiano Brahmagupta trovò la
soluzione più piccola per il caso d = 92. Bisogna inoltre segnalare
che Brahmagupta scrisse il Bramasphuta Siddhanta (628), un
trattato su aritmetica e numeri negativi - secondo termini ana¬
loghi a quelli della matematica moderna - dove compare per la
prima volta il concetto di «zero». Nell’opera, che fu tradotta in
arabo nel 773 e in latino nel 1126, utilizzò il metodo chakravala
per risolvere le equazioni diofantee quadratiche, comprese quelle
della forma 6Lr2 + 1 = y2.
Una versione modificata del metodo di Brahmagupta fu uti¬
lizzata da Bhaskara II (1114-1185 ca.) per trovare, nel 1150, la
soluzione generale di altre equazioni quadratiche intermedie in¬
determinate ed equazioni diofantee quadratiche. Ottenne anche la
soluzione di altre equazioni quadratiche indeterminate, cubiche,
quartiche e polinomiche di gradi maggiori. Verso la metà del xiv
secolo, un altro matematico indiano, Narayana Pandit (1340-1400
ca.), perfezionò le restanti equazioni quadratiche indeterminate
per le equazioni di gradi superiori.
Più tardi, Pierre de Fermat avrebbe approfondito le equazio¬
ni diofantee e, per esempio, propose come problema l’equazione
6LT2 + 1 = y2 creata da Bhramagupta. Nel 1657, ormai alla fine della
sua carriera, Fermat lanciò la seguente sfida alla comunità mate¬
matica d’Inghilterra:
Dato un numero qualsiasi che non sia un quadrato, esiste un nu¬
mero infinito di quadrati tali per cui se il quadrato è moltiplicato
per il numero dato e l’unità è aggiunta al prodotto, il risultato è
un quadrato.
EQUAZIONI DIOFANTEE
81
Cioè dato d, che non è un quadrato, esistono infiniti quadrati,
x2, tali per cui se si moltiplicano per de si aggiunge 1 a questo
prodotto, il risultato è un quadrato che viene indicato con y2.
Questo conduce all’equazione d -x2 + 1 = y2, che è precisamente
l’equazione di Peli. Dato che all’epoca di Diofanto le soluzioni
razionali erano prese come quelle valide per queste equazioni, gli
inglesi risolsero molto presto la sfida di Fermat. Tuttavia, questi
aveva incluso un preambolo, che non arrivò ai suoi destinatari,
dove chiariva che si chiedevano soluzioni intere. I matematici
inglesi, ben lontani dal farsi scoraggiare dalla difficoltà, raddop¬
piarono i loro sforzi, e non solo riuscirono a risolvere i casi
particolari, ma offrirono anche un procedimento generale per
ottenere la soluzione di qualsiasi valore di d.
Alla fine, il metodo generale per calcolare soluzioni di questo
tipo fu attribuito al matematico inglese John Peli (1611-1685), dal
quale prende il nome questa equazione. A tale proposito esiste
un’aspra controversia, perché probabilmente il merito sarebbe
dovuto andare al matematico irlandese William Brouncker (1620-
1684), cui un malaugurato errore, che si è mantenuto per molto
tempo, aveva tolto la gloria matematica.
TECNICHE PER RISOLVERE EQUAZIONI LINEARI
Le tecniche odierne per risolvere ciascuna delle equazioni dio-
fantee in precedenza descritte implicano una serie di teoremi di
grande importanza. Questi servono per risolvere inizialmente le
equazioni diofantee lineari, cosa che verrà debitamente illustrata
con esempi, e sono formulati di seguito. Si tratta, da una parte,
del concetto e del calcolo del cosiddetto «massimo comune di¬
visore», che si ottiene attraverso l’algoritmo di Euclide, e dall’al¬
tro della cosiddetta «identità di Bézout». Il massimo comune
divisore di due numeri a e b viene indicato come «mcd(a, b)» e
deve essere inteso come il più grande dei numeri interi naturali
che divide entrambi senza lasciare resto. Per esempio, si abbia
per a = 30 e per ò = 18. Il 3 è il divisore comune, ma non il più
82
EQUAZIONI DIOFANTEE
L'ERRORE A DISCAPITO DI WILLIAM BROUNCKER
William Brouncker è stato un eminente matematico irlandese del xvm secolo e il
primo presidente della Royal Society, fondata a Londra il 28 novembre 1660. Si
distinse soprattutto per la sua notevole capacità nel risolvere problemi mate¬
matici. In effetti, ideò un metodo per calcolare soluzioni intere di equazioni della
forma x2-dy2 = n dove d è un intero positivo che non è un quadrato perfetto e n
è un intero diverso da zero. Tuttavia, il matematico svizzero Eulero (Leonhard
Euler, 1707-1783) nelle sue opere scrisse
che, per questo tipo di equazioni, il me¬
todo per calcolare le soluzioni era stato
ottenuto dal matematico inglese John
Peli (1611-1685). Il prestigio di Eulero fece
sì che l'errore, frutto di una malaugurata
confusione, avesse una grande diffusio¬
ne e che la comunità matematica la rite¬
nesse un fatto assodato, portando come
conclusione il fatto che le equazioni che
hanno la forma x2-dy2-n siano chiamate
«di Peli», e non «di Brouncker». L’espres¬
sione «equazione di Peli» è ancora oggi
in vigore in matematica.
Si ritiene che William Brouncker sia stato
il vero scopritore del metodo generale
per risolvere le «equazioni di Peli».
grande, che è il 6. Ciò viene espresso nella seguente maniera:
mcd(18, 30) = 6. Come si ottiene questo risultato? Mediante il già
citato algoritmo di Euclide, che consiste nel dividere entrambi i
numeri e, successivamente, realizzare divisioni tra il quoziente
precedente e il nuovo resto. Il processo termina quando qual¬
che resto è 0. Il divisore di quest’ultima divisione rappresenta,
allora, il massimo comune divisore di entrambi i numeri. Per
esempio, il processo per trovare la soluzione a mcd(48,30) è il
seguente. Prima si divide 48 per 30, ottenendo come resto 18 e
di quoziente 1. Poi, si divide 30 per 18, che dà un resto di 12 e di
quoziente 1. Quindi si divide 18 per 12, ottenendo come resto 6
e di quoziente 1. Infine, dividendo 12 per 6, si ottiene come resto
EQUAZIONI DIOFANTEE
83
0 e di quoziente 2. Per questo, la soluzione a mcd(48, 30) è 6. Nel
caso in cui il mcd(a, ft) = 1, si dice che a e b sono primi tra loro.
Da parte sua, l’identità di Bézout stabilisce che:
Se a e ft sono interi maggiori di 0, esistono interi x e y tali per cui se
mcd(a, ft) = d, allora d = ax + by.
Di seguito viene presentato un esempio di come si usa l’i¬
dentità di Bézout con il seguente enunciato: dati i numeri 1.769 e
551, trovare i valori xey che verificano che se d = mcd(1769, 551),
allora d = 1769 x + 551 • y. La prima cosa da fare sarà calcolare il
mcd(1769, 551). Se si applica l’algoritmo di Euclide e si realizzano
le successive divisioni, si ottiene:
1769 = 3-551 + 116,
551 = 116-4 + 87,
116 = 87-1 + 29,
87 = 3-29 + 0.
Per cui la soluzione cercata è:
mcd(1769, 551) = 29.
L’identità di Bézout afferma che vi sono valori xey che verificano
29= 1769-^ + 551-2/.
A partire dalle espressioni precedenti, il 29 si scrive come la
combinazione di 1.769 e 551. In questo modo:
29 = 116-87 - 1 = 116-(551 - 116 - 4) = (1 769 - 3 ■ 551)-
-(551-(1769-3-551)-4) = (1769-3-551)-551 + 4-1769-
-12-551= 5-1-69+ (-16). 551.
Da cui si ottiene:
29= 1769-(5)+ 551-(-16).
84
EQUAZIONI DIOFANTEE
Si deve osservare che dell’espressione 1.769 a:+ 551 2/= 29
sono state trovate due soluzioni intere:
x = 5, y = —16.
Per calcolare le soluzioni delle equazioni diofantee lineari si
deve in primo luogo enunciare un risultato o un teorema aventi le
condizioni che determinano quando un’equazione diofantea lineare
è risolvibile, e, a sua volta, come si calcola la soluzione generale.
Per esempio, si consideri l’equazione diofantea generale ax+by = c.
Se d = mcd (a, b) è tale per cui d divide c - cioè il resto risultante
dal dividere c per d è zero -, e se si conoscono x0 e y0 soluzioni
particolari dell’equazione, allora le soluzioni sono date da
a ,
y=yQ--t,
d
dove t è un numero intero, cioè per ogni valore di t si avrà una
soluzione. Di fatto, il teorema stabilisce che:
Una equazione diofantea della forma ax + by = c ha soluzione intera
se, e solamente se, d divide c essendo d = mcd(a, b).
In questo modo, l’equazione 2x + 1C\y =17 non ha soluzione per¬
ché 2 = mcd(2, 10) non divide 17.
Un altro esempio sarebbe 1.769a:+ 551 y = 29. Mediante l’al¬
goritmo di Euclide e l’identità di Bézout si ottiene che nell’equazio¬
ne diofantea 29= 1.769 -x+ 551 y, i valori a:0 = 5e i/0 = —16 saranno
soluzioni particolari. Cioè:
29 =1769-(5)+ 551-(-16).
Pertanto, l’insieme di soluzioni dell’equazione diofantea sa¬
rebbe quella che genera i diversi valori interi di t.
x = 5 + ——t = 5+ 19 t,
29
EQUAZIONI DIOFANTEE
85
1769, 1ß ßl ♦
y = -16 1 = -16 + 61 t.
29
È necessario insistere sul fatto che per garantire 1’esistenza di
soluzioni è necessario che d divida c. In caso contrario, l’equazione
non ha una soluzione. Con questo risultato, basta conoscere x0 e
y0 per generare tutte le soluzioni. L’identità di Bézout ci aiuterà a
calcolare x0 e y0 A tal fine, di seguito sarà presentato un esempio
di soluzione per visualizzarlo in modo più chiaro.
UNA SOLUZIONE PARTICOLARE
L’obiettivo è cercare la soluzione particolare di un’equazione diofan-
tea lineare con due incognite. Il teorema che useremo afferma che:
Siano a, b, c tre numeri interi. L’equazione lineare ax + by = c ha
soluzione intera se, e solo se, il massimo comune divisore di a e
b divide c.
La dimostrazione avviene in questo modo. Supponiamo che
gli interi xQ e y0 siano soluzioni dell’equazione ax + by = c, cioè
axQ+ by0 = c. Ebbene, se d = mcd (a, b), allora
d = mcd (a, b) => d\a e d\b => dl(aa:0+ by0) => die.
In maniera reciproca, supponiamo che d = mcd (a, b) sia divi¬
sore di c. Allora,
mcd (a, b) = d
mcd(a/d, b/d)=1 ^>3 p,gEZ:— p +—q = l=
“d
d d
essendo c/d intero poiché, per ipotesi, d è divisore di c. Ora baste¬
rebbe prendere
x0 = cp/d e yfì = cq/d
86
EQUAZIONI DIOFANTEE
e si avrà che ax() + by0 = c. Cioè gli interi x0 e y0 sono soluzioni dell’e¬
quazione. La soluzione che abbiamo trovato deve essere conside¬
rata, quindi, la «soluzione particolare» del sistema. Si deve con¬
siderare che questo teorema assicura 1’esistenza di una soluzione
per una equazione di questo tipo e, inoltre, offre un metodo per
calcolarla. L’esempio successivo chiarirà la questione. Si tratta di
trovare una soluzione per l’equazione diofantea 525#+ 100?/ = 50.
Come prima cosa si calcola il massimo comune divisore di 525 e
100 mediante l’algoritmo di Euclide:
525 = 5(100)+ 25
100 = 4(25)+ 0.
Cioè mcd(525,100) = 25. Poiché 25 divide 50, il teorema prece¬
dente garantisce 1’esistenza di una soluzione intera per l’equazione.
Ora, seguendo il metodo esposto nella dimostrazione del teorema,
bisogna trovare i coefficienti della combinazione lineare del mas¬
simo comune divisore di 525 e 100. Basterebbe seguire a ritroso
l’algoritmo di Euclide:
25 =1(525)+ (-5)100.
Pertanto, i coefficienti che cerchiamo sono p = 1 e q = -5. Per
cui, secondo il teorema, una soluzione per l’equazione sarà:
x0 = cp/d e yQ = cq/d,
dove c è il termine indipendente dell’equazione e d il massimo
comune divisore dei coefficienti di x e y. Di conseguenza:
*o = ^ = 2
2/o =
25
50(-5)
25
= -10.
Riassumendo, è possibile concludere che una equazione dio-
fantea lineare ha la forma generale:
EQUAZIONI DIOFANTEE
87
alxl+a^c2 + ... + anxn = ft,
dove ava2,...,ati sono interi, non tutti nulli, e sono necessarie
soluzioni anch’esse intere. Ha soluzione se, e solamente se,
mcd(aj, a2,..., an) divide b. La più semplice equazione diofantea è
quella diofantea lineare con due incognite, ax+by=c, dove a e b
sono interi dati, ed entrambi non possono essere zero.
EQUAZIONI NON LINEARI
Nei casi precedenti sono state spiegate le equazioni diofantee
lineari e alcuni metodi per risolverle. Tuttavia, la questione si
complica enormemente nel caso delle equazioni non lineari. In
realtà, la loro difficoltà ha fatto sì che il matematico tedesco
David Hilbert (1862-1943) le includesse nel suo celebre elenco
di 23 problemi ancora non risolti, che presentò alla comunità
matematica nel 1900, durante il II Congresso Mondiale dei Ma¬
tematici, tenutosi a Parigi. In sostanza, il decimo problema espo¬
neva quanto segue:
Trovare un algoritmo che determini se una equazione diofantea
polinomica data con coefficienti interi ha soluzione intera.
Il suo sviluppo e la sua dimostrazione hanno un grande va¬
lore per la matematica moderna, poiché include concetti della
teoria dei numeri e della logica matematica, e fece aumentare
l’interesse per questa e altre equazioni diofantee. Bisogna cita¬
re, per esempio, il matematico statunitense John Forbes Nash
(1928-2015), che durante i suoi studi presso il Carnegie Tech si
appassionò alle equazioni diofantee prima di rivoluzionare la te¬
oria dei giochi con la sua soluzione di equilibrio.
Alla fine, il matematico russo Jurij Matijasevich (San Pietro¬
burgo, 1947), nel 1970 ha dimostrato l’impossibilità di risolverlo:
non c’è alcun algoritmo capace di determinare se un’equazione
diofantea polinomica sia risolvibile. Pertanto, non è neppure
88
EQUAZIONI DIOFANTEE
DIOFANTO E I 23 PROBLEMI DI DAVID HILBERT
Il giorno 8 agosto del 1900, sedici secoli
dopo la morte di Diofanto, il matematico
tedesco David Hilbert (1862-1943) tenne
una conferenza al Congresso Internazio¬
nale dei Matematici, dal titolo «Proble¬
mi matematici». Durante la conferenza,
presentò una lista di 23 sfide matema¬
tiche la cui risoluzione avrebbe rappre¬
sentato un significativo avanzamento
per diversi rami della matematica. Il
decimo problema chiedeva di provare
l’esistenza di un algoritmo universale
che indicasse se era possibile risolvere
qualsiasi tipo di equazione diofantea. La
risposta si fece attendere 70 anni e ven¬
ne data dal matematico russo Jurij Vla¬
dimirovich Matijasevich. Nato nel 1947
a San Pietroburgo, Matijasevich si era
già reso protagonista di una folgorante
carriera scientifica, laureandosi campio¬
ne nella VI Olimpiade Internazionale di
Matematica a Mosca a soli diciassette
anni. Nel 1969 si laureò all’Università Statale di San Pietroburgo (all’epoca
ancora Leningrado) con una tesi dottorale che dimostrava che non c’è al¬
cun algoritmo generico che fornisca criteri generali per risolvere qualsiasi
equazione diofantea. Con questo risultato venne definitivamente chiusa una
questione della cui possibile soluzione dubitava lo stesso Hilbert, che previ¬
de che non esisteva alcun algoritmo ancora prima di presentare la lista dei
problemi: «Talvolta accade che cerchiamo la soluzione basandoci su ipotesi
insufficienti, o su un senso scorretto, e per questo motivo falliamo. Allora
sorge il problema: dimostrare l’impossibilità di ottenere una soluzione con
tale ipotesi o nel senso preso in considerazione».
possibile trovare un metodo generale che ottenga le soluzioni.
Questa impossibilità giustifica il fatto che qui vengano trattati
casi particolari di equazioni che ammettono un metodo semplice
per risolverle, che abbondano nell’opera di Diofanto. Nel caso di
equazioni indeterminate di secondo grado, e sulla base dell’analisi
del Libro II dell’Aritmetica, emerge il seguente risultato:
EQUAZIONI DIOFANTEE
89
Ogni equazione indeterminata di secondo grado a due variabili o
non ha soluzioni razionali, oppure ha una quantità infinita di solu¬
zioni. Nell’ultimo caso, tutte le soluzioni si esprimono come fun¬
zioni di un parametro che si indica con k, in modo che x = cp (/c);
y = (k). Pertanto, cp e sono funzioni che dipendono da k.
Diofanto, per esempio, propose nell’ottavo problema del Li¬
bro II áe\Y Aritmetica di scomporre il 16 - un quadrato - come
somma di due quadrati, oppure, che è la stessa cosa, trovare
x e y in modo tale che x2 + y2 = 16. Per risolverlo, il matematico
alessandrino prese in considerazione l’intersezione della famiglia
di rette della forma y = k x-4(k parametro) che passano per il
punto (0,-4) intersecate con la circonferenza x2 + y2= 16, così
come si vede nella figura 1.
Le soluzioni sono della forma:
x =
8 k
/c2+r
y = 4-
k2-1
k2 + l'
essendo k un parametro.
In questo modo, assegnando valori a k si ottengono le solu¬
zioni. Per esempio, per k = 0 si ottiene x = 0 e y = -4. Nel caso di
k=l, si ha a? = 4 e t/ = 0. Per k = 2 si ha x - 16/5 ey = 12/5. Per k = 3
si ottiene x = 12/5 e y = 16/5 ecc. Con questo è possibile genera¬
re tutti i punti che verificano x2 + y2 = 16. Nel caso generale di
x? + y2 = a2, si tratta dell’equazione di una circonferenza con cen¬
tro nel punto (0,0) e raggio a, per cui basta considerare la fami¬
glia di rette della forma
y = k-x-a,
dove A: è il parametro, e trovare l’intersezione delle rette con la cir¬
conferenza. Nel trattamento geometrico, si stanno caratterizzando
tali punti, che sono generati dai valori:
2 ak k2 -1
x = —— y = a • ——.
k2 +1 k2 +1
Così, a ogni valore razionale di k corrisponde un unico punto
di coordinate razionali della curva x2 + y2 = a2.
90
EQUAZIONI DIOFANTEE
EQUAZIONI DEL TIPO x2-dy2 = 1
In generale, una equazione di Peli, così come è stato indicato nei
paragrafi precedenti, è della forma aP-d- y2=n. A titolo illustrativo
si include un esempio dell’equazione di Peli ^—29z/2 = 7. È possibi¬
le dimostrare facilmente che le coppie (-6,1), (-6,-1), (6,1), (6,-1)
sono soluzioni intere dell’equazione. Un buon risultato stabilisce
che se la coppia (xvyt) è una soluzione, allora le successive so¬
luzioni (xk, yk) verificano la relazione xk + yk\fd = (x{ + yx-4d)k.
Nell’ambito della teoria dei numeri, risultano particolarmente
interessanti le equazioni di Peli di aspetto x2-dy2=n, in cui n
divide d e che, denotando il quoziente tra den con il carattere a,
cioè d/n = a, assumono l’aspetto di x2-ay2= 1.
In precedenza è stato spiegato che l’equazione x2-ay2= 1,
dove a è un numero intero che non è un quadrato perfetto, è nota
come equazione di Peli. L’importanza della stessa risiede nel fatto
EQUAZIONI DIOFANTEE
91
che qualsiasi altra equazione di secondo grado a due incognite
può essere ridotta a una equazione di Peli del tipo mostrato.
Chiaramente, qualsiasi equazione di questo tipo ha per soluzione
(X, 2/) = (1,0), il che può essere osservato mediante una semplice
sostituzione.
Nel caso in cui si trovasse un’altra soluzione diversa da que¬
sto, esiste un metodo complesso basato sulla teoria delle «frazioni
continue», con cui si generano le restanti soluzioni, ma che qui
non verrà sviluppato per mancanza di spazio. Per l’ipotesi in cui a
invece sia un quadrato perfetto, basterà scrivere
x2 - ay2 = (x- yfãy) • (x + 4ãy\
per poi denotare
x + yfãy = m
x-y/ãy = n,
e infine ottenere che:
m + n m-n
2 y 2Æ
Con ciò, l’equazione diventa m • n = 1.
In tale ambito è necessario sottolineare l’importanza di un
esponente. Per esempio, è possibile osservare una certa analo¬
gia tra oc2 = 2y4-ì e l’equazione di Peli x1 = 2y2 + 1. Effettivamente,
la differenza risiede nell’esponente, il che rappresenta una dif¬
ferenza visiva minima, e tuttavia decisiva. Così, nell’equazione
oc2 = 2y*-\ si è ottenuto in forma naturale che la coppia x = 1 e y = 1
era una soluzione. Successivamente, nel 1942, è stato trovato che
anche la coppia x = 239 e y = 13 era una soluzione, ed è stato di¬
mostrato che tale equazione non ha altre soluzioni intere. Invece,
l’equazione x2 = 2yl +1 ha infinite soluzioni intere:
x=3,y = 2,
x= 17, y= 12,
3?=99, y = 70,
92
EQUAZIONI DIOFANTEE
La spiegazione a questa disparità di risultati tra entrambe
le equazioni venne offerta dal matematico norvegese Axel Thue
(1863-1922), che stabilì il seguente risultato:
Le equazioni diofantee irriducibili a due variabili con grado maggiore
o uguale a tre possono solo avere un numero finito di soluzioni.
EQUAZIONE DEL TIPO x2-y2 = a
Si tratta di un caso particolare dell’equazione di Peli nella quale si
verifica il seguente risultato:
L’equazione x2-y2 = a, dove a è un numero naturale, ha soluzioni
intere se, e solamente se, a può essere scomposto nel prodotto di
numeri della stessa parità. Semen sono due di tali numeri della
. v , N , . m + n m-n v
stessa panta (m • n = a), la coppia x = ew = e una solu-
2 2
zione dell’equazione.
Bisogna scomporre l’equazione oc?-y2, che può essere scritta
oc1-y2 = (x + y)-(x-y'),
e denominando
allora risulta
x+y = m, x-y=n
mn = a.
Si osservi che men devono avere la stessa parità, in modo
tale che xey siano interi. Dall’espressione precedente si ottiene:
m+n m-n
Un esempio di ciò si ha dal risolvere l’equazione x2-y2- 8.
Cioè m-n = 8, con cui si ottengono le seguenti possibilità per
men:
EQUAZIONI DIOFANTEE
93
(1, 8), (8, 1), (-1, -8), (-8, -1), (2, 4), (4, 2), (-2, -4), (-4, -2).
Scartando quelle che non hanno la stessa parità, rimangono:
(2, 4), (4, 2), (-2, -4), (-4, -2).
I valori possibili per x e y sono mostrati nella seguente tabella:
m
n
m + n
x =
2
m-n
y- 2
2
4
3
-1
4
2
3
1
-2
-4
-3
1
-4
-2
-3
-1
Si noti che se (a, b) è una soluzione, lo è anche (±a,±b).
EQUAZIONE DI FERMAT xn + yn=zn
È la più classica delle equazioni diofantee di grado maggiore di 1 e
con tre variabili (quella di grado 2 rappresenta il teorema di Pitago¬
ra). La più famosa è quella presente nell’ultimo teorema di Fermat.
Data l’equazione diofantea x” + y" = z”, con n > 3, non ha soluzione nei
numeri interi positivi x, y, z.
Particolarmente interessante è il caso n- 2, noto come«e-
quazione pitagorica», che si esprime oc1 + y2 = z1. Le soluzioni sono
chiamate «teme pitagoriche» e si accerta che è possibile generare
soluzioni mediante
x = 2 mn,
y = m2-n2,
z = ri1 + m2,
94
EQUAZIONI DIOFANTEE
se assumono valori interi di m maggiori di n. Nella seguente tabella
sono illustrate alcune soluzioni.
m
n
x-2 mn
y-m7-n7
z=n7 + m7
x2+y2 = z2
2
1
4 .
3
5
16 + 9 = 25
4
2
16
12
20
162+122 =202
5
2
20
21
29
202 + 212 =292
Per il lettore più esperto in la matematica, presentiamo il
ragionamento che stabilisce l’uguaglianza mostrata. Il metodo
di risoluzione consiste nello scomporre l’equazione come due
quozienti, dove il numeratore e il denominatore sono funzioni
lineari. In questa forma, xl + y2 = 22 equivarrebbe all’espressione
x1 = z2-y2= (z-y)-(z + y). Quindi è possibile scrivere:
x _ z+y_m
z-y x n ’
per cui si ha
nx=m-z-m-y,
mx = nz + ny,
e riducendo il sistema a una equazione che non contenga x, cosa
che si ottiene moltiplicando la prima equazione per m, la seconda
per n e quindi sottraendo, si arriva a:
(m2 -n2) • z- (n2 + m2) • y.
Pertanto:
z = n2 + m2, y = ml-rìl, x = 2mn.
Si può osservare che esistono infinite soluzioni dell’equa¬
zione che dipendono da men. Pertanto, se si ha una soluzione
(X, ?/, z) = (a, by c)y anche qualsiasi tema della forma (ka, kb, kc)
sarà una soluzione. Come si già affermato in precedenza, si tratta
EQUAZIONI DIOFANTEE
95
delle teme pitagoriche, che sono le lunghezze dei lati di un trian¬
golo rettangolo in termini geometrici.
EQUAZIONI DELLA FORMA y* = x3 + a
Questa equazione, nella quale compare a come numero naturale, è
chiamata «equazione di Mordell» in onore del matematico britan¬
nico, naturalizzato statunitense,
Louis Mordell (1888-1972), che
tenne numerose conferenze sui
lavori di Diofanto e le raccol¬
se in un’opera di riferimento,
Equazioni diofantee (1969).
La rappresentazione gra¬
fica dell’equazione di Mordell
è una curva denominata «ellit¬
tica» sul piano reale. Per ogni
a possiede un numero finito di
soluzioni intere, e il calcolo del¬
le stesse fa parte di sofisticati
studi della teoria dei numeri.
Nella figura 2 viene mostrato
il grafico della curva ellittica
y2=a? + 4.
EQUAZIONI DELLA FORMA y* + x3 = a
In questo tipo di equazioni, se a è un cubo perfetto - a della forma
a = b3- risulta evidente che ha per soluzioni (0, ò) e (ò, 0). Colpi¬
sce il caso in cui a= 1729, essendo dunque y3+x3 = 1.729. Questa
equazione si chiama «cubica di Ramanujan», dal nome del mate¬
matico indiano Srinivasa Ramanujan (1887-1920), che, mentre era
in ospedale, gravemente malato, ricevette la visita del suo unico
96
EQUAZIONI DIOHANTEE
protettore all’Università di Cambridge, il professore e matematico
britannico Godfrey Harold Hardy (1877-1947). Questi disse che era
venuto in taxi il cui numero era 1.729, e Ramanujan, dotato di una
prodigiosa velocità di calcolo, rispose che 1.729 era il numero più
piccolo che si potesse esprimere come la somma di due cubi di
due forme diverse. Aveva ragione, poiché 1.729= 13+ 123 = 93 + IO3.
In seguito, Hardy gli chiese se conosceva la risposta per le quarte
potenze, e Ramanujan rispose che doveva trattarsi di un numero
estremamente grande. Di fatto, la risposta, che chiarì il suo otte¬
nimento mediante calcoli al computer, è:
635.318.657 = 1344 +1334 = 1584 + 594
In altri ordini, Ramanujan scoprì una identità, che permette
di costruire esempi della soma di tre cubi equivalente a un quarto
cubo:
(3z2 + 5 xy - 5 y2y] + (4z2 - 4xy + 6?/2)3 + (5oc2 - 5xy - 3 ?/2)3 =
(6x2-4xy + 4y2y\
Questa uguaglianza, che generalizza la coincidenza numerica
per cui 33 + 43 + 53 = 63 = 216, viene verificata mediante un semplice
sviluppo algebrico, ma sembra impossibile da ottenere senza di¬
sporre di una teoria generale. Tuttavia, Ramanujan vi riuscì.
EQUAZIONE DEL TIPO xz + y* = z*
Questo è un altro problema interessante, che chiede di trovare una
tema di numeri tali per cui la somma di due cubi dia un quadrato.
Le soluzioni vengono generate stabilendo valori per i parametri
s e t per, di seguito, fare:
x=s4+6s2
y- -s4 + 6s212 + 3t4,
z = 6st(s4 + 3t4).
EQUAZIONI DIOFANTEE
97
Prendendo il valore s = 3 e t = 2, si ottiene:
2493 + 1833 = 46442.
Se si prende il valore s = 4 e t = 5, si ricava 7813+ 40193 = 255 7202.
EQUAZIONE DEL TIPO x4 + y2 = z3
La bellezza di questa equazione risiede nel fatto che appaiono tre
potenze diverse, quadrati, cubi e di quarto grado. La soluzione si
genera assegnando valori arbitrari ai parametri set, in modo tale
che i valori di x, y, z che verificano l’equazione sono:
x=6st(3s4-4t4),
y= (3s4+ 414) ■ (9s8-408s4£4 + 16«8),
z= 9s8+ 168s4^4 + 16£8.
Prendendo s = 3 e t = 2 si ha la relazione
64444+ 1429462612 = 2808733.
Per s=ì e t=ì si ottiene la scomposizione
64 +2 6812= 1933.
EQUAZIONE DEL TIPO x8 + y8 + z8 = fB
Questo problema propone di trovare quattro cubi in modo tale
che la somma di tre di essi sia il quarto cubo. Nel 1591, François
Viète ottenne una formula che facilitò la generazione di soluzioni
per questo tipo di equazione, per la quale considerò valori per
men qualsiasi. In tal caso, i valori definiti generano soluzioni
della seguente equazione:
98
EQUAZIONI DIOFANTEE
FOTO IN ALTO
A SINISTRA
Eulero trovò
metodi di
risoluzione
generale per
diversi problemi
dellVAr/f/nef/ca
di Diofanto.
FOTO IN ALTO
A DESTRA
Monumento a
Joseph-Louis de
Lagrange,
creatore di un
algoritmo per
risolvere
equazioni
diofantee non
lineari di un tipo
particolare.
FOTO IN BASSO:
John Forbes Nash
studiò a fondo
le equazioni
diofantee
alla Carnegie
Tech prima di
rivoluzionare la
teoria dei giochi.
99
EQUAZIONI DIOFANTEE
xi + y3+z3= t3,
x=m(m3-2n3),
y = n(2m3-n3))
z = n{m3+n3),
t = m(m3 + n3).
Per esempio, se si prende m = 2en=lsi ottiene che
x= 12, y= 15, z-9, t- 18.
Cioè
123 + 153 + 93 = 183.
Se si prende m = 3 e n = 2, si ottiene
333 + 703 + 923 = 105:).
In merito a questo tipo di equazione, Diofanto affermò che «la
differenza di qualsiasi di due cubi è la somma di due cubi». Di fatto,
faceva riferimento alla soluzione dell’equazione x'+ yl= à3-b3t con
a > b > 0 e con x e y positivi. L’equazione x'+ y'+ z3 = t3 rimanda, per
analogia, a Platone, cui si attribuisce la soma di tre cubi di numeri
a, b, c che danno un cubo di un quarto numero: a3+ b3+ c3 = d\ Si
basò sul fatto che il cubo, in termini di volume, il cui lato sono 6
unità - cioè 6:* -, equivale alla somma dei volumi di tre cubi i cui
lati siano 3, 4 e 5 unità, cioè 3:) + 43+ 53 = 6:}.
IL CONTRIBUTO DI EULERO
Il matematico svizzero Eulero diede preziosi contributi ai lavori di
Diofanto sulle equazioni indeterminate di secondo e terzo grado,
soprattutto perché analizzò in maniera sistematica la risoluzione
in numeri razionali. Inoltre, ampliò tanto il campo dei numeri interi
quanto quello di quelle equazioni indeterminate la cui forma non
ha sempre soluzioni intere:
100
EQUAZIONI DIOFANTEE
y2 = aoc2 + bx+c,
y3=ox? + boc2 + ex + d.
La figura 3 mostra che le soluzioni intere per y2=x?+x+ 1 sono
i punti A (-1,1), B (-1,-1), C (0,-1), D (0,1)- Inquanto all’equazione
?/3= ax?+bx2+cx+dì Eulero affermò che «non è possibile trovare la
soluzione generale, né l’insieme infinito di tutte le soluzioni». Inol¬
tre, notò che in alcune curve di terzo grado, non tutte, era possibile
trovare una espressione per x e per y che generasse le soluzioni a
partire da un parametro. In questo senso, lavorò al problema sesto
del Libro IV di Diofanto, y3 = x3+ 16#2, le cui soluzioni per valori
arbitrari di a diversi da 1 sono della forma:
16
16-a
y = a'X = ^~T
a — 1
Eulero realizzò i suoi ragionamenti mediante strumenti alge¬
brici, non geometrici: proprio come il suo predecessore Diofanto.
EQUAZIONI DIOFANTEE
101
CAPITOLO 4
Problemi e soluzioni
d e\YAritmetica
Nella sua Aritmetica, Diofanto affrontò la risoluzione
di equazioni indeterminate, quelle che possiedono
un numero infinito di soluzioni e che sarebbero state
chiamate «equazioni diofantee». A tale scopo utilizzò una
simbologia e una notazione proprie, e dimostrò
che era possibile operare tra aree e volumi senza
ricorrere alla geometria, un’innovazione assoluta
per la costruzione dell’algebra.
In questo capitolo, dedicato alla presentazione dell’opera di
Diofanto, V Aritmetica, i principali protagonisti saranno i proble¬
mi in essa contenuti. Si cercherà di stabilire con il lettore una
serie di «dialoghi», tramite i quali spiegare i problemi e le soluzio¬
ni che caratterizzano l’opera principale di Diofanto, dal momento
che i suoi esercizi sono i veri protagonisti dell’eredità scritta che
il matematico alessandrino ci ha lasciato. Una delle principali ca¬
ratteristiche degli stessi è il fatto di essere scritti in una forma
generica, sebbene nella loro risoluzione Diofanto abbia utilizzato
numeri concreti. In realtà, esponeva un caso generale e risolveva
un caso particolare con abilità non sempre giustificate, e perfino
con ragionamenti talvolta contorti. Ciononostante, le soluzioni
soddisfanno sempre le condizioni proposte nel problema.
Nel capitolo, gli enunciati e la soluzione generale sono interpre¬
tati con il linguaggio matematico attuale, rispettando, per quanto
possibile, l’originale di Diofanto. Perciò, in alcuni casi sarà mantenu¬
to il termine arithmos per indicare l’incognita o un gruppo di inco¬
gnite, così come avveniva nel linguaggio algebrico sincopato usato
dal matematico alessandrino, che costituisce, senza alcun dubbio,
uno dei suoi principali tratti distintivi. Si deve segnalare che Varith¬
mos sarà qui denotato con il simbolo a, sebbene Diofanto utilizzasse
il simbolo ç. Inoltre, si sottolinea che la maggior parte delle soluzio¬
ni generiche sono state date da Bachet de Méziriac.
PROBLEMI E SOLUZIONI DELL'ARITMETICA
105
PROBLEMI DEL LIBRO I
I 39 problemi compresi nel Libro I de\YAritmetica rappresenta¬
no l’avvio di una vera e propria pietra miliare della matematica,
nella quale Diofanto aumentò la difficoltà delle sfide con il pro¬
gressivo avanzare dell’opera. Di seguito sono enumerati i prin¬
cipali problemi presenti nel primo volume, sottolineando i loro
corrispondenti sviluppi e le conclusioni, con una maggiore o
minore estensione a seconda dell’interesse che offrono e della
loro semplicità o complessità.
1.1. Scomporre un numero dato in due parti, di cui sia data la dif¬
ferenza.
Questo problema, esposto in forma generale, nel linguaggio
matematico odierno si traduce in questo modo: dati due valori
a e ö, trovare i valori di x e y in modo tale che
x+y=aI
y-x = b\
In origine, Diofanto lo aveva risolto prendendo a = 100 e b= 40.
Considerò come arithmos la parte piccola x e la chiamò a, per cui
la parte maggiore è y = a + 40. Di seguito considerò a + a + 40 = 100,
cioè 2a + 40 = 100. In questo modo, a = 30 e la parte maggiore è 70.
Oggi si risolverebbe come
y =
a + b
~2~
x-
a-b
~2~'
Sostituendo questi valori nel sistema si verificano in maniera
simultanea le uguaglianze. Affinché le soluzioni siano intere è ne¬
cessario che a e b abbiano la stessa parità.
1.2. Scomporre un numero dato in due parti che siano in un rap¬
porto dato.
106
PROBLEMI E SOLUZIONI DELL'ARITMETICA
Con la simbologia odierna, il problema risulterebbe così: dati
due valori a era maggiori di 1, trovare due valori x e y in maniera
tale che x + y = a, x = my. Diofanto lo risolse per il caso particolare
in cui a = 60 e ra = 3 («rapporto di 3 a 1»). Se x=3y, si ha che
3y +y = 60, 4y = 60. Quindi y = 15, per cui x = 45. Oggi, in maniera
generale, si hanno i valori
x - am ; y = a come soluzioni,
ra+l’ ra+1
1.3. Scomporre un numero dato in due parti tali per cui la differen¬
za tra la maggiore e un multiplo dato della minore sia data.
Cioè, dati a, ö, ra>l, si tratta di trovare due valori x e y tali
per cui
x + y = a I
x = my + b\‘
Diofanto scelse di prendere valori concreti e optò per a = 80,
m = 3 e b = 4. Proponendo y- a come la parte piccola, quella più
grande è 3a+4, per cui ottenne 4a+4=80. Pertanto, a= 19, e allo¬
ra y= 19, ,r = 61.
Nei termini attuali, la soluzione generale è:
a-b ma+b
y = , x = .
m +1 m +1
Questo problema, risolto con notevole abilità da Diofanto,
serve per sottolineare uno dei fattori fondamentali per cui l’A¬
ritmetica costituisce un elemento essenziale nella storia della
matematica: l’uso da parte di Diofanto del linguaggio algebrico
sincopato. Nella tabella riportata di seguito è illustrata la sua
equivalenza rispetto al linguaggio attuale.
PROBLEMI E SOLUZIONI DELL'ARITMETICA
107
Sia il numero 80 e lo si scomponga in due parti,
tali per cui la maggiore sia tripla di quella
minore e, inoltre, la superi di 4 unità
Se x rappresenta la parte
maggiore ey la minore,
allora
x+y=80, x=3y+4.
Se la parte minore è un ahthmos, la maggiore
sarà 3 ahthmos più 4 unità
y=a x-3a +4
E poiché la somma di entrambe deve essere
uguale a 80 unità e quella delle due parti è 4
arihmos e 4 unità, risulta che 4 ahthmos e 4
unità valgono 80 unità
Sommando
x+y=4a +4,
4a + 4 = 80
Sottraendo i termini simili dei simili, le 76 unità
Riducendo
rimanenti equivalgono a 4 ahthmos
4a = 76
E, pertanto, 1 ahthmos vale 19 unità, che
è la parte minore
a = 19
Quindi la maggiore è 61
3a + 4=3-19 + 4 = 61
1.4. Trovare due numeri in un rapporto dato, e la cui differenza sia
anch’essa data.
Cioè dati m > 1 e a, trovare x e y tali per cui
x-y = a]
x = my ['
Diofanto considerò il rapporto di 5 a 1 e la differenza 20 (m=5,
a = 20). La parte maggiore è x = 5a e denominò la minore y = a. In
questo modo, considerò 4a = 20, cioè a = 5, e concluse che x = 25 e
y- 5. Attualmente è possibile considerare i valori
a am
che verificano le condizioni.
1.5. Scomporre un numero dato in due parti tali per cui la somma
di differenti frazioni date di ciascuna delle parti sia un altro nume¬
ro dato.
108
PROBLEMI E SOLUZIONI DELL’ARITMETICA
Detto in altri termini, dati i valori a, ò, m, n (m * n), bisogna
risolvere il sistema
a = x + y
o^+y
m n
= b
Diofanto prese come valori particolari a = 100 e ò = 30, m = 3e
n = 5. Designò come arithmos y/5 = a, per cui si aveva y = 5a e
x = 90-3a. Dedusse quindi che a = 5. Con ciò, y = 25 e x - 75.
Nella notazione odierna, è facile dimostrare che i valori che
verificano la condizione sono
m(bn-a) n§ n(a-bm)
x = , y =
n-m n-m
con la restrizione a/n<b<a/m.
Il problema I.6., che chiede di scomporre un numero dato in
due parti tali per cui la differenza di diverse frazioni date di
ciascuna delle parti sia un altro numero dato, è analogo al pre¬
cedente, considerando tuttavia la differenza. In questo caso, le
soluzioni sono:
m(bn + a)
x -, y =
n + m
n(a-bm)
n + m
Come è possibile osservare nella tabella successiva, i primi
sei problemi presentati sono casi particolari di un sistema di equa¬
zioni lineari con due equazioni e due incognite della forma:
lx + ay = a1
$'X + ry = bì’
Problema
Problema
Problema
Problema
Problema
Problema
1
O
il
-Q
3
Ob = 0)
5
6
a
1
1
1
-1
1
1
ß
1
1
1
1 /m
1 /m
1 /m
Y
-1
-m
-m
-m/n
1 /n
-1 /n
PROBLEMI E SOLUZIONI DELL’ARITMETICA
109
Per questo motivo, le soluzioni dei primi sei problemi possono
essere riassunte come:
av-ba
x =—
Y-crß
b-aß
y = -.
Y-a-ß
In termini attuali si tratta, dunque, dello stesso problema. In
termini geometrici, un’espressione della forma Ax+By=C rappre¬
senta una retta, e i casi che sono stati esposti cercano i punti co¬
muni. Per esempio, come viene mostrato nella figura 1, il sistema
del problema 1.4 può essere rappresentato graficamente:
x-y = 201
x = 5 y ]'
È giunto il momento di aprire una parentesi e di spiegare che
un sistema lineare a due equazioni e a incognite è, in generale,
un’espressione della forma
xl'X + yl'y = a
x2‘X + y2-y = b
no
PROBLEMI E SOLUZIONI DELL’ARITMETICA
I valori numerici xv xv yv y2 sono noti come «coefficienti del
sistema», e i caratteri x e y, come «incognite». Risolvere il sistema
implica calcolare i valori numerici di x e y in maniera tale che
sostituendoli verifichino le uguaglianze e i valori trovati siano so¬
luzioni. Non tutti i sistemi hanno una soluzione. Se ce l’hanno, si
classificano come «compatibili»; se la soluzione è unica, come
«compatibili determinati»; e se non hanno soluzione, come «in¬
compatibili». Una condizione necessaria e sufficiente affinché ab¬
biano soluzione unica è che xì • y2-x2 • y1 *0. In tal caso, la soluzio¬
ne viene determinata dai valori
a-y9 - b y, x,‘b-x.}-a
X ^y ! è ,
xx-y.,-x.,- y, x^y.-x,- yt
come, per esempio:
3x+y=9 1
2x + 3y = 13 J‘
In questo caso si ha:
9-3-1 13 _ 13-3-9-2
= 2, y =
3-3-1-2 * 3-3-1-2
= 3.
Nella sua trasposizione geometrica, la soluzione è il punto co¬
mune che è verificato dalle due soluzioni, che rappresentano rette.
1.7. Sottrarre due numeri dati di un stesso numero in modo tale che
le differenze siano in un rapporto dato.
Cioè se si considera a eb con a < b y m > 1, trovare x tale per
cui x-a=m(x-b). Come d’abitudine, Diofanto affrontò valori con¬
creti: a = 20, b = 100 e m = 3. Ottenne così x = 140. Si tratta di una
equazione di primo grado, per cui il valore generico che verifica
l’uguaglianza è
mb-a
x = .
m-1
Anche questa forma di esprimere la soluzione coincide con
quella proposta da Bachet de Méziriac, che come si è già segna¬
PROBLEMI E SOLUZIONI DELL'>*/?/rM£77C4
111
lato andò oltre l’edizione pura dell'Aritmetica: incluse infatti una
serie di proposizioni, sviluppi e risultati che, senza dubbio, contri¬
buirono in maniera decisiva alla diffusione dell’opera, così come
all’impatto di questa versione commentata all’interno della comu¬
nità matematica intemazionale. Da parte sua, François Viète, uno
dei più grandi rinnovatori del linguaggio algebrico, scrisse l’espres¬
sione proposta da Bachet de Méziriac nella forma
, b-a
x = b + .
m-1
Se si eseguono queste operazioni, è possibile dimostrare facilmen¬
te che sono lo stesso valore.
1.12. Scomporre per due volte un numero dato in due numeri in modo
tale che un numero della prima scomposizione si trovi in un rappor¬
to dato con una della seconda e il numero risultante di questa secon¬
da scomposizione si trovi in un rapporto dato con il numero risul¬
tante della prima scomposizione.
Formalmente, è possibile scrivere: dati a, m, n (m> 1, n> 1),
trovare xv x2, yv y2 in modo tale che xx >x2, yx >y2 tali per cui
a=xl+x2=yl + y2, conxx = my2, yx = nx2.
Diofanto affermò che se si scomponeva due volte il numero
100, in modo che il numero maggiore della prima scomposizione
fosse il doppio del minore della seconda, il maggiore della secon¬
da fosse il triplo del minore della prima, e il minore della seconda
y2 = a, allora il maggiore della prima (a^) sarebbe stato x{ = 2a e,
chiamando x2 il minore della prima, sarebbe stato x2 = 100-2a. Il
numero maggiore della seconda sarebbe stato yx = 3x2 = 300-6a.
Dato che la somma dei numeri della seconda scomposizione era
anch’essa 100, questa somma equivaleva a 300 unità meno 5 ari-
thmos, cioè 300-5a= 100. In sintesi, Diofanto ottenne il numero
a= 40, per cui la scomposizione di 100 è: 100 = 80 + 20 = 60 + 40.
La soluzione generale è stata data da Bachet de Méziriac:
am(n-1) _ a(ra-l) _ an(m-1) _ a(n-1)
x\= \ > > Vi ~ i » y > ~ ■
nm -1 nm -1 nm -1 nm -1
112
PROBLEMI E SOLUZIONI DELL'ARITMETICA
L’IMPORTANZA DEL LIBRO II
Il Libro II raccoglie 35 problemi, e di essi tratteremo se i primi
sette sono originali. Paul Tannery ha infatti sostenuto che non lo
fossero, e altri storici hanno avanzato l’ipotesi che furono scritti
da qualche commentatore o traduttore di autori greci o latini, sem¬
pre di epoca antica ma comunque posteriore a Diofanto. Per que¬
ste ragioni passeremo direttamente all’ottavo problema.
II.8. Scomporre un quadrato dato in due quadrati.
Cioè dato a, trovare x, y tali per cui x2 + y2 = a2. Questo è il
problema che ha dato origine all’ultimo teorema di Fermat: l’e¬
quazione x" + y" = z" non ha soluzioni intere non nulle per n, fat¬
ta eccezione per n = 2.
Lo stesso Fermat ha lasciato una nota sul margine della sua
copia dell'Aritmetica affermando che non poteva riportare la
dimostrazione per mancanza di spazio.
Diofanto risolse il problema con a = 4. Con la retorica che lo
caratterizzava, espose il procedimento in questa forma:
Se vogliamo scomporre 16 in due quadrati e supponiamo che il primo
è 1 arithmos, l’altro avrà 16 unità meno 1 quadrato di arithmos, e,
pertanto, 16 unità meno 1 quadrato di arithmos sono un quadrato.
Formiamo il quadrato di un insieme qualsiasi di arithmos diminuito
di tante unità quante ne ha la radice di 16 unità, e sia il quadrato di 2
aiithmos meno 4 unità. Questo quadrato avrà, dunque, 4 quadrati di
arithmos e 16 unità meno 16 arithmos, che uguagliamo a 16 unità
meno 1 quadrato di arithmos, e, aggiungendo all’uno e all’altro lato i
termini negativi e sottraendo quelli simili, risulta che 5 quadrati di
arithmos equivalgono a 16 arithmos, e, pertanto, 1 arithmos vale
16/5; quindi uno dei numeri è 256/25 e l’altro 400/25, numeri la cui
somma è 144/25. Cioè: 16 unità, e ciascuna di esse è un quadrato.
Per risolvere l’equazione oc2 +y2 = 16, Diofanto prese come in¬
cognita x=a. Pertanto, è y2 = 16-a2, che identifica con una espres¬
sione avente la forma ( ma - Vl6 ) . Questa, per m = 2, è
PROBLEMI E SOLUZIONI DELL'ARITMETICA
113
(2a-4)2 = 4a2 + 16-16a = 16 -a2
e, semplificando, 5a2=16a, a = 16/5. Pertanto,
per cui risulta
400
25
16 = 42.
Un bellissimo ragionamento geometrico per risolvere questo
problema si basa, da un lato, su teme pitagoriche, e dall’altro sul
fatto che a partire dall’osservazione di triangoli rettangoli è possibi¬
le stabilire una relazione di proporzionalità. Per esempio, conside¬
riamo ima coppia di triangoli rettangoli, n primo di essi è il classico
triangolo pitagorico: (3)2+ (4)2 =52, e il problema da risolvere è
(x)2+ (y)2=42= 16. È possibile osservare le loro rispettive raffigu¬
razioni grafiche nella figura 2.
A partire dai due triangoli, è possibile stabilire che la tema
(oc, y, 4) deve essere proporzionale alla tema (3, 4, 5). Quindi
Or, 2/, 4)=k(3,4,5). Confrontandoli, si ha che x=3k ey=4k, 4=5/c.
Risolvendo k dà k=4/5, per cui si stabilisce che
(X, y, 4)=4/5 (3,4, 5) = (12/5,16/5, 4),
FIG. 2
114
PROBLEMI E SOLUZIONI DELL'ARITMETICA
con cui, effettivamente, si verifica (12/5)2 + (16/5)2 = 42 = 16. Bachet
de Méziriac presentò una soluzione generale per scomporre un
quadrato come somma di due:
Sia a > 0, m > n. Da questo, si ha x =
che verifica che x1 + y2 = a2.
2 mn
——7^ y =
m +n~
(ra2 - n2
2 ~ ^ ’
m +n~
Per esempio, se si considera a=7 e si desidera scomporlo come
somma di due quadrati, si prendono in maniera arbitraria valori per
m, n, come possono essere m - 3, n=2, e allora si ottiene
il che produce
12 7
x =— -7, y =
13
II.9. Scomporre un numero dato che è una somma di due quadrati in
altri due quadrati.
Cioè dato a2 + ò2, trovare x, y tali per cui a2 + ò2=x? + y2. Fede¬
le al suo stile, Diofanto commentò:
Sia 13, soma di due quadrati, 4 e 9, il numero che desideriamo
scomporre in altri due quadrati. Prendiamo le radici 2 e 3 di questi
supposti quadrati, ipotizziamo che il lato di uno dei quadrati sia
i=a + 2e che il lato dell’altro sia ma-3 con m arbitrario; per esem¬
pio, y = 2ct — 3. Allora uno dei quadrati è xl = a2 + 4a + 4 e l’altro
4a2 + 9 - 12a; poiché la somma di questi quadrati è uguale a 13, ri¬
sulta 5a2 + 13-8a= 13, da dove a= 8/5. Tornando alle posizioni, il
lato del primo quadrato è x = a + 2= 18/5 e il lato del secondo
y = 2ct—3= 1/5; quindi i quadrati sono a:2=324/25, y2= 1/25, la cui som¬
ma è 325/25, il numero dato.
Questo problema attirò l’attenzione del matematico svizzero
Eulero, che vi apportò un notevole miglioramento. Eulero stabilì
PROBLEMI E SOLUZIONI DELL'ARITMETICA
115
che se si prendono men come numeri razionali arbitrari, allora i
valori x e y che verificano la scomposizione sono:
x =
2nmb + a(m2 - n2) 2nma + b(n2-m2)
* -, y = * -
2 2
n +m
2 2
n + m
Eulero chiarì che sem = n, oppure m = a-b, n=a+b, la scom¬
posizione proposta è quella di partenza.
II. 10. Trovare due numeri quadrati che abbiano una differenza data.
Cioè dato d, trovare x, y tali per cui oc2-y2 = d. Come esempi,
si ha 60 = 82-22 = 162-142, il che mostra che la scomposizione in
differenza di quadrati di uno stesso numero non è unica. Se si
esamina l’equazione diofantea proposta e si soddisfano i metodi
di risoluzione, dato un valore m arbitrario si ha che
m2 + d
x =
2 m
y-
m2 -d
2 m
con la restrizione per cui d < ni2.
Il problema non ammette soluzioni intere sedè della forma
4n + 2, dato che x2 - y2 = {x + y)(x-y) - dove entrambi i fattori
hanno la stessa parità se x e y sono interi - e un numero pari
moltiplicato per un altro numero pari è multiplo di 4; mentre un
numero dispari moltiplicato per un altro numero dispari è dispa¬
ri. Invece, se d è dispari o un multiplo di 4 maggiore di 4, il
problema avrà sempre soluzioni intere, come si è visto nel capi¬
tolo precedente.
II. 19. Trovare tre quadrati tali per cui la differenza tra il maggiore
e quello medio si trova in un rapporto dato con quello tra il medio
e il minore.
Cioè, dato m> 1, trovare x, y, z, con x>y>z, tali per cui
oc2-y2 =m(y2- z2). Per il caso m = 3 si ottiene x= 11, y= 7, z-5. Si
osserva inoltre che per m = 1 risultano tre quadrati in progressione
aritmetica Alla luce di questo risultato, è possibile enunciare:
116
PROBLEMI E SOLUZIONI DELL'ARITMETICA
JACQUES DE BILLY
Il matematico e astronomo francese Jacques de Billy (1602-1679) mostrò
un talento naturale per l’aritmetica, sebbene provasse una speciale predi-
lezione per l’elaborazione di tavole astronomiche. Le sue doti per l’inse¬
gnamento lo portarono a impartire lezioni in diverse scuole gesuite fran¬
cesi, da Reims fino a Pigione e
Grenoble, e infine sarebbe divenuto
rettore delle scuole gesuite di Sens e
Langres. Tra i suoi alunni più noti va
citato Claude Gaspard Bachet de Méz-
iriac, il principale traduttore e divulga¬
tore dell’opera di Diofanto. Inoltre,
mantenne anche una corrispondenza
epistolare con Pierre de Fermat. Con
loro condivise una passione assoluta
per i contenuti de\YAritmetica, alla cui
diffusione contribuì attraverso diversi
commenti e con la dimostrazione di un
problema concreto. Oggi, il prezioso
lascito di Jacques de Billy fa parte del¬
la teoria dei numeri.
Il gesuita francese Jacques de Billy dimostrò il
risultato del problema 11.19 de\VAritmetica.
È impossibile trovare quattro quadrati in progressione aritmetica.
Questo risultato è stato dimostrato dal matematico e astrono¬
mo francese Jacques de Billy (1602-1679).
11.20. Trovare due numeri tali per cui il quadrato di ognuno di essi
aumentato nell’altro numero formi un quadrato.
Cioè trovare x, y tali per cui x2 + y = «un quadrato»,
y2+x= «un quadrato». Con le equazioni, risulta essere un problema
indeterminato di secondo grado
oc2 + y=a2J y2+x=b2.
PROBLEMI E SOLUZIONI DELL'ARITMETICA
117
Diofanto lo risolse mediante la relazione lineare y= 2+x, che
impose affinché il problema fosse risolvibile, cioè determinato. La
sua soluzione era:
*=3/13, y= 19/13, a= 16/13, 6 = 20/13,
Eulero, da parte sua, risolse il problema in maniera più gene¬
ralizzata nel suo libro Algebra, dove affrontò l’equazione
x2+y = (p-x)2, y2+x = (q-y)2
e realizzò diverse operazioni, fino a concludere che:
2qp2 - q2 2pq2 - p2
x = —, y = —^.
4 pq - 1 4 pq - 1
Per esempio, nel caso dip=2 eq=3 si ottenne x= 15/23 e y=32/23.
11.30. Trovare due numeri tali per cui il loro prodotto aumentato o
diminuito in una somma formi un quadrato.
Cioè trovare x, y tali per cui xy + (x + y) = «quadrato»,
xy-(x + y) = «un altro quadrato». Diofanto ragionò in maniera
molto elegante considerando i numeri 2 e 3, e osservando che
22 + 32 = 13, che 13 + 12 = 52 e che 13 - 12 = l2. Scisse allora
xy= 13a2, in modo tale che se uno dei numeri è x- a, l’altro sia
13a. Poiché si verifica che 13a2± 12a2 è un quadrato, identificò
12a2 con la somma dei numeri, cioè scrisse che x + y= 12a2. Al¬
lora, 12a2 = 14a, da dove risulta a = 14/12 = 7/6, e i numeri sono
x= 7/6, ?/= 91/6.
UNA BREVE ESCURSIONE NEL LIBRO III
I primi quattro problemi del Libro III sono analoghi agli ultimi due
del libro precedente, il che diede adito allo storico Paul Tannery
di speculare su una possibilità: che neppure questi problemi fos-
118
PROBLEMI E SOLUZIONI DELL'ARITMETICA
sero del tutto originali di Diofanto, ma che sarebbero stati intro¬
dotti nelle traduzioni a partire da documenti precedenti ai lavori
del matematico alessandrino. Per questo motivo, in questo para¬
grafo passeremo direttamente al quinto problema
III.5. Trovare tre numeri la cui somma sia un quadrato e tali per cui
la somma di ogni due di essi superi l’altro di un quadrato.
Cioè trovare x, y, z tali per cui le espressioni successive siano
un quadrato:
x+y + z, x+y-z, y + z-x, z + x-y.
Diofanto propose come soluzione x=ì7/2, y= 65/2, z =40.
III.6. Trovare tre numeri la cui somma sia un quadrato e tali per cui
la somma di ogni due di essi sia anch’essa un quadrato.
Cioè trovare x, y, z di forma tale per cui le espressioni che
sono indicate siano quadrati:
x + y + z, x + y, y + z, z + x.
Diofanto ragionò nella maniera seguente. Come era solito fare,
introdusse Yarithmos a in modo che x + y + z=(a+ì)2 e che la
somma dei primi fosse x+y=á2, per cui il terzo sarà z = 2a + 1. Dato
che la condizione è che y + z sia «un quadrato», scrisse:
y + z- (a—1)2= a2+ l-2a. Così,
x=(x + y + z)-(y + z) = 4a, y=(x + y)-x = a2-4a.
Risulta tuttavia che x + z - 6a + 1 sia «un quadrato». Diofanto
impose che questo quadrato fosse 121. Con ciò, a = 20, e i numeri
sono x=80, y=320, z = 41.
III.8. Dato un numero, trovarne altri tre in modo tale che la somma
di due qualsiasi di questi numeri aumentata nel numero dato formi
PROBLEMI E SOLUZIONI DELL'ARITMETICA
119
un quadrato, e che la somma dei tre numeri aumentata nel nume¬
ro dato formi anch’essa un quadrato.
Cioè dato a, trovare x, y, z in modo tale che le seguenti espres¬
sioni siano un quadrato:
x + y + z + a, x+y + a, y + z + a, x + z + a.
Diofanto lo risolse per il caso a = 3. Scrisse la somma dei primi
due numeri come # + ?/=a2 + 4a + 1, Affinché aggiungendo 3 unità
risulti un quadrato; per la somma del secondo e del terzo,
y + z = a2 + 6a + 6, e per quella dei tre numeri x+y+z= a2 +8a + 13
in modo tale che queste somme, aumentate di tre unità, formino
anch’esse quadrati. Cioè, rispettivamente, x + y + 3 = (a + 2)2,
y+z+3 = (a + 3)2, x+y+z+3=(a+ 4)2.
Si deduce allora che il terzo numero è z = (x+y+z) -
(x+y) = 4a + 12, che il primo è x = (pc+y+z) - (y+z) = 2a + 7 e che al¬
lora il secondo è
y = {x+y)-x = a2 + 2a - 6.
Rimane da soddisfare chex+z+3 sia «un quadrato». Uguaglian¬
do questa somma, che è 6a + 22, a un quadrato numerico come 100,
come propose Diofanto, risulta a = 13.1 numeri saranno quindi:
x = 33,y = 189, 2 = 64.
Il problema III.9 è analogo al precedente, poiché chiede che il
numero dato sia diminuito e non aumentato, cioè sottraendo a.
Con un ragionamento simile, Diofanto giunse al risultato x = 23,
y = 80, z = 44 per a = 3.
III. 15. Trovare tre numeri tali per cui il prodotto di due qualsiasi di
essi, aumentato nella somma di questi due, formi un quadrato.
Si noti che il prodotto di due quadrati qualsiasi consecutivi
aumentato nella sua somma è un quadrato. Supponiamo che il
120
PROBLEMI E SOLUZIONI DELL'ARITMETICA
primo numero sia 4 e il secondo 9, il cui prodotto 36, aumentato
nella sua somma, forma un quadrato. Si ha l’identità
a2 (a+1)2+a2 +(a+l)2=(a2 +a+1)2.
Per a2=4, (a+l)2=9 si ottiene, effettivamente,
36+ 4 + 9 = 49 = 72 = (4+ 2 + l)2.
Diofanto lo sviluppò in questo modo:
È necessario che il prodotto del secondo per il terzo, aumentato nel¬
la sua somma, e quello del terzo per il primo, aumentato anch’esso
nella sua somma, siano numeri quadrati. Se il terzo è 1 arithmos, il
prodotto del secondo per il terzo, aumentato nella sua somma, avrà
10 arithmos e 9 unità uguali a un quadrato, e il prodotto del terzo per
11 primo, aumentato nella sua somma, 5 arithmos e 4 unità, uguali
ad un quadrato, dando quindi come risultato una doppia equazione
la cui differenza è 5 arithmos e 5 unità. Due numeri il cui prodotto
sia 5 arithmos e 5 unità (cioè: questa differenza) sono: 1 arithmos
più 1 unità e 5 unità; quindi si avrà, come prima, che la semisomma di
questi numeri, moltiplicata per se stessa, è il quadrato maggiore, e la
semidifferenza, moltiplicata per se stessa, il quadrato minore, e poiché
1 arithmos vale 28 unità, il primo numero è 4, il secondo 9 e il terzo 28.
Espresso per mezzo di equazioni, si ha:
xy + (x+y) = a2, yz+(y + z) = b2, zx + (z + x) = c2.
E tenendo presente la nota precedente, se si ipotizza z- a, la
seconda e la terza equazione diventano
10a + 9 = ò2, 5a + 4 = c2,
da cui deriva
62-c2=(ò + c) (ò-c) = 5(a+vl),
e, postulando b + c= a + 1, b-c- 5, si ha:
PROBLEMI E SOLUZIONI DELL'ARITMETICA
121
2
a- 4
2
E, pertanto,
10ct + 9 = ^y^ , 5a + 4 = |
entrambe equazioni che danno lo stesso valore, a = 28. Di conse¬
guenza, x - 4, y = 9, z = 28.
Fermat, in merito a questo problema, affermò che era possi¬
bile andare maggiormente in profondità:
Così, io posso fornire infinite soluzioni del seguente problema:
trovare quattro numeri tali per cui il prodotto di due qualsiasi di
essi, aumentato nella somma degli stessi due, sia un quadrato.
Il matematico francese propose i primi tre numeri in modo
identico a quello in cui sono presenti nel problema V.5: 25/9, 64/9,
196/9,... Per il quarto numero, Thomas Little Heath trovò una so¬
luzione negativa.
Attualmente è stato rilevato che esiste un quarto numero
razionale dell’ordine di 120 cifre nel numeratore e di 118 nel
denominatore.
Eulero considerò l’identitàxy + x+y = (x+Y)(y+l)-\e: rifor¬
mulò il problema di Diofanto e il commento di Fermat chiedendo
di trovare tre numeri A, B, C - o quattro numeri, A, B,C,D- tali
per cui il prodotto di ciascuno dei due diminuito di una unità fosse
un quadrato perfetto.
III. 16. Trovare tre numeri tali per cui il prodotto di due qualsiasi
di essi, diminuito nella somma di questi due numeri, formi un
quadrato.
Come d’abitudine, i quadrati sono denotati come a2, b2, c2 per
risolvere il sistema:
xy-(x + y) = a2, yz-(y + z) = ò2, zx-(z + x) = c2.
122
PROBLEMI E SOLUZIONI DELL'/4/?/7A/£T/G4
Diofanto diede sfoggio della sua abilità e trovò due numeri
ausiliari x' e y' che soddisfano le condizioni
x'y'-(x'+y') = p\
x'-l
y-1
La seconda delle quali viene soddisfatta da x',=y+ 1, ?/’=4?/+l,
dal momento che è
y +1-1 11
4?/ + l-l_4_22
Impostando
P2 = (2y-2f,
la prima condizione diventa
(y + 1) (4y + 1)- (y + 1 + 4y + 1) = (2y - 2)2
da cui y = 5/8.
Pertanto,
x'
13 , 28
Ty=-s
7
2
Questi valori soddisfano la prima equazione del sistema, che
è identica alla prima condizione. Eseguendo
13 7
X = , .V = - , 2 = 0L
8 y 2
la seconda e la terza equazione del sistema diventano:
5 7 2 5a 13 2
-a — = b, = c.
2 2 8 8
Moltiplicando per 4 e 16:
10a-14 = 4ò2 = ò’2, 10a-26= 16c2 = c’2
sottraendo:
ò’2-c’2= (ò’+c’) (6-c’) = 12 = 2-6,
PROBLEMI E SOLUZIONI DELL'ARITMETICA
123
e scrivendo ò’ + c’ = 6, 6’ -c' = 2, si ottiene
6’2 = (8/2 )2 = 64/4, 10a-14 = 16,
da cui a = 3, per cui allora,
z = 3 = 24/8, x = 13/8, y = 28/8.
III. 19. Trovare quattro numeri tali per cui il quadrato della loro som¬
ma, aumentato o diminuito di ciascuno di essi, formi un quadrato.
Cioè trovare x, y, z, t tali per cui (x+ y + z + i)2 ±x = á2,
(x + y + z +1)2 ±y = b2, (x + y + z +1)2 ±z = c2, (x + y + z +1)2± t = d2.
Per risolverlo, Diofanto applicò, eccezionalmente, un bel ri¬
sultato di geometria su triangoli rettangoli, basato sul teore¬
ma di Pitagora, dove si afferma che «il quadrato dell’ipotenusa
di ogni triangolo rettangolo aumentato o diminuito del dop¬
pio del prodotto dei cateti forma un quadrato». Se si deno¬
ta l’ipotenusa con h e i cateti con p e q, il risultato stabilisce:
h2 ± 2pq = «un quadrato».
Per il teorema di Pitagora si ha che k2=p2 + q2. Allora, sosti¬
tuendo nell’espressione precedente si può impostare
p2 + q2± 2pq = «un quadrato» = (p ± q)2.
Fermat realizzò un commento a tale risultato:
Ogni numero primo della forma 4n + 1 è l'ipotenusa di un triangolo
rettangolo una sola volta; il suo quadrato lo è due volte; il suo cubo
lo è tre volte; il suo biquadrato quattro volte, e così di seguito.
Per esempio, per n=lsiha4n+l = 41 + l = 5, i cateti saranno
3 e 4, e si avrà: 32 + 42 = 52.
Per n = 2siha4tt+l=4-2+l = 9, che non è primo e, pertanto,
il risultato non è valido.
124
PROBLEMI E SOLUZIONI DELL'ARITMETICA
Ç> f *òì>7«ß7TVf»>>Ç-tTi/^CvVeì-x- V:^^>û^7e^-X ^^V*'C<*A>vaùr’»W«|>>
yyf^Caontf. >CUv’À>7À{tìOji^>»JJi(-i(o/r<>i--t-[3 tÛ|j£, A - (&*».£
^orfry t» C^**iS*vt <«»-t ®tòXy-irOu,t «*ì"r»< V>>r< f* ^/xì7o|LiCA’ttÌViTou <J<; 1° £ <^Ç' I ■“*'
*yn(T^ì-J- aU»\M£4v T»7»*/Ì6,r«»-pl>^oì »»AJ»i,-»Jka^<Ji<^<tV>ìVAr^Alt»
(liAJtK I. ui?lijÌAtf <7v-3<- i^juc^I ò4^Ao<^fn7^T^rov60rcy^/ È CyVA«/<r\r» vi7**£byvSit*jL
-7^*y»t *V ÇfñìTovJtxxAlôt'ml CÌtìT^ò. fa& ne»- v‘«jV ✓ÇO*' |ct,aXTf*«Ai«M rxAc ~Yj ju»^/W> >» *♦ Ò^’i 4 v'VofJ
<_t9i/» A*>v^ ^Vq7^yw’i<TtJm»^^jÌjL-(>j^j'ili.À/a^cM-^ri v<TOti O
|Wc A |^v<ra*V^7o'^ i7ao»0* ( £ Lf K *<ìt JuiVjcr^ '—•
. . ^ f./T< /-w ! a rJ ~ r«*5 > /•_ ,
V
o'r—lorTó fj£{. 7i7a/^iccioL,Ç^^XfJum xmri**7owo^ci^joAr* *. *cu*âo,r *
-T>7çA /*»vo> Jr<w7J?Äjilf^«vTt^o^,yãor«i(^V-T?«»/Ìu>>,-Mie*%«jr* ot/o-^i5-ju#\jul cA^ {jj’ jmJp»®
—pi vì/«fe£)^*c* •nlg/i'faz r » c cj veç • «avW'Sv^ob j£fa *TllßAToo *• vAvi'v^ku jr yr
oi'v ^otef>Xj~»j liaoy £ Afr« V^‘Æf fl a£ i’Tcì^ «' &Tf 24 ßo ra> £tuJ3t 'AiA JU-fC^Ç
Ç-f ^ujjpico7uZ^xtjSLjttÁt-i-i A jlL x^f A* \|^ciV»> A,outf»Ç* ^c«/ì\ì}»6io^f'--t£ 1^
ty JUS pV od/Lj A x/j/kuA>i>C^ 5 vi*t TtJfi',«pJUSV^Jhsl/aÇ- ffJ&vìçCy SL -pii «W «uüT® • ♦\'i«v7Qyi/?/^
•JiWiit ■)*> « C_aVOüV«^«» vtJtf\ 7d ?e vJ^v'fcldi- r. w ü / i .£ Jk‘ .Åà"«U5 ?" TI OÙ JLo i^ji. « i m^o «ir. 2L^ pmxf'-iS-t
Particolare di una
pagina in greco dei
preziosi testi di
Diofanto,
conservato presso
la Biblioteca
Apostolica
Vaticana.
Busto di Pitagora, il
cui teorema venne
utilizzato in maniera
eccezionale da
Diofanto per
risolvere un
problema del Libro
III dell’Ar/tmet/ca.
PROBLEMI E SOLUZIONI DELL'ARITMETICA
125
Per n = 3 si ha 4n+1= 4-3+1=13, che è invece primo e, pertan¬
to, il risultato è valido. In questo caso si ha 52+122=132.
Diofanto realizzò diversi calcoli, fino a ottenere che
1 713 600 _ 12 675 000 _ 15 615 600 8 517 600
X 163 021 824 ’ V 163 021 824 ’ Z 163 021 824 ’ 163 021 824 '
ALCUNI ASPETTI DEL LIBRO IV
Il Libro IV offre 40 problemi, dei quali, per motivi di spazio, sono
stati scelti i principali. Tra loro sottolineano quelli in cui si ri¬
corre a una «falsa posizione», come i problemi IV.8 e IV.9, come
il problema IV.29, sul quale Bachet de Méziriac avrebbe realizza¬
to un prezioso contributo.
Emergono anche alcuni problemi, nei quali Diofanto ottenne
le soluzioni in maniera confusa, ma tuttavia meritoria, come il pro¬
blema IV.31.
IV.3. Moltiplicare uno stesso numero per un quadrato e per la radice
di questo [il suo lato] in modo tale che il prodotto per il lato sia un
cubo e il prodotto per il quadrato dia il lato di questo cubo.
Cioè trovare x, y tali per cui xy = l3 y x?y = l.È facile osservare
che
X- ì/l2, y = l5.
Il problema può essere impostato in maniera più generale nel
modo seguente: dato l, trovare x, y in modo che xl-y, xnl = yn+l.
La soluzione è:
x=l/V\ y= 1 /ln-\
IV. 19. Trovare tre numeri indeterminati tali per cui il prodotto di
due qualsiasi di essi, aumentato di una unità, formi un quadrato.
126
PROBLEMI E SOLUZIONI DELL'ARITMETICA
In questo caso l’enunciato, nel quale i quadrati sono denotati
come a2, b2, c2, chiede di trovare x> y, z tali per cui
xy + 1 = a2, yz + 1 = b\ zx + 1 = c2.
Il problema è indeterminato - possiede infinite soluzioni - e
Diofanto propose di generare le soluzioni a partire dai valori arbi¬
trari a, m della forma
x = m2a + 2ra, y = a, z =v(m+1)2 a + 2(m + 1).
IV.29. Trovare quattro numeri [quadrati] la cui somma aumentata di
quella dei suoi lati formi un numero dato.
Dato a, trovare x, y, z, t tali per cui x2 + y2 +z2 + t2 +(x + y
+ z + t) = a.
Diofanto optò per il 12 come «numero dato». Dal momento che
ogni quadrato (m2), aumentato della sua radice e di 1/4 di unità, for¬
ma un quadrato la cui radice diminuita di 1/2 unità è la radice del
quadrato originario; cioè ra2+ra+1/4 = (ra +1/2)2, identità che appli¬
cata all’equazione oc2 +y2 + z2 + t2 + (x+y+z+t) = 12 risulta
x2 + x + 1/4 + y2 + y + 1/4 + zr + z + 1/4 +12 +1 + 1/4 =
= 12+4 -1/4 =13,
che può essere raggruppata come
fix + 1/2)2 + (y + 1/2)2 + O + 1/2)2 + (t + 1/2)2 = 13 =
= 64/25 + 36/25 + 144/25 + 81/25;
identificando i termini, è:
x + 1/2 = 8/5, y + 1/2 = 6/5, z + 1/2 = 12/5, t + 1/2 = 9/5,
da cui
x = 11/10, y = 7/10, z = 19/10, t = 13/10.
PROBLEMI E SOLUZIONI DELL'ARITMETICA
127
Diofanto scrisse le operazioni precedenti in questa forma:
La somma dei quattro numeri aumentata delle sue radici vale 12
unità, e aumentata, inoltre, di 4 quarti, cioè: 1 unità, avrà valore 13,
numero che dovremo scomporre in quattro quadrati, in modo tale
che se sottraiamo 1/2 unità dalla radice di ciascuno di questi quadrati
avremo le radici dei quattro quadrati. Scomponendo 13 in 4 e 9, e
ciascuno di questi quadrati in due:
13 = 4+ 9 = (64/25+ 36/25) (144/25 + 81/25).
E prendendo le radici di questi quadrati si ha:
8/5, 6/5, 12/5, 9/5.
Sottraendo 1/2 unità di questi, le radici dei quadrati richiesti sono
11/10,7/10, 19/10, 13/10,
e la soluzione è:
x1- 121/100,2/2 = 49/100, 22 = 361/100, *2= 169/100.
Rispetto a questo problema, Bachet de Méziriac realizzò una
tabella in cui viene illustrata la scomposizione in uno, due, tre o
quattro quadrati interi di tutti i numeri tra 1 e 120, ed enunciò un
teorema:
Ogni numero intero [positivo] è un quadrato, o somma di due, tre o
al massimo di quattro quadrati.
Come è possibile osservare, Diofanto era abbastanza «creativo»
e realizzò varie ipotesi che, apparentemente, non sono giustificate.
IV.38. Trovare tre numeri tali per cui il prodotto della loro somma
per il primo, per il secondo e per il terzo sia un numero triangolare,
quadrato e cubico, rispettivamente.
128
PROBLEMI E SOLUZIONI DELL'ARITMETICA
In questo enunciato, «triangolare» significa che ha forma
n(n +1)
2
per n naturale, come sarà spiegato nel prossimo capitolo. In lin¬
guaggio algebrico equivale a trovare x, y, z in modo tale che
(x+y+z) x = n(n + ^) >
2
(x+y+z) y = «numero quadrato»,
(x+y+z) z=«\m cubo».
«Confesso che non sono ancora riuscito a ottenere una
dimostrazione, cosa per cui sarò molto grato a chi vi riesca,
perché non solo in questo problema, ma anche in alcuni del
Libro V, si vede che Diofanto la dava per scontata.»
— Bachet de Méziriac.
Diofanto realizzò i calcoli pertinenti e propose i seguenti
valori:
x= 153/81, y = 6400/81, z = 8/81.
Per la sua soluzione, il matematico alessandrino utilizzò un
bellissimo risultato:
Ogni numero triangolare preso otto volte e aumentato di 1 unità è
un quadrato.
Cioè 1/2 n(n+1)8 +1 = (2n+1)2.
Diofanto, inoltre, presuppose, sebbene non lo avesse indicato
in maniera esplicita nell’enunciato, che x+y+z fosse un numero
quadrato. In questo senso, i valori proposti verificavano che la sua
somma fosse 81, cioè 92.
PROBLEMI E SOLUZIONI DELL'ARITMETICA
129
LA COMPLESSITÀ DEL LIBRO V
Il Libro V propone 30 problemi. Per via del suo elevato li¬
vello di difficoltà, in alcuni casi verrà esposto solo l’enun¬
ciato e la soluzione corrispondente, omettendo il proces¬
so di risoluzione. Bisogna segnalare che Bachet de Méziriac
inserì alcune soluzioni e rifletté soprattutto su un problema di cui
si è già parlato in queste pagine, il V.30, legato ai prezzi del vino.
V.l. Trovare tre numeri in proporzione geometrica, tali per cui, sot¬
traendo da ognuno di essi un numero dato, risulti un quadrato.
Come prima cosa si deve specificare che una successione di
numeri av a2, a3, ... è una progressione geometrica quando ogni
termine è ottenuto moltiplicando il precedente per un numero fisso,
chiamato «rapporto» della progressione. Pertanto, in una progres¬
sione geometrica il quoziente tra due termini consecutivi è sempre
uguale al rapporto. Di conseguenza, una progressione geometrica
risulta essere determinata dando qualsiasi termine e il rapporto. Se
il primo termine di una progressione geometrica è a{ e il rapporto
è r, la progressione sarà:
a, a =a,r a =a.,r a =a.,r a =a .r
12 1 3 2 4 3 N H-l
a2 = axr a3 = a{ri a4 = alri an = alrH~l
Il «termine generale» della progressione geometrica è:
an = aìr"-1. Si noti che a{ -a;t = (a2)2. Esempio: La successione 1, 2,
4, 8, 16, 32,... è una progressione geometrica di rapporto r=2.
In quanto alla somma di n termini consecutivi di una progres¬
sione geometrica, sia una progressione geometrica di primo ter¬
mine dj e di rapporto r. Per trovare il valore della somma degli n
primi termini S = a, + a2 + a3 + a4 +... + a,M + an si utilizza:
s Q|(l-r") -1)
1 - r r -1
Per esempio, la somma dei primi 10 termini della progressione
1, 2, 4, 8, ...è:
130
PROBLEMI E SOLUZIONI DELL'ARITMETICA
s =
2-1
= 1023.
Nel caso della somma di infiniti termini, è possibile realizzare
solamente se il rapporto verifica -1 <r< 1. Questa condizione si
scrive come I r k 1, e il suo valore è
s ai(-i) «i
r -1 1 - r
Per esempio, la somma 100 + 50 + 25 +12,5 +... - infiniti termi¬
ni, con r= 1/2 -, vale:
1-1/2
Una volta dati questi chiarimenti, per il problema V. 1 i quadra¬
ti saranno denotati come b2, c2, d2.
Tradotto nel linguaggio analitico: dato a, trovare x, y, z in
modo tale che xz = y2- condizione che si trova in una progressione
geometrica - e in modo che x-a = b2, y-a = c2, z-a = d2. Diofanto
prese 12 come «numero dato» e con esso ottenne i valori:
x = 169/4, y = 4693/208, z= 130321/10816.
Bachet de Méziriac lo risolse per qualsiasi valore di a e trovò
la soluzione:
x =
(a+i)2
2/ =
er + 18a + l
"Te ’
(cr + 18a + l)“
64(a + l)2
V. 11. Scomporre l’unità in tre parti tali per cui, sommando a ognuna
di esse uno stesso numero, risulti un quadrato.
Cioè dato a, trovare x, y, z tali per cui x+y + z - 1, in maniera
tale che le seguenti espressioni siano un quadrato: x+a, y + a,
z + a. Diofanto affermò che hanno soluzione se il numero a non è
2 né un multiplo di 8 più 2. Dall’enunciato emerge che
x + a + y + a + z + a deve essere la somma di tre quadrati, e poiché
x + a + y + a + z + a = (x+y + z) + 3a= 1 +3a, allora 1 +3adeve esse¬
PROBLEMI E SOLUZIONI DELL'ARITMETICA
131
re la somma di tre quadrati. Diofanto lo risolse per il caso a = 3. La
sua idea fu di scomporre il numero 10 come somma di tre quadra¬
ti, e ottenne i valori
*=228478/505521, y= 134662/505521, *=142381/505521.
Bachet de Méziriac scoprì che il problema non può essere ri¬
solto neppure per a=9 e valori della forma a = 32n + 9, poiché 1 + 3a
non è un somma di tre quadrati; lo dimostrò per valori di a da 1
fino a 325. Lo stesso Bachet de Méziriac arricchì ulteriormente il
problema, generalizzandolo, con il seguente contributo:
Siano dea numeri tali per cui d + Sa sia una somma di tre
quadrati. Trovare x, y, * tali per cui x+y + z = de\e espressio¬
ni successive siano un quadrato: x + a, y +a, z +a.
Per il caso d = 5, a = 3, diede la soluzione
* = 934/625, y = 1041/625, * = 46/25.
V. 29. Trovare tre quadrati tali per cui la somma dei suoi quadrati
formi un quadrato.
Cioè trovare x2, y2, z1 tali per cui l’espressione oci + y4+zi sia un
quadrato. Diofanto considerò Yarithmos a in maniera tale che i qua¬
drati fossero a2, 4 e 9. Giunse all’espressione 20a2=3, che non viene
soddisfatta da alcun valore razionale di a, e cercò il modo di sostitu¬
ire la frazione á2=3/20 con quella di due quadrati. Osservando che era
3 (10)~ — (42 + 9a)
20 2 10
ipotizzò che si deve arrivare a un numero k che sia della forma
k2-(m2 + n2) p2
2 k q2
per certi valori di k, m, n, p, q. Diofanto introdusse allora le
relazioni
132
PROBLEMI E SOLUZIONI DELL'ARITMETICA
m2 = ß2, n2= 16, /c = ß2 + 4,
con cui scrisse:
(ß2 +4)2 -(ß4 + 16) p2_ 4ß2
2(ß2+4) <T ß2+4’
dovendo essere ß2 + 4 un quadrato. Ipotizzando ß2 + 4= (ß + l)2, ot¬
tenne ß = 3/2, con cui
k=25/4, m2=9/4,
e poiché si è preso n = 4, i quadrati di questi numeri sono: 25, 9 e
16. Con tutto ciò concluse il problema deducendo:
^=144/25, y2=9, ^2=16.
Diofanto non espose il problema con la condizione che un
quadrato fosse la somma di due biquadrati, la cui impossibilità fu
dimostrata da Fermat. Questo fece pensare ad alcuni storici della
matematica che forse Diofanto conosceva questo risultato, ma che
non abbia lasciato testimonianza di ciò. La dimostrazione del pro¬
blema fu data da Eulero nel 1849.
V.30. Una persona ha comprato un certo numero di misure di
vino, alcune da otto dracme ciascuna e altre da cinque, pagando
in totale un numero quadrato di dracme. Questo numero, aumen¬
tato di 60 unità, dà un altro quadrato, che ha per lato il numero
totale di misure di vino comprate. Quante misure di vino ha com¬
prato di ogni prezzo?
Questo problema, enunciato in forma di epigramma, rappre¬
sentò un indicatore per delimitare l’epoca in cui visse Diofanto a
partire dal rapporto qualità/prezzo del vino dell’epoca. Comune¬
mente, il suo significato è il seguente: si comprano due qualità di
vino, da 8 e da 5 dracme alla caraffa, e in totale si paga un numero
quadrato che, aumentato di 60 unità, forma un quadrato la cui ra¬
dice è la quantità totale di caraffe. La sfida è verificare quante sono
state acquistate per ogni qualità. Tradotto in linguaggio algebrico,
se x e y sono le incognite, a: è il numero di misure da 5 dracme e
PROBLEMI E SOLUZIONI DELL'ARITMETICA
133
y quello da 8 dracme, il problema si riduce ipotizzando il sistema
di equazioni della forma &r+5y = n2, con ri2 + 60 = (x+y)2. Da dove,
&r + 52/ = Or+2/)2-60.
Impostando x+y = m, si ottiene m2-60 = 5ra + 3.r = 8m-3?/.
ra2-60>5ral
Quindi \, da cui si ottiene 11 < m < 12.
m2 -60 < 8mJ
Poiché m2-60 è un quadrato, se si ha m2-60 = (m-n)2, allora
n2 +60
m =
2 n
Il che dimostra necessariamente che n si trova in 19<n<21. Dio-
fanto prese il valore n- 20 e, pertanto, m = 23/2. In questa maniera
giunse alla soluzione:
x = 59/12, y = 79/12.
LIBRO VI: TRIANGOLI RETTANGOLI DAI LATI
RAZIONALI
Nonostante Diofanto avesse «spogliato la geometria», tutti i pro¬
blemi di questo libro fanno riferimento a triangoli rettangoli
aventi lati razionali che, oltre a soddisfare l’equazione pitagorica
a2 = b2 + c2, devono adempiere alle condizioni imposte dai rispet¬
tivi enunciati. In generale, per la versione odierna delle soluzio¬
ni i cateti saranno indicati anche come x, y, indistintamente, e
z per l’ipotenusa. Diofanto utilizzò, quindi, l’uguaglianza - equa¬
zione pitagorica - à2 = b2 + c2, dove, come d’abitudine, a rappre¬
senta l’ipotenusa, essendo òeci cateti di un triangolo rettango¬
lo. Utilizzò questa uguaglianza anche in una di queste due forme
V
2 J
2
V /
134
PROBLEMI E SOLUZIONI DELL'ARITMETICA
(2 k + if + [2 k(k + l)]2 = (2 K2 + 2 k+ 1 )2,
e considerò, come faceva spesso, che dati due numeri men, era
possibile prendere come cateti i valori b = m2-n2 i c = 2mn. Allora
l’ipotenusa è a = m2 + n2, poiché è facile dimostrare che si verifica
(m2-n2)2 + (2mn)2 = (m2 + n2)2. Infine, in alcuni problemi utilizzò
anche l’identità
che anch’essa soddisfa l’equazione pitagorica.
VI.8-9. Trovare un triangolo rettangolo tale per cui aumentando [dimi¬
nuendo] la sua area alla somma dei due cateti si formi un numero dato.
Cioè dato a, trovare x, y, z tale per cui o^ + y2 = z2.
Diofanto lo risolse per a = 6; ottenne, rispettivamente, come
risultato:
x = 28/18 (x= 168/35), y = 45/18 (2/ = 270/35), ^ = 53/18 (* = 318/35).
Attualmente è possibile dimostrare che, senza fare riferimento
a un caso particolare di un valore concreto di a, si può ottenere una
soluzione generale per qualsiasi valore di a * 1, che è rispettivamente:
Pierre de Fermat, sulla base di tale problema, propose il seguente:
Trovare un triangolo (x, y, z) rettangolo tale per cui la somma dei
cateti diminuita dell’area sia un numero dato.
2
2
Cioè:
PROBLEMI E SOLUZIONI DELL'ARITMETICA
135
x2 + y2=z2.
Il matematico francese non trovò nessuna soluzione generale,
ma lo risolse per a = 6 e trovò due soluzioni per il problema:
/143 278 1441 1745438521\ /146160 137514 10472631126\
( 22919* 12180’279153420 J 6 [ 1441 ’71639’ 103231799 j
VI. 14-15. Trovare un triangolo rettangolo tale per cui sottraendo
[sommando] dall’area l’ipotenusa, oppure uno dei cateti, si formino
quadrati.
In questo caso si chiede di trovare (x, y, z) tale per cui
jc2 + y2 = z2, 1/2 xy^-z, l/2xy=fx formino un quadrato. Questi due
problemi hanno dato luogo alla seguente nota di Fermat:
Per mezzo del mio metodo si potrebbe risolvere il problema, più
difficile, di trovare un triangolo rettangolo tale che sottraendo l’area,
o dall’ipotenusa oppure da uno dei cateti, si ottenga un quadrato.
La soluzione, che non fu mai data da Fermat, si deve a Eulero.
Il matematico svizzero affermò che vi sono infinite soluzioni e pro¬
pose come la soluzione minore:
x = 697/1045, y = 696/1045, z = 985/1045.
Diofanto fece precedere il problema VI. 15 di un lemma che
sostiene che se ci sono tre numeri, come m = 3, n = 11 ep = 5, con
i quali è possibile formare un quadrato scrivendo q2=p2 • m-n = 82,
allora vi è un altro quadrato, r2>p2, con cui è possibile formare un
altro quadrato nella stessa maniera: r2-m-n= 1162.
In quanto alle soluzioni concrete dei problemi VI. 14 e VI. 15,
sono le seguenti. Per il problema VI. 14:
x = 8/3, y = 15/3, z = 17/3.
Rispetto al problema VI. 15, il matematico alessandrino ottenne:
136
PROBLEMI E SOLUZIONI DELL'ARITMETICA
.r = 8/77,y =15/77, z= 17/77.
VI. 16. Trovare un triangolo rettangolo tale per cui se si divide uno
dei suoi angoli acuti in due parti uguali si ottenga che la lunghezza
di tale retta sia un numero razionale.
Questo problema, l’unico del libro che si allontana dal tipo
generale, adotta una forma geometrica nell’enunciato, che oggi
risulterebbe scritto così:
Trovare un triangolo rettangolo tale per cui la bisettrice di uno dei
suoi angoli acuti abbia per lunghezza un numero razionale.
In questa occasione Diofanto definì, in maniera implicita, il con¬
cetto che oggi è noto come «bisettrice di un angolo». Secondo lo
storico e matematico italiano Gino Loria (1862-1954), Diofanto do¬
veva sapere che il problema non ha soluzione se si considera la bi¬
settrice dell’angolo retto, poiché si ottiene sempre un numero irra¬
zionale. La soluzione di Diofanto fu la seguente. Sia BD la bisettrice
dell’angolo acuto B del triangolo rettangolo ABC. Supponendo che
BD = 5a, AD = 3a,
si ha, per il teorema di Pitagora,
AB = ^(5 oc)2-(3 oc)2 =4 oc;
e se AC è un multiplo di 3, prendendo AC=3, risulta DC=3 -3a.
Diofanto si occupò della proposizione di Euclide mostrata negli
Elementi, e concretamente la VL3:
AB/BC = c/a=AD/DC,
e sostituendo qui i valori precedenti, scrisse:
PROBLEMI E SOLUZIONI DELL'ARITMETICA 137
Applicando ancora una volta il teorema di Pitagora, ottenne:
(4-4a)2=(4a)2+32, a=7/32.
In modo che adottando le omologhe 32 volte maggiori, per
cui realizzo proporzioni, il triangolo cercato e:
AB 28 AC-96 £C=100
BD- 35 AD 21 DC-Ih
Nella figura 3 si osserva che la bisettrice (BD) ha una lunghez
za di unità.
VI 17. Tro ar ' un triangolo rettangolo tale p r ui il valore della sua
ar a aum ntato del ^alor dell ipot nusa, formi un quadrato e il
alor ; d 1 uo pennv ro ia un ubo
Ciò tro ar rx y, z) in modo che oc1+y2- 2.1/2 2/+ sia un
quadrato, ~x\ y+z ia un cubo. Diofanto si imbattè in un equazione
di terzo rado "h nr ol se, enza conoscere alcuna tecnica, dando
VI
80
60
\40
«
20
o|
U \d
-40 -20
0 2\ 40 60 80 *00 120
-20
38
PROBLEMI E SOLUZIONI DELL'ARITMETICA
come soluzione la radice ß = 4 senza alcuna spiegazione. Poiché la
formula per risolverle sarebbe divenuta nota solo nel Rinascimento,
è possibile che abbia trovato la soluzione con la seguente equazione:
4ß2 + 4 = ß;} + ß.
Il ragionamento è plausibile, poiché era in grado di trasporre
termini e ridurre quelli simili, per cui si sarebbe osservato che
4(ß2 + l) = ß(ß2+ 1),
da cui, dividendo per ß2 + 1, si ottiene ß = 4, e le altre due radici
ß=± V-T sono a lui ignote. Probabilmente ignorava che la somma
del quadrato di 5 e di 2 unità è il cubo di 3, cioè 52 + 2 = 27 = 32, e che
è l’unica soluzione del problema, come avvisò Fermat:
Vi è solo un quadrato intero che, aumentato di 2, dà un cubo.
Il che è vero, ma non fu dimostrato da lui, bensì da Eulero. Di
fatto, si tratta di un caso particolare dell’equazione di Mordell. Una
volta ottenuto ß = 4, si hanno ß +1 = 5, ß — 1 =3, per i lati del quadra¬
to e del cubo, per cui questi sono 25 e 27. Poiché per ipotesi l’area
è l'arithmos a e i cateti sono ancora b = 2, c = a, ma l’ipotenusa è
ora 25-a, per il teorema di Pitagora si ha:
(25 - a)2 = a2 + 625 - 50a = 22 + a2 = 4 + a2,
da cui a = 121/50, e la soluzione, che non fu data da Diofanto, è:
a = 629/50, ft = 621/50, c = 2.
Alla luce del lavoro sxùYAritmetica, Bachet de Méziriac pro¬
pose 22 suoi problemi sui triangoli rettangoli e, tra gli altri contri¬
buti, scrisse il seguente enunciato:
Trovare un triangolo rettangolo (x, y, z) con lati razionali, la cui area
sia un numero dato a.
PROBLEMI E SOLUZIONI DELL’ARITMETICA
139
Alla fine, Bachet de Méziriac stabilì che, perché avesse solu¬
zione, era sufficiente che esistessero numeri positivi razionali x e
y, tali per cui y2=oâ + 4a2. Allora, Viète notò anche un’altra condi¬
zione necessaria e sufficiente per 1’esistenza di un triangolo rettan¬
golo razionale di area a: che esistano x e y razionali, con y diverso
da zero, tali per cui y2=xì-à2x. Da parte sua, Fermat aggiunse:
L’area di un triangolo rettangolo con queste caratteristiche non può
essere un quadrato.
In definitiva, e come chiusura a questo capitolo, si può affer¬
mare che i 189 problemi della versione greca dell’Aritmetica po¬
sero le basi per la risoluzione delle equazioni lineari con due o più
incognite, che, in onore a chi le formalizzò, strutturò e risolse in
casi particolari, sono chiamate equazioni diofantee. Questo termi¬
ne comprende anche le equazioni non lineari, che aprirono una
strada matematica complessa e affascinante, poiché la totalità dei
suoi punti interrogativi non trovò risposte conclusive fino alla fine
del xx secolo. L’orizzonte aperto dall 'Aritmetica mantiene la sua
validità e il suo potere di seduzione anche diciotto secoli dopo
1’esistenza del suo autore, Diofanto. Con ciò, l’enigmatico mate¬
matico alessandrino si conquistò, per meriti propri, un posto d’o¬
nore tra i più grandi della storia della matematica universale.
140
PROBLEMI E SOLUZIONI DELL'ARITMETICA
CAPITOLO 5
Il lascito di Diofanto
e la sua validità nel xxi secolo
Oltre ÆAritmetica, ci è pervenuta un’altra notevole
opera di Diofanto: Numeri poligonali. Insieme,
rappresentano un lascito che ha ispirato per secoli
i più grandi matematici e ha fatto avanzare l’aritmetica
fino alle soglie dell’attuale teoria dei numeri. Le equazioni
diofantee sono presenti nella dittologia e nei sistemi
di sicurezza, come transazioni bancarie e codici
a barre, per esempio.
Una volta trattati approfonditamente i contenuti dell 'Aritmetica,
una biografìa di Diofanto, per essere completa, richiede che ven¬
ga trattato anche un altro prezioso testo del grande matematico
alessandrino che ci è pervenuto: Numeri poligonali. Nell’Anti¬
chità, i pitagorici erano soliti rappresentare i numeri mediante
punti su una pergamena o collocando dei sassolini nella sabbia,
e li classificavano a seconda delle forme poligonali di queste
distribuzioni di punti. Cioè associavano i numeri a figure geome¬
triche. Queste si ottenevano tramite la disposizione regolare di
punti, la cui somma determinava il numero rappresentato. In
questo modo, ottennero i diversi tipi di numeri poligonali o figu¬
rati, a partire dai numeri triangolari e proseguendo con i nume¬
ri quadrati, i numeri pentagonali ecc. Per i matematici preceden¬
ti a Diofanto, che erano sostanzialmente geometri, le
espressioni «numeri triangolari» o «numeri quadrati» non costi¬
tuivano semplici metafore, bensì numeri che, effettivamente,
erano triangoli e quadrati.
Come si è già spiegato, un numero poligonale è un numero
naturale che può essere espresso mediante un poligono regolare.
Sarà triangolare se forma un triangolo; pentagonale se genera un
pentagono; esagonale se crea un esagono, e così via. In generale,
si è soliti fare riferimento a essi come a numeri «m-gonali». Così,
un «3-gonale» sarò triangolare; un «4-gonale» quadrangolare; un
IL LASCITO DI DIOFANTO E LA SUA VALIDITÀ NEL XXI SECOLO
143
MARIN MERSENNE
Il sacerdote, filosofo e matematico fran¬
cese Marin Mersenne (1588-1648), noto
anche come Marin Mersennus, frequentò
i suoi studi presso l’università gesuita di
La Fiòche, dove fece amicizia con Carte¬
sio (René Descartes, 1596-1650). A par¬
tire da lì, sarebbe divenuto una delle
principali figure della comunità scientifi¬
ca internazionale, mantenendo una nutri¬
ta corrispondenza con Cartesio, Fermat,
Galileo Galilei e Christiaan Huygens, tra
gli altri. Mersenne non esitò a informarli
delle sue idee e dei rispettivi lavori, con
il proposito di aprire un confronto e sti¬
molarli nelle proprie ricerche. La sua
azione non solo favorì il flusso di infor¬
mazione tra scienziati sparsi in vari Paesi,
ma contribuì anche ad arricchire notevol¬
mente le conoscenze dell'epoca. Autore
di diversi libri teologici e del Trattato
dell’armonia universale (1627), conside¬
rato come la principale fonte teorica della musica del xvn secolo, i suoi inte¬
ressi matematici lo portarono anche pubblicare l’opera Cogitata physico-ma-
thematica (1641), dove introdusse i cosiddetti «numeri primi di Mersenne»,
congetturando con grande abilità su di essi; tanto che la sua raffinatezza e la
sua dimostrazione sarebbero rimaste valide per secoli.
Marin Mersenne, in una incisione
del xvn secolo realizzata
da Balthasar Moncornet.
«5-gonale» sarà pentagonale ecc. I numeri poligonali sono stati
uno degli argomenti più affascinanti della storia dell’aritmetica.
Oltre a Diofanto, furono affrontati da matematici del calibro di
Gauss, Eulero, Lagrange e Marin Mersenne, solo per citarne alcu¬
ni. I numeri poligonali fanno parte di diversi campi della cono¬
scenza matematica, come la teoria dei numeri, la combinatoria e
lo studio delle probabilità. Oggi, il loro studio approfondito ha
raggiunto un enorme valore pratico, nonostante si tratti di una
materia ancora emergente: l’applicazione della crittografìa nell’am¬
bito della sicurezza nelle comunicazioni.
144
IL LASCITO DI DIOFANTO E LA SUA VALIDITÀ NEL XXI SECOLO
TIPI Dl NUMERI POLIGONALI
In questo paragrafo saranno spiegate le tipo¬
logie più semplici di numeri poligonali, come
i triangolari, i quadrangolari e i pentagonali. Il
primo gruppo è formato dai numeri triangola¬
ri, che si formano per addizione successiva dei
termini della progressione aritmetica naturale
1, 2, 3, 4, 5, 6, 7,..., così come viene illustrato ,
nella figura 1. j
Come si può osservare, nella prima fila del
triangolo vi è un elemento; nella seconda vi
sono due elementi; nella terza sono tre elementi ecc. Il totale del¬
la prima fila è 1. Il totale della prima più la seconda è 1 + 2=3, cioè
la somma di due termini della progressione aritmetica. Il totale
della prima fino alla terza èl + 2 + 3 = 6(la somma di tre termini
della progressione aritmetica). In questa forma, I numeri 1, 3, 6,
10,15,... sono triangolari, come è possibile osservare nella figura
2. n numero 10 è triangolare dal momento che 10 = 1 + 2+ 3+ 4.
In generale, Yn numero triangolare viene definito dalla somma
degli n primi termini della somma della progressione aritmetica
Con ciò si ha
n(n+l)
* 2
In questo modo, si ottengono Tv
T2, Ty ..., che equivalgono a 1, 3, 6,
10,15, 21,28,...
Con quanto esposto, la rappre¬
sentazione grafica si otterrebbe pro¬
lungando due lati del triangolo e
aggiungendo un terzo lato, cosa che
ci dà un bel risultato:
La somma di due numeri triangola¬
ri consecutivi è un quadrato perfet¬
to, inoltreT +T . =n2.
1 n Tir-1
10
15
IL LASCITO DI DIOFANTO E LA SUA VALIDITÀ NEL XXI SECOLO
145
In effetti:
w(w + l) (w-l)(w-l + l) 2
« »-1 2 2
La somma degli n primi numeri triangolari è nota come «nu¬
mero tetraedrico». La sua espressione viene determinata dalla
formula:
c n(n + ì)(n + 2)
6 '
Così, per esempio, T{ + T2 + T:ì = 1 + 3 + 6 = 10, il che utilizzando
la formula dà:
5 = 3(3 + l)(3 + 2) _1q
•’ 6
A titolo di curiosità, un numero primo di tipo 2”-l è chia¬
mato «numero primo di Mersenne», tuttavia non tutti i numeri
ottenuti in questa maniera sono primi. Per esempio, per n = 3, il
numero 23-l = 7 è primo; tuttavia, per w = 4, il numero 24-l = 15
non è primo.
Fu Pierre de Fermat a scoprire che il numero triangolare
più grande del tipo 2"-l è il 4.095, che corrisponde a n- 12.
Da parte sua, Cari Friedrich Gauss (1777-1855) nel 1796 di¬
mostrò che ogni intero positivo può essere rappresentato come
la somma di un massimo di tre numeri triangolari, non necessa¬
riamente diversi. Per esempio, 20 = 10 + 10. Il matematico tedesco
riportò nei suoi quaderni la felice scoperta con il termine greco
«Eureka», come già aveva fatto lo scienziato greco Archimede
nell’Antichità. Ciononostante, si deve segnalare che questo ri¬
sultato è un caso particolare del teorema del numero poligonale
di Fermat, che affermò che ogni numero naturale n può essere
espresso al massimo come la somma di n numeri poligonali, non
necessariamente della stessa specie. Per esempio, il numero 17
si può esprimere come la somma di tre triangolari: 17=10 + 6+1.
Anche come la somma di due quadrati: 17= 16+ 1. Inoltre, si può
esprimere come la somma di due pentagonali: 17 = 12 + 5.
146
IL LASCITO DI DIOFANTO E LA SUA VALIDITÀ NEL XXI SECOLO
NUMERI QUADRANGOLARI
I numeri quadrangolari si forma¬
no sommando i termini della pro¬
gressione aritmetica 1, 3, 5, 7, 9,...
In generale, il numero n quadran¬
golare verrà definito dalla soma
degli n primi termini della somma ì 4
della progressione aritmetica.
Con questo si ha Qn= n1 2, e da que¬
sta forma si ottengono Q2, Q3,
...: 1, 4, 9, 16, 25, ..., come viene
illustrato nella figura 3. Tali nu¬
meri sono noti anche come «qua¬
drati perfetti». Una proprietà di 16
un quadrato perfetto è che tale
quadrato, n2, è la somma degli n
primi numeri dispari. Per esempio: 25 = 52 è la somma dei cinque
primi numeri dispari: 1+3 + 5 + 7 + 9. Nel linguaggio formale, si
esprime come:
n2 = £(2fc-l).
A>1
Si noti che un quadrato perfetto è anche la somma dei due nu¬
meri triangolari, per cui si deve ricordare che Tn+ Tn l=n2. Per esem¬
pio: 52= Tb + T4 = 15 +10.
Dei numeri quadrangolari vale la pena citare, brevemente, al¬
meno altre due belle proprietà:
1. Il prodotto di due dispari consecutivi aggiungendo una uni¬
tà è im quadrato perfetto. Cioè,
(2 n-1) (2n + 1) +1 = 4n2-1 + 1 = 2r*2.
Ciò può essere dimostrato, per esempio, con:
7-9+1 = 63+1 = 64 = 82.
IL LASCITO DI DIOFANTO E LA SUA VALIDITÀ NEL XXI SECOLO
147
2. D prodotto di quattro interi consecutivi aumentato di ima
unità è anch’esso un quadrato perfetto:
(n -1) n (n +1 )(n + 2) +1 = (n2+n-1)2.
Così per esempio, pern= 14 si ha che il prodotto dà:
13 • 14 • 15 • 16+1 = 43 681 = 2092.
NUMERI PENTAGONALI
In maniera analoga ai numeri triangolari e a quelli quadrati, i
numeri pentagonali si ottengono sommando i termini della pro¬
gressione aritmetica 1, 4, 7,10,13,16,..., la cui espressione gene¬
rale è la seguente:
D (3n-l)n
rn~ n »
FIG 4
1
5
12
148
IL LASCITO DI DIOFANTO E LA SUA VALIDITÀ NEL XXI SECOLO
dal che risulta, come viene illustrato nella figura 4, che i numeri
pentagonali sono 1, 5, 12, 22, 35, 51, 70,...
Esiste un criterio per verificare se un numero è pentagonale.
Se si ha un numero x e si desidera sapere se è pentagonale, si re¬
alizza l’operazione
1 + n/24.x + 1
6 ‘
Allora, se il risultato è un numero naturale k, questo valore k
indica che x è il k-esimo numero pentagonale. Per esempio: il 63
è un numero pentagonale? Risolvendo
1 + V24-63 + 1
6
si dimostra che il risultato non è un valore naturale, per cui il 63
non è un numero pentagonale. Invece, se si realizza lo stesso pro¬
cesso per il 70,
1 + V24-70 + 1
6
si verifica che 70 invece è un numero pentagonale; concretamente,
è il settimo dei numeri pentagonali.
Oltre ai numeri pentagonali, l’espressione della formula gene¬
rale per trovare l’n-esimo numero m-gonale è la seguente:
p,n =-n(2 + (m-2)(n-l)) = ——n —n.
Per i casi m = 3, m = 4, m = 5 si ottengono le formule illustra¬
te in precedenza per i numeri triangolari, quadrati e pentagona¬
li, rispettivamente.
PROPOSIZIONI E REGOLE PRATICHE DI DIOFANTO
Diofanto, nel suo testo Numeri poligonali, lavorò con una serie
di concetti relazionati con le progressioni aritmetiche e con i cita¬
li. LASCITO DI DIOFANTO E LA SUA VALIDITÀ NEL XXI SECOLO
149
ti numeri poligonali. Nella sua opera, oltre a definire i numeri m-go-
nali, dimostrò cinque proposizioni - attualmente sono chiamate
«proprietà» - e trasmise un paio di quelle che lui stesso chiamò
«regole pratiche». Nel linguaggio attuale, la prima proposizione
viene enunciata così:
1. Trovare il numero poligonale a partire da un lato.
Cioè se P è il numero m-gonale di lato n, si ha, come già
indicato:
Per esempio, per trovare l’esagonale di lato 10, basta sostitu¬
ire nella formula precedente m = 6, n= 10. Con ciò, risulta P= 190.
2. Trovare il lato a partire dal numero poligonale.
Cioè se P è il numero m-gonale di lato n, si ha:
Per esempio, dato un numero esagonale P= 190, si ha n= 10.
SICUREZZA E CODIFICA
Oggi, una gran parte del lascito matematico di Diofanto viene mol¬
to spesso applicata nei sistemi di sicurezza. Si tratta, concretamen¬
te, delle equazioni diofantee, la cui gamma è rappresentata da
quelle più note, della forma ax +by = c, fino a quelle più sofisticate,
come quelle citate da Louis Mordell nella sua opera Equazioni
diofantee, del tipo y 2 = afì+ ax+b. I grafici di queste ultime pren¬
dono il nome di «curve ellittiche», e si utilizzano nei sistemi di si¬
curezza avanzati per la criptatura di grandi sequenze di dati. Qui
non saranno descritti per il loro elevato grado di complessità: ba¬
sti citare il fatto che sono coinvolti nella maggior parte dei cosid-
(m-2) 2 (to-4)
1 {sj8P(m-2)+(m-4f -2 | '
m-2
150
IL LASCITO DI DIOFANTO E LA SUA VALIDITÀ NEL XXI SECOLO
FOTO IN ALTO
A SINISTRA
Cari Friedrich
Gauss dimostrò
che ogni intero
positivo può
essere
rappresentato
come la somma di
un massimo di tre
numeri triangolari,
non
necessariamente
diversi.
FOTO IN ALTO
A DESTRA
Whitfield Diffie,
creatore insieme a
Martin Heilman
del protocollo
crittografico
Diffie-Hellman,
durante una
conferenza nel
2007.
FOTO IN BASSO
Le equazioni
diofantee
sviluppano lo
standard della
cifratura delle
transazioni
economiche sicure
che sono usate da
milioni di persone
in tutto il mondo.
IL LASCITO DI DIOFANTO E LA SUA VALIDITÀ NEL XXI SECOLO 151
detti «sistemi RSA», con chiave pubblica, e del protocollo critto¬
grafico Diffie-Hellman, elementi abitualmente utilizzati nella
trasmissione di dati attraverso Internet, soprattutto nelle transa¬
zioni bancarie e nelle comunicazioni altamente riservate.
Le equazioni del tipo ax +by = c sono imprescindibili per lavo¬
rare nell’aritmetica modulare, ramo che rivela la correttezza o la
falsità dei diversi codici a barre. Nei sistemi di sicurezza compaio¬
no espressioni della forma ax=b(m), dove a, b, m sono valori noti.
In altre parole, equivalgono a risolvere equazioni della forma
ax+my = b. Il concetto di «congruenza» in aritmetica modulare
può essere espresso come ax=b(rn), dove m è un intero positivo,
a e b sono numeri interi e x + un valore intero. Si legge «ax è con¬
gruente con b modulo m». Per risolvere questa equazione, è op¬
portuno trovare tutti gli interi x che soddisfino l’equazione diofan-
tea equivalente a.ax+my = b. Per esempio: 3#=^ (10). In questo
caso, l’equazione diofantea è 3a; + 10i/=-4. Infine, applicando i
metodi di risoluzione si ottiene x = 2.
Come esempi dell’applicazione pratica di queste congruenze
è possibile citare: il codice o cifrario di Cesare, il calcolo del codi¬
ce fiscale, la verifica delle cifre di controllo dei conti bancari e i
codici EAN-10 ed EAN-13 dei prodotti e dei sistemi di sicurezza
odierni, a partire dal già citato RSA. Tutti questi sistemi si basano
sulla soluzione delle cosiddette «equazioni di congruenze», che
rimandano alle equazioni diofantee per essere risolte. Per esempio,
il codice a barre EAN di un prodotto è composto da dieci cifre
ABCDEFGHIJ, e ne consegue che il criterio stabilito per la sua
autenticità è:
10A+9B + 8C + 7D + 6E + 5F + 4G + 3H + 2I + J =0 (11).
Tutti i libri pubblicati e posti in vendita devono disporre di un
ISBN, acronimo di International Standard Book Number («nume¬
ro di riferimento intemazionale del libro»). Se una delle cifre del
numero ISBN risultasse illeggibile, è possibile verificare di quale
cifra si tratti. Supponiamo che il numero ISBN di un esemplare sia
«8485a;60459», dove a:èun valore sconosciuto. Se si applica il
criterio precedente, si ottiene la congruenza (xr=-276 (11), e que¬
152
IL LASCITO DI DIOFANTO E LA SUA VALIDITÀ NEL XXI SECOLO
sta corrisponde all’equazione diofantea (-6).x + (-11)?/= 276. La
soluzione è x = 9 e ci dà il numero che mancava per avere l’ISBN
corretto: «8485960459». Un altro semplice esercizio, in relazione
con il precedente, è la verifica di un codice EAN-13 della forma
ABCDEFGHIJKLM. Il criterio di veridicità è:
A + C + E + G + I + K + 3(B + D + F + H + J + L) +M=0 (10),
dove le prime due cifre rappresentano il codice del Paese e le ul¬
time due sono la cifra che è denominata di controllo.
Società
c
D
E
F
G
Prodotto
H
1
J
K
L
D.C.
M
Si dispone di un prodotto con il codice «40-13320-03:r49-7»,
dove la cifra x risulta illeggibile. Come lo possiamo verificare?
Applicando il criterio dell’EAN-13 si ottiene: 3a; = -4(10), che equi¬
vale all’equazione diofantea (-3)#+ (—10)2/ = 4. La soluzione della
stessa è a; = 2. Quindi il codice corretto è «40-13320-03249-7».
IL VALORE ATTUALE DI UN MATEMATICO
DEL III SECOLO
Oltre al suo testo sui numeri poligonali e alle applicazioni pra¬
tiche delle equazioni diofantee, che abbiamo appena visto, la par¬
te principale del lascito di Diofanto è presente nell 'Aritmetica, la
cui lettura è vivamente consigliata al lettore. In questo modo potrà
ampliare le sue conoscenze matematiche, e, nel caso possegga una
mente inquieta, potrebbe trovare soluzioni per i problemi che Dio¬
fanto risolse in forma particolare. In quanto alla ricerca dei meto¬
di generali di risoluzione delle equazioni diofantee, esigono un li¬
vello così elevato che fu alla portata solo di alcuni dei più grandi
matematici della storia. Tuttavia, risulta molto interessante cono¬
scere e usare i metodi che questi matematici apportarono e trarre
IL LASCITO DI DIOFANTO E LA SUA VALIDITÀ NEL XXI SECOLO
153
conclusioni da essi. In questo senso, si deve ricordare che non
esiste alcun algoritmo generale che permetta di determinare se le
equazioni diofantee non lineari siano risolvibili, come ha dimostra¬
to Jury Matyasevich nel 1970.
Nel corso di queste pagine si è potuto verificare che i matema¬
tici che affrontarono le equazioni diofantee furono personaggi il¬
lustri: Bachet de Méziriac, Viète, Fermat, Eulero, Lagrange... Tutto
ciò conferma l’importanza dei lavori di Diofanto per la storia della
matematica, in generale, e per il progresso dell’aritmetica o teoria
dei numeri, in particolare, senza dimenticare altre aree in cui le
equazioni diofantee sono presenti. Diofanto fu il grande anello di
congiunzione per il passaggio dal linguaggio geometrico a quello
algebrico. Introdusse inoltre una simbologia e una notazione che
rivoluzionarono la scrittura dei testi matematici, fu un pioniere nel
ricorrere a processi algebrici per risolvere equazioni non lineari
indeterminate, e fu il primo a utilizzare notazioni algebriche con¬
crete ed estese. Prima di Diofanto, era inconcepibile sommare un
quadrato e un cubo, aree con volumi. Dopo Diofanto, l’algebra si
liberò della visione geometrica e abbracciò, con forza e per sem¬
pre, l’aritmetica.
154
IL LASCITO DI DIOFANTO E LA SUA VALIDITÀ NEL XXI SECOLO
Letture consigliate
AA.W., Antologia Palatina, Mondadori, 1992.
Bachet de Méziriac, C.G., Diophante Alexandrini Arithmeticorum
libri sex, et de numeris multangulis liber unus. Nunc pri¬
miera graecé et latiné editi, atque absolutissimis. Commen-
tariis ilustrati, Parigi, H. Drouart, 1621.
Boyer, C., Storia della matematica, Mondadori, 1990.
Cajori, F., A History of Mathematical Notations, Chicago, Open
Court Company Publishers, 1928.
Christianidis, J., Classics in the History of Greek Mathematics,
Dordrecht, Kluwer Academic Publishers, 2004.
Diofanto di Alessandria, De poligonys numeris, Fabrizio Serra Edi¬
tore, 2011.
Fermat, P., Osservazioni su Diofanto, Bollati Boringhieri, 2006.
Heath, T.L., Diophantus of Alexandria: A Study in the History of
Greek Algebra, Cambridge, Cambridge University Press, 1910.
Mordell, L., Diophantine equations, Massachusetts, Academic
Press, 1969.
Tannery, P., La Geometrie Grecque, Part 1: Histoire Generate
de La Geometrie Elementaire, Kessinger Pub Co., 2010.
155
Indice
Alessandria, 7, 8, 11, 12, 15, 17,
19-24, 26, 31, 32
Biblioteca di, 7, 15, 19-23, 26
Scuola di, 20, 31, 32
faro di, 19, 20, 22, 23
Museo di, 15, 17-20, 22, 24, 31
Alessandro Magno, 7, 19, 20, 23
algebra, 31-34, 4245, 47, 48, 62
algoritmo, 13, 25, 79-85, 87, 88, 89,
99, 154
Al-Khwarizmi, 33, 52
Apastamba, 77, 78
Apollonio di Perga, 11, 17, 24, 31
aritmetica, 9, 34, 41, 67, 77-79, 81
modulare, 41, 60, 152
arithmos, 41, 50, 62, 63, 66-68, 105,
106, 108, 109, 112, 113, 119, 121,
132, 139
Archimede, 11, 22, 24, 31, 69, 80, 146
Aryabhata, 78, 80, 81
Bachet de Méziriac, Claude Gaspard,
9, 11-13, 39, 43, 45, 46, 58,71,
105, 111, 112, 115, 117, 126, 128,
129, 130-132, 139, 140, 154
Bhaskara, 81
Baudhayana, 77, 78
Bell, Eric Tempie, 72
Billy, Jacques de, 117
Bombelli, Rafael, 13, 30, 45
Boyer, Carl, 79
Brahmagupta, 78, 81
Brouncker, William, 13, 82, 83
Cartesio (René Descartes), 9, 12,
33, 43, 70-72, 79, 144
Castelnuovo, Emma, 25
Cefala, Costantino, 36
cilindro, 19, 20, 28
cono, 19, 28
cubo, 8, 9, 33, 49, 51, 54, 55, 58,
66-69, 96-98, 100, 124, 126, 128,
157
129, 138, 139, 154
Diffie, Whitfield, 151, 152
Dionisio, 18, 43, 47, 49, 67
epigramma, 36-38, 133
equazione,
di Fermat, 59, 94-96
di Peli, 13, 80-83
equazioni,
cubiche di Ramanqjan, 13, 96,
97
diofantee, 10-13, 25, 32, 42, 46,
48-50, 75, 76, 78-80
indeterminate, 10, 11, 33, 44, 78,
89, 90, 100, 103
lineari, 33, 48, 49, 51, 55, 73, 78,
81-88, 140
non lineari, 10, 11, 33, 34, 56,
88-100, 140, 154
Eratostene, 17
Erone di Alessandria, 17, 24, 26,
28-31, 35
Euclide, 8, 9, 11, 17, 19, 22, 24, 25,
27, 31, 32, 34, 42, 82-85, 87, 137
Eudosso di Cnido, 22, 24
Eulero (Leonhard Euler), 9, 31, 39,
43, 59,73, 83, 99-101, 115, 116,
118, 122, 133, 136, 139, 144, 154
Fermat, Pierre de, 9, 10, 12, 13, 26,
34, 39, 43, 45, 46, 48, 51, 58-61,
71,73,81,82, 113, 117, 122, 124,
133, 135, 136, 139, 140, 144, 146,
154
ultimo teorema di, 45, 48, 51,
58-61, 75, 94-96
Gauss, Cari Friedrich, 22, 31, 77,
144, 146, 151
Gosselin, Guillaume, 45
Hardy, Godfrey Harold, 97
Heath, Thomas Little, 32, 122
Heilman, Martin, 151, 152
Hilbert, David, 10, 13, 88, 89
Huygens, Christiaan, 54, 55, 144
identità di Bézout, 82-86
Ipazia di Alessandria, 11, 18, 24, 26,
31,32
Ipparco, 24
Ipsicle di Alessandria, 18
Keplero (Johannes Kepler), 22
Kummer, Emst, 59
Lagrange, Joseph-Louis de, 9, 13,
79, 99, 144, 154
Legendre, Adrien-Marie, 27, 59
Leibniz, Gottfried Wilhelm, 24
massimo comune divisore, 25,
82-87
Matijasevich, Yurij, 13, 88, 89, 154
metodo, 13, 51-53, 76, 99, 108
di riduzione, 51-53, 108
di risoluzione generale, 13, 76,
99
di restaurazione, 51-53
Mersenne, Marin, 144, 146
Mordeil, Louis, 13, 96, 139, 150
Nash, John Forbes, 88, 99
Newton, Isaac, 22, 24, 61
158
INDICE
numeri
quadrangolari, 145, 147
interi, 10, 25, 26, 28, 44, 48, 50,
55, 58, 59, 76-79, 82, 84-88,
93-95, 100, 152
immaginari, 8, 13, 30
pentagonali, 143, 145, 146, 148,
149
poligonali, 11, 12, 13, 15, 18, 35,
42, 45, 141, 143-146, 149, 150
teoria dei, 11, 25, 27, 41, 45, 46,
54, 59, 60, 75, 88,91,96, 117,
141, 144, 154
triangolari, 143, 145-149
Pandit, Narayana, 81
Pappo di Alessandria, 18, 24, 26, 31
Peli, John, 13, 80-83, 91-93
Pitagora, 125
teorema di, 25, 30, 60, 94, 124,
137, 138, 139
Platone, 27, 36, 100
progressione, 55, 116, 117, 130, 131,
145, 147, 148
aritmetica, 116, 117, 145, 147,
148
geometrica, 55, 130, 131
quadrato, 8-10, 13, 25, 26, 30, 33, 35,
46-49, 51, 53-55, 58, 66-69, 77,
78,80-82,90-92, 97,98, 113,
115-122, 124, 126-134, 136,
138-140, 154
Qusta ben Luqa, 13, 44
Ramanqjan, Srinivasa, 13, 96, 97
rettangolo, 25, 29, 30, 54, 60, 96,
124, 134-140
Regiomontano, Johann Müller, 13,
44, 45
simbologia, 8, 9, 62, 66-72, 103, 107,
154
Sostrato di Cnido, 19
Tannery, Paul, 13, 17, 18, 43, 46, 47,
113, 118
Teone di Alessandria, 11, 18, 24, 26,
31
tema pitagorica, 60
Tolomeo, Claudio, 17, 18, 24, 31
triangolo, 8, 9, 25, 26, 28-30, 54, 60,
96, 114, 124, 134-140, 143, 145
Viète, François, 9, 34, 43, 47, 48, 70,
79, 98, 112, 140, 154
Vogel, Kurt, 34
Wiles, Andrew, 60, 61
Xylander, Guilielmus, 13, 45, 70
INDICE
159