Автор: Арустамов Х.А.
Теги: математика решение задач учебное пособие самообразование начертательная геометрия
Год: 1978
Текст
Проф, X. А. АРУСТАМОВ
СБОРНИК ЗАДАЧ
ПО НАЧЕРТАТЕЛЬНОЙ
ГЕОМЕТРИИ
С РЕШЕНИЯМИ ТИПОВЫХ ЗАДАЧ
Допущено Министерством высшего и среднего специального образования СССР >
в качестве учебного пособия для высших учебных заведений
ИЗДАНИЕ ДЕВЯТОЕ, СТЕРЕОТИПНОЕ
Москва «МАШИНОСТРОЕНИЕ» 1978
515
А86
УДК 515 (076.1)
Арустамов X. А.
А8б Соорпик задач по начертательной геометрии. Изд. 9-е,
стереотип. Учебное пособие для студентов вузов. М., «Маши-
ностроение», 1978. 445 с. с ил.
В каждой главе сборника даны краткие сведения по начертательной геометрии,
решенные типовые примеры, знакомящие студентов с методикой решения
задач и графическим оформлением эпюров, задачи для самостоятельного
решения студентами, а в некоторых главах приведены вопросы для самопро-
верки.
Книга допущена Министерством высшего и среднего специального образо-
вания СССР в качестве учебного пособия для студентов вузов.
А
30105-037
038(01)-78
037-78
515
ПРЕДИСЛОВИЕ
Этот сборник предназначен для студентов, изучающих курс начертательной
геометрии по программе, утвержденной Министерством высшего и среднего спе-
циального образования СССР для высших учебных заведений. !
В сборнике, кроме задач для самостоятельного решения и типовых примеров,
знакомящих студентов с методикой решений задач и графическим оформлением
эпюров, в каждой главе помещено краткое изложение теории, а в некоторых
главах (I, II, IV и XIX) приведены вопросы для самопроверки.
На основании личного многолетнего наблюдения занятий студентов автор
настоятельно рекомендует всем, начинающим изучать начертательную геометрию,
следующий порядок работы:
1) изучить теорию соответствующего раздела по учебным пособиям, рекомен-
дованным Министерством высшего и среднего специального образования СССР;
2) прочитать краткое изложение теории, приведенное в прорабатываемой
главе сборника, и ответить на вопросы для самопроверки;
3) лично полностью проделать все построения по примерам, решенным
в данной главе, придерживаясь текста сборника;
4) приступить к систематическому решению задач — по указанию преподава-
теля или по личному выбору.
Сборник задач могут использовать также лица, изучающие начертательную
геометрию самостоятельно или обучающиеся в заочных институтах.
Наличие в сборнике значительного числа задач облегчает подбор материала
для упражнений, контрольных, домашних и экзаменационных заданий, в чем
особенно нуждаются начинающие педагоги.
РАЗДЕЛ ПЕРВЫЙ
Глава I
ОСНОВНЫЕ ПОНЯТИЯ ОРТОГОНАЛЬНОГО
ПРОЕКТИРОВАНИЯ
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
Изобразить две плоскости, принимаемые в ортогональном проектировании
за плоскости проекций, написать на них названия и обозначения плоскостей, пол,
четвертей пространства (фиг. 1, 2) и полностью формулировать ответы на сле-
дующие вопросы.
1. Что называется осью проекций?
2. Какими полами плоскостей проекций ограничены четверти пространства:
первая, вторая, третья и четвертая?
3. Что служит границей между указанными четвертями пространства: между
первой и второй, между третьей и четвертой, между первой и четвертой, между
второй и третьей?
4. Перечислить четверти пространства, расположенные над горизонтальной
плоскостью проекций, под горизонтальной плоскостью проекций, перед верти-
кальной (фронтальной) плоскостью проекций, з а вертикальной плоскостью
проекций.
5. Какое положение занимает относительно плоскостей проекций произвольная
точка, находящаяся в первой четверти пространства, во второй, в третьей,
в четвертой четвертях пространства?
6. Где лежит точка, если она находится между первой и четвертой четвертями
пространства, между второй и третьей, между первой и второй, между третьей
и четвертой четвертями пространства?
7. Где лежит точка, находящаяся на границе всех четырех четвертей прост-
ранства?
8. Что называется прямоугольной проекцией пространственной точки на про-
извольную плоскость?
9. Что называется горизонтальной проекцией точки, вертикальной проекцией
точки?
10. На каких полах плоскостей проекций лежат проекции произвольной точки,
находящейся в первой четверти пространства, во второй, в третьей, в четвертой?
И. Где находятся проекции точки, лежащей на передней поле горизонтальной
плоскости проекций, на задней поле горизонтальной плоскости проекций, на верхней
поле вертикальной плоскости проекций, на нижней поле вертикальной плоскости
проекций, на оси проекций?
12. Что характерно для всех точек горизонтальной плоскости проекций,
вертикальной плоскости проекций?
13. Где может находиться точка, если ее горизонтальная проекция лежит
на передней поле горизонтальной плоскости проекций, на задней поле горизон-
тальной плоскости проекций; ее вертикальная проекция лежит на верхней поле
вертикальной плоскости проекций, на нижней поле вертикальной плоскости
проекций?
14. Что такое эпюр точки и как перейти от пространственного чертежа
к эпюру?
5
15. Какие полы плоскостей проекций после их совмещения находятся над
осью проекций, под осью проекций?
16. Где находится точка, если ее горизонтальная проекция на эпюре распо-
ложена н а д осью проекций, под осью проекций; ее вертикальная проекция
расположена над осью проекций, под осью проекций?
Глава II
ТОЧКА
Точки пространства обозначают большими буквами латинского алфавита: А,
В, С, D и т. д.
Проекции этих точек обозначают соответственно малыми буквами: я, b,c,dn т. д.
При этом обозначение вертикальной (фронтальной) проекции точки, в отличие от
обозначения ее горизонтальной проекции, всегда снабжают знаком ' («прим»).
Например, горизонтальную проекцию точки А. обозначают через а, вертикальную
же ее проекцию — через а'.
Обе проекции одной и той же точки — горизонтальная и вертикальная —
лежат на общем перпендикуляре к оси проекций.
Если в пространстве
1) точка находится в первой чет-
верти,
2) точка находится во второй чет-
верти,
то на эпюре1
горизонтальная проекция точки лежит
под осью проекций, а вертикальная ее
проекция — над осью проекций;
обе проекции точки — горизонтальная и
вертикальная — лежат над осью проек-
ций;
1 Наоборот, если на эпюре горизонтальная проекция точки лежит иод осью
проекций, а вертикальная ее проекция — над осью проекций, то в пространстве
точка находится в первой четверти.
Если на эпюре обе проекции точки — горизонтальная и вертикальная — лежат
над осью проекций, то в пространстве точка находится во второй четверти и т. д.
Указанные условия (между пространством и эпюром) сохраняют в каждом
случае свою закономерность и для обратной зависимости (между эпюром и
пространством).
6
3) точка находится в третьей чет-
верти,
4) точка находится в четвертой чет-
верти,
горизонтальная проекция точки лежит
над осью проекций, а вертикальная ее
проекция — под осью проекций;
обе проекции точки — горизонтальная и
вертикальная — лежат под осью проек-
ций.
Любая точка горизонтальной плоскости проекций имеет свою вертикальную
проекцию на оси проекций.
Любая точка вертикальной плоскости проекций имеет свою горизонтальную
проекцию на оси проекций.
Если обе проекции точки совпадают и лежат на оси проекций, то точка
находится на оси проекций.
Расстояние у — от горизонтальной проекции точки до оси проекций — равно
расстоянию от самой точки до вертикальной плоскости проекций.
Расстояние z — от вертикальной, проекции точки до оси проекций — равно
расстоянию от самой точки до горизонтальной плоскости проекций.
Координата z положительна для точек, расположенных над горизонтальной
плоскостью проекций, и отрицательна для точек, расположенных под горизон-
тальной плоскостью проекций.
Координата у положительна для точек, расположенных перед вертикальной
плоскостью проекций, п отрицательна дня точек, расположенных за вертикальной
плоскостью проекций.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
Полностью формулировать ответы на следующие вопросы:
1. Как принято обозначать точки пространства?
2. Как обозначают проекции пространственной точки и по какому признаку
их различают между собой?
3. Как расположены на эпюре проекции одной и той же пространственной
точки относительно оси проекций?
4. Имеет ли смысл эпюр, когда перпендикуляры, опущенные из проекций
точки на ось проекций, взаимно смещены?
5. Как понимать выражение: «дана пространственная точка»?
6. Где на эпюре лежат проекции произвольной точки, находящейся в первой
четверти пространства, во второй, в третьей, в четвертой четверти пространства?
7. При каком задании точки в пространстве возможно совпадение вне оси
проекций ее горизонтальной и вертикальной проекций?
8. Как восстановить положение пространственной точки по ее проекциям?
9. Где на эпюре лежат проекции точки, находящейся на передней поле
горизонтальной плоскости проекций, на задней поле горизонтальной плоскости
проекций, на верхней поле вертикальной плоскости проекций, на нижней поле
вертикальной плоскости проекций?
10. Как обозначают расстояние от точки в пространстве до горизонтальной
плоскости проекций, до вертикальной плоскости проекций?
11. Чем измеряется на эпюре расстояние от точки в пространстве до гори-
зонтальной плоскости проекций, до вертикальной плоскости проекций?
12. В каких четвертях пространства координата z точки положительна, отри-
цательна?
13. В каких четвертях пространства координата у точки положительна, отри-
цательна?
14. Какие знаки имеются у координат у, z точки, находящейся в первой
четверти пространства, во второй, в третьей, в четвертой четверти пространства?
15. Какую координату определяет на эпюре горизонтальная проекция точки,
вертикальная проекция точки?
16. Как откладывать на эпюре отрезок, определяющий координату г, если она
положительна, отрицательна; отрезок, определяющий координату у, если она
положительна, отрицательна?
7
ПРИМЕРЫ
Пример 1
Построить эпюр произвольной точки А, находящейся во второй чет-
верти пространства и удаленной от горизонтальной плоскости проекций
на 32 мм, а от вертикальной плоскости проекций на 18 мм (фиг. 3).
- Решение. Задаем на оси проекций произвольную точку ах и через нее
проводим перпендикулярно оси проекций прямую. Обе проекции (а, а1) искомой
точки А будут лежать на этом перпендикуляре и находиться над осью проекций.
Для того чтобы выдержать заданные расстояния от точки до плоскостей проекций,
необходимо, чтобы расстояние от горизонтальной проекции точки до оси проекций
равнялось 18 мм (расстояние от точки до вертикальной плоскости проекций),
а расстояние от вертикальной проекции точки до оси проекций — 32 мм (расстояние
от точки до горизонтальной плоскости проекций). Теперь остается отложить
вверх на перпендикуляре от точки ах отрезок длиной 18 мм и получить гори-
зонтальную проекцию (а) точки, а затем отложить вверх отрезок длиной 32 мм
и получить вертикальную проекцию (o') точки.
?а‘ Фиг. 3 ра фиг. 4 I
1 1 1 1 1 1 1 1 1 । X 0 1 1
1 1 1 1 X 1 0 1 1 1 1
X Пример 2 0 L 1 1 Фиг. 5 6 а'
Построить эпюр произвольной точки А ( — 24, —13) (фиг. 4).
Решение. Так как координаты точки (а, а') отрицательны, она находится
за вертикальной плоскостью проекций и под горизонтальной плоскостью проек-
ций, т. е. в третьей четверти пространства. Задаем на оси проекций произвольную
точку ах. Проведя через нее перпендикулярно оси проекций прямую, откладываем
на ней, вверх отрезок аха длиной 24 мм (у) и вниз отрезок аха' длиной
13 мм (z). Полученные проекции точки действительно соответствуют расположению
точки в третьей четверти,
Пример 3
Дана горизонтальная проекция (я) точки А, находящейся в третьей
четверти пространства. Построить ее вертикальную проекцию (а') согласно
условию (фиг. 5)
2 = у + 15 мм.
Решение. Вертикальная проекция искомой точки должна лежать под осью
проекций на прямой, проходящей через заданную горизонтальную проекцию точки
перпендикулярно оси проекций. Расстоянием от горизонтальной проекции точки
до оси проекций измеряется расстояние от точки А до вертикальной плоскости
проекций (у). Следовательно, чтобы получить вертикальную проекцию (а') точки,
достаточно провести через горизонтальную проекцию (я) точки перпендикуляр к оси
проекций и отложить на нем от точки ах вниз отрезок яля' длиной
аха + 15 мм.
8
<?a' a'<?b'
I b
A----------------0 J
I
b^ct
l
,i
bt>
Фиг. 6
I»
. I
1
t
X—4^—0
I
I
1
ia
к
Фиг. 8
X------------------------0
I
I
I
I
nd
Фиг. 7
Пример 4
Дана точка А (12, 20). Построить эпюр точки В, симметричной точке А
относительно: горизонтальной плоскости проекций (фиг. 6), вертикальной
плоскости проекций (фиг. 7), оси проекций (фиг. 8).
-20). Построив эпюр точки (а, а'),
Решение. Точка (а, o') задана в первой четверти.
1. Точка, симметричная ей относительно горизонтальной плоскости проекций,
находится в четвертой четверти, т. е. В (12, —
откладываем на общем перпендикуляре
вниз отрезки ахЬ длиной 12 мм (у) и ахЪ'
длиной 20 мм (z).
2. Точка, симметричная ей относи-
тельно вертикальной плоскости проекций,
находится во второй четверти, т. е. В
( — 12, 20). Построив, как и прежде, эпюр
точки (а, а"), откладываем на общем пер-
пендикуляре вверх отрезки ахЬ длиной
12 мм (у) и ахЬ' длиной 20 мм (z).
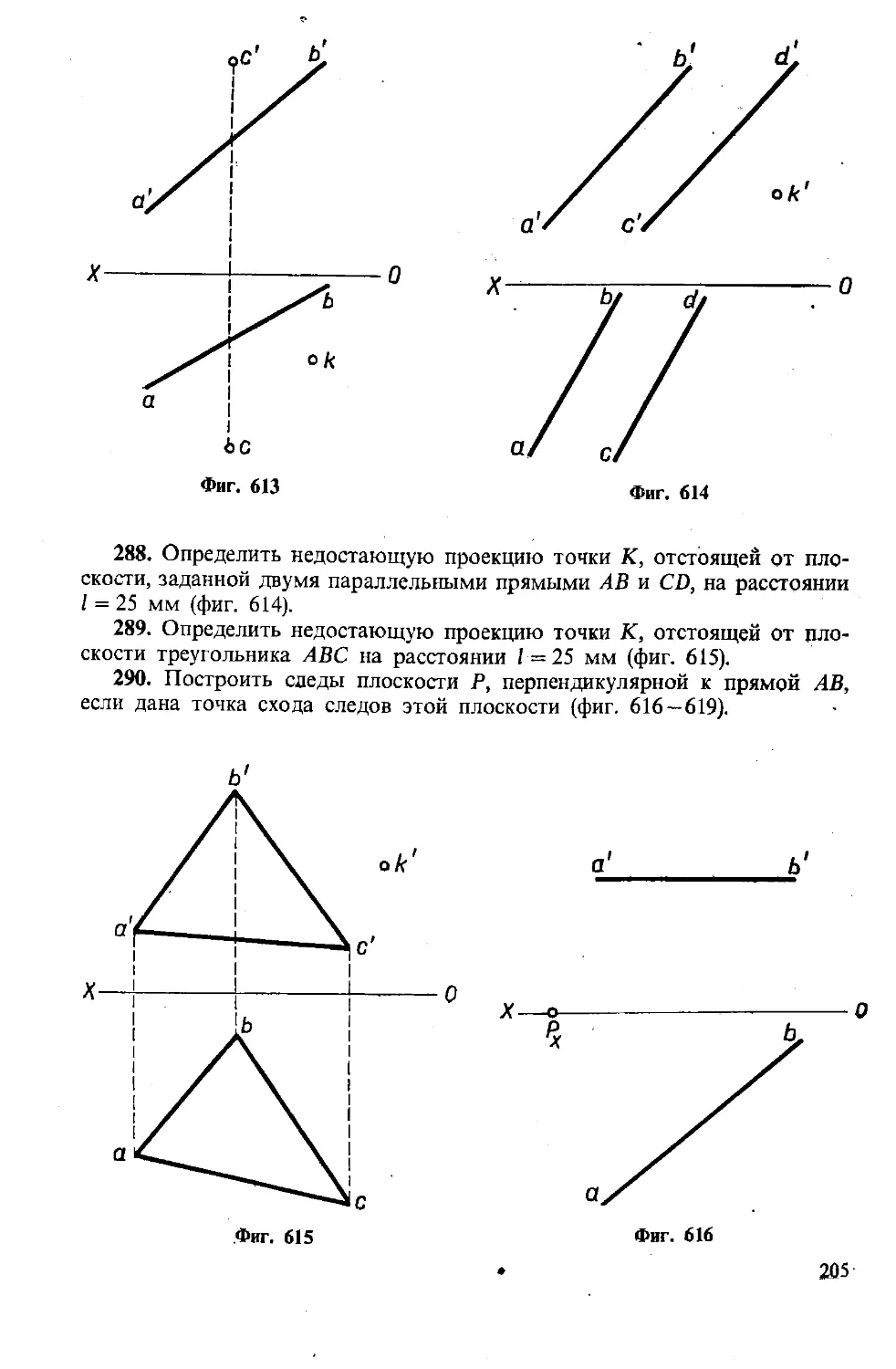
3. Точка, симметричная ей относи-
тельно оси проекций, находится в третьей
четверти, т. е. В ( —12, —20). Построив, как
и прежде, эпюр точки (я, а'), откладываем
на общем перпендикуляре: вверх отре-
зок ахЬ длиной 12 мм (у) и вниз отрезок
ахЬ' длиной 20 мм (z).
Пример 5
Даны точка А и горизонтальная проекция точки В. В какой четверти
находится точка В, если расстояние между их вертикальными проекциями
равно 25 мм (фиг. 9)?
Решение. Необходимо прежде всего найти вертикальную проекцию (Ь')
точки В. Так как расстояние между вертикальными проекциями точек должно
быть равно 25 мм, то точка Ь' должна лежать где-то на Окружности радиуса
25 мм, описанной из точки а'. Вместе с тем точка Ь' должна лежать и на перпен-
дикуляре, опущенном на ось проекций из точки Ь. Таким образом, точку Ь'
получаем на пересечении этого перпендикуляра с окружностью. Этими точками
являются Ь' и bi. Точка В может находиться в первой или в четвертой четверти
пространства.
В частном случае может подучиться одно решение (когда?) или вообще не
получиться ни одного решения (когда?).
9
ЗАДАЧИ
1. Построить проекции точки А, находящейся в первой четверти про-
странства, во второй, в третьей, в четвертой четверти пространства, и дать
ее эпюр (фиг. 10 — 13).
2. Построить проекции точки А при условии z = 0 (фиг. 10 и 12), при
условии у = 0 (фиг. 11 и 13) и дать их эпюр.
3. Построить эпюр произвольной точки А по заданным координатам:
у 15 25 25 -25 -20 -30 35 0 -30 0
_ 25 -40 -25 - 15 35 30 0 -30 0 30
4. Построить эпюр точки А, находящейся в указанной четверти, если
дана одна из ее проекций и зависимость между координатами (у = z + и)
(фиг. 14—17).
5. Построить эпюр точки А, находящейся в указанной четверти, если
дана одна из ее проекций и отношение расстояний от этой точки до
плоскостей проекций I — = ш| (фиг. 18—21).
10
1ч п-15
Кч П-20
аа
О О
Фиг. 14
О Q'
Фиг. 15
X-------------------О
Пч п-10
Фиг. 16
оа‘
Шч п-25 &ч. т-1,5
X------------------О X------------------О
X------------------О
оа' 1ч т-2 оа
Фиг. 17 Фиг. 18 Фиг. 19
Ob'
о а'
/
оа
X----1----------о
X—--------------о *---------------3-----о
Пч. т=1 |
Фиг. 20 Фиг. 21 да Фиг. 22
6. Построить эпюр точки В, симметричной точке А (—25, 30), относи-
тельно горизонтальной плоскости проекций, вертикальной плоскости про-
екций, оси проекций.
7. Даны точка А и вертикальная проекция точки В. В какой четверти
находится точка В, если расстояние между их горизонтальными проекциями
равно 25 мм (фиг. 22)?
Глава III
ПРЯМАЯ
Если в пространстве
1) прямая параллельна горизонталь-
ной плоскости проекций,
то на эпюре1
вертикальная проекция прямой парал-
лельна оси проекций, а горизонтальная
ее проекция образует с осью проекций
произвольный угол;
1 См. сноску на стр. 6.
11
2) прямая параллельна вертикаль-
ной плоскости проекций,
3) прямая параллельна оси проекций,
4) прямая расположена в плоскости,
перпендикулярной к оси проекций (про-
фильная прямая),
5) прямая перпендикулярна горизон-
тальной плоскости проекций (горизон-
тально-проектирующая прямая),
6) прямая перпендикулярна верти-
кальной плоскости проекций (вертикаль-
но-проектирующая прямая),
горизонтальная проекция прямой парал-
лельна оси проекций, а вертикальная ее
проекция образует с осью проекций
произвольный угол;
обе проекции прямой — горизонтальная
и вертикальная — параллельны оси про-
екций;
обе проекции прямой — горизонтальная
и вертикальная — лежат на общем пер-
пендикуляре к оси проекций;
горизонтальная проекция прямой —
точка, а вертикальная ее проекция —
прямая, перпендикулярная к оси проек-
ций;
вертикальная проекция прямой — точка,
а горизонтальная ее проекция — прямая,
перпендикулярная к оси проекций.
ЗАДАЧИ
8. Построить проекции прямой АВ и дать ее эпюр, если она:
1) параллельна горизонтальной плоскости проекций (фиг. 23);
2) параллельна вертикальной плоскости проекций (фиг. 24);
3) параллельна оси проекций (фиг. 25);
4) перпендикулярна горизонтальной плоскости проекций (фиг. 26);
5) перпендикулярна вертикальной плоскости проекций (фиг. 27).
9. Прочитать эпюр отрезка АВ (заполнить пропущенное):
1) Отрезок АВ находится в (?) четверти пространства и концом А
упирается в (?) полу (?) плоскости проекций (фиг. 28).
2) Отрезок АВ находится в (?) четверти пространства и концом А
упирается в (?) (фиг. 29).
3) Отрезок АВ находится в (?) четверти пространства, расположен
параллельно (?) плоскости проекций и концом А упирается в (?) плоскость
проекций (фиг. 30).
4) Отрезок АВ находится в (?) четверти пространства, расположен
перпендикулярно (?) плоскости проекций и концом В упирается в (?) полу
(?) плоскости проекций (фиг. 31).
5) Отрезок АВ находится в (?) четверти и концом А упирается в (?)
полу (?) плоскости проекций (фиг. 32).
Фиг. 23
12
Фиг. 24
13
a
x
О
Фиг. 35
Фиг. 36
6) Отрезок АВ лежит на (?) поле (?) плоскости проекций (фиг. 33).
7) Отрезок АВ находится в (?) четверти, расположен параллельно (?)
плоскости проекций и концом А упирается в (?) полу (?) плоскости
проекций (фиг. 34).
8) Отрезок АВ находится в (?) четверти, расположен перпендикулярно
(?) плоскости проекций и концом А упирается в (?) полу (?) плоскости
проекций (фиг. 35).
9) Отрезок АВ находится в (?) четверти и расположен параллельно (?)
(фиг. 36).
10) Отрезок АВ лежит на (?) поле (?) плоскости проекций (фиг. 37).
И) Отрезок АВ находится в (?) четверти и упирается концом А в (?)
полу (?) плоскости проекций и концом В - в (?) полу (?) плоскости проек-
ций (фиг. 38).
12) Отрезок АВ лежит на (?) поле (?) плоскости проекций и располо-
жен параллельно (?) (фиг. 39).
13) Отрезок АВ лежит на (?) поле (?) плоскости проекций и расположен
параллельно (?) (фиг. 40).
10. Построить эпюр отрезка АВ, если он:
1) общего положения, находится во второй четверти и упирается
концом А в вертикальную плоскость проекций;
2) находится в первой четверти, расположен параллельно вертикальной
плоскости проекций и упирается концом А в плоскость проекций;
14
b
a
Фиг. 39
В
a
b
a
Фиг. 40
3) лежит произвольно на передней поле горизонтальной плоскости
проекций;
4) находится в четвертой четверти, расположен перпендикулярно гори-
зонтальной плоскости проекций, и его конец А, одинаково удален от
плоскостей проекций;
5) находится в третьей четверти, расположен параллельно горизонталь-
ной плоскости проекций и его конец А упирается в плоскость проекций;
6) находится в плоскости биссектора первой четверти и параллелен оси
проекций;
7) находится в четвертой четверти, расположен параллельно вертикаль-
ной плоскости проекций и его конец А одинаково удален от плоскостей
проекций;
8) общего положения, находится в третьей четверти, упирается концом А
в горизонтальную плоскость проекций и его конец В одинаково удален
от плоскостей проекций;
9) лежит на верхней поле вертикальной плоскости проекций и парал-
лелен оси проекций;
10) находится во второй четверти, упирается концом А в ось проекций
и его конец В одинаково удален от плоскостей проекций;
11) находится в третьей четверти, расположен перпендикулярно верти-
кальной плоскости проекций и упирается концом В в плоскость проекций.
15
Глава IV
ПРОЕКТИРОВАНИЕ НА ТРИ ПЛОСКОСТИ ПРОЕКЦИЙ
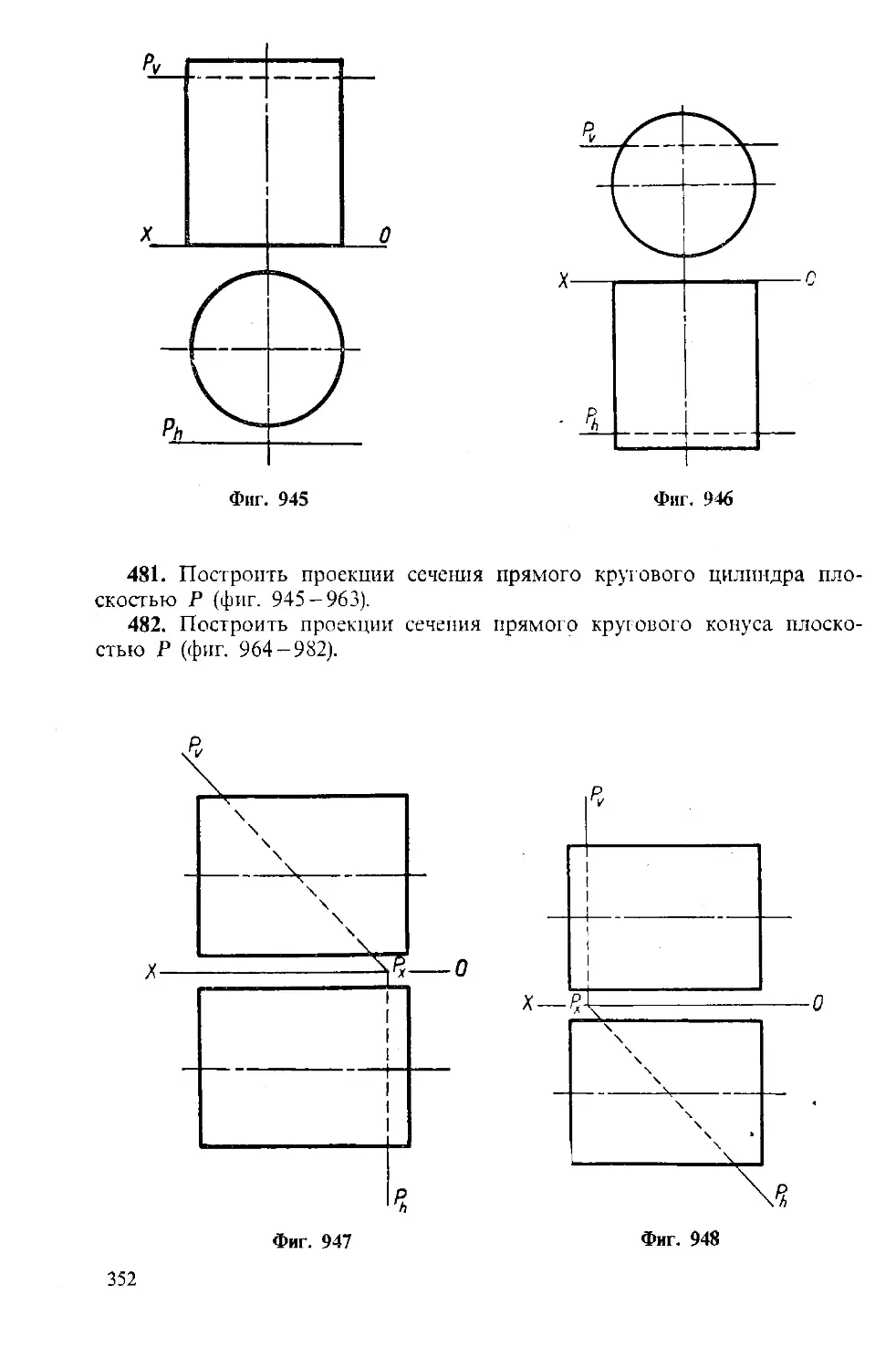
Изобразить три плоскости, принимаемые в ортогональном проектировании
за плоскости проекций, написать на них названия и обозначения плоскостей!, осей
проекций, пол плоскостей проекций, октантов пространства (фиг. 41).
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
Полностью формулировать ответы на следующие вопросы.
1. По какой оси пересекаются плоскости проекций: горизонтальная и верти-
кальная, горизонтальная и профильная, вертикальная и профильная?
2. Какими координатными плоскостями являются плоскости проекций: гори-
зонтальная, вертикальная, профильная?
3. Какими полами плоскостей проекций ограничены первый октант, второй
и т. д.—до восьмого?
4. Что служит границей между указанными октантами: первым и четвертым,
вторым и третьим, пятым и восьмым, шестым и седьмым; первым и вторым,
третьим и четвертым, пятым и шестым, седьмым и восьмым; первым и пятым,
вторым и шестым, третьим и седьмым, четвертым и восьмым?
5. Перечислить октанты, расположенные над горизонтальной плоскостью
проекций, под горизонтальной плоскостью проекций, перед вертикальной
плоскостью проекций, за вертикальной плоскостью проекций; слева от про-
фильной плоскости проекций, справа от профильной плоскости проекций.
6. Какое положение занимает относительно плоскостей проекций произволь-
ная точка, находящаяся в первом октанте, во втором и т. д, в восьмом?
7. Каким октантам принадлежит точка, лежащая на положительной оси ОХ,
OY, OZ; отрицательной оси OX, OY, OZ?
8. На каких полах плоскостей проекций лежат проекции произвольной точки,
находящейся в первом октанте, во втором и т. д, в восьмом?
16
9. Где находятся проекции произвольной точки, лежащей на плоскости: Н
(или на Н1г Н2, Я3); Г (или на Vlt V2, F3); PF(или на Wt, W2, W3); ±OX; ±OY;
+ OZ1
10. Что- характерно для всех точек горизонтальной плоскости проекций,
вертикальной плоскости проекций, профильной плоскости проекций?
11. Где может находиться точка в пространстве, если ее горизонтальная
проекция лежит на Н (или на Яь Н2, Н3); ее вертикальная проекция лежит на V
(или на Vit V2, V3); ее профильная проекция лежит на W (или на Ж1( W2, 1У3)?
12. Какие полы плоскостей проекций после их совмещения будут находиться
над осью ОХ, под осью ОХ; справа от оси OZ, слева от оси OZ?
13. Начертить в совмещенном положении полы плоскостей проекций, ограни-
чивающих первый октант, второй и т. д., восьмой?
14. При каком задании точки в пространстве ее горизонтальная проекция на
эпюре будет находиться над осью ОХ, под осью ОХ; слева от оси OZ,
справа от оси OZ?
15. При каком задании точки в пространстве ее вертикальная проекция на
эпюре будет находиться над осью ОХ, под осью ОХ; слева от оси OZ,
справа от оси OZ?
16. При каком задании точки в пространстве ее профильная проекция на
эпюре будет находиться над осью ОХ, под осью ОХ; слева от оси OZ,
справа от оси OZ?
17. При каком задании точки, не лежащей на оси проекций, возможно
совпадение ее вертикальной и горизонтальной проекций, ее вертикальной и про-
фильной проекций, всех ее трех проекций?
Прежде чем ответить на дальнейшие вопросы (18—28), следует построить на
пространственном чертеже в первом октанте проекции точки А йа три плоскости
проекций и указать координаты самой точки и ее проекций (фиг. 42).
18. Какие координаты определяют горизонтальную проекцию точки, верти-
кальную проекцию точки, профильную проекцию точки?
19. Какие проекции точки расположены, после совмещения плоскостей проек-
ций, на общем перпендикуляре к оси OX, OZ1
20. Каков порядок нахождения по двум заданным проекциям точки ее третьей
проекции? Как, например, по горизонтальной и вертикальной проекциям точки
найти ее профильную проекцию и т. д.?
21. Чем измеряется на эпюре расстояние от точки в пространстве до про-
фильной плоскости проекций?
22. Что означает равенство нулю двух каких-либо координат точки (например,
х = 0; z = 0)?
23. Что означает равенство нулю какой-либо координаты точки (например,
У = 0)?
24. В каких октантах координата х точки положительна, отрицательна?
25. В каких октантах координата у точки положительна, отрицательна?
26. В каких октантах координата г точки положительна, отрицательна?
27. Какие знаки имеют координаты х, у, z точки, находящейся в первом октанте,
во втором и т. д., в восьмом?
28. Как откладывать на эпюре: отрезок, определяющий координату х, если
она положительна, отрицательна; отрезок, определяющий координату у, при опре-
делении профильной проекции точки, если эта координата положительна, отри-
цательна?
ПРИМЕРЫ
Пример б
Построить эпюр точки А (15, -24, 15) (фиг. 43).
Решение. Откладываем на положительной оси ОХ отрезок Оах длиной
15 мм (х) и, проведя через точку ах прямую перпендикулярно этой оси, откладываем
на ней вверх отрезки аха данной 24 мм (у) и аха‘ длиной 15 мм (z). Для опре-
деления профильной проекции (а") точки проводим через точку а' перпендикулярно
оси OZ прямую и откладываем на ней влево отрезок а2а" длиной 24 мм (у).
-------- —----------------- 17
" - • ti «J . - _______
Пример 7
Дана точка Я (—15, —24, —15). Построить эпюр точки В, симметрич-
ной точке А, относительно плоскостей проекций: горизонтальной (фиг. 44),
вертикальной (фиг. 45) и профильной (фиг. 46).
Решение. Точка А находится вправо от профильной плоскости проекций,
за вертикальной плоскостью проекций и под горизонтальной плоскостью проек-
ций, т. е. в седьмом октанте. Строим ее эпюр. Откладываем на отрицательной
оси ОХ отрезок Оах длиной 15 мм (х) и, проведя через точку ах прямую
перпендикулярно оси ОХ, откладываем на ней отрезки вверх аха длиной 24 мм
(у) и вниз аха' длиной 15 мм (z). Затем проводим через точку а' прямую
перпендикулярно оси OZ и откладываем влево отрезок а.а." длиной 24 мм (у).
1. Точка В, симметричная данной точке относительно горизонтальной плоскости
проекций, находится в шестом октанте, т. е. В (-15, —24, 15). Откладываем на
общем перпендикуляре вверх отрезки ахЬ длиной 24 мм (у) и ахЬ' длиной 15 мм
(’) и затем находим профильную проекцию (/>") точки В.
2. Точка В, симметричная данной точке относительно вертикальной плоскости
проекций, находится в восьмом октанте, т. е. В (—15, 24, —15). Построив, как
18
Фиг. 47
Фиг. 46
2
।
I
i
i
i
i
i
i
i
i
a'b-
i
oi
Z
0
и выше, эпюр точки А, откладываем иа общем перпендикуляре вниз отрезки
ахЬ длиной 24 мм (у) и ахЬ' длиной 15 мм (z). Затем, проведя через точку Ь'
перпендикулярно оси 0Z прямую, откладываем на ней вправо отрезок а:Ь"
длиной 24 мм (у).
3. Точка В, симметричная данной точке относительно профильной плоскости
проекций, находится в третьем октанте, т. е. В (15, —24, —15). Построив, как
и выше, эпюр точки А, откладываем на положительной оси ОХ отрезок 0Ьх
длиной 15 мм (х) и, проведя через точку Ьх прямую перпендикулярно оси ОХ,
откладываем на ней отрезки вверх bxb длиной 24 мм (у) и вниз bxb' длиной
15 мм (z). Затем находим профильную проекцию (Ь") точки В.
Пример 8
Дана точка А (15, 24, —15). Построить эпюр точки В, симметричной
точке А, относительно оси проекций ОХ (фиг.-47), О У (фиг. 48), 0Z (фиг. 49).
19
Решение. Точка А находится влево от профильной плоскости проекций
перед вертикальной плоскостью проекций и под горизонтальной плоскостью
проекций, т. е. в четвертом октанте. Строим ее эпюр. Откладываем на положи-
тельной оси ОХ отрезок 0ах длиной 15 мм'(х) и, проведя через точку ах прямую
перпендикулярно оси ОХ, откладываем на ней вниз отрезки аха длиной 24 мм (у)
и аха' длиной 15 мм (г). Затем находим профильную проекцию (а") точки А.
1. Точка В, симметричная данной точке относительно оси ОХ, находится
во втором октанте, т. е. В (15, —24, 15). Откладываем на общем перпендикуляре
вверх отрезки ахЬ длиной 24 мм (у) и ахЬ' длиной 15 мм (z). Затем находим
профильную проекцию (Ь") точки В.
2. Точка В, симметричная данной точке относительно оси ОУ, находится
в пятом октанте, т. е. В (-15, 24, 15). Построив, как и выше, эпюр точки А,
откладываем на отрицательной оси ОХ отрезок ОЬХ длиной 15 мм (х) и, проведя
через точку Ъх прямую перпендикулярно оси ОХ, откладываем на ней отрезки
вниз ЪХЬ длиной 24 мм (у) и вверх ЪХЪ' длиной 15 мм (z). Затем находим
профильную проекцию (!>") точки В.
3. Точка В, симметричная данной точке относительно оси 0Z, находится
в седьмом октанте, т. е. В (—15, —24, —15). Построив, как и выше, эпюр точки А,
откладываем на отрицательной оси ОХ отрезок ОЪХ длиной 15 мм (х) и, проведя
через точку Ьх прямую перпендикулярно оси ОХ, откладываем на ней отрезки
вверх bxb длиной 24 мм (у) и вниз bxb' длиной 15 мм (z). Затем находим
профильную проекцию (Ь") точки В.
Пример 9
Дана горизонтальная проекция (а) точки А, находящейся в третьей
четверти. Построить две ее другие проекции, зная условие: z = х + 12 мм
(фиг. 50).
Решение. Вертикальная проекция (л') точки должна лежать под осью ОХ
и на перпендикуляре к ней, проходящем через горизонтальную проекцию точки.
Координата х определяет расстояние от горизонтальной проекции (л) точки до
оси OZ.
Координата z определяет расстояние от вертикальной проекции (д') точки до
оси ОХ. Поэтому проводим через точку а прямую перпендикулярно оси ОХ
до пересечения с ней в точке ах. От точки ах откладываем па этом перпендикуляре
вниз отрезок аха', равный аау + 12 мм.
Конец этого отрезка дает нам вертикаль-
ную проекцию («') точки.
Затем по двум проекциям (а и я')
точки А находим ее профильную проек-
цию (а")-
Пример 10
Построить ось 0Z и горизонталь-
ную проекцию точки А, находящейся
во второй четверти пространства, зная
проекции а и а" и отношение ее коор-
динат — = 3 (фиг. 51).
Решение. Заданные проекции точ-
ки А должны лежать слева от оси OZ.
Так как расстояние от вертикальной про-
екции (а') точки до оси OZ есть х, а рас-
стояние от профильной проекции (а") точ-
ки до оси OZ есть у, то отрезок между
z
2
Фиг. 52
проекциями точки, т. е. я'я", равен разности (х — у). Пользуясь заданным условием
-у = 3, составляем производную пропорцию ——— = ^ —2, откуда —^-=У-
Теперь остается разделить отрезок а'а" пополам и провести ось OZ перпен-
дикулярно оси ОХ на расстоянии справа от профильной проекции [а")
точки. Затем находим горизонтальную проекцию (а) точки А.
Пример И
Построить ось ОХ и профильную проекцию точки А, находящейся
в четвертой четверти пространства, зная проекции а и а' и отношение ее
У 1
координат — — — (фиг. 52).
Решение. Заданные проекции точки А должны лежать под осью ОХ.
Так как расстояние от горизонтальной проекции точки до оси ОХ есть у, а рас-
стояние от вертикальной проекции точки до оси ОХ есть z, то отрезок между
проекциями точки, т. е. а'а, равен разности (z — у). Пользуясь заданным условием
у 1
— = —, составляем производную пропорцию, куда войдет разность z — у, для чего
z 3
у 1 z 3 z-y 3 — 1 „ z—у
перепишем условие — = — в виде — = —, откуда —- = —— = 2 или —— = у.
z 3 У 1 У 1 2
Теперь остается разделить отрезок а'а пополам и провести ось ОХ над
точкой а на расстоянии Затем находим профильную проекцию (я") точки А.
ЗАДАЧИ
11. Построить проекции точки А, находящейся в первом октанте, во вто-
ром и т.д., в восьмом, и дать ее эпюр (фиг. 53-60).
12. Построить проекции точки А: при условии, что 2^ = 0 (фиг. 53, 55,
58, 60); при условии, что уА = 0 (фиг. 54, 56, 57, 59);. при условии, что
хА = 0 (фиг. 54, 56, 57, 59), и дать ее эпюр.
21
13. Построить эпюр точки А по заданным координатам.
X 20 15 15 20 -15 -20 -20 -15 25 -25
У' 15 -25 -25 20 25 -15 -15 25 -25 25
Z 25 35 -20 -30 20 25 -25 -35 25 -25
X 15 -15 20 -15 0 0 0 0 0 -20
У -25 25 0 0 —20 25 -20 -20 0 0
Z 0 0 -30 30 30 -35 20 0 20 0
Фиг. 54
Фиг. 56
22
14. Найти недостающие проекции точки А, если известны: одна из ее
проекций, соотношение между координатами точки (или другие данные)
и четверть, в которой она находится (фиг. 61-66).
15. Нанести недостающую ось проекций и определить проекцию точки
А, если дано соотношение между ее координатами (фиг. 67 — 72).
16. Построить третью проекцию — прямой АВ, треугольника АВС
(фиг. 73-78).
17. Построить проекции треугольника АВС, если даны координаты его
вершин А (20, 0, 0), В (0, 30, 0) и С (0, 0, 25).
18. Построить проекции треугольника АВС, если даны координаты его
вершин А (20, 30, 0), В (20, 0, 30) и С (0, 20, 30).
19. Дана точка А (20, 30, 20). Построить эпюр точки В, симметричной
точке А, относительно горизонтальной плоскости проекций, вертикальной
плоскости проекций, профильной плоскости проекций (дать три эпюра).
23
z
z
Фиг. 61
z
z
a'
о
X----------
Пч
X=Y + 15
Фиг. 64
Фиг. 62
Z
z
a'
9
Фиг. 67
X__±
Y 2
6
a
Фиг. 68
1ч
Z-X+10
Y
Фиг. 69
Y
24
25
2
2
26
20. Дана точка А (20, 30, 20). Построить эпюр точки В, симметричной
точке А, относительно осей OX, OY, OZ (дать три эпюра).
21. Построить проекции куба с основанием ABCD на вертикальной
плоскости проекций, если дана диагональ АС его основания, и указать
проекции каждой грани, каждого ребра (фиг. 79).
22. Построить проекции правильной треугольной прямой призмы высо-
той 50 мм, если дана сторона АВ ее основания, лежащего на горизон-
тальной плоскости проекций, указать проекции каждой грани, каждого
ребра (фиг. 80).
23. Построить проекции прямой правильной треугольной пирамиды
высотой 60 мм, если дана сторона АВ ее основания, лежащего на верти-
кальной плоскости проекций, и указать проекции каждой грани, каждого
ребра (фиг. 81).
24. Построить проекции прямого кругового цилиндра с основанием на
вертикальной плоскости проекций и с центром С (30, 0, 30), если дана его
высота 60 мм, а радиус основания равен 20 мм.
25. Построить геометрическое место прямых пространства, проходящих
через точку S (30, 30, 50) и образующих с горизонтальной плоскостью
проекций угол, равный 70°.
26. Построить геометрическое место точек пространства, удаленных
от точки С (30, 30, 35) на 20 мм.
Глава V
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ТОЧКИ
Если в пространстве то на эпюре1
точка лежит на прямой, проекции точки лежат на одноименных
проекциях прямой.
Примечание. В случае профильной прямой обратная теорема справедлива
только в системе Н, V, W. Необходимо, имея две проекции, проверить, лежит
ли профильная проекция точки на профильной проекции прямой.
Вывод
Если в пространстве то на эпюре1
прямая проходит через точку, проекции прямой проходят через одно-
именные проекции точки.
ПРИМЕРЫ
Пример 12
Лежат ли точки А, В, С, Ь на прямой MN (фиг. 82)?
Решение. Проекции (а, а ) точки А лежат на одноименных проекциях прямой
(тп, т'п'), следовательно, точка А лежит на прямой MN.
Проекции (Ь, Ь') точки В лежат на разноименных проекциях прямой (тп, т'п’),
следовательно, точка В на прямой MN не лежит.
Не лежат на прямой MN также и точки С и D (почему?)
Пример 13
Лежит ли точка С на профильной прямой АВ (фиг. 83)?
1 См. сноску на стр. 6.
37
z
Решение. Так как заданная прямая - профильная, необходимо проверить
дополнительно взаимное положение профильной проекции точки и профильной
проекции прямой. Построив профильную проекцию прямой и профильную проекцию
точки, видим, что профильная проекция точки не лежит на профильной проекции
прямой, а следовательно, точка С на прямой АВ не лежит.
Пример 14
Даны профильная прямая АВ и вертикальная проекция (с*) точки С,
лежащей на прямой. Найти горизонтальную проекцию (с) этой точки
(фиг. 84).
Решение. Для того чтобы можно было найти горизонтальную проекцию
(с) точки, нужна ее профильная проекция (с"), которая должна лежать на профиль-
ной проекции (а"Ь") прямой и на перпендикулярной к оси OZ прямой, проведенной
через точку с'. Отсюда находим профильную проекцию (d'b") прямой и на ее
пересечении с перпендикуляром к оси OZ, проведенным через точку с', получаем
профильную проекцию (с") точки. Затем находим горизонтальную проекцию (с)
точки.
Пример 15
Даны профильная прямая АВ и горизонтальная проекция (с) точки С,
лежащей на прямой. Найти вертикальную проекцию (с') этой точки
(фиг. 85).
Решение. Для того чтобы можно было найти вертикальную проекцию (с')
точки, нужна ее профильная проекция (с"), которая должна лежать на профиль-
ной проекции (d'b") прямой и находиться на расстоянии (у) слева (почему?) от оси
OZ. Отсюда — находим профильную проекцию (d'b") прямой и на пересечении
с прямой, параллельной оси OZ, проведенной слева от нее на расстоянии схс
(т. е. у), получаем профильную проекцию (с") точки, затем находим вертикальную
проекцию (с’) точки.
Пример 16
Провести через точки А и В прямую (фиг. 86).
Решение. Проводим проекции искомой прямой: горизонтальную — через
точки а и Ь, вертикальную — через точки а' и V.
28
Пример 17
Даны точка А и разноименные проекции точек В и С. Найти недостаю-
щие проекции точек В и С, если все они должны лежать на прямой MN
(фиг. 87).
Решение. Проводим проекции прямой MN: горизонтальную (тп) — через
точки а и с, вертикальную (т'п') — через точки а' и Ь'. Затем находим горизонталь-
ную проекцию (Ь) точки В на прямой тп и вертикальную проекцию (с') точки С
на прямой т'п'.
•29
Пример 18
z 1
Найти на прямой АВ точку С, зная отношение ее координат: —= —
(фиг. 88).
Решение. Координаты z и у определяют профильную проекцию (с") точки С.
Геометрическое место точек плоскости в системе ZOY с отношением координат
z 1
— = — есть прямая линия, уравнение которой у = 2z. Профильная проекция (с")
Г 2
точки С должна лежать на профильной проекции (с;"Л") заданной прямой АВ и на
прямой у = 2z, т. е. на их пересечении. Следовательно, по заданным проекциям
прямой АВ находим ее профильную проекцию (а"Ь"), проводим в системе ZOY
прямую у = 2: и на их пересечении получаем профильную проекцию (с") точки С.
Затем уже по с" находим горизонтальную и вертикальную проекции искомой
точки на одноименных проекциях прямой АВ.
ЗАДАЧИ
27. Найти на прямой АВ точку, если дано ее расстояние от какой-
либо плоскости проекций (фиг. 89 — 91).
28. Найти на прямой АВ точку С, одна из проекций которой известна
(фиг. 92, 93).
29. Что характерно на эпюре для всех точек, лежащих на горизонтально-
проектирующей прямой, на вертикально-проектирующей прямой, на про-
фильно-проектирующей прямой?
30. Всегда ли по одной проекции точки, лежащей на прямой, можно
найти другую ее проекцию в системе (Н, Г); (Н, V, W)?
31. Найти на прямой АВ точку С с отношением координат — = т
(фиг. 94, 95).
30
31
32. Провести через точку С прямую АВ параллельно горизонтальной
плоскости проекций (фиг. 96), параллельно вертикальной плоскости проек-
ций (фиг. 97), параллельно профильной плоскости проекций (фиг. 98).
Глава VI
СЛЕДЫ ПРЯМОЙ
Следами прямой называют точки ее пересечения с плоскостями проекций.
Горизонтальным следом прямой называют точку ее пересечения
с горизонтальной плоскостью проекций.
Вертикальным следом прямой называют точку ее пересечения
с вертикальной плоскостью проекций.
Горизонтальный след прямой обозначают буквой Н, а его проекции буквами
(/;, /1').
Вертикальный след прямой обозначают буквой V, а его проекции — буквами
(г, v').
Правило. Для нахождения горизонтального следа прямой поступаем так:
продолжаем вертикальную проекцию прямой до пересечения с осью ОХ в точке h';
в этой точке восставляем перпендикуляр к оси проекций до пересечения с гори-
зонтальной проекцией прямой в точке /1 (Н). Эта точка и является горизонтальным
следом прямой.
Для того чтобы найти вертикальный след прямой, поступаем так: продолжаем
горизонтальную проекцию прямой до пересечения с осью ОХ в точке v. В этой
точке восставляем перпендикуляр к оси проекций до пересечения с вертикальной
проекцией прямой в точке v' (7). Эта точка и является вертикальным следом
прямой.
Примечание. По указанному правилу для профильной прямой можно
найти только точки h’ и v. Для нахождения /1 и v' необходимо сначала найти /Г
и v" на пересечении а"Ь" с осями О У и 0Z, а затем по /»' и й" найти h (Н) и по
v и v” найти v’ (7).
ПРИМЕРЫ
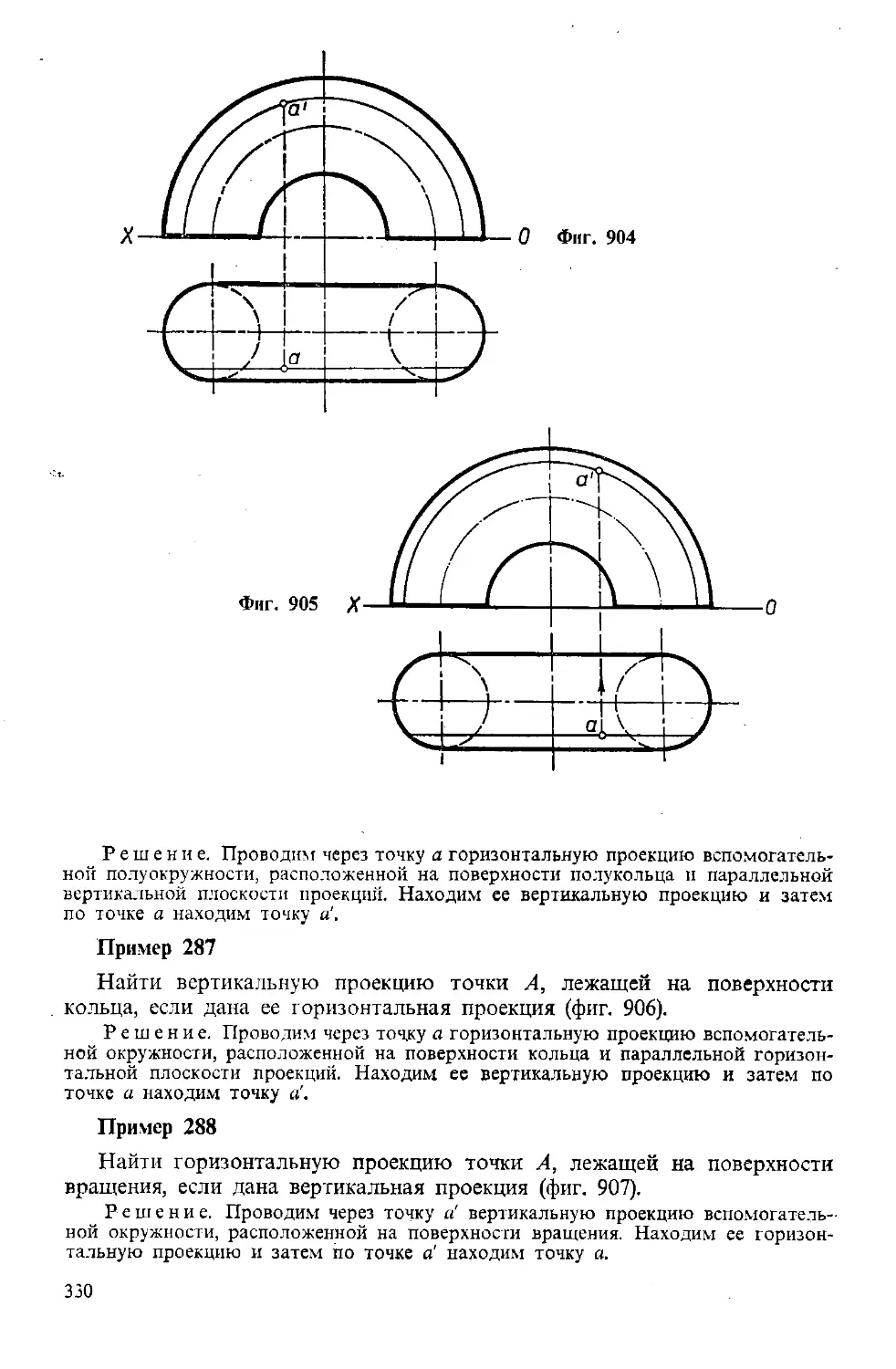
Пример 19
Построить проекции прямой, зная ее следы (фиг. 99).
Решение. Искомая прямая проходит через следы — точки Н и V. Следова-
тельно, проекции прямой должны пройти через одноименные проекции этих точек.
Находим проекции (й, й’) и (г, v') этих точек и проводим горизонтальную проекцию
прямой через точки h и v и вертикальную проекцию прямой — через точки v' и h’.
Пример 20
Найти следы прямой АВ и отделить видимую ее часть от невидимой
(фиг. 100).
Решение. Продолжаем горизонтальную проекцию (ab) прямой до пересече-
ния с осью ОХ в точке v. В этой точке восставляем перпендикуляр к оси проекций
до пересечения с вертикальной проекцией прямой в точке v’ (7). Получаем верти-
кальный след прямой. Затем продолжаем вертикальную проекцию (а'й') прямой
до пересечения с осью проекций в точке й'.'В этой точке восставляем перпендикуляр
к оси проекций до пересечения с горизонтальной проекцией прямой в точке h (II).
Получаем горизонтальный след прямой.
Следовательно, искомая прямая имеет горизонтальный след на заднем поле
горизонтальной плоскости проекций и вертикальный след — на верхнем поле
вертикальной плоскости проекций. Такая прямая проходит через первую, вторую
и третью четверти пространства. Отрезок ее между следами невидим. После верти-
кального следа прямая видима, а после горизонтального следа — невидима.
32
Пример 21
Дана профильная прямая АВ. Найти ее следы (фиг, 101).
Решение. Продолжаем заданные проекции до пересечения с осью проекций
в точках h' и V. Строим профильную проекцию заданной прямой и продолжаем
до пересечения с осью О У в точке /г" и с осью OZ в точке v“, а затем по h' и h"
находим h (Н) и по v и v" находим v' (У).
Пример 22
Построить проекции прямой, зная следы — точки Н и W. Найти верти-
кальный след прямой и отделить видимую ее часть от невидимой (фиг. 102).
Решение. По заданным следам — точкам Н и W— находим их проекции
и затем проводим проекции искомой прямой через одноименные проекции точек
Н и W.
2 Арустамов X. А.
33
V
Для того чтобы получить вертикальный след прямой, находим точку г на
пересечении горизонтальной проекции прямой с осью ОХ и восставляем в этой
точке перпендикуляр к оси до пересечения в точке v' с вертикальной проекцией
прямой. Получаем вертикальный след прямой. Прямая — невидима.
ЗАДАЧИ
33. Перечислить прямые, имеющие в системе плоскостей И и V только
один след, и назвать — какой.
34. Перечислить прямые, имеющие в системе плоскостей Н, У и И':
1) только один след (назвать — какой),
2) два следа (назвать — какие).
35. Что характерно на эпюре для следов профильной прямой?
36. В каких случаях возможно совпадение на эпюре следов профильной
прямой?
37. Привести пример, когда прямая не определяется горизонтальным
и вертикальным следами, и указать, какие нужно задать дополнительные
условия для полного определения этой прямой.
х—--------------»—о
Фиг. 103 о (Н)
34
X-------—----------г----(
Он)
Фиг. 104
а о
I
1
I
Ab'
Фиг. 106
0
b'
I
I
I
x-------------;------------о
।
।
।
।
Фиг. 109 о ab
Фиг. ПО
38 ., Перечислить случаи совпадения следа прямой с какой-либо из ее
протекций.
39. Построить проекции прямой по заданным ее следам (фиг. 103, 104).
40. Найти следы прямой, проходящей через точки А и В (фиг. 105, 106).
35
41. Найти следы прямой АВ (фиг. 107 — 113).
42. Даны следы (или след и отдельная проекция каждого из дву:
других следов) прямой. Построить три проекции искомой прямо!
(фиг. 114-117).
36
Глава VII
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ
то на эпюре1
Если в пространстве
1) прямые пересекаются,
2) прямые параллельны,
одноименные проекции прямых пересе-
каются и точки их пересечения лежат
на одном перпендикуляре к оси проек-
ций;
одноименные проекции прямых парал-
лельны.
В частном случае пересекающиеся прямые могут быть перпендикулярны между
собой.
Теорему о проектировании двух перпендикулярных прямых см. в гл. X.
Если прямые не пересекаются и не параллельны, то они скре-
щиваются.
Пр имечание. Взаимное расположение двух прямых при наличии хотя бы
одной профильной прямой устанавливается по третьей проекции. Например, две
профильные прямые параллельны, если их профильные проекции между собой
параллельны.
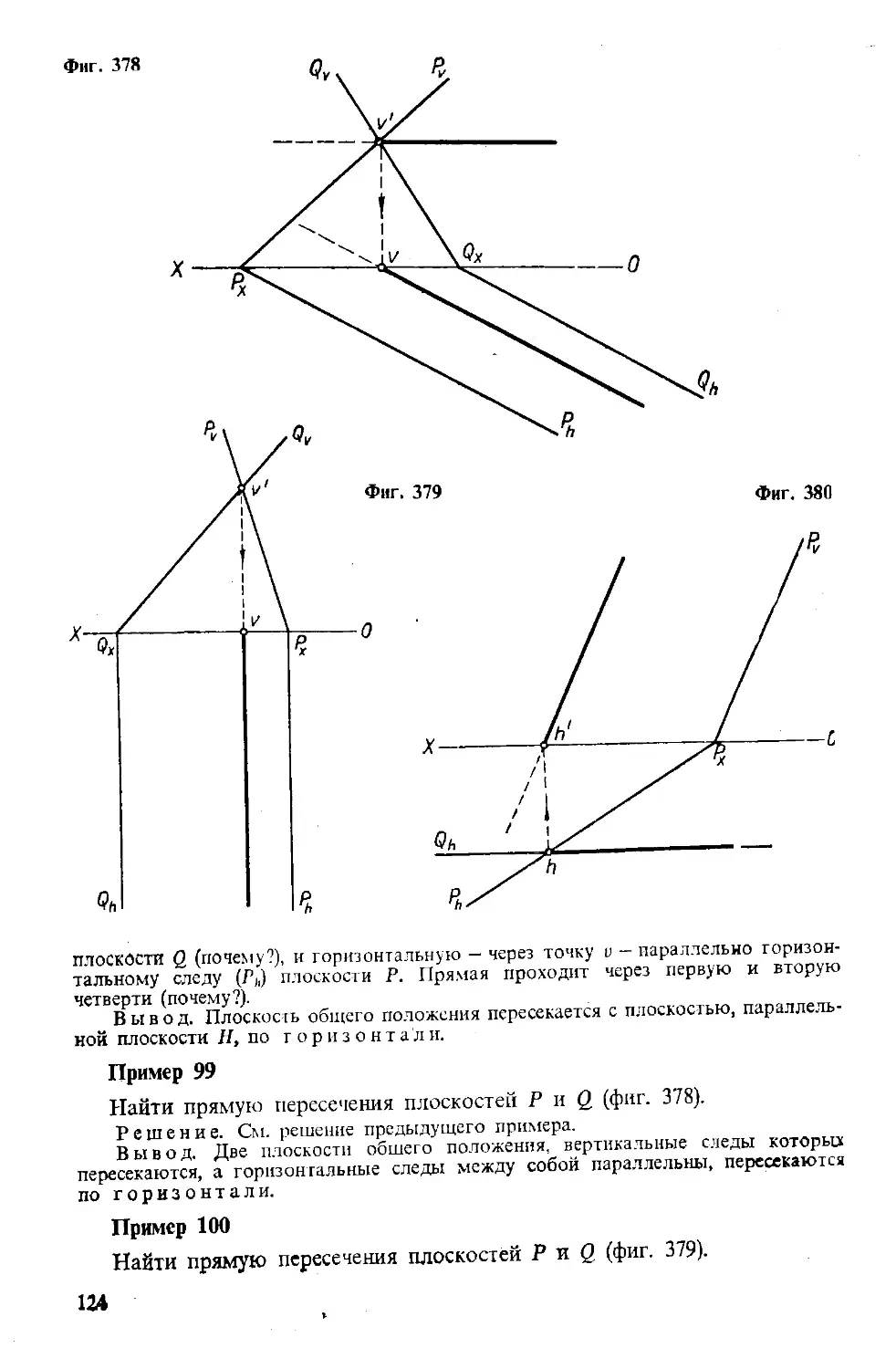
ПРИМЕРЫ
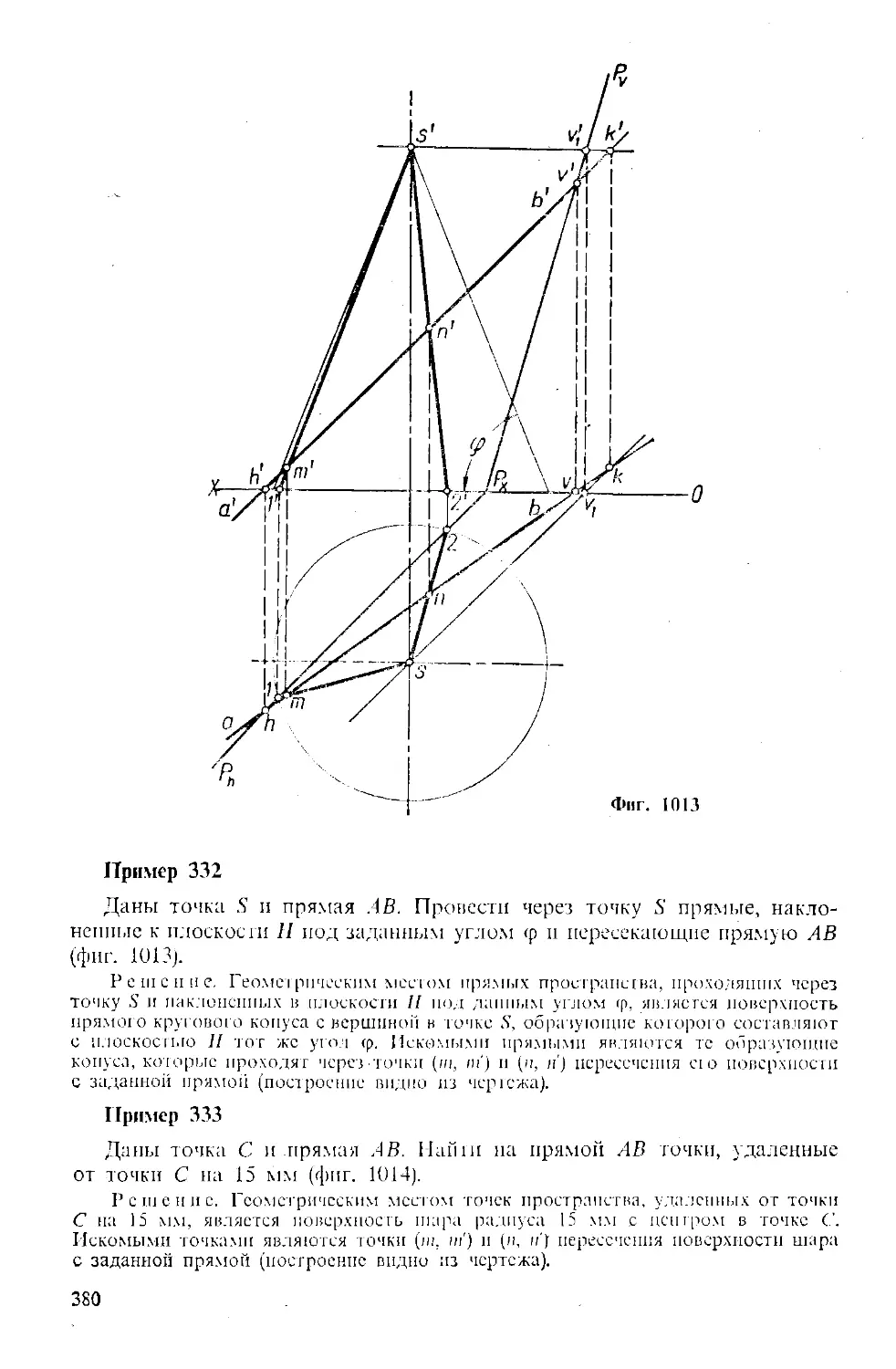
Пример 23
Выяснить взаимное расположение прямых АВ ii CD в пространстве
(фиг. 118).
1 См. сноску на стр. 6.
37
Решение. Точки пересечения одноименных проекций заданных прямых лежат
на одном перпендикуляре к оси проекций. Обозначаем пересечение горизонтальных
проекций прямых через к и пересечение вертикальных их проекций — через к'.
Точка (к, к') лежит на прямых АВ и CD, т. е. является общей их точкой. Отсюда:
прямые АВ и CD в пространстве пересекаются.
Пример 24
Выяснить взаимное расположение прямых АВ и CD (фиг. 119).
Решение. Точки пересечения одноименных проекций прямых лежат на одном
перпендикуляре к оси проекций. Обозначаем пересечение горизонтальных проекций
через к и пересечение их вертикальных проекций — через к'. Точка (к, к') лежит
на прямой (ab, а'Ь'). Для выяснения положения точки (к, к') относительно про-
фильной прямой CD строим профильные проекции прямой (cd, c'd') и точки (к, к).
Профильная проекция (к") точки не лежит на профильной проекции (c"d") прямой
CD, т. е. точка (fc, к') на профильной прямой (cd, c'd] не лежит и точка (к, к )
не является обшей точкой для заданных прямых АВ и CD. Отсюда: прямые
АВ и CD в пространстве скрещиваются,
Пример 25
Выяснигь взаимное расположение прямых ,4В и CD (фиг. 120).
Решение. Горизонтальные и вертикальные проекции заданных прямых АВ
и CD между собой параллельны. Следовательно, в пространстве прямые АВ и CD
параллельны.
Пример 26
Выяснить взаимное расположение прямых .4В и CD (фиг. 121).
Решение. Горизонтальные и вертикальные проекции двух профильных
прямых, не лежащих в одной плоскости, между собой всегда параллельны,
а потому для выяснения взаимного расположения таких прямых необходимо
построить их профильные проекции: (а"Ь“) и (c"d"). Профильные проекции прямых
(ah, а'Ь') и (cd, c'd’) между собой пересекаются. Отсюда прямые АВ и CD в простран-
стве скрещиваются.
3?
Даны прямая АВ и точка С. Провести через точку С произвольную
прямую, пересекающую прямую АВ (фиг. 122).
Решение. Берем произвольную точку К на прямой АВ. Так как заданная
прямая АВ — профильная, строим ее профильную проекцию и на ней задаем
произвольно профильную проекцию (к") точки К. По профильной проекции (к")
точки находим горизонтальную и вертикальную проекции (к, к') точки на одно-
именных проекциях прямой АВ. Затем проводим проекции искомой прямой:
горизонтальную проекцию прямой — через точки с и к; вертикальную проекцию
прямой — через точки с' и к'.
39
Пример 28
Даны прямая АВ и точка С. Провести через точку С прямую, пере-
секающую прямую АВ, параллельно вертикальной плоскости проекций
(фиг. 123).
Решение. Проекции искомой прямой должны проходить через одноименные
проекции точки С; так как прямая должна быть параллельна вертикальной
плоскости проекций, ее горизонтальная проекция будет параллельна оси проекций.
Отсюда — проводим через точку с горизонтальную проекцию искомой прямой
параллельно оси проекций до пересечения с прямой ah в точке к. По точке к
находим точку к' и проводим вертикальную проекцию прямой через точки к', и с'.
Пример 29
Даны прямая АВ и точка К. Провести через точку К прямую парал-
лельно прямой АВ (фиг. 124).
Решение. Проекции искомой прямой должны проходить через одноимен-
ные проекции точки К. При этом одноименные проекции прямых, заданной
и искомой, должны быть между собой параллельны. Отсюда — проводим проекции
искомой прямой: горизонтальную {кт} через точку к параллельно прямой ab
и вертикальную (к'т’) через точку к' параллельно прямой а'Ь'.
Пример 30
Даны прямая АВ и точка К. Провести через точку К прямую парал-
лельно прямой АВ (фиг. 125).
Решение. Искомая прямая — тоже профильная. Условием параллельное!и
двух профильных прямых, как известно, является параллельность их профильных
проекций. Отсюда — находим профильную проекцию (а"Ь") прямой АВ и профиль-
ную проекцию (к") точки К. Проводим через точку к" профильную проекцию
искомой прямой параллельно прямой а”Ь"\ ограничиваем ее произвольным отрез-
ком c”d" и затем строим по профильной проекции прямой ее горизонтальную {cd)
и вертикальную (cd') проекции.
Пример 31
Параллельные прямые ,1В и CD пересечь произвольной прямой (фиг. 126).
Решение. Берем на каждой из заданных прямых АВ и CD по произвольной
точке. Прямая, проведенная через эти две точки, будет искомой. Отсюда — задаем
произвольную точку (ш, т') на прямой АВ и точку (н, и') на прямой CD. Затем
проводим горизонтальную проекцию искомой прямой через точки типи верти-
кальную проекцию прямой через точки т и п'. ,
т --Ь
40
41
Эту задачу можно решить несколько иначе. Пересекаем вертикальные проекции
произвольной прямой и отмечаем точки пересечения т' и л'. По точке т' находим
т на горизонтальной проекции прямой АВ и по точке п' находим п на горизон-
тальной проекции прямой CD. Проводим через полученные точки тип горизон-
тальную проекцию искомой прямой. Можно было бы начать решение задачи также
с проведения произвольно горизонтальной проекции искомой прямой, а затем
поступить так же, как и выше.
Пример 32
Прямые АВ и CD пересечь прямой, параллельной горизонтальной
плоскости проекций (фиг. 127).
Решение. Искомая прямая должна быть параллельна горизонтальной
плоскости проекций, а следовательно, ее вертикальная проекция должна быть
параллельна оси ОХ. О гсюда — проводим произвольно вертикальную проекцию
искомой прямой параллельно оси проекций; точки пересечения с прямыми ah'
и с А обозначаем через /<’ н. т'. Но точкам к’ и ш’ находим на прямых ab и с<1
точки к и т. Проводим через точки к и т горизонтальную проекцию (кт) искомой
прямой.
ЗАДАЧИ
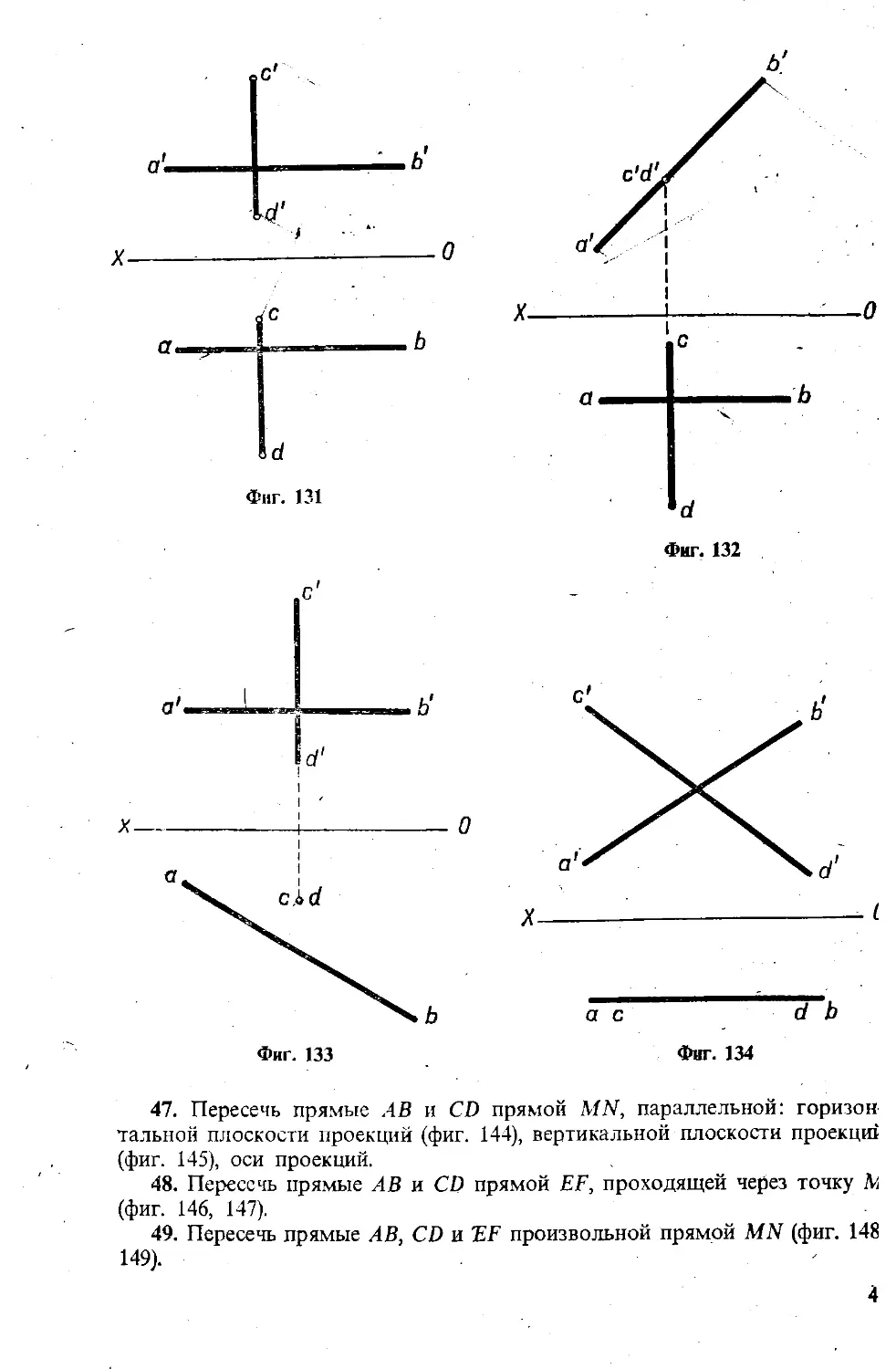
43. Определить взаимное расположение прямых АВ и CD (фиг. 128 — 137).
44. Пересечь прямую АВ прямой MN, проходящей через точку С
и параллельной: горизонтальной плоскости проекций (фиг. 138), вертикаль-
ной плоскости проекций (фиг. 139).
45. Провести через точку С прямую, пересекающую прямую АВ и ось
проекций (фиг. 140, 141).
46. Провести через точку С прямую, параллельную прямой АВ
(фиг. 142, 143).
фиг. 128 Фиг. 129 -Фиг. 130
42
ас d b
Фиг. 134
47. Пересечь прямые АВ и CD прямой MN, параллельной: горизон
тальной плоскости проекций (фиг. 144), вертикальной плоскости проекцш
(фиг. 145), оси проекций.
48. Пересечь прямые АВ и CD прямой EF, проходящей через точку
(фиг. 146, 147).
49. Пересечь прямые АВ, CD и FF произвольной прямой MN (фиг. 148
149). '
4
44
45
46
Глава VIII
ДЛИНА ОТРЕЗКА ПРЯМОЙ И УГЛЫ НАКЛОНА ПРЯМОЙ
К ПЛОСКОСТЯМ ПРОЕКЦИЙ
Отрезок прямой, расположенный в пространстве параллельно какой-либо
плоскости проекций, проектируется на эту плоскость в действительную величину
(т. е. без искажения).
Если отрезок параллелен горизонтальной плоскости проекций, то угол между
горизонтальной проекцией этого отрезка и осью проекций равен углу наклона
самого отрезка к вертикальной плоскости проекций.
Если отрезок параллелен вертикальной плоскости проекций, то угол между
вертикальной проекцией этого отрезка и осью проекций равен углу наклона самого
отрезка к горизонтальной плоскости проекций.
Длину отрезка прямой по его проекциям определяют как гипотезу прямо-
угольного треугольника, одним катетом которого является одна из проекций
данного отрезка, а другим катетом — абсолютная величина алгебраической разности
расстояний от копцов другой проекции отрезка до оси проекций.
Угол в треугольнике между катетом — горизонтальной проекцией отрезка —
и гипотенузой — его действительной величиной — равен углу наклона самого отрезка
к горизонтальной плоскости проекций.
Угол в треугольнике между катетом — вертикальной проекцией отрезка — и
гипотенузой — его действительной величиной — равен углу наклона самого отрезка
к вертикальной плоскости проекций.
ПРИМЕРЫ
Пример 33
Определить действительную длину отрезка АВ (фиг. 150).
Реше ни е. Строим прямоугольный треугольник по двум катетам. За один'
катет принимаем горизонтальную проекцию (ab) отрезка, а за другой катет —
отрезок, длина которого равна |z + zi|. Гипотенуза этого прямоугольного тре-
угольника дает нам действительную длину отрезка.
Тот же результат получаем, построив прямоугольный треугольник, одним
катетом которого является вертикальная проекция (а'Ь') отрезка, а другим кате-
том — отрезок длиной |ут — у|. Гипотенуза этого треугольника дает нам действи-
тельную длину отрезка.
В обоих случаях получается один и тот же результат.
Пример 34
Отложить на прямой АВ от точки К отрезок длиной 28 мм по направ-
лению от точки А к точке В (фиг. 151).
Решение. Выделяем на прямой АВ (условно) произвольный отрезок КМ
и определяем его действительную величину. Для этого строим прямоугольный'
треугольник по двум катетам (к’т’) и | у — У11. Откладываем на гипотенузе
построенного треугольника отрезок КС длиной 28 мм и опускаем из точки С
перпендикуляр на прямую а’Ь1 до пересечения с ней в точке с’. По точке с'
находим точку с на прямой ab. Проекциями искомого отрезка являются (кс, к'с').
Пример 35
Провести через точку С прямую, параллельную горизонтальной плоско-
сти проекций и составляющую с вертикальной плоскостью проекций
угол, равный 45° (фиг. 152).
Решение. Так как искомая прямая АВ параллельна горизонтальной плоско-
сти проекций, ее вертикальная проекция должна быть-параллельна оси проекций.
Для того чтобы прямая составляла с вертикальной плоскостью проекций угол,
47
48
равный 45°, необходимо, чтобы ее горизонтальная проекция составляла с осью
проекций угол, равный 45°. Отсюда — проводим через точку с' вертикальную
проекцию (а'Ь') прямой параллельно оси проекций, а через точку с — горизонталь-
ную проекцию (afe) прямой под углом 45° к оси проекций. Таких прямых - две,
а на чертеже проведена только одна прямая.
Пример 36
Определить углы наклона прямой АВ к плоскостям проекций (фйт. 153).
Решение. Строим, как было указано, прямоугольные треугольники аЬВ
и а'Ь'А. Угол а является углом наклона данной прямой к горизонтальной
плоскости проекций; угол 0 является углом наклона той же прямой к вертикаль-
ной плоскости проекций.
Пример 37
Провести через точку С прямую, составляющую с горизонтальной
плоскостью проекций угол а, а с вертикальной плоскостью проекций —
угол р [а + р < 90°] (фиг. 154).
Решение. Предварительно проводим в стороне прямую, наклоненную
к плоскостям проекций под заданными углами. Для этого берем произвольную
точку А на вертикальной плоскости проекций и проводим через ее вертикальную
проекцию (а') прямую a'blt составляющую с осью проекций угол а. На этой прямой,
как на гипотенузе, строим прямоугольный треугольник с углом 0 при вершине а',
а'Ь1
для чего делим прямую а о1 пополам и радиусом, равным ——, описываем по-
луокружность. Затем проводим через точку а' катет, составляющий с прямой a'fej
угол 0, до пересечения с дугой в точке К и соединяем точки. К и bt. Катет Ка'
49
равен по величине вертикальной проекций вспомогательной прямой. Для того
чтобы установить ее положение, описываем из точки а' радиусом а'К дугу до
пересечения с осью проекции в точке £>'; а'Ь' — вертикальная проекция вспомога-
тельной прямой.
Катет Kbi определяет разность расстояний от концов горизонтальной проек-
ции прямой до оси проекций. Для того чтобы установить положение горизонтальной
проекции прямой, из точки /У восставляем к оси проекций перпендикуляр и на
нем откладываем отрезок bb', равный отрезку Kbt. Соединив точки а и />, полу-
чаем горизонтальную проекцию (ah) вспомогательной прямой. Теперь остается
провести через проекции (с, с') точки С проекции (inn, т'п') искомой прямой
параллельно проекциям ранее построенной прямой (ab, а'Ь').
Примечание. Точку А можно взять и на горизонтальной плоскости
проекций. Предлагаем учащимся решить этот случай.
Пример 38
Даны прямая ВС и точка А. Провести через точку А прямую, пере-
секающую прямую ВС под заданным утлом <р (фиг. 155).
Решение. Заключаем прямую (be, Ъ’с') и точку (а, а') в треугольник (abc,
а'Ь'с') и находим его действительную величину. Построив вспомогательный тре-
угольник АВС, проводим через точку А прямые AM и AN, составляющие с пря-
мой ВС заданный угол <р. Затем, отложив на прямой ЬС от точки b отрезки ЬМ
и bN, равные отрезкам ВМ и BN, и опустив перпендикуляры из точек М и N
на прямую Ьс, получаем точки т и п. По ним находим точки т' и п'.
Прямые (ат, а'т') и (ап, а'п') являются искомыми.
50
Пример 39
Даны прямая ВС и точка А. Найти на ВС точку, удаленную от точки
А на заданное расстояние / мм (фиг. 156).
Решение. Заключаем прямую (Ьс, Ь'с') и точку (a, o’) в треугольник (abc,
а'Ь'с'} и находим его действительную величину. Построив вспомогательный тре-
угольник АВС, описываем из точки А дугу радиуса I мм, пересекающую сторону
ВС в точках М и N. Отложив на прямой ЬС от точки Ь отрезки ЬМ и bN,
равные отрезкам ВМ и BN, и опустив перпендикуляры из точек и W на пря-
мую Ьс, получаем точки т и п. По ним находим точки т' и и'. Точки (т, т')
и (п, п') являются искомыми.
В частном случае может получиться одна точка (когда?) или вообще не
получится ни одной точки (когда?).
Пример 40
Дан треугольник АВС. Провести биссектрису угла А (фиг. 157).
Решение. Находим действительную величину треугольника (abc, а'Ь'с').
Строим вспомогательный треугольник АВС и проводим биссектрису угла А, кото-
рая пересекает сторону ВС в точке М. Отложив на прямой Ь'С от точки Ъ'
отрезок Ъ'М, равный ВМ, опускаем из точки М перпендикуляр на прямую Ь'с'.
и получаем точку т'. По ней определяем точку т. Прямая (ат, а'т') является
искомой.
Пример 41
Дана прямая АВ, пересекающая ось проекций. Провести биссектрису
угла между прямой АВ и осью проекций (фиг. 158).
51
Решение. Задаем произвольную точку (с с') на осп проекций и, соединив
ее с точкой (Ь, Ь'), получаем треугольник (abc, а'Ь'с'). Находим действительную
величину этого треугольника. Дальнейшее понятно из чертежа (см. пример 40).
Пример 42
Даны точка А и прямая MN. Построить прямоугольную трапецию
ABCD, зная, что большее основание ВС лежит па прямой MN, меньшее
основание AD равно АВ, а боковая сторона DC равна 1,15ЛВ (фиг. 159).
Решение. Для определения вершин В, С, D трапеции пользуемся вспомо-
гательным треугольником, для чего заключаем прямую (тп, т'п') и точку (а, а')
в треугольник (атп, а'т'п') и определяем его действительную величину. Строим
отдельно треугольник AMN. Вершиной В служит основание перпендикуляра, опу-
щенного из точки А на сторону MN. Проведя через точку А прямую параллельно
стороне MN и отложив на пей отрезок длины АВ, получаем вершину D. Для
определения вершины С описываем из точки D дугу радиуса, равного 1,15ЛВ,
пересекающую прямую MN. Теперь остается все это проделать последовательно
на эпюре.
Построение видно из чертежа.
Я
ЗАДАЧИ
50. Определить действительную длину отрезка прямой АВ и углы ее
наклона к плоскостям Н и V (фиг. 160).
51. Какой геометрический смысл имеет параллельность на эпюре про-
екций прямой общего положения? '
52. Провести через точку А (20, 35) прямую, равнонаклоненную
к плоскостям Н и V (задача неопределенная).
53. Построить действительную величину треугольника АВС (фиг. 161).
54. Провести через точку А (20, 35) прямую, параллельную вертикаль-
ной плоскости проекций и составляющую с горизонтальной плоскостью
проекций угол, равный 45°. Сколько таких прямых?
- 55. Провести через точку А (20, 30) прямую, составляющую с гори-
зонтальной плоскостью проекций угол 30° и с вертикальной плоскостью
проекций угол 45°. Сколько таких прямых?
56. Отложить на прямой АВ отрезок длиной 15 мм от точки А
к точке В (фиг. 162).
57. Найти центр круга, описанного около треугольника АВС (фиг. 163).
58. Найти центр круга, вписанного в треугольник АВС (фиг. 163).
59. Построить биссектрису угла АВС (фиг. 164, 165).
60. Опустить из точки А перпендикуляр на прямую ВС (фиг. 166).
61. Определить расстояние от точки А до прямой ВС (фиг. 166).
62. Определить расстояние между параллельными прямыми АВ и CD
(фиг. 167).
63. Построить шар с центром в точке С, касательный к прямой АВ
(фиг. 168).
Указание. См. задачу 61.
64. Найти на прямой АВ точку, отстоящую от точки С на 30 мм
(фиг. 168). Какие возможны случаи?
65. Найти точку пересечения прямой MN с поверхностью шара (фиг. 169).
Какие возможны случаи?
Указание. См. задачу 64.
54
66. Описать из точки С шар, отсекающий на заданной прямой АВ
отрезок длиной 40 мм (фиг. 168).
67. Построить прямоугольный треугольник АВС с прямым углом С
на прямой MN (фиг. 170). Какие возможны случаи?
68. Провести через точку С прямую, пересекающую прямую АВ под
острым углом <р, равным 30°, или 45°, или 60° (фиг. 168). Сколько может
быть таких прямых?
55
Фиг. 166
ba
Фиг. 168
69. Построить равнобедренный треугольник АВС с основанием ВС на
прямой MN, исходя из условия, что длина боковой стороны составляет
1,25 высоты (фиг. 171).
70. Построить равнобедренный треугольник АВС с основанием ВС
на прямой MN, исходя из условия, что длина этого основания составляет
1,5 высоты (фиг. 171).
71. Построить равнобедренный треугольник АВС с основанием ВС
на прямой MN, исходя из условия, что угол при основании равен 30°
(фиг. 171).
56
Фиг. 171
72. Построить равносторонний тре-
угольник АВС с основанием ВС на
прямой MN (фиг. 171).
73. Построить прямоугольный тре-
угольник АВС с катетом ВС на прямой
MN, исходя из условия, что длина ги-
потенузы равна 1,25/г (фиг. 172).
74. Построить прямоугольный тре-
угольник АВС с катетом ВС на пря-
мой MN, исходя из условия, что
ia
острый угол С равен 30° (фиг. 172).
75. Построить прямоугольный равнобедренный треугольник АВС
с гипотенузой ВС на' прямой MN (фиг. 171).
76; Построить прямоугольный равнобедренный треугольник АВС
с катетом ВС на прямой MN (фиг. 172).
77. Построить прямоугольник ABCD с большим основанием ВС на
прямой MN, исходя из условия, что его площадь равна 1,5 АВ2 (фиг. 172).
78. Построить прямоугольник ABCD с большим основание^ ВС на
прямой MN, исходя из условия, что отношение его сторон равно 1,5
(фиг. 172).
S7
79. Построить квадрат ABCD со стороной ВС на прямой MN (фиг. 172).
80. Построить квадрат ABCD с диагональю BD на прямой MN (фиг. 171).
81. Построить ромб ABCD со стороной ВС на прямой MN, исходя
из условия, что длина его стороны составляет 1,2 высоты (фиг. 171).
82. Построить ромб ABCD со стороной ВС на прямой MN, исходя
из условия, что острый угол В равен 60° (фиг. 171).
83. Построить ромб ABCD с большей диагональю BD на прямой MN,
исходя из условия, что отношение его диагоналей равно 2 (фиг. 171).
84. Построить параллелограмм ABCD с основанием ВС на прямой MN,
исходя из условия, что острый угол В равен 60°, а длина диагонали АС
на 5 мм превышает величину боковой стороны (фиг. 171).
. 85. Построить параллелограмм ABCD с основанием ВС на прямой MN,
исходя из условия, что длина боковой стороны равна 1,25/’, а отношение
сторон равно 2 (фиг. 171).
86. Построить прямоугольную трапецию ABCD с большим основанием
ВС на прямой MN, исходя из условия, что AD = АВ,, a DC = 1,15АВ
(фиг. 172).
87. Построить прямоугольную трапецию ABCD с большим основанием
2
ВС на прямой MN, исходя из условия, что AD =АВ — ~ВС (фиг. 172).
88. Построить прямоугольную трапецию ABCD с большим основанием
ВС на прямой MN, исходя из условия, что AD = АВ и угол С — 45°
(фиг. 172).
89. Построить равнобедренную трапецию ABCD с большим основанием
ВС на прямой MN, исходя из условия, что АВ = AD — DC — 40 мм
(фиг. 171).
90. Построить равнобедренную трапецию ABCD с большим основанием
ВС на прямой MN, исходя из условия, что острый угол В = С равен 45°,
а меньшее основание равно боковой стороне (фиг. 171).
Глава IX
ДЕЛЕНИЕ ОТРЕЗКА В ДАННОМ ОТНОШЕНИИ
Е ,П
Если точка делит в пространстве отрезок в отношении —, то и проекции
п
Точки делят одноименные проекции отрезка в том же отношении.
Следовательно, для деления (па эпюре) отрезка в данном отношении опреде-
лять его действительную величину не нужно.
ПРИМЕРЫ
Пример 43
Даны прямая MN и точка С. Провести через точку С прямую, пере-
секающую заданную прямую в точке, делящей ее отрезок между следами
в отношении 2:3 в направлении от Я к У (фиг. 173).
Решение. По известному правилу находим следы заданной прямой (»ш, т'С)
и делим одну из ее проекций, например горизонтальную, в заданном отношении
2:3 точкой к. По точке к находим вертикальную проекцию (!') точки на верти-
58
калькой проекции (т'п1) прямой MN. Затем проводим проекции искомой прямой
через одноименные проекции точек К и С, а именно: горизонтальную проекцию
прямой через точки к и с; вертикальную проекцию прямой через тсгФси к' и с'.
ЗАДАЧИ
а
Фиг. 175
59
Фиг. 174
ьа
92. Провести через точку С прямую, пересекающую отрезок АВ в точке,
„ ml.,
делящей его в заданном отношении — = -у (фиг. 176).
93. Найти центр тяжести площади треугольника АВС (фиг. 163).
Указание. Центр тяжести площади треугольника лежит в точке пересечения его'
медиан.
94. Найти центр тяжести периметра треугольника АВС (фиг. 163).
Указание. Центр тяжести периметра треугольника находится в центре круга,
вписанного в треугольник, вершины которого лежат на срединах сторон данного
треугольника.
Глава X
НЕКОТОРЫЕ СЛУЧАИ ПРОЕКТИРОВАНИЯ УГЛОВ
Любой угол, стороны которого расположены параллельно плоскости проекций,
проектируется на эту плоскость без искажения.
Прямой угол, у которого хотя бы только одна сторона параллельна
плоскости проекций, проектируется на эту плоскость тоже прямым углом
(т. е. без искажения).
Таким образом, если в пространстве даны две взаимно перпендикулярные
пересекающиеся прямые, из которых одна расположена параллельно’ плоскости
проекций, то их проекции на этой плоскости тоже будут взаимно перпендикулярны
(см. гл. VII, о перпендикулярности двух прямых).
ПРИМЕРЫ
Пример 44
Даны прямая АВ и точка С. Провести через точку С прямую, пере-
секающую прямую АВ под прямым углом (фиг. 177).
Решение. Искомая прямая должна удовлетворять в пространстве трем
условиям, а именно: проходить через точку С, быть перпендикулярной К прямой
АВ, параллельной вертикальной плоскости проекций, и пересекать прямую АВ.
На эпюре проекции искомой прямой должны пройти через одноименные проекции
точки С; вертикальные проекции прямых, заданной и искомой, должны быть
взаимно перпендикулярны, и, наконец, точки пересечения одноименных проекций
должны лежать на общем перпендикуляре к оси проекций.
Следовательно, проводим через точку с' вертикальную проекцию искомой
прямой — перпендикулярно прямой а'Ь' до пересечения с ней в точке к'. По точке к?
находим точку к на горизонтальной проекции (ab) прямой АВ и через нее про*
водим горизонтальную проекцию (ск) искомой прямой.
Пример 45
Прямые АВ и CD пересечь третьей прямой, перпендикулярной к ним
(фиг. 178).
Решение. Искомая прямая MN — профильная, так как она должна быть перпен-
дикулярна прямой АВ, которая параллельна оси проекций. Для того чтобы иско-
мая прямая MN была перпендикулярна также прямой CD, необходимо, чтобы
профильные их проекции (т"п" и c"d") были взаимно перпендикулярны (теорема
проектирования прямого угла).
Отсюда — через а"Ь" проводим лийию т"п" перпендикулярно с"4" до их взаим-
ного пересечения в точке п". Затем, найдя по точке в" точки п и п' на одно-
именных проекциях прямой CD, проводим прямые /ив и т'п'.
Пример 46
Даны прямая АВ и точка С. Определить расстояние от точки С до
прямой АВ (фиг. 179).
61
п'
О
Фиг. 179
П
Решение. Опускаем из точки (е, с)
перпендикуляр на прямую (ab, а’Ь') и
находим его основание (/с, к'\ для чего про-
водим через точку с прямую перпендику-
лярно прямой at>; получив на их пересе-
чении точку к, по ней находим точку к'-
после этого определяем действительную
длину отрезка (ск, с'к').
Фиг. 180
Пример 47
Даны прямая MN, параллельная горизонтальной плоскости проекций,
п вертикальная проекция перпендикулярной к ней прямой АВ. Построить
прямоугольник ABCD с основанием ВС на прямой MN, исходя из условия,
что его длина равна 1,5ЛВ (фиг. 180).
Решение. Определяем точку b и, проводя через нее прямую, перпендикуляр-
ную к прямой тп, находим горизонтальную проекцию (лЬ) боковой стороны.
Найдя истинную величину аВ стороны (ab, а’Ь’), откладываем на прямой (тп, т'п)
от точки (Ь, Ь’) отрезок длиной 1,5 аВ. Получив точку (с, с'), проводим через эту
точку и точку (<т, а’) прямые параллельно сторонам (ab, а'Ь') и (Ъс, Ь'с').
ЗАДАЧИ
95. Провести через точку С прямую, пересекающую прямую АВ и пер-
пендикулярную к ней (фиг. 181 — 185).
96. Пересечь прямые АВ и CD прямой, к ним перпендикулярной
(фиг. 186, 187).
62
a A t
Фиг. 181
63
97. Опустить из точки С перпендикуляр на прямую АВ (фиг. 188, 189).
98. Определить расстояние от точки С до прямой АВ (фиг. 188, 189).
99. Определить расстояние между параллельными прямыми АВ и CD
(фиг. 190— 194).
100. Определить расстояние между скрещивающимися прямыми АВ
и CD (фиг. 195, 196).
64
к
f
i-
6 I
ab ।
।
cd
Фиг. 190
3 Арустамов X'. A.. 65
b'
I
1
ab
Фиг. 197
101. Определить недостающую проекцию точки С, исходя из условия,
что расстояние I от точки С до прямой АВ равно 30 мм (фиг. 197—201).
Какие возможны случаи?
102. Определить недостающую проекцию прямой CD, параллельной
прямой АВ, исходя из условия, что между ними расстояние I = 20 мм
(фиг. 202—206). Какие возможны случаи?
66
103. Построить шар с центром в точке С, касательный к прямой А В
(фиг. 207, 20S).
Указание. См. задачу 98.
104. Найти на прямой АВ точку, отстоящую от точки С на 40 мм
(фиг. 209). Какие возможны случаи?
105. Найти точку пересечения прямой АВ с поверхностью тара
(фиг. 210). Какие возможны случаи'?
Указание. См. задачу 104.
106. Описать из точки С шар, отсекающий на заданной прямой АВ
отрезок длиной / = 40 мм (фиг. 211).
69
107. Построить прямоугольный треугольник ЛВС с прямым углом В
на прямой EF (фиг. 212). Какие возможны случаи?
108. Провести через точку С прямую, пересекающую прямую MN под
острым углом (р, равным 30°, или 45°, или 60° (фиг. 213), Сколько может
быть таких прямых?
109. Построить равнобедренный треугольник ЛВС с основанием ВС
на прямой Л/Л7, исходя из условия, что длина боковой стороны равна
l,25/i (фиг. 214)
110. Построить равнобедренный треугольник ЛВС с основанием ВС
на прямой Д/Л7. исходя из условия, что его д шпа рлвш 1,5/) (фиг. 215).
111. Построить равнобедренный треугольник .-1ВС с основанием ВС
на прямой MN, исходя из условия, что угол при основании равен 30э
(фиг. 214).
112. Построить равнобедренный треугольник АВС с основанием ВС
на прямой Л/Л’, исходя из условия, что его боковая сторона больше
высоты АВ на 10 мм (фиг. 214).
113. Построить равнобедренный треугольник АВС с основанием ВС
на прямой MN и с вершиной А на прямой EF, исходя из условия, что
точка К является основанием высоты АК, а боковая сторона равна
1,15АК (фиг. 216).
114. Построить равнобедренный треугольник ЛВС, исходя из условия,
что его основание ВС, длина которого равна 60 мм, расположено на
прямой A1N, вершина А — на прямой EF, перпендикулярной к MN, причем
высота треугольника равна 40 мм (фиг. 217).
Фиг. 213 Фиг. 214
70
115. Построить равнобедренный треугольник АВС с основанием ВС
на прямой MN, исходя из условия, что его высота AD, равная 40 мм,
лежит на прямой EF и угол при основании равен 30' (фиг. 217).
116. Построить равнобедренный треугольник АВС с вершиной А на
прямой EF (фиг. 218).
117. Построить равносторонний треугольник АВС с основанием ВС,
лежащим на прямой MN (фиг. 214).
118. Построить равносторонний треугольник АВС с основанием ВС
на прямой MN, исходя из условия, что точка К является основанием
высоты (фиг. 219).
119. Построить прямоугольную трапецию ABCD с большим основанием
ВС па прямой MN, исходя из условия, что AD = АВ; DC — 1,15ЛВ
(фиг. 220).
120. Построить равносторонний треугольник АВС с основанием ВС,
лежащим на прямой MN, исходя из условия, что его высота AD, равная
40 мм, лежит на прямой EF (фиг. 217).
121. Построить равносторонний треугольник АВС с основанием ВС,
равным 50 мм и лежащим на прямой MN, и с вершиной А на прямой
EF, перпендикулярной к MN (фиг. 217).
122. Построить прямоугольный треугольник АВС с катетом ВС на
прямой MN, исходя из условия, что длина гипотенузы равна 1,25 h
(фиг. 220).
123. Построить прямоугольный треугольник АВС с -катетом ВС на
прямой MN, исходя из условия, что острый угол С равен 30° (фиг. 220).
124. Построить прямоугольный равнобедренный треугольник АВС
с гипотенузой АС на прямой MN. (фиг. 221).
125. Построить прямоугольный равнобедренный треугольник АВС
с катетом ВС на прямой MN (фиг. 220).
126. Построить прямоугольный треугольник АВС с катетом ВС на
прямой MN, исходя из условия, что радиус круга, описанного около тре-
угольника, равен 0,75АВ (фиг. 220).
127. Построить прямоугольный, равнобедренный треугольник АВС с ка-
тетом ВС на прямой ВМ и с вершиной А на прямой EF (фиг. 222).
128. Построить прямоугольный треугольник АВС с основанием ВС
на прямой MN, исходя из условия, что катет АВ, длина которого равна
30 мм, лежит на прямой EF и площадь треугольника составляет 0,75ЛВ2
(фиг. 223).
129. Построить прямоугольник ABCD с большим основанием ВС на
прямой MN, исходя из условия, что его площадь равна 1,5 АВ2 (фиг. 220).
130. Построить прямоугольник ABCD с большим основанием ВС на
прямой MN, исходя из условия, что отношение его сторон равно 1,5
(фиг. 220).
73
131. Построить прямоугольник ABCD с большей стороной ВС на пря-
мой ВМ, исходя из условия, что отношение его сторон равно 2 (фиг. 224).
132. Построить прямоугольник ABCD с большей стороной ВС на
прямой ВМ и с вершиной А на прямой EF, исходя из условия, что его
диагональ равна 2АВ (фиг. 222).
133. Построить прямоугольник ABCD с большей стороной ВС на пря-
мой MN, исходя из условия, что сторона АВ, длина которой составляет
40 мм, лежит на прямой EF и отношение его сторон равно 1,5 (фиг. 223).
134. Построить прямоугольник ABCD с вершиной А на прямой EF
и вычислить его площадь (фиг. 225).
135. Построить квадрат ABCD со стороной ВС на прямой MN (фиг. 220).
136. Построить квадрат ABCD с диагональю BD на прямой MN
(фиг. 214).
137. Построить квадрат ABCD со стороной АВ на прямой BE (фиг. 226).
138. Построить квадрат ABCD со стороной ВС па прямой ВМ (фиг. 224).
139. Построить квадрат ABCD со стороной ВС на прямой ВМ, исходя
из условия, что вершина А лежит на прямой EF (фиг. 227).
140. Построить квадрат ABCD с диагональю BD на прямой MN, исходя
из условия, что вершина А лежит на прямой EF и точка К есть пере-
сечение диагоналей (фиг. 216).
141. Построить квадрат ABCD с диагональю BD на прямой MN
(фиг. 228).
142. Построить параллелограмм ABCD с основанием ВС на прямой MN,
исходя из условия, что острый угол В равен 60, а длина диагонали АС
на 5 мм больше боковой стороны (фиг. 220).
143. Построить параллелограмм-ABCD с основанием ВС на прямой MN,
исходя из условия, что длина боковой стороны равна 1,25/1 и отношение
сторон равно 2 (фиг. 220).
74
75
144. Построить прямоугольную трапецию 4 BCD с большим основанием
2
ВС на прямой MN, исходя из условия, что AD = AB=— ВС (фиг. 220).
145. Построить параллелограмм ABCD с большей стороной ВС на
прямой MN и с вершиной А на прямой EF, исходя из условия, что
сторона АВ больше высоты АК па 5 мм и сторона ВС равна 1,5АК
(фиг. 229).
146. Построить параллелограмм ABCD со стороной ВС длиной 60 мм
и расположенной на прямой ВМ, исходя из условия, что его высота АК
лежит на прямой EF и длина боковой стороны равна 40 мм (фиг. 230).
147. Построить ромб ABCD со стороной ВС на прямой MN, исходя
из условия, что длина его стороны равна 1,2ft (фиг. 220).
148. Построить ромб ABCD со стороной ВС на прямой MN, исходя
из условия, что острый угол В равен 60° (фиг. 220).
149. Построить ромб ABCD с большей диагональю BD на прямой MN,
исходя пз условия, что отношение его диагоналей равно 2 (фиг. 215).
150. Построить ромб ABCD со стороной ВС на прямой MN, исходя
из условия, что длина его стороны равна 1,2 высоты АК (фиг. 219).
151. Построить прямоугольную трапецию ABCD с большим основанием
ВС на прямой MN, исходя пз условия, что AD = АВ и угол С равен 45°
(60°, 30°) (фиг. 220).
152. Построить ромб ABCD с большей диагональю BD на прямой MN,
исходя из условия, что меньшая диагональ, длина которой равна 40 мм,
лежит на прямой EF, а площадь ромба равна АС2 (фиг.^17).
153. Построить ромб ABCD с вершиной А на прямой EF (фиг. 231).
154. Построить равносторонний треугольник АВС с основанием ВС,
лежащим на прямой MN, и с вершиной А на прямой EF, исходя из
условия, что точка К является основанием высоты АК (фиг. 232).
155. Построить параллелограмм ABCD с большей стороной ВС на
прямой MN, шсходя из условия, что точка К — основание высоты — делит
ее в отношении 1:2 от точки В к точке С и угол В равен 60° (фиг. 233).
156. Построить ромб ABCD с большей диагональю BD на прямой MN
и с вершиной А на прямой EF, исходя из условия, что точка. К есть
пересечение диагоналей, а их отношение равно 2 (фиг. 232).
157. Построить прямоугольную трапецию ABCD с большим основанием
ВС на прямой ВМ, исходя из условия, что AD = АВ; CD = 1,2АВ; В = 90°
(фиг. 224).
158. Построить прямоугольную трапецию ABCD с большим основанием
ВС на прямой ВМ, исходя из условия, что вершина А лежит на прямой
EF; AD = АВ; В = 90°; С = <р° (фиг. 227).
159. Построить прямоугольную трапецию ABCD с большим основанием
ВС на прямой MN и со стороной АВ на прямой EF, исходя из условия,
чего В = 90°; AD = АВ = 40 мм; С = 45° (фиг. 223).
77
160. Построить равнобедренную трапецию ABCD с большим основа-
нием ВС на прямой MN, исходя из условия, что АВ = AD = DC — 40 мм
(фиг. 220).
161. Построить равнобедренную трапецию ABCD с большим основанием
ВС на прямой MN, исходя из условия, что острый угол равен 45° и мень-
шее основание равно боковой стороне (фиг. 220).
162. Провести через точку В прямую, расположенную под углом 70°
к горизонтальной плоскости проекций и удаленную от прямой АВ на 20 мм
(фиг. 234).
РАЗДЕЛ ВТОРОЙ
Глава XI
ПЛОСКОСТЬ
Плоскость может быть задана в пространстве следующими геометрическими
элементами:
1) тремя точками, не лежащими на одной прямой;
2) прямой и точкой, не лежащей на этой прямой;
3) двумя пересекающимися прямыми;
4) двумя параллельными прямыми.
Плоскость, произвольно наклоненную к плоскостям проекций, называют
плоскостью общего положения.
Плоскость, перпендикулярную к горизонтальной плоскости проекций, называют
горизонта л ьно-проект и рующей плоскостью.
Плоскость, перпендикулярную к вертикальной плоскости проекций, называют
вертикальпо-проектирующей плоскостью.
Плоскость, перпендикулярную к профильной плоскости проекций, называют
профилыю-проектпрующей плоскостью.
Точка, взятая на какой-либо из прямых, определяющих плоскость, лежит на
этой плоскости.
Прямая лежит в плоскости, если она имеет с плоскостью две общие точки.
Г ори зон талью плоскости называют прямую, лежащую в этой плоскости
и параллельную горизонтальной плоскости проекций.
Ф р о и т а л ыо плоскости называют прямую, лежащую в этой плоскости
и параллельную' вертикальной плоскости проекций.
Линией наибольшего ската плоскости называют лежащую в этой
плоскости прямую, которая перпендикулярна произвольной горизонтали плоскости.
Произвольная точка лежит на плоскости, если она взята на прямой, лежащей
в этой плоскости.
До решения помещенных ниже примеров необходимо предварительно разобрать
задачи 163-171.
ПРИМЕРЫ
Пример 48
В плоскости, заданной параллельными прямыми АВ и CD, провести
произвольную прямую (фиг. 235).
Решение. Задаемся на прямых (ab, а'Ь') и (cd, c’d') произвольными точками
(т, ш') и (п, п') и проводим через них прямую (тп, т'п').
Пример 49
Дана плоскость пересекающимися прямыми АВ и CD. Лежит ли пря-
мая MN в этой плоскости (фиг. 236)?
Решение. Обозначаем точки пересечений вертикальных проекций прямых
79
АВ и MN через к’ и прямых CD и MN через Г. Строим горизонтальные их
проекции — точки к и I на горизонтальной проекции (mn) прямой MN. Из построе-
ния видно, что точки (к, к') и (Z, Г) прямой MN на заданной плоскости не лежат.
Следовательно, прямая MN в плоскости не лежит.
Решение этой задачи можно начать и с пересечений горизонтальных
проекций — точек к и I.
Пример 50
Даны плоскость параллельными прямыми АВ и CD и горизонтальная
проекция прямой MN, лежащей в этой плоскости. Найти ее вертикальную
проекцию (фиг. 237).
Решение. Обозначаем точки пересечений горизонтальных проекций прямых
АВ и MN через к и прямых CD и MN — через I.
Определив по точкам к и I точки к' на прямой а'Ь' и I' на прямой c'd’,
проводим искомую вертикальную проекцию (т'п) прямой через найденные точки
к' и Г.
Пример 51
В плоскости, заданной прямой АВ и точкой С, провести горизонталь
на расстоянии 15 мм от горизонтальной плоскости проекций (фиг. 238).
Решение. От задания плоскости прямой и точкой прежде всего переходим
к заданию плоскости двумя прямыми, например пересекающимися. Для этого,
задавшись произвольной точкой (к, к') на прямой (ab, а'Ь'), проводим проекции
прямой (ск, с'к'). Затем на расстоянии 15 мм от оси проекций проводим парал-
лельную ей вертикальную проекцию (н/п) горизонтали, которая пересекает прямые
а'Ь' и с'к' в точках d’ и е'. Наконец, находим точки d и е на прямых ab и ск
и через них проводим горизонтальную проекцию (тп) горизонтали (на чертеже
дано одно решение).
81
Пример 52
В плоскости, заданной двумя параллельными прямыми АВ и CD, про-
вести фронта ль на расстоянии 15 мм от вертикальной плоскости проекций
(фиг. 239).
Решение. Проводим на расстоянии 15 мм от оси проекций параллельную
ей горизонтальную проекцию (тп) фронтали, которая пересекает прямые ah и cd
в точках к и к Затем находим точки к' и Г на прямых а'Ь' и с'сГ и проводим
через них вертикальную проекцию (ш'н') фронтали (дано одно решение).
Пример 53
В плоскости, заданной пересекающимися прямыми АВ и CD, провести
линию наибольшего ската (фиг. 240).
Решение. Проводим произвольную горизонталь [тп, т’п’) плоскости. Так как
линия наибольшего ската должна быть перпендикулярна этой горизонтали, прово-
дим ее горизонтальную проекцию, например (И<). перпендикулярно горизонтальной
проекции (/mi) горизонтали (теорема проектирования прямого утла), а затем по
горизонтальной проекции (ск) — .шшш наибольшего ската — находим ее вертикаль-
ную проекцию (е’к’).
Пример 54
Взять на плоскости треугольника АВС произвольную точку К (фиг. 241).
Решение. Проводим в плоскости треугольника bciiomoiаш.тьную прямую,
например (тн, /пн'), и на ней берем произвольную точку (/<, /<’) Последняя и лежит
на плоскости треугольника.
82
Пример 55
Даны плоскость точкой С и прямой АВ и точка К. Лежит ли точка К
на плоскости (фиг. 242)?
Решение. Проводим через точки с' и к' вертикальную проекцию вспомога-
тельной прямой до пересечения с прямой а'Ь' в точке т'. Находим точку т
на прямой ab и проводим через точки с и т горизонтальную проекцию (ст)
вспомогательной прямой. Прямая (ст, с'т') лежит в заданной плоскости и, как
видно из чертежа, точка (к, к') на этой прямой не лежит. Следовательно, точка
(к, к') на данной плоскости не лежит.
Пример 56
Даны плоскость пересекающимися прямыми АВ и CD и горизонталь-
ная проекция (к) точки К, лежащей на этой плоскости. Найти ее верти-
кальную проекцию (к'), пользуясь фронталью (фиг. 243).
Решение. Проводим через точку к параллельно оси проекций горизонталь-
ную проекцию (ши) фронтали, которая пересекает прямые ab и cd в точках ей/.
Находим точки е' и /' на прямых а'Ь' и c'd' и проводим через них вертикальную
проекцию (т'п') фронтали. Фронталь (нш, т'п') лежит в заданной плоскости; для
того, чтобы точка (к, к') лежала на плоскости, берем точку к' на прямой т'п'.
ЗАДАЧИ
163. Задать произвольную горизонтально-проектирующую плоскость:
1) двумя пересекающимися прямыми;
2) прямой и точкой.
83
164. Задать плоскость, параллельную вертикальной плоскости проекций:
I) двумя параллельными прямыми;
2) тремя точками.
165. Что на .эпюре характерно для геометрических элементов, опре-
деляющих горизонтально-проектирующую плоскость?
166. Задать произвольную вертикально-проектпрующую плоскость:
1) двумя параллельными прямыми;
2) тремя точками.
167. Задать плоскость, параллельную горизонтальной плоскости проек-
ций :
1) двумя пересекающимися прямыми;
2) прямой п точкой.
168. Ч го на эпюре характерно для геометрических элементов, опре-
деляющих вертикально-проектпрующую плоскосгь?
169. Задать произвольную профильно-проектирующую плоскость:
1) двумя пересекающимися прямыми;
2) двумя параллельными прямыми;
3) прямой и точкой;
4) тремя точками.
170. Что на эпюре характерно для геометрических элементов, опреде-
ляющих профильно-проектирующую плоскость?
171. Задать плоскость общего положения;
1) двумя пересекающимися прямыми;
2) двумя параллельными прямыми;
3) прямой и точкой;
4) тремя точками.
172. Построить на заданной плоскости геометрическое место точек,
удаленных от плоскости Н на 15 мм (фиг. .244 -247).
84
85
173. Построить на заданной плоскости геометрическое место точек,
удаленных от плоскости У на 15 мм (фиг. 244-247).
174. Дана вертикальная проекция точки, лежащей на плоскости, задан-
ной двумя параллельными прямыми АВ и CD. Найти ее горизонтальную
проекцию (фиг. 248).
86
175. Дана горизонтальная проекция точки, лежащей на плоскости, за-
данной прямой АВ и точкой С. Найти ее вертикальную проекцию (фиг. 249).
176. Дана вертикальная проекция треугольника KMN, лежащего в пло-
скости, заданной двумя параллельными прямыми АВ и CD. Найти его
горизонтальную проекцию (фиг. 250).
177. Выяснить, лежат ли все четыре точки А, В, С и D на одной пло-
скости (фиг. 251).
178. Определить горизонтальную проекцию плоского пятиугольника
ABCDE, зная вертикальную его проекцию п горизонтальную проекцию
двух смежных сторон (фиг. 252).
179. Дана пирамида SABCD (фиг. 253):
1) Взять произвольную точку К на ее грани SBC;
2) Найти вертикальную проекцию (ш ) точки М, лежащей на грани SCD,
по ее горизонтальной проекции (ш); «
3) Найти горизонтальную проекцию (е) точки Е, лежащей на грани SAB,
по ее вертикальной проекции (/);
4) Провести через точку N грани SAD ее линию наибольшего ската.
Глава XII
ЗАДАНИЕ ПЛОСКОСТИ СЛЕДАМИ.
ПРЯМАЯ И ТОЧКА В ПЛОСКОСТИ
В частном случае прямые, определяющие плоскость, могут лежать в самих
плоскостях проекций. Тогда эти прямые называют следами плоскости, потому что
по этим прямым определяемая ими плоскость пересекается с плоскостями проекций.
Прямую, лежащую в данной плоскости и в горизонтальной плоскости проек-
ций, называют горизонтальным следом плоскости.
Прямую, лежащую в данной плоскости и в вертикальной плоскости проекций,
называют вертикальным следом плоскости.
4 Общую точку следов плоскости называют точкой схода следов пло-
скости.
Плоскость, заданную следами, обозначают буквами Р, Q, R, S, Т и т. д.
Горизонтальный след плоскости обозначают так: Р(„ Q>„ R^, Sh, Th и т. д.
Вертикальный след плоскости обозначают так: Рс, Qv, Rm S„, Т„ и т. д.
Точку схода следов плоскости обозначают так: Рх, Qx, Rx, Sx, Тх и т. д.
Любая точка, лежащая на горизонтальном или вертикальном следе плоскости,
лежит на этой плоскости.
Прямая лежит в плоскости, если ее следы лежат на одноименных следах
плоскости.
Горизонталь плоскости и горизонтальный след плоскости между собой парал-
лельны. Отсюда — проекции горизонтали параллельны одноименным проекциям
горизонтального следа плоскости.
Фронталь плоскости и вертикальный след плоскости между собой параллельны.
Отсюда — проекции фроптали параллельны одноименным проекциям вертикаль-
ного следа плоскости.
Линия наибольшего ската плоскости и горизонтальный след плоскости между
собой перпендикулярны. Отсюда: горизонтальная проекция линии наибольшего
ската плоскости перпендикулярна горизонтальному следу плоскости (точнее, гори-
зонтальной проекции горизонтального следа плоскости).
ЗАДАЧИ
180. Задать следами произвольную горизонтально-проектирующую
плоскость. Чему равен на эпюре угол между горизонтальным следом
этой плоскости и осью проекций?
87
181. Задать следами плоскость, параллельную вертикальной плоскости
проекций, проходящую через первую и четвертую четверти, вторую и
третью четверти.
182. Задать следами произвольную вертикально-проектирующую пло-
скость. Чему равен на эпюре угол между вертикальным следом этой
плоскости и осью проекций?
183. Задать следами плоскость, параллельную горизонтальной плоскости
проекций и проходящую через первую и вторую четверти, третью и чет-
вертую четверти.
184. Задать следами ирофильно-проектирующую плоскость, проходя-
щую через четверти: вторую, первую и четвертую; первую, вторую и
третью; первую, четвертую и третью; вторую, третью и четвертую.
185. Что означает слияние на эпюре следов профи.тьно-проектирующей
плоскости?
186. Задать плоскость, проходящую через ось проекций и через четверти:
первую и третью, вторую и четвертую.
187. Задать плоскость общего положения: остроугольную, тупоуголь-
ную, ио слившимися следами.
188. Плоскость, параллельная горизонтальной (или вертикальной) пло-
скости проекций, задается единственным следом. Однако прямая, как
извеепто, нс определяет собой единственной’ плоскости в простран-
стве. Нет ли в этом противоречия?
189. Какое требуется дополнение при задании следами плоскости,
проходящей через ось проекций?
19(1. Какие две прямые являются следами:
Г) плоскости общего положения;
2) горизонтально проектирующей плоскости;
3) вер 1 икалыю-проектирующей плоскости;
41 и роф| 1.11; т ю -1i роектиру ющей плоскост и ?
191. Чт о па эпюре характерно для т очек, линий, плоских фигур, лежащих;
1) в । оризон гально-проектирующей плоскости;
2) н вер гика л и но-проект ирующей плоскости;
3) в профильно-проектирующей плоскости?
192. Как па эпюре расположены проекции горизонтали плоскости общего
положения, заданной следами? (Почему?)
193. Как ла эпюре расположены проекции фронтали плоскости общего
положения, заданной следами? (Почему'?)
194. Какая прямая является горизонталью вертикалыто-ироектирутощей
плоское! и?
195. Какая прямая является фронталыо грризон гально-проектирующей
плоскости?
196. Какая прямая является горизонталью нрофи.тыто-проектирующей
плоское in'?
197. Какая прямая является фронталыо профильно-цроектирующей
плоскости?
198. Какая прямая является линией наибольшего ската профилыю-
проект прующей илоскост и?
88
ПРИМЕРЫ
Пример 57
Построить следы плоскости, заданной прямой АВ и точкой С,(фиг. 254).
Решение. Искомые следы плоскости обозначаем через Ph и Р„. Для того
чтобы провести вертикальный след (Р„) плоскости, необходимо иметь две точки
этой плоскости, лежащие на вертикальной плоскости проекций. Одна такая точка
(с, с') уже дана. Второй точкой будет служить вертикальный след (и, и') прямой
(ah, a'b'). Находим точку (г, г') п проводим проекции искомого вертикального следа
(Р„) плоскости: вертикальную - через точки с’ и г' до пересечения с осью проекций
в точке Рх и горизонтальную — через точки сиг, совпадающую с осью проекций.
Одну точку (Рх) горизонтального следа Ph имеем; находим горизонтальный след
(й, 11') прямой (ab, а'Ь'). Получаем вторую точку горизонтального следа плоскости.
Проводим проекции искомого горизонтального следа (Ph) плоскости: горизон-
тальную - через точки h и Рх п вертикальную — через точки Рх и К, совпадаю-
щую с осью проекций.
Вывод. С осью проекций всегда совпадают горизонтальная проекция
вертикального следа плоскости и вертикальная проекция горизонтального следа
плоскости (Почему?).
Пример 58
Построить следы плоскости, заданной двумя пересекающимися пря-
мыми АВ и CD (фиг. 255).
Решение. Находим следы (й, Л') и (и. г7) прямой (ab, а'Ь1) и след (hlt h\)
прямой (cd, c'd'). Проводим горизонтальный след (Ph) искомой плоскости Р —
через точки h и й, и вертикальный след
(P.J-- через точку |/, параллельно прямой
подтверждает правильность решения за-
Фиг. 255
Фиг. 254
89
Пример 59
Построить следы плоскости, заданной прямой А В и точкой С (фиг. 256).
Решение. Прямая АВ и точка С определяют плоскость общего положения
(почему?).
Обозначаем ее следы через Р,, и Р,„ Переходим от задания плоскости прямой
и точкой к заданию ее двумя пересекающимися прямыми, для чего проводим
через точку (с, с') прямую (горизонталь) параллельно 1 оризонталыюй плоскости
проекций, пересекающую прямую (ah, ah') в точке (к, к'}. Точкой схода следов
(PJ плоскости будет служить точка прямой (ab, ah'), лежащая на оси проекций
(почему?). Найдя вертикальный след (г, г') горизонтали, проводим вертикальный
след (Р,.) плоскости через точки Р, и v'; горизонт альный след (Р,,} плоскости
проводим через точку Рх параллельно горизонтальной проекции горизонтали.
90
Пример 60
Построить следы плоскости, заданной двумя параллельными прямыми
АВ и CD (фиг. 257).
Решение. Прямые АВ и CD определяют плоскость, параллельную оси
проекций (почему?), следы которой Р,, и Р„ параллельны оси проекций. Для того
чтобы провести горизонтальный след (Pj, нужна только одна точка плоскости,
лежащая па горизонтальной плоскости проекций; для того чтобы провести верти-
кальный след (Рг), нужна только одна точка плоскости, лежащая на вертикальной
плоскости проекций. Прямые (</(>, а'Ь’) и (с<7, c'd') не могут пересекать плоскости Н
и И; пересекаем их произвольно вспомогательной прямой MN и находим ее
следы. Действительно, точки (/?, /1') и (г, с') лежат на заданной плоскости, потому
что они находятся на прямой, лежащей в плоскости. Проводим через точку v'
вертикальный след (PL) плоскости — параллельно оси проекций и через точку h —
горизонтальный след (Р(]) плоскости — тоже параллельно оси проекций.
В ы в о д. Для того чтобы перейти от задания плоскости не следами (напри-
мер, двумя пересекающимися или двумя параллельными прямыми) к заданию ее
следами, нужно найти следы заданных прямых и провести через них одноименные
следы плоскости. В тех случаях, когда плоскость задана прямой и точкой или
тремя точками, нс лежащими на одной прямой, следует предварительно перейти
к заданию ее двумя пересекающимися или двумя параллельными прямыми,
а затем поступить гак, как указано выше.
Пример 61
Найти профильный след плоскости Р (фиг. 258).
Решение. Профильный след (Р„) плоскости должен проходить через про-
фильные следы прямых (следов) Р,, и Р„. Прямая Р„ не имеет профильного следа.
Находим профильный след (И’> прямой Ph и проводим профильный след (Pw)
плоскости через точку W параллельно осп OZ.
Точку W обозначают также буквой Р с индексом у (Ру).
Пример 62
Найти профильный след плоскости Р
Р е ш с н и с. 11аходим профильные
следы (И') и (Il'j) прямых (следов) Р(, и
Р^. и проводим через точки Ifu 1Ц искомый
профильный след (PJ плоскости.
Точки W и И) обозначают также че-
рез Р, и Р-.
Пример 63
Лежит ли прямая АВ в плоскости
Р (фиг. 261)?
Решение. Строим следы прямой
АВ: горизонтальный (й, /,') и вертикальный
(с, г'). Следы заданной прямой (ab, а’Ь')
лежат на одноименных следах плоскости.
Следовательно, прямая АВ лежит в
плоскости (по теореме).
Пример 64
Лежит ли прямая АВ в плоскости
Р (фиг. 262)?
Решение. Прямая (ah, a'b') имеет
единственный профильный след. Построим
(фиг. 259, 260).
91
след прямой и профильный след плоскости. Профильный след ([Г) прямой лежит
на профильном следе (Р„.) плоскости. Следовательно, прямая АВ лежит в пло-
ское i n В.
Ниже показано решение этой же задачи без профильной плоскости проекций.
Пример 65
В плоскости Р провести произвольную прямую, проходящую через
вторую, первую и четвертую четверти пространства (фиг. 263).
Решение. Известно, что следы искомой прямой должны лежать на одно-
именных следах плоскости. Любая прямая, проходящая через вторую, первую
и четвертую четверти пространства, имеет горизонтальный след на передней поле
92
горизонтальной плоскости проекций и вертикальный следчна верхней поле верти-
кальной плоскости проекций, которые на эшоре располагаются так: вертикальный —
над осью проекций, а горизонтальный — под осью проекций.
Задаемся произвольно на горизонтальном следе (PJ плоскости точкой-следом
(й, h'), а на вертикальном следе (Р„) - точкой-следом (с, </) и проводим проекции
искомой прямой: горизонтальную — через точки h и v и вертикальную — через
точки /1' и и'.
Пример 66
В плоскости Р провести произвольную прямую, проходящую через
третью и четвертую четверти (фиг. 264).
Решение. Прямая, проходящая через третью и четвертую четверти про-
странства, имеет единственный вертикальный след на нижней поле вертикальной
плоскости проекции, который па эпюре располагается под осью проекций.
Задаемся па вертикальном следе (Рг) плоскости точкой (г, г') и проводим через
нее проекции искомой прямой (горизонтали): вертикальную — через точку v'
параллельно оси проекций и горизонтальную — через точку г параллельно гори-
зонтальному следу (Р,,) плоскости.
93
В плоскости Р провести произвольную прямую, проходящую через
вторую и третью четверти (фиг. 265).
Решение. Прямая, проходящая через вторую и третью четверти простран-
ства, имеет единственный горизонтальный след на задней поле горизонтальной
плоскости проекций, который на эпюре располагается над осью проекций.
Задаемся на продолжении горизонтального следа (PJ плоскости точкой (h, /1')
и проводим через нее проекции искомой прямой (фронтали): горизонтальную —
через точку h параллельно оси проекций и вертикальную — через точку Л' парал-
лельно вертикальному следу (Pj плоскости.
Пример 68
В плоскости Р провести прямую, параллельную оси проекций, нахо-
дящуюся в третьей четверти (фиг. 266).
94
Решение. Профильная проекция искомой прямой, изображаемая в виде
точки, должна лежать на профильном следе данной плоскости. Построив профиль-
ный след (PJ плоскости, берем произвольно точку и обозначаем ее через m"n".
Имея профильную проекцию (in"n") искомой прямой, строим ее горизонтальную
(inn) и вертикальную (т'п‘) проекции — по общему правилу.
Пример 69
Даны плоскость Р и точка А. Лежит ли точка на плоскости (фиг. 267)?
Решение. Горизонтальная проекция любой точки горизонтально-проектиру-
ющей плоскости, как известно, лежит на горизонтальном следе плоскости.
В данном случае горизонтальная проекция (а) точки лежит на продолжении
горизонтального следа (PJ плоскости. Следовательно, заданная точка (а, а') лежит
на плоскости Р.
Пример 70
Даны точка А и плоскость Р. Лежит ли точка на плоскости (фиг. 268)?
Решение. Вертикальная проекция любой точки вертикально-проектирующей
плоскости, как известно, лежит на вертикальном следе плоскости. В данном случае
вертикальная проекция (а’) точки не лежит на вертикальном следе (PJ плоскости.
Следовательно, заданная точка (а, а') ц е лежит на плоскости Р.
Пример 71
Даны плоскость Р и точка А. Лежит ли точка на плоскости
(фиг. 269-271)?
Решение. Так как плоскость — общего положения, то пользуемся какой-либо
вспомогательной прямой.
1. Через вертикальную проекцию (а') точки проводим произвольную верти-
кальную проекцию (h'v') вспомогательной прямой. По h'v' находим горизонтальную
проекцию (hv) вспомогательной прямой. Горизонтальная проекция (а) точки не
лежит на прямой hv. Следовательно, заданная точка (а, а') _не лежит на
плоскости Р.
Решение задачи можно также начать с проведения горизонтальной проекции
(hv) вспомогательной прямой через горизонтальную проекцию (а) точки и т. д.
95
2, Решение при помогли горизонтали. Проводим через вертикальную проек-
цию (Д) точки вертикальную проекцию горизонтали - параллельно осп проекций,
до пересечения с вертикальным следом (Рс) плоскости в точке и'. По точке и'
находим на осп проекции точку с и проводим через нее горизонтальную проекцию
горизонтали — параллельно горизонтальному следу (/’,,) плоскости. Точка (о, д') не
лежит на горизонтали плоскости. Следовательно, заданная точка (а, а') не лежит
на плоскости Р.
Решение задачи можно начать и с проведения горизонтальной проекции
горизонтали через iоризонюльную проекцию (у/) точки - параллельно горизонталь-
ному следу плоскости и т. д.
3. Решение при помощи фронталп. Проводим через горизонтальную проекцию
(и) точки горизонтальную проекцию фронтами — параллельно оси проекции, до
пересечения с i орпзоптальпым следом (Ph) пл едкости в точке /к По точке h находим
па оси проекций точку h' и проводим через нее вертикальную проекцию фронталп
параллельно вертикальному следу (Р,) плоскости. Точка («, о') не лежит на фрон-
тали плоскости. Следовательно, точка (а, а') нс лежит па плоскости Р.
Решение задачи можно начать и с проведения вертикальной проекции фронталп
через вертикальную проекцию (а') точки - - параллельно вертикальному следу
плоскости и т, д.
96
Даны плоскость Р и точка А. Лежит ли точка на плоскости (фиг. 272,273)?
Решение. Пользуемся вспомогательной прямой (тк, т'к'), лежащей в плоско-
сти Р. Через вертикальную проекцию (д') точки проводим вертикальную проекцию
вспомогательной прямой, проходящей через точку к', до пересечения с осью проек-
ций в точке (;и, т’). Через точки т и к проводим горизонтальную проекцию
вспомогательной прямой. Точка (а, д') на вспомогательной прямой (тк, т'к1) не
лежит. Следовательно, точка (а, а') не лежит на плоскости Р.
Эту же задачу можно решить и другим способом. Профильная проекция .
любой точки профильнопроектирующей плоскости, как известно, лежит на про-
фильном следе плоскости. Находим профильный след (Р„) плоскости и профиль-
ную проекцию (а") точки. Из сказанного выше вытекает, что точка (д, д') не лежит
на плоскости Р.
Пример 73
Даны плоскость Р и прямая MN. Лежит ли прямая в плоскости
(фиг. 274)?
Решение. Решаем эту задачу, не пользуясь профильной плоскостью проек-
ций. Задаем на вертикальной проекции (т'п') прямой произвольную точку д' и
проводим через нее вертикальную проекцию (h'v’) вспомогательной прямой, лежа-
щей в плоскости Р; по проекции (h'vr) находим горизонтальную проекцию (hv)
прямой и на ней по д' — точку а. Точка (д, д') лежит на прямой (hv, h'v'). Следо-
вательно, прямая (тп, т'п') проходит через точку (д, д'), лежащую в плоскости Р,
и потому лежит в этой плоскости.
Пример 74 - ‘
Даны плоскость Р и горизонтальная проекция (а) точки А, лежащей
в этой плоскости. Найти ее вертикальную проекцию а' (фиг. 275).
Решение. Так как данная плоскость — общего положения, пользуемся' какой-
либо вспомогательной прямой (например, горизонтальной). Проводим через гори-
зонтальную проекцию (д) точки горизонтальную проекцию горизонтали парал-
лельно горизонтальному следу (Ря) плоскости до пересечения с осью проекций
в точке V. По точке v находим на вертикальном следе (Р,) плоскости точку t/
и проводим через нее вертикальную проекцию горизонтали параллельно оси проек-
97
ций. По точке а находим точку а' на вертикальной проекции горизонтали.
В случае задания вертикальной проекции точки решение задачи начинаем с про-
ведения вертикальной проекции горизонтали через вертикальную проекцию точки
параллельно оси проекций и т. д.
Пример 75
Даны плоскость Р и вертикальная проекция (я) точки А, лежащей
на этой плоскости. Найти ее горизонтальную проекцию а (фиг. 276).
Решение. Решаем задачу при помощи фронтали. Проводим через вертикаль-
ную проекцию (д') точки вертикальную проекцию фронтали — параллельно вертикаль-
ному следу (PJ плоскости до пересечения с осью проекций в точке h'. По точке h’
находим на горизонтальном следе (Ph) плоскости точку h и проводим через нее
горизонтальную проекцию фронтали — параллельно оси проекций. По точке а'
находим точку а на горизонтальной проекции фронтали.
98
В случае задания горизонтальной проекции точки решение задачи начинаем
с проведения горизонтальной проекции фронтали через горизонтальную проекцию
точки параллельно оси проекций и т. д.
Пример 76
Даны плоскость Р и вертикальная проекция (д') точки А, лежащей
на этой плоскости. Найти ее горизонтальную проекцию а (фиг. 277).
Решение. Проводим через вертикальную проекцию (д') точки вертикальную
проекцию (h'v) вспомогательной прямой плоскости Р. По h'v' находим горизон-
тальную проекцию (hv) прямой и на ней по точке а' находим горизонтальную
проекцию (а) точки.
Эту же задачу можно решить и другим способом. Известно, что профильная
проекция (л") точки должна лежать на профильном следе (PJ плоскости. Имея
профильный след (PJ плоскости, по вертикальной проекции (а') точки находим
профильную проекцию (о") точки, а затем, по общему правилу, по проекциям а'
и а" находим горизонтальную проекцию (а) точки (чертеж нужно выполнить
самостоятельно).
Пример 77
Даны плоскость Р и горизонтальная проекция (а) точки А, лежащей
на этой плоскости. Найти ее вертикальную проекцию а' (фиг. 278, 279).
Решение. Проводим через горизонтальную проекцию (а) точки горизонталь-
ную проекцию (ак) вспомогательной прямой, пересекающей ось проекций в точке
(т, т'). По горизонтальной проекции (кт) прямой находим ее вертикальную
проекцию (к'т) и на ней — искомую вертикальную проекцию (д') точки. Эту задачу
можно решить и другим способом. Зная, что профильная проекция (д") точки
4*
99
г
должна лежать на профильном следе (PJ плоскости, находим этот след и на
нем — профильную проекцию (а") точки, а затем — искомую вертикальную проек-
цию (o') точки.
Пример 78
Даны вертикальный след (PJ плоскости Р и точка А, лежащая на
этой плоскости. Найти горизонтальный след (РЛ) плоскости (фиг. 280).
Решение. Вертикальный след (Р„) плоскости перпендикулярен оси проекций,
и, следовательно, сама плоскость — горизонтально-проектирующая. Так как задан-
ная точка (а, а') лежит на плоскости Р, проводим искомый горизонтальный след
(РА) плоскости через горизонтальную проекцию (а) точки и точку Рх.
Фиг. 280
100
z
Пример 79
Даны горизонтальный след (РЛ) плоскости Р и точка А, лежащая на
этой плоскости. Найти вертикальный след (Р„) плоскости (фиг. 281).
Решение. Горизонтальный след (Рь) плоскости перпендикулярен оси проек-
ций, и, следовательно, сама плоскость — вертикально-проектирующая. Так как
заданная точка (а, а') лежит на плоскости Р, проводим искомый вертикальный след
(Р/,) плоскости через вертикальную проекцию (а‘) точки и точку Рх.
Пример 80
Даны вертикальный след (Р„) плоскости Р и точка А, лежащая на этой
плоскости. Найти горизонтальный след (Рл) плоскости (фиг. 282, 283).
Решение. Вертикальный след (Рв) плоскости параллелен оси проекций,
а следовательно, сама плоскость — профильно-проектирующая. Так как заданная
точка (а, а1) лежит на плоскости Р, ее профильная проекция (а") должна лежать
на профильном следе (PJ плоскости.
Проводим профильный след (Р,„) плоскости через профильный след прямой Р„
и профильную проекцию (а") заданной точки. Зная след Pw плоскости, проводим
101
искомый горизонтальный след (Ph) плоскости через горизонтальную проекцию его
профильного следа параллельно оси проекций.
Эту же задачу можно решить, не пользуясь профильной плоскостью проекций,
но в таком случае пользуются какой-либо вспомогательной прямой. Проводим
в плоскости Р через вертикальную проекцию (д') точки вертикальную проекцию
(й'г') вспомогательной прямой. По вертикальной проекции (h'v') прямой находим
ее горизонтальную проекцию (hv) и проводим искомый горизонтальный след (Ph)
плоскости через горизонтальный след прямой — параллельно оси проекций.
Пример 81
Даны горизонтальный след (Р„) плоскости Р и точка А, лежащая на
этой плоскости. Найти вертикальный след (Р,,) плоскости (фиг. 284-286).
Решение. Так как плоскость — общего положения, то пользуемся какой-либо
вспомогательной прямой.
1. Проводим в плоскости Р через горизонтальную проекцию (а) точки гори-
зонтальную проекцию (hv) вспомогательной прямой и по ней находим ее верти-
кальную проекцию (h'v'). Затем проводим искомый вертикальный след (Р„) плоско-
сти через точки v и Рх.
Проще решить эту задачу при помощи главных линий плоскости - горизон-
тали или фронтали.
2. Проводим проекции горизонтали плоскости через проекции точки (а, д'):
горизонтальную — через точку а - параллельно горизонтальному следу (РЛ) плоско-
сти и вертикальную — через точку а' — параллельно оси проекций. Найдя след
(г, и') горизонтали, проводим искомый вертикальный след (Рс) плоскости через
точки v' и Рх.
3. Проводим через горизонтальную проекцию (а) точки горизонтальную про-
екцию фронтали (как?) — до пересечения с горизонтальным следом (Ph) плоскости
в точке h. Найдя по точке h на оси проекций точку h', проводим через точки h'
и а' вертикальную проекцию фронтали, а параллельно ей — искомый вертикаль-
ный след (Р„) плоскости через точку Рх.
Пример 82
Даны вертикальный след (PJ) плоскости Р и точка А, лежащая на этой
плоскости. Найти горизонтальный след (Ph) плоскости (фиг. 287, 288).
102
Решение. 1. Проводим через вертикальную проекцию (д') точки вертикаль-
ную проекцию горизонтали плоскости Р — параллельно оси проекций, до пересе-
чения с вертикальным следом (Р,.) плоскости в точке v'. Найдя по точке v на оси
проекций точку v, проводим через точки а и v горизонтальную проекцию гори-
зонтали, а параллельно ей — искомый горизонтальный след (Ph) плоскости через
точку Рх.
2. Проводим через проекции точки (а, д') проекции фронтали плоскости:
вертикальную — через точку д', параллельно вертикальному следу (Р„) плоскости
и горизонтальную через точку а — параллельно оси проекций. Найдя горизонталь-
ный след (Ji, Ji') фронтали, проводим искомый горизонтальный след (Ph) плоскости
через точки h и Рх.
Пример 83
Даны точка А, лежащая на горизонтально-проектирующей плоскости,
и точка схода ее следов (Рл). Построить следы плоскости (фиг. 289).
Решение. Так как искомая плоскость — горизонтально-проектирующая, то
горизонтальная проекция (д) точки А должна лежать на горизонтальном следе (Pft)
плоскости; вертикальный след (PJ должен быть перпендикулярен оси проекций.
Проводим следы плоскости: горизонтальный (РА) — через точки Ph и д; вертикаль-
ный (PJ — через точку Рх перпендикулярно оси проекций.
103
Вывод. Если горизонтально-проектирующая плоскость проходит через неко-
торую точку, то горизонтальный след этой плоскости проходит через горизон-
тальную проекцию этой точки.
Пример 84
Дана точка А. Провести через нее плоскость Р, перпендикулярную
к горизонтальной плоскости проекций п составляющую с вертикальной
плоскостью проекций угол, равный 30° (фиг. 290).
Решение. Угол между горизонтальпо-проектирующей плоскостью и верти-
кальной плоскостью проекций определяется углом между горизонтальным следом
плоскости и осью проекций. Отсюда — проводим через горизонтальную проекцию
(</) точки горизонтальный след (Р,,) плоскости под заданным углом 30° к оси
проекций до пересечения с ней в точке Рх: затем проводим через точку Рх
вертикальный след (PJ плоскости перпендикулярно оси проекций. (Дано одно
решение.)
Пример 85
Провести через точку А плоскость Р, перпендикулярную к вертикальной
плоскости проекций (фиг. 291).
Решение. Так как точка (а, а') должна лежать па вертикально-проектиру-
ющей плоскости, то, как известно, ее вертикальная проекция должна лежать на
вертикальном следе {/’,) плоскости; кроме того, горизонтальный след (Р(1) должен
быть перпендикулярен оси проекций. Через точку можно провести множество
плоскостей, а потому задаем произвольно на оси проекций точку Рх и проводим
следы плоскости: вертикальный (PJ — через точки а и Рх и горизонтальный
(РА) -- через точку Рх перпендикулярно оси проекций.
Вывод. Если вертикально-проектирующая плоскость проходит через точку,
то вертикальный след этой плоскости проходит через вертикальную проекцию
точки.
Пример 86
Дана точка А. Провести через нее плоскость Р, перпендикулярную
к вертикальной плоскости проекций и составляющую с горизонтальной
плоскостью проекций угол, равный 60° (фиг. 292).
104
Решение. Угол между вертикально-проектирующей плоскостью и горизон-
тальной плоскостью проекций определяется углом между вертикальным следом
плоскости и, осью проекций. Поэтому проводим через вертикальную проекцию (д')
точки вертикальный след (Р„) плоскости под заданным углом 60° к оси проекций,
до пересечения с пей в точке Рх; затем проводим через точку Рх горизонтальный
след (Р(|) плоскости перпендикулярно оси проекций. (Дано одно решение.)
Пример 87
Провести через точку А плоскость Р, параллельную оси проекций и про-
ходящую через первую, вторую и третью четверти пространства (фиг. 293).
Решение. Так как плоскость Р — профильно-проектирующая, то ее профиль-
ный след (Рн) должен проходить через профильную проекцию («'') заданной точки.
Следы (Ph и РА плоскости должны быть параллельны оси проекций. Любая
плоскость, проходящая через первую, вторую и третью четверти, имеет горизон-
тальный след (Р(|) на задней поле горизонтальной плоскости проекций и верти-
кальный след (Р„) — на верхней поле вертикальной плоскости проекций, которые
на эпюре располагаются (оба) над осью проекций. Находим профильную проек-
цию (а") заданной точки и проводим через нее произвольно профильный след (Рн.)
плоскости, пересекающий оси OZ и О У в точках W (профильный след прямой Р^
и W (профильный след прямой Р„), а затем определяем Ph и Р„ (см. чертеж).
Примечание. Ниже указано, как проводить через точку плоскость общего
положения (см. стр. 108).
Пример 88
Заключить прямую АВ в горизонтально-проектир^ющую плоскость Р
(фиг. 294).
Решение. Известно, что горизонтальная проекция произвольной прямой,
лежащей в горизонтально-проектирующей плоскости, совпадает с горизонтальным
следом плоскости, а следовательно, и наоборот: горизонтальный след (РА плоско-
сти, заключающей произвольную прямую, совпадает с горизонтальной проекцией
(ab) заданной прямой. Отсюда — продолжаем горизонтальную проекцию (ab) пря-
мой до пересечения с осью проекций в точке Pt и через нее проводим вертикаль-
ный след (Р„) плоскости — перпендикулярно оси проекций.
' Пример 89
Заключить прямую АВ в вертикально-проектпрующую плоскость Р
(фиг. 295).
105
Решение. Известно, что вертикальная проекция произвольной прямой, лежа-
щей в вертикально-проектирующей плоскости, совпадает с вертикальным следом
плоскости, а следовательно, и наоборот: вертикальный след (Pj плоскости, заклю-
чающей произвольную прямую, будет совпадать с вертикальной проекцией (а'Ь’)
заданной прямой. Отсюда — продолжаем вертикальную проекцию (а'Ь') прямой
до пересечения с осью проекций в точке Рх и через нее проводим горизонталь-
ный след (Ph) плоскости — перпендикулярно оси проекций.
Пример 90
Заключить прямую АВ в плоскость Р, параллельную оси проекций
(фиг. 296).
Решение. Известно, что профильная проекция произвольной прямой, лежа-
щей в профильно-проектирующей плоскости, совпадает с профильным следом
плоскости, а следовательно, и наоборот: профильный след (Р„.) плоскости, заклю-
чающей произвольную прямую, совпадает с профильной проекцией (а"Ь") заданной
прямой. Отсюда — находим профильную проекцию (а’Ь") прямой и продолжаем
Фиг.
106
тальный след (Ph) плоскости и вертикальный след (PJ плоскости параллельно оси
проекций (см. чертеж).
Примечание. Ниже показано решение этой задачи без использования
профильной плоскости проекций.
Вывод. Через произвольную прямую можно провести: единственную гори-
зонтально-проектирующую плоскость, единственную вертикально-проектирующую
плоскость, единственную профильно-проектирующую плоскость (почему9.).
Пример 91
Заключить прямую АВ в плоскость Р общего положения, зная точку
схода следов (Рх) плоскости (фиг. 297).
Решение. Известно, что следы прямой, лежащей в плоскости, находятся на
одноименных следах плоскости и наоборот: следы плоскости, заключающей пря-
мую, должны проходить через одноименные следы прямой.
Находим след (и, и') прямой и проводим вертикальный след (PJ плоскости
через точки Рх и v и горизонтальный след (PJ плоскости через точку Рх —
параллельно горизонтальной проекции (ab) прямой (почему?).
Пример 92
Прямую АВ заключить в плоскость Р общего положения (фиг. 298).
Решение. Находим след (/i, /Г) прямой и, задав на оси проекций произвольно
(почему?) точку Рх, проводим следы плоскости: горизонтальный (/',,) — через точки
Рх и h и вертикальный (Pj — через точку Рх - параллельно вертикальной проекции
(а'Ь'} прямой (почему?).
Пример 93
Построить следы плоскости Р общего положения, проходящей через
точку А, зная точку схода следов (Рл) плоскости (фиг. 299, 300).
Решение 1. Используем горизонталь плоскости. Проводим проекции произ-
вольной горизонтали через одноименные проекции точки (а, а') и находим ее след
ф, г'). Проводим вертикальный след (PJ плоскости через точки Рх и v1 и гори-
зонтальный след (Ph) — через точку Рх - параллельно горизонтальной проекции
горизонтали (почему?).
2. Используем фронталь плоскости. Проводим проекции произвольной фрон-
тали через одноименные проекции заданной точки (а, а') и находим ее след (/i, /1').
Проводим горизонтальный след (Рк) плоскости через точки Рх и Ь и вертикальный
след (Pv) - через точку Рх - параллельно вертикальной проекции фронтали (по-
чему?).
Примечание. Через точку А можно провести любую прямую.
107
Пример 94
Построить следы плоскости Р общего положения, проходящей через
точку А (фиг. 301 — 303).
Решение. 1. Проводим проекции произвольной прямой через одноименные
проекции точки (а, а') и находим ее следы (li, h') и (у, v'). Так как через точку
можно провести множество плоскостей, задаем на оси проекции" произвольную
точку Рх и проводим следы плоскости: горизонтальный (Р(1) — через точки Рх и h
и вертикальный (Рj — через точки Рх и v'.
2. Используем горизонталь плоскости. Проводим проекции произвольной гори-
зонтали через одноименные проекции точки (а, а') и находим ее след (в, в’)-
Задаем иа оси проекции произвольно точку Рх и проводим следы плоскости:
вертикальный (Р„) — через точки Рх и v' и горизонтальный (Р,,) — через точку Рх —
параллельно горизонтальной проекции горизонтали (почему?).
3. Используем фронталь плоскости. Проводим проекции произвольной фрон-
тали через одноименные проекции точки (а, а’) и находим се след (h, h'). Задаем
иа оси проекций произвольную точку Рх и проводим следы плоскости: горизон-
тальный (Р(1) — через точки Рх и h и вертикальный (Ро) - через точку Рх — парал-
лельно вертикальной проекции фронтали (почему?).
ЗАДАЧИ
199. Перечислить прямые, которые можно провести в плоскости Р
(фиг. 304-311).
200. Найти следы плоскости, заданной: двумя пересекающимися пря-
мыми, двумя параллельными прямыми, прямой и точкой (фиг. 312 — 317).
201. Найти профильный след плоскости Р (фиг. 318 — 327).
202. Провести в плоскости Р произвольную прямую, проходящую
через указанные четверти (фиг. 328 — 332).
203. Построить на плоскости Р геометрическое место точек, удаленных
от горизонтальной плоскости проекций на 15 мм (фиг. 332, 333).
204. Построить на плоскости Р геометрическое место точек, удаленных
от вертикальной плоскости проекций на 15 мм (фиг. 332, 333).
205. Построить на плоскости Р точку А с заданными координатами
(фиг. 332, 333):
108
109
Фиг. 309
0
Фиг. 311
х---------------------------------о
Фиг. 310
НО
Ill
€ Z
Ъ У _ 0 у
Фиг. 320 Y
7
1 Z
х 0
Фиг. 323 ой' 1 1 1 1 1 1 у 1 РЛ Y Z 0
1 1 1 1 1 6 а Фиг. 324 Y
Z
«-У
И
Фиг. 325
112
113
206. Определить недостающие проекции точек, лежащих на плоскости Р
(фиг. 334-341).
207. Дана горизонтальная проекция треугольника АВС, лежащего
в плоскости Р. Определить его вертикальную проекцию (или наоборот):
не пользуясь главными линиями плоскости; пользуясь горизонталями
и фронталями плоскости (фиг. 342, 343).
208. Дана одна из проекций треугольника АВС, лежащего в профиль-
но-проектирующей плоскости. Определить другую его проекцию: не
пользуясь профильной плоскостью проекций; пользуясь профильной
плоскостью проекций (фиг. 344, 345).
209. Определить недостающий след плоскости Р, заданной одним следом
и точкой, лежащей на этой плоскости (фиг. 346-355).
210. Построить следы плоскости Р, проходящей через точку А, если
дана точка их схода и известно, что плоскость:
1) общего положения (фиг. 356— 359);
114
115
116
1
I г
4° I
I I
х--------------------1-------------------о X----------------------1
Фиг. 354
I
ia'
Фиг. 355
О
?xT3
Фиг. 356
ia
Фиг. 357
<? а'
।
I
I
| 9а'
।
I
!
1 Рх 1
i а х------J; о
Фиг. 358 Фиг. 359
118
----------------,— о
I
I
<[>a'
i
i
i
Aa
Фиг. 360
?a
0
i 1,П,Шч
ba
Фиг. 362
Фиг. 364
|_________________0
I
I
I
l 1,ПГ,Шч
I
I
oa
Фиг. 363
I
la'
I 1,П,№ч
I
la
Фиг. 365 j
211. Построить следы профильно-проектирующей плоскости Р, прохо-
дящей через точку А и через указанные четверти пространства (фиг. 362 —
365). Задача неопределенная.
212. Провести через точку Л (—30, —20) горизонтально-проектирующую
плоскость Р, составляющую с вертикальной плоскостью проекций у?Ьл,
равный 453.
119
213. Провести через точку А (30, —20) вертикально-проектирующую
плоскость Р, составляющую с горизонтальной плоскостью проекций угол,
равный 30°.
214. Провести через точку А ( — 20, 30) профильно-проектирующую
плоскость, составляющую с горизонтальной плоскостью проекций угол,
равный 30°; с вертикальной плоскостью проекций угол, равный 45°.
215. Построить следы плоскости Р, проходящей через прямую АВ,
исходя из условия, что плоскость:
1) горизонтально-проектирующая (фиг. 366, 367);
2) вертикально-проектирующая (фиг. 368, 369);
3) общего положения (фиг. 370 — 372).
216. Построить следы профильно-проектирующей плоскости, проходя-
щей. через прямую АВ: пользуясь профильной плоскостью проекций; не
пользуясь профильной плоскостью проекций (фиг. 373).
120
a'
b
Глава ХШ
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ, ЗАДАННЫХ СЛЕДАМИ
Две плоскости пересекаются по прямой линии. Прямая линия в пространстве
определена, если известны одна точка этой прямой и ее направление или же две
точки этой прямой.
Отсюда следует, что найти прямую пересечения двух плоскостей означает
найти две точки, общие для пересекающихся плоскостей, или же найти одну
такую точку и направление прямой.
В частном случае точками прямой могут служить следы этой прямой.
Следы прямой пересечения двух плоскостей находятся на пересечении одно-
именных следов этих плоскостей, а именно:
горизонтальный след прямой пересечения находится на пересечении горизон-
тальных следов плоскостей;
вертикальный след прямой пересечения находится на пересечении вертикальных
следов плоскостей;
121
профильный след прямой пересечения находится на пересечении профильных
следов плоскостей.
В зависимости от расположения в пространстве пересекающихся плоскостей,
прямая пересечения может иметь в системе плоскостей Н и V следы: и горизон-
тальный и вертикальный; единственный горизонтальный; единственный вертикаль-
ный; может не иметь ни горизонтального, ни вертикального следов.
Если прямая пересечения имеет и горизонтальный и вертикальный следы, то
это — или прямая общего положения, или профильная прямая, или прямая, пере-
секающая ось проекций.
Если прямая пересечения имеет единственный горизонтальный след, то это —
прямая, параллельная вертикальной плоскости проекций (фронталь); в частном
случае она может быть перпендикулярна горизонтальной плоскости проекций.
Если прямая пересечения имеет единственный вертикальный след, то это —
прямая, параллельная горизонтальной плоскости проекций (горизонталь); в частном
случае она может быть перпендикулярна вертикальной плоскости проекций.
Если прямая пересечения имеет единственный профильный след, то это —
прямая, параллельная оси проекций.
В тех случаях, когда прямая пересечения — проектирующая, т. е. перпендику-
лярна какой-либо плоскости проекций, не следует забывать, что одна из
проекций прямой совпадает со следом прямой, а именно: если прямая пересечения
перпендикулярна плоскости Н, то ее горизонтальная проекция совпадает с гори-
зонтальным следом этой прямой; если прямая пересечения перпендикулярна
плоскости V, то ее вертикальная проекция совпадает с вертикальным следом
этой прямой.
Если прямая пересечения перпендикулярна плоскости И' (параллельна оси
проекций), то ее профильная проекция совпадает с профильным следом этой
прямой.
Если одноименные следы плоскостей (или горизонтальные, или вертикальные,
или и горизонтальные и вертикальные) в пределах чертежа не пересекаются,
необходимо найти одну или две произвольные точки, принадлежащие прямой
пересечения заданных плоскостей.
Произвольную точку, принадлежащую прямой пересечения двух плоскостей,
определяют, вводя вспомогательную плоскость (см. примеры).
ПРИМЕРЫ
Пример 95
Найти прямую пересечения плоскостей Р и Q (фиг. 374).
Решение. Плоскости Р и О пересекаются по прямой общего положения,
проходящей через точки-следы (Л, IP) и (г, г'), находящиеся на пересечении гори-
зонтальных и вертикальных следов плоскостей. Проводим проекции искомой пря-
мой: горизонтальную — через точки h и г и вертикальную — через точки /Г и г',
которая совпадает с вертикальным следом (О.) плоскости Q (почему?). Прямая
проходит через вторую, первую и четвертую четверти (почему?).
Пример 96
Найти прямую пересечения плоскостей Р и Q (фиг. 375).
Решение. Плоскости Р и О пересекаются по прямой общего положения,
проходящей через точки-следы (/1, Л') и (г, г’), находящиеся на пересечении гори-
зонтальных и вертикальных следов плоскостей. Проводим проекции искомой
прямой: горизонтальную — через точки h и г, которая совпадает с горизонтальным
следом (Q;,) плоскости Q (почему?), и вертикальную — через точки и г'. Прямая
проходит через первую, четвертую и третью четверти (почему?).
Пример 97
Найти прямую пересечения плоскостей Р и Q (фиг. 376).
Решение. Плоскости Р и Q пересекаются по профильной прямой, прохо-
дящей через точки-следы l/i./i) и (г, г'), находящиеся на пересечении горизонталь-
ных и вертикальных следов плоскостей и расположенные на одном перпендикуляре
122
к оси проекций. Проводим проекции искомой прямой: горизонтальную — через
точки й и к и вертикальную — через точки /;' и v'. Строим также ее профильную
проекцию (/Ги").
Указать, через какие четверти проходит прямая и что означает совпадение
ее следов на эпюре.
Пример 98
Найти прямую пересечения плоскостей Р и Q (фиг. 377).
Решение. Плоскости Р и О пересекаются по прямой — горизонтали, про-
ходящей через точку-след (v, i>'), находящуюся на пересечении вертикальных следов
плоскостей. Проводим проекции искомой прямой: вертикальную — через точку v' —
параллельно оси проекций, которая совпадает с вертикальным следом (QJ
123
плоскости Q (почему?), и горизонтальную — через точку и — параллельно горизон-
тальному следу (Г,,) плоскости Р. Прямая проходит через первую и вторую
четверти (почему?).
Вывод. Плоскость общего положения пересекается с плоскостью, параллель-
ной плоскости Я, по горизонтали.
Пример 99
Найти прямую пересечения плоскостей Р и Q (фиг. 378).
Решение. См. решение предыдущего примера.
Вывод. Две плоскости общего положения, вертикальные следы которых
пересекаются, а горизонтальные следы между собой параллельны, пересекаются
по горизонтали.
Пример 100
Найти прямую пересечения плоскостей Р и Q (фиг. 379).
124
Решение. Плоскости Р и Q пересекаются по прямой — горизонтали, кото-
рая перпендикулярна вертикальной плоскости проекций (почему?).
Вертикальная проекция искомой прямой совпадает с точкой v' (почему?);
горизонтальная ее проекция проходит через точку и и перпендикулярна оси
проекций. Прямая проходит через первую и вторую четверти.
Вывод. Две вертикально-проектирующие плоскости пересекаются по прямой,
перпендикулярной к вертикальной плоскости проекций.
Пример 101
Найти прямую пересечения плоскостей Р и Q (фиг. 380).
Решение. Плоскости Р и Q пересекаются по прямой — фронтали, проходя-
щей через точку-след (й, й'), находящуюся на пересечении горизонтальных следов
плоскостей. Проводим проекции искомой прямой: горизонтальную — через точку
й, параллельно оси проекций, которая совпадает с горизонтальным следом (Qjj
плоскости Q (почему?), и вертикальную — через точку й', параллельно вертикаль-
ному следу (Р„) плоскости Р. Прямая проходит через первую и четвертую чет-
верти (почему?).
Вывод. Плоскость общего положения пересекается с плоскостью, параллель-
ной плоскости V, по фронтали.
Пример 102
Найти прямую пересечения плоскостей Р и Q (фиг. 381).
Решение. См. решение предыдущего примера.
Вывод. Две плоскости общего положения, горизонтальные следы которых
пересекаются, а вертикальные следы. между собой параллельны, пересекаются
по фронтали.
Пример 103
Найти прямую пересечения плоскостей Р и Q (фиг. 382).
Решение. Горизонтально-преектирующие плоскости Р и Q пересекаются
по прямой — фронтали, которая перпендикулярна горизонтальной плоскости проек-
ций. Горизонтальная проекция искомой прямой совпадает с точкой й (почему?),
а вертикальная ее проекция проходит через точку й' и перпендикулярна оси
проекций. Прямая проходит через первую и четвертую четверти (почему?).
125
Вывод. Две горизонтально-проектирующие плоскости пересекаются по пря-
мой, перпендикулярной к горизонтальной плоскости проекций.
Пример 104
Найти прямую пересечения плоскостей Р и О (фиг. 383, 384).
Решение. Плоскости Р и Q пересекаются по прямой MN, параллельной
оси проекций (почему?).
Первый способ. Профильная проекция (т"п") искомой прямой совпадает
с профильным следом этой прямой, который, как известно, находится на пересе-
чении профильных следов (Pw и 2„) плоскостей. Находим профильные следы
заданных плоскостей. Их пересечением является профильная проекция (т'п")
искомой прямой. Затем по профильной проекции прямой находим ее горизонталь-
ную (mu) и вертикальную (ni'n'J проекции, которые должны быть параллельны оси
проекций (почему?).
Второй способ. Так как искомая прямая MN лежит в плоскости О. то
ее вертикальная проекция (ni'/i) совпадает с вертикальным следом (Qt) этой
126
плоскости (почему?). Имея вертикальную проекцию (т'п') прямой, можем найти
ее горизонтальную проекцию не пользуясь профильной плоскостью проекций
Для этого задаем произвольную точку к' на прямой т'п’ и находим горизонталь -
ную проекцию (к) точки, зная, что точка (к, к) лежит и на плоскости Р. Найдя
точку к, проводим через нее горизонтальную проекцию (>нп) искомой прямой —
параллельно осп проекций.
Пример 105
Найти прямую пересечения плоскостей Р и Q (фиг. 385).
Решение.
Первый способ. См. решение предыдущего примера.
Второй способ. Так как искомая прямая лежит в плоскости Q, то ее гори-
зонтальная проекция (тп) совпадает с горизонтальным следом (OJ этой плоскости
(почему?). Имея горизонтальную проекцию (тп) прямой, можем найти ее верти-
кальную проекцию (т'п’), не пользуясь профильной плоскостью проекций. Для
этого задаем на прямой тп точку к и находим вертикальную проекцию (С) точки,
зная, что точка (к, к') лежит и на плоскости Р. Найдя точку к', проводим через
нее вертикальную проекцию (т'п') искомой прямой — параллельно оси проекций.
Пример 106
Найти прямую пересечения плоскостей Р и О (фиг. 386).
Решение. Плоскости Р и О пересекаются по прямой MN, параллельной
оси проекций (почему?). Находим ее профильную проекцию (т"п") на пересечении
профильных следов плоскостей, а затем по профильной проекции прямой опре-
деляем ее горизонтальную (тп) и вертикальную (т'п') проекции, которые парал-
лельны оси проекций.
Пример 107
Найти прямую пересечения плоскостей Р n Q (фиг. 387).
Решение. Плоскости Р и Q пересекаются по прямой общего положения,
проходящей через точку-след (h, h') пересечения горизонтальных следов плоскостей.
Точка-след (г, г') пересечения вертикальных следов плоскостей недоступна,
так как эти следы плоскостей, по заданию, в пределах чертежа не пересекаются
Вместо точки (г, с') необходимо найти другую — произвольную точку прямой
пересечения, общую для заданных плоскостей. Для этого поступаем следующим
образом. Вводим вспомогательную плоскость R, например, параллельную плоско-
сти Н, которая, как известно, пересекает каждую из данных плоскостей по горн-
127
зонтали. На их пересечении получаем вспомогательную точку (к, к"), общую для
данных плоскостей. Найдя эту вторую точку (к, к') прямой, проводим ее проекции:
горизонтальную — через точки h и к и вертикальную — через точки h' и к'.
Через какие четверти проходит прямая пересечения?
Примечание. В случае необходимости можно, пользуясь указанным выше
способом, найти и две произвольные точки прямой пересечения, вводя после-
довательно две плоскости; проще всего ввести их параллельно плоскости Н
или параллельно плоскости V.
Пример 108
Найти прямую пересечения плоскостей Р и Q (фиг. 388).
128
Решение. Плоскости Р и Q пересекаются по прямой, пересекающей ось
проекций в точках (й, й') и (у, iX), совпадающих с точкой (щ т') и находящихся
на пересечении горизонтальных и вертикальных следов плоскостей. Цзвестдо, дто
точки-следы (й, й') и (г, и’), как совпавшие; не определяют прямую и что не о б к,От
д и м о найти еще одну точку этой прямой, общую для заданных плоскостей.
Точка (а, а') по заданию лежит на плоскости Р. Проверяем прежде всего, не
лежит ли точка (а, а1) и на плоскости Q. Проверку выполняем хотя бы при
помощи горизонтали. Точка (а, а ) действительно лежит и на плоскости Q, т. е.
является общей точкой для данных плоскостей. Проводим проекции цсгщмой
прямой: вертикальную — через точки in и а' и горизонтальн ую — через тощи m
и а. Прямая проходит через первую и третью четверти (почему?).
Пример 109
Найти прямую пересечения плоскостей Р и Q (фиг. 389).
Решение. Плоскости Р и Q пересекаются по прямой, проходящей через
точку (/, Г), с которой совпадают точки (й, Й) и (и, v') пересечений одноименных
следов плоскостей. Точка (a, o') лежит, по условию, на плоскости Р\ на плоскости Q
эта точка не лежит, в чем можно убедиться, например, при помощи фронтали.
5 Арустамов X. А.
129
Следовательно, для определения прямой необходимо naitTii еще одну ее точку.
Вводим вспомогательную плоскость К, параллельную вер,пкa.’ii.noii плоскосн!
проекций и проходящую через точку (’л. </'): горизонт а ль ими се след (/?,,) проходит
через точку <i — параллельно осп проекций. Плоскосн. R пересекает плоскость Р
по прямой (пт, т'п'). параллельной оси проекций, проходящей через точку (и. и ).
а плоскость О — по фронтали, прохо л.чщей через точку (/1,, Ь\). На пересечении
прямой А/У и фронтащ получаем точку (А , А"). черед которую также до окна
пройти,прямая пересечения. Проводим проекции искомой прямой: горизонталь-
ную — через точки / и к и вертикальную — через точки /' и к'.
Пример ПО
Найти линию пересечения плоскостей Р и Q. не пользуясь профильной
плоскостью проекций (фиг. 390).
Решение. Плоскости Р и Q пересекаются по прямой MN, параллельной
оси проекций (почему?).
Зная направление искомой прямой, необходимо найти сисе одну ее точку, для
чего вводим вспомогательную вертикальпо-просктирующую плоскость R. проходя-
щую через точку (л, <т'). Вспомогательная плоскость R пересекает плоскость Р
по прямой (л/, а'Г), а плоскость Q — по вертпкально-проектиругощей прямой,
проходящей через точку (г, г'). На их пересечении получаем точку (А, А). Прово-
дим проекции (тп, т'п') искомой прямой, параллельно оси проекций, через одно-
именные проекции найденной точки (А, А'). Как и следовало ожидать, вертикальная
проекция (ш'н') искомой прямой совпадает с вертикальным следом (0) плоскости О
(почему?).
Пример 111
Найти линию пересечения плоскостей Р и Q, не пользуясь профильной
плоскостью проекций (фиг. 391).
Решение. Плоскости Р и О пересекаются по прямой MN, параллельной
оси проекций (почему.’).
Зная направление искомой прямой, 1еобходимо найти еще одну ее точку ,ддя
чего вводим произвольную горизонтально-проектирующую плоскость Н. Плоскость
R пересекает плоскость О по прямой (/ir, h’P), а плоскость Р — по горизонтально-
проектирующей прямой, проходящей через точку (/ц, h\). На их пересечении
получаем точку (к, к'). Проводим проекции (тп, т'п') искомой прямой — параллельно
оси проекций — через одноименные проекции найденной точки (к, к').
130
Пример 112
Найти линию пересечения плоскостей Р и Q, не пользуясь профиль-
ной плоскостью проекций (фиг. 392).
Решение. Плоскости Р и Q пересекаются по прямой MN, параллельной
оси проекций (почему?). Зная направление искомой прямой, необходимо найти
еще одну ее точку, для чего вводим вспомогательную вертикально-проектирующую
плоскость R, которая пересекает плоскость Р по прямой (ho, h'v'), а плоскость
й — по прямой (/цщ, h\v\). На их пересечении получаем точку (к, к'). Проводим
проекции (тп, т'п'), искомой прямой — параллельно оси проекций — через одно-
именные проекции найденной точки (к,
5* 131
ЗАДАЧИ
217. Найти линию пересечения плоскостей Р и Q:
1) не вводя вспомогательной плоскости (фиг. 393—413);
2) не ввода вспомогательной плоскости и не пользуясь профильной
плоскостью проекций (фиг. 410-413);
3) ввода вспомогательную плоскость (фиг. 414—421).
U3
Фиг. 415
218. Найти горизонтальные следы двух пересевающихся плоскостей Р
и <2, если известны их вертикальные следы и точка К, принадлежащая
линии их пересечения (фиг. 422, 423).
Глава XIV
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПЛОСКОСТЬЮ
Для того чтобы найти точку пересечения прямой с плоскостью, поступают
так:
1) заданную прямую заключают в произвольную вспомогательную плоскость
(про ще - в проектирующую);
2) находят прямую пересечения плоскостей — заданной и вспомогательной;
3) на пересечении прямых — заданной и полученной — получается искомая
точка.
Указание. Если один из элементов пересечения — или плоскость, или прямая —
проектирующие, то пользование изложенным правилом не рекомен-
дуется, так как в большинстве таких случаев нахождение точки пересечения
значительно упрощается (сгл. примеры).
ПРИМЕРЫ
Пример ИЗ
Найта точку пересечения прямой АВ с плоскостью Р (фиг. 424).
Решение. Обозначаем искомую точку через М (т, т'). Так как точка М
лежит на горизонтально-проектпрующей плоскости, ее горизонтальная проекция
(т) должна лежать где-то на горизонтальном следе (/’,,) плоскости. Вместе
с тем, так как эта же точка Af лежит и на прямой АВ, то ее горизонтальная
проекция (т) должна лежать и где-то на горизонтальной проекции (ab) прямой.
Отсюда — горизонтальная проекция (т) искомой точки должна лежать на горизон-
тальном следе (Рй) плоскости и па горизонтальной проекции (ab) прямой, т. е. на
их пересечении. Зная горизонтальную проекцию (т) искомой точки, находим ее
вертикальную проекцию (irf) на вертикальной проекции (а'Ь’) прямой.
Вывод. Горизонтальная проекция точки пересечения любой прямой с гори-
зонтально-проектирующей плоскостью находится на пересечении горизонтального
следа плоскости с горизонтальной проекцией прямой. (Схематическая запись:
т-> х ab.)
Hl
Пример 114
Найти точку пересечения прямой АВ с плоскостью Р (фиг. 425).
Решение. Обозначаем искомую точку через М (т, т'). Плоскость Р,
параллельная вертикальной плоскости проекций, горизонтально-проектирующая.
Поэтому горизонтальную проекцию (;и) искомой точки находим на пересечении
прямых Р,, и ab. Так как заданная прямая (ab, а’Ь') — профильная, то, пользуясь
профильной плоскостью проекции, по точке т находим точку т" на прямой а"Ь",
затем но точке т: — точку т' на прямой а'Ь'.
Пример 115
Найти точку пересечения прямой АВ с плоскостью Р (фиг. 426).
Решение. Обозначаем искомую точку через М (т, т'). Так как точка М
лежит на вертпка.тыю-иросктпрующей плоскости, то ее вертикальная проекция (»/)
должна лежать где-то па вертикальном следе (Р) плоскости. Вместе с тем, так
как эта точка М лежит и па прямой АВ, ее вертикальная проекция (nf) должна
лежать также где-то па вертикальной проекции (а'Ь') прямой. Отсюда — верти-
кальная проекция (т') искомой точки должна лежать на вертикальном следе (PL.)
плоскости и на вертикальной проекции (а’Ь1) прямой, т. е. на их пересечении.
Зная вертикальную проекцию (и/) искомой
точки, находим ее горизонтальную про-
екцию (ш) на горизонтальной проекции
(ab) прямой.
Вывод. Вертикальная проекция точ-
ки пересечения любой прямой с верти-
кально-проектирующей плоскостью нахо-
дится на пересечении вертикального следа
плоскости с вертикальной проекцией пря-
мой. (Схематическая запись: Pv х а'Ь'.)
Z
Y Фиг. 425
138
Пример 116
Найти точку пересечения прямой АВ с плоскостью Р (фиг. 427).
Решение. Обозначаем искомую точку через М (т, пГ). Заданная плоскость
Р — вертпкально-проектпрующая. Отсюда вертикальную проекцию- («') искомой
точки находим па пересечении прямых Р„ и а'Ь'. Так как заданная прямая —
профильная, то, пользуясь профильной плоскостью проекций, по точке т' находим
точку т" на прямой d’b", а затем по точке т" — точку т на прямой ab.
Пример 117
Найти точку пересечения прямой АВ с плоскостью Р (фиг. 428).
Решение. Обозначаем искомую точку через М (т, т'). Так как точка М
лежит на профильно-проектирующей плоскости, то ее профильная проекция (т")
должна лежать где-то на профильном следе (Pw) плоскости. Вместе с тем, так
как эта же точка лежит и на ттрямой АВ, то ее профильная проекция (и") должна
лежать также где-то на профильной проекции (а”Ь") прямой. Отсюда — про-
фильная проекция (/п") искомой точки должна лежать на профильном следе (Pw)
плоскости и на профильной проекции (а"й") прямой, т. е. на их пересечении.
Найдя профильный след плоскости и профильную проекцию прямой,1 получаем
на их пересечении профильную проекцию (ш") искомой точки. Зная профильную
проекцию (hi") искомой точки, находим две другие ее проекции на одноимённых
проекциях прямой.
В ы в о д. Профильная проекция точки пересечения л ю б о й прямой с про-
фильно-проектирующей плоскостью находится на пересечении профильного следа
плоскости с профильной проекцией прямой. (Схематическая запись: т' -> Р„ х д"Ь''.)
Примечание. Ниже показано, как можно решить эту же задачу, не
пользуясь профильной плоскостью проекций.
Пример 118
Найти точку пересечения прямой АВ с плоскостью Р (фиг. 429).
139
140
Решение. Обозначаем искомую точку через М (т, nf). Заданная плоскость
Р, проходящая через ось проекций, — профильно-проектирующая. Отсюда — про-
фильную проекцию (т") искомой точки находим на пересечении профильного следа
(РД плоскости и профильной проекции (а"Ь") прямой.
Зная профильную проекцию («Г) искомой точки, находим две другие ge проек-
ции на одноименных проекциях прямой.
Примечание. Данную задачу можно решить и без профильной плоскости
проекций, но решение изложенным способом значительно проще.
Пример 119
Найти точку пересечения прямой АВ с плоскостью Р (фиг. 430).
Решение. Обозначаем искомую точку через М (т, т'). Так как эта точка
лежит на горизонтально-прректирующей прямой (ab, а'Ьг), то ее горизонтальная
проекция (»i) должна совпадать с горизонтальной проекцией (ab) прямой. Зная
горизонтальную проекцию (т) точки, находим ее вертикальную проекцию ,(т’)
из условия, что точка (т, т') лежит и на заданной плоскости. Для этого
пользуемся фронталью (или горизонталью). Дальнейшее построение видно из
чертежа.
Пример 120
Найти точку пересечения прямой АВ с плоскостью Р (фиг. 431).
Решение. Обозначаем искомую точку через М (т, т'). Так как эта точка
лежит на вертикалыю-проектирующей прямой, ее вертикальная проекция (т')
совпадает с вертикальной проекцией (а'Ь') прямой. Зная вертикальную проекцию
(т") точки, находим ее горизонтальную проекцию (т) из условия, что точка
(т, т') лежит на заданной плоскости. Для этого пользуемся горизонталью (или
фронталью). Дальнейшее построение видно из чертежа.
141
Пример 121
Найти точку пересечения прямой АВ с плоскостью Р (фиг. 432).
Решение. Обозначаем искомую точку через М (т, т'). Так как эта точка
лежит на горизонталыю-проектирующей прямой, то ее горизонтальная проекция
(т) совпадает с горизонтальной проекцией (лЛ) прямой. Зная горизонтальную
проекцию (т) точки, находим ее вертикальную проекцию (т'), пользуясь условием,
что эта точка лежит и на заданной плоскости. Для этого используем вспомога-
тельную прямую (nk, п'к'). Дальнейшее построение видно из чертежа.
Пример 122
Найти точку пересечения прямой АВ с плоскостью Р.(фиг. 433).
Решение. Обозначаем искомую точку через Л/ (m, in'). Так как эта точка
лежит на вертпка.тьно-проектпрующей прямой, то ее вертикальная проекция (т')
совпадает с вертикальной проекцией (я'/Х) прямой. Зная вертикальную проекцию
(т') точки, находим ее горизонтальную проекцию (т), пользуясь условием, что эта
точка лежит и на заданной плоскости. Для этого используем вспомогательную
прямую (/;г, /и')- Хотя плоскость Р — профилыто-проектпрующая, задача решена
без профильной плоскости проекций. В данном случае использовано не свойство
точек плоскости, а свойство точек проектирующей прямой.
142
Пример 123
Найти точку пересечения прямой АВ с плоскостью Р (фиг. 434).
Решение. Обозначаем искомую точку через М (т, т'). Заключаем прямую
АВ в горизонтально-проектирующую плоскость R (можно и в вертикально-
проектирующую), которая пересекает заданную плоскость пр прямой (hv, h’v').
На пересечении вертикальных проекций (h'v1 и а'Ь') прямых получаем вертикальную
проекцию (т‘) искомой точки. Затем по вертикальной проекции (т’) точки
находим ее горизонтальную проекцию (т) на горизонтальной проекции (ab) прямой.
Пример 124
Найти точку пересечения прямой АВ с плоскостью Р (фиг. 435).
Решен и е. Обозначаем искомую точку через М (т, nf). Заключаем прямую
АВ в плоскость R, параллельную горизонтальной плоскости проекций, которая
пересекает заданную плоскость Р по горизонтали. На пересечении горизонтальных
проекций горизонтали и заданной прямой получаем горизонтальную проекцию (т)
искомой точки. По горизонтальной проекции (т) точки находим ее вертикальную
проекцию (т’) на прямой а'Ь'.
Прямую АВ можно заключить и в горизонтально-проектирующую плоскость,
но это усложняет решение задачи. (Предлагаем учащимся убедиться в этом.)
Пример 125
Найти точку пересечения прямой АВ с плоскостью Р (фйг. 436).
Решение. Обозначаем искомую точку через М (т, т'). Заключаем прямую
АВ в плоскость R, параллельную вертикальной плоскости проекций, которая
пересекает заданную плоскость Р по фронтали. На пересечении вертикальных
проекций - фронтали и заданной прямой — получаем вертикальную проекцию (т1)
искомой точки. По вертикальной проекции (т) точки находим ее горизонтальную
проекцию (т) на горизонтальной проекции (ab) прямой.
143
Пример 126
Найти точку пересечения прямой АВ с плоскостью Р (фиг. 437).
Решение. Обозначаем искомую точку через М (т, Заключаем прямую
АВ в горизонтально-проектирующую плоскость R, которая пересекает заданную
плоскость Р по прямой (hr, h't').
На пересечении вертикальных проекций прямых — вспомогательной и задан-
ной — получаем вертикальную проекцию (т') искомой точки. По вертикальной
проекции (ж') точки находим ее горизонтальную проекцию (т) на горизонтальной
проекции (ab) прямой.
Пример 127
Найти точку пересечения прямой АВ с плоскостью Р (фиг. 438).
Решение. Обозначаем искомую Точку через М (т, т'). Заключаем прямую
АВ в вертикально-проектирующую плоскость R, которая пересекает заданную
плоскость по прямой (lw, h'v'). На пересечении горизонтальных проекций прямых —
заданной и вспомогательной — получаем горизонтальную проекцию (,и) искомой
точки. Затем по горизонтальной проекции (ш) точки находим ее вертикальную
проекцию (т') на вертикальной проекции (а'Ь') прямой.
Пример 128
Найти точку пересечения прямой АВ с плоскостью Р (фиг. 439).
Решение. Обозначаем искомую точку через М (т, т'). Так как заданная
прямая АВ — профильная, то при решении этой задачи нельзя избежать
профильной плоскости проекций, а потому решаем ее так, как было указано
в примере 117, а именно: строим профильный след (Р„) плоскости и профильную
проекцию (а''Ь") прямой. На их пересечении получаем профильную проекцию (т")
искомой точки, а затем по профильной проекции (т") точки находим две ее
другие проекции (т и т’) на одноименных проекциях (ah и а'Ь') прямой.
144
Пример 129
Найти точку пересечения прямой АВ с плоскостью Р (фиг. 440).
Решение. Обозначаем искомую точку через М (т, т'). Заключаем прямую
АВ в профильную плоскость R, которая пересекает заданную плоскость Р по
профильной прямой (hv, h'v'). Так как обе прямые — заданная и вспомогательная —
профильные, находим профильную проекцию (ni") искомой точки на пересечении
профильных проекций (а”Ь" и h"v”) этих прямых, а затем по профильной проекции
(т’) точки находим две ее другие проекции (т и т') па одноименных проекциях
(ab и db") прямой.
Пример 130
Найти точку пересечения прямой MN с плоскостью, заданной парал-
лельными прямыми АВ и CD (фиг. 441).
Решение. Обозначаем искомую точку через К (к, к'). Так как заданная
плоскость — горизонтально-проектирующая (почему?), находим горизонтальную
проекцию (к) точки на пересечении прямых тп и ab (почему?), или, что то же,
прямых пт и cd. По горизонтальной проекции (к) точки находим ее вертикальную
проекцию (к') па вертикальной проекции (т'п') прямой.
Пример 131
Найти точку пересечения прямой MN с плоскостью треугольника АВС
(фиг. 442).
Решение. Обозначаем искомую точку через К (к, к'). Так как заданная
плоскость — вертикально-проектирующая (почему?), находим вертикальную проек-
цию (к') точки на пересечении прямой т’п’ с вертикальной проекцией (а'Ь'сг)
треугольника (почему?). По вертикальной проекции (к') точки находим ее
горизонтальную проекцию (к) на горизонтальной проекции (тп) прямой (как?).
Пример 132
Найти точку пересечения прямой MN с плоскостью, заданной точкой А
и прямой ВС (фиг. 443).
145
Решение. Обозначим искомую точку через К (к, fc')- Так как эта точка
должна лежать на вертикально-просктирующей прямой (пт, т'п'), то ее вертикаль^
ная проекция (к') должна совпадать с точкой т'п' (почему?). По вертикальной
проекции (к1) точки находим ее горизонтальную проекцию (к) на прямой тп,
пользуясь условием, что точка (к, к’) лежит и на заданной плоскости. Дальнейшее
решение видно из чертежа.
146
Пример 133
• Найти линию пересечения плоскости Р с плоскостью треугольника АВС
(фиг. 444).
Решение. Первый способ. Линия пересечения будет определена, если найдем
две точки, принадлежащие заданным плоскостям. Находим точки (т, т') и (п, п’)
пересечения сторон (ас, а'с') и (Ьс, Ь'с') треугольника с плоскостью Р. Прямая
(тп, т'п'), проходящая через найденные точки (т, т') и (л, п), является искомой.
Второй способ. Так как плоскость Р — вертикально-проектирующая, то верти-
кальная проекция (т'п1) линии пересечения совпадает с вертикальным следом (Рц)
плоскости. Пользуясь условием, что искомая прямая (тп, т'п') принадлежит
к плоскости треугольника АВС, по вертикальной проекции (т'п') линии пересечения
находим ее горизонтальную проекцию (win).
Пример 134
Найти линию пересечения плоскости Р с плоскостью, заданной прямой
АВ и точкой С (фиг. 445). '
Решение. Первый способ. Линия пересечения будет определена, если найдем
две точки, принадлежащие заданным плоскостям. Точку (с, с') нельзя принять
за точку липни пересечения (почему?). Для того чтобы найти такие, точки, проще
всего перейти предварительно от задания плоскости прямой и точкой
к заданию ее двумя параллельными прямыми (ab, а’Ь') и (cd, c'd’), а затем найти
точки (т, т’) и (п, п') пересечения этих прямых с плоскостью Р. Прямая (тп, т'п'),
проходящая через найденные точки (т, т') и (и, и'), является искомой.
Второй способ. Так как плоскость Р — горизонтально-проектирующая, то го-
ризонтальная проекция (тп) линии пересечения совпадает с горизонтальным сле-
дом (Рь) плоскости. Теперь, пользуясь условием, что искомая прямая (тп, т'п')
принадлежит также другой плоскости, по горизонтальной проекции (ши) прямой
находим ее вертикальную проекцию (т'п').
147
Фиг. 446
Пример 135
Найти точку пересечения прямой MN с плоскостью, заданной парал-
лельными прямыми АВ и CD (фиг. 446).
Решение. Так как заданная плоскость — общего положения (почему?), то
прямую MN заключаем во вспомогательную плоскость R, например, параллельную
горизонтальной плоскости проекций, и находим линию (е/, e'f) пересечения
плоскостей. Искомую точку (к, к') получаем на пересечении прямых (пт, т'п')
и (е/, e'f). (См. пример 133.)
Пример 136
Найти точку пересечения прямой MN с плоскостью треугольника АВС
(фиг. 447).
Решение. Прямую MN заключаем во вспомогательную горизонтально-
проектирующую плоскость R и находим линию (de, d'e') пересечения плоскостей.
Искомую точку (к, к') получаем на пересечении прямых (тп, т'п') и (de, d'e').
Пример 137
Найти линию пересечения плоскости Р с плоскостью, заданной парал-
лельными прямыми АВ и CD (фиг. ,448).
Решение. Эту задачу можно решить тремя способами.
Первый способ. Переходим предварительно от задания плоскости не
следами к заданию ее следами, а затем решаем задачу так, как было указано
выше (см. примеры 95—112).
Второй способ. Находим точки пересечения прямых АВ и CD с плоскостью Р,
которые и определяют линию пересечения.
Третий способ. Находим точки, определяющие линию пересечения, введя
последовательно две вспомогательные плоскости.
Из этих трех способов проще всех третий. Вводим вспомогательную
плоскость R, параллельную горизонтальной плоскости проекций, пересекающую
плоскость Р по горизонтали (ut, v't'), и вторую плоскость — по горизонтали
(ди, д’и'); на их пересечении получаем точку (т, т'). Затем вводим вторую
вспомогательную плоскость — S, например, параллельную вертикальной плоскости
проекций, пересекающую плоскость Р по фронтали (rh, r'h'), и другую плоскость —
по фронтали (ке, к'е'); на их пересечении получаем точку (п, ri). Прямая (тп, т'п'),
проходящая через найденные точки (ш, т') и (п, и'), является искомой.
148
149
Пример 138
Найти линию пересечения плоскостей, заданных пересекающимися пря-
мыми FE и FG и параллельными прямыми АВ и CD (фиг. 449).
Решение. Находим точки (ш, т') и (и, п'), общие для заданных плоскостей,
для чего вводим вспомогательную плоскость R, параллельную горизонтальной
плоскости проекций и пересекающую заданные плоскости по горизонталям (кр, к'р')
и (Й, Г;'); на их пересечении получаем точку (ш, т'). Затем вводим вторую
вспомогательную плоскость — S, параллельную вертикальной плоскости проекций
и пересекающую заданные плоскости по фропталям (qs, q's") и (ru, г'и'); на их
пересечении получаем точку (и, п'). Прямая (ши, т'п'), проходящая через найденные
точки рп, т) и (и, и), является искомой.
ЗАДАЧИ
219. Найти точку пересечения прямой АВ с плоскостью Р (фит. 450 — 467).
220. Найти точку пересечения прямой АВ с плоскостьщ, заданной
не следами (фиг. 468 — 473).
150
151
152
154
221. Найти линию пересечения плоскости треугольника АВС с пло-
скостью Р и указать, через какие четверти проходит искомая линия
(фиг. 474).
222. Найти линию пересечения плоскости, заданной двумя параллель-
ными прямыми KLh MN, с плоскостью, заданной двумя пересекающимися
прямыми АВ и АС, и указать, через какие четверти проходит искомая
линия (фиг. 475).
155
156
Г л aefi XV
ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ Й ПЛОСКОСТИ.
ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ
Прямая и плоскость параллельны, если в плоскости можно провести прямую,
параллельную заданной прямой.
Две плоскости Р и Q, заданные следами, взаимно параллельны, если их одно-
именные следы между собой параллельны.
Обратная теорема не всегда справедлива в системе плоскостей И И V.
Например, две профильно-нроектирующие плоскости взаимно дараллсльда только
тогда, когда их профильные следа между собой параллельны.
Главные линии - горизонтали и фронта ли-двух параллельных плоскостей
между собой параллельны. Этой особенностью главных линий параллельны*
плоскостей удобно пользоваться для выяснения параллельности двух плоскостей,
когда одна из плоскостей или обе плоскости заданы не следами (нахождение
следов плоскости необязательно),
Параллельность плоскостей можно проверить и при'помощи произвольных
прямых.
ПРИМЕРЫ
Пример 139
Даны плоскость Р н точка А. Провести Через точку прямую, парал-
лельную плоскости (фиг. 476). -t
Решение. Задаем в плоскости какую-нибудь прямую (hv, htf), а затем через
точку (а, д') проводим прямую (аЬ, а'Ь1), параллельную ей. Так как прямая (A®, nV)
задается в плоскости произвольно, то, следоватедьно, через точку можно
провести множество прямых, параллельных плоскости Р. Однако через точку
можно провести только одну горизонталь и только одну фронталь, парал-
лельную заданной плоскости (почему?).
157
Пример 140
Даны точка А и плоскость — прямой DE и точкой С. Провести через
точку произвольную прямую, параллельную заданной плоскости (фиг. 477).
Решение. Задаем в плоскости какую-нибудь прямую (ск, е'к1) и через точку
(а, а') проводим прямую (ab, а'Ь'), параллельную ей. (Задача неопределенная.)
Пример 141
Даны плоскость Р и прямая АВ. Параллельны ли они между собой
(фиг. 478)?
Решение. Прямая АВ параллельна плоскости Р, если в последней можно
провести прямую, параллельную заданной прямой АВ. Проводим вертикальную
проекцию (/('с') прямой, лежащей в плоскости, параллельно прямой (а'Ь') и затем
находим ее горизонтальную проекцию (hv). Если последняя параллельна прямой
ab, то и прямая (ab, а'Ь') параллельна плоскости Р, и наоборот. В данной задаче
прямая АВ и плоскость Р не параллельны.
Решение задачи можно начать и с проведения горизонтальной проекции (М
прямой и т. д.
Пример 142
Даны прямая MN и плоскость - параллельными прямыми АВ и CD.
Параллельны ли они между собой (фиг. 479)?
Решение. Проводим произвольно вертикальную проекцию (е'к') вспомога-
тельной прямой, лежащей в заданной плоскости, параллельную прямой т'п’,
и находим сс горизонтальную проекцию (с/<). Так как прямые (efc, е'к') и (тп, т'п')
не параллельны (почему?), то и заданная прямая и плоскость тоже не парал-
лель н ы.
Решение задачи можно начать и с проведения произвольно горизонтальной
проекции (el'.) вспомогательной прямой и т. д.
158
159
Пример 143
Даны прямая АВ и топка С. Провести через точку С плоскость Р общего
положения со слившимися следами, параллельную прямой АВ (фиг. 480).
Решение. Для того чтобы плоскость Р, проходящая через точку С, была
параллельна прямой АВ, она должна заключать прямую, параллельную прямой
АВ. Проводим через точку (с, с') прямую (тп, m'lf), параллельную прямой (ab, а'Ь'),
п заключаем ее в плоскость. Для этого находим следы (h, h’) и (г, v’) прямой
(тп, т’п’) и проводим через точки (h, /1') и (у, с') следы Ph и Ре искомой плоскости,
слившиеся в одну прямую.
Примечание. В общем случае, если нет дополнительных указаний о пло-
скости, задача - неопределенная; в таких случаях точку Рх задаем произвольно.
Пример 144
Даны прямые АВ и СВ. Провести через прямую АВ плоскость, парал-
лельную прямой CD (фиг. 481).
Решение. Для того чтобы плоскость, проходящая через прямую АВ, была
параллельна прямой CD, она должна заключать прямую, параллельную прямой CD.
Проводим через произвольную точку (к, к’) прямой (ab, а'Ь1) прямую (тк, т'к'),
параллельную прямой (cd, cd’)- прямые (ab, а'Ь') и (тк, т’к’) определяют искомую
плоскость.
Точно так же можно провести и через прямую CD -единственную
плоскость, параллельную прямой АВ.
Эти плоскости можно задать и следами, для нахождения которых нужно
использовать ранее указанный способ. (Как?)
Вывод. Через две скрещивающиеся прямые можно провести только одну
пару параллельных плоскостей (плоскости параллелизма).
160
Пример 145
Даны плоскость Р и точка схода следов плоскости Q, параллельной
плоскости Р. Построить следы плоскости Q (фиг. 482, 483).
Решение. Следы плоскости Q должны быть параллельны одноименным
следам плоскости Р. Проводим через точку Qx следы: Qh— параллельно Рк и Q„ —
параллельно Р„.
Пример 146
Даны плоскость Р и точка А. Провести через точку А плоскость Q,
параллельную плоскости Р (фиг. 484).
Решение. Искомая плоскость Q — горизонтально-проектирукицая. Так как
эта плоскость должна проходить через точку (а, а'), то прежде всего проводим
горизонтальный след (Qh) плоскости через точку а — параллельно следу Рк,
до пересечения с осью проекций в точке Qx; затем через эту точку проводим
вертикальный след (Qj плоскости параллельно следу Р„.
Примечание. Если точка Qx выходаг за пределы чертежа, то проводить
вертикальный след необязательно.
Пример 147
Даны плоскость Р и точка А. Провести через точку А плоскость Q,
параллельную плоскости Р (фиг. 485).
Решение. Искомая плоскость Q — профильно-проектирующая. Известно, что
необходимым условием параллельности двух профильно-проектируюших плоско-
стей является параллельность их профильных следов. Находим профильный след
(PJ плоскости Р и профильную проекцию («") точки А. Так как плоскость Q
должна проходить через точку (а, а'), то проводим профильный след (()„.)
плоскости Q параллельно следу Рт через профильную проекцию (а") точки. Затем,
имея след Qm находим следы Qk и Qv, параллельные оси проекций.
Примечание. Данную задачу можно решить, не пользуясь профильной
плоскостью проекций (см. пример 149 — первый способ).
161
Пример 148
Даны плоскость Р и точка А. Провести через точку А плоскость Q,
параллельную плоскости Р (фиг. 486).
Решение. Искомая плоскость Q — общего положения, со слившимися сле-
дами. Так как точка (а, а'), через которую проходит плоскость Q, лежит на гори-
зонтальной плоскости проекции, то она должна лежать и на горизонтальном
следе (Oh) плоскости. Отсюда — проводим через точку а горизонтальный след (О(.)
плоскости до пересечения с осью проекций в точке Q,.; его продолжение является
вертикальным следом (Qj плоскости.
Пример 149
Даны плоскость Р и точка А. Провести через точку А плоскость Q,
параллельную плоскости Р (фиг. 487 — 489).
Решен и е. Общий прием решения заключается в том, что через точку А
проводят вспомогательную прямую, параллельную заданной плоскости Р (см. при-
мер 139), и ее заключают в плоскость, удовлетворяющую условию задачи.
Первый способ. Задаем в данной плоскости Р произвольную прямую (he, h'er)
и через точку (а, а’) проводим прямую, параллельную ей. Найдя следы (/ц, /ф)
и (щ, г)) этой прямой, проводим через них следы искомой плоскости Q: горизон-
тальный (Qft) — через точку hlt параллельно следу Р(, и вертикальный (Qt.) — через
точку г), параллельно следу Р... При правильном решении следы Q,, и О„ искомой
плоскости должны пересекаться на оси проекций в точке Ох. Проще решить
задачу при помощи главных линий плоскости — горизонтали пли фропталп.
Второй способ. Проводим через точку (а, а') горизонталь искомой плоскости
О — параллельно произвольной горизонтали плоскости Р. Ее горизонтальная проек-
ция должна проходить через точку а, параллельно следу Р,„ а вертикальная
проекция — через точку а1, параллельно оси проекций. Найдя след (г, г') этой
горизонтали, проводим следы искомой плоскости: сначала вертикальный след
(2с) через точку г', параллельно следу Рг, до пересечения с осью проекций
в точке Qx, а затем через эту точку — горизонтальный след (().), параллельно
следу Ph.
Третий способ. Проводим через точку (л, «') фронталь искомой плоскости Q —
параллельно произвольной фропталп плоскости Р. Ее горизонтальная проекция
162
Фиг. 486
должна проходить через точку а параллельно оси проекций, а вертикальная
проекция — через точку а', параллельно следу Р„. Найдя след (h, h') этой фронтали,
проводим следы искомой плоскости: сначала горизонтальный след (QJ —
через точку h, параллельно следу до пересечения с осью проекций в точке Qx,
а потом через эту точку — вертикальный след (2„), параллельно следу Р„.
Примечания. 1. Через заданную точку можно провести горизонтали и фрон-
тали искомой плоскости, не проводя этих линий на заданной плоскости (почему?).
2. Иногда при пользовании горизонталью или фронталью точка Qx
выходит за пределы чертежа; в этих случаях следы Qh и Q„ искомой плоскости
проводим независимо от точки Qx, для чего пользуемся и фронталью и
горизонталью.
6* 163
Фиг. 490
Пример 150
Даны точка А и плоскость — прямой ВС и точкой D. Провести через
точку А плоскость, параллельную заданной плоскости (фиг. 490).
Решенне. Переходим предварительно от задания плоскости прямой”
п точкой к заданию ее двумя пересекающимися прямыми ВС и DE. Проводим
затем через точку (д, а') прямые а'т') и (ап, а’п), соответственно параллельные
прямым (Ьс, Ь'с') и (de, d'e'). Искомая плоскость задана пересекающимися прямыми
AM п ЛА'. Она же может быть задана и следами, построение которых проводим
по общему правилу (как?).
Пример 151
Даны точка А и плоскость — параллельными прямыми ВС и DE.
Провести через точку А плоскость, параллельную заданной плоскости
(фиг. 491).
Решение. Проводим произвольную прямую (fk, fid) заданной плоскости
(для чего?), а затем проводим через точку (а, а') прямые (am, a'nd) и (ап, а'п'),
параллельные прямым (Ьс, Ь'с') или (de, d'e') и (fk, fid).
Пример 152
Даны треугольник АВС и плоскость Р. Параллельны ли плоскость
треугольника и плоскость Р (фиг. 492)?
Решение. Задачу можно решить двумя способами.
Первый способ. Находим предварительно следы плоскости треугольника,
а затем, пользуясь теоремой о расположении одноименных следов плоскостей,
выясняем расположение и самих плоскостей.
Второй способ. Пользуемся условием, что в параллельных плоскостях можно
провести параллельные прямые. Проводим произвольно горизонтали пло-
скости Р и плоскости треугольника АВС. В случае параллельности горизонталей
164
Фиг. 491
проводим произвольно фронтали тех же плоскостей. Если фроитали тоже
параллельны, то и сами плоскости между собой параллельны. Если же первая
пара главных линий (или горизонтали или фронтали) не параллельна, то следует
на этом прекратить решение задачи и сделать заключение, что плоскости уже
не параллельны. В данной задаче имеем случай, когда плоскость Р и плоскость
треугольника АВС не п а р а л л е л ьн ы;- .
Фиг. 492
165
Пример 153
Параллельны ли плоскости, заданные параллельными прямыми АВ и CD
и пересекающимися прямыми EF и GK (фиг. 493)?
Решение. Решаем задачу, не находя следов заданных плоскостей. Проводим
произвольно горизонтали в заданных плоскостях. Так как горизонтали
плоскостей не параллельны, то и сами плоскости уже не параллельны.
ЗАДАЧИ
223. Провести через точку А прямую, параллельную плоскости Р
(фиг. 494).
224. Провести через точку А прямую, параллельную плоскости, задан-
ной прямой ВС и точкой D (фиг. 495).
166
225. Провести через точку А прямую, параллельную плоскости, задан-
ной параллельными прямыми ВС и DE (фиг. 496).
226. Провести через точку А прямую, параллельную плоскости тре-
угольника BCD (фиг. 497).
227. Провести через точку А прямую, параллельную плоскости Р
и одинаково наклоненную к плоскостям проекций (фиг. 498).
228. Параллельны ли прямая АВ и плоскость Р (фиг. 499)?
Фиг. 497
а.
Фиг. 499
167
229. Параллельны ли прямая АВ и плоское 1ь, заданная прямой CD
и точкой К (фиг. 500)?
230. Параллельны ли прямая .41? и плоскость, заданная параллельными
прямыми CD и ЕЕ (фиг. 501)?
231. Параллельны ли прямая АВ п плоскость треугольника CDE
(фиг. 502)?
232. Провести через точку А плоскость Q, перпендикулярную к гори-
зонтальной плоскости проекций и параллельную прямой ВС (фиг. 503).
233. Провести через прямую АВ плоскость Р, параллельную прямой
CD (фиг. 504).
Фиг. 502
168
234. Через заданные прямые АВ и CD провести взаимно параллельные
плоскости Р и Q (фиг. 505, 506).
235. Построить следы плоскости Q, параллельной плоскости Р, если
дана точка схода следов (gx) плоскости (фиг. 507-510).
236. Выяснить, параллельны ли плоскости Р и Q (фиг. 511, 512):
1) пользуясь профильной плоскостью проекций;
2) не пользуясь профильной плоскостью проекций.
X
169
171J
237. Найти недостающий след плоскости Q, исходя из условия, что
плоскости Р и Q параллельны между собой (фиг. 513, 514):
1) пользуясь профильной плоскостью проекций;
2) не пользуясь профильной плоскостью проекций.
238. Построить следы плоскости, проходящей через точку К и парал-
лельной плоскости Р (фиг. 515 — 518).
239. Построить следы плоскости, проходящей через точку К и парал-
лельной плоскости Р (фиг. 519, 520):
1) пользуясь профильной плоскостью проекций;
2) не пользуясь профильной плоскостью проекций.
240. Провести через точку К плоскость, параллельную плоскости,
заданной прямой АВ и точкой С (фиг. 521).
172
241. Провести через точку К плоскость, параллельную плоскости,
заданной двумя параллельными прямыми АВ и CD (фиг. 522).
242. Провести через точку К плоскость, параллельную плоскости тре-
угольника АВС (фиг. 523).
Указание. В задачах 241, 242 и 243 искомую плоскость задать не следами
и следами.
Фиг. 524
Фиг. 525
173
243. Провести через Wikv С прямую, пересекающую прямую АВ
и параллельную плоскости Р (фиг. 524).
244. Провести через точку С прямую, пересекающую прямую АВ
и параллельную плоскости, заданной прямой DE и точкой К (фиг. 525).
245. Провести через точку К прямую, пересекающую прямую EF
и параллельную плоскости, заданной параллельными прямыми АВ н CD
(фиг. 526).
174
246. Провести через точку D прямую, пересекающую прямую EF
и параллельную плоскости треугольника АВС (фиг. 527).
247. Провести плоскость Q, параллельную плоскости Р, так, чтобы
отрезок заданной прямой АВ, заключенный между плоскостями, имел
Длину, равную 20 мм (фиг. 528, 529).
175
Фиг. 532
248. Провести плоскости Р, параллельную плоскости, заданной прямой
АВ и точкой С, так, чтобы отрезок заданной прямой ЕЕ, заключенный
между плоскостями, имел длину, равную 25 мм (фиг. 530).
249. Провести плоскость Р, параллельную плоскости, заданной парал-
лельными линиями АВ и CD, так, чтобы отрезок заданной прямой ЕЕ,
заключенный между плоскостями, имел длину, равную 30 мм (фиг. 531).
250. Провести плоскость Р, параллельную плоскости треугольника АВС,
так, чтобы отрезок заданной прямой ЕЕ, заключенный между плоскостями,
имел длину, равную 30 мм (фиг. 532).
Глава XVI
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ и плоскости.
ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
Если прямая перпендикулярна плоскости, заданной следами, то проекции этой
прямой перпендикулярны соответствующим следам плоскости; вместе с тем гори-
зонтальная проекция прямой перпендикулярна также горизонтальной проекции
горизонтали (почему?), а вертикальная проекция прямой перпендикулярна также
вертикальной проекции фронтали (почему?).
Этой особенностью проекций главных линий плоскости, перпендикулярной
к прямой, следует пользоваться для:
1) выяснения перпендикулярности прямой к плоскости, заданной не следами,
без определения следов плоскости;
2| опускания перпендикуляра из точки на плоскость, заданную не следами
(см. ниже примеры).
Обратная теорема не всегда справедлива в системе плоскостей Н и V.
Исключение. Прямая перпендикулярна профильпо-проектирующей пло-
скости, если дополнительно профильная проекция прямой перпендикулярна
профильному следу плоскости.
Плоскости Р и Q взаимно перпендикулярны, если плоскость Р содержит
прямую, перпендикулярную к плоскости Q.
176
ПРИМЕРЫ
Пример 154
Даны плоскость Р и точка А. Опустить из точки А перпендикуляр
на плоскость Р (фиг. 533).
Решение. Проводим через проекции заданной точки (а, а’) одноименные
проекции искомой прямой перпендикулярно соответственным следам плоскости,
т. е. ab ± Ph и a'b' 1 Р„.
Пример 155
Даны плоскость Р и точка А. Опустить из точки А перпендикуляр на
плоскость Р (фиг. 534).
Решение. ' Искомая прямая — про-
ф и льна я. Ее проекции должны проходить
через одноименные проекции заданной точки
(а, д') и должны быть перпендикулярны
соответствующим следам плоскости. Однако
нужно иметь в виду, что для любой про-
фильной прямой, хотя бы и не перпендику-
лярной к профильно-проектирующей плос-
кости, горизонтальная и вертикальная про-
екции на эпюре всегда перпендикулярны
следам плоскости. Вот почему нужно начинать
решение задачи с профильной плоскости
проекций и обеспечить перпендикулярное
положение профильной проекции искомой
прямой к профильному следу плоскости; за-
тем уже по профильной проекции прямой нуж-
но найти две ее другие проекции. Отсюда —
находим профильный след (/\) плоскости л
профильную проекцию (а") точки и опускаем
перпендикуляр из точки а" на след Р„. Огра-
ничиваем профильную проекцию прямой про-
извольным отрезком а"Ь" и затем находим
другие его проекции: горизонтальную (ab)
и вертикальную (й'Ь).
177
Пример 156
Даны плоскость двумя параллельными прямыми .4В п CD и точка К.
Опустить перпендикуляр из точки на эту плоскость (фиг. 535).
Решение. Проводим сначала произвольно горизонталь и фронталь данной
плоскости. Затем проводим проекции перпендикуляра: горизонтальную (А.7) — через
точку к. перпендикулярно горизонтальной проекции горизонтали (почему?), и вер-
тикальную (к'Г) - через точку к1, перпендикулярно вертикальной проекции фрон-
тали (почему?).
Пример 157
Даны плоскость Р и точка А. Определить расстояние от точки до
плоскости (фиг. 536).
Решение. Известно, что расстояние от точки до плоскости измеряется
отрезком перпендикуляра от его основания па плоскости до заданной точки.
Опускаем из точки (п, а') перпендикуляр на плоскость Р и находим его основание
(b, Ь'), т. е. точку пересечения перпендикуляра с плоскостью. Так как отрезок (ab,a'h 1.
расположен параллельно горизонтальной плоскости проекций, его горизонтальная
проекция (ab) дает нам истинное расстояние.
В ы в о д. Расстояние от произвольной точки до горизонтально-проектирующей
плоскости измеряется па эпюре расстоянием от горизонтальной проекции точки
до горизонтального следа плоскости.
Аналогично этому можно сделать вывод, что:
1) расстояние от произвольной точки до вертикально-проектирующей плоскости
измеряется на эпюре расстоянием от вертикальной проекции точки до вертикаль-
ного следа плоскости;
178
2) расстояние от произвольной точки до профильно-проектирующеи плоскости
измеряется на эпюре расстоянием от профильной проекции точки до профильного
следа плоскости.
Пример 158
Даны плоскость Р и точка А. Определить расстояние от точки до
плоскости (фиг. 537).
Решепи е. Опускаем из точки (а, а') перпендикуляр на плоскость Р и находим
его основание на этой плоскости, для чего ищем точку (/>, Ь') пересечения перпен-
дикуляра с плоскостью. Имея проекции (ab, а'Ь") отрезка перпендикуляра, определим
его действительную величину построением треугольника.
Пример 159
Даны треугольник АВС и точка К. Определить расстояние от точки
до плоскости треугольника (фиг. 538).
Реше и п е. Опускаем из заданной точки (к, к1) перпендикуляр на плоскость
треугольника (см. пример 156) и находим точку (р, р') — основание перпендикуляра.
Определяем истинную величину отрезка перпендикуляра (кр, к'р1).
Пример 160
Даны параллельные плоскости Р и Q. Определить расстояние между
ними (фиг. 539).
Реше н и е. Общий прием решения заключается в том, что на одной из
плоскостей берут произвольную точку и определяют ее расстояние до другой
плоскости (см. пример 157).
179
Вывод. Расстояние между параллельными вертикально-проектирующими
плоскостями измеряется на эпюре расстоянием между их вертикальными следами.
Аналогично этому расстояние между параллельными горизонтально-проекти-
рующими плоскостями измеряется на эпюре расстоянием между их горизонталь-
ными следами; расстояние между параллельными профильно-проектирующими
плоскостями измеряется на эпюре расстоянием между их профильными следами.
Пример 161
Даны плоскость Р и точка А этой плоскости — ее вертикальной проек-
цией. Восставить из точки А перпендикуляр к плоскости длиной I мм
(фиг. 540).
Решение. Находим горизонтальную проекцию (а) заданной точки, например
при помощи горизонтали, и проводим проекции перпендикуляра к плоскости через
точку (а, а'). Ограничив его условным отрезком (ат, ат), строим этот отрезок
в натуральную величину и откладываем на нем отрезок AN дайной I мм. Затем
находим его проекции (ап, ап).
Пример 162
Даны плоскость прямой АВ с точкой С и точка К этой плоскости —
ее горизонтальной проекцией. Восставить из точки К перпендикуляр
к плоскости длиной I мм (фиг. 541).
180
181
Решение. Переходим предварительно от задания плоскости прямой
и точкой к заданию ее двумя параллельными прямыми АВ и CD. Находим при
помощи фронтали вертикальную проекцию (//) заданной точки и затем проводим
через точку (к, к') горизонталь плоскости. Проводим проекции перпендикуляра
к плоскости: горизонтальную — перпендикулярно горизонтальной проекции гори-
зонтали и вертикальную — перпендикулярно вертикальной проекции фронтали.
Ограничиваем перпендикуляр условным отрезком (кт, к'т'); строим этот отрезок
в натуральную величину и откладываем на нем отрезок KN заданной длины I мм;
затем находим его проекции (кп, к'п’).
Пример 163
Даны прямая АВ и точка Рх. Построить следы плоскости Р, перпен-
дикулярной к прямой АВ (фиг. 542).
Решение. Искомая плоскость — горизонтально-проектирующая. Проводим
ее следы через точку Рх: горизонтальный (7<) — перпендикулярно прямой ab и
вертикальный (PL) — перпендикулярно прямой а'Ь1.
Пример 164
Даны прямая АВ и точка Рх. Построить следы плоскости Р, перпен-
дикулярной к прямой АВ (фиг. 543).
Решение. Искомая плоскость — вертикально-проектирующая. Проводим ее
следы через точку Рх: горизонтальный (Р(|) — перпендикулярно прямой ab и вер-
тикальный (PJ — перпендикулярно прямой а'Ь'.
Пример 165
Даны прямая АВ и точка Рх. Построить следы плоскости Р, перпен-
дикулярной к прямой АВ (фиг. 544).
Решение. Искомая плоскость — общего положения. Проводим ее следы через
точку Рх: горизонтальный (Ph) — перпендикулярно прямой ab и вертикальный
(PJ — перпендикулярно прямой а’Ь'.
Пример 166
Даны прямая АВ и точка С. Провести через точку плоскость Р, пер-
пендикулярную к прямой (фиг. 545).
Решение. Искомая плоскость — горизонтально-проектирующая. Так как эта
плоскость должна проходить через точку (с, с'), проводим сначала ее горизонталь-
ный след (Р,,) через точку с — перпендикулярно прямой ab, до пересечения с осью
проекций в точке Р„ а затем вертикальный след (Р„) через эту точку — перпенди-
кулярно прямой а'Ъ'.
Прим еч а н и е. Если точка Рх выходит за пределы чертежа, то проводить
вертикальный след плоскости необязательно (почему?).
Пример 167
Даны прямая АВ и точка С. Провести через точку плоскость Р, пер-
пендикулярную к прямой (фиг. 546).
Решение. Искомая плоскость — вертикально-проектирующая. Так как эта
плоскость должна проходить через точку (с, с'), проводим сначала ее вертикаль-
ный след (PJ через точку с' — перпендикулярно прямой а’Ь’, до пересечения
с осью проекций в точке Рх, а затем горизонтальный след (Ph) - через эту точку,
перпендикулярно прямой аЬ.
Примечание. Если точка Рх выходит за пределы чертежа, то прово-
дить горизонтальный след плоскости необязательно (почему?).
Пример 168
Даны прямай АВ и точка С. Провести через эту точку плоскость Р,
перпендикулярную к прямой АВ (фиг. 547).
183
Решение. Искомая плоскость - профильно-проектируюгцая. Находим про-
фильную проекцию (d'b"] прямой и профильную проекцию (с") точки; так как эта
плоскость должна проходить через точку (с, с’), проводим профильный след (Р„.)
плоскости через точку с" — перпендикулярно прямой d'b" и затем по следу Pw
находим два других следа (РЛ и 7ф) плоскости.
Пример 169
Даны прямая АВ и точка С. Провести через точку плоскость Р, пер-
пендикулярную к прямой (фиг. 548, 549).
Решение. Первый сноса'). Проводим проекции горизонтали искомой плоско-
сти через одноименные проекции заданной точки: вертикальную — через точку с',
параллельно осп проекций, и горизонтальную — через точку с, перпендикулярно
прямой аЬ.
Найдя след (с, г') горизонтали проводим следы плоскости сначала верти-
кальный (Р,.) — через точку г', перпендикулярно прямой а'Ь', до пересечения
с осью проекций в точке Рх, а затем горизонтальный (РЛ) - через эту точку,
перпендикулярно прямой ab.
Второй способ. Проводим проекции фронтали искомой плоскости через одно-
именные проекции заданной точки: горизонтальную — через точку с, параллельно
оси проекций, и вертикальную — через точку с', перпендикулярно прямой а'Ь'.
Найдя след (/;, /:') фронтали, проводим следы плоскости: сначала горизонтальный
(РА) — через точку /:, перпендикулярно прямой ab, до пересечения с осью проекций
в точке Рх, а затем вертикальный (Рг) — через эту точку,- перпендикулярно
прямой аЬ'.
Примечание. Иногда при пользовании горизонталью или фронтальна
•точка Рх в ы х о л и т за пределы чертежа; в этих случаях следы Ph и Р„ искомой
плоскости проводим независимо один от другого, для чего пользуемся
и фронталыо и горизонталью.
184
Пример 170
Даны прямая АВ п точка С. Опустить из точки С перйендикуляр на
прямую АВ (фиг. 550).
Опустить перпендикуляр из точки на прямую непосредственно можно
только в том случае, когда заданная прямая параллельна какой-либо плоскости
проекций (но какой теореме?). В общем же случае задача решается следующим
образом.
Решепие. Проводим через заданную точку (с, o') плоскость Р, перпендику-
лярную к прямой (ab, а'Ь"), и находим точку (к, к') их пересечения. Прямая,
проходящая через точки (с, с') и (к, к'), является искомой.
Указание. Для определения расстояния от точки С до прямой АВ остается
найти длину отрезка СК.
Пример 171
Даны плоскость Р и точка А. Провести через -точку А плоскость R,
перпендикулярную к данной плоскости (фиг. 551).
Решеяпе. Если плоскость R должна быть перпендикулярна плоскости Р,
то она должна заключать прямую, перпендикулярную к этой плоскости. Прово-
дим через точку (а, а') прямую, перпендикулярную к плоскости Р. Заключая ее
в плоскость R. получаем плоскость, перпендикулярную к данной плоскости
(задача — неопределенная).
Вывод. Плоскость, проходящая через точку перпендикулярно другой пло-
скости, единственная, если искомая плоскость — какая-либо проектирующая
или общего положения, но со слившимися следами (почему?).
185
я
Фиг. 550
Пример 172
Даны прямая АВ и плоскость Р. Провести через прямую АВ плоскость,
перпендикулярную к данной плоскости Р (фиг. 552).
Решение. Из произвольной точки (к, к') заданной прямей опускаем перпен-
дикуляр на плоскость Р. Пересекающиеся прямые (ак, а'к') и (kni, k'in') определяют
искомую плоскость.
Пример 173
Даны прямая DE и плоскость — прямой АВ и точкой С. Провести
через прямую плоскость, перпендикулярную к данной плоскости (фиг. 553).
Решение. Проводим через точку С горизонталь и фронталь плоскости
и из произвольной точки, например (к, к’), прямой опускаем перпендикуляр на
плоскость, для чего проводим через точку к прямую kf, перпендикулярную
к горизонтальной проекции горизонтали, и через точку к' - прямую kf, перпен-
дикулярную к вертикальной проекции фронтали. Искомая плоскость определена
двумя пересекающимися прямыми (е</, е'й) п (kf, kf).
Пример 174
Дана плоскость Р. Построить геометрическое место точек пространства,
отстоящих от плоскости на расстоянии I = 40 мм (фиг. 554).
186
Фиг. 553
187
Решение. Искомым геометрическим местом является плоскость, парал-
лельная данной плоскости и отстоящая от нее на расстоянии I = 40 мм. Отсюда
ход построений таков:
1) берем на заданной плоскости произвольную точку;
2) восставляем из этой точки перпендикуляр к плоскости;
3) откладываем па этом перпендикуляре отрезок длиной I = 40 мм (достаточно
дать одно решение);
4) проводим через конец перпендикуляра плоскость, параллельную данной
плоскости.
Учащимся рекомендуется произвести построение самостоятельно.
Пример 175
Построить геометрическое место точек па плоскости Р, отстоящих от
плоскости Q иа расстоянии I — 40 мм (фиг. 555).
Геше и и е. Искомым геометрическим местом является прямая пересечения
плоскости Р с плоскостью R, параллельной дайной плоскости Q и отстоящей
от псе па заданное расстояние. Отсюда ход построений таков:
1) берем па плоскости О произвольную точку;
2) восставляем из этой точки перпендикуляр к плоскости О;
3) откладываем па этом перпендикуляре отрезок длиной I = 40 мм (достаточно
дать одно решение);
4) проводим через конец перпендикуляра плоскость R, параллельную плоскости
О;
5) находим прямую пересечения плоскостей Р и R, которая и является
искомым геометрическим местом.
Пример 176
Найти иа прямой АВ точку, отстоящую от плоскости Р иа расстоянии
I = 40 мм (фиг. 556).
Решение. Искомой точкой является точка пересечения прямой АВ и пло-
скости R, параллельной данной плоскости Р и отстоящей от нее на расстоянии
I = 40 мм. Отсюда ход построений таков:
1) берем па заданной плоскости произвольную точку;
2) восставляем пз этой точки иерпсн,-щкуляр к плоскости;
188
3) откладываем на этом перпендикуляре отрезок длиной I = 40 мм (достаточно
дать одно решение);
4) проводим через конец перпендикуляра плоскость JR, параллельную плоско-
сти Р;
5) находим точку пересечения прямой АВ с плоскостью Л.
Пример 177
Найти недостающую проекцию точки К, отстоящей от плоскости Р
на расстоянии I = 40 мм (фиг. 557).
Решение. Искомую проекцию точки К находим, как недостающую проек-
цию, при одной заданной проекции, произвольной точки плоскости R, параллельной
данной плоскости и отстоящей от пее на расстоянии I = 40 мм. Отвода ход
построений таков:
1) берем на заданной плоскости произвольную точку;
2) восставляем из этой точки перпендикуляр к плоскости;
3) откладываем па этом перпендикуляре отрезок длиной 1 = 40 мм (достаточно
дать одно решение);
4) проводим через конец перпендикуляра плоскость R, параллельную плоско-
сти Р;
5) по заданной проекции точки К плоскости К находим другую ее проекцию.
Пример 178
Построить геометрическое место точек пространства, равноудаленных
от концов отрезка АВ (фиг. 558).
Решение. Искомым геометрическим местом является плоскость, перпендику-
лярная к данному отрезку и проходящая через его середину. Отсюда ход
построений таков:
1) делим заданный отрезок точкой К пополам;
2) проводим через эту точку плоскость, перпендикулярную к данному отрезку.
Пример 179
Построить геометрическое место точек на плоскости Р, равноудален-
ных от концов отрезка АВ (фиг. 559).
189
Решение. Искомым геометрическим местом является прямая пересечения
плоскости Р с плоскостью R, перпендикулярной к отрезку АВ и проходящей
через его середину. Отсюда ход построений таков:
1) делим заданный отрезок точкой К пополам;
2) проводим через эту точку плоскость R, перпендикулярную к данному
отрезку;
3) находим прямую пересечения плоскостей Р и R.
Пример 180
Найти на прямой CD точку, равноудаленную от концов отрезка АВ
(фиг. 560).
Решение. Искомой точкой является точка пересечения прямой CD с пло-
скостью R, перпендикулярной к отрезку АВ и проходящей через его середину.
Отсюда ход построений таков:
1) делим заданный отрезок точкой К пополам;
2) проводим через эту точку плоскость R, перпендикулярную к данному
отрезку;
3) находим точку пересечения прямой CD с плоскостью К.
Пример 181
Найти недостающую проекцию точки К, равноудаленной от концов
отрезка АВ (фиг. 561).
Решение. Искомую проекцию точки К находим, как недостающую проек-
цию при одной заданной проекции произвольной точки плоскости R, перпенди-
кулярной к отрезку АВ и проходящей через его середину. Отсюда ход построений
таков:
1) делим заданный отрезок точкой М пополам;
2) проводим через точку плоскость К, перпендикулярную к данному' отрезку;
3) по заданной проекции точки К плоскости R находим другую ее проекцию.
190
Пример 182
Найти на прямой АВ точку, отстоящую от точки К на расстоянии
I 40 мм (фиг. 562).
Решение. В общем случае искомых точек имеются две, например М и N,
которые являются вершинами равнобедренного треугольника KMN с основанием
MN на прямой АВ. Отсюда ход построений таков:
1) опускаем из точки К перпендикуляр на прямую АВ и находим точку' Й —
основание перпен,ни.у.ляра — высоты KD;
2| находим натуральную величину высоты KD и строим (в стороне) в нату-
ральную величину вспомогательный треугольник KMN с боковой стороной
длиной / = 40 мм.
3) откладываем па прямой АВ от точки D отрезки DM и DN. Точки М и N
являются искомыми.
Какие еше возможны случаи? V
Пример 183
Провести через точку К прямую, пересекающую прямую АВ под
заданным углом о (фиг. 562). . .2
Реше и и е. Искомых прямых имеются две, например КМ и KN, которые
являются боковыми сторонами равнобедренного треугольника KMN с основанием
МЫ па прямой АВ, с углами <р при основании. Отсюда ход построений таков:
1) опускаем из точки К перпендикуляр на прямую АВ И находим точку D-
оСиоваипс перпендикуляра — высоты KD-,
2) находим натуральную величину высоты KD и ггроим (в стороне) в нату-
ральную величину вспомогательный треугольник KMN с углом <р при основании;
3) откладываем на прямой АВ от точки D отрезки DM и DN и проводим,
прямые через точки К и М; К и N.
191
Пример 184
Найти недостающую проекцию прямой CD, пересекающей прямую АВ,
исходя из условия, что эти прямые между собой перпендикулярны (фиг. 563).
Решение. Геометрическим местом прямых пространства, перпендикулярных
к какой-либо прямой и пересекающих ее, является плоскость R, перпендику-
лярная к этой прямой и проходящая через точку пересечения прямых.
Искомую проекцию прямой CD находим, как недостающую проекцию произ-
вольной прямой, лежащей в плоскости R.
Отсюда ход построений таков:
1) находим проекции точки пересечения прямых;
2) проводим через эту точку плоскость R, перпендикулярную к прямой АВ;
3) по заданной проекции прямой плоскости R находим другую ес проекцию.
Пример 185
Определить расстояние между скрещивающимися прямыми АВ и CD
(фиг. 564).
Решение. Расстояние между скрещивающимися прямыми измеряется рас-
стоянием между плоскостями параллелизма, или, что то же, расстоянием от одной
из прямых до плоскости, проходящей через другую прямую параллельно первой
прямой.
Отсюда ход построений таков:
1) проводим через прямую АВ плоскость, параллельную прямой CD
(одна из плоскостей параллелизма);
2) берем на прямой CD произвольную точку К;
3) находим расстояние от этой точки до плоскости.
Примечание. Таким способом решения задачи определяем только рас-
стояние между заданными скрещивающимися прямыми, но не положение крат-
чайшего расстояния.
192
ЗАДАЧИ
251. Опустить из точки К перпендикуляр на плоскость Р (фиг. 560 — 569).
252. Опустить перпендикуляр из точки К на плоскость треугольника
АВС (фиг. 570, 571).
253. Опустить перпендикуляр из точки К на плоскость, заданную
параллельными прямыми АВ и CD (фиг. 572).
254. Опустить из точки К перпендикуляр на плоскость, заданную пря-
мой АВ и точкой С (фиг. 573).
255. Определить расстояние от точки К до плоскости Р (фиг. 565 — 569).
256. Определить расстояние от точки К до плоскости треугольника
АВС (фиг. 570, 571).
257. Определить расстояние от точки К до плоскости, заданной двумя
параллельными прямыми АВ и CD (фиг. 572).
194
258. Определить расстояние от точки К до плоскости, заданной пря-
мой АВ и точкой С (фиг. 573).
259. Определить расстояние между параллельными плоскостями Р и Q
(фиг. 574-577).
260. Определить расстояние между скрещивающимися прямыми АВ
и CD (фиг. 578).
261. Определить недостающий-след плоскости Р, исходя из условия,
что ее расстояние от точки К равно 15 мм (фиг. 579 — 581).
196
262. Описать из точки С шар, касательный к плоскости Р (фиг. 582 — 584).
263. Описать из точки С шар, касательный к плоскости, заданной пря-
мой MN и точкой К (фиг. 585).
264. Описать из точки С шар, касательный к плоскости, заданной
двумя параллельными прямыми K.L и MN (фиг. 586).
265. Описать из точки С шар, касательный к плоскости треугольника
KMN (фиг. 587).
197
198
266. Восставить из точки К перпендикуляр длиной I = 40 мм к пло- .
скости Р, исходя из условия, что горизонтальная проекция точки К
плоскости известна (фиг. 557).
267. Восставить из точки К перпендикуляр длииой I = 40 мм к плоскости,
заданной прямой АВ и точкой С, исходя из условия, что горизонтальная
проекция точки К плоскости известна (фиг. 588).
268. Восставить из точки К перпендикуляр длиной / — 40 мм к плоскости,
заданной двумя параллельными прямыми АВ и CD, исходя из условия,
что вертикальная проекция точки К плоскости известна (фиг. 589).
269. Восставить из точки К перпендикуляр длиной I = 40 мм к пло-
скости треугольника АВС, исходя из условия, что вертикальная проекция
точки К плоскости треугольника известна (фиг. 590).
270. Построить проекции прямой треугольной призмы с основанием
АВС на плоскости Р, если даны горизонтальная проекция основания и ее
высота /? = 40 мм (фиг. 591).
271. Построить геометрическое место точек пространства, отстоящих
•от плоскости Р на расстоянии I = 20 мм (фиг. 592 — 597).
272. Построить геометрическое место точек пространства, отстоящих
от плоскости, заданной прямой АВ и точкой С, на расстоянии I = 30 мм
(фиг. 598).
273. Построить геометрическое место точек пространства, отстоящих
от плоскости, заданной параллельными прямыми АВ и CD, на расстоянии
I = 30 мм (фиг. 599).
274. Построить геометрическое место точек пространства, отстоящих
от плоскости треугольника АВС на расстоянии I = 30 мм (фиг. 600).
275. Построить на плоскости Q геометрическое место точек, отстоящих
от плоскости Р на расстоянии / = 30 мм (фиг. 393, 394).
200
276. Построить на плоскости, заданной прямой АВ и точкой С, гео-
метрическое место точек, отстоящих от плоскости Р на расстоянии
I = 25 мм (фиг. 601).
Фяг. 601
201
277. Построить на плоскости, заданной двумя параллельными прямыми
АВ и CD,, геометрическое место точек, отстоящих от плоскости Р на
расстоянии I = 25 мм (фиг. 602).
278. Построить на плоскости треугольника АВС геометрическое место
точек, отстоящих от плоскости Р на расстоянии I = 25 мм (фиг. 603).
279. Построить на плоскости Р геометрическое место точек, отстоящих
от плоскости, заданной прямой АВ и точкой С, на расстоянии I = 25 мм
(фиг. 601).
202
280. Построить на плоскости Р геометрическое место точек, отстоящих
от плоскости, заданной двумя параллельными прямыми АВ и CD, на
расстоянии I = 30 мм (фиг. 602).
281. Построить на плоскости Р геометрическое место точек, отстоящих
от плоскости треугольника АВС на расстоянии I = 20 мм (фиг. 603).
282. Найти на прямой АВ точку, отстоящую от плоскости Р на рас-
стоянии I = 25 мм (фиг. 604, 605).
283. Найти на прямой MN точку, отстоящую от плоскости, заданной
прямой АВ и точкой С, на расстоянии I = 20 мМ (фиг. 606).
’203
284. Найти па прямой MN точку, отстоящую от плоскости, заданной
двумя параллельными прямыми АВ и CD, на расстоянии I = 25 мм
(фиг. 607).
285. Найти на прямой MN точку, отстоящую от плоскости треуголь-
ника АВС на расстоянии I = 25 мм (фиг. 608).
286. Определить недостающую проекцию точки А, отстоящей от пло-
скости Р на расстоянии 1 = 25 мм (фиг. 609-612).
287. Определить недостающую проекцию точки К, отстоящей от пло-
скости, заданной Прямой АВ и точкой С, на расстоянии I = 20 мм
(фиг. 613).
204
288. Определить недостающую проекцию точки К, отстоящей от пло-
скости, заданной двумя параллельными прямыми АВ и CD, на расстоянии
/ = 25 мм (фиг. 614).
289. Определить недостающую проекцию точки К, отстоящей от пло-
скости треугольника АВС на расстоянии I = 25 мм (фиг. 615).
290. Построить следы плоскости Р, перпендикулярной к прямой АВ,
если дана точка схода следов этой плоскости (фиг. 616 — 619).
205
Фиг. 618
291. Построить недостающий след (элемент) плоскости Р, перпендику-
лярной к прямой АВ (фиг. 620, 621).
292. Построить следы плоскости, проходящей через точку С и перпен-
дикулярной к прямой АВ (фиг. 622 — 624).
293. Перпендикулярны ли прямые АВ и CD (фиг. 625)?
Указание. Угла между прямыми не находить.
294. Определить недостающую проекцию прямой CD, исходя из условия,
что она пересекает прямую АВ под углом 90'’ (фиг. 563).
295. Провести через точку А плоскость, перпендикулярную к плоско-
стям Р и Q (фиг. 626).
296. Построить геометрическое место точек пространства, равноудален-
ных от концов отрезка АВ (фиг. 558, 627).
297. Построить иа плоскости Р геометрическое место точек, равно-
удаленных от концов отрезка АВ (фиг. 628).
298. Построить на плоскости, заданной прямой АВ и точкой С, гео-
метрическое место точек, равноудаленных от концов отрезка MN (фиг. 629).
299. Построить на плоскости, за-
, данной двумя параллельными пря-
мыми АВ и CD, геометрическое
место точек, .равноудаленных от
^Ч. - концов отрезка MN (фиг. 630).
^Ч. 300. Построить на плоскости
треугольника АВС геометрическое
у. ь'ь место точек, равноудаленных от
концов отрезка MN (фиг. 631).
у о____________________________ _ 301. Найти недостающую про-
р екцию точки К, одинаково удален-
х ной от концов отрезка АВ (фиг.
Фиг. 619 632, .633).
206
207
208
I
209
302. Найти на прямой CD точку, одинаково удаленную от концов
отрезка АВ (фиг. 634, 635).
303. Опустить из точки С перпендикуляр иа прямую АВ (фиг. 636 — 638).
304. Определить расстояние от точки С до прямой АВ (фиг. 636 — 638).
210
305. Построить шар с центром в точке С, касательный к прямой АВ
(фиг. 636-638).
306. Определить расстояние между параллельными прямыми АВ и CD
(фиг. 639).
307. Найти на прямой АВ точку, отстоящую от точки С на расстоянии
I = 30 мм. Какие возможны случаи (фиг. 636)?
308. Провести через точку С прямую, пересекающую прямую АВ под
углом 45°. Сколько может быть таких прямых (фиг. 637)?
309. Провести через точку К перпендикулярно плоскости Р:
1) горизонтально-проектирующую плоскость R (фиг. 640);
2) вертикально-проектирующую плоскость S (фиг. 641).
211
310. Провести через точку К перпендикулярно плоскости, заданной
прямой АВ и точкой С, горизонтально-проектирутощую плоскость К
(фиг. 642).
311. Провести через точку К перпендикулярно плоскости, заданной
двумя параллельными прямыми АВ и CD, вершкалыю-проектирующую
плоскость S (фиг. 643).
312. Провести через точку К перпендикулярно плоскости треугольника
АВС профильно-проектирующую плоскость S (фиг. 644).
212
Фиг. 643
313. Провести через точку К перпендикулярно плоскости Р плоскость
Q общего положения со слившимися следами (фиг. 645).
314. Провести через прямую Хв плоскость, перпендикулярную к пло-
скости Р (фиг. 646, 647).
315. Провести через прямую MN плоскость, перпендикулярную к пло-
скости, заданной прямой АВ и точкой С (фиг. 648).
Указание. Искомую плоскость задать следами.
213
316. Провести через прямую MN плоскость, перпендикулярную к пло-
скости, заданной двумя параллельными прямыми АВ и CD (фиг. 649).
Указание. Искомую плоскость задать следами.
317. Провести через прямую MN плоскость, перпендикулярную к пло-
скости треугольника АВС (фиг. 650).
Указание. Искомую плоскость задать следами.
214
318. Построить равнобедренный треугольник АВС с основанием ВС
на прямой MN, исходя из условия, что длина боковой стороны равна
1,25 его высоты (фиг. 651).
319. Построить равнобедренный треугольник АВС с основанием ВС
на прямой MN, исходя из условия, что его длина составляет 1,5 высоты
(фиг. 651).
320. Построить равнобедренный треугольник АВС с основанием ВС
на прямой MN, исходя из условия, что угол при основании равен 30°
(фиг. 651).
321. Построить равносторонний треугольник АВС с основанием ВС
на прямой MN (фиг. 651).
322. Построить прямоугольный треугольник АВС с катетом ВС на пря-
мой MN, исходя из условия, что длина гипотенузы равна 1,25 высоты
(фиг. 652).
323. Построить прямоугольный треугольник АВС с катетом ВС на
прямой MN, исходя из условия, что острый угол С равен 30° (фиг. 652).
324. Построить прямоугольный равнобедренный треугольник АВС
с гипотенузой ВС на прямой MN (фиг. 651).
325. Построить прямоугольный равнобедренный треугольник АВС
с катетом ВС на прямой MN (фиг. 652).
326. Построить прямоугольник ABCD с большим основанием ВС на
прямой MN, исходя из условия, что его площадь равна 1,5.4В2 (фиг. 652).
327. Построить прямоугольник ABCD с большим основанием ВС на
прямой MN, исходя из условия, что отношение его сторон равно 1,5
(фиг. 652).
215
328. Построить квадрат ABCD со стороной ВС на прямой MN (фиг. 652).
329. Построить квадрат ABCD с диагональю BD на прямой MN
(фиг. 651).
330. Построить параллелограмм ABCD с основанием ВС на прямой MN,
исходя из условия, что острый угол В равен 60°, а длина диагонали АС
на 5 мм превышает величину боковой стороны (фиг. 651).
331. Построить параллелограмм ABCD с основанием ВС на прямой MN,
исходя из условия, что длина боковой стороны равна 1,25 высоты и отно-
шение сторон равно 2 (фиг. 651).
332. Построить ромб ABCD со стороной ВС на прямой MN, исходя
из условия, что длина его стороны равна 1,2 высоты (фиг. 651).
333. Построить ромб ABCD со стороной ВС на прямой MN, исходя
из условия, что острый угол В равен 60° (фиг. 651).
334. Построить ромб ABCD с большей диагональю BD на прямой MN,.
исходя из условия, что отношение его диагоналей равно 2 (фиг. 651).
335. Построить прямоугольную трапецию ABCD с большим осно-
ванием ВС на прямой MN, исходя из условия, что AD = АВ; DC = 1,15АВ
(фиг. 652).
336. Построить прямоугольную трапецию ABCD с большим основанием
э
ВС на прямой MN при условии, что AD = АВ = ВС (фиг. 652).
j
337. Построить прямоугольную трапецию ABCD с большим основанием
ВС на прямой MN, если дано AD = АВ и угол С равен 45° (фиг. 652).
338. Построить равнобедренную трапецию ABCD с большим основа-
нием ВС иа прямой MN, если дано АВ = AD = DC = 40 мм (фиг. 651).
339. Построить равнобедренную трапецию ABCD с большим основа-
нием ВС на прямой MN при условии, что острый угол равен 45' и
меньшее основание равно боковой стороне (фиг. 651).
340. Построить равнобедренный треугольник АВС с основанием ВС
на прямой MN, если его боковая сторона больше высоты AD на 10 мм
(фиг. 651).
341. Построить равносторонний треугольник АВС с основанием ВС
на прямой MN. исходя из условия, что точка К является основанием
высоты (фиг. 653).
342. Построить прямоугольный треугольник АВС с катетом ВС на пря-
мой MN, если радиус круга, описанного около треугольника, равен О,75ЛВ
(фиг. 651).
343. Построить прямоугольник ABCD с большей стороной ВС на пря-
мой ВМ, исходя из условия, что отношение его сторон равно 2 (фиг. 654).
344. Построить квадрат ABCD со стороной ВС па прямой MN (фиг. 652).
345. Построить квадрат ABCD со стороной ВС на прямой ВМ (фиг. 654).
346. Построить параллелограмм ABCD с большей стороной ВС на
прямой MN, исходя из условия, что точка К — основание высоты — делит
ее в отношении 1:2 от точки В к точке С и угол В = 60 (фиг. 653).
347. Построить ромб ABCD со стороной ВС па прямой MN, если
длина его стороны равна 1,2 высоты (фиг. 651).
348. Построить прямоугольную трапецию ABCD с большим основанием
ВС на прямой ВМ, если В = 90°; AD = АВ; CD = 1,2ЛВ (фиг. 654).
349. Построить прямоугольную трапецию ABCD с большим основанием
216
ВС на прямой MN и со стороной АВ на прямой EF, если угол В = 90°;
AD = АВ = 40 мм и угол С = 45° (фиг. 655).
350. Построить ромб ABCD с большей диагональю BD на прямой MN,
если меньшая диагональ имеет длину, равную 40 мм, и лежит на прямой
EF, а площадь ромба равна АС2 (фиг. 656).
351. Построить параллелограмм ABCD со стороной ВС, длина которой
равна 60 мм и которая расположена на прямой ВМ, если высота парал-
лелограмма АК лежит на прямой EF, а длина боковой стороны равна
40 мм (фиг. 657).
352. Построить квадрат ABCD с диагональю BD на прямой MN
(фиг. 658).
353. Построить прямоугольник ABCD с большей стороной ВС, лежащей
на прямой MN, если сторона АВ имеет длину, равную 40 мм и лежит
на прямой EF, а отношение сторон прямоугольника равно 1,5 (фиг. 655).
354. Построить прямоугольный треугольник АВС с основанием ВС,
лежащим на прямой MN, если катет АВ имеет длину, равную 30 мм,
и лежит на прямой EF, а площадь треугольника равна 0,75ЛВ2 (фиг. 655).
355. Построить равносторонний треугольник АВС с основанием ВС,
которое имеет длину, равную 50 мм, и лежит на прямой MN, если вер-
шина А лежит на прямой EF, перпендикулярной к MN (фиг. 656).
356. Построить равносторонний треугольник АВС с основанием ВС
на прямой MN, если его высота AD равна 40 мм и лежит на прямой EF
(фиг. 656).
217 .
218
Фиг. 660
357. Построить равнобедренный треугольник АВС с основанием ВС
на прямой MN, если его высота AD равна 40 мм и лежит на прямой EF
и угол при основании равен 30° (фиг. 656).
358. Построить равнобедренный треугольник АВС с основанием ВС
длиной 60 мм, лежащим на прямой MN, если вершина А лежит на
прямой EF, перпендикулярной к MN, а высота равна 40 мм (фиг. 656).
359. Построить равнобедренный треугольник АВС с основанием ВС,
лежащим на прямой MN, и с вершиной А на прямой EF, исходя из
условия, что точка К является основанием высоты АК и боковая сторона
равна 1,15Л.К (фиг. 659).
360. Построить равносторонний треугольник АВС с основанием ВС,
лежащим на прямой MN, и с вершиной А на прямой EF, исходя из
условия, что точка К является основанием высоты Л К.(фиг. 659).
361. Построить прямоугольный равнобедренный треугольник АВС
с катетом ВС, лежащим на прямой ВМ, и с вершиной А на прямой EF
(фиг. 660).
362. Построить прямоугольник ABCD с большей стороной АС, лежащей
на прямой ВМ, и с вершиной А на прямой EF, если диагональ прямо-
угольника равна 2АВ (фиг. 660).
219
363. Построить квадрат ABCD со стороной ВС, лежащей на прямой
ВМ, если вершина .4 лежит на прямой EF (фиг. 660).
364. Построить квадрат ABCD с диагональю BD, лежащей на прямой
MN, если вершина А лежит иа прямой EF, а точка К является пересе-
чением его диагоналей (фиг. 659).
365. Построить параллелограмм ABCD с большей стороной ВС иа
прямой MN и с вершиной А иа прямой EF, если сторона АВ больше
высоты АК па 5 мм, а сторона ВС равна 1,5.4К (фиг. 659).
366. Построить ромб ABCD с большей диагональю BD, лежащей па
прямой MN, и с вершиной А иа прямой EF, если точка К является
пересечением его диагоналей, а отношение диагоналей равно 2 (фиг. 659).
367. Построить прямоугольную трапецию ABCD с большим основанием
ВС, лежащим на прямой ВМ, если вершина А лежит на прямой EF,
AD = АВ; В =9(Г; С = ср (фиг. 660).
368. Построить равнобедренный треугольник АВС с вершиной А, лежа-
щей на прямой EF (фиг. 661).
369. Построить прямоугольник ABCD с вершиной А, лежащей на пря-
мой EF, и вычислить его площадь (фиг. 661).
370. Построить ромб ABCD с вершиной А, лежащей на прямой EF
(фиг. 662).
РАЗДЕЛ ТРЕТИЙ
Глава XVII
ВРАЩЕНИЕ.
ПЕРЕМЕЩЕНИЕ ПАРАЛЛЕЛЬНО ПЛОСКОСТЯМ ПРОЕКЦИЙ
ПРИМЕРЫ
Пример 186
Повернуть точку А вокруг оси I, перпендикулярной к плоскости Н,
на угол 120° по направлению движения часовой стрелки (фиг. 663).
Решение. Точка (а, а') при ее вращении вокруг оси (i, i) описывает
в плоскости R, перпендикулярной к оси вращения, т. е. в плоскости, параллельной
плоскости II, окружность радиуса ai. Горизонтальная проекция (а) точки описывает
дугу aat окружности радиуса ai с центральным углом а = 120°. Вертикальная
проекция (л') точки движется по прямой, параллельной оси проекций (z = const).
Зная повое положение горизонтальной проекции (йД точки, находим ее вертикаль-
ную, проекцию («)).
Пример 187
Повернуть точку А вокруг оси I, перпендикулярной к плоскости V,
на угол 120° по направлению движения часовой стрелки (фиг. 664).
Решенпе. Точка (а, а1) при ее вращении вокруг оси (i, i') описывает в пло-
скости R, перпендикулярной к оси вращения, т. е. в плоскости, параллельной
плоскости V, окружность радиуса a'i'. Вертикальная проекция (а') точки описывает
дугу fl'n) окружности радиуса a'i' с центральным углом а = 120°. Горизонтальная
проекция (я) точки движется по прямой, параллельной оси проекции (у = const).
Зная новое положение вертикальной проекции (я)) точки, находим ее горизонталь-
ную проекцию (nJ.
Пример 188
Повернуть отрезок АВ вокруг оси I, перпендикулярной к плоскости И,
на угол 120° по направлению движения часовой стрелки (фиг. 665).
Решенп е. Для того чтобы повернуть отрезок на заданный угол, достаточно
повернуть на этот угол, обязательно в одном направлении, точки А и В
отрезка. Для этого поступаем так, как было указано выше. Из построения видно,
что длина горизонтальной проекции (ni&i) отрезка не изменяется; изменяется
только ее положение относительно оси проекций. Это обстоятельство дает нам
возможность ограничиться поворотом на заданный угол одной только точки
(к, к') отрезка, ближайшей к оси (i, i'). Повернув точку к на угол 120° —в поло-
жение fcj, проводим через нее прямую, перпендикулярную к радиусу iklt и на ней
откладываем отрезки atkt = ак и ЬА^ = Ьк. Зная горизонтальную проекцию (ajbJ
отрезка, находим его вертикальную проекцию (n'jb'i). Построение видно из чертежа.
Пример 189
Повернуть отрезок АВ вокруг оси I, перпендикулярной к плоскости V,
на угол 60° по направлению движения часовой стрелки (фиг. 666).
221
Решение. Для того чтобы повернуть отрезок на заданный угол, достаточно
повернуть на этот угол, обязательно в одном направлении, точки А и В
отрезка. Для этого поступаем так, как было указано выше. Из построения видно,
что длина вертикальной проекции (alb'j) отрезка не изменяется; изменяется только
ее положение относительно оси
проекции. Это обстоятельство
дает нам возможность ограни-
читься поворотом на заданный
угол одной только точки (/с, к')
отрезка, ближайшей к оси (;, г).
Повернув точку к' на угол 60°,
в положение к\, проводим через
нее прямую, перпендикулярную
к радиусу i’k'i, и па пей откла-
дываем отрезки «i/<i — о'к' и
b'jk'j = Ь'к'. Зная вертикальную
проекцию (ci'ib'i) отрезка, нахо-
дим горизонтальную проекцию
(аМ. Построение видно из чер-
тежа.
Пример 190
Повернуть треугольник
АВС вокруг оси I, перпенди-
кулярной к плоскости Н, на
угол 120° по направлению
движения часовой стрелки
(фиг. 667).
Реше п и е. Поворачиваем
вершины А, В и С треугольника
на угол 120°. Зная горизонталь-
ные проекции (aj, (bj) и (ci)
точек, находим их вертикальные
222
к>
u>
проекции (a'j), (bi) и (ci). Соединяя одноименные проекции вершин треугольника,
получаем его проекции: горизонтальную (ajbxCj) и вертикальную (aibicj). Следует
обратить внимание на то, что треугольники abc и д1Ь1с1 между собой равны.
Примем а н и е. При вращении треугольника вокруг оси I, перпендикулярной
к плоскости V, были бы равны между собой треугольники а'Ь'с' и
Выводы:
1. При вращении точки вокруг осп I, перпендикулярной к плоскости 11,
вертикальная ее проекция движется по прямой, параллельной осп проекций.
2. При вращении точки вокруг оси 1, перпендикулярной к плоскости V,
горизонтальная ее проекция движется по прямой, параллельной осп проекций.
3. При вращении отрезка вокруг оси I, перпендикулярной к плоскости Я,
длина горизонтальной проекции отрезка не изменяется, а следовательно,
не изменяется и угол наклона отрезка к горизонтальной плоскости проекций.
4. При вращении отрезка вокруг оси /, перпендикулярной к плоскости V,
длина вертикальной проекции не изменяется, а следовательно, не изменяется и угол
наклона отрезка к вертикальной плоскости проекций.
5. При вращении плоской фигуры (например, треугольника) вокруг оси I,
перпендикулярной к плоскости Я, горизонтальная проекция фигуры по
изменяется, а следовательно, ие изменяется и угол наклона плоскости фигуры
к горизонтальной плоскости проекций.
6. При вращении плоской фигуры вокруг оси I, перпендикулярной к плоскости
V, вертикальная проекция фигуры не изменяется, а следовательно, не изме-
няется и угол наклона плоскости фигуры к вертикальной плоскости проекций.
7. При вращении системы геометрических элементов (точек, прямых или их
комбинаций) вокруг оси, перпендикулярной к плоскости Я (или V), взаимное
положение горизонтальных (вертикальных) проекций заданных элементов
не изменяется, изменяется только их положение относительно оси проекций.
В ряде случаев, при вращении системы геометрических элементов вокруг оси,
перпендикулярной к плоскости проекций, происходит наложение получаемой проек-
ции на первоначальную. Для того чтобы избежать этого, целесообразно пере-
мещать систему параллельно плоскости проекций, а не прибегать к вращению.
Пример 191
Даны точка А и плоскость R, параллельная плоскости II, проходящая
через эту точку. Проследить за движением точки по плоскости (фиг. 668).
Решение. Какую бы линию точка (а, а') ни описывала в плоскости R, вер-
тикальная проекция такой линии (траектории) изображается в виде прямой, совпа-
дающей со следом А’„ плоскости. Вертикальная проекция (а') точки движется по
прямой, параллельной оси проекций; горизонтальная се проекция (а) движется по
такой же точно линии, как и сама точка А, в плоскости R (почему?). Допустим,
что точка а перешла по линии 1 в положение <гп> зная это, нетрудно найти
положение вертикальной проекции (и)) точки.
Если точка а переходит в т о ж е положение по линии II, то это никак
не отражается на положении вертикальной проекции (а)) точки. Отсюда, видим,
что достаточно указать повое положение горизонтальной проекции (aJ точки,
чтобы точно определить положение (я)) ее вертикальной проекции. В данном
случае происходит не движение точки вокруг оси, а произвольное ее перемещение
по плоскости, параллельной плоскости Я.
В дальнейшем называем такое перемещение точки «перемещением точки
параллельно плоскости Я». Из чертежа видно, что расстояние от вертикальной
проекции (а)) точки до осп проекций, как и при вращении вокруг оси I, перпен-
дикулярной к плоскости Я, не изменяется.
Пример 192
Даны точка А и плоскость Д, параллельная плоскости V, проходящая
через эту точку. Проследить за движением точки по плоскости (фиг. 669).
Решение. Какую бы линию точка (а, а') ни описывала в плоскости R,
горизонтальная проекция такой линии (траектории) изображается в виде прямой,
224
совпадающей со следом плос-
кости. Горизонтальная проекция
(а) тонки движется по прямой,
параллельной оси проекций; вер-
тикальная ее проекция (аг) дви-
жется по такой же точно липли,
как и сама точка А, в плоскости
R (почему?). Допустим, что точка
а' перешла по линии 1 в поло-
жение «i; зная это, нетрудно
найти положение горизонталь-
ной проекции (щ) точки. Если
точка а! переходит в то же
положение а\ по линии II, то это
никак не отражается на положе-
нии горизонтальной проекции
(щ) точки. Отсюда видим, что
достаточно указать новое
положение вертикальной проек-
ции (а)) точки, чтобы точно опре-
делить положение (ах) ее гори-
зонтальной проекции.
В данном случае опять-таки происходит не движение точки вокруг оси, а про-
извольное ее перемещение по плоскости, параллельной плоскости К В дальнейшем
называем такое перемещение точки «перемещением точки параллельно плоскости
К». Из чертежа видно, что расстояние от горизонтальной проекции (ах) точки
до оси проекции, как и при вращений вокруг оси, перпендикулярной к плоскости
F, не изменяется.
Пример 193
Дана точка А в третьей четверти. Привести ее в первую четверть
(фиг. 670).
Решение. Для того чтобы привести точку (а, «9 в первую четверть, нужно
выполнить последовательно два перемещения. Первое — параллельно вертикаль-
8 Арустамов X. А.
225
пои плоскости проекции, чтобы привести точку (а, а') во вторую четверть;
второе — параллельно горизонтальной плоскости проекций, чтобы привести точку
(<?!, ai) в первую четверть (можно идти и в обратном порядке: сначала — парал-
лельно плоскости Н, а затем — параллельно плоскости V). Отсюда — при перенесе-
нии точки во вторую четверть обе ее проекции должны быть над осью проек-
ций; горизонтальная проекция точки движется по прямой, параллельной оси
проекций. Задавшись произвольно вертикальной проекцией (ai) точки, нахо-
дим ее горизонтальную проекцию (щ). При втором перемещении вертикальная
проекция (й’х) точки движется по прямой, параллельно оси проекций; задав
произвольно горизонтальную проекцию (а2) точки под осью проекций
(почему?), находим вертикальную проекцию (ai) точки. Точка (a2ai) является
искомой.
Пример 194
Отрезок АВ перемещением параллельно горизонтальной плоскости про-
екций привести в произвольное положение (фиг. 671).
Решение. При перемещении отрезка параллельно горизонтальной плоскости
проекций длина его горизонтальной проекции, как и при вращении отрезка вокруг
оси, перпендикулярной к плоскости II, не изменяется. Задаем под осью проекций
(чтобы оставить отрезок в первой четверти) отрезок djit в произвольном
положении, равным отрезку ab, и затем по горизонтальной проекции отрезка
находим его вертикальную проекцию (a'jbi).
Примечай и е. При решении такпх задач нужно стремиться оставлять
заданные элементы в первой четверти и приводить их в первую четверть, если
они заданы в других четвертях.
Пример 195
Отрезок АВ перемещением параллельно вертикальной плоскости про-
екций привести в произвольное положение (фиг. 672).
Решение. При перемещении отрезка параллельно вертикальной плоскости
проекции длина его вертикальной проекции, как и при вращении отрезка вокруг
осп, перпендикулярной к плоскости V, не изменяется. Задаем в произвольном
положении отрезок a'J^, равный отрезку а'й',-и затем по вертикальной проекции
(ait'J отрезка находим его горизонтальную проекцию ta-Jji)-
Пример 196
Отрезок АВ привести в положение, параллельное вертикальной пло-
скости проекций (фиг. 673).
Решение. Перемещаем отрезок параллельно горизонтальной плоскости про-
екций. Так как он должен находиться в положении, параллельном вертикальной
плоскости проекций, его горизонтальная проекция должна быть параллельна оси
проекций. Задаем под осью проекций отрезок а1Ь1 в положении, параллельном
оси проекций, равный отрезку ab, и затем по горизонтальной проекции (ait>i)
отрезка находим его вертикальную проекцию (aib'J.
Пример 197
Отрезок АВ привести в положение, параллельное горизонтальной
плоскости проекции (фиг. 674).
Решение. Перемещаем отрезок параллельно вертикальной плоскости про-
екций. Так как отрезок должен находиться в положении, параллельном горизон-
тальной плоскости проекций, его вертикальная проекция должна быть параллельна
оси проекций. Задаем над осью проекций отрезок ai?/, в положении, параллель-
ном оси проекций, равный отрезку а’Ь', и затем по вертикальной проекции (ai£>i)
отрезка находим его горизонтальную проекцию (ajbJ.
226
Пример 198
Отрезок АВ привести в положение, перпендикулярное К горизонталь'
НОЙ плоскости проекций (фиг. 675).
Решение. Так как отрезок АВ задан в положении, параллельном верти-
кальной плоскости проекций, то достаточно одного его перемещения парал-
лельно вертикальной плоскости проекций. Задаем отрезок а\Ъ\ в положении, пер-
пендикулярном к оси проекций (почему?), равный отрезку а'Ь', и затем по верти-
кальной проекции (a’Ai’A отрезка находим его горизонтальную проекцию (atbA
в виде точки.
Пример 199
Отрезок АВ привести в положение, перпендикулярное к вертикальной
плоскости проекций (фиг. 676).
Решение. Так как отрезок АВ задан в положении, параллельном горизон-
тальной плоскости проекций, достаточно одного его перемещения параллельно
горизонтальной плоскости проекций. Задаем отрезок в положении, перпенди-
кулярном к оси проекций (почему?), равный отрезку ab, и затем по горизонталь-
ной проекции (ajbj) отрезка находим его вертикальную проекцию (а^Ь'А в виде
точки.
Пример 200
Отрезок АВ привести в положение, перпендикулярное к горизонталь-
ной плоскости проекций (фиг. 677).
Решение. Так как заданный отрезок (ab, а'Ь1) — общего положения, для того
чтобы привести его в положение, перпендикулярное к плоскости Н, нужно выпол-
нить последовательно два перемещения. Первое — параллельно горизонтальной
плоскости проекций, чтобы привести отрезок (ab, а'Ь1} в положение, параллельное
вертикальной плоскости проекций; второе — параллельно вертикальной плоскости
проекций, чтобы привести отрезок (<цЬ1, flibl) в положение, перпендикулярное
к горизонтальной плоскости проекций. Отсюда: располагаем, где угодно, в поло-
жении, параллельном оси проекций, отрезок равный отрезку ab, и определяем
228
вертикальную проекцию (aib'j) отрезка. Затем располагаем в положении, перпен-
дикулярном к оси проекций, отрезок а'2Ъ'2, равный отрезку fl'jb'i, ц находим гори-
зонтальную проекцию (а2Ьг) отрезка в виде точки. Отрезок является
искомым.
Пример 201
Отрезок АВ привести в положение, перпендикулярное к вертикальной
плоскости проекций (фиг. 678).
Решение. Так как заданный отрезок (аЪ, а’Ь') — общего положения, дня того
чтобы привести его в положение, перпендикулярное к плоскости V, нужно выпол-
229
нить последовательно два перемещения: первое — параллельно вертикальной плоско-
сти проекций, чтобы привести отрезок (ab, а'Ь') в положение, параллельное гори-
зонтальной плоскости проекций; второе — параллельно горизонтальной плоскости
проекций, чтобы привести отрезок (а^, a'l&l) в положение, перпендикулярное
к вертикальной плоскости проекций. Отсюда: располагаем, где угодно, в положе-
нии, параллельном оси проекций, отрезок а)Ь\, равный отрезку а'Ь', и определяем
горизонтальную проекцию отрезка. Затем располагаем- в положении, перпен-
дикулярном к оси проекций, отрезок а2Ь2, равный отрезку а^, и находим верти-
кальную проекцию (а2Ь2) отрезка в виде точки. Отрезок (а2Ь2, а'2Ь2) является
искомым.
Пример 202
Плоскость Р привести в положение, перпендикулярное к плоскости Н
(фиг. 679).
Решение. Для того чтобы заданную плоскость привести в положение, пер-
пендикулярное к плоскости Н, проводим в ней фронталь и ставим ее в положе-
ние, перпендикулярное к плоскости Н. Тогда и заданная плоскость занимает
положение, тоже перпендикулярное к плоскости II. Проводим в плоскости Р
произвольную фронталь, перемещаем ее параллельно плоскости V так, чтобы
фронталь стала в положение, перпендикулярное к плоскости Н. Вертикальная
проекция фронтали, а следовательно, и вертикальный след (P„t) плоскости перпен-
дикулярны оси проекций, горизонтальная проекция фронтали сливается в точку.
Так как при перемещении плоскости параллельно вертикальной плоскости проек-
ций утол ее наклона к этой плоскости проекции, как и при вращении плоскости
вокруг оси, перпендикулярной к плоскости V, не изменяется, необходимо, чтобы
при любом положении плоскости не изменялось и расстояние между ее вертикаль-
ным следом и вертикальной проекцией фронтали.
Задаем на оси проекций произвольно точку схода Рх и проводим через
нее перпендикулярно оси проекций вертикальный след (P„J плоскости, а парал-
лельно ему, на расстоянии I — вертикальную проекцию фронтали. Найдя горизон-
тальный след фронтали, т. е. точку hlt проводим горизонтальный след (РЛ])
плоскости через точки Рх и 1^.
230
Фиг. 680
Пример 203
Плоскость Р привести в положение, перпендикулярное к плоскости V
(фиг. 680).
Решение. Для того чтобы заданную плоскость привести в положение,
перпендикулярное к плоскости V, проводим в ней горизонталь и ставим ее
в положение, перпендикулярное к плоскости V. Тогда и заданная плоскость зани-
мает положение, тоже перпендикулярное к плоскости V. Проводим в плоскости Р
произвольную горизонталь и перемещаем ее параллельно плоскости И так, чтобы
горизонталь стала в положение, перпендикулярное к плоскости V. Горизонтальная
проекция горизонтали, а следовательно, и горизонтальный след (РЛ1) плоскости
перпендикулярны оси проекций; вертикальная проекция горизонтали сливается
в точку. Так как при перемещении плоскости параллельно горизонтальной пло-
скости проекций угол ее наклона к этой плоскости проекций не изменяется,
необходимо, чтобы при любом положении плоскости не изменялось и расстояние
между ее горизонтальным следом и горизонтальной проекцией горизонтали.
Отсюда: задаем на осп проекций произвольную точку схода Рх и проводим
через нее перпендикулярно оси проекций горизонтальный след (Phl) плоскости,
а параллельно ему, на расстоянии I — горизонтальную проекцию горизонтали.
Найдя.вертикальный след горизонтали, т. е. точку v'lt проводим вертикальный след
(РВ1) плоскости через точки г) и PXl. '
Пример 204
Найти центр круга, описанного около треугольника АВС (фиг. 681).
Решение. Центр круга, описанного около треугольника, находится на пере-
сечешш перпендикуляров, проведенных к его сторонам через их середины. Для
того чтобы можно было провести эти перпендикуляры, нужна натуральная вели-
чина треугольника, для чего необходимо привести плоскость треугольника в поло-
жение, параллельное одной из плоскостей проекций, например плоскости Н.
Такого положения достигаем, выполнив два последовательных перемещения:
первое — параллельно горизонтальной плоскости проекции и второе — параллельно
вертикальной плоскости проекций.
231
Фиг. 681
Отсюда: проводим горизонталь в плоскости треугольника через точку (а, д')
и перемещаем ее параллельно плоскости Н до положения, перпендикулярного
к плоскости V. При перемещении треугольника параллельно плоскости Н его
горизонтальная проекция, как известно, не должна изменяться, а потому приво-
дим горизонтальную проекцию треугольника в положение a^biCi так, чтобы
горизонтальная проекция горизонтали была перпендикулярна оси проекций: по
a^Ct находим вертикальную проекцию (aib'xci) треугольника, которая получается
в виде прямой линии (почему?). 'Затем перемещаем треугольник (ахЬхсх, п'хУхс'х)
параллельно вертикальной плоскости проекций и приводим вертикальную проекцию
G12&2C2) треугольника в положение, параллельное осп проекций; по а'2Ь'2с'2 находим
оД>2с2 — натуральную величину треугольника. Проведя перпендикуляры через сере-
дины сторон а2Ь2 и а2с2, находим на пх пересечении точку (d2d’2) — центр круга,
которую затем переносам в первоначальное положение. Построение видно
пз чертежа.
Пример 205
Параллельные прямые АВ и CD переместить в такое положение, при
котором их горизонтальные проекции сливаются в одну прямую линию
(фиг. 682).
Решение. Параллельные прямые АВ и CD определяют плоскость; пх
горизонтальные проекции сливаются в одну прямую линию, когда эта плоскость
занимает положение, перпендикулярное к горизонтальной плоскости проекций.
Отсюда: проводим фронталь этой плоскости и перемещением всей системы
параллельно плоскости V ставим фронталь в. положение, перпендикулярное
к плоскости И. Взаимное положение вертикальных проекций элементов при этом
не изменяется. Имея вертикальные проекции и (с'х<7'х) прямых, находим пх
горизонтальные проекции (яхЬх) и (сх</х), слившиеся в одну прямую.
Пример 206
Опустить перпендикуляр пз точки С па прямую АВ (фиг. 683).
232
Решение. Опушить перпендикуляр из точки на прямую непосредственно
на эпюре можно только в том случае, когда заданная прямая параллельна
какой-либо плоскости проекций (по какой теореме?). Отсюда: перемещаем задан-
ную систему параллельно вертикальной плоскости проекций до положения, когда
прямая (ai?»!, становится параллельной горизонтальной плоскости проекций.
Имея проекции точки Ct и прямой Л1ВЬ опускаем из точки Cj перпендикуляр
на прямую и на их пересечении получаем горизонтальную проекцию (dt) —
основание перпендикуляра. Найдя его проекции (d, d') в первоначальном задании,
проводим проекции искомого перпендикуляра: горизонтальную — через точки end,
вертикальную — через точки с' и d'.
233
Пример 207
Пересечь прямые АВ и CD перпендикулярной к ним прямой MN
(фиг. 684).
Решение. Перемещаем прямые (аЪ, а’Ь') и (cd, c’d') так, чтобы одна из пря-
мых, например (ab, а'Ь'), заняла положение, перпендикулярное к горизонтальной
плоскости проекций. Так как прямая (ab, а’Ь1) — общего положения, следует, как
известно, произвести два последовательных перемещения заданной системы:
первое — параллельно плоскости II, при котором прямая аАА) параллельна
вертикальной плоскости проекций, и второе — параллельно вертикальной плоскости
проекций, при котором прямая (а2Ь2, а'2Ь'2) перпендикулярна горизонтальной
плоскости проекций. Пересекаем прямые (а2Ь2, а'2Ъ'2) и (c2d2, c'2d'2) перпендикулярной
прямой (nyi2, >11'211'2), а затем находим прямую (пи, ш'п') в первоначальном
задании. Построение видно из чертежа.
Пример 208
Построить линию пересечения пирамиды плоскостью Р (фиг. 685).
Решение. Для построения линии пересечения нужно найти точки пересече-
ния боковых ребер пирамиды с плоскостью; так как и ребра пирамиды и сама
плоскость Р — общего положения, целесообразно изменить положение заданной
системы так, чтобы плоскость Р2 стала вертикалыю-проектпрующей. Проводим
горизонталь плоскости и, перемещая систему параллельно горизонтальной плоско-
сти проекций, приводим горизонталь в положение, перпендикулярное к плоскости
V, а плоскость Pi — в положение, перпендикулярное к плоскости V. Построив
элементы заданной системы, после перемещения находим по известному правилу
проекции (аА^е^, а'АА'А’А линия пересечения пирамиды плоскостью Р2; затем
находим проекции линии пересечения в первоначальном задании. Построе-
ние видно из чертежа.
Пример 209
Построить проекции правильной шестиугольной пирамиды с основа-
нием на плоскости Р, исходя из условия, что сторона основания равна
10 мм и высота h — 30 мм (фиг. 686).
234
235
Фпг. 687
Решение. Строим предварительно проекции пирамиды с основанием на
горизонтальной плоскости проекций. Переместив плоскость Р в положение верти-
ка льно-проектирующей плоскости Рп строим проекции пирамиды с основанием
на плоскости Pt. Остается теперь перейти от положения плоскости Pi к перво-
начальному заданию. Построение видно из чертежа.
Пример 210
Плоскости Р и Q привести в положение, перпендикулярное к горизон-
тальной плоскости проекций (фиг. 687).
Решение. Для того чтобы заданные плоскости Р и Q были перпендикулярны
горизонтальной плоскости проекций, нужно, чтобы линия их пересечения была
перпендикулярна этой плоскости. Отсюда: находим линию пересечения заданных
плоскостей и, как уже было указано (см. пример -200), пользуясь двойным пере-
мещением, приводим ее вместе со всей системой в положение, перпенди-
кулярное к плоскости Н. При таком расположении линии пересечения плоскости
Р3 п Q2 тоже перпендикулярны плоскости Н. Построение видно из чертежа.
Примечапие. Если линия пересечения плоскостей — горизонталь пли
фронталь, то задача решается одним перемещением.
Вывод. Из анализа задач, решенных методом перемещения, видно, что
основным действием в них является нахождение такого положения заданных эле-
ментов, которое приводит к простому решению задачи при данном условии.
В дальнейшем расположите геометрических элементов относительно плоскостей
проекций, при котором решение задачи вытекает без каких-либо дополнитель-
ных построений, называем «наивыгоднейшим» положением заданных элементов.
ЗАДАЧИ
Указание. Помещенные ниже задачи решить вращением и перемещением.
371. Прямую АВ поставить в положение, параллельное горизонтальной
плоскости проекций (фиг. 688, 689).
372. Прямую АВ поставить в положение, параллельное вертикальной
плоскости проекций (фиг. 688, 689).
236
>b'
I
x--------------!----------------о
b
Фиг. 691
373. Прямую AB поставить в положение, перпендикулярное к горизон-
тальной плоскости проекций (фиг. 690, 691).
374. Прямую АВ поставить в положение, перпендикулярное к верти-
кальной плоскости проекций (фиг. 691, 692).
375. Плоскость Р поставить в положение, пернендакулярное к горизон-
тальной плоскости проекций (фиг. 693, 694). '
376. Плоскость Р поставить в положение, перпендикулярное к верти-
кальной плоскости проекций (фиг. 693, 694).
237
377. Треугольник АВС поставить в такое положение, чтобы его гори-
зонтальная (вертикальная) проекция сливалась в прямую линию (фиг. 600).
378. Параллельные прямые АВ и CD поставить в такое положение,
чтобы их вертикальные (горизонтальные) проекции сливались в одну
прямую линию (фиг. 639).
379. Прямые АВ и CD поставить в такое положение, чтобы их гори-
зонтальные (вертикальные) проекции были параллельны между собой
(фиг. 578).
380. Прямые АВ и CD поставить в такое положение, чтобы прямая
АВ была перпендикулярна: к горизонтальной плоскости проекций (фиг. 578);
к вертикальной плоскости проекций (фиг. 144).
381. Плоскости Р и Q поставить в положение, перпендикулярное:
к горизонтальной плоскости проекций (фиг. 393, 394); к вертикальной
плоскости проекций (фиг. 400, 408).
382. Пересечь прямые АВ и CD прямой MN, перпендикулярной к пря-
мой АВ, так, чтобы отрезок прямой MN между заданными прямыми имел
длину, равную 20 мм (фиг. 578).
383. Найти точку пересечения прямой АВ с плоскостью Р (фиг. 466, 467).
238
Глава XVIII
СОВМЕЩЕНИЕ.
ВРАЩЕНИЕ ВОКРУГ ГОРИЗОНТАЛИ И ФРОНТАЛИ
ПРИМЕРЫ
Пример 211
Даны горизонтальный след (PJ плоскости Р и точка А этой плоскости.
Найти совмещенное положение точки А на горизонтальной плоскости
проекций. Вертикальный след плоскости не находить (фиг. 695).
Решение. Проводим через точку (a, o') плоскость R, перпендикулярную
к оси вращения Ph, и находим центр вращения (а, а') на пересечении плоскости
R со следом Ph. Определяем натуральную величину радиуса вращения (яа, я’о<)
и описываем из точки а дугу радиуса г до пересечения со следом R/, в искомой
точке Ао. Дано одно решение.
Выводы. При совмещении плоскости с горизонтальной плоскостью проек-
ций:
1) радиус вращения есть гипотенуза прямоугольного треугольника, одтгм
катетом которого является расстояние от горизонтальной проекции точки до
горизонтального следа плоскости, а другим катетом — отрезок z;
2) положение любой точки плоскости находится на горизонтальном следе (R)
плоскости вращения — на расстоянии радиуса вращения;
3) в частном случае, когда плоскость — горнзонтально-проектирующая, пос = О
и г = 2.
239
Пример 212
Дана вертикально-просктирующая плоскость Р и на ней точка А.
Найти совмещенное положение точки А на плоскости Н (фиг. 696).
Решение. Так как ст = Рхпх, то радиус вращения точки (а, а') равен Рха’.
Отсюда: опускаем из горизонтальной проекции («) точки перпендикуляр на гори-
зонтальный след (PJ плоскости и откладываем на нем с/.А0=Рла’. Дано одно
решение.
Пример 213
Даны вертикальный след (Рг) плоскости Р и точка А этой плоскости.
Найти совмещенное положение точки А на вертикальной плоскости про-
екций. Горизонтальный след плоскости не находить (фиг. 697).
Решение. Проводим через точку (а, а') плоскость R, перпендикулярную
к оси вращения Pv, и находим центр вращения (Р, р ) на пересечении плоскости К
со следом Р„. Определяем натуральную величину радиуса вращения (ар, а'р)
и описываем из точки Р' дугу радиуса г до пересечения со следом R„ в искомой
точке Ао. Дано одно решение.
Выводы. При совмещении плоскости с вертикальной плоскостью проекций:
1) радиус вращения есть гипотенуза прямоугольного треугольника, одним
катетом которого является расстояшк от вертикальной проекции точки до верти-
кального следа плоскости, а другим катетом — отрезок у;
2) положение любой точки плоскости находится на вертикальном следе (R.)
плоскости вращения — па расстоянии радиуса вращения;
3) в частном случае, когда плоскость — вертикально-просктирующая, а'Р' = О
и г = у.
Пример 214
Дана горизопталыю-проектпрующая плоскость Р и ла ней точка А.
Найти совмещенное положение точки А па плоскости Г (фиг. 698).
240
Решение, Так как а'р' = Рхах, то радиус вращения точки (a, а*) равен Рха.
Отсюда: опускаем из вертикальной проекции (д') точки перпендикуляр на верти-
кальный след (Р„) плоскости и откладываем на нем р'Л0 = Рха. Дано одно решение.
Пример 215
Даны точка А и прямая MN. Точку А вращением вокруг прямой MN
совместить с плоскостью Т, параллельной горизонтальной плоскости
проекций и проходящей через прямую MN (фиг. 699).
Решение. Проводим через точку (а, а1) плоскость R, перпендикулярную
к оси вращения (mn, т'п'), и находим центр вращения (а, а') на пересечении
плоскости R с прямой (тп, т'п'). Определяем натуральную величину радиуса вра-
щения (аа, а'а') и описываем из точки а дугу радиуса г до пересечения со следом
Rk в искомой точке Ао. Дано одно решение.
Вывод. Радиус вращения есть гипотенуза прямоугольного треугольника,
одним катетом которого является расстояние от горизонтальной проекции точки
до горизонтальной проекции горизонтали, а другим катетом — расстояние от вер-
тикальной проекции точки до вертикальной проекции горизонтали.
Пример 216
Даны точка А и прямая MN. Точку А вращением вокруг прямой MN
совместить с плоскостью Т, параллельной вертикальной плоскости проек-
ций и проходящей через прямую MN (фиг. 700).
Решение. Проводим через точку (а, д') плоскость R, перпендикулярную
к оси вращения (тп, т'п1), и находим центр вращения (0, 0') на пересечении
плоскости R с прямой (тп, т'п’). Определяем натуральную величину радиуса вра-
щения (ар, а'р') и описываем из точки р' дугу радиуса г до пересечения со следом
R,, в искомой точке Аа. Дано одно решение.
Вывод. Радиус вращения есть гипотенуза прямоугольного треугольника,
одним катетом которого является расстояние от вертикальной проекции точки
до вертикальной проекции фронтали, а другим катетом — расстояние от горизон-
тальной проекции точки до горизонтальной проекции фронтали.
Пример 217
Совместить плоскость Р с горизонтальной плоскостью проекций
(фиг. 701).
Решение. Вращаем плоскость Р вокруг горизонтального следа (РЛ) пло-
скости. Чтобы найти совмещенный вертикальный след (Рг ) плоскости, задаем на
след'е Р,. произвольную точку (г, г') и находим ее совмещенное положение Vo
на плоскости Н (построение видно из чертежа). Проводим через точки Рх и V&
искомый совмещенный вертикальный след (РС)) плоскости.
Угол <р — истинный угол между следами плоскости.
Из чертежа видно, что PXVO = Pxv'. Пользуясь этим, можно упростить решение
задачи. Опускаем из точки v перпендикуляр на след Ph и из точки Рх радиусом,
равным Рхг', описываем дугу до пересечения с перпендикуляром в точке Ко.
Проводим совмещенный след Pt. через точки Рх и Ро.
Пример 218
Совместить плоскость Р с вертикальной плоскостью проекций (фиг. 702).
Реше н и е. Вращаем плоскость Р вокруг вертикального следа (Рг) плоскости.
Для того чтобы найти совмещенный горизонтальный след (Р/,^ плоскости, задаем
на следе Ph произвольную точку (А, А') и находим се совмещенное положение Н„
на плоскости V (построение видно из чертежа). Проводим через точки Рх и Но
искомый совмещенный горизонтальный след |Р/(]) плоскости.
Угол ф — истинный угол между следами плоскости.
Из чертежа видно, что РХНО = ЛА Пользуясь этим, можно упростить решение
задачи. Опускаем из точки h’ перпендикуляр па след Pv и из точки Рх радиусом,
равным PJi, описываем дугу до пересечения с перпендикуляром в точках Но и Но1.
Проводим совмещенный след Р1:. че-
рез точки Рх и Но и след Р/,, —
через точки Рх и Но1.
242
Пример 219
Даны плоскость Р и точка А, принадлежащая ей. Найти совмещенной
положение этой точки на горизонтальной плоскости проекций, не опре-
деляя радиуса вращения (фиг. 703, 704).
Решение.
Первый способ. Пользуемся горизонталью. Находим точку Уо — совмещенное
положение точки (с, t>'), и проводим через нее совмещенную горизонталь парал-
лельно горизонтальному следу (РЛ) плоскости. Опускаем.из точки а перпендикуляр
на след У,, до пересечения с совмещенной горизонталью в искомой точке Ао.
Второй способ. Пользуемся фронталью. Находим совмещенное положение вер-
тикального следа (Р„ ) плоскости, и проводим через точку h совмещенную фронталь
параллельно совмещенному вертикальному следу плоскости. Опускаем из точки а
перпендикуляр па след РА до пересечения с совмещенной фронталью в искомой
точке Ао.
Вывод. При совмещении плоскости с плоскостью Н положение любой
точки плоскости находим на пересечении совмещенной главной линии с перпен-
дикуляром, опущенным из горизонтальной проекции точки на горизонтальный след
плоскости.
Пример 220
Даны плоскость Р и точка А, принадлежащая ей. Найти совмещенное
положение этой точки на вертикальной плоскости проекций, не определяя
радиуса вращения (фиг. 705, 706).
Решение.
Первый способ. Находим совмещенный горизонтальный след (Р/ц) плоскости
и через точку v' проводим совмещенную горизонталь параллельно следу Ph^
Опускаем из точки а' перпендикуляр на след Pv до пересечения с совмещенной
горизонталью в искомой точке Ао.
243
Второй способ. Пользуемся фронталью. Находим точку Но, совмещенное поло-
жение точки (h, h') и проводим через нее совмещенную фронталь параллельно
вертикальному следу (Р„) плоскости. Опускаем из точки а' перпендикуляр на след
Ро до пересечения с совмещенной фронталью в искомой точке Aq.
Вывод. При совмещении плоскости с плоскостью V положение любой точки
плоскости находим на пересечении совмещенной главной линии с перпендикуляром,
опущенным пз вертикальной проекции точки на вертикальный след плоскости.
Указание. На основании решений последних примеров, как видно из выполнен-
ных эпюр, нетрудно решить и обратную задачу, т. е. по заданному совмещенному
положению точки на горизонтальной (вертикальной) плоскости проекций пайти
проекции этой точки (см. следующие пршмеры).
Пример 221
Даны плоскость Р и совмещенное положение ее точки Ао на горизон-
тальной плоскости проекций. Найти проекции этой точки (фиг. 707).
Решение. Находим совмещенный вертикальный след (P„J плоскости и про-
водим через точку Ао совмещенную горизонталь — параллельно горизонтальному
следу (?<,) плоскости, до пересечения со следом P„t в точке Fo- По точке Va
находим ее проекции (е, г') и проводим через них проекции горизонтали (как?).
Затем опускаем из точки Ао перпендикуляр на след Ph и па его пересечении
с горизонтальной проекцией горизонтали получаем горизонтальную проекцию («)
точки; зная ее, находим и вертикальную проекцию (я') точки.
Задачу можно решить и при помощи' фроитали.
Пример 222
Даны плоскость Р и совмещенное положение ее точки Ао на плоскости
Н. Найти проекции этой точки (фиг. 708).
Решение. Точка Ао лежит на задней поле горизонтальной плоскости про-
екций. Находим совмещенный вертикальный след (Т\. ) плоскости и проводим
244
Фиг. 707 Фиг. 708
через точку Ао совмещенную фронталь параллельно вертикальному следу (PV1)
плоскости до пересечения со следом Ph в точке На. По точке Ло находим ее
проекции (h, h') и проводим через них проекции фронтали (как?). Опускаем из
точки Ао перпендикуляр на след Ph и на его пересечении с горизонтальной
проекцией фронтали получаем горизонтальную проекцию (а) точки; зная ее, нахо-
дим и вертикальную проекцию (а') точки.
Задачу можно решить и при помощи горизонтали.
Пример 223
Даны плоскость Р и совмещенное положение ее точки Ао на плоскости
V. Найти проекции этой точки (фиг. 709).
Решение. Находим совмещенный горизонтальный след (Р^^) плоскости и
проводим через точку Ао совмещенную горизонталь параллельно совмещенному
горизонтальному следу (Phi) плоскости до пересечения со следом Р„ в точке Vo.
По точке Vo находим ее проекции (у, в) и проводим через них проекции гори-
зонтали (как?). Опускаем из точки Ло перпендикуляр на след Р„ и на его пере-
сечении с вертикальной проекцией горизонтали получаем вертикальную проекцию
(д') точки; зная ее, находим и горизонтальную проекцию (а) точки.
Задачу можно решить и при помощи фронтали.
Пример 224
Даны плоскость Р и совмещенное положение ее точки Ао на плоскости
У (фиг. 710). Найти проекции этой точки.
Решение. Точка Ао лежит на нижней поле вертикальной плоскости проекций.
Находим совмещенный горизонтальный след (P^J плоскости и проводим через
точку Ао совмещенную фронталь параллельно следу Р„ до пересечения со следом
в точке Hq. По точке Но находим ее проекции (/;, /1') и проводим через них
245
проекции фронтали (как?). Опускаем из точки Аа перпендикуляр на след Р„ и на его
пересечении с вертикальной проекцией фронтали получаем вертикальную проекцию
(д') точки; зная ее, находим и горизонтальную проекцию (а) точки.
Задачу можно решить и при помощи горизонтали.
Пример 225
Построить проекции прямоугольного треугольника АВС, лежащего на
плоскости Р, исходя из условия, что даны вертикальная проекция гипо-
тенузы АС и угол С = 60° (фиг. 711).
Решение. Находим совмещенное положение Ао и Со точек (a, o') и (с, с1)
на плоскости Н. Строим в натуральную величину треугольник А0В0С0 и затем,
зная точку Во, находим ее проекции (Ь, Ь1). Соединяя точку (Ь, Ь') с точками (а, а')
и (с, с'), получаем проекции (abc) и (a'b’c'j искомого треугольника.
Эта же задача решена на фиг. 712; плоскость Р совмещена с плоскостью V.
Построение видно из чертежа.
Пример 226
Построить проекции равностороннего треугольника АВС, лежащего на
плоскости Р, исходя из условия, что дана горизонтальная проекция сто-
роны АВ (фиг. 713).
Решение. Находим совмещенное положение А0В0 стороны треугольника
на плоскости V. Строим в натуральную величину треугольник А0В0С0 и затем,
зная точку Со, находим ее проекции (с, с'). Соединяя точку (с, с') с концами
стороны (ab, а'Ь'), получаем проекции (abc) и (a'b'c') искомого треугольника.
Эта же задача решена на фиг. 714; плоскость Р совмещена с плоскостью Н.
Построение видно из чертежа.
Пример 227
Найти натуральную величину треугольника АВС, лежащего на плоско-
сти Р, параллельной оси проекций, если дана горизонтальная его проек-
ция (фиг. 715).
246
Фиг. 711
Фиг. 715
248
Рете кие. Находим проекции (а'Ь'с') и (а"Ь"с*) треугольника. Совмещаем
плоскость Р с профильной плоскостью проекций: положение точки Ао находим,
восставив из профильной проекции точки перпендикуляр к следу Р„ и отложив
на нем отрезок а''А0, равный координате х точки (а, д'). Аналогично находим
точки Во и Со. Соединив полученные точки, получаем треугольник AqBqCq —
натуральную величину треугольника (abc, а'Ь'с').
Задачу можно решить и совмещением плоскости Р с плоскостью Н (фиг. 716)
или с плоскостью V (фиг. 717). Построение видно из чертежа.
Велпчппы радиусов вращения вершин треугольника найдены при помощи
профильной плоскости проекции (как?).
В ы в о д. Радиус вращения любой точки плоскости, параллельной оси проекций,
при ее совмещении:
1) с профильной плоскостью проекций — равен координате х точки;
2) с горизонтальной плоскостью проекций — равен Р.а", РЛ", Р?с" и т.д.;
3) с вертикальной плоскостью проекций — равен Рад, РгЬ, Рг<г и т.д.
Пример 228
Построить проекции квадрата ABCD, лежащего на плоскости Р, если
дана вертикальная проекция его диагонали АС (фиг. 718).
249
Решение. Совмещаем плоскость Р с вертикальной плоскостью проекций
и находим положение точек Аа и Со. На диагонали А0С0 строим квадрат A0BQC0D0,
а затем, в обратном порядке, находим проекции (abed) и (а'Ь'с’сГ) квадрата. Эта
же задача решена на фиг. 719, где плоскость Р совмещена с горизонтальной
плоскостью проекций.
Пример 229
Построить проекции окружности, лежащей в плоскости Р, если даны
ее центр С и радиус 20 мм (фиг. 720).
Решение. Окружность проектируется па плоскости проекций эллипсами,
причем большая ось эллипса всегда равна диаметру окружности. Так как окруж-
ность лежит в плоскости общего положения, то невозможно выделить тот ее
диаметр, который на обе плоскости проектируется без искажения. Следовательно,
главные оси эллипсов на горизонтальной плоскости проекций и на вертикальной
плоскости проекций следует находить независимо одну от другой. На гори-
зонтальную плоскость проекций без искажения проектируется в большую ось
тот диаметр окружности, который расположен на горизонтали плоскости;
диаметр, перпендикулярный к этому диаметру, проектируется с искажением в малую
ось перпендикулярно (на основании теоремы проектирования прямого угла) боль-
шой оси. Аналогично на вертикальную плоскость проекций без искажения проек-
250
Фиг. 718 Фиг. 719
тируется в большую- ось эллипса тот диаметр окружности, который расположен
на фронтали плоскости; диаметр, перпендикулярный к этому диаметру, проекти-
руется с искажением в малую ось . эллипса перпендикулярно большой его оси.
Отсюда ход построений таков:
1) совмещаем заданную плоскость, например с горизонтальной плоскостью
проекций, и находим положение точки Со — центра окружности;
2) описываем из точки Со окружность заданного радиуса и проводим две
пары взаимно перпендикулярных диаметров — диаметр, параллельный следу Ph
и ему перпендикулярный, и диаметр, параллельный следу Р„ и ему перпендику-
лярный; затем находим горизонтальные проекции первой пары диаметров окруж-
ности и вертикальные проекции второй пары диаметров.
Дальнейшее построение видно из чертежа.
Выводы:
1. Главными осями эллипса на горизонтальной плоскости проекций являются
горизонтальные проекции двух взаимно перпендикулярных диаметров, из которых
один расположен параллельно горизонтальной плоскости проекций.
2. Главными осями эллипса на вертикальной плоскости проекций являются
вертикальные проекции двух взаимно перпендикулярных диаметров, из которых
один расположен параллельно вертикальной плоскости проекций.
Пример 230
Построить проекции прямого кругового конуса с основанием на пло-
скости Р, исходя пз условия, что радиус его основания равен 20 мм,
высота h = 55 мм и его ось совпадает с прямой (1, Г) (фиг. 721).
251
Фиг. 720
Решение. Находим точку (с, с) пересечения прямой (1, Г) с плоскостью Р,
т. е. центр основания конуса. Совмещаем плоскость Р с вертикальной плоскостью
проекций и, найдя положение точки Со, описываем из этой точки окружность
заданного радиуса 20 мм. Зная совмещенное положение основания конуса, находим
его проекции (подробно см. пример 229).
Для того чтобы найти точку (s, s') — вершину конуса — откладываем на прямой
(/, Г) от точки (с, с') отрезок длиной 55 мм. Проводим проекции крайних обра-
зующих через точки s и s', касательные к каждому эллипсу.
Пример 231
Построить проекции куба с основанием ABCD, одно из боковых ребер
которого совпадает с прямой (/, Г), если дана вертикальная проекция
диагонали АС (фиг. 722).
252
Фиг. 721
Решение. Основание ABCD куба лежит в плоскости Р, перпендикулярной
к прямой (/, Г), проходящей через точку (а, а'). Зная вертикальную проекцию (д')
вершины (а, а') основания, находим ее горизонтальную проекцию (а) на горизон-
тальной проекции прямой (/, Г). Проводим через точку (а, а') плоскость Р, пер-
пендикулярную к прямой (1, Г), и находим горизонтальную проекцию (ас) диаго-
нали. Совместив эту плоскость с горизонтальной плоскостью проекций, находим
положение диагонали А0С0 и на ней строим квадрат /10B0C0D0 — основание куба.
Зная совмещенное положение A0B0C0D0 основания куба, находим его проекции
(abed} и (a'b'c'd1). Восставляем из точек (Ь, Ь'), (с, с') и (d, d'} перпендикуляры
к плоскости Р, откладываем на них отрезки, равные стороне основания куба,
и соединяем концы этих перпендикуляров. На чертеже выделены видимые и не-
видимые линии.
253
Пример 232
Опустить из точки С перпендикуляр на прямую АВ. Решить пример
вращением около горизонтали и фронтали (фиг. 723, 724).
Р е ш е н и е.
1. Вращение около горизонтали.
Проводим через точку (с, с') горизонталь, пересекающую прямую (ab, а'Ь')
в точке (к, к'), и вращением данной прямой около горизонтали совмещаем ее
с плоскостью R, проходящей через эту горизонталь и параллельной горизонталь-
ной! плоскости проекций. Так как точка (к, к') прямой (ab, а’Ь') уже лежит на
плоскости R, нужно найти на этой плоскости положение другой ее точки (а, а').
Для этого из точки а опускаем перпендикуляр на горизонтальную проекцию (ск)
горизонтали и из точки а. радиусом с/.А. равным радиусу вращения точки (а, а),
описываем дугу до пересечения с перпендикуляром в точке Ао. Соединяем точки
к и Ао прямой кА0 и опускаем на нее из точки с перпендикуляр; в точке их
254
255
пересечения получаем основание перпендикуляра — точку Do. Опускаем обратно
из точки Do перпендикуляр на горизонтальную проекцию (с/с) горизонтали и на
пересечении его с прямой ab получаем горизонтальную проекцию (d) основанияj
перпендикуляра; по ней находим ее вертикальную проекцию (</') на прямой а'Ь'.
Соединяя точки (с, с') и (</, d'), получаем искомую прямую (al, c'd').
2. Вращение около фронтали.
Проводим через точку (с, с') фронталь, пересекающую прямую (ab, а'Ь')
в точке (к, к'), и вращением данной прямой около фронтали совмещаем ее
с плоскостью R, проходящей через эту фронталь и параллельной вертикальной
плоскости проекций. Так как точка (к, к') прямой (ab, а'Ь') уже лежит на плоскости
R, то нужно найти на этой плоскости положение другой ее точки (я, а'). Для этого
опускаем из точки а' перпендикуляр на вертикальную проекцию (с'к') фронтали
и из точки Р' радиусом Р'Л, равным радиусу вращения точки (й, а'), описываем
дугу до пересечения ее с перпендикуляром в точке Ао. Соединив точки к' и Ао
прямой к'А0, опускаем на нее из точки с' перпендикуляр; в точке их пересечения
получаем основание перпендикуляра — точку Do. Опускаем обратно из точки Do
перпендикуляр на вертикальную проекцию (с'к1) фронтали и на пересечении его
с прямой а'Ь' получаем вертикальную проекцию (d') основания перпендикуляра;
по ней находим ее горизонтальную проекцию (d) на прямой ab. Соединяя точки
(с, с') и (d, d'), получаем искомую прямую (cd, c'd').
Вывод. Вращением около горизонтали или фронтали удобно пользоваться
при решении задач, когда заданные элементы находятся в одной плоскости.
ЗАДАЧИ
384. Совместить плоскость Р с плоскостью Н и найти совмещенное
положение точки А, лежащей^па этой плоскости (фиг. 725 — 730).
385. Совместить плоскость Р с плоскостью V и найти совмещенное
положение точки А, лежащей на этой плоскости (фиг. 725 — 730).
386. Построить проекции точки А, лежащей на плоскости Р, если дано
совмещенное положение этой точки на плоскости Н (фиг. 731 — 734).
387. Построить проекции точки А, лежащей на плоскости Р, если дано
совмещенное положение этой точки на плоскости V (фиг. 735 — 738).
256
pv
388. Построить на плоскости Р геометрическое место точек, равно-
удаленных от следов этой плоскости (фиг. 739, 740).
389. Построить геометрическое место точек пространства, равноудален-
ных от вершин треугольника АВС (фиг. 741).
390. Построить проекции треугольника АВС, лежащего в плоскости Р,
если дано совмещенное положение этого треугольника на плоскости Н
(фиг. 742).
391. Определить центр круга, описанного около треугольника АВС,
лежащего в плоскости Р (фиг. 743).
392. Построить проекции квадрата ABCD, лежащего в плоскости Р,
зная его сторону АВ (фиг. 744).
9 Арустамов X. А. 257
258
°д0
х----------------------О
р.
Фиг. 737
393. Построить проекции равностороннего треугольника АВС, лежащего
в плоскости Р, если дано совмещенное положение его стороны Л0В0 на
плоскости Н (фиг. 745).
394. Построить проекции треугольника АВС, лежащего в плоскости Р,
если дано совмещенное положение треугольника на плоскости V (фиг. 746).
395. Построить на плоскости Р геометрическое место точек, удаленных
от ее точки С на 20 мм (фиг. 747).
396. Построить на плоскости Р окружность с центром в ее точке С,
касательную к вертикальному следу этой плоскости (фиг. 747).
397. Построить окружность радиуса 20 мм на плоскости Р, касательную
к ее следам (фиг. 739).
398. Построить окружность, вписанную в треугольник АВС, лежащий
в плоскости Р (фиг. 741).
9*
259
399. Построить окружность, описанную около треугольника АВС, лежа-
щего в плоскости Р (фиг. 741).
400. Построить окружность, касательную к следам плоскости Р и про-
ходящую через точку А этой плоскости. Дать одно решение (фиг. 730).
401. Определить действительную величину треугольника АВС (фиг. 615).
Указание. Задачи 401 —412 решить вращением около горизонтали „ли фронтали.
402. Провести биссектрису угла А треугольника АВС (фиг. 615).
260
403. Найти центр окружности, вписанной в треугольник АВС (фиг. 615).
404. Найти центр окружности, описанной около треугольника АВС
(фиг. 61.5).
405. Опустить перпендикуляр из точки С на прямую АВ (фиг. 636, 637).
406. Найти на прямой АВ точку, удаленную от точки С на 25 мм
(фиг. 636, 637).
261
407. Провести через точку С прямую, пересекающую прямую АВ под
заданным углом ср, равным 30, или 45, или 60° (фиг. 637).
408. Построить равносторонний треугольник АВС с основанием ВС на
прямой MN (фиг. 651).
409. Построить равнобедренный треугольник АВС с основанием ВС
на прямой MN, если угол В — С = ср (фиг. 651).
410. Построить квадрат ABCD со стороной ВС на прямой MN (фиг. 652).
411. Пересечь параллельные прямые Kbit MN двумя другими прямыми
так, чтобы получился квадрат ABCD (фиг. 748).
412. Пересечь параллельные прямые КЬи MN двумя другими прямыми
так, чтобы получился ромб ABCD с острым углом В = 60° (фиг. 748).
Глава XIX
ПЕРЕМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ
При замене какой-либо плоскости проекций новой перпендикулярность между
ними в новой системе необходимо всегда сохранять. Тогда обе проекции точки
и в новой системе расположены на общем перпендикуляре к новой осн проекций.
/ И V \
При замене старой горизонтальной плоскости проекций новой->----I:
\ fl Hi /
1) точка может перейти из первой четверти в четвертую, из второй — в третью,
и обратно;
2) положение вертикальной проекции точки не изменяется;
3) расстояние от горизонтальной проекции точки до оси проекций в новой
и старой системах не изменяется (а1а11 = аах).
„ .. „ „ ( V J/, \
При замене старой вертикальной плоскости проекции новой I —
1) точка может перейти из первой четверти во вторую, из третьей — в чет-
вертую, и обратно;
2) положение горизонтальной проекции точки не изменяется;
3) расстояние от вертикальной проекции точки до оси проекций в новой
и старой системах не изменяется (a']flx| = a'or).
Правило. Для того чтобы найти вертикальную (горизонтальную) проекцию
точки на новой вертикальной (горизонтальной) плоскости проекций, нужно опустить
из горизонтальной (вертикальной) проекции точки перпендикуляр на новую ось
проекций и от точки пересечения отложить на нем в соответствующую
сторону (см. примеры) отрезок, равный расстоянию от старой вертикальной
(горизонтальной) проекции точки до старой оси проекций.
ПРИМЕРЫ
Пример 233
JZ.
Дана точка А в первой четверти. Найти ее проекции в системе
(фиг. 749).
Решение. Определяем прежде всего, в какой четверти будет находиться
точка в новой системе. Горизонтальная проекция (а) точки в старой системе
находится под осью проекций, т. е. на передней поле горизонтальной плоскости
проекций; в новой же системе горизонтальная проекция (а) точки оказывается
над осью (OjXi) проекций, т. е. на задней поле горизонтальной плоскости проек-
ций. Следовательно, искомая точка в новой системе находится во второй
четверти.
262
Отсюда: проводим через точку а перпендикуляр к оси OjA", и откладываем
на нем вверх от точки отрезок, равный а'ах-, конец его и является новой
вертикальной проекцией (ai) точки.
Пример 234
V
Дана точка А в первой четверти. Найти ее проекции в системе —
(фиг. 750).
Решение. Определим, в какой четверти будет находиться точка в новой
системе. Вертикальная проекция (а') точки в старой системе находится над осью
проекций, т. е. на верхней поле вертикальной плоскости проекций; в новой же
системе вертикальная проекция (а') точки оказывается под осью проекций,
т. е. на нижней поле вертикальной плоскости проекций. Следовательно, искомая
точка в новой системе находится в четвертой четверти.
Отсюда: проводим через точку а' перпендикуляр к оси О-.Х^ и откладываем
на нем вниз от точки aXl отрезок, равный аах; конец его и является новой
горизонтальной проекцией (аД точки.
Пример 235
Дан отрезок АВ. Найти его проекции, если в новой системе он должен
быть расположен параллельно вертикальной плоскости проекций (фиг. 751)
Решение. Для того чтобы отрезок был параллелен вертикальной плоскости
проекций нужно, чтобы горизонтальная его проекция была параллельна оси про-
екций. Проводим ось проекций OjXj параллельно горизонтальной проекции (ab)
отрезка и, как было указано выше, найдя вертикальные проекции (а)) и (i>i) точек,
получаем вертикальную проекцию (a'jfci) отрезка в новой системе.
263
264
Пример 236
Дан отрезок АВ. Найти его проекции, если в новой системе он должен
быть расположен параллельно горизонтальной плоскости проекций
(фиг. 752).
Решение. Для того чтобы отрезок был параллелен горизонтальной плоско-
сти проекций, нужно, чтобы его вертикальная проекция была параллельна оси
проекций. Проводим ось проекций OiXt параллельно вертикальной проекции (а'Ь')
отрезка и, как было указано, найдя горизонтальные проекции (а А и (bt) точек,
получаем горизонтальную проекцию (а^) отрезка в новой системе.
Пример 237
Дан отрезок АВ. Найти его проекции, если в новой системе он должен
быть расположен перпендикулярно горизонтальной плоскости проекций
(фиг. 753).
Решение. Для того чтобы отрезок был перпендикулярен горизонтальной
плоскости проекций, нужно, чтобы его вертикальная проекция была перпендику-
лярна оси проекций. Проводим ось проекций QiXi перпендикулярно вертикальной
проекции (а'Ь') отрезка и, как было указано, находим его горизонтальную проек-
цию (а^) в виде точки.
Пример 238
Дан отрезок АВ. Найти его проекции, если в новой системе он должен
быть расположен перпендикулярно вертикальной плоскости проекций
(фиг. 754).
Решение. Для того чтобы отрезок был перпендикулярен вертикальной
плоскости проекций, нужно, чтобы его горизонтальная проекция была перпендику-
лярна оси проекций. Проводим ось проекций OtXi перпендикулярно горизонталь-
ной проекции (ab) отрезка и, как было указано, находим его вертикальную про-
екцию (a'jb'j) в виде точки.
Пример 239
Дан отрезок АВ. Найти его проекции, если в новой системе он должен
быть расположен перпендикулярно вертикальной плоскости проекций
(фиг. 755).
Решение. Для решения задачи нужно произвести последовательно две
перемены плоскостей проекций ( ). Строим проекции отрезка (ab, а'Ь')
V „
в системе --, в которой он расположен параллельно горизонтальной плоскости
Hi
jz,
проекций; затем строим проекции отрезка (ajbj, а'Ь') в системе ——, в которой он
Hi
расположен перпендикулярно вертикальной плоскости проекций. Построение видно
из чертежа.
Пример 240
Дан отрезок АВ. Найти его проекции, если в новой системе он должен
быть расположен перпендикулярно горизонтальной плоскости проекций
(фиг. 756).
Решение. Для решения задачи нужно произвести последовательно две
перемены плоскостей проекций (—-^-М. Строим проекции отрезка (ab, а’Ь')
\ Н Нг /
265
266
в системе , в которой он расположен параллельно вертикальной плоскости
л
проекций. Затем строим проекции отрезка (ab, а'^) в системе в которой он
В 2
расположен перпендикулярно горизонтальной плоскости проекций. Построение
видно из чертежа.
Пример 241
Построить следы плоскости Р в системе (фиг. 757).
Н
Решение. Горизонтальный след (PJ плоскости остается без изменения.
На пересечении горизонтального следа (Ph) плоскости с новой осью проекций OiXj
получаем новую точку схода (РХ1) следов. По заданию Ph перпендикулярен OiXlt
а это означает, что в новой системе заданная плоскость должна быть верти-
кально-проектирующей. Для того чтобы найти направление нового верти-
кального следа (Р ), берем на плоскости произвольную точку (а, а') и находим ее
новую вертикальную проекцию (a'J. Проводим через точки Рх и a't новый верти-
кальный след (Р ) плоскости.
Пример 242
у
Построить следы плоскости Р в системе —— (фиг. 758).
•Hi
Решение. Вертикальный след (PJ плоскости остается без изменения. На пере-
сечении вертикального следа (Р„) плоскости с новой осью проекций OLXL получаем
новую точку схода (РХ1) следов. Для того чтобы найти направление нового
горизонтального следа (Pftj) плоскости, берем на плоскости при птГмощи фронтали
какую-нибудь точку (а, а’) и, найдя ее в новой системе, проводим фронталь через
эту точку. Затем находим горизонтальный след этой фронтали и проводим новый
горизонтальный след (Р?11) плоскости через точки Рх и hL. .
Примечание. Иногда точка Рх выходит за пределы чертежа; в этих
случаях пользуются двумя фронталями и, найдя точки hL и h2, проводят через
них след Ph
Пример 243
Дана плоскость Р. Построить ее следы, если в новой системе она
должна быть перпендикулярна плоскости Н (фиг. 759).
. Решение. Известно, что вертикальный след горизонтально-проектирующей
плоскости должен быть перпендикулярен оси проекций. Проводим новую ось
проекций OjXl перпендикулярно следу Р„. Точка Рх их пересечения является новой
точкой схода следов. Для того чтобы найти направление нового горизонтального
следа (Phj) плоскости, берем на следе Ph произвольную точку (h, h') и находим ее
новую горизонтальную проекцию (йД. Через точки Рх и h2 проводим новый горизон-
тальный след (Phl) плоскости.
Пример 244
Опустить перпендикуляр из точки С на прямую АВ (фиг. 760).
Решение. Опустить перпендикуляр из точки на прямую непосредственно
на эпюре можно только в том случае, если заданная прямая параллельна какой-
либо плоскости проекций (почему?). Отсюда: заменяем, например, вертикальную
плоскость проекций новой Vlt которая параллельна прямой АВ. Проводим ось
(Oj-Yi) проекций параллельно (почему?) прямой ab и находим вертикальные про-
екции прямой (а^ЬД и точки (с'Д. Опускаем из точки с\ перпендикуляр на прямую
a'tbi и на их пересечении получаем вертикальную проекцию (4Д точки — основания
перпендикуляра. Найдя его проекции (d, d') в первоначальном задании, проводим
267
268
проекций искомого перпендикуляра: горизонтальную — через точки с и d, верти-
кальную — через точки с' и d‘.
Пример 245
Заменить плоскости проекций новыми так, чтобы вертикальный проек-
ции параллельных прямых АВ и CD слились в одну прямую (фйг. 761).
Решение. Параллельные прямые АВ и CD определяют плоскость, и их
вертикальные проекции сливаются в одну прямую линию, если только эта плоскость
в новой системе перпендикулярна вертикальной плоскости проекций. Пересекаем
прямые (ab, а'Ь') и (cd, c'd') произвольной горизонталью (кт, к'т') и, проведя новую
ось (OiXJ проекций перпендикулярно (почему?) прямой кт, находим их новые
вертикальные проекции (a)fci) и (с) di), которые при точном построении сли-
ваются в одну прямую линию.
Пример 246
Найти центр окружности, описанной около треугольника АВС (фиг. 762).
Решение. Центр окружности, описанной около треугольника, находится на
пересечении перпендикуляров, проведенных к его сторонам через их середины.
Для того чтобы провести эти перпендикуляры, нужно иметь натуральную величину
треугольника, а для этого необходимо, чтобы одна из плоскостей проекций^
например горизонтальная, была параллельна плоскости треугольника. Пользуемся
последовательно двумя переменами плоскостей проекций. Сначала заменяем верти-
кальную плоскость проекций новой (I/j), которая перпендикулярна плоскости
треугольника, а затем заменяем горизонтальную плоскость проекций новой (НА,
которая параллельна плоскости треугольника. Проводим горизонталь (Ьк, Ък)
треугольника и, задавшись осью (OjXj) проекций, перпендикулярной (почему?)
к горизонтальной проекции (Ьк) горизонтали, находим вертикальную проекцию
(aibic)) треугольника в виде прямой. Затем проводим ось (02Х2) проекций парал-
лельно (почему?) вертикальной проекции (aiZ>ici) треугольника и находим его
горизонтальную проекцию. Треугольник а2Ь2с2 — натуральная величина заданного
треугольника АВС. Найдя центр (d2) окружности, описанной около треугольника
а2Ь2с2, находим проекции (d, d') этой точки в первоначальном задании (построение
видно из чертежа).
Пример 247
Пересечь скрещивающиеся прямые АВ и CD перпендикулярной к ним
прямой MN (фиг. 763). )
Решение. Заменой плоскостей проекций новыми приводим их в такое поло-
жение, когда одна из плоскостей проекций, например вертикальная, перпендикулярна
прямой АВ (можно и прямой CD). Заменяем горизонтальную плоскость проек-
ций новой (Hi), которая параллельна прямой АВ; проводим ось (OjA'j) проекций
параллельно прямой а'Ь' и находим горизонтальные проекции (а^А и (cjdJ.
заданных прямых. Затем заменяем вертикальную плоскость проекций новой (И2),
которая перпендикулярна прямой Л1В1; проводим ось (О2Х2) проекций перпенди-
кулярно прямой a2bi и находим вертикальные проекции (а'2Ь'2) и (c'2d'2) заданных
прямых. Полученные прямые (а1Ь1, а'2Ь'2) и (c2di, c'2d2) пересекаем перпендикуляр-
ной прямой (m^i, т'2п'2), а затем находим проекции (тп, т’п') искомой прямой
в первоначальном задании. Построение видно из чертежа.
Примечание. Если одна из прямых параллельна какой-либо плоскости
проекций, то достаточно одной замены плоскостей проекций.
Пример 248
Найти линию пересечения поверхности пирамиды с плоскостью Р
(фиг. 764).
Решение. Для построения линии пересечения нужно искать точки пересе-
чения боковых ребер пирамиды с плоскостью. Так как плоскость Р — общего
269
270
положения, целесообразно заменить плоскости проекций так, чтобы в новой
системе заданная плоскость являлась вертикально-проектирующей. Заменяем вер-
тикальную плоскость проекций новой (Р\); проводим ось (Oi-Xi) проекций перпен-
дикулярно следу Рь, находим вертикальный след PVI и вертикальную проекцию
пирамиды. Найдя вертикальную проекцию (aibicjdi) линии пересечения, получаем
проекции (abed) и (a'b'c'd') искомой линии пересечения в первоначальном задании.
Построение видно из чертежа.
Пример 249
Заменить плоскости проекций новыми так, чтобы плоскости Р и Q были
вертикально-проектирующими (фиг. 765).
Решение. Для того чтобы плоскости Р и Q были вертикально-проектирую-
щими, нужно, чтобы вертикальная плоскость проекций новой системы была пер-
пендикулярна линии пересечения этих плоскостей. Находим линию (hv, h'v') пере-
сечения плоскостей Р и Q. Заменяем горизонтальную плоскость проекций новой
(HJ, которая параллельна найденной линии пересечения плоскостей; проводим ось
(01X1) проекций параллельно прямой h'v' и находим горизонтальные следы (Phl)
и (QhJ заданных плоскостей, параллельные прямой Затем заменяем верти-
кальную плоскость проекций новой (У2). Проводим ось (02Х2) проекций перпен-
271
дикулярно прямой йдд и находим вертикальные следы (РГ1) и (Q,,) заданных
плоскостей, проходящие через точку h'2v'2.
Примечание. Если заданные плоскости пересекаются по горизонтали или
по фронтали, то достаточно одной (какой?) замены плоскостей проекций.
Из анализа задач, решенных методом перемены плоскостей проекций, как и
при вращении (перемещении), видно, что основное действие в них заключается
в выяснении «наивыгоднейшего положения» заданных элементов, которые приводят
к простому решению задачи при данном условии.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Чем измеряется на эпюре расстояние от точки до горизонтально-проекти-
рующей прямой?
2. Чем измеряется на эпюре расстояние от точки до вертикально-проектирую-
щей прямой?
3. Какое положение элементов является наивыгоднейшим при определении
расстояния от точки до прямой?
4. Чем измеряется на эпюре расстояние между двумя горизонтально-проек-
тирующими прямыми?
5. Чем измеряется на эпюре расстояние между двумя вертикально-проекти-
рующими прямыми?
б. Какое положение элементов является наивыгоднейшим при определешш
расстояния между двумя параллельными прямыми?
7. Чем измеряется на эпюре расстояние между двумя скрещивающимися
прямыми, из которых одна — горизонтально-проектирующая?
8. Чем измеряется на эпюре расстояние между двумя скрещивающимися
прямыми, из которых одна — вертикально-проектирующая?
9. Какое положение элементов является наивыгоднейшим при определении
расстояния между двумя скрещивающимися прямыми?
10. Чем измеряется на эпюре расстояние от точки до горизонтально-проек-
тируюшей плоскости?
11. Чем измеряется на эпюре расстояние от точки до вертикально-проектирую-
щей плоскости?
12. Какое положение элементов является наивыгоднейшим при определении
расстояния от точки до плоскости?
272
13. Чем измеряется на эпюре расстояние между двумя параллельными гори-
зонтально-проектирующими плоскостями?
14. Чем измеряется на эпюре расстояние между двумя параллельными верти-
кально-проектирующими плоскостями? '
15. Какое положение элементов является наивыгоднейшим при определении
расстояния между двумя параллельными плоскостями?
16. Чем измеряется на эпюре угол наклона горизонтально-проектирующей
плоскости к вертикальной плоскости проекций?
17. Чем измеряется на эпюре угол наклона вертикально-проектирующей
плоскости к горизонтальной плоскости проекций?
18. Какое положение плоскости является наивыгоднейшим при определении
углов ее наклона к плоскостям' проекций?
19. Чем измеряется на эпюре угол между двумя горизонтально-проектирую-
щими плоскостями?
20. Чем измеряется на эпюре угол между двумя вертикально-проектирующими
плоскостями?
21. Какое положение плоскостей является наивыгоднейшим при определении
угла между ними?
ЗАДАЧИ
413. Построить проекции точек А и В в заданной новой системе
(фиг. 766-773). -
414. Построить проекции прямой АВ в новой системе, если прямая
должна быть параллельна горизонтальной плоскости проекций (фиг. 774,
775).
415. Построить проекции прямой АВ в новой системе, если прямая
должна быть параллельна вертикальной плоскости проекций (фиг. 774, 775).
416. Построить проекции прямой АВ в новой системе, если прямая
должна быть перпендикулярна горизонтальной плоскости проекций
(фиг. 776, 777).
Фиг. 766
273
417. Построить проекции прямой АВ в новой системе, если прямая
должна быть перпендикулярна вертикальной плоскости проекций (фиг. 777.
778).
418. Построить следы плоскости Р в заданной новой системе (фиг. 779,
780).
419. Построить следы плоскости Р в новой системе так, чтобы она
являлась горизонтально-проектирующей (фиг. 739, 740).
420. Построить следы плоскости Р в новой системе так, чтобы она
являлась вертикально-проектирующей (фиг. 739, 740).
421. Построить проекции параллельных прямых АВ и CD в новой
системе, если их горизонтальные проекции сливаются в одну прямую
линию (фиг. 639).
422. Построить проекции параллельных прямых АВ и CD в новой
системе, если их вертикальные проекции сливаются в одну прямую линию
(фиг. 639).
275
д'bf
Фиг. 779
423. Построить проекции прямых
АВ и CD в новой системе, если их
горизонтальные проекции параллель-
ны между собой (фиг. 578).
424. Построить проекции прямых
АВ и CD в новой системе, если их
вертикальные проекции параллельны
между собой (фиг. 578).
425. Построить проекции треуголь-
ника АВС в новой системе, если его
горизонтальная проекция сливается в
прямую линию (фиг. 600).
426. Построить проекции треугольника АВС в новой системе, если его
вертикальная проекция сливается в прямую линию (фиг. 600).
427. Найти точку пересечения прямой АВ с плоскостью Р (фиг. 466, 467).
428. Построить проекции треугольника АВС в новой системе, если его
горизонтальная проекция представляет натуральную величину треуголь-
ника (фиг. 600). -
429. Построить проекции треугольника АВС в новой системе, если его
вертикальная проекция представляет натуральную величину треугольника
(фиг. 600).
430. Найти центр тяжести периметра треугольника АВС (фиг. 600).
431. Найти центр окружности, вписанной в треугольник АВС (фиг. 600).
432. Найти центр окружности, описанной около треугольника АВС
(фиг. 600).
276
433. Построить проекции прямых АВ и CD в новой системе, если
прямая АВ перпендикулярна вертикальной плоскости проекций (фиг. 578).
434. Построить проекции прямых АВ и CD в новой системе, если
прямая АВ перпендикулярна вертикальной плоскости проекций (фиг. 144).
435. Пересечь прямые АВ и CD прямой MN, перпендикулярной к пря-
мой АВ, так, чтобы ее отрезок между заданными прямыми имел длину,
равную 20 мм (фиг. 578).
436. Построить следы плоскостей Р и Q в новой системе, если они
должны быть горизонтально-проектирующими (фиг. 393, 394).
437. Построить следы плоскостей Р и Q в новой системе, если они
должны быть вертикально-проектирующими (фиг. 400, 408).
Глава XX
ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ
Расстояние между двумя точками, измеряемое длиной отрезка, соеди-
няющего эти точки, можно определить одним из следующих способов:
1) построением прямоугольного треугольника (см. пример 33);
2) вращением или перемещением; нужно привести отрезок в поло-
жение, параллельное одной из плоскостей проекций (см. примеры 196, 197);
3) совмещением; нужно заключить отрезок в какую-нибудь плоскость
(проще — в горизонтально- или же в вертикальпо-проектирующую) и совместить эту
плоскость с какой-либо плоскостью проекций;
4) переменой плоскостей проекций; нужно заменить одну из
плоскостей проекций новой, которая должна быть параллельна данному отрезку
(см. примеры 235 и 236).
ПРИМЕРЫ
Пример 250
Даны точки А и В. Определить расстояние между ними (фиг. 781).
Решение. Применяем способ совмещения. Проводим через точки (а, д')
и (Ь, Ь') горизонтально-проектирующую плоскость R и совмещаем эту плоскость
с горизонтальной плоскостью проекций. Находим положения Аа и Ва точек (в, а1)
и (Ь, Ь'); соединив их отрезком А0В0, получаем искомое расстояние.
Расстояние от точки до прямой можно определить одним из следую-
щих способов:
1) прямым путем; нужно провести через точку плоскость, перпендикуляр-
ную к прямой, найти пересечение заданной прямой с этой плоскостью и опреде-
лить длину отрезка между точками — найденной и заданной (см. пример 170);
2) вращением или перемещением; нужно привести заданную систему
в положение, когда заданная прямая перпендикулярна какой-либо плоскости проек-
ций, или плоскость, определяемая прямой и точкой, параллельна какой-либо
плоскости проекций;
3) совмещением; нужно найти один из следов плоскости, заданной прямой
и точкой, и вращением около этого следа найти совмещенное положение точки
и прямой;
4) вращением вокруг горизонтали или фронтали; нужно про-
вести через горизонталь (фронталь) плоскости, определяемой заданными элемен-
тами, плоскость К, параллельную горизонтальной (вертикальной) плоскости проек-
ций, и вращением Вокруг горизонтали (фронтали) найти совмещенное положение
точки и прямой на этой плоскости;
5) переменой плоскостей проекций; нужно заменить плоскости
проекций новыми, чтобы одна из них была перпендикулярна заданной прямой
или параллельна плоскости, определяемой прямой и точкой.
277
Пример 251
Определить расстояние от точки С до прямой АВ (фиг. 782-784).
Решение.
1. Способ вращения вокруг горизонтали (фиг. 782). Проводим через точку (с, с1)
горизонталь (cfc, c'k'), пересекающую прямую (ab, а'Ь') в точке (/с, к'), и заключаем
ее в плоскость R, параллельную горизонтальной плоскости проекций. Точки (с, с1)
и (к, к') уже лежат на плоскости R; для того чтобы найти совмещенное положение
прямой на плоскости R, достаточно найти положение еще одной произвольной
точки этой прямой, например (Ь, Ь'). Опускаем из точки Ь перпендикуляр на пря-
мую ск и радиусом, равным «В, описываем из точки а дугу, пересекающую этот
перпендикуляр в точке Во. Соединив точки к и Во, получаем совмещенное поло-
жение (кВ0) заданной прямой. Искомым расстоянием является отрезок I.
2. Способ перемещения (фиг. 783, 784). Перемещаем заданные элементы
параллельно горизонтальной плоскости проекций и ставим прямую в положение,
параллельное вертикальной плоскости проекций. Затем перемещаем их параллельно
вертикальной плоскости проекций и ставим прямую в положение, перпендикуляр-
ное к горизонтальной плоскости проекций. Искомым расстоянием I является рас-
стояние между точкой с2 и отрезком а2Ь2. Построение видно из чертежа.
Пользуясь перемещением, можно задачу решить и таким образом; заключаем
точку (с, с') и прямую (ab, а'Ь') в треугольник (abc, а'Ь'с1) и двумя последователь-
ными перемещениями приводим его в положение, параллельное, например, гори-
зонтальной плоскости проекций. Высота c2d2 треугольника а2Ь2с2 является искомым
расстоянием. Построение видно из чертежа. - — »• -
, Расстояние между параллельными прямыми можно определить
одним из тех способов, которые были приведены для определения расстояния
от точки до прямой.
278
Пример 252
Найти расстояние между параллельными прямыми АВ и CD (фиг. 785,
Решение.
1. Способ совмещения (фиг. 785). Находим горизонтальные следы (й, й*)
и (й„ й)) прямых (ab, а'Ь1) и (cd, c'd') и проводим через эти точки горизонтальный
след (РЛ) плоскости, определяемой данными прямыми. Вращением около следа Ph
находим совмещенные положения прямых (аЪ, а'Ь') и (cd, c'd') на горизонтальной
плоскости проекций. Так как одна точка (й, й') прямой (ab, а'Ь') лежит на горизон-
тальной плоскости проекций, находим совмещенное положение Во точки (Ь, Ь’)‘
точки й и Во определяют совмещенное положение ЙВО прямой (ab, а'Ь'). Совме-
279
d'
щенное положение прямой (cd, c'd') находим, проведя через точку прямую
параллельно прямой /гВ0 (почему?); расстояние I между ними является искомым.
2. Способ перемены плоскостей проекций (фиг. 786, 787). Заменяем горизон-
тальную плоскость проекций новой (Hi), которая параллельна заданным прямым;
затем заменяем вертикальную плоскость проекций новой (1'2), которая перпенди-
кулярна тем же прямым. Расстояние I между вертикальными проекциями (а'2Ь'2)
и (c2d'2) прямых является искомым. Построение видно из чертежа.
280
Пользуясь способом перемены плоскостей проекций, задачу можно решить
и таким образом: заменяем горизонтальную плоскость проекций новой (Hi),
которая перпендикулярна плоскости, определяемой заданными прямыми АВ и CD.
Затем заменяем вертикальную плоскость проекций новой (V2), которая параллельна
заданной плоскости. Расстояние / между параллельными прямыми а'2Ь’2 и c'2d'2
является искомым. Построение видно из чертежа.
Расстояние между скрещивающимися прямыми можно определить
одним из следующих способов:
1) прямым путем; нужно провести через одну из заданных прямых
плоскость R параллельно другой прямой и определить расстояние от произволь-
ной точки второй прямой до плоскости;
2) вращением или перемещением; нужно привести заданные прямые
в положение, когда одна из них перпендикулярна какой-либо плоскости проекций;
3) переменой плоскостей проекций; нужно заменить плоскости
проекций, чтобы одна из них была перпендикулярна какой-либо из данных прямых.
Пример 253
Определить расстояние между скрещивающимися прямыми АВ и CD
(фиг. 788).
Решение. Способ перемены плоскостей.
Заменяем вертикальную плоскость проекций новой (Pi), которая параллельна
прямой АВ. Затем заменяем горизонтальную плоскость проекций новой (Н2),
которая перпендикулярна той же прямой. Расстояние I между горизонтальными
проекциями прямых является искомым. Построение видно из чертежа.
Расстояние от точки до плоскости можно определить одним из сле-
дующих способов:
1) прямым путём; нужно опустить перпендикуляр из точки на плоскость,
найти основание перпендикуляра и определить расстояние между точками — задан-
ной и найденной;
2) вращением или перемещением; нужно привести заданную систему
в положение, когда плоскость перпендикулярна какой-либо плоскости проекций;
281
3) совмещением; нужно провести
через точку горизонтально- или верти-
ка.тьно-проектирующую плоскость, пер-
пендикулярную к заданной плоскости, и
совмещением вспомогательной плоскости
с какой-либо плоскостью проекций найти
положение заданной точки и линии пере-
сечения плоскостей; расстояние I между
ними является искомым;
4) переменой плоскостей
проекций; нужно заменить одну из
плоскостей проекций новой, которая пер-
пендикулярна заданной плоскости.
Пример 254
Определить расстояние от точки А
до плоскости Р (фиг. 789, 790).
Решение.
1. Способ перемещения (фиг. 789). Про-
водим в плоскости Р произвольную фрон-
таль и, перемещая ее параллельно пло-
скости V вместе со всей системой, при-
водим в положение перпендикулярное к
плоскости Н.. Задаем на оси проекций
произвольную точку Рх и проводим через
нее перпендикулярно оСи проекций верти-
кальный след (РГ1) и параллельно ему на
расстоянии Ц — вертикальную проекцию
фронтали. Новое положение а\ точки (я, а') находим на расстоянии Z от
следа Р, на произвольном расстоянии от оси проекций, а затем по а\ получаем
точку at (см. построение). Проводим горизонтальный след (Phl) через точки Рл
282
и й; перпендикуляр, опущенный из точки ах на след РА1, определяет искомое
расстояние.
2. Способ совмещения (фиг. 790). Проводим через точку (a, o') горизонтально-
проектирующую плоскость Я, перпендикулярную к плоскости Р. Находим линию
(hv, h'v1) пересечения плоскостей Р и R и, совмещая плоскость R с горизонтальной
(вертикальной) плоскостью проекций, находим положение Ао точки (а, а") и /1К0
прямой (hv, h'v'). Опускаем из точки Ай перпендикуляр на прямую 'hVa. Отрезок I
является искомым расстоянием.
Примечание. Можно провести через точку А вертикально-проектирующую
плоскость R и т. д.
Пример 255
Определить расстояние от точки К до плоскости треугольника АВС
(фиг. 791).
Решение.
Способ перемены плоскостей проекций.
Заменяем вертикальную плоскость проекций новой (Pi). Проводим через вер-
шину (а, а') горизонталь (ат, а’т') плоскости треугольника и проводим новую ось
(О1УГ) проекций, перпендикулярную к горизонтальной проекции (ат) горизонтали.
Находим вертикальные проекции (&)) точки (кк') и (aiftici) треугольника (abc, а'Ь'с').
Опускаем из точки к\ перпендикуляр на вертикальную проекцию a'lbici треуголь-
ника. Отрезок I является искомым расстоянием.
Расстояние между параллельными плоскостями можно опреде-
лить одним из приведенных способов определения расстояния от точки до
плоскости.
283
Пример 256
Определить расстояние между параллельными плоскостями Р и О
(фиг. 792).
Решение. Перемещением приводим заданные плоскости в положение, пер-
пендикулярное к вертикальной (можно и к горизонтальной) плоскости проекций.
Проводим на плоскости Р горизонталь и, перемещая всю систему параллельно
горизонтальной плоскости проекций, ставим горизонталь в положение, перпенди-
кулярное к вертикальной плоскости проекций. Расстояние I между вертикальными
следами (Р„ ) и (2„t) плоскостей является искомым. Построение видно из чертежа.
Примечание. Таким путем можно определить и расстояние между
скрещивающимися прямыми, как расстояние между плоскостями парал-
лелизма.
Пример 257
Даны точка А и горизонтальный след (Рй) плоскости Р, удаленной от
точки Л на 18 мм. Найти вертикальный след этой плоскости (фиг. 793, 794).
Решение.
1. Способ совмещения (фиг. 793). Проводим через точку (л, д') горизонтально-
проектирующую плоскость R, перпендикулярную к плоскости Р, и, совместив эту
плоскость с горизонтальной (можно и с вертикальной) плоскостью проекций,
находим точку Ао и след Rt. . Так как расстояние от точки до плоскости изме-
ряется расстоянием от точки до линии пересечения плоскостей Р и R, описываем
из точки Ао как из центра окружность радиусом 18 мм и проводим через точку h
пересечения следов Ph и Rh прямую, касательную к этой окружности, до пересе-
чения со следом Р1( в точке Уо (дано одно решение). Затем, найдя по точке Vo
точку v' на следе Рь, проводим через точки Рх и г' искомый вертикальный след (Р„)
плоскости.
2. Способ перемещения (фиг. 794). Перемещаем заданную систему параллельно
горизонтальной плоскости проекций и приводим ее в положение, когда плоскость
Р — вертикально-проектирующая. Задаемся положением горизонтальной проекции
(di) точки и горизонтальным следом (Phl) плоскости, находим вертикальную про-
екцию (а)) точки. Так как расстояние от точки до вертикально-проектирующей
плоскости на эпюре измеряется расстоянием от вертикальной проекции точки
284
до вертикального следа плоскости, описываем из точки а\, как из центра, окруж-
ность радиуса 18 мм и проводим через точку РХ1 след Р„1, касательный к этой
окружности (дано одно решение).
Проводим произвольную горизонталь плоскости Pj и, найдя ее ? первона-
чальном задании, проводим через точки Рх и v' искомый вертикальный след (Р„)
плоскости.
Пример 258
Даны плоскость Р и вертикальная проекция точки А, удаленной от
плоскости Р на 18 мм. Найти горизонтальную проекцию этой точки
(фиг. 795, 796).
286
Решение.
1. Способ совмещения (фиг. 795). Проводим через точку (а, а') вертикально-
проектирующую плоскость R, перпендикулярную к плоскости Р, и, совместив ее
с вертикальной плоскостью проекций, находим прямую v'Ha пересечения плоскостей
Р и R. Так как совмещенное положение точки Ао должно находиться на расстоянии
18 мм от прямой v'H0 и на перпендикуляре, восставленном из точки а' к следу Rv,
проводим параллельно прямой v'HQ вспомогательную прямую на расстоянии 18 мм
(дано одно решение) и на ее пересечении с перпендикуляром получаем точку Ао.
Зная точку Ао, находим горизонтальную проекцию (а) точки А.
1. Способ перемены плоскостей проекций (фиг. 796). Заменяем горизонтальную
плоскость проекций новой (Hi), которая перпендикулярна плоскости Р. Проведя
вспомогательную прямую, параллельную следу Phl, на расстоянии 18 мм от него
(дано одно решение), получаем на пересечении с перпендикуляром, опущенным
из вертикальной проекции (а') точки на OiXlt точку по точке находим
искомую горизонтальную проекцию (а) точки.
Пример 259
Даны прямая АВ и горизонтальная проекция (cd) прямой CD, парал-
лельной АВ. Найти вертикальную проекцию прямой CD, если расстояние
между заданными прямыми равно I мм (фиг. 797-799).
Решение.
1. Способ перемены плоско-
стей проекций (фиг. 797). Заменой
плоскостей проекций новыми
приводим их в такое положение,
когда горизонтальная плоскость
проекций перпендикулярна за-
данным прямым. В таком случае
расстояние между этими пря-
мыми измеряется расстоянием
между их горизонтальными про-
екциями (а2Ь2) и (c2d2), изобра-
жаемыми в виде точек. Отсюда:
заменяем вертикальную плос-
кость проекций новой (Pj), кото-
рая параллельна заданным пря-
мым, и находим пока только вер-
тикальную проекцию (a'lfci) пря-
мой АВ. Затем заменяем гори-
зонтальную плоскость проекций
новой (Н2), которая перпендику-
лярна заданным прямым, и нахо-
дим опять только горизонталь-
ную проекцию (а2Ь^) той же
прямой. Описав из этой точки
окружность радиуса / мм и про-
ведя прямую, параллельную оси
(О2-^2) проекций на расстоянии
cctl (см. чертеж), получаем на
пересечении с окружностью точ-
ку с2, она же d2 — горизонталь-
ную проекцию (c2d2) прямой CD
(дано одно решение). Найдя вер-
тикальную проекцию (с'^\) пря-
мой обратным построением,
получаем ее вертикальную про-
екцию (c'd') в первоначальном
задании.
Фиг. 797
287
Фиг. 798 vf
288
2. Способ совмещения (фиг. 798). Задаем на прямой (ab, а'Ь') произвольную
точку (к, /с') и проводим через нее плоскость Р, перпендикулярную к этой прямой.
Для того чтобы найти основание (т, т') прямой (cd, c'd') на плоскости Р, заклю-
чаем эту прямую в горизонтально-проектирующую плоскость R и находим прямую
(hv, h'v1) пересечения этих плоскостей. Совместив плоскость Р с горизонтальной
(можно — с вертикальной) плоскостью проекций, находим точку Ко и из этой
точки, как из центра, описываем окружность радиуса I мм, которая на пересече-
нии с прямой лГ0 дает основание Мо прямой (cd, c'd') на плоскости Р. Находим
вертикальную проекцию (т') этой точки и проводим через нее вертикальную про-
екцию (c'd1) прямой. Дано одно решение.
3. Способ перемещения (фиг. 799). Перемещаем заданную систему параллельно
горизонтальной плоскости проекций и приводим ее в положение, при котором
прямая АВ параллельна вертикальной плоскости проекций. Затем перемещаем
систему параллельно вертикальной плоскости проекций и приводим ее в положение,
при котором та же прямая АВ перпендикулярна горизонтальной плоскости проек-
ций. Горизонтальные проекции прямых в таком положении изображаются в виде
точек (а2Ь2) и (c2d2), и расстояние между ними должно.равняться / мм. Отсюда:
для нахождения точки (c2d2) описываем из точки (а2Ь2) окружность радиуса I мм;
на ее пересечении с прямой Cjd1; параллельной оси проекций, получаем точку (c2d2)
(дано одно решение), горизонтальную проекцию прямой CD. Найдя вертикальную
проекцию (c'2d'2) прямой, обратным построением получаем ее вертикальную проек-
цию (c'd1) в первоначальном задании.
ЗАДАЧИ
438. Определить расстояние между точками А и В (фиг. 800 — 803).
439. Найти недостающую проекцию точки В, если расстояние между
точками А и В равно 25 мм (фиг. 804, 805).
440. Определить расстояние от точки С до прямой АВ (фиг. 636, 637).
441. Определить недостающую проекцию точки А, если расстояние'от
точки А до прямой ВС равно 25 мм (фиг. 806, 807).
442. Определить расстояние между параллельными прямыми АВ и CD
(фиг. 599, 639).
?а'
Фиг. 800
10 Арустамов X. А.
289
Фиг. 801
I
I
I
1°
I
I
X------1-----------!-------0
I
0
X
i
I
I
I
I
Ab'
Фиг. 802
b'
r-
] A
I b
I
I
ba'
Фиг. 803
?a'
>b'
X
0
; ।
I Ab
।
ьа
Фиг. 804
ba
Фиг. 805
443. Определить недостающую проекцию прямой CD, если расстояние
между параллельными прямыми АВ и CD равно 25 мм (фиг. 808, 809).
444. Построить проекции прямой MN, параллельной прямым АВ и CD
и удаленной от прямой АВ на 20 мм и от прямой CD на 30 мм
(фиг. 599, 639).
445. Найти проекции прямой MN, параллельной прямой АВ и удален-
ной от нее на 20 мм „и от точки С на 30 мм (фиг. 636, 637).
446. Найти проекции прямой MN, параллельной заданным прямым АВ,
CD, EF и равноудаленной от них (фиг. 810).
290
10*
291
447. Найти проекции прямой MN., параллельной прямой АВ и равно-
удаленной от этой прямой и от точек С и D (фиг. 811).
448. Определить расстояние между скрещивающимися прямыми АВ
И CD (фиг. 560, 578).
449. Найти на прямой АВ точку, удаленную от прямой CD на 25 мм
(фиг. 560, 578).
450. Определить расстояние от точки К до заданной плоскости
(фиг. 641-645).
451. Описать из точки С шар, касательный к заданной плоскости
(фиг. 582-587).
292
452. Определить недостающую
проекцию точки К, удаленной от за-
данной плоскости на 25 мм (фиг. 557
588-590).
453. Найти недостающий след пло-
скости Р, если расстояние от точки А
до этой плоскости равно 20 мм (фиг.
812, 813).
454. Определить недостающий след
плоскости Р, если она касательна к
поверхности шара (фиг. 814).
455. Определить расстояние между
параллельными плоскостями Р и Q
(фиг. 577).
456. Построить геометрическое
место точек пространства, отстоящих
от заданной плоскости на 25 мм
(фиг. 596-600).
457. Найти на прямой MN точку,
удаленную от заданной плоскости на
25 мм (фиг. 606-608).
Глава XXI
ОПРЕДЕЛЕНИЕ УГЛОВ
Угол между двумя пересекающимися прямыми можно опре-
делить одним из следующих способов:
1) заключением угла в треугольник; нужно пересечь стороны угла
произвольной прямой и определить натуральную величину полученного треуголь-
ника, откуда определяем натуральную величину заданного угла;
2) вращением (или перемещением); нужно поставить плоскость угла
в положение, параллельное какой-либо плоскости проекций;
3) совмещением; нужно найти один из следов плоскости угла — горизон-
тальный или вертикальный — и вращением около этого следа совместить с соот-
ветствующей плоскостью проекций;
4) вращением около горизонтали или фронтали;. нужно
совместить заданный угол с плоскостью R, параллельной горизонтальной (верти-
кальной) плоскости проекций, проходящей через произвольную горизонталь (фрон-
таль) плоскости угла;
5) переменой плоскостей проекций; нужно изменить плоскости
проекций так, чтобы одна из них стала параллельной плоскости заданного угла.
Указание. Из всех перечисленных способов решений наиболее просто и быстро
приводит к цели четвертый.
Для прямых, не лежащих в одной плоскости мерой угла между
ними служит угол между двумя пересекающимися прямыми, параллельными
данным.
ПРИМЕРЫ
Пример 260
Определить натуральную величину угла АВС (фиг. 815).
293
Фиг. 815
Фиг. 816
Решение. Способ вращения около горизонтали.
Проводим горизонталь (тп, т'п') в пдоскости угла и заключаем ее в плоскость
Т, параллельную горизонтальной плоскости проекций. Совмещаем стороны угла
(mb, m'b') и (nb, п'Ь') с плоскостью Т. Точки (т, т') и (п, и') уже лежат на плоскости
Т; остается совместить с этой плоскостью вершину (Ь, Ь') угла. Угол тВоп
является искомым. Построение видно из чертежа.
Пример 261
Провести биссектрису угла С треугольника АВС (фиг. 816).
Решение. Способ перемещения.
Для того чтобы провести биссектрису угла, требуется его натуральная вели-
чина. А для этого необходимо привести плоскость треугольника в положение,
параллельное какой-либо плоскости проекций, например горизонтальной.
Проводим горизонталь в плоскости треугольника через точку (а, а') и пере-
мещаем ее параллельно горизонтальной плоскости проекций до положения, пер-,
пендикулярного к вертикальной плоскости проекций. При перемещении треуголь-
ника параллельно горизонтальной плоскости проекций его горизонтальная проек-
ция, как известно, не должна изменяться, а потому приводим горизонтальную
проекцию треугольника в положение ajbjCj так, чтобы горизонтальная проекция
горизонтали была перпендикулярна оси проекций; по a^Ci находим вертикальную
проекцию (а\Ь\с'1) треугольника, которая получается в виде прямой линии. Затем
перемещаем треугольник (alblc1, а'^с'А параллельно вертикальной плоскости
проекций и приводим вертикальную проекцию (а'2Ь'2с2) треугольника в положение,
параллельное оси проекций; по d2b'2c'2 находим а2Ь2с2. Проведя биссектрису угла
(с2, с'Д, находим ее проекции (cd, c'd') обратным построением в первоначальном
задании (построение видно из чертежа).
Углом между прямой и плоскостью называется острый угол,
заключенный между-этой прямой и ее проекцией на данную плоскость.
Прямой путь определения этого угла требует ряда дополнительных построе-
ний (каких?) и потому очень длинен. Его можно значительно сократить, определяя
не искомый угол а, а его дополнение до 90°, т. е. острый угол ср, заключенный
между заданной прямой и перпендикуляром, опущенным из ее произвольной
точки на плоскость. Последний можно определить одним из приведенных выше
способов, но, как уже было указано, проще всего, применить вращение около
горизонтали или фронтали.
В тех случаях, когда найденный угол <р оказывается тупым, для получения
искомого угла а следует вычесть из найденного угла <р угол, равный 90° (фиг. 817)
(почему)?
Пример 262
Определить угол между прямой АВ и плоскостью Р (фиг. 817).
Решение. Опускаем из точки (а, д') перпендикуляр на плоскость Р. Так как
плоскость Р — профильно-проектирующая, то строим профильный след (Pw) плоско-
сти и профильную проекцию (а") точки; проводим через точку а" перпендикулярно
следу Pv прямую а"т" и по ней находим горизонтальную (ат) и вертикальную (а'т1)
проекции перпендикуляра. Затем, найдя вращением около горизонтали (тп, т'п')
натуральную величину угла получаем искомый угол а как дополнение этого
угла до 90°.
Указание. Точно так же определяем угол между прямой и плоскостью, когда
последняя задана не следами.
Угол между двумя пересекающимися плоскостями измеряется одним из его
линейных углов, обычно меньшим (а°). Определение линейного угла требует
ряда дополнительных построений (каких?), и потому прямой путь решения очень
длинен. Его можно значительно^ократить, определяя угол ср, заключенный между
перпендикулярами, опущенными из произвольной точки на заданные
плоскости; при этом найденный угол <р является искомым, если он острый;
если же найденный угол <р оказывается тупым, то искомый угол является допол-
нением к нему до 180° (фиг. 818).
295
При определении угла между двумя пересекающимися плоско-
стями с направленными сторонами (например, между гранями много-
гранника) перпендикуляры на заданные плоскости нужно опускать из произ-
вольной точки, взятой внутри двугранного угла. Искомый угол всегда является
дополнением до 180° к найденному углу <р.
Угол между двумя плоскостями можно определить также:
1) вращением или перемещением; нркно поставить заданные плоско-
сти (т. е. линию их пересечения) в положение, перпендикулярное к какой-либо
плоскости, проекций (см. пример 210);
2) переменой плоскостей проекций; нужно изменить плоскости
'проекций так, чтобы однаtиз них стала перпендикулярна заданным плоскостям,
т. е. линии их пересечения ‘(см. пример 249).
296
297
Фиг. 820
Пример 263
Определить угол между плоскостями Р и Q (фиг. 819).
Решение. Опускаем из произвольной точки (<?, а') перпендикуляры (ab, а’Ь')
и (ас, ас) на плоскости Р и Q и вращением около фронтали (пт, т'п) определяем
натуральную величину утла (Ъас, Ь'а’с'). Искомый угол равен углу а.
Пример 264
Определить угол при ребре SA пирамиды SABCD (фиг. 820).
Решение. Способ перемещения.
Перемещаем пирамиду параллельно горизонтальной плоскости проекций и
ставим ее в положение, когда ребро SA параллельно вертикальной плоскости
проекций. Затем перемещаем ее -параллельно вертикальной плоскости проекций
и ставим в положение, когда ребро S.4 перпендикулярно горизонтальной плоскости
проекций. Угол b2a2d2 является искомым. Построение видно из чертежа.
ЗАДАЧИ
458. Определить угол между пересекающимися прямыми АВ и АС
(фиг. 164, 165).
459. Определить угол между скрещивающимися прямыми АВ и CD
(фиг. 560, 578).
460. Определить угол между прямой АВ и заданной плоскостью
(фиг. 451-458; 470-473).
461. Определить углы наклона заданной плоскости к плоскостям про-
екций (фиг. 596-600).
298
462. Найти недостающий след плоскости Р, если угол, образуемый этой
плоскостью с вертикальной плоскостью проекций, равен 60° (фиг. 821, 822).
463. Найти недостающий след плоскости Р, если угол, образуемый этой
плоскостью с горизонтальной плоскостью проекций, равен 45° (фиг. 823,
824).
464. Провести через точку А (20, 30) произвольную плоскость Р,
наклоненную к горизонтальной (вертикальной) плоскости проекций под
углом 45°.
465. Определить: двугранный угол пирамиды при ребре SA (SB, SC, SD);
угол наклона грани SAB (SBC, SCD, SAD) к ее основанию (фиг. 820).
466. Определить угол между заданными плоскостями (фиг. 393, 394,
398 - 401, 408, 409, 474, 601-603).
РАЗДЕЛ ЧЕТВЕРТЫЙ
Глава XXII
СЕЧЕНИЕ МНОГОГРАННИКОВ ПЛОСКОСТЬЮ.
РАЗВЕРТКИ МНОГОГРАННИКОВ
Разверткой многогранника называется плоская фигура, полученная последо-
вательным совмещением всех граней многогранника с плоскостью чертежа; пло-
щадь полученной фигуры равна поверхности развернутого многогранника.
Вывод. На развертке многогранника все его грани должны быть построены
в натуральную величину.
ПРИМЕРЫ
Пример 265
Найти линию пересечения поверхности призмы с плоскостью Р (фиг. 825).
Решение. Для того чтобы построить линию пересечения, нужно найти точки
пересечения ребер призмы с данной плоскостью. Находим точку (л, а') пересечения
ребра (/, Г) с плоскостью. Горизонтальная проекция (а) этой точки совпадает
с горизонтальной проекцией ребра; зная это, находим вертикальную проекцию (а')
точки, пользуясь условием, что точка (а, а') лежит и на плоскости Р. Аналогичным
порядком находим точки (Ь, Ь'), (с, с') и (<•/, <Г) пересечений остальных ребер
с плоскостью Р. Соединив последовательно найденные точки, получаем
проекции искомой линии пересечения: горизонтальную (abed) и вертикальную
(a'b'c'd1). Из чертежа видно, что горизонтальная проекция (abed) линии пересечения
совпадает с горизонтальной проекцией (/, 2, 3, 4) призмы._
Пример 266
Найти линию пересечения поверхности призмы с плоскостью Р (фиг. 826).
Решение. Нужно найти точки пересечения ребер призмы с плоскостью Р.
Находим точку (а, а') пересечения ребра (/, Г) с плоскостью; заключаем ребро
в плоскость R, параллельную вертикальной плоскости проекций, которая пересекает
плоскость Р по фронтали. На пересечении вертикальных проекций ребра и фронтали
получаем вертикальную проекцию (д') точки; зная ее, находим горизонтальную
проекцию (а) точки на горизонтальной проекции ребра. Аналогичным образом
находим точки (Ь, Ь'), (с, с') и (d, d') пересечений остальных ребер с плоскостью.
Соединив последовательно найденные точки, получаем проекции искомой
линии: горизонтальную (abed) и вертикальную (a'b'c’d').
Пример 267
Найти линию пересечения поверхности призмы плоскостью Р (фиг. 827).
Решение. Так как и боковые ребра призмы и плоскость Р — общего поло-
жения, то обычный прием решения, т. е. нахождение точек пересечения всех боко-
вых ребер с плоскостью, выглядит громоздко (почему?), и потому для упро-
щения построений полезно учесть следующее. Призма поставлена основанием на
горизонтальную плоскость проекций, и горизонтальная проекция каждой стороны
основания призмы является горизонтальным следом соответствующей боковой
300
301
Фиг. 828
грани призмы, а точка их пересечений с горизонтальным следом )Ph) плоскости —
одной точкой горизонтальной проекции стороны линии пересечения. Отсюда:
обычным путем находим, например, точку (а, а') пересечения ребра (Z, Г) с пло-
скостью. Затем продолжаем прямую 1, 4 до пересечения со следом Ph в точке й;
соединив точки а и /| прямой ah, на ее пересечении с iоризонтальной проекцией
ребра^(4, 4') получаем горизонтальную проекцию (Ь) точки пересечения ребра (4, 4 )
с плоскостью; зная ее, находим вертикальную проекцию (/>') точки. Аналогичным
образом продолжаем прямую 4, 3 до пересечения со следом Ph в точке ht;
соединив точки b и /it прямой bht. на се пересечении с горизонтальной проекцией
ребра (3, 3') получаем горизонтальную проекцию (с) точки пересечения ребра (3, 3 )
с плоскостью; зная ее, находим вертикальную проекцию (i') точки. Наконец
продолжаем прямую 2, 3 до пересечения со следом Ph в точке /о; соединив точки
с и h2 прямой c/i2, на ее пересечении с горизонтальной проекцией ребра (2, 2‘)
получаем горизонтальную проекцию (d) точки пересечения ребра (2, 2') с плоскостью;
зная ее, находим вертикальную проекцию (J'J точки. Соединив последова-
тельно найденные точки, получаем проекции искомой' линии пересечения:
горизонтальную (abed) и вертикальную (a'b'c'd).
Пример 268
Найти линию пересечения поверхности пирамиды с плоскостью R
(фиг. 828).
Решение. Находим точки пересечения боковых ребер пирамиды с горизон-
тально-проектирующей плоскостью. Соединив последовательно найденные точки,
получаем проекции искомой линии: горизонтальную (abed) и вертикальную (a'b'c'd').
Из чертежа видно, 'по горизонтальная проекция (abed) линии пересечения сливается
со следом Rh (почему?).
302
z
Пример 269
Найти линию пересечения поверхности пирамиды с плоскостью Р
(фиг, 829).
Решение. Находим точки пересечений боковых ребер пирамиды с про-
фильно-проектирующей плоскостью. Строим профильную проекцию пирамиды и
профильный след (Р„.) плоскости. На пересечении профильных проекций ребер
пирамиды со следом Р„ получаем профильные проекции точек пересечений ребер
с плоскостью; зная их, находим горизонтальные и вертикальные проекции этих
точек. Соединив последовательно найденные точки, получаем проекции
искомой линии пересечения: горизонтальную (abed) и вертикальную (а'Ь'c'd').
Решение задачи без профильной плоскости проекции усложнило бы построение
(почему?).
Пример 270
Дать полную развертку поверхности четырехугольной призмы (фиг. 830).
Решение. Полная поверхность заданной призмы состоит из четырёх прямо-
угольников и двух четырехугольников. Проводим произвольную прямую NN и на
ней от точки А откладываем отрезки АВ, ВС, CD, DA, равные сторонам основания
призмы, т. е. АВ = ah; ВС = Ьс и т. д. Через точки А, В, С, D, А проводим'перпен-
дикуляры к прямой NN и на них откладываем одинаковые (почему?) отрезки
длиной й; соединив концы перпендикуляров, получаем прямую Д1В1С1О141,
параллельную прямой ABCDA, Затем пристраиваем, например при стороне AD,
нижнее основание призмы, а при стороне ALDt — верхнее ее основание.
303
Полученная фигура является полной разверткой поверхности призмы.
' Показываем дополнительно, как перенести точку (/с, к'), заданную на грани
BB,CtC призмы, на се развертку. Откладываем на стороне ВС отрезок ВМ,
равный Ьт, и, восставив перпендикуляр, откладываем на нем отрезок МК, равный
т'к’.
Пример 271
Дать полную развертку поверхности наклонной четырехугольной
призмы (фиг, 831).
Решение. Так как боковые грани наклонной призмы — параллелограммы,
то для их построения в натуральную величину необходимо дополнительно
определить — для каждого параллелограмма — угол между его сторонами или
длину одной из его диагоналей. Этого можно избежать, введя вспомогатель-
ную плоскость R, перпендикулярную к боковым ребрам, которая рассекает
304
наклонную нриз.му па две прямые усеченные призмы с общим основанием в пло-
скости перпендикулярного сечения. Найдя проекции такого сечения (называемого
«нормальным») и его натуральную величину способом совмещения приступаем к раз-
вертке поверхности наклонной призмы; она слагается из поверхностей двух прямых
призм, расположенных по обе стороны перпендикулярного сечения.
Проводим произвольную прямую NN и на пей от точки' Е откладываем
отрезки EF; FK; KL; LE, равные сторонам нормального сечения наклонной призмы,
т. е. EF = E0F0; FK = FQK0 и т. д. Через точки Е, F, К, L, Е проводим перпен-
дикуляры к прямой NN и па них откладываем длины боковых ребер верхней
и нижней призм. Соединив концы перпендикуляров, получаем ломаные линии
ABCDA и AlBiC1DiAl с параллельными сторонами, т. е. АВ || AjStJ ВС ||-S1Cl п т. д.
305
Фиг. 832
Затем пристраиваем к какой-либо грани верхнее и нижнее основания призмы,
заданные в натуральную величину.
Показываем дополнительно, как перенести точку (р, р'), заданную на грани
BBLCCt наклонной призмы, на ее развертку. Откладываем на стороне ВС отрезок
ВМ = Ьт; проведя через точку М прямую параллельно ребру, откладываем на ней
отрезок МР = тр’.
Примечание. Если боковые • ребра наклонной призмы не параллельны
плоскости проекций, то, пользуясь перемещением, ставим их в положение, при
котором они параллельны одной из плоскостей проекций.
Пример 272
Дать полную развертку четырехугольной пирамиды (фиг. 832).
Решение. Для того чтобы можно было построить натуральные величины
боковых граней пирамиды, необходимо определить натуральные величины ее
боковых ребер. Откладываем на оси проекций от произвольной точки отрезки
з1<з1, .Sjbj, SjCi, s^!, равные длинам горизонтальных проекций боковых ребер;
соединив точки с1э с точкой s), получаем натуральные величины этих
ребер. Задаем произвольную точку S и строим последовательно грани SAB, SBC,
306
SCb, SAb, зная три Стороны каждой грани. Затем пристраиваем основание АВСЬ
пирамиды при какой-либо стороне, например ВС. Полученная фигура является
полной разверткой поверхности пирамиды.
Показываем дополнительно, как перенести точку (к, к'), заданную на грани
(she, s'b'c') пирамиды, на ее развертку. Откладываем на стороне ВС отрезок
ВМ = Ьт, а затем, соединив точки S и М прямой SM, откладываем. на ней
отрезок SK = s'jfc'i.
Пример 273
Пересечь призму плоскостью Р и дать развертку какой-либо ее части
(фиг. 833).
Решение. Находим точки пересечений ребер призмы с плоскостью Р.
Например, для того чтобы найти точку (к, к') пересечения ребра (aalt а'а\)
с плоскостью, заключаем зто ребро в плоскость К, параллельную горизонтальной
плоскости проекций, которая пересекает плоскость Р по горизонтали. На пересе-
чении горизонтальных проекций ребра и горизонтали получаем горизонтальную
проекцию (А) точки, зная ее, находим вертикальную проекцию (к') точки на верти-
кальной проекции ребра. Аналогичным образом находим точки (/, /’), (т, т') и (», и')
пересечений остальных ребер с плоскостью. Соединив последовательно
найденные точки, получаем проекции линии сечения. Находим совмещением
плоскости Р с горизонтальной плоскостью проекций истинную величину K0L0M0N0.
Прежде чем приступить к развертке усеченной призмы, находим истинную
величину основания ABCD, расположенного параллельно профильной плоскости
проекций. Для этого находим его профильную проекцию (d'b"c"d“).
Проводим произвольную прямую MjMi и на ней от точки А откладываем
отрезки АВ, ВС, CD, DA, равные сторонам основания призмы, т. е. АВ — а"Ь";
ВС = Ь"с" и т. д. Через точки А, В, С, D, А проводим перпендикуляры к прямой
М1М1 и на них откладываем соответствующие длины боковых ребер, т. е. АК — а’к';
BL= Ь'Г и т. д. Соединив концы перпендикуляров, получаем ломаную линию
KLMNK. Затем пристраиваем, например при стороне MN, основание KLMN,
а при стороне CD — основание ABCD.
Пример 274
Пересечь пирамиду плоскостью Р и дать развертку какой-либо ее части
(фиг. 834).
Решение. Находим точки пересечений ребер пирамиды с плоскостью Р.
Так как секущая плоскость — вертикально-проектирующая, то на пересечении вер-
тикальных проекций (s'b', s'c’, s'd') ребер с вертикальным следом (Р,) плоскости
получаем вертикальные проекции (A', nf, н') точек пересечения, а зная их, находим
горизонтальные проекции (к, т, и) этих точек; ребро (sa, s'a') секущей плоскостью
не пересекается. Основание пирамиды секущей плоскостью пересекается по прямой
(ef, e'f). Находим натуральные величины всех боковых ребер пирамиды — пере-
мещением, фигуры сечения — совмещением. >
Для того чтобы получить развертку боковой поверхности усеченной пирамиды,
строим развертку боковой поверхности заданной пирамиды и переносим на нее
найденные точки Е, F, К, М, N. Определяем истинные величины отрезков (sk, s'k'),
(sm, s'm'), (s/i, s'iT) и откладываем их на прямых SA, SC, SD. Затем откладываем
BE = be на стороне АВ и DF = df на стороне DA. Пристраиваем верхнее и нижнее
основания усеченной пирамиды при какой-либо грани. Полученная фигура является
полной разверткой поверхности усеченной пирамиды.
При м е ч а н и е. Если секущая плоскость — общего положения, рекомендуется
проекции сечения находить вращением (перемещением) или переменой плоскостей
проекций (см. примеры 208 и 248).
307
Фиг. 833
308
ЗАДАЧИ
467. Пересечь многогранник (призму или пирамиду) плоскостью Р
и дать полную развертку одной из его частей (фиг. 835-886).
г,------ ----------------------------------- Р/
Фиг. 836
Фиг. 835 Фиг. 837
310
311
312
313
314
•315
Фиг. 861 Фиг. 862
Фиг. 863
316
317
319
Глава ХХПГ
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТИ И ПОВЕРХНОСТИ
Для того чтобы построить линию пересечения любой поверхности с плоско-
стью, нужно найти ряд точек, принадлежащих как поверхности, так и плоскости,
и затем эти точки соединить плавной кривой линией.
Для того чтобы найти произвольную точку линии пересечения, поступают так:
1) проводят вспомогательную плоскость;
2) находят линии пересечения этой плоскости с поверхностью и с заданной
плоскостью;
3) на пересечении найденных линий получают искомые точки (чаще всего —
Две).
Последовательно проводя ряд вспомогательных плоскостей, можно найти
необходимое число точек.
Указание. Вспомогательную плоскость следует выбирать так, чтобы ее линия
пересечения с поверхностью проектировалась на плоскости проекций в виде
простейших линий — прямой или окружности.
Если заданная поверхность имеет прямолинейные образующие, то линию пере-
сечения можно найти также следующим образом: наносим на поверхность ряд
образующих и находим точки их пересечения с плоскостью, а затем соединяем
эти точки плавной кривой линией.
СЕЧЕНИЕ ЦИЛИНДРА
Любая плоскость пересекает поверхности прямого кругового цилиндра:
1) ио окружности, если плоскость перпендикулярна осп цилиндра;
2) по эллипсу, если плоскость произвольно наклонена к осп цилиндра:
3) по двум образующим, если плоскость параллельна оси цилиндра
и отстоит от нее на расстоянии /, которое меньше радиуса г цилиндра;
4) по одной образующей, если плоскость параллельна оси цилиндра
и отстоит от нее на расстоянии I, которое равно радиусу г цилиндра (плоскость —
касательная к поверхности цилиндра).
322
Указание. Любая цилиндрическая поверхность может быть пересечена по
прямым плоскостью, параллельной ее образующей.
СЕЧЕНИЕ КОНУСА
Обозначаем угол наклона образующей конуса к его основанию через а,
л угол наклона плоскости к основанию конуса — через <р.
Любая плоскость, проходящая через вершину прямогр кругового
конуса, пересекает его поверхность:
1) в точке, если <р меньше а;
2) по одной образующей, если <р = а, т. е. когда плоскость является
касательной к поверхности конуса;
3) по двум образующим, если <р больше а или <р=90’, т.е. когда
плоскость проходит через ось конуса.
Указание. Любая коническая поверхность может быть пересечена по пря-
мым плоскостью, проходящей "через ее вершину.
Любая плоскость, не проходящая через вершину прямого кругового
конуса, пересекает его поверхность:
1) по окружности, если плоскость перпендикулярна оси конуса, т. е. <р = 0;
2) по эллипсу, если <р меньше а;
3) по параболе, если <р = а, т. е. плоскость параллельна одной из обра-
зующих конуса;
4) по гиперболе, если <р больше а или ср = 90’, т. е. когда плоскость
параллельна оси конуса.
Указание. Для выявления вида линии пересечения, когда секущая плоскость —
общего положения, вращают плоскость вокруг оси конуса и приводят ее в такое
положение, чтобы она стала вертикально-проектирующей, если ось конуса перпен-
дикулярна горизонтальной плоскости проекций, и горизонтально-проектирующей,
если ось конуса перпендикулярна вертикальной плоскости проекций.
СЕЧЕНИЕ ШАРА
Любая плоскость пересекает поверхность шара по окружности, если рас-
стояние I от плоскости до центра шара меньше радиуса R щара.
В частном случае плоскость является касательной к поверхности шара,
если I = R.
Указание. Любая поверхность вращения может быть пересечена по окруж-
ности плоскостью, перпендикулярной к ее оси.
В дальнейшем при решении задач придется задавать точку на поверхности.
Для этого поступают так: проводят на поверхности вспомогательную
линию (прямую, окружность) и затем на этой линии берут точку (конкретно —
см. примеры).
ПРИМЕРЫ
Пример 275
Задать на поверхности наклонного цилиндра произвольную точку А
(фиг. 887).
Решение. Задаем произвольную точку (т, т') на основании цилиндра и
проводим через нее вспомогательную образующую. На этой образующей берем
точку (а, а'), которая и лежит на заданной поверхности.
Пример 276
Найти вертикальную, проекцию точки А, лежащей' на поверхности
наклонного цилиндра, если дана ее горизонтальная проекция (фиг. 888).
Решение. Проводим через точку а Горизонтальную проекцию (ат) вспомо-
гательной образующей. Находим вертикальную проекцию (iri) точки М и проводим
через нее вертикальную проекцию образующей; затем на ней по точке а находим
точку а'
11*.
323
Фиг. 887
Фиг. 888
324
Пример 277
Задать на поверхности конуса произвольную точку А.
Решение.
Первый способ (фиг. 889). Задаем произвольную точку (т, т') на основании
конуса и проводим вспомогательную образующую через точки (in, т') и (s, s').
На этой образующей берем точку (а, а'), которая и лежит на заданной поверх-
ности.
Второй способ (фиг. 890). Проводим на поверхности конуса вспомогательную
окружность; ее вертикальная проекция является прямой линией, параллельной оси
проекций, а ее горизонтальная проекция — окружностью. На этой окружности
берем точку (а, а'), которая и лежит на заданной поверхности.
Пример 278
Лежит ли точка А на поверхности усеченного конуса?
Решение.
Первый способ (фиг. 891). Проводим через точку а горизонтальную проекцию
вспомогательной окружности, расположенной на поверхности конуса, и затем
находим ее вертикальную проекцию. Из чертежа видно, что точка а' не лежит
на вертикальной проекции вспомогательной окружности. Следовательно, точка
(а, а') на поверхности конуса не лежит. (Решение задачи можно начать также
с проведения вертикальной проекции вспомогательной окружности и т. д.)
Второй способ (фиг. 892). Проводим через тЪчку а' вертикальную проекцию
(т'пг) вспомогательной образующей и находим ее горизонтальную проекцию (ши).
Из чертежа видно, что горизонтальная проекция (а) точки не лежит на гори-
зонтальной проекции (тн) образующей. Следовательно, точка (а, а') на поверхности
конуса не лежит. (Можно ли начать решение задачи с проведения горизонтальной
проекции образующей, не достраивая горизонтальной проекции вершины конуса?)
325
Пример 279
Найти вертикальную проекцию точки А, лежащей на поверхности
усеченного конуса, если дана ее горизонтальная проекция.
Решение.
Первый способ (фиг. 893). Проводим через точку а горизонтальную проекцию
(тп) вспомогательной образующей и находим ее вертикальную проекцию (т'п).
Затем по точке а находим точку а'.
Второй способ (фиг. 894). Проводим через точку а горизонтальную проекцию
вспомогательной окружности, расположенной на поверхности конуса, и находим
ее вертикальную проекцию. Затем по точке а находим точку а'.
(Можно ли первым способом решить обратную задачу — т. е. по вертикальной
проекции точки найти ее горизонтальную проекцию, не достраивая вертикальной
проекции вершины конуса?)
Пример 280
Найти вертикальную проекцию точки А, лежащей на поверхности
наклонного конуса, если дана ее горизонтальная проекция (фиг. 895).
Решение.
Проводим через точку а горизонтальную проекцию (sm) вспомогательной
образующей. Находим вертикальную проекцию (;«') точки М и проводим через
нее вертикальную проекцию (s'm') образующей; затем на ней по то аде а находим
точку а’.
Пример 281
Найти горизонтальную проекцию точки А, лежащей на поверхности
конуса, если дана ее вертикальная проекция.
Решение.
Первый способ (фиг. 896). Строим профильную проекцию конуса. Проводим
через точку а' вертикальную проекцию вспомогательной окружности, расположен-
ной на поверхности конуса, и затем находим ее профильную проекцию. По точке
д' находим точку а", а затем по двум этим проекциям - точку а.
326
Второй способ (фиг. 897). Строим профильную проекцию конуса. Проводим
через точку а’ вертикальную проекцию (s'm'j вспомогательной образующей. Нахо-
дим профильную проекцию (т") точки М, а затем по точкам т' и т" — точку т.
Проводим горизонтальную проекцию (sm) образующей и на ней находим точку а.
Пример 282
Задать на поверхности шара произвольную точку А.
Решение.
Первый способ (фиг. 898). Проводим на поверхности шара вспомогательную
окружность, расположенную па-
раллельно горизонтальной пло-
скости проекций; ее вертикаль-
ная проекция является прямой
линией, параллельной оси проек-
ций, а ее горизонтальная проек-
ция — окружностью. На вспомо-
гательной окружности берем
произвольную точку (a,o'), кото-
рая и лежит на заданной поверх-
ности.
Второй способ (фиг. 899).
Проводим на поверхности шара
вспомогательную окружность,
расположенную параллельно
вертикальной плоскости проек-
ций. Ее горизонтальная проек-
ция является прямой линией,
параллельной оси проекций, а ее
вертикальная проекция — окруж-
ностью. На вспомогательной
окружности берем произволь-
ную точку (а, а'), которая и ле-
жит на заданной поверхности.
327
Пример 283
Найти горизонтальную проекцию точки А, лежащей на поверхности
шара, если дана ее вертикальная проекция.
Решение.
Первый способ (фиг. 900). Проводим через точку а’ вертикальную проекцию
вспомогательной окружности, расположенной на поверхности шара и параллель-
ной горизонтальной плоскости проекций. Находим ее горизонтальную проекцию
и затем по точке а' находим точку а.
Второй способ (фиг. 901). Проводим через точку а' вертикальную проекцию
вспомогательной окружности, расположенной на поверхности шара и параллель-
328
ной вертйкальной плоскости проекций. Находим ее горизонтальную проекцию
и затем по точке а' находим точку а.
Пример 284
Найти вертикальную проекцию точки А, лежащей на поверхности шаро-
вого сегмента, если дана ее горизонтальная проекция.
Решение.
Первый способ (фиг. 902). Проводим через точку а горизонтальную проекцию
вспомогательной окружности, расположенной на поверхности шарового сегмента
и параллельной горизонтальной плоскости проекций. Находим ее вертикальную
проекцию и затем по точке а находим точку а'.
Второй способ (фиг. 903). Дополняем шаровой сегмент до получения полу-
шара и. проводим через точку а горизонтальную проекцию вспомогательной,
полуокружности, расположенной на поверхности полушара и параллельной верти-
кальной плоскости проекций. Находим ее вертикальную проекцию и Затем по
точке а находим точку а'.
Пример 285
Задать на поверхности полукольца произвольную точку А (фиг. 904).
Решение. Проводим на поверхности Полукольца вспомогательную полу-
окружность, расположенную параллельно вертикальной плоскости проекций; ее
горизонтальная проекция является прямой линией, параллельной оси проекций,
а ее вертикальная проекция — полуокружностью. На вспомогательной полуокруж-
ности берем точку (б, а'), которая и лежит на заданной поверхности.
Пример 286
Найти вертикальную проекцию точки А, лежащей на поверхности полу-
кольца, если дана ее горизонтальная проекция (фиг. 905).
329
Решение. Проводим через точку а горизонтальную проекцию вспомогатель-
ной полуокружности, расположенной на поверхности полукольца и параллельной
вертикальной плоскости проекций. Находим ее вертикальную проекцию и затем
по точке а находим точку а'.
Пример 287
Найти вертикальную проекцию точки А, лежащей на поверхности
кольца, если дана ее горизонтальная проекция (фиг. 906).
Решение. Проводим через точку а горизонтальную проекцию вспомогатель-
ной окружности, расположенной на поверхности кольца и параллельной горизон-
тальной плоскости проекций. Находим ее вертикальную проекцию и затем по
точке а находим точку а'.
Пример 288
Найти горизонтальную проекцию точки А, лежащей на поверхности
вращения, если дана вертикальная проекция (фиг. 907).
Решение. Проводим через точку а' вертикальную проекцию вспомогатель-
ной окружности, расположенной на поверхности вращения. Находим ее горизон-
тальную проекцию и затем по точке а' находим точку а.
330
X
Фиг. 906
Фиг. 907
о
Фиг. 908
О
X
Пример 289
Найти горизонтальную проекцию
точки А, лежащей на поверхности
вращения, если дана ее вертикальная
проекция (фиг. 908).
Решение. Проводим через точку d
вертикальную проекцию вспомогательной
окружности, расположенной на поверх-
ности вращения. Находим ее горизонталь-
ную проекцию и затем по точке d нахо-
дим точку а.
Пример 290
Провести через прямую АВ пло-
скость, пересекающую поверхность
наклонного цилиндра по образую-
щйм, и найти эти образующие
(фиг. 909).
Решение. Задаем на прямой (ab, а'Ь') произвольную точку (к, к1) и проводим
через нее прямую (kl, к'Г), параллельную оси цилиндра. Прямые (ab, db') и (kl, к’Г)
определяют искомую плоскость. Находим горизонтальные следы (h, h') и (йь h'j
этих прямых и проводим через точки h и горизонтальный след (Ph) плоскости;
на его пересечении с основанием цилиндра получаем точки (ni, т') и (и, п'), через
которые проводим искомые образующие.
Примечание. В частном случае (когда?) горизонтальный след (РЛ) плоскости
может касаться основания цилиндра, тогда эта плоскость является касатель-
ной к поверхности цилиндра.
Пример 291
Провести через точку А плоскость, касательную к поверхности наклон-
ного цилиндра (фиг. 910).
331
Фиг. 909
Фиг. 910
Решение. Проводим через точку (а, а1) прямую, параллельную Оси цилиндра,
и находим ее вертикальный след (и, v'). Проводим через точку v' прямые v'k' и v'k),
касательные к вертикальной проекции основания цилиндра в точках т' и mi.
Через точки (т, т') и (т1г т\) проводим образующие цилиндра (тп, т'п') и (m^,
mini) — линии касания. Прямые (vk, v'k') и (yklt v'k)) с соответствующими линиями
касания определяют искомые плоскости.
Эти плоскости можно изобразить также следами (как?).
Пример 292
Провести произвольную плоскость, пересекающую поверхность конуса
по образующим, и найти эти образующие (фиг. 911).
Решение. Секущая плоскость Р должна проходить через вершину (.?, s')
конуса. Проводим через точку (s, s') произвольную горизонталь и находим ее
вертикальный след (и, v'). Задаем на оси проекций произвольную точку Рх
и проводим следы этой плоскости Ph и Pv. Плоскость Р пересекает основание
конуса по хорде (ти, т'п'). Соединив вершину (s, s') конуса с концами (т, т')
и (и, п') хорды, получаем искомые образующие (sm, s'm') и (sn, s'n').
Примечание. Точку Рх можно задать так, что горизонтальный след (РА)
плоскости касается основания конуса; тогда эта плоскость является касатель-
н о й к поверхности конуса.
Пример 293
Даны конус и вертикальный след плоскости Р, пересекающей поверх-
ность конуса по образующим. Найти эти образующие (фиг. 912).
Фиг. 912
333
Решение. Так как плоскость Р должна проходить через вершину (s, s') конуса,
лежащую на горизонтальной плоскости проекций, проводим горизонтальный след
(РА) плоскости через точки Рх и з. Находим линию пересечения плоскости Р
с плоскостью основания конуса и отмечаем точки (in, т') и (и, д') ее пересечения
с окружностью основания. Соединив вершину (s, s') конуса с точками (т, т’) и
(и, д'), получаем искомые образующие (sm, s'm') и (sh, s'n').
Пример 294
Провести плоскость, касательную к поверхности конуса, если дана
вертикальная проекция (а') точки линии касания (фиг. 913).
Решение. Проводим через точку а' вертикальную проекцию (s'/д') образую-
щей и находим ее горизонтальную проекцию (sm). Проводим через точку (т, тг)
фронталь, касательную к окружности основания конуса. Фронталь и образующая
(sm, s'm') определяют искомую плоскость. Эту плоскость можно изобразить
и следами (как?).
Пример 295
Построить проекции линии пересечения плоскости Р с поверхностью
цилиндра (фиг. 914).
Решение. Плоскость Р пересекает поверхность цилиндра по эллипсу, верти-
кальная проекция которого совпадает с вертикальным следом (Р„) плоскости,
а горизонтальная проекция — с горизонтальной проекцией цилиндра. Истинную
величину эллипса можно построить по главным осям: большая ось равняется
отрезку а'0', а малая ось — диаметру цилиндра. Точка (ос, а') является низшей
точкой линии пересечения, а точка (0, 0') — ее высшей точкой.
334
Пример 296
Построить проекции линии пересечения плоскости Р с поверхностью
цилиндра (фиг. 915). .
-Решение. Проводим через ось цилиндра горизонтально-лроектирующую
плоскость R, перпендикулярную к плоскости Р; плоскость R пересекает
поверхность цилиндра по образующим, а плоскость Р — по прямой (hv, h'v'); на
их пересечении получаем низшую точку (а, а*) и высшую точку (Р, р*) пинии
335
пересечения. Проводим через ось цилиндра плоскость Rt, параллельную верти-
кальной плоскости проекций; плоскость R, пересекает поверхность цилиндра
по крайним образующим, а плоскость Р — по фронталй; на их пересечении
получаем точки (а, а') и (b, Ьг) линии пересечения.
Находим точки пересечения профильных образующих цилиндра с плоскостью Р.
Горизонтальные проекции (с) и (rf) этих точек известны (почему?); по ним,
пользуясь горизонталями, находим вертикальные проекции (с') и (d')- Аналогично
находим точки пересечения еще нескольких образующих цилиндра с плоскостью.
Соединив последовательно вертикальные проекции всех найденных точек,
получаем вертикальную проекцию линии пересечения — эллипс. Истинную величину
эллипса можно построить по главным осям; большая ось равна длине отрезка
(ар, «xPi), а малая ось —диаметру цилиндра.
Пример 297
Построить проекции линии пересечения плоскости Р с поверхностью
конуса (фиг. 916).
Решение. Плоскость Р пересекает поверхность конуса по эллипсу,
вертикальная проекция которого совпадает с вертикальным следом (PJ плоскости.
Горизонтальную проекцию эл.тшгса строим по точкам: задаем вертикальные
проекции ряда его точек и находим их горизонтальные проекции (см. примеры
279 — 281). Затем через горизонтальные проекции точек проводим плавную кри-
вую — эллипс. Горизонтальную проекцию линии пересечения, как эллипс, можно
построить также по главным осям: по большой оси оф и по малой оси ab.
Истинную величину эллипса можно построить по двум его главным осям:
по большой оси а'р' и по малой оси ab, которую находим по вертикальной
проекции (а'Ь'). ,
Пример 298
Построить проекции линии пересечения плоскости Р с поверхностью
конуса (фиг. 917).
Решение. Плоскость Р пересекает поверхность конуса по гиперболе
с вершиной в точке (<?, а'), горизонтальная проекция которой совпадает с гори-
зонтальным следом (PJ плоскости. Вертикальную проекцию линии пересечения
строим по точкам: задаем горизонтальные проекции ряда точек линии пересечения
и находим их вертикальные проекции (см. пример 279 — 281). Затем через верти-
кальные проекции точек проводим плавную кривую - гиперболу.
Пример 299
Построить проекции линии пересечения плоскости Р с поверхностью
конуса (фиг. 918).
Решение. Плоскость Р пересекает поверхность конуса по параболе
с вершиной в точке (а, а'), горизонтальная проекция которой совпадает с гори-
зонтальным следом (Р(1) плоскости. Вертикальную проекцию параболы строим
по точкам: задаем горизонтальные проекции ряда точек линии пересечения и нахо-
дим их вертикальные проекции. Затем через вертикальные проекции точек про-
водим плавную кривую - параболу.
Пример 300
Построить проекции линии пересечения плоскости Р с поверхностью
конуса.
Решение.
Первый способ (фиг. 919). Проводим через ось конуса горизонтально-проекти-
рующую плоскость К, перпендикулярную к плоскости Р; плоскость К
пересекает поверхность конуса по образующим, а плоскость Р — по прямой (hv, h'v")',
на их пересечении получаем низшую точку (а, а') и высшую точку (Р, Р') линии
пересечения. Проводим через ось конуса плоскость R;, параллельную плоскости К;
плоскость Rx пересекает поверхность конуса по крайним образующим а плоскость
336
Р — по фронтали; на их пересечении получаем еще две точки (а, а') и (Ь, У)
линии пересечения. Для того чтобы найти точки линии пересечения, лежащие на
профильных образующих, заменяем вертикальную плоскость проекций новой (КД,
где плоскость Р — вертикально-проектирующая, и находим точки (с, ci) и (d, di)
пересечения этих образующих с плоскостью Рр Затем находим точки (с, с') и (d, d1).
Для того чтобы найти промежуточные точки линии пересечения, поступаем так:
вводим между точками (а, а') и (р, р') вспомогательную плоскость Q, параллель-
ную плоскости Я; плоскость О пересекает поверхность конуса по окружности,
а плоскость Р — по горизонтали; на их пересечении получаем две точки (к, к')
и (т, m'). Аналогично находим еще несколько точек и затем через одноименные
проекции найденных точек проводим плавные кривые — эллипсы.
Второй способ (фиг. 920). Перемещаем заданную систему параллельно гори-
зонтальной плоскости проекций и приводим ее в положение, при котором плоскость
Р является вертикально-проектирующей. Находим проекции линии пересечения
и затем, обратным перемещением, находим проекции пересечения в первоначаль-
ном задании (подробнее см. чертеж).
Третий способ (фиг. 921). Точки (а, а1) и (Ь, Ь1) на крайних образующих
и точки (с, с') и (</, d') на профильных образующих конуса находим так, как было
указано в первом способе. Для того чтобы найти промежуточные точки, поль-
зуемся вспомогательными плоскостями, проходящими через вершину (s, s') конуса,
горизонтальные следы которых параллельны следу Ph. Каждая такая плоскость
пересекает поверхность конуса по двум образующим, а плоскость Р — по горизон-
тали; на пересечении полученных линий получаем по две точки. Для того чтобы
найти точки (а, а’) и (0, 0'), проводим вспомогательные плоскости, касательные
к конусу; на пересечении линий касания —
образующих с соответствующими гори-
зонталями — получаем эти точки. Затем
через одноименные проекции всех найден-
ных точек проводим плавные кривые —
эллипсы.
Фиг. 918
Фиг. 917
'338
Пример 301
Построить проекции линии пересечения плоскости Р с поверхностью
шара (фиг. 922).
Решение. Плоскость Р пересекает поверхность шара по окружности
горизонтальная проекция (cd) которой совпадает с горизонтальным следом (PJ
плоскости. Вертикальную проекцию окружности — эллипс — строим по главным
339
Фиг. 920
его осям; большой осью является вертикальная проекция (а'Ь1) диаметра, распо-
ложенного перпендикулярно горизонтальной плоскости проекций, а малой осью —
вертикальная проекция (с'сГ) диаметра, расположенного параллельно горизонталь-
ной плоскости проекций. Вертикальную проекцию окружности можно построить
также по толкам; задаем горизонтальные проекции ряда точек окружности и
находим их вертикальные проекции (см. примеры 283, 284). Затем полученные
точки соединяем плавной кривой — эллипсом.
Для того чтобы отделить на вертикальной проекции кривой видимую ее
часть от невидимой, находим вертикальные проекции (»/) и (д') ее точек, располо-
женных на главном меридиане.
Пример 302
Построить проекции линии пересечения плоскости Р с поверхностью
шара (фиг. 923).
Решение. Плоскость Р пересекает поверхность шара по окружности, верти-
кальная проекция (с', rf'-) которой совпадает с вертикальных! следом (PL.) плоскости.
Горизонтальную проекцию окружности — эллипс — строим по главным осям; боль-
шой осью является горизонтальная проекция (ab) диаметра, перпендикулярного
к вертикальной плоскости проекций, а малой осью — горизонтальная проекция (al)
диаметра, расположенного параллельно вертикальной плоскости проекций. Гори-
зонтальную проекцию окружности можно построить также по точкам; задаем
вертикальные проекции ряда точек окружности и находим их горизонтальные
проекции (см. примеры 283, 284). Затем полученные точки соединяем плавной
кривой — эллипсом.
340
341
Фиг. 923
Для того чтобы отделить на горизонтальной проекции кривой видимую ее
часть от невидимой, находим горизонтальные проекции (ш) и (п) ее точек, распо-
ложенных на экваторе.
Пример 303
Построить проекции линии пересечения плоскости Р с поверхностью
шара.
Решение.
Первый способ (фиг. 924). Проводим через центр шара горпзонтально-проек-
тирующую плоскость R, перпендикулярную к плоскости Р; плоскость R
пересекает поверхность шара по окружное™, а плоскость Р — по прямой (Ju; h'с');
на их пересечении получаем низшую точку (а, а‘) и высшую точку (Р, Р') линии
пересечения. Для того чтобы не строить эллипса на вертикальной плоскости
проекций, совмещаем плоскость R с горизонтальной плоскостью проекций и
находим предварительно эти точки в совмещенном положении (см. чертеж).
Для того чтобы найти промежуточные точки линии пересечения, проводим
между точками (а, а') и (Р, р') ряд вспомогательных плоскостей Q, Qi и т. д.,
параллельных горизонтальной плоскости проекций. Например, плоскость Q пере-
секает поверхность шара по окружности, а плоскость Р — по горизонтали; на их
пересечении получаем две точки: (Ц 1') и (2, 2').
Для того чтобы на вертикальной проекции кривой отделить видимую ее часть
от невидимой, проводим через центр шара плоскость RJt параллельную верти-
кальной плоскости проекции; плоскость Pj пересекает поверхность шара по
главному меридиану, а плоскость Р — по фронтали. На их пересечении
получаем точки (а, а') и (Ь, Ь'). Для того чтобы на горизонтальной проекции
342
кривой отделить видимую ее часть от невидимой, проводим: через центр тара
плоскость S, параллельную горизонтальной плоскости проекций; плоскость S
пересекает поверхность шара по экватору, а плоскость Р — по горизонтали.
На их пересечении получаем точки (/», /«') и (и, п'). Затем одноименные проекции
всех найденных точек соединяем плавными кривыми — эллипсами. ,
343
Фиг. 925
Второй способ (фиг. 925). Перемещаем заданную систему параллельно гори-
зонтальной плоскости проекций и приводим ее в положение, при котором
плоскость Р является вертикально-проектнрующей. Затем находим проекции линии
пересечения и обратным перемещением находим ее проекции — эллипсы — в перво-
начальном задании (построение видно из чертежа).
Третий способ (фиг. 926). Опускаем пз центра шара перпендикуляр на плоскость
Р и находим его основание (с, с') — центр окружности. Пользуясь вспомогательным
построением (см. чертеж), определяем радиус г этой окружности по натуральной
величине расстояния I от центра шара до плоскости Р и по радиусу R шара.
Совмещаем плоскость Р с горизонтальной плоскостью проекций и находим поло-
жение (Со) центра окружности. Строим в совмещенном положении эту окружность,
а затем находим ее проекции (см. пример 229).
Пример 304
Провести на плоскости Р прямую, составляющую с осью проекций
угол, равный ср (фиг. 927).
Решение. Геометрическим местом прямых в пространстве, составляющих
с осью проекций заданный угол, является поверхность прямого кругового конуса
произвольной высоты и с углом 2<р при вершине в точке Рх. Искомыми прямыми
являются те образующие конуса, по которым плоскость Р пересекает эту. поверх-
ность (построение видно из чертежа).
344
Пример 305
Даны точка S и плоскость Р. Провести через точку S прямую, парал-
лельную плоскости Р и составляющую с вертикальной плоскостью проек-
ций угол <р (фиг. '928).
Решение. Геометрическим местом прямых в пространстве, проходящих
через точку S .и наклоненных к вертикальной плоскости проекций под углом <р,
является поверхность прямого кругового конуса с вершиной в точке S, образующие
которого наклонены к вертикальной плоскости проекций под углом <р. Искомыми
прямыми являются те образующие конуса, по которым плоскость Q. проходящая
через точку 5 параллельно плоскости Р, пересекает его поверхность (построение
видно из чертежа).
345
Фиг. 929 фиг. 928
346
* Пример 306
Даны точка S и прямая АВ. Провести через точку S плоскость Р,
наклоненную к горизонтальной плоскости проекций под заданным углом Ф
и параллельную прямой АВ (фиг. 929).
Решение. Плоскостью, наклоненной к горизонтальной плоскости проекций
под заданным углом ф и проходящей через точку S, является любая плоскость,
касательная к поверхности прямого кругового конуса с вершиной в точке S,
образующие которого составляют с горизонтальной плоскостью проекций тот же
угол ф. Искомой плоскостью является та из этих плоскостей, которая заключает
прямую, параллельную АВ. Отсюда — проводим через точку S — вершину конуса —
прямую MN, параллельную прямой АВ, и эту прямую заключаем в плоскости,
касательные к поверхности конуса. Задача имеет два решения (построение
видно из чертежа).
Пример 307
Провести к поверхности шара касательную плоскость Р, параллельную
плоскости R (фиг. 930).
Решение. Проводим через центр (с, с*) шара прямую, перпендикуляр-
ную к плоскости R, и находим точки (т, т') и (и, и') ее пересечения с поверхностью
шара; это проще сделать, отложив на проведенной прямой отрезки (ст, с'т')
и (си, с'п'), равные радиусу шара. Затем проводим через полученные точки (т, т')
и (п, п') плоскости Р и Plt параллельные плоскости R, или, что то же,
плоскости, перпендикулярные к прямой (тп, т'п') (построение видно из чертежа).
Пример 308
Провести через точку S прямую, составляющую с горизонтальной пло-
скостью проекций угол ф и перпендикулярную к прямой CS (фиг. 931).
347
Решение. Геометрическим местом прямых, проходящих через точку S и
составляющих с горизонтальной плоскостью проекций угол <р, является поверхность
прямого кругового конуса с вершиной в точке S, образующие которого накло-
нены к горизонтальной плоскости проекций под углом <р. Вместе с тем геометри-
ческим местом прямых пространства, проходящих через точку S и перпендикуляр-
ных к прямой CS, является плоскость, перпендикулярная к прямой CS. Отсюда —
искомые прямые получаем как результат пересечения с поверхностью конуса
плоскости, перпендикулярной к прямой CS (построение видно из чертежа),
ЗАДАЧИ
468. Провести через точку А плоскость Р, пересекающую поверхность
наклонного цилиндра по образующим, и найти эти образующие (фиг. 932).
469. Провести через точку А плоскость Р, параллельную прямой MN
и пересекающую поверхность наклонного цилиндра по образующим,
и найти эти образующие (фиг. 933).
470. Провести через прямую АВ плоскость, пересекающую поверхность
наклонного цилиндра по образующим, и найти эти образующие (фиг. 934).
471. Провести произвольную плоскость Р, пересекающую поверхность
наклонного цилиндра по образующим, и найти эти образующие (фиг. 935).
348
349
472. Построить следы плоскости, касательной к поверхности цилиндра
и проходящей через точку К, лежащую на его поверхности (фиг. 936).
473. Построить следы плоскости, касательной к поверхности цилиндра
и проходящей через точку К (фиг. 937).
474. Построить следы плоскости, касательной к поверхности наклонного
цилиндра и параллельной прямой АВ (фиг. 938).
475. Провести через точку А плоскость Р, пересекающую поверхность
конуса по образующим, и найти эти образующие (фиг. 939).
476. Провести плоскость Р, пересекающую поверхность конуса по обра-
зующим и параллельную прямой АВ, и найти эти образующие (фиг. 940). *
350
477. Провести плоскость Р, пересекающую поверхность конуса по обра-
зующим и параллельную плоскости Q: найти эти образующие (фиг. 941).
478. Построить следы плоскости, касательной к поверхности конуса
и проходящей через точку К, лежащую на его поверхности (фиг. 942).
479. Провести через точку К плоскость, касательную к поверхности
конуса (фиг. 943).
480. Провести плоскость, параллельную прямой АВ и касательную
к поверхности конуса (фиг. 944).
Фиг. 943
481. Построить проекции сечения прямого кругового цилиндра пло-
скостью Р (фиг. 945-963).
482. Построить проекции сечения прямого кругового конуса плоско-
стью Р (фиг. 964-982).
Фиг. 948
Фиг. 947
352
Фиг. 953
Фиг. 954
354.
356
357
358
Фиг. 974
Фиг. 977
359
Фиг. 978
Фиг. 979
Фиг. 980
Фиг. 981
360
361
483. Построить проекции сечения шара плоскостью Р (фиг. 983).
484. Построить следы плоскости, касательной к поверхности шара
и- проходящей через прямую АВ (фиг. 984).
485. Построить следы плоскости, касательной к поверхности шара, если
дана вертикальная проекция (/с') точки касания (фиг. 985).
486. Провести плоскость Р, параллельную плоскости Q и касательную
к поверхности шара (фиг. 986).
Глава XXIV
РАЗВЕРТКИ КРИВЫХ ПОВЕРХНОСТЕЙ
ПРИМЕРЫ
Пример 309
Дать развертку боковой поверхности прямого кругового цилиндра
(фиг. 987).
Решение. Разверткой боковой поверхности прямого кругового цилиндра,
радиус основания которого равен г, а высота является прямоугольник
с основанием длиной 2rtr и высотой h. Для того чтобы избежать вычислений,
связанных с определением длины окружности, обычно вписывают в основание
цилиндра правильный 12-угольник (на чертеже показываем только вершины 0, 1,
2 и т. д.), и его периметр принимают за длину основания прямоугольника. Таким
образом развертку боковой поверхности прямого кругового цилиндра заменяют
с достаточной для практики точностью разверткой боковой поверхности прямой
правильной 12-угольной призмы, вписанной в данный цилиндр.
Показываем дополнительно, как перенести точку (к, к) с поверхности
цилиндра на его развертку. Откладываем на основании прямоугольника отрезок
ОМ, равный длине выпрямленной дуги От, и, восставив в точке М перпендикуляр,
откладываем на нем отрезок МК, равный т'к'.
.362
Пример 310
Дать развертку боковой поверхности усеченного прямого кругового
цилиндра (фиг. 988)
Решение. Делим основание цилиндра на 12 равных частей и проводим
через точки деления образующие. Проводим в стороне прямую и на ней откла-
дываем последовательно от ее произвольной точки 0 (нуль), стороны правильного
12-угольника, вписанного в основание цилиндра. Проводим через точки 0,1, 2 и т. д,
включая точку 12, перпендикуляры к прямой и на них откладываем длины соот-*
ветствующих образующих. Соединив концы образующих плавной кривой, получаем
развертку боковой поверхности усеченного цилиндра.
Пример 311
Дать полную развертку нижней части прямого кругового цилиндра,
усеченного плоскостью R (фиг. 989).
Решение. Делим основание цилиндра на 12 равных частей и проводим
через точки деления образующие. Из построения видно, что только на участке
дуги 1 0 II образующие цилиндра пересекаются с плоскостью R. Проводим
в стороне прямую и на ней откладываем последовательно от ее произвольной
точки 0 равные отрезки 01, 12 и т. д. и два промежуточных равных отрезка 0 1
и 12 II. Проводим через точки 0,1 ... 12, I, II перпендикуляры к прямой и на них
откладываем длины соответствующих образующих. Соединив концы образующих,
расположенных на участке I— II, прямой линией, а на остальном участке — плавной
кривой, получаем развертку боковой поверхности усеченного цилиндра.
Для того чтобы получить полную развертку, необходимо добавить к развертке
боковой поверхности цилиндра: нижнее основание — круг, часть верхнего основа-
ния - сегмент и фигуру сечения — часть эллипса, найдя предварительно его нату-
ральную величину (см. чертеж).
Указание. Если секущая плоскость — общего положения, то целесообразно
предварительно, вращением всей системы вокруг оси цилиндра на соответствую-
щий угол <р, привести ее в положение, когда плоскость является проектирующей.
Фиг. 988
363
Б
Пример 312
Дать полную развертку боковой поверхности наклонного цилиндра
с круговым основанием (фиг. 990).
Решение. Развертку боковой поверхности наклонного цилиндра производим
по правилу развертки наклонной призмы (см. пример 271). Проводим вспомога-
тельную плоскость R, перпендикулярную к оси цилиндра, и разбиваем его на два
прямых цилиндра с общим основанием. Находим натуральную величину пер-
пендикулярного (нормального) сечения. Делим основание цилиндра на 12 рав-
ных частей и через точки деления проводим образующие цилиндра, которые делят
периметр нормального сечения на 12 неравных частей: I—II, II—III и т. д.
Проводим в стороне прямую линию и на ней от произвольной точки откладываем
прямолинейные отрезки I —II, II— III и т. д., равные сторонам многоуголь-
ника I, II, III...I, вписанного в кривую нормального сечения. Проводим через
полученные точки I, II, III ...I перпендикуляры к прямой 1—1, и на каждом из них
оз кладываем длины образующих верхнего и нижнего цилиндров, заданные в нату-
ральную величину (почему?). Соединив концы образующих плавной кривой,
получаем развертку боковой поверхности наклонного цилиндра.
Показываем дополнительно, как перенести на развертку цилиндра точку К,
лежащую на его поверхности, зная горизонтальную проекцию (к) этой точки.
Проводим через точку к горизонтальную проекцию (кп) вспомогательной обра-
зующей, а затем на ее вертикальной проекции по точке к находим точку к'.
Точку (tn, т‘) образующей (кп, к'п), лежащую на линии нормального сечения,
переносим на развертку, и через точку М проводим перпендикуляр к прямой 1—Г,
на этом перпендикуляре откладываем вверх отрезок MK = m'k'.
Указание. Если ось цилиндра не параллельна какой-либо плоскости проекций,
то предварительно ставим цилиндр в положение, когда его ось парал-
лельна плоскости Н или V (для чего)?
364
365
Пример 313
Дать развертку боковой поверхности прямого кругового конуса (фиг. 991).
Решение. Разверткой боковой поверхности прямого кругового конуса
с радиусом основания, равным г, и длиной образующей I является сектор
, 2пг ТТ с-
радиуса I с центральным углом <р = —-—. Для того чтобы избежать вычислении,
связанных с определением длины дуги сектора или угла ср, обычно вписывают
в основание конуса правильный 12-угольник (на чертеже показываем только
вершины 0, 1, 2 и т. д.) и затем, описав из произвольной точки S дугу радиуса I,
засекают последовательно от любой ее точки 12 дуг, хорды которых равны
стороне 12-угольника. Таким образом развертку боковой поверхности прямого
кругового конуса заменяют, с достаточной для практики точностью, разверт-
кой правильной 12-угольной пирамиды, вписанной в данный конус.
Показываем дополнительно, как перенести на развертку конуса точку К, лежа-
щую на его поверхности, зная горизонтальную проекцию (к) этой точки. Проводим
через точку к горизонтальную проекцию (s»h) вспомогательной образующей и
находим ее вертикальную проекцию (s'»i'); затем по точке к находим точку к'
на прямой s’m’. Находим образующую SM на развертке и на ней- откладываем
натуральную величину отрезка (sk, s‘k’) образующей-
Пример 314
Дать развертку боковой поверхности наклонного конуса с круговым
основанием (фиг. 992).
Решение. Делим основание конуса на 12 равных частей и проводим через
точки деления образующие. Таким образом всю боковую поверхность разбиваем
на 12 криволинейных треугольников, которые с достаточной для практики
точностью можно заменить плоскими треугольниками; следовательно, боковая
поверхность конуса заменяется боковой поверхностью 12-угольной пирамиды,
вписанной в этот конус. Находим натуральные величины всех образующих конуса
(см. чертеж) и строим последовательно плоские треугольники SOI, S12 и т. д.
Соединив концы образующих плавной кривой, получаем развертку боковой поверх-
ности наклонного конуса. Дополнительно на чертеже показан перенос произволь-
ной точки К с поверхности конуса на его развертку.
366
Пример 315
Дать развертку боковой поверхности усеченного наклонного конуса,
не пользуясь его вершиной (фиг. 993).
Решение. Делим верхнее и нижнее основания конуса на 12 равных частей
и соединяем прямыми (образующими) точки I—I, 2— II и т. д., т. е. вписываем
в усеченный конус 12-угольную усеченную пирамиду. Заменив каждую криво-
линейную трапецию плоско й, разбиваем их на треугольники и находим
натуральные величины всех образующих и диагоналей (см. чертеж). Строим
последовательно прямолинейные треугольники 1 2 II, 1 III пт. д.; соединив концы
I, II, III, ... и 1, 2, 3, ... образующих плавными кривыми, получаем с достаточной
для практики точностью развертку боковой поверхности усеченного конуса.
Указание. Подобное разложение кривых поверхностей на треугольники с успе-
хом можно применять и прп более сложных развертках.
Пример 316
Дать полную развертку нижней части прямого кругового конуса, усе-
ченного плоскостью Р (фиг. 994).
Решение. Делим основание конуса на 12 равных частей и, проводя через
точки деления образующие, находим точки их пересечения с плоскостью Р.
Строим развертку полного конуса (см. пример 313) и на каждой образующей
откладываем натуральную величину длины отрезка соответствующей образующей
конуса от его вершины до точки пересечения с плоскостью. Затем концы этих
367
! отрезков соединяем плавной кривой. Для того чтобы получить полную развертку
нижней части конуса, нужно добавить к развертке его боковой поверхности:
основание — круг и фигуру сечения — эллипс, найдя предварительно его натураль-
ную величину (см. чертеж).
Указание. Если секущая плоскость — общего положения, то целесообразно
предварительно, вращением всей системы около оси конуса на соответствующий
угол <р, привести ее в положение, когда плоскость является проектирующей.
Пример 317
Дать полную развертку нижней части прямого кругового конуса, усе-
ченного плоскостью Р (фиг. 995).
Решение. Делим основание конуса на 12 равных частей и проводим через
точки деления образующие. Из построения видно, что только на участке дуги
368 "
I О II образующие конуса пересекаются с плоскостью Р. Строим развертку пол-
ного конуса и проводим на ней дополнительно промежуточные образующие SI
и SII. На каждой образующей, пересекающейся с плоскостью Р, откладываем
натуральную величину длины отрезка соответствующей образующей конуса от его
вершины до точки пересечения с плоскостью; затем концы этих отрезков соединяем
плавной кривой. Для того чтобы получить полную развертку нижней части конуса,
нужно добавить к развертке его боковой поверхности: части основания — сегмент
и фигуру сечения — параболу, найдя предварительно ее натуральную величину
(см. чертеж).
369
ЗАДАЧИ
487. Пересечь прямой круговой цилиндр плоскостью Р и дать полную
развертку одной из его частей (фиг. 945-963).
488. Пересечь прямой круговой конус плоскостью и дать полную раз-
вертку одной из его частей (фиг. 964 — 982).
Глава XXV
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПОВЕРХНОСТЬЮ
Для того чтобы найти точки пересечения прямой с поверхностью любого
тела (призма, пирамида, цилиндр, конус, шар и т. д.), поступают точно так же,
как и при нахождении точки пересечения прямой с плоскостью, а именно;
1) заданную прямую заключают во вспомогательную плоскость;
370
2) находят линию (прямую или кривую) пересечения заданной поверхности
со вспомогательной плоскостью;
3) на пересечении заданной прямой с линией пересечения получают искомою
точки.
В частном случае прямая линия может быть карательной к поверхности.
Указание. При заключении прямой во вспомогательную плоскость последнюю
следует выбирать так, чтобы ее линия пересечения с поверхностью проектиро-
валась на плоскости проекций в виде простейших линий — прямой или окруж-
ности.
ПРИМЕРЫ
Пример 318
Найти точки пересечения поверхности призмы с прямой АВ (фиг. 996).
Решение. Заключаем прямую АВ в вертикально- (или горизонтально-)
проектирующую плоскость R, которая пересекает поверхность призмы по четырех-
угольнику. На пересечении горизонтальных проекций полученного четырехуголь-
ника и заданной прямой находим горизонтальные проекции (т) и (и) искомых
точек; зная их, находим вертикальные проекции (т‘) и (и) точек на прямой а'Ь':
В данном случае искомые точки можно найти и не вводя плоскость R (почему?).
Пример 319
Найти точки пересечения поверхности пирамиды с прямой АВ (фиг. 997).
Решение. Заключаем прямую АВ в горизонтально-проектирующую пло-
скость R, которая пересекает поверхность пирамиды по четырехугольнику.
На пересечении вертикальных проекций полученного четырехугольника и заданной
прямой находим вертикальные проекции (т') и (п') искомых точек; зная их, находим
горизонтальные проекции (т) и (п) точек на прямой ab.
Пример 320
Найти точки пересечения прямой АВ с поверхностью пирамиды
(фиг. 998).
Решение. Заключаем прямую АВ в профильную плоскость R, которая
пересекает поверхность пирамиды по треугольнику CDE. На пересечении профиль-
ных проекций полученного треугольника и заданной прямой находим профильные
проекции (т") и (п") искомых точек; зная их, находим точки т и п на прямой ab
и точки т' и п' на прямой а'Ь'.
Пример 321
Найти точки пересечения прямой АВ с поверхностью цилиндра (фиг. 999).
Р е ш е н и е. Заключаем прямую АВ в горизонтально-проектирующую пло-
скость R, которая пересекает поверхность цилиндра по двум образующим.
На пересечении вертикальных проекций этих образующих и заданной прямой
находим вертикальные проекции (т) и (л') искомых точек. Зная точки т' и л',
находим точки т и п на прямой ab (прямую АВ можно было заключить и
в вертикально-проектирующую плоскость}.
372
Найти точки пересечения прямой АВ с поверхностью наклонного
цилиндра (фиг. 1000).
Решение. Заключаем прямую АВ в плоскость R, параллельную оси
цилиндра; для этого задаем на прямой (ab, а'Ь") произвольную точку (с, с')
и проводим через нее прямую (cd, c'd'), параллельную оси цилиндра. Эта плоскость,
заданная двумя пересекающимися прямыми, пересекает поверхность цилиндра по
двум образующим. Находим горизонтальные следы (h, h') и (/ц, h,) прямых
(ab, а'Ь') и (cd, c'd') и проводим через точки h и ht горизонтальный след (Rh)
плоскости [вертикальный след плоскости для решения данной задачи не нужен
(почему?)]. Плоскость R пересекает основание цилиндра по хорде (12, 1'2'). Через
точки (1, 1') и (2, 2') проводим образующие цилиндра. На пересечении вертикальных
проекций этих образующих с вертикальной проекцией (а'Ь') заданной прямой
находим вертикальные проекции (т') и (и') искомых точек. Зная точки т' и л',
находим точки т и п на прямой ab. [Заключение прямой АВ в горизонтально-
или вертикально-проектирующую плоскость усложнило бы решение задачи
(почему?).]
Указание. В частном случае (когда?) вспомогательную плоскость, проходящую
через прямую АВ, удобнее задать двумя прямыми, параллельными оси
цилиндра.
Пример 323
Найти точки пересечения прямой АВ с поверхностью конуса (фиг. 1001).
Решение. Заданная прямая пересекает боковую поверхность конуса в един-
ственной точке (т, т'). Заключаем прямую АВ в вертикально-проектирующую
плоскость R, проходящую через вершину 5 конуса; эта плоскость пересекает
поверхность конуса по двум прямым — образующим (на эпюре показана только
одна образующая). На пересечении горизонтальных проекций прямых — заданной
и найденной — находим горизонтальную проекцию (т) искомой точки. Зная точку
т, находим точку т, совпадающую с вертикальной проекцией (а'Ь') заданной
прямой (почему?).
373
Пример 324
Найти точки пересечения прямой АВ с поверхностью конуса (фиг. 1002).
Решение. Заключаем прямую АВ в плоскость R, параллельную плоскости
Н; плоскость R пересекает поверхность конуса по окружности. На пересечении
горизонтальных проекций найденной окружности и заданной прямой находим
горизонтальные проекции (т) и (и) искомых точек. Зная точки т и п, находим
точки т' и п' на прямой а'Ь'. Прямую АВ можно было заключить и в горизон-
тально-проектируюшую плоскость, но это значительно усложнило бы решение
задачи (почему?). >
Пример 325
Найти точки пересечения прямой АВ с поверхностью конуса (фиг. 1003).
Решение. Заключаем прямую АВ в профильную плоскость R, которая
пересекает поверхность конуса по окружности. На пересечении профильных про-
екций найденной окружности и заданной прямой находим профильные проекции
(nt") и (и") искомых точек. Зная их, находим горизонтальные и вертикальные
проекции искомых точек на одноименных проекциях прямой (ab, а'Ь').
Пример 326
Найти точки пересечения прямой АВ с поверхностью наклонного конуса
(фиг. 1004).
Решение. Заключаем прямую АВ в плоскость R, проходящую через вершину
S конуса. Эта плоскость, заданная прямой АВ и точкой 5, пересекает поверхность
конуса по двум прямым — образующим.
374
Для того чтобы их найти, поступаем следующим образом. От задания
вспомогательной плоскости прямой АВ и точкой S переходим к заданию ее двумя
пересекающимися прямыми АВ и SC (точку С на прямой АВ берем произвольно).
Находим горизонтальные следы (/i, h') и (ht, h\) прямых (ab, a h') и (sc, s'c') и про-
водим через точки /1 и горизонтальный след (R*) плоскости [вертикальный
след плоскости для решения данной задачи не нужен (почему?)]. Плоскость R
пересекает основание конуса на хорде (12, Г2'), а поверхность конуса по прямым —
образующим (si, s'/') и (s2, s'2'). На пересечении вертикальных проекций этих
образующих с -вертикальной проекцией (а'Ь') заданной прямой находим вертикаль-
ные проекции (т') и (и') искомых точек. Зная точки т' и п', находим точки тип
375
на прямой ab. [Заключение прямой ЛВ в горизонтально- или вертикально-проек-
тнрующую плоскость значительно усложнило бы решение задачи (почему?).]
Указание. В частном случае (когда?) вспомогательную плоскость, проходящую
через прямую ЛВ и. точку S, удобнее задать двумя прямыми, пересекающимися
в точке 5.
Пример 327
Найти точки пересечения прямой ЛВ с поверхностью конуса (фиг. 1005).
Ре те и и с. Заключаем прямую АВ в плоскость R, проходящую через вершину
S конуса. Находим следы (/i, Ь'} и (г, у') прямой (ab, а'Ь'} и проводим следы
плоскости: горизонтальный (RJ — через точки h, s и вертикальный (Rt.) — через
точки Rx, v'. Находим линию пересечения плоскости R с плоскостью основания
конуса. Плоскость R пересекает основание конуса по хорде • (12, 1'2'}, а его поверх-
ность — по образующим (si, s'Г} и (s2, s'2'). На пересечении вертикальных проекций
этих образующих с вертикальной проекцией (а'Ь'} заданной прямой находим вер-
тикальные проекции (т'} и (п') искомых точек. Зная точки т' и и', находим точки
т и п на прямой ab.
376
Пример 328
Найти точки пересечения прямой АВ с поверхностью шара (фиг. 1006).
Решение. Заключаем прямую АВ в плоскость R, параллельную плоскости
Н, которая пересекает поверхность шара по окружности. На пересечении гори-
зонтальных проекций найденной окружности и заданной прямой находим горизон-
тальные проекции (ш) и (н) искомых точек. Зная точки т и п, находим точки т
и п‘ на прямой а'Ь'.
Пример 329
Найти точки пересечения прямой АВ с поверхностью шара.
Решение.
1. Способ совмещения (фиг. 1007). Заключаем прямую АВ в горизонтально-
проектирующую плоскость R, которая пересекает поверхность шара по окружности
радиуса г с центром в точке (с, с').
Для того чтобы избежать построе-
ния кривой по лекалу (какой?), совме-
щаем плоскость R с плоскостью Н.
Находим в совмещенном положении
окружность и заданную прямую и на
их пересечении получаем точки Ма и
No; по ним находим искомые точки
(ш, т') и (и, и').
2. Способ перемены плоскостей
проекций (фиг. 1008). Заменяем, напри-
мер, вертикальную плоскость проекций
новой (Ц), параллельной
заданной у
Фиг. 1008
'о
Фиг. 1007
377
Фиг. 1009
прямой- Заключаем прямую (ah, a'jb)) в плоскость R, параллельную плоскости 1);
плоскость R пересекает шар по окружности. На пересечении вертикальных проекций
прямой и окружности получаем точки т[ и п\; по ним находим искомые точки
(те, т) и (л, п').
Способ перемещения (фиг. 1009). Перемещаем заданную систему, например
параллельно горизонтальной плоскости проекций, и приводим ее в положение,
когда прямая параллельна плоскости Г. Заключаем прямую (а^, а\Ь\) в плоскость
R, параллельную плоскости 1'; плоскость R пересекает поверхность шара по
окружности. На пересечении вертикальных проекций окружности и прямой находим
точки nil и ni- По точкам те) и л) в обратном порядке находим точки те' и п’
на прямой а'Ь’, а по ним — точки те и п на прямой ab. Точки (те, те’) и (л, л') —
искомые.
Пример 330
Найти точки пересечения прямой АВ с поверхностью кольца (фиг. 1010).
Решение. Заключаем прямую АВ в плоскость R, параллельную плоскости V;
плоскость Я пересекает поверхность кольца по окружности. На пересечении
вертикальных проекций окружности и заданной прямой находим вертикальные
проекции (те') и (л') искомых точек. Зная точки те' и и', находим точки т и л на
прямой ab. (Прямую АВ можно было заключить и в вертикально-проектирующую
плоскость, но это значительно усложнило бы решение задачи.)
Пример 331
Найти точки пересечения прямой АВ с поверхностью вращения (фиг. 1011).
Решение. Заключаем прямую АВ в вертикально-проектируюшую плоскость
Я и находим проекции линии пересечения. На пересечении горизонтальных про-
екций этой линии и заданной прямой получаем точки те и л: по ним находим
точки те' и л' на прямой а'Ь'.
На фиг. 1012 задача решена заключением прямой в горизонтально-проекти-
рующую плоскость R.
378
379
Пример 332
Даны точка S и прямая АВ. Провести через точку S прямые, накло-
ненные к плоскоеги II иод заданным углом <р и пересекающие прямую АВ
(фиг. 1013).
Решение. Геометрическим местом прямых пространства, проходящих через
точку .S' и наклоненных в плоскости II под данным углом <р, является поверхность
прямого кругового конуса с вершиной в точке .S', образующие которого сосгавпяют
с плоскостью II тот же угол <р. Искомыми прямыми являются тс образующие
конуса, которые проходят через'Точки (in, in") и (п, п') пересечения сю поверхности
с заданной прямой (построение видно из чертежа).
Пример 333
Даны точка С и прямая АВ. Наши на прямой АВ точки, удаленные
от точки С на 15 мм (фиг. 1014).
Решение. Геометрическим местом точек пространства, эталонных от точки
С на 15 мм, является поверхность шара радиуса 15 мм с центром в точке С.
Искомыми точками являются точки (ш. ш') и (и, п') пересечения поверхности шара
с заданной прямой (построение видно из чертежа).
380
ЗАДАЧИ
489. Найти точки пересечения прямой с поверхностью тела (призмы,
пирамиды, цилиндра, конуса, шара и т. д., фиг. 1015 — 1034).
382
383
Фиг. 1025
384
Фиг. 1030
Глава XXVI
ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
Для того чтобы построить линию пересечения двух поверхностей, нужно
найти ряд общих точек, принадлежащих им, и затем эта точки соединить
в определенной последовательности.
Линией пересечения может быть:
1) пространственная к р и в а я — при пересечении двух кривых поверх-
ностей или кривой поверхности и многогранника;
2) пространственная ломаная линия — при пересечении двух много-
гранников.
И [тогда линия пересечения двух поверхностен может оказаться плоской —
прямой линией, окружностью, эллипсом и т. д. (см. ниже).
Для того чтобы найти произвольную точку линии пересечения, поступают так:
1) вводят вспомогательную плоскость;
2) находят линии пересечения этой плоскости с каждой поверхностью;
3) на пересечении найденных линий получают искомые точки.
Последовательно вводя ряд вспомогательных плоскостей, можно найти необхо-
димое число точек.
Указание. Вспомогательную плоскость следует выбирать так, чтобы ее линия
пересечения с каждой поверхностью проектировалась на плоскости проекций
в виде простейших линий — прямой или окружности.
Линию пересечения двух многогранников (А и В) можно найти и так:
1) находят точки пересечения ребер одного многогранника (Л) с гранями
другого (В);
2) находят точки пересечения ребер второго многогранника (В) с гранями
первого (Л); •
3) найденные точки последовательно соединяют между собой прямыми
линиями.
Указание. Соединяют между собой обязательно только те точки, которые
лежат на одних и тех же гранях каждого многогранника.
Если хотя бы одна из поверхностей имеет прямолинейные образующие, то
линию пересечения можно найти и таким образом: наносят на этой поверхности
386
ряд образующих и находят точки их пересечения с другой поверхностью, а затем
соединяют эти точки кривой, линией.
Иногда для того, чтобы найти точки линии пересечения кривых поверхностей,
проще ввести не плоскость, а поверхность — цилиндрическую, коническую или
шаровую. . ...
Любая поверхность вращения пересекается с поверхностью шара по окруж-
ности, если центр шара лежит на оси вращения.
ПРИМЕРЫ
Пример 334
Найти линию пересечения двух цилиндров (фиг. 1035).
Решение. Вводим вспомогательную плоскость R, параллельную плоскости
Н и пересекающую поверхность вертикального цилиндра по окружности, а поверх-
ность горизонтального цилиндра — по образующим; на их пересечении получаем
точки (1, Г) и (2, 2'). Аналогично находим еще ряд точек (см. чертеж). Соединив
эти точки кривой линией, получаем искомую линию пересечения..
Указание. Можно воспользоваться также вспомогательной плоскостью, парал-
лельной плоскости V.
Пример 335
Найти линию пересечения двух цилиндров (фиг. 1036).
Решение. Вводим вспомогательную плоскость R, параллельную плоскости V
и пересекающую поверхности цилиндров по образующим. На их пересечении
получаем точки (/, /’) и (2, 2"). Аналогично находим еще ряд произвольных
13’
точек. Затем находим характерные точки А, В, С, D, Е. F при помощи вспомога-
тельных плоскостей St, S2, S3 и S4 (см. чертеж). Соединив все найденные точки
кривой линией, получаем искомую линию пересечения.
Указание. При построении линии пересечения следует каждый раз обращать
внимание на отыскание тех ее точек, которые позволяют полнее характеризовать
кривую линию.
Пример 336
Найти линию пересечения двух цилиндров и дать развертки их боковых
поверхностей (фиг. 1037).
Решение. Делим основание наклонного цилиндра на 12 равных частей и,
проведя через точки деления образующие, находим точки их пересечения с поверх-
ностью вертикального цилиндра. Затем вводим вспомогательную плоскость R,
параллельную плоскости V и проходящую через ось вертикального цилиндра. Эта
плоскость пересекает поверхности цилиндров по образующим, на пересечении
которых получаем характерные точки (а, а') и (Ь, Ь'). Соединив все найденные точки
кривой линией, получаем искомую линию пересечения.
Развертки боковых поверхностей цилиндров строятся по общему правилу
(построение видно из чертежа).
Пример 337
Найти линию пересечения цилиндра с конусом (фиг. 103S).
388
Фиг. 1037
Решение. Вводим вспомогательную плоскость R, параллельную плоскости
W; плоскость R пересекает поверхность конуса по окружности, а поверхность
цилиндра — по образующим; на их пересечении получаем точки (1, Г) и (2, 2').
Аналогично находим еще ряд произвольных точек. Затем находим характерные
точки А, В; С, D; Е, F при помощи вспомогательных плоскостей Р, Q, S (на чер-
теже не обозначены). Соединив все найденные точки кривой линией, получаем
искомую линию пересечения.
Использование вспомогательной плоскости, параллельной плоскости Н или V,
значительно усложняет решение (почему?).
Пример 338
Найти линию пересечения цилиндра с конусом и дать развертки их
боковых поверхностей (фиг. 1039).
Решение. Делим основание цилиндра на 12 равных частей и, проведя через
точки деления образующие, находим точки их пересечения с поверхностью конуса.
Соединив эти точки кривой линией, получаем искомую линию пересечения.
Развертки боковых поверхностей цилиндра и конуса строятся по общему
правилу (построение видно из чертежа).
390
z
Пример 339 •
Найти линию пересечения цилиндра с конусом (фиг. 1040).
Решение. Проводим на поверхности конуса 12 образующих и находим
точки их пересечения с поверхностью цилиндра. Затем находим характерные точки
А, В Соединив все найденные точки кривой линией, получаем искомую линию
пересечения (построение видно из чертежа).
Пример 340
Найти линию пересечения цилиндра с конусом, пользуясь шаровыми
поверхностями (фиг. 1041).
Решение. Принимаем точку (с, с') пересечения осей цилиндра и конуса
за центр вспомогательных шаровых поверхностей. Описываем из точки (с, с') шар
произвольного радиуса R, который (шар) пересекает каждую из данных
поверхностей по окружности; вертикальные их проекции — прямые линии, а гори-
зонтальные проекции — эллипсы (последние для решения задачи не нужны и потому
их не строим). На пересечении этих прямых линий получаем вертикальные про-
екции (Г) и (2') точек; по ним, пользуясь вспомогательными образующими (или
окружностями), находим горизонтальные проекции (1) и (2) точек. Аналогично,
392
изменяя только радиус шара, получаем еще ряд точек. Соединив эти точки кривой
линией, находим искомую линию пересечения.
Линию пересечения можно найти также при помощи вспомогательных плоско-
стей. Для того чтобы избежать построения кривых по лекалу (каких?), эти плоскости
проводим через вершину конуса параллельно оси цилиндра. Такой способ значи-
тельно усложняет решение задачи.
Указания. ‘
1. Если оси пересекающихся поверхностей не расположены параллельно
какой-либо плоскости проекций, то целесообразно предварительно привести
их в такое положение (зачем?).
2. Если оси цилиндра и конуса не пересекаются, то пользуемся указанными
вспомогательными плоскостями.
3. Если цилиндр и конус не являются поверхностями вращения, тоже поль-
зуемся указанными вспомогательными плоскостями независимо от взаимного
положения их осей.
Пример 341 ,
Найти линию пересечения двух конусов (фиг. 1042).
Решение. Так как оси конусов пересекаются в точке (с, с”), принимаем эту
точку за центр вспомогательных шаровых поверхностей. Описываем из точки (с, с)
шар произвольного радиуса R, который (шар) пересекает каждую из данных
поверхностей по окружности. Горизонтальные проекции этих окружностей —
прямые линии, а вертикальные проекции — эллипсы (последние для решения задачи
не нужны и поэтому их не строим). На пересечении этих прямых линий получаем
горизонтальные проекции (1) и (2) точек; по ним, пользуясь вспомогательными
образующими (или окружностями), находим вертикальные проекции (Г) и (2') точек.
Аналогично, изменив только радиус шара, получаем еще ряд точек. Соединив эти
точки кривой линией, находим искомую линию пересечения.
393
Фиг. 1044
Линию пересечения можно найти также при помощи вспомогательных
плоскостей. Для того чтобы избежать построения кривых по лекалу (каких?), эти
плоскости проводим через вершины конусов. Такой способ значительно усложняет
решение задачи.
Указания.
1. Если оси двух конусов не пересекаются, to пользуемся указанными вспо-
могательными плоскостями.
2. Если конусы не являются поверхностями вращения, то тоже пользуемся
указанными вспомогательными плоскостями независимо от взаимного положения
их осей.
Пример 342
Найти линию пересечения цилиндра с шаром (фиг. 1043).
Решение. Вводим вспомогательную плоскость R, параллельную плоскости
Н; плоскость R пересекает обе поверхности по окружностям; на их пересечении
получаем точки (1, 73 и (2, 2'). Аналогично находим еще ряд произвольных точек.
Затем — характерные точки; низшую (а, а*), высшую (0, 03, а также (а, д') и (Ь, Ь1)
(см. чертеж). Соединив все найденные точки кривой линией, получаем искомую
линию пересечения.
Можно пользоваться также вспомогательной плоскостью, параллельной пло-
скости V.
Пример 343
Найти линию пересечения цилиндра с шаром (фиг. 1044).
Решение. Вводим вспомогательную плоскость R, параллельную плоскости
V; плоскость R пересекает поверхность шара по окружности, а поверхность
цилиндра —по образующим; на их пересечении получаем точки (7, 7') и (2, 23.
Аналогично находим еще ряд произвольных точек. Затем находим характерные
точки А, В; С, D; Е, F (см. чертеж). Низшую точку (а, а') и высшую точку (0, Р')
находим на пересечении с поверхностью шара тех образующих цилиндра, которые
расположены в горизонтально-просктирующей плоскости S, проходящей через ось
цилиндра и центр шара. Соединив все найденные точки кривой линией, получаем
искомую линию пересечения.
Пример 344
Найти линию пересечения конуса с шаром (фиг. 1045).
Решение. Вводим вспомогательную плоскость Л, параллельную плоскости
Н; плоскость R пересекает данные поверхности по окружностям; на их пересе-
чении получаем точки (7, Е) и (2, 23- Аналогично находим еще ряд произвольных
точек (см. чертеж). Для того чтобы найти точки (а, аЗ и (0, 03, вращаем заданные
поверхности вокруг оси шара, перпендикулярной к плоскости Н, на соответствую-
щий угол <р (см. чертеж) и строим вертикальную проекцию конуса в новом
положении (вертикальная проекция шара не изменяется). Найдя точки (а1( а'О
и (0i> 01)> вращением в обратную сторону получаем проекции искомых точек (а, аЗ
и (0, 03- Затем находим точки (а, а') й (Ь, Ь') пересечения профильных образующих
конуса с поверхностью шара (см. чертеж).
Соединив все найденные точки кривой линией, получаем искомую линию
пересечения. Точки (а, о/) и (0, 03 можно найти также способом перемены плоско-
стей проекций (как?); точки (а, а') й (Ь, Ъ') можно также найти, не пользуясь
профильной плоскостью проекций (как?).
395
ЗАДАЧИ
490. Даны две поверхности (см. ниже). Построить линию их пересече-
ния, развертки этих поверхностей и нанести на них линии пересечения:
1) призма и призма (фиг. 1046—1048);
2) призма и пирамида (фиг. 1049 — 1051);
3) пирамида и пирамида (фиг. 1052-1054);
4) призма и цилиндр (фиг. 1055—1057);
5) призма и шар (фиг. 1058, 1059); у
6) призма и конус (фиг. 1060—1062);
7) пирамида и цилиндр (фиг. 1063, 1064);.
8) пирамида и шар (фиг. 1065);
9) пирамида и конус (фиг. 1066);
10) цилиндр и цилиндр (фиг. 1067-1080);
11) цилиндр и конус (фиг. 1081 — 1094);
12) цилиндр и шар (фиг. 1095 — 1100);
13) конус и шар (фиг. 1101-1107);
14) конус и конус (фиг. 1108 — 1110).
491. Построить проекции линии пересечения шара с прямым круговым
цилиндром радиуса г = 20 мм, ось которого совпадает с заданной прямой,
а центр верхнего основания —с точкой (с, с') (фиг. 1100).
396
X-
Фиг. 1048
Фиг. 1049
397
Фиг. 1050 Фиг. 1051
Фиг. 1053
398
399
Фиг. 1058
400
401
492. Построить проекции линии пересечения шара с прямым круговым
конусом с вершиной в точке S, если ось конуса совпадает с заданной
прямой и угол при его вершине равен 60°.
493. Пользуясь вспомогательными шаровыми поверхностями, построить
проекции линии пересечения:
1) двух цилиндров (фиг. 1067, 1069, 1072, 1074);
2) цилиндра и конуса (фиг. 1079, 1081, 1083, 1086,-1087, 1090, 1091).
Фиг. 1068
Фиг. 1069
402
403
494. Построить проекции линии пересечения двух конусов, пользуясь
вспомогательными шаровыми поверхностями (фиг. 1108, 1109).
495. Построить проекции линии пересечения поверхности кольца с ци-
линдром (фиг. 1111, 1112).
496. Построить линии пересечения поверхности кольца с конусом
(фиг. 1113).
497. Построить проекции линии пересечения поверхности кольца с ци-
линдром, переходящим в шар (фиг. 1114).
404
405
406
407
Фиг. 1091
410
Фиг. 1102
Фиг. 1104
411
412
413
X-
Фиг. 1114
414
РАЗДЕЛ ПЯТЫЙ
Глава XXVII
СМЕШАННЫЕ ЗАДАЧИ
(для всех разделов)
Решить различными способами каждую из помещенных ниже задач.
498. Найти точку пересечения плоскостей Р, Q и R (фиг. 1115, 1116).
499. Провести через точку А прямую параллельно плоскостям Р и Q
(фиг. 1117).
500. Провести через точку К прямую, параллельную горизонтально-
проектирующей плоскости R и плоскости, заданной прямой АВ и точкой С
(фиг. .1118).
501. Провести через точку К прямую, параллельную вертикально-
проектирующей плоскости R и плоскости, заданной двумя параллельными
прямыми АВ и CD (фиг. 1119).
502. Провести через точку К прямую, параллельную профильно-проек-
тирующей плоскости Р и плоскости, заданной пересекающимися прямыми
АВ и АС (фиг. 1120).
503. Провести через точку М прямую, параллельную плоскостям, задан-
ным пересекающимися прямыми АВ и CD и параллельными прямыми EF
и КЬ(фиг. 1121).
504. Провести на плоскости Р через ее точку А прямую, параллельную
плоскости Q (фиг. 1122).
505. Провести через точку К прямую MN, пересекающую заданные
прямые АВ и CD (фиг. 1123).
506. Пересечь заданные прямые АВ, CD и EF произвольной
прямой MN (фиг. 1124).
507. Пересечь заданные прямые АВ и CD прямой MN, параллельной
прямой EF (фиг. 1124).
508. Пересечь заданные прямые АВ и CD прямой MN, параллельной
оси проекций (фиг. 1125).
Указание. Профильной плоскостью проекций не пользоваться.
509. Пересечь заданные прямые АВ и CD произвольной прямой
MN, одинаково наклоненной к плоскостям проекций (фиг. 1125).
510. Пересечь заданные прямые АВ и CD прямой, составляющей с гори-
зонтальной плоскостью проекций угол 45° и с вертикальной плоскостью
проекций угол 30° (фиг. 1125).
511. Пересечь прямые АВ, АС и AD прямой AM, образующей равные
углы с данными прямыми (фиг. 1126).
415
416
512. Провести через точку М прямую KL, одинаково наклоненную
к произвольным прямым АВ, CD и EF (фиг. 1127).
513. Найти на плоскости Р геометрическое место точек, равноудаленных
от точек А и В этой плоскости (фиг. 1128).
514. Построить на плоскости Р равнобедренный треугольник АВС
с вершиной А на горизонтальном следе плоскости, если дана вертикальная
проекция стороны ВС (фиг. 1129).
515. Провести через точку М прямой АВ перпендикулярную к ней
прямую MN, пересекающую прямую CD (фиг. ИЗО).
516. Построить проекции шара, радиус которого равен 25 мм, закры-
вающего круглое отверстие радиуса 20 мм, вырезанное на плоскости Р
(фиг. 1131).
418
517. Построить проекции шара радиуса 25 мм, касательного к пло-
скости Р, если дана вертикальная проекция точки С — центра шара
(фиг. 1132).
518. Построить проекции шара радиуса 25 мм, касательного к плоско-
сти,'заданной прямой АВ и точкой D, если дана горизонтальная проекция
точки С —центра шара (фиг. 1133).
519. Построить проекции шара радиуса 30 мм, касательного к плоско-
сти, заданной двумя параллельными прямыми АВ и DE, если дана верти-
кальная проекция точки С —центра шара (фиг. 1134).
14* 419
X---------------------------------
Фиг. 1134
Фиг. 1135
520. Построить проекции шара радиуса 25 мм, касательного к пло-
скости треугольника KLM, если дана горизонтальная проекция точки С —
центра шара (фиг. 1135).
420
521. Построить проекции шара радиуса 25 мм, касательного к плоско-
сти Р с центром на прямой АВ (фиг. 466).
522. Построить проекции шара радиуса 25 мм, касательного к плоскости,
заданной прямой АВ и точкой D, и с центром на прямой MN (фиг. 1136).
523. Построить проекции шара радиуса 25 мм, касательного к пло-
скости, заданной параллельными прямыми АВ и DE, и с центром на
прямой MN (фиг. 1137).
524. Построить проекции шара радиуса 25 мм, касательного к плоскости
треугольника DEF с центром на прямой АВ (фиг. 1138).
525. Провести через точку К плоскость Q, перпендикулярную к плоско-
сти Р и одинаково наклоненную к плоскости проекций (фиг. 640, 641).
526. Провести через точку К. плоскость Р, перпендикулярную к плоско-
сти, заданной прямой АВ и точкой С, одинаково наклоненную к плоскостям
проекций (фиг. 642).
527. Провести через точку К плоскость Р, перпендикулярную к пло-
скости, заданной параллельными прямыми АВ и CD, одинаково наклонен-
ную к плоскости проекций (фиг. 643).
528. Провести через точку К плоскость Р, перпендикулярную к пло-
скости треугольника АВС, одинаково наклоненную к плоскостям проекций
(фиг. 644).
529. Провести через точку М плоскость Р, перпендикулярную к пло-
скостям, заданным пересекающимися прямыми АВ и CD и параллельными
прямыми EF и KL (фиг. 1139).
530. Провести через точку М плоскость, перпендикулярную к плоскости
Р и к плоскости треугольника АВС (фиг. 1140).
531. Провести через точку М плоскость, перпендикулярную к плоскости
Р и к плоскости, заданной прямой АВ и точкой С (фиг. 1141).
532. Провести через точку М плоскость, перпендикулярную к плоскостям
Р и <2 (фиг. 1142).
421
°? е'
фиг. 1138 Фиг. 1139
422
533. Провести через точку М плоскость Q, перпендикулярную к пло-
скости Р и к плоскости, заданной параллельными прямыми АВ и CD
(фиг. 1143).
534. Построить геометрическое место точек пространства, равноуда-
ленных от параллельных прямых АВ и CD (фиг. 599).
535. Построить на плоскости Р геометрическое место точек, равно-
удаленных от параллельных прямых АВ и CD (фиг. 602).
536. Найти на прямой MN точку К, равноудаленную от параллельных
прямых АВ и CD (фиг. 607).
537. Провести прямую MN, перпендикулярную к плоскости Р и пере-
секающую прямые АВ и CD (фиг. 1144).
538. Пересечь произвольные прямые АВ и CD перпендикулярной к ним
прямой MN (фиг. 578).
539. Провести плоскость Р, равноудаленную от двух произвольных
прямых АВ и CD (фиг. 578).
540. Построить геометрическое место точек пространства, равноудален-
ных от ближайших точек двух произвольных прямых АВ и CD (фиг. 578).
541. Найти на плоскости Р геометрическое место точек, равноудаленных
от ближайших точек произвольных прямых АВ и CD (фиг. 1144).
542. Найти на прямой EF точку, равноудаленную от ближайших точек
произвольных прямых АВ и CD (фиг. 1124).
543. Провести на плоскости Р прямую, перпендикулярную к прямой АВ
и проходящую через точку ее пересечения с плоскостью (фиг. 556).
544. Провести на плоскости треугольника АВС прямую, перпендикуляр-
ную к прямой MN и проходящую через точку ее пересечения с плоскостью
(фиг. 698).
423
545. Провести на плоскости, заданной параллельными прямыми АВ
и CD, прямую, перпендикулярную к прямой MN и проходящую через
точку ее пересечения с плоскостью (фиг. 607).
546. Провести на плоскости, заданной прямой АВ и точкой С, прямую,
перпендикулярную к прямой Л-LV и проходящую через точку ее пересе-
чения с плоскостью (фиг. 606).
424
547. Найти на плоскости Р точку, равноудаленную от внешних точек А,
В, С (фиг. 1145).
548. Найти на плоскости, заданной прямой DE и точкой F, точку К,
равноудаленную от внешних точек А, В, С (фиг. 1146).
549. Найти на плоскости, заданной параллельными прямыми DE и FK,
точку М, равноудаленную от внешних точек А, В, С (фиг. 1147).
550. Найти на плоскости, заданной пересекающимися прямыми DE
и EF, точку К, равноудаленную от внешних точек А, В, С (фиг. 1148).
551. Построить геометрическое место точек пространства, равноудален-
ных от пересекающихся прямых АВ и АС (фиг. 1149).
552. Построить на плоскости Р геометрическое место точек, равно-
удаленных от пересекающихся прямых АВ я АС (фиг. 1150).
553. Построить на плоскости, заданной прямой АВ и точкой С, гео-
метрическое место точек, равноудаленных от пересекающихся прямых DE
и EF (фиг. 1151). .
554. Построить на плоскости треугольника DEF геометрическое место
точек, равноудаленных от пересекающихся прямых АВ и АС (фиг. 1152).
555. Построить на плоскости, заданной двумя параллельными пря-
мыми DE и FК, геометрическое место точек, равноудаленных от пересе-
кающихся прямых АВ и АС (фиг. 1153).
556. Найти на внешней прямой MN точку, равноудаленную от пере-
секающихся прямых АВ и АС (фиг. 1154).
557. Построить геометрическое место точек пространства, равноудален-
ных от следов плоскости Р (фиг. 596, 597).
558. Построить геометрическое место точек на плоскости Q, равно-
удаленных от следов плоскости Р (фиг. 393, 394).
559. Построить геометрическое место точек на плоскости, заданной
двумя параллельными прямыми АВ и CD, равноудаленных от следов
плоскости Р (фиг. 602).
425
560. Построить геометрическое место точек на плоскости треугольника
АВС, равноудаленных от следов плоскости Р (фиг. 603, 474).
561. Построить геометрическое место точек на плоскости, заданной
прямой АВ и точкой С, равноудаленных от следов плоскости Р (фиг. 601).
42а
562. Найти на прямой АВ плоскости Р точку, равноудаленную от следов
этой плоскости (фиг. 340, 341).
563. Найти на внешней прямой АВ точку, равноудаленную от следов
плоскости Р (фиг. 499).
564. Построить геометрическое место точек пространства, равноудален-
ных от плоскостей Р и Q (фиг. 393, 394).
565. Построить на плоскости Р геометрическое место точек, равно-
удаленных от плоскостей Q и R (фиг. 1115, 1116).
566. Найти на прямой АВ точку, равноудаленную от плоскостей Р и Q
(фиг. 1155).
567. Провести через точку К плоскость, одинаково наклоненную к пло-
скостям проекций, на которую параллельные прямые АВ и CD проекти-
руются в одну прямую линию (фиг. 643).
568. Провести через точку К плоскость, параллельную прямой EF,
на которую параллельные прямые АВ и CD проектируются в одну прямую
линию (фиг. 526).
569. Провести через прямую EF плоскость, на которую параллельные
прямые АВ и CD проектируются в одну прямую линию (фиг. 531).
570. Провести через точку К плоскость, одинаково наклоненную к пло-
скостям проекций, на которую произвольные прямые АВ и CD проекти-
руются параллельными прямыми (фиг. 1123). А
571. Провести через прямую АВ плоскость, на которую произвольные
прямые CD и EF проектируются параллельными прямыми (фиг. 1124).
572. Провести через точку К плоскость, параллельную прямой АВ, на
которую произвольные прямые CD и EF проектируются параллельными
прямыми (фиг. 1156).
573. Найти точку, равноудаленную от четырех точек А, В, С и D, про-
извольно заданных в Пространстве (фиг. 251).
427
574. Найти на плоскости Р точку, равноудаленную от точки Рх и от
следов прямой АВ, лежащей в этой плоскости (фиг. 340, 341).
575. Построить на плоскости Р прямоугольный треугольник АВС
с вершиной В прямого угла на горизонтальном следе плоскости, если
дана вертикальная проекция стороны АС (фиг. 1157).
576. Провести на плоскости Р через ее точку А прямую, составляющую
со следами этой плоскости равные углы <р (фиг. 352, 353).
577. Найти на плоскости Р точку, удаленную от ее точек А и В соот-
ветственно на 20 и 30 мм (фиг. 1158). Какие возможны случаи?
578. Найти на плоскости Р точку, удаленную от ее точки С на 20 мм
и от ее прямой АВ на 10 мм (фиг. 1159). Какие возможны случаи?
579. Провести на плоскости Р через ее точку А прямую, удаленную
от другой ее точки С на 20 мм (фиг. 1160).
580. Провести на плоскости Р прямую, удаленную от ее точек А и В
соответственно на 20 и 15 мм (фиг. 1161).
581. Построить на плоскости Р геометрическое место точек, удаленных
от внешней точки А на 60 мм (фиг. 1162).
582. Найти на прямой АВ плоскости Р точку, удаленную от внешней
точки С на 60 мм (фиг. 1163).
583. Найти на плоскости Р точку, удаленную от точки С этой плоскости
на 15 мм и от внешней точки А на 60 мм (фиг. 1164).
584. Найти на плоскости Р точку, удаленную от внешних точек А и В
соответственно на мм и 12 мм (фиг. 1165).
585. Провести через точку М прямую, пересекающую в точках К и L
прямую АВ и плоскость Р, earn МК = KL (фиг. 1166).
430
586. Построить равнобедренный треугольник АВС с вершиной С на
плоскости Р, если его высота равна 40 мм (фиг. 1167).
587. Построить равносторонний треугольник АВС, если его вершина С
лежит на плоскости Р (фиг. 1167).
588. Построить траекторию точки С, движущейся вокруг прямой АВ
(фиг. 1168).
589. Построить траекторию ближайшей точки М прямой АВ, вращаю-
щейся около произвольной прямой CD (фиг. 578).
590. Построить проекции прямой призмы, высота которой равна 60 мм,
исходя из условия, что ее основание — квадрат ABCD с диагональю BD
на прямой MN (фиг. 658).
591. Построить проекции прямой призмы, высота которой равна 60 мм,
исходя из условия, что ее основание. — равнобедренный треугольник АВС
с вершиной А на прямой EF (фиг. 661).
592. Построить проекции куба с основанием ABCD со стороной ВС
на прямой ВМ, если даны отрезок АВ и горизонтальная проекция перпен-
дикулярной к нему прямой ВМ (фиг. 1169).
593. Построить пирамиду SABC высотой h = 60 мм, исходя из условия,
что ее основание — равнобедренный треугольник АВС с вершиной А на
прямой EF, а проекция вершины S на основание совпадает с центром
окружности, описанной около треугольника АВС (фиг. 661).
594. Построить проекции.пирамиды SABC, исходя из условия, что длина
бокового ребра SA равна 65 мм, а проекция вершины S на основание
совпадает с центром окружности, вписанной в треугольник АВС (фиг. 163).
431
595. Построить проекции пирамиды SABC высотой h = 60 мм, исходя
из условия, что проекция вершины S на основание совпадает с центром
окружности, описанной около треугольника АВС (фиг. 163).
596. Построить проекции пирамиды SABC, исходя из условия, что
проекция его вершины S на основание совпадает с центром тяжести его
площади, а боковое ребро SC наклонено к плоскости основания под углом
ср (фиг. 163).
597. Построить проекции прямой правильной призмы высотой h = 60 мм
и с основанием АВС на плоскости Р, если дана вертикальная проекция
стороны АВ ее основания (фиг. 1170).
598. Построить проекции прямой призмы высотой h = 60 мм и с осно-
ванием АВС на плоскости R, если дано основание в совмещенном поло-
жении на плоскости Н (фиг. 1171).
599. Построить проекции куба с основанием ABCD на плоскости Р,
если дана вертикальная проекция стороны ВС его основания (фиг. 1172).
600. Построить проекции куба с основанием ABCD на плоскости Р,
если дана горизонтальная проекция диагонали BD его основания (фиг. 1173).
601. Построить проекции куба с основанием ABCD на плоскости Р,
если дана сторона АВ его основания в совмещенном положении на
плоскости У (фиг. 1174).
602. Построить проекции куба с основанием ABCD на плоскости Р,
если дана диагональ BD его основания в совмещенном положении на
плоскости Н (фиг. 1175).
603. Построить проекции прямой правильной треугольной призмы
высотой h = 60 мм, исходя из условия, что два ее боковых ребра совпадают
с заданными прямыми (1, Г) и (2, 2'), а точка Рх — точка схода следов
плоскости основания (фиг. 1176).
432
604. Построить проекции куба с основанием ABCD, исходя из условия,
что одна из его боковых сторон совпадает с прямой (1, Г), и дана верти-
кальная проекция перпендикулярного к ней отрезка АС (фиг. 1177).
605. Построить проекции прямой призмы высотой h = 60 мм, исходя
из условия, что ее основание — квадрат ABCD и одна из ее боковых сторон
совпадает с заданной прямой (7, Г), и дана горизонтальная проекция
отрезка AD, перпендикулярного к прямой (1, Г) (фиг. 1178).
606. Построить проекции тетраэдра с основанием АВС на плоскости Р,
если дана сторона АВ его основания в совмещенном положении на пло-
скости V (фиг. 1179).
607. Построить проекции треугольной пирамиды высотой h = 60 мм
и с основанием АВС на плоскости Р, если даны вертикальные проекции
ее основания и вершины S (фиг. 1180).
608. Построить проекции прямой правильной треугольной пирамиды
высотой h = 60 мм и с основанием АВС на плоскости Р, если дана гори-
зонтальная проекция стороны АВ ее основания (фиг. 1181).
609. Построить проекции прямой правильной пирамиды высотой h =
= 60 мм и с основанием АВС на плоскости Р, если дана сторона АВ
ее основания в совмещенном положении на плоскости Я (фиг. 1182).
610. Построить проекции прямого кругового конуса, основание которого
имеет радиус, равный 20 мм, и лежит на плоскости Р, если дана точка
S —вершина конуса (фиг. 1183).
611. Построить геометрическое место прямых в пространстве, прохо-
дящих через точку S и наклоненных к плоскости Р под заданным углом <р
(фиг. 1183).
612. Построить проекции прямого кругового конуса, высота которого
/г = 60 мм, а основание имеет радиус, равный 20 мм, и лежит на плоскости
Р, если дана вертикальная проекция центра основания (фиг. 1184).
613. Построить проекции прямого кругового конуса, высота которого
h = 60 мм, а основание имеет радиус, равный 20 мм, и лежит на плоскости
Р, если дано совмещенное положение точки С — центра его основания
на плоскости Я (фиг. 1185).
614. Построить проекции прямого кругового конуса, высота которого
h = 60 мм, а ось расположена на заданной прямой (1, I1), если даны'
точка А окружности его основания в совмещенном положении на плоскости
Я и точка Рх — точка схода следов плоскости основания (фиг. 1186).
615. Построить проекции прямого кругового конуса, высота которого
h = 60 мм, а основание имеет радиус, равный 20 мм, и лежит на плоскости
Р с осью на заданной прямой (1, 1'), если дана точка Рх —точка схода
следов плоскости основания (фиг. 1187).
435
о До
Фиг. 1186
х—S----------О
616. Построить проекции прямого кругового конуса, высота которого
/1 = 60 мм, а ось расположена па заданной прямой (I, Г), если дана точка
С — центр его основания радиуса 20 мм (фиг. 1188).
617. Построить проекции прямого кругового конуса, высота которого
h = 60 мм, а ось расположена на заданной прямой (1, Г), если точка А
лежит на окружности основания конуса (фиг. 1189).
436
618. Построить пирамиду SABC, если даны ее основание АВС и длины
боковых ребер: S.4 = 55 мм; SB = 60 мм; SC = 60 мм (фиг. 1190).
Указание. Решить задачу, пользуясь разверткой поверхности пирамиды («звез-
дочкой»),
619. Провести в плоскости Р прямую, пересекающую ось проекций под
углом 30° (фиг. 1191).
437
620. Провести через точку S на плоскости Р прямую, составляющую
с плоскостью Н угол 60° (фиг. 1192).
621. Провести через точку S прямую, параллельную плоскости Р
и составляющую с плоскостью V угол 60°-(фиг. 1193).
Фиг. 1194
438
1 уаёявии
622. Провести через точку S прямую, параллельную шюсжосп?
и составляющую с прямой АВ угол 30° (фиг. 1194).
623. Провести плоскость Q, параллельную плоскости Р и пересекаю-
шую шар по кругу радиуса г = 20 мм (фиг. 1195).
624. Найти на прямой АВ точки, удаленные от точки С на 25 мм
(фиг. 1196) (пользоваться геометрическим местом точек).
625. Провести через точку S прямую, пересекающую прямую АВ и
составляющую с плоскостью Р угол 60° (фиг. 1197).
626. Найти на прямой CD точку, удаленную от прямой АВ на 20 мм
(фиг. 1198).
627. Провести ч'ерез точку S прямую, пересекающую прямую CD
и составляющую с прямой АВ угол 30° (фиг. 1199).
628. Построить прямоугольный треугольник CDK с вершиной К пря-
мого угла на прямой АВ (фиг. 1200).
629. Построить проекции шара радиуса г = 20 мм, касательного к дан-
ному шару, если центр искомого шара лежит на прямой АВ (фиг. 1201).
630. Провести через прямую АВ плоскость, составляющую с плоскостью
Н угол 60° (фиг. 1202).
631. Построить следы плоскости Q, касательной к поверхности конуса
и перпендикулярной к плоскости Р (фиг. 1203).
632. Провести через точку S плоскость Р, наклоненную к плоскости Н
под заданным углом <р и перпендикулярную к плоскости Q (фиг. 1204).
Фиг. 1196
439
Фиг. 1199
440
633. Провести через точку S плоскость Р, наклоненную к плоскости Н
под заданным углом <р и параллельную прямой АВ (фиг. 1205).
634. Провести через точку С плоскость Р, удаленную от прямой АВ
на 20 мм (фиг. 1206).
441
442
635. Провести через прямую АВ плоскость Р, удаленную от точки С
на 20 мм (фиг. 1207).
636. Построить проекции прямого кругового цилиндра с осью на пря-
мой CD, если прямая АВ — касательная к этому цилиндру (фиг. 1208).
637. Провести через прямую АВ плоскость, пересекающую шар по
кругу радиуса г = 20 мм (фиг. 1209).
638. Провести через точку М плоскость, параллельную прямой АВ
и удаленную от точки С на 20 мм (фиг. 1210).
639. Провести через прямую АВ плоскость Р, удаленную от прямой CD
на 20 мм (фиг. 1211).
ОГЛАВЛЕНИЕ
№ Предисловие- решенного примера '№ задачи Стр. 3
РАЗДЕЛ ПЕРВЫЙ
Глава I. Основные понятия ортогонального проектирования 5
Глава II. Точка 1—5 1—7 6
Глава III. Прямая — 8—.10 И
Глава IV. Проектирование на три плоскости проекций 6-11 11—26 16
Глава V. Взаимное положение прямой и точки 12 — 18 27 — 32 27
Глава VI. Следы прямой 19 — 22 33 — 42 32
Глава VII. Взаимное положение прямых в про- странстве 23 — 32 43—49 37
Глава VIII. Длина отрезка прямой и углы наклона прямой к плоскостям про- екций 33 — 42 50—90 47
Глава IX. Деление отрезка в данном отноше- нии 43 91-94 58
Глава X. Некоторые случаи проектирования углов 44 — 47 95 — 16.2 60
Глава РАЗДЕЛ ВТОРОЙ XI. Плоскость 48—56 163-179 79
Глава XII. Задание плоскости следами. Прямая и точка в плоскости 57 — 94 180 — 216 87
Глава XIII. Пересечение плоскостей, заданных следами 95 — 112 217 — 218 121
Глава XIV. Пересечение прямой с плоскостью 113 — 138 219 — 222 137
Глава XV. Параллельность прямой и плоско- сти. • Параллельность плоскостей 139 — 153 223-250 157
Глава . XVI. Перпендикулярность прямой и пло- скости. Перпендикулярность пло- скостей 154 — 185 251—370 176
РАЗДЕЛ ТРЕТИЙ
Глава XVII. Вращение. Перемещение параллель-
но плоскостям проекций . . . . 186—210
Глава XVIII. Совмещение. Вращение вокруг го-
ризонтали и фронтали........................... 211—232
371—383 221
384-412 239
444
Глава XIX. Перемена плоскостей проекций 233 — 249
Глава XX. Определение расстояний .... 250—259
Глава XXI. Определение углов ...... 260—264
РАЗДЕЛ ЧЕТВЕРТЫЙ
Глава XXII. Сечение многогранников плоско-
стью. Развертки многогранников 265—224
Глава XXIII. Взаимное положение плоскости и
поверхности'......................... 275 — 308
Глава XXIV. Развертки кривых поверхностей 309—317
Глава XXV. Пересечение прямой с поверхно-
стью ..................................... 318 — 333
Глава XXVI. Пересечение поверхностей . . . . 334 — 344
РАЗДЕЛ ПЯТЫЙ
Глава XXVII. Смешанные задачи (для всех раз-
делов) ............................
413 — 437 262
438 — 457 277
458 — 466' 293
467 300
468 — 486 322
487-488 362
489 370
490 — 497 386
498-639 415
ИБ № 2028
Христофор Артемьевич Арустамов
СБОРНИК ЗАДАЧ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Редактор издательства О. Д. Горчакова
Технический редактор Ф. II. Мельниченко
Корректор И. М. Боретиа
Переплет художника Е. В. Бекетова
Сдано в набор 8.06.77. Подписано в печать 16.01.78. Формат 60x90V16
Бумага типографская № 2. Гарнитура тайме. Печать высокая. Усл. печ. л. 28,0
Уч.-изд. л. 29,9.Тираж 190 000 экз. Зак. 1280. Цена 1 р. 10 к.
Издательство «Машиностроение»: 107885, ГСП, Москва, Б-78, 1-й Басманный пер., 3
Ордена Октябрьской Революции, ордена Трудового Красного Знамени Ленинградское
производственно-техническое объединение «Печатный Двор» имени А. М. Горького Союзпо-
лиграфпрома при Государственном комитете Совета Министров СССР по делам издательств,
полиграфии и книжной торговли. 197136, Ленинград, П-136, Гатчинская ул., 26.
Издательство «Машиностроение»
НОВЫЕ КНИГИ
ПО ДЕТАЛЯМ МАШИН
Выпуск 1978 года
Андреев А. В: Передачи трением. Изд. 2-е, перераб. и доп. 14 изд.
, л. 75 к.
Балтер М. А. Упрочнение деталей машин. Изд. 2-е, перераб. и доп.
13 изд. л. 70 к.
Боренштейн Ю. П. Механизмы для воспроизведения сложного
профиля. Справочное пособие. 17 изд. л. 1 р. 10 к.
Вейц В. Л., Волженская А. М., Колчин Н. И. Геометрия
зацепления зубчатых передач. Изд. 3-е, перераб. и доп. 7 изд. л.
(Б-чка зубореза). 30 к.
Булгаков Э. Б., Васина Л. М. Эвольвентные зубчатые передачи
в обобщающих параметрах. Справочник по геометрическому расчету.
16 изд. л. 1 р. 05 к.
Доводка прецизионных деталей машин. 22 изд. л. (Б-ка технолога).
1 р. 55 к. Авт.: П. Н. Орлов, П. Н. Савелова, В. А. По-
лухин и др.
Допуски и посадки. Справочник. Изд. 5-е, перераб. и доп. 55 изд. л.
3 р. 30 к. Авт.: В. Д. Мягков, М. А. Палей, В. А. Бра-
гинский и др. ~
Карпухин И. М. Посадки приборных и шпиндельных шарикоподшипников.
Справочное пособие. 12 изд. л. 95 к.
Клебанов Б. М., Гинзбург А. Е. Зубчатые передачи в ма-
шиностроении. 7 изд. л. (Б-чка зубореза). 30 к.
Леонов А. И. Инерциальные автоматические трансформаторы вращаю-
щего момента. 16 изд. л. 1р. 05 к.
Мальцев В. Ф. Механические импульсные передачи. Изд. 3-е, перераб.
и доп. 21 изд. л. 1 р. 05 к.
Суворов А. А. Обработка деталей из вольфрама и его сплавов.
12 изд. л. 70 к.
Тайц Б. А., Марков Н. Н. Точность и контроль зубчатых
передач. Изд. 2-е, перераб. и доп. 9 изд. л. (Б-ка технолога). 35 к.
Уравновешивание роторов и механизмов. Сборник статей. Пбд ред.
В. А. Щепетильникова. 20 изд. л. 1 р. 50 к.
Приобретайте новые книги издательства «Машиностроение» в магазинах,
распространяющих техническую литературу I
ИЗДАТЕЛЬСТВО «МАШИНОСТРОЕНИЕ»
НОВЫЕ КНИГИ
ПО КОНСТРУИРОВАНИЮ МАШИН
И ПРИБОРОВ
Выпуск 1978 года
Анурьев В. И. Справочник конструктора-машиностроителя.
В 3-х томах. Изд. 5-е, перераб. и доп. 150 изд. л. (Б-ка
конструктора). Цена комплекта 9 р.
Борисов В. И. Общая методология конструирования машин.
10 изд. л. и65 к.
Ипатов М. И., Проскуряков А. В., Семенов В. В.
Снижение себестоимости машин. 14 изд. л. 1 р. 20 к.
Ковалев А. П., К о чалое Н. К., Колобов А. А.
Экономическая эффективность новой техники в машинострое-
нии. 19 изд. л. 1 р. 50 к.
Милосердии Ю. В., Лакин Ю. Г. Расчет и конструиро-
вание механизмов, приборов и установок. Учебник для вузов.
20 изд. л. 1 р. 10 к.
О р г о В. М. Основы конструирования и расчета на проч-
ность гидротурбин. Учебное пособие для вузов. 19 изд. л.
1 р. 03 к.
Петров В. А., Медведев Г. И. Системная оценка
эффективности новой техники. 15 изд. л. 90 к.
П у з ы и я К. Ф., Запасник А. С. Экономическая эф-
фективность научно-исследовательских и опытно-конструктор-
ских разработок в машиностроении. 21 изд. л. 1 р. 20 к.
Расчет и конструирование расходомеров. Под ред. П. П. Крем-
левского. 19 изд. л. 1 р. 10 к. Авт.: П. П. Крем-
левский, Е. М. Аристов, Д. В. Беляев и др.
Ш т а и к о М. Г. Материалоемкость продукции машиностроения.
16 изд. л. 1 р.
Приобретайте новые книги издательства «Машиностроение»
в магазинах, распространяющих техническую литературу!