Текст
АКАДЕМИЯ НАУК СССР
ИНСТИТУТ ИСТОРИИ ЕСТЕСТВОЗНАНИЯ И ТЕХНИКИ
А.П. ЮШКЕВИЧ
СТОРИЯ
МАТЕМАТИКИ
Р В
1оссии
ДО 1Q1J ГОДА
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва 1968
Ю 96
ЛМШМ min mm
АННОТАЦИЯ
Книга содержит историю математических
исследований в России до начала XX века.
Вначале рассматриваются рукописные памятники
средних веков и начала нового времени, до сих
пор опубликованные только частично. Далее
последовательно анализируется научное
творчество петербургских академиков XVIII века
во главе с Эйлером, открытия Лобачевского,
деятельность математической школы Чебыше-
ва, труды математиков, работавших в Москве,
Киеве, Харькове и других университетских
центрах. Помимо печатных трудов, в книге
использованы и архивные материалы, например,
неопубликованные сочинения Остроградского.
Книга иллюстрирована портретами
отечественных математиков, некоторыми факсимиле;
в ней также имеется обширная библиография.
Книга рассчитана на студентов и
преподавателей университетов и педагогических
институтов, учителей средних школ и научных
работников.
82-68
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ 7
ЧАСТЬ ПЕРВАЯ
МАТЕМАТИЧЕСКАЯ КУЛЬТУРА В РОССИИ ДО НАЧАЛА XVIII ВЕКА
Глава 1. Математические знания в Древней Руси 9
Древнерусская нумерация (9). Метрология (13). Первые системы
дробей (15). Математические памятники Киевской Руси (16). Кирик
Новгородец (17). Вопросы «философии математики» (20). Татарское иго
(22).
Глава 2. Рукописи XV—XVII вв 23
Подъем Московского государства (23). Арифметика в рукописях XVII века
(24). Инострументальный счет (27). Строка тройная (30). Строка
фальшивая (32). Задачи для развлечения (36). Геометрические прогрессии
(36). Задача «о деньгах в куче ведати» (37). Терминология (40). Оценка
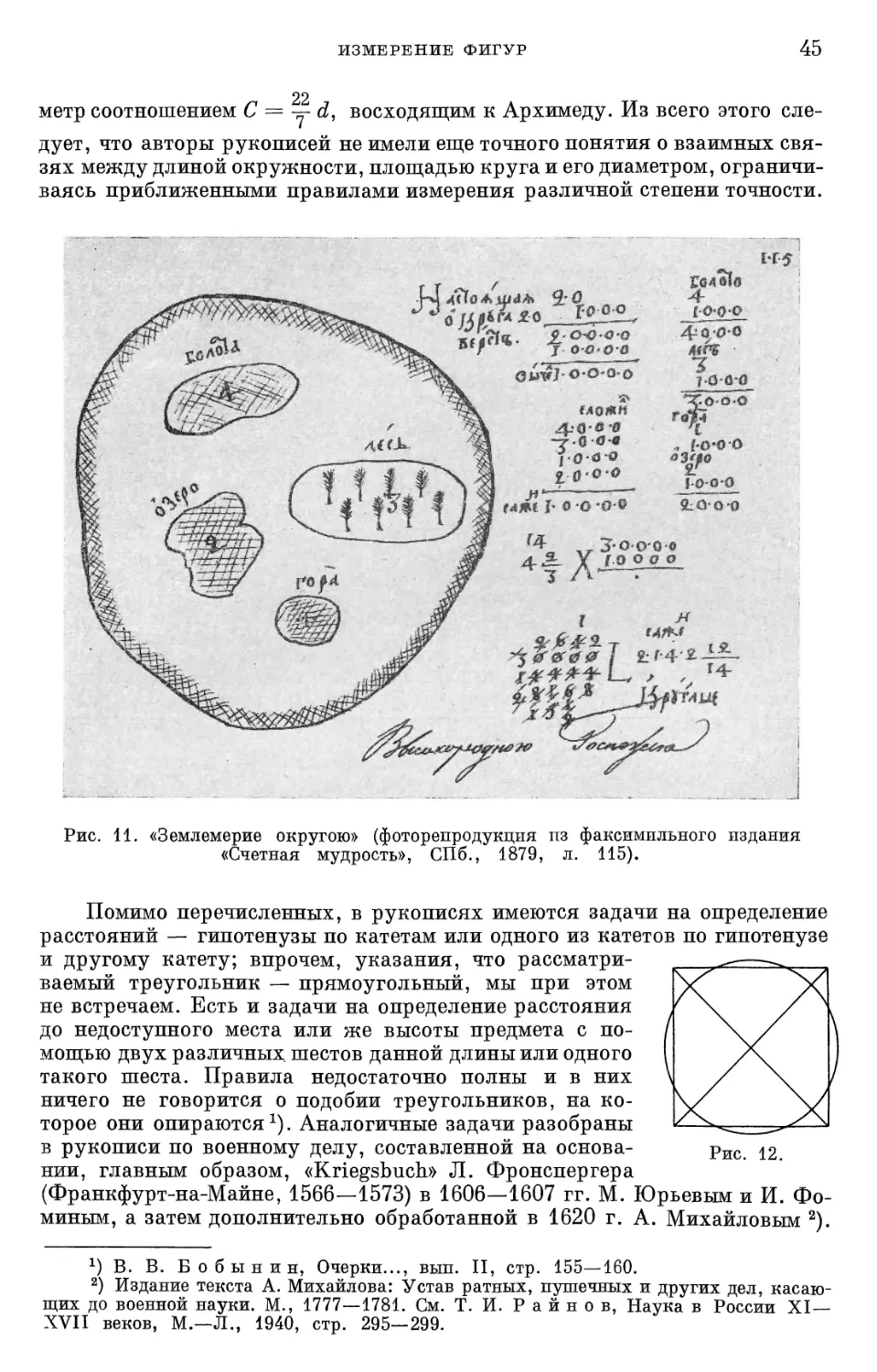
арифметических рукописей (41). Измерение фигур (42). Геометрическая
рукопись «Синодальная № 42» (47). Проблемы непрерывного и
неделимых (49). Итоги (51).
Глава 3. Государство и математика в эпоху Петра Первого ..... 52
Подготовка военных и технических кадров (52). Новые школы (52).
Я. В. Брюс (54). Л. Ф. Магницкий (55). А. Д. Фархварсон (56).
«Арифметика» Магницкого (58). Алгебра и тригонометрия у Магницкого (65).
Первые учебники геометрии и тригонометрии (71).
ЧАСТЬ ВТОРАЯ
МАТЕМАТИКА В ПЕТЕРБУРГСКОЙ АКАДЕМИИ НАУК В XVIII ВЕКЕ
Глава 4. Петербургская Академия наук 74
Основание Академии наук (74). Математика в Академии наук (75).
Академия наук и математическое просвещение (76). Учебная литература
(79).
Глава 5. Первые академики-математики . 83
Математика на рубеже XVII и XVIII веков (83). Первые академики (85).
Я. Герман (86). Дифференциальные уравнения (87). Вопросы геометрии
(88). Ф.-Х . Майер и разработка тригонометрии (90). Н. Бернулли (90).
Г.-В. Крафт (91). X. Гольдбах и учение о рядах (92). Проблемы
Гольдбаха в теории чисел (95). Интегрирование дифференциального бинома (96).
Даниил Бернулли (97). Проблемы теории колебаний (99). Численное
решение уравнений (100). Теория вероятностей и статистика (101).
Кривая распределения ошибок (102).
Глава 6. Леонард Эйлер 103
Начало карьеры (103). Переезд в Петербург (103). Эйлер в Берлине (106).
Возвращение Эйлера в Петербург (108). Общая характеристика творче^
ства (110).
Глава 7. Бесконечные ряды 114
Интерполирование последовательностей и рядов; специальные функции
(114). Формула суммирования Эйлера (117). Дзета-функция (119).
Суммирование расходящихся рядов (121).
4
ОГЛАВЛЕНИЕ
Глава 8. Математическая трилогия Л, Эйлера 128
«Введение в анализ бесконечных» (128). Понятие функции (130).
Исследование элементарных функций (134). Начала теории функций
комплексного переменного (135). Основная теорема алгебры (137). Логарифмическая
функция (138). Новые приложения комплексных чисел (139). Конформные
отображения (139). Вычисление определенных интегралов и уравнения
Даламбера — Эйлера (140). Проблема интерпретации комплексных чисел
(141). Основания дифференциального исчисления (142). «Исчисление
нулей» Эйлера (145). Разработка дифференциального исчисления (148).
Интегральное исчисление (150). Эллиптические интегралы (152).
Определенные интегралы (154). Кратные интегралы (156).
Глава 9. Дифференциальные уравнения и вариационное исчисление .... 157
Обыкновенные дифференциальные уравнения (157). Уравнение Риккати
(157). Линейные уравнения с постоянными коэффициентами (158).
Линейные уравнения с переменными коэффициентами (159).
Интегрирующий множитель (160). Особые решения (161). Численное решение
дифференциальных уравнений (161). Уравнения с частными производными (163).
Проблема колебания струны. Метод Даламбера — Эйлера (164). Принцип
наложения колебаний Д. Бернулли (167). Аналитическая представимость
функций (170). Тригонометрические ряды (172). Вариационное
исчисление (174).
Глава 10. Другие математические работы Л. Эйлера 181
Элементарная геометрия и тригонометрия (181). Аналитическая
геометрия (181). Дифференциальная геометрия поверхностей (183).
Топологические задачи (185). Теория чисел (185).
Глава И. Ученики и первые преемники Эйлера 190
Школа Эйлера (190). С. К. Котельников и С. Я. Румовский (190). А. И. Лек-
сель (195). Н. И. Фусс (196). Ф. И. Шуберт (198). Мемуар С. Е. Гурьева
(199). Вопросы обоснования анализа на рубеже XVIII—XIX веков (201).
С. Е. Гурьев и его последователи (203). Математика в Академии наук
в начале XIX века (214).
ЧАСТЬ ТРЕТЬЯ
МАТЕМАТИКА В РОССИИ В ПЕРВОЙ ПОЛОВИНЕ XIX ВЕКА
Глава 12. Общие условия развития математики 216
Реформа системы образования (216). Физико-математические факультеты
(218). Академия наук (224). Особенности развития математики в России
и за рубежом (225).
Глава 13, Н. И. Лобачевский и открытие неевклидовой геометрии .... 229
Постулат Евклида о параллельных (229). Н. И. Лобачевский (232).
Мировоззрение Н. И. Лобачевского (235). Пространство и действительность
(237). Начальные понятия геометрии (238). Открытие неевклидовой
геометрии (240). Лобачевский о геометрии действительного мира (247).
Первые применения геометрии Лобачевского (248). Непротиворечивость
гиперболической геометрии (249). Н. И. Лобачевский и современники
(250). Теория поверхностей К. Ф. Гаусса (252). Исследования Ф. Г. Мин-
динга по теории поверхностей (255). Дальнейшее развитие неевклидовой
геометрии (257). Геометрия и физика XX века (262). Аксиоматический
метод (263). «Алгебра» Лобачевского (265). Сочинения по алгебре
М. В. Остроградского и О. И. Сомова (269). Студенческая работа П. Л. Че-
бышева (270). Исследования Лобачевского по теории рядов Фурье
(270). Признак сходимости Лобачевского (272).
Глава 14. Новый подъем исследований в Академии наук; М. В,
Остроградский и В. Я. Буняковский 274
Жизнь М. В. Остроградского (274). Работы Остроградского по теории
теплоты (278). Вариационное исчисление (285). Дифференциальные
уравнения (287). Кратные интегралы (289). Интегрирование алгебраических
функций (293). Жизнь и творчество В. Я. Буняковского (296).
Неравенство Буняковского (298). Буняковский и теория параллельных (299).
Теория вероятностей (300). Вычислительные устройства (302).
ОГЛАВЛЕНИЕ
5
ЧАСТЬ ЧЕТВЕРТАЯ
МАТЕМАТИКА В РОССИИ ВО ВТОРОЙ ПОЛОВИНЕ XIX
И В НАЧАЛЕ XX века
Глава 15. Общие условия и особенности развития математики 306
Математическое образование; средняя школа (306) . Математика в
университетах (311). Математические общества и научные съезды (316).
Математические журналы и другие издания (320). Основные направления
математических исследований в России и за рубежом (324).
Глава 16. П. Л. Чебышев и петербургская математическая школа .... 332
Жизнь П. Л. Чебышева (332). О творчестве Чебышева (337). Чебышев
и его ученики (341).
Глава 17. Теория чисел 343
Исследования П. Л. Чебышева по теории распределения простых чисел
(343). Диофантовы приближения (348). Работы Н. В. Бугаева (349).
А. Н. Коркин и Е. И. Золотарев (350). Работы А. Н. Коркина и Е. Н.
Золотарева по теории квадратичных форм (353). А. А. Марков и его
магистерская диссертация (357). Г. Ф. Вороной и геометрия чисел (363). Теория
алгебраических чисел (366). Новые исследования по аналитической
теории чисел (376).
Глава 18. Интегрирование алгебраических функций 380
Исследования П. Л. Чебышева (380). О. И. Сомов (383). Преемники
Чебышева (384).
Глава 19. Теория вероятностей 387
Закон больших чисел и центральная предельная теорема (387). П. Л.
Чебышев и теория вероятностей (390). Проблемы теории моментов (394).
Предельные теоремы А. А. Маркова и А. М. Ляпунова (398). Цепи
Маркова (401). Е. Е. Слуцкий (403). Аксиомы теории вероятностей С. Н. Берн-
штейна (404).
Глава 20. Теория приближения функций , 405
Исследования П. Л. Чебышева (405). Работы Е. И. Золотарева, А. А.
Маркова и В. А. Маркова (411). Интерполирование и ортогональные
многочлены (413). Механические квадратуры (418) С. Н. Бернштейн и
конструктивная теория функций (421).
Глава 21. Дифференциальные уравнения 427
Классические методы; А. Ю. Давидов (427). В. Г. Имшенецкий (429).
A. В. Летников и приложения «междупредельных производных» (433).
М. Е. Ващенко-Захарченко и символическое исчисление (435). Новые
направления в теории дифференциальных уравнений (437). СВ.
Ковалевская (438). Теорема Ковалевской (440). Задача о вращении твердого
тела (443). В. А. Анисимов (444). С. Н. Бернштейн и проблемы
Гильберта (445). Качественная теория дифференциальных уравнений и
теория устойчивости (446). Работа Н. Е. Жуковского (448). Жизнь
A.M. Ляпунова (448). Фигуры равновесия вращающейся жидкой массы
и их устойчивость (451). Грушевидные фигуры (454). Устойчивость
систем с конечным числом степеней свободы (455). П. Г. Боль и метод
неподвижных точек (458). Квазипериодические функции (462). Жизнь
B. А.Стеклова (463). Задачи математической физики (464). Теория
замкнутости (467). Н. М. Гюнтер (471). Интегральные уравнения (472). Младшее
поколение петербургской школы (475). Методы В. Ритца и Б. Г. Га-
лёркина (476). А. Н. Крылов (477).
Глава 22. Сходимость и суммирование рядов 483
Н. В. Бугаев и учение о сопряженных рядах (483). В. П. Ермаков и его
признак сходимости (486). Параллелограмм Ньютона (489). Метод
суммирования Г. Ф. Вороного (489). Улучшение сходимости ряда Фурье по
А. Н. Крылову (490).
ОГЛАВЛЕНИЕ
Глава 23. Теория аналитических функций; специальные функции ....
Распространение теории аналитических функций (492). М. Е. Ващенко-
Захарченко (493). Ю. В. Сохоцкий (494). Теорема Сохоцкого (495.)
Граничные свойства аналитических функций (496). Эллиптические и
гиперэллиптические функции (498). Б. Я. Букреев (499). Другие работы (500).
Историк теории аналитических функций И. Ю. Тимченко (501).
Исследования по цилиндрическим функциям; Н. Я. Сонин (502). Гамма-функция
(506). Функции и числа Вернул ли (506).
Глава 24. Геометрические исследования; вопросы математической логики
О. И. Сомов и векторное исчисление (509). Сети Чебышева (510). К. М. Пе-
терсон и московская геометрическая школа (511). Лекции В. Я. Цингера
(513). Работы по проективной геометрии К. А. Андреева и А. К. Власова
(513). Дифференциально-геометрические исследования Б. К. Млодзеев-
ского (515). Д. Ф., Егоров и его ученики (517). Геометрия в Казани;
Ф. М. Суворов (519). А. В. Васильев (520). А. П. Котельников и теория
векторов в неевклидовых пространствах (521). Д. Н. Зейлигер и
геометрия линейчатых пространств (525). Работы Д. М. Синцова по теории
коннексов (526). Основания геометрии (527). Геометрия в Одессе;
аксиоматика В. Ф. Кагана (528). С. О. Шатуновский и теория измерения
многогранников (531). Аксиомы учения о величине (533). П. С. Порецкий
и алгебра логики (534). И. В. Слешинский (535). Проблема закона
исключенного третьего (536).
Глава 25. Исследования по алгебре
Вычисление корней (538). Решение алгебраических уравнений в
трансцендентных функциях (539). Теория групп (540). Распространение теории
групп в России (545). Возникновение Киевской алгебраической школы
(547). Д. А. Граве (547). Ученики Д. А. Граве; О. Ю. Шмидт (552).
С. О. Шатуновский и теория Галуа (554). Гиперкомплексные числа
(555). Диссертация П. Э. Ромера (557). Ф. Э. Молил (557).
Глава 26. Возникновение московской школы теории функций
Теория множеств и теория функций (559). Первые работы по теории
функций в России (562). Теория функций в Московском университете (563).
Теорема Д. Ф. Егорова (565). Н. Н. Лузин (565). Теорема о С-свойстве (566).
«Интеграл и тригонометрический ряд» (567). Ученики и последователи
Лузина (573).
Заключение
Именной указатель
492
509
538
559
578
579
6
ПРЕДИСЛОВИЕ
Русские математики вступили на путь самостоятельного научного
творчества в двадцатые годы прошлого столетия. К этому времени
относятся исключительные по идейной глубине и смелому новаторству
исследования Н. И. Лобачевского, открывшего целый мир неевклидовой
геометрии, и выдающиеся труды М. В. Остроградского по
математической физике и интегральному исчислению. Вскоре затем (в середине
ж второй половине XIX века) П. Л. Чебышев получил фундаментальные
результаты в теории чисел, далеко продвинулся в разработке созданной
им теории наилучшего приближения функций и поднял на неизмеримо
более высокий уровень теорию вероятностей. Вместе с тем он организовал
и возглавил Петербургскую математическую школу, к которой
принадлежали крупнейшие математики конца XIX и начала XX вв.: А. А. Марков,
проложивший новые пути в теории вероятностей (марковские цепи),
А. М. Ляпунов, творец важных отделов математической теории
устойчивости, Е. И. Золотарев и Г. Ф. Вороной, авторы замечательных
открытий в теории квадратичных форм и в алгебраической теории чисел и
другие ученые. Петербургская школа пользовалась всемирным признанием.
Будучи ведущей в России до самой Великой Октябрьской
социалистической революции, она не являлась единственной. В университетах Москвы,
Казани, Киева, Одессы, Тарту, Харькова складывались другие
направления, подготовлялись большие научные школы анализа, геометрии,
алгебры и т. д., которым предстояло в дальнейшем сыграть
первостепенную роль. Так, еще до 1917 г. в Москве началось формирование школы
теории функций действительного переменного, особенно ярко
представленной в то время Н. Н. Лузиным.
Необычайный расцвет математического творчества наступил после
Октябрьской революции. Успехи, достигнутые в течение первых же лет
после 1917 г., были немыслимы в других общественных условиях.
Повсеместное расширение сети средних и высших школ, создание научных
институтов и разветвленной системы аспирантуры, широкая
демократизация образования, ставшего доступным всем слоям населения и всем
национальностям, издание огромной учебной и научной литературы,—
все это, вместе с революционным творческим порывом учащейся
молодежи и многих ученых старших поколений, быстро выдвинуло советскую
математику на одно из самых первых мест в мире. По размаху, качеству
и значимости математических исследований Советский Союз ныне не
уступает ни одной стране.
Вместе с тем успехи математики в СССР и его отдельных республиках
тесно связаны с предшествующим развитием математики и
математической культуры в России. Скромная и почти забытая теперь работа
математиков допетровского времени, в частности безымянных
авторов рукописей XVII века, явилась предпосылкой первого
изданного у нас печатного руководства — энциклопедической «Арифметики»
8
ПРЕДИСЛОВИЕ
Л. Ф. Магницкого (1703). Возникшие при Петре I военно-технические
школы сразу стали важным рассадником математической образованности.
Основание в 1725 г. Академии наук в Петербурге сообщило мощный толчок
усвоению и дальнейшему развитию у нас математических открытий
Декарта и Ферма, Ньютона и Лейбница. Гений Л. Эйлера, для которого
Россия стала родной страной, оказывал из Петербурга мощное влияние на
прогресс математических наук во всей Европе. Научно-просветительная
и педагогическая работа Эйлера и его учеников, последователей или
ближайших преемников — С. К. Котельникова, С. Я. Румовского,
Н. Г. Курганова, Н. И. Фусса, С. Е. Гурьева и др. немало содействовала
улучшению преподавания во всех учебных заведениях страны, число
которых на протяжении XVIII века постепенно возрастало. Эта работа
подготовляла и ту реформу системы образования, которая была начата
еще в конце XVIII века, но проведена лишь в начале XIX века.
Составной частью реформы явилось открытие первых
физико-математических факультетов, в которых получили свои путевки в научную жизнь
в Казани Лобачевский, в Харькове — Остроградский, в Москве —Чебышев.
Предлагаемая вниманию читателей книга посвящена истории
математики в России со времен, от которых сохранились в нашей стране
первые математические памятники, т. е. с XI — XII вв., до Октябрьской
революции. Основное место занимает изложение собственно научных
исследований с учетом развития математики за рубежом. Истории
математической культуры — образования, литературы, обществ, съездов
и т. д., естественно, отведено меньше места. Описание отдельных, даже
весьма крупных открытий, ограничивается, как правило,
характеристикой основных идей и результатов; проведение доказательств увеличило
бы объем книги во много раз. Читатель, желающий ознакомиться с каким-
либо вопросом подробнее, найдет в книге необходимые литературные
ссылки, как на первоисточники, так и на исторические работы о них.
Я ограничиваюсь историей математики в России и не касаюсь
математики в Средней Азии или Закавказье, тем более, что по этому вопросу
имеется своя собственная литература. Как известно, имеются также
подробные обзоры развития математических наук в СССР, доведенные до 1957 г.
Подготовляя книгу к печати, я опирался как на собственные работы
в этой области, которые веду уже свыше 25 лет, так и на работы других
исследователей. При подготовке настоящей книги литература, изданная
до начала 1966 г., учтена по мере возможности полностью. Как правило,
я старался знакомиться с первоисточниками. Там, где материал
приходилось брать из вторых рук, это указано в литературных ссылках.
Календарные даты приведены по новому стилю, за редкими, особо
оговоренными исключениями.
Я не претендую на исчерпывающую полноту описания. Многое
просто не умещалось в установленный объем книги, многое — и, быть
может, еще большее, до сих пор вовсе не изучено. За любые указания
на пробелы в изложении я буду благодарен каждому, кто пожелает мне
об этом письменно или устно сообщить.
Я весьма благодарен Г. Ф. Рыбкину и А. Ф. Лапко за большую
работу при подготовке книги к печати.
Москва,
май 1966 г.
А. Юшкевич
ЧАСТЬ ПЕРВАЯ
МАТЕМАТИЧЕСКАЯ КУЛЬТУРА В РОССИИ
ДО НАЧАЛА XVIII ВЕКА
ГЛАВА ПЕРВАЯ
МАТЕМАТИЧЕСКИЕ ЗНАНИЯ В ДРЕВНЕЙ РУСИ
Первые сведения о развитии математики, именно арифметики, на
Руси относятся к IX — XII вв., к эпохе процветания и упадка киевской
«империи Рюриковичей».
Арифметических знаний требовала практическая деятельность людей:
расчеты в торговле, выкладки, связанные с обложением податью, а также
с нуждами строительства и военного дела. Без них невозможно было
составление календаря. Без них, так же как без знакомства с некоторыми
свойствами геометрических фигур, невозможно было понимание ряда
основных фактов в астрономии.
Древнерусская нумерация. В то время как народы средневековой
Западной Европы переняли римскую нумерацию, в России получила
распространение десятичная алфавитная нумерация, сходная с той,
которой пользовались вслед за древними греками византийцы. В Византии
была в ходу так называемая теперь ионийская нумерация, восходящая
примерно к V веку до н. э. и основанная на греческом алфавите из
24 букв, обозначавших по порядку числа от 1 до 9, десятки и сотни,
с тремя исключениями из этого правила: 6, 90 и 900 обозначались
с помощью особых знаков «вау», «коппа» и «сампи», которые в греческом
письме не употреблялись х). Возможно, что до создания специальной
азбуки, приспособленной к фонетическим особенностям славянской речи,
славяне, находившиеся в тесных связях с византийцами, пользовались
при письме греческими алфавитом и нумерацией. Затем в
южнославянских землях были разработаны два славянских алфавита — глаголица,
буквы которой имели также числовое значение, и кириллица, в короткое
время вытеснившая глаголицу.
На Руси кириллица получила распространение вскоре после ее
введения у балканских славян, вероятно, при великом князе киевском
Владимире Святославиче (978—1015); ею написаны уже древнейшие
рукописи XI века. Создатели кириллицы использовали греческий алфавит,
но в широкой мере учли потребности славянского языка. На этой
азбуке основывалась и древнерусская нумерация, применявшаяся без
х) Об ионийской нумерации см. М. Я. Выгодский, Арифметика и алгебра
в древнем мире, М., 1967.
10
ГЛ. 1. МАТЕМАТИЧЕСКИЕ ЗНАНИЯ В ДРЕВНЕЙ РУСИ
существенных изменений до XVII века включительно х). Числа от 1 до 9,
десятки и сотни изображались с помощью последовательных букв.
Из этого правила имелось несколько исключений. Так, число 2
обозначалось третьей буквой «веди», а не второй «буки», не получившей числового
значения, ибо у византийцев это число выражалось буквой Р, которую
на Руси передавали звуком В. «Фита», стоящая в славянском алфавите
предпоследней, соответствовала 9, подобно греческой 0, а буква «живете»,
которой нет в греческом алфавите, числового значения не получила.
Отступления от правила имеются также в обозначениях десятков и сотен.
Так, знаком 90 долго служила упомянутая «коппа» q , а затем, не
позднее XIV века, ее сменила похожая буква «червь», сначала лишенная
числового значения. 900 вначале изображались «малым юсом», несколько
сходным с «самни», позднее же буквой «цы», быть может, под влиянием
глаголицы, в которой графема «цы» изображала 900.
Приведенная здесь таблица (рис. 1) дает ясное представление о
славянском алфавите в цифрах. Буквы написаны в ней строгим уставом,
который с XIV века все чаще заменяется более простым и беглым
полууставом, а затем скорописью. Для выделения чисел и записи над их
знаками ставился еще особый значок ~ — титло. Титло, которому в
греческой нумерации соответствовала черта, ставилось иногда над каждой
буквой —цифрой, иногда только над первой или же над всем числом.
В некоторых рукописях числа выделялись с обеих сторон точками.
Тысячи обозначались теми же буквами алфавита, у которых внизу слева
ставился знак в виде перечеркнутой черточки, например ^ = 1000,^=3000.
Греки и византийцы применяли с той же целью значок в виде штриха.
При помощи цифр и этого знака можно было непосредственно обозначить
все целые числа до одного миллиона 2).
При записи чисел больше 10 цифры писали слева направо в порядке
убывания десятичных разрядов так, как теперь. Описанный порядок не
всегда соблюдался только для чисел от 11 до 19. В согласии с
произношением этих девяти чисел, при котором единицы называются ранее десяти
(одиннадцать — один на десять и т. п.), числа 11, 12 и т. д. иногда
записывали так: д| ? bj и т. д. Знак тысяч слева ставился при каждой цифре,
означающей то или иное количество тысяч: пропуск этого знака повлек
бы за собой изменение числового значения записи. Например,
ТКЛ = 321
Д КЛ = 300021
Д^КЛ =320001
7ДЛ = 321000
Для единиц более высоких десятичных разрядов имелись специальные
названия и обозначения. Описание развитой системы таких числительных
г) Р. А. Симонов, О некоторых особенностях нумерации, применявшейся
в кириллице; JI. П. Жуковская, К истории буквенной цифири и алфавитов
у славян. В сб.: Источниковедение и история русского языка, М., 1964.
2) Иногда значок тысяч перечеркивали только один раз, а случалось, что и
три раза.
ДРЕВНЕРУССКАЯ НУМЕРАЦИЯ
11
и знаков мы находим в рукописях XVII века, но несомненно, что она
возникла не позднее XV века. Наиболее употребительный счет велся
на тьмы (десять тысяч), легионы или легеоны (десять тем) и леодры (десять
Рис. 1. Славянский алфавит и цифры (звездочкой помечены буквы,
исключенные впоследствии из русского алфавита; двумя звездочками — буквы, у
которых изменилось начертание).
легионов) 1). Вот как именовалось при этом число 9 876 543 210: «девять
тысящ леодров и восмьсот леодров и семьдесят леодров и шесть леодров
г) Слово тьма означало в обычной речи огромное, не поддающееся пересчету
количество; в смысле 10 000 оно встречается уже в XII веке. Слово легион,
вероятно, связано с наименованием крупного римского воинского подразделения,
состоявшего из 10 когорт. Происхождение термина леодр — неясно.
12 ГЛ. 1. МАТЕМАТИЧЕСКИЕ ЗНАНИЯ В ДРЕВНЕЙ РУСИ
и пять легионов и четыре тьмы и три тысящи и двесте и десять»*). Нередка
в рукописях встречаются и более высокие разряды той же системы —
враны, т. е. вороны (десять леодров), и колоды (десять вранов). Тьмы
обозначали (рис. 2), обводя знаки единиц кружком, легионы с помощью
кружков из точек, леодры — кружками с лучиками 2), а враны —
кружками из крестиков, или же ставя по бокам знака единиц букву «како».
Колоду иногда обозначали, как показано на рисунке, но имелись и другие»
Тьмы (д), (в), . . .
Легионы { А }, (' В } • • .
Леодры = А с, |В |, ...
Враны i Дх5, {KJ, . . . , или же КАК, КЕК
Колода А
Рис. 2. Примеры обозначения древнерусских
единиц для высоких девятичных разрядов.
обозначения. Наиболее ранняя запись десятков тысяч с помощью кружков
встречается в одной новгородской грамоте на бересте XIV века (рис. 3) 3).
Наряду с такой системой, иногда называвшейся «малым числом»,,
существовала и другая —«великое число», применявшаяся «коли
прилучался великий счет и перечень» (перечень значит число). Здесь тьма
Рис. 3. Фоторепродукция прориси берестяной грамоты № 342 первой половины
XIV в. В верхнем ряду изображены цифры 1, 2, 3 (частично) 7, 8, 9, 10, 20, 30, 40,
(частично); в среднем 60, 70, 80, 90, 100, 200 (частично), 300, . . ., 700; в нижнем
ряду 2000, . . ., 9000, 10 000, . . ., 40 000 (от 50 000 остался след).
означала тысячу тысяч, т. е. 106, легион — тьму тем, т. е. 1012, леодр —
легион легионов, т. е. 1024, вран —леодр леодров, т. е. 1048, и колода —
десять вранов, т. е. 1049.
О границе счета в рукописях нередко сказано: «И боле сего несть
человеческому уму разумети, токмо един бог весть» 4), но не в том смысле,
что больших чисел не существует, а в том, что «сего боле несть числа
х) Рукопись Арханг. Д. — 478 Библиотеки АН СССР в Ленинграде, л. 51.
2) Иногда, наоборот, для легионов применялись кружки с черточками, а для
леодров — кружки с точками.
3) Р. А. Симонов, Числовые грамоты на бересте XIII—XIV вв. и
некоторые вопросы истории кирилловской нумерации. В сб.: Хиляда и сто години сла-
вянска писменост, София, 1963, стр. 290.
4) Рукопись Э/РБ—40 Отделения ист. русской культуры Государственного
Эрмитажа, л. е^ об.
МЕТРОЛОГИЯ
13
в словенстем языце» х). Как «малое», так и «великое число» в XVII веке
уже начинали выходить из употребления вместе с алфавитной нумерацией.
Следует заметить, что с двоякими значениями названий высших
десятичных разрядов мы встречаемся и в древнекитайском и в
западноевропейском счете, который также начал обогащаться на исходе средних
веков новыми числительными. Так, вслед за появлением в Италии
XIV века слова «миллион», во Франции в конце XV века вводятся
термины: биллион, триллион, квадриллион и т. д. для степеней миллиона:
(106)2, (106)3, (106)4, ... В XVII веке во Франции (и в XIX веке в США)
слова: биллион, триллион, квадриллион и т. д. получили значения
степеней тысячи: 109, 1012, 1015, . . ., между тем как в Германии и Англии
они продолжали обозначать по-прежнему 1012, 1018, 1024, . . .
Алфавитная славянская нумерация применялась несколько веков,
и ньшешняя десятичная система, основанная на применении десяти цифр
О, 1, 2, . . ., 9 и принципа поместного или позиционного значения
(согласно которому значение всякой цифры определяется ее местом в записи
числа), начала вытеснять ее лишь в XVII веке. Алфавитная нумерация
менее совершенна, чем современная, и значительно менее удобна для
обозначения больших чисел и действий над ними. В IX—XI вв.
десятичная позиционная система была известна еще только в Индии и в
мусульманских государствах. Проникать в Западную Европу она начала
в XII веке. Вычисления при помощи алфавитной системы с небольшими
числами труда не представляют. В случае больших чисел она удобнее
для записи и выкладок, чем широко распространенная до XV века
в Западной Европе римская нумерация.
Метрология. Большую роль во всей хозяйственной жизни имеют
системы мер; они участвуют и в различных математических расчетах
и измерениях 2).
Три основные древнерусские меры длины носят названия частей тела.
Меньшая мера — малая пядь — является расстоянием между
раздвинутыми большим и указательным пальцами и соответствует примерно 19 см;
большая пядь — расстояние между большим пальцем и мизинцем —
около 22—23 см (отсюда название икон, имеющих в ширину 19 или 23 см,—
«пядницы»). Большая часть кирпичей XII века имеют ширину также
пядь в 19 см. Локоть есть расстояние от локтевого сочленения до концов
вытянутых пальцев и соответствует двум большим пядям; и эта единица
измерения имела свой вариант — локоть со сжатыми пальцами, размером
в две малые пяди. Такова обычная ширина холста, чрезвычайно
устойчивая и повсеместная, идущая из глубокой древности.
Единица сажень — расстояние от ступни до конца вытянутой вверх
руки (примерно 215 см) при росте человека 170—172 см. Величина другого
вида этой единицы измерения, так называемой простой сажени, определена
историками при помощи надписи на Тмутараканском камне, содержащей
сведения о промере ширины Керченского пролива. Результат этого
интересного измерения «по леду от Тмутороканя до Корчева» (Керчи),
произведенного в 1068 г., выразился в 14 000 сажен. Величину простой
сажени определяют отсюда в 150—158 см. Она составляет расстояние
между большими пальцами рук человека среднего роста, вытянутых в
г) Рукопись Э/РБ — 40 Отделения ист. русской культуры Государственного
Эрмитажа, л. д. об.
2) Подробнее см. Л. В. Ч е р е п н и н, Русская метрология, М., 1944. Он же,
Русская хронология, М., 1944.
14
ГЛ. 1. МАТЕМАТИЧЕСКИЕ ЗНАНИЯ В ДРЕВНЕЙ РУСИ
стороны. При последовательном делении ее на 4 и на 8 получаются
известные уже нам малые локоть и пядь. По-видимому, простая сажень
предшествовала обыкновенной, трехаршинной.
Для определения больших расстояний в Древней Руси существовала
верста, или поприще. Все эти термины: пядь, локоть, сажень, верста,
поприще встречаются уже в XI — XII вв. Меры длины, как и другие
меры, не отличались устойчивостью и в период феодальной
раздробленности в России колебались от одного княжества к другому, а вместе
с тем изменялись во времени. Подобная же пестрота мер характерна
была и для других феодальных стран в средние века, а иногда и позднее.
Система мер, употреблявшаяся в России до введения метрических мер
по декрету Совета Народных Комиссаров РСФСР от 14 сентября 1918 г.,
в основном установилась в XVII веке; установление ее явилось одним
из следствий объединения различных частей страны в единое
централизованное государство с единым рынком, валютой и законами 1).
Меры поверхности находились в тесной связи с мерами сыпучих тел,
прежде всего зерновых культур. В Киевском государстве и феодальных
княжествах XIII — XV вв. главными мерами сыпучих тел служили кадь
(киевская кадь — примерно 14 пудов ржи, а московская— примерно 24 пуда)
и ее подразделения: 1 кадь = 2 половникам = 4 четвертям = 8
осьминам. В XVI — XVII вв. кадь и половник из обихода исчезают и
основной мерой становится четверть (равная примерно 6 пудам ржи) и ее
двоичные или троично-двоичные подразделения: 1 четверть = 2
осьминам =4 полуосьминам = 8 четверикам = 16 получетверикам и т. д.=
= 3 третям = 6 полтретям = 12 пол-полтретям и т. д. Меры земельной
поверхности определялись первоначально тем средним количеством ржи,
которая на них высевалась. Основные дореволюционные меры
поверхности— десятина и четверть появляются в XIII —XV вв., причем две
четверти составляли десятину2). Четверть (или четь) представляла собой
площадь, на которой высевалась четверть ржи. Четверти — меры
поверхности — делились на более мелкие меры совершенно так же, как
четверти — меры сыпучих тел. Мы еще вернемся к некоторым
особенностям старинной русской системы земельных мер, ибо с ними впоследствии
связана была раскладка налогов, а денежные расчеты податного
обложения сыграли немалую роль в развитии некоторых частей арифметики.
У всех народов на определенной ступени культуры наблюдается
тесная зависимость между весовой и денежной единицами.
Весовой и одновременно денежной единицей в Киевском государстве
была гривна. Происхождение ее не византийское, а скорее всего
восточное — результат тесных торговых связей Руси с Востоком. Находимые
в изобилии в кладах серебряные слитки — русские гривны — по весу
соответствуют почти в точности арабскому фунту — ротлю (409,5 г),
который арабы заимствовали в Ираке. Вес золотой монеты Владимира
Святославича составляет 1/96 часть позднейшего русского фунта, или
золотник, т. е. соответствует арабскому золотому динару. Следовательно,
древнерусская гривна соответствует позднейшему фунту и представляет
собой очень давнюю единицу русских мер веса. Слово золотник
встречается в ряде документов Киевской эпохи, так же как пуд и берковец.
Однако неясно, означал ли первоначально золотник специфическую
г) В стандартной дореволюционной системе русских мер одна верста =500 саж.^
«1066,8 ж, одна сажень = 3 арш. « 213,4 см, один аршин = 16 вершкам «71,1 см.
2) Одна десятина = 80 X 30 кв. саж. = 2400 кв. саж. = 1 га 925 кв. ж.
ПЕРВЫЕ СИСТЕМЫ ДРОБЕЙ
15
весовую единицу или золотую монету. Точно так же не известен
первоначальный вес пуда и берковца. Впоследствии установились
соотношения: 1 берковец = 10 пудам, 1 пуд = 40 фунтам, т. е. 16,4 кг.
Более древними обозначениями понятия «деньги» в русском языке
были слова «скот» и «куны», так как первыми мерилами ценности и
платежными знаками при возникновении обмена у славянских племен
явились домашний скот и меховые шкурки лесных зверей («куны»— куницы).
Вплоть до XV века, а кое-где и позднее, шкурки куниц и белок или
только их мордочки —«мордки» и отрезки —«резаны» продолжали
служить мелкой монетой. Вместе с тем уже в Киевской Руси денежная или
кунная система существенно опиралась на систему металлических единиц,
слитков или монет. Вначале, видимо, основная крупная единица — гривна
подразделялась на 20 ногат х), а также на 25 кун и 50 резан. Чеканка
монет прекратилась в конце XI века и возобновилась два или три века
спустя. В период феодальной раздробленности в Москве, Новгороде,
Пскове и т. д. имелась своя особая валюта, затем в ходе объединения
страны постепенно создается общая денежная система.
В XIII — XV вв. основной единицей в Москве становится рубль —
серебряный слиток, представлявший собой половинный обрубок прежней
гривны, весом в полфунта или 48 золотников, т. е. 204,76 г. Более мелкими
единицами являлись полтина (1/2 рубля) и деньга (сначала 1/100 рубля).
В Новгороде рублем тогда служил слиток или монета почти вдвое
большего веса. В обращении были также алтыны, монета в 6 денег 2). Иван III
(1462—1505) запретил удельным князьям чеканку собственной монеты,
а в начале царствования Ивана Грозного (1533—1584) была установлена
денежная система, единая для всего государства. Были введены
серебряные копейки в 1/100 рубля 3), деньга получила значение полкопейки,
гривна, гривенник — десяти копеек. В ходу долгое время, частью до наших
дней, сохраняются деньги, алтыны, полтины и другие единицы, но
основными оказываются рубль, гривенник и копейка. Тем самым русская
денежная система приобрела в главном десятичную структуру. Мы
увидим, что это отразилось и на судьбе русских счетов.
Первые системы дробей. Простейшие из дробей, 1/2 и 1/3, были
известны с незапамятных времен. Затем путем деления пополам этих
основных в обиходе дробей возникли два ряда дробей — двоичный
и троично-двоичный. Оба они возникли вместе с описанными выше
аналогичными подразделениями мер, особенно мер сыпучих тел и земельных
поверхностей. Эти два ряда были: а) 1/2, 1/4 (четь или четверть), 1/8
(полчети или полчетверти), 1/16 (пол-полчети), 1/32 (пол-пол-полчети,
или малая четь) и т. д. и б) 1/3, 1/6 (полтрети), 1/12 (пол-полтрети), 1/24
(пол-пол-полтрети, или малая треть) и т. п.
При помощи сложения или вычитания таких основных дробей нередко
выражали другие дроби, например: 11/24 есть треть и пол-полтрети и
х) От арабского «нагд», что значит полноценная, хорошая монета.
2) Слово деньга произошло от названия татарской монеты «данги» или «тенга»
и т. п., в свою очередь восходящего к наименованию весовой и денежной единицы
«данг», бывшей в употреблении в Средней Азии и Иране. Татарского же
происхождения, вероятно, слово алтын, от «алтын» — шесть или «алтун» — золото. Имеются
и другие гипотезы о происхождении этого термина.
3) Слово «копейка» в русском языке встречается с XV века и возникло из
татарского названия монеты «динарь — копеки» =1/6 тенги. С 1704 г. копейки
изготовляли уже из меди.
16
ГЛ. 1. МАТЕМАТИЧЕСКИЕ ЗНАНИЯ В ДРЕВНЕЙ РУСИ
11 1 1 1
пол-пол-полтрети, т. е. ^ = у+ 79 + 97» а ^^ есть тРеть ^ез пол"пол"
29 1 1
полчетверти, т. е. об = ~з"~~з2- ^ти ДБа Ряда ДР°бей играли особенную
роль при расчете податей и составляли важную часть сошного письма,
как именовалась в XVI — XVII вв. совокупность приемов поземельного
налогового обложения.
Для названия целого числа единиц без половины ставилась перед
названием этого числа единиц приставка «пол». Полтретьи (не полтрети)
обозначало, таким образом, 2 1/2, полчетверты — 3 1/2, полшесты —
5 1/2 и т. п. До сих пор говорят: полтора (пол-втора) и при счете времени:
полтретьего, полшестого.
Математические памятники Киевской Руси, В X—XI вв. Киевское
государство достигло высокой степени могущества и культурного
расцвета. Оно поддерживало связи с Византией и Западной Европой.
При Владимире Святославиче в Киеве была основана для детей
приближенных к нему людей школа, в которой обучение велось по образцам
византийских школ; при Ярославе Мудром (1019—1054), как
свидетельствует летопись, переписывалось много книг. При княжеских дворах,
в церквах и монастырях появляются библиотеки. Наряду с Киевом
крупным культурным центром страны был Новгород, с его высоко
развитыми ремеслами и торговлей, которую он в широких размерах вел
и с заморскими странами. Летопись сообщает об открытии школы в
Новгороде Ярославом Мудрым, который «прииде к Новугороду собра от
старост и поповых детей триста учити книгам». Начальная
арифметическая грамотность не была редкостью даже среди простых новгородцев
XII — XIII вв.1). Однако до нас почти не дошло сведений о
математических знаниях того времени: в бесчисленных пожарах и разрушениях,
которые принесли с собой нашествия татар, погибли почти все рукописи,
за редчайшими исключениями. Сохранились только единичные
письменные свидетельства, знакомящие нас с математикой Киевской Руси далеко
не полностью.
Одним из исторических документов является «Правда Русская»—
сборник юридических установлений, регламентирующий наказания,
в частности, штрафы за всякого рода преступления. «Правда Русская»
была составлена в XI — XII вв. и дошла до нас в нескольких редакциях,
рукописи которых восходят к XIII — XV вв. Сочинение служит
драгоценным источником по метрологии. Наиболее интересные вычисления
имеются в статьях, входящих в состав так называемой Софийской
летописи 2), в которых идет речь о приплоде от скота и пчел и его стоимости,
о прибытке от высева хлебных злаков и т. п. Несомненно, что эти статьи,
по характеру совершенно отличные от всех других параграфов сборника,
и во многих редакциях отсутствующие, являются произвольной вставкой
каких-то переписчиков. В нескольких случаях здесь находится сумма
геометрической прогрессии со знаменателем 2. Так, указано потомство
от 22 овец за 12 лет, при невысказанном допущении, что вначале было
также 22 (или 21) барана, что каждая овца приносит за год по овце и
барану и что все потомство выживает. Через 12 лет овец будет 90112, баранов
столько же или на одного меньше. Указана также цена всего стада через
х) Л. Е. Майстров, О математических знаках и терминах, встречающихся
в археологических памятниках Древней Руси.— Ист.-матем. исслед., вып. X, 1957.
2) «Правда Русская», под ред. Б. Д. Грекова, М.—Л., 1940, стр. 352 и след.
КИРИК НОВГОРОДЕЦ
17
12 лет, если овца стоит 6 ногат, а баран 10 резан; цена —«40 000 гривен
и 5000 гривен и 50 гривен и 5 гривен и 40 резан» г) подсчитана для случая,
когда баранов вначале было 21. Принятая скорость размножения овец
недалека от действительной. Вместе с тем практического значения такой
подсчет, сделанный в допущении выживания всего стада за 12 лет, иметь
не мог. Статья возникла как обобщение и вместе с тем упрощение
наблюдаемых явлений. Такова же статья о приплоде от 22 коз. В аналогичной
статье о свиньях числовые данные между собою не согласуются и
внушают недоверие 2), но, по-видимому, и тут имелась в виду прогрессия
со знаменателем 2. В нескольких других статьях числовые данные не
подходят под какое-либо простое правило; возможно, что эти данные при
переписке были искажены.
Задачи на геометрические прогрессии привлекали математиков
с древнейших времен. Как вычисляли авторы математических статей
«Правды Русской», неизвестно. Впрочем, им требовалось немногое:
складывать, умножать на 2, 6 и 10, делить на 50. Более сложные расчеты нужны
были в календарных и хронологических расчетах, результаты которых
мы находим в древнейшем русском математическом сочинении, дошедшем
до нас целиком и принадлежащем новгородскому ученому Кирику.
Кирик Новгородец. В хозяйственной и гражданской жизни всех
народов большое значение имеет календарь, который является основой
и всякой хронологии. Свой календарь имели с древности и славянские
народы; о нем мы почти ничего не знаем. С принятием христианства
в Киевской Руси получил распространение юлианский календарь,
введенный в Римской империи в I веке до н. э. и слегка модифицированный
в Византии. Счет лет велся от «сотворения мира», именно с 5508 г. до
н. э., а днем Нового года было, как и в Византии, 1 сентября. В народе,
впрочем, широко принято было новый год начинать по старинному обычаю
в марте, когда наступает весенняя погода. Современное летосчисление
ввел с 1 (11) января 1700 г. Петр Великий, а старый юлианский стиль
был заменен новым григорианским с 14 (1) февраля 1918 г.
Календарь нужен был не только для регулирования земледельческих
работ и всей гражданской жизни, но и для своевременного отправления
церковных праздников. Эти праздники делятся на неподвижные, которые
имеют место всегда в одни и те же дни года, и переходящие, которые
в разные годы могут падать на разные дни. Переходящими являются
и дни некоторых постов. Все переходящие праздники и посты твердо
связаны с наступлением пасхи. Крупные деятели христианской церкви
неоднократно посвящали труды вычислению пасхалий. Уже английский
клирик Беда, прозванный Достопочтенным (672—735), считал нужным
обучать в церковных школах астрономии и арифметике, чтобы
разбросанные по разным местностям священники могли сами правильно
назначать переходящие праздничные дни.
Вычисление дня наступления пасхи представляет собой довольно
сложную математическую задачу. Согласно старинным правилам пасха
должна праздноваться в первое воскресенье вслед за весенним
полнолунием, наступающим не ранее дня весеннего равноденствия 21 марта и не
х) Автор этого текста не пользуется для обозначения 10 000 словом тьма, как
и для 100 000 словом легион. Видимо, эти термины были еще мало употребительны,
а второй из них, быть может, тогда вовсе не существовал (ср. стр. 11).
2) А. П. Юшкевич, О некоторых статьях «Правды Русской»,— Труды Ин-та
ист. естеств., т. II, 1948.
18
ГЛ. 1. МАТЕМАТИЧЕСКИЕ ЗНАНИЯ В ДРЕВНЕЙ РУСИ
позднее 18 апреля. Поэтому первый день пасхи бывает не ранее 22 марта
и не позднее 25 апреля. Не вдаваясь в некоторые, впрочем, существенные,
детали, мы отметим следующие наиболее важные для вычисления пасхалии
моменты. Прежде всего, лунный месяц, который длится чуть более
29,5 суток, почти целое число раз содержится в 19 солнечных годах
по 365,25 суток. По истечении 19-летнего «лунного круга» в 235 месяцев
фазы Луны всякий раз пробегают одни и те же числа юлианского
календаря. С другой стороны, в календарном году содержится 52 недели и один
или два дня, в зависимости от того, простой год или високосный. Поэтому
какой-либо день недели, например, первое мартовское воскресенье,
перемещается по различным числам, совершая периодический цикл
в 28 лет, так называемый «солнечный круг». В результате дни пасхи
перемещаются по числам календаря в определенной последовательности за
период в 28 х 19 = 532 года. По прошествии этого «великого круга»
или «великого индиктиона» весь цикл передвижения дня пасхи
повторяется *). Заметим еще, что при определении дней мартовских воскресений
исходили из того, что в году, предшествовавшем началу христианского
летоисчисления, воскресеньями были 7, 14, 21 и 28 марта.
С математической точки зрения вычисление дня пасхи приводится
к решению в целых числах линейных неопределенных уравнений.
Пасхалии рассчитывали на много лет вперед, неоднократно проверяли
уже сделанные таблицы. В народе производили вычисления по руке
и пальцам. Составление простых и удобных формул, учитывающих
различные не упомянутые нами обстоятельства,— дело, требующего немалого
остроумия. Этой задачей не пренебрегали самые крупные ученые. К. Гаусс
опубликовал без доказательства найденные им правила в 1802 г. Н. И.
Лобачевский посвятил этой задаче несколько параграфов «Алгебры или
вычисления конечных» (Казань, 1834). Н. Я. Сонин напечатал в томе V
«Математического сборника» (1870) перевод большой статьи Г. Кинкелина
«Вычисление христианской пасхи».
Вопросам хронологии и календаря и посвящено «Учение им же ведати
человеку числа всех лет», т. е. «Наставление, как человеку познать
счисление лет» Кирика — первого русского математика, известного нам
по имени 2).
Мы располагаем о Кирике очень немногими сведениями. Родился
он в 1110 г.3), а в 1136 г., когда написал свое «Учение», состоял диаконом
Новгородского Антониева монастыря. Он был близок ко двору
новгородского епископа Нифонта, которому адресовано другое сохранившееся
его сочинение, содержащее вопросы относительно церковных обрядов
и допустимости некоторых обычаев. Кирик участвовал также в
составлении первой Новгородской летописи. Из «Вопрошаний Нифонту» видно,
что их автор был человеком болезненным.
Сочинение Кирика о счислении лет состоит из 27 пунктов. В начале
указан год, в котором оно написано, именно 6644 г. от «сотворения мира».
Далее указано, что от этого момента до настоящего времени прошло
79 728 месяцев, или 346 673 недели,— тут разъясняется, что в году
х) Мы не касаемся небольших отклонений от этих целых чисел, которые
сказываются лишь по истечении больших промежутков времени.
2) Текст этого сочинения был впервые опубликован в 1828 г. по неполному списку.
Более полный список (начало XVI века) издали с русским переводом Т. И. Коншина
и В. П. Зубов; примечания принадлежат последнему. См. Ист.-матем. исслед., вып. VI,
1953.
3) А не в 1108 г., как указывали прежде.
КИРИК НОВГОРОДЕЦ
19
52 недели и один с четвертью день, или 2 426 721 день или 29 120 652
дневных часа и столько же ночных, считая по 12 часов в дне и в ночи. 29
миллионов Кирик называет 290 несведиями. Этот термин для 100 000
встречается только в рассматриваемом сочинении, слово же легион здесь не
Рис. 4. Фоторепродукция страницы рукописи «Наставления»
Кирика Новгородца (рукопись начала XVI в. из Погодинского
собрания, № 76 в Гос. публ. библиотеке в Ленинграде, л. 343).
употребляется. С числовой записью в рукописи можно познакомиться
по прилагаемой фотографии (рис. 4). Такие выкладки были в XII веке
нелегким делом. Недаром Кирик сопровождает подсчет числа часов
замечанием: «по малу бо созидается град, и великий бывает, тако и
20
ГЛ. 1. МАТЕМАТИЧЕСКИЕ ЗНАНИЯ В ДРЕВНЕЙ РУСИ
видение [знание] по малу на много приходит»1). Все приводимые
результаты вычислены точно.
Затем сообщается, как находить солнечный и другие круги, что
«от Адама» прошло 237 солнечных кругов и нового круга идет 8-й год,
349 —«полчетвертаста без одиного»— лунных кругов и нового круга
идет 13-й год, а также 12 великих кругов и 13-го прошло 260 лет. В
заключение приведены данные о пасхалии, рассчитанной самим Кириком на
6644 г. В этом году пасха пришлась на 22 марта, т. е. была наиболее
ранней возможной. Кирик говорит, что так бывает редко и в ближайший раз
это повторится через 248 лет. Очевидно, что пасхальные таблицы были
вычислены по крайней мере на два с половиной века вперед. В последних
строках автор сообщает свой возраст в годах, месяцах, неделях, днях
и часах. Вычисления с большими числами доставляли ему несомненное
удовольствие.
Любопытно применяемое Кириком деление часа на пятые, двадцать
пятые и т. д. доли, которые он называл «дробными часами» или «часцами».
Доходит он до седьмых дробных часов, которых в дне или ночи 937 500,
причем говорит, что от седьмых дробных уже ничего не получается.
Это, кажется, единственная пятеричная система деления часа; мы находим
ее затем лишь в некоторых русских рукописях XVI — XVII вв., уже
наряду с делением на минуты и секунды.
Почему же Кирик остановился на седьмых дробных? В. П. Зубов
объяснил это, предположив, что Кирик применил свои пятеричные
«часцы» к измерению длины астрономического года, исходя из
продолжительности 19-летнего цикла в 6940 суток2). Деление 6940 на 19 дает
в частном 365 суток и в остатке 5-24 = 120 часов. Деление 120 на 19
дает в частном 6 часов и в остатке 6. Остаток обращается в первые дробные
часы и 6-5 = 30 делится на 19 и т. д. Получив при седьмых дробных
в остатке 1, Кирик увидел, что умножение на 5 дает число, меньшее 19»
и потому объявил, что «не ражаются от седьмых дробных» 3).
Астрономический год выразится при этом как 365 дней 6 часов 1 первый дробный
час, 2 вторых дробных, 4 третьих, 2 четвертых, 1 пятый, 4 шестых и 1
седьмой. А. Е. Раик отметила еще, что от девятых дробных при делении
5-5 = 25 на 19 в остатке получается снова 6, как вначале, т. е. начинается
новый период бесконечной пятеричной дроби, так что «седьмые дробные
являются как бы естественным порогом, за пределами которого через
два шага картина циклически повторяется» 4). Не исключено, что Кирик
обратил внимание на такую цикличность.
Вопросы «философии математики». Математика в Древней Руси
не была ограничена кругом чисто практических вопросов и
хронологических вычислений. В образованных кругах пробуждался интерес и к более
отвлеченным вопросам.
В развитии европейской мысли средних веков большую роль сыграло
распространение воззрений Аристотеля. Идеи Аристотеля, в частности,
его учение о количестве, получили известность и в Киевском государстве.
х) Кирик Новгородец, Учение им же ведати человеку числа всех лет.—
Ист.-матем. исслед., вып. VI, стр. 178.
2) В. П. Зубов, Кирик Новгородец и древнерусские деления часа.—Ист.-
матем. исслед., вып. VI, 1953.
3) См. Ист.-матем. исслед., вып. VI, стр. 188.
4) А. Е. Р а и к, К вопросу о делении часа у Кирика Новгородца.— Ист.-матем.
исслед., вып. XVI, 1965, стр. 188.
ВОПРОСЫ «ФИЛОСОФИИ МАТЕМАТИКИ»
21
Об этом прежде всего свидетельствует сборник болгарского
происхождения, составленный в 1073 г. для черниговского князя Святослава Яросла-
вича (1054—1076), так называемый «Изборник Святослава», самый ранний
Рис. 5. Фоторепродукция страницы из факсимильного издания
«Изборника Святослава» (СПб., 1880, л. 164).
памятник древнерусской письменности х). Наряду с текстами по
грамматике, логике, поэтике и пр. здесь имеются статьи, восходящие к
«Категориям» Аристотеля и трактующие о количестве как мере, посредством
х) Изборник Великого князя Святослава Ярославича 1073 года, СПб., 1880.
22
ГЛ. 1. МАТЕМАТИЧЕСКИЕ ЗНАНИЯ В ДРЕВНЕЙ РУСИ
которой производится измерение и счисление, и о количественном, как
о том, что является измеряемым и счисляемым (рис. 5). «Количества же,—
сказано в сборнике,— ова суть разлучаема [одни дискретные], ова же
содержима [одни же непрерывные]» *); далее приводятся примеры и
пояснения. Более подробно те же вопросы рассмотрены в переводе
«Диалектики» византийского философа и богослова первой половины VIII века
Иоанна Дамаскина (ум. 749), дошедшем во многих списках. Хотя эти
списки начинаются с XV века, но сделаны со значительно более ранних
рукописей. У Иоанна Дамаскина даны античное определение числа как
собрания единиц, аристотелево определение непрерывных количеств,
как таких, чьи части соединяются общей границей («их же части к некоему
общему пределу совокупляются» 2)), указаны различные виды дискретного
{«содержащеся») и непрерывного («определеное») количеств. Последнее
делится на пять видов: тело, поверхность («явление»), линия («черта»),
место и время. В этой связи объяснено, что точка («срока») не имеет
измерения («расстояния»), линия — одно измерение и т. д. Количество
расчленяется также на конечное («убо есть в пределе») и бесконечное
(«беспредельно») и т. д.3).
Татарское иго. Так в X—XII вв. поднимались первые ростки
математики в России. Как в странах Западной Европы, так и в Киевском
государстве начиналось культурное пробуждение. На Западе знакомятся
с математикой арабоязычных народов, возникает борьба за внедрение
позиционной десятичной системы, переводятся арабские сочинения по
алгебре и тригонометрии. Около 1200 г. необычайно математически
одаренный пизанский купец Леонардо пишет знаменитый труд по
арифметике и алгебре Liber Abaci. В России, первоначально более связанной
с Византией, чем со странами ислама, развитие математики пошло иным
путем. Установление довольно оживленных государственных и
культурных контактов с рядом стран Западной Европы, казалось, предвещало
€ближение в ходе развития и в области математических наук.
Исторические судьбы сложились иначе. Раздираемая феодальными
междоусобицами, Киевская Русь не смогла противостоять полчищам татар. Она
заслонила собою лежащие к западу части Европы, но сама попала с середины
XIII века под тяжкое иго, которое на долгий срок задержало ее
культурный и научный прогресс. А. С. Пушкин как-то заметил, что татары не
походили на мавров: завоевав Россию, они не подарили ей ни алгебры,
ни Аристотеля. В общем итоге к началу Нового времени наша страна
значительно отстала от Западной Европы в науке вообще и в математике
в частности.
х) Изборник Великого князя Святослава Ярославича, л. 231 об. См. также
В. П. Зубов, К вопросу о характере древнерусской математики.— УМН, VII,
(3) 1952, стр. 84.
2) В. П. Зубов, цит. соч., стр. 86.
3) Там же, стр. 87—89.
ГЛАВА ВТОРАЯ
РУКОПИСИ XV—XVII вв.
Подъем Московского государства. Еще до разгрома войск Золотой
Орды Дмитрием Донским (1359—1389) в 1380 г. и окончательного
свержения татарского ига в 1480 г., его пагубное влияние постепенно слабеет,
хотя и продолжает тормозить развитие Русского государства. В XV веке
крепнет экономическое и политическое могущество Москвы и Новгорода.
В 1478 г. «Господин Великий Новгород» подчиняется Московскому
великому князю. Московское княжество уже со времен Ивана Калиты (1325—
1340) становится организующим началом Русского централизованного
государства, которое быстро расширяет свои границы, преодолевая
сопротивление русских феодальных князей и возвращая силой земли на
востоке и западе, на юге и севере, захваченные в период ига. С
укреплением и объединением Русского государства в XV — XVI вв., с
постепенным экономическим подъемом страны и ростом городов были связаны новые
запросы общества к математике. Большое государственное значение
приобрели межевание и измерение земель и раскладка податей. Увеличивался
торговый оборот внутри страны и с иноземными государствами, а
вследствие этого рос интерес к практической арифметике и практической
геометрии. Коммерческие и землемерные задачи оказывали длительное
и плодотворное влияние на развитие средневековой математики во всех
странах, в том числе и в России. Усиливается потребность в
математических знаниях среди строителей и военных. Исследователи истории
русской иконописи, а также гражданского, церковного и военного зодчества
подчеркивают выдающееся значение для этих отраслей искусства навыков
в практической геометрии, соблюдения определенных пропорций.
Организация войска и, особенно, артиллерии также требовали определенного
минимума математических знаний. В военной литературе тех времен
решен ряд задач на определение расстояний от далеких предметов или
высоты недоступных построек и т. п. Предъявляла свои запросы к
математике и церковь. Так, в конце XV века в Москве и Новгороде были
продолжены на несколько десятков лет вперед пасхальные таблицы
ранее доведенные до 1492 г., а в 1538 г. священник новгородского
Софийского собора Агафон рассчитал пасхальные даты до 7980 г., т. е. до 2472 г.
Наконец, и в сочинениях «светского», натурфилософского и
естественнонаучного содержания, которые имели довольно широкое
распространение среди интеллигентных людей, встречаются сведения по
математике.
Математических документов XV — XVI вв. сохранилось крайне
мало, но в книгохранилищах Советского Союза имеется много
десятков рукописных учебников математики, написанных неизвестными нам
24
ГЛ. 2. РУКОПИСИ XV—XVII ВЕКОВ
авторами в разное время на протяжении всего XVII века г). Книги эти не
тождественны между собою. Одни включают арифметику и геометрию,
другие только арифметику или ее отдельные вопросы, либо же только
геометрию. В одних задач больше, в других меньше; есть рукописи с
пространными предисловиями на нескольких страницах, есть сочинения
с коротенькими введениями в несколько строк. Основное арифметическое
и геометрическое содержание в большинстве случаев почти одинаково.
Нередко правила и задачи во всех рукописях изложены в одних и тех же
выражениях. Можно с уверенностью сказать, что все эти учебники
восходят к одному или немногим прототипам, которые до сих пор не
обнаружены. Все же между рукописями имеются различия в составе задач
и даже общих правил. Кроме того, на протяжении XVII в. наблюдается
постепенно вытеснение алфавитной нумерации современной. В более
ранних сочинениях славянская нумерация применяется еще довольно
широко и переплетается с так называемой арабской; к концу столетия
она становится все более редкой и сохраняется почти исключительно для
ознакомления с современными цифрами.
Арифметика в рукописях XVII века. Изложению арифметики
предшествовало введение, в котором специально подчеркивалась
общественная полезность и ценность этой науки. Арифметика рассматривается как
одно из семи «свободных искусств», составлявших в средневековой Европе
основу высшего образования: грамматики, риторики (искусства
красноречия), диалектики (искусства вести спор), музыки (учения о гармонии),
арифметики, геометрии и астрономии. В рукописи № 681 из собрания
В. М. Ундольского, хранящегося в Государственной библиотеке
им. В. И. Ленина (это рукопись первой половины XVII века), арифметика
именуется «пятой мудростью в семи великих мудростях» и о ней сказано:
«Сия мудрость есть изыскана древними философи остропаримого разума,
нарицается арифметика, сиречь счетная — арифмос по-гречески счет
толкуется. Ею же состоится численная всякая мудрость: сим бо числом
может числить всякой счет малой и великой, елико мощно постигнути
человеческому разуму» 2). Отмечается общее воспитательное значение
арифметики: «Сия мудрость... и честь дарует, и ум человеческий высоко-
парив творит, и память укрепляет, и острых острее творит в разум».
Несколько далее арифметика разъясняет от своего лица приносимую
ею пользу: «Аз заочные, невидимые и предъочные дела объявляю: в
солнечном же и в лунном течении разум многим подаваю; и в морском
плавании и в земном верстании наставляю и меру указую; и в купеческих
вещех и во всяких числех недоумени разрешаю...», а далее вновь
подчеркивается: «Без сея мудрости ни един философ, ни доктор не может быти.
По сей мудрости гости по Государствам торгуют» 3) и т. д. При этом
сказано, что арифметика — слово греческое, что по-немецки она называется
алгоризма, а по-русски — цыфирная счетная мудрость.
г) Ср. К. I. Швецов, Б1бл1ограф1я староруських математичных рукопкпв.—
Станиславський Державний педагопчний шститут. Науков1 Записки, Ф1зико-мате-
матична cepia, вып. 1, Кшв, 1955.
В личной библиотеке проф. И. К. Андронова имеется рукопись, содержащая
большой отдел арифметики и относящаяся ко второй половине XVI века. Эта
рукопись, во многом сходная с позднейшими, остается пока, к сожалению,
неопубликованной.
2) Цит. по кн.: В. В. Б о б ы н и н, Очерки истории развития
физико-математических знаний в России (далее: Очерки...), вып. I, М., 1886, стр. 5.
3) Там же, стр. 6.
АРИФМЕТИКА В РУКОПИСЯХ XVII ВЕКА
25
Руководства по арифметике предназначались, впрочем, не столько
для изучения навигации и астрономии, хотя были люди, знавшие и
любившие астрономию, сколько для торговцев, чиновников государственных
учреждений, землемеров, управителей имений, ремесленников и т. п.
Этим определялось и содержание учебников.
Весь материал распределен на «статьи», следующие в общем порядку
возрастающей трудности вопросов и содержащие «строки» х) — правила,
поясняемые затем многочисленными и обычно весьма хорошо
подобранными задачами, опять-таки следующими в порядке усложнения. Во
многих случаях задачи позволяли не только усвоить, но и понять механизм
действия правила.
Однако никаких теоретических выводов или разъяснений не
сообщалось. В те времена во всем мире был чрезвычайно широко
распространен подобный метод обучения и изложения, обращенный более
к памяти, чем к уму учащихся. В западноевропейской литературе
руководства такого рода часто назывались «Практическими арифметиками»
(или геометриями), а немногочисленные учебники, содержащие
доказательства, именовались «Теоретическими арифметиками» (или,
соответственно, геометриями).
Прежде всего разъясняется современная десятичная позиционная
нумерация (рис. 6). Введение новой нумерации, обусловленное ростом
связей со странами Западной Европы, явилось событием огромного
культурного и научного значения. В XVII веке в России новая нумерация
употреблялась еще только узким кругом знатоков математики. Детей,
вместе со славянской грамотой, обучали алфавитной нумерации, которая
применялась почти во всех печатных книгах и в общежитии. К изучению
арифметических рукописей приступали, уже владея алфавитной
нумерацией. Об этом свидетельствует тот факт, что новые цифры поясняются
в рукописях не только словами, но и надписанными сверху алфавитными
знаками чисел.
В статье о нумерации читатель знакомился также с
произношением чисел. Здесь приводились сведения об упоминавшемся уже выше
счете тьмами, легионами и леодрами, как в «малом» числе, так и в
«большом».
Слова: миллион, биллион, триллион и т. п. введены были
Л. Ф. Магницким в его «Арифметике» 1703 г.
Отметим здесь же, что в книгопечатании, официальной
документации, монетном деле переход к позиционной системе происходил
постепенно.
Если не считать славянских книг, изданных за границей в 1611 и
последующих годах, то датой появления новых цифр в собственно русской
печати был 1638 г. (Псалтирь, изданная в местечке Евю). Затем эти цифры
встречаются на многих чертежах и текстах к ним в «Учении и хитрости
ратного строения пехотных людей» (М., 1647). Таблицы произведений до
100 х 100 в «Считании удобном, которым всякий человек купующий
и продающий зело удобно изыскати может число всякие вещи» (М., 1682)
даны еще в славянской нумерации. Даже в 1702 г. половина тиража
«Юрнала» об осаде Нотебурга была выпущена с алфавитными цифрами,
между тем как другая половина — с новыми. В «Арифметике»
Магницкого применяется лишь новая нумерация, но пагинация алфавитная
г) Слово строка, вероятно, есть перевод латинского regula, обозначающего
и правило, и линейку.
26
ГЛ. 2. РУКОПИСИ XV—XVII ВЕКОВ
и так же дан год издания на титульном листе. После этого старая
нумерация исчезает из печати. В частности, «Книга считания удобного» была
Рис. 6. Примеры записи чисел славянскими и «арабскими» цифрами в
арифметической рукописи XVII в. (Гос. библиотека им. В. И. Ленина в Москве).
переиздана в новой нумерации (СПб., 1714). На русских монетах новые
цифры появились впервые в 1654 г.; в последний раз славянские цифры
были вычеканены на медных деньгах в 1718 г.
ИНСТРУМЕНТАЛЬНЫЙ СЧЕТ
27
Вслед за нумерацией излагались четыре первых действия над целыми
числами. Проверка вычитания производилась путем сложения разности
с вычитаемым, проверка прочих действий посредством числа 9. Проверка
девятью, известная еще древнегреческим и индийским ученым, основана
на том, что остатки от деления на 9 любого натурального числа и суммы
значений его цифр одинаковы. Если назвать такой остаток поверочным
числом, то, например, поверочное число суммы должно быть равно сумме
поверочных чисел слагаемых или, если эта вторая сумма более или
равна 9, поверочному числу этой второй суммы. При неравенстве названных
поверочных чисел сложение произведено безусловно неверно. Однако
это необходимое условие правильности результата не является
достаточным: поверочные числа могут оказаться равными и при неправильно
произведенном сложении. В этом легко убедиться хотя бы на примере
равенства 25 + 71 = 96 и 25 + 71 = 87, из которых первое — верное,
а второе — неверное. Впрочем, авторы рукописей формулировали
равенство поверочных чисел, как достаточное условие правильности выкладки;
так оно и бывает чаще всего в практике вычислителей. Для умножения
и деления правила проверки девятью формулируются сходно с правилом
проверки сложения (и вычитания).
При инструментальном счете (см. далее) все действия проверялись
€ помощью обратных. Так, в упомянутой на стр. 12—13 рукописи Э/РБ-40
Государственного Эрмитажа после описания умножения «костьми»
говорится: «А пытати хошь, гораздо ли счел или не гораздо умножал, и ты
пытай деловою строкою, которым перечнем умножал, тем и дели. Буде
з делу выдет такожде перечень, каков умножал, то гораздо столко.
Не таков, то не гораздо. Опять считай.» *). При действиях над дробями
каждая операция проверялась с помощью обратной.
Свойства арифметических операций были в то время выделены только
частично. В рукописях иногда упоминаются переместительное свойство
сложения (на примере 3 + 4 = 4 + 3) и умножения (на примере 1/3-1/4 =
= 1/4-1/3) 2).
Инструментальный счет. Производству арифметических действий
в письменном виде или в уме всюду предшествовали простейшие формы
инструментального счета: на пальцах, при помощи камешков или палочек,
зарубок на палке или узелков на веревке и т. п. и уже в древности
(Египет, Греция, Китай) появляются специальные счетные приборы, широко
распространенные в быту и особенно в торговом деле. В рассматриваемых
нами рукописях обычно кратко описываются два приема
инструментального счета. Один из них —«счет костьми», другой —«дощаной счет».
Счет костьми применялся во всей средневековой Европе, и в
западноевропейских странах его именовали счетом на линиях 3). Состоял этот
прием в следующем. На доске или столе проводили мелом несколько
горизонтальных прямых линий — для единиц, десятков, сотен и т. д.,
х) Цит. рукопись, л. к—к об., ср. также л. кв. Знаки препинания
поставлены мною. См. еще рукопись Рог. 23 Гос. библиотеки им. В. И. Ленина, л. 38
(согласно задаче на подсчет числа часов, прошедших от «сотворения мира», до 7138
(т. е. 1630) г. протограф или один из протографов этой рукописи 1681 г. относится
к 1630 г.; см. л. 252) и рукопись 17.6.24 Библ. АН СССР в Ленинграде, л. 16
(рукопись 1645 г.).
2) См. рукопись Э/РБ-40 Отд. ист. русск. культуры Государственного Эрмитажа
л. з об. и В. В. Б о б ы н и н, Очерки..., вып. I, стр. 66.
3) Кости в наших рукописях нередко именуются «пенязи» или «пеняги» —
от немецкого названия счетных жетонов Rechenpfennige.
28
ГЛ. 2. РУКОПИСИ XV—XVII ВЕКОВ
следуя снизу вверх. На каждую линию полагалось класть до четырех:
костей или жетонов; кость, помещенная между двумя линиями, означала
пять единиц того разряда, который откладывается на более близкой
к вычислителю линии. Далее доска расчерчивалась вертикальными
прямыми на несколько столбцов, в которые клали кости, выражающие
отдельные слагаемые или сомножители и т. д. Результат действия или
составляющие результат числа отмечались в свободных отделениях доски.
Мы приводим здесь (рис. 7) схему умножения 66 х 96 = 6336 (= 36 -f-
+ 540 +360 +5400).
Хотя счет костьми и был известен в России, но гораздо большей
популярностью пользовался дощаной счет — вычисления при помощи
прибора, бывшего прообразом русских счетов. Старинные русские счеты
•
•
1_*—
•
•
—*_
•
•
•
•
•
АЛЛА
•
• "
ШЛА
•
Рис. 7. Схема умножения при счете костьми или на линиях.
отличались от позднейших менее совершенным устройством, но и в
начальном виде позволяли быстро и легко производить .сложные арифметические
действия. Дощаной счет имел весьма широкое распространение среди
торговцев, служащих московских приказов, «мерщиков»— землемеров,
монастырских экономов и т. д. Как показывают новейшие исследования,
дощаной счет возник в связи с потребностями сошного письма, о котором
мы уже говорили ранее (стр. 16) *). Налог взимался поземельный, в
зависимости от количества и качества земельной площади, которую переводили
в условные единицы — сохи, по некоторым коэффициентам,
определявшимся не только качеством земли, но и социальным положением ее
владельца. Так, соха земли среднего качества, принадлежавшая церкви
или царю, составляла 1000 четвертей, земли помещичьей — 700
четвертей, а земли, обрабатывавшейся казенными крестьянами,— 600
четвертей. Измерением земель, их переводом в сохи и подсчетом налогов
занималась целая армия специальных чиновников, для которых составлено
было руководство —«Книга сошному письму» 2). Понятие сохи
своеобразно применялось и при обложении доходов горожан, не имевших
земельных угодий.
Дощаной счет в первоначальной форме был специально приспособлен
к нуждам сошной арифметики. Обычно прибор состоял из четырех
счетных полей, расположенных по два в двух ящиках, в каждом из которых
протянуто было по 14 параллельных веревок или проволок. Иногда таких
полей было два. На проволоках, предназначенных для счета целых
чисел, нанизывалось по 9 (иногда по 10) костяшек; на прочих — меньшее
1) И. Г. Спасский, Происхождение и история русских счетов.— Ист.-
матем. исслед., вып. V, 1952.
2) С. Б. В е с е л о в с к и й, Сошное письмо. Исследование по истории
кадастра и посошного обложения Московского государства, т. 1—2, М., 1915—1916.
ИНСТРУМЕНТАЛЬНЫЙ СЧЕТ
29
количество костяшек. В одном из полей имелась проволока с четырьмя
костяшками, а, кроме того, три проволоки с одной костью каждая: здесь
велся счет четвертям (земли), полчетвертям, пол-полчетвертям; в
соседнем поле, где имелась проволока с тремя костями, аналогично велся счет
с третями, полтретями и т. д. В другом ящике, назначавшемся для
денежных расчетов, имелись проволоки с пятью и шестью костями (1 алтын,
как уже говорилось, содержит 6 денег) и ряд проволок с одной костью
(рис. 8). Такие приборы уже в середине XVII века назывались просто
счетами и в рукописях более или менее подробно объяснено, как ими
Рис. 8. «Дощаной счет» с четырьмя счетными полями
(фотокопия из рукописи № 1664 Погодинского
собрания в Гос. публ. библиотеке в Ленинграде).
пользоваться. Способ вычислений в дощаном счете таков же, ^ак в
нынешних русских счетах. Отметим только, что сложение двух одинаковых
«сошных» дробей дает дробь ближайшего высшего разряда, например,
111
-гк + jo — ~а и т. п. На счетах сложению двух таких дробей соответствует
переход к ближайшей вышестоящей костяшке.
В сошной арифметике приходилось иметь дело и с более мелкими
дробями. В некоторых рукописях приводятся чертежи и описания «дщиц
счетных», аналогичных только что рассмотренным, но с большим числом
рядов с одной костью, так что на них можно откладывать доли до 1/128
и 1/96. Несомненно, что изготовлялись и соответствующие приборы.
Для удобства вычислителей приводилось много правил «свода мелких
костей», т. е. сложения употребительных в сошном счете дробей, вроде:
три чети сохи да полчети сохи да пол-полчети сохи и т. д. вплоть до пол-
пол-пол-пол-полчети сохи составляют соху без пол-пол-пол-пол-полчети,
т. е. 3/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 = 1 - 1/128 и т. п.1).
Сошное письмо вышло из употребления во второй половине XVII века
в связи с введением в 1646 г. подворного обложения (в 1722 г. замененного
подушным). Но русские счеты не исчезли вместе с сошным письмом.
Уже в XVII веке они прочно вошли в житейский обиход. Изменилась
лишь форма счетов, которые были теперь приспособлены прежде всего
х) И. Г. Спасский, цит. соч., стр. 346,
30
ГЛ. 2. РУКОПИСИ XV—XVII ВЕКОВ
к денежным выкладкам в наиболее употребительных валютных единицах:
осталось одно счетное поле и исключены лишние ряды костей. До сих пор
сохранились два ряда из четырех костей, применявшиеся ранее для счета
полушек — четвертей копеек и, быть может, четвертаков (четвертак —
25 копеек).
О происхождении русских счетов были высказаны различные
мнения. Некоторые, в том числе В. В. Бобынин, полагали, что они пришли
с Востока, от китайцев, быть может, через посредство татар. Однако
китайский суанпан существенно отличается от русских счетов
применением пятеричного принципа: в нем на каждой проволоке имеются пять
шариков со значением единицы соответствующего разряда и один или
два шарика со значением пяти таких единиц. Более вероятно мнение
И. Г. Спасского о самобытном возникновении счетов, как инструмента,
приспособленного для сошного письма. Идея устройства счетов могла
быть навеяна, согласно И. Г. Спасскому, четками, которые, как
свидетельствуют исторические памятники, носили многие русские люди.
Ритуальное применение четок соединялось, видимо, с их употреблением,
как простейшего счетного прибора *).
Вслед за описанием инструментального счета во многих рукописях
идут важные для торговцев и потому весьма обширные таблицы денежных,
весовых, сыпучих и иных мер Московского государства, Венеции,
Антверпена, Нюрнберга и других городов, с примерами перевода
больших мер в меньшие и обратно или перехода от мер одной системы к
другой 2). Разделы, посвященные счету, заканчиваются подробнейшим
изложением действий над обыкновенными дробями, первым из которых
служило «вынимание дробовое»— определение одной или нескольких долей
данного целого или дробного числа: такие величины участвовали затем
в остальных действиях над дробями. Особенно детально рассмотрено
сложение. Здесь дается 10 правил, начиная со случая, когда слагаемые имеют
общий знаменатель и кончая сложением выраженной смешанным числом
части смешанного числа с несколькими долями дроби (на примере: 32/3
от 21/2 плюс 4/5 от 6/7). В пояснение сложения в рукописях говорится:
«О разумении, что есть сложение долям. Буди же ти ведомо сице. Возми
число шесть. Что же половина изо шти; то есть три. Что есть треть изо
шти; то есть два. Сложи же половину с третью. Станет пять шестин» 3).
Строка тройная. Остальное содержание арифметических руководств
почти полностью составляют задачи коммерческой арифметики. Задачи
разбиты на многочисленные «статьи». Названия этих статей часто
покажутся странными нынешнему читателю, но в свое время они помогали
ориентироваться при поисках приема решения того или иного вопроса.
Например, в «Статье складной торговой» рукописей даны решения задач,
в которых требуется распределить прибыль между участниками
предприятия, внесшими в складчину определенные взносы (в более поздних
учебниках такие задачи объединялись под рубрикой «Правила
товарищества»). «Статья о нечисти во всяких овощах и товарех»— это статья на
правило смешения (название связано с тем, что в задачах смешивается,
г) И. Г. Спасский, цит. соч., стр. 372.
2) Таблицы восходят к «Торговой книге», составленной, вероятно, в XVI веке.
См. Записки отделения русской и славянской археологии Русского археологического
общества, т. 1, отд. 3, СПб., 1851, стр. 106—114.
3) Рукопись Арханг. Д—478 Библиотеки АН СССР в Ленинграде, л. 94 об»
СТРОКА ТРОЙНАЯ
31
скажем, чистый перец с нечистым). Впрочем, иногда под одной рубрикой
собраны были задачи различного содержания.
С математической точки зрения все задачи решаются при помощи
немногих приемов: тройного правила и правил ложного положения.
Тройное правило применялось при решении задач, в которых ищется
величина я, находящаяся в геометрической пропорции с тремя данными
величинами: — = —. Отсюда и наименование правила — правила трех
величин. Задачи такого рода встречались и решались с незапамятных
времен. В древнем Китае и особенно в Индии решению их был придан
характер регулярного правила, затем не позднее IX века оно попадает
в страны ислама, а в Европе с тройным правилом познакомились в XII веке
по сочинениям на арабском языке. И еще в Индии к простому тройному
правилу были добавлены обратное, а также правила 5, 7, 9 и т. д. величин.
Так, по правилу пяти величин находят величину х, удовлетворяющую
двум пропорциям:
х d у Ъ
у е ' а с '
abd -г-, г>
сразу в виде частного х = . Б задачах на обратное тройное правило
величины одной категории находятся в отношении, обратном отношению
соответствующих им величин другой категории.
В средние века, да и много позже, до XIX века включительно,
тройное правило с различными его вариантами занимало при обучении
арифметике одно из главных мест. Авторы европейских арифметических
сочинений XV и следующих веков расточали этому правилу похвалы, называли
его наиболее полезным правилом своей науки, «золотым». Сочинители
русских арифметических руководств также писали: «Та строка тройная
похвальная и лутчая строка изо всех иных строк. Философы ее зовут
златою строкою» *).
Описанию правила в рукописях не предпосылается объяснение
пропорции и ее свойств. Это стали делать много позднее, в середине
XVIII века. Общий прием решения задач на тройное правило сразу
формулируется в следующих словах: «Она [строка тройная] ставится
в три перечня [т. е. числа], ражает собою четвертый перечень. Поставит
первой перечень, а другим перечнем третей умножает, и что родится во
умножении, то первым перечнем делит и оттуды выходит четвертый
перечень». Непосредственно за этим следовал разъяснительный пример:
«Смотри: восмь; цена им, или добыли, или потеряли, или дали, или дадут,
или заняли, или платили. g[ . [12]. Что дадут, или платят, или что ни
есть десять? И ты умножай 12 с 10, придет 120; то дели ж на 8, придет 15,
мно стало сколь дорого 8, по той цене стало и 10». Самое вычисление
располагалось так: «Указ счету:
8 12 10
12
^15
120
8
2).
г) Этот текст из рукописи Ундольского № 681 цит. по кн.: В. В.Бобынин,
Очерки..., вып. I, стр. 8.
2) Этот текст из рукописи Ундольского № 681 цит. по кн.: В. В. Б о б ы н и н,
Очерки..., вып. I, стр. 8—9. Знаки препинания расставлены мною. (—А. Ю.)
32
ГЛ. 2. РУКОПИСИ XV—XVII ВЕКОВ
Как видно, в примере речь шла об отыскании, скажем, цены 10
предметов по известной (12) цене 8 таких же предметов:
х 10 12-10 ,к
¦j2" = -g-, откуда х = —g— =15.
В рукописях нет указания на круг вопросов, к которым применимо
тройное правило; где и как следует его применять, показывали
многочисленные дальнейшие задачи. При внимательном чтении подробного
решения таких задач учащийся вполне мог разобраться в механизме
действия тройного правила.
Не всегда, впрочем, решение задач достаточно мотивировано. Такова,
например, задача: при цене меры ржи 4 алтына, т. е. 12 коп., за 2 деньги
продается хлеб весом в 3V3 фунта; каков должен быть вес хлеба в ту
же цену, если мера ржи стоит 2 гривны, т. е. 20 коп.? Эта задача, по
существу, на обратное тройное правило. В рукописях, однако, без всякого
пояснения вопрос решается, как если бы имела место прямая
пропорциональность: «А считай сице. Постави на строку тройную и молви: 2 гривны
даст 3V3 фунта, что даст 4 алтына?» х), откуда искомый вес получается
равным 3-о---^г = 2 фунтам. Еще менее понятен без дополнительных
разъяснений ход решения задачи, составляющей «статью спрашивалную
со времены»: во сколько дней выпьет кадь кваса жена, если вместе с мужем
они ее выпивают за 10 дней, а один муж может выпить кадь за 14 дней.
Эта задача — типа старинных греческих задач на бассейны с трубами,
сохранившихся и в наших задачниках арифметики. И здесь приводится
только один рецепт: «А считай сице. Выни 10 из 14: останется 4. Молви:
4 даст 10. Что даст 14? Умножи 14 с 10, придет 140; дели ж ту 140 на 4,
станет 35 дней. В столько дней одна жена его кадь квасу выпьет» 2).
Решение задачи, таким образом, производится по тройному правилу, но
о самом приведении задачи к этому правилу ничего не сказано 3). Такое
решение могло быть усвоено только механически.
Строка фальшивая. Догматически излагалось в рукописях и другое
важное правило —«ложного положения», или, как оно в них называлось,
статья «вымышленая или затейчивая», а также «фальшивая». Правила
ложных положений, попавшие в Европу с Востока через посредство
переводов с арабского языка, применялись к решению задач, которым
соответствуют уравнения первой степени. Различались два вида этого
правила. Правило одного ложного положения применимо к задачам,
которые по-современному выражаются уравнением ах = с. Если
приписать искомому х произвольное «ложное» значение х± и обозначить ах{
через с4, то истинное значение х найдется по тройному правилу из
пропорции
X с
х^ с±
Возник этот прием в связи со стремлением избежать действий с дробями
в задачах, в которых коэффициент при неизвестном является суммой
г) Текст из рукописи Ундольского № 681 цит. по кн.: В. В. Б о б ы н и н,
Очерки..., вып. I, стр. 82.
2) Там же, стр. 83.
3) Муж с женой выпивают в день 1/10 кади, один муж — 1/14 кади; следова-
1 1 14—10 4
тельно, одна жена может выпить в день —— -— , т.е. ———_—__ кади и т. д.
10 14 14-10 14-10
СТРОКА ФАЛЬШИВАЯ
33
нескольких дробей:
\ 41 42 Чп )
В качестве ложного положения выбирали здесь число, нацело делящееся
на все знаменатели qu q2, . . ., qn. Правило распространяли и на задачи,
в которых коэффициент при неизвестном целый.
В. В. Бобынин, который впервые исследовал русские математические
рукописи XVII века, не усмотрел в них правила одного ложного
положения 1). Это правило в них, действительно, не сформулировано, но
фактически используется. Таковы, например, задачи «статьи деловой» рукописи
Рог. № 23 2). В одном случае 12 рублей делятся между тремя братьями
так, что доли их относятся, как 4:2:1. Мы бы выразили вопрос
уравнением -г + -7г + -г = 12. Автор принимает xt = 4, так что сумма всех
долей будет 7, а затем «ставит на строку», т. е. применяет для отыскания
каждой доли тройное правило. В другом случае требуется разбить число
100 на части так, чтобы треть одной из них равнялась учетверенной
другой. Если в уравнении х/3 = 4z/ взять х^ = 12, то у± = 1 и сумма
xi + У± = 13 вместо 100. «Ставя на строку», автор находит х = 92 4/13
и у = 7 9/13, добавляя: «Сице всегда ищи». Задача трактуется, по
существу, как система двух уравнений: уравнение с одним неизвестным
х/3 = 4(100 — х) по шаблонному правилу одного ложного положения
потребовало бы предварительного сведения к форме ах = с. Задачи»
подобные первой из приведенных, имеются во многих рукописях, иногда
под рубрикой «статьи фалшивой торговой складной» 3). Любопытно, что
в одной рукописи неизвестная величина именуется «столко», т. е.
количество 4). Гораздо чаще, однако, употреблялось правило двух ложных
положений.
Мы только что упомянули, что к задачам, непосредственно
выражающимся уравнением ах -\- Ъ = с, правило одного ложного положения
неприменимо. Для их решения издавна пользовались правилом двух
ложных положений, которое ранее всего встречается в китайской
литературе, не позднее начала н. э. Из Китая правило было перенесено много
веков спустя в страны ислама и отсюда попало в Европу. Искомой
величине х даются последовательно какие-либо два значения xt и х2. При ах± +
-\- Ъ = Ci и ах2 + b — с2 из данного уравнения и только что написанных
равенств следует, что
X — Х{ с — с±
х — х2 с — с2
Если с — ci = di, c — c2 = d2, то искомое значение
d2 — di
Мы вывели значение неизвестной алгебраически. В старинных
рукописях давалось только словесное предписание, без вывода. При этом
1) В. В. Бобынин, Очерки истории развития физико-математических знаний
в России, ч. III. Физико-математические науки в их настоящем и прошедшем, т. 7,
1888, стр. 307—308.
2) Рукопись Рог. № 23 Гос. библиотеки им. В. И. Ленина, лл. 95—97.
3) Например, в рукописях Арханг. Д — 478 (л. 178 об. —180 об.) и Арханг.
Д —479 (л. 176—177 об.) Библ. АН СССР в Ленинграде.
4) «Счетная мудрость». Труды Общества любителей древней письменности,
т. 43, СПб., 1879, л. 72 об.— Заметим, что в индийской алгебре неизвестная величина
нередко называлась «яват — тават», по-санскритски «столько — сколько».
34
ГЛ. 2. РУКОПИСИ XV—XVII ВЕКОВ
авторы, не знавшие еще отрицательных чисел, формулировали правило»
двух ложных положений отдельно для случая, когда с^ и с2 оба больше-
или меньше, чем с (т. е. ошибки db d2 — одинакового знака), и для
случая, когда одно из чисел си с2 больше с, а другое меньше (du d2 — разных
знаков). В первом случае неизвестная находится путем деления разностей,
а во втором — путем деления сумм.
Правило двух ложных положений дает точное решение для уравнения
первой степени с одним неизвестным и определенных систем таких
уравнений со многими неизвестными. Этот момент в некоторых рукописях
особо подчеркивается наряду с высокими требованиями, предъявляемыми
к тем, кто применяет правило ложных положений. Так, в одном
манускрипте конца XVII века мы читаем: «Статья цыфирная еже именуется
вымышленая или затейчивая высокого остропамятного разума, и любо-
трудного умного прилежания. Ее же нецыи фалшивой строкой нарекоша,
иже ни малым чим погрешается» х). Популярность правила в средние-
века и даже в XVII — XVIII вв. объяснялась тем, что оно позволяет
автоматически находить точное решение задач первой степени с одним
или несколькими неизвестными, не составляя уравнений и не анализируя
вопрос по существу. Правило двух ложных положений нередко
применялось также, да и теперь применяется, для приближенного вычисления
корней нелинейных уравнений, и его можно найти в любом современном
курсе приближенных вычислений. Из школьных программ его исключили
в начале XIX века.
Фальшивое правило описано в рукописях весьма подробно и общая
вычислительная схема иллюстрируется многими задачами. Ошибки имеют
специальные названия и обозначения. Если принятое «ложное положение»-
дает результат больше требуемого в условии, ошибка d помечается
«знаменем», т. е. знаком —\—, а если меньше, то знаком —'-—. Приведем ход.
решения задачи, которую можно записать уравнением *L = 18. Вначале
за х принимается 8, что дает для левой части уравнения 24 вместо 18,—
«ино тут много —}— 6», а затем берется число 7, причем получается 21,—
«ино много ж—¦—3» 2). Неизвестная я = 6 находится следующим образом:
3деловое Ч I 6 -то есть число.
о
~24
Знаки —|— и —\— характеризуют не сложение и вычитание, а
избыток и недостаток по отношению к числу, данному в условии.
Несомненно, что они, как и выражения «много» и, соответственно (в случае-
недостатка), «мало» восходят, как и вся схема вычисления, включая форму
записи, прежде всего к немецкой учебной литературе. Знаки -\- и —
появляются в ней в конце XV века, а знак —;— впервые встречается
у А* Ризе в 1525 г.; они использовались как в правиле ложного
положения, так и для действий сложения и вычитания. В 1489 г. И. Видман
г) Рукопись Арханг. Д — 479 Библ. АН СССР в Ленинграде, л. 126. Судя
по задаче об определении числа часов от сотворения мира до 7138 г. (л. 21—21 об.)г
протограф или один из протографов этой рукописи относится к 1630 г. Ср. стр. 27.
2) В. В. Б о б ы н и н, Очерки..., вып. I, стр. 92—93.
аз 42
__24__
вы 18 ни »
СТРОКА ФАЛЬШИВАЯ
35
писал: «das ¦+- das ist mer» и «was — ist das ist minus» x). Еще ранее схемой
с крестом и терминами plus (больше) и minus (меньше) пользовался
Леонардо Пизанский (1202) 2).
Приведем еще решение по фальшивому правилу задачи на отыскание
двух неизвестных по двум условиям: два купца, Петр и Иван, желают
приобрести двор ценой 38 руб. У Петра недостает до этой суммы 2/3
наличных денег Ивана, а у Ивана 3/4 наличности Петра. Задача может
быть записана системой уравнений:
*+-|-г/ = 38' (1)
У + 3. х = 38, (2)
где х — наличность Петра, у — наличность Ивана. В качестве первого
положения берется х<± = 24, тогда по (1) у± = 21; эти значения при
подстановке в левую часть (2) дают 39, т. е. на d± = 1 больше, чем следует.
В качестве второго положения берется х2 = 20, тогда по (1) у2 = 27;
это для левой части (2) дает 42, т. е. на d2 = 4 больше, чем следует. После
этого х и у вычисляются согласно правилам:
^24.4-20.1^1 21^2L1 = 19>
4—1 3 ' * 4—1
Авторы рукописей применяли правило ложных положений и к
задачам, которые мы выразили бы системами трех уравнений с тремя
неизвестными (статья фальшивая в три перечня) и даже четырех уравнений
с четырьмя неизвестными (статья фальшивая в четыре поставки, или
статья фальшивая четвертная). Не приводя безукоризненных вычислений
(они довольно длинны), мы только сформулируем на языке современной
символики одну такую задачу с четырьмя неизвестными:
x+±-(y + z + u) = 100,
y + ±(x + z + u) = 100,
z + ±(x + y + u) = 100,
u+±(x + y + z) = 10Q.
Здесь x = 2 26/37 рубля или 2 рубля 23 алтына 2 деньги и 1 3/37
полуденьги 3). Подобного рода задачи, восходящие к Диофанту, нередко
встречаются у средневековых западноевропейских математиков, начиная
с Леонардо Пизанского. Иногда к ним применялось, как позднее в наших
рукописях, правило двух ложных положений 4).
В некоторых случаях задачи, сводящиеся к двум линейным
уравнениям с двумя неизвестными, решаются без фальшивого правила.
г) J. Tropfke, Geschichte der Elementar — Mathematik, В. II, 3 Aufl.,
Berlin und Leipzig, 1933, стр. 22.
2) F. С a j о г y, A history of mathematical notations, vol. I, Chicago, 1928,
стр. 230—256.
3) В. В. Б о б ы н и н, Очерки..., вып. I, стр. 98—104.
4) См. К. V о g е 1, Die Practica des Algorismus Ratisbonensis, Munchen, 1954,
стр. 171—173, 187—188.— Practica представляет собой сборник задач, составленный
в Германии в середине XV века.
36
ГЛ. 2. РУКОПИСИ XV—XVII ВЕКОВ
В «Счетной мудрости» Общества любителей древней письменности имеется,
например, такая задача: «Идет корабль по морю, на нем мужеска полу
и женска 120 человек. Найму дали 120 гривен, мущины дали по 4 алтына,
а женщины дали по 3 алтына с человека. Сколько мужеска полу было
и женска порознь» *). Далее следует выкладка. Все суммы переводятся
в копейки, берется разность между оплатой проезда с мужчины и с
женщины, т. е. 3 к., 120 умножается на 9 и произведение 1080 к. вычитается
из 1200 к.; разность 120 по делении на 3 и дает число мужчин, равное 40.
Все завершается проверкой: 12-40 -\- 9-80 = 1200, за которой следует
одно слово: «правда». Здесь мы имеем дело с продуманным
арифметическим решением вопроса. Нам не встречались такого рода решения
линейных задач с 2 неизвестными в западноевропейских руководствах.
Задачи для развлечения. В конце многих рукописей, а иногда и в самом
тексте, приводятся еще задачи для развлечения и развития смекалки.
Есть среди них задачи на определение времени и места встречи
путешественников, движущихся с определенными скоростями друг за другом
или навстречу друг другу, на геометрические прогрессии, неопределенные
задачи на отыскание трех неизвестных по двум линейным зависимостям
и другие. Некоторые задачи можно найти в арифметических задачниках
вплоть до нашего времени, вроде задачи о гусях: «Летело стадо гусей,
навстречу им один гусь и рече: бог в помочь летети сту гусям. И гуси
яму сказали: не сто нас гусей всем стадом летит: нас летит стадо и как
бы и нам еще столко, да полстолка, да четверть столка, да ты, гусь, и то
было б сто гусей» (ответ: 36) 2). В одних рукописях ответ приводится
без вывода, в других он получен по правилу ложных положений.
Геометрические прогрессии. Мы рассмотрим здесь две группы задач.
Одна из них представляет собой излюбленные у многих народов, начиная
с древних египтян, задачи на суммирование геометрических прогрессий.
Уже в более ранней русской литературе встречались прогрессии,
знаменатель которых равен 2. В рукописях XVII века содержатся задачи на
прогрессии со знаменателями 2 (последний член прогрессии доходит до 224
и даже до 240), 3, 4, 5, 7, 8, 12, 40. Выбор знаменателей 7, 12, 40 не
случаен: эти числа занимали особое место в древнейшем счете, о чем
свидетельствуют различные поговорки и выражения, вроде «семь раз отмерь,
один отрежь», «сорок сороков»— в смысле очень большого числа и т. п.
Задачи часто приводятся в шутливой форме. Вот одна из них:
«Идет семь баб: 7
У всякия бабы по семи посохов: 49
На всяком посохе по семи сучков: 343
На всяком сучку по семи кошелей: 2401
Во всяком кошеле по семи пирогов: 16807
Во всяком пироге по семи воробев: 117649
Во всяком воробе по семи пупков: 823543
И всего — 960799» 3).
г) «Счетная мудрость», л. 86.
2) «Памятники древней письменности», СПб., 1878—1879. Вкладные листы
€ факсимиле арифметических задач, л. 315.
3) «Памятники древней письменности», СПб., 1878—1879. Вкладные листы с
факсимиле арифметических задач, л. 314.— В рукописи Арханг. Д — 478 Библ.
АН СССР в Ленинграде эта задача доведена до 78. Ср. там же прогрессию 40 +
_j_ 402 + . . . + 408 с суммой 6 721 641 025 640 (л. 228 об.).
ЗАДАЧА «О ДЕНЬГАХ В КУЧЕ ВЕДАТИ»
37
Первоначально сумму прогрессий находили, складывая подряд все
ее члены. Но русские арифметики XVII века знали и правило
сокращенного суммирования геометрической прогрессии. Именно,
Sn=l + q+...+qn
при целом д>2, находится следующим образом: целая часть от
деления qn на q—1 умножается на q и к результату прибавляется остаток,
т. е. 1. В самом деле,
-^ = l + q + q2+...+q"-i + —LT
(l + q+...+q--i).q + l=,Sn.
При q = 2 сумма вычисляется по правилу
1 + 2+ ¦ • ¦ +2?г = 2-2п —I1).
Такой прием суммирования встречается и в западноевропейской
литературе, например у итальянца Бельдоманди в «Algorismus de integris»
(1410; опубл. в 1483 и 1540 гг.) и в немецкой анонимной арифметике,
изданной в Бамберге в 1483 г.
Задача «о деньгах в куче ведати». В другой группе задач,
сводящихся к решению в целых числах неопределенных уравнений первой
степени, особый интерес представляет задача «О деньгах в куче ведати».
Она впервые встречается у китайского математика Сунь-цзы, жившего
примерно в III веке н. э.: требуется найти число, которое при делении
на 3, 5 и 7 дает соответственно остатки 2, 3 и 2. Китайские математики
уже знали общий метод ее решения. Неизвестными путями задача попала
в Византию, где мы ее находим в одной рукописи конца XIV или начала
XV века, а также в Европу. Здесь она имеется в «Книге об абаке»
Леонардо Пизанского (1202), который мог с ней познакомиться во время своих
поездок в арабские страны и Византию, позднее в немецких арифметиках
XV века, у французского математика Баше де Мезириака (1612) и т. д.
Ею занимался Эйлер, а полное обоснование способа ее решения при
любом числе делителей дал К. Гаусс (1801). В терминах теории сравнений
Гаусса для случая 3 попарно взаимно простых делителей задача Сунь-цзы
формулируется так: ищется решение системы сравнений
х = rd (modft),
х= r2(modq2),
x = r3(modq3).
Основным является определение вспомогательных чисел N±, N2, N3.
удовлетворяющих другой системе,
Niq2q3= 1 (mod ft),
#2?1?з= l(modg2).
N3qiq2= l(modgr3).
Решение дается сравнением
x = {Niq2q3ri + N2qiq3rz + N3qtq2r3) (mod д&ЯзЬ
г) «Счетная мудрость», л. 24 об., 25.
38
ГЛ. 2. РУКОПИСИ XV—XVII ВЕКОВ
откуда легко находится наименьшее положительное решение, которое
только и интересовало средневековых математиков.
Во многих русских рукописях механизм решения описан весьма
лаконично. «Аще хочеши в куче деньги ведати, и ты вели перевести по
3 деньги. А что останется от 3-х, 2 или 1, и ты за 1 по 70. Да опять вели
перевести по 5, и что останется 4 или 3, или 2, или 1, и ты за 1 клади
по 21. Да опять вели перевести по 7, и что останется, 6 или 5, или 4, или
3, или 2, или 1, и ты тако же за всякий 1 клади по 15. Да что в остатках
перечни родились, и те перечни сочти вместо; а сколько станет и ты из
того перечню вычитай по 105, и что останется от 105 или сама 105,
то столько в куче и есть» 1). Как видно, здесь сразу названы числа
А^^Мз = 70, N2qiq3 = 21 и N^q2 = 15, после чего предлагается
составить сумму 70^ -f- 21г2 + 15г3; ответ находится, как наименьшее
положительное значение разности 70г± -f- 21r2 -f- 15г3 — ЮЫ при целом t.
По цитированному правилу можно решить задачу с данными делителями
3, 5 и 7, но не с какими-либо другими делителями, так как не сказано,
ни как находить числа N±, N2, N3, а по ним А^д2#з и т. д., ни как
образовано число 105 = gi<72#3-
Задача Сунь-цзы была известна у нас и в других числовых вариантах.
В рукописи Рог. 23 (лл. 227 об.—228 об.) с той же краткостью приведены
правила решения еще для двух троек делителей 5, 7, 9 и 15, 28, 19. Здесь
также без всяких объяснений даются в первом случае N^qz = 126,
-^2<Мз = 225, N3q1q2 = 280 и gig2#3 = 315, а во втором соответственно
6916, 4845, 4200 и 7980.
Однако мы можем утверждать, что наши арифметики XVII века
полностью владели общим алгоритмом решения задачи 2). Об этом
свидетельствует «Счетная мудрость», изданная Обществом любителей древней
письменности. Данная рукопись вообще весьма интересна, так как
написана учеником. Об этом говорят отличия от стандартных текстов других
рукописей, язык, очень близкий к устной речи, необычная подробность
многих выкладок и объяснений, сокращения слов, обилие описок и т. д.
Иногда писавший как бы пересказывает то, что слышал от учителя и
благодаря тому знакомит нас хотя бы отчасти с процессом обучения. И вот
в «Счетной мудрости» в деталях объяснено, как находить
вспомогательные числа iVi, iV2, N3 и заодно числа А^д2д3, называемые «примерами»,
а также модуль дадг^з» именуемый «деловым числом». Решение получается
как остаток от деления iV"1g2g3ri + -^2?19зг2 + Лгз?1?2гз на деловое число 3).
Все это иллюстрируется на самом частом и старинном случае делителей
3, 5, 7. Так, чтобы отыскать «пример» для 3, составляется произведение
5-7 = 35 и с помощью проб ищется такое наименьшее Ni4 чтобы А^-35
при делении на 3 давало в остатке 1: «Будет же от того деления останется
одна [т. е. 1], то пример будет тому числу, коим делил то число, что делил,
или хотя без доль придет. А будет же сперва не придет, не останется
одного числа от первого деления... и ты тот перечень зачни умножать с.2.
и дели тем числом, которому пример станешь искать, чтоб одно число
в долях осталось. А будет из.2. ум[ножил], а одного числа от делу не
останется, и ты тот перечень хотя до.30. [нужно: до 3] умножай, по
единому числу прибавливай впрет, вдугорет [в другой ряд] с.З. ум[ножь],
г) Цит. по кн.: В. В. Б о б ы н и н, Очерки..., вып. I, стр. 117.
2) А. П. Юшкевич, Об одной задаче теории чисел в русских математических
рукописях XVII века— Труды Ин-та ист. естеств. и техн., т. 17, 1957.
3) При делении нацело искомым оказывается, как мы видели, само «деловое
число».
ЗАДАЧА «О ДЕНЬГАХ В КУЧЕ ВЕДАТИ»
39
в трете с.4. и впред потому же и от которого ум[ножил] от делу останется
одно число, то ум[ноженное] число и пример станет» *).
В «Счетной мудрости» (лл. 100—101 об.) задача решена еще во
многих вариантах, с тройками делителей 5, 7, 9; 15, 19, 28 (обе тройки
Рис. 9. Фоторепродукция таблицы для решения задачи «О деньгах в куче
ведати» (рукопись Э/РБ — 40 Государственного Эрмитажа в Ленинграде, л. 24).
имеются в рукописи Рог. 23); 7, 9, 11 («примеры» 99, 154, 441); 9, 11, 17
<«примеры» 748, 1530,1089) и, наконец, И, 13,17 («примеры» 221, 1496, 715).
*) «Счетная мудрость», л. 99. Разумеется, чтобы найти N± в случае делителя 3,
достаточно использовать iV4 = 1, 7V4 = 2, iV^ = 3 (последнее для случая деления
без остатка).
40
ГЛ. 2. РУКОПИСИ XV—XVII ВЕКОВ
В западноевропейских книгах по арифметике дается такое же
правило подыскания чисел Л^д2<7з и т. д.*). Но в них не встречается решение,
записанное в виде таблицы, которое имеется в уже не раз упоминавшейся
рукописи Государственного Эрмитажа. Текст задачи на остатки совпадает
с цитированным выше, а за ним на отдельном листе следует заполненная
славянскими цифрами таблица с тремя входами, в которую занесены все
наименьшие числа, дающие при делении на 3, 5, 7 соответственно остатки
от 1 до 3, от 1 до 5, от 1 до 7. Таблица окаймлена указателями остатков
в современном начертании. Под таблицей разъяснено, как ею
пользоваться: «по 3 перевесть и на той стране смотри, где по три стоит. В другой
ряд перевесть по 5 и на другой стране смотри, где стоит по пяти и в той
полосе друг против друга стоит. А в третью статью перевесть по 7. Итого
смотри сверху, что скажет и по полосе поди и как до той полосы дойдет,
то и укажет» 2) (рис. 9). Например, чтобы найти число, дающее остатки
2, 3, 4, следует в строке, соединяющей число 2 в левом указателе остатков
от деления на 3, и число 3 в правом указателе остатков от деления на 5,
взять число, стоящее под 4 в верхнем указателе остатков от деления на 7,
т. е. число 53. Всего в таблице 105 чисел, дающих наименьшие значения
х = 70г± + 21г2 + 15г3 —105*.
Вдоль каждой строки следуют числа в арифметической прогрессии с
разностью 15 (так как г4 и г2 постоянны), причем, если числа больше 105,
то вычитается 105. Вдоль каждого столбца (где г3 постоянно) числа
возрастают на 91, с той же оговоркой относительно вычитания 105. При
переходе от последнего члена строки к первому члену следующей число
увеличивается на 1. Составление таблицы было, по-видимому, делом одного
из русских математиков.
Терминология. Математическая терминология XVII века была еще
во многом несходна с установившейся позднее. Число часто называлось
перечнем, нуль — оном, оником (название буквы «о»). Дроби — обычна
«доли»— 1/5, 1/7... именовались пятиной, седьминой и т. п., а 12/13 либо
двенадцать тринадцатин, либо двенадцать тринадцатых жеребьев
(т. е. частей). Вместо «сумма» говорили исподний большой перечень,,
т. е. нижнее большое число (сумма подписывалась под слагаемыми —
перечнями), вместо «уменьшаемое» и «вычитаемое»— заемный и
платежный перечень, вместо «делимое», «делитель» и «частное»— большой,
деловой и жеребейный перечень. Специальных названий для множителей
не было. Числитель дроби назывался верхним числом, а знаменатель —
нижним. Появлялись и некоторые иностранные термины. Так, мы
встречаем статьи: «Нюмерасие [лат. numeratio], или считание словесем и
начертание числом цыфирным», «адитсие [лат. additio], или считание», но также
сложение; «сюстряксие» [лат. substractio], по-русски вынимание или
вычитание, «мюлтипликасие [лат. nmltiplicatio], или умножение числу
всякому», «статия дивизие [лат. divisio] или деловая, или росчетная» 3).
Основы современной русской математической терминологии были далее
развиты в XVIII веке.
г) Ср. К. V о g е 1, Die Practica des Algorismus Ratisbonensis, стр. 120—121.
Решение поясняется здесь на том же примере делителей 3, 5, 7. Все остальные
примеры (их 8) отличаются от имеющихся в наших рукописях.
2) Рукопись Э/РБ — 40 Отделения истории русской культуры
Государственного Эрмитажа, л. 24.
3) Цит. по кн. В. В. Бобынин, Очерки..., вып. I, стр. 6—7, 62—63.
ОЦЕНКА АРИФМЕТИЧЕСКИХ РУКОПИСЕЙ
41
Оценка арифметических рукописей. Как видно из нашего обзора,
русские арифметические учебники XVII века сообщали большую сумму
знаний, начиная с элементарных правил нумерации и действий над
целыми дробями и кончая приемами решения задач, приводящихся
к системам четырех уравнений первой степени с четырьмя неизвестными.
Мы подчеркивали, что изложение арифметики носило в рукописях
догматический характер. Учащемуся предлагались готовые правила,
поясняемые многочисленными задачами. Способ умножения и деления
дробей, столь смущающих, как известно, новичков, не мотивировался;
понятия отношения и пропорции не вводились и т. д. С современной нам
точки зрения такую методику можно было бы подвергнуть критике, так
же как и некоторые другие недостатки изложения (неоправданное иногда
существом дела распределение задач по «статьям» и т. п.).
Подчеркивая эти методические недостатки, В. В. Бобынин высказал
в свое время мнение о «низком состоянии интеллектуальных средств»,
имевшихся «в распоряжении наших арифметиков XVII столетия и более
ранних времен», об отсутствии у них «ясного представления о сущности
предмета и о том общем, что скрывается под видимым разнообразием
частных случаев» *). Сознательное употребление тройного правила,
например, он считал для них немыслимым. Здесь, однако, смешиваются
два различных вопроса — об уровне изложения предмета, с одной
стороны, и об уровне знаний составителя учебника, с другой.
Догматизм изложения был присущ почти всей тогдашней литературе
по «практической» математике. Математика средневековой Европы
развивалась прежде всего как наука купцов, строителей, художников,
горных техников, военных инженеров, чиновников, мастеров. Эти люди
не были знакомы с античным идеалом математической строгости, да и не
испытывали нужды в такой строгости. Математика была нужна им как
средство решения сравнительно простых задач, встречавшихся в
практической деятельности, и в учебной литературе они искали предписаний
и правил для таких типичных задач.
Воспитание мышления стояло в педагогике тех времен на заднем
плане, хотя его значение иногда декларировалось самими авторами
практических руководств. Даже в XVII и XVIII вв. сохранялся большой
спрос на руководства, содержавшие только правила арифметики и
геометрии, поясняемые на примерах и задачах.
Самое беглое сопоставление русских арифметических рукописей
с наиболее популярными сочинениями по практической арифметике
в Германии, Франции, Англии XVII века показывает их тесное
внутреннее родство. Это была литература одного стиля — и по содержанию
и по форме. Везде мы встречаем рецептурную манеру изложения, везде
в центре стоит тройное правило, а за ним — правило ложного положения;
везде, наконец, мы находим классификацию задач по правилам —
тройному, товарищества, смешения и пр., классификацию, сохранявшуюся
до конца XIX века и отвергнутую лишь новой методикой. Сходны многие
задачи в книгах на разных языках. Они нередко отличаются только
числовыми данными.
Несомненно, что составители русских рукописей знали и
использовали западноевропейскую учебную литературу по арифметике. Точно
назвать сочинения, бывшие в их распоряжении, мы не можем, но это
не столь важно. Различия между русскими, немецкими, французскими,
г) В. В. Бобынин, Очерки..., вып. I, стр. 67—68.
42
ГЛ. 2. РУКОПИСИ XV—XVII ВЕКОВ
итальянскими и т. д. арифметиками были менее существенны, чем то,
что имелось в них общего. Скорее всего наши авторы примыкали к немец-
жим учебникам. В пользу этого говорят как изложение ряда вопросов
в наших рукописях (счет костьми, правило ложных положений и др.),
так и общие исторические соображения: оживленные торговые связи,
сравнительная географическая близость немецких стран и т. д. Весьма
вероятно, что в распоряжении наших авторов были также польские
и голландские учебники. Но, во всяком случае, наши рукописи не
являлись переводом или переложением какого-либо одного труда. Все они
заметно отличаются от любого из нам известных зарубежных учебников.
Русские авторы тщательно и вдумчиво перерабатывали доступные им
материалы, учитывая запросы своего читателя и уже сложившиеся в
стране традиции. Отметим, прежде всего, переделку всех задач применительно
к русской системе мер. Уже одно это требовало большой предварительной
расчетной работы, невозможной без ясного понимания соответствующих
приемов. Далее, наши рукописи выделяются во всей европейской
арифметической литературе обилием подробно решенных задач. Эта
особенность, обусловленная потребностями самоучек и недостаточным в то время
числом школ, сохранилась и во многих русских учебниках XVIII века.
Можно отметить целый ряд более частных отличий. Так, в
противоположность ряду зарубежных учебников, наши рукописи не содержат
распределения задач на тройное правило по рубрикам прямого и обратного,
а также пятерного, семерного и т. п. правил. Небольшой популярностью
пользовалось у нас правило одного ложного положения,
распространенное в западных странах. То же следует сказать о счете на линиях;
наоборот, широко распространился в России самобытный «дощаной счет».
Наконец, мы находим в рукописях оригинальные вещи, вроде таблицы
решений задачи на остатки.
Если к сказанному добавить, что при устном обучении, несомненно,
давались дополнительные объяснения, то становится очевидным, что
высказанная В. В. Бобыниным оценка «интеллектуальных средств»
русских математиков XVII века несправедлива. Конечно,
арифметические рукописи подобно большинству учебников представляли собой
компиляции, но их составление могло быть посильно только людям,
свободно владевшим всей системой тогдашней практической арифметики
и способным к ее сознательному употреблению. И если упоминавшаяся
«статья спрашивалная со времены» помещалась среди задач на тройное
правило, то не потому, что авторы рукописей не понимали сути этой
не столь уж трудной задачи, но по невниманию (в данном случае) к
методической стороне обучения.
Мы обязаны авторам арифметических руководств XVII века многим.
Эти люди явились в России пионерами распространения десятичной
позиционной нумерации и построенной на ней «алгорифмической» арифметики.
Они во многом подготовили почву, на которой выросли учебная
литература и школа XVIII столетия.
Измерение фигур. В рассматриваемых рукописях имеются также
сведения по геометрии, преимущественно об измерении площадей и
объемов1).
г) Подробнее см. В. В. Б о б ы н и н, Очерки..., вып. II, М., 1893; К. I. Ш в е-
ц о в, Навчальш поспбники з геометрп та викладання геометрп в Pocii в XVII ст.—
Науково-дослщний шститут педагогши. Науков1 записки, т. XIII, Ф1зико-матема-
тична cepin, вып. II, 1959.
ИЗМЕРЕНИЕ ФИГУР
43
Для измерения земельных участков их разбивали на простейшие
фигуры. Были известны точные правила измерения площади
прямоугольника, прямоугольного треугольника и прямоугольной трапеции.
Площадь треугольника вычисляется по различным правилам: как
произведение половины меньшей стороны на большую, как произведение
половины большей стороны на полусумму двух других и еще по так
называемой формуле Герона. В рукописи Ленинградской публичной
библиотеки им. Салтыкова-Щедрина F — IX.47 оба последних способа
применяются к треугольнику со сторонами 13, 14, 15. По формуле Герона
площадь равна 84, а формула S = —^—^ дает 101 1/4 (с погрешностью
около 20%). В рукописи на это расхождение не обращено внимания *).
В других задачах погрешность менее значительна, но приближенный
характер ряда правил нигде не отмечается. Четырехугольник иногда
разделяется на треугольники; применяется также выражение его площади
в виде произведения полусумм противолежащих сторон, что дает (кроме
случая прямоугольника) результат с избытком. Невнимание к точности
правил сопровождается иногда пренебрежением к условиям задач и
некоторые грубые ошибки повторяются во многих рукописях. Такова,
например, задача на вычисление площади четырехугольника со сторонами
256 1/2, 26 1/2, 467 1/2 и 65 1/2. Здесь произведен полный расчет по
правилу S = а~^~с ^—. Между тем такой четырехугольник явно
невозможен, ибо третья сторона больше суммы остальных (рис. 10) 2).
Площади произвольных многоугольников измеряли, разбивая их
на треугольники и четырехугольники, или же по общему правилу,
включавшему невысказанное допущение, что любые плоские фигуры с равным
периметром имеют одинаковую площадь. Именно, принимали, что всякий
многоугольник равновелик квадрату со стороной, равной четверти его
периметра. Правило рекомендовалось как точное. В рукописи из собрания
В. М. Ундольского № 682 (Гос. библиотека им. В. И. Ленина) говорится,
что, вычисляя таким образом, «единую сажень не потеряешь» 3). На самом
деле ошибка при этом может быть весьма значительной. В случае круга
(С \ 2
-г\ ,
соответствующей приближению я ^ 4, дает результат, меньший истинного
С2
S = -т-г- примерно на 20% 4). В «Счетной мудрости» встречается
аналогичный, только еще ухудшенный прием «землемерия округою» 5),
происхождение которого неизвестно: сторона квадрата, равновеликого данной
фигуре, берется равной ее периметру, деленному на 4 2/3. Фигура может
быть при этом многоугольной или криволинейной, притом не обязательно
г) К. I. Швецов, цит. соч., стр. 92—93.— Заметим, что в данной рукописи
есть несколько задач на построение: перпендикуляра в конце отрезка, середины
отрезка, центра круга и др.
2) На это не обратили внимания ни В. В. Бобынин (цит. соч., вып. II,
стр. 96), ни К. I. Швецов (цит. соч., стр. 102).
В «Счетной мудрости», изданной Обществом любителей древней письменности,
эта ошибка повторяется в случае четырехугольника со сторонами 256 1/2, 26 1/2,
367 1/2 и 35 1/2 (л. 117 во второй пагинации).
3) В. В. Бобынин, Очерки..., вып. II, стр. 111.
4) Это грубое приближение иногда применялось в Западной Европе еще в
_Х-Х1 вв.
5) «Счетная мудрость», л. 114 об.
44
ГЛ. 2. РУКОПИСИ XV—XVII ВЕКОВ
выпуклой. Так находится, например, размер пахотной земли участкаг
на котором имеются болота, озеро, лес и гора (рис. 11).
Наряду с этим для измерения круга применялись и более
совершенные приемы. В рукописях Ундольского № 682 и F — IX.47
Ленинградской публичной библиотеки им. Салтыкова-Щедрина площадь круга
Рис. 10. Задача на измерение площади четырехугольника с неправильными
числовыми данными (фоторепродукция из факсимильного издания «Счетная
мудрость», СПб., 1879, л. ИЗ).
(7 \ 2
что соответствует приближению я ^ 3 1/16 = 3,0625. Там же приводится
построение круга, равновеликого квадрату (как иногда выражаются,
циркулатура квадрата), для чего в качестве диаметра круга принимается
4/5 диагонали квадрата. В рукописи F — IX.47 мы читаем (рис. 12):
«Землю четвероуголною хошь круглину учинити и ты из угла в угол положи
черты на крест и размерь из угла в угол на 10 мер, а в четверти по 5 и от
угла остави 5-ю меру очерти цыркулем и стала она из четвероуголного
кругла» х); как видно, при построении пользовались циркулем. Этой
циркулатуре квадрата соответствует приближение я = 3 1/8 = 3,125.
Обе только что указанные квадратуры известны были еще в древней
Индии и неоднократно применялись западноевропейскими математиками
средних веков 2). И, наконец, длина окружности выражается через диа-
х) К. I. Швецов, цит. соч., стр. 105.
2) См. М. Cantor, Vorlesungen liber Geschichte der Mathematik, B-de I—II,
Leipzig, 1899—1906; по указателю (число я).
ИЗМЕРЕНИЕ ФИГУР
45
22
метр соотношением С = -=- d, восходящим к Архимеду. Из всего этого
следует, что авторы рукописей не имели еще точного понятия о взаимных
связях между длиной окружности, площадью круга и его диаметром,
ограничиваясь приближенными правилами измерения различной степени точности.
Рис. 11. «Землемерие округою» (фоторепродукция из факсимильного издания
«Счетная мудрость», СПб., 1879, л. 115).
Помимо перечисленных, в рукописях имеются задачи на определение
расстояний — гипотенузы по катетам или одного из катетов по гипотенузе
и другому катету; впрочем, указания, что
рассматриваемый треугольник — прямоугольный, мы при этом
не встречаем. Есть и задачи на определение расстояния
до недоступного места или же высоты предмета с
помощью двух различных шестов данной длины или одного
такого шеста. Правила недостаточно полны и в них
ничего не говорится о подобии треугольников, на
которое они опираются1). Аналогичные задачи разобраны
в рукописи по военному делу, составленной на
основании, главным образом, «Kriegsbuch» Л. Фронспергера
(Франкфурт-на-Майне, 1566—1573) в 1606—1607 гг. М. Юрьевым и И.
Фоминым, а затем дополнительно обработанной в 1620 г. А. Михайловым 2).
г) В. В. Б о б ы н и н, Очерки..., вып. II, стр. 155—160.
2) Издание текста А. Михайлова: Устав ратных, пушечных и других дел, касаю-
щих до военной науки. М., 1777—1781. См. Т. И. Р а й н о в, Наука в России XI—
XVII веков, М.—Л., 1940, стр. 295—299.
46
ГЛ. 2. РУКОПИСИ XV—XVII ВЕКОВ
Как упоминалось, в рукописи F — IX.47 есть задачи на построениег
которые не встречаются в других: перпендикуляра в конце отрезка,
середины отрезка, центра окружности, а также задачи на преобразование фигур
в равновеликие, например, прямоугольника в квадрат. Пояснения
отсутствуют и чертежи, иллюстрирующие преобразования фигур,
несовершенны. Точно так же без всяких объяснений решена в этой рукописи задача
на вычисление высоты h прямоугольного треугольника по данным катетам
и г. аЪ г)
а, о ж гипотенузе с: п = — '.
Сообщаются в наших рукописях и правила нахождения некоторых
объемов: куба, прямоугольного параллелепипеда, прямого цилиндра
(здесь площадь основания исчисляется по диаметру при я = 3), бочки.
Объем бочки определяется, исходя из допущения, что она равновелика
цилиндру, имеющему ту же высоту и диаметр основания
diJr2d2-\-d3
4
где du d3 — диаметры нижнего и верхнего оснований бочки, a d2 —
диаметр параллельного основаниям сечения, проходящего через воронку.
Результат получается меньший истинного.
К задачам на измерение площадей и теорему Пифагора примыкает
в некоторых рукописях описание извлечения квадратного корня-«радикса
геометрического» из многозначного целого числа, последовательные цифры
корня устанавливаются на основании правила возведения в квадрат
двучлена. В случае иррационального корня У а2-{-г, где г < 2а +1,
дробная часть приближенно вычисляется по своеобразному правилу,
нигде более, кажется, не встречающемуся. Если, для простоты, целая
часть корня двузначна а = 10а + Р> то )/~a2-\-r представляется в виде-
10а + р + /on 4- r\ ft ' аналогично находится дробная часть в других
случаях 2). В немногих примерах с дробями дело приводится по
приближению к целым числам. Например, в треугольнике с катетами 9 1/2 и 6 3/4
квадрат гипотенузы 135 52/64 заменяется на 136, после чего значение
]/436 получается равным 11 15/21.
Точно так же в стереометрической части рукописей иногда
сообщается прием извлечения «кореня осмоу го лного», т. е. кубического корня на
основе правила возведения двучлена в куб. Дробная часть
иррационального кубического корня находится по правилу ]/а3 + г = а -\- ^ .
Как видно, в целом геометрические знания в России XVI — XVII вв.
значительно уступали арифметическим. Рукописи по геометрии нередко
содержат ошибки. Переписывались они весьма некритически. Чертежи
часто плохого качества. Такое различие в состоянии арифметики и
геометрии объяснялось, по-видимому, следующим. Арифметика в
значительной мере обслуживала предприимчивый торговый люд, высоко
ценивший точность в денежных расчетах. А землемерной геометрией занимались
чиновники, пользовавшиеся прадедовскими приемами, не придавая
большого значения их точности и не будучи заинтересованными в ней. Обилие
свободной земли также не стимулировало аккуратности измерений.
г) К. I. Швецов, цит. соч., стр. 86—90.
2) Напомним, что общепринятые приближенные формулы суть ~\/а2 + r ^
Г / т
^ а + 7л—ПГ (по неД°статку) и у а2 + г s а + — (по избытку).
ГЕОМЕТРИЧЕСКАЯ РУКОПИСЬ «СИНОДАЛЬНАЯ № 42» 47
Геометрическая рукопись «Синодальная № 42». Все же
рассмотренные рукописи недостаточно полно отражают геометрические знания
в России того времени. Имелись и высокообразованные любители наук,
стремившиеся поднять уровень математического просвещения в стране.
Попытку такого рода предпринял составитель первого русского
систематического курса геометрии, точнее, планиметрии, в котором около
350 страниц и множество чертежей, и рукопись которого
«Синодальная № 42» хранится в Московском государственном историческом музее.
Судя по первому из двух предисловий к рукописи, составителем был
князь Иван Елизарьев; согласно второму — свое сочинение он писал,
в 1625 г.1)'.
Елизарьев был очень начитанным в геометрии человеком. В своей
работе он использовал многие источники. Первое предисловие начинается
с указания, что оно «собрано» «от многих учителей и их книги у меня все»
и далее говорится: «Начало философеи и ритории и иных мудростей, что
подобает к геометрии, собрал я от различных многих старинных
мудростей и книг» 2). Особенно опирался Елизарьев на «Резюме геометрии»
(Geometrical extraction, London, 1616) англичанина Дж. Спейделя и
весьма известные в ту пору «Двадцать семь книги геометрии» (Geometriae
libri XXVII, Basileae, 1569) французского философа и математика
Пьера ла Рамэ или, в латинизированной форме, Петра Рамуса,
выдающегося педагога, стремившегося к упрощению изложения геометрии и ее
приспособлению к нуждам практики. Свой труд Елизарьев рассматривал
как элементарное руководство, советуя затем изучать Евклида, «Рамеюса»
и иных «учителей»3).
Геометрия определяется в первом предисловии, как «мастерство
чтобы было добро положено» 4),— так перевел Елизарьев слова, с которых
начинается книга ла Рамэ: «Geometria est ars bene metiendi», т. е.
«Геометрия есть искусство хорошо измерять». Значительная часть этого
предисловия является переводом или пересказом текста ла Рамэ, в
котором говорится о предмете геометрии, о мерах, о смысле, придаваемом
термину «геометрия» разными авторами — Платоном, Плутархом и др.
Язык предисловия труден, а порой даже неясен. Отчасти это можно
объяснить терминологическими трудностями, которые приходилось
преодолевать Елизарьеву.
Собственно геометрический текст рукописи начинается с 47
определений, называемых «совершениями» 5),— линии, поверхности, тела,
перпендикуляра, различных видов углов, треугольников и
четырехугольников» окружности, касательной, параллельных прямых, подобия фигур
и т. д. Тут же вводятся понятия об измерении площади квадрата и
градусной мере углов.
Приведем для примера определения прямого угла и
перпендикуляра: «Аще прямая черта упадет на другую прямую черту, сотворяет
углы на всякие страны равны и всякой угол нарицается прямой угол,
а та прямая черта, которая справлена, нарицается стоячея» 6). К
определениям иногда добавлены указания на свойства фигур, Так.
*) Ю. А. Белый иК. И. Швецов, Об одной русской геометрической
рукописи первой четверти XVII века.— Ист.-матем. исслед., вып. XII, 1959, стр. 186—188.
2) Там же, стр. 194.
3) Там же, стр. 208.
4) Там же, стр. 193.
5) Греческое 'opog — граница, предел; латинское definitio происходит от defi-
nire — ограничивать, устанавливать и т. п.
6) Ю. А. Б е л ы й и К И. Ш в е ц о в, цит. соч., стр. 204.
48
ГЛ. 2. РУКОПИСИ XV—XVII ВЕКОВ
определив равносторонний треугольник, автор указывает, что каждый
из его углов составляет шестую часть «венца»— окружности.
Далее следует 74 планиметрические теоремы —«видения» х), по
большей частью восходящие к первым шести книгам «Начал» Евклида.
Формулировки теорем сопровождаются пояснениями, иногда включающими
элементы доказательств. Мы особо отметим 59—61 теоремы, а именно
неравенства 3 10/71 < я < 3 1/7, приближение п = 22/7, выражение
площади круга через радиус и длину окружности и приближенное
выражение площади квадрата на диаметре круга через 14/11 площади последнего
(все это со ссылками на Архимеда), а также 66 теорему об отношении
площадей кругов (она доказана в XII книге «Начал»).
Определения и теоремы составляют две части первой книги рукописи.
Две другие части, образующие вторую книгу, содержат 132 построения —
«провидения». Помимо простейших построений, мы находим здесь,
например, деление отрезка в среднем и крайнем
отношении (№ 20), деление окружности на
равные части — до 10 частей (№ 25),
преобразование пятиугольника в равновеликий
четырехугольник (№ 26), проведение касательной
к окружности из внешней точки (№ 31),
построение треугольника и вычисление высоты
С по трем данным сторонам (№№ 42—43),
построение треугольника по различным условиям,
Рис. 13. Задача о делении скажем, подобного данному треугольнику
треугольника на пять рав- и равновеликого данному квадрату (№ 81),
ных частей. деление треугольника на данное число
равновеликих частей прямыми, выходящими из точки
на одной из его сторон (№ 123; ср. рис. 13, где число частей пять и
сторона ВС разделена на пять равных частей).
Даже это неполное перечисление говорит о замечательном богатстве
руководства Елизарьева как в теоретической части, так и в отделе
построений. Мы не будем подробно останавливаться на его терминологии, которую
он должен был в значительной мере создавать впервые. Иногда он
подбирает русские слова, иногда копирует латинские и английские термины.
Подобие называется «сподоблением», касательная —«притирающей
чертой», слово «основанный» означает пропорциональный; есть «паралле-
лицкие черты», «дегриис» (англ. degrees) или «степени», т. е. градусы,
«скара» (англ. square) — квадрат либо площадь и т. д.
Елизарьев надеялся на издание книги в типографии. Обращаясь
к царю Михаилу Федоровичу (1613—1645), он писал: «А буде твое
государьское жалованье будет, велишь к печати ту книгу отдать и толды еще
стану смотреть у справки. Надеюсь, государь, на милость божию и на
твое государьское жалованье, что не будет та книга виновата, хотя без
помощника справлена» 2). Царь и его приближенные не сочли этого
нужным и рукопись осталась в единственном экземпляре, который
автор не отредактировал окончательно. Первый печатный учебник
геометрии вышел в России более чем 80 лет спустя, а равноценные
по содержанию руководства еще позднее, после основания
Академии наук.
г) Греческое слово Фешрт^а (от Фесорбсо— смотрю, вижу) означает зрелище,
видение, а также доказываемое предложение.
2) Ю. А. Белый и К. И. Швецов, цит. соч., стр. 201.
Ж
ПРОБЛЕМЫ НЕПРЕРЫВНОГО И НЕДЕЛИМЫХ
49
Проблемы непрерывного и неделимых. В XV—XVII вв. среди части
русской интеллигенции вновь усиливается, как некогда в Киевской Руси,
интерес к естествознанию и философии. Упоминавшаяся выше
«Диалектика» Дамаскина переписывалась в то время неоднократно, а в XVI веке
был сделан новый ее перевод (с латинского перевода). В последние
десятилетия XV и начале XVI вв. в Новгороде, Пскове, Москве и других
городах появилась рационалистическая ересь «жидовствующих», сторонники
которой изучали по рукописным переводам астрономию, медицину,
логику и т. д. В одной такой космографической рукописи XVI века
имеются некоторые сведения по математике. Так, в ней приведено
определение сферы по «премудрому Клидасу», т. е. Евклиду: «И то нарицается
круг, половина обыходу кругового и около снура, олны дойдеть до местьца
своего, тогда ся наречеть круг равен в частках своих, а плоть одержанаа
в обыходе том наречеться круг» х). Здесь слово круг имеет значение шара;
в этом смысле в других местах рукописи кругами называются небесные
сферы и небеса (латинское orbis также обозначало круг и небо). Это
определение весьма близко к данному Евклидом в XI книге «Начал»: «Сфера
будет: если при неподвижности диаметра полукруга, вращающийся
полукруг снова вернется в то же самое [положение], из которого он начал
двигаться, то охваченная фигура [и есть сфера]» 2).
Слова «равен в частках своих» выражают, быть может, равенство
радиусов сферы. Не ограничиваясь этим, автор рукописи определяет
еще сферу по «премудрому Феодосию», автору «Сферики» (ок. 100 г. до
н. э.), который «зоветь кругом то, что [в] своей тычьце равен по своим
сторонам; тычка же насереднейшаа, то есть — тычька кругови, а снур —
то, что приходить с одной стороны круговой и до другое через тычьку его».
«Снур», определение которого дается попутно, означает здесь диаметр;
это же слово обозначало тогда более общим образом линию. В рукописи
упоминаются прямые и непрямые углы и приведено градусное деление
зодиака. Каждый его знак, «задея», делится на 30 «степеней», т. е.
градусов, степень — на 60 «дробниц», т. е. минут, далее идут 60 «уторых»—
секунд и 60 «третьих»— терций.
В тех же «еретических» кругах был выполнен перевод части
«Стремления философов» (Маккасид ал-Фаласифа) мусульманского богослова
второй половины XI и начала XII века ал-Газзали, именно входящей
в состав этого труда «Логики» и части «Метафизики». Сочинения
ал-Газзали, в натурфилософии близкого к Аристотелю, оказали заметное влияние
на средневековую европейскую мысль. Математические вопросы
затрагиваются ал-Газзали многократно. Так, в «Логике» попутно упоминается
теорема о равенстве суммы углов треугольника двум прямым («...також
отлучится мыслию будущу углом треснурии ровно двема стоящим») 3).
Перевод «Метафизики» сделан с древнееврейского перевода; он сохранился
в нескольких списках, доходящих до XVIII века 4). Как и в «Диалектике»
*) А. И. Соболевский, Переводная литература Московской Руси XIV—
XVII вв., СПб., 1903, стр. 409—412. Здесь даны лишь отрывки из «Космографии»,
полностью еще не изученной. Об астрономическом содержании ее см. Т. И. Рай-
нов, Наука в России XI—XVII вв., стр. 239 и след. Однако Т. И. Райнов ошибочно
принял это определение за дефиницию круга (стр. 209—210).
2) «Начала Евклида», книги XI—XV, перев. и комментарии Д. Д. Мордухай-
Болтовского, при ред. участии И. Н. Веселовского, М.—Л., 1950, стр. 10.
3) С. Л. Неверов, Логика иудействующих.— Киевские унив. изв., 1909,
№ 8, стр. 46. Перевод Неверова сделан по рукописи второй половины XV века.
4) В. П. Зубов, Вопрос о «неделимых» и бесконечном в древнерусском
литературном памятнике XV века.— Ист.-матем. исслед., вып. III, 1950. В. П. Зубов
взял за основу одну рукопись XVII века.
50
ГЛ. 2 РУКОПИСИ XV—XVII ВЕКОВ
Дамаскина, мы находим здесь определения тела («плотного»), поверхности
(«простора») и линии («снура»); в теле можно разместить «три снуры
врезных на углы стоящий» (три пересекающиеся под прямыми углами
линии — прямые) 2), поверхность имеет «должину» и «ширину», а линии
только «должину»; к этому добавлено далее, что «тычка не имать меры»,
т. е. величины 2). Характеризуются виды углов —«стоящих», «острых»
и «широких» (тупых). Количество делится на «урезное»— дискретное
и «прилепное»— непрерывное. Обсуждается вопрос, есть ли линия
результат движения точки, причем ответ гласит, что это на самом деле
не так, хотя и мыслимо.
Наибольший интерес представляет анализ проблемы строения
непрерывных тел. Эта проблема обсуждалась в греческой философии и науке
еще с V века до н. э. Здесь боролись две основные концепции. Согласно
одной все состоит из физически или же мысленно неделимых частей;
по второй континуум потенциально бесконечно делим, так что не состоит
из атомов. Первый удар по учению о неделимых нанесли знаменитые
парадоксы Зенона Элейского. Развитие математики в Греции опиралось
на признание неограниченной делимости непрерывных величин. Лишь
в вопросах, относящихся к вычислению площадей и объемов
криволинейных фигур, отдельные ученые, например, Архимед, прибегали к идее
неделимых, как удобному средству исследования и открытия, но не
убедительного доказательства. Ряд аргументов против учения о
неделимых развили Аристотель и его последователи. Эта аргументация перешла,
в научную литературу на арабском, древнееврейском и латинском языках
и оживленно обсуждалась в средневековой схоластике. С нею же мы
встречаемся в русском переводе сочинения ал-Газзали.
Вслед за Аристотелем ал-Газзали критикует мнение, что непрерывное
тело состоит из неделимых в действительности или в мысли атомов.
Для этого выдвигается шесть аргументов, имеющих целью показатьу
что допущение неделимых приводит к противоречиям, например, к тому,
что диагональ квадрата оказывается равной его стороне, а это ложно,
«занеже мерою наугольник [диагональ] долже стран его много и се ведомо
с премудрости мерныя [из геометрии]» 3). Как и Аристотель, ал-Газзалн
принимает лишь потенциальную бесконечную делимость непрерывного:
тело имеет части не актуально («в деле»), а потенциально («в силе»).
В «Метафизике» разбирается и вопрос о бесконечно большом. Ал-Газзали:
отвергает «безконечьство» (также «безконечие») пустого или наполненного
пространства и цепи причин, но признает бесконечность времени и
мирового движения, и еще числа душ за бесконечное время существования.
Вселенной.
Проблемы непрерывного и дискретного, актуальной и потенциальной
бесконечности обсуждались не только инакомыслящими любителями
натурфилософии. Они излагались в учебных курсах физики, которые
читались в Киево-Могилянской академии, основанной в 1631 г. и Славяно-
греко-латинской академии, учрежденной в Москве в 1687 г. Эти учебные
заведения долгое время готовили образованных людей не только для
церкви, но и для государства, и лишь в начале XIX века были
преобразованы в чисто духовные высшие школы. В Славяно-греко-латинской.
г) В. П. Зубов, Вопрос о «неделимых» и бесконечном в древнерусском:
литературном памятнике XV века—Ист.-матем. исслед., вып. III, 1950, стр. 411, 412.
2) Там же, стр. 413.
3) Там же, стр. 420.
итоги
51
академии, как и в Киево-Могилянской, наряду с арифметикой читались
лекции и по курсу геометрии. Так, например, Феофан Прокопович
(1681—1736), сам бывший воспитанником Киевской Академии, в начале
XVIII века читал в ней на латинском языке довольно обширный
математический курс, в программу которого входили планиметрия,
излагавшаяся в духе обработки «Начал» Евклида, сделанной Хр. Клавием (1574),
сведения о квадратуре круга с помощью квадратрисы, понятия о
конических сечениях и спиралях. В Московской Академии обучался некоторое
время М. В. Ломоносов, впервые познакомившийся здесь с античными и
средневековыми воззрениями на континуум и атомистику1).
Итоги. Подводя итоги развития математической культуры в России
до XVIII века, мы видим, что к этому времени были удовлетворены лишь
первые потребности в сравнительно элементарных областях. Возникла
рукописная литература по практической арифметике и геометрии, но
попытка создания более совершенных руководств по геометрии не
получила официальной поддержки. Отдельные любители математики не
выходили за пределы решения любопытных частных задач и изучения
вопросов, связанных с натурфилософией. Правительства московских
царей, плохо понимавшие экономические и технические потребности
страны и неприязненно относившиеся к светской культуре Запада, почти
ничего не сделали для распространения в России технических и научных
знаний, соответствующих запросам эпохи. Духовенство решительно
поддерживало и нередко направляло царскую власть в этих вопросах.
В надгробном похвальном слове Петру I, произнесенном 29 июня (10 июля)
1725 г., Феофан Прокопович не очень сгущал краски, восклицая: «Тыя
прежде были ли? Не ведаю во всем государстве, был ли хотя один цирклик,
а протчаго орудия и имен не слыхано; а есть ли бы где некое явилося
арифметическое или геометрическое действие, то тогда волшебством нари-
цано» 2). В итоге наука в целом, и математика в частности, резко
отставали у нас от передовых стран Западной Европы, где на протяжении
XVII столетия достигнуты были большие успехи в астрономии и механике,
химии и биологии, где Декарт и Ферма заложили начала аналитической
геометрии, Ньютон и Лейбниц, завершая труды целой плеяды ученых,
разработали основы дифференциального и интегрального исчисления,
и где успешно исследовались проблемы теории чисел, теории
вероятностей, проективной геометрии и т. д. При всем том, перелом в истории
России, одним из важных элементов которого явился и перелом в развитии
у нас науки, был в конце XVII века уже не за горами.
г) В. П. Зубов, Ломоносов и Славяно-греко-латинская академия,— Труды
Ин-та ист. естеств. и техн., т. I, 1954.
2) Феофан Прокопович, Сочинения, М.—Л., 1961, стр. 135, 136.
ГЛАВА ТРЕТЬЯ
ГОСУДАРСТВО И МАТЕМАТИКА В ЭПОХУ ПЕТРА ПЕРВОГО
Подготовка военных и технических кадров. В первой четверти
XVIII века математическому просвещению в России было сообщено новое
направление. Математика перестает быть частным делом и обучение ей
ставится на службу политическим, военным, экономическим задачам
государства. За распространение светского образования борется с
большой энергией правительство во главе с царем, позднее императором
Петром I (1682-1725).
Одним из главных пунктов постепенно складывавшейся программы
деятельности Петра было создание кадров технической и
административной интеллигенции. Спешная подготовка специалистов была необходима
для новой регулярной армии, строившегося мощного флота,
насаждавшихся мануфактур, дорожного дела, для подвергнутого коренной
переделке правительственного аппарата. Петр столкнулся с отдельными
элементами этой задачи в юношеских военных играх с «потешными»,
а завершил свою просветительскую деятельность указом о создании
Академии наук.
Еще в молодости Петр с охотой изучал математику и овладел ею по
крайней мере в объеме, нужном для квалифицированного инженера,
архитектора и навигатора. По-русски он писал с ошибками, но с чертежами
и математическими приборами обращался свободно. В этом, как и во
многих других отношениях, он на голову превосходил не только своих
предшественников на русском престоле, но и других монархов.
Практическое значение математики ему было ясно и в организованных при нем
первых специальных школах она стала одним из основных предметов,
за преподаванием которого постоянно и пристально следили он сам и его
сподвижники.
Новые школы. О роли, которая придавалась математическому
образованию, говорит даже название некоторых школ. Первой была основана
по указу 14 (25) января 1701 г. школа «математических и навигацких,
то есть мореходно хитростно искусств учения» в Москве. Математико-
навигацкая школа, помещавшаяся с 1702 г. в снесенной в тридцатые
годы нашего века Сухаревской башне (рис. 14), была своего рода
политехникумом, откуда ежегодно выходили многие десятки молодых людей
различных сословий во все роды военной, морской и гражданской службы.
В 1714 г. приступили к организации в ряде городов низших «цыфирных»
школ. В 1711 г. в Москве начала функционировать инженерная школа
и в 1712 г. артиллерийская; обе они впоследствии были переведены
в Петербург. В 1715 г. от Навигацкой школы отделилась Морская
академия в Петербурге, которой поручено было готовить специалистов для
флота: Россия стала к тому времени крупнейшей морской державой.
НОВЫЕ ШКОЛЫ
53
Тогда же возникло несколько горных училищ на Урале. Несмотря на
многие трудности — недостаточную квалификацию преподавателей,
нехватку книг и приборов, суровый школьный режим, нежелание дворян,
Рис. 14. Сухаревская башня, в которой помещалась
Московская Навигацкая школа при Петре I.
чтобы их дети учились вместе с ребятами «неблагородного»
происхождения, несмотря на нерадивость самих учеников, иногда бегством
спасавшихся от горьких корней учения, не дожидаясь его сладких плодов,—
названные школы дали стране первые сотни и тысячи столь необходимых
ей специалистов, в том числе и учителей. В Сухаревской школе препода-
54 ГЛ. 3. ГОСУДАРСТВО И МАТЕМАТИКА В ЭПОХУ ПЕТРА ПЕРВОГО
вание математики с самого начала включало арифметику, геометрию,
тригонометрию, пользование таблицами логарифмов, счетными
линейками. Обучение на первых порах и еще долгое время носило механический
характер: требовалось только запоминать правила и уметь применять
их к соответствующим задачам.
Я. В. Брюс. Петр Великий имел в этом деле ряд помощников.
Ближайшим был генерал Яков Вилимович Брюс (1670—1735), из «потешных»
выросший в крупного государственного деятеля — начальника всей
артиллерии, президента берг- и
мануфактур-коллегии и т. д. Брюс
получил хорошее образование в доме отца,
прибывшего в середине XVII века из
Шотландии в Россию и здесь
назначенного командиром одного из
полков. В 1697—1698 гг. около года
Брюс занимался в Англии с
преподавателем математики и астрономии.
Обе науки он изучил весьма
глубоко. Он много читал и оставил после
себя большую библиотеку (около
1500 книг), а также собрание
научных инструментов, которые завещал
Академии наук. В Сухаревской
башне он оборудовал первую в России
обсерваторию, сам изготовлял для
нее инструменты и вел наблюдения
и составил звездную карту. Он
выпускал календари, занимался научными
переводами и руководил как Нави-
гацкой школой, так и изданием
многих книг. Ему принадлежит за-
Я. В. Брюс. слуга пропаганды в России коперни-
канства, враждебно встреченного
православной церковью, и идей Ньютона г). Любопытны письма, которыми
обменивался этот замечательный человек с академиками И. Г. Лейтма-
ном, механиком и оптиком (1667—1736) и Л. Эйлером2).
К преподаванию в Навигацкой школе было привлечено несколько
человек. Во главе дела был поставлен А. Д. Фархварсон. Его ближайшим
помощником являлся Л. Ф. Магницкий; с ними работал также Стефан
Гвин, перешедший затем в Морскую академию (ум. 1720) и Грейс
(ум, 1709) 3). Фархварсону и особенно Магницкому принадлежат
почетные места в истории нашего просвещения.
1)Б. Е. Райков. Очерки по истории гелиоцентрического мировоззрения
в России, 2-е изд., М.—Л., 1947; В. Л. Ченакал, Яков Вилимович Брюс —
русский астроном начала XVIII века.— Астроном, журнал, т. XXVIII, вып. 1, 1951.
2) Научное наследство, т. 2, М., 1951, стр. 1083—1101 и Ист.-матем. исслед.,
вып. X, 1957, стр. 95—116.
3) Гвин и Грейс прибыли в Россию из Англии вместе с Фархварсоном (см. далее);
оба были, насколько известно, воспитанниками Оксфордского университета.
Возможно, что это были Sackvill Gwynne, поступивший в университет в 1689 г. в
возрасте 15 лет, и Robert Gray, поступивший в 1679 г., будучи 16 лет [письменное
сообщение д-ра Симпсона (W. D. Simpson) через посредство д-ра Уайтмана —
(W. P. D. Wiffhtman); оба — сотрудники университета в Абердине, Шотландия].
Л. Ф. МАГНИЦКИЙ
55
Л. Ф. Магницкий. Леонтий Филиппович Магницкий родился 19 июня
1669 г. Он происходил из тверских крестьян. По-видимому, самоучкой
он изучил многие науки и среди них математику, а также несколько
европейских языков х). В Навигацкой школе он работал с начала 1702 г.,
Рис. 15. Титульный лжет второго издания тригонометрических и логарифмических
таблиц (Москва, 1716).
преподавая арифметику, геометрию и тригонометрию, иногда и
мореходные науки. С 1716 г. до конца жизни Магницкий руководил школой,
б которой была тогда прекращена подготовка морских кадров. К осени
1702 г. он уже закончил свою знаменитую «Арифметику», о которой
говорится далее. Вместе с Фархварсоном и Гвином он опубликовал «Таблицы
логарифмов и синусов, тангенсов и секансов» (М., 1703). Эти таблицы
(рис. 15), воспроизводящие известные таблицы А. Флакка, вышедшие
в 1628 г. (А. V 1 а с q, Tabulae sinuum, tangentium et secantium, et
logarithm! sinuum, tangentium et numerorum ab unitate ad 10 000), содержали
1) Возможно, что Магницкий обучался в Славяно-греко-латинской академии;
«однако в списках ее учеников его имя не встречается.
56 ГЛ. 3. ГОСУДАРСТВО И МАТЕМАТИКА В ЭПОХУ ПЕТРА ПЕРВОГО
семизначные десятичные логарифмы чисел до 10 000, а затем логарифмы
и натуральные значения названных функций (с тем отличием, что у Флак-
ка первыми шли таблицы тригонометрических величин). «Во употребление
и знание математико-навигацким ученикам», как сказано на титульном
листе, было выпущено через 13 лет второе издание этой книги (М., 1716).
Фархварсон и Магницкий подготовили также русское издание
голландских «Таблиц горизонтальных северные и южные широты восхождения
солнца...» (М., 1722), содержащих нужные мореплавателям таблицы
с объяснением, как ими пользоваться. Скончался Магницкий, проработав
в Навигацкой школе почти сорок лет, 30 октября 1739 г. и был похоронен
в одной из московских церквей, ныне не существующей.
Учеником Магницкого по Сухаревской школе был продолжатель
его дела — один из самых выдающихся русских педагогов XVIII
столетия Н. Г. Курганов г).
Как второе издание логарифмических таблиц, так и только что
названные таблицы для мореходов были напечатаны в типографии Василия Ано-
фриевичаКиприанова(ум. 1728), издателя многих первых русских научно-
технических книг. Киприанов принимал участие и в печатании
«Арифметики» Магницкого. Частично используя последнюю, он подготовил
увлекательно составленный математический плакат «Новый способ
арифметики феорики или зрителныя» (М., 1705), украшенный многими
рисунками, изображениями геометрических инструментов, видами Кремля
и только что основанного в 1703 г. «Петрополиса»— Петербурга, а также
воображаемыми портретами Пифагора, Архимеда, Птолемея, Тихо Браге
и еще нескольких знаменитых ученых, среди них даже Коперника.
Рисунки служили для характеристики различных наук — арифметики,,
геометрии, астрономии, оптики, фортификации и т. д.; к ним давались
подписи, объясняющие значение этих наук. Главное содержание плаката
составляло краткое описание правил действий над целыми и дробями,
включая «децимальные», т. е. десятичные, а также тройного и фальшивого*
правил, с примерами ко всему этому.
А. Д. Фархварсон. Андрей Данилович Фархварсон (Henry или Harry
Farquharson, ок. 1675—9 дек. 1739), уроженец Милна близ Абердина,,
обучался в 1691—1695 гг. в Маришал-Колледже Абердинского
университета и затем преподавал в нем математику2). Во время пребывания
Петра I в 1698 г. в Англии, он познакомился каким-то образом с Фарх-
варсоном и пригласил его с собой в Россию. Здесь шотландский математик
помогал царю в организации Навигацкой школы, где читал некоторые
разделы математики, астрономию и мореходное дело. В 1716 г. его перевели
профессором в Петербургскую морскую академию. Многие русские
моряки были его воспитанниками. В 1737 г. по представлению Адмиралтейств-
коллегий его произвели в бригадиры — чин, промежуточный между
полковником и генерал-майором и позднее упраздненный3).
Фархварсон был связан в своей деятельности с Академией наук.
Он составил по-латыни несколько руководств, оставшихся в рукописи
или в рукописном русском переводе. Участие его в издании учебной лите-
г) Биографию Магницкого см. в кн.: В. Е. Прудников, Русские педагоги-
математики XVIII—XIX веков, М., 1956; А. П. Денисов, Леонтий Филиппович-
Магницкий, 1669—1739, М.7 1967.
2) Этими данными я обязан опять-таки д-рам Симпсону и Уайтману.
3) Краткую,биографию Фархварсона см. в кн.: В. Н. Верх, Жизнеописания»
первых российских адмиралов, ч. 1, СПб., 1831, стр. 71—78.
А. Д. ФАРХВАРСОН
57
ратуры не ограничилось книгами, названными выше. Под его редакцией
вышел первый русский печатный теоретический курс геометрии, именно
«Эвклидовы элементы из двенадцати нефтоновых книг выбранные и в осмь
книг чрез профессора математики Андрея Фархварсона сокращенные,
с латинского на российский язык хирургиусом Иваном Сатаровым
преложенные» (СПб., 1739) г). На самом деле эти «Элементы» представляют
собой, хотя это нигде в них не отмечено, переработку соответствующих
отделов «Начал плоской и пространственной геометрии, с приложением
избранных теорем Архимеда» (Elementa Geometriae planae et solidae.
Quibus accedunt selecta ex Archimede theoremata, 1654) А. Такэ, которые
пользовались широким распространением во второй половине XVII
и первой половине XVIII вв. Основную часть учебника Такэ образует
адаптированное для юношества изложение I—VI и XI—XII книг
«Начал» Евклида. Особенно значительной переработке (в сторону арифме-
тизации) Такэ подверг теорию пропорций в V книге, заменив
классическое определение равенства отношений по Евдоксу другим, более
отвечавшим запросам вычислительной математики XVII века: как равные,
определяются отношения, предыдущие члены которых содержат свои
последующие или их любые равночастные доли (скажем, десятые, сотые,
и т. д.) равное число раз. Большое внимание Такэ уделил измерению фигур,
снабдив его числовыми примерами, причем оригинально изложил учение
об измерении пирамиды, круга и круглых тел. Как и многие его
предшественники и современники, он понимал, что общим содержанием
античных доказательств по методу исчерпывания служит предельный
переход, проведение которого, однако, весьма усложнялось из-за
отсутствия общих понятий и теорем. Из-за этого всякий раз приходилось
подтверждать правильность предельного перехода с помощью приведения
к нелепости допущения, что искомая величина не больше и не меньше
некоторой данной величины, фактически находимой при предельном
переходе. Предельный переход Такэ называл «окончанием» одной фигуры
в другую и основную роль у него играет общее предложение, которое мы
можем записать в таком виде: если xly = А/В, где А ж В суть постоянные,
lini зс А
тор— =7Г- ^а этои основе Такэ перестроил школьное учение округе,
пирамиде и круглых телах. В русском переводе соответствующее
определение таково: «Величины в некоторой фигуре написанные или описанные,
или фигуры меншие или болшие на фигуру окончатися глаголются
[in figuram desinere dicuntur], егда наконец от оные разнитися могут
количеством меншим каково нибудь даного, или коликим нибудь малым» 2).
А «общая поризма» гласит: «Буде оные которые в двух фигурах (А, В)
выписуются в тех окончаюца, какую пропорцию меж собой всегда имеют
написанные, ту же имеют и фигуры» 3). Это было первое у нас изложение
идей метода пределов, который нашел многих сторонников в России на
рубеже XVIII и XIX вв.
К материалу «Начал» Такэ присоединил изложение ряда
предложений из сочинений Архимеда «Об измерении круга» и «О шаре и цилиндре»
и еще некоторых вопросов (приближенное построение любых правильных
многоугольников, построение нескольких средних пропорциональных
и т. д.). Это добавление появилось на русском языке через несколько лет
г) О Сатарове известно еще только, что он работал переводчиком в
Академии наук.
2) Эвклидовы элементы..., СПб., 1739, стр. 259—260.
3) Там же, стр. 263.
58 ГЛ. 3. ГОСУДАРСТВО И МАТЕМАТИКА В ЭПОХУ ПЕТРА ПЕРВОГО
после смерти Фархварсона. Однако теперь его имя на титульном листе
не было названо, зато появились имена Такэ и Домкино: «Архимедовы
теоремы Андреем Таккветом езуитом выбранные и Георгием Петром Дом-
кино сокращенные, с латинского на российский язык хирургиусом
Иваном Сатаровым преложенные» (СПб., 1745). Пагинация здесь
продолжает пагинацию «Элементов» и можно думать, что обе части готовились
одновременно. Какое участие принял Фархварсон в подготовке второй
части — неясно. Не удалось также узнать, о каком «ньютоновом» издании
говорится на титульном листе «Элементов». Что касается Домкино,
именем которого подписано и краткое историческое введение к «Эвклидовым
элементам», то установлено лишь, что это был Г. П. Домке — G. P. Dom-
cke, о личности которого более подробных сведений пока не имеется1).
По сравнению с книгой Такэ в русском тексте «Элементов» есть
небольшие изменения. Сокращен вводный отдел по истории математики,
исключены критика Евклида в V книге и рассуждения о модной в XV—XVII вв.
проблеме угла касания. Увеличено количество числовых примеров во
II книге (так называемая геометрическая алгебра) и в V книге. Добавлены
некоторые полезные предложения, вроде теоремы Птолемея. Возможно,
что книга предназначалась для учащихся Морской академии, в
типографии которой печатались обе ее части. И впоследствии, как мы увидим,
преподаватели этой Академии использовали «Начала» Евклида в учебных
целях (стр. 80) 2).
Перу Фархварсона принадлежит небольшая «Книжица о сочинении
и описании сектора, скал плоской и гунтерской со употреблением оных
инструментов в решении разных математических проблем» (СПб., 1739).
Сектор — это пара вращающихся вокруг общего центра и подходящим
образом разграфленных линеек, т. е. пропорциональный циркуль,
изобретенный почти одновременно в конце XVI века в Италии, Германии
и Бельгии; гунтерская скала есть логарифмическая шкала, которую ввел
в начале XVII века Э. Гунтер. Фархварсон учит построению и
применению натуральных и логарифмических шкал чисел и тригонометрических
величин, а также сектора. Затем он решает задачи на отыскание
неизвестного члена пропорции, деление отрезка на данное число частей, точечное
построение эллипса по данным осям, на решение прямоугольных
треугольников и т. п. Изложенные в книге Фархварсона элементарные
номографические построения, видимо, входили в курс Морской академии.
«Арифметика» Магницкого. Первое печатное руководство по
арифметике на русском языке было издано за границей. В 1700 г. Петр I дал
голландцу Я. Тессингу право печатать и ввозить в Россию книги
светского характера, географические карты и т. д. По математике Тессинг
выпустил «Краткое и полезное руковедение во аритметыку» (Амстердам,
1699) Ильи Федоровича Копиевича или Копиевского, родом из
Белоруссии. Однако арифметике здесь отведено лишь 16 страниц, где даны
краткие сведения о новой нумерации и первых четырех действиях над целыми
числами, причем сообщаются весьма лаконичные определения операций.
Нуль зовется оником или же, как вскоре и у Магницкого, цифрою; это
слово перешло в Европу из арабской литературы и долгое время
означало нуль. Остальные 32 страницы книжечки содержат нравоучительные
х) И. Я. Д е п м а н, Георг Петр Домкино.—Труды Ин-та ист. естеств.,
т. 2, 1948.
2) А. П. Юшкевич, О первом русском издании трудов Евклида и
Архимеда.— Труды Ин-та ист. естеств., т. 2, 1948.
«АРИФМЕТИКА» МАГНИЦКОГО
59
изречения (вроде: «жену свою ты должен любити, от любодеицы себя
сохранити») и притчи.
«Руковедение» Копиевича не имело успеха и не могло идти ни
в какое сравнение с появившейся вскоре «Арифметикой» Магницкого,
жзданной очень большим для того времени тиражом — 2400 экз. Эта
«Арифметика сиречь наука числительная. С разных диалектов на сла-
ьенский язык преведеная, и во едино собрана, и на две книги
разделена», изданная в Москве в январе 1703 г., сыграла в истории русского
математического образования чрезвычайную роль 1). Популярность
сочинения была необыкновенная, и около 50 лет оно не имело конкурентов
как в школах, так и в более широких читательских кругах. «Арифметику»
Магницкого и грамматику Смотрицкого называл «вратами своей учености»
Ломоносов. Вместе с тем, «Арифметика» явилась связующим звеном
между традициями московской рукописной литературы и влияниями
жовой, западноевропейской. Она оказала немалое влияние на учебные
руководства русских авторов, начиная с Киселева XVIII века — Н.
Курганова, до Курганова XX века — А. Киселева.
С внешней стороны «Арифметика» представляет собой большой том
in 4° в 331 лист, т. е. 662 страницы, набранный еще славянским шрифтом
(рис. 16); пагинация также славянская. Имея в виду интересы не только
школы, но и самоучек, каким в математике являлся он сам, Магницкий
снабдил все правила действий и решения задач очень большим числом
подробно решенных примеров 2). Таких примеров в ней значительно
больше, чем в соответствующих заграничных руководствах. В
предисловии автор, по примеру своих предшественников, разъясняет пользу
математики, и общегражданскую для всех людей — купцов,
ремесленников и т. д., и государственную, особо подчеркивая притом ее значение
ъ военном деле и мореплавании. Именно учитывая нужды практики
Магницкий придал своему труду полуэнциклопедический характер,
включив в него, помимо собственно математического материала,
многочисленные сведения по естествознанию и технике.
«Арифметика» делится на две книги. Первая из них, большая (в ней
218 листов),— состоит из пяти частей и посвящена преимущественно
арифметике в собственном смысле слова. Сам автор о ней писал: «В первой
_яже именуется политика, вся гражданские потребы, купецкие убо и
воинские, и различных чинов ради людей многие приклады и образы положи-
х:ом, пропорции руд, и различных царств и времен разнство денег, и весов,
и мер, разливающихся вещей тяготу, и ины многи образцы» 3) (л. 18).
Во второй книге (насчитывающей 87 листов) три части, включающие
алгебру с геометрическими приложениями, начала тригонометрии,
космографию, географию и навигацию. Тут все было новым для русского
1) Магницкому посвятили работы В. В. Бобынин (см. его Очерки истории
развития физико-математических знаний в России.— Физико-математические науки
ъ их настоящем и прошедшем, тт. VII—X, 1888—1891), а также Д. Д. Галанин
(Л. Ф. Магницкий и его арифметика, вып. I—III, М., 1914). Я во многом
расхожусь в оценке «Арифметики» с обоими исследователями.
2) В том, что автор предназначал книгу для самого широкого круга читателей,
убеждает уже титульный лист, где сказано, что она «ради обучения мудролюбивых
российских отроков и всякого чина и возраста людей... произведена». К тому же
Магницкий работал над нею еще в 1700 г. до открытия первой из петровских школ.
На л. 272 об. говорится о 1700 г., как «преходящем», а на л. 273 об. о 1701 г., как
о «предлежащем».
3) Термин «арифметика политика», т. е. гражданская ([хёфобосг поХтк&у
^OYapiaajxuv), восходит к византийской литературе XIV века.
Рис. 16. Первая страница «Арифметики» Л. Ф. Магницкого
(Москва, 1703).
«АРИФМЕТИКА» МАГНИЦКОГО
61
читателя. Мы ограничимся в дальнейшем разбором математического
содержания этого замечательного труда.
На титульном листе сам Магницкий характеризовал свое сочинение
как перевод — лучше сказать, переложение — с различных языков,
оставляя за собой лишь «во едино собрание». Эти слова, говорящие о
скромности автора, нужно понимать в том смысле, что, подобно всем авторам
учебных книг, Магницкий изучил и использовал целый ряд более ранних
руководств, причем он не ограничился старыми нашими рукописями, но
привлек и иностранную литературу. Фактически, «собирая во едино»
арифметические, алгебраические, геометрические и иные материалы, будь
то отдельные задачи или методы решения задач — он все подверг весьма
тщательному отбору и существенной обработке. В результате возник
вполне оригинальный курс, учитывавший запросы и возможности русских
читателей того времени и вместе с тем открывавший перед ними, как
выразился Ломоносов, врата к дальнейшему углублению знаний. Вопрос
о зарубежных книгах, которыми располагал Магницкий, исследован
не до конца. С большой вероятностью можно полагать, что он имел под
руками по крайней мере сочинения по арифметике Я. ван дер Шуере
(Arithmetica, Haarlem, 1601), И. Фаульгабера (Arithmetischer Wegweyser
zu...Rechenkunst, Ulm, 1614), А. Такэ (Arithmeticae Theoria et Praxis,
Lovanii, 1656), И. С. Фарманковича (Arithmetica practica bipartita...,
Cracoviae 1669; включало алгебру), труды по алгебре М. Штифеля
(Arithmetica integra, Nurnberg, 1544) и того же И. Фаульгабера или
других немецких авторов, Дж. Валлиса (1657) и К. Ф. Дешаля (1674)х). Таким
образом, Магницкий имел весьма основательную математическую
подготовку.
В первой книге «Арифметики» очень многое почерпнуто, в
обработанном виде, также из рукописей, о которых говорилось выше. Такая
преемственность имела большое воспитательное значение. Вместе с тем
уже в первых четырех частях этой книги немало нового, начиная с
обучения арифметическим действиям. Весь материал расположен гораздо более
систематически, существенно обновлены задачи 2), исключены сведения
о счете костьми и дощаном счете, современная нумерация окончательно
вытесняет алфавитную и старый счет на тьмы, легионы и пр. заменен
общепринятыми в Европе миллионами, биллионами, триллионами и
квадриллионами (каждый класс содержит шесть десятичных разрядов).
Далее этого Магницкий не идет, ибо
«Довлеет числа сего
к вещем всем мира всего».
Тут же, впервые в наших учебниках, высказана идея бесконечности
натурального ряда:
«Число есть бесконечно,
умом нам недотечно
Ни кто не знает конца,
Кроме всех Бога творца».
Стихи вообще нередко встречаются в «Арифметике»: в такой форме
Магницкий любил высказывать поучения, общие выводы и советы читателю.
*) Несомненно, что имелись и другие источники (например, по тригонометрии).
2) Среди задач на арифметические правила (тройное и др.) из рукописей взято
около половины. См. К. I. Швецов, Першоджерелы «Арифметики» Л. Магнщь-
кого.— 1сторико-математичний зб1рник, III, Кшв, 1962, стр. 122.
62 ГЛ. 3. ГОСУДАРСТВО И МАТЕМАТИКА В ЭПОХУ ПЕТРА ПЕРВОГО
Главную роль в первой книге «Арифметики» играют, как и в
рукописях, тройное правило и правило двух ложных положений, а несколько
задач решено по правилу одного ложного положения, которое, впрочем,
в общем виде не формулируется. Однако, в отличие от рукописей,
различаются «возвратительное», т. е. обратное тройное правило и правила
пяти, а также семи величин. Все это вместе с правилом «соединительным»г
т. е. смешения, объединено под именем «правил подобных». Подобие или
подобенство — термин, означающий пропорциональность, а также
пропорцию. Еще ла Рамэ в 1555 г. писал, что пропорция есть подобие
отношений — proportio est similitudo rationum, а в XVII веке ряд авторов
именовал тройное правило со всеми его вариантами «правилами
пропорций». Действительно, решения основаны здесь на свойствах
пропорциональных величин. Магницкий обстоятельно описывает простое тройное
правило, которое характеризует, как «некий устав о трех перечнях, их же
друг к другу подобием учит изобретати четвертый, третьему подобный»
(л. 60 об.). Эти три данные числа называются количество, цена и
изобретатель; первое и третье должны быть «единого качества», а третье
«изобретает иный перечень подобный себе, таковым же подобием яковым и вторый
первому подобен есть» (там же). Правило поясняется примером: 1 фунт
стоит 20 алтын, сколько стоят 3 фунта? — и формулируется в следующих
выражениях: «И тому третьему перечню по подобию второго к первому,
изобретается тако: средний перечень сиречь вторый, умножай с третьим,.
а первым раздели» (л. 60 об.—61).
Как видно, Магницкий прямо связывает тройное правило с
пропорциональностью величин, и читатель, усваивая правило, заодно свыкался
с представлением о свойствах «подобия» двух пар чисел. Сама
формулировка правила конкретно выражала одно из свойств пропорции. Однако
Магницкий не выделил и не разъяснил предварительно применяемые им
общие свойства пропорциональных величин. Так поступало подавляющее
большинство авторов арифметических руководств. Только немногие,
вроде Такэ и Дешаля, предпосылали тройным правилам более или менее
развитое учение о пропорциях.
К «подобенствам» или, как он их теперь называет, пропорциям,
Магницкий возвращается в пятой части, озаглавленной «О прогрессиях
и радиксах квадратных и кубических». Эти вопросы, указывал Магницкий,
относятся собственно к алгебре, но, поскольку изучать ее смогут немногие,
он решил изложить их здесь «в дополнение многих, в прешедших частех
различных правил, и гражданских числительных потреб паче же
воинских» (л. 179).
Определив общим образом «прогрессио» или «шествование», как
«пропорцию, или подобенство числ к числам в примножении, или во умен-
шении яковых либо перечнев», Магницкий разделяет прогрессии на
арифметические, геометрические и «армонические» (л. 179 об.), последние,
впрочем, оставлены далее в стороне. «Арифметическое прогрессио или
пропорция есть, егда три или многая числа коеждо их друг от друга равное
разнство, но разные пропорции имать, и сие или единаким пошествием
яко 2.4.6.8.10.12 или не единаким, яко 2.4.5.7.8.10.11.13» (л. 179 об.).
Применение здесь слова «пропорция» в двух различных смыслах, как
прогрессии, т. е. некоторой последовательности чисел, и как
геометрического отношения двух чисел, разумеется, создавало трудности; через
несколько страниц это же слово означает также знаменатель
геометрической прогрессии или же ее «умножителное число». Непривычное для нас
включение в число арифметических прогрессий арифметических рядов
«АРИФМЕТИКА» МАГНИЦКОГО
63
с переменной разностью (в данном случае принимающей поочередно
значения 2 и 1) встречалось ранее, например у Дж. Кардано (1539)
и М. Штифеля (1544), который именовал их progressions intercisae —
прерывными прогрессиями1). Фактически все же Магницкий занимается
только обыкновенными арифметическими прогрессиями, решая типичные
задачи на вычисление суммы, первого члена («предела», от латинского
terminus), разности и т. д. по тем или иным данным; вводится и понятие
среднего пропорционального числа.
Аналогично арифметической определяется геометрическая
прогрессия или пропорция, «егда три или многая числа, едину и туюжде между
собою пропорцию, но разнства различные имут, и сие или единаким
пошествием, яко 2.4.8.16.32.64.128. или не единаким, яко 2.4.6.12.18.»
(л. 179 об.). Сумма обыкновенной геометрической прогрессии находится
по правилу S = nq ai . В одной из задач, именно на отыскание
знаменателя прогрессии по условию д7 = 2187, допущена, по недосмотру,
грубая ошибка: Магницкий делит 2187 на 7 и говорит, что остаток 3
дает «разнство» (опять недосмотр!) прогрессии.
Далее следует правило извлечения квадратного корня, само
название которого объясняется тем, что «от него вся пропорция всея алгебры
начинается или раждается» (л. 185 об.). Здесь, очевидно, имеется в виду
прогрессия степеней неизвестной, т. е. ж, х2, х3,. . . К этому примыкает
описание десятичных дробей, после чего приводится правило извлечения
кубического корня. Если квадратный корень или радикс определяется как
выраженный числом «бок» «четверобочной и равномерной фигуры», та
кубический корень вводится, как число, выражающее «бок» «кубичного
корпуса». Как видно, хотя Магницкий перенес извлечение корней,
излагавшееся ранее в геометрических рукописях, в арифметику, само
определение квадратного и кубического корня сохраняло след происхождения
этих понятий из геометрии. В качестве примеров приведено много задач
на теорему Пифагора и ее пространственный аналог, на определение
цилиндра с равными высотой и диаметром, а также сферы, равновеликих
данному кубу и другие. Есть здесь и задачи, не требующие извлечения
корней; например, на отыскание боковой поверхности конуса («шатра») по
окружности основания и образующей (к ней примыкает задача, в которой
даны диаметр основания и высота конуса) и на вычисление объема и
поверхности шара по его диаметру и «пропорции архимедовой» (я = 22/7).
Представляет интерес изложение системы десятичных дробей,
помещенное вслед за извлечением квадратного корня, несомненно в связи:
с употреблением в приближенных вычислениях правила, выражаемого
формулой
Vn =
Vamqs"
10'1
«Зде потребно есть,— писал Магницкий,— кратко о ином чине
арифметики рещи, яже децималь или десятная именуется, сиречь в десятных.
частях, или в сотых, или в тысячных, и множайше» (л. 202 об.). С. Стевин,
который в 1585 г. выступил с пропагандой системы десятичных дробей,
также говорил, что «десятая есть вид арифметики» 2), но Магницкий
г) М. Cantor, Vorlesungen uber Geschichte der Mathematik, B. II, стр. 501;
J. T г о p f k e, Geschichte des Elementar — Mathematik, B. VI, 2 Aufl., стр. 13.
2) The principal works of Simon Stevin, vol. II A. Amsterdam, 1958, стр.. 402.
64 ГЛ. 3. ГОСУДАРСТВО И МАТЕМАТИКА В ЭПОХУ ПЕТРА ПЕРВОГО
следовал не Стевину, а немецким ученым, вроде И. Г. Бейера (1603) и др.,
которые применяли десятичные дроби в форме геометрических мер.
Многие,— говорится в «Арифметике»,— употребляют «сей чин... во искании
количества линий, и арей или суперфиций плоских» (л. 202 об.).
Магницкий излагает этот вопрос очень коротко, пример дает только на
сложение и остальное предоставляет читателю. Следует учесть, что в то время
десятичные дроби лишь начинали входить в более широкое употребление
и в курсы элементарной математики. Меры, употребляемые Магницким,
в порядке убывания, таковы: рута (немецкое Ruthe) или сажень, фут
или стопа, цолль или палец, гран или зерно и скрупул или дробь;
их «признаками» служат в случае линейных мер соответственно [0, [1, [2
и т. д. При этом вслед за числом пишется только знак наименьшей меры,
так что, например 82.3.9.3.8 [4 означает 82 руты 3 фута 9 цоллей 3 грана
и 8 скрупулов. Указание одного лишь последнего разряда десятичной
дроби встречается у ряда авторов, в том числе Бейера, писавшего над
последней цифрой латинский номер разряда, но употребление значка [,
как у Магницкого, я у других математиков не обнаружил. Дешаль
применял такой знак, но по-иному, отделяя им дробную часть десятичного
числа от целой.
Пятой частью заканчивается первая книга «Арифметики». Как видно,
она отличается от прежних русских арифметических рукописей не только
гораздо большим богатством содержания, но и самой манерой подачи
материала. В рукописях отсутствовали не только доказательства, но почти
полностью даже определения понятий; самое большее, некоторые
иностранные термины пояснялись русскими знакомыми словами, как «адитсие
или считание». У Магницкого также не было доказательств в строгом
смысле слова, но в очень многих случаях он, растолковывая свои
правила, подводит к их сознательному применению. Так поступает он,
например, при изложении тройного правила. Особенно важным средством
содержательного изложения и воспитания мышления стали у Магницкого
определения, которыми он пользуется не только, когда вводит такие
неизвестные читателю даже понаслышке понятия, как прогрессия или
радикс, но и в случае вполне, казалось бы, обиходных понятий и действий.
«Аддицио или сложение,— разъяснял он,— есть двух или многих числ
во едино собрание, или во един перечень совокупление» (л. 4).
«Умножение есть, им же что в числах умножаем, или коликим вещем по множеству
иных вещей раздаем, и количество их числом показуем» (л. 11 ), т\ е. есть
повторение данного количества столько раз, сколько вещей в другом
данном множестве. Такие же определения даются в иностранных
учебниках того времени и, с небольшими уточнениями, в школьной
литературе наших дней. Из этих определений, обобщенных на абстрактные
множества произвольных элементов, возникли современные определения
операций над количественными и порядковыми числами. Приведем еще
определение дроби: «Число ломаное ничтоже ино есть, токмо часть вещи,
числом обявленная, сиречь полтина есть половина рубля, а пишется сице:
1/2 рубля, или четь 1/4, или пятая часть 1/5, или две пятые части 2/5,
и всякие вещи яковая либо часть, обявлена числом» (л. 42). Отдел о дробях
следовал за метрологическим. И теперь детей учат дробям, отправляясь
от деления на равные части единичных конкретных величин, и в
частности, различных мер.
Уже в первой книге «Арифметики» Магницкий проделал большую
работу по обогащению и улучшению русской математической
терминологии. Многие термины впервые встречаются у Магницкого или, во всяком
АЛГЕБРА И ТРИГОНОМЕТРИЯ У МАГНИЦКОГО
65
случае, благодаря ему вошли в наш математический словарь: множитель,
произведение (также продукт), делимый и частный перечни (также квотус),
делитель, квадратное число, среднее пропорциональное число, извлечение
корня (ранее говорили: деление радиксом), пропорция, прогрессия и т. д.
Алгебра и тригонометрия у Магницкого. Вторая книга «Арифметики»
впервые знакомила нашего читателя с обширным кругом знаний, которые
Магницкий назвал «арифметикой астрономской» и которые включали,
среди прочего, алгебру и тригонометрию. В предисловии Магницкий
подчеркивал значение всего этого комплекса сведений для России его
времени. «Астрономская» арифметика, писал он, «в настоящая времена
есть потребнейшая в нашем всероссийском государстве быти, неже в
прежде бывшем», ибо без нее невозможно быть хорошим геодезистом, инженером
и воином, «паче же ни навигатор будет без сея науки, не может бо добро
кораблеходствовати, и к желаемому пристанищу достигнути, и уречен-
ное место получити...» (л. 219 об.). Изучение алгебры он рассматривал
как «некий высочайший и тщаливейшим токмо свойственный жребий,
зане не всякому общенародному человеку есть сия потребна, яко купцем,
икономом, ремесленником и таковым» (л. 225 об.).
Мы остановимся только на алгебре и тригонометрии, оставив в
стороне извлечение корней высшей степени с помощью таблицы
биномиальных коэффициентов до 10 степени двучлена, которое он поясняет на
примерах от 4 до 8 степени х), а также изложение шестидесятеричной
системы дробей и целых чисел, высшие единицы которой, начиная с 602,
называются первой, второй и т. д. сексагенами 2), и некоторые другие
вопросы.
Слово алгебра Магницкий производил, как и многие, от имени якобы
йзобревшего ее Гебера (на самом деле севильский астроном Гебер, точнее,
Джабир ибн Афла, живший в XI веке, к этому не имел никакого
отношения). Итальянцы, добавлено в «Арифметике», зовут ее коссика, от слова
косса, т. е. вещь. В самом деле, итальянское название неизвестной
величины cosa — вещь — перевод соответствующего арабского Термина, было
распространено на всю науку алгебры, в латинской форме ars cossica
или просто cossa, а в немецкой — Gosse или die Coss. И прежде всего
Магницкий знакомит с коссическими названиями, а также обозначениями
степеней неизвестной вплоть до 25-й включительно. Этот «вид» алгебры 3)
он называет нумерацией — numeratio, поясняя: «Нумерацио или
счисление алгебраики есть числа алгебраическая или коссика именованиями
и характирами объявленная, от единицы коею либо пропорциею примно-
жаемая, и в не оконченое проходящая, и тою равною пропорциею ею же
при искренное единицы саму ону превосходит, их же расстояние от
х) Этот раздел излагался во многих сочинениях немецких алгебраистов.
2) Такая система возникла еще в древнем Вавилоне, а затем шестидесятеричные
дроби вошли в широкое употребление через эллинистическую астрономию. В странах
ислама астрономы с X—XI вв. применяли и шестидесятеричные разряды целых
чисел, так называемые первые, вторые и т. д. «поднятые»; попытки ввести шестидеся-
теричный счет целых делались и в Европе. В дальнейшем Магницкий сексагенами не
пользуется.
3) Слово «вид» есть перевод латинского species, означавшего со времени Ф. Вие-
та, с одной стороны, знаки алгебраических величин, а с другой — операции
арифметики и алгебры. Магницкий понимает под видом как раз последние, относя к действиям
наименование и обозначение. Знаки алгебраических величин он иногда называет
характирами, от characteres тогдашней латинской терминологии, что восходит к
греческому %арахтт]р — изображение и т. п.
66 ГЛ. 3. ГОСУДАРСТВО И МАТЕМАТИКА В ЭПОХУ ПЕТРА ПЕРВОГО
единицы числа естественным порядком поступающая показуют» (л. 226).
Здесь появляется упоминавшаяся ранее геометрическая прогрессия
степеней неизвестной; Магницкий отмечает, что отношение (у него —
пропорция) к единице ближайшей к ней степени таково же, как между
соседними членами прогрессии, а также что стоящие в таблице
натуральные числа, нумерующие члены прогрессии, показывают их
расстояние от единицы. Мы не будем приводить все эти коссические знаки х).
После того Магницкий переходит к другому способу обозначения —
«знаменованию алгебраики»— notatio, которое «ничто же ино есть, токмо
литеры гласныя, полагаемыя за количество непознаное числ, или о немже
взыскание есть. Такожде и согласные, полагаемыя за количества даных
чисел, или познаных» (л. 227). На прилагаемой фотографии (рис. 17)
изображены различные приводимые Магницким символы первых пяти
и далее для четырех степеней неизвестной и данной величины.
Обозначение неизвестных величин прописными гласными и данных величин
прописными согласными ввел (1593) Ф. Виет, который характеризовал
степени, ставя рядом с буквой полное или сокращенное латинское название
степени. Т. Герриот заменил прописные буквы строчными (опубл. 1631)
и его обозначение степеней простым повторением букв дается в 7 и 9
строках фотографии. П. Эригон ставил показатель степени в одну строку
вслед за основанием (1634 и 1644), как в 12 и 15 строках снимка (или
перед основанием), причем пользовался строчными буквами. В 8, 10, 13
и 16 строках содержатся коссические знаки, иногда в форме, несколько
отличной от той, в какой они появились в конце XV века. Различие в 7
и 9 строках, а также в 12 и 15 строках между прописными и строчными
буквами следует отнести за счет ошибки типографии.
Магницкий приводит два примера алгебраических выражений в
буквенном обозначении, предупреждая, что числовой коэффициент (этого
термина у него нет) ставится впереди соответствующей буквы. В
дальнейшем он употребляет коссические знаки и излагает на многих
примерах основы алгебраического исчисления — вплоть до деления
многочленов; в примерах иногда встречаются ошибки или опечатки. Особенно бегло
и недостаточно ясно написан параграф о дробных алгебраических выра-
3 3
жениях. -р— он пишет -^б- и читает «три пятины радиксов».
В алгебре Магницкий пользуется знаками —{— (называемом «болше»)
и —'-— («менше») и чертой для деления (ср. стр. 34). Сообщаются правила
извлечения корней высших степеней и излагается учение о шестидесяте-
ричных дробях.
За всем этим следует вторая часть второй книги «О геометрических
чрез арифметику действующих», прежде всего 18 задач, среди которых
задачи на вычисление площадей параллелограмма, правильных
многоугольников (по стороне и «перпендикуляру» к ней из центра), сегмента
круга, объемов круглых тел; сообщены диаметр, поверхность и объем
Земли в итальянских милях, которых в градусе 64, 363 (рис. 18). Попутно
приведены некоторые теоремы — о равенстве стороны правильно
вписанного в круг шестиугольника «семидиаметру» и о равенстве отношения
площадей двух кругов отношению квадратов их диаметров. Для русского
читателя здесь было много новых важных сведений. А далее Магницкий
переходит к решению трех канонических видов квадратных уравнений
с положительными коэффициентами при членах: «Первое, егда едино есть,
г) См. А. П. Юшкевич, История математики в средние века, М., 1961,
стр. 412—413.
Рис. 17. Алгебраические знаки в «Арифметике» Л. Ф. Магницкого (л. 227).
68 ГЛ. 3. ГОСУДАРСТВО И МАТЕМАТИКА В ЭПОХУ ПЕТРА ПЕРВОГО
или многая q —¦— единым, или многими радиксы равняются числу. Якоже
q —|— R о или q о —|— R или о —{— q Д» (л. 252). Знаки неизвестной
(от radix — корень) и квадрата (от quadratum) следует понимать во
множественном числе, т. е. R это наше Ъх и q — наше ах2; знак о для
произвольного свободного члена —«праздного числа» возник, вероятно, из
соответствующего коссического знака, имевшего форму перечеркнутого
кружка. Здесь же впервые появляется удлиненный знак равенства,
предложенный Р. Рекордом (1557). Рассмотрение по отдельности указанных
трех форм квадратных уравнений, восходящее к греческой и арабской
математике, все еще сохранялось во многих учебниках, хотя с середины
XVI века в Европе была известна и единообразная трактовка вопроса. Для
каждой формы имелось свое правило решения; так поступает и Магницкий.
Решение высказано словесно; учитываются лишь положительные корни1).
Затем разобрано несколько задач, выражающихся линейными,
квадратными и биквадратными уравнениями. Геометрические задачи
объединены заглавием «О различных линиях в фигурах сущих».
Большинство из них относится к определению элементов
прямоугольных или произвольных треугольников по тем или иным данным
(например, катетов по их произведению и разности или высоты по
трем сторонам и т. п.). Любопытно введение в нескольких случаях
двух неизвестных, обозначаемых 1R и 1а или 1R и 1А: тут
сочетаются различные типы символов. Такое обозначение второй
неизвестной, как и приписывание коэффициента 1, восходит к
немецкому алгебраисту М. Штифелю (1544), который иногда обозначал
неизвестные и их степени гласными и согласными прописными готиче-
0 12 3
скими буквами, вроде 1, 121, 12Ш, 12ИШ и т. д. (1553). В примерах
алгебраической части «Арифметики» немало опечаток и есть отдельные
неточности. Вообще эта часть была составлена, как писал сам автор,
«не по мнозе времени» (л. 179).
Каковы же были здесь источники Магницкого? Скорее всего, как
уже упоминалось, он использовал «Математический курс или мир» (Cursus
seu Mundus mathematicus, Lugduni, 1674 и др. изд.) К. Ф. Дешаля,
сочинения коссистов М. Штифеля и И. Фаульгабера, а также «Общую
математику» (Mathesis universalis, Oxoniae 1657) Дж. Валлиса. Все это весьма
распространенные в XVII веке руководства, причем книги Дешаля и
Валлиса могли иметься у Фархварсона и Брюса.
Алгебраический отдел своего «Курса» Дешаль также начинает с
наименования и обозначения коссических чисел, которое называет denomi-
natio numerorum cossicorum, а следом в королларии знакомит с
обозначением данных и неизвестных величин при помощи прописных согласных
и гласных букв, причем в обеих формах записи: А, АА, AAA, . . .
и А, А2, A3, ... и т. п. Соответствующие объяснения у Магницкого
и Дешаля звучат весьма сходно. У Дешаля есть и термин numeratio
numerorum cossicorum, означающий коссическую запись алгебраических
выражений с помощью знаков действий. Как у Дешаля, так и у
Магницкого особо выделена нумерация «алгебраических чисел в долях»
(соответственно, numeratio fractionum cossicorum), начинающаяся с записи одно-
8 12
членов вроде -^-(Магницкий) или -^= (Дешаль) 2). Результат действий
г) Почему и не рассмотрено уравнение вида ах2 + Ъх + с = 0 при
положительных а, &, с.
2) С. F. D е с h a 1 е s, Cursus seu mundus mathematicus, Lugduni, 1690,
стр. 571—583.
Рис. 18. Размеры земного шара; измерение объема и поверхности некоторых тел
(«Арифметика» Л. Ф. Магницкого, л: 236).
70 ГЛ. 3. ГОСУДАРСТВО И МАТЕМАТИКА В ЭПОХУ ПЕТРА ПЕРВОГО
оба автора рекомендуют проверять с помощью обратных операций.
Сходство обнаруживается и в предпочтении, отдаваемом коссическим знакам,
и в применении символа равенства Рекорда, и в ряде геометрических
задач. У Валлиса мы также находим таблицу алгебраических обозначений
под названием De notatione algebrica (ср. «Знаменование алгебраики»
Магницкого): в левом столбце ее стоят наименования (nomina) степеней,
затем самые знаки — characteres (вначале коссические, затем в виде
A, Aq, Ас и т. п., герриотовы и, наконец, декартовы а, а2, а3, . . .),
а в правом столбце указан еще показатель степени — potestas seu gradus х).
Впрочем, сам Валлис предпочитал символику Декарта (1637). Наконец,
у коссических авторов Магницкий мог найти таблицу биномиальных
коэффициентов с приложением к извлечению корней (он, как и Штифель,
останавливается на корне 8-й степени), а также, как говорилось,
обозначение двух неизвестных li?, 1А, которое, восходя к Штифелю, встречается
и у Фаульгабера2), с тем отличием, что последний писал не \А, но, в
соответствии с готическим алфавитом, 1SI.
При оценке изложения алгебры у Магницкого следует помнить, что
столь привычная теперь символика Декарта находила в те времена
признание еще немногих и повсеместно укореняется только в XVIII веке.
В курсах авторитетных педагогов XVII столетия преобладали то
коссические обозначения, то символы Виета и его последователей, иногда
комбинации тех и других, а иной раз собственные специально
придуманные знаки. Далее, одни авторы уже принимали отрицательные и мнимые
числа, другие еще отвергали их употребление, по крайней мере в школе;
а это, естественно, отражалось на учении о квадратных уравнениях.
Если оставить в стороне описки и опечатки в алгебраическом тексте
«Арифметики», то он стоит в одном ряду со множеством других учебников
алгебры своего времени.
Вслед за алгеброй Магницкий на нескольких страницах дает решения
семи тригонометрических «проблем», служащих для вычисления таблиц
синусов, тангенсов и секансов. Он сообщает правила вычисления по
синусу дуги а, меньшей 90°, косинуса дуги 90° — а («синуса дополнения») 3),
затем теоремы о синусах и хордах дуг 2а, За и 5а, которые с помощью
приведенного в книге чертежа могут быть распространены на (2п -{-1) а.
тз . а l/sin2a + sm vers2 а г
Выразив затем sin -^ = — , он далее приближенно
вычисляет с помощью правила двух ложных положений хорду 10° по хорде 30°
и хорду 2° по хорде 10°, а отсюда сразу получается синус 1°. Это первое
изложение тригонометрии на русском языке в силу своей чрезмерной
краткости вряд ли было доступно большинству читателей. В последней
части «Арифметики» содержатся различные сведения, полезные для
моряков (таблицы магнитных склонений, таблицы широты точек восхода
и захода Солнца и Луны, координаты важнейших портов, часы прилива
и отлива в них и т. д.).
«Арифметика» Магницкого удовлетворила важной государственной
и общественной потребности своего времени, ее изучали много и прилежно,
о чем свидетельствуют многочисленные сохранившиеся списки и
конспекты книги. Разделив судьбу родственных учебников в Западной
Европе, она прослужила до середины XVIII века. Все же, несмотря на свой
х) J. W а 11 i s, Operum mathematicorum pars prima, Oxoniae, 1657, стр. 72.
2) Ср., например, J. Faulhaber, Academia algebrae, Ulm, 1631.
3) А также по хорде («субтензе») дуги, меньшей 180°, хорды дополнения до 180°.
ПЕРВЫЕ УЧЕБНИКИ ГЕОМЕТРИИ И ТРИГОНОМЕТРИИ 71
энциклопедический характер, «Арифметика» и в Петровскую эпоху
оказалась для школы недостаточной: в ней было слишком мало геометрического
материала.
Первые учебники геометрии и тригонометрии. В Петровское время
на русском языке напечатаны были два геометрических руководства.
Одним из них был перевод австрийской книги А. Э. Буркгарда фон Пюр-
кенштейна «Ertzherzogliche Handgriffe des Zirckels und Lineals», Wien,
(1686), дважды изданный в Москве в 1708 г. под названием «Геометриа
славенски землемерие» и со шмуцтитулом: «Приемы циркуля и линейки
или избраннейшее начало во математических искусствах, им же возможно
легким и новым способом вскоре доступити землемерия и иных из оного
происходящих искусств» *). Эта была первая книга, набранная новым
русским шрифтом. Она была переиздана в 1709 г. под вторым из
приведенных названий, причем дополнена главой «О превращении фигур плоских
во иные такого же содержания» (отдельно изданной еще в 1708 г.), а также
главой об изготовлении солнечных часов. Четвертое издание вышло
в 1725 г. Переводчиком книги был Я. В. Брюс, который составил и
дополнение о преобразовании с помощью циркуля и линейки одних плоских
фигур в другие равновеликие фигуры с некоторыми данными элементами
{всего 39 задач). Сам Петр также принял деятельное участие в
издании, тщательно отредактировав весь текст книги и написав главу о
часах 2).
«Приемы циркуля и линейки» начинаются с объяснения тесной
взаимной связи между «геометрией феоретикой» и «геометрией практикой»
и пользы этой науки. За этим следуют многочисленные определения или
описания ряда геометрических понятий, «общественные знаемности»
(общепринятые положения, аксиомы) и «обещания или допущения»
(постулатов). В этой части сочинения, занимающей вместе с прекрасными
рисунками около 50 страниц, характерно сочетание математических
формулировок в стиле Евклида с практическими чертежными советами
и не претендующими на какую-либо точность аналогиями. Первым стоит
определение: «Пункт есть мнейшая точка, о ней же мыслити возможно,
и не может вящще мнейши разделена быти» и тут же добавляется: «А ради
недовольной остроты очес, делается она иногда довольно велика» 3).
О плоскости сказано: «Плоская суперфициа или наружность есть такое
величество, которое долго и широко есть без толстоты. Солнечная стень
изображает нам подлинную плоскость» 4). Даются графические
представления о винтовой линии («гелика или шурупная»), спиралях («спира-
лис или улитковая»), о линиях «эллиптике», «параболике» и «гиперболике»,
о которых сообщается еще, что они принадлежат к коническим сечениям.
Эллипсоид —«сфероид или раздавленный глобус»,— говорит автор,—
«изображает подлинное яйцо» 5), конус сравнивается с заостренным
караваем и т. п. Аксиомы — те же, что у Евклида, только нет аксиомы
о целом и части. Список постулатов заметно отличается от евклидова,
например, нет постулатов о равенстве прямых углов и о параллельных.
Приведем только первый постулат «Приемов»: «Допущается и признается
х) Ср. И. Я. Д е п м а н, О первом печатном руководстве по геометрии на
русском языке.— Труды Ин-та ист. естеств., т. III, 1949.
2) С. Е. Ф е л ь, Петровская геометрия.— Труды Ин-та ист. естеств., т. IV, 1952.
3) Приемы циркуля и линейки..., М., 1709, стр. 15.
4) Там же, стр. 26.
5) Там же, стр. 42.
72 ГЛ. 3. ГОСУДАРСТВО И МАТЕМАТИКА В ЭПОХУ ПЕТРА ПЕРВОГО
свободно без всякого прекословия, еже ли кто имеет прямую линейку,
к тому же карандаш, или перо, то может он тем на бумаге из даныя точки
прямую линею начертить» *), причем рекомендуется плотно приложить
линейку к бумаге и т. п.
Основное содержание «Приемов», разделенных на шесть книг,
образуют около сотни точных или приближенных построений при помощи
циркуля и линейки. Помимо простейших построений, отметим проведение
прямой через две точки, которые из-за большого расстояния между ними
Рис. 19. Пропорциональное увеличение и уменьшение изображений («Приемы
циркуля и линейки», Москва, 1709, стр. 238, 239).
нельзя соединить линейкой, черчение спиралей из полуокружностей
с растущими в арифметической или геометрической прогрессии
радиусами, веревочное построение эллипса, отыскание центра и осей данного
эллипса, приближенное построение данной плоской фигуры в данном
масштабе (рис. 19). Доказательства отсутствуют.
Богатство построений, содержащихся в «Приемах», очевидно. Книга
имела успех. Она не только трижды переиздавалась, но и много раз
переписывалась; один из сохранившихся списков сделан в Смоленске
в 1768 г.
Важным дополнением к «Приемам» явилась изданная в 1714 г. в
Петербурге «Геометрия практика», в четырех главах которой решено 68 задач
1) Приемы циркуля и линейки..., М., 1709, стр. 54.
ПЕРВЫЕ УЧЕБНИКИ ГЕОМЕТРИИ И ТРИГОНОМЕТРИИ
73
на измерение фигур х). В 1-й главе решаются треугольники и вычисляется
высота удаленных предметов с помощью натуральных таблиц синусов,
тангенсов и секансов. Тригонометрические линии эти вводятся,
соответственно, как горизонтальный катет, вертикальный катет и гипотенуза
прямоугольного треугольника. Во 2-й главе те же и аналогичные задачи
решены с помощью таблиц логарифмов. Главы 3—4 содержат правила
вычисления площадей и прямолинейных фигур, круга и его частей,
эллипса по неточной формуле S = я \—к— ) L поверхностей круглых тел,
а затем объемов правильных многогранников и круглых тел. И здесь
доказательства приемов решения задач не приведены.
И в этих книгах наша математическая терминология обогатилась
большим количеством слов. Многие из них укоренились, как плоскость,
катет, гипотенуза, высота, цилиндр, конус и т. д. Другие термины,
которые легко могли быть заменены русскими словами, вроде: сунерфиция
(площадь, поверхность), корпуленция (объем) и т. д. с течением времени
выпали из обихода.
Мы подробно остановились на учебных руководствах петровского
времени, чтобы показать, насколько шире стал кругозор русских
математиков за первую четверть XVIII века, насколько тем самым
подготовлена была почва для дальнейшего быстрого роста русской математической
культуры, связанного с учреждением Академии наук.
!) И. Я. Д е п м а н, «Геометрия практика», — Ист.-матем. исслед., вып.
VIII, 1955.
ЧАСТЬ ВТОРАЯ
МАТЕМАТИКА В ПЕТЕРБУРГСКОЙ АКАДЕМИИ
НАУК В XVIII ВЕКЕ
ГЛАВА ЧЕТВЕРТАЯ
ПЕТЕРБУРГСКАЯ АКАДЕМИЯ НАУК
Основание Академии наук. Поворотным пунктом в развитии науки
в России явилось основание Петербургской Академии наук (рис. 20).
Событие это Петр I и его помощники подготовляли долгие годы. 22 января
(2 февраля) 1724 г. император утвердил проект положения об Академии.
Рис. 20. Академия наук и Кунсткамера (гравюра Мальтона, 1789).
Ему не довелось, однако, быть свидетелем открытия Академии наук,
первые собрания которой начались в августе 1725 г., через полгода после
его смерти.
Академия наук состояла из трех классов: первый объединял
математику, астрономию, механику с географией, второй — физику, химию
и естественные науки, третий — гуманитарные дисциплины. Академии
предназначалась роль не только научного учреждения, но и основного
центра подготовки ученых и вспомогательного персонала для ее
многочисленных учреждений — обсерватории, лабораторий, инструментальных
мастерских, библиотеки, музея, ботанического сада, издательства и
типографии. С этой целью при Академии учреждались университет и
гимназия, а на академиков возлагались преподавание в них и индивидуальные
занятия с более способными студентами х).
г) Подробнее см.: История Академии наук СССР, т. 1, М.—Л., 1958, а также
П. Пекарский, История Императорской Академии наук в Петербурге, т. I, СПб.,
1870 (эта книга содержит ценные биографические сведения о первых академиках).
МАТЕМАТИКА В АКАДЕМИИ НАУК
75
Математика в Академии наук. К началу XVIII века стало очевидным
значение большого математического аппарата для разработки многих
теоретических и практических проблем науки и техники, имеющих
государственное и общественное значение. При организации Петербургской
Академии наук это обстоятельство учитывалось в полной мере. Среди
23 академиков, приглашенных на работу в течение первых лет, семь
являлись математиками. Это были (по старшинству рождения) Я. Герман,
X. Гольдбах, Ф.-Х. Майер, Г.-В. Крафт, молодые братья Н. и Д. Бер-
нулли и их совсем еще юный друг Л. Эйлер. Вначале академиков
пришлось выписывать из-за рубежа, в данном случае из Швейцарии и
Германии. Позднее в Академии в XVIII веке работали математики В. Е. Адо-
дуров, С. К. Котельников, С. Я. Румовский, И. А. Эйлер, Н. И. Фусс,
М. Е. Головин, А. И. Лексель, Ф. И. Шуберт и С. Е. Гурьев. Все они
внесли больший или меньший вклад в развитие математических наук и
образования. Начиная с 1728 г., когда вышел первый том «Записок»
Петербургской Академии за 1726 г. (рис. 21), по 1806 г., когда был издан последний,
XV том ее «Новых трудов» за 1802 г. х), в изданиях Академии было
напечатано более 700 научных мемуаров и отдельных книг по математике
и механике, среди них около 400 работ Л. Эйлера, около 40 — Д. Бер-
нулли, по 2—3 десятка — Лекселя, Гурьева, Фусса и Шуберта, по
несколько статей Я. Германа, Г.-В. Крафта, С. К. Котельникова, С. Я. Румов-
ского и т. д. 2). Дело было, однако, не только и не столько в количестве
этих публикаций, сколько в их исключительно богатом и разнообразном
научном содержании. Вряд ли можно назвать какой-либо отдел
математики (и механики), который бы не был представлен в изданиях
Петербургской Академии первоклассными изысканиями. Это относится к
теории чисел и теории вероятностей с приложениями к статистике и
страхованию, к элементарной тригонометрии и тригонометрическим рядам,
к сферической геодезии и картографии, к небесной механике и морской
науке, к геометрии и теории машин, а главное, ко всем областям
математического анализа: интегральному исчислению, дифференциальным
уравнениям, вариационному исчислению, специальным функциям и т. д.
Печатные издания Академии оказывали огромное влияние на общий
прогресс математических наук и ученые Западной Европы с нетерпением
ожидали появления ее трудов. В 1734 г., всего лишь через шесть лет
после выхода первого тома «Записок», Д. Бернулли, возвратившийся
в Швейцарию, писал Эйлеру: «Не могу Вам довольно объяснить, с какой
жадностью повсюду спрашивают о Петербургских Мемуарах...
Желательно, чтобы их печатание было ускорено» 3).
Но международная научная информация передавалась не только
через посредство печатных изданий. В тот век, когда периодические
органы большинства академий выходили не чаще раза в год и нередко
с большим опозданием, очень большую роль играла научная переписка.
Ученая корреспонденция Петербургской Академии с Парижем, Лондоном,
х) Всего вышло 14 томов Commentarii Academiae Scientiarum Imperialis Petro-
politanae, затем 20 томов Novi Commentarii, 12 книг Acta и 15 томов Nova Acta —
все на латинском языке. В дальнейшем они цитируются сокращенно: GAP, NCAP,
АР, NAP, соответствующий год тома приводится в скобках, а за ним указан без
скобок фактический год издания.
2) См. библиографический указатель: Математика в изданиях Академии наук.
1728—1935. Сост. О. В. Динзе и К. И. Шафрановский, под ред. В. И. Смирнова,
М.—Л., 1936.
3) Correspondance mathematique et physique de quelques celebres geometres du
XVIIie siecle, publiee par P. H. Fuss, t. II, St.-Petersbourg, 1843, стр. 415—416.
76
ГЛ. 4. ПЕТЕРБУРГСКАЯ АКАДЕМИЯ НАУК
Берлином, Веной и т. д. колоссальна и в ней участвовали почти все
крупные математики того времени. Иные письма представляют собой
небольшие мемуары, с полными доказательствами теорем.
Рис. 21. Титульный лист первого тома «Записок Имп.
Петербургской Академии наук» за 1726 г., 1728.
Таким образом, уже вскоре после основания Академии наук в
Петербурге, молодая русская столица, только что возникшая «из тьмы лесов
и топи блат», превратилась в крупнейший международный центр физико-
математических исследований.
Академия наук и математическое просвещение. Как сказано, при
Академии функционировали университет и гимназия. Их история полна
трудной и далеко не всегда успешной борьбы передовых ученых с
бюрократическим и косным аппаратом, во главе которого долгие годы стоял
советник академической канцелярии И. Д. Шумахер (1690—1761), немало
АКАДЕМИЯ НАУК И МАТЕМАТИЧЕСКОЕ ПРОСВЕЩЕНИЕ 77
препятствовавший воспитанию русских научных кадров. К тому же
материальное положение учащихся было весьма тяжелое, а
перспективы перед большинством из них — незавидные. Государственные деятели
послепетровского времени, которых историк В. О. Ключевский метко
охарактеризовал нулями, потерявшими со смертью Петра I свою
передовую единицу, почти не заботились о подготовке национальной
интеллигенции. Дворянство, даже столичное,
гналось по большей части только за внешним
светским лоском, а тысячи разбросанных
по отцовским поместьям Митрофанушек
старались увильнуть от всякой службы. Купцы
и мещане нередко просили освободить их
детей от учения, детям же крепостных доступ
к образованию и вовсе был закрыт. Учащиеся
набирались по большей части среди детей
солдат, мещан, мастеровых, бедных
священников. Гимназистов и студентов было
немного, и они нередко по своей воле или
невольно не кончали курса и направлялись на
работу переводчиками, канцеляристами,
наборщиками, мастеровыми академических
учреждений. В 1745 г. академики
жаловались на Шумахера, что «при академии
довольного числа студентов никогда не бывало,
о сем не токмо теперь, но еще с начала
академии от всех профессоров происходили в* ?• АД°ДУР0В» первый рус-
г> г\ г -к г г гл скии адъюнкт Академии наук
жалобы. Однако-ж, об отвращении сего вреда (силуэт работы неизвестного
никогда довольного старания не было» и что художника).
пополнение университета присланными из
Москвы молодыми людьми, уже несколько подготовленными к занятиям,
оказалось почти безрезультатным, так как «большая часть из них вместо
обучения наукам сделаны переводчиками, подъячими и ремесленными
людьми». Шумахер, заявляли академики, «только думает о художествах,
которые глазами можно чувствовать и дабы тем себя показать, старание
имеет» *). В. Е. Адодуров (26 марта 1709—16 ноября 1780), первый русский
студент, получивший звание адъюнкта Академии 2) и работавший в ней
в 1733—1741 г., писал: «Кроме языков, обучался я при Академии наук
истории, географии, философским, математическим и физическим наукам,
а именно: логике, метафизике, арифметике, геометрии, тригонометрии
плоской и сферической, алгебре и некоторым другим. И может быть,
чтоб в оных науках не посредственное познание получить мог, ежели
бы для неискусства в тех науках академических переводчиков, не
принужден был касающих до оных наук переводов почти всегда отправлять,
которые не малую часть времени у меня занимали» 3).
1) С. В. Рождественский, Очерки по истории систем народного
просвещения в России в XVIII—XIX вв., т. I, СПб., 1911, стр. 166—167.
2) Младшие по должности члены Академии именовались адъюнктами, далее шли
по старшинству экстраординарные профессора и профессора (в XIX веке
—экстраординарные и ординарные академики). Звание члена-корреспондента введено в 1759 г.
3) П. Пекарский, История Императорской Академии наук в Петербурге,
т. I, стр. 511—512. По-видимому, Адодуров не был лишен математического дарования.
В Академии, помимо переводов, он должен был заниматься главным образом
преподаванием языков. В 1762—1771 гг. он состоял куратором (попечителем) Московского
университета.
78
ГЛ. 4. ПЕТЕРБУРГСКАЯ АКАДЕМИЯ НАУК
Общая математическая подготовка в университете ограничивалась
кругом элементарных предметов, но студенты, специализировавшиеся
в физико-математических науках, изучали и высшую математику.
Заканчивая университет, математики представляли пробные работы, решая
задачи, требовавшие хорошего владения аналитической геометрией,
дифференциальным и интегральным исчислением, обыкновенными
дифференциальными уравнениями, бесконечными степенными рядами и т. п.
Некоторые молодые люди
направлялись для
усовершенствования в Германию.
Как ни трудны были
условия деятельности академических
учебных заведений, они
сыграли весьма важную роль в
развитии науки и просвещения
в XVIII веке, вплоть до их
закрытия в самом начале XIX
столетия. Не говоря о гениальном
М. В. Ломоносове и других
представителях естественных
и гуманитарных наук, только
математическим наукам первый
наш университет дал В. Е. Адо-
дурова, А. А. Барсова, Б. А.
Волкова, М. Е. Головина,
Я. П. Козельского, С. К. Ко-
тельникова, С. Я. Румовского,
М. Софронова, Н. И. Фусса,
И. Юдина. Эти люди и другие,
здесь не названные, много
потрудились для распространения
математических знаний, а неко-
Н. Г. Курганов - «навигатор, обсерватор, Т0РЫе пеРвыми из РУССКИХ вы-
астроном, морской ходитель, корабельной ступили на научном поприще,
водитель, небесных звезд считатель» с руко- Почти все питомцы академи-
водством по навигации в руках (зарисовка, ческого университета вели заня-
сделанная в 1789 г. одним из учеников). тияне только в неми состоявшей
при нем гимназии, но и в других
учебных заведениях. А. А. Барсов (1730—1791) стал первым профессором
математики в основанном в 1755 г. Московском университете. Математику
он преподавал здесь шесть лет *), после чего его заменил в 1762 г. его
же ученик Д. С. Аничков (ум. 1788), автор нескольких учебников по
элементарной математике и философской диссертации, содержавшей
вольнодумные рассуждения о земном происхождении религий и о том, что
человеку по природе несвойственно верить тому, чего нельзя себе представить
мысленно или в воображении2). М. Е. Головин (1756—1790), племянник
Ломоносова и ученик Эйлера, активно участвовал в организации системы
1) Барсов, более интересовавшийся филологией, перешел на освободившуюся
кафедру русской словесности.
2) Заметим здесь же, что в XVIII веке математика была в Московском
университете второстепенным вспомогательным предметом и студенты проходили только
ее элементарные отделы. См. А. П. Юшкевич, Математика в Московском
университете за первые сто лет его существования,— Ист.-матем. исслед., вып. I, 1948.
УЧЕБНАЯ ЛИТЕРАТУРА
79
народных училищ, начатой в 1782 г., и был профессором основанной
в 1786 г. Учительской семинарии в Петербурге, первом рассаднике
преподавателей общей гражданской школы в России. Уроженец Украины
Я. П. Козельский (ок. 1728—ок. 1794), видный философ материалисти-
чески-сенсуалистского направления, обучал математике и механике
в Артиллерийском и инженерном кадетском корпусе, возникшем в 1762 г.
из слияния Артиллерийской и Инженерной школ. С. К. Котельников вел
занятия в Морском кадетском корпусе, открытом в 1752 г. на базе
Морской академии. В Сухопутном (открыт в 1731 г.) и Морском кадетских
корпусах преподавал Н. И. Фусс, который также принял активное
участие в реформе системы образования, произведенной в начале XIX века.
С. Я. Румовский в 1803—1812 гг. был первым попечителем Казанского
учебного округа и оказал большую помощь при организации Казанского
университета.
Наряду с этим к работе в Академии наук привлекались сотрудники
военных и морских школ. Так было, например, с учеником Магницкого
по Навигацкой школе, а затем слушателем Морской академии Н. Г.
Кургановым (1725 или 1726—1796), автором популярнейшей хрестоматии —
«Письмовника» (1769) и многих учебников для Морского корпуса, где
он преподавал математические и мореходные науки с 1743 г. до самой
смерти. На протяжении почти 20 лет Курганов участвовал в
астрономических и картографических работах и экспедициях Академии наук, был
тесно связан со многими ее учеными и в 1774 г. получил от Л. Эйлера
и С. К. Котельникова весьма лестную характеристику, на основании
которой ему присвоили звание профессора высшей математики и
навигации Морского корпуса *).
Учебная литература. Большой вклад внесла Академия наук в
создание учебной математической литературы. На протяжении XVIII века
количество русских руководств по математике постепенно возрастало.
За первую половину века их вышло около 30, за следующие 25 лет 32,
а в последнюю четверть столетия 66, т. е. больше, чем за предыдущие
75 лет.
Общей тенденцией европейской учебной литературы XVIII века
было стремление перейти от догматического преподнесения правил
решения задач, рассчитанного на механическое заучивание отдельных
рецептов, к систематическому научному изложению. В разных странах эта
тенденция принимала различные формы. В Германии, особенно под
влиянием Хр. Вольфа, автора весьма распространенных руководств по всему
циклу математических наук (1710 и след.) 2), была на первый план
выдвинута логическая тренировка учащихся. Вольфианство в педагогике,
справедливо отвергавшее обучение математике как совокупности
ремесленных правил, страдало переоценкой формальной и часто к тому же
иллюзорной строгости в ущерб наглядным представлениям и интуиции.
В погоне за мнимым логическим совершенством начальные отделы
учебников загромождались не применяющимися далее и потому бесполезными
и педагогически даже вредными аксиомами, постулатами и
многочисленными определениями, за которыми следовали плохо связанные с ними
и между собой теоремы, следствия и поучения, с одной стороны, и сугубо
х) Подробнее см.: А. П. Денисов, Н. Г. Курганов — выдающийся русский
ученый и просветитель XVIII века, Л., 1961.
2) К математическим наукам Вольф относил не только механику, физику и
астрономию, но также пиротехнику и архитектуру.
80
ГЛ. 4. ПЕТЕРБУРГСКАЯ АКАДЕМИЯ НАУК
деловые советы землемерного или расчетного характера, с другой.
Педантическая псевдострогость приводила Вольфа и его последователей к
курьезам, вроде изложения архитектуры more geometrico, причем
доказывались, как «теоремы» утверждения, что окно не должно быть выше трех
футов от пола или что высота комнаты не должна быть ни слишком велика,
ни слишком мала. Это направление стало быстро отставать от требований
жизни и развития математики. Довольно скоро в самой Германии на смену
курсам Вольфа пришли изданные в 1758—1766 гг. руководства А. Г. Кест-
нера, гораздо менее педантические и более содержательные. В Англии
тогда же велась усиленная работа над приспособлением к преподаванию
«Начал» Евклида, доставивших немалые мучения многим поколениям
ребят. Наконец, в предреволюционной Франции шла борьба за
демократизацию преподавания и предпринимались энергичные и успешные усилия
соединить простоту и наглядность обучения математике с убедительностью
доказательств. Здесь во главе этого движения, истоки которого восходят
еще к XVI веку и П. ла Рамэ, стояли А. Клеро и Ж. Даламбер, которые
считали вообще лишним начинать курс с какой-либо аксиоматики.
Все эти тенденции отразились, хотя и с различной силой, в
оригинальной и переводной русской литературе. Мы встречаемся в ней и с
несколько ослабленным вольфианским направлением, например в учебниках
Д. С. Аничкова для Московского университета, и с попытками применения
в Морском корпусе обработок «Начал» Евклида, изданных Фархварсоном
и Кургановым *), а также преподавателями того же корпуса В. Н.
Никитиным (1739—1809) и П. И. Суворовым (1750—1815) 2), и с переводами
французских учебников. Вместе с тем в России складывалось и
собственное направление, по духу родственное французскому, но от него
независимое. Ведущими были руководства Л. Эйлера, оказавшие
исключительное воздействие на мировую учебную литературу. Характерными
особенностями курсов Эйлера являются, наряду со строгой последовательностью
и систематичностью, поразительная доходчивость и прозрачность
изложения. Теоретические положения доказываются с редкой простотой
и всегда сопровождаются увлекательными и подробно разобранными
примерами. Читатель вводится в самую суть проблемы как бы наиболее
естественным путем и все время с живым интересом следит за
рассуждениями автора, возбуждающими работу собственной интуиции читателя
и вместе с тем обучающими его мыслить математически. Так же писал
Эйлер свои научные мемуары.
Мы рассмотрим подробнее творчество Эйлера далее. Здесь мы назовем
для примера прежде всего «Руководство к арифметике, для употребления
в гимназии при Императорской Академии наук», вышедшее вначале
на немецком языке (СПб., 1738—1740), а затем в русском переводе
В. Е. Адодурова (ч. 1, СПб., 1740) и студента В. Кузнецова (ч. 2, СПб.,
1760). Хотя Эйлер, в 1741 г. переехавший в Берлин, не закончил книгу
и изданные части ее содержали лишь действия над целыми, дробями и над
именованными числами, она положила начало новому течению в нашей
учебной литературе. В предисловии Эйлер противопоставил свою
педагогическую установку авторам зарубежных учебников, которые либо
«содержат только правила с многими при них положенными примерами»,
х) Елементы геометрии,... состоящие из осьми Евклидовых книг, изъясненные
новым способом, удобопонятнейшим юношеству. Перев. с французского Н.
Курганова, СПб., 1769.
2) Евклидовых стихий осьмь книг... Переведены с греческого и поправлены
(В. Н. Никитиным и П. И. Суворовым), СПб., 1784; изд. 2-е, 1789.
УЧЕБНАЯ ЛИТЕРАТУРА
81
либо же, если и разъясняют основания арифметики, «однакож так
трудным и непонятным образом, что ежели кто к математическому порядку
не привык, так не можно почти того и выразуметь» (ч. 1, стр. 4). Свое
влияние «Руководство» Эйлера оказало особенно через две книги
Курганова, одобренные и изданные Академией. Это «Универсальная
арифметика» (1-е изд., СПб., 1757), содержащая, подобно труду Магницкого,
также геометрическую и алгебраическую части, и «Арифметика или
числовник» (1-е изд., СПб., 1771), отличающаяся от предыдущей книги
главным образом исключением геометрических задач и алгебры. В
изложении действий над отвлеченными и именованными числами Курганов
непосредственно примкнул к Эйлеру.
Еще большее значение получила «Универсальная арифметика»
Л. Эйлера (два тома, СПб., 1768—1769), вышедшая сначала в русском
переводе студентов П. Б. Иноходцева (1742—1806), позднее академика
по кафедре астрономии, и И. Юдина, а через два года в немецком
оригинале1). Это учебное руководство по алгебре включает большой отдел,
посвященный решению в целых числах неопределенных уравнений
и содержит, особенно в названном отделе, ряд открытий самого Эйлера.
О высоких достоинствах книги говорят ее многократные переиздания
и переводы на французский, английский, голландский и латинский языки.
В письме к Эйлеру от 30 декабря 1773 г. Ж. Лагранж писал: «Я в
особенном восхищении от части, касающейся неопределенных задач, и нахожу
ее тем более ценной, что, насколько мне известно, еще не существует
книги, в которой эта область анализа была бы рассмотрена сколько-
нибудь удовлетворительно» 2). Изданный в следующем году французский
перевод книги вышел с ценными дополнениями Лагранжа по диофантову
анализу. Но и в собственно алгебраической части «Универсальная
арифметика»— мастерский труд, существенно отличающийся от других
выдающихся курсов алгебры, вышедших ранее, таких, как «Универсальная
арифметика» И. Ньютона (Arithmetica universalis, 1707), развернутым
комментарием к которой является «Трактат по алгебре» (Treatise on
Algebra, 1748) К. Маклорена и «Начала алгебры» (Elements d'algebre, 1746)
А. Клеро. Отбор, расположение и способ изложения материала, данные
Эйлером, в значительной мере определили курс элементарной алгебры
в течение последующих полутораста лет. В первом томе Эйлер с
необычной ранее полнотой рассматривает основные понятия и операции алгебры
многочленов и развивает соответствующее исчисление; сюда же входят
соединения и бином Ньютона, пропорции и прогрессии, десятичные дроби
и логарифмы; второй том посвящен уравнениям до четвертой степени
включительно, приближенному вычислению корней и неопределенному
анализу. Позднее Н. И. Фусс составил по Эйлеру учебник для
Сухопутного кадетского корпуса на французском языке —«Уроки алгебры» (Legons
d'algebre, СПб., 1783). Переработка Фусса состояла, главным образом,
в сокращении объема, особенно в части диофантова анализа. По-русски
«Начальные основания алгебры» (СПб., 1798) Фусса вышли как первая
х) До того Академия выпустила в свет первый русский учебник алгебры —
«Начальное основание математики» (СПб., 1752) крупного военного инженера
Н. Е. Муравьева (1724—1770). Редактором книги, содержавшей и некоторые сведения
по высшей алгебре (связь корней и коэффициентов уравнения, правило Декарта,
отделение корней, кубические уравнения, приближенный метод Ньютона), но не
отличавшейся большими педагогическими достоинствами, был астроном академик
Н. И. Попов (1720—1782).
2) С. Я. Лурье, Неопубликованная научная переписка Леонарда Эйлера.—
Сборник: Леонард Эйлер, М.— Л., 1935, стр. 116.
82
ГЛ. 4. ПЕТЕРБУРГСКАЯ АКАДЕМИЯ НАУК
часть курса, охватывавшего также геометрию, тригонометрию,
аналитическую геометрию и анализ и употреблявшегося в начале XIX века
в гимназиях.
В нескольких своих сочинениях Эйлер придал тригонометрии
современный вид — и по форме и по содержанию. На этой основе М. Е. Головин
написал «Плоскую и сферическую тригонометрию с алгебраическими
доказательствами», изданную по решению Академии наук (СПб., 1789).
Этот учебник превосходил по научному уровню все более ранние и даже
некоторые изданные позднее.
Наконец, сжатым конспектом трудов Эйлера явилось и первое на
русском языке изложение основ математического анализа, принадлежащее
С. К. Котельникову и включенное им во второй том переведенных и
переработанных им «Сокращений первых оснований мафиматики» (Auszug aus
den Anfangsgrunden aller Mathematischen Wissenschaften, Halle, 1713)
Xp. Вольфа (два тома, СПб., 1770—1771). На полусотне страниц
Котельников приводит сведения о функциях —«объятиях» и их разложениях
в степенные ряды, «дифференциальном калкулусе» (правила
дифференцирования, ряд Тейлора, экстремумы) и «интегральном калкулусе»
(вычисление неопределенных интегралов, применение рядов, отдельные
определенные интегралы и обыкновенные дифференциальные уравнения).
Объяснения, вообще очень сжатые, иногда вовсе недостаточны;
доказательства почти отсутствуют. Вскоре появились и другие, более полные
книги по высшей математике на русском языке, особенно нужные для
Учительской семинарии, военных школ, а с начала XIX века для физико-
математических факультетов. Студенты академического университета
нуждались в руководствах на русском языке в меньшей степени, так как
основательно изучали иностранные языки, включая латынь, на которой
написаны почти все работы Эйлера.
Не задерживаясь далее на истории математического образования *),
мы обратимся к научной деятельности петербургских академиков,
предпослав этому несколько замечаний о состоянии и задачах математики
к началу XVIII века.
г) Подробнее см. А. П. Юшкевич, Математика и ее преподавание в России
XVIII—XIX вв.— Математика в школе, 1947, № 3—4; А. П. Ю ш к е в и ч, Эйлер
и русская математика в XVIII веке.— Труды Ин-та ист. естеств., т. III, 1949.
ТЛАВА ПЯТАЯ
ПЕРВЫЕ АКАДЕМИКИ-МАТЕМАТИКИ
Математика на рубеже XVII и XVIII веков. Основание Петербургской
Академии наук пришлось на время бурного расцвета математики и
механики. В XVII—XVIII вв., как писал Энгельс, «первое место заняло
элементарнейшее естествознание — механика земных и небесных тел,
а наряду с ней, на службе у нее, открытие и усовершенствование
математических методов. Здесь были совершены великие дела» х).
XVII век ознаменован был многими замечательными открытиями
в математике, механике, оптике и астрономии. В его первые годы Кеплер,
исходя из коперниканской картины мира, установил основные законы
движения планет по эллиптическим орбитам. Галилей, усовершенствовав
зрительную трубу, произвел на небе наблюдения, укрепившие коперни-
канство, а изучая падение тяжелых тел, заложил основы динамики. Вслед
за тем, как Галилей доказал, что наклонно брошенное в пустоте тело
движется по параболе, его ученик Торричелли установил, что
параболическую форму имеет и струя жидкости, вытекающая из отверстия в
боковой стенке сосуда: это был первый закон гидродинамики. Изготовление
телескопов и микроскопов выдвинуло ряд проблем геометрической оптики.
Гюйгенс исследовал, в связи с техникой изготовления часов, задачу
о малых колебаниях; попутно он выяснил, что траекторией маятника
постоянного периода служит циклоида. Изучение формы тяжелой, гибкой
и нерастяжимой нити, подвешенной за два конца, привело к другой новой
трансцендентной кривой — цепной линии. Наконец, Ньютон в
бессмертных «Математических началах натуральной философии» (Philosophiae
naturalis principia mathematica, 1686) сформулировал три классических
закона динамики и закон всемирного тяготения, вывел отсюда законы
Кеплера и заложил прочный фундамент классической небесной механики,
завещав, впрочем, потомству ряд трудных проблем теории движения
Луны, планет и комет, теории взаимного притяжения неточечных масс.
Развитие механики и физики непосредственно переплеталось, часто
в творчестве одних и тех же людей, с разработкой математических
методов. В центре внимания оказывается изучение быстро увеличивающегося
в объеме класса функций, этого математического эквивалента движения
и изменения. В 1637 г. Декарт и одновременно Ферма создают аналитико-
геометрический метод изучения геометрических образов при помощи
уравнений между переменными координатами их точек и показывают
образцы его применения на плоских кривых второго порядка и
нескольких других линиях; Ньютон, привлекая также проективный метод,
г) Ф. Энгельс, Диалектика природы, М., 1953, стр. 5.
34
ГЛ. 5. ПЕРВЫЕ АКАДЕМИКИ-МАТЕМАТИКИ
исследует затем кривые третьего порядка. Тот же Декарт совершенствует
алгебру и ее символику. Целая плеяда математиков при решении вопросов
геометрии и естествознания создает два рода приемов для решения
двух групп задач. Одна из них в более отвлеченном выражении сводится
к дифференцированию (проведение касательных и нормалей,
определение скорости движения, экстремумы, кратные корни уравнений, эволюты),
а другая — к интегрированию (квадратуры и кубатуры, центры тяжести,
определение пути, давление). Быстро выясняется — в геометрическом
или механическом выражении — взаимообратная связь между этими
группами задач и соответствующими им математическими приемами.
Для представления иррациональных и трансцендентных функций и
для приближенных вычислений начинают применять бесконечные
степенные ряды.
В только что упомянутых приемах не было, однако, единства.
Им недоставало, как вскоре обнаружилось, общих аналитических
понятий и подходящей символики, без чего невозможно было создание
достаточно сильных и общих, а вместе с тем единообразных и простых методов,
пригодных для исследования всех этих задач. Новый и решающий шаг
был сделан Ньютоном и Лейбницем, которые выявили центральные общие
идеи, содержавшиеся в инфинитезимальных приемах их
предшественников. Следуя различными путями, употребляя различную терминологию
и обозначения, оба они независимо и почти одновременно установили
основные понятия и правила операций метода флюксий и флюент
(по выражению Ньютона) или дифференциального и интегрального
исчисления (как говорил Лейбниц). Они же первые стали употреблять
в широком масштабе бесконечные ряды, а также применили новое
исчисление к множеству новых вопросов, положив при этом начало
дифференциальной геометрии плоских кривых и решению обыкновенных
дифференциальных уравнений. Работы основоположников математического
анализа были почти немедленно продолжены их последователями,
особенно Яковом Бернулли и его младшим братом Иоганном Бернулли.
В конце XVII века исчисление бесконечно малых было приложено к
проблемам вариационного исчисления, а в начале XVIII века к одной из
важнейших в истории математической физики задач — о малых колебаниях
струны.
Успехи анализа были столь велики, что подавали надежду на быстрое
исчерпание главных математических задач. В 1691 г. Лейбниц писал
Гюйгенсу: «Я хочу, чтобы мы могли еще в этом веке довести до
завершения анализ чисел и линий, по крайней мере в главном, дабы избавить
от этой заботы человеческий род, чтобы отныне вся проницательность
человеческого разума обратилась к физике» х). Однако в
действительности, на протяжении всего XVIII века и вплоть до наших дней постоянно
возникали все новые проблемы, требовавшие новых понятий и методов
математического анализа.
Открытие дифференциального и интегрального исчислений явилось
основным, но не единственным крупным событием в математической
жизни XVII века. Это столетие было отмечено также большими
достижениями в алгебре и возрождением интереса к теории чисел, многие
замечательные предложения которой сформулировал, не сообщив
доказательства, Ферма. Тот же Ферма, вместе с Б. Паскалем и Гюйгенсом, сооб-
г) Leibnizens mathematische Schriften, hsg. von С. Gerhardt, В. II. Halle, 1850,
S. 107—108.
ПЕРВЫЕ АКАДЕМИКИ
85
гцил первый толчок развитию теории вероятности, как отдельной науки,
а Я. Бернулли высказал и точно доказал носящий теперь его имя закон
больших чисел. Наконец, помимо аналитической геометрии, были сделаны
первые шаги в область проективной геометрии. Однако блестящий почин
Дезарга почти не нашел в ту эпоху продолжателей.
В Петербургской Академии наук XVIII века, кроме работ по
математическому анализу, преобладающее значение получили исследования,
связанные с его приложениями к проблемам механики, астрономии,
физики и техники. Именно это направление ярко выражено в трудах
Д. Бернулли, который был в первой группе ученых, приглашенных
из-за границы. Центральной фигурой в этой области был великий
Л. Эйлер, творчество которого охватило все области
физико-математических знаний. В этой сфере человеческой деятельности XVIII столетие
с полным правом может быть названо веком Эйлера.
Наряду с математическим анализом и его приложениями в Академии
разрабатывались вопросы теории чисел. Здесь основополагающими
явились опять-таки труды Эйлера. Другое важное направление изысканий
было связано с понятием вероятности и его приложениями в статистике.
Все отмеченные направления, возникшие в первый же период
существования Академии, получили широкое развитие в дальнейших ее работах
вплоть до настоящего времени. Наиболее яркий и влиятельный
представитель математических наук в Академии наук в XIX веке, П. Л. Чебышев.
сделал блестящие открытия во всех указанных областях: теории чисел,
теории вероятностей и математическом анализе, особенно в теории
приближения функций и ее приложениях к теории механизмов и машин.
Первые академики. Мы уже сказали, что с 1725—1727 гг. в составе
Академии наук работали Герман, Гольдбах, Майер, Крафт, два брата
Бернулли, к именам которых, быть может, следует добавить еще имя
механика и физика Г. В. Бюльфингера (1695—1750). Всем им, хотя и в
разной мере, Петербургская Академия наук обязана первыми своими
замечательными достижениями в сфере механико-математических наук.
Но и эти ученые, как и другие иностранные члены Академии, чрезвычайно
многим обязаны были России. Только здесь, в Академии, они нашли
подходящие условия для теоретических и экспериментальных
исследований, для публикации своих трудов, а потребности русского государства
и общества нередко непосредственно стимулировали и направляли
их занятия. В Академии был собран большой по тем временам коллектив,
члены которого имели постоянную возможность почти каждодневных
встреч, взаимного духовного обогащения и вместе с тем критики;
еженедельно, а то и два раза в неделю на конференциях обсуждались научные
доклады.
Петербург, как магнит, притягивал многих западноевропейских
ученых, не только начинающих, но и маститых, особенно из Германии
и Швейцарии. В немецких университетах первой половины XVIII в.
ничто, в сущности, не содействовало творческой деятельности по
математике; ни отношение властей, ни запросы студентов, ни среда, в которой
математик оказывался, как правило, в единственном числе. В
Швейцарии даже самые одаренные молодые математики не могли рассчитывать
на одну из крайне немногочисленных университетских должностей (они
насчитывались единицами), пока не скончается занимающий ее профессор,
и нередко вынуждены были браться за другие дела — юриспруденцию,
медицину, философию, богословие. Блестящие перспективы работы
86
ГЛ. 5. ПЕРВЫЕ АКАДЕМИКИ-МАТЕМАТИКИ
в России ясны были уже И. Бернулли, который стал профессором
математики Базельского университета в 1705 г., когда умер состоявший в этой
должности его старший брат. В связи с переездом своих сыновей Николая
и Даниила в Петербург, И. Бернулли писал: «...лучше несколько
потерпеть от сурового климата страны льдов, в которой приветствуют муз,
чем умереть от голода в стране с умеренным климатом, в которой муз
обижают и презирают»1).
Выразительно подчеркнул значение, которое имела работа в
Петербургской Академии наук для ее членов, Л. Эйлер. В письме к Шумахеру
от 18 ноября 1749 г., отправленном из Берлина, где он тогда жил, Эйлер
писал: «...я и все остальные, имевшие счастье некоторое время состоять
при русской императорской Академии, должны признать, что всем, чем
являемся, мы обязаны благоприятным обстоятельствам, в которых там
находились. Что касается собственно меня лично, то при отсутствии этой
превосходной возможности, я был бы вынужден отдаться главным образом
другим занятиям, в которых, судя по всему, оказался бы только
дилетантом. Когда его корол. величество [Фридрих II Прусский] недавно
спросил меня, где я изучил то, что знаю, я, согласно истине, ответил, что
всем обязан своему пребыванию при Академии в Петербурге» 2).
Участие-академиков в развитии математики и в трудах самой Академии
было неодинаковым. Не говоря уже о различиях в даровании, некоторые
работали в Академии недолго, как Герман, Майер и особенно Н.
Бернулли, а Гольдбах занимался больше научно-организационными делами
Академии, чем научными исследованиями. Тем не менее и эти ученые
оставили значительный след в развитии математики.
Я. Герман. Старейший из академиков Яков Герман (16 июля 1678 —
14 июля 1733), первый из иностранных академиков заключивший
контракт, обязывавший его проработать в Академии пять лет, ко времени
приезда в Петербург был уже видным математиком. Его учителем по
Базельскому университету был Я. Бернулли, с ним переписывался
Лейбниц, по предложению которого Герман в 1701 г. был избран членом
только что основанной Берлинской Академии наук. В 1707 г. Герман
был приглашен в Падуанский университет, а в 1713 г. в университет
во Франкфурте-на-Одере, где он закончил свою «Форономию, или о силах
и движениях твердых и жидких тел» (Phoronomia, seu de viribus et motibus
corporum solidarum et fluidorum, Amstelodami, 1716). Этот труд, в
котором содержалось систематическое, хотя и весьма сжатое, изложение
механики, пользовался в свое время большой известностью. В
предисловии к своей «Механике» (1736) Эйлер писал: «Я не знаю, вышла ли в свет
какая-либо другая работа, кроме «Форономии» Германа, в которой это
учение о движении было бы разобрано совершенно отдельно и обогащено
столь многими блестящими вновь открытыми положениями»3). Вместе
с тем Эйлер отмечал, как недостаток сочинения, что автор не применил
анализа и все излагал при помощи синтетических геометрических
доказательств.
г) L.— G. du Pasquier, Leonard Euler et ses amis, Paris, 1927, стр. 9.
2) Die Berliner und die Petersburger Akademie der Wissenschaften im Briefwechsel
Leonhard Eulers, T. II, hsg. und eingeleitet von A. P. Juskevic und E. Winter,
Berlin, 1961, стр. 182.
3) Л. Эйлер, Основы динамики точки. Перев. В. С. Гохмана и С. П.
Кондратьева, под ред. В. П. Егоршина, М.— Л., 1938, стр. 33.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
87
Математические труды Германа стали появляться в 1700 г., когда
•он выступил с защитой дифференциального исчисления от голландца
Б. Ныовентиита, подвергнувшего критике понятие бесконечно малых
и принцип пренебрежения таких слагаемых, а также применение
дифференциалов высших порядков (1694 и след. годы). За этим последовали
статьи по дифференциальной геометрии плоских кривых (1702—1703),
вывод теорем сложения тангенса и секанса, откуда Герман индуктивно
получил разложения тангенса и секанса кратной дуги (1706), улучшенное
изложение открытого Лейбницем правила решения задачи об
ортогональных траекториях, т. е. об отыскании кривых, ортогонально пересекающих
данное однопараметрическое семейство плоских кривых (1717—1719)
и еще некоторые работы.
В Петербурге, куда Герман прибыл вместе с Бюльфингером в августе
1725 г., он, согласно контракту, должен был «о приращении Академии
генерально старание иметь, особливо же части высшей математики
в совершенство приводить, о том систему написать и ежедневно по оной,
выключая праздники, в пользу учащегося юношества по одному часу
читать и в своей науке одного или двух студентов в совершенство при-
весть» г). Как первый ученый, ставший у нас академиком [его патент
датирован 4(15) мая 1725 г.], он назывался нередко professor primarius
et matheseos sublimioris.
«Системы» высшей математики Герман не написал, но был весьма
деятельным членом Академии и оказал несомненное влияние на интересы
более молодых своих коллег. Первый сохранившийся протокол
конференции Академии гласит, что 13(24) ноября 1725 г. Герман сделал доклад
об аналитическом выводе сфероидальной формы Земли, которую Ньютон
выводил синтетическим методом. Его статья о мере живых сил открывает
собой первый том академических «Записок». В публичном собрании
Академии 1(12) августа 1726 г. он выступил с речью о происхождении и
развитии геометрии (De ortu et progressu Geometriae; опубликована в Ser-
mones in secundo solenni Academiae scientiarum... recitati., Petropoli,
1728). Из-за происков Шумахера Герман вместе с тем же Бюльфингером,
с которым приехал в Петербург, покинул в январе 1731 г. русскую
столицу, сохранив звание почетного академика, и пенсию, обязывавшие его
присылать в Академию некоторые свои труды.
Дифференциальные уравнения. В первых шести томах «Записок»
Академии напечатано 15 работ Германа, из них 12 по разным вопросам
математики, Несколько статей посвящено обыкновенным
дифференциальным уравнениям, которыми занимались и другие академики. В одной
статье предложен своеобразный прием преобразования уравнения
первого порядка, с помощью которого Герман проинтегрировал, правда,
довольно громоздко, уравнение в полных дифференциалах с целыми
рациональными коэффициентами [САР I (1726) 17281. Вскоре затем он
впервые рассмотрел [САР II (1727) 1729] уравнение
y = P(z)x + Q(z), где dy = zdx,
которое теперь известно под именем Даламбера, решившего его на
двадцать лет позднее [1748 (1750)] в порядке обобщения так называемого
уравнения Клеро [случай Р (z) = z; 1734 (1736)], или под именем Лагран-
жа, занявшегося им еще позднее. Для решения Герман прежде всего
1) П. П е к а р с к и й, История Ими. Академии наук в Петербурге, т. I, стр. 67.
88
ГЛ. 5. ПЕРВЫЕ АКАДЕМИКИ-МАТЕМАТИКИ
дифференцирует уравнение по х (прием, употребленный также Клеро
и Даламбером), после чего получается вспомогательное уравнение,
линейное относительно х, которое затем интегрируется несколько иначе, чем
по обычному способу. Решение исходного уравнения, которое было бы
правильнее называть уравнением Германа, записывается в форме двух
выражений для х ж у в функции параметра z, точно так, как и теперь.
Случай обращения Р (z) — z в нуль Герман не рассмотрел, пройдя поэтому
мимо возможных особых решений и уравнения Клеро *).
Вопросы геометрии. Ряд работ Германа относится к различным
отделам геометрии. В том же первом томе «Записок» он поместил статьи о
задаче Кеплера разделить полукруг в данном отношении (Герман это делает
двумя способами: с помощью одной специальной кривой и аналитически,
посредством быстро сходящегося ряда) и о сферических эпициклоидах,
т. е. кривых, описываемых фиксированной точкой окружности радиуса Ь,
катящейся по неподвижной окружности радиуса а на поверхности шара.
Незадолго перед тем В. Вивиани показал, что сферическая лемниската,
возникающая в пересечении шаровой поверхности с касающимся его
внутренним образом цилиндром, диаметр которого равен радиусу шара,
вырезает из шарового октанта точно квадрируемую область (1692). Эта
изящная задача привлекла в свое время внимание Лейбница, И. Бернулли
и др. Герман занялся сферической эпициклоидой в связи с проблемой
спрямления кривых на шаре; он показал, что длина этой линии I весьма
просто выражается через радиусы обеих окружностей и косинус угла ф
между их плоскостями:
у_4&Уа2 — 2a&cos(p + b2
I — ш
а
Спустя некоторое время сферические эпициклоиды исследовал И.
Бернулли (1735), а позднее академики Лексель [АР (1779 : 1) 1782] и Фусс
(Mem. Acad. Petersb., VIII, 1822). Вообще, изучение кривых на шаре
стало в конце XVIII века одной из главных областей занятий учеников
Эйлера.
В IV т. «Записок» [1729 (1735)] Герман дал более полное, по сравнению
с прежними, аналитическое рассмотрение кривых второго порядка.
Он развил способ, предложенный еще Декартом (1637), и исходил из
уравнения
ат/2 + 2|in/ + ух2 + 28у + 2гх + ср = О,
разрешенного относительно у. Герман показывает, что кривая бывает
эллипсом, параболой или гиперболой, смотря по тому, меньше нуля,
равна ему или больше его величина J32 — ay. Случаи вырождения, вообще
говоря, остались вне поля зрения, но Герман знал, что когда в выражении
для у корень извлекается, уравнение может представлять пару прямых.
Декарт, не учтя двузначности квадратичного радикала, считал, что
уравнение при этом выражает одну прямую. Анализ Германа несколько
улучшил и дополнил В. Риккати (1757), который, в частности, подробно
разобрал один гиперболический случай, упущенный петербургским
1)М. I. Симонов, Про nepini дослщження з диференщальних р1внянь
у Петербурзыай Академп наук.— 1сторико-математичний збарник, IV, Кшв, 1963.—
Возможно, что уравнение Германа — Даламбера проинтегрировал еще в 1694 г.
И. Бернулли, не опубликовавший, однако, своего результата (ср. Г. В и л е й т-
н е р, История математики от Декарта до середины XIX столетия. Перев. под ред.
А. П. Юшкевича, 2-е изд., М., 1966, стр. 189).
ВОПРОСЫ ГЕОМЕТРИИ
89
академиком. В ином плане и с большим совершенством построил теорию
кривых второго порядка Эйлер, о чем будет сказано далее.
В том же томе «Записок» Герман распространил метод полярных
координат, примененных Я. Бернулли только к спиралям (1691), на любые
плоские кривые, подчеркнув, что с его помощью можно так же изящно
исследовать свойства линий, как и обычным методом. Попутно Герман
записал формулы, выражающие декартовы координаты точки через
полярные в виде х = nz, у = mz, где z —«радиус проекции», а п и тп —
косинус и синус «угла проекции». Среди кривых, рассмотренных таким
образом, были парабола — первое применение полярных координат
к коническим сечениям — и декартов лист. В употреблении таких
координат за Германом последовали многие и, пожалуй, прежде всего
петербургские математики — Крафт, в одной статье которого появляется
термин полярное уравнение — aequatio polaris [GAP VI (1732—1733) 1738],
Эйлер и затем его преемники до Гурьева включительно.
Наконец, Герман одним из первых приступил к систематической
разработке аналитической геометрии в пространстве. В статье,
присланной уже из Базеля и напечатанной посмертно в VI томе «Записок», ониссле-
довал, отправляясь от их уравнений, ряд поверхностей, начиная с
плоскости
az + by + ex — е2 = О,
параболического цилиндра
z2—ах— Ъу = 0
и конусов
z2 = xy и az2 — bxz — cyz + су2 = 0.
Поверхности с более сложными уравнениями
z2 — ах2 — Ъху — су2 — ех — fy = 0
и
az2 + byz + су2 — exz + fx2 + gz — bx = 0
он лишь бегло охарактеризовал как «коноидальные», имеющие
конические сечения. Поверхности
и2 — х2 — у2 = 0,
где и есть функция z, Герман называл «круглыми телами»; позднее стали
говорить о поверхностях вращения. С большей полнотой изучена
плоскость, но для некоторых поверхностей Герман выявляет также форму
с помощью плоских сечений, находит вершины и, в одном случае,
касательную плоскость, а также сообщает дифференциальное уравнение
геодезической (проблема, которой до него занимались оба старшие брата
Бернулли и Эйлер). Из высших поверхностей рассмотрена в первом
октанте поверхность с уравнением
(Ь — z) У а2 — у2 = Ъх.
Валлис, впервые изучивший эту поверхность без записи уравнения,
называл ее «конусоклином». По-видимому, Герман не знал появившейся
в 1731 г. замечательной работы по геометрии пространства А. Клеро,
во многом пересекавшейся с его собственными исследованиями. И в этом
направлении труды Германа, какиКлеро, были далеко продолжены прежде
всего Л. Эйлером.
90
ГЛ. 5. ПЕРВЫЕ АКАДЕМИКИ-МАТЕМАТИКИ
Ф.-Х. Майер и разработка тригонометрии. Недолго, всего четыре
с половиной года, продолжалась деятельность в Академии и Фридриха-
Христофа Майера (10 окт. 1697—5 дек. 1729), прибывшего в августе
1725 г. вместе с Бюльфингером, у которого он учился в Тюбингене.
Несколько месяцев молодой магистр числился в Академии студентом,
но уже в январе 1726 г. был назначен экстраординарным профессором
математики.
В I—V томах «Записок» Майер опубликовал 14 статей по астрономии
и математике, преимущественно по тригонометрии [САР II (1727) 1729;
III (1729) 1735; V (1730—1731) 1738]. Несмотря на неясности и ошибки
в установлении знаков тригонометрических функций углов, больших
прямого (вопрос этот в то время еще не был решен окончательно), Майер
заметно содействовал прогрессу тригонометрии. Подобно другим авторам
он старался упростить символику этой науки и для этого обозначал
функции инициалами их наименований, не указывая, однако, аргумента.
гр Sc+Cs
1ак, синус суммы и разности он писал в виде —=^— , причем прописная
буква употреблялась для большего угла, а г — есть радиус
тригонометрического круга. Эти обозначения, которые при большем числе углов
приходилось пополнять все новыми и новыми буквами, применялись и другими
академиками, а также некоторыми зарубежными авторами. Майер, далее,
улучшил аналитическое изложение тригонометрии, большая часть формул
которой выводилась тогда каждая по отдельности на основе специального
геометрического построения. Он вполне отчетливо понимал значение
аналитического построения тригонометрии и утверждал, например, что
из теоремы косинусов сферической тригонометрии можно вывести все
формулы для прямоугольного и косоугольного треугольников.
(Последовательная аналитическая трактовка плоской и сферической тригонометрии
и создание современной символики явились, как упоминалось, заслугой
Эйлера.) Майеру принадлежит также несколько новых формул, удобных
для приведения к логарифмическому виду. Занимался он и
суммированием рядов.
Н. Бернулли. Всего лишь несколько месяцев успел проработать
в Академии Николай II Бернулли (27 янв. 1695—9 авг. 1726), неожиданно
скончавшийся в расцвете сил. Две работы его напечатаны в первом томе
«Записок»— одна о движении тел под действием удара и другая о
дифференциальных уравнениях, главным образом Риккати и линейном. Заслу-
живает внимания новый прием решения уравнения -*- = by -f ах
с помощью подстановки у = cbxz (заменой у = и (х) v (х) Лейбниц решил
линейное уравнение еще в конце XVII века). Такие
экспоненциальные подстановки сыграли затем большую роль в исследованиях
Эйлера.
Заметим тут же, что семья Бернулли сыграла большую роль в
развитии математических наук с конца XVII до конца XVIII столетия. Как
мы знаем, братья Яков и Иоганн I Бернулли стали ближайшими
сподвижниками Лейбница в разработке исчисления бесконечно малых, а братья
Николай II и Даниил, сыновья Иоганна I, принадлежали к числу наших
первых академиков. Видным математиком были также племянник и
ученик старших братьев Бернулли Николай I (1687—1759), одно время
занимавший кафедру математики в Падуе, а затем получивший профессуру
в Базеле, сперва на кафедре логики, а затем — юриспруденции; его имя
Г.-В. КРАФТ
91
нам еще встретится в дальнейшем. Наконец, внук Иоганна I Бернулли
и сын Иоганна II (1710—1790), физика, Яков II Бернулли (17 окт. 1759—
14 июля 1789) приглашен был после смерти Лекселя в Петербургскую
Академию наук. Деятельность его была здесь недолгой: он приехал весной
1786 г. и через три с небольшим года погиб во время купания в Неве.
В I—VI томах «Новых трудов» Петербургской Академии напечатано его
11 работ по механике.
Г.-В. Крафт. Георг Вольфганг Крафт (16 июля 1701 — 18 июля 1754),
как и Майер, был учеником Бюльфингера и прибыл в Петербург в конце
1725 г. Вначале он состоял адъюнктом, с 1731 г. профессором математики,
а с 1733 г. профессором физики. Он
преподавал в академических учебных
заведениях, вел метеорологические и
астрономические наблюдения, ставил физические
опыты в лаборатории, которую привел
в образцовый порядок. Для академических
гимназистов Крафт написал учебники
географии и механики, а также «Краткое
руководство к теоретической геометрии»,
сначала вышедшее по-немецки (СПб., 1740),
а затем в русском переводе студента И. Го-
лубцова, отредактированном М. В.
Ломоносовым (СПб., 1748). Это неплохая по тем
временам книга, написанная довольно
просто и, кроме теоретического материала,
содержащая многие весьма полезные
практические советы. Она была переиздана
в 1762 г.
Крафту принадлежат большие заслуги
в популяризации научных знаний. В
«Исторических, генеалогических и географи- Г-"в- ^Ра*т (гравюра И Гайда
^ ' гч тт с портрета работы В. Манера,
ческих примечаниях» к газете «С.-Петер- Конец 40-х, начало 50-х годов
бургские ведомости» — первом научно-по- XVIII в.).
пулярном журнале на русском языке,
издававшемся Академией наук, помещено много превосходных статей
Крафта и среди них обзоры истории и современного состояния
классических задач о квадратуре круга, трисекции угла и удвоении куба.
Автор склонялся к мнению, что элементарное решение этих задач
невозможно и вместе с тем подчеркивал, что поиски таких решений
могут привести к другим важным открытиям. По поводу
квадратуры круга он, в частности, писал: «Ежели о вопросе нашем в протчей
истории наук посмотрим, то признаемся, что знатнейшие изобретения,
которые мы ныне имеем, не того ради изобретены, что их искали, но понеже
нечто иное напрасно искали, а между тем некоторые попалися, которые
будто незваные гости сами пришли и с собою великую пользу принесли.
Тако и о сем вопросе надеятися можно, что скорее иное что незнаемое
по случаю квадратуры циркуля найдется, нежели как она сама» 1). Это
предвидение Крафта полностью оправдалось. Известно, что он занимался
по требованию невежественной и суеверной императрицы Анны Иоаннов-
ны астрологией и составлением гороскопов. Вспомним, что веком раньше
г) Примечания в Ведомостях, 1729, стр. 261.
92
ГЛ. 5. ПЕРВЫЕ АКАДЕМИКИ-МАТЕМАТИКИ
гороскопы по горькой необходимости вычислял и другой воспиганник
Тюбингенского университета — великий Кеплер.
В 1744 г. Крафт занял кафедру математики в Тюбингене, причем
за ним было сохранено звание почетного члена Академии. В качестве
такового он присылал в Петербург статьи до конца жизни. В «Записках»
и «Новых записках» помещено около 60 работ Крафта, из них примерно
треть по математике — элементарной геометрии, эволютам и каустикам,
дружественным и совершенным числам, интегральному исчислению.
Все они посвящены решению сравнительно нетрудных частных задач.
С Эйлером, после его отъезда в Берлин в 1741 г., Крафт вел дружескую
научную переписку, в которой обсуждались вопросы суммирования
рядов, решения дифференциальных уравнений, задачи механики и многое
другое. Нередко Эйлер разъяснял своему приятелю более трудные
вопросы. Так, встретившись в задаче о вычислении боковой поверхности
наклонного конуса, поставленной еще Я. Германом, с интегралом вида
е У(г2 + Ьд)2 + а2г2
\ ——' — ах, Крафт в 1742 г. просил разъяснить, нельзя ли его
<у 2~|/г2— х2
выразить посредством «квадратуры эллипса». Ответ Эйлера не сохранился,
но в статье Крафта [САР XIV (1744—1746) 1751] правильно сказано,
что интеграл не сводится к квадратуре конических сечений. Эйлер также
напечатал работу о поверхностях различных тел, в которой преобразует
интегралы, выражающие площади, к интегралам, выражающим дуги
плоских кривых [N САР I (1747—1748) 1750]. В 1748 г. Эйлер предложил
Крафту доказать найденную им незадолго до того теорему: сумма
квадратов сторон четырехугольника равна сумме квадратов его диагоналей,
сложенной с учетверенным квадратом расстояния между серединами
диагоналей. Оригинальное доказательство Крафта, как и собственный
вывод Эйлера, появились одновременно в т. I «Новых записок» *).
X. Гольдбах и учение о рядах. Своеобразна фигура Христиана
Гольдбаха (18 марта 1690—1 дек. 1764). Он окончил юридический факультет
Кенигсбергского университета, но еще в студенческие годы увлекся
математикой. В долгие годы странствий чуть ли не по всей Европе
Гольдбах завязал знакомство и переписку со многими геометрами, в том числе
Лейбницем и братьями Николаем и Даниилом Бернулли. С 1717 г. начали
появляться его небольшие статьи в лейпцигских Acta Eruditorum. Летом
1725 г. он приехал по собственному почину в Россию и был принят в
Академию в качестве профессора математики и первого ученого секретаря.
Назначенный благодаря своим приятным светским манерам воспитателем
наследника, вскоре императора Петра II (1728—1730), Гольдбах провел
1728—1731 гг. вместе с двором в Москве, переписываясь оттуда с Д.
Бернулли и Эйлером. В начало 1732 г. он возвратился в Академию, где
считался старшим среди ее членов. Через десять лет он был переведен на
крупный пост по ведомству иностранных дел и здесь дослужился до высокого
чина тайного советника. Связи его с Академией, кроме чисто личных,
на этом оборвались. Но он продолжал почти до кончины научную
переписку с Эйлером, жившим в 1741—1766 гг. в Берлине.
В I—III и VI томах «Записок» напечатаны шесть работ Гольдбаха,
из них две о дифференциальных уравнениях и две, наиболее интересные,
г) Ср. A. Juskevifi, Zu den russisch — deutschen Beziehungen auf mathematischem
Gebiet in der Mitte des 18. Jahrhundrts.— Jahrbuch fur Geschichte der UdSSR und
der Volksdemokratischen Lander Europas, B. 7, Berlin, 1963.
X. ГОЛЬДБАХ И УЧЕНИЕ О РЯДАХ
93
о бесконечных рядах. Первая из них «О преобразовании рядов»,
доложенная конференции Академии еще осенью 1725 г., содержит два метода
преобразования [САР 111(1727) 1729]. Один из них состоит в построении
по ряду А с данной суммой другого ряда, имеющего ту же сумму. Он
основан на почленном вычитании рядов В ж С, имеющих общую сумму,
а затем в почленном сложении (или вычитании) ряда А с рядом В — С = О,
так что А -± (В — С) = А. Это иллюстрируется примерами вроде
2
1
S
п(п-\г2) 4J 4л (и+1)
71 = 1 71=1
и, значит,
-*-! Ап(п + 1)(п + 2)
71=1
= 0.
-Заметим, что ряды, члены которых суть рациональные функции своего
номера с целыми коэффициентами, давно занимали Гольдбаха. Другой
прием основан на своеобразном почленном умножении ряда А = а -\-
+ &-fc-f^+---Ha ряд 1 + а — а +Р — Р + 7 — Т + * • •» в котором
а, Р, у» • • • монотонно убывают к нулю, так что его сумма равна 1.
Преобразованный ряд А получается в виде
Ш+Ъ) ( + (c + d)
[ +аа {
+ (* + /) ( + (g + h)+...
+ (е — с)а | +(g— е)а+ .
1 + ар ] +(с —а)Р {+(*-<•) р+..
1 + ау I +(с — а) у+ .,
+ (с — а) а
{ + а6+...
Беря А = 1 — т + т2 — т3 + ... = -г-;— и полагая
т2-\-т—1 п тг-\-т—1 т2-\-т—1
а~ ^+2 ' Р" (m + 2)2 ' Y (^г + 2)3 ' *
Гольдбах преобразует по этому методу прогрессию А в ряд
А=—hr + Tzrr™-*
2 ^(w+2)2^ (m+2)3^"' 7?i+l '
Все операции производятся формально. Гольдбах замечает, что, по
мнению многих, хотя ряд А возникает путем деления 1 на 1 + ти, он все же
неравен значению этой дроби при т > 1. Однако сам Гольдбах не видит
оснований отказываться от употребления расходящихся рядов, поскольку
их можно бывает преобразовать в сходящиеся. В защиту употребления
расходящихся рядов Гольдбах выступал ранее в переписке с Николаем I
и Даниилом Бернулли х). Мы скажем теперь, что ряд А: сходящийся
при —1 < т < 1, и ряд Аи сходящийся при т > —1 или т <— 3,
имеют общую сумму в общей части их областей сходимости; вместе с тем
второй ряд дает аналитическое продолжение первого 2).
г) Эта переписка опубликована в кн.: Correspondance mathematique et physique
de quelques celebres geometres du XVIIIе siecle, publiee par P. H. Fuss, t. II
St.-Petersbourg, 1843. Ср. особенно стр. 210, 213—216, 219—222.
2) Ср. Г. X a p д и, Расходящиеся ряды, перев. Д. А. Райкова, с
предисловием С. Б. Стечкина, М., 1951, стр. 31—32.
94
ГЛ. 5. ПЕРВЫЕ АКАДЕМИКИ-МАТЕМАТИКИ
Другая саатья, частью подготовленная еще в 1721 г., но в России
переработанная и дополненная, называется «Об общих членах рядов»
1САР III (178 )1732]. В ней рассмотрен вопрос об интерполировании
последовательностей я1? а2, а3, . . . или рядов а± -f а2 + аз + • • •
(те и другие в то время назывались series), т. е. о нахождении функции
/ (тг), при всяком целом положительном п принимающей значение ап;
при п дробном значения «общего члена» / (п) дают «промежуточные члены»
с дробными индексами. В столь общей постановке задача неопределенна
и допускает бесчисленное множество решений; здесь дело зависело от
конкретных условий вопроса и интуиции исследователя.
Первое такое интерполирование произвел Валлис (1656). Он выразил
(мы пользуемся нашим математическим языком) квадратуру круга инте-
f -
гралом \ (1—x2)2dx = ~y- и получил новое представление я в форме
о
бесконечного произведения, проинтерполировав таблицу чисел
1:{{1-*Г*х=<г±01
О
С помощью остроумной индукции Валлис нашел, что при к = п—--у
4 3-3 5-5 7-7
J_, I я 2-4 4-6 6-8 "• *
2 '
1
1
и строго обосновал этот результат. Поскольку 1 : \ (1 — xk)ndx при
о
1 3 3 5
к =-гг ж п = 0, 1,2, ... принимает значения 1. ~о~ »1Г " т ' ' ' *' ^аллис
1
тем самым выразил член этой последовательности, имеющей индекс п = — .
Последовательность, п-ж член которой есть произведение п неравных
возрастающих или убывающих чисел, Валлис назвал
гипергеометрической; другим примером гипергеометрической последовательности у него
является последовательность факториалов {п\}.
Проблема интерполирования последовательностей вновь
заинтересовала математиков XVIII века, в частности, в связи с суммированием
рядов: если для ряда а± -\- а2 + • • • + ап + • • • известно аналитическое
п
выражение общего члена последовательности частных сумм 2 ak =
= S (п), то сумма ряда оказывается значением этого выражения при
п = оо. Гольдбах представил общий член произвольной
последовательности {ап} в форме
/(*) = fll+2 СГ1^!'
т. е., в случае дробного п, в виде бесконечного ряда; среди его примеров
фигурирует и гипергеометрическая последовательность {га!} Валлиса.
Для [у]! подучилось выражение в виде расходящегося ряда, но Гольдбах
ПРОБЛЕМЫ ГОЛЬДБАХА В ТЕОРИИ ЧИСЕЛ
95
обошел эту трудность, представив сходящимся рядом обратную величину:
J _, i_ _1 1_ J_ _1_ 1-3
3\ , 2! ' 2 3! '2-4+ 4! '2-4-6~f_ ' ' *
В 1728—1729 гг. проблема и статья Гольдбаха обсуждались в его
переписке с Д. Бернулли, причем последний поставил задачу выразить общий
член последовательности факториалов «в конечном виде» г). Это оказалось
не под силу ни Гольдбаху, ни самому Бернулли, который нашел, правда,
очень важное представление в форме некоторого бесконечного
произведения. Лишь Эйлер сумел найти совершенно неожиданное и чрезвычайно
глубокое решение вопроса,— о нем будет идти речь далее.
Мы остановились несколько подробнее на проблеме
интерполирования, как характерной для творчества Гольдбаха. Несмотря на свой
несомненный талант, он все же всегда был только любителем математики и
занимался ею недостаточно систематически, часто в часы досуга от других —
служебных или придворных — обязанностей. Иногда ему не доставало
и более солидной подготовки, пробелы которой ясны из его переписки.
Но идеи, носящиеся в воздухе, он подхватывал налету, а главное, обладал
удивительной интуицией в постановке важных и плодотворных задач.
Недаром Эйлер переписывался с Гольдбахом на протяжении более 30 лет.
Вообще, научная переписка Гольдбаха интереснее и значительнее его
напечатанных статей и в ней мы встречаем замечательные мысли,
стимулировавшие творчество не только его корреспондентов, но и позднейших
ученых, а также открытия, не появившиеся своевременно в печати.
Проблемы Гольдбаха в теории чисел. Имя Гольдбаха известно теперь
главным образом в связи с знаменитой «проблемой Гольдбаха». В письме
к Эйлеру от 27 мая (7 июня) 1742 г. он высказал предположение, что
всякое целое число, большее двух, есть сумма трех простых чисел,
понимая под простым числом также единицу 2); как видно из ответного письма
Эйлера от 30 июня, Гольдбах еще ранее сообщил ему, что любое четное
число есть сумма двух простых, откуда следовала бы истинность
предыдущей гипотезы3). Проблема Гольдбаха оставалась неприступной еще
в начале нашего столетия и только новые мощные аналитические методы
теории чисел позволили сдвинуть дело с мертвой точки. В двадцатые
годы английские ученые Г. Харди и Дж. Литлвуд установили связь этой
проблемы с другими задачами теории чисел и анализа. В 1930 г. советский
математик Л. Г. Шнирельман (1905—1938) с помощью специального
разработанного им метода доказал, что каждое целое число есть сумма
не более, чем к простых чисел (включая единицу), где к — некоторое
фиксированное число. Впрочем, доказать, что к = 3 по способу Шнирель-
мана не удается; установлено только, что к не больше 20. В 1937 г.
И. М. Виноградов, пользуясь совершенно другим методом тригонометри-
х) Gorrespondance mathematique et physique de quelques celebres geometres du
XVIIIe siecle, t. II, p. 278. Подробнее о работах Гольдбаха по теории рядов см.
J. Е. Hofmann, Um Eulers erste Reihenstudien.— Sammelband zu Ehren des250.
Geburtstages Leonhard Eulers. Unter Red. von K. Schroeder, Berlin, 1959.
2) Гольдбах не подозревал, что такое же наблюдение сделал еще Декарт. Запись
Декарта была опубликована по его черновым бумагам только в 1908 г.
3) См. Leonhard Е и 1 е г und Christian Goldbach, Briefwechsel. 1729—
1764. Hsg. und eingeleitet von A. P, Juskevic und E. Winter. Berlin, 1965, S.
104, 110. Во введении к этой книге содержится разбор математического творчества
Гольдбаха.
96
ГЛ. 5. ПЕРВЫЕ АКАДЕМИКИ-МАТЕМАТИКИ
ческих сумм, доказал, что всякое достаточно большое нечетное число есть
сумма трех простых. Методы Шнирельмана и, особенно, Виноградова
получили замечательные приложения и в исследовании других
арифметических задач1). Задача о представлении четного числа суммой двух
простых пока не решена.
В переписке Гольдбаха с Д. Бернулли содержатся еще два
арифметических предложения, которые были доказаны только много спустя,
28 апреля 1729 г. Д. Бернулли заметил, что натуральные логарифмы
рациональных чисел не могут быть выражены ни рациональными
числами, ни иррациональными корнями из них, т. е., по-нашему, что они
трансцендентны. В ответ на это Гольдбах 20 октября 1729 г. 2) привел
111
новый пример трансцендентного числа, именно 775 + 7752 + Ш* + • • • +
Н йч + • • ¦ Первые критерии трансцендентности чисел дал в 1844—
1851 гг. Ж. Лиувилль, причем построенные им примеры трансцендентных
чисел имеют сходство с числом Гольдбаха. Утверждение Д. Бернулли
следует из более общей теоремы Ф. Линдемана: натуральный логарифм
любого алгебраического числа, отличного от единицы, есть число
трансцендентное (1882). Предложение Гольдбаха доказал в 1938 г.
ленинградский ученый Р. О. Кузьмин (1891—1949) 3).
Интегрирование дифференциального бинома. Мы отметим еще два
открытия Гольдбаха, одно из которых относится к интегральному
исчислению, а другое к теории рядов. Еще в письме к Лейбницу
1676 г. Ньютон указал, что биномиальный дифференциал ят (а + bxn)v dx,
где т, 72, р — рациональные числа, интегрируется в конечном виде, если
т или т +/? есть целое положительное число; тривиальный случай
целого положительного р он просто не упомянул. Поисками условий
интегрируемости биномиального дифференциала с помощью его
рационализации занимались затем многие, в том числе И. Бернулли, Герман,
Д. Бернулли, Гольдбах и Эйлер. В письмах к Д. Бернулли от 1 июня
и к Эйлеру от 6 ноября 1730 г. Гольдбах показал, что посредством
некоторых подстановок биномиальный дифференциал преобразуется в
рациональный дифференциал, если хотя бы одно из трех указанных выражений
есть любое целое число, тем самым фактически исчерпав случаи конечной
интегрируемости \ хт (а -\- bxn)v dx. Эти условия обыкновенно связывают
с именем Эйлера, который, однако, сам признал полноту результата
Гольдбаха 4). Эйлер позднее записал в первом томе своего «Интегрального
исчисления» (1769) условия в обычном для нас виде, между тем как
у Гольдбаха они выглядят несколько иначе. Заметим, что при обсуждении
с Гольдбахом этого вопроса, Эйлер со всей ясностью подчеркнул
необходимость расширить смысл термина «интегрируемость». Под этим в те вре-
*) Н. Г. Чудаков, О проблеме Гольдбаха.— УМН, вып. IV, 1938;
Б. Н. Делоне, Петербургская школа теории чисел, М.— Л., 1947, стр. 365 и след.
2) Correspon dance mathematique et physique de quelques celebres geometres du
XVIIIе siecle, t. II, стр. 301, 326.
3) P. О. Кузьмин, О трансцендентных числах Гольдбаха.— Труды
Ленинградского индустр. ин-та, разд. физ.-матем., 1938.
4) См. Correspondance mathematique et physique de quelques celebres geometres
du XVIIIе siecle, t. II, стр. 368—370; Leonhard Euler und Christian Gold-
h а с h, Briefwechsel, стр. 43—50.
ДАНИИЛ БЕРНУЛЛИ
97
мена понимали интегрируемость в алгебраических функциях и,
например, Д. Бернулли говорил, что рациональные дифференциалы либо
интегрируются, либо приводятся к квадратуре круга или гиперболы.
Эйлер предложил понимать под интегрируемыми функциями также и те,
интегралы которых выражаются в логарифмах. Позднее он присоединил
к этому круговые функции.
Итог изучению задачи интегрирования дифференциального бинома
в случае рациональных показателей подвел П. Л. Чебышев, который
в 1853 г. доказал, что давно известные достаточные условия
интегрируемости в элементарных функциях вместе с тем необходимы (стр. 381).
Наконец, в письме к Эйлеру от 20 сентября (1 октября) 1742 г. Гольдбах
сделал любопытное замечание о гармоническом ряде: 1, "Т ' Т ' Т ' ? ' ' " '*
путем подходящей расстановки в нем знаков + и — сумму такого ряда
можно сделать равной любому числу г). Общая теорема, согласно которой
условно сходящийся ряд можно, переставляя его члены, преобразовать
в ряд с наперед заданной конечной или бесконечной суммой, была
доказана в 1853 г. Б. Риманом.
Даниил Бернулли. Уже не раз упоминавшийся нами Д. Бернулли
родился 8 февраля 1700 г. в Гронингене (Голландия), где в то время его
отец Иоганн Бернулли занимал университетскую кафедру. Математику
Д. Бернулли изучал под руководством отца и старшего брата Николая.
Окончив в 1716 г. Базельский университет со степенью магистра
философии, он дополнительно изучил медицину и в 1721 г. сдал в том же Базеле
установленные экзамены. Затем он отправился в Италию для
усовершенствования в медицине. Одновременно Д. Бернулли продолжал занятия
математикой и вскоре выпустил «Математические этюды» (Exercitationes
quaedam mathematicae, Venetiae, 1724). Здесь, среди прочего, дано
решение поставленной незадолго перед тем Дж. Риккати задачи об отыскании
случаев, в которых уравнение
интегрируется путем разделения переменных, т. е. в квадратурах. Решение
нашли независимо и почти одновременно сам Риккати, И. Бернулли и его
сыновья Николай и Даниил, а также его племянник Николай Бернулли.
В печати первым выступил Д. Бернулли, который показал, что разде-
ление переменных достигается при п = —?Гг, где к — любое целое или к=оо.
В 1841 г. Лиувилль доказал, что эти случаи являются единственными.
Не найдя применения своим дарованиям ни на родине, ни в Италии,
Д. Бернулли охотно принял приглашение в Петербург на кафедру
физиологии, причем предполагалось, что он применит в этой науке
математические методы. Начало таким исследованиям, в частности по механике
движения животных, положил в конце XVII века итальянец Дж. Борелли
и это направление приобрело большую популярность. Плодом недолгих
занятий Д. Бернулли физиологией явились две статьи в первом томе
«Записок»— по теории движения мускулов и о зрительном нерве. Но уже
с самого приезда осенью 1725 г. он занялся почти исключительно
механикой и математикой и в 1728 г. был назначен профессором математики.
х) Leonhard Е и 1 е г und Christian Goldbach, Briefwechsel, стр. 123; ср.
также письмо Гольдбаха от июня — июля 1752 г. на стр. 350.
98
ГЛ. 5. ПЕРВЫЕ АКАДЕМИКИ-МАТЕМАТИКИ
Д. Бернулли провел в Петербурге восемь лет до лета 1733 г. и вернулся
в Базель главным образом из-за враждебного отношения со стороны
Шумахера. В Базеле ему снова пришлось занять кафедру анатомии
и медицины; только в 1750 г. он перешел на освободившуюся кафедру
физики. Вместе с тем Д. Бернулли остался почетным членом Петербургской
Академии и поддерживал с нею научные связи до конца жизни. Из 75 работ
его в России вышло 50, а в последние годы он печатался почти
исключительно в петербургских изданиях. Академик Н. И. Фусс был в юные годы
учеником Д. Бернулли и получил
приглашение в Россию по его рекомендации.
Десять трудов Д. Бернулли
получили премию на различных научных
конкурсах. Он был одним из восьми
иностранных членов Парижской Академии
наук, членом Берлинской Академии,
Лондонского королевского общества.
Только Эйлер был удостоен таких же
научных почестей и отличий. Скончался
Д. Бернулли в глубокой старости в
Базеле 17 марта 1782 г.
Д. Бернулли был «геометром» в том
широком смысле, какое это слово имело'
в XVIII веке, т. е. занимался, как
и большинство математиков того
времени, различными
физико-математическими науками. Более всего его привлекали
физика и механика, а в математике —
методы исследования
естественнонаучных, технических и вообще практиче-
Даниил Бернулли (гравюра И. Гайда ских задач. Он предпочитал физическую
с портрета работы И. Губера, первая модель и рассуждение математической
половина XVIII в., Государствен- выкладке и стремился обойтись воз-
ныи Эрмитаж).
г ' можным минимумом математических
средств. Характерны названия многих
работ, представленных им на соискание премий Парижской Академии,
вроде: «О наилучшем устройстве якорей», «О наиболее выгодном способе
усилить действие ветра на больших кораблях», «О наилучшем способе
уменьшения боковой и килевой качки судна». К более отвлеченным
вопросам самой математики Д. Бернулли относился равнодушно
и даже несколько иронически; со временем это усиливалось. 18 марта
1778 г. он писал Фуссу по поводу занятий Эйлера теорией чисел:
«То, что Вы потрудились сообщить мне по этому вопросу, показалось мне
весьма тонким и достойным нашего великого метра. Но не находите
ли Вы, что расточать такие богатства на простые числа, значит, пожалуй,
оказывать им слишком много чести, и не является ли это данью
рафинированному вкусу нашего времени?» х).
Главным делом Д. Бернулли в Академии явилась подготовка труда
по гидродинамике, окончательная редакция которого была опубликована
через несколько лет в Страсбурге, причем на титульном листе стояло:
«Академический труд, составленный автором в период пребывания его
2) Correspondance mathematique et physique de quelques celebres geometres du
XVIIIе siecle, t. II, стр. 676—677.
ПРОБЛЕМЫ ТЕОРИИ КОЛЕБАНИЙ
99
в Петербурге» (Hydrodynamica sive de viribus et motibus fluidorum com-
mentarii, Argentorati, 1738 1)). Эта классическая книга содержит
описание многих опытов над движением воды и воздуха, а также вывод на основе
некоторых гипотез ряда основных законов. По существу, только в ней
было положено начало гидродинамике как науке. К исследованию
движения жидкостей Д. Бернулли применяет закон сохранения живых сил.
Он впервые проводит различие между гидростатическим и
гидродинамическим давлением. Одним из важнейших результатов является вывод
знаменитого уравнения Бернулли, выражающего связь между давлением
и скоростью идеальной тяжелой жидкости на данной глубине под
поверхностью; оно широко применяется для решения практических задач и из
него следует закон истечения, открытый Торричелли. Здесь же заложены
основы кинетической теории газов, рассмотрен вопрос о реактивных
силах. Дифференциальных уравнений движения жидкости еще нет; они
были через 20 лет установлены Эйлером [Memoires de l'Acad. de Berlin,
XI (1755)1757]. Впрочем, Д. Бернулли сам писал: «Я рассматриваю
настоящий трактат скорее как физический, чем как математический» 2).
Ранее говорилось об отдельных математических открытиях Д.
Бернулли, изложенных в его переписке с Гольдбахом. Добавим, что 30
января (10 февраля) 1729 г. Д. Бернулли указал, что
есть основание натуральных логарифмов, которое Эйлер позднее обозна-
1-j ) = ех [Miscellanea Beroli-
nensia, VII, 17431. Большой интерес имеет также переписка Д. Бернулли
с Эйлером в 1726—1768 гг., опубликованная до сих пор не полностью 3)„
Впрочем, ее основное содержание включено в печатные труды обоих
корреспондентов.
Проблемы теории колебаний. Наряду с механикой жидкостей и газок
основное место в творчестве Д. Бернулли занимают исследования о
колебаниях систем с конечным или бесконечным числом степеней свободы.
В решении таких вопросов он руководствовался одним принципиально
важным положением, а именно рассматривал всякое колебание системы
как результат суперпозиции (наложения) колебаний специального вида
(теперь их называют главными), которые могут быть найдены
сравнительно просто. В истории математической физики особое место занимает
задача о струне. Математической трактовке ее подверг впервые Б. Тейлор,
который в несколько отличной от теперешней форме выразил
дифференциальное уравнение малых поперечных колебаний (1713, опуб. в 1714).
Допустив, что все точки струны возвращаются в первоначальное
положение на одной прямой одновременно, Тейлор заключил, что струна
в каждый момент имеет форму синусоиды. И. Бернулли, бывший
почетным членом Петербургской Академии, в письме к сыну Даниилу, напеча-
г) Д. Бернулли, Гидродинамика или записки о силах и движениях
жидкостей. Дерев. В. С. Гохмана, комм, и ред. А. И. Некрасова и К. К. Баумгарта, статья
В. И. Смирнова, М., 1959. Статья В. И. Смирнова содержит разбор
математического творчества Д. Бернулли.
2) Д. Бернулли, Гидродинамика, стр. 34.
3) Correspondance mathematique de quelques celebres geometres du XVIIIе1
siecle, t. II.
100
ГЛ. 5. ПЕРВЫЕ АКАДЕМИКИ-МАТЕМАТИКИ
танном во II томе ее «Записок», обратил его внимание на задачу о струне,
а в III томе посвятил ей специальную статью, в которой, впрочем, не
продвинулся существенно далее Тейлора. Таким образом, уже в первых
выпусках петербургских «Записок» был возбужден вопрос об этой задаче,
сыгравшей несколько позднее столь большую роль в развитии математики,
благодаря, прежде всего, Ж. Даламберу, Эйлеру и Д. Бернулли. Но на
первом этапе своей деятельности Д. Бернулли обратился к другому
вопросу теории колебаний, именно к задаче о малых колебаниях
дискретных систем грузов, связанных с вертикально подвешенной гибкой
невесомой нитью и, в предельном случае, когда число грузов неограниченно
растет, о малых колебаниях однородной тяжелой нити или цепи.
В двух работах, посвященных этим задачам [САР VI (1732—1733)
1738 и VII (1734—1735) 1740], Д. Бернулли положил начало теории
цилиндрических функций. Определение фигуры колебаний нити
приводится к частному случаю так называемого уравнения Бесселя, именно
к уравнению
dx2 dx n '
где x есть разность между длиной I нити и длиной части ее дуги,
отсчитываемой от точки подвеса, у — отклонение точки нити от вертикального
положения равновесия, а — представляет собой квадрат частоты
колебания, деленный на ускорение силы тяжести. Решение этого уравнения
находится по методу неопределенных коэффициентов в форме
л X , X2 хъ я4
2/ = 1--
1 4тг2 4-9тгЗ > 4-9-16и4 '"''
а это не что иное, как цилиндрическая функция первого рода нулевого
порядка/0 (1/ •—) • Поскольку у = 0 прия = Z, Д. Бернулли получает для
отыскания п уравнение, в левой части которого стоит бесконечный ряд.
Он заключает, что существует бесконечное число действительных корней
такого уравнения и два первых значения корня вычисляет с помощью
собственного приближенного метода, изобретенного незадолго перед
тем г).
Мы не будем останавливаться на последующих работах Д. Бернулли
по колебаниям упругих стержней и по колебаниям воздуха в трубах.
Заметим лишь, что в статье о колебаниях стержней [САР XIII (1741 —
1743) 1751] Бернулли проинтегрировал как с помощью бесконечных рядов,
так и в конечном виде линейное уравнение с постоянными коэффициентами
—-^ = /с4г/. Вполне общие результаты в этом направлении тогда же или
несколько ранее получил и Эйлер. Мы отложим пока рассмотрение работ
Д. Бернулли, посвященных задаче о струне.
Численное решение уравнений. Только что упомянутый
приближенный метод решения уравнений для случая, прежде всего, алгебраических
уравнений Д. Бернулли сообщил без вывода в третьем томе «Записок».
Он основан на применении рекуррентных (возвратных)
последовательностей или рядов, впервые подвергнутых подробному исследованию
х) Подробнее см. В. В. Гуссов, Развитие теории цилиндрических функций в
России и СССР.— Ист.-матем. исслед., вып. VI, 1953.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СТАТИСТИКА
101
А. де Муавром, которому принадлежит и термин «рекуррентный» (1722).
В случае уравнения хп + а^х71'1 + .. . -\-ап = 0 берут п произвольных
действительных чисел ри р2, ..., рп и с помощью рекуррентного
соотношения рп+т + сцРп+т-1+"•+апрт = 0 образуют числа рп+и рп+2, ...
Наиболее удаленный от нуля действительный корень уравнения
находится как предел отношения ^^ при к-^оо. В т. V «Записок» Д. Бер~
Pk
нулли распространил свой метод на отыскание корней функций, задан-
ных бесконечными степенными рядами. Более детально метод Бернулли
исследовал Эйлер в т. I «Введения в анализ» (1748), рассмотрев случаи,
когда этот метод не ведет непосредственно к цели (предел не существует),
именно когда наибольшим модулем обладают два действительных
корня различных знаков или пара сопряженных комплексных корней.
Дальнейшая разработка метода принадлежит Ж. Лагранжу (1798)
и К. Г. Греффе (1837).
Теория вероятностей и статистика. В том же т. V «Записок» появилась
первая работа Д. Бернулли по теории вероятностей, посвященная
поставленной в 1713 г. его двоюродным братом Николаем задаче, получившей
название «петербургской игры». Бросается монета до тех пор, пока не
выпадет герб, после чего игра закончена. Петр выплачивает Павлу 2П~1
дукатов, если герб выпадает при п-ж бросании. Спрашивается, какую ставку
должен выплатить Павел Петру перед началом игры, чтобы игра была
безобидной? Игра считается безобидной, если за участие в ней платится
ставка, равная математическому ожиданию игрока. В данном случае
111
математическое ожидание Павла есть 1 -=- + 2-7-+ 4,_о~ + • • •» т- е-
Павел должен был бы за право игры внести бесконечную ставку. Такоо
расхождение с практическим здравым смыслом побудило Д. Бернулли
ввести другую оценку надежды на увеличение или уменьшение имущества
в зависимости от исходного имущества. Моральное значение у перехода
имущества а в имущество х выражается равенством y=b-log— , где Ъ >0
есть коэффициент пропорциональности; иными словами, бесконечно
малое приращение dy принимается обратно пропорциональным
имуществу х и пропорциональным бесконечно малому приращению самого
имущества dx. Исходя из этого выводится величина, которую Д. Бернулли
назвал «законно ожидаемой выгодой», а Лаплас в 1812 г. нравственным
ожиданием. Именно, если лицо, имеющее имущество а, ожидает с
вероятностями ри р2, . . ., рп, причем pi + р2 + ... + рп = 1,
соответственные приращения имущества а±, а2, . • ., ап, то нравственное ожидание
его есть (а + а1)Р1(а + а2)Р2 . . . (а + ад)Рп —а. Нравственное ожидание
Павла в петербургской игре оказывается при этом конечным.
Понятие нравственного ожидания, которое пытались применить
и к другим вопросам, например, страхованию, себя не оправдало и вышло
из научного употребления. Были предложены и другие объяснения
парадокса петербургской игры, в частности, советским математиком А. Я. Хин-
чиным (1925). Все же следует добавить, что сама идея применения
логарифмической функции к измерению вероятностных величин была недавно
с успехом развита в современной теории информации. В качестве меры
неопределенности опыта А с п возможными исходами Аи А2, . . ., Ап,
имеющими вероятности ри р2, . . ., рп (Pi + Р2 + ... + рп = 1)г
в теории информации служит так называемая энтропия Н(А), определяв-
102
ГЛ. 5. ПЕРВЫЕ АКАДЕМИКИ-МАТЕМАТИКИ
п
мая формулой Н (А) = —^] pklog pk. На эту аналогию указал
fe=i
Ю. В. Линник1).
В последующем Д. Бернулли не раз обращался к проблемам теории
вероятностей и статистике. Большой заслугой его явилось первое
применение в теории вероятностей исчисления бесконечно малых [NCAP XII
{1766—1767)1768 и XIV(1769) 1770]. Решение дискретных задач этой
науки комбинаторными методами нередко затруднительно, а кроме того,
приводит к громоздким выражениям. Д. Бернулли предложил пренебрегать
конечными числами, например единицей, в сравнении с большими
числовыми параметрами задач, как пренебрегают бесконечно малыми в анализе;
это позволяет заменять комбинаторные рассуждения и выкладки более
простыми дифференциальными и интеграционными операциями и получать
приближенные формулы, содержащие главные члены соответствующих
комбинаторных выражений. Несколько ранее, чем Д. Бернулли развил
общие соображения по данному вопросу, он показал первое их
применение в работе о смертности от оспы и действия прививок [Memoires de
Г Acad, de Paris (1760)1766]. Впоследствии методы анализа стали играть
в теории вероятностей решающую роль.
Кривая распределения ошибок. Другая важная работа Д. Бернулли
посвящена теории ошибок и обработке наблюдений, которой он занимался
еще в тридцатые годы [АР (1778 : 1)1780]. Кривая распределения ошибок
должна, по мнению Д. Бернулли, удовлетворять пяти условиям: она имеет
ось симметрии, монотонно убывает по обе ее стороны, касательная в
центре параллельна оси абсцисс, на которой откладываются значения
ошибок, на некотором расстоянии от оси симметрии кривая пересекает ось
абсцисс, и, наконец, касательная в точках пересечения параллельна
оси симметрии. В качестве такой кривой Д. Бернулли выбрал окружность;
радиус ее, т. е. возможный предел ошибок, устанавливается из
наблюдений. Первые три условия сохранил и К. Ф. Гаусс, предложивший так
называемый теперь нормальный закон распределения ошибок (1809).
Для определения центра окружности, которому соответствует наибольшая
ллотность вероятности, Д. Бернулли употребил метод максимального
лравдоподобия, который вновь применял затем Гаусс и который в общем
виде был разработан уже в XX веке Р. Фишером (1912) и др.
Прием Д. Бернулли основан на отыскании максимума некоторого
произведения и приводит к уравнениям высоких степеней. Эйлер
в том же томе «Трудов» указал другой способ, требующий решения
уравнения третьей степени.
Помимо упомянутой работы об оспопрививании, Д. Бернулли
принадлежит еще несколько ценных исследований по демографии.
Мы обратимся теперь к жизни и творчеству младшего по возрасту
члена академической группы математиков — великого Леонарда Эйлера.
г) См. статью В. И. Смирнова в кн.: Д. Бернулли, Гидродинамика, стр. 465.
ГЛАВА ШЕСТАЯ
ЛЕОНАРД ЭЙЛЕР
Начало карьеры. Леонард Эйлер родился 15 апреля 1707 г. в Базеле
в семье сельского пастора. Отец, обучавшийся математике у Якова Бер-
нулли, дал сыну первые уроки по этому предмету, но предназначал его
к духовной карьере. В 1720 г. Эйлер приступил к слушанию лекций
в Базельском университете. Здесь он изучал древние языки и классиков,
философию и богословие, но интерес к математике взял верх, и юноше
в конце концов было дозволено отдаться любимой науке. Необыкновенные
способности Леонарда Эйлера обратили на себя внимание знаменитого
Иоганна Бернулли, который стал давать ему уроки. С сыновьями своего
профессора Николаем и Даниилом Эйлер завязал тесную дружбу.
В 1724 г. Эйлер окончил университет, а в 1726—1728 гг. появились
его первые работы — об изохронных кривых в сопротивляющейся среде,
об одном специальном виде траекторий, о звуке и о наилучшем способе
расположения мачт на корабле. Последняя работа была представлена
на конкурс Парижской Академии и принята к печати. Отметим здесь же,
что впоследствии Эйлер, как и Д. Бернулли, многократно получал премии
или почетные отзывы на конкурсах Парижской Академии. К 12 премиям,
присужденным Эйлеру Парижской Академией в 1738—1772 гг., следует
прибавить премию 1765 г. от английского парламента; ему также, по
существу, обязан своими семью премиями его сын Иоганн-Альбрехт, который
лишь излагал и обрабатывал идеи отца. Некоторые из премированных
работ Л. Эйлера относятся, как и первое конкурсное сочинение, к
кораблестроению и навигации, многие — к небесной механике, особенно теории
движения планет.
Только что упомянутая диссертация о звуке была представлена
Базельскому университету в связи с намерением Эйлера участвовать
в конкурсе на замещение должности профессора физики. Вакансии в этом
университете тогда замещались путем жребия среди отобранных
кандидатов. Эйлер не был допущен к жеребьевке; как пишет его биограф,
базельский профессор О. Шпис, это было для Эйлера счастьем, так как
перед ним в это же время открывалась неизмеримо более широкая арена
деятельности х).
Переезд в Петербург. Николай и Даниил Бернулли убедили
руководство Петербургской Академии пригласить их молодого приятеля на
свободную должность адъюнкта физиологии. Несколько месяцев Эйлер усиленно
штудировал медицину. 5 апреля 1727 г. он навсегда распростился со Швей-
г) О. S р i е s s, Leonhard Euler. Frauenfeld-Leipzig, 1929, стр. 51. Другие
биографии Эйлера: N. Fuss, Eloge de Monsieur Leonard Euler, St. Petersbourg, 1783;
L. G. du P a s q u i e r, Leonard Euler et ses amis, Paris, 1927.
104
ГЛ. 6. ЛЕОНАРД ЭЙЛЕР
царией и после полуторамесячного путешествия по Рейну, Германии
и Балтийскому морю 24 мая прибыл в Петербург. С этого времени и до
самой кончины личная судьба Эйлера и его научное творчество оказались
теснейшим образом связанными с русской Академией наук, с Россией
вообще. Не в пример многим приглашенным в Россию иностранцам Эйлер
в первые же годы петербургской жизни изучил русский язык, на котором
мог говорить и писать.
Хотя Эйлера пригласили в качестве физиолога, но ему, как и Д. Бер-
нулли, сразу предоставили возможность работать по любимой им
специальности. Вскоре это было оформлено официально: с января 1731 г.
он был назначен профессором физики, а летом 1733 г. заменил уехавшего
Д. Бернулли на кафедре математики. По приезде в Россию Эйлер
немедленно приступил к научной работе, а также включился в педагогическую
и просветительскую и научно-организационную деятельность Академии.
Он читал лекции студентам академического университета, экзаменовал в
кадетском корпусе, рецензировал поступающие на отзыв работы молодых
ученых, руководил занятиями студентов, писал учебники и популярные статьи.
Этой стороны деятельности Эйлера мы отчасти коснулись уже ранее.
Активное участие Эйлер принял в тридцатые годы в деятельности
географического департамента Академии, на которьр возложено было
составление карт России. Этой работе правительство придавало огромное
значение и с выполнением ее непрестанно торопило Академию. В
географическом департаменте Эйлер работал много лет подряд. Блестящий
вычислитель, он нередко проводил кропотливые расчеты без помощников
и с необычайной быстротой и точностью. Но он занимался не только
выкладками и решением чисто математических задач, но картографией
в целом и даже сам вычертил немало карт.
Эйлер неоднократно участвовал и в технических экспертизах —
по устройству пильных машин, пожарных насосов, в комиссии о мерах
и весах, где изучал вопрос о чувствительности весов для взвешивания
монет. С конца тридцатых годов по особому поручению Академии Эйлер
приступил к подготовке большого труда по корабельной архитектуре
и кораблевождению, который закончил в 1743 г.
С необычайным успехом шла и научная работа по математике и
механике. В первый раз Эйлер прожил в Петербурге 14 лет. За это время
он получил блестящие результаты во многих областях: учении о
бесконечных рядах и бесконечных произведениях, в решении
дифференциальных уравнений, вариационном исчислении, теории чисел, динамике
точки, теории музыки. Здесь следует подчеркнуть благотворные условия
работы в Петербурге. Если первые стимулы к научным изысканиям Эйлер
получил от своего учителя И. Бернулли, с которым продолжал
регулярную переписку почти до его смерти х), то общение с другими
петербургскими учеными обратило внимание молодого Эйлера на ряд новых проблем.
Нигде в мире Эйлер не мог бы оказаться в кругу столь
квалифицированных и одаренных математиков с общими интересами. Выше мы не раз
отмечали интенсивность духовного обмена между ними, в котором участвовал
и Эйлер. Упомянем, что ряд лет он жил в одной квартире с Д. Бернулли.
Литературная продукция Эйлера в первые пятнадцать лет научной
работы была в сравнении с последующим временем не очень велика.
К 1741 г. из печати вышло около 55 трудов и среди них двухтомная
г) Она опубликована в Gorrespondance mathematique et physique de quelques
celebres geometres du XVIIIе siecle, t. II и в Bibliotheca mathematica, 3 Folge, B. 4—
6, 1904—1905.
Леонард Эйлер (гравюра В. Соколова с портрета И. Брукера, сделанного
в Петербурге в 1737 г., Государственный Эрмитаж).
106
ГЛ. 6. ЛЕОНАРД ЭЙЛЕР
«Механика» (Mechanica sive motus scientia analytice exposita, Petropoli,
1736), в которой дано первое последовательно аналитическое построение
динамики точки. Но уже в тридцатые годы XVIII века Эйлер наметил
программу многих последующих исследований.
Открытия молодого Эйлера, благодаря его переписке нередко
становившиеся известными задолго до появления в печати, произвели
сильнейшее впечатление на современников. Слава его быстро росла. Это
своеобразно отразил в письмах к Эйлеру И. Бернулли. В 1728 г. письмо
адресуется «ученейшему и даровитейшему юному мужу Леонарду Эйлеру»,
в 1731 г.—«славнейшему и ученейшему господину профессору,
дражайшему другу», в 1741 г.—«знаменитейшему и превосходнейшему мужу»
и, наконец, в 1746 г.—«главе математиков Леонарду Эйлеру», Mathema-
ticorum principi Leonhardo Eulero. К этому времени Эйлер был членом
двух академий — в Петербурге и Берлине. В 1749 г. он был избран членом
Лондонского королевского общества, в 1755 г. Парижской Академии
наук; кроме того, он был членом еще четырех других научных обществ.
В 1734 г. Эйлер женился и в том же году родился его старший сын
Иоганн-Альбрехт (27 ноября 1734—18 сентября 1800), впоследствии ученик
и сотрудник своего отца. Теперь Л. Эйлер обзавелся собственным домом
невдалеке от Академии. Казалось, он прочно обосновался в Петербурге.
Однако в регентство Анны Леопольдовны (с ноября 1740 г. по декабрь
1741 г.) в столице сложилась неустойчивая политическая обстановка,
которую весьма остро переживали иностранные жители. По словам
автобиографии Эйлера, «положение начало представляться довольно
неуверенным» 1). Это обстоятельство, а отчасти тяжелая обстановка в Академии,
постоянно поддерживавшаяся Шумахером, побудили Эйлера
воспользоваться предложением прусского короля перейти на работу в
Берлинскую Академию.
Эйлер в Берлине. Летом 1741 г. Эйлер с семьей прибыл в Берлин, где
ему предстояло прожить 25 лет. В Берлинской Академии он вел очень
большую научную и организационную работу. С 1746 г. он состоял
директором математического отделения и нередко исполнял президентские
обязанности. Помимо этого, Эйлеру приходилось по поручению короля
заниматься вопросами баллистики, гидротехническими задачами,
связанными с каналостроением и водоснабжением резиденции Фридриха Сан-
Суси, расчетами для организации государственных лотерей и т. д.
При всем том, Эйлер сохранял регулярную и тесную связь с
Петербургской Академией, если не считать вынужденного перерыва в течение
нескольких военных лет. Он оставался почетным членом нашей Академии
и ему выплачивалась крупная пенсия. Формально являясь почетным
членом Академии, он фактически работал, как ее иногородний
действительный член. Сил Эйлера с избытком хватало для полноценного
«совместительства» в обеих академиях. Свои сочинения он публиковал почти
поровну в берлинских и петербургских изданиях: даже обе академии
вместе не справлялись с колоссальным потоком его трудов 2).
1) Ю. X. К о п е л е в и ч, Материалы к биографии Леонарда Эйлера.— Ист.-
матем. исслед., вып. X, 1957, стр. 17.
2) Эти связи Эйлера, а через него и Берлинской Академии, с Академией наук
в Петербурге ярко отражены в его обширной переписке с должностными лицами
последней. См. Die Berliner und die Petersburger Akademie der Wissenschaften im
Brieiwechsel Leonhard Eulers. Teil I—II, hsg. und eingeleitet von A. P. Juskevic und
E. Winter, Berlin, 1959—1961.
ЭЙЛЕР В БЕРЛИНЕ
107
Проживая в Берлине, Эйлер постоянно информировал Петербургскую
Академию о новинках научной и технической мысли за границей,
редактировал математический раздел ее записок, рецензировал дипломные
сочинения академических студентов и адъюнктов. На квартире у него
подолгу жили присланные к нему для завершения образования
Котельников, Румовский и Софронов. Эйлер приобретал для Академии книги,
аппаратуру и оборудование; он подыскивал кандидатов на замещение
вакансий в Академии. В последнем вопросе он никогда не становился
на сторону Шумахера и немецкой академической партии. Эйлер понимал,
что России нужны национальные кадры ученых, и поддерживал русских
кандидатов. Когда в 1754 г. встал вопрос о замещении вакантной кафедры
математики, Эйлер, сравнивая Котельникова с некоторыми зарубежными
претендентами, писал в Академию: «...во всяком случае несомненно, что
во всей Германии не найти более трех человек, которые в математике
заслуживали бы предпочтение перед Котельниковым, но я надеюсь,
что в течение года добьюсь с ним того, что он превзойдет и этих людей» *).
К этому времени относится и переписка Эйлера с М. В. Ломоносовым
(1711—1765), свидетельствующая об их глубоком взаимном уважении.
Ломоносов делился с Эйлером своими идеями, например, о
корпускулярном строении материи, своей теорией тепла, возражениями против лейб-
ницевой теории монад. В ряде пунктов физические взгляды Ломоносова
и Эйлера совпадали. В 1747 г. Шумахер послал две работы Ломоносова
на заключение Эйлера, надеясь получить отрицательный отзыв. Ответ
Эйлера разбил планы Шумахера. Великий математик писал: «Все сии
сочинения не токмо хороши, но и превосходны, ибо он [т. е. Ломоносов]
изъясняет физические и химические материи самые нужные и трудные,
кои совсем неизвестны и невозможны были к истолкованию самым
остроумным ученым людям, с таким основательством, что я совсем уверен
в справедливости его изъяснений. При сем случае я должен отдать
справедливость г-ну Ломоносову, что он одарован самым счастливым
остроумием для объяснения явлений физических и химических» 2).
Энергия Эйлера в зрелые годы кажется неиссякаемой. Продолжая
осуществлять планы, намеченные в Петербурге, он вместе с тем включает
в круг занятий новые вопросы. Так, например, он впервые строит
теорию элементарных функций комплексного переменного, соревнуясь с
Ж. Даламбером и Д. Бернулли, разрабатывает задачу о колебании струны
и вместе с тем приемы решения уравнений с частными производными
и разложения в тригонометрические ряды, получает важные результаты
по эллиптическим интегралам, развивает алгоритм вариационного
исчисления, предложенный молодым Лагранжем, углубляется в
дифференциальную геометрию поверхностей и делает первые шаги в топологии. В
механике, соперничая с Клеро и другими, он решает трудные задачи теории
движения Луны и больших планет, а кроме того, закладывает
математические основания механики твердого тела и гидродинамики и решает ряд
задач теории упругости. Все это переплетается с построением первых
ахроматических рефракторов, изучением зубчатых передач,
совершенствованием гидравлической реактивной турбины, изобретенной И. А. Зег-
нером.
г) Die Berliner und die Petersburger Akademie der Wissenschaften im Briefwechsel
Leonhard Eulers, Teil I, стр. 57.
2) Цит. по кн.: M. В. Ломоносов, Избранные философские произведения
М., 1950, стр. 709—710.
108
ГЛ. 6. ЛЕОНАРД ЭЙЛЕР
В то же время Эйлер пишет одну за другой большие сводные
монографии, вскоре ставшие классическими руководствами для многих
поколений. Он публикует в Швейцарии «Метод нахождения кривых линий,
обладающих свойствами максимума, либо минимума» (1744) и два тома
«Введения в анализ бесконечных» (1748), в Германии немецкий перевод
с обширными собственными дополнениями «Новых начал артиллерии»
(1745) Б. Робинса и «Теорию движения твердого тела» (1765), в
Петербурге заказанную нашей Академией двухтомную «Морскую науку»;
по поручению и за счет нашей же Академии он, для удобства чтения
корректур, печатает в Берлине «Теорию движения Луны» (1753) и
«Дифференциальное исчисление» (1755). За исключением книги по баллистике,
остальные написаны по-латыни.
Возвращение Эйлера в Петербург. Во время пребывания в Берлине
Эйлер несколько раз ставил вопрос о возвращении в Петербург.
Отношения его с королем чаще всего оставляли желать лучшего; эти
два человека слишком расходились во всем: в мировоззрении, в
отношении к математике (Фридрих не ценил сколько-нибудь отвлеченные
изыскания), в личных вкусах и манерах и т. д. Все это усиливало
разногласия в чисто деловых вопросах, касавшихся управления Берлинской
Академией, в которое король постоянно вмешивался. В 1766 г. Эйлер
решительно потребовал увольнения, с тем чтобы возвратиться в
Петербург. Опасаясь скандала и не желая конфликта с русским правительством,
стоявшим за спиной Эйлера, король с досадой отпустил ученого, бывшего
лучшим украшением и главной силой его Академии. 28 июля 1766 г.
Эйлер был снова в Петербурге.
Эйлер вернулся в нашу Академию под шестьдесят лет. Осенью
1766 г. он почти целиком потерял зрение на второй глаз, а первым не видел
с конца тридцатых годов. Это несчастье, впрочем, не отразилось на era
творчестве сколько-нибудь заметно. Эйлера выручали его
изумительная память, а также писавшие под его диктовку и проводившие
численные расчеты ученики — старший сын Иоганн-Альбрехт, Головин,.
Фусс и др.
Среди математиков всех времен Эйлер выделяется не только
гигантской продуктивностью, но и не слабевшей со временем активностью.
Наоборот, литературная продукция его с годами росла. За 1725—1744 гг. он
подготовил, считая по названиям, приблизительно 15 % своих сочинений,,
за 1745—1764 гг. около 35%, а за 1765—1783 гг. примерно 50%. Когда
ему было семьдесят лет, в 1777 г., Эйлер подготовил с помощью
секретарей чуть ли не сотню статей, по две в неделю. Мы назовем здесь только
большие книги, изданные во второй период петербургской жизни Эйлера.
Это — популярные «Письма о разных физических и филозофических
материях» в трех частях (франц. изд., СПб., 1768—1772; русский перевод
С. Я. Румовского, 1768—1774), трехтомное «Интегральное исчисление»
(1768—1770), известная уже нам «Универсальная арифметика» в двух
томах (1768 — 1769), трехтомная «Диоптрика» (1769—1771), огромная
«Новая теория движения Луны», составленная под руководством Эйлера
его старшим сыном Иоганном-Альбрехтом и академиками В.-Л. Крафтом
(1743—1814), сыном математика, упоминавшегося ранее Г.-В. Крафта,
и А. И. Лекселем, и, наконец, учебник «Полное умозрение строения
и вождения кораблей» (франц. изд., СПб., 1773, русский перевод
М. Е. Головина 1778 г.). «Интегральное исчисление», «Диоптрика» и книга
о движении Луны написаны по-латыни.
ВОЗВРАЩЕНИЕ ЭЙЛЕРА В ПЕТЕРБУРГ
109
Эйлер продолжал участвовать и в других занятиях Академии. Так,
он работал вместе с выдающимся изобретателем И. П. Кулибиным (1735 —
1818) над изготовлением по собственному проекту нового микроскопа.
В 1776 г. при экспертизе проекта постоянного одноарочного моста через
Рис. 22. Мемориальная доска, установленная 16 апреля
1957 г. на доме, в котором проживал Л. Эйлер во второй
петербургский период жизни (Ленинград, Набережная
лейтенанта Шмидта, 15).
Неву, предложенного Кулибиным, Эйлер оказал ему поддержку и дал
теоретическое обоснование найденного Кулибиным правила пересчета
результатов испытания моделей на натуру. Заметим, что Эйлер вообще
высоко ценил технические дарования русских мастеров 1). Вместе с сыном
Иоганном-Альбрехтом, назначенным в 1769 г. секретарем Академии,
г) А, П. Юшкевич, Жизнь и математическое творчество Леонарда
Эйлера.— УМН, XII (4), 1957, стр. 14.
110
ГЛ. 6. ЛЕОНАРД ЭЙЛЕР
Эйлер был в 1766—1774 гг. членом Комиссии, управлявшей всеми делами
Академии.
Последние годы жизни Эйлер уже не мог посещать заседания
конференции, хотя и продолжал работать дома, на углу 10 линии и
набережной Большой Невы,— этот дом сохранился в перестроенном виде до сих
пор (рис. 22). Эйлер был окружен большой семьей: кроме старшего сына,
в Петербурге жили и два других — врач Карл Эйлер (1740—1790) и
Христофор Эйлер (1743—1808)— офицер (потом генерал-лейтенант) русской
Рис. 23. Надгробие на могиле Л. Эйлера
в Ленинградском некрополе.
армии, а также их многочисленные дети, потомки которых и сейчас
проживают в Советском Союзе. Эйлер скончался скоропостижно, от
кровоизлияния в мозг, 18 сент. 1783 г. Его похоронили на Смоленском
лютеранском кладбище, в получасе ходьбы от его дома. Осенью 1956 г. могила
Эйлера и воздвигнутый на ней в 1837 г. памятник (рис. 23) были
перенесены в Ленинградский некрополь, по близости от могилы другого
крупнейшего деятеля Петербургской Академии — М. В. Ломоносова.
Общая характеристика творчества. При жизни Эйлера было
напечатано около 560 его трудов, из них около 400 в изданиях Петербургской
Академии. Эйлер как-то заметил в шутку, что оставит после себя столько
ОБЩАЯ ХАРАКТЕРИСТИКА ТВОРЧЕСТВА
111
статей, что их придется печатать еще в течение двадцати лет. На самом
деле публикация его научного наследия, в подготовке которой
участвовали Н. И. Фусс, В. Я. Буняковский, П. Л. Чебышев и П. Н. Фусс,
продолжалась в изданиях нашей Академии до 1862 г.; некоторые работы
были выявлены еще позднее. Список трудов Эйлера, составленный в 1910—
1913 гг. шведским историком математики Г. Энестремом, насчитывает
более 850 названий, не считая 31 труда Иоганна-Альбрехта, написанных
под руководством отца; к этому следует
добавить многие сотни чисто научных
писем Л. Эйлера, нередко
представляющих собой подлинные научные тру
ды г). Полное собрание сочинений
Эйлера (без переписки), Leonhardi Euleri
Opera omnia, издающееся с 1911 г.
Швейцарским обществом
естествоиспытателей, должно содержать 72 больших
тома. Полностью завершена публикация
только математической серии в 29
томах, из которых один в двух частях2).
Не менее поразителен, чем
количественный размах, грандиозный
диапазон творческих интересов Эйлера,
распространявшихся не только на весь
цикл физико-математических наук, но
и на технику и даже на сельское
хозяйство — в одной статье он описывает
особый способ сева зерновых культур,
а вместе с тем на логику и
философию 3). При всем том, главным делом
Эйлера была разработка математики.
Из 72 томов его сочинений лишь 29
относятся, как сказано, к «чистой»
математике, 31—к механике и астрономии
и 12— к физике и разным вопросам.
Однако следует иметь в виду, что
значительная часть работ по механике, астрономии и оптике состоит в
точной математической постановке и математическом же решении их проблем.
Л.'Эйлер (бюст работы Д. Рашетта,
1784. Оригинал находится в здании
Президиума АН СССР в Москве,
авторская копия 1788 г. в
Государственном Эрмитаже).
х) Список трудов Эйлера, а также многочисленные сведения о его рукописях,
служебной карьере и участии в заседаниях Академии наук имеются в книге:
Рукописные материалы Л. Эйлера в Архиве Академии наук СССР, т. I. Составители
Ю. X. Копелевич, М. В. Крутикова, Г. К. Михайлов и Н. М. Раскин, М.— Л., 1962.
2) Помимо изданий переписки, указанных выше, см. еще: Леонард Эйлер,
Письма к ученым. Составили Т. Н. Кладо, Ю. X. Копелевич, Т. А. Лукина, под
ред. В. И. Смирнова, М.— Л., 1963. Резюме почти всех сохранившихся писем Эйлера
опубликованы в кн.: Леонард Эйлер. Переписка. Аннотированный указатель, под
редакцией В. И. Смирнова и А. П. Юшкевича, Л., 1967.
3) О работах Эйлера по механическим и физическим наукам и технике см.:
А. Т. Г р и г о р ь я н, Очерки по истории механики в России, М., 1961; С. П. Т и-
м о ш е н к о, История науки о сопротивлении материалов с краткими сведениями
из истории теории упругости и теории сооружений. Перев. под ред. А. Н.
Митинского, М., 1957; А. П. М а н д р ы к а, Баллистические исследования Леонарда
Эйлера, М.—Л., 1958; М. Ф. Субботин, Астрономические^ работы Леонарда
Эйлера; Я. Г. Д о р ф м а н, Физические воззрения Леонарда Эйлера; Г. Г. С л ю-
с а р е в, «Диоптрика» Эйлера; Н. М. Раскин, Вопросы техники у Эйлера
(последние четыре статьи в сб.: Леонард Эйлер, под ред. М. А. Лаврентьева, А. П. Юшкевича,
А. Т. Григорьяна, М., 1958).
112
ГЛ. 6. ЛЕОНАРД ЭЙЛЕР
Все творчество Эйлера пронизывает идея тесной связи математики
с естественными науками и техникой. Как и Д. Бернулли, Эйлер в своих
работах осуществлял тесную связь теории и практики. Он с
непревзойденным искусством умел выделять в частных, конкретных задачах зерно
широких общих теорий и всегда стремился доводить теоретическое
исследование до числового результата, дающего вполне эффективное решение
вопроса. В отличие от Д. Бернулли, Эйлер, математик по преимуществу,
обращался к математике не от случая к случаю, но неустанно и
систематически развивал ее как единое целое. В значительной степени этим
определялся великолепный успех его трудов.
В математическом творчестве Эйлера на первом месте стоит анализ
бесконечно малых, которому отведено 18 томов собрания сочинений,
из них один двойной; далее следуют теория чисел — четыре с половиной
тома, геометрия — четыре тома, алгебра — полтора тома и комбинаторика
с теорией вероятностей — один том. Очень многие исследования по
геометрии проведены при помощи алгебры и исчисления бесконечно малых.
Таким образом, в главном Эйлер был аналистом и арифметиком.
Разрабатывая анализ, он обогатил его не только множеством отдельных важных
формул, теорем и приемов во всех ранее наметившихся направлениях,
не только последовательно систематизировал его в своих
фундаментальных руководствах, но и явился основателем нескольких больших
дисциплин: вариационного исчисления, учения об элементарных функциях
комплексного переменного, теории дифференциальных уравнений, учения
о специальных функциях, учения о тригонометрических рядах и др.
А теория чисел на протяжении полувека принадлежала к самым любимым
предметам занятий Эйлера, как и многих других крупнейших
математиков, на другом полюсе интересов которых находились прикладные
проблемы, например К. Ф. Гаусса, П. Л. Чебышева и Д. Гильберта.
Широко распространено представление об Эйлере как великом
вычислителе и виртуозе формальных преобразований. Он действительно
был таковым. Но облик Эйлера-математика далеко не исчерпывается этим.
Искуснейшим образом манипулируя аппаратом формул, создавая
замечательные расчетные алгоритмы, он вместе с тем был творцом новых важных
понятий и глубоких идей. В математике XVIII века относительная роль
«понятийного» элемента в сравнении с формально-алгоритмическим была
гораздо менее значительна, чем в последующем столетии и особенно
в наше время. Это отражено и в творчестве Эйлера. Но развитие
математики и в XVIII веке включало совершенствование старых и создание
новых фундаментальных понятий этой науки и проходило в борьбе мнений
по многим принципиальным вопросам — о содержании и объеме понятий
функции, дифференциала и интеграла, о значении сходящихся и
расходящихся рядов, о роли комплексных чисел, и т. д. В этой работе Эйлеру
принадлежат очень большие заслуги, наряду с некоторыми неудачами.
Точно так же нередко встречается мнение, что Эйлер-математик
был эмпирик, всецело полагавшийся на неполную индукцию. М. Я.
Выгодский писал: «... тогда, когда Эйлеру нужно установить какой-либо закон,
имеющий место для целочисленных значений аргумента, он поступает
не так, как поступил бы математик нашего времени. Он ограничивается
наблюдением этого закона для некоторого (притом довольно
небольшого) числа значений, подобно тому как естествоиспытатель
устанавливает всеобщий закон природы из конечного числа наблюдений». Так,
увидев, что закон образования коэффициентрв в формулах конечных
разностей до пятого порядка тот же, что в биноме Ньютона, Эйлер делает вывод
ОБЩАЯ ХАРАКТЕРИСТИКА ТВОРЧЕСТВА
113
о тождестве этих коэффициентов для разности любого порядка. М. Я.
Выгодский заключает: «Не нужно думать, что Эйлер не дает в таких случаях
общего доказательства ввиду его трудности или, наоборот,
предоставляет проведение легкого доказательства читателю. Нет, для него самого
„неполная индукция" вполне убедительна» г).
Совершенно верно, что Эйлер, как и другие математики всех времен,
широко использовал индуктивные обобщения, нестрогие аналогии,
наблюдения над эмпирическим числовым материалом и т. п. Но при этом он
прекрасно понимал, что это — эвристические приемы, не имеющие сами
по себе доказательной силы. В одной из ранних работ по теории чисел
Эйлер писал по поводу предложений Ферма: «По-видимому, сам Ферма
пришел к большей части своих теорем посредством индукции, которая
представляет собой едва ли не единственный путь нахождения этих
положений. Однако я мог бы показать, как мало значения приходится
придавать индукции в этих вопросах», и Эйлер указывает на опровергнутое
им предложение, что все числа вида 22т + 1 простые. Эйлер добавляет:
«По указанной причине все такие свойства чисел, которые опираются
на одну только индукцию, я считаю недостоверными, пока они не будут
либо подкреплены аподиктическими доказательствами, либо вовсе
опровергнуты» 2). Это далеко не единственное высказывание Эйлера такого
рода 3). Я не буду пока входить в вопрос о том, насколько
удовлетворительны с нашей точки зрения многие доказательства, казавшиеся Эйлеру
строгими. Свободные переходы по аналогии из области конечного в область
бесконечного, применение формул без разбора условий, в которых они
имеют реальный смысл, и т. п. недостатки метода вывода Эйлера были
позднее подвергнуты критике, во многом правильной, кое в чем
односторонней. Но так или иначе, неполная индукция, вопреки мнению
М. Я. Выгодского, была для Эйлера не приемом точного математического
доказательства, но только средством математического поиска.
Эйлер оказал огромное влияние на все развитие математических
наук. Выдающийся французский ученый Лаплас не раз говорил молодым
математикам: «Читайте Эйлера, читайте Эйлера, он наш общий учитель» 4).
И Эйлера читали все крупнейшие математики XIX века, щедро черпая
в его трудах и знания, и проблемы для собственных изысканий, и методы,
подлежащие дальнейшему совершенствованию. Особое значение имело
творчество Эйлера для науки в России. Мы увидим далее, что оно нашло
великолепное и оригинальное развитие у П. Л. Чебышева и его учеников.
г) Л. Эйлер, Дифференциальное исчисление, перев. и вступительная статья
М. Я. Выгодского, М.— Л., 1949, стр. 23.
2) L. Е и 1 е г i Opera omnia, ser. I, vol. II, стр. 33.
3) Подробнее см.: Д. П о и а, Математика и правдоподобные рассуждения.
Перев. И. А. Вайнштейна, под ред. С. А. Яновской, М., 1957; см. также
И. Г. Мельников, Леонард Эйлер о математической строгости. — Ист.-матем.
исслед., вып. XVII, 1966.
4) Так вспоминал лично знавший Лапласа итальянский математик Г. Либри.
См. Journal des savants, 1846, стр. 51.
ГЛАВА СЕДЬМАЯ
БЕСКОНЕЧНЫЕ РЯДЫ
Мы начнем разбор математического творчества Эйлера с бесконечных
рядов, которые очень быстро приобрели в его исследованиях совершенно
исключительное значение. Уже Ньютон и Лейбниц видели в бесконечных
рядах не только средство приближенных вычислений, но своего рода
универсальный ключ к задачам анализа, которые не удается решить
в конечной форме. Ряды оказались пригодными для вычисления корней
уравнений, не разрешающихся в радикалах, для представления
неэлементарных интегралов, интегрирования дифференциальных уравнений,
не выражающихся в квадратурах и т. д. Эйлер необычайно умножил
приложения бесконечных рядов, впервые приступил в широком масштабе
к исследованию с их помощью функций и внес в теорию рядов новые идеи
и методы, разработка которых продолжается до сих пор.
Интерполирование последовательностей и рядов; специальные
функции. Первые и сразу же замечательные успехи Эйлера были связаны
с интерполированием рядов и последовательностей. Выше говорилось
о поставленной Д. Бернулли задаче найти конечное выражение для
общего члена последовательности факториалов 1,1-2,1-2-3, . . . Эйлер
решил эту задачу, обратив, в некотором смысле, ход мыслей Валлиса.
Английский математик применил интерполирование к вычислению
данного определенного интеграла; Эйлер выразил общий член
последовательности #1, а2, . . ., аП1 ... некоторым определенным интегралом
ь
р {х, п) dx, зависящим от переменного параметра п и при п целом
а
и положительном совпадающим с ап. Работа на эту тему была готова еще
осенью 1729 г. и тут же представлена Петербургской Академии, но
увидела свет много позднее (САР V (1730—1731) 1738). Прежде всего Эйлер
выражает общий член последовательности п\ бесконечным произведением,
которое в несколько ином виде нашел и Д. Бернулли:
/j.2n 21~n-3n З1-71-^
1 + п 2 + п 3 + п "'
Затем, не задерживаясь на обосновании этого результата, которое Эйлер
доложил лишь в 1776 г. [NAP VII (1789) 1793], он переходит к главной
1
цели. Отправляясь от интеграла \ xv (1 — x)q dx, отдельные случаи
о
которого рассматривал Валлис и который при целых положительных
ИНТЕРПОЛИРОВАНИЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ 115
(P+q + lY.
р, q равен /п_^^_^ , Эйлер с помощью преобразований и предельных
i
переходов получил интеграл \ (—In х)п dx, при целом положительном п
о
равный п\ Именно этот интеграл, который он впоследствии иногда
обозначал [/г], Эйлер принял за общий член последовательности
факториалов; что п должно быть здесь больше —1, он указал позднее. Тут же
Эйлер приводит основное свойство функции [п], общее с обыкновенным
факториалом: [п + 1] = (п + 1) [п]. Сравнение найденного для [п]
произведения при п = у с валлисовым бесконечным произведением для —
дало, в частности, «конечное выражение» члена, промежуточного между
первым и вторым, именно Г у 1 = (у )! = -у- .
Учение о бесконечных последовательностях и произведениях
переплетается в данной работе Эйлера, как и во многих последующих, с
теорией специальных функций, начало которой было положено в нашей
Академии наук. Вслед за Лежандром (1809 и след.) мы зовем теперь
1
\ (—In х)п dx эйлеровым интегралом второго рода или гамма-функцией
о
1
Г (п + 1), а интеграл \ xv (1 — x)q dx, где/? > —1, q > —1, эйлеровым
о
интегралом первого рода или, по предложению Ж. Бине (1839), бета-
функцией В(р + 1, q + 1). Эйлер открыл многие свойства обоих классов
функций. Так, в письме к Гольдбаху от 4 июля 1744 г. он привел
разложения логарифмической производной гамма-функции
d In Г (х + 1) _ , я х х
dx ~" ~~У ~т~ 1 + ж + 2(2 + х)+Ъ(3 + х) + "'
И
dlnr<?+1) = -V + E(2)s-e(3)s» + S(4)a;8-...
dx
1
Здесь у — так называемая постоянная Эйлера, а ? (п) = ^ ^ ~ дзета-
функция, о которых говорится далее. В том же письме содержится
асимптотическое разложение логарифма гамма-функции
In
Г(х+1) = ±1п2л+(х+±)Ых-х+-±-
3-4-5-б.гЗ г 5.6-7-6^5
которое для целых положительных п было дано еще в 1730 г. Дж.
Стерлингом и А. де Муавром. Эти результаты Эйлер включил в
«Дифференциальное исчисление» *) (1755).
х) Где коэффициенты разложения In Г {х + 1) по степеням 1/х уже выражены*
явно через бернуллиевы числа И, SB, (?,..., о которых см. далее:
1 / 1 ^ 21 SB .
6яб
116
ГЛ. 7. БЕСКОНЕЧНЫЕ РЯДЫ
Эйлеру принадлежит и другое, более употребительное интегральное
оо
представление Г (п) = \е"ххп"1 dz (представл. 1781, опубл. 1794), а также
о
многие важные формулы, среди которых укажем лишь две:
Г (и) Г (1-л) = -^— и В(р, q) = V^)V{q}
[NCAP XVI (1771) 1772]. Его исследования были продолжены многими
отечественными и зарубежными математиками, в частности Н. Я. Сони-
ным. Интенсивная разработка учения о гамма-функции была связана
с ее большой ролью в анализе и теории чисел. Через Г (п) выражаются
многие суммы рядов, бесконечные произведения и определенные
интегралы; она тесно связана с другими специальными функциями —
цилиндрическими, дзета-функцией и проч.
Несколько работ [САР V, VI и др.] Эйлер посвятил интерполирова-
11 1
нию и исследованию гармонических рядов —1-"~тт+ л. 91 ~^~ • • •'
названных так лордом Броункером (1668) потому, что любые три
последовательные члена их образуют гармоническую пропорцию, т. е. ak-±: ak+i =
= (uft-i — ak) : (ak — ak+i). Расходимость ряда 1 + 1/2 + 1/3 + . . . была
доказана около 1350 г. Н. Оремом и три века спустя вновь открыта
П. Менголи (1650) и старшими братьями Бернулли (1689). Тот же Менголи
заметил связь гармонического ряда с логарифмами (1659). Вскоре (1668)
Н. Меркатор открыл знаменитое разложение
1п(1+ж) = ж —-у- + -| ...
В статье, напечатанной в Acta Eruditorum за 1720 г., Гольдбах установил,
П оо
чт0 у = у ZL—г не зная, что этот результат был известен еще Мен-
АЛ к *-* к (к-\-п)
k=l k=i
голи и Я. Бернулли. В 1729 г. гармонические ряды явились одним из
предметов переписки Гольдбаха с Д. Бернулли; здесь х) мы находим некоторые
1
1
оценки Д. Бернулли для суммы 2 Т ' а также изложение открытого его
т-{-п
младшим братом Иоганном II свойства величины ^ у стремиться при
i . 1 гп-\-п
постоянном т/п и тп + п —> оо к «асимптотическому числу» In .
Эйлер продвинулся значительно дальше своих друзей. С помощью
разложения Меркатора он выразил частную сумму гармонического ряда
в виде
п п п п
i k=l k=i fc=l
x) Correspondance mathematique et physique de quelques celebres geometres du
XVIII« siecle, t. II, стр. 252-253, 300-302.
ФОРМУЛА СУММИРОВАНИЯ ЭЙЛЕРА
117
П
ХП 1
При п~-> оо разность 2j "т.— 1П (и + 1) стремится к конечному пределу
именно упомянутой постоянной у, носящей теперь имя Эйлера. Так было
открыто важное асимптотическое равенствох)
i+-r+T+---+4—lnn+v-
С помощью формулы
Y—|-С(2)—^С(3)+4-С(4)---.
Эйлер вычислил у = 0,577 218 (вместо 0,577 215 7 . . . ).
Формула суммирования Эйлера. В начале тридцатых годов Эйлер
открыл формулу суммирования, связывающую частные суммы ряда
с интегралом и производными его общего члена. Эйлер доложил ее
Петербургской Академии летом 1732 г. и она была напечатана в т. VI «Записок»,
вышедшем в 1738 г.; к тому же результату независимо пришел не позднее
1738 г. Маклорен, опубликовавший его в 1742 г. Первоначально Эйлер
привел формулу без доказательства в виде
Р л , , л . 0 dt , dH , я dH . dH .
здесь s — сумма n первых членов ряда с общим членом t(n), s = t = 0
при тг = 0, а коэффициенты определяются рекуррентными соотношениями
__1_ р__^ L — JL — _Ё 5L_L_i- —о
а~ 2 ' |J— 2! 3! ~ 12 ' У~ 2! 3! + 4! ~~U'
s_jl P. _i_ з L_ L 8-o
(вообще, начиная с 7, коэффициенты через один равны нулю).
Через три года, осенью 1735 г., Эйлер сообщил вывод формулы
суммирования и показал первые замечательные ее приложения [САР VIII
п
(1736) 1741]. Он выразил с ее помощью степенные суммы Sm = 2А:7П
до т = 16 включительно, еще не зная, видимо, что эта задача была
решена ранее Я. Вернул ли (опубл. в 1713), а затем частную сумму гармониче-
п
ского ряда 2т » причем, положив к = 10, подсчитал постоянную ус 16-ю
верными знаками. Расходимость доставляемого при этом формулой
суммирования бесконечного ряда Эйлеру была ясна и он умело взял
подходящее для его цели число членов. В этой же статье он привел весьма точные
приближения для ? (2), ? (3) и ? (4). Однако в то время Эйлер еще не
заметил и, во всяком случае, не указал, что коэффициенты формулы сумми-
г) Говорят, что / (х) асимптотически равна ер (х) при х ->- х0 (где х0 может быть
/ (я)
бесконечным), и пишут / (х) ~ ф (я), если lim —^ = 1. Иными словами, ф (х) выра-
жает / (х) при х->х0 со сколь угодно малой относительной ошибкой lim , , У = 0.
х J \х)
118
ГЛ. 7. БЕСКОНЕЧНЫЕ РЯДЫ
рования непосредственно связаны со входящими в разложения для
степенных сумм S2m числами Бернулли х) и на эту связь указал лишь в
«Дифференциальном исчислении», где формула записана в виде
21 dz Ъ d*z , (? d*z
S(z)= J *<**+_* + _.-?-
1-2-3.4 dx* ¦ 1.2-3.4.5.6 dx*
причем SI = B2, ® = — iS4, © = ?9, ...
Как показал Эйлер, с ростом индекса 2п абсолютные величины чисел
В2п неограниченно возрастают, притом быстрее, чем члены любой
возрастающей геометрической прогрессии [САР XI (1739) 1750]. Поэтому
ряд, входящий в правую часть формулы суммирования, вообще говоря,
расходится. Вместе с тем во многих случаях формула суммирования
является превосходным инструментом приближенных вычислений. Это
удивительное обстоятельство обнаружил еще Стирлинг, разложение
которого для In (п\) представляет собой частный случай формулы
суммирования. Эйлер, как мы видели, встретился с тем же фактом в работе,
напечатанной в т. VIII «Записок», как и в только что упомянутой статье
t
в т. XI, где он, отправляясь от интеграла arctg t= \ , ,ц 2 и его при-
b
ближенного выражения суммой
nt Tit , nt , nt
S = -
s + *a"r" ^2 + 4*2 ~r w2 + 9?2 -r • • • ~r ^24-722*2
(она получается при делении отрезка интегрирования на п равных частей),
выразил разность arctg 1 — s по формуле суммирования и нашел
представление
п
я хч п i 1 I в2 BQ Bi0
у,
4 ZJ п* + № ^ 4п^ 2-2-п* 23.6./гб ~ гМО-лЮ
Особенность этого представления сам Эйлер характеризовал следующим
образом: чем больше п, тем точнее получается значение зг, однако ряд
следует обрывать на подходящем месте, ибо он расходится, причем так
сильно, что даже ряд, возникающий при умножении /тг-ro члена на х ,
остается расходящимся, как бы мало ни было х. Взяв п = 5, Эйлер
вычислил п с 12-ю верными десятичными знаками; при этом он совершенно
правильно оборвал суммирование на члене, имеющем наименьшую
абсолютную величину.
Ряды, обладающие таким свойством, Лежандр назвал
полусходящимися, теперь их чаще именуют расходящимися асимптотическими
1) Я. Бернулли ввел числа, названные по его имени Муавром (1730) и Эйлером
п
(1755), как коэффициенты при первой степени п в выражениях для ?2771 =
k=l
Теперь числами Бернулли обычно зовут все числа, возникающие из символической
формулы (В + 1)т — Вт = 0 (В0 = 1; т = 2, 3, . . .), если после возведения
в степень заменить Вк на В^. Кроме В±=—^ все B2h+i = 0. Сам Я. Бернулли привел
111 15
первые пять чисел В2 = — , В4 = —— , В6= —,В8=— ^, Bi0 = —.
ДЗЕТА-ФУНКЦИЯ
119
рядами х). Эйлер оперировал ими с величайшим мастерством, хотя и не
располагал выражением остаточного члена формулы суммирования.
Формула суммирования Эйлера — Маклорена явилась в XIX—
XX вв. предметом многочисленных изысканий; вместе с числами Бернулли
она широко применяется в различных вопросах анализа, теории конечных
разностей и теории чисел. Строгое обоснование теории асимптотических
разложений, нашедших важные приложения и в небесной механике, дал
впервые в 1886 г. А. Пуанкаре2).
Дзета-функция. Необыкновенно красивые результаты принадлежат
оо
Эйлеру в исследовании так называемых обратных рядов 2 ш» гДе п —
целое, большее единицы, т. е. функции, которую мы, вслед за Б. Риманом
(1859), называем теперь дзета-функцией ? (п) 3). Вопрос о суммировании
ряда обратных квадратов ? (2) поставил Менголи (1659); Я. Бернулли
доказал, что этот ряд сходится (1689). В 1728—1729 гг. вопрос вновь
обсуждался в переписке Гольдбаха с Д. Бернулли и оба они
приближенно подсчитали ? (2), но не точнее, чем до 0,01. Год спустя Стирлинг
вычислил восемь верных десятичных знаков.
Не зная еще вычисления Стирлинга, Эйлер вначале также занялся
приближенным вычислением, найдя ? (2) = 1,644934 [САР V (1730—
1731) 1738]; затем, как упоминалось, он нашел более точные значения
С (2), ?(3) и ? (4),— первое из них с 20-ю знаками. Вскоре Эйлер
продвинулся гораздо дальше, установив, что для всех четных степеней
отношение ? (2п) : п2п рационально. Вот схема одного из рассуждений в
первой из статей Эйлера, посвященных этому вопросу [САР VII (1734—1735)
1740], Зная, что функция
sin х л х2 , х*
3! ^ 5!
'*) Говорят, что ряд V, —— есть асимптотическое разложение функции / (х)/
jLJ xh
оо П
и пишут / (х) ~ yj —?-, если разность rn (х) —f (х) — *S\ -А при любом фиксирован-
k=0 ft=i
ном n удовлетворяет условию lim xnrn (x) = 0. Иначе: при x -> оо разность rn (х)
ЭС->оо
есть бесконечно малая более высокого порядка, чем —^; тем самым характеризуется
п оо
степень приближения к f (х), которое дает *S\ —— . Разумеется, всякий ряд V, —— ,
fe=0 k=0
сходящийся к / (х), есть ее асимптотическое разложение, но это разложение может
быть и расходящимся рядом.
2) В. В. Л и х и н, Теория функций и чисел Бернулли и ее развитие в трудах
отечественных математиков.— Ист.-матем. исслед., вып. XII, 1959; М. В. Ч и р и
ков, Из истории асимптотических рядов.— Там же, вып. XIII, 1960.
оо
й) Ряд J>j -j— , где z = x-\-yi, определяет ? (z) лишь при # > 1. Риман, который
&=1
впервые стал рассматривать ? (z) при мнимых значениях аргумента, распространил
ее определение как однозначной аналитической функции, на всю комплексную
плоскость (за исключением простого полюса z = 1).
120
ГЛ. 7. БЕСКОНЕЧНЫЕ РЯДЫ
Sin я
имеет нули (корни) ±я, ±2я, ±3я, . . ., Эйлер применяет к
бесконечному ряду, стоящему в правой части, способ разложения на множители
обыкновенного алгебраического многочлена. Это немедленно дает
разложение в бесконечное произведение
4 — — Л- — — — (\ ——\ [\ х2 \ (\ х2 \
1_3!+5! •••-^ П2) (,1~4я2 ) [г - 9^2-j ••'
Затем Эйлер применяет зависимости между суммами обратных степеней
корней алгебраических уравнений и их коэффициентами и таким образом
выводит, что
11 я2
? (2) = 1 + -^г" + "32" + • • • = "ё~ »
с(4)=1+4г+ж+••¦=¦?¦
и т. д. до ? (12). Другое, аналогичное рассуждение давало точно такие же
результаты. Однако Эйлер сознавал недостаточную надежность своих
выводов, которые были подвергнуты критике и его корреспондентами.
И. Бернулли указал, что нужно еще выяснить, являются ли числа вида
±тгя единственными нулями функции sin х. Д. Бернулли подверг
сомнению законность переноса на бесконечные степенные ряды свойств
конечных алгебраических многочленов. В т. VII Miscellanea Berolinensia (1743)
Эйлер предложил новый способ разложения —- в бесконечное
произведение, основываясь на открытой им перед тем зависимости между синусом
и показательной функцией:
sin х = ^ •
r^ „ sin х
оилер рассматривает как значение выражения
(<+#)4'-f)"
2xi
при п = оо. Последнее выражение он преобразует в произведение,
применяя разложение на множители двучлена вида zn — ап х). Переходя к
пределу при п = оо, Эйлер получил прежний результат.
Несколько ранее Эйлер установил, что отношение ? (2п) : я2п весьма
просто выражаются через коэффициенты формулы суммирования (САР XII
(1740) 1750). В «Дифференциальном исчислении» они записаны также-
с помощью чисел Бернулли. В наших обозначениях выражения для
? (2/г) таковы:
г/о \ ( — 1)п-12*п-1В2пл2п
Помимо
и ряды
С(2в)
, Эйлер
1 1
ЬУ
*1Ь).
(2/г)!
просуммировал ряды
Г +
1
/[71
1
' 32П
!
+ Г
1
42rt
1 ,
-3)" '
•+
1
5П
22п-1_
• • • = 2ъп-
1 1 !
1 (— iyi 1 '
-1
-1
• • ?
-?(2»)
х) Разложения двучленов я4 =F яп на действительные множители 1-й и 2-й степенш
впервые нашел ученик Ньютона Р. Котес (опубл. в 1722).
СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ
121
суммы которых также равны пп с некоторым рациональным
коэффициентом. Однако все его попытки определить арифметическую природу сумм
рядов обратных нечетных степеней, т. е. ? (2п + 1) оказались тщетными.
Этот вопрос остается нерешенным по сей день.
В теории дзета-функции Эйлер получил и другие замечательные
результаты. Прежде всего, его имя носит знаменитое тождество
е<*)=2трг= П —А-
где бесконечное произведение справа распространено на все простые
числа р (САР IX (1737) 1744). С помощью этого тождества Эйлер
определил суммы новых рядов и произведений, а для ряда чисел, обратных
1 1 1 1
простым, -^- + ^ + -?-+---Н Ь •••> получил асимптотическое
равенство
2 4~ь.2 4-
1
из которого следует, что названный ряд расходится. Функция ? (п) и
тождество Эйлера стали впоследствии важнейшим средством исследования
проблем распределения простых чисел в натуральном ряде и
арифметических прогрессиях, особенно благодаря П. Л. Чебышеву и Б. Риману.
Чебышев же продолжил изучение сходимости рядов, члены которых суть
функции простых чисел.
Мы отметим еще одно открытие Эйлера в теории дзета-функции,
именно его вывод функционального уравнения
[1 —ги-^ + З^1—4n-i+... __ Г(га —1)! (2П —1) пп_
1_ J 1_ яп(2п-1 —1) C0S 2
2П Зп 4П
или, в другой записи,
? (1 _^) =_А- .COS-^- Г (72) I (П).
Этот результат был доложен Берлинской Академии в 1749 г.,
опубликован почти через 20 лет (Mem. Ac. Berlin, XVII (1761) 1768) и затем надолго
забыт. Риман вновь получил его и доказал в общем случае в 1859 г.,
и только в конце прошлого века заметили, что функциональное уравнение
Римана имелось еще у Эйлера. Эйлер пришел к своему открытию,
сравнивая суммы прямых и обратных степеней натурального ряда. На строгое
доказательство он не претендовал, но, проверив равенство для всех
целых п и некоторых дробных, пришел к убеждению в его
справедливости и для других действительных значений аргумента.
Суммирование расходящихся рядов. Весьма интересна эта проверка
Эйлера, в которой применяется суммирование расходящихся рядов.
Дело в том, что при целом п > 1 ряд в числителе левой части уравнения
Эйлера расходится. Выражаясь на современном языке, можно сказать,
122
ГЛ. 7. БЕСКОНЕЧНЫЕ РЯДЫ
что Эйлер вычислил сумму такого расходящегося ряда, как предел
l_2^-i + 3n-1-4n-1+...= lim (l-2n-1x+3n-1x2+in'1x3 + ...)¦
х->1-0
Это дало ему
1 _ 271"1 + З""1 — 472-1 + ... = 2^—JL ^
1 п
н, в частности,
1 — 1 + 1 — 1+--- =4"» 1-22* + 32* — 42*+...=0,
l_22fc-i + 32*-i-42*-1+ ... =^=±ДаЛ.
Такие равенства многие современники Эйлера считали бессмысленными.
Как может быть, спрашивали они, 1—4 + 9 — 16+ . . . = О, если
частные суммы 1, —3, 6, —10, . . . чем дальше, тем больше и притом
неограниченно удаляются от нуля? Однако вычисление суммы ряда
лосредством указанного предельного перехода и вытекающие из него
парадоксальные равенства имеют совершенно точный смысл. Каковы же
были взгляды Эйлера на общие проблемы сходимости рядов?
Математики XVIII века, как и мы, различали сходящиеся ряды
п
^о + а>\ + • • • + ап + • • ¦» частные суммы которых sn = ^j ak при
п—> оо стремятся к конечному пределу, от расходящихся. Правда, тогда
нередко называли сходящимися все ряды, члены которых стремятся
к нулю, но эта нечеткость терминологии не имела еще решающего
значения. Главное было в том, что отсутствовала общая теория сходимости.
Чаще всего сходимость ряда определялась на глаз и точно так же
оценивалась погрешность приближения суммы сходящегося ряда какой-либо
его частной суммой. Только в редких случаях оценки обосновывались
с помощью точных неравенств, например, в отдельных вычислениях
Эйлера. Несколько известных достаточных критериев сходимости —
Лейбница, Даламбера (сформулированный не вполне корректно) и Макло-
рена — почти не применялись, как и высказанный Эйлером в связи
с изучением знакоположительных гармонических рядов необходимый
критерий
l\m(shn— sn) = 0,
где к — фиксированное целое, большее единицы [САР VII (1734—1735)
1740] г). Хотя для отдельных функциональных рядов была фактически
известна область сходимости, но само это понятие выделено не было.
Действия над рядами — умножение, деление, обращение,
дифференцирование и интегрирование — производили по тем же правилам, что и над
конечными многочленами, без каких-либо ограничений, полагая, что
все операции алгебры и анализа в обоих случаях управляются одними
х) Некоторые авторы полагают, что в написанном равенстве Эйлер трактует к
как пробегающее все натуральные значения 1, 2, 3, ..., и соответственно считают его
условие равносильным общему критерию сходимости Больцано — Коши (с оговоркой,
что Эйлер имел в виду лишь знакоположительные ряды). Ср. введение G. Faber
bL. Euleri Opera omnia, Ser. I, vol. 16—2, p. XIV. Однако ни формулировка
критерия у Эйлера (довольно нечеткая), ни примеры его употребления не дают оснований для
столь широкого толкования.
СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ
123
и теми же законами. Все же поскольку из области аналитических
функций выходили редко и в конце концов разложения рассматривали в
интервале абсолютной сходимости, такой формальный подход обычно не
приводил к ошибкам.
В трактовке сходящихся рядов ученые XVIII века были почти
единодушны. Иначе обстояло дело с расходящимися рядами. П. Вариньон,
Д. Бернулли (в молодые годы), его кузен Н. Бернулли, Даламбер, Лаг-
ранж (в зрелом возрасте) отвергали расходящиеся ряды. По их мнению,
под суммой бесконечного ряда было допустимо понимать только
результат последовательного сложения его членов, т. е. предел частных сумм,
если он существует.
Однако уже Лейбниц пытался рационально истолковать равенство
1 — 1 + 1 — 1+ ... = 1/2, формально получающееся из разложения
7--j— = 1 — х + х2, — xs -f- ..., при х = 1. Доводы в пользу
расходящихся рядов, правда, не отличающиеся убедительностью, приводил
Гольдбах в письмах к Д. Бернулли 1724 г. Главным сторонником
применения расходящихся рядов выступил Эйлер, который разработал
некоторые общие принципы их теории и первые эффективные приемы
суммирования.
Убедившись на собственном опыте в полезности асимптотических
и иных расходящихся рядов, Эйлер поставил целью обосновать
законность их употребления. Эту задачу он считал возможным решить при
помощи естественного обобщения понятия суммы ряда. В самой
постановке вопроса он занял позицию, отличную от всех его современников.
Он не спрашивал подобно другим, что есть сумма 1 — 1 +1 — . . .,
как если бы такая сумма была некоей заранее данной вместе с рядом
сущностью. Он считал нужным выяснить, как надлежит,— если это
возможно и целесообразно,— определить понятие суммы для расходящихся
рядов. «Современному математику,— пишет Г. Харди,— и не придет
в голову, что какое-либо соединение математических символов может
иметь «смысл» до того, как ему придан смысл с помощью определения» *).
Подход Эйлера гораздо ближе к нашему, чем его осторожных
противников, хотя развитая им концепция и не безупречна с точки зрения
математики нашей эпохи.
Свои соображения Эйлер прежде всего изложил в письмах к
Николаю I Бернулли (1743), который выдвинул некоторые возражения,
и к Гольдбаху (1745), который выразил полное согласие, а затем в
«Дифференциальном исчислении». Эйлер отправляется от примера ряда, порож-
даемого функцией т—— при неограниченном делении. На каждом шагу
деления получается точное равенство
¦=1+х+ . . . +хп
1-х ~ " ' " ' * " ' ' ' 1-
т. е.
гп+1
При — 1 < я < 1 и п—> оо разность стремится к нулю и сумма
1 тт
ряда, понимаемая как предел частных сумм, равна j—— . Для остальных
г) Г. Харди, Расходящиеся ряды. Дерев. Д. А. Райкова, с пред. С. Б. Стечки-
на, М., 1951, стр. 19.
124
ГЛ. 7. БЕСКОНЕЧНЫЕ РЯДЫ
значений х разность -j—— к нулю не стремится и ряд 1 + х -f- • • -
. . . -\-хп -\- . . . расходится. Далее Эйлер пишет следующее. Из того, что,
выполняя последовательное сложение членов, мы не имеем при|я[>1
п
приближения 2 ж* к какому-либо пределу, некоторые заключают, что
оо
в этом случае ряд 2 хк вовсе не имеет суммы. Однако, отказавшись от рас-
ходящихся рядов, мы лишились бы многих замечательных открытий,
которые удается произвести с их помощью. Вместе с тем непонятно, как
такие суммы, если они ложны, всегда приводят к правильным
результатам. «Развязать этот труднейший узел» и избежать «кажущихся
противоречий» можно, «если мы припишем слову «сумма» значение, отличное
от обычного. А именно, мы скажем, что сумма некоторого бесконечного
ряда есть конечное выражение, из разложения которого возникает этот
ряд. В этом смысле у бесконечного ряда 1 -\- х -\- х2 -\- хъ -\- и т. д.
истинная его сумма будет равна -. , ибо этот ряд происходит из разложения
этой дроби, какое бы число ни подставлять вместо х. При этом
соглашении, если ряд будет сходящимся, новое определение слова сумма совпадет
с обычным, а так как расходящиеся ряды не имеют никакой суммы в
собственном смысле слова, то из этого нового наименования не проистечет
никаких неудобств. Приняв это определение, мы сможем сохранить
выгоды пользования расходящимися рядами и в то же время защититься
от всяческих обвинений» х).
Таким образом, Эйлер накладывает на понятие обобщенной суммы
ряда требование, теперь называемое условием регулярности: обобщенная
сумма ряда должна, если ряд сходится, совпадать с его обыкновенной
суммой, т. е. пределом частных сумм. Все же эйлерово определение
обобщенной суммы, как «конечного выражения, из разложения которого
возникает этот ряд», связано с некоторыми трудностями. Еще Н. Бер-
нулли выразил сомнение: не может ли один и тот же ряд оказаться
разложением двух разных аналитических выражений, значения которых при
одинаковых аргументах не равны? В этом случае определение Эйлера
потеряло бы смысл. Эйлер был убежден, что всякий ряд порождается
одним-единственным выражением, хотя доказать этого и не мог. Теперь
мы знаем, что для степенных рядов, которые главным образом имел в виду
Эйлер, его утверждение, при правильном понимании, верно: сходящемуся
степенному ряду соответствует одна порождающая его аналитическая
функция. Несостоятельность некоторых указанных позднее примеров,
казалось бы, противоречащих сказанному, была правильно выяснена
еще Лагранжем. Однако для других рядов утверждение Эйлера, вообще
говоря, утрачивает силу и суммирование в указанном смысле уже не
удовлетворяет условию регулярности 2).
Понимание обобщенной суммы ряда, как порождающего этот ряд
конечного выражения, приобрело точный математический смысл в теории
функций комплексного переменного XIX столетия, на основе учения
К. Вейерштрасса об аналитическом продолжении. Если / (z) — функция,
аналитическая в области g, и существует функция F (z), аналитическая
в более широкой области G, а в g тождественно равная / (z), то F (z) назы-
г) Л. Эйлер, Дифференциальное исчисление, стр. 101.
2) Г. X а р д и, Расходящиеся ряды, гл. 1 и 2.
СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ
125
вают аналитическим продолжением f(z). Аналитическое продолжение
обладает свойством единственности, поэтому естественно F(z) обозначать
просто f(z). Область g может лежать на действительной оси х, т. е. можно
говорить об аналитическом продолжении функций действительного
переменного на комплексную область. Так, степенной ряд 1 + х -f- х2 -f- . . .,
сходящийся к f(x) = -г—— в интервале (—1, -\-1) и вне этого интервала
на оси х расходящийся, имеет аналитическим продолжением на всю
плоскость комплексного переменного, исключая точку z = 1, функцию
f(z) = г——, совпадающую с / (х) в интервале (—1, +1). Таким образом,
эйлерова обобщенная сумма данного ряда есть в этом смысле не что иное,
как аналитическое продолжение его суммы в интервале (—1, +1).
Эйлеру принадлежат два регулярных метода суммирования. Один
яз них был упомянут в связи с функциональным уравнением дзета-функ-
оо оо
ции: обобщенная сумма ряда 2 ап определяется, как lim 2 akxki если
/е=0 эс-*1—О k=0
этот предел существует. Другой метод описан в гл. I части 2
«Дифференциального исчисления». Данный ряд
ах— Ьх2 + сх3 — dx* + • • •
с помощью подстановки х= .v__ преобразуется в другой,
ау — Аау2 + А2а • у3 — А3а • у* + . . .,
где у = ——,&Аа—Ь—а, А2а = с — 2Ь-\-а, A3a = d—Зс + ЗЬ — а и т. д.
суть разности последовательности чисел а, Ь, с, d, . . . При х=1 будет
у = 1/2 и в качестве суммы ряда
а—Ъ-\-с— d-\- . . .
Эйлер принимает сумму ряда
^¦а — -^-Аа + ^А2а — ^гА3а+ . ..,
если последний сходится. Этот метод позволяет преобразовывать медленно
сходящиеся ряды в другие, сходящиеся быстрее, а также суммировать
многие расходящиеся ряды. Вот два примера Эйлера. Для ряда 1 — 1 +
+ 1 — ... все разности равны нулю, и, значит, обобщенная сумма
равна 1/2. Для ряда 1 — 4-J-9 — 16 + • ¦ • первые разности суть
нечетные числа 3, 5, 7, . . ., вторая разность постоянно равна 2 и третья —
нулю, так что обобщенная сумма есть 1/2 — 3/4 + 2/8 = 0.
Даниил Вернул ли, в молодости отвергавший расходящиеся ряды,
позднее, вероятно, под влиянием Эйлера, также оценил их пользу,
сравнивая их при этом с мнимыми числами. В статье, напечатанной в XVI т.
«Новых записок» Петербургской Академии (1771 (1772)), он писал: «Если
мы применим это парадоксальное решение как промежуточное звено
для определения при помощи его других величин, значение которых
не подвергается никакому сомнению, то определенное нами значение явно
окажется правильным,— это будет совершенно так же, как в тех
случаях, когда вещественные количества получаются при помощи мнимых
количеств» х). Заслуживает внимания метод суммирования, примененный
х) См. статью В. И. Смирнова в кн.: Д. Б е р н у л л и, Гидродинамика, стр. 475.
126
ГЛ. 7. БЕСКОНЕЧНЫЕ РЯДЫ
им к периодическим колеблющимся рядам У] ak, у которых при некотором
фиксированном р имеет место а0 + #i + #2 + ... + #p-i = 0 и при
любом /2 справедливо а^+р = ар. Обобщенную сумму такого ряда он
вычислял как предел среднего арифметического частных сумм, т. е. как
Km g°-»"** + ¦ • • -~Tsn ^ g специальном случае ряда 1 — 1 +1 — 1 -f- ...
этот способ, дающий опять-таки 1/2, употребил еще Лейбниц (1713).
Д. Бернулли признавал, что не в состоянии обосновать свой «принцип»
и подтверждал его полезность примерами. Более глубокое развитие этот
метод получил у вновь открывшего его Э. Чезаро (1890).
Разыскание условий, в которых правомерны обобщенные приемы
суммирования, было непосильно для математики XVIII века. Между тем
неограниченное применение расходящихся рядов порождало, особенно
в руках менее глубоких и осторожных ученых, ошибки. Даже у Эйлера
встречаются промахи. В упоминавшейся статье о вычислении числа зт,
содержащей столь тонкие мысли о полусходящихся рядах (САР XI (1739)
1750), Эйлер высказал утверждение, что сумма любой геометрической
прогрессии, продолженной в обе стороны, равна нулю, т. е. что всегда
оо —1 оо
П=—оо 71=—оо 71=0
В 1753 г. этот парадокс обсуждался в переписке Эйлера с Г.-В. Крафтомг
который, наоборот, полагал, что такая сумма бесконечно велика.
В ходе реформы оснований анализа, начавшейся на рубеже XVIII
и XIX вв., расходящиеся ряды были почти полностью исключены из
рассмотрения. На первое место выдвинулась разработка теории сходимости
рядов (Б. Больцано, О. Коши, Н. Абель и др.). Построение этой теории,
а также теории аналитических функций, явилось необходимой
предпосылкой современной теории суммирования расходящихся рядов. В конце
XIX века выяснилось, что изучение многих вопросов теории рядов
нуждается в обобщении методов суммирования и на этом пути были
получены замечательные результаты. Новая теория суммирования была
построена на гораздо более прочной основе, чем в XVIII веке, и в гораздо
более обширных размерах. Теперь расходящиеся ряды стали не только
сильным, но и вполне безопасным средством исследования. Это повлекло
за собой радикальный пересмотр господствовавшей десятки лет
отрицательной оценки идей и методов Эйлера. Вот что писал в 1826 г. Абель:
«Расходящиеся ряды суть целиком изобретение дьявола и это позор,
что на них решаются основывать какие-либо доказательства. Применяя
их, можно вывести все, что угодно, и именно они породили столько
неудач и парадоксов. Можно ли вообразить себе что либо более
возмутительное, чем утверждение, будто
0 = l_2n + 3n-4n+ и т. д.,
где п — целое положительное число. Risum teneatis, amici»1). А вот
высказывание, сделанное в той же связи Г. Харди в наше время: «Ошибочно
х) То есть удержитесь ли Вы от смеха, друзья? (слова Горация). См. W. A h-
rens, Scherz und Ernst in der Mathematik, Leipzig, 1904, S. 46.
СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ
127
считать Эйлера «нестрогим» математиком, хотя его язык может иногда
показаться нестрогим на современный слух... Затруднения того времени
относительно расходящихся рядов возникали большей частью не из-за
какой-либо особой таинственности расходящихся рядов, как таковых,
но из-за несклонности давать формальные определения и недостаточности
тогдашней теории функций» 1).
Начала современной теории суммирования положили на рубеже XIX
и XX вв. ученые разных стран — итальянец Э. Чезаро, француз Э. Бо-
рель, наш математик Г. Ф. Вороной, венгр Л. Фейер и другие 2).
х) Г. X а р д и, Расходящиеся ряды, стр. 29—30.
2) По истории проблемы до начала XX века см. также Е. В о г е 1, Logons sur
les series divergentes, 2е ed., Paris, 1928.
ГЛАВА ВОСЬМАЯ
МАТЕМАТИЧЕСКАЯ ТРИЛОГИЯ Л. ЭЙЛЕРА
«Введение в анализ бесконечных». Мы обратимся теперь к другим
исследованиям Эйлера по анализу, по возможности группируя изложение
вокруг трех фундаментальных трудов, в значительной части
подытоживших его достижения в этой области —«Введения в анализ бесконечных»,
«Дифференциального исчисления» и «Интегрального исчисления», к
которым можно было бы еще отнести более ранний «Метод изучения кривых
линий, обладающих свойствами максимума, либо минимума». Эти
сочинения составили эпоху в развитии математики и ее преподавания. В них
впервые математический анализ был представлен как единая система.
Исключительно ясное изложение теории иллюстрировалось множеством
примеров. Главную особенность педагогического мастерства Эйлера
правильно подчеркнул еще один из его младших современников,
французский математик и социолог Ж. А. де Кондорсе. В похвальном слове,
произнесенном вскоре после кончины великого ученого, Кондорсе
заметил, что Эйлер предпочитал обучение своих учеников тому небольшому
удовлетворению, какое получил бы, изумляя их, и потому счел нужным
добавить к своим открытиям чистосердечное изложение идей, к ним его
приводивших х). Особенно ярко великий учительский талант Эйлера
проявился во «Введении в анализ», которое до сих пор остается одной
из наиболее увлекательных книг для начинающих изучать так
называемую высшую математику.
«Введение в анализ бесконечных» (Introductio in analysin infinito-
rum, t. I—II, Lausannae, 1748) 2) состоит из двух томов. Второй посвящен
аналитической геометрии и мы оставим его пока в стороне. Предметом
первого тома (рис. 24) служит в основном теория элементарных
функций, которые изучаются при помощи алгебры и разложений в степенные
ряды и произведения. При этом используются понятия бесконечно малой
и бесконечно большой величины, но их определения и свойства не
высказаны, многочисленные предельные переходы производятся без
теоретического обоснования и само слово «предел» здесь не встречается.
Цель «Введения» Эйлер охарактеризовал в следующих словах
предисловия: «Нередко мне приходилось замечать, что большая часть
трудностей, с которыми сталкиваются в анализе бесконечных изучающие
математику, возникает оттого, что, едва усвоив элементарную алгебру,
х) J.-A. de Gondorcet, Eloge de M. Euler, 1786 (переиздано в L. Euleri
Opera omnia, Ser. Ill, vol. 12, 1960).
2) Л. Эйлер, Введение в анализ бесконечных, т. I, изд. 2. Перев. Е. Л. Пацанов-
ского, Вступит, статья А. Шпайзера. Ред. перев. И. Б. Погребысский, М., 1961. Тоже,
т. II, перев. В. С. Гохмана. Ред. перев., вступит, статья и примечания И. Б. Погре-
бысского, М., 1961.
Рис. 24. Титульный лист первого тома «Введения в анализ бесконечных»
Л. Эйлера (Лозанна, 1748).
130
ГЛ. 8. МАТЕМАТИЧЕСКАЯ ТРИЛОГИЯ ЭЙЛЕРА
они направляют свои мысли к этому высокому искусству, вследствие
чего они не только как бы остаются стоять на пороге, но и составляют
себе превратные представления о том бесконечном, идея которого здесь
используется... Есть много вопросов, разрешение которых важно для
подготовки изучающих к более высокой науке и которые, однако, в
элементарной алгебре либо пропускаются, либо рассматриваются
недостаточно обстоятельно... Я старался не только пространнее и отчетливее,
чем обычно, изложить все, что, безусловно, требует анализ бесконечных,
но развил также довольно много вопросов, благодаря которым читатели
незаметно и как бы сверх ожидания могут освоиться с идеей
бесконечного. Много вопросов, разбираемых обычно в анализе бесконечных,
я здесь разрешил при помощи правил элементарной алгебры, чтобы
впоследствии тем лучше выявилась сущность того и другого метода» *).
В том же предисловии Эйлер впервые отчетливо определил предмет
анализа. «Весь анализ бесконечных,— говорится там,— вращается вокруг
переменных количеств и их функций» 2). Наш выдающийся историк
математики И. Ю. Тимченко правильно характеризовал заслугу Эйлера:
«До Эйлера математический анализ был лишь системой методов,
служивших для решения различных конкретных вопросов, системой слабой,
без прочной внутренней связи — самостоятельного абстрактного объекта.
Эйлер нашел такой объект в понятии о функции — великой идее
Лейбница и Бернулли и тем положил основание математического анализа как
отдельной науки» 3).
Понятие функции. С отдельными видами функций математика имела
фактически дело с глубокой древности. Астрономические таблицы
вавилонян, древних греков и индийцев могут служить примерами табличного
задания функций, а теорема о постоянстве отношения площадей круга
и квадрата на его диаметре или же античные определения конических
сечений — примерами словесного задания функции, причем сами эти
кривые выступали как геометрический образ соответствующей
зависимости. Однако древность не выработала общего понятия функции, которое
впервые возникло, хотя и в недостаточно четкой форме, на протяжении
XIV века в учении о широтах и долготах форм (Р. Суайнсхед, Н. Орем:
и др.).
В XVII веке идея функции становится доминирующей в
математическом естествознании и математике. Важнейшее значение имело при
этом введение нового способа задания функции при помощи формул,
предпосылкой чего явилось развитие алгебры и ее символики. У Декарта
(1637) понятие функции уже фигурирует в виде уравнений между х и г/,
ограничиваясь, впрочем, почти исключительно явными или неявными
алгебраическими зависимостями. Ньютон трактовал функцию, как
флюенту — текущую величину, аргументом которой является равномерно
текущая величина, подобная времени. Здесь сказалось влияние механики;
возможно, что и генетически механическая трактовка идеи функции
восходит к упомянутому учению о широтах и долготах форм. Иногда Ньютон
говорил о величинах соотнесенной и отнесенной, которым соответствуют
наши аргумент и функция. Область изучаемых функций в XVII веке
х) Л. Эйлер, Введение в анализ бесконечных, т. 1, стр. 19.
2) Там же.
3) И. Ю. Тимченко, Основания теории аналитических функций, ч. 1.
Исторические сведения о развитии понятий и методов, лежащих в основании теории
аналитических функций, Одесса, 1899, стр. 259.
ПОНЯТИЕ ФУНКЦИИ
131
быстро растет. Нередко функции представляли под видом площадей
или квадратур кривых, иногда их задавали с помощью степенных рядов.
Слово функция х) ввел в 1673—1694 гг. Лейбниц, назвав так различные
отрезки, связанные с данной кривой, как, например, абсциссы и
ординаты ее точек, или отрезки касательных и нормалей.
В печати чисто арифметическое определение функции сформулировал
впервые И. Бернулли (1718): функция переменной величины есть
количество, составленное каким бы то ни было образом из этой переменной
и постоянных 2). В первой главе «Введения» Эйлер раскрывает
определение своего учителя с большей полнотой: «Функция переменного
количества есть аналитическое выражение, составленное каким-либо образом
из этого переменного количества и чисел или постоянных количеств»3).
Здесь особо подчеркнуто, что функции задаются посредством
аналитических выражений, формул. При этом Эйлер делает шаг вперед
принципиального значения, заявляя, что «переменное количество», т. е.
аргумент, «охватывает собой решительно все числа», даже мнимые 4). Тем
самым функции комплексного переменного были объявлены
равноправными с функциями действительного переменного.
Более точно объем приведенного определения функции одного
переменного раскрывается в дальнейших пояснениях Эйлера. Что значит
«аналитическое выражение?» Ответ вначале гласит, что функции
образуются с помощью алгебраических операций, а также трансцендентных
действий, которые мы теперь называем элементарными, и бесчисленных
других, доставляемых интегрированием. Классифицируя разные типы
функций, Эйлер выделяет функции алгебраические и трансцендентные,
алгебраические подразделяются на рациональные и иррациональные,
рациональные — на дробные и целые. Особо выделяются функции
однозначные и многозначные. Все это знакомые теперь вещи. Также знакомы
ныне каждому студенту втуза неявное и параметрическое (термина этого
у Эйлера не было) задание функций и обратные функции. Несколько
далее Эйлер заявляет, что общим средством аналитического выражения
функций служат степенные ряды
A + Bz + Cz2 + Dz3 + ...
Тут Эйлер ссылается на опыт математиков: если кто-нибудь сомневается
в сказанном, то «сомнение устранится самим разложением той или иной
функции». Но для совершенной общности следует допустить еще любые
другие показатели: «не будет никакого сомнения в том, что всякая
функция z может быть преобразована в такое бесконечное выражение
Az* + Bz$ + CzV + Dzb +
где показатели а, р, у, б и т. д. обозначают любые числа» 5).
г) Латинское fungor, functus sum буквально значит осуществлять, исполнять.
2) Впрочем, еще в 1697 г. И. Бернулли писал о «количестве X, составленном из х
и постоянных» (Acta Fruditorum, стр. 115), употребляя знак X, чтобы сразу было
видно, какое количество служит аргументом данной функции. В той же статье 1718 г.,
в которой И. Бернулли сформулировал приведенное в тексте определение функции,
он применил символ ух (Joh. Bernoulli, Opera, vol. II, Lausannae et Genevae,
1742, стр. 241—243). Обозначение / ( [-a J с употреблением скобок принадлежит
Эйлеру [GAP VII (1734-1735) 1740].
3) Л. Эйлер, Введение в анализ бесконечных, т. I, стр. 24. Слова «каким-либо
образом» было бы лучше передать: «каким бы то ни было образом» (quomodocunque).
4) Там же.
5) Там же, стр. 67.
132
ГЛ. 8. МАТЕМАТИЧЕСКАЯ ТРИЛОГИЯ ЭЙЛЕРА
Итак, аналитически выразимая по Эйлеру функция в нашей
терминологии оказывается функцией аналитической во всей области своего
определения, кроме, быть может, отдельных значений аргумента, для
которых она пред ставима обобщенным степенным рядом. Сам термин
«аналитическая функция» восходит к Лагранжу, который в конце
XVIII века сделал попытку доказать в общем случае выдвинутое
Эйлером утверждение, в справедливости которого не сомневались и другие
математики вплоть до Коши, опровергнувшего «доказательство» Лагранжа.
Однако Эйлер не ограничился, да и не мог ограничиться, одними
аналитическими функциями* Нужды математики и ее приложений (об этом
нам придется говорить позднее), требовали более широкой трактовки
понятия функциональной зависимости. Эйлеру это было известно еще
до выхода в свет тома I «Введения» и в его томе II понятие функции
берется в большем объеме. В начале тома II плоские кривые и вместе с ними
функции подразделяются на непрерывные (functiones continuae) и
прерывные (discontinuae). Эти термины Эйлер употребляет не в нашем смысле.
Непрерывной он называет линию, природа которой выражается одной
определенной функцией, одним аналитическим законом, а прерывная
или смешанная линия определяется, как составленная из частей
различных непрерывных кривых. Речь идет, таким образом, о непрерывности
или неизменности «закона» линии или функции. Так, две ветви
гиперболы у = — составляют одну непрерывную линию, подобно параболе или
эллипсу (пример Эйлера), между тем как сплошная линия, составленная
из полупрямой у =— х для x^Cl и полупрямой у = х для #> 1,
разрывна. В анализе, замечает Эйлер, рассматриваются главным образом
«непрерывные» линии. Геометрически непрерывные, сплошные линии Эйлер
именовал иногда связными. Если эйлеровы непрерывные и аналитически
выразимые функции соответствуют нашим аналитическим, то разрывные,
которые он называл также смешанными и неправильными, оказываются
кусочно-аналитическими.
Любопытно, что Эйлер весьма рано встретился с функциями, которые
заведомо не являются аналитическими, т. е. не пред ставимы бесконечным
степенным рядом, даже обобщенным, хотя могут быть записаны одной
формулой и в этом смысле «непрерывны». Такова функция у = (— 1)*,
о парадоксальных особенностях которой Эйлер писал еще в письме
к И. Бернулли от 5(16) ноября 1727 г. х), и о которой вновь идет речь
в томе II «Введения». График этой функции, определенной лишь для
т
рациональных чисел вида 9 , , , состоит из двух множеств дискретных
точек, всюду плотно покрывающих прямые у = =pl, однако так, что,
по выражению самого Эйлера, «никакие две из этих точек не являются
смежными» 2). Подобного рода «аномалии», нарушавшие установленные
схемы классификации, еще мало интересовали Эйлера и других
математиков XVIII века.
Определение функции как аналитического выражения является
во «Введении» основным. Вместе с тем, Эйлеру приходится с самого начала
книги рассуждать о функциях, аналитическое выражение которых
неизвестно, например, когда формулируются теоремы о существовании
обратной функции или функции, заданной параметрически (теперь мы знаем,
что обе теоремы справедливы только при некоторых ограничениях).
~ !) Bibliotheca mathematica, 3 Folge, Bd. 4, S. 346—348.
2) Л. Эйлер, Введение в анализ бесконечных, т. II, стр. 276.
ПОНЯТИЕ ФУНКЦИИ
133
В последнем случае, как специально замечает Эйлер, функцию весьма
часто нельзя «из-за несовершенства алгебры» выразить явно, «тем не менее
эта взаимность функций имеет такой характер, как если бы все уравнения
могли быть решены» 1). Итак, функция может существовать и тогда, когда
аналитическое выражение ее неизвестно. С другой стороны, различные
аналитические выражения, вроде ]/rl-\-z2jrz и t , могут на деле
У 1 + Z2 — Z
представлять одну и ту же функцию 2). Во всех таких случаях под
функцией понимается соответствие между элементами двух числовых
множеств, независимо от способа задания соответствия и от того, удалось ли
его представить аналитически.
Разумеется, сама по себе идея соответствия не была новой, она
присутствует во всяком способе задания функции, но до Эйлера она не была
выделена в общей форме, Эйлер сделал это в «Дифференциальном
исчислении»: «Когда некоторые количества зависят от других таким образом,
что при изменении последних и сами они подвергаются изменению, то
первые называются функциями вторых. Это наименование имеет
чрезвычайно широкий характер; оно охватывает все способы, какими одно
количество может определяться с помощью других» 3). Новое определение,
не ограничивавшее способа задания функций, раскрывало необходимый
простор для исследований, прежде всего самого Эйлера. В том же
«Дифференциальном исчислении» ему приходится иметь дело с
«непредставимыми функциями», аналитическое выражение которых заранее неизвестно
(хотя в конце концов они оказываются аналитическими). К этому
определению Эйлера восходят классические дефиниции Н. И. Лобачевского
(1834) и П. Лежен Дирихле (1837), которые мы находим и в теперешних
учебниках. Впрочем, Эйлер не вкладывал в свои слова тот почти
безбрежный смысл, который они приобрели в теории функций
действительного переменного конца XIX и начала XX вв. 4).
Первые главы «Введения» содержат сведения «о функциях вообще»
и их преобразованиях. Многие теоремы, среди них об обратной функции
и о параметрическом задании, не доказываются. Среди недоказанных
теорем находится и утверждение, что целая рациональная функция
принимает все значения, промежуточные между какими-либо двумя ее
значениями. Это предложение пытались затем доказать для функций
неопределенно широкого класса, а Б. Больцано действительно доказал
его для функций, непрерывных в нашем смысле (1817). Опираясь на это
свойство, Эйлер выводит теоремы о существовании действительного корня
у алгебраического уравнения нечетной степени и положительного и
отрицательного корней у уравнения четной степени с отрицательным
свободным членом. Тут же Эйлер утверждает, что всякая целая рациональная
функция может быть разложена на действительные множители первой
или второй степени и что мнимые корни такой функции встречаются
сопряженными парами; в то время Эйлер готовил работу об
основной теореме алгебры. Здесь эти предложения нужны для разложения
г) Л. Эйлер, Введение в анализ бесконечных, т. I, стр. 29.
2) Более того, можно показать, что функция, представимая одним аналитическим
выражением, имеет бесчисленное множество аналитических выражений.
3) Л. Эйлер, Дифференциальное исчисление, стр. 38. О понятии функции
у Эйлера см.: А. И. Маркушевич, Основные понятия математического анализа
и теории функций в трудах Эйлера.— В сб.: Леонард Эйлер, М., 1958.
4) Подробнее см.: А. П. Ю ш к е в и ч, О развитии понятия функции.— Ист.-
матем. исслед., вып. XVII, 1966.
134
ГЛ. 8, МАТЕМАТИЧЕСКАЯ ТРИЛОГИЯ ЭЙЛЕРА
рациональной дроби в сумму простых. Среди преобразований упомя-
(, m
,_, ) п и V ах* -\-Ъх -\-с\ все это
применяется в интегральном исчислении.
Исследование элементарных функций. Далее Эйлер переходит к
бесконечным рядам и произведениям и их применению к теории элементарных
функций. Прежде всего раскладываются в рекуррентные ряды
рациональные функции и сообщается без вывода разложение в ряд любой
действительной степени бинома ь) и полинома. Впервые дается определение
логарифмической функции, как обратной для показательной функции ах,
причем а > 0. Тригонометрические функции рассматриваются только
в круге радиуса 1, т. е. как отвлеченные числа, и, опять-таки впервые,
вносится совершенная ясность в вопрос о знаках круговых функций
при любых действительных значениях аргумента. Формулы Муавра (1722)
даются в простой и удобной современной записи 2)
(cos х ± i sin х)п = cos пх ± i sin пх.
Доказательство проводится только для натурального п. Из формул
Муавра, переписанных в виде
(cos х + i sin х)п + (cos х — i sin x) n
cosnx = - ¦ '
smnx =
2
(cos x + i sin x)n — (cos x — i sin x}n
2i
при помощи теоремы о биноме и предельного перехода, в котором х
берется бесконечно малой, а п бесконечным, так чтобы z = хп оставалось
конечным (цри этом, как пишет Эйлер, sin х = х и cos х = 1), выводятся
известные разложения для cos z и sin z в степенные ряды. Из тех же
формул, учитывая, что (1± —] при п = оо есть e±ix, Эйлер выводит
знаменитые зависимости между круговыми функциями и показательной
COS z = ^ , sin z = -
2 ' 2*
или
e±iz _. cos z + I sin z%
Мы егце вернемся к этим формулам Эйлера несколько далее.
г) Впоследствии Эйлер предложил различные выводы теоремы о биноме, с точки
зрения XIX века нуждающиеся в уточнениях. Особенно интересно доказательство
в NCAP XIX (1774) 1775, основанное на рассмотрении функционального уравнения
Ф(а)ф(р) = ф(сс + (3) и более строго проведенное Коши (1821).
2) Сам Муавр писал:
1
4 Пу .
где х = cos В, I = cos А = cos пВ.
Обозначая "]/—1 = i, mbi следуем Эйлеру, который, впрочем ввел знак i для
мнимой единицы много позднее (1777, опублик. в 1794). Во «Введении» этот символ
обозначает бесконечность.
НАЧАЛА ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 135
В качестве примера разложений в бесконечные произведения
приведем изящные представления для гиперболических функций х)
shx=Jl_fL=xji (l + ^gy) ,
k=l
ch^ =
ex-\-e x y-r / . 4r2
11 V + (2k — 1)2я2 j
2 11 V ' (2k —1)2 я2
ft=i
Отсюда, полагая показатели мнимыми, Эйлер чрезвычайно просто вывел
разложения
оо оо
SinX = Z П (1-Щг) И С°" = П (*~ (2к-1)*п*) '
fc=l fe=l
первое из них нам уже встречалось.
Во «Введении» Эйлер учит также третьему важному приему
разложения функций — в бесконечные суммы простейших дробей, которые он
использовал и в более ранних работах, например,
= 1 . 1 , 1 . 1 1 ,
® х * х — я ' х-\-ы х — 2п*х-{-2к
Большое место отведено дзета-функции. В связи с разбором задачи
о том, сколькими различными способами данное целое число представимо,
как сумма данного количества неравных или равных слагаемых,
вводится ряд
2 (-!)** —=П (!-**)•
h=-oo k=l
Это — одна из так называемых тэта-функций, учение о которых развил
почти сто лет спустя (1840) К. Якоби, применивший тэта-функции в
теории эллиптических функций.
Специальная глава отведена непрерывным дробям, которые еще
ранее были предметом важных изысканий Эйлера и получили у него
многочисленные применения2). Здесь, в частности, показано
преобразование в непрерывные дроби различных бесконечных рядов. В другой
главе развит, как упоминалось, метод Бернулли решения алгебраических
уравнений. Все это, как и многое другое, нам придется оставить в стороне.
Первый том «Введения в анализ бесконечных» оказал большое
влияние на преподавание анализа в высшей школе и на учебную литературу,
сначала непосредственно, а затем через различные примыкавшие к нему
руководства, вроде замечательного «Курса алгебраического анализа»
О. Коши (1821).
Начала теории функций комплексного переменного. Мнимые и
комплексные числа 3) были открыты в середине XVI века в алгебре и первое
применение получили в исследовании кубических уравнений. В 1629 г.
г) Обозначения chz, sh х ввел в 1757 г. В. Риккати, сын Дж. Риккати.
Гиперболические функции были выделены в особый класс В. Риккати и И. Ламбертом (опублик.
в 1769 г.).
2) Подробнее см. А. Н. Хованский, Работы Л. Эйлера по теории цепных
дробей.— Ист.-матем. исслед., вып. X, 1957.
3) Термин nombre imaginaire — мнимое число принадлежит Декарту;
«комплексное количество» встречается в 1803 г. у Л. Карно, а «комплексное число»
ш 1831 г. у Гаусса; о «сопряженных» выражениях писал Коши (1821).
136
ГЛ. 8. МАТЕМАТИЧЕСКАЯ ТРИЛОГИЯ ЭЙЛЕРА
А. Жирар и в 1637 г. Декарт высказали основную теорему алгебры
в таком виде: всякое алгебраическое уравнение может иметь столько
корней, какова его степень, и если действительных корней меньше, то
недостающие корни модшо себе вообразить. Это означало, что многочлен
хп -\- а^х71-1 + . . . + ап разлагается в произведение п множителей вида
х — хк, где xk есть число действительное или мнимое. Долгое время была
неясно, какова природа мнимых корней, т. е. все ли они того же вида
а -\- Ы, что и корни квадратного уравнения?
Занимаясь интегрированием рациональных функций, Лейбниц
и И. Бернулли ввели мнимые числа в анализ. Интегрирование такой
функции основано на ее разложении в сумму простых дробей. Лейбниц
(1702) поставил вопрос: всегда ли интеграл рациональной функции
выражается в логарифмах и арктангенсах (не считая рациональных функций)
или, как он говорил сам, в квадратурах гиперболы и круга? Ответ зависел
от того, всякий ли алгебраический многочлен с действительными
коэффициентами разлагается на действительные линейные и квадратичные
множители? Лейбниц ответил отрицательно. Уже для простого случая
многочлена я4 + а4 он не нашел такого разложения. Получив
х* + а4 = (х2 + аЧ) (х2 — аЧ) =
= (х + а Уъ) (х — а У г) (х + а У — i) (х — а У — i)
он высказал мнение, что правую часть невозможно представить как
произведение двух действительных квадратичных множителей. На
самом деле
(х ±а>УГ)(х ±о>У—i) = x2 ±У2ах-{-а2, так как "]/"& +У—г = ]/"2.
Этого Лейбниц не знал, несложное же преобразование
х* + а4 = (х2 + а2)2 — 2а2х2 = (х2 + У2ах + а2) (х2 — У2ах + а2)
он упустил из вида по случайному недосмотру. Как бы то ни было,
Лейбниц пришел к заключению, что область мнимых корней уравнений вовсе
не ограничена числами вида а -\- Ы.
Интегрирование рациональных функций привело также к вопросу
о природе логарифмов отрицательных и комплексных чисел. Что следует
понимать под \ —г, когда я-<0? Было известно, что при х > 0 интеграл
выражается логарифмом, но в толковании случая х < 0 Лейбниц и И.
Бернулли разошлись.
И. Бернулли сделал первый важный шаг в учении об элементарных
трансцендентных функциях комплексного переменного. Преобразовав
дифференциал арктангенса в сумму двух логарифмических
дифференциалов
dx _ 1 dx ,( 1 dx
а2-\-х2 ~~ 2а a-\-xi~r 2а а — xi '
он заключил (1703), что мнимые логарифмы заменяют собой
действительные круговые секторы; в пояснение И. Бернулли указал, что при сложении
мнимые величины здесь взаимно уничтожаются и сумма их оказывается
действительной 1). Однако он не развил эту замечательную идею. В 1712—
1713 гг. в полемике с Лейбницем И. Бернулли утверждал, что логарифмы
х) J oh. Bernoulli Opera omnia, vol. I, Lausannae et Genevae, 1742,
стр. 399—400.
ОСНОВНАЯ ТЕОРЕМА АЛГЕБРЫ
137
отрицательных чисел действительны и log (— а) = log (+а). Лейбниц
полагал, что такие логарифмы мнимы, не уточняя, в каком смысле.
Эйлер начал обсуждение проблемы в переписке с И. Бернулли 1727—
1728 гг. В ответ на совершенно точное эйлерово описание графика
функции у =(— 1)х, о котором говорилось выше, И. Бернулли заявил, что
у = (— 1)* = 1, так как log у = х log (— 1), a log (— 1) = log (1) =
= 0; вообще log (— х) = log х, поскольку d log (— х) = d log х, Эйлер
10/21 декабря 1728 г. возразил, что из последнего равенства следует лишьг
что log (— х) = log х -f- Const, где Const = log (— 1), между тем
допущение log (— 1) = log 1 = 0 ведет к противоречию. Используя метод
самого Бернулли «для приведения квадратуры круга к логарифмам»,
Эйлер вывел в других обозначениях формулу
1 -, cosz+tsinz
# = -777- Ш Ч— ,
2i cos х — isini
а из нее при х = -^- получил In (— 1) = яг. Попытки И. Бернулли
согласовать эти выводы, сделанные при помощи его же метода, с равенством
log (—х) = log х были неясны и неудовлетворительны1). Эйлер
продолжал следовать правильному пути.
Только что написанная формула, по существу, содержит в себе
знаменитые формулы Эйлера, связывающие между собой синус, косинус
и показательную функцию, однако в явном виде он пришел к ним
позднее 2). Несомненно, что Эйлер ими владел в 1739—1740 гг. Они
применяются в указанной ранее работе, посвященной ? (2п) и представленной
Петербургской Академии осенью 1739 г. (но напечатанной лишь в XII т.
«Записок» в 1750 г.). Вскоре затем, 18 октября 1740 г. Эйлер писал И.
Бернулли, что 2cos х и ехг -\- е~хг раскладываются в один и тот же ряд и
потому представляют собой фактически одно и то же решение некоторого
линейного дифференциального уравнения с постоянными
коэффициентами 3). В печати формулы Эйлера появились прежде всего в также
упоминавшейся ранее статье в т. VII Miscellanea Berolinensia, 1743, а широкую
известность приобрели благодаря «Введению в анализ бесконечных».
В сороковые годы Эйлер, а также Даламбер, завершили в главном
создание начал теории элементарных функций комплексного переменного.
Важным результатом было установление того факта, что мнимые
величины алгебры и анализа всегда имеют вид а + Ы.
Основная теорема алгебры. 1 сентября 1742 г. в письме к Н. Бернулли
Эйлер впервые высказал основную теорему алгебры вполне отчетливое
всякий алгебраический многочлен любой степени с действительными
коэффициентами разлагается на действительные же множители 1-й и 2-й
степени, иными словами, корни многочлена, число которых равно его
степени, суть действительные или мнимые числа вида а + Ы. Правда,
добавлял Эйлер, он еще не располагает полным доказательством этой теоремы,
столь полезной и для анализа. Вскоре, 15 декабря, он оповестил о своем
открытии Гольдбаха. Характерно, что первоначально оба корреспондента
Эйлера усомнились в теореме и постарались подобрать примеры, ее
опровергающие. Лишь после разъяснений Эйлера они признали свои ошибки,
х) Bibliotheca mathematica, 3 Folge, В. 4, стр. 348—361.
2) Р. Котес обнародовал равенство In (cos х + ъ sins) = ъх еще в 1716 г., но у него
это равенство упоминается мимоходом и не получило ни развития, ни применения..
3) Bibliotheca mathematica, 3 Folge, В. 6, стр 76—77.
138
ГЛ. 8. МАТЕМАТИЧЕСКАЯ ТРИЛОГИЯ ЭЙЛЕРА
-аналогичные допущенной Лейбницем. Теорема была опубликована
б статье Эйлера в т. VII Miscellanea Berolinensia, 1743, посвященной
жнтегрированию линейных однородных дифференциальных уравнений
с постоянными коэффициентами при помощи алгебраического уравнения,
которое теперь называют характеристическим 1).
Доказательство основной теоремы алгебры Эйлер нашел,
по-видимому, через несколько лет: он представил его Берлинской Академии 10
ноября 1746 г., а появилось оно в Mem. Ac. Berlin V (1749) 1751. Тремя
годами ранее, в томе II того же издания (1746) 1748 было напечатано
доказательство теоремы, предложенное Даламбером. По своему характеру эти
два доказательства существенно различны. В то время как вывод Далам-
бера чисто аналитический, у Эйлера он в большой своей части
алгебраический, хотя и опирается на аналитические теоремы о корнях уравнений
нечетной степени и четной степени с отрицательным свободным членом,
о которых говорилось раньше. Обе работы содержали чрезвычайно
глубокие и плодотворные идеи, обе недостаточно строги с точки зрения
позднейшей математики, и оба доказательства были впоследствии
усовершенствованы крупнейшими математиками XIX века 2).
Логарифмическая функция. Статья Эйлера заканчивается теоремами,
ъ которых показано, что все алгебраические и основные трансцендентные
действия над комплексными числами порождают снова комплексные
числа. С утверждением, что любая функция величины х + iy есть также
комплексная величина р + iq, выступил в своей статье и Даламбер.
Однако в учении о логарифмах знаменитые математики разошлись. В
переписке с Эйлером 1747—1748 гг. Даламбер, подобно И. Бернулли, отстаивал
мнение, что log (— а) = log (+ а). Эйлер решительно оспаривал эту
точку зрения и развил полную теорию логарифмической функции
комплексного переменного, которая вошла, с некоторыми изменениями в
деталях изложения, в математику. Соответствующий мемуар Эйлера появился
в том же V томе записок Берлинской Академии.
Уже говорилось, что Эйлер определил логарифмическую функцию
как функцию, обратную показательной, т. е. у = In х, если х = еу,
причем х ф0. Комплексное число а + Ы Эйлер представляет в знакомой
теперь каждому школьнику тригонометрической форме а + Ы = с (cos ср+
+ i sin ф), где модуль с, термин, введенный в 1814—1815 гг. Ж. Арганом,
есть + У а2 + б2, cos ф = — , sin ср = —. Если с = ес, то In (а + Ы) =
= С + In (cos ф + i sin ф). Пусть cos ф + i sin ф = еи, т. е. и =
= In (cos ф + i sin ф). Записывая cos ф + isin ф в виде е®1= (l + -^-J
(и \п
1 -| ] , где п — бесконечно большая
величина, Эйлер получил двучленное уравнение бесконечно высокой степени
(* + v)"-(*+-?-)*-o.
бесконечное множество корней которого обнимается формулой
и = In (cos ф + i sin ф) = (ф ± 2%ri) i,
г) Leonhard Euler und Christian Goldbacn. Briefwechsel. 1729—1764,
S. 130—132.
2) И. Г.. Б а ш м а к о в а, О доказательстве основной теоремы алгебры.— Ист.-
матем. исслед., вып. X, 1957.
КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
139
тде X может принимать все значения 0, 1, 2, 3, ... Поэтому
ln.(a + bi) = C + (y±2Xn)i, Л = 0, 1, 2, 3, ...
Таким образом, логарифм всякого отличного от нуля числа имеет
бесконечное множество значений. Среди значений логарифма любого
положительного числа есть одно действительное, другие же все мнимы;
логарифмы остальных чисел имеют только мнимые значения.
Новые приложения комплексных чисел. Эйлер не ограничился
разработкой учения об элементарных аналитических функциях комплексного
переменного. Ему, как и Даламберу, принадлежат новые приложения
комплексных величин в анализе, механике и геометрии, а также ряд
результатов весьма общего характера.
В 1752 г. Даламбер впервые применил комплексные величины в
гидромеханике. Исследуя установившееся плоское движение несжимаемой
жидкости, он получил, что слагающие скорости частицы потока и и v,
параллельные осям координат х и z/, удовлетворяют системе уравнений
с частными производными
f)u ди ди ди
dx ду ' ду дх
Решение этой системы он выразил при помощи двух произвольных
функций комплексного переменного, неявно предполагаемых аналитическими.
В гидродинамических работах 1755—1757 гг. Эйлер развил метод Далам-
бера далее и у него уже появились две важные величины, которые позднее
получили название потенциала скоростей и силовой функции. В одной
пз этих работ [Mem. Ac. Berlin XI (1755) 1757] Эйлер записал
составляющие скорости в виде
тде ф и г|) — произвольные функции, удовлетворяющие условию, что при
замене аргумента на комплексно сопряженный они сами принимают
комплексно сопряженные значения. Это означает, что рассматриваемые
Эйлером аналитические функции действительны на действительной оси.
Конформные отображения. Методы интегрирования уравнений
с частными производными, развитые в гидродинамике, оказались
полезными при изучение проблемы ортогональных траекторий, занимавшей
Эйлера еще в юности. Посредством функций комплексного переменного
Эйлер преобразует одни пары семейств ортогональных траекторий
в другие сначала в общем виде, а затем рассматривает некоторые частные
случаи [NCAP XIV (1769) 1770]. Так, например, ортогональные семейства
прямых переводятся с помощью целых многочленов в семейства
алгебраических кривых, а посредством дробно-линейной функции — в семейства
окружностей (или прямых). Такие отображения конформны, но в данной
работе Эйлер еще не подчеркнул это важное свойство, которое вскоре
выступило на передний план в его работах по картографии.
Начало общей теории картографических проекций положили в
течение немногих лет, с 1772 по 1779 г., Ламберт, Эйлер и Лагранж, причем
Эйлеру принадлежит заслуга употребления здесь аналитических функций.
140
ГЛ. 8. МАТЕМАТИЧЕСКАЯ ТРИЛОГИЯ ЭЙЛЕРА
В первой из своих трех статей по картографии [АР (1777 : 1) 1778] *)
Эйлер прежде всего доказывает невозможность конгруентного
отображения части сферической поверхности на плоскость. Затем он решает двумя:
способами задачу об отображении, при котором «малейшие» части земной
поверхности представляются на карте подобными им фигурами. Излагая
второй способ, он показывает, что такое отображение может быть
произведено посредством произвольной аналитической функции комплексного
переменного. В качестве примеров Эйлер рассмотрел ряд важных
употребительных проекций и, в частности, использовал круговое свойство
дробно-линейного преобразования, которое всегда отображает
окружности в окружности же (прямая считается окружностью бесконечно
большого радиуса). В последней статье Эйлер специально разобрал
достоинства и недостатки карты Российской империи, выполненной в конической
проекции французского астронома Ж. Н. Делиля, состоявшего в 1725—
1747 гг. членом Петербургской Академии.
Картографические работы Эйлера были продолжены многими
учеными, в том числе П. Л. Чебышевым и Д. А. Граве. Мы отметим пока статьи
академика Ф. И. Шуберта о проектировании на плоскость поверхности
эллипсоида вращения, в одной из которых появилось и выражение рго-
jectio conformis, конформная проекция [NAP V (1787) 1789].
Впоследствии учение о конформных отображениях выросло в один из главных
отделов теории аналитических функций и получило чрезвычайно важные
приложения в механике жидкостей и газов, теории упругости,
электростатике и т. д., а также в технике. Здесь весьма значительны достижения
советской научной школы, первыми руководителями которой были
Н. Е. Жуковский и С. А. Чаплыгин.
Вычисление определенных интегралов и уравнения Даламбера —
Эйлера. В те же семидесятые годы Эйлер открыл еще одну область
применения функций комплексного переменного: вычисление определенных
интегралов. Принципы и первые примеры нового метода интегрирования
изложены в двух статьях Эйлера, доложенных нашей Академии весной
1777 г., но напечатанных лишь посмертно [NAP VII (1789) 1793 и X (1792)
1797]. Успехи теории мнимых, подчеркивал Эйлер, основаны главным
образом на том свойстве функций комплексного переменного, что при
замене значения аргумента на сопряженное меняется на сопряженное
и значение функции. Выше было отмечено, что Эйлер рассматривал именно
такие функции. Сам способ интегрирования состоит в следующем. В
интеграле \ / (z) dz = F (z) производится подстановка z = х ± yi\ если
/ (х ± у г) = и ЧЬ vi и F (х ± yi) = U ± Vi, то сравнение
действительных и мнимых частей содержащего интеграл равенства приводит к двум
новым интегральным соотношениям:
U=\udx — vdy и "Р= \ vdx-\-udy.
Из этих равенств Эйлер извлекает важное теоретическое заключение.
Чтобы выражения v dx + и dy и и dx — v dy были интегрируемы,
требуется выполнение условий
ди _ dv ди __ dv
дх ду ' ду дх '
г) Все три опубликованы на русском языке в кн.: Л. Эйлер, Избранные
картографические статьи, перев. Н. Ф. Булаевского, под ред. Г. В. Багратуни, М., 1959.
ПРОБЛЕМА ИНТЕРПРЕТАЦИИ КОМПЛЕКСНЫХ ЧИСЕЛ 141
т. е. условий полного дифференциала [которые Эйлер привел еще в одной
статье в САР VII (1734—1735) 1740]. Тем самым Эйлер впервые выявил
общим образом, что действительная и мнимая части произвольной
(аналитической) функции и + vi удовлетворяют тем двум уравнениям,
которые встретились ему и, несколько раньше, Даламберу при решении
задач гидромеханики. Это свойство функций комплексного переменного
Эйлер справедливо назвал замечательным. Однако глубокое
теоретическое значение уравнений Даламбера — Эйлера выяснилось только в общей
теории аналитических функций Коши и Римана, по именам которых
чаще всего их и называют. Эйлер вывел эти условия, как необходимое
свойство функций комплексного переменного, недостаточно строго
и к тому же недостаточно определенно трактуя само понятие
аналитической функции. У Коши и Римана те же условия оказываются не только
необходимыми, но и достаточными (при некоторых дополнительных
требованиях) для аналитичности функции; вместе с тем действительная и
мнимая части функции оказываются сопряженными гармоническими
функциями. При этом однозначная функция, по определению, называется
аналитической в некоторой области, если она во всех точках этой области
дифференцируема. Функция, аналитическая в смысле Коши и Римана,
разлагается в некоторой окрестности каждой точки области
аналитичности в степенной ряд, т. е. является аналитической и в смысле Эйлера.
С помощью своего метода Эйлер вычислил несколько трудных
несобственных интегралов для случаев, когда первообразные не выражаются
в элементарных функциях. Примеры такого рода нам еще встретятся,
пока же мы ограничимся упоминанием, что эти работы Эйлера (и почти
одновременные — Лапласа) повлекли за собой классические
исследования об интегрировании в комплексной области Гаусса, Пуассона и,
особенно, Коши, в которых было разработано центральное понятие о
криволинейном интеграле, взятом вдоль кривой на комплексной плоскости,
у Эйлера еще отсутствовавшее.
Таким образом, Эйлеру принадлежит открытие столь
фундаментальных общих свойств класса аналитических функций, как выполнение
для них уравнений Коши — Римана и конформность производимых
посредством них отображений. Если к этому добавить пионерские
исследования Эйлера по интегрированию, фактическое применение
аналитического продолжения, его разложения в степенные ряды, бесконечные
произведения и суммы простых дробей и т. д., то ясной становится
огромная роль работ великого математика в подготовке общей теории
аналитических функций, многие идеи и методы которой явились прямым
развитием заложенных им начал.
Проблема интерпретации комплексных чисел. Новые успехи теории
функций комплексного переменного в XIX веке были тесно связаны
с уточнением основных понятий и приемов математического анализа
в действительной области и тех особенностей, которые возникают при их
переносе в комплексную область. Существенную роль сыграло
геометрическое истолкование мнимых и комплексных чисел. В XVII и XVIII вв.
эти числа рассматривали как вспомогательные символы, удобные и даже
необходимые в исследовании, но представляющие собой чистейшие
фикции. Правда, еще Валлис в конце XVII века пытался дать
геометрическое истолкование мнимых величин и аналогичную попытку предпринял
немецкий математик Г. Кюн в NCAP III (1750—1751) 1753. Примитивная
и путаная трактовка Кюна, в которой чисто мнимое число выступает
142
ГЛ. 8. МАТЕМАТИЧЕСКАЯ ТРИЛОГИЯ ЭЙЛЕРА
в качестве стороны квадрата с отрицательной площадью, а операции
над мнимостями вовсе не изучены, успеха не имела. Эйлер резко возражал
против нее. Для Эйлера мнимое число как таковое не име^хо реального
смысла, который присущ лишь его действительной части и коэффициенту
в мнимой части, взятым по отдельности. Разумеется, в работах по
гидродинамике и геометрии Эйлер переходил от комплексного числа z = х + yi
к точке М (х, у) и обратно, и в этом была уже некоторая основа для
геометрического истолкования. Но для Эйлера здесь речь шла не о
сопоставлении комплексного числа z с точкой М, но действительных чисел
х, у с ее координатами. Точно так же содержалась в скрытом виде
возможность геометрической интерпретации и в применявшейся Эйлером
тригонометрической форме комплексного числа z = г (cos ф + i sin ф).
В позднейшие годы жизни Эйлер, по-видимому, несколько ближе подошел
к мысли о геометрическом изображении мнимостей *). Однако
полноценная интерпретация должна включать истолкование операций, а этой
мысли у Эйлера мы не находим. Современная геометрическая модель
комплексных чисел была независимо предложена на рубеже XVIII
и XIX вв. несколькими учеными — датчанином К. Весселем в 1799 г.,
французом Ж. Арганом в 1806 г., Гауссом и другими.
Основания дифференциального исчисления. Через несколько лет
после издания «Введения в анализ бесконечных» Эйлер опубликовал
продолжение курса —«Дифференциальное исчисление» (Institutiones
calculi differentialis), которое он начал писать еще в Петербурге, но
закончил в Берлине, где оно и вышло в 1755 г. на средства Петербургской
Академии. Мы прежде всего остановимся на проблемах обоснования
математического анализа.
Лейбниц и его ученики строили дифференциальное исчисление на
принципе пренебрежения бесконечно малыми слагаемыми в сравнении с
конечными и бесконечно малыми высшего порядка в сравнении с величинами
более низкого порядка. Дифференциалы трактовались при этом как
бесконечно малые приращения, как разности двух ближайших друг к другу
значений какой-либо величины. Так, для вычисления дифференциала
функции у = х2 в уравнении
dy = Ay = (x-\- dx)2 ¦—xz = 2xdx-\- dx2
пренебрегали членом dx2 и получали dy = 2х dx. С современной точкж
зрения, если dy есть знак приращения г/, то уравнение dy = 2х dx
неточное. Если dy есть знак дифференциала, то это уравнение точное, но зато
неточно уравнение dy = 2х dx + dx2.
Первый учебник дифференциального исчисления, составленный
в 1691—1692 гг. И. Бернулли, открывается тремя постулатами:
1° Величина, уменьшающаяся или увеличивающаяся на бесконечно
меньшую, чем она, величину, не уменьшается и не увеличивается.
2° Всякая кривая линия состоит из бесконечно многих прямых,
которые сами бесконечно малы.
*) И. Ю. Тимченко, цит. соч., стр. 644. О работах Л. Эйлера по
аналитическим функциям, помимо труда И. Ю. Тимченко, см. А. И. Маркушевич,
Очерки по истории теории аналитических функций, М.— Л., 1951; С. Е. Б е л о з е р о в,
Основные этапы равития общей теории аналитических функций, Ростов-на-Донуv
1962.
ОСНОВАНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
143
3° Фигура, содержащаяся между двумя ординатами, разностью
абсцисс и бесконечно малой частью любой кривой, рассматривается
как параллелограмм х).
Последний постулат относится собственно к интегральному
исчислению. Под интегралом в школе Лейбница понимали прежде всего сумму
бесконечного числа бесконечно малых дифференциалов, т. е.
определенный интеграл. Вместе с тем, при вычислении интегралов пользовались,
когда это удавалось, взаимно обратной зависимостью между
дифференцированием и интегрированием, т. е., говоря по-нашему, находили
определенный интеграл как разность значений неопределенного интеграла
при верхнем и нижнем пределах интегрирования.
Приведенные постулаты и понятия вызывали немало сомнений и
возражений. Что такое бесконечно малая величина? Если она отлична от
нуля, то первый постулат несовместим с арифметическими свойствами
равенства величин. Непонятно, далее, как с помощью неточного
постулата получаются результаты, истинность которых во многих случаях
может быть строго подтверждена при помощи других приемов. А при
понимании бесконечно малой как нуля возникают другие трудности.
Все нули одинаковы, так что 0:0 = 1 и любые отношения бесконечно
малых, играющие главную роль в дифференциальном исчислении, также
сводятся к единице. Кроме того, ицтеграл оказывается суммой нулей,
а значит, нулем, и т. д.
Лейбниц в разное время обосновывал принцип отбрасывания
бесконечно малых и дифференциальное исчисление различными способами.
Мы находим у него и толкование бесконечно малых как просто крайне
малых величин, и замечание, что это актуально бесконечно малые
величины, не удовлетворяющие так называемой теперь аксиоме Архимеда.
В первом мемуаре по дифференциальному исчислению (1684) он ввел
дифференциал величины у как отрезок dy, удовлетворяющий равенству
7 ydx « „7
ау = -— , где St — подкасательная кривой с ординатой у и ах — про-
извольный отрезок абсциссы. Однако при вычислении и употреблении
дифференциалов следует исходить из того, что dy пропорционален
«мгновенному» приращению величины у. В других случаях Лейбниц ссылался
на то, что все результаты, получаемые с помощью бесконечно малых,
можно, независимо от природы последних, доказать с помощью
безупречного метода исчерпывания древних геометров. Он развивал также мысль,
что в математике действует своеобразный «закон непрерывности»,
лежащий в основании всех предельных переходов 2).
Для Ньютона и его последователей главными понятиями были
флюента — текущая переменная величина и ее флюксия, скорость ее течения
или изменения, т. е. наша производная, по отношению к которой флюента
есть неопределенный интеграл или первообразная. Наряду с флюксией
основным рабочим понятием был момент —«мгновенное приращение»,
«едва едва зарождающееся начало» текущей величины. В практике
вычислений момент не отличался от бесконечно малого дифференциала
г) Этот учебник, широко использованный Г. Ф. Лопиталем при написании
первого печатного руководства по дифференциальному исчислению: Analyse des infiniments
petits pour l/intelligence des lignes courbes (Paris 1696), увидел свет только в XX веке.
См. J. Bernoulli, Die Differentialrechnung, nsg. von P. Schaiheitlin,
Leipzig, 1924.
2) А. П. Юшкевич, Лейбниц и основание исчисления бесконечно малых.—
УМН, 3 : 1 (23), 1948, стр. 162, 187-196.
144
ГЛ. 8. МАТЕМАТИЧЕСКАЯ ТРИЛОГИЯ ЭЙЛЕРА
Лейбница. Однако Ньютон высказывался осторожнее. Флюксии,— писал
он,— относятся почти как приращения флюент за «крайне малые» и
равные приращения времени1), а точнее говоря, флюксии находятся в
«первом отношении» зарождающихся приращений или в «последнем отношении»
исчезающих приращений. Эти первые и последние отношения суть не что
иное как предел, который мы обозначаем lim ¦—-; Ньютон пользовался
Дя:->0 Дж
словом «предел», но не употреблял таких обозначений. Флюксия
величины у = х2 вычисляется так: образуется отношение
¦^- = 2х + Ах,
Ах ' '
а затем «приращения исчезают», т. е. Ах и Ау полагаются оба равными
нулю. Отбрасывание в дифференциальных равенствах бесконечно малых
заменяется здесь переходом к пределу в указанной форме.
В методе пределов и флюксий Ньютона, разумеется, была налицо
бесконечно малая величина, как переменная, имеющая пределом нуль
ж в конце концов с ним совпадающая. Изменение величин Ньютон
представлял себе, подобно движению в механике, непрерывным, так что
переменные, вообще говоря, достигают своих предельных значений, как
движущееся конечное время тело достигает конца своего пути. Флюксия
приводится тем самым к отношению двух нулей. Могут возразить,—
говорил Ньютон,— что когда величины исчезли, между ними уже нет
никакого отношения, а пока они не исчезли, отношение еще не есть
последнее, т. е. предельное отношение. На это он отвечал, что отношение величин
существует и в самый момент их исчезновения, подобно тому, как,
очевидно, существует скорость движущегося тела в момент его остановки,
жли в момент начала движения 2).
Дифференциальное и интегральное исчисление Лейбница взяло
в XVIII веке верх над методом флюксий ж флюент Ньютона повсюду,
кроме Англии, где большинство ученых упорно придерживалось теории
и обозначений их великого соотечественника. В значительной мере это
было связано с оперативными преимуществами символики Лейбница 3).
Другой причиной победы дифференциального исчисления над флюксион-
ным была прямая необходимость в непосредственном употреблении
дифференциалов как элементарных частей величин, изучаемых в самой
математике и в математическом естествознании.
г) Временем Ньютон называл здесь отвлеченную величину, служащую общим
аргументом текущих величин и возрастающую равномерно, подобно времени.
2) А. Н. Колмогоров, Ньютон и современное математическое мышление,
в сб.: «Московский университет — памяти Исаака Ньютона», Москва 1946; А. П. Ю ш-
к е в и ч, Идеи обоснования математического анализа в XVIII веке. В кн.: Л. К а р-
н о, Размышления о метафизике исчисления бесконечно малых, перев. Н. Соловьева
под ред. А. П. Юшкевича, М.—Л., 1936, стр. 25—40.
3) Ньютон обозначал флюксии величины г/, ставя над ней равное порядку флюксии
число точек, а интеграл (флюенту) писал в виде у или
, не указывая аргумента
интеграции. Это неудобно или непригодно для производных высших порядков, замены
переменных и особенно для распространения на функции многих переменных.
Замечательно гибкая символика Лейбница, отражающая самую суть понятий дифференциала
(d — инициал слова differentia — разность) и интеграла (S — первая буква слова
Summa), была тщательно продумана ее творцом, который вообще придавал
обозначениям первостепенное значение. Ньютоново обозначение производных используется до
сих пор в механике и векторном анализе.
«ИСЧИСЛЕНИЕ НУЛЕЙ» ЭЙЛЕРА
145
Однако ни лейбницево обоснование исчисления бесконечно малых,
ни ньютоново обоснование метода флюксий не получили единодушного
признания. Едва-едва зарождающиеся начала величин или мгновенные
приращения, выступающие как некая неуловимая грань между бытием
и небытием, отбрасывание «ничтожно малых» или «исчезающе малых»
величин, отношения бесконечно малых при их становлении нулями, все
это вызывало недоумения, возражения и споры. К. Маркс писал об этом:
«Итак сами верили в мистический характер новооткрытого исчисления,
которое давало правильные (и притом в геометрическом применении
прямо поразительные) результаты математически положительно
неправильным путем. Таким образом сами себя мистифицировали и тем более
ценили новое открытие, тем более бесили толпу старых ортодоксальных
математиков и вызвали таким образом враждебный крик, отдавшийся
даже в мире несведущих в математике людей и бывший необходимым,
для того, чтобы проложить путь новому» х).
Особенное впечатление произвела остроумная критика оснований
математического анализа в небольшом сочинении «Аналист» (Analyst,
London, 1734) известного философа идеалиста Дж. Беркли. Всякое
дифференциальное уравнение, полученное путем отбрасывания слагаемых
бесконечно малых, содержит, согласно Беркли, ошибку. Точность
результатов анализа объясняется только взаимной компенсацией нескольких
таких ошибок в двух или более дифференциальных уравнениях, которые
составляются в ходе решения задачи. Эту идею оригинально и подробно
развил 60 лет спустя Л. Карно. Нестрогим, согласно Беркли, является
также метод пределов и флюксий, ибо не может быть отношения между
несуществующими вещами. Кроме того, логически порочно само
определение флюксии; ведь отношение ~~ образуется в предположении, что
Ах ф0, между тем для получения флюксии в нем затем полагают Ах = 0.
Памфлет Беркли вызвал в Англии бурные споры, в частности о том,
достигает переменная своего предельного значения или нет? Первую
точку зрения отстаивал Дж. Джюрин, а вторую Б. Робине. В дискуссии
выступил и Маклорен, посвятивший защите теории Ньютона
значительную часть своего «Трактата о флюксиях» (A treatise of fluxions, Edinburgh,
1742).
«Исчисление нулей» Эйлера. В одной своей брошюре (1739) Робине
задел и Эйлера, упрекая его в ошибках, будто бы допущенных в
«Механике» при употреблении принципа отбрасывания бесконечно малых,
который Эйлер-де воспринял от своего учителя, т. е. И. Бернулли. Если
обвинение в ошибках было неверным, то справедливо, что первоначально
Эйлер разделял взгляды И. Бернулли на вопросы обоснования анализа.
Сохранилась латинская рукопись, озаглавленная «Calculus differentialis»
и являющаяся незаконченным наброском курса дифференциального
исчисления, составленного Эйлером, вероятно, еще до 1730 г.
Дифференциальное исчисление трактуется здесь как специальный случай
исчисления конечных разностей, возникающий, когда разности бесконечно малы.
Формулы дифференцирования выводятся из формул конечных разностей
с помощью принципа отбрасывания бесконечно малых, причем Эйлер
доказывает этот принцип в немногих словах, опираясь на понимание
бесконечно малых, как величин, которые меньше любой данной конечной
) Сб. Марксизм и естествознание, М., 1933, стр. 54.
146
ГЛ. 8. МАТЕМАТИЧЕСКАЯ ТРИЛОГИЯ ЭЙЛЕРА
величины и потому не могут быть назначены или указаны.
Дифференциалом называется бесконечно малое приращение величины г).
Эйлер снова обратился к основаниям анализа в «Дифференциальном
исчислении». К этому времени он хорошо изучил литературу вопроса,
в частности, полемику, связанную с «Аналистом» Беркли, несомненно,
оказавшую влияние на эволюцию его взглядов. Теперь он развивает
своеобразное «исчисление нулей» и вводит в дифференциальное
исчисление Лейбница ряд идей теории флюксий Ньютона2). Главным объектом
дифференциального исчисления объявляется не дифференциал, но
производная функция, только, в отличие от Ньютона, Эйлер вводит ее чисто
арифметически, без каких-либо ссылок на понятие скорости.
Дифференциальное исчисление, подчеркивает Эйлер, есть «метод определения
отношения исчезающих приращений, получаемых какими-либо функциями,
когда переменному количеству, функциями которого они являются,
дается исчезающее приращение» 3). Несколько далее, опять-таки в духе
Ньютона, производная характеризуется как предел: сначала приращения
берутся конечными, а «затем нужно мысленно представить, что эти
приращения становятся все меньшими и меньшими, и тогда мы найдем, что
их отношение все более и более приближается к некоторому
определенному пределу, которого они достигают, однако, лишь тогда, когда
полностью обращаются в нуль. Этот предел, который составляет как бы
последнее отношение упомянутых приращений, и является истинным
объектом дифференциального исчисления» 4).
Эйлер следует за Ньютоном и в понимании бесконечно малых
величин. Функции мыслятся как непрерывные и, вообще говоря, достигают
своих предельных значений. Соответственно бесконечно малая величина
определяется как нуль (чего Ньютон не делал). При понимании
бесконечно малых как величин, отличных от нуля, возражения против
дифференциального исчисления были бы справедливы, но именно потому, что
они суть нули, дифференциальное исчисление безошибочно. Производная
может быть вычислена путем приравнивания нулю приращения
аргумента Ах в отношении -~-. Вместе с тем производная может
рассматриваться и как отношение ~- , где dy= О и dx = 0. Эйлер отвергает возражения,
будто деление нуля на нуль не имеет смысла. Нули можно сравнивать
между собой двояко. Арифметическое отношение, т. е. разность двух
нулей, есть нуль, но частное -^ может быть, вообще говоря, любым числом5),
г) Рукопись содержит четыре главы и заканчивается правилами
дифференцирования логарифмических и показательных функций. См. А. P. Juschkewitsch,
Euler and Lagrange tiber die Grundlagen der Analysis.— Sammelband zu Ehren des 250.
Geburtstages Leonhard Eulers. Unter der Redaktion von K. Schroder. Berlin, 1959.
2) Любопытно замечание Эйлера в начале первого тома его «Интегрального
исчисления». Указывая на различия в терминологии и символике между математиками Англии
и континента Европы, он отдает предпочтение наименованиям первых (например,
«текущим количествам», т. е. флюентам, перед «переменными количествами») и обозначениям
вторых. Правда, — добавляет Эйлер,—множество книг, написанных тем и другим
способом, делает такое согласование обеих теорий бесполезным. См. Л. Эйлер,
Интегральное исчисление, т. I, перев. С. Я. Лурье и М. Я. Выгодского. М., 1956, стр. 10—11.
3) Л. Эйлер, Дифференциальное исчисление, стр. 39.
4) Там же, стр. 41.
5) В поле действительных чисел частное 0 : 0 может равняться его любому
элементу. Ср. И. В. Проскуряков, Понятия множества, группы, кольца и поля.
Теоретические основы арифметики.— Энциклопедия элементарной математики, кн. 1,
М.—Л., 1951, стр. 115.
«ИСЧИСЛЕНИЕ НУЛЕЙ» ЭЙЛЕРА
147
поскольку для любого конечного п справедливо п-0 = 0. Однако в
дифференциальном исчислении частное, выступающее под видом отношения
дифференциалов -j-, перестает быть неопределенным. Эйлер выводит
основные правила отыскания таких частных как в форме принципа
отбрасывания бесконечно малых, так и в форме, соответствующей переходу
к пределу, именно:
a±ndx = a и
а также (при п>т)
adxm-hbdxn = adxm и " "* Т™" *"" =1-
— a dxm
По существу, эти рассуждения Эйдера законны, поскольку он
предполагает всякий раз, что рассматриваемые непрерывные величины
принимают свои предельные значения. Для нас функция, заданная формулой
f(x)=^—^- ,
Jv ' х — а
определена для всех хфа. Мы можем построить другую функцию,
2—,7.2
а + п dx
а
adxm
и
— 1
*-•)
ЧЬ Ъ dxn
F{x) = { х~а
{ 2а
определенную и непрерывную для всех действительных значении х и
совпадающую с / (х) для всех хфа. Ньютон и за ним Эйлер заранее
принимали, что функция / (х), заданная формулой / (х) = ~а , определена
и непрерывна также при х = а, т. е. для них она совпадала с нашей
функцией F (х). Это и только это они имели в виду, говоря, что выражение
о. о
при х = а принимает значение 2а, которое Эйлер именовал отно-
х — а
шением двух нулей.
Эйлер, как и Ньютон, не дал явного определения понятия предела
и не сформулировал каких-либо теорем о свойствах пределов. Он
ограничился приведенными выше весьма общими соображениями, считая их
достаточными для разрешения всех сомнений в точности
дифференциального исчисления. Затем он распространяет исчисление нулей на
дифференциалы высших порядков.
Фактическое вычисление производных и дифференциалов
основывается на разложении функций в бесконечные степенные ряды.
Дифференциальное исчисление, как и в первоначальном эскизе курса,
рассматривается как частный случай метода конечных разностей, который
«наступает тогда, когда разности, которые мы раньше считали конечными,
полагаются бесконечно малыми» х). В связи с этим первые две главы
«Дифференциального исчисления» посвящены изложению начал теории
конечных разностей, причем Эйлер вводит современное удобное их
обозначение. Он показывает на примерах, как разлагаются конечные разности
функций в ряды по степеням конечной разности аргумента со и утверждает»
что такое представление
Аг/ = Рсо + (?со2 + Лсо3+ . ..
2) Л. Эйлер, Дифференциальное исчисление, стр. 102—103.
148
ГЛ. 8. МАТЕМАТИЧЕСКАЯ ТРИЛОГИЯ ЭЙЛЕРА
имеет место для любой функции. Для отыскания дифференциала dy
или производной функции Р достаточно знать первый член этого
разложения. Например, чтобы вычислить d In х=Ы (x-\-dx) — lnx = In (l + —) ,
Эйлер использует приведенное во «Введении в анализ бесконечных»
разложение
ln(l + 2) = z~? + -|—....
dx dx
и, беря z = —, сразу получает, что din я = — . Также производится
дифференцирование и некоторых других элементарных функций. Отсюда
был один шаг к определению производной, как коэффициента в члене
степенного разложения / (х + dx), линейном относительно dx. Этот шаг,
отправляясь от идей Эйлера, сделал в 1772 г. Лагранж.
Концепцию Эйлера (и Даламбера, о которой говорится далее) Маркс
характеризовал как некоторый шаг вперед. Оба математика брали за
исходный пункт не прежнее неточное равенство х^ = х + dx, где dx есть
бесконечно малая величина с ее неясными и противоречивыми
свойствами, а правильное равенство х± = х + Ах, где Ах есть какое-либо конечное
приращение, которое только под конец превращается в нуль. В этом
смысле Маркс говорил о рациональном исчислении Даламбера и Эйлера.
Однако эйлерова попытка обоснования анализа могла явиться только
одним из этапов в его развитии. Исчисление нулей маскировало
производившиеся фактически предельные переходы и дифференциал,
превратившийся в нуль, был, по сути дела, бесполезен в анализе и в его
приложениях. Дифференциал функции dy есть главная линейная часть ее
приращения Az/, и разность Аг/ — dy при бесконечно малом Ах и
производной, отличной от нуля, есть бесконечно малая высшего порядка
в сравнении с Ах. Эта современная формулировка появилась только
в XIX веке, но фактически указанным свойством дифференциала
пользовались с самого возникновения исчисления бесконечно малых. Сам
Эйлер писал: «Пусть приращение со, которое получает переменное х,
будет чрезвычайно малым... Тогда, зная первый дифференциал Р dx,
мы знаем с весьма большим приближением и конечную разность, ибо
и она будет равна Рсо; это дает немалую пользу во многих случаях, в
которых анализ применяется на практике» х). И хотя Эйлер тут же повторяет,
что дифференциал есть нуль, такая трактовка не согласуется со смыслом
цитированного отрывка. В применениях дифференциального исчисления
Эйлер широко использовал ряд Тейлора и при этом ему приходилось
всякий раз оперировать с величинами, достаточно и произвольно малыми,
но отличными от нуля и не с предельными равенствами, но, так сказать,
с допредельными соотношениями и с оценками неравенств. Такие оценки
производились, правда, без применения 8, б — техники Вейерштрасса,
иногда на глаз, но, во всяком случае, в них применялись не нулевые
бесконечно малые, а бесконечно малые величины в нашем понимании
этого слова.
Разработка дифференциального исчисления. «Дифференциальное
исчисление» чрезвычайно содержательно и многое в нем принадлежит лично
Эйлеру. В первой части подробно изложены приемы дифференцирования
¦) Л. Эйлер, Дифференциальное исчисление, стр. 105,
РАЗРАБОТКА ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 149
функций одного и многих переменных. Отметим здесь: правило
дифференцирования функции нескольких величин, зависящих от одного
аргумента, доказательство теоремы о независимости значения частных
производных от порядка дифференцирования (высказанной еще Николаем I
Бернулли— двоюродным братом Даниила—- в 1721 г.), выводы общей
теоремы об однородных функциях (для двух переменных Эйлер высказал
ее в 1736 г.) и необходимого условия, при котором выражение Р dx +
+- Q dy является точным дифференциалом, которое Эйлер пишет здесь
в форме
/dP_\ = /dQ\
\ dy ) \ dx )
Такое обозначение частных производных вслед за Эйлером стали
применять и другие математики, хотя еще долгое время, вплоть до середины
XIX века, частные производные писали чаще всего так же, как обыкно-
тт -, dv dv
венные. Наше современное обозначение, вроде -,-ит.п., встречающееся
у Лежандра в 1786 г., ввел в обиход Якоби, начиная с одной работы
1841 г.
Во второй части труда рассмотрены приложения дифференциального
исчисления; здесь выводятся и используются ряд Тейлора, а также
формула суммирования Эйлера — Маклорена. Как и в других сочинениях
Эйлера, поражают разнообразие и богатство примеров, частью
опубликованных ранее, частью новых. Большое место отведено учению об
экстремумах. Необходимые и достаточные условия экстремума функции у = f (х)
Эйлер получает, рассматривая знак разности
f(x±a)-f(x) = ±a^r + 4-^
dx 2 dx2
в достаточно малой окрестности соответствующего значения аргумента.
При этом он опирается на предложение (справедливое на деле только
при существенных ограничениях), которое применяется и в других
случаях и которое аналогично принципу отбрасывания бесконечно малых:
при достаточно малом а (абсолютная) величина какого-либо члена ряда
больше суммы всех следующих за ним членов. Впоследствии прием
Эйлера был уточнен: бесконечный ряд Тейлора был заменен так называемой
формулой Тейлора с остаточным членом, и на этой основе производится
требуемая оценка разности f(x ± а) — f(x). Эйлер исследует также
экстремумы функций двух и многих переменных. Удивительным образом
он допускает при этом ошибку, утверждая, что f(x, у) имеет максимум
(или минимум), если она имеет в этой точке максимум (или минимум)
относительно каждого из аргументов при постоянстве другого, т. е. если
^H-«*pfi<H$<»H3>^>»]. Более
точное исследование достаточных условий экстремума функций многих
переменных произвел вскоре Лагранж (1759).
Не останавливаясь на других вопросах (приложения ряда Тейлора
к численному решению уравнений, раскрытие различных форм
неопределенностей, анализ особых случаев, когда дифференциал функции
оказывается неравносильным ее приращению х) и т. д.), мы отметим еще
г) Это имеет место, если производная равна нулю или если функция в данной
точке не дифференцируема. Более детальный разбор таких случаев произвел Лагранж.
150
ГЛ. 8. МАТЕМАТИЧЕСКАЯ ТРИЛОГИЯ ЭЙЛЕРА
одну особенность «Дифференциального исчисления». Подобно первому
тому «Введения в анализ бесконечных» оно не содержит ни
геометрических приложений, ни даже каких-либо геометрических или механических
иллюстраций основных понятий и приемов. Все изложение имеет
исключительно арифметико-алгебраический характер. Аналогично строилось
и «Интегральное исчисление». Можно оспорить методические достоинства
такого изложения, однако для развития математики оно имело важное
значение. Отражая объективную тенденцию к выделению анализа в
самостоятельную дисциплину, оно прокладывало дорогу его арифметизации.
Для раннего исчисления бесконечно малых характерны были
геометрическая и механическая трактовка многих основных понятий и
обоснование некоторых принципиально важных теорем ссылками на
геометрическую или механическую очевидность. Мы видели, например, что Ньютон
пытался обосновать существование отношения исчезающих приращений,
апеллируя к идее скорости тела в мгновение его остановки. Лагранж
позднее заметил, что изучение движения тел является предметом
механики, которая сама опирается на анализ и что понятие скорости в любое
мгновение неравномерного движения нуждается в определении. Другой
пример: площади (или пути) вычисляли с помощью интегралов, а
существование интеграла обосновывали тем, что интеграл есть площадь
(или путь), которая, очевидно, существует. В итоге ни понятия скорости,
ни производной, ни площади, ни интеграла не получали
удовлетворительного определения и нельзя было точно исследовать «проблемы
существования» этих и других основных объектов. Недостаточная отвлеченность
и общность понятий анализа ограничивала вместе с тем его возможные
применения в различных областях естествознания.
Эйлер намеревался посвятить геометрическим приложениям
дифференциального исчисления отдельную третью часть своего труда. Эту
работу он не закончил, а подготовленная им еще около 1750 г. часть рукописи,
в которой речь идет главным образом о касательных к кривым и об их
бесконечных ветвях, увидела свет только в 1862 г.
Когда математики начала XIX века приступили к коренному
пересмотру оснований анализа, построение его на арифметическом
фундаменте, начатое Эйлером и продолженное Лагранжем, сыграло решающую
роль. При этом выяснилось, что наши геометрические или механические
представления весьма ограничены и в более тонких случаях могут
привести к неверным заключениям. Так, нельзя наглядно представить себе
непрерывное движение, в любой момент лишенное скорости (или
непрерывную кривую, нигде не имеющую касательной), но Больцано и затем
Вейерштрасс аналитически построили непрерывные функции, ни в одной
точке не имеющие производной.
Интегральное исчисление. Серию руководств Эйлера по
математическому анализу завершили три тома «Интегрального исчисления» (Insti-
tutiones calculi integralis, Petropoli, 1768—1770): том I, в котором
«излагается метод интегрирования от первых начал до интегрирования
дифференциальных уравнений первого порядка», том II, в котором «излагается
метод отыскания функций одного переменного по данному соотношению
между дифференциалами второго и высших порядков», и том III, в
котором «излагается метод отыскания функций двух и большего числа
переменных по данному соотношению между дифференциалами любого
порядка, с приложением о вариационном исчислении и с дополнением,
содержащим разбор весьма замечательных случаев, встречающихся при
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
151
интегрировании дифференциальных уравнений» 2). При вторичном
издании этого труда (Petropoli, 1792—1794) был добавлен том IV, куда вошли
статьи Эйлера, дополнявшие содержание первых трех томов.
Интегральное исчисление Эйлер определяет как «метод, посредством
которого по данному соотношению между дифференциалами количеств
находят соотношение между самими количествами» 2). Таким образом,
интегральное исчисление обнимает и интегрирование дифференциальных
уравнений. Именно так понимал интегральное исчисление, «обратный
метод флюксий» и Ньютон. Мы сейчас рассмотрим лишь работы Эйлера
по интегрированию функций одного переменного. В «Интегральном
исчислении» этому посвящены все девять глав первого раздела I тома
и пятая — шестая главы его второго раздела.
В интегральном исчислении в узком смысле слова основным является
у Эйлера понятие, которое теперь называется неопределенным
интегралом. Интегралом данной функции f(x) Эйлер называет функцию,
имеющую дифференциал f(x)dx. Он отвергает лейбницево понимание
интеграла как суммы бесчисленного количества малых дифференциалов, ибо
для Эйлера дифференциал есть нуль, а сумма любого числа нулей есть
снова нуль. Лучше сказать, говорит Эйлер, что интеграл находится
не по дифференциалу f(x)dx, который есть нуль, а по данной функции
f(x). Интеграл,, содержащий произвольную постоянную, Эйлер называл
полным, а тот, в котором эта постоянная получает в соответствии с
начальными данными (вроде: у = у0 при х = х0) фиксированное значение,—
частным. Величина, которую мы называем определенным интегралом,
выступает как значение частного интеграла при данном значении
аргумента.
Впрочем, концепция определенного интеграла как суммы, вернее,
как предела интегральной суммы, по необходимости выступает в
главе 7-й, посвященной приближенному вычислению интегралов. Здесь,
предполагая, что подынтегральная функция изменяется «мало» вместе
с «весьма малым» изменением аргумента, Эйлер приближенно выражает
X
интеграл \ f(x) dx, при х = х0 равный у0, т. е. \ f(x) dx + z/0, суммой
п п
^ / (х) dx = у о + 2 / (Zft-i) (я* — xk-±) = у о + 2 / (*ft-i) Axk-i-
k=i fc=l
Приближение тем точнее, чем меньшими берутся разности kxk, если
только при этом значения функции также изменяются на малые
разности: «Если же этого не происходит, то указанное определение будет
крайне ненадежным» 3). Как видно, Эйлер имеет в виду, что
подынтегральная функция непрерывна в нашем смысле слова. Несколько далее он
специально подчеркивает, что в окрестности точки бесконечного разрыва
такой способ приближенного вычисления «непозволителен» 4). Затем,
предполагая подынтегральную функцию монотонной, он заключает
1) Л. Эйлер, Интегральное исчисление, т. I, перев. С. Я. Лурье иМ. Я.
Выгодского. Предисловие М. Я. Выгодского, М., 1956; т. II, перев. и предисловие И. Б. По-
гребысского, М., 1957; т. III, перев. и комментарии Ф. И. Франкля, М., 1958.
2) Там же, стр. 9.
3) Там же, стр. 162.
4) Там же, стр. 164. На эти мысли Эйлера, кажется, в трудах по истории анализа
не обращали внимания.
152
ГЛ. 8. МАТЕМАТИЧЕСКАЯ ТРИЛОГИЯ ЭЙЛЕРА
интеграл между нижней и верхней интегральными суммами, т. е,
п п
У о + 2 / (xk-i) A#a-i и г/о + S / (xk) A#a-i; в следующем за этим примере
ft=i ft=i
он добавляет, что при бесконечно большом числе делений обе эти суммы
дают истинное значение интеграла. В специальном пояснении Эйлер
здесь принимает лейбницеву концепцию интеграла, приспособляя ее
к своему пониманию бесконечно малой: «интегрирование,— пишет он,—
можно получить из суммирования с любой точностью; точно же его нельзя
совершить иначе, как положив, что разности являются бесконечно
малыми, т. е. нулями» х). Отправляясь от этих соображений Эйлера, Лакруа
в своем курсе дифференциального и интегрального исчисления (1798)
еще ближе подошел к трактовке определенного интеграла как предела
интегральной суммы, подготовляя вслед за своим великим
предшественником почву для классического определения интеграла непрерывной
функции и доказательства его существования, данных Коши (1823) 2).
Техника вычисления неопределенных интегралов разработана в т. I
«Интегрального исчисления» с большой подробностью и систематически.
Практически Эйлер исчерпал случаи интегрирования в элементарных
функциях, круг которых он сам очертил, и потомству осталось добавить
в этом отношении только немногое. Изложение мало отличается от
теперешнего и содержание соответствующих глав труда великого ученого
без существенных изменений было включено в последующие руководства,
в которых, впрочем, гораздо меньшее место отводится интегрированию
при помощи бесконечных рядов. Многие приемы принадлежат самому
Эйлеру или получили от него свою окончательную форму,— это
относится к интегрированию \ R (х, У ах2 + Ъх + с) dx, дифференциального
бинома, различных трансцендентных функций, в частности,
тригонометрических, к разнообразным новым рекуррентным формулам и т. д.
Эллиптические интегралы. Из многочисленных открытий Эйлера
в интегральном исчислении мы остановимся на немногих и, прежде всего,
на теории эллиптических интегралов, т. е. интегралов вида
х
П (ж)=Л R(x, VP~(x))dx,
о
где R — рациональная функция, а Р (х) — многочлен 3-й или 4-й степени
без кратных корней. Такие интегралы начали встречаться во второй
половине XVII века в задачах на спрямление кривых (в частности, дуги
эллипса), а вскоре выяснилась также их важность в механике и теории
упругости. Ученые быстро убедились, что эллиптические интегралы
являются трансцендентными функциями нового типа и обладают
замечательными особенностями. В работах 1716 и следующих годов итальянец
Дж. К. ди Фаньяно, занимаясь спрямлением эллипсов,
гипербол и лемнискат, установил, что при определенных условиях
сумма или разность дуг одной и той же кривой выражается
алгебраически. Это означало, что алгебраически интегрируется
соответствующее дифференциальное уравнение с разделенными переменными,
г) Л. Эйлер, Интегральное исчисление, т. I, стр. 163.
2) А. П. Ю ш к е в и ч, О возникновении понятия об определенном интеграле
Коши.— Труды Ин-та ист. естеств., т. I, 1947.
ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
153
вроде
dx dlJ =0
dx
гэ ax
хотя \ л/\ _ 4 сам п0 се^е и не берется в конечном виде.
В серии работ, печатание которых началось в шестидесятые годы,
в частности в томе I «Интегрального исчисления», Эйлер далеко
продвинулся в направлении, указанном Фаньяно. Постепенно распространяя
свои результаты на более сложные случаи, Эйлер пришел к общей
теореме, позднее названной теоремой сложения эллиптических интегралов:
сумма или разность таких интегралов, отличающихся лишь своими
пределами, выражается интегралом того же вида, сложенным с некоторой
алгебраической функцией, т. е.
U(x) + U(y) = U(a) + f(x, z/, а),
где / (х, г/, а) есть функция алгебраическая1), и пределы х, у, а также
связаны алгебраическим уравнением. Эти исследования, переплетавшиеся
с изысканиями Лагранжа (1766, опубл. в 1769), Эйлер вел почти до конца
жизни. Они были блестяще продолжены в XIX веке, в первую очередь
Н. Абелем, который в 1826 г. представил Парижской Академии мемуар,
содержащий широкое обобщение теоремы сложения на так называемые
абелевы интегралы \ R (х, у) dx, где х, у связаны любым алгебраическим
уравнением F (х, у) = 0. Сумма таких интегралов, если они не
эллиптические, уже не может быть представлена одним интегралом того же вида,
но некоторым определенным числом таких интегралов, которое зависит
от природы уравнения F (х, у) = 0.
Эйлер и Лагранж обратили внимание на аналогию между
рассмотренными ими «эллиптическими» дифференциальными уравнениями и более
простым уравнением теории круговых функций
dx dy ^
уrz^2 — УГ1Г^2 ~~ '
интеграл которого можно записать и в алгебраической форме
х VT^y* ± У V~i — x* = а
и с помощью арксинусов
arcsin х + arcsin у = arcsin а.
Обращая функцию арксинуса
С3 dt (* dt
u = dLicsmx= \ . , v=diYCsmy =
0T/i-*2 " JVi-*2
т. е. переходя к тригонометрическим функциям x = sinu, y = sinv,
последнее равенство можно выразить как теорему сложения синусов,
алгебраически связывающую sin и = ]/"l—cos2 и, smv=Y^l — cos2z; и sin(u + z;):
sin и cos v + sin v cos и = sin (u±v).
x) В конце XVIII века выяснилось, что для некоторых видов интегралов
функция / (х, у, а) — логарифмически-алгебраическая.
154
ГЛ. 8. МАТЕМАТИЧЕСКАЯ ТРИЛОГИЯ ЭЙЛЕРА
Однако ни Эйлеру, ни Лагранжу не пришла мысль об обращении эллип-
х
тических интегралов z = П (х) = \ R(t, Р (t)) dt, т. е. о рассмотрении
о
функций х = ф (z), получивших позднее название эллиптических. Эта
идея была выдвинута опять-таки Абелем и одновременно Якоби (1827),
которые создали новую дисциплину — теорию эллиптических функций,
явившуюся затем предметом занятий многих крупнейших математиков —
Лиувилля, Вейерштрасса, Эрмита и других.
Второй круг вопросов учения об эллиптических интегралах связан
с проблемой сравнения между собою дуг различных конических сечений,
т. е. с преобразованием одних эллиптических интегралов в другие.
Основной целью было выделение среди всего разнообразия этих интегралов
по возможности немногих нормальных типов. Эту мысль Эйлер отчетливо
высказал в специальном мемуаре, в котором впервые предложил
рассматривать дуги эллипсов как функции, равноправные с логарифмической
и круговыми [NCAP X (1764) 1766]. За основное принимается кониче-
х2
ское сечение у2 = 2х , которое, в зависимости от значений а, может
быть эллипсом, параболой или гиперболой; длину дуги сечения Эйлер
обозначает особым символом ГЫа]. Преобразовав Пх[а] к форме
\ у т. f*^dz, Эйлер различает 12 случаев, в зависимости от знаков
и относительной величины постоянных. Классификацией эллиптических
интегралов занимались и другие, в том числе наш академик А. И. Лек-
сель. Окончательное решение вопроса дал А. М. Лежандр (1793—1794),
который показал, что любой эллиптический интеграл может быть
приведен к одному из трех основных родов, умноженному, быть может, еще на
постоянную, и сложенному с элементарной функцией. Эти три рода
Лежандр записал в виде
Т ^ _^Е_ ТТ ?M4-7?sin2co^ ТП е А + В sin* у dy
L ) АФ ' J \А + "8т Ч) Аф ' Ш' ) l-f-rcsin^ Д^ '
где Аф = "j/Ч — c2sin2cp, 0<с<1.
Определенные интегралы. Большое место в творчестве Эйлера
занимало изучение специальных определенных интегралов. Мы уже говорили
об эйлеровых интегралах 1-го и 2-го рода, т. е. функциях В(р, q) и Т(п).
С помощью дифференцирования и интегрирования под знаком интеграла,
а также мнимых подстановок он вычислил ряд новых важных интегралов.
Так, в статье, представленной в 1781 г., но напечатанной лишь в
четвертом томе «Интегрального исчисления» (1794), Эйлер, отправляясь от
равенства
оо
\ xnile-xdx = T (п)
о
и произведя подстановку х = ку, k = p±iq = r (cos а + i sin а), нашел
значения трех интегралов:
оо оо оо
С3 cos a da ? sin a da i/ я Р sin я 7 тс
о v о v о
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ 155
Первые два он получил после соответствующих преобразований и срав-
нения действительной и мнимой частей, принимая тг = -% , р = 0, q =1,
т. е. г = 1, а=-^-, и учитывая, что Г ( —) = ]/"я. Третий интеграл
получается при р = 0, q = 1, исходя из того, что для бесконечно малого п
будет Т(п) = ±Т(1 + п) = Ш=±.
Упомянем еще, что в первом томе «Интегрального исчисления» рас-
ос In X
-,— = \ —- , изучавшийся затем итальянским
О — оо
математиком Л. Маскерони (1792). И. фон Зольднер назвал эту новую
трансцендентную интегральным логарифмом и обозначил li х (1809) *).
Следует заметить, что выводы Эйлера, относящиеся к вычислению
несобственных интегралов, обоснованы, с нашей точки зрения, нестрого;
правомерность фактически производимых предельных переходов при этом
не контролируется. Эйлер обращался с несобственными интегралами как
€ обыкновенными.
В последние годы жизни Эйлера вычисление и изучение свойств
определенных интегралов приобретает все большее и большее значение.
Определенный интеграл трактуется уже не только как одно из значений
«частного» интеграла, он становится самостоятельным предметом анализа.
Характерна в этом отношении одна статья Эйлера 1775 г., напечатанная
посмертно в Opuscula analytica, II (Petropoli, 1785). В ней впервые явно
формулируются основные свойства определенного интеграла,
выражаемые в наших обозначениях формулами
и и, и о и
<\Pdx= — *\Pdx, $Pdx+*{Pdx=^P
dx
(аЪ или
и, -
I
и им аналогичные. Примерно в то же время (1777) Эйлер ввел для опре-
Г Vab х = а~
деленного интеграла специальное обозначение 1 Pdx , _
<z = ot, ad = Ro), сходное с предложенным на год ранее Лапласом
х = а
dx {Р} h . Нижний предел Эйлер называл terminus a quo (предел,
X — о
от которого), верхний — terminus ad quem (предел, до которого). Вскоре
Лаплас ввел термины «определенный интеграл» и «пределы
интегрирования»— limites (Гintegration (1782, опубл. 1785), а С. Лакруа
—«неопределенный интеграл» (1798). Впрочем, еще в седьмой главе I тома
«Интегрального исчисления» Эйлер писал, что всякое интегральное выражение
само по себе «неопределенно» и делается «определенным», когда интеграл
получает данное значение Ъ при данном значении аргумента а 2). Слова
«производная» функция — fonction derivee и «первообразная» функция —
ь
fonction primitive принадлежат Лагранжу (1772). Обозначение \ / (х) dx
а
ввел в 1819—1820 гг. Фурье.
х) Мы еще встретимся с применением интегрального логарифма в работах
П. Л. Чебышева по теории чисел.
2) Л. Эйлер, Интегральное исчисление, т. I, стр. 161.
156
ГЛ. 8. МАТЕМАТИЧЕСКАЯ ТРИЛОГИЯ ЭЙЛЕРА
Кратные интегралы. Наконец, Эйлер положил начало теории кратных
интегралов, введя двойные интегралы; ему принадлежит и этот термин.
В посвященной этому статье (NGAP XIV (1769) 1770) он учит находить
внутренние и внешние пределы интегрирования по уравнению границы
области, дает формальный вывод правила замены переменных, и
применяет двойные интегралы к вычислению объемов и поверхностей.
Следующим шагом явилось введение тройных интегралов Лагранжем (1773,
опубл. в 1775). Теория многомерных интегралов сразу стала одним
из важных средств механики и математической физики и ее успешно
развивали далее Гаусс, Коши, Дж. Грин и другие. В России
крупнейший вклад в разработку этой теории сделал М. В. Остроградский,
который, среди прочего, дал геометрическое истолкование приема Эйлера
для преобразования переменных в двойном интеграле и исправил одну
неточность, допущенную Лагранжем при выводе правила замены
переменных в тройном интеграле (1836).
ГЛАВА ДЕВЯТАЯ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
И ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Обыкновенные дифференциальные уравнения. Еще Ньютон,
разрабатывая свой метод флюксий и флюент для нужд небесной механики,
увидел, что главным инструментом последней является не просто
интегрирование функций одного переменного, а решение дифференциальных
уравнений. Сам второй закон ньютоновой механики, устанавливающий
пропорциональность ускорения движущейся точки и действующей на нее
силы, выражается, как известно, дифференциальным уравнением
второго порядка.
Первое развитие методы решения дифференциальных уравнений
получили у Ньютона, Лейбница и братьев Бернулли. Эйлер обогатил
теорию дифференциальных уравнений новыми первостепенными
результатами. Можно сказать, что благодаря его трудам теория
дифференциальных уравнений выделилась в особую математическую науку.
Интегрированию дифференциальных уравнений Эйлер посвятил много статей
и большую часть «Интегрального исчисления».
В конце XVII и начале XVIII в. были разработаны приемы решения
весьма немногих классов обыкновенных дифференциальных уравнений.
Это были уравнения с разделяющимися переменными, приводящиеся
к ним однородные и линейные уравнения первого порядка, простейшие
линейные уравнения второго порядка с постоянными коэффициентами
и еще некоторые. Для таких уравнений были найдены решения в
элементарных функциях или квадратурах. В частных случаях был применен
метод интегрирующего множителя. Найдены были также способы
понижения порядка уравнений второго порядка, не содержащих одной из
переменных. К уравнениям, неинтегрируемым в квадратурах, применяли
решения с помощью бесконечных рядов.
Уравнение Риккати. Важный толчок дальнейшим исследованиям
положило изучение специального уравнения Риккати, которым
занимались и наши академики Д. Бернулли и X. Гольдбах. Это уравнение, как
и общее уравнение Риккати
% = P(x)y* + Q(x)y + R(x)
(термин Даламбера), десятилетиями привлекало также Эйлера. Еще
в тридцатые годы он исследовал специальное уравнение Риккати,
представляя его решение в форме бесконечных рядов или непрерывных дробей.
В шестидесятые годы он установил, что, зная одно частное решение общего
158 ГЛ. 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
уравнения Риккати, его можно свести к линейному уравнению первого
порядка, а зная два частные решения, найти общее решение одной
квадратурой. Эйлеру была известна и тесная зависимость между уравнением
Риккати и линейным уравнением второго порядка и способ
преобразования первого во второе.
Линейные уравнения с постоянными коэффициентами. Линейные
дифференциальные уравнения играли важную роль в работах Эйлера по
механике и математической физике и он уделил этому классу уравнений и его
отдельным видам много внимания. Укажем прежде всего, что Эйлеру
принадлежит современный метод решения однородного уравнения с
постоянными коэффициентами
dny . dn~iy . . dy , л
Этим методом он овладел не позднее 1739 г., а соответствующая работа
увидела свет в т. VII Miscellanea Berolinensia, 1743 г. В этой статье
впервые появились термины «частный интеграл» и «полный интеграл»,
соответствующий нашему общему решению, причем в применении именно
к дифференциальным уравнениям. Вначале Эйлер устанавливает, что
линейная комбинация частных решений рассматриваемого уравнения
является в свою очередь его решением и что общее решение должно
содержать п произвольных постоянных; впрочем, более точный анализ
соответствующих понятий (линейная независимость, ее критерии и т. д.)
выпал уже на долю ученых XIX века. Затем применяется подстановка
у = ekx, приводящая к так называемому теперь характеристическому
уравнению
а0кп + а^к71'1 + . . . + ctn-ik + ап = О,
во всех подробностях разбираются случаи однократных и многократных
действительных или мнимых корней. Метод преобразования переменных
с помощью показательных функций Эйлеру был известен еще с 1728 г.г
когда он применил его для приведения некоторых уравнений второго
порядка к уравнению первого порядка [САР III (1728) 1732]. Перед тем
экспоненциальная подстановка была, как говорилось, употреблена
Николаем Бернулли (младшим).
Для решения неоднородного уравнения
Эйлер предложил метод последовательного понижения порядка [NCAP
III (1750—1751) 1753], суть которого мы поясним на примере уравнения
второго порядка:
Уравнение умножается на етх и интегрируется, причем результат ищется
в виде уравнения 1 порядка
emx(^ + ^y) = lf(x)e^dx,
где cti и а2 — некоторые постоянные, подлежащие, как и т, отысканию.
Дифференцирование последнего уравнения и сравнение результата с левой
частью данного уравнения позволяет найти все три постоянные. Далее
ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ 159
процесс повторяется применительно к возникшему уравнению, и т. п.
Излагаемый в теперешних учебниках способ вариации постоянных был
разработан Лагранжем (1775, опубл. в 1777), но к уравнению ~ +
+ ау = / (х) Эйлер применил его еще ранее в работе о приливах и
отливах (опубл. в 1741), а также в нескольких других случаях. Независимо
от Эйлера и одновременно с ним метод вариации постоянных применил
к только что написанному уравнению и Д. Бернулли, который, как
упоминалось, самостоятельно нашел также решение однородного уравнения
с постоянными коэффициентами. Добавим, что в томе II «Интегрального
исчисления», посвященном обыкновенным уравнениям выше первого
порядка, Эйлер впервые исследовал линейные уравнения с постоянными
коэффициентами бесконечного порядка, теория которых успешно
развивается и в наши дни.
Вслед за Даламбером (1743—1747), но применяя иные методы, Эйлер
разрабатывал также методы решения систем линейных уравнений с
постоянными коэффициентами [GAP I (1747—1748) 1750] *). Позднее в этом
направлении у нас работал А. И. Лексель.
Линейные уравнения с переменными коэффициентами. Среди
изученных Эйлером линейных уравнений с переменными коэффициентами
мы особо отметим уравнение
(а + Ъхп) х* -0- + (с + fxn) х -g- + (g + hxn)y = 0,
которое содержит, как частные случаи, целый ряд важных типов
уравнений математической физики и самого анализа:
1) уравнение Бесселя
2) уравнение Лежандра
(1-х
3) гипергеометрическое уравнение Гаусса
*(i-*)g+i
4) уравнение Чебышева
(1-*)-Й-2*? + Лу = 0,
х(1-х)^ + [(1 + а + $)х-у]% + афу = 0,
5) уравнение Чебышева—Эрмита
В томе II «Интегрального исчисления» Эйлер интегрирует свое уравнение
прежде всего с помощью рядов, беря искомое частное решение в виде
ряда с неопределенными коэффициентами
y = xm(A + Bxn + Cs*n + Dx*n + ...)
х) Н. И. Симонов, О первых исследованиях Ж. Даламбера и Л. Эйлера по
теории линейных систем дифференциальных уравнений с постоянными
коэффициентами.— Ист.-матем. исслед., вып. IX, 1956.
160 ГЛ. 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
(или же аналогичного ряда, в котором п заменено на —п). Это
приводит к определяющему т квадратному уравнению
am (т — 1) + cm + g = 0,
а также к рекуррентным соотношениям между коэффициентами А, В,
С, D, .... Если корни определяющего уравнения неравны и разность
их не делится на п, получаются два различных частных решения,
позволяющие составить общее; в противном случае второе частное решение
содержит, как показывает Эйлер, помимо степеней х, еще In х.
Сходимости возникающих рядов Эйлер не исследовал. Специальное внимание
он уделяет случаям, когда ряды обрываются и решения оказываются
конечными многочленами. Замечательный и важный метод Эйлера был
подробнее и глубже развит в XIX веке, в частности Г. Фробениусом
(1873); Эйлер применяет к тому же уравнению и другой изобретенный
им прием, в котором решение ищется в форме определенного интеграла
функции, зависящей от параметра 1). Этот прием Лаплас перенес на
линейные уравнения с частными производными второго порядка (1773, опубл.
в 1777).
Несколько ранее «Интегрального исчисления» появилась статья
Эйлера, в которой задача о колебании упругой мембраны была сведена
к решению уравнения Бесселя:
(NCAP X (1764) 1766). Найденное им в форме бесконечного ряда решение
этого уравнения представляет собой цилиндрическую функцию первого
рода /р ( — ] с любым действительным индексом (3. Напомним, что до того
Д. Бернулли встретилась цилиндрическая функция первого рода
нулевого порядка. В томе II «Интегрального исчисления», решая в одном
частном случае все то же общее уравнение второго порядка, Эйлер пришел
к цилиндрической функции второго рода нулевого порядка YQ (х),
которую представил рядом, содержащим In ж2). Цилиндрические функции,
наряду с гамма- и дзета-функцией, принадлежат к наиболее важным
видам специальных функций и постоянно встречаются в математическом
естествознании. В их дальнейшем исследовании и обобщении
участвовали Ф. В. Бессель и многие иные зарубежные ученые, а в России А. В.
Летников и Н. Я. Сонин, которому принадлежат здесь особые заслуги.
Интегрирующий множитель. Мы упоминали, что Эйлер, наряду
с Клеро, нашел необходимое условие, при котором выражение М (х, y)dx+
+ N (х, у) dy является полным дифференциалом. В томе I
«Интегрального исчисления» Эйлер показал, как при выполнении этого условия
—-=——найти функцию, имеющую указанное выражение своим
дифференциалом и тем самым установил достаточность условия. Стремясь
свести к уРавнению полного дифференциала возможно более широкие
классы дифференциальных уравнений, Эйлер развил метод
интегрирующего множителя, примененный до того в отдельных случаях И. Бернулли
и его сыном Николаем. В первую очередь Эйлер (одновременно с
г) Н. И. Симонов, Прикладные методы анализа у Эйлера, М., 1957, гл. II.
2) В. В. Гуссов, Развитие теории цилиндрических функций в России и СССР,
Ист.-матем. исслед., вып. VI, 1953, стр. 357 и след.
ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 161
Даламбером) доказывает теорему о существовании для каждого
обыкновенного дифференциального уравнения первого порядка интегрирующего
множителя; при этом предполагается существование общего решения.
После этого он находит интегрирующие множители для ряда уже
проинтегрированных видов уравнений, а затем по заданным множителям того
или иного вида находит соответствующие им классы дифференциальных
уравнений. Метод интегрирующего множителя Эйлер распространил на
уравнения высших порядков. При этом он использовал найденное им
несколько ранее [NCAP X (1764) 1766] условие, при котором функция
F (х, у, у'', . . ., у М) является полной производной некоторой другой
функции, содержащей производные у до (п — 1)-го порядка. То же
условие нашел в 1765 г. французский математик Кондорсе, а новый вывод
его предложил А. И. Лексель. Позднее работы Эйлера по теории
интегрирующего множителя были продолжены многими, у нас, в частности,
Ф. Г. Миндингом.
Особые решения. Перечислить все открытия Эйлера в учении об
обыкновенных дифференциальных уравнениях здесь невозможно. Упомянем
еще только два его результата. Один касается особых решений уравнений
первого порядка, примеры которых встретились прежде всего Тейлору
(1715), а затем Клеро и самому Эйлеру (1736). Мы имеем в виду первые
критерии, позволяющие установить, не зная общего интеграла
уравнения, является ли какое-либо данное его решение частным интегралом
или нет. Эйлер придавал таким признакам важное значение, поскольку
«во всех тех задачах, решение которых приводится к дифференциальному
уравнению, произвольное постоянное количество, присоединяемое в
результате интегрирования, определяется из условий, присоединяемых
к каждой задаче, так что всегда требуется только такой частный
интеграл» 1). Вопрос исследован в томе I «Интегрального исчисления», причем
Эйлер постепенно переходит от простейших видов уравнений с
разделяющимися переменными к уравнению Р (х, у) dx = Q (х, у) dy, где «какие
угодно» функции Р и Q фактически ограничены довольно широкими
условиями. Все дело сводится к установлению расходимости некоторых
несобственных интегралов, связанных с соответствующим
дифференциальным уравнением.
Эти исследования Эйлера были вскоре продолжены Лапласом и Ла-
гранжем. Последний разработал основы более общей теории особых
решений и, в частности, дал их геометрическое истолкование. Много спустя
критерий Эйлера для уравнения Р (х, у) dx = Q (х, у) dy был вновь
высказан С. Пуассоном, под именем которого иногда и встречается в
литературе 2).
Другой важный результат Эйлера лежит в области приближенного
интегрирования уравнений первого порядка.
Численное решение дифференциальных уравнений. Потребность в
приближенном интегрировании дифференциальных уравнений весьма остро
ощущалась в небесной механике,— в теории движения Луны и планет.
Именно в этой связи Эйлер разработал свой метод, изложенный все
г) Л. Эйлер, Интегральное исчисление, т. I, стр. 305.
2) Н. И. С и м о н о в, О научном наследии Леонарда Эйлера в области
дифференциальных уравнений.— Ист.-матем. исслед., вып. VII, 1954, стр. 543.
162 ГЛ. 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
в том же томе I «Интегрального исчисления». Задача о приближенном
интегрировании на отрезке (x0l х) уравнения
•?=/<*.*>
с начальным условием х = х0, у = у0 решается в предположении, что
/ (х, у) непрерывна (в нашем смысле слова) и что искомый интеграл
разлагается близ точки (х0, г/о) в ряд Тейлора:
СО dlj 0)2 d?lj
У - Уо -t-jr •¦^ + "2Г ' ~Ш + ' ' '
Переходя от х0 к х± = х0 + со и считая со весьма малым, Эйлер находит
приближенное значение уи вычисляя по функции f(x, у) производные
dy d2u о
j- , -г-j , . . . и подставляя в них начальные значения х0, у0. оатем,
отправляясь от значений хи у± и переходя к следующему близкому значению
х2, он аналогично находит приближенное значение у2 и т. д., пока для у,
соответствующего конечному значению х = хп, не получится
приближенное значение уп. Если ограничиться членами первой степени
относительно со, то возникает последовательность приближений
У1 = Уо + /(*о, У о) {xl — Xq),
y2 = yi + f(zi, г/i) (х2 — х±),
Уп — Уп-1 ~"Г / \Xn-li Уп-\) \Хп — Хп-1),
так что, в конце концов,
п
Уп = Уо+ 2 /(Sft-i, Ук-i) (Xk — Zk-i).
k=i
Этот метод излагается теперь под именем метода ломаных Эйлера, так как
искомая интегральная кривая, проходящая через точку (х0, у0),
аппроксимируется проходящей через ту же точку ломаной линией.
Исследование сходимости процесса Эйлер не производит; он ограничивается, как
и в случае приближенного вычисления определенных интегралов,
замечанием о способах преодоления трудностей, возникающих, когда
функция f(x, у) обращается в бесконечность (а также в нуль); затрагивается
и случай обращения в бесконечность коэффициентов ряда Тейлора, т. е.
dy d2y
Метод ломаных Эйлера, распространенный им самим в томе II
«Интегрального исчисления» на уравнения второго порядка, был затем развит
далее в XIX веке. Следует особо подчеркнуть, что этот метод лежит
в основе первого доказательства существования решения уравнения
Л = f(x, у) с начальными условиями, данного в двадцатые годы XIX века
Коши (опублик. в 1844) и впоследствии улучшенного Р. Липшицем (1876).
Доказательство Коши — Липшица приводится теперь во многих
руководствах г).
г) Подробнее см. Н. И. Симонов, Прикладные методы анализа у Эйлера,
гл. III.
УРАВНЕНИЯ С ЧАСТНЫМИ^ ПРОИЗВОДНЫМИ
163
О применении Эйлером к решению дифференциальных уравнений
метода степенных рядов с неопределенными коэффициентами,
восходящего к Ньютону и Лейбницу, уже говорилось.
Уравнения с частными производными. В XVIII веке началась
интенсивная разработка приемов решения уравнений с частными
производными. Первыми успехами в этом направлении мы обязаны Эйлеру и Далам-
беру. В томе III «Интегрального исчисления» сведена значительная часть
всех результатов, полученных к концу шестидесятых годов, и он явился
первым курсом по этой тогда новой дисциплине.
Более ранние работы Эйлера тридцатых годов посвящены отдельным
уравнениям первого порядка, к которым он пришел, занимаясь
некоторыми вопросами геометрии [например, САР VII (1734—1735) 1740]; этим
кругом вопросов он занимался и позднее. Установленные им связи между
нелинейными и линейными уравнениями и прием решения последнего
в случае
% = V(x,y)? + U{x,y)
(«Интегральное исчисление», т. III) послужили отправным пунктом
дальнейших работ Лапласа и Лагранжа. Но с середины XVIII века
центральное место заняли линейные уравнения второго порядка, к
которым сводятся важнейшие задачи математической физики, в частности,
разнообразные вопросы теории колебаний. Только для примера мы
упомянем основное в гидродинамике уравнение, которому удовлетворяет
так называемое объемное расширение и:
д2и д2и . д2и д2и
dt2 ~~"дх2~^~ду2"^г dz2
[Mem. Ac. Berl., XV (1759) 1766], уравнение колебаний мембраны
d2z _ d2z дЧ
dt2 ~ дх2 "Г" ду2 '
решенное Эйлером с помощью цилиндрических функций первого рода
[NGAP X (1764) 1766] и еще уравнение
исследованное в томе III «Интегрального исчисления». Эйлер получил
это уравнение несколько ранее, изучая колебания струн переменной
толщины и движение воздуха в трубах. Позднее оно явилось предметом
изысканий Лапласа (1777), Пуассона (1823), Римана (1850), Г. Дарбу
(1877) и других ученых, вплоть до работ наших дней по газовой динамике.
Эйлер представил общее решение этого уравнения в форме ряда
z = А(х + у)х [f(x)+F (у)] + В (x + y)*+l[f (x) + F'(y)] +
+ C(x + y)x+2[f'(x) + F"(y)]+...,
где f(x) и F (у) — произвольные функции, вывел рекуррентные формулы
для коэффициентов и определяющее X уравнение
№ + (2т— 1)Л + тг = 0,
а в заключение рассмотрел случаи, когда ряд обрывается.
164 ГЛ. 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Мы остановимся более подробно только на знаменитой в истории
математической физики и хронологически первой задаче о колебании струны1).
Проблема колебания струны. Метод Даламбера — Эйлера. Как
говорилось, вопрос о малых поперечных колебаниях бесконечно тонкой
однородной струны был впервые математически рассмотрен в 1713 г. Тейлором,
решение которого, однако, оказалось весьма частным и недостаточным.
За этим последовали две статьи И. Бернулли о колебаниях нагруженных
струн во II и III томах «Записок» нашей Академии. Принципиально
по новому подошел к задаче Даламбер. В работе 1746 г., изданной в Mem.
Ac. BerL, III (1747) 1749, он впервые записал дифференциальное
уравнение свободного колебания, которое теперь мы зовем волновым, в форме,
немногим отличающейся от современной,
<% д*у
dt* и дх* '
и с помощью остроумных преобразований вывел его решение в виде
у(х, t) = f1{x + at) + f2{x — at),
где /i и /2 — любые функции, подчиненные некоторым ограничениям,
о которых мы скажем далее. Так было найдено общее решение уравнения
колебаний струны, содержащее две произвольные функции. Эти
произвольные функции играют в интегралах уравнений с частными
производными роль, сходную с ролью произвольных постоянных в интегралах
обыкновенных дифференциальных уравнений. Даламбер подчеркнул
отличие своего решения, включающего бесконечное множество кривых, от
единственного синусоидального решения, указанного Тейлором.
Колебание струны вполне определяется при наличии дополнительных
условий, наложенных на струну. Уже Даламбер различал те два типа
условий, которые впоследствии назвали граничными (они относятся
к закрепленным концам струны, если только она не считается
бесконечной) и начальными (они характеризуют состояние струны в начальный
момент времени). Если концы струны длины/ неподвижны, то граничные
условия можно взять в виде
г/(0, t) = y(h 0=о.
Это позволяет выразить одну из произвольных функций через другую,
поскольку /2 ( — и) = — Д (и), так что решение будет
у(х, t) = fi(at + x) — fi(at — x).
Кроме того, функция /i(i^), если подставлять в нее произвольные
значения аргумента, оказывается четной и периода 21:
/i(-") = /i(«), /i(« + 2Z) = /i(u).
Начальные условия Даламбера заключались в задании исходной формы
струны и скорости ее точек:
у(х, 0) = у0(х), ду{*! 0) = vQ(x),
г) Подробнее см. Ф. И. Франк ль, Об исследованиях ^Л. Эйлера в области
теории уравнений в частных производных, в кн.: Л. Эйлер, Интегральное
исчисление, т. III; Н. И. С и м о н о в, Об исследованиях Л. Эйлера по интегрирова-
лию линейных уравнений и систем линейных уравнений с частными производными.—
Лст.-матем. исслед., вып. X, 1957.
ПРОБЛЕМА КОЛЕБАНИЯ СТРУНЫ. МЕТОД ДАЛАМБЕРА — ЭЙЛЕРА 165
где известны функции у0(х), v0(x). Это дает уравнения
/i(*) —/i( —s) = Sfo(*). h(x) + h( — x) = -j[ v°(x)dx>
определяющие остававшуюся еще произвольной функцию Д (и).
Описанный прием теперь именуют методом характеристик. В другой
статье, напечатанной в томе VI «Записок« Берлинской Академии (1750)
1752, Даламбер наметил идею еще одного важного приема, отправным
пунктом которого служит представление искомого решения в форме
у (х, t) = ф (ж)-ф (?), что приводит к интегрированию двух обыкновенных
линейных уравнений второго порядка с постоянными коэффициентами.
Этот «метод разделения переменных» был развит много спустя Фурье,
Пуассоном, Остроградским и другими.
Как сказано, произвольные функции, входящие в общий интеграл
волнового уравнения, Даламбер подчинил некоторым ограничениям.
Во-первых, произвольные функции, входящие в решение, оказывались
четными и периода 21, а функции, выражающие начальную форму и
скорость струны, должны были быть нечетными и того же периода.
Во-вторых, он требовал, чтобы каждая рассматриваемая функция определялась
одним уравнением (т. е. была «непрерывна» в уже известном нам смысле
этого слова) и даже более, чтобы она представлялась степенным рядом.
Во всех остальных случаях Даламбер считал свой метод неприменимым.
Тем самым исключались даже столь естественные начальные фигуры,
как защепленная струна, оттянутая вначале за одну из точек без
начальной скорости, или такая простая форма, как параболическая дуга, и т. п.
Дело в том, что аналитическое выражение, задающее кривую на каком-
либо одном участке, Даламбер считал автоматически определяющим
ее повсюду.
В следующем томе IV берлинских «Записок» [(1748) 1750] с работой
по тому же вопросу выступил Эйлер, который решительно отверг
требование «непрерывности», выдвинутое Даламбером. Эйлер указывал, что
по самому физическому существу дела, начальной фигурой струны может
служить произвольная линия, описанная свободным движением руки,
даже и непредставимая одним уравнением; то же относится к линии,
изображающей начальную скорость. Но такой произвол ничуть не мешает
употреблению описанного метода решения, ибо в нем имеет значение
лишь та часть данной линии у0 или же v0, которая соответствует отрезку
(0, Z). Продолжение этих линий вне участка (0, Z), каково бы оно ни было,
не приходится принимать во внимание. Найденное по начальным и
граничным условиям решение у распространяется (при всяком
фиксированном t) с отрезка (0, Z) на отрезок (—Z, 0) по закону нечетности, а вне
участка (—Z, Z) повторяется с периодом 21. Таким образом, устранялась
трудность, связанная с тем обстоятельством, что все функции, по самому
смыслу задачи, заданы на (0, Z), между тем как численные значения
аргументов at ± х в решении уравнения могут лежать вне этого промежутка.
«Непрерывные» функции, заданные одним аналитическим
выражением, обладали и с точки зрения Эйлера тем свойством, что задание их
на любом, сколь угодно малом отрезке однозначно определяет их повсюду.
В XIX веке выяснилось, что это свойство присуще аналитическим
функциям комплексного переменного. Эйлер считал, что во многих вопросах
анализа можно обойтись «непрерывными» функциями. Однако в
математической физике и решении уравнений с частными производными
необходимым становится применение линий, изображаемых произвольными
166 ГЛ. 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
кривыми, и, следовательно, «разрывных» функций. По-видимому, Эйлер
имел в виду не только простые «разрывы» закона непрерывности, когда
функция может быть определена в области существования несколькими
различными формулами, так называемые «смешанные линии», но и еще
более произвольные «разрывные» функции1). Так или иначе, для
решения волнового уравнения нет нужды знать аналитические выражения
начальных функций. Эйлер специально подчеркивает, что
рассматриваемый метод интегрирования позволяет графически построить струну
в любой момент ее колебания безо всякого вычисления, только по
начальным фигурам кривых на отрезке (О, I).
По сути дела, допускаемые Эйлером произвольные линии
соответствуют нашим непрерывным функциям с кусочно-непрерывными первой
и второй производными, т. е. непрерывным кривым с
кусочно-непрерывными наклоном касательной и кривизной. Тем самым Эйлер впервые
сознательно ввел в употребление неаналитические функции. Это был шаг
вперед принципиального значения. Несколько лет спустя Эйлер писал:
«Особенная сила интеграции [уравнений с частными производными.—
А. Ю.], рассматриваемых в данной книге, в том и состоит, что при них
могут встречаться и разрывные функции, так что надо полагать, что
благодаря этому существенно новому исчислению границы анализа
значительно расширяются» 2). Здесь от идей Эйлера нити протягиваются
к новейшим методам XX века, к обобщенным функциям С. Л. Соболева
и французского математика Л. Шварца, позволяющим представить
решение волнового уравнения в классической форме /i (х + at) + /2 (х — а0
даже тогда, когда функции f± (х) и /2 (х), будучи непрерывными, недиф-
ференцируемы в обычном смысле слова.
Наряду с общими глубокими мыслями, чрезвычайно расширявшими
сферу приложения метода характеристик, статья Эйлера содержала
математический анализ физической картины колебания струны (установление
97
периода колебания во времени Т = —, подтвердившее результат
Тейлора, существование последовательности собственных частот колебания
vk = kvi, Vi = у , соответствующих основному тону и обертонам, и т. д.).
Попутно Эйлер отметил, что в некоторых случаях решением может
служить сумма простых гармонических колебаний
2. пкх nnat
ап sin — cos —j— ,
причем начальная фигура струны имеет уравнение
Уо= 2j Oti sin-р.
Однако такое представление Эйлер считал весьма частным и в подробности
не вошел. Он даже не указывает, имеются ли в виду конечные
тригонометрические суммы или бесконечные ряды.
Позднее Эйлер открыл совершенно иной прием решения уравнения
д*У _„2 д2У
dt* ~а дх*
г) См. статью Эйлера о применении в анализе разрывных функций в NCAP XI
(1765) 1767.
2) Л. Эйлер, Интегральное исчисление, т. III, стр. 28.
ПРИНЦИП НАЛОЖЕНИЯ КОЛЕБАНИЙ Д. БЕРНУЛЛИ 167
с помощью преобразования к так называемым теперь характеристическим
координатам и = х -\- at, v = х — at [Misc. Taur., Ill (1762—1765) 1766].
Данное уравнение переходит в более простое
ди dv '
общее решение которого получается почти сразу в виде
y = h (и) + h {») = /i (х + at) + h (х — at).
Принцип наложения колебаний Д. Бернулли. Вскоре после выхода
из печати первых статей Даламбера и Эйлера в обсуждение задачи о
струне включился третий крупнейший геометр того времени Д. Бернулли,
который выдвинул утверждение, что наиболее удобным и вместе с тем
совершенно общим является решение в виде бесконечного
тригонометрического ряда. Это внесло новый элемент в завязавшийся тем временем
спор между Даламбером и Эйлером и поставило перед математикой новые
чрезвычайно важные проблемы.
В томе IX берлинских «Записок» [(1753) 1755] Д. Бернулли выступил
с критикой метода Даламбера и Эйлера, которые, по его мнению, с помощью
труднейших абстрактных вычислений получают не более того, что можно
вывести почти без выкладок из содержательного рассмотрения самой
природы колебаний струн. Ни дифференциальное уравнение колебаний,
ни приемы его решения не вызвали интереса у Бернулли. Он отправляется
от синусоидального решения задачи, предложенного Тейлором, и того
положения, что звучание всех тел вообще складывается из бесчисленного
множества элементарных звуков, обусловленных некоторыми
регулярными колебаниями. Так, звук струны состоит из основного тона и всех
обертонов, которые она способна издавать и которые являются основными
тонами для струн в 2, 3, 4, ... раз более коротких, чем данная. В
соответствии с этим любое колебание струны оказывается суммой
бесчисленного множества простых гармонических колебаний — синусоид с
частотами, следующими в арифметической прогрессии, т. е. суммой
тригонометрического ряда. Таким образом, Д. Бернулли выдвинул на первый
план уже упоминавшийся принцип наложения или суперпозиции
колебаний.
Принцип суперпозиции Бернулли считал чуть ли универсальным
законом природы. В нескольких работах он показал его приложения,
не разрабатывая, впрочем, в деталях математическую сторону дела.
В частности, за только что изложенной была помещена статья,
посвященная задаче о колебаниях нескольких грузов, связанных с невесомой
натянутой нитью. Весьма выпукло Д. Бернулли высказал свою
концепцию в письме к Эйлеру, написанном не позже сентября 1754 г.: «Вот
каково мое мнение по этому вопросу: мы доказали, что любая кривая,
выраженная уравнением
пх п . 2пх , . Зпх ,
у = a sm Ь Р sin \- у sm f- и т. д.,
удовлетворяет условию, о котором идет речь. Но разве нельзя сказать,
что это уравнение обнимает все возможные кривые: нельзя ли,
распоряжаясь произвольными количествами а, р, у и т. д., заставить кривую
пройти через любое количество данных по положению точек? Разве
уравнение такой природы имеет меньшую сферу действия, чем
неопределенное уравнение
у = ах-{-§хх-\-ух3-{- . . . и т. д.?
168 ГЛ. 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
...Итак, я утверждаю, что для решения Вашей задачи: по любой данной
начальной форме найти последующее движение нужно определить
количества а, Р, y» отождествляющие данную кривую с нашим
неопределенным: уравнением, и мы тотчас получим частные изохронные колебания,
из которых составится искомое движение». И далее Д. Бернулли
выражал восхищение «скрытым ранее физическим сокровищем», а именно
«возможностью сводить встречающиеся в природе движения, которые
кажутся не подчиненными какому-либо закону, к простым изохронным
движениям, которыми видимо пользуется природа в большей части своих
действий» 1).
Идея Д. Бернулли была чрезвычайно плодотворна. В. И. Смирнов
пишет: «пример колебания натянутой нити не был, по существу,
выигрышным для Даниила Бернулли. Метод Даламбера — Эйлера не использует
бесконечных рядов и при заданных начальных условиях он дает решение
задачи в известном смысле в конечном виде. Но круг задач, при решении
которых этот метод применим с такой простотой, весьма ограничен,
и Даниил Бернулли был вполне прав, когда подчеркивал общность своего
метода по сравнению с методом Даламбера — Эйлера» 2). Все это, однако,
стало выясняться лишь в XIX веке благодаря работам Фурье и его
последователей, которые синтезировали и развили далее метод разделения
переменных Даламбера и принцип суперпозиции колебаний Д. Бернулли.
Сам Бернулли, как сказано, не имел в виду предложить метод
интегрирования волнового дифференциального уравнения. Вместе с тем он не мог
обосновать утверждение о представимости любой (в некотором смысле)
кривой или функции в форме ряда по синусам. Он даже не располагал
общим способом вычисления коэффициентов такого ряда.
Ни Даламбер, ни Эйлер не согласились с Бернулли. В том же томе
берлинских «Записок», что и статьи Бернулли, появился ответ Эйлера.
Эйлер признает, что физическую картину процесса звукообразования
Д. Бернулли по своему методу характеризует и объясняет превосходно
и гораздо лучше своих предшественников. Все то же можно, однако,
получить из решения дифференциального уравнения колебаний по
способу Даламбера — Эйлера. Именно дифференциальное уравнение, решение
которого Бернулли обходит, является для Эйлера основой теории
колебаний струны,— это относится и к другим задачам математической
физики. Эйлер признает и ценность принципа суперпозиции. Но между тем как
у Д. Бернулли этот принцип выступает как чрезвычайно общий закон
природы, Эйлер трактует его как свойство решений линейных однородных
дифференциальных уравнений, причем доказывает соответствующую
теорему: линейная комбинация частных решений такого уравнения сама
является его решением. Поэтому принцип суперпозиции применим к
явлениям, которые можно описать линейными однородными
дифференциальными уравнениями.
Что касается решения в форме ряда по синусам, то Эйлер отказывает
ему как раз в той общности, на которой с такой решительностью настаивал
Д. Бернулли. Согласно Эйлеру ряды по синусам годятся для
представления весьма ограниченного класса непрерывных (в его смысле) нечетных
и периодических функций. Здесь Эйлер допустил ошибку, сходную с той,
в которой упрекал Даламбера. Возражения Эйлера опирались все на то же
г) Correspondance physique et mathematique de quelques celebres geometres du
XVIIIе siecle, t. II, стр. 654—655.
2) В. И. Смирнов, Даниил Бернулли, в кн.: Д. Бернулли,
Гидродинамика, стр. 482—483.
ПРИНЦИП НАЛОЖЕНИЯ КОЛЕБАНИЙ Д. БЕРНУЛЛИ 169
В
*Ч7*
убеждение, что формула, определяющая функцию в некотором интервале,
должна определять ее повсюду. Отход от этого положения Эйлер считал
возможным лишь в случае кривых (функций), заданных геометрически
произвольным свободным движением руки. А Бернулли не мог привести
в пользу своего утверждения,— справедливого, как выяснилось много
спустя, при некоторых ограничениях,—
убедительных доводов.
Спор между Даламбером, Эйлером
и Д. Бернулли распространился и на
другие задачи математической физики и типы
дифференциальных уравнений. Полемика
велась как в печати, так и в частной
переписке. Каждая сторона оставалась
в главном при своем мнении. В
дискуссию, кроме того, включились Лагранж,
Лаплас, Монж и другие математики, в той
или иной степени примыкавшие к ее
инициаторам, а иногда занимавшие
колеблющиеся позиции. В ходе обсуждения были
выдвинуты некоторые важные новые
соображения. Так, Эйлер указал, что его
решение задачи основано на допущении
бесконечной малости не только самого
колебания струны у, в.о и. наклона
касательной j- . Он весьма подробно
рассмотрел геометрическую картину
распространения и отражения волн (Miscellanea
Taurinensia, 3 (1762—1765) 1766; Mem.
de Berlin, 21 (1765) 1767), в частности,
для струны, защепленной в одной точке
(NCAP XVII (1772) 1773); этот пример
вошел впоследствии в курсы
математической физики (рис. 25). В качестве
дополнительного аргумента против метода
Д. Бернулли Эйлер в письме к Иоганну III
Бернулли (племяннику Даниила) от 24 мая
1764 г. привел такое возражение: вообще
говоря, невозможно определить
бесконечное множество коэффициентов ряда синусов, выражающего какую-либо
кривую. Д. Бернулли в письме к тому же адресату от 25 июля 1765 г.
заявил в ответ, что он все более убеждается в общности своего метода,
но только потенциальной, ибо согласен, что отыскание этих
коэффициентов по большей части превосходит возможности анализа г). В то
время Эйлеру еще не были известны формулы так называемых теперь
«коэффициентов Фурье».
Полемика продолжалась и после смерти всех трех ее инициаторов.
Еще в 1787 г. Петербургская Академия, как бы отдавая долг памяти
скончавшегося за четыре года до того Эйлера, объявила на 1789 г.
конкурсную тему (мы приводим ее в переводе с французского): «Определить,
D
Е/
* S
G \т?
\*
ff Ч^
Рпс. 25. Построение графика
колебаний защепленной струны (из
статьи Л. Эйлера в XVII т.
«Новых записок» Петербургской
академии наук; нижний рисунок
служит диаграммой для определения
движения).
г) См. С. Trues dell, The Rational Mechanics of Flexible or Elastic Bodies,
1638—1788 (L. Euleri Opera omnia, Ser. II, vol. llbis, 1960), стр. 277—278.—
Полностью эти письма не опубликованы.
170 ГЛ. 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
принадлежат ли произвольные функции, вводимые при интегрировании
дифференциальных уравнений более чем с двумя переменными, каким бы
то ни было кривым или поверхностям, алгебраическим, трансцендентным
или механическим, разрывным или произведенным свободным движением
руки, или же их можно законным образом отнести лишь к кривым
непрерывным и способным быть выраженными алгебраическими или
трансцендентными уравнениями?». В 1790 г. премия была присуждена страсбург-
скому профессору Л. Арбогасту за его «Мемуар о природе произвольных
функций, входящих в интегралы уравнений с частными
дифференциалами» (Memoire sur la nature des fonctions arbitraires qui entrent dans les
integrales des equations aux differentielles partielles. St.-Petersbourg, 1791).
Арбогаст выступил на стороне Эйлера. Один из аргументов Даламбера
и его приверженцев был тот, что при отсутствии единого закона для всей
кривой не существуют, вообще говоря, значения производных в точках
разрыва, т. е. в точках перехода от одного закона к другому. Опровергая
этот довод, Арбогаст фактически пришел к понятию производной слева
и справа, хотя не ввел соответственных терминов.
Эти левые и правые производные первого, второго и высших
порядков могут удовлетворять данному дифференциальному уравнению точно
так же, как в случае, когда их значения совпадают, т.е. когда существуют
производные в точке. Арбогаст пошел дальше. Он полагал, что не только
у производных, но и у самих функций, служащих интегралами
уравнений, можно допустить в отдельных точках скачки. Такие функции он
называл несмежными — discontigues. Впрочем, и Арбогасту не удалось
решить все трудности, возникшие во время этой дискуссии, тогда
имевшей уже сорокалетнюю давность х).
Спор о решении волнового уравнения является одним из ярких
примеров того, как математическое естествознание порождает вопросы
глубочайшего теоретического значения, касающиеся самых оснований
математики. Комплекс этих вопросов велик и мы можем кратко
остановиться лишь на некоторых моментах истории их решения.
Аналитическая представимость функций. Ответ на вопрос, какие
функции могут быть выражены аналитически, зависит от операций,
которые допускается производить при составлении аналитических выражений
над переменными и постоянными. Подготовляя свою классификацию
функций, Эйлер в первом томе «Введения в анализ бесконечного» прежде
всего относит к действиям анализа алгебраические операции, от
сложения до решения уравнений, основные трансцендентные и интегрирование
всех элементарных функций. Затем он утверждает, что все такие
перечисленные типы функций представимы степенными рядами, мы бы сказали,
с помощью счетного множества сложений, умножений и предельного
перехода. Еще далее он включает в класс аналитических выражений
обобщенные степенные ряды. А. И. Маркушевич по этому поводу писал:
«Пользуясь современной терминологией, можно так резюмировать этот
взгляд Эйлера..., характерный для всего анализа XVIII века:
аналитически представимые функции суть функции аналитические» 2).
х) Подробнее см. И. Ю. Тимченко, Исторические сведения о развитии
понятий и методов, лежащих в основании теории аналитических функций, стр. 473 и след.;
С. Truesdell, The Rational Mechanics of Flexible or Elastic Bodies, part. III.
2) А. И. Маркушевич, Элементы теории аналитических функций, М.,
1944, стр. 22.
АНАЛИТИЧЕСКАЯ ПРЕДСТАВИМОСТЬ ФУНКЦИЙ
171
Дополняя класс употребительных в анализе функций «разрывными»
функциями Эйлер, как отмечалось, фактически вводил всевозможные
непрерывные в нашем смысле слова функции с кусочно-непрерывными
первой и второй производными, представленные под видом плоских
кривых, проведенных «свободным» движением руки. При этом Эйлер
полагал, что «разрывные» или «смешанные» функции аналитически
невыразимы и, в частности, непредставимы тригонометрическими рядами,
которые он, естественно, относил к разряду допустимых аналитических
выражений. Однако Эйлер ошибался, думая, что его «разрывные»
функции действительно «разрывны» в его же понимании этого термина. Уже
Фурье показал, что многие функции, заданные на разных участках
отрезка [а, Ь] различными формулами, могут быть представлены на этом отрезке
одним тригонометрическим рядом, т. е. одним аналитическим
выражением (1822). Ему же принадлежит первая попытка доказать теорему
о разложимости произвольной функции в тригонометрический ряд. В
действительности такое разложение возможно не для всякой функции; сам
Фурье предполагал, по существу, функцию аналитической, а такое
ограничение чрезмерно. Вскоре были предложены многочисленные другие
доказательства теоремы о разложимости функции в соответствующий ей
«ряд Фурье» для функций тех или иных весьма широких классов. Так,
Н. И. Лобачевский доказал, что теорема верна для любой непрерывной
(в нашем смысле) на отрезке [а, Ъ] функции, вторая производная которой
обращается в бесконечность лишь конечное число раз (ср. стр. 272).
Тем самым «разрывные» функции Эйлера оказались аналитически
выразимыми с помощью рядов Фурье, правда, не всюду, а на отрезке конечной
произвольной длины. Такая же теорема имеет место и для непрерывных
функций с ограниченной кусочно-непрерывной производной. Одной
непрерывности, впрочем, уже недостаточно: существуют непрерывные функции,
ряды Фурье которых расходятся на конечных и даже бесконечных
множествах точек; первый пример такого рода был построен в 1873 г. П. Дюбуа-
Реймоном.
Проблема аналитической выразимости функций имеет долгую
историю. Важным этапом явилась теорема Вейерштрасса (1886), согласно
которой всякая непрерывная на отрезке [а, Ь] функция / (х) может быть
на нем выражена как сумма равномерно сходящегося ряда целых
алгебраических многочленов Рп(х):
оо
/(*)= 2 *>.(*)•
Спрашивалось, как обстоит дело с функциями, имеющими конечное
или бесконечное множество точек разрыва? Этот вопрос подробно
исследовал в 1898 г. Р. Бэр. Построенная Бэром классификация функций
позволила решить в известном смысле проблему аналитической
выразимости функций. В 1905 г. А. Лебег доказал, что всякая функция,
аналитически выразимая при помощи счетного множества сложений, умножений
и предельных переходов, входит в классификацию Бэра и, обратно,
всякая функция, принадлежащая к этой классификации, аналитически
выразима указанным образом. Но, как показал тот же Лебег, имеются
функции, аналитически невыразимые в его смысле *).
г) Подробнее см. А. И. М а р к у ш е в и ч, Элементы теории аналитических
функций, стр. 20—32.
172 ГЛ. 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Тригонометрические ряды. В заключение скажем несколько слов
о первом этапе развития учения о тригонометрических рядах, которое
заложено было все тем же Эйлером г). Первые разложения в
тригонометрические ряды Эйлер сообщил Гольдбаху в письме от 4 июля 1744 г. Это
было записанное в несколько иной форме разложение
я х . . sin2;z . sin Зге .
___==31ПЖ+__+__ + ...
(ряд сходится при О < х < 2я) и разложение
-тг + cos х + cos 2х + cos Зх + ...
(расходящееся всюду). Оба они были включены в «Дифференциальное
исчисление», а также в первую статью по тригонометрическим рядам,
представленную Эйлером весной 1752 г. Берлинской Академии, а год
спустя — Петербургской, в «Записках» которой она и увидела свет
(NGAP V (1754—1755) 1760). В этой статье Эйлер показал, что по
известной сумме ряда
оо
2 anzn = f(z),
п=0
где ап — действительные числа и z = o,osx-\-ismx можно, приравнивая
действительные и мнимые части, найти суммы рядов
оо оо
2 а>п cos пх и 2 ап sin пх.
П=0 71=1
Для геометрической прогрессии
оо
V anzn= 1_
^—I 1 — az '
71=0
таким образом, получаются два разложения
оо оо
XI п 1 — acosx утл п . a sin х
>. ап cosпх=т-.—s—о и >, ап smпх = -г-.—ъ—^ .
ZJ i_j_a2_2a cos а; ^-1 1 + а2 — 2а cos ж
71=0 71=1
Если а= —1, то первое разложение дает
cos х — cos 2х + cos Зх — ...=—.
Интегрируя почленно последнее равенство, Эйлер вывел новое
разложение
х . sin2z , sin3;r
а вторичное интегрирование дало ему
cos 2х . cos Зх
COS?-
22 ~ З2 ' ' ' 12 4
(что верно для —я<;^<я). Сходимость полученных рядов Эйлер,
как обычно, не исследует.
*) Подробнее см. статью G. F a b е г, в кн.: L. Е и 1 е г i Opera omnia,Ser. I,
vol. XVI2, а также А. Б. Паплаускас, Тригонометрические ряды от Эйлера fro
Лебега, М., 1966.
ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ
173
В те же годы, как мы видели, Эйлер впервые применил
тригонометрические ряды к решению уравнения колебаний струны.
То обстоятельство, что тригонометрический ряд в силу своей
периодичности может представлять непериодическую функцию только на
конечном отрезке, было, разумеется, ясно с самого начала. Со всей
определенностью подчеркнул это Д. Бернулли в одной из своих более поздних
работ по рядам (NGAP XVII (1772) 1773). Здесь вновь получены
некоторые разложения, найденные раньше Эйлером, и по поводу разложения
линейной функции 4^-—2Г0В0РИТСЯ' что равенство
. sin2z . sin3;r . п х
Sina: + —g—+—g—+ . . . =-2~-J-
верно только при 0 < х < 2я, а на последующих промежутках длины 2я
сумма рядов есть (2п — 1) у —о" • Д- Бернулли отметил и скачок суммы
ряда от значения — ук у ПРИ переходе через точку х = 2я. Эти мысли
не получили, однако, в то время развития.
Первые разложения в тригонометрические ряды были найдены с
помощью частных приемов, и мы знаем, что Эйлер и Д. Бернулли долгое
время полагали, что нахождение всех коэффициентов ряда синусов,
изображающего произвольную данную функцию, превосходит возможности
математического анализа. Все же Эйлер решил и эту важную задачу,
именно в статье 1777 г., вышедшей в NAP XI (1793) 1798. Предполагая,
что / (х) разлагается на отрезке [0, дх] в ряд по косинусам (мы пользуемся
принятой теперь записью)
/(я)=-у- + 2 ancosnxi
n=l
он, умножая обе стороны равенства на cosmx и интегрируя почленно
от 0 до it, получил выражение для коэффициентов
хп = — \ / (х) cos пх dx, п = 0, 1, 2,
Все это,— указывал Эйлер,— легко прилагается и к разложению в ряд
по синусам. Тем самым Эйлер нашел формулы для разложения в
неполные ряды Фурье и значения так называемых коэффициентов Фурье,
носящие теперь имя французского математика, который вновь получил эти
результаты, показал фундаментальное значение тригонометрических рядов
для математической физики и начал разработку связанных с ними
теоретических проблем. Статья Эйлера, видимо, не была известна Фурье.
Следует добавить, что Эйлеру в свою очередь осталась неизвестной более
ранняя работа А. Клеро по небесной механике (1759), в которой уже были
опубликованы формулы коэффициентов Фурье в разложении в ряд
по косинусам.
В XVIII веке тригонометрические ряды привлекли сравнительно
небольшое внимание. Положение резко изменилось после работ Фурье,
когда изучением этих рядов занялись первоклассные математики — Коши,
Пуассон, П. Лежен Дирихле, Лобачевский, Риман, Г. Кантор и др.
Большие заслуги принадлежат и советским ученым, прежде всего Н. Н. Лузину
174 ГЛ. 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
и Д. Е. Меньшову. С развитием теории тригонометрических рядов
оказались связанными многие важнейшие открытия в области
математического анализа, как в его глубочайших основаниях — теории множеств
и теории функций действительного переменного, так и в приложениях
к естествознанию и технике. В конечном счете, истоки этого мощного
идейного потока восходят к Эйлеру и Д. Бернулли.
Вариационное исчисление. Одной из наиболее выдающихся заслуг
Эйлера в математике явилась разработка новой науки, которую он
впоследствии назвал вариационным исчислением.
Предметом вариационного исчисления является особый круг задач
о наибольших и наименьших величинах, существенно отличных от
обыкновенных задач на максимумы и минимумы, решаемых в
дифференциальном исчислении. В дифференциальном исчислении ищутся значения
аргумента, при которых принимает наибольшие или наименьшие (по
сравнению с ближайшими) значения данная функция f(x). Говоря на языке
геометрии, здесь ищутся вершины данной плоской кривой у = f(x). Эта
задача легко обобщается на функции многих переменных. В вариационном
исчислении ищутся экстремумы так называемых функционалов —
величин, значения которых определяются выбором уже не числового
аргумента, а некоторой функции или кривой (что опять-таки обобщается
на случай зависимости функционала от нескольких функций). Так,
площадь, ограниченная замкнутой и не пересекающей себя плоской кривой
данной длины, зависит от выбора этой линии. Вариационная задача об
отыскании замкнутой плоской кривой, которая при данной длине
(периметре) охватывает наибольшую площадь,— простейшая из так
называемых изопериметрических задач,— была поставлена и решена еще
древними греками. Искомой кривой является в этом случае окружность.
В конце XVII века было выдвинуто и частью решено несколько
вариационных задач. Ньютон рассмотрел вопрос о форме кривой, вращение
которой вокруг данной оси дает тело, испытывающее при движении
в жидкости в направлении этой оси наименьшее сопротивление. И.
Бернулли предложил задачу о разыскании кривой, соединяющей две не
лежащие на одной вертикали точки А и В, и обладающей тем свойством, что
падающая по ней тяжелая точка скатывается из верхнего положения
в нижнее за кратчайшее время. Братья Бернулли, Лейбниц и Ньютон
установили, что искомой кривой быстрейшего ската — брахистохроной
является циклоида. Я. Бернулли сформулировал и решил одну новую
трудную изопериметрическую задачу, а И. Бернулли предложил задачу
о геодезических линиях, т. е. об отыскании кривой кратчайшей длины,
лежащей на данной поверхности и соединяющей две какие-либо ее точки
(на шаре, скажем, такой кривой будет одна из дуг большого круга,
проходящего через две взятые точки) и нашел, что в точках геодезической
кривой ее соприкасающаяся плоскость содержит нормаль к поверхности.
Дифференциальное уравнение геодезических линий первым опубликовал
Эйлер (САР III (1728) 1732), но оно было известно и его учителю.
До Эйлера не существовало сколько-нибудь общих приемов решения
вариационных задач, которые к тому же не ставились в сколько-нибудь
общей форме. В ряде статей и затем в специальной монографии Эйлер
заложил начала вариационного исчисления как самостоятельной науки.
Монография называлась «Метод нахождения кривых линий, обладающих
свойствами максимума, либо минимума или решение изопериметрической
задачи, взятой в самом широком смысле» (Methodus inveniendi lineas
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
175
curvas maximi minimive propietates gaudentes, sive solutio problematis
isoperimetrici latissimo sensu accepti. Lausannae et Genevae, 1744).
Интересной особенностью этого сочинения является очень тесное переплетение
геометрического и аналитического изложения, от которого автор отошел
в более поздних курсах дифференциального и интегрального исчисления.
«Хотя вопросы этого рода могут быть сведены к чистому анализу, все же
полезно связать их с учением о кривых линиях. Ибо если бы мы
пожелали отвлечься от кривых линий и сосредоточить внимание на одних
только чистых величинах, то, во-первых, самые задачи стали бы
запутанными и неизящными и менее усматривался бы их практический смысл;
во-вторых, и метод разрешения такого рода вопросов, если бы он
применялся к одним только абстрактным величинам, был бы слишком запутан
и труден, тогда как рассмотрение фигур и линейное изображение величин
удивительно помогают ему и облегчают его понимание» 1). В общих
теоретических рассуждениях функции часто выступают здесь под видом
кривых линий и вне связи с каким-либо аналитическим выражением.
Фактически уже в этом сочинении Эйлер встал на путь введения
«разрывных» функций, ибо метод его основан на произвольном бесконечно малом
изменении кривой в окрестности одной или нескольких ее точек,
изменении, которое невозможно, как он утверждал позднее, без нарушения
«непрерывности» кривой 2).
Термина функционал у Эйлера нет, он появился только в XX веке,
но ему полностью соответствует выражение «формула максимума и
минимума». Первой ставится задача об отыскании проходящей через две
данные точки с абсциссами а и Ъ кривой у = f (х), сообщающей экстремум
интегралу
\z{x, y,*L,...,^)dx,
а
значения которого зависят от выбора функции у; функция предполагается
известной. Примером может служить брахистохрона с закрепленными
концами. Это задачи на абсолютный метод максимумов и минимумов,
когда кривая, дающая экстремум функционала, определяется «среди всех
вообще кривых, отнесенных к одной и той же абсциссе» 3), т. е.
определенных на одном и том же отрезке [а, Ъ]. В относительном методе
максимумов рассматривается иной класс задач, в которых экстремум функционала
ищется при дополнительном условии, наложенном на функцию у и ее
производные, или, как выражается Эйлер, только для тех кривых,
«которые имеют какое-либо наперед указанное общее свойство» 4). Таковы,
в частности, изопериметрическая задача и задача о геодезических.
Все эти понятия сформулированы в первой главе книги. Здесь же
вводятся еще два важнейших понятия, соответствующих варьированию
кривой (экстремали) в точке и вариации функционала. Для первой
операции Эйлер не имеет еще специального названия, он лишь описывает, как
производится переход от одной кривой к другой, бесконечно мало отли-
х) Л. Эйлер, Метод нахождения кривых линий, обладающих свойствами
максимума, либо минимума или решение изопериметрической задачи, взятой в самом
широком смысле, перев. Н. С. Кошлякова. М.—Л., 1934, стр. 43.
2) А. И. Маркушевич, Основные понятия математического анализа и
теории функций в трудах Эйлера, в сб.: Леонард Эйлер, М., 1958, стр. 108—109.
3) Л. Эйлер, Метод нахождения кривых линий, стр. 29.
4) Там же, стр. 31.
176 ГЛ. 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
чающейся от нее в окрестности некоторой точки (рис. 26). Вызванное
таким переходом бесконечно малое изменение функционала именуется
дифференциальным значением, соответствующим данной формуле
максимума и минимума. Устанавливается, что необходимое условие экстремума
состоит в обращении в нуль дифференциального
значения, т. е. вариации функционала.
Достаточные условия Эйлер вообще не рассматривал.
В следующей, второй главе изложен общий
метод отыскания абсолютных экстремумов. Мы
кратко поясним, следуя Эйлеру, этот метод на
примере интеграла
А
М N О
Рис. 26. Варьирование
экстремальной кривой (из
«Метода нахождения кривых
линий...» Л. Эйлера, 1744).
и
W(y)=l Z(x, y,%)dx.
Кривую y = f (х), сообщающую W(y) максимум
или минимум, Эйлер фактически рассматривает
как предельную линию, к которой стремится
последовательность ломаных Ln с вершинами в точках Мъ (xk, yh), где
Xk = а + к dx, dx = -^- , к = О, 1, 2, . . ., п.
Именно, интеграл заменяется «эквивалентной», как говорит Эйлер,
суммой вида
Wn (у0, гЛ, . . ., уп) = 2 Z (xh, yk, Щр^) dx,
h=Q
зависящей от переменных у0, уи . . ., уп. Вариация интеграла,
обусловленная вариацией кривой в точке, заменяется соответственно бесконечно
малым приращением суммы Wn, обусловленным бесконечно малым
изменением одной из ординат yk. Таким образом, дело сводится к отысканию
обыкновенного экстремума функции многих переменных Wn,— задаче,
которую Эйлер более общим образом рассмотрел в «Дифференциальном
исчислении». Если теперь какой-либо ординате yk дается бесконечно малое
приращение пи (рис. 26), в сумме
п-1
У\ Z(xk, yk, pk) dx,
k=0
где
Pk
yk+j — Uk
dx
изменяются лишь два слагаемых
Z/fr-^dx
Zkdx
(мы отмечаем с помощью индексов соответствующие значения
аргументов х, у, р, чего Эйлер не делал). Дифференциальное значение
величины Wn, эквивалентной функционалу, вычисляется при помощи
обычных правил анализа, как сумма полных дифференциалов этих
слагаемых в виде
[Nk dx — (Pk — iVO] ¦ пи = (Nk dx — dPk) • nv,
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
177
где Nh = — и Pk = ——. Условие экстремума выражается уравнением
Nfrdx—dPk = 0 или, поскольку оно должно выполняться для любой
ординаты,
ах
Мы пишем это дифференциальное уравнение второго порядка в форме
dz d (w)
ду dx
- = 0
или
d2Z d2y d2Z dy d2Z dZ _ Q
dz/'2 dx2 dy dy' dx дх ду' dy
Его общий интеграл содержит две произвольные постоянные, которые
определяются из условия, что искомая кривая проходит через две данные
точки. Приведенное уравнение, как и его обобщение на случай
функционала
ъ
\z(x, у,%, ..., g) dx,
именно
\ду' } , Уду") . , ..„ а \дУ™)
• + (-1)" Z =Q.
dy dx dx2 • • • г v. / fi^
также данное Эйлером, носят имя своего изобретателя. Для
определенности задачи в общем случае требуется задание 2п добавочных условий,
по которым определяются все произвольные постоянные, входящие
в общий интеграл уравнения порядка 2п, например, задание 2п точек,
через которые должна пройти искомая экстремаль.
Таким образом, отыскание экстремума функционала указанного вида
приводится к решению обыкновенных дифференциальных уравнений.
В главе V Эйлер изложил относительный метод максимумов и
минимумов, позволяющий свести эту задачу к нахождению абсолютного
экстремума. Здесь, среди прочего, исправлена ошибка Я. Бернулли, который
полагал, что кривая, которой присуще некоторое свойство максимума
или минимума, обладает им в любых сколь угодно малых своих частях.
Эйлер ранее стоял на той же точке зрения, теперь он показал, что принцип
Бернулли имеет ограниченную сферу действия. Все изложение снабжено
множеством превосходных примеров и задач из области геометрии и
механики.
К основному тексту книги добавлены два приложения, содержащие
применения вариационного исчисления к теории упругости и движению
тел в среде без сопротивления. В начале первого приложения Эйлер
высказывает метафизический принцип, согласно которому «в мире не
происходит ничего, в чем не был бы виден смысл какого-нибудь максимума
или минимума; поэтому нет никакого сомнения, что все явления мира
с таким же успехом можно определить из причин конечных при помощи
метода максимумов и минимумов, как и из самых причин производящих» х).
г) Л. Эйлер, Метод нахождения кривых линий, стр. 447.
178 ГЛ.9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Но далее идут совершенно конкретные вещи: решается задача об изгибе
однородной упругой пластинки, в которой требуется найти экстремум
интеграла
ds
Ж'
где R — радиус кривизны кривой изгиба, выведено и подробно
исследовано уравнение упругой линии, получена известная в учении о
сопротивлении материалов формула для определения критической нагрузки,
допускаемой без изгиба колонной данной высоты и с данным коэффициентом
упругости, и, наконец, рассмотрен изгиб неоднородной упругой
пластинки. Во втором приложении Эйлер впервые точно сформулировал принцип
наименьшего действия, решив тем самым вопрос, поставленный перед
ним в 1741 г. Д. Бернулли: можно ли исследовать орбиты, описываемые
телом под действием центральных сил, посредством «изопериметрическо-
го» метода? Эйлер дал утвердительный ответ, показав, что движение
совершается по траекториям, которые сообщают наименьшее значение
интегралу
Mvds,
где М— масса тела и v— его скорость. На этой основе Эйлер решает
несколько задач1).
Вслед за Эйлером вариационным исчислением занялся Лагранж.
Существенным нововведением, которое легло в основу алгоритма
варьирования, было обозначение изменений, претерпеваемых величинами при
переходе от одной кривой к другой, бесконечно близкой, специальной
характеристикой б, для отличия от знака d, выражающего изменения
величин при бесконечно малом перемещении вдоль одной и той же
кривой. Лагранж без доказательства установил основные правила операций
над символом б, совпадающие с правилами обыкновенного
дифференцирования, и, опираясь на переместительность б и d (также не обоснованную)
и интегрирование по частям, дал очень простой аналитический вывод
ъ
вариации интеграла \ F (х, г/, j-, . . ., ^-|J dx и уравнения Эйлера.
а
Свои первые результаты Лагранж сообщил в письме от 12 августа 1755 г.
Эйлеру, который немедленно оценил значение нового алгорифма,
позволявшего дать общее аналитическое выражение прежним способам,
опиравшимся на геометрически-инфинитезимальные рассмотрения. В ответном
письме от 6 сентября, горячо поддержав своего молодого корреспондента,
которому не было и 20 лет, Эйлер отметил следующую особенность
варьирования по Лагранжу. Тогда как Эйлер, переходя от искомой кривой
к соседней, изменял одну или несколько ординат, Лагранж изменяет все
ординаты сразу. Эйлер советовал Лагранжу продолжать исследования
и сам с увлечением занялся разработкой нового метода. Вскоре он
продвинулся далеко, но терпеливо выжидал с публикацией, чтобы не перебить
дорогу молодому ученому. Через семь лет появилась первая статья Лаг-
ранжа (1762). Кратко и совершенно формально описав принципы
алгоритма варьирования, Лагранж знакомил с его первыми приложениями.
При этом был разобран ряд новых вопросов: экстремумы с подвижными
г) Об истории принципа наименьшего действия и роли Эйлера в его разработке
см. сб.: «Вариационные принципы механики», под ред. Л. С. Полака, М., 1959.
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
179
концами, одна задача на экстремум двойного интеграла. Тогда же Лагранж
опубликовал большую статью, в которой принцип наименьшего действия
распространялся на систему тел и открывались новые перспективы
приложения вариационного исчисления в динамике. Однако эти первые
публикации Лагранжа не обратили на себя должного внимания из-за
чрезмерной сжатости и трудности изложения начал. Вариационный алгоритм
Лагранжа получил известность, прежде всего, благодаря Эйлеру.
В томе X NCAP (1764) 1766 Эйлер дал собственное, очень подробное
и ясное изложение нового метода, трактуя его как новую отрасль анализа,
как новое исчисление, которому присвоил имя вариационного. В частности,
он впервые доказал основные равенства 8dy = dSy и б\И^= \ 8W1).
В томе III «Интегрального исчисления» Эйлер поместил обширное
«Приложение о вариационном исчислении». Здесь было впервые выведено
общее необходимое условие абсолютного экстремума двойного интеграла
с постоянными пределами, которое Лагранж получил лишь в одном
частном случае, именно в задаче о минимальных поверхностях 2). В
простейшем случае интеграла
Ь d
dz dz
^ J V(z, г/, z, p, q)dxdy, где p--
dx ' У ~dy
искомая функция (поверхность) z = f (х, у), которая может сообщить
ему экстремальное значение, должна удовлетворять уравнению в частных
производных второго порядка (типа Монжа — Ампера)
dz dx \ dp ) dy \ dq )
Вопроса о краевых условиях, служащих для выделения среди всех
решений уравнения искомого, Эйлер коснулся мельком. В качестве примера
он взял задачу об отыскании минимальной поверхности, под которой
Ъ d
на плоскости хОу находится данный объем, так что интеграл \ Kzdxdy
а с
задан. Решение возникающего при этом эллиптического нелинейного
уравнения превосходило возможности тогдашней математики и Эйлер
отметил только, что уравнение выполняется для отдельных классов
поверхностей второго порядка.
Эйлер ограничился двойными интегралами с постоянными пределами
и случай переменных пределов интегрирования оставил в стороне. Дело
в том, что при вычислении вариаций частных производных функции
z (х, у) он ошибочно получил для б д—т- и S^-o- два различных выражения
вместо одного (как потом выяснилось, оба неверных) и, во избежание
этого противоречия, принял, что Ьх не зависит от у, а 8у не зависит от х.
Поэтому формулы Эйлера для вариаций частных производных оказались
г) В своих работах по вариационному исчислению Эйлер и Лагранж фактически
оперировали только слабыми вариациями, считая бесконечно малой вместе с 6у и ду'.
Так называемые сильные вариации, при которых бесконечно малому перемещению
точки соответствует конечный поворот касательной, не рассматривались.
2) То есть задачи об отыскании среди всех поверхностей, проходящих через
данный пространственный контур, поверхности с наименьшей площадью. Лагранж вывел
дифференциальное уравнение в частных производных для таких поверхностей;
впоследствии их изучали многие.
180 ГЛ. 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
непригодными для отыскания вариации двойного интеграла с
произвольными переменными пределами. Только много спустя Пуассон
распространил результаты Эйлера на общий случай двойного интеграла.
Еще через несколько лет Эйлер предложил другой способ
построения вариационного исчисления, который сам назвал «легким» [NGAP XVI
(1771) 1772; также в томе IV «Интегрального исчисления»]. Здесь были
заложены начала трактовки операции варьирования, которая
впоследствии стала употребительной. Функции (кривые), среди которых ищется
та, которая сообщает экстремум данному однократному интегралу,
представляются в виде семейства, зависящего от одного параметра у = у (х, t);
предполагается, что искомая функция получается при t = t0. Этой
кривой соответствует вариация
Таким образом варьирование оказывается дифференцированием по
параметру с последующим предположением, что t = t0. На этом пути весьма
просто выводятся основные формулы вариационного исчисления, в
частности, переместительность операций дифференцирования и варьирования.
Решение дифференциальных уравнений, выражающих необходимые
условия экстремума функционалов, во многих случаях наталкивается
на практически непреодолимые трудности. В этой связи примечательно,
что первый конечно-разностный метод, с помощью которого Эйлер вывел
свое дифференциальное уравнение, сам заключает возможности как
приближенного, так и точного решения вариационных задач. Такие
«прямые» методы, в которых вариационная задача трактуется, как
предельная для задачи на обыкновенный экстремум функции конечного
числа переменных, получили большое развитие в XX веке. Более того,
эти методы доставляют прием решения проблем теории
дифференциальных уравнений путем приведения их к соответствующим вариационным
задачам, которые затем решаются с помощью прямых методов. Первым
по времени является прямой метод Эйлера, который, извлеченный из
забвения и усовершенствованный, излагается теперь во многих учебных
руководствах. Весьма употребителен также метод, предложенный в 1908 г.
В. Ритцем, а затем обоснованный и развитый далее советским ученым
Н. М. Крыловым в 1918 и следующих годах.
Нам еще придется говорить о вариационном исчислении в связи
с работами М. В. Остроградского об экстремумах кратных интегралов г).
г) Подробнее см. К. А. Р ы б н и к о в, Первые этапы развития вариационного
исчисления,— Ист.-матем. исслед., вып. II, 1949, и А. В. Дорофеева, Развитие
вариационного исчисления, как исчисления вариаций.— Ист.-матем. исслед.,
вып. XIV, 1961.
ГЛАВА ДЕСЯТАЯ
ДРУГИЕ МАТЕМАТИЧЕСКИЕ РАБОТЫ Л. ЭЙЛЕРА
Элементарная геометрия и тригонометрия. Хотя Эйлер был по
преимуществу арифметиком и аналистом, ему принадлежат работы почти
во всех областях современной ему геометрии, правда, в большей части
основанные на применении алгебры и анализа. Он не пренебрегал и
элементарными задачами. Примерами могут служить уже упоминавшаяся
его теорема о том, что сумма квадратов четырех сторон четырехугольника
равна сумме квадратов обеих диагоналей, сложенной с учетверенным
квадратом отрезка, соединяющего середины диагоналей [NCAP I (1747—
1748) 1750] и теорема: точки пересечения высот, центр тяжести и центр
описанного круга любого треугольника лежат на одной прямой [NCAP
XI (1765) 1767]. Несколько работ Эйлера относятся к геометрии на сфере
и аналитическому построению сферической тригонометрии. Последнее
Эйлер выполнил двумя способами: во-первых, трактуя стороны
сферических треугольников как геодезические, т. е. средствами
вариационного исчисления [Mem. Ac. Berlin, IX (1753) 1755], а во-вторых, на
элементарной основе [АР (1779 : 1) 1782]. Во второй статье впервые
выведена полная система основных формул сферической тригонометрии.
О заслугах Эйлера в плоской тригонометрии говорилось ранее.
Аналитическая геометрия. Аналитической геометрии посвящен весь
второй том «Введения в анализ бесконечных». Здесь в первый раз было
последовательно реализовано то стремление к алгебраическому
исследованию кривых и поверхностей, которое наметили еще Декарт и Ферма,
и постепенно проводили в жизнь их последователи в течение целого
столетия. В предисловии, помещенном в первом томе труда, Эйлер писал:
«я не пользуюсь (во II томе.— А. Ю.) никакими другими средствами,
кроме уравнения, выражающего природу той или иной кривой линии,
и показываю, как из этого уравнения можно вывести как фигуру кривой,
так и ее основные свойства» х); точно так же изучаются и поверхности.
Книга начинается с некоторых общих рассуждений о природе
функций и кривых линий, которых нам приходилось отчасти касаться; за этим
следует вывод формул преобразования координат, которые впервые
предстают в современной записи, и общего уравнения прямой. Классификация
алгебраических кривых сопровождается разбором основных свойств
линий любого порядка, например, о числе точек, определяющих кривую
га-го порядка,— вопроса, который Эйлер более подробно рассмотрел
тогда же в специальной статье (Mem. Ac. Berlin, IV (1748) 1750). После
этого Эйлер переходит к кривым второго порядка. Алгебраически иссле-
!) Л. Эйлер, Введение в анализ бесконечных, т. I, стр. 21.
182 ГЛ. 10. ДРУГИЕ МАТЕМАТИЧЕСКИЕ РАБОТЫ Л. ЭЙЛЕРА
дуя общее уравнение кривых второго порядка, которое пишется в виде
7/2 i (гх + У)У , frr2 + [fo + a _ п
У -h с -h с -и,
Эйлер строит теорию диаметров, центра, касательных и т. д., попутно
по-новому доказывая ряд теорем Декарта и Ньютона. С помощью
преобразования координат общее уравнение приводится к форме
г/2 = а + Р# + 7^2
и, в зависимости от условий у > 0, 7 < 0» У = 0» определяющих наличие
и характер бесконечных ветвей или их отсутствие, кривые второго
порядка подразделяются на гиперболы, эллипсы и параболы, свойства которых
изучаются с большой подробностью. Изложение, как всегда у Эйлера,
очень ясно, хотя еще во многом отличается от принятого в наших
учебниках. Например, записав уравнение эллипса относительно вершины
у> = 2сх-е{2*-е) х*
(с — полупараметр, d — расстояние фокуса от вершины), Эйлер
переходит к параболе, полагая 2d = с, причем оси эллипса становятся
бесконечно большими. После этого он выводит ряд свойств параболы,
рассматривая ее как бесконечно растянутый эллипс.
Далее Эйлер детально исследует вопрос о бесконечных ветвях и
асимптотах алгебраической кривой п-то порядка, применяя разложение на
множители совокупности старших членов уравнения, имеющих относительно
обеих координат измерение п. Здесь он попутно замечает, что общее
уравнение 2-й степени п
ау2 + §ху + ух2 + 6 у + гх + ? = 0
при P2<4(xy представляет эллипс, а при P2>4c&y гиперболу (ср. стр.88).
Однако учение об инвариантах кривых второго порядка не получило еще
у Эйлера какого-либо развития и осталось на долю геометров XIX века.
Теория бесконечных ветвей и асимптот затем используется для
классификации кривых третьего порядка, глубоко изученных еще Ньютоном
и его последователями, а также для классификации кривых четвертого
порядка, впервые успешно разработанной только Эйлером. Исследуется
также кривизна линий, причем используются лишь алгебраические
средства, и некоторые виды особых (кратных) точек кривых. Здесь
заметим, что с помощью простого примера у = У~х ± "j/я3 Эйлер показал
ошибочность мнения некоторых математиков, которое одно время
разделял и сам, будто алгебраические кривые не могут иметь тЬчек возврата
2-го рода. Наконец, рассмотрены условия, при которых плоские кривые
имеют одну или несколько осей симметрии, а также преобразования
подобия, определяемые формулами х = X/m, y = Y/m и аффинные
преобразования x = X/m, y = Y/n. Особая глава посвящена наиболее
употребительным трансцендентным кривым, и среди них кривой с уравнением
ху = ух, которая двадцатью годами ранее фигурировала в переписке
Д. Бернулли и Гольдбаха. Включение трансцендентных линий в курс
аналитической геометрии было методическим новшеством, как и широкое
применение в нем полярных координат (для спиралей, конхоиды и т. д.).
К основному тексту Эйлер добавил приложение о поверхностях. Эта
область геометрии была в то время почти не разработана. Первое
уравнение поверхности — параболоида вращения — появилось только в 1679 г.
у Ф. де Лагира, а после него можно отметить отдельные достижения
немногих ученых, среди них Я. Германа и А. Клеро, о которых
говорилось выше. Эйлер занялся вопросами пространственной геометрии и тео-
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТЕЙ 183
рии поверхностей одновременно с двумя последними математиками,
и, например, в его статье о геодезических линиях речь идет об отдельных
классах поверхностях вращения, цилиндрических и конических. Во
втором томе «Введения» те же и некоторые другие общие классы
поверхностей трактуются более общим образом. Впрочем, главное внимание
уделено квадрикам, т. е. поверхностям второго порядка. Форма
поверхностей исследуется с помощью их плоских сечений. Для упрощения общего
уравнения квадрики выводятся формулы преобразования координат,
причем поворот осей определяется тремя углами, сохранившими до сих пор
название углов Эйлера. Совокупность старших членов общего
уравнения квадрики
az2 + $yz + yxz + by2 + гху + ?>х2 + щ + 0г/ + ix + к = О
в силу однородности уравнения
az2 + (Зг/z + yxz + бг/2 + гху -\-?)х2 = 0
принадлежит так называемому асимптотическому конусу, пользуясь
которым, Эйлер характеризует поведение квадрики в бесконечности, подобно
тому как с помощью асимптот изучаются бесконечные ветви кривых.
Канонические уравнения невырожденных квадрик получаются в форме,
мало отличной от принятой ныне. Уравнение
Ap2 + Bq2 + Cr2 + K = 0
при тех или иных комбинациях знаков соответствует эллипсоиду, эллипти-
ко-гиперболической и гиперболико-гиперболической поверхностям (наши
однополостный и двухполостный
гиперболоиды), а уравнение
Ар2 ± Bq2 = аг
—эллиптико-параболическим и
параболически-гиперболическим
поверхностям (наши эллиптический и
гиперболический параболоид);
учитываются соответствующие конусы
и цилиндры. Описание
поверхностей кратко и нет указаний на
системы прямолинейных
образующих однополостного гиперболоида
и гиперболического параболоида,
который рассмотрен здесь,
по-видимому, впервые. Впрочем, две
прямые, лежащие в пересечении
последнего с плоскостью г = 0, указаны
(на рис. 27 это прямые Ее, Ff).
Приложение заканчивается краткими замечаниями о пространственных
кривых, к изучению которых первым приступил А. Клеро в «Исследованиях
о кривых двоякой кривизны» (Recherches sur les courbes a double courbure,
Paris, 1731). Термин «кривая двоякой кривизны» ввел в 1726 г. А, Пито.
Дифференциальная геометрия поверхностей. Первые исследования
по дифференциальной геометрии были неразрывно связаны с разработкой
дифференциального исчисления. К концу XVII века удалось решить
основные задачи: определение касательных и нормалей к плоской кривой,
ее экстремумов, точек перегиба и заострения, радиуса кривизны и
соприкасающегося круга, эволют и огибающих семейства кривых. Клеро
Рис. 27. Различные плоские сечения
«параболически-гиперболической
поверхности», по Л. Эйлеру (из второго тома
«Введения в анализ бесконечных»,
Лозанна, 1748).
184 ГЛ. 10. ДРУГИЕ МАТЕМАТИЧЕСКИЕ РАБОТЫ Л. ЭЙЛЕРА
приступил к изучению пространственных кривых, рассматривая их как
пересечения поверхностей; он привел для кривой двоякой кривизны
формулу дифференциала дуги и подкасательной. Эйлер встретился с задачами
дифференциальной геометрии на первых же порах деятельности, в
частности, в связи с задачей о геодезических линиях. Ряд задач этой науки
он решил в ходе занятий механикой, изучая несвободное движение
точки по поверхности, а также в связи с картографией. Но он посвятил
дифференциальной геометрии и ряд специальных работ, имевших
основоположное значение.
К таким работам относится прежде всего статья о кривизне
поверхностей в томе XVI Mem. Ac. Berlin, (1760) 1767, с которой собственно
и начинается дифференциальная геометрия поверхностей. Эйлер прежде
всего выводит формулу радиуса кривизны произвольного плоского
сечения поверхности, затем переходит к случаю нормального сечения (т. е.
сечения, проходящего через нормаль к поверхности в данной точке),
устанавливает существование двух экстремальных сечений, лежащих
в двух взаимно-перпендикулярных плоскостях и, наконец, дает
выражение радиуса кривизны г любого нормального сечения через
наибольший и наименьший радиусы / и g:
f + g — (f — g)cos2cp *
здесь ф — угол между этим нормальным сечением и одним из
экстремальных направлений. Результаты Эйлера были развиты в школе Мон-
жа, особенно Ж. Менье, теорема которого (1776, опубл. в 1785) наряду
с теоремой Эйлера приводится во всех современных учебниках, и Ш.
Дюпеном, который, в частности, сообщил формуле Эйлера употребительный
ныне вид. Введение понятия полной кривизны поверхности явилось уже
заслугой Гаусса (1827).
В следующей важной работе Эйлера изучены развертывающиеся
поверхности, которые можно наложить на плоскость без складок и
разрывов [NCAP XVI (1771) 1772]. Таковы, например, цилиндры и конусы.
Эйлер доказывает существование бесчисленного множества других
развертывающихся поверхностей, и выводит условия развертываемости.
Отправным пунктом служит положение, что бесконечно малый
треугольник на такой поверхности должен быть конгруентен соответствующему
треугольнику на плоскости. Здесь впервые вводится и используется
линейный элемент поверхности и впервые же декартовы координаты
x,y,z точек поверхности выражены в функции двух параметров t, и; вновь
так их выразил Гаусс, со времени которого эти «гауссовы» координаты
вошли в общее употребление. Окончательный результат данной работы
Эйлера состоит в том, что касательные к любой пространственной кривой
образуют развертывающуюся поверхность; кроме таких поверхностей,
развертываются на плоскость еще лишь цилиндрические и конические
поверхности. В более поздней статье 1776 г. [NAP VI (1788) 1790] Эйлер
изучил поверхности, которые получаются при движении центра данного
круга вдоль плоской кривой, если плоскость круга при этом все время
перпендикулярна к кривой в соответственной точке. Эйлер назвал такие
поверхности «искривленными цилиндрами», теперь их именуют
трубчатыми. Эйлер приступил также к изучению кривизны пространственных
кривых [АР (1782 : 1) 1786] и нашел первую из трех формул, данных
в 1847 г. Ж. Френе; эта формула устанавливает зависимость между
направляющими косинусами касательной и главной нормали и кривизной линии.
ТЕОРИЯ ЧИСЕЛ
185
Труды Эйлера по теории поверхностей были особенно успешно
продолжены Монжем и затем Гауссом. К сожалению, один из наиболее
замечательных результатов Эйлера оставался неизвестным почти сто лет
и увидел свет только в томе I Opuscula postuma, 1862. Он содержится
в заметке, написанной около 1770 г. и в современных обозначениях
гласит, что две поверхности наложимы одна на другую, если у них равны
коэффициенты Е, F, G первой дифференциальной квадратичной формы
Гаусса для линейного элемента. Эти условия были снова получены
Гауссом в его классической работе по теории поверхностей (1827), о которой
мы уже упоминали и которая еще встретится нам далее.
К Эйлеру восходит и так называемая естественная геометрия
плоских кривых, в которой свойства кривых изучаются с помощью
уравнений между величинами, непосредственно принадлежащими самим кривым,
например, между длиной дуги и радиусом кривизны. Эйлер применил
естественные координаты плоской кривой еще в САР VIII (1736) 1741.
Этим кругом вопросов занимался также Н. И. Фусс. В конце прошлого
века естественная геометрия получила широкое развитие у Э. Чезаро
и других.
Топологические задачи. Наконец, Эйлеру принадлежат первые
исследования по топологии,— науке, в которой изучаются свойства фигур,
не меняющиеся при любых взаимно однозначных и взаимно непрерывных
(или топологических) преобразованиях. Такова решенная им задача
о переброшенных через несколько рукавов реки мостах, которые
требуется перейти все, причем каждый не более чем один раз [САР VIII
(1736) 1741]; она вошла во многие занимательные книги по математике.
Но главный результат Эйлера в этой области относится к теории
многогранников [NCAP IV (1752—1753) 1758]. Здесь среди многих теорем
о свойствах и условиях существования многогранников Эйлер
формулирует и доказывает предложение, впервые высказанное им в письме к
Гольдбаху от 14 ноября 1750 г.: число вершин S, ребер А и граней Н любого
многогранника (предполагаемого выпуклым) связаны равенством
S + H = A + 2.
Равенство сохраняется для всех фигур, которые можно топологически
преобразовать в выпуклые многогранники. Эта теорема Эйлера (без
вывода встречающаяся в бумагах Декарта, опубликованных в 1860 г.)
явилась одним из первых предложений топологии, которая стала
складываться в самостоятельную науку лишь с середины XIX века. Число
S — A -f- Н, называемое теперь эйлеровой характеристикой, есть
основной топологический инвариант многогранника и играет важную роль
в исследовании общих свойств поверхностей1).
Теория чисел. Эта наука неизменно привлекала интерес крупнейших
математиков мира, начиная с древнейших времен, когда круг ее
интересов был еще ограничен только целыми числами. Древние греки
разработали важные алгоритмы разыскания общего наибольшего делителя
и общего наименьшего кратного, выявили существование простых чисел,
т.е. чисел, отличных от 1 и не имеющих делителей, кроме 1 и самих себя.
х) Подробнее см. Б. Н. Делоне, Эйлер, как геометр. В сб.: Леонард Эйлер,
М., 1958; Б. А. Розенфельд, Геометрические преобразования в работах
Леонарда Эйлера.— Ист.-матем. исслед., вып. X, 1957.
186 ГЛ. 10. ДРУГИЕ МАТЕМАТИЧЕСКИЕ РАБОТЫ Л. ЭЙЛЕРА
Простые числа 2, 3, 5, 7, 11, 13, 17, 19, . . ., из которых путем
перемножения получаются все остальные натуральные числа, привлекали особое
внимание ученых. Древность оставила, однако, только два
фундаментальных результата в учении о простых числах, которые оба содержатся
в «Началах» Евклида. Одним из них было утверждение, что любое
натуральное число единственным образом, если отвлечься от порядка,
разлагается в произведение простых сомножителей. Другое предложение
гласило, что число простых чисел неограниченно велико. Современник
Евклида Эратосфен предложил всем известный способ составления
таблицы простых чисел («решето Эратосфена»). Видное место в античной теории
чисел занимало также решение неопределенных уравнений. Не позднее
V века до н. э. удалось найти полную систему целых решений уравнения
х2 -)- у2 = z2, т. е. построить прямоугольные треугольники со сторонами,
выражающимися целыми числами. Весьма остроумные приемы решения
в рациональных числах неопределенных уравнений первых трех степеней
изложены в «Арифметиках» Диофанта, жившего примерно в III веке.
Это сочинение оказало большое влияние на возрождение интереса к
теории чисел в XVII веке. Неопределенные уравнения изучались также
в Древнем Китае (задача об остатках) и Индии (уравнения первой и
второй степени), а также в странах ислама и в средневековой Европе.
Систематические работы по теории чисел начались только в XVII
и XVIII вв. благодаря трудам Ферма и особенно Эйлера. Ферма не
оставил доказательств многих высказанных им теорем, и эти доказательства
в ряде случаев были даны Эйлером, сделавшим также много новых
фундаментальных открытий. «Открытия Фермата, — писал П. Л. Чебышев,—
служили только вызовом геометрам на изыскания в теории чисел. Но,
несмотря на весь интерес этих изысканий, до Эйлера на них никто не вызывался.
И это понятно: эти изыскания требовали не новых приложений приемов,
уже известных, и не новых развитии приемов, прежде употреблявшихся;
эти изыскания требовали создания новых приемов, открытия новых начал,
одним словом, основания новой науки. Это сделано было Эйлером» г).
Теории чисел Эйлер посвятил почти полтораста работ и
значительную часть научной переписки. Особенно интересна переписка Эйлера
с Гольдбахом, по которой можно проследить за становлением и
развитием многих арифметических идей великого математика.
Среди утверждений Ферма, сообщенных им без вывода, важное место
занимает так называемая теперь малая теорема Ферма, одна из основных-
в современной теории сравнений, в которой изучаются вопросы делимости
чисел. По отношению к данному числу т, рассматриваемому как
делитель, все числа можно разбить на т классов вида
km, кт-{-1, кт-\-2, ..., кт-{-(т—1),
где к — любое число. Два числа одного и того же класса, а и Ь,
характеризуются тем, что их разность а — Ъ делится на т, т. е. а — Ъ = пт.
Такие два числа называются сравнимыми по модулю т и этот факт
записывается сравнением
а = Ъ (mod т),
причем говорят, что а есть вычет Ъ или Ъ есть вычет а по модулю т. Слова
вычет и невычет (по-латыни residuum и поп residuum) ввел еще Эйлер,
а термин сравнение (congruentia) и его знак принадлежат Гауссу, кото-
х) П. Л. Чебышев, Полное собрание сочинений, т. I, М., 1944, стр. 10.
ТЕОРИЯ ЧИСЕЛ
187
рый разработал аппарат теории сравнений (1801), оказавшийся
чрезвычайно удобным, особенно потому, что сравнения по своим свойствам
подобны равенствам.
Малая теорема Ферма гласит, что если р простое и а не делится
на р, то а?'1 — 1 делится на р, т. е. а?'1 = 1 (mod р). Эйлер дал два
доказательства теоремы [САР VIII (1736) 1741; NCAP VII (1758-1759) 1761]
и затем ее обобщение: если функция ср (т) обозначает число чисел,
меньших и взаимно простых с т, то а® <т> = 1 (modт) [NGAP VIII
(1760-1761) 1763].
Ферма нашел, что всякое простое число вида in -\-1 есть сумма
двух целых квадратов или, как говорят, представимо формой х2 -|- у2.
В ходе доказательства этой теоремы Эйлер пришел к рассмотрению
остатков от деления на простое число р последовательности квадратов чисел
и так называемых квадратичных вычетов; как раз в этой работе
появились и слова вычет и невычет [NCAP V (1754—1755) 1760]. Если
двучленное сравнение второй степени х2 = а(то&т) имеет решение, т. е.
существует такое х, что х2 — а делится на т, то а называется квадратичным
вычетом по модулю т; если решения нет, то говорят, что а —
квадратичный невычет. Например, 5 есть квадратичный вычет по модулю
11, так как 42 — 5 делится,на 11, а 7 есть невычет по модулю 11, так как
х2 — 7 ни при каком целом х не делится на 11. Особую важность имеют
квадратичные вычеты по простому нечетному модулю. Аналогично
вводится понятие вычетов более высокой степени.
Эйлер заложил начала общей теории степенных вычетов и открыл,
хотя и не доказал, основной в теории квадратичных вычетов закон
взаимности (1772, опубл. в Opuscula analytica, 1, 1783). Этот закон
устанавливает, для каких нечетных простых чисел р данное нечетное простое
число q служит квадратичным вычетом. Именно, если хотя бы одно из
чисел р и q имеет вид in -\-1, то q будет квадратичным вычетом или
невычетом р, смотря по тому, будет ли р квадратичным вычетом или
невычетом q; если же оба они вида in +3, то q есть квадратичный вычет или
невычет р, смотря по тому, будет ли р квадратичный невычет или вычет q.
Например, пусть р = 11, q = 5; тогда 5 есть вычет по модулю 11 и вместе
с тем 11 — вычет по модулю 5. А если взять р = 11, q = 7, то 11 есть
вычет по модулю 7, так как 52 — 11 делится на 7, между тем, как было
сказано, 7 есть невычет по модулю 11.
Это открытие Эйлера оставалось незамеченным, пока на него не
указал в 1849 г. Чебышев. Квадратичный закон взаимности был вновь найден
Лежандром (1785) и доказан Гауссом (1801); он имеет фундаментальное
значение в теории делимости. Дальнейшие исследования в этом
направлении привели к созданию теории алгебраических чисел, лежащей на
стыке между теорией чисел и алгеброй. Квадратичный закон взаимности
получил широкие обобщения — у Гаусса на биквадратичные вычеты,
у Э. Куммера — на поля деления круга и т. д. В наиболее общей форме —
для любых полей алгебраических чисел — закон взаимности был
установлен в 1950 г. советским математиком И. Р. Шафаревичем.
Отправляясь от упомянутой проблемы Ферма о простых числах вида
in -|-1, Эйлер рассмотрел вопрос о представлении простых, а также
составных чисел и другими квадратичными формами вида ах2 -f- су2
и использовал свойства этих форм для исследования того, является ли
данное большое число N простым или составным. Более общей трактовке
бинарные формы с двумя переменными ах2 -f- 2bxy -f- су2 подверг Лаг-
ранж. К трудам обоих ученых восходит обширная теория квадратичных
188 ГЛ. 10. ДРУГИЕ МАТЕМАТИЧЕСКИЕ РАБОТЫ Л. ЭЙЛЕРА
форм, о которой нам еще придется говорить в связи с работами ряда
представителей школы П. Л. Чебышева.
Большое место в арифметических изысканиях Эйлера занимает
решение неопределенных уравнений. Мы уже упоминали, что он указал общий
прием решения древней задачи об остатках, которую можно выразить
системой линейньгх сравнений с различными попарно взаимно простыми
модулями
х = а>1 (mod mi), х = а2 (mod т2), ..., х = ak (mod mk)
[GAP VII (1734 — 1735) 1740]. Полный анализ вопроса дал Гаусс.
С помощью непрерывных дробей Эйлер исследовал задачу о решении
уравнения
х2 — dy2 = 1,
где d — неквадратное число [NCAP XI (1765) 1767]. Отыскание
наименьшего решения этого уравнения, которым до того, не говоря о древних
и индийцах, занимались Ферма и Валлис, Эйлер поставил в зависимость
от разложения в непрерывную дробь Y~d, причем указал на
периодичность такой дроби,— факт, вскоре доказанный Лагранжем. Решение
общего уравнения второй степени с двумя неизвестными
ах2 + Ъху -f су2 + dx -f- еу + / = 0
тесно связано с решением только что указанного частного случая; и здесь
изыскания Эйлера были завершены Лагранжем.
Особенной известностью пользуется в широких кругах так
называемая великая теорема Ферма: уравнение хп -\-yn = zn при п>3
и xyz ^0 не имеет целых решений. Ферма утверждал, что располагает
доказательством этого предложения, но его не оставил. Эйлер доказал
теорему по методу неограниченного спуска, принадлежащему Ферма,
для п = 4 (что было сделано, впрочем, еще в XVII в.) и для п = 3 [NCAP
VIII (1760—1761) 1763]. В этом втором случае Эйлер впервые рассмотрел
выражения вида a -f- b]f— 3, где а и Ъ — натуральные числа, как своего
рода целые числа,— прием, обобщенный затем Гауссом, Куммером и др.
творцами теории алгебраических чисел. В значительной части эти
исследования были связаны с пр од о лжавшимися усилиями доказать великую
теорему Ферма.
Наконец, к Эйлеру восходят первые применения в теории чисел
аналитических методов, которые он использовал в некоторых вопросах так
называемого partitio numerorum, т. е. в аддитивных задачах о
разложениях чисел в суммы чисел того или иного вида. В 1740 г. берлинский
математик Ф. Ноде поставил перед Эйлером вопрос: сколькими
различными способами можно данное число N представить суммами к равных
или неравных чисел? Эйлер привел решение в томе I «Введения в анализ
бесконечных». Оно основано на разложении некоторых бесконечных
произведений в бесконечные ряды, коэффициенты которых и дают ответ
на поставленные вопросы. Например, в разложении
1 = 1 + х + 2х2 + Зх3 + 5я4 + 7х5 + 11х6 + 15х7+ ...
П (1 —хП)
71=1
каждый коэффициент показывает, сколькими способами можно
представить в виде суммы равных или неравных чисел показатель степени х;
ТЕОРИЯ ЧИСЕЛ
189
так, число 7 представимо таким образом 15 способами. Мы уже
говорили, что знаменатель только что написанной дроби разлагается в ряд
[] (1-х")= 2 (-!)*•* 2 •
71=1 fe= — оо
Эта формула теории тэта-рядов также применяется к анализу
рассматриваемых вопросов. С ее же помощью Эйлер вывел важную рекуррентную
формулу для определения суммы делителей данного числа N, впервые в
письме к Гольдбаху от 1 апреля 1747 г. [NGAP V (1754—1755) 1760].
В переписке с Гольдбахом Эйлер, по-видимому, впервые поставил
вопрос, насколько часто встречаются в ряду натуральных чисел простые
числа: 28 октября 1752 г. Эйлер отмечает, что число простых, меньших
данного N, примерно есть In N. Эта оценка оказалась довольно грубой.
Но Эйлер же, как говорилось, дал те аналитические средства, которые
оказались основными в дальнейшем исследовании этой проблемы: дзета-
функцию и интегральный логарифм. Наконец, в развитии аналитической
теории чисел важную роль сыграло выдвинутое Эйлером предположение,
что во всякой бесконечной арифметической прогрессии со взаимно
простыми первым членом и разностью содержится бесконечно много простых
чисел (Opuscula analytica, 11, 1783). Эту теорему доказал в 1837 г.
Дирихле.
Нельзя пройти также мимо заслуг Эйлера в изучении
арифметической природы некоторых замечательных постоянных и в постановке
проблем теории трансцендентных чисел. Установленная им зависимость
между числами е и я и разложения е в бесконечные непрерывные дроби
имели решающее значение для доказательства иррациональности обоих
этих чисел И. Ламбертом (1768), а первая названная зависимость — для
доказательства Ф. Линдеманом трансцендентности я (1882). Как мы
знаем, Д. Бернулли и Гольдбах выразили уверенность, что натуральные
логарифмы рациональных чисел трансцендентны. В томе I «Введения
в анализ бесконечных» Эйлер высказал такое утверждение: логарифм
рационального числа при рациональном основании есть либо
рациональное число, либо трансцендентное. На рубеже XIX и XX вв. Д. Гильберт
сформулировал среди труднейших и актуальных проблем математики
и вопрос об арифметической природе чисел вида аь, где а и Ъ —
алгебраические. Ответ дал в 1934 г. советский математик А. О. Гельфонд,
доказавший, что всякое алгебраическое число, отличное от нуля и единицы,
в алгебраически-иррациональной степени есть число трансцендентное.
Благодаря Эйлеру теория чисел превратилась в подлинную
математическую науку. Исследования, начатые им в столь многих
направлениях, были продолжены затем крупнейшими математиками всего мира1).
Мы перейдем теперь к разбору работ учеников и первых преемников
Эйлера, деятельность которых охватила почти семьдесят пять лет от
середины XVIII и до конца первой четверти XIX века.
г) Подробнее см. А. О. Гельфонд, Роль работ Л. Эйлера в развитии теории
чисел. В сб.: Леонард Эйлер, М., 1958; И. Г. Б а ш м а к о в а, Обоснование теории
делимости в трудах Е. И. Золотарева, § 1—5.— Ист.-матем. исслед., вып. II, 1949.
ГЛАВА ОДИННАДЦАТАЯ
УЧЕНИКИ И ПЕРВЫЕ ПРЕЕМНИКИ ЭЙЛЕРА
Школа Эйлера. Большой вклад в развитие математической культуры
и науки внесли ученики и ближайшие сотрудники Эйлера — академики
С. К. Котельников, С. Я. Румовский, М. Софронов, М. Е. Головин,
Н. И. Фусс, А. И. Лексель, Ф. И. Шуберт, а также С. Е. Гурьев и В. И. Вис-
коватов. Они преподавали в учебных заведениях, писали руководства
и популярные статьи по математике, механике и астрономии. Об этом
уже упоминалось ранее. Им принадлежит ряд научных исследований,
в значительной части примыкающих к тематике Эйлера. При этом из
приблизительно 200 математических работ Лекселя, Фусса, Шуберта
и Гурьева более 70 посвящено различным вопросам геометрии; можно
сказать, что на рубеже XVIII и XIX вв. в Петербурге работала сильная
геометрическая школа. Особенно интересные открытия сделаны были
в сферической геометрии, полигонометрии, а также некоторых отделах
дифференциальной геометрии1).
С. К. Котельников и С. Я. Румовский. Старшим учеником Эйлера
был Семен Кириллович Котельников (1723 — 13 апреля 1806). Сын
рядового Преображенского полка, обучившего его чтению, он 11-летним
мальчиком был принят в школу, учрежденную Феофаном Проконовичем
для детей бедняков и сирот. Здесь его выучили писать и началам
латинской грамматики. Еще три года он учился в семинарии при Алевхандро-
Невской лавре. Перед самым поступлением в академическую гимназию
18-летний Котельников сообщал о себе, что в семинарии «синтаксиму
и поэтику прошел и в риторику вступил. Сверх тех наук никакому
искусству и художеству не обучен» 2). Несмотря на столь слабую подготовку,
в гимназии и университете, куда его перевели осенью 1742 г.,
Котельников быстро выдвинулся как один из лучших студентов, а его
математические способности обратили на себя внимание известного физика
академика Г. Рихмана (1711—1753).
В октябре 1750 г. Котельников представил ученой Конференции
работу на латинском языке «О квадратуре и спрямлении конхоиды
посредством касательной». Название диссертации связано с тем, что за аргумент
г) В. И. Лысенко, Из истории первой Петербургской математической
школы.—Труды Ин-та ист. естеств. и техн., т. 43, 1961.
2) М. И. Сухомлинов, История Российской Академии, вып. 3, СПб., 1876,
стр. 4 (в этом сочинении имеются подробные биографии Котельникова, Румовского
и нескольких других математиков, состоявших членами Российской Академии,
организованной в 1783 г. и в 1840 г. объединенной с Академией наук; задачей этой
академии было изучение русской словесности).
С. К. КОТЕЛЬНИКОВ и С Я. РУМОВСКИЙ
191
принимается длина отрезка касательной в вершине между вершиной
и точкой пересечения с радиусом-вектором соответствующей точки
кривой; существенную роль в исследовании играет разложение
интегрируемых алгебраических функций в степенные ряды. Академики одобрили
сочинение, и молодой человек был произведен в 1751 г. в адъюнкты. Эйлер,
которому работу послали на отзыв, также хорошо оценил ее и было
решено направить Котельникова для
дальнейшего усовершенствования в Берлин к
великому математику.
В семье своего наставника Котельников
прожил четыре года, начиная с лета 1752 г.
Вместе с ним проходил курс математических
наук старший сын Эйлера Иоганн-Альбрехт
(27 ноября 1734 — 17 сентября 1800). 8
августа 1752 г. Эйлер, сообщая Шумахеру о своих
ежедневных занятиях с Котельниковым
анализом (за чем последуют механика,
гидромеханика и астрономия), писал: «Из его
прилежания и природной одаренности я могу
уже заключить, что в короткое время он
настолько продвинется, что Императорская
Академия сможет быть им вполне довольна.
Я даю ему уроки всегда в обществе моего
Альбрехта и замечаю, что небольшое
соревнование немало полезно обоим, так как они
примерно одинаковой силы» *). Летом 1754г.
группа «аспирантов» Эйлера еще выросла: из
Петербурга прибыли Степан Яковлевич Румовский (9 ноября 1734 —
18 июля 1812) и Михаил Софронов (1729 — 21 февраля 1760). Оба
выходцы из среды бедного духовенства, обучавшиеся вначале подобно Котель-
никову в духовных семинариях, Румовский и Софронов поступили в 1748 г.
в академический университет и кончили его с блестящим успехом.
На выпускном экзамене в январе 1753 г. Софронов по математике и физике
оказался даже первым. В его характеристике отдельно отмечалось:
«Да он же сверх того имеет особливые заслуги, что девять человек
студентов обучились у него геометрии и алгебре довольно» 2). Диссертации
Румовского «Решение Кеплеровой задачи об определении полуординаты
(эллипса) по данному сектору» и Софронова «О спрямлении эллиптических
дуг» были одобрены Эйлером; в конце 1753 г. оба они были произведены
в адъюнкты. Софронову, больному алкоголизмом, пришлось менее чем
через год вернуться в Петербург, где он еще несколько лет занимался
преподаванием и переводами. Его несомненное дарование не смогло
раскрыться из-за болезни; печатных трудов он не оставил. Котельников
и Румовский возвратились летом 1756 г. В том же году Котельников
был избран профессором математики. Деятельность его была
разнообразной. В 1761—1766 гг. он руководил Академической гимназией, 17 лет
состоял членом управлявшей Академией комиссии, работал в Географи-
С. К. Котельников (силуэт
работы Ф. Антинга, 1780-е
годы).
х) Die Berliner und die Petersburger Akademie der Wissenschaften in Briefwech-
sel Leonhard Eulers, B. 2, hsg. von A. P. Juschkewitsch und E. Winter, Berlin, 1961,
стр. 281.
2)B. И. Смирнов иЕ. С. Кулябко, Михаил Софронов, русский
математик середины XVIII века. М.—Л., 1954, стр. 21—22.
192
ГЛ. 11. УЧЕНИКИ И ПЕРВЫЕ ПРЕЕМНИКИ ЭЙЛЕРА
ческом департаменте, с 1771 г. заведовал библиотекой и музеем, читал
в Академии студентам и вольнослушателям вплоть до 1796 г. лекции
по высшей математике и механике, преподавал в Морском кадетском
корпусе. Мы упоминали о написанном им кратком изложении
дифференциального и интегрального исчисления, которое он включил в свой перевод
курса Вольфа; ему принадлежат и другие учебные руководства —«Первых
оснований мафиматических наук часть первая, содержащая в себе
арифметику» (СПб., 1766), «Молодой геодет или первые основания геодезии»
(СПб., 1766) и «Книга, содержащая в себе учение о равновесии и
движении тел» (СПб., 1774) х). В учебнике арифметики число трактуется по
Ньютону, как «содержание», т. е. отношение двух количеств и потому
большое внимание отведено изложению теории пропорций; применяется
буквенное обозначение количеств; приводятся правило ложных
положений, доказываемое алгебраически, сведения об извлечении корней,
прогрессиях, логарифмах. Начиная с 1783 г. Котельников отдавал много
времени работе в только что созданной тогда Российской академии,
а в 1797 г. был назначен цензором и в связи с этим перешел в Академии
наук на положение почетного члена.
Научная продукция Котельникова была невелика. В VII—VIII томах
«Новых записок» академии напечатаны три статьи его по механике и
физике, а в NCAP X (1764) 1766 математическая работа, в которой рассмотрена
задача Эйлера о числе Рп возможных способов разбиения га-угольника на
треугольники посредством непересекающихся диагоналей. Еще в письме
к Гольдбаху от 4 сентября 1751 г. Эйлер привел формулу
р _ 2-6-10. ..(4га —10) о
^п~ 2-3-4...(п-1) ' П>6'
которую затем опубликовал без доказательства в NCAP VII (1758—
1759) 1761. Котельников предложил вывод этой формулы, которую привел
также в своем учебнике геодезии вместе с несколькими теоремами о
построении га-угольника по тем или иным данным 2га — 3 его элементам, именно:
1) га сторонам и га — 3 углам, 2) га — 2 сторонам и га — 1 углам, 3) га
сторонам и га — 3 диагоналям. Обобщениями задачи Эйлера (например,
вопросом о разбиении га-угольника на гаг-угольники) занимались
впоследствии многие — Н. И. Фусс (1810, Mem. Ac. Sciences XI, 1830), Лиувилль
и др., а общие основы полигонометрии разработал другой петербургский
академик — Лексель.
В 1761 г. Котельников произнес яркую публичную речь о пользе
математики. Значение математики для других наук, «о пользе которых
никто не сумневается» 2), раскрывается с помощью исторического обзора
ее достижений и их приложений с древних времен до середины XVIII века.
Развивая замечательные мысли, высказанные за десять лет до того
в «Слове о пользе химии» (1751) М. В. Ломоносова (1711—1765),
призывавшего к объединению усилий математиков и химиков, Котельников
подчеркивает, что успехи наук были бы еще большими, если бы теоретики
и практики не были столь разобщены в своей деятельности. О роли
отвлеченных математических идей для познания природы Котельников писал:
«И понеже математики рассуждают вообще о всех вещах, ничего не назы-
1)А. А. Космодемьянский, Очерки по истории механики в России. —
Уч. записки МГУ, вып. 122. М., 1848, стр. 203—206.
2) С. К. Котельников, Слово о пользе упражнения в чистых
математических рассуждениях, СПб. 1761, стр. 6.
С. К. КОТЕЛЬНИКОВ и С. Я. РУМОВСКИЙ
193
вая своим именем, или поколику они [вещи] в рассуждении их величины
или количества их свойств переменяются, яко тягости, твердости,
движения, теплоты, упругости и прочих качеств; то можно оные рассуждения
их во всех употреблять науках, глядя по обстоятельствам случающихся
в телах перемен. Ибо к полезному оных в других науках употреблению
почти ничего больше не надобно, как каждое количество назвать своим
именем, которых уже свойства и их перемены исследованы и включены
в формулы аналитические. Итак, вся
трудность состоит в искусстве употреблять
в нужном случае исследованные уже в
математике и изображенные аналитическими
характерами [знаками] тел свойства»*).
Стихийно-материалистические установки
автора проявляются во всей речи.
Котельников принадлежал к той группе
русских математиков XVIII века, которые
почти всю свою энергию отдавали
просветительской деятельности в ее различных
проявлениях. Понятно, что, например, в декабре
1763 г., отвечая на запрос, почему он не
дает статей для «Новых ежемесячных
сочинений» Академии наук, Котельников писал:
«...порученное мне дело в рассуждении
гимназии, такожде и чтение лекций оставляют
весьма мало времени, в которое бы мне
в науке моей профессии можно было
упражняться в покое».
Более активно было научное творчество _ _,
С. Я. Румовского, хотя и он много времени с- я- Р^0ВТ1&м°КМпм^'
J ' ^ * менцова, литография М. Момар-
уделял преподаванию, учебно-литературной, ского? 183о-е годы).
и научно-организационной работе.
Отметим его «Сокращения математики, часть
первую, содержащую начальные основания арифметики, геометрии и
тригонометрии» (СПб., 1760), составленную с учетом, в частности,
тригонометрических исследований Эйлера и под несомненным влиянием руководств
профессора И. А. Зегнера. Профессор по кафедре астрономии с 1763 г.,
Румовский в последние годы работы в Академии состоял ее
вице-президентом (1800—1803). После того, оставаясь почетным членом Академии,
он плодотворно трудился до конца жизни на посту члена Главного
правления училищ, проводившего большую реформу системы
образования, а так же, как упоминалось, был попечителем Казанского
университета. Как и Котельников, Румовский был активным членом
Российской Академии 2).
Научные заслуги Румовского лежат главным образом в области
астрономии и географии. Почти 40 лет он возглавлял Географический
департамент Академии, занимался составлением карт, 25 лет руководил
изданием ежегодных астрономических словарей. В 1761 и 1769 гг. он
участвовал в экспедициях по наблюдению прохождения Венеры по Солнцу
в Селенгинске и, соответственно, на Коле, из которых вторая дала богатые
х) С. К. Котельников, Слово о пользе упражнения в чистых
математических рассуждениях, СПб., 1761, стр. 17.
2) Подробная биография С. Я. Румовского имеется в кн.: М. Сухомлинов,
История Российской Академии, вып. 2, СПб., 1875.
194 ГЛ. 11. УЧЕНИКИ И ПЕРВЫЕ ПРЕЕМНИКИ ЭЙЛЕРА
результаты. Изданные им в 1786 г. таблицы географического положения
многочисленных пунктов отличались замечательной точностью и высоко
ценились еще долгое время спустя. По математике он опубликовал семь
статей, тесно примыкающих к работам Эйлера.
Первая из математических работ Румовского [NCAP VIII (1760—
1761) 1763] содержит решение поставленной Эйлером задачи: определить
контур основания конуса данной высоты, имеющего при данном объеме
наименьшую боковую поверхность; употребляя полярные координаты,
Румовский свел дело к отысканию условного экстремума интеграла
\ ]/ a*\-j-y + (а2 + г2)г2 dcp, обращающегося в нуль, когда ф = 0 при
заданной величине \ г2йф; уравнение Эйлера интегрируется при этом
в квадратурах. Заметим, что в конце статьи приведено было решение
Эйлера, применившего прямолинейные координаты и что несколько
спустя Иоганн-Альбрехт Эйлер напечатал в Abh. d. Bayer. Akad. d.
Wissenschaften, 1764 решение задачи об отыскании контура основания
конуса данной высоты, имеющего при данной боковой поверхности
наибольший объем. Это — одна из трех математических работ И.-А. Эйлера;
остальные 28 принадлежат физике, астрономии и механике и в
составлении всех их почти несомненно значительное участие его отца.
В других статьях по математике, которые Румовский стал
представлять после двадцатилетнего перерыва, речь идет о решении некоторых
видов обыкновенных дифференциальных уравнений первого порядка,
которые с помощью тех или других подстановок приводятся к линейному
[АР (1781 : 1)1784; NAP XII (1794) 1801] х), о суммировании
расходящихся рядов [NAP VI (1788) 1790] и об интегрировании посредством
подходящих рационализирующих подстановок алгебраических функций,
1 1 (Л 22\2
вроде , _ _ \ } и т. п.
[NAP X (1792) 1797 и XI (1793) 1798; Mem. Ac. Sc. Petersb. II, 1810].
Такие интеграции имеют весьма частный характер, но в те времена,
когда лишь подходила к завершению выработка основных приемов
интегрирования в конечном виде, ими занимались многие математики во главе
с Эйлером. Например, в том же X томе «Новых трудов» помещена статья
из наследия Эйлера об интегрировании функции rL
(3 + Z2) У 1 ± 3*2
В статье о суммировании рядов вида 1П — 2п + Зп — 4П + ...
Румовский опять-таки применил один из характерных приемов Эйлера,
упоминавшихся нами ранее (ср. статью Эйлера о суммировании рядов
1п + 2п + Зп + 4П + ... в том же VI томе «Новых трудов»). Именно,
Румовский полагает
si = l — 2x + 3x2 — 4:x3+ ...
и, интегрируя, находит \sLdx = тт^. ; далее дифференцирование дает
*i = {1 + х)2 и> прия= 1,
1-2 + 3-4+...=!.
х) Эти уравнения, вроде (1 — р)(п2 — s2)dp + (?г2+ р3 + ps + p2s)ds = 0, были
несколько иначе до того решены Эйлером.
А. И. ЛЕКСЕЛЬ
195
Затем аналогично рассматриваются
s2 = l — 22х + 32х2 — 4.2х3 + ..., s3 = l — 23х + 33х2 — 4V+ ...
и устанавливается закон перехода от sn к sn+i. В дополнение находятся
обобщенные суммы рядов 1 — Зп + 5П — 1п + . . . *).
А. И. Лексель. Астроном и математик Андрей Иванович (Андрей-
Иоганн) Лексель (4 января 1741 — 11 декабря 1784) был приглашен
в Академию в 1769 г. по совету Эйлера. До того он работал в
университете и в Морском училище в Упсале, а еще раньше в университете своего
родного города Або. В истории астрономии имя Лекселя связано с
исследованием носящей его имя кометы 1770 г., а также с установлением того
важнейшего факта, что обнаруженная в 1781 г. Гершелем около созвездия
Близнецов движущаяся звездочка есть не комета, как думал сначала
знаменитый наблюдатель, а новая планета, которую вскоре назвали
Ураном. Эйлеру Лексель оказал большую помощь при подготовке «Новой
теории движения Луны», об этом уже упоминалось.
Многие статьи Лекселя по математике и механике (всего их 28,
причем по геометрии 9) тесно связаны с тематикой Эйлера. Они посвящены
новому выводу условия, при котором функция F (х, г/, -^ , -т-| , . . ., -j^A
является полной производной (NCAP XVI (1770) 1771), без помощи
вариационного исчисления, как это сделал Эйлер, решению систем
линейных обыкновенных дифференциальных уравнений второго порядка
с постоянными коэффициентами [АР (1777 : 1) 1778 и (1779 : II) 1783],
классификации и свойствам эллиптических интегралов [АР (1778 : 1) 1780
и (1778 : II) 1781] и интегрированию с помощью их рационализации
/[ хт—1
иррациональных функций, вроде г [АР (1781 : II) 1785].
(1 — хт) у2хт—1
Вслед за тригонометрией внимание математиков — Ламберта (1770)
и др.— привлекла тетрагонометрия, т. е. решение четырехугольников.
Лексель построил первую общую систему полигонометрии [NGAP XIX
(1774) 1775 и XX (1775) 1776]. Он систематически рассмотрел вопрос
о решении плоского несамонересекающегося тг-угольника по данным
2п — 3 сторонам и углам между ними, причем по меньшей мере п — 2
являются сторонами, и подразделили все имеющие место случаи на три
основных класса, а классы в свою очередь на порядки. Решения опираются
на два общих уравнения, получающиеся при проектировании
многоугольника на две взаимно перпендикулярные оси, из которых одна совпадает
с какой-либо стороной. Если обозначить стороны а, Ь, с, . . ., I ж
соответствующие внешние углы , |3, у, . . ., Я, причем а + |3 + 7 + • • •
... + К = 360°, то уравнения имеют вид
a sin a-\-b sin (а +13) + с sin (а + (i + у) + ... + I sin (а + Р + у + .. . + Ц = 0,
a cos а + Ъ cos (a -f (3) + с cos (а +13 + у) + ... + / cos (а + Р + у + ... + Ji) = 0;
они сохраняют силу и для невыпуклых и самопересекающихся
многоугольников. Из этих уравнений Лексель вывел главные формулы
тригонометрии и тетрагонометрии, демонстрируя заодно ряд весьма простых
способов решения задач, затем все это распространяется на 5-, 6- и 7-уголь-
ники. Он изучил и вопрос о решении тг-угольников по данным диагоналям
г) См. подробнее: А. П. Юшкевич, Эйлер и русская математика в XVIII
веке.— Труды Ин-та ист. естеств., т. III, 1949.
196
ГЛ. 11. УЧЕНИКИ И ПЕРВЫЕ ПРЕЕМНИКИ ЭЙЛЕРА
и их углам со сторонами, указав общие правила решения, а также
принципы классификации задач. Попутно разобраны комбинаторные
проблемы, которыми, как мы видели, занимались Эйлер и Котельников,
п(п— 3) „ п*(п — 3)
вроде определения числа —Ц>—-диагоналей тг-угольника и числа ——^—-
углов, образуемых ими между собой и со сторонами, а также другие,
более сложные задачи. Все это составило содержание первой статьи
Лекселя по полигонометрии; во второй решен ряд частных задач, особенно
на четырехугольники, в том числе когда среди данных элементов имеется
одна диагональ. В 1789 г. результаты Лекселя существенно дополнил
швейцарец С. Люилье, в исследовании которого основную роль играло
некоторое выражение для площади многоугольника, определением
которой петербургский академик не занимался г).
Лексель существенно обогатил сферическую геометрию. Он начал
с изучения сферических эпициклоид, которыми занимался еще Я. Герман
[АР (1779 : 1) 1782], а затем перешел к анализу свойств различных
сферических треугольников [АР (1781 : 1) 1784, (1782 : 1) 1786 и (1782 : II)
1786]. Среди многих открытых им предложений, обобщающих формулу
Герона, теорему Птолемея и т. д., особенно замечательна теорема,
которую он доказал двумя способами: геометрическое место вершин
сферических треугольников с общим основанием и одинаковой площадью есть
малый круг шара. Лежандр поместил эту теорему вместе с собственным
ее доказательством в одном из приложений к своим «Началам геометрии»
(Elements de geometrie, 1 изд., Paris, 1794), а впоследствии ее применяли
в своих исследованиях по сферической геометрии Я. Штейнер (1837)
и другие. Попутно Лексель вывел большое число новых важных формул
сферической тригонометрии 2).
Н. И. Фусс. Крупным представителем школы Эйлера является
Николай Иванович Фусс (29 янв. 1755 — 4 янв. 1826), который в возрасте
17 лет был по совету своего учителя Д. Бернулли приглашен в Петербург,
чтобы помогать Эйлеру в качестве секретаря. Фусс прожил у Эйлера
десять лет, работая с ним ежедневно по 8—9 часов. С семьей Эйлера он
породнился, женившись на одной из его внучек. В 1776 г. Фусс стал
адъюнктом, в 1783 г.— академиком, а с 1800 г., после смерти старшего
сына Эйлера, занял пост непременного секретаря академии. В
восьмидесятые и девяностые годы Фусс был профессором Сухопутного и Морского
кадетских корпусов, в начале XIX века принял деятельное участие
в реформе системы образования в качестве члена Главного правления
училищ. Его учебники по элементарной математике и началам высшей,
написанные под сильнейшим влиянием трудов Эйлера, употреблялись
во многих школах на рубеже XVIII и XIX вв.
Человек способный и еще более работоспособный, Фусс в научном
отношении стал как бы малым спутником Эйлера. Перу Фусса
принадлежит более 100 мемуаров по различным вопросам математики, механики
и физики. Почти все они так или иначе примыкают к тематике Эйлера.
Первым трудом Фусса явилась составленная на основании работ Эйлера
инструкция об изготовлении оптических линз и микроскопов (1774)у
г) В. И. Л ы с е н к о, Работы по полигонометрии в России XVIII веке.— Ист.-
матем. исслед., вып. XII, 1959.
2) В. И. Лысенко, О работах петербургских академиков А. И. Лекселя,
Н. И. Фусса и Ф. И. Шуберта по сферической геометрии и сферической
тригонометрии.—Труды Ин-та ист. естеств. и техн., т. 34, 1960.
Н. И. ФУСС
197
за ней последовало написанное под руководством Эйлера сочинение
об устройстве страховых касс и лотерей (1776). Первая статья по мате-
хт
матике посвящена была разложению рациональной дроби -. ^ ^...
\рс a j [зс — О)
на простые [АР (177 : 1) 1778], последняя, написанная за два месяца
до смерти автора,— приведению к рациональному виду некоторых
иррациональных выражений и вычислению двойных интегралов (Mem. Ас.
А. И. Лексель, Н. И. Фусс и И. А. Эйлер
(силуэт работы Ф. Антпнга, 1784 г.) перед
современным памятником Л. Эйлеру.
Sciences XI, 1830). Величайший пиэтет к своему учителю Фусс хранил
до конца дней. Перу Фусса принадлежит известная биография Эйлера
[Eloge de Monsieur Euler. St.-Petersbourg, 1783], содержащая первый
список его трудов, и он очень многое сделал для публикации
колоссального посмертного наследия Эйлера, напечатав около 170 его статей.
Наиболее интересны геометрические работы Фусса. В общей
сложности их 33. Вслед за Лекселем он занялся сферической геометрией
и в томе II NAP (1784) 1788 решил три задачи о сферическом
треугольнике, построенном на данной дуге большого круга и удовлетворяющем
одному из трех экстремальных условий: чтобы 1) угол при
противолежащей вершине был наибольшим, 2) сумма двух сторон при вершине
198
ГЛ. 11. УЧЕНИКИ И ПЕРВЫЕ ПРЕЕМНИКИ ЭЙЛЕРА
была наименьшей и 3) площадь была наибольшей. Отправляясь от
второй задачи, Фусс пришел к сферическим эллипсам, т. е. геометрическим
местам вершин сферических треугольников с данными основанием и
суммой двух других сторон и исследовал свойства этих любопытных кривых
[NAP III (1785) 1788].
Из дифференциально-геометрических работ Фусса отметим
относящиеся или близкие к так называемой естественной геометрии, о которых
мы уже упоминали. В них изучены некоторые случаи задачи об
определении и спрямлении кривой, радиус кривизны которой есть степенная
функция радиуса-вектора [NAP IV (1786) 1789], а также об определении
кривых по уравнениям между радиусом кривизны г, радиусом-вектором z,
длиной дуги 5, вроде
т2г2 ± ft2s2 — const, m2r2 + m2s2 = z2
и т. п. (1799, опубл. Mem. Ac. Sciences 1, 1809). Сходными задачами
занимался также Шуберт.
Оставляя в стороне целый ряд статей Фусса по элементарной
геометрии (например, новое решение задачи о круге, касающемся трех
данных кругов) и аналитической геометрии, мы укажем еще на
поставленную Фуссом «проблему замыкания». Прежде всего он занялся задачей
о четырехсторонниках, около которых можно описать и в которые можно
вписать окружности [NAP X (1792) 1797]; вскоре последовала работа,
в которой задача обобщается на некоторые виды многоугольников с более
чем четырьмя сторонами [NAP XIII (1795—1796) 1802]. Затем задачей
занялся Я. Штейнер (1827). Полное решение проблемы замыкания для
круга дал с помощью эллиптических функций Якоби в 1828 г. Сама
проблема ставится так. Внутри данного круга лежит другой данный
круг. Из точки внешней окружности
проводятся хорда, касательная к внутренней
окружности, из конца этой хорды —
следующая касательная, и т. д.
Спрашивается, при каких условиях образуемый
хордами многоугольник замкнутый? Пон-
селе в своем классическом труде по
проективной геометрии распространил
проблему на конические сечения (1822) 1).
Ф. И. Шуберт. Федор Иванович
(Фридрих-Теодор) Шуберт (30 октября 1758 —
22 октября 1825), подобно Румовскому
и Лекселю, соединял занятия математикой
с астрономией. В Петербург он приехал
из Германии в возрасте 25 лет, а к работе
в Академии приступил в 1785 г.; в
следующем году он был произведен в
адъюнкты, в 1789 г. стал академиком и с 1803 г.
руководил академической обсерваторией.
Ф. И. Шуберт. Диапазон математических интересов
Шуберта был довольно широк, но
значительная часть из его 31 статьи по математике, именно 20, относится
опять-таки к геометрии. Упомянем в первую очередь работу о
свойствах локсодромы, т. е. линии на шаре, пересекающей все меридианы
г) Подробнее см. указанные выше статьи В. И. Лысенко.
МЕМУАР С. Е. ГУРЬЕВА
199
под данным углом [NAP IV (1786) 1789], и напечатанную вместе с нею
статью по картографии, где рассмотрены свойства некоторых проекций
меридианов и параллелей, лежащих на эллипсоиде вращения, и где
впервые появляется слово «конформная проекция». Там же и еще в томе XII
NAP (1794) 1801 помещены две статьи Шуберта по сферической
геометрии, примыкающие к работам Лекселя и Фусса. Во второй из них
решены задачи о геометрическом месте вершин сферических треугольников
с данным основанием и данным отношением: 1) синусов двух других
сторон, 2) их косинусов, 3) синусов половин двух других сторон и 4) их
косинусов. В первом случае получается кривая двоякой кривизны —
пересечение шара с некоторым конусом, во втором — большой круг,
перпендикулярный к основанию, а в остальных — два параллельных
и равных малых круга, также перпендикулярных к основанию
треугольника. В томе XII имеется еще статья Шуберта о построении системы
сферической тригонометрии на основе теоремы Менелая. Наконец,
заслуживает внимания более поздняя работа о точках возврата плоской
кривой (Mem. Ac. Sciences, VIII, 1822), в которой Шуберт впервые указал,
что точки возврата кривой / (ж, у) = 0 должны удовлетворять системе
уравнений
/ d2f \2__ d2f d2/
\дхду) "~ дх* ' ду* '
и рассмотрел все возможные случаи такой особой точки, кроме случая
самоприкосновения *).
В истории алгебры известна работа Шуберта о разыскании целых
линейных и квадратичных множителей алгебраического многочлена
с целыми коэффициентами [NAP XI (1793) 1798]; этой задачей,
поставленной Ньютоном, занимались многие математики. Статья Шуберта была
надолго забыта и в 1882 г. Л. Кронекер дал общее решение вопроса,
применив метод, сходный с приемом петербургского академика.
Позднее Шуберт заинтересовался проблемами обоснования анализа
и к этому мы еще вернемся,
Мемуар СЕ. Гурьева. Среди работ по геометрии заслуживает
упоминания мемуар С. Е. Гурьева по дифференциальной геометрии плоских
кривых, уравнения которых даны в полярных координатах [NAP XII (1794)
1801]. До того каждая дифференциально-геометрическая формула такого
рода выводилась по отдельности из рассмотрения соответствующих
бесконечно малых фигур. Гурьев впервые систематически вывел всю систему
основных дифференциально-геометрических формул в полярных координатах
аналитически, отправляясь от формул в декартовой прямоугольной
системе. В начале работы он писал: «Все авторы, насколько мне известно,
для проведения касательной, определения радиуса кривизны,
спрямления и квадратуры кривых, все ординаты которых выходят изнеподвиж-
ной точки, употребляли прием, отличный от того, которым они пользуются
для всего этого, если ординаты берутся параллельными; всегда
присоединяют какое-либо более или менее сложное построение, вводя маленькие
криволинейные треугольники, иногда столь затрудняющие доказатель-
г) В. И. Л ы с е н к о, Из истории вопроса о точках возврата плоской кривой.—
Ист.-матем. исслед., вып. XIV, 1961.
200 ГЛ. 11. УЧЕНИКИ И ПЕРВЫЕ ПРЕЕМНИКИ ЭЙЛЕРА
ство, что его почти невозможно запомнить... Мне пришло в голову вывести
все это из принципов, имеющих место для кривых с параллельными
ординатами» *). Гурьев рассматривает кривую AM (рис. 28), заданную
уравнением между радиусом-вектором FM = zk углом 2? AFM = со, здесь
он сделал некоторый шаг вперед по сравнению с многими своими
предшественниками, которые пользовались не полярным углом, а дугой круга
какого-либо радиуса. Отрезки АР = х, РМ = у суть прямоугольные
декартовы координаты точки.
Прежде всего Гурьев выводит формулу угла касательной МТ с
радиусом-вектором FM, вводя вспомогательные угол 2(.FTM = ср и отрезок
PF = v = AF — х. Так как X TMF =
= 2d — ф — со, то
tg<TMF=-sin(y + (*\;
СОЗ(ф+С0) '
далее,
dy dx
Sin ф = :Г7==== , COS ф :
VdxZ + dy*
Ydx^ + dy*
= z cos со сле-
Рис. 28. Чертеж к работе
С. Е. Гурьева (в полярных
координатах) .
и из равенств у = z sin со;
дует, что
dy = z cos со dco -f- sin со dz,
dx= — dv = z sin со dco — cos со dz.
Это после небольших выкладок дает
известную формулу
tg^TMF = ^.
Вслед затем выводятся выражения для
полярной подкасательной FR, радиуса
кривизны, дифференциала дуги и площади
Р = AFM = AMP + MPF (исходятиз того,
4TodP = ydx+d^ = y-^±^ и т. п.),
2 2
а также поверхности и объема тела вращения дуги AM и площади AMP
вокруг оси АР. Все это сопровождается примерами, в которых фигурируют
квадратриса, спирали, конхоида и конические сечения. Эта небольшая
статья Гурьева (в ней 15 страниц) получила довольно широкую
известность. Отметим еще его работу, содержащую новые выражения объема
трехгранной пирамиды через ее шесть ребер или через три ребра,
выходящие из одной вершины, и углы между ними («Умозрительные
исследования», 1, 1808). Особенно просты выражения в последнем случае:
V = -?r- У~1 — cos2 а — cos2 р — cos2 у -\- 2 cos a cos |3 cos у
и, если положить
я + Р + ?
= со,
аЪс -
V = -~- ]/sin со sin (со — a) sin (со — (3) sin (со-
¦?)•
Впервые выразил объем пирамиды через ее шесть ребер Эйлер в
упоминавшемся ранее письме к Гольдбаху от 14 ноября 1750 г., содержащем
знаменитую теорему о зависимости между числами вершин, ребер и гра-
*) NAP XII, стр. 176-177.
ВОПРОСЫ ОБОСНОВАНИЯ АНАЛИЗА
201
ней многогранника [см. NCAP IV (1752—1753) 1758]. В статье о
поверхностях второго порядка Гурьев дал первое на русском языке изложение
этого отдела аналитической геометрии в пространстве («Умозрительные
исследования» 1, 1808); здесь приведены некоторые критерии для
суждения по общему уравнению о характере поверхности. Нам придется еще
говорить о других геометрических трудах Гурьева, но его главные
интересы лежали совсем в другой области — в области оснований
математики, которые в то время приобрели особую актуальность.
Вопросы обоснования анализа на рубеже XVIII—XIX веков. Мы
говорили ранее о взглядах на этот вопрос Лейбница и Ньютона и об
эйлеровом «исчислении нулей». Ньютонова теория первых и последних
отношений получила в середине XVIII века дальнейшее развитие у Даламбе-
ра. Даламбер считал, что дифференциальное исчисление недопустимо
строить на неясном понятии лейбницевой бесконечно малой величины.
Он отвергал трактовку бесконечно малых как ничтожно малых величин,
пренебрежение которыми не нарушает точности равенств. Отвергал он
и ньютоновы «исчезающие» величины, говоря, что величина есть или что-
нибудь или ничто.
Вслед за Ньютоном Даламбер в качестве центрального выдвигает
понятие предела, которое определяет в следующих словах: «Говорят,
что одна величина является пределом другой величины, если эта вторая
может стать к первой ближе, чем на любую данную величину, как бы
ни была мала эта последняя, причем, однако, приближающаяся величина
никогда не может превзойти величину, к которой приближается. Таким
образом, разность такого количества и его предела абсолютно неуказуема».
К этому добавляется, что «предел никогда не совпадает или не становится
равным величине, для которой он является пределом» 1). В основе
определения лежали представления, связанные с наиболее употребительными
в то время предельными переходами, вроде приближения площади круга
с помощью последовательностей правильных вписанных или описанных
многоугольников. Площади вписанных многоугольников с увеличением
числа сторон возрастают, а описанных — убывают, но ни при каком
числе сторон многоугольник не совпадает в точности с кругом. Таким
образом, переменная мыслилась изменяющейся монотонно, и предел,
рассматриваемый как «односторонний предел» последовательности, не
должен был совпадать с каким-либо значением переменной. Последнее
требование было частью обусловлено стремлением избежать трудности,
связанные с делением друг на друга двух нулей: для Даламбера, в отличие
от Эйлера, бесконечно малая не достигает своего предельного нулевого
значения.
В анализе, говорил Даламбер, не требуется, по существу,
дифференцировать отдельные величины (т. е. вычислять бесконечно малые
дифференциалы), но лишь определять пределы отношений конечных величин,
именно приращений функции и ее аргумента. «В дифференциальном
исчислении речь идет вовсе не о бесконечно малых величинах, но только
о пределах конечных величин... Словами «бесконечно малые» пользуются
лишь для сокращения выражений»2). Таким образом, Даламбер, как
г) Статья «Limite» в Encyclopedie, Dictionnaire des Sciences, des arts et des metiers,
т. IX (1765). Эта статья написана Даламбером совместно с де ла Шапеллем.
2) Статья «Difierentiel» в Encyclopedie, т. IV (1759).
202 гл. ii. ученики и первые преемники эйлера
и Эйлер, выдвигал на первый план вычисление производных. Но каковы
свойства этих умаляющихся конечных приращений, Даламбер не выяснял,
ясного определения дифференциала не дал, а на практике оперировал
с дифференциалами, как и Эйлер. Точно так же почти не исследованы
были свойства пределов. В цитированной статье о пределе указаны лишь
две теоремы: о равенстве двух величин, служащих пределом одной и той же
переменной, и о равенстве предела произведения двух величин
произведению их пределов.
Идеи Даламбера нашли некоторых сторонников и на их основе
Ж. Кузен составил «Уроки дифференциального и интегрального
исчисления» (Lemons de calcul differentiel et de calcul integral, Paris, 1777),
имевшие успех, о чем свидетельствует их переиздание в 1796 г. *¦).
Однако большинство современников не пошло за Даламбером. Отказ
от пользования лейбницевой бесконечно малой при отсутствии нового
определения бесконечно малой величины естественно воспринимался
как отказ от применения какого бы то ни было исчисления бесконечно
малых. Математики справедливо считали невозможным пойти на это.
«Методу пределов,— писал в конце XVIII века Карно,— свойственно
одно серьезное затруднение, не имеющее места в анализе бесконечно
малых; именно, в нем нельзя, как в этом последнем, отделять бесконечно
малые количества друг от друга, и так как эти количества в нем всегда
связаны друг с другом, то невозможно ни использовать при вычислениях
свойства, принадлежащие каждому из них в отдельности, ни подвергать
уравнения, в которых они встречаются, преобразованиям,
способствующим их исключению» 2). Синтез идей исчисления бесконечно малых и
метода пределов удался только в начале XIX века. Сам Карно, оригинально
развивая мысль, высказанную еще Беркли, сделал попытку обосновать
лейбницево исчисление, раз навсегда доказав, что производимые в нем
отбрасывания бесконечно малых не только могут, но и должны
приводить к точным соотношениям между конечными величинами в силу
происходящей при вычислениях компенсации ошибок, которые, по его
мнению, имеют место при таких отбрасываниях.
Новая концепция была выдвинута Лагранжем, сначала в одной
статье 1772 г. и затем в большом труде «Теория аналитических функций,
содержащая принципы дифференциального исчисления, освобожденные
от всякого рассмотрения бесконечно малых, исчезающих количеств,
пределов и флюксий, и приведенные к алгебраическому анализу конечных
количеств» (Theorie des fonctions analytiques contenant les principes du
calcul differentiel, degages de toute consideration d'infiniment petits,
d'evanouissants, de limites et de fluxions, et reduits а Г analyse algebrique
des quantites finies. Paris, 1797), к которому примыкают «Уроки
исчисления функций» (Legons sur le calcul des fonctions. Paris, 1801). Отвергая
применение бесконечно малых в духе школы Лейбница, пределов
Ньютона и Даламбера, а также исчисление отношений нулей Эйлера, Лагранж
стремится построить анализ на двух принципах, по существу,
высказанных еще Эйлером. Прежде всего он хочет доказать, что всякая функция
/ (х), понимаемая как аналитическое выражение, есть аналитическая
функция, т. е. представима, за исключением, быть может, отдельных
г) Русский перевод этой книги с собственными дополнениями выпустил С. Е.
Гурьев: Кузен, Дифференциальное и интегральное исчисления, СПб., 1801.
2) Л. Карно, Размышления о метафизике исчисления бесконечно малых, перев.
Н. М. Соловьева,'под ред. А. П. Юшкевича, М.—Л., 1936, стр. 243.
С. Е. ГУРЬЕВ И ЕГО ПОСЛЕДОВАТЕЛИ
203
значений аргумента, бесконечным степенным рядом вида
f(x + h) = f(x)+ph + qh2 + rh3 + sh*+ ...
Определяя первую производную функцию f{x) данной первообразной
функции f(x) просто как коэффициент при первой степени h в этом
разложении f(x) = р, Лагранж с помощью чисто формальных
преобразований устанавливает зависимости между всеми коэффициентами
разложения 2q = р', Зг = q', 4s = г', ... ив результате получает
f(x + h) = f(x)+f'(x).h + ?®? + f^&h»+...,
где /" (х) есть первая производная функции /' (х) или вторая производная
/ (х), и т. д. Другое основное предложение, на котором основаны
приложения теории аналитических функций, гласит, что при достаточно малых
значениях h любой член разложения (по модулю) больше (модуля)
суммы всех последующих, так что f{x + h) может быть приближена с любой
данной степенью точности некоторым конечным алгебраическим
многочленом по h. Пользуясь этими принципами, Лагранж строит всю технику
дифференцирования и затем применяет теорию к решению основных
задач дифференциального и интегрального исчисления, с приложениями
к геометрии и механике.
«Алгебраическое», по словам Маркса, исчисление Лагранжа занимает
видное место в истории математического анализа. Лагранж первый вывел
формулу остаточного члена в разложении функций в конечный ряд
Тейлора, т. е. дал общее средство оценки разности между / (х + Ь) и суммой п
первых членов ряда. Он первый действительно, а не на словах, сделал
производную функцию самостоятельным объектом анализа, ввел в
употребление знаменитую теорему о среднем f(x + h) — f(x) = f(c) h (где с
лежит между х и х + К) и развил те методы исследования задач на
экстремумы, на соприкосновение кривых и т. д., которые вошли в обиход
математиков XIX века. Вместе с тем, в принципе Лагранж потерпел неудачу.
Доказательство основной теоремы было, как вскоре выяснил Коши,
несостоятельным и опиралось на молчаливую предпосылку о разложимости
всякой функции в ряд Тейлора. Проблема сходимости рядов была
обойдена, и найденная Лагранжем форма остаточного члена, получившая
впоследствии решающее значение, использована почти не была: остаточный член
иногда применяется для оценки точности отдельных конкретных
разложений, но не для исследования сходимости ряда к данной функции.
Оперирование рядами по-прежнему носило формальный характер.
Наконец, Лагранж прошел мимо того обстоятельства, что в его теории
неизбежно сохранялись фактически и предельные переходы и скрытое
пользование (переменной!) бесконечно малой величиной, без чего нельзя было
обойтись ни в основных теоремах, ни при выводе правил
дифференцирования, ни в приложениях.
С. Е. Гурьев и его последователи. Исследования по обоснованиям
анализа получили у нас дальнейшее развитие на рубеже XVIII и XIX вв.,
особенно в трудах С. Е. Гурьева.
Семен Емельянович Гурьев (1764 — 23 декабря 1813) происходил
из небогатого дворянского рода. В 1784 г. он окончил Артиллерийский
и инженерный кадетский корпус в Петербурге, после чего стал
преподавать навигацию, артиллерию и математику. В 1796 г. он приступил
к работе в Академии наук в должности адъюнкта, а через два года был
204 гл. и. ученики и первые преемники Эйлера
избран ординарным академиком. Деятельность Гурьева в Академии была
чрезвычайно активной. Протоколы академической Конференции пестрят
сообщениями о его научных докладах, выступлениях по
научно-организационным вопросам, о его отзывах на различные сочинения. В трудах
Академии он опубликовал около 30 статей по анализу, геометрии и
механике. Некоторые его работы по дифференциальной, аналитической и
элементарной геометрии мы упоминали.
Гурьев особенно заботился о подготовке национальных кадров
русских ученых, о распространении научной и учебной литературы на
русском языке. Еще в 1799 г. он предложил целиком переводить на русский
язык издававшийся тогда по-латыни научный орган Академии. Это
предложение принято не было, но через девять лет, по новому его настоянию,
Академия приступила к выпуску «Умозрительных исследований». В пяти
томах этого издания (1808—1819) было помещено много ценных статей
по естествознанию и математике. К сожалению, после смерти Гурьева
выпуск «Умозрительных исследований» прекратился, и научные записки
Академии в течение ряда лет вновь издавались только на иностранном
(французском) языке.
Большое участие Гурьев принял в реформах в области просвещения.
Он преподавал в различных учебных заведениях Петербурга, подготовил
немало преподавателей математики и инженеров и написал ряд учебников
по элементарной и по высшей математике. Особенно заслуживают
упоминания его весьма содержательные «Основания дифференциального
исчисления с приложением оного к аналитике» (СПб., 1811) и «Основания
трансцендентной геометрии кривых поверхностей» (СПб., 1806) — первое
русское руководство по дифференциальной геометрии; в последнем
рассматривалось также вычисление площадей поверхностей и объемов с
помощью двойных интегралов.
Главный труд Гурьева «Опыт о усовершении елементов геометрии»
(СПб., 1798) посвящен вопросам обоснования математики (рис. 29).
Издание этого труда сопряжено было с большими спорами в Академии наук,
в результате которых часть сочинения света не увидела. Дело в том,
что Гурьев выступил с рядом критических замечаний по адресу Эйлера.
Ученики Эйлера — Фусс, Румовский и другие,— категорически
возражали против публикации такой критики.
С неизданной частью «Опыта» Гурьева довольно подробно знакомит
отзыв, составленный в марте 1797 г. Румовским. Из этого отзыва видно,
что Гурьев критиковал употребление Эйлером расходящихся рядов
и данные им доказательства теоремы о биноме. Вот, например, как
передает Румовский замечания Гурьева о выводе этой теоремы в статье
Эйлера, помещенной в т. V NAP:
«Это доказательство простое и носит общий характер, но именно
поэтому несправедливо. В самом деле,— говорит он,— ряд 1 + тх +
. т(т — 1) о . т(т — 1) (т — 2) Q , ^
Н—, 2 ; х2-\ —т-гг-к Lx3 + и т. д. либо выражает неизменное
количество (1 + х)ш в случае, когда m есть число целое и положительное,
либо — сходящееся и лишь приближающееся в случае, когда ш есть
дробь или отрицательное число и<1; либо, когда m есть дробь или
отрицательное число и ж>1, он ничего не означает, а отсюда само собой
вытекает, что столь различные случаи не могут допустить общего
доказательства.
Недостаток этого доказательства,— говорит он,— следует, без
сомнения, искать в том, что делается допущение (1 + х)п = 1 + Ах + Вх2 +
С. Е. ГУРЬЕВ И ЕГО ПОСЛЕДОВАТЕЛИ
205
+ Сх* + Dx^ + и т. д., которое можно принять лишь в отдельных
примерах, подставляя вместо п определенное целое число или
положительную или отрицательную дробь. Но среди таких примеров имеется лишь
один случай, в котором получается совершенное равенство между (1 + х)п
Рис. 29. Титульный лист «Опыта» С. Е. Гурьева.
и 1 + Ах + Вх2 + Схг + Dx* + . . . + Nxn, а в других случаях оно
может иметь место, как мы показали выше, только если к ряду прибавить
член Рхп, природа которого весьма отличается от природы количества А,
Б, С ж т. д., и когда п есть положительная или отрицательная дробь,
это количество является скрытым и нам вовсе не известно» х). Гурьев
г) См. Архив АН СССР. Дело С. Е. Гурьева, ф. 1, оп. 2, § 84. Отзыв С. Я. Румов-
ского написан по-французски.
206 ГЛ. 11. УЧЕНИКИ И ПЕРВЫЕ ПРЕЕМНИКИ ЭЙЛЕРА
предлагает новое доказательство теоремы, но Румовский в нем не успел
разобраться.
Эти мысли Гурьева для своего времени были весьма замечательными.
По существу, он здесь возражал против «доводов, извлеченных из общности
алгебры», против приписывания «алгебраическим формулам
неопределенной области действия, между тем как в действительности большинство
из них имеет силу лишь при известных условиях и для некоторых
значений входящих величин». Все это подверг энергичной критике 25 лет
спустя Коши, слова которого мы здесь процитировали1). Более того,
правда, в недостаточно ясной форме, Гурьев подчеркнул важность оценки
остаточного члена разложения бинома, природа которого, как он
выражался, отличается от природы членов с коэффициентами А, В, С, . . .
Значение критики Гурьева не ослабляет то обстоятельство, что
собственное его доказательство, опубликованное в XII томе NAP, было
неудовлетворительным. Не забудем, что первый строгий вывод формулы бинома
для действительного показателя дал только Гаусс в 1812 г., а основы
общей теории сходимости рядов были заложены Коши в 1821 г.
Мы узнаем из того же отзыва, что в рукописи Гурьева содержался
критико-исторический обзор различных способов обоснования исчисления
бесконечно малых вплоть до Эйлера. Это же отмечалось в почти
одновременной рецензии Фусса. Любопытно в этой рецензии замечание Фусса,
связанное с тем, что Гурьев, вслед за Даламбером, отказывался от
применения бесконечно малых:
«Мне кажется, что г. Гурьев впадает в иллюзию, когда, исключая
слово «бесконечно малое», полагает, будто исключил саму эту вещь.
Мы находим идею бесконечно малого, в том смысле, какой ей придают
пользующиеся ею геометры, уже в первой лемме о равенстве пределов;
и вновь находим ее во всех последующих доказательствах, основанных
на этой лемме» 2). Речь идет о свойстве единственности предела, которое
Гурьев в «Опыте» назвал «основательной истиной способа пределов»
и о котором там же писал: «Новые геометры давно уже заметили, что способ
архимедов доказательств не в ином чем состоит, как в следующей истине,
что когда возрастающая или убывающая величина имеет два предела,
то оные равны между собою» 3). И Фусс продолжает: «Суть этих
доказательств заключается в установлении предела возрастающей или
убывающей величины и в переходе от величины к пределу, когда удалось
доказать, что эта разность может стать меньше всякой данной величины.
Но... величина, меньшая всякой данной величины, которой автор здесь
заменяет бесконечно малые, сама есть бесконечно малая; ибо, если бы
это была величина конечная, то можно было бы указать величину еще
меньшую, а это противоречит допущению». Как видно, Фусс, вслед за
Эйлером, понимал под бесконечно малой величину меньшую, чем всякая
данная величина, т. е. абсолютный нуль. Такая критика теории пределов
Гурьева не попадала в цель.
После долгого обсуждения, Конференция дала согласие на печатание
труда Гурьева, при условии исключения выпадов против «наших
величайших геометров» 4) и через несколько месяцев книга увидела свет.
А свой критико-исторический обзор, вероятно, в несколько переработан-
*) А. С а и с h у, Exercices d/analyse, t. II, Paris, 1841, стр. 220.
2) См. Архив АН СССР. Дело С. Е. Гурьева, ф. 1, оп. 2, § 76.
3) С. Е. Гурьев, Опыт о усовершении елементов геометрии, стр. 28 и 35.
4) Протоколы Конференции Имп. Академии наук в Петербурге, т. IV, протокол
от 27 марта (ст. Ст.) 1797 г.
С. Е. ГУРЬЕВ И ЕГО ПОСЛЕДОВАТЕЛИ
207
ном виде, Гурьев представил Академии много спустя, в 1813 г., за
несколько месяцев до кончины. Это «Краткое изложение различных способов
изъяснять дифференциальное исчисление» («Умозрительные
исследования», IV, 1815) содержит довольно подробный анализ взглядов Барроу,
Лейбница, Ньютона, Маклорена, Эйлера и Даламбера. «Опыт» Гурьева
начинается словами: «Читая математические откровения нынешних времен
и обращаясь к началам, на коих оные обыкновенно утверждаются, всегда
я представлял себе огромное здание, непрестанно возвышающееся на
слабых основаниях, всегда сокрушался о преклонности к падению сей
чрезвычайной громады полезнейших роду человеческому знаний» г).
Точным основанием анализа и отделов геометрии, посвященных
измерению фигур, Гурьев считал метод пределов, развивавшийся Далам-
бером. Однако в определении предела у Даламбера Гурьев видел
некоторые недостатки, главным из которых было отсутствие указания на то,
что предел есть величина постоянная. Собственное определение Гурьева,
относящееся опять-таки к одностороннему пределу монотонной
переменной величины, гласит: «Есть ли какая-нибудь величина от какого ни есть
известного без конца продолжаться могущего действия всегда возрастает
или убывает, и от того к другой непременной величине приближается,
так что может разниться с нею меньше, нежели всякая по произволению
данная или взятая того же роду величина, и со всем тем никогда ее не
достигает, то сия другая непременная величина есть то, что пределом
первой (возрастающей или убывающей величины) мы называем» 2).
Приведенное определение предела, как видно, относится к монотонно
изменяющимся величинам, а также рациональным числам: Гурьев
отвергал существование иррациональных чисел и оставил в стороне
возникающие при этом трудности. Фактически, конечно, он пользовался более
широким пониманием предела немонотонной функции, например, когда
1 1
рассматривал значение функции -г—— при х = -~- как предел суммы п
1 —{— х Z
111
первых членов ряда 1 —^- + -^ я~~Ь - • • (сумма эта колеблется около
своего предельного значения 2/3) или когда число е (т. е. иррациональное
число) выступало как предел, который он писал в виде
Основываясь на определении понятия предела, Гурьев доказывает
свойство его единственности и затем, привлекая принцип наложения,
выводит ряд теорем: о равенстве круга треугольнику, основание которого
равно окружности и высота — радиусу, о поверхностях прямых цилиндра
и конуса, а также шара, о равенстве объемов призм с равными
основаниями и высотами, об объемах пирамид и тех же трех круглых тел.
Подробно разобран вопрос о равенстве призм, много занимавший комментаторов
Евклида в XVIII веке. Теорема об объеме шара высказана в такой форме:
шар равен пирамиде, у которой основание — поверхность шара, а высота —
радиус его. Все это составляет содержание первой главы сочинения.
Вторая глава «Опыта» посвящена теории пропорций и ее
применениям. Подобно многим математикам средних веков и нового времени
Гурьев считал классическое общее определение геометрической
пропорции, данное в V книге евклидовых «Начал», недостаточно естественным
г) С. Е. Гурьев, Опыт о усовершении елементов геометрии, СПб., 1798, стр. 1.
2) Там же, стр. 34.
208 гл. ii. ученики и первые преемники Эйлера
и прямым. Напомним, что в переводе на наши обозначения это определен
ние гласит: две пары величин А, В и С, D образуют пропорцию, если
для любых пар целых положительных чисел т, п при выполнении какого-
либо из трех условий пА = тВ выполняется одноименное из условий
nC = mD. Гурьев определил пропорцию следующим образом: «Четыре
величины Ау В, С и D называются пропорциональными, когда, в случае
соизмеримости А с В и С с D, сами А и С суть равнократные каких ни есть
из равночастных Е и F величин В и D, а в случае несоизмеримости,
приближенные их X, Y и Z, V, по всяким равночастным Е и F величин В
и D взятые, суть равнократные оных равночастных Е и F» г). При этом
величины X и Y называются меньшей и большей приближенными
величины А, несоизмеримой с В, когда они удовлетворяют условиям X =
= тЕ <A<i(m-\-l)E = Y, где Е есть какая-либо «частная» В,
¦р
Е = — . Таким образом, несоизмеримые величины образуют пропорцию
А: В = С \D, если для любых целых положительных п и соответствующих
m одновременно выполняются неравенства
На основе такого определения, напоминающего свойство пропорций,
указанное еще Такэ и названное им первым и непогрешимым (1654),
Гурьев развивает свою теорию пропорций и затем применяет ее к учению
о подобии и измерению площадей многоугольников. Далее он доказывает
в качестве основного второго предложения метода пределов теорему:
х С АС
если— =7j"' 1™ж —A, \\т.у = В, то-^ =^-, после чего выводит теоремы
об отношении площадей кругов и об отношении поверхностей подобных
цилиндров и конусов. «Сим,— писал он,— я оканчиваю вторую главу сея
книги, поелику все прочее, к сей главе относящееся, после предложенного
здесь не заключает в себе уже никакой трудности» 2).
В «Общем заключении и прибавлениях» содержится критико-методи-
ческий разбор «Начал» Евклида и незадолго до того изданных «Начал
геометрии» (1794) Лежандра, а также развернутая оригинальная
программа курса геометрии самого автора, реализованная затем в его
собственных учебниках 3). Самым слабым пунктом этой программы было
требование, чтобы обучение геометрии (без прямых вычислений!)
предшествовало арифметике 4), но в ней имеются и важные положительные моменты,
оказавшие влияние на наши учебники XIX века. К таким моментам
относится, прежде всего, систематическое применение метода пределов.
1) С. Е. Гурьев, Опыт о усовершении елементов геометрии, стр. 119.
2) Там же, стр. 161.
3) С. Е. Гурьев, Морского учебного курса часть первая, содержащая
основания геометрии, 2 тт., СПб., 1804—1807; он же, Основания геометрии, СПб., 1811.
4) Эта методическая установка связывалась и с методологическими воззрениями
Гурьева, изложенными в его речи «Рассуждение о мафематике и ее отраслях» (СПб.,
1809). Описывая предмет математики и ее классификацию, Гурьев отводил первое место
среди математических дисциплин геометрии, поскольку первыми свойствами тел, как
показывает их действие на наши чувства, являются протяженность и движимость.
Процесс отвлечения приводит далее к науке исчисления и ее подразделениям —
арифметике, алгебре и анализу с его частями; за этим следуют прикладные математические
науки.
С. Е. ГУРЬЕВ И ЕГО ПОСЛЕДОВАТЕЛИ
209
Не останавливаясь на этой стороне «Опыта», мы отметим лишь первую
в русской литературе постановку вопроса о доказательстве постулата
о параллельных. В первом издании своего руководства геометрии Лежандр
сделал попытку доказать постулат о параллельных в форме предложения,
что наклонная АС ж перпендикуляр BD к одной прямой обязательно
пересекаются. Для этого он берет на АС точки F, С, Р и опускает из них
на прямую перпендикуляры FG, CM, PN (рис. 30). Основания
перпендикуляров G, М, N падают последовательно между А и В, удаляясь от
первой точки, а предположить, что есть граница их расстояний, скажем,
AM, нелепо. В самом деле, если бы СМ был последний перпендикуляр,
то, взяв Р справа от С и опустив перпендикуляр PN, мы получили бы,
что N лежит от А дальше, чем М.
Поэтому основания перпендикуля
ров G, М, N, , ... удаляются от А
сколь угодно и среди них найдется
совпадающее с В, что и
доказывает пересечение АС и BD.
Гурьев правильно заметил
недостаток рассуждения, из которого
следует лишь невозможность
существования последнего
перпендикуляра, опущенного из точек АС
на АВ, а не существования
границы расстояний AM.
Неизвестно еще, соответствуют ли равным отрезкам
равные AG = GM = MN и т. д
D
G М N
Рис. 30.
AF = FC = СР и т. д.
Быть может, величина AN = AG +
1,1.1
+ GM+ MN +. . . растет как сумма членов ряда 1 + у + ~7" + 1Г~Ь **•'
так что при любом удалении точка С никогда не достигает 2AG1 Эта
остроумная критика не помешала Гурьеву допустить в его собственном
доказательстве постулата о параллельных аналогичную ошибку х).
В последующих изданиях «Начал геометрии» Лежандр предложил другие
доказательства и также поступил Гурьев в своих «Основаниях
геометрии» (СПб., 1804—1807; 2-е изд. 1811).
«Основания дифференциального исчисления» Гурьева базируются
на более развитом учении о пределах, которое он изложил еще в одной
статье 1797 г., где, обобщая простейшие теоремы о предельных
переходах,— пределе суммы, разности, произведения и т. д.— сформулировал
правило вычисления предела функции путем подстановки в функцию
предельного значения аргумента: «согласно 12 вспомогательным истинам
метода пределов, видно, что если над какой-нибудь увеличивающейся
или уменьшающейся величиной, имеющей предел, производят некоторую
операцию, то результат этой операции имеет пределом результат той же
операции, произведенной над пределом увеличивавшейся или
уменьшавшейся величины» 2). Однако даже доказательство теоремы о пределе
суммы двух переменных на основе определения предела Даламбера —
Гурьева в общем случае не проходит. Гурьев по отдельности доказывает
теорему для случаев, когда обе переменные возрастают или обе убывают.
Но если они меняются в разных направлениях, то их сумма, вообще
г) С. Е. Гурьев, Опыт о усовершении елементов геометрии, стр. 189—190.
2) NAP, т. XIII, стр. 187. Статья содержит попытку более строгого вывода усло-
дЧ дЧ
вия полного дифференциала и теоремы = .
210
ГЛ. 11 УЧЕНИКИ И ПЕРВЫЕ ПРЕЕМНИКИ ЭЙЛЕРА
говоря, не монотонна и к ней неприменимо названное определение.
Большое число (12) теорем о пределах объясняется тем, что, например,
теоремы о пределе суммы или разности переменной и постоянной величин
формулировались и доказывались особо. Исходное определение понятия
предела не позволяло, без его расширения, говорить о пределе
постоянной величины.
Наряду с пределом основным понятием дифференциального
исчисления у Гурьева служит lim -~, т. е. производная; дифференциалы
вводятся как произвольные числа, отношение которых равно этому
пределу. Гурьев пытается доказать, что для функции, предполагаемой
непрерывной (в нашем смысле), всегда существует производная. При этом он
опирается на существование у непрерывной кривой касательной,—
свойство, в то время ни у кого не вызывавшее сомнения. А. М. Ампер
несколькими годами ранее сделал попытку доказать дифференцируемость
произвольной функции всюду, за исключением отдельных точек, чисто
аналитически. Лишь много позднее выяснилось, что все эти доказательства обречены
на неудачу, так как непрерывные функции могут быть и недифференци-
руемыми. Бесконечно малые в курсе Гурьева, в явном виде не вводятся.
Учебник Гурьева очень богат фактическим материалом. Это был
первый на русском языке полный, хотя, к сожалению, тяжелый в
изложении, курс дифференциального исчисления для функций одной и многих
переменных. Вскоре, однако, стало очевидным, что теория пределов
Даламбера и его первых последователей недостаточна ни для построения
анализа в его наличном тогда состоянии, ни особенно для его дальнейшей
обработки. Само определение предела, ограниченное монотонными
переменными, было недостаточным, а отказ от применения бесконечно малых
был не только лишним по существу, но и лишал анализ одного из наиболее
эффективных его средств. В книге не было определения непрерывной
функции и по-прежнему формальный характер носили операции с рядами,
хотя формула Тейлора приводилась с остаточным членом. Прогрессивная
по своим тенденциям теория пределов нуждалась еще в существенном
развитии. Для построения общей теории сходимости последовательностей
и бесконечных рядов недоставало основного критерия сходимости Боль-
цано — Коши, открытие которого, впрочем, не заставило себя долго
ждать. Больцано пришел к нему в поисках доказательства теоремы о том,
что непрерывная функция, на концах отрезка имеющая разные знаки,
по крайней мере один раз обращается внутри отрезка в нуль (1816),
а Коши — в исследованиях по теории сходимости рядов (1821); вслед
затем Коши применил этот критерий в доказательстве существования
интеграла непрерывной функции (1823). Именно с критерия Больцано —
Коши ведет свое начало современная теория пределов, которая из
средства, позволяющего более или менее точно уяснить смысл начальных
операций дифференцирования и передоказывать уже известные теоремы,
стала действенным орудием новых теоретических изысканий.
Работы С. Е. Гурьева привлекли внимание русских математиков
к проблемам обоснования анализа. Это относится прежде всего к его
ученику, преподавателю математики и механики в Артиллерийском
кадетском корпусе Василию Ивановичу Висковатову (6 января 1780 —
20 октября 1812), в 1803 г. избранному адъюнктом Академии наук, а
четыре года спустя академиком. Висковатов дал изложение теории
аналитических функций Лагранжа, впервые употребив при этом русский термин
«производная функция» («Умозрительные исследования», II, 1810). Другой
С. Б. ГУРЬЕВ И ЕГО ПОСЛЕДОВАТЕЛИ
211
термин Висковатова «начальная функция» не удержался; мы говорим:
«первообразная». В своем изложении Висковатов, в отличие от Лагранжа,
широко пользовался сравнениями с обычными понятиями исчисления
бесконечно малых и чертежами. Это сближало обе теории и облегчало
изучение предмета. В двух других больших статьях Висковатов знакомил
наших читателей с вариационным исчислением («Умозрительные
исследования», II, 1810 и III, 1812). Несколько ранее он опубликовал, следуя
Амперу, вывод формулы Тейлора («Умозрительные исследования», I,
1808). К тому же кругу вопросов примыкают две статьи Шуберта об
основах дифференциального исчисления и теореме Тейлора (Mem. Ac. Sciences,
VI, 1818 и VII, 1820).
Вне стен Академии наук энергичную литературную и
педагогическую деятельность развил Петр Александрович Рахманов (ум. 1813 г.),
происходивший из старинной дворянской фамилии. Получив образование
в известной московской частной школе Е. Войтяховского, автора
«Теоретического и практического курса чистой математики» (4 тома, М., 1787—
1790), Рахманов поступил на военную службу, но главные интересы его
принадлежали математике. В значительной мере под влиянием Гурьева,
он написал свой первый труд «Новая теория содержания и пропорции
геометрической соизмеримых и несоизмеримых количеств, и в последнем
случае основанная на способе пределов» (М., 1803); напомним, что слово
«содержание» здесь означает отношение. Впрочем, Рахманов не во всем
следовал за Гурьевым. Определение пропорции, данное последним, он
считал недостаточно ясно выражающим суть дела и для определения
равенства несоизмеримых отношений ввел понятие «приближенной к А,
по мере а сыскиваемой» х). Под этим он понимал приближающую А по
недостатку переменную сумму, составленную из кратных а и ее все
меньших «частных»— долей, именно сумму вида
Хр=т0а + т^ + т2^+...+тРп1п^Пр,
где числа щ, п2, ... при сравнении двух каких-либо отношений
предполагаются одними и теми же, а кратности т0, ти т2, . . . — наибольшие
возможные, при которых Хр < А. Практически имеются в виду
приближения с помощью десятичных дробей. Величина А является пределом
своих приближенных (естественно, что доказательство этого предложения
у Рахманова не могло быть полноценным). После этого равенство
иррациональных отношений —«приближенных содержаний»— определяется
через равенство приближающих рациональных отношений:
приближенные содержания равны, «когда приближенные к предыдущим, сысканные
по последующим за меру взятым, с сими последующими при каждом своем
изменении всегда будут составлять равные содержания» 2). Так, — = —- ?
А С
если, скажем, десятичные приближения по недостатку для j- и для -=г ,
взятые с одинаковой степенью точности, всегда равны. Из своего
определения Рахманов выводит затем определение Гурьева.
Иррациональные числа Рахманов, вслед за Кестнером, рассматривал
как пределы выражающих их десятичных дробей3). Точно так же
г) П. Рахманов, Новая теория содержания и пропорции геометрической...,
М., 1803, стр. 45—46.
2) Там же, стр. 59—60.
3) Там же, стр. X.
212
ГЛ. 11. УЧЕНИКИ И ПЕРВЫЕ ПРЕЕМНИКИ ЭЙЛЕРА
смотрели на дело многие выдающиеся математики первой половины
XIX века, в частности, Коши. Только позднее выяснилось, что
классическая теория пределов сама нуждается для своего обоснования в
независимой теории иррациональных и вообще действительных чисел (Дедекинд,
Кантор, Вейерштрасс).
Одной из своих заслуг сам Рахманов считал доказательство всех
упоминавшихся выше 12 основных теорем метода пределов, которые
Гурьев доказал тогда еще не все. Некоторые выводы Рахманова по форме
сходны с употребительными поныне. Например, теорему о пределе суммы
нескольких (у него — трех) переменных он доказывает, выбирая
произвольно малое s и предполагая переменные меньшими своих пределов,
так: можно сделать одновременно
Л-Х<у, Я-У<±, C-Z<y
и, значит,
(A + B + C)-(X + Y + Z)<e.
Для вывода теоремы о пределе произведения используются, в том же
предположении, неравенства
АВ-БХ<у и ?Х-ХУ<у,
причем второе следует из возможности сделать В — У < -к-j и условия
X < А. Впрочем, как и другие математики того времени, при
формулировке теоремы о пределе частного, Рахманов не делал оговорки, что
предел знаменателя не есть нуль; это подразумевалось.
1803—1805 гг. Рахманов провел в Париже, где слушал в различных
учебных заведениях лекции лучших математиков», с которыми завел
и личное знакомство. За границей он выпустил брошюру «Опыт
некоторых приложений метода пределов» (Essay sur quelques usages de la metho-
de des limites, par P. de R., Vienne, 1805). Опираясь на геометрические
представления, иллюстрируемые чертежами, он здесь вывел при помощи
предельного перехода интегралы, выражающие в декартовых
прямоугольных координатах площадь криволинейной трапеции и объем тела
вращения вокруг оси абсцисс. Постановка преподавания во Франции, особенно
в Политехнической школе, и размах научных исследований произвели
на Рахманова сильное впечатление. В Россию он вернулся убежденным
и пылким пропагандистом передовых направлений французской научной
и педагогической мысли. Он завязал связи с Московским университетом
и Академией наук и приступил к интенсивной научно-литературной
работе. В ряде статей, брошюр и книг он стал излагать дифференциально-
геометрические работы Монжа и теорию аналитических функций Лагран-
жа, которую соединял с теорией пределов. Несколько таких работ он
поместил в своем «Собрании сочинений» (СПб., 1807), другие появились
отдельно или в «Артиллерийском журнале» (1808). В «Московских ученых
ведомостях», издававшихся Московским университетом, и в «Военном
журнале», выходившем под редакцией (и некоторое время на средства)
Рахманова, он опубликовал ряд блестящих рецензий на новые книги
по анализу и аналитической геометрии. Наконец, в своей квартире
в Петербурге Рахманов читал для желающих студентов Педагогического
института, учителей и офицеров курс анализа, из которых составились
С. Е. ГУРЬЕВ И ЕГО ПОСЛЕДОВАТЕЛИ
213
«Лекции г. Рахманова о дифференциальном исчислении» (СПб., 1810),
составленные одним из его слушателей, бывшим воспитанником
Академии наук Н. Тенигиным. За этим последовал «Опыт о различных теориях
дифференциального исчисления и о сравнении оных» (СПб., 1812).
Собственные взгляды Рахманова были эклектичны и его доказательства часто
не строже тех, которые он считал лишенными точности, но вместе с тем
его труды широко содействовали у нас распространению новейших
математических идей и открытий.
В последние годы жизни Рахманов разошелся с Гурьевым и
напечатал в «Военном журнале» за 1812 г. несколько весьма колких отзывов
о его трудах, в частности, об «Основаниях геометрии». Достоинства
руководств Гурьева оттесняются здесь на задний план и подчеркиваются их
недостатки: отсутствие правил измерения фигур в курсе геометрии и его
растянутость и тяжелый язык, неполнота труда по дифференциальной
геометрии, в котором не учтены работы Монжа, и т. д. Это повлекло
ответные выступления в печати Висковатова и другого ученика
Гурьева — Николая Михеевича Архангельского, воспитанника и впоследствии
профессора прикладной математики Харьковского университета (1787—
1857). Однако полемика оборвалась со смертью Рахманова, погибшего
в битве под Лейпцигом в октябре 1813 г.
Помимо названных ученых, проблемами обоснования анализа у нас
занимался в ту пору целый ряд других преподавателей и любителей
математики. Назовем прежде всего магистра Московского университета
Александра Дмитриевича Барсова (ум. около 1800 г.), племянника
упоминавшегося ранее профессора Барсова. Подобно Кестнеру, руководства
которого оказали на него несомненное влияние, А. Д. Барсов пытался
построить анализ на основе понятия предела, хотя и не столь
последовательно и систематично, как это сделал несколько позже Гурьев. Его
«Новая алгебра, содержащая в себе не только простую аналитику,
но также дифференциальное, интегральное и вариационное исчисление»
(М., 1797), при составлении которой автор опирался и на сочинения
Эйлера, несмотря на ряд недостатков в изложении, представляла в то
время заметное явление в русской математической литературе. Она
сыграла роль и в формировании воззрений Рахманова, хотя последний
критиковал в своей книге по теории пропорций Барсова за нечеткое определение
предела и связанные с этим неточности (не требуя постоянства предела,
Барсов, как и Кестнер, писал, что пределом величины аит + Ъ при и —>оо,
т > 0 является аит).
В Москве теория пределов вводилась иногда и в преподавание. Так,
в 1804—1806 гг. молодой профессор Иоганн Иде, ученик Кестнера (1775 —
13 октября 1806), излагал ее в университетском курсе анализа. Учитель
Фед. Кузьмин опубликовал книгу «Способ пределов и его употребление
или предложения, касающиеся до заменения способа бесконечно малых»
(М., 1804), где просто и кратко изложены были начала учения о пределах
по Гурьеву, а также их приложения к измерению круга и круглых тел.
Об успехе этой книги, предназначенной для юношества, говорит ее
несколько переработанное переиздание, вышедшее два года спустя под
названием «Начала способа пределов и применение его к началам
геометрии» (М., 1806). Упомянем еще одного любителя математики —
доктора Геттингенского университета и, по роду службы, как и Рахманов,
военного, Павла Акимовича Сулиму (1779 — 3 ноября 1812). В год окончания
университета, перед возвращением в Россию, Сулима опубликовал в Гет-
тингене небольшой «Мемуар о сближении теории аналитических функций
214 ГЛ. 11. УЧЕНИКИ И ПЕРВЫЕ ПРЕЕМНИКИ ЭЙЛЕРА
или исчисления дериваций *) с развитой но методу пределов теорией
дифференциального исчисления, на примере теоремы Тейлора» (Memoire
sur le rapprochement de la theorie des fonctions analytiques ou du calcul
des derivations avec la theorie du calcul differentiel developpee par la me-
thode des limites en prenant pour exemple le theoreme de Taylor. Gottin-
gue, 1804) 2).
Математика в Академии наук в начале XIX века. Труды Гурьева,
Висковатова и других только что названных математиков, к которым
мы могли бы добавить еще несколько имен 3), оказали серьезное влияние
на преподавание в России анализа и геометрии и учебную литературу,
влияние, ощущавшееся несколько десятков лет. Несомненно также
плодотворное воздействие работ петербургских академиков по сферической
геометрии, тригонометрии и другим геометрическим дисциплинам. Однако
в целом со смертью Леонарда Эйлера уровень математического творчества
в Академии наук заметно понизился. Положение дел еще ухудшилось,
когда в Академии остались лишь Фусс, загруженный административными
делами и продолжавший разработку мало актуальных частных задач,
и Шуберт, большую часть времени отдававший астрономии. Непременный
секретарь решил восполнить поредевшие ряды математиков ближайшими
родными, состоявшими «элевами»—«учениками», мы бы сказали теперь —
аспирантами — Академии. В 1814 г. был избран адъюнктом и в 1820 г.
академиком племянник Фусса Эдуард Давыдович Коллинс (14 июля
1791 — 16 августа 1840), а в 1823 г. стал академиком сын Фусса Павел
Николаевич (1 июня 1798 — 22 января 1855), который в 1826 г. занял
освободившийся со смертью отца пост непременного секретаря.
Первые печатные работы Коллинса и П. Н. Фусса имели ученический
характер и вряд ли Эйлер допустил бы их публикацию. Позднее Коллинс
выпустил ряд более солидных статей, но все они имеют небольшую
научную ценность. Упомянем лишь одну «Основные черты типического
счисления» (Grundlagen des typischen Kalkiils, СПб., 1823), где автор пытается
изучить свойства математических операций и символов с весьма общей
точки зрения. В этой работе заметно воздействие комбинаторной школы,
процветавшей в Германии на рубеже XVIII и XIX вв.; оно чувствуется
и в других работах Коллинса. Научная активность Коллинса была
незначительной и с количественной стороны. С 1824 г. он все больше времени
отдавал работе в Петербургской немецкой школе — Peterschule. Что
касается П. Н. Фусса, то он после избрания непременным секретарем
почти вовсе не вел научную работу. Пожалуй, главной заслугой Коллинса
и П. Н. Фусса перед математикой явилось привлечение к работе в
Академии наук М. В. Остроградского и В. Я. Буняковского, которые вновь
подняли здесь уровень математических исследований на большую высоту.
Обозревая в заключение результаты деятельности математиков в
России XVIII века, мы видим, что за 100 лет произошел сдвиг огромного
1) Исчисление дериваций Арбогаста (1800) — формальный способ разложения
в ряды различных функций, при котором из данных функций формально же выводятся
их деривации — производные функции и их свойства. Метод дериваций имеет много
общего с теорией аналитических функций Лагранжа. На русском языке его изложение
см.: В. Я. Буняковский, Лексикон чистой и прикладной математики, т. I,
СПб., 1839, стр. 348—354.
2)Е. С. Шатунова, О работе П. А. Сулимы по обоснованию
математического анализа.— Ист.-матем. исслед., вып. XII, 1959.
3) Подробнее см. А. П. Юшкевич, Академик С. Е. Гурьев и его роль в
развитии русской науки.— Труды Ин-та ист. естеств., т. I, 1947.
МАТЕМАТИКА В АКАДЕМИИ НАУК В НАЧАЛЕ XIX ВЕКА 215
значения. В начале XVIII века были изданы первые печатные учебники
по элементарным отделам математики; к началу XIX века в изданиях
Петербургской Академии наук было опубликовано большое число
монографий и многие сотни статей по всем актуальным проблемам
математических наук. Петербургская Академия наук стала крупнейшим центром
математических исследований. В нашей стране получили дальнейшее
блестящее развитие идеи Декарта и Ферма, Ньютона и Лейбница; здесь
заложены были основы математической физики, теории
дифференциальных уравнений, учения о функциях комплексного переменного,
вариационного исчисления, теории чисел; фундаментальные открытия были сделаны
в алгебре, в учении о специальных функциях и других отделах анализа,
в тригонометрии, аналитической и дифференциальной геометрии и т. д.
Последние годы рассмотренного нами периода совпали с началом
нового широкого общественного подъема в России, который нашел свое
выражение и в области просвещения. С этим общественным подъемом
и с реформой преподавания математики связано начало нового периода
в развитии русской математики.
ЧАСТЬ ТРЕТЬЯ
МАТЕМАТИКА В РОССИИ
В ПЕРВОЙ ПОЛОВИНЕ XIX ВЕКА
ГЛАВА ДВЕНАДЦАТАЯ
ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
Реформа системы образования. В истории математики в России
рассматриваемый период был отмечен новыми замечательными достижениями,
которым суждено было оказать решающее влияние не только на мировую
математику в целом, но и на все математическое естествознание.
После смерти Л. Эйлера (1783) Петербургская Академия наук на
некоторое время утратила значение крупнейшего европейского центра в области
математических наук. На первое место теперь выдвинулась поднятая
волной французской буржуазной революции парижская школа
математиков во главе с Ж. Лагранжем, Г. Монжем, П. Лапласом, Ж. Фурье
и О. Коши, а затем немецкая школа во главе с К. Ф. Гауссом. Но уже
в двадцатые годы XIX века начался новый подъем математики в нашей
стране.
Одной из важных предпосылок этого подъема явились изменения
в системе образования, которые произошли в самом начале XIX столетия.
Особенное значение имела организация новых университетов и создание
физико-математических факультетов.
В XVIII веке немногочисленных специалистов-математиков готовили
при Академии наук. К концу XVIII века академические учебные
заведения почти прекратили свою работу, а в начале XIX века были закрыты
в связи с общей реформой системы народного просвещения. При
Академии наук сохранилось только небольшое число «элевов» для подготовки
ее адъюнктов, но и этот институт несколько позднее был устранен.
В Московском университете почти полстолетия преподавание математики
не выходило за пределы элементарных отделов. В военных и морских
учебных заведениях обучали исчислению бесконечно малых и высшей
геометрии, но специалисты математики выходили из таких школ редко.
Одним из них, кроме С. Е. Гурьева, был Платон Яковлевич Гамалея
(29 ноября 1766 — 21 июля 1817), автор пятитомной «Вышней теории
морского искусства» (СПб., 1801—1808), первые два тома которого
представляют собой весьма содержательный и доступно написанный курс
алгебры, конических сечений и анализа, до начал теории обыкновенных
дифференциальных уравнений включительно, а третий посвящен теоре-
РЕФОРМА СИСТЕМЫ ОБРАЗОВАНИЯ
217
тической и прикладной механике. Заслуги этого даровитого и
просвещенного профессора Морского корпуса были по инициативе Гурьева отмечены
его избранием в 1799 г. почетным членом Академии наук. «Речь о науках
вообще, о пользе их и о способе упражняться в оных», произнесенная
Гамалеей на выпуске воспитанников корпуса в конце 1806 г. (СПб.,
1807) — речь, вся проникнутая передовыми идеями материализма второй
половины XVIII века, представляла собой красноречивый панегирик
науке вообще, математике в частности. Заслуживает упоминания его
совет соединять изучение науки и ее истории.
Потребность страны в расширении системы общего образования была
велика и в 1782 г. правительство создало Комиссию об учреждении
училищ. Были открыты двухклассные малые народные училища в уездных
городах и четырехклассные главные училища с пятилетним сроком
обучения — в губернских. В первый год начало работать всего восемь школ,
имевших 518 учеников и 26 учителей, к 1800 г. в 315 школах имелось
около 20 000 ребят и 800 учителей. Рост — несомненный, но для
государства с 26-миллионным населением это было совсем немного. Важную
роль сыграло созданное в 1782 г. при Петербургском главном училище
отделение для подготовки учителей, преобразованное в 1786 г. в
Учительскую семинарию со сроком обучения в два с половиной года. Мы
говорили, что в ней преподавал М. Е. Головин; другим ее профессором
был Петр Иванович Гиларовский, автор «Сокращения высшей
математики» (СПб., 1796). За первые пятнадцать лет Учительская семинария
подготовила свыше 400 педагогов и одним из ее воспитанников был
выдающийся деятель математического просвещения Т. Ф. Осиповский. В 1804 г.
семинария была преобразована в Педагогический институт и в 1816 г.
в Главный педагогический институт, на основе которого еще полтора
десятка лет спустя возник Петербургский университет. Впрочем, в 1829 г.
Главный педагогический институт был открыт вновь и из него вышло
немало преподавателей не только гимназий, но и высших учебных
заведений. Вторично закрыт он был в 1859 г.
Комиссия об учреждении училищ подготовила и проект об
учреждении университетов. Однако революционная буря, разразившаяся во
Франции и потрясшая всю Европу, заставила царское правительство
отложить в сторону более широкие планы народного образования. «Черни,—
заявляла Екатерина II,— не должно давать образования, поколику будет
знать столько же, сколько вы да я, то не станет повиноваться нам в такой
мере, как повинуется ныне». Все же военные успехи французских армий
наглядно демонстрировали всему свету важность быстрого
совершенствования технического оснащения войск и флота, которое опиралось на
огромную работу, проводившуюся французскими химиками, физиками,
математиками и инженерами, а также на создание нового, гораздо более
высокого типа школ для подготовки высококвалифицированной научной
и технической интеллигенции. Когда Наполеон, сохранив экономические
завоевания революции, установил единовластие, казавшееся более
прочным, чем при династии Бурбонов, монархические правительства других
европейских государств решились пойти на некоторые реформы системы
образования. В России эти реформы провело правительство молодого
Александра I, вступившего на престол в 1801 г. Наибольшая сумма
знаний предназначалась для дворянства. Прочие сословия допускались
к знаниям в той мере, какая требовалась их родом деятельности, причем
в удел «нисшим» оставались, в лучшем случае, закон божий и начальная
грамота. В лучшем случае — потому, что даже начальное образование
218 ГЛ. 12. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
не было обязательным, а сеть начальных школ была ничтожной. Наиболее
способным одиночкам из простых людей предоставлялась весьма
сомнительная возможность перехода в высшее сословие, если им удавалось
попасть в высшее учебное заведение и его закончить. Тем не менее, эти
реформы при всей их недостаточности имели большое значение для
прогресса культуры и науки в России и их решительно поддерживали лучшие
люди страны. В середине десятых годов правительство убедилось, что
новые школы стали рассадниками философского, научного и политического
свободомыслия и от показного либерализма перешло к суровым
репрессиям, к покровительству мистике и мракобесию. В Харькове, Казани,
Петербурге были уволены многие передовые профессора и в университетах
введен жестокий полицейский режим. Попечитель Казанского округа
М. Л. Магницкий (1778—1844), недостойный потомок автора
«Арифметики», предлагал в 1819 г. вовсе закрыть подчиненный ему крамольный
университет; на это правительство все же не решилось. Резкие колебания
в университетской и вообще образовательной политике имели место
и в дальнейшем; за временными послаблениями всякий раз шло
преследование передового студенчества и профессуры; потом правительство опять
невольно отступало под напором экономической необходимости и
общественного давления и т. д.; все это продолжалось вплоть до свержения
самодержавия.
В 1802 г. было основано Министерство народного просвещения и при
нем Главное правление училищ, в которое вошли, как упоминалось,
Румовский и Фусс. План реформы начали осуществлять сравнительно
быстро. В уездных городах открывались уездные училища, в губерниях —
гимназии, а в шести городах — по числу учебных округов —
университеты. Один из них — Московский, существовал уже с 1755 г., другие
учреждались в Дерпте — Тарту (1802), Вильно — Вильнюсе, где до того
имелась иезуитская академия (1803), в Харькове и Казани (1805) и в
Петербурге (1819). Впрочем, Виленский университет был по политическим
соображениям закрыт в 1832 г.; вместо него в 1834 г. учрежден был
Киевский. Помимо того, было основано несколько новых высших технических
учебных заведений в Петербурге и Москве.
Важной чертой новой системы учебных заведений была ее
непрерывность: из уездного училища можно было перейти в гимназию, а
гимназическая подготовка была в принципе достаточной для начала
университетских занятий. Другой стороной реформы было новое деление
университетов и расширение их программ. Для примера мы кратко остановимся
на Московском университете.
Физико-математические факультеты. Московский университет
первые полвека работал в составе трех факультетов: юридического,
медицинского и философского. По уставу 1804 г. в нем появилось уже четыре
факультета или отделения: нравственных и политических наук, словесных
наук, врачебных или медицинских наук и, наконец, физических и
математических наук. На последнем отделении учреждались кафедры: 1)
опытной и теоретической физики, 2) чистой математики, 3) прикладной
математики, 4) астрономии, 5) химии, 6) ботаники, 7) минералогии и
сельского домоводства и 8) технологии и наук, относящихся к торговле
и фабрикам. Отделение готовило гимназических учителей, а также кадры
ученых, способных вести самостоятельные исследования и преподавать
в университете. Впервые вводились ученые степени: кандидата (для особо
успешно окончивших университетский курс), магистра и доктора. Как
ФИЗИКО-МАТЕМАТИЧЕСКИЕ ФАКУЛЬТЕТЫ
219
видно, преподавание на отделении охватывало весьма широкий круг
знаний и всей подготовке студентов сообщен был в значительной мере
прикладной характер. Это делалось с учетом интересов сельского
хозяйства и развивавшейся промышленности. Технических учебных заведений,
как и агрономических, в Москве тогда еще не было.
Слушателей физико-математического факультета обучали алгебре,
аналитической геометрии, дифференциальному и интегральному
исчислению; в течение довольно продолжительного времени на первом году
Д. М. Перевощиков. П. С. Щепкин.
обучения читали повторительный курс элементарной математики, ибо
студенты нередко поступали с плохим знанием школьного курса. Срок
обучения вначале был трехгодичный; с 1835 г. добавили еще один,
четвертый год; тогда же, в связи с улучшением преподавания в гимназиях
прекратили чтение повторительного элементарного курса. В это же время
расширили программу по математическому анализу, включив теорию
дифференциальных уравнений, обыкновенных и с частными производными,
а также вариационное исчисление. Кроме того, студенты с III курса
разделялись на математиков и естественников, и далее обучение
следовало различным программам. Еще десять лет спустя добавлен был курс
начертательной геометрии, а с 1850 г.— теория вероятностей с
приложениями к обработке наблюдений и к страховому делу. Вскоре затем
стали читать лекции по теории поверхностей и исчислению конечных
разностей.
Параллельно с расширением программ по математике,
совершенствовалось и углублялось содержание лекций. Большие заслуги во всем
этом принадлежали профессорам Д. М. Перевощикову и П. С. Щепкину,
а особенно Н. Е. Зернову и Н. Д. Брашману, которые поставили
преподавание математики и механики на уровень современной им науки.
Дмитрий Матвеевич Перевощиков (28 апреля 1790 — 15 сентября 1880),
воспитанник Казанского университета, был автором ряда учебников, среди
которых широкой известностью пользовалась «Ручная математическая
220 ГЛ. 12. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
энциклопедия» в 13 томиках, из которых первые семь содержали курсы
элементарной и высшей математики, следующие три — механики, а
остальные были посвящены физике и астрономии (М., 1826—1837). Об одном
из томиков Н. В. Гоголь в 1827 г. писал: «Не знаю, как воздать хвалу
этому образцовому сочинению. Верите ли, что я, только читая ее, понял
все то, что мне казалось темным, неудовлетворительным, когда проходил
математику» г). В Московском университете Перевощиков работал с 1818 г.г
читая разнообразные курсы по математике, астрономии и механике.
Главные труды его относятся к астрономии; в 1852 г. он был избран
академиком и переехал в Петербург. Павел Степанович Щепкин (1793 — 27 июля
1836), окончивший Московский университет в 1811 г., преподавал в нем
математику с 1817 по 1833 г. В 1834 г. освободившуюся с уходом Щепкина
вакансию занял другой воспитанник университета, ученик Перевощикова
Николай Ефимович Зернов (19 ноября 1804 — 5 декабря 1862), первый
московский доктор математических наук. Докторская диссертация 3ер-
нова «Рассуждение об интеграции уравнений с частными
дифференциалами» (М., 1837) содержала тщательное и не лишенное оригинальности
изложение классических методов; в течение многих лет она служила
учебником. Преподавание анализа Зернов поднял на значительно более
высокий уровень, чем его предшественники, которые, подобно авторам
распространенных тогда французских учебников — С. Лакруа (1 изд.
1797—1800), Ж.-Л. Бушарла (1815) и Л.-Б. Франкеру (1819),
эклектически соединяли идеи и методы исчисления бесконечно малых Лейбница,,
теории аналитических функций Лагранжа, способа пределов Даламбераг
а иногда и учения о компенсации ошибок Карно, которое высоко ценил,
например, Перевощиков. «Дифференциальное исчисление с приложениями
к геометрии» (М., 1842) Зернова в широкой мере отразило ту реформу
оснований анализа, которую проводил в своих лекциях и научной
деятельности Коши; в него включены и многие важные результаты последнего,
как классический пример функции е х2 (предполагаемой при х = 0
равной нулю), которая не раскладывается (при всех х ф§) в
соответствующий ей сходящийся ряд Маклорена. М. В. Остроградский писал об этом
сочинении, что оно «есть первое, в котором на русском языке изложена
дифференциальное исчисление с приложением его к геометрии с
надлежащей полнотою и отчетливостью и с приспособлением метод, признанных
за лучшие. Курс г. Перевощикова, хотя и заслуживает всякого
уважения, слишком сокращен; книга же Гурьева весьма тяжелая в
изложении» 2). Все же Остроградский отмечал неясности и неточности во
введении к учебнику; в самом деле, идеи обоснования анализа Коши изложены
здесь не вполне отчетливо и переплетаются с мотивами теории Карно.
В результате руководству Зернова была присуждена половинная
Демидовская премия Академии наук (эти премии, учрежденные богачем
П. Н. Демидовым, присуждались в 1832—1865 гг.: полная премия
составляла 5000 руб.).
Последний из четырех названных деятелей Московского
университета, Николай Дмитриевич Брашман (25 июня 1796 — 25 мая 1866),
уроженец Моравии и воспитанник Политехнического института и университе-
х) Н. В. Гоголь, Полное собрание сочинений, т. X, изд. АН СССР, 1940,
стр. 109.
2)М. В. Остроградский, Полное собрание трудов, т. III, Киев, 1961,
стр. 321.
ФИЗИКО-МАТЕМАТИЧЕСКИЕ ФАКУЛЬТЕТЫ
221
та в Вене, приехал работать в Петербург в 1823 г. С весны 1825 г. он
преподавал в Казанском университете, а в начале учебного 1834—1835 гг.
перешел на кафедру прикладной математики Московского университета.
Здесь он превосходно поставил курс механики, которой также посвящен
ряд его научных работ. Вместе с Зерновым он уделял много сил и времени
улучшению преподавания математики. Два руководства Брашмана были
удостоены Демидовской премии: «Курс аналитической геометрии» (М.,
1836) и, на основании отзыва Остроградского, «Теория равновесия тел
Н. Е. Зернов. Н. Д. Брашман.
твердых и жидких» (М., 1837). Оба они отличаются высокими
достоинствами. Руководство Брашмана по аналитической геометрии далеко выходило
за пределы обязательной университетской программы и вводило читателя
в новейшие исследования по проективной геометрии (принцип
двойственности, теория полюсов и поляр с приложениями к коническим сечениям).
В последней главе его изложены собственные исследования автора о
геометрическом истолковании неравенств. Пристально следя за новинками
математической литературы, Брашман знакомил с ними студентов на
лекциях, в частных беседах и, наконец, публикациях. Математические статьи
его в «Ученых записках» Московского университета, которые стали
выходить в 1833 г., содержат отдельные результаты по теории
дифференциальных уравнений, примыкающие к исследованиям Штурма, по
интегрированию алгебраических функций, теории экстремумов функций многих
переменных, и другим вопросам. Эти работы, печатавшиеся на
протяжении 1834—1835 гг., имели для студентов несомненное стимулирующее
значение.
Интересы Брашмана распространялись и на прикладную механику.
В своих курсах, наряду с проблемами аналитической механики, он уделял
большое внимание ее техническим применениям, знакомя слушателей
с принципами расчета работы различных машин, гидравликой, задачами
баллистики и т. д. При его участии на факультете были введены в 1844 г.
222 ГЛ. 12. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
курсы начертательной геометрии и практической механики, чтение которых
было поручено его ученику Александру Степановичу Ершову (1818—
1867), впоследствии одному из организаторов Московского высшего
технического училища. Добавим, что по настоянию Брашмана же
в 1850 г. на кафедру математики был принят другой талантливый
его ученик, А. Ю. Давидов, начавший тогда же чтение курса теории
вероятностей.
Нам еще придется говорить о выдающихся заслугах Брашмана в
подготовке научных кадров, а также в создании Московского математического
общества и его печатного органа —«Математического сборника». Здесь
добавим, что Брашман находился в постоянном контакте с Академией
наук и, в частности, с Остроградским, который оказывал несомненное
воздействие на его научные интересы. В 1855 г. Брашман был избран
членом-корреспондентом Академии. В Московском университете он
работал до 1864 г., но и после того до конца жизни сохранял с ним самую
тесную связь.
В двадцатые и особенно в тридцатые и сороковые годы значительно
улучшилась подготовка студентов физико-математического факультета,
возросли требования, предъявляемые на экзаменах, особенно
магистерских, более содержательными и глубокими стали магистерские
диссертации. В то время такие диссертации, как правило, представляли собой
обзоры развития и состояния той или иной дисциплины: вариационного
исчисления, интегрирования алгебраических функций, теории кривизны
поверхностей, теории вероятностей, теории равновесия тел в жидкости,
теории водяных колес и т. п. Некоторые диссертации могли служить
хорошими учебниками, иные содержали самостоятельные научные
результаты.
А. И. Герцен, учившийся на факультете в 1829—1833 гг. и
специализировавшийся по астрономии, вспоминал: «Молодежь была прекрасная
в наш курс. Именно в это время пробуждались у нас больше и больше
теоретические стремления» 2). Сам Герцен, как и некоторые его товарищи,
вступил на трудный и опасный путь идейной и политической борьбы
с самодержавием и крепостничеством,— наука,— говорил он,—не
отвлекала их от вмешательства в жизнь, страдавшую вокруг. Другая часть
студенчества той эпохи, не столь радикально настроенная и вместе с тем
преданная «теоретическим стремлениям» в сфере физико-математических
наук, видела свой способ служения родине и человечеству в научной
и педагогической работе. Уже в то время факультет окончил ряд
выдающихся ученых: уже названные А. С. Ершов и А. Ю. Давидов, механик
и математик О. И. Сомов, механик И. И. Рахманинов, баллистик Н. В. Маи-
евский,— этот список, во главе которого следует поставить великого
П. Л. Чебышева, можно было бы продолжить 2).
Уровень и успехи преподавания математики в различных
университетах естественно зависели во многом от профессорско-преподавательского
состава. Так, в Харьковском университете в 1804—1820 гг. кафедру
математики возглавлял выдающийся по своей эрудиции и
педагогическому дарованию воспитанник Учительской семинарии Тимофей Федо-
х) А. И. Герцен, Былое и думы, т. 1, М., 1937, стр. 204.
2) Подробнее см. А. П. Юшкевич, Математика в Московском университете
за первые сто лет его существования.— Ист.-матем. исслед., вып. II, 1949; И. И. Л и -
холетов иС. А. Яновская, Из истории преподавания математики в
Московском университете (1804—1860).— Ист.-матем. исслед., вып. VIII, 1955.
ФИЗИКО-МАТЕМАТИЧЕСКИЕ ФАКУЛЬТЕТЫ
223
рович Осиповский (2 февраля 1765 — 24 июня 1832), автор очень хорошего
«Курса математики» (три тома, 1801—1823), обнимавшего все читавшиеся
тогда в гимназиях и университете предметы, и человека широких научных
и философских интересов. Вместе со своим помощником Андреем
Федоровичем Павловским (1788—1856), Осиповский превосходно
поставил преподавание математики в Харькове, но после его увольнения
в 1820 г. уровень преподавания несколько понизился, вплоть до прихода
в 1845 г. Евгения Ильича Бейера (1819—1899), получившего образование
в Главном педагогическом институте в Петербурге под руководством
Остроградского *). Высокими качествами отличались лекции по различным
математическим дисциплинам
воспитанника Геттингенского университета
профессора Мартина Федоровича Бар-
тельса (23 авг. 1769—19 дек. 1836),
работавшего по приглашению Румовско-
го в 1808—1820 гг. в Казани, а с начала
1821 г. до конца жизни в Дерптском
университете2). С середины десятых
годов XIX века до 1846 г. в Казанском
университете математику преподавал
Н. И. Лобачевский. В Дерпте с 1837 г.
читал математические курсы ученик
Бартельса Карл-Эдуард Зенф (1810—
1849), к которому в 1843 г.
присоединился крупный геометр Ф. Г. Миндинг.
В Петербургском университете, где
вначале курсы чистой и прикладной
математики вели воспитанники
Главного педагогического института Дмитрий
Семенович Чижов (1785—1852) и Викен-
тий Александрович Анкудович (1799—
1855), студенты получали в двадцатых
и тридцатых годах посредственную под- т ф осиповский.
готовку. Только в середине тридцатых
годов Анкудович пополнил курс анализа началами вариационного
исчисления, но еще ряд лет почти не уделял места дифференциальным уравнениям.
Правда, он же в 1837 г. поставил здесь курс теории вероятностей. Чижов
и Анкудович вышли в отставку один за другим в 1846 и, соответственно,
1847 г., но еще до того на факультете начались перемены к лучшему.
В 1840 г. здесь начал свою долгую 35-летнюю преподавательскую
деятельность прибывший из Москвы О. И. Сомов, прежде всего обновивший
и углубивший курсы высшей алгебры и аналитической геометрии, а затем
открывший новый курс теории эллиптических функций. С 1846 г.
профессором университета состоял В. Я. Буняковский, в том же году
приступивший здесь к чтению лекций по теории вероятностей; три года спустя
он начал чтение большого курса интегрирования дифференциальных
уравнений. Наконец, в 1847 г. на факультет пришел еще один воспитанник
*) См. сб.: Физико-математический факультет Харьковского университета за
первые 100 лет его существования. Харьков, 1908; Э. Я. Б а х м у т с к а я, Тимофей
Федорович Осиповский.— Ист.-матем. исслед., вып. V, 1952.
2) И, Я. Д е п м а н, М. Ф. Бартельс — учитель И. И. Лобачевского.— Ист.-
матем. исслед., вып. III, 1950.
224 ГЛ. 12. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
Московского университета — П. Л. Чебышев, первым курсом которого
явилась теория чисел; из этих лекций вскоре выросла докторская
диссертация Чебышева по теории сравнений, ставшая на долгое время
классическим руководством по этому предмету. Буняковский и Чебышев,
проработавший в университете до 1882 г., читали самые разнообразные курсы
по математике; Сомов вел также занятия по механике. Благодаря этим
трем ученым, особенно Чебышеву, преподавание всего цикла механико-
математических наук, существенно расширенного, было поднято на самый
высокий уровень 1).
В результате организации физико-математических факультетов в
России, наряду с Петербургом возникают новые математические центры —
в Казани, Москве, Харькове. В первой половине XIX века эти
факультеты дали гимназиям тысячи квалифицированных учителей и высшей
школе многих профессоров и ученых. Из университетов вышли
крупнейшие наши математики рассматриваемого времени: из Казанского—Н. И.
Лобачевский, из Харьковского — М. В. Остроградский, из Московского —
О. И. Сомов, П. Л. Чебышев и А. Ю. Давидов, из Дерптского — К. М. Пе-
терсон. Деятельность некоторых из названных лиц выходит, впрочем,
за рамки этого периода.
Академия наук. В Академии наук после смерти в 1825 г. Шуберта
и в 1826 г. старшего Фусса оставался фактически один математик —
Коллинс, продолжавший изредка печатать статьи в духе немецкой школы
формально-комбинаторного анализа. П. Н. Фусс был почти полностью
поглощен своими обязанностями непременного секретаря; впрочем,
отдавая дань памяти своего великого предка и его соратников, он
опубликовал в двух томах часть хранившейся в академическом архиве научной
переписки Эйлера, И. Бернулли, Д.Бернулли, Гольдбаха и других ученых —
Correspondance mathematique et physique de quelques celebres geometres
du XVIIIе siecle (St.-Petersbourg, 1843). Позднее, вместе с братом,
учителем математики Николаем Николаевичем Фуссом (1810—1867), он
выпустил в свет два тома неизданных рукописей Эйлера (Opera postuma mathe-
matica et physica, Petropoli, 1844). Новый подъем работ по математике
в Академии наук был связан с избранием в нее в 1828 г. М. В.
Остроградского и В. Я. Буняковского, а затем, в 1853 г., П. Л. Чебышева.
С их приходом Академия вновь становится крупнейшим математическим
центром, оказывающим мощное влияние на развитие математики в
России и за рубежом. Как мы видели, новые академики-математики вели
преподавание в университетах и других высших учебных заведениях
страны; это относится и к последующим членам Академии наук, по
большей части ученикам Чебышева. С другой стороны, если не считать
Буняковского и позднее А. Н. Крылова, то с 1828 г. все наши академики-
математики вышли из русских университетов.
Научная и педагогическая деятельность Лобачевского,
Остроградского, Буняковского, Чебышева отличалась очень высокой
интенсивностью. Вместе с ними и другие названные профессора многое сделали
для подъема математической культуры в России. Все же первая половина
XIX века явилась эпохой творчества немногих одиночек. Создание
отечественных математических школ еще только подготовлялось и первая
из них после эйлеровской — школа Чебышева возникла лишь во второй
1)Р. И. Галченкова, Математика в Ленинградском (Петербургском)
университете в XIX веке.— Ист.-матем. исслед., вып. XIV, 1961.
ОСОБЕННОСТИ РАЗВИТИЯ МАТЕМАТИКИ В РОССИИ И ЗА РУБЕЖОМ 225
половине столетия, в другой общественной обстановке, изменившихся
условиях университетской жизни, на почве нового духовного подъема
русской интеллигенции. «Жизнь русских университетов,— писал А. В.
Васильев,— всегда зависела от уставов и тех рамок, в которые их ставила
этими уставами власть, почти всегда невежественная»1). Устав 1804 г.
предоставил университетам самостоятельность, хотя и весьма ограниченную,
позволил им оказывать прогрессивное влияние на средние учебные
заведения и на все просвещение. Реакция, наступившая вскоре после
Отечественной войны 1812 года, и еще усилившаяся в ответ на восстание
декабристов в 1825 г., а затем на революционные события в Западной Европе
1848 г., вновь полностью подчинила университеты царскому
Министерству просвещения, ввела в них полуказарменный режим, а сверх того,
резко ограничила доступ как в высшие, так и в средние училища. Число
студентов было невелико и рост его сознательно сдерживался, количество
вакансий на преподавательские должности в университетах ничтожно,
а материальное и общественное положение гимназических учителей было
незавидное. И над всей духовной жизнью тяготело иго николаевского
жандармского режима, безжалостно преследовавшего малейшие
проявления вольного духа в любой сфере культуры и науки. Тот же А. В.
Васильев справедливо подчеркивал: «Математика, ценность которой для
баллистики и даже для интендантского дела нельзя было отрицать,
терпелась более, чем другие науки, но и она только терпелась» 2). В глазах
царя и его окружения любой ученый был вольнодумцем, по крайней
мере потенциальным 3).
Особенности развития математики в России и за рубежом. В
развитии математики в России этого периода можно отметить некоторые
своеобразные моменты. В разработке одних направлений исследования
русских ученых тесно переплетаются с исследованиями за рубежом. Здесь,
как, например, в математической физике и в ряде отделов математического
анализа или в теории чисел, имеет место довольно регулярная связь
между русскими и зарубежными исследованиями, хотя иногда
результаты, полученные в России, остаются незамеченными и с запозданием
переоткрываются за границей.
В других случаях русские ученые, отправляясь от проблем,
поставленных в мировой математике, уходят далеко вперед, оставляя позади
западноевропейских математиков. Так было с работами по неевклидовой
геометрии Лобачевского, которые получили признание и дальнейшее
развитие только много спустя после их публикации, так случилось позднее
с фундаментальными трудами Чебышева и его учеников по теории
вероятностей и теории приближения функций.
Вместе с тем некоторые новые направления математики еще не были
представлены или мало разрабатывались в России первой половины
XIX века. Это относится, например, к теории функций комплексного
переменного и проективной геометрии. Такое отставание на одних
участках фронта математических исследований, соединявшееся с далеким
продвижением вперед на других, объяснялось прежде всего малочисленностью
русских математиков в первой половине XIX века. С течением времени
х) А. В. Васильев, Математика, вып. 1 (1725—1826—1863). Птг., 1921,
стр. 70.
2) Там же, стр. 62.
3) Ср. А. И. Д е л ь в и г, Воспоминания, М.-Л., 1930, стр. 115.
226 ГЛ. 12. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
деятельность наших ученых распространялась на новые и новые области
математики, но сплошной фронт, охватывающий все или почти все отделы
математики, был создан в стране лишь после Великой Октябрьской
социалистической революции.
В развитии математического анализа в первой половине XIX века
выделяются два решающих момента. Во-первых, значительно
расширяется область применения его методов в естествознании. Если ранее
главными областями приложения математического анализа были механика
(в том числе небесная) и оптика, то теперь на первый план выдвигаются
также разнообразные проблемы математической физики, В связи с
обострением интереса к тепловым, электрическим и магнитным явлениям,
математические методы получают новое поле приложений в термодинамике,
электродинамике и т. д. Все это обусловливает прогресс теории уравнений
с частными производными, а в связи с нею теории тригонометрических
рядов, некоторых отделов интегрального исчисления, учения о
специальных функциях и пр. Первыми по времени здесь являются работы
французской школы, особенно Фурье по теплопроводности. В России эту
проблематику с большим успехом разрабатывает Остроградский. С другой
стороны, в аналитической механике получают важное значение
вариационные принципы, развиваемые ирландцем У. Гамильтоном, М. В.
Остроградским и немецким ученым К. Якоби; это стимулировало разработку
вариационного исчисления и опять-таки теории дифференциальных
уравнений.
Другим характерным моментом в развитии математического анализа
была перестройка его оснований. Огромный накопленный в XVIII веке
материал, а также многочисленные трудности, обнаружившиеся (особенно
в связи с решением задач математической физики) в теории рядов, в
интегрировании разрывных функций и пр. вызвали в начале XIX века
постановку новых проблем или новую постановку уже ранее возникших
вопросов. От изучения отдельных разложений в ряды и отдельных более частных
видов функций математики обращаются к общим проблемам сходимости
рядов, разложимости функций в ряды того или иного вида, к изучению
общих свойств широких классов функций, прежде всего непрерывных,
к удовлетворяющему возросшему стандарту строгости решению так
называемых «проблем существования» различных объектов анализа и
других математических наук. Математики убеждаются в необходимости
доказывать теоремы анализа на арифметической основе, а не на
обращении к наглядным, но далеко не всегда точным представлениям
геометрии и механики (хотя они и не отказываются от пользования
геометрическими или физическими моделями в своей творческой
работе).
Чешский философ и математик Б. Больцано и француз О. Коши дают
определение непрерывной функции в современном смысле слова и
устанавливают необходимый и достаточный критерий существования предела
последовательности. В «Курсе алгебраического анализа» (Cours (Гanalyse
algebrique, Paris, 1821) Коши, среди прочего, излагает основания
современной теории сходимости рядов, а в «Резюме лекций по анализу
бесконечно малых» (Resume des legons sur le calcnl infinitesimal, Paris, 1823)
реализует в основных чертах программу построения анализа на базе
новой теории пределов, включающей и учение о бесконечно малых
величинах, как переменных, имеющих пределом нуль. В этих же лекциях
Коши дал свое известное доказательство существования определенного
интеграла непрерывной функции, как предела интегральных сумм, и впер-
ОСОБЕННОСТИ РАЗВИТИЯ МАТЕМАТИКИ В РОССИИ И ЗА РУБЕЖОМ 227
вые рассмотрел более общим образом условия существования
несобственных интегралов; в другом месте он доказал первые теоремы о
существовании решений дифференциальных уравнений. Эти и другие работы Коши
повлекли за собой коренные перемены в методах исследования анализа
в целом. Отныне теоремы анализа стремятся доказывать в точно
определенных границах их правомерности, а при введении новых понятий
требуется выяснение возможности их существования. В России идеи Коши
были вскоре восприняты Остроградским и Лобачевским, которые развили
их далее. Лобачевский почти в одно время с Дирихле формулирует
современное общее определение функции и значительно продвигается
в исследовании достаточных условий разложимости функций в ряды
Фурье.
В связи с занятиями математической физикой и вариационным
исчислением Остроградский существенно обогатил теорию кратных интегралов.
Наряду с этим Остроградский разрабатывал теорию интегрирования
алгебраических иррациональностей, в которой первые фундаментальные
результаты были получены норвежцем Н. Абелем; впоследствии эта
область анализа стала одним из предметов занятий Чебьппева. Теория
эллиптических функций, в той форме, какую ей сообщили Абель и Якоби,
излагалась в курсах Сомова и Чебьппева, а первый из них дал ее
оригинальное изложение в специальной монографии.
В середине двадцатых годов Коши приступил к разработке общей
теории аналитических функций комплексного переменного, которую
затем с успехом развивали в новых направлениях К. Вейерштрасс,
Б. Риман и др. Эта молодая отрасль анализа, в подготовке которой столь
многое сделал Эйлер, не сразу нашла у нас продолжателей в
рассматриваемое время. Только Остроградский посвятил ей несколько ранних
своих работ; позднее в лекциях по теории определенных интегралов,
читанных в Инженерной академии, он отводил видное место теории
вычетов.
Крупные успехи достигнуты были в области алгебры. В 1799 г. Гаусс
почти безупречно доказал основную теорему о существовании
комплексного корня у всякого алгебраического уравнения. Итальянский
математик П. Руффини (с некоторой неполнотой) и Абель (совершенно строго)
доказали неразрешимость в радикалах общего уравнения пятой и высших
степеней, положив конец тщетным стараниям многих ученых XVII—
XVIII вв. найти такое решение. Исследуя вопрос о классах уравнений
высших степеней, допускающих решение в радикалах, французский
математик Э. Галуа заложил начала общей теории групп, которая наряду
с неевклидовой геометрией во многом определила развитие математики
второй половины XIX века. Одновременно в алгебре велись исследования
и в других направлениях. Большое развитие в связи с запросами
практики получили численные методы решения алгебраических уравнений
(Фурье, Ш. Штурм, К. Греффе). Результаты принципиального значения
достигнуты были в общей теории операций над алгебраическими
величинами (У. Гамильтон, Дж. Пикок, Г. Грассман). Оба эти последние
направления разрабатывал и Лобачевский.
Мы не будем пока касаться новых открытий в теории вероятностей
(Лаплас, С. Пуассон) и теории чисел (Гаусс, Дирихле, Э. Куммер), ибо
к глубокой разработке этих областей русские математики приступили
только в самом конце рассматриваемого периода и полученные
здесь Чебышевым результаты удобнее будет разобрать в следующей
части. Но еще до работ Чебьппева некоторые исследования по теории
228 ГЛ. 12. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
вероятностей и теории чисел были проведены Лобачевским, Остроградским
и Буняковским.
Наконец, в развитии геометрии в первой половине XIX века
выделяются три основных момента. Это, во-первых, разработка Гауссом внутренней
геометрии поверхностей; впервые изложенной им в одной работе 1827 г.
Вскоре дифференциально-геометрические исследования Гаусса были
успешно продолжены Ф. Г. Миндингом и к концу рассматриваемого периода —
К. М. Петерсоном. Вторым направлением явилось проективно-геометриче-
ское (Ж.-В. Понселе, М. Шаль, Я. Штейнеридр.). Третьим и важнейшим
событием в истории геометрии явилось открытие Лобачевским первой
системы неевклидовой геометрии. Обзор развития русской математики
в рассматриваемый период мы и начнем с трудов Лобачевского.
ГЛАВА ТРИНАДЦАТАЯ
Н. И. ЛОБАЧЕВСКИЙ И ОТКРЫТИЕ НЕЕВКЛИДОВОЙ ГЕОМЕТРИИ
Постулат Евклида о параллельных. На первых же страницах «Начал»
Евклида приводится перечень исходных положений геометрии. Одни из них
характеризуют общие свойства величин, вроде того, что целое больше
части, что при прибавлении к равным величинам равных получаются
равные и т. п. Их Евклид называл общими понятиями, их называли также
аксиомами. Другие исходные положения — специально геометрические,
их Евклид именовал требованиями, а его латинские переводчики —
постулатами. В разных списках «Начал» число аксиом и постулатов
несколько колеблется. Вот пять постулатов, несомненно, имевшихся
в оригинале труда александрийского геометра:
I. От всякой точки до всякой точки можно провести прямую линию.
П. Ограниченную прямую можно непрерывно продолжать по
прямой.
III. Из всякого центра и всяким радиусом может быть описан круг.
IV. Все прямые углы равны между собой.
V. Если при пересечении двух лежащих в одной плоскости прямых
третьей сумма внутренних односторонних углов меньше 2d, то названные
две прямые при достаточном продолжении пересекаются, и притом с той
стороны, где сумма указанных углов менее 2d.
Две лежащие в одной плоскости прямые, которые не пересекаются,
сколько бы их ни продолжать в обе стороны, называются параллельными.
В V постулате Евклида *), таким образом, идет речь о некотором условии,
при выполнении которого две лежащие в одной плоскости прямые не
параллельны. Это и есть знаменитый в истории науки постулат о параллельных
Евклида.
Значение V постулата о параллельных в евклидовой геометрии
огромно. Лишь немногие начальные теоремы в «Началах» Евклида
доказываются без его применения. С его помощью выводится теорема о том, что сумма
углов во всяком треугольнике равна 2d; на нем основана возможность
существования прямоугольников и квадратов, а также подобных и в то
же время неравных фигур; из него следует теорема Пифагора и он
определяет характер формул для измерения площадей и объемов, вообще всю
метрику евклидова пространства. В частности, из V постулата легко
вывести 31-е предложение первой книги «Начал»: через точку, лежащую
вне прямой, можно в их общей плоскости провести одну и только одну
прямую ей параллельную. Утверждением о единственности параллельной
один комментатор Евклида предложил в XVIII веке заменить V посту-
г) В некоторых рукописях «Начал» V постулат фигурирует как XI аксиома.
230 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
лат, поскольку и обратно из этого предложения можно вывести V
постулат, а значит, и все основанные на нем теоремы.
Более чем 2000 лет никто не сомневался, что все постулаты Евклида
представляют собой абсолютные и незыблемые истины. В этом
отношении V постулат также не вызывал никаких сомнений. Тем не менее уже
с древности именно постулат о параллельных привлек особое внимание
ряда геометров, считавших неестественным помещение его среди
постулатов. Вероятно, это было связано с относительно меньшей очевидностью
и наглядностью V постулата: в неявном виде он предполагает
достижимость любых, как угодно далеких частей плоскости, выражая свойство,
которое обнаруживается только при бесконечном продолжении прямых.
Попытки доказательства V постулата начались еще в древности и затем
производились неоднократно крупными математиками.
Одни математики старались доказать постулат о параллельных,
применяя только другие постулаты или те теоремы, которые можно вывести
из последних, не используя сам V постулат. Все такие попытки
оказались неудачными. Их общий недостаток состоял в том, что в доказательстве
неявно применялось какое-нибудь предположение, равносильное
доказываемому постулату.
Другие предлагали по-новому определить параллельные прямые
или же заменить V постулат каким-либо по их мнению более очевидным,
предложением. Так, например, в XI веке поэт и ученый Омар Хайям
ввел вместо V постулата «принцип», согласно которому две лежащие
в одной плоскости и сходящиеся прямые пересекаются и не могут
расходиться в направлении схождения. С помощью этого принципа Хайям
доказывает, что в четырехугольнике A BCD, в котором углы при
основании А и В — прямые и стороны А С, BD равны, углы С и D также прямые,
а из этого предложения о существовании прямоугольника довольно просто
выводится V постулат. Рассуждения Хайяма получили оригинальное
развитие в XIII веке у Насирэддина ат-Туси, работы которого в свою
очередь стимулировали исследования Дж. Валлиса. В 1663 г. Валлис
доказал постулат о параллельных, исходя из явного допущения, что
для каждой фигуры существует подобная ей фигура произвольной
величины. Это допущение он считал вытекающим из существа
пространственных отношений.
С логической точки зрения результаты Хайяма или Валлиса лишь
выявляли равносильность V постулата и некоторых других предложений
геометрии. Так, Хайям, по существу, установил эквивалентность
постулата и предложения о сумме углов треугольника, а Валлис показал, что
не только из V постулата можно вывести учение о подобии, но и обратно —
из евклидова учения о подобии следует V постулат. Это раскрывало
глубокие взаимные связи между различными предложениями геометрии
Евклида. Однако вопрос о том, можно ли вывести постулат о параллельных
из других постулатов Евклида, не прибегая к каким бы то ни было новым
предпосылкам, оставался открытым.
Итальянец Д. Саккери подробно разработал идею обосновать
постулат о параллельных от противного, показав, что отказ от него приводит
к некоторому противоречию. В сочинении, изданном в 1733 г., он вновь
рассматривает четырехугольник Хайяма — ат-Туси. Углы С ж D в этом
четырехугольнике равны (это доказывается без обращения к V постулату
или равносильному предложению) и могут быть априори предположены
либо оба тупыми, либо острыми, либо прямыми. Установив, что в последнем
случае имеет место V постулат, Саккери стремился доказать, что гипотезы
ПОСТУЛАТ ЕВКЛИДА О ПАРАЛЛЕЛЬНЫХ
231
тупого и острого углов приводят к противоречиям. Гипотеза тупого угла
влечет за собой следствие, что через две точки могут проходить две
различные прямые. Считая несомненным, что две прямые не могут
пересекаться в двух точках, Саккери пришел к выводу, что гипотеза тупого
угла должна быть отвергнута х). Итальянский математик думал, что он
сумел привести к противоречию и гипотезу острого угла, но в этой части
рассуждений незаметно для себя допустил довольно трудно уловимую
ошибку. Развивая следствия из гипотезы острого угла, Саккери
при этом фактически получил некоторые предложения неевклидовой
геометрии.
Несколько дальше Саккери продвинулся в теории параллельных
работавший в Германии эльзасец И. Г. Ламберт. В одном труде,
опубликованном посмертно (1786) он получил новые следствия из гипотезы
острого угла, например, предложение о пропорциональности площади
треугольника и разности между 2d и суммой его углов, а также тот весьма
парадоксальный результат, что должна существовать абсолютная мера
отрезков. Ламберт не допустил ошибки, сделанной Саккери, и не признал
справедливым ни одно из «доказательств» евклидова постулата. Всякий
раз,— указывал он,— в этих доказательствах остается как будто
ничтожная мелочь, в которой, однако, и заключается вся трудность, ибо она
содержит либо доказываемый постулат, либо равносильное ему
положение. Более того, Ламберт высказал предположение, что гипотеза острого
угла справедлива на «мнимой сфере»,— замечание, глубокий смысл
которого смог стать ясным только после установления Лобачевским связи
между формулами неевклидовой и сферической тригонометрии.
Проблемой доказательства V постулата интенсивно занимались
во второй половине XVIII века и другие ученые. Много усилий на его
доказательство потратил в конце XVIII и в первой трети XIX века
А. Лежандр, поставив в центр вопрос о сумме углов треугольника. Если
эта сумма равна 2d, то V постулат справедлив, и Лежандр хочет доказать,
что эта сумма не может быть ни больше, ни меньше двух прямых. Он
прежде всего показывает, что при допущении всех постулатов Евклида, кроме
постулата о параллельных, сумма углов в треугольнике не может
превосходить 2d. Оставалось доказать, что она не может быть и менее 2d,
но все многочисленные доказательства, предложенные с этой целью
Лежандром, были неудовлетворительны. Так, в одном из них
предполагается, что через точку, лежащую внутри острого угла, всегда можно
провести прямую, пересекающую обе стороны угла, а это допущение
равносильно V постулату. Мы упоминали выше о критике другого
доказательства Лежандра и попытке собственного доказательства С. Е.
Гурьева (стр. 209).
В результате проблема параллельных оставалась к началу XIX века
неразрешенной и положение казалось безвыходным. Большой знаток
вопроса венгерский математик Фаркаш Бояи в 1820 г. писал своему
сыну Яношу: «Молю тебя, не делай только и ты попыток одолеть теорию
параллельных линий: ты затратишь на это все свое время, а предложения
этого вы не докажете все вместе. Не пытайся одолеть теорию
параллельных линий ни тем способом, который ты сообщаешь мне, ни каким-либо
1) В некоторых рукописях «Начал» Евклида имеется аксиома о том, что две
прямые не могут замыкать пространства, и во всех рукописях это предложение
фигурирует при доказательстве равенства двух треугольников, имеющих по две равные
стороны, заключающие равные углы. Отказ от этого предложения лежит в основе одной
систем неевклидовой геометрии.
232 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
другим. Я изучил все пути до конца: я не встретил ни одной идеи, которой
бы я не разрабатывал. Я прошел весь беспросветный мрак этой ночи,
и всякий светоч, всякую радость жизни я в ней похоронил... Этот
беспросветный мрак... никогда не прояснится на земле, и никогда несчастный
род человеческий не будет владеть чем-либо совершенным даже в
геометрии. Это большая и вечная рана в моей душе...» 1). Беспросветный мрак,
о котором с горечью писал старший Бояи, рассеял Лобачевский и,
несколько позднее, Я. Бояи.
Н. И. Лобачевский. Величайший геометр XIX века Николай
Иванович Лобачевский родился 1 декабря 1792 г. в Нижнем Новгороде (г.
Горький) в семье мелкого чиновника. В 1802 г. он был принят в Казанскую
гимназию, а в феврале 1807 г., 15-ти лет, поступил в незадолго перед
тем открывшийся Казанский университет.
В гимназии и университете Лобачевский имел хороших наставников.
Математике его первоначально обучал воспитанник Московского
университета Григорий Иванович Карташевский (29 сентября 1779 — 24
августа 1840), человек большой культуры и выдающегося педагогического
таланта, а с 1808 г.— профессор М. Ф. Бартельс, который привлек
молодого Лобачевского к изучению классических трудов Эйлера, Лагранжа,
Монжа, Лапласа, Гаусса. Это было превосходной математической школой
для юноши: он знакомился с современной ему наукой в самом лучшем
изложении, из первых рук.
Огромное влияние на формирование мировоззрения великого геометра
имел патриотический подъем, который переживала в начале XIX века
русская интеллигенция. В молодые годы в среде гимназических и
университетских друзей Лобачевский проникся убеждением, что человек обязан
стремиться к гармоническому совершенствованию своих способностей,
а силы и знания свои ставить на службу отечеству. Глубокое уважение
к человеческой личности, к просвещению и науке, любовь к отчизне
Лобачевский ярко и образно высказал впоследствии в замечательной
«Речи о важнейших предметах воспитания» (1828; Казанский вестник,
1832). Преданность научной истине, в искании и распространении которой
Лобачевский видел свой способ служения народу и человечеству,
поддерживала его и в борьбе за свои новаторские научные идеи и в трудной
работе на посту ректора университета.
Успехи Лобачевского в занятиях были блестящие, и в 1811 г. он был
произведен, минуя степень кандидата, в магистры. В 1814 г. он был
назначен адъюнктом по математике в родном университете и приступил к чтению
лекций. Еще через два года ему было присвоено звание профессора.
В течение 30 с лишним лет, до 1846 г., он читал все основные курсы по
математике, а иногда механику, астрономию, физику.
Педагогическая и просветительная деятельность Лобачевского далеко
выходила за пределы обычных обязанностей профессора. Ряд лет он
работал деканом физико-математического факультета, с 1827 по 1846 —
ректором университета, а затем, до своей смерти, помощником попечителя
Казанского учебного округа. Плодотворная административная и
организаторская работа Лобачевского, которая смогла развернуться во всю
ширь только после отстранения в 1826 г. архиреакционера М. Л.
Магницкого, оказавшегося к тому же архиплутом, от должности попечителя
г) Цит. по кн.: В. Ф. Каган, Лобачевский. Изд. 2-е, М.—Л., 1948, стр. 168.
Эта книга является наиболее полной научной биографией великого математика.
Николай Иванович Лобачевский
(портрет маслом, Л. Д. Крюков, 1839).
234 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
Казанского округа, одна могла бы обеспечить ему выдающееся место
в истории русской культуры. Около четверти века Лобачевский стоял
во главе всей учебной жизни обширного Казанского округа. Он посещал
занятия в школах, вел переписку с директорами низших и средних
учебных заведений. Для учителей математики он написал «Наставление»,
свидетельствующее о передовом характере и глубине его педагогических
воззрений 1).
Особенно многим обязан Лобачевскому Казанский университет
(рис. 31). Лобачевский поднял на большую высоту преподавание
математики и естественных наук; он руководил университетским
строительством: при нем выстроены были анатомический театр, химическая
лаборатория с физическим кабинетом и библиотекой, астрономическая и
магнитная обсерватории и т. д. Он следил за оборудованием физического
Рис. 31. Казанский университет в 1840-е годы (с литографии В. Турина).
кабинета и обсерватории, за пополнением библиотеки университета, и он
же в 1834 г. положил начало «Ученым запискам» Казанского университета,
в которых опубликована большая часть его собственных трудов.
Преданность Лобачевского как ученого и администратора интересам
университета, тактичное руководство работой преподавателей, постоянное
внимание к занятиям и нуждам студенчества снискали ему глубокое
уважение товарищей по работе и популярность среди молодежи. В июле
1846 г. исполнилось 30 лет работы Лобачевского в звании профессора.
Согласно тогдашнему уставу за этим должна была последовать отставка.
Совет университета возбудил перед министром просвещения ходатайство
об оставлении Лобачевского на кафедре еще в течение пяти лет, с тем,
чтобы он мог сохранить за собой пост ректора. Совет почитает,—
говорилось в ходатайстве Совета Казанского университета, направленном
управляющему Казанским учебным округом от 11(23) июня 1846 г.,—
1)В. М. Нагаева, Педагогические взгляды и деятельность Н. И.
Лобачевского.— Ист.-матем. исслед., вып. III, 1950.
МИРОВОЗЗРЕНИЕ Н. И. ЛОБАЧЕВСКОГО
235
за особенную честь для университета иметь в числе профессоров столь
отличного ученого и опытного преподавателя г). Министерство, однако,
не сочло нужным удовлетворить просьбу Совета университета, и
Лобачевский был назначен на второстепенный пост помощника попечителя
Казанского округа, где начальником его оказался местный помещик
тенерал-лейтенант В. П. Молоствов. Отстранение от любимого дела,
которому было отдано более 30 лет жизни, оскорбительное для достоинства
великого ученого и педагога подчинение малокультурному Молоствову,
наконец, большое личное горе — смерть в 1852 г. любимого старшего сына,—
все это пагубно отразилось на здоровье Лобачевского, и ранее растроенном
непомерными трудами. Силы его начали быстро падать. К этому
присоединилось заметное ослабление зрения. В последний год жизни
Лобачевский ослеп и предсмертную свою работу «Пангеометрия» уже
продиктовал двум своим ученикам. Скончался Лобачевский 24 февраля 1856 г. 2).
Мировоззрение Н. И. Лобачевского. Геометрические исследования
Лобачевского, к которым мы вскоре обратимся, имели не только
математическое и естественнонаучное, но и широкое философское значение.
Предпосылкой открытия неевклидовой геометрии, которое явилось
тлавным делом Лобачевского, был его материалистический подход к
проблемам познания. Основной чертой научного мировоззрения Лобачевского
была твердая уверенность в объективном и не зависящем от человеческого
сознания существовании материального мира и в возможности его познания,
В своей речи «О важнейших предметах воспитания» 1828 г.
Лобачевский сочувственно приводит слова Ф. Бэкона: «Оставьте трудиться
напрасно, стараясь извлечь из одного разума всю мудрость; спрашивайте
природу, она хранит все истины и на вопросы ваши будет отвечать вам
непременно и удовлетворительно» 3). Основой наших представлений о природе,
согласно Лобачевскому, служат ощущения, внешней, объективной
причиной которых является мир движущихся материальных вещей. «Мы познаем
в природе одни только тела»4),— заявлял Лобачевский, и именно тела,
находящиеся в движении, как это пояснял в другом высказывании: «В
природе мы познаем собственно только движение, без которого чувственные
впечатления невозможны» 5). Все наши знания о мире — опытного
происхождения, все основные понятия науки суть отвлечения реальных свойств
движущейся материи. Лобачевский решительно критиковал
идеалистическое представление, согласно которому исходные научные понятия —
это врожденные идеи, с которыми человек уже появляется на свет. «Первые
понятия, с которых начинается какая-нибудь наука,— заявлял он,—
должны быть ясны и приведены к самому меньшему числу. Тогда только
они могут служить прочным и достаточным основанием учения. Такие
понятия приобретаются чувствами; врожденным — не должно верить»6).
Лобачевский подчеркивал глубокую важность правильного решения
вопроса о природе начальных понятий для математики. В обозрении
преподавания математики на 1825—1826 гг. он писал: «Здесь место
х) Материалы для биографии Н. И. Лобачевского. Собрал и редактировал
Л. Б. Модзалевский, М.—Л., 1948, стр. 512.
2) Мы располагаем ныне превосходно комментированным и снабженным ценными
статьями изданием трудов великого математика: Н. И. Лобачевский, Полное
собрание сочинений, тт. I—V. Гл. ред. В. Ф. Каган. М.—Л., 1946—1951.
3) Материалы для биографии Н. И. Лобачевского, стр. 323.
4) Там же, стр. 204.
5) Н. И. Лобачевский, Полное собрание сочинений, т. II, стр. 158.
6) Н. И. Лобачевский, Полное собрание сочинений, т. I, стр. 186.
236 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
говорить о понятиях, которые должны быть положены в основания
математических наук, потому что решение сего вопроса всего важнее для
геометрии». И, отвечая на этот вопрос, Лобачевский утверждал: «То неоспоримо,
что мы всеми нашими понятиями о телах одолжены чувствам.
Подтверждается истина сего и тем, что там останавливается наше суждение, где*
перестают руководствовать нас чувства, и что мы отвлекаем от тел и такие-
понятия, к которым наклоняют нас чувства; хотя существо вещей инаково...
Отсюда надобно вывести то заключение, что в основание математических
наук могут быть приняты все понятия, каковы бы они ни были,
приобретаемые из природы, и что математика на сих основаниях по справедливости,
может назваться наукою точною». Наоборот, «все математические начала,
которые думают произвести из самого разума, независимо от вещей мира,
останутся бесполезными для математики, а часто даже не
оправдываемые ею» г).
Итак, начальные понятия математики имеют свои корни в природе,
в свойствах материальных тел. Чем же объясняется, по Лобачевскому,
дедуктивный характер математических наук? Ведь «точные науки
отличаются тем, что в начале их полагаются те понятия, откуда производится
все учение силою нашего суждения» 2).
Крупнейший философ-идеалист второй половины XVIII века И. Кант
утверждал, что истинное познание, обладающее внутренней
необходимостью и обязательностью, является априорным и не зависимым от опыта.
Математика в его глазах являла пример априорного познания,
принципиально не нуждающегося в опытной проверке. Математические истины,,
по Канту, суть априорные синтетические суждения 3) о свойствах
априорных же форм созерцания пространства и времени, свободных от всякой
чувственности.
Лобачевский решает вопрос о дедуктивном характере и точности
математических наук с материалистических позиций. Для него сами
правила логических умозаключений суть отражения реальных
закономерностей мира. В речи «О важнейших предметах воспитания» он говорил:
«разум, это значит, известные начала суждения, в которых как бы
отпечатались первые действующие причины вселенной и которые
соглашают, таким образом, все наши заключения с явлениями в природе, где
противоречия существовать не могут»4). В конечном счете, таким
образом, критерий истины Лобачевский видел в согласии между научной
теорией и реальной действительностью. Математику он определяет как
«науку об измерении», добавляя: «все то, что существует в природе,
подчинено необходимому условию быть измеряему»5). Такое понимание
предмета математики теперь представляется ограниченным, однако и оно
свидетельствует о материалистических установках великого геометра.
С этих общих материалистических позиций подошел Лобачевский
к проблеме пространства и его геометрических свойств.
г) Материалы для биографии Н. И. Лобачевского, стр. 203—204.
2) Там же, стр. 177.
3) Кант назвал аналитическими суждения, не расширяющие нашего познания,
поскольку их сказуемые содержатся в подлежащем (например, все тела протяженны;
здесь понятие протяженности входит в понятие тела). В синтетических суждениях
сказуемое не содержится в подлежащем, хотя и связано с ним. Таково апостериорное,
вытекающее из опыта синтетическое суждение: тело имеет тяжесть, или априорное
синтетическое суждение: 7 + 5 = 12 (понятие 12 не входит ни в понятие 7 и 5, ни
в понятие суммы двух чисел).
4) Материалы, для биографии Н. И. Лобачевского, стр. 323.
5) Там же, стр. 205.
ПРОСТРАНСТВО И ДЕЙСТВИТЕЛЬНОСТЬ
237
Пространство и действительность. До XIX века, как уже
говорилось, никто не сомневался, что единственно возможной является система
теометрии изложенная у Евклида, что пространство может быть только
«евклидовым». И. Кант попытался сообщить евклидовой геометрии
принципиальную незыблемость, заявив, что пространство, как и время,
является априорной формой человеческого созерцания. В соответствии
с этим исходные положения геометрии Евклида, как и вытекающие из них
теоремы, обладают аподиктической достоверностью и принципиально
не нуждаются в опытной проверке, ибо составляют необходимую
предпосылку самого опыта.
Взгляды Канта были хорошо известны в России и даже нашли
отдельных последователей, в том числе и в Казани, где их придерживался
один из учителей Лобачевского, физик Иван Ипатович Запольский
(1773—1811). В России же кантианство нашло и решительных
критиков. Первый удар кантовскому учению с материалистических позиций
нанес в России профессор Харьковского университета Т. Ф. Осиповский.
Осиповский опровергал кантовское учение об априорном и субъективном
характере наших представлений о пространстве и времени. Он доказывал
объективную реальность пространства и времени. «Пространство и время,—
писал он,— суть условия бытия вещей, в самой природе и в них самих,
а не в нашем только образе чувствования существующие» х).
Делая известную уступку агностицизму, Осиповский утверждал,
что «пространство в своей сущности» нам не известно, однако «сущность
его имеет постоянное отношение к тому впечатлению, которое оно в наших
чувствах производит»; а потому, сравнивая впечатления, которые
производят на нас части пространства, мы приходим к тому же результагу,
как и при сравнении самих частей пространства 2).
Свойства пространства и времени даны нам с принудительной
необходимостью и всеобщностью: «Не в нашей воле состоит родить или
не родить в нас понятие о месте какой-либо действующей на наши чувства
вещи» или расположить вещи в таком положении друг к другу, «как нам
за благо рассудится. Притом сии явления усматриваем так, что ежели
которое-либо из них усматривает один из нас, то усматривает его и другой
совершенно соответственным образом и порядком. Каким же образом сие
произойти может, когда в природе нет ничего сим явлениям
соответствующего?» 3). Учение о субъективности пространства и времени,— утверждал
Осиповский,— неизбежно должно привести к лейбницианскому учению
о предустановленной гармонии («предустроенном согласии») между
познающими субъектами. Но «такая система невольным образом извлечет слова,
сказанные Альфонсом X, королем Кастильским, по случаю рассуждения
его о системе мира, изложенной Птолемеем» 4).
Критикуя тезис Канта, согласно которому эмпирические суждения
не имеют характера всеобщности и необходимости, Осиповский указывал,
что такое утверждение было бы правомерно лишь в том случае, если бы
опыт («опытность») ограничивался частными случаями, действительно
1) Т. Ф. Осиповский, О пространстве и времени (1807).— Ист.-матем.
исслед., вып. V, 1952, стр. 16.
2) Там же, стр. 16.
3) Там же, стр. 12.
4) Там же, стр. 14. Осиповский намекал на приписываемый Альфонсу X отзыв
о системе Птолемея: «Если бы господь бог посоветовался со мною при сотворении
мира, я предложил бы ему что-нибудь лучшее». Слова эти не были включены в речь
Осиповского, видимо, по цензурным условиям.
238 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
не несущими на себе «печати всеобщности». Но понятие о пространстве
приобретается совсем иначе: оно начинается с целого и притом такого,
которое непрерывно и «единообразно во всех своих частях». «Сие и
доставляет возможность и удобство приложения к частям его как аналитических,
так и синтетических исследований». То же относится и ко времени:
«Хотя понятие о нем начинается и не от целого, но единообразие его и
непрерывность налагают на него печать всеобщности, а потому и
способности как к аналитическим, так и к синтетическим о нем
суждениям» г).
Подобно Осиповскому и Лобачевский неоднократно отмечает опытное
происхождение геометрических абстракций и критикует идеалистическую,
в частности, кантовскую, концепцию пространства (не называя, правдаг
Канта по имени). Геометрия как учение о пространстве и его свойстваху
по мнению Лобачевского, отображает действительные отношения в мире
действительных вещей: «Основания геометрии должны быть почерпнуты
из свойства тел, которое открываем в воображении, представляя
пространство и в нем троякое деление» 2). Но великий обновитель геометрии
дал более глубокий анализ понятия пространства, чем Осиповский,
который еще придерживался ньютоновского представления об
абсолютном пустом пространстве, как вместилище всех вещей. По Осиповскому,
«есть ли бы при каком либо отношении вещей сии вещи и уничтожились,
то бы оные отношения остались. Следовательно, есть нечто особенное
от вещей, что производит в нас понятие об оных отношениях; и сие
особенное, что бы оно ни было, будет пространство» 3). Для Лобачевского
пустое пространство, от материи независимое, не существует. Говоря,
что мы познаем в природе лишь движение тел (эти слова приведены были
выше), Лобачевский продолжает: «Все прочие понятия, например,
геометрические, произведены нашим умом искусственно, будучи взяты в
свойствах движения; а потому пространство, само собой, отдельно, для нас
не существует» 4).
Начальные понятия геометрии. Наряду с обрисованными
материалистическими воззрениями важной предпосылкой открытия Лобачевского
было стремление его к точному исследованию основных понятий
математики. Мы отмечали выше, что в начале XIX века резко усилился интерес
к принципиальным методологическим вопросам, что математики, и среди
них тот же Лобачевский, в это время приступили к новому обоснованию
анализа и алгебры, без которого был невозможен дальнейший прогресс
науки. Существенный недостаток точности и строгости Лобачевский
усмотрел и в самих начальных понятиях геометрии. В первом печатном
труде по неевклидовой геометрии —«О началах геометрии» (1829) —
он писал: «В самом деле, кто не согласится, что никакая математическая
наука не должна бы начинаться с таких темных понятий, с каких,
повторяя Евклида, начинаем мы Геометрию, и что нигде в Математике нельзя
терпеть такого недостатка строгости, какой принуждены были допустить
в теории параллельных линий» 5). Математики, утверждал он,— не
соединяют еще ясного понятия с такими словами, как пространство,
поверхность, линия, точка, угол и т. д. К этому выводу Лобачевский пришел,
*) Ист.-матем. исслед., вып. V, стр. 14.
2) Материалы для биографии Н. И. Лобачевского, стр. 178.
3) Ист.-матем. исслед., вып. V, стр. 13.
4) Н. И. Лобачевский, Полное собрание сочинений, т. II, стр. 158—159.
5) Н. И. Лобачевский, Полное собрание сочинений, т. I, стр. 185.
НАЧАЛЬНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ
239
размышляя над теорией параллельных и постепенно разматывая сложное
переплетение применяемых в ней геометрических идей.
Мы не можем здесь подробно останавливаться на предложенном
Лобачевским определении первых понятий геометрии. Заметим лишь,
что в «Новых началах геометрии» (1835) он сделал первую в истории
математики попытку в качестве отправного пункта избрать наиболее
общие, как теперь говорят,— топологические свойства трехмерных
геометрических тел, рассматриваемых как абстракции твердых движущихся
тел действительного мира. В основу кладутся понятие трехмерного тела
и отношение прикосновения тел, а также их сечения. «Прикосновение,—
говорит Лобачевский,— составляет отличительную принадлежность тел
и дает им название геометрических, когда в них удерживаем это свойство,
не принимая в рассуждение все другие, существенные ли то будут или
случайные» 1). Это представление исходное, далее не определяемое через
другие, более простые, «получаемое прямо в природе чувствами»; оно
«не происходит из других, а потому не подлежит уже толкованию» 2).
Что касается сечения тела на части, то под ним, по Лобачевскому, мы
уже «не разумеем какую-нибудь новую принадлежность тела; но тоже
прикосновение, выражая в этот раз уже деление тела на две
прикосновенные части»3). Исходя из этих первых понятий, Лобачевский затем
определяет с их помощью понятия поверхности, линии, точки, расстояния
и ряд других.
В своей критике идеалистической концепции пространства
Лобачевский, таким образом, пошел гораздо дальше Осиповского, ибо не
ограничился общим философским рассмотрением проблемы, но дал ее анализ
и наметил пути ее решения на основе конкретного математического
исследования.
Главный удар по кантианству Лобачевский, однако, нанес в своей
новой теории параллельных. И здесь мы должны выделить два момента.
С одной стороны, материалистическое понимание предмета геометрии
явилось предпосылкой открытия Лобачевским новой системы геометрии.
Кантовская трактовка пространства препятствовала допущению самой
возможности новой, неевклидовой геометрии, поскольку Кант объявил
евклидову геометрию единственной и притом априорной формой
пространственного созерцания. С другой стороны, построение системы
неевклидовой геометрии наносило сокрушительный удар по кантианству
на базе математики, ибо фактически доказывало возможность различных
геометрических систем4).
1) Н. И. Лобачевский, Полное собрание сочинений, т. II, стр. 168.
Подробный критический разбор системы определений Лобачевского см. там же в
примечаниях, стр. 465 и след.
2) Там же, стр. 168.
3) Там же.
4) Интересно отметить, что и Гаусс, об отношении которого к неевклидовой
геометрии мы говорим ниже, указывал, что невозможность априорно решить вопрос об
евклидовой или неевклидовой природе реального пространства «доказывает самым
ясным образом, что Кант был неправ, утверждая, что пространство является лишь
формой нашего созерцания» (К. F. Gaus s, Werke, Leipzig, 1900, т. VIII, стр. 224.
Письмо к Ф. Бояи от 6 марта 1832 г.). Я. Бояи также критиковал учение Канта о
пространстве и времени (см. Imre Toth, Johann Bolyai, Bukarest, 1955, стр. 43—44).
Подробный анализ философских и методологических взглядов Лобачевского см.
в кн.: С. А. Яновская, Передовые идеи Н. И. Лобачевского — орудие борьбы
против идеализма в математике. М.—Л., 1950. См. также Г. Ф. Р ы б к и н,
Материализм—основная черта мировоззрения Н. И. Лобачевского.— Ист.-матем. исслед.,
вып. III, 1950. С. А. Я н о в с к а я, О мировоззрении Н. И. Лобачевского.—
Ист.-матем. исслед., вып. III—IV, 1950—1951.
240 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
Открытие неевклидовой геометрии. Теорией параллельных
Лобачевский заинтересовался рано. В лекциях по геометрии 1816—1817 гг. он
еще пытался доказать равносильное постулату о параллельных
предложение о равенстве суммы углов треугольника 2d. Попутно он доказывает
без пользования V постулатом теорему: если сумма углов равна 2d в каком-
либо одном треугольнике, то она равна 2d и во всяком другом х). Но не
позднее 1822 г. Лобачевский приходит к убеждению, что все известные
попытки доказать постулат о параллельных несостоятельны. А еще четыре
года спустя, в знаменательный для истории науки день 6 (18) февраля
1826 г., Лобачевский представил Отделению физико-математических
наук Казанского университета написанное по-французски «Краткое
изложение начал геометрии...», в котором изложил главные идеи и вывел ряд
теорем новой, неевклидовой геометрии (рис. 32). 23 февраля Отделение,
заслушав Лобачевского, передало его работу на рассмотрение астроному
Ивану Михайловичу Симонову (1794—1855), физику Адольфу Яковлевичу
Купферу (1799—1865) и Н. Д. Брашману. Члены комиссии никакого
отзыва, однако, не дали, вероятно не разобрав как следует сочинение,
поражавшее новизной исходных положений и парадоксальностью
выводов и, вследствие сжатости, особенно трудное для понимания. Три года
спустя основное содержание «Краткого изложения» было включено в
классический труд Лобачевского «О началах геометрии», опубликованный
в «Казанском вестнике» за 1829—1830 гг. и открывший новую эпоху
в истории не только геометрии, но и математики в целом. Как указывал
сам Лобачевский, первые 16 из 104 уравнений этого труда содержались
в «Кратком изложении».
Когда Лобачевский писал мемуары «О началах геометрии» (рис. 33),
новая геометрическая система была им продумана уже не только в
основных чертах, но и далеко развита. Именно с точки зрения полученных
им результатов упрекал он прежнюю теорию, или теории, параллельных
линий в недостатке строгости. Этот недостаток заключается не только
в том, что безуспешными оказывались все попытки доказать V постулат.
Дело было глубже: Лобачевский пришел к выводу, что V постулат
принципиально недоказуем при помощи других аксиом и постулатов Евклида,
ибо возможна стройная геометрическая система, основанная на новом
постулате о параллельных, система, свободная от внутренних
противоречий и вместе с тем не противоречащая опытным данным. Новый
постулат при этом не исключал евклидов постулат, но включал его как
предельный случай, и все евклидовы соотношения могли выполняться с любой
заданной степенью точности в достаточно малых частях пространства
Лобачевского.
В свете своего открытия Лобачевский естественно усматривал наличие
произвола в системе Евклида. Греческий математик допускал лишь
«частный случай, когда две параллельные должны быть вместе перпен-
дикулами к одной прямой» 2), без необходимости, произвольно отвергая
возможность параллельности перпендикуляра и некоторой наклонной
к данной прямой. Произволом страдали и «доказательства» V постулата,
поскольку их авторы основывались на допущении каких-либо
равносильных ему предложений, которые не являются необходимыми и отказ
ют которых не ведет к противоречиям. Новую теорию параллельных
г) Ни Лобачевский, ни Лежандр, опубликовавший эту теорему в 1833 г., не
знали, что она была известна Саккери. См.: Б. Л. Лаптев, Теория параллельных
прямых в ранних работах Н. И. Лобачевского.— Ист.-матем. исслед., вып. IV, 1951.
2) Н. И. Лобачевский, Полное собрание сочинений, т. II, стр. 267.
ОТКРЫТИЕ НЕЕВКЛИДОВОЙ ГЕОМЕТРИИ
241
Лобачевский желал построить так, чтобы она не содержала более
элементов произвола и охватывала проблему во всей полноте.
Постулат параллельных Лобачевского заключается, коротко говоря,
в том, что в данной плоскости через точку D можно провести по меньшей
Рже. 32. Сопроводительная записка Н. И. Лобачевского к его
докладу, представленному 6(18) февраля 1826 г.
мере две прямые, не пересекающие данную прямую L'L. Разъясним это
несколько подробнее.
Пусть в плоскости даны прямая V AL и вне прямой точка D, и пусть
AD есть перпендикуляр к L'AL (рис. 34). Представим себе, что через D
проводятся различные прямые. Одни из них, вроде BDB', соединяющей D
242 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
с точкой В луча AL, пересекают AL. Безусловно, не пересекает UAL
прямая E'DE, перпендикулярная AD (это и есть, по Евклиду, единственная
Рис. 33. Первые две страницы сочинения «О началах геометрии» («Казанский
вестник», кн. 2—3 за 1829 г., стр. 178 и 179).
параллель в точке D к прямой UAL). Лобачевский принимает, что
в данной плоскости имеется по крайней мере одна отличная от E'DE
прямая, скажем, CDC,
проходящая через D и не пересекающая
AL. В этом и заключался новый
постулат Лобачевского. В таком
случае и все прямые, проходящие
через D внутри вертикального
угла CDE, не пересекают AL. Но
тогда прямые, проходящие через D
в прямом углу EDA, разбиваются
на два класса: пересекающих AL
(вроде В'В) и не пересекающих AL
(вроде С С). Отсюда следует, что
существует граничная прямая K'DK, отделяющая прямые первого класса
от прямых второго, причем сама эта прямая K'DK не может пересекать AL
(если бы она пересекала AL где-либо в точке М, то на AL можно бы взять
Рис. 34.
ОТКРЫТИЕ НЕЕВКЛИДОВОЙ ГЕОМЕТРИИ
243
справа от М точку iV, и луч DN, лежащий в углу EDK, оказался бы
пересекающим AL, т. е. прямая K'DK не была бы граничной). В силу
симметрии должна существовать тогда и граничная прямая KJ)K[, отделяющая
в прямом углу E'DA проходящие через точку D прямые, пересекающие
AL', от непересекающих. Эти две граничные прямые K'DK и KJ)K[
Лобачевский и назвал параллельными к L'AL соответственно в сторону
параллельности AL и AL'. Лучи вроде DB он называл встречными или
сводными с AL, а лучи вроде DC — невстречными или разводными с ней.
«Под этим видом,— писал Лобачевский,— параллельность уже
рассматривается во всей обширности» х). В предельном случае, когда
граничная прямая К'К совпадает с перпендикуляром к AD, т. е. Е'Е (тогда
совпадает с ним и К\К'^), имеет место обычный евклидов постулат.
Таким образом, в плоскости геометрии Лобачевского через точку D
можно провести параллельно данной прямой AL две прямые K'DK,
K\DK'X. В одну сторону, именно в сторону параллельности, два
параллельных луча (DK и AL, DK[ и AL') неограниченно сближаются между
собой, а в другой они (DK' и AL', DKt и AL) неограниченно удаляются
одна от другой. В евклидовой геометрии, как известно, две параллельные
прямые являются всюду равноотстоящими одна от другой.
Угол ф параллельного луча DK с перпендикуляром AD называется
углом параллельности в точке D относительно прямой UL. В евклидовой
геометрии угол параллельности равен прямому; в ней перпендикуляр
и любая наклонная к AL при достаточном продолжении встретятся.
В плоскости Лобачевского угол параллельности отличен от прямого.
Он обязательно острый и, как показал Лобачевский, зависит от
расстояния точки D от прямой AL, т. е. от длины х перпендикуляра AD. Чем
больше х, тем угол параллельности меньше, а чем х меньше, тем угол
цараллельности ближе к прямому. Если обозначить угол
параллельности ф через Щх), то
где е — основание натуральных логарифмов, а к — некоторая
положительная постоянная. Величина этой постоянной к теоретически может
быть произвольной, и различным ее значениям соответствуют различные
пространства Лобачевского, в которых, однако, действуют общие
закономерности. При к, стремящемся к положительной бесконечности, и любой
х
выбранной длине отрезка AD величина ~ стремится к нулю, е k —
к единице, и, значит, Щх) — к прямому углу. В этом смысле геометрия
Евклида опять-таки является предельным случаем геометрии
Лобачевского, которая переходит в евклидову при к—>+°°-
Последовательно развивая следствия из этих посылок, Лобачевский
вывел основные теоремы новой геометрии. Многие предложения в ней
удивляли своей неожиданностью. Сумма углов треугольника, как ясна
из сказанного ранее, оказывается меньше двух прямых; для разных
треугольников, вообще говоря, она различна и может быть сколь угодно
г) Н. И. Лобачевский, Полное собрание сочинений, т. II, стр. 267.—
Со времени Б. Римана известно, что существуют геометрические системы, отличные от
систем как Евклида, так и Лобачевского. Мнение Лобачевского, что его геометрия
всеобщая, справедливо лишь в том смысле, что какая-либо другая теория параллельности
невозможна, если сохраняются остальные постулаты евклидовой геометрии.
244 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
близка к нулю (при неограниченном увеличении трех высот). Площадь
треугольника S выражается не произведением половины основания
на высоту, а пропорциональна разности между двумя прямыми углами
и суммой углов треугольника а + Р + у:
S = к2 (я — а — (3 — у);
поэтому на плоскости Лобачевского площадь треугольника, как бы далеко
ни отстояли одна от другой его вершины, не может превзойти к2п. Теорема
Пифагора, определяющая метрику геометрии Евклида, заменяется
уравнением между гиперболическими функциями1) катетов а, Ъ и гипотенузы с
ch?-ch? = chlT'
причем с2>а2-\- Ь2, тригонометрическая зависимость между катетом,
противолежащим углом а и гипотенузой принимает вид
sh -т- = sh -у- sin а,
к к
длина окружности I выражается через радиус г равенством
l = 2nksh.-r
к
и т. д. В связи с той фундаментальной ролью, какую играют в геометрии
Лобачевского гиперболические функции, ее впоследствии стали нередко
именовать гиперболической.
Подобные неравные фигуры в геометрии Лобачевского не существуют,
и к признакам равенства треугольников, известным из геометрии Евклида,
здесь присоединяется еще один: при равенстве всех трех углов
треугольники равны.
Как видно, длины отрезков в геометрии Лобачевского связаны
определенным образом с углами. Например, выбор суммы углов правильного
треугольника при фиксированном к определяет длину его стороны. При
всей парадоксальности этих и иных теорем новой геометрии (например,
линия равных расстояний от данной прямой есть не прямая, а некоторая
кривая —«эквидистанта»), ее можно было столь же последовательно
и логично развивать как евклидову, причем никаких внутренних
противоречий в ней не обнаруживалось.
Большинство теорем геометрии Лобачевского отличается от
евклидовых. Вместе с тем в достаточно малых частях плоскости Лобачевского
все соотношения оказываются приближенно евклидовыми. В самом деле,
если в основной формуле для угла параллельности взять х весьма малым
по сравнению с /с, то tg—¦— = е к будет близок к единице, а угол
параллельности П (х) — к прямому, т. е. параллель DK в смысле Лобачевского
будет весьма мало уклоняться от перпендикуляра DE — единственной
параллели в смысле Евклида. С большим приближением будут
выполняться при этом и другие соотношения обычной геометрии. Сумма углов
в малых треугольниках будет почти равна 2d; зависимость для сторон
прямоугольного треугольника будет мало отличаться от зависимости,
х) Напомним, что спж = ^ » shz
ОТКРЫТИЕ НЕЕВКЛИДОВОЙ ГЕОМЕТРИИ
245
выраженной теоремой Пифагора, а длина окружности — от 2лг, и т. д.
В самом деле, если разложить гиперболические функции в степенные
ряды, то приведенные несколько выше формулы для прямоугольного
треугольника и окружности будут
а2 + &2 g4-f ба2Ь2 + &4 , _ с2 с*
2/с2 + 24&4 + " * e ~2p+24F + ' ' ''
Я CL / С С \
T4-6p+... = (T + 6p+...)sina,
z=2rt4x+^+---)-
Полагая величины т~' Т' Т ' Т бесконечно малыми и пренебрегая
в написанных равенствах членами высших порядков, мы получим хорошо
знакомые соотношения евклидовой геометрии
а2 + й2 = с2, а = с sin a, Z = 2jtr.
В том же первом своем труде Лобачевский показал, что евклидова
планиметрия полностью реализуется в его системе на так называемой
предельной поверхности. В евклидовой плоскости окружность,
проходящая через фиксированную точку, при неограниченном удалении ее
центра в бесконечность вдоль диаметра, проходящего через эту точку,
сколь угодно приближается по форме к прямой. В геометрии Лобачевского
такая окружность при удалении ее центра в бесконечность переходит
в особую кривую — предельную линию. Можно сказать также, что
предельные линии это ортогональные траектории пучка прямых,
параллельных какой-либо прямой в заданную ее сторону. Всякая прямая пучка
служит осью предельной линии. Точно так же сфера, центр которой
удаляется в бесконечность, переходит здесь не в плоскость, как в
пространстве Евклида, а в особую предельную поверхность, которая в
пересечении с плоскостью дает предельные линии или окружности.
Предельная поверхность получается также при вращении предельной линии
вокруг одной из своих осей. Предельные линии служат на предельных
поверхностях линиями кратчайшего расстояния, все равны между собою
и вообще обладают теми свойствами, какие присущи прямой на плоскости
в геометрии Евклида.
Предельная поверхность играет важную роль в геометрии
Лобачевского. Все геометрические соотношения на предельной поверхности,
если только заменить в формулировках теорем планиметрии прямые
на предельные линии, точно совпадают с соотношениями евклидовой
планиметрии; например, сумма углов треугольника из частей предельных
линий будет равна 2d и т. д. Таким образом, соотношения двумерной
евклидовой геометрии не только приближенно выполняются в достаточно
малых частях пространства Лобачевского, но и совершенно точно
воспроизводятся на предельных поверхностях. Пользуясь последним
обстоятельством, Лобачевский и вывел основные тригонометрические формулы
в новой системе. Он построил также аналитическую геометрию на
плоскости в новой системе и получил формулы для дифференциалов дуги,
площади и объема, необходимые при вычислении размеров фигур. Все
эти формулы имеют иной вид, чем в геометрии Евклида,— выше мы
привели выражения площади треугольника и длины окружности.
Укажем еще только основную в дифференциальной геометрии формулу
246 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
дифференциала дуги ММ' плоской кривой, где точка М имеет
координаты х, у.
ds* = ch2-^dx2 + dy*.
С ее помощью Лобачевский вычислил длину окружности.
Среди различных следствий нового постулата о параллельных
особенно неожиданным являлось одно, которого мы коснулись ранее, отмечая,
что заданием углов треугольника, при выбранном значении постоянной к,
определяются длины его сторон. В пространстве Евклида единицу
измерения углов можно определить чисто геометрически, например, взять
за такую единицу прямой угол. Но единицу длины в евклидовом
пространстве невозможно установить на основании одних геометрических
соображений: она задается выбором некоторого физического объекта,
например, эталона метра или, как поступают астрономы, отрезка,
проходимого светом в одну секунду. Иначе обстоит дело в пространстве
Лобачевского. Здесь, при выбранном значении постоянной /с, можно задать
единицу длины чисто геометрически. Можно, например, принять за
единицу длины сторону правильного треугольника с данной суммой углов или
же взять отрезок AD = х, которому соответствует угол параллельности
И(х) = -г радианов, так что
х
tg— = e h и AD = х = к In ctg -~- .
Сама постоянная к, неоднократно уже встречавшаяся нам, представляет
собой некоторую линейную величину, непосредственно зависящую от
установленной единицы длины1).
Одна из попыток Лежандра доказать V постулат, опровергнутая
Лобачевским, основана была на принципе однородности, согласно которому
отрезок, т. е. величина линейная, не может определяться только углом,
который выражается отвлеченным числом (например, если взять прямой
угол за единицу). Так, равенство вида с = f (А, В, С), где с — сторона
треугольника и А, 5, С его углы, противоречит принципу однородности
и, по мнению Лежандра, невозможно, поскольку единицы длин и углов
мы вправе выбирать независимо друг от друга; при изменении этих единиц
приведенное равенство, вообще говоря, нарушилось бы. В частности,
согласно Лежандру, нелепо думать, что одним заданием угла а
равностороннего треугольника может быть определена длина его стороны х.
Однако на деле в гиперболической геометрии принцип однородности
не нарушается. Заданием угла а равностороннего треугольника
определяется отношение его стороны к некоторому отрезку постоянной длины,
именно отрезку к. Конкретно, сторона х в данном случае определяется
неявным уравнением:
, х cos а + cos2 а
СП — = г-5 ,
к sin2 а
и принцип однородности соблюдается, поскольку -у является отношением
двух отрезков. Аналогично обстоит дело и с другими равенствами
х) Эта постоянная к имеет различные геометрические истолкования, выражая,
в частности, расстояние между двумя концентрическими предельными дугами,
лежащими между двумя осями, когда отношение длин дуг равно числу е. Подробнее см. в
любом специальном сочинении по неевклидовой геометрии.
ЛОБАЧЕВСКИЙ О ГЕОМЕТРИИ ДЕЙСТВИТЕЛЬНОГО МИРА 247
б геометрии Лобачевского, в том числе и с основным равенством:
1 - —
tg-g Щх) = е k ,
б котором угол параллельности опять-таки выступает как функция
отношения отрезка х к отрезку /с, различному в различных пространствах
Лобачевского, но имеющему постоянное значение в каждом из них.
Таким образом, в геометрии Лобачевского однородность сохранилась,
но вместе с тем во всех ее формулах содержится некоторая линейная
постоянная величина к, при выборе которой длины линий уже
оказываются зависящими от углов. Впрочем, указывал Лобачевский, не следует
удивляться возможности такой зависимости между линиями и углами:
ведь в природе силы, например, сила всемирного тяготения, зависят
от разнородных с ними расстояний.
Лобачевский о геометрии действительного мира. Далеко проведя
разработку новой геометрической системы, Лобачевский, естественно,
поставил вопрос о геометрических свойствах реального пространства.
Он обсуждается уже в труде «О началах геометрии».
Лобачевский выбирает ту из теорем, которую он считал в принципе
проверяемой на опыте, всегда имеющем дело с конечными участками
мира,— теорему о сумме углов треугольника. Если бы оказалось, что
в некотором реально наблюдаемом треугольнике эта сумма менее 2d,
то в физическом мире имела бы место новая геометрия.
Лобачевский оценивает по данным астрономических наблюдений
сумму углов огромного треугольника, вершинами которого служат два
диаметрально противоположных положения Земли на ее орбите и звезда
Сириус. Луч света считается прямолинейным.
Произведенные Лобачевским подсчеты не показали приметного
уклонения суммы углов такого треугольника от 2d. Результат этот означал,
что в доступных обозрению частях Вселенной геометрия Евклида
выполняется с совершенно удовлетворительной точностью. Однако при очень
больших значениях постоянной к в сравнении с основным масштабом
наблюдаемого явления метрические соотношения в обеих геометрических
системах различаются столь мало, что различия эти могут быть
неуловимы и для самых чувствительных приборов.
Непосредственное обращение к опыту не дало Лобачевскому ответа
на вопрос о том, осуществляются ли в реальном пространстве
геометрические законы созданной им системы. За евклидовой геометрией все же
оставалось в этих условиях преимущество большей простоты ее формул.
В сочинении «О началах геометрии» Лобачевский в результате склоняется
к выводу, что физическое пространство в наблюдаемых его частях является
евклидовым, хотя и этого точно доказать невозможно, учитывая
ничтожность различия формул обеих геометрий при достаточно больших
значениях к. Поэтому Лобачевский на первых порах называет новую
геометрию воображаемой. «Итак,— писал он,— очень вероятно, что евклидовы
положения одни только истинные, хотя и останутся навсегда
недоказанными. Как бы то ни было, новая Геометрия, основание которой здесь
положено, если и не существует в природе, тем не менее может
существовать в нашем воображении...» г) и, добавлял Лобачевский, уже приносит
г) Н. И. Лобачевский, Полное собрание сочинений, т. I, стр. 209.—
Ср. новую трактовку астрономических соображений Лобачевского у А. П. Н о р-
д е н а, Вопросы обоснования геометрии в работах Н. И. Лобачевского.— Ист.-матем.
<исслед., вып. XI, 1958.
248 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
пользу в анализе (к этому мы вскоре обратимся). Но уже в этом труде
он высказал предположение, что новая геометрия сможет найти
применение в изучении механических явлений. С большой четкостью эта
гениальная догадка Лобачевского сформулирована в «Новых началах геометрии
с полной теорией параллельных» (Уч. зап. Казанского ун-та, 1835—
1838). Говоря, что свойства пространства определяются свойствами
движущихся тел, Лобачевский во вступлении писал: «В нашем уме не может
быть никакого противоречия, когда мы допускаем, что некоторые силы
в природе следуют одной, другие своей особой Геометрии. Чтобы пояснить
эту мысль, полагаем, как и многие в этом уверены, что силы
притягательные слабеют от распространения своего действия по сфере. В
употребительной Геометрии величину сферы принимают 4яг2 для полупоперечника г,
от чего сила должна уменьшаться в содержании [отношении] к квадрату
расстояния. В воображаемой Геометрии нашел я поверхность шара
л(вг-*-г)2
и такой Геометрии, может быть, следуют молекулярные силы, которых
за тем все разнообразие будет зависеть от числа е, всегда весьма
большого» *). Развивая эти соображения, Лобачевский указывал, что
неевклидовы пространственные соотношения, быть может, имеют место «либо
за пределами видимого мира, либо в тесной сфере молекулярных
притяжений» 2).
Идеи, высказанные в этих словах, далеко опережали науку того
времени. Только в результате дальнейшего развития неевклидовой
геометрии — уже за пределы той первой системы, которую разработал сам
Лобачевский,— и новых успехов физики подтвердилась принципиальная
правота его предвидений.
Мы еще вернемся к этому вопросу.
Первые применения геометрии Лобачевского. Не найдя приложений
новой геометрии в физических науках, Лобачевский, однако, смог
показать, что она «открывает новое, обширное поле для взаимных применений
Геометрии и Аналитики» 3). Он вычислил ряд определенных интегралов,
выражая последние как значения длины, площади или объема некоторой
фигуры (в его геометрии), а затем определяя сами эти значения
геометрическими методами. Применяет Лобачевский и другие геометрические
приемы, комбинируя их с аналитическими преобразованиями.
Примеры вычисления определенных интегралов содержались в трудах
«О началах геометрии» и «Воображаемая геометрия» (Уч. зап. Казанского
ун-та, 1835), но особенно много интегралов вычислено в специальной
работе «Применение воображаемой геометрии к некоторым интегралам»
(Уч. зап. Казанского ун-та, 1836). В общей совокупности Лобачевский
нашел значения около пятидесяти сложных определенных интегралов.
Некоторые из них были ранее вычислены чисто аналитически, и
совпадение результатов, полученных обоими методами, укрепляло уверенность
в непротиворечивости неевклидовой геометрии. Большинство интегралов,
вычисленных Лобачевским, являлись новыми и свидетельствовали о
полезности его геометрических открытий.
1) Н. И. Лобачевский, Полное собрание сочинений, т. II, стр. 159. Число
е в данной формуле Лобачевского не есть основание натуральных логарифмов,
значение его зависит от пространственной постоянной к.
2) Там же, стр. 160.
3) Н. И. Лобачевский, Полное собрание сочинений, т. I, стр. 210.
НЕПРОТИВОРЕЧИВОСТЬ ГИПЕРБОЛИЧЕСКОЙ ГЕОМЕТРИИ 249
Найденные Лобачевским интегралы были включены в таблицы,
изданные Д. Биеренс де Хааном в 1858 г. в Амстердаме. Из этих Tables
d'integrales definies многие формулы попали в позднейшие справочники,
вплоть до новейших. Нередко имя Лобачевского при этом не указывается.
Мы не будем приводить образцы интегралов Лобачевского х). Укажем
только, что многие интегрирования он произвел при помощи введенной
им трансцендентной функции
оо
L(x) = я In 2 —у 2 —р sin2A:^.
k=i
Ряд справа сходится при всех действительных х и на отрезке ( —|г? тг)
х
его сумма совпадает с интегралом — \ In cos t dt. Функция L (x) играет
о
особую роль в гиперболической геометрии прежде всего потому, что служит
для выражения через ребра и углы объемов пирамид и других
многогранников; одних элементарных и общеупотребительных специальных
функций для этого недостаточно.
Впоследствии геометрия Лобачевского получила новые чрезвычайно
важные применения в математическом анализе.
Непротиворечивость гиперболической геометрии. Ни вычисление
трудных определенных интегралов, ни далекое развитие новой
геометрической системы, при котором не обнаруживалось внутренних
противоречий, не давали еще доказательства ее логической правомерности.
Правильные результаты, в данном случае верные значения интегралов,
могли быть получены из неверных посылок. Возможность получить
противоречие при дальнейшем развертывании предложений новой
геометрии принципиально исключена еще не была. Это было Лобачевскому
ясно.
Попытка Лобачевского доказать непротиворечивость новой системы
геометрии, точнее, новой планиметрии, намеченная в сочинении «О началах
геометрии» и развитая в «Воображаемой геометрии», состояла, коротко
говоря, в следующем. Лобачевский устанавливает, что из некоторой
системы уравнений сферической тригонометрии в пространстве Евклида
можно, заменив стороны сферических треугольников а, 6, сна-,-,-,
где i = У — 1, получить другую систему уравнений, совпадающих с
уравнениями тригонометрии на плоскости Лобачевского. Новая система
уравнений непротиворечива (совместна) в той же мере, как система
уравнений обычной сферической тригонометрии. Затем аргументы новой системы
истолковываются как стороны и углы плоского прямолинейного
треугольника; при этом стороны имеют положительные значения, если
сумма углов меньше я. Наконец, Лобачевский показывает, что из этих
тригонометрических формул и предложений абсолютной геометрии, т. е.
предложений, не зависящих от V постулата, можно вывести теоремы его
планиметрии. Он считает тем самым доказанным, что «обыкновенная
Геометрия, Тригонометрия и эта новая Геометрия всегда будут согласны
между собой» 2).
г) Н. И. Лобачевский, Полное собрание сочинений, т. III, стр. 412—425.
2) Н. И. Лобачевский, Полное собрание сочинений, т. I, стр. 261.
250 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
Как пишут А. П. Норден и А. Н. Хованский, в «Воображаемой
геометрии» Лобачевский «близко подошел к тому методу введения новых
геометрических систем, который является господствующим в настоящее
время и сводится к заданию некоторого соотношения аналитического
характера, определяющего геометрию в абстрактном пространстве. Точка
зрения Лобачевского вполне совпала бы с современной, если бы он начал
не с задания конечных тригонометрических соотношений, из которых
он сейчас же получает линейный элемент плоскости, а с задания этого
линейного элемента,— из него тригонометрические соотношения могли бы
быть получены интегрированием. К такой
дифференциально-геометрической постановке вопроса, приведшей впоследствии Римана к созданию
его системы, Лобачевский был особенно близок, указав на то, что строение
его пространства и пространства Евклида тождественны в бесконечно
малом» *).
Рассуждения Лобачевского содержали весьма плодотворную идею
интерпретации гиперболической геометрии, но не давали все же строгого
доказательства ее непротиворечивости. Как заметил А. П. Норден,
«Лобачевский не учел одного существенного момента: формулы обычной
сферической тригонометрии, из которых вытекает, что сумма углов
треугольника больше двух прямых, если рассматривать эти формулы как
формулы тригонометрии на плоскости, противоречат аксиомам
абсолютной геометрии. Поэтому соображения Лобачевского имеют смысл, только
если понимать под непротиворечивостью внутреннюю непротиворечивость
тригонометрических формул, а одного этого для доказательства
непротиворечивости геометрии недостаточно» 2). Первые доказательства
непротиворечивости гиперболической геометрии были получены уже после
смерти ее творца.
После публикации названных сочинений Лобачевский интенсивно
продолжает работу по геометрии, уточняя и развивая отдельные вопросы.
Наиболее широкое изложение дается в «Новых началах геометрии с
полной теорией параллельных». В 1840 г. на немецком языке издается
сравнительно более доступное изложение вопроса в «Геометрических
исследованиях по теории параллельных линий» (Geometrische Untersuchungen
zur Theorie der Parallellinien, Berlin, 1840). Последней работой была,
как упоминалось, «Пангеометрия», т. е. «Всеобщая геометрия» (Уч. зап.
Казанского ун-та, 1855), вышедшая также в несколько переработанном
виде на французском языке в сборнике, изданном в Казани в 1856 г.
Термин «воображаемая геометрия» Лобачевский здесь отбросил: новое
название лучше выражало суть его системы, которая включала обычную
теометрию как предельный случай 3).
Н. И. Лобачевский и современники. В истории математики, как
и других наук, многие великие открытия производились независимо
и близко по времени несколькими учеными. Так было с аналитической
геометрией Декарта и Ферма, с дифференциальным и интегральным
г) Н. И. Лобачевский, Полное собрание сочинений, т. III, стр. 12.
2) Б. А. Розенфельд. Интерпретации геометрии Лобачевского. Сб. «Исто-
рико-математические исследования», вып. IX, 1956, стр. 176. В этой статье показано,
что, отправляясь от соображений Лобачевского, можно доказать непротиворечивость
его планиметрии, рассматривая формулы его тригонометрии как формулы
тригонометрии на сфере мнимого радиуса в комплексном евклидовом пространстве.
3) Термин «пангеометрия» не является все же вполне подходящим, ибо, как уже
отмечалось, существуют другие неевклидовы системы, отличные от системы
Лобачевского.
Н. И. ЛОБАЧЕВСКИЙ И СОВРЕМЕННИКИ
251
исчислением Ньютона и Лейбница. К идеям неевклидовой геометрии
также подходили различные ученые.
Одновременно с Лобачевским и независимо от него успешно
занимался теорией параллельных молодой венгерец Янош Бояи. На два года
позднее Лобачевского, в 1831 г., Я. Бояи опубликовал брошюру,
содержавшую изящное и весьма краткое изложение начал новой геометрии,
совпадающей с геометрией Лобачевского. Бояи следовал пути,
существенно отличному от избранного Лобачевским. Останавливаться на
особенностях его построения гиперболической геометрии мы не будем1).
Заметим лишь, что в последующем развитии ученые отправлялись от
трудов Лобачевского, в которых идеи новой геометрии были выражены
проще, отчетливее и с неизмеримо большей полнотой. В «Приложении»
Бояи выводятся в строго геометрическом стиле только основные теоремы,
аналитические методы почти не развиты. Никаких внегеометрических
приложений в труде Бояи не имеется, нет и попытки доказательства
непротиворечивости новой системы.
Занимался теорией параллельных и К. Гаусс. При жизни Гаусс
публично ни разу не высказался по этому вопросу. Но из посмертно
изданной его переписки (1865), а затем из дневника и черновых записей
выяснилось, что он с конца XVIII века заинтересовался теорией
параллельных, а около 1817 г. пришел к убеждению в недоказуемости V
постулата и уже овладел основными фактами неевклидовой геометрии. Свои
соображения по этим вопросам Гаусс несколько раз сообщал в переписке,
решительно требуя, однако, чтобы его мысли сохраняли в строгом секрете.
В 1829 г., т. е. в год публикации труда «О началах геометрии»
Лобачевского, Гаусс писал астроному Бесселю, что еще не скоро отработает свои
мысли, чтобы их можно было опубликовать. «Возможное дело,—
продолжал Гаусс,— что я не решусь на это всю свою жизнь, потому что я боюсь
крика беотийцев [т. е. невежд], который поднимется, когда я выскажу
свои воззрения целиком» 2). В 1831 г., т. е. через два года после выхода
классической работы Лобачевского, Гаусс начал записывать некоторые
свои открытия по неевклидовой геометрии, но эти разрозненные
фрагменты были опубликованы лишь после его смерти, наступившей в 1856 г.
Гаусс, судя по его письмам и заметкам, не ожидал, что неевклидова
теометрия получит существенные приложения. Быть может, этим отчасти
объясняется молчание, которое он хранил всю жизнь. В итоге
размышления Гаусса над вопросами теории параллельных долгое время оставались
моментом его биографии, а не истории науки, на прогресс которой не
оказали своевременно влияния. Более того, опасаясь того же «крика
беотийцев», Гаусс не решился оказать публичной поддержки ни Лобачевскому,
ни Бояи, хотя труды их привлекали его пристальное внимание и в
переписке с друзьями он дал этим трудам самую высокую оценку. Косвенно,
тем не менее, Гаусс выразил свое восхищение научным подвигом
Лобачевского, предложив в 1842 г. избрать его членом-корреспондентом Гет-
тингенского научного общества. Это избрание явилось, кажется,
единственной формой прижизненного признания научных заслуг Лобачевского
за границей.
х) Сочинение Бояи имеется в русском переводе: Я. Б о л ь а и. Appendix.
Приложение, содержащее науку о пространстве, абсолютно истинную. Перев. с латинского,
вступит, статья и примечания В. Ф. Кагана. М.—Л., 1950. Название труда Я. Бояи
объясняется тем, что большая часть тиража была издана в качестве приложения к
руководству по геометрии его отца Ф. Бояи в 1832 г.
2) С. F. Gauss, Werke, т. VIII, стр. 200.
252 ГЛ. 13, Н. И, ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
Лобачевскому принадлежит, таким образом, безусловный приоритет
в открытии неевклидовой геометрии. Но дело не только в первенстве-
опубликования и не только в великолепной смелости Лобачевского,
отличавшей его от Гаусса, или в его выдержке, отличавшей его от Бояи,
который, нигде не встретив поддержки, после 1832 г. не опубликовал
более ни одной работы по геометрии. Дело еще и в том, что в трудах
Лобачевского гиперболическая геометрия получила неизмеримо более широкое
и глубокое развитие, нежели в черновиках Гаусса и брошюре Бояи *).
И лишь Лобачевский показал пользу новой геометрии для других частей
математики и предвидел ее применение в физике.
Среди современников Лобачевского только Гаусс и Я. Бояи сумели
оценить глубину его открытия, хотя и не высказались о нем в печати 2).
Остальные математики того времени, даже самые крупные из них,
отнеслись к созданию неевклидовой геометрии либо с безразличным
недоверием к ее значению, либо отрицательно, считая ее беспочвенной фантазией,
сплетением нелепостей и парадоксов. Более того, его основоположный
труд «О началах геометрии» был грубо высмеян на страницах журнала
«Сын отечества» за 1834 г.: рецензент или рецензенты, укрывшись за
инициалами С. С, заявляли, что Лобачевский изображает в своей геометрии
черное белым, круглое — четыреугольным и издевательски приписывали
ему намерение написать сатиру или карикатуру на геометрию. При этОхМ
они ссылались, не называя их, на первоклассных наших математиков,
которые, прочитав сочинение Лобачевского, ничего в нем не поняли
(речь шла, несомненно, о Буняковском и Остроградском, о чем будет
сказано далее) 3). Известно только одно публичное выступление того
времени, автор которого решился положительно оценить исследования
Лобачевского по геометрии. Это была актовая речь окончившего
Харьковский университет казанского профессора прикладной математики Петра
Ивановича Котельникова (1809—9 июня 1879), произнесенная и
опубликованная в 1842 г. В своей речи Котельников отмечал, что Лобачевский
предпринял «изумительный труд построить целую науку, геометрию,
на новом предположении: сумма углов в прямоугольном треугольнике
менее двух прямых — труд, который рано или поздно найдет своих
ценителей»4). Такие ценители появились, однако, уже после кончины
великого геометра.
Теория поверхностей К. Ф. Гаусса. Для дальнейшего развития
неевклидовой геометрии важное значение имели новые успехи в
дифференциальной геометрии, в частности, теории поверхностей.
г) Ср. В. Ф. Каган, Строение неэвклидовой геометрии у Лобачевского, Гаусса
и Больаи.— Труды Ин-та ист. естеств., т. 2, 1948; А. П. Н о р д е н, Гаусс и
Лобачевский. Ист.-матем. исслед., вып. IX, 1956.
2) Высказывания Гаусса, как было сказано, содержатся в его ученой переписке;
заметки Бояи, как он сам об этом упоминает, не предназначались для опубликования.
Приведем для примера оценку, данную Гауссом «Геометрическим исследованиям»
Лобачевского в письме к Шумахеру от 28 ноября 1846 г.: «В развитии [системы неэвклидовой
геометрии] автор следует другому пути, отличному от того, которым шел я сам; оно
выполнено Лобачевским мастерски в подлинном геометрическом духе. Я считаю
должным обратить Ваше внимание.на эту книгу, которая наверное доставит Вам совершенно
исключительное наслаждение» (G. F. Gans s, Werke, т. VIII, стр. 239). Гаусс,
владевший русским языком, знал и другие работы Лобачевского.
3) Возможно, что рецензию написали С. А. Бурачек и С. И. Зеленый. См. мнение
А. П. Котельникова в кн.: Н. К. Лобачевский, Полное собрание сочинений,
т. I, стр. 406—409.
4) Цит. по кн.: Материалы для биографии Н. И. Лобачевского, стр. 440.
ТЕОРИЯ ПОВЕРХНОСТЕЙ К. Ф. ГАУССА
253
В мемуаре 1827 г. «Общие исследования по теории поверхностей»
(Disquisitiones generales circa superficies cnrvas) Гаусс заложил глубокие
основы так называемой теперь внутренней геометрии поверхностей,
т. е. изучения тех свойств, которые определяются только метрическими
отношениями на самой поверхности и не зависят от метрических
соотношений в пространстве вне нее. Такой подход был связан с многолетними
занятиями Гаусса геодезическими измерениями. Основную роль во
внутренней геометрии играет изгибание и наложение поверхностей, о котором
нам уже приходилось говорить в связи с дифференциально-геометрическими
работами Эйлера. Некоторым обобщением изгибания является
изометрическое отображение одной поверхности на другую, при котором
сохраняются длины всех отображаемых дуг кривых. Всякое изгибание есть
нзометрия, но две изометрические поверхности не обязательно наложимы
друг на друга. Несколько упрощая, можно сказать, что изгибание есть
изометрдя без разрывов и складок. Важность изометрии определяется
тем, что все изометричные между собой поверхности имеют в известном
смысле одну и ту же геометрию. Например, для поверхностей, изометрич-
ных плоскости, справедливы теоремы обыкновенной планиметрии, если
в них вместо прямых линий говорить о геодезических линиях
соответствующих поверхностей.
При изометрическом отображении поверхности некоторые
геометрические величины изменяются, например, кривизна линий: прямой
отрезок, проведенный в прямоугольнике, при изгибании последнего в цилиндр
перейдет в кусок винтовой линии или в окружность (если этот отрезок
ле принадлежит одной из образующих цилиндра). Другие величины
пе изменяются при изгибании; к ним, по определению, относится длина
кривой на поверхности, а также площадь куска поверхности, углы между
линиями и т. д. Изучение инвариантных, не изменяющихся при изометрии
свойств поверхностей и является делом внутренней геометрии
поверхностей.
Гаусс создал разветвленный аппарат аналитического изучения
внутренней геометрии поверхностей. Не зная об упоминавшейся выше работе
Эйлера, опубликованной в 1862 г., он снова вводит криволинейные
координаты на поверхности. Применение декартовых координат точки
поверхности х, у, z неудобно во внутренней геометрии, ибо они при изометрии
меняются. Вместо этого положение точки на поверхности определяется
парой чисел и, v, которые связаны с этой точкой и при изгибании остаются
неизменными. Если одной из величин, допустим, и, придать постоянное
значение С1? а другую непрерывно изменять, точка опишет на
поверхности некоторую кривую с уравнением и = С±; точно так же при
фиксированном значении v получается другая линия с уравнением v = С2,
При различных значениях С±, С2 на поверхности образуется сетка
координатных линий и = С1? v = С2, причем координатные линии выбирают
так, чтобы линии каждого из семейств и = С± (и v = С2) не пересекались
между собой, но всякие две линии различных семейств имели одну точку
пересечения. Аналогия с сеткой координатных прямых х = Ci} у = С2
в декартовой системе на плоскости очевидна. Простым примером
криволинейных координат могут служить географические координаты — широта
и долгота; координатными линиями служат здесь меридианы и
параллели. Любая точка земной поверхности, за исключением полюсов
(которые не имеют определенной долготы при широте ±90°), однозначно
определяется парой определенных географических координат. Декартовы
координаты точек поверхности при введении какой-либо системы отсчета
254 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
выражаются в функции координат криволинейных
x = f±(u, v),
V = h К v),
z = f3(u, v).
Наряду с криволинейными координатами решающим в работе Гаусса
было введение (опять-таки независимо от Эйлера) первой квадратичной
формы, через которую выражается линейный элемент, т. е. дифференциал
дуги кривой на поверхности:
ds2 = Edu2 + IF dudv + G dv2,
где E, F, G суть некоторые функции и, v. Через коэффициенты первой
квадратичной формы выражается не только дифференциал дуги, но и
элемент площади поверхности, и угол между двумя кривыми и ряд других
важных величин. Огромная роль первой квадратичной формы в теории
изгибания определяется тем, что задание ее, т. е. задание коэффициентов
Е, F, G, полностью определяет всю внутреннюю геометрию
соответствующих ей изометрических поверхностей: всякая величина, выражающаяся
через эти коэффициенты (и их производные), инвариантна при изгибании.
Вторая дифференциальная форма также принадлежит Гауссу.
Гаусс ввел, далее, понятие полной кривизны поверхности в какой-
либо ее точке. Проведем через нормаль к поверхности в какой-либо ее
точке все возможные плоскости. Возникающие при этом плоские кривые
сечения будут, вообще говоря, различной кривизны. Мы говорили, что
среди значений кривизны имеются наибольшее kt и наименьшее к2
(«главные кривизны»), которые изучал еще Эйлер. Полную кривизну К
поверхности в данной точке Гаусс определил через произведение главных кривизн
1л. = гС\ • А^2«
Величина К характеризует форму поверхности в окрестности данной
точки М. Если К > 0, то все нормальные сечения в М обращены
вогнутостью в одну сторону и поверхность располагается с одной стороны
от касательной плоскости в М. Точка М в этом случае называется
эллиптической; поверхность близ М чашевидна и сходна с поверхностью
эллипсоида. Если К < 0, то часть нормальных сечений обращена вогнутостью
в одну сторону, часть — в противоположную, касательная плоскость
рассекает поверхность, которая имеет близ М седловидную форму,
наподобие гиперболического параболоида. Точка М называется при этом
гиперболической. При К = О точка называется параболической. Таковы,
например, точки цилиндрической поверхности, а также плоскости.
Одним из главных результатов рассматриваемой работы Гаусса
является теорема о том, что полная кривизна выражается через
коэффициенты Е, F,Gm их производные по координатам, а значит, при изометрии
не меняется (хотя главные кривизны каждая по отдельности изменяются);
таким образом, совпадение значений К в соответственных точках двух
поверхностей является необходимым условием их изометрии, а значит,
наложимости друг на друга. Поэтому, например, кусок плоскости {К = 0)
нельзя изогнуть в шар какого-либо радиуса R (К = -^) , нельзя также
изогнуть шар одного радиуса в шар другого радиуса или же в эллипсоид
и т. п.
Работы Гаусса получили дальнейшее развитие в трудах многих
ученых и прежде всего Ф. Г. Миндинга.
ИССЛЕДОВАНИЯ Ф. Г. МИНДИНГА ПО ТЕОРИИ ПОВЕРХНОСТЕЙ 255
Исследования Ф. Г. Миндинга по теории поверхностей. Фердинанд
Готлибович Миндинг (23 января 1806—13 мая 1885) родился в польском
городе Калише, в то время принадлежавшем Пруссии; учился он в
университетах Галле и Берлина. С 1831 по 1843 г. он был приват-доцентом
Берлинского университета, а затем переехал на работу в Дерптский
университет, где преподавал в течение 40 лет. Многие труды его
опубликованы в изданиях Петербургской Академии наук,
членом-корреспондентом которой он состоял с 1864 г. и почетным членом с 1879 г.
В Дерпте Миндинг занял кафедру прикладной математики и вместе
с профессором кафедры чистой математики геометром К. Э. Зенфом поднял
здесь преподавание на весьма высокий
уровень. Работы Миндинга разнообразны;
они относятся к теории непрерывных
дробей (Bull. Ac. Sc.-Petersb., 1869), высшей
алгебре, абелевым интегралам,
вариационному исчислению и т. д. Главные свои
открытия он сделал в теории обыкновенных
дифференциальных уравнений и особенно
в геометрии.
«Исследования об интегрировании
дифференциальных уравнений первого
порядка с двумя переменными» (СПб.,
1862) Миндинга получили по отзыву
Остроградского высокую оценку нашей
Академии наук и были отмечены Демидовской
премией. Отправляясь от отдельных
замечаний Эйлера, Миндинг развил метод
отыскания общего интеграла уравнения
М(х, y)dx +N(x, y)dy, где Ми N —
целые многочлены, старший член которых
имеет степень тг, когда известен п -\- 1
частный интеграл. Из этих интегралов _ ,,
Ф. Г Миндинг.
при определенных условиях составляется А
интегрирующий множитель уравнения и
дело сводится к квадратурам. М. В. Остроградский охарактеризовал
данную работу, как «самый важный шаг» в интегрировании
дифференциальных уравнений после Эйлера г). Метод Миндинга разработали далее
французский математик Г. Дарбу (1878), а также А. Н. Коркин (Math.
Ann., 48, 1897).
Геометрические изыскания Миндинга непосредственно примыкают
к работам Гаусса по внутренней геометрии поверхностей.
При решении задачи о разыскании на данной поверхности замкнутой
кривой с данным периметром, ограничивающей наименьшую площадь,
Миндинг ввел понятие геодезической кривизны линии на поверхности
(термин О. Бонне, 1848), получившее большое значение в
дифференциальной геометрии (Grelle's Journ., 5, 1829) 2). Год спустя Миндинг доказал
*) М. В. О с тр о г рад ский, Полное собрание трудов, т. III, стр. 328.
2) Геодезическую кривизну кривой на поверхности в данной точке М можно
определить как кривизну в соответствующей точке проекции этой кривой на касательную
плоскость к поверхности. На плоскости решение указанной задачи дает окружность,
в общем случае искомой кривой будет так называемая геодезическая окружность —
кривая постоянной геодезической кривизны. Crelle's Journal — это Journal fur die
reine und angewandte Mathematik, основанный в 1826 г. А. Л. Крелле.
256 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
инвариантность геодезической кривизны при изгибании поверхности
(Grelle's Journ., 6, 1830).
Замечательные результаты были получены Миндингом в теории изо-
метрии. Он дал полное решение общей проблемы о необходимых и
достаточных условиях изометричности двух поверхностей. Аналитически
проблема может быть выражена вопросом: существуют ли такие
непрерывные функции ф (и, г;), я|) (и, г;), что уравнение
Е± ди\ + 2F± du^ dv± + GL dv\ = Edu2 + IF dudv + G dv2
оказывается следствием уравнений
ul = (^)(u, г;), vi = ty(u, v)l
Имя Миндинга носит, в частности, теорема, вошедшая в позднейшие
курсы дифференциальной геометрии: поверхности с равной постоянной
полной кривизной наложимы друг на друга; при этом поверхность
постоянной кривизны может передвигаться по самой себе подобно плоскости
(Crelle's Journ., 19, 1839). Миндинг изучал также изгибания и свойства
некоторых специальных классов поверхностей: поверхностей вращения
и среди них поверхностей постоянной положительной кривизны, изо-
жетричных с шаром, а также поверхностей постоянной отрицательной
кривизны (Grelle's Journ., 18, 1838 и 19, 1839).
Многие примеры Миндинга вошли затем (нередко без упоминания
автора), в учебные руководства. Упомянем еще, что в 1838 г. Миндинг,
вслед за Эйлером, высказал предположение о жесткости, неизгибаемости
поверхности полного шара, доказанное лишь в 1899 г. Г. Либманом (любая
часть сферы, однако, изгибаема).
Работы Гаусса и Миндинга легли в основу позднейших исследований
по дифференциальной геометрии О. Бонне, Э. Бура, Д. Кодацци, Э. Бель-
трами и др. и явились предпосылкой учения Б. Римана о многомерных
пространствах и их кривизне. Эти работы сообщили также толчок
геометрическим трудам ученика Миндинга и Зенфа — К. М. Петерсона,
который после переезда из Дерпта в Москву положил начало московской
школе дифференциальной геометрии. Первые результаты Петерсона
приходятся на границу рассматриваемого периода (1853). Для связности
изложения удобнее рассмотреть деятельность Петерсона в следующей
части. Сейчас мы обратимся к одному моменту в трудах Миндинга,
сыгравшему большую роль в дальнейшем развитии неевклидовой геометрии.
Исследуя поверхности постоянной отрицательной кривизны, Миндинг
сделал мимоходом одно интересное наблюдение. - Он заметил (Grelle's
Journ., 20, 1840), что формулы сферической тригонометрии для
треугольников, образованных геодезическими линиями на поверхности постоянной
положительной кривизны (например, теорема косинусов), переходят
в формулы тригонометрии геодезических треугольников на поверхностях
постоянной отрицательной кривизны, если только заменить в
тригонометрических функциях действительные аргументы, выражающие стороны,
на мнимые, т. е. заменить эти функции гиперболическими. Такого рода
связь, как мы видели, была установлена Лобачевским между формулами
тригонометрии на шаре и в гиперболической тригонометрии. Замечание
Миндинга, по существу, означало, что геометрия на поверхности
постоянной отрицательной кривизны совпадает с геометрией на (части) плоскости
Лобачевского. У самого Миндинга, далекого от круга идей Лобачевского,
этого вывода нет.
ДАЛЬНЕЙШЕЕ РАЗВИТИЕ НЕЕВКЛИДОВОЙ ГЕОМЕТРИИ 257
Любопытно, что в 17-м томе того же журнала Крелле был напечатан
французский перевод «Воображаемой геометрии» Лобачевского,
содержавший его тригонометрические формулы, совпадающие с формулами Миндин-
га для поверхностей постоянной отрицательной кривизны. Видимо, ни
один из обоих геометров не обратил внимания на статью другого и, во
всяком случае, на глубокую связь между полученными ими результатами.
Но то же замечание Миндинга стало исходным пунктом Бельтрами,
который через четверть века нашел первую геометрическую
интерпретацию гиперболической геометрии на поверхности, принадлежащей
евклидову пространству.
Дальнейшее развитие неевклидовой геометрии. Во второй половине
шестидесятых годов XIX века неевклидова геометрия начала привлекать
интерес, возраставший очень быстро. Несмотря на враждебное отношение
отдельных влиятельных математиков старших поколений, к ее изучению
и разработке приступает все большее число выдающихся молодых ученых.
Некоторую роль в этом сыграло посмертное издание писем Гаусса,
содержащих чрезвычайно лестную оценку геометрических работ Лобачевского
и полное признание его принципиальной правоты. Во Франции, Германии,
Англии, Италии идеи русского геометра воспринимаются теперь с
энтузиазмом и появляются переводы его сочинений х). Одновременно меняется
отношение к гиперболической геометрии и на родине ее творца. Изданные
вначале по-немецки «Геометрические исследования» печатаются в переводе
профессора А. В. Летникова в III томе московского «Математического
сборника» за 1868 г. (рис. 35), причем в предисловии к переводу
геометрические труды Лобачевского характеризуются как «весьма
замечательные, но мало известные», и подчеркивается, что они должны оказать
влияние на улучшение методов преподавания, а также уничтожить всякую
надежду доказать априори постулат Евклида о параллельных. В том же
году воспитанник и профессор математики Казанского университета
Эраст Петрович Янишевский (17 марта 1829 — февраль 1906) публикует
«Историческую записку о жизни и деятельности Н. И. Лобачевского»
(Казань, 1868) — речь, произнесенную им в торжественном собрании
университета в ноябре 1868 г. (она появилась вскоре во французском
и итальянском переводах). И тогда же выходит в свет «Опыт
истолкования неевклидовой геометрии» (Saggio di interpretazione della geometria
noneuclidea, Giorn. di matem., 1868) итальянского геометра Э. Бельтрами.
Опираясь, как уже говорилось, на работы Миндинга, Бельтрами
доказывает, что в самом евклидовом пространстве существуют
поверхности, именно поверхности постоянной отрицательной кривизны, на
которых выполняются все соотношения, имеющие место в конечных частях
плоскости Лобачевского. Нетрудно составить представление об одной
из таких поверхностей — псевдосфере (рис. 36), по форме напоминающей
бесконечно вытянутую граммофонную трубу. Плоская кривая, у которой
отрезок касательной между точкой касания и некоторой прямой—
основанием имеет постоянную длину а, называется трактрисой; при вращении
трактрисы вокруг основания и возникает псевдосфера с постоянной
1) Например, «Геометрические исследования» были переведены на французский
язык Ж. Гуэлем (1866), а «Пангеометрия» на итальянский Дж. Баттальини (1867); до
того «Пангеометрия» вышла в немецком переводе (1858).
Подробнее см. Э. К. X и л ь к е в и ч, Из истории распространения идей
Н. И. Лобачевского в 60—70-х годах XIX столетия.— Ист.-матем. исслед., вып. TI,
1949.
Рис. 35. Из предисловия к русскому переводу «Геометрических исследований» Н. И. Лобачевского
в «Математическом сборнике», т. 3, 1868,
ДАЛЬНЕЙШЕЕ РАЗВИТИЕ НЕЕВКЛИДОВОЙ ГЕОМЕТРИИ 259
полной кривизной
Внутренняя геометрия псевдосферы — гиперболическая и для геоде^
зических треугольников на ней выполняются все предложения
геометрии и тригонометрии Лобачевского. Геометрия Лобачевского
получает тем самым истолкование, как внутренняя геометрия поверхности
псевдосферы. Каждая теорема Лобачевского выражает некоторое
предложение о свойствах евклидовых фигур на псевдосфере, причем прямые
Лобачевского (геодезические на плоскости) заменяются на
геодезические линии псевдосферы. Поэтому если бы где-либо в планиметрии
Лобачевского встретилось противоречие, то должно было бы иметься
соответствующее ему противоречивое предложение в евклидовой геометрии,
именно, в системе теорем внутренней геометрии псевдосферы. Иными
словами, гиперболическая планиметрия могла
бы оказаться противоречивой только в случае
противоречивости евклидовой х).
Однако интерпретация Бельтрами все же
не решала вопрос до конца. Во-первых, в ней
речь шла только о планиметрии, а не о
трехмерной геометрии Лобачевского. Во-вторых,
как уже было отмечено, эта интерпретация
является не полной, а локальной: на
псевдосферу отображается не вся плоскость
Лобачевского, но лишь ее часть. Это легко
представить себе ПО аналогии С геометрией про- Рис. 36. Псевдосфера,
стого круглого цилиндра. Внутренняя
геометрия круглого цилиндра, поверхности нулевой кривизны, совпадает с
геометрией части евклидовой плоскости, ибо цилиндр, разрезанный вдоль
какой-нибудь образующей, можно изогнуть не в целую плоскость, но
лишь в плоскую полосу. Точно так же, если разрезать одну из полостей
псевдосферы вдоль ее меридиана, то возникающей при этом разомкнутой
поверхности будет соответствовать лишь некоторая часть плоскости
Лобачевского.
Бельтрами указал на возможность другой интерпретации
гиперболической тригонометрии, которую вскоре развил немецкий математик
Ф. Клейн в работе «О так называемой неевклидовой геометрии»
(Ober die sogenannte Nicht-Euklidische Geometrie, Math. Ann. 4, 1871;
6, 1873). В интерпретации Клейна соотношения, имеющие место на всей
бесконечной плоскости Лобачевского, истолковываются в обыкновенном
евклидовом круге.
*) Постоянная к, фигурировавшая в приведенных ранее^ формулах геометрии
Лобачевского, связана с кривизной поверхностей постоянной отрицательной
кривизны соотношением
А - R ,
т. е. в данном случае
&2 = а2
и
к = а (ибо к >0).
260 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
Образом, или, как говорят, моделью, бесконечной плоскости
Лобачевского Клейн выбирает (рис. 37) внутренность круга радиуса 1 (без
самой окружности). Точки плоскости Лобачевского изображаются точками
внутри круга, прямые Лобачевского — хордами с выключенными
концами, как PQ, PR, QS. Измерение отрезков в модели производится по
особому закону: именно за длину отрезка АВ на хорде PQ принимается
In(— : ~rj) ; при таком законе измерения хорда PQ оказывается бесконеч-
ной длины. По особому правилу измеряются также углы,— приводить
его не будем.
В этой модели выполняются все постулаты геометрии Евклида, за
исключением пятого, место которого занимает постулат о параллельных
Лобачевского. В самом деле, через любую точку
М внутри круга можно провести бесчисленно
много «прямых»— хорд, не пересекающих
данную «прямую»— хорду АВ: это все «прямые»,
проходящие внутри вертикальных углов PMS
и QMR. Сами «прямые» MP и MQ служат
образами двух параллелей в смысле Лобачевского
к А В, причем параллель MP неограниченно
сближается с ней в сторону АР ж параллель
MQ — в сторону BQ (не забудем, что точки Р, Q
модели не принадлежат: хорда рассматривается
без концов).
Рис 37. Интерпретация Клейна дает полное
доказательство логической равноправности
планиметрии Лобачевского и планиметрии Евклида. Каждое предложение
Лобачевского переходит при указанном истолковании в некоторое
предложение евклидовой геометрии. Поэтому если бы при
развертывании системы гиперболической геометрии на плоскости мы когда-либо
пришли к двум взаимно противоречащим предложениям, то и в евклидовой
геометрии оказалось бы два соответствующих взаимно противоречивых
предложения. Модель Клейна для трехмерного пространства Лобачевского
строится внутри шара аналогично двумерной модели. Так было
окончательно установлено, что геометрия Лобачевского столь же
непротиворечива, как и геометрия Евклида, и что V постулат Евклида принципиально
невыводим из других его постулатов. Другие две важные интерпретации
геометрии Лобачевского предложил французский математик А. Пуанкаре
в 1882 и 1887 гг.; существует еще целый ряд работ зарубежных и
отечественных ученых по этому вопросу 1).
Лобачевский построил первую систему неевклидовой геометрии.
За полтора года до его смерти Б. Риман в лекции, прочитанной на право
преподавания в Геттингенском университете, сделал следующий шаг
вперед и показал возможность еще более общих неевклидовых систем.
Эта лекция «О гипотезах, лежащих в основании геометрии» (Uber die
Hypothesen, welche der Geometrie zu Grunde liegen), была опубликована
в 1866 г. В ней содержалось дальнейшее обобщение понятия о
пространстве, отправным пунктом которого явились гауссово учение о внутренней
геометрии поверхностей и некоторые идеи первой неевклидовой геометрии.
Мы не можем здесь входить в детали римановой геометрии. Ограничимся
1)Б. А. Розенфельд, Интерпретации геометрии Лобачевского.— Ист.
матем. исслед., вып. IX, 1956.
ДАЛЬНЕЙШЕЕ РАЗВИТИЕ НЕЕВКЛИДОВОЙ ГЕОМЕТРИИ 261
следующими замечаниями. Объектом исследования Римана были
непрерывные множества элементов — точек, каждая из которых
характеризуется п (72, вообще говоря, больше 3) числами—координатами1). Эти
множества называются гс-мерными пространствами, ибо между
координатами их элементов имеют место соотношения, сходные с теми,
которые существуют между координатами точек в двух- или трехмерной
пространстве.
Обобщая формулу Гаусса для дифференциала дуги на поверхности-
и его учение о кривизне поверхности, Риман вводит закон определения
расстояния между двумя бесконечно близкими точками, так называемое
мероопределение в гс-мерном пространстве, и развивает общую теорию
его кривизны. Если обозначить координаты двух бесконечно близких
точек #!, х2, . . ., хп и Xi -\-dxi, х2 + dx2, . . ., хп + dxlt, то расстояние
между ними определяется формулой
ds2 = 2 Stk dxi dxk, (i, A = 1, 2, . . ., ri),
где gik суть функции координат xi4 x2, . . ., xn, а квадратичная форма
справа для любых различных точек имеет положительное значение.
Гиперболическая геометрия Лобачевского при этом оказывается
частным случаем общей римановой геометрии — геометрией трехмерного
пространства постоянной отрицательной кривизны. Риман указал на
возможность и нового вида трехмерной неевклидовой геометрии, отличной
от гиперболической. Это — геометрия пространства постоянной
положительной кривизны, сходная с геометрией на шаре. Такое пространство
является безграничным, но вместе с тем имеет конечные размеры. В нем
через точку вне данной прямой нельзя провести в их общей плоскости
ни одной прямой, не пересекающей данной, т. е. не существует
параллельных прямых. В этой системе два перпендикуляра к одной и той же прямойу
лежащие в одной и той же плоскости, пересекаются, сумма углов
треугольника больше 2d, а два отличных от прямых угла в четырехугольнике
Хайяма-ат-Туси оказываются тупыми.
Мы говорили, что Саккери показал несовместимость гипотезы тупого
угла в четырехугольнике Хайяма-ат-Туси с тем положением, что две
прямые не могут пересекаться в двух различных точках. Считая
последнее положение очевидным, Саккери полагал, что доказал логическую
невозможность гипотезы тупого угла. Исходя из допущения бесконечности
прямой, Лежандр позднее доказывал, что сумма углов треугольника
не может быть более 2d. Благодаря Риману стало понятным, что можно
построить непротиворечивую геометрию, в которой имеет место названная
гипотеза. Системы аксиом геометрии Лобачевского и геометрии Евклида
различаются только в аксиоме параллельности. Аксиоматика геометрии
пространства постоянной положительной кривизны во многом несходна
с евклидовой. Не входя в подробности, укажем, что эти существенные
отличия связаны именно с конечностью такого пространства, в частности,
и всякой расположенной в нем прямой, имеющей замкнутый характер.
2) Одним из примеров многомерного пространства может служить фазовое
пространство состояний множества п частиц, движущихся в обычном трехмерном
пространстве. В каждый момент времени состояние этой механической системы определяется
6/г координатами, ибо состояние каждой частицы можно определить тремя
обыкновенными координатами и тремя проекциями ее скорости на координатные оси. Точка в
фазовом пространстве есть не что иное, как совокупность 6п чисел, определяющих в
каждый момент времени состояние системы.
262 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
Геометрию пространства постоянной положительной кривизны нередко
также называют римановой в узком смысле слова. Ф. Клейн (1873)
указал на существование двух разновидностей римановой геометрии.
В обеих разновидностях два перпендикуляра к одному отрезку
пересекаются по обе стороны от отрезка. В сферической системе эти точки
пересечения различны, в эллиптической — они сливаются в одну.
Так, с конца шестидесятых годов начинается триумфальное развитие
идей Лобачевского, а имя его приобретает мировую славу. Открытие
Лобачевского признается в области математики равнозначащим открытию
Коперника в астрономии. Английский математик У. Клиффорд писал:
«Чем Коперник был в отношении Птолемея, тем был Лобачевский в
отношении Евклида... Каждый из них произвел в научных идеях столь
значительную революцию, что она может быть сравнена только с деянием
другого» х).
Геометрия и физика XX века. Первым общим результатом открытия
и развития неевклидовой геометрии явилось, как мы видели, обогащение
самого учения о математическом пространстве. Изменение тех или иных
аксиом позволило строить новые и новые геометрические системы
произвольного — и даже бесконечного — числа измерений. Геометрия стала
общей наукой о пространственных отношениях и формах тел, а также
о других отношениях и формах действительности, сходных по своим
свойствам с обыкновенными, давно известными отношениями и формами
трехмерного евклидова пространства. Такое обогащение содержания
геометрии имело поистине гигантское значение для дальнейшего прогресса
естественных наук, и многие геометрические системы получили
плодотворные приложения в различных областях математики и физики.
Замечательным примером таких приложений явилось построение
Г. Минковским (1909) кинематики специальной теории относительности,
основы которой были заложены незадолго перед тем А. Эйнштейном (1905).
Основную роль в исследовании Минковского играет квадратичная
дифференциальная форма
ds2 = с2 dt2 — dx2 — dy2 — dz2
(с — скорость света), выражающая линейный элемент четырехмерного
пространственно-временного многообразия, точки которого, или
«мировые моменты», определяются четырьмя координатами х, у, z, t.
Вскоре в общей теории относительности Эйнштейна (1916 и след.
годы) была установлена глубокая и неразрывная связь между геометрией
физического пространственно-временного многообразия и существующими
в мире полями тяготения, которые, как и электромагнитные поля, не
учитывались еще в специальной теории относительности. Метрика этого
общего риманова многообразия, зависящая от распределения
гравитационных масс, характеризуется квадратичной формой
ds2 = 2 gih dxt dxk (i, к = 1, 2, 3, 4),
где коэффициенты представляют собой некоторые функции координат,
четвертая из которых, #4, выражает время. Мы оставляем здесь в стороне
трудности, выявившиеся при попытках создания единой теории
гравитационных и электромагнитных процессов.
г) W. К. Clifford, Lectures and Essays, New York, 1901, v. I, стр. 356
(1-е изд. 1879).
АКСИОМАТИЧЕСКИЙ МЕТОД
263
Связанные с общей теорией относительности космологические
исследования, опирающиеся на некоторые данные о распределении плотности
материи и о движении галактических систем, позволили советскому
ученому А. А. Фридману (1922) и другим построить несколько гипотез
о неевклидовом характере доступного наблюдениям мирового
пространства в целом. Одной из возможностей явилось при этом гиперболическое
по типу пространство с огромным значением к = 1,8 -109 световых лет.
Если учесть, что наиболее точные существующие инструменты не
позволяют заметить уклонение от двух прямых суммы углов рассмотренного
Лобачевским астрономического треугольника при к > 60 световых лет,
то, как ни приблизительна указанная оценка к, понятно, что от простых,
непосредственных измерений углов ожидать решения вопроса не
приходится. Впрочем, эти попытки определить характер геометрии мирового
пространства основаны пока на недостаточно прочных основаниях.
Предположение Лобачевского, что реальные геометрические
отношения зависят от физической структуры материи, нашло подтверждение
не только в космических масштабах. Современная теория квант все с
большей настоятельностью выдвигает необходимость применения геометрии,
отличной от евклидовой, к проблемам микромира. По мнению ряда ученых,
возникает задача заменить для микромира геометрию, исходным элементом
которой является безразмерная точка, другой геометрией, в которой
имелась бы фундаментальная наименьшая длина.
Аксиоматический метод. Чрезвычайно важным следствием открытия
неевклидовой геометрии явилось новое развитие аксиоматического метода,
впервые созданного древними греками. После того как непротиворечивость
неевклидовых систем была поставлена в прямую зависимость от
непротиворечивости обычной геометрии, математики приступили к тщательному
исследованию определений и аксиом, на которых основана последняя.
Выяснилось, что общепринятых аксиом далеко недостаточно для
последовательного доказательства большинства предложений геометрии Евклида,
если не пользоваться наглядными представлениями, содержащими
скрытые допущения, что геометры в течение двух тысячелетий незаметно для
самих себя использовали целые группы аксиом, без которых нельзя
логически вывести даже первые теоремы «Начал». Попутно изучались
особенности простейших геометрических понятий, зависимости между
аксиомами, постулатами и определениями, принципы употребления метода
моделей и т. д. Аналогичные изыскания велись в области теоретической
арифметики.
В ходе этой работы и сам аксиоматический метод подвергался
значительному усовершенствованию. Были установлены основные
требования, которые предъявляются ко всякой системе аксиом, именно
требования совместности, полноты и, по мере возможности, независимости, было
введено понятие изоморфизма двух систем математических объектов,
получившее самые широкие применения в разных областях, и т. д.
Проблема непротиворечивости была поставлена и по отношению
к евклидовой геометрии. В результате труда многих ученых были
достигнуты выдающиеся результаты. Первые итоги были подведены в Италии
М. Пиери (1899), в Германии Д. Гильбертом (1899) и в России В. Ф.
Каганом (1902), которые предложили, каждый по-своему, полную систему
аксиом обычной геометрии; впоследствии в эти системы были внесены
некоторые улучшения. Совместность аксиом геометрии Евклида была
доказана с помощью ее арифметической интерпретации. Каждое понятие
264 ГЛ. 13 Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
и отношение геометрии истолковывается арифметически, например, точка
как пара или тройка действительных чисел — ее координат,
принадлежность точки прямой как выполнение некоторого уравнения и т. д. Все
аксиомы геометрии переходят при этом в некоторые правильные
арифметические предложения и тем самым доказывается, что евклидова
геометрия непротиворечива в той же мере, как ее арифметическая модель.
Мы только в самых общих чертах обрисовали первый этап разработки
современного аксиоматического метода на примере геометрии, оставляя
в стороне многие первоклассные открытия, например, создание новой
теории измерения плоских и пространственных фигур, включающей
анализ понятия величины, или конструкция новых геометрических систем,
например, неархимедовых. Подчеркнем здесь другое: аксиоматический
метод исследования был распространен, как сказано, на арифметику
(особенно Д. Гильбертом), затем на теорию множеств, теорию
вероятностей (С. Н. Бернштейн, А. Н. Колмогоров и другие), в общем на всю
математику. Первые образцы аксиоматической разработки механики были
известны издавна. Так строил статику еще Архимед, а классическую
динамику Ньютон. Теперь аксиоматический метод стали применять
и в других достаточно математизированных областях физики.
А. Н. Колмогоров пишет: «Овладеть всем разнообразием образований,
изучаемых современной математикой, нельзя без аксиоматического
метода, позволяющего систематически обозреть различные возможности
развития той или другой теории, открывающиеся в зависимости от того,
как видоизменяются исходные допущения, положенные в ее основу
(аксиомы). Первым примером последовательного проведения таких
аксиоматических исследований, которые стали привычными не только
математикам, но и механикам и физикам, явилась неевклидова геометрия
Лобачевского» *).
Аксиоматический метод имеет свои границы действия. Внутренняя
непротиворечивость какой-либо теории всякий раз доказывается
проверкой ее аксиоматики на какой-нибудь модели, соотношения которой
принимаются за непротиворечивые. Моделью геометрии Лобачевского
послужили образы евклидова пространства, моделью евклидовой геометрии —
арифметика. Цепь таких математических моделей, очевидно, без конца
продолжать невозможно. В конечном итоге истинность математических
теорий проверяется широкой практикой всего человеческого опыта,
соответствием теории и действительности. Помимо этого, как замечает
А. Н. Колмогоров, «можно говорить лишь о системах аксиом отдельных
математических теорий, а не о системе аксиом всей математики в целом.
Математика в целом не может быть до конца аксиоматизирована, т. е.
выведена из раз и навсегда данной конечной системы аксиом. Решающей
причиной этого является все более глубокое, никогда не
останавливающееся изучение свойств объектов реального мира» 2). И не все
математические теории могут быть построены на полных системах аксиом.
Добавим в заключение, что в дальнейшем развитии математики
с большой широтой оправдалась уверенность Лобачевского в полезности
неевклидовой геометрии для анализа. Сам Лобачевский дал здесь, как
мы знаем, многочисленные примеры вычисления определенных
интегралов. В работах восьмидесятых годов А. Пуанкаре с помощью геометрии
г) Цит. по кн.: А. П. Н о р д е н. Элементарное введение в геометрию
Лобачевского, М.—Л., 1953, стр. 231.
2) «Большая Сов. Энциклопедия», изд. 2-е, т. 1, стр. 616.
«АЛГЕБРА» ЛОБАЧЕВСКОГО
265
Лобачевского решил ряд труднейших проблем теории автоморфных
функций — важного класса аналитических функций комплексного
переменного z, удовлетворяющих условию, что их значения не меняются при
дробно-линейной замене аргумента:
(ad — be фО). Частным видом автоморфных функций являются, между
прочим, любые периодические функции периода Ь, ибо при с = 0,
а = 1, d= 1
f(z + b) = f(z).
Пуанкаре сам указывал, что ключом к решению поставленных им задач
явилась неевклидова геометрия. При этом Пуанкаре предложил одну
из своих интерпретаций геометрии Лобачевского, упоминавшихся выше.
Геометрия Лобачевского получила применение и в других отделах
математики.
«Алгебра» Лобачевского. Открытие и разработка неевклидовой
геометрии были главным делом Лобачевского. Но ему принадлежат также
ценные исследования по алгебре и анализу. Первые из них изложены
в большой монографии «Алгебра, или Вычисление конечных» (Казань,
1834) 1).
В книге Лобачевского, представляющей собой одновременно
университетский курс и научную монографию, отразились как характерное
для великого ученого внимание к точному анализу исходных понятий,
так и интерес к практическим приложениям. «Алгебру и Геометрию,—
писал в предисловии Лобачевский,— постигла одинаковая участь
За быстрыми успехами в начале следовали весьма медленные и оставили
науку на такой степени, где она еще далека от совершенства. Это
произошло, вероятно, от того, что Математики все свое внимание обратили
на высшие части Аналитики, пренебрегая началами... Где-нибудь,
однако ж, надобно воротиться снова к началам и теперь уже всю строгость
почитать у места». И тут же он разъяснял, что, поскольку «Алгебра
первая начинает Математику со всею точностию понятий и со всей обширно-
стию взгляда», в его сочинении «говорится о числах, счете, четырех
действиях Арифметических. Понятие о положительных и отрицательных
я не почел нужным заимствовать прямо из природы вещей, перейдя уже
раз к отвлеченным; но рассматриваю их как числа, искусственно
соединенные со знаками, и единственно в намерении правила сложения и
вычитания сделать общими» 2). Из этих слов видно, что Лобачевский одним
из первых понял значение логического исследования коренных свойств
натуральных и иных видов чисел, а также действий над ними, и подходил
к этой проблеме с позиций, близких к современной теоретической
арифметике.
Трактуя алгебру как «вычисление конечных» и своего рода введение
в анализ, и в этом примыкая к традиции Эйлера, к которой был близок
и Коши, Лобачевский включил в свой курс элементы теории конечных
разностей, теории чисел и элементарные трансцендентные функции, для
г) Подробнее см. А. П. Юшкевич и И. Г. Б а ш м а к о в а, Алгебра, или
Вычисление конечных Н. И. Лобачевского.— Ист.-матем. исслед., вып. II, 1949.
2) Н. И. Лобачевский, Полное собрание сочинений, т. IV, стр. 24—25.
266 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
исследования которых широко применял бесконечные ряды. Главным
предметом алгебры он считал по-прежнему решение уравнений. В этой
области, именно в численном решении уравнений, ему принадлежит
изобретение собственного метода, о котором в предисловии сказано, что
он, «кажется, заслуживает внимания по краткости и легкости
вычисления в сравнении с другими известными мне способами»1).
В первых шести главах «Алгебры» Лобачевский подверг разбору
главные свойства арифметических действий над целыми и дробями, законы
которых удалось полностью выявить только в XIX веке. Мы
находим здесь, например, оригинальное определение нуля равенствами;
а + 0 = а и 0 + а = а (обычно нуль определяли через вычитание:
а — а = 0). Это определение используется затем в принадлежащем
Лобачевскому первом доказательстве основного свойства сложения —
коммутативности: а + Ъ = Ъ + а, базирующемся на допущении
ассоциативности сложения (а + Ъ) + с = а + (Ь + с). Исследуя действие
вычитания, Лобачевский считает необходимым показать, что а — а = 0,
и установить однозначность этого действия, так что разность двух чисел
есть одно определенное число.
Примечательно, что и в алгебре Лобачевский возражает против
немотивированных «произвольных» допущений. Равенство а-0 = 0
не вытекает из общего определения умножения натуральных чисел как
действия, посредством которого по двум данным числам находится третье,
происходящее из первого так, как второе происходит из единицы. Ведь,
замечает Лобачевский,— нуль никак не происходит из единицы. Желая
распространить действие умножения на случай умножения на нуль,
Лобачевский принимает равенство а-0 = 0 не в качестве произвольного
соглашения, но мотивирует его следующим образом: «Выбор, однако же,
значения для какого-нибудь частного случая, не заключающегося в общем
определении, не произволен, но ограничивается известным правилом,
принятым везде в математике и состоящим в том, чтобы почитать за
значение выражения в таком частном случае ту границу, к которой подходит
значение общего выражения, когда вместе приближаются и коликие
[относительные числа] в выражении к той границе, которая составляет
частный случай, не подходящий под общее определение». И так как
«в нашем примере а X 0 представляет границу, к которой приближается
произведение а X Ъ с уменьшением Ъ . . . следовательно, нуль и должно
принять за произведение а X 0» 2).
Упомянем еще, что Лобачевский отказался от попыток доказать
правила знаков при действиях над относительными числами, как это
постоянно и безуспешно делали математики XVIII века. Правила знаков
он высказывает как своего рода определения. Теперь нам ясно, что
относительные числа являются определенными лишь после того как для них
введены основные правила операций. К числу первых ученых, это
осознавших, принадлежал Лобачевский.
Одновременно с Лобачевским над изучением оснований арифметики
и алгебры работали многие зарубежные ученые: М. Ом, Дж. Пикок,
У. Гамильтон, Г. Грассман и др. Эти работы подготовили почву для
настоящего переворота в арифметике. Их результатом явилось широкое
обобщение понятие о числе, введение кватернионов и гиперкомплексных
числовых систем, создание некоммутативных и неассоциативных алгебр,
х) Н. И. Лобачевский. Полное собрание сочинений, т. IV, стр. 27.
2) Там же, стр. 51.
«АЛГЕБРА» ЛОБАЧЕВСКОГО
267
а также позднейшее аксиоматическое построение арифметики. Эти
исследования нашли важные применения и в механике и в физике.
В главах VII и VIII книги Лобачевского говорится соответственно
о десятичных и непрерывных дробях. В главе IX изложено решение систем
линейных уравнений при помощи определителей — «представительных
выражений», без подробного исследования случаев неопределенных или
несовместных систем, которые были общим образом изучены много позднее.
Один способ определения детерминанта Лобачевский взял из курса
алгебраического анализа Коши. Другой, по существу совпадающий с
определением детерминанта, как суммы вида 2 i я1а #23 • • • anv, гДе a» Р, ¦ • ., v
есть какая-либо из перестановок чисел 1, 2, . . ., 7г, он считал своим
собственным, не зная, что Коши развил эту же идею в одном мемуаре 1815 г.
В X главе, посвященной линейным диофантовым системам, для
однородной системы предложен оригинальный способ решения, вновь найденный
и опубликованный в 1862 г. итальянским ученым Э. Бетти 1).
После того Лобачевский переходит к возведению в степень и
извлечению корня, а затем к элементарным трансцендентным, причем, начиная
с гл. XI, употребляет при надобности минимальный аналитический
аппарат, а именно «исчезающие строки», т. е. сходящиеся степенные ряды,
в которых «всегда можно найти член, за которым сумма последующих,
сколько бы их ни было взято, будет менее всякого данного числа» 2);
из действий используется сложение и умножение таких рядов.
Иррациональные числа фактически рассматриваются как пределы своих
рациональных приближений, мнимые вводятся формально. В главе XI
заслуживает быть отмеченным строгий и во многом оригинальный вывод
теоремы о степени бинома для любого рационального показателя (сама идея
вывода, основанного на использовании функционального уравнения
Ф (х) ср (у) = ф (х + г/), восходила к Эйлеру). В следующей главе
формула бинома распространяется на мнимые и комплексные показатели.
В главе XIII строится теория логарифмической и показательной функций,
а в главе XIV дается чисто аналитическое определение
тригонометрических функций, принадлежащее Лобачевскому. Косинус и синус любого
действительного аргумента вводятся, как величины L и М в равенстве
ехУ~-^ = Ь-\-МУ—1; все свойства их устанавливаются на этой основе.
В предисловии к книге подчеркивалось: «О тригонометрических функциях
я также захотел говорить, не выходя впрочем из пределов Алгебры.
Надеюсь, что меня одобрят, потому что не только решение уравнений
требует такого пособия, но даже и учение о степенях осталось бы иначе
неполным» 3).
В главе XV приведены начальные сведения по теории конечных
разностей. В главе XVI, где речь идет о решении двучленных уравнений
деления круга хп — 1 = 0, теория которых была развита Гауссом (1801),
опять-таки содержатся собственные исследования автора о понижении
€тепени уравнения в случае, когда п = 4т?г + 1, полученные им еще
1)П. Г. КонторовичиД. И. Мильман, Об одном методе Н. И.
Лобачевского нахождения целых решений целочисленных линейных однородных
уравнений.— УМН, VIII, 1 (53) 1953.
2) Н. И. Лобачевский, Полное собрание сочинений, т. IV, стр. 194.
3) Там же, стр. 26. Н. Г. Чеботарев указал, что такой способ введения
тригонометрических функций обусловлен был еще тем, что они необходимы как инструмент
в геометрии Лобачевского, между тем их геометрическое определение в
гиперболической плоскости непросто (там же, стр. 15).
268 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
в 1813 г.; в специальной статье в Уч. зап. Казанского ун-та, 1, 1834г
Лобачевский рассмотрел еще случай п = 8т + 1.
Наконец, в главе XVII доказывается основная теорема алгебры, ряд
теорем о симметрических функциях и об отделении корней, а в последнем
параграфе книги коротко описан открытый Лобачевским способ
приближенного решения уравнений с численными коэффициентами.
Численные методы решения алгебраических уравнений высших
степеней уже давно привлекали внимание математиков. Первый
систематический прием был предложен китайскими учеными не позднее VII века;
по существу, он совпадает с методом, вновь открытым итальянцем П. Руф-
фини в 1804 г. и англичанином У. Горнером в 1819 г. В разработке
различных приемов вычисления действительных корней уравнений
участвовали И. Ньютон, Д. Бернулли, Л. Эйлер и другие; специальные сочинения
этому вопросу посвятили Лагранж и Фурье.
Сущность метода Лобачевского такова. Допустим, для простоты,
что корни уравнения
хп + а^71"1 + а2хп-2 + . . . + ап = 0 (1)
суть действительные различные числа #l7 х2, ..., хп, расположенные
в порядке убывания абсолютных значений: | х± | > | х2 | > . . . Если
составить уравнение
y" + Aiyn-i + A2yn-*+...+An = 0, (2)
корни которого суть достаточно высокие r-е степени корней уравнений (1),.
то каждое из чисел i/i = х\, у2 = х\, ... будет весьма велико в
сравнении со всеми, за ним следующими. С другой стороны, сумма
У1 + У2+.- +Уп=—А
и поэтому имеет место приближенное равенство
yitt — Ai,
из которого уже легко находится наибольший по модулю корень х^ (знак
Xi определяется подстановкой в данное уравнение). Зависимости между
суммами произведений пар, троек и т. д. корней уравнения (2) и
коэффициентами А2, А3 и т. д. позволяют затем по порядку найти приближенные
значения у2, у3, • • • и х2, хг . . .
Для составления вспомогательного уравнения (2) Лобачевский
последовательно образует уравнения, корни которых являются квадратами,
четвертыми, восьмыми и т. д. степенями корней начального уравнения (1).
Коэффициенты вспомогательных уравнений вычисляются тогда весьма
просто. Так, если корни уравнения (2) суть квадраты корней
уравнения (1), то
А = — а1 + 2а2, А2 = а\ — 2aia3 + 2а4,
А3= — а\ -f- 2а2а4 — 2aia5 + 2а6,... (3)
Для примера Лобачевский вычислил путем возведения в 8-степень
наибольший по модулю корень уравнения
именно х = у^242067 = 4,70968. Здесь верны все цифры, по знаку же
корень отрицательный. Перед тем тот же корень был найден с помощью
непрерывных дробей и затем уточнен по способу Ньютона. Вычисления
наглядно показывали удобство нового метода.
СОЧИНЕНИЯ ПО АЛГЕБРЕ М. В. ОСТРОГРАДСКОГО И О. И. СОМОВА 269
Значение метода Лобачевского в том, что он позволяет достаточно
просто и, главное, одновременно находить все, в том числе и комплексные,
корни уравнения, не имеющего кратных корней. Сам Лобачевский не
указал на возможность получать с помощью его приема сразу все корни.
Между тем это свойство выгодно отличало его прием от других, служащих
для вычисления каждого корня по отдельности и требующих их
предварительного отделения. Вероятно, из-за краткости изложения это
открытие Лобачевского долго оставалось незамеченным. Теперь метод
возведения в квадрат можно найти в любом современном курсе
вычислительной математики.
Открытие изложенного приема Лобачевский разделяет с двумя
учеными. Несколько ранее, в 1826 г., вычисление корней путем
последовательного возведения в квадрат было мимоходом предложено
бельгийским математиком Ж. Данделеном, который, однако, не придал этому
приему существенного значения и рассматривал его лишь как
вспомогательный момент другого вычислительного метода. Данделен даже не
выписал формулы (3), употребление которых придает методу систематический
характер. Несколько позднее Лобачевского швейцарский математик
К. Греффе в ответ на конкурс, объявленный Берлинской Академией наук,
с большой подробностью изложил тот же метод в специальной книге
(1837), благодаря которой он и получил широкую известность. Все три
ученых работали независимо друг от друга. Позднее этот метод
технически усовершенствован рядом ученых.
Сочинения по алгебре М. В. Остроградского и О. И. Сомова. Вскоре
после книги Лобачевского на русском языке вышли еще два больших
труда по алгебре: «Лекции алгебрического и трансцендентного анализа»,
т. I (СПб., 1837) М. В. Остроградского х), изданные по записям его
публичного курса преподавателями Морского корпуса Степаном Анисимовичем
Бурачком (1800—1876) и Семеном Ильичем Зеленым (1809—1892) и
«Теория определенных алгебраических уравнений высших степеней» (М., 1838)
О. И. Сомова. Мы коротко остановимся на них здесь же для сравнения
с трудом Лобачевского. Сочинения по алгебре Остроградского и Сомова
менее оригинальны, чем монография Лобачевского, но оба составлены
с большим мастерством и чрезвычайно богаты материалом.
«Лекции» Остроградского поражают высоким уровнем изложения:
в них учтены самые новейшие тогда достижения алгебры. В первой части
рассмотрены отделение и приближенное вычисление корней, включая
опубликованную в 1829 г. теорему Ш. Штурма, которая здесь впервые
появляется в учебной литературе. Для вычисления корней уравнения
/ (х) = 0 рекомендуется наряду со способом Ньютона «второе
приближение», т. е. отыскание поправки у к приближенному значению корня а
путем приравнивания нулю первых трех членов разложения / (а + у)
в ряд Тейлора, что дает
Jf _ -Г (а) + УГ (a)*-2f (а) Г (а)
У~ Г (а)
Так поступал Фурье (1831), а еще ранее Э. Галлей (1694). Оценки
погрешности сам Остроградский не привел и издатели попытались найти ее
границу сами, но допустили ошибку, вскоре замеченную Чебышевым.
г) В том I вошли алгебра и теория чисел; лекции по «трансцендентному анализу»,
кроме двух, света не увидели. «Лекции» были переизданы: М. В.
Остроградский, Полное собрание сочинений, т. II, изд. АН СССР, 1940.
270 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
Вторая часть посвящена проблеме разрешимости уравнений в радикалахг
которая после работ Лагранжа и особенно П. Руффини и Н. Абеля стала
в центре алгебраических исследований. Здесь Остроградский дает
несколько измененное (и не вполне завершенное) доказательство теоремы Абеля
о неразрешимости в общем случае буквенного уравнения пятой степени
в радикалах. Бурачек и Зеленый легко распространили это
доказательство на любое уравнение простой степени выше четвертой. Общий
критерий разрешимости уравнений в радикалах открыл Э. Галуа, но его работы
1830—1832 гг. еще долго оставались неизвестными. Отдельные классы
уравнений, решающихся в радикалах, были все же изучены; к ним
относятся упоминавшиеся двучленные уравнения деления круга. В последних
лекциях Остроградский сообщает довольно большой круг сведений по
теории чисел, необходимых для изложения гауссовой теории этих уравнений
(общая теория сравнений, степенные вычеты, первообразные корни,
индексы), которая и венчает его лекции. Все это было совершенно новым
в учебном курсе алгебры. Заметим, что алгебраические результаты
Лобачевского в «Лекциях» нигде не упоминаются.
Монография Сомова, который опирался на труды французских
математиков и лекции Остроградского, представляет собой более сжатый курс.
Книга написана на высоком уровне (в нее вошла, например, теорема
Абеля) и благодаря своим педагогическим достоинствам вполне могла
применяться в качестве учебника. И в ней открытия и само имя
Лобачевского нигде не названы. Академия наук наградила это сочинение
Демидовской премией 1).
Студенческая работа П. Л. Чебышева. Интересную работу
«Вычисление корней уравнения» написал на конкурсную тему, объявленную на
1840/1841 учебный год физико-тематическим факультетом Московского»
университета, П. Л. Чебышев (ср. стр. 332). Основываясь на обращении
степенных рядов, он выразил значение корня х уравнения / (х) = 0 рядом
у_„ /(*) Г/(Д)12 Г (а)
Х~а /'(*) L/'WJ "2/'(«) "''
где а есть приближенное значение х. Беря то или иное число членов этой
формулы и оценивая остаток, Чебышев получил приближенную формулу
Ньютона с оценкой погрешности лучшей, чем данная Фурье,
приближение второго порядка, опять-таки с оценкой погрешности (причем
он показывает упомянутую ошибку в «Лекциях» Остроградского),
а также некоторые другие известные в то время формулы. На конкретных
примерах Чебышев показал эффективность своих приемов вычисления
и предложенных им оценок точности приближения. К сожалению, эта
работа увидела свет только в пятом томе Полного собрания сочинений
П. Л. Чебышева, изданном в 1951 г.
Исследования Лобачевского по теории рядов Фурье. Выше
говорилось, что одной из актуальных проблем математики первой половины
XIX века была разработка теории рядов. Крупный вклад в эту теорию
внес Н. И. Лобачевский. Первые исследования его в этой области содер-
х) Подробнее см. А. К. С у ш к е в и ч, Материалы к истории алгебры в России
в XIX веке и в начале XX века.— Ист.-матем. исслед., вып. IV, 1951; И Г. Башма-
кова и Л. А. Сорокина, О лекциях по алгебраическому анализу М. В.
Остроградского, в сб.: Михаил Васильевич Остроградский. Педагогическое наследие.
Документы о жизни и деятельности. Под ред. И. Б. Погребысского и А. П. Юшкевича,
М., 1961.
ИССЛЕДОВАНИЯ ЛОБАЧЕВСКОГО ПО ТЕОРИИ РЯДОВ ФУРЬЕ 271
жатся еще в «Алгебре»; специально теории рядов Лобачевский посвятил
три большие статьи 1834—1841 гг. *).
Работы Лобачевского по теории рядов свидетельствуют о большой
глубине его аналитических идей. Одним из примеров передовых
воззрений Лобачевского в этой области может служить его понимание
функциональной зависимости.
Ранее уже говорилось о постепенном расширении понятия функции.
Определение функции как произвольно заданного соответствия между
двумя множествами чисел, вовсе не обязательно выраженного
аналитически, восходящее к Эйлеру, Лобачевский высказал с полной
отчетливостью. Оно сформулировано в статье «Об исчезании тригонометрических
строк» (Уч. зап. Казанского ун-та, 1834). Здесь Лобачевский писал:
«Кажется, нельзя сомневаться ни в истине того, что все в мире может быть
представлено числами; ни в справедливости того, что всякая в нем
перемена и отношение выражается аналитической функцией. Между тем
обширный взгляд теории допускает существование зависимости только
в том смысле, чтобы числа, одни с другими в связи, принимать как бы
данными вместе». Лагранж, который понимал под функцией только
зависимость, выраженную аналитически (преимущественно степенным рядом)т
«столько же, следовательно, повредил обширности понятия, сколько
думал выиграть в строгости суждения» 2). П. Л ежен Дирихле
сформулировал аналогичное определение в печати на три года позднее, в 1837 г.
В той же статье Лобачевский провел различение между
непрерывностью функции, которую он называл «постепенностью», и ее дифферен-
цируемостью —«непрерывностью». Впрочем, Лобачевский, вероятно,
представлял себе, что непрерывная функция может иметь лишь
отдельные точки недифференцируемости. Первый пример непрерывной и нигде
не дифференцируемой функции был опубликован Вейерштрассом много
позднее, в 1872 г. 3).
Главные результаты Лобачевского в теории рядов относятся к
проблеме представимости функции / (х) тригонометрическим рядом Фурье:
П=оо
fk(x) = -у- + 2 (ап cos пх + Ьп sin пх).
71=1
Эта проблема, возникшая, как мы знаем, еще в XVIII веке, изучалась
в начале XIX века Фурье, Коши, Пуассоном и другими. В 1829 г. Дирихле
точно сформулировал достаточные условия, при которых такое
разложение имеет место. В условиях Дирихле требуется, чтобы / (х) на
рассматриваемом конечном отрезке была равномерно ограничена и имела
не более чем конечное число экстремумов и конечное же число точек
разрыва первого рода — конечных скачков. В доказательстве
Дирихле имелся один пробел4), который он исключил позднее (1837).
г) Подробнее см. Г. Л. Л у н ц, О работах Н. И. Лобачевского по
математическому анализу.— Ист.-матем. исслед., вып. II, 1949, и его же статьи и примечания
в томе V Полного собрания сочинений Н. И. Лобачевского.
2) Н. И. Лобачевский, Полное собрание сочинений, т. V, стр. 44.
3) Лишь в XX веке стало известно, что в рукописях Б. Больцано начала
тридцатых годов XIX века содержался уже пример непрерывной и нигде не
дифференцируемой функции (сам Больцано доказал недифференцируемость построенной им функции
на всюду плотном множестве точек).
оо
„ч тт ? sinxdx п
4) Именно, оно опиралось на равенство \ = -~- , установленное еще Эиле-
о
ром, но недостаточно строгим образом.
272 ГЛ. 13. Н. И. ЛОБАЧЕВСКИЙ И НЕЕВКЛИДОВА ГЕОМЕТРИЯ
Лобачевский заметил этот пробел и пошел по другому пути
исследования.
В статье 1834 г. Лобачевский доказывает теорему о разложимости
данной на конечном интервале функции в ряд Фурье при условиях,
отличных от условий Дирихле. В некоторых отношениях условия Лобачевского
более жесткие: вывод предполагает равномерную ограниченность /(я),
не более чем конечное число точек разрыва первого рода и двукратную
дифференцируемость функции (причем f'(x) и f\x) могут конечное число
раз обращаться в бесконечность) 1). Но, с другой стороны, в
доказательстве Лобачевского не требуется ограниченность числа экстремумов.
В дальнейшем исследовании Лобачевский показывает, что теорема
сохраняет силу, если в окрестности отдельных точек f(x) делается
неограниченной, оставаясь интегрируемой. Наконец, все в той же работе
Лобачевский доказывает, что почленное интегрирование ряда Фурье для
функции /(х), безразлично, сходящегося или расходящегося, дает сходящийся
ряд, сумма которого равна интегралу функции f(x). Эта теорема в более
общей трактовке была вновь найдена в 1906 г. А. Лебегом. В следующей
статье (Уч. зап. Казанского ун-та, 1835) Лобачевский провел
доказательство теоремы о разложении функции в ряд Фурье при условии, что f(x)
дифференцируема на данном отрезке, за исключением конечного числа
точек, где /' (х) = ± оо, и ограничена; при этом f(x) может иметь конечное
число разрывов первого рода и бесконечно много экстремумов.
Признак сходимости Лобачевского. Работы Лобачевского по теории
рядов основываются на точных оценках неравенств и на постоянном
внимании к сходимости встречающихся рядов 2). Интересно заметить, что
исследование сходимости Лобачевский во многих случаях производит
с помощью открытого им признака сходимости числовых рядов,
опирающегося на разложение членов ряда в двоичные дроби. Этот признак
Лобачевский применил в одном случае в «Алгебре» и подробнее рассматривает
в статье 1834 г. Сам Лобачевский доказывал достаточность указанного
им признака. В более современной формулировке принцип Лобачевского
71= оо
гласит: ряд 2 / (п)' гДе / (п) положительная, монотонная и не возрастаю-
71=1
71= оо
щая функция, сходится или расходится одновременно с рядом ^ |^ , где
71=1
числа рт определяются неравенствами
1 1
Вопросы сходимости рядов привлекали внимание и других русских
математиков. В. Я. Буняковский изложил новейшие работы о
сходимости рядов (в том числе признаки Раабе, Дюамеля, Моргана) в одном
из приложений к своим «Основаниям математической теории
вероятностей» (СПб., 1846) и предложил собственный критерий сходимости,
основанный на рассмотрении предела ип In п~ при п = оо. К этому же
1) Как сказано, существование производной (и производных любых порядков)
всюду, за исключением отдельных точек, Лобачевский считал естественным свойством
непрерывных функций.
2) Правда, формулировки Лобачевского не всегда полны и ясны; об этом
см. в статьях Г. Л. Лунца, названных выше.
ПРИЗНАК СХОДИМОСТИ ЛОБАЧЕВСКОГО
273
кругу проблем отчасти примыкает «Мемуар об определенных
квадратурах» Остроградского (Mem. Ac. Sc. Petersb., VI ser., t. 2, 1839—1841),
где он вывел в употребительной теперь форме остаточный член формулы
суммирования Эйлера — Маклорена, в менее удобном виде впервые
найденный незадолго до того Пуассоном (1827), а также остаточный член
ряда Лежандра (1811 и 1825), аналогичного ряду Эйлера — Маклорена.
Остроградский не знал, что равносильный результат для оценки
остатка формулы Эйлера — Маклорена в 1834 г. нашел Якоби.
Исследования по теории рядов составляют лишь часть открытий,
сделанных в России первой половины XIX века в обширной области
математического анализа. Наиболее значительные успехи в этом
направлении достигнуты были в разработке проблем математической физики,
вариационного и интегрального исчислений. Здесь неувядаемую славу
приобрели труды М. В. Остроградского, проводившиеся им в Академии
наук.
ГЛАВА ЧЕТЫРНАДЦАТАЯ
НОВЫЙ ПОДЪЕМ ИССЛЕДОВАНИЙ В АКАДЕМИИ НАУК;
М. В. ОСТРОГРАДСКИЙ И ВГЯ. БУНЯКОВСКИЙ
Жизнь М. В. Остроградского. Мы уже говорили, что математическая
жизнь в Академии наук в середине десятых годов почти замерла и
возродилась в конце двадцатых с приходом в Академию Остроградского
и Буняковского, особенно первого из них. Познакомимся коротко с
далеко необычной биографией этого выдающегося аналитика 1).
Михаил Васильевич Остроградский родился 24 сентября 1801 г.
на Украине, в деревне Пашенной Кобелякского уезда Полтавской губ.
(ныне Козелыцанского района Полтавской области) в семье помещика.
В 1816 г. он поступил в Харьковский университет, где преподавали уже
упоминавшиеся Т. Ф. Осиповский и А. Ф. Павловский. В 1820 г.
Остроградский успешно сдал кандидатские экзамены, и перед ним, казалось,
открывалась прямая дорога к университетской профессуре. Однако
острая идейная борьба, которая в те годы велась в Харьковском
университете, помешала спокойному течению научной карьеры
Остроградского.
Выше говорилось, что Осиповский подверг критике идеалистическую
немецкую философию, сторонники которой имелись и среди работавших
в Харьковском университете иностранцев. В устных выступлениях
Осиповский разоблачал и высмеивал мистиков, стоявших во главе
министерства просвещения и учебных округов. Свое враждебное отношение к Оси-
повскому реакционная часть харьковской профессуры перенесла и на его
лучшего ученика, также не любившего ни метафизики, ни мистики
и бывшего, надо полагать, уже тогда «полным материалистом и атеистом»2).
Когда ректор университета Осиповский Предложил присвоить
Остроградскому заслуженную им степень кандидата, в Совете университета
произошли резкие столкновения. Один из реакционных профессоров,
А. И. Дудрович, письменно донес попечителю округа 3. Я. Карнееву,
что по вине Осиповского студенты-математики не занимаются богословием,
а Остроградского обвинил в том, что он, несмотря на предписание
начальства, не слушал богопознания и христианского учения. Дело дошло
до министра «духовных дел и народного просвещения» А. Н. Голицына,
*) Подробнее см. Б. В. Г н е д е н к о, И. Б. П о г р е б ы с с к и й, Михаил
Васильевич Остр о градский. М., 1963; А. И. К р о п о т о в и И. А. Марон,
М. В. Остроградский и его педагогическое наследие. М., 1961.
2) Так характеризовал свои взгляды сам М. В. Остроградский в беседе с химиком
А. М. Бутлеровым. Лишь в последние годы жизни знаменитый математик стал
религиозным человеком. См.: Г. Ф. Рыбкин, Материалистические черты
мировоззрения М. В. Остроградского и его учителя Т. Ф. Осиповского.— УМН, VI (2), 1952.
жизнь М. В. ОСТРОГРАДСКОГО
275
по указанию которого Осиповский был уволен из университета,
Остроградскому отказали в присуждении степени кандидата, издевательски
предложив заново сдать экзамены, якобы сданные им раньше в
неправильном порядке.
Остроградский мужественно перенес эти испытания и решил,
несмотря ни на что, посвятить свою жизнь науке. Еще в Харьковском
университете его особенно увлекали вопросы прикладной математики и в 1822 г.
он отправился в Париж, где работали Лаплас и Фурье, Лежандр и
Пуассон, Бине и Коши и другие первоклассные ученые, пролагавщие новъш
пути в математике, математической физике
и механике. Курсы, читавшиеся в
Политехнической школе, Сорбонне, Коллеж
де Франс были образцовыми и привлекали
молодежь из многих стран.
Быстрые успехи Остроградского
завоевали ему дружбу и уважение многих
французских математиков, как старших
поколений, так и сверстников. Время
парижской жизни явилось для
Остроградского не только «годами странствий и
учения», но и интенсивного творчества.
В 1824—1827 гг. он представил Академии
наук в Париже несколько замечательных
мемуаров на французском языке. В
«Замечаниях об определенных интегралах»
(1824) он дал вывод незадолго перед тем
опубликованной Коши формулы для
вычета функции относительно полюса тг-го
порядка, вывод, по сути дела совпадающий
с принятым ныне. В «Доказательстве одной
теоремы интегрального исчисления» (1826) м- в- Остроградскии.
он разработал весьма важную составную
часть общего метода разделения переменных для интегрирования
уравнений математической физики. В том же году Остроградский
подготовил «Мемуар о распространении волн в цилиндрическом бассейне»,
где развил исследования Коши и Пуассона, изучивших движение
малых волн в бассейне бесконечной глубины и не ограниченном
стенками, а год спустя «Мемуар о распространении тепла внутри твердых
тел», содержавший новое сжатое изложение метода разделения и решение
новой задачи о распространении тепла в некоторой треугольной призме.
Из них только работа по гидродинамике увидела свет в издании
Парижской Академии (Mem. div. sav. Ac. Sc. de Paris, 3, 1832), другие же
остались в ее архиве. Но и неопубликованные тогда его открытия по
математической физике оказали существенное влияние на развитие математики.
Основные результаты вошли в последующие печатные труды самого
Остроградского; кроме того, в рукописи или в устном изложении самого
Остроградского с ними ознакомились тогда же или вскоре Коши,
Пуассон, Г. Ламе и другие *).
Перечисленные работы показывают, что Остроградский в первые же
годы парижской жизни не только полностью овладел новейшим аппаратом
х) А. П. Юшкевич, О неопубликованных ранних работах М. В.
Остроградского.— Ист.-матем. исслед., вып. XVI, 1965.
276 ГЛ. 14. М. В. ОСТРОГРАДСКИЙ и в. Я. БУНЯКОВСКИЙ
анализа и механики, но существенно развил его и мастерски применил
к решению как весьма общих актуальных проблем, так и частных трудных
задач. Копти с высокой похвалой отзывался о работах своего молодого
ученика и сотрудника. Например, в основоположном мемуаре по теории
интегралов в комплексной области 1825 г., Коши, рассказывая о своих
предыдущих результатах, писал: «Наконец, один молодой русский,
одаренный большой проницательностью и весьма искусный в анализе
бесконечно малых, г. Остроградский, также прибегнув к употреблению этих
интегралов [именно интегралов между мнимыми пределами.— А. Ю.]
ж их преобразованию в обыкновенные, дал новое доказательство формул,
мною выше упомянутых, и обобщил другие формулы, которые я
представил в 19-й тетради «Журнала Политехнической школы». Г. Остроградский
любезно сообщил нам главные результаты своей работы» г). Столь же
уважительны отзывы Коши об Остроградском в статьях по теории вычетов.
Много позднее, в работе, в которой установлен ряд общих свойств
интегралов линейных уравнений с частными производными, Коши
вспоминал о парижских открытиях Остроградского: «Я хотел бы иметь
возможность сравнить полученные мною здесь результаты с результатами,
полученными г. Остроградским в мемуаре, в котором он установил несколько
общих предложений относительно интегрирования линейных уравнений
в частных производных. Но я только смутно помню этот мемуар и, так
как не знаю, был ли он где-либо опубликован, я лишен возможности
произвести это сравнение» 2).
Весной 1828 г. Остроградский приехал в Петербург и здесь на
протяжении нескольких месяцев представил Академии наук три работы. Первая
содержала оригинальный, основанный на .новой концепции интеграла
{Коши), вывод уравнения Пуассона, которому удовлетворяет объемный
потенциал поля тяготения в точке, лежащей внутри притягиваемой массы
жли на ее границе. Следующая посвящена вопросу о перестановке порядка
интегрирований в двойном интеграле в случае бесконечного разрыва
лодынтегральной функции и примыкает к аналогичным исследованиям
Коши. Третьей был уже упомянутый мемуар «Доказательство одной
теоремы интегрального исчисления», который автор вскоре взял обратно
для переработки и затем опубликовал под названием «Заметки по теории
теплоты». Все они появились в первом томе VI серии Mem. Ac. Sc. Petersb.
в 1831 г. 3). Коллинс представил о трудах Остроградского блестящий
отзыв и 29 декабря 1828 г. молодой ученый был избран адъюнктом по
прикладной математике. Два года спустя он был выбран экстраординарным
академиком и в 1831 г.— ординарным.
Деятельность Остроградского в Академии была весьма
разносторонней. Он сделал более 85 научных сообщений, частью неопубликованных;
читал, как мы знаем, публичные лекции; писал подробные отзывы на
поступавшие в Академию работы, участвовал в комиссиях по введению
григорианского календаря и десятичных мер (что было сделано лишь после
Великой Октябрьской социалистической революции), по водоснабжению
1) А. С а и с h у, Oeuvres completes, II ser., t. II, Paris, 1958, стр. 58.
2) A. G a u с h y, Exercices d'analyse et de physique mathematique, t. II, Paris,
1841, стр. 333.
3) В дальнейшем мы, как правило, указываем только год публикации статей
Остроградского. Все они имеются в издании: М. В. Остроградский, Полное
собрание трудов, т. I—III, отв. ред. И. 3. Штокало, Киев, 1959—1961. В этом издании
имеются обстоятельные статьи и комментарии, освещающие научное творчество
Остроградского.
жизнь М. В. ОСТРОГРАДСКОГО
277
Петербурга и т. д., занимался по поручению правительства изысканиями
по внешней баллистике, и т. д. Вместе с тем Остроградский много времени
уделял преподаванию. С 1828 г. он начал читать лекции в Морском
корпусе (впоследствии Морской академии), где преемниками его
последовательно были В. Я. Буняковский, А. Н. Коркин, А. Н. Крылов. С годами
педагогическая деятельность Остроградского становилась все более
интенсивной. Он вел занятия по математике и механике в Институте
инженеров путей сообщения, Главном инженерном и Главном
артиллерийском училищах, Главном педагогическом институте. С 1847 г. и до
своей смерти он работал на посту главного наблюдателя по преподаванию
математических наук во всех военных учебных заведениях страны. Ему
принадлежат несколько руководств по элементарной и высшей математике.
Мы только что упоминали о его превосходном курсе алгебры.
Педагогические взгляды Остроградского были весьма прогрессивными.
Он считал, что в гимназиях и кадетских корпусах нужны лаборатории
и мастерские, где учащиеся приобретали бы трудовые навыки,
производили опыты и наблюдения. Он выступал за наглядность обучения
математике, особенно в раннем возрасте, и критиковал сухое и формальное
изложение этого предмета в современной ему школе. Он был сторонником
введения в специальных старших классах средних военных учебных
заведений идеи функции и начал анализа; курс математики, с его точки
зрения, должен быть связан с другими предметами, как физика, в которых
применяются математические методы. Как видно, в ряде пунктов
Остроградский предвосхитил идеи так называемого движения за реформу
преподавания, возникшего в начале XX века. Кое-чего Остроградский
добился в этом направлении в кадетских корпусах. Однако более широкая
реализация педагогических установок Остроградского стала возможной
лишь много позднее. Свое общее педагогическое credo Остроградский
изложил в написанной совместно с парижским математиком и инженером
И.-О. Блюмом (1812—1877) брошюре «Размышления о преподавании»,,
вышедшей на французском языке («Considerations sur l'enseignement»,
Петербург — Париж, 1860). Чтение этого блестящего по изложению
и глубокого по содержанию сочинения интересно и в наши дни.
Школьное преподавание арифметики, алгебры и геометрии,— писали авторы,—
ничем «не напоминает о насущной необходимости изучения этих предметов
для практической жизни» и на деле дает «только тот результат, что их
усваивает очень небольшое число учеников»1). Этому в брошюре ярко
противопоставлены принципы обучения, воспитывающего
наблюдательность и любознательность, техническую сноровку и научное мышление.
Для повышения интереса и привлечения внимания учеников Блюм
и Остроградский рекомендовали использовать историю наук и биографии
выдающихся людей, «принесших пользу наукам и искусству»: «Это в одна
и то же время отличная разрядка и средство с помощью живого рассказа
запечатлеть то или иное основное положение, либо удачное приложение
теоретических принципов» 2). Школьная математика должна учитывать
особенности детского восприятия, но следует избегать общепринятой
недооценки возможностей детей уже с семилетнего возраста. В
брошюре разобран вопрос об обучении ребят до 12 лет, причем только в
гимназиях или специальных учебных заведениях; более массовые школы, где
учат началам чтения, письма и счета, оставлены были в стороне.
х) См. сб.: Михаил Васильевич Остроградский, М., 1861, стр. 35 .
2) Там же, стр. 37.
278 ГЛ. 14. М. В. ОСТРОГРАДСКИЙ И В. Я. БУНЯКОВСКИЙ
Остроградский оказал значительное влияние на развитие математики
и механики. Он, в частности, подготовлял условия для создания
математической школы, организованной Чебышевым, и сам основал русскую
школу механики. К его исследованиям примыкают многие последующие
работы по математической физике (казанского математика А. Ф. Попова,
О. И. Сомова и др.), по теории интегрирования иррациональных функций
(Брашмана, Сомова, Чебышева), по теории кратных интегралов (Н. Н. Зи-
нина) и даже по теории чисел и теории вероятностей, которыми сам
он занимался немного. Прямыми учениками Остроградского были
создатель теории автоматического регулирования И. А. Вышнеградский
{1831—1895), автор классических исследований по теории трения и
влияния на него смазки и по теории механизмов Н. П. Петров (1822—1889),
профессор математики Артиллерийского училища и позднее выдающийся
публицист-народник П. Л. Лавров (1823—1900), профессора
Киевского университета А. Н. Тихомандрицкий, Харьковского университета
Е. И. Бейер и Д. М. Деларю, Новороссийского университета в Одессе
Е. Ф. Сабинин и другие. Все перечисленные математики вышли из
Главного педагогического института, где Остроградский преподавал с 1832
по 1859 г.
Научные заслуги Остроградского были высоко оценены и за рубежом.
Он был избран членом-корреспондентом французской Академии наук
в 1856 г., а еще ранее членом Американской академии наук и академий
е Турине и в Риме. Скончался он 1 января 1862 г.
Работы Остроградского по теории теплоты. Остроградский мечтал
<о грандиозном синтезе в области математической физики. В записке,
поданной Академии наук 24 марта (ст. ст.) 1830 г. он писал, что собрал
уже материалы по движению и равновесию упругих тел, по
распространению волн на поверхности несжимаемых жидкостей, по
распространению тепла внутри твердых тел. Но эти теории образуют лишь часть
труда, который должен также включить разработанные однородным
методом электростатику, электродинамику, учение о распространении тепла
в жидкости, теорию капиллярности и т. д. х). Понятно, что Остроградский
выполнил только часть этого плана, но и сделанного достаточно для
увековечения его имени.
Главный вклад Остроградского в математическую физику содержится
в его пяти работах по теории теплоты, начиная с двух упомянутых статей,
представленных французской Академии наук в 1826—1827 гг. 2). В статье
«Доказательство одной теоремы интегрального исчисления» впервые была
изложена общая схема решения уравнений математической физики
посредством метода разделения переменных, который восходит еще
к Даламберу и Д. Бернулли, но систематическим применением и
развитием которого мы обязаны в первую очередь Фурье (1807—1822). До сих
пор полагали, что Остроградский сообщил свои результаты в данной
области прежде всего в «Заметке по теории теплоты», доложенной
Петербургской Академии наук 5(17) ноября 1828 г. и увидевшей свет
в 1831 г. Об этой «Заметке» В. А. Стеклов писал: «После того как Фурье
было составлено дифференциальное уравнение распространения теплоты
в твердом теле, явилась необходимость указать прием определения иско-
х) См. сб.: Михаил Васильевич Остроградский, стр. 275—276.
2) Русский перевод обеих статей опубликован в Ист.-матем. исслед., вып. XVI,
1965; ко второй статье приложены подробные комментарии В. И. Антроповой.
РАБОТЫ ОСТРОГРАДСКОГО ПО ТЕОРИИ ТЕПЛОТЫ
279
мой температуры тела согласно с условиями задачи. Эта задача в общем
случае представляла громадные трудности, и исследования,
естественно, начались с возможно простых случаев, на которых отчетливее
выступают особенности задачи. Сам Фурье, а также Пуассон рассмотрели
случаи охлаждения твердого тела: шара, цилиндра, куба и
прямоугольного параллелепипеда.
Во всех этих случаях Фурье применял один и тот же прием, известный
теперь под именем метода Фурье, но едва ли сам он усматривал всю
общность своего приема. По крайней мере из исследований Фурье этого
не видно, и я едва ли ошибусь, если скажу, что метод Фурье во всей
общности впервые был формулирован Остроградским, а затем уже (в 1829 г.)
Ламе и Дюамелем»1).
Эти последние слова Стеклова приобретают теперь еще большую
силу, если учесть, что метод Фурье был сообщен Парижской Академии
наук Остроградским дважды, 13 февраля 1826 г. в «Доказательстве...»
и затем 6 августа 1827 г. во второй части «Мемуара о распространении
тепла внутри твердых тел». Между тем статья Г. Ламе была доложена той
же Академии наук 8 мая 1829 г., а статья Ж. Дюамеля 9 февраля 1829 г.
и 5 апреля 1830 г., причем обе вышли из печати в Journ. Ее. Polyt.,
t. XIV, cahier XXII, 1833, т. е. на два года позднее «Заметки по теории
теплоты» Остроградского.
Мы изложим основные рассуждения Остроградского в обеих первых
работах по теории тепла, несколько отступая от его собственных
обозначений (рис. 38 и 39). Пусть твердое тело, ограниченное какой-либо
замкнутой поверхностью, помещено в среду с нулевой температурой и его
начальная температура выражается какой-либо данной функцией / (я, у, z).
Тогда согласно Фурье температура тела v (х, г/, z, t) удовлетворяет
уравнению
1»=к Ш + -д^ + ^) (ВН^ТРИ тела)' (*)
-^- cos А, + -J- cos I1 + 4— cos 7 + hv = 0 (на его поверхности) (2)
и при t = 0
v\t=o = f(x1 г/, z). (3)
Здесь к2 и h — некоторые физические постоянные, а Я, [i, у — углы
внешней нормали к поверхности с положительными направлениями осей
координат.
«Определение величины v,— писал Остроградский в «Мемуаре о
распространении тепла...»,— сопряжено с большими трудностями, которые,
однако, можно уменьшить» 2). Именно, величина v представляется в виде
произведения
v = e-k 0 tu(Xi у^ 2);
в таком случае функция и удовлетворяет уравнениям
с) и д и г) и
-^cos^ + -^cos[i + -^cosу + /ш = 0 (на его поверхности). (5)
1)В. А. Стеклов, О работах М. В. Остроградского в области математической
физики. В кн.: П. И. Т р и п о л ь с к и й, Михаил Васильевич Остроградский,
Полтава, 1902, стр. 122.
2)М. В. Остроградский, Мемуар о распространении тепла внутри
твердых тел.— Ист.-матем. исслед., вып. XVI, 1965, стр. 85.
Рис. 38. Фотокопия десятой страницы рукописи М. В. Остроградского
«Доказательство одной теоремы интегрального нечисления» (оригинал
хранится в Архиве Академии наук в Париже).
Рис. 39. Фотокопия второй страницы второго раздела рукописи М. В.
Остроградского «Мемуар о распространении тепла внутри твердых тел»
(оригинал хранится в Архиве Академии наук в Париже).
282 ГЛ. 14. М. В. ОСТРОГРАДСКИЙ и в. Я. БУНЯКОВСКИЙ
Предполагая, что существует бесконечная последовательность чисел
Qn и соответствующих им функций ип, удовлетворяющих уравнениям (4)
и (5) (их теперь называют собственными значениями и собственными
функциями данной краевой задачи), Остроградский ищет решение
исходного уравнения в виде бесконечного ряда по собственным функциям
*= 2 с^-^Ч, (6)
71=1
где Сп — неопределенные коэффициенты, подлежащие определению.
В силу начального условия
оо
f(x,y,z)=4%Cnun (7)
71*= 1
и вопрос сводится к отысканию коэффициентов Сп разложения
«произвольной» функции f(x, г/, z) в ряд по собственным функциям ип, в так
называемый теперь обобщенный ряд Фурье. Именно эта важная проблема,
частным случаем которой является задача разложения данной функции
f(x) в тригонометрический ряд Фурье, и стоит в центре работ
Остроградского по теории тепла.
Остроградский получил два важных результата. Прежде всего он
доказывает ортогональность системы собственных функций, т. е. то
свойство, что для различных ит, ип, соответствующих числам 0^ и 0^, причем
ft2 =?= А2
^ итип-(й = 0; (8)
здесь \ —знак тройного интеграла по объему тела, со — элемент объема.
Затем находятся коэффициенты
_lf(x, у, z)un.g
J Мп-СО
Таким образом, разложение (7) имеет вид
,, ч ^ ип I f (х, у, z)un.®
f(x, if, Z)= 2 ^—5-5 • (Ю)
n=l W°°
а решение задачи, согласно (6) и (9),
^ -k2e2nt ип \ f (х, у, Z) Un.(0
v=2je Г"2 • v11)
71=1
J Мп'СО
Доказательство ортогональности проводится с помощью некоторых
интегральных преобразований, из которых Остроградский выделил, как
особую теорему, предложение, которое стало впоследствии краеугольным
в теории кратных интегралов. Это предложение, полностью доказанное
уже в первой из названных статей, во второй сформулировано
следующим образом: «Обозначая через /?, g, г функции от х, у и z, конечные
ж непрерывные для всех точек тела, получим
I (1г + 1г + 4г) • Ю= I (P^sX + qcoSli + rcosy) • s,
РАБОТЫ ОСТРОГРАДСКОГО ПО ТЕОРИИ ТЕПЛОТЫ
283
где со — элемент объема и s — элемент поверхности; интеграл левой
части берется по всему объему тела, а интеграл правой — по всему
протяжению поверхности» *). Это и есть знаменитая формула Остроградского
для преобразования тройного интеграла по объему от выражения типа
дивергенции, в двойной интеграл по поверхности, ограничивающий
объем. Дюамель, Ламе и другие математики долгое время выводили
свойство ортогональности, не применяя эту формулу, которая как бы
скрывалась в их выкладках над кратными интегралами и только Остроградский
понял ее широкое значение. В настоящее время оно общепризнано и
современное доказательство ортогональности не отличается, по существу,
от данного в 1826—1827 гг. Остроградским 2). Мы еще вернемся к этой
теореме.
Вторая статья Остроградского посвящена почти целиком задаче
о распространении тепла в прямой призме, в основании которой лежит
равнобедренный прямоугольный треугольник. Решение Остроградского
оставалось неопубликованным до 1965 г. и о нем было известно только
благодаря Ламе, которому его сообщил сам Остроградский 3). Ламе
упомянул об этом решении в статье, посвященной аналогичной задаче для
случая равностороннего треугольника (1833), и затем провел полное
доказательство в курсе лекций по теории тепла, изданном в 1861 г.
Мы говорили, что Остроградский представил «Доказательство одной
теоремы интегрального исчисления» Петербургской Академии наук,
но после взял обратно для переработки и вместо него опубликовал
«Заметку по теории тепла (1831). Основная задача этой работы — прежняя,
но все результаты существенно обобщены и сформулированы более
отчетливо. Сжато характеризуя метод разделения переменных, Остроградский
в самом начале статьи писал: «Сначала ищут частные решения,
удовлетворяющие как уравнению, относящемуся ко всему рассматриваемому объему,
так и уравнению, относящемуся к его поверхности; оказывается, что
этих решений бесконечное множество и каждое из них содержит, как
множитель, произвольную постоянную. Затем берут сумму всех этих
частных решений и пытаются так определить произвольные множители,
чтобы получить заданное для некоторого данного момента состояние. Этой
последней части проблемы и посвящается наша заметка»4). Сразу после
этих слов выводится интегральная формула для объемного интеграла и с ее
помощью так называемая формула Грина для произвольных сопряженных
в трехмерном пространстве линейных дифференциальных операторов
с постоянными коэффициентами. Далее доказывается ортогональность
системы собственных функций соответствующей краевой задачи для
линейных уравнений с частными производными любого порядка 5). Затем
Остроградский применяет общие результаты к уравнению
теплопроводности. О самом разложении типа (10) он замечает, что такой ряд, по его
Х)М. В. Остроградский, цит. соч.—Ист.-матем. исслед., вып. XVI,
1965, стр. 86.
2) Точнее говоря, формула Остроградского непосредственно применяется в
названном доказательстве во второй статье. В первой статье она служит для вывода другой
теоремы (представляющей собой частный случай так называемой теоремы Грина)
и здесь доказательство ортогональности основано именно на этой последней, по которой
статья и названа «Доказательством одной теоремы интегрального исчисления».
3) Ламе познакомился с Остроградским в годы своей работы в Петербургском
Институте инженеров путей сообщения, где он преподавал в 1820—1831 гг.
4)М. В. Остроградский, Полное собрание трудов, т. I, стр. 62.
б) Столь же общие результаты были получены Коши в указанной ранее статье
1841 г.
284 ГЛ. 14. М. В. ОСТРОГРАДСКИЙ И В. Я. БУНЯКОВСКИЙ
мнению, всегда сходится, но доказать это замечательное свойство в общем
случае очень трудно. Сам Остроградский ограничивается попыткой
доказательства сходимости для случая тригонометрического ряда Фурье.
Действительно, доказательство сходимости для более широких систем
собственных функций (так же как доказательство полноты этих систем)
весьма трудно и при тогдашнем состоянии анализа вообще не было
возможно; в разработке этих проблем большие заслуги принадлежат
В. А. Стеклову.
В «Заметке», как и в предшествовавших статьях, температура
окружающей среды принималась равной нулю,— этому соответствует так
называемое однородное граничное условие (2). В непосредственно
примыкающей к ней «Второй заметке по теории теплоты» (1831, предст. 1829)
задача о распространении тепла в теле, помещенном в среду с
произвольной переменной температурой Т(х, г/, z, t) х), сведена к предыдущей
совершенно так же, как делают теперь. Дюамель решил эту задачу в
упоминавшейся статье, напечатанной в 1833 г. Ранее Фурье ограничился
предположением Т = 0. Лаплас принимал температуру среды зависящей
лишь от координат ее точек, а Пуассон рассмотрел некоторые случаи,
когда температура является периодической функцией времени.
Наконец, в 1836 г. Остроградский представил Академии работу о
распространении тепла в движущейся жидкости, несжимаемой при давлении
и свободной от внутреннего трения — невязкой (1838). Тем самым он
нашел решение вопроса в более общем случае, чем Фурье, вывод которого
относится к идеальной жидкости (опубл. в 1833). Еще более общий
случай вязкой жидкости был исследован много спустя Г. Кирхгофом (1894) 2).
В. А. Стеклов обратил особое внимание на метод, примененный
в этой работе. Он писал: «Вместо того чтобы рассматривать элементарные
параллелепипеды, как это практикуется и до сих пор многими
французскими математиками, Остроградский выделяет из тела некоторый
произвольный объем и составляет интегральное уравнение, характеризующее
особенность явления для этого объема. Замечая затем, что это уравнение
должно быть справедливо для какого угодно объема, выделенного из тела,
он приравнивает нулю подынтегральную функцию и получает таким
образом искомый результат. Это самый изящный, строгий и простой
метод, который вошел теперь в употребление только после исследований
Неймана и Кирхгофа. Мы можем теперь утверждать, что идея применения
этого метода к вопросам, подобным рассматриваемому, принадлежит
М. В. Остроградскому» 3).
Две работы Остроградского по теории упругости тесно связаны
с работами Пуассона. В первой статье, доложенной в 1829 г.,
Остроградский решил задачу о распространении малых колебаний в
бесконечной изотропной упругой среде, характеризуемой одной постоянной (1831),
не зная, что задачей занимался перед тем Пуассон (1829). И здесь дело
сводится к интегрированию уравнений с частными производными. Метод
решения, предложенный русским математиком, был более общим и
формулы его проще. Продолжая свои исследования, Пуассон получил решение
в новой более удобной форме и рассмотрел важные частные случаи.
1) При этом однородное условие на границе заменяется на неоднородное, в
котором вместо нуля в правой части (2) стоит функция Т.
2) В. И. Антропова, О работах Фурье, Остроградского и Пуассона по
теплопроводности в жидкостях.— Впоросы истории естествознания и техники, вып. 3, 1957.
3) См. кн.: П. И. Трип о лье кий, Михаил Васильевич Остроградский.
Празднование столетия дня его рождения, стр. 126.
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
285
Далее в 1832 г. была представлена вторая работа Остроградского
{1833), который, применяя свой метод, получил и развил решение
Пуассона. Этот метод состоял в обобщении способа Коши интегрирования
одного линейного однородного уравнения в частных производных с одной
неизвестной функцией и с постоянными коэффициентами на систему таких
уравнений. Искомые решения представляются в виде интегралов Фурье
и это приводит к системе обыкновенных линейных дифференциальных
уравнений. Немного спустя такое же обобщение метода дали Коши
ж Пуассон.
Вариационное исчисление. Фундаментальные работы Остроградского
по вариационному исчислению тесно переплетались с его исследованиями
по аналитической механике и ее вариационным принципам х). Не касаясь
этой стороны дела, мы рассмотрим его знаменитый «Мемуар об исчислении
вариаций кратных интегралов» (1838; предст. 1834).
Выше говорилось, что Эйлер вывел уравнение, которому должна
удовлетворять функция двух переменных z (х, у), сообщающая
экстремум двойному интегралу с постоянными пределами
Ь d
I lu[x,y,z, -?-, -fi, -gl, ...)dxdy.
а с
Результат Эйлера мог быть перенесен на интегралы с переменными
пределами, если правильно выразить вариации частных производных
функции z(x, у), учитывая, что 8х и ду зависят от обоих аргументов х, у.
Впервые решил эту задачу общим образом Пуассон (1833); вариацию
интеграла, взятого по произвольной области, он представил в форме
Вывод Пуассона основывался на введении вспомогательных независимых
переменных, функциями которых он считал аргументы х и у. Кроме того,
французский математик ограничился двойными интегралами; обобщение
уже полученных результатов на интегралы более высокой кратности
было невозможно без новых средств общей теории кратных интегралов.
Отправляясь от результатов Пуассона, Остроградский подтвердил
их на другом пути и распространил на n-кратные интегралы. В начале
своего мемуара Остроградский писал, что Пуассон добавил к принципам
вариационного исчисления, как их установил Лагранж, «нечто вроде
нового принципа», состоящего во введении новых вспомогательных
переменных, которые исключаются затем в ходе выкладок. «Между тем
предположение, что 8х не зависит от г/, а 8у от х, кажется вытекающим из самых
простых и элементарных принципов дифференциального исчисления
и пока не доказано, что эти принципы недостаточны или что их
неправильно применяли, останется открытым вопрос, следует ли предпочесть
формулы Пуассона для вариации частных производных функции двух
переменных формулам Эйлера и других математиков, относящимся к тому же
вопросу. В сущности, последние формулы являются частными случаями
первых; но, может быть, этот частный случай должен иметь место всегда» 2).
а) А. Т. Григорьян, Очерки истории механики в России, М., 1961, гл. 9.
2) М. В. О с т р о г р а д с к и й, Полное собрание трудов, т. III, стр. 45.
286 ГЛ. 14. М. В. ОСТРОГРАДСКИЙ И В. Я. БУНЯКОВСКИЙ
Остроградский решает вопрос в пользу Пуассона, однако отвергает
введение вспомогательных переменных, как лишнее, и пользуется только
классическим аппаратом вариационного исчисления —«принципами,
сочетающими всю желаемую общность с наибольшей простотой» х). Следует
отметить, что и Остроградский всегда рассматривал так называемые
слабые вариации.
Прежде всего Остроградский вычисляет указанным способом
вариации частных производных функции z(x, у). Так, подобно Пуассону,
он находит, что
* dz dbz dz дбх dz dby
дх дх дх дх ду дх '
между тем Эйлер и его преемники выводили формулу
о dz ddz dz дбх
дх дх дх дх '
которая на самом деле вытекает из предыдущей в предположении, что
8у не зависит от х. Вслед затем вычисляются вариации частных
производных функции и(х, у, z, . . .) любого числа переменных, и вариация
функции U, зависящей от и и х, у, z, . . ., а также частных производных
функции и представляется в виде
где DU «зависит от приращения Du величины и, которое следует придать
к и всюду, где эта функция содержится в U» 2).
После этого Остроградский впервые приступает к отысканию
необходимого условия экстремума определенного интеграла любой кратности
V = \ Udxdy dz...,
взятого по области, координаты которой удовлетворяют неравенству
L(x, г/, z,...)<0,
и получает вариацию интеграла в виде
Выражение под знаком первого n-мерного интеграла — того же
типа дивергенции, что и в формуле Остроградского для преобразования
тройного интеграла в двойной, уже встречавшейся ранее. Для
дальнейшего преобразования вариации 8V Остроградский обобщает свою формулу
на интегралы произвольной кратности и решает еще два вопроса теории
кратных интегралов (см. далее). Это позволяет ему представить 8V в
другом виде:
V(?)'+(v),+(?)•+¦••
где первый из интегралов правой части (п — 1)-кратный и берется по
границе области интегрирования 5, а второй га-кратный — по самой области,
Х)М. В. Остроградский, Полное собрание трудов, т. III, стр. 46.
2) Там же, стр. 51.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
287
после чего этот второй интеграл в свою очередь выражается как сумма
двух интегралов, взятых соответственно по области и по ее границе
DUdxdydz... = [ WDUdxdydz... + { Qds.
Уравнение W = О, если его выписать в развернутом виде, есть не что
иное, как обобщенное уравнение в частных производных Эйлера, которому
должна удовлетворять функция, сообщающая экстремум функционалу V.
Из формул и указаний Остроградского можно также получить и те
граничные условия, которые служат для выделения среди решений
уравнения W = 0 искомой функции и (х, у, z, . . .), если она существует.
Однако ни обобщенного уравнения Эйлера, ни краевых условий
вариационной задачи Остроградский не приводит. Многие труды его написаны
чрезвычайно лаконично и это, в частности, относится к последним
параграфам рассматриваемого мемуара.
Работа Остроградского появилась на французском языке также
в Crelle's Journ., т. 16, 1836 и позднее в английском переводе в книге
А. Тодгентера по истории вариационного исчисления History of the
Progress of the Calculus of Variations during the 19 Century (Cambridge and
London, 1861). Однако чрезвычайная сжатость, а в конце работы и
незавершенность изложения настолько затрудняла ее понимание и применение,
что в 1840 г. Парижская Академия наук объявила конкурс на тему:
«Найти предельные уравнения, которые должно присоединить к уравнениям
неопределенным для того, чтобы вполне определить максимумы и
минимумы кратных интегралов». В 1844 г. премия была присуждена страсбург-
скому профессору П. Саррюсу (опубл. в 1848 г.), который, не внеся чего-
либо принципиально нового в сравнении с Остроградским, подробнее
развил необходимые вычисления. Кроме того, почетным отзывом отмечена
была работа преподавателя Политехнической школы Ш. Делоне, который
сам указывал, что его прием мало отличается от метода Остроградского,
уже преодолевшего главные трудности вопроса. Профессор университета
в Одессе и ученик Остроградского Егор Федорович Сабинин (1831—1909),
работы которого продолжают исследования его учителя по вариационному
исчислению, подробно разобрал мемуар Саррюса и указал на
содержащиеся в нем неточности (Матем. сборн., XIV, 1888—1889 и XXII, 1902).
Мы лишь упомянем большой «Мемуар о дифференциальных
уравнениях, относящихся к изопериметрической задаче», представленный
Остроградским в 1848 г. (1850). По содержанию он в равной мере
принадлежит аналитической механике и вариационному исчислению; важное
место в нем занимают приведение дифференциальных уравнений
вариационной задачи об экстремуме интеграла, зависящего от нескольких
неизвестных функций одного аргумента, к канонической форме и
обобщение метода Гамильтона — Якоби интегрирования канонических систем.
Дифференциальные уравнения. В теории обыкновенных
дифференциальных уравнений заслуживают внимания два результата
Остроградского. В «Заметке о методе последовательных приближений» (1838, предст.
в 1835), предложен метод решения нелинейных уравнений с помощью
разложения решения в ряд по малому параметру, позволяющий избегать
так называемых вековых членов, содержащих аргумент вне
тригонометрических функций. Такие члены нередко появляются при употреблении
обыкновенных приемов интегрирования с помощью степенных рядов;
неограниченно возрастая вместе с аргументом, они порождают ошибочные
288 ГЛ. 14. М. В. ОСТРОГРАДСКИЙ И В. Я. БУНЯКОВСКИЙ
приближения, а содержащее их решение оказывается неподходящим.
С этим явлением встречались еще астрономы XVIII в. и задачей
уничтожения вековых членов занимались Лаплас, Лагранж и другие. Свой
метод, основанный на одновременном разложении по параметру как самого
решения, так и периода входящих в него периодических функций,
Остроградский кратко пояснил на примере:
dy
< = ays, y\t=o = U
-О,
dt2 1*-"*. * |Г=и—-И dt
который записал в несколько иной форме:
?+(!_!¦),_,.(,._.•,),
совпадающей с данным уравнением при со = а. Решение с точностью
до величин первого порядка относительно а, найденное обычным
способом, содержит вековой член:
у = cos t -f- -qir (12* sin t -f cos t — cos 3t);
решение по способу Остроградского от него свободно:
у = cos nt + -gTv^ (vosnt — cos3nt), n2 = l г- .
Найденное приближение Остроградский сопоставил с точным решением
уравнения в эллиптических функциях Якоби. Остроградский
ограничился получением первого приближения; в конце статьи он высказал
намерение приложить этот метод к движению планет вокруг Солнца.
Намерение это, видимо, не осуществилось, но как раз в работах по
определению орбит небесных тел идея Остроградского получила дальнейшее
развитие. Одним из первых таких трудов явилось исследование по теории
возмущений шведского ученого А. Линдстедта, работавшего в 1879—
1886 гг. в Дерптском университете (Mem. Ac. Sc. Petersb., VII ser., t.
31, 1883). За этим последовали глубокие исследования А. Пуанкаре
и А. М. Ляпунова и, уже в советский период, Н. М. Крылова и Н. Н.
Боголюбова. Пример Остроградского рассматривался многими, в частности,
в книге «Вибрация судов» (СПб., 19G8) А. Н. Крылова, который применил
к нему и другим, более общим классам линейных неоднородных уравнений
второго порядка, содержащих малый параметр, несколько
модифицированный им метод Ляпунова. В настоящее время метод малого параметра
широко применяется к исследованию нелинейных задач механики, физики
и техники.
Небольшая «Заметка о линейных дифференциальных уравнениях»
Остроградского (1839, предст. 1838) содержит классическую теорему,
которая излагается теперь в любом курсе дифференциальных уравнений.
Дано уравнение
ж п его решений г/ь у2, . . ., г/п, которые предполагаются линейно
независимыми. Согласно теореме Остроградского определитель
Д(*) =
J/i г/2 ... уп
У[ У\ ••• Уп
y(n-l) y^n-i) . . . j,<n-D
КРАТНЫЕ ИНТЕГРАЛЫ
289
выражается через коэффициент при (п—1)-й производной:
л / \ - \ Р dx
Д (х) = ае J ,
где а — постоянная. Мы называем определитель А (х) по имени
впервые рассмотревшего его (в другой связи и более общей форме) польского
математика Г. Вронского (1812). Та же теорема была одновременно
получена из несколько иных соображений Ж. Лиувиллем (1838).
Кратные интегралы. Мы дважды говорили о работах Остроградского
по кратным интегралам. Остановимся на них несколько подробнее.
Формула Остроградского для преобразования тройного интеграла
в двойной, которую мы пишем теперь обычно в виде
I I I {^- + ^ + ^) d*dydz= I I (Pcosa + <?cosP + i?cosY) ds (1)
(V) (S)
или
\\\ divA dv = \ \ An ds,
(V) (S)
где div A — дивергенция поля вектора A, An — скалярное произведение
вектора А на единичный вектор внешней нормали п к граничной
поверхности, в математической литературе нередко связывалась ранее с именами
Гаусса или Грина. На самом деле в работе Гаусса о притяжении
сфероидов (1813) можно усмотреть только весьма частные случаи формулы (1),
например при Р = х, Q = R = О и т. п. Что касается Дж. Грина, то
в его труде по теории электричества и магнетизма (1828) формулы (1)
вовсе нет; в нем выведено другое соотношение между тройным и
двойным интегралами, именно, формула Грина для оператора Лапласа
Аи = -г"2 +-*-2 +-т-2 » которую можно записать в виде
HI (uAv-vAu)dxdydz= Ц {u^-v^)ds. (2)
Конечно, можно вывести формулу (1) из (2), полагая
dv ди -п dv ди ~ dv ди п
U- у-—= Р, и- р—- = (/, u-z V—r = R
дх дх ду ду х dz oz
и точно так же можно получить формулу (2) из (1), но Грин этого и не думал
делать.
Все же вопрос об авторе интегральной формулы (1) оставался не
вполне ясным. Дело в том, что, как было недавно замечено, в мемуаре
Пуассона по теории упругости, доложенном Парижской Академии наук
14 апреля 1828 г. и опубликованном в Mem. Ac. Sc. de Paris, t. VIII, 1829,
выводится формула
S(*+-?+^)*-S <л+и>.+"".>*.
где слева стоит интеграл по объему, а справа интеграл по граничной
поверхности, причем а, |3, у суть направляющие косинусы внешней
нормали. Между тем, как мы помним, «Заметка по теории теплоты
Остроградского была представлена Петербургской Академии наук 5 (17) ноября
1828 г. и напечатана в 1831 г. И хотя Пуассон не претендовал на открытие
290 ГЛ. 14. М. В. ОСТРОГРАДСКИЙ И В. Я. БУНЯКОВСКИЙ
приведенной только что формулы, а также, как подчеркнула В. И.
Антропова, «нигде не рассматривает это соотношение, как некоторую общую
теорему математического анализа» 1), получалось, что он несколько
опередил Остроградского.
Парижские рукописи Остроградского свидетельствуют, однако,
с полной несомненностью, что ему принадлежит и открытие, и первое
сообщение интегральной теоремы (1). Впервые она была высказана
и доказана, точно так, как это делают теперь, не в «Заметке по теории
теплоты», но в «Доказательстве одной теоремы интегрального
исчисления», представленном Парижской Академии наук 13 февраля 1826 г.,
после чего еще раз была сформулирована в той части «Мемуара о
распространении тепла внутри твердых тел», которую Остроградский
представил 6 августа 1827 г. «Мемуар» был дан на отзыв Фурье и Пуассону,
причем последний его, безусловно, читал, как свидетельствует запись
на первых страницах обеих частей рукописи. Разумеется, Пуассону
и не приходила мысль приписывать себе теорему, с которой он
познакомился в сочинении Остроградского за два года до представления своей
работы на теории упругости.
Что касается взаимоотношения работ по кратным интегралам
Остроградского и Грина, напомним, что в «Заметке по теории теплоты» выведена
формула, обнимающая собственную формулу Грина, как весьма частный
случай. Непривычная теперь символика Копти, употребленная
Остроградским в «Заметке», до недавнего времени скрывала от исследователей
это важное его открытие 2). Разумеется, за Грином остается честь
открытия и первой публикации в 1828 г. носящей его имя формулы для
операторов Лапласа.
Открытие формулы преобразования тройного интеграла в двойной
помогло Остроградскому решить проблему варьирования тг-кратного
интеграла, именно, вывести понадобившуюся там общую формулу
преобразования интеграла от выражения типа дивергенции по тг-мерной
области и интеграл по ограничивающей ее (п — 1)-мерной
сверхповерхности S с уравнением L (х, z/, z, . . .) = 0. Если придерживаться прежних
обозначений, то формула имеет вид
$(?+?+?+•••)***••-
=)vm+m+m+-' <3>
Впрочем, Остроградский не применял геометрических образов и терминов,
которыми пользуемся мы: геометрия многомерных пространств в то
время еще не существовала.
В «Мемуаре об исчислении вариаций кратных интегралов»
рассмотрены еще два важных вопроса общей теории таких интегралов. Во-первых,
Остроградский выводит формулу замены переменных в многомерном
интеграле; во-вторых, впервые дает полное и точное описание приема
вычисления тг-кратного интеграла с помощью п последовательных
интеграции по каждой из переменных в соответствующих пределах. Наконец,
г) В. И. Антропова, К истории интегральной теоремы М. В.
Остроградского.— Труды Ин-та ист. естеств. и техн., т. 17, 1957, стр. 263.
2) В. И. Антропова, цит. соч., стр. 255.
КРАТНЫЕ ИНТЕГРАЛЫ
291
Uh
\
F
Е .
^М
Л
N
А
\м"' \
—•—\В
R
х
из формул, содержащихся в этом мемуаре, легко выводится общее
правило дифференцирования по параметру многомерного интеграла, когда
от этого параметра зависит не только подынтегральная функция, но и
граница области интегрирования. Как пишет Е. Я. Ремез, названное правило
вытекает из наличных в мемуаре формул «настолько естественным
образом, что позднейшие математики даже отождествляли его с одною из
формул этого мемуара» г).
Замене переменных в кратных интегралах Остроградский посвятил
специальную работу. Для двойного интеграла соответствующее
правило вывел с помощью формальных преобразований Эйлер, для
тройного — Лагранж. Однако, хотя результат Лагранжа верен, рассуждения
его были неточными: он как бы
исходил из того, что элементы объемов
в старых и новых переменных —
координатах — между собою равны.
Аналогичную ошибку допустил
вначале в только что упомянутом выводе
правила замены переменных
Остроградский. В статье «О
преобразовании переменных в кратных
интегралах» (1838, предст. 1836)
Остроградский раскрыл ошибку Лагранжа,
а также впервые изложил тот
наглядный геометрический метод
преобразования переменных в двойном
интеграле, который, в несколько
более строгом оформлении, излагается
и в наших руководствах. Именно, при замене переменных в интеграле
\\ V(x, у) dy dx по формулам х = х(и, v), у = у(и, v), область
интегрирования (рис. 40) разбивается координатными линиями двух систем
и = const, v = const (именно линиями BF, СЕ, ... и ММ', М"МШ, . . .)
на бесконечно малые криЕ о линейные четырехугольники ММ' М"М'\
Тогда интеграл можно получить, складывая сначала те его элементы,
«которые отвечают бесконечно узкой криволинейной полосе BCEF, а затем,
продолжая суммировать элементы полосами, подобными BCEF, пока
они все не будут исчерпаны» 2). Несложный подсчет дает для площади
ММ'М"М'", которая с точностью до малых высшего порядка может
. (дхду дхду\ , j
рассматриваться как параллелограмм, выражением I — ^—~didu) dv аи,
где i = ±1, выбирается так, чтобы площадь была положительной.
В итоге получается известная формула
Так дифференциальное выражение i (-р-^ — у у\ &v &и-> которое Эйлер
формально подставлял вместо dydx, а следуя рассуждениям Лагранжа
для трехмерного случая, нужно было бы считать равным dydx, приобрело
у Остроградского простой и ясный геометрический смысл. Завершив
Рис. 40.
1)М. В. Остроградский, Полное собрание трудов, т. III, стр. 380.
2)М. В. Остроградский, Полное собрание трудов, т. III, стр. 111.
292 ГЛ. 14. М. В. ОСТРОГРАДСКИЙ и В. Я. БУНЯКОВСКИЙ
выкладки, Остроградский замечает, что предшествующие соображения
легко распространяются на тройные интегралы, но они неприменимы
к многократным интегралам, «по причине геометрической теоремы,
которую мы с ними связали» 1): как уже говорилось, многомерной геометрии
еще не было. Поэтому на примере двойного интеграла Остроградский дает
и чисто аналитический вывод, который можно распространить на интеграл
любой кратности. Как и во многих других случаях, Остроградский
ограничивается замечаниями, достаточными, по его мнению, для
компетентного читателя.
Позднее, в публичных лекциях по теории определенных интегралов,
читанных в 1858—1859 г., Остроградский почти всю вторую половину
курса отвел теории кратных интегралов и здесь, среди прочего, вывел
формулу преобразования переменных в тройном интеграле на
геометрической основе, а также дал аналитический вывод для многомерного
интеграла.
В этой части теории кратных интегралов исследования
Остроградского переплетались с работами Якоби и льежского математика Э. Ката-
лана. Формулу преобразования переменных в тг-кратном интеграле
опубликовал без вывода первым Якоби (1833); чисто аналитическое
доказательство дали затем он же и Каталан в одном году (1841). Остроградский
получил свои результаты независимо и ему принадлежит построение
геометрической картины проблемы 2).
Исследования Остроградского по кратным интегралам были
продолжены многими исследователями. В России к ним принадлежал, помимо
его прямых учеников, Николай Николаевич Зинин (26 июня 1854—22
апреля 1910), сын выдающегося казанского химика. Воспитанник
Петербургского университета, Н. Н. Зинин более четверти века, с 1880 по 1907 г.,
преподавал в Варшавском университете, а последние годы жизни провел на
посту директора только что основанного Донецкого политехнического
института в Новочеркасске. В статье «О формулах М. В. Остроградского в
теории кратных интегралов и об их приложении» (Математ. сб., т. 15, 1891)
он дал систематическое и развернутое изложение этой теории, включая
теорему о дифференцировании интеграла по параметру и применения
к вариационному исчислению. Эта статья легла в основу докторской
диссертации Зинина (Варшавские университетские изв., 1891—1892) 3).
В конце XIX века значение интегральных теорем Остроградского, так же
как и формул Грина и др., стало очевидным, и они вошли в состав
классического аппарата анализа функций многих переменных. Например,
формула (1) имеется в трактате по электричеству и магнетизму (1873)
знаменитого английского физика Дж. К. Максвелла и в курсе анализа (1882)
французского математика К. Жордана. Оба они связывали эту формулу
с именем Остроградского, в чем, к сожалению, за ними последовали далеко
не все зарубежные, да иногда и русские авторы. Но интегральная формула
Остроградского не только одна из классических в анализе. В еще более
обобщенном виде она получила уже в наше время новые применения
*) М. В. Остроградский, Полное собрание трудов, т. III, стр. 112.
2) Г. М. Ф и х т е н г о л ь ц, О преобразовании переменных в кратных
интегралах.— Ист.-матем. исслед., вып. V, 1952; «Записки интегрального исчисления,
составленные с публичных лекций господина академика Остроградского»,
опубликованы с комментариями В. И. Антроповой в сб.: Михаил Васильевич Остроградский,
М., 1961.
3) О Зинине см. некролог, написанный П. Кузнецовым, в «Известиях Донск.
политехи, института», т. 2, 1913.
ИНТЕГРИРОВАНИЕ АЛГЕБРАИЧЕСКИХ ФУНКЦИЙ
293
в геометрии римановых пространств и расположенных в них многообразий
различного числа измерений,— особенно благодаря французскому
математику Э. Картану (1922 и след. годы) х).
Интегрирование алгебраических функций. В XVIII века были
разработаны основные приемы выражения интегралов элементарных функций
в конечном виде. При этом стало ясно, хотя и не было доказано, что многие
такие интегралы не берутся в элементарных функциях. В начале XIX века,
прежде всего с развитием теории эллиптических интегралов, был заложен
фундамент теории интегрирования в конечном виде. В интегрировании
алгебраических функций основополагающие результаты получил в конце
двадцатых годов Абель. В письме к Лежандру от 25 ноября 1828 г. Абель
сформулировал, как особо важное, следующее предложение:
«Если \ ydx, где у связан с х каким-нибудь алгебраическим
уравнением, может быть явно или неявно выражен при помощи алгебраических
и логарифмических функций, то всегда можно положить
\ у dx = u + A1lnvi + A2lnv2+ ... -\-Amln vmi
где Аи А2, . . ., Ат — постоянные и и, у4, у2, . . ., vm —
рациональные функции х и у» 2). Поэтому, если этот интеграл алгебраический, он
представляет собой рациональную функцию х, у. Абель указал также,
что когда у = -?=, где г ж R — рациональные функции х, то во всех слу-
Р v dx
чаях, когда интеграл \ —j=. интегрируется, он представляется конечной
суммой
Pk—qkVR
где р, pk и qk — рациональные функции х и Ah — постоянные. Менее
чем через полгода Абель скончался и вскоре затем письмо было напечатано
в журнале Крелле. Доказательства теорем в письме отсутствовали и
эффективные приемы определения функций, входящих в указанные Абелем
выражения, приведены не были.
С лета и до конца 1826 г. Абель находился в Париже, где тогда жил
Остроградский. Весьма возможно, что они здесь встречались и беседовали.
Как бы то ни было, теория интегрирования алгебраических функций живо
заинтересовала Остроградского и он посвятил ей шесть работ 1833—1850 гг.
Мы отметим лишь некоторые содержащиеся в них результаты.
Две первые работы носят для нас несколько неожиданное название:
«Мемуар об интегрировании рациональных дробей» и «Продолжение
мемуара об интегрировании рациональных дробей» (1833), но речь идет
в них не о рациональных функциях одного независимого переменного,
но об интегралах вида \ R (х, у) dx, где R (х, у) есть рациональная
функция х ж у, причем у определяется неприводимым алгебраическим
уравнением п-ж степени с целыми относительно х коэффициентами.
Остроградский устанавливает, что если этот интеграл есть алгебраическая
1)С. П. Фиников, Метод внешних форм Картана в дифференциальной
геометрии, М.—Л., 1948.
2) N. Abel, Oeuvres completes, t. II, Christiania, 1881, стр. 275.
294 ГЛ. 14. М. В. ОСТРОГРАДСКИЙ и в. Я. БУНЯКОВСКИЙ
функция х, то он должен быть целой рациональной функцией у степени
п — 1с рациональными относительно х коэффициентами; вместе с тем
показано, как вычислить последние. При п=1 получается, что
алгебраический интеграл обыкновенной рациональной дроби R (х) есть
рациональная функция, т. е.
где все функции — целые рациональные относительно х и степень X ниже,
чем Y. Слагаемое Q находится, как известно, весьма просто; Y есть общий
наибольший делитель М и — , а X, как показывает Остроградский,
есть решение некоторого линейного дифференциального уравнения
первого порядка с целыми рациональными относительно х коэффициентами
и может быть вычислен по способу неопределенных коэффициентов или,
проще, посредством непрерывных дробей. Попутно Остроградский
замечает, что интеграл рациональной функции не может быть алгебраическим,
если степень числителя L только на единицу меньше степени
знаменателя М, а также если знаменатель и его производная не имеют общего
делителя, т. е. М не имеет кратных корней (дробь считается сокращенной).
Отсюда, между прочим, следует трансцендентность интегралов функций
1 1
— и 2 , т. е. 1п х и arctg х. В конце статьи разобраны примеры
Р (г2 + 15а:4 —14^7) dx _ xz_j
д (1 + Я5)10 — 3 (*5+1)9
И
Р (30 + 150^4+17.г164-7а:17 — Ъ'бх*1) dx _ х™ — 3
\ (ХЬ + Х^\)11 — (я5_|_я_Л_1)10-
Как видно, Остроградский всюду стремился здесь доводить изложение
до расчетного алгоритма, позволяющего найти конкретное решение
задачи — тенденция, которая стала затем характерной для творчества
Чебышева.
т. Р Ldx
Во второй статье специально исследован интеграл \——, где
у2 = R (х), причем многочлен R не имеет кратных корней. Здесь п = 2
и легко выясняется, что когда интеграл алгебраический, он имеет вид
Р L dx X
\ тг — = тг V + const.
J М у у * ~
Аналогично предыдущему развиваются приемы вычисления целых
рациональных функций X, Y, разбирается пример
х(хЬ + х* — 4г2 — 4z — 4) dx 2"ТД5 —1 ,
х* + х*-х-1 У^ГГ- *2-1 +C°nSt
и отмечается, что \ — не может быть алгебраическим, если степень В
выше единицы. О случае, когда тот же интеграл сводится к
алгебраическим и логарифмическим функциям, Остроградский писал, что, как он
недавно обнаружил, интеграл всегда можно найти, и обещал изложить
свои исследования в другом мемуаре. Однако он не выполнил это
намерение и полный разбор этого случая вошел в состав диссертации Чебышева
на право чтения лекций (1847).
ИНТЕГРИРОВАНИЕ АЛГЕБРАИЧЕСКИХ ФУНКЦИЙ
295
Две следующие статьи посвящены изучению соотношений между
интегралами алгебраических функций,— проблеме, которую Абель
обогатил своей классической теоремой сложения этих интегралов. В первой
статье Остроградского (1833) доказано следующее предложение. Пусть
tk = \yk dx суть трансцендентные интегралы п алгебраических функций
yi(x), г/2(^), . . ., уп{х) и не существует алгебраической зависимости
между х, tu t2, . . ., tn. В таком случае, если интеграл алгебраической
функции z = \ ydx алгебраически выражается через «г, U, t2, . . ., ?n,
n
то z = 2 cktk рациональная функция x, z/, z/i, y2, . - ., yn, причем ck —
постоянные. Это предложение, как выяснилось впоследствии, содержится
в одной работе Абеля, увидевшей свет лишь в 1881 г.
К только что рассмотренной статье Остроградского примыкает статья
его «Об интегралах алгебраических функций» (1843, предст. 1842), где
тот же вопрос рассмотрен несколько более общим образом. Понимая здесь
под прямой и, соответственно, обратной трансцендентной функцией такую,
производная которой есть алгебраическая функция аргумента или,
соответственно, самой функции, Остроградский доказывает, что, во-первых,
прямые и обратные функции не могут быть связаны алгебраической
зависимостью, и, во-вторых, что алгебраическая зависимость между
прямыми функциями всегда может быть сведена к линейному уравнению
между ними с постоянными коэффициентами и со свободным членом,
который есть алгебраическая функция аргумента. Простым следствием
первого предложения является то, что интеграл алгебраической функции
не может содержать показательных и тригонометрических функций
(в действительной области). Мы оставим в стороне еще одну, последнюю
работу этого цикла (1853, предст. 1850).
Первые исследования Остроградского по интегрированию
алгебраических функций шли параллельно с изысканиями Лиувилля, который
в том же 1833 г., что и Остроградский, опубликовал ряд результатов,
частью совпадающих, частью более общих, и затем успешно продолжал
работать в этом направлении. С помощью построенной им классификации
элементарных трансцендентных функций Лиувилль нашел, как выражаются,
в тех случаях, когда это возможно, интегралы алгебраических функций
через элементарные, глубоко рассмотрел проблему алгебраической
представимости этих интегралов, в том числе специально для эллиптических
интегралов и т. д. Весьма общие методы Лиувилля были развиты другими
зарубежными математиками. Со своей стороны, Остроградский оказал
большое влияние на разработку того же круга проблем в России, особенно
через посредство Сомова и, как упоминалось, Чебышева. Пока мы
отметим еще, что магистерская диссертация О. И. Сомова «Рассуждение
об интегралах алгебраических иррациональных дифференциалов с одной
переменной» (М., 1841) содержала первое на русском языке
систематическое изложение соответствующих работ Абеля и Лиувилля, а также
теории эллиптических функций по Якоби.
В заключение остановимся коротко на замечательной статье
Остроградского «Об интегрировании рациональных дробей», где этот термин
надлежит понимать уже в обычном смысле (1845, предст. 1844). Казалось,
что вопрос был окончательно решен еще в XVIII веке Лейбниц выдвинул
идею метода, состоящего в разложении данной рациональной дроби,
после выделения целой части, в сумму элементарных дробей, и разобрал
296 ГЛ. 14. М. В. ОСТРОГРАДСКИЙ И В. Я. БУНЯКОВСКИЙ
менее сложные частные случаи; И. Бернулли преодолел некоторые
возникшие на этом пути трудности; Эйлер разработал метод во всех деталях
и придал ему классическую форму. После разложения данной дроби
в сумму элементарных дробей, почленное интегрирование дает сумму
рациональной функции с логарифмическими и круговыми. Остроградский
решает в данной статье два вопроса. Прежде всего, он подробно разбирает
условия алгебраической интегрируемости рациональной дроби, чего
он касался уже в предыдущих работах. Затем, и это главное, он излагает
способ нахождения алгебраической, т. е. рациональной части интеграла,
если она существует, не требующий предварительного разложения данной
дроби на элементарные. Интеграл выражается в виде
(степень Y ниже, чем Q, и Q уже не имеет кратных корней), причем
знаменатели Р и Q и, после того, числители X и Y находятся посредством
рациональных действий над данными целыми рациональными функциями
и дифференцирований. В 1872 г. Эрмит самостоятельно пришел к тому же
методу, с несущественными отличиями, а год спустя изложил его в своем
курсе анализа. С тех пор этот прием излагается в зарубежной литературе
под именем Эрмита.
Некоторые работы Остроградского были связаны с конкретными
задачами современной ему военной техники. Так, например, в 1839—
1842 гг. он по поручению артиллерийского ведомства занимался изучением
стрельбы эксцентрическими сферическими снарядами, у которых центр
фигуры отличен от центра инерции. Этому вопросу Остроградский
посвятил три небольшие статьи, из которых одна содержала таблицы
интегралов, нужных для решения задачи о движении снаряда в воздухе при
квадратичном законе сопротивления. К работам по баллистике в свою
очередь примыкали исследования Остроградского по приближенным
вычислениям, в том числе и упоминавшаяся работа 1839 г., содержащая
вывод остаточного члена формулы суммирования Эйлера — Маклорена.
Жизнь и творчество В. Я. Буняковского. Большое значение для
прогресса математики в России имела деятельность Виктора Яковлевича
Буняковского (16 декабря 1804—12 декабря 1889). Как и Остроградскийг
он был родом с Украины: он родился в г. Баре Могилевского уезда
Подольской губернии (ныне Винницкой области) в семье подполковника
одного из кавалерийских полков. Высшее математическое образование
он получил в Париже, где в 1825 г. ему была присуждена степень доктора
математики за две работы, из которых одна имела своим предметом теорию
распространения теплоты внутри твердых тел, а другая — задачу о
вращении в сопротивляющейся среде некоторой плоской системы. В Париже
Буняковский познакомился с Остроградским, с которым ему пришлось
впоследствии много и дружно работать.
В 1826 г. Буняковский вернулся в Россию и вскоре начал преподавать
математику в Морском корпусе, где работал до 1864 г. В 1846—1860 гг.
он состоял профессором Петербургского университета, читая лекции
по дифференциальному и интегральному исчислению, аналитической
механике, теории дифференциальных уравнений, вариационному
исчислению, теории вероятностей и теории конечных разностей: Работал
Буняковский и в других учебных заведениях Петербурга. В один год с
Остроградским (1828)' Буняковский был избран адъюнктом Академии наук
ЖИЗНЬ И ТВОРЧЕСТВО в. Я. БУНЯКОВСКОГО
297
и в 1830 г.— академиком. С 1864 г. он почти до самой кончины
работал на посту вице-президента Академии наук х).
Буняковский многое сделал для распространения математических
знаний не только как педагог, но и как автор учебных руководств, в том
числе для гимназий, а также популярных статей по математике, например
для «Энциклопедического словаря» под редакцией П. Л. Лаврова (СПб.,
1861—1863), который, впрочем, прекратился на шестом томе из-за
цензурных условий. К сожалению, незавершенным, уже по другой причине,
осталось замечательное начинание
самого Буняковского,— его «Лексикон
чистой и прикладной математики»
(т. I, СПб., 1839). Расположенный по
алфавиту французских терминов, этот
словарь, по замыслу Буняковского,
должен был явиться своего рода
энциклопедией всех математических наук.
«Главная цель издания,— говорилось
в предисловии,—состояла в том, чтобы
доставить моим соотечественникам,
занимающимся Математикою, и уже
несколько знакомым с нею, такую книгу,
в которой они могли бы почерпнуть
достаточные сведения о всех важнейших
теориях, как старых, так и новейших»;
при этом автор не ограничивался
собственно математикой, но захватывал
большое число слов и «из других наук,
более или менее соприкосновенных
с Математикою»2). Другой целью этого
труда было обогащение русской мате- в я Б вский>
матическои терминологии, ь первый
том, объемом в 462 страницы с восемью
листами чертежей вошли статьи на буквы А —D. Кроме того,
Буняковский подготовил обширные материалы по буквам от Е до L; однако
они не были еще готовы к печати и Буняковский их оставил для справок
тем, кто возьмется за продолжение его словаря. Материалы эти хранятся
в Архиве Академии наук СССР в Ленинграде, так никем и не
использованные: никто не решился единолично продолжить столь трудное и для
одного человека, в сущности, непосильное дело.
Статьи «Лексикона», часто весьма обстоятельные и содержащие
ценные исторические сведения, говорят о колоссальной эрудиции автора,
знакомого со всей тогдашней литературой вопроса. В изложении, как
правило, учтена, реформа математического анализа, проводившаяся
Коши 3). Иногда, однако, новые концепции эклектически соединяются
г) В. Е. П р у д н и к о в, В. Я. Буняковский, ученый и педагог, М., 1954.
2) В. Я. Буняковский, Лексикон чистой и прикладной математики, т. I,
СПб., 1839, стр. VII.
3) Распространению идей Коши, бывшего в Париже одним из его руководителей,
Буняковский способствовал также переводом курса анализа французского математика:
А. Коши, Краткое изложение уроков о дифференциальном и интегральном
исчислении, СПб., 1831.
Другое основоположное руководство Коши вышло на русском языке значительно
позднее: А. Коши, Алгебраический анализ, перевод Ф. Эвальда, В. Григорьева,.
А. Ильина, Лейпциг, 1864.
298 ГЛ. 14. М. В. ОСТРОГРАДСКИЙ и В. Я. БУНЯКОВСКИЙ
с прежними, устарелыми. Так, определив прежде всего непрерывную
функцию по Коши, Буняковский считает необходимым дополнить данное
определение условием представимости функции во всей области задания
одним и тем же выражением, т. е. условием непрерывности в смысле
Эйлера. Для историка науки «Лексикон» интересен и в наше время.
Буняковскому принадлежит около 150 работ по разным вопросам
математики и ее приложений. Более 40 из них относится к теории чисел *);
они примыкают к тематике Эйлера. Он дал новое, очень простое
доказательство теоремы Эйлера, обобщающей малую теорему Ферма, и
предложил в удобной форме целое решение давно уже изученного уравнения
ах ± Ъу = с с целыми взаимно простыми коэффициентами; рассмотрел
ряд частных нелинейных задач диофантова анализа; занимался
проблемами представления чисел квадратичными формами и partitio numerorum;
в теории квадратичных вычетов нашел новые теоремы о свойствах так
называемого символа Лежандра и оригинальный вывод закона
взаимности, и т. д. Результаты Буняковского не раз упоминаются в известном
руководстве по теории чисел П. Бахмана и в истории этой науки,
составленной Л. Диксоном2). Вместе с Чебышевым Буняковский опубликовал
в двух томах теоретико-числовые работы Эйлера, некоторые — впервые.
В этой связи следует отметить поддержку, которую благожелательный
по природе Буняковский оказывал тем, в ком видел научное дарование.
Так, благодаря ему получили известность открытия уральского любителя
математики священника Ивана Михеевича Первушина (2 февраля 1827—
29 июня 1900), который занимался изучением делимости чисел вида
2п±1и 22т + 1, интересовавших еще Ферма и Эйлера. В 1877—1878 гг.
Первушин сообщил Академии наук первые после Эйлера примеры
составных чисел последней указанной формы, именно 2212 + 1,
делящегося на 7-214 + 1 = 114 689, и 2223 + 1, делящегося на 5.225 + 1 =
= 167 772 161. Оба результата были опубликованы в специальных
заметках Буняковского (1878); первый из них тогда же нашел
французский математик Э. Люка. В 1883 г. Первушин прислал Академии
записку, в которой устанавливалось, что девятнадцатизначное число
261 _ 1 = 2 305 843 009 213 693 951 является простым. В 1887 г. это
доказал также немецкий математик П. Зеельгоф. До того наибольшим
известным простым числом было 231 — 1=2 147 483 647 (Эйлер,
1772). Следует заметить, что проверка для таких громадных чисел,
являются ли они простыми, практически была неосуществима с помощью
примитивных способов разложения на множители. Она потребовала открытия
различных тонких приемов, имеющих более общий интерес3).
Неравенство Буняковского. Мы упоминали о занятиях Буняковского
признаками сходимости рядов. Ему принадлежат и другие работы по
анализу, частью непосредственно примыкающие к исследованиям
Остроградского по интегрированию алгебраических функций (некоторые случаи
oj _1_ п. П,Х
интегрируемости | 1—у= -, алгебраическое
суммировала+с2 ух^ -\- ахъ -f- bx2 -f- ex -f- d
x) И. Г. Мельников, О работах В. Я. Буняковского по теории чисел.—
Труды Ин-та ист. естеств. и техн., т. 17, 1957.
2) P. Bach man n, Niedere Zahlentheorie, Bd. I—II, Leipzig, 1902—1910;
L. E. Dickson, History of the theory of numbers, v. I—III, Washington,
1919—1923.
3) A. E. Раик, Уральский математик И. М. Первушин. Ист.-матем. исслед.,
вып. VI, 1953,
БУНЯКОВСКИЙ И ТЕОРИЯ ПАРАЛЛЕЛЬНЫХ
299
ние рациональной дроби в теории конечных разностей). Один из
результатов, содержащихся в статье «О некоторых неравенствах,
относящихся к определенным интегралам или интегралам в конечных
разностях» (Bull. Ac. Sc. Petersb., CI. phys.-mathem., XVII, 1859) прочно
вошел в современную математику. Здесь Буняковский вывел
замечательное неравенство
ъ ъ ъ
\ f (х) Ч> (%) dx \ < \ /2 (х) dx \ ср2 (х) dx,
а а а
являющееся интегральным аналогом арифметического неравенства Коши
(|аА)2<(1!4)(Ь?),
где ak, bk — любые действительные числа. Неравенство Буняковского,
которое все еще нередко зовут по имени Г. Шварца, вновь нашедшего
его в 1884 г., принадлежит к числу наиболее употребительных в
классическом и функциональном анализе. О. Гёльдер распространил его на произ-
1 1
вольные степени р и д, связанные условием —| = 1:
ъ ъ 1 ъ I
I f(x)y(x)dx<([fp(x)dxy (J q*(x)dxy .
а а а
Другого типа обобщением является неравенство Сонина
ъ ъ ъ
о < j е (х) ф2 {х) dx- J е (х) dx— (jj е (я) ф (х) dx}2 <
а а а
Ъ Ъ
< ? 0 (х) [G— ф (х)] dx-^Q (х) [ф (х) — g] dx,
а а
где 9 (х) > 0, a G и g суть наибольшее и наименьшее значения ф (х) на
отрезке интегрирования (Зап. Академии наук по физ.-матем. отд., VIII
сер., т. VI, 1898). При 0 (х) = /2 (х), ф (х) f (х) = г[з (ж) отсюда получается
неравенство Буняковского.
Буняковский и теория параллельных. В этом вопросе, которому
Буняковский посвятил несколько работ, его позиция не была передовой.
В труде «Параллельные линии» (1853) он дал содержательный
исторический обзор вопроса и критически рассмотрел различные попытки
доказательства постулата о параллельных Насирэддина ат-Туси, Кастильона,
Бертрана, Лежандра, Гурьева и др. Все известные ему доказательства
Буняковский относит по характеру употребляемых в них приемов к
четырем группам: это 1) сравнение бесконечных пространств, 2)
непосредственные построения, 3) принцип однородности и 4) применение понятия
силы и движения. Остроумно раскрывая недостатки рассуждений своих
предшественников, Буняковский в заключение предлагает собственное
доказательство, основанное на определении прямой как линии, ни одна
точка которой никакой особенностью не может отличаться от другой,
определении, которое он высказывает на различные лады и связывает
с принципом однородности. Это произвольное и неясное представление
300 ГЛ. 14. М. В. ОСТРОГРАДСКИЙ и в. Я. БУНЯКОВСКИЙ
Буняковский считал «свойством, совершенно согласным с нашими
первоначальными понятиями о прямой»1).
Имя Лобачевского в этом сочинении не упоминается, но, разумеетсяг
труды великого реформатора геометрии были Буняковскому давно хорошо
известны. Мемуар Лобачевского «О началах геометрии» был еще в 1832 г.
направлен Казанским университетом Академии наук. Отзыв был поручен
Остроградскому, который сообщил Конференции, что понял в книге
только следующее: можно допустить, что сумма углов в треугольнике
меньше двух прямых, откуда проистекает более трудная, чем
обыкновенная, геометрия, которая может служить особенно для вычисления
определенных интегралов. Однако из двух приводимых автором интегралов
один неверен (А. Н. Колмогоров в 1948 г. показал, что этот упрек
несправедлив). И Остроградский заключал: «Все, что я понял в геометрии г-на
Лобачевского, ниже посредственного», книга изложена небрежно,
«опорочена ошибкой» и, «следовательно, не заслуживает внимания Академии»2).
Буняковский вполне разделял эту несправедливую оценку; более
того, как сказано, он пытался доказать постулат о параллельных. Он не
переменил свое мнение и тогда, когда геометрия Лобачевского получила
довольно широкое признание. В работе, специально посвященной
неевклидовой геометрии (Mem. Ac. Sc. Petersb., VII ser., t. VIII, 1872),
он пытался доказать ее противоречие с наглядными представлениями:
о пространстве и, вслед за французским математиком Ж. Бертраном,
характеризовал ее, как «логическую распущенность»— une debauche
de logique. Новое доказательство V постулата, предложенное здесь Буня-
ковским, опиралось на его прежнее понимание прямой, как бесконечной
линии, во всех своих частях тождественной, и, по существу, предполагало,
что эквидистантой прямой служит прямая. Впрочем, решительно отвергая:
неевклидову геометрию, Буняковский теперь уважительно отзывался
о дарованиях творца. В этом смысле его статья выгодно отличается от
упомянутой ранее рецензии в «Сыне отечества» за 1834 г., написанной не без
влияния Буняковского и Остроградского.
Теория вероятностей. Видное место в деятельности Буняковского^
занимают труды по теории вероятностей и ее приложениям. После Д. Бер-
нулли и Л. Эйлера в исследованиях по теории вероятностей в России
наступил перерыв. Развитие в XIX веке статистических, особенно
демографических, исследований и организация первых обществ, страховавших
от огня, несчастных случаев, потери посылок и т. д., вновь привлекли
внимание к теории вероятностей. В 1821 г. появилось первое на русском
языке выступление по этому предмету — речь харьковского профессора
А. Ф. Павловского «О вероятности» (Харьков, 1821). Павловский
популярно изложил основные понятия и теоремы теории вероятностей, в том
числе закон больших чисел Я. Бернулли. Пропаганде страхового дела,
которое поощрялось правительством, но не вызывало еще доверия у
населения, посвящена была специальная речь Н. Е. Зернова «Теория
вероятностей с приложением преимущественно к смертности и страхованию»,
в печатном виде занимающая 85 страниц (М., 1843). В ней прежде всего
излагаются основные понятия и теоремы теории вероятностей, а затем
как математические, так и административные аргументы и даже ссылки
на Библию используются для убеждения в выгодности различных видов
1) Уч. записки Ими. Академии наук по первому и третьему отделениям, т. II,
вып. 3, СПб., 1853, стр. 405—406.
2) Материалы для биографии Н. И. Лобачевского, стр. 333—334.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
301
страхования. Особенно интенсивно страховое дело и статистика начали
развиваться в России после Крымской войны.
В тридцатые и сороковые годы появляются отдельные оригинальные
работы по теории вероятностей, как, например, статья Н. И. Лобачевского
о вероятности средних результатов, полученных из повторных
наблюдений (1842), и несколько статей М. В. Остроградского. В одной из них
решается следующая задача: сосуд содержит п шаров, различающихся
только белой или черной окраской; требуется определить вероятности
того или иного состава сосуда, если при извлечении ш шаров среди них
оказалось к белых и I черных? (1848, предст. в 1846). Остроградский сам
отмечал важность этого вопроса для контроля качества продукции с
помощью выборочного метода. Его работа принадлежала к числу первых 1).
Занимался статистикой и задачами страхового дела также Э. Коллинс.
В речи о значении математических наук, произнесенной Н. Д. Браш-
жаном 17 (29) июня 1841 г. в торжественном собрании Московского
университета, специально подчеркивалось неудовлетворительное положение
о преподаванием теории вероятностей, столь необходимой для финансового
дела, страхования и проч. «Кто,— говорил он,— не видит с крайним
сожалением совершенное небрежение в учебных заведениях одной из
важнейших частей математики? Едва в некоторых университетах дают
понятие о теории вероятностей, и до сих пор нет на русском языке ни одного
сочинения, ни перевода не только ученой, но даже элементарной теории
вероятностей... Надеемся, что русские ученые постараются скоро
восполнить этот недостаток» 2). Мы знаем, что вскоре, действительно, этот
предмет был введен в университетский курс и одно за другим вышли два
пособия по этому предмету, одно, более краткое, Чебышева (1845), и дру-
тое — Буняковского. Это — уже упоминавшиеся «Основания теории
вероятностей» (СПб., 1846), вместе с дополнениями содержащие почти
500 страниц. Для своего времени «Основания» представляли собой
чрезвычайно богатое материалом руководство, охватывавшее все отделы
теории вероятностей и ее многочисленных приложений к теории ошибок
наблюдений, демографии, страхованию, военной статистике и т. д. Буня-
ковский, как и Остроградский, не избежал модных тогда применений
теории вероятностей к определению правдоподобия свидетельских
показаний и преданий, а также правильности судебных решений, выносимых
большинством голосов. Такие задачи, решение которых опиралось на
неверные предпосылки о связях между показаниями и суждениями отдельных
лиц, еще долго сохранялись на страницах солидных книг и статей.
Теории вероятностей и статистике Буняковский посвятил около
20 работ 1835—1876 гг., ас 1858 г. состоял правительственным экспертом
по этим вопросам. Он изучал движение народонаселения и его возрастной
состав, предложил эмпирическую формулу закона смертности, вычислял
вероятные контингенты мужчин призывного возраста и производил
расчеты, которые были положены в основу деятельности целого ряда
пенсионных касс. Занимался такими расчетами и Остроградский.
Буняковский не получил существенных оригинальных результатов
в теории вероятностей, но в целом очень многое сделал для развития
этой науки в России. Современники высоко ценили его заслуги. На празд-
х) Б. В. Гнеденко, О работах Н. И. Лобачевского по теории вероятностей.—
Ист.-матем. исслед., вып. II, 1949; Он ж е, О работах М. В. Остроградского по теории
вероятностей.— Ист.-матем. исслед., вып. IV, 1951.
2) Н. Д. Б р а ш м а н, О влиянии математических наук на развитие
умственных способностей. М , 1841, стр. 30—31.
302 ГЛ. 14. М. В. ОСТРОГРАДСКИЙ и в. Я. БУНЯКОВСКЙЙ
новании полувекового юбилея присуждения Буняковскому докторской
степени в 1875 г. знаменитый астроном Ф. А. Бредихин (1831—1904),
выступая от имени Московского математического общества, говорил:
«Вы обогатили литературу классическим сочинением по теории
вероятностей. Этим сочинением вы водворили эту науку у нас и не переставали
оставаться ее представителем до настоящего времени. Выводы и
основания ее не были Вами оставлены в сфере одного теоретического
рассмотрения. Вы приложили ее законы и заключения к решению важных задач
нашей государственной и общественной жизни. Вы содействовали
научному разрешению многих вопросов русской статистики» 1).
Вычислительные устройства. В середине XIX века некоторые успехи
были достигнуты у нас в разработке вычислительных устройств. В этом
принимали участие и конструкторы-самоучки, и инженеры, и математики,
прежде всего те же Буняковский и Остроградский, частью собственными
трудами, частью помощью другим людям.
Мы прежде всего отметим содействие, оказанное обоими академиками
и их коллегами трем изобретателям арифметических машин, начало
конструкции которых было положено еще Б. Паскалем и Лейбницем, но
которые долго еще не находили практического употребления. В 1845 г.
Академия наук рассмотрела машину для четырех арифметических действий,
построенную белостокским ученым Зиновием Яковлевичем Слонимским
(1810—1904), впоследствии видным деятелем еврейского просвещения
в России и Польше. П. Фусс и Буняковский дали весьма благоприятное
заключение как о самой машине, так и о теоретической работе,
проведенной изобретателем. В отзыве Фусса и Буняковского подчеркнуто
«остроумное доказательство» основной теоремы Слонимского, раскрывающей
«весьма примечательное свойство кратных чисел». Теорема формулируется
так: «Положим, что произвольное целое число, состоящее из скольких
угодно цифр, умножено в каком ни есть порядке на 1, 2, 3, . . . до 9;
подписав все эти произведения одни под другими, не отступая в левую
сторону..., получим полные девятицифренные вертикальные столбцы.
Условимся для краткости называть видом расположение цифр в подобном
столбце. В силу теоремы г. Слонимского число р различных видов
определится весьма простою формулою р = 10 (q -}- 1), в которой q
изображает число правильных дробей, различных между собою и имеющих
знаменателями множители 2, 3, 4, ...доЭ.В настоящем случае простое
вычисление покажет, что различных по виду девятицифренных столбцов
будет только 280» 2). Ограниченность этого числа,— добавляли
рецензенты,— навела Слонимского на мысль об устройстве машины, «и успех
вполне оправдал его предположение». Недостаток прибора, который
быстро и сразу давал произведения любых семизначных чисел на числа от 1
до 9, был тот, что в случае многозначного множителя отдельные
произведения приходилось складывать дополнительно. Наряду с этой машиной
Слонимский построил меньшую, для одних сложений и вычитаний,
которую, наряду с Фуссом и Буняковским, одобрили также Остроградский
и Б. С. Якоби (1801—1874), брат математика, отмечая ее преимущества
перед известным в то время инструментом д-ра Д. Д. Рота (1843).
1) Описание празднования докторского юбилея... В. Я. Буняковского..., СПб.,
1876, стр. 14.
2)М.И. Радовский, Из истории вычислительных устройств (по материалам
Архива АН СССР).— Ист.-матем. исслед., вып. XIV, 1961, стр. 566—567.
См. также 3. Слонимский, Описание нового числительного инструмента»
СПб., 1845.
ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
303
В 1846 г. варшавский часовой мастер Израиль Штоффель (ум. после
1875 г.) представил Академии наук свою машину для четырех действий
арифметики. Буняковский и Якоби отмечали в своем отзыве, что этот
прибор, хотя не имеет такого теоретического интереса, как большая
машина Слонимского, зато свободен от только что указанного ее
недостатка. По их мнению, он мог бы быть весьма полезен в учреждениях, «где
длинные и кропотливые вычисления и, главным образом, умножения
и деления должны производиться быстро и точно» *). Наконец,
Остроградский в том же году одобрил «счетчик» петербургского учителя музыки
Куммера, технически улучшившего и упростившего меньшую машину
Слонимского. По предложению рецензентов Слонимскому была присуждена
половинная Демидовская премия, Штоффелю — награда в 1500 руб.,
а Куммеру признано возможным выдать патент. Однако все эти
вычислительные устройства не смогли в то время получить широкого
распространения, частью из-за технических несовершенств, частью из-за
экономической нецелесообразности.
Добавим, что над совершенствованием счетных машин успешно работал
П. Л. Чебышев. В августе 1876 г. он представил на V съезде Французской
ассоциации содействия преуспеванию наук доклад о суммирующей
машине с непрерывным движением (текст его до сих пор не обнаружен), а в
августе 1882 г. на XI съезде той же Ассоциации — доклад «О новой
арифметической машине», в которой имелся дополнительный механизм для
умножений и делений. Как подчеркивал сам Чебышев, его машина отличалась
от предшествующих, в том числе от машины Рота, непрерывным
переносом десятков. В прежних инструментах с прерывным изменением цифр
суммы колесо старшего разряда сразу поворачивается на одно делениеу
когда колесо предшествующего разряда переходит с 9 на 0, между тем в
арифмометре Чебышева колесо старшего разряда, при полном обороте
предшествующего колеса, поворачивается на одно деление непрерывно.
Сохранилось два экземпляра машины Чебышева. Один хранится в парижском
Музее ремесел и искусств, Conservatoire des Arts et Metiers (рис. 41), другой,
более ранний, в московском Государственном Историческом музее 2).
Арифмометр Чебышева во многом предвосхищал устройство
современных счетных машин. Это особенно относится к удачно решенной Чебы-
шевым задаче автоматического действия всех элементов машины при
умножении. Принцип десятичного переноса, выдвинутый Чебышевым,
через несколько лет был вновь применен Э. Зеллингом (1886). Больший
успех, однако, выпал тогда на долю арифмометра, изобретенного
инженером Петербургской экспедиции заготовления государственных бумаг
Вильгодтом Теофиловичем Однером (ум. около 1906 г.), по
происхождению шведом. Однер занялся усовершенствованием арифмометра в
середине семидесятых годов, первые патенты получил в 1878—1880 гг. и затем
еще несколько лет работал над улучшением его конструкции. В 1890 г.
машина уже не отличалась, если не считать технических деталей, от
наиболее распространенного теперь типа ручных арифмометров (рис. 42)
и тогда же в Петербурге открылся завод для ее массового производства.
«Основной успех арифмометра был обеспечен изобретением
оригинального колеса с переменным числом зубцов, ныне называемого именем
1) М. И. Р а д о в с к и й, цит. публикация, стр. 572.
2) Л. Е. Майстров, Первый арифмометр П. Л. Чебышева.— Ист.-матем.
исслед., вып. XIV, 1961; см. также В. Г. Б о о л ь, Приборы и машины для
механического производства математических действий. М., 1896. В. Г. Бооль (1836—1899) дал очень
подробное описание арифмометра Чебышева.
Рис. 41. Арифметическая машина П. Л. Чебышева, хранящаяся в Музее
ремесел и искусств в Париже.
Рис. 42. Арифмометр Однера.
ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
305
изобретателя, а также работающей без отказа скачкообразной
(единовременной) системы переноса десятков» *).
Делались попытки модифицировать чрезвычайно популярные у нас
счеты, современная форма которых установилась уже к началу XVIII века.
Одна из таких попыток была предпринята еще в 1867 г. Буняковским,
построившим при помощи системы из трех колес «самосчеты», в которых
он механизировал процесс переноса единиц из низших разрядов в высшие,
для чего в счетах сбрасывают косточки на одной проволоке, заменяя
одной косточкой на другой. В самосчетах единицы различных разрядов
сами размещались по соответствующим местам. Однако этот инструмент
сильно уступал в простоте обращения обыкновенным счетам и в обиход
не вошел 2). Заметим, что сообщение о самосчетах, сделанное
Буняковским в 1876 г., побудило Чебышева заняться арифметическими машинами.
Русские изобретатели внесли вклад и в усовершенствование
планиметров, которые позволяют механически измерять площади нарисованных
фигур путем обвода специальным элементом прибора периметра фигуры.
В 1854—1856 гг. оригинальный планиметр был создан конструктором-
самоучкой, впоследствии журналистом и автором нескольких
беллетристических произведений, Павлом Алексеевичем Зарубиным (1816—1886).
По отзыву Буняковского, астронома В. Я. Струве (1793—1864), Якоби
и Чебышева этот и другие инструменты Зарубина были отмечены
присуждением ему Демидовской премии. Особенное внимание обратили академики
на простоту устройства, точность результатов, скорость в применении
и недорогую цену на линейку-планиметр, преобразующую многоугольник
в равновеликий треугольник. Заметим, что в те же годы швейцарский
математик И. Амслер построил (1854) и описал (1856) полярный
планиметр, носящий его имя. Несколько позднее своеобразный по конструкции
планиметр предложил Буняковский (1860, опубл. в 1866) 3).
* *
*
Деятельность М. В. Остроградского и В. Я. Буняковского вновь
подняла на высокий уровень математические исследования в Академии наук.
Своим творчеством Остроградский подготовлял почву для возникновения
новой математической школы в Петербурге. Оба они многое сделали для
улучшения преподавания в столичных высших учебных заведениях, что
было также необходимым условием дальнейших успехов. Вторая
Петербургская математическая школа не заставила себя долго ожидать. Ее
непосредственным организатором и признанным главой стал П. Л. Чебышев, имя
которого встречалось нам уже не раз. Его исключительно яркая научная
и педагогическая деятельность развернулась преимущественно во второй
половине XIX столетия, и мы обратимся к ней в следующей части.
х) Л. Е. С а д о в с к и й, Из истории развития машинной математики в
России.— УМН, т. V, вып. 2 (36), 1950, стр. 63; В. Т. О д н е р, Арифмометр,
привилегированный во всех странах. Изд. 2-е, СПб., 1892; В. Г. Б о о л ь, пит. соч.
2) В. Я. Буняковский, О самосчетах и о новом их применении. СПб.,
1876; В. Г. Б о о л ь, цит. соч.
3) П. Л. Чебышев, Полное собрание сочинений, т. V, М.— Л., 1951, стр. 302—
307; см. также В. Г. БоольиЛ. Б. Садовский, цитированные сочинения.
ЧАСТЬ ЧЕТВЕРТАЯ
МАТЕМАТИКА В РОССИИ ВО ВТОРОЙ
ПОЛОВИНЕ XIX И В НАЧАЛЕ XX ВЕКА
ГЛАВА ПЯТНАДЦАТАЯ
ОБЩИЕ УСЛОВИЯ И ОСОБЕННОСТИ
РАЗВИТИЯ МАТЕМАТИКИ
Математическое образование; средняя школа. Развитие наук в России,
начиная примерно с 1860 г. и до 1917 г., происходило в новых
общественных условиях. В 1855 г. в разгар Крымской войны умер Николай I, а год
спустя закончилась эта война, наглядно показавшая банкротство
проводившейся императором политики, а также глубокую экономическую
и техническую отсталость охранявшегося им крепостнического режима.
Опасаясь революции, правительство Александра II пошло на ряд реформ,
главной из которых явилась отмена в 1861 г. крепостного права. Россия
вступила в период быстрого развития капитализма и в ней, как писал
В. И. Ленин, «в несколько десятилетий совершились превращения,
занявшие в некоторых старых странах Европы целые века» х). Промышленность
и сельское хозяйство, строительство и транспорт, армия и
государственный аппарат нуждались во все большем количестве квалифицированных
специалистов. Под давлением необходимости, с одной стороны, и
передовой общественности, с другой, правительство пошло на некоторое
расширение сети учебных заведений и улучшение их организации и программ,
как это имело уже место в начале XIX века. И так же, как тогда, за
реформами быстро последовала реакция. В 1864 г. был введен новый устав
для гимназий, расширявший права педагогических советов и отменявший
сословные ограничения при поступлении; наряду с «классическими»
гимназиями с одним или двумя древними языками учреждались
«реальные» гимназии без древних языков и с несколько усиленными курсами
математики и естественных наук. Но всего лишь через 7—8 лет
правительство, напуганное ростом революционных настроений среди молодежи,
перешло в контрнаступление. Все гимназии вновь стали «классическими»
с двумя древними языками, число часов на которые сильно
увеличивалось, преподавание естественной истории прекращалось, курс математики
несколько уменьшался. «Реальным» училищам сообщался резко
выраженный профессиональный уклон, срок обязательного обучения в них
урезался на год. В 80-е годы при Александре III и эти меры были призна-
х) В. И. Ленин, Сочинения, т. 17, стр. 95—96.
МАТЕМАТИЧЕСКОЕ ОБРАЗОВАНИЕ; СРЕДНЯЯ ШКОЛА 307
ны недостаточными. В дополнение к ним была повышена плата за
обучение, директорам было предложено освободить подведомственные им
гимназии «от поступления в них,— говоря словами официального
распоряжения,— детей кучеров, лакеев, поваров, прачек, мелких лавочников
и тому подобных людей, детей коих, за исключением разве одаренных
необыкновенными способностями, вовсе не следует выводить из среды,
к коей они принадлежат», а для евреев введена ограничительная норма
приема. Все это повлекло за собой заметное сокращение общего числа
гимназистов и повышение среди них процента дворян почти до 60.
Впоследствии «классицизм» гимназических программ был снова несколько
ослаблен: греческий язык стал необязательным, восстановлено в
скромных размерах естествоведение. Улучшено было преподавание в реальных
училищах, которые, однако, с начала и до конца их существования не
давали права на поступление в университет: для этого требовалось сдать еще
экзамен по латыни. Все же, несмотря на все препятствия, «разночинная»
молодежь проникала в среднюю и высшую школу, и именно из ее среды
выходило теперь большинство деятелей русской науки и просвещения.
Для детей рабочих и крестьян гимназии были, за редкими исключениями,
недоступны.
Как видно, власти боялись не только «кухаркиных детей»
(«циркуляром о кухаркиных детях» прозвали цитированное только что
распоряжение 1887 г.), но и естествознания. Что математика, физика, химия,
биологические науки необходимы государству, что без них не может успешно
развиваться хозяйство страны, а особенно крупная промышленность
и новые виды транспорта, понимали даже царские чиновники. Однако,
с другой стороны, распространение естественнонаучных знаний в широких
кругах населения содействовало росту влияния материализма и атеизма.
Появление «нигилистов», провозглашавших, подобно тургеневскому
Базарову, что природа не храм, а мастерская и человек в ней работник,
и ниспровергавших принципы казенной морали и религии, а вместе с тем
и слепую веру в традиционные авторитеты, внушало самые серьезные
опасения сменявшим друг друга царским правительствам. Сегодняшний
нигилист завтра становился революционером. Недаром революционные
демократы Н. А. Добролюбов (1836—1861), Н. Г. Чернышевский (1828—
1889) и Д. И. Писарев (1840—1868) придавали пропаганде естествознания
не только образовательное, но и передовое общественное значение.
Знаменитый физиолог И. П. Павлов (1849—1936) писал: «Под влиянием
литературы шестидесятых годов, в особенности Писарева, наши
умственные интересы обратились в сторону естествознания, и многие из нас,
в числе этих и я, решили изучать в университете естественные науки» х).
Рассматриваемый период был временем блестящих успехов
естествознания в России. Прогресс математики был одним из элементов всего
научного и, шире, социального прогресса в целом. Как и в других областях
знания, он находил выражение во всей сфере народного образования,
в организации научных обществ и съездов, росте специальной и учебной
литературы, активизации исследований, появлении новых научных
центров и усилении связей между ними и т. д.
На преподавании математики существенно отражались общие
судьбы средней школы. Число часов по математике менялось
незначительно. В первых трех классах гимназии проходили арифметику, в третьем
уже приступали к алгебре, в четвертом — к геометрии и в седьмом —
г) И. П. Павло в, Полное собрание трудов, т. V, М.—Л., 1949, стр. 371.
308 ГЛ. 15. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
к тригонометрии; в реальных училищах, кроме того, изучали элементы
аналитической геометрии и анализа. Но на методике обучения и
содержании программ сказывались достижения педагогической мысли, внедрению
которых нередко противодействовал косный министерский аппарат.
Мы можем только мельком коснуться этого вопроса г).
Уже в тридцатые годы вопросы преподавания математики становятся
предметом более постоянного, чем прежде, обсуждения и здесь следует
назвать Петра Семеновича Гурьева (1807—21 сент. 1884) сына академика
С. Е. Гурьева. О работе в этой области Остроградского и Буняковского
уже говорилось. В середине XIX столетия русская педагогическая мысль
достигла высокого расцвета, ее яркими представителями были хирург
Н. И. Пирогов (1810—1881) и основоположник научной педагогики
в России К. Д. Ушинский (1824—1871). В это время усиливается и
разработка вопросов преподавания математики, в которой принимали участие
и школьные учителя, и крупные ученые, в том числе П. Л. Чебышев,
который в течение 17 лет (с 1856 по 1873 г.) состоял членом Ученого
комитета Министерства народного просвещения. Своими докладами
о программах и методах преподавания и многочисленными рецензиями
на учебные пособия по математике, физике и космографии, от которых
он всегда требовал точности и ясности изложения, Чебышев оказывал
большую помощь русскому образованию. Немало сил и времени отдали
средней школе А. Ю. Давидов, В. П. Ермаков, К. А. Поссе, Б. К. Млод-
зеевский, Д. М. Синцов, В. Ф. Каган, Д. Д. Мордухай-Болтовской
и другие университетские деятели. Математические общества также много
сделали для средней школы. Например, в начале XX века по
предложению Б. К. Млодзеевского, Н. Е. Жуковского, Н. В. Бугаева и других
членов Московского математического общества было создано при
Московском университете Педагогическое общество, оформившееся в 1906 г.
в Московский педагогический кружок. Председателем его был Б. К. Млод-
зеевский, который привлек к работе многочисленных учителей и
работников университета. Кружок издавал журнал «Математическое
образование» и наряду с возникшим в 1885 г. Отделом математики
Петербургского педагогического музея военно-учебных заведений сыграл серьезную
роль в разработке проблем преподавания математики в средней школе.
Рост общественного интереса к вопросам математического
образования нашел свое выражение в появлении специальных журналов,
из которых первым был недолговечный «Учебный математический
журнал», издававшийся в Ревеле (ныне Таллин) в 1833—1834 гг. Издателем
его был уроженец Митавы Карл-Генрих Купфер (1789—1838),
защитивший в 1813 г. в Дерптском университете диссертацию по суммированию
рядов на степень доктора философии. Впоследствии Купфер ряд лет
преподавал в ревельской гимназии, а в конце жизни в Нежинском лицее,
которому тогда (1832—1840) был придан характер физико-математического
института с трехлетним курсом обучения. Любопытно, что в те же 1833—
1834 г. г. в Петербурге выходил первый русский специальный
«Педагогический журнал», одним из редакторов и активным участником
которого был П. С. Гурьев.
В рассматриваемый период научно-популярные и методические
материалы по математике печатались в различных общих и специальных
журналах, вроде «Педагогического сборника» (СПб., 1864—1917), который
х) А. В. Ланков, К истории развития передовых идей в русской методике
математики, М., 1951.
МАТЕМАТИЧЕСКОЕ ОБРАЗОВАНИЕ; СРЕДНЯЯ ШКОЛА 309
долгое время редактировал выдающийся методист Алексей Николаевич
Острогорский (род. 1840), или «Математического листка» (М., 1879—
1882) кандидата Московского университета Александра Ивановича
Гольденберга (1837—1902). Следует отметить второй отдел 2—10 томов
«Математического сборника», органа Московского математического
общества, где с 1867 по 1882 г. публиковались статьи по вопросам элементарной
математики, по истории математики, рецензии на учебники. Затем второй
отдел навсегда исчезает со страниц «Математического сборника»,
вероятно, в связи с появлением новых аналогичных изданий, в первую очередь
«Журнала элементарной математики» (Киев, 1884—1886), основанного
В. П. Ермаковым и быстро завоевавшего симпатии широкого круга
читателей. Непосредственным продолжением журнала Ермакова явился
«Вестник опытной физики и элементарной математики» (Киев, 1886—1891;
Одесса, 1891—1917), до 1898 г. редактировавшийся воспитанником
Киевского университета Эразмом Корнелиевичем Шпачинским (1848—1912),
а затем В. Ф. Каганом. «Вестник» был очень популярен среди учителей
и учащихся. В нем публиковались статьи и заметки по самым различным
вопросам элементарной математики, высшей алгебры, началам анализа
и пропагандировались неевклидова геометрия, новые направления
в основаниях геометрии, теории функций, философии математики;
дебатировались вопросы методики преподавания; помещались интересные
задачи. Прекрасно поставлен был отдел рецензий. Наряду с «Вестником»
в последние годы перед Октябрьской революцией заслуженную
известность приобрел издававшийся в 1912—1917 гг. в Москве журнал
«Математическое образование», редактором которого был. И. И. Чистяков
(1870—1942). В обоих журналах участвовали многие видные ученые
и учителя х).
Во второй половине XIX века создан был ряд учебных руководств
для средней школы, среди них передовая для своего времени
«Элементарная геометрия в объеме гимназического курса» А. Ю. Давидова (М., 1864),
39-е издание которой вышло в 1922 г., и его же «Начальная алгебра»,
переиздававшаяся с 1865 по 1922 г., а также руководства воспитанника
Петербургского университета Андрея Петровича Киселева (1852—1940):
«Систематический курс арифметики для средних учебных заведений»
(СПб., 1884), «Элементарная алгебра» (СПб., 1888) и «Элементарная
геометрия» (СПб., 1892). Киселев совершенствовал свои руководства от
издания к изданию, и они постепенно стали основными математическими
учебниками русских школ. По учебникам Киселева обучались десятки
миллионов школьников; после некоторой переработки эти учебники
были приняты в 1937—1938 гг. в школах Советского Союза.
В девяностые годы XIX в. программы средней школы стали
предметом острой критики со стороны многих педагогов и ученых, которые
требовали освобождения курса математики от лишнего балласта и его
обогащения новым актуальным научным материалом. Особенно
настаивали на введении в школьный курс идеи функциональной зависимости.
В 1891 г. в журнале «Русская школа» с такого рода требованиями
выступил педагог и методист Семен Ильич Шохор-Троцкий (1853—1923).
Вскоре этому же вопросу посвятил яркую статью крупный деятель
математического просвещения, позднее профессор Московского городского
х) И. Я. Д е п м а н, Русские математические журналы для учителя.— Матем.
в школе, 1951, № 6; С. А. Д а х и я, Журнал элементарной математики и Вестник
опытной физики и элементарной математики.— Ист.-матем. исслед., вып. IX, 1956.
310 ГЛ. 15. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
народного университета им. Шанявского В. П. Шереметевский (умер
в 1919). Шереметевский подчеркивал, что центральные идеи современной
математики и математического естествознания остаются за рамками
гимназических программ. Он писал: «Молодые люди конца XIX века,
готовящиеся принять официальное удостоверение в умственной зрелости,
искусственно задерживаются на средневековом уровне математической
мысли» и подробно обосновывал тезис, что «и элементарный курс должен
группироваться вокруг основного понятия о функциональной
зависимости» х).
В начале XX века движение за реформу преподавания, ставившее
своими задачами воспитание в школьниках функционального мышления
и внесение в школьные программы элементов высшей математики, успешно
развивалось за рубежом. В Германии его возглавлял Ф. Клейн, во
Франции его деятельными сторонниками были такие видные ученые, как
П. Аппель и Э. Борель 2). На IV Международном математическом
конгрессе в Риме (1908) была создана Международная ассоциация
преподавателей математики, в работах которой участвовала и русская
национальная делегация, подготовившая дляУ Конгресса в Кембридже (1912)
тринадцать отчетных докладов.
Методико-математическая деятельность достигла в царской России
высшей своей точки вскоре после революции 1905 г. Свидетельством
этого явились два Всероссийских съезда преподавателей математики,
из которых первый состоялся в Петербурге в январе 1912 г., а второй
в Москве в январе 1915 г. Съезды были весьма многолюдны, например,
в первом приняло участие 1217 работников средней и высшей школ.
На съездах было обсуждено большое число вопросов — о преподавании
геометрии и изложении идей неевклидовой геометрии, о введении новых
сведений по теоретической арифметике, приближенных вычислениях,
реформе курса алгебры, исторических элементах в преподавании,
подготовке учителей и т. д. Всего на I съезде был сделан 71 доклад, на II
съезде — 32 доклада. Решения I съезда призывали поднять активность и
самодеятельность учащихся, усилить как наглядность преподавания, так
и роль логического элемента в старших классах. Вынесена также была
рекомендация, опустив некоторые второстепенные вопросы, провести
через курс средней школы идею функции и, для сближения преподавания
с требованиями науки и жизни, знакомить учащихся с простейшими
и, несомненно, доступными им идеями аналитической геометрии и
анализа 3). Открывая второй съезд, Б. К. Млодзеевский вновь подчеркивал,
что «успехи естествознания и техники выдвинули вопрос о введении
в среднюю школу вопросов, изучаемых теперь обыкновенно в высшей
школе; стало очевидным, что в настоящее время основные понятия
исчисления бесконечно малых, аналитической геометрии и теории вероятностей
должны быть достоянием каждого образованного человека» 4). С. Н. Берн-
штейн посвятил на втором съезде специальное сообщение возможным
приемам введения в школе понятия о функции.
1)В. П. Шереметевский, Математика как наука и ее школьные
суррогаты.—«Русская мысль», 1895, № 5, стр. 106 и 118.
2) См. статью В. Ф. Кагана, Реформа преподавания математики в средних
школах Франции и Германии (1910) в кн.: Э. Борель — П. Штеккель,
Элементарная математика, I. Арифметика и алгебра. Изд. 2-е, Одесса, 1923.
3) Труды 1-го Всероссийского съезда преподавателей математики, т. I—III, СПб.,
1913.
4) Доклады, читанные на 2-м Всероссийском съезде преподавателей математики
в Москве, М., 1915, стр. 3.
МАТЕМАТИКА В УНИВЕРСИТЕТАХ
311
Передовые педагоги старались проводить в жизнь новые идеи хотя бы
в отдельных школах и создавали новые замечательные руководства.
Одним из таких борцов за реформу был воспитанник Киевского
университета — К. Ф. Лебединцев (1878—1925), работавший в гимназиях Киева
и Москвы, а в последние годы жизни — в киевской высшей школе.
В своем «Курсе алгебры для средних учебных заведений» (ч. I—II, Киев,
1909—1910) и примыкающих к нему руководствах он последовательно
развивал понятие о числе, переменной величине, функциях и их
графиках. В последние годы перед Великой Октябрьской социалистической
революцией вышел ряд других учебных книг по гимназическому курсу
математики и вопросам методики преподавания, которые мы не можем
здесь перечислять.
Однако в условиях все нараставшей тогда реакции сколько-нибудь
широкая и последовательная реализация прогрессивных педагогических
взглядов была немыслима. Только в реальных училищах (с 1906 г.)
и в кадетских корпусах (в 1911 г.) введены были начала аналитической
геометрии и анализа. Выходили за рамки установленных программ
и отдельные частные средние учебные заведения. В подавляющем же
большинстве государственных школ дело оставалось по-прежнему. Когда
в 1915—1916 гг. Министерство народного просвещения под давлением
передовых общественных кругов попыталось разработать проект общей
реформы преподавания, министр был уволен в отставку.
Затронутый Б. К. Млодзеевским вопрос о преподавании в школе
теории вероятностей вызвал вскоре ожесточенную полемику. П. А.
Некрасов, в прошлом — профессор математики Московского университета,
а в рассматриваемое время член Ученого совета Министерства народного
просвещения, задумал использовать теорию вероятностей для поддержки
самодержавия и православия. Вместе со своим коллегой по Ученому
совету министерства В. Г. Алексеевым, профессором математики в
Юрьеве, и некоторыми педагогами П. А. Некрасов стал добиваться включения
в курс гимназии теории вероятностей, принципы которой самым
ненаучным образом извращались в идеалистическом духе. Как открыто
заявляли Алексеев и Некрасов, их целью была борьба с материализмом,
который завоевывал симпатии учащейся молодежи.
Против Некрасова и его единомышленников выступили крупнейшие
математики во главе с академиком А. А. Марковым. В «Журнале
Министерства народного просвещения» за 1915 г. велся резкий спор между
обоими лагерями. В октябре того же года Академия наук, по
предложению Маркова, создала комиссию, в которую вошли он сам, академики
А. М. Ляпунов, В. А. Стеклов, члены-корреспонденты механик
Д. К. Бобылев (1842—1917), А. Н Крылов и астроном Н. Я. Цингер
(1842—1918). В ноябре комиссия вынесла решение, категорически
осуждавшее лженаучное использование теории вероятностей П. А.
Некрасовым, как «злоупотребление математикой с предвзятой целью превратить
науку в орудие религиозного и политического воздействия» *).
Осуществить свои планы П. А. Некрасову не удалось.
Математика в университетах. В рассматриваемое время возросло
число университетов. В 1865 г. был учрежден по инициативе Пирогова
х) М. Я. Выгодский, Математика и ее деятели в Московском университете во
второй половине XIX века — Ист.-матем. исслед., 1948, вып. 1, стр. 178; В. Л. Ми н-
к о в с к и й, Педагогические идеи и деятельность академика А. А. Маркова.
Математика в школе, 1952, № 5, стр. 11—12.
312 ГЛ. 15. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
Новороссийский университет в Одессе, затем последовали открытие
в 1869 г. университета в Варшаве и в 1915 г. в Ростове-на-Дону. Мы не
касаемся здесь Томского (1888) и Саратовского (1909) университетов,
так как физико-математические факультеты в них были организованы
только в 1917 и соответственно 1918 г., а также Пермского университета,
открытого перед Октябрьской революцией. Своеобразным учреждением
явился Московский городской народный университет, основанный в 1908 г.
на средства, завещанные для этого филантропом А. Л. Шанявским. Здесь
могли обучаться люди, недопущенные по формальным причинам в
государственные университеты. Это учебное заведение существовало до 1918 г.,
когда в нем отпала надобность. Во второй половине XIX и начале XX вв.
появился также ряд новых высших технических учебных заведений,
например, Московское Высшее техническое училище, организованное
в 1868 г. на базе прежнего ремесленного училища; так как из втузов
почти не выходили специалисты математики, мы можем оставить их
в стороне.
Деятельность университетов протекала в тех трудных общих
условиях, которые только что были описаны. Устав 1863 г. позволил
преподавателям и студентам недолгие годы работать и учиться в более
свободной обстановке. Были расширены права университетских и факультетских
советов, ослаблено постоянное мелочное вмешательство попечителей.
Революционное движение среди студенчества, с тех пор никогда не
угасавшее, а также попытки более демократически настроенной части
профессуры противодействовать начальственной «опеке», привели в
нескольких университетах к репрессиям, увольнению непокорных ученых
и исключению неблагонадежных студентов. Власть попечителей была
полностью восстановлена уставом 1884 г., действовавшим, с некоторыми
послаблениями, до 1917 г. Все это задерживало, но не могло остановить
прогресса науки и образования.
На физико-математических факультетах план обучения математике
до 1850 г. был примерно таков: высшая алгебра, аналитическая
геометрия, общий курс математического анализа с геометрическими
приложениями, интегрирование дифференциальных уравнений (обыкновенных
и с частными производными), вариационное исчисление; около 1850 г.
добавляются начертательная геометрия, конечные разности, теория
вероятностей, а в отдельных университетах и другие предметы. Со
временем постепенно обогащается содержание обязательных курсов и
вводятся некоторые новые. В 70-е годы организуются обязательные
практические занятия с решением задач, в обычай входит чтение факультативных
специальных дисциплин и возникают студенческие научные семинары
и кружки. Обучение было четырехгодичным.
Первое место на протяжении всего этого времени занимает теперь
Петербургский университет. Мы говорили, что в сороковые годы здесь
начали преподавание Сомов, Буняковский и Чебышев, который оказал
решающее влияние на всю деятельность факультета, привлекая к научной
работе и преподаванию талантливую молодежь. 35 лет Чебышев читал
различные лекционные курсы: по сферической тригонометрии,
аналитической геометрии, высшей алгебре, интегральному исчислению,
эллиптическим функциям, теории чисел, теории вероятностей и некоторые
другие. В 60-е годы на факультете появляются ученики Чебышева,
а затем ученики этих учеников: в 1861 г, А. Н. Коркин, с блеском
излагавший почти все учебные предметы от сферической тригонометрии
до вариационного исчисления; в 1868 г. Ю. В. Сохоцкий, тогда же прочи-
МАТЕМАТИКА В УНИВЕРСИТЕТАХ
313
тавший специальный курс теории функций комплексного переменного,
а впоследствии поставивший очень интересный курс алгебры (он вел
и другие предметы); в том же году Е. И. Золотарев, впервые поставивший
в 1877—1878 уч. г. как особый курс «Введение в анализ». В 1873 г. на
физико-математическом факультете появился К. А. Поссе, в 1880 г. А. А.
Марков, в 1882 г. И. Л. Пташицкий, в 1891 г. И. И. Иванов, в 1905 г.
Д. Ф. Селиванов и в 1906 г. В. А. Стеклов, поставивший большой и
глубокий курс математической физики. Это — поистине первоклассный
состав лекторов. Все они (кроме Стеклова) были воспитанниками
Петербургского университета, из которого вышли также многие профессора
других университетов и технических школ — М. А. Тихомандрицкий,
А. М. Ляпунов, Г. Ф. Вороной, А. В. Васильев, Д. А. Граве, Д. Д. Морду-
хай-Болтовской, Н. М. Гюнтер и иные. Некоторые из только что названных
ученых недолгое время преподавали и в родном университете х).
В Московском университете передовые традиции, заложенные
Н. Д. Брашманом и Н. Е. Зерновым, были продолжены прежде всего
A. Ю. Давидовым, а затем их учеником Н. В. Бугаевым, приступившим
к преподаванию в 1865 г. Бугаев поставил чтение лекций по теории
функций комплексного переменного, а также вводил новые научные идеи
в другие свои курсы — по эллиптическим функциям, конечным
разностям и др. С 1862 г. на факультете начал работать механик и геометр
B. Я. Цингер, заслуживший общую признательность слушателей яркими
лекциями по проективной геометрии. В 1885 г. специальным курсом
по синтетической теории конических сечений начал блестящую
лекторскую деятельность Б. К. Млодзеевский и одновременно с ним пришел
на факультет П. А. Некрасов. В 90-е годы к преподаванию приступили
Д. Ф. Егоров (1893), Л. К. Лахтин (1896), К. А. Андреев (1898), в 1902 г.—
И. И. Жегалкин и в 1914 г. Н. Н. Лузин. Млодзеевский, Егоров и Лузин
внесли в преподавание математики на факультете новейшие идеи
анализа и теории функций и в корне изменили характер студенческих
занятий. Об этом будет сказано в своем месте. Добавим, что в 1882 г. В. В. Бобы-
нин впервые в России стал читать здесь факультативный курс истории
математики.
Мы говорим здесь об истории математики, но картина жизни физико-
математического факультета Московского университета на рубеже XIX—
XX вв. была бы неполной, если не сказать хотя бы несколько слов и о
других его деятелях. Механика и физика были в то время представлены
знаменитым теоретиком воздухоплавания Н. Е. Жуковским, автором
выдающихся исследований по магнетизму и электричеству А. Г. Столетовым
(1839—1896), прославившимся открытием давления света П. Н.
Лебедевым (1866—1912), а также разносторонним физиком-теоретиком Н. А. Умо-
вым (1846—1915), который уже в преклонных летах, одним из первых
воспринял идеи теории относительности и стал ее убежденным
пропагандистом. Лекции Умова производили сильнейшее впечатление. Сын Бугаева,
писатель Андрей Белый, учившийся в начале века на естественном
отделении физико-математического факультета, в 1921 г. вспоминал:
И было: много, много дум;
И метафизики, и шумов.
И строгой физикой мой ум
Переполнял: профессор Умов.
г) Р. И. Г а л ч е н к о в а, Математика в Ленинградском (Петербургском)
университете,— Ист.-матем. исолед., вып. XIV, 1961.
314 ГЛ. 15. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
Над мглой космической он пел,
Развив власы и выгнув выю,
Что парадоксами Максвелл
Уничтожает энтропию,
Что взрывы, полные игры,
Таят томсоновые вихри,
И что огромные миры
В атомных силах не утихли,
Что мысль, как динамит, летит
Смелей, прикидчевей и прытче...
Развитие математики на факультете в те годы имело столь же
динамический и бурный характер, но никто не рассказал об этом стихами.
Все упомянутые математики вышли из стен Московского
университета, но многие его воспитанники работали в других городах. Это
относится, например, к Н. Я. Сонину, К. А. Андрееву, В. А. Анисимову,
П. С. Назимову, В. В. Преображенскому.
В Казанском университете освободившуюся в 1846 г. с уходом
Лобачевского кафедру занял его ученик А. Ф. Попов, специалист по
математической физике; еще ранее, в 1838 г., на кафедре прикладной
математики начал работать воспитанник Харьковского университета
П. И. Котельников, читавший лекции и по математическим дисциплинам.
В 1860—1871 гг., с некоторым перерывом, вел занятия В. Г. Имшенецкий,
покинувший университет по политическим причинам, а с 1871 до 1911 г.
работал ученик всех трех названных профессоров геометр Ф. М. Суворов.
Тремя годами позже Суворова пришел А. В. Васильев,
организовавший здесь в 1900 г. первый научный студенческий кружок; он читал
в Казани лекции до 1907 г. Несколько позднее на факультете работали
П. С. Назимов, А. П. Котельников (сын П. И. Котельников а),
воспитанник Одесского университета Д. Н. Зейлигер (оба эти геометра провели
в Казани около 20 лет, до 1914 г.), Д. М. Синцов и др. г).
В Харьковском университете, после увольнения в 1820 г. Осипов-
ского, долгое время не было профессоров высокой квалификации.
Положение несколько изменилось к лучшему с приходом ученика
Остроградского по Главному педагогическому институту Евгения Ильича Бейера
(1819—1899), который преподавал на факультете с 1845 по 1872 г., и затем
ученика последнего Д. М. Деларю, читавшего лекции с 1861 г. В 1872 г.
профессором механики был избран В. Г. Имшенецкий, в 1874 г. кафедра
математики пополнилась К. А. Андреевым, работавшим здесь в течение
25 лет, и в 1883 г. М. А. Тихомандрицким; благодаря им уровень
преподавания значительно повысился. Решающий перелом в жизни
факультета наступил с приходом в 1885 г. на кафедру прикладной математики
A. М. Ляпунова и вскоре его ученика по Харьковскому же университету
B. А. Стеклова. Оба они оказали мощное влияние на развитие всего цикла
механико-математических наук. Ляпунов перешел на работу в Академию
наук в 1902 г., Стеклов в Петербургский университет в 1906 г. Но и в
дальнейшем работа факультета проводилась на очень высоком уровне: с 1893 г.
до 1906 г. здесь работал В. П. Алексеевский, в 1903 г. приступил к
лекциям Д. М. Синцов, а в 1907 г. С. Н. Бернштейн 2).
1)Ср.Б.Л. Лаптев, Математика в Казанском университете за 40 лет (1917—
1957).— Ист.-матем. исслед., вып. XII, 1959.
2) М. Н. М а р ч е в с к и й, История математических кафедр в Харьковском
университете за 150 лет его существования, а также другие статьи в сб.: Записки матем.
отд. физ.-матем. факультета и Харьковского матем. о-ва, т. XXIV, сер. 4, 1956.
МАТЕМАТИКА В УНИВЕРСИТЕТАХ
315
В более молодом Киевском университете преподавание математики
обязано своими первыми серьезными успехами его воспитанникам
П. Э. Ромеру и М. Е. Ващенко-Захарченко, которые начали читать
лекции в 1861 и, соответственно, с 1863 г., а затем В. П. Ермакову (с 1874 г.)
и Б. Я. Букрееву (с 1886 г.). Особенно яркого расцвета математика
достигла здесь благодаря блестящей педагогической деятельности Д. А. Граве,
который пришел в университет в 1901 г. х).
В Новороссийском университете в Одессе основные математические
курсы долгое время, с 1867 до 1889 г., вели уже упоминавшийся ученик
Остроградского Е. Ф. Сабинин и ученик Сабинина С. П. Ярошенко
(с 1870 г.). В 1876 г. начал работу В. В. Преображенский, в 1883 г.
И. В. Слешинский (вышедший в отставку тридцать лет спустя). В 1888 г.
на кафедре математики стал работать И. Ю. Тимченко, в 1894 г.
В. И. Циммерман, в 1898 г. В. Ф. Каган, в 1904 г. Е. Л. Буницкий
ив 1905 г. С. О. Шатуновский. Жизнь физико-математического факультета
в Одессе была весьма интенсивной. Это относится прежде всего к кафедре
физики, которую возглавлял с 1872 по 1893 г. Н. А. Умов, и к кафедре
прикладной математики, где выдающиеся исследования по кинематике
механизмов вели В. Н. Лигин (1846—1900), X. И. Гохман (1851—1916)
и И. М. Занчевский (1861—1928). Несколько позднее, с середины
девяностых годов на высокий уровень поднята была вся работа и в области
«чистой» математики 2).
Ряд крупных математиков преподавал в Варшавском университете:
в 1872—1893 гг. Н. Я. Сонин, в 1880—1907 гг. Н. Н. Зинин, в 1890—
1907 гг. В. А. Анисимов, в 1894—1908 гг. Г. Ф. Вороной, с 1909 г.
Д. Д. Мордухай-Болтовской (оба из Петербургского университета)
и В. П. Вельмин (из Киевского университета). Два последних математика
с 1915 г. работали в университете в Ростове-на-Дону 3). Из математиков
Дерптского (Юрьевского) университета заслуживают особого
упоминания Ф. Э. Молин, которому из-за политической обстановки после
недолгих лет работы пришлось переехать в Томск, москвичи Л. К. Лахтин
(1892—1896) и В. Г. Алексеев (1895—1917) и, наконец, Г. В. Колосов
(из Петербурга), профессор кафедры прикладной математики в 1902—
1913 гг. 4).
Мы кратко перечислили здесь наиболее крупных университетских
математиков второй половины XIX и начала XX вв. Следует подчеркнуть,
и об этом нам придется говорить позднее, что с течением времени развитие
математики в каждом университете приобретало свои особенности. Если
в Петербургском университете распространялись преимущественно идеи
математической школы, созданной Чебышевым, то в Москве, Киеве,
Одессе и т. д. закладывались основы развития других направлений
математики. Это в первую очередь находило отражение в обязательных
лекционных курсах, по содержанию нередко существенно отличавшихся
в различных университетах, в постановке специальных курсов и в выборе
диссертационных тем.
х) Л. Н. Грацианская и И. 3. Штокало, Разделы по истории
математики в кн.: IcTopin Ки'гвського ушверситету. Кигв, 1959.
2) С. М. К i р о, Математика в Одеському Новоросшському ушверситет1, 1сто-
рико-математичний зб1рник, II. Ки'гв, 1961.
3)С. Е. Белозеров, Математика в Ростовском университете.— Ист.-ма-
тем. исслед., вып. VI, 1953.
4) Ср. Г. Р и г о, Из жизни и деятельности четырех замечательных математиков
Тартуского Университета.— Уч. зап. Тартуского университета, вып. 37, 1955.
316 ГЛ. 15. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
Учебный процесс необходимо было обеспечить руководствами. Многие
курсы выходили в литографских изданиях, их мы касаться не будем.
Из всей большой учебной литературы того времени мы назовем для
примера только немногие, особенно замечательные сочинения, такие как
«Теория сравнений» П. Л. Чебышева (СПб., 1849); «Основания теории
эллиптических функций» О. И. Сомова (СПб., 1850); «Исчисление
конечных разностей» А. А. Маркова (СПб., 1889—1891) и его же классическое
«Исчисление вероятностей» (СПб., 1900); курсы А. Н. Крылова «Лекции
о приближенных вычислениях» (СПб., 1911) и «О некоторых
дифференциальных уравнениях математической физики, имеющих приложение
в технических вопросах» (СПб., 1913); «Элементарный курс теории чисел
(Киев, 1909) и «Высшая алгебра» (Киев, 1915) Д. А. Граве. Учебными
пособиями нередко служили диссертации, например, только что
названная книга П. Л. Чебышева, работы В. Г. Имшенецкого «Об
интегрировании уравнений с частными производными первого порядка» (Казань,
1865) и «Исследование способов интегрирования уравнений с частными
производными второго порядка функций двух независимых переменных»
(Казань, 1868), а также «Общие методы решения основных задач
математической физики» (Харьков, 1901) В. А. Стеклова.
Успехи в создании учебной математической литературы были
значительны. Вместе с тем на русском языке еще недоставало многих
учебников. Основная работа по обеспечению высшей школы всеми
необходимыми руководствами была проведена уже в советское время.
Математические общества и научные съезды. Большая роль в
развитии математики за рассматриваемый период принадлежала, наряду
с Академией наук и университетами, тесно связанным с последними
математическим обществам. Первое из них, Московское, было создано все
в те же шестидесятые годы. Если не считать старейшего Московского
общества испытателей природы, возникшего в 1805 г., то математики
Москвы, объединившиеся в свободный научный коллектив в 1864 г.,
опередили ученых других специальностей: Русское техническое общество
было учреждено в 1866 г., Русское химическое общество в 1868 г.,
Русское физическое общество в 1872 г. (все три в Петербурге).
Московское математическое общество, начавшее свою деятельность
в 1864 г. (протокол первого заседания датирован 15(27) сентября этого
года), а юридически оформленное в 1867 г., является также старейшим
среди крупных математических обществ мира1). Лондонское
математическое общество было учреждено в 1865 г., Математическое общество
Франции — в 1872 г., Математический кружок Палермо в Италии в 1884 г.
х) Первая попытка создания в России математического общества была сделана
еще в 1810 г., по инициативе группы преподавателей и студентов Московского
университета, в частности Михаила Николаевича Муравьева (1796—1866), который в
молодости был близок к кругам декабристов, а затем стал одним из наиболее реакционных
и жестоких царских слуг. Председателем общества был отец только что названного
студента подполковник Николай Николаевич Муравьев (1768—1840), весьма
просвещенный человек, который организовал у себя на дому чтение лекций по математике, в
том числе высшей, военным и другим наукам. Среди членов общества были П. А.
Рахманов и П. А. Сулима. Главной задачей общества стало распространение математических
знаний и подготовка молодежи к военной службе. В 1816 г. на базе общества возникло
Московское учебное заведение для колонновожатых, т. е. офицеров Генерального
штаба, через несколько лет из-за болезни Н. Н. Муравьева переведенное в Петербург, где
оно функционировало до 1826 г. Н. Н. Муравьев — сын Н. Е. Муравьева, автора
первого русского учебника алгебры, о котором говорилось ранее.
МАТЕМАТИЧЕСКИЕ ОБЩЕСТВА И НАУЧНЫЕ СЪЕЗДЫ 317
Американское (вначале Нью-Йоркское) математическое общество —
б 1888 г., Германское объединение математиков — в 1890 г.
Инициаторами создания Московского математического общества
явились Н. Д. Брашман и А. Ю. Давидов, к которым присоединились
другие университетские работники—астроном Ф. А. Бредихин,
Н. В. Бугаев, В. Я. Цингер, механик Ф. А. Слудский (1841—1897), физик
Н. А. Любимов (1830—1898), профессор Московского Высшего
технического училища А. В. Летников, К. М. Петерсон и др. В числе членов-
учредителей Общества был и П. Л. Чебышев. Первым президентом был
жзбран Н. Д. Брашман, вице-президентом — А. Ю. Давидов и
секретарем В. Я. Цингер. Работе Общества с самого начала был придан
регулярный характер. Ежемесячно происходили заседания, посвященные
научным докладам и рефератам, и сразу начата была подготовка к изданию
печатного органа —«Математического сборника», первый том которого
вышел в октябре 1866 г., еще до официального утверждения устава
Общества. Работа Общества наталкивалась на трудности, особенно
финансовые. П. Л. Чебышеву удалось исхлопотать небольшую субсидию, но денег
не хватало, и одно время Общество вынуждено было даже отказаться
от ежегодного издания «Математического сборника», который четверть
ъека печатался на средства, собранные среди членов Общества.
В течение долгого времени деятельность Московского
математического общества охватывала математику, механику, астрономию и физику,
что, естественно, определялось его составом и интересами руководителей.
Постепенно, однако, Общество становилось все более и более
математическим или, точнее, математико-механическим. Об этом говорит хотя бы
то обстоятельство, что в первых десяти томах «Математического
сборника» математике посвящено почти 50% статей, а в следующих пяти
томах около 85%. В общей сложности на заседаниях Общества по 1917 г.
было сделано 971 сообщение, причем по математике —640 (или 66%),
по механике —217 (или 22%), остальные 12% приходятся на физику
и астрономию.
Действительными членами Московского математического общества
могли быть магистры и доктора математических наук, а также «лица,
заявившие себя трудами в этих науках». Первоначально в обществе было
всего 14 человек, в 1901 г. в нем состоял уже 101 член, а в 1913 г. число
членов достигло 112, из них 34 жили в Москве, 57— в других городах
России, остальные 21 были иностранными учеными. В дореволюционное
время общество было несколько замкнутым, и научная молодежь
допускалась в его состав редко.
Московское математическое общество было тесно связано, даже чисто
персонально, с физико-математическим факультетом университета, но его
рамки были значительно шире факультетских, оно служило центром
всей московской математической жизни. Напомним, что уже среди
первых организаторов общества имелись и не университетские работники,
как Летников или учительствовавший в гимназии Петерсон.
По своему значению Московское математическое общество уступало
только Академии наук. Деятельность Общества не ограничивалась
научными собраниями и публикацией «Математического сборника». Оно
поддерживало тесные связи с научными объединениями и отдельными
математиками Петербурга и других городов, а также зарубежных стран,
содействовало реферированию и публикации работ русских математиков
в иностранных журналах, занималось вопросами преподавания в средней
школе, вело регулярный обмен изданиями с редакциями различных
318 ГЛ. 15. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
журналов, находилось в тесном контакте с Обществом распространения
технических знаний и т. д.
Президентами Московского математического общества в
рассматриваемый период после Н. Д. Брашмана были последовательно А. Ю.
Давидов (1866-1886), В. Я. Цингер (1886-1891), Н. В. Бугаев (1891-1903),
затем два года П. А. Некрасов, вскоре вынужденный из-за переезда
в Петербург сложить с себя это звание и, наконец, Н. Е. Жуковский
(1905—1921). Николай Егорович Жуковский (17 января 1847—17 марта
1921), как и другой замечательный механик, его ученик Сергей
Алексеевич Чаплыгин (5 апреля 1869—8 октября 1942), были очень активными
членами Общества, которое сыграло видную роль и в развитии механики
в нашей стране. Всего с 1873 по 1920 гг. Жуковский выступил в
заседаниях Общества со 114 докладами. Некоторые из них относятся и к
математике — вариационному исчислению, дифференциальной геометрии,
непрерывным дробям 1).
Следующим по старшинству явилось Харьковское математическое
общество, основанное в 1879 г. Е. И. Бейером, В. Г. Имшенецким,
Д. М. Деларю, К. А. Андреевым и другими; позднее в него вступили
A. М. Ляпунов, В. А. Стек лов, Д. М. Синцов, С. Н. Бернштейн и другие
выдающиеся ученые. Харьковское общество к 1914 г. насчитывало
146 членов. Общество содействовало публикации диссертаций своих
членов — в своих «Сообщениях» или отдельным изданием; так увидели свет
докторские диссертации А. М. Ляпунова, М. А. Тихомандрицкого,
B. А. Стеклова и С. Н. Бернштейна. Предметом постоянного и особого
внимания общества служили вопросы преподавания в средней школе.
Председателями его были Бейер, Имшенецкий, Андреев (с 1884 по 1899 г.),
Ляпунов, Стеклов и с 1906 г. бессменно до кончины Синцов 2).
В Казани общество возникло в 1880 г. вначале как
физико-математическая секция Общества естествоиспытателей. 10 лет спустя секция
была преобразована в физико-математическое общество, насчитывавшее
к 1915 г. 126 членов. Весьма активным председателем Общества в 1884—
1907 гг. был А. В. Васильев. В значительной мере по его инициативе
и под его руководством Общество вместе с Казанским университетом
содействовало переизданию трудов Лобачевского и распространению его
идей. Мы не будем останавливаться на основанном в 1889 г. Киевском
физико-математическом обществе и начавшем еще ранее, в 1876 г., свою
деятельность Математическом отделении Новороссийского общества
естествоиспытателей 3). Скажем лишь несколько слов о Математическом
обществе в Петербурге.
Петербургское математическое общество, созданное в 1890 г. по
предложению В. Г. Имшенецкого, который стал его первым председателем
(после смерти его в 1892 г. сменил Ю. В. Сохоцкий), работало примерно
до 1905 г., но протоколы его опубликованы лишь за 1890—1899 гг. Вел
эти протоколы секретарь Общества (до 1903 г.), профессор Артиллерий-
г) Подробнее см.: П. С. Александров, Московское математическое
общество.— УМН, т. I, вып. 1, 1946; Л. А. Л ю с т е р н и к, Московский математический
сборник (там же); М. Я. Выгодский, Математика и ее деятели в Московском
университете во второй половине XIX века.— Ист.-матем. исслед., вып. 1, 1948;
П. С. Александров и О. Н. Головин, Московское математическое
общество.— УМН, т. XII, вып. 6, 1957.
2) М. Н. М а р ч е в с к и й, Харьковское математическое общество за первые
75 лет его существования.— Ист.-матем. исслед., вып. IX, 1956.
3) Э. Б. Л е й б м а н, Математическое отделение Новороссийского общества
естествоиспытателей (1876—1928).— Ист.-матем. исслед., вып. XIV, 1961.
МАТЕМАТИЧЕСКИЕ ОБЩЕСТВА И НАУЧНЫЕ СЪЕЗДЫ 319
ской академии и Высших женских курсов Петр Алексеевич Шифф (1849—
1910), автор нескольких работ по анализу и механике. В состав общества
вошли не только крупные столичные математики, механики, астрономы,
но и любители, а также учителя гимназий; к концу XIX века в нем
состояло около 100 человек, в том числе 13 женщин. Среди последних
большинство составляли астрономы-вычислители Пулковской обсерватории, три
же пользовались в свое время немалой известностью. Елизавета Федоровна
Литвинова (1845—1922), окончившая университет в Швейцарии,
преподавала затем в одной из Петербургских женских гимназий; ее ученицей
была Н. К. Крупская. Перу Литвиновой принадлежит немало статей
в «Педагогическом сборнике» и брошюр в издававшейся Ф. Ф. Павленко-
вым (1839—1900) серии биографий, среди них — жизнеописания Эйлера,
Даламбера, Лапласа, Лобачевского и Ковалевской. Вера Иосифовна
Шифф (ум. около 1919 г.), жена секретаря Общества, воспитанница и
преподавательница Высших женских курсов, составила два задачника,
не раз переиздававшихся и бывших в ходу еще несколько лет после
Октябрьской революции: «Сборник упражнений по дифференциальному
и интегральному исчислениям» (1—2 чч., СПб., 1889—1900) и «Сборник
упражнений по аналитической геометрии» (СПб., 1904). Наконец, Любовь
Николаевна Запольская (1871—1943), закончившая Высшие женские
курсы в Петербурге, впоследствии работала в Геттингене у Д. Гильберта
и защитила под его руководством диссертацию по алгебраической теории
чисел (1902); к этой же области относится ее магистерская диссертация,
защищенная в Москве в 1905 г. Л. Н. Запольская преподавала на
Высших женских курсах в Москве и в ряде периферийных высших учебных
заведений х).
Необычна была судьба одного из членов Общества — Михаила
Михайловича Филиппова (1858—26 июля 1903), воспитанника
Новороссийского университета, защитившего докторскую диссертацию по
интегральным инвариантам линейных дифференциальных уравнений
у Л. Кенигсбергера в Гейдельберге (1892). Помимо диссертации,
Филиппову принадлежат и другие работы по математике, но большую часть сил
он отдал распространению знаний. Он писал по вопросам естествознания,
философии, экономических наук; для павленковской серии составил
биографии Паскаля и Ньютона; переводил Дарвина; производил
химические опыты и был тесно связан с подпольными революционными
кругами, примыкая к марксистам. В 1894—1903 гг. он издавал журнал
«Научное обозрение», в котором сотрудничали В. И. Ленин и Г. В.
Плеханов, а также многие крупные математики и естествоиспытатели,—
В. А. Стеклов, Д. И. Менделеев и другие. Среди статей самого Филиппова
в этом журнале отметим «Пространство Лобачевского и многомерное
пространство», печатавшуюся в пяти номерах за 1894 г. Журнал и
редактор находились под бдительным надзором полиции; 1901—1902 гг.
Филиппов провел в ссылке. Он погиб, производя в домашней лаборатории опыты
по передаче взрыва на далекие расстояния.
Петербургское общество собиралось, не считая каникул, примерно раз
в месяц, за 1890—1899 гг. было заслушано 172 сообщения. Чаще других
1) У Гильберта в то время занимались еще две русские женщины-математика:
Надежда Николаевна Гернет (1877—1943), ставшая позднее профессором в Ленинграде
(она защитила диссертацию по вариационному исчислению) и Вера Евгеньевна
Лебедева (род. 1881), вышедшая замуж за крупного румынского математика А. Миллера
и получившая профессуру в Ясском университете (ее диссертация была по
интегральным уравнениям).
320 ГЛ. 15. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
выступали с докладами Д. А. Граве, Н. Я. Сонин, Ю. В. Сохоцкий,
П. А. Шифф, А. А. и В. А. Марковы, Д. Ф. Селиванов, И. И. Иванов;
активными участниками собраний были механики Н. Б. Делоне (1856—
1931) и И. В. Мещерский (1859—1935) и астроном О. А. Баклунд (1846—
1916). В 1892 г. сделал доклад о приближенном вычислении интегралов
Чебышев. Почему общество прекратило свою деятельность, не известно г).
Наряду с собраниями научных обществ весьма важной формой
прямых контактов между учеными, охватывающей к тому же весьма широкий
круг участников, работающих в большинстве своем в различных городах
и даже странах, служат научные съезды. В Германии первый съезд
естествоиспытателей произошел в 1822 г., в Англии в 1831 г. Русские ученые
смогли добиться разрешения на организацию 1-го Всероссийского съезда
естествоиспытателей и врачей только после долгих усилий; он
происходил в январе 1868 г. в Петербурге. С тех пор состоялось еще двенадцать
съездов, собиравшихся в обеих столицах, в Киеве, Казани, Варшаве,
Одессе и, наконец, в Тифлисе, где в июне 1913 г. был устроен последний
перед революцией и по счету 13-й съезд. На всех съездах имелась
математическая секция, где слушались доклады также по механике и
астрономии2). Число участников секции постепенно возрастало, примерно
с 50 на первых съездах до 400—500 на последних. С докладами выступали
почти все крупные математики страны, начиная с Чебышева, который был
активным участником 1—3 и 5—6 съездов. Число докладов по математике
было невелико, особенно вначале, и росло медленно. На первом съезде
их было всего 6, на двух следующих, в 1869 и 1871 гг., соответственно 10
и 12; на двенадцатом съезде в 1911 г.—27 и на тринадцатом —31. Для
сравнения укажем, что членами Первого Всесоюзного съезда математиков
в Харькове в 1930 г. состоял 471 советский ученый, а общее число докладов
достигло 164, из них 13 докладов принадлежало иностранным членам
съезда 3).
Русские математики участвовали и в зарубежных научных съездах.
Так, Чебышев многократно выступал в 1873—1882 гг. на сессиях
Французской ассоциации содействия преуспеванию наук — Association Fran-
§aise pour Tavancement des sciences. Наши ученые регулярно делали
сообщения и на Международных математических конгрессах, из которых
первый происходил в 1897 г. в Цюрихе, а последний за рассматриваемое
время, именно пятый, в 1912 г. в Кембридже.
Математические журналы и другие издания. Рост математических
исследований и увеличение числа научных центров повлекли за собой
во многих странах еще в первой половине XIX века появление
специальных математических журналов. Одних академических записок, которыми
можно было в общем удовлетвориться в XVIII веке, в XIX столетии
оказывалось недостаточно. Вместе с тем становилось нецелесообразным
публиковать вместе статьи по математике и, скажем, по химии или
биологии.
Математические журналы возникают в Европе в конце XVIII века
и начале XIX века. Старейшими были два французских издания: Jour-
г) И. Я. Д е п м а н, С.-Петербургское математическое общество.— Ист.-матем.
исслед., вып. XIII, 1960.
2) С. Н. Кир о, Математика на съездах русских естествоиспытателей и врачей.—
Ист.-матем. исслед., вып. XI, 1958; А. А. Киселев и Е. П. Ожигова,
П. Л. Чебышев на съездах русских естествоиспытателей и врачей.— Ист.-матем. исслед.,
вып. XV, 1963.
3) Труды Первого Всесоюзного съезда математиков. М.-Л., 1936, стр. 358—376.
МАТЕМАТИЧЕСКИЕ ЖУРНАЛЫ И ДРУГИЕ ИЗДАНИЯ 321
nal de ГЕсоге Polytechnique, выходивший с 1795 г.; и основанные в 1810 г.
геометром Ж. Д. Жергонном Annales des mathematiques pures et appli-
quees (1810—1831), которые после недолгого перерыва, наступившего
в 1831 г., продолжил с 1836 г. Journal des mathematiques pures et appli-
quees, иногда называемый по имени его основателя «Журналом Лиувилля».
В Германии инженер и математик А. Крелле положил в 1826 г. начало
Journal fur die reine und angewandte Mathematik, также часто
называемому просто «Журналом Крелле». Организующая и стимулирующая роль
этих изданий была столь очевидной, что вскоре число математических
журналов начинает расти, и они появляются и в других странах —
Англии, Италии и России. Разумеется, всюду продолжали играть очень
важную роль и академические записки. Именно в журналах Академии
наук печаталась в России большая часть работ Чебышева и его
петербургских учеников. Записки нашей Академии наук разделяются на серии,
по отделениям Академии; выход их становится более регулярным и
частым. Наряду с этим все возрастающее значение приобретают серийные
издания, чаще всего «Ученые записки», университетов и математических
обществ.
Первым русским математическим научным журналом явился
«Вестник математических наук», который издавал в 1860—1863 гг. в Вильнюсе
воспитанник Казанского университета астроном М. М. Гусев (1826—1866);
в нем участвовали Брашман, Бугаев, Ващенко-Захарченко, Сабинин
и другие математики. Выход этого журнала, где помещались также
популярные статьи, рецензии, задачи, довольно скоро прекратился
вследствие денежных затруднений издателя.
Следующим по времени был уже знакомый нам орган Московского
математического общества —«Математический сборник», первый том
которого вышел в 1866 г. (рис. 43). В рассматриваемое время в «Сборнике»
было опубликовано много замечательных работ Чебышева, Петерсона,
Коркина, Млодзеевского, Егорова, Лузина, Жуковского, Чаплыгина
и других. 30-й том «Математического сборника», который начали готовить
в 1916 г., вышел в 1918 г.
Несколько позднее стали выпускать свои труды другие
математические общества. Таковы, например, «Записки Математического отделения
Новороссийского общества естествоиспытателей» (23 тома за 1878—
1916 гг.) и «Сообщения Харьковского математического общества» (с 1879
по 1918 г. вышло 16 томов). В этих изданиях публиковались статьи
не только местных, но и иногородних математиков, и, скажем, в
харьковских «Сообщениях» мы находим работы Чебышева, Коркина, братьев
Марковых, Ермакова и вообще многих ученых, в Харькове не работавших.
Упомянем еще первый русский журнал по истории математики
«Физико-математические науки в их настоящем и прошедшем»,
издававшийся в Москве В. В. Бобыниным, который был одновременно и автором
всех статей, биографических очерков, некрологов, рецензий, информации
о текущей математической жизни в России и за рубежом, и составителем
подробных библиографических обзоров. В 1885—1898 гг. вышли 13 томов
журнала, в 1899—1904 гг. еще один том его продолжения
«Физико-математические науки в ходе их развития». Бобынин выпускал журнал на
собственные средства, а жил он с семьей на преподавательское жалованье;
в конце концов расходы по изданию стали для него непосильными.
Скажем несколько слов об этом человеке, беззаветно преданном
истории наук, интерес к которой заметно возрос во многих
европейских странах в середине XIX века. Сын небогатого дворянина Виктор
Рис. 43. Титульный лист и содержание «Математического сборника», т. 1, 1866.
МАТЕМАТИЧЕСКИЕ ЖУРНАЛЫ И ДРУГИЕ ИЗДАНИЯ 323
Викторович Бобынин (20 ноября 1849—25 ноября 1919) окончил Тульскую
гимназию в 1867 г. и Московский университет в 1872 г. и стал преподавать
в военно-учебных средних заведениях, сначала в Нижнем-Новгороде,
затем в Москве. В 1882 г. он защитил в Московском университете
магистерскую диссертацию «Математика у древних египтян» (Математический
листок, М., 1881—1882) и осенью того же года приступил в качестве
приват-доцента к чтению необязательного курса истории математики. Особые
заслуги принадлежат ему в разработке истории математики и астрономии
в России до основания Академии наук, области, ранее почти неизученной.
Этому он посвятил «Очерки истории
развития физико-математических знаний в России.
XVII столетие» (вып. 1—2, М., 1886—1890)
и много статей в собственном (тт. VII—XI)
и других журналах, причем привлек
обширные рукописные материалы. Большую
ценность имеет «Русская физико-математическая
библиография» от начала книгопечатания
до 1816 г., печатавшаяся в его журнале
и вышедшая также отдельным изданием
в трех томах (М., 1886—1900). Общее число
его работ, включая превосходные статьи
в Энциклопедическом словаре Брокгауза
и Ефрона, превышает 550. Имя Бобынина
пользовалось большой известностью в
России и за рубежом, но его выдающиеся
научные заслуги получили официальное
признание уже после Октябрьской революции.
35 лет он оставался приват-доцентом
Московского университета и лишь в 1917 г. получил
профессорское звание *). в> в. Бобынин.
С количественным ростом и
международным распространением математических
исследований (в XVIII веке они печатались в 210 периодических
изданиях, в XIX веке — в 950) связано было появление реферативных
журналов. Небезуспешные попытки такого рода предпринимались
и ранее, но прочную основу регулярное реферирование приобрело
в последней трети прошлого столетия. В 1871 г. вышел первый том
основанного берлинским математиком К. Ортманом ежегодника Jahrbuch
tiber die Fortschritte der Mathematik, в котором работы реферировались
за 2—3 прошедших года. А. В. Васильев об этом издании вспоминал:
«Трудно, думаю, оценить ту громадную пользу, которую оно принесло;
в частности, конечно, особенно обязана ему русская наука. При
поразительном незнании нашего языка иностранцами... только благодаря этому
Jahrbuch'у русская математическая литература могла сделаться
известной математикам других стран» 2). В ежегоднике Ортмана с его второго
тома (1873) участвовали многие русские ученые, начиная с А. Н. Коркина
и Е. И. Золотарева, а затем К. А. Поссе; поистине гигантскую работу
выполнил Д. М. Синцов, поместивший в нем с 1893 г. более 2000 рефератов.
г) К. А. Рыбников, Виктор Викторович Бобынин; А. М. Л у к о м с к а я,
Библиографический указатель... работ В. В. Бобынина.— Ист.-матем. исслед., вып.
III, 1950.
2)А. В. Васильев, Математика за последние 50 лет.— «Математическое
образование», т. 2, 1958, стр. 56, 57.
324 ГЛ. 15. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
Постепенно число реферативных изданий стало возрастать; так, с 1893 г.
стало выходить под покровительством Математического общества в
Амстердаме Revue sernestrielle des publications mathematiques, в котором тоже
активно сотрудничали русские математики. Мы здесь назвали только два
наиболее известных реферативных органа по математике того времени.
Значительную роль в подъеме математической культуры в России
сыграло издание разнообразной оригинальной и переводной литературы
по актуальным вопросам науки, исторических обзоров, отдельных
классических сочинений. Большой известностью пользовались книги,
выходившие в начале XX века в одесском издательстве «Матезис», в
работе которого участвовали многие математики, особенно В. Ф. Каган
и С. О. Шатуновский. Немало хороших книг вышло в Казани, Киеве,
Харькове и других городах. В 10 сборниках «Новых идей в математике»
(СПб., 1912—1915), выпускавшихся А. В. Васильевым и П. С.
Юшкевичем, помещены были переводы работ Г. Кантора по теории множеств,
А. Пуанкаре и Г. Минковского по теории относительности, дискуссионные
статьи по математической логике и т. д. У молодежи заслуженную любовь
приобрели две книги. Одной из них была обработка «Элементов высшей
математики» Г. А. Лоренца, выполненная В. П. Шереметевским (1—2 тт.,
1-е изд., М., 1898—1901; 4-е изд., М., 1919—1926); среди дополнений
Шереметевского особенно замечателен превосходный очерк истории
математики, переизданный еще раз в 1940 г. Другая книга — это
увлекательная и очень разнообразная по содержанию «Энциклопедия математики.
Очерк ее современного состояния» (Киев, 1912) Д. А. Граве, возникшая
из публичных лекций автора.
Основные направления математических исследований в России и за
рубежом. Развитие математики в России второй половины XIX и начала
XX века характеризуется значительным расширением области творчества,
а также возникновением научных коллективов с отчетливо выраженными
идейными устремлениями. Среди этих коллективов первым по
времени и по значению была петербургская математическая школа во главе
с П. Л. Чебышевым, возглавлявшим ее на протяжении более трех
десятков лет. В творчестве Чебышева мощное развитие получили теория чисел,
теория вероятностей, интегрирование алгебраических функций. В
непосредственной связи с техническими задачами Чебышев создал теорию
наилучшего приближения функций. Ученики и последователи Чебышева
успешно продолжили разработку его тематики и вместе с тем расширили
круг интересов школы. А. Н. Коркин, Е. И. Золотарев, А. А. Марков,
Г. Ф. Вороной продвигают далее теорию квадратичных форм, Золотарев —
теорию алгебраических чисел, А. А. Марков и А. М. Ляпунов глубоко
исследуют круг проблем, связанных с предельными теоремами теории
вероятностей; в 900-е годы Марков кладет начало большому новому
отделу этой науки — так называемой теории цепей Маркова. В теории
наилучшего приближения функций работали братья Марковы и Золотарев.
В связи с одной задачей, поставленной Чебышевым, Ляпунов, начиная
с 80-х годов, создал громадный цикл работ по фигурам равновесия
вращающейся жидкой массы. Он же блестяще развил классическую теорию
устойчивости и качественные методы исследования систем
обыкновенных дифференциальных уравнений. Ляпунову принадлежат также
основополагающие исследования по уравнениям математической физики.
Ученик Ляпунова В. А. Стеклов получил первоклассные результаты в области
математической физики и теории ортогональных функций. Значительный
ОСНОВНЫЕ НАПРАВЛЕНИЯ МАТЕМАТИЧЕСКИХ ИССЛЕДОВАНИЙ 325
вклад в теорию дифференциальных уравнений внес А. Н. Коркин; его
ученику А. Н. Крылову принадлежат ценные работы по прикладной
математике.
Петербургская математическая школа группировалась в основном
вокруг Академии наук, состав которой между 1876 и 1915 гг. пополнился
академиками Золотаревым, Имшенецким, Марковым, Сониным,
Ляпуновым, Стекловым, Крыловым, и вокруг Петербургского университета. Эта
школа оказала чрезвычайно сильное и плодотворное влияние на
дальнейшее развитие математики. Укажем для примера Харьковский
университет, где в течение многих лет работали Ляпунов и Стеклов и где в начале
XX века сообщил новое направление теории наилучшего приближения
функций С. Н. Бернштейн. Тематику школы разрабатывали и математики,
в главном примыкавшие к другим направлениям, как Сонин или Имше-
нецкий.
Блестящие результаты Чебышева и его последователей явились
в рассматриваемое время наиболее крупным национальным вкладом
в мировую математику и до известной степени оставили в тени работы
других русских математических школ. В историчеркой перспективе
следует, однако, высоко оценить деятельность и других научных
коллективов. Университеты и ученые общества Москвы, Казани, Харькова,
Киева, Одессы вырастают в крупные научные центры. Многие математики
этих городов, менее тесно связанные со школой Чебышева и потому менее
подверженные ее духовному притяжению, живо откликались на
различные новые направления и идеи за рубежом, пропагандировали их в своих
лекциях, руководствах и диссертациях и тем самым раскрывали перед
молодежью перспективы творчества в ряде других важных областей
математики. Эти ученые, к которым принадлежали и некоторые питомцы
петербургской школы, явились в России пионерами теории
аналитических функций Римана и Вейерштрасса, операционного исчисления,
учения о кватернионах и гиперкомплексных числовых системах, теории
инвариантов, математической логики, абстрактной алгебры и теории
групп, теории множеств и функций действительного переменного,
интегральных уравнений и т. д. Эти же ученые продолжили у нас
разработку неевклидовой геометрии, а от нее перешли к основаниям
геометрии. Теперь видно, что педагогическая и научная деятельность во всех
указанных областях имела гораздо большее значение, чем казалось
полвека назад: она существенно подготовила почву для возникновения
и расцвета ряда советских математических школ, часть которых свои
первые шаги сделала еще перед Октябрьской революцией.
Одним из основных предметов занятий русских математиков
рассматриваемого периода явилась теория дифференциальных уравнений,
обыкновенных и с частными производными. Ею занимались не только
в петербургской школе. Замечательные результаты в аналитической
теории дифференциальных уравнений были получены в семидесятых —
восьмидесятых годах С. В. Ковалевской и в девятисотых годах С. Н. Берн-
штейном. Различные проблемы теории дифференциальных уравнений
разрабатывали в Москве А. Ю. Давидов, А. В. Летников, К. М. Петерсон,
Д. Ф. Егоров, в Казани и позднее в Петербурге — В. Г. Имшенецкий,
в Казани, а затем в Харькове — Д. М. Синцов, в Киеве — В. П. Ермаков,
в Одессе — Е. Л. Буницкий.
В шестидесятые годы складывается геометрическая школа в Москве.
Дерптский ученик Миндинга К. М. Петерсон основал здесь сильную
школу дифференциальной геометрии, крупнейшими представителями
326 ГЛ. 15. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
которой явились Б. К. Млодзеевский и Д. Ф. Егоров. В Москве же
В. Я. Цингер возбудил интерес к проективной геометрии и привлек к
занятиям ею К. А. Андреева и А. К. Власова. В 70-е годы, полтора десятилетия
спустя после кончины Лобачевского, возрождаются исследования по
геометрии в Казани, где учение о неевклидовых пространствах
разрабатывают Ф. М. Суворов и А. П. Котельников, неевклидову механику —
Котельников, теорию коннексов — Д. М. Синцов и линейчатую
геометрию — Д. Н. Зейлигер. Следует заметить, чтоК. А.Андреев и Д. М.
Синцов основную научную и педагогическую работу вели затем в Харькове.
На рубеже XIX и XX вв. В. Ф. Каган и С. О. Шатуновский в Одессе
ведут работы по основаниям геометрии.
Незадолго до Октябрьской революции возникли два коллектива,
которым предстояло блестящее будущее. Это, во-первых, московская
школа теории функций, созданная Д. Ф. Егоровым и Н. Н. Лузиным,
и, во-вторых, школа алгебры и теории групп, начало которой было
положено в Киеве Д. А. Граве.
Преемственные связи и вместе с тем своеобразие нового периода
ясны из сказанного. От Лобачевского протягиваются нити к казанским
и одесским геометрам, от Миндинга — к московской геометрической
школе, от занятий Буняковского и Остроградского теорией
вероятностей, теорией чисел и интегрированием иррациональностей — к
соответствующим направлениям петербургской школы. Разумеется, все эти
исследования велись на новом уровне и охватывали новый круг задач.
В геометрии изучаются свойства трехмерного пространства Римана
и га-мерных пространств, а также аксиоматика этой науки. В теории чисел
переходят от решения частных задач к разработке целых ее отраслей
и созданию принципиально новых методов. В теории вероятностей
проводятся основоположные изыскания по ее предельным теоремам, которые
впервые распространяются на зависимые случайные величины (цепи
Маркова). А наряду со всем этим русские ученые впервые приступают
к разработке проективной геометрии, теории гиперкомплексных чисел,
теории групп. Наконец, в России возникают новые научные направления,
например, в теории наилучшего приближения функций, геометрической
теории чисел, качественной теории дифференциальных уравнений.
Сравнение состояния и тенденций математики в России 1850—1917 гг.
с положением за рубежом показывает, во-первых, значительную
оригинальность проблематики русских ученых и, во-вторых, сохранение,
хотя и в меньшей степени, чем ранее, неравномерности в развитии
отдельных дисциплин. Эта неравномерность постепенно ослабевала и чем далее,
тем больше. Нужно, впрочем, иметь в виду, что математические науки
неравномерно развивались и в любой другой европейской стране, в том
числе в Германии и во Франции, сохранявших на протяжении этого
времени ведущее положение в математике.
В развитии мировой математики рассматриваемого периода следует
выделить три наиболее значительных момента: развитие теории групп
и новой алгебры, бурный расцвет теории функций комплексного
переменного, создание теории функций действительного переменного и теории
множеств. Эти моменты наряду с дальнейшим развитием неевклидовой
геометрии определили в главном облик современной математики.
Как уже говорилось, идеи теории групп подстановок, с
особенным блеском развитые около 1830 г. Э. Галуа, первоначально остались
вне поля зрения математиков. Не сразу привлекли внимание и труды
А. Кэли, четверть века спустя приступившего к изучению абстрактных
ОСНОВНЫЕ НАПРАВЛЕНИЯ МАТЕМАТИЧЕСКИХ ИССЛЕДОВАНИЙ 327
групп, а также предшествовавшие им работы Д. Пикока, А. де Моргана
и У. Гамильтона, приступивших к построению общей теории
алгебраических операций. Положение вещей изменилось в семидесятые годы,
когда С. Ли создал теорию непрерывных групп и применил ее в теории
дифференциальных уравнений, а также, наряду с Ф. Клейном, в
геометрии. С этих пор теоретико-групповые методы получают все более
широкое распространение в математике, а в последние десятилетия
и в физике.
Новая алгебра — весьма разветвленная дисциплина, в которой
исторически начальная задача вычисления корней алгебраических
уравнений составляет лишь одну из глав. Лагранж, Руффини, Абель, Галуа
выдвинули на передний план проблему разрешимости уравнений в
радикалах; эти исследования велись теоретико-групповыми методами. Видное
место в алгебре, начиная с появившихся в середине сороковых годов
работ Г. Грассмана и У. Гамильтона, заняла теория гиперкомплексных
числовых систем, своеобразных обобщений обыкновенных комплексных
чисел; одной из разновидностей таких систем, ныне называемых
«алгебрами», является алгебра векторов. На границе между алгеброй и теорией
чисел лежит теория алгебраических чисел, начало которой положил
К. Гаусс и которую затем разрабатывали Э. Куммер, Р. Дедекинд, Л. Кро-
некер, Д. Гильберт и другие.
Судьбы алгебры в России в известной мере характерны для тех
направлений, которые находились вне круга интересов петербургской
школы. Прежде всего началось усвоение и распространение новых идей,
главным образом в периферийных университетах. В 1864 г. молодой
харьковский магистрант Д. М. Деларю изложил идеи теории Галуа. Через
двадцать лет эта теория явилась предметом магистерской диссертации
Д. Ф. Селиванова (Петербург, 1885); тогда же теорию групп стали
пропагандировать в своих лекциях, учебниках и монографиях А. В. Васильев
в Казани, М. Е. Ващенко-Захарченко и В. П. Ермаков в Киеве. Вскоре
затем начинается творческая разработка и применение новых
алгебраических методов. В конце XIX столетия идеи Ли использует в своих
исследованиях по теории коннексов Д. М. Синцов; в начале XX века работы
С. Ли и Ф. Клейна были изложены и нашли свое применение в трудах
В. Ф. Кагана по основаниям геометрии. В начале же нынешнего века
создал новую алгебраическую школу в Киеве Д. А. Граве, ученик
которого О. Ю. Шмидт выпустил оригинальный труд по «Абстрактной теории
групп» (1916). Годом позже С. О. Шатуновский опубликовал в Одессе
магистерскую диссертацию, содержавшую оригинальное построение
алгебры и, в частности, теории Галуа.
Сходная картина наблюдается и в учении о гиперкомплексных
числовых системах. Первое изложение гамильтоновой теории кватернионов
на русском языке мы находим в докторской диссертации киевского
ученого П. Э. Ромера, опубликованной в 1868 г. почти через 25 лет после
первых публикаций У. Гамильтона (1844). Еще четверть века спустя
(1892) дерптский математик Ф. Э. Молин выступил с глубокими работами
о системах высших комплексных чисел; тогда же А. П. Котельников
в Казани детально разрабатывал теорию бикватернионов и ее приложения
к механике и геометрии неевклидовых пространств (1895).
Что касается теории алгебраических чисел, то блестящие работы
в этой области Е. И. Золотарева (1874—1878), которые публиковались
одновременно с родственными им работами Р. Дедекинда, положили
начало целой серии исследований русских математиков — И. И. Иванова,
328 ГЛ. 15. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
Ю. В. Сохоцкого, А. А. Маркова, Г. Ф. Вороного, Д. А. Граве, В. П. Вель-
мина и других.
Русские математики вели отдельные исследования и в других
областях алгебры, например, в изучении разрешимости некоторых видов
уравнений при помощи тех или иных специальных функций (П. А.
Некрасов и Л. К. Лахтин).
Примерно таким же, как в области алгебры, было в России положение
в области теории функций действительного и комплексного переменных.
Основным отправным пунктом здесь явились работы Коши, который
первый в широком объеме приступил к укреплению оснований всего
математического анализа и дальнейшей его разработке методами новой
теории пределов. Исходя как из внутренних потребностей исчисления
бесконечно малых, так и из новых проблем и методов математической
физики, Коши поставил на реальную почву решение различных «проблем
существования» анализа. Важные результаты в реформе анализа, наряду
с Коши и работавшим независимо от него Б. Больцано, получены были
в теории рядов Н. Абедем, П. Дирихле, Н. И. Лобачевским и другими.
Но все это было только началом. Скоро обнаружилось, что в построениях
Коши недоставало весьма существенных элементов, доказательства
страдали неполнотой, а некоторые утверждения были даже ошибочны.
Так, Коши не выделил еще понятия равномерной сходимости и
равномерной непрерывности и не усмотрел, что необходимой частью фундамента
анализа должно быть развернутое учение о действительном числе. С
середины XIX столетия исследования по обоснованию анализа резко
усиливаются и вместе с тем все более полно и эффективно используются в тех
его отделах, которые обслуживают математическое естествознание,
например, в теории дифференциальных уравнений и вариационном исчислении.
Выдающееся значение имела деятельность К. Вейерштрасса, который
в своих лекциях и мемуарах впервые строго установил основные свойства
непрерывных функций *), а также показал значение и ввел в постоянный
обиход применение неравенств, дающих строгие оценки разнообразных
предельных переходов и приближений. В начале семидесятых годов
К. Вейерштрасс, Р. Дедекинд и Г. Кантор, принимая понятие
натурального числа за исходное, независимо друг от друга и каждый по-своему
строят современное учение о действительном числе, завершая в известном
смысле процесс арифметизации анализа, начавшийся еще в XVIII веке.
Более детальное изучение свойств непрерывных и разрывных
функций и процессов дифференцирования и интегрирования, в значительной
мере связанное с разработкой теории тригонометрических рядов, привело
во второй половине XIX века к выделению в самостоятельную науку
общей теории функций действительного переменного. Главным образом
с этим же кругом проблем было связано создание в восьмидесятые годы
теории множеств, основателем которой был Г. Кантор. Все это
подготовило почву для чрезвычайно продуктивной и влиятельной французской
школы теории функций во главе с Э. Борелем, Р. Бэром и А. Лебегом,
а также для многочисленных исследований в других странах. Наконец,
логические трудности, встретившиеся в самой теории множеств, и более
глубокий анализ оснований геометрии и арифметики обусловили быстрое
развитие математической логики — общей теории математических
доказательств, которая в наши дни приобрела не только теоретическую, но
2) Отдельные важные теоремы Вейерштрасса встречаются уже в рукописях
Больцано тридцатых годов, увидевших свет лишь сто лет спустя.
ОСНОВНЫЕ НАПРАВЛЕНИЯ МАТЕМАТИЧЕСКИХ ИССЛЕДОВАНИЙ 329
и практическую актуальность, в частности, в теории математических
машин.
Теоретико-функциональные идеи начали привлекать пристальное
внимание русских ученых на самом рубеже XIX и XX вв. В 1900 г.
Б. К. Млодзеевский прочитал в Московском университете первый курс
лекций по теории функций действительного переменного. В 1907 г.
выходят в свет первые русские монографии по теории множеств —
магистерские диссертации И. И. Жегалкина о трансфинитных числах (Москва)
и В. Л. Некрасова о строении и мере линейных точечных областей (Томск).
Теория действительного числа, учение о трансфинитных числах и другие
вопросы находили освещение также в лекциях Д. Ф. Егорова, книгах
А. В. Васильева, статьях и лекциях С. О. Шатуновского. В 1911 г.
Д. Ф. Егоров опубликовал известную теорему о почти всюду сходящейся
на данном отрезке последовательности измеримых функций. С этого же
года начинается блестящий цикл работ по теории функций Н. Н. Лузина,
среди которых выделяется его классическая диссертация об интеграле
и тригонометрическом ряде (1915). В 1915—1916 гг. выступают в печати
ученики Егорова и Лузина — Д. Е. Меньшов, П. С. Александров
и А. Я. Хинчин. Все значение деятельности этой очень сильной, хотя
первоначально и небольшой группы математиков раскрылось уже в
послереволюционный период.
Наряду с функциями действительного переменного огромное место
в развитии математики новейшего времени занимают функции
комплексного переменного, общую теорию которых разработали с различных точек
зрения прежде всего Коши (1825 и след. годы) и несколько позже, начиная
с середины XIX века, Риман и Вейерштрасс. Методы ее глубоко проникли
почти во все области математики, от теории чисел до геометрии, и стали
одним из главных средств теоретической физики и технических наук.
В России теория аналитических функций приобретала популярность
постепенно, хотя еще Остроградский в лекциях пятидесятых годов излагал
приложения теории вычетов Коши к вычислению определенных
интегралов. В 1860 г. магистерскую диссертацию по интегрированию в
комплексной области защитил в Москве К. И. Карастелев. Одним из ранних
пропагандистов идей Римана явился работавший в Киеве М. Е. Ващенко-
Захарченко (1866). В Киеве же В. Я. Букреев развивал идеи теории
аналитических функций Вейерштрасса (1883 и след. гг.). Однако в разработке
общей теории аналитических функций русские математики
рассматриваемого периода приняли еще мало участия. П. Л. Чебышев и ряд его
учеников избегали по возможности функций комплексного переменного. Все же
одному из членов петербургской математической школы, Ю. В. Сохоц-
кому, принадлежит в этой области несколько ценных открытий,
изложенных в двух его диссертациях (1868 и 1873 гг.), о которых будет сказано
в дальнейшем. Вместе с тем методы общей теории функций — именно
теории Вейерштрасса — получили важные применения в аналитической
теории дифференциальных уравнений у С. В. Ковалевской, в
классических исследованиях А. М. Ляпунова, в работах по линейным
дифференциальным уравнениям В. А. Анисимова, в теории цилиндрических
функций Н. Я. Сонина и еще в некоторых случаях. Перед самой Октябрьской
революцией ученик Д. Ф. Егорова В. В. Голубев выступил в Москве
с магистерской диссертацией (1916), в которой рассматривались вопросы,
пограничные для теории функций действительного и комплексного
переменных. Диссертация Голубева явилась первой в большой серии
дальнейших исследований советских ученых. Очень важную роль, особенно
330 ГЛ. 15. ОБЩИЕ УСЛОВИЯ РАЗВИТИЯ МАТЕМАТИКИ
в дальнейшем развитии геометрической теории функций, сыграли ее
применения в гидро- и аэродинамике. Здесь большое стимулирующее
влияние оказали исследования Н. Е. Жуковского и С. А. Чаплыгина
(1902). Приложениями той же теории к проблемам теории упругости
занимался Г. В. Колосов (1908 и след. гг).
Таким образом, если три только что рассмотренных больших
направления математической мысли не были в рассматриваемое время в России
главными, то каждое из них было в той или иной мере представлено в
университетском образовании и научной деятельности, в каждом были
получены отдельные важные результаты, а незадолго перед Октябрьской
революцией у нас уже началось формирование подлинных школ новой
алгебры и теории функций.
В этом кратком обзоре мы пропустили многое. Укажем для примера,
что в последние десятилетия XIX века в России началось развитие
математической логики, первые значительные успехи в которой за рубежом
были достигнуты незадолго перед тем А. де Морганом, Д. Булем, С. Дже-
вонсом и Э. Шредером. Здесь на первом по времени и значению месте
следует назвать казанского астронома П. С. Порецкого, продвинувшегося
в алгебре логики существенно дальше, чем его предшественники (1883
и след. гг.) и поставившего в Казанском университете первый в стране
курс лекций по этому предмету. На рубеже XIX—XX вв. проблемы
математической логики разрабатывали также одесские ученые — И. В. Сле-
шинский, Е. Л. Буницкий и С. О. Шатуновский. В настоящее время
советская школа математической логики (П. С. Новиков, А. И.
Мальцев (1909—1967), А. А. Марков и др.) является одной из сильнейших.
С восьмидесятых годов в ряде университетов начинаются работы
по истории математики. О В. В. Бобынине уже говорилось. В Киеве ею
занимались М. Е. Ващенко-Захарченко и профессор древней истории
Николай Михайлович Бубнов (род. 1858), автор оригинальной гипотезы
о происхождении и распространении наших цифр («Арифметическая
самостоятельность европейской культуры», Киев, 1908) и издатель
сочинений средневекового математика Герберта (Gerberti... Opera mathema-
tica. Berlin, 1899). В Одессе глубокие исследования по истории учения
о функциях комплексного переменного вели И. Ю. Тимченко и по истории
неевклидовой геометрии и оснований геометрии — В. Ф. Каган.
Историей математики, в частности неевклидовой геометрии, много занимался
также А. В. Васильев.
В целом русские математики были лучше знакомы с работами своих
зарубежных коллег, чем последние с достижениями наших ученых.
Частью это объяснялось недостаточным распространением русских
журналов и в еще большей мере незнакомством иностранцев с русским языком.
Многие важные исследования, опубликованные на русском языке, долго
оставались за границей неизвестными или же их знали только по кратким
аннотациям в реферативных журналах. Несомненное значение имела
также неравномерность развития математики в различных странах.
Более близкие по тематике сочинения русских ученых получали
распространение на Западе довольно быстро. Очень широкую известность
получили открытия П. Л. Чебышева в теории чисел и интегрирования
алгебраических функций или, скажем, Н. Я. Сонина в теории
цилиндрических функций. Всеобщее внимание сразу привлекли печатавшиеся
за границей труды С. В. Ковалевской. Знали за рубежом и исследования
по геометрии Ф. М. Суворова, А. П. Котельникова, В. Ф. Кагана,
С. О. ШатуноЁского. Во Франции и Германии популярны были в силу
ОСНОВНЫЕ НАПРАВЛЕНИЯ МАТЕМАТИЧЕСКИХ ИССЛЕДОВАНИЙ 331
их педагогических достоинств даже менее значительные монографии
В. Г. Имшенецкого, содержавшие изложение классических методов
интегрирования уравнений с частными производными первого и второго
порядков.
Иначе обстояло дело с русскими работами, тематически или по методу
далекими от исследований западноевропейских ученых. Такие труды,
даже первоклассные, нередко долго оказывались вне поля зрения за
рубежом. Так обстояло, например, дело вплоть до начала XX века с
исследованиями Чебышева по теории наилучшего приближения функций
и с работами его же и его учеников по теории вероятностей, которые
приобрели всемирную славу и были продолжены за рубежом только
в последние десятилетия, после того как эта наука под влиянием запросов
естествознания, статистики и техники повсюду, а не только в России,
выдвинулась на одно из первых мест 1).
Результатом недостаточного знакомства с русской математической
литературой являлась иногда напрасная трата усилий зарубежных
ученых на разработку давно решенных проблем. Некоторые теоремы
Б. К. Млодзеевского по теории многомерных многообразий вновь были
получены через 15—20 лет итальянскими и французскими геометрами,
важные результаты в теории чисел Г. Ф. Вороного через сорок с лишним
лет опять были найдены немецким ученым Буллигом. Таких примеров
немало.
Общая тенденция вела, однако, ко все более широкому и полному
международному сотрудничеству. Центральные идеи, развивавшиеся
русскими математиками во всех основных направлениях их творчества,
рано или поздно находили продолжение и за пределами нашего отечества.
Особенно важные сочинения, написанные по-русски, переводились
на другие европейские языки: так, магистерская диссертация А. М.
Ляпунова 1884 г. была издана на французском языке в 1904 г., а его
докторская работа 1892 г.— в 1907 г.; этот последний перевод был вновь издан
в Соединенных Штатах Америки сорок лет спустя.
Перед Октябрьской революцией лучшие достижения наших
отечественных ученых пользовались заслуженным признанием во всем мире.
г) Некоторую роль играла и научная конкуренция. Характерно, например,
отношение к исследованиям Е. И. Золотарева, который совершенно самостоятельно и
своеобразно разрабатывал общую теорию алгебраических чисел параллельно с Р. Дедекин-
дом. Даже такие знатоки вопроса, как Л. Кронекер или П. Бахман, не изучив, как
следует, сочинения Золотарева, высказывали о них превратные суждения.
ГЛАВА ШЕСТНАДЦАТАЯ
П. Л. ЧЕБЫШЕВ И ПЕТЕРБУРГСКАЯ
МАТЕМАТИЧЕСКАЯ ШКОЛА
Жизнь П. Л. Чебышева. Крупнейший наряду с Н. И. Лобачевским
русский математик XIX века Пафнутий Львович Чебышев родился
16 мая 1821 г. в сельце Окатово Боровского уезда Калужской губернии,
где отец его имел небольшое поместье. Когда мальчику было около 10 лет,
семья переехала в Москву. Здесь он получил домашнее образование
и в 1837 г. поступил на физико-математический факультет университета,
который окончил в 1841 г. кандидатом. Еще при переходе на второй курс
он написал свою первую работу о вычислении корней уравнений, о
которой шла речь выше (стр. 270). За это сочинение Чебышев был награжден
на конкурсе 1841 г. серебряной медалью; впрочем, оно было вполне
достойно золотой.
Годы занятий в Москве наложили печать на всю последующую
деятельность Чебышева. В Московском университете он не только приобрел
весьма солидные знания, но и получил важные творческие стимулы. Вскоре
после окончания университета Чебышев опубликовал две первые свои
работы по анализу, непосредственно примыкавшие к тематике Коши,
а именно «Заметку об одном классе кратных определенных интегралов»
(в журнале Лиувилля, 1843) и «Заметку о сходимости ряда Тейлора»
(в журнале Крелле, 1844); вторая из них, между прочим, представляет
собою единственный труд Чебышева, в котором широко используется
теория аналитических функций Коши1). Два следующих сочинения
московского периода были посвящены теории вероятностей, об интересе
к которой в математических кругах обеих наших столиц уже говорилось.
Одним из них явился «Опыт элементарного изложения теории
вероятностей» (М., 1845), задуманный как руководство для студентов
Демидовского лицея в Ярославле, где преподаванию сообщен был юридический
уклон 2). Летом 1846 г. Чебышев защитил «Опыт» в качестве магистерской
диссертации, оппонентами выступили Н. Е. Зернов и Н. Д. Брашман.
1) Труды Чебышева изданы в советское время в пяти томах: П. Л. Чебышев,
Полное собрание сочинений, М.—Л., 1944—1951 (председ. ред. коллегии С. Н. Берн-
штейн); издание снабжено многими комментариями. В V томе имеется хронологический
перечень сочинений Чебышева с указанием соответствующего тома собрания; здесь же
собраны многие биографические материалы и переписка. Глубокие обзоры творчества
Чебышева см. в кн.: Научное наследие П. Л. Чебышева. Вып. I. Математика, вып. II.
Теория механизмов. М.— Л., 1945. В Полное собрание сочинений не вошли некоторые
записанные слушателями курсы лекций, а также небольшие заметки в
«Энциклопедическом словаре» П. Л. Лаврова.
2) Ярославский лицей был основан в 1805 г. на средства П. Г. Демидова (1738—
1821); в 1833—1845 гг. Демидовский лицей был подчинен Московскому университету.
Мысль о написании элементарного курса теории вероятностей была подана, кажется,
тогдашним попечителем Московского учебного округа С. Г. Строгановым (1794—1882).
Пафнутий Львович Чебышев.
334
ГЛ. 16. П. Л. ЧЕБЫШЕВ И ЕГО ШКОЛА
Добавлением к диссертации явилось «Элементарное доказательство
одного общего предложения теории вероятностей», именно закона
больших чисел Пуассона (журнал Крелле, 1846). Впоследствии, как мы знаем,
теория вероятностей стала одним из главных по значению, если не по
объему, направлений творчества Чебышева.
В Москве же П. Л. Чебышев написал свою первую работу по теории
алгебраических функций, примыкавшую к кругу вопросов,
разрабатывавшихся Остроградским, Брашманом и Сомовым. Это сочинение «Об
интегрировании помощью логарифмов», подготовленное (быть может,
в первом варианте) в конце 1843 г., послужило позднее диссертацией
Чебышева на право чтения лекций в Петербургском университете. В свое
время оно опубликовано не было *) и содержавшиеся в нем результаты
вошли в другие работы Чебышева по интегрированию иррациональных
функций,— проблеме, которой он с увлечением занимался на
протяжении более двадцати лет.
Влияние физико-математического факультета Московского
университета отразилось и на исключительном интересе Чебышева к задачам
прикладной механики, в которую он внес впоследствии значительный
вклад и которая привела его к созданию теории наилучшего приближения
функций.
Первое место среди учителей Чебышева принадлежало Н. Д. Браш-
ману. Великий математик сам засвидетельствовал это в заметке
«Разложение в ряды при помощи непрерывных дробей», напечатанной в форме
письма к Брашману в первом томе «Математического сборника» (1866),
а перед тем доложенной самим автором на заседании Московского
математического общества 18(30) сентября 1865 г. Статья завершалась
обращением к Н. Д. Брашману: «Сказанного мною достаточно, чтобы увидеть,
как много интереса пред став лгяет предмет, на который я был наведен
Вашими лекциями и всегда драгоценными для меня беседами с Вами» 2).
В 1847 г. Чебышев переехал в Петербург. Весной он защитил в
Петербургском университете только что упоминавшуюся диссертацию на право
чтения лекций, вскоре был утвержден доцентом и в сентябре начал первые
свои учебные курсы — по алгебре и теории чисел,—последний он читал в
течение 35 лет. Научные исследования Чебышева в этот новый,
петербургский период жизни сосредоточились прежде всего именно на теории чисел,
которую он вновь поднял в России на уровень, столетием ранее
достигнутый в нашей стране благодаря гению Эйлера. Толчок сообщило,
по-видимому, изучение эйлеровского арифметического наследия, к которому
в том же 1847 г. Чебышева привлек Буняковский; однако некоторые
вопросы теории чисел встретились Чебышеву еще в ходе подготовки
второй диссертации. Он указал на это в тезисах работы, а во вступительном
слове к ее защите специально отметил, что «такая зависимость
интегрирования дифференциалов от свойств чисел весьма замечательна 3).
Буняковский и Чебышев в короткие сроки подготовили полное
собрание трудов Эйлера по теории чисел и подробный систематический
указатель к нему, так что двухтомные Leonhardi Euleri Commentationes
arithmeticae collectae, в которые вошли и многие неопубликованные
заметки и фрагменты Эйлера, увидели свет уже в 1849 г. Одновременно
появилась докторская диссертация Чебышева — замечательное по ори-
г) Эта диссертация была напечатана впервые в «Известиях АН СССР», VII серия,
отд. физ.-матем. наук, 8 (1930).
2) П. Л. Чебышев, Полное собрание сочинений, т. II, стр. 415.
3) Там же, т. V, стр. 144. Мы коснемся этого вопроса в дальнейшем.
ЖИЗНЬ П. Л. ЧЕБЫШЕВА
335
гинальности построения и выводов изложение теории сравнений,
содержавшее многие собственные результаты автора. Благодаря своим высоким
достоинствам «Теория сравнений» Чебышева, защищенная в
Петербургском университете 15(27) мая 1849 г. и через несколько дней отмеченная
половинной Демидовской премией Академии наук, десятки лет служила
основным университетским руководством предмета. Она была переиздана
в 1879 и 1907 гг., переведена на немецкий язык в 1888 г. и на итальянский
в 1895 г. В приложении к «Теории сравнений» вышел знаменитый мемуар
Чебышева «Об определении числа простых чисел, не превосходящих
данной величины», французский перевод которого в записках Академии наук
(1848, опубл. в 1851) и в журнале Лиувилля (1852) обратил на себя
внимание всего ученого мира. За этим в 1850 г. последовал непосредственно
примыкающий к предыдущему мемуар «О простых числах», напечатанный
прежде всего в журнале Лиувилля (1852). Еще несколько статей по
теории чисел появилось тогда же. Впоследствии Чебышев обращался к
теории чисел редко.
В 1850 г. П. Л. Чебышев был избран экстраординарным профессором
Петербургского университета и в 1860 г.— ординарным. Это десятилетие
было временем исключительно интенсивной деятельности его в различных
направлениях. Еще продолжая исследования по теории чисел, он
возвращается к теории алгебраических функций и уже первая его работа
«Об интегрировании иррациональных дифференциалов», появившаяся
в журнале Лиувилля за 1853 г., далеко позади оставила результаты
диссертации на право чтения лекций. В 1849—1851 гг. Чебышев читал
на «реальном отделении» Петербургского университета г) курс
практической (прикладной) механики, а в 1852—1856 гг. читает его ив
Александровском лицее, который был открыт в 1811 г. в Царском Селе и в котором
некогда учился А. С. Пушкин. Из программы, составленной Чебьппевым
в январе 1850 г., видно, что уже тогда он заинтересовался кругом
вопросов, которые вскоре привели его к созданию новых отделов теории
механизмов и, в прямой связи с нею, теории приближения функций; этот
интерес еще более возрос во время пятимесячной командировки за
границу в 1852 г., о которой еще будет речь впереди. Вскоре после
возвращения из-за границы Чебышев представил Академии наук мемуар
«Теория механизмов, известных под названием параллелограммов»,
напечатанный в академических записках 1854 г., а в 1857 г.— основоположный
труд «Вопросы о наименьших величинах, связанные с приближенным
представлением функций», который появился в тех же записках в 1859 г.
К этому следует добавить, что, откликаясь на нужды Родины,
Чебышев в самом начале 1856 г. приступил к работе в Артиллерийском
отделении Военно-ученого комитета, а через несколько недель принял на себя
также и обязанности члена Ученого комитета Министерства народного
просвещения, которые с усердием выполнял до 1873 г. Работа Чебышева
в Артиллерийском комитете, продолжавшаяся до 1869 г., имела серьезное
значение для баллистики и вообще для артиллерийской науки. Например,
в 1867 г. Чебышев вывел хорошо согласовавшуюся с опытами
приближенную формулу дальности полета в воздухе сферических снарядов с
начальными скоростями, не превосходящими некоторого предела. Его
математические консультации широко использовал, между прочим, крупнейший
русский баллистик Николай Владимирович Маиевский (1823—1892),
г) Это отделение существовало только в 1839—1843 и 1849—1851 гг. и набор
студентов произвело лишь дважды — в 1839 и 1849 гг.
336
ГЛ. 16. П. Л. ЧЕБЫШЕВ И ЕГО ШКОЛА
бывший питомец Московского университета, а с 1878 г.—
член-корреспондент Академии наук. С занятиями артиллерией, а именно с вопросом
о составлении таблиц стрельбы по опытным данным, отчасти связаны были
важные работы Чебышева по теории интерполирования.
Начиная с 1853 г. в творчестве Чебышева все с большей силой
преобладают теория механизмов и теория приближения функций, которым,
взятым вместе, принадлежит более 2/3 его работ. Исследования по теории
приближения функций переплетались с работами по ортогональным
многочленам, оценкам определенных интегралов, приближенным квадратурам,
отделению корней алгебраических уравнений и т. д. Наряду с этим в 60-е
годы, отчасти в связи с курсом теории вероятностей, который ранее вел
Буняковский и который сам он читал с 1860/61 до 1881/82 учебного года,
Чебышев вновь обратился и к этому предмету. В работе «О средних
величинах», напечатанной во втором томе «Математического сборника» (1866),
он дал широкое обобщение закона больших чисел. Вслед за тем он после
долгих поисков предложил соответствующее обобщение центральной
предельной теоремы, которой посвятил статью «О двух теоремах
относительно вероятностей» в «Записках Академии наук» (1887),
подготовленную, когда автору было уже 66 лет. Два этих труда принадлежат к числу
классических.
Чебышев не раз представлял русскую науку за рубежом. Наиболее
тесны были его контакты с французскими математиками. С 1873 по 1882 г.
он сделал 16 докладов на четырех сессиях Французской ассоциации
содействия преуспеванию науки. Здесь, как упоминалось, он
демонстрировал свой арифмометр, конструкции и улучшению которого он в то
время уделил немало времени. Мы говорили также об активном участии
Чебышева в съездах русских естествоиспытателей и врачей.
Замечательные открытия П. Л. Чебышева принесли ему громкую
славу в России и за границей. 13 апреля 1853 г. он был избран адъюнктом
Академии наук. Любопытно, что в своем представлении Буняковский,
Струве, Фусс и Якоби наряду с заслугами Чебышева в области
математики особо отмечали, что он «ревностно занимается практической
механикой» и писали: «При быстром развитии фабричной промышленности
в наше время и успехах практической механики, Академия, конечно,
признает чрезвычайно полезным усилить последний предмет, приобретя
ученого, которого дознанные математические знания ручались бы вместе
за основательность практических его сведений» х). Три года спустя
Чебышев был избран экстраординарным академиком по кафедре прикладной
математики, а 22 декабря 1858 г. ординарным. Помимо того, он состоял
почетным членом всех русских университетов и Артиллерийской
Академии. О признании заслуг Чебышева за рубежом говорят его избрание
членом-корреспондентом (1860) и иностранным членом (1874) Академии
наук Института Франции, членом-корреспондентом Берлинской
Академии наук (1871), членом Лондонского королевского общества (1877),
Итальянской королевской академии (1880) и Шведской Академии наук
(1893). Мы назвали здесь далеко не все научные отличия Чебышева.
В 1890 г. Ш. Эрмит, бывший тогда президентом Французской Академии
наук, обратился к своему правительству с просьбой о награждении
Чебышева командорским крестом ордена Почетного легиона. Просьба была
уважена. Извещая об этом Чебышева, Эрмит 21 мая 1890 г. писал: «Все
члены Академии, которым было представлено возбужденное мною хода-
) П. Л. Чебышев, Полное собрание сочинений, т. V, стр. 276—277.
О ТВОРЧЕСТВЕ ЧЕБЫШЕВА
337
тайство, поддержали его своей подписью и воспользовались случаем
засвидетельствовать живейшую симпатию, которую Вы им внушаете.
Все они присоединились ко мне, заверяя, что Вы являетесь гордостью
науки в России, одним из первых геометров Европы, одним из
величайших геометров всех времен» *).
Летом 1882 г. Чебышев оставил после 35-летней службы
Петербургский университет и занялся исключительно научной работой.
Интенсивность его занятий несколько ослабела, но и в последующие годы он
опубликовал еще 14 работ из 82, напечатанных им за полстолетия. Скончался
П. Л. Чебышев на семьдесят четвертом году жизни 8 декабря 1894 г.
и еще в феврале того же года он представил Академии наук свой
последний труд.
О творчестве Чебышева. Чебышев был математиком очень широких
интересов, простиравшихся от теории чисел до баллистических задач.
Вместе с тем все его творчество было проникнуто некоторыми общими
идейными устремлениями и свидетельствует о
стихийно-материалистическом подходе великого математика к науке вообще и избранной им
области знания в частности.
Быть может, особенно характерно для Чебышева было поразительное
уменье находить в частных практических, нередко технических, задачах
истоки глубоких математических теорий. В полушутливой форме он
незадолго до кончины высказал свой взгляд на взаимоотношения теории
с практикой в беседе с А. В. Васильевым. Математика,— говорил
Чебышев,— пережила ранее два периода. В первом — задачи ставились богами
(делосская задача об удвоении куба), во втором — полубогами (Паскаль,
Ферма). Мы вошли теперь в третий период, когда задачи ставит нужда.
При этом Чебышев был уверен, что чем труднее естественно поставленная
задача, тем плодотворнее должны быть методы ее решения и тем шире
область их последующих применений в других вопросах 2).
Глубокий интерес Чебышева к прикладным вопросам нашел
выражение в его отчете о заграничной командировке во Францию, Англию и
Германию в июле — ноябре 1852 г. Поразительно, как много вообще успел
Чебышев сделать за эти пять месяцев, и еще поразительнее, как соединял
он занятия вопросами теории чисел, интегрирования иррациональных
функций и теории двояко-периодических функций с изучением
промышленности и техники, с тщательным осмотром металлургических
заводов и мельниц, лабораторий и технических музеев, а в них—паровых
машин, гидравлических турбин и колес, бумагопрядильных и
льнопрядильных машин, механизмов для передачи движения, арифмометра
Паскаля и автоматов изобретателя XVIII века Вокансона. Описывая
содержание своих бесед с лучшими математиками Парижа, Лондона и Берлина,
Чебышев вместе с тем высказывает соображения о качестве работы машин
и рассказывает о ходе собственных изысканий. Чтение отчета вызывает
равное восхищение как необыкновенной интенсивностью и размахом
работы его автора, так и гениальным раскрытием математического
существа конкретных практических задач.
Приведем некоторые выдержки из отчета, пересказ которого не может
дать сколько-нибудь адекватного представления об оригинале.
х) П. Л. Чебышев, Полное собрание сочинений, т. V, стр. 434.
2) С. Н. Б е р н ш т е й н, Чебышев, его влияние на развитие математики.—
Ученые записки МГУ, 1947, вып. 91, стр. 39.
338
ГЛ. 16. П. Л. ЧЕБЫШЕВ И ЕГО ШКОЛА
«...до 8 августа занятия мои ограничивались предметами, которые
находятся в Париже и его окрестностях. При всей ограниченности
времени, которое я должен был делить между Conservatoire des arts et metiers,
мастерскими Каве и многими предметами по части практической механики,
в высшей степени интересными, как-то: атмосферическою железною
дорогою в Сен-Жермене, дорогою Со, замечательною по своим изгибам,
машиною Марли и другими, я счел необходимым не упускать из виду и того,
что мог приобресть для моего теоретического образования из беседования
с знаменитыми французскими геометрами. Посему, дообеденные часы
проводил я или в Conservatoire des arts et metiers, или на фабриках,
большею частью у Каве, вечера же посвящал частью на беседование
с гг. Коши, Лиувиллем, Биенэме, Термитом, Серре, Лебегом и другими
учеными, частью же на теоретические занятия, которые имели или
непосредственное отношение с данными, полученными мною из
рассматривания различных систем машин, или с вопросами анализа, на которые был
наведен разговором с кем-либо из ученых. Таким образом, по желанию
гг. Лиувилля и Термита, я занялся развитием тех начал, на которых
написана была моя диссертация, представленная в С.-Петербургский
университет в 1847 г. pro venia legendi 1)>> 2). Сообщив о результатах,
полученных в этом направлении (в частности, о полном решении проблемы
интегрируемости в элементарных функциях дифференциального двучлена),
Чебышев рассказывает о начале своих занятий теорией механизмов
и связанными с нею математическими проблемами:
«Из многих предметов исследования, которые представились мне при
рассматривании, и сличения между собою различных механизмов
передачи движения, особенно в паровой машине, где и экономия в топливе
и прочность машины много зависят от способов передачи работы пара,
я особенно занялся теорией механизмов, известных под названием
параллелограммов» 3).
Мы не будем сейчас задерживаться на свойствах этих
параллелограммов, отметив лишь, что «предположивши вывести правила для устройства
параллелограммов прямо из свойства этого механизма», Чебышев
«встретил вопросы анализа, о которых до сих пор знали очень мало» 4), и что
первым результатом его исследований в этом направлении и явился
упоминавшийся уже мемуар «Теория механизмов, известных под названием
параллелограммов», подготовленный еще во время командировки.
Приведенные выдержки показывают, как соединялись задачи
практики и теории в самой деятельности Чебышева. Единство теории и
практики было определяющим в его математическом творчестве и принципы
этого единства он выпукло сформулировал в речи «Черчение
географических карт», написанной для торжественного акта в Петербургском
университете в 1856 г. «Науки математические,— говорил Чебышев,— с самой
глубокой древности обращали на себя особенное внимание; в настоящее
время они получили еще более интереса по влиянию своему на искусства
и промышленность. Сближение теории с практикою дает самые
благотворные результаты, и не одна только практика от этого выигрывает; сами
науки развиваются под влиянием ее: она открывает им новые предметы
для исследования, или новые стороны в предметах давно известных.
Несмотря на ту высокую степень развития, до которой доведены науки
2) На право чтения лекций. (— А. Ю.)
2) П. Л. Чебышев, Полное собрание сочинений, т. V, стр. 247—248.
3) Там же, стр. 248—249.
4) Там же, стр. 249.
О ТВОРЧЕСТВЕ ЧЕБЫШЕВА
339
математические трудами великих геометров трех последних столетий,
практика обнаруживает ясно неполноту их во многих отношениях; она
предлагает вопросы, существенно новые для науки, и таким образом
вызывает на изыскание совершенно новых метод. Если теория много
выигрывает от новых приложений старой методы или от новых развитии
ее, то она еще более приобретает открытием новых метод, и в этом случае
науки находят себе верного руководителя в практике» *).
Среди тех вопросов, которые ставит перед математикой практика,
Чебышева преимущественно привлекали различные экстремальные
задачи — задачи о наибольших или наименьших значениях величин. В той же
речи он отмечал, что особенную важность имеют те методы, «которые
необходимы для решения различных видоизменений одной и той же
задачи, общей для всей практической деятельности человека: как
располагать средствами своими для достижения по возможности большей выгоды?
Решение задач этого рода составляет предмет как называемой теории
наибольших и наименьших величин. Эти задачи, чисто практического
характера, имеют особенную важность и для теории: все законы,
определяющие движение материи весомой и невесомой, представляют решение
задач этого рода. Нельзя не заметить особенно благотворного влияния
их на развитие наук математических» 2).
Эти положения, напоминающие цитированные ранее слова Эйлера
о том, что все происходящее в мире можно определить при помощи метода
максимумов и минимумов, но свободные от прежнего налета метафизики
и телеологии, Чебышев поясняет примерами из истории математики.
Он напоминает, прежде всего, о роли задач на отыскание наибольших
и наименьших величин в создании дифференциального исчисления,
затем о задачах, приведших к открытию вариационного исчисления
и, наконец, о новом роде таких задач, существенно отличном от
предыдущих, к которым пришел он сам, изучая вопрос о наилучшем устройстве
параллелограмма Уатта, и в которых, как мы говорим теперь, требуется
минимализировать на данном отрезке наибольшее уклонение функции
данного класса от некоторой определенной функции. Другой пример
вопросов этого рода представляет черчение географических карт. Именно,
Чебышев ставит проблему выбора той из бесчисленно многих возможных
конформных проекций на плоскость данного участка земной поверхности,
при которой различия масштаба, в разных частях карты неодинакового
будут наименьшими, так что изображение участка окажется наилучшим.
Эта практически важная задача подобна задачам, возникшим в теории
параллелограммов, но относится, так сказать, к высшему разряду: там
отыскивалось несколько постоянных величин, характеризующих искомую
функцию данного класса, здесь же требуется найти две неизвестные
функции, что,— писал Чебышев,— соответствует определению бесконечного
множества постоянных. Задача приводится к решению некоторого
уравнения в частных производных при данном значении его интеграла на
контуре. Ответ, приведенный Чебышевым без доказательства, гласил, что
наилучшей в указанном смысле будет проекция, при которой на границе
г) П. Л. Чебышев, Полное собрание сочинений, т. V, стр. 150. С. А.
Яновская указала на связь этих идей П. Л. Чебышева со взглядами А. С. Ершова,
выраженными в его статье «О содержании и преподавании теоретической механики» («Журнал
Министерства народного просвещения», 1845). Ершов, однако, гораздо более
ограниченно трактовал вопрос, подчеркивая преимущественно значение науки для
промышленной практики. См. С. А. Яновская, Два документа из истории Московского
университета.— Вестник Московского университета, 1952, № 8, стр. 43—44, 56.
2) П. Л. Чебышев, Полное собрание сочинений, т. V, стр. 150—151.
340
ГЛ. 16. П. Л. ЧЕБЫШЕВ И ЕГО ШКОЛА
изображения масштаб сохраняет одну и ту же постоянную величину1).
Указав, что для изображения всякой страны на карте получается одна
наиболее выгодная проекция, зависящая от положения страны
относительно экватора и формы ее границ, Чебышев особо остановился на карте
европейской части России, приведя основные результаты
соответствующих расчетов. Свою речь он закончил словами: «Подобно этому,
милостивые государи, большая часть вопросов практики приводится к задачам
наибольших и наименьших величин, совершенно новым для науки, и только
решением этих задач мы можем удовлетворить требованиям практики,
которая везде ищет самого лучшего, самого выгодного» 2).
С описанным подходом Чебышева к математике связано было его
постоянное стремление к строгому и вместе с тем эффективному решению
ее задач, к построению алгоритмов, которые позволяют реально доводить
исследование либо до точного числового ответа, либо до вполне пригодного
приближенного решения. При этом строгость любой теории, имеющей
дело с приближениями, Чебышев понимал в смысле возможности точного
установления пределов погрешностей, доставляемых этой теорией.
Характерной для математических работ Чебышева является
сравнительная простота и элементарность используемых им математических
средств. Чебышев применял, в частности, почти исключительно функции
действительного аргумента 3), а среди них — по возможности простейшие.
С особенным искусством он использовал средства алгебры и специально —
аппарат непрерывных дробей, который стал в его руках великолепным
орудием исследования различных вопросов теории наилучшего
приближения функций и примыкающих к ней проблем.
Говоря о Чебышеве, нам несколько раз пришлось называть Эйлера.
При всем своеобразии их индивидуальностей, принадлежавших к тому
же различным этапам развития математики, в творчестве обоих
петербургских академиков наблюдается глубокая преемственность. Интересы обоих
охватывали необыкновенно широкий круг общих вопросов,
простиравшихся от теории механизмов до теории чисел. Для обоих характерна
была тесная связь между насущными вопросами естествознания и техники
и значительной частью их собственно математической проблематики; оба
соединяли прикладную по преимуществу направленность исследований
и преимущественный интерес к конкретным задачам с отличающим
великих математиков стремлением к построению широких обобщающих
теоретических систем; оба постоянно стремились, на различных уровнях
математической строгости, к эффективному и практически наиболее
выгодному решению задач, доведенному до числового ответа. Эта идейная
преемственность нередко переходила в прямое продолжение разработки
отдельных проблем, примеры чего нам уже встречались и еще встретятся
далее. Мы здесь подчеркиваем общее, оставляя в стороне различия,
которые бросаются в глаза даже при одном сопоставлении списков работ
обоих ученых. Сказанное о Чебышеве распространяется на всю его школу,
представители которой столь же основательно знали и высоко ценили
научное наследие Эйлера, как их учитель. И для А. А. Маркова, напри-
х) Доказательство этой теоремы, как и ряда других утверждений, содержащихся
в этой речи Чебышева и в кратком мемуаре «О построении географических карт» (1856),
дал сорок лет спустя Д. А. Граве. Об этом будет сказано далее.
2) П. Л. Чебышев, Полное собрание сочинений, т. V, стр. 157.
3) Заметим, что в виде редкого исключения функции комплексного переменного
применяются Че.бышевым вслед за Эйлером и Лагранжем в только что упоминавшемся
картографическом мемуаре.
ЧЕБЫШЕВ И ЕГО УЧЕНИКИ
341
мер, было совершенно естественно в списке литературы к различным
главам его «Исчисления конечных разностей» (2-е изд., Одесса, 1911) привести
наряду с новейшими работами многочисленные сочинения Эйлера, да
не только Эйлера, но и Ньютона, Котеса, Стирлинга, Маклорена и т. д.
Чебьппев и его ученики. Помимо печатных трудов Чебышева,
большую роль в распространении его влияния, и особенно в создании его
школы, сыграла педагогическая работа ученого в Петербургском
университете. А. М. Ляпунов вспоминал: «Курсы его не были обширными,
и при изложении их он заботился не столько о количестве сообщаемого
материала, сколько о выяснении принципиальных сторон трактуемых
вопросов. Отличаясь живым и увлекательным изложением, лекции его
сопровождались множеством интересных замечаний относительно
значения и важности тех или других вопросов или научных методов.
Замечания эти высказывались иногда мимоходом по поводу какого-либо
конкретного случая, но всегда глубоко западали в умах его слушателей.
Вследствие этого лекции его имели высокое развивающее значение, и слушатели
его после каждой лекции выносили нечто существенно новое в смысле
большей широты взгляда и новизны точек зрения» х). В своих лекциях
Чебышев нередко давал обширные исторические справки о разработке
того или иного вопроса.
Чебьппев был не только вдохновляющим лектором, но и
замечательным научным руководителем. Он помогал студентам и начинающим
ученым ценными советами, предлагал им темы для самостоятельного изучения,
обещавшие привести к важным и интересным результатам, рецензировал
конкурсные студенческие сочинения, магистерские и докторские
диссертации. Раз в неделю Чебьппев принимал у себя дома всех Желающих
получить совет и, как писал К. А. Поссе, «редко кто-нибудь от него
уходил, не унося с собою новых мыслей и поощрения к дальнейшей работе»,
если только вопрос принадлежал к областям математики, интересовавшим
самого Чебышева. В противном случае беседа быстро прекращалась
и гость «уходил не вполне удовлетворенный результатами своего
посещения» 2). Умение поставить перед молодым ученым богатую возмояшостями
и увлекательную задачу — редкий дар, без которого создание научной
школы немыслимо, и этим дарованием Чебьппев обладал в самой высокой
степени. Эту черту Чебышева ярко характеризовал Е. И. Золотарев,
говоривший: «В математике... найти и верно поставить вопрос несравненно
труднее, чем его решить; как скоро вопрос поставлен и поставлен верно,
решение его так или иначе отыщется. Пафнутий Львович отличается
изумительной способностью и уменьем ставить новые вопросы в
математике» 3).
Непосредственными учениками Чебышева были А. Н. Коркин,
Ю. В. Сохоцкий, Е. И. Золотарев, А. А. Марков, А. М. Ляпунов, И. Л. Пта-
шицкий, И. И. Иванов, К. А. Поссе, Д. А. Граве, Г. Ф. Вороной, А. В.
Васильев и еще ряд математиков. Научная деятельность этих ученых
протекала под сильнейшим воздействием Чебышева, многие прямо продолжали
разработку его тематики, и все они распространяли идеи своего учителя
в университетах и других высших школах Петербурга, Казани, Киева,
Харькова, Варшавы.
г) А. М. Ляпунов, Жизнь и труды П. Л. Чебышева. В кн.: П. Л.
Чебышев, Избранные математические труды, М.—Л., 1946, стр. 18.
2) П. Л. Чебышев, Полное собрание сочинений, т. V, стр. 210.
3) Е. П. Ожигова, Егор Иванович Золотарев, М.— Л., 1966, стр. 25.
342
ГЛ. 16. П. Л. ЧЕБЫШЕВ И ЕГО ШКОЛА
Единство петербургской математической школы определялось, с одной
стороны, близостью тематики и методов ее деятелей к тематике и методам
Чебышева (хотя со временем круг их занятий становился все шире)
и, с другой, общим подходом к математике, который А. М. Ляпунов
выразил в таких словах:
«П. Л. Чебышев и его последователи остаются постоянно на реальной
почве, руководясь взглядом, что только те изыскания имеют цену,
которые вызываются приложениями (научными или практическими), и только
те теории действительно полезны, которые вытекают из рассмотрения
частных случаев.
Детальная разработка вопросов, особенно важных с точки зрения
приложений и в то же время представляющих особенные теоретические
трудности, требующие изобретения новых методов и восхождения к
принципам науки, затем обобщение полученных выводов и создание этим
путем более или менее общей теории — таково направление большинства
работ П. Л. Чебышева и ученых, усвоивших его взгляды» 1).
При всем величии достижений петербургской математической школы
ей, однако, была свойственна и некоторая ограниченность. Чебышев
и многие видные его ученики безразлично и даже скептически относились
к отдельным важным направлениям западноевропейской математики. Это
относится не только к Маркову, идейно особенно близкому к Чебышеву,
но и к Ляпунову, который, вообще говоря, высоко ценил многие новые
методы западноевропейских математиков. Например, идеи Римана в
теории функций представлялись Ляпунову «весьма отвлеченными», и он
полагал, что углубление последователей знаменитого немецкого
математика в «функционально-теоретические исследования» и в
«псевдогеометрические» изыскания в многомерных пространствах заходит иногда столь
далеко, что «теряется всякая возможность видеть их значение по
отношению к каким-либо приложениям не только в настоящем, но и в
будущем» 2).
В начале XX века отдельные молодые представители чебышевской
школы приступили к сближению ее тематики и методов с другими
направлениями математической мысли, и это вскоре принесло новые богатые
результаты.
г) А. М. Ляпунов. Жизнь и труды П. Л. Чебышева. В кн.: П. Л. Ч е б ы-
шев, Избранные математические труды, стр. 20.
2) Там же, стр. 19, 20. Следует сказать, что при этом Ляпунов высоко ценил
глубокие геометрические исследования Лобачевского и полагал, что великий геометр
«едва ли мог увидеть развитие своих идей» в упомянутых «изысканиях
трансцендентального характера» (там же, стр. 20).
ГЛАВА СЕМНАДЦАТАЯ
ТЕОРИЯ ЧИСЕЛ
Исследования П. Л. Чебышева по теории распределения простых
чисел. В системе математических наук теория чисел занимает несколько
особое место. Возникла она из рассмотрения простейших свойств целых
чисел, дробей и квадратичных иррациональностей, и первые теоремы ее
незаменимы в самых элементарных вычислениях. Вместе с тем, в отличие
от других математических дисциплин, прямые приложения теории чисел
в естествознании долгое время отсутствовали. Для развития самой
математики теория чисел всегда имела, однако, большое значение. Разработка
задач теории чисел влечет за собой совершенствование, а иногда и
возникновение новых методов алгебры, математического анализа, теории
аналитических функций и т. д. Гармоничное развитие математики без прогресса
теории чисел немыслимо. В наше время теория чисел получила важное
применение ив естественных науках, например, кристаллографии, и в
некоторых вопросах машинной математики. Основы теории чисел как
самостоятельной науки были заложены Леонардом Эйлером. После Эйлера
в теории чисел были достигнуты новые успехи. Лагранж и особенно
Гаусс замечательно развили далее теорию квадратичных форм. Гаусс
разработал аппарат и символику теории сравнений, дал доказательство
квадратичного закона взаимности Эйлера — Лежандра, создал теорию
делимости целых комплексных чисел; в его трудах содержалась целая
программа работ, продолжающихся до наших дней.
Одним из центральных в теории чисел издавна был вопрос о
распределении простых чисел, но именно здесь со времен древних греков
достигнуты были весьма скромные успехи. Основной результат содержался еще
в «Началах» Евклида, где доказано, что множество простых чисел
бесконечно. Новое доказательство теоремы Евклида следовало из тождества
Эйлера, определяющего дзета-функцию:
оо
где в произведении множители следуют по всем простым числам р = 2, 3,
5, 7, . . ., а слагаемые в сумме — по всем натуральным п 1). Функция ?(s)
х) При 5 > 1 и s -+ 1 сумма ряда 2j ~^Г неограниченно возрастает, и, значит,
71=1
произведение в знаменателе правой части не может содержать лишь конечное числа
множителей.
344
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
в XIX веке стала одним из основных средств исследования в теории
чисел.
Важный шаг вперед в учении о простых числах сделал в 1837 г.
П. Лежен Дирихле, при помощи средств анализа (так называемых рядов
оо
Дирихле вида 2~т) » обобщивший теорему Евклида (ср. стр. 189) он
Докати 1
зал, что в любой арифметической прогрессии с общим членом a -f nb,
где а и Ъ взаимно просты, содержится бесконечно много простых
чисел.
С конца XVIII века математиков (и еще ранее — Эйлера) живо
занимал вопрос, насколько часто встречаются прбстые числа в натуральном
ряде. Известно, что простых чисел бесконечно много. Но сколько их
имеется в тех или иных границах? Или, другими словами, если
обозначить число простых чисел, не превосходящих числа х, через п(х), какова
природа функции п(х)?
Ценное, хотя, как потом выяснилось, недостаточно точное
приближенное решение поставленной задачи получил в 1798—1808 гг. А. Ле-
жандр, который, опираясь на довольно обширные таблицы простых чисел,
пришел к выводу, что для больших х функция я (х) выражается
приближенной формулой
%УХ)- ins-1,08366 #
Результат Лежандра носил эмпирический характер. Не ясно было,
пригодна ли его приближенная формула для чисел #, выходящих за
границы изученных им таблиц, которые достигали только миллиона.
Гаусс, опять-таки основываясь на табличных подсчетах, пришел
к несколько иному (и, как оказалось, более точному) выводу: отношение
п^х' для больших х приближенно выражается функцией -,— , так что
для я(х) приближением служит интегральный логарифм
х
Однако письмо Гаусса 1849 г., в котором он поделился с И. Энке
своими мыслями, увидело свет лишь в 1863 г. Между тем в том же 1849 г.
глубокие теоретические результаты в изучении функции п(х) получил
Чебышев.
В статье «Об определении числа простых чисел, не превосходящих
данной величины», П. Л. Чебышев, используя свойства функции ?(s)
вблизи ее особой точки s = 1, доказал, что при 2<^< сю функция л(х)
бесконечное множество раз удовлетворяет неравенствам
X X
, ч f5 dx ах , у. ^ (* dx . ах
2 2
сколь бы мало ни было а > 0 и сколь бы велико ни было п. Из этой
теоремы Чебышев получил другую теорему, показывающую
принципиальную неточность эмпирической формулы Лежандра для всех достаточно
РАСПРЕДЕЛЕНИЕ ПРОСТЫХ ЧИСЕЛ
345
больших х. Согласно этой теореме выражение
X
л (х)
¦Ых
не может при х —> оо иметь предела, отличного от —1.
«Доказанное нами относительно предела значений1)
¦ log х
фМ
при х = оо,— заключал Чебьппев,— противоречит формуле,
предложенной Лежандром для приближенного определения числа простых чисел,
меньших данного.
По его мнению, при х большом значение ф(я) может быть
определено с достаточной точностью уравнением
ф(*) =
log х —1,08366
Но отсюда для предела —^ — log х и при х = оо находим — 1,08366
вместо — 1» 2).
Из теорем Чебышева следовало также, что отношение п(х) к функции
Li# или к функции -, не может при х —> оо иметь предела,
отличного от 1.
Заметим, что в пределах наличных тогда таблиц разность выражения
Лежандра
In х —1,08366
? dx
J ln#
незначительна. Чебьппев показал, что эта разность, достигая минимума
при х ^ 1 247 689, далее постоянно и беспредельно возрастает.
В конце мемуара, принимая для приближенного выражения функции
х
п(х) интеграл \ ^ , Чебьппев выводит еще две асимптотические формулы
для
(ср. стр. 121) и для
2 ,— = 1п1пх + С
р^х
П(»~)-й-.
р^х
где С и С0 — постоянные. При этом опять-таки-были исправлены
соответствующие результаты Лежандра, содержавшие вместо lux разность
Ых — 1,08366.
Следующая статья Чебышева «О простых числах» (1850, опубл.
в 1852) содержала новые глубокие результаты. В начале автор отмечал,
что все вопросы, зависящие от закона распределения простых чисел
г) У Чебышева ф(#) обозначает число простых чисел, меньших х, а
натуральный логарифм обозначен log х. (— А. Ю.)
2) П. Л. Ч е б ы ш е в, Полное собрание сочинений, т. I, стр. 182.
346
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
в натуральном ряде, представляют большие трудности. Предметом статьи
являются два таких вопроса. Первым является так называемый постулат
Ж. Бертрана — высказанное названным французским математиком
в 1845 г. и проверенное в пределах нескольких миллионов
предположение, что между числами п и 2п — 2 при п > 3 всегда имеется по крайней
мере одно простое число 1).
Другой вопрос относится к критерию сходимости числовых рядов,
члены крторых суть функции последовательных простых чисел,— мы
об этом скажем далее. Но кульминационным пунктом мемуара был новый
вклад Чебышева в учение о распределении простых чисел. «Мы даем,—
писал он,— также формулу для вычисления по приближению числа
простых чисел, не превышающих данного предела, и указываем предел
погрешности этой формулы, что до сих пор еще не было сделано» 2).
Основную роль в работе играют устанавливаемые Чебышевым
неравенства для функции Q(x) = In (2. 3. 5. 7 . . .) = 2 hi/?, т. е. натураль-
ного логарифма произведения всех простых чисел, не превосходящих
данного числа х; эти неравенства получаются с помощью носящих имя
Стерлинга неравенств для логарифма произведения всех натуральных
чисел, не превосходящих х; между обоими логарифмами существует
довольно простая связь. Неравенства Чебышева имеют вид
Ах р- Ах2 — 81 6 1п2х т-In я — 3<0 (х) <
<-^-Ах — Ах2 +~т^-77 In2.г+ 4-к*я+ 2,
^5 ' 41nb '2 ' *
1 J. 1
где А = In—'—^— = 0,92129 . . .; при выводе использовались частные
30М
свойства числа 30.
С помощью своих неравенств Чебышев прежде всего доказывает
постулат Бертрана, а затем исследует сходимость рядов, номера членов
которых пробегают по простым числам. Первые результаты в этом
направлении принадлежали Эйлеру, на которого Чебышев ссылается в начале
статьи. Эйлер доказал, что ряд У\ — делается расходящимся при тех же
рк
Р^2 *
оо
значениях показателя /с, что и ряд У\ — , —он сходится при/с>1 и рас-
71=2
оо
ходится при ft<;l. Однако сходимость ряда 2 Un не является, вообще
71=2
говоря, необходимой для сходимости ряда 2 Up. Например, как пока-
Р^2
зывает далее Чебышев, ряд
1111
х) Самому Бертрану этот «постулат» понадобился при доказательстве одной
теоремы в теории групп подстановок.
2) П. Л. Чебышев, Полное собрание сочинений, т. I, стр. 192.
РАСПРЕДЕЛЕНИЕ ПРОСТЫХ ЧИСЕЛ
347
сходится и сумма его есть 1,63 с точностью до 0,1, между тем как ряд
11111
ТТпТ+1ПпТ + 41п4 + 51п5 + 1ПпТГ + ' "•
расходится. Критерий сходимости, который устанавливает Чебышев,
г./ \ r> F (х)
гласит: если F(x) для достаточно больших х положительна и .
убывает, то для сходимости ряда
F(2) + F(3) + F(5)+F(7)+...
необходимо и достаточно, чтобы сходился ряд
F(2) F(3) F(4) F(5)
In 2 "*" In 3 "*"" In 4 'r In 5 ^ " "
Доказательство основывается на оценке снизу и сверху суммы HF(p),
где простые числа р лежат между некоторыми пределами I и L.
Наконец, полагая F(x) ==1,1 = 2жЬ = х, Чебышев в конце статьи
устанавливает пределы, между которыми заключается функция я(#).
Незначительно преобразуя соответствующее предложение Чебышева, его
можно выразить неравенствами:
А -т^— <л(х)<с-гА -^—
In a; v ' 5 In х
или же
0,92129 <1^< 1,10555;
иными словами, л(х) может отклоняться от ,— немногим более, чем
' v ' In х
на 10%.
Добавим, что в письме к П. Н. Фуссу, напечатанном в 1853 г., Чебышев
поставил вопрос о распределении простых чисел в различных
арифметических прогрессиях и сам привел один результат, относящийся к разности
числа простых чисел в прогрессии с общим членом An -f- 3 и в прогрессии
с общим членом in -\- 1, когда эти простые числа меньше некоторого
предела.
Все эти открытия Чебышева произвели сильнейшее впечатление
на современников, и, например, Ж. Серре в известном курсе высшей
алгебры (Cours d'algebre superieure, t. 2,1866) дал полное изложение второго
мемуара Чебышева. Улучшить результаты Чебьппева оказалось нелегким
делом, и этим занимались выдающиеся математики вплоть до наших дней.
Немецкий математик Ф. Мертенс (1874) уточнил асимптотические
формулы Чебышева для ^ — и JT (1 ) , а также распространил
их на простые числа в арифметических прогрессиях ах-\- Ъ со взаимно
простыми а и Ъ. Англичанин Дж. Сильвестр в работах 1881 и 1892 гг.
заключил отношение я (х) : -,— в более тесные границы 0,95695 < я (х) : ,— <
< 1,04423 и снизил границу в постулате Бертрана, доказав, что при
достаточно больших п между п и 1,092п всегда есть простое число.
Большое число работ было посвящено установлению границ числа простых
чисел в арифметических прогрессиях. Так, преподаватель Петербургского
Института инженеров путей сообщения В. И. Станевич нашел (1899)
соответствующие оценки для прогрессий An ± 1, а И. И. Иванов (1901)
348
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
для прогрессий 6п ± 1; этой проблематикой занимался и ряд
зарубежных ученых, в том числе А. Пуанкаре (1892).
Исследования Чебышева о функции п (х) и непосредственно
продолжавшие их работы оставляли все же открытым вопрос: существует ли
предел отношения л(х) к ^— (или к Их)? Пока было доказано лишь,
что если предел существует, то он равен единице. Установление
существования этого предела потребовало новых, более сильных
аналитических методов, а именно применения свойств той же дзета-функции,
которую применял и Чебышев, но уже как функции комплексного
переменного.
Б. Риман в 1859 г. показал тесную связь свойств функции л(х)
со свойствами дзета-функции, рассматриваемой на плоскости
комплексного переменного, и особенно с распределением нулей последней. Мемуар
Римана, в том числе некоторые высказанные им без доказательства
предложения о свойствах функции ? (s), оказал чрезвычайно плодотворное
влияние на развитие как теории аналитических функций, так и теории
чисел.
Применение аналитических функций и специально ?(s) позволило
дать полное доказательство так называемого асимптотического закона
распределения простых чисел, т. е. теоремы, согласно которой при х—> оо
х
предел отношения п(х) к ^— или к \ у— есть единица. Асимптотиче-
2
ский закон был доказан в 1896 г. независимо друг от друга французским
математиком Ж. Адамаром и бельгийцем Ш. де ла Валле-Пуссеном.
Сравнительно недавно было получено доказательство при помощи средств,
не выходящих за пределы анализа функций действительного переменного
(норвежский математик А. Сельберг, а также венгерский математик
П. Эрдеш в 1949 г.; технически сложный вывод Сельберга упростили
в 1955 г. А. Г. Постников и Н. П. Романов). Эти так называемые
элементарные доказательства закона распределения простых чисел, в
которых применяются и асимптотические формулы типа Чебышева и Мертенса,
положили начало целому большому циклу новых работ.
Диофантовы приближения. Мы далеко не полностью рассмотрели
работы Чебышева по теории чисел. Отметим еще статью «Об одном
арифметическом вопросе» (1866), относящуюся, по терминологии Г. Минковско-
го, к теории диофантовых приближений. Эта теория имеет своим
предметом решение в целых числах алгебраических уравнений или неравенств
с действительными коэффициентами, а также их систем; к ней относится,
таким образом, и приближение любых действительных чисел числами
р ациона л ьными.
Однородное линейное уравнение
у — ах = 0,
в котором а — иррациональное число, точно решить в целых числах
невозможно. Непрерывные дроби дают наилучшие приближения разности
у — ах к нулю в том смысле, что если — — какая-либо подходящая дробь
Як
числа а, то для всякого д, меньшего gfe, и любого целого р, будет иметь
РАБОТЫ Н. В. БУГАЕВА
349
место неравенство
\qa — p\>\qka — pk\;
другими словами, любая дробь —, где q < qk, отстоит от а дальше, чем — 1).
Чебышев в названной выше работе исследовал простейшую линейную
неоднородную задачу теории диофантовых приближений: «По данной
степени приближения разности у — ах к нулю,— писал он,—
наименьшие числа х, у, при которых такое приближение имеет место, легко
определяются разложением количества а в непрерывную дробь. Вопрос более
сложный, когда числа х, у ищутся под условием, чтобы разность у — ах
до желаемой степени приближения привелась бы к данной величине Ъ,
отличной от нуля, тоже может быть решен при помощи непрерывных
дробей» 2). Чебышев доказывает, что при иррациональном а существует
бесконечное множество целых чисел х, г/, для которых
\у — ах — Ъ |< —.
Ш. Эрмит в 1879 г. характеризовал этот результат, как обобщение
основного результата теории непрерывных дробей, открывающее дорогу для
многочисленных дальнейших изысканий. И в самом деле, исследование
Чебышева породило целую литературу. Улучшением постоянной в его
оценке или обобщениями теоремы занимались многочисленные
математики: Эрмит (1879), Г. Минковский (1896), опиравшийся на теорию парал-
лелоэдров Вороного, Р. Ремак (1923), Н. Г. Чеботарев (1934) и другие.
А. Я. Хинчин (1935) и более просто И. И. Жогин (1944) показали, что
имеется бесконечное множество пар целых решений неравенства
\у — ах— Ь[<-
"1/5 х
Дальнейшее уменьшение стоящей справа постоянной —^= уже невоз-
|/5
можно.
Работы Н. В. Бугаева. Мы упомянем здесь же о некоторых теоретико-
числовых работах уже встречавшегося нам выше московского математика
Н. В. Бугаева, тем более что они частично связаны с проблематикой
Чебышева. Называя первичными натуральные числа, не делящиеся
на квадраты целых чисел (кроме единицы), Бугаев поставил вопрос о
свойствах функции Hi(n), выражающей число первичных чисел, не
превосходящих п. На третьем съезде русских естествоиспытателей и врачей в Киеве
(1871) Бугаев сообщил ряд своих открытий, относящихся к первичным
и А:-ичным числам (не делящимся на (к -f- 1)-е степени других чисел),
и среди них формулу
Я1(П) + Я1(?)+Я1(-?-) + ...=п.
г) Использование величины \ да — р |, а не величины
для оценки приб-
Я .
лижения числа а дробью p/q имеет определенные преимущества. См. А. Я. Хинчин,
Элементы теории чисел, в кн.: Энциклопедия элементарной математики. I, Арифметика,
под ред. П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина, М.—Л., 1951,
стр. 326.
2) П. Л. Чебышев, Полное собрание сочинений, т. I, стр. 237.
350
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
На это Чебышев заметил, что по способу, изложенному в его работе
«О простых числах», можно, используя приведенное только что
равенство, найти пределы, в которых заключена Н^ (п) в виде
ад-В(?)_«(?)_В(?)+*Щ<*1М<«»*+2.??
(здесь Е(х) означает целую часть х), причем вместо нижнего предела
539
можно взять меньшую величину — п — 3.
Функцией Hi(n) занимался раньше Дирихле, который из теоретико-
вероятностных соображений пришел к мнению, что асимптотическим
выражением для нее при п—-^ оо является —-^ п. Узнав об этом в 1872 г.
из беседы с Куммером, Бугаев год спустя вывел асимптотическую формулу
Н±(п)ъ —у ' а также асимптотические формулы для других Hk(n), где
Нь — число /с-ичных чисел, не превосходящих п, например, Н3(п) « — п.
Бугаев поставил также задачу об оценке разности Н±(п) ^ » которую
в 1906 г. с использованием закона распределения простых чисел Адама-
ра — Валле-Пуссена вывел в виде otyx) Э. Ландау и элементарным
методом, аналогичным методу А. Сельберга, Е. П. Ожигова (1962) г).
Эти результаты Бугаева изложены в цикле из четырех статей «Учение
о числовых производных» (Матем. сборн., тт. 5—6, 1870—1873), где
выведен также целый ряд весьма общих арифметических тождеств, и среди
них таких, которые применяются в современных элементарных
доказательствах асимптотического закона распределения простых чисел. Эти
открытия Бугаева были хорошо известны русским математикам прошлого
столетия. Например, А. А. Марков в представлении Бугаева в члены-
корреспонденты Академии наук, подписанном также Н. Я. Сониным,
говорил, что особого внимания среди трудов кандидата заслуживает
«...обстоятельно им разработанное учение о числовых производных,
в котором найдены им многие интересные и общие результаты» 2).
Впоследствии формулы Бугаева перестали в большинстве случаев связывать с его
именем и лишь в самое последнее время его работы по теории чисел вновь
привлекли внимание математиков и историков математики.
А. Н. Коркин и Е. И. Золотарев. Новые успехи русских математиков
в теории чисел были достигнуты прежде всего А. Н. Коркиным и Е. И.
Золотаревым. Александр Николаевич Коркин (3 марта 1837 — 1 сентября
1908) был старшим из учеников Чебышева 3). Он происходил из зажиточной
крестьянской семьи Вологодской губернии. Петербургский университет
Коркин окончил в 1858 г. и преподавал в нем с 1860 по 1908 г., причем
с 1868 г. в звании профессора. Более 30 лет он состоял также профессором
Морской Академии, где его сменил в 1900 г. его ученик А. Н. Крылов.
г) Н. Д. Беспамятных, Арифметические исследования в России в XIX
веке.— Уч. зап. Гродненского пед. института, вып. II, сер. матем., Минск, 1957;
А. А. Киселев и Е. П. О ж и г о в а, П. Л. Чебышев на съездах русских
естествоиспытателей и врачей.— Ист.-матем. исслед., вып. XV, 1963.
2) Архив АН СССР, ф. 2, оп. 1 (1897), № 16. Избрание Бугаева состоялось в том
же году.
3) К. А. Поссе, А. Н. Коркин (некролог). — Отч. о сост. и деят.
С.-Петербургского университета за 1908 г., СПб., 1909.
А. Н. КОРКИН И Е. И. ЗОЛОТАРЕВ
351
Глубокий знаток классиков математики, от Эйлера до Дирихле, Кор-
кин подобно Чебышеву не ценил исследований Римана и Вейерштрасса,
казавшихся ему «декадентскими».
Работы Коркина относятся к двум областям: дифференциальным
уравнениям и теории чисел. К первой области принадлежат обе его
диссертации — магистерская «Об определении произвольных функций в
интегралах линейных уравнений с частными производными» (СПб., 1860),
высоко оцененная в официальном отзыве Чебышева, и докторская «О
совокупных уравнениях с частными производными первого порядка и о
некоторых вопросах механики» (СПб., 1868), а также ряд статей. Эти труды
Коркина продолжили начатые в Петербурге
ранее исследования по уравнениям с
частными производными. Высоким качеством
отличались лекции Коркина, которые частью
включил в свои руководства А. Н. Крылов.
Так, например, в широко известном курсе
дифференциальных уравнений
математической физики Крылова изложены, следуя
Коркину, методы интегрирования линейных
дифференциальных уравнений в частных
производных с постоянными коэффициентами.
В начале третьей главы этого курса А. Н.
Крылов писал:
«В 1901 г. я попросил Александра
Николаевича объяснить мне непонятое мною место
в одном из мемуаров Пуассона, помещенных
в 19-й тетради журнала Политехнической
школы. Александр Николаевич не только
в нескольких словах разъяснил то, что мне
представлялось непонятным, но еще и прочел
мне целую лекцию, в которой дал свое
изложение метода Пуассона. В какой мере он а Н Ко -н
владел этим предметом, читатель может судить
по тому, что эта лекция, составляющая § 40, 41
и 43 этой главы, была им прочитана в ответ на мой вопрос, для Александра
Николаевича неожиданный, немедленно, без всякой подготовки, причем
Александр Николаевич почти не пользовался карандашом, который
держал в руке, а лишь следя глазами за моею записью, продиктовал мне
все изложенное ниже со всеми выкладками и формулами» х).
Коркину принадлежат ценные работы в теории чисел2). Они были
проведены им вместе с Е. И. Золотаревым, который вначале слушал у него
лекции, а затем стал его сотрудником и другом.
Егор Иванович Золотарев родился 12 апреля 1847 г. в Петербурге,
где отец его, часовщик, держал небольшой магазин. После окончания
пятой гимназии, одной из лучших в столице по составу учителей (физику
в ней преподавал, например, К. Д. Краевич (1833—1892), автор
популярнейшего до революции учебника), Золотарев в 1863 г. поступил в
Петербургский университет. Физико-математический факультет он окончил
в 1867 г.; здесь главными учителями его были Чебышев, Сомов, Коркин.
х) А. Н. Крылов, О некоторых дифференциальных уравнениях
математической физики, имеющих приложение в технических вопросах. Л., 1933, стр. 135.
2) А. Н. Коркин, Собрание сочинений, т. 1, СПб., 1911.
352
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
Осенью 1868 г. Золотарев защитил диссертацию на право чтения лекций
по теории наилучшего приближения функций (о ней речь впереди), с
успехом прочитал две пробные лекции и начал работу в Петербургском
университете в качестве приват-доцента. Через год он сдал магистерские
экзамены и защитил магистерскую диссертацию «Об одном
неопределенном уравнении третьей степени» (СПб., 1869), получившую хорошую
оценку оппонентов — П. Л. Чебышева и Ю. В. Сохоцкого. В это же
время он начал преподавание вначале механики, а затем и математики
в Институте инженеров путей сообщения. В университете он читал теорию
эллиптических функций, анализ, механику, алгебру и, впервые, курс
введения в анализ. Сохранились
литографированные издания некоторых его курсов х).
Магистерская диссертация Золотарева
имела предметом решение в целых числах
неопределенного уравнения
х3 + Ау3 + АН3 — ЪАхуг = 1,
где А — данное некубическое число. Говоря
на языке теории алгебраических чисел,
требовалось найти основную единицу
кубического поля R (у А). Эту задачу Золотарев
решил, приведя ее к разысканию
минимумов некоторой квадратичной формы с тремя
переменными, зависящей от параметра.
Таким образом, в этой работе намечены были
два главные направления изысканий
Золотарева. Вскоре Золотарев вместе с Коркиным
занялся теорией минимумов квадратичных
форм. Их совместные статьи печатались на
протяжении 1872—1877 гг. Параллельно
Золотарев разрабатывал теорию алгебраиче-
Е. И. Золотарев. ских чисел и в 1874 г. защитил в качестве
докторской диссертации главный свой труд
в этой области —«Теорию целых комплексных чисел с приложениями
к интегральному исчислению» (СПб., 1874). Оппонентами были Че-
бышев и Коркин. Результаты этого труда были дополнены затем в двух
статьях, одна из которых, переданная Золотаревым в редакцию
журнала Лиувилля летом 1876 г. во время поездки за границу, увидела свет
только посмертно в 1880 г., а другая, представленная Академии
наук в 1877 г., вышла из печати в следующем году, т. е. в самый год его
смерти. Заметим, что решенная Золотаревым проблема интегрального
исчисления непосредственно примыкала к исследованиям Чебышева
по интегрированию алгебраических функций, в ходе обобщения которых
Золотарев и пришел к созданию своей теории целых комплексных чисел.
В апреле 1876 г. Золотарев получил в Петербургском университете
профессуру и в том же году, в декабре, был избран членом Академии
наук в звании адъюнкта на место, освободившееся после кончины О. И.
Сомова. В отзыве, составленном Чебышевым и подписанном также Буня-
ковским, Перевощиковым и астрономом А. Н. Савичем (1811—1883),
г) Подробнее см. Р. О. Кузьмин, Жизнь и научная деятельность Егора
Ивановича Золотарева.— УМН, II, 6 (22), 1947; Е. П. Ожигова, Егор Иванович
Золотарев, М.—Л., 1966.
ТЕОРИЯ КВАДРАТИЧНЫХ ФОРМ
353
отмечалось, что Золотарев, подобно Сомову, «представляет в себе также
замечательное соединение познаний по Чистой Математике и по
Аналитической Механике» и что наука обязана Золотареву «многими весьма
важными трудами, доставившими его имени лестную известность и у нас
и за границею» 1). Не прошло и двух лет, как те же Чебышев, Буняков-
ский и Савич вошли в физико-математическое Отделение Академии с
представлением о повышении Золотарева в звание экстраординарного
академика, хотя по уставу для этого полагался шестилетний срок работы
в звании адъюнкта. Избрание прошло 14 мая 1878 г. в собрании
Отделения единогласно и на август был заготовлен протокол для баллотировки
в общем собрании Академии наук. Протокол этот, однако, остался
незаполненным: в начале июля Е. И. Золотарев попал под поезд и 19 июля
скончался от заражения крови всего 31 года от роду.
Таким образом, научная деятельность Золотарева продолжалась
всего около десяти лет, но за этот короткий срок он сделал много
первоклассных открытий. Уже в советское время основные его труды и часть
переписки, представляющей выдающийся научный и биографический
интерес, были собраны в двух томах. К сожалению, вопреки своему
названию, это издание не является полным 2).
Обратимся прежде всего к работам Золотарева и Коркина по теории
квадратичных форм.
Работы А. Н. Коркина и Е. И. Золотарева по теории квадратичных
форм. Однородный многочлен второй степени с п переменными
i j=n
2 CLijXfXj = а^хх -)-...-}- аппхп -f- ai2XiX2 -\- #21^2^1 ~t~ • • •
где dij = dji, называется квадратичной формой; коэффициенты здесь —
действительные числа. В зависимости от числа переменных различаются
двоичные (бинарные), троичные (тернарные) и т. д. формы. В
арифметической теории форм рассматриваются формы, переменные которых
принимают только целые рациональные значения. Величина
D= -
ап ai2 • • • ат
*>nl «п2
называется определителем формы (мы ставим знак в соответствии с тем,
как поступали в XIX веке). Поясним некоторые нужные далее понятия
на примере двоичной формы, которую запишем в виде
ах2-\-2Ъху-\-су2.
Легко показать, что если определитель этой формы
а Ъ
D= —
Ъ с
= Ь2 — ас<0,
г) Е. П. Ожигова, Егор Иванович Золотарев, стр. 50.
2)Е. И. Золотарев, Полное собрание сочинений с биографическим
очерком Б. А. Венкова. Вып. 1—2, изд. АН СССР, 1931—1932.
354
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
то, исключая тривиальный случай обращения формы в нуль приз; = у = О,
форма принимает значения только одного знака. В этом случае форма
называется определенной. Например, при а>0 (тогда и с > 0) форма
будет положительно определенной или, короче, положительной. Если же
D > 0, то при одних значениях ж, у форма положительна, а при
других — отрицательна. Такая форма называется неопределенной. Случай
D = 0 мы оставим в стороне. Отрицательные формы получаются из
положительных умножением на —1, так что можно ограничиться
рассмотрением одних положительных форм.
Линейное преобразование
переводит данную форму в другую квадратичную форму:
a1x21 + 2bix1yi + Ciy21.
Если при целых а, р, у, б определитель преобразования
а р
d =
= а6 — Ру
V
равен 1 или —1, то множества чисел, представляемых этими двумя
формами, одинаковы. Такие формы Лежандр назвал эквивалентными. Две
эквивалентные формы обязательно обладают одним и тем же
определителем, ибо
а,! Ъ^
bi ct
D,
= D-d2.
Однако две формы с одним и тем же определителем могут и не быть
эквивалентными. Для эквивалентности двух форм с одним и тем же
определителем необходимо и достаточно, чтобы существовало хотя бы одно
линейное преобразование с d = + 1, переводящее одну форму в другую.
Множество форм данного определителя, между собою эквивалентных,
называется классом форм. Для форм данного определителя число различных
классов конечно. Все эти понятия распространяются на квадратичные
формы с числом переменных, большим двух, и с любыми действительными
коэффициентами.
Изучение арифметики квадратичных форм началось с форм двоичных.
Ранее говорилось о работах Эйлера, посвященных проблеме
представимости такими формами целых чисел. Исследования Эйлера продолжил
и обобщил Лагранж, который начал разработку вопроса об отыскании
экстремумов форм (1769 и след. годы), а затем Гаусс, которому
принадлежат основные понятия и терминология современной теории и множество
важных открытий в этой области (1801). К Гауссу, в частности, восходит
развитое учение об эквивалентности форм. От «Арифметических
исследований» Гаусса отправлялись все, кто работал в этой области в первой
половине XIX века: Дирихле, Якоби, Эйзенштейн, Эрмит и другие.
Работы Коркина и Золотарева были посвящены исследованию минимумов
положительных квадратичных форм. Возьмем множество положительных
г, j=n
форм 2 aijxixj данного определителя/) <0. Если действительные коэф-
фициенты dtj, фиксированы, а переменные х^ принимают всевозможные
целые рациональные значения, не равные одновременно все нулю, то среди
ТЕОРИЯ КВАДРАТИЧНЫХ ФОРМ
355
значений, получаемых формой, имеется некоторое наименьшее. Этот
минимум формы зависит от ее коэффициентов и непрерывно меняется
с непрерывным изменением последних; при этом для эквивалентных
между собой форм минимум одинаков. В своем изменении этот минимум
может иметь один или несколько максимумов, соответствующих
неэквивалентным формам (число которых зависит от числа переменных п).
Разыскание минимумов квадратичных форм принадлежит к числу
важных задач их арифметической теории и от него зависит решение
многих других вопросов. В письме к Якоби, напечатанном в 40-м томе
журнала Крелле, Ш. Эрмит указал на значение, которое имело бы
определение минимумов двоичной и троичной форм,
(у-ах)2 + ^- и A(z-ax)2 + B(y-bx)2 + -^-,
где А ж В — положительные числа, а жЪ — действительные и параметр Д
непрерывно меняется от 0 до оо. Далее Эрмит сообщал, что для
положительных форм с п переменными он получил для границы минимумов
число (-тН У | D | и высказал предположение, что коэффициент в этом
2
выражении следует заменить на п . К отысканию минимумов квадра-
уп + 1
тичных форм,— заключал Эрмит,— приводится, в частности, решение
в целых числах неопределенных уравнений вида Norme cp(ct) = 1, где
ф(а) — целое комплексное число, зависящее от корня а неприводимого
уравнения F{x) = 0 п-ж степени с целыми коэффициентами и старшим
коэффициентом, равным 1. Под целым комплексным числом ср (а) здесь
понимается многочлен а0 + а±а + а2а2 + . . . + а-^-^а71'1 с целыми
рациональными коэффициентами. Нормой числа ф(а) называется
произведение ф(а!) ф(а2) . • . ф(ал)> гДе аь «2» - . ., ал — все корни
уравнения F(x) = 0. Так, нормой обыкновенного комплексного числа а + Ы
служит произведение (а + Ы) (а — Ы), ибо корни g&i, ос2 уравнения
х2 + 1 = 0 суть i ж —i.
А. Н. Коркин заинтересовался теорией квадратичных форм еще
во время заграничной поездки 1862—1863 гг.; под его влиянием занялся
ею Е. И. Золотарев. Только что упомянутое письмо Эрмита послужило
отправным пунктом магистерской диссертации Золотарева «Об одном
неопределенном уравнении третьей степени» (СПб., 1869), посвященной
решению в целых числах уравнения
х3 + Ау3 + АН3 — ЪАхуъ = 1,
где А — целое некубическое число, левая часть которого есть норма
целого комплексного числа х + уу^А + z У А2, зависящего от корня
уравнения и3 — -4 = 0. Было известно, что бесчисленное множество
решений рассматриваемого уравнения можно вывести, зная одно
основное. В первой части работы Золотарев нашел все последовательные
минимумы двоичной и троичной форм, о которых шла речь в письме Эрмита,
и получил некоторые предварительные результаты, касающиеся
предположения Эрмита о границах минимумов тг-ичных форм. Во второй части
Золотарев показал, что искомое основное решение изучаемого им
кубического уравнения содержится среди значений, сообщающих минимумы
некоторой квадратичной троичной форме, зависящей от параметра. Умея
356
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
находить последовательные минимумы последней, он до конца решил
поставленную задачу.
Попытка проверить предположение Эрмита относительно
коэффициента в выражении для точной верхней границы минимумов
у и + 1
форм с п переменными вскоре повлекла за собой серию совместных работ
обоих русских математиков, продолжавшихся около 8 лет.
В статье «О четверичных положительных квадратичных формах»
(Mathematische Annalen, В. 5, 1872), Коркин и Золотарев исследовали
вопрос Эрмита для случая четырех переменных и установили, что
минимум таких форм не превосходит числа -j/4|.D|, причем это значение
принимается формой
l/41 D | (х\ + х\ + х\ + х\ + х±х2 + х±х3 + х±Хь),
например, при х± = — 1, х2 = х3 = х± = 1. Вместе с тем было
показано, что предположение Эрмита, верное для п = 2 и п = 3, не
оправдывается уже при тг = 4, так как ^—= < У"4. Величина V\D\ при
у 5 /л +1
w > 3 является точной верхней границей только для некоторого класса
эквивалентных форм данного определителя.
В двух последующих работах (Math. Annalen, В. 6, 1873; В. 11,
1877) Коркин и Золотарев распространили эти результаты. Здесь вводится
важное понятие предельных форм, минимумы которых при любых
бесконечно малых изменениях коэффициентов (не меняющих D) могут тодько
уменьшаться. Та предельная форма, минимум которой является
наибольшим, доставляет точную верхнюю границу минимумов всех форм данного
определителя. В более ранней из этих двух работ авторы с помощью
приведения формы к некоторому простейшему виду, которое они назвали
разложением формы по ее минимумам, нашли лучшую, чем Эрмит,
верхнюю границу минимумов для любого п, дающую точный наибольший
минимум при п = 4. В последней статье они решили ту же задачу для
п = 5 (здесь получается У 8|2) |) и установили все предельные формы
для форм с 2, 3, 4 и 5 переменными, причем оказалось, что при п = 2
и п = 3 их по одной, в случае четырех переменных — две и в случае пяти —
три. Здесь применено было не разложение формы по минимумам, а
разыскание совокупностей значений переменных, при которых форма имеет
минимум, так называемых представлений минимума. Число представлений
минимума тг-ичной формы не меньше n{<nj~ * и, зная эти представления,
а также значение минимума, можно полностью определить коэффициенты
соответствующей предельной формы.
Открытия Коркина и Золотарева были очень высоко оценены Эрми-
том, Чебышевым и другими современниками, и положили начало работам
многих русских и зарубежных ученых, которые в различных
направлениях продолжаются до наших дней. В частности, благодаря усилиям целого
ряда исследователей были найдены наибольшие минимумы форм с 6, 7,
8, 9 и 10 переменными (Г. Блихфельдт, 1925—1934; Н. Гофрейтер, 1934;
Л. Морделл, 1946—1948). При этом оказалось, что минимумы
предельных форм, приведенные в качестве примеров для гг = 6итг = 7во второй
статье Коркина и Золотарева, являются для этих случаев наибольшими.
В конце XIX века немецкий математик Г. Минковский, уроженец
городка Алексоты Минской губернии (теперь в Литовской ССР), присту-
А. А. МАРКОВ И ЕГО МАГИСТЕРСКАЯ ДИССЕРТАЦИЯ 357
пил к разработке дисциплины, которую назвал геометрией чисел.
Оказалось, что существует глубокий параллелизм между свойствами
квадратичных форм и правильных точечных решеток в евклидовом пространстве,
число измерений которого равно числу переменных формы. Так, двоичной
форме соответствует плоская решетка параллелограммов с вершинами
в целочисленных точках косоугольной декартовой системы, определяемой
коэффициентами формы. В трехмерном пространстве троичной форме
соответствуют параллелепипеды. Все понятия теории квадратичных форм
имеют свои аналоги в геометрии чисел и, например, минимум формы
выступает как квадрат наименьшего расстояния между точками ее
решетки. В 1904 г. Минковский показал, что задачу Коркина и Золотарева
можно высказать и как задачу о наиболее плотном заполнении га-мерного
пространства одинаковыми тг-мерными шарами, центры которых лежат
в точках решетки 1).
Геометрия чисел, в которой плодотворно взаимодействуют
арифметические и геометрические представления и методы, выросла в большую
науку. В России это направление первым стал развивать Г. Ф. Вороной.
Но прежде чем перейти к его работам, мы должны рассмотреть более
ранние исследования о минимумах неопределенных форм,
принадлежащие А. А. Маркову.
А. А. Марков и его магистерская диссертация. Андрей Андреевич
Марков, имя которого нам встречалось уже неоднократно, был
крупнейшим среди прямых учеников Чебышева. Родился Марков в Рязани 14 июня
1856 г. Отец его вначале служил в Лесном
департаменте, а затем работал в качестве
частного поверенного. В начале
шестидесятых годов семья переехала в
Петербург, и когда мальчику исполнилось
десять лет, его определили в гимназию,
ту самую, в которой ранее обучался
Золотарев. Любимым предметом Маркова
стала математика, другие его мало
интересовали. Он самостоятельно изучал
высшую математику и сам нашел один
способ интегриров ания обыкнов енных
линейных дифференциальных уравнений
с постоянными коэффициентами.
Впрочем, способ этот не был новым, как
разъяснили гимназисту Коркин и
Золотарев, которым он сообщил о сделанном
им открытии. Кроме математики, юноша
увлекался произведениями Добролюбова,
Чернышевского и Писарева, передовые
идеи которых оказали несомненное
влияние на его мировоззрение.
В 1874 г., по окончании гимназии, А" А' МаРков-
А. А. Марков поступил в
Петербургский университет, где слушал лекции Чебышева, Коркина и
Золотарева и работал под руководством двух последних в студенческом
кружке. В 1878 г. ему была присуждена золотая медаль за сочинение «Об-
) Б. Н. Делоне, Петербургская школа теории чисел, М.—Л., 1947.
358
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
интегрировании дифференциальных уравнений при помощи непрерывных
дробей с приложением к уравнению (1 -\-х2)-^ = п (1 + у2)», содержавшее,
среди прочего, новый признак сходимости непрерывных дробей. Золотарев
в своем отзыве отмечал, что эта работа занимает видное место среди
студенческих сочинений, отмеченных награждением их авторов медалями
в различное время. В том же году Марков окончил
физико-математический факультет со степенью кандидата и, по представлению Коркина
(Золотарева уже не было в живых), был оставлен при университете для
подготовки к профессорскому званию.
Всего через два года Марков защитил магистерскую диссертацию
«О бинарных квадратичных формах положительного определителя» (СПб.,
1880), примыкавшую к работам Коркина и Золотарева. Это сочинение
высоко оценил Чебышев, особо подчеркнувший искусство автора в
применении непрерывных дробей, средства, которым столь успешно
пользовался он сам и «от которого прямо или косвенно зависит решение многих
весьма важных вопросов, еще не решенных» г). В год защиты этой
диссертации Марков приступил к преподаванию в Петербургском университете
в должности приват-доцента. Вскоре теория непрерывных дробей
получила новое развитие и применение в докторской диссертации Маркова
«О некоторых приложениях алгебраических непрерывных дробей» (СПб.,
1884), где доказаны и обобщены важные неравенства Чебышева в учении
о предельных величинах интегралов. Этот труд открыл большую серию
работ Маркова по теории моментов, ставшей важным средством
исследования в теории вероятностей, по интерполированию и наилучшему
приближению функций. Два года спустя Марков был избран профессором
университета и, по предложению Чебышева, адъюнктом Академии наук. В 1890 г.
он был выбран экстраординарным академиком и в 1896 г.— ординарным.
Занятия в указанных направлениях математики соединялись с
отдельными исследованиями по дифференциальным уравнениям, приближенным
вычислениям, теории алгебраических чисел. Постепенно на первый план
выдвигается теория вероятностей — ее предельные теоремы, метод
наименьших квадратов, вопросы математической статистики. С конца
девяностых годов Марков посвящает этому кругу проблем все больше времени
и сил, а в начале девятисотых закладывает основания теории зависимых
случайных величин. В этой области, которую Марков систематически
и глубоко разрабатывал до самого конца жизни, ему принадлежат
открытия непреходящего значения. Марковские цепи и обобщающие их
марковские процессы известны теперь каждому математику и физику.
В 1905 г. Марков по собственному желанию вышел в отставку в
университете со званием заслуженного профессора: он не желал занятием
штатной должности загораживать путь другим, более молодым людям.
Вместе с тем он сохранял связь с университетом и продолжал в качестве
приват-доцента, т. е. без твердого оклада, вести курсы по теории
вероятностей и другим интересовавшим его специальным вопросам вплоть до
тяжелого заболевания, особенно обострившегося в 1920—1921 гг., когда
он в последний раз читал лекции по любимому предмету и готовил новое
издание своего труда «Исчисления вероятностей». А. А. Марков скончался
20 июля 1922 г.
Как педагога, Маркова отличало умение излагать мысли с
замечательной точностью и ясностью. Такими же качествами обладали и руко-
-) П. Л. Чебышев, Полное собрание сочинений, т. V, стр. 300.
А. А. МАРКОВ И ЕГО МАГИСТЕРСКАЯ ДИССЕРТАЦИЯ 359
водства Маркова, из которых особенно прославилось только что названное
«Исчисление вероятностей» (СПб., 1900; изд-е 4, значительно
дополненное автором, М., 1924), составленное на основе курса лекций,
неизменно читавшегося им после выхода в отставку в 1883 г. Чебышева. Это
классическое руководство написано с совершенной полнотой выводов
is. простотой изложения, снабжено подробно разобранными примерами,
и вместе с тем включает первоклассные научные результаты самого
автора, не говоря уже о новых доказательствах многих ранее известных
теорем. В 1912 г. курс Маркова был издан в немецком переводе Г. Либ-
мана (Wahrscheinlichkeitsbrechnung, Lpz.— Berl., 1912). Замечательными
достоинствами обладает также «Исчисление конечных разностей» (СПб.,
1889—1891; 2-е дополн. изд., Одесса, 1910), содержащее не только вполне
оригинальное изложение многих вопросов, но и дальнейшее развитие
их Марковым. Сказанное относится, например, к главе о приложении
двукратных сумм к преобразованию сходящихся рядов с целью их
быстрого и точного приближенного суммирования, в которой рассмотрено и
преобразование Эйлера 1); здесь замечательна и безукоризненная техника
весьма точных приближенных вычислений. Эта книга Маркова оказала
сильное влияние на распространенный в свое время в России и Германии
«Курс исчисления конечных разностей» (СПб., 1908) его университетского
коллеги еще со студенческих лет Д. Ф. Селиванова (немецкое издание
ъышло раньше в Лейпциге, 1904).
Некоторые лекции Маркова — о введении в анализ, о
дифференциальном исчислении и др.— были литографированы. Два специальных курса,
«Лекции о функциях, наименее уклоняющихся от нуля» и «Лекции о
непрерывных дробях», переизданы по литографированным запискам 1906 г.
в советское время2). К сожалению, до сих пор не существует полного
собрания его научных трудов.
Марков был не только большим ученым, но и мужественным
гражданином, решительно отстаивавшим свои передовые убеждения. К числу
таких проявлений гражданского мужества Маркова относятся
например, его протест против исключения М. Горького из почетных членов
Академии наук (а исключения этого потребовал царь Николай II)
и его отказ принять участие в выборах в III Государственную Думу
в связи с роспуском II Думы и изданием нового реакционного закона
о выборах.
Академик А. Н. Крылов в письме к С. Ф. Ольденбургу говорил: «Вы,
конечно, помните его (т. е. А. А. Маркова.— А. Ю.) резкий протест,
заявленный Академии по поводу исключения, по распоряжению
министра Сипягина, Горького из Академии. Наверное, Вы помните также,
что в первое же мартовское 1917 г. заседание Академии наук Андрей
Андреевич внес предложение, единогласно принятое, о включении вновь
Горького в число почетных академиков. Сколько раз выступал Марков
в университете с протестами против мероприятий бывшего правительства
и полиции по отношению к университету и студентам,— одно время он
даже был отставлен от должности профессора за эти выступления.
Припомните его протест против Синода по поводу отлучения Толстого от
г) Ср. статью Маркова «Мемуар о преобразовании медленно сходящихся рядов
в быстро сходящиеся ряды» (на франц. языке, Mem. Ac. Sc. Petersb., VII ser., t.37, № 9,
1890).
2) А. А. Марков, Избранные труды по теории непрерывных дробей и
теории функций, наименее уклоняющихся от нуля. Биографич. очерк и примеч. Н. И. Ахи-
езера. М.—Л., 1948.
360
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
церкви; ведь таких протестов, всегда заявлявшихся открыто и явно,
не перечислить и, конечно, самое имя и ученая слава Маркова придавали
им силу и распространение, не способствовавшие упрочению бывшего
правительства»1). Ранее говорилось уже о публичных выступлениях
А. А. Маркова против реакционных предложений П. А. Некрасова,
касавшихся средней школы.
Добавим к этому, что А. А. Марков был решительным атеистом.
Ярким свидетельством этого является его требование об отлучении его
от церкви, которое он выразил в специальном прошении от 12 февраля
(ст. ст.) 1912 г. Текст прошения весьма примечателен:
«Честь имею покорнейше просить Святейший Синод об отлучении
меня от церкви.
Надеюсь, что достаточным основанием для отлучения может служить
ссылка на мою книгу «Исчисление вероятностей», где ясно выражено
мое отрицательное отношение к сказаниям, лежащим в основании
еврейской и христианской религии.
Вот выдержка из этой книги (стр. 213—214): «Независимо от
математических формул, на которых мы не остановимся, не придавая им
большого значения, ясно, что к рассказам о невероятных событиях, будто бы
происшедших в давно минувшее время, следует относиться с крайним
сомнением. И мы никак не можем согласиться с акад. Буняковским
(«Основания математической теории вероятностей», стр. 326), что
необходимо выделить известный класс рассказов, сомневаться в которых
он считает предосудительным.
Чтобы не иметь дело с еще более строгими судьями и избежать
обвинений в потрясении основ, мы не останавливаемся на этом предмете,
не относящемся непосредственно к математике».
Чтобы не оставалось никаких сомнений, о чем идет здесь речь,
приведу соответствующую выписку из книги Буняковского: «Некоторые
философы, в видах предосудительных, пытались применять формулы,
относящиеся к ослаблению вероятности свидетельств и преданий, к
верованиям религиозным и тем поколебать их.
Если приведенной выдержки недостаточно, то покорнейше прошу
принять во внимание, что я не усматриваю существенной разницы между
иконами и идолами, которые, конечно, не боги, а их изображения, и не
сочувствую всем религиям, которые, подобно православию,
поддерживаются огнем и мечом и сами служат им»2).
После безуспешных попыток отговорить А. А. Маркова церковным
властям пришлось исключить его из списка верующих3).
По тематике научного творчества, по характеру применявшихся
им методов Марков был наиболее близким к Чебышеву, его
последователем. Он далеко продолжил исследования основателя петербургской
математической школы по теории непрерывных дробей, теории моментов,
теории вероятностей, теории приближения функций и т. д. Вместе с тем
Марков выдвинул ряд новых плодотворных идей во всех основных
г) Цит. по биографии А. А. Маркова, составленной его сыном, известным советским
математиком А. А. Марковым: А. А. Марков, Избранные труды. Изд-во АН СССР,
1951, стр. 610. См. также: А. В. Кольцов, Некоторые материалы к биографии
академика А. А. Маркова.— Вопросы истории естествознания и техники, вып. 1, М., 1956,
стр. 204—207.
2) А. А. Марков, Избранные труды, стр. 608—609.
3) Ф. П. Отрадных, Эпизод из жизни академика А. А. Маркова.— Ист.-
матем. исслед., вып. VI, 1953.
А. А. МАРКОВ И ЕГО МАГИСТЕРСКАЯ ДИССЕРТАЦИЯ 361
областях, которыми занимался. Пока мы остановимся только на его
магистерской диссертации.
Во второй из статей о квадратичных формах Коркин и Золотарев
коротко коснулись вопроса о минимумах неопределенных форм, указав
для случая двух переменных на одну их специфическую особенность.
В этом направлении их первый поиск был продолжен в
диссертации Маркова «О бинарных квадратичных формах положительного
определителя» (1880), которую Чебышев, Коркин и Сохоцкий
характеризовали в одном документе как «весьма замечательное и трудное
исследование» г).
В диссертации Маркова рассматриваются неопределенные двоичные
квадратичные формы
ах2 + 2Ъху + су2
с действительными коэффициентами, определитель которых
D = b2 — ac>0.
Было известно, что для определенных двоичных форм с определите-
л ем D<C.O точный верхний предел минимумов есть у -о- \D |,
соответствующий форме
V'
4-|л|(*"+^+0*).
а для неопределенных форм с определителем Z?>>0 точный верхнивг
предел ес^ь I/ — D и соответствует форме
у о
Коркин и Золотарев заметили существенное различие между двоичными
формами отрицательного и положительного определителей. В случае
D < 0 для любого положительного числа Z, не превосходящего 4/3,
существуют формы, минимумы которых равны ]/ I- \D |. Иначе обстоит дело
с неопределенными формами. Минимум у -f-25 имеет, как сказано, форма
/
— D(x2-~ ху — у2),
а также ей эквивалентные; все же остальные двоичные квадратичные
формы того же определителя D таковы, что точный верхний предел их
минимумов естьТ/^-/), и этот предел является минимумом формы
у у? (х2 — 2ху — у2). Для значений I между 1/2 и 4/5 не существует
форм с D > 0, минимумами которых являются числа У ID.
Отправляясь от немногих и кратких замечаний Коркина и
Золотарева о свойствах неопределенных двоичных квадратичных форм, Марков
продвинул исследование вопроса далее и выяснил основные законы
дискретного распределения минимумов названных форм.
^П.Л. Чебышев, Полное собрание сочинений, т. V, стр. 300.
362
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
Марков доказывает, что точный верхний предел минимумов форм,
же эквивалентных ни форме
ни форме
V-
-^-D(x2—xy — y2),
V-
4rD(x*-2xy-y*),
есть 1/ ?р. D и соответствует форме
/:
A-D(bx2—llxy--by2)
и ей эквивалентным. Числа 4/5, 1/2, 100/221 представляют собой
первые члены бесконечной последовательности убывающих положительных
чисел
N„ N2, ...,Nk, ...,
обладающих следующими свойствами:
1. Число классов двоичных квадратичных форм, для каждой из
которых определитель равен данному положительному числу D и минимум
равен Y^NkD, не может быть ни нулем, ни бесконечно большим.
2. Если некоторая двоичная квадратичная форма положительного
определителя D не может быть сделана по абсолютной величине меньше
YNkD, то минимум ее равен одному из чисел
V7f\D, \ГЩр, ..., УЖф.
3. Предел Nk при неограниченном возрастании к равен 4/9.
4. Для предельного значения чисел Nk существует бесчисленное
множество классов двоичных квадратичных форм положительного опре-
ел
делителя Z), минимум которых есть -n-V^D
Числа Nk зависят от некоторых периодических непрерывных дробей,
изучение которых показывает, что эти числа пред ставимы в виде
1
_9_ 1_
4 <?2
где Q — некоторое целое число. При этом, если целые числа т, п,
удовлетворяют неопределенному уравнению
х2 + у2 + z2 = 3xyz,
то среди чисел Nk наверное встречаются числа
1 1 1
_9 1_ ' 9 1_ ' _9 1_ '
4 т2 4 п2 4 р2
Наоборот, если некоторое Nk равно -= т-, где т — целое, то можно
4 т2
Г. Ф. ВОРОНОЙ И ГЕОМЕТРИЯ ЧИСЕЛ
363
найти бесконечное множество пар целых чисел п, р, для которых
т2 + ^2 + р2 = Зтпр.
Введенные Марковым периодические непрерывные дроби позволяют
найти все целые решения неопределенного уравнения
%2 + У2 + 22 = 3xyz,
не превосходящие по абсолютной величине заданного предела.
Как видно, Марков рассмотрел распределение минимумов, не мень-
ших -^-]ЛО. Вопрос о распределении минимумов, меньших этой
величины, оказался весьма трудным и до сих пор почти не исследован. Большие
трудности представляет также изучение минимумов неопределенных
форм с числом переменных, превосходящим два, а также форм более
высоких степеней. Сам Марков нашел в 1901—1909 гг. первые четыре
предельные формы для неопределенных троичных квадратичных форм
и две первые предельные формы в случае четверичных форм.
Исследования Маркова были продолжены в России и за рубежом. В частности,
Б. Н. Делоне дал геометрическое истолкование результатов Маркова,
обобщил постановку его задач и
открыл новые пути их изучения,
а Б. А. Венков в 1945 г. установил
с помощью геометрического метода
еще семь следующих предельных форм
для неопределенных троичных
квадратичных форм. Добавим, что
результаты диссертации Маркова, как
показал немецкий математик А. Гурвиц
(1891), непосредственно связываются
также с теорией рациональных
приближений действительных чисел *).
Г. Ф. Вороной и геометрия чисел.
Новые успехи в теории квадратичных
форм были достигнуты Георгием
Феодосьевичем Вороным (28 апреля
1868—20 ноября 1908), уроженцем
с. Журавка Полтавской губернии,
где он родился в имении своего отца,
в то время профессора русской
словесности Нежинского лицея. Еще г- ф- Вороной,
в Прилукской гимназии, которую он
окончил в 1885 г., Вороной полюбил математику. В том же году он
поступил в Петербургский университет. Занимался он с необыкновенным
прилежанием, вернее, страстностью; доходило до того, что он колол
себе пальцы булавкой, чтобы не уснуть в ночные часы, отведенные для
работы. Он с исключительным вниманием слушал лекции и, не
ограничиваясь тем, что для студента было обязательно, изучал новейшую
г) Магистерская диссертация и некоторые статьи Маркова о троичных формах
переизданы и комментированы в кн.: А. А. Марков, Избранные труды. Теория
чисел. Теория вероятностей. Ред. Ю. В. Линника, изд. АН СССР, 1951. См. также
Б. Н. Делоне, Петербургская школа теории чисел; о н ж е, О работе А. А.
Маркова «О бинарных квадратичных формах положительного определителя».— УМН,
т. III, вып. 5 (27), 1948.
364
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
литературу и мемуары классиков, тренировался в решении трудных задач,
а заодно овладевал иностранными языками. В 1888 г. Вороной занялся
теорией чисел Бернулли, к которой его внимание привлекли лекции
Маркова по исчислению конечных разностей. В декабре он сделал в
студенческом кружке, руководимом Марковым, свое первое научное
сообщение о новом доказательстве одного свойства чисел Бернулли. Под новый
год, 31 декабря (ст. ст.), получив еще другие результаты в том же
направлении, он писал в дневнике: «Я много, очень много работал и убедился,
что могу работать, и, кажется, успел в этом убедить других...» и, далео
говоря о счастье научного творчества: «Я твердо верю, что новый год
мне принесет еще больше радостей в этом отношении, потому что я
заметил, что моими последними успехами я обязан привычке мыслить без
пера и бумаги. Все предложения, доказанные таким образом, возникли
совершенно независимо и мне оставалось их только поверять» х). Теории
чисел Бернулли Вороной посвятил свое кандидатское сочинение,
поданное осенью 1889 г. и напечатанное во втором томе «Сообщений
Харьковского математического общества» (1890). По представлению Маркова,
Коркина, Сохоцкого и Поссе Вороной был оставлен при университете-
для подготовки к профессорскому званию.
За небольшой статьей о числах Бернулли последовали две
монографии: магистерская диссертация «О целых алгебраических числах,
зависящих от корня уравнения третьей степени» (СПб., 1894) и докторская
диссертация «Об одном обобщении алгорифма непрерывных дробей»
(Варшава, 1896), которую Вороной защитил в 1897 г. Обе они примыкают
к исследованиям Золотарева, Маркова и Сохоцкого по теории
алгебраических чисел и будут рассмотрены далее. Заметим лишь, что за эти работы
Академия наук присудила их автору премию имени Буняковского. После
магистерской защиты летом 1894 г. Вороной получил профессуру в
Варшавском университете, где и работал до конца своей жизни (с годичным
перерывом, когда в 1907—1908 гг. он преподавал в Донском
политехническом институте в Новочеркасске). Вороной отдавал преподаванию много
сил и времени. Одним из его учеников является крупнейший современный
польский математик В. Серпинский. Незадолго до кончины, в 1907 г.
Вороной был избран членом-корреспондентом Академии наук. Академия
наук УССР воздала должное этому замечательному ученому, собрав
все его научные труды, в том числе неопубликованные записи, в одном
издании 2).
На годы жизни в Варшаве приходятся исследования Вороного
по теории квадратичных форм. Вороной задумал обширную серию работ
под общим названием «Новые приложения непрерывных параметров
к теории квадратичных форм». Фактически он успел подготовить к печати
два больших мемуара. Первый из них —«О некоторых свойствах
положительных совершенных квадратичных форм»— вышел в 1908 г. в 133-м
томе журнала Крелле.
Коркин и Золотарев решили задачу Эрмита об отыскании верхних
границ минимумов положительных квадратичных форм данного
определителя с п переменными при п, равном 4 и 5, и, введя понятие
предельных форм, изучили многие важные их свойства. Общего приема вычисле-
г) Цит. по статье И. 3. Штокало и И. Б. Погреб ысского «Жизнь
и научная деятельность Г. Ф. Вороного» в кн.: Г. Ф. Вороной, Собрание
сочинений, т. III, Киев, 1953, стр 274.
2) Г. Ф. Вороной, Собрание сочинений, тт. I—III. Гл ред. И. М.
Виноградов. Киев, 1952—1953.
Г. Ф. ВОРОНОЙ И ГЕОМЕТРИЯ ЧИСЕЛ
365
ния всех предельных форм при любом п до Вороного не знали. Целью
первого мемуара Вороного является эффективное решение задачи Эрмита.
Коркин и Золотарев доказали, что каждая предельная форма
определяется значением своего минимума и всеми его представлениями. Вороной
заметил, что это свойство при числе переменных до пяти включительно
определяет только предельные формы, но при п>6 встречаются
положительные квадратичные формы, которые, обладая этим свойством,
не являются предельными. Отправляясь от этого, он выделил как особый
тип положительных квадратичных форм так называемые совершенные
формы, которые вполне определяются значениями своего минимума
и всеми его представлениями. Всякая предельная форма есть
совершенная, но совершенная форма (при гс>6) может и не быть предельной.
Оказалось, что исследование более широкого класса совершенных форм
ведет к более общим результатам, чем изучение форм предельных.
Совершенствуя и развивая далее методы Эрмита и других своих
предшественников, Вороной построил алгоритм, при помощи которого можно при любом
п найти в конечное число шагов все неэквивалентные совершенные формы7
число которых для данного п всегда ограничено. Кроме того, он
установил необходимые и достаточные условия, при которых совершенная
форма оказывается предельной. Создав стройную и законченную теорию
совершенных форм, в которой учение о предельных формах является
одним из отделов, Вороной продвинул далеко вперед работы Эрмита,
Коркина и Золотарева.
Создание алгоритма отыскания различных совершенных форм
опиралось у Вороного на геометрические методы, именно на исследование
областей и их границ в многомерном евклидовом пространстве,
координатами точек которого служат коэффициенты формы ^аах1хз- Во
введении к своему мемуару 1908 г. Вороной указывал, что «множеству (ф)
всех совершенных форм от п переменных приводится в соответствие
множество (R) областей п ^ ^ ' измерений, определенных с помощью
линейных неравенств» х) — линейных относительно atj. Области,
рассматривавшиеся Вороным, представляют собой (обобщенные) многогранники
и отыскание совершенных форм сводится к отысканию соответствующих
им граней, причем уравнения последних доставляют коэффициенты
форм. Следует добавить, что алгоритм Вороного, принципиально решая
задачу об отыскании минимумов положительных квадратичных форм,
связан при больших значениях п со значительными расчетными
трудностями. Результаты, относящиеся к значениям п от 6 до 10, о которых
упоминалось выше, были найдены с помощью приемов, аналогичных
методам Коркина и Золотарева.
Изучение свойств многогранников в многомерном пространстве
глубоко захватило Вороного. На протяжении многих лет он исследовал
эти свойства и им посвятил свой второй и последний мемуар о
квадратичных формах «Исследования о примитивных параллелоэдрах»,
напечатанный, как и предыдущий, в журнале Крелле (тт. 134, 1908 г. и 136,1909 г.).
Параллелоэдры — это выпуклые многогранники, посредством
параллельного и смежного расположения которых по целым граням можно
заполнить все пространство так, что они не входят друг в друга и между
ними не остается пустот. Параллелоэдры обыкновенного евклидова
пространства были впервые глубоко исследованы знаменитым русским
*) Г. Ф. Вороной, Собрание сочинений, т. Ц, стр. 175.
366
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
кристаллографом академиком Евграфом Степановичем Федоровым (22
декабря 1853—21 мая 1919). В «Началах учения о фигурах» (СПб., 1885)
Федоров показал, что имеется пять типов трехмерных параллелоэдров:
давно известные параллелепипед, правильная шестигранная призма и еще
два вида 12-гранников и один 14-гранник *). В 1896 г. важные свойства
многомерных параллелоэдров установил Г. Минковский.
Г. Ф. Вороной перенес задачу о параллелоэдрах на пространство п
измерений. В сохранившемся черновике его письма в редакцию журнала
Крелле от 1907 г. он говорил: «Трехмерные параллелоэдры играют теперь
важную роль в теории строения кристаллических тел..., но до сих пор
кристаллографы удовлетворялись описанием параллелоэдров с чисто
геометрической точки зрения. Я уже давно заметил, что задача разбиения
n-мерного аналитического пространства на выпуклые конгруэнтные
многогранники тесно связана с арифметической теорией положительных
квадратичных форм» 2).
В своем мемуаре Вороной полностью решил проблему заполнения
тг-мерного евклидова пространства при условии, что параллелоэдры
примитивные, т. е. сходятся в каждой вершине в возможно меньшем
для данного п числе, именно в числе п -j- 1. Для примера укажем, что
кубы не дают примитивного заполнения трехмерного пространства,
так как при этом в каждой вершине встречается 8 кубов, а не 4; вообще,
среди пяти федоровских тел только 14-гранник является примитивным.
Исследование примитивных параллелоэдров непосредственно
переплетается в мемуаре с рассмотрением соответствующих положительных
квадратических форм и методы их теории применяются для создания
алгоритма, с помощью которого можно найти все примитивные
параллелоэдры при любом п. Непримитивные заполнения пространства, даже при
п = 4, Вороной оставил неизученными. Преждевременная смерть не
позволила ему завершить уже начатые дальнейшие исследования.
Рассматриваемая работа Вороного сыграла огромную роль, и автор
ее, вслед за Г. Минковским, является одним из основателей геометрии
чисел. Эти изыскания Вороного были продолжены в советское время
Б. Н. Делоне, Б. А. Венковым, А. Д. Александровым и многими другими 3).
Вороной занимался и неопределенными квадратичными формами,
однако опубликовать по этому вопросу ничего не успел.
Соответствующие его заметки напечатаны только в последнее время 4). Ему
принадлежат также ценные открытия в аналитической теории чисел, к которым
мы обратимся позднее.
Теория алгебраических чисел. Начало работам в этой области
математики, пограничной между теорией чисел и алгеброй, в России положил
Е. И. Золотарев. Важный, хотя и частный, вопрос этой теории,
относящийся к кубическому полю, был рассмотрен в магистерской
диссертации Золотарева 1869 г. Вскоре затем занятия одной задачей Чебышева
в интегрировании алгебраических функций привели Золотарева к
фундаментальному результату — построению теории делимости для общего
числового алгебраического поля. Непосредственным отправным пунктом
*) Б. Н. Д е л о н е, Е. С. Федоров как геометр.— Труды Ин-та ист. естеств.
и техн., т. 10, М., 1956.
2) Цит. по статье И. 3. Штокало и И. Б. Погребысского в кн.: Г. Ф.
Вороной, Собрание сочинений, т. III, стр. 289 (подлинник письма на французском языке).
3) Б. Н. Делоне, Петербургская школа теории чисел, М.—Л., 1947.
4) В третьем томе цитированного ранее Собрания сочинений Вороного.
ТЕОРИЯ АЛГЕБРАИЧЕСКИХ ЧИСЕЛ
367
исследований Золотарева, в основной части проведенных с молниеносной
быстротой, в течение лета 1873 г., послужил вопрос: при каких
значениях постоянной А интеграл
Р (х + A) dx Р (х -\- A) dx
J yxbJraX3 + px2 + yxjrb~ J УЩх) '
с данными коэффициентами а, (3, у, 6, интегрируется в конечном виде
(предполагается, что корни многочлена в знаменателе различные, в
противном случае интеграл берется легко)?
Абель установил, что этот интеграл при подходящем значении А
(которое является единственным) интегрируется в конечном виде тогда
и только тогда, когда радикал в знаменателе раскладывается в
периодическую непрерывную дробь, которая имеет вид
VR {x) = x2 + ax + b +
1
а^х-\-Ъ^-
Bx^ + Cx^D 1
а1ж + &1-
В этом случае интеграл выражается в логарифмах по формуле
Р (x + A)dx = 1 1п р + дУЩх)
J УЯ(Х) 2Я р — дУЁЩ '
где р (х) и q (х) суть соответственно числитель (степени К) и
знаменатель подходящей дроби
^М- = х2 + ах+Ь +
q{x) l
1
а1х + Ь± +
апг + Ъп
Однако число членов периода заранее неизвестно и если периодичность
разложения фактически не обнаруживается, то нельзя сказать, происходит
ли это потому, что дробь не периодична или потому, что еще не дошли
до конца периода. В 1861 г. Чебышев сообщил без доказательства прием,
позволяющий при помощи конечного числа алгебраических действий
либо найти, при каком значении постоянной А этот интеграл выражается
через элементарные функции, либо установить, что он не интегрируется
ни при каких значениях А; при этом данные коэффициенты многочлена
считались рациональными. Число требуемых действий зависит от
обязательно ограниченного числа решений в целых числах некоторой системы
двух уравнений второй и шестой степени с тремя неизвестными. В 1872 г.
368
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
Золотарев опубликовал в 5 т. Mathematische Annalen полное
доказательство теоремы Чебышева, применив теорию эллиптических функций
Якоби. В докторской диссертации 1874 г. Золотарев распространил
решение задачи Чебышева на случай любых действительных
коэффициентов, причем многочлен в знаменателе с помощью некоторой
подстановки представил в виде х (х — 1) (х — а) (х — Р). Для этого ему
пришлось развить новую теорию делимости алгебраических чисел.
В письме к Коркину в 1873 г. Золотарев писал: «Чтобы доказать
конечность действий в этом случае, мне пришлось составить новую теорию
комплексных чисел, зависящих от корней уравнения..., которое можно
считать неприводимым. Этой теории я приписываю гораздо большее
значение, чем обобщению методы Чебышева» *). Уравнение, о котором
идет речь, алгебраическое с целыми рациональными коэффициентами,
из которых старший равен единице; параметры аир связаны
определенным образом с корнями этого уравнения. Заканчивая письмо,
Золотарев выражал уверенность, что новая теория получит и другие
приложения, кроме методы Чебышева.
Будет удобнее дать представление о работах Золотарева по теории
делимости, если ввести некоторые употребляемые теперь понятия и
термины.
Множество элементов, например, чисел или функций, называется
кольцом (термин Р. Дедекинда), если в нем определены две операции,
называемые сложением и умножением, причем они обе коммутативны
и ассоциативны, умножение дистрибутивно относительно сложения,
т. е. а(Ъ + с) = аЪ -\- ас и, наконец, для сложения имеется обратная
операция — вычитание. Во всяком кольце существует элемент, сумма
которого с любым другим элементом а равна тому же а; этот элемент О
называют нулем кольца. Для всякого элемента а кольца есть
противоположный элемент —а, в сумме с ним дающий 0.
Числовыми кольцами являются, например, множества всех целых
чисел, или только всех четных чисел. Натуральные числа не образуют
кольца (разность двух натуральных чисел может и не быть натуральным
числом), так же как и нечетные (сумма двух нечетных чисел — четное
число). Здесь операции сложения и умножения имеют обыкновенный
арифметический смысл.
Кольцо, в частности, называется полем, если в нем для любых двух
элементов а, Ъ (причем а — не нуль) возможна однозначная операция
деления Ъ на а, т. е. существует такой элемент х, что ах = Ъ. В каждом
поле существует его единица, т. е. элемент, произведение которого на любой
элемент а дает а\ эта единица единственная. В кольцах единица может
и не существовать, как, например, в кольце четных чисел. В каждом
поле для любого элемента а, отличного от нуля, имеется обратный а-1,
т. е. такой, что их произведение аа-1 = 1.
Если часть элементов Р' поля Р сама есть поле по отношению к тем
же операциям сложения и умножения, то эта часть поля Р' называется
подполем Р, а поле Р — расширением поля Р'. Так, множество
рациональных чисел есть подполе поля действительных чисел, а множество
комплексных чисел есть расширение поля действительных чисел.
Если к рациональному полю R присоединить все числа, являющиеся
рациональными функциями с рациональными коэффициентами от корня
со какого-либо неприводимого алгебраического уравнения п-и степени
г) Е. И. Золотарев, Полное собрание сочинений, вып. 2, стр. 211.
ТЕОРИЯ АЛГЕБРАИЧЕСКИХ ЧИСЕЛ
369
F (х) = 0 с целыми коэффициентами *), то получается расширение этого
поля R (со), и говорят, что это новое поле, зависящее от со, возникло
от присоединения к R числа со и имеет степень п. Так, квадратичное
поле рациональных комплексных чисел R (]/" — 1) получается от
присоединения к R корня уравнения
я2 + 1 = 0.
Если старший коэффициент уравнения с целыми коэффициентами есть 1,
то его корень называется целым алгебраическим числом п-ж степени.
Все целые алгебраические числа поля R (со) образуют кольцо. В этом
кольце всегда существуют такие п целых чисел (Оь со2, . . ., соп, что
любое другое целое число единственным образом представляется в виде
^о)! -\-а2(й2 + • • • +a7iC07i» гДе ak — целые рациональные числа;
говорят, что числа ©i, со2, . . ., соп образуют базис кольца целых чисел
поля R (со).
Выше мы определили уже понятие нормы алгебраического числа.
Единицей какого-либо кольца целых алгебраических чисел называется
число, норма которого равна 4=1; всякая единица а обладает тем свой-
ством, что а = —. Таких единиц в кольце целых рациональных чисел,
т. е. корней уравнения F (х) = х -J- а± = 0, две, 1 и —1. Вообще говоря,
в кольцах, зависящих от уравнений высших степеней, единиц бесконечно
много, но в каждом кольце имеется определенное конечное количество
так называемых основных единиц, а все остальные представляются
произведениями степеней основных единиц, умноженными на какую-либо
особую единицу — некоторый корень из единицы (теорема Дирихле, 1846).
Теория делимости в кольце целых рациональных чисел имеет
основное значение во всей обыкновенной арифметике. Ее центральным
предложением служит древняя теорема о возможности и единственности
разложения всякого такого числа в произведение простых чисел (и одной
из основных единиц, т. е. 1 или —1). Теория алгебраических чисел,
имеющая обширные и глубокие приложения, сводится к построению
арифметики различных колец, содержащих в себе кольцо всех целых
рациональных чисел. Для такого построения требовалось в первую
очередь для каждого кольца найти его единицы и разработать в нем
теорию делимости.
К расширению понятия целостности привели исследования,
посвященные обобщению квадратичного закона взаимности, а затем — большой
теореме Ферма. Первое такое расширение было дано Гауссом в связи
с изучением закона взаимности для биквадратичных вычетов (1832).
Гауссовы целые числа — это комплексные числа вида а -f- Ы, где а и Ъ —
целые рациональные числа, i = У—1.
Арифметика кольца гауссовых чисел имеет свои особенности.
Например, в нем составными оказываются не только обыкновенные составные
числа, но и некоторые обыкновенные простые числа, как 2 = (1 + i) х
X (1 — &)• Однако, как показал Гаусс, на целые комплексные числа
можно распространить все основные законы обыкновенной арифметики —
алгоритм Евклида, понятие о наибольшем общем делителе и т. д. В
частности, в кольце гауссовых чисел всякое составное число единственным
г) Алгебраическое уравнение / (х) = 0 с коэффициентами из поля Р называется
неприводимым в поле Р, если левая часть не раскладывается на множители низших
степеней с коэффициентами в Р.
370
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
образом разлагается в произведение простых гауссовых чисел и его
четырех единиц 1, —1, i, —i. Гауссовы простые числа таковы:
а) простые действительные числа вида 4га -f- 3,
б) комплексные множители чисел вида 4тг -)- 1,
в) число 1 — г.
Гаусс изучил кольцо целых комплексных чисел, принадлежащее
полю рациональных комплексных чисел R (У—1).
Ученик Гаусса Ф. Эйзенштейн для доказательства кубического*
закона взаимности рассмотрел целые числа поля R (х), где х —
комплексный корень уравнения х3 — 1 = 0, т. е.
_ 1 У^з
Попытки доказать знаменитую большую теорему Ферма привели
П. Лежен Дирихле (1846), Э. Куммера (1847) и других математиков
к рассмотрению целых чисел еще более общего вида
а = а0 + сцх + а2х2 + . . . + ап-\хП~х->
где а0, аь . . ., an_i — целые рациональные числа, а х — какой-либо
хп /[
отличный от 1 корень гауссова уравнения деления круга = 0.
Эти числа образуют кольцо в поле R (ж), где х — по-прежнему корень
уравнения деления круга. Однако установить законы делимости,
аналогичные обычным, в кольце куммеровых чисел оказалось нелегко.
Трудность здесь связана со своеобразным расщеплением понятия простоты
в этом кольце. Обыкновенные простые числа, неразложимые на целые
рациональные множители, отличные от них самих и единицы, обладают
тем свойством, что если произведение двух целых рациональных чисел аЪ
делится на простое jo, то по крайней мере один из множителей делится
на р. В кольце же куммеровых целых чисел имеются такие, что их
произведение делится на число, не имеющее делителей в этом кольце, кроме
единицы, но ни один из сомножителей на него не делится. Поясним
сказанное аналогией.
Рассмотрим кольцо четных чисел. Числа, вроде 2, 6, 10, 14, 22 и т. п.,
не имеют делителей в этом кольце и в этом смысле могут считаться в нем
«простыми». Вместе с тем существуют числа кольца, которые
представляются в виде произведений различных «простых» чисел, т. е. для которых
не имеет места теорема об однозначности разложения на простые
множители и не выполняется упомянутое свойство. Так, 60 = 6-10 = 2-30;
ни 6, ни 10 не делятся на 2 в нашем кольце, а 60 делится.
В только что рассмотренном кольце можно восстановить закон
однозначности разложения на множители, присоединив к его элементам
другие, именно все нечетные числа. Для восстановления того же закона
у целых чисел поля деления круга Куммер вводит особые множители,,
названные им «идеальными числами». Если в таком дополненном поле
произведение аЪ делится, а числа а и Ъ не делятся на р, неразложимое
в поле деления круга, то это объясняется тем, что р является
произведением идеальных множителей, скажем, тп, а числа а и Ъ — идеальных
множителей тг и, соответственно, ns, причем множители ттг, г, п, s
полю деления круга не принадлежат.
Куммер применил свою теорию делимости (1847) к доказательству
теоремы Ферма для всех показателей, не превосходящих 100, а также
ТЕОРИЯ АЛГЕБРАИЧЕСКИХ ЧИСЕЛ
371
для многих других показателей, именно — для простых чисел, не
делящих числители некоторых чисел Бернулли (1850). Мы еще будем говорить
о работах русских математиков по теории чисел Бернулли.
Следующим этапом явилась разработка общей теории делимости
целых алгебраических чисел. Решение этой трудной задачи и дал в своей
диссертации «Теория целых комплексных чисел с приложением к
интегральному исчислению» (1874) Золотарев.
В первой главе диссертации строится аппарат функциональных
сравнений по двойному модулю, восходящий в идейном смысле к Галуа
и Гауссу и довольно подробно развитый в курсе алгебры Серре. Два
многочлена с целыми коэффициентами А(х) и В(х) называются
сравнимыми по простому модулю р, если по этому модулю попарно сравнимы
коэффициенты при одинаковых степенях переменного. Если, далее,
А = BQ (mod/?), то говорят, что А делится на В по модулю р;
многочлен же, не делящийся по модулю р ни на какой многочлен низшей
степени, называется простым по этому модулю. Наконец, пусть при делении
А на многочлен В степени п, простой по модулю /?, получается остаток R
(степени не выше п — 1), т. е. А = BQ -\- R (mod р); тогда R называется
наименьшим вычетом А по модулю р и функции В. Две функции, имеющие
одинаковые вычеты, называются сравнимыми по модулю р и функции В.
Мы лишь сформулировали для ясности основные определения. У
Золотарева свойства и некоторые применения функциональных сравнений
занимают более 30 страниц.
Во второй главе вводятся основные понятия теории целых
алгебраических чисел: само понятие целого числа, зависящего от корней
неприводимого уравнения F (х) = 0 п-ж степени с целыми коэффициентами
и старшим коэффициентом 1, затем понятия нормы, комплексной единицы
и другие. Здесь же выводится необходимая для дальнейшего теорема
Дирихле об алгебраических единицах, причем предложено совершенна
оригинальное доказательство, основанное на эрмитовом методе
непрерывного параметра и предложении о границе минимумов положительных
квадратичных форм.
Основной является третья глава книги «Идеальные множители
комплексных чисел», в которой строится полная теория делимости для
алгебраических полей, зависящих от весьма обширного класса «неособых»
уравнений F (х) = 0. Уже в то время Золотарев располагал средствами,
позволявшими строить эту теорию без каких-либо ограничений, однако
некоторые «особые» случаи он счел полезным исключить пока из
рассмотрения, чтобы «представить теорию комплексных чисел в самом простом
виде» г). Здесь при введении основных понятий используются
функциональные сравнения. Так, обыкновенное простое число рассматривается
в поле, зависящем от уравнения F (х) = 0, как простое, если F (х) —
простая функция по модулю р\ такое простое число делится только на само-
себя и на единицы поля. Остальные обыкновенные простые числа
считаются составными. Для сохранения однозначности разложения на
множители целых чисел таких полей, Золотарев, вслед за Куммером, вводит
(опять-таки с помощью функциональных сравнений) обобщенные
идеальные множители, подробно разбирает их свойства и показывает, что целые
числа Гаусса и Куммера являются частными случаями тех весьма
общего вида «целых комплексных чисел», арифметику которых он создал
в этой главе.
) Е. И. Золотарев, Полное собрание сочинений, вып. 1, стр. 249.
372
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
Наконец, в четвертой главе дано решение задачи Чебышева, по
объему занимающее 2/5 всего сочинения. В своем отзыве Чебышев, вполне
признавая высокое значение в науке общей теории Золотарева, обратил
специальное внимание на ее применение к интегральному исчислению,
как по достоинству решенного при этом вопроса, так и потому, что «до сих
пор мы знаем еще очень мало приложений теории чисел к вопросам
определенного анализа и эти приложения считаются весьма важными
приобретениями для математики» х).
В докторской диссертации Золотарева теория делимости была
построена еще не для самого общего случая; но ограничения, наложенные на
уравнения F(x) = 0, были сняты в мемуарах «О комплексных числах»
(1877) и особенно «О теории комплексных чисел» (1876; опубл. в 1880),
дающих окончательное завершение
общей теории делимости Золотарева.
Одновременно с Золотаревым над
построением общей теории делимости
работал немецкий ученый Р. Дедекинд,
который шел путями, совершенно
отличными от Золотарева. Свои открытия
Дедекинд в неполном изложении
опубликовал в 1871 г.; в более общем виде
он развил свою теорию идеалов в 1879 г.
В 1881—1882 гг. другой немецкий
математик, Л. Кронекер, дал третье
обоснование теории делимости. Уже то
обстоятельство, что три столь крупных
математика почти одновременно и
независимыми путями шли к общей цели,
свидетельствует о значительности и
актуальности самой проблемы.
За границей труды Золотарева
получили признание нескоро, в России же
его идеи и методы нашли
продолжателей быстро.
И. И. Иванов. Большую роль в распространении
теории Золотарева сыграл Иван
Иванович Иванов (11 августа 1862—17 декабря 1939). Выходец из
бедной семьи, с 14 лет живший на собственные скудные заработки, Иванов
окончил уездное училище и учительский институт. По-видимому, Чебы-
шеву и Коркину удалось исхлопотать небольшое пособие, позволившее
Иванову заниматься в университете в качестве вольнослушателя. За два
года Иванов сдал здесь все экзамены и в 1886 г. был оставлен для
подготовки к профессорскому званию. В магистерской диссертации Иванова
«Целые комплексные числа» (СПб., 1891) содержался вывод теории
Золотарева из теории Дедекинда, в статье «К теории целых комплексных
чисел» (Записки Акад. наук, т. 72, № 9, 1893) — вывод второй теории
из первой. Таким образом была установлена равносильность результатов
обеих теорий, несмотря на глубокое различие их методов, которые сообщают
каждой из них свои особые преимущества в различных приложениях.
Докторская диссертация Иванова «О некоторых вопросах,
находящихся в связи со счетом простых чисел» (СПб., 1901) содержала весьма
г) П. Л. Ч е б ы ш е в, Полное собрание сочинений, т. V, стр. 299.
ТЕОРИЯ АЛГЕБРАИЧЕСКИХ ЧИСЕЛ
373
полное изложение открытий, сделанных в этой области без употребления
функций комплексного переменного, и ряд обобщений результатов Чебы-
шева. Об одном из них, относящемся к распределению простых чисел
в прогрессии 6п ± 1, уже говорилось. Другое обобщение связано с
теоремой Чебьппева, согласно которой отношение наибольшего простого
делителя чисел 1 + 22, 1 + 42, . . ., 1 + 4/V2 к числу N неограниченно
возрастает вместе с N. Эту теорему со слов Чебьппева привел в
четвертом издании своего известного курса Эрмит в 1891 г. Марков в 1895 г.
восстановил по черновикам Чебьппева ее вывод. Тогда же Иванов
доказал, что если целые А и а взаимно простые, то отношение наибольшего
простого делителя чисел А + а-12, А -\-a-22, . . ., A -J- aN2 беспредельно
растет вместе с N.
В 1891 г. Иванов работал в Петербургском университете,
позднее также в Политехническом институте и на Высших женских
курсах; в 1924 г. он был избран членом-корреспондентом Академии
наук СССР.
Распространению теории делимости Золотарева одним из первых
содействовал также Ю. В. Сохоцкий, книга которого «Начало общего
наибольшего делителя в применении к теории делимости алгебраических
чисел» (СПб., 1893) содержит превосходное по ясности и полноте
изложение вопроса х).
К обеим диссертациям Золотарева, магистерской и докторской,,
примыкает ряд работ петербургских математиков по теории полей,
зависящих от уравнений третьей степени.
В 1892 г. А. А. Марков выступил с исследованием «О целых числах,
зависящих от корня кубического из цедого рационального числа».
Он определил простые идеальные множители всех целых чисел чисто
кубического поля и фундаментальный базис для этого случая. Именно,
он показал, что все целые алгебраические числа, зависящие от угАг
где А не есть целый куб, можно, по выделении из А квадратного
множителя, так что А = а2Ь, представить в виде
х + У VvPb + z У ab2,
если А не сравнимо с ±1 по модулю 9 и в виде
если А == ± 1 (mod 9). Здесь х, у, z — целые рациональные. В конце
работы дана таблица алгебраических единиц для чисел от А = 2 до
А = 70. «Я убежден,— писал Марков,— что почти все эти единицы:
являются основными» 2).
Исследования Маркова и Сохоцкого стали в свою очередь
отправными для Вороного, который, в отличие от своих предшественников,
изучавших специальные кубические поля и кольца, избрал предметом самый
общий случай. В магистерской диссертации «О целых алгебраических
числах, зависящих от корня уравнения третьей степени» (1894) он
определил фундаментальный базис поля, зависящего от корней неприводимога
х) История всего этого цикла проблем подробно рассмотрена в статье И. Г. Б а ш-
маковой, Обоснование теории делимости в трудах Е. И. Золотарева.—Ист.-матем„
исслед., вып. II, 1949.
2) А. А. Марков, Избранные труды. Теория чисел. Теория вероятностей,,
стр. 133.
374
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
уравнения р3 = гр + s. Теорему Вороного можно формулировать так:
каждое целое алгебраическое число общего кубического поля имеет вид
к
х + уа + z— , где х, у, z — целые рациональные, а есть подходящим
образом выбранное в поле целое алгебраическое число, а & — наименьшее
натуральное число, для которого частное к/а есть целое алгебраическое г).
Здесь же, используя упомянутый труд Сохоцкого, Вороной предложил
удобный способ разложения на простые идеальные множители всех целых
чисел поля.
Оставался вопрос об отыскании единиц общего кубического поля.
Эта трудная задача была полностью решена в докторской диссертации
Вороного «Об одном обобщении алгорифма непрерывных дробей» (1896).
Вычисление основной единицы квадратичного поля, равносильное
решению уравнения Пелля х2, — А у2 = 1, производится с помощью алгоритма
непрерывных дробей, именно разложения в непрерывную периодическую
дробь квадратного корня из числа А (которое предполагается
неквадратным). Этот алгоритм, восходящий к Валлису (1657), был глубоко изучен
Эйлером, Лагранжем и другими. С середины XIX века предпринимался
ряд попыток обобщения алгорифма непрерывных дробей для решения
задач теории кубических полей. В предисловии к докторской диссертации
Вороной подробно разобрал сравнительные достоинства и недостатки
этих обобщений, принадлежащих Якоби, Дирихле, Кронекеру, Пуанкаре,
Эрмиту и другим ученым. «Полагая в основание наших исследований
особенную точку зрения на алгорифм непрерывных дробей,— писал
Вороной,— мы предлагаем новое его обобщение» 2). Руководящей идеей
явилось при этом установление понятия об относительных минимумах
так называемых ковариантных форм и способа их вычисления. Все это
связывается с общей теорией квадратичных форм. Алгоритм Вороного
позволяет для всякого предложенного уравнения сразу найти основную
систему его алгебраических единиц, которых бывает одна, когда
уравнение имеет только один действительный корень, и две, когда все три корня
действительные. Другие приемы давали системы единиц, из которых
основные приходилось выбирать путем проб.
Во всех рассмотренных работах Золотарева, Маркова и Вороного
ярко проявляются уже отмечавшиеся нами особенности чебышевской
школы, именно построение широких обобщающих теорий на основе
решения трудных конкретных задач и стремление к созданию практически
наиболее выгодных расчетных приемов, позволяющих в возможно
меньшее число шагов дать исчерпывающий числовой ответ для каждого частно-
то случая. Д. А. Граве рассказывает, что когда Марков, бывший вместе
с Сохоцким оппонентом по докторской диссертации Вороного,
находившегося еще в Варшаве, познакомился с его работой, он пригласил
диссертанта в Петербург и когда тот пришел, посадил его в своем кабинете,
предложив вычислить основную единицу для поля, зависящего от >/23.
Через три часа Вороной назвал результат, совпавший с ранее найденным
самим Марковым с помощью другого, более частного способа. Не знаю,
насколько точен этот рассказ 3), но он по-своему отражает
алгоритмический стиль всего творчества петербургских математиков.
*) Д. А. Граве, Элементарный курс теории чисел. Изд. 2-е, Киев, 1913,
стр. 263.
2) Г. Ф. Вороной, Собрание сочинений, т. I, стр. 206.
3) Д. А. Граве, Про узагальнення алгоритма Вороного.— Журнал матем.
циклу ВУАН, III, № 2, 1933.
ТЕОРИЯ АЛГЕБРАИЧЕСКИХ ЧИСЕЛ
375
Данная работа Вороного написана в чисто аналитическом духе.
Б. Н. Делоне полагает, что, подготовляя ее, Вороной «мыслил и находил
свои результаты геометрически» и лишь потому все перекладывал затем
на арифметический язык, что «в то время геометрия была в Петербурге,
особенно в вопросах теории чисел, не в фаворе» х).
Исследования по теории кубического поля были продолжены
многими советскими учеными: Б. Н. Делоне, Д. К. Фаддеевым, Б. А. Венковым
и другими. Некоторые американские и немецкие математики, не зная
работ Вороного, вновь выводили его теоремы с опозданием на десятки лет.
В дальнейшем развитии теории алгебраических чисел большую роль
сыграла алгебраическая школа Д. А. Граве, который сам много
способствовал популяризации этой дисциплины и идей ее русских
представителей своими лекциями, семинарами и книгами: уже названным курсом
теории чисел и в еще большей мере курсом «Арифметическая теория
алгебраических величин», из пяти задуманных томов которого свет
увидели два: «Квадратичная область» (с приложением статьи В. П. Вельмина
«Об идеалах квадратичной области») и «Теория идеалов» (Киев, 1910—
1913). Только что упомянутый Владимир Петрович Вельмин (род. 20 июля
1885), ученик Б. Я. Букреева, работавший с 1909 г. доцентом и с 1913 г.
профессором Варшавского (Ростовского) университета, издал по своим
лекциям «Введение в теорию алгебраических чисел» (Варшава, 1913)
и магистерскую диссертацию «О квадратичном законе взаимности в
произвольной квадратичной области» (Варшава, 1913), содержащую
оригинальное изложение и собственные результаты автора в так называемой
теории полей классов.
В эти же годы начали свои первые работы по теории чисел ученики
Д. А. Граве: Б. Н. Делоне, Н. Г. Чеботарев и другие.
Борис Николаевич Делоне (род. 15 марта 1890), сын профессора
механики Н. Б. Делоне (1856—1931) 2), окончил Киевский университет
в 1913 г. Учителями его были В. П. Ермаков и Д. А. Граве. Еще в
студенческие годы Б. Н. Делоне успешно занялся вопросами новой алгебры
ж теории алгебраических чисел. В 1915—1916 гг. он начал исследования
по диофантову анализу. Наиболее общий результат здесь был получен
в начале XX века скандинавским математиком А. Туэ, который показал
(1909 и последующие годы), что уравнение
а0хп + а±хп-гу + . . . + апуп = С,
тде п > 2, все ak, а также С — целые, и многочлен a0zn + a^z71'1 +...
... + ап неприводим в поле рациональных чисел,— может иметь только
конечное число целых решений. Однако вопрос о числе и границах
возможных решений Туэ не рассмотрел.
Б. Н. Делоне исследовал случай кубического аналога уравнения
Пелля, т. е. уравнение
ах3 + у3 = 1,
тде а — целое некубическое число. Он доказал, что, помимо очевидного
решения х = 0, у = 1, это уравнение может иметь не более одного цело-
численного решения. Метод Делоне позволяет найти такие решения,
г) Б. Н. Делоне, Петербургская школа теории чисел, стр. 213.
2) Которому принадлежит, между прочим, книга на немецком языке о работах
Чебышева по теории механизмов: N. Delaunay, Die Tschebyschefschen Arbeiten
in der Theorie der Gelenkmechanismen, Leipzig, 1900.
376
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
если они существуют. Работы в этом направлении были продолжены
как самим Делоне, так и другими учеными.
Опубликованы эти и примыкающие к ним результаты Б. Н. Делоне
были уже в советское время, в 1922 и последующие годы. В 1929 г.
Делоне был избран членом-корреспондентом Академии наук СССР.
Николай Григорьевич Чеботарев (15 июня 1894 — 2 июля 1947),
впоследствии крупнейший советский алгебраист, работавший в Киеве,
Одессе и с 1927 г. в Казани, с 1929 г. член-корреспондент Академии наук
СССР, внес в теорию алгебраических чисел очень значительный вклад.
Все основные работы его появились уже после 1917 г. и мы
рассматривать их здесь не будем. Скажем только, что Чеботарев очень многое
сделал для распространения и развития идей Золотарева. Ему, в
частности, принадлежат статьи «Новое обоснование теории идеалов (по
Золотареву)» (Казань, Изв. физ.-матем. о-ва, 25(2), 1925) и «Об основании
теории идеалов по Золотареву». Во второй из них Чеботарев писал:
«Интерес, который представляет теория Золотарева в настоящее время,
заключается в том, что в ней впервые была развита теория, получившая
в настоящее время название локальной теории идеалов. Последняя
оказалась весьма плодотворной в теории полей классов, а также в теории
алгебраических функций» 1). Исследования самого Н. Г. Чеботарева, И. Р. Ша-
фаревича и других математиков в полной мере подтверждают
справедливость этих слов.
Мы еще вернемся к Д. А. Граве и его киевским ученикам в отделе,
посвященном алгебре.
Новые исследования по аналитической теории чисел. Г. Ф. Вороной
сообщил новый толчок работам русских математиков и в аналитической
теории чисел, прежде всего в той ее области, которую теперь именуют
асимптотической геометрией чисел.
В статье «Об одной задаче из теории асимптотических функций»
(1903) Вороной занялся задачей, рассмотренной еще Дирихле в 1849 г.
Задача состоит в асимптотической оценке для больших п функции
S(/0 = T(l) + T(2) + ...+T(#i)f
где х(к) — число делителей натурального числа к. Задачу легко
сформулировать на языке геометрии, ибо S (п) есть число точек с целыми
координатами (х, у), для которых
?>0, г/>0, ху^п,
т. е. число целых точек в области, ограниченной ветвью гиперболы ху = п
и осями координат, за исключением точек на осях.
Дирихле показал, что функция S(n) асимптотически изображается
выражением
S(n) = n(lnn + 2C—l) + 0(Vn),
где С ¦= 0,577 . . . есть постоянная Эйлера 2). Вороной, применяя так
.называемые ряды Фарея (последовательность некоторых несократимых
г) УМН, т. II, 6 (22), 1947, стр. 52.
2) Напомним, что запись вида f{x) = О(х) означает, что для всех достаточно
' ^ к, где к — некоторая положительная постоянная.
больших х имеет место
х
f (х)
Запись f(x) = о (х) означает, что lim ; v ' = 0.
АНАЛИТИЧЕСКАЯ ТЕОРИЯ ЧИСЕЛ
377
дробей alb) и формулу суммирования Н. Я. Сонина, улучшил оценку
приближения, показав, что
S(n) = n(lnn + 2C— 1) + О (Уп In п).
Заметим, чтобы не возвращаться к этому впоследствии, что формула
суммирования Н. Я. Сонина, обобщающая формулу Эйлера —Маклорена,
имеет вид
п^Ъ Ъ Ъ
2 /(») = §/(*) dx + ro (b)f(b)-r0 (a) /(a)- J r0 (х) df(x).
п>а а а
Здесь г0(х) = [х] — х + ~2 » гДе Ь] есть целая часть # или само число #,
если оно целое, так что \г0 (х)\ не превосходит 1/2; функция / (х) имеет
непрерывную производную в интервале а <С х <С Ь, где а и 6 —
положительные числа («Об одном определенном интеграле, содержащем
числовую функцию Ы». (Варшавские унив. известия, 1885).
Мы не будем касаться других статей Вороного по аналитической
теории чисел, в которых он впервые применил к ее проблемам
цилиндрические функции. Заметим лишь, что работа, посвященная задаче Дирихле,
имела большое значение в дальнейшем развитии теории чисел в России.
Первым продолжением этой работы явилась статья уже упомянутого
нами польского математика В. Серпинского. Вороной поставил перед
ним восходящую еще к Гауссу задачу о подсчете числа целых точек
в круге ?2 + г/2<лг. При помощи методов Вороного Серпинский нашел
(Ргасе Mat.-fiz., 17, 1906), что это число if> (п) определяется
асимптотической формулой
ty (п) = т-\-0 (т/я).
Несколько позднее та же работа Вороного послужила отправным
пунктом замечательных исследований И. М. Виноградова.
Иван Матвеевич Виноградов родился 14 сентября 1891 г. в семье
священника в селе Милолюб Великолукского уезда Псковской губернии.
По окончании в 1910 г. реального училища в Великих Луках И. М.
Виноградов поступил в Петербургский университет и в 1915 г. был оставлен
здесь для подготовки к профессорскому званию. Решенные Виноградовым
задачи и созданные им мощные аналитические методы оказали глубокое
влияние на все развитие современной теории чисел и принадлежат к
наиболее ярким ее достижениям. С 1929 г. И. М. Виноградов является
действительным членом Академии наук СССР, он является также иностранным
членом Академии наук в Париже, Лондонского королевского общества,
Академии наук США и других научных корпораций. С 1932 г.
И. М. Виноградов руководит Математическим институтом Академии наук
СССР; в 1945 г. ему было присвоено звание Героя Социалистического Труда.
Обратимся к первым выдающимся работам И. М. Виноградова,
опубликованным в самом конце рассматриваемого периода.
В работе «Новый способ для получения асимптотических выражений
арифметических функций», появившейся в «Известиях Академии наук»
за 1917 г., Виноградов писал:
«При изысканиях асимптотических выражений арифметических
функций особенную трудность представляет оценка верхнего предела
допускаемой погрешности. Такое обстоятельство объясняется несовершенством
применяемых методов исследования и выдвигает важный и трудный вопрос
378
ГЛ. 17. ТЕОРИЯ ЧИСЕЛ
об улучшении последних. Вороной в своей замечательной работе развил
новый метод, применимый к целому ряду асимптотических задач, дающий
предел погрешности значительно меньший, чем получается по классическому
способу Дирихле». Указав затем результаты Вороного и Серпинского,
И. М. Виноградов продолжает: «Несмотря на необыкновенное остроумие
и глубину, метод Вороного слишком сложен, что сильно затрудняет его
применение. В настоящей работе мы развиваем новый метод, значительно
более простой, нежели метод Вороного, и дающий почти те же верхние
пределы погрешностей. Так, для случая Вороного верхний предел
погрешности по нашему методу оказывается у a (In а)5, а для случая
Серпинского — У a (In а) 2/з» 1).
Уже в начальный период своего творчества Виноградов поставил
себе целью создание более общих методов решения задач аналитической
теории чисел. В данной работе он
предложил общий способ подсчета числа целых
точек, расположенных в областях,
ограниченных контурами весьма обширного
класса. Для области, ограниченной дугой
линии у =/ (х) над осью'абсцисс,
прямыми х = Q, х = R (<? < R) и отрезком оси
абсцисс, число целых точек в ней
(исключая точки на левой и нижней частях
контура) выражается суммой
x>Q
Если обозначить {/ (х)} дробную часть / (х),
так что
lf(x)] = f(x)-{f(x)},
то вычисление суммы 2 [/(ж)] можно свести
к вычислению суммы 2/(ж) (с помощью
формулы Сонина) и суммы дробных
долей 2{/ (х)}.
И. М. Виноградов. И- М- Виноградов при некоторых
условиях относительно / (х) нашел весьма
простую оценку для этой суммы дробных долей, а затем и для числа
точек в указанной области, от которой уже нетрудно было перейти
к замкнутым областям овального вида. Свои результаты он
распространяет затем и на случай Вороного. Вот одна из основных теорем
Виноградова. Если область с площадью S ограничена замкнутым контуром,
на котором отношение наибольшего радиуса кривизны г к наименьшему
не превосходит данного постоянного числа, то число Т целых точек этой
области выражается асимптотическим равенством
T = S + 0((rlnr)2/3).
Для круга
х2 -f- у2 <; п
немедленно получается
Г = я:л + 0(л1/8(111Л)"/8).
г) И. М. Виноградов, Избранные труды, М., 1952, стр. 3.
АНАЛИТИЧЕСКАЯ ТЕОРИЯ ЧИСЕЛ
379
В конце работы Виноградов применил свой метод к задаче о
вычислении среднего значения функции h(—А), выражающей число классов
неэквивалентных двоичных квадратичных форм
ах2 -f 2Ъху + су2
с данным отрицательным определителем — А, причем а > 0; 6, с —
целые и а, 26, с не имеют общего делителя. В 1801 г. Гаусс без
доказательства сообщил, что в приближенном выражении суммы
h(-l)+h(-2)+...+h(-n)
оо
главный член есть -к-.— тг3/а, где е= 2 ~Р~'в 1865 г. это доказали Р. Лип-
шиц и Ф. Мертенс. В 1912 г. Э. Ландау дал более точное
асимптотическое выражение:
-^п*/*--^п + 0(п*/*Ып).
Виноградов получает для добавочного члена оценку О (тг5/е (In тг)2/з).
Вскоре, в 1918 г. в томе 16 «Сообщений» Харьковского математического
общества вышла другая статья Виноградова, специально посвященная
задаче Гаусса. В этой работе автор использовал новый, более сильный
метод, основанный на разложении {f(x)} в ряд Фурье, что сводит
оценку 2 {/(#)} к оценке некоторых тригонометрических сумм, и понизил
добавочный член асимптотической формулы для задачи Гаусса до
0(п3/*(Ы п)2). Дальнейшее улучшение оценки И. М. Виноградов получил
в виде 0(rc°'7+s) в 1934 г.
На последующих блестящих открытиях И. М. Виноградова в теории
чисел мы не останавливаемся: они целиком принадлежат советскому
времени.
ГЛАВА ВОСЕМНАДЦАТАЯ
ИНТЕГРИРОВАНИЕ АЛГЕБРАИЧЕСКИХ ФУНКЦИЙ
Исследования П. Л. Чебышева. В предыдущей главе мы видели, что
вопрос о выражении эллиптических интегралов в элементарных функциях
потребовал чисто арифметических изысканий и для Золотарева явился
непосредственным поводом для разработки общей теории алгебраических
чисел. В творчестве Чебышева занятия этим вопросом хронологически
явились одними из первых, Мы коротко остановимся на этом
направлении Петербургской школы.
В истории математики неоднократно возникала потребность выяснить,
разрешимы ли те или иные задачи при помощи данных средств. Целый
ряд накопившихся с древности задач подобного рода был до конца
исследован только в XIX веке. Сюда относится, например, доказательства
невозможности деления произвольного угла на три равные части
(трисекции угла) или построения стороны квадрата, по площади равного
кругу данного радиуса (квадратуры круга), при помощи циркуля и
линейки. В том же столетии, как мы знаем, была доказана невозможность
решения общих алгебраических уравнений выше четвертой степени
при помощи основных четырех действий и извлечения корня (т. е. их
решения в радикалах). К этому же кругу проблем принадлежит вопрос
о выразимости в элементарных функциях интегралов различных классов
иррациональностей, который встал вместе с появлением интегрального
исчисления, а также о выражении в квадратурах решений
дифференциальных уравнений.
Мы уже говорили о вкладе, внесенном в теорию интегрирования
алгебраических функций Абелем, Остроградским и Лиувиллем, а также
коснулись диссертации на право чтения лекций Чебышева (1847), в
которой он подробно разобрал вопрос, поставленный Остроградским: как
Р / (x)dx
определить все члены в конечном выражении интеграла \ — ' , если
J F (я?) yrQ(x)
известно, что он берется в алгебраических и логарифмических функциях
(здесь функции f(x), F(x), Q(x) — целые рациональные и последняя
без кратных корней). После этого Чебышев опубликовал по теории абе-
левых интегралов г) еще шесть работ, которые все имеют своим предметом
установление условий конечной интегрируемости тех или иных видов
*) Абелевыми называют интегралы вида \ Щх, y)dx, где R(x, у) —
рациональная функция я, у, аг/ определяется неприводимым уравнением п-й степени с целыми
или рациональными относительно х коэффициентами. Если у2= F{x) и F(x) многочлен
3-й или 4-й степени, абелев интеграл — эллиптический, если степень F(x) выше
четвертой — гиперэллиптический.
ИССЛЕДОВАНИЯ П. Л. ЧЕБЫШЕВА
381
интегралов, а также отыскание самого конечного выражения, если оно
возможно. Заметим, что этот круг вопросов частично освещался в курсе
теории эллиптических функций, который Чебышев читал с 1849/50 по
1859/60 гг. 1).
Результаты упомянутой диссертации Чебышев включил в свой
первый печатный мемуар по данному вопросу «Об интегрировании
иррациональных дифференциалов», вышедший в 1853 г. Здесь решается
проблема, обобщающая задачу, решенную в диссертации. В начале
мемуара Чебышев указывает, что согласно Абелю и Лиувиллю, если
интеграл вида
Р f(x) dx
где все три функции опять-таки целые рациональные и в(х) не имеет
корней кратности выше т — 1, берется в алгебраических и
логарифмических функциях, то его конечное выражение имеет вид
U + A0lnv0 + Ailnvi + A2liiv2 + .. .,
где U, v0, Vi, v2, . . . — рациональные функции х и у~0 (я), А0, Аи А2 . . -
— постоянные. Как замечает Чебышев, определение алгебраического члена,
Р(х) ^=i
который имеет вид х|^9 п (х), где Р и Q —- целые функции, произво-
V \х)
дится без труда. Далее же дается полное решение двух основных вопросов:
«1°. Определить число логарифмических членов в выражении
данного интеграла...
2°. Найти аналитические условия, определяющие каждый член
в отдельности» 2).
Из данного Чебышевым общего ответа на первый вопрос,
сформулированного в виде I и II теорем, вытекала, как частное следствие,
упоминавшаяся уже теорема Абеля, высказанная им без доказательства: «Если
интеграл вида \ ?-Д , в котором р и R — целые функции от х,
выражается через логарифмы, то его всегда можно представить следующим
образом:
i
pdl =A\np + ql^R
где A — постоянная, арид — целые функции от х» 2).
Г» 4tx\ fix
III теорема гласила, что \ ^ ' не приводится к алгебраической
е) у 0 (х)
7TV"fl ( \
и логарифмическим функциям, если степень f(x) ниже степени ——— ;
под степенью алгебраической функции у(х) здесь, как и у Абеля,
понимается такое число б, что lim ^^- есть конечное число, отличное от нуля.
Я-юо X
Доказанные теоремы позволили Чебышеву решить в том же мемуаре
восходящий к Ньютону, Гольдбаху и Эйлеру вопрос об условиях
интегрируемости биномиального дифференциала хт(а + bxn)vdx. Как уже
говорилось, Чебышев установил, что, кроме давно известных случаев
х) Ср. программу этого курса: П. Л. Чебышев, Полное собрание сочинений,
т. V, стр. 223—224.
2) П. Л. Чебышев, Полное собрание сочинений, т. II, стр. 53—54.
382
ГЛ. 18. ИНТЕГРИРОВАНИЕ АЛГЕБРАИЧЕСКИХ ФУНКЦИЙ
интегрируемости, интеграл \ xm(a + bxn)pdx с рациональными
показателями 7?г, тг, р представляет собой новую трансцендентную функцию и в
элементарных функциях не выражается, Этот классический результат
вошел во все современные курсы математического анализа.
К рассмотренному мемуару примыкают две статьи Чебышева 1865
и 1867 гг. об интегрировании в элементарных функциях интегралов,
содержащих кубический корень из целого многочлена; в частности, во
второй статье высказано (без доказательства) утверждение, что интегралг
Р Q dx
¦' у/Xs-|-ах-\-Ъ
выражается в элементарных функциях лишь при условии, что по
крайней мере одно из уравнений
Ъ2 \2 ™ , п Ъ2
3(-^r)aZ^ + 6ir(^ + 2Z) = l
Ъ2
удовлетворяется выражением X, рациональным относительно -д. Поэтому
если -д рациональная дробь, необходимо, чтобы по крайней мере одно
из указанных двух уравнений имело рациональный корень.
Чебышеву принадлежат также важные исследования по
эллиптическим интегралам. В статье «Об интегрировании дифференциалов,
содержащих квадратный корень из многочлена третьей или четвертой степени»
(1857) он показал, что вопрос об интегрировании в конечном виде
дифференциала
/ (х) dx
F(x) У ах* + ряз + ух2 + дх +JT
f(x) i/i
приводится к разысканию интегралов, в которых у~ = х -\- А, где
постоянная А определяется требованием, чтобы такой интеграл выра-
жалсяв конечномвиде. Эту задачу Чебышев рассмотрел в работе «С Об интег-
(х-\-А) dx
рировании дифференциала ; > (1861), которой мы
ух* -\- ах3 + $х2 + ух + б
уже коснулись в связи с работами Золотарева по теории алгебраических
чисел. Такой дифференциал, в предположении, что целая функция под
радикалом не имеет равных корней, когда он интегрируется без труда,
либо вовсе не интегрируется в конечном виде ни при каком значении А,
либо же интегрируется при одном единственном значении этой
постоянной. Метод Абеля, позволявший фактически провести интегрирование
и найти значение А, когда радикал разлагается в периодическую
непрерывную дробь, не давал эффективного решения вопроса (см. выше,
стр. 367). Такое решение в случае рациональных а, (3, у, б удалось найти
Чебышеву. Он сводит эту задачу к интегрированию аналогичного диффе-
(х~\-B)dx „ п/ \
ренциала v ' ' , где многочлен четвертой степени К(х) имеет целые
~]/R(x)
коэффициенты и неразложим на два рациональных множителя второй
степени. Применяя, вслед за Абелем, разложение ]Лй {х) в
непрерывную дробь, Чебышев установил, что данный дифференциал не
интегрируется в конечном виде ни при каком В, если среди некоторого вполне
о. и. СОМОВ
383
определенного числа первых знаменателей разложения отсутствует
знаменатель второй степени. Упомянутое число весьма просто связано с
непременно конечным числом целых решений неопределенной системы двух
уравнений шестой степени с тремя неизвестными, свободные члены которой
выражаются через коэффициенты R{x). В противном случае интеграл
при некотором значении В выражается в виде логарифма алгебраической
функции по формуле Абеля, причем и здесь можно назначить, как писал
Чебышев, предел числа операций, которые приходится произвести. В ходе
выкладок, строгую последовательность которых указывает Чебышев,
находится искомое значение постоянных В и А.
Свой алгоритм Чебышев проиллюстрировал двумя примерами на оба
разобранных случая, однако обоснования его не привел. Это сделал,
как говорилось, Золотарев (1872), использовав связь рассматриваемой
интеграционной задачи с задачей деления периода эллиптических
функций, связь, на которую указал ранее Вейерштрасс (1857). Золотарев
применил здесь эллиптические функции Якоби. Вскоре затем — и об этом
также было сказано выше — Золотарев дал полное алгоритмическое реше-
(х 1 jV\dx
ние вопроса об интегрируемости дифференциала Т^ при любых
УЩх)
действительных коэффициентах в знаменателе.
О. И. Сомов. Выдающуюся роль в распространении интереса к
проблемам интегрирования алгебраических функций сыграл старший товарищ
Чебышева по занятиям в Московском университете и по работе в
Петербургском университете Осип (Иосиф)
Иванович Сомов (13 июня 1815 —
8 мая 1876), избранный
членом-корреспондентом Академии наук в начале
1853 г. и ординарным академиком
в 1862 г. на вакансию,
освободившуюся со смертью Остроградского.
Основные научные труды Сомова
принадлежат к теоретической механике,
но он оставил по себе добрую память
и как математик. Его магистерская
диссертация 1841 г., как мы знаем,
была первым на русском языке
сводным трудом по интегрированию
алгебраических иррациональностей.
Докторская диссертация по
теоретической физике (1847) доставила
Сомову профессуру по кафедре
прикладной математики. В Петербургском
университете, где он работал в
течение 35 лет почти до самой кончины,
Сомов читал различные лекции по
механике и математике и в 1847 г. О- И. Сомов.
впервые поставил курс эллиптических
функций. «Основания теории эллиптических функций» (СПб., 1850)
Сомова были отмечены Демидовской премией, так же как его «Теория
определенных алгебраических уравнений высших степеней» (1838) и докторская
диссертация. В своем отзыве об «Основаниях теории эллиптических
функций» Остроградский и Буняковский подчеркивали полноту и
384 ГЛ. 18. ИНТЕГРИРОВАНИЕ АЛГЕБРАИЧЕСКИХ ФУНКЦИЙ
систематичность изложения, опиравшегося преимущественно на теории
Абеля и Якобиг). Еще четверть века спустя ученик Сомова Е. И. Золотарев
писал, что это сочинение остается украшением русской математической
литературы 2). Сомову принадлежат и некоторые частные результаты
в этой области.
Мы здесь не можем входить в разбор трудов Сомова по механике,
которые содержат и ценные математические результаты. Мы еще
рассмотрим позднее работы Сомова по геометрии и векторному исчислению,
пока же заметим, что, применяя эллиптические функции, Сомов завершил
решение знаменитой задачи о движении твердого тела вокруг
неподвижной точки — полюса в тех двух случаях, которые к тому времени были
изучены, именно в случае Эйлера — Пуансо (1758; 1834), когда центр
тяжести тела совпадает с полюсом и равнодействующая всех сил
проходит через полюс, и в случае Лагранжа — Пуассона (1788; 1815), когда
центр тяжести тела лежит на его оси симметрии, на которой находится
также точка приложения силы тяжести, отличная от полюса. В обоих
случаях дело было сведено к квадратурам, которые Сомов довел до конца,
выразив их в эллиптических функциях (1851, 1856). Как известно,
исследование третьего случая задачи принесло позднее бессмертную славу
С. В. Ковалевской. Сомову принадлежат и отдельные специальные
работы по эллиптическим функциям.
Преемники Чебышева. Рассматриваемым кругом вопросов занимались
и другие ученые. Так, Александр Васильевич Бессель (1839—1870),
окончивший Петербургский университет в 1861 г., защитил
магистерскую диссертацию «О приведении интегралов иррациональных функций
к эллиптическим» (СПб., 1865). В Петербургском университете Бессель
начал преподавание в 1865 г. с нового курса теории определителей; затем
он читал также лекции по эллиптическим функциям, используя в
изложении и методы теории функций комплексного переменного. Золотарев
слушал курс эллиптических функций именно у Бесселя 3). После защиты
докторской диссертации по теории инвариантов двоичных форм (1868)
Бессель перешел на работу в Новороссийский университет и вскоре
скончался. Не остался чуждым той же тематики А. А. Марков, исследовавший
вопрос об интегрируемости в конечном виде дифференциала ———у====
{х6-\-с)у х6-\~д
(Зап. Акад. наук, т. 75, 1895). Особенно много работ посвятил
интегрированию алгебраических функций воспитанник (1853) и профессор
математики (1896) Горного института Иван Петрович Долбня (12 февраля
1853—15 февраля 1912). В 1890 г. он с помощью эллиптических функций
Вейерштрасса дал новое, более простое доказательство теоремы Чебышева
(х+А) Ах
об интегрировании ¦ ,———, где R (х) — многочлен четвертой степени.
Применяя аналогичный метод Долбня в 1893 г. исследовал
вопрос об интегрируемости ~у==- , где Р (х) = (х—а) (х—Ъ) (х—Ъ)
1)М. В. Остроградский, Полное собрание трудов, т. 3, стр. 326.
2) Е. И. 3 о л о т а р е в, Об ученых трудах академика И. И. Сомова.— Записки
Академии наук, т. 31, 1878.
3) О занятиях Золотарева теорией эллиптических функций см. М. Б. Н а л б а н-
д я н, Теория эллиптических функций и ее приложения в трудах Е. И. Золотарева.—
Ист.-матем. исслед., вып. XVI, 1965.
ПРЕЕМНИКИ ЧЕБЫШЕВА
385
(х—I—Д) dx
и зл——-. , где Q (х) = (х — а)2 (х — Ъ)2 (х — с)2. Эти и многие другие
работы Долбни были напечатаны во французских журналах и после его
смерти собраны в одном томе *). В диссертации Долбни «Исследование по
теории абелевых интегралов» (СПб., 1896) суммированы только более
ранние результаты, полученные им по проблеме приводимости этих
интегралов к элементарным функциям. Учеником Долбни был
выдающийся советский математик Н. М. Крылов 2).
Не касаясь работ по абелевым и эллиптическим интегралам и
функциям М. А, Тихомандрицкого, в меньшей мере относящихся к вопросу
И. П. Долбня. И. Л. Пташицкий.
об интегрировании в конечном виде, мы коротко остановимся еще на
ученике Чебышева и Золотарева Иване Львовиче Пташицком, по
происхождению — поляке (2 сентября 1854 — 30 апреля 1912). Пташицкий окончил
университет в 1876 г., получив премию, учрежденную в память I съезда
русских естествоиспытателей и врачей, за сочинение об интегрировании
в конечном виде алгебраических дифференциалов: Той же проблеме были
посвящены его магистерская и докторская диссертации: «Об
интегрировании в конечном виде иррациональных дифференциалов» (СПб., 1881)
и «Об интегрировании в конечном виде эллиптических дифференциалов»
(СПб., 1888). В этих и других трудах Пташицкий дал новое, часто более
простое и полное изложение открытий своих предшественников от Абеля
до Золотарева, которые дополнил собственными оригинальными
изысканиями. В Петербургском университете, где он начал преподавание в 1882 г.
приват-доцентом (в 1897 г. он получил здесь профессуру), Пташицкий
нередко вел курс эллиптических функций 3). Этой тематикой занимался
1) I. D olbnia, Oeuvres mathematiques, Paris, 1913.
2) H. M. Крыло в, И. H. Долбня. СПб., 1912; Д. Д. Мор духай-Бо л-
т о в с к о й, Очерк научной деятельности И. П. Долбни. М., 1912.
3) К. А. П о с с е, И. Л. Пташицкий (некролог).— Сообщ. Харьк. матем. о-ва,
т. 13, 1913.
386 ГЛ. 18. ИНТЕГРИРОВАНИЕ АЛГЕБРАИЧЕСКИХ ФУНКЦИЙ
также воспитанник и преподаватель Московского университета, с 1871 г.
профессор университета в Варшаве Николай Николаевич Алексеев (17 мая:
1829—14 марта 1881), в 1879 г. избранный адъюнктом Академии наук.
Скажем еще несколько слов о работах ученика К. А. Поссе и А. А.
Маркова — Дмитрия Дмитриевича Мордухай-Болтовского (9 августа 1876—
7 февраля 1952), с 1898 г. ассистента и с 1909 г. профессора Варшавского
университета, а затем, с 1915 г., профессора университета в Ростове-на-
Дону. Первые работы Мордухай-Болтовского относились к общей теории
абелевых интегралов и его магистерская диссертация «О приведении
абелевых интегралов к низшим трансцендентным» (Варшава, 1905—1906)
содержала ряд новых результатов.
Вслед затем Мордухай-Болтовской занялся проблемой
интегрирования в конечном виде обыкновенных дифференциальных уравнений (Изв.
Варшавского ун-та, 1909—1911). В 1913 г. он начал цикл доставивших
ему впоследствии большую известность работ по теории трансцендентных
чисел и тогда же доказал, что дзета-функция гипертрансцендентна, т. е.
не может быть решением какого-либо алгебраического
дифференциального уравнения, коэффициенты которого суть целые многочлены (Изв.
Варш. политехи, ин-та, 1913). Укажем еще, что в 1926 г. Мордухай-
Болтовской исследовал вопрос об интегрируемости в конечном виде
биномиального дифференциала, когда показатели иррациональны,
распространив на этот общий случай классические результаты Чебышева (Изв.
Казан, физ.-матем. о-ва, 1, 3, 1926).
Диапазон интересов Мордухай-Болтовского был весьма обширен
и обнимал, помимо указанных областей математики, теорию функций
комплексного переменного, геометрию, особенно в пространстве
Лобачевского, историю и философию математики. Большинство его работ
падает на советское время, когда он развил кипучую научную,
педагогическую и литературную деятельность *).
х) См. М. П. Черняев, Н. М. Несторович и Н. М. Ляпин,
Дмитрий Дмитриевич Мордухай-Болтовской.— УМН, т. VIII, 4(56), 1953.
ГЛАВА ДЕВЯТНАДЦАТАЯ
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Закон больших чисел и центральная предельная теорема. Первые
общие предложения теории вероятностей — теоремы сложения и
умножения — были установлены в XVII веке; тогда же было введено понятие
математического ожидания случайной величины. Пионерами в этой
области были П. Ферма, Б. Паскаль, X. Гюйгенс. Применяя
комбинаторные подсчеты, Я. Бернулли в своем «Искусстве предугадывания» (Ars
conjectandi), опубликованном посмертно в 1713 г., доказал замечательную
теорему, известную ему еще до 1690 г. Теорема Бернулли, простейший
случай более общего предложения, которое С. Пуассон в 1837 г. назвал
законом больших чисел, содержит первое математическое выражение тех
закономерностей, которые возникают при наступлении большого числа
отдельных независимых случайных событий. Мы приведем теорему
Бернулли в современной формулировке. Допустим, что производится
последовательность независимых испытаний, в каждом из которых некоторое
событие Е может появиться с постоянной вероятностью р\ скажем,
бросается правильная монета, причем вероятность ее падения гербом вверх
всякий раз равна 1/2. По теореме Бернулли с вероятностью, как угодно
близкой к 1, можно утверждать, что при достаточно большом числе п
независимых испытаний случайное число т появлений события Е
будет удовлетворять неравенству
т
<е,
где е — любое как угодно малое положительное число. Другими
словами, почти достоверно, что при достаточно большом числе испытаний
частота события Е, т. е. число т/п, сколь угодно мало отклонится от его
вероятности р.
С. Пуассон распространил теорему Бернулли на более общий
случай, когда вероятность появления события Е меняется от испытания
к испытанию. Если эта вероятность при первом испытании есть р±, при
втором /?2, . . ., вообще при п-м испытании рп, то величину^ в
предыдущем неравенстве следует заменить на среднюю арифметическую
Pi-rP2^r ••¦ -гРп . ИСПЫТания по-прежнему предполагаются независимыми,
п
Теорема Бернулли есть частный случай теоремы Пуассона, когда все рп
равны одному и тому же числу р. К своему обобщению Пуассон пришел,
изучая вопросы теории стрельбы.
Закон больших чисел, устанавливая связи между вероятностями
и частотами событий при массовых испытаниях, имеет основное значение
в теории вероятностей и ее приложениях.
388
ГЛ. 19. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Другим основным предложением этой науки является так
называемая центральная предельная теорема, дающая теоретическое объяснение
широкой распространенности в природе так называемого нормального
распределения вероятностей. Первоначальная форма центральной
предельной теоремы относилась к схеме, изученной еще Я. Бернулли, т. е.
к последовательности независимых испытаний, в каждом из которых
наступление события Е имеет постоянную вероятность р.
Для формулировки этой теоремы и других предложений, которые
нам встретятся далее, мы введем некоторые понятия и термины.
Величина ? называется случайной, если она принимает те или иные
значения с определенными вероятностями. Случайная величина может
быть дискретной, т. е. принимать только дискретные числовые значения
(например, число очков, выпадающих при бросании правильной игорной
кубической кости), и непрерывной, т. е. принимать любые значения
в некотором промежутке (например, величина отклонения точки
попадания центра снаряда от центра цели при стрельбе).
Случайная величина характеризуется совокупностью своих
возможных значений и их вероятностями, или, как говорят, распределением
вероятностей своих значений. Функция F(x), выражающая вероятность
того, что случайная величина | принимает значение, меньшее какого-либо
действительного числа х, называется функцией распределения величины ?.
Вероятность принять какое-либо значение в промежутке между числами а
и Ъ {а < ? < Ъ) для непрерывной случайной величины с функцией рас-
ъ
пределения F (х) есть F(b) — F(a) = \ dF(x) *). Если нанести значения
а
непрерывной случайной величины на ось абсцисс, то вероятность того,
что величина g примет какое-нибудь значение в промежутке (а, Ь),
выразится площадью S, ограниченной дугой кривой у = f{x), где f(x) = F'(x),
отрезками прямых х = а, х = Ъ и отрезком оси абсцисс; при этом пло-
ъ
щадь S есть J f(x) dx. Функция f(x) называется плотностью вероятности.
а
Среди различных функций распределения особое по важности место
занимает впервые изученный Гауссом (1809) и Лапласом 2) так
называемый нормальный закон распределения вероятностей, в простейшем
варианте которого плотность вероятности есть
у к
График кривой вероятности y=f(x) представляет собой похожую
на колокол кривую, которая симметрична относительно оси ординат
и имеет асимптотой ось абсцисс; площадь между кривой и асимптотой
равна 1 (это означает, что случайная величина достоверно принимает
какое-либо действительное значение). Нормально распределенной
называется также величина с плотностью вероятности
f(x) = -^=-e-h2(x-a)\
уп
Соответствующий график отличается от предыдущего сдвигом вдоль оси
абсцисс и сжатием или растяжением вдоль осей координат.
1) Требование существования производной функции распределения F(x) входит
в более точное определение непрерывной случайной величины.
2) А также американским ученым Р. Эдрейном, который, как и Гаусс, пришел
к этому закону, разрабатывая теорию ошибок (1808).
ЗАКОН БОЛЬШИХ ЧИСЕЛ
389
Нормально распределены весьма многие случайные величины. По этой
схеме часто распределяются случайные ошибки измерений и наблюдений,
отклонения размеров деталей механизма от номинала и т. д. Для
интеграла вероятностей, так называемого интеграла Лапласа
— оо
который нередко пишут в виде
— оо
(пользование такой формой интеграла вероятностей удобнее), составлены
подробные таблицы, позволяющие быстро находить вероятность того,
что нормально распределенная случайная величина | заключена в
числовом промежутке (а, Ъ).
Центральная предельная теорема, относящаяся к схеме испытаний
Бернулли, была высказана для любого значения вероятности р Муавром
в 1733 г., а затем вторично Лапласом в его «Аналитической теории
вероятностей» (Theorie analytique des probabilities, Paris, 1812). Теорема Муавра —
Лапласа позволяет оценить вероятности различных отклонений
частоты т/п некоторого случайного события от его вероятности р при п
независимых испытаниях, в каждом из которых вероятность появления
события Е равна р. Согласно этой теореме вероятность неравенства
. т—пр . ,
\/npq
стремится при п —> оо к интегралу
Ъ t2
а
т. е. распределение вероятностей названных отклонений стремится к
нормальному распределению.
Предельная теорема Муавра — Лапласа имеет асимптотический
характер. На практике ею пользуются, исходя из того, что при достаточно
больших конечных п интеграл Лапласа дает вполне удовлетворительные
приближения для вероятности только что написанных неравенств.
Существуют весьма точные оценки степени приближений, доставляемых
теоремой Муавра — Лапласа, например, данные С. Н. Бернштейном (1943).
Теорема Муавра — Лапласа была распространена и на схему испытаний
Пуассона.
Установление обеих предельных теорем — закона больших чисел
и теоремы Муавра — Лапласа — было главным достижением в развитии
теории вероятностей за два века после первых шагов, сделанных в
середине XVII столетия.
Выдающимися событиями в развитии теории вероятностей XVIII века
явились также известные уже нам работы Д. Бернулли, впервые
заменившего при решении ряда задач громоздкие комбинаторные
подсчеты методами анализа бесконечно малых. Большое значение имели
390
ГЛ. 19. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
исследования Д. Бернулли, Л. Эйлера и других по теории ошибок,
увенчанные трудами Гаусса, Эдрейна и Лапласа.
Несмотря на довольно значительные успехи теории вероятностей
и постепенное распространение круга ее применений в артиллерии,
статистике, страховом деле, астрономии и т. д., развитие этой дисциплины
в первой половине XIX века значительно отставало от других
математических наук. Обоснование предельных теорем было недостаточным, не были
выяснены границы их применимости и возможности дальнейшего
обобщения. В приложениях не учитывалась необходимость соответствия между
условиями теорем и реальными условиями тех явлений, к которым их
желали применить. Даже Лаплас и Пуассон допускали в приложениях
теории вероятностей принципиальные ошибки. Это особенно относится
к применению ее методов для оценки вероятностей свидетельских
показаний, правильности судейских решений и некоторых других явлений
общественной жизни. Такого рода темам, как говорилось, посвящено было много
работ и большие отделы в учебных руководствах, например, в
«Основаниях математической теории вероятностей» В. Я. Буняковского им
отведено более полусотни страниц. Подобные приложения, основанные
на произвольных и даже прямо неверных допущениях, сильно
компрометировали саму теорию вероятностей х).
В итоге в теории вероятностей создавалось положение, аналогичное
тому, какое возникло в начале XIX века в математическом анализе:
дальнейшее ее развитие требовало существенного уточнения основных
положений и совершенствования средств исследования. Преобразование
теории вероятностей в строгую математическую науку было предпринято,
прежде всего, П. Л. Чебышевым. Основное внимание Чебышев
сосредоточил на предельных теоремах.
П. Л. Чебышев и теория вероятностей. Первая работа Чебышева
в этой области, магистерская диссертация «Опыт элементарного анализа
теории вероятностей» (1845), явилась только его начальным шагом в этом
направлении. Непосредственной задачей диссертации было дать
изложение предмета, в наименьшей степени использующее аппарат
математического анализа. В предисловии к сочинению, помеченному 17 октября
(ст. ст.) 1844 г., Чебышев писал: «Дать возможность поверить все эти
заключения анализом строгим и простым, доступным для большей части
учащихся, есть большой шаг в способе элементарного изложения теории
вероятностей»2). Автор опирался почти исключительно на алгебру и
комбинаторику; из средств, которые мы относим к анализу, он применил
лишь разложение в степенной ряд In (1 + ж), что в его времена нередко
включалось в дополнения к алгебраическому курсу. Содержание книги
составили основные теоремы теории вероятностей, закон больших чисел
для случая ограниченного числа различных вероятностей и центральная
предельная теорема для случая биномиального распределения. Но уже
в этой работе проявилась та руководящая идея Чебышева, о которой
мы говорили, характеризуя его творчество в целом: при доказательстве
предельных теорем он стремился давать возможно более точную оценку
доставляемых ими приближений, т. е. заключать допредельные
соотношения в строго определенные неравенства. Эта идея отчетливо выступает
г) Критику таких приложений см. в кн.: А. А. Марков, Исчисление
вероятностей, изд. 4-е, М., 1924, стр. 314 и след., а также в кн.: С. Н. Б е р н ш т е й н,
Теория вероятностей, изд. 3-е, М.—Л., 1934, стр. 179—180.
2) П. Л. Чебышев, Полное собрание сочинений, т. V, стр. 28.
П. Л. ЧЕБЫШЕВ И ТЕОРИЯ ВЕРОЯТНОСТЕЙ
391
ъ примыкавшей к диссертации статье Чебышева «Элементарное
доказательство одного общего предложения теории вероятностей» (1846), где дано
новое и строгое доказательство теоремы Пуассона. О доказательстве самого
Пуассона, основанном на приближенном вычислении «одного довольно
сложного интеграла», Чебышев писал: «Однако, как ни остроумен способ,
употребленный знаменитым геометром, он не доставляет предела
погрешности, которую допускает этот приближенный анализ, и вследствие такой
неизвестности величины погрешности доказательство не имеет надлежащей
строгости» 1). При помощи элементарных средств Чебышев дал
оригинальное доказательство теоремы вместе с необходимой для ее приложений
оценкой числа испытаний, при котором можно гарантировать
определенную близость к единице вероятности того, что частота события уклонится
от средней арифметической его вероятностей не более, чем на заданную
величину.
В последующие годы Чебышев занялся другими работами, которые
не прошли, однако, даром и для теории вероятностей. В это время он
успешно разрабатывает теорию непрерывных дробей и некоторые вопросы
оценки интегралов, позволившие ему далеко продвинуть исследование
предельных теорем. К теории вероятностей он вновь обратился около
1860 г. в связи с чтением соответствующего курса и занятиями вопросами
баллистики. В знаменитой работе «О средних величинах», доложенной
Академии в 1866 г. и опубликованной год спустя во втором томе
«Математического сборника» и в журнале Лиувилля, Чебышев доказал одно
ъажное неравенство и при его помощи вывел новый, более широкий закон
больших чисел, распространенный на последовательности независимых
случайных величин.
Мы сформулируем результаты Чебышева в современной
терминологии, напомнив предварительно смысл некоторых терминов.
Математическим ожиданием или средним значением М(Е,) или ? дискретной
случайной величины ?, принимающей значения ?1? ?2» • • •> ??г с вероятностями
п
Pi, Рг, • • -7 рп называется сумма 2 IkPk- Для непрерывной случайной
k=i
величины, которая принимает значения в промежутке (а, Ь), математи-
ь
ческое ожидание определяется интегралом \ xf(x) dx, где f(x) — ПЛОТ-
ность вероятности распределения ?. Среднее значение случайной
величины — весьма важная ее характеристика, которая дополняется еще
так называемой дисперсией. Дисперсия D(?,) величины ? есть
математическое ожидание квадрата отклонения случайной величины от ее
среднего значения, т. е.
D&) = M[l-M{l)\* или D{l) = M{l-\)\
Дисперсия является мерой рассеяния значений случайной величины
около ее среднего значения: чем более вероятны большие отклонения ?
от |, тем больше D(Q. Наконец, момент тг-го порядка величины ?
относительно с есть математическое ожидание тг-й степени разности ? — с,
т. е. момент
|in = M(g-c)n;
х) П. Л. Чебышев, Полное собрание сочинений, т. II, стр. 14.
392
ГЛ. 19. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
для непрерывной величины ? момент га-го порядка выражается интегралом
ъ
\ (x-c)nf(x)dx.
а
При п = 1 и с = О момент совпадает с математическим ожиданием, при
п = 2жс=^ — с дисперсией.
Упомянутое нами основное неравенство Чебышева *) состоит в
утверждении, что для случайной величины ?, имеющей конечную дисперсию
Z>(|), при любом данном е > О
Р{\1-1\<г}>1-Ш-
Если в этом неравенстве взять в качестве величины ? среднее
арифметическое п независимых случайных величин ?1? ?2? • • •? ?п> то и
получается закон больших чисел Чебышева. Приведем собственную
формулировку Чебышева:
«Если математические ожидания величин
х, у, Z, ..., х , у , Z , . . .
суть
а, Ь, с, ..., а1? ol7 Cj[, . ..,
то вероятность, что среднее арифметическое N величин х, у, z, ... от
среднего арифметического математических ожиданий этих величин
разнится не более как на
1 / 4 + h + Ci+.:. fl2 + fr2+c2+...
t V N N '
t2
при всяком значении ?, будет превосходить 1 — -~ » 2).
Короче говоря, закон Чебышева устанавливает, что при достаточно
больших п с вероятностью, близкой к достоверности, можно полагать,
что среднее арифметическое случайных величин сколь угодно мало
колеблется около некоторого постоянного числа — среднего их
математических ожиданий. Теоремы Пуассона, а значит, и Берну л ли, являются
частными случаями закона больших чисел Чебышева и получаются
из него, когда п-я случайная величина принимает значение 1, если
некоторое событие Е при п-ж испытании наступает, и значение 0, если Е
не наступает.
Последняя из четырех работ Чебышева по теории вероятностей была
отделена от монографии о средних величинах промежутком почти в двадцать
лет. За это время Чебышев далеко продвинулся в разработке метода
оценки интегралов, который уже послужил ему при доказательстве
закона больших чисел (мы расскажем об этих оценках далее), и смог применить
этот метод к распространению на суммы случайных величин теоремы
Муавра — Лапласа. Центральная предельная теорема Чебышева,
опубликованная им в статье «О двух теоремах относительно вероятностей» 3)
х) В несколько менее общей форме неравенство, о котором говорится, было
получено французским математиком Ж. Бьенэме в работе, посвященной
теоретико-вероятностному обоснованию метода наименьших квадратов (1853). Применение этого
неравенства к обобщению закона больших чисел принадлежит всецело Чебышеву.
2) П. Л. Чебышев, Полное собрание сочинений, т. II, стр. 435.
3) Первая теорема из двух, подразумеваемых в заглавии статьи, есть закон
больших чисел.
П. Л. ЧЕБЫШЕВ И ТЕОРИЯ ВЕРОЯТНОСТЕЙ
393
в 1887 г. в «Записках Академии наук» и в 1890—1891 гг. в «Acta mathe-
matica» Миттаг-Леффлера, гласит:
«Если математические ожидания величин
и^ и2, щ, . . .
равны нулю, а математические ожидания всех их степеней имеют
числовую величину ниже какого-либо конечного предела, вероятность, чта
сумма п величин
^1 + ^2 + ^3+ ... +ВЛ,
деленная на квадратный корень из удвоенной суммы математических
ожиданий их квадратов, заключается между двумя какими-нибудь
величинами t и f, с возрастанием числа п до оо имеет пределом величину
интеграла
v
-4= \ е-хЫх»1).
~|/зх J
Вторая теорема Чебышева открывала возможности широкого
применения теории вероятностей к задачам математической статистики и
естественных наук, в которых изучаемое явление рассматривается как
результат суммарного действия очень большого количества случайных
факторов, влияние каждого из которых весьма мало по сравнению с влиянием
их в совокупности. Согласно этой теореме такое суммарное действие
с большим приближением следует нормальному закону распределения.
Исследования Чебышева по предельным теоремам были по
достоинству оценены современными ему русскими математиками. Его
замечательный по своей простоте и доступности вывод закона больших чисел
был принят в распространенных тогда «Элементарном курсе теории
вероятностей» В. П. Ермакова (Киев, 1878 и 1879), «Курсе теории вероятностей»
М. А. Тихомандрицкого (Харьков, 1898) и учебнике П. А. Некрасова
(Москва, 1896). А ученики великого математика А. А. Марков и А. М.
Ляпунов значительно продвинули далее изучение предельных теорем, тем
более необходимое, что и в формулировке и в доказательстве центральной
предельной теоремы, данных самим Чебышевым, еще имелись пробелы2).
Мы подведем краткий итог работам Чебышева в области теории
вероятностей словами крупнейшего современного специалиста в этой области
академика А. Н. Колмогорова: «Вывел русскую теорию вероятностей
на первое место в мире Пафнутий Львович Чебышев. С методологической
стороны основной переворот, совершенный Чебышевым, заключался
не только в том, что он впервые с полной настойчивостью выдвинул
требование абсолютной строгости доказательства предельных теорем
(выводы Муавра, Лапласа и Пуассона были с формально-логической стороны
совсем не безупречны, в отличие, впрочем, от Бернулли, который свою
предельную теорему доказал с исчерпывающей арифметической
строгостью), но главным образом в том, что Чебышев всюду стремился получать
точные оценки отклонений от предельных закономерностей, возможных
2) П. Л. Чебышев, Полное собрание сочинений, т. III, стр. 230.
2) Например, в точной формулировке теоремы, помимо условия взаимной
независимости случайных величин, нужно добавить условие, что среднее арифметическое
дисперсий стремится при п -> оо к некоторому конечному положительному пределу.
Подробнее см. примечания А. Н. Колмогорова в третьем томе Полного собрания
сочинений П. Л. Чебышева, стр. 404—409.
394
ГЛ. 19. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
:хотя бы и при большом, но конечном числе испытаний, в виде безусловно
правильных при любом числе испытаний неравенств.
Далее, Чебышев впервые ясно оценил и использовал всю силу
понятий «случайной величины» и «математического ожидания» (среднего
значения) случайной величины. Понятия эти были известны и ранее
и являются производными от основных понятий «события» и «вероятности».
Но случайные величины и их математические ожидания подчинены
гораздо более удобному и гибкому алгоритму» *).
Проблемы теории моментов. Выше говорилось, что при
доказательстве предельных теорем Чебышев опирался на свои исследования по
оценкам интегралов. Укажем постановку задачи, на которую впервые обратил
Бнимание Бьенэме, но которая получила глубокую разработку и
широкие применения у Чебышев а и его учеников.
Допустим, что даны значения интегралов — моментов —
в в в
со= \ f(x) dx, ci = \ xf(x) dx, . . ., cm = \ xmf(x) dx,
A A A
в промежутке (А, В), причем неизвестная функция / (х) положительна.
Требуется по заданным числам с0, с1? . .., ст найти границы, между
которыми лежит значение интеграла
ъ
^ / (х) dx,
а
где А < а < Ъ < В.
В первой работе, специально посвященной этой проблеме («О
предельных величинах интегралов», 1874 г.), Чебышев указывает следующую
простую механическую интерпретацию задачи при т = 2: «Даны: длина,
вес, место центра тяжести и момент инерции материальной прямой линии
с неизвестною плотностью, изменяющеюся при переходе от одной точки
к другой. Требуется найти наиболее тесные пределы для веса некоторого
отрезка этой прямой» 2).
Чебышев привел полное решение этой частной задачи при различном
выборе данных чисел. Исследование общего вопроса он связал с
аппаратом непрерывных дробей, пользуясь которым получил теорему,
определяющую наибольшие и наименьшие значения интеграла I f(x) dx при
некоторых значениях нижнего и верхнего пределов интегрирования.
Именно, если ут~т есть 6п-на из подходящих дробей непрерывной дроби
1
пгг 1
az 4- р + л
а2*+Р2+---
в которую разлагается интеграл
в
,} Z — X
г) А. Н. Колмогоров, Роль русской науки в развитии теории
вероятностей.— Уч. зап. МГУ, 1947, вып. 91, стр. 56.
2) П. Л. Чебышев, Полное собрание сочинений, т. III, стр. 65. Заметим, что
термин «момент» вошел в употребление в связи с этим механическим истолкованием
задачи.
ПРОБЛЕМЫ ТЕОРИИ МОМЕНТОВ
395
ж если z±, z2, . . ., zi, . . ., zn, . . ., zm суть расположенные в порядке
возрастания корни уравнения i|)(z) = 0 (степени 7тг), а функция f(x)
в промежутке (А, В) положительна, то
п— 1 zn п
Чебышев не сообщил доказательства своих неравенств; это сделал
10 лет спустя Марков. Но к задачам оценки интегралов Чебышев
возвращался не раз.
Вот один из его результатов, непосредственно использованный при
выводе центральной предельной теоремы и изложенный в работе «Об
интегральных вычетах, доставляющих приближенные величины интегралов»
(1887). Если неизвестная положительная функция f(x) удовлетворяет
условиям
? f(x)dx=l, . .., \ x2m~2f(x)dx--
\
1.3-5... (2т — 3)
x*L-1f(x)dx = 0 (1 = 1, 2, ..., га),
или же при & = 0, 1, 2, . . ., 2га—1, условиям
1/2jc
\ xkf(x)dx = -j=' \ хке 2" da;, (1)
то
\т
д2х2
d# j=- \ в 2 dx
<
3Т/3 (т2 — 2/гг + 3) /2 (q2v2 +1)3
2 (m — 3)3 у^—Г
Это значит, что при т —-> со разность между интегралами слева
стремится к нулю не медленнее, чем величина порядка 1/j/ra.
Центральную предельную теорему Чебышев опубликовал в том же
1887 г. Приведенное неравенство имело при выводе этой теоремы
основное значение, давая ключ к решению вопроса о том, в какой мере
определен закон распределения вероятностей некоторой случайной величины,
когда известны ее моменты любого порядка. Из неравенства Чебышева
следовало, что при выполнении равенств (1) для любого га функция f(x)
представляет собой нормальный закон распределения. Показав, что
моменты величины .и± п (ак = D(uk)) стремятся в пределе при
у2(а±-\ \-ап)
п —¦> оо к интегралам вида
+°
—\=- \ xke-x2dx,
Чебышев и получил центральную предельную теорему.
Дальнейшее развитие теория моментов получила у Маркова.
Первой работой Маркова по теории моментов была статья
«Доказательство некоторых неравенств П. Л. Чебышева» (1884), в которой
396
ГЛ. 19. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
содержался вывод неравенств, опубликованных Чебышевым в 1874 г. г).
Затем Марков дал решение задачи Чебышева для любого т при а = А ш
произвольном Ъ на [А, В], а также получил большое число новых
результатов, причем, подобно Чебышеву, использовал аппарат непрерывных
дробей, теорию которых обогатил рядом важных открытий (например, в
изучении сходимости таких дробей, исследовании корней знаменателей
подходящих дробей, обращении рядов в непрерывные дроби и т. д.). Эти
результаты Маркова входят в его докторскую диссертацию 1884 г.,
в статьи «Новые приложения непрерывных дробей» (1896) и «О
предельных величинах интегралов в связи с интерполированием» (1898) и другие
работы. Заметим, что исследования Маркова шли параллельно с работами
выдающегося голландского математика Т. Стилтьеса, которому также
принадлежат важнейшие исследования по непрерывным дробям и теории
моментов. В частности, почти одновременно с Марковым и не зная о его
статье, Стилтьес вывел основные неравенства Чебышева, которые
самостоятельно открыл вновь через 10 лет после публикации мемуара
последнего «О предельных величинах интегралов» в журнале Лиувилля.
Задачу Чебышева Марков обобщил в различных направлениях.
В постановке Чебышева речь шла об определении точных границ для
интеграла
ъ
\ f(x) dx
а
при данных значениях моментов функции на интервале (А, В), где А <
< а <С Ъ < В и неизвестная функция f(x) предполагается в пределах
интегрирования положительной. А. А. Марков изучил случай, в котором
функция f(x) удовлетворяет условию 0 < f(x) < L, определил
наибольшие и наименьшие значения
ъ
[ F(x) • f(x) dx,
а
где F(x) — данная функция, неотрицательная в интервале (а, Ъ) вместе
со своими производными до некоторого порядка, и для этой задачи
исследовал случай, в котором заданы уже не значения моментов функции f(x),
но значения
ъ
f(x) Xk(x) dx,
а
где Xk(z) — СУТЬ некоторые функции, удовлетворяющие неравенствам
определенного вида.
Приведем один из характерных результатов Маркова, относящихся
к этому циклу исследований (он опубликован в названной работе 1896 г.):
при заданных значениях интегралов
ь
Со = 5 КУ) dy,
а
Ъ Ъ
Ci = J уКу) dy, ..., сп_± = J г/п_1/Ы dy
а а
1) Эти и другие примыкающие к ней работы переизданы в кн.: А. А. Марков,
Избранные труды по теории непрерывных дробей и теории функций, наименее
уклоняющихся от нуля, М.—Л., 1948.
ПРОБЛЕМЫ ТЕОРИИ МОМЕНТОВ
397
и условии
o<m<L
интеграл
ъ
\ упт dy
а
достигает экстремального значения для таких функций /(г/), для которых
интервал (а, Ъ) делится на п + 1 частей, в которых f(y) попеременно
равна 0 и L, если только подобное разбиение на меньшее число частей
невозможно при заданных числах с0, си с2, • • •» cn-i- В последнем из
интервалов нужно, чтобы f (у) = L для
максимума и / (у) = 0 для минимума
интеграла
ъ
I ynf(y) dy.
а
Вопросами оценки интегралов
-занимались и другие русские
математики. К ним прежде всего следует
отнести Константина Александровича
Поссе (9 ноября 1847—11 октября 1928),
кандидата (1868), доцента (1873) и
затем профессора (1883) Петербургского
университета, работавшего также
в Институте инженеров путей
сообщения, на Высших женских курсах
и в других учебных заведениях.
Более широким кругам имя Поссе
известно по его «Курсу
дифференциального и интегрального исчисления»
(СПб., 1891), дважды
переиздававшемуся в советское время. Поссе
К А ТТпгрр
принадлежат ценные научные иссле- Г1, л- 11и1ЛДЗ-
дования по ортогональным
функциям1), а также по проблеме моментов и другим родственным вопросам,
которые высоко ценили Марков и другие современники: в 1916 г. Поссе
был избран почетным членом Академии наук. В частности, в статье
«К вопросу о предельных значениях интегралов или сумм» (Сообщ. Харьк.
матем. о-ва, 1885) Поссе существенно упростил и дополнил результаты
Маркова2). К этой статье отчасти примыкает монография Поссе «О
некоторых приложениях алгебраических непрерывных дробей» на
французском языке (Sur quelques applications des fractions continues algebriques,
СПб., 1886).
Оценками интегралов занимался также Н. Я. Сонин. В статье «О
точности определения предельных величин интегралов» (Зап. Акад. наук,
т. 69, 1892) он существенно улучшил и упростил неравенство, данное
*) О его магистерской диссертации 1873 г., посвященной многочленам Якоби,
мы скажем далее. Докторскую диссертацию «О функциях 6 от двух переменных и о
задаче Якоби» (об обращении ультраэллиптических интегралов) Поссе защитил в 1882 г.
2) Статья эта переиздана в приложении к кн.: А. А. Марков, Избранные
труды по теории непрерывных дробей и теории функций, наименее уклоняющихся от нуля.
398
ГЛ. 19. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Чебышевым в 1887 г., показав, что
— оо —оо
Эта работа особо отмечена в представлении Сонина в академики,
подписанном Чебышевым, Бредихиным и еще одним астрономом — О. А. Бак-
лундом (1846—1916). Неравенство Сонина, называя его «замечательным»,
использовал в своих исследованиях о центральной предельной теореме
Марков. Позднее Сонин нашел другие важные неравенства в теории
определенных интегралов, содержащие, как частные случаи, неравенство
Буняковского и еще одно неравенство Чебышева (Зап. Акад. наук по
физ.-матем. отд., т. VI, 1898); об этом упоминалось на стр. 299 х).
Теория моментов, начало которой положили Чебышев, Марков
и Стилтьес и которая весьма тесно связана не только с теорией
вероятностей, но и с теорией приближения функций, ортогональными
многочленами и т. д., интенсивно развивалась и в XX веке. Основное место в
теории моментов занимает следующая общая степенная проблема моментов:
дана конечная или бесконечная последовательность действительных чисел
с0, ci, . . ., сп, ... и требуется определить неубывающую функцию F(x)t
для которой на конечном или бесконечном промежутке (а, Ъ) выполняются
равенства
ъ
J xmdF{x) = cm.
а
При этом ставятся вопросы об условиях разрешимости проблемы,
о единственности решения, если оно существует, о фактическом
отыскании и изучении свойств функции F(x), и другие.
Применяя метод моментов, Марков продолжил далее работы
Чебышева по предельным теоремам теории вероятностей.
Предельные теоремы А. А. Маркова и А. М. Ляпунова. Закон
больших чисел Чебышева представлял собой широкое обобщение
соответствующих теорем Бернулли и Пуассона. Однако условия, содержащиеся в
формулировке Чебышева, все же не охватывают все классы случайных
величин, к которым применим закон больших чисел, и могут быть ослаблены.
В теореме Чебышева закон распространялся на независимые случайные
величины с равномерно ограниченными дисперсиями D(^) < С. В третьей
главе «Исчисления вероятностей» Марков доказал, что закон больших
чисел выполняется для последовательности случайных величин ?ь ?2>- • -
. . ., ^п и при выполнении менее стеснительного условия
Ит D(Zl) + D(l2) + ...+D(tn)_Qm
П->оо П
Закон больших чисел применим и в ряде случаев, когда дисперсии не
существуют, например, если при любом т существует такое б > 0, что М | |т |1+б<
< С, где С — некоторая постоянная.
Исследования Маркова поставили вопрос о необходимых и
достаточных условиях применимости закона больших чисел. Интерес к проблеме
г) Подробнее см. Н. И. А х и е з е р, Работы Н. Я. Сонина по приближенному
вычислению определенных интегралов, в кн.: Н. Я. Сонин, Исследования о
цилиндрических функциях и специальных полиномах. Ред. и комментарии Н. И. Ахиезера.
М., 1954. В этой книге переиздана первая из двух упоминаемых нами статей Сонина.
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ А. А. МАРКОВА И A. M. ЛЯПУНОВА 399
определялся все более расширявшимися приложениями теории
вероятностей в естествознании, статистике и технике. Такие условия были
установлены в различной форме А. Н. Колмогоровым (1928) и А. Я. Хинчи-
ным (1929).
Перейдем к работам Маркова, посвященным центральной предельной
теореме. Первое доказательство этой теоремы Марков изложил в 1898 г.,
через 11 лет после выхода в свет мемуара Чебышева, в письмах к
профессору А. В. Васильеву, опубликованных в «Известиях» Казанского
физико-математического общества за 1899 г. В начале работы Марков
отмечал, что важное значение мемуара Чебышева ослабляется сложностью
содержащихся в нем выводов и недостаточной строгостью суждений,
в силу которой теорема Чебышева не может считаться доказанной;
написанный Васильевым очерк трудов Чебышева,— продолжал Марков,—
укрепил его давнишнее желание упростить и вместе с тем сделать вполне
строгим вывод Чебышева. Применяя метод моментов, Марков
безукоризненно доказал центральную предельную теорему в формулировке, кото-
dme—я2
рую мы приведем по его мемуару «О корнях уравнения ех2 —, т =0» (1898);
«Вероятность, что сумма
Щ + и2 + . . . -f ип
независимых величин
содержится между
a У 2 (а± + а2 + .. . + ап) и р У 2 (^ + а2 + . . . + ап),
где а1? а2, . . ., ап — математические ожидания величин и\, и\,...,и\
и а и (3 — две какие-либо заданные величины, стремится при
неограниченном возрастании п к пределу, равному
lkle-x2dx>
а
если бесконечная последовательность независимых величин
удовлетворяет следующим условиям:
1) математические ожидания величин
UU u2i • • • 7 Un
равны нулю;
2) математические ожидания величин
uhi uki uh' • • •
остаются конечными для конечных значений к в случае, когда к
неограниченно возрастает;
3) математическое ожидание величины
2
Uk
не делается бесконечно малым, когда к неограниченно возрастает» х),
г) А. А. Марков, Избранные труды. Изд-во АН СССР, 1951, стр. 267—268.
400
ГЛ. 19. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Заканчивая статью, Марков подчеркивал: «до исследования Чебышева
предложение о пределе вероятности было доказано только для самых
простых частных случаев» 1).
Фактически при выводе Марков пользуется не третьим условием,
но следующим из него более слабым условием: для всех целых т > 2
М(и?)+Щи™) + ...+Щи%)
lim ^— = 0,
п-и» [D(Ul) + D(u2)+... +D(un)]m^2
которое обыкновенно и приводится теперь в литературе.
Вскоре после появления статей Маркова в журналах Академии наук
за 1900 и 1901 гг. были напечатаны одна за другой две работы А. М.
Ляпунова: «Об одной теореме теории вероятностей» и «Новая форма теоремы
о пределе вероятностей», в которых центральная предельная
теорема была доказана новым методом и в значительно более общих
условиях 2). Вместо метода моментов Ляпунов применил глубоко
разработанный им метод характеристических функций, восходящий к Лагранжу
и Лапласу 3).
Характеристической функцией случайной величины | называется
математическое ожидание величины eitx, т. е. интеграл
-j-oo
J eiixdF(x),
— оо
тде F(x) есть функция распределения ?. Характеристическая функция
•существует для всякой случайной величины ? и полностью определяет ее
моменты любого порядка, если они существуют; вместе с тем эта функция
однозначно определяет функцию распределения F(x), независимо от того,
существуют или не существуют те или иные моменты. Метод
характеристических функций Ляпунова оказался чрезвычайно мощным и позволил
ему избавиться в доказательстве центральной предельной теоремы от
некоторых ограничений. Уже в первой из названных статей Ляпунов
указывал, что предлагаемая им формулировка теоремы значительно более
общая, чем у Чебышева и Маркова, так как не требует не только того,
чтобы моменты любого порядка были меньше некоторого постоянного
предела, т. е. равномерно ограничены, но даже, чтобы существовали
моменты выше третьего порядка. Третье условие Маркова также
заменялось более слабым требованием. Во второй статье Ляпунов ослабил
ограничения далее, и в окончательном виде его результат гласил, что
центральная предельная теорема справедлива, если для
последовательности независимых случайных величин |i,^2» ¦ . ., 5ш ¦ • • существует
хотя бы одно такое число б > 0, что
М{Ъ*+*) + M(tl+6) + .. • +М(^+б)
lim тиль = 0.
х) А. А. Марков, Избранные труды, Изд-во АН СССР, 1951, стр. 269.
2) Обе статьи имеются в кн.: А. М. Ляпунов, Избранные труды. Редакция
В. И. Смирнова, Изд-во АН СССР, 1948.
3) В одной работе 1892 г. о способе наименьших квадратов попытку в сходном
направлении (но в более ограничительных условиях) предпринял профессор Одесского
университета И. В. Слешинскии, о чем А. М. Ляпунов упоминает в первой
из названных статей. Об этой работе Слешинского см.: Б. В. Гнеденко и
И. И. Г и х м а н, Развитие теории вероятностей на Украине.— Ист.-матем. исслед.,
вып. IX, 1956.
ЦЕПИ МАРКОВА
401
Ляпунов дал также оценку ошибки при замене для конечных значений п
точного закона распределения предельным; много позднее более точные
оценки были получены шведским ученым Г. Крамером.
А. А. Марков приложил много усилий, чтобы доказать центральную
предельную теорему в условиях Ляпунова при помощи метода моментов.
Введением вспомогательных случайных величин, определенным образом
связанных с данными и обладающих моментами всех порядков, Маркову
в 1908 г. удалось достичь цели.
Свое доказательство теоремы Ляпунова Марков опубликовал в
приложении к третьему изданию «Исчисления вероятностей» в 1913 г. Тем
самым, как выразился Марков, восстанавливалось поколебленное было
значение метода математических ожиданий 1). Преобразованный Марковым
метод моментов применяется и поныне, хотя основное место в изучении
случайных величин приобрел метод характеристических функций
Ляпунова.
Исследования границ действия центральной предельной теоремы для
различных классов независимых случайных величин продолжались в
широком масштабе и позднее (С. Н. Бернштейн, 1926; А. Я. Хинчин и др.) 2).
Мы оставляем в стороне работы Маркова по обоснованию метода
наименьших квадратов (о чем идет речь, например, в упомянутых выше
письмах к А. В. Васильеву) и его многолетние занятия практическими
задачами страхового дела, чтобы прямо перейти к главному делу его жизни:
основоположным изысканиям по теории зависимых случайных величин.
Цепи Маркова. Особое значение для дальнейшего развития теории
вероятностей и ее приложений имело введение Марковым «испытаний,
связанных в цепь». Учение о марковских цепях выросло в большой новый
отдел теории вероятностей, в котором изучаются зависимые случайные
величины, между тем как ранее основным предметом исследования
служили последовательности независимых случайных величин.
Последовательность случайных величин называется простой цепью Маркова, если
условные вероятности значений, принимаемых (п + 1)-й величиной
(вероятности перехода), оказываются вполне определенными, когда
известны значения, принятые п-ж величиной, непосредственно ей
предшествующей, т. е. при известном значении п-ж. величины (п + 1)-я величина
делается независимой от значений, принимавшихся величинами от первой
до (п — 1)-й. Такую цепь образует, например, случайная величина ?п,
которая может принимать значения только 1 или 0 так, что вероятность
значения 1 есть pi, если ?>n-i = 1 и р2, если ?n_i = 0. В сложной цепи
Маркова к-то порядка вероятности значений величины определяются
значениями к предшествующих ей величин. Наконец, в однородной цепи
вероятностная зависимость последующей величины от предыдущей или к
предыдущих не зависит от ее номера, в неоднородной же может меняться
от номера к номеру.
Частные задачи, в которых фактически рассматривались примеры
цепей Маркова, встречались еще до его работ, например, в применениях
теории вероятностей к некоторым статистическим задачам биологии
и физики; такие задачи рассматривал и А. Пуанкаре. Однако при этом
дело не вышло за пределы отдельных примеров; общая структура их
не только не была подвергнута изучению, но даже не была отчетливо
1) А. А. Марков, Исчисление вероятностей, 4-е изд., М., 1924, стр. 535.
2) Б. В. Гнеденко, Развитие теории вероятностей в России.— Труды Ин-та
ист. естеств., т. II, 1948.
402
ГЛ. 19. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
выделена. Марков развивает, начиная с 1906 г., общую теорию цепей,
которые теперь носят его имя.
Многочисленные работы Маркова по теории цепей имеют своим
главным предметом распространение обеих предельных теорем на суммы
зависимых случайных величин, подчиненных тем или иным условиям.
Первой была статья «Распространение закона больших чисел на
величины, зависящие друг от друга», законченная весной 1907 г. и
опубликованная в том же году. Здесь закон больших чисел обобщается на простые
однородные цепи с двумя возможными значениями (состояниями)
случайной величины 1 или 0, а затем и с большим, чем два, числом состояний.
При этом вводится и определяется само понятие «величин, связанных
в цепь». В ходе рассуждений было установлено так называемое эргодиче-
ское свойство рассматриваемых цепей и тем положено начало
многочисленным эргодическим теоремам, получившим особенное значение в
современных приложениях теории вероятностей. Статья заканчивается
словами: «Итак, независимость величин не составляет необходимого условия
для существования закона больших чисел» х). Почти одновременно Марков
опубликовал «Исследование замечательного случая зависимых
испытаний», где на цепь случайных величин с двумя возможными состояниями
была распространена центральная предельная теорема (Изв. Акад. наук,
VI сер., т. 1, 1907). Доказательства велись по методу моментов. Год
спустя, применяя для вычисления моментов сумм случайных величин,
по существу, характеристические функции, Марков доказал ту же
теорему для однородных цепей с тремя и более состояниями случайной
величины. В конце этой работы, озаглавленной «Распространение предельных
теорем исчисления вероятностей на сумму величин, связанных в цепь»,
отмечено, что ее результаты можно перенести «на сложные цепи, в
которых каждое число непосредственно связано не с одним, а с несколькими
предшествующими ему числами» 2). Это выполнено в статье «Об одном
случае испытаний, связанных в сложную цепь» (1911). Годом ранее,
в 1910 г., обе предельные теоремы были доказаны в некоторых условиях
и для неоднородных цепей в «Исследовании общего случая испытаний,
связанных в цепь» 3). И в дальнейшем Марков продолжал разработку
теории, прочные основания которой заложил в перечисленных мемуарах.
Физические приложения теории цепей были тогда еще делом
будущего. Для иллюстрации своих схем Марков рассмотрел чередование
20 000 гласных и согласных букв в первой главе и 16 начальных строфах
второй главы «Евгения Онегина», исходя из того, что вероятность
появления в данном месте текста гласной и согласной зависит от характера
одной или двух предыдущих букв («Пример статистического исследования
над текстом «Евгения Онегина», иллюстрирующий связь испытаний
в цепь», Изв. Акад. наук, VI сер., т. 7, 1913). В то время такой пример
мог казаться мало значительным и даже несколько искусственным. Теперь
теоретико-вероятностное исследование чередований букв в различных
языках стало актуальной задачей, например, в вопросах наиболее
рационального кодирования при передаче сообщений по телеграфу и т. п.
Этот пример, вместе с некоторыми основными результатами по теории
цепей, Марков включил в приложения к подготовленному им незадолго
до кончины 4-му изданию «Исчисления вероятностей», вышедшему в 1924 г.
1) А. М. Марков, Избранные труды. Теория чисел. Теория вероятностей,
стр. 361.
2) Там же, стр. 397.
3) Обе статьи помещены в тех же «Избранных трудах» А. А. Маркова.
Е. Е. СЛУЦКИЙ
403
Несколько позднее теория цепей Маркова получила чрезвычайно
широкое развитие и многообразные применения в различных вопросах
физики, техники и биологии, в которых вероятность того, что система,
состояния которой меняются дискретно в моменты времени tn, в момент
времени tn+i окажется в одном из возможных для нее состояний, зависит
от фактически имевшего место состояния системы в момент времени tn
или в моменты tn,tn-u . . ., tn-k+i, но не зависит от ее состояния в более
ранние моменты.
Весьма важным для приложений явилось обобщение первоначальной
дискретной схемы случайных процессов на непрерывные случайные
процессы, так называемые процессы Маркова, именно такие, для которых
знание состояния системы в момент времени t0 определяет закон
распределения вероятностей возможных состояний этой системы в последующие
моменты времени t > t0, независимо от того, каковы были состояния
системы в моменты времени, предшествовавшие t0. Цепи Маркова
являются частным случаем такого рода процессов, когда состояния системы
изменяются скачками в отдельные моменты времени tQ,tL, . . ., tnl . . . и само
число возможных состояний системы конечно. Академик А. Н.
Колмогоров, автор многих выдающихся исследований по марковским
процессам, писал: «Значение работ Чебышева, Маркова и Ляпунова было вполне
оценено в Западной Европе лишь с большим опозданием — в 20-х и даже
30-х годах нашего века. Теперь они повсюду воспринимаются как
исходный пункт всего дальнейшего современного развития теории
вероятностей. В частности, основная предельная теорема Ляпунова и теория
цепей Маркова были именно тем, что было наиболее необходимым для
солидного обоснования развившейся статистической физики» г).
В конце рассматриваемого периода к работе по теории вероятностей
приступили еще два математика, основная деятельность которых в этой
области развернулась уже после Октябрьской революции. Мы имеем
в виду Е. Е. Слуцкого и С. Н. Бернштейна.
Е. Е. Слуцкий. Евгений Евгеньевич Слуцкий (19 апреля 1880 —
10 марта 1948), сын учителя, поступил в 1899 г. на
физико-математический факультет Киевского университета. Ему не удалось, однако,
окончить факультет, так как он принимал участие в студенческом движении
и через два года вместе со многими другими студентами был отдан в
солдаты за участие в запрещенной сходке. Только в 1911 г. Слуцкий смог
окончить университет, впрочем, уже по другому, юридическому
факультету. Он не прекратил все же занятий математикой и опубликовал
незадолго до Октябрьской революции несколько работ по теории вероятностей
и статистике, из которых мы отметим монографию «Теория корреляции
и элементы учения о кривых распределения» (Киев, 1912), содержавшую
точное и ясное изложение этих основных в математической статистике
вопросов и этим выгодно отличавшуюся от многих зарубежных книг.
После этого Слуцкий смог начать преподавать в Киевском
коммерческом институте. Наиболее важные исследования Слуцкого по теории
случайных процессов, основанные на применении методов теории
функций действительного переменного, были начаты примерно в середине
20-х годов 2).
1)А. Н. Колмогоров, Роль русской науки в развитии теории
вероятностей.— Уч. зап. МГУ, вып. 91, 1947, стр. 59.
2) А. Н. Колмогоров, Евгений Евгеньевич Слуцкий. Некролог.— УМН,
т. III, 4 (26), 1948.
404
ГЛ. 19. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Аксиомы теории вероятностей С. Н. Бернштейна. Ко времени
появления первых работ С. Н. Бернштейна по теории вероятностей (1911 и
последующие годы) он уже приобрел большую известность работами по
дифференциальным уравнениям и теории приближения функций. Мы здесь
несколько остановимся на его «Опыте аксиоматического обоснования
теории вероятностей» (Сообщ. Харьк. матем. о-ва, т. 15, 1917).
Аксиоматический метод к началу XX века сделал уже весьма
серьезные успехи. В порядок дня поставлена была и проблема обоснования
теории вероятностей, первое решение которой дал С. Н. Бернштейн.
Помимо постулата о существовании математической вероятности,
именно — таких комплексов условий, при которых наступление
некоторого факта имеет определенную вероятность, выражающуюся
действительным числом, Бернштейн вводит три аксиомы, из которых должны
быть получены затем прочие предложения теории. Аксиомы эти таковы:
1. Аксиома сравнения вероятностей. Если а есть вид (частный случай
в узком смысле слова) события А, то вер. а< вер. А; обратно, если между
вероятностями фактов aL и А существует неравенство вер. а± << вер. А,
то оно означает, что вер. а± = вер. а, где а есть некоторый вид события А.
2. Аксиома о несовместимых событиях. Если известно, что события
А и А± несовместимы между собой, и, с другой стороны, события В и Bi
также между собой несовместимы, причем вер. А = вер. В и вер. А± =
= вер. Ви то вероятность факта С, заключающегося в наступлении
события А или события А±, равна вероятности факта Си заключающегося
в наступлении В или Ви т. е. вер. (А или А^) = вер. (В или В±).
Из этих аксиом выводится, что вероятность события, которому
благоприятствуют т случаев из п единственно возможных несовместимых
Y т
и равновероятных случаев, есть возрастающая функция аргумента —,
в качестве которой удобно выбрать просто дробь —. Выводится также
теорема сложения. Теорема умножения доказывается на основании
следующей аксиомы:
3. Аксиома совмещения событий. Вероятность совмещения события А
и события В (при данных условиях) зависит исключительно от
вероятности А (при тех же условиях) и от вероятности, которую приобретает
факт В после осуществления А.
Свою аксиоматику С. Н. Бернштейн изложил в первых главах
написанного им известного руководства «Теория вероятностей» 1). Система
аксиом Бернштейна получила некоторое развитие у советского математика
В. И. Гливенко (1897—1940), но все же она не решала полностью
проблему обоснования теории вероятностей 2). Впоследствии были выдвинуты
и другие системы аксиом теории вероятностей, например, работавшим
в Вене Р. Мизесом. В настоящее время общепринята аксиоматика,
предложенная А. Н. Колмогоровым (1929—1933) и основанная на важных
аналогиях между понятиями теории вероятностей и теории меры.
г) Мы привели аксиомы С. Н. Бернштейна по первому изданию «Теории
вероятностей» (М.—Л., 1927, стр. 2—25); изд. 4-е этого руководства вышло в 1946 г.
2) Ср. Б. В. Гнеденко и И. И. Гихман, Развитие теории вероятностей
на Украине.— Ист.-матем. исслед., вып. IX, 1956, стр. 498—500.
ГЛАВА ДВАДЦАТАЯ
ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
Исследования П. Л. Чебышева. Вопросы приближенного выражения
одних функций посредством других функций, в каком-либо смысле более
простых, занимали математиков издавна. Одним из важнейших приемов
служили при этом разложения функции в окрестности какого-либо
значения аргумента в степенные или тригонометрические ряды, другим —
различные интерполяционные формулы (Ньютона, Лагранжа и др.), при
помощи которых данная функция заменяется конечным алгебраическим
или тригонометрическим многочленом, при нескольких заданных
значениях аргумента точно совпадающим с соответствующими значениями
функции. Чебышев, отправляясь от задач машиностроения, подошел
к проблеме приближения функций совершенно по-новому, поставив
и решив некоторую задачу экстремального характера.
Среди различных шарнирных механизмов, применяемых в
машиностроении, большую роль играет так называемый параллелограмм Уатта,
который служит для превращения вращательного движения кривошипа
в прямолинейное движение поршня и обратно. Однако на самом деле
движение поршня не удается при этом сделать строго прямо линейным,
что порождает вредные и разрушительные боковые давления. Точки
поршня описывают кривые, более или менее отклоняющиеся от прямых.
Конструкторы стремились эмпирически подобрать соотношения
между звеньями механизмов так, чтобы по возможности уменьшить эти
отклонения. Но, как указывал Чебышев, надежных правил для
определения наиболее выгодных элементов параллелограмма не
существовало.
Параллелограмм Уатта, как мы только что сказали, принадлежит
к числу шарнирных механизмов. Оставляя в стороне все технические
подробности, приведем для иллюстрации пример простого четырехзвен-
ного механизма ABCD, играющего основную роль и в устройстве Уатта
(рис. 44). Стержни АВ и CD могут вращаться около неподвижных точек А
и/) и соединены подвижными шарнирами в точках В и С со стержнем ВС;
все стержни расположены в одной плоскости. При движении точек В
и С по окружностям жестко связанная со стержнем ВС точка М будет
описывать некоторую кривую. Например, если взять АВ = CD и М
в середине ВС, то траекторией точки М будет кривая шестого порядка,
которая, однако, на некотором участке весьма мало уклоняется от
прямой линии.
Мы описали так называемый сокращенный параллелограмм Уатта.
Если к стержню АВ добавить стержень BE, а в точке С добавить
стержень CF, равный и параллельный BE, и соединить Е и F стержнем EF
406
ГЛ. 20. ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
(так что фигура BEFC есть параллелограмм), то получается так
называемый полный параллелограмм Уатта (рис. 45). При BE = АВ точка F
здесь описывает линию, подобную траектории точки М, т. е. также мало
уклоняющуюся от прямой на некоторой дуге.
На параллелограмм Уатта и его различные видоизменения Чебышев
обратил, как мы знаем, пристальное внимание во время заграничной
командировки 1852 г. С этого времени он посвящает теории механизмов большое
число работ. Одни из них имели непосредственно конструкторский
характер. В частности, великий ученый построил четырехзвенный шарнирный
Рис. 44.
механизм САА^С^ (рис. 46), в котором центр М отрезка АА± при
определенных размерах элементов механизма описывает дуги, столь мало
отклоняющиеся от прямых, что разница почти не заметна: на участке
в 20 см отклонение не превосходит 1 мм х). Стоит заметить для сравнения,
что семизвенное прямило уроженца
Ковенской губернии и доктора Иен-
ского университета Либмана Из-
раилевича Липкина (1841—1875),
сконструированное последним
одновременно с французским
инженером Ш. Поселье и в принципе
преобразующее круговое
движение в прямолинейное совершенно
точно, дает из-за сложности
конструкции практически меньшую
точность, чем четырехзвенник Че-
бышева 2). Другие исследования
Чебышева содержали новую
математическую дисциплину, которую он разработал, глубоко обобщив
постановку проблем, встретившихся ему в этой области техники.
1) П. Л. Чебышев, Об одном механизме (1868).— Полное собрание сочинений,
т. IV, М.—Л., 1948. —На рис. 46 звенья АС и AiCi равны.
2) Статья Липкина «Uber eine Gelenkgeradeftinning» («Об одном прямиле»)
появилась в Melanges mathem. de Г Acad, de St.-Petersb., 1870; Поселье сообщил о своем
открытии в письме в редакцию Nouvelles annales des mathematiques в 1864 г., но решение
опубликовал только в 1873 г. За этим последовал ряд исследований по теории
шарнирных механизмов Сильвестра, А. Кемпе и др.
Укажем, что после защиты в Иене диссертации о пространственных строфоидах
(1872) Липкин сдал в 1873 г. в Петербурге магистерские экзамены; закончить
магистерскую работу по математическим проблемам картографии ему помешала
преждевременная смерть.
О работах П. Л. Чебышева и его последователей по теории механизмов и их
конструированию см. сб. «Научное наследие П. Л. Чебышева». Вып. П. Теория
механизмов; А. Н. Боголюбов, История механики машин, Киев, 1964.
ИССЛЕДОВАНИЯ П. Л. ЧЕБЫШЕВА
407
«Принцип, лежащий в основании современной теории
параллелограмма,— писал Чебышев, — далеко не сводит к minimum'y предел его
уклонений, столь вредных благодаря происходящим от них боковым
давлениям на поршневой стержень. Поэтому не только для теории, но и для
практики очень важно заменить в исследованиях о параллелограммах этот
принцип, который стараются оправдать при помощи не точных
рассуждений прямой методой»1). Эта метода была теорией наилучшего приближения
функций. Как создатель этой теории, Чебышев является одним из
основоположников нового широкого направления
в той области математики, которая занимается
экстремальными задачами, т. е. задачами,
относящимися к исследованию наименьших
и наибольших значений некоторых величин.
Значение таких исследований Чебышев
подчеркнул с особой силой в уже
цитированном выше сочинении «Черчение
географических карт».
Применительно к механизму Уатта была
поставлена задача о таком определении его
элементов, чтобы наибольшее отклонение
движения некоторых связанных с ним точек ^ „
от движения по прямой было возможно
меньшим на некотором определенном участке. Рпс. 46.
Математически задача состояла в
определении функций некоторого класса, наименее уклоняющихся в данном
промежутке от данной функции.
Классический инструмент для приближения функций представляет
собой так называемый многочлен Тейлора. Пусть функция / (х),
определенная в некотором промежутке, содержащем точку х0, имеет в х0
производные до порядка п включительно. Тогда разность между функцией
f(x) и многочленом Тейлора степени не выше п
я*)-[/ы+^-+...+ ^«-«а* ]=о[(*-,оГ],
т. е. при бесконечно малом значении х — х0 есть бесконечно малая более
высокого порядка, чем (х — х0)п. Это свойство характерно для
многочлена Тейлора.
В своем первом мемуаре по теории наилучшего приближения
функций —«Теории механизмов, известных под названием параллелограммов»
(1854), Чебышев ставит вопрос о приближениях совсем иного рода. Среди
всех многочленов Рп(х) степени не выше п он ищет такой, чтобы
максимальное из их «уклонений» от данной непрерывной функции f(x) на
промежутке (а, Ь), т. е. значение
maLx\f(z) — Pn(x)\,
зависящее от выбора коэффициентов многочлена, было наименьшим.
Теорию Чебышева нередко называют в настоящее время теорией
равномерного приближения функций: в равной мере для всех х на
*) П. Л. Чебышев, Полное собрание сочинений, т. II, стр. 24.
408
ГЛ. 20. ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
интервале (а, Ъ) искомый многочлен Рп(х) должен сообщить наименьшее
значение величине тах|/(#) — Рп(х) | •
Мы приведем постановку задачи словами Чебышева: «Когда
разлагаем функцию f(x) по степени х — а, сумма первых членов дает полиномг
который между всеми другими той же степени наиболее приближается
к f(x) вблизи х = а. Этот полином принимают за приближенное значение
функции f(x), когда требуется представить
ее в виде целой функции. Но для
вычисления f(x) под видом целой функции следует
этому полиному предпочесть другой, если
вместо наиболее приближенного выражения
f(x) вблизи х = а требуется увеличить
предел точности ее приближенного выражения
внутри данного для х промежутка. Этот
второй полином определяется условием, чтобы
предел его уклонений от f(x) в данном
промежутке был менее предела уклонений всех
других полиномов той же степени. По мере
Рис. 47. уменьшения этого промежутка второе
приближенное выражение f(x) приближается
к выражению, находимому из разложения f(x) по степеням х — а, при
прилично выбранном а. Но пока промежуток остается конечным,
коэффициенты этих двух приближенных выражений f(x) отличаются друг от
друга, и их разностями, даже в случае, когда они малы, нельзя
пренебрегать в теории механизмов, которыми мы
будем заниматься» г).
Поясним сказанное двумя простыми
примерами. Возьмем / (х) = хг и будем
приближать ее в окрестности (—/г, К) начала
координат двучленом первой степени у = ах +6.
Приближающий двучлен Тейлора у = f (0) +
+ /' (0) х в данном случае сводится к нулю;
его наибольшее уклонение в промежутке
(— h, К) от / (х) равно h2 и достигается на
концах промежутка. Двучлен, дающий
наилучшее приближение в смысле Чебышева,
здесь есть г/ = -^-; его наибольшее уклоне-
/г2
ние, имеющее место при х = 0, ±/&, равно у,
т. е. вдвое меньше наибольшего уклонения,
доставляемого двучленом Тейлора. За счет некоторого ухудшения
приближения в соседстве с началом достигается улучшение приближения во всем
интервале (рис. 47). Если взять / (х) = х3 и степень приближающего
многочлена опять равной 1, то двучлен Тейлора снова есть у = 0, а дву-
член Чебышева у = j h2x. Наибольшее уклонение последнего от х3 здесь
Рис. 48.
2) П. Л. Ч е б ы ш е в, Полное собрание сочинений, т. II, стр. 25. Заметим, что
в конце названного мемуара Чебышев обещал дать его продолжение, в котором
собирался применить формулы теории приближения функций к отысканию элементов
параллелограммов, обладающих наилучшей точностью хода. Такое продолжение не было
опубликовано. Соответствующие расчеты произвели И. И. Артоболевский и Н. И. Ле-
витский в комментариях к работам П. Л. Чебышева по теории механизмов в т. IV его
Полного собрания сочинений.
ИССЛЕДОВАНИЯ П. Л. ЧЕБЫШЕВА
409
есть jh3 (оно достигается при х = ± h/2 и х = ± h) и вчетверо меньше
наибольшего уклонения двучлена Тейлора, равного h3 (рис. 48).
Первые задачи о равномерном приближении были поставлены
Лапласом и Фурье в связи с приближенным решением линейных систем
уравнений, число которых превосходит число неизвестных, а затем Понселе
в связи с изучением действия некоторых машин (1835). Однако Понселе
ограничился решением весьма частных задач, и создание обширной
теории равномерного приближения функций явилось делом Чебышева 1).
В мемуаре 1854 г. Чебышев привел без вывода важное свойство
целых многочленов наилучшего приближения: если для многочленов
Рп(х) = РохП + Pi^'1"1 + • • • Л~ Рп степени п наименьшее значение
шах | f(x) — Рп(х) |
в промежутке (а, Ъ) есть L, то уклонение \f(x) — Рп(х)\ принимает это
значение L по крайней мере в п -\- 2 различных точках интервала (а, 6).
Опираясь на это свойство и некоторые другие соображения, Чебышев
решает задачу о наилучшем приближении функции / (х) = хп в
интервале — h < х < h при помощи многочленов степени п — 1 или, что
то же, об отыскании многочлена хп -\- р^-1 -\- . . . + Рп степени п
со старшим коэффициентом, равным 1, наименее уклоняющегося на этом
промежутке от нуля. Искомый многочлен находится как решение
некоторого обыкновенного дифференциального уравнения первого порядка,
и имеет вид
hnTn\h) hn I х\
2^1 = 2^rcos(^-arccos7T j =
= ^[{х + У^-^)п + {х-УхС1-^)п]
(T — первая буква фамилии Чебышева во французской транскрипции) 2).
Само наименьшее значение уклонения L = 9п_1 . Вот первые
четыре таких многочлена (из которых второй и третий нам фактически уже
встретились):
/г2 3 /i4
sy /у а /у>0 ул ? /у» -у>4 In Z/y>2 1 .
чА/, tAs j-v , tX/ . to iAy , cX/ IL iAs q
В следующем, самом большом своем мемуаре по теории равномерного
приближения —«Вопросы о наименьших величинах, связанные с
приближенным представлением функций» (1859) 3), Чебышев продвинулся
х) В одной задаче Понселе требуется подобрать коэффициенты аир, сообщающие
наименьшее значение
ая + р
max
ТД2 + 1
-1
Другая задача Понселе о наилучшем приближении ух2 + у2 + z2 линейной функцией
ах + $у + yz (при некоторых условиях) явилась предметом детального анализа
А. А. Маркова (Изв. Акад. наук, V сер., т. 24, 1906). Подробнее см.; А. А. Гусак,
Предыстория и начало развития теории приближения функций.— Ист.-матем. исслед.,
вып. XIV, 1961.
2) Тригонометрическая форма многочлена Чебышева встречается в более позднем
мемуаре «О квадратурах» (1874). Обозначение многочленов ЧебышеваТп(х) предложил
С. Н. Бернштейн в докторской диссертации 1912 г.
3) Краткая заметка под тем же названием, содержавшая изложение части
результатов большого мемуара, вышла еще в 1857 г.
410
ГЛ. 20. ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
значительно далее. Он ставит здесь задачу весьма общим образом. Пусть
дана функция F (х, р±, р2, • • ., рп) = 0 независимой переменной х,
изменяющейся в промежутке — h ^ х ^ h, тп параметров р1ч р2, . . ., рп\
предполагается, что функция имеет конечные и непрерывные
производные по х и параметрам. Требуется найти такие значения параметров,
при которых наибольшее уклонение функции от нуля, т. е. значение
max | F (х, p±J pz, . .., рп) \
будет наименьшим.
Чебышев установил здесь необходимое условие, при котором
искомая система параметров дает решение задачи, доказав, в частности,
приведенное выше свойство многочленов наилучшего приближения, и дал
новый вывод наименее уклоняющегося от нуля многочлена 72-й степени
со старшим коэффициентом !, основанный на разложении функции
"(Лг2 — /г2 в непрерывную дробь, а также рассмотрел новые важные
конкретные случаи. Так, он решает вопрос об отыскании наименее
уклоняющейся от нуля рациональной дроби
Xn-\-PiXn-~L+ ...+ Рп
R{x)
где R (х) — данный многочлен степени т < 72, не обращающийся в нуль
в интервале — h < х ^ h. Решается и задача об отыскании наименее
уклоняющейся от нуля рациональной функции вида
когда заданы только коэффициенты А±, . . ., Ат. Исследуя функции,
наименее уклоняющиеся от нуля, Чебышев получил несколько теорем
о пределах корней алгебраических уравнений. Так, уравнение с одними
нечетными степенями
х21+1 + Ах21-1 + ят и + К = 0
имеет по крайней мере один корень между —2 1/ уи + 2 V"2~#
Другая теорема гласит, что уравнение
f(x)=xn + Axn-1+ ...+К = 0,
все корни которого действительны, имеет, каково бы ни было t, по край-
,2nfWi)
ней мере один корень в промежутке между t и t -f 4 "J/ -пр* где радикал
взят со знаком, обратным знаку jTrlr. Впоследствии только что приве-
денные границы были сближены самим Чебышевым (1872) и Марковым
(1903).
На искомую функцию наилучшего приближения можно накладывать
и другие требования, например, чтобы она принимала заданные
значения при заданных значениях х, и т. д. Так, в статье «О функциях, мало
удаляющихся от нуля при некоторых величинах переменной» (1881),
Чебышев определил наименее уклоняющийся от нуля в промежутке
(—/г, -\-h) многочлен степени 72, принимающий данное значение в
точке вне этого промежутка, и затем решил аналогичную задачу для
РАБОТЫ Е. И. ЗОЛОТАРЕВА, А. А. МАРКОВА И В. А. МАРКОВА 411
тригонометрического многочлена
п п
А0 + 2 Akcosky + 2 Bhsmky,
fc=i /i=i
приведя последний к алгебраическому виду подстановкой tg-~ = x.
Исследования Чебышева по теории равномерного приближения
функций, продолжавшиеся до 1882 г., довольно быстро получили известность
ж в России и за границей, где, например, Ж. Бертран включил в свой
жзвестный «Traite du calcul differentiel» (Paris, 1864) второй чебышевский
вывод многочлена, наименее уклоняющегося от нуля. Однако творческая
разработка этого цикла идей Чебышева была успешно продолжена прежде
всего его русскими учениками; зарубежные ученые оценили важность
новой математической дисциплины уже после кончины великого
математика. В первую очередь русские математики решили ряд новых
конкретных задач большой трудности, непосредственно примыкавших к
проблематике Чебышева.
Работы Е. И. Золотарева, А. А. Маркова и В. А. Маркова. Задача
об определении наименее уклоняющегося от нуля многочлена данной
степени была решена Чебьппевым для случая, когда задан коэффициент
(равный хотя бы 1) при старшей степени. В 1877 г. Е. И. Золотарев в
работе «Приложение эллиптических функций к вопросам о функциях,
наименее и наиболее отклоняющихся от нуля», включавшей содержание его
диссертации на право чтения лекций (1868), обобщил, по совету
Чебышева, задачу на случай, когда задан еще один коэффициент многочлена.
Отыскание многочлена
хп + о±хп~1 + р2хп^+...+рп,
где с»! — заданное число, наименее уклоняющегося от нуля в данном
лромежутке, потребовало решения некоторого дифференциального
уравнения посредством эллиптических функций. К этой задаче сводится
другой решенный Золотаревым вопрос о наименее уклоняющемся в (—fe, -\-h)
от нуля многочлене степени п со старшим коэффициентом 1, принимающем
данное значение для некоторого данного значения аргумента вне
данного промежутка.
В 1887 г. знаменитый химик Д. И. Менделеев (1834—1907) в труде
«Исследование водных растворов по удельному весу» поставил задачу,
явившуюся отправным пунктом новых исследований по теории
приближения функций. Задача Менделеева состояла в следующем: найти точные
пределы числовых значений коэффициентов квадратного трехчлена у =
= ах2, + 2Ъх + с ПРИ условии, что этот трехчлен уклоняется от нуля
не более, чем на А в данном промежутке а < х <; |3. На языке геометрии
вопрос формулируется так: найти точные пределы значений
коэффициентов указанной параболы, дуга которой в промежутке (а, |3) лежит между
отрезками АВ и CD, параллельными оси абсцисс и отстоящими от нее
по обе стороны на расстоянии А.
Нетрудно показать, что при а > 0 искомые границы дают
коэффициенты параболы, касающейся нижнего отрезка CD в его середине и
проходящей через точки А и В с абсциссами а и (3 и, например,
^ 8А
412
ГЛ. 20. ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
Простое геометрическое решение вопроса дал в 1891 г. на VIII съезде
русских естествоиспытателей и врачей Д. А. Граве х).
В статье «Об одном вопросе Д. И. Менделеева» (1889) А. А. Марков,
обобщая задачу Менделеева на многочлены высших степеней, подверг
изучению связи между предельными значениями многочленов и их
производных 2). Проблема состояла в определении верхнего предела
значений производной для многочленов п-ж степени Рп(х) = р0хп -\-р^хп~х + . . .
... -\-~рп, которые сами при а < х < Ъ лежат в пределах L' <
< Рп (х) < L. Марков решил вопрос и для случая, когда значение х дано,
и для случая, когда х есть любое число
между а и Ь. Во втором случае
выполняется известное «неравенство Маркова»
Указанная граница величины Р'п (х) =
= р0пхп-1 + р±(п - I)*""2 + . . . +Рп-±
достигается для некоторого многочлена,
наименее уклоняющегося от нуля.
Решение вопроса в первом случае давало ответ
на обобщенную задачу Менделеева: найти
точный верхний предел числового
значения одного из коэффициентов pk
многочлена Рп(х) данного уклонения L.
Задача Менделеева — Маркова была
распространена на высшие производные
братом академика — Владимиром
Андреевичем Марковым, чрезвычайно
даровитым математиком, скончавшимся от
туберкулеза всего 26 лет от роду (19 мая
В. А. Марков. 1871—30 января 1897).
В работе «О функциях, наименее
уклоняющихся от нуля в данном
промежутке» (СПб., 1892), написанной незадолго до окончания
университета, В. А. Марков дал решение вопроса об определении по уклонению
многочлена верхнего предела значений его производной любого порядка.
В прежних обозначениях неравенство В. А. Маркова имеет вид
\rn Wl"^ (Ь__а)п- (т + 1)...(2т)
Предметом этой работы В. А. Маркова является поставленная им весьма
общая проблема отыскания наименее уклоняющегося в данном
промежутке от нуля многочлена Рп(х) степени тг, коэффициенты которого
связаны данной линейной зависимостью аоРп + aiPn-i + - . - + ыпРо —
= е (или, что то же, проблема отыскания точного верхнего предела
соответствующей линейной функции при данном пределе L уклонений
многочлена от нуля).
Задача Чебышева о наименее уклоняющемся от нуля многочлене
при условии ро — 1 = 0 (ро — старший коэффициент многочлена Рп{х))
х) Д. А. Граве, Энциклопедия математики, Киев, 1912, стр. 441—443.
2) А. А. Марков, Избранные труды по теории непрерывных дробей и теории
функций, наименее уклоняющихся от нуля. В этом издании опубликованы марковские
«Лекции о функциях, наименее уклоняющихся от нуля», в которых подведены
основные итоги его собственных и иных исследований в этой области до 1906 г.
ИНТЕРПОЛИРОВАНИЕ И ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ 413
является частным случаем этой проблемы. В. А. Марков далеко
продвинулся в решении общей проблемы и, в частности, решил вопрос об
отыскании наименее уклоняющегося от нуля многочлена данной степени с одним
заданным коэффициентом при любой степени переменного. В
рассматриваемом труде В. А. Марков, подобно Чебышеву, встретился с задачами
алгебры; здесь содержится одна замечательная теорема о распределении
корней, включенная позднее Д. А. Граве в его «Элементы высшей
алгебры» (Киев, 1914). Говорят, что корни двух функций перемежаются, если
все эти корни действительные и между любыми двумя
последовательными корнями одной функции лежит один корень другой. Согласно
теореме В. А. Маркова, если корни двух многочленов перемежаются,
то перемежаются и корни их производных. В. А. Марков дал и
некоторые обобщения своей теоремы1).
Исследования в указанных направлениях велись и позднее; они
продолжаются вплоть до нашего времени. Так, С. Н. Бернштейн доказал
в 1912 г. для многочленов Рп(х) неравенство
\Р2(х)\<-7=Ц== (а<х<Ъ),
у (х — а) (Ъ — х)
значительно более сильное, чем неравенство Маркова, для значений
аргумента, не очень близких к концам промежутка. Для тригонометрических
многочленов порядка п
k=n
SJq) = а0 + 2 (ak cos &ф 4- bk sin Acp) (0 < cp < 2n),
fc=i
Бернштейн вывел неравенство
|?;(ф)|<гатах|?л|.
Эти неравенства Бернштейна имеют большое значение; их
обобщениями занимались многие ученые в СССР и за границей. Заметим еще,
что харьковский профессор Антон Павлович Пшеборский (1871—1942)
распространил упоминавшиеся исследования Е. И. Золотарева на другие
случаи двух линейных соотношений между коэффициентами многочлена
(Сообщ. Харьк. матем. о-ва, т. 14, 1913).
Интерполирование и ортогональные многочлены. С теорией
наилучшего приближения тесно связаны интерполирование и ортогональные
многочлены, методы квадратур, теория моментов. С теорией моментов
мы уже встретились и сейчас остановимся на разработке Чебышевым
и его последователями других названных областей.
Ортогональные многочлены представляют собой весьма важный класс
ортогональных функций, классическим примером которых служат
системы тригонометрических функций 1, sin пх, cos пх (п = 1, 2, 3, . . .)
на отрезке (—я, я). Система многочленов Рп(х) степени п
называется ортогональной в интервале (а, &), который может быть и
бесконечным, относительно так называемой весовой функции р(х) > 0,
*) Добавим, что в год кончины В. А. Маркова вышла еще одна ценная его работа
«О положительных тройничных квадратичных формах» (СПб., 1897).
414
ГЛ. 20. ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
если для любых двух различных функций системы Рт(х), Рп(х)
выполняется равенство
ъ
\ Рт (х) Рп (х) р (х) dx = 0 (т Ф п),
а
так называемое условие ортогональности с весом р (х). Первым примером
ортогональных многочленов были многочлены А. Лежандра (1784),
которые он получил, как частные решения Рп(х) уравнения второго порядка
он же доказал их ортогональность на промежутке (—1, 1) с весом р(х) =1.
Многочлены Лежандра могут быть введены также с помощью
производящей функции, как коэффициенты разложения
= P0(x)+Pi(x)s+P2(x)s*+...
VI — 2sx + s*
Теорию этих многочленов разрабатывал одновременно с Лежандром
Лаплас; шаровые функции являются их обобщением.
В конце XVIII и первой половине XIX вв. в связи с решением тех
или иных задач математического естествознания введены были и другие
системы ортогональных многочленов, например, многочлены Якоби
(опубл. в 1859) Jn(x), производящей функцией которых служит
(1 + 5+ "l/l — 2sx + s*)k(l — s+Yl — 2sx + s^ г / \ . Г / \ I Г / \ 2 .
У1_2*Г+,2 ±-±-=Jo(x)+Ji(x)s + J2(x)s*+...
Чебышев называл эти многочлены «функциями, подобными функциям
Лежандра» и в заметке под таким названием (1870) доказал их ортого-
нальность в промежутке (—1, +1) относительно веса ,, )h .
При % = [х = 0 получаются многочлены Лежандра, как частный случай.
Многочлены Чебышева Тп(х) = cos п (arccos х) также обладают свойством
1
ортогональности в промежутке (—1, +1) с весом . и могут рассмат-
1/1—х2
риваться, как частный вид многочленов Якоби при X = \х = -к .
В ряде работ Чебышев рассмотрел как частные виды ортогональных
многочленов, так и их некоторые общие свойства. Основную роль играл
при этом аппарат непрерывных дробей. Если интеграл
ь
р(х)
dx,
где р (х) > 0 есть данная функция, обладающая моментами любого
ъ
порядка sn = \ хпр (х) dx, разложить в ряд вида
z ~^~ z* "*" z3 ^
ИНТЕРПОЛИРОВАНИЕ И ОРТОГОНАЛЬНЫЕ многочлзны 415
в соответствующую этому ряду непрерывную дробь
Ро
I Pi
z — а± i о
то знаменатели Рп (х) подходящих дробей Qn(x)/Pn(x) этой непрерывной
дроби образуют систему многочленов, ортогональных в интервале (а, Ъ)
с весом р(х) > О1).
Ортогональные многочлены получили у Чебышева основное
применение в задаче о приближении функций по способу наименьших квадратов,
который был впервые предложен Лежандром (1806) и Гауссом (1808)
в связи с определением орбит небесных тел по данным наблюдений, а
также в связи с задачами геодезических измерений. Укажем коротко
постановку задачи в интересующем нас случае приближения функций.
Допустим сначала, что требуется построить целый многочлен, значения
которого в п + 1 данной точке x0l х±, х2, . . ., хп точно совпадают со
значениями некоторой заданной функции f(x). Степень приближающего
функцию многочлена, вообще говоря, не может быть меньше п; если взять ее
равной п, то многочлен находится по так называемой интерполяционной
формуле Лагранжа (1792—1793). При больших п вычисление
интерполяционного многочлена Лагранжа затруднительно; кроме того, степень
самого многочлена становится высокой и его применение неудобным.
В таких случаях целесообразно применять многочлен Р(х) степени,
меньшей чем п, и, вообще говоря, уже не совпадающий со значениями
/ (х) в данных точках, но зато такой, чтобы сумма квадратов его
уклонений от / (х) в этих точках, умноженных, быть может, на некоторый вес
р (х) > 0, была наименьшей, т. е. чтобы выражение
2!р(*1Н/(*«)-ад]'
г=0
принимало наименьшее значение 2). Все это переносится на случай
функции f(x), заданной в целом промежутке (а, Ъ): здесь приближающий
многочлен Р(х) ищется из условия обращения в минимум интеграла
ъ
\p(x)[f{x)-P{x)\*dx.
а
Здесь мы также имеем дело с построением многочлена данной степени,
наименее уклоняющегося в известном смысле от функции f(x) на
промежутке (а, Ь); но определение наилучшего приближения теперь другое.
Связь приближений по способу наименьших квадратов с теорией
ортогональных многочленов основана на следующем. Оказывается, что
многочлен Р(х) степени п, обращающий в минимум интеграл
ъ
lp(x)U(x)-P(x)]*dz,
а
г) Как ряд, так и дробь, указанные в тексте, могут расходиться. Эти разложения
могут быть чисто формальными; назначение их—в получении соответствующих дробей
Qn{x)lPn(x). Подробнее см: Н. И. А хи е з е р, Общая теория полиномов П. Л.
Чебышева. В сб. «Научное наследие П. Л. Чебышева», вып. I, М.—Л., 1945.
2) Мы не останавливаемся здесь на применении способа наименьших квадратов
в теории ошибок измерений. Как упоминалось, в этом направлении провел ряд важных
исследований А. А. Марков, подытоживший их в своем «Исчислении вероятностей».
416
ГЛ. 20. ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
может быть представлен в виде суммы
Р(х)= %AkPh(x),
тде Pk (х) — ортогональные многочлены, являющиеся знаменателями тех
лодходящих дробей, которые возникают при разложении в непрерывную
дробь интеграла
ь
а
коэффициенты Аъ определяются по формулам типа формул Фурье в
теории тригонометрических рядов:
ъ
I /(*) Ph(*) Р(*) dx
ЛЪ — ь
J Pk(x) р(х) dx
а
Из многочисленных мемуаров П. Л. Чебышева, посвященных этим
вопросам, мы назовем следующие: «О непрерывных дробях» (1855), «Об
интерполировании по способу наименьших квадратов» (1859), «Об
интерполировании» (1864), «Об интерполировании величин равноотстоящих» (1875).
В статье «О разложении функций одной переменной» (1859) содержатся,
среди прочего, первые разложения по новым введенным им системам
полиномов, о которых сейчас будет речь. Чебышев подробно разбирает
случай дискретно заданных значений f(x) в отдельных точках, но его
результаты непосредственно переносятся на случай функции /(#),
заданной в целом промежутке.
В мемуаре «Об интерполировании в случае большого числа данных,
доставленных наблюдениями» (1859) Чебышев рассмотрел еще один вид
интерполирования, в ряде случаев приводящий к более простым
вычислениям, чем способ наименьших квадратов, и достаточно точный.
«Невозможно,— писал он в начале мемуара,— дать способ интерполирования,
который был бы вообще предпочтительнее всех других, ибо, смотря по
обстоятельствам, приходится заботиться преимущественно об упрощении
вычислений или о точности результатов» г). Свой метод Чебышев
применил к определению орбит планет по многим наблюдениям, о чем
докладывал в 1876 г. на V съезде русских естествоиспытателей и врачей. Текст
доклада, к сожалению, не сохранился, но известно, что он привлек
внимание. Астрономы — О. А. Баклунд и другие — с успехом использовали
метод Чебышева, а Марков дал ему дальнейшее развитие в статье «О
предельных величинах интегралов в связи с интерполированием» (1898) 2).
Данный метод Чебышева приводит к разложению функции в биортого-
нальные ряды.
Приведем некоторые системы ортогональных многочленов, изученные
Чебышевым. Это, прежде всего, уже известные нам многочлены Чебышева
Тп(х). Это, далее, многочлены Чебышева — Эрмита Нт(х), ортогональ-
__0С2
ные в промежутке (—оо, оо) с весом е 2 . Чебышев рассмотрел их в статье
1)П.Л. Чебышев, Полное собрание сочинений, т. II, стр. 244.
2) Статья имеется в кн.: А. А. Марков, Избранные труды по теории
непрерывных дробей и теории функций, наименее уклоняющихся от нуля.
ИНТЕРПОЛИРОВАНИЕ И ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ 417
«О разложении функций одной переменной» 1859 г., а Эрмит — в статье
1864 г. Это, наконец, многочлены Чебышева — Лагерра Ln(x),
ортогональные в промежутке (0, оо) с весом е~х. У Чебышева многочлены Ln(x)
рассмотрены в той же статье 1859 г., Э. Лагерр (1834—1886) их
исследовал в 1879 г. Следует добавить, что сам Чебышев вводил ортогональные
многочлены, отправляясь от ставившихся им задач и применяя, как
сказано, метод непрерывных дробей. Определение таких многочленов
условием ортогональности в данном промежутке относительно данной весовой
функции было ему чуждым.
Рассмотренный цикл исследований Чебышева был продолжен,
начиная с семидесятых годов, Сохоцким, Поссе, Марковым, Сониным и
другими. К. А. Поссе посвятил многочленам Якоби магистерскую диссертацию
«О функциях, подобных функциям Лежандра» (СПб., 1873), в которой
установил ряд новых свойств ортогональных многочленов разных типов
и связей между ними. Ю. В. Сохоцкий в докторской диссертации «Об
определенных интегралах и функциях, употребляемых при разложениях
в ряды» (СПб., 1873), впервые ввел обобщенные многочлены Чебышева —
Лагерра, соответствующие в промежутке (0, оо) весу р(х) = е~хха,
где а > — 1. Эти же функции были вскоре исследованы в работе Н. Я. Со-
нина по цилиндрическим функциям (1880), о которой еще будет сказано
далее; при этом, помимо их выражения через цилиндрические функции,
Сонин дал также разложения по многочленам Т^(х), носящим теперь
его имя. В этой же работе дано обобщение многочленов Чебышева —
Эрмита на случай веса р(х) = е~х2\х\2с, с> —~~ в промежутке (— оо, оо).
В другом мемуаре «О приближенном вычислении определенных
интегралов и входящих при этом вычислении целых функциях» (Варш.
универс. изв., 1887) Сонин предложил новый подход к определению
и исследованию ортогональных многочленов. В то время как Чебышев,
а за ним Поссе, Марков и другие вводили такие многочлены, отправляясь
ъ
от разложения интеграла \ _ х в непрерывную дробь, Сонин стал
а
вводить их как целые функции Ц)п(х), однозначно определяемые
условием ортогональности относительно веса р(х) на промежутке (а, Ь), так,
как делают теперь. Это обстоятельство специально отмечено в
предисловии к мемуару. «В настоящем труде,— писал Сонин,— мы старались
держаться на самой общей теоретической почве и имели в виду довести
до последней степени строгости, простоты и ясности решения всех
вопросов относительно приближенного вычисления определенных интегралов
по методу интерполирования. Целые функции уп(х) (имеющие важное
значение в этом вопросе) мы определяем их интегральным свойством,
а о разложении в непрерывную дробь интеграла
ъ
Р F (z) dz
<J x — z
a
(знаменатель п-ж подходящей дроби, которой обыкновенно принимался
за определение полинома q>n(x)) упоминаем лишь вскользь, приводя
не только самую дробь, но и остаток при вычислении интеграла по этой
дроби» *).
г) Варшавские университетские известия, 1887, № 1—3, стр. 4.
418
ГЛ. 20. ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
Важную роль в дальнейшем изучении свойств ортогональных
многочленов играет их представление в виде производной
Ъ(х) = !яЬг*Ш- (" = 0,1,2, ...),
F(x) dxn
где
л.
F0(x)=F(x), Fn(x)=Vx-t)^~1ifn(t)F(x)dt (« = 1,2, ...),
<J in — 1)
a
и применение уравнений в конечных разностях. В том же мемуаре
решены две следующие задачи: найти все системы ортогональных многочленов
фо(я) = 1» 9i(#)» фг(^)5 фз(#)» • • ¦» Для которых система многочленов 2^р>
Фз^2^ фд|г) ^ ... 1) также ортогональна в том же промежутке
относительно некоторого веса (который может быть и другим) или 2)
удовлетворяет конечно-разностному уравнению того же вида, что и данные
многочлены. Сонин показал, что единственными тремя системами,
удовлетворяющими поставленным условиям, являются многочлены Якоби, Чебы-
шева — Лагерра и Чебышева — Эрмита. Тот же результат был вновь
доказан в 1935 г. В. Ханом, не знавшим работы Н. Я. Сонина. Не имея
возможности входить в подробности, мы отсылаем за ними к литературе1).
С проблемами общей теории ортогональных многочленов нам придется еще
раз встретиться при разборе теории замкнутости В. А. Стеклова.
Механические квадратуры. Потребность в приближенном вычислении
определенных интегралов — приближенных, или механических,
квадратурах — возникла одновременно с их введением. Приближенное
вычисление величин, которые, по существу, выражаются определенными
интегралами, производилось даже до создания интегрального исчисления
(например, вычисление логарифмов Непером).
Формулы механических квадратур для интеграла ?)
+1
\ f(x) dx
-l
строятся в виде
1
^ f(x) dx « А^(х±) + ... + Anf(xn),
-l
где коэффициенты At и точки деления промежутка хг не зависят от f(x).
Первые формулы квадратур (так называемые формулы Д. Грегори —
Т. Симпсона, И. Ньютона — Р. Котеса и др.), широко употребительные
г) Например, Я. Л. Геронимус, Теория ортогональных многочленов. Об"
зор достижений отечественной математики. М.—Л., 1950; Н. И. А х и е з е р, Работы
Н. Я. Сонина по приближенному вычислению определенных интегралов, в кн.:
Н. Я. Сонин, Исследования о цилиндрических функциях и специальных
полиномах. Ред. и комментарии Н. И. Ахиезера, М., 1954.
2) Специальный выбор пределов интервала —1 и +1 принципиального значения
Ъ—а , Ъ-\-а
не имеет; в случае пределов х = а, х = Ъ подстановка х = —^— у+—к~ немедленно
ведет к интегралу с пределами z/ = — 1, у = -J-1.
МЕХАНИЧЕСКИЕ КВАДРАТУРЫ
419
и ныне, основаны были на делении промежутка (—1, +1) на равные
части; при этом коэффициенты отдельных членов оказывались
неодинаковыми. Новый прием был предложен Гауссом, который, исходя из
условия, чтобы формула давала точное значение интеграла для многочлена
не выше (2тг — 1)-й степени, получил формулы с неравноотстоящими
значениями х±, х2, . . ., хп.
Формулы Гаусса (1816) обладают высокой степенью приближения
и особенно употребительны, когда необходимо использовать возможно
меньшее число значений fix); но и в этих формулах коэффициенты Аи
выражающиеся через корни многочленов Лежандра, различны между
собой.
В мемуаре «О квадратурах» (1874) Чебышев, отправляясь от одного
исследования Эрмита, разработал новые общие формулы квадратур,
коэффициенты которых либо одинаковы, либо же отличаются только
знаком. Наиболее известная из его формул такова:
1
J f(x) dxzzk [fix,) + f(x2) + . . . + /(*„)].
-1
Коэффициент к и точки х±, х2, . . ., хп определяются требованием, чтобы
написанное приближенное равенство было точным для любого многочлена
степени не выше п. Это дает к = 21 п, а хи х2, • • ••> %п оказываются
корнями некоторого уравнения степени п. Чебышев нашел значения
аргумента х для п = 2, 3, 4, 5, 6, 7. Так, при п = 4 значения х являются
корнями уравнения
и приближенно будут х, = —х^ = — 0,794654 и х2 = — хг = — 0,187592.
Впоследствии выяснилось, что при п = 8 и п > 9 значения х
представляют собой комплексные числа и формула становится непригодной.
Для п > 9 это доказал в 1937 г. С. Н. Бернштейн.
Равенство всех коэффициентов At делает формулу Чебышева в ряде
случаев весьма удобной для практических вычислений, особенно, когда
значения f(xt) содержат сравнительно большие погрешности. Чебышев-
ские формулы квадратур были использованы А. Н. Крыловым в
исследованиях по теории корабля и применяются морскими строителями во
всем мире.
Приведенную формулу Чебышев получил, исследуя более общий
случай механической квадратуры
1
I f(x) Р(х) dx = k [fix,) + fix2) +...+ fixn)\
-l
с данной весовой функцией pix) и полагая затем pix) = 1. Для этого
общего случая г) он предложил два типа формул квадратур. Если интеграл
1
от весовой функции \ pix) dx не равен нулю, то коэффициенты квадра-
-1
турной формулы одинаковы и она имеет только что указанный вид. Если же
) В упомянутом исследовании Эрмита был рассмотрен частный случаи
420 ГЛ. 20. ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
1
\ р(х) dx = 0, то коэффициенты, имея одинаковое абсолютное значение,
—1
разделяются на две равночисленные группы разного знака и формула
принимает вид
1
I /И Р(Я) dxttk [f(x±) + . . . + f(Xm) — f{Zm+l) — ... — f(x2m)]',
-1
предполагается, что он& точная для многочлена степени не выше 2т + 1.
1
Выводы в значительной мере основаны на рассмотрении интеграла \ ^^dx.
-1
Применение своих общих формул второго типа Чебышев показывает
прежде всего на примере веса р(х) = х. Интеграл
1
\ xf(x) dx
-l
приближенно выражается двучленной формулой:
J */(*)&«/1[/(/т)-/(-/т)]'
-1
далее приводится четырехчленная формула. Другим примером служит
вес р(х) = —. , что приводит к весьма простым и удобным прибли-
жениям для интеграла
^ cos0/(cose)d9, вроде y72[/(cos "f") —/(cos-у*)] »
о
а затем и для интеграла
\ cos nQ 9(cos 8) dQ,
где n — целое число: Формулы квадратур с весом, отличным от 1,
находят применение в приближенном вычислении интегралов от разрывных
функций.
Механические квадратуры с весом изучались затем К. А. Поссе
(1875, 1886), Н. Я. Сониным (1887), А. А. Марковым (1885, 1896) и
другими. При этом были тщательно исследованы методы Гаусса и Чебышева,
построены новые формулы квадратур, даны выражения остаточных членов
и т. д. Упомянем, что Сонин по-новому вывел из своих более общих
формул формулы Чебышева обоих типов; он и Поссе выяснили, что только
1
для веса р(х )= >- -вообще возможны формулы, при любом п имеющие
одинаковые коэффициенты. Марков в уже встречавшейся нам статье
по проблеме моментов «Новые приложения непрерывных дробей»
применил полученные в ней результаты к выводу формул, аналогичных
формулам Чебышева второго типа. Требуя, чтобы формула была точной для
С. Н.БЕРНШТЕЙН И КОНСТРУКТИВНАЯ ТЕОРИЯ ФУНКЦИЙ 421
многочленов степени не выше 2т, Марков мог гарантировать, что все
встречающиеся в вычислениях числа действительные; его формулы
снабжены остаточными членами. Наши математики и позже успешно
занимались этой проблематикой. В самом конце рассматривамого времени
и начале советского периода ценные результаты опубликовал В. А. Стек-
лов (Изв. Акад. наук, тт. 10—13, 1916—1919). Помимо новых удобных
квадратурных формул, он предложил весьма общую оценку остаточного
члена, а также рассмотрел вопрос об условиях, в которых для
непрерывных функций или же функций, интегрируемых по Риману, квадратурный
процесс сходится к точным значениям интегралов при стремлении числа
точек деления промежутка интегрирования к бесконечности г).
С. Н. Бернштейн и конструктивная теория функций. В начале XX века
теория наилучшего приближения функций получила развитие в
совершенно новом направлении, которое явилось результатом установления
связи между чебышевской теорией и идеями общей теории функций,
разрабатывавшейся в Германии и Франции. Основными явились здесь
работы С. Н. Бернштейна.
Чебышев и его ближайшие ученики поставили и исследовали задачу
об отыскании многочлена тг-й степени Рп(х), наименее уклоняющегося
от данной непрерывной функции f(x) на данном отрезке (а, Ъ). Если
обозначить максимум модуля уклонения для такого многочлена Рп(х)
через En[f(x)] 2), то с увеличением степени многочлена п уклонения
EnU(x)] не увеличиваются и, вообще говоря, уменьшаются.
Петербургские математики, однако, не занимались вопросом о поведении Еп с
ростом п: их интересовало отыскание наилучшего приближения для данной
функции при заданной степени многочлена в тех или иных конкретных
условиях.
В 1885 г. К. Вейерштрасс доказал, что всякая непрерывная на
отрезке (а, Ъ) функция f(x) может быть разложена в равномерно сходящийся
ряд степенных многочленов; поэтому при любом 8 > 0 имеется
многочлен Р(П)(х) степени тг(е), для которого \f(x) — Р(П)(#)|< 8, каково бы
ни было значение х, принадлежащее рассматриваемому отрезку. Из этой
теоремы непосредственно следует, что для всякой непрерывной функции
значения Еп [f(x)], соответствующие аппроксимации многочленами
наилучшего приближения, стремятся к нулю при п ->оо.
В первые годы XX века интерес к проблемам приближения функций
степенными многочленами в странах Западной Европы быстро возрастает
благодаря работам Э. Бореля, А. Лебега и Ш. де Валле-Пуссена.
Основное значение имела постановка вопроса об оценке порядка величины
наилучшего приближения En[f(x)] непрерывной функции f(x) при
неограниченном росте п. Одним из исходных пунктов явилось новое
доказательство теоремы Вейерштрасса, данное Лебегом. Произвольную
непрерывную функцию у = f{x) Лебег приближенно представлял функцией вида
Уп = Ах + В+ 2 Ch\x — ak\
(это соответствует аппроксимации графика кривой у = f(x) некоторой
ломаной, составленной из прямолинейных отрезков), а функцию уп в свою
х) Подробнее см. Я. Л. Г е р о н и м у с, Теория ортогональных многочленов.
Обзор достижений отечественной математики.
2) От французского слова ecart — уклонение.
422
ГЛ. 20. ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
очередь приближал степенными многочленами. Задача сводилась, таким
образом, к приближению в некотором интервале, скажем от —1 до 1,
функции \х\. Изучая характер приближения \х\ многочленом п-ж степе-
к
ни, Валле-Пуссен установил, что Е[ \ х | ] ^ — , где к — некоторая
постоянная. Возникал вопрос об оценке величины снизу, и по рекомендации
Валле-Пуссена Бельгийская Академия наук в 1908 г. объявила конкурс
на тему о разложении действительных или аналитических функций в ряды
многочленов, которую сам Валле-Пуссен сформулировал так: возможно
или нет представить ординату многоугольной линии, или, что сводится
к тому же, \х\ в промежутке (—1, +1), посредством многочлена степени п
с приближением более высокого порядка, чем 1/га? Два года спустя Валле-
Пуссен получил для 2?п[|ж| ] оценку снизу:
па „ <?„[Ы],
п(\пп)3 nil JJ'
которую год спустя С. Н. Бернштейн заменил несколько лучшей:
!ГШТ<*Л1*11
(здесь а и at — постоянные), а еще через год — оценкой еще более точной
и принципиально не подлежащей улучшению.
Сергей Натанович Бернштейн, о первых трудах которого по теории
вероятностей уже говорилось, родился в Одессе 6 марта 1880 г.; отец
его был доцентом анатомии и физиологии. В силу трудностей, связанных
в царской России с поступлением в университет для евреев, С. Н.
Бернштейн временно уехал за границу. Он окончил в 1899 г. университет
и в 1901 г. Высшую электротехническую школу в Париже и потом
занимался еще в Геттингене. По возвращении на родину со степенью доктора
наук, полученной в 1904 г. в Париже, он должен был вновь защитить
магистерскую и докторскую диссертацию, так как степени, полученные
за границей, не давали прав в России. Первая защита состоялась в 1908 г.
при оппонентах Д. М. Синцове и А. П. Пшеборском, вторая — в 1913 г.,
причем оппонентамина этот раз были тот же А. П. Пшеборский иН.Н.
Салтыков (1870—1961), специалист по механике и уравнениям с частными
производными. В 1907 г. Бернштейн приступил к преподаванию в
Харьковском университете в качестве приват-доцента. Среди курсов, впервые
им здесь поставленных, отметим интегрирование уравнений
математической физики, аналитическую теорию дифференциальных уравнений
и интегральные уравнения; он регулярно читал также лекции по теории
вероятностей. Профессуру Бернштейн смог получить только после
революции, в 1917 г. В Харькове Бернштейн заложил основы большой
математической школы. Он работал здесь до 1933 г., когда переехал в
Ленинград, где преподавал в университете и Политехническом институте;
с 1941 г. он живет в Москве. В 1925 г. С. Н. Бернщтейн был избран
членом Академии наук УССР, а'в 1929 — действительным членом Академии
наук СССР. Заслуги Бернштейна высоко ценятся и за рубежом.
Парижская Академия наук избрала его в 1928 г. своим корреспондентом
и в 1955 г. иностранным членом.
Первые исследования Бернштейна, в том числе и магистерская
диссертация, относились к области дифференциальных уравнений, и мы
о них скажем далее. Сейчас мы обратимся к его основополагающим
изысканиям по теории наилучшего приближения функций.
С. Н. БЕРНШТЕЙН И КОНСТРУКТИВНАЯ ТЕОРИЯ ФУНКЦИЙ 423
Работа Бернштейна, представленная в 1911 г. Бельгийской
Академии наук в связи с проблемой Валле-Пуссена, была премирована
Бельгийской Академией, а Валле-Пуссен характеризовал ее как «наиболее
существенный вклад из всех, какие были сделаны в области разложения
функций действительного переменного в ряды полиномов, как по числу,
так и по значительности содержащихся в ней результатов» *). Эта работа
составила главную часть докторской диссертации Бернштейна «О
наилучшем приближении непрерывных
функций посредством многочленов данной
степени» (Харьков, 1912) и тогда же
была напечатана в Mem. publ. par la
classe des sciences Acad, de Belgique,
t. 4, 1912, под названием «О порядке
наилучшего приближения непрерывных
функций многочленами данной степени»
(Sur l'ordre de la meilleure approximation
des fonctions continues par des polynomes
de degre donne).
Прежде всего укажем на решение,
которое получила задача Валле-Пуссена
о порядке величины Еп[\ х\]. Бернштейн
показал, что вопрос бельгийского
математика решается в отрицательном
смысле, так как при всяком п имеет место
неравенство
1 2
4(1 + У2)(2ге-1)<адЖ|1<^ + 1) '
Кроме того, Бернштейн доказал, что С. Н. Бернштейн.
при неограниченном возрастании п
произведение 2п-Е2п[\ х\] стремится к пределу X, который равен 0,282
с точностью до 0,004. Отсюда для достаточно больших п следует, что
0,278 Е г. яП ^0,286
Но еще важнее, чем эти блестящие результаты, были выдвинутые
Бернштейном новые общие идеи, в разработке которых существенную
вспомогательную роль играли приводившиеся выше неравенства
Бернштейна, связывающие максимумы абсолютных значений многочлена
(целого или тригонометрического) и его производных в данном интервале.
В докладе на V Международном конгрессе математиков в Кембридже
(1912) Бернштейн, подобно Чебышеву, говорил: «Пример задачи о
наилучшем приближении \х\, предложенной Валле-Пуссеном, дает еще одно
подтверждение того факта, что хорошо поставленный частный вопрос
способен быть отправной точкой для далеко идущих теорий»2). Именно,
в процессе изучения величины En[f (х)] для различных классов функций
х) Цит. по статье: В.Л. Гончаров, Теория наилучшего приближения
функций. В сб. «Научное наследие П. Л. Чебышева», вып. 1, Математика, стр. 159,
2) См. русский перевод доклада: С. Н. Бернштейн, О новых исследованиях,
относящихся к наилучшему приближению непрерывных функций многочленами.—
УМН, т. V, вып. 4 (38), 1950, стр. 126. Сам доклад напечатан на французском языке
в Ргос. 5 Intern. Math. Congress, t. I, 1913.
424
ГЛ. 20. ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
f(x) выяснилось, что между аналитическими и дифференциальными
свойствами f(x) и асимптотическим законом убывания величины En[f(x)}
при п ->- оо имеется весьма тесная связь.
Одновременно с Бернштейном аналогичными проблемами занимался
находившийся тогда в Геттингене американец Д. Джексон. Результаты
Бернштейна показали, что по быстроте убывания En[f(x)] можно судить
о таких свойствах f(x), как аналитичность, существование непрерывных
производных до определенного порядка, выполнение обобщенных условий
Липшица и т. д. Бернштейну же и Джексону принадлежало решение ряда
обратных задач, в которых речь идет об изучении быстроты убывания
En[f(x)] в зависимости от свойств f(x).
Уже первые открытия в новой проблематике были столь значительны,
что на V Международном математическом конгрессе, состоявшемся всего
через год после публикаций Бернштейна, был поставлен только что
цитированный его обзорный доклад. В небольшой таблице автор подвел
краткий итог своим исследованиям и исследованиям Джексона. Мы
приведем часть таблицы, содержащей необходимые или достаточные условия,
при которых функция обладает тем или иным аналитическим свойством.
Всего в таблице содержалось 10 результатов, из которых Бернштейну
принадлежали 7, Джексону два и Лебегу один. Заметим, что из
результатов Вейерштрасса следовало, что для непрерывности f(x) необходимо
и достаточно выполнение условия lim En[f(x)] = 0.
Для того чтобы
функция действительной
переменной
1) была
аналитической,
2) обладала
производными всех
порядков,
3) обладала
непрерывной
производной порядка р
Необходимое
условие
lim Дп[/(*)1рп = 0
(р>1)
limEn[f(x)]nP = 0
(каково бы ни
было р)
En[f(x)]nP<Bn
(где еп -> 0 при
п -> оо)
Автор
С. Н. Берн-
штейн
С. Н. Берн-
штейн
Д.
Джексон
Достаточное
условие
То же
То же
оо
2 En[f(x)]nP-i
71=1
сходится
Автор
С. Н. Берн-
штейн
С. Н. Берн-
штейн
С. Н. Берн-
штейн
Анализируя таблицу, Бернштейн говорил: «Достаточно бросить
беглый взгляд на таблицу, чтобы отдать себе отчет в точности сказанного
мною выше по поводу тесной связи, существующей между наилучшим
приближением и дифференциальными свойствами функции. Вы видите
прежде всего, что с точки зрения действительной переменной
аналитические функции могут быть определены как функции, наилучшее
приближение которых посредством многочленов убывает наиболее быстро;
это — функции, которые среди всех непрерывных функций наименее
отличаются от многочленов» *). Класс бесконечно дифференцируемых
функций также однозначно определяется природой убывания
величины Еп. Иначе обстоит дело с функциями третьего класса нашей таблицы,
г) См. УМН, т. V, вып. 4 (38), 1950, стр. 123.
С. Н. БЕРНШТВЙН И КОНСТРУКТИВНАЯ ТЕОРИЯ ФУНКЦИЙ 425
для которых необходимое и достаточные условия не совпадают; эти
функции, как писал Бернштейн, не могут быть полностью охарактеризованы
с помощью наилучшего приближения. В целом таблица
свидетельствовала, что чем проще дифференциальная природа функции f(x), тем быстрее
убывает с ростом п величина En[f(x)], и наоборот.
Укажем попутно, что в докторской диссертации Бернштейна
результат, содержащийся в первой строке таблицы, был частично распространен
на аналитические функции комплексного переменного в следующей
формулировке: если для всякого п величина Еп [/ (х)] на отрезке (—1, +1)
не превосходит АТ/рп, где р > 1 и М — некоторая постоянная, то f(x) —
голоморфна внутри эллипса с фокусами в точках —1 и +1 и с
полусуммой осей, равной р. Справедливо и обратное предложение.
Основные работы Бернштейна относятся к трем довольно далеким,
вообще говоря, друг от друга областям математики —
дифференциальным уравнениям, теории наилучшего приближения функций и теории
вероятностей. Но, как и у всякого крупного математика, между работами
Бернштейна в этих направлениях существуют глубокие связи. Укажем
для примера, что в 1912 г. он с помощью методов теории вероятностей
дал простое доказательство теоремы Вейерштрасса о равномерном
приближении непрерывной функции f(x) на отрезке (0,1) некоторой
последовательностью многочленов (Сообщ. Харьк. матем. о-ва, т. 13). Бернштейн
показал, что в качестве таких многочленов могут быть взяты
Bn{x) = ^l[±)chnx\l-x\n-\
Эти «многочлены Бернштейна» явились позднее предметом дальнейших
изысканий и приложений различных ученых. В свою очередь к
многочленам Вп Бернштейн пришел, отправляясь от изучения так называемых
нормальных рядов, введенных им в работах по дифференциальным
уравнениям для определения аналитичности функций в действительной
области.
Еще в рассматриваемый период Бернштейн продвинулся дальше
в разработке нового направления теории приближения функций. Так,
в 1914 г. (Math. Annal. В. 75) он ввел в рассмотрение новый класс
квазианалитических функций, для которых на отрезке (а, Ъ)
EnAf{x)]<~ (* = 1,2,3, ...),
Р г
где р>1, а натуральные числа
Всякая аналитическая функция является квазианалитической; именно,
для аналитических функций последовательность чисел щ, п2, п3, - - .
совпадает с натуральным рядом, но квазианалитическая функция может
даже не быть дифференцируемой. Бернштейн указал на основное
свойство квазианалитических функций, с которым связано их наименование:
подобно аналитической всякая квазианалитическая в интервале (а, Ъ)
функция однозначно определяется в нем своими значениями на любом
как угодно малом его участке1).
г) Существует ряд классов квазианалитических функций; функции,- о которых
здесь идет речь, Бернштейн называет квазианалитическими класса (Р).
426
ГЛ. 20. ТЕОРИЯ ПРИБЛИЖЕНИЯ ФУНКЦИЙ
Особенное развитие деятельность Бернштейна получила уже после
Октябрьской революции. В настоящее время конструктивная теория
функций (термин, предложенный для нового направления самим Берн-
штейном в 1938 г.) представляет собой развитую математическую
дисциплину, в которой изучаются зависимости между свойствами различных
классов функций и характером их приближения в той или иной (конечной
или бесконечной) области при помощи других, более простых функций;
эта теория включает, как часть, и классическую проблематику,
непосредственно продолжающую чебышевскую. В дальнейшем развитии
теории принимали участие многие ученые, в том числе ученики С. Н.
Бернштейна Н. И. Ахиезер, В. Ф. Бржечко (1891—1954), Я. Л. Геронимус,
В. Л. Гончаров (1896—1955), а затем — целый ряд других советских
математиков; это направление интенсивно разрабатывалось и за
рубежом х).
*) Подробнее см. Н. И. Ахиезер, Академик С. Н. Бернштейн и его работы
по конструктивной теории функций. Харьков, 1955.
ГЛАВА ДВАДЦАТЬ ПЕРВАЯ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Классические методы; А. Ю. Давидов. В разработку теории
дифференциальных уравнений русские ученые, главным образом более молодые
представители петербургской школы, внесли вклад огромного значения.
Исследования в этой области охватили широкий круг вопросов —
систематизацию и совершенствование классических приемов интегрирования,
изучение различных специальных уравнений, теоремы существования
решений, новые краевые задачи, качественную теорию дифференциальных
уравнений, приближенные приемы интегрирования и т. д.
Как мы знаем, в Москве интерес к теории дифференциальных
уравнений возбудил Н. Е. Зернов, в 1837 г. защитивший докторскую
диссертацию «Рассуждение об интеграции уравнений с частными
дифференциалами» (М., 1837). Эта книга представляет собой не оригинальное
исследование, но систематическое изложение основных методов интегрирования
уравнений в частных производных первого и второго порядков от Эйлера
и Лагранжа до Фурье, Пуассона и Якоби; рассматриваются отдельные
примеры уравнений высших порядков. Указывая в заключение, что
уравнения с частными дифференциалами лежат в основании теории тепла
и других отделов математической физики, автор писал, что свой труд
«желал сделать приготовлением к изучению сих любопытных теорий,
составляющих торжество наук математических» х). Мы упоминали, что
некоторое время диссертация Зернова служила в Московском
университете пособием для студентов, но уже в пятидесятые годы она вышла
из употребления.
Оригинальный вклад внес в теорию уравнений с частными
производными ученик Зернова и Брашмана Август Юльевич Давидов (27 декабря
1823—3 января 1886),. окончивший университет в 1845 г. и
преподававший в нем с 1850 г., сначала в звании адъюнкта, а потом
экстраординарного (1853) и ординарного (1859) профессора. Мы говорили уже о
выдающихся заслугах Давидова, как одного из организаторов и долговременного
руководителя Московского математического общества, а также как
деятеля народного образования, по учебникам которого изучали геометрию
и алгебру несколько поколений русских школьников 2). Главные научные
интересы Давидова принадлежали механике. В магистерской
диссертации «Теория равновесия тел, погруженных в жидкость» (М., 1848) он,
продолжая исследования Ш. Дюпена, который шел преимущественно
2) Н. Е. Зернов, Рассуждение об интеграции уравнений с частными
дифференциалами, М., 1837, стр. 125.
2) Р. А. Симонов, Педагогическое наследие профессора математики
Московского университета А. Ю. Давидова, М., 1957.
428
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
геометрическим путем, разработал современный аналитический метод
определения положений устойчивого равновесия плавающих тел с помощью
поверхности центров (геометрического места центров тяжести
постоянного объема, отсеченного плоскостью от тела). Эта работа,
вдохновленная мастерским изложением вопроса в «Теории равновесия тел твердых
и жидких» (М., 1837) Н. Д. Брашмана, стала отправным пунктом
дальнейших исследований того же Брашмана и других русских механиков.
Позднее (1855) Давидов специально рассмотрел вопрос о числе
положений равновесия погруженной в
жидкость однородной прямой трехгранной
призмы. Буняковский незадолго до
того (1852) показал, что это число не
превосходит 15; Давидов установил, что
максимальное число таких
положений равно 12. В докторской
диссертации «Теория капиллярных явлений»
(М., 1851) Давидов систематизировал
и дополнил изыскания Лапласа,
Пуассона и Гаусса, связав эту теорию с общей
теорией равновесия жидкостей. За
каждую диссертацию Давидову была
присуждена половинная Демидовская
премия *).
Работы Давидова по механике
свидетельствуют о свободном владении им
всем соответствующим аппаратом
математического анализа, включая теорию
дифференциальных уравнений.
Математике вообще посвящена большая
А. Ю. Давидов. часть его трудов. Мы особо отметим
здесь статью «Об уравнениях с
частными дифференциалами какого-нибудь порядка» (Матем. сборник, т. 1,
1866), которая содержит новые результаты в теории характеристик,
играющей важную роль в интегрировании уравнений с частными
производными. Начало этой теории фактически положил Эйлер в третьем томе
«Интегрального исчисления», а подробнее развил ее, особенно
применительно к уравнениям второго порядка, Г. Монж (1784; 1807). Монж ввел
и самый термин «характеристика», как в теории поверхностей (где это —
линия пересечения двух бесконечно близких поверхностей данного одно-
параметрического семейства), так и в теории уравнений с частными
производными (где характеристика есть линия, через которую проходит
бесконечное множество поверхностей, удовлетворяющих данному
Дифференциальному уравнению). Для рассмотренных им типов уравнений
с частными производными Монж вывел соответствующие обыкновенные
дифференциальные уравнения их характеристик. Геометрическая теория
решения уравнений с частными производными, своими первыми
большими успехами обязанная Лагранжу и еще более Монжу,
разрабатывалась затем многими учеными. Давидов обобщил результаты, полученные
для уравнений 1 и 2 порядков, выведя уравнения характеристик для
произвольного дифференциального уравнения ?г-го порядка с двумя неза-
х) См. отзывы М. В. Остроградского в кн.: М. В. Остроградский,
Полное собрание трудов, т. I, стр. 35—45.
В. Г. ИМШЕНЕЦКИЙ
429
висимыми переменными. Его работа вызвала еще несколько других
в том же направлении.
Первым откликнулся воспитанник Московского университета
Владимир Васильевич Преображенский (1846—1905), работавший
преимущественно в Одесском университете (1876—1882, 1889—1900) и в нем же
защитивший докторскую диссертацию по теории логарифмического
потенциала (Зап. Новоросс. унив., т. 28, 1879). В статье «Об интегрировании
уравнений с частными производными высших порядков», послужившей
его магистерской диссертацией (Матем. сборник, т. 7, 1874),
Преображенский получил результаты Давидова с помощью более простого приема,
который распространил на системы уравнений первого порядка с
произвольным числом независимых переменных. Другой изящный вывод
тех же результатов предложил К. М. Петерсон, решивший с помощью
уравнений характеристик несколько сложных уравнений с частными
производными (Матем. сборник, тт. 8—10, 1877—1882). Теория
характеристик разрабатывалась также Н. Я. Сониным, Д. Ф. Егоровым и
другими русскими учеными.
Мы не можем останавливаться здесь на работах Давидова по
различным вопросам анализа (определенные интегралы, абелевы функции и др.)
ж теории вероятностей с приложениями к демографии и медицине. Укажем
только, что в статье «Приложение теории вероятностей к статистике»
(Учебно-литературные статьи профессоров и преподавателей Московского
университета... М., 1855) он, кажется, впервые, ввел понятия функции
распределения и плотности распределения случайной величины, не
применяя, впрочем, эти современные нам термины г).
В. Г. Имшенецкий. Большое внимание русских математиков
продолжало привлекать совершенствование классических приемов
интегрирования уравнений с частными производными 1 и 2 порядков.
Несомненные заслуги в этой области принадлежат В. Г. Имшенецкому.
Василий Григорьевич Имшенецкий (16 января 1832—5 июня 1892)
родился в семье врача в Ижевске. После окончания гимназии в Казани
он в 1848 г. поступил на физико-математический факультет Казанского
университета, где на него большое влияние оказал профессор Александр
Федорович Попов (29 ноября 1815—12 января 1879), ученик
Лобачевского. Главные работы Попова, в том числе докторская диссертация
«Об интегрировании уравнений гидродинамики, приведенных к
линейному виду» (Казань, 1845), получившая хорошую оценку Лобачевского 2),
относятся к механике жидкостей; ему принадлежат также статьи по
частным вопросам анализа: вычисление некоторых определенных интегралов,
оригинальный вывод остаточного члена Лагранжа и другие. В Казанском
университете Попов преподавал, заменив здесь своего учителя, с 1846
по 1866 г., до выхода в отставку по болезни; в том же 1866 году он был
избран членом-корреспондентом Академии наук 3).
х) Этими сведениями я обязан устному сообщению X. О. Ондара. О научном
творчестве Давидова см.: Н. Е. Ж у к о в с к и й, П. А. Н е к р а с о в, П. М.
Покровский, Жизнь и труды А. Ю. Давидова. — Матем. сборник, т. 15, 1890;
Ф. И. Франкль, О работах русских математиков по теории характеристик
уравнений в частных производных, УМН, т. VI, 2 (42), 1951, стр. 154—155.
2) Н. И. Лобачевский, Полное собрание сочинений, т. 5, стр. 381—394.
3) В. П. Б ычк о в, Казанский математик Александр Федорович Попов.
Ученые зап. Тираспольского гос. пед. института им. Т. Г. Шевченко, вып. V, 1957
(имеется список сочинений Попова).
430
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Имшенецкий окончил университет в 1853 г. и вначале вел занятия
в гимназии, к которым в 1860 г. добавилось чтение лекций в родном
университете. В 1862—1864 гг. он провел два года в заграничной
командировке и слушал в Париже лекции Ламе по математической физике
и Бертрана по дифференциальным уравнениям и теории потенциала.
В 1865 г. он защитил магистерскую диссертацию «Об интегрировании
уравнений с частными производными первого порядка» (Казань, 1865),
а три года спустя докторскую —«Исследование способов интегрирования
уравнений с частными производными второго порядка функции двух
независимых переменных» (Казань, 1868).
С 1865 г. Имшенецкий был доцентом,
а с 1868 г. — профессором Казанского
университета. Однако здесь его
деятельность была неожиданно прервана. В начале
семидесятых годов попечителем Казанского
округа состоял П. Д. Шестаков, который
сам говорил о себе, что его назовут вторым
Магницким. В 1871 г. физиолог П. Ф. Лес-
гафт (1837—1909) выступил с
разоблачением злоупотреблений и недостойных
поступков попечителя и поддерживавшей
его реакционной части профессоров. «Дело
Лесгафта» было доложено императору,
и Александр II приказал уволить
Лесгафта из университета. Ответом на этот
акт произвола явилась коллективная
подача в отставку шести прогрессивных
профессоров, в том числе Имшенецкого.
Вскоре, в 1872 г., Имшенецкий был
„ ^ тт „ избран профессором механики Харьков-
В. Г. Имшенецкий. х- х- -г х- *¦
^ ского университета, где в течение десяти
лет вел активную педагогическую работу
и принял участие в создании Харьковского математического общества.
В 1881 г. он по предложению Чебышева, Буняковского и Савича был
избран академиком и в 1882 г. переехал в Петербург. Здесь он продолжал
работы по дифференциальным уравнениям и специальным функциям
и вместе с тем с 1884 г. читал лекции на Высших женских курсах;
в конце жизни он принял активное участие в организации Петербургского
математического общества г).
Работы Имшенецкого по уравнениям с частными производными
посвящены систематизации, упрощению и дополнению методов
интегрирования, начало которым положили Эйлер и Лагранж и целью которых было
нахождение решения в возможно более общей и конечной форме. В
магистерской диссертации значительно упрощен и развит метод Якоби
интегрирования уравнения с частными производными первого порядка
т? ( dz dz dz \ —О
? \х^хг,. . . ,хп, z, — , — , . . ., дХп J - и,
опубликованный уже после смерти Якоби в 1862 г. 2). В докторской
х) К. А. Андреев и др., Жизнь и научная деятельность Василия
Григорьевича Имшенецкого, М., 1896.
2) Независимо рт Якоби и почти одновременно с ним тот же метод разрабатывал
в сороковые годы М. В. Остроградский.
В. Г. ИМШЕНЕЦКИЙ
431
диссертации Имшенецкий улучшил ряд классических приемов решения
уравнений второго порядка, созданных Лапласом, Монжем и Ампером.
Выход обеих работ явился значительным событием в литературе вопроса
и они привлекли внимание как в России, так и за границей. Первый
пропагандист идей Лобачевского во Франции Ж. Гуэль перевел обе
диссертации Имшенецкого на французский язык (1869 и 1872), а вторая из них
издана также в немецком переводе Ф. Мазера в 1892 г. Для учебных
целей обе диссертации были переизданы Московским математическим
обществом в 1916 г. В настоящее время проблематика, интересовавшая
Имшенецкого, утратила прежнее ведущее значение и разрабатывается
мало, но многие его приемы интегрирования прочно вошли в учебную
литературу.
В исследованиях Имшенецкого мы находим и первые ростки
некоторых новых больших идей, а именно — так называемой теории
касательных преобразований, с 1873 г. развивавшейся знаменитым норвежским
математиком С. Ли. Касательное преобразование Имшенецкий
использовал в докторской диссертации для преобразования уравнений типа
Монжа — Ампера
*?+^+*?+*+*[ё-?-(:йг)гИ
где Н, К, L, М, N — функции х, у, z, -^, -^, к виду
да2 ' даду 1 ду2 '
в предположении, что известен какой-либо частный интеграл
Z = cd(x, у, а, у, т))
данного уравнения, содержащий три производных параметра а, у, г\.
К сожалению, эта весьма важная идея Имшенецкого долго оставалась
незамеченной. Сам С. Ли впоследствии, ознакомившись с результатами
Имшенецкого, дал им высокую оценку. В 1894 г. он, с похвалой
отозвавшись о магистерской диссертации Имшенецкого, писал: «Еще большее
значение имеет произведение Имшенецкого о дифференциальных
уравнениях с частными производными второго порядка, которое вносит новый
вклад в теории, обоснованные Лапласом, Монжем и Ампером (я лично
должен, конечно, сожалеть, что познакомился с этим произведением
лишь после того, как я пришел к эквивалентным результатам частично
благодаря собственным исследованиям, частично благодаря работам
Дарбу»1).
Теории уравнений с частными производными был посвящен в это
время еще ряд диссертаций и монографий, обобщавших и уточнявших
классические методы интегрирования: обе диссертации В. П. Ермакова
«Общая теория интегрирования линейных дифференциальных уравнений
высших порядков с частными производными и с постоянными
коэффициентами» (Спб., 1873) и «Интегрирование дифференциальных уравнений
механики» (Киев, 1877), докторская диссертация Н. Я. Сонина «Об
интегрировании уравнений с частными производными второго порядка» (Матем.
сборник, т. 7, 1874), опубликованная Ф. Энгелем на немецком языке
г) В. А. К о ч е в, Академик В. Г. Имшенецкий (автореферат диссертации)г
Свердловск, 1953, стр. 13.
432
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
в «Mathematische Annalen» за 1897 г., магистерская диссертация
москвича Д. Ф. Егорова «Уравнения с частными производными второго
порядка по двум независимым переменным. Общая теория интегралов;
характеристики» (М., 1898), содержащая оригинальное геометрическое
изложение теории, обе диссертации Н. Н. Салтыкова по уравнениям
первого порядка (Харьков, 1899 и 1905), содержащие разработку
теорий С. Ли, докторская диссертация (1903) петербургского математика
Бориса Михайловича Кояловича (1867—1941), и др.
Заслуживающие упоминания результаты были получены в отдельных
вопросах теории обыкновенных уравнений. Д. Ф. Егоров на лекциях
в Московском университете излагал новый прием интегрирования
уравнения Якоби:
Ax + By + O)dx + (Aix + Biy + Ci)dy + (A2x + B2y + C2)(xdy — ydx) = 09
вошедший в современные учебные руководства1). В. П. Ермаков указал
ряд случаев решения в квадратурах однородного линейного уравнения
второго порядка
А{х)%г + В(х)? + С(х)у = 0
с целыми рациональными коэффициентами (Киевск. унив. изв., № 9,
1880). Вслед за Миндингом целый ряд ученых — Коркин, Ермаков,
Сонин и др.— разрабатывали учение об интегрирующем множителе;
Сонин, например, исследовал с его помощью уравнение
dy __л , #М
которым до него занимались многие, начиная с Эйлера (Изв. Акад. наук,
1895) 2).
К исследованию систем линейных дифференциальных уравнений
€ постоянными коэффициентами относится один из важных результатов
О. И. Сомова. Вопрос о малых колебаниях системы материальных точек
вокруг положения устойчивого равновесия приводится к такой системе
уравнений второго порядка, причем ее интегралы определяются корнями
алгебраического уравнения частот (характеристического уравнения).
В случае кратных корней, при решении по обычным методам, появляются
вековые члены, содержащие аргумент, т. е. время вне знаков периодиче-
€ких функций, синуса и косинуса, и так как эти члены при п ->- оо
неограниченно возрастают, то устойчивость равновесия представляется
невозможной. Даламбер (1761) и Лагранж (1788) заключили отсюда, что
вековое уравнение не должно иметь кратных корней; это мнение утвердилось
надолго. Только К. Вейерштрасс и, независимо от него и по-другому,
Сомов выяснили, что для консервативной динамической системы наличие
кратных корней на самом деле не влечет за собой вековых членов, и
показали, как составлять в этом случае общие интегралы уравнений
движения. Вышли обе работы почти одновременно: статья Вейерштрасса,
в 1858 г., а Сомова через несколько месяцев спустя (Mem. Ac. Sc. Petersb.,
г) См., например, В. В. Степанов, Курс дифференциальных уравнений,
М., 1953, стр. 41.
2) См., например, К. Я. Л а т ы ш е в а, О работах В. П. Ермакова по теории
дифференциальных уравнений.— Ист.-матем. исслед., вып. IX, 1956; А. И. К р о -
потов, Николай Яковлевич Сонин. Л., 1967.
А. В. ЛЕТНИКОВ И ПРИЛОЖЕНИЯ «МЕЖДУ ПРЕДЕЛЬНЫХ ПРОИЗВОДНЫХ» 433
7 ser., I, № 14, 1859) 1). Напомним, что проблемой избавления от
вековых членов занимался в другой связи М. В. Остроградский.
Возвратимся к Имшенецкому. Начиная с 1887 г. он посвятил ряд
работ отысканию дробно-рациональных интегралов линейных
дифференциальных уравнений
где все коэффициенты и свободный член суть целые рациональные
функции х (Зап. Акад. наук, т. 55, 1887; т. 58, 1888; т. 64, 1891). Способ
решения этой задачи для уравнений первого и второго порядков был
предложен еще в тридцатые годы Лиувиллем, который пришел к ней в связи
с интегрированием алгебраических функций. Однако реализация идеи
Лиувилля при п > 2 наталкивалась, вообще говоря, на практически
непреодолимые вычислительные трудности. Имшенецкий разработал
собственный прием решения посредством некоторого специального
интегрирующего множителя, прием, который, однако, также не был лишен
недостатков. Сообщения Имшенецкого вызвали острую полемику о
сравнительной силе обоих методов. В ней приняли участие А. А. Марков, А. Н. Кор-
кин, К. А. Поссе (выступавшие против Имшенецкого), К. А. Андреев,
П. А. Некрасов (отстаивавшие его метод) и многие другие, как Д. А.
Граве, Н. В. Бугаев, Н. М. Гюнтер и В. П. Ермаков. Работы названных
лиц печатались в журналах Петербурга, Москвы, Киева и Харькова
еще в течение ряда лет. Метод Имшенецкого был при этом несколько
усовершенствован. Особенно детально сопоставлены и разработаны были
приемы Имшенецкого и Лиувилля в докторской диссертации Д. М.
Синцова «Рациональные интегралы линейных уравнений» (Казань, 1898).
Все же эти исследования не привели к удобному и безотказно
действующему алгоритму нахождения рациональных решений линейных
уравнений с многочисленными коэффициентами. Позднее Д. Д. Мордухай-Бол-
товской предложил искать решения в форме произведения рациональной
функции на показательную функцию и на некоторую степень аргумента;
эта идея не так давно (1952) получила развитие в докторской диссертации
и других трудах киевского математика К. Я. Латышевой (1897—1956).
А. В. Летников и приложения «междупредельных производных».
Среди исследований, посвященных специальным линейным уравнениям
второго порядка, мы отметим работы Алексея Васильевича Летников а
(13 января 1837—10 марта 1888), воспитанника Межевого института
и вольнослушателя Московского университета, одного из учредителей
Московского математического общества и с 1868 г. профессора математики
Московского Высшего технического училища. Наиболее оригинальным
делом Летникова явилась разработка теории дифференцирования
произвольного порядка. Его исследования по этому вопросу получили у нас
широкую известность и были особо подчеркнуты в представлении в
члены-корреспонденты Академии наук, составленном Имшенецким и
подписанном также Буняковским и Баклундом2). Избран в Академию
Летников был в начале 1885 г.
х) Я. Л. Г е р о н и м у с, Очерки о работах корифеев русской механики, М.,
1952, стр. 60—74.
2)Р.Я. Шостак, Алексей Васильевич Летников.— Ист.-матем. исслед.,
вып. V, 1952, стр. 237—238.
434
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Своеобразные обобщения понятия о производной функции fln) (х)
на дробные значения п были даны еще Лейбницем и затем Эйлером;
в XIX веке этим вопросом занимались Лаплас (1812), Фурье (1822),
Лиувилль (1832—1835), применивший введенное им определение
производной дробного порядка к задачам математической физики,
пражский математик А. К. Грюнвальд (1867)
и другие. Первый вариант своей новой
теории Летников изложил в магистерской
диссертации 1868 г. (Матем. сб., т. 3) х).
Шесть лет спустя он дал иное, более
совершенное изложение с многочисленными
применениями в докторской диссертации
«Исследования, относящиеся к теории
х
интегралов вида \ (х — u)p~i f(u) du» (Ма-
b
тем. сб., т. 7, 1874).
Летников определяет производную
с любым отрицательным показателем — р
формулой
л.
где f(x) непрерывна в промежутке
интегрирования, но при х = а может обра-
А. В. Летников. щаться в бесконечность порядка г<1.
При целом р эта производная совпадает
с р-кратным интегралом функции f(x). Производная с положительным,
в том числе дробным, показателем вводится как
dn \D-Pf(x)]*
где n — целое положительное и О <С р < 1. При р = 0 выражение,
как и должно быть, совпадает с обыкновенной производной тг-го порядка.
Выяснив ряд свойств таких «междупредельных» производных,
Летников с их помощью развивает новый метод нахождения решений и
изучения их особенностей для уравнения
{х-а){х-Ъ)^ + (с + кх)% + ку = 0,
которое при соответствующем выборе постоянных переходит в следующие
весьма важные классы уравнений: гипергеометрическое уравнение
x(x-l)^ + l(a + f> + l)x-y}%L + a$y = 0,
уравнение многочленов Лежандра
г) Напомним, что в этом же томе «Математического сборника» появился
сделанный Летниковым перевод «Геометрических оснований теории параллельных»
Лобачевского со вступительной статьей переводчика, содержавшей высокую оценку трудов
казанского геометра.
М. Е. ВАЩЕНКО-ЗАХАРЧЕНКО И СИМВОЛИЧЕСКОЕ ИСЧИСЛЕНИЕ 435
уравнение многочленов Чебышева
и, наконец (путем некоторых преобразований), в уравнение Бесселя
Дальнейшим приложениям между предельных производных (например,
к теории сферических функций и их обобщений на произвольные индексы)
посвящено еще несколько статей Летникова в 10—12 тт. «Математического
сборника» (1882—1885).
Обобщение понятия производной можно реализовать по-разному.
В современной теории тригонометрических рядов нашло применение иное
определение интегралов и производных дробных порядков, данное
в 1917 г. Г. Вейлем. В других вопросах, например, теории
преобразования Лапласа, используется определение, в сущности, очень близкое
к предложенному Летниковым и восходящее к одной юношеской работе
Римана г).
М. Е. Ващенко-Захарченко и символическое исчисление. Работы
Летникова во многом близки к символическому исчислению, которое
незадолго перед тем начали применять в теории дифференциальных
уравнений и теории конечных разностей. Это исчисление, позднее названное
операционным, с 30-х годов XIX века разрабатывали, отправляясь от
идей Лапласа и Коши, Лобатто (1837), Д. Грегори (1838), затем Дж. Буль
(1844) и другие. Символические методы упрощали решение некоторых
задач, прежде всего линейных дифференциальных или разностных
уравнений с постоянными коэффициентами, а также давали новые результаты.
В символическом исчислении основную роль играет оператор, обозна-
« d у
чаемый -j- = р, над которым производится ряд формальных операции
dn
алгебраического характера, вроде рп = -т^г , и который переводит данную
функцию f(t) путем «умножения» в ее производную p-f(t) = ^ ,
t
1 (* 1
а путем «деления»— в интеграл — -f(t) = \ f(t) dt. Например,— -1 = t
р J р
о
1 tn
и вообще — • 1=—р. Таким образом, результаты всех символических
операций получают требуемый смысл. Линейное дифференциальное урав-
п
утл dn~h fit)
нение с постоянными коэффициентами ^j ak —л+п-ъ. -Сие начальным
условием , fe =0 (к = 0, 1, . . ., тг — 1) записывается в виде
п
P(p)-f(t) = 0, где Р(р) = 2 akpn-h, а его решение есть-^гу ¦/(*); далее
г) В незаконченном опыте обобщения действий интегрирования и
дифференцирования, написанном в 1847 г., Риман, следуя другому ходу мыслей и применяя
расходящиеся ряды, пришел к формулам, в основном совпадающим с определением
Летникова. Набросок Римана был опубликован посмертно в 1876 г.
436
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
вступают в действие правила исчисления, допускающие, в частности,
формальные разложения в ряды.
Свидетельством большой отзывчивости русских математиков
рассматриваемого времени к только созревавшим научным теориям, сулившим
богатые плоды лишь. в будущем, явилась магистерская диссертация
М. Е. Ващенко-Захарченко «Символическое исчисление и приложение
его к интегрированию линейных дифференциальных уравнений» (Киев,
1862). Ващенко-Захарченко правильно оценил важность нового
исчисления для дальнейшего развития анализа. Многие думали тогда, что
символическое исчисление лишь позволяет более коротко получать уже
известные результаты!. В предисловии к диссертации киевский магистрант
подчеркивал: «Символическое исчисление не есть сокращение, но есть
такой же могущественный инструмент для исследований, как и другие
методы чистого анализа». Любопытно заметить, что несколько ранее этой
работы Ващенко-Захарченко напечатал небольшую статью на английском
языке «О дробном дифференцировании» (On fractional differentiation, The
Quarterly Journal of pure and appl. Mathematics, IV, 1866).
Четверть века спустя, с 1887 г., началась серия работ английского
инженера и физика О. Хевисайда, в широком плане развившего
операционное исчисление и показавшего его пользу в решении многочисленных
задач теории электричества и электротехники. Исследования Хевисайда,
обоснованные совершенно недостаточно, были встречены большинством
математиков либо отрицательно, либо без интереса. Но через некоторое
время польза операционного исчисления стала несомненной и в десятые-
двадцатые годы нашего столетия Т. Бромвич, Н. Винер, Дж. Карсон,
П. Леви и другие приступили к его более строгому построению и
дальнейшей разработке. При этом основную роль сыграло применение
преобразования Лапласа
оо
О
где р = х + yi, которое переводит «оригинал» f(t) в его «изображение»
F(p), в частности, дифференциальный оператор в оператор умножения
на комплексную переменную. В настоящее время операционное
исчисление стало отделом теории операторов функционального анализа; его методы
теперь повседневно применяются в математической физике и технике и
соответствующие учебные курсы введены во многих высших технических школах.
Мы охарактеризуем сочинение Ващенко-Захарченко словами
академика АН УССР И. 3. Штокало: «В начале этой книги рассматривается
вопрос о символах и их свойствах, затем решаются линейные
дифференциальные уравнения с постоянными и переменными коэффициентами —
обыкновенные и в частных производных, выводится формула,
выражающая, согласно современной терминологии операционного исчисления,
оригинал в виде суммы, взятой по корням знаменателя изображения,
причем рассмотрен также случай кратных корней, чего не сделал в своей
работе Хевисайд. К тому же следует заметить, что Хевисайд в своем мемуа-
ре привел указанную формулу без вывода, а Ващенко-Захарченко дал
полное ее доказательство. Кроме того, в книге Ващенко-Захарченко
рассмотрено применение символического метода при интегрировании
линейных дифференциальных уравнений с помощью бесконечных рядов» 1).
г) И. 3. Ш.т окало, Операционные методы и их развитие в теории линейных
дифференциальных уравнений с переменными коэффициентами, Киев, 1961, стр. 4—5.
НОВЫЕ НАПРАВЛЕНИЯ В ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 437
Новые направления в теории дифференциальных уравнений. На
протяжении долгого времени основные усилия в области обыкновенных
дифференциальных уравнений были устремлены на поиски их решений
в элементарных функциях или в интегралах от элементарных функций —
квадратурах. Для практически важных классов уравнений эта задача
была к середине XIX века в основном решена. Если найти решение
в таком виде не удавалось, его получали в виде бесконечного ряда или же
применяли численные методы решения.
В первой половине XIX века окончательно выяснилось, что решения
дифференциальных уравнений, вообще говоря, не выражадотся
элементарными функциями и их квадратурами, что дифференциальные уравнения
являются источником новых трансцендентностей. Первые результаты
здесь получил Лиувилль, в 1841 г. доказавший, что специальное
уравнение Риккати интегрируется в квадратурах только в тех случаях, которые
были установлены еще Д. Бернулли. В России задачами интегрируемости
обыкновенных дифференциальных уравнений в конечном виде занимались,,
как мы видели, В. П. Ермаков, а затем работавший в Казанском
(1882—1885) и Киевском (1887) университетах профессор Владимир
Павлович Максимович (1850—1889), который в 1885 г. доказал невозможность
нахождения в квадратурах интеграла общего линейного уравнения
второго порядка, и Д. Д. Мордухай-Болтовской (Варш. унив. изв., 1909—
1911; 1914).
Если проблема решения дифференциальных уравнений в конечном
виде постепенно отодвигалась на второй план, то все более значительную
роль начинало играть изучение свойств их решений непосредственно до
определяющим свойствам самих дифференциальных уравнений. Здесь,
в соответствии с общим духом реформы математического анализа,
предпринятой в начале XIX века, первым был поставлен вопрос о
существовании решений тех или иных классов дифференциальных уравнений.
После того как Коши выяснил, что при довольно общих условиях
решения дифференциальных уравнений суть аналитические функции,
а сама теория аналитических функций получила мощное развитие в
трудах Коши, Вейерштрасса и Римана, возникает прежде всего
аналитическая теория дифференциальных уравнений. Характерная черта этого
направления — изучение свойств решений дифференциальных уравнений
методами теории функций комплексного переменного, начиная с вопросов
о существовании и однозначности решения, о типе и расположении его
особых точек и т. д.
Другим новым направлением в теории дифференциальных уравнений,
по времени несколько более поздним, явилась качественная теория
обыкновенных дифференциальных уравнений. Теоремы существования Коши
и других авторов, а также численные методы интегрирования, позволяли
характеризовать поведение функции, являющейся решением
дифференциального уравнения или системы таких уравнений, только локально,
в некоторой близости от тех или иных заданных значений аргументов.
Между тем проблемы механики все более требовательно выдвигали новую
задачу — изучение свойств решений в целом, во всей области их
существования. Здесь существенную роль сыграло геометрическое представление
решений (в простейшем случае — в виде кривых на плоскости),
позволившее применить геометрические и топологические методы, сочетавшие
с большой эффективностью и высокую степень наглядности.
Наконец, в исследовании задач механики и математической
физики центральное место в рассматриваемый период занимает усиление
438
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
и уточнение методов решения краевых задач, разработанных в первой
половине XIX века Фурье, Пуассоном, Остроградским, Штурмом и др.
С этой проблематикой связано было и углубленное изучение вопросов
о разложении функций в ряды по ортогональным системам.
Во всех этих направлениях русским ученым принадлежат
фундаментальные результаты. Мы начнем с основоположных работ С. В.
Ковалевской по теоремам существования.
С. В. Ковалевская. Выдающийся математик Софья Васильевна
Ковалевская родилась 15 января 1850 г. в семье богатого помещика, отставного
генерал-лейтенанта В. В. Корвин-Круковского; ее прадедом с
материнской стороны был упоминавшийся ранее академик Шуберт. Уже с детских
лет С. В. Ковалевская проявила интерес к математике и полюбила эту
науку. Передовые общественные идеи 60-х годов оказали на юную
Ковалевскую сильное влияние, прежде всего через ее старшую сестру Анну
Васильевну (1843—1887), впоследствии писательницу и активную
участницу Парижской коммуны, членом правительства которой был муж
Анны Васильевны В. Жаклар х). Еще молодой девушкой С. В.
Ковалевская прониклась глубоким сочувствием к борьбе лучших представителей
русской интеллигенции с самодержавным крепостническим строем
и к идеям утопического социализма. Возмущало ее неравноправное
положение женщин, с которым ей пришлось рано познакомиться на
собственном опыте. Впоследствии она писала: «Я чувствую, что предназначена
служить истине-науке и прокладывать новый путь женщинам, потому
что это значит служить справедливости» 2).
Первые уроки высшей математики Ковалевской давал талантливый
педагог Александр Николаевич Страннолюбский (10 февраля 1839—
19 мая 1903), поклонник Чернышевского и Писарева, позднее — один
из организаторов Высших женских курсов в Петербурге, открывшихся
в 1878 г.3). Доступ в университеты был женщинам запрещен. Для
получения высшего образования Ковалевская решила уехать за границу. Чтобы
освободиться от отцовской власти, она, вступила в фиктивный брак
с В. О. Ковалевским, впоследствии знаменитым палеонтологом (1842—
1883). В 1869 г. она отправилась в Германию. Своего мужа Ковалевская
полюбила и брак перестал быть фиктивным.
Вскоре математическим образованием Ковалевской взялся руководить
крупнейший немецкий математик того времени Вейерштрасс. Занятия
ее шли успешно, и она часто поражала своего учителя быстротой и
оригинальностью мысли. В 1874 г. Вейерштрасс направил в Геттингенский
университет три работы Ковалевской, за которые ей была присвоена
степень доктора философии «с высшей похвалой». Одна из них была
посвящена общей теории уравнений с частными производными (опубл. в 1875),
другая — приведению некоторого класса абелевых интегралов к
эллиптическим (опубл. в 1884) и третья — дальнейшей разработке исследования
Лапласа о форме кольца Сатурна, рассматриваемого как жидкое (опубл.
х) В дни Парижской коммуны С. В. Ковалевская провела почти 40 дней в
осажденном Париже, ухаживала в госпитале за ранеными бойцами. После падения
коммуны она вместе с мужем участвовала в спасении сестры и В. Жаклара.
2) Цит. по статье: П. Я. Полубаринова-Кочина, Жизнь и
научная деятельность С. В. Ковалевской. В сб. «Памяти С. В. Ковалевской», М., 1951,
стр. 27.
3) О Страннолюбском см.: В. Е. Прудников, Русские педагоги-математики
XVIII—XIX веков, М., 1956.
С. В. КОВАЛЕВСКАЯ
439
в 1885) *) — одному из вопросов теории формы небесных тел, которую
несколько позднее стал разрабатывать у нас А. М. Ляпунов. Во всех трех
работах широкое применение получали методы и теоремы Вейерштрасса.
Вернувшись в 1874 г. на родину, Ковалевская завязала знакомство
с Чебышевым, Жуковским и другими учеными, выступала с научными
докладами на VI и VII съездах русских естествоиспытателей и врачей
в 1880 и 1883 гг., публиковала
научные обозрения в журналах, занималась
литературной деятельностью. В 1881 г.
Московское математическое общество
избрало ее своим членом. В
семидесятые годы она написала роман
«Нигилистка», в котором с любовью и
уважением обрисовала жизнь и моральный
облик современных ей русских
революционеров 2). Но все усилия
Ковалевской получить работу по
специальности оставались тщетными: женщине
в тогдашних царских университетах
места не было. Министр просвещения
отказал ей даже в праве держать
магистерские экзамены при Московском
университете. Математические занятия
Ковалевской стали менее интенсивными.
Весной 1883 г. трагически
скончался В. О. Ковалевский, и Софья
Васильевна с маленькой дочерью
оказалась в трудном материальном
положении. В это время она получила от СВ. Ковалевская,
шведского математика Г.
Миттаг-Леффлера приглашение на должность доцента в незадолго перед тем
открытый Стокгольмский университет и в ноябре того же года переехала
в Стокгольм.
Ковалевская вновь с энергией взялась за научную работу. В 1884 г.
она состоит уже профессором — первым в мире профессором математики
среди женщин. С блестящим успехом читает она математические курсы
по различным отделам теории дифференциальных уравнений, в том числе
по качественным методам (следуя Пуанкаре), а также по эллиптическим,
абелевым и тэта-функциям, механике и др. В 1886—1887 г. она читала
курс по теории движения твердого тела и вела собственные изыскания
в этой области, начатые еще ранее. По предложению Миттаг-Леффлера
Ковалевская вошла в состав редакции основанного им в 1882 г. журнала
Acta mathematica.
1888 год приносит С. В. Ковалевской подлинный научный триумф:
ей присуждают премию Парижской Академии наук за лучшую работу
о вращении твердого тела; при этом премия была почти вдвое увеличена.
Работа была представлена под девизом: «Говори, что знаешь; делай, что
обязан; будь, чему быть». В 1889 г. Ковалевская получила премию
Шведской Академии за вторую работу на ту же тему.
г) Все они имеются в русском переводе: СВ. Ковалевская, Научные
работы. Ред. и комментарии П. Я. Полубариновой-Кочиной, изд. АН СССР, 1948.
2) Этот роман не мог увидеть свет в царской России. Он был издан на немецком
языке в 1896 г., а на русском — уже после Октябрьской революции (Харьков, 1928).
440
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Эти исследования принесли Ковалевской мировую славу. По
предложению Чебышева, Имшенецкого и Буняковского Петербургская Академия
наук вынесла специальное решение о допущении женщин к избранию
в члены-корреспонденты, и 7(19) ноября 1889 г. Ковалевской присудили
это почетное звание. Чебышев, с которым Софья Васильевна была в частом
научном общении, известил ее об избрании на следующий день
телеграммой. Он писал: «Наша Академия наук только что избрала Вас членом-
корреспондентом, допустив этим нововведение, которому не было до сих
пор прецедента. Я очень счастлив видеть исполненным одно из моих самых
пламенных желаний» 1).
Ковалевская продолжала мечтать о возвращении на родину, живя
и работая в Стокгольме лишь «наполовину добровольно», как выразился
ее большой друг и однофамилец М. М. Ковалевский (1851—1916),
известный историк и социолог. Хлопоты в этом направлении не
увенчались, к сожалению, успехом. Скончалась Софья Васильевна 10 февраля
1891 г. в расцвете сил на 42-м году жизни от воспаления легких. В речи
на ее похоронах М. М. Ковалевский сказал:. «Софья Васильевна!
Благодаря Вашим знаниям, Вашему таланту и Вашему характеру, Вы всегда
были и будете славой нашей родины. Недаром оплакивает Вас вся ученая
и литературная Россия. Со всех концов обширной империи, из
Гельсингфорса и Тифлиса, из Харькова и Саратова, присылают венки на Вашу
могилу... Вам не суждено было работать в родной стране. Но, работая
по необходимости вдали от родины, Вы сохранили свою национальность.
Вы остались верной и преданной союзницей юной России, России мирной,
справедливой и свободной, той России, которой принадлежит будущее» 2).
Теорема Ковалевской. Основной математический результат
Ковалевской содержится в одной из трех работ, поданных ею на соискание
докторской степени: «К теории дифференциальных уравнений в частных
производных» (Zur Theorie der partiellen Differential — Gleichungen, Crelle's
Journal, B. 80, 1875), работе, которую Э. Пикар назвал впоследствии
классической 3). Это — известная теорема Ковалевской о существовании
решений нормальной системы уравнений с частными производными.
В лекциях 1820—1830 гг. Коши впервые доказал существование
и единственность решения обыкновенного дифференциального уравнения
первого порядка у' = f(x, у) при начальных условиях х = х0, у = у&
df (х у)
в области непрерывности f(x, у) и ;. Вывод Коши, опубликованный
в кратком изложении в 1835 г. и подробнее в 1844 г. его учеником
Ф. Муаньо, положил начало многочисленным исследованиям. Теоремы
существования и единственности имели глубокий принципиальный
интерес. Их значение, однако, отнюдь не ограничивалось рамками общей
теории. Они были важны и для приложений, выясняя условия, в которых
законно применение методов дифференциальных уравнений к задачам
математического естествознания. Эти теоремы были тесно связаны с
разработкой методов приближенного решения, поскольку в самом ходе их
доказательства использовались выражения, приближающие искомое
х) Цит. по статье: В. Е. П р у д н и к о в, С. В. Ковалевская и П. Л. Чебышев.
В сб. «Памяти С. В. Ковалевской», стр. 118.
2) Цит. по статье: П. Я. Полубаринова-Кочина, Жизнь и научная
деятельность С. В. Ковалевской. В сб. «Памяти С. В. Ковалевской», стр. 60.
3)Э. Пикар, О развитии за последние сто лет некоторых основных теорий
математического анализа. Перев. С. Н. Бернштейна, Харьков, 1912, стр. 36.
ТЕОРЕМА КОВАЛЕВСКОЙ
441
решение с любой степенью точности. Свое доказательство Коши
распространил на более общие случаи. В 1842 г. он опубликовал доказательство
существования при некоторых ограничениях решения линейной системы
уравнений с частными производными в комплексной области,
представляя решения в форме степенных рядов и применяя мажорирующие
функции; нелинейную систему он привел к линейной.
В память этих исследований Коши изучавшаяся им проблема
называется теперь задачей Коши.
Для уравнения с частными производными
-^-f^XbXi, ...,*,., ср, ...,-^-^-—Л, ...j=0
(a+a1+... + ar<iV, а<л) задача Коши заключается в нахождении такого
решения ц>(х,х±,Х2, ¦••, хг), что при данном значении аргумента х = х0
функцииф, •—-,. . ., _^ обращаются в некоторые заданные функции
аргументов х±, . . ., хт\ эти функции, как и/, считаются аналитическими.
Аналогично ставится вопрос для системы уравнений.
Результаты Коши, относившиеся к существованию решений в
комплексной области, остались многим неизвестными. Вейерштрасс вновь дал
несколько отличное решение задачи Коши для системы обыкновенных
уравнений в комплексной области. Ковалевская, применяя методы вейер-
штрассовой теории функций, занялась исследованием вопроса для
уравнений с частными производными.
Напомним, что функция F(zil z2, . . ., zm) называется аналитической
или голоморфной функцией комплексных аргументов z1? z2l . . ., zm
в окрестности их значений а1? а2, . . ., ат, если для всех zu
удовлетворяющих неравенству \zt — а% | <С б, где б — некоторое положительное
число, она разлагается в сходящийся в этой окрестности степенной ряд
^jAklk2...km(zi — ai) г{4~ a2)ft2 . .. (zm — am) т,
где каждый из индексов kt пробегает последовательность чисел 0, 1, 2Г
3, . . ., /г, ... Как и в обыкновенном ряде Тейлора, коэффициенты
А^ я а чкм выражаются через значения производных функций F в точке
(<Zi, a2, . . ., am).
Во втором параграфе своей работы Ковалевская доказывает
существование единственного аналитического решения задачи Коши для уравнения
с частными производными указанного выше вида при условиях, что
аналитическими являются / в окрестности точки (х0, аи . . ., аТ) и все
функции, входящие в начальные условия, в окрестности точки (а1? . . ., ат)
и что, кроме того, само уравнение имеет нормальную форму. При этом
уравнение называется нормальным, если а + cxi + . . . + ат < п, т. е.
если в функцию / не входят производные более высокого порядка, чем
старшая производная по основному переменному х, относительно которой
уравнение считается разрешенным.
В следующем отделе диссертации показано, как при помощи
линейного преобразования аргументов уравнение, не имеющее нормальной формы,
приводится к ней, после чего задача Коши ставится уже относительно
некоторой новой независимой переменной. Здесь же Ковалевская
сообщила особенно поразивший своей неожиданностью и весьма простой пример
степенного ряда, формально удовлетворяющего некоторому уравнению,.
442
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
но, вообще говоря, расходящегося. Пример строится для уравнения
теплопроводности
дф д2ф
дх ду2,
с начальным условием: при х = а
Ф = Фо(г/[&),
где ф (у | Ъ) — аналитическая функция в окрестности у = Ъг). Как
выяснила Ковалевская, степенной ряд
У d2v9o (у [ Ь) (х-аУ
А ду2* ' v! '
v = 0 *
формально удовлетворяющий условиям задачи, сходится только при
весьма специальном выборе функции ф0 (у | Ъ)\ вообще же говоря, ни при какой
системе значений (х, у) он не имеет определенной конечной суммы. Так
обстоит дело, в частности, если взять а = О, Ъ = О и
степенной ряд принимает тогда вид
V=-oo
у (2v)l х"*
v = 0 v Vf
и расходится, сколь бы малыми ни взять х и у.
В четвертом параграфе работы решение задачи Коши
распространялось на нормальные системы уравнений с частными производными.
Работы Коши 1842 г. оставались некоторое время неизвестны
Ковалевской, как и Вейерштрассу. Впоследствии французские математики
указали на близость исследований Коши и Ковалевской. Результаты
Ковалевской оказались при этом более общими. По поводу возникшего
вопроса о приоритете Ковалевская писала 15 июля 1885 г. Миттаг-Леффле-
ру, что он «обстоятельно обсуждался во Французской Академии наук
в связи с работой Дарбу по тому же вопросу, написанной и представленной
несколькими месяцами позже меня... Когда я писала свою работу, я,
действительно, как и Вейерштрасс, не знала, что Коши занимался этим
вопросом, и это было большой ошибкой с нашей стороны. Однако в свое время
Вейерштрасс указал Эрмиту, что ни Коши, ни Дарбу не заметили
главных условий, при которых дифференциальное уравнение в частных
производных всегда имеет интеграл, или, иными словами, когда оно может
быть приведено к нормальному виду. Ни один из них не подозревал даже,
что возможны случаи, как, например,
дф д2ф
когда формально существует ряд от х, г/, удовлетворяющий этому
уравнению, если при х = а взять произвольное значение функции ф = %(у\ Ъ),
но что этот ряд будет сходящимся только при очень частном выборе
г) Знаком у(у\Ъ) Ковалевская обозначила степенной ряд по целым
положительным степеням у — Ъ.
ЗАДАЧА О ВРАЩЕНИИ ТВЕРДОГО ТЕЛА
начальной функции; в общем случае ряд будет расходящимся. Именно
этому результату моих исследований Вейерштрасс всегда придавал
наибольшее значение» х).
Теорему Ковалевской изучают теперь все студенты-математики.
Дальнейшим исследованием задачи Коши в тех или иных условиях
занимались очень многие крупные математики.
Задача о вращении твердого тела. Упоминавшиеся работы
Ковалевской о вращении твердого тела также относятся к аналитической теории
дифференциальных уравнений. Мы коротко остановимся на них. Оба
соответствующих мемуара —«Задача о вращении твердого тела около
неподвижной точки» (Sur le probleme de la rotation d'un corps solide autour d'un
point fixe) и «Об одном свойстве системы дифференциальных уравнений,
определяющей вращение твердого тела около неподвижной точки» (Sur
line propriete du systeme d' equations differentielles qui definit la rotation
d'un corps solide autour d'un point fixe) были напечатаны на французском
языке в шведском журнале Acta mathematica (t. 12, 1889; t. 14, 1890).
Пусть масса тела есть М, постоянная силы тяжести g; Ox^y^Z\. —
неподвижная система координат с началом в неподвижной точке, Oxyz —
подвижная система, оси которой направлены по главным осям А, В, С
эллипсоида инерции тела относительно точки О; х0, у0, z0 — координаты
центра тяжести тела в подвижной системе; р, q, г — проекции мгновенной
угловой скорости вращения тела в ней же и у±, у2, 7з — направляющие
косинусы оси Oz с осями подвижной системы. Тогда уравнения движения
тела суть
A^=-{B-C)qr+ Mg (у0у"- z0y'),^=ry'-qy",
B^=(C-A)rp + Mg (Zoy - x0y"), ^f = PV" ~ ry,
C-^r=(A-B)pq + Mg(x0y'-y0y), ±f = qy-py'.
Движение тела будет определено, если удастся выразить шесть искомых
величин, р, q, г, у\ у", у"\ как известные функции времени t.
Мы уже говорили, что в двух случаях решение было получено в
эллиптических функциях: в случае Эйлера—Пуансо, когда х0= у0= z0 = 0, ив
случае Лагранжа — Пуассона А = В, х0 = у0 = 0, когда тело
представляет собой симметрический тяжелый гироскоп (волчок).
С. В. Ковалевская применила к исследованию проблемы методы
теории аналитических функций, рассматривая аргумент-время как
комплексную величину. Заметив, что в двух известных случаях интегралы,
выражающиеся эллиптическими функциями, суть однозначные функции
времени, не имеющие других особенностей, кроме полюсов, для всех
конечных значений аргумента, она поставила вопрос: имеются ли еще
случаи такого же рода? Это и привело ее к открытию третьего случая,
в котором два момента инерции равны удвоенному третьему, А = В = 2С,
так что эллипсоид инерции есть тело вращения, и центр тяжести тела
лежит в плоскости экватора этого эллипсоида, z0 = 0. Интегралы системы
уравнений получаются с помощью эллиптических и ультраэллиптических
функций. На поставленный вопрос Ковалевская дала такой ответ: три
г) Цит. по статье: П. Я. Полубаринова-Кочина, Научные работы
С. В. Ковалевской.— УМН, т. V, вып. 4(38), 1950, стр. 5.
444
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
указанных случая, в которых действительные функции р, q, г, у', у", у"г
при любых начальных значениях однозначны и без особенных точек,
кроме полюсов, являются единственными из всех возможных. Полное-
доказательство этого факта провели в 1893 г. А. М. Ляпунов (Сообщ.
Харьк. матем. о-ва, т. 4, 1894—1895) и ученик Жуковского профессор
Московского университета Герман Германович Аппельрот (1866—1943)
в книге «Задача о движении тяжелого твердого тела около неподвижной
точки» (М., 1893). Весьма наглядную и простую иллюстрацию случаев
Эйлера, симметричного гироскопа Лагранжа и несимметричного гироскопа
Ковалевской предложил Н. Е. Жуковский (рис. 49; Матем. сборник,,
Рис. 49. Гироскопы, соответствующие случаям Эйлера,
Лагранжа и Ковалевской, по Н. Е. Жуковскому.
т. 19, 1896). Дальнейшей разработкой теории гироскопов и специально
случая Ковалевской (дополнением ее работ, рассмотрением некоторых
его видов, геометрическими интерпретациями и т. д.) занимались, помимо
названных, многие другие русские и зарубежные ученые вплоть до нашего
времени.
В. А. Анисимов. Разрабатывались в России и отдельные вопросы
аналитической теории линейных дифференциальных уравнений с
аналитическими коэффициентами, начало которой положил Риман и вслед
за ним особенно ученик Вейерштрасса Л. Фукс, а затем Пуанкаре, Клейн
и другие; изучались также различные классы нелинейных уравнений.
Именно в этой связи Пуанкаре и Клейн пришли к разработке теории
автоморфных функций, о которых мы упоминали, когда речь шла о
приложениях неевклидовой геометрии Лобачевского. Методы Фукса у нас
пропагандировал и развил воспитанник Московского университета
Василий Афанасьевич Анисимов (10 марта 1860—9 сентября 1907)г
прослушавший курс лекций немецкого математика во время заграничной
командировки. Уравнениям класса Фукса, решения которых имеют только
регулярные особые точки, Анисимов посвятил свою магистерскую
диссертацию «Основания теории линейных дифференциальных уравнений»
(Уч. зап. МГУ, отд. физ.-матем., вып. 9, 1889). После защиты диссертации
в Москве Анисимов работал в Варшавском университете и здесь продолжал
исследования в той же области, тесно переплетавшиеся с изысканиями
другого московского математика П. А. Некрасова. При изучении функций,
определяемых линейными дифференциальными уравнениями, применяется
так называемый предельный круг, радиус которого Фукс находил по
корням некоторого уравнения. Некрасов (Матем. сборник, т. 11, 1883)
показал, что теорема Фукса о радиусе предельного круга неверна. Более
подробно тот же вопрос был рассмотрен в магистерской диссертации
С. Н. БЕРНШТЕЙН И ПРОБЛЕМЫ ГИЛЬБЕРТА
445
Анисимова. Фукс в 1890 г. видоизменил свое правило, но и в нем Некрасов
обнаружил неточность (Math. Annalen, В.38, 1890), а в деталях проблема
была разобрана в докторской диссертации Анисимова «Предельный круг
Фукса» (Варш. унив. изв., 1892, № 1). В 1896 г. Анисимов подверг
анализу особые точки решений уравнения Риккати, которое, как известно,
приводится к линейному дифференциальному уравнению 2 порядка (Варш.
унив. изв., 1896, № 3) х).
С. Н. Бернштейн и проблемы Гильберта. В начале XX века появились
-замечательные исследования С. Н. Бернштейна о решениях
дифференциальных уравнений с частными производными эллиптического типа.
Примером таких уравнений служит встречавшееся еще Эйлеру, но
детально изученное только Лапласом линейное уравнение
д2и . д2и д2и ^
Их* + ~ду* + ^Г = U>
имеющее основное значение в (стационарных) задачах теории потенциала,
теплопроводности, электростатики, гидродинамики. Задачи эти
математически формулируются в виде краевых задач, в которых требуется найти
решение, удовлетворяющее в некоторой области данному
дифференциальному уравнению и в точках ее границы некоторому данному условию.
В первой краевой задаче, носящей имя Дирихле, ищется решение
уравнения Лапласа или вообще уравнения эллиптического типа, принимающее
на границе области данные значения. Во второй задаче — задаче
Неймана — на границе области задаются значения производной искомого
интеграла по нормали к границе. В третьей задаче заданными являются
соотношения между значениями на границе искомого интеграла и его
нормальной производной. Так, задачей Дирихле является задача о
стационарном распределении температуры в однородном теле с постоянной
теплопроводностью при заданной температуре на поверхности, задачей
Неймана — аналогичная задача при данном распределении на
поверхности теплового потока.
Давно было известно, что (при некоторых ограничениях) решения
уравнения Лапласа с двумя переменными
д2и д2и ^
дх2 ду2
являются аналитическими функциями. Аналитическими являются и
дважды непрерывно дифференцируемые решения более общего уравнения
д2и . д2и . , ч ди . 7 / ч ди . , ч п
тде а, Ъ и с — аналитические функции. Это было доказано Э. Пикаром
в 1890 г. В 1900 г. Д. Гильберт среди других ожидающих решения проблем
в двух из них, 19-й и 20-й, поставил вопрос о характере решений более
общих эллиптических уравнений и о разрешимости для них задачи
Дирихле. Вскоре эти две проблемы были решены С. Н. Бернштейном.
В работе «Об аналитической природе решений дифференциальных
уравнений с частными производными второго порядка», напечатанной на
французском языке (Sur la nature analytique des solutions des equations
1)C. E. Белозеров, Математика в Ростовском университете.— Ист.-ма-
тем. исслед., вып. VI, 1953.
446
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
aux derivees partielles des second ordre, Leipzig, 1904) и затем в первой
части магистерской диссертации, защищенной в Харькове «Исследование
я интегрирование дифференциальных уравнений с частными производными
второго порядка эллиптического типа» (Сообщ. Харьк. матем. о-ва, т. И,
1908), С. Н. Бернштейн дал решение 19-й проблемы Гильберта. Он
доказал, что решение уравнения
F(x, у, и, р, q, г, s, t) = 0,
п y ди ди д2и д2и
где ^-аналитическая функция и р-=-^, 9 = -щч Г = -^Г> s = d^djj '
а также выполнено определяющее эллиптический тип уравнения
д*и
условие
*?•?-(?)'>¦¦¦
будет аналитическим, если оно (т. е. решение) имеет непрерывные
производные до третьего порядка включительно. Средством исследования
служат так называемые нормальные ряды
ОО ОО
2 2 Anx'iR-x)*,
v=0 q=0
равномерно и абсолютно сходящиеся при 0< х< i?, и критерий,
позволяющий судить об аналитичности функции по ее разложению в такой ряд.
Во второй части магистерской диссертации С. Н. Бернштейн дал
решение 20-й проблемы Гильберта, доказав существование аналитического
решения задачи Дирихле для очень широкого класса нелинейных
эллиптических уравнений в предположении, что решение имеет непрерывные
производные первых двух порядков.
С. Н. Бернштейн продолжал работать над проблемами аналитичности
решений уравнений с частными производными и в дальнейшем. Его
результаты стали отправным пунктом новых изысканий, продолжающихся до
наших дней; его методы изучения условий аналитичности решений, а
также их поведения, получили значительное развитие и были распространены
на другие классы уравнений. Выдающиеся исследования в этой области
принадлежат советским математикам, особенно И. Г. Петровскому и его
школе, а также О. А. Ладыженской и другим *).
В первой части магистерской диссертации, как следствие общих
теорем, формулируется предложение дифференциальной геометрии: всякая
поверхность, налагающаяся на аналитическую поверхность
положительной кривизны, сама аналитическая. Для поверхностей отрицательной
и нулевой кривизны этого утверждать нельзя. И это более специальное,
но весьма интересное предложение, впервые опубликованное в Math.
Annalen, В.60, 1905, послужило источником последующих работ как
автора, так и некоторых советских математиков.
Качественная теория дифференциальных уравнений и теория
устойчивости. Создание качественной теории дифференциальных уравнений
явилось делом двух математиков — А. Пуанкаре и А. М. Ляпунова.
Общая цель теории, как говорилось, состоит в исследовании функций,
г) С. С. Д е м и д о в, К истории проблем Гильберта.— Hgt.-матем. исслед.,
XVII, 1966.
ТЕОРИЯ УСТОЙЧИВОСТИ
447
являющихся решением уравнения или системы уравнений во всей области
существования, по самим уравнениям, не зная аналитического выражения
этой функции, которое удается найти лишь в специальных случаях.
Термин «качественная теория» принадлежит Пуанкаре.
Качественное исследование общего поведения функций или кривых,
определяемых дифференциальными уравнениями, указывал Пуанкаре,
может иметь значение и для последующего вычисления функций, но имеет
первостепенную важность само по себе, поскольку к такому исследованию
приводят чрезвычайно важные задачи анализа и механики. Еще к Ньютону
и Лапласу восходит, например, вопрос об устойчивости солнечной системы
или более частный вопрос о движении системы трех тел, подчиняющихся
законам небесной механики. Старые методы, ограничившиеся изучением
решения в окрестности отдельных значений аргументов, принципиально
не позволяли ответить на вопрос о поведении такой системы в течение
сколь угодно больших промежутков времени, т. е. для t ->¦ оо, и выяснить,
остаются ли взаимные расстояния этих тел всегда ограниченными или же
некоторые из членов системы в конце концов неограниченно сближаются
или удаляются в бесконечность и т. д. Качественное исследование
призвано было дать ответ на вопросы такого рода.
В простейшем случае уравнения ~ = f(x, у) или системы
% = Х(х,у),
задача состоит в изучении поведения семейства интегральных кривых
на всей плоскости только по свойствам функций Х(х, у) и Y(x, у),
которые предполагаются целыми многочленами относительно своих
аргументов. В серии работ, начатых в 1878 г., Пуанкаре существенно продвинул
решение вопроса для указанного случая и для некоторых уравнений
высшего порядка (которые можно привести к системам уравнений первого
порядка с тем или иным числом неизвестных функций). Большую роль
играет анализ поведения интегральных кривых близ особых точек
дифференциальных уравнений, изучение которых начали в середине XIX века
Ш. Врио и Ж. Буке. Для уравнения первого порядка особые точки можно
определить как такие, через которые проходит более чем одна или не
проходит ни одна интегральная кривая. Для написанной выше системы
особыми могут быть точки, в которых Х(х, у) и Y(x, у) одновременно
обращаются в нуль.
Пуанкаре установил основные критерии, при которых особая точка
уравнения первого порядка является, по его терминологии, узлом, седлом,
фокусом или центром, а также изучил возможные типы расположения
интегральных кривых около особой точки. Аналогичный анализ он провел
для уравнения второго порядка, или, что то же, системы
% = X(x,y,z); ^r = Y(x,y,z); ^ = Z(x,y,z).
Пуанкаре, далее, ввел весьма важное понятие предельного цикла —
замкнутой интегральной кривой, к которой по спирали приближаются
все достаточно близкие интегральные кривые и которая имеет важное
значение при изучении периодических процессов.
448
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Наконец, Пуанкаре положил начало обширным исследованиям
вопроса об устойчивости или неустойчивости интегральных кривых или,
как говорят, траекторий систем дифференциальных уравнений.
Созданные методы Пуанкаре применил затем к задаче трех тел,
построив теорию периодических орбит. Проблема периодических решений
занимала его до самой кончины в 1912 г. Весьма глубоко изучил Пуанкаре
задачу трех тел и с точки зрения устойчивости ее движений (так
называемой устойчивости по Пуассону). Исследования Пуанкаре в значительной
мере опирались на топологические рассмотрения, и с ними было связано
обострение интереса к топологии и первые ее успехи как
самостоятельной науки в трудах самого Пуанкаре.
Работа Н. Е. Жуковского. В России разработка проблем
качественной теории дифференциальных уравнений началась одновременно с
разработкой ее во Франции. Первым исследованием в этой области мы
обязаны Н. Е. Жуковскому, который в магистерской диссертации «Кинематика
жидкого тела», опубликованной в VIII т. «Математического сборника»
(1876), пришел к результатам, частично опередившим изыскания
Пуанкаре. Рассматривая в некоторых условиях плоскопараллельное движение
несжимаемой жидкости, Жуковский пришел к классификации особых
точек уравнений первого порядка, в которой имелись все четыре основных
вида особых точек, указанных Пуанкаре, а также исследовал поведение
интегральных кривых в окрестности особой точки каждого вида.
Дальнейшего развития учение об особых точках у Жуковского не получило: оно
было лишь побочным и частным результатом его занятий механикой.
Поэтому его результат остался незамеченным, пока через 50 лет на него
вновь не обратил внимание Д. М. Синцов х), который в своих работах
по геометрической теории дифференциальных уравнений и сам внес
существенные дополнения в классификацию особых точек уравнений первого
порядка.
Основное значение для качественной теории дифференциальных
уравнений имели труды А. М. Ляпунова, который во многих направлениях
пошел значительно дальше Пуанкаре.
Жизнь А. М. Ляпунова. Александр Михайлович Ляпунов родился
6 июня 1857 г. в Ярославле в семье директора Демидовского лицея,
астронома М. В. Ляпунова, ранее работавшего в Казанском университете.
Два младших брата А. М. Ляпунова также приобрели большую
известность: Сергей Михайлович (1859—1924) как композитор, Борис
Михайлович (1864—1942) как филолог-славист.
Окончив гимназию в Нижнем Новгороде, А. М. Ляпунов в 1876 г.
поступил на физико-математический факультет Петербургского
университета. По рекомендации своего руководителя профессора механики
Д. К. Бобылева (1842—1917) Ляпунов в 1880 г. был оставлен при кафедре
механики для подготовки к званию профессора. Наибольшее впечатление
в университетские годы на Ляпунова произвели лекции Чебышева —
по записям молодого Ляпунова мы, между прочим, знаем курс теории
вероятностей, читанный Чебышевым в 1879—1880 гг. (этот конспект был
издан академиком А. Н. Крыловым в 1936 г.). Чебышев, естественно,
1) Д. М. Синцов, Н. Е. Жуковский и классификация особенных точек
дифференциальных уравнений первого порядка.— Ученые записки
научно-исследовательских кафедр Украины, Отдел математический, вып. 1, 1924.
ЖИЗНЬ А. М. ЛЯПУНОВА
449
оказал сильное влияние на научные интересы и воззрения Ляпунова.
Чебышев же поставил перед Ляпуновым задачу, из которой выросла
магистерская диссертация последнего «Об устойчивости эллипсоидальных
форм равновесия вращающейся жидкости» (СПб., 1884). К этой задаче
и ее решению мы еще вернемся ниже.
Защитив в 1885 г. диссертацию, Ляпунов перешел на работу в
Харьковский университет, где приступил к чтению лекций по механике вместо
избранного академиком В. Г. Имшенецкого. Ближайший ученик
А. М. Ляпунова академик В. А. Стек-
лов в речи, произнесенной 3 мая 1919г.,
вспоминал о первой лекции своего
учителя, которого студенты ожидали с
настороженным любопытством, опасаясь,
что это какой-либо ставленник
реакционного министра Делянова: «... курс
механики мне был уже знаком.
Но с самого начала лекции (по
динамике точки. — А. Ю.) я услыхал то,
чего раньше не слыхал и не встречал
нив одном из известных мне руководств.
И все недружелюбие курса сразу
разлетелось прахом; силою своего
таланта, обаянию которого в
большинстве случаев бессознательно поддается
молодежь, Александр Михайлович, сам
не зная того, покорил в один час
предвзято настроенную аудиторию.
С этого же дня Александр
Михайлович занял совершенно особое
положение в глазах студентов: к нему стали
относиться с исключительно почтитель- А м Ляпунов
нымуважением. Большинство, которому
не были чужды интересы науки, стали
напрягать все силы, чтобы хоть немного приблизиться к той высоте,
на которую влёк Александр Михайлович своих слушателей» г).
Активная педагогическая работа и исключительно тщательная
подготовка лекций недолго мешали научным занятиям молодого доцента. Два
года спустя он приступил к разработке новой области — теории
устойчивости движения механических систем с конечным числом степеней
свободы и уже в 1888 г. опубликовал первую свою статью по этому
вопросу. В 1892 г. при оппонентах Н. Е. Жуковском и Б. К. Млодзеевском
Ляпунов защитил в Московском университете докторскую диссертацию
«Общая задача об устойчивости движения» (Харьков, 1892),
принадлежащую к числу наиболее выдающихся достижений математической мысли
XIX века 2). Проблемы устойчивости привлекали его внимание еще 10 лет,
до 1902 г.
По возвращении в Харьков Ляпунов продолжал чтение лекций по
различным предметам. В 1893 г. он был утвержден профессором. Чтение
х) В. А. С т е к л о в, Александр Михайлович Ляпунов, в кн.: А. М. Ляп у-
н о в, Работы по теории потенциала. М.—Л., 1949, стр. 16.
2) Как говорилось, обе диссертации Ляпунова были переведены на французский
язык: магистерская в Ann. de la Faculte des Sciences de Г Univ. de Toulouse, t. VI, 1904;
докторская там же, 2 ser., t. IX, 1907 (переиздано в США, 1947).
450
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
курса теории вероятностей явилось одним из поводов для его известных
уже нам замечательных работ 1900—1901 гг. о центральной предельной
теореме. Он работал также над вопросами математической физики и
значительно продвинул дальнейшую разработку теории потенциала, особенно
в статье «О некоторых вопросах, относящихся к задаче Дирихле» (1898).
Эти исследования Ляпунова получили блестящее продолжение в трудах
его лучшего ученика по Харьковскому университету — В. А. Стеклова.
Деятельное участие принимал Ляпунов в жизни Харьковского
математического общества — с 1891 по 1898 гг. в качестве товарища председателя,
а в 1899—1902 как председатель и редактор его «Сообщений».
В октябре 1901 г. Ляпунов, в начале того же года выбранный членом-
корреспондентом Академии наук, был избран академиком по кафедре
прикладной математики, остававшейся вакантной в течение семи лет
после кончины Чебышева. Нельзя было найти более достойного преемника
по академической кафедре для основателя и главы петербургской школы.
Весной следующего года Ляпунов переехал в Петербург. Здесь он уже
более не преподавал, а занялся научной работой, главным образом общей
проблемой фигур равновесия вращающейся жидкости, связанной с тем
вопросом, который поставил перед ним Чебышев в начале его научной
деятельности. В результате неустанного труда, продолжавшегося около
15 лет, Ляпунов чрезвычайно далеко продвинул решение этой проблемы.
Несколько слов о Ляпунове, сказанных В. А. Стекловым, прекрасно
характеризуют основную черту Ляпунова — глубокую преданность
избранной науке:
«Воспитанный сначала своим отцом, сотоварищем Н. И. Лобачевского
по Казанскому университету, затем в кругу лиц, близких к нашему
знаменитому физиологу И. М. Сеченову, которому, кстати сказать,
Александр Михайлович одно время давал уроки математики, проведший свою
юность в среде наиболее просвещенной части нашего тогдашнего общества,
на умы которого еще продолжали влиять Н. А. Добролюбов и Н. Г.
Чернышевский, А. М. Ляпунов олицетворял собой лучший тип идеалиста
шестидесятых годов.
Все из ряда вон выходящие силы свои он отдавал на беззаветное
служение науке, ею он жил, в ней одной видел смысл жизни и часто
говорил, что без научного творчества и самая жизнь для него ничего не стоит.
С самого начала своей ученой деятельности он работал изо дня в день
до 4 или 5 часов ночи, а иногда являлся на лекции (в Харьковском
университете), не спав всю ночь. Он не позволял себе почти никаких
развлечений и если появлялся иногда (раз или два в год) в театре или в
концерте, то лишь в самых исключительных случаях, как, например, на
редких концертах своего брата, известного композитора СМ. Ляпунова» *).
Летом 1917 г. ввиду обострения туберкулеза у его жены, племянницы
И. М. Сеченова, Ляпунов переехал на юг, в Одессу. В день кончины жены
Ляпунов застрелился, оставив записку, в которой просил похоронить
себя в одной могиле с женой. Через три дня, 3 ноября 1918 г., Ляпунов
скончался. Заслуги его перед наукой и Родиной поистине огромны, и чем
далее, тем яснее становится значение его неутомимой научной работы,
которую чрезвычайно высоко ценили и его современники. Он состоял
не только членом нашей Академии наук, но также иностранным членом
Римской Academia dei Lincei, членом-корреспондентом Академии наук
в Париже, почетным членом ряда русских университетов, членом многих
г) См. в кн.: А. М. Ляпунов, Работы по теории потенциала, стр. 31 — 32.
ФИГУРЫ РАВНОВЕСИЯ ВРАЩАЮЩЕЙСЯ ЖИДКОЙ МАССЫ 451
научных обществ. Академия наук СССР издала «Собрание сочинений»
А. М. Ляпунова в 5 томах (М., 1954—1965).
Мы уже говорили об одном направлении работ Ляпунова, недолго,
правда, занимавшем его внимание,— теоретико-вероятностном. Мы
видели, что в исследовании центральной предельной теоремы он избрал путь,
отличный от того, каким шел, следуя Чебышеву, А. А. Марков.
Между методами обоих наиболее выдающихся учеников Чебышева,
несмотря на их принадлежность к одной школе, имелись существенные
различия. Ляпунов не придерживался методов Чебышева с такой
исключительностью, как Марков, и лучше многих других деятелей петербургской
школы оценил важность некоторых новых течений западноевропейской
математики, например, теории функций комплексного переменного.
Поэтому, как указывает академик С. Н. Бернштейн, «Ляпунов более независимо
подходил к проблемам Чебышева» 1). Вместе с тем, отправным пунктом
исследований Ляпунова, который привел его к созданию большого
нового направления в рамках петербургской школы, явился, как мы
сказали, вопрос, выдвинутый Чебышевым.
Фигуры равновесия вращающейся жидкой массы и их устойчивость.
Поставленная Чебышевым задача имела за собой долгую историю. В
лекции «О форме небесных тел», вступительной к курсу, который Ляпунов
начал в Новороссийском университете незадолго до кончины, он говорил:
«По известной гипотезе, каждое такое тело первоначально было в жидком
состоянии, причем настоящую свою форму оно приобрело раньше
отвердения, предварительно получивши, вследствие внутреннего трения,
неизменную форму. В этом предположении фигура небесного тела должна
представлять одну из тех, которые может принять жидкая вращающаяся
масса, частицы которой взаимно притягиваются по закону Ньютона,
или, по крайней мере, должна мало отличаться от такой фигуры
равновесия вращающейся жидкости. Ввиду этого вопросы о формах равновесия
вращающейся жидкости при сказанных условиях приобретают важное
значение». Тут же Ляпунов отмечал математическую трудность вопроса,
«для которого не существует общего решения и еще не найдено приемов,
при посредстве которых можно было бы искать такое решение.
Действительно, здесь все приводится к решению некоторого функционального
уравнения, принадлежащего к классу уравнений, известных в настоящее
время под названием интегральных, но не принадлежащих к тому
простейшему классу этих уравнений, которым так много занимались математики
в последние годы» 2). Вращение предполагается равномерным.
Еще Ньютон и его преемники в XVIII веке, Маклорен и другие,
установили, что такими формами равновесия могут быть эллипсоиды
вращения. Даламбер показал, что всякой угловой скорости, не превышающей
некоторого предела, соответствуют два эллипсоида вращения, сжатые
в направлении оси вращения. Этот цикл исследований завершил Лаплас.
Затем Якоби выяснил, что фигурами равновесия однородной вращающейся
жидкости могут быть и трехосные эллипсоиды при некоторых отношениях
между осями; Лиувилль рассмотрел этот случай до конца. Существует
некоторая угловая скорость вращения со0? за которой невозможны
эллипсоидальные фигуры равновесия. При со = 0 фигурой равновесия служит
сфера; для всех со, 0 < со < соь где со± —- некоторая величина, меньшая
г) С. Н. Б е р н ш т е й н, О работах П. Л. Чебышева по теории вероятностей.
В сб. «Научное наследие П. Л. Чебышева», вып. 1, стр. 62.
2) А. М. Ляпунов, Избранные труды, изд. АН СССР, 1948, стр. 303.
452
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
(о0> имеются три фигуры равновесия — два эллипсоида Маклорена и один
Якоби. При со = coi эллипсоид Якоби переходит в один из эллипсоидов
Маклорена, в промежутке coi < со<со0 имеются два эллипсоида
Маклорена, которые при со = со о сливаются в один.
Когда Ляпунов, искавший подходящую тему для магистерской
диссертации, обсуждал в 1882 г. этот вопрос с Чебышевым, тот предложил
задачу: «Известно, что при некоторой величине угловой скорости
вращения эллипсоидальные формы равновесия перестают служить формами
равновесия вращающейся жидкости. Не переходят ли они при этом
в какие-либо новые формы равновесия, которые при малом увеличении
угловой скорости мало отличались бы от эллипсоидов?» г). Ранее Чебышев
ставил ту же задачу перед Золотаревым и Ковалевской, но неизвестно,
пытались ли они приступить к ней. Сам далекий от данного круга
вопросов, Чебышев с удивительной прозорливостью предложил эту труднейшую
проблему, исследование которой явилось одним из замечательных
триумфов математики и механики.
В то время Ляпунов смог решить задачу Чебышева только в первом
приближении. Как он сам писал, математические его ресурсы тогда, всего
через два года после окончания курса, были недостаточны. Но полагая,
что судить q существовании фигур равновесия по первому приближению
рискованно и не имея средств продвинуться глубже, он отложил задачу
и перешел к другой — об устойчивости эллипсоидов равновесия. Этой
проблемой, существенной для выяснения действительно возможных в
природе фигур равновесия, занимались крупные ученые, как Лиувилль
и Риман, но при этом рассматривались либо частные случаи, либо методы
не были строги. Ляпунов дал точную постановку проблемы, недостававшую
ранее, определив устойчивую форму равновесия вращающейся
жидкости, как такую, «для которой, после сообщения движению жидкости
достаточно малых возмущений, форма жидкости остается на сколько
угодно мало отличающейся от этой формы равновесия, по крайней мере до тех
пор, пока на поверхности жидкости не образуется на сколько угодно тон-
ких нитеобразных или листообразных выступов» 2). Математическая
формулировка этого определения лежит в основе дальнейшего исследования.
Дело приводится к вопросу о существовании минимума некоторого
выражения и установленный таким образом критерий устойчивости позволил
разобрать вопрос об устойчивости эллипсоидов Маклорена и Якоби. Среди
прочего здесь устанавливается ряд новых свойств функций Ламе (1839),
имеющих большое значение при рассмотрении различных физических
явлений в областях, ограниченных эллипсоидальной поверхностью. Что
касается самой задачи Чебышева, то о ней Ляпунов с большой
осторожностью упомянул лишь в одном из тезисов диссертации: «Для всякого
целого п, превосходящего 2, между эллипсоидами Якоби можно найти
по крайней мере один, а между эллипсоидами Маклорена Е I ~Г") таких»
к которым бесконечно близки некоторые алгебраические поверхности
п-го порядка, для которых можно в первом приближении удовлетворить
условию равновесия». Однако, как сказано, Ляпунов не счел возможным
заключить отсюда о существовании этих новых форм равновесия.
На этой стадии исследований Ляпунов встретился с параллельными
работами Пуанкаре, который в 1885 г. нашел те же новые формы равнове-
*) А. М. Ляпунов, Избранные труды, стр. 314.
2) А. М. Л я п у н о в, Об устойчивости эллипсоидальных форм равновесия
вращающейся жидкости. СПб., 1884, стр. VII.
ФИГУРЫ РАВНОВЕСИЯ ВРАЩАЮЩЕЙСЯ ЖИДКОЙ МАССЫ 453
сия по первому приближению и, основываясь на некоторых аналогиях,
пришел к уверенности в том, что они действительно возможны. Между
обоими учеными завязалась переписка. Дать строгое обоснование своему
утверждению Пуанкаре в ней не мог. Последовавшая через два года
публикация Пуанкаре также не удовлетворила Ляпунова. В противоположность
Пуанкаре, который полагал, что в механике нельзя требовать такой же
строгости, как в чистом анализе, Ляпунов требовал, чтобы любая задача
механики или физики, поставленная с точки зрения анализа совершенно
определенно, трактовалась с полной строгостью, как чисто аналитическая
задача.
После того наступил долгий перерыв в занятиях Ляпунова фигурами
равновесия, к которым он снова обратился уже после избрания в
Академию наук, приобретя необходимый для этого досуг. Затем на протяжении
15 лет он неустанно работал в этом направлении, последовательно
опубликовав «Исследования в теории фигуры небесных тел» (Зап. Акад. наук
по физ.-матем. отд., VIII сер. т. XIV, 1903), «Об уравнении Клеро и более
общих уравнениях теории фигуры планет» (там же, т. XV, 1904), «Об одной
задаче Чебышева» (там же, т. XVII, 1905), «О фигурах равновесия
однородной вращающейся жидкости, мало отличающихся от эллипсоидальных»
(четыре части, СПб., 1906—1914) и «О некоторых фигурах равновесия
неоднородной вращающейся жидкости» (посмертно изданное В. И.
Смирновым; две части, Л., 1925—1927). Вместе с еще несколькими меньшими
мемуарами, эти работы, все написанные на французском языке,
составляют цикл, насчитывающий около 1500 страниц большого формата,— труд
поистине гигантский.
В двух первых работах Ляпунов, продолжая исследования, начатые
Клеро и развитые с помощью последовательных приближений Лежандром
и Лапласом, доказал существование близких к сфере фигур равновесия
достаточно медленно вращающейся неоднородной жидкости и изучил
решения цепи появляющихся при этом интегро-дифференциальных
уравнений, т. е. уравнений, в которых неизвестная функция входит под
знаками как интегралов, так и производных. Первым из этих уравнений
является уравнение Клеро вида
хх А
f(x) J ф) х2 dx — ^ J ф) d [x*f(x)] — .J- J <p(s) df{x)=Nx\
0 0 x
где f(x) — искомая функция, позволяющая определить форму фигуры
равновесия, а ф(я) выражает данный закон распределения плотности
жидкой массы. Другие уравнения обобщают приведенное, которое служит
лишь для первого приближения. Рассмотрение этих уравнений привело
Ляпунова в силу самой физической сущности задачи к расширению поня-
b
тия интеграла Стилтьеса, т. е. интеграла вида \ ф(ж) df(x), который
с1
а
сам Стилтьес ввел в 1894 г. как предел (при maxA^->0) сумм
п-1
2 ф(&) [f(xi+i) — f(xt)]f xt < Е| < xi+u
i=0
где ф(я) — функция, непрерывная на отрезке [а, Ь], а / (х) —
возрастающая. Ляпунову нужен был интеграл Стилтьеса, в котором интегрируемая
функция подчинена лишь условиям ограниченности и монотонности. Для
454
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
такого интеграла он доказывает теорему существования и некоторые
свойства. Затем существенно ослабляются ограничения, наложенные на
функцию f(x). Все это в работе 1904 г. делается попутно и потому не
привлекло в свое время внимания специалистов по теории функций.
Обобщение Ляпунова подводило к понятию интеграла Стилтьеса — Римана х).
В последующих работах Ляпунов, возвращаясь к проблеме Чебыше-
ва, установил следующий факт: среди эллипсоидов Маклорена и Якоби
существуют такие «эллипсоиды бифуркации», что наряду с близкими к ним
эллипсоидальными же фигурами равновесия существуют и
неэллипсоидальные. Здесь дается и ряд методов последовательного определения таких
фигур, уравнения которых, естественно, не выражаются в конечном виде
через элементарные функции, как для эллипсоидов. Наконец, в последней
работе доказано, что всякий эллипсоид Маклорена и Якоби, отличный
от эллипсоидов бифуркации, порождает новые близкие по форме фигуры
равновесия, причем их плотность непостоянна, но изменяется не сильно.
Добавим, что в большой работе «Задача минимума в одном вопросе
устойчивости фигур равновесия вращающейся жидкой массы» (Зап. Акад.
наук по физ.-матем. отд., VIII сер., т. XXII, 1908) уточнена и развита
далее теория устойчивости, изложенная в магистерской диссертации,
и изучена устойчивость новых найденных фигур равновесия, близких
к эллипсоидальным.
При решении этих задач и соответствующих нелинейных
интегральных уравнений Ляпунов преодолевал чрезвычайные математические
трудности. Он изобрел особый метод получения последовательных
приближений при решении того уравнения гидростатики, которому должны
удовлетворять фигуры равновесия, и точно доказал сходимость этих
приближений. Вообще говоря, Ляпунову пришлось провести первое
большое исследование по теории нелинейных интегральных уравнений,
которые впоследствии явились предметом многочисленных работ. В ходе
исследований получались также новые важные теоремы о рядах
многочленов, о свойствах сферических функций (уравнение замкнутости) и др.
Грушевидные фигуры. Работы Ляпунова этого периода вновь
встретились с работами Пуанкаре. При некоторой угловой скорости от
эллипсоида Якоби ответвляются фигуры равновесия, которые Пуанкаре назвал
грушевидными. Астроном Дж. Дарвин, сын великого биолога, в своей
гипотезе о возникновении двойных звезд путем разделения вращающейся
жидкой массы на два тела встретился с проблемой устойчивости
грушевидных форм. Пуанкаре, исследовавший ранее вопрос в пределах,
доставляемых вторым приближением, пришел к мнению, что эти формы
устойчивы. Дарвин, произведя сложные вычисления на основе общих формул
Пуанкаре, полагал, что подтвердил это мнение, укреплявшее его гипотезу.
Ляпунов в 1905 г., пользуясь не приближенными, а точными формулами,
опроверг мнение Пуанкаре и Дарвина; в статье «Об одной задаче Чебыше-
ва» он сообщил, что для грушевидных форм не имеет минимума та
величина, обращение которой в минимум служит условием устойчивости.
Возникшая полемика первоначально не привела к окончательному
результату, так как Ляпунов не опубликовал полностью все соответствующие
выкладки. Незадолго до смерти Пуанкаре писал, что не уверен в
правильности своего более раннего мнения, а для решения вопроса требуется
г) Ф. А. М.е д в е д е в, Вклад А. М. Ляпунова в теорию интеграла Стилтьеса.—
Ист.-матем. исслед., вып. XIV, 1961.
ТЕОРИЯ УСТОЙЧИВОСТИ СИСТЕМ
455
вновь начать исключительно сложные вычисления. В 1912 г. Ляпунов
опубликовал необходимые расчеты, но проверить их никто не решался.
Характерны слова знаменитого Пикара в написанном им представлении
Ляпунова в члены-корреспонденты Академии наук в Париже (1915).
Высоко оценивая строгость приемов Ляпунова, он все же считал желательным
повторение выкладок: «Исследование устойчивости здесь весьма тонко.
Чтобы ее изучить, Пуанкаре ограничился вторым приближением, и с
неравенством, к которому он пришел, было трудно обращаться. Следуя тому
же пути, сэр Джордж Дарвин счел возможным сделать вывод об
устойчивости. Не таково мнение г. Ляпунова, метод которого неоспоримо более
строг, чем метод его предшественников; он делает вывод о неустойчивости.
Однако поскольку окончательный результат мог быть получен лишь путем
трудных численных выкладок, было бы хорошо, чтобы эти вычисления
были вновь проделаны другими» г). В 1917 г., когда уже не было в живых
ни Дарвина, ни Пуанкаре, Дж. Джине обнаружил дефект в вычислениях
Дарвина.
Устойчивость систем с конечным числом степеней свободы. Работы
Ляпунова об устойчивости фигур равновесия вращающейся жидкости
относятся к одной из проблем устойчивости движения сплошной среды.
Вообще, проблема устойчивости равновесия и движения сплошной среды
до настоящего времени еще мало изучена даже в отношении самой
постановки вопроса. Принципиально более простым является вопрос об
устойчивости равновесия и движения механической системы с конечным числом
степеней свободы, состояния которой (т. е. положения и скорости ее
элементов) определяются конечным числом параметров, например,
вращающегося волчка или движения планеты вокруг Солнца. Но даже этот
вопрос, которым занимались многие выдающиеся ученые, до работ
Ляпунова не получил сколько-нибудь общего и строгого решения. Перейдем
к этим исследованиям Ляпунова.
Среди работ Ляпунова по этому вопросу, публиковавшихся в 1888—
1902 гг., главной является докторская диссертация «Общая задача об
устойчивости движений» (1892). Приведем математическую постановку
задачи.
Рассматривается система п обыкновенных дифференциальных
уравнений первого порядка с п неизвестными функциями x^t) действительного
аргумента (времени t). Принимается, что уравнения решены относительно
производных, т. е. система имеет вид
~df = ^fc (^' ж1» X2i • • •» xn)i А = 1, 2, . .., п, (1)
причем данные функции Xk для всех достаточно малых по модулю
значениях х±, х2, . . ., хп (которые могут быть комплексными) и любом t > t0
голоморфны и суть степенные ряды по Xk без свободного члена,
коэффициенты же могут зависеть от t. Решение системы вполне определяется
заданием начальных значений искомых функций xk (t) при t = t0.
Очевидно, что уравнения (1) имеют нулевое решение xt = х2 = . . . = хп = 0.
В настоящее время систему (1) называют динамической, так как
к ней можно привести уравнения движения конечного числа материальных
точек или твердых тел, движущихся по законам динамики; решения
х) А. П. Юшкевич, А. М. Ляпунов и Академия наук Института Франции
{по неопубликованным архивным документам).— Ист.-матем. исслед., вып. XVI,
1965, стр. 386-387.
456
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
системы называют траекториями. Ляпунов пользовался следующей
терминологией. Каждое частное решение системы (1) он называл
движением; исследуемое решение, соответствующее начальному условию t = t0,—
невозмущенным движением; решения, соответствующие некоторым
образом измененному начальному условию,— возмущенными движениями.
Нулевое решение системы (1) называется устойчивым по Ляпунову,
если при всех t > tQ для любого сколь угодно малого 8 > О можно
подобрать такое б > 0, что все решения системы xh(t) будут по модулю
меньше 8, когда начальные данные xk(t0) по модулю меньше 6. Другими
словами, невозмущенное нулевое решение устойчиво, если на всем
бесконечном промежутке времени t > t0 траектории возмущенного движения
остаются при достаточно малых | xk(t0) | в сколь угодно малой окрестности
нулевой точки.
Следует заметить, что до Ляпунова рассматривались лишь частные
случаи устойчивости движения и соответственно вводились частные
определения самого этого понятия. На основе приведенного общего
определения «устойчивости по Ляпунову» и строится все дальнейшее исследование
в его докторской диссертации.
Если система (1) проинтегрирована и ее решение найдено в простой
форме, исследование устойчивости не представляет затруднений. Мы
говорили, однако, что такое интегрирование удается только в сравнительно
редких случаях. Общепринятый способ изучения устойчивости
динамических систем до Ляпунова заключался в том, что данные функции Xk
разлагались в ряды, а затем отбрасывались члены выше первого
порядка. Таким образом, вместо системы (1) изучалась соответствующая ей
система первого приближения, именно — линейная однородная система
с переменными коэффициентами
^ = Pki(t)xi + Pk2(t)z2+...+Pim(t)zn, к = 1, 2, .. ., п. (2)
Так поступали еще незадолго до Ляпунова У. Томсон и П. Тэт (1879),
Э. Рауз (1877 и 1884) и Н. Е. Жуковский в статье «О прочности движения»
(Уч. зап. Моск. ун-та, отд. физ.-матем., вып. 4, 1882).
«Конечно,— писал Ляпунов,— указанный сейчас прием вносит весьма
существенное упрощение, в особенности в тех случаях, когда
коэффициенты в дифференциальных уравнениях суть постоянные величины. Но
законность такого упрощения a priori ничем не оправдывается, ибо дело
приводится к замене рассматриваемой задачи другою, с которою она может
не находиться ни в какой зависимости. Во всяком случае, очевидно, что
если решение новой задачи и может давать ответ на первоначальную, то
только при известных случаях, а последние обыкновенно не
указываются»-1). Привлечение членов второго порядка и некоторых следующих
(так поступал, например, Рауз) и повышение тем самым точности
приближений на конечном промежутке времени также не позволяло, вообще
говоря, судить об устойчивости или неустойчивости для бесконечного
промежутка времени. Здесь требовалось создание совершенно новых
методов, которые и разработал Ляпунов.
В своей диссертации Ляпунов решил при весьма общих
предположениях вопрос о том, когда вопрос об устойчивости решения системы (1)
решается по первому приближению, путем исследования линейной систе-
г) А. М. Ляпунов, Общая задача об устойчивости движения, М.—Л., 1950,
стр. 10.
ТЕОРИЯ УСТОЙЧИВОСТИ СИСТЕМ
457
мы (2). Далее он решил вопрос об устойчивости и в ряде «сомнительных»
случаев, когда первое приближение не позволяет решить вопрос об
устойчивости для общей системы (1). Он подробно разобрал особенно важные
в приложениях системы с постоянными коэффициентами Pkmi не
зависящими от времени (установившиеся движения), или же с периодическими
коэффициентами с одним и тем же периодом, а также рассмотрел случай
произвольных коэффициентов, ограниченных по абсолютной величине
при t > t0. Мы не можем входить в существо применявшихся при этом
методов и лишь укажем отдельные результаты и, прежде всего, две
теоремы, относящиеся к установившимся движениям. Для системы с
постоянными коэффициентами
^J- = Pkl%l + Pk2%2 + - - • + PknZn (3)
составляется «определяющее» (вековое) уравнение
I Pll — И Pl2 • • • Pin
fti Р22 — К • • • Р2п
I Pnl Pn2 • • • Рпп — К
имеющее степень п относительно величины к. Ляпунов показывает, что
если действительные части всех корней этого «определяющего» уравнения
отрицательны, то невозмущенное движение системы (3) и вместе с ним
невозмущенное движение системы (1) х), удовлетворяющее тем же
начальным условиям, устойчиво, и притом всякое возмущенное движение,
достаточно близкое к устойчивому, асимптотически стремится к нему при
t -> 00. Если же среди корней имеется хотя бы один с положительной
действительной частью, то невозмущенное движение неустойчиво.
Первое приближение не позволяет решить вопрос об устойчивости
решений системы (1), если уравнение (4), не имея корней с
положительными действительными частями, имеет корни, действительная часть которых
равна нулю. Ляпунов рассмотрел при этом два случая: 1) когда один
корень равен нулю, а действительные части всех остальных корней
отрицательны, и 2) когда уравнение имеет два чисто мнимых сопряженных
корня, а прочие корни имеют отрицательные действительные части. Изучая
последний случай, Ляпунов пришел к исследованию важного в
приложениях вопроса о существовании периодических решений некоторых
нелинейных систем обыкновенных дифференциальных уравнений довольно
общего вида. Для периодических коэффициентов Ляпунов глубоко
изучил два частных случая, особенно трудных: когда характеристическое
уравнение имеет один корень, равный 1, или два мнимых сопряженных,
с модулем, равным 1.
К докторской диссертации Ляпунова примыкает несколько статей,
посвященных глубокому анализу уравнения ~^- + p(i)x = 0 с
периодическим действительным коэффициентом p(t), бывшего ранее предметом
исследования Н. Е. Жуковского (1882—1891) и рассматривавшегося
Ляпуновым еще в диссертации (Сообщ. Харьк. матем. о-ва, т. 5, 1896;
Зад. Акад. наук по физ.-матем. отд., VIII сер., т. XIII, 1902).
Исследования по качественной теории дифференциальных уравнений
Ляпунова тесно переплетались с работами Пуанкаре. В предисловии
) Из которой (3) получается при отбрасывании нелинейных членов правой части.
=о,
(4)
458
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
к докторской диссертации русский математик отмечал, что Пуанкаре
принадлежит единственная попытка строгого решения проблемы устойчивости
для некоторых систем. Ссылаясь на мемуар Пуанкаре о кривых,
определяемых дифференциальными уравнениями, Ляпунов писал: «Хотя
Пуанкаре и ограничивается очень частными случаями, но методы, которыми он
пользуется, допускают значительно более общие приложения и способны
привести еще ко многим новым результатам. Идеями, заключающимися
в названном мемуаре, я руководствовался при большей части моих
изысканий» г).
Несмотря на тесную связь между исследованиями Ляпунова и
Пуанкаре, они велись все же в существенно отличных направлениях. Для
Пуанкаре было характерно применение геометрически-топологических
методов, для Ляпунова — аналитическая трактовка проблем и выработка
соответствующих алгоритмов. Отдельные результаты их совпадают, но
это не касается основного содержания. В целом результаты обоих
математиков прекрасно дополняли друг друга.
Первое время упомянутые работы Ляпунова не получили широкого
отклика. Но с начала тридцатых годов нынешнего столетия стало
появляться большое число работ математиков, механиков и физиков,
непосредственно связанных с его исследованиями по устойчивости динамических
систем. Докторская диссертация Ляпунова является редкой книгой
в отношении влияния, которое она оказывала и оказывает. Вообще,
методы, развитые Пуанкаре и Ляпуновым, имеют первостепенное значение
для механики, физики и техники. Роль проблем устойчивости в технике
растет в наше время изо дня в день. Конструкция устойчивых и прочных
при взлете, полете и посадке самолетов, различные точные приборы,
прочность коленчатых валов авиационных моторов, теория автоколебаний
электрических систем и многое другое требуют математического
исследования устойчивости движения. Всем этим вопросам за последние
десятилетия посвящена была чрезвычайно обширная литература 2).
П. Г. Боль и метод неподвижных точек. Работы Пуанкаре по
качественной теории дифференциальных уравнений содействовали развитию
особого раздела геометрии — топологии. Ценные результаты в этом
направлении получены на рубеже XIX и XX вв. в нашей стране
П. Г. Болем.
Топология — сравнительно молодая наука. От других геометрических
дисциплин она отличается подходом к изучению пространственных
образов. В обычной геометрии изучаются свойства фигур, инвариантные при
их любом перемещении — движении (например, длина отрезка, угол
между прямыми), так называемые метрические свойства. Две окружности
одинакового радиуса с точки зрения метрической геометрии тождественны,
независимо от их положения, и одна может быть преобразована в другую
с помощью обыкновенного перемещения; однако две окружности
различного радиуса отличаются по величине. Аффинная геометрия имеет
предметом свойства фигур, инвариантные относительно всех аффинных
преобразований, при которых прямые линии переходят в прямые,
например, относительно равномерного сжатия фигур данной плоскости к некото-
г) А. М. Ляпунов, Общая задача об устойчивости движения, стр. 11.
2) Подробнее о трудах Ляпунова по теории устойчивости см-. В. И. Смирнов,
Очерк научных трудов А. М. Ляпунова в кн.: А. М. Ляпунов, Избранные труды.
См. также: Александр Михайлович Ляпунов. Библиография. Состав. А. М. Луком-
ская, под ред. В. И. Смирнова. М.—-Л., 1953.
П. Г. БОЛЬ И МЕТОД НЕПОДВИЖНЫХ ТОЧЕК
459
рой ее прямой или параллельного проектирования фигур одной плоскости
на другую, ей не параллельную, или же центрального проектирования
одной плоскости на другую, ей параллельную. Аффинные свойства
окружностей различного радиуса одинаковы, так же как свойства окружности
и эллипса. Аффинная геометрия обнимает метрическую как частный
случай. Более общей является проективная геометрия — наука о свойствах
фигур, инвариантных по отношению к проективным преобразованиям,
при которых точки, лежащие на одной прямой, переходят в точки, опять-
таки лежащие на одной прямой. Таково центральное проектирование
фигур плоскости на другую плоскость, ей не параллельную. При
проективном преобразовании не сохраняется, вообще говоря, и параллелизм
прямых. Проективная геометрия не проводит различия не только между
окружностью и эллипсом, но и между этими линиями и параболой или
гиперболой. Вместе с тем, принадлежность к классу линий второго
порядка — проективное свойство кривых, так как проективное преобразование
линии второго порядка переводит ее в линию того же порядка.
Еще более общие геометрические свойства являются предметом
топологии. Говорят, что фигура F± топологически преобразуется в фигуру F2
если: 1) каждая точка М± фигуры F± преобразуется в одну и только одну
точку М2 фигуры F2 и обратно (преобразование взаимно однозначно),
и 2) если при неограниченном сближении двух точек М± и М[ фигуры Fi
неограниченно сближаются соответствующие им образы — точки М2
и М'2 фигуры F2 и обратно (преобразование взаимно непрерывно). В
топологии изучаются свойства фигур, инвариантные относительно
топологических преобразований, так называемых гомеоморфизмов, и, разумеется,
сами эти преобразования. Две фигуры, переходящие одна в другую при
топологическом преобразовании, называют гомеоморфными. Если
вообразить себе какую-либо фигуру сделанной из резины и затем подвергнуть
ее любым растяжениям, сжатиям и кручениям, без склеиваний и
разрывов, то будут возникать фигуры, гомеоморфные первоначальной.
Склеивания и разрывы исключаются, так как первые нарушают взаимную
однозначность преобразования, а вторые его непрерывность. С топологической
точки зрения всякая плоская область, ограниченная одной замкнутой
не пересекающей саму себя кривой, гомеоморфна кругу, а любой выпуклый
многогранник, эллипсоид и т. п.— шару. Важным топологическим
инвариантом является число измерений фигуры.
Интерес к топологическим свойствам фигур стал возрастать во второй
половине XIX века. Риман встретился с топологическими проблемами
в своей геометрической теории функций комплексного переменного.
Особенное внимание стали привлекать вопросы топологии в связи с
исследованиями Пуанкаре по качественной теории дифференциальных уравнений.
Топология постепенно выделяется в особую науку, прежде всего
благодаря самому Пуанкаре и голландскому математику Л. Э. Брауеру, а ее
методы получают все более широкие приложения в различных вопросах
анализа, начиная с теории динамических систем. Среди этих методов
важное место занимает метод неподвижных точек, впервые разработанный
П. Г. Болем. В теоремах о неподвижных точках доказывается, что в
некоторых условиях при непрерывном (не обязательно взаимно однозначном)
преобразовании фигур в самих себя, переводящем всякую точку фигуры в
точку той же фигуры, всегда имеется по крайней мере одна точка,
переходящая в саму себя — неподвижная точка преобразования. Приложение
таких теорем к доказательству существования решений дифференциальных
уравнений и их систем основывается, коротко говоря, на следующем.
460
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Уравнения записываются в виде р = А(р), где А — оператор, а р —
та или иная функция, рассматриваемая как точка функционального
пространства. Например, уравнение j- = f(x, у) с начальными условия-
х
ми х = ж0, у = г/о пишется в виде у = у0 + \ /(#» */) йж, и т. п. В таком
случае отыскание решения уравнения р = А(р) равносильно отысканию
неподвижной точки р преобразования, определяемого оператором А,
Если такое преобразование имеет неподвижную точку, то доказано
существование решения рассматриваемого уравнения.
Латвийский математик Пирс Георгиевич Боль (23 октября 1865 —
25 декабря 1921) окончил в 1887 г. Дерптский университет и в 1893 г.
защитил в нем магистерскую диссертацию, о которой будет сказано
несколько позднее. Два года спустя он был приглашен читать лекции
в Рижский политехникум. В 1900 г., после защиты докторской
диссертации, ему присвоили звание профессора. Последние годы жизни он работал
в Латвийском университете, основанном в Риге в 1919 г. х).
Главное место в творчестве Боля заняла теория дифференциальных
уравнений с ее приложениями к механике. Развивая качественные методы
этой теории, он и получил свои топологические результаты. Наиболее
ранние из них содержатся в его докторской работе «О некоторых
дифференциальных уравнениях общего характера, применимых к механике»
(Юрьев, 1900; франц. перевод в Bull, de la Societe mathematique de France,
1910), тематически примыкавшей к исследованиям А. Пуанкаре и
немецкого математика А. Кнезера, который в 1890—1900 гг. был профессором
в Дерптском университете и с которым Боль поддерживал тесную научную
связь. Кнезер и замечательный алгебраист Ф. Э. Молин, о трудах которого
будет речь впереди, выступили официальными оппонентами на докторской
защите Боля. Теория устойчивости Ляпунова была, разумеется, Болю
хорошо известна, но их работы шли в различных направлениях.
В докторской диссертации Боль аналитически формулирует и
доказывает теорему, согласно которой нельзя непрерывно преобразовать круг
вместе с его окружностью в эту окружность так, чтобы все точки
последней остались неподвижными. Эта теорема тут же обобщается на п-мерный
шар и его поверхность. Однако строгим доказательством обобщенного
предложения Боль в то время не располагал и мог лишь привести
геометрические доводы, обосновывающие его для случая п = 3, т. е.
обыкновенного шара. Поэтому, хотя он уже тогда понимал значение теоремы для
теории дифференциальных уравнений, основную задачу диссертации он
решил по-иному. Центральное место в работе занимает исследование
системы дифференциальных уравнений первого порядка
-ff = Phi*! + Pk2%2 + • • - + PhnXn + ?(*, a*, . . . , Xn) (к = 1, 2, ..., n),
где коэффициенты pkm постоянны, и функции ?, заданные для — оо <
< t < сю, непрерывно дифференцируемы по всем xk и удовлетворяют
еще некоторым условиям, а корни векового уравнения имеют
действительные части, отличные от нуля. Боль доказал существование решений
системы, рассмотрел структуру множества решений в зависимости от числа
корней с положительной и отрицательной действительной частью, а также
г) А. Д. М ы ш к и с, И. М. Рабинович, Математик Пирс Боль из Риги,
Рига, 1965.
П. Г. БОЛЬ И МЕТОД НЕПОДВИЖНЫХ ТОЧЕК
461
выяснил их асимптотическое поведение для бесконечного времени. Общие
результаты он применил к отдельным важным случаям, в частности,
к движению механической системы под действием возмущающих сил
вблизи положения неустойчивого равновесия.
Четыре года спустя Боль вернулся к топологическим теоремам
в статье «О движении механической системы вблизи положения
равновесия» (Uber die Bewegung eines mechanischen Systems in der Nahe einer
Gleichgewichtslage. Crelle's Journal, B. 127, 1904). Здесь доказана теорема
о невозможности непрерывного преобразования тг-мерного куба в его
поверхность, при котором точки последней остаются неподвижными,
а затем обобщение этой теоремы на любое замкнутое ограниченное
точечное множество в ^-мерном пространстве (и тем самым упомянутая теорема
об тг-мерном шаре из докторской диссертации). Несомненно, что Боль
располагал еще рядом топологических теорем, которые не приводит, так
как они не связаны непосредственно с предметом данного исследования.
Об этом свидетельствует он сам:
«Я ограничился в первой главе лишь тем, что являлось необходимым
для цели моей работы и воздержался от высказывания дальнейших
соображений. Все же я хочу здесь заметить, что с помощью соображений,
сходных с теми, которые встречаются в первой главе, может быть доказана
следующая теорема:
Если точки шаровой поверхности переводятся снова в точки шаровой
поверхности и если это происходит посредством непрерывного движения,
которое не затрагивает центра шара, то по крайней мере одна точка
возвращается в свое исходное положение. Под непрерывным движением здесь
подразумевается такое, при котором прямоугольные координаты суть
непрерывные функции времени и начальных значений.
Эту теорему можно перенести на случай других поверхностей;
возможно также ее распространение на многообразия нечетной размерности.
Как последняя теорема, так и предыдущая могут служить для
установления периодических дифференциальных уравнений» г). Заметим, что, как
видно, геометрический язык не был чужд Болю, хотя в основном он
формулировал и выводил свои теоремы аналитически.
Из предложений Боля, которые он затем прилагает к рассматриваемой
проблеме механики, нетрудно вывести теорему о существовании
неподвижной точки при непрерывном преобразовании шара в самого себя. Сам
Боль, однако, не сформулировал эту теорему, которую высказал и
доказал, наряду с другими предложениями о неподвижных точках, Л. Э. Брау-
ер в работах 1909 и следующих годов. Вряд ли можно сомневаться в том,
что Брауеру результаты Боля, высказанные попутно, как
вспомогательные в статье по механике, остались неизвестными. Вообще, замечательные
топологические открытия рижского математика не привлекли того
внимания, какого заслуживали. Существенный толчок развитию топологических
методов в теории дифференциальных уравнений дал в 1912 г., незадолго
до своей смерти, А. Пуанкаре. Исследуя ограниченную задачу трех тел 2),
Пуанкаре высказал одну теорему о неподвижных точках в случае пре-
х) П. Г. Боль. Избранныв труды. Вступительная статья А. Д. Мышкиса
и И. М. Рабиновича. Рига, 1961, стр. 88—89. См. также доклад названных авторов
в Московском математическом обществе: Первое доказательство теоремы о
неподвижной точке при непрерывном отображении шара в себя.— УМН, т. X, 3 (65), 1955, а
также их книгу: Математик Пирс Боль из Риги. Рига, 1965.
2) То есть движение тела бесконечно малой массы под действием двух конечных
притягивающих масс, из которых одна обращается около другой по окружности.
462
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
образования в самого себя кругового кольца; из этой теоремы следовало
существование бесконечного числа периодических орбит. Пуанкаре не
успел дать вывода своей топологической теоремы и это сделал год спустя
Дж. Биркгоф, один из создателей современной теории динамических
систем. В дальнейшем теория непрерывных отображений разрабатывалась
многими и ее метод неподвижных точек стал основным в качественной
теории дифференциальных уравнений. В наше время этот метод вошел
в университетские руководства.
Квазипериодические функции. Большую известность до недавнего
времени имело открытие Болем класса функций, которые сам он называл
«периодическими в расширенном смысле», а мы, вслед за французским
математиком Э. Эсклангоном (1903), именуем квазипериодическими. Эти
функции Боль впервые рассмотрел в магистерской диссертации «О
представлении функций одного переменного тригонометрическими рядами
с несколькими аргументами, пропорциональными одной независимой
переменной» (Uber die Darstellung von Fuktionen einer Variablen durch trigo-
nometrische Reihen mit mehreren einer Variablen proportionalen Argumen-
ten. Dorpat, 1893). Здесь изучены функции, раскладывающиеся в
равномерно сходящиеся тригонометрические ряды 2 uk, где uk суть целые
2зтсс 2зхсс
рациональные функций выражений cos , sin (\х = 1, 2, . . ., т)
с заданным числом независимых г) коэффициентов пропорциональности— .
При т = 1 функция является обыкновенной периодической, при т > 1
возникает более обширный класс квазипериодических функций. Простым
примером квазипериодической, но уже не периодической функции может
служить сумма нескольких периодических функций с несоизмеримыми
периодами, вроде sin х -f- sin]/2 х -f sinJ/Зж; впрочем, множество
квазипериодических функций не ограничивается суммами такого рода. Боль
глубоко исследовал свойства введенных им функций и применял последние
в работах по теории дифференциальных уравнений. Так, в статье «Об одном
дифференциальном уравнении из теории возмущений» (Uber eine Diffe-
rentialgleichung der Storungstheorie, Crelle's Journal, B. 131, 1906) он
рассмотрел решения уравнения
-#Г + /(0* = Ф(*)>
где /(/) и ср(г) квазипериодичны.
Теория квазипериодических функций Боля явилась основой, на
которой датский математик Г. Бор, брат знаменитого физика, начал в 1923 г.
строить еще более общую теорию почти-периодических функций, т. е.
грубо говоря, функций, значения которых весьма мало меняются, когда
аргумент изменяется на некоторое постоянное приращение —«почти-пери-
од» 2). Вскоре существенный вклад в теорию почти-периодических функций
внесли советские ученые В. В. Степанов и Н. Н. Боголюбов, а за ними
и другие.
х) То есть неудовлетворяющих какому-либо линейному однородному уравнению
с целыми коэффициентами.
2) Точнее: функция f(x) называется почти-периодической, если для любого s;>
>¦ 0 имеется такое значение Z(e), что в любом промежутке оси х длины I содержится по
крайней мере один почти-период т, для которого |/(я + т) —f(x)\ < 8, каково
бы ни было значение х. Это свойство для случая квазипериодических* функций было
известно еще Болю.
ЖИЗНЬ В. А. СТЕКЛОВА
463
Сказанным далеко не исчерпываются ценные открытия Боля.
Упомянем только, что в связи с задачами теории вековых возмущений он пришел
к изучению распределения дробных частей заданных некоторым образом
функций (Crelle's Journal, В. 135, 1909). Установленная при этом Болем
теорема была независимо выведена год спустя В. Серпинским и Г. Вейлем
и существенно обобщена последним в 1916 г.
Впоследствии теорию распределения дробных частей функций успешно
разрабатывали И. М. Виноградов и другие советские специалисты в
теории чисел.
Жизнь В. А. Стеклова. Ряды деятелей петербургской математической
школы получили на рубеже XIX и XX вв. блестящее пополнение в лице
воспитанника Харьковского университета В. А. Стеклова *).
Владимир Андреевич Стеклов, сын преподавателя Нижегородской
духовной семинарии и по матери племянник Н. А. Добролюбова, родился
в Нижнем-Новгороде (г. Горький)
9 января 1864 г. Он поступил на
физико-математический факультет
Харьковского университета в 1883 г.,
где с третьего курса стал заниматься
под руководством А. М. Ляпунова.
Ляпунов оказал решающее влияние
на выбор Стекловым области его
исследований. После окончания в 1887 г.
Харьковского университета Стеклов
был оставлен на кафедре механики
для подготовки к профессорскому
званию. За магистерской
диссертацией «О движении твердого тела
в жидкости>> (Харьков, 1893), защита
которой состоялась в 1894 г.,
последовал ряд исследований Стеклова по
математической физике, ставшей
затем его главной специальностью. Ряд
мемуаров в этой области и особенно
докторская диссертация по
прикладной математике —«Общие методы
решения основных задач математи- В. А. Стеклов.
ческой физики» (Харьков, 1901),
защищенная в 1902 г., принесли Стеклову большую известность, и в начале
1903 г. он был избран членом-корреспондентом Академии наук.
В 1891 г. Стеклов стал приват-доцентом и в 1896 г. профессором
Харьковского университета. В 1902—1905 гг. он состоял председателем
Харьковского математического общества (до него этот пост занимал Ляпунов).
Он избирался деканом факультета, участвовал в составлении нового
университетского устава. В 1906 г. после выхода в отставку А. А. Маркова
Стеклов возглавил кафедру математики в Петербургском университете,
где воспитал многих учеников, ставших впоследствии крупными учеными.
Более того, он создал здесь новую ветвь петербургской математической
школы, выросшую затем в большую советскую школу математической
физики.
г) Г. И. И г н а ц и у с, Владимир Андреевич Стеклов, М., 1967.
464
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
В 1910 г. Стеклов были избран адъюнктом Академии наук, а летом
1912 г.— ординарным академиком.
В Петербургском университете Стеклов вел не только научную и
учебную работу. Много раз он выступал в Ученом совете по общим вопросам
университетской жизни, далеко выходя за границы одних университетских
дел и нередко поднимая голос протеста против полицейско-бюрократиче-
ского режима в высшей школе. В годы реакции он не боялся резко
критиковать действия министра просвещения Кассо, брать под защиту
студенческие революционные сходки и т. д. г).
Последние девять лет жизни Стеклова относятся к советскому
периоду. Сразу после Великой Октябрьской социалистической революции
Стеклов занял выдающееся место в ряду лучших представителей русской
интеллигенции, ставших на сторону советской власти и отдавших свои
знания и дарования народу. В 1919 г. он был избран вице-президентом
Академии наук и на этом посту вел до самой смерти огромную научно-
организационную работу. Детищем В. А. Стеклова явился
Физико-математический институт, созданный в 1921 г. и впоследствии разделенный
на три, из которых Математический институт, крупнейший в своей
области научный центр СССР, носит его имя.
Стеклов был одним из замечательных математиков, работавших в тех
областях своей науки, которые непосредственно связаны с
естествознанием. В своих выступлениях он подобно Чебышеву ярко и талантливо
пропагандировал важность единения науки и практики. Собственная научная
деятельность Стеклова являлась живым примером такого единства. Вместе
с тем он оставался верен и другой традиции петербургской школы
математиков, постоянно стремясь к совершенной строгости математического
исследования и к постановке широких проблем на основе конкретных
задач. Искренний и горячий патриот, он был большим знатоком и
любителем русской культуры и истории. Ученик Стеклова, академик В. И.
Смирнов пишет: «Любовь к русской музыке, привычка приводить изречения
Петра Великого, Ломоносова, Лобачевского — все это было у В. А.
Стеклова не просто любовью к «русскому стилю», а выражением подлинной,
кровной связи его с русской культурой, и сам В. А. Стеклов являлся
одним из крупнейших представителей этой культуры» 2).
Умер Стеклов 30 мая 1926 г.
Задачи математической физики. Важнейшие труды Стеклова
посвящены математической физике. Особенное внимание ученых в конце
прошлого столетия здесь привлекали: задача об определении поверхностной
плотности электричества, находящегося в равновесии на данной
проводящей поверхности, задача об определении электростатического
потенциала внутри данной поверхности по его известным значениям на самой
поверхности, при условии, что внутри поверхности заряды отсутствуют,
и, наконец, задача гидромеханики, состоящая в исследовании
установившегося (не зависящего от времени) движения жидкости, обтекающей
данное твердое тело. В этих задачах приходится иметь дело с решением
уравнения Лапласа при тех или иных дополнительных условиях на
границе рассматриваемой области. Функции, удовлетворяющие уравнению
г) И. Я. Д е п м а н, В. А. Стеклов в Петербургском университете.—Ист. -
матем. исслед., вып. VI, М., 1953.
2) См. сб.: Люди русской науки, Математика. Механика. Физика. Химия. Под
ред. И. В. Кузнецова, М., 1961, стр. 276.
ЗАДАЧИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
465
Лапласа, называют гармоническими, а всякая гармоническая функция
может быть представлена с помощью некоторых несобственных
интегралов — так называемых потенциалов простого и двойного слоя. Поэтому
для изучения гармонических функций первостепенное значение приобрело
исследование свойств названных потенциалов и специально их
нормальных производных.
В 1877 г. К. Нейман предложил метод последовательных приближений
(«метод арифметических средних») решения задачи Дирихле и задачи,
носящей его имя, для случая поверхностей, выпуклых во всех точках.
Этот метод опирался на применение потенциалов двойного слоя и их
нормальных производных, существование которых для более общих
поверхностей не было обосновано. В 1889 г. Пуанкаре предложил прием
«выметания», применимый к более широкому классу случаев, но не дающий
аналитического выражения искомой функции, в отличие от метода
Неймана. Несколько ранее Г. Шварц (1885) внес в изучение вопроса новые
идеи, широко развитые Пуанкаре в работах 1894—1897 гг., которые,
как писал Н. М. Гюнтер, «полны творческих мыслей, но строго
доказанного, что можно было бы счесть фундаментом будущего здания, в них почти
нет» х). Мемуар Пуанкаре 1897 г., в частности, содержал нестрогое
распространение метода Неймана на невыпуклые поверхности. Но основным был
в нем метод фундаментальных (собственных) функций, восходящий
к Фурье, разработанный по-новому Пуанкаре и получивший дальнейшее
развитие у Г. Робена, Э. Леруа, В. А. Стеклова и польского ученого
С. Заремба.
Для строгого рассмотрения задач математической физики решающее
значение имели работы А. М. Ляпунова. Сам Стеклов рисовал обстановку,
сложившуюся на самом рубеже XIX и XX веков, так:
«Начиная с 1895 г., среди членов Харьковского математического
общества проявился живой интерес к вопросам математической физики,
в разработке которых А. М. Ляпунов принял деятельное участие, и здесь,
как и во всем, за что брался, он оказал услуги первостепенной
важности.
Все предшествовавшие изыскания об основных задачах
математической физики (электростатическая задача, задача Дирихле, основная задача
гидродинамики) основывались на некоторых свойствах так называемого
потенциала двойного слоя, которые, как заметил А. М. Ляпунов,
оказывались иногда неверными даже в простейших примерах.
Я имею в виду вопрос о существовании так называемых нормальных
производных от потенциала двойного слоя.
Это обстоятельство делало сомнительными все методы решения
указанных выше задач, ставшие теперь, после изысканий А. М. Ляпунова,
классическими. Он впервые указал общие условия как относительно
напряжения слоя, так и относительно поверхности его распределения,
при которых нормальные производные действительно существуют (в 1897
в Comptes rendus и Journal de mathematiques).
Пользуясь этими результатами, я доказал затем (в 1899 г. в Comptes
rendus и в 1900 г. в Journal de Toulouse), что принцип Неймана
действительно приложим ко всем поверхностям, удовлетворяющим условиям
А. М. Ляпунова, если только напряжение исходного слоя в методе
Неймана может быть представлено под видом потенциала простого слоя.
х) Н. М. Гюнтер, Труды В. А. Стеклова по математической физике. УМН,
т. 1, 3—4 (13—14), 1946, стр. 23. Впервые напечатано в «Сборнике памяти В. А.
Стеклова», Л., 1928.
466
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
В 1902 г. Александр Михайлович предпринял новое исследование х)
и указал новые свойства потенциала двойного слоя, которые позволили
освободиться от только что указанного ограничения, что привело к
решению задачи Дирихле в самом общем виде.
В своем знаменитом мемуаре «О некоторых вопросах, относящихся
к проблеме Дирихле» (Journal de mathem., 1898), А. М. Ляпунов дал ряд
других важных теорем относительно потенциалов двойного и простого
слоя и указал, между прочим, необходимые и достаточные условия для
того, чтобы функция, решающая задачу Дирихле внутри данной
области, имела нормальные производные на поверхности, ограничивающей
область» 2). Класс поверхностей, удовлетворяющих трем условиям
Ляпунова, называется теперь его именем.
Исследования, о которых мы рассказали, Стеклов подытожил в
докторской диссертации 1901 г., полное название которой гласило: «Общие
методы решения основных задач математической физики. Задача о
распределении электричества. Основная задача гидродинамики. Задача об
установившейся температуре. Задачи Дирихле (метода К. Неймана) и Гаусса.
Фундаментальные функции и их приложения». Решение всех
перечисленных проблем поставлено здесь на прочное основание в первой главе, где
доказаны необходимые общие теоремы, в частности, о свойствах
потенциала простого и двойного слоя. Во второй главе обосновывается метод Робе-
на и с его помощью решается основная электростатическая задача об
определении поверхностной плотности электричества, упомянутая выше.
В третьей главе, среди прочего, дано точное решение новых задач
аналитической теории тепла, причем поставлено на прочную основу и дополнено
исследование, проведенное незадолго до того (1894) Пуанкаре. Следующая
глава посвящена задаче Дирихле и методу Неймана.
Наиболее важной частью рассматриваемой диссертации, как
подчеркивал в своем отзыве А. М. Ляпунов, один из оппонентов на ее защите,
была последняя, пятая глава по теории функций, которые Пуанкаре
в мемуаре 1897 г. назвал фундаментальными, а мы именуем теперь
собственными 3). Фундаментальные функции, широко обобщающие различные
классы функций, применявшихся при решении краевых задач ранее
(тригонометрических, шаровых и т. д.), вводились Пуанкаре, Леруа
и Стекловым различными условиями. Первоначально Стеклов определил
их как потенциалы простого слоя, для которых отношение внутренней
нормальной производной к значению потенциала на данной поверхности
постоянно. В диссертации фундаментальные функции определены более
общим образом. Пусть даны поверхность 5, удовлетворяющая
определенным условиям, и на ней непрерывная положительная функция ф(М),
где М — точка поверхности. Функции Стеклова uh — это потенциалы
простого слоя, удовлетворяющие условию -=^- = kk(puk, где Xk —
dJif
характеристическое число. Стеклов строго доказывает существование
бесконечного счетного множества положительных характеристических
чисел и соответствующих им фундаментальных функций, зависящих
только от взятых поверхности S и на ней функции ф; эти функции образуют
г) «Об основном принципе метода Неймана в задаче Дирихле» (Сообщ. Харьк.
матем. о-ва, т. VII, 1902). [Эта статья, как и названная непосредственно далее,
помещены в кн.: А. М. Ляпунов, Работы по теории потенциала, М.—Л., 1949. А. Ю.].
2) В. А. Стеклов, Александр Михайлович Ляпунов. В кн.:-А. М.
Ляпунов, Работы по теории потенциала, стр. 21—22.
3) Этот отзыв напечатан в той же книге.
ТЕОРИЯ ЗАМКНУТОСТИ
467
на поверхности замкнутую ортогональную систему с весом ф. Он исследует
вопрос о разложении какой-либо данной функции / в ряд по
фундаментальным функциям и показывает, что такое разложение всегда возможно, если
полученный ряд — обобщенный ряд Фурье — на поверхности равномерно
сходится. Наконец, он дает при помощи своих функций решение задач
Дирихле и Неймана.
Примером стекловской трактовки какой-либо частной задачи может
служить данное им еще в 1896 г. решение задачи о распространении тепла
в неоднородном ограниченном твердом стержне а ^ х ^ 6, выражающейся
уравнением
где v(x, i) — искомая температура стержня, р(х) и q(x) — некоторые
данные непрерывные неотрицательные функции и р(х) имеет непрерывную
производную (Сообщ. Харьк. матем. о-ва, т. 5, 1896). Цусть на концах
стержня температура нулевая v(a, t) = v(b, t) = 0 и в начальный момент
v(x, 0) = f(x). Если искать частное решение в виде е-Н*ик(х), то uk(x)
есть решение линейного уравнения второго порядка Штурма — Лиувилля
с граничными условиями и (а) = и (Ъ) = 0; название объясняется тем, что
в 1837 г. Штурм и Лиувилль исследовали краевые задачи такого типа.
Решение исходного уравнения, отвечающее всем условиям, ищется в виде
оо
ряда v = 2 ^ке~%^ик(х). Тогда функция f(x) должна в силу начального
условия быть представима рядом по собственным (фундаментальным)
оо
функциям краевой задачи f(x)= 2 akuk(x)', здесь коэффициенты Фурье
b b
ak = \ p(x) f(x) uk{x) dx : \ p (x) u\{x) dx. Применяя метод Шварца — Пу-
а а
анкаре, Стеклов строго доказывает существование бесконечной
последовательности положительных собственных значений (характеристических
чисел) {kk} и соответствующих им собственных функций {uh(x)},
ортогональных с весом р(я), а также замкнутость системы этих функций и схо-
оо
димость ряда 2 ап^к{х) к функции f(x). Стеклов рассмотрел эту задачу
и для трехмерного тела.
Теория замкнутости. Еще в середине двадцатых годов XIX века
в математической физике приобрел центральное значение вопрос о
разложении какой-либо данной функции (например, выражающий начальное
распределение температуры) в ряд по функциям некоторой ортогональной
системы (например, по собственным функциям соответствующей краевой
задачи). Остроградский полагал, что возникающий при этом ряд всегда
сходится. Вместе с тем он подчеркивал трудность доказательства этого,
как он писал, замечательного свойства в общем случае. После того были
изучены для отдельных ортогональных систем проблемы сходимости
к данной функции, подчиненной тем или иным ограничениям. Строгое
исследование ортогональных систем под этим углом зрения в весьма
468
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
широком объеме было проведено В. А. Стекловым. Этому вопросу он
посвятил множество работ, регулярно появлявшихся в течение тридцати
лет, начиная с 1896 г.
Постепенно распространяя круг исследований, В. А. Стеклов построил
обширную теорию замкнутости систем ортогональных функций,
рассматриваемых в областях 1, 2 и 3 измерений. Это выражение он впервые применил
в заметке «Об условии замкнутости ортогональных функций», появившейся
на французском языке в Gomptes rendus за 1910 г. Мы коротко поясним
некоторые руководящие идеи в случае функций одного переменного.
Пусть дана произвольная непрерывная (или подчиненная другому
определенному условию) функция f(x) и ортогональная система функций
{uh(x)} с непрерывным весом р(х) > 0. Всегда можно принять для про-
ь
стоты, что система нормальная, т. е. \ р(х) и^{х) dx = 1; приведение
а
ортогональной системы к нормальной форме вполне элементарно. Говорят,
что система функций {uk(x)} — ортонормированная на промежутке (а, Ъ)
с весом р(х), если
0, к ф U
{ р(х) uk(x) щ(х) dx = \ ' '
о I 1, А —и
Итак, основная проблема состоит в разложении произвольной непре-
оо
рывной на (а, Ъ) функции f(x) в ряд вида ^j ak uk(x)- Эту проблему
k=i
В. А. Стеклов связал с замкнутостью системы {uk(x)}.
Если допустить возможность разложения
оо
f(x)= S cikuk(x),
k=l
а также почленного интегрирования этого ряда, то без труда
получаются коэффициенты Фурье разложения
ak = \ р(х) f(x) uk(x) dx.
Коэффициенты Фурье обладают тем свойством, что средняя квадратичная
погрешность с весом р(х) приближения f(x) суммой
п
2 Akuk(x)
k=i
имеет наименьшее значение, если все коэффициенты Ak суть
соответственные коэффициенты Фурье, т. е. Ak = ak. Эту наименьшую среднюю
квадратичную погрешность можно записать в виде \ р(х) f(x) dx — ^ а^\
а
оо b
2 а\ < j р(х) f(x) dx.
k=i
поэтому
k=i
ТЕОРИЯ ЗАМКНУТОСТИ
469
Последнее неравенство носит имя Бесселя. Когда средняя квадратичная
Ъ п
погрешность \ р(х) f(x) dx —2#fe стремится к нулю при тг-э-оо , орто-
а h=l
тональная нормированная система функций называется замкнутой. Иными
словами, условие замкнутости есть
оо Ь
2 a\=^p(x)f*(x)dx.
h=l а
Это равенство Стеклова широко обобщает давно известное равенство
Парсеваля для тригонометрической системы
1, cos#, sin#, cos2х, sin2х, cos3^, sin3^, ...
и промежутка ( — я, jt), имеющее вид
Я оо
где ak, bk — известные коэффициенты Эйлера — Фурье; последнее было
найдено в 1805 г. М. Парсевалем (в допущении разложимости функции
в тригонометрический ряд) и доказано А. М. Ляпуновым в 1896 г. (в
предположении интегрируемости ограниченной функции /(#)).
Условие замкнутости можно высказать в различных формах, помимо
стремления к нулю указанной средней квадратичной погрешности или,
оо
как говорят, сходимости ряда ^ ak uk(x) к f(x) в среднем. Например,
это условие выражает так называемую полноту системы, именно тот факт,
что она не может быть расширена присоединением новой функции, не
равной тождественно нулю, без нарушения ортогональности системы.
Стеклов доказал замкнутость многих встречающихся в анализе и его
приложениях ортогональных систем, в частности, собственных функций
уравнения Штурма — Лиувилля, при некотором однородном граничном
условии, относительно всех интегрируемых по Риману функций и
различных ортогональных многочленов, рассматриваемых на конечном или
бесконечном промежутке — многочленов Чебышева, Якоби, Чебышева —
Лагерра, Чебышева — Эрмита; при этом исследовались разнообразные
свойства этих систем.
Свойство замкнутости играет существенную роль в работах В. А. Стек-
лова по теоремам разложения в ряды собственных функций: замкнутость
ортогональной системы необходима, хотя и не всегда достаточна, для
возможности разложения данной функции по функциям этой системы.
Укажем две важные теоремы Стеклова. Первая гласит: если ряд Фурье
для непрерывной функции f(x) по функциям uk(x) замкнутой ортонорми-
рованной системы сходится на промежутке {а, Ъ) равномерно, то его сумма
на (а, Ъ) равна f(x). Непрерывность f(x) может быть заменена менее
жестким требованием. Во второй теореме утверждается, при тех же
условиях, что если ряд Фурье для функции/(ж) расходится, то его почленное
интегрирование на (а, Ъ) дает сходящийся ряд, сумма которого равна
интегралу функции f(x), т. е., с точностью до постоянного множителя
дает среднее значение f(x) на промежутке (а, Ъ). Это — обобщение
аналогичной теоремы о тригонометрических рядах, о которой говорилось ранее
470
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
по поводу соответствующих работ Лобачевского. Оно играет роль в так
называемом методе сглаживания, о котором сказано далее.
Исследование разложимости В. А. Стеклов производил не только
с помощью общих предложений теории замкнутости, но и путем
непосредственной оценки остаточного члена разложения. Изучению асимпотических
свойств ортогональных систем функций uk(x), т. е. поведения uk(x) при
к —> оо, он посвятил обширный мемуар «Об асимптотических выражениях
некоторых функций, определенных линейными дифференциальными
уравнениями второго порядка, и их приложении к задаче разложения
произвольной функции в ряды по названным функциям» (на франц.
языке; Сообщ. Харьк. матем. о-ва, т. 10, 1907) и ряд других работ. Здесь
с помощью метода асимптотических выражений Лиувилля, незадолго
перед тем аналогично использованного также А. Кнезером (1903),
получены асимптотические формулы для собственных функций уравнений
Штурма — Лиувилля и общие результаты применены к названным выше
классам многочленов. При этом выведены не только главные члены
асимптотических выражений, но и последующие, а также произведены требуемые
оценки.
Начиная с 1910 г. В. А. Стеклов стал применять в теории замкнутости
еще один важный метод, идея которого заключается в следующем. При
изучении вопроса о разложении функции f(x) с некоторыми «плохими»,
неудобными свойствами, она заменяется усредненной функцией
ЭС+/1
X
Такие «функции Стеклова», как их предложил называть Н. М. Гюнтер,
строятся и в случае многих переменных. Функция Fh(x) обладает более
удобными свойствами, чем f(x), например, первая непрерывна, когда
вторая только интегрируема, а если f(x) непрерывна, то Fh(x) имеет
непрерывную производную и т. д. Вместе с тем для непрерывной функции
f(x) модуль разности Fh(x) — f(x) при h-+0 равномерно стремится
к нулю. Прием Стеклова получил название метода сглаживания или
усреднения; сглаживание может быть произведено несколько раз.
Как мы говорили, работы В. А. Стеклова по теории замкнутости
и разложениям функций продолжались три десятилетия: две последние
вышли в самый год его кончины. В 1918—1920 гг. он читал для небольшой
квалифицированной группы слушателей курс математической физики,
который обработал для печати. В этих «Основных задачах математической
физики» (2 тт., Птг., 1922—1923) резюмированы многие его исследования
по рассмотренному кругу вопросов. Уже посмертно вышли «Основы теории
интегрирования обыкновенных дифференциальных уравнений» (М.— Л.,
1927). О работах по теории квадратур, также относящихся к последнему
десятилетию жизни В. А. Стеклова, говорилось выше.
Понятия и предложения теории ортонормированных систем функций
нашли в начале XX века весьма удобное истолкование в так называемом
пространстве Гильберта, бесконечномерном пространстве вектор-функций.
Между свойствами функций и векторов здесь устанавливается далеко
идущая и плодотворная аналогия. Скалярному произведению двух
обыкновенных векторов, равенство которого нулю выражает их взаимную
перпендикулярность (ортогональность), соответствует интеграл произведения
двух функций по соответствующей области, именно поэтому функции,
для которых такой интеграл равен нулю, называют ортогональными. Раз-
Н. М. ГЮНТЕР
471
ложению любого вектора по единичным векторам — ортам соответствует
разложение произвольной функции по функциям ортонормирован-
ной системы и т. д. Условие замкнутости оказывается здесь аналогом
теоремы Пифагора: квадрат длины вектора (интеграл в правой части
условия), равен сумме квадратов его проекций на орты (сумма в левой части
условия). Замкнутости соответствует полнота системы ортов: не
существует еще какой-либо ненулевой орт, ортогональный ко всем ортам системы
и т. д. Пространство Гильберта получило Свои первые применения в теории
линейных интегральных уравнений, бурно развивавшейся на самом
рубеже XIX и XX вв. Теория интегральных уравнений с симметрическим
ядром сразу же оказалась мощным средством исследования вопроса
о разложении функций в ряды по системам ортогональных функций.
В. А. Стеклов шел в этом вопросе собственными путями, не используя
новую теорию и получая аналогичные результаты другими средствами.
Академик В. И. Смирнов подвел итог его работам в следующих
словах:
«Исследования по математической физике естественно привели к общей
проблеме разложения по ортонормированным системам функций. Этому
вопросу и смежным с ним посвящены наиболее значительные по объему
и значению работы Владимира Андреевича. Ему принадлежат создание
теории замкнутости, ряд общих результатов по теоремам разложения
и подробное исследование вопросов разложения по специальным
ортонормированным системам. Методы доказательства этих теорем разложения
весьма разнообразны и оригинальны и подчас неожиданны, но просты,
особенно в позднейших работах. В некоторых из них можно видеть зачатки
будущих приемов функционального анализа. До появления работы Кнезе-
ра, связанной с асимптотикой функций Штурма — Лиувилля (1903)
и работ Гильберта по интегральным уравнениям (1904), работы Владимира
Андреевича были основными во всей математической литературе по
теоремам разложения.
Проблемы, которые трактовались в работах Владимира Андреевича,
были актуальными проблемами не только для его времени. В настоящее
время имеется огромная литература по теоремам разложения. Теория
функций вещественного переменного и функциональный анализ подвели
общую теоретическую базу и раскрыли новые перспективы для
исследования различных функциональных пространств. Работы Владимира
Андреевича с введенными в них операциями замыкания и усреднения немало
способствовали развитию этих новых областей математики» х).
Н. М. Гюнтер. Широкое применение метод сглаживания получил
в руках Николая Максимовича Гюнтера (17 декабря 1871 — 4 мая 1941),
ученика Коркина и Маркова, с 1894 г. и до кончины работавшего в
Петербургском, затем Ленинградском университете, с 1922 г.
члена-корреспондента Академии наук СССР. Работы Гюнтера, выполненные в
рассматриваемое время, относились главным образом к общей теории
дифференциальных уравнений. Так, его магистерская диссертация «О приложениях
теории алгебраических форм и интегрированию линейных
дифференциальных уравнений» (СПб., 1903), защищенная в 1904 г., посвящена
установлению случаев интегрируемости обыкновенных линейных уравнений в
алгебраических функциях; докторская диссертация «К теории характеристик
х) В. И. Смирнов, Памяти Владимира Андреевича Стеклова.— Труды Ма-
тем. ин-та АН СССР 73, 1964, стр. 11-12.
472
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
систем уравнений в частных производных» (СПб., 1913), защита которой
состоялась в 1915 г., содержит полное исследование задачи: найти
значения производных любого порядка от неизвестных функций щ, u2l . . ., ип
на данной поверхности хт = i|)(#i, х2, . . ., хт-±), имея значения только
некоторых первых из этих производных. В советское время Н. М. Гюнтер
обратился к математической физике и,
начиная с 1924 г., стал употреблять
метод сглаживания Стек лов а.
Классические понятия
математического анализа нередко описывают
явления, рассматриваемые в
математической физике, недостаточно адекватно.
Например в действительности мы всегда
измеряем среднюю температуру
некоторой области за некоторое время;
температура в данной точке и в данный
момент — понятие идеализированное.
То же относится и ко многим другим
наблюдаемым величинам. В таких и
аналогичных случаях приходится иметь
дело с функциями, лишенными тех
свойств, которые требуются для
применения обычных методов анализа. В связи
с этим возникает потребность в
приспособлении математического аппарата
к изучению различного рода средних
величин и не функций точек, но функ-
М. Гюнтер. цИ? областей. Именно в этом
направлении развивал Н. М. Гюнтер метод
сглаживания, в котором функция заменяется обобщенным интегралом Стилтье-
са по малой переменной области, поделенным на меру этой области *).
Интегральные уравнения. Теория интегральных уравнений была
в начале XX века очень молодой математической дисциплиной.
Интегральным называется уравнение, в котором искомая функция входит под
знаком интеграла. Задачи такого рода встречались еще Фурье, Абелю
и Лиувиллю. Абель, в частности, рассмотрел в 1826 г. задачу об
определении лежащей в вертикальной плоскости кривой, по которой должна падать
без трения тяжелая точка с данной высоты до нулевой за данное время.
«Прямое решение» этого вопроса ставил в особую заслугу Абелю еще
П. Л. Чебышев 2). Если время падения точки по кривой с высоты х до
наинизшей точки 0 есть данная функция /(ж), а неизвестная производная
ds
длины дуги ¦=- = и(х), то уравнение Абеля имеет вид
dx
u(t) dt
о о
V2g(x-t)
:f(X).
x) См. Биографический очерк, написанный В. И. Смирновым и С. Л. Соболевым,
в кн.: Н. М. Гюнтер, Теория потенциала и ее применение к основным задачам
математической физики. М., 1953.
2) В статье об Абеле в «Энциклопедическом словаре» П. Л. Лаврова; см. Ист.-ма-
тем. исслед., вып.. VI, стр. 226.
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
473
Это — частный случай уравнений, именуемых теперь линейными
интегральными уравнениями Вольтерра первого рода
X
^ К(х, t)u{t)dt = f(x).
а
Здесь искомой является функция u(t)\ даны функци и f (х) и К(х, t),
причем последняя называется ядром уравнения. Линейное интегральное
уравнение Вольтерра второго рода имеет вид
X
и(х) + А, ^ К(х, t) u(t) dt = f(t);
a
здесь X есть некоторая постоянная. Если в интегралах взять верхний
предел постоянным, то это будут, соответственно, уравнения первого
и второго рода Фредгольма. Все эти типы уравнений распространяются
на функции многих переменных. Ядро называется симметричным, если
К(х, t) = K(t, х). Значения X, при которых уравнение второго рода
имеет ненулевые решения, называются собственными значениями, а
соответствующие решения — собственными функциями уравнения.
Общая теория линейных интегральных уравнений разрабатывались
начиная с 1896 г. итальянцем В. Вольтерра для уравнений с переменным
верхним пределом, затем с 1900 г. шведом Э. Фредгольмом и в
последующие годы (1904, 1907 и след.) особенно Д. Гильбертом и Э. Шмидтом.
Мы уже говорили о первостепенном значении теории линейных
интегральных уравнений с симметричным ядром для математической физики и
теории разложения по ортогональным функциям. Но еще до создания общей
теории, получившей в наш век огромное развитие, был получен ряд
частных результатов. Отдельные важные открытия здесь принадлежат
и нашим отечественным ученым.
В первую очередь назовем докторскую диссертацию петербургского
математика Ю. В. Сохоцкого «Об определенных интегралах и функциях,
употребляемых при разложениях в ряды» (СПб., 1873), в которой было
положено начало изучению сингулярных интегральных уравнений
(с ядрами, обращающимися в бесконечность в области интегрирования),
находящей теперь обширные приложения в задачах математического
естествознания. К числу сингулярных относится, между прочим, и
уравнение Абеля. Применяя методы теории функций комплексного переменного,
Сохоцкий получил некоторые теоремы, относящиеся к сингулярным
уравнениям с так называемым ядром Коши
а
здесь х лежит в области интегрирования и знак интеграла, берущегося
по некоторой кривой, следует понимать в смысле так называемого
главного значения интеграла типа Коши. Эта работа Сохоцкого долгое время
оставалась совершенно незамеченной; мы к ней еще возвратимся. Основы
теории сингулярных уравнений были вне связи с исследованиями
Сохоцкого разработаны Гильбертом, Пуанкаре и другими1).
*) А. И. М а р к у ш е в и ч, Вклад Ю. В. Сохоцкого в общую теорию
аналитических функций. — Ист.-матем. исслед., вып. III, 1950, стр. 404—406.
474
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Другая работа по теории интегральных уравнений была
опубликована в 1884 г. Н. Я. Сониным. В статье «Об обобщении формулы Абеля»
(на франц. языке, Acta mathem., 1884) Сонин дал с помощью степенных
рядов решение уравнения первого рода с переменным верхним пределом
для случая, когда ядро К(х, t) есть функция разности х — t,
удовлетворяющая некоторым дополнительным условиям 2).
В начале нынешнего столетия интегральными уравнениями в России
занялся ряд ученых. Напомним прежде всего, что трудные нелинейные
интегральные и интегро-дифференциальные уравнения пришлось решать
А. М. Ляпунову в работах по фигурам равновесия. Следует упомянуть
также воспитанника Новороссийского университета, с 1904 г. его приват-
доцента и с 1915 г.— профессора Е. Л. Буницкого (1874—1952). Во время
заграничной командировки 1906—1907 гг. Буницкий познакомился в
в Геттингене с Гильбертом и под его влиянием занялся теорией линейных
интегральных уравнений. Различным вопросам ее, в том числе уравнениям
с разрывными ядрами, он посвятил, начиная с 1907 г., ряд работ,
печатавшихся как в зарубежных журналах, так и в одесских изданиях. Они
рассмотрены и в его магистерской диссертации «К теории функций Грина
для обыкновенных линейных дифференциальных уравнений» (Зап. матем.
отд. Новоросс. о-ва естествоиспытателей, т. 21, 1913), продолжением
которой, в значительной части, явилась и докторская диссертация
«К вопросу о решении обыкновенных линейных дифференциальных
уравнений при данных предельных условиях» (Приложение к т. 23 тех же
Записок, 1916). В 1922 г. Буницкий переехал в Прагу и работал здесь
в Карловом университете 2).
Мы писали, что в Харькове читал в 1912 г. необязательный курс
теории интегральных уравнений С. Н. Бернштейн. В Москве ее
пропагандистом явился Д. Ф. Егоров. В советское время наши ученые внесли
в теорию интегральных уравнений много нового, особенно в разработку
сингулярных интегральных уравнений, которую вела и ведет большая
научная школа, возглавляемая Николаем Ивановичем Мусхелишвили
(род. 16 февраля 1891). Деятельность этого ученого почти целиком
приходится уже на послереволюционный период. Поэтому здесь мы можем
сказать лишь немногое. В 1914 г. он окончил Петроградский университет,
несколько лет работал в Петрограде, но уже в 1920 г. вернулся на родину
в Тбилиси. Здесь он вместе с воспитанником Московского университета
Андреем Михайловичем Размадзе (11 августа 1890 — 2 октября 1929),
автором ценных работ по вариационному исчислению (1914 и след. годы),
приступил в незадолго перед тем основанном Тифлисском университете
(1918 г.) к подготовке национальных грузинских кадров математиков
и механиков. Выдающиеся исследования Мусхелишвили по теории
упругости, начатые им еще в 1915 г. совместно с Г. В. Колосовым, по
интегральным уравнениям и теории аналитических функций принесли ему широкую
известность. В 1933 г. он был избран членом-корреспондентом и в 1939 г.
действительным членом Академии наук СССР, а с 1941 г. бессменно состоит
президентом Академии наук Грузинской ССР 3).
г) Г. Мюнц, Интегральные уравнения, ч. 1, М.—Л., стр. 144—146.
2) С. М. К i р о, Математика в Одеському (Новоросшському) Ушверситет1.—
Историко-математичний зб1рник, II, Кшв, 1961, стр. 39—41.
3) М.В. Келдыш и С. Л. Соболев, Николай Иванович Мусхелишвили.—
УМН, т. 6, 2(42), 1951.— Об А. М. Размадзе см. «Математика», М.—Л., 1932,
стр. 114—115, 133—134.
МЛАДШЕЕ ПОКОЛЕНИЕ ПЕТЕРБУРГСКОЙ ШКОЛЫ
475
Младшее поколение петербургской школы. В последние годы перед
Октябрьской революцией возникают новые интересы и среди молодых
учеников великих «петербуржцев». Так, на физико-математическом
факультете Петербургского университета был создан математический
кружок, участники которого, изучая классиков от Лиувилля до Пуанкаре,
вместе с тем с увлечением приступили к овладению новыми методами
теории функций и идеями геттингенской школы Гильберта, в особенности
в области вариационного исчисления и интегральных уравнений. В этом
кружке работали многие будущие видные ученые, как братья А. С.
ж Я. С. Безиковичи, Н. М. Крылов (не принадлежавший, собственно,
к университету), В. И. Смирнов, Я. Д. Тамаркин, Я. В. Успенский,
A. А. Фридман и другие.
Николай Митрофанович Крылов (29 ноября 1879—11 мая 1955),
ученик И. П. Долбни по Петербургскому горному институту, бывший
б нем профессором в 1912—1917 г., преподавал затем несколько лет
в Крымском университете в Симферополе; в 1922 г. он был избран
академиком Академии наук УССР и с этого времени работал в Киеве; в 1929 г.
он был избран также членом Академии наук СССР. В Киеве Н. М. Крылов
положил основание большой школы, разрабатывающей приближенные
методы интегрирования уравнений математической физики, интегральных
уравнений, а также нелинейной механики*).
Владимир Иванович Смирнов (род. 10 июня 1887 г.), ученик
B. А. Стеклова и издатель посмертных трудов А. М. Ляпунова, с 1915 г.
по настоящее время состоит профессором Ленинградского университета;
с 1932 г. он член-корреспондент Академии наук СССР и с 1943 г. академик.
Исследования В. И. Смирнова принадлежат в основном к теории функций
комплексного переменного и ее приложениям 2). Работы Якова Самойлови-
ча Безиковича (17 июля 1886—23 июля 1958), профессора
Ленинградского университета и Текстильного института, относились к области
приближенных вычислений. Недолгой была блестящая деятельность
Александра Александровича Фридмана (29 июня 1888—16 сентября
1925), талант которого высоко ценил его учитель В. А. Стеклов и который
особенно прославился своими исследованиями по гидромеханике,
аэродинамике (динамической метеорологии) и теории относительности.
Что касается А. С. Безиковича (род. 1891), Я. Д. Тамаркина (10 июля
1888—18 ноября 1945) и Я. В. Успенского (11 мая 1883—27 января 1947),
то они в двадцатые годы уехали за границу, где и прошла в большей
своей части их научная деятельность3).
Научное творчество молодых петербургских математиков
развернулось во всей полноте уже после Октябрьской революции, но некоторые
из них опубликовали или же получили свои первые результаты еще
до конца рассматриваемого периода. Так, А. А. Фридман вместе
с Я. Д. Тамаркиным еще гимназистами напечатали две небольшие статьи
по теории чисел (1905). В 1911 г. А. А. Фридман опубликовал в
«Сообщениях Харьковского математического общества» работу об особого вида
частных решениях уравнения Лапласа, в которой решил один вопрос,
г) О. В. Крылова, Николай Митрофанович Крылов, М., 1945.
2) С. Л. С о б о л е в и А. П. Епифанова, Владимир Иванович Смирнов,
М.—Л., 1949; О. А. Ладыженская, С. М. Лозинский и С. Г. Михлин,
Владимир Иванович Смирнов, УМН, т. 23, вып. 4 (142), 1968.
3) О работах Я. В. Успенского по теории чисел см. Е. П. О ж и г о в а,
Математика в Академии наук в первые годы советской власти. Ист.-матем. исслед., вып. XVII
1966, стр. 387—388.
476
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
поставленный в докторской диссертации В. А. Стеклова; несколько спустя
с 1913 г., он начал серию исследований по метеорологии и гидродинамике,
для которых находил время даже в годы первой мировой войны,
проведенные им на фронте, где он служил летчиком 1). В. И. Смирнов занимался
задачами униформизации аналитических многозначных функций
(выражения аргумента и функции с помощью аналитических однозначных
функций некоторого параметра). С этим находилась в связи и его магистерская
диссертация «Задачи обращения линейного дифференциального уравнения
второго порядка с четырьмя особыми точками» (Пгр., 1918). Подобно тому
как эллиптические функции возникают при обращении эллиптических
интегралов, новые важные типы функций представляют собой результат
обращения решений линейных дифференциальных уравнений. Так,
обращение некоторых линейных однородных уравнений второго порядка
приводит к автоморфным функциям. Этой проблематикой занимались
крупнейшие математики — Пуанкаре, Клейн и другие. Задачу обращения
уравнения класса Фукса с тремя особыми точками, так называемого
уравнения Гаусса, рассмотрел Г. Шварц; В. И. Смирнов детально исследовал
уравнение с четырьмя особыми точками, приведя его к виду
?[z(z-a)(,-i)*L] + (* + b)V = 0
(особые точки суть 0, 1, а и оо; X — действительный параметр). В 1918 г.
в «Сообщениях Харьковского математического общества», т. 16 появилось
исследование В. И. Смирнова об униформизации любого неприводимого
алгебраического уравнения f(x, у) = 0 с помощью автоморфных функций.
Более других опубликовал в то время старший из этого поколения
петербургских математиков Н. М. Крылов. Его тогдашние работы
охватили довольно большой круг актуальных вопросов анализа: разложения
решений дифференциальных уравнений с частными производными в ряды
фундаментальных функций, теорию замкнутости, интегральные уравнения,
формулы механических квадратур, а также прямые методы решения
вариационных задач и краевых задач математической физики.
Методы В. Ритца и Б. Г. Галёркина. Мы говорили ранее о прямом
методе ломаных Эйлера, с помощью которого он вывел свое
дифференциальное уравнение, выражающее необходимое условие экстремума
вариационной задачи, и в этой связи упоминали о другом весьма важном прямом
методе решения вариационных задач и приводящихся к ним
дифференциальных уравнений, предложенном В. Ритцем (1908). Общая схема
метода вкратце такова. Для отыскания экстремума функционала F(y(x))
(мы берем простейший случай), т. е. нахождения сообщающей ему
экстремальное значение функции у(х), принимающей на концах данного
промежутка данные значения у {а) = а, у(Ъ) = |3, выбирается подходящим
образом некоторая система функций (р±(х), фг(ж), . . ., <pn(#)> • • • и из пер-
п
вых п этих функций образуется линейная комбинация уп{х) = 2 сь.щ(х)
с постоянными коэффициентами сь с2, . . ., сп, причем требуется, чтобы
Уп(а) == ai Уп(Ь) = |3. Функции уп(х) принимаются за приближенные
значения искомой у(х). Таким образом, дело сводится прежде всего
г) См. Письма А. А. Фридмана Б. Б. Голицыну и В. А. Стеклову. Публикация
и вводная статья Л. С. Полака, примечания А. Ф. Гаврилова.— Труды Ин-та ист.
естеств. и техн., т. 22, 1959; Отзыв академика В. А. Стеклова о трудах А. А.
Фридмана, в сб.: Очерки истории математики, и механики, М., 1963.
А. Н. КРЫЛОВ
477
к задаче дифференциального исчисления — отысканию экстремума
функции F{yn(x)), зависящей от п параметров си с2, . . ., сп, которые
определяются из системы п уравнений
При некоторых условиях полученные приближенные решения образуют
последовательность у±(х), Уг{х), • • •> УЛх)-> • • •? сходящуюся к искомой
функции у(х). Этот метод, практическую важность которого отметил
Пуанкаре, быстро получил широкое распространение среди ученых,
решавших технические задачи.
Ритц не привел должного обоснования своего метода. Н. М. Крылов
посвятил его применению и исследованию несколько работ 1915—1917 гг.,
а в статье «О методе В. Ритца приближенного решения задач
математической физики» (на франц. языке, Изв. Росс. Академии наук, 1918),
написанной вместе с Я. Д. Тамаркиным, доказал для целого ряда задач
сходимость последовательности приближений к искомому решению. В
дальнейшем Н. М. Крылов распространил метод и на интегральные уравнения.
В работах Н. М. Крылова содержатся необходимые оценки приближений,
в том числе и для небольших значений п.
Существенное видоизменение и обобщение метода Ритца предложил
специалист по теории упругости Борис Григорьевич Галёркин (1871 —
1945), воспитанник Петербургского технологического института,
впоследствии профессор Ленинградского политехнического института (1920)
и академик (1935). Метод Галёркина, изложенный им в статье «Стержни
и пластинки. Ряды в некоторых вопросах упругого равновесия стержней
и пластинок» (Вестник инженеров, 1915, № 19), применимый и к ряду
краевых задач, не сводящихся к вариационным, также вошел в широкое
употребление. Несколько ранее в 1913 г. такой же прием использовал
в решении отдельных задач теории упругости корабельный инженер
и профессор Петербургского политехнического института, а также Морской
академии, Иван Григорьевич Бубнов (1872—1919). В. Г. Галёркин
изложил метод в общей форме. Дальнейшее развитие и обоснование метод
Бубнова — Галёркина нашел в трудах советских математиков, в частности
академика М. В. Келдыша (1942).
Многое сделал для пропаганды и разработки численных методов
анализа один из наиболее своеобразных представителей петербургской
математической школы — А. Н. Крылов, к жизни и творчеству которого мы
теперь обратимся.
А. Н. Крылов. Алексей Николаевич Крылов — замечательный
представитель науки о корабле в ее самых различных аспектах, выдающийся
морской инженер, и вместе с тем крупный математик прикладного
направления — родился 15 августа 1863 г. в поместье своего отца,
артиллерийского офицера, в Ардатовском, уезде Симбирской губернии. По матери,
С. В. Ляпуновой, А. Н. Крылов приходился двоюродным племянником
А. М. Ляпунову. В 1878 г. Крылов поступил в Петербургское морское
училище и окончил его в 1884 г. Дополнительно он изучал математику
под руководством Ляпунова.
В 1888 г. А. Н. Крылов поступил в Морскую академию, где
наставником его по математике был А. Н. Коркин. Коркин оказал большое влияние
на своего ученика и, будучи сам большим знатоком и поклонником
классиков математики XVIII—XIX вв., воспитал в Крылове глубокий интерес
478
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
к тем вечно живым идеям, которые заключаются в творчестве Эйлера,.
Коши, Пуассона и других корифеев науки. Одновременно Крылов слушал:
многие курсы в университете — Коркина, Маркова, Граве и других.
Через два года Крылов блестяще окончил Морскую академию и был
оставлен при ней для подготовки к профессорскому званию, а с 1892 г.
начал читать в Морской академии курс теории корабля, рассматривая,
в частности, проблему качки корабля. Его теоретические исследования
о поведении корабля при волнении
имели и важное практическое
значение; они доставили Крылову мировую
известность. Можно сказать, что
молодой ученый явился достойным
преемником автора «Морской науки»—
великого Эйлера.
А. Н. Крылов был специалистом
по кораблестроению, теории компаса,
инженером, математиком; к этому
добавим, что он был механиком,
астрономом и историком науки.
Объединяющим всю его деятельность,
направленную на решение весьма практических
задач, было применение
математических методов, приводящих решение
к окончательной вычислительной схеме
или возможно простейшей системе
формул. Перед наукой рубежа XIX
и XX вв. стояло большое число
разнообразных проблем. Одни требовали
разработки новых теорий, новых мето-
А. Н. Крылов. д0В? учитывающих тонкие особенности
исследуемых функций, решения
вопросов существования при возможно менее стеснительных условиях и т. п.
Но имелось огромное количество вопросов естествознания и техники,
которые нуждались в решении алгоритмического характера и могли
быть решены совершенствованием одних классических методов. А. Н.
Крылова привлекла именно последняя проблематика. В предисловии к своему
замечательному курсу лекций по уравнениям математической физики,
прочитанному в 1912 г. в Морской академии и ставшему настольной
книгой многих русских ученых и инженеров, Крылов писал:
«Из этого общего обзора содержания предлагаемого курса видно, что
я придерживался главным образом способов изложения «старых авторов»
Фурье, Пуассона, Коши, для которых главная цель состояла в нахождении
решения, а не в безукоризненно строгом его обосновании и не в
доказательстве его существования в общем случае или при установленных
необходимых ограничениях. Эта часть мне представлялась имеющей лишь
специально математический интерес», и далее автор отсылал к трудам
В. А. Стек л ов а 1).
1) А. Н. Крылов, О некоторых дифференциальных уравнениях
математической физики, имеющих приложение в технических вопросах. Изд. 3-е, Л., 1933, стр. 3.
Первое издание вышло в 1913 г., второе, значительно расширенное,— в 1932 г.; книга
издавалась и позднее, в последний раз в 1950 г. Заметим, что Крылов тут же
специально отмечает, что не включил в свой курс развитую Гильбертом «особую методу
интегральных уравнений», поскольку по этому вопросу имеется книга А. Кнезера, «вполне
приспособленная для учебных целей».
А. Н. КРЫЛОВ
479
Мы теперь вряд ли согласимся с мыслью, высказанной в конце
приведенной цитаты. Время внесло поправки в эти оценки, но вместе с тем
всей своей деятельностью Крылов убедительно доказывал, что решение
стоявших перед ним вопросов могло быть успешно и кратчайшим путем
достигнуто на избранном им пути.
Было бы неправильно при этом думать, что Крылов не ценил широту
и общность методов математики. С большой яркостью он подчеркивает
роль методов широкого охвата в одном из своих блестящих исторических
этюдов, посвященном Лагранжу. Лагранж,— говорил Крылов,—
поступил правильно, сообщив изложению механики самую общую
аналитическую форму: поэтому-то методы его аналитической механики оказались
в равной мере приложимыми к определению орбит небесных тел и
электронов в атоме, к качанию корабля на волнении, к расчету гребного вала
на корабле и к расчету полета тяжелого артиллерийского снаряда1).
В собственных исследованиях, относящихся главным образом к теории
колебаний, Крылов использовал метод разделения переменных, который
распространил на случай вынужденных колебаний (свободные колебания
рассматривались ранее). Из ряда его работ мы отметим мемуар «О
вынужденных колебаниях упругих стержней постоянного сечения»,
опубликованный на немецком языке в Mathematische Annalen за 1905 г. Основное
содержание этого мемуара, написанного в связи с изучением колебаний
корабля, включено было затем в VII главу курса уравнений математической
физики. Задача эта выражается линейным уравнением в частных
производных четвертого порядка с правой частью, зависящей от двух
переменных
d2z , о д4? г / +\
«г+ь,-йг = /(*.')
(z— есть стрелка прогиба стержня в точке с абсциссой х в момент
времени t\ f(x,t) характеризует внешнюю нагрузку), при граничных
и начальных условиях (стержень, подпертый в обоих концах):
при х = 0 и x=l z = 0, -jfY — 0,
dz
при t = 0 Z = ф (х), -т- = г|) (х).
Решение ищется в виде суммы z = z± + z2, причем z± выражает свободные
колебания стержня, т. е. удовлетворяет написанному уравнению без
правой части, при данных начальных и граничных условиях, а второе
слагаемое z2 выражает вынужденные колебания, но уже при нулевых
начальных условиях.
Отыскание
оо
*i= S Tn(t)Xn{x)
71=1
приводится к решению двучленных однородных линейных уравнений
с постоянными коэффициентами как обычно и не представляет труда.
Оно дает
тг . ппх т . bn2n2t . г, • bn2n2t
Xn = sin—j-, Тп = Апcos—jj~+Bnsin—^— ,
где An, Bn находятся по начальным условиям. Чтобы найти функцию z2,
Крылов представляет ее в виде разложения по собственным функциям
г) См. сб.: Жозеф Луи Лагранж, М.—Л., 1937, стр. 16.
480
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
свободных колебаний Хп(х) с коэффициентами Sn(t), зависящими лишь
от времени,
оо
z2== 2j SnXn-
71=1
Одновременно также представляется правая часть уравнения
п=1
так что
i
о
а это дает для определения Sn(t) обыкновенное неоднородное линейное
уравнение второго порядка с постоянными коэффициентами
с нулевыми начальными условиями Sn(0)=0, —It"^1®' так чт0
t
Sn = ИГ I Нп^ sin -Т"(*—а) d°m
о
Найденные значения z* и z2 дают общее решение вопроса о вынужденных
колебаниях упругого стержня.
Разобрав различные случаи закрепления стержня и действующей
на него нагрузки, упомянув об исследованиях Стокса, связанных с одним
конкретным случаем обрушения железнодорожного моста, Крылов
применяет затем тот же метод к задаче о прямолинейном движении тяжелого
тела, подвешенного к концу растяжимой нити. Пуассон изучил здесь
случай свободных колебаний. Крылов опять-таки рассматривает
колебания вынужденные; сама задача выражается уравнением колебания струны
с правым членом. Вместе с тем Крылов показывает, что к той же задаче
приводят другие важные вопросы техники: теория индикатора паровой
машины, крутильные колебания вала с закрепленным в конце его
маховиком и другие. Тот же метод применяется далее к задаче распространения
тока по кабелю, изучавшейся ранее Кирхгофом, К. А. Поссе и др., а также
к изучению продольных колебаний орудия при выстреле и вредных
вибраций корабля, вызванных работой поршневых машин1). Все это
сопровождается подробно проведенными числовыми расчетами и чертежами.
С этими трудами Крылова были тесно связаны его работы по
приближенным вычислениям. Все направление творчества Крылова, естественно,
наталкивало его на занятия этим отделом математики. Читая лекции по
теории корабля, он еще в конце XIX века увидел, что инженеры
производят выкладки чрезвычайно неэкономно, используя 10 и более значащих
цифр там, где верны только первые три, применяя неудобные схемы
вычислений и т. д. В некоторых кораблестроительных расчетах, как
выяснил Крылов, до 97% цифр, участвовавших в выкладках, были
ненужны.
г) Корабль при этом рассматривается как упругий стержень, поперечные
размеры которого весьма малы по сравнению с длиной.
А. Н. КРЫЛОВ
481
Распространение в России различных совершенных методов
приближенного вычисления — решения алгебраических уравнений,
механических квадратур, численного интегрирования дифференциальных
уравнений — явилось большой заслугой Крылова. Его «Лекции о приближенных
вычислениях» (СПб., 1911), явившиеся обработкой курса, впервые
прочитанного в 1906 г., представляют собой превосходную и во многом
оригинальную по изложению монографию, которая несколько раз издавалась
вплоть до наших дней 1).
Крылов не только усовершенствовал изложение уже известных
методов приближенных вычислений, особенно численного интегрирования
дифференциальных уравнений по способу норвежского геофизика и
математика К. Штёрмера, но и сделал в этой области ценные оригинальные
открытия. Об одном из них — методе улучшения сходимости рядов
Фурье — мы расскажем в следующей главе.
В 1904 г. Крылов спроектировал и подробно описал в печати, а затем
и построил машину для приближенного интегрирования некоторых типов
обыкновенных дифференциальных уравнений, которая могла также
применяться для гармонического анализа (т. е. вычисления коэффициентов
разложения функции в тригонометрический ряд) и нахождения
действительных корней алгебраических уравнений. Опытный экземпляр этой
машины, к сожалению, погиб во время первой мировой войны. Этот
прибор был одним из изобретений Крылова-конструктора.
Мы упоминали, что Крылов проявлял живейший интерес к трудам
классиков науки. В рассматриваемое время он с особенной глубиной
изучил «Математические начала» Ньютона, к которым обратился в начале
XX века, как первому источнику учения о сопротивлении жидкости.
В 1915 г. он напечатал в «Известиях Морской академии» мастерский
перевод всего этого труда, снабженный глубокими математическими и
историческими комментариями. В мире не существует подобного издания
«Математических начал натуральной философии», и никогда еще этот труд не
находил столь проницательного толкователя. Несколько ранее А. Н.
Крылов выявил практический интерес, который представляет для
современного исследователя ньютонов метод определения кометных и планетных
орбит по малому числу наблюдений («Беседы о способах определения
орбит комет и планет по малому числу наблюдений», СПб., 1911). И в
дальнейшем Крылов отводил много времени исследованию творчества
классиков математики, того же Ньютона, Эйлера, Лагранжа, Гаусса, которым
посвящен ряд его блестящих устных и печатных выступлений и
переводных работ. В сочинениях великих геометров прошлого Крылов видел
не только прекрасное средство воспитания и направления широких
идейных интересов читателя, но и богатейшую сокровищницу эффективных
методов решения проблем прикладной математики. И он действительно
находил в трактатах старых авторов идеи и приемы, которые развивал
затем в форме, полезной для науки наших дней.
Место А. Н. Крылова в школе, основанной Чебышевым, ярко
характеризует В. И. Смирнов: «Создатель петербургской математической школы
П. Л. Чебышев был начинателем разнообразных направлений в
математике и, в частности, он неоднократно указывал на необходимость сближения
г) Этот курс А. Н. Крылов прочитал в помещении частной гимназии К. Мая,
когда власти временно закрыли Петербургский университет ввиду студенческих
волнений. Занятия были организованы по предложению Н. М. Гюнтера; помимо его самого
и Крылова, лекции читали А. А. Марков, С. Е. Савич и П. А. Шифф. Издание
«Лекций» в 1933 г. было значительно дополнено; они переиздавались еще в 1950 и 1954 гг.
482
ГЛ. 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
теории и практики. Но почти все представители петербургской школы
развивали чисто теоретические направления в математике... А. Н. Крылов
со всей силой своего своеобразного и исключительного таланта проложил
от петербургской школы дорогу к проблемам, поставленным человеческими
потребностями» *).
В 1914 г. по инициативе Н. Е. Жуковского Московский университет
присвоил А. Н. Крылову степень доктора прикладной математики, в
начале 1915 г. он был избран членом-корреспондентом Академии наук. Весной
1916 г. состоялось его избрание академиком. Великую Октябрьскую
социалистическую революцию он встретил немолодым, но полным энергии
человеком и без колебаний отдал свои знания и талант служению новой,
Советской России. В 1943 г. ему было присвоено звание Героя
Социалистического Труда.
До самой кончины своей, последовавшей 26 октября 1945 г. на 82-м
году жизни, Крылов продолжал неутомимую научную деятельность
в области математики и механики с их приложениями, а также по истории
науки. Свою жизнь он описал в блестящей по литературным достоинствам
и чрезвычайно интересной книге «Мои воспоминания», первое издание
которой вышло в 1942 г. 2).
Перейдем к исследованиям русских математиков в других областях
классического математического анализа. Здесь мы уже не встретим в
рассматриваемый период больших школ и непрерывной цепи работ, но будем
иметь дело с отдельными открытиями.
г) В. И. Смирнов, Математические работы А. Н. Крылова.— Труды Ин-та-
ист. естеств. и техн., т. 15, 1956. В этом томе помещены и другие статьи об А. Н.
Крылове и его творчестве.
2) Сочинения А. Н. Крылова, включая переводы классиков математики, см.
в издании: А. Н. Крылов, Собрание трудов, тт. 1—11, М.—Л., 1936—1951.
Анализ творчества см. в кн.: Я. Л. Г е р о н и м у с, Очерки о работах корифеев русской
механики.
ГЛАВА ДВАДЦАТЬ ВТОРАЯ
СХОДИМОСТЬ И СУММИРОВАНИЕ РЯДОВ
Н. В. Бугаев и учение о сопряженных рядах. После выхода в свег
«Курса алгебраического анализа» Коши (1821), в котором проблемы общей
теории рядов были впервые исследованы на современной основе, и работ
Абеля многочисленные математики обратились к отысканию достаточных:
критериев сходимости числовых рядов.
К признакам, установленным ранее
Даламбером, самим Коши и Гауссом,
было добавлено немало новых —
признаки сходимости Лобачевского, А. де
Моргана, И. И. Раабе, Куммера и т. д.
Первая сводка результатов в этой
области в русской литературе была дана
в 1846 г. В. Я. Буняковским в одном
из приложений к его курсу теории
вероятностей.
Оригинальную работу посвятил
теории рядов уже не раз
встречавшийся нам Н. В. Бугаев. Остановимся
прежде всего на жизненном пути этого
оригинального человека и ученого,
имя которого в свое время
пользовалось большой известностью, затем было
предано забвению, а теперь вновь все
чаще появляется на страницах исто-
рико-математических трудов.
Николай Васильевич Бугаев
(14 сентября 1837—11 июня 1903), сын и В Б
военного врача и уроженец
кавказского с. Душети, в возрасте 10 лет был
отправлен в Москву для обучения в гимназии; уже с четвертого класса
ему пришлось зарабатывать себе на жизнь частными уроками. В 1855—
1859 гг. он учился в Московском университете у Брашмана, Зернова
и Давидова; потом занимался еще в Инженерной академии в Петербурге^
но вскоре покинул ее, вернулся в Москву и с тех пор полностью
отдался математике. В 1863 г., после сдачи магистерских экзаменов, он
защитил диссертацию по теории рядов и после того в течение двух с
половиной лет провел в заграничной командировке, где посещал лекции
лучших французских и немецких математиков. В 1866 г. Бугаев защитил
докторскую работу «Числовые тождества, находящиеся в связи с свой-
484
ГЛ. 22. СХОДИМОСТЬ И СУММИРОВАНИЕ РЯДОВ
ствами символа Е» (Матем. сб., т. 1, 1866), и вскоре был избран
профессором Московского университета. Мы говорили о его активном участии
в организации Московского математического общества и в руководстве
последним, вначале в качестве секретаря (1869), потом вице-президента
(1886) и, наконец, президента (с 1891 г. до кончины). Добавим, что он
был одним из самых постоянных авторов «Математического сборника»
и что именно по его настоянию статьи русских авторов в этом издании
с самого начала стали публиковаться на русском языке. На факультете
Бугаев играл очень видную роль и в расширении программы, и в
усилении практических занятий, и в привлечении кончающих курс студентов
к научной работе, для чего с 1892 г. с ними проводились дополнительные
занятия . Его учениками были Сонин, Андреев, Некрасов, Анисимов,
Преображенский, Лахтин, Млодзеевский, Егоров и др., многим из них
он сообщил первые стимулы к самостоятельным исследованиям.
Сын Бугаева, уже цитированный нами Андрей Белый, рисовал облик
отца в таких стихах:
...И мой отец, декан Летаев,
Руками в воздух разведя:
«Да, мой голубчик,— ухо вянет:
Такую, право, порешь чушь.»
И в глазках крошечных проглянет
Математическая сушь.
Широконосый и раскосый
С жестковолосой бородой,
Расставит в воздухе вопросы:
Вопрос — один; вопрос — другой;
Неразрешимые вопросы...
Белый в то время увлекался буддизмом, мистическими аллегориями
и проч. и, как он говорит, перед всеми развивал «свои смесительные
мысли», которые отец кратко и решительно квалифицировал «чушью».
Рационализм Н. В. Бугаева оборачивался в глазах будущего писателя
«математической сушью», но суши как раз не было. Н. В. Бугаев был очень
живым человеком, с разносторонними научными и общественными
интересами. Это был живой и деятельный организатор и на деканском посту,
который занимал долгие годы; страстный спорщик и сочинитель общей
системы математики, предсказывавший в недалеком будущем бурное
развитие математики прерывного или аритмологии, которая не уступит
анализу непрерывного по общности приемов и красоте результатов и лишь
начальной фазой которой служит теория чисел (Математика и научно-
философское миросозерцание. Вопросы философии и психологии, 1889).
Не ограничиваясь всем этим, Бугаев врывался в область философии,
проповедуя здесь некую «эволюционную монадологию» наподобие
монадологии Лейбница.
Как ведущий московский математик и один из руководителей
математического общества, Бугаев вел обширнейшую переписку со многими
учеными России, Франции, Германии. Ему, наконец, принадлежит
немалая заслуга в организации реферирования работ наших ученых в
зарубежных журналах.
В математике Н. В. Бугаев стремился выбирать собственные дороги.
Выше упоминались его работы по теории чисел, получившие
уважительную оценку со стороны А. А. Маркова, хотя по своей тематике они в
большей части были далеки от петербургской школы теории чисел. Другие
Н. В. БУГАЕВ И УЧЕНИЕ О СОПРЯЖЕННЫХ РЯДАХ 485
работы его относятся к приложениям эллиптических функций к теории
чисел, позволившим ему доказать многие формулы, сообщенные Лиувил-
лем без доказательства (Матем. сборник, тт. XI—XII), к интегрированию
дифференциальных уравнений в конечной форме, к алгебре и т. д. 1). Свою
оценку деятельности Бугаева крупнейшие русские математики того
времени официально выразили дважды, сначала присудив ему на основании
заключения Буняковского и Сомова почетный отзыв за магистерскую
диссертацию по рядам (1864), а потом избрав его членом-корреспондентом
Академии наук по представлению Маркова и Сонина (1898). Вместе с тем,
с годами духовный облик Бугаева менялся. По-видимому, ему
недоставало в более молодые годы авторитетного научного руководителя,
а позднее конгениальной научной среды. Интересы Давидова, Летникова,
Петерсона лежали в других сферах, собственные ученики, едва
оперившись, уезжали работать в дальние университеты и там нередко обращались
к другой тематике. У Н. В. Бугаева, несомненно, имелось чувство
одиночества и обособленности; об этом свидетельствуют некоторые письма
Е. И. Золотарева к А. Н. Коркину. И вот оригинальность Н. В. Бугаева
переходила постепенно в оригинальничанье, авторитетность в
авторитарность, обида из-за непризнания тех или иных заслуг в их некритическую
переоценку, и так выросла к старости лет фигура талантливого чудака —
сын прозвал его «московским чудаком» 2).
Обратимся к диссертации «Сходимость бесконечных рядов по их
внешнему признаку» (М., 1863). На первой же странице сочинения Бугаев
указывает, что его цель найти «в одном общем методе или каком-нибудь
общем понятии регулирующее начало, из которого бы развивались все
предложенные признаки сходимости», связи между которыми до того были
плохо изучены. Такое общее начало Бугаев усмотрел в разработанной
им теории сопряженности. Диссертация состоит из двух частей.
В курсе алгебраического анализа Коши, среди прочего, доказал
теорему: если числа щ, и2, . . ., ип, . . . положительны и монотонно убываютг
оо оо
то ряды 2 ипж 2 2П и2п либо оба сходятся или же оба расходятся.
Дергать 1 71=0
ский математик Магнус-Георг Паукер (26 ноября 1787—31 августа 1855),
член-корреспондент Петербургской Академии наук, использовал эту теорему
для нового вывода признаков сходимости де Моргана и Бертрана, заметив,,
что вместо числа 2 можно поставить и любые другие натуральные числа
(Журнал Крелле, т. 42, 1851). Именно теорема Коши кладется Бугаевым
оо
в основу первой части работы, где из данного ряда 2 ип с монотонно убываю-
71=1
щими положительными членами образуются последовательности рядов,
сходящихся или расходящихся одновременно с ним, или, как выражается
Бугаев, рядов сопряженных. Примером двух сопряженных рядов служат
оо оо
2 ип и 2 2ии2п» причем первый относительно второго именуется предше-
71=1 71=0
ствующим, а второй относительно первого последующим. Из данного ряда
оо
2 ип можно составить сколько угодно предшествующих друг другу или
71=1
х) Ср. Краткое обозрение ученых трудов профессора Н. В. Бугаева
(составленное им самим), публикация Ф. Я. Шевелева.— Ист.-матем. исслед., вып. XII, 1959.
2) О Бугаеве см. статьи в Математическом сборнике, т. XXV, 1904—1905;
М. Я. Выгодский, Математика и ее деятели в Московском университете во
второй половине XIX века.—Ист.-матем. исслед., вып. I, 1948.
486
ГЛ. 22. СХОДИМОСТЬ И СУММИРОВАНИЕ РЯДОВ
последующих друг за другом рядов с общими членами
ип1°Еп ип log п - г>п = 9П-
(логарифм берется по основанию 2); ряды эти являются сопряженными.
Двойка, как сказано, может быть заменена другими натуральными
числами. Отправляясь от тех или иных известных простейших рядов, Бугаев
таким путем систематически выводит как известные ранее, так и некоторые
ловые признаки сходимости. Среди них сам он особо выделяет критерии
Iim-5^L<1? iimJ^L<i и т. д.
Специальный параграф отведен признаку Лобачевского, способ которого
Бугаев ценил выше многих других «по стремлению затронуть вопрос
с большей общностью и по рациональности основной мысли привести
условия сходимости к определению высшего предела ряда» *).
Во второй части Бугаев, отправляясь от интегрального
признака Коши — Маклорена, обобщает свой прием и выводит теорему: если
*ф(#) — положительная, дифференцируемая и монотонно возрастающая
оо оо
функция, причем о|)(оо) = оо, то ряды 2 Щь и ^jty'(n) Щ(П) сопряженные 2).
71=1 71=1
Предыдущая теорема получается при г|)(л) = 2П.
Бугаев не был одинок в разработке общих схем признаков сходимости.
Эта проблема интересовала Куммера и других ученых, а сравнением
различных критериев занимались и ранее. Исследования в этом
направлении ведутся и в наше время. В частности, советский математик Г. С. Сале-
хов предложил весьма общую схему однообразного вывода ряда признаков
сходимости, оценки остаточного члена и улучшения сходимости медленно
сходящихся рядов; эта схема обнимает, в частности, все признаки,
получающиеся из теории сопряженных рядов Бугаева 3).
Диссертация Бугаева послужила отправным пунктом дальнейших
исследований, в которых были попутно исправлены некоторые неточности,
имеющиеся в формулировках и рассуждениях Бугаева.
В. П. Ермаков и его признак сходимости. Новый сильный признак
сходимости был открыт Василием Петровичем Ермаковым (11 марта 1845—
16 марта 1922), имя которого нам уже встречалось, как основателя
«Журнала элементарной математики», автора работ по дифференциальным
уравнениям и участника одной из связанных с ними дискуссий. Сын учителя
церковно-приходской школы, В. П. Ермаков в 1869 г. окончил Киевский
университет, где его учителями были М. Е. Ващенко-Захарченко
и П. Э. Ромер. Перед двухлетней заграничной командировкой в Париж
ж Берлин в 1871—1873 гг. он некоторое время пробыл в Петербурге, где
беседы с А. Н. Коркиным и П. Л. Чебышевым укрепили его в уже ранее
созревавшем намерении заняться механикой и дифференциальными урав-
г) Н. В. Бугаев, Сходимость бесконечных рядов по их внешнему виду. М.,
1863, стр. 42.
2) Там же, стр. 55.
3) Г. С. Салехов, К теории вычисления рядов.— УМН, т. 4, 32, 1949; о к
ЭК'?, Вычисление рядов. М., 1955.
В. П. ЕРМАКОВ И ЕГО ПРИЗНАК СХОДИМОСТИ
487
нениями. Именно дифференциальным уравнениям, как уже говорилось,
посвящены обе диссертации Ермакова, из которых магистерскую он
защитил в Петербурге в 1873 г., а докторскую в Киеве в 1877 г. В Киевском
университете он преподавал тридцать лет с 1874 до 1909 г., читая
разнообразные курсы от теории векторов на плоскости до теории вероятностей;
в 1877 г. ему было присвоено профессорское звание. Двадцать лет, с 1899
по 1919 г., он проработал также в Киевском политехническом институте,
основанном в 1898 г. Вместе с М. Е. Ващенко-Захарченко, Б. Я. Букрее-
вым и другими В. П. Ермаков основал
в 1890 г. Киевское
физико-математическое общество и в последующем был
одним из активнейших его членов.
Помимо сказанного, Ермаков
занимался вариационным исчислением,
проективной геометрией; в книге «Теория
векторов на плоскости. Приложение
к исследованию конических сечений»
(Киев, 1887) он дал первое на русском
языке векторное изложение теории
конических сечений. Он составил немало
учебных руководств и написал множество
популярных статей *). Однако было что-то
общее в судьбах Ермакова и Бугаева,
да, быть может, и не только этих двух
периферийных математиков. Вот что
пишут о Ермакове нынешние исследователи
развития математики на Украине:
«Недооценка достижений современных ему
математиков, стремление идти своим
путем независимо от того, насколько этот в п Ермаков
путь подходил по сути дела, в
известной мере научное одиночество (в начале
своей деятельности Ермаков слишком явно превосходил коллег-земляков)
отрицательно сказались на его творчестве. В итоге этот крупный талант,
несмотря на любовь к науке и большую работоспособность, дал гораздо
меньше, чем мог бы дать» 2).
Наибольшую известность Ермакову доставила его работа по теории
¦сходимости рядов, которая, несомненно, возникла под влиянием теории
сопряженных рядов Бугаева.
Впервые о своем признаке сходимости Ермаков доложил на одном
из заседаний III съезда русских естествоиспытателей и врачей в сентябре
1871 г. Он показал, что ряд, общий член которого f(n) есть положительная
убывающая функция, причем lim f(n) = 0, сходится, если
lim^gL<l,
я_юо 7\х)
и расходится, если тот же предел больше единицы. Этот критерий он вывел
из более общего, опирающегося в свою очередь на признак сходимости
*) Л. Н. Грацианская, Василий Петрович Ермаков.— Ист.-матем. исслед.,
вып. IX, 1956, стр. 667—690.
2) Б. В. Гнеденко и И. Б. Погреб ы секи й, О развитии математики
на Украине.— Ист.-матем. исслед., вып. IX, 1956, стр. 414.
488
ГЛ. 22. СХОДИМОСТЬ И СУММИРОВАНИЕ РЯДОВ
несобственного интеграла \ f(x) dx, который Ермаков высказал в форме:
а
если для положительной функции ср(#), которая больше х для всех я>аг
отношение '/ 'хч при х—> оо стремится к пределу, меньшему еди-
Т\х)
оо
ницы, то интеграл \ f(x) dx конечен; если же при х>а отношение
а
Ф ^X'J^X" >1, то интеграл бесконечен. В силу интегрального признака
1\х)
оо
Коши —Маклорена ряд 2 f(n) ПРИ тех же условиях соответственно схо-
п=а
дится или расходится. Выше приведенный критерий получается, если
взять «сопряженную функцию» ср(#) = ех. Ермаков высказал на съезде
убеждение, что для всех употребляемых в анализе рядов предел отноше-
ния \ ' равен нулю либо бесконечности, так что сомнительные случаи,
Т\х)
когда предел этого отношения есть 1, представиться не могут.
Сообщение Ермакова весьма заинтересовало присутствовавших
математиков. П. Л. Чебышев, в частности, отметив особенно важное значение
этого критерия, показал его связь с критерием особенности решения
дифференциального уравнения первого порядка: если у = О удовлетворяет
уравнению -^- = F(x, у), то решение это является особым или неособым,
смотря по тому, будет ли выражение
е vF(x,y)
_1
У2Р(х, е У)
обращаться при у = 0 в нуль или в бесконечность 1).
В 1872 г. Ермаков опубликовал более подробное изложение своих
результатов. В начале статьи он ссылается на диссертацию Бугаева,
а затем выводит свой критерий, который, как он справедливо писал,
«по чувствительности и простоте превосходит все доселе известные
признаки сходимости» 2).
Признак Ермакова является действительно чрезвычайно сильным.
Но, как и в докладе на съезде, так и в статье Ермаков переоценил его
силу, утверждая, что для его признака «на практике никогда не
встречается сомнительного случая, хотя теоретически доказать это трудно и вряд
ли возможно»3). Впрочем, он скоро исправил эту ошибку, и в своем «Отчете
о путешествии за границу», написанном уже в июне 1872 г., а
напечатанном в № 1 Киевских «университетских известий» за 1874 г., привел
пример ряда, для которого его признак не решает вопрос о сходимости. Ори-
г) Ср. А. А. Киселев и Е. П. О ж и г о в а, П. Л. Чебышев на съездах
русских естествоиспытателей и врачей.— Ист.-матем. исслед., вып. XV, 1963, стр.
302—303.
2)В.П. Ермаков, Новый признак сходимости и расходимости бесконечных
знакопостоянных рядов.— Универ. известия, Киев, 1872, № 3, стр. 2; ср. е г о ж е,
Теория сходимости бесконечных строк и определенных интегралов.— Матем. сб.,
т. VI, 1872.
3) Университетские известия, Киев, 1872, № 3, стр. 16.
МЕТОД СУММИРОВАНИЯ Г. Ф. ВОРОНОГО
489
гинальные выводы признака Ермакова даны были впоследствии и другими
авторами — А. Н. Коркиным (1882), А. Прингсгеймом (1890), Д. М.
Синцовым (1899), В. Я. Букреевым (1917 и 1930); он привлекает внимание
математиков и в наши дни (В. А. Зморович, 1956). Н. В. Бугаев в
специальной статье показал, что критерий Ермакова может быть выведен
из его, Бугаева, теории сопряженности рядов (Матем. сборник, т. 14, 1888);
данное при этом доказательство было уточнено В. А. Зморовичем в 1956 г.
Параллелограмм Ньютона. К рассматриваемому кругу вопросов
отчасти примыкают работы о «начале наибольших и наименьших
показателей», как назвали у нас метод параллелограмма Ньютона, служащий
для разложения неявно заданной функции /(#, у) = 0 (у Ньютона эта
был целый многочлен) по дробным степеням разности х—а. Метод Ньютона,
имеющийся уже в его работах семидесятых годов XVII века, был в XVIII
веке использован для исследования алгебраических кривых в
окрестности их особых точек. В XIX веке он получил широкое развитие и
применение в изучении ветвей аналитических функций и специально
алгебраических функций и был систематически разработан рядом ученых, в
частности, В. А. Пюизё, который в 1850 г. впервые исследовал сходимость
возникающих разложений. Лиувилль применил метод к нахождению целых
рациональных интегралов линейных дифференциальных уравнений с
многочленными коэффициентами и в этой-то связи он привлек внимание
русских математиков, занимавшихся, как мы знаем, этим вопросом.
Н. В. Бугаев предложил обобщение метода параллелограмма Ньютона
на систему двух уравнений с тремя переменными Д(#, г/, z) = 0,
f2{x1 2/, z) = 0, показав, как разложить у и z в ряды по дробным
степеням х, без предварительного исключения неизвестных (Матем. сб., т. 14,
1888). Затем он использовал этот метод для отыскания частных целых
и дробных решений названных дифференциальных уравнений (Матем.
сб., т. 16, 1891; Изв. Акад. наук, т. 67, 1892), а также их
алгебраических интегралов (Матем. сб., т. 17, 1893). В уже встречавшейся
нам докторской диссертации Д. М. Синцова (1898) развит изящный
геометрический метод, распространяющий прием Ньютона на два уравнения
с тремя неизвестными1).
Мы уже останавливались ранее на некоторых других исследованиях
по теории рядов, в частности, П. Л. Чебышева о рядах, члены которых
имеют простые номера. Укажем теперь на одну замечательную работу
Г. Ф. Вороного по суммированию расходящихся рядов.
Метод суммирования Г. Ф. Вороного. Как мы знаем, в конце XIX века
математики пришли к убеждению в ценности обобщенных приемов
суммирования, начало которым положил Эйлер. К этому приводили
исследования некоторых действий над рядами, проблемы теории рядов Фурье,
задачи операционного исчисления и т. д. Работы Э. Чезаро, Э. Бореля,
Л. Фейера и других положили начало современной теории суммирования
рядов, ныне выросшей в особый отдел математики.
Вороной пришел к проблемам суммирования рядов в связи со своими
работами по аналитической теории чисел. Новый созданный им метод
суммирования он доложил в начале 1902 г. на XI съезде русских
естествоиспытателей и врачей в Петербурге, а краткая заметка «Расширение
1)Н. Г. Чеботарев, Многоугольник Ньютона и его роль в современном
развитии математики. В сб.: Исаак Ньютон, под ред. С. И. Вавилова, М.—Л., 1943.
490
ГЛ. 22. СХОДИМОСТЬ И СУММИРОВАНИЕ РЯДОВ
понятия о пределе суммы членов бесконечного ряда» была опубликована
в «Дневнике» этого съезда в 1902 г.
оо
Вороной определяет обобщенную сумму ряда 2 uk следующим обра-
оо п
зом. Пусть числа рп>0, р0 > 0 и 2 Pk=°°. Обозначим 2 uk = sn-
h=Q k=0
оо
«Значением символа 2 uh>> Вороной называет предел при п —» оо выражения
PnSo-rPn-i4-r •.. -rPosn ^ Метод Вороного регулярен (т. е. для сходя-
Ро -г Pi ~г • • • "Г Рп
щегося ряда обобщенная сумма совпадает с обыкновенной), когда
lim ¦ j^ : = 0. Если при различном выборе чисел pk две обоб-
п_юо Р0 I Pl-r • ---ГРп
щенные суммы Вороного существуют, то они численно равны. В качестве
частных случаев метод Вороного содержит метод Чезаро (рп = 1) и более
поздний (1909) метод венгра М. Рисса.
Заметка Вороного осталась в свое время неизвестной, и его метод
был вновь в 1919 г. предложен скандинавским ученым, также
профессором в Лунде Н. Э. Нёрлундом, исследования которого были
продолжены другими. Только после того как Я. Д. Тамаркин опубликовал
в Annals of mathematics английский перевод заметки Вороного с
подробными пояснениями (vol. 33, № 3, 1932), за рубежом узнали, что так
называемый метод суммирования Нёрлунда был впервые предложен
Г. Ф. Вороным х).
Улучшение сходимости ряда Фурье по А. Н. Крылову. Решения
механических, физических и технических задач нередко представляются в виде
весьма медленно сходящихся рядов Фурье, которые поэтому практически
непригодны в приближенных вычислениях, или же рядов, которые при
дифференцировании дают медленно сходящиеся и даже расходящиеся
ряды. В рассмотренной в конце предыдущей главы статье о колебании
стержней А. Н. Крылов отмечал, что такие плохо сходящиеся, особенно
близ концов промежутка, ряды получаются по его методу, когда
вынуждающая сила не отвечает некоторым условиям. Это побудило его
заняться поисками приема, усиливающего сходимость рядов Фурье. Такой
прием, применимый в большом числе довольно общих случаев, он изложил
в своих курсах приближенных вычислений и уравнений математической
физики. В предисловии ко второму из них А. Н. Крылов писал: «Этот
прием [изложенный в гл. VI.— А. Ю.\ не только дает практическую
возможность с удобством пользоваться такими рядами в приложениях,
получая желаемую степень точности, взяв самое ограниченное число
(3—5) членов преобразованного ряда, но часто приводит к
представлению суммы предложенного ряда в замкнутой форме под видом разрывной
функции. Этот же прием дает возможность находить производные от
функций, представленных такими рядами Фурье, почленное
дифференцирование которых недопустимо» 2).
г) Г. Ф. Вороной, Собрание сочинений, т. III, стр. 9—10, 206—207; Г. X а р-
д и, Расходящиеся ряды, гл. IV — V.
2) А. Н. Крылов, О некоторых дифференциальных уравнениях
математической физики, имеющих приложение в технических вопросах, стр. 2.
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДА ФУРЬЕ ПО А. Н. КРЫЛОВУ 491
Суть дела в следующем. Быстрота сходимости ряда Фурье какой-
либо функции
оо
/ (х) = 4р -4- ^ а">cos пх + ^ s^n П;Г
п = 1
или, иначе говоря, порядок малости коэффициентов ап, Ъп прига—>оо
зависит от аналитических свойств функции/(я). Пусть, например, на
промежутке (—я, я) непрерывная функция f(x) имеет непрерывные
производные до (к — 1)-го порядка включительно, причем для всех /<т) (х),
0<7?г<& — 1 предельные значения на концах промежутка равны,
/(т)(_я -f 0) = /<т)(я — 0) (случай любого другого промежутка легко
приводится к рассматриваемому). Тогда коэффициенты Фурье ап, Ъп
функции f(x) будут при п—> оо бесконечно малыми порядка выше, чем—^-.
Но если f(x) имеет на (—я, я) хотя бы один скачок, или ее предельные
значения на концах неравны, то коэффициенты ап, Ъп будут при п-^оо
бесконечно малыми лишь порядка — и ряд Фурье этой функции
становится неудобным для вычисления его суммы. Почленное же
дифференцирование ряда Фурье понижает порядок малости его коэффициентов
на единицу, так как дает ряд
оо
2 (— пап sin пх + пЪп cos пх).
71=1
Если, скажем, коэффициенты Фурье функции f(x) будут порядка -^,
то при двукратном дифференцировании ряда получается ряд,
коэффициенты которого не стремятся к нулю. Между тем при изучении
колебаний или изгиба стержней и многих других вопросов приходится
пользоваться производными нескольких первых порядков от решения,
выраженного тригонометрическим рядом.
На этих свойствах и основан метод А. Н. Крылова, состоящий в том,
что из данной функции f(x) вычитается другая, известная функция ср(ж),
имеющая те же скачки, что и данная, и производные которой вплоть до
некоторого порядка, определяемого условиями вопроса, имеют скачки,
совпадающие со скачками соответственных производных данной
функции. В таком случае разность F(x) данной и подобранной функции
F(x) = f(x) — ф(я) будет на (—я, я) непрерывно дифференцируема
требуемое число раз и ряд Фурье для F(x) окажется с коэффициентами
желательного порядка малости. Обыкновенно ф(я) берется в виде
кусочно-многочленной функции подходящей степени.
Крылов показал, как поступать, если функция задана только своим
рядом Фурье. Он снабдил изложение метода прекрасными примерами,
а также отметил, что с его помощью можно проверить, удовлетворяет ли
выраженная рядом функция тому дифференциальному уравнению, как
решение которого она была получена, хотя бы сам ряд нельзя было
почленно дифференцировать нужное число раз. Метод А. Н. Крылова давно
вошел в руководства для университетов и высших технических школ.
ГЛАВА ДВАДЦАТЬ ТРЕТЬЯ
ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ;
СПЕЦИАЛЬНЫЕ ФУНКЦИИ
Распространение теории аналитических функций. Общая теория
функций комплексного переменного находилась в стороне от главных линии
развития математики в России в 1860—1917 гг. П. Л. Чебышев не
проявлял интереса к теории аналитических функций и занятия ею не были
в чести ни в его школе, ни долгое время в Петербургском университете.
Конечно, А. М. Ляпунов, В. А. Стеклов, Н. Я. Сонин широко
применяли методы теории аналитических функций Коши и Вейерштрасса —
мы не говорим уже о С. В. Ковалевской. Однако и эти ученые не
занимались специально разработкой самой теории функций. Все же русские
ученые получили в теории аналитических функций комплексного
переменного заслуживающие внимания результаты. Важные открытия были
сделаны одним из учеников Чебышева — Ю. В. Сохоцким. Большая
работа велась по распространению этой теории в университетах.
Специальные курсы по функциям комплексного переменного введены
были в различных университетах в разное время. В Петербурге его
прочитал впервые в 1869 г. Сохоцкий, а в 80-е и 90-е годы его читали также
А. Н. Коркин и другие лекторы. Сохоцкий опирался в своем курсе
на руководство профессора университета в Праге Г. Дюрежа
«Элементарная теория функций одной комплексной переменной величины, со
специальным учетом работ Римана» (Elemente der Theorie der Functionen
einer Complexen veranderlichen Grosse, mit besonderer Beriicksichtigung
der Schopfungen Riemann's. Leipzig, 1864; 5-е изд., 1906). Это
руководство, содержавшее одно из самых первых систематических изложений
геометрической теории функций Римана, рекомендовал слушателям,
наряду с классическим «Курсом анализа» К. Жордана (Cours d'analyse
a l'Ecole Polytechnique, tt. 1—3, Paris, 1882—1887), и Коркин; им
пользовались также в других университетах. В Москве курс теории функций
поставил в 1864 г. А. Ю. Давидов, с 1869 г. его читал Н. В. Бугаев,
а позднее П. А. Некрасов и П. М. Покровский; в Киеве с конца
шестидесятых годов курс вел М. Е. Ващенко-Захарченко, затем П. Э. Ромер,
и еще позднее — Б. Я. Букреев; в Казани в 1867 г. П. И. Котельников,
а вслед за ним А. В. Васильев (1874) и В. П. Максимович; в Харькове
первым, по-видимому, Д. М. Деларю (1874), в Одессе И. В. Слешин-
ский (1889) и затем И. Ю. Тимченко *). Напомним, что теория вычетов
Коши ранее входила в состав курса теории определенных интегралов,
г) С. Е. Белозеров, Основные этапы развития общей теории аналитических
функций, Ростов н/Д., 1862, стр. 252—253; там же, стр. 150—154, см. о руководстве-
Дюрежа.
М. Е. ВАЩЕНКО-ЗАХАРЧЕНКО
493
который еще в середине пятидесятых годов читал в Главном
педагогическом институте М. В. Остроградский и который нередко ставился затем
в университетах.
Первой работой, посвященной теории функций, явилась
магистерская диссертация К. И. Карастелева «Теория интегралов функций
мнимого переменного количества» (М., 1860), содержавшая изложение
теории Коши. Корнелий Иванович Карастелев (1829—1886), окончивший
Московский университет в 1851 г., преподавал долгие годы в Одессе,
сперва в Ришельевском лицее и затем, с самого его основания до 1885 г.,
в Новороссийском университете. Более значительный след в нашей
математической культуре оставила вторая по счету диссертация по теории
функций, именно — докторская диссертация М. Е. Ващенко-Захарчен-
ко. Имя этого ученого нам встречалось уже не раз.
М. Е. Ващенко-Захарченко. Михаил Егорович (или Юрьевич) Ващен-
ко-Захарченко (12 ноября 1825—27 августа 1912), уроженец с. Малиевки
Полтавской губернии, проучившись два года в Киевском университете
и затем примерно столько же в
Сорбонне и Коллеж де Франс, по
возвращении в Киев сдал в 1852 г. экзамены
за университетский курс и начал
преподавательскую деятельность в
средних учебных заведениях. О его
магистерской диссертации 1862 г. по
•символическому исчислению мы
говорили ранее. Осенью 1863 г. Ващенко-
Захарченко стал приват-доцентом
Киевского университета; его первые
лекции были по теории вероятностей
и затем по теории чисел, а
впоследствии он перечитал почти все
математические курсы. Профессуру он
получил в 1867 г. вскоре после защиты
докторской диссертации и неутомимо
работал в университете до 1902 г.
Характерной чертой научной
деятельности Ващенко-Захарченко был
пристальный интерес к новым
направлениям математики. Он первым или
одним из первых пропагандировал М. Е. Ващенко-Захарченко.
в России символические методы,
геометрическую теорию функций, проективную геометрию, теорию
инвариантов, теорию групп и т. д. К сожалению, глубина его эрудиции не
всегда соответствовала ее широте, и многочисленные курсы его сделаны
иногда наспех и содержат промахи. Отметим еще, что
Ващенко-Захарченко живо интересовался и историей математики. Заслугой его был
перевод книг «Начал» Евклида, правда, вольный и содержащий
неточности («Начала Евклида с пояснительным введением и толкованиями»,
Киев, 1880). В предисловии к этому переводу Ващенко-Захарченко
дал одно из наиболее ранних у нас изложений неевклидовой
геометрии, придерживаясь «Начал абсолютной геометрии» профессора
в Граце И. Фришауфа х). «История математики» (т. I, Киев, 1883)
х) J. Frischauf, Elemente der Absoluten Geometrie, Leipzig, 1876.
494 ГЛ. 23. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ; СПЕЦИАЛЬНЫЕ ФУНКЦИИ
Ващенко-Захарченко, доведенная в основном до эпохи Возрождения,
была полезной и богатой сведениями, хотя в большей части своей:
компилятивной книгой.
«Риманова теория функций составного переменного» (Киев, 1867)
явилась, как и упоминавшаяся книга Дюрежа, одним из первых в
мировой учебной литературе изложений вопроса. Ващенко-Захарченко
останавливается здесь на основных разделах теории, начиная с
геометрического истолкования комплексных («составных») чисел, условий Коши —
Римана, понятия о конформном отображении, продолжая интегральной
теоремой Коши и кончая римановыми поверхностями и многозначными
функциями1). Диссертация некоторое время употреблялась и как
учебное пособие.
Ю. В. Сохоцкий. Почти одновременно с Ващенко-Захарченко, но
с гораздо большим научным успехом, теорией функций занялся.
Ю. В. Сохоцкий.
Юлиан Васильевич Сохоцкий (5 февраля 1842—14 декабря 1927),
уроженец Варшавы, где он окончил гимназию, получил высшее
образование в Петербургском университете. По-
видимому, уже вскоре после окончания
в 1866 г. университета основные результаты
его магистерской диссертации были готовы.
Однако П. Л. Чебышев не сразу дал
согласие на постановку защиты работы,
основанной на методах функций комплексного
переменного. Диссертация «Теория
интегральных вычетов с некоторыми приложениями»
(СПб., 1868) была защищена в 1868 г., и вскоре
Сохоцкий, осенью того же года избранный
доцентом, прочитал в Петербургском
университете свои первые курсы по теории функций
и по теории непрерывных дробей с
приложением к интегрированию. Позднее
Сохоцкий читал лекции по другим предметам; так,
с 1876 г. он в течение 40 лет читал высшую
алгебру, и его лекции по специальным главам
этой науки сыграли немалую роль в
воспитании Г. Ф. Вороного. Другим излюбленным.
Ю В Сохо к " курсом Сохоцкого, который он читал с 1884 г.,
была теория определенных интегралов. В
университете он проработал более пятидесяти:
лет, до двадцатых годов нынешнего столетия, сначала в качестве приват-
доцента, а с 1873 г., после защиты докторской диссертации, в звании,
профессора.
Первым пропагандистом теории вычетов Коши в России явился,
как мы знаем, М. В. Остроградский. В курсе теории функций Сохоцкого
учение о вычетах и их приложениях с самого начала заняло центральное
место: ему отведена вся вторая часть программы, первая часть которой
посвящена общим теориям об аналитических функциях и третья —
эллиптическим функциям.
1) Л. Н. Грацианская, Михаил Егорович Ващенко-Захарченко.— Ист.-
матем. исслед., вып. XII, 1961.
ТЕОРЕМА СОХОЦКОГО
495
В предисловии к магистерской диссертации Сохоцкий, отметив
недостаточное внимание современных ему ученых к разработке теории
вычетов, писал, что намерен изложить общие начала теории и показать
новые ее применения. Такие приложения относились к обращению
степенных рядов, именно ряду Лагранжа, а также к разложениям функции
в непрерывные дроби вида
где ak — постоянные числа и qk — целые многочлены. При этом
Сохоцкий получил новым методом ряд результатов Чебышева, содержащихся
в мемуаре «О непрерывных дробях» (1855).
Любопытно заметить, что аппарат теории функций комплексного
переменного изредка и ограниченно все же использовался П. Л. Чебыше-
вым. В частности, интегральная теорема Коши применяется в статье
«О ряде Лагранжа» (1857). Самый ряд Лагранжа, дающий разложение
F(x) по возрастающим степеням величины г/, определяемой уравнением
х = а + уц(х),
где ф(я) — данная функция, Чебышев выводит, не прибегая к теории
функций комплексного переменного. Но при оценке остаточного члена
формулы Лагранжа в случае разложения по степеням эксцентриситета е
величины я, определяемой уравнением Кеплера
x = a + esinx
(х — так называемая эксцентрическая аномалия, а — средняя
аномалия). Чебышев применяет теорему Коши (для некоторого частного
случая). Интегральные вычеты встречаются еще в двух статьях Чебышева
по оценкам интегралов, опубликованных в 1885 и 1887 гг.
Теорема Сохоцкого. Важнейшим — с точки зрения теории
аналитических функций — результатом магистерской диссертации Сохоцкого явилось
все же не применение теории вычетов к различным вопросам, но
проведенное в ней попутно исследование свойств аналитической функции
в соседстве с существенно особой точкой. Обобщая теоремы Коши о
разложении функций в бесконечные ряды в окрестности особых точек,
Сохоцкий пришел к следующей теореме: «Если данная функция f(z)
в некоторой точке z0 обращается в оо бесконечного порядка, то
непременно в этой же точке функция f(z) должна принимать всевозможные
значения» *). Здесь точка, в которой функция обращается в бесконечность
бесконечного порядка, есть существенно особая (по современной
терминологии), а «значения f(z) в точке zQ»—это множество предельных
значений f(z) в этой точке. Теорему Сохоцкого можно передать в более
современном виде следующим образом: в сколь угодно малой
окрестности своей существенно особой точки однозначная функция f(z)
принимает значения, сколь угодно близкие к любому данному комплексному
числу (конечному или бесконечному). Вывод Сохоцкого близок к обычно
принятому теперь доказательству.
*) Ю. В. Сохоцкий, Теория интегральных вычетов с некоторыми
приложениями. СПб., 1868, стр. 17.
496 ГЛ. 23. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ; СПЕЦИАЛЬНЫЕ ФУНКЦИИ
Одновременно с Сохоцким тот же результат опубликовал итальянский
математик Ф. Казорати 1). Более широкую известность теорема получила
благодаря вновь открывшему ее Вейерштрассу, который сформулировал
ее в работе, представленной Берлинской Академии наук в 1876 г. и по
имени которого она до сих пор называется в большинстве руководств.
Эта работа Вейерштрасса стала отправным пунктом многочисленных
и важных исследований, связанных с вопросом о поведении однозначной
функции в окрестности существенно особой точки. Первым крупным
шагом вперед явилось доказательство теоремы Э. Пикара (1879), согласно
которой в сколь угодно малой окрестности существенно особой точки
однозначная функция в точности принимает любое конечное значение,
кроме, быть может, одного. В настоящее время обе эти теоремы, как
и другие применяющиеся к ним результаты, стали предметом
университетских курсов. В двадцатые годы XX века теория распределения значений
целых функций переросла в теорию распределения значений мероморф-
ных функций (финский математик Р. Неванлинна и его школа).
Докторская диссертация Ю. В. Сохоцкого «Об определенных
интегралах и функциях, употребляемых при разложениях в ряды» (СПб., 1873)
также связана с тематикой Чебышева. Посвящена она исследованию
специальных функций, возникающих при разложении в непрерывные
дроби интегралов некоторого вида, и рядов, составленных из таких
функций, а именно функций, подобных функциям Лежандра (многочленов
Якоби), обобщенных полиномов Чебышева — Лагерра и др., о которых
говорилось ранее. Результаты Сохоцкого в этом направлении, и, в
частности, общность положенного в основу их вывода приема, получили
высокую оценку Чебышева 2).
Граничные свойства аналитических функций. Особенно
примечательны исследования Сохоцкого по теории граничных свойств аналитических
функций, т. е. их свойств в окрестности границы области, в которой
функция предполагается однозначной и аналитической (особые точки
принадлежат этой границе). Именно в докторской диссертации Сохоцкого
были впервые изучены граничные значения интегралов типа Коши.
Интегралом Коши называют выражение
1 Р № dl
2ju J ? — z '
L
где f(z) — функция, аналитическая в некоторой области G и на
ограничивающем ее замкнутом контуре L, удовлетворяющем некоторым
условиям. Во всякой точке z внутри области G интеграл Коши выражает саму
аналитическую функцию /(z), а во всякой внешней точке он равен нулю.
Интегралом типа Коши называется выражение
1 Р /(?)<%
2ni j ? — z '
L
причем контур L может быть как замкнутым, так и разомкнутым, а
функция /(?) задана только на L, причем она не обязательно аналитическая,
г) А. Дингхас указывает, что к этой же теореме пришли несколько ранее
(между 1854 г. и 1859 г.) Брио и Буке. См. A. D i n g h a s, Der Weierstraj3sche Satz
und die Anfange der Werteverteilungstheorie. Festschrift zur Gedachtnisfeier fur Weierstra|3.
1815—1865. Hsg. von H. Behnke und K. Kopfermann. Koln und Opladen, 1966, стр. 171.
2) П. Л. Ч e б ы ш е в, Полное собрание сочинений, т. V, стр. 288—289.
ГРАНИЧНЫЕ СВОЙСТВА АНАЛИТИЧЕСКИХ ФУНКЦИЙ
497
а скажем, только непрерывная на L или даже разрывная, но
интегрируемая; точка z предполагается лежащей не на контуре L.
Если взять контур L снова замкнутым, то интеграл типа Коши
определяет две, вообще говоря, различные аналитические функции: одну,
Fi(z), внутри контура L, другую, F2(z), вне контура. На самом контуре
L интеграл не имеет смысла, поскольку функция J , вообще говоря,
не интегрируема вдоль L, если точка z0 лежит на контуре. Однако выра-
С / (С) dl « гл
жению \ хо/ можно придать подходящий смысл. <Зто достигается
следующим образом. Вокруг точки z0 как центра описывается окружность
бесконечно, малого радиуса е и из L исключается отсекаемая этой
окружностью бесконечно малая дуга I. Тогда интеграл \ }" » взятый по
L-l
оставшейся части контура L—Z, при 8 —> О стремится к определенному
конечному пределу, который и принимается за значение интеграла
\ rZ-z (главное значение в смысле Коши). Функции F^z) и F2{z)
L
стремятся к определенным конечным пределам Fi(z0) и Fe(z0), если
точка z стремится к какой-либо точке z0 контура, оставаясь при этом
в первом случае внутри L и во втором вне L. Оказывается, между этими
предельными значениями интеграла типа Коши Fi(z0), Fe(z0) и
значениями граничной функции f(z0) существуют зависимости, установление
которых и составило содержание двух теорем Сохоцкого. Согласно первой
из них разность предельных значений интеграла типа Коши в точке zQ
равна значению данной граничной функции f(z0) в этой точке, т. е.
Fi(z0)-Fe(z0) = f(z0).
Вторая теорема выражает внутренние и внешние предельные значения
интеграла типа Коши через его главное значение и значение граничной;
функции:
L L'
вместе с главным значением интеграла типа Коши здесь выступает и
соответствующее сингулярное интегральное уравнение, о чем упоминалось
выше. Мы передали основное содержание теорем Сохоцкого в том виде,
как они приводятся в руководствах нашего времени. У него самого они
сформулированы в, несколько отличных терминах и условиях.
Открытия Ю. В. Сохоцкого по теории граничных свойств
аналитических функций оставались забытыми долгие десятилетия, пока на них
не обратили внимание советские специалисты Г. М. Голузин (1906—1952)
и А. И. Маркушевич х). Проблемы, разработку которых начал Сохоцкий,
получили новое развитие в начале XX века, причем в основу были
положены методы теории функций действительного переменного. Интеграл
типа Коши и другие выражения, служащие для представления
аналитических функций, например, интеграл Пуассона, стали рассматривать
х) А. И. Маркушевич, Очерки по истории теории аналитических функций,
М.—Л., 1951, стр. 80—83; о н ж е, Вклад Ю. В. Сохоцкого в общую теорию
аналитических функций.—Ист.-матем. исслед., вып. III, 1950.
498 ГЛ. 23. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ; СПЕЦИАЛЬНЫЕ ФУНКЦИИ
при более общих предположениях относительно граничной функции
f(z) и контура L, рассматривая различные множества точек разрыва
этой функции, понимая интеграл в смысле Лебега, и т. п. Первые
существенные результаты были получены французским математиком П. Фату
в 1906 г., затем через два года И. Племель занялся изучением
предельных значений интегралов типа Коши при предположении непрерывности
f(z); Племель при этом вывел вновь соотношения, содержащиеся во
второй и первой теоремах Сохоцкого. Нам придется еще говорить о
дальнейших исследованиях в этом направлении, проведенных на самом рубеже
рассматриваемого периода В. В. Голубевым и И. И. Приваловым.
Ю. В. Сохоцкому принадлежат и другие работы в теории функций,
в частности, по эллиптическим и тэта-функциям, напечатанные на
польском языке. Они до сих пор не изучены историками математики х).
Эллиптические и гиперэллиптические функции. В конце XIX века
большое влияние и распространение получили идеи теории
аналитических функций Вейерштрасса, в частности, его теория эллиптических
и гиперэллиптических функций. Одним из
ее пропагандистов выступил и Сохоцкий,
который в более ранних работах исходил
от исследований Коши. В 1896—1897 гг.
он выступил в Петербургском
математическом обществе, председателем которого
состоял после смерти Имшенецкого, с
несколькими сообщениями, посвященными
упрощению изложения теории
эллиптических функций по Вейерштрассу.
Построение, предложенное Сохоцким, положил
в основу своего «Опыта элементарной
теории вейерштрассовых функций <§>и, 1ц
и ои с приложением статей об
эллиптических функциях sn и, сп и и dn и» (М., 1898)
профессор Артиллерийской академии и член
Петербургского математического общества
Сергей Георгиевич Петрович (1869—1926)2).
Вейерштрассовой теории
эллиптических и гиперэллиптических функций3)
были посвящены труды и других русских
М. А. Тихомандрицкий. ученых того времени. Сюда относятся,
например, исследования Матвея
Александровича Тихомандрицкого (1844—1921), сына одного из первых киевских
профессоров Александра Николаевича Тихомандрицкого (1800—1888),
который, впрочем, в Киевском университете работал недолго, а затем
занимал различные должности в Главном педагогическом институте»
Казанском учебном округе и Министерстве народного просвещения.
В 1865 г. М. А. Тихомандрицкий окончил Петербургский университет
и при нем же в 1876 г., защитил магистерскую диссертацию о гипергео-
х) И. Я. Д е п м а н, С.-Петербургское математическое общество.— Ист.-
матем. исслед., вып. XIII, 1960, стр. 36.
2) Там же, стр. 37.
3) Гиперэллиптические функции получаются при обращении гиперэллиптических
интегралов, т. е. интегралов от рациональных функций R(x, у), где у есть квадратный
корень из многочлена выше четвертой степени.
Б. Я. БУКРЕЕВ
499
метрических рядах. Несколько лет он был доцентом Петербургского
университета, где, в частности, читал курс эллиптических функций,
а также вел занятия на Высших женских курсах. В 1883 г. он был избран
доцентом Харьковского университета и здесь преподавал до 1903 г.,
с 1885 г. в звании профессора. После того он возвратился в Петербург
и вновь взял на себя отдельные приватдоцентские курсы в здешнем
университете. Среди работ Тихомандриц-
кого выделяется его докторская
диссертация «Обращение гиперэллиптических
интегралов» (Харьков, 1885),
базирующаяся на теории Вейерштрасса, лекции
которого он слушал в 1883—1884гг.
Большой известностью пользовались
учебники Тихомандрицкого, в том числе «Теория
эллиптических интегралов и
эллиптических функций» (Харьков, 1895) и
«Основания теории абелевых
интегралов» (Харьков, 1895). Ему принадлежат
еще ценные статьи по истории
математики в Харьковском университете,
написанные в связи со 100-летним юбилеем
этого учебного заведения. Они
помещены в сборнике
«Физико-математический факультет Харьковского
университета за первые 100 лет
существования», под ред. И. П. Осипова и Д. И.
Багалей (Харьков, 1908).
Тем же кругом вопросов занимался „ „ „
ученик Бугаева Петр Михайлович П' М' ПокРов™
Покровский (1857—1 марта 1901),
в 1881 г. оставленный при кафедре математики для подготовки к
профессорскому званию. В течение нескольких лет Покровский был приват-
доцентом Московского университета и в 1887 г. защитил в нем
магистерскую диссертацию «Теория ультраэллиптических функций I класса» (Матем.
сборник, т. 13), за которой последовала докторская: «О преобразованиях
ультраэллиптических интегралов и функций I класса» (Матем. сборник,
т. 15, 1891). И на Покровского оказал сильное влияние Вейерштрасс,
лекции которого он слушал во время заграничной командировки 1889—
1890 гг. С 1891 г. Покровский был профессором Киевского
университета; работая здесь, он опубликовал еще несколько статей по той же
тематике, а также лекционный курс «Теория функций комплексного
переменного» (Киев, 1892).
Упомянем еще магистерскую работу другого ученика Бугаева — Петра
Сергеевича Назимова (1851 —1901) «О приложениях эллиптических
функций к теории чисел» (М., 1884), за которую диссертанту была
присуждена степень доктора чистой математики.
Б. Я. Букреев. В Киевском университете занятия теорией функций
были продолжены учеником Ермакова и Ващенко-Захарченко — Борисом
Яковлевичем Букреевым (24 августа 1859—2 октября 1962). В 1883—
1886 гг. Б. Я. Букреев опубликовал свои первые статьи по общей теории
целых и мероморфных функций. В упоминавшейся работе 1876 г.
Вейерштрасс распространил основную теорему алгебры о разложении
500 ГЛ. 23. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ; СПЕЦИАЛЬНЫЕ ФУНКЦИИ
многочлена на множители на любые целые трансцендентные функции, а его
ученик Миттаг-Леффлер год спустя дал обобщение теоремы о разложении
рациональной дроби в сумму элементарных дробей на случай
произвольной мероморфной функции (мероморфная функция является аналогом
дробно-рациональной функции и может быть представлена как
отношение двух целых функций). Магистерская диссертация Букреева «О
разложении трансцендентных функций на
частные дроби» (Университ. известия,
Киев, 1886) содержала, помимо
изложения общей теории, многочисленные
примеры конкретных разложений.
Вскоре Букреев защитил докторскую
диссертацию «О фуксовых функциях
нулевого ранга с симметрическим
основным полигоном» (Киев, 1889),
явившуюся первой русской работой по
теории автоморфных функций,
фундамент которой за несколько лет до того
заложили Ф. Клейн и А. Пуанкаре.
Б. Я. Букреев и позднее
продолжал заниматься отдельными
вопросами теории функций комплексного
переменного. Ему принадлежат также
исследования по теории рядов,
вариационному исчислению, неевклидовой
геометрии и др. Курсы его были
значительно выше по уровню
математической строгости, чем киевских мате-
„ а л матиков старшего поколения. Сохра-
Ъ. Ул.. JbVKpeGB. -* ^
няя редкую работоспособность до
самого конца своей долгой жизни,
В* Я. Букреев продолжал публиковать работы еще в столетнем возрасте.
В Киевском университете он преподавал с 1885 г. около 75 лет.
Другие работы. Наши математики разрабатывали и другие отделы
теории аналитических функций. Так, Иван Романович Брайцев (14 января
1870—4 января 1947), окончивший Московский университет в 1896 г.
и некоторое время преподававший в Варшавском университете, а с 1918 г.
профессор основанного в том же году Нижегородского (Горьковского)
университета, продолжил исследования Ж. Адамара и Э. Бореля об
особых точках функции, заданной рядом Тейлора. Свой новый метод Брайцев
развил в целой серии работ: «Изыскание особых точек функции,
определяемой рядом Тейлора» (М., 1907), «Новый метод изыскания
особых точек функции, определяемой строкой Тейлора» (Варшава, 1910),
«Об особых точках аналитических функций» (Варшава, 1915) и других.
К этим изысканиям примыкает статья Михаила Федоровича Субботина
(28 июня 1893—26 дек. 1966), окончившего Варшавский университет
в 1914 г. (Матем. сборник, т. 30, 1916). Брайцев работал в том же
направлении и других областях теории аналитических функций и в советское
время; ему принадлежат также ценные результаты по цилиндрическим
функциям. М. Ф. Субботин переключился позднее на небесную
механику, к которой относятся его главные достижения; в 1946 г. он был
избран членом-корреспондентом Академии наук СССР.
ИСТОРИК ТЕОРИИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ И. Ю. ТИМЧЕНКО 501
В конце XIX века в теории аналитических функций выросло еще
одно направление — теория роста функций, в которой изучаются связи
между порядком роста функции и различными ее свойствами,
проведением коэффициентов ее ряда Тейлора и т. д. Первые основоположные
результаты здесь получил в 1883 г. А. Пуанкаре, затем Ж. Адамар (1893),
Э. Борель и другие. В России этому кругу вопиосов посвятил
магистерскую диссертацию «Исследование по теории
роста функций» (Казань, 1910) воспитанник
Казанского университета и ученик А. В.
Васильева Николай Николаевич Парфентьев
(31 марта 1877—22 января 1943),
работавший в родном университете с 1904 г.,
вначале приват-доцентом, а с 1911 г.—
профессором.
В Одессе особые точки аналитических
функций изучал И. В. Слешинский (Матем.
сборник, т. 18, 1893) и ему же принадлежит
несколько работ о разложениях
аналитических функций в непрерывные дроби
и о сходимости и особых точках
непрерывных дробей на плоскости комплексного
переменного. Одна из этих работ «О
сходимости непрерывных дробей» (Зап. Матем.
отд. Новоросс. о-ва естествоиспытателей,
т. X, 1889) явилась магистерской
диссертацией Слешинского.
Наше изложение было бы неполным,
если бы мы не отметили еще работы н* н> ПаРФентьев.
Н. Е. Жуковского по гидро-и
аэродинамике, его замечательного ученика, впоследствии академика, Сергея
Алексеевича Чаплыгина (5 апреля 1869—8 октября 1942) по аэродинамике
и теории упругости и профессора Гурия Васильевича Колосова
(1867—1936), а также Н. И. Мусхелишвили по теории упругости. По
своему содержанию эти исследования лежат за пределами нашего
рассмотрения. Мы упоминаем их потому, что в них было положено начало
чрезвычайно плодотворным приложениям теории аналитических функций,
которые получили особенное развитие уже в советское время, причем
оказали мощное влияние на разработку ряда проблем самой этой теории1).
Историк теории аналитических функций И. Ю. Тимченко. В заключение
скажем несколько слов об одной работе, стоящей несколько особняком
— «Основаниях теории аналитических функций». Это — магистерская
диссертация воспитанника (1885), затем доцента (1888) и профессора
(1914) Новороссийского университета Ивана Юрьевича Тимченко (1862—
1939). Занявшись под влиянием Слешинского теорией аналитических
функций, Тимченко задумал большой труд, который должен был
систематически охватить эту науку в целом в ее связях с основными понятиями
математического анализа. Первую часть предполагалось отвести истории,
вторую — общей теории, построенной в соответствии с принципами
*) Ср. А. И. М а р к у ш е в и ч, Очерки по истории аналитических функций
(очерк пятый); СЕ. Б е л о з е р о в, Основные этапы развития общей теории
аналитических функций, Ростов н/Д., 1962, стр. 252—277.
502 ГЛ. 23. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ; СПЕЦИАЛЬНЫЕ ФУНКЦИИ
Вейерштрасса; в одной из глав автор намеревался изложить идеи молодой
тогда теории множеств Г. Кантора. Полностью осуществить свой замысел
Тимченко не удалось и свет увидел только первый том первой части.
Эта работа «Основания теории аналитических функций. Часть I.
Исторические сведения о развитии понятий и методов, лежащих в основании
теории аналитических функций, т. I» печаталась в 1892—1899 гг. в
«Записках» Математического отделения Новороссийского общества
естествоиспытателей (тт. XII, XVI, XIX) и в 1899 г. вышла отдельной книгой.
История вопроса доведена здесь до знаменитого мемуара Коши 1825 г.
об определенных интегралах, взятых между мнимыми пределами. «Эпоха
точной разработки математического анализа; основание новой теории
функций», как кратко характеризовал Тимченко девятый, по его счету,
период развития теории аналитических функций, должна была стать
предметом второго тома первой части. Единственный опубликованный
том, в котором более 650 страниц, замечателен по исключительному
богатству исследованного в нем материала и по точности его анализа.
Книгой Тимченко, ныне являющейся библиографической редкостью,
широко пользовались последующие историки математики, и она
получила большую известность за рубежом. К сожалению, этот
фундаментальный труд никто пока не решается продолжить с той исчерпывающей
полнотой, с которой его выполнил выдающийся одесский историк
математики.
Исследования по цилиндрическим функциям; Н. Я. Сонин. Начала
теории специальных функций заложены были в России частью Д. Бернул-
ли и особенно Л. Эйлером. Значительное развитие некоторые отделы
теории специальных функций получили в нашей стране в
рассматриваемый период; существенную роль сыграли при этом методы теории
аналитических функций. Мы остановимся сначала на цилиндрических
функциях, введенных названными петербургскими академиками.
Цилиндрической функцией первого рода с индексом п называется
частный интеграл Jn(x) дифференциального уравнения
*|?+*-? + (*-»')у=о, (1)
ограниченный при х = 0. Частный интеграл Yn(x) того же уравнения,
при х = 0 неограниченный, называют цилиндрической функцией второго
рода с индексом п.
В первой половине XIX века цилиндрические функции получили
новые применения в теории теплопроводности Фурье, в исследованиях
но теории возмущений в движении планет Ф. Бесселя (1824) х), в
работах по гидродинамике М. В. Остроградского (1826). В это время создается
общая теория цилиндрических функций первого рода, в дальнейшей
разработке которой принимают участие немецкие ученые О. Шлемильх
(1857, случай целого индекса), Э. Ломмель (1868, любые вещественные
1) Цилиндрические функции нередко называют до сих пор по имени Бесселя,
так же как уравнение (1). Несмотря на заслуги Бесселя в общей теории функций
Jn(x) при целом индексе и ее приложений, такая терминология, введенная в 1857 г.
О. Шлемильхом, исторически не оправдана. Другой немецкий математик, Э. Гейне,
в 1868 г. предложил название «цилиндрические функции», ибо они играют в теории
теплоты и притяжения для цилиндра ту же роль, какую шаровые функции играют в
случае шара. Подробнее см.: В. В. Г у с с о в, Развитие теории цилиндрических
функций в России и СССР.— Ист.-матем. исслед., вып. VI, 1953.
ИССЛЕДОВАНИЯ ПО ЦИЛИНДРИЧЕСКИМ ФУНКЦИЯМ; н. я. сонин 503
индексы), Г. Ганкель (1869, комплексные индексы). Несколько позднее
началась разработка общей теории функций второго рода: для целых
индексов это сделал К. Нейман (1867), для произвольных комплексных
индексов Г. Ганкель (1869), один пробел в исследовании которого
восполнил Г. Вебер (1873). В результате работы Ганкеля учение о
цилиндрических функциях в дальнейшем развивается в тесной связи с теорией
функций комплексного переменного.
В этих исследованиях заметна тенденция построения все более
широкого класса цилиндрических функций. Оригинальное изложение теории
функций Jn (х) дал при помощи своего
метода обобщенного дифференцирования
А. В. Летников (Матем. сборник, т. 7,1874).
Вскоре затем выступил с классическими
работами в этой области Сонин г).
Николай Яковлевич Сонин родился в
небогатой дворянской семье в г. Туле 22
февраля 1849 г. Учился он в одной из москов-
скихгимназий, где математику преподавали
известные педагоги Александр Федорович
Малинин (1835—7 марта 1888) и
Константин Петрович Буренин (ум. в 1882 г.),
авторы распространенных и много раз
издававшихся «Руководства к арифметике»,
«Собрания арифметических задач» (1 изд., М., 1866)
ж «Руководства алгебры и собрания
алгебраических задач» (1 изд., М., 1870). В
университете учителем Сонина был Н. В.
Бугаев, предложивший ему для конкурсного
сочинения тему «Теория функций
комплексного переменного». н я с н
За это сочинение Сонин получил в
1869 г. золотую медаль. В том же году он
окончил университет. Впоследствии он широко применял методы теории
функции комплексного переменного. В 1869 г. Сонин выступил на II съезде
русских естествоиспытателей и врачей в Москве с докладом о
дифференцировании с произвольным индексом, в котором подверг критике теорию
А. В. Летникова. В 6 томе Математического сборника (1872) помещены статья
Сонина и ответ Летникова с разбором собственной конструкции его критика.
В 1871 г. Сонин защитил магистерскую диссертацию «О разложении
функций в бесконечные ряды» (Матем. сб., т. 5) ив 1872 г. перешел
tl& работу приват-доцентом в Варшавский университет. Здесь он работал
20 лет. В 1874 г. в Москве состоялась защита уже упоминавшейся
докторской диссертации Сонина, посвященной уравнениям с частными
производными; в 1877 г. он получил звание профессора. Как педагог, Сонин
сыграл очень большую роль в истории физико-математического
факультета Варшавского университета. В 1885 и 1888 гг. он избирался на пост
декана; был первым председателем физико-математического отделения
Варшавского общества естествоиспытателей; участвовал в редактировании
ч<Варшавских университетских известий».
Варшавский период жизни Сонина отмечен активной научной
деятельностью. В эти годы появляются его блестящие мемуары по цилиндри-
х) А. И. К р о п о т о в, Николай Яковлевич Сонин, Л., 1967.
504 ГЛ. 23. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ; СПЕЦИАЛЬНЫЕ ФУНКЦИИ
ческим функциям и Г-функциям, по оценкам определенных интегралов,
по теории ортогональных многочленов, где он указал новые пути
исследования, о точности формул суммирования Эйлера — Маклорена и т. д.
Одной из особенностей творчества Сонина было стремление к возможно
более общей и широкой трактовке проблем. Мы увидим это далее,
говоря о его работах по специальным функциям.
Исследования Сонина высоко ценились современниками.
Совокупность семи работ Сонина по определенным интегралам, ортогональным
многочленам и некоторым другим смежным вопросам анализа была,
по представлению Имшенецкого, Чебышева и Маркова, награждена
Академией наук в 1890 г. премией им. Буняковского *); в начале 1892 г.
он был избран ее членом-корреспондентом, а в 1893 г. ординарным
академиком. В 1894—1899 гг. Сонин читал лекции на Высших женских курсах.
В 1899—1907 гг. он вместе с А. А. Марковым издал собрание сочинений
П. Л. Чебышева в двух томах. Он активно участвовал в работе
Петербургского математического общества и за 1894—1897 гг. выступил в нем
с 15-ю докладами. Деловые качества Н. Я. Сонина и вместе с тем
политические консервативные взгляды позволили ему занять высокие
административные посты в Министерстве народного просвещения. В 1899—1901 гг.
он был попечителем Петербургского учебного округа, а затем до конца
жизни членом совета Министерства и председателем его Ученого комитета,
главной задачей которого было рассмотрение программ и учебных
руководств для средней школы. Этому делу Сонин отдавал много времени.
При его участии, среди прочего, пересмотрены были программы реальных
училищ и в их старших классах с 1907—1908 уч. г. введены начала ана-
дитической геометрии и анализа. Н. Я. Сонин скончался 27 февраля
1915 г.
Цилиндрические функции встречаются у Сонина впервые в
магистерской диссертации 1870 г. Используя формулу Коши
Т{ ' 2ni J а—z '
L
Сонин приводи! задачу разложения аналитической функции f(z) по тем
или иным функциям Zn (z) к разложению одной лишь функции ——-
оо
п=0
причем коэффициенты разложения Ап зависят от а, функции Zn — от z.
В качестве функций Zn(z) берутся цилиндрические функции, функции
Лежандра и др.
Основной труд Сонина в рассматриваемой области, «Исследования
о цилиндрических функциях и о разложении непрерывных функций
в ряды» появился на французском языке в 16-м томе «Mathematische
Annalen» за 1880 г. Он изобилует новыми открытиями.
Сонин дал совершенно новое и весьма общее построение всей теории
цилиндрических функций, определив последние, как частные
решения некоторых функциональных рекуррентных уравнений. Прежде
всего вводятся функции (позднее названные полуцилиндрическими)
х) См. отзыв в кн.: П. Л. Ч е б ы ш е в, Полное собрание сочинений, т. V,
стр. 307—310.
ИССЛЕДОВАНИЯ ПО ЦИЛИНДРИЧЕСКИМ ФУНКЦИЯМ; н. я. сонин 505
SQ(x)f St(x), S2(x), . . ., удовлетворяющие уравнению
Sn+l(x) + 2^-Sn.l(x) = 0
и условию Si(x)= ~d~* 3Десь SQ(x) — произвольная
аналитическая функция, х — комплексная переменная. Полуцилиндрическая
функция Sn может быть записана в символической форме
о (-D + yW^i)n+{-D-yW+i)n с
ол = ^ о0,
где Z) = — . Для функции S0(a + x), разложимой в ряд Тейлора, а затем
и для Sp (а + х) выводятся разложения в ряды
S0(a + х)= J0(a) S0(x) + 2 § (- 1)п Jn(a) Sn(x),
n=l
oo
Sp{a + x)= 2 Jn(a)Sp-.n(x),
причем Jn(a) оказываются в точности цилиндрическими функциями
первого рода с целым индексом. Вторая написанная формула выражает
теорему сложения. После этого функции Sn(x) обобщаются на случай
произвольного индекса, а именно — общие цилиндрические функции
определяются, как решения системы двух функциональных уравнений,
первое из которых написано выше, а второе есть
nSn(x) = | [Sn.t(x) + Sn+i(x)l
причем в обоих уравнениях п может быть уже произвольным числом;
заметим, что второму условие при целом п удовлетворяют функции
Jn(x). В рассматриваемом мемуаре Сонин вывел многие свойства общих,
а также специальных цилиндрических функций, среди них указанную
теорему сложения, различные интегральные представления и
разложения в ряды, новые разложения по этим функциям, вычислил ряд новых
определенных интегралов, содержащих цилиндрические функции и т. д.
Наряду с методами теории аналитических функций Сонин широко
применял методы символического исчисления, первым пропагандистом
которых у нас явился Ващенко-Захарченко. Позднее Сонин еще
несколько развил свои исследования в этом направлении (Math. Annalen^
В. LIX, 1904) !).
Некоторые результаты Сонина были заново получены, иногда с
запозданием на много лет, за рубежом 2). В целом, однако, как общие идеи,
так и частные открытия Сонина получили большую известность и
дальнейшее развитие повсюду. Они включены в известные трактаты Н.
Нильсена (N. Nielsen, Handbuch der Theorie der Cylinderfunktionen,
Leipzig, 1904) и Г. H. Ватсона (G. N. W a t s о n, Theory of Bessel Functions,
Cambridge, 1922; русский перевод вышел в 1949 г.). В дальнейшем
вопросами теории цилиндрических функций занимались многие наши ученые.
!) Эти и другие работы опубликованы в кн.: Н. Я. Сонин, Исследования
о цилиндрических функциях и специальных полиномах. Редакция и комментарии
Н. И- Ахиезера, М., 1954.
2) Подробнее см.: В. В. Гуссов, Развитие теории цилиндрических функций
в России и СССР.— Ист.-матем. исслед., вып. VI, 1953.
506 ГЛ. 23. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ; СПЕЦИАЛЬНЫЕ ФУНКЦИИ
Асимптотические разложения с помощью дифференциальных уравнений
вывели И. Р. Брайцев (Изв. Варш. политехи, ин-та, 1902—1903) и, в
рамках большого исследования об асимптотических выражениях многих
классов ортогональных функций, определяемых линейными уравнениями
второго порядка, В. А. Стеклов (Сообщ. Харьк. матем. о-ва, т. 10, 1907).
Цилиндрические функции многих переменных изучал М. И. Акимов
(1916 и след. гг.). Новые разложения по цилиндрическим функциям нашел
(1911 и след. гг.) Владимир Сергеевич Игнатовский (20 марта 1875—1943),
впоследствии профессор Ленинградского университета и с 1932 г. член-
корреспондент Академии наук СССР. Г. Ф. Вороной впервые применил
цилиндрические функции в аналитической теории чисел, установив их
связь с суммированием функции %(п), выражающей число делителей
натурального числа п («Об одной трансцендентной функции и ее
приложениях к суммированию некоторых рядов»; Ann. Scient. Ее. Normale,
t. 21, 1904). С другой стороны, цилиндрические функции получали все
более обширные приложения в гидродинамике, небесной механике, теории
упругости и других отраслях науки.
Гамма-функция. Широкими обобщающими идеями и применением
конечноразностных методов отмечены также работы Н. Я. Сонина по
теории гамма-функции и по функциям Бернулли. Основные результаты,
относящиеся к гамма-функции, содержатся в работе «О прерывной
функции [х] и ее применениях» (Варш. универс. изв., 1889). Сама эта функция
[х] вводится как частное решение разностного уравнения [х -f 1] —
— [х] = 1, обращающееся в нуль, когда 0<? < 1. С ее помощью Сонин
получил ряд своих результатов, в том числе носящую его имя формулу
суммирования, о которой говорилось ранее по поводу работ Г. Ф.
Вороного и И. М. Виноградова по аналитической теории чисел. Отправным
пунктом исследования гамма-функции у Сонина служит опять-таки
уравнение в конечных разностях
F(x + l)-F(x) = f(x),
рассматриваемое при некоторых ограничениях, наложенных на данную
функцию f(x). Установив ряд свойств функции F(x), Сонин затем
исследует решения уравнения, возникающие при том или ином выборе f(x)
и таким образом (при f(x) = log х) получает обобщения многих предложений
теории гамма-функции, новые интегральное представление и
асимптотические разложения, а также значительно более точные оценки остаточных
членов ранее найденных разложений. Позднее оригинальное построение
всей теории гамма-функции разработал на основе одного соотношения,
вытекающего из исследований по теории замкнутости, В. А. Стеклов;
при этом также были найдены новые результаты (Annali di mathem. рига
е applicata, т. 21, 1913). Класс специальных функций, по своим многим
свойствам сходных с гамма-функцией, ввел и изучил в магистерской
диссертадии «О функциях, подобных функции гамма» (Харьков, 1892)
и других работах Владимир Петрович Алексеевский (1858—1916),
работавший в 1893—1906 гг. в Харьковском университете, а после в Томском
технологическом институте.
Функции и числа Бернулли. Остановимся в заключение на функциях
Бернулли и связанных с ними числах Бернулли. Исторически первыми
были введены числа Я. Бернулли Bk, о которых уже говорилось в главе,
посвященной Л. Эйлеру. К. Г. Якоби (1834) и М. В. Остроградский
ФУНКЦИИ И ЧИСЛА БЕРНУЛЛИ
507
{Мемуар об определенных квадратурах, 1841), исследуя остаточный член
формулы суммирования Эйлера — Маклорена, пришли к так
называемым многочленам Бернулли, которые для натуральных п можно
определить символической формулой
Вп(х) = (х + В)п,
где Вк следует заменить везде на Вк.
Последующие работы И. Раабе (1851), О. Шлемильха (1856) и других
положили начало общей теории чисел и функций Бернулли. Функции
Бернулли с отрицательным индексом ввел в статье «Об обобщении
функций Я. Бернулли» (Зап. Акад. наук, сер. VII, т. 31, 1883) В. Г. Имше-
нецкий, показавший также их применения к вычислению интегралов
(Прилож. к Запискам Акад. наук, т. 52, 1886). Еще более широкие
обобщения были предложены Д. М. Синцовым — вначале на дробные
рациональные (Изв. Казанск. физ.-матем. о-ва, 1890) и затем на произвольные
комплексные индексы, причем были использованы обобщенные производные
в форме, предложенной Сониным («Бернуллиевы функции с произвольными
указателями», там же, 1891). Сам Н. Я. Сонин также внес вклад в эту
теорию, применив в ней методы теории конечных разностей, которые он так
успешно использовал при изучении цилиндрических и Г-функций.
Многочлен Бернулли Вп(х) Сонин (Варш. Унив. изв., 1888) определил, как
многочленное решение уравнения в конечных разностях
F(x + 1)—F(x)=nxn-1 (71 = 1,2, ...).
обращающееся в нуль при х = 0; он показал также, как аналогичным
способом определить функции Имшенецкого. Такой подход позволил
развить теорию функций Бернулли с особенной простотой, и с тех пор
эта теория становится одной из глав теории конечных разностей
(А. А. Марков, Н. Э. Нерлунд и др.). В той же работе 1888 г. «О бернул-
лиевых полиномах и их приложениях» Сонин дал обобщение формулы
•суммирования Эйлера — Маклорена, в которой вместо чисел Бернулли
участвуют многочлены Бернулли, а отсюда получил разложения в ряды
¦('+т)
функций для In—р/~л и 1п—г ( \ • Эти же разложения вновь
получил в 1895 г. Ш. Эрмит.
Мы упомянем еще обобщающие исследования В. А. Стеклова (Сообщ.
Харьк. матем. о-ва, т. 8, 1902) о формулах суммирования, связанные как
с его работами по теории Г-функции, так и с оригинальным применением
функций Бернулли.
Числа Бернулли находят приложения в теории чисел; например,
с ними тесно связана большая теорема Ферма. Так, еще Куммер доказал
б 1850 г. справедливость этой теоремы для всякого нечетного простого
показателя/?, не делящего числителей бернуллиевых чисел В2, В k, . . ., 2?р_3.
Изучением чисел Бернулли с арифметической точки зрения занимался
ряд исследователей. Введем положительные числа &&, которые также
обычно называют по имени Бернулли и которые связаны с В2к
соотношением
(-l)k-i bk = B2k.
В 1840 г. немецкий математик Хр. Штаудт доказал, что (—l)kbk = Т -\-
+ 2 1/Х, где Т — целое, а 1 — простые числа, такие, что 2к делится
1111
на X — 1; например, Ь3 = 1 —у —-о Т = 42' Позднее английский
508 ГЛ. 23. ТЕОРИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ; СПЕЦИАЛЬНЫЕ ФУНКЦИИ
ученый Дж. Адаме (1878) высказал без доказательства утверждение1
о некоторых свойствах числителей чисел bk.
Г. Ф. Вороной в статье «О числах Бернулли» (Сообщ. Харьк. матем.
о-ва, т. 2, 1890) дал новый, более простой вывод теоремы Штаудта и
одновременно доказал теорему о составе числителей бернуллиевых чисел Ьд,
обобщающую теорему Адамса* Теорема Вороного гласит, что если т —
индекс числа Ът —делится на к = р?, р$ , . . ., /#, где ри р2, . . ., pL —
простые числа, не делящие знаменатель числа Ът, то его числитель
делится на к. В «Элементарном курсе теории чисел» Д. А. Граве (изд. 2-е,
Киев, 1913) числам Бернулли посвящена специальная глава, в которой
приведены результаты Штаудта и Вороного, причем исправлена одна
неточность, вкравшаяся в рассуждения последнего *).
Мы рассмотрели чрезвычайно обширный круг исследований,
проведенных несколькими поколениями ученых, принадлежащих к
петербургской математической школе или с нею тесно связанных; в некоторых
случаях нам приходилось касаться и работ, более далеких от основных
интересов этой школы. В заключение обратимся к трем циклам
изысканий, проводившихся главным образом вне рамок этой школы — по
геометрии, алгебре и теории функций действительного переменного. Эти
направления, связанные частью с классическими, частью с новыми
течениями математической мысли, развивались в университетах Москвыг
Казани, Киева, Харькова, Одессы.
х) Подробнее см. В. В. Л и х и н, Теория функций и чисел Бернулли и ее
развитие в трудах отечественных математиков.— Ист.-матем. исслед., вып. XII, 1959.
ГЛАВА ДВАДЦАТЬ ЧЕТВЕРТАЯ
ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ;
ВОПРОСЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
О. И. Сомов и векторное исчисление. П. Л. Чебышев и его ученики
занимались геометрией немного. Наиболее яркими геометрами в России
первой половины XIX столетия были Н. И. Лобачевский и Ф. Г. Миндинг.
Все же и представители петербургской школы внесли свой вклад и в
дифференциальную геометрию. Мы имеем в виду некоторые работы О. И.
Сомова и самого П. Л. Чебышева.
О. И. Сомов первый в нашей стране и один из первых в мире начал
систематически применять векторное исчисление к механике и геометрии.
В дальнейшем развитии векторного исчисления выдающуюся роль
сыграли глубокие исследования У. Гамильтона и Г. Грассмана. Но в то время
труды этих ученых еще не привлекли широкого внимания (только в
Англии нашлись последователи Гамильтона) и особенные заслуги в
распространении векторного исчисления и его применений выпали на долю
Б. де Сен-Венана (1845, 1847) и его последователя А. Резаля (1862),
которые разработали начала векторной алг/ебры (включая операцию
умножения), а также дифференцирования и интегрирования векторных функций
скалярного аргумента. С работами обоих названных авторов Сомов был
хорошо знаком. В обширной статье «Об ускорениях высших порядков»
(Зап. Акад. наук, т. V, 1864) Сомов строит аппарат дифференцирования
лектор-функций и применяет его к изучению кривых двоякой кривизны,
используя при этом связанный с ней основной подвижной трехгранник.
В предисловии он писал: «Эти начала (т. е. векторное исчисление.—
А. Ю.) во многих отношениях расширяют средства аналитической
геометрии и аналитической механики, доставляя возможность исследовать
свойства кривых линий и обстоятельства движения или независимо
от координат или в координатах произвольных».
К названной статье примыкает другая работа Сомова «Прямой
способ для выражения дифференциальных параметров первого и второго
порядка и кривизны поверхности в каких-либо координатах
ортогональных или косоугольных». (Зап. Акад. наук, т. VIII, 1865).
Дифференциальные параметры были впервые широко использованы
Г. Ламе в его общей теории ортогональных криволинейных координат,
которую он развивал применительно к задачам математической физики
и упругости. Для функции f(x, г/, z) дифференциальным параметром
первого порядка Ламе назвал величину
510 ГЛ. 24. ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ; МАТЕМАТИЧЕСКАЯ ЛОГИКА
(на языке векторного исчисления — модуль вектора grad/), а параметром
второго порядка —
д2/ д2/ д2/
дх* "*~ ду2 "~ dz2 '
т. е. оператор Лапласа данной функции. Оба параметра суть
дифференциальные инварианты ортогонального преобразования координат. После
первых работ Ламе (1837, 1840), продолженных им самим, Э. Бельтрами
(1864) и др., теория дифференциальных инвариантов получила большое
развитие и применения в дифференциальной геометрии. Сомов изложил
учение о дифференциальных параметрах в рамках векторного исчисления.
Многие приемы и формулы О. И. Сомова, вначале не привлекшие
внимания, употребляются теперь в руководствах по теории поля. Его
несомненной заслугой было также последовательное построение на векторной
основе системы формул классической дифференциальной геометрии
кривых и поверхностей.
В России теория ускорений высших порядков была впервые
применена к одному чебышевскому механизму Н. Е. Жуковским,
принадлежавшим, как известно, к лагерю решительных сторонников применения
векторного исчисления в механике и ее преподавании1). К числу их
принадлежал, как отмечалось, и В. П. Ермаков, а позднее сын О. И.
Сомова — профессор механики в Варшаве и затем в Петербурге (1905) Павел
Осипович Сомов (1852—1919), специализировавшийся по кинематике
механизмов. Одно время П. О. Сомов читал в Петербургском университете
лекции по «векториальному анализу», распространению которого
способствовали и его учебные руководства.
Сети Чебышева. С весьма важной работой по дифференциальной
геометрии поверхностей выступил П. Л. Чебышев. Это доклад —«О
кройке одежды» сделанный во Французской ассоциации содействия
преуспеванию наук в 1878 г., но увидевший свет только в 1936 г. В связи с
сообщением Э. Люка о применении математического анализа к тканям,
сделанный в той же ассоциации двумя годами ранее (1876), П. Л. Чебышев
исследовал задачу об одевании какой-либо поверхности тканью, которая
в первоначальном плоском состоянии образована двумя параллельными
системами взаимно перпендикулярных нерастяжимых нитей-линий. Когда
такая ткань одевается на поверхность, прямоугольные клетки, из
которых состоит ткань, переходят в параллелограммы: при сохранении длин
сторон меняются углы между ними. Так на поверхности возникает «чебы-
шевская сеть», две системы линий которой в пересечении дают
криволинейные четырехугольники с равными противоположными сторонами.
Одевание поверхности — более общее преобразование, чем изгибание,
при котором сохраняются длины всех изгибаемых линий, так как
расстояния между точками одеваемой ткани (поверхности), лежащими на разных
нитях (линиях), вообще говоря, изменяются, например по диагонали.
Свое теоретическое исследование Чебышев сопроводил демонстрацией
чехла для шара, изготовленного в соответствии с найденными им
формулами. Он закончил доклад словами: «Два куска указанной формы, будучи
скроены и сшиты сообразно с тем, что мы описали, дали результат,
не оставляющий желать лучшего, как вы сами можете судить. Это дока-
*) Я. Л. Геронимус, Очерки о работах корифеев русской механики, стр.
78—95; 209—215; Ф. Д. Крамар, И. Д. М о л ю к о в, Иосиф Иванович Сомов
(1815—1876) — математик, механик, педагог. Алма-Ата, 1965, стр. 44—57.
К. М. ПЕТЕРСОН И МОСКОВСКАЯ ГЕОМЕТРИЧЕСКАЯ ШКОЛА 511
зывает, насколько вышеизложенные соображения согласуются с
практикой» х).
Чебышевские сети имеют большое значение для внутренней
геометрии поверхностей. В частности, две системы асимптотических линий
любой поверхности постоянной отрицательной кривизны образуют такую
сеть. Это используется при доказательстве того, что геометрия плоскости
Лобачевского в целом не может быть реализована на регулярной
поверхности постоянной отрицательной кривизны (теорема Гильберта, 1901) 2).
Теория сетей Чебышева стала предметом специальных исследований
многих отечественных и зарубежных математиков в советское время 3).
К. М. Петерсон и московская геометрическая школа. Мы уже говорили
о работах по геометрии поверхностей Миндинга и несколько раз
упоминали имя его ученика К. М. Петерсона, положившего начало московской
геометрической школы. Познакомимся
с жизнью и творчеством этого выдающегося
математика несколько подробнее 4).
Карл Михайлович Петерсон, по
национальности — латыш, родился 25 мая 1828 г.
в семье рижского мещанина, ранее бывшего
крепостным. После окончания Рижской
гимназии Петерсон в 1847—1852 гг.
обучался в Дерптском университете, где его
учителями были К. Э. Зенф и Ф. Г. Миндинг.
В 1853 г. Петерсон защитил кандидатскую
диссертацию.
С 1865 г. Петерсон преподавал
математику в Петропавловском училище в Москве.
Университетским работником он не стал, но
принял деятельное участие в кружке,
группировавшемся около Н. Д. Брашмана
и А. Ю. Давидова и был одним из членов-
учредителей Московского математического
общества. В первом же томе
«Математического сборника» Петерсон выступил
с ценной статьей по дифференциальной К. М. Петерсон.
геометрии; в «Математическом сборнике»
было напечатано вообще большинство его работ, из них последняя —
в десятом томе за 1882 г., т. е. уже после его кончины, последовавшей
19 апреля 1881 г. За работы по интегрированию уравнений с частными
производными Новороссийский университет по предложению В. В.
Преображенского и физика Н. А. Умова присудил Петерсону в 1879 г.
степень доктора чистой математики.
Уже кандидатская диссертация Петерсона «Об изгибании
поверхностей» явилась весьма значительным научным трудом. Странная судьба
постигла это сочинение. Несмотря на высокую оценку ее, данную самим
х) П. Л. Ч е б ы ш е в, Полное собрание сочинений, т. V, стр. 170.
2) В. Ф. Каган, Основания геометрии, часть вторая, М., 1956, стр. 33—35.
3) В. П. Б ы ч к о в, О развитии геометрических идей П. Л. Чебышева.— Ист.-
матем. исслед., вып. XVII, 1966.
4) С. Д. Российский, Карл Михайлович Петерсон.—УМН, IV, 5 (33),
1949; И. Я. Д е п м а н, Карл Михайлович Петерсон и его диссертация.— Ист.-ма-
тем. исслед., вып. V, 1952.
512 ГЛ. 24. ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ; МАТЕМАТИЧЕСКАЯ ЛОГИКА
Миндингом, назвавшим ее исключительной, работа не была при жизни
автора напечатана. Диссертация хранилась в архиве и первым после
Миндинга ознакомился с ней, по-видимому, А. Кнезер, когда он работал
в конце XIX века в Юрьеве. Некоторые сведения о диссертации,
полученные от Кнезера, опубликовал в 1901 г. П. Штеккель. И только в 1952 г.
диссертация К. М. Петерсона увидела свет в русском переводе с
рукописного немецкого оригинала 1).
Тематически диссертация примыкает к исследованиям Гаусса и
Миндинга по теории изгибания поверхностей.
Ранее говорилось о результате Гаусса, согласно которому задание
первой квадратичной формы
Е du2 + 2Fdudu + G dv2 = ds2,
поверхности x = fi(u, v), у = f2(u, v), z = /3(w, v) определяет
внутреннюю геометрию поверхности. Наряду с первой формой существенную
роль играет вторая дифференциальная форма:
D du2 + 2D' du dv + D" dv\
Она выражает удвоенную главную часть расстояния точки поверхности
до касательной плоскости в бесконечно близкой точке. Коэффициенты
D, D', D", как и Е, F, G, являются функциями координат и их
производных.
В диссертации Петерсона выведены основные свойства
коэффициентов второй квадратичной формы поверхности и решен вопрос об
аналитических условиях, определяющих поверхность с точностью до ее положения
в пространстве, т. е. саму геометрическую форму поверхности. Уже Гаусс
установил некоторое алгебраическое соотношение между коэффициентами
обеих форм, которое, например, можно записать в виде
Ks=* EG — F2
где К — полная кривизна поверхности в данной точке. Петерсон дополнил
алгебраическое соотношение между коэффициентами/), D', В" и Е, F, G
еще двумя дифференциальными соотношениями. Эти уравнения Гаусса —
Петерсона являются основными в теории поверхностей. Однако, как мы
сказали, результат Петерсона остался незамеченным. Два его уравнения
были вновь открыты и опубликованы в 1857 г. Г. Майнарди, а полный их
вывод дал еще позднее другой итальянский математик Д. Кодацци
в 1868-1869 гг.
С внешней стороны уравнения Петерсона отличны от уравнений
Майнарди и Кодацци, так как вместо величин D, D', D" он использовал
в своем выводе значения главных радиусов кривизны т^ и г2 в данной
точке поверхности и угла v между одной из линий кривизны и одной
из координатных линий на поверхности 2). Однако это внешнее отличие
не имеет значения, так как от величин rb г2, v можно перейти к
величинам D, D', D".
г) См. Ист.-матем. исслед., вып. V, 1952, где даны перевод работы, выполненный
И. Я. Депманом при участии Я. X. Сарва, и комментарии к ней С. Д. Российского.
2) В каждой обыкновенной точке поверхности имеются два нормальных сечения
с наибольшей и наименьшей кривизнами, так называемые главные сечения.
Направления касательных к главным сечениям в данной точке также называются главными.
Кривая на поверхности называется линией кривизны, если в каждой ее точке
касательная параллельна одному из главных направлений в этой точке.
РАБОТЫ К. А. АНДРЕЕВА и А. К. ВЛАСОВА
513
Другой важнейший результат своего исследования Петерсон выразил
следующим образом. Если даны шесть величин Е, F, G, ru г2, v, то
поверхность определена вплоть до ее положения в пространстве. Это
фундаментальное предложение, согласно которому геометрическая форма
поверхности вполне определяется заданием обеих основных квадратичных форм,
вновь получил в 1866 г. французский математик О. Бонне, под именем
которого оно и известно теперь в литературе.
Диссертация Петерсона содержала крупнейший вклад в общую
теорию поверхностей. В статье «Об отношениях и сродствах между кривыми
поверхностями» (Матем. сборник, т. 1, 1866) он положил начало большому
циклу работ по теории изгибания на главном основании. Первый пример
такого рода изгибания был найден еще Миндингом при изучении
изгибания поверхностей вращения в поверхности вращения (Crelle's Journ.,
B. 18, 1838). Исследования Петерсона в этом направлении продолжили
многие московские математики: Б. К. Млодзеевский, Д. Ф. Егоров,
C. П. Фиников, С. С. Бюшгенс, Н. Н. Лузин и др. Некоторые
опубликованные результаты Петерсона позднее вновь получили крупные
зарубежные геометры, такие как Г. Дарбу и др.
Более широкую известность открытия
Петерсона получили благодаря обзорным
статьям Б. К. Млодзеевского и Д. Ф.
Егорова, опубликованным в 1903 г. в т. 24
«Матем. сборника» и тогда же в Annales
de la Faculte des Sciences de Toulouse. После
этого в том же издании в 1905 г. появился
французский перевод основных работ
Петерсона, которые ныне пользуются общим
признанием.
Лекции В. Я. Цингера. В годы
творчества Петерсона лекции по геометрии в
Московском университете читал Василий
Яковлевич Цингер (23 февраля 1836—1 марта
1907), большой поклонник и знаток
проективной геометрии, автор ряда работ не
только в этой области и по механике, но также
по ботанике, которую он любил едва ли
не меньше своей прямой специальности1). в- я- Цингер.
Блестящий лектор, увлекательно
развивавший идеи Шаля 2) и Штейнера, В. Я. Цингер был учителем ряда
московских геометров: К. А. Андреева, А. К. Власова, Б. К.
Млодзеевского, Д. Ф. Егорова. Из них первые два работали в области
проективной геометрии, а два других — в области дифференциальной
геометрии.
Работы по проективной геометрии К. А. Андреева и А. К. Власова.
Константин Алексеевич Андреев (26 марта 1848—29 октября 1921) вскоре
после окончания в 1871 г. Московского университета поступил на работу
в Харьковский университет, где провел 25 лет с 1874 до 1898 г. После
этого он почти до конца жизни преподавал в Московском университете.
г) К. А. Андреев, В. Я. Цингер (некролог).—Матем. сб., т. 28, 1911.
2) Цингер перевел на русский язык известный труд М. Шаля «Исторический
обзор происхождения и развития геометрических методов», М., 1888.
514 ГЛ. 24. ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ; МАТЕМАТИЧЕСКАЯ ЛОГИКА
Харьковский период жизни был временем наибольшей активности
Андреева как ученого и общественного деятеля. Здесь он защитил магистерскую
диссертацию «О геометрическом образовании плоских кривых» (Харьков,
1875), здесь же подготовил докторскую работу, защищенную в 1879 г.
в Москве. В том же 1879 г. он был утвержден профессором. В 1884—1899 гг.
он был председателем Харьковского математического общества и
редактором его «Сообщений». Из его руководств особую известность получил
«Основной курс аналитической геометрии» (Харьков, 1888, 5-е изд., 1909).
Построение высших алгебраических кривых по данным их
точкам (обыкновенным или кратным) и касательным стало предметом
геометрических исследований, начиная
с Ньютона, который решил несколько
таких задач для кривых третьего
порядка. С помощью двух проективных
пучков прямых можно образовывать
кривые второго порядка, как места
пересечения соответственных прямых.
Для применения этого метода к высшим
кривым были предложены два различных
способа обобщения. С одной стороны,
можно заменять прямые обоих пучков
другими линиями; с другой, — можно
повысить порядок соответствия между
прямыми пучков. М. Шаль для
образования кривых высшего порядка употреблял
проективные соотношения между
элементами пучка прямых и пучка
конических сечений. Видоизменение этого
приема содержится в статье В. Я. Цин-
гера «Построение кривой третьего
порядка по девяти данным точкам» (Матем.
сборник, т. 3, 1868). К. А. Андреев пошел
К. А. Андреев. по ВТОрОМу пути, близкому к идеям
Ж. Понселе, применяя так называемый
метод многозначных соответствий, в котором прямым одного пучка ставятся
в соответствие по две или более прямых другого. Последовательному
развитию этого метода посвящены обе его диссертации. Мы
охарактеризуем докторскую работу «О геометрических соответствиях в применении
к вопросу о построении кривых линий» (Матем. сборник, т. 9, 1879)
небольшой выдержкой из отзыва, подписанного О. А. Баклундом, В. Г. Имшенец-
ким и В. Я. Буняковским в связи с представлением К. А. Андреева в члены-
корреспонденты Академии наук (избрание состоялось в 1884 г.):
«...диссертация г. Андреева составляет продолжение его
самостоятельных исследований в вопросе о построении высших кривых по точкам,
который Шаль считал одним из основных вопросов. Обобщение теории
построения кривых приводит к теории геометрического соответствия:
высших порядков. От теории взаимного двузначного соответствия,
изложенной в предыдущем труде, автор переходит на основании тех же
геометрических принципов к таким многозначным соответствиям, где число
элементов геометрической формы, соответствующих одному элементу
другой формы, доходит до четырех... В этом сочинении предлагается
оригинальный, весьма общий способ построения не только кривых
четвертого порядка по 14 точкам, но также кривых пятого порядка по 20 точкам.
Б. К. МЛОДЗБЕВСКИЙ
515
Кроме того, дается построение многих частных форм кривых еще высших
порядков» г).
Перу К. А. Андреева принадлежит несколько историко-биографиче-
ских очерков — о его учителе В. Я. Цингере, названный выше, о его друге
В. Г. Имшенецком (Матем. сборник, т. 18, 1896), о М. Шале (Сообщ.
Харьк. матем. о-ва, т. I, 1881) и др.
В ином направлении лежали изыскания другого ученика Цингера —
Алексея Константиновича Власова (1868—21 мая 1922), работавшего
вначале в Московском университете, затем
в 1911—1917 гг. в Московском коммерческом
институте и далее опять в университете.
В магистерской (1901) и докторской (1909)
диссертациях А. К. Власов дал строгое
проективное исследование линейных систем
конических сечений и полярных систем
высших порядков в формах первой ступени.
Видное место в его творчестве занимают
проблемы, связанные с теоремой Паскаля
о конических сечениях: им посвящены и
первая его студенческая работа и последняя
статья, вышедшая через три года после
его кончины (Матем. сборник, т. 32, 1925).
Для теоремы Паскаля Власов нашел
своеобразный аналог в четырехмерном
пространстве. Особое значение имеет
оригинальное и простое доказательство Власова
основной теоремы аксонометрии, высказанной
в 1860 г. немецким геометром К. Польке
и в 1864 г. обобщенной Г. Шварцем: всякий А. К. Власов.
полный четырехсторонник есть
параллельная проекция некоторого тетраэдра. Эта работа Власова, также
напечатанная посмертно (Матем. сб., т. 32, 1925), положила у нас начало применению
методов высшей синтетической геометрии к начертательной геометрии
и номографии. Учеником Власова был крупный специалист во всех трех
областях геометрии профессор Московского университета Н. А. Глаголев
(3 декабря 1888—2 июля 1945), окончивший этот университет в 1912 г.
Многие студенты и теперь изучают «Курс высшей математики»
А. К. Власова (М., 1914; 5-е изд., 1952).
Дифференциально-геометрические исследования Б. К. Млодзеевского»
Научные интересы Болеслава Корнелиевича Млодзеевского (10 июля
1858—18 января 1923), сына профессора медицинского факультета
Московского университета, складывались в большой мере под воздействием идей
Петерсона. После окончания университета в 1880 г. он был по
рекомендации своего учителя В. Я. Цингера оставлен при нем и с 1885 г. начал
здесь в должности приват-доцента преподавательскую деятельность,
длившуюся без малого 40 лет. Магистерская диссертация Млодзеевского
посвящена теории изгибания поверхностей; тему он выбрал по совету
Цингера, который вместе с Жуковским выступали оппонентами на защите
2) Цит. по кн. Д. 3. Г о р д е в с к о г о, К. А. Андреев — выдающийся
русский геометр, Харьков, 1955, стр. 35—36.—«Предыдущий труд» Андреева — это его
магистерская диссертация (1875). См. также М. П. Черняев, Константин
Алексеевич Андреев как геометр. Ист.-матем. исслед., вып. IX, 1956.
516 ГЛ. 24. ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ; МАТЕМАТИЧЕСКАЯ ЛОГИКА
(1886). После защиты докторской работы по общей теории тг-мерных
многообразий (1889), Млодзеевский полтора года провел в заграничной
командировке в Париже, Геттингене и Цюрихе. В 1892 г. он был избран
профессором.
Б. К. Млодзеевский был человеком яркого общественного
темперамента и передовых взглядов. Вместе с А. К. Власовым он много сил отдал
Московскому математическому кружку, сыгравшему столь большую роль
в развитии среднего образования. С 1891 г. он был одним из руководителей
Московского математического общества в должности его секретаря,
с 1906 г. как вице-президент при президенте Жуковском, а после кончины
знаменитого механика в 1921 г. в качестве президента. 1911 год был
ознаменован в жизни Московского
университета бурными событиями.
Вспыхнувшие студенческие волнения были
грубо подавлены полицией, введенной
в помещение университета, ректор и его
ближайшие помощники были уволены
министром просвещения Л. А. Кассо.
В знак протеста университет покинуло
более 100 преподавателей, среди них
П.Н. Лебедев, Н. А. Умов, С А.
Чаплыгин, Б. К.Млодзеевский, А. К.
Власов, СП. Фиников и многие другие. До
1917 г., когда Млодзеевский смог
вернуться (как и Власов, и Фиников) в
университет, он преподавал на Высших
женских курсах и в Университете им.
Шанявского.
В магистерской диссертации
«Исследования об изгибании поверхностей»
(М., 1886) Млодзеевский впервые бе-
_, ТР ,, „ зупречно вывел общее дифференциаль-
Б. К. Млодзеевский. J г ~^ п w v *л
ное уравнение изгибания—уравнение
типа Монжа — Ампера, которое
выражает координаты точек всех поверхностей с данным линейным
элементом ds2 = Е du2 -\- 2F du dv -\- G dv2 в функции параметров и, v. Здесь
же были начаты, а в докторской работе «О многообразиях многих
измерений» (М., 1889) продолжены исследования Млодзеевского по
дифференциальным инвариантам.
Дифференциальными инвариантами называют такие выражения,
образованные из функций точек какого-либо многообразия (пространства)
и их производных либо дифференциалов, которые не изменяются при том
или ином преобразовании переменных (координат). Порядок инварианта
есть порядок высших входящих в него производных и дифференциалов.
Так, при изометрии дифференциальным инвариантом первой квадратичной
формы, притом второго порядка, является полная кривизна К
поверхности, так как она выражается через коэффициенты Е, F, G и их первые
производные, а Е, F, G в свою очередь сами содержат производные
первого порядка. Как говорилось, дифференциальными инвариантами
являются также дифференциальные параметры, изучавшиеся О. И. Сомовым.
В России дифференциальные инварианты трехмерного риманова
пространства были впервые изучены Ф. М. Суворовым,— об этом мы
скажем далее. Б. К. Млодзеевский распространил исследование инвариантов
Д. Ф. ЕГОРОВ И ЕГО УЧЕНИКИ
517
и условий наложимости на пространства и поверхности многих измерений.
Он в деталях изучил взаимные связи между дифференциальными
инвариантами линейного элемента ds2 = V gik dxt dxk тг-мерного многообразия
и показал, что всякий инвариант можно выразить через дифференциальные
параметры первого порядка данного многообразия. Ту же теорему
независимо получил Г. Дарбу (1894). Млодзеевский успешно исследовал
также изгибания различных частных классов поверхностей,
непосредственно развивая работы Миндинга и Петерсона (Матем. сборник, т. 21,
1900; т. 24, 1904). Ему принадлежат также работы по отдельным вопросам
анализа, механики и алгебраической геометрии, которой он занимался
в последние годы жизни г).
Вместе с Д. Ф. Егоровым Б. К. Млодзеевский воспитал многих
молодых геометров, составивших ядро большой научной школы. В этом деле
большую роль сыграл организованный Млодзеевским в 1905 г.
специальный семинар.
Д. Ф. Егоров и его ученики. Младший из четырех названных выше
учеников Цингера, Дмитрий Федорович Егоров (22 декабря 1869— 10
сентября 1931), окончивший университет в 1891 г., специализировался
вначале также по дифференциальной геометрии. Его докторская
диссертация «Об одном классе ортогональных систем» (М., 1901) посвящена триор-
тогональным потенциальным поверхностям. Три семейства поверхностей
образуют триортогональную систему, если в каждой точке пространства
любые две поверхности двух различных семейств пересекаются под
прямым углом. Таковы, например, системы плоскостей, параллельных
координатным, в декартовых прямоугольных координатах и координатные
поверхности в случае полярных либо цилиндрических координат. Триор-
тогональные системы, помимо чисто математического интереса, весьма
важны в механике, теоретической физике и т. д. Рассмотренные Д. Ф.
Егоровым триортогональные системы так называемых потенциальных
поверхностей — системы Е определяются с помощью рассмотрения течения
на поверхности жидкости с потенциалом скоростей относительно сети
линий кривизны, по которым пересекаются поверхности различных
семейств. Основные результаты Егорова включены в трактат Г. Дарбу:
Legons sur les systemes orthogonaux et les coordonnees curvilignes (2 ed.,
Paris, 1910).
Как и Млодзеевский, Егоров продолжал исследования Петерсона
по изгибанию на главном основании.
С 1893 г. Д. Ф. Егоров состоял приват-доцентом Московского
университета и с 1903 г.— профессором. Здесь еще большее значение, чем работа
в области геометрии, имела его деятельность, направленная на внедрение
у нас новых направлений в вариационном исчислении, теории
интегральных уравнений и общей теории функций. Новые идеи Егоров излагал
и в своих лекциях, всегда безукоризненно отделанных до последнего слова
речи и последнего значка на доске, но особенное значение имел созданный
им в 1910 г. семинар, где каждый год избиралась для работы со
слушателями очередная актуальная тема. Постепенно Егоров стал одним из
руководящих профессоров, и влияние его сильно сказывалось на всей жизни
физико-математического факультета, особенно после смерти Жуковского
г) С. Д. Российский, Болеслав Корнелиевич Млодзеевский, изд.
Московского ун-та, 1950. См. также А. Ф. Лапко, Л. А. Люстерник, Из истории
советской математики.—УМН, т. 22, вып. 6(133), 1967, стр. 40—47.
518 ГЛ. 24. ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ; МАТЕМАТИЧЕСКАЯ ЛОГИКА
и Млодзеевского. С 1922 г. и почти до конца жизни он руководил
Московским математическим обществом как его президент; вице-президентом
был тогда Н. Н. Лузин. Научная репутация Д. Ф. Егорова была высокой.
В 1924 г. он был избран членом-корреспондентом Академии наук СССР,
в 1929 г.— почетным членом.
Д. Ф. Егоров (стоит справа; слева от него польский
математик В. Серпинский; сидит Н. Н. Лузин).
Многие крупные советские математики являются учениками Д. Ф.
Егорова: Н. Н. Лузин, В. В. Степанов, И. И. Привалов, И. Г. Петровский,
геометры С. С. Бюшгенс, С. П. Фиников и другие.
Сергей Сергеевич Бюшгенс (24 сентября 1882—29 марта 1963)
и Сергей Павлович Фиников (15 ноября 1883—27 февраля 1964)
выстудили с оригинальными исследованиями уже в конце рассматриваемого
ГЕОМЕТРИЯ В КАЗАНИ; Ф. М. СУВОРОВ
519
периода. В 1917 г. вышли их магистерские диссертации, продолжавшие
летерсоновскую линию: «Об изгибании поверхностей на главном
основании» С. С. Бюшгенса и «Общая задача изгибания на главном основании»
С П. Финикова. Оба они начали в 1906 г. преподавать в Московском
университете. После смерти Егорова Фиников заменил его в качестве
руководителя большой дифференциально-геометрической школы, в работу
которой внес ряд новых идей.
Геометрия в Казани; Ф. М. Суворов. Одновременно с московской
создается и казанская геометрическая школа, возникновение которой
было во многом связано с пробуждением интереса к творчеству
Лобачевского. Уже в 1867 г. В. Г. Имшенецкий и другие математики подняли
вопрос об издании трудов великого геометра, что удалось осуществить,
впрочем, несколько позднее. В семи-
десятые-восьмидесятые годы Казань
становится видным центром
пропаганды и развития неевклидовой
геометрии. Основная заслуга здесь
принадлежала Ф. М. Суворову, А В.
Васильеву, А. П. Котельникову и
Д. М. Синцову. В 1883—1886 гг.
издается в двух томах «Полное собрание
сочинений по геометрии» Лобачевского
лод редакцией А. В. Васильева и с
биографическим очерком Ф. М.
Суворова. В Казани публикуется много
оригинальных и переводных работ по
неевклидовой геометрии. В 1893 г.
в Казани было торжественно
отпраздновано столетие со дня рождения
Лобачевского и учреждена премия его
имени, которой начиная с 1897 г.,
были удостоены С. Ли, Ф. Клейн,
А. Пуанкаре, Д. Гильберт и другие
крупнейшие ученые.
Старший из только что назван- ф* м- СУВ0Р0В-
ных казанских математиков — Федор
Матвеевич Суворов (26 сентября 1845—2 июля 1911), ученик А. Ф.
Попова, В. Г. Имшенецкого и П. И. Котельникова, у которого он слушал
лекции по проективной геометрии и теории векторов, приступил к работе
в Казанском университете в 1869 г. Занявшись по совету Имшенецкого
неевклидовой геометрией, он посвятил свою магистерскую диссертацию
«О характеристиках систем 3-х измерений» (Казань, 1871) изучению
общих трехмерных пространств и особенно теории их кривизны. Это
была первая в России и одна из первых в мировой литературе работ,
развивавших неевклидову дифференциальную геометрию. Тем же кругом
вопросов, что и Суворов, занимались тогда Л. Кронекер, Р. Липшиц,
Э. Кристофель (1869) и другие.
Центральное место в диссертации Суворова занимает выяснение
свойств инвариантов дифференциальных квадратичных форм римановых
многообразий. Независимо от Кристофеля и другим способом Суворов
установил основные условия эквивалентности квадратичных форм для
трехмерного пространства. В некоторых пунктах Суворов предварил
520 ГЛ. 24. ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ; МАТЕМАТИЧЕСКАЯ ЛОГИКА
выдающегося итальянского геометра Г. Риччи, который в 1886 г.
приступил к разработке так называемого абсолютного дифференциального
(тензорного) исчисления, в XX веке ставшего основным аппаратом
дифференциальной геометрии и теории относительности.
Магистерская диссертация Суворова, резюме которой он опубликовал
на французском языке в 1873 г. в 4-м т. «Bulletin des sciences mathema-
tiques et astronomiques», получила известность и за границей; ссылки
на нее можно встретить в соответствующей статье немецкой Encyklopadie
der Mathematischen Wissenschaften (В. III3, Heft 7, 1923), у знаменитого
французского геометра Э. Картана и др.
Докторская диссертация Суворова «Об изображении воображаемых
точек и воображаемых прямых на плоскости и о построении кривых линий
второй степени, определяемых с помощью воображаемых точек и
касательных» (Казань, 1884) посвящена теории мнимых элементов проективной
геометрии, впервые получивших реальное геометрическое истолкование
в глубоких исследованиях Хр. Штаудта (1856—1860). Несколько ранее
Суворова этими вопросами занимался у нас воспитанник и с 1871 г.
профессор Новороссийского университета Семен Петрович Ярошенко (1846—
1917) в работе «Алгебраические операции в области элементарных
геометрических форм» (Одесса, 1878) А).
А. В. Васильев. Крупным деятелем математической культуры был
Александр Васильевич Васильев (2 июля 1853—6 октября 1929). Сын
известного китаиста и, по матери,
внук астронома И. М. Симонова,
Васильев был воспитанником
Петербургского университета, который окончил
в 1874 г. Его магистерская (1880)
и докторская (1884) диссертации
относятся к алгебре и о них будет
сказано далее. В Казанском университете
Васильев работал с 1875 г. в звании
приват-доцента. Профессуру он получил
в 1887 г. и оставался здесь до 1907 г.,
когда переехал в Петербург. Васильев
был одним из активнейших членов
и с 1884 г.—председателем
физико-математической секции Казанского
общества естествоиспытателей, которая по
его предложению была преобразована
в 1890 г. в Казанское
физико-математическое общество. В течение 17 лет, до
самого отъезда, А. В. Васильев состоял
его председателем. Одновременно он
участвовал в работах земских учреж-
аспльев. дений Казанской губернии в области
народного просвещения. В1907—1917 гг.
Васильев состоял выборным членом Государственного совета, где
занимал либерально-буржуазную позицию.
Основной сферой деятельности Васильева была неустанная
пропаганда передовых математических теорий, в частности, неевклидовой гео-
1) П. М. Q л о н и ч е в, Казанский геометр Федор Матвеевич Суворов.—Ист.-
м. исслетт.. вып. ТХ. М.. IQ.Sfi.
/ XX. J.YX. V/ ш)Х KJ XX XX Т. С/ JD, XUIAI
матем. исслед., вып. IX, М., 1956.
А. П. КОТЕЛЬНИКОВ И ТЕОРИЯ ВЕКТОРОВ
521
метрии. В ряде работ на русском и иностранных языках Васильев
популяризировал геометрические открытия Лобачевского. Он первый обратил
внимание на выдающиеся труды Лобачевского по алгебре и
математическому анализу, более подробно изученные уже в советское время. Первое
собрание геометрических сочинений Лобачевского было выпущено, как
уже говорилось, под его редакцией. Ему же принадлежит первая научная
биография Лобачевского (Николай Иванович Лобачевский. СПб., 1914).
В своих лекциях и курсах он знакомил с новыми проблемами алгебры
и теории групп, теории гиперкомплексных чисел, теории множеств
и т. д. В 1900 г. А. В. Васильев организовал студенческий
физико-математический кружок. Соединяя большую математическую эрудицию с
интересом к истории математики, Васильев включал в свои курсы целые
отделы, в которых рисовал широкую картину исторического развития
вопроса. Таково, например, очень интересное его «Введение в анализ»,
в двух выпусках которого (Казань, 1904—1908) дается весьма
содержательное и столь же увлекательное систематическое и историческое
изложение учения о числе и его обобщениях. Мы уже говорили о выпусках
«Новые идеи в математике», которые он издавал вместе с П. С.
Юшкевичем. В советское время он опубликовал очерк истории теории чисел
«Целое число» (Птг., 1919) и небольшую, но богатую фактическим
материалом книгу по истории математики в России с основания Академии
наук до 1863 г.— первый обобщающий труд в этой области (Математика.
Вып. 1, 1725—1826—1863. Птг., 1921). А. В. Васильев был первым из
русских ученых выбран членом-корреспондентом Международной академии
истории наук, основанной в 1929 г. 1).
А. П. Котельников и теория векторов в неевклидовых пространствах.
Большие заслуги в разработке проблем неевклидовой геометрии и
механики принадлежали Александру Петровичу Котельникову (20 октября
1856—6 марта 1944), сыну П. И. Котельникова и ученику А. В. Васильева
и Ф. М. Суворова. Вскоре после окончания Казанского университета
(1889) Котельников приступил к разработке проблем механики
неевклидовых пространств, результатом чего и явились его магистерская
диссертация «Винтовое счисление и некоторые его применения к геометрии
и механике» (Казань, 1895), а затем и докторская диссертация
«Проективная теория векторов». В 1893—1899 гг. он преподавал в Казанском
университете в звании приват-доцента. После защиты второй диссертации,
за которую ему присудили степени доктора чистой и прикладной
математики, Котельников некоторое время работал профессором в Киевском
политехническом институте, с 1904 по 1914 г.— в Казани, затем в течение
10 лет вновь в Киеве (в университете и в Политехническом институте).
С 1924 г. и до конца жизни он руководил кафедрой механики в Московском
Высшем техническом училище, преподавал и в других втузах и работал
в ЦАГИ. Продолжая научные работы по механике и геометрии, он вместе
с тем принял деятельное участие в подготовке Полного собрания
сочинений Н. И. Лобачевского, а также, в качестве главного редактора, Полного
собрания сочинений Н. Е. Жуковского. В 1934 г. ему было присвоено
звание заслуженного деятеля науки и техники РСФСР.
В самом конце шестидесятых годов XIX века итальянский математик
А. Дженокки и бельгиец Ж. де Тилли занялись вопросами неевклидовой
1)Н. Н. Парфентьев, Заслуженный профессор математики Александр
Васильевич Васильев (Изв. Казанск. физ.-матем. о-ва, (2) т. 24 (1924); о н ж е,
А. В. Васильев как математик и философ (там же, (3) т. 4, 1929—1930).
522 ГЛ. 24. ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ; МАТЕМАТИЧЕСКАЯ ЛОГИКА
механики, на необходимость разработки которой указывал еще сам
Лобачевский. Правда, первоначальной целью обоих авторов была
попытка доказать от противного евклидов постулат о параллельных, получив
при отказе от этого постулата какое-либо противоречие в системе
механики. Но противоречие такого рода, естественно, не обнаруживалось,
и, убедившись в тщетности поисков, Дженокки и де Тилли положили
начало неевклидовой механике. Проблема привлекла внимание ряда
ученых. В России первые работы по этому вопросу принадлежали
А. П. Котельникову и Павлу Соломоновичу Юшкевичу (11 июля 1873—
6 декабря 1945), опубликовавшему работу «О сложении сил в
гиперболическом пространстве» (Вестн. опытной
физики и элем, математики, сем. 22,
1898). Сложение сил, скоростей, вообще
векторов в евклидовом пространстве
выражается правилом параллелограмма.
В пространстве Лобачевского
параллелограммов нет и необходимо иное
определение векторной суммы.
Проблема сложения векторов в
пространствах постоянной кривизны
явилась одним из отправных пунктов
творчества А. П. Котельникова.
Во введении к докторской
диссертации он, характеризуя наиболее
существенные пункты, отличающие ее от
работ других авторов, указывал,
во-первых, что рассматривает кинематику
и динамику твердого тела не по
отдельности, но соединяет их в одну более
отвлеченную теорию векторов, и, во-
вторых, что «все указанные мною авторы
А. П. Котельников. задавали силу и скорость совокупностью
прямой и числа, и только де Тилли и
П. Юшкевич изобразили силы и скорость им пропорциональными отрезками
прямой. Такое геометрическое представление у названных авторов,
однако, не играет никакой существенной роли и даже простейшим законом
сложения сил и скоростей эти авторы, подобно всем другим, пользовались
в его аналитической форме. Никто, насколько мне известно, не задавался
вопросом, не следует ли, изображая силы и скорости прямолинейным
отрезком, принять какую-нибудь другую зависимость между длиной этих
отрезков и величиной изображаемых ими сил и скоростей вместо прямой
пропорциональности, никто не задавался вопросом, нельзя ли основной
закон механики — закон сложения сил и скоростей — выразить в столь же
простой геометрической форме, как и правило параллелограмма в
евклидовом пространстве и, таким образом, придать механике твердого тела
в неевклидовых пространствах более геометрический характер. Эти
вопросы следует считать исходными вопросами моей работы. Они повели
меня в свою очередь к более глубокому анализу тех предположений,
которые необходимы с точки зрения проективной геометрии для
формального обоснования теории векторов» х).
г) А. П. Котельников, Проективная теория векторов. Введение к
докторской диссертации (отд. оттиск.), Казань, 1899, стр. 29.
А. П. КОТЕЛЬНИКОВ И ТЕОРИЯ ВЕКТОРОВ
523
Построение теории векторов с приложениями к механике и геометрии
~и составляет содержание обеих диссертаций А. П. Котельникова, причем
основным аппаратом служит винтовое исчисление и арифметика особого
рода комплексных чисел с двумя единицами. Корни винтового
исчисления восходят к теории кватернионов Гамильтона, о которой нам еще
шридется говорить (см. стр. 555 и след.), и развивающим ее трудам У.
Клиффорда и Р. Болла, которые начали появляться в семидесятые годы
XIX века. Были введены общие комплексные числа вида а +&со, где
вторая единица со для пространств Евклида, Римана и Лобачевского
определяется соответственно равенствами
0)2 = 0, со* = ?2>0, со2 = ?2<0
(к2 — кривизна пространства). Эти числа были названы, следуя тому, же
порядку, параболическими, эллиптическими и гиперболическими; частным
случаем последних являются обыкновенные комплексные числа, к2 = —1.
Выражения q± + cog27 в которых q± и q2 суть гамильтоновы кватернионы,
именуются бикватернионами и последние, подобно общим комплексным
числам а + Ью, подразделяются на параболические, эллиптические
и гиперболические. Для характеристики системы приложенных к телу
сил и его движения в пространстве Евклида было предложено понятие
винта, как пары скользящего и свободного векторов, которые можно
выбрать ко л линеарными. Между всеми тремя категориями объектов
существует тесная взаимосвязь: параболический кватернион можно
рассматривать как сумму параболического комплексного числа и винта.
В свою очередь винт, определяемый скользящим вектором г и свободным
вектором г', есть комплексный вектор г-\-<х>г'. В случае пространства
постоянной ненулевой кривизны систему приложенных сил можно
заменить двумя скользящими векторами, направленными по двум взаимно
полярным прямым. Такой винт получил название мотора х). Только что
указанные связи между бикватернионами, общими комплексными
числами, винтами и векторами имеют место и для моторов. Заметим еще,
что вторая единица общего комплексного числа со является оператором
некоторого преобразования вектора, на который умножается со.
Двукратное применение этой операции в евклидовом пространстве дает нуль-вектор,
так что со2 = 0; вообще же со2 = к2.
Магистерская диссертация А. П. Котельникова, предметом которой
служили векторы, винты и их приложения для случая пространства
Евклида, явилась как бы вступлением к докторской. В «Проективной
теории векторов» дана общая теория векторов пространств постоянной
кривизны, трактуемых как метрические проективные пространства.
Метризация, т. е. измерение длин и углов, достигается тем, что в
рассматриваемом проективном пространстве фиксируется так называемый абсолют —
действительная или мнимая поверхность второго порядка, которая
переходит сама в себя при проективном преобразовании, переводящем точки,
лежащие на одной прямой, в точки, расположенные опять-таки на прямой.
Для пространства Евклида абсолют есть бесконечно удаленная плоскость
вместе с принадлежащей ей мнимой линией пересечения всех сфер, для
пространства Римана — некоторая мнимая поверхность и для
пространства Лобачевского — поверхность замкнутая.
*) Дело в том, что мотор характеризует произвольное движение (лат. motio) в
рассматриваемом пространстве. Напомним, что вектор характеризует перемещение (лат.
vectio) вдоль прямой.
524 ГЛ. 24. ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ; МАТЕМАТИЧЕСКАЯ ЛОГИКА
В докторской диссертации подробно изложены арифметика общих
комплексных чисел, учение об их элементарных функциях и
геометрические интерпретации на плоскости и поверхностях второго порядка. Далее-
последовательно разрабатывается теория векторов и операций над ними.
Сложение производится по правилу четырехугольника: на рис. 50 сумма
векторов ох и оу определяется как диагональ oz; следует иметь в виду, чта
точки а и Ъ находятся в пересечении прямых, несущих ох и оу с
плоскостью О, полярной с точкой о относительно абсолюта. В пространстве-
Евклида плоскость О бесконечно удаленная и четырехугольник переходит
в параллелограмм.
Для векторов, моторов и еще третьего вида- основных объектов,
роторов, которые вводятся как пары плоскостей, пересечение
которых называется осью ротора х),
определяются различные характеризующие-
их величины, которые, так же как и
операции над ними, во многом сходны со
свойствами обыкновенных векторов и
служат их обобщениями. Все это
осуществляется с помощью исчисления
бикватернионов, которые Котельников
предпочитает рассматривать не в форме
4i +о>д2> а в форме q= со -\-ix -\-jy-\-kz,
где со, х, г/, z суть общие комплексные
числа а -\- Ьа>. Это позволяет весьма
просто переводить формулы теории
кватернионов в формулы теории бикватернио-
Рис. 50. Сложение векторов в тео- нов и, на основе сходства обеих теорий,
рии А. П. Котельникова. установить параллелизм геометрических
систем, которые служат их
геометрической интерпретацией, т. е. теории векторов и теории моторов. В более
поздней работе, опубликованной уже посмертно, А. П. Котельников писал:
«Мы приходим, таким образом, к мысли перенести из теории векторов
такие элементарные понятия, как длина вектора, проекция вектора,
координаты вектора, угол между двумя векторами и т. д. в теорию моторов
и внести в эту последнюю соответствующие понятия: тензор мотора,
проекции мотора, комплексные координаты мотора, комплексный угол
между прямыми и т. д. 2). Вместе с тем получается возможность каждому
построению и теореме теории связки векторов сопоставить построение
и теорему теории моторов и, пользуясь первыми, находить новые, ещо
не известные теоремы теории моторов. Таким образом, мы приходим
к принципу перенесения» 3).
х) Ротор характеризует вращение (лат. rotatio) тела около оси. Заметим, что
мотор можно вводить и как пару, составленную из вектора и ротора с осью, проходящей
через начало вектора. Всякое движение в рассматриваемых пространствах можно в любой
момент рассматривать как перемещение вдоль прямой вместе с вращением вокруг нее.
2) Тензор мотора, определяемого парой скользящих векторов с углом ср между
ними и кратчайшим расстоянием d, есть комплексное число tgcp +-^tg (kd); комплексным
углом между двумя прямыми называется число ср + cod; проекция мотора на ось равна
произведению его тензора на косинус комплексного угла между осью мотора и осью
проекции.
3) А. П. Котельников, Теория векторов и комплексные числа. Ь кн.:
А. П. Котельников, В. А. Фок, Некоторые применения идей Лобачевского
в механике и физике, М.—Л., 1950, стр. 42.
Д. Н. ЗЕЙЛИГЕР И ГЕОМЕТРИЯ ЛИНЕЙЧАТЫХ ПРОСТРАНСТВ 525
Принцип перенесения имеет большое значение в исследовании Котель-
никова, устанавливая соответствие между простыми геометрическими
фигурами и более сложными. Если взять комплексную сферу единичного
радиуса в евклидовом пространстве, координаты которого суть общие
комплексные числа а -\- Ьсо, то один из основных результатов А. П. Котель-
никова можно высказать следующим образом: множество лучей
неевклидова пространства взаимно однозначно изображается комплексной сферой,
причем комплексный угол между прямыми равен сферическому
расстоянию соответственных точек сферы, а щетки прямых (множества
перпендикуляров к одной прямой) изображаются большими кругами сферы.
Вместе с тем, движения неевклидова пространства изображаются вращениями
комплексной сферы, и обратно.
Исследования Котельникова развивались одновременно с
аналогичными изысканиями немецкого математика Э. Штуди, начатыми в 1891 г.
ж завершенными в наиболее важных частях в 1899—1901 гг. 1).
Так в той же Казани, где Лобачевский положил начало неевклидовой
геометрии, в широком плане была разработана теория векторов и
механика трехмерных пространств
постоянной кривизны. Неевклидова механика
привлекала внимание и других русских
ученых, помимо названных. Укажем для
примера статью Н. Е. Жуковского
«О движении материальной
псевдосферической фигуры по поверхности
псевдосферы» (1902) 2).
Д. Н. Зейлигер и геометрия
линейчатых пространств. Работы
Котельникова оказали сильное влияние на одного
из официальных оппонентов,
выступавшего на защите обеих его диссертаций —
Дмитрия Николаевича Зейлигера (24 мая
1864—25 июля 1936), воспитанника
Новороссийского университета,
работавшего сначала в Одессе, затем
профессором в Казани (1892—1914), Пегро-
граде (1914—1917), снова в Казани (до
1929 г.) и в последние годы во втузах
Донецка и Новочеркасска.
Первоначально Зейлигер занимался механикой, Д- Н. Зейлигер.
но с середины 90-х годов приступил
к систематической разработке комплексной геометрии линейчатых
пространств, элементами которых служат не точки, а прямые. Основную
роль здесь играют арифметика параболических комплексных чисел,
винты и метод переноса, согласно которому геометрия сферы единичного
радиуса переходит в геометрию линейчатого пространства при замене
в ее формулах действительных чисел параболическими. В
рассматриваемое время Д. Н. Зейлигер опубликовал по линейчатой геометрии две
работы (Уч. зап. Казанск. ун-та, т. 64, 1897 и т. 75, 1908). Он в
подробностях развил аналитическую геометрию линейчатых поверхностей вто-
х) Б. А. Розенфельд, Александр Петрович Котельников.— Ист.-матем.
исслед., вып. IX, 1956.
2)Н. Е. Жуковский, Собрание сочинений, т. I, М.—Л., 1948.
526 ГЛ. 24. ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ; МАТЕМАТИЧЕСКАЯ ЛОГИКА
рого порядка, а также дифференциальную геометрию линейчатых
поверхностей и конгруэнции, т. е. систем прямых, зависящих от двух параметров»
Итоги исследований в этой области Д. Н. Зейлигер подвел в книге
«Комплексная линейчатая геометрия» (М.—Л., 1934). В том же направлении,
несколько позднее Зейлигера начал работать немецкий геометр В. Бляшкег
который наряду с новыми ценными результатами получил, не зная
русского языка, и некоторые результаты Котельникова и Зейлигера *).
Котельников оказал влияние также на работы выдающегося
советского геометра, воспитанника и профессора Казанского университета
Петра Алексеевича Широкова (9 февраля 1895—26 февраля 1944) и отчасти
на окончившего Московский университет Александра Петровича Нордена
(род. 24 июля 1904 г.), заменившего П. А. Широкова на кафедре геометрии
Казанского университета.
Работы Д. М. Синцова по теории коннексов. В Казани же получил
образование (1900) и начал свою деятельность крупный геометр Дмитрий
Матвеевич Синцов (28 ноября 1867—28 января 1946)— ученик Ф. М.
Суворова и А. В. Васильева. Синцов занял в
Казанском университете должность приват-
доцента в 1894 г., а после защиты в 1898 г.
докторской диссертации о рациональных
интегралах дифференциальных уравненийг
о которой, как и о некоторых других
работах Синцова, уже говорилось, переехал на
работу в качестве профессора в Высшее
горное училище в Екатеринослав (ныне
Днепропетровск). Через несколько лет, в
1903 г., Д. М. Синцов перешел в
Харьковский университет, с которым была связана
вся его дальнейшая жизнь. Здесь он с 1906 г.
был председателем Математического
общества, а в советское время создал новую
геометрическую школу. В 1939 г. Синцов был
избран членом Академии наук УССР.
Магистерская диссертация Синцова
«Теория коннексов в пространстве в связи
с теорией дифференциальных уравнений
в частных производных первого порядка»
Д. М. Синцов. (Казань, 1894) была посвящена
сравнительно новому кругу проблем. Начало этому
направлению в геометрии, в котором основными элементами
конфигураций служат сочетания простейших геометрических образов, положил
в начале семидесятых годов XIX века немецкий математик А. Клебш.
Он разработал геометрию тернарных комплексов, т. е. плоских
конфигураций из элементов (точка, прямая), удовлетворяющих уравнению
/ (#4, ?2» #3» Щ* U2i Щ) =0,
где / — однородная функция по отдельности относительно xk и yk, xk —
однородные координаты точки, a yh — однородные координаты прямой.
*) Ср. Д. Н. Зейлигер, Современное состояние комплексной геометрии
линейчатого пространства, в кн.: Труды Первого Всесоюзного съезда математиков
(Харьков, 1930), М.— Л., 1936.
ОСНОВАНИЯ ГЕОМЕТРИИ
527
Теория коннексов тесно связана с теорией инвариантов, с одной
стороны, и с теорией дифференциальных уравнений,— с другой.
Первая работа по теории коннексов в России принадлежала
А. В. Васильеву (Уч. Зап. Казанск. ун-та, 1878), изложившему результаты
Клебша и, в частности, приложения к особым решениям
дифференциальных уравнений. Васильев привлек к этой тематике Синцова. В
магистерской диссертации Синцов впервые разработал общую теорию кватер-
нарного комплекса с элементом (точка, плоскость), предварив исследования
зарубежных математиков Л. Оттона и Стюверта (1900). В последующих
работах Синцов изучил коннексы с элементами (точка, прямая) и (точка,
прямая, плоскость) в пространстве, причем детально исследовал ряд
проблем теории интегральных кривых дифференциальных уравнений *).
Основания геометрии. Мы уже отмечали, что после того как вопрос
о непротиворечивости неевклидовой геометрии был сведен к вопросу
о непротиворечивости геометрии Евклида, особое внимание привлекло
исследование оснований геометрии вообще и аксиоматики евклидова
пространства в особенности.
Традиционная система аксиом «Начал» Евклида, в течение более
двухтысячелетий мало затронутая критикой (если не считать постулат
о параллельных), была подвергнута тщательному анализу, причем
обнаружились существенные пробелы. Ряд исследователей (среди них в первую
очередь следует назвать немецкого ученого М. Паша и итальянца Дж. Пеа-
но) установили многие скрытые допущения, применяемые в
доказательствах теорем, были выяснены требования, которым должна удовлетворять
аксиоматика: совместность аксиом, полнота системы и, по возможности,
независимость аксиом, при которой число их приводится к минимуму.
В одном и том же 1899 г. вышли два первых труда, содержавших достаточно
разработанную систему аксиом евклидовой геометрии: «Об элементарной
геометрии, как гипотетико-дедуктивной системе» (Delia geometria elemen-
tare come sistema ipotetico-deduttivo) ученика Пеано — M. Пиери
и «Основания геометрии» (Die Grundlagen der Geometrie) Д. Гильберта.
Аксиоматика Пиери — довольно громоздкая и успеха не имела,
Гильберту же удалось создать образцовую систему, которая, правда,
потребовала некоторых уточнений. Список аксиом Гильберта (всего их в
окончательной редакции 20) разделяется на пять основных групп. Это —
группы аксиом соединения или принадлежности, порядка, конгруэнтности,
параллельности и непрерывности. Основные объекты геометрии — точки,
прямые и плоскости, из которых строятся другие фигуры, не
определяются; аксиомы дают полное описание взаимоотношений между ними.
Гильберт глубоко исследовал значение каждой группы аксиом и каждой из них
по отдельности. Непротиворечивость доказывается путем построения
арифметической модели, в которой интерпретируются все основные
объекты и отношения геометрии. Например, точке на плоскости соответствует
пара чисел (х, у), прямой — отношение трех чисел (и : v : w), причем
и и v не равны оба нулю, а принадлежность точки (х, у) прямой (и : v : w)
выражается уравнением их -)- vy -j- w = 0, и т. п. Так устанавливается,
что геометрия непротиворечива, если непротиворечива и арифметика.
Помимо того, Гильберт разработал целый ряд важных отделов метриче-
г) И. А. Наумов, Д. М. Синцов (очерк жизни и научно-педагогической
деятельности), Харьков, 1955. См. также Д. М. Синцов, Современное состояние
теории коннексов, в кн.: Труды Первого Всесоюзного съезда математиков (Харьков»
1930), М.- Л., 1936.
528 ГЛ. 24. ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ; МАТЕМАТИЧЕСКАЯ ЛОГИКА
ской и проективной неархимедовой геометрии, в которой не выполняется
аксиома измерения Евдокса — Архимеда. В последующем автор
«Оснований» внес отдельные улучшения в систему аксиом и многие дополнения,
как в тексте, так и в приложениях — об измерении объемов, об аксиомах
арифметики и др. Благодаря простоте формулировок отдельных аксиом,
их естественной группировке и непосредственным связям с
установившимся построением геометрии, аксиоматика Гильберта стала
классической х). Однако она не была единственной. Кроме Пиери, почти в одно
время с Гильбертом и совершенно самостоятельно другое обоснование
евклидовой геометрии предложил одесский ученый В. Ф. Каган.
Геометрия в Одессе; аксиоматика В. Ф. Кагана. Вениамин
Федорович Каган (9 марта 1869—8 мая 1953) родился в литовском городе
Шавли (ныне Шауляй). В 1887 г. он поступил
в Новороссийский университет.
Пребывание его здесь оказалось недолгим. За
участие в студенческих сходках по поводу
кончины Н. Г.Чернышевского Каган был
в 1889 г. исключен из университета с
запрещением поступать в другой и выслан под
надзором полиции в Екатеринослав
(Днепропетровск). В 1892 г. он окончил экстерном
Киевский университет и несколько позже
приступил к сдаче в Петербурге
магистерских экзаменов. А. А. Марков и К. А. Поссе
обратили внимание на способности
магистранта и рекомендовали привлечь его к
преподаванию в Петербургском университете.
Министерство просвещения отклонило это
предложение из-за еврейской
национальности В. Ф. Кагана. Все же ему была
предоставлена приват-доцентура в том самом
Новороссийском университете, из кото-
В. Ф. Каган. рого его исключили десятью годами ранее.
Здесь В. Ф. Каган работал с 1898 г.
приват-доцентом и с 1917 г. в звании профессора, которое ему было
присвоено только после революции.
В Одессе В. Ф. Каган занял видное положение, как превосходный
лектор, активный ученый и общественный деятель. О его работе в
издательстве «Матезис» (что значит «знание», «наука») и в «Вестнике опытной
физики и элементарной математики» уже говорилось. Добавим, что он был
страстным борцом за реформу преподавания в средней школе и сам вел
занятия в одной из школ с 1903 по 1917 г. В 1906 г., вместе с другими
передовыми учеными, он организовал в Одессе Высшие женские курсы.
Геометрией Лобачевского В. Ф. Каган заинтересовался еще на втором
курсе университета. В возрасте 24 лет он начал публиковать в «Вестнике
опытной физики и элементарной математики» серию посвященных ей статей
{1893—1898), которые составили затем обширный «Очерк геометрической
системы Лобачевского» (Одесса, 1900). Это было первое общедоступное
и вместе с тем полное изложение системы гиперболической геометрии,
г) Д. Гильберт, Основания геометрии, перев. И. С. Градштейна, под ред.
и со вступит, статьей П. К. Рашевского, М.— Л., 1948. Сочинение Гильберта (2-е изд.)
на основании отзыва Пуанкаре было удостоено в 1904 г. премии имени Лобачевского.
ГЕОМЕТРИЯ В ОДЕССЕ; АКСИОМАТИКА В. Ф. КАГАНА 529
в китором имеется ряд оригинальных теорем и доказательств автора.
Переход от неевклидовой геометрии к проблемам об основании геометрии
был для В. Ф. Кагана естественным, особенно в той обстановке, в которой
он оказался в Одессе. Здешние математики во главе с И. В. Слешинским
с увлечением занимались вопросами обоснования математических наук,
вплоть до математической логики х).
В 1902 г. В. Ф. Каган напечатал статью «Система посылок,
определяющая евклидову геометрию», в которой предложил новую систему
аксиом и определений (Зап. Матем. отд. Новорос. о-ва естествоиспытателей,
т. 20; также в Jahresbericht d. Deutsch. Math.-Vereinigung, В. 11, 1902).
Той же проблеме посвящена его магистерская диссертация «Основания
геометрии» (2 тт., Одесса, 1905—1907), защищенная в 1907 г. В первом
томе «Опыт обоснования евклидовой геометрии» 2) содержится анализ
системы аксиом и определений, разработанной Каганом. Здесь очень
полно рассмотрен вопрос о совместности и взаимной независимости аксиом,
что достигается с помощью аналитических моделей — различного рода
пространств, точки которых суть совокупности того или иного
количества действительных чисел — координат, и в которых введены
определенным образом расстояние между двумя точками и движения, т. е.
преобразования координат 3). Самое построение геометрической системы
проведено с чрезвычайной полнотой: в книге без малого 800 страниц.
Второй том диссертации посвящен обстоятельному историко-крити-
ческому очерку развития учения об основаниях геометрии, вплоть до Паша,
Пиери и Гильберта; он сохраняет большой интерес и в наше время.
Как сказано, в основу аксиоматики В. Ф. Кагана положено понятие
о пространстве, как точечном многообразии, «в котором (согласно Риману)
каждым двум точкам отнесено арифметическое число — расстояние и
(согласно Ли) установлена система преобразований, относящих каждую точку
некоторой другой точке (движений)»4). Точка, основной элемент, из
которого образуются другие фигуры, не определяется.
Мы приведем систему аксиом Кагана:
1. Между любыми двумя точками пространства С и D на всяком
расстоянии, меньшем CD, от любой из них имеется точка, прямолинейно
относительно них расположенная 5).
2. Если две точки в пространстве расположены каждая
прямолинейно относительно двух других точек, то они образуют с последними
прямолинейный образ. (Исключается геометрия Римана в узком смысле.)
3. Если некоторое движение приводит две различные точки М и N
в совмещение с двумя различными же точками пространства М' и N',
то расстояния MN и М''N' равны. (Расстояние есть инвариант движения.)
4. Никакое движение не совмещает всех точек пространства с одной
и той же точкой.
г) Ср. Э. Б. Л е и б м а н, Математическое отделение Новороссийского общества
естествоиспытателей,— Ист.-матем. исслед., вып. XIV, 1961, стр. 431—437 (список
докладов, читанных на заседаниях отделения до 1919 г.).
2) В «Записках Новороссийск, ун.-та» первый том был опубликован в тт. 97
(1904) и 101 (1905).
3) Предисловие к первому тому и заключительная глава о независимости аксиом
переизданы в кн.: В. Ф. Каган, Очерки по геометрии, изд. Московского ун-та
1963, стр. 522—568.
4) В. Ф. Каган, Основания геометрии, т. II, Одесса, 1907, стр. 551.
5) Точки А, В, С расположены прямолинейно, если АВ-\^ВС = АС\ при этом В
лежит между А и С.
530 ГЛ. 24. ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ; МАТЕМАТИЧЕСКАЯ ЛОГИКА
5. Каковы бы ни были движения S и S' в пространстве, имеется
движение SS', заменяющее последовательное их производство. (Движения
образуют полугруппу г).)
6. Вращением вокруг двух точек А ж В всякая третья точка С может
быть приведена в совмещение с любой точкой С, если АС = АС'
и ВС = ВС'.
7. В пространстве существует плоскость.
8. Если три точки, А, В и С, расположены в одной плоскости и из
трех пар точек: АВ, ВС ж АС две пары расположены в этой плоскости
по одну сторону точек М ж N, то точки третьей пары также расположены
по одну сторону точек М ж N. (Так называемый постулат Паша,
исключающий пространства более трех измерений.)
9. В пространстве существует плоскость, в пределах которой всяким
трем точкам, не имеющим прямолинейного расположения, отвечает по
крайней мере одна точка пространства, одинаково от них удаленная.
(Пространство евклидово.)
10. В пространстве существует плоскость, при неподвижности которой
все пространство остается в покое.
Предполагается заданной система действительных чисел.
Позднее система аксиом Кагана вновь привлекла внимание геометров
в связи с построением теории метрических пространств 2).
Незадолго до «Оснований геометрии» В. Ф. Каган опубликовал статью
по вопросу об измерении объемов. Дело было в следующем. Д. Гильберт
разработал теорию измерения площадей прямолинейных плоских фигур,
в которой основную роль играют определения равновеликости двух
многоугольников по разложению (когда их можно разбить на конечное числа
попарно конгруэнтных треугольников) и по дополнению (когда к ним
можно присоединить конечное число таких равновеликих по разложению
многоугольников, что получающиеся в результате многоугольники
равновелики по разложению). Доказывается, что для любого данного треугольника
половина произведения какой-либо стороны на соответствующую ей
высоту имеет одно и то же значение и это произведение, однозначно
определяемое данным треугольником, принимается за его меру площади;
коэффициент 1/2 взят для того, чтобы в дальнейшем площадь квадрата с
единичной стороной оказалась равной единице 3). Мера площади треугольника
является аддитивным инвариантом относительно его любого разбиения
на конечное число заполняющих его и взаимно не перекрывающихся
треугольников; при всяком таком разбиении мера площади данного
треугольника равна сумме мер составляющих его частей. Мера площади
любого многоугольника определяется как сумма мер площадей
треугольников, на которые он может быть разбит при каком-нибудь определенном
разложении; эта мера площади инвариантна относительно любого
разбиения данного многоугольника. В этой инвариантности вся суть дела: мера
площади многоугольника есть такая однозначно определяемая им
величина, которая не меняется ни при каком его разложении на треугольники
г) См. определение на стр. 543.
2) См. замечания Г. Б. Гуревича в кн.: В. Ф. Каган, Очерки по геометрии,
стр. 520—521.
3) Следует добавить, что Гильберт характеризует здесь меру площади не
действительным числом, а некоторым отрезком, выражающим полупроизведение стороны и
высоты (в смысле разработанного им исчисления отрезков). Особенность этого исчисления
в том, что оно стр.оится без аксиом непрерывности, при помощи частного случая
теоремы Паскаля.
С. О. ШАТУНОВСКИЙ И ТЕОРИЯ ИЗМЕРЕНИЯ МНОГОГРАННИКОВ 531
и их перегруппировке. Резюмирующая теорема гласит: два равновеликих
по разложению или по дополнению многоугольника имеют одинаковую
меру площади и два многоугольника с одинаковой мерой площади
равновелики по разложению или по дополнению. Мы только что употребили
слово величина. В самом деле, определенная указанным способом мера
площади обладает характерным свойством величины. Два произвольных
многоугольника всегда можно путем разложения или дополнения
преобразовать в такие, которые либо конгруэнтны либо один есть часть другого,
а при этом их меры площади либо равны либо одна меньше другой.
В своем докладе о математических проблемах 1900 г. Гильберт под
номером 3 высказал предположение, что аналогичное построение теории
измерения многогранников невозможно, так как могут существовать
тетраэдры с равными основаниями и равными высотами, которые нельзя
разложить на конечное число попарно конгруэнтных тетраэдров или
дополнить попарно конгруэнтными тетраэдрами до многогранников,
разложимых на попарно конгруэнтные тетраэдры. В 1900—1902 гг. немецкий
математик М. Ден подтвердил предположение Гильберта. Доказательства
Дена очень сложно и длинно. В. Ф. Каган в 57-м томе Mathematische Аппа-
len, 1903, опубликовал новое по идее, весьма изящное и вдесятеро более
короткое доказательство теоремы Дена. Исследования В. Ф. Кагана па
теории многогранников получили сравнительно недавно, с конца
сороковых годов, продолжение в работах швейцарских геометров, установивших
достаточные условия равносоставленности двух таких тел (необходимое
условие привел Ден) г).
В 1922 г. Каган переехал в Москву и вскоре стал профессором
Московского университета. Еще ранее, в связи с изучением теории
относительности, он приступил к исследованиям по дифференциальной геометриж
многомерных пространств и разработке ее современного аппарата —
тензорного исчисления. Перед отъездом из Одессы он прочитал в здешнем
университете первый в нашей стране курс лекций по теории
относительности. В 1927 г. он организовал в МГУ семинар по векторному и
тензорному анализу, который явился как бы школой для многих выдающихся
советских геометров — Якова Семеновича Дубнова (30 ноября 1887—
13 декабря 1957), П. К. Р ашевского (род. 27 июля 1907), А. П. Нордена
(род. 24 июня 1904), В. В. Вагнера (род. 4 ноября 1908) и др. С 1934 г.
В. Ф. Каган руководил в университете кафедрой геометрии, пятью годами
ранее ему было присвоено звание заслуженного деятеля науки РСФСР.
В. Ф. Каган без устали работал до самой глубокой старости. Наряду
с геометрией он много внимания уделял ее истории. Особой заслугой его
явилась организация издания Полного собрания сочинений
Лобачевского,— здесь ему принадлежат главная редакция, многие статьи и
комментарии. Мы упоминали также написанную им большую биографию
Лобачевского 2).
СО. Шатуновский и теория измерения многогранников.
Значительный вклад в основания геометрии внес и другой одесский математик
Самуил Осипович Шатуновский (13 марта 1859—27 марта 1929).
х) В последующем В. Ф. Каган еще более упростил доказательство теоремы Дена.
Ср. работу «О преобразовании многогранников» (1913) и дополнения редакции к ней,
в кн.: В. Ф. Каган, Очерки по геометрии.
2) А. М. Л о п ш и ц, Вениамин Федорович Каган, в кн.: В. Ф. К а г а ят
Очерки по геометрии.
532 ГЛ. 24. ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ; МАТЕМАТИЧЕСКАЯ ЛОГИКА
Замечательна судьба этого человека. Шатуновский родился в семье
бедного ремесленника и окончив реальное училище в Херсоне, поступил
в одно из высших технических учебных заведений Петербурга. Техника,
однако, его не привлекала; он заинтересовался математикой. Шатуновский
слушал лекции в Петербургском университете. Однако поступить в
университет он не мог и сделал попытку завершить своей образование в
Швейцарии. Крайняя нужда заставила его вскоре вернуться на родину, и он
жил здесь в городах юга России на средства от частных уроков. Самоучкой
он изучал математику, и уже в девяностые годы некоторые его работы
привлекли одесских математиков. С 1895 г. он регулярно выступал с
докладами в Математическом отделении Новороссийского общества
естествоиспытателей, стал его членом в 1897 г.
и секретарем в 1898 г. Работники
Новороссийского университета — Ярошен-
ко, Слешинский, Тимченко, Каган
добились от Министерства народного
просвещения разрешения на сдачу
Шатуновским магистерских экзаменов,
к которым он по правилам не мог
быть допущен, так как не имел
аттестата зрелости. То была эпоха первой
русской революции, и министр
уступил. После сдачи магистерских
экзаменов Шатуновский преподавал с
1905 г. в качестве приват-доцента
в университете. Он вел также занятия
на Высших женских курсах. Звание
профессора он получил после
установления Советской власти 1).
Шатуновский был ученым тон-
С. О. Шатуновский. кого логического склада мышления
и более всего его привлекали вопросы
обоснования математики — арифметики, геометрии, анализа и
математической логики. Это как нельзя лучше соответствовало общему
направлению интересов ведущих одесских математиков. В геометрии ему
принадлежат исследования по теории измерения площадей, в которых он
встретился с Гильбертом, а также объемов. Свое учение об измерении
площадей Шатуновский впервые изложил в собрании Математического
отделения Новоросс. о-ва естествоиспытателей в 1895 г. и затем под
названием «Основания теории площадей и объемов» на 10 съезде
русских естествоиспытателей и врачей (1898), в «Дневнике» которого
(Киев, 1898) были напечатаны ее главные положения. Как указывал
впоследствии сам Шатуновский в начале статьи «Об измерении объемов
многогранников», его теория измерения площадей прямолинейных фигур
тождественна с гильбертовой. Вероятно, выход «Оснований геометрии»
Гильберта в 1899 г. удержал Шатуновского от опубликования собственной
теории. Изложение ее дал в «Этюдах по основаниям геометрии» В. Ф. Каган
(Вестник опытной физ. и элем, матем., 1901) 2). В передаче Кагана теория
Шатуновского отличается от гильбертовой применением действительных
чисел, как мер длин отрезков и мер площадей. В главном обе теории совер-
*) Н. Г. Чеботарев, Самуил Осипович Шатуновский.— УМН, вып. VII, 1940.
2) «Этюды» переизданы в кн.: В. Ф. Каган, Очерки по геометрии.
АКСИОМЫ УЧЕНИЯ О ВЕЛИЧИНЕ
533
шенно сходны. Вместо слов «мера площади» Шатуновский говорил об
«инварианте прямолинейной фигуры».
Доклад «Основания элементарной теории объемов» Шатуновский
сделал в Одессе в 1898 г., а статью «Об измерении объемов
многогранников», в которой смогли быть учтены результаты Дена, опубликовал
в «Вестнике опытной физики и элем, математики» за 1902 г. и год спустя
на немецком языке в Mathematische Annalen, в. 57. Из теоремы Дена
следует, что построение теории измерения объемов на основе одного только
метода разложения и дополнения невозможно и что оно требует особого
подхода. С этой целью некоторые авторы привлекали инфинитезимальные
методы, например, принцип Кавальери. Шатуновский поставил задачу
развить элементарную теорию измерения объемов. Существенную роль
у него играло тщательно разработанное учение о величине. Мы видели,
что метод разложения и дополнения позволяет трактовать меру площадж
как величину. В силу теоремы Дена для многогранников дело обстоит
иначе: могут быть два такие многогранника, что при любом их
преобразовании возникают пары многогранников, которые и не конгруэнтны и не
таковы, что один есть часть другого. Таким образом, названный метод
не позволяет сравнивать два произвольных многогранника по величине
их объемов. Шатуновский оригинально преодолел встретившуюся
трудность.
Доказывается, что для любого данного тетраэдра треть произведения:
какого-либо основания на соответствующую ему высоту имеет одно
и то же значение; это произведение, однозначно характеризуемое данным
тетраэдром, определяется как его объемный инвариант. Коэффициент
1/3 берется, чтобы в дальнейшем объем куба с единичной стороной
оказался равным единице. Затем устанавливается, что при любом разбиении
данного тетраэдра на конечное число тетраэдров сумма инвариантов
последних равна его инварианту. Аналогичная теорема доказывается для
любого многогранника и вводится понятие объемного инварианта
многогранника. Два равновеликих по разложению или дополнению
многогранника имеют одинаковый инвариант. Объем многогранника, определяемый
как его инвариант, обладает характерными свойствами величины.
Аксиомы учения о величине. Одновременно с этими исследованиями
Шатуновский впервые аксиоматически построил учение о величине,
необходимое ему для измерения многогранников. Тысячелетиями математики
ограничивались представлением, что величина есть то, что может быть
больше и меньше и отношения равенства и неравенства величин не
подвергались логическому анализу. В 1902 г. С. О. Шатуновский сделал
устное сообщение «О постулатах, лежащих в основании понятия о
величине», напечатанное в «Зап. Матем. отд. Новорос. о-ва
естествоиспытателей», т. 26, 1904. Множество элементов а, Ь, с, ... называется скалярной
величиной (или множеством значений скалярной величины), если между
ними имеются отношения а (равно), р (больше) и 7 (меньше), которые
удовлетворяют следующим восьми аксиомам количественного сравнения:
1. Каждые два элемента множества находятся друг с другом по
крайней мере в одном из отношений а, |3, у-
2, 3. Отношение а исключает |3 и исключает у
4. Отношение а рефлексивно, т. е. всегда ааа.
5. Отношение а обратимо, т. е. при ааЪ и baa.
6—8. Отношения а, р, 7 транзитивны, т. е. при aab и Ъас будет ассс;
аналогично обстоит дело с |3 и 7-
534 ГЛ. 24. ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ; МАТЕМАТИЧЕСКАЯ ЛОГИКА
Шатуновский доказал совместимость и независимость этих аксиом
и вывел из них основные свойства отношений равно, больше и меньше.
Объем многогранника удовлетворяет всем восьми аксиомам.
Учение Шатуновского о скалярной величине, которое он докладывал
и на I Всероссийском съезде преподавателей математики, получило
широкое признание. С. О. Шатуновский включил его в свой курс «Введения
в анализ» (литогр. изд., Одесса, 1906; печ. изд. Одесса, 1923). Оно
изложено также в «Теоретической арифметике» (2-е изд., Москва, 1939) его
ученика Игоря Владимировича Арнольда (19 марта 1900—20 октября 1948),
работавшего ряд лет в Московском университете и в 1947 г. избранного
членом-корреспондентом Академии педагогических наук. Заметим, что
И. В. Арнольд обработал для печати только что названное «Введение
в анализ».
Мы закончим эту главу краткими сведениями о развитии в
рассматриваемый период математической логики, началом развития которой в нашей
стране мы обязаны — и это неудивительно — как раз математикам
Казани и Одессы.
П. С. Порецкий и алгебра логики. Некоторые идеи математической
логики восходят еще к средним векам. Успехи буквенной алгебры и ее
применение к геометрии Декартом повлекли за собой первые успешные
попытки представить в виде буквенного исчисления классическую логику
Аристотеля. Набросок такого логического исчисления дал Лейбниц, но
систематические исследования начались полутора столетиями позднее,
в середине XIX века. Пионерами были ученые, примыкавшие к
английской алгебраической школе, прежде всего А. де Морган и Дж. Буль,
а затем У. С. Джевонс и немецкий математик Э. Шредер. В созданной ими
алгебре логики отношения между высказываниями или классами
(множествами предметов, для которых выполняется тот или иной предикат)
выражаются формулами, составленными из символов, в значительной части
заимствованных из алгебры. Процесс логического вывода передается
в форме преобразования начальных или полученных из них данных формул
в новые по строго определенным правилам, во многом сходным с
алгебраическими, но имеющим другое истолкование.
В России интерес к алгебре логики развивался параллельно с
работами по основаниям геометрии и других математических наук. Рефераты
зарубежных работ стали появляться в различных журналах уже с 1881 г.;
б 1886—1889 гг. подробное изложение идей Буля и Джевонса дал
В. В. Бобынин. В это время в Казани работал выдающийся исследователь
проблем математической логики П. С. Порецкий.
Платон Сергеевич Порецкий (15 октября 1846—22 августа 1907),
сын врача, окончил в 1870 г. физико-математический факультет
Харьковского университета. Специализировался он по астрономии, которой
посвятил целый ряд работ, включая докторскую диссертацию,
подготовленную уже в Казани (1886), где он приступил к астрономическим
наблюдениям в 1876 г. В Казанском университете он читал лекции по
астрономии и математике, здесь же, как упоминалось, он прочитал первый у нас
курс математической логики. Этой молодой тогда наукой П. С.
Порецкий занялся еще до 1880 г., когда вышла из печати его первая статья
реферативного характера. На протяжении 1884—1904 гг. Порецкий
опубликовал на русском и французском языках большой цикл статей: «О
способах решения логических равенств и об обратном способе математической
логики» (Собр. протоколов заседаний секции физ.-матем. наук при Казан-
И. В. СЛЕШИНСКИЙ
535
ском ун-те, т. 2, 1884), «Семь основных законов теории логических
равенств» (Изв. физ.-матем. о-ва при Казанском ун-те, 2 сер., т. 8, 1898—
1899) и другие; уже посмертно вышла его «Объединенная теория
логических равенств и неравенств» (там же, т. 16, 1908). Критически развивая
и обобщая исследования Буля и Шредера, П. С. Порецкий внес весьма
значительный вклад в логику высказываний и в логику классов. Его
особой заслугой явилось создание алгоритмов, которые решают вопрос
о множестве следствий, вытекающих из данных посылок и, обратно,
позволяют установить посылки, следствием
которых является данное логическое
равенство.
Труды П. С. Порецкого привлекли
в свое время внимание лишь немногих.
Весьма сочувственно отнесся к ним
В. Г. Имшенецкий, который, однако,
сам не занимался математической
логикой. Некоторое продолжение они
получили у одесских математиков. За
рубежом их высоко оценил прежде всего
французский специалист по
математической логике Л. Кутюра, значительная
часть «Алгебры логики» которого (L'al-
gebre de la logique, Paris, 1905) отведена
методу Порецкого. Приступая к его
изложению, Кутюра писал: «...Буль
и Шредер преувеличивали аналогию
алгебры логики с обыкновенной
алгеброй. В логике различие терминов
известных и неизвестных является
искусственным и почти бесполезным: все термины,
в сущности, известны, и речь идет толь- П. С. Порецкий.
ко о том, чтобы из данных между ними
отношений вывести новые отношения (т. е. отношения неизвестные или
неявно известные). Такова цель метода Порецкого» г). Метод Порецкого
нашел применение и в позднейших исследованиях по алгебре логики
американского ученого А. Блейка (1938) и немецкого ученого О. Беккера (1950),
как более совершенный в сравнении с методами его предшественников.
А. Блейк указывает, что в то время как метод Шредера неполно
характеризует множество всех заключений, которые выводимы из данного
логического равенства, таблица следствий Порецкого дает решение этой задачи 2).
И. В. Слешинский. В Одессе инициатором исследований в этой области
явился не раз упоминавшийся выше Иван Владиславович Слешинский
(1854—1931), окончивший Новороссийский университет в 1875 г. и
преподававший в нем до 1909 г., а с 1911 г. работавший в Кракове. Интересы
Слешинского были очень широки и примыкали к нескольким
направлениям русской математической мысли. Вслед за Остроградским и одним из
своих учителей Сабининым он занимался вариационным исчислением
к разработке которого привлек еще одного одесского ученого Владимира
х) Л. Кутюра, Алгебра логики. Дерев, с прибавлениями И. Слешинского
Одесса, 1909, стр. 68.
2) Н. И. С т я ж к и н, Становление идей математической логики, М. 1964
стр. 214. "' '
536 ГЛ. 24. ГЕОМЕТРИЧЕСКИЕ ИССЛЕДОВАНИЯ; МАТЕМАТИЧЕСКАЯ ЛОГИКА
Иоахимовича Циммермана (1866—1939). Затем И. В. Слешинский занялся
вопросом о применении непрерывных дробей к исследованию уравнения
Риккати (тема, восходящая к Эйлеру) и отсюда перешел к изучению
сходимости и аналитических свойств функциональных непрерывных дробей;
полученные в этом направлении результаты он резюмировал в
магистерской диссертации, о которой говорилось в предыдущей главе (1889).
Докторская диссертация Слешинского «К теории способа наименьших
квадратов» (Зап. Матем. отд. Новоросс. о-ва естествоиспытателей, т. 14, 1892),
в которой он применил метод, по идее совпадающий с методом
характеристических функций, хотя и разработанный в недостаточной мере, нами
также упоминалась х). В 1890—1892 гг. он
выступил в заседаниях Математического
отделения с докладами по теории
иррациональных чисел и о невозможности
выведения аксиомы Евклида о параллельных
из других аксиом. Влияние его на
направление начатых вскоре исследований Шату-
новского, Кагана, Буницкого и других
одесских ученых несомненно. В 1893 г.
Слешинский сделал в Математическом
отделении сообщение «Логическая машина
Джевонса», напечатанное в том же году
в «Вестнике опытной физики и элем,
математики». К выполненному им русскому
переводу «Алгебры логики» Кутюра
приложено дополнение Слешинского, в
котором дана оригинальная система аксиом
этой науки и с их помощью доказан ряд
основных формул, вывод которых у Кутюра
был недостаточно ясным.
И. В. Слешинский. Вскоре после издания в Одессе
перевода книги Кутюра петербургский
математик Б. М. Коялович выступил с критикой алгебры логики,
утверждая, что она бесполезна и, более того, содержит противоречия. Это
последнее утверждение И. В. Слешинский опроверг, показав прямую
ошибку критика; это вызвало в свою очередь ответ Кояловича. Полемика
между Кояловичем и Слешинским велась на страницах «Журнала
Министерства народного просвещения» за 1910 г. Наоборот, крупный
австрийский физик-теоретик П. Эренфест, в 1904—1912 гг. работавший в
Петербурге, весьма положительно оценил книгу и в своем подробном отзыве
о ней прозорливо указал на возможные приложения алгебры логики
в физике и технике (Журн. Русск. физ.-хим. о-ва, отдел физики, т. 42,
1910)2). Во Франции также развернулась оживленная дискуссия о значении
математической логики между Кутюра и Пуанкаре; русский перевод их
статей появился в 10-м сборнике «Новых идей в математике» (Птг., 1915).
Проблема закона исключенного третьего. Несколько статей по алгебре
логики и ее приложению к арифметике опубликовал в «Вестнике опытной
физики и элем, математики» за 1896—1899 гг. Е. Л. Буницкий. Но осо-
х) Ср. Б. В. Гнеденко и И. И. Гихман, Развитие теории вероятностей
на Украине.— Ист.-матем. исслед., вып. IX, 1956, стр. 490—491.
2) Н. И. Стяжки н, В. Д. Силаков, Краткий очерк истории общей и
математической логики в России, М., 1962, стр. 70—74.
ПРОБЛЕМА ЗАКОНА ИСКЛЮЧЕННОГО ТРЕТЬЕГО
537
бенный интерес представляют идеи С. О. Шатуновского, именно — его
анализ вопроса о применимости закона исключенного третьего к элементам
бесконечных множеств. С докладом на эту тему Шатуновский выступил
в заседании Математического отделения Новорос. о-ва естествоиспытателей
еще в 1901 г., но печатно высказал свои соображения много позднее, во
введении к магистерской диссертации «Алгебра как учение о сравнениях
по функциональным модулям» (Одесса, 1917). Здесь он указывает, что
применение закона исключенного третьего к элементам бесконечных
множеств требует чрезвычайной осторожности. Возможность выбора
между двумя предложениями «А есть 5» и «А не есть 5», в которых А
есть некоторый предмет, а В — множество предметов, зависит не только
от определения множества В, но и от определения предмета А. Каково бы
ни было множество В (если только оно не есть множество всех вообще
предметов), можно всегда определить предмет А так, чтобы из его
определения нельзя было сделать заключения о принадлежности или
непринадлежности А к множеству В. Например, если предмет А определен как
целое число, оканчивающееся шестеркой, а В есть множество точных
квадратов, то об А нельзя сказать ни того, что А принадлежит В, ни того,
что А не принадлежит В. Но если дополнить определение Л, например,
сказав, что предмет А есть целое число, оканчивающееся шестеркой
с предшествующим четным числом десятков, то уже можно сказать, что
одно из двух предложений «А есть В» и «А не есть Z?», а именно второе,
истинно. С. А. Яновская по этому поводу пишет: «С. О. Шатуновский
предлагает использовать закон исключенного третьего как определение
индивидуума или логической единицы, по отношению к предикату В.
Именно, предмет А является индивидуумом или логической единицей
относительно предиката В, если из двух предложений «А есть В» и «А не
есть В» по крайней мере одно верно. Но это значит, что применимость
закона исключенного третьего нуждается всякий раз в особой проверке» *).
Как мы сказали, с устным сообщением по данному вопросу С. О.
Шатуновский выступил в 1901 г., в печати же — в 1917 г. В промежутке
между этими двумя датами, начиная с 1908 г., стали появляться работы
Л. Брауера, который пришел к гораздо более радикальному
пересмотру проблемы применимости закона исключенного третьего к
бесконечным множествам и положил начало так называемому
интуиционистскому направлению в основаниях математики. В дальнейшем изучение
условий и границ действия закона исключенного третьего сыграло большую
роль в развитии математической логики.
С конца XIX и начала XX вв. судьбы математической логики тесно
переплетаются с разработкой теории множеств. Содержание
математической логики чрезвычайно расширяется. Алгебра логики становится лишь
одной из начальных глав математической логики, как общей весьма
разветвленной теории математических доказательств.
2) С. А. Яновская, Основания математики и математическая логика, в кн.:
«Математика в СССР за тридцать лет», М.— Л., 1948, стр. 28. Ср. также Э. Я. Б а х-
мутская, О ранних работах С. О. Шатуновского по основаниям математики. Ист.-
матем. исслед., вып. XVI, 1965.
ГЛАВА ДВАДЦАТЬ ПЯТАЯ
ИССЛЕДОВАНИЯ ПО АЛГЕБРЕ
Вычисление корней. Основным событием в развитии алгебры за
рассматриваемое время явилась разработка теории групп и
теоретико-групповых методов исследования, а в России в конце этого периода возникновение
крупной школы современной алгебры. Предварительно мы остановимся
на некоторых других работах более специального характера.
В предыдущем упоминались некоторые алгебраические теоремы
П. Л. Чебышева об отделении действительных корней уравнений, и
теорема о перемежающихся корнях, открытая В. А. Марковым. В
рассматриваемое время также появилось несколько работ об отделении корней
алгебраических уравнений и среди них статьи А. А. Маркова (Сообщения и
протоколы Харьк. матем. о-ва, т. 11, 1886), П. С. Назимова о методе Штурма
(Матем, сборник, т. 13, 1886) и В. А. Стеклова (Сообщ. Харьк. матем.
о-ва, т. 3, 1893). К этому кругу вопросов отчасти примыкают диссертация
на право чтения лекций (Уч. записки Казанск. ун-та, год 41, 1874) и
докторская диссертация «Теория отделения корней систем алгебраических
уравнений» (Казань, 1884) А. В. Васильева, в которых изложен и
дополнен метод характеристик Л. Кронекера и общие результаты применены
к отделению комплексных корней одного алгебраического уравнения.
Определение числа корней трехчленного уравнения, по модуле не
превосходящих данного предела, произвел П. Г. Боль (Math. Annalen, В. 65,
1908), перед которым этот вопрос встал при изучении одной проблемы
небесной механики. Речь шла об уравнении ахп + Ъхт + с = 0 с
комплексными коэффициентами. Еще ранее в другом плане проблемой
отделения корней расчлененных уравнений занимался П. А. Некрасов (см.
далее).
Выходили работы, посвященные численному решению уравнений
высших степеней. Так, Бугаев предложил оригинальный итерационный
процесс и некоторые его модификации в «Матем. сборнике», тт. 18—19
(1896—1897). Д. А. Граве в 1883 г. применил к решению трехчленных
уравнений с действительными коэффициентами видоизмененный способ
Гаусса (1849). Метод итерации Граве, пригодный для вычисления
действительных корней, представляет собой некоторое обобщение алгоритма
непрерывных дробей. Он был впервые изложен в двенадцатой главе
«Элементов высшей алгебры» Граве (Киев, 1914), причем подробно пояснен
на примере вычисления трех действительных корней уравнения хь — ix —
-2 = 0.
Для решения линейной системы уравнений с большим числом
неизвестных удобный метод последовательных приближений дал немецкий
математик П. Зейдель (1874). П. А. Некрасов нашел несколько практически
РЕШЕНИЕ УРАВНЕНИЙ В ТРАНСЦЕНДЕНТНЫХ ФУНКЦИЯХ 539
выгодных правил установления сходимости этого метода (Зап. Акад. наук,
т. 69, № 5, 1892, приложение; также Матем. сборник, т. 16, 1892). Способ
Зейделя можно найти в большинстве современных курсов приближенных
вычислений.
Решение алгебраических уравнений в трансцендентных функциях.
П. А. Некрасов и Л. К. Лахтин, оба ученики Бугаева, исследовали также
другой круг проблем. Магистерская диссертация Павла Алексеевича
Некрасова (1 февраля 1858—20 декабря 1924), окончившего Московский
университет в 1878 г. и оставленного при кафедре чистой математики,
-а затем преподававшего в нем с 1885 г. в течение двадцати лет (с 1886 г.
в звании профессора) *) носит название «Исследование уравнений
вида ит — рип — q = 0» (Матем. сборник, т. 22, 1884). Мы только что
товорили о численном решении трехчленных уравнений. Напомним, что
еще Ламберт (1758) и затем Эйлер вывели разложения корней и
степеней корней таких уравнений в бесконечные ряды. В простейших случаях
п = 2, 3, 4 трехчленное уравнение решается в радикалах и в
тригонометрических функциях. Уравнение хъ + ах + Ъ = 0, к которому
сводится с помощью преобразования Э. С. Бринга (1786), вновь открытого
Дж. Джеррардом (1834), полное уравнение пятой степени, с
совершенно новой точки зрения исследовал Ш. Эрмит, который показал (1858), что
его корни выражаются в эллиптических модулярных функциях. Одно-
ъременно к тому же результату пришел Л. Кронекер. Это открытие по-
ълекло за собой целую серию блестящих исследований, первые итоги
которых подвел Ф. Клейн, установивший здесь глубокую связь с группой
вращения правильного икосаэдра вокруг его осей симметрии (1884).
Для произвольного трехчленного уравнения сколько-нибудь общая
теория отсутствовала. П. А. Некрасов применил к изучению такого
уравнения методы теории аналитических функций и на этом пути выявил
жногие свойства его корней. Он произвел отделение его корней, т. е.
определил на плоскости комплексного переменного области, заключающие
каждая по одному корню уравнения; рассмотрел свойства и сходимость
рядов, выражающих корни и их степени, и показал приложения этих
рядов к интегралам и дифференциальным уравнениям. Здесь указана
также связь между трехчленными уравнениями и рядом Лагранжа,
который явился предметом докторской диссертации Некрасова (Матем.
сборник, т. 12, 1886). Рассматриваемая работа была высоко оценена
современниками. Академия наук по собственному почину наградила автора
премией Буняковского; подробный разбор ее представил В. Г. Имшенец-
кий. На немецком языке Некрасов изложил свои результаты в 29 томе
Mathem. Annalen.
Несколько позже Некрасов выразил корни трехчленного уравнения
посредством определенных интегралов от логарифмических функций
(Матем. сборник, т. 13, 1888). Вскоре Лахтин также представил эти корни
в виде определенных интегралов, с помощью иного приема, используя,
вслед за Дж. Булем (1864), дифференциальное уравнение, порядок
которого тот же, что степень данного уравнения (Матем. сборник, т. 15, 1890).
За этим последовали другие работы Лахтина в том же направлении.
г) В 1905 г. Некрасов, с 1897 г. бывший попечителем Московского учебного окру-
та, переехал в Петербург, где работал в Министерстве народного просвещения. О
политических взглядах Некрасова в то время мы уже говорили.
540
ГЛ. 25. ИССЛЕДОВАНИЯ ПО АЛГЕБРЕ
Леонид Кузьмич Лахтин (1853—1927), в 1892—1896 гг. состоявший
профессором в Юрьеве, а затем до конца жизни в Московском университете,
посвятил несколько больших работ решению алгебраических уравнений
высших степеней в специальных
функциях, зависящих от интегралов
дифференциальных уравнений, главным образом
линейных уравнений второго и третьего
порядков 1). Такие дифференциальные
уравнения называют дифференциальными
резольвентами соответствующих
алгебраических уравнений, которые пишутся в виде
Ф (х, у) = 0, где х — один из
коэффициентов, у — неизвестное.
Первая статья, по существу, целая:
книга в 430 страниц, «Алгебраические
уравнения, разрешимые в
гипергеометрических функциях», завершающаяся
исследованием уравнений 3, 4, 5-й степеней и
одного вида 6-й степени, вышла в 1892—
1893 гг. (Матем. сборник, т. 16—17), за
нею последовала столь же обширная
монография «Дифференциальные резольвенты
алгебраических уравнений высших родов»
(там же, т. 19, 1896—1897) и еще несколько
Л. К. Лахтин. лет спустя две статьи о резольвентах
общего уравнения 6-й степени (там же, т. 22г
1901). В работах Лахтина нашли применение и теория функций, и
дифференциальные уравнения и теоретико-групповые методы, распространение
которых явилось, как сказано, важнейшим событием в развитии алгебры
рассматриваемого периода.
Теория групп. В течение долгих веков задачей алгебры было
отыскание корней алгебраических уравнений. Почти триста лет после того как
были решены в радикалах уравнения 3 и 4-й степени, математики
занимались поисками аналогичного решения буквенных уравнений выше
четвертой степени, прежде всего уравнений пятой степени. Однако все
попытки такого рода оставались безуспешными. И еще Лагранж в конце
XVIII века пришел к мысли, что в такой постановке задача, вообще
говоря, неразрешима, что корни общего уравнения пятой степени нельзя
точно выразить формулой, в которой над коэффициентами уравнения
производится конечное число сложений, вычитаний, умножений, делений
и извлечений корня с натуральным показателем. Как говорилось,
предположение Лагранжа оказалось правильным. Первое, еще недостаточно
полное его доказательство предложил в 1799 г. итальянский ученый
П. Руффини, а в 1824 г. это вполне строго доказал Н. Абель. Теорема
Руффини — Абеля, по-другому доказанная М. В. Остроградским, стала
отправным пунктом большого нового течения алгебраической мысли.
Согласно этой теореме нет общей формулы, выражающей в радикалах
г) В последние годы жизни Л. К. Лахтин занимался также математической
статистикой. На первом курсе университета (1923) мне довелось еще слушать его
неторопливые лекции по введению в анализ, доступные даже совсем мало подготовленному
человеку, но резко контрастировавшие с духом «лузитании», который пронизывал тогда?
всю атмосферу на математическом отделении (см. об этом далее).
ТЕОРИЯ ГРУПП
541
корни любого данного уравнения п-ж степени при п > 5. Но это не
означает, что среди таких уравнений нет классов уравнений, допускающих
решение в радикалах. Абель также показал, что неприводимое уравнение
простой степени, корни которого рационально выражаются через один из
них, разрешимо в радикалах. Возникла проблема: выделить и
охарактеризовать класс тех уравнений данной п-ж. степени, которые разрешимы
в радикалах. Эту проблему поставил и решил в 1830—1832 гг. Э. Галуа.
Работы Галуа произвели подлинный переворот в алгебре и оказали
сильное влияние на математику в целом. Для решения указанной задачи
Галуа глубоко разработал основы носящей теперь его имя теории.
Центральными в ней являются понятия группы и поля.
Множество G каких-либо элементов а, Ь, с, ... называется группой,
если в нем введена некоторая операция, называемая «умножением» (ее
принято обозначать обычным способом), и если выполняются условия:
1) произведение двух элементов множества G является элементом
того же множества;
2) умножение ассоциативно, т. е. для любых трех элементов а, Ь, с
выполняется соотношение (а-Ь)-с = а-(Ь-с);
3) существует хотя бы один элемент множества, называемый
«единицей» (е), при перемножении с которым любой элемент множества
не меняется: ае = еа = а;
4) для каждого элемента а в G существует хотя бы один такой
элемент, обозначаемый а-1 и именуемый «обратным элементом», что
произведение а и а~г дает единицу: а-а'1 = а'1-а = е 1).
В каждой группе имеется только одна единица е и для каждого
элемента а имеется только один обратный элемент а'1. Группы с конечным
числом элементов называют конечными, число элементов — порядком
группы; бесконечные группы — это группы с бесконечным числом
элементов. Если операция умножения коммутативна, т. е. аЪ = Ъа, группа
называется коммутативной или абелевой.
Исторически первыми изучены были конечные группы подстановок.
Если имеется множество п элементов, которые мы обозначим 1, 2, 3, ...
. . ., п, то, как известно, существует ровно 1-2-3 . . . п = п\ различных
расположений этих п элементов. Подстановкой называется переход от
«основного» расположения элементов 1, 2, 3, 4, . . ., п к какому-либо
другому (включая и основное расположение); это, собственно, взаимно
однозначное преобразование данного множества на себя.
Кольца и поля (о них говорилось в связи с работами Е. И. Золотарева
по теории делимости) обладают групповыми свойствами: все элементы
кольца образуют коммутативную группу относительно операции
сложения, а все отличные от нуля элементы поля также и группу относительно
операции умножения.
Развивая идеи Лагранжа и Абеля, Галуа свел вопрос о критерии
разрешимости уравнений в радикалах к исследованию свойств некоторой
группы подстановок. Пусть дано уравнение п-ж степени
xn + pixn-1 + p2xn^+...+Pn = 0, (1)
коэффициенты которого принадлежат полю комплексных чисел, так
называемому основному полю данного уравнения. Рассмотрим целые
многочлены Щхи х2, . . ., хп) от независимых переменных хи х2, . . ., хп,
коэффициенты которых принадлежат основному полю и которые обращаются
) Это определение восходит к А. Кэли (1857).
542
ГЛ. 25. ИССЛЕДОВАНИЯ ПО АЛГЕБРЕ
в нуль при замене независимых переменных корнями ?ь ?2> ?з> • • •> ^
уравнения (1); равенства
Л^, х2, ..., хп) = 0 (2)
называются рациональными соотношениями между корнями. Множество
всех подстановок корней ?i, ?г» • • •» ?л» переводящих каждое из
рациональных соотношений (2) в рациональное же соотношение, образует так
называемую группу Галуа данного уравнения. Галуа установил, что
уравнение (1) разрешимо в радикалах, если его группа Галуа разрешима.
Мы не можем дать здесь определения разрешимости группы и скажем
только, что, зная числовые значения коэффициентов уравнения (1), можно
построить соответствующую группу Галуа и фактически проверить ее
разрешимость. Для неприводимого в основном поле уравнения простой
степени Галуа получил критерий: необходимое и достаточное условие
разрешимости в радикалах состоит в том, чтобы все корни уравнения,
рационально выражались через любые два из них. Лриведенная несколько
выше теорема Абеля представляет собой частный случай теоремы Галуа.
Идеи Галуа, высказанные им чрезвычайно кратко и без доказательств,
получили широкое распространение только после выхода в 1870 г.
«Трактата о подстановках и алгебраических уравнениях» (Traite des substitutions
et des equations algebriques) К. Жордана. До 1870 г. были достигнуты
некоторые новые результаты в теории групп, а в начале семидесятых
годов С. Ли положил начало новой обширной ее области — теории
непрерывных групп преобразований. Пусть данное множество элементов,
скажем, точек евклидова пространства, или плоскости, или прямой,
отображается в себя с помощью некоторого взаимно однозначного
преобразования (движения), которое непрерывно переводит каждый определенный
элемент М (и только его) в определенный же его элемент М (и только
в него). В случае плоскости это могут быть ее параллельный перенос или
вращение вокруг неизменного начала и т. д. Такие непрерывные
преобразования обладают групповыми свойствами. Простым примером может
служить совокупность всех преобразований Т двух переменных х, у,
определяемых формулами
х' = х cos ф + у sin фэ
у' = — х sin ф + у cos ф.
Это преобразование вращения плоскости при неизменном начале.
Лод умножением двух преобразований Т и Т будем понимать
последовательное применение Т± и Г2. Множество преобразований Т образует
группу относительно группового умножения, причем произведением
преобразований с поворотами ф! и ф2 будет преобразование с поворотом на угол
Ф = Ф1 + фг- Групповой единицей служит тождественное преобразование
х' = х,у' = г/,
т. е. отсутствие поворота, или покой. Для преобразования с поворотом на
угол ф обратным элементом является преобразование с поворотом на
угол —ф. Рассмотренная группа преобразований называется еще группой
вращений плоскости, она зависит от параметра ф. Лри этом
преобразовании функция х2 + у2 (квадрат расстояния между точками) остается
неизменной
х'2 + у'2 = х2 + у2;
она называется .инвариантом данной группы преобразований.
ТЕОРИЯ ГРУПП
54а
Вообще, пусть многообразие, элементы которого определяются
заданием п чисел хи х2, . . ., хп, подвергается преобразованию Г,
переводящему его в себя. Если Т осуществляется с помощью функций
/а(#ь #2> • • ., #Л; аи а2, • • ., On), к = 1, 2, . . ., я, непрерывных
относительно аргументов х% и параметров at, причем последовательное
проведение двух преобразований Т± и Т2 (их произведение Т^Т2)
xk — Jk (#i» x4i • ¦ • ? %п\ Q>i, 0*2, • • • i Q>m)i
x'k = h (x'v x'2, . . ., x'n- b±, b2, . . ., bm), к = 1, 2, . . ., n
есть преобразование того же вида
%k ~ Jk \xli x2i • • • ч хп'ч cii c2i • • • » cm)i к = 1, 2, . . . , ft,
где cfe = i^ (av a2, . . ., am; &1? &2> • • •, bm), к = 1, 2, ..., тг; если, далее,
существует всегда обратное преобразование Г"1
%k == Jk (^i> ^2' * ' ' ' ^w» &±ч ^2' ' • • ' ^mj» /С = 1» ^» • • • > 72-
(т. е. уравнения #& = fk (хи х2, . . ., хп; ab а2, . . ., ат) разрешимы
указанным образом относительно всех xk) и, значит, тождественное
преобразование (единица) ТТ~г = Т~гТ, переводящее каждый элемент
в самого себя, то говорят, что Т образуют непрерывную
га-параметрическую группу или группу Ли. Функции fk считаются
дифференцируемыми по переменным и параметрам требуемое в том или ином вопросе число
раз, обычно дважды. Функция F(xu х2, . . ., д^), удовлетворяющая
относительно Т равенству F(x'2, х2, . . ., х^) = F(xi, х2, . . ., хп),
называется инвариантом группы преобразований. Если преобразование Т
удовлетворяет только первому из указанных условий, то говорят о
полугруппе преобразований.
Софус Ли применил разработанную им теорию непрерывных групп
к теории дифференциальных уравнений, достигнув при этом большой
общности в изучении проблемы интегрирования в квадратурах. Ф. Клейн
и А. Пуанкаре показали важность новой теории в исследовании авто-
морфных функций. Все трое названных ученых, а за ними многие другие
приложили непрерывные группы к геометрии. В так называемой Эрлан-
генской программе — вступительной лекции, прочитанной в 1872 г.
Клейном в Эрлангенской высшей политехнической школе — была выдвинута
идея обозреть и классифицировать при помощи непрерывных групп с
единой точки зрения различные системы геометрии и их взаимные связи.
Пространство рассматривается как многообразие элементов (точек, или
прямых или окружностей и т. д.), в котором задана та или иная группа
преобразований (движений), переводящих его в самого себя. Предметом
каждой геометрии является изучение свойств фигур, инвариантных
относительно данной группы преобразований; две фигуры, переводящиеся
одна в другую при таком преобразовании, считаются «равными» или
конгруэнтными.
Так, группа обыкновенных движений определяет евклидову
метрическую геометрию, группа аффинных преобразований евклидова
пространства, при которых прямые переходят в прямые,— аффинную геометрию,
в которой на плоскости «равны» два любых треугольника, а в пространстве-
два любых тетраэдра, и т. д. Сам Клейн уделил особенное внимание
проективной геометрии, которая в случае, скажем, плоскости характеризуется
группой проективных преобразований
, _ flis+biy + ci ,_ а2,х-\-Ъ2у + с2
а3х + Ъ3у-\-с3 ' У а3х + Ъ3у + съ '
544
ГЛ. 25. ИССЛЕДОВАНИЯ ПО АЛГЕБРЕ
причем определитель из коэффициентов числителей и знаменателя отличен
от нуля, а плоскость дополняется бесконечно удаленной прямой, в
которую преобразуется прямая а3х + Ь3у + с3 = 0. Инвариантом этой группы
служит двойное отношение четырех точек, лежащих на одной прямой.
Метрическая геометрия пространств Евклида, Лобачевского и Римана
входит, как говорилось, в состав проективной геометрии, и
характеризующие их группы преобразований являются частями (подгруппами) группы
проективных преобразований.
Программа Клейна в значительной мере определила развитие
геометрии на полстолетия; одним из направлений ее реализации служило и
доказательство непротиворечивости неевклидовых геометрий с помощью
интерпретаций самого Клейна и Пуанкаре, упоминавшихся нами ранее.
На этом пути были построены и новые геометрические системы. При всем
своем значении программа Клейна не универсальна и в дальнейшем, уже
в XX веке созданы были новые типы пространств, при построении которых
применение групп преобразований явилось лишь одной из
руководящих идей.
Общая теория инвариантов возникла в связи с развитием теории форм
и аналитической геометрии: простейшие инварианты кривой второго
порядка изучают все инженеры. Благодаря английским математикам,
особенно Дж. Булю, А. Кэли и Дж. Сильвестру (который ввел само слово
«инвариант») эта теория в середине XIX века выделилась в особую
дисциплину, разработкой которой занимались Г. Аронгольд, П. Гордан,
Д. Гильберт и многие другие и которая оказалась в высшей степени
полезной не только в геометрии и теории групп, но и в других математических
науках.
Как мы видели, понятие группы обладает высокой степенью
абстрактности. В конкретных случаях элементами групп могут быть числа,
подстановки, геометрические фигуры и т. д. Вместе с тем групповая операция
умножения может иметь различный смысл — под ней можно понимать
и арифметическое умножение, и сложение, и последовательную
реализацию подстановок и разнообразные движения в пространстве и т. д. Если
в XVII веке математики пришли к понятию переменной величины,
значениями которой служат постоянные числа, то в XX веке наука поднялась
на более высокую ступень абстракции и приступила к изучению свойств
общего понятия операции, частными случаями которого могут быть
различные рассмотренные нами и иные действия. Именно чрезвычайной
общностью теории групп объясняется широкое приложение ее методов
в математике и физике, прежде всего в кристаллографии, а в XX веке
в теории относительности и в квантовой теории.
Итогом развития в рассматриваемый период явилось создание
абстрактной теории групп, в которой свойства группы изучаются
совершенно независимо от природы составляющих ее элементов. Основную роль
при этом играет понятие изоморфизма. Две группы G и G' называют
изоморфными, если между их элементами а, Ь, с, . . . и а', V, с', ... можно
установить такое взаимно однозначное соответствие, что произведению
аЪ соответствует произведение а'Ъ''. Две изоморфные группы могут отли1
чаться только природой элементов, но не структурно. С точки зрения
абстрактной теории групп все изоморфные между собой группы
неотличимы, а изучение всех их сводится к изучению какой-либо одной. Так,
каждая конечная группа изоморфна некоторой группе подстановок.
Результатом всего этого развития явилось изменение самого облика
алгебры. В прежней, классической алгебре символический аппарат, бук-
РАСПРОСТРАНЕНИЕ ТЕОРИИ ГРУПП В РОССИИ
545
венное исчисление имели значение вспомогательного орудия и изучались
в узком плане, а единственной реализацией буквенных символов а, &,
с, . . , были действительные или комплексные числа, единственными
допустимыми операциями а + &, ab, . . ., были обычные действия арифметики.
В абстрактной алгебре, включающей теорию групп, на первый план
выдвинулось изучение множеств элементов произвольной природы, над
которыми производятся те или иные операции, сходные с действиями
классической алгебры. Эта эволюция связана была не только с рассмотренными
нами моментами; существенную роль играло здесь развитие теории
алгебраических чисел, теории гиперкомплексных чисел, векторного исчисления.
Решение алгебраических уравнений и вообще теория алгебраических
многочленов не утратили, разумеется, практического значения и
теоретического интереса. Но эта теория теперь рассматривается лишь как одна из
глав алгебры и новые результаты в ней получаются новыми, более
мощными методами.
Распространение теории групп в России. Проникновение теории
групп и теории инвариантов и связанных с ними областей началось в
России довольно рано и в разных местах. Первой во времени явилась
магистерская диссертация воспитанника (1860) и с 1861 г. преподавателя,
а затем профессора Харьковского университета Даниила Михайловича
Деларю (1839—1905) «Общая теория алгебраического решения
уравнений» (Харьков, 1864). На 114 страницах автор изложил историю проблемы
решения уравнений в радикалах, важнейшие предложения теории Галуа
и, в частности, теории «абелевских» уравнений, которые теперь называют
циклическими (мы зовем абелевым уравнение, если каждый из его корней
рационально выражается через один; абелевы уравнения приводятся
к циклическим). Несмотря на то, что в работе Деларю отсутствовали
существенные оригинальные результаты, заслуга его была весьма значительна.
Напомним, что первое систематическое и подробное изложение теории
Галуа, благодаря которому она и получила более широкую известность,
дал в 1870 г. К. Жордан. До того существовала только специальная
мемуарная литература.
Большую известность новые алгебраические идеи начинают получать
в восьмидесятые и девяностые годы. Примером может служить курс
высшей алгебры, читанный тогда в Казанском университете профессором
А. В. Васильевым, где, наряду с учением о симметрических функциях,
основное место отводилось теории групп подстановок («субституций»)
и исследованиям Лагранжа и Абеля. В своем курсе Васильев вплотную
подходил к теории Галуа, упоминая его теорему о разрешимости в
радикалах уравнений, все корни которых рационально выражаются через
произвольные два. Такой же характер имел его печатный курс лекций
«Алгебраический анализ. Теория буквенных уравнений в связи с теорией
субституций» с приложением «Теория деления круга» (Казань, 1886).
Еще ранее, в 1880 г., Васильев опубликовал в 47-м томе «Ученых записок»
Казанского университета магистерскую диссертацию «О функциях
рациональных, аналогичных с функциями двоякопериодическими», в которой
конечные группы линейных преобразований применяются к исследованию
рациональных автоморфных функций. Теории групп Васильев придавал
первостепенное значение в современной математике. Пишущий эти строки,
будучи еще студентом второго курса, впервые услышал о первых
понятиях этой теории и о ее важности в беседах с покойным казанским
математиком, который в то время (в 1925 г.) был уже на склоне лет.
546
ГЛ. 25. ИССЛЕДОВАНИЯ ПО АЛГЕБРЕ
В Петербурге пропагандистом теории Галуа явился воспитанник,,
с 1885 г. доцент и с 1905 г. проффессор Петербургского университета
Дмитрий Федорович Селиванов (1855—1932). В магистерской
диссертации Селиванова «Теория алгебраического решения уравнений» (Спб., 1885}
содержится довольно подробное изложение теории конечных групп и
специально теории Галуа. В докторской диссертации «Об уравнениях пятой
степени с целыми коэффициентами» (СПб., 1899) основной задачей
является установление необходимых и достаточных условий разрешимости
в радикалах уравнений пятой степени. Применительно к поставленной
цели изложены главные предложения
теории Галуа. Обе работы представляли
собой в основном изложение уже
известных результатов.
Вообще Д. Ф. Селиванов известен
более как автор учебных руководств. Мы
упоминали о его курсе теории конечных
разностей. Перу его принадлежит и
соответствующая глава в «Encyklopadie der
Mathematischen Wissenschaften»,
содержащая подобно другим отделам этого
издания очень большой справочный
материал. В эти же годы (1888—1901) задачами
разрешимости в радикалах уравнений
того или иного вида в Петербурге
занимался И. П. Долбня.
Работы в этом же направлении
велись и в Юрьеве (Тарту). Не касаясь
исследований преподававшего одно время
в местном университете немецкого
математика А. Кнезера и работ Ф. Э. Молина
по гиперкомплексным числам (о послед-
Д. Ф. Селиванов. них будет речь идти ниже), мы отметим
здесь очень обстоятельное изложение
теории инвариантов в докторской диссертации Виссариона
Григорьевича Алексеева (1866—1943) «Теория рациональных инвариантов
бинарных форм в направлении Софуса Ли, Кэли и Аронгольда» (Юрьев,
1899). Алексеев был воспитанником и с 1891 г. приват-доцентом
Московского университета, а в 1895 г. перешел на работу в Юрьев, где
получил профессуру в 1901 г. и преподавал до 1918 г. По теории
инвариантов он опубликовал несколько специальных статей, из которых одна
(1900), написанная совместно с П. Горданом, посвящена аналогиям между
формулами теории инвариантов и химическими формулами.
Теория непрерывных групп Ли также нашла отражение в
специальной русской математической литературе. Подробное изложение ее, вместе
с приложениями к геометрии, дал в первом томе «Оснований геометрии»
(Одесса, 1907) В. Ф. Каган. Некоторые сведения по теории инвариантов
имеются в главе о линейных и квадратичных формах обширных «Оснований
теории определителей» того же автора (Одесса, 1922), подготовленных
еще до 1917 г. Оригинальное применение методы С. Ли получили в
геометрических исследованиях Д. М. Синцова, тесно связанных с теорией
дифференциальных уравнений.
В Московском университете также возрос интерес к новой алгебре,
свидетельством чего являются читавшиеся здесь в начале XX века спе-
Д. А. ГРАВЕ
547
циальные курсы о решении уравнений в радикалах, теории
гиперкомплексных чисел и теории инвариантов (его читал Д. Ф. Егоров). Основным
центром развития теоретико-групповой алгебры в рассматриваемый
период явился, однако, Киевский университет.
Возникновение Киевской алгебраической школы. Зачинателем здесь
явился М. Е. Ващенко-Захарченко. В расширенном для печати курсе-
лекций «Теория определителей и теория форм» (Киев, 1877) он дал
подробное и отвечавшее в то время состоянию вопроса изложение теории
определителей х) и теории инвариантов в связи с теорией бинарных форм.
Во второй части курса алгебры Ващенко-Захарченко (первая вышла
в 1887 г. под названием «Алгебраический анализ или высшая алгебра»)
«Высшая алгебра. Теория представлений и приложение ее к
алгебраическим вопросам» (Киев, 1890) содержится также детальное, хотя иногда
неаккуратное изложение теории групп подстановок, теории Галуа,
и, наконец, решение уравнений пятой степени в эллиптических функциях
(по Кронекеру).
Вслед за руководствами Ващенко-Захарченко появляются работы
других киевских математиков, частью компилятивные, частью
оригинальные.
Это прежде всего сравнительно простое, хотя и не очень строгое
изложение теории Галуа в статье В. П. Ермакова «Алгебраические уравнения,
решаемые в радикалах» (Киевск. универс. изв., 1901) и его же работа
«Общая форма радикального выражения, имеющего 3, 4, 5, 6, 7, 8
и 9 значений» (Киев, 1904), в которой по возможности элементарно
рассмотрен вопрос о разрешимости в радикалах некоторых видов уравнений,,
главным образом циклических. В начале XX века алгеброй занялся Георгий
Васильевич Пфейффер (1872—1946), с 1900 г. работавший в Киевском
университете. В «Киевских университетских известиях» за 1902 г. он
напечатал две статьи о решении абелевых и двучленных уравнений, и там же год
спустя магистерскую диссертацию «Группы многогранников». Группы
вращений правильных многогранников изоморфны группам подстановок,
характеризующим свойства алгебраических уравнений. Как говорилось,
замечательные связи между группой вращений икосаэдра
(двадцатигранника) и теорией решения уравнений 5-й степени были раскрыты во второй
половине XIX века Ф. Клейном, опиравшимся на предшествующие
изыскания Ш. Эрмита и Л. Кронекера. Диссертация Пфейффера содержит
общую теорию групп вращений многогранников в оригинальном
изложении; в ней есть и собственные результаты автора.
Впоследствии Пфейффер занялся теорией алгебраических функций
и поверхностей (докторская диссертация 1910 г.). В 1920 г. он был избран
членом Академии наук УССР; его работы советского времени лежат почти
исключительно в области дифференциальных уравнений с частными
производными.
Д. А. Граве. В 10-е годы XX века в Киеве создается научная
алгебраическая школа. Главная роль в ее организации принадлежала
Д. А. Граве.
Дмитрий Александрович Граве родился в г. Кириллове Новгородской
губернии 6 сентября 1863 г. Научную работу он начал, будучи студентом
г) Еще ранее этому предмету посвятил свою докторскую диссертацию «Теория
определителей и ее приложения» (Одесса, 1871) С. П. Ярошенко.
548
ГЛ. 25. ИССЛЕДОВАНИЯ ПО АЛГЕБРЕ
Петербургского университета, который окончил в 1885 г. Свои первые
работы по дифференциальной геометрии и дифференциальным уравнениям
он напечатал в «Записках физико-математического общества студентов
С.-Петербургского университета» (т. I—II, 1884—1885). Среди учителей
Д. А. Граве особое место занимал в первом периоде его деятельности
А. Н. Коркин.
В магистерской диссертации Д. А. Граве «Об интегрировании частных
дифференциальных уравнений первого порядка» (СПб., 1889), развивающей
методы Якоби и Коркина, дано, среди
прочего, решение одного вопроса
задачи трех тел, поставленного перед
ним Коркиным. После защиты в том
же 1889 г. Граве приступил к
преподаванию в Петербургском
университете в звании приват-доцента.
Докторская диссертация Граве также была
написана на тему, предложенную
Коркиным и примыкавшую к
картографическим изысканиям Эйлера, Лагран-
жа и Чебышева. Коркин предложил
Граве найти эквивалентные проекции
шара на плоскость, при которых
меридианы и параллели изображаются
прямыми и окружностями; при этом
проекции называются эквивалентными,
если площади криволинейных фигур
на шаре переходят в точно подобные
им на карте. В диссертации «Об
основных задачах математической
теории построения географических карт»
Д. А. Граве. (СПб., 1896) Граве выразил задачу
Коркина некоторым уравнением с
частными производными и дал ее полное решение. Всего он получил 11
возможных видов проекций. Несколько ранее, в 1894 г., Граве дал
простое доказательство высказанной за сорок лет до того без доказательства
теоремы Чебышева о том, что уклонение масштаба, т. е. разность между
наибольшими и наименьшими его значениями внутри данной карты, будет
наименьшим для такой карты, на которой масштаб вдоль границы имеет
постоянную величину х).
Защита прошла успешно. Коркин в своем неофициальном отзыве
писал, что «этой работой Д. А. (Граве) укрепил традиции, установленные
у нас Эйлером и которым следуют все математики нашего университета» 2).
В 1911 г. Граве распространил свои исследования на поверхности с
гауссовой кривизной постоянного знака. (Journ. fur die reine und angewandte
Mathematik, B. 140).
г) Любопытно, что первое свое сообщение об этом Д. А. Граве сделал на 23 сессии
Французской ассоциации преуспеванию наук, в которой нередко выступал ранее
П. Л. Чебышев. Краткое изложение этих результатов Д. А. Граве включил в свою
«Энциклопедию математики» (Киев, 1912, стр. 439—441).
2) Газета «Новости», 22 апреля 1896 г. См. В. А. Добровольский, Научно-
педагогическая деятельность Д. А. Граве.— Ист.-матем. исслед., вып. XV, 1963,
стр. 323.
Д. А. ГРАВЕ
549
Д. А. Граве интересовался и некоторыми элементарными задачами.
Так, Эйлер, изучая функцию со(#), предельную для последовательности
«сверхстепеней» со^я) = а , (о2(х) = а>а*\ <*>з(#) = аа<1 , - . ., указал без
доказательства свойства со(х). Граве снабдил предложения Эйлера
требуемым выводом (Nouv. Ann. des mathem., 3 ser., v. 17, 1898). Несколько
ранее Граве из соображений, относящихся к делителям чисел вида х2, + 1,
пришел к заключению, что уравнение
я . 1 . . 1
_- = ттг • arctg 1- тг • arctg —
имеет только пять издавна известных решений в целых числах: 1) т = 1,
п = 1, р = 2, q = 3; 2—4) ттг = 2, л = 1 и р = 1, д = — 1, или р = 2,
q = ~ 1 (случай Я. Германа, 1706) или р = 3, д = 7 (случай Эйлера,
1738; опубл. в 1744); 5) т = 4, п = 1, р = 5, q = — 239 (случай Дж. Мэ-
чина, опубл. в 1706). Формула для последнего случая была применена
еще самим Мэчином для быстрого вычисления я со 100 знаками (1706).
В Intermediare des mathematiciens за 1895 г. Д. А. Граве предложил
доказать свое предположение. Это вскоре выполнил К. Ф. Штёрмер, тогда
еще бывший студентом.
После докторской защиты Граве еще три года прожил в столице.
В 1891—1899 гг. он был весьма активным членом Петербургского
математического общества. В 1899 г. он перешел на работу профессором
в Харьковский университет, а с начала* 1902 г.— в Киевский университет,
с которым оказалась связана вся его дальнейшая деятельность.
В Киеве, отчасти под влиянием здешних интересов, отчасти в
результате бесед за границей с Г. Фробениусом, К. Гензелем, Э. Ландау и др.,
Граве отошел от прежней тематики и сосредоточился на новой алгебре
и теории чисел. Он расширил рамки обычного лекционного курса алгебры,,
написал новые руководства, организовал студенческие семинары.
Блестящий лектор и превосходный научный руководитель, Граве быстро добился
больших результатов: всего через несколько лет вокруг него образуется
сильный коллектив из молодых преподавателей и студентов. Специальный
семинар по теории групп, основанный им в 1911 г., превращается в
научную школу, членами которой были В. П. Вельмин, Б. Н. Делоне,
Е. И. Жилинский, А. М. Островский, Н. Г. Чеботарев, О. Ю. Шмидт
и другие.
Мы приведем слова самого Граве, рисующие работу его семинара:
«В моем стремлении поднять преподавание чистой математики в Киевском
университете я столкнулся с большими препятствиями известной косности
официальных программ. Теории групп не было места в обязательном
преподавании.
Желая, тем не менее, дать серьезным студентам, занимающимся
наукой, возможность практически познакомиться с теорией групп и получить
таким образом в свое распоряжение сильное орудие исследования, я
выделил один день в неделю из моего семинара, который посвятил теории групп.
Я назвал занятия по теории групп просеминаром, желая этим подчеркнуть
элементарность указанной теории: элементарность не в смысле простоты
ее, а в том смысле, что основы теории групп не требуют почти никаких
предварительных сведений по другим предметам.
Занятия в этом просеминаре происходили в осеннем полугодии 1911 г.
по субботам. Самый характер занятий был таков. Мы взяли книгу Pascal,
«Repertorium der hoheren Analysis», в которой заключается статья проф!
Loewy об абстрактной теории групп. В этой статье перечислены теоремы
550
ГЛ. 25. ИССЛЕДОВАНИЯ ПО АЛГЕБРЕ
без доказательства с подробными литературными ссылками. Эти теоремы
выставлялись в русском переводе в книге, находившейся в помещении
математического семинара. Студенты должны были пробовать сами
доказать теоремы, и если встречали затруднение, то могли обращаться к
литературе» г).
Один из лучших учеников Граве — Н. Г. Чеботарев — позднее
вспоминал: «Д. А. приучал молодежь к самостоятельной
исследовательской работе с самого начала, не заботясь об эрудиции ученика, которая
приходила впоследствии сама собой... В выборе темы Д. А. проявлял
большую смелость, давая ученикам большие отделы алгебры, в которых
они сами должны были искать нерешенные задачи. При этом он всегда
рекомендовал сразу брать для разрешения трудные вопросы, и это
большей частью приводило к прекрасным результатам. Исключительно велико
также количество студентов, которых Д. А. ежегодно оставлял при
университете, справедливо считая, что отбор научных работников должен
производиться не в процессе учебы, а в процессе творческой работы» 2).
В своей «Математической автобиографии» Н. Г. Чеботарев ярко обрисовал
обстановку тесного сотрудничества в руководимом Граве молодом и друж-
яом коллективе 3).
С 1901 г. начинают появляться отдельные статьи Д. А. Граве по
частным вопросам алгебры, например, о классах алгебраически разрешимых
уравнений 5-й степени вида хъ -\-10/??3 + Юдя2 + Ъгх -\- s = 0, где
р, q, г рациональны, а 5 произвольно, которых он получает два, именно
хъ -{- s = 0 и хъ + i-Opx3 -f- 20р2х -[-5=0 (Bull, des Sciences mathem.,
2 ser., t. 34, 1910). По большей части эти статьи содержат методические
упрощения и уточнения в изложении тех или иных высших отделов
алгебры, как, скажем, статья «Об алгебраических единицах» (Киевск.
универс. изв., 1912). Педагогическая и учебно-литературная работа
-захватывает Граве почти целиком и к этому времени относится создание
«го замечательных курсов, весьма популярных среди учащейся молодежи,
ж не только молодежи.
Руководства Граве отличались полнотой, свежестью содержания
ж особой, ему свойственной доходчивостью и оригинальностью
изложения. Он дал, между прочим, первый образец популяризации теории групп
среди любителей математики, посвятив ей несколько параграфов в
«Энциклопедии математики», в которых ярко показал на немногих примерах
идейную сторону этой науки.
Первым алгебраическим руководством Граве были «Элементы
алгебраического анализа», печатавшиеся в «Университетских известиях»
в 1904—1908 гг. и затем отдельно изданные под названием «Теория
конечных групп» (Киев, 1908). Это была первая у нас книга специально по
теории групп. В 1914 г. он издал фундаментальные «Элементы высшей
алгебры» (698 страниц). Основной алгебраической монографией того времени
был огромный курс Г. Вебера, далеко выходивший за пределы
потребностей и возможностей студентов. Вебер издал также сокращенное издание
своей книги, которое не удовлетворило Граве неполнотой, отчасти
нечеткостью и громоздкостью доказательств. Монография Граве обладает
г) Этот отрывок из отзыва Д. А. Граве о книге О. Ю. Шмидта по теории групп
любезно предоставил нам В. А. Добровольский (отзыв хранился в одном из архивов
УССР).
2) Н. Г. Чеботарев, Академик Дмитрий Александрович Граве (К 50-летию
«го научно -не дагогической деятельности).— УМН, вып. III, 1937, стр. 231.
3) См. УМН, т. III, вып. 4, 1948.
Д. А. ГРАВЕ
551
высокими достоинствами. Большое место отведено здесь, наряду с
классическими вопросами, теории групп подстановок, теории инвариантов,
квадратичным формам, теории полей и особенно теории Галуа. Изложение
теории Галуа Граве подверг значительной переработке.
Вот что он писал по этому поводу В. А. Стеклову: «Изложение у Вебе-
ра я не могу назвать строгим. Вплоть до последних своих работ, он
определяет группу Галуа (по Галуа) двойным свойством: 1) не нарушать
зависимости между корнями, 2) давать рациональное значение всякой
функции, принадлежащей группе Галуа. Из моего изложения с простотой
и ясностью Вы увидите, что группу Галуа можно определить так: «Группа
Галуа есть совокупность подстановок, из которых каждая не нарушает
¦всякого соотношения между корнями». Второе свойство есть теорема,
а потому включение его в определение есть логическая ошибка. В
последнее время моего преподавания я упростил теорию Галуа в такой степени,
что дальше идти некуда... Изложение Вебера я не могу назвать общим,
потому что оно относится к численным уравнениям, коэффициенты
которых — постоянные числа, а потому переход к случаю коэффициентов
функциональных требует добавочных рассуждений. У меня получается
теория строгая, совершенно общая и... простая...» *). Принципы своего
построения Д. А. Граве разъяснил в специальной работе «Об основных
положениях теории Галуа», напечатанной в 29 томе «Математического
сборника» за 1914 г. Монография Граве оказала серьезное влияние
на изложение теории Галуа у советских авторов и сохраняет интерес
и в наши дни.
Выдающимися достоинствами обладало и второе издание
«Элементарного курса теории чисел» Граве (Киев, 1913; первое издание вышло
в 1909 г.), содержащее главы по теории полей, непрерывным дробям,
бинарным квадратичным формам, общей теории алгебраических чисел и
исчислению матриц. В частности, в седьмой главе, «Теория полей»,
Граве знакомит читателя с такой научной новинкой, как поле /?-адических
чисел Гензеля, т. е. символов вида
^¦ + %Г+ ¦ - +bo + aiP + a2p*+ . . . +апРп+ . . .,
р р
Где р — простое число. Гензель построил теорию формальных операций
над этими символами (которые при бесконечном числе членов
представляют собой, вообще говоря, расходящиеся ряды), а также показал
применение jp-адических разложений в алгебре и теории чисел. Граве один
из первых правильно оценил аппарат Гензеля, который приобрел
большое значение в теории алгебраических чисел. В главе по общей теории
алгебраических чисел автор излагал исследования Маркова, Вороного,
Дедекинда, Золотарева. В книге — редкий случай — приведены три
теоремы, незадолго перед тем доказанные учениками Граве — студентами
Б. Н. Делоне, Е. И. Жилинским и О. Ю. Шмидтом 2). Следует добавить,
что ученики Граве помогали ему в подготовке его книг к печати. Среди
больших руководств Д. А. Граве назовем еще упомянутую ранее
«Арифметическую теорию алгебраических величин», из намеченных пяти томов
х) Цит. по статье В. А. Добровольского. Научно-педагогическая
деятельность Д. А. Граве.— Ист.-матем. исслед., вып. XV, стр. 331.
2) Б. Н. Делоне доказал теорему, высказанную В. П. Ермаковым: особенным
числом кубического поля может быть только 2. Е. И. Жилинский доказал общую теорему:
особенные простые числа поля меньше его степени. Теорема О. Ю. Шмидта относится
к теории групп подстановок элементов конечного поля (см. Д. А. Г р а в е,
Элементарный курс теории чисел, Киев, 1913, стр. 264—265, 171—172).
552
ГЛ. 25. ИССЛЕДОВАНИЯ ПО АЛГЕБРЕ
которой были изданы два: «Квадратичная область» и «Теория идеалов»
(Киев, 1910-1913).
Все руководства Д. А. Граве содержат много интересных
исторических справок, а иногда и более подробных экскурсов в историю проблемы.
Для средней школы Д. А. Граве написал «Начала алгебры» (Киев,
1915), план которой была задуман вместе с В. А. Марковым еще в
девяностые годы. Целью было дать строго логическое и вместе с тем доступное
изложение основных вопросов, в частности, учения об иррациональных
числах и пределах. В учебнике приводится способ Н. Я. Сонина
извлечения корней высших степеней, рассказано о проблеме решения
уравнений в радикалах (теорема Абеля), сообщаются понятие о функции
и ее графике и элементарные способы отыскания экстремумов.
После Октябрьской революции Граве продолжал свою плодотворную
научно-педагогическую работу. В 1920 г. он был избран членом Академии
наук УССР, в 1924 — членом-корреспондентом и в 1929 г.— почетным
членом Академии наук СССР. Скончался Д. А. Граве 19 декабря 1939 г. х).
Ученики Д. А. Граве; О. Ю. Шмидт. В последнее пятилетие перед
Октябрьской революцией молодые участники киевской алгебраической
школы выступили с первыми работами. Некоторые из них представляли
собой усовершенствования выводов уже
известных теорем или упрощенные
изложения трудных отделов современной
алгебры. Проделанная в этом
направлении работа, непосредственно
примыкавшая к научно-литературной
деятельности самого Граве, была затем
использована в лекциях и руководствах
советского времени. Другие работы
молодых киевлян содержали
оригинальные результаты. Не останавливаясь на
статьях по теории /ьадических чисел
Е. И. Жилинского (1914), впоследствии
работавшего в Польше, и А. М.
Островского (1913), осевшего в первую
мировую войну за границей (он стал
профессором университета в Базеле), мы
остановимся на деятельности О. Ю. Шмидта
и Н. Г. Чеботарева.
Отто Юльевич Шмидт (30 сентября
1891—7 сентября 1956) начал свою
научную деятельность еще в
студенческие годы (1909—1913). Первым его
О. Ю. Шмидт. успехом явилось новое и значительно
более простое доказательство важной
теоремы немецкого алгебраиста Р. Ремака (1911) о центральном
изоморфизме разложений конечной группы в прямое произведение
неразложимых множителей, опубликованное в «Отчетах и протоколах физико-
математического общества при Киевском университете» за 1912 г. В
следующем году Шмидт напечатал в «Университетских известиях» подробное
изложение исследований по весьма трудной и почти неизученной задаче
х) См. Сборник, посвященный памяти академика Д. А. Граве, М.—Л., 1940.
УЧЕНИКИ Д. А. ГРАВЕ; О. Ю. ШМИДТ
553
Галуа о типах разрешимых в радикалах уравнений, степень которых
есть степень простого числа; здесь он новым методом получил основные
результаты К. Жордана и дополнил их некоторыми своими1). В 1913 г.
Шмидт дал еще одно доказательство теоремы Ремака (Bull. Soc. Math,
de France, v. 41). Следует заметить, что оба доказательства и особенно
второе, отличающееся чрезвычайной простотой, получили большую
известность и повторялись в советских и зарубежных руководствах
по теории групп; второе из них включено, например, в широко
распространенное сочинение базельского профессора А. Шпайзера Die Theorie
der Gruppen von endlicher Ordnung (3-е изд., 1937).
Вслед за этим в киевских «Университетских известиях» за 1914—
1915 гг. была напечатана «Абстрактная теория групп» Шмидта, в 1916 г.
вышедшая отдельным изданием и переизданная в 1933 г. в Москве. Здесь
многие доказательства принадлежали автору. Главной особенностью
монографии было первое в мировой литературе изложение основ теории
групп, одновременно для групп конечных и бесконечных (специально
конечным группам посвящены главы, начиная с пятой).
В то же время теория бесконечных групп была мало разработана;
выбрав такой способ изложения, молодой автор правильно предвидел
(и сам подготовил) ход дальнейшего развития теории групп.
Как отмечает крупный современный специалист в этой области
А. Г. Курош, многие поколения советских алгебраистов учились теории
групп по труду О. Ю. Шмидта 2).
В 1916 г. Шмидт стал приват-доцентом Киевского университета
и начал чтение курса по теории групп. Но во всей широте кипучая
общественная и научная деятельность академика О. Ю. Шмидта развернулась
уже после Октябрьской революции, которую он принял с открытой
душой. В 1918 г. он вступил в Коммунистическую партию. Он вел очень
большую и разнообразную политическую и общественную работу и для
научных занятий в первые годы Советской власти у него оставалось
мало времени. Лишь в 1920 г. он вновь приступил к преподаванию
математики, а с 1924 г. стали опять появляться его статьи по алгебре. В 1928 г.
он дал важное обобщение теоремы Ремака на бесконечные группы особого
вида (обладающие главным рядом); эта теорема Ремака — Шмидта,
одна из основных в общей теории групп, явилась отправным пунктом
исследований многих советских и зарубежных ученых. С 1923 г.
О. Ю. Шмидт работал в Московском университете и в течение многих
лет до 1949 г. руководил здесь кафедрой алгебры, а также организованным
им в 1930 г. алгебраическим семинаром.
Заслуги его в создании советской алгебраической школы очень
велики. Однако с годами О. Ю. Шмидт все больше сил и времени отдавал
исследованию Арктики, а затем проблемам геофизики и космологии.
Его научные заслуги были отмечены избранием членом-корреспондентом
АН СССР в 1933 г. и через два года — ее действительным членом.
Арктические экспедиции принесли О. Ю. Шмидту всемирную славу и звание
Героя Советского Союза (1937) 3).
Скажем несколько слов о работах других учеников Граве.
Н. Г. Чеботарев начал заниматься в семинаре Граве будучи
студентом второго курса, после того как летом 1913 г. самостоятельно изучил
1) Одну из теорем Шмидта, содержащихся в этой работе, Граве и включил в свой
курс теории чисел.
2) А. Г. Курош, Отто Юльевич Шмидт (некролог).— УМН, т. XI, 6 (72), 1956.
3) См. сб. «Отто Юльевич Шмидт. Жизнь и деятельность», М., 1959.
554
ГЛ. 25. ИССЛЕДОВАНИЯ ПО АЛГЕБРЕ
по краткому курсу Вебера теорию Галуа. До Октябрьской революции
Чеботарев не успел ничего опубликовать, но фактически приступил
к научной работе на том же втором курсе. Так, уже второй его доклад
на семинаре Граве содержал новое и простое доказательство теоремы
Бертрана о границе индексов симметрической группы, которое Чеботарев
впоследствии воспроизвел в своих «Основах теории Галуа» (ч. 1, Л.— М.,
1934). Вообще, еще до окончания университета у Чеботарева (отчасти
под влиянием бесед с Д. А. Граве и особенно с Б. Н. Делоне) созрел ряд
идей в области новой алгебры, которые он затем реализовал на
протяжении многих лет. В 1916 г. Чеботарев защитил дипломную работу по
теории jo-адических чисел и был оставлен при Киевском университете. Все
это подробно описано в уже упоминавшейся «Математической
автобиографии» Н. Г. Чеботарева, доведенной до 1927 г. О некоторых других работах
и жизненном пути этого выдающегося ученого говорилось, когда речь
шла об исследованиях по теории делимости Е. И. Золотарева.
В школе Граве, как мы видели, разрабатывались не только
алгебраические, но и арифметические вопросы, а также пограничные проблемы.
Занятий В. П. Вельмина теорией алгебраических чисел нам пришлось
коснуться ранее. Мы отметим еще две статьи молодых киевских
математиков. Одна из них, написанная Б. Н. Делоне, содержит оригинальное
доказательство с помощью закона взаимности Эйзенштейна теоремы
Кронекера, согласно которой каждый корень абелева уравнения простой
степени рационально выражается через некоторый корень из единицы.
Другая, принадлежащая М. Ф. Кравчуку, имеет своим предметом
свойства перестановочных групп матриц. Обе они напечатаны в «Сообщ. Харьк.
матем. о-ва», т. 14 (1915). Б. Н. Делоне в дальнейшем занимался
преимущественно теорией чисел и ее приложениями к кристаллографии, но
обращался также и к алгебраической тематике, в частности, развивая
геометрическую трактовку теории Галуа. Михаил Филиппович Кравчук
(21 ноября 1892—9 марта 1942), впоследствии профессор Киевского
университета (1922) и академик Академии наук УССР (1929), продолжая
в дальнейшем работы по алгебре, в том числе по группам перестановочных
матриц, работал и в других областях математики, особенно в теории
дифференциальных уравнений.
С. О. Шатуновский и теория Галуа. Своеобразное построение теории
Галуа дал в самом конце рассматриваемого времени С. О. Шатуновский.
Речь идет об уже -известной нам его диссертации «Алгебра как учение
о сравнениях по функциональным модулям» (1917), во введении к которой
автор высказал свои взгляды на условия применимости закона
исключенного третьего. Основное содержание этой книги составляет новое
построение теории Галуа, не предполагающее, как обычные изложения,
существования корня алгебраического уравнения, в доказательствах
которого применяется закон исключенного третьего. Вместо уравнения
f(x) = xn + aixn-1+ ... +ап = 0
изучаются сравнения
f(x) = 0[mod(pk(xi, х2, . . . хп)\, ?=1.2, - . ., п,
где модули ф(^1? х2, . . ., хп) представляют собой левые части некоторых
соотношений между корнями уравнения, рассматриваемыми как
независимые переменные. Введение определенной «натуральной системы
модулей» позволяет полностью развить теорию Галуа без теорем о суще-
ГИПЕРКОМПЛЕКСНЫЕ ЧИСЛА
555
ствовании корней, которые особо доказываются в заключительной главе
диссертации. Мысль о таком подходе была выдвинута несколько ранее
П. Мертенсом, но Шатуновский провел ее подробно и весьма оригинально.
Ряд исходных понятий и идей его работы предвосхищает понятия и идеи,
получившие через несколько лет основное значение, благодаря Эмми
Нётер и созданной ею школе 1). Н. Г. Чеботарев в «Основах теории Галуа»
(гл. 2) последовал в своем выводе свойств группы Галуа за Мертенсом
и Шатуновским, считая такое изложение более удобным и естественным.
Аналогичное данному Шатуновским построение теории Галуа
независимо разработал немецкий математик А. Леви в 1925—1927 гг.
Гиперкомплексные числа. Важное значение для развития алгебры
и математики в целом имели работы по обобщению понятия о числе.
Открытые в середине XVI века комплексные числа получили всем теперь
известное геометрическое истолкование на рубеже XVIII и XIX вв.,
причем выяснилось, что операции над комплексными числами выражают
некоторые преобразования на плоскости. Сложение комплексных чисел
соответствует параллельному сдвигу плоскости; умножение на
комплексное число — вращению плоскости вокруг начала с некоторым
растяжением (или сжатием) всех отрезков в одном и том же отношении.
После этого возник вопрос: нельзя ли ввести такие новые числа, которые
выражают основные преобразования в трехмерном пространстве?
Положительный ответ на этот вопрос дали в 1843 г. ирландский математик
и физик У. Гамильтон, создатель теории кватернионов 2).
Обычные комплексные числа суть числа с двумя основными
единицами: 1 и i, причем при действиях над комплексными числами, законы
которых почти ничем не отличаются от законов, управляющих действиями
над вещественными числами, имеет место равенство i2 = — 1.
Кватернионы Гамильтона должны были прежде всего отобразить вращение
с растяжением в пространстве, характеризуемое четырьмя параметрами.
Кватернион Гамильтона, т. е. четверное гиперкомплексное число,
жмеет форму
q = а + ib + jc + kd,
где а, 6, с, d — действительные числа и i, /, А—мнимые единицы,
удовлетворяющие условиям
i2 = j* = k2=—l; ij =—ji = k\ jk =—kj = i; ki=—ik = j.
Отличие кватернионов от действительных чисел глубже, чем
комплексных чисел. Из существенных свойств действительных чисел для
комплексных чисел не выполняются лишь скалярные соотношения
«больше» или «меньше», и комплексные числа, как и действительные,
образуют поле. Для кватернионов, как это видно уже из правил
умножения основных единиц, нарушается коммутативность операции
умножения. Здесь произведение зависит от порядка сомножителей и, вообще
товоря,
*) Н. Г. Чеботарев, Самуил Осипович Шатуновский.— УМН, вып. VII,
стр. 318—319. О замечательном математике Э. Нётер и связях ее с московской
математикой см. П. С. Александров, Памяти Эмми Нётер.— УМН, вып. II, 1936.
2) Первоначальная попытка Гамильтона построить систему чисел с тремя
единицами, обладающую основными свойствами обыкновенных комплексных чисел, была
неудачной. Причина этого обстоятельства выяснилась много позднее (см. далее).
556
ГЛ. 25. ИССЛЕДОВАНИЯ ПО АЛГЕБРЕ
Приходится поэтому отличать умножение слева от умножения справа.
Кватернионы не образуют поля в том смысле, как мы определили
последнее ранее. Нередко говорят, впрочем, что кватернионы образуют
некоммутативное поле. Роль открытия кватернионов (к которому
подходили Гаусс и еще ранее Эйлер) в алгебре Пуанкаре сравнил с ролью
открытия Лобачевского в развитии геометрии.
В кватернионе q = а -\- ib -\- jc -\-kd Гамильтон назвал член а —
скаляром, а трехчлен ib -f jc + kd — вектором. Он показал ряд
приложений кватернионов в механике и геометрии. Учение о кватернионах
явилось одним из источников векторного исчисления.
Укажем на одну важную формулу: произведение двух векторов т^
и г>2, рассматриваемых как кватернионы, непосредственно связано с их
скалярным (vl7 v2) и векторным [vu v2] произведениями:
Кватернионы Гамильтона представляют собой частный вид еще
более общих гиперкомплексных числовых систем, теорию которых
впервые опубликовал в 1844 г. немецкий математик Г. Грассман.
Для понимания дальнейшего напомним, что обыкновенные
комплексные числа можно строить как пары действительных чисел (а, &), действия
над которыми определяются правилами:
1. (а, Ъ) = (с, d), если а = с и b = d,
2. (а, Ь) + (с, d) = (a + c, b + d),
3. (а, Ь)-(с, d)=(ac — bd, ad + bc).
Пара (а, 0) считается совпадающей с действительным числом а. Из
третьего условия следует, что
(0, 1). (0,1) = (0,1)2 =-1;
эта пара (0, 1) обозначается i. Тогда пара (а, Ъ) может быть записана
в обычной форме a -f- bi. Аналогично можно построить кватернионы
как некоторые четверки чисел. Гиперкомплексное число а ранга п
вводится как совокупность п действительных чисел (аи а2, . . ., ап),
удовлетворяющих условиям, определяющим подходящим образом равенство,
сложение и умножение на действительное число. Если обозначить
совокупности п чисел (1, 0, . . ., 0) = е1? (0, 1, 0, . . ., 0) = е2, ...
. . ., (0, 0, . . ., 0, 1) = 8П, то гиперкомплексное число а(а1? а2, . . ., ап)
можно записать в форме линейной комбинации основных единиц е&:
а = а^! + а2е2 + ... + апеп.
Дальнейшее построение системы гиперкомплексных чисел связано
с условиями, которые налагаются на операцию умножения. Прежде
всего принимаются дистрибутивность умножения по отношению к
сложению и ассоциативность при умножении единиц между собой и на
действительные числа. Тогда произведение двух гиперкомплексных чисел имеет вид
Но произведения основных единиц могут быть, по условию, приняты
за некоторые новые единицы или же сводиться к линейным
комбинациям самих основных единиц. В последнем случае говорят, что кольца
гиперкомплексных чисел образуют линейную ассоциативную алгебру
над полем действительных чисел. От выбора коэффициентов в равенстве
с о л(1)р Л_^?>р -4- 4-cWp
Ф. э. молин
557
зависит конкретная форма закона умножения соответствующей алгебры.
Частными случаями линейных ассоциативных алгебр являются алгебра
комплексных чисел или алгебра кватернионов.
Мы не можем рассматривать здесь ни дальнейшую общую историю
теории гиперкомплексных чисел, ни тесно связанное с ними исчисление
матриц и теорию векторных пространств. Мы приведем еще только
важную теорему Г. Фробениуса (1878) и американского математика и логика
Ч. Пирса (1881), обобщающую результат К. Вейерштрасса, объяснивший
неудачу Гамильтона в первоначальной попытке построить систему чисел
с тремя единицами. Эта теорема выясняет место комплексных чисел
и кватернионов среди остальных гиперкомплексных чисел: над полем
действительных чисел существуют только две системы гиперкомплексных
чисел, обладающих свойствами коммутативного поля, именно поля
действительных и комплексных чисел, и только одна система, образующая
некоммутативное поле, именно система кватернионов. Все прочие системы
гиперкомплексных чисел более существенно отличаются по своим
свойствам от чисел в обычном смысле слова. Так, во всех них существуют
элементы, которые Вейерштрасс назвал делителями нуля, т. е. отличные
от нуля элементы, произведение которых равно нулю.
Диссертация П. Э. Ромера. Первое на русском языке изложение
теории кватернионов дал воспитанник, адъюнкт (1861) и затем (1867)
профессор Киевского университета Павел Эмильевич Ромер (1835—1899)
в своем отчете о заграничной командировке, напечатанном в
«Университетских известиях» за 1864 г., и, более подробно, в докторской диссертации
«Основные начала метода кватернионов» (Киев, 1867). Здесь в первой
части строится общая теория, а во второй
дано довольно подробное векторное
изложение основ дифференциальной геометрии
пространства. И в этом случае один из
киевских математиков выступил как
пропагандист новых математических идей.
Об исследованиях А. П. Котельникова
по теории бикватернионов и особого рода
двоичных чисел а + &со говорилось выше.
Ф. Э. Молин. Новые, очень важные
результаты в теории гиперкомплексных
числовых систем были получены Ф. Э. Мо-
лином. Федор Эдуардович Молин (11
сентября 1861—25 декабря 1941) окончил
Дерптский университет в 1883 г. и здесь
же в 1885 г. защитил магистерскую
диссертацию по теории эллиптических функций,
подготовленную им под руководством
Ф. Клейна во время заграничной коман-
дировки в Лейпциг. После нескольких лет ¦ ' олин-
работы в Дерптском университете он был
в 1900 г. переведен на работу профессором в Томский технологический
институт, а с 1917 г. работал в Томском университете. В 1934 г. ему было
присвоено звание заслуженного деятеля науки.
В 1892 г. Молин защитил докторскую диссертацию «О системах
высших комплексных чисел» (Matliem. Annalen, В. 41, 1892), в которой дал
558
ГЛ. 25. ИССЛЕДОВАНИЯ ПО АЛГЕБРЕ
классификацию и исследовал структуру этих систем и установил их связи
с группами и матрицами. Основная теорема Молина гласит: всякая простая
ассоциативная алгебра над полем комплексных чисел ранга 2 или выше
изоморфна алгебре всех матриц некоторого порядка над этим полем.
Через несколько лет в небольшой статье «Об инвариантах линейных групп
подстановок» (Sitzungsber. der Berl. Akademie, 1897) Молин решил вопрос
о числе представлений неприводимой группы подстановок. Это была одна
из первых работ по теории линейного представления групп, тесно
связанной с теорией алгебры и теорией матрицы; одновременно в том же
направлении вел изыскания Фробениус. В последующем теория представления
групп, в которой каждому элементу группы ставится в соответствие
некоторая матрица, выросла в большую дисциплину, получившую широкие
приложения в современной физике и прежде всего в квантовой механике.
Многие результаты Молина в теории гиперкомплексных чисел были
заново получены и далеко развиты выдающимся французским
математиком Э. Картаном (1898 и следующие годы), а затем рядом американских
ученых, один из которых Дж. Ведерборн распространил упомянутую
теорему Молина на случай произвольного поля (1907). Открытия Молина
высоко ценятся математиками нашего времени г).
Советские ученые впоследствии внесли много нового в разработку
различных алгебраических систем, которые, как мы видели, не
исчерпываются линейными ассоциативными алгебрами, а также в теорию
представлений групп.
г) Н. Б у р б а к и, Очерки по истории математики. Перевод И. Г. Башмаковой
под ред. К. А. Рыбникова, М., 1963, стр. 116—118; Н. Ф. К а н у н о в, О работах
Ф. Э. Молина по теории представлений конечных групп.— Ист.-матем. исслед.,
вып. XVII, 1966.
ГЛАВА ДВАДЦАТЬ ШЕСТАЯ
ВОЗНИКНОВЕНИЕ МОСКОВСКОЙ школы
ТЕОРИИ ФУНКЦИЙ
Теория множеств и теория функций. Как уже говорилось, начало
XX века было ознаменовано новым подъемом научного творчества на
физико-математическом факультете Московского университета. В
области физики это время отмечено работами П. Н. Лебедева, в механике —
великими открытиями по гидро- и аэродинамике Н. Е. Жуковского
и С. А. Чаплыгина, в математике — созданием московской школы теории
функций, деятельность которой оказала мощное и плодотворное влияние
на все последующее развитие математических наук в Советском Союзе,
да и за его пределами.
После того как Лобачевский и Дирихле сформулировали общее
определение функции как заданного любым способом соответствия между
парами элементов двух множеств чисел, в математике стало выдвигаться
на передний план исследование понятия функции и ее свойств во все
более широком аспекте. Еще в анализе Коши основное место занимали
функции непрерывные или имеющие конечное число точек разрыва.
Дальнейшее развитие анализа потребовало применения и изучения
гораздо более сложных функций с бесконечным множеством точек разрыва.
Опираясь на механические аналогии и геометрические
представления, математики долгое время полагали, что дифференцируемость
является, за исключением отдельных точек, естественным свойством
непрерывных функций. В начале XIX века были сделаны даже попытки доказать
это (Ампер, С. Е. Гурьев, и другие). Но уже Б. Больцано около 1835 г.
и затем независимо от него К. Вейерштрасс в 1871 г. открыли функции
непрерывные и вместе с тем не имеющие производной ни в одной точке
промежутка непрерывности. Так возник вопрос об условиях
существования производных функций и об их свойствах.
В 1853 г. Б. Риман, изучая проблему представимости разрывных
функций тригонометрическими рядами, коэффициенты которых
выражаются по формулам Фурье через интегралы, содержащие эту функцию,
поставил вопрос об условиях интегрируемости функций, обладающих тем или
иным множеством точек разрывов. Риман распространил классическое
определение интеграла, данное Коши, на максимально широкий класс
ограниченных функций и установил критерий интегрируемости «в смысле
Римана». Он же впервые привел пример функции со всюду плотным
множеством точек конечного разрыва и вместе с тем интегрируемойх).
!) Множество точек называется всюду плотным на промежутке (а, Ь), если в
любом как угодно малом промежутке внутри (а, Ъ) имеются точки этого множества.
Например, множество рациональных точек или чисел всюду плотно на любом отрезке.
560 ГЛ. 26. ВОЗНИКНОВЕНИЕ московской ШКОЛЫ ТЕОРИИ ФУНКЦИЙ
Проблема интегрируемости стала одной из ведущих в формировавшейся
тогда теории функций действительного переменного.
Детальный анализ свойств предельных переходов и непрерывных
функций показал неудовлетворительность их доказательств даже у Коши.
В середине XIX века стало ясным, что само определение непрерывности
функции нуждается в более строгом учении о действительном числе.
Одним из первых обратил на это внимание немецкий математик Р. Деде-
кинд, в печати изложивший свою теорию иррациональных чисел,
рассматриваемых как сечения во множестве чисел рациональных, в 1872 г.
Проблема созрела настолько, что в том же году были предложены
другие приемы определения иррациональных чисел и операций над ними
К. Вейерштрассом, Г. Кантором и Ш. Мерэ. Построение теории
действительных чисел явилось одним из основных моментов в укреплении
фундамента математического анализа.
Исследование вопроса о представимости функций
тригонометрическими рядами и о сходимости таких рядов привело Г. Кантора к созданию
общей теории множеств, принципы которой он изложил в серии работ,
начиная с 1874 г. Эта новая дисциплина, к идеям которой подходили также
в алгебре, теории чисел и т. д., приобрела огромное значение в
дальнейшем развитии математики. Кантор детально разработал теорию операций
над множествами, состоящими из бесконечного числа элементов, обобщил
в понятии мощности множества понятие конечного количественного
числа, а в учении о трансфинитных числах распространил на некоторые
классы бесконечных множеств понятие конечного порядкового числа.
Особое значение имела разработка теории точечных множеств,
элементами которых служат точки того или иного тг-мерного пространства1).
Теория множеств легла в основу общей теории функций
действительного переменного, главной задачей которой на протяжении ряда
десятилетий было исследование в возможно более широком плане таких понятий,
как функция, производная, первообразная, определенный интеграл, сумма
ряда функций и т. п. В процессе развития теории множеств и теории
функций возникли и серьезные трудности. Уже в середине девяностых
годов XIX века ученые встретились с логически противоречивыми
предложениями, возникающими при некоторых операциях над множествами.
Изучение таких противоречий и попытка их преодоления привели
в XX веке к созданию различных направлений в методологии математики.
Споры по вопросам обоснования теории функций продолжаются и в наши
дни, и логические трудности, о которых мы упомянули, не удалось в
полной мере преодолеть и поныне. Мы можем, однако, оставить в стороне
эти вопросы, не имеющие прямой связи с историей математики в нашей
стране в начале XX века. Ограничимся замечанием, что анализ
парадоксов теории множеств повлек за собой расцвет математической логики
как общей теории математических доказательств. Об этом мы уже
говорили ранее.
Важным шагом в развитии теории функций была разработка на
рубеже XIX и XX вв. Э. Борелем и А. Лебегом теории меры точечных
множеств. Мера множества явилась обобщением понятия длины отрезка.
Внешняя мера множества точек М, лежащего в промежутке (а, Ь),
строится так. Множество М покрывают конечной или бесконечной
совокупностью промежутков tu t2, . . ., tn, . . ., с тем, чтобы каждая точка
х) См. Ф. А. Медведев, Развитие теории множеств в XIX веке, М.,
1965.
ТЕОРИЯ МНОЖЕСТВ И ТЕОРИЯ ФУНКЦИЙ
561
множества М попала внутрь хотя бы одного из них. Для каждого из
возможных покрытий составляется сумма длин промежутков. Нижняя грань
таких сумм называется внешней мерой. Затем берется внешняя мера
множества всех точек промежутка (а, &), не принадлежащих М, так
называемого множества, дополнительного к М, Внутренняя мера
множества М определяется как разность между длиной промежутка (а, Ъ)
и внешней мерой дополнительного множества. Множество называют
измеримым, если его внутренняя и внешняя мера равны между собой.
Общее значение этих мер называют мерой множества. Множество
нескольких отдельных точек имеет меру нуль, мера промежутка совпадает с его
длиной. Существуют всюду плотные множества меры нуль, например
множество всех точек промежутка (а, Ъ) с рациональными абсциссами.
Наряду с приведенным понятием меры множества Лебег ввел понятие
измеримой функции. Функция /(#), определенная для множества М
значений аргумента х, называется измеримой, если измеримо множество
тех значений х, принадлежащих М, для которых f(x) > а, где а — любое
действительное число. Класс измеримых функций, гораздо более
широкий, чем класс непрерывных или, скажем, интегрируемых по Риману
функций, стал предметом особого внимания ученых, работавших в теории
функций. Две измеримые функции f(x) и ф(#), значения которых
отличаются лишь на множестве меры нуль, называются эквивалентными
функциями. В теории Лебега такие функции, по существу, не
различаются; обычно все теоремы относятся не к одной функции, а к классу
эквивалентных функций. Измеримые функции являются основным объектом
современной теории функций. За пределы измеримых функций в
математическом анализе практически не выходят.
Лебег существенно обобщил понятие интеграла (1902). Интеграл
ь
Лебега, обозначаемый привычным символом \ f(x) dx, определяется сле-
а
дующим образом. Пусть у = /(ж), ограниченная и измеримая на отрезке
(а, Ъ) функция, изменяется на отрезке 7?г< г/< М. Разобьем множество
значений у на части возрастающими числами
т = 1\0<щ< . .. <г\п = М.
Обозначим через \ik меру множества тех точек х, для которых
!]*_!< у < r\ki и возьмем любое значение yh, t\k-±< У к < Ци- Интеграл
Лебега определяется как
п
lim 2 УкРн
k=i
при условии max (r\k — v}k-i) ->- 0- Для всякой ограниченной измеримой
на отрезке (а, Ъ) функции этот предел, т. е. интеграл Лебега, существует.
Он содержит в себе как частный случай интеграл Римана и, значит,
интеграл Коши от непрерывной функции. Но функции, интегрируемые
по Лебегу, могут не быть интегрируемыми по Риману 1). Ограниченная
на (а, Ъ) функция имеет интеграл Римана тогда и только тогда, когда
множество ее точек разрыва на (а, Ъ) имеет меру нуль; измеримая же
г) Примером функции, интегрируемой по Лебегу и не интегрируемой по Риману,
может служить функция/ (я), определенная на отрезке (0,1):
Г 1 в рациональных точках,
7 \х) = ^ о в ИррацИональных точках.
562 ГЛ. 26. ВОЗНИКНОВЕНИЕ МОСКОВСКОЙ ШКОЛЫ ТЕОРИИ ФУНКЦИЙ
функция может иметь множество точек разрыва с положительной мерой.
Понятие интеграла Лебега распространяется и на бесконечные
промежутки, а также на некоторые виды неограниченных измеримых функций.
Интеграл Лебега стал важнейшим средством исследования не только
в теории функций и непосредственно связанных с ней областях, например,
теории тригонометрических рядов, но и во многих других отделах
современной математики, включая теорию дифференциальных уравнений,
теорию вероятностей и т. д.
Еще более общее определение интеграла предложил в 1912 г.
французский математик А. Данжуа.
Первые работы по теории функций в России. Идеи теории множеств
и теории функций начинают распространяться в России с конца XIX
и начала XX вв. В это время выходят переводы таких классических
работ, как «Непрерывность и иррациональные числа» Р. Дедекинда,
выполненный С. О. Шатуновским (I изд., 1894), который приложил ко
второму изданию (Одесса, 1906) свою статью «Доказательство
существования трансцендентных чисел», опубликованную ранее в «Вестнике опытной
физики и элем, математики» за 1896 г.; «Парадоксы бесконечного» Б. Боль-
цано (Одесса, 1911; перевод И. В. Слешинского); статьи П. Лежен
Дирихле, Б. Римана и Р. Липшица по теории тригонометрических рядов в
переводе харьковского математика Григория Алексеевича Грузинцева (1880 —
22 августа 1929) 2) и С. Н. Бернштейна (сб. «Разложение функций в
тригонометрические ряды», Харьков, 1914); первая работа Г. Кантора
«Основы общего учения о многообразиях» (перевод П. С. Юшкевича;
сб. «Новые идеи в математике», № 6, СПб., 1914) и другие. В некотором
объеме сведения по теории множеств и теории функций излагаются
в отдельных руководствах, например, во «Введении в теорию рядов»
Б, Я. Букреева (Киев, 1906) или во «Введении в анализ» А. В. Васильева
(вып. 1—2, Казань, 1904—1908). Особого внимания заслуживает
упоминавшийся ранее курс лекций по введению в анализ С. О. Шатунов-
ского, литографированное издание которого появилось еще в 1906—
1907 гг. и который в переработанном виде вышел в 1923 г.
«Введение в анализ» Шатуновского, в основе которого лежит теория
множеств и теория действительного числа, во многом представляет собой
оригинальный научный труд. Особенностью его является стремление
автора использовать минимум исходных посылок и дать широкое
обобщение ряда основных теорем. Учение о числе Шатуновский строит не на
обычном понятии об упорядоченной последовательности, но на понятии
«расположенного комплекса». Множество называется упорядоченным, если
в нем установлено отношение порядка (следования или предшествования)
между двумя любыми его элементами. Множество расположено, по Шату-
новскому, если для двух любых его элементов можно указать третий,
следующий за ними обоими, хотя бы для этих двух отношение следования
установлено и не было. Например, условимся считать дробь у следующей
за дробью -т тогда и только тогда, когда # + d > Ь + с. В случае а + d =
= Ъ + с дроби -т- и -г- не расположены в указанном смысле друг относи-
г) С 1910 г. Г. А. Грузинцев работал в Харьковском университете в качестве
приват-доцента; с 1918 г. он профессор Днепропетровского института народного
образования.
ТЕОРИЯ ФУНКЦИЙ В МОСКОВСКОМ УНИВЕРСИТЕТЕ
563
тельно друга, но всегда можно привести дробь а ° , которая следует
за каждой из дробей-г-и— • Обобщается на расположенные множества
и понятие предела. Обобщенный в смысле Шатуновского предел был
независимо введен также в работах 1915—1922 гг. американскими
математиками Э. Г. Муром и Г. Л. Смитом. Понятие обобщенного предела,
использованное самим Шатуновским в построении учения о
действительном числе, было применено затем к расширению понятия об интеграле.
Первые шаги в этом направлении сделал в 1913—1916 гг. одесский
математик, в то время приват-доцент, а позднее профессор, Дмитрий
Антонович Крыжановский (26 октября 1883—1938), который применил
обобщенный предел к определению обыкновенных интегралов. Уже в
советское время (1930) А. Н. Колмогоров с помощью обобщенного предела
дал принципиальное расширение понятия интеграла 1). С теорией предела
Шатуновского — Мура читатель может познакомиться по изложению
во втором томе «Курса дифференциального и интегрального исчисления»
другого воспитанника одесской математической школы, впоследствии
профессора Ленинградского университета Григория Михайловича Фих-
тенгольца (5 июня 1888—26 июля 1959). В курсе С. О. Шатуновского
имеются и другие научные результаты, относящиеся к изложению
основных свойств функций, как обобщение теоремы Больцано — Вейерштрасса
для одномерного и тг-мерного пространства и др.
Следует назвать как одного из первых русских математиков,
занявшихся теорией множеств, воспитанника Казанского университета,
работавшего долгие годы профессором Томского технологического института
Владимира Леонидовича Некрасова (1864—1922). Главным трудом его
в этой области была магистерская диссертация «Строение и мера
линейных точечных областей» (Томск, 1907), содержащая и собственные
результаты автора 2). Защита ее состоялась в 1908 г. в Москве.
Теория функций в Московском университете. Таким образом, интерес
к новой области математики возникал во многих городах. Но главным
центром развития теории функции стала Москва.
Ознакомление московских математиков с исследованиями в этом
направлении началось с постановки курса лекций «Теория функций
действительного переменного», который впервые прочитал осенью 1900—
1901 учебного года Б. К. Млодзеевский, продолжавший его вести и в
последующие годы. Живой интерес возбудила теория множеств у Ивана
Ивановича Жегалкина (3 августа 1869—28 марта 1947), окончившего
Московский университет в 1893 г. и в 1902 г. ставшего в нем
приват-доцентом. Магистерская диссертация Жегалкина «Трансфинитные числа»
(«Москва», 1907), защищенная в один год с диссертацией В. Л.
Некрасова 3), содержала очень полное и во многом самостоятельное изложение
абстрактной теории множеств и трансфинитных чисел. Книга
заканчивается описанием парадокса о множестве всех вещей и указанием, что
ни одна из попыток решения этого и аналогичных парадоксор не является
г) Подробнее см. В. И. Г л и в е н к о, Интеграл Стилтьеса, М.— Л., 1936,
стр. 191 и след.; Ф. А. М е д в е д е в, О формировании понятия обобщенного предела.—
Труды Ин-та ист. естеств. и техн., т. 34, 1960.
2)Ф. А. Медведев, Первые руководства по теории множеств.— Труды
Ин-та ист. естеств. и техн., т. 28, 1959.
з) Одним из официальных оппонентов в обоих случаях выступал Б. К.
Млодзеевский.
564 ГЛ. 26. ВОЗНИКНОВЕНИЕ московской ШКОЛЫ ТЕОРИИ ФУНКЦИЙ
удовлетворительной. Исследование их причины, указывал в предисловии
автор, относится к задачам логики.
В 1911 г. профессор Жегалкин вместе со многими другими ушел
из университета (см. стр. 516) и вновь стал работать в нем в 1917 г. Его
исследования в послереволюционное время относились преимущественно
к математической логике, к которой он естественно пришел от занятий
теорией множеств. Руководимый им в последние годы жизни семинар
сыграл немалую роль в развитии математической логики в стенах
Московского университета. В 1945 г. И. И. Жегалкину было присвоено
почетное звание заслуженного деятеля науки РСФСР.
Весьма значительны в создании московской школы теории функции
заслуги Д. Ф. Егорова. Он правильно оценил широкие перспективы,
открывавшиеся в этой области и привлек
к ней целый ряд высоко одаренных
студентов, которым оказывал помощь не
только своими беседами и советами, но
и содействием в оставлении их при
университете, получении стипендий и т. д. В
течение нескольких лет семинар Д. Ф. Егорова
был основным центром занятий теорией
функций. В нем выступали с обзорными
и оригинальными сообщениями многие
студенты и молодые ученые. П. С.
Александров, тогда студент второго семестра,
вспоминает о семинаре Д. Ф. Егорова,
темой которого в 1914 г. служили
«Бесконечные последовательности»: «В том же
семинаре участвовали А. Я. Хинчин,
Д. Е. Меньшов и др. Участники этого
семинара получили в нем первое
соприкосновение с настоящей живой математиче-
ской наукой — впечатление, которое уже
. . Жегалкин. не может никогда изгладиться! Они
знакомились сначала с элементарными
свойствами числовых последовательностей и рядов, переходили затем к различным
случаям сходимости последовательностей функций и в заключение
знакомились с такими животрепещущими в те времена достижениями
математики, как сходимость в среднем, сходимость по мере, теорема
Фишера — Рисса и т. п. Семинар Д. Ф. Егорова разбивался на группы по
темам, а результаты коллективной разработки каждой группы своей темы
докладывались одним из членов группы на общем собрании семинара.
Сложилась традиция, по которой на общие собрания семинара приходили
не только студенты, но и молодые математики, окончившие курс и
«оставленные при универсигете» или даже приват-доценты (Привалов,
Степанов). На этих собраниях происходили обсуждения научных проблем,
волновавших тогда математиков» *). Немало докладов по теории функций
ставилось также на заседаниях Московского математического общества —
всего с 1905 по 1917 г. их состоялось более сорока 2).
1)П. С. Александров, Математика в Московском университете в первой
половине XX века.— Ист.-матем. исслед., вып. VIII, 1955, стр. 13.
2) Ф. А. Медведев, Подготовка теоретико-множественных и теоретико-
функциональных исследований в России. Очерки истории математики и механики
(сборник статей), М., 1963.
Н. Н. ЛУЗИН
565
Теорема Д. Ф. Егорова. В теории функций Д. Ф. Егорову
принадлежит одна из основных теорем, опубликованная им в «Comptes Rendus»
в 1911 г. в заметке «О последовательности измеримых функций» и
вошедшая теперь во все учебники по этому предмету. Теорема Егорова состоит
в следующем. Если последовательность измеримых функций сходится
почти всюду (т. е. за исключением множества меры нуль) на отрезке (а, Ь),
то из этого отрезка можно исключить такое точечное множество сколь
угодно малой меры, что на оставшемся множестве последовательность
будет сходящейся равномерно. Мы охарактеризуем значение этой теоремы
словами Н. Н. Лузина:
«Это важное предложение имеет фундаментальное значение для
математического анализа, будучи применяемым во многих его отделах.
Причина этому лежит в том, что именно лишь с равномерно
сходящимися последовательностями мы по преимуществу и встречаемся в
математическом анализе, так как только для них имеются простые и постоянно
употребляемые предложения. В частности, эта теорема встречает частое
употребление в теории интегральных уравнений, теории функций
комплексного переменного, теории
интеграла, теории производных чисел и др.
и влечет быстрые доказательства
многих ценных общих предложений» г).
Н. Н. Лузин. Главным идейным
вдохновителем и признанным главой
новой московской математической
школы явился Н. Н. Лузин.
Николай Николаевич Лузин
родился 9 декабря 1883 г. в Томске. Дед его
был крепостным крестьянином, отец—
торговым служащим. Окончив в 1901 г.
гимназию в Томске, Лузин в том же году
поступил в Московский университет.
Как вспоминал сам Лузин,
математику в гимназии он не любил, так
как учитель требовал заучивания
наизусть формулировок теорем и
доказательств в точности по учебнику, а
механическая память у Лузина была плохая.
Дело несколько изменилось благодаря
репетитору, который показал молодому узин,
гимназисту внутренние логические
связи между предложениями математики. На математическое отделение
Лузин поступил с целью приобрести хорошую общую подготовку для
последующих занятий; он собирался стать инженером. Судьба его
сложилась, однако, по-иному. Блестящие лекции московских профессоров,
особенно геометров Б. К. Млодзеевского и К. А. Андреева, произвели на
него сильное впечатление и навсегда поставили в центр его интересов
математику.
В университете, «Н. Н. Лузин как одаренный студент,— пишут
биографы Лузина,— сразу же обратил на себя внимание профессоров.
г) Н. Н. Лузин, О последовательностях измеримых функций. В кн.:
Н. Н. Лузин, Интеграл и тригонометрический ряд. Редакция и комментарии
Н. К. Бари и Д. Е. Меньшова, М.—Л., 1951, стр. 336.
566 ГЛ. 26. ВОЗНИКНОВЕНИЕ МОСКОВСКОЙ ШКОЛЫ ТЕОРИИ ФУНКЦИЙ
Он, будучи еще студентом младших курсов, был избран секретарем
студенческого математического кружка, председателем которого был
знаменитый механик Н. Е. Жуковский. В этом кружке разрабатывались
вопросы, представлявшие в то время особую научную актуальность.
Лузин и его университетский товарищ С. С. Бюшгенс были активными
участниками этого кружка; у них преобладали в докладах вопросы
обоснования математики, вопросы теории множеств, вопросы ариф-
метизации математики, которые тогда привлекали внимание
математиков, и начавшие вызывать интерес вопросы аксиоматики. На
заседания кружка часто приходили профессора Б. К. Млодзеевский,
Д. Ф. Егоров и только что вступивший в число приват-доцентов
И. И. Жегалкин» х).
В 1905—1906 гг. Лузин вместе с В. В. Голубевым по совету Егорова
несколько месяцев провели в Париже, где посещали лекции Э. Бореля,
А. Пуанкаре и др. и изучали новинки научной литературы. В это время
Лузин уже занимался вопросами теории функций. В 1906 г. Лузин
окончил университет и был по рекомендации Егорова оставлен для подготовки
к профессорскому званию. В 1910 г. он сдал магистерские экзамены
и, после прочтения двух пробных лекций, получил в начале 1911 г. звание
приват-доцента по кафедре чистой математики. Последующие годы Лузин
посвятил углубленному изучению теории функций, в частности, проблем
теории тригонометрических рядов.
С осени 1910 до весны 1914 г. Лузин был в командировке в Геттингене
и в Париже, где слушал некоторые лекционные курсы и познакомился
с крупнейшими деятелями французской школы теории функций — А.
Лебегом, Э. Борелем, А. Данжуа и другими выдающимися учеными.
Одновременно он вел интенсивную научную работу. В 1912 г. он выступил
с несколькими заметками в парижских «Gomptes rendus» и с двумя
статьями в 28-м томе «Математического сборника», привлекшими большое
внимание ученого мира.
Теорема о С-свойстве. В статье «К основной теореме интегрального
исчисления» Лузин сообщил замечательную теорему о так называемом
«С-свойстве» измеримых функций (С — начальная буква французского
слова «continuite», что означает непрерывность). Согласно теореме Лузина
всякая измеримая и почти всюду конечная на отрезке (а, Ъ) функция
непрерывна на совершенном множестве точек, которое лежит на (а, Ъ)
и получается из (а, Ъ) путем исключения из него множества сколь угодно
малой меры 2).
Эта теорема Лузина, к которой он пришел, по его собственному
указанию, на основе бесед с Д. Ф. Егоровым, раскрывала глубокое
структурное свойство измеримых функций и устанавливала их тесную связь
с гораздо более простыми и хорошо изученными непрерывными
функциями. В настоящее время в некоторых руководствах по теории функций
С-свойство берется за определение измеримой функции.
В той же статье Лузин получил новые результаты в задаче об
отыскании первообразных функций, о которой будет идти речь далее.
г) См. биографический очерк В. В. Голубева и Н. К. Бари в книге: Н. Н.
Лузин, Интеграл и тригонометрический ряд, М.— Л., 1951, стр. 14.
2) Множество М называется замкнутым, если в его состав входят все его
предельные точки, т. е. точки, в любой окрестности которых имеется хотя бы одна точка
множества М (не считая их самих). Замкнутое множество называется совершенным,
если оно состоит только из своих предельных точек.
«ИНТЕГРАЛ И ТРИГОНОМЕТРИЧЕСКИЙ РЯД»
567
Другая статья «Об одном случае ряда Тейлора», напечатанная в том
же номере журнала, что предыдущая, содержала первые выдающиеся
открытия Лузина в теории степенных и тригонометрических рядов.
Здесь содержался пример тригонометрического ряда
оо
21 Ап cos пх + Вп sin пх,
71=0
коэффициенты которого Ап и Вп при п ->¦ оо стремятся к нулю и который
почти всюду расходится. Этот результат поразил математиков своей
неожиданностью. Пример Лузина дал ответ на вопрос, поставленный
в 1906 г. П. Фату, который высказал на первый взгляд естественное
предположение, что условия lim Ап = 0 и lim Вп = 0 обеспечивают
п-^оо п->оо
сходимость тригонометрического ряда почти всюду. Пример Лузина
непосредственно вытекал из другого, относящегося к степенным рядам.
Лузин построил степенной ряд, коэффициенты которого стремятся к нулю
и который расходится во всех точках окружности своего круга сходимости.
«Интеграл и тригонометрический ряд». Весной 1914 г. Лузин
возвратился в Москву и приступил к работе в университете. Отчет о
заграничной командировке, представленный им, ярко характеризует богатство
сделанных за это время молодым ученым открытий г). Значительная
часть их вошла в его знаменитую монографию «Интеграл и
тригонометрический ряд» (М., 1915), защищенную им в качестве магистерской
диссертации. Защита состоялась в мае 1916 г. при официальных
оппонентах Д. Ф. Егорове и Л. К. Лахтине. Она прошла с исключительным
успехом: в виде редкого исключения диссертанту присудили сразу степень
доктора чистой математики. Еще ранее физико-математический факультет
и Московское математическое общество наградили Лузина за его
монографию премией имени А. Ю. Давидова. В 1917 г. Лузин был избран
профессором.
Во введении к диссертации Н. Н. Лузин прежде всего разбирает
вопрос о взаимоотношениях между классическим анализом и теорией
функций: «Обычно противополагают классический анализ и теорию
функций действительного переменного. Хотя главный объект, с которым
имеет дело та и другая ветвь математики, один и тот же, именно понятие
функции, есть, однако, существенная разница в тех способах, которыми
пользуются для изучения функции анализ и теория функций.
В то время как функции классического анализа являются данными
посредством тех или других уравнений, разложений в ряды и т. д., говоря
вообще, являются определенными тою или другою системой
аналитических выражений, формул, в это самое время теория функций
действительного переменного отправляется от самого общего определения понятия
функции, данного Дирихле, понятия функции, как соответствия,
совершенно независимо от того, каким образом это соответствие на самом деле
может быть установлено»2).
Однако,— указывает Лузин,— такое определение функции имеет
слишком общий характер и о нем удается высказать лишь немногие
суждения 3). Поэтому теория функций должна рассматривать лишь
г) См. «Историко-математические исследования», вып. VIII, 1955 (стр. 55—76).
2) Н. Н. Лузин, Интеграл и тригонометрический ряд, М.— Л., 1951, стр. 49.
3) В наше время столь общее понятие функции было неоднократно подвергнуто
критическому разбору.
568 ГЛ. 26. ВОЗНИКНОВЕНИЕ московской ШКОЛЫ ТЕОРИИ ФУНКЦИЙ
более или менее обширные классы функций, вроде функций непрерывных,
точечно-разрывных, интегрируемых, дифференцируемых и т. д. Различие
методов классического анализа и теории функций состоит в том, что
первый выводит свойства функций из определяющих их аналитических
выражений, тогда как вторая — из общего свойства рассматриваемого
класса функций, заранее характеризующего этот класс. «Какова,—
продолжает автор,— применимость результатов теории функций
действительного переменного?» И он отвечает: «...если не хотят, чтобы теория
функций действительного переменного была теорией, замкнутой в себе
и не оказывающей влияния на другие математические теории, нужно
поставить в связь аналитические выражения, с одной стороны,
определения и понятия теории функций действительного переменного, с другой
стороны» х).
В результате Лузин формулирует две главные задачи теории функций:
1. Дано структурное свойство функции. Требуется найти аналитические
выражения, изображающие эту функцию. 2. Обратная, и более важная
задача: дан класс аналитических выражений. Требуется найти
необходимое и достаточное структурное свойство функций, изображаемых
этим классом аналитических выражений.
В качестве примера такого рода исследования Лузин указал на
теорему французского ученого Р. Бэра, в 1898 г. нашедшего необходимые
и достаточные условия представимости функции f(x) суммой сходящегося
оо
всюду ряда целых многочленов 2 Рп(х): такая функция точечно-разрыв-
п=1
на на всяком совершенном множестве.
Таким образом, Лузин видел главную задачу теории функций в том,
чтобы ее методы и понятия получили развитие, при котором
содействовали бы развитию математики в целом, и особенно математического
анализа. Дальнейшая разработка теории функций в его собственных трудах
и в трудах основанной им научной школы показала, что Лузин правильно
наметил главные цели этой новой тогда отрасли математики и что теория
функций на самом деле оказалась призванной не только дать более
глубокое обоснование анализа, но и служить эффективному развитию
анализа и других наук.
Как видно из названия книги Лузина, специальное внимание уделено
в ней важнейшему в анализе классу аналитических выражений, именно
тригонометрическим рядам и прежде всего рядам Фурье, т. е. для
функции f(x), определенной на отрезке (0, 2я), рядам вида
оо
-т~ + 2 ап cos пх ~Ь bn sin пх
71=1
с коэффициентами
2я 2я
ап = — \ / (х) cos пх dx, bn = — \ / (х) sin пх dx
—JT —я
(п = 0, 1, 2, ...)•
*) Н. Н. Лузин, Интеграл и тригонометрический ряд, стр. 50.
«ИНТЕГРАЛ И ТРИГОНОМЕТРИЧЕСКИЙ РЯД»
569
Значительная часть книги посвящена вопросам, связанным с
выяснением необходимых и достаточных условий того, чтобы функция f(x)
была представима ее рядом Фурье. Вместе с тем, как отмечал Лузин,
задача о тригонометрических рядах Фурье, их сходимости,
суммируемости и свойствах изображаемых ими функций тесно связана с задачей
возможно более общего определения интеграла. Коэффициенты ряда
Фурье выражены интегралами, в которые входит функция f(x) и чем
шире применяемое определение интеграла — Коши, Римана, Лебега,
Данжуа,— тем шире соответствующий класс рядов Фурье. В работе
рассматривались и общие тригонометрические ряды.
Содержание диссертации Лузина очень богато и во многом весьма
специально. Мы остановимся лишь на части содержащихся в ней
результатов.
В первой главе работы Лузина излагается С-свойство и на его основе
выводятся некоторые теоремы об аналитическом представлении
измеримых и почти всюду конечных функций.
Вторая глава посвящена центральной проблеме интегрального
исчисления — отысканию первообразных функций. В XVIII веке удалось
создать почти все известные методы интегрирования элементарных
функций в конечном виде.
Более общая постановка задачи принадлежит Коши, который в 1823 г.
впервые аналитически доказал существование первообразной F(x) для
любой непрерывной на отрезке (а, Ъ) функции f{x) и дал способ
построения F(x). Первообразной является в этом случае интеграл с переменным
верхним пределом
X
а
гда С — любая постоянная. Затем встал вопрос о существовании и об
отыскании первообразных для широких классов функций.
Определение первообразной по данной на отрезке (а, Ъ) ее
производной оказалось сложной проблемой. Интеграл Римана не дает полного
ее решения: имеются функции с ограниченными производными, не
интегрируемыми по Риману. Более мощным средством построения
первообразных служит интеграл Лебега.
Вместе с тем существуют функции, для которых первообразные
не могут быть построены при помощи интеграла Лебега или даже более
общего интеграла, с этой целью введенного Данжуа в 1912 г. В то же
время интеграл Лебега с переменным верхним пределом почти всюду
имеет производную, равную подынтегральной функции.
Ввиду этих и других соображений Н. Н. Лузин различает точную
первообразную, имеющую данную функцию своей производной во всех
точках рассматриваемого промежутка, и первообразную, под которой
понимается непрерывная функция, имеющая данную функцию своей
производной почти всюду. Как он доказал, для существования у данной
функции f(x) первообразной необходимо и достаточно, чтобы f(x) была
измерима и почти всюду конечная.
Теорема о первообразной получила в той же главе применение к
решению задачи Дирихле о гармонической функции для круга, в том весьма
общем случае, когда эта искомая функция должна принимать на
граничной окружности почти всюду значения какой-либо данной измеримой
и почти всюду конечной функции f{x). Фату решил ранее задачу для
570 ГЛ. 26. ВОЗНИКНОВЕНИЕ московской ШКОЛЫ ТЕОРИИ ФУНКЦИЙ
случая, когда f(x) суммируема на отрезке 0< #< 2я. Вместе с
упомянутой выше статьей о ряде Тейлора этот результат Лузина и выдвинутые
им попутно вопросы положили начало исследованиям по теории
граничных свойств аналитических функций, которые он проводил уже в
советское время, отчасти вместе с И. И. Приваловым.
В третьей главе работы продолжается изучение первообразных
функций. Здесь ставится вопрос о тех особенностях, которые выделяют
интегралы с переменным верхним пределом среди бесконечного множества
первообразных функций F(x) данной функции f(x), которые разнятся
не на постоянную величину. Лузин решил вопрос для интегралов Лебега
и Данжуа полностью. Мы приведем характерное свойство интеграла
Лебега в геометрической формулировке: если функция f(x) суммируема,
то среди всех кривых, выражающих ее первообразные, интеграл Лебега
есть кривая с наименьшей длиной.
Четвертая глава содержит, среди прочего, постановку некоторых
вопросов относительно обобщения понятия неопределенного интеграла,
а также раздел, посвященный обобщениям понятия производной. Здесь
автор рассказывает об одной работе А. Я. Хинчина, к которой мы еще
возвратимся.
В пятой главе устанавливаются необходимые и достаточные условия
для сходимости почти всюду ряда Фурье для функции f{x) с
интегрируемым квадратом, т. е. такой, что на отрезке (0, 2я) существует
конечный интеграл Лебега от квадрата функции f(x). В 1907 г. Э. Фишер
и Ф. Рисе установили носящую теперь их имя теорему, согласно
которой необходимым и достаточным условием того, что
тригонометрический ряд
оо
-у-+ 2 On cos пх + Ъп sin пх
п=1
есть ряд Фурье для некоторой функции с интегрируемым квадратом,
является сходимость ряда
п=1
Теорема Фишера — Рисса имеет место и для других ортогональных
систем и играет важную роль в общей теории замкнутости.
Для функции f(x) с интегрируемым квадратом и рядом Фурье
оо
"1Г+ 2 ап cos nx-\-bn sin пх
п= 1
Лузин назвал сопряженной функцию g(x), определяемую сопряженным
тригонометрическим рядом
оо
2 (— Ъп cos пх + ап sin пх),
71=1
который, по теореме Фишера — Рисса, очевидно, также является рядом
Фурье функции с интегрируемым квадратом. С помощью этой
сопряженной функции g(x) Лузин формулирует условие сходимости почти всюду
ряда Фурье: для того чтобы ряд Фурье данной функции f(x) с
интегрируемым квадратом был сходящимся почти всюду на отрезке (0, 2я),
необходимо и достаточно, чтобы почти всюду на этом отрезке имело место
«ИНТЕГРАЛ И ТРИГОНОМЕТРИЧЕСКИЙ РЯД»
571
равенство
2я
lim С g (*+«)-g(«-«) cosnada = 0,
2jt
при этом интеграл понимается, как lim \ . Только что указанный инте-
8-^0 *
8
грал, названный Лузиным «особым», в его руках стал сильным
средством теории функций. В частности, Лузин получил с его помощью
новое свойство измеримых множеств — так называемое свойство почти
симметричности.
Наконец, в шестой главе работы исследуется общий вопрос об
условиях представимости функций тригонометрическими рядами. В тех
случаях, когда сумма ряда в обычном смысле не существует, стали
применять обобщенные приемы суммирования. Мы упоминали ранее в этой
связи работы Л. Фейера, который с успехом использовал в теории
тригонометрических рядов определение обобщенной суммы, как
S(X) = Hm Ы*) + Ы')+Г+Ы*) f
где Sn(x) — сумма n +1 первых членов ряда
oo
~1Г~Ь 2 anCOsnx-{- bnsin пх.
n= 1
Так, например, всякая непрерывная в промежутке (0, 2я) функция f(x)
пред ставима суммой тригонометрического ряда Фурье, если сумму
понимать в смысле Фейера.
Лузин продвинулся значительно далее своих предшественников,
показав, что всякая измеримая конечная почти всюду функция может
быть в известном смысле почти всюду представлена, причем
неединственным образом, некоторым тригонометрическим рядом. Именно,
функция f(x), обладающая только что указанными свойствами, представима
почти всюду на отрезке (0, 2я) тригонометрическим рядом
оо
-у-+ 2 йп cos пх "Ь bn sin пх, (Т)
71=1
почти всюду суммируемым к ней методами Римана и Пуассона.
Суммирования по Пуассону и Риману представляют собой также обобщенные
приемы суммирования расходящихся рядов. Мы поясним для примера
смысл суммирования по Пуассону. Рассмотрим связанный с рядом (Т)
ряд Р(р, х)
оо
Р(р, х) = Ц- + 2 9п (ап cos пх + Ъп sin пх), (Р)
71=1
предполагаемый голоморфным внутри единичного круга с центром в
начале. Суммой ряда (Р) в смысле Пуассона называется предел / (х) =
= lim Р(р, х), если он существует почти всюду на отрезке (0, 2я).
Книга Н. Н. Лузина, написанная с редкой ясностью и характерным
для автора наглядно геометрическим стилем мышления, явилась
572 ГЛ. 26. ВОЗНИКНОВЕНИЕ московской ШКОЛЫ ТЕОРИИ ФУНКЦИЙ
богатейшим источником новых проблем, из которого ученые долгое
время черпали и продолжают черпать задачи.
«Интеграл и тригонометрический ряд» явился ценнейшим вкладом
Лузина в метрическую теорию функций, в которой на основе понятия
меры изучаются свойства измеримых функций, интеграла, производной
и других центральных понятий анализа. В 1915 г. Лузин начинает
заниматься другим направлением теории функции — дескриптивным. В
дескриптивной теории функций изучается структура и мощности
различных сложных точечных множеств, образуемых некоторыми
специальными способами из замкнутых множеств. В последующие же годы Лузин
вместе с учениками развернул широкие исследования в этом
направлении, которые продолжал до самой смерти.
Мы не можем здесь подробно осветить деятельность Н. Н. Лузина
в послереволюционное время. До 1929 г. он работал преимущественно
в Московском университете, а затем в Математическом и других
институтах Академии наук СССР, членом-корреспондентом которой был избран
в 1927 г. и действительным членом в 1929 г. Помимо исследований по
теории функций, он занимался также некоторыми вопросами теории
приближенных вычислений, дифференциальной геометрии и истории
математики. Большую популярность приобрело переработанное им
издание учебника В. Грэнвиля, из которого возник собственный курс
дифференциального и интегрального исчислений Н. Н. Лузина; по этим
руководствам обучались и обучаются многие будущие инженеры и
учителя. Н. Н. Лузин скончался 28 февраля 1950 г.
Трудно переоценить роль Лузина в развитии современной
математики, прежде всего в формировании советской математической школы.
Его прямыми или косвенными учениками являются почти все наши
выдающиеся московские математики. Чрезвычайное богатство своих
идей Лузин использовал не в одиночку. Он охотно делился занимавшими
его вопросами с молодежью, щедро разбрасывая на лекциях, семинарах
и в личных беседах с учениками новые вопросы, новые подходы к их
решению. «В методах научно-педагогической работы,— рассказывал
В. В. Степанов,— Лузин произвел настоящую революцию: двери
профессорской комнаты широко раскрылись для студентов, лектор проводил
все перерывы между лекциями в оживленной научной беседе со своими
слушателями, причем слушателям предлагалось решать проблемы,
решение которых в данный момент не удавалось руководителю» х). А после
занятий члены «Лузитании», как шутливо прозвали коллектив учеников
Лузина, провожали молодого профессора домой, прогулка и живая
научная беседа затягивались надолго.
Вместе с тем Н. Н. Лузин был удивительным лектором. Его
слушатели, в том числе и пишущий эти строки, никогда не забудут
необыкновенного увлечения, которое они испытывали на его лекциях. Казалось,
он заново творил на глазах аудитории излагаемую теорию — так оно
действительно бывало в специальном курсе теории функций, когда он
рассказывал о только что полученных и еще не до конца развитых или
обоснованных результатах. К тому же Лузин обладал очень красивым и
проникновенным голосом. Впечатление от его лекций было сравнимо с
впечатлением от монологов знаменитых мастеров Художественного
театра.
г) В. В. Степанов, Московская школа теории функций.— Уч. зап. МГУ*
1947, вып. 91, стр. 49.
УЧЕНИКИ И ПОСЛЕДОВАТЕЛИ ЛУЗИНА
573
Ученики и последователи Лузина. Очень быстро вокруг Лузина
составилась группа талантливых последователей из товарищей и
студентов. Перед самой Октябрьской революцией
эта еще небольшая, но яркая и сильная
московская школа теории функций
выступила публично. Мы имеем в виду
первые работы А. Я. Хинчина, Д. Е.
Меньшова, П. С. Александрова и М. Я. Сусли-
на, а также магистерскую диссертацию
университетского товарища Лузина —
В. В. Голубева.
Александр Яковлевич Хинчин (20 май
4894—18 ноября 1959) приступил к
научной работе еще в студенческие годы. Его
первый результат был включен в
диссертацию Лузина. Речь шла о поставленном
в 1904 г. Б. К. Млодзеевским вопросе:
обобщить на недифференцируемые в
обычном смысле функции понятие производной
так, чтобы обобщенная производная
обладала основными свойствами
обыкновенной производной. Хинчин дал решение
вопроса в устном сообщении студенческому
математическому кружку осенью 1914 г.
Пусть М — некоторое измеримое множе- Хинчин.
ство и N — подмножество множества точек
М, принадлежащих промежутку (х0 — h, х0 + h). Плотностью множества
М в точке х0 называется Нш. Мера N . Асимптотической производной функ-
ции f(x) в точке х0 Хинчин назвал
lim К*>-К*о> ,
причем х принимает значения на множестве Е, для которого точка х
служит точкой плотности 1. Хинчин тогда же доказал необходимую
для корректности определения независимость значения асимптотической
производной от того или другого выбора множества Е, имеющего точку х0
точкой единичной плотности. Впервые эти результаты были
опубликованы в § 60 книги Н. Н. Лузина. Вскоре в заметке, напечатанной в «Сотр-
tes rendus» Парижской Академии наук за 1916 г., Хинчин применил
понятие асимптотической производной к дальнейшему обобщению понятия
интеграла Данжуа (одновременно с самим Данжуа). Обобщенный
интеграл Данжуа — Хинчина позволяет восстанавливать первообразную
функцию по ее данной асимптотической производной. В 1916 г. А. Я.
Хинчин был оставлен при университете по предложению Д. Ф. Егорова,
подчеркивавшего, наряду с математическим дарованием молодого ученого,
его «талант необыкновенно ясного и свободного изложения» 1). В
Московском университете Хинчин преподавал с 1922 г., а с избранием в члены-
корреспонденты Академии наук СССР (1939) он работал также в Мате-
х) Ф. А. Медведев, Подготовка теоретико-множественных и теоретико-
функциональных исследований в России. Сб. «Очерки истории математики и механики»,
М., 1963, стр. 63.
574 ГЛ. 26. ВОЗНИКНОВЕНИЕ московской ШКОЛЫ ТЕОРИИ ФУНКЦИЙ
матическом институте им. Стеклова. Ему принадлежат первоклассные
труды по теории функций, теории чисел и теории вероятностей х).
Теории интеграла Данжуа посвящена была и первая опубликованная
работа Дмитрия Евгеньевича Меньшова (род. 18 апреля 1892 г.),
появившаяся в 30-м томе «Математического сборника» за 1916 г., год окончания
им университета. В том же году Меньшов напечатал в «Gomptes
rendus» заметку, посвященную проблеме
единственности представления функции
тригонометрическим рядом.
Проблема единственности
тригонометрического ряда, представляющего данную
функцию / (х), сводится к другой задаче —
о существовании тригонометрического ряда,,
не все коэффициенты которого равны нулю,
но сумма которого есть нуль. Этой задачей
занимались такие математики, как Б. Ри-
ман, Г. Кантор и А. Лебег.
В. Юнг доказал, что у
тригонометрического ряда, сумма которого равна нулю,
всюду, за исключением, быть может,
счетного множества точек, все коэффициенты
равны нулю. При обобщенном понимании
суммы дело обстоит иначе; например, как
показал Лузин, тригонометрический ряд
с коэффициентами, отличными от нуля,
может быть суммируем методом Пуассона
к нулю. Однако существование ряда, схо-
Д. Е. Меньшов. дящегося почти всюду к нулю и имеющего
коэффициенты, отличные от нуля, казалось
маловероятным. Это отметил в своей диссертации Лузин. Через год после
публикации «Интеграла и тригонометрического ряда» Меньшов в
упомянутой заметке построил неожиданный пример тригонометрического ряда,
почти всюду сходящегося к нулю и имеющего коэффициенты, отличные
от нуля.
Последующие изыскания Д. Е. Меньшова были посвящены
тригонометрическим и вообще ортогональным рядам, а также свойствам
аналитических функций. С 1922 г. он работает в Московском университете,
с 1953 г. является членом-корреспондентом Академии наук СССР 2).
Работы П. С. Александрова и М. Я. Суслина принадлежали к
дескриптивной теории функций.
Первым предметом изучения дескриптивной теории функций явились
так называемые множества Бореля. Суммой двух или большего числа
множеств называется множество элементов, которые принадлежат хотя бы
одному из слагаемых множеств; произведением множеств называется
множество, элементы которого принадлежат обоим исходным множествам.
Борелевские множества — это множества, которые получаются в
результате применения к конечному или счетному числу замкнутых множеств
конечного или бесконечного числа действий сложения и умножения
(исследование их основано на учении о трансфинитных числах).
1)Б. В. Гнеденко, Александр Яковлевич Хинчин.— УМН, т. X,
3 (65), 1955.
2) Н. К. Бари и Л. А. Л ю с т е р н и к, Дмитрий Евгеньевич Меньшов.—
УМН, т. VII, 3 (49), 1952.
УЧЕНИКИ И ПОСЛЕДОВАТЕЛИ ЛУЗИНА
575
Всякое несчетное замкнутое множество имеет мощность континуума,
Н. Н. Лузин поставил вопрос о мощности борелевских множеств.
Ответ была дан П. С. Александровым.
Павел Сергеевич Александров (род.
7 мая 1896 г.) получил свой результат
в 1915 г., еще будучи студентом третьего
курса, и опубликовал его в «Comptes
rendus» в 1916 г. Он доказал, что всякое
несчетное борелевское множество, содержа,
подобно обыкновенному несчетному
замкнутому множеству, совершенную часть,
имеет мощность континуума. Еще большее
значение имел использованный
Александровым прием задания борелевских
множеств при помощи так называемой А
-операции. Лузин поставил вопрос: является
ли борелевским всякое множество,
возникающее при А -операции над замкнутыми
множествами? Этот вопрос решил
талантливый, очень рано скончавшийся Михаил
Яковлевич Суслин (15 ноября 1894—1919),
вышедший из крестьянской семьи
Саратовской губернии. В 1916 г., будучи сту- П. С. Александров
дентом третьего курса, Суслин построил
при помощи А -операции над отрезками неборелевское множество, которое
предложил назвать аналитическим или Л-множеством.
Сам М. Я. Суслин, безвременно скончавшийся от сыпного тифа,
успел опубликовать лишь заметку в «Comptes rendus» за 1917 г.; его
результаты были изложены и развиты
подробнее уже посмертно немецким ученым Ф. Хаус-
дорфом, который назвал ^1-множества суслин-
скими, Н. Н. Лузиным и другими. Теория
аналитических множеств была затем развита
Лузиным и его учениками. Еще более
широкий класс множеств образуют так называемые
проективные множества, впервые введенные
и изученные Лузиным; проблемы учения
о проективных множествах весьма трудны
и носят характер, пограничный с методологией
математики и математической логикой.
П. С. Александров после окончания
университета в 1917 г. ненадолго отошел от
математики, но уже в 1920 г. вновь обратился
к ней. Вместе с Павлом Самуиловичем Уры-
соном (3 февр. 1898—17 августа 1924) он
положил начало большой топологической школе,
М. Я. Суслин. которую возглавляет и в настоящее время.
С 1921 г. он работает в Московском
университете., В 1929 г. он был избран членом-корреспондентом Академии наук
СССР ив 1953г. академиком; в 1932—1964 гг. он руководил деятельностью
Московского математического общества в качестве его президента х).
х) Л. С. П о н т р я г и н, Е. Ф. Мищенко, Павел Сергеевич Александров.—
УМН, т. XI, 4 (70), 1956.
576 ГЛ. 26. ВОЗНИКНОВЕНИЕ московской ШКОЛЫ ТЕОРИЙ ФУНКЦИЙ
В работах Н. Н. Лузина метрическая теория функций была
применена к исследованию граничных свойств аналитических функций, т. е. их
свойств в окрестности множества граничных точек. К этому направлению
относятся также многие работы
товарища Лузина — Владимира
Васильевича Голубева (3 декабря 1884—4
декабря 1954), окончившего Московский
университет в один год с ним,
впоследствии профессора университетов в
Саратове (1917—1930) и в Москве (с 1930 г.)
и с 1934 г. члена-корреспондента
Академии наук СССР. В магистерской
диссертации В. В. Голубева «Однозначные
аналитические функции с совершенным
множеством особенностей» (М., 1916)
были значительно обобщены
упоминавшиеся нами результаты Племеля о
предельных значениях интегралов типа
Коши (работы Ю. В. Сохоцкого еще
долго оставались забытыми).
Исследования по теории особых точек Голубев
продолжал и в дальнейшем. Ему
принадлежат также работы по
аналитической теории дифференциальных
уравнений и аэродинамике.
В. В. Голубев. Граничные свойства аналитических
функций явились предметом изысканий
еще одного ученика Егорова—Ивана Ивановича Привалова (11 февраля
1891 — 13 июля 1941), который окончил университет в 1913 г. И. И.
Привалов глубоко продвинулся в анализе свойств
интеграла типа Коши уже к концу
рассматриваемого периода, но сделанные в то время
открытия опубликовал несколько позднее в книге
«Интеграл Cauchy» (Саратов, 1918). В ряде
последующих работ, частью в соавторстве
с Н. Н. Лузиным, Привалов рассмотрел
широкий круг вопросов теории граничных свойств.
Несколько лет И. И. Привалов был
профессором в Саратовском университете, а с 1922 г.
читал лекции в Московском университете.
В 1939 г. он вошел в состав Академии наук
СССР как ее член-корреспондент г).
Мы назвали здесь имена и первые открытия
только немногих учеников или последователей
Лузина, именно тех, которые начали свою
научную деятельность до 1917 г.
Значение московской школы теории
функций далеко не ограничивается открытиями в са- И. И. Привалов,
мой теории функций. Методы теории функций
были эффективно использованы в теории аналитических функций
и топологии, в теории чисел и теории вероятностей, в качественной
г) О работах В. В. Голубева, Н. Н. Лузина и И. И. Привалова см. в сб.
«Математика в СССР за тридцать лет»., М.— Л., 1948.
УЧЕНИКИ И ПОСЛЕДОВАТЕЛИ ЛУЗИНА
577
теории дифференциальных уравнений и вариационном исчислении
и т. д. «Всякой научной школе со специализированной тематикой,—
писал В. В. Степанов,— в процессе ее развития угрожает
опасность эпигонства... после того как основные проблемы разрешены и
исчерпаны трудами ряда талантливых ученых, эти же ученые и их ученики
добирают оставшиеся крохи. Московская школа в целом преодолела эту
опасность расширением области исследования и применением методов
теории функций и теории множеств к
другим отраслям математики» х).
В дальнейшем развитии теории
функций и распространении ее методов на
другие области математики главную роль
в первую очередь сыграли названные
ученики Н. Н. Лузина. К группе учеников
Егорова и товарищей Лузина принадлежал
и только что цитированный Вячеслав
Васильевич Степанов (4 сентября 1889 —-
22 июля 1950), в 1913 г. оставленный при
университете. После Октябрьской
революции Степанов явился одним из главных
организаторов всей работы
физико-математического факультета Московского
университета. В 1946 г. он был избран членом-
корреспондентом Академии наук СССР.
Научная деятельность его, однако, выходит
за границы рассматриваемого периода2).
Влияние столь сильной школы, как
школа ^Лузина, не могло ограничиться
кругом московских математиков. Методы в- в- Степанов,
теории функций после Октябрьской
революции получают признание и в других советских научных центрах,
в частности, в Ленинграде, где вначале с неодобрением смотрели
на московское увлечение, казалось бы, слишком общими и
отвлеченными идеями, лишенными прямой связи с другими конкретными
проблемами математики и математического естествознания. Многие
москвичи, со своей стороны, безразлично относились к традиционной тематике
ленинградцев. Но уже в двадцатые годы началось сближение обоих
главных течений русской математической мысли. Московская школа теории
функций оказала немалое воздействие и за рубежом. Особенно
значительным было влияние на польскую математику, где возникла сильная
школа теории функций (В. Серпинский, Г. Штейнгауз, С. Мазуркевич,
А. Райхман, А. Зигмунд и другие); оно сказывалось и на творчестве
французских, английских, немецких и японских ученых.
1)В. В. Степанов, Московская школа теории функций.— Уч. зап. МГУ,
1947, вып. 91, стр. 51.
2) П. С. Александров и В. В. Немыцкий, Вячеслав Васильевич
Степанов, М., 1956.
ЗАКЛЮЧЕНИЕ
Подведем в нескольких словах итоги развития математики в России
в XIX и начале XX вв.
К Октябрьской революции отечественная математика имела
выдающиеся достижения. Русские математики, отправляясь от задач, которые
ставила на очередь дня теория и практика, в ряде важнейших
направлений далеко продвинулись вперед. Лобачевский, открыв пути построения
новых геометрических систем и поставив математику перед
необходимостью развития аксиоматических методов исследования, во многом
определил все дальнейшее развитие математической мысли.
Остроградский с блеском разрабатывал математическую физику, интегральное
исчисление и другие отделы анализа. Благодаря трудам Чебышева и его
учеников — Золотарева, Вороного, Маркова, Ляпунова и других —
русские школы теории чисел и теории вероятностей выдвинулись на первое
место в мире. Чебышев же, показав один из наиболее замечательных
примеров математического анализа задач техники, создал новую теорию,
приближения функций. Основополагающие труды Ляпунова по теории
устойчивости динамических систем и качественным методам составили
новую крупнейшую главу теории дифференциальных уравнений.
Ляпунов и Стеклов мощно продвинули вперед математическую физику. В
начале XX века возникла московская школа теории функций действительного
переменного во главе с Лузиным, в Киеве школа алгебраическая, в
Харькове сообщено было новое направление исследованиям по теории
вероятностей и теории приближения функций; в Москве, Казани, Одессе и других
центрах проводились исследования по геометрии.
Вместе с тем еще более широкому развитию математики по всему
ее фронту, как и других естественных наук, в нашей стране
препятствовала вся система царского режима. Народные массы не имели доступа
к просвещению вообще и тем более к высшему образованию. На огромное
государство приходилось лишь около десятка физико-математических
факультетов; обучались на математических отделениях немногочисленные
студенты. Научно-исследовательских математических институтов не
существовало. Редко кого оставляли для подготовки к профессуре при
университетах, и многим талантливым математикам после окончания
университета не было пути к научной деятельности. Связь математики с
народнохозяйственными нуждами была еще слабой, несмотря на деятельность
отдельных замечательных «прикладников», как Жуковский, Чаплыгин
и Крылов.
Коренной поворот в развитии отечественной математики мог быть
обусловлен только коренным общественным поворотом в судьбах всей
страны. После Великой Октябрьской социалистической революции
начался новый период истории нашей математики. Его рассмотрение лежит
за пределами этой книги.
именной указатель
Абель Н. (Abel N. Н., 1802—1829) 126,
153, 154, 227, 270, 293, 295, 327, 328,
367, 380-385, 472-474, 483, 540-
542, 545, 552
Агафон (16 в.) 23
Адамар Ж. (Hadamard J., 1865—1963)
348, 350, 500, 501
Адаме Дж. (Adams J.) 508
Адодуров В. Е. (1709-1778) 75, 77, 78, 80
Акимов М. И. 506
Ал-Газзали (1058—1111) 49, 50
Александр I (1777—1825) 217
Александр II (1818—1881) 306, 430
Александр III (1845—1894) 306
Александров А. Д. (род. 1912) 366
Александров П. С. (род. 1896) 318, 329,
349, 555, 564, 573—575, 577
Алексеев В. Г. (1866—1943) 311, 315, 546
Алексеев Н. Н. (1829—1881) 386
Алексеевский В. П. (1858—1916) 314, 506
Альфонс X Кастильский (1221—1284) 237
Ампер А. М. (Ampere А. М., 1775—1836)
179, 210, 211, 431, 559
Амслер И. (Amsler J., 1823—1912) 305
Андреев К. А. (1848—1921) 313, 314,
318, 326, 430, 433, 484, 513—515, 565
Андронов И. К. (род. 1894) 24
Анисимов В. А. (1860—1907) 314, 315,
329, 444, 445, 484
Аничков Д. С. (ум. 1788) 78, 80
Анкудович В. А. (1799—1855) 223
Анна Иоанновна (1693—1740) 91
Анна Леопольдовна (1718—1746) 106
Антинг Ф. (18 в.) 191, 197
Антропова В. И. (род. 1924) 278, 284,
290 292
Аппель П. (Appell Р., 1855—1930) 310
Аппельрот Г. Г. (1866—1943) 444
Арбогаст Л. (Arbogast L. F. А., 1759—
1803) 170, 214
Арган Ж. (Argand J. R., 1768—1822)
138, 142
Арене В. (Ahrens W.) 126
Аристотель (384—322 до н. э.) 20—22,
49, 50, 534
Арнольд И. В. (1900—1948) 534
Аронгольд Г. (Aronhold S. Н., 1819—1884)
544, 546
Артоболевский И. И. (род. 1905) 408
Архангельский Н. М. (1787—1857) 213
Архимед (287—212 до н. э.) 45, 48, 50,
56—58, 143, 264, 528
Ат-Туси Насирэддин (1201—1274) 230,
261 299
Ахиезер Н. И. (род. 1901) 359, 398, 415,
418, 426, 505
Бага л ей Д. И. 499
Багратуни Г. В. 140
Баклунд О. А. (1846—1916) 320, 398,
416, 433, 514
Бари Н. К. (1901—1961) 565, 566, 574
Барроу И. (Barrow I., 1630—1677) 207
Барсов А. А. (1730—1791) 78, 213
Барсов А. Д. (ум. ок. 1800) 213
Бартельс М. Ф. (1769—1836) 223, 232
Баттальини Дж. (Battaglini G., 1826—
1894) 257
Баумгарт К. К. 99
Бахман П. (Bachmann Р., 1837—1920)
298 331
Бахмутская Э. Я. (род. 1916) 223, 537
Баше де Мезириак (Bachet de Meziriac
С. G., 1587—1638) 37
Башмакова И. Г. (род. 1921) 138, 189,
265, 270, 373, 558
Беда Достопочтенный (672—735) 17
Безикович А. С. (род. 1891) 475
Безикович Я. С. (1886—1958) 475
БейерЕ. И. (1819—1899)223,278,314,318
Бейер И. Г. (Beier J. Н., 1563—1625) 64
Беккер О. (Becker О., род. 1889) 535
Белозеров С. Е. (род. 1904) 142, 315,
445, 492, 501
Белый (Бугаев) А. Н. (1880—1934)313, 484
Белый Ю. А. 47, 48
Бельдоманди П. (Beldomandi Р., род. ок.
1370) 37
Бельтрами Э. (Beltrami Е., 1835—1900)
256, 257, 259, 510
Бенке Г. (Behnke Н.) 496
Беркли Дж. (Berkeley G., 1684—1753)
145, 146, 202
Бернулли Д. (Bernoulli D., 1700—1782)
75, 85, ?6, 90, 92, 93, 95—104, 107,
112, 114, 116, 119, 120, 123, 125, 126,
149, 157, 159, 160, 167—169, 173,
174, 178, 182, 189, 196, 224, 268, 278,
300, 364, 371, 389, 390, 437, 502
Бернулли И. I. (Bernoulli Joh., 1667 —
1748) 84, 8Q, 88—90, 96, 97, 99, ЮЗ,
104, 106, 116, 120, 130—132, 135—
138, 142, 145, 160, 164, 174, 224, 296
580
ИМЕННОЙ УКАЗАТЕЛЬ
Бернулли И. II (Bernoulli Joh., 1710—
1790) 91, 116
Бернулли И. HI (Bernoulli Joh., 1744—
1807) 169
Бернулли Н. I (Bernoulli N., 1687—1759)
90,93, 97, 101, 123, 124, 137, 149
Бернулли Н. II (Bernoulli N., 1695—
1726) 75, 85, 86, 90, 92, 97, 103, 157,
158, 160
Бернулли Я. I (Bernoulli J., 1654—1705)
84—86,89,90,103, 116—119, 174, 177,
300, 387—389, 392, 393, 398, 506—508
Бернулли Я. II (Bernoulli J., 1759—1789)
91
Бернштейн С. Н. (род. 1880) 264, 310,
314, 318, 325, 332, 337, 389, 390, 401,
403, 404, 409, 413, 419, 421—426,
440, 445, 446, 451, 474, 562
Бертран Ж. (Bertrand J. L. F., 1822—
1900) 299, 300, 346, 347, 411, 430,
485, 554
Берх В. Н. 56
Беспамятных Н. Д. (род. 1910) 350
Бессель А. В. (1839—1870) 384
Бессель Ф. В. (Bessel F. W., 1784—1846)
159, 160, 251, 435, 469, 502, 505
Бетти Э. (Betti Е., 1823—1892) 267
Биеренс де Хаан Д. (Bierens de Haan D.,
1822—1895) 249
Бине Ж. (Binet J. Ph. M., 1786—1856)
115 275 338
Биркго'ф Дж. Д. (Birkhoff G. D., 1884—
1947) 462
Блейк A. (Blake A.) 535
Блихфельдт Г. (Bleichfeldt H. F.) 356
Блюм И.-О. (Blum J.-A., 1812—1877) 277
Бляшке В. (BlaschkeW., 1885—1962)526
Бобылев Д. К. (1842—1917) 311, 448
Бобынин В. В. (1849—1919) 24, 27, 30—
35, 38, 40—43, 45, 59, 313, 321, 322,
330, 534
Боголюбов А. Н. (род. 1912) 406
Боголюбов Н. Н. (род. 1909) 288, 462
Болл P. (Boll R.) 523
Боль П. Г. (1865—1921) 458—463, 538
Больцано Б. (Bolzano В., 1781—1848)
122, 126, 133, 150, 210, 226, 271, 328,
559 562 563
Бонне'О. (Bonnet Р. О., 1819—1892)
255, 256, 513
Бооль В. Г. (1836—1899) 303, 305
Бор Г. (Bohr Н., 1887—1951) 462
БореллиДж. (BorelliG. А., 1608—1679)^97
БорельЭ. (Borel Е., 1871—1956) 127, 310,
328, 421, 489,500,501,560,566,574
Бояи Ф. (Bolyai F., 1775—1856) 231,
232 239 251
Бояи Я. (Bolyai J., 1802—1860) 231,
232, 239, 251, 252
Браге Тихо (Brahe Tycho, 1546—1601) 56
Брайцев И. Р. (1870—1947) 500, 506
Брауер Л. Э. (Brower L. Е. J., род. 1882)
459 461 537
Брашман Н. Д. (1796—1863) 219—222,
240, 278, 301, 313, 317, 318, 321,
332, 334, 427, 428, 483, 511
Бредихин Ф. А. (1831—1904) 302, 317, 398
Бржечко В. Ф. (1891—1954) 426
Бринг Э. С. (Bring Е. S., 1736—1798) 539
Врио Ш. (Briot Gh., 1817—1882) 447, 496
Брокгауз 323
Бромвич Т. (Bromwich Т., 1875—1929) 436
Броункер В. (Brouncker W., 1620?—
1684) 116
Брукер И. 105
Брюс Я. В. (1670—1735) 54, 68, 71
Бубнов И. Г. (1872—1919) 477
Бубнов Н. М. (род. 1858) 330
Бугаев Н. В. (1837—1903) 308, 313,
317, 318, 321, 349, 350, 433, 483—489,
492, 499, 503, 538, 539
Буке Ж. (Bouqet J. С., 1819—1885) 447,
496
Букреев Б. Я. (1859—1962) 315, 329,
375, 487, 489, 492, 499, 500, 562
Булаевский Н. Ф. 140
Буллиг (Bullig) 331
Буль Дж. (Boole G., 1815—1864) 330,
435, 534, 535, 539, 544
Буницкий Е. Л. (1874—1952) 315, 325,
330, 474, 536, 537
Буняковский В. Я. (1804—1889) 111,
214, 223, 224, 228, 252, 272, 274, 277,
296—303, 305, 308, 312, 326, 334,
336, 352, 353, 360, 364, 383, 390,
398, 428, 430, 433, 440, 483, 485,
504, 514, 539
Бур Э. (Bour Е., 1831—1866) 256
Бурачек С. А. (1800—1876) 252, 269, 270
Бурбаки Н. (Bourbaki N.) 558
Буренин К. П. (ум. 1882) 503
Буркгард фон Пюркенштейн А. Э. (Burc-
khard von Piirckenstein A. E.) 71
Бутлеров A. M. (1828—1886) 274
Бушарла Ж.-Л. (Boucharlat J. L., 1775?—
1848) 220
Бычков В. П. 429, 511
Бьенэме Ж. (Bienayme I. J., 1796—1878)
392 394
Бэкон' Ф. (Bacon F., 1561—1626) 235
Бэр P. (Baire R., 1879—1932) 171, 328,
568
Бюльфингер Г. В. (1695—1750) 85, 87,
90 91
Бюшгенс С. С. (1882—1963) 513, 518, 519,
566
Вавилов С. И. (1891—1951) 489
Вагнер В. В. (род. 1908) 531
Вайнштейн И. А. (род. 1917) 113
Валле-Пуссен Ш. де ла (Vallee Poussin
Gh. J. de la, 1866—1962) 348, 350,
421—423
Валлис Дж. (Wallis J., 1616 — 1703) 61,
68, 70, 89, 94, 114, 141, 188, 230, 374
Вариньон П. (Varignon P. de, 1654—1722)
123
Васильев A. B. (1853—1929) 225, 313,
314, 318, 323, 324, 327, 329, 330,
337, 341, 399, 401, 492, 501, 519—521,
526, 527, 538, 545, 562
ИМЕННОЙ УКАЗАТЕЛЬ
581
Ваасон Г. Н. (Watson G. N.) 505
Ващенко-Захарченко М. Е. (1825—1912)
315, 321, 327, 329, 330, 435, 436, 486,
487, 492—494, 499, 505, 547
Вебер Г. (Weber Н., 1842—1913) 503,
550, 551, 554
Ведерборн Дзк. (Wedderburn J. Н. М.,
1882—1948) 558
Вейерштрасс К. (Weierstrass К. Th. W.,
1815-1897) 124, 148, 150, 154, 171,
212, 227, 271, 325, 328, 329, 351, 383,
384, 421, 424, 425, 432, 437—439,
441-444, 492, 496, 498, 499, 502,
557, 559, 560, 563
Вейль Г. (Weyl Н., 1885—1955) 435, 463
Вельмин В. П. (род. 1885) 315, 328, 375,
549, 554
Венков Б. А. (род. 1900) 353, 363, 366, 375
Веселовский И. Н. (род. 1892) 49
Веселовский С. Б. (1876—1952) 28
Вессель К. (Wessel К., 1745—1818) 142
Вивиани В. (Viviani V., 1622—1703) 88
Видман И. (Widman L, род. ок. 1460) 34
Виет Ф. (Viete, Vieta F., 1540—1603)
66, 70
Вилейтнер Г. (Wieleitner Н., 1874—1931)
88
Винер Н. (Wiener N., 1894—1964) 436
Виноградов И. М. (род. 1891) 95, 96,
364, 377—379, 463, 506
Винтер Е. (Winter Е., род. 1896) 86, 95,
106
Висковатов В. И. (1780—1812) 190, 210,
211, 213, 214
Владимир Святославич (ум. 1015) 9,
14, 16
Власов А. К. (1868—1922) 326, 513, 515,
516
Войтяховский Е. (18 в.) 211
Вокансон (Vaucanson J., 1709—1782) 337
Волков Б. А. (18 в.) 78
Вольтерра В. (Volterra V., 1860—1940)473
Вольф Хр. (Wolff Ch. F. von, 1679—1754)
79, 80, 82, 192
Вороной Г. Ф. (1868—1908) 7, 127, 313,
315, 324, 328, 331, 341, 349, 357, 363—
366, 373—378, 489, 490, 494, 506,
508, 551, 578
Вронский Г. (WronskyH., 1778—1853)
289
Выгодский М. Я. (1898—1965) 9, 112,
ИЗ, 146, 151, 309, 485
Вышнеградский И. А. (1831—1895) 278
Гаврилов А. Ф. (род. 1887) 476
Гайд И. 91, 98
Галанин Д. Д. 59
Галёркин Б. Г. (1871—1945) 476, 477
Галилей Г. (Galilei G., 1564—1642) 83
Галлей Э. (Halley Е., 1656—1742) 269
Галуа Э. (Galoys Е., 1811—1832) 227,
270, 326, 327, 371, 541, 542, 545—547,
551, 554, 555
Галченкова Р. И. 224, 313
Гамалея П. Я. (1766-1817) 216, 217
Гамильтон У. (Hamilton W. R., 1805—
1865) 226, 227, 266, 287, 327, 509,
523 555 557
Ганкель Г. (Hankel Н., 1839—1873) 503
Гаусс К. Ф. (Gauss К. F., 1777—1855)
18, 37, 102, 112, 135, 141, 142, 156,
159, 184—188, 206, 216, 227, 228,
232, 239, 251—257, 261, 267, 289,
327, 343, 344, 354, 369—371, 377,
379, 388, 390, 415, 419, 420, 428, 466,
476, 481, 483, 512, 538, 556
Гвин С. (Gwynne S.) 54, 55
Гейне Э. (Heine Н. Е., 1821—1881) 502
Гельфонд А. О. (род. 1906) 189
Гензель К. (Hensel К., 1861—1941) 549,
551
Герберт (Gerberti, 950—1003) 330
Герман Я. (Hermann J., 1678—1733) 75,
85-89, 92, 96, 182, 196, 549
Гернет Н. Н. (1877—1943) 319
Герон (I век н. э.) 43, 196
Геронимус Я. Л. (род. 1898) 418, 421,
426, 433, 482, 510
Герриот Т. (Harriot Т., 1560—1621) 66
Герхард К. (Gerhardt С, 1816—1899) 84
Герцен А. И. (1812—1870) 222
Гершель В. (Herschel W., 1738—1822) 195
Гёльдер О. (Holder О., 1859—1937) 299
Гиларовский П. И. 217
Гильберт Д. (Hilbert D., 1862—1943)
112, 189, 263, 264, 319, 327, 445, 446,
470, 471, 473-475, 478, 511, 519,
527—532, 544
Гихман И. И. (род. 1918) 400, 404, 536
Глаголев Н. А. (1888—1945) 515
Гливенко В. И. (1897—1940) 404, 563
Гнеденко Б. В. (род. 1912) 274, 301, 400,
401, 404, 487, 536, 573
Гоголь Н. В. (1809—1852) 220
Голицын А. Н. (1773—1844) 274
Голицын Б. Б. (1862—1916) 476
Головин М. Е. (1756—1790) 75, 78, 82,
108, 190, 217
Головин О. Н. (род. 1916) 318
Голубев В. В. (1884^-1954) 329, 498,
566, 573, 576
Голубцов И. (18 в.) 91
Голузин Г. М. (1906—1952) 497
Гольдбах Ш. (Goldbach Ch., 1690—1764)
75, 85, 86, 92—97, 99, 115, 116, 119,
123, 137, 138, 157, 172, 182, 185, 186,
189, 200, 224, 381
Гольденберг А. И. (1837—1902) 309
Гончаров В. Л. (1896—1955) 423, 426
Гордан П. (Gordan Р., 1837—1912) 544, 546
Гордевский Д. 3. (род. 1908) 515
Горнер У. (Horner W. G., 1786—1837) 268
Горький М. (Пешков А. М., 1868—1936) 359
Гофман (Hofmann J. Е., род. 1900) 95
Гофрейтер Н. (Hofreiter N.) 356
Гохман В. С. (1880—1956) 86, 99, 128
Гохман X. И. (1851—1916) 315
Граве Д. А. (1863—1939) 140, 313, 315,
316, 320, 324, 326—328, 340, 341,
374—376, 412, 413, 433, 478, 508,
547—554
582
ИМЕННОЙ УКАЗАТЕЛЬ
Грассман Г. (Grassman Н. G., 1809—
1877) 227, 266, 327, 509, 556
Градштейн И. С. (1899—1958) 528
Грацианская Л. Н. (род. 1894) 315, 487,
494
Грегори Дж. (Gregori J., 1638—1675) 418
Грегори Д. (Gregory D. F., 1813—1844)
435
Грейс P. (Gray R.) 54
Греффе К. Г. (Graffe К. Н., 1799—1873)
101, 227, 269
Григорьев В. 297
Григорьян А. Т. (род. 1910) 111, 285
Грин Дж. (Green G., 1793—1841) 156,
283, 289, 290, 292, 474
Грузинцев Г. А. (1880—1929) 562
Грэнвиль В. 572
Грюнвальд А. К. (Grunwald А. С., 19 в.) 434
Губер И. 98
Гунтер Э. (Gunter Е., 1581—1626) 58
Гурвиц A. (Hurwits А., 1859—1919) 363
Гуревич Г. Б. (род. 1898) 530
Гурьев П. G. (1807—1884) 308
Гурьев С. Е. (1764—1813) 75, 89, 190,
199—214, 216, 217, 220, 231, 299, 559
Гусак А. А. 409
Гусев М. М. (1826—1866) 321
Гуссов В. В. (род. 1911) 100, 160, 502, 505
Гуэль Ж. (Houel J., 1825—1886) 257, 431
Гюйгенс X. (Huygens Ch., 1629—1695)
83, 84, 387
Гюнтер Н. М. (1871—1941) 313, 433, 465,
470-472, 481
Давидов А. Ю. (1823—1886) 222, 224,
308, 309, 313, 317, 318, 325, 427—429,
483, 485, 492, 511, 567
Даламбер Ж. (d'Alembert J., 1717—1783)
80, 87, 88, 100, 107, 122, 123, 137—
141, 146, 157, 159, 161, 162, 164, 165,
167—170, 201, 202, 206, 207, 209,
210, 220, 278, 319, 432, 451, 483
Дамаскин Иоанн (ум. 749) 22, 49, 50
Данделен Ж. (Dandelin G. Р., 1794—
1887) 269
Данжуа A. (Danjoy А., род. 1884) 562,
566, 569, 570, 573, 574
Дарбу Г. (Darboux G., 1842—1917) 163,
255, 434, 442, 513, 517
Дарвин Дж. (Darwin G., 1845—1912) 454,
455
Дарвин Ч. (Darwin Ch., 1809—1882) 319
Дахия С. А. (род. 1918) 309
Дедекинд P. (Dedekind J. W. R., 1831—
1916) 212, 327, 328, 331, 368, 372,
551, 560, 562
Дезарг (Desargues G., 1591—1661) 85
Декарт P. (Descartes R., 1596—1650)
8, 51, 70, 83, 84, 88, 95, 130, 135, 136,
181, 182, 185, 215, 250, 534
Деларю Д. M. (1839—1905) 278, 314,
318, 327, 492, 545
Делиль Ж. Н. (Delisle J. N., 1688—1768)
140
Делоне Б. Н. (род. 1890) 96, 185, 357,
363, 366, 375, 376, 549, 551, 554
Делоне Н. Б. (1856—1931) 320, 375
Делоне Ш. (Delaunay Ch. Е., 1816—1872)
287
Дельвиг А. И. (1813—1887) 225
Делянов И. Д. (1818—1897) 449
Демидов П. Н. (1738—1821) 220, 332
Демидов С. С. 446
Ден М. (Dehn М., 1878—1952) 531, 533
Денисов А. П. 56, 79
Депман И. Я. (род. 1885) 58, 71, 73, 223,
309, 320, 464, 498, 511, 512
Деталь К. Ф. (Dechales CI. F. М., 1621 —
1678) 61, 62, 64, 68
Джабир ибн Афла (Гебер, 11 в.) 65
Джевонс У. С. (Jevons W. S., 1835—1882)
330, 534, 536
Джексон Д. (Jackson D., 1888—1946) 424
Дженокки A. (Denocchi А., 1817—1889)
521, 522
Джеррард Дж. (Jerrard G. В., ум. 1863)
539
Джине Дж. (Jeans J., 1877—1946) 455
Джюрин Дж. (Jurin J., 1684—1750) 145
Диксон Л. (Dickson L. Е., 1874—1954) 298
Дингхас A. (Dinghas А.) 496
Динзе О. В. 75
Диофант (3 в. н. э.) 35, 186
Дирихле Л ежен (Dirichlet P. G. Lejeune,
1805—1859) 133, 173, 189, 227, 271,
328, 344, 350, 351, 354, 370, 371, 374,
376—378, 445, 446, 450, 465—467,
559, 562, 567, 569
Дмитрий Донской (1350—1389) 23
Добровольский В. А. 548, 550, 551
Добролюбов Н. А. (1836—1861) 307, 357,
450, 463
Долбня И. П. (1853—1912) 384, 385,
475, 546
Домке (Домкин) Г. П. (Domcke G. Р.) 58
Дорофеева А. В. 180
Дорфман Я. Г. (род. 1898) 111
Дубнов Я. С. (1887—1957) 531
Дудрович А. И. (первая половина 19 в.)
274
Дюамель (Duhamel J. М. С, 1797—1872)
272, 279, 283, 284
Дюбуа-Реймон П. (Du Bois Reymond P.,
1831—1889) 171
Дюпен Ф. Ш. (Dupin F. P. Ch., 1784—
1873) 184, 427
ДюрежГ. (Durege H., 1821—1893) 492, 493
Евдокс (4 в. до н. э.) 57, 528
Евклид (365 — ок. 300 до н. э.) 47—49,
51, 57, 58, 71, 80, 186, 207, 208,
229—231, 237, 240, 242—247, 250,
257, 260—263, 343, 344, 369, 493,
523, 524, 527, 536, 544
Егоров Д. Ф. (1869—1931) 313, 321, 325,
326, 329, 429, 432, 484, 513, 517—519,
547, 564—567, 573, 576, 577
Егоршин В. П. 86
Екатерина II (1729—1796) 217
Елизарьев И. (17 в.) 47, 48
Епифанова А. П. 475
ИМЕННОЙ УКАЗАТЕЛЬ
583
Ермаков В. П. (1845—1922) 308, 309,
315, 321, 325, 327, 375, 393, 431—433,
437, 486-489, 499, 510, 547, 551
Ершов А. С. (1818—1867) 222, 339
Ефрон 323
Жаклар В. 438
Жегалкин И. И. (1869—1947) 313, 329,
563, 564, 566
Жергон Ж. Д. (Gergonne J. D., 1771 —
1859) 321
Жилинский Е. И. 549, 551, 552
Жирар A. (Girard А., 1595—1632) 136
Жогин И. И. (род. 1907) 349
Жордан К. (Jordan С., 1838—1922) 292,
492, 542, 545, 553
Жуковская Л. П. 10
Жуковский Н. Е. (1847—1921) 140,
308, 313, 318, 321, 330, 429, 439, 444,
448, 449, 456, 457, 482, 501, 510,
515—517, 521, 525, 559, 566, 578
Занчевский И. М. (1861—1928) 315
Запольская Л. Н. (1871—1943) 319
Запольский И. И. (1773—1811) 237
Заремба С. (Zaremba S., род. 1863) 465
Зарубин П. А. (1816—1886) 305
Зегнер И. A. (Segner J. A. von, 1704—
1777) 107, 193
Зеельгоф П. (Seelhoff Р., 1829—1896) 298
Зейдель П. (Seidel P. v., 1821—1896) 538,
539
Зейлигер Д. Н. (1864—1936) 314, 326,
525, 526
Зеленый G. И. (1809—1892) 252, 269, 270
Зеллинг Э. (Selling Е., 1834—1920) 303
Зенон Элейский (ок. 450 до н. э.) 50
Зенф К. Э. (1810—1849) 223, 255, 256, 511
Зернов Н. Е. (1804—1862) 219—221,
300, 313, 332, 427, 483
Зигмунд A. (Zygmund А., род. 1900)
577
Зинин Н. Н. (1854-1910) 278, 292, 315
Зморович В. А. (род. 1909) 489
Золотарев Е. И. (1847—1878) 7, 189,
313, 323—325, 327, 331, 341, 350—
358, 361, 364-368, 371—374, 376,
380, 382-385, 411, 413, 452, 485,
541, 551, 554, 578
Зольднер И. фон (Soldner J. von, 1776 —
1833) 155
Зубов В. П. (1899—1963) 18, 20, 22, 49,
50, 51
Иван I Калита (ум. 1340) 23
Иван III Васильевич (1440—1505) 15
Иван IV Васильевич Грозный (1530—
1584) 15
Иванов И. И. (1862—1939) 313, 320,
327, 341, 347, 372, 373
Игнатовский В. G. (1875—1943) 506
Игнациус Г. И. (ум. 1967) 463
Иде И. (Ide J., 1775—1806) 213
Ильин А. (19 в.) 297
Имшенецкий В. Г. (1832—1892) 314, 316,
318, 325, 331, 429-431, 433, 440,
449, 498, 504, 507, 514, 515, 519, 535,
439
Иноходцев П. Б. (1742—1806) 81
Кавальери Б. (Gavalieri В., 1598?—1647)
533
Каве 338
Каган В. Ф. (1869-1953) 232, 235, 251,
252, 263, 308-310, 315, 324, 326,
327, 330, 511, 528—532, 536, 546
Казорати Ф. (Gasorati F., 1835—1890)
496 '
Каменцов М. 193
Кант И. (Kant I., 1724—1804) 236—239
Кантор Г. (Cantor G., 1845—1918) 173,
502, 560, 562, 574
Кантор М. (Gantor М., 1829—1920) 44,
63, 212, 324, 328
Канунов Н. Ф. 558
Карастелев К. И. (1829—1886) 329, 493
Кардано Дж. (Cardano G., 1501—1576) 63
Карнеев 3. Я. (1748—1828) 274
Карно Л. (Carnot L. N. М., 1753—1823)
135, 144, 145, 202, 220
Карсон Дж. (Carson J. R., род. 1887) 436
Картан Э. (Gartan Е., 1869—1951) 293,
520, 558
Карташевский Г. И. (1779—1840) 232
Кассо Л. А. (1865—1914) 464, 516
Кастильон Ж. (Castillion G. F., 1708—
1794) 299
Каталан Э. (Catalan Е. Ch., 1814—1894)
292
Келдыш М. В. (род. 1911) 474, 477
Кемпе А. (Кетре А. В., 1849—1922) 406
Кенигсбергер Л. Konigsberger L., 1837—
1921) 319
Кеплер И. (Kepler J., 1571—1630) 83,
88, 92, 495
Кестнер А. Г. (Kastner A. G., 1775—
1806) 80, 211, 213
Кинкелин Г. (Kinkelin Н., род. 1832) 18
Киприанов В. А. (ум. 1728) 56
Кирик Новгородец (род. 1110) 17—20
Киро С. Н. (род. 1926) 315, 320, 474
Кирхгоф Г. (Kirchhoff G. R., 1824—1887)
284, 480
Киселев А. А. (род. 1916) 320, 350, 488
Киселев А. П. (1852—1940) 59, 309
Клавий Хр. (Clavius Gh., 1537—1612) 51
Кладо Т. Н. 111
Клебш A. (Klebsch R. F. А., 1833—1872)
526, 527
Клейн Ф. (Klein F., 1849—1925) 259,
260, 262, 310, 327, 444, 476, 500, 519,
539, 543. 544, 547, 557
Клеро A. (Clairaut А. С., 1713—1765)
80, 81, 87—89, 107, 160, 161, 173,
182, 183, 453
Клиффорд У. (Clifford W. К., 1845—
1879) 262, 523
Ключевский В. О. (1841—1911) 77
584
ИМЕННОЙ УКАЗАТЕЛЬ
Кнезер A. (Kneser А., 1862—1930) 460,
470, 471, 478, 512, 546
Ковалевская С. В. (1850—1891)
319, 325, 329, 330, 384, 438-444, 452,
492
Ковалевский В. О. (1842—1883) 438, 439
Ковалевский М. М. (1851—1916) 440
Кодацци Д. (Godazzi D., 1824—1873)
256, 512
Козельский Я. П. (1728—1794) 78, 79
Коллинс Э. Д. (1791—1840) 214, 224,
276, 301
Колмогоров А. Н. (род. 1903) 144, 264,
300, 393, 394, 403, 404, 563
Колосов Г. В. (1867—1936) 315, 330,
474, 501
Кольцов А. В. (род. 1927) 360
Кондорсе Ж. А. де (Condorcet М. J. А.
N. К. de, 1743-1794) 128, 161
Кондратьев С. П. 86
Конторович П. Г. (1905—1968) 267
Коншина Т. И. 18
Копелевич Ю. X. 106, 111
Коперник Н. (Coppernicus N., 1473—1543)
56, 262
Копиевич (Копиевский) И. Ф. 58, 59
Копферман К. (Kopfermann К.) 496
Корвин-Круковская А. В. (Жеклар)
(1843—1887) 438
Корвин-Круковский В. В. 438
Коркин А. Н. (1837—1908) 255, 277,
312, 321, 323—325, 341, 350—352,
354—358, 361, 365, 368, 372, 432,
433, 471, 477, 478, 485, 486, 489, 492,
548
Космодемьянский А. А. 192
Котельников А. П. (1856—1944) 252,
314, 326, 327, 330, 519, 521—526, 557
Котельников П. И. (1809—1879) 252,
314, 492, 519, 521
Котельников С. К. (1723—1806) 75, 78,
79, 82, 107, 190—193, 196
Котес P. (Cotes R., 1682—1716) 120, 137,
341, 418
Кочев В. А. 431
Коши О. (Cauchy A- L., 1789—1857) 122,
126, 132, 134, 135, 141, 152, 156, 162,
173, 203, 206, 210, 212, 216, 220, 226,
227, 265, 267, 271, 275, 276, 283, 285,
290, 297—299, 328, 329, 332, 338, 435,
437, 440-443, 473, 478, 483, 485,
486, 488, 492-498, 502, 504, 559—561,
569, 576
Кошляков Н. С. (1891—1958) 175
Коялович Б. М. 536
Кравчук М. Ф. (1892—1942) 554
Краевич К, Д. (1833—1892) 351
Крамар Ф. Д. (род. 1911) 510
Крамер Г. (Cramer G., 1704—1752)
401
Крафт В. Л. (1743—1814) 108
Крафт Г. В. (Krafft G. W., 1701—1754)
75, 85, 89, 91, 92, 108, 126
Крелле А. Л. (Crelle A. L., 1780—1855)
255, 293, 321, 332, 334, 355, 364—
366, 485
Кристофель Э. (Christoffel Е. В. 1829—
1900) 519
Кронекер Л. (Kronecker L., 1823—1891)
199, 327, 331, 372, 374, 519, 538, 539,
547, 554
Кропотов А. И. (род. 1909) 274, 432, 503
Крупская Н. К. (1869—1939) 319
Крутикова М. В. 111
Крыжановский Д. А. (1883—1938) 563
Крылов А. Н. (1863—1945) 224, 277,
288, 311, 316, 325, 350, 351, 359, 419,
448, 477—482, 490, 491, 578
Крылов Н. М. (1879—1955) 180, 288, 385,
475—477
Крылова О. В. 475
Крюков Л. Д. 233
Кузен Ж. (Cousin J. А., 1739—1800) 202
Кузнецов В. (18 в.) 80
Кузнецов И. В. 464
Кузнецов П. 292
Кузьмин Р. О. (1891—1949) 96, 352
Кузьмин Ф. 213
Кулибин И. П. (1735—1818) 109
Кулябко Е. С. 191
Куммер (19 в.) 303
Куммер Э. (Rummer Е. Е., 1810—1893,
187, 188, 227, 327, 350, 370, 371, 483,
486, 507
Купфер А. Я. (1791—1865) 240
Купфер К. Г. (1789—1838) 308
Курганов Н. Г. (1725?—1796) 8, 56, 59,
78-81
Курош Г. А. (род. 1908) 553
Кутюра Л. (Couturat L., 1868—1914) 535,
536
Кэджори Ф. (Cajory F., 1859—1930) 35
Кэли A. (Cayley А., 1821—1895) 326,
541, 544, 546
Кюн Г. (Kiinn Н., 1690—1769) 141
Лаврентьев М. А. (род. 1900) 111
Лавров П. Л. (1823—1900) 278, 297, 332,
472
Лагерр Э. (Laguerre Е., 1834—1886) 417,
418, 469, 496
Лагир Ф. де (Lahire F., 1640—1718)
182
Лагранж Ж. Л. (Lagrange J. L., 1736—
1813) 81, 87, 101, 107, 123, 124, 132,
139, 146, 148—150, 153—156,159, 161,
163, 169, 178, 179, 187, 188, 202, 203,
210—212, 214, 216, 220, 232, 268, 270,
271, 285, 288, 291, 327, 340, 343, 354r
374, 384, 400, 405, 415, 427—430, 432,
443, 444, 479, 481, 495, 539—541, 545,
548
Ладыженская О. А. (род. 1922) 446, 475
Лакруа С. (Lacroix S. F., 1765—1843) 152,
155 220
Ламберт И. Г. (Lambert J. Н., 1728—1777)
135, 139, 189, 195, 231, 539
Ламе Г. (Lame G., 1795—1870) 275, 279,
283, 430, 452, 509, 510 ,
Ландау Э. (Landau Е., 1877—1938) 350,
379, 549
ИМЕННОЙ УКАЗАТЕЛЬ
585
Ланков А. В. 308
Лапко А. Ф. (род. 1919) 8, 517
Лаплас П. (Laplace P. S. de, 1749—1827)
101, 113, 141, 155, 160, 161, 163, 169,
216, 227, 232, 275, 284, 288—290, 319,
388—390, 392, 393, 400, 409, 414, 428,
431, 434-436, 438, 445, 447, 451, 453,
464, 465, 475, 510
Лаптев Б. Л. (род. 1905) 240, 314
Латышева К. Я. (1897—1956) 432, 433
Лахтин Л. К. (1853—1927) 313, 315, 328,
484, 539, 540, 567
Лебег A. (Lebesgue Н., 1875—1941) 171,
172, 272, 328, 338, 421, 424, 498, 560—
562, 569, 570, 574
Лебедев П. Н. (1839—1896) 313, 516, 559
Лебедева В. Е. (род. 1881) 319
Лебединцев К. Ф. (1878—1925) 311
Леви A. (Lewy Н.) 549, 555
Леви П. (Levy Р., род. 1886) 436
Левитский Н. И. 408
Лежандр А. М. (Legendre А. М., 1752—
1833) 115, 118, 149, 154, 159, 187—
196, 208, 209, 231, 240, 246, 261, 273,
275, 293, 298, 299, 343—345, 354, 414,
415, 417, 419, 431, 453, 496, 504
Лейбман Э. Б. 318, 529
Лейбниц (Leibniz G. W. von, 1646—1716)
8, 51, 84, 86-88, 90, 92, 96, 114, 122,
123, 126, 130, 131, 136—138, 142—144,
146, 157, 163, 174, 201, 202, 207, 215,
220, 250, 295, 302, 434, 484, 534
Лейтман И. Г. (1667—1736) 54
Лексель А. И. (Lexell A. J., 1741—1784)
75, 88, 91, 108, 154, 159, 161, 190, 192,
^[95 199
Ленин В. И. (1870—1924) 306, 319
Леонардо Пизанский (Leonardo Pisano,
ок. 1170 — ок. 1230) 22, 35, 37
Леруа Э. (Leroy Е.) 465, 466
Лесгафт П. Ф. (1837—1909) 430
Летников А. В. (1837—1888) 160, 257,
317, 325, 433-435, 485, 503
Ли С. (Lie S., 1842—1899) 327, 431, 432,
519, 529, 542, 543, 546
Либман Г. (Liebmann К. О. Н., 1874—
1939) 256, 359
Либри Г. (Libri G., 1803—1869) ИЗ
Лигин В. Н. (1846—1900) 315
Линдеман Ф. (Lindemann F., 1852—1939)
96, 189
Линдстед А. 288
Линник Ю. В. (род. 1915) 102, 363
Липкин Л. И. (1841—1875) 406
Липшиц P. (Lipschitz R. 1832—1903)
162, 379, 424, 519, 562
Литвинова Е. Ф. (1845—1922) 319
Литлвуд Дж. (Littlewood J., род. 1885)
95
Лиувилль Ж. (Liouville J., 1809—1882)
96, 97, 154, 192, 289, 295, 321, 332,
335, 338, 352, 380, 381, 391, 396,
433, 434, 437, 451, 452, 467, 469-472,
475, 485, 489
Лихин В. В. (род. 1905) 119, 508
Лихолетов И. И. (род. 1910) 222
Лобатто (Lobatto R., род. 1797) 435
Лобачевский Н. И, (1792—1856) 7, 8,
18, 133, 171, 173, 223—225, 227—229,
231—252, 256—272, 300, 301, 314,
318, 319, 326, 328, 332, 342, 386, 429,
431, 434, 444, 450, 464, 470, 483, 486,
509, 511, 519, 521—525, 528, 531, 544,
556, 559, 578
Лозинский С. М. (род. 1914) 475
Ломмель Э. (Lommel Е., 1837—1899) 502
Ломоносов М. В. (1711—1765) 51, 59,
78, 91, 107, 110, 192, 464
Лопиталь Г. Ф. (L'Hospital G. F. de,
1661—1704) 143
Лопшиц А. М. (род. 1897) 531
Лоренц Г. A. (Lorentz Н., 1853—1928)
324
Лузин Н. Н. (1883—1950) 7, 173, 313.
321, 326, 329, 513, 518, 565—578
Лукина Т. А. 111
Лукомская А. М. 323, 458
Лунц Г. Л. (род. 1910) 271, 272
Лурье С. Я. (1890—1965) 81, 146, 151
Лысенко В. И. 190, 196, 198, 199
Любимов Н. А. (1830—1898) 317
Люилье С. (L'Huilier S., 1750—1840) 196
Люка Э. (Lucas Е., 1842—1891) 298, 510
Люстерник Л. А. (род. 1899) 318, 517, 574
Ляпин Н. М. 386
Ляпунов А. М. (1857—1918) 7, 288, 311,
313, 314, 318, 324, 325, 329, 331, 341,
342, 393, 398, 400, 401, 403, 439,444,
446, 448—458, 460, 463, 465, 466,
469, 474, 475, 492, 578
Ляпунов Б. М. (1864—1942) 448
Ляпунов М. В. (1820—1868) 448
Ляпунов С. В. 477
Ляпунов С. М. (1859—1924) 448, 450
Магницкий Л. Ф. (1669—1739) 8, 25, 54,
55, 58—71, 79, 81
Магницкий М. Л. (1778—1844) 218, 232,
430
Мазер Ф. (Maseres F., 1731—1824) 431
Мазуркевич С. 577
Маиевский Н. В. (1823—1892) 222,
335
Май К. 481
Майер В. 91
Майер Ф. X. (Majer F. К., 1697—1729)
75, 85, 86, 90, 91
Майнарди Г. (Mainardi G., 1800—1879)
512
Майстров Л. Е. (род. 1920) 16, 303
Маклорен К. (Maclaurin С, 1698—1746)
81, 117, 119, 122, 145, 149, 207, 220,
273, 296, 341, 377, 451, 452, 454, 486,
488, 504, 507
Максвелл Дж. К. (Maxwell J. С., 1831—
1879) 292, 314
Максимович В. П. (1850—1889) 437, 492
Малинин А. Ф. (1835—1888) 503
Мальтон 74
Мальцев А. И. (1909—1967) 330
Мандрыка А. П. 111
586
ИМЕННОЙ УКАЗАТЕЛЬ
Марков А. А. (1856—1922) 7, 311, 313,
316, 320, 321, 324—326, 340-342,
350, 357—364, 373, 374, 384, 386,
390, 393, 395—403, 409—412, 415—
417, 420, 421, 433, 451, 463, 471, 478,
481, 484, 485, 504, 507, 528, 538, 551,
578
Марков А. А. (род. 1903) 330, 360
Марков В. А. (1871—1897) 320, 321,
324, 411-413, 538, 552
Маркс К. (1818—1883) 145, 148, 203, 328
Маркушевич А. И. (род. 1908) 133, 142,
170, 171, 175, 349, 473, 497, 501
Марон И. А. (род. 1911) 274
Марчевский М. Н. (род. 1884) 314, 318
Маскерони Л. (Mascheroni L., 1750—
1800) 155
Медведев Ф. А. (род. 1923) 454, 560,
563, 564, 573
Мельников И. Г. (род. 1916) 113, 298
Менголи П. (Mengoli Р., 1625—1686)
116, 119
Менделеев Д. И. (1834—1907) 319, 411,
412
Менелай (1 в. н. э.) 199
Менье Ж. (Meusnier J. В., 1754-1793)
184
Меньшов Д. Е. (род. 1892) 174, 329, 564,
565, 573, 574
Меркатор Н. (Mercator N., 1620—1687)
116
Мертенс П. (Mertens Р.) 555
Мертенс Ф. (Mertens F., 1840—1927) 347,
348, 379
Мерэ Ш. (Мёгеу С, 1835—1911) 560
Мещерский И. В. (1859—1935) 320
Мизес P. (Mises R. v., 1883—1953) 404
Миллер A. (Miller А.) 319
Мильман Д. И. 267
Миндинг Ф. Г. (Minding F. А., 1806—
1885) 161, 223, 228, 254—267, 325,
326, 432, 509, 511—513, 517
Минковский В. Л. (род. 1911) 311
Минковский Г. (Minkowski Н., 1864—
1909) 262, 324, 348, 349, 356, 357, 366
Митинский А. Н. 111
Миттаг-Леффлер Г. (Mittag-Leffler G.)
399, 439, 442, 500
Михаил Федорович (1597—1645) 48
Михайлов А. (17в.) 45
Михайлов Г. К. (род. 1929) 111
Михлин С. Г. (род. 1908) 475
Мищенко Е. Ф. (род. 1922) 575
Млодзеевский Б. К. (1858—1923) 308,
310, 311, 313, 321, 326, 329, 331, 449,
484, 513, 515-518, 563, 565, 566,
573
Модзалевский Л. Б. 235
Молин Ф. Э. (1861—1941) 315, 327, 460,
546, 558
Молоствов В. П. (1794—1863) 235
Молюков И. Д. 510
Момарский М. 193
Монж Г. (Monge G., 1746—1816) 169,
179, 184, 185, 212, 213, 216, 232, 428,
431
Морган А. де (Morgan A. de, 1806—1871)
272, 327, 330, 483, 485, 534
Морделл Л. (Могdell L. J., род. 1888)
356
Мордухай-Болтовской Д. Д. (1876—1952)
49, 308, 313, 315, 385, 386, 433, 437
Муавр А. де (Moivre A. de, 1667—1754)
101, 115, 118, 134, 389, 392, 393
Муаньо Ф. (Moiagno F. N. М., 1804—
1884) 440
Мур Э. Г. (Moore Е. Н., 1862—1932) 563
Муравьев М. Н. (1796—1866) 316
Муравьев Н. Е. (1724—1770) 81, 316
Муравьев Н. Н. (1768—1840) 316
Мусхелишвили Н. И. (род. 1891) 474, 501
Мышкис А. Д. (род. 1920) 460, 461
Мэчин Дж. (Machin J., 1680—1751) 549
Мюнц Г. 474
Нагаева В. М. (род. 1901) 234
Назимов П. С. (1851—1901)314, 499, 538
Налбандян М. Б. 384
Наполеон I (1769—1821) 217
Наумов И. А. (род. 1923) 527
Неванлинна P. (Nevanlinna R., род.
1895) 496
Неверов С. Л. 49
Некрасов А. И. (1883—1957) 99
Некрасов В. Л. (1864—1922) 329, 563
Некрасов П. А. (1858—1924) 311, 313,
318, 328, 360, 393, 429, 433, 444, 445,
484, 492, 538, 539
Немыцкий В. В. (1900—1967) 577
Непер (Neper, Napier J., 1550—1617) 418
Несторович Н. М. (1891—1955) 386
Нейман К. (Neumann С, 1832—1925)
284, 445, 465—467, 503
Нёрлунд Н. Э. (Norlund, род. 1885) 490,
507
Нётер Э. (Noether Е., 1882—1935) 555
Никитин В. Н. (1739—1809) 80
Николай I (1796—1855) 306
Николай II (1868—1918) 359
Нильсен Н. (Nielsen N.) 505
Нифонт (11—12 в.) 18
Новиков П. С. (род. 1901) 330
Ноде Ф. (Naude Ph., 1684—1745) 188
Норден А. П. (род. 1904) 247, 250, 252,
264, 526, 531
Ньювентиит Б. (Nieuwentijt В., 1654—
1718) 87
Ньютон И. (Newton I., 1642—1727) 8,
51, 54, 81, 84, 87, 96, 114, 120, 130,
143—147, 150, 151, 157, 163, 174,
182, 192, 199, 201, 202, 207, 215,
251, 264, 268—270, 319, 341, 381,
405, 418, 447, 451, 481, 489, 514
Однер В. Т. (ум. ок. 1906) 303—305
Ожигова Е. П. (род. 1923) 320, 341,
350, 352, 353, 475, 488
Олоничев П. М. (род. 1920) 520
Ольденбург С. Ф. (1863—1934) 359
Ом М. (Ohm М., 1792—1872) 266
ИМЕННОЙ УКАЗАТЕЛЬ
587
Ондар X. О. 429
Орем Н. (Oresme N., 1323?—1382) 116,
130
Ортман К. 323
Осипов И. П. 499
Осиповский Т. Ф. (1765—1832) 217, 223,
237, 239, 274, 275, 314
Островский А. М. (род. 1893) 549, 552
Острогорский А. Н. (род. 1840) 309
Остроградский М. В. (1801—1862) 7, 8,
156, 165, 180, 214, 220—224, 226, 227,
228, 252, 255, 269, 270, 273—296, 298,
300-303, 305, 308, 314, 315, 326, 329,
334, 380, 383, 384, 428, 430, 433, 438,
467, 493, 494, 502, 506, 535, 540, 578
Отрадных Ф. П. 360
Оттон Л. (Autone L.) 527
Павленков Ф. Ф. (1839—1900) 319
Павлов И. П. (1849-1936) 307
Павловский А. Ф. (1788—1856) 223, 274,
300
Паплаускас А. Б. (род. 1931) 172
Парсеваль М. (Parseval М. А.) 469
Парфентьев Н. Н. (1877—1943) 501,
521
Паскаль Б. (Pascal В., 1623—1662) 84,
302, 319, 337, 387, 515, 530, 549
Паскье (Pasquier L. G.) 86, 103
Паукер М. Г. (1787—1855) 485
Пацановский Е. Л. 128
Паш М. (Pasch М., 1843—1930) 527, 529,
530
Пеано Дж. (Peano G., 1858—1932) 527
Пекарский П. П. (1827—1872) 74, 77, 87
Пелль (Pell J., 1610—1685) 374, 375
Первушин И. М. (1827—1900) 298
Перевощиков Д. М. (1790—1880) 219,
220, 352
Петерсон К. М. (1828—1881) 224, 228,
256, 317, 321, 325, 429, 485, 511-
513 515 517
Петр i'Великий (1672—1725) 8, 17, 51 —
54, 56, 58, 71, 74, 77, 464
Петр II (1716—1730) 92
Петров Н. П. (1822—1889) 278
Петрович С. Г. (1869—1926) 498
Петровский И. Г. (род. 1901) 446,
518
Пиери М. (Pieri М. 1860—1904) 263,
527 529
Пикар' Э. (Picard Е.) 440, 445, 455,
496
Пикок Дж. (Peacock G., 1791—1858) 227,
266, 327
Пирогов Н. И. (1810—1881) 308, 311
Пирс Ч. (Peirce С. S., 1839—1914) 557
Писарев Д. И. (1840—1868) 307, 357,
438
Пито A. (Pitot Н., 1695—1771) 183
Пифагор (6 в. до н. э.) 56, 63, 244, 245,
471
Платон (429 — 348 до н. э.) 47
Племель И. 498, 576
Плеханов Г. В. (1856—1918) 319
Плутарх (ок. 50—ок. 125) 47
Погребысский И. Б. (род. 1906) 128, 151,
270, 274, 364, 366, 487
Пойа Д. (Polya G., род. 1887) ИЗ
Покровский П. М. (1857—1901) 429, 492,
499
Полак Л. С. (род. 1909) 178, 476
Полубаринова-Кочина П. Я. (род. 1899)
438—440, 443
Польке К. (РоЫке К., 1810—1877) 515
Понселе Ж.-В. (Poncelet J. V., 1788—
1867) 198, 228, 409, 514
Понтрягин Л. С. (род. 1908) 575
Попов А. Ф. (1815—1879) 278, 314, 429,
519
Попов Н. И. (1720-1782) 81
Порецкий П. С. (1846—1907) 330, 534,
535
Поселье Ш. (Peaucellier А., 19 в.) 406
Поссе К. А. (1847—1928) 308, 313, 323,
341, 350, 364, 385, 386, 397, 417, 420,
433, 480, 528
Постников А. Г. (род. 1921) 348
Преображенский В. В. (1846—1905) 314,
315, 429, 484, 511
Привалов И. И. (1891—1941) 498, 518,
564, 570, 576
Прингсгейм A. (Pringsheim А., 1850—
1941) 489
Прокопович Феофан (1681—1736) 51, 190
Проскуряков И. В. (род. 1910) 146
Прудников В. Е. (род. 1895) 56, 297, 438,
440
Пташицкий И. Л. (1854—1912) 313, 341,
385
Птолемей К. (2 в. н. э.) 56, 58, 196, 237,
262
Пуанкаре A. (Poincare Н., 1854—1912)
119, 260, 264, 265, 288, 324, 348, 374,
401, 444, 446—448, 452—455, 458-
462, 465—467, 473, 475—477,
500, 501, 519, 528, 536, 543, 544, 556,
566
Пуансо Л. (Poinsot L., 1777—1859) 384,
443
Пуассон С. (Poisson S. D., 1781—1840)
141, 161, 163, 165, 173, 180, 227, 271,
273, 275, 276, 279, 284—286, 289,
290, 334, 351, 384, 387, 389—393, 398,
427, 428, 438, 443, 448, 477, 478,
497, 571, 574
Пушкин А. С. (1799—1837) 22, 335
Пфейффер Г. В. (1872—1946) 547
Пшеборский А. П. (1871—1942) 413, 422
Пюизё В. A. (Puiseux V., 1820—1883)
489
Раабе И. И. (Raabe J., 1801—1859) 272,
483, 507
Рабинович И. М. (род. 1911) 460, 461
Радовский М. И. (1903—1964) 302, 303
Размадзе А. М. (1890—1929) 474
Раик А. Е. (род. 1903) 20, 298
Райков Б. Е. 54
Райков Д. А. (род. 1905) 93, 123
588
ИМЕННОЙ УКАЗАТЕЛЬ
Райнов Т. И. (1888—1958) 45, 49
Райхман А. 577
Рамэ П. ла (Рамус П.) (Ramus, Ramee P.
de la, 1515—1572) 47, 62, 80
Раскин H. M. (род. 1906) 111
Рауз Э. (Routh Е. L, 1831—1907) 456
Рахманинов И. И. (1829—1897) 222
Рахманов П. А. (ум. 1813) 211—213, 316
Рашевский П. К. (род. 1907) 528, 531
Рашетт Д. 111
Резаль A. (Resal Н., 1828—1896) 509
Рекорд P. (Recorde R., 1510—1558)
68, 70
Ремак P. (Remak R., 1888—ум. в годы
2-й мир. войны) 349, 552, 553
Ремез Е. Я. (род. 1896) 291
Риго Г. 315
Ризе A. (Riese А., 1492—1559) 34
Риккати В. (Riccati V., 1707—1775) 88,
135, 437, 445, 536
Риккати Дж. (Riccati J., 1676—1754) 90,
97, 135, 157, 158
Риман Б. (Riemann В., 1826—1866) 97,
119, 121, 141, 163, 173, 227, 243, 250,
256, 260, 261, 325, 326, 329, 342,
348, 351, 421, 435, 437, 444, 452, 454,
459, 469, 492, 494, 523, 529, 544, 559,
561, 562, 569, 571, 574
Рисе М. (Riesz М., род. 1886) 490
Рисе Ф. (Riesz F., 1880—1956) 564, 570
Ритц В. (Rith W.) 180, 476, 477
Рихман Г. (1711—1753) 190
Риччи Г. (Ricci М. М. G., 1853—1925)
520
Робен Г. 465, 466
Робине Б. (Robins В., 1707—1751) 108,
145
Рождественский С. В. 77
Розенфельд Б. А. (род. 1917) 185, 250,
260, 525
Романов Н. П. (род. 1907) 348
Ромер П. Э. (1835—1899) 315, 327, 486,
492 557
Российский С. Д. (род. 1897) 512, 517
Рот Д. Д. (19 в.) 302, 303
Румовский С. Я. (1734—1812) 8, 75, 78,
79, 107, 108, 190, 191, 193, 194, 204—
206, 218, 223
Руффини П. (Ruffini Р., 1765-1822)
227, 268, 270, 327, 540
Рыбкин Г. Ф. (род. 1903) 8, 239, 274
Рыбников К! А. (род. 1913) 180, 323,
Сабинин Е. Ф. (1831—1909) 278, 287,
315 321 535
Савич А. Н. (1811—1883) 352, 353, 430
Савич С. Е. 481
Садовский Л. Е. (род. 1916) 305
Саккери Д. (Saccheri G., 1667—1733)
230, 231, 240, 261
Салехов Г. С. (род. 1913) 486
Салтыков Н. Н. (1870—1961) 422, 432
Сарв Я. X. (1877—1954) 512
Саррюс П. (Sarrus P. F., 1798—1861) 287
Сатаров И. (18 в.) 57, 58
Святослав Ярославич (1027—1076) 21
Селиванов Д. Ф. (1855—1932) 313, 320,
327, 359, 546
Сельберг A. (Selberg А., род. 1917) 348, 350
Сен-Венан Б. де (Barre de Saint-
Venant A. J. CL, 1797—1886) 509
Серпинский В. (Serpinski W., род. 1882)
364, 377, 463, 518, 577
Ceppe Ж. (Serret J. A., 1819—1885) 338,
347, 371
Сеченов И. M. (1829—1905) 450
Силаков В. Д. 536
Сильвестр Дж. (Sylvester J. J., 1814—
1897) 347, 406, 544
Симонов И. М. (1794—1855) 240, 520
Симонов Н. И. (род. 1910) 88, 159—162,
164
Симонов Р. А. (род. 1929) 10, 12, 427
Симпсон В. (Simpson W. D.) 54, 56
Симпсон Т. (Simpson Т., 1710—1761) 418
Синцов Д. М. (1867—1946) 308, 314, 318,
323, 325—327, 422, 433, 448, 489, 507,
519, 526, 527, 546
Сипягин Д. С. (1853—1902) 359
Слешинский И. В. (1854—1931) 315,
330, 400, 492, 501, 529, 532, 535,
536, 562
Слонимский 3. Я. (1810—1904) 302, 303
Слудский Ф. А. (1841—1897) 317
Слуцкий Е. Е. (1880—1948) 403
Слюсарев Г. Г. 111
Смирнов В. И. (род. 1887) 75, 99, 102,
111, 125, 168, 191, 400, 453, 458, 464,
471, 472, 475, 476, 481, 482
Смит Г. Л. (Smith Н. L.) 563
Смотрицкий М. Г. (ок. 1578—1633) 59
Соболев С. Л. (род. 1908) 166, 472, 474,
475
Соболевский А. И. (1856—1929) 49
Соколов В. 105
Соловьев Н. М. 144, 202
Сомов О. И. (1815—1876) 222—224, 227,
269, 270, 278,295, 312, 316, 334,351 —
353, 383, 384, 432, 485, 509, 510, 516
Сомов П. О. (1852—1919) 510
Сонин Н. Я. (1849—1915) 18, 116, 160,
299, 314, 315, 320, 325, 329, 330, 350,
377, 378, 397, 398, 417, 418, 420, 429,
431, 432, 474, 484, 485, 492, 502—507,
552
Сорокина Л. А. 270
Софронов М. (1729—1760) 78, 107, 190,
191
Сохоцкий Ю. В. (1842—1927) 312, 318,
320, 328, 329, 341, 352, 361, 364, 373,
374, 417, 473, 492, 494—498, 576
Спасский И. Г. (род. 1904) 28—30
Спейдель Дж. (Speidell J., 16—17 вв) 47
Станевич В. И. 347
Стевин С. (Stevin S., 154S—1620) 63, 64
Стеклов В. А. (1864—1926) 278, 279,
284, 311, 313, 314, 316, 318, 319, 324,
325, 418, 421, 449, 450, 463—472,
475, 476, 478, 492, 506, 507, 538, 551,
574, 578
ИМЕННОЙ
Степанов В. В. (1889—1950) 432, 462,
518, 564, 572, 577
Стечкин С. Б. (род. 1920) 93, 123
Стилтьес Т. (Stieltjes Т. J., 1856—1894)
396, 398, 453, 454, 472, 563
Стирлинг Дж. (Stirling J., 1696?—1770)
115, 118, 119, 341, 346
Стоке (Stokes G., 1819—1903) 480
Столетов А. Г. (1839—1896) 313
Страннолюбский А. Н. (1839—1903) 438
Строганов С. Г. (1794—1882) 332
Струве В. Я. (1793—1864) 305, 336
Стюверт (Stuyvaert) 527
Стяжкин Н. И. (род. 1932) 535, 536
Суайнсхед P. (Suineshead R., 14 в.) 130
Субботин М. Ф. (1893—1966) 111, 500
Суворов П. И. (1750—1815) 80
Суворов Ф. М. (1845—1911) 314, 326,
330, 516, 519—521, 526
Сулима П. А. (1779—1812) 213, 214, 316
Сунь-цзы (3 в.) 37, 38
Суслин М. Я. (1894—1919) 573—575
Сухомлинов М. И. (1828—1901) 190, 193
Сушкевич А. К. (1889—1961) 270
Такэ A. (Tacquet А., 1612—1680) 57,
58, 61, 62, 208
Тамаркин Я. Д. (1888—1945) 475, 477, 490
Тейлор Б. (Taylor В., 1685—1731) 99,
100, 148, 149, 161, 162, 164, 167, 203,
210, 211, 214, 269, 332, 407—409,
441, 500, 501, 505, 567, 570
Тенигин Н. 213
Тессинг Я. 58
Тилли Ж. де (Tilly J. de, 19 в.) 521, 522
Тимошенко С. П. (род. 1878) 111
Тимченко И. Ю. (1862—1939) 130, 142,
170, 315, 330, 492, 501, 502, 532
Тихомандрицкий А. Н. (1800—1888) 278,
385, 498
Тихомандрицкий М. А. (1844—1921) 313,
314, 318, 393, 498, 499
Тодгентер A. (Todhunter J., 1820—1884)
287
Толстой Л. Н. (1828—1910) 359
Томсон У. (Thomson W., 1824—1907) 456
Торричелли (Torricelli Е., 1608—1647)
83 99
Трипольский П. И. 279, 284
Тропфке И. (Tropfke J., 1866—1939) 35, 63
Трусделл (Truesdell С, род. 1919) 169, 170
Турин В. 234
Туэ A. (Thue А., 1863-1922) 375
Тэт П. (Tait P. G., 1831—1901) 456
Уайтхман У. (Wightmann W. P. D.) 54, 56
Уатт (Watt J., 1736—1819) 339, 405 — 407
Умов Н. А. (1846—1915) 313, 315, 511,
516, 538
Ундольский В. М. (1815—1864) 24, 31,
32, 43, 44
Урысон П. С. (1898 — 1924) 575
Успенский Я. В. (1883—1947) 475
Ушинский К. Д. (1824—1871) 308
589
Фабер Г. (Faber G., 1877—1966) 122,
172
Фаддеев Д. К. (род. 1907) 375
Фаньяно Дж. К. ди (de Toschi di Fag-
nano G. C, 1682—1766) 152, 153
Фарей Д. (Farey J.) 376
Фарманкович И. С. 61
Фархварсон А. Д. (Farquharson Н., 1675- -
1739) 54—58, 68, 80
Фату П. (Fatou Р., 1878—1929) 498, 567,
569
Фаульгабер И. (Faulhaber J., 1580—
1635) 61, 68, 70
Федоров Е. С. (1853—1919) 366
Фейер Л. (FejerL., 1880—1959) 127, 489,
571
Фель С. Е. 71
Феодосии (1 в. до н. э.) 49
Ферма П. (Fermat P. de, 1601—1665) 8,
51, 83, 84, ИЗ, 181, 186—188, 215,
250, 298, 337, 369, 370, 387
Филиппов М. М. (1858—1903) 319
Фиников С. П. (1882—1964) 293, 513,
516 518 519
Фихтенгольц Г. М. (1888—1959) 292,
563
Фишер P. (Fischer R. А., род. 1890) 102
Фишер Э. (Fischer Е., род. 1875) 564,
570
Флакк A. (Vlacq А., 1600?—1667) 55,
56
Фогель К. (Vogel К., род. 1888) 35, 40
Фок В. А. (род. 1898) 524
Фомин И. (17 в.) 45
Франкер Л. Б. (Francoeur L. В., 1773—
1849) 220
Франкль Ф. И. (1905—1961) 151, 164,
429
Фредгольм Э. (Fredholm Е.) 473
Френе Ж. (Frenet J. F., 1816—1900)
184
Фридман А. А. (1888—1925) 263, 475,
476
Фридрих II Прусский (1712—1786) 86,
106, 108
Фришауф И. (Frischauf J., 1837—1924)
493
Фробениус Г. (Frobenius G., 1849—1917)
160, 549, 557, 558
Фронспергер Л. (Fronsperger L., 16 в.)
45
Фукс Л. (Fuchs L., 1833—1902) 444, 445,
476
Фурье Ж. (Fourier J. В. J., 1768—1830)
155, 165, 168, 169, 171, 173, 216, 226,
227, 268—272, 275, 278, 279, 282,
284, 285, 290, 409, 416, 427, 434, 438,
465, 467—469, 472, 478, 481, 489—491,
502, 559, 569, 570
Фусс Н. И. (Fuss N., 1755—1826) 8, 75,
78, 79, 81, 88, 97, 103, 108, 111, 185,
190, 192, 196—199, 204, 206, 214,
218, 224
Фусс Н. Н. (1810—1867) 224
Фусс П. Н. (Fuss P. N., 1798—1859)
93, 111, 214, 224, 302, 336, 347
590 ИМЕННОЙ
Хайям Омар (1048—1131?) 230, 261
Хан В. (Hahn W.) 418
Харди Г. (Hardy G. Н., 1877—1947) 93,
95, 123, 124, 126, 127, 490
Хаусдорф Ф. (Hausdorff F.) 575
Хевисайд О. (Heaviside О., 1850—1925)
436
Хилькевич Э. К. (род. 1895) 257
Хинчин А. Я. (1894-1959) 101, 329,
349, 399, 401, 564, 570, 573, 574
Хованский А. Н. (род. 1916) 135, 250
Циммерман В. И. (1866—1939) 315,
536
Цингер В. Я. (1836—1907) 313, 317, 318,
326, 513-515
Цингер Н. Я. (1842—1918) 311
Чаплыгин С. А. (1869—1942) 140, 318,
321, 330, 501, 516, 559, 578
Чеботарев Н. Г. (1895—1947) 267,
349, 475, 489, 532, 549, 550, 552—
555
Чебышев П. Л. (1821—1894) 7, 8, 85,
97, 111—113, 121, 140, 155, 159, 186—
188, 222, 224, 225, 227, 269, 270, 278,
294, 295, 298, 301, 303—305, 308,312,
315—317, 320, 321, 324, 325, 329-353,
356—361, 366—368, 372, 373, 375,
380—386, 391—396, 398—400, 403,
405—421, 423, 430, 435, 439, 440,
448—454, 464, 469, 472, 481, 486,
488, 489—492, 494—496, 504, 509—
511 548 578
Чезаро Э. (Cesaro Е., 1859—1906) 126,
127, 185, 489, 490
Ченакал В. Л. 54
Черепнин Л. В. 13
Чернышевский Н. Г. (1828—1889) 307,
357, 438, 450, 528
Черняев М. П. (род. 1891) 386, 515
Чижов Д. С. (1785—1852) 223
Чириков М. В. 119
Чистяков И. И. (1870—1942) 309
Чудаков Н. Г. (род. 1904) 96
Шаль М. (Chasles М., 1793—1880) 228,
513-515
Шанявский А. Л. 312, 516
Шапелль де ла (Chapelle de la, 1710—
1792) 201
Шатунова Е. С. 214
Шатуновский С. О. (1859—1929) 315,
324, 326, 327, 329, 330, 531—534, 536,
537, 554, 555, 562, 563
Шафаревич И. Р. (род. 1923) 187, 376
Шафрановский К. И. 75
Шафхайтлин П. (Schafheitlin Р.) 143
Шварц Г. A. (Schwarz Н., 1843—1921)
299, 465, 467, 476, 515
Шварц Л. (Schwarz L., род. 1915) 166
Швецов К. И. (род. 1913) 24, 42—44,
46—48, 61
Шевелев Ф. Я. 485
Шереметевский В. П. (ум. 1919) 310,
324
Шестаков П. Д. (1826—1889) 430
Широков П. А. (1895—1944) 526
Шифф В. И. (ум. ок. 1919) 319
Шифф П. А. (1849—1910) 319, 320,
481
Шлёмильх О. (Schlomilch О. X., 1823—
1901) 502, 507
Шмидт О. Ю. (1891—1956) 327, 549—
553
Шмидт Э. (Schmidt Е., 1876—1959)
473
Шнирельман Л. Г. (1905—1938) 95,
96
Шостак Р. Я. (род. 1902) 433
Шохор-Троцкий С. И. (1853—1923)
309
Шпайзер A. (Speiser А., род. 1885) 128,
553
Шпачинский Э. К. (1848—1912) 309
Шпис О. (Spiess L. О., 1878—1966) 103
Шредер К. (Schroder К., род. 1909) 95,
146
Шредер Э. (Schroder Е., 1841—1902)
330, 534, 535
Штаудт Хр. (Staudt К. G. С. v., 1798—
1867) 507, 508, 520
Штейнгауз Г. (Steinhaus Н.) 577
Штейнер Я. (Steiner J., 1796—1863) 196,
198, 228, 513
Штеккель П. (Stackel Р., 1862—1919)
310 512
Штёрмер К. (Stormer С, 1874—1957) 481,
549
Штифель М. (Stifel М., ок. 1486—1567)
61, 63, 68, 70
Штокало И. 3. (род. 1897) 276, 315, 364,
366, 436
Штоффель И. (ум. после 1875) 303
Штуди Э. (Study Е., 1862—1922) 525
Штурм Ш. (Sturm J. Ch. F., 1803—1855)
221, 227, 269, 438, 467, 469-471,
538
Шуберт Ф. И. (Schubert F. J. v., 1758—
1825) 75, 140, 190, 196, 198, 199, 211,
214, 224, 438
Шуере Я. ван дер 61
Шумахер (Schumacher Н. С, 1780—1850)
252
Шумахер И. Д. (1690—1761) 76, 77, 86,
87, 97, 106, 107, 191
Щепкин П. С. (1793—1836) 219, 220
Эвальд Ф. 297
Эдрейн P. (Adrain R., 1775—1843)388,
390
Эйзенштейн Ф. (Eisenstein F. G. М.,
1823—1852) 354, 370, 554
Эйлер И. A. (Euler J. А., 1734-1800)
75, 103, 106, 108, 109, 111, 191,
194
ИМЕННОЙ УКАЗАТЕЛЬ
591
Эйлер К. (1740-1790) 110
Эйлер Л. (Euler L., 1707—1783) 8, 37,
54, 75, 78-82, 85, 86, 88-90, 92,
95—135, 137—142, 145-197, 199—
202, 204, 206, 207, 213, 214, 216, 224,
227, 232, 253-256, 265, 267, 268,
271, 273, 285, 287, 291, 296, 298—300,
319, 334, 339—341, 343, 344, 346,
351, 354, 359, 374, 376, 377, 381, 384,
390, 427, 428, 430, 432, 434, 443—445,
469, 476, 478, 481, 489, 502, 504, 506,
507, 536, 539, 548, 549, 556
Эйлер X. (1743—1808)
Эйнштейн A. (Einstein А., 1879—1955)
262
Энгель Ф. (Engel F., 1861—1941) 431
Энгельс Ф. (1820—1895) 83
Энестрем Г. (Enestrom G., 1852—1923)
111
Энке И. (Encke J. F., 1791—1865) 344
Эратосфен (276—195? до н. э.) 186
Эрдеш П. (Erdos Р.) 348
Эренфест П. (Ehrenfest Р., 1880—1933)
536
Эригон П. (Herigone Р., ок. 1640) 66
Эрмит Ш. (Hermite Ch., 1822—1901) 154,
159, 296, 336, 338, 349, 354—356, 364,
365, 373, 374, 416—419, 442, 469, 507,
539, 547
Эсклангон Э. (Esclangon Е., 1876—1954)
462
Юдин И. (18 в.) 78, 81
Юрьев М. (17 в.) 45
Юшкевич А. П. (род. 1906) 17, 38,
58, 66, 78, 82, 86, 88, 92, 95, 106,
109, 111, 133, 143, 144, 146, 152, 191,
195, 202, 214, 222, 265, 270, 275,
455
Юшкевич П. С. (1873—1945) 324, 521,
522, 562
Якоби Б. С. (1801—1874) 302, 303, 305,
336
Якоби К. Г. (Jacobi К. G. J., 1804—1851)
135, 149, 154, 198, 226, 227, 273,
287, 288, 292, 295, 354, 355, 368, 374,
383, 384, 397, 414, 417, 418, 427, 430,
432, 451, 452, 454, 469, 496, 506,
548
Янишевский Э. П. (1829—1906) 257
Яновская С. А. (1896—1966) ИЗ, 222,
239 339 537
Ярослав Мудрый (978—1054) 16
Ярошенко С. П. (1846—1917) 315, 520,
532, 547
Адольф Павлович Юшкевич
История математики в России (до 1917 г.)
М., 1968 г., 592 стр. с илл.
Редакторы А. Ф* Лапко и Г. Ф. Рыбкин
Техн. редактор К. Ф. Брудно
Корректоры Е. А. Белицкая и В. П. Сорокина
* * *
Сдано в набор 26/1 1968 г.
Подписано к печати 28/VIII 1968 г.
Бумага 70xl08Vie- Физ. печ. л. 37.
Условн. печ. л. 51,8. Уч.-изд. л. 48,76.
Тираж 11000 экз. Цена 3 р. 28 к.
Т-13121. Заказ № 118.
* * *
Издательство «Наука»
Главная редакция
физико-математической литературы
Москва, В-71, Ленинский проспект, 15.
* * *
Московская типография № 16 Главполиграфпрома
Комитета по печати при Совете Министров СССР
Москва, Трехпрудный пер., 9