Автор: Бузулук В.И.
Теги: авиация и космонавтика летательные аппараты ракетная техника космическая техника воздушный транспорт авиация и воздушные соединения воздушные линии и аэропорты авиация космические аппараты
ISBN: 978-5-89845-012-0
Год: 2008
В.И. БУЗУЛУК
ОПТИМИЗАЦИЯ ТРАЕКТОРИЙ
ДВИЖЕНИЯ АЭРОКОСМИЧЕСКИХ
ЛЕТАТЕЛЬНЫХ АППАРАТОВ
В.И. Бузулук
ОПТИМИЗАЦИЯ ТРАЕКТОРИЙ
ДВИЖЕНИЯ АЭРОКОСМИЧЕСКИХ
ЛЕТАТЕЛЬНЫХ АППАРАТОВ
Москва - Жуковский
2008
УДК 629.782.015
ББК 39.53
Б-904
Бузулук В.И
Б-904 Оптимизация траекторий движения аэрокосмических ле-
тательных аппаратов. - М. - 2008. - 476с.
ISBN 978-5-89845-012-0
В монографии изложены приближенные методы оптимиза-
ции траекторий движения крылатых систем выведения на орби-
ту и других типов аэрокосмических летательных аппаратов.
Рассматриваются основные этапы полета: взлет, разгон и
выведение на орбиту с ЖРД и ВРД, крейсерский полет, спуск с
орбиты и планирование, возврат первых ступеней вертикально
стартующих систем выведения к точке старта.
Приводятся общие положения динамики полета. Разрабаты-
ваются методы расчета, основанные на применении прибли-
женно оптимальных (близких к оптимальным) законов управ-
ления. На примере решения модельных задач дается сравнение
с точными решениями, полученными с использованием прин-
ципа максимума.
Предназначена для научных работников и инженеров авиа-
ционно-космической отрасли, специализирующихся в области
оптимизации траекторий движения аэрокосмических летатель-
ных аппаратов. Может быть полезна аспирантам и студентам
соответствующих специальностей ВУЗов.
Автор книги - доктор технических наук, член-
корреспондент Российской академии им. К.Э. Циолковского,
свыше 30 лет проработал в ЦАГИ в области исследования пер-
спектив развития аэрокосмической техники.
Рецензент - д.т.н. профессор А.Г. Милованов
Издание осуществлено при поддержке
ФГУП «Центральный аэрогидродинамический
институт имени профессора Н.Е. Жуковского»
ISBN 978-5-89845-012-0
© В.И. Бузулук, 2008
© ФГУП «Центральный аэрогидродина-
мический институт им. проф.
Н.Е. Жуковского», 2008
Посвящается 90-летию
Центрального аэрогидродинамического
института имени профессора Н.Е. Жуковского
ОГЛАВЛЕНИЕ
Предисловие.............................................. 9
Предисловие автора....................................... 11
Основные обозначения, сокращения, индексы .............. 15
Глава 1. Аэрокосмический летательный аппарат как объект
исследования траекторий движения ....................... 21
1.1. Классификация аэрокосмических ЛА ............. 25
1.2. Основные типы топлива и двигателей аэрокосмических
ЛА ................................................ 28
1.3. Состояние работ по созданию многоразовых систем
выведения на орбиту и гиперзвуковых ЛА............. 45
Глава 2. Общие положения динамики полета аэрокосмиче-
ских ЛА ................................................ 53
2.1. Уравнение движения в векторной форме.......... 53
2.2. Движение, форма и гравитационное поле Земли .. 55
2.3. Модель атмосферы.............................. 64
2.4. Основные системы координат.................... 69
2.5. О разделении результирующей силы на аэродинамиче-
скую и силу тяги двигателя ........................ 77
2.6. Исходные уравнения движения в траекторной системе
координат ......................................... 89
2.7. Упрощенные уравнения движения. Первые интегралы
уравнений оптимального пространственного движения. 95
2.8. Оптимальное пространственное движение на квазиста-
ционарных режимах................................. 102
2.9. Оптимальное плоское движение на квазистационарных
режимах........................................... 106
2.10. Расчет траектории движения ЛА с ВРД в режиме от-
слеживания заданной программной траектории.......... 122
6
Оглавление
Глава 3. Разгон и выведение на орбиту ЛА с использованием
ЖРД..................................................... 129
3.1. Исходные данные............................... 130
3.2. Постановка задачи............................. 136
3.3. Оптимальная программа выведения в плоскопарал-
лельном поле тяготения в отсутствии атмосферы ..... 138
3.4. Основные участки выведения. Довыведение на орбиту . 142
3.5. Формирование приближенно оптимального управления
на активном участке полета......................... 149
3.6. Решение модельной задачи с использованием принципа
максимума............................:............. 159
3.7. Примеры расчетов. Сравнение приближенного решения
с оптимальным ..................................... 161
Глава 4. Программа выработки компонентов топлива при
разгоне ЛА с ЖРД............................... 167
4.1. Постановка задачи............................. 169
4.2. Решение задачи в общем виде................... 170
4.3. Решение краевой задачи в частных случаях.... 172
4.4. Оптимальные условия переключения двух типов топ-
лива............................................... 174
4.5. Связь функционала с удельными весовыми параметра-
ми ЛА ............................................. 176
4.6. Определение эффективности последовательного при-
менения двух типов топлива ........................ 179
4.7. Определение эффективности оптимальной выработки
горючего и окислителя двухкомпонентного топлива..... 184
Глава 5. Траектория движения дозвукового самолета-
носителя перед стартом воздушно-космического
аппарата с ЖРД ......................................... 191
5.1. Постановка общей задачи. Выделение частной задачи
оптимизации траектории на участке совместного поле-
та ДСН и ВКА....................................... 193
5.2. Линеаризация функционала для различных типов ВКА. 194
5.3. Оптимизация траектории от взлета ДСН до точки стар-
та ВКА............................................. 199
5.4. Расчет траектории разгона - набора высоты ДСН с ис-
пользованием приближенно оптимального управления.. 206
5.5. Исследование предстартового маневра ДСН с исполь-
зованием принципа максимума........................ 208
5.6. Формирование приближенно оптимального управления
на траектории предстартового маневра ДСН .......... 212
Оглавление
7
Глава 6. Исходные данные для расчета траекторий полета
аэрокосмических ЛА с ВРД ...................... 215
6.1. Два способа задания компонентов результирующей си-
лы. Аэродинамические характеристики планера .. 216
6.2. Проспектные характеристики ВРД............... 218
6.3. Входной импульс потока. Характеристики воздухоза-
борника .......................................... 224
6.4. Выходной импульс потока. Характеристики реактивно-
го сопла. Эффективная тяга ВРД ................... 235
Глава 7. Разгон ЛА с ВРД со свободной дальностью полета .... 241
7.1. Постановка задачи............................ 243
7.2. Упрощение задачи в случае фиксированных диапазонов
работы двигателей................................. 244
7.3. Взлетные характеристики...................... 246
7.4. Оптимизация траекторий на участке работы турбоком-
прессорных ВРД.................................... 267
7.5. Оптимизация траекторий на участке работы прямоточ-
ных ВРД........................................... 282
7.6. Условия включения и выключения ВРД........... 299
Глава 8. Полет ЛА с ВРД на заданную дальность.......... 307
8.1. Постановка задачи............................ 308
8.2. Максимизация коэффициента крейсерской дальности ... 308
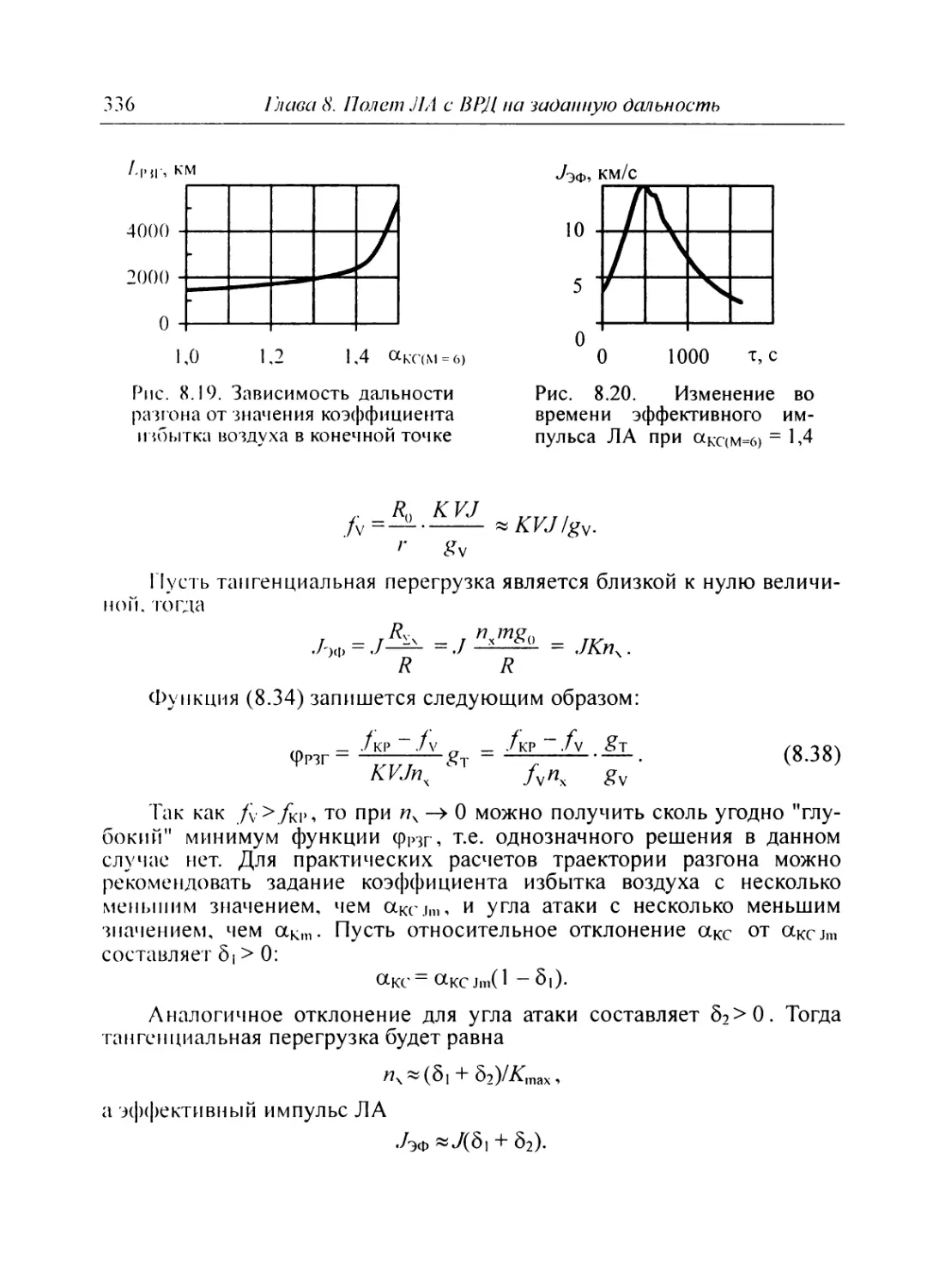
8.3. Оптимизация траекторий на участке разгона.... 326
8.4. Оптимизация траекторий на участке планирования.. 337
Глава 9. Возвращение ЛА с орбиты. Планирование в атмо-
сфере .................................................. 341
9.1. Уравнения движения в ортодромической системе коор-
динат. Продольная и боковая дальности планирования . 343
9.2. Начальные и конечные условия ................ 346
9.3. Аэродинамические характеристики планирующего ЛА 351
9.4. Постановка задачи............................ 359
9.5. Приближенно оптимальное управление углом крена и
аэродинамическим качеством в отсутствии ограниче-
ний на фазовые переменные......................... 360
9.6. Оптимизация траекторий планирования при наличии
фазовых ограничений .............................. 365
9.7. Планирование с максимальной продольной дальностью 375
9.8. Планирование с максимальной боковой дальностью . 384
8
Оглавление
9.9. Планирование с минимальной продольной дальностью. 397
9.10. Упрощенный расчет достижимой области земной по-
верхности ......................................... 400
9.11. Спуск с геостационарной орбиты гиперзвукового лета-
тельного аппарата с большим аэродинамическим каче-
ством ............................................. 406
Глава 10. Возврат крылатых ступеней к точке старта МКТС .. 417
10.1. Постановка задачи............................ 418
10.2. Решение модельной задачи оптимизации траектории
возврата, лежащей в вертикальной плоскости, с исполь-
зованием принципа максимума........................ 423
10.3. Решение модельной задачи оптимизации пространст-
венной траектории возврата с использованием принци-
па максимума....................................... 433
10.4. Формирование приближенно оптимального управления
движением. Сравнение приближенного решения с точ-
ным решением ...................................... 448
10.5. Примеры расчетов для различных скоростей отделения
от МКТС............................................ 454
Приложения..............................................459
1. Алгоритм определения параметров стандартной атмо-
сферы .......................................... 459
2. Газодинамические функции .................... 466
Литература..............................................468
Предисловие
Одним из направлений дальнейшего развития ракетно-космической
техники является создание нового поколения многоразовых систем
выведения на орбиту - аэрокосмических летательных аппаратов, и в
перспективе возможно слияние аэрокосмической и гиперзвуковой
авиационной техники.
Разработка сложных технических систем требует проведения ши-
рокомасштабных научных исследований по всем основным фундамен-
тальным дисциплинам. Причем роль начального этапа проектирования
повышается, так как на этом этапе должно быть принято большинство
концептуальных и схемных решений, которые будут определять эффек-
тивность и экономичность будущей аэрокосмической техники. Широта
решаемых задач определяется большим многообразием вариантов
летательных аппаратов и комбинаций их двигателей - как ВРД, так и
ЖРД.
Основная особенность аэрокосмических летательных аппаратов
заключается в большом потребном запасе маршевого топлива и в зна-
чительном аэродинамическом нагревании. В связи с этим неотъемлемой
частью процесса формирования облика таких аппаратов является опти-
мизация траекторий движения на основных этапах полета, включающая
в себя определение массы и объема компонентов топлива, маневренных
возможностей, характеристик, необходимых для последующего опреде-
ления силового и теплового воздействия на аппарат. Для решения таких
задач необходимо иметь простые, но достаточно точные методы расче-
та, позволяющие повысить эффективность процесса проектирования.
Автор книги В.И. Бузулук, доктор технических наук, член-
корреспондент Российской академии им. К.Э. Циолковского, свыше
30 лет проработал в ЦАГИ в области исследования перспектив разви-
тия аэрокосмической техники. Данная книга развивает сложившиеся в
ЦАГИ подходы к анализу сложных технических систем и является
весомым вкладом в разработку приближенных методов оптимизации
траекторий аэрокосмических летательных аппаратов на этапе формиро-
вания облика.
10
Предисловие
Теоретические положения и методы, разработанные автором, ис-
пользовались при формировании облика авиационно-космической
системы МИГАКС (РСК ”МИГ” им. А.И. Микояна) и воздушно-
космических самолетов Ту-2000 (АНТК им. А.Н. Туполева), МАКС-М
(НПО "Молния”), Interim HOTOL (фирма ВАе, Великобритания), а
также при исследовании демонстраторов гиперзвуковых технологий и
других типов аэрокосмических летательных аппаратов.
Книга предназначена для научных работников и инженеров авиа-
ционно-космической отрасли, специализирующихся в области оптими-
зации траекторий различных типов аэрокосмических летательных
аппаратов и систем на этапе формирования облика. Может быть полез-
на аспирантам и студентам соответствующих специальностей ВУЗов.
Директор ЦАГИ
доктор техн, наук
С.Л. Чернышев
Предисловие автора
На этапе формирования облика аэрокосмических летательных ап-
паратов (ЛА) и систем в соответствии с итерационной процедурой
возникает необходимость проведения многочисленных расчетов траек-
торий движения на основных участках полета: при разгоне с ЖРД и
ВРД, в крейсерском полете, при спуске с орбиты и т.д. Причем расчеты
должны проводиться быстро и достаточно точно. Один из способов
решения таких задач основан на применении приближенно оптималь-
ного управления. Под этим термином в данной книге понимается такое
управление, которое по своей структуре является близким к оптималь-
ному и обеспечивает значение функционала (критерия оптимальности),
близкое к точному решению. Оптимизация траекторий проводится по
критериям, учитывающим массы полезного груза и конструкции.
Рассмотрена первая группа задач динамики полета-о наивыгод-
нейших траекториях ЛА. При этом использовался сложившийся в
динамике полета подход, когда сложное явление схематизируется:
выделяются только главные черты явления. Вопросы исследования
"второстепенных" факторов, в том числе вопросы исследования движе-
ния вокруг центра масс ЛА, выходят за рамки данной книги.
Широко используется принцип декомпозиции, позволяющий раз-
делить исходную задачу оптимизации траектории на несколько частных
и выделить в траектории полета наиболее характерные участки.
В первой главе дается классификация аэрокосмических ЛА и сис-
тем с точки зрения оптимизации траекторий. Рассматриваются возмож-
ные типы топлива, двигателей и диапазоны их работы по скорости
полета. Кратко излагается состояние работ в области создания многора-
зовых систем выведения на орбиту и гиперзвуковых ЛА.
Во второй главе приводятся общие положения динамики полета,
необходимые для последовательного изложения дальнейшего материа-
ла. Излагается способ приближенного учета вращения Земли в упро-
щенных уравнениях движения. Исследуется оптимальное движение на
квазистационарных режимах в общем виде. Разрабатывается метод
расчета траекторий движения ЛА с ВРД, основанный на отслеживании
12
Предисловие автора
программной траектории с учетом фазовых ограничений, заданных в
координатах "высота - скорость".
В третьей и четвертой главах оптимизируются траектории выведе-
ния на орбиту ЛА с ЖРД. В третьей главе разрабатывается приближен-
ный метод оптимизации траекторий выведения аэрокосмических ЛА в
предположении постоянного соотношения компонентов топлива. Рас-
сматриваются горизонтальный (воздушный) и вертикальный типы
старта. Применительно к активному участку полета воздушно-
космического самолета с воздушным стартом решается модельная
задача. Дается сравнение приближенного решения с точным решением,
полученным с использованием принципа максимума.
В четвертой главе с использованием принципа максимума решает-
ся задача оптимизации циклограммы работы ЖРД на многокомпонент-
ном топливе. Подробно исследуются решения задачи для двухкомпо-
нентного (водород + кислород) и трехкомпонентного (керосин +
водород + кислород) типов топлива. Определяется эффективность
программы оптимальной выработки компонентов топлива. Формирует-
ся рациональная программа выработки топлива.
В пятой главе исследуются траектории движения дозвукового са-
молета-носителя с ТРД перед стартом на орбиту воздушно-
космического аппарата с ЖРД. Задача решается применительно к раз-
личным типам ракетно-космических систем воздушного старта. Рас-
сматривается пример расчета оптимальной траектории (с использова-
нием принципа максимума) от взлета дозвукового самолета-носителя до
точки старта воздушно-космического аппарата. Подробно исследуется
предстартовый участок полета самолета-носителя. Формируется про-
грамма приближенно оптимального управления.
В шестой главе освещены вопросы задания исходных тягово-
экономических характеристик ВРД. Рассматриваются проспектные
характеристики турбокомпрессорных и прямоточных двигателей, ха-
рактеристики входного и выходного устройств комбинированной сило-
вой установки. Приводятся соотношения, необходимые для расчета
эффективной тяги ВРД.
В седьмой главе оптимизируются траектории разгона ЛА с ВРД со
свободной дальностью полета. Рассматривается выведение на орбиту
воздушно-космического самолета с комбинированной силовой установ-
кой, состоящей из разнотипных ВРД и ЖРД. Формируется алгоритм
расчета взлетных характеристик самолета с учетом возможного отказа
Предисловие автора
13
одного двигателя. Рассматриваются особенности оптимизации траекто-
рий разгона на участках работы турбокомпрессорных ВРД (при малых
скоростях полета) и прямоточных ВРД (при больших скоростях полета).
Определяются оптимальные условия включения и выключения различ-
ных типов ВРД.
В восьмой главе разрабатывается приближенный метод оптимиза-
ции траекторий на основных участках полета гиперзвукового ЛА с ВРД
с заданной суммарной дальностью. Решается задача максимизации
коэффициента крейсерской дальности. Проводится совместная оптими-
зация управляющих переменных и площади входа в двигатель. Разраба-
тываются приближенные методы оптимизации управления движением
на участках разгона и планирования с использованием ВРД. Проводятся
расчеты траекторий разгона и планирования для различных вариантов
задачи.
В девятой главе исследуются траектории спуска с орбиты и плани-
рования ЛА с большим аэродинамическим качеством. Рассматриваются
основные варианты задания начальных условий и аэродинамических
характеристик планирующих ЛА. Подробно исследуются траектории
планирования с максимальной и минимальной продольной дальностью,
с максимальной боковой дальностью. Разрабатывается метод упрощен-
ного построения достижимой области земной поверхности. Формиру-
ется приближенно оптимальный закон управления ЛА при его прямом
возврате с высоких околоземных орбит. Решается задача прямого воз-
врата с геостационарной орбиты летательного аппарата типа "конус".
В десятой главе разрабатывается приближенный метод оптимиза-
ции траекторий пассивного возврата первых крылатых ступеней верти-
кально стартующих систем выведения с ЖРД к их точке старта. Рас-
сматривается возврат в вертикальной плоскости и пространственный
возврат. Вначале решаются модельные задачи с использованием прин-
ципа максимума. Затем на основе полученных решений формируются
приближенно оптимальные законы управления.
При численном решении задач использовались вычислительные
программы, созданные автором для персональной ЭВМ.
По мнению автора, книга предназначена для специалистов в облас-
ти оптимизации траекторий, и может быть полезной при исследовании
перспективных аэрокосмических ЛА на этапе формирования облика.
Вместе с тем она будет полезной для аспирантов и студентов соответст-
вующих специальностей ВУЗов.
14
Предисловие автора
Ряд результатов, приведенных в книге, получен в коллективе, руко-
водимом В.П. Плохих, совместно с С.В. Володиным, К.А. Червоненко и
В.В. Скипенко.
Автор выражает благодарность ученым ЦАГИ, учеником которых
он себя считает: Л.М. Шкадову, В.Ф. Илларионову, В.Е. Денисову,
В.В. Лазареву, В.П. Плохих, Б.Х. Давидсону.
Автор признателен В.В. Сонину за помощь в подготовке материала
книги и А.С. Филатьеву, высказавшему ценные замечания по ее содер-
жанию, а также А.П. Дьячевскому, оказавшему помощь в редактирова-
нии книги.
Автор выражает глубокую благодарность за поддержку и помощь в
издании книги директору ЦАГИ С.Л. Чернышеву, научному
руководителю ЦАГИ В.Г. Дмитриеву, первому заместителю директора
ЦАГИ ГА. Павловцу, начальнику отдела ЦАГИ В.В. Подлубному и
генеральному директору ЗАО "АЭРОКОН” Э.Г. Багдасаряну.
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ, СОКРАЩЕНИЯ, ИНДЕКСЫ
Основные обозначения
А - коэффициент "отвала" поляры;
Ах - коэффициенты аппроксимации;
а - скорость звука, большая полуось эллипса;
В - коэффициент, учитывающий нелинейность;
b -оптимизируемый параметр в законе управления углом крена, коэф-
фициент;
Вх - коэффициенты аппроксимации;
С, - константы интегрирования;
Сг - функция переключения, равная ±1;
cR - коэффициент тяги ВРД;
сх - коэффициент лобового сопротивления;
су - коэффициент аэродинамической подъемной силы;
суо - коэффициент аэродинамической подъемной силы при а = 0°;
суа - производная коэффициента су по углу атаки при а = 0°;
Су - коэффициент, учитывающий несимметричность поляры;
с^, с^у - коэффициенты составляющих вектора результирующей силы Rz
(проекции на оси скоростной системы координат);
Е - удельная энергия ЛА: Е= Н + H2/(2gT);
е - эксцентриситет орбиты, эллипса;
F -площадь входа воздухозаборника, поперечная площадь потока воз-
духа, функционал, характерная площадь двигателя;
f - коэффициент расхода воздуха, коэффициент трения, функция;
G - вес ЛА: G = mgQ;
G/S -удельная нагрузка на характерную площадь ЛА;
g -ускорение гравитационного притяжения;
go ~ стандартное ускорение свободного падения;
gr, g<p - радиальная и меридиональная составляющие ускорения g;
gv-ускорение гравитационного притяжения с учетом разгрузки:
gv = g[l - ^A2/(gr)];
gT - ускорение силы тяжести;
Н -функция Гамильтона;
Н - высота полета;
Яи - теплотворная способность;
Яют- высота первого отражения;
//без ~ безопасная высота при взлете;
/ -импульс потока воздуха (газа), вычисленный через избыточное дав-
ление, энтальпия, момент инерции;
16
Обозначения, сокращения, индексы
i - наклонение орбиты, относительная величина, характеризующая
входной импульс потока;
J -удельный импульс двигателя;
<7эф - эффективный удельный импульс ЛА;
]цб - вектор центробежного ускорения;
К - аэродинамическое качество;
/Стах - максимум аэродинамического качества по углу атаки;
Ки - коэффициент поджатия;
к - отношение теплоемкостей для воздуха: к = сР /cv;
кт - отношение секундных расходов окислителя и горючего;
L - путевая дальность полета;
Lq - стехиометрический коэффициент;
Lx , Lz - продольная и боковая дальности планирования;
/ - управляющая переменная, коэффициент;
М - число Маха;
М -логарифмическая масса, масса полезного груза, молярная масса;
т - масса;
in -относительная масса;
N - сила реакции;
п - параметр, характеризующий "разгрузку": п = (Р7ККР)2- 1;
/?х, пу - тангенциальная и нормальная скоростная перегрузки;
цх), цу1 - продольная и нормальная перегрузки (проекции на оси связанной
системы координат);
Р - вектор сопряженных переменных;
Р, - сопряженные переменные;
р -давление атмосферы (газа), параметр орбиты;
Q - секундный расход массы;
q - скоростной напор;
q\, q2 - переменные, характеризующие пространственное движение;
91 - универсальная газовая постоянная, удаление от точки старта, тяго-
вооруженность ЛА: 91 = R/(mgo);
Re - число Рейнольдса;
R - сила, тяга двигателя;
Ro -средний радиус шарообразной Земли;
радиус затупления в критической точке ЛА;
Rs - вектор результирующей силы ЛА;
- радиус общего земного эллипсоида;
г - расстояние от центра Земли до центра масс ЛА;
S - характерная площадь ЛА, площадь;
5 - угловое расстояние по дуге большого круга Земли;
Т - температура воздуха, конечное время, период;
7W - температура в критической точке ЛА;
Обозначения, сокращения, индексы
17
U - вектор управления;
U -силовая функция, соотношение сопряженных переменных;
щ - управляющие переменные;
V - скорость;
W -объем;
X - вектор фазовых координат;
X, Ад - сила лобового сопротивления ЛА;
Xi - продольная сила сопротивления (проекция на связанную ось <2х|);
Xj - фазовые переменные;
Y, УА - аэродинамическая подъемная сила ЛА;
Ki - нормальная сила (проекция на связанную ось Oyi);
у - относительный коэффициент подъемной силы: у = су!су^т •
а -угол атаки, удельный весовой параметр, градиент, сжатие земного эл-
липсоида;
акс - коэффициент избытка воздуха (окислителя) в камере сгорания двигате-
ля;
Р -параметр атмосферы, угол установки двигателя относительно плоскости
симметрии ЛА, удельный весовой параметр, угол косого скачка;
% -истинная аномалия, условный угол, связанный с углом атаки;
у -угол крена, удельный весовой параметр, градиент;
А - приращение;
S -угол заклинения вектора тяги относительно оси О*] (на виде сбоку),
отклонение переменной в относительном виде, относительный пара-
метр, характеризующий зависимость коэффициента cxmin от высоты,
рассогласование между углами курса и визирования на заданную точку,
угловое расстояние между ЛА и плоскостью /7;
8 -геометрическая степень расширения сопла, относительная "сухая” масса
ЛА, относительная величина, степень черноты, угол между мгновенной
плоскостью движения ЛА и плоскостью 77;
0 -угол наклона траектории (неограниченная величина);
0 - угол наклона траектории (|б I < я/2);
0 -угол тангажа, угол отклонения импульса схода с орбиты;
А - ортодромическая долгота, вспомогательная функция;
X -геоцентрическая долгота, приведенная скорость, вспомогательная функ-
ция;
ц -относительная конечная масса, относительная масса ПГ, произведение
универсальной гравитационной постоянной на массу Земли, динамиче-
ская вязкость;
18
Обозначения, сокращения, индексы
v - коэффициент дросселирования секундного расхода массы топлива,
поправочная функция;
р - плотность воздуха, газа, топлива;
о - коэффициент полного давления, постоянная Стефана-Больцмана;
стх -баллистический коэффициент: стх= cx5/(wg0);
су - параметр планирования: сту = cyS7(wg0);
т - время полета;
Ф - ортодромическая широта, промежуточный функционал;
ср - геоцентрическая широта, максимизируемая функция;
Т - ортодромический угол курса;
Ч'виз-угол визирования;
- угол курса;
со -угловая скорость вращения.
Сокращения
АКС - авиационно-космическая система;
ВЗ - воздухозаборник;
ВКА - воздушно-космический аппарат;
ВКС - воздушно-космический самолет;
ВПП - взлетно-посадочная полоса;
ВРД - воздушно-реактивный двигатель;
ВРУ - возвращаемый ракетный ускоритель;
ВСХ - высотно-скоростные характеристики;
ВТБ - внешний топливный бак;
ГЛ А - гиперзвуковой летательный аппарат;
ГПВРД - гиперзвуковой прямоточный ВРД (со сверхзвуковым горением);
ГРПД - гиперзвуковой ракетно-прямоточный двигатель;
ГС - гиперзвуковой самолет;
ГСО - геостационарная орбита;
ГСР - гиперзвуковой самолет-разгонщик;
ГТД - газотурбинный двигатель;
ДГПВРД - двухрежимный ГПВРД (с до- и со сверхзвуковым горением);
ДСН - дозвуковой самолет-носитель;
ЖВРД - жидкостно-воздушный реактивный двигатель с сжижением вход-
ного воздуха;
ЖРД - жидкостный ракетный двигатель;
ИСЗ - искусственный спутник Земли;
КА - космический аппарат;
КС - камера сгорания;
КСУ - комбинированная силовая установка;
ЛА - летательный аппарат;
МКТС - многоразовая космическая транспортная система;
Обозначения, сокращения, индексы
19
ОС - орбитальный самолет;
ПВРД - прямоточный ВРД (с дозвуковым горением);
ПГ - полезный груз;
РБ - ракетный блок;
РД - ракетный двигатель;
РДТТ - ракетный двигатель твердого топлива;
PH - ракета-носитель;
РПД - ракетно-прямоточный двигатель;
PC - реактивное сопло;
РТД - ракетно-турбинный двигатель;
РТДп - ракетно-турбинный двигатель пароводородной схемы;
с.к. - система координат;
ТПД - турбопрямоточный двигатель;
ТРД - турбореактивный двигатель;
ТРДДФ - двухконтурный турбореактивный двигатель с форсажной камерой;
ТРДДФТ - ТРДДФ с теплообменником на входе в двигатель;
ц.м. - центр масс.
Индексы
О - стартовый, начальный, на уровне моря;
(-1) - взлет с одним отказавшим двигателем;
Е - переносный;
Н - на высоте Я;
Нб - на безопасной высоте;
Jm - на режиме Jmax;
Km - на режиме /Стах;
тахД - максимально допустимый;
ттД - минимально допустимый;
opt - оптимальный;
q - с постоянным скоростным напором q ;
А - абсолютный, аэродинамический;
В - вертикальный, воздух, воздушный;
ВЗЛ - взлет;
ВКЛ - включение;
ВХ - вход;
Г - газ, геопотенциальный, горло, горючее, гравитационный;
ГО - грузовой отсек;
Д - довыведение, допустимый, донный;
ДВ - двигатель;
Ж - "жидкий";
3 - Земля;
И - изотермический, инерциальный, идеальный;
ИЗ - изолированный;
20
Обозначения, сокращения, индексы
К - конечный;
кв - квазистационарный;
КЕР - керосин;
КР - круговой, крейсерский, критическое сечение;
М - молярный;
ОК - окислитель;
ОМ - орбитальное маневрирование;
ОРТ - ортодромический;
ОТБ - отбор;
ОТР - отрыв от ВПП;
П - переключение, плоскость /7, характеризующая пространственное
движение ЛА, потери, прямоточный, пустотный;
п.ст - отрыв передней стойки;
пл - планирование, пластина;
пос - посадочный;
ПР - приведенный, программный, проспектный;
ПРЕР - прерванный взлет;
ПРОД - продолженный взлет;
ПТР - потребный;
р - разбег, расчетный;
РЗГ - разгон;
с - сопло, сваливание;
сж - сжиженный воздух;
СР - средний;
ст - стандартный, стояночный;
СУХ - "сухой”;
сх - сход;
т - топливо, торможение;
тк - турбокомпрессорный;
У - узел, условный;
уд - удельный;
УС - усиление;
ХАР - характеристический;
э - эквивалентный, экстремум;
ЭФ - эффективный;
а - апогей;
л - перигей;
Z - суммарный;
00 - невозмущенный.
ГЛАВА 1
АЭРОКОСМИЧЕСКИЙ ЛЕТАТЕЛЬНЫЙ АППАРАТ КАК
ОБЪЕКТ ИССЛЕДОВАНИЯ ТРАЕКТОРИЙ ДВИЖЕНИЯ
Зарождение аэрокосмической техники произошло на стыке самоле-
та- и ракетостроения. Соответственно механика полета аэрокосмиче-
ских летательных аппаратов базируется на теории полета самолетов и
ракетных ЛА.
Начало создания теории полета самолетов (крылатых летательных
аппаратов тяжелее воздуха) относится к концу XIX века, к годам зарож-
дения авиации. Большой вклад в разработку теоретических основ поле-
та в атмосфере был внесен российским ученым проф. Н.Е. Жуковским.
В работе "О парении птиц” (1891 г.) он впервые установил связь между
углом атаки, скоростью и углом наклона траектории при планировании
самолета. В работе ”О наивыгоднейшем угле наклона траектории аэро-
плана” (1897 г.) им был рассмотрен установившийся горизонтальный
полет и обоснованы условия такого полета. Н.Е. Жуковский создал
графоаналитический метод аэродинамического расчета самолета, так
называемый метод тяг (1913 г.), который широко применяется до на-
стоящего времени.
В 1918 г. в России по инициативе Н.Е. Жуковского был создан Цен-
тральный аэрогидродинамический институт (ЦАГИ) [21], в котором
зародилась основа новых отраслей науки и техники, в дальнейшем
ставших фундаментом для развития современной авиации. Ученым
ЦАГИ принадлежит большая роль в развитии аэромеханики самолетов.
В последующие годы из ЦАГИ выделились институты авиацион-
ного моторостроения (ЦИАМ), летно-исследовательский (ЛИИ) и др.
Был создан ряд авиационных КБ. Авиация в России начала развиваться
бурными темпами.
К концу 30-х годов самолет стал уже надежным транспортным
средством. В предвоенные годы и в годы Великой отечественной войны
в нашей стране были созданы высококлассные самолеты, обеспечившие
превосходство над авиацией противника: штурмовики Ил-2 и Ил-10,
истребители МиГ-3, Ла-7, Як-3, бомбардировщики Пе-2, Пе-8, Ту-2 и
др. В послевоенные годы в кратчайшие сроки отечественная авиация
осуществила переход на реактивные двигатели. В начале 50-х годов
22 Глава 1. Аэрокосмический ЛА как объект исследования траекторий
были созданы первые боевые сверхзвуковые самолеты. В 1968 г. впер-
вые в мире взлетел пассажирский сверхзвуковой самолет Ту-144. Все-
мирную известность получили самолеты, созданные конструкторскими
коллективами, возглавляемыми А.Н. Туполевым, С.В. Ильюшиным,
А.И. Микояном, А.С. Яковлевым, П.О. Сухим, В.М. Мясищевым,
О.К. Антоновым, другими заслуженными авиаконструкторами.
Помимо России в практическое самолетостроение большой вклад
внесли США, Германия, Франция, Великобритания.
Скорость первых аэропланов составляла несколько десятков кило-
метров в час, скорость полета современных самолетов измеряется
тысячами километров в час. По мере развития авиационной техники
вместе со скоростью и высотой увеличивались дальность полета, взлет-
ная масса и масса полезного груза (ПГ). Так, созданный в СССР дозву-
ковой самолет Ан-225 "Мр!я" с массой 600 т имеет грузоподъемность
до 250 т. Практическая дальность пассажирских и грузовых перевозок в
настоящее время достигает 15-J-20 тысяч километров. Использование
дозаправки в воздухе позволяет достигнуть практически любой точки
земной поверхности. Рекорд скорости, поставленный на самолете SR-71
(США), составляет 3529 км/ч. Рекордная высота 37,65 км была достиг-
нута на самолете Е-266М (СССР). Экспериментальный аппарат воз-
душного старта Х-15 (США) достиг скорости полета, соответствующей
числу Маха 7.
Одновременно с развитием самолетов совершенствовались авиа-
ционные двигатели - от поршневых до современных воздушно-
реактивных (ВРД). Так как для создания подъемной силы самолета и
силы тяги его двигателя необходим атмосферный воздух, то полет
крылатых летательных аппаратов
0 1 8 Г, км/с
Рис. 1.1. Области полета современ-
ных самолетов и ракет-носителей в
координатах "высота - скорость"
>жет осуществляться только в плот-
ных слоях атмосферы (рис. 1.1).
Теоретическое обоснование
возможности полетов в космиче-
ском пространстве впервые было
дано К.Э. Циолковским задолго до
создания ракетно-космической
техники. В своем труде "Исследо-
вание мировых пространств реак-
тивными приборами" (1903 г.), в
дальнейших работах К.Э. Циол-
ковский показал реальность тех-
нического осуществления косми-
ческих полетов и дал
принципиальное решение ряда
основных проблем космонавтики
[49].
Фундаментальной стала фор-
мула Циолковского, показываю-
щая, что энергетика ракеты зави-
Глава 1. Аэрокосмический ЛА как объект исследования траекторий 23
сит от удельного импульса ее двигателя и весового совершенства кон-
струкции, обеспечивающего наибольший бортовой запас топлива:
Ихар = -Лп— или Гхар=Лп—4^- (1-1)
ц 1-
Здесь Кхар- характеристическая скорость ракеты;
J - удельный импульс двигателя (отношение тяги к секундному
расходу массы топлива);
ц = mK/mQ - относительная конечная масса летательного аппара-
та; и mQ - конечная и начальная (стартовая) масса ЛА;
тТ = т^/то - относительный запас топлива.
Формула (1.1) - основное уравнение движения одноступенчатой
ракеты, определяющее ее максимальную скорость, которая может быть
достигнута при прямолинейном движении в пустоте в отсутствии
внешних сил (идеальный случай).
Вопросам теории реактивного движения и космонавтики посвяще-
ны также работы Н.Е. Жуковского, И.В. Мещерского, Ю.В. Кондратюка,
Ф.А. Цандера и других российских ученых. За рубежом ранние труды
по космонавтике были опубликованы Р. Эно-Пельтри, Р. Годдардом,
Г. Обертом [49].
Началом космической эры считается дата запуска в СССР первого
искусственного спутника Земли (ИСЗ) - 4 октября 1957 г. Освоению
космического пространства в значительной мере способствовало воен-
ное соперничество СССР и США. В дальнейшем космонавтика превра-
тилась в самостоятельную совокупность отраслей науки и техники и
была поставлена на службу в первую очередь общечеловеческим инте-
ресам. За первые десятилетия космической эры наша страна, США и
другие развитые страны достигли небывалых успехов в развитии ракет-
но-космической техники и в осуществлении различных космических
программ. В 1961г. Ю. А.Гагарин совершил первый в мире полет в
космос. В 1969 г. Н. Армстронг, 3. Олдрин и М. Коллинз (США) выпол-
нили первую лунную экспедицию. В СССР, начиная с 1971 г., для кос-
мических исследований успешно использовались долговременные
орбитальные станции ’’Салют” и ’’Мир”. Всего в космос было выведено
несколько тысяч искусственных спутников и межпланетных космиче-
ских аппаратов (КА). В процессе развития ракетно-космической техни-
ки масса выводимого на околоземную орбиту полезного груза увеличи-
лась от 84кг (первый ИСЗ) до 140т (программа ’’Аполлон”, США),
стартовая масса ракет-носителей возросла от 300 т (PH ’’Восток”) до
3000т (PH "Сатурн-V”, США). Скорости полета ракет-носителей и
спускаемых космических аппаратов в атмосфере превысили скорость
сверхзвуковых самолетов в несколько раз.
В СССР первые ракетно-космические комплексы были созданы под
руководством С.П. Королева, с именем которого связана эпоха первых
достижений в ракетостроении и космонавтике. Большой вклад в разви-
24 Глава 1. Аэрокосмический ЛА как объект исследования траекторий
тие ракетно-космической техники внесли В.П. Глушко, М.К. Янгель,
В.Н. Челомей, др. советские ученые и конструкторы.
Одновременно с совершенствованием конструкции PH повышалась
эффективность ракетных двигателей (РД), основными типами которых
являются жидкостные (ЖРД) и твердотопливные (РДТТ). В отличие от
самолета все топливо ракеты является бортовым, т.е. атмосферный
воздух не используется для создания силы тяги. Вследствие этого тра-
ектория PH формируется таким образом, чтобы как можно быстрее
выйти из плотных слоев атмосферы (см. рис. 1.1).
Долгие годы основным транспортным средством доставки полез-
ных грузов на орбиту являлись одноразовые ракеты-носители. Удельная
стоимость выведения на орбиту (стоимость выведения, отнесенная к
массе полезного груза) для таких систем практически достигла своего
предела. В связи с этим в 80-е годы начался этап постепенного перехода
от одноразовых PH к многоразовым средствам выведения. Так, в США
с 1981 г. эксплуатируется частично многоразовая аэрокосмическая
система выведения "Space Shuttle", состоящая из двух РДТТ, пилоти-
руемого орбитального самолета с маршевыми ЖРД и внешнего топлив-
ного бака (ВТБ), который является единственным одноразовым элемен-
том этой системы. После завершения космического полета
орбитальный самолет "Space Shuttle" совершает планирующий спуск и
бездвигательную посадку на аэродром.
На следующих этапах развития аэрокосмической техники могут
быть созданы полностью многоразовые космические транспортные
системы (МКТС). Освоение горизонтального старта МКТС и гиперзву-
кового полета с применением ВРД позволит значительно сократить
потребный запас топлива выведения на орбиту по сравнению с ракет-
ными системами вертикального старта. Однако создание аэрокосмиче-
ских ЛА, способных осуществлять длительный высокоскоростной
полет в плотных слоях атмосферы, потребует решения целого комплек-
са научно-технических проблем, таких как защита от аэродинамическо-
го нагревания, обеспечение многоразовости конструкции, широкое
внедрение водородной технологии и т.д. В связи с этим необходимы
широкомасштабные научные исследования аэрокосмических ЛА по
всем фундаментальным дисциплинам, включая механику полета.
Применительно к аэрокосмическим летательным аппаратам роль
этапа формирования облика (начального этапа проектирования) повы-
шается, так как здесь должно быть принято большинство концептуаль-
ных и схемных решений, определяющих эффективность и экономич-
ность будущей аэрокосмической техники. Одной из составных частей
формирования облика перспективных аэрокосмических ЛА является
оптимизация траекторий их движения, в процессе которой могут быть
быстро и точно определены масса и объем маршевого топлива, а также
основные траекторные характеристики на всех участках полета от
старта до посадки.
1.1. Классификация аэрокосмических ЛА
25
1.1. Классификация аэрокосмических ЛА
Прежде чем перейти к исследованию траекторий движения аэро-
космических летательных аппаратов, необходимо получить общее
представление о назначении таких ЛА и их возможном облике. В на-
стоящее время сложилась определенная терминология, которая будет
использоваться в книге. Термин "летательный аппарат" является наибо-
лее общим и соответствует любому средству передвижения в атмосфере
и космическом пространстве. ЛА может быть крылатым и бескрылым,
беспилотным и пилотируемым, с ВРД или с комбинацией ВРД и ЖРД, и
т.д. Чаще под аппаратом понимается одноступенчатое средство пере-
движения. Многоступенчатый ЛА обычно называется системой. В
процессе развития техники сложилось так, что самолет практически
всегда был многоразовым крылатым и одноступенчатым. В связи с этим
уместно называть самолетом только такой ЛА, который имеет эти при-
знаки и обладает высокой несущей способностью.
На рис. 1.2 показана укрупненная классификация аэрокосмических
летательных аппаратов по их назначению, типу старта и числу ступе-
ней. Аэрокосмические ЛА разделены на 2 класса:
- гиперзвуковые самолеты (ГС) и системы, не выходящие на ор-
биту;
- системы выведения на орбиту.
Основное назначение гиперзвуковых самолетов и систем - это дос-
тавка полезного груза на заданное расстояние или полет с заданным
радиусом действия с посадкой в точке взлета. Взлет и посадка ГС -
горизонтальные. В качестве двигателей для ГС обычно рассматривают-
ся только ВРД. При этом важнейшим параметром ГС является макси-
мальное число М полета, которое теоретически лежит в пределах от
5-6 до 15-20.
Гиперзвуковые системы (чаще двухступенчатые) в общем случае
могут иметь как горизонтальный, так и вертикальный старт. При верти-
кальном старте первой ступенью системы является ракетный ускори-
тель, при горизонтальном старте в качестве первой ступени использу-
ется самолет-носитель. Вторая ступень гиперзвуковой системы
представляет собой ГС или планирующий летательный аппарат.
В случае полета на заданное расстояние альтернативой ГС может
служить ракетоплан - одноступенчатый ЛА с ЖРД. Такой аппарат по
достижении максимальной скорости полета осуществляет планирова-
ние в атмосфере без использования двигателя.
К гиперзвуковым системам относятся экспериментальные ЛА и
демонстраторы, предназначенные для отработки техники гиперзвуково-
го полета. Старт таких ЛА чаще всего предполагается с использованием
дозвукового самолета-носителя (ДСН).
Траекторию полета гиперзвуковых самолетов и систем обычно раз-
деляют на три участка:
26 Глава 1. Аэрокосмический ЛА как объект исследования траекторий
Рис. 1.2. Укрупненная классификация аэрокосмических
ЛА по их назначению, типу старта и числу ступеней
- участок разгона до максимальной скорости;
- участок крейсерского полета;
- участок планирования (с использованием или без использования
ВРД).
При оптимизации траекторий движения ГС необходимо учитывать,
что названные участки полета связаны между собой условием обеспе-
чения суммарной дальности полета.
В отличие от гиперзвуковых самолетов МКТС предназначены для
доставки полезного груза на околоземную орбиту. Облик МКТС в
значительной мере определяется типом применяемых двигателей и
типом старта. МКТС могут быть как многоступенчатыми (обычно не
более двух - трех ступеней), так и одноступенчатыми.
По типу старта МКТС подразделяются на системы вертикального и
горизонтального старта. В МКТС вертикального старта в качестве
маршевых обычно рассматриваются ракетные двигатели, хотя теорети-
чески возможно использование ВРД (например, на второй ступени
1.1. Классификация аэрокосмических ЛА
27
системы). В варианте использования ракетных двигателей траектория
выведения МКТС (рис. 1.3) имеет такой же характер, как у современ-
ных ракет-носителей, хотя условие возврата первой ступени к месту
старта оказывает некоторое влияние на траекторию движения после-
дующих ступеней.
Одноступенчатую МКТС вертикального старта часто называют
воздушно-космическим аппаратом (ВКА). Посадка многоразовых
ступеней МКТС вертикального старта, как правило, предполагается
горизонтальной, хотя в некоторых проектах рассматриваются варианты
вертикальной посадки.
Применительно к МКТС горизонтального старта обычно рассмат-
ривается комбинация ВРД и ЖРД. Траектории выведения на орбиту
таких систем существенно отличаются от траекторий МКТС, на кото-
рых установлены только ЖРД (см. рис. 1.3).
Одноступенчатый аппарат горизонтального старта чаще называют
воздушно-космическим самолетом (ВКС). Многоступенчатые МКТС
горизонтального старта называются авиационно-космическими систе-
мами (АКС). При этом уже в самом названии отражен принцип авиаци-
онного (самолетного) старта с аэродрома. В качестве первой ступени
АКС возможно использование дозвукового самолета-носителя, сверх-
звукового или гиперзвукового самолета-разгонщика (ГСР).
На первой ступени АКС, как правило, предусматривается исполь-
зование только ВРД, на второй ступени - ЖРД или комбинации ВРД и
ЖРД.
Вторая ступень АКС может быть полностью многоразовой или со-
держать одноразовые элементы. В первом случае вторую ступень АКС
называют ВКС. Таким же термином обозначаются и другие многоразо-
вые крылатые летательные аппараты, которые при помощи собственно-
го топлива выходят на орбиту и затем возвращаются с нее, например
одноступенчатый аппарат
горизонтального старта с
использованием наземного
разгонного устройства.
В качестве одноразо-
вого элемента в МКТС
может входить внешний
топливный бак или ракет-
ный блок (РБ). Многоразо-
вый ЛА, не имеющий
маршевого топлива, но
выходящий на орбиту и
затем осуществляющий
планирование в атмосфере,
называют орбитальным
кораблем. Крылатый ко-
рабль называется орби-
Рис. 1.3. Траектории выведения
на орбиту различных типов МКТС
в координатах "высота - скорость"
28 Глава 1. Аэрокосмический ЛА как объект исследования траекторий
тальным самолетом (ОС). При наличии в системе выведения одноразо-
вого РБ маршевые ЖРД на орбитальном самолете отсутствуют, как на
ОС ’’Буран". При наличии в системе внешнего топливного бака марше-
вые ЖРД устанавливаются на ОС, как в МКТС "Space Shuttle".
Траектория движения МКТС имеет три самостоятельных участка:
- разгон и выведение на орбиту;
- орбитальный полет;
- возвращение с орбиты.
Задачу оптимизации траекторий движения МКТС (в отличие от
аналогичной задачи для ГС) можно разделить на три самостоятельных в
соответствии с выделенными участками. Определяющее влияние на
облик МКТС оказывают траекторные характеристики выведения на
орбиту и возврата с нее (в отличие от орбитального движения). В связи
с этим в данной книге основное внимание уделено оптимизации траек-
торий на этих режимах полета.
При выведении на орбиту дальность полета обычно не фиксирует-
ся, что облегчает решение задачи по сравнению со случаем фиксиро-
ванной дальности. К МКТС может быть выдвинуто требование выведе-
ния на орбиту с параллаксом, т.е. с боковым удалением плоскости
орбиты от точки старта. Очевидно, что существенный параллакс можно
обеспечить только на участке полета с ВРД. При таком выведении на
орбиту траектория становится пространственной и задача выведения
усложняется. Траектории планирования в общем случае являются
пространственными и могут содержать участки полета с ВРД.
Из предварительного обзора различных типов аэрокосмических ЛА
видно, что при их исследовании возникает широкий спектр задач опти-
мизации траекторий движения. Необходимо уметь рассчитывать траек-
тории разгона как с ЖРД, так и с ВРД, траектории крейсерского полета
и планирования в атмосфере. При этом движение может быть плоским
(в вертикальной плоскости) или пространственным, дальность полета
может быть как свободной, так и фиксированной, и т.д. Большинство
этих траекторных задач рассмотрено в данной книге.
1.2. Основные типы топлива и двигателей
аэрокосмических ЛА
Для обеспечения активного полета ЛА как в авиационной, так и в
ракетной технике применяется принцип реактивного движения: дви-
жущая сила образуется за счет истечения реактивной струи. Чтобы
создать такую струю, необходимо иметь запас расходуемого вещества
(рабочего тела) и запас энергии. В соответствии с этим двигатель дол-
жен включать в себя генератор, служащий для преобразования первич-
ной энергии в кинетическую энергию реактивной струи, и движитель -
устройство преобразования полученной механической энергии струи в
полезную работу силы тяги.
1.2. Основные типы топлива и двигателей аэрокосмических ЛА
29
В общем случае потребные ресурсы энергии и расходуемой массы
могут находиться как на борту ЛА, так и в окружающей среде. Двига-
тель, использующий для создания реактивной тяги атмосферный воз-
дух, называется воздушно-реактивным. Автономный реактивный дви-
гатель, использующий только бортовые ресурсы энергии и расходуемой
массы, называется ракетным. Термин ’’ракетный” в данном случае
используется вследствие исторически сложившейся традиции и под-
черкивает, что такой тип двигателя наиболее характерен для движения
ракет. Теория двигателей подробно изложена в соответствующей лите-
ратуре (см. например, [5], [90]). Ниже даны основные сведения о двига-
телях и топливах, необходимые для расчета траекторий.
Ракетные двигатели. В РД для создания тяги могут использовать-
ся различные виды первичной энергии: химическая, ядерная, электри-
ческая и др. В соответствии с этим различают химические, ядерные,
электрические ракетные двигатели и т.д. Во всех случаях первичная
энергия сначала превращается в тепловую, а затем при помощи рабоче-
го тела преобразуется в кинетическую энергию реактивной струи.
Источники энергии и рабочего тела могут быть как раздельными, так и
совмещенными.
Первый случай характерен для ядерных и электрических двигате-
лей. Так, например, продукты превращений ядерного топлива не преду-
сматриваются к использованию в качестве рабочего тела ввиду малости
их массы и опасности заражения окружающей среды. В ядерных РД
должно использоваться специальное рабочее тело, воспринимающее
энергию от независимого источника. Наиболее эффективным является
рабочее тело, обладающее минимальной молекулярной массой, напри-
мер водород. Ядерные РД пока не нашли применения в ракетной техни-
ке вследствие большой массы реактора и радиационной защиты, а
также из-за повышенного риска заражения окружающей среды. Элек-
трические двигатели имеют малую тягу и предназначены в первую
очередь для полета в космическом пространстве.
В химических топливах источники энергии и рабочего тела явля-
ются совмещенными: тепло, выделяемое в результате химической
реакции, сообщается продуктам этой реакции. Тепловая энергия в
химических РД может быть получена в результате реакций разложения,
восстановления и окисления (горения), а также - в результате рекомби-
нации атомов или радикалов (химические реакции перечислены в
порядке возрастания тепловыделения). Теплотворная способность Ну
(количество тепла, получаемое в результате химической реакции, в
которой участвует 1 кг топлива) является одним из основных показате-
лей топлива. Большей величине Нц соответствует больший удельный
импульс двигателя: J- ^2Нц .
Наибольшее тепловыделение теоретически может быть получено в
результате реакции рекомбинации. Так, при рекомбинации атомарного
водорода Ни = 215 МДж/кг, что на порядок больше, чем при горении
30 Глава 1. Аэрокосмический ЛА как объект исследования траекторий
топлива. Однако способы получения и сохранения свободных атомов и
радикалов пока не найдены и топлива на их основе не созданы [116].
Самое широкое применение в ракетно-космической технике нашли
химические РД, тепловая энергия в которых получается в результате
горения. Чтобы осуществить такую реакцию, необходимо наличие
окислителя и горючего. Для полного окисления горючего требуется
вполне определенное количество окислителя, определяемое стехиомет-
рическим коэффициентом £0, который показывает, во сколько раз масса
окислителя должна превышать массу горючего. Реальное соотношение
массы окислителя и горючего кт, как правило, отличается от стехио-
метрического. Наряду с величиной кт используется коэффициент из-
бытка окислителя, который по определению равен
<*кс = £?ок/(£?п£о) “ кт1Ьц.
Здесь 2ок и Q\ - секундные расходы массы окислителя и горючего.
С точки зрения агрегатного состояния топлива бывают твердыми,
жидкими или смешанными (гибридными). В соответствии с этим ра-
кетные двигатели подразделяются на РДТТ, ЖРД и гибридные, причем
наиболее освоенными являются первые два типа РД. В РДТТ окисли-
тель и горючее в виде одного вещества размещаются непосредственно в
камере сгорания двигателя. Для обеспечения горения топливному
заряду придается специальная форма. Компоненты топлива ЖРД хра-
нятся раздельно в топливных баках, откуда они подаются при помощи
насосов по отдельным магистралям в камеру сгорания двигателя. Наи-
более широко в ЖРД используется двухкомпонентное топливо. Воз-
можно также применение многокомпонентных жидких топлив (как
правило, рассматривается трехкомпонентное топливо).
В современной ракетно-космической технике в качестве маршевых
двигателей используются только ЖРД и РДТТ. Одним из основных
преимуществ РДТТ является высокая плотность его топлива
(рт = 1600н-2300 кг/м3), в связи с чем такой тип двигателя наиболее
эффективен при установке на первых ступенях PH.
Наиболее широкое применение в системах выведения получили
жидкостные ракетные двигатели. ЖРД могут устанавливаться как на
первых, так и на последних ступенях PH. С точки зрения экономично-
сти и дросселирования тяги ЖРД обладают существенно лучшими
характеристиками, чем РДТТ. Кроме того, использование в ЖРД таких
компонентов, как кислород, водород, керосин, приводит к существенно
меньшему загрязнению окружающей среды. Вследствие этих преиму-
ществ при исследовании перспективных многоразовых систем выведе-
ния на орбиту из класса ракетных двигателей рассматриваются, как
правило, только ЖРД.
В настоящее время известно большое число жидких топлив. Ос-
новные требования к топливу заключаются в следующем. Оно должно
обладать высокой теплотворностью и иметь малую молекулярную
массу, обеспечивая тем самым высокий удельный импульс. Топливо
1.2. Основные типы топлива и двигателей аэрокосмических ЛА
31
должно иметь высокую плотность, что будет приводить к уменьшению
габаритов и массы топливных баков ЛА. Кроме того, топливо должно
быть способным к охлаждению двигателя, к самовоспламенению,
иметь хорошие эксплуатационные свойства и быть сравнительно деше-
вым. В настоящее время таких топлив, которые удовлетворяли бы всем
перечисленным свойствам, не существует. В зависимости от основного
назначения ЛА приходится отказываться от удовлетворения одних
требований в пользу других. Очевидно, что из всех требований к топ-
ливам для перспективных систем выведения на первое место необхо-
димо поставить высокие энергетические возможности и отсутствие
отрицательного воздействия на окружающую среду (или сведение к
минимуму такого воздействия).
По температуре кипения компоненты жидких топлив подразделя-
ются на высококипящие, низкокипящие и криогенные. Высококипящи-
ми называют компоненты, находящиеся в жидкофазном состоянии в
обычных условиях (при давлении 0,1013 МПа и температуре 25°С).
Такие компоненты, как правило, допускают длительное хранение.
Низкокипящие вещества в обычных условиях находятся в газообразном
состоянии. Низкокипящие компоненты с температурой кипения меньше
120К называются криогенными.
По энергетическому признаку компоненты жидких топлив подраз-
деляются на низкотеплотворные и высокотеплотворные. Такое разделе-
ние, как правило, сочетается с разделением по степени криогенности
(высокотеплотворные компоненты являются криогенными жидкостя-
ми).
Из широкого многообразия топливных компонентов можно выде-
лить широко применяемые в ракетно-космической технике и перспек-
тивные компоненты. Число используемых окислителей сравнительно
невелико; основные показатели этих веществ приведены в табл. 1.1 (по
данным работ [49], [116]). Как видно из таблицы, единственным неток-
сичным окислителем является кислород. Кроме того, кислород имеет
наибольшее значение Иц (обеспечивает наибольший удельный импульс
ЖРД) и является относительно дешевым. Производство жидкого кисло-
рода хорошо освоено (в настоящее время его получают из сжиженного
воздуха). Именно этими достоинствами определяется широта примене-
ния жидкого кислорода в ракетно-космической технике, например, на
PH "Восток”, ’’Союз”, "Энергия” (СССР), "Сатурн-V”, "Space Shuttle”
(США). Основным недостатком кислорода является его криогенность.
По плотности жидкий кислород также несколько уступает другим
окислителям. Высококипящие окислители, несмотря на свою токсич-
ность, в силу различных исторических причин долгие годы применя-
лись в ракетно-космической технике, например, азотный тетраксид - на
PH "Титан” (США).
32 Глава 1. Аэрокосмический ЛА как объект исследования траекторий
Основные характеристики окислителей
Таблица 1.1
Наименование Молекулярная масса Плотность жидкого ком- понента р, кг/м3 Температура плавле- ния/кипения, К Теплотворность топлива на основе водорода Нц > МДж/кг Токсичность
Азотная кислота HNO3 63 1513 231,4 359 8,1 Токсична
Перекись водорода н2о2 34 1448 273 424 8,25 Слабо токсична
Азотный тетраксид n2o4 92 1447 262 294 9,45 Очень токсичен
Кислород О2 32 1140 54 90 13,0 Нетоксичен
Что касается перспективных окислителей, то в лабораторных усло-
виях открыто и проверено несколько десятков высокотеплотворных
химических веществ: фтор, производные фтора, новые синтезирован-
ные окислители и др. Одним из самых высококалорийных окислителей
является озон: в паре с водородом он дает теоретически до
16,15 МДж/кг (на ~25% больше, чем у топлива Н2 + О2). Однако при
использовании перспективных окислителей в работающих двигателях
возникает ряд серьезных технических и эксплуатационных трудностей.
Главные из них - высокая токсичность, взрывоопасность, коррозионная
активность, дороговизна, трудности производства и т.д. [116].
В соответствии с вышесказанным можно заключить, что с точки
зрения наибольшего удельного импульса и отсутствия токсичности
наилучшим окислителем является жидкий кислород. Именно такой
окислитель и рассматривается в большинстве случаев применительно к
перспективным МКТС.
Основу всех используемых и перспективных горючих составляют
семь наиболее теплотворных химических элементов, находящихся в
первых трех группах и первых четырех периодах периодической систе-
мы элементов Менделеева: водород, литий, бериллий, бор, углерод,
магний и алюминий. Наивысшей массовой теплотой сгорания обладает
водород. Вследствие этого большое значение с точки зрения возможно-
го использования в качестве горючих компонентов имеют различные
химические соединения с водородом, например: углеводороды (соеди-
1.2. Основные типы топлива и двигателей аэрокосмических ЛА
33
нения углерода с водородом); бороводороды (соединения бора с водо-
родом); тройные соединения водорода, бора, углерода и др. [90].
В настоящее время известно большое число горючих компонентов,
однако практическое применение нашли только некоторые из них.
Основные характеристики таких горючих представлены в табл. 1.2 (по
данным работ [49], [116]).
Таблица 1.2
Основные характеристики горючих
Наименование Молекулярная масса Плотность жидко- го компонента р, кг/м3 Температура плавле- ния/кипения, К Теплотворность 1 топлива на основе кислорода Яц, МДж/кг Токсичность
Высококипящие
Гидразин N2H4 32,048 1008 275 387 8,1 Токсичен
Метилгидразин CH3N2H3 46,075 875 220 360 9,0 Токсичен
Несимметричный диметил гидразин (CH3)2N2H2 Аэрозин 50 (50 % НДМГ + 50 % N2H4) 60,102 791 216 336 9,3 Очень токсичен
- 900 266 343 - Очень токсичен
Спирт этиловый С2Н5ОН 46,07 780 159 351 8,7 Слабо токсичен
Пентаборан ста- бильный В5Н9 63,172 630 226 332 12,7 Очень токсичен
Керосин 164-188 800-850 200-220 420-550 9,5 Слабо токсичен
Низкокипящие и криогенные
Аммиак NH3 17,032 681 195 240 7,0 Токсичен
Диборан В2Нб 27,688 430 108 181 - Очень токсичен
Метан СН4 16,043 422 91 112 - Нетоксичен
Водород Н2 2,016 71 13,9 20,4 12,6 Нетоксичен
34 Глава I. Аэрокосмический ЛА как объект исследования траекторий
К группе высококипящих (долгохранимых) горючих относятся
гидразин и его производные, представители группы бороводородов,
спирты, керосин. К числу низкокипящих горючих относятся аммиак,
диборан; к числу криогенных - метан, водород. Большинство долгохра-
нимых горючих высокотоксичны. Применение таких горючих было
связано с тем, что они позволили достичь сравнительно высокого
удельного импульса ЖРД и одновременно были способны к длительно-
му хранению, что было важно на определенных этапах развития ракет-
ной техники. Большое распространение получили гидразин и его про-
изводные (метилгидразин, несимметричный диметилгидразин и др.).
Так, например, топливо на основе несимметричного диметилгидразина
(НДМГ), являющегося очень токсичным, имеет более высокий удель-
ный импульс, чем топливо на основе керосина. Из числа долгохрани-
мых горючих и окислителей наибольший удельный импульс обеспечи-
вает самовоспламеняющееся топливо НДМГ + N2O4. Такое топливо
широко применяется в ракетно-космической технике, например, на PH
"Протон" (СССР), "Ариан-1" (Франция). Бороводородные соединения
(пентаборан, диборан и др.), несмотря на высокую теплотворность, не
получили широкого применения в ракетной технике вследствие высо-
кой токсичности и сложности производства.
Наименее токсичными из долгохранимых горючих являются спир-
ты и керосин. Спирты как горючие компоненты топлива сыграли боль-
шую роль в начале развития ракетной техники. Затем они уступили
свое место керосину, который имеет большую теплотворную способ-
ность.
Топливо на основе керосина в удельном импульсе лишь незначи-
тельно уступает топливу на основе НДМГ. Плотность керосина при-
мерно такая, как и у других долгохранимых горючих. Он весьма досту-
пен и дешев, прост в эксплуатации. Вследствие своих положительных
свойств керосин нашел широкое применение в ракетно-космической
технике. Используется в паре как с жидким кислородом, например, на
PH "Восток", "Союз" (СССР), "Атлас", "Сатурн" (США), так и с
высококипящими окислителями.
Так как керосин - это смесь индивидуальных углеводородов, полу-
чаемых при перегонке или крекинге нефти, то его химический состав
непостоянен и зависит от месторождения нефти. Молекулярная масса,
плотность и другие характеристики керосина могут изменяться в неко-
тором диапазоне. В авиационной и ракетной технике используются
несколько сортов керосина: ТС-1, РТ, Т-6, Т-8В, РГ-1, отличающихся
своими свойствами. Большую плотность имеет керосин марки Т-6
(р > 840 кг/м3). Стехиометрический коэффициент керосина при сгора-
нии в кислороде составляет 3,41. Вместо керосина естественного неф-
тяного происхождения возможно получение синтетических углеводоро-
дов, свойства которых могут быть сформированы в соответствии с
заданными требованиями. Так, например, топливо Шелдайн (США)
имеет плотность 1080 кг/м3.
1.2. Основные типы топлива и двигателей аэрокосмических ЛА
35
Характерным представителем группы криогенных высокотепло-
творных горючих является жидкий водород (нетоксичный в отличие от
высококипящих горючих). Водородно-кислородное топливо, предло-
женное впервые К.Э. Циолковским в 1903 г., обеспечивает наибольший
удельный импульс из всех освоенных типов топлива. Сравнение других
типов топлива обычно проводят с водородно-кислородным топливом,
которое является общепризнанным международным эталоном. Стехио-
метрический коэффициент водорода при сгорании в кислороде состав-
ляет 7,94.
Наряду с положительными свойствами жидкий водород имеет су-
щественные недостатки. Основным из них является его малая плот-
ность, что вместе с криогенной температурой приводит к существенно-
му увеличению габаритов и массы водородных баков по сравнению с
высококипящими горючими. Наибольший удельный импульс водород-
но-кислородного ЖРД реализуется при существенном переобогащении
топлива горючим (аКс < 1), что не позволяет снизить среднюю плот-
ность топлива за счет более плотного окислителя. В результате плот-
ность водородно-кислородного топлива составляет 3504-390 кг/м3, в то
время как керосиново-кислородное топливо имеет плотность
- 1000 кг/м3. Вследствие этого суммарная масса баков водородно-
кислородного топлива существенно больше, чем масса баков, соответ-
ствующая другому типу топлива (при равной массе топлива). В отличие
от других жидкостей водород сжимается при увеличении давления, что
вызывает серьезные трудности в работе и конструировании насосов.
Водород представляет собой пожароопасную жидкость, так как дает с
кислородом и воздухом легковоспламеняющиеся смеси. При использо-
вании водорода на практике возникают трудности, связанные с его
сохранением в жидком состоянии длительное время. Водород вызывает
охрупчивание материалов. Вследствие растворимости водорода в неко-
торых металлах усложняется решение вопросов герметизации. Стои-
мость жидкого водорода пока еще остается очень большой.
Однако, несмотря на перечисленные недостатки, успехи, достигну-
тые в ракетной технике, позволили в значительной мере реализовать
главное преимущество водородно-кислородного топлива-его удель-
ный импульс. Наряду с жидким водородом возможно использование
шугообразного водорода (грубодисперсной смеси жидкого и твердого
водорода). При этом могут быть увеличены как хладоресурс топлива,
так и его плотность (до 82 кг/м3). В настоящее время накоплен доста-
точный опыт применения криогенных компонентов топлива (как кисло-
рода, так и водорода) в результате эксплуатации таких систем выведе-
ния, как "Сатурн", "Space Shuttle" (США), "Энергия" (СССР), "Ариан"
(Франция). Наибольший эффект достигается в случае применения
водородно-кислородного топлива на последних ступенях систем выве-
дения.
С учетом вышесказанного можно заключить, что из числа освоен-
ных горючих компонентов наиболее эффективными для многоразовых
36 Глава 1. Аэрокосмический ЛА как объект исследования траекторий
систем выведения на орбиту являются водород и керосин. Возможно
также рассмотрение жидкого метана, который имеет большую темпера-
туру кипения, чем водород. С целью повышения эффективности жид-
ких топлив изучаются их сочетания с легкими металлами (литий, бе-
риллий, алюминий) и гидридами этих металлов. Такие топлива,
возможно, будут использоваться в перспективе.
В ракетно-космической технике по существу применяется один тип
ЖРД - двухкомпонентный двигатель с соплом Лаваля. При этом для
маршевых ЖРД наиболее широко используется схема двигателя с на-
сосной подачей топлива и с дожиганием генераторного газа. Основные
элементы ЖРД - турбонасосный агрегат, камера сгорания (КС) и реак-
тивное сопло (PC) - рис. 1.4. Горючее и окислитель под высоким давле-
нием подаются из топливных баков
в двигатель. Давление в магистра-
лях создается при помощи турбо-
насосного агрегата, рабочее тело
для питания которого генерируется
в газогенераторе. Через газогенера-
тор обычно пропускается один
компонент и часть другого компо-
нента с получением либо восста-
новительного, либо окислительно-
го газа. Генераторный газ, пройдя
через турбонасосный агрегат,
Рис. 1.4. Схема ракетного двигателя
направляется в камеру сгорания.
Оставшаяся часть второго компонента также поступает в камеру сгора-
ния, где и происходит дожигание. В результате сгорания топливной
смеси температура в КС увеличивается. После выхода из КС продукты
сгорания расширяются в реактивном сопле. Камера ЖРД обычно охла-
ждается одним из компонентов топлива, проходящим до поступления в
КС через тракт охлаждения.
В теории РД для вывода уравнения тяги используется идеализиро-
ванное представление двигателя (без учета выхлопных патрубков и
других элементов, через которые происходит истечение) - см. рис. 1.4.
Тягой ракетного двигателя называют результирующую газодинамиче-
ских сил, действующих на внутренние поверхности двигателя во время
его работы, и сил воздействия окружающей среды на наружную по-
верхность двигателя (за исключением сил внешнего аэродинамического
сопротивления). В теории РД показано, что тяга двигателя равна
7? - (?т Кс + (рс - /?н) Fc.
(1.2)
Здесь Qy - секундный расход массы топлива;
Рс - скорость истечения реактивной струи;
рс - давление на срезе сопла;
рн - атмосферное давление на высоте Н\
Fc - площадь среза реактивного сопла.
1.2. Основные типы топлива и двигателей аэрокосмических ЛА
37
Удельный импульс ракетного двигателя по определению равен
J= R IQ, =Vc + (pc-Рн) Fc/Qt (1.3)
и определяется главным образом первым слагаемым - скоростью исте-
чения реактивной струи.
Основным весовым показателем ЖРД является его удельная масса
Удв = m^JR , где издв - масса двигателя, R - тяга ЖРД на уровне моря
или в пустоте.
В соответствии с формулой Циолковского (1.1) важнейшим показа-
телем ЖРД является его удельный импульс в пустоте Jn При выбран-
ном типе топлива удельный импульс Jn определяется главным образом
геометрической степенью расширения сопла £ = FC/FKP, где FKP-
площадь критического сечения PC. Величина Jn тем больше, чем боль-
ше 8. Тяга ЖРД в пустоте связана с 7П и параметрами потока на срезе
сопла следующим образом:
~ £?т-Л1= Ст^с + PcFq .
От скорости тяга и удельный импульс ЖРД (как и других типов РД)
практически не зависят. При уменьшении высоты эти величины
уменьшаются по отношению к своим пустотным значениям, причем в
соответствии с формулой (1.2) величина уменьшения тяги прямо про-
порциональна давлению атмосферы и площади среза сопла:
^н = ^п — Рн^с- (1-4)
Вследствие этого на первых ступенях PH используются ЖРД с
умеренными значениями 8, обеспечивающими приемлемые потери
тяги, связанные с противодавлением атмосферы. Уменьшить величину
противодавления можно также путем увеличения давления в камере
сгорания ркс, так как площадь Fc обратно пропорциональна р«с • При
увеличении ркс удельный импульс в пустоте несколько улучшается.
Однако вместе с этим увеличивается удельная масса двигателя.
На последних ступенях (при рн » 0) используются ЖРД с больши-
ми значениями 8 с тем, чтобы добиться большего удельного импульса в
пустоте. Однако увеличение размеров сопла приводит к увеличению
удельной массы двигателя. Выбор основных параметров ЖРД (давле-
ния в камере сгорания, геометрической степени расширения сопла,
размерности двигателя и др.) является самостоятельной задачей проек-
тирования, которая тесно связана с оптимизацией траекторий (см.
например, работы [5], [19]).
В случае рассмотрения перспективных одноступенчатых систем
выведения с ЖРД двигатели должны работать во всем диапазоне высот.
С целью уменьшения противоречий между тягово-экономическими
характеристиками ЖРД на малых и больших высотах рассматриваются
различные схемы двигателей со скачкообразным увеличением в полете
геометрической степени расширения сопла. Например, в ЖРД с двухпо-
38 Глава 1. Аэрокосмический ЛА как объект исследования траекторий
зиционным соплом на первом участке полета используется PC с мень-
шим срезом, на втором участке - PC с большим срезом. В двухкамер-
ном ЖРД с коаксиальным расположением камер и сопел на первом
участке работают внутренняя и внешняя камеры, на втором участке
внешняя камера отключается, в результате чего уменьшается площадь
критического сечения PC. Рассматриваются различные варианты ЖРД с
центральным телом или ЖРД линейной схемы. Ожидается, что такие
двигатели способны к саморегулированию при изменении атмосферно-
го давления. Возможны и другие схемы ЖРД.
Воздушно-реактивные двигатели. В отличие от ракетных двига-
телей для работы ВРД используется атмосферный воздух, который
составляет основную часть рабочего тела двигателя. Основным окисли-
телем для ВРД служит атмосферный кислород. В сухом воздухе массо-
вая доля кислорода составляет 23,1 %. На борту ЛА с ВРД, как правило,
расположено только горючее, хотя в некоторых случаях в дополнение к
атмосферному кислороду возможно применение бортового окислителя.
В связи с этим необходимо подчеркнуть разницу терминов примени-
тельно к топливам РД и ВРД. Так как все компоненты топлива ракетно-
го двигателя являются бортовыми, то топливо РД включает в себя как
горючее, так и окислитель. Топливом ЛА с ВРД называются только те
компоненты, которые являются бортовыми. Поэтому в авиации по
сложившейся традиции понятие "топливо” ВРД отождествляется с
понятием ’’горючее". При определении теплотворной способности
топлива ВРД подразумевается, что выделенное в результате горения
тепло относится к 1 кг горючего. Стехиометрический коэффициент £0
топлива ВРД определяется как масса воздуха, необходимого для полно-
го сжигания 1 кг горючего. Коэффициент избытка воздуха по определе-
нию равен
<^кс = Qb/(QtLq).
Здесь £?в и - секундные расходы воздуха и бортового топлива.
Основным типом горючего в современной авиации является керо-
син, который является удобным в эксплуатации и обеспечивает прием-
лемые характеристики авиационных двигателей. Жидкий водород в
авиации, в отличие от ракетно-космической техники, пока еще не нашел
практического применения, несмотря на то, что его теплотворная спо-
собность в ~ 2,8 раза больше, чем у керосина. Это связано с нескольки-
ми причинами. Основная из них заключается в том, что плотность
водорода на порядок меньше, чем плотность керосина. Если у ракетных
ЛА при переходе от керосина к водороду плотность топлива (в паре с
кислородом) уменьшается примерно в 3 раза, то у ЛА с ВРД аналогич-
ное уменьшение становится 12-кратным. В результате при использова-
нии водорода будут существенно увеличиваться объем топливных баков
и мидель самолета, что приведет к ухудшению его аэродинамических
характеристик. Удельная масса водородных баков, как уже было отме-
чено выше, существенно больше керосиновых. Наконец, стоимость
1.2. Основные типы топлива и двигателей аэрокосмических ЛА
39
водорода в настоящее время существенно больше по сравнению с
керосином.
Тем не менее, в будущем отношение к водороду как к универсаль-
ному энергоносителю может и должно измениться. Во-первых, нефтя-
ные запасы на Земле ограничены, во-вторых, в результате сжигания
углеводородного горючего увеличивается загрязнение окружающей
среды. В отличие от этого использование водородной технологии в
промышленности и на транспорте - это путь к экологическому равно-
весию на Земле. С одной стороны, для производства водорода путем
электролиза воды имеются практически неограниченные запасы сырья
(необходимы только мощные и дешевые источники электроэнергии). С
другой стороны, при сжигании водорода с дозированным количеством
кислорода не создается вредных выбросов, ликвидируется опасность
парникового эффекта. После сжигания водород в виде воды вновь
возвращается в кругооборот природы. Таким образом, вследствие на-
званных факторов в обозримом будущем может произойти вынужден-
ный переход дозвуковой и сверхзвуковой авиации на водородное топли-
во, равно как и других видов транспорта и промышленности [24].
В отличие от современных дозвуковых и сверхзвуковых самолетов
аэрокосмические ЛА при числах М > 5-ьб будут подвергаться сущест-
венно большему аэродинамическому нагреванию. Для охлаждения
конструкции самолета и двигателя наиболее рационально использовать
бортовое топливо, из всех типов которого наибольшим хладоресурсом
обладает жидкий водород (примерно в 20 раз больше, чем у керосина и
в 5 раз больше, чем у метана, с учетом пределов возможного подогрева
топлива). Вследствие этого водород является практически единствен-
ным типом горючего для обеспечения больших гиперзвуковых скоро-
стей полета в атмосфере [15]. Керосин как альтернатива водороду
может рассматриваться только применительно к начальным участкам
разгона аэрокосмических ЛА. Жидкий метан, имеющий большую
плотность, чем водород, но меньшие теплоту сгорания и хладоресурс,
может оказаться эффективным в диапазоне скоростей, соответствую-
щих переходу от керосина к водороду (рис. 1.5). Опыт применения
метана в авиации обеспечит предпосылки для перехода в перспективе к
жидкому водороду.
Основные характеристики керосина, метана и водорода приведены
в табл. 1.3 (по данным работы [68]). Более подробные характеристики
водорода приведены в справочнике [24].
Удельный импульс ВРД по определению равен отношению тяги к
секундному расходу массы бортового топлива. Так как секундный
расход бортового топлива ВРД существенно меньше, чем соответст-
вующий расход всей топливной смеси, то удельный импульс у ВРД
существенно больше, чем у ракетных двигателей. Это главная причина,
по которой ЖРД не нашли широкого применения в авиации.
40 Глава 1. Аэрокосмический ЛА как объект исследования траекторий
Рис. 1.5. Диапазоны возможного использования по числу
М полета различных типов горючего и окислителя ВРД
Таблица 1.3
Основные характеристики топлив ВРД
Показатель Керосин Метан Водород
Молекулярная формула ~15%Н ~ 85 % С СН4 Н2
Температура плавления/кипения, К 2134-223 90,7 11,2
при давлении 0,1013 Мпа 400-590 111,7 20,3
Плотность топлива рт, кг/м3 775-840 422 70,8
при температуре, К (293) (111,7) (20,3)
Плотность 50% шуги, кг/м3 437 78,1
при температуре, К (91) (11,2)
Теплота сгорания горючего низшая Ни, МДж/кг 42,9-43,3 50,1 120
Тепловой эффект сгорания криотоплива, МДж/кг - 48,8 116,1
Хладоресурс, МДж/кг при нагреве в диапазоне температуры, К Стехиометрический коэффициент £0 при сгорании в воздухе 0,93 (293-533) 14,7-14,9 2,95 (112-922) 17,21 18,0 (20-1273) 34,38
В современной авиации наибольшее распространение получили
различные типы газотурбинных двигателей (ГТД). Самым простым
типом ГТД является турбореактивный двигатель (ТРД). ТРД состоит из
воздухозаборника (ВЗ), компрессора, камеры сгорания, турбины и
реактивного сопла. При полете со скоростью V набегающая струя воз-
1.2. Основные типы топлива и двигателей аэрокосмических ЛА
41
духа частично сжимается в воздухозаборнике. Затем сжатие воздуха
происходит в компрессоре, приводимом во вращение турбиной. Из
компрессора воздух поступает в камеру сгорания, где в него впрыскива-
ется горючее и осуществляется сгорание топливовоздушной смеси, в
процессе которого температура продуктов сгорания повышается до
величины, допускаемой жаропрочностью горячей части двигателя. В
турбине часть потенциальной энергии газов преобразуется в механиче-
скую работу на валу, передаваемую компрессору. Расширение продук-
тов сгорания происходит в реактивном сопле, причем скорость истече-
ния продуктов сгорания больше скорости полета, что и обусловливает
появление тяги реактивного двигателя.
В теории ВРД тяга двигателя, определенная по внутренним пара-
метрам (без учета внешнего сопротивления двигателя), записывается
следующим образом:
Я = (0в + 0т) Рс + (рс ~Рн) Fq- Q^V. (1.5)
Здесь 0в-секундный расход массы воздуха. В отличие от выражения
(1.2) для тяги РД в (1.5) входит количество движения входной струи
воздуха со знаком минус.
В теории ВРД широко используется удельная тяга 7?уд (тяга, отне-
сенная к секундному расходу воздуха). Если пренебречь величиной 0Т
по сравнению с 0в, то удельную тягу в случае полного расширения
струи (рс = Рн) можно записать как
7?уд«Гс-Г. (1.6)
В ВРД прямой реакции располагаемая работа термодинамического
цикла равна разности значений кинетической энергии газа на выходе из
двигателя и на входе в него:
Ае = (Гс2 - Г2)/2 . (1.7)
Здесь работа Ае соответствует 1 кг воздуха. Выражение (1.6) с учетом
(1.7) можно переписать следующим образом:
Луд® -j2Ae+V2 - V. (1.8)
Так как величина Ле является ограниченной (в частности, опреде-
ляется максимально допустимой температурой горячей части ВРД), то
из (1.8) следует, что при увеличении скорости полета тяга ВРД будет
убывать. Это является одним из главных недостатков ВРД по сравне-
нию с ЖРД, тяга и удельный импульс которого практически не зависят
от скорости полета. Кроме того, удельная масса ВРД в несколько раз
больше аналогичного показателя ЖРД. Вследствие этих недостатков в
определенных случаях ВРД может проигрывать ЖРД.
Для полета со сверхзвуковой скоростью полета в авиации приме-
няются одно- и двухконтурные турбореактивные двигатели с форсажем
(ТРДФ и ТРДДФ). Схемы этих двигателей несколько отличаются от
42 Глава 1. Аэрокосмический ЛА как объект исследования траекторий
схемы ТРД, однако принцип создания тяги аналогичен. Современные
ТРДФ и ТРДДФ могут обеспечить разгон самолета только до чисел
М = 34-3,5; при дальнейшем увеличении скорости полета их тяга резко
уменьшается. Для полета самолета с большими скоростями (М > 34-3,5)
должны использоваться другие типы двигателей, например прямоточ-
ные (бескомпрессорные) ВРД, ракетные или комбинированные двигате-
ли. В настоящее время известно большое число различных типов пер-
спективных ВРД и их комбинаций. Схемы таких двигателей, принципы
их работы и возможные характеристики изложены в соответствующей
литературе: [39], [53], [68], [90].
Каждый тип ВРД имеет свой диапазон наивыгоднейшего примене-
ния. На рис. 1.6 показаны примерные диапазоны работы по числу М
полета основных типов двигателей, которые наиболее часто рассматри-
ваются применительно к аэрокосмическим ЛА. Дадим краткую харак-
теристику этим двигателям.
В диапазоне чисел Маха от взлетных значений до значений 3,04-3,5
наиболее рациональным является ТРДДФ. Однако такой двигатель
должен иметь определенные отличия от своего аналога, применяюще-
гося на современных сверхзвуковых самолетах. Отличие заключается
Рис. 1.6. Диапазоны работы по числу М полета различных типов двигателей
1.2. Основные типы топлива и двигателей аэрокосмических ЛА
43
прежде всего в более низком уровне степени повышения давления в
компрессоре и степени двухконтурности и большей температуре газа
перед турбиной. Основным требованием к такому ТРДДФ является
простота и малая удельная масса двигателя. Двигатель, либо должен
работать на криогенном топливе (метан, водород), либо должен иметь
двухтопливную систему, когда в основной камере сгорания использует-
ся керосин, а в форсажной - водород.
Для полета ЛА в диапазоне чисел М = 34-6 наиболее рациональным
является сверхзвуковой прямоточный воздушно-реактивный двигатель
с дозвуковой скоростью потока внутри камеры сгорания (ПВРД). Сжа-
тие воздуха осуществляется в сверхзвуковом воздухозаборнике, расши-
рение продуктов сгорания - в регулируемом сверхзвуковом сопле.
Компрессор в ПВРД отсутствует, что приводит к уменьшению эффек-
тивности двигателя при малых (дозвуковых) скоростях полета. Кроме
того, при уменьшении начальной скорости работы ПВРД увеличивается
площадь поперечного сечения камеры сгорания, отнесенная к площади
входа в воздухозаборник, что приводит к увеличению массы двигателя.
Вследствие этого ПВРД может рассматриваться только в комбинации с
другими типами двигателей, например с ТРДДФ. Число М включения
ПВРД является оптимизируемым параметром. В качестве топлива
ПВРД может использоваться как керосин, так и водород. В настоящее
время ПВРД нашли применение в основном на беспилотных ЛА, ис-
пользуемых при больших сверхзвуковых скоростях полета.
Вместо комбинации ГТД + ПВРД возможно использование комби-
нированного турбопрямоточного двигателя (ТПД), который имеет два
контура: турбореактивный и прямоточный. Такой двигатель сочетает в
себе преимущества ГТД в диапазоне чисел М < 3,04-3,5 с преимущест-
вами ПВРД при М > 3,04-3,5. Расположение контуров может быть па-
раллельным или коаксиальным (тандемным). Преимущество коакси-
альной схемы - в меньших лобовых размерах двигателя и наличии
общих элементов, упрощающих конструкцию двигательной установки.
Недостаток - невозможность одновременной работы обоих контуров в
широком диапазоне чисел М полета. Число М переключения контуров
является оптимизируемым параметром.
В диапазоне чисел М = 04-6 может использоваться ракетно-
турбинный двигатель (РТД), который объединяет в себе циклы и эле-
менты ГТД и РД. Компрессор РТД приводится во вращение турбиной,
работающей от ракетного двигателя, играющего роль генератора газа.
Возможны различные схемы РТД. Наиболее изученными являются
газогенераторная (РТДгг), парогазогенераторная (РТДпг) и пароводо-
родная (РТДп) схемы. Топливом РТДгг и РТДпг являются жидкий
водород и жидкий кислород. В РТДп в качестве топлива используется
только водород, который перед выходом на турбину газифицируется и
нагревается до высокой температуры в теплообменнике, установленном
в основной камере сгорания. У этой схемы больше как удельный им-
пульс, так и удельная масса двигателя по сравнению с РТДпг и РТДгг.
44 Глава 1. Аэрокосмический ЛА как объект исследования траекторий
Применение сжижения атмосферного воздуха в РТДп позволяет еще
более увеличить его удельный импульс. Общим недостатком всех схем
РТД является неблагоприятное протекание дроссельных характеристик,
что вызывает ухудшение экономичности двигателя в крейсерском поле-
те.
До чисел М » 6 способен работать двухконтурный двигатель с ох-
лаждением воздуха на входе и с форсажной камерой (ТРДДФТ). Топли-
вом такого двигателя является водород. Весовые и высотно-скоростные
характеристики ТРДДФТ близки к соответствующим характеристикам
РТДп. Дроссельные характеристики являются более благоприятными
по сравнению с РТД.
Ракетно-прямоточный двигатель (РПД), органически сочетающий в
себе свойства ПВРД и РД, в отличие от ПВРД, может работать, начиная
от взлета ЛА. В данном случае ракетный двигатель является струйным
эжектором прямоточного ВРД. Продукты сгорания РД за счет энергооб-
мена увеличивают сжатие атмосферного воздуха, поступающего в
ПВРД, и смешиваются с этим воздухом (в схеме РПД со смешением)
или догорают в смеси с воздухом в камере сгорания ПВРД (в схеме РПД
с догоранием). При малых скоростях полета тягово-экономические
характеристики такого двигателя лучше, чем у ЖРД, но выигрыш дос-
тигается ценой увеличения удельной массы РПД. При больших сверх-
звуковых скоростях характеристики РПД и ПВРД близки. Топливом
РПД является керосин + О2 или Н2+ О2.
Жидкостно-воздушный ракетный двигатель (ЖВРД) отличается от
обычного ЖРД тем, что бортовой окислитель полностью или частично
заменяется атмосферным воздухом, предварительно сжиженным и
сжатым до высокого давления перед его подачей в камеру сгорания.
Охлаждение и сжижение атмосферного воздуха осуществляется в
специальном теплообменнике, установленном за воздухозаборником.
Эффективное сжижение атмосферного воздуха возможно только в
случае использования криогенного бортового топлива, обладающего
большим хладоресурсом. Наиболее подходящим для этой цели является
водородно-кислородное топливо. Режим сжижения эффективен до
чисел М = 64-7. При больших числах М полета воздушный тракт двига-
теля перекрывается и включается режим работы обычного ЖРД. Таким
образом, данный тип двигателя способен работать во всем диапазоне
скоростей полета вплоть до орбитальных. Удельная масса ЖВРД мень-
ше, чем комбинации РТДп + ЖРД. Однако удельный импульс на режи-
ме сжижения значительно уступает аналогичной величине РТДп. Объ-
ясняется это тем, что располагаемый хладоресурс бортового топлива
позволяет сжижать воздух со значительно меньшей массой, чем нужно
для полного сгорания водорода. В результате в камеру сгорания должно
подаваться топливо либо переобогащенное горючим, либо с дополни-
тельным бортовым окислителем.
Все вышеперечисленные воздушно-реактивные двигатели способ-
ны работать до чисел М полета, не превышающих 64-7. Единственным
1.2. Основные типы топлива и двигателей аэрокосмических ЛА
45
типом ВРД, способным эффективно работать при числах М > 6-5-7,
является гиперзвуковой прямоточный воздушно-реактивный двигатель
(ГПВРД). В отличие от ПВРД в камере сгорания такого двигателя ско-
рость потока является сверхзвуковой. Теоретически ГПВРД может
использоваться в диапазоне чисел Маха от ~ 6 до 154-20. Топливом
ГПВРД является водород.
Гиперзвуковой ракетно-прямоточный двигатель (ГРПД) представ-
ляет собой разновидность ГПВРД. В таком двигателе для форсирования
тяги используется бортовой кислород. В результате, несмотря на неко-
торое уменьшение удельного импульса, скорость выключения ГРПД
может быть увеличена по сравнению с ГПВРД [13]. При больших ско-
ростях полета после отключения воздушного тракта ГРПД способен
работать на режиме ЖРД. Таким образом, в отличие от комбинации
"ПВРД + ЖРД, масса силовой установки на базе ГРПД может быть
уменьшена на величину массы ЖРД.
Альтернативой комбинации ПВРД и ГПВРД является двухрежим-
ный ГПВРД (ДГПВРД) с единым воздушным трактом. В таком двигате-
ле дозвуковая камера сгорания устанавливается за сверхзвуковой КС.
Объединение двух трактов в одном позволяет уменьшить массу двига-
теля, однако диапазон работы ДГПВРД будет несколько меньше, чем у
комбинации ПВРД и ГПВРД.
Итак, разгон ЛА до больших гиперзвуковых скоростей
(М > 6-5-7) может быть осуществлен только путем использования не-
скольких типов ВРД. При этом заключительный этап выведения на
орбиту возможен только с использованием ЖРД, который, по существу,
является единственным типом двигателя, работоспособным во всем
диапазоне скоростей полета аэрокосмических ЛА. Следует оговориться,
что теоретически возможно выведение на орбиту без использования
маршевых ЖРД. Для этого необходимы такие характеристики ГПВРД,
которые могли бы обеспечить эффективный разгон ЛА на высотах
404-50 км до скорости, большей, чем орбитальная. После отключения
ГПВРД высота ЛА будет увеличиваться в баллистическом полете до
заданного конечного значения высоты. Импульс довыведения в апогее
переходной орбиты в этом случае может быть осуществлен при помощи
ЖРД орбитального маневрирования.
1.3. Состояние работ по созданию многоразовых систем
выведения на орбиту и гиперзвуковых ЛА
В настоящее время все системы выведения на орбиту, за исключе-
нием "Space Shuttle" (США), являются одноразовыми. С целью даль-
нейшего снижения удельной стоимости выведения, являющейся одним
из основных технико-экономических показателей таких систем, во
многих странах мира ведутся исследования различных типов многора-
зовых систем выведения на орбиту. При этом рассматриваются как
46 Глава 1. Аэрокосмический ЛА как объект исследования траекторий
вертикальный, так и горизонтальный способы старта, одно- и двухсту-
пенчатые системы, различные комбинации ВРД и ЖРД. Вместе с этим в
авиации идет последовательное освоение гиперзвуковых скоростей
полета, в результате чего в перспективе возможно слияние гиперзвуко-
вой авиационной и многоразовой ракетно-космической техники. На-
пример, гиперзвуковой самолет может использоваться как для полета на
заданную дальность, так и в качестве первой ступени МКТС. Важней-
шим достоинством гиперзвукового полета является существенное
сокращение времени движения по сравнению с дозвуковым полетом. В
настоящее время известно большое число проектов гиперзвуковых
самолетов. Исследуются одно- и двухступенчатые схемы ЛА. Выбира-
ется рациональная крейсерская скорость полета. Рассматриваются
различные типы топлива и двигателей. Изучаются основные проблемы
гиперзвукового полета, одной из которых является проблема звукового
удара [112].
Очевидно, что для создания нового поколения аэрокосмических
ЛА необходим существенный скачок в развитии авиационно-
космической отрасли и смежных с ней отраслей промышленности. В
нашей стране и за рубежом к настоящему времени уже накоплен боль-
шой научно-технический потенциал для создания многоразовых систем
выведения и гиперзвуковых самолетов. Теоретические и эксперимен-
тальные работы в этой области были начаты еще задолго до начала
космической эры. Впервые концепция воздушно-космического самоле-
та была сформулирована советским ученым Ф.А. Цандером в статье
"Описание межпланетного корабля системы Ф.А. Цандера" (1924 г.).
Первый проект воздушно-космического самолета с ЖРД был разрабо-
тан в Германии в 40-х годах (авторы Е. Зенгер и И. Бредт). Предполага-
лось, что суборбитальный ВКС, разгоняемый при помощи ракетного
ускорителя, будет использоваться в качестве антиподного бомбарди-
ровщика. Старт двухступенчатой системы должен был осуществляться
с использованием монорельсовой катапульты длиной 2,9 км. Расчетный
угол наклона траектории равнялся 30°, число М старта-1,5. Этот
проект намного опережал свое время.
В СССР углубленные проработки аэрокосмических ЛА и их сило-
вых установок были начаты в 50-60-х годах. В этот период разрабаты-
вался проект авиационно-космической системы "Спираль", состоящей
из гиперзвукового самолета-разгонщика и орбитального самолета с
ракетным ускорителем (головной разработчик - ОКБ А.И. Микояна).
Построенный аналог ОС успешно испытывался в полете в ЛИИ (старт
осуществлялся с дозвукового самолета Ту-95) [21]. В связи с разработ-
кой АКС "Спираль" были начаты проектные исследования пароводо-
родных РТД в ОКБ А.М. Люльки и Н.Д. Кузнецова [54].
Проектные разработки аэрокосмических ЛА требовали соответст-
вующей экспериментальной базы. В соответствии с этими потребно-
стями в ЦАГИ в 60-80-х годах была создана мощная гиперзвуковая
экспериментальная база, позволяющая проводить исследования аэро-
1.3. Состояние работ по созданию многоразовых систем выведения 47
динамических характеристик, моделируя числа Маха и Рейнольдса
практически во всем диапазоне их изменения по траектории полета
орбитального самолета. Так, например, крупноразмерная гиперзвуковая
аэродинамическая труба Т-117 позволила проводить отработку аэроди-
намической компоновки аэрокосмических ЛА в условиях, близких к
полетным [21].
В 80-х годах в СССР был разработан и построен многоразовый ор-
битальный самолет "Буран” (головной разработчик - НПО "Молния”,
главный конструктор - Г.Е. Лозино-Лозинский). В 1988 г. ОС "Буран”
был выведен на орбиту при помощи ракеты-носителя "Энергия", а
затем осуществил планирующий спуск в атмосфере и посадку на аэро-
дром в автоматическом режиме.
В период 1993-2003 гг. по заказу Федерального космического
агентства в ЦНИИМаш и ЦАГИ были проведены комплексные иссле-
дования перспектив создания многоразовых космических транспортных
систем - НИР "Орел" [115], [121] и "Гриф" [77], [78]. В результате этих
работ из возможного многообразия концепций были выбраны несколько
базовых МКТС и затем в конструкторских бюро разработаны техниче-
ские предложения по этим системам выведения.
В классе МКТС вертикального старта подробно проработаны две
системы (головной исполнитель ЦНИИМаш) [121] - рис. 1.7:
МВРН - двухступенчатая всеазимутальная PH (с многоразовой
первой ступенью), предназначенная для выведения транспортных
грузов массой до 25 т или многоразового орбитального самолета;
МКР - многоразовый космический ракетоплан.
В классе МКТС горизонтального старта (головной исполнитель
ЦАГИ) подробно проработаны три базовые МКТС горизонтального
старта [115].
МАКС (НПО "Молния") предполагает создание многоцелевой
авиационно-космической системы, состоящей из двух ступеней: дозву-
кового самолета-носителя и ракетно-космической ступени, которая
может быть выполнена в различной конфигурации и комплектации с
высоким уровнем унификации [132]. Стартовая масса АКС составляет
630 т, масса второй ступени - 275 т. В базовом варианте МАКС
(рис. 1.8) в качестве второй ступени используется орбитальный самолет
МКР
Рис. 1.7. МКТС
вертикального старта
48 Глава /. Аэрокосмический ЛА как объект исследования траекторий
Рис. 1.8. Многоцелевая авиационно-
космическая система МАКС в варианте с
орбитальным самолетом и внешним
топливным баком
с внешним одноразовым топливным баком. В дальнейшем по мере
развития системы предполагается разработка других вариантов ракет-
ной ступени, в том числе многоразового воздушно-космического само-
лета с перспективным уровнем технологии.
В качестве первой ступени МАКС предусматривается использова-
ние модифицированного самолета-носителя Ан-225 "Мр!я" с двигате-
лями Д-18Т или TRENT. На орбитальном самолете планируется уста-
новка трехкомпонентных ЖРД РД-701 (разработка НПО ’’Энергомаш").
Топливом ЖРД являются керосин, водород и кислород [115].
В НПО "Молния" в процессе разработки ОС "Буран", а также в
рамках проекта МАКС и других концепций авиационно-космических
систем накоплен большой практический опыт в области ключевых
гиперзвуковых технологий: по конструкции и теплозащите ОС, по
криогенным топливным бакам, по трехкомпонентному ЖРД и др. [2].
МИГАКС (КБ "МИГ" им. А.И. Микояна) представляет собой двух-
ступенчатую АКС, состоящую из гиперзвукового самолета-разгонщика
с ВРД и ВКС с ЖРД (рис. 1.9) [115]. Разделение ступеней осуществля-
ется при числе М = 6. Стартовая масса АКС составляет 420 т. Самолет-
разгонщик имеет комбинированную силовую установку (КСУ). На
первом участке разгона до числа М = 3,5 используются ТРДДФ и час-
тично ПВРД. На втором участке разгона (М = 3,5ч-6,0) применяются
только ПВРД (вход в ТРДДФ при этом закрыт). В ТРДДФ в качестве
топлива используется керосин (в основной камере сгорания) и водород
(в форсажной камере). Топливом ПВРД является водород. Применение
на ГСР двух типов топлива придает дополнительные возможности
АКС: автономность при перебазировании, использование существую-
щих аэродромов, обеспечение дозаправки в воздухе для выведения ПГ
на приэкваториальные орбиты.
Аэродинамическая компоновка ГСР является интегральной с ниж-
ним расположением КСУ. Носовая часть фюзеляжа используется для
поджатия входной струи воздуха, хвостовая часть - в качестве реактив-
ного сопла КСУ Двухконтурный плоский воздухозаборник с внутрен-
ней створкой, распределяющей в области горла поток по контурам
ТРДДФ и ПВРД, отработан экспериментально в аэродинамических
трубах ЦАГИ. Концепция МИГАКС была сформирована из условия
максимума выводимого на орбиту ПГ с учетом последующего возвра-
щения ГСР на стартовый аэродром. При такой схеме полета параллакс
выведения составляет 620 км.
Ту-2000 (АНТК им. А.Н. Туполева) представляет собой односту-
пенчатый ВКС с ВРД и ЖРД (рис. 1.10) [137]. Стартовая масса ВКС
1.3. Состояние работ по созданию многоразовых систем выведения 49
Рис. 1.9. Двухступенчатая авиационно-
космическая система МИГАКС с ГСР
Рис. 1.10. Одноступенчатый
ВКС ТУ-2000
составляет 250^-350 т. На первом участке разгона работают ТРД, далее -
широкодиапазонный ПВРД с до- и сверхзвуковым горением (до чисел
М=12-Н5), на последнем участке - ЖРД. Аэродинамическая компо-
новка ВКС является интегральной с нижним расположением КСУ, что
позволяет изменять тягу ПВРД при помощи угла атаки.
В АНТК им. А.Н. Туполева накоплен значительный потенциал в
области разработки ВКС на жидководородном топливе, имеется опыт
по использованию на дозвуковом самолете сжиженного природного
газа.
Помимо базовых концепций МКТС горизонтального старта в Рос-
сии исследовались альтернативные варианты аэрокосмических систем,
например, одноступенчатый ВКС МИГ-2000 с ЖВРД (КБ "МИГ"
им. А.И. Микояна и ИЦ им. М.В. Келдыша) [121], ЛА "Аякс" (НПО
"Ленинец") [54] и др.
Наибольшие трудности при создании АКС и ВКС связаны с разра-
боткой их силовых установок [12]. В этой области накоплен большой
опыт. Так, например, в СНТК им. Н.Д. Кузнецова создан эксперимен-
тальный двигатель НК-88, работающий на жидком водороде, и его
модификация, использующая в качестве топлива сжиженный природ-
ный газ; эти двигатели прошли летные испытания на самолете Ту-155
[68]. В ЦИАМ проведены стендовые испытания турбопрямоточного
двигателя (М = 4,5) и несколько летных испытаний водородного осе-
симметричного двухрежимного ГПВРД (в диапазоне чисел М = 3,0-?-6,5)
[54]. Имеются и другие важные разработки в обеспечение создания
МКТС, ГС и их силовых установок.
Очевидно, что создание таких аппаратов, как Ту-2000, подразуме-
вает наличие суперперспективных технологий, материалов, конструк-
ции, оборудования и относится к дальней перспективе. В настоящее
время из-за отсутствия ряда технологий и неточного знания исходных
данных имеется большой технический и финансовый риск создания
перспективных аэрокосмических ЛА. В результате исследований МКТС
в России и за рубежом пришли к выводу, что обязательным этапом
создания таких систем должна стать разработка экспериментального
аппарата - демонстратора гиперзвуковых ключевых технологий. Боль-
шинству из требований, предъявляемых к экспериментальному ЛА,
отвечает концепция многоцелевой летающей лаборатории EMPL, пред-
ложенная ЦАГИ совместно с ЭМЗ им. В.М. Мясищева и НПО "Сатурн"
им. А.М. Люльки в 1992 году [113]. В этой концепции летающая лабо-
ратория представляет собой многоразовый гиперзвуковой разгонщик
50 Глава 1. Аэрокосмический ЛА как объект исследования траекторий
____ воздушного старта (рис. 1.11) с собст-
венными маршевыми ЖРД, обеспечи-
вающими разгон до чисел М = 6н-8.
Разгонщик должен стартовать с дозвуко-
вого самолета-носителя, например,
Рис. 1.11. Гиперзвуковая Ил-76МФ и способен нести на себе
летающая лаборатория EMPL свободнолетающую крупномасштабную
модель гиперзвукового летательного
аппарата или неотделяемые испытуемые
объекты: модуль ГПВРД или элемент конструкции. Кроме того, гипер-
звуковой разгонщик EMPL может быть использован для выведения на
орбиту малоразмерных спутников, что будет способствовать быстрой
окупаемости затрат на создание такой системы.
Помимо EMPL в России проработан целый ряд демонстраторов:
МАКС-Д (НПО "Молния”), ИГЛА (ЦИАМ) и др. [18], [141].
Значительный научно-технический задел в области создания ги-
перзвуковых самолетов и аэрокосмических систем накоплен также в
США. В начале 60-х годов экспериментальный самолет Х-15 в кратко-
временном полете достигал чисел М = 54-7. В период 1960-1975 гг.
велась отработка концепции орбитального пилотируемого самолета,
входа в атмосферу и самой посадки (экспериментальные аппараты
Х-24, М-2, HL-10 и др.). Результаты этих исследований были использо-
ваны при создании системы выведения "Space Shuttle”.
В начале 80-х годов в США фирмой Boeing был предложен проект
двухступенчатой АКС на базе дозвукового самолета-носителя В-747.
Фирмой Pratt & Whitney построен и испытан демонстрационный вари-
ант пароводородного РТД. В НИЦ им. Лэнгли разработан и испытан
модульный двухрежимный ГПВРД, который при числах М = 5-^-6 рабо-
тал в режиме ПВРД, а при больших скоростях (до чисел М= 10) - в
режиме ГПВРД. Полученный экспериментальный материал частично
подтвердил работоспособность ГПВРД до чисел М « 10 [68].
Большой шаг сделан в середине 80-х годов в ходе 8-летней про-
граммы NASP [129], цель которой состояла в создании технического
задела для широкого круга трансатмосферных и воздушно-космических
ЛА различного назначения. Этой программой предусматривалось соз-
дание экспериментального самолета-демонстратора Х-30, способного
после взлета с обычного аэродрома разгоняться в атмосфере до скоро-
сти, соответствующей числу М = 25, выходить на низкую орбиту и
возвращаться, маневрируя в атмосфере Земли. Предполагалось, что
Х-30 будет иметь массу около 120 т, оснащаться комбинированной
силовой установкой на базе двухрежимного ГПВРД и использовать в
качестве топлива шугообразный водород. В продолжение этих работ
фирма Lockheed Martin возглавила разработку экспериментального ЛА
Х-33 с водородно-кислородными ЖРД. Такой аппарат должен был
продемонстрировать полеты до чисел М = 15.
1.3. Состояние работ по созданию многоразовых систем выведения 51
В середине 80-х годов фирмой McDonnell Douglas разрабатывался
проект гиперзвукового пассажирского самолета "Ориент-экспресс" с
числом Мтах = 5.
Программа NASA Hyper-Х предусматривает летные испытания во-
дородного ГПВРД при числах М = 5, 7 и 10 с применением малораз-
мерных моделей гиперзвукового самолета [138]. Проработки такого
самолета, рассчитанного на число Мтах=10, проведены фирмой
Boeing.
В США разработан перспективный план реализации американских
гиперзвуковых ЛА с ВРД до 2025 года [135]. По этому плану в 2020 г.
должен быть создан стратегический (коммерческий) самолет с числом
М = 10, в 2025 г. должны быть созданы АКС и ВКС с комбинированны-
ми силовыми установками.
В Японии также ведутся работы в данной области. Так, программа
исследований и разработок японского водородного ВКС JASP охваты-
вает все основные направления ключевых технологий, включая созда-
ние водородно-метанового испытательного комплекса и проведение
экспериментальных исследований крупномасштабных моделей ГПВРД
при числах М < 8 [133]. Водородные технологии исследуются примени-
тельно к пароводородному РТД ATREX-500. В рамках программы
HYPR Япония совместно с США, Францией и Великобританией разра-
батывает турбопрямоточный двигатель, способный работать до чисел
М = 5 (основная камера сгорания работает на керосине, форсажно-
прямоточная - на метане) [134].
В Германии национальная программа в области перспективных
космических транспортных систем в течение нескольких лет ориенти-
ровалась на создание двухступенчатой системы SANGER, где первая
ступень с ВРД должна была достигать скорости, соответствующей
числу М = 6-е-7 [131]. Программа предусматривала также постройку
самостоятельно взлетающего пилотируемого демонстратора первой
ступени HYTECH массой около 7 т.
В Великобритании в конце 80-х годов фирмой ВАе проводились
исследования одноступенчатого ВКС HOTOL с ЖВРД. Старт ВКС
предполагался с разгонной тележки. До числа М = 5 двигатель должен
был работать в режиме сжижения, затем - как обычный ЖРД. После
завершения этих исследований фирма ВАе предложила проект одно-
ступенчатого ВКС Interim HOTOL с водородно-кислородными ЖРД
[136]. ВКС должен был стартовать с дозвукового самолета-носителя
Ан-225. В разработке проекта ВКС участвовали Россия и Украина.
В 1998 г. в рамках исследовательской программы PREPHA (Фран-
ция) проведены стендовые испытания ГПВРД (М = 7,5), который рабо-
тал 10 секунд.
Большая часть работ по созданию многоразовых аэрокосмических
систем не получила дальнейшего развития вследствие ограниченности
финансирования в данной области. Однако, основываясь на далеко
неполном перечне различных разработок, можно заключить, что веду-
52 Глава 1. Аэрокосмический ЛА как объект исследования траекторий
щими аэрокосмическими державами накоплен большой научно-
технический задел для создания многоразовых аэрокосмических лета-
тельных аппаратов и систем. В настоящее время основные усилия
направляются на разработку ключевых технологий, а также на их де-
монстрацию в условиях, близких к реальным. Такой подход позволит
значительно снизить технический и финансовый риск, и в ближайшем
будущем может появиться основа для создания многоразовых систем
выведения на орбиту.
ГЛАВА 2
ОБЩИЕ ПОЛОЖЕНИЯ ДИНАМИКИ
ПОЛЕТА АЭРОКОСМИЧЕСКИХ ЛА
В данной главе приводятся общие положения динамики полета и
даются основные определения, необходимые для последовательного
изложения дальнейшего материала (см. также работы [7], [56], [63],
[71], [86], [111] и др.).
2.1. Уравнение движения в векторной форме
Движение летательного аппарата с неработающим двигателем
осуществляется под действием главного вектора внешних сил R. (Здесь
и далее векторные величины обозначаются жирным шрифтом). Для
описания движения ЛА в данном случае используется основное урав-
нение динамики:
(2.1)
dx
Здесь т - масса ЛА; VA-вектор абсолютной скорости полета в инер-
циальной системе отсчета; т - время полета.
Внешние силы можно разделить на массовые G и поверхностные
силы П:
R = G + H.
Массовые силы обусловлены притяжением Земли и других небес-
ных тел, их величина пропорциональна массе ЛА. Поверхностные силы
возникают вследствие воздействия внешнего потока при движении ЛА
в достаточно плотных слоях атмосферы. При неработающем двигателе
поверхностные силы по существу являются аэродинамическими. Со-
гласно ГОСТу 20058-80 [28] главный вектор аэродинамических сил
называется аэродинамической силой планера и обозначается RA [64].
Аэродинамическая сила представляет собой интеграл сил давления и
54
Глава 2. Общие положения динамики полета
трения по всей смачиваемой поверхности ЛА и определяется формой
внешней поверхности, скоростью движения и параметрами атмосферы.
Летательный аппарат с работающим двигателем с точки зрения ме-
ханики представляет собой тело переменного состава. Движение ЛА
осуществляется под действием главного вектора внешних сил R и
вследствие изменения своего внутреннего состава. В процессе движе-
ния от ЛА могут отделяться частицы с некоторой скоростью или при-
соединяться к нему. При этом масса ЛА может как уменьшаться, так и
увеличиваться (в общем случае), а может оставаться постоянной (при
равенстве масс отделяемых и присоединяемых частиц в единицу вре-
мени). Понятие о теле переменного состава включает в себя, как част-
ный случай, понятие о теле переменной массы (последнее одновремен-
но будет и телом переменного состава).
В основе теории тела переменного состава лежит уравнение Ме-
щерского для точки переменной массы:
d V
т ----=И + Ф. (2.2)
d т
При выводе этого уравнения используется гипотеза быстродейст-
вия процесса присоединения и отделения частиц. Принцип записи
уравнения (2.2) заключается в следующем: для любого момента време-
ни т при движении точки переменной массы в инерциальной системе
отсчета произведение текущей массы точки на ее ускорение равно
геометрической сумме всех внешних сил R и дополнительной реактив-
ной силы Ф. Для точки переменной массы реактивная сила в общем
случае равна
Ф = -01 Vi + 02 v2. (2.3)
Здесь Q\ - масса отделяемых частиц в единицу времени; Vi - скорость
отделения частиц по отношению к движущемуся ЛА; Qi -масса при-
соединяемых частиц в единицу времени; V2 - скорость присоединения
частиц по отношению к ЛА. Полагается, что Q\ > 0 и 02 > 0.
Внутри реального тела переменного состава, в пределах его внеш-
них контуров, постоянно происходит перемещение частиц, находящих-
ся в газообразном и жидком состоянии. Кроме того, центр масс ЛА, как
правило, изменяет свое положение относительно внешней оболочки.
Все это приводит к усложнению уравнения движения, которое записы-
вается для тела переменного состава в следующем виде (см. работы [7],
[56], [71]):
т + ф + RKOP + 2т <oxVr. (2.4)
dx dx
Здесь, в отличие от уравнения (2.2), в правой части добавлено несколь-
ко слагаемых, которые представляют собой дополнительные силы,
действующие на ЛА.
2.1. Уравнение движения в векторной форме
55
Силы, главный вектор которых равен (-5Кг/б/т), называются вариа-
ционными. Эти силы возникают вследствие нестационарности относи-
тельного движения внутренней среды и обусловлены изменением
(вариациями) количества движения К относительно корпуса ЛА. Про-
изводная 8/б/т вычислена в системе координат, жестко связанной с
корпусом ЛА. Если относительное движение среды стационарное, т.е. в
каждой точке ЛА плотность среды и скорость движения частиц не
меняется с течением времени, то вариационные силы равны нулю.
Кориолисовы силы Rkop обусловлены движением топлива и про-
дуктов горения внутри ЛА, вращающегося с угловой скоростью со в
инерциальной системе отсчета.
Последние два слагаемые в правой части уравнения (2.4) отражают
перемещение центра масс ЛА относительно его корпуса (Vr и аг -
скорость и ускорение центра масс ЛА относительно корпуса).
Дополнительные силы имеют наибольшее значение при движении
ЛА с ракетным двигателем, т.е. когда имеет место быстрое изменение
массы аппарата. В большинстве случаев при расчете траекторий дви-
жения ЛА дополнительные силы в правой части уравнения (2.4) значи-
тельно меньше по абсолютной величине, чем векторная сумма R + Ф. В
связи с этим с достаточной для практики точностью в качестве уравне-
ния движения ЛА переменного состава используется уравнение для
точки переменной массы
d V
т ---=G + Re. (2.5)
dx
Здесь Vа - скорость движения центра масс ЛА в инерциальной системе
отсчета; RE-главный вектор поверхностных и реактивных сил
(Re = П + Ф).
Согласно ГОСТу 20058-80 вектор RE называется ’’результирующей
силой” летательного аппарата [64]. При неработающем двигателе
(Ф = 0) уравнение (2.5) превращается в уравнение (2.1).
Перейдем к рассмотрению сил, действующих на ЛА.
2.2. Движение, форма и гравитационное поле Земли
Рассмотрим вначале массовые силы. При исследовании полета ЛА
в околоземном пространстве основным притягивающим телом является
Земля. Силы притяжения, действующие со стороны других небесных
тел, на несколько порядков меньше. Так, притяжение Луны (ближайше-
го небесного тела) на поверхности Земли составляет всего около
0,3-10'3% земного притяжения. Основным возмущающим небесным
телом является Солнце вследствие своей большой массы. Его притяже-
ние составляет примерно 0,06% земного притяжения (~ 0,006 м/с2), что
соизмеримо с поправками на нешарообразность Земли. Тем не менее
при рассмотрении полета ЛА на высотах до 10004-2000 км согласно
56
Глава 2. Общие положения динамики полета
сложившейся практике [71] можно ограничиться учетом только силы
гравитационного притяжения Земли:
G = mg.
Здесь g - ускорение гравитационного притяжения Земли.
Для определения силы гравитационного притяжения, а также сил
инерции, вызванных вращением Земли, необходимо принять соответст-
вующие вычислительные модели.
Движение Земли. В общем случае Земля совершает сложное дви-
жение, состоящее в основном из следующих составляющих [56].
1. Вращение вокруг собственной оси с запада на восток. При этом
период вращения в абсолютной системе координат (звездные сутки)
составляет 23 ч 56 мин 4,091 с среднего звездного времени.
2. Годичное обращение вокруг Солнца со средней скоростью дви-
жения 29,893 км/с.
3. Нутационные колебания земной оси с периодом около 18,6 лет и
с амплитудой, не превышающей 9,2".
4. Прецессионное движение относительно оси эклиптики с перио-
дом 25800 лет.
5. Движение с солнечной системой относительно других звезд.
Кроме того, на движение Земли влияют Луна и другие планеты.
Основной составляющей движения Земли
является вращение вокруг собственной оси.
Влияние других составляющих движения
Земли на траекторию ЛА чрезвычайно мало, и
ими можно пренебречь [56]. В связи с этим
будем полагать, что Земля вращается с посто-
янной угловой скоростью
со3 = 72,921158-10’6 рад/с
с запада на восток, а центр масс Земли дви-
жется прямолинейно и равномерно в абсо-
лютной системе координат (рис. 2.1). Вектор
угловой скорости (Оз направлен по оси враще-
ния от южного полюса Ps к северному PN в
соответствии с правилами знаков для правых систем координат.
Геометрическая форма и гравитационное поле Земли. Вследст-
вие своего вращения Земля представляет собой сплюснутое тело, у
которого расстояние между полюсами меньше диаметра экватора.
Реальная поверхность Земли со всеми ее неровностями называется
физической поверхностью. Так как физическую поверхность Земли
описать простой математической моделью невозможно, то вместо
физической поверхности используется поверхность тела, которое наи-
более близко подходит к Земле в целом по форме и размерам, а сама
м ш3 = const
Ps
Рис. 2.1. Модель
движения Земли
2.2. Движение, форма и гравитационное поле Земли
57
поверхность может быть описана простой математической зависимо-
стью.
Наиболее близко к реальной Земле подходит геометрическое тело,
получившее название геоид. Для определения геоида используется
понятие уровенной поверхности потенциала силы тяжести. Как извест-
но, в системе координат, жестко связанной с вращающейся Землей, на
любое тело с массой т помимо силы гравитационного притяжения
Земли G действует сила инерции J = -m jE, вызванная суточным вра-
щением Земли (здесь jE - переносное ускорение, направленное к оси
вращения Земли). Эти две силы проявляются в виде результирующей,
которая называется силой тяжести GT= ^gi- Причем экспериментально
невозможно отделить силу инерции от силы гравитационного притяже-
ния, так как их действие физически проявляется одинаково.
Для удобства введем в рассмотрение
вектор центробежного ускорения ]ц.б = -]е,
направление которого совпадает с силой
инерции J. Модуль вектора jUB равен
co32r coscp, где г - расстояние от центра Земли,
<р - геоцентрическая широта (ее определение
будет дано в разделе 2.4). Ускорение силы
тяжести в векторной форме записывается
следующим образом (рис. 2.2):
Рис. 2.2. К определению
ускорения силы тяжести
gT = g + ju.B • (2.6)
Анализ зависимости (2.6) показывает,
что вектор gT в общем случае не проходит через центр Земли, а его
модуль зависит от широты. Ускорение силы тяжести (ускорение сво-
бодного падения) можно определить экспериментально. В качестве
стандартного принято ускорение свободного падения на уровне моря на
средних широтах, равное g0 = 9,80665 м/с2. Согласно ГОСТу 4401-81
[29] такое ускорение реализуется на широте ф45 = 45 °32'33". Междуна-
родным астрономическим союзом (МАС) в 1964 году принята следую-
щая зависимость ускорения свободного падения от широты:
gT = 9,780319 (1 + 0,0053024 sin2<p - 0,00000585 sin22<p), (2.7)
согласно которой среднее ускорение силы тяжести на экваторе равно
9,780319 м/с2, а на полюсах - 9,8321782 м/с2.
Зависимость (2.7) можно использовать для проверки правильности
принятой модели гравитационного поля Земли. Будем далее называть
значение gT, определенное по формуле (2.7), действительным.
Геометрическое место точек, в которых потенциал силы тяжести
имеет одинаковое значение, называется уровенной поверхностью по-
тенциала силы тяжести. Во всех своих точках уровенная поверхность
ортогональна к вектору силы тяжести, направление которого на практи-
ке можно определить при помощи отвеса. Очевидно, что поверхность
58
Гпава 2. Общие положения динамики полета
океанов совпадает с уровенной поверхностью потенциала силы тяже-
сти. В противном случае произошло бы перетекание воды под действи-
ем силы тяжести, являющейся основной силой, действующей на вод-
ный слой.
Геоидом называется геометрическое тело, ограниченное уровенной
поверхностью потенциала силы тяжести, совпадающей со свободной
поверхностью океанов (невозмущенной приливами, волнами и др.) и
продолженной под материками. Поверхность геоида непрерывна, замк-
нута и не имеет резких перегибов и складок. Однако потенциал силы
тяжести в общем случае зависит от неоднородности внутреннего
строения Земли, поэтому поверхность геоида оказывается довольно
сложной и ее так же, как и физическую поверхность Земли, невозможно
описать простой математической зависимостью. По этой причине геоид
заменяют более простым телом.
Плоская Земля. Простейшим приближением является представле-
ние фигуры Земли в виде тела, ограниченного плоскостью. При этом
полагается, что гравитационное поле и поле силы тяжести являются
однородными и плоскопараллельными: векторы ускорений g и gT не
зависят от высоты и направлены по нормали к поверхности Земли. В
данном случае естественно считать, что gT = go- Модель плоскопарал-
лельного поля Земли служит для формирования структуры управления
и используется при оценке траекторий, протяженность которых суще-
ственно меньше радиуса Земли.
Шарообразная Земля. Следующим приближением геометрической
модели Земли является шар.
Модель гравитационного поля Земли тесно связана с ее геометри-
ческой моделью. Сила гравитационного притяжения является консерва-
тивной, т.е. имеющей силовую функцию. Силовая функция материаль-
ной точки массой т называется ньютоновским потенциалом и равна
U=fm/r,
где /-универсальная гравитационная постоянная; г-расстояние от
материальной точки до рассматриваемой точки пространства.
Будем полагать, что в шарообразной модели Земли плотность зем-
ного вещества имеет сферическое распределение. Тогда, как показано в
работе [7], потенциал гравитационного поля Земли будет совпадать с
ньютоновским потенциалом материальной точки. Такое гравитацион-
ное поле называется центральным или полем ньютонова тяготения. В
этом случае ускорение гравитационного притяжения Земли направлено
строго к ее центру и определяется следующей формулой:
g = g/r2, (2.8)
где ц - произведение универсальной гравитационной постоянной f на
массу Земли: ц =//773 = 3,986004-Ю14 м/с2 [56].
2.2. Движение, форма и гравитационное поле Земли
59
Модель шарообразной Земли широко используется при оптимиза-
ции управления, а также во многих случаях расчета траекторий. При
этом радиус шара 7?0 обычно задается из условия равенства объемов
Земли и ее шарообразной модели: Rq = 6371,11 км ([7], [56], [71] и др.).
Однако при таком значении Ro ускорение силы тяжести на средней
широте отличается от стандартного ускорения свободного падения go на
~ 0,03 %.
В данной работе предлагается радиус шарообразной модели Земли
выбирать из условия, чтобы ускорение силы тяжести gT на широте
Ф45 = 45°32'33" на уровне моря равнялось стандартному ускорению
свободного падения:
gT = Ц / Ro2 - (®з COS(P45)2 Ro = go • (2.9)
Такому условию соответствует RQ = 6370,0218 км, при этом ускоре-
ние гравитационного притяжения на поверхности Земли равно
gR0=ц/7?о2 = 9,823267 м/с5.
Общий земной эллипсоид. Наиболее ра-
циональным приближением к реальной
фигуре Земли является эллипсоид, получен-
ный вращением эллипса вокруг малой оси.
Такая модель называется ’’общим земным
эллипсоидом" (рис. 2.3).
Общий земной эллипсоид определяют
исходя из следующих условий [56]:
- центр эллипсоида совпадает с центром
Рис. 2.3. Общий земной
масс Земли, а плоскость его экватора - с эллипсоид
плоскостью экватора Земли;
- объемы эллипсоида и Земли равны;
-сумма квадратов отклонений (по высоте) поверхности общего
земного эллипсоида от поверхности геоида должна быть минимальной.
Определение размеров общего земного эллипсоида является одной
из основных задач геодезии. Обычно используют параметры общего
земного эллипсоида, принятые МАС в 1964 году и несколько уточненью
в последующие годы [72]: большая (экваториальная) полуось равна
7?е = 6378,137 км, сжатие эллипсоида составляет
а = (7^e-7?p)/7?e = 1/298,25.
Малая (полярная) полуось такого эллипсоида равна
Rp = Re(1 - а) = 6356,752 км.
Радиус Земли в зависимости от геоцентрической широты <р опре-
деляется следующим образом:
Я
R3 = , р-------------------- • (2.10)
7(1 - a)2 cos2 <р + sin2 <р
60
Глава 2. Общие положения динамики полета
На средней широте (<р45 = 45°32'33") радиус общего земного эллип-
соида составляет 6367,215 км, что на ~ 3 км меньше, чем радиус шаро-
образной Земли.
Сохранив в разложении в ряд правой части (2.10) слагаемые только
первого порядка относительно сжатия а, можно получить приближен-
ную формулу
Я3 = Яе(1 ~asin2<p), (2.11)
которая дает несколько завышенные значения 7?3 по сравнению с фор-
мулой (2.10). Наибольшая погрешность имеет место при ф»45° и не
превышает 27 м.
Если предположить, что плотность Земли обладает осевой симмет-
рией, то, используя потенциал силы тяжести, можно получить уравне-
ние, приближенно описывающее поверхность геоида [71], [72]. Такую
поверхность называют нормальным сфероидом или эллипсоидом Кле-
ро. Можно также показать, что уравнение поверхности нормального
сфероида преобразуется к виду (2.11), если в его правой части отбро-
сить величины выше первого порядка малости. Это и является доказа-
тельством правомочности замены геоида эллипсоидом вращения. Сжа-
тие а зависит от моментов инерции и скорости вращения Земли:
3 Iz-Ix^Rl
а =------—+ —-—- .
2 7773 R~ 2ц
Здесь /z, /х- моменты инерции Земли относительно оси вращения и
оси, лежащей в плоскости экватора; т? - масса Земли.
Модель общего земного эллипсоида широко используется при про-
ведении расчетов траекторий, протяженность которых соизмерима с
размерами Земли. В некоторых более ограниченных задачах оказывает-
ся целесообразным повысить точность локального описания поверхно-
сти Земли, например, на территории одного государства. Для этой цели
используют "референц-эллипсоид”, который ориентируют таким обра-
зом, чтобы его поверхность наилучшим образом совпадала с поверхно-
стью геоида в заданной области. При этом центр масс референц-
эллипсоида может не совпадать с центром масс Земли, однако их оси
должны быть параллельны. В СССР в 1940 году принят референц-
эллипсоид, предложенный Ф.Н. Красовским, с параметрами
Re = 6378,245 км, a = 1/298,3.
Современные данные геодезии и астрономии свидетельствуют о
том, что действительная фигура Земли достаточно хорошо описывается
трехосным эллипсоидом со значениями осей [72]
Rc(i) = 6378,26630 км; Яе(2) = 6378,0537 км; Rp = 6356,77472 км.
Для реальной Земли, имеющей сложную форму и неравномерное
распределение масс, задача определения потенциальной функции U
2.2. Движение, форма и гравитационное поле Земли
61
оказывается довольно трудной. Обычно потенциал Земли представляют
в виде бесконечного ряда:
W(sin<p)], (2.12)
п=2 \ '
где Jn-безразмерные постоянные коэффициенты; Рп (sincp) представля-
ют собой полиномы Лежандра, определяемые следующим образом:
Ро(х) = 1; Р\(х)=х- /*2 (х) = (Зх2 - 1 )/2;
Л(х) = (35х4 -ЗОх2 + 3)/8; . . .; Р„(х) = ^-^(х2 “ «У • (2-13)
Первое слагаемое в (2.12) соответствует шару со сферическим рас-
пределением плотности. Члены выражения (2.12), содержащие Pn(sin(p),
называются второй, третьей и т.д. зональными гармониками. Порядок
величин этих членов определяется величинами безразмерных коэффи-
циентов [7]:
Л= 1,0827-10’3; J3 = -2,56-10'6; Л = -1,58-10’6; ...
Зональные гармоники нечетного порядка учитывают асимметрию
Земли относительно плоскости экватора. Вторая зональная гармоника
учитывает полярное сжатие Земли и является самой существенной
поправкой при переходе к нецентральному полю тяготения (на три
порядка превышает остальные возмущающие члены).
Обычно предполагается, что Земля является симметричной отно-
сительно плоскости экватора, и в ряде (2.12) оставляют только слагае-
мые с полиномами Р2(*) и Р4(х) [56]. Однако, так как коэффициенты
разложения убывают весьма медленно, то ряд (2.12) сходится также
медленно. В результате простое ’’урезание” ряда приводит к тому, что
расчетное ускорение силы тяжести на уровне моря отличается от своего
действительного значения, например, на полюсе или на экваторе.
В данной работе предлагается другой способ формирования фор-
мулы для потенциала Земли. Будем использовать вторую и четвертую
гармоники, записав при этом полином Р4 (х) в виде
Л(х)=Лх4 + Лх2 + С.
Для определения коэффициентов А, В и С вместо формулы (2.13)
воспользуемся условием совпадения расчетного (по формулам (2.14)-
(2.16)) и действительного (по формуле (2.7)) значений gT на уровне
моря в трех характерных точках: на экваторе, на полюсе и на средней
широте. При этом коэффициент С однозначно определяется из условия
совпадения расчетного и действительного значений gT на экваторе,
сумма коэффициентов А и В - из условия, записанного при (р = 90°. В
результате получим
62
Глава 2. Общие положения динамики полета
А = 17,110277; В = -16,164195; С = 0,48261979.
Коэффициенты А, В и С вычислены с двойной точностью. В расче-
тах с одинарной точностью достаточно использовать не более четырех
значащих цифр. Следует заметить, что расчетные значения коэффици-
ентов А, В и С превышают не более чем в пять раз коэффициенты поли-
нома Р4 (х), которые согласно формуле (2.13) равны А = 4,375; В = -3,75;
С = 0,375.
Из выражения (2.12) видно, что потенциал U зависит не только от
удаления точки пространства от центра Земли, но и от геоцентрической
широты (р этой точки. Это означает, что вектор гравитационного уско-
рения g, как и вектор gT, не проходит через центр Земли (за исключе-
нием точек, лежащих на экваториаль-
ной плоскости и на оси вращения
Земли). Этот вектор лежит в плоскости
меридиана, проходящего через ось
вращения Земли и рассматриваемую
точку пространства.
Представим вектор g в виде суммы
двух составляющих: радиальной gr,
направленной к центру Земли, и мери-
диональной gm, перпендикулярной
вектору gr (рис. 2.4). Тогда
Рис. 2.4. Гравитационное поле
общего земного эллипсоида
dU 3 Т ( R, У _ . 2
gr = -— =-т[1 - -Л — (3sin ср — 1) —
or г 2 v г )
/ R Л4
- 5J4 — (^sin4(p + Bsin2(p + С)];
I г )
(2.14)
&ф ~
гбф
- — j Ззтф 4-
r к г J
4- J4 — (4Аsin\p 4- 2Взтф)]со8ф. (2.15)
\ г J
Из формулы (2.14) следует, что основной член радиальной состав-
ляющей совпадает с ускорением гравитационного притяжения для
шарообразной Земли (2.8). На экваторе (при ф = 0) поправка к основно-
му члену составляет ~ 0,15 %, причем направление возмущающего
воздействия совпадает с направлением основного воздействия. На
полюсах поправка составляет ~ 0,3 % от основного воздействия и про-
тивоположна ему по направлению.
Вектор g(p всегда направлен в сторону экватора. На полюсах и эква-
торе £ф= 0. Знак gip в (2.15) выбран так, что в северном полушарии эта
переменная отрицательная, а в южном - положительная. Максимальное
2.2. Движение, форма и гравитационное поле Земли
63
значение модуля g^ составляет —0,15% от основного слагаемого и
соответствует широте (р « 45°.
Таким образом, для общего земного эллипсоида радиус Земли оп-
ределяется по формуле (2.10), составляющие вектора ускорения грави-
тационного притяжения - по формулам (2.14) и (2.15). Сила гравитаци-
онного притяжения приложена в центре масс ЛА.
При проведении более точных траекторных расчетов для потенци-
альной функции используется выражение, учитывающее как отклоне-
ние реальной формы Земли от общего земного эллипсоида, так и нали-
чие в отдельных районах Земли гравитационных аномалий [7].
Зная составляющие вектора ускорения гравитационного притяже-
ния, можно вычислить ускорение силы тяжести, используя следующее
соотношение:
(gi-)2 = (gr - ®32 Г cos2(p)2 + (g<p - со32 Г coscp sincp)2. (2.16)
Радиальная составляющая центробежного ускорения максимальна
на экваторе (-0,34% от g0) и направлена против гравитационного
притяжения. Меридиональная составляющая центробежного ускорения
максимальна на средних широтах (~ 0,17% от go) и направлена в ту же
сторону, что и вектор . Таким образом, составляющие центробежного
ускорения имеют один порядок с поправками, учитывающими нецен-
тральность поля гравитационного притяжения.
На рис. 2.5 показано изменение расчетных ускорений гравитацион-
ного притяжения g и силы тяжести gT от геоцентрической широты на
уровне моря для двух моделей Земли. Для шарообразной Земли раз-
ность между значениями gT на полюсе и экваторе меньше, чем для
общего земного эллипсоида. Наибольшее отличие ускорений для двух
сравниваемых моделей Земли имеет место на экваторе и на полюсах
(~ 0,1 % от go).
Рис. 2.5. Зависимости ускорения гравитационного притяжения и
ускорения силы тяжести от геоцентрической широты на уровне моря
для двух моделей Земли; формулы (2.8), (2.9) и (2.14)-(2.16)
64
Глава 2. Общие положения динамики полета
2.3. Модель атмосферы
Если массовые силы, действующие на ЛА, определяются гравита-
ционным полем Земли, то поверхностные силы зависят главным обра-
зом от параметров земной атмосферы: плотности р, давления р, скоро-
сти звука а и др. Для их определения необходимо принять модель
атмосферы Земли.
В общем случае параметры атмосферы определяются высотой по-
лета, географической широтой, временем года и временем суток, а
также рядом других факторов, таких как степень солнечной активности.
Описание реальной атмосферы Земли математической моделью вызы-
вает значительные трудности из-за сложной природы распределения
атмосферного вещества во времени и пространстве и ограниченности
знаний об этом распределении. Однако известно, что основным факто-
ром, определяющим реальную атмосферу, является высота//.
Для расчета номинальных траекторий ЛА обычно используется
модель стандартной атмосферы СА-81 по ГОСТу 4401-81 [29]. Ее пара-
метры получены путем осреднения многолетних измерений, проведен-
ных на большой территории. СА-81 описывает средние значения пара-
метров спокойной атмосферы в зависимости только от высоты в
диапазоне от минус 2 км до 1200 км. Такая модель атмосферы называ-
ется стационарной и сферической; стационарность подчеркивает ее
независимость от времени, а сферичность - независимость от геогра-
фических координат. Зависимость параметров атмосферы от высоты в
СА-81 подобрана так, что наиболее близко подходит к условиям в сред-
них широтах северного полушария в предположении среднего уровня
солнечной активности. За нулевую высоту принят уровень моря. Значе-
ния основных параметров атмосферы при Н=0 приведены в табл. 2.1.
Таблица 2.1
Основные параметры стандартной атмосферы на уровне моря
Наименование Обозначение Значение
Температура То 288,15 К
Скорость звука во 340,294 м/с
Давление Ро 101325,0 Па
Плотность ро 1,2250 кг/м3
Ускорение свободного падения 9,80665 м/с2
на широте 45°32'33" OV
Молярная масса м0 28,964420 кг/кмоль
Параметры атмосферы в СА-81 представлены в зависимости от
высоты в табличном виде. При этом в качестве определяющих взяты
температура и молярная масса. По характеру зависимости температуры
2.3. Модель атмосферы
65
и давления от высоты стандартная атмосфера разделена на два диапа-
зона: до 120 км и от 120 км и выше.
Диапазон Н< 120 км. В данном диапазоне для определения зави-
симости параметров атмосферы от высоты в СА-81 используется урав-
нение статического равновесия неподвижной относительно Земли
атмосферы
dp = -pgTdH. (2.17)
Давление воздуха связано с плотностью р и температурой Т урав-
нением состояния идеального газа
р = р<ПТ/М. (2.18)
Здесь М- молярная масса; 91 = 8314,32 Дж-К’кмоль’1 - универсальная
газовая постоянная.
Исключив из уравнения (2.17) плотность при помощи (2.18) и
проинтегрировав левую часть уравнения, получим
1п(р/р) = - dH, (2.19)
/7*
где давление р* соответствует высоте Н*. Для того чтобы можно было
проинтегрировать правую часть полученного выражения, в СА-81
делается несколько предположений.
1. Предполагается, что ускорение силы тяжести gT зависит от высо-
ты Я так же, как и ускорение гравитационного притяжения g для шаро-
образной Земли:
где Ry = 6356,767 км-условный радиус Земли, выбранный из условия
совпадения градиента gT по Н с истинным градиентом на уровне моря
на широте 45°32'33".
Следует заметить, что реальная зависимость gT от высоты (от ра-
диуса Земли) для шарообразной Земли описывается формулой (2.9).
2. Используется понятие геопотенциальной высоты Яг, физический
смысл которой заключается в том, что она пропорциональна удельной
работе, совершаемой против силы тяжести при перемещении единич-
ной массы по нормали к геопотенциальной поверхности (т.е. к уровен-
ной поверхности потенциала силы тяжести). Геопотенциальная и гео-
метрическая высоты связаны следующим образом:
Нг= , (2.21)
Ry + Н
66
Глава 2. Общие положения динамики полета
производная Hv по Нс учетом (2.20) равна
dHvldH=gdgQ. (2.22)
3. Вводится понятие молярной температуры, которая связана с
обычной термодинамической температурой следующим образом:
Tm = TMq/M. (2.23)
В результате после замены переменных в (2.19) с учетом (2.22) и
(2.23) получаем
1п(^//) = - (2.24)
91 н'г
Заданная в СА-81 непрерывная кусочно-линейная зависимость
Гм = Тм* + ам(//г-//г*) (2.25)
позволяет аналитически проинтегрировать правую часть уравнения
(2.24). В соответствии с изломами этой зависимости до высоты 120 км
атмосфера разделена на 11 слоев. Индекс * в (2.24) и (2.25) соответст-
вует нижней границе рассматриваемого слоя; ам = dT^/dHv - градиент
молярной температуры по Hv. Три слоя - 3, 6 и 9-й - изотермические
(ам=0).
После интегрирования правой части уравнения (2.24) в СА-81 по-
лучены два выражения для определения давления: для изотермического
слоя
р=р‘ехр[- ^0 (Яг -Я^)], (2.26)
Тм
для слоя с линейным изменением Тм по Нг
MQg0
р=р\Тм/Тм)*а" . (2.27)
Однако, если с использованием этих выражений определить давле-
ние на высоте 120 км, последовательно перебирая все слои и используя
заданную в СА-81 зависимость Тм от Нг, то между расчетным и таб-
личным значениями р обнаружится расхождение в 0,013 %. По сущест-
ву это означает разрыв давления на высоте 120 км, так как в следующем
диапазоне высот в СА-81 используются другие расчетные зависимости.
Чтобы исключить имеющийся в СА-81 разрыв параметров атмо-
сферы предлагается следующий способ. Возьмем формулы (2.26) и
(2.27) за основу и перепишем их с использованием параметра слоя р.
Для изотермического слоя
р=р ехр[-ри(Яг-Яг*)], (2.28)
2.3. Модель атмосферы
67
для слоя с линейным изменением Гм по Hv
p=p(TM,/TMf. (2.29)
Параметр ри в формуле (2.28) имеет размерность 1/м, параметр Р в
формуле (2.29) - безразмерная величина. Значения Р и ри для каждого
слоя будем определять с использованием табличных данных СА-81 в
начале и в конце этого слоя (т.е. в начале следующего слоя):
Ри = In (р7р**) / ( 77г** - Нг ) - для изотермического слоя;
Р = 1п(/?7р**) / 1п(Гм*7гм*) - для слоя с линейным изменением
Гм по /7г-
Здесь индекс ** соответствует верхней границе рассматриваемого слоя.
При использовании параметров р и ри расчетное давление будет
автоматически совпадать с табличным давлением СА-81 в граничных
точках каждого слоя. При этом гарантируется непрерывное изменение
параметров атмосферы по высоте. Приближенные равенства
х и R - Мо^о
~ *ГМ ~ *ам
в первых 10-ти слоях (до высоты 104 км) выполняются с точно-
стью до 0,0009%, в 11-м слое (77= 104ч-120 км) - с точностью до
0,003%.
Во многих задачах динамики полета при использовании стандарт-
ной атмосферы возникает необходимость решения обратной задачи,
заключающейся в определении высоты полета по заданному давлению
или плотности. Зависимости (2.28) и (2.29) позволяют решить такую
задачу без использования итерационной процедуры. Выпишем соответ-
ствующие формулы. Для изотермического слоя
/7Г = //г* - In (р //?*)/Ри или 77г = //г* - In (р /р*)/Ри.
Для слоя с линейной зависимостью Тм от Нг по заданному давле-
нию или плотности сначала определяется молярная температура
ТМ = ТМ* (р*/р)У* или Тм = Тм’(р*/р),/(₽+1),
затем - геопотенциальная и геометрическая высоты
Нг = Нг+(Тм- Гм*)/ам ; Н= Ry Hv /(7?у - /7Г).
Диапазон Н> 120 км. В СА-81 в качестве определяющей задается
кусочно-линейная зависимость термодинамической температуры Т от
геометрической высоты 77. В соответствии с изломами этой зависимо-
сти верхняя часть атмосферы разделена на 9 слоев. Давление вычисля-
ется с использованием концентрации частиц, зависимость которой от
68
Глава 2. Общие положения динамики полета
высоты аппроксимируется полиномом четвертой степени. Такая зави-
симость р от Н не позволяет аналитически определять высоту по задан-
ному давлению или плотности. Чтобы эту задачу можно было решить
без итераций не только в нижнем, но и в верхнем диапазоне высот,
предлагается иной способ построения зависимости р(Н).
В качестве исходных данных используются табличные значения
СА-81 в граничных точках девяти слоев в соответствии с зависимостью
Т от Н. Для определения давления применена экспоненциальная функ-
ция, показатель которой является дробно-линейной функцией геомет-
рической высоты:
(2.30)
• ( аН~Н*
В формулу (2.30) входят два неизвестных параметра слоя - Р и
Н* - на один больше, чем в формуле (2.28) для изотермического слоя.
Для определения второго параметра воспользуемся давлением рСр в
промежуточной точке слоя с высотой ЯСр • Таким образом, для каждого
слоя расчетная зависимость будет совпадать с табличной в трех узло-
вых точках. В остальных точках отличие расчетных значений от таб-
личных данных СА-81 не превышает 2ч-3%. Формулы для определения
параметров слоя имеют следующий вид:
Н" - Нср
и>-нсг-цНс'-н
\n(pcf/p)
₽ ЯСР - н' н” - н
1п(рСр//) 1п(/’//)
При заданном давлении высота определяется следующим образом:
я y + ff>(//p)/p
1-1п(//р)/р
Зависимость типа (2.30) можно использовать и для плотности. От-
личие расчетных значений от табличных в этом случае также не пре-
вышает 2ч-3%. При таком подходе зависимость молярной массы от
высоты не используется в качестве определяющей (в отличие от СА-81).
При необходимости молярную массу можно определить из уравнения
состояния идеального газа через давление, плотность и температуру.
При этом отличие расчетных значений М от табличных данных СА-81
также не превышает 2-^-3 %.
Полный алгоритм определения параметров атмосферы по заданной
высоте и определения высоты по давлению и плотности изложен в
приложении 1. Далее такая модель атмосферы будет использоваться в
качестве основной.
2.3. Модель атмосферы
69
В некоторых случаях наряду с СА-81 будет использоваться про-
стейшая модель изотермической атмосферы с экспоненциальным изме-
нением плотности:
р = р0ехр(-р/7). (2.31)
Здесь параметр атмосферы р = -р'н/р обычно равен 1,41-10 ^*м-1.
Следует подчеркнуть, что реальная атмосфера является несферич-
ной и динамичной. Истинные значения ее параметров отличаются от
стандартных. Эти отклонения называют вариациями параметров. Мо-
дель вариаций параметров атмосферы (сезонно-широтных, суточных и
случайных) описывается в работе [86]. Способ учета возмущений
параметров атмосферы изложен в работе [56].
2.4. Основные системы координат
Исходное уравнение движения ЛА (2.5) записано в векторной фор-
ме в инерциальной системе отсчета. Для записи уравнений движения в
общепринятой форме необходимо ввести в рассмотрение несколько
неинерциальных систем координат. Классификация и описание основ-
ных систем координат приведены в работах [27], [28], [64], [71] и др.
Следует отметить, что некоторые системы координат в разных источни-
ках называются по-разному. Дадим краткое описание используемых
ниже систем координат, а также определение используемых величин.
В общем случае для характеристики системы отсчета задается на-
чало координат, основная плоскость и главное направление. В соответ-
ствии с [28] все используемые системы координат правые. При изуче-
нии траекторного движения ветер и скольжение ЛА обычно не
учитываются. Поэтому дальнейшее изложение будет вестись сразу с
учетом этих упрощений.
Абсолютной системой координат принято называть прямоуголь-
ную декартову с.к., начало которой совпадает с центром масс солнца, а
оси неподвижны относительно звезд. Всякая система координат, пере-
мещающаяся прямолинейно и равномерно относительно абсолютной,
называется инерциальной.
Геоцентрической называется система координат, начало которой
совпадает с геометрическим центром Земли. Для задания положения
ЛА относительно Земли используются три геоцентрические системы
координат: инерциальная, вращающаяся экваториальная и вращающая-
ся ортодромическая. Все системы координат являются прямоугольны-
ми, однако положение ЛА в них задается при помощи сферических
координат. Некоторые понятия, используемые в различных геоцентри-
ческих системах координат, являются общими. Местной вертикалью
называется линия, проходящая через центр Земли. Местной горизон-
тальной плоскостью называется плоскость, ортогональная местному
геоцентрическому радиусу.
70
Глава 2. Общие положения динамики полета
Одной из координат в геоцентрической с.к. является расстояние г
от центра Земли. Вместо расстояния г может задаваться высота Н,
которая отсчитывается от поверхности Земли вдоль геоцентрического
радиуса:
H=r-R3, (2.32)
где радиус 7?3 общего земного эллипсоида вычисляется по формуле
(2.10).
Следует подчеркнуть, что вертикаль в геоцентрической системе
координат не ортогональна к поверхности общего земного эллипсоида,
в отличие от геодезической с.к., в которой направление вертикали
совпадает с вектором силы тяжести. В связи с этим в геодезической
системе координат высота отсчитывается по нормали к земному эллип-
соиду, а широта (ргд задается как угол между местной геодезической
вертикалью и плоскостью экватора. Геодезическая и геоцентрическая
широты связаны между собой соотношением
s 1п(срГд - ср) = е2 Бшсргд coscp,
где е - эксцентриситет меридианного эллипса общего земного эллип-
соида.
Далее геодезическая система координат использоваться не будет.
ЛА-центрической называется система координат, начало которой
совпадает с центром масс ЛА. Для задания направления вектора скоро-
сти и углового положения ЛА используются четыре ЛА-центрические
прямоугольные системы координат: нормальная, траекторная, скорост-
ная и связанная. Перейдем к описанию используемых систем отсчета.
Геоцентрическая инерциальная (экваториальная) система коор-
динат (рис. 2.6). Начало координат находится в центре Земли.
Основной является плоскость экватора ОхцуИ- Ось ОхИ (опорное на-
правление) параллельна линии Земля - Солнце в день весеннего равно-
денствия. Ось направлена вдоль оси вращения Земли в сторону
северного полюса. Систему координат Охцуи^и можно считать инерци-
альной, так как выше было принято допущение о равномерном и пря-
молинейном движении центра масс Земли. Данная система координат
используется для описания движения ЛА на околоземной орбите.
Геоцентрическая вращающаяся (экваториальная) система коор-
динат Ox0yoZo (рис. 2.7). Ось OzQ совпадает с осью Oz^ инерциальной
системы координат. В отличие от инерциальной с.к. эта система коор-
динат жестко связана с вращающейся Землей, т.е. вращается с угловой
скоростью со3 вокруг оси Ozq. Основной является плоскость экватора
Ох0уо. Опорное направление Ох0 пересекает гринвичский меридиан.
Положение ЛА в данной системе координат задается тремя сфери-
ческими координатами: расстоянием ЛА от центра Земли г, геоцентри-
ческими долготой X и широтой ср (см. рис. 2.7). Угол X отсчитывается от
гринвичского меридиана в восточном направлении в основной плоско-
сти (0 < X < 2л или -л < X < л). Угол ср отсчитывается по меридиану от
2.4. Основные системы координат
71
Рис. 2.6. Геоцентрическая инер-
циальная система координат
Рис. 2.7. Геоцентрическая вращаю-
щаяся система координат
основной плоскости, положи-
тельный в северном полушарии и
отрицательный в южном полуша-
рии (-71 /2 < (р < 71 /2).
Нормальная (ЛА-центри-
ческая ориентированная) система
координат OxgXgZg (рис. 2.8).
Начало координат совпадает с
ц.м. ЛА. Основная плоскость
OxgZg параллельна местной гори-
зонтальной плоскости. Основное
направление Oxg параллельно
касательной к местной геоцен-
трической параллели и направле-
но на восток. Ось Ozg лежит в
плоскости местного меридиана и
направлена с севера на юг. Ось
совпадает с местной геоцен-
трической вертикалью. Нормаль-
ная система координат служит
для задания направления вектора
воздушной скорости. В работе [71]
ся земной.
Рис. 2.8. Ориентация нормальной
системы координат относительно
геоцентрической вращающейся с.к.
иная система координат называет-
Траекторная (ЛА-центрическая вертикально-скоростная) система
координат ОхкУк^к (рис. 2.9) движется вместе с ЛА с воздушной скоро-
стью V относительно геоцентрической вращающейся с.к. Эта система
координат является наиболее употребительной для записи уравнений
движения ЛА в атмосфере. Основная плоскость ОхкУк совпадает с
72
Глава 2. Общие положения динамики полета
Рис. 2.9. Ориентация траекторной системы координат
относительно нормальной с.к.
вертикальной плоскостью, проходящей через вектор воздушной скоро-
сти V и местную геоцентрическую вертикаль, при этом ось Оук, как
правило, направлена вверх от поверхности Земли. Ось Охк (основное
направление) совпадает с вектором воздушной скорости ЛА.
Положение траекторной системы координат по отношению к нор-
мальной характеризуют два угла:
- угол наклона траектории 0 между вектором скорости V и местной
горизонтальной плоскостью (положительный угол соответствует поло-
жительной проекции вектора скорости на ось Оу^ нормальной с.к.).
Угол наклона траектории лежит в диапазоне -к/2 < 0 < л/2;
- угол курса \|/ между проекцией вектора скорости на местную го-
ризонтальную плоскость и осью Oxg нормальной сж. (отсчитывается
против часовой стрелки, изменяется в диапазоне -л < \|/ < л).
В работе [71] данная система координат называется скоростной, в
[56] - полускоростной, в [111] - сферически-скоростной.
При рассмотрении движения ЛА на орбите, как правило, использу-
ется абсолютная скорость, заданная в инерциальной системе координат.
В связи с этим часто возникает задача пересчета фазовых переменных
из геоцентрической вращающейся в инерциальную систему координат
и обратно.
Пусть модуль абсолютной скорости в инерциальной системе коор-
динат равен ИА. По аналогии с углами, задающими направление вектора
воздушной скорости V в нормальной системе координат, зададим на-
правление вектора абсолютной скорости VA при помощи двух углов:
2.4. Основные системы координат
73
- угла наклона траектории 0А между вектором скорости VA и мест-
ной горизонтальной плоскостью;
- угла курса уА между проекцией вектора скорости VA на местную
горизонтальную плоскость и осью Oxg нормальной системы координат.
Положение орбиты в инерциальной системе координат задается
при помощи наклонения i (угла между плоскостью орбиты и плоско-
стью экватора ОхцУи)- Наклонение орбиты связано с геоцентрической
широтой ср и углом \рА следующим образом:
cosz = coscp cosyA. (2.33)
Плоскость орбиты пересекается с плоскостью экватора в двух точ-
ках: в восходящем и нисходящем узлах. Для определенности будем
полагать, что в окрестности восходящего узла знаки углов курса и
наклонения орбиты совпадают. В этом случае наклонение орбиты, как и
угол курса, будет изменяться от минус л до л. Из формулы (2.33) следу-
ет, что всегда ср < z и уА < /.
Для определения связи между фазовыми координатами в инерци-
альной системе координат и геоцентрической вращающейся с.к. вос-
пользуемся теоремой о сложении скоростей. В проекции на оси нор-
мальной системы координат можно записать
ИА sin0A = V sin0;
VA cos0А sinyA = V cos0 si nv|/;
VA cos0A cosyA = V cos0 cosy + KE, j
где KE- переносная скорость:
(2.34)
KE = co3r coscp. (2.35)
После преобразования выражений (2.34) получим формулы для пе-
рехода из геоцентрической вращающейся с.к. в инерциальную систему
координат:
КА2 = И2[1 +2COS0COS4/ ИЕ///+(ГЕ/И)2]; ]
sin0A= sin0 V/VK; [ (236)
tg\|/A = cos0sinvy /(cos0 cosv|/ + VE/V). 1
Формулы для перехода из инерциальной с.к. в геоцентрическую
вращающуюся систему координат имеют следующий вид:
V2 = ГА2[1 -2cos0acosv|/a Ке/Ка + (Ие/Га)2] ;
sin0 = sin0A ИА/К;
tg\|/ = cos0A sini|/A /(cos0A cosv|/A - ГЕ/ИА).
(2.37)
74
Глава 2. Общие положения динамики полета
Найдем приближенную дифференциальную связь между величи-
нами ИА и К В большинстве случаев можно пренебречь изменением
кинематических параметров 0, у и ср по сравнению со скоростью. Тогда
dV^/dV^(V+ VE cos0 cos\|/)/KA ;
dV/dVx ~ (ГА - ИЕ cos0A cos\|/A)/K
(2.38)
Скоростная (ЛА-центрическая) система координат 6>ХдуАгА
(рис. 2.10). Основная плоскость Ох&уА совпадает с плоскостью симмет-
рии ЛА, при этом ось ОуА направлена вверх. Ось ОхА (основное на-
правление), также как и в траекторной системе координат, совпадает с
вектором воздушной скорости V. Относительно траекторной скорост-
ная система координат повернута на угол крена у между плоскостью
симметрии ЛА и местной вертикальной плоскостью. Положительный
угол у соответствует положительной проекции подъемной силы на ось
OzK траекторной системы координат (крен на правое крыло). В общем
случае угол крена лежит в диапазоне -к < у < л.
В скоростной системе координат, как правило, задаются аэродина-
мические силы, поэтому часто она называется аэродинамической. В
работе [71] скоростная с.к. называется поточной, в [56] - полускорост-
ной. В данной работе при использовании скоростной системы коорди-
нат индекс "А” будет опускаться.
Связанная (ЛА-центрическая) система координат Ox\y\Z\
(рис. 2.11). Основная плоскость Oxiyi является плоскостью симметрии
ЛА. Основное направление Ох{ направлено вперед по продольной оси
ЛА, ось Оу\ - в сторону верхней части ЛА. Обычно оси связанной
Вертикальная плоскость
Плоскость симметрии ЛА
Рис. 2.10. Ориентация скоростной системы координат
относительно траекторной с.к.
2.4. Основные системы координат
75
системы координат близки к главным центральным осям инерции ЛА,
хотя могут выбираться и из других соображений. При полете без
скольжения ось Oz\ совпадает со скоростной осью Oz. Относительно
скоростной с.к. связанная система координат повернута на угол атаки а.
Положительный угол атаки соответствует отрицательной проекции
вектора скорости на ось Оу\. В общем случае угол атаки лежит в диапа-
зоне -л < ос < л.
Положение связанной системы координат по отношению к нор-
мальной с.к. характеризуют два угла:
-угол рыскания v|/( между проекцией оси Ох\ на местную горизон-
тальную плоскость и осью Ох& нормальной системы координат;
-угол тангажа 9 между осью Ох} и местной горизонтальной плос-
костью.
При нулевом угле крена углы рыскания и курса совпадают, угол
тангажа равен
9 = 6 + а. (2.39)
Из анализа уравнений движения, записанных в траекторной систе-
ме координат (см. раздел 2.6), следует, что при прохождении траектории
вблизи полюса Земли могут возникнуть вычислительные трудности,
если в уравнениях движения используются геоцентрические координа-
ты. В точке над полюсом (при ср = ±л /2) в уравнениях движения, слу-
жащих для определения угла курса и геоцентрической долготы, возни-
кает деление на ноль. Для избежания этих трудностей введем в
рассмотрение ортодромическую систему координат, жестко связанную с
вращающейся Землей. Эта система координат будет использоваться при
исследовании траекторий спуска ЛА с орбиты.
Рис. 2.11. Ориентация связанной системы координат
относительно скоростной с.к.
76
Глава 2. Общие положения динамики полета
Ортодромическая (геоцентрическая вращающаяся) система коор-
динат ОхдудИд (рис. 2.12). От экваториальной геоцентрической вра-
щающейся системы координат ортодромическая с.к. отличается тем,
что ее основная плоскость (плоскость ортодромии) повернута относи-
тельно экваториальной плоскости на некоторый угол /Орт, который
изменяется в диапазоне - л < /Орт^ я. Плоскость ортодромии пересека-
ется с плоскостью экватора в двух точках: в восходящем и нисходящем
узлах. За опорное принимается направление, проходящее через восхо-
дящий узел ортодромии. Ось Oz% направлена в сторону северного орто-
дромического полюса.
Для задания положения ортодромической системы координат отно-
сительно экваториальной с.к. помимо наклонения zOpt используется
долгота восходящего узла Ху. Диапазон ее изменения составляет от
минус л/2 до л/2. При нулевом наклонении плоскости ортодромии
будем полагать Ху=0°. В этом случае ортодромическая и экваториаль-
ная системы координат полностью совпадают. При /’орт = л и при
/орт = -л также будем полагать, что Ху = 0°.
Положение ЛА в ортодромической системе координат задается так
же, как и в экваториальной с.к., при помощи трех сферических коорди-
нат. Ортодромическая долгота А отсчитывается от восходящего узла в
восточном направлении в плоскости ортодромии (0<А<2л или
-л < А < л). Ортодромическая широта Ф отсчитывается по ортодроми-
ческому меридиану от плоскости ортодромии. Угол Ф - положительный
в северном ортодромическом полушарии и отрицательный в южном
(-л/2 < Ф < л/2).
ортодромии
Рис. 2.12. Ориентация ортодромической системы координат
относительно экваториальной с.к.
2.4. Основные системы координат
77
Ориентация вектора воздушной скорости в ортодромической сис-
теме координат, также как и в экваториальной с.к., задается при помощи
двух углов:
- ортодромического угла курса Ч7;
- угла наклона траектории 0.
Очевидно, что модуль скорости, высота и угол 0 в ортодромиче-
ской и экваториальной системах координат одинаковы.
Связь между геоцентрическими и ортодромическими координата-
ми устанавливается при помощи формул сферической тригонометрии.
При переходе из экваториальной с.к. в ортодромическую систему коор-
динат широта, долгота и угол курса соответственно равны
Ф = arcsin(sincp cosz'opt - coscp sinAX sin/орт) ;
Л = arctg[(coszOPT coscp sinAX + sinzOpT sincp)/(coscp cosAX)];
Ч7 = у - Ay;
Ay = arctg[sinz0PT coscp cosAX/(coszOPt - sincp sinO)].
Здесь AX = X-Xy; Ay-угол между ортодромическим и геоцентриче-
ским меридианами.
При переходе от ортодромических к геоцентрическим координатам
формулы принимают следующий вид:
ср = arcsin(sin0 coszOPT + cos0 sinA sinz0PT);
X = Xy + arctg[(coszOPT cosO sinA - sinz0PT 5шФ)/(со5Ф cosA)];
y = 47 + Ay;
Ay = arctg[sinz0PT со$Ф cosA/(cos z0Pt - sincp sinO)].
2.5. О разделении результирующей силы на
аэродинамическую и силу тяги двигателя
В правую часть уравнения движения (2.5) помимо массовых сил G
входит главный вектор поверхностных и реактивных сил - результи-
рующая сила JIA Rv. В общем случае главный вектор поверхностных
сил П определяется как интеграл сил давления и трения по всей смачи-
ваемой поверхности аппарата:
П= jpnt/54- Rf(5z).
5'v
Здесь S^- площадь смачиваемой поверхности ЛА, включая внутренний
тракт двигателя; р- давление (абсолютное) в каждой точке поверхно-
сти; п - единичный вектор нормали к поверхности ЛА; Rf-главный
вектор сил трения.
78 Глава 2. Общие положения динамики полета
В процессе работы двигателя (при расходовании бортового запаса
топлива) реактивная сила приложена к топливным форсункам и равна
Ф г = -Qx vT,
где Qx = I dm^/dx | - секундный расход массы топлива; vT- вектор скоро-
сти подачи топлива в камеру сгорания.
В случае отбора входящего воздуха, например, при сжижении и на-
коплении атмосферного воздуха за счет использования бортового хла-
доресурса, реактивная сила приложена к патрубку забора сжиженного
воздуха и равна
Ф(7Ж = £?СЖ ¥СЖ ,
где (2сж= I dmcx/dx | - масса накапливаемого сжиженного воздуха в
единицу времени; уСж- вектор скорости забора сжиженного воздуха из
ожижителя.
Рассмотрим наиболее общий случай, когда на ЛА установлен ВРД.
Пусть при этом расходуется бортовое топливо и одновременно идет
процесс накопления сжиженного воздуха. Главный вектор поверхност-
ных и реактивных сил равен
Re~ JpudS + Rf(Ss) + Фт + Фсж • (2.42)
Здесь полагается, что силы давления, действующие на срезе сопел
топливных форсунок и на срезе патрубков забора сжиженного воздуха,
включены в интеграл сил давления по площади S%.
При записи (2.42) основную долю в результирующей силе Re со-
ставляют поверхностные силы, вызванные аэродинамическим воздей-
ствием на внешнюю поверхность ЛА и газодинамическим воздействи-
ем на внутреннюю поверхность двигательного тракта. Теоретически
возможен прямой расчет вектора Re (с использованием соответствую-
щих расчетных методов). Однако более распространен другой подход,
когда вектор Re представляют в виде суммы аэродинамической силы
планера и силы тяги двигателя.
Форма записи Re зависит от выбора контрольной поверхности, от-
деляющей ЛА, как тело переменного состава, от внешней среды. Так,
при записи формулы (2.42) полагается, что контрольная поверхность
совпадает с твердой смачиваемой поверхностью ЛА, включая внутрен-
ний тракт КСУ.
Для выделения аэродинамической силы планера и силы тяги ВРД
из Re контрольную поверхность проводят так, чтобы она охватывала
внутренний тракт КСУ. При увеличении максимальной скорости полета
до сверх- и гиперзвуковой роль входного и выходного устройств ВРД в
создании силы тяги существенно возрастает. Их размеры значительно
увеличиваются, и становится целесообразным объединить конструк-
тивно элементы силовой установки с планером. При этом в результате
2.5. О разделении результирующей силы
79
интеграции планера с силовой установкой ВРД возникает возможность
получения положительных эффектов, направленных на улучшение
летно-технических характеристик ЛА. Наилучшая интеграция силовой
установки и планера ЛА достигается при нижнем расположении ВРД
(рис. 2.13). В этом случае носовая часть фюзеляжа используется для
предварительного сжатия входного потока, а хвостовая часть-для
расширения продуктов сгорания. Вопросы разделения сил и интеграции
планера и силовой установки основательно изучены в ЦАГИ [106].
Дадим краткое изложение этих вопросов.
Пусть скорость полета ЛА равна V. Проведем контрольную по-
верхность, охватывающую внутренний тракт ВРД, и разделим ее на
четыре участка (см. рис. 2.13):
1 - поперечное сечение входной струи воздуха с площадью ;
2 - внешняя поверхность ЛА (та ее часть, которая совпадает с кон-
трольной поверхностью) с площадью 5А. Обозначена жирной линией;
3 - поверхность жидкого контура от входного сечения до кромки
обечайки воздухозаборника ВРД. Обозначена коротким пунктиром.
Площадь этой поверхности равна ;
4-выходное сечение с площадью Fc. Это сечение, как правило,
является косым.
Поток в сечении 1 (см. рис. 2.13) при числе М > 1 является невоз-
мущенным. Параметры невозмущенного потока обозначаются индек-
сом оо. Через входное сечение в контрольное пространство втекает
воздух со скоростью Voo = -V и с секундным расходом
2b = PooKoFoo. (2.43)
Это означает, что к сечению 1 со стороны внешней среды приложе-
на реактивная сила (2bV«>. Кроме того, на поверхность сечения 1 со
стороны внешней среды действует интеграл сил давления fpvn dF.
А.
На поверхность 2 действует интеграл сил давления и трения, рав-
ный j/7Anrf5 + Rf(5A). На поверхность 3 действует интеграл сил давле-
Рис. 2.13. К определению вектора результирующей силы Ry
80
Глава 2. Общие положения динамики полета
ния Здесь величиныр\,рж и п являются функциями геомет-
Л’ж
рических координат.
К выходному сечению приложена реактивная сила (-jgrVc), где
Vc - вектор средней скорости истечения из реактивного сопла; Qy -
секундный расход газа (продуктов истечения), который связан с се-
кундными расходами воздуха и топлива следующим образом:
Qv = Qb — (2сж + (?т • (2.44)
Для записи реактивной силы в общем виде введем в рассмотрение
единичный вектор нормали к сечению потока к. Вектор к направлен по
потоку, т.е. угол между к и вектором скорости единичной струйки тока
меньше 90°. Очевидно, что в сечении 1 имеет место равенство к = п, а в
выходном сечении к = -n. С учетом вышесказанного можно написать
-CrVc = - Jpr(Vr • k)VrJF .
''с
Здесь запись (а-b) соответствует скалярному произведению векторов а
и Ь.
Кроме реактивной силы к сечению 4 со стороны внешней среды
приложен интеграл сил давления jprndF. В общем случае параметры
'*С
потока рг,/?г и Vr являются функциями геометрических координат.
Запишем уравнение Мещерского для выделенного контрольного
объема:
т— = G + Rz = G + + \p.,ndF + J pAn dS +
+ Rf (SA) + J ЛИ dS - Jpr (Vr • k)Vr dF + J prn dF. (2.45)
•Sk г г
Заметим, что, строго говоря, масса т в (2.45) складывается из мас-
сы летательного аппарата и массы той части воздуха (газа) тв,
которая оказалась внутри контрольного объема:
т = тм + тв •
Очевидно, что в большинстве случаев масса тв пренебрежимо ма-
ла по сравнению с массой ЛА, поэтому далее под массой т , входящей в
уравнения движения, будем понимать массу летательного аппарата.
Необходимо отметить, что процессы, происходящие внутри контроль-
ного объема (подача топлива в камеру сгорания и забор сжиженного
воздуха), прямо никак не отражены в уравнении (2.45) в отличие от
уравнения (2.42).
2.5. О разделении результирующей силы
81
Выделим из уравнения (2.45) вектор R^:
Re = 2bVm+ \p.rpdF + + Rf(SA) +
F.
+ - Jpr(Vr-k)VrJF+ JprnJF. (2.46)
•Sc /с FC
В аэродинамике при вычислении сил давления принято использо-
вать избыточное по отношению к атмосферному давление (р-р^). В
связи с этим добавим к правой части уравнения (2.46) равный нулю
интеграл по всей контрольной поверхности
=- ndS - \p, ndF.
F. '•’л «ж P
В результате получим
Rs= J(/’A-.P»)na® +Rf(5’A)+ \(p-K-p„)ndS +
+ 2bVm-[ Jpr(Vr-k)VrdF + f(pr-pJkrfF]. (2.47)
Fc FC
Здесь в последнем слагаемом было использовано равенство к = -п.
Первые два слагаемые в правой части выражения (2.47) представ-
ляют собой аэродинамическую силу, действующую на планер ЛА:
Ra= J(PA “ Р Jn + Rf (SA).
Третье слагаемое в (2.47) представляет собой силу, действующую
на жидкий контур входной струи воздуха:
R»= /(Рж-pJndS.
‘Sk
Проекции вектора аэродинамической силы RA на оси скоростной
системы координат называются силой лобового сопротивления ХА и
аэродинамической подъемной силой УА (для упрощения записи индекс
"А” будем опускать). Сила X всегда положительна и направлена против
вектора скорости ЛА.
Вместо размерных сил используются безразмерные коэффициенты,
определяемые следующим образом:
сх = X!(qS)\ су= Y/{qS).
Здесь сх - коэффициент лобового сопротивления; су- коэффициент
аэродинамической подъемной силы; q - скоростной напор; 5 - харак-
82
Глава 2. Общие положения динамики полета
терная площадь ЛА (обычно площадь в плане или площадь базовой
трапеции крыла).
Скоростной напор равен
q = рИ2/2 = 0,7рМ2.
Аналогично, проекции вектора Rx на оси скоростной системы ко-
ординат называются силой лобового сопротивления по жидкому конту-
ру и подъемной силой жидкого контура:
Х^ = cK^qF; Y-^-cy-^qF.
Здесь схЖ, суж~ безразмерные коэффициенты; F - характерная площадь
тракта ВРД (обычно площадь входа в воздухозаборник).
Сила Хж всегда положительная и направлена против вектора скоро-
сти ЛА. Следует отметить, что модуль силы Иж является довольно
значительным в общем балансе сил. В трансзвуковом диапазоне скоро-
стей сопротивление по жидкому контуру может превышать сопротивле-
ние планера ЛА.
В газовой динамике широко используется понятие импульса потока
[1]. По определению полным импульсом единичной струйки с попереч-
ным сечением F называется сумма количества движения газа, проте-
кающего в единицу времени, и силы абсолютного давления:
IA = pF2F + pF.
Импульс потока газа, вычисленный через избыточное давление, в
общем случае равен
1= Jpr(vr -k)Vr6ZF+ j(pr - pK)kdF, (2.48)
/• /’•
где F- площадь косого сечения, через которое протекает поток.
Сравнение выражений (2.48) и (2.47) показывает, что последние
два слагаемые в выражении (2.47) представляют собой импульс 1с
потока газа, вытекающего из реактивного сопла. Вектор 1с входит в
(2.47) со знаком минус.
Импульс потока, вычисленный через избыточное давление во
входном сечении, совпадает с входным количеством движения воздуха,
протекающего в единицу времени:
loo “ •
В теории ВРД используется понятие коэффициента расхода возду-
ха, который по определению равен
f-F^IF.
С учетом этого модуль входного импульса равен
L = 2fqF,
2.5. О разделении результирующей силы
83
а направление вектора !«, всегда противоположно вектору скорости
полета V.
Вектор Rc = -1с называется тягой реактивного сопла. Вместо раз-
мерной силы часто используется коэффициент тяги сопла, который
определяется следующим образом:
Crc= 7?с/(<7^)-
С использованием введенных выше обозначений перепишем выра-
жение (2.47) как векторную сумму четырех слагаемых (рис. 2.14я):
Re - Ra + R>k + I® + Rc,
(2.49)
или в проекции на оси скоростной системы координат
(2.50)
^zx = cRC <?Fcos(a + 8) - 2fqF- cxqS-c^qF;
7?zy = cyqS + суЖ qF + cRC (yFsin(a + 8).
Здесь a-угол атаки; 8-угол между вектором тяги сопла и осью Ох\
(положительный угол соответствует положительной проекции тяги
сопла на ось Оу\). Запись (2.50) более характерна для ЛА с прямоточ-
ным ВРД.
Если контрольное сечение 1 перенести от носка фюзеляжа к на-
чальному сечению воздухозаборника (рис. 2.146), то формула (2.49)
примет вид
Рис. 2.14. Возможные формы представления вектора результирующей силы Rv:
сечение 1 входной струи воздуха проведено через носовую точку ЛА (а), через
точку первого клина воздухозаборника ВРД (6)
84
Глава 2. Общие положения динамики полета
(2.52)
Ке ~ Кж+11 + Кс • (2.51)
Здесь при вычислении вектора RA предполагается, что в 5А включена
нижняя поверхность носовой части фюзеляжа. При вычислении векто-
ра Rx используется жидкий контур входной струи, относящийся только
к воздухозаборнику.
В проекции на оси скоростной системы координат запись (2.51)
примет вид
^Ех = CRC <7^cos(a + 5) - Ц cos (a + си) - cx qS - qF\
2?sy = cyqS + + cRC<7^sin(a + 8) - Л sin (a + aj).
Форма разделения сил, соответствующая (2.51) и (2.52), удобна в
тех случаях, когда на одном ЛА рассматриваются различные типы
двигателей или изменяются параметры двигательного тракта.
В выражениях (2.49) и (2.51) тяга ВРД явно не выделена. Если все
слагаемые вектора Rs известны, то нет никакой необходимости в выде-
лении тяги двигателя для проведения траекторных расчетов. Однако в
случае необходимости вектор тяги можно выделить из Rs различными
способами. Например, можно ввести понятие условной тяги:
Нврд = loo + Rc или Rвpд = 11 + Rc •
В этом случае выражение для вектора Rsпримет простой вид:
Re = Кд + Иж + Кврд ,
однако модуль тяги и направление вектора тяги будут зависеть от выбо-
ра контрольной поверхности.
Основной (классический) способ разделения основывается на оп-
ределении тяги, принятом в теории ВРД: тяга двигателя - это разность
между тягой Rc реактивного сопла и входным импульсом Ц при усло-
вии, что векторы Rc и la, коллинеарны оси двигателя. Примем выраже-
ние (2.51) в качестве исходного. Проведем единичный вектор пдв,
параллельный оси двигателя. Этот вектор заклинен к оси ЛА под углом
8дВ (см. рис. 2.146). Прибавим к правой части уравнения (2.51) две
равные нулю векторные суммы:
R^ = Ra + Rx + Ii + Rc + I Ло I Пдв — I Л» I Пдв +1 Rc I пдв — I Rc I пдв,
в результате получим:
Re = Ra + Иж+ Rвpд + ARj + AR2, (2.53)
где
Кврд = ( I Rc I — I Zoo I ) Пдв ;
AR] = Ii + | Zoo I Пдв; AR2 = Rc — I Rc I пдв.
2.5. О разделении результирующей силы
85
Здесь следует помнить, что величине Rc соответствует расход газа
Qr, который может отличаться от входного расхода воздуха Qb на вели-
чину 0сж - см. соотношение (2.44). Если в расчетах используется тяга
ВРД, вычисленная без учета отбора воздуха из тракта КСУ, то в (2.53)
под 7?Врд необходимо понимать тягу, меньшую на величину АЦ = 0сжК,
где £>сж - секундный расход воздуха, отбираемого на самолетные нуж-
ды, или сжижаемого и накапливаемого на борту ЛА.
В скоростной системе координат компоненты вектора
Rs записываются следующим образом:
7?хх = 7?врд cos(a + 8ДВ) + ДЯ|х + \R2x-cxqS-cxyKqF; 1
7?xy = ЯВрд sin(a + 8ДВ) + Д Riy + Д7?гу + су q S + суЖ qF, ]
где
Д7?1Х = Л,соз(а + 8дв)-/1 cosCa + aJ; 1
ДЯ|У = Л, sin (а+ 5дв)-Л sin(a+ ai), J (2.55)
ДТ?2х = Rc cos(a + 8) - Rc cos (a + 8ДВ); 1
i (2.56)
A7?2y = Rc sin (a + 8) - Rc sin (a + 8ДВ). J
(2.57)
Приведенная запись характерна для случая, когда все компоненты
определяются расчетным путем. При экспериментальном определении
аэродинамических характеристик ЛА с ВРД силы, действующие на
жидкий контур, и силы, учитывающие поворот вектора входного им-
пульса, не выделяют из аэродинамических сил. В этом случае выраже-
ния (2.54) примут вид
7?sx = ^врд cos(a + Здв) — cxs q S + Д/?2х j
= Яврд Sin(a + Здв) + cys qS + \Rly.
Здесь аэродинамические коэффициенты cxs и cys учитывают разворот
вектора входного импульса и силы, действующие на жидкий контур.
Если в полете угол 8 изменяется незначительно, то можно считать,
что ось двигателя параллельна вектору выходного импульса. В этом
случае (8 = 8ДВ) слагаемые в (2.57), учитывающие разворот вектора
выходного импульса, становятся равными нулю и выражения для ком-
понентов вектора Rs примут обычный вид, характерный для дозвуковых
самолетов с ТРД:
7?Sx ~ ^врд cos(a + 8дв) — cxqS\
Rty = Яврд sin(a + 8Дв) + cyqS.
Здесь коэффициенты сх и су имеют тот же смысл, что и в выражениях
(2.57), и зависят от выбранного угла 8ДВ.
(2.58)
86
Глава 2. Общие положения динамики полета
(2.59)
В случае, когда на ЛА установлен ЖРД (!« = 0 и Иж = 0), выраже-
ние (2.49) принимает вид
Re — Ra + R>k^ •
Модуль тяги ЖРД совпадает с модулем выходного импульса. Для
случая ЖРД с соплом Лаваля правую часть выражения (2.48) можно
проинтегрировать. В результате получается выражение для модуля тяги
ЖРД
^жрд — 2т Ис + (Pc - Р^) Fс •
Здесь 2т - расход массы бортового топлива ЖРД; Кс- средняя скорость
истечения продуктов сгорания на срезе сопла; рс- давление на срезе
сопла; Fc~ площадь среза сопла.
Проекции вектора Rs на оси скоростной системы координат запи-
сываются следующим образом:
Яех = Яжрд cos(a + 8) - сх qS\
R^y = ЯЖрд sin(a + 8) + су qS .
Здесь 8-угол установки ЖРД. При вычислении аэродинамических
коэффициентов сх и су в (2.59) используется вся внешняя поверхность
ЛА, включая донную, за исключением среза сопел ЖРД.
Для ЛА с неработающим двигателем из (2.49) получим
Rz = Ra ,
проекции вектора Rs на оси скоростной системы координат
7?sx = -cx^1Sr; R^y= cyqS. (2.60)
Здесь при вычислении коэффициентов аэродинамических сил исполь-
зуется вся внешняя поверхность ЛА, включая донную.
Таким образом, возможны различные формы задания компонентов
результирующей силы ЛА. Кроме того, форма задания может изменять-
ся по траектории полета вследствие смены типов двигателя или изме-
нения внешней геометрии ЛА. Для корректного задания вектора Rs
необходимо следить за тем, чтобы контрольная поверхность была замк-
нутой. Необходимо также точно знать, каким образом определены
коэффициенты сх и су, учтены ли в них силы, действующие на жидкий
контур, и силы, связанные с разворотом вектора входного импульса.
Подробнее о задании исходных характеристик ЛА с ВРД будет изложе-
но в гл. 6.
Зависимость коэффициентов аэродинамических сил от угла
атаки. В общем случае аэродинамические характеристики зависят от
внешней формы ЛА, от угла атаки и от фазовых переменных. Вместо
фазовых переменных, как правило, используются критерии подобия:
число Маха М = Via и число Рейнольдса Re = р Р7/ц, где I - характер-
ный размер ЛА; ц - динамическая вязкость.
2.5. О разделении результирующей силы
87
При оптимизации траекторий движения обычно полагается, что
рассматривается конкретный аппарат с фиксированной формой внеш-
ней поверхности, т.е. аэродинамические характеристики являются
известными. При этом следует отметить, что в процессе проектирова-
ния ЛА (в результате уточнения массы и объема топлива) внешняя
форма аппарата, как правило, изменяется, и аэродинамические характе-
ристики должны уточняться. В связи с этим, говоря об аэродинамиче-
ских характеристиках, будем полагать, что они уже соответствуют той
итерации внешней формы аппарата, для которой проводится цикл
расчетов траектории движения.
При решении задач динамики полета целесообразно иметь анали-
тические зависимости коэффициентов сх и су от угла атаки. Их вид
прямо влияет на процедуру определения оптимального управления.
В ограниченном диапазоне углов атаки зависимость коэффициента
су от угла атаки близка к линейной. Однако при гиперзвуковых скоро-
стях полета и при рассмотрении широкого диапазона углов атаки ис-
тинная зависимость су(а) может быть существенно нелинейной. В связи
с этим в качестве основного варианта примем квадратичную зависи-
мость су(а):
су = суо+ су а+ 2?а2. (2.61)
Здесь суо - коэффициент аэродинамической подъемной силы при а = 0°;
Су - производная коэффициента су по углу атаки при а = 0°;
В - коэффициент, характеризующий отклонение зависимости
су(ос) от линейной.
В некоторых случаях будет использоваться линейная зависимость
су(а), при которой 2? = 0.
Важнейшей характеристикой самолета является его аэродинамиче-
ское качество, которое по определению равно
К = Су /сх .
Максимальное аэродинамическое качество ЯГтах (максимум по углу
атаки или по коэффициенту су) определяется из условия
— Су (<?х) Су ~ 0 • (2.62)
Силу лобового сопротивления представляют в виде двух состав-
ляющих, одна из которых связана с созданием аэродинамической подъ-
емной силы и называется индуктивным сопротивлением (ее безразмер-
ный коэффициент сх/). Другая составляющая не зависит от подъемной
силы (ее коэффициент cxmin). Таким образом, сх = cxmin + сХ1.
Зависимость сх от су называется полярой самолета, которая в боль-
шинстве случаев с достаточной точностью может быть представлена в
виде квадратичной функции
С\ ~ сх min А (су - Су ) . (2.63)
88
Глава 2. Общие положения динамики полета
Здесь А - коэффициент отвала поляры;
с* - коэффициент, учитывающий несимметричность поляры.
В случае квадратичной поляры уравнение (2.62) решается аналити-
чески. Формулы, связывающие /Стах с основными аэродинамическими
коэффициентами, имеют следующий вид:
Сх min~ ЖСуК1п)2 - А (Су ) = 2 + У ’
^тах
к 1 ___________________________1________.
2ДсуКт-су) 2ЛА/схт1П/Л + (су)2-су
СуКт — Су + лМхтт -А + (Су ) >
СУ
ктГ
. 1 С
^хКт 2у4СуК.т(СуКт ^у ) — 2 Сх min
^тах
Здесь аэродинамические коэффициенты сукт и схКт соответствуют
режиму /Стах .
При известном значении су угол атаки определяется в результате
решения квадратного уравнения (2.61). Так, на режиме /Стах имеем
2(СуКт Сур)
(2.65)
ОСКт ।------------------
+WyKm-^yo)
В частном случае, когда поляра - симметричная (су* = 0), формулы
(2.64) упрощаются:
<^х min ' ^(^yKm) 2 ’
^АК. max
К - 1 - 1 •
2Ymax I----- »
2Лс 2 J Ac
у Km vyi^xmin
СуКт О J Г'' д/Сх min A J
^^“^тах
^хКт min 2у4(СуКт) 2
2АКтах
(2.66)
С учетом приближенного соотношения А ® 1/суа и при су0=0 из
формул (2.66) можно получить
2.5. О разделении результирующей силы
89
СуКш ~ \1СХ minCy ’ aKm ~ • (2-67)
^^шах
В некоторых случаях вместо коэффициента су удобнее использо-
вать относительный коэффициенту = су/суКт. Тогда зависимость (2.63)
для симметричной поляры примет следующий вид:
^xrninO У ),
а аэродинамическое качество будет связано с Ктах следующим образом:
К=2Ктту/(\+у2). (2.68)
Значения аэродинамических коэффициентов обычно получают в
результате испытаний моделей ЛА в аэродинамических трубах или
расчетным путем (см. работы [8], [50] и др.).
2.6. Исходные уравнения движения в траекторной
системе координат
Подытожим основные упрощающие предположения, с использова-
нием которых будут записаны уравнения движения ЛА.
1. Внешняя среда, в которой происходит полет ЛА, считается неиз-
менной во времени, а характеристики этой среды - однозначно извест-
ными.
2. Масса летательного аппарата сосредоточена в его центре масс,
т.е. перемещения внутренней среды (компонентов топлива, других
жидкостей) относительно внешней оболочки не учитываются.
3. Движение ЛА рассматривается без учета скольжения и ветра.
4. Предполагается, что в каждой точке траектории аппарат сбалан-
сирован относительно боковой оси Oz (момент тангажа равен нулю).
При записи уравнений движения обычно используется понятие пе-
регрузки. По определению вектор перегрузки равен
nz = Rs /(т go).
Проекции вектора пЕ на оси Ох и Оу скоростной системы коорди-
нат называются тангенциальной и нормальной (скоростной) перегруз-
ками и равны
= R^x К™ go); пу = R^y Кт g0). (2.69)
Проекции вектора ns на оси Ог| и Oyi связанной системы коорди-
нат называются продольной и нормальной перегрузками. Эти компо-
ненты обычно используются для задания ограничений на вектор пере-
грузки. Связь между компонентами вектора ns в связанной и
скоростной системах координат имеет следующий вид:
пх\ = пх cosa + пу sina; иу1 = пу cosa - пх sina. (2.70)
90
Глава 2. Общие положения динамики полета
Для записи уравнений движения будем использовать траекторную
систему координат. Подробный вывод уравнений изложен во многих
работах (см., например, [71], [111]). В отличие от большинства работ в
приведенные ниже уравнения движения входят две составляющие
вектора ускорения гравитационного притяжения (вместо одной ради-
альной), так как в качестве основной модели Земли принят общий
земной эллипсоид.
При записи уравнений движения в качестве аргумента использует-
ся текущее время т. Фазовыми координатами являются:
V - модуль вектора скорости ЛА в геоцентрической вращающейся
системе координат (воздушная скорость);
0 - угол наклона траектории к местной горизонтальной плоскости
(полагается, что |0| < л/2);
Н - высота над поверхностью Земли, отсчитываемая вдоль геоцен-
трического радиуса;
т - масса летательного аппарата;
ср - угол курса (отсчитывается от местной геоцентрической парал-
лели);
ср, X- геоцентрические широта и долгота;
L - путевая дальность полета.
Дифференциальные уравнения пространственного движения ЛА с
работающим двигателем в траекторной системе координат имеют
следующий вид:
dV/dx = go пх- gT sinO + g<p cosO simp + A v;
dQ/dx = gonycosy/V-gT[\ - K2/(grr)] cosO/И-
- g9 sinO simp + Д0;
dH/dx = Г sinO;
dm/dx Qt 9 >(271)
d\\jldx = -go Пу siny /(VcosO) - VcosO tgcp coscp lr +
+ g9 coscp + Avp;
dcp /б/т = V cosO simp lr;
dk/di = V cosO coscp/(r coscp);
dL IdT = V cosO 7?з /r.
Здесь в правые части уравнений движения входят:
go - стандартное ускорение свободного падения (g0 = 9,80665 м/с2);
gr,g(p- компоненты вектора ускорения гравитационного притяжения,
вычисляемые по формулам (2.14) и (2.15);
7?з- радиус Земли на данной широте в соответствии с форму-
лой (2.10);
г - расстояние от центра Земли (г = 7?3 + //);
2.6. Исходные уравнения движения в траекторной системе координат 91
Qx - расход массы топлива в единицу времени (QT > 0).
Слагаемые, учитывающие силы инерции, обусловленные вращени-
ем Земли, в системе уравнений (2.71) равны
Av = coscp (sinO coscp - cosO sincp si my);
Де = co32r coscp (cosO coscp + sinO sincp simy)/V +
+ 2co3 coscp coscy;
ДК|/ = - co32r coscp sincp cosvy /(KcosO) -
- 2co3 (sincp - tgO coscp simy).
(2.72)
Здесь слагаемые, пропорциональные co32r coscp, представляют собой
компоненты вектора центробежного ускорения. Слагаемые, пропорцио-
нальные 2со3, представляют собой компоненты вектора кориолисова
ускорения (входят только в Д0 и Дм/).
Следует отметить, что правые части уравнений движения (2.71) не
зависят от фазовых переменных Z и к Кроме того, они также не зависят
от времени полета т, т.е. система уравнений (2.71) является автономной.
В зависимости от решаемой задачи исходные уравнения движения
могут видоизменяться. В некоторых случаях при интегрировании урав-
нений (2.71) фазовые переменные имеет смысл обезразмерить следую-
щим образом:
x=Xi/x^ (2.73)
где х, - i-я фазовая переменная; х* - ее максимальное или некоторое
характерное значение. При таком подходе система уравнений движения
примет следующий вид:
dxjdx = (dxjdx) /х,\ (2.74)
где dxjdx - правые части системы (2.71). Интегрируемые переменные
х, по модулю не будут превышать единицу или близкое к ней число.
В некоторых задачах вместо одного уравнения расхода массы ЛА
необходимо интегрировать несколько уравнений. Такая ситуация имеет
место, если соотношение расходов масс компонентов топлива перемен-
но или на ЛА используется несколько типов топлива. Тогда вместо
четвертого уравнения (2.71) должны интегрироваться п уравнений в
соответствии с числом компонентов топлива:
dmrjdx = gTj; J = и. (2.75)
Здесь zwTj - масса у-го компонента топлива; £>Tj — его расход в единицу
времени.
Текущая масса ЛА равна
w = w0-SwTj, (2.76)
где то - стартовая масса ЛА (в начальной точке интегрирования).
92
Гпава 2. Общие положения динамики полета
Суммарный объем топлива определяется следующим образом:
= L тГ) /pTj, (2.77)
где pTj - плотностьу-го компонента топлива.
В случае сжижения и накопления воздуха уравнение расхода массы
ЛА примет вид
dmldx = 0сж_ Qx •
В этом случае, а также в случае отбора воздуха из тракта КСУ, не-
обходимо учесть, что соответствующая часть входного импульса (РсжЮ
тормозится до нулевой скорости.
Для варианта движения ЛА с постоянной массой (т - const) чет-
вертое уравнение в (2.71) отсутствует.
Запишем уравнения движения ЛА в общем виде:
dxjdx -f(x\, х2, ..., хп, щ , и2 , ...,ur); i= 1, ..., п,
или
rfX/rfr = F(X, U) , (2.78)
где X = (х[, х2, ..., хп) - вектор фазовых координат; U = (щ, и2, .... иг)-
вектор управляющих воздействий (далее будет называться вектором
управления); F = (/1,J2, •••, Л) _ вектор, координатами которого явля-
ются правые части уравнений движения.
Для определения фазовых координат в виде функций времени
X = Х(т) на отрезке т0 < т < тк необходимо задать граничные условия и
вектор управления как функцию времени: U = U(t); т g [т0, тк].
В общем случае каждая из фазовых координат как на левом конце
(при т = То), так и на правом конце траектории (при т = тк) может быть
фиксированной, свободной или подвижной (принадлежать некоторому
многообразию). Так как система уравнений движения автономна, то без
ограничения общности можно считать, что т0 = 0. Конечное время в
общем случае может быть свободным или фиксированным.
Если закон управления известен, т.е. выбрано некоторое допусти-
мое управление U = U(t), то уравнения (2.78) примут вид
rfX/rfT = F(X,U(T)), (2.79)
откуда при заданных начальных условиях Х(т0) = Хо траектория движе-
ния X = Х(т) будет определяться как решение задачи Коши. Граничные
условия в зависимости от постановки задачи могут изменяться.
Критерием выбора функции U(t) в большинстве задач является
максимум (или минимум) некоторой функции конечных и/или началь-
ных значений фазовых переменных. В частном случае может максими-
зироваться одна фазовая переменная, например конечная масса или
дальность полета.
Основными координатами вектора U, как правило, являются угол
атаки а, угол крена у и величины, определяющие режим работы двига-
2.6. Исходные уравнения движения в траекторной системе координат 93
теля (двигателей) и ориентацию его вектора тяги. Угол крена у входит в
уравнения движения (2.71) явно. От угла атаки а и от режима работы
двигателя в общем случае зависят расход массы топлива Qy и перегруз-
ки пх и пу.
Задача оптимизации траекторий обычно решается с учетом огра-
ничений, наложенных на угол атаки, угол крена и режим работы двига-
теля:
О^гппД — Ct — О^тахД » I У I — УтахД , С?Т — £?ТтахД • (2.80)
Ограничения могут быть наложены также и на фазовые перемен-
ные или на некоторые их функции, например:
Q — *7тахД •> Пх\ — Пх\ шахД , ^yl — ^yl тахД • (2.81)
При полете с большими скоростями в атмосфере летательный ап-
парат подвергается значительному аэродинамическому нагреванию.
Расчет нагревания всей поверхности ЛА представляет самостоятельную
сложную задачу и выходит за рамки данной книги. Поэтому будем
учитывать только температуру Ты в критической точке (в носке ЛА). На
эту величину может быть наложено ограничение: Ты < Аутахд •
Одним из простейших способов определения температуры Ты яв-
ляется решение уравнения Кэмп-Ридделла [130]. Согласно [111] урав-
нение теплового баланса записывается следующим образом:
ф(Гад) - Cw (Д - 7W) /10 - е orw4 = 0 , (2.82)
где Cw - коэффициент теплопередачи; /0, 4, /w- энтальпия торможе-
ния, энтальпия восстановления и энтальпия газа при температуре стен-
ки; 8 - степень черноты поверхности; и = 0,56696-10'7 Вт/(м2-К4) -
постоянная Стефана-Больцмана.
Коэффициент Cw для ламинарного обтекания выражается следую-
щей зависимостью от плотности воздуха и скорости полета:
Cw = 0,2595-10'4 K3’25(p/y?w )0'5, (2.83)
где Яы - радиус затупления носовой части аппарата;
Здесь все величины задаются в системе СИ.
Энтальпия торможения /0 зависит от скорости полета и температу-
ры воздуха Т:
/о = 1000Г+К2/2 .
Энтальпия восстановления /е в критической точке равна энтальпии
торможения /0- Энтальпия /w в пределах изменения температуры до
2500 К может быть аппроксимирована следующей зависимостью:
1ы = 0,124-10% - 0,161 -106.
94
Глава 2. Общие положения динамики полета
При известных значениях V, р и Т (т.е. в каждой точке траектории)
уравнение (2.82) является уравнением четвертой степени относительно
и его можно решить, например, с использованием метода Ньютона.
В случае задания ограничения 7\у1пахд можно построить соответст-
вующую зависимость максимально допустимого скоростного напора от
скорости полета дт\у(Ю- Определим эту зависимость из (2.82) с исполь-
зованием выражения для скоростного напора (<? = рК2/2):
9tw = 0,5 /?w (е о)%1ШхД8/[(0,2595-1(Г4 Q)2V4 5], (2.84)
где Ci = 1 — Zw/Zo -
Производная ^Tw по скорости равна
dq^ldV=-q™ [4,5 IV + 2VI^/{C{ /02)].
Из полученных выражений следует, что по мере увеличения скорости
полета величина <?Tw уменьшается с высоким темпом.
Уравнение Кэмп - Ридделла (2.82) является очень удобным, так как
при проведении траекторных расчетов можно легко определить харак-
терную температуру конструкции без привлечения сложных вычисли-
тельных программ, основанных на решении уравнений аэротермодина-
мики. Однако расчеты, проведенные с применением более точных
методик, показали, что температура, определенная с использованием
уравнения Кэмп - Ридделла, отличается как по величине, так и по
характеру зависимости от скорости полета (см., например, работу [23]).
Для того чтобы сохранить удобство подхода, основанного на реше-
нии уравнения Кэмп - Ридделла, в данной работе предложен следую-
щий способ. Уравнение Кэмп - Ридделла записывается с использовани-
ем поправочной функции v(K):
8О[Т\у(1 +v)]4 = CW(/e-/w)//o.
Функция v(V) определяется для конкретного ЛА в результате кон-
трольного расчета температуры с использованием точных методов
расчета и расчетно-экспериментальных данных. В дальнейшем, при
необходимости, функция v(K) может уточняться. Практика расчетов
показала, что при таком подходе погрешность определения температу-
ры в критической точке (или выдерживания заданного ограничения на
температуру в критической точке) не превышает 10-^20 К.
На рис. 2.15 в качестве примера приведена поправочная зависи-
мость, полученная в результате расчетных исследований возвращаемого
с орбиты крылатого космического корабля [23].
Зависимость ^tw(K) можно использовать в качестве исходного ог-
раничения вместо величины Туутахд- Будем далее полагать, что фазовые
ограничения заданы в координатах "Н- V" или "Я-M". Такие ограни-
чения удобно представить в виде единой кусочно-гладкой кривой, что
значительно упрощает решение задачи.
2.6. Исходные уравнения движения в траекторной системе координат 95
В общем случае уравнения
движения можно проинтегриро-
вать численно только на ЭВМ.
Громоздкость дифференциальных
уравнений в некоторой степени
влияет на суммарное время вы-
числений. Однако, имея в виду
достигнутый уровень быстродей-
ствия современных ЭВМ (в том
числе и персональных), можно
заключить, что это не является
существенным фактором. Поэто-
му в дальнейшем (если не сдела-
но других оговорок) предполага-
ется, что интегрируются исход-
ные уравнения (2.71), записанные
с учетом сил инерции. Правые
Рис. 2.15. Поправочная функция в
уравнении Кэмп-Ридделла, полу-
ченная применительно к крылатому
космическому кораблю
части уравнений движения могут иметь изломы, например, вследствие
изломов исходных зависимостей параметров атмосферы от высоты (в
соответствии с СА-81). Компоненты вектора перегрузки могут иметь
разрывы в точках отключения или переключения двигателей и др. При
необходимости траектория движения разделяется на несколько участ-
ков. Для интегрирования уравнений движения используется любая
стандартная процедура, например метод Рунге-Кутта 4-го порядка
точности.
2.7. Упрощенные уравнения движения. Первые
интегралы уравнений оптимального пространственного
движения
При определении структуры оптимального управления, а также
при решении некоторых задач динамики полета, целесообразно исполь-
зовать упрощенные уравнения движения. В качестве модели Земли
обычно используется шар с центральным полем тяготения. Это значит,
что в уравнениях (2.71) можно положить
Яз = я0; gr = g; gq>=o, (2.85)
где g и Rq соответствуют шарообразной модели Земли.
При движении ЛА с большими скоростями углы наклона траекто-
рии, как правило, малы, поэтому при необходимости (например, в
случае аналитического интегрирования уравнений движения) можно
считать, что
sinO « 0; cos0 » 1.
(2.86)
96
Глава 2. Общие положения динамики полета
Выражения (2.72), учитывающие центробежное и кориолисово ус-
корения, являются довольно громоздкими, поэтому целесообразно
положить Av = До = Д1|/ = 0. При этом некоторые составляющие сил
инерции можно учесть в уравнениях движения приближенно, в частно-
сти, в первом и во втором уравнениях движения (2.71).
В слагаемое Де входят составляющие как кориолисова, так и цен-
тробежного ускорений. Эти составляющие можно учесть, если подста-
вить в слагаемое, учитывающее кривизну Земли, вместо воздушной
скорости V абсолютную скорость КА, вычисленную в инерциальной
геоцентрической системе координат:
-g [1 - VA2/(gr)] cos9/^»-g[l - V2/(gr)] cosO/K+Де. (2.87)
Здесь приближенное равенство становится точным при 0 = 0, в чем
можно убедиться, воспользовавшись соотношениями (2.36) и (2.35).
В слагаемое Ду входит составляющая только центробежного уско-
рения. Разложим вектор ]ЦБ на две компоненты: на радиальную jT (на-
правленную к центру Земли) и меридиональную уф (касательную к
местному меридиану):
7г = - (со3 cos(p)2 г ; уф = - со32созф siп<р г.
Для учета jT в первом уравнении движения необходимо вместо ус-
корения гравитационного притяжения подставить ускорение силы
тяжести, приняв для него приближенную зависимость от высоты, ана-
логичную (2.20):
gT = go(^o/r)2; r = R0 + H. (2.88)
Это равносильно тому, что радиальная составляющая вектора ]ЦБ при-
нята постоянной и равной своему значению на широте <р » 45°.
Меридиональная составляющая вектора jUB входит в 1-е и 5-е урав-
нения движения. Примем 7Ф=0 и определим погрешность, которая при
этом возникает. Меридиональная составляющая вектора ]ЦБ максималь-
на по модулю при полете вдоль меридиана на широте ф = 45°. Ее мак-
симальное значение по модулю составляет со32г/2, что не превышает
0,17% отg0.
Определим погрешность, которая возникает в пятом уравнении
(2.71) вследствие обнуления Дф . В слагаемое Дф входят составляющие
как векторауф, так и кориолисова ускорения. Вектор кориолисова уско-
рения полностью проецируется на боковую ось OzK при полете над
одним из полюсов, его модуль при этом равен 2со3 V. При движении с
круговой скоростью эта величина достигает 1,2 м/с2 (-12% от go), что
существенно в общем балансе сил. Однако, как правило, ЛА летают на
меньших широтах и с меньшими скоростями, поэтому реально погреш-
ность в правой части пятого уравнения (2.71) будет иметь меньшее
значение. Так, при полете на средних широтах при числе М « 15 модуль
произведения КДФ составляет -4% от g0. Данное упрощение может
2.7. Упрощенные уравнения движения. Первые интегралы уравнении 97
сказаться только при рассмотрении проекции траектории на земную
поверхность.
Таким образом, можно заключить, что упрощенные уравнения
движения в плоскости развертки практически соответствуют исходным
уравнениям.
Перепишем систему уравнений движения (2.71) с учетом принятых
упрощений:
dV ldx = g^-g? sinO;
б/0 /б/т = go пу cosy / V - g[ 1 - KA2/(g r)]cos0 / И;
dH/dx = V sinO; dm/dx = -Qt,
(2.89)
dxy/dx =-gony siny /(V cos0) - Kcos0 tgcp cosy /r;
б/ф /dx = V cos0 sin 14/ /r;
dX/dx = V cosO cos\|//(r coscp);
dL /dx = V cos0 7?o lr.
В общем случае движение, описываемое уравнениями (2.89) и
(2.90), является пространственным. Теоретические основы исследова-
ния оптимального пространственного движения ЛА в атмосфере под-
робно изложены в монографии Л.М. Шкадова, Р.С. Бухановой,
В.Ф. Илларионова, В.П. Плохих [111]. Ниже будут приведены некото-
рые результаты этой работы.
Как показано в [111], в случае пренебрежения вращением Земли
(при Рд = V) правые части системы (2.89) не зависят от фазовых пере-
менных у, ср, X, Z, и это позволяет систему уравнений движения разде-
лить на две части. Уравнения (2.89) описывают некоторое фиктивное
плоское движение (движение в плоскости развертки), а уравнения
(2.90) определяют проекцию траектории ЛА на поверхность Земли, т.е.
форму изгиба плоскости развертки.
Пусть решается следующая задача оптимального управления: сре-
ди всех траекторий, удовлетворяющих уравнениям (2.89), (2.90), при
заданной области изменения вектора управления U требуется опреде-
лить траекторию, обеспечивающую в конечной точке минимальное
значение некоторой функции начальных и конечных значений фазовых
координат:
^(*/0, */к) —>min; Z= 1, п < 8. (2.91)
Воспользуемся принципом максимума Понтрягина [79]. Как пока-
зано в работе [111], задача минимизации функции (2.91) решается так
же, как и в случае минимизации конечного значения одной из фазовых
переменных. Оптимальные значения координат вектора U в каждый
момент времени определяются из условия абсолютного максимума
функции Гамильтона
98
Глава 2. Общие положения динамики полета
8 Их
(2-92)
7^ dx
и выражаются в виде некоторых функций фазовых координат и сопря-
женных переменных Р,, определяемых системой уравнений
dPJdx = - сГН/дх,; i = 1, 8. (2.93)
Структура оптимального управления определяется поведением ре-
шения сопряженной системы (2.93) совместно с уравнениями (2.89),
(2.90) при граничных условиях, вид которых зависит от конкретной
формулировки задачи.
Представим функцию Гамильтона (2.92) в виде суммы:
Н = НХ + Н2,
где
4 8
(2.94)
Zi Л dx
В работе [111] показано, что если правые части системы уравнений
(2.89) не зависят от фазовых переменных системы (2.90), определяю-
щей форму изгиба плоскости развертки (в данном случае от перемен-
ных <|/, <р, X и Z), то система уравнений (2.93) для определения сопря-
женных переменных разделяется на две части:
dPJdx =-д(Н\ +Н2)/8х^ i= 1, ...,4; (2.95)
dPJdx = -&Н21дх^ z = 5, ...,8, (2.96)
причем система уравнений (2.96) не зависит от системы уравнений
(2.95). Таким образом, как система уравнений движения ЛА, так и
сопряженная с ней система распадаются на две части, одна из которых
отделима. Причем характерно, что в фазовой системе отделяются урав-
нения (2.89), описывающие движение в плоскости развертки, которые
могут быть решены независимо от уравнений (2.90). Для сопряженной
системы уравнений (2.95), (2.96) имеет место обратная картина, т.е.
отделяется система (2.96), соответствующая фазовой системе (2.90),
которая определяет форму изгиба плоскости развертки. Это обстоятель-
ство позволило получить в работе [111] несколько первых интегралов
уравнений оптимального пространственного движения.
Проанализируем правые части системы уравнений (2.89) с точки
зрения их зависимости от фазовых переменных \у, <р, X и L для случая
вращающейся Земли. Выше уже было отмечено, что переменные X и L
не входят в правые части уравнений движения. Естественно полагать,
что как аэродинамические коэффициенты, так и тягово-экономические
характеристики, в том числе расход массы топлива (2т, не зависят от
2.7. Упрощенные уравнения движения. Первые интегралы уравнений 99
фазовых переменных ф и у. Так как выше была принята модель стан-
дартной атмосферы СА-81, являющейся стационарной и сферичной, и,
кроме того, влияние ветра не учитывается, то можно заключить, что
скоростной напор и, следовательно, перегрузки их, пу также не зависят
от этих переменных. Ускорения g и gT в соответствии с формулами (2.8)
и (2.88) зависят только от высоты. Таким образом, от переменных и ср
явно зависит только абсолютная скорость ЙЛ в соответствии с форму-
лами (2.36) и (2.35). Чтобы избавиться от этой зависимости, воспользу-
емся первой формулой (2.36) и пренебрежем в ней последним слагае-
мым. Это равносильно тому, что радиальная составляющая
центробежного ускорения не учитывается. Однако эту составляющую
можно учесть приближенно, как и в первом уравнении движения, заме-
нив ускорение g HagT. Тогда, используя соотношение (2.36) и учитывая,
что
cos z’opt = coscp cosy, (2.97)
второе уравнение (2.89) перепишем следующим образом:
dQ/di = g0 лу cosy/И-gT (1 - V2 + C°S*0РТ )cos6/ К
Здесь z’opt - наклонение плоскости ортодромии, в которой лежит вектор
воздушной скорости V в каждый момент времени.
В плоском движении (в полете без крена) угол /Орт практически по-
стоянен. В пространственном движении этот угол изменяется по траек-
тории в соответствии с соотношением (2.97). Если ^гол z’opt зафиксиро-
вать, приняв в качестве характерного значение /*, соответствующее
максимальной скорости полета, то таким образом можно обеспечить
приближенный учет кориолисова ускорения, который будет наиболее
точным на тех участках полета, где величина кориолисова ускорения
максимальна.
Следует отметить, что слагаемое, учитывающее кривизну Земли во
втором уравнении (2.89), можно было не записывать через абсолютную
скорость КА. Это равносильно тому, что кориолисово ускорение было
бы принято равным нулю. Однако цель математических преобразова-
ниий состояла в том, чтобы получить уравнения движения, максималь-
но близкие к исходным, т.е. наиболее полно учесть силы инерции при
условии обеспечения независимости правых частей уравнений (2.89) от
переменных у и ср.
Таким образом, в системе уравнений
dV/dz = go пх- gT sinO;
dd /dx = go ny cosy /Г- gT (1 - V1 )cos0 /К;
dH/dx = HsinO; dm/dx = -Qt
(2.98)
100
Глава 2. Общие положения динамики полета
(2.99)
правые части не зависят от фазовых переменных \|/, ср, А, и L.
Это означает, что при рассмотрении пространственного движения
можно воспользоваться результатами работы [111], в соответствии с
которыми первые интегралы для сопряженной системы уравнений
(2.96) записываются следующим образом:
PL= С| ; С2; Лр = С3 sinA,- С4 cosA,;
= (С3 cosA, + С4 sinX) coscp + С2 sincp,
где С, (z = 1, ..., 4) - некоторые константы интегрирования, значения
которых определяются граничными условиями конкретной задачи.
Если по условию задачи конечное время фиксировано, то в качест-
ве независимой переменной удобнее взять угловое расстояние s9 как это
было сделано в работе [111]. Угловое расстояние отсчитывается по
длине большого круга и связано со временем следующим образом:
ds = (КcosQlr) dx.
Уравнения движения при этом примут вид
dVIds = (go п* - gT sinO) г I (V cosO);
dQ/ds =gor z?y cosy/(K2cos0) -gyr/V2 + 1 + 2 co3 r cosz 7K;
dH/ds = r tgO; dm!ds =-Qt^I(VcosO);
d\\f/ds =-gorny siny /(TcosO)2 - tgcp cosy;
<7cp Ids = sin\|/;
d\ Ids = cos\|/ /coscp; dxlds = r! (TcosO).
(2.100)
(2.101)
(2.102)
Вместо первого соотношения в (2.99) необходимо записать Рх= С\.
Дифференциальное уравнение для определения времени в (2.102)
отнесено к пространственной части системы уравнений движения
условно. Основная особенность времени как фазовой переменной
заключается в том, что оно не входит в правые части всех уравнений
движения. Если оно также не входит в минимизируемую функцию
F(x/o, Х/к), то последнее уравнение в (2.102) можно исключить из рас-
смотрения. То же самое относится к последнему уравнению системы
(2.90) для дальности полета.
В работе [111] введены в рассмотрение переменные q\ и q2, кото-
рые играют важную роль при исследовании пространственного движе-
ния ЛА:
<71 =Лр= C2sincp + C3cosA, coscp + C4sinX coscp; (2.103)
</2 = C2 coscp cos\|/ + C3 (sinA, sinv|/ - cosA, sincp cosy) -
- C4 (cosA, sinvjj + sinA, sincp cosy). (2.104)
2.7. Упрощенные уравнения движения. Первые интегралы уравнений 101
С использованием этих переменных функцию Н2 можно записать в
виде
772 = -<7igo«ySiny/(Kcos0) + (^2 + Ci2?o) 7cos0/r. (2.105)
Для случая, когда аргументом является переменная s, функция 772
записывается следующим образом:
772 = ~q\gvr пуsiny /(7cos0)2 + q2 + С\ г/(VcosO). (2.106)
Переменные q\ и q2 имеют определенный геометрический смысл.
Проведем через центр земной сферы некоторую плоскость 77и зададим
значения трех независимых констант С2, С3 и С4, входящих в (2.103) и
(2.104), при помощи трех других независимых переменных А, Хп, /’п
посредством соотношений
С2 = Л cosz'n; С3 = A sinz’n sinXn; G = -A sinzn cosXn ; A > 0, (2.107)
где Хп - долгота восходящего узла плоскости 77; zn - угол наклона 77к
экваториальной плоскости (рис. 2.16).
Пусть ЛА в некоторый момент времени находится в точке М. Тогда,
как показано в работе [111],
^i = ^4sin5; q2 = A cos 8, (2.108)
где 8 - угловое расстояние между ЛА и плоскостью 77; 8 - угол между
плоскостью 77 и мгновенной плоскостью движения, содержащей век-
тор воздушной скорости V. На рис. 2.16 углы 8 и 8 показаны положи-
тельными.
Так как решение сопряженной системы уравнений (2.93) в силу ее
линейности и однородности относительно Р( определяется с точностью
до положительного множителя, то без ограничения общности можно
положить Л = 1. Таким образом, переменные q\ и q2, от которых зависит
Рис. 2.16. К геометрической интерпретации переменных qx и q2
102
Глава 2. Общие положения динамики полета
оптимальное управление, определяются только положением ЛА и
направлением вектора его скорости относительно плоскости /7, фикси-
руемой в пространстве значениями параметров Хп и /п, которые, в свою
очередь, определяются граничными условиями конкретной задачи.
В работе [111] показано, что полученные результаты могут быть
обобщены на класс задач с фазовыми ограничениями типа
G(x,,U)<0 или G(x,)<0; z=l,...,4, (2.109)
т.е. если фазовые переменные vg, (р, X и L не входят в уравнение грани-
цы. В этом случае система уравнений (2.96), использовавшаяся при
получении первых интегралов, не изменит своего вида, и эти интегралы
сохранятся.
Наличие выписанных выше первых интегралов значительно облег-
чает решение задачи и позволяет в ряде случаев устранить дополни-
тельные трудности, вызываемые пространственностью движения.
Основные трудности, связанные с поиском оптимального управления в
пространственном движении, обусловливаются не столько пространст-
венностью движения, сколько сложностью решения уравнений, соот-
ветствующих движению в плоскости развертки.
2.8. Оптимальное пространственное движение на
квазистационарных режимах
Если уравнения, описывающие движение в плоскости развертки,
достаточно просты, то исследование специфики оптимального про-
странственного движения может быть облегчено. В частности, всегда,
когда движение ЛА в плоскости развертки описывается одним уравне-
нием (система (2.98) или (2.101) вырождается в одно дифференциаль-
ное уравнение), все сопряженные переменные (и, следовательно, опти-
мальное управление ЛА) могут быть выражены в функции фазовых
координат и некоторых констант. Действительно, в этом случае из
четырех сопряженных переменных Pv, Ре, Рн и Рт остается только
одна, значение которой в любой точке траектории может быть выраже-
но в функции фазовых координат и констант С], С2, С3 и С4 из условия
Н = const.
Существенно упростить уравнения движения позволяет гипотеза
квазистационарности, заключающаяся в предположении, что
и 0«О. (2.110)
Такие режимы полета в действительности имеют место, например,
в крейсерском полете и при планировании ЛА с высоким аэродинами-
ческим качеством. В этом случае второе дифференциальное уравнение
системы (2.89) превращается в конечное соотношение:
go«ycosy =g[l - VA2/(gr)\ COS0 . (2.111)
2.8. Оптимальное пространственное движение
103
Аналогично, из второго уравнения (2.98) получим:
Tz2 l + 2co3rcosz*/K _
go ny cosy = gT (1 - V ------------) cosO, (2.112)
gT''
где
gT = g0(/?0/r) ; r = Ro + H.
Третье уравнение движения относительно высоты полета, как бу-
дет показано ниже, также можно свести к конечному соотношению. В
некоторых случаях ввиду малости угла 0 это уравнение исключают из
рассмотрения. При этом в (2.111) и (2.112) необходимо положить
cosO = 1.
Таким образом, если число исходных дифференциальных уравне-
ний, описывающих движение в плоскости развертки, равно трем, то
использование гипотезы квазистационарности позволяет свести систе-
му уравнений вида (2.98) или (2.101) к одному дифференциальному
уравнению. Кроме того, если время и путевая дальность заранее не
зафиксированы и не входят в функционал (при этом будут справедливы
соотношения Н = 0 и С\ = 0), то семейство экстремалей для таких задач
при любых граничных условиях будет не более чем двухпараметриче-
ским [111].
Систему уравнений (2.98) или (2.101) можно свести к одному диф-
ференциальному уравнению, например, для случая пассивного плани-
рования в атмосфере (т = const). Траектории движения такого класса
были подробно исследованы в работе [111]. При этом было показано,
что гипотеза квазистационарности является эффективным средством
получения структуры приближенно оптимального управления, которое
затем можно использовать для интегрирования полной системы урав-
нений.
Вначале в работе [111] с использованием асимптотических методов
была исследована полная система уравнений вида (2.101), (2.102) для
случая невращающейся Земли. Предполагалось, что планирование
осуществляется с малыми углами наклона траектории (0 « 0), управле-
ние осуществляется углами крена и атаки с неограниченным диапазо-
ном изменения. Аэродинамические коэффициенты су и сх зависят от
угла атаки и не зависят от высоты и числа Маха.
Было показано, что оптимальные значения угла крена в процессе
полета ЛА совершают "быстрые” колебания относительно некоторой
"медленно” меняющейся во времени величины, определяемой выраже-
нием
tgYcp = -«?i/?2, (2.113)
где п = g0 R^/V2- 1 >0.
Оптимальный угол атаки колеблется около значения, соответст-
вующего максимальному аэродинамическому качеству:
104
Глава 2. Общие положения динамики полета
КсР^пах. (2.И4)
Далее задача была решена с использованием гипотезы квазиста-
ционарности. При этом применялись уравнения движения следующего
вида:
dV/ds =-Vnl (К cosy); d\\j/ds = -п tgy- tgcp cosy;
t/ср Ids = siny; d'kids = cosy /cosy; dx Ids = RJV,
1 (2.П5)
которые можно получить из уравнений (2.101), (2.102) с использовани-
ем (2.112) при т = const; 0 = 0; со3 = 0; gT = gQ; г = Ro и с учетом того,
что в данном случае К = -пу/пх.
В качестве управляющих переменных использовались угол крена у
и аэродинамическое качество К. На управляющие переменные были
наложены ограничения
1у1 — Утахд < ^/2; 0 < Кт|Пд К < Ктах, (2.116)
так как при К = 0 и при у = ±л/2 правые части уравнений разрывны и
уравнения теряют физический смысл.
Зависимость аэродинамических коэффициентов от высоты не учи-
тывалась. В результате были получены условия оптимальности, кото-
рые в частном случае, когда время т и длина дуги s заранее не зафикси-
рованы и не входят в функционал, имеют следующий вид:
Yopt = у * = - arctg(n qx/q2} при q2 < -1 п qx /tgymaxA I;
Yopt = УтахД signal при q2 > -1 n qx I;
^iopt — ^Чпах При t/2 — I 77 qX tgyma^ I ,
^opt — -^ЧптД При 6/2 > I 77 qX tgy1naxД I •
(2.117)
При этом было показано, что режим особого управления отсутствует.
Условия (2.117) записаны в соответствии со стандартным опреде-
лением знаков угла крена, когда положительный угол у соответствует
правому крену (см. раздел 2.4). В работе [111] положительный угол у
соответствует левому крену.
Соотношения (2.117) выделяют в плоскости [<71, q2] три характер-
ные области (рис. 2.17), в каждой их которых реализуется определен-
ный режим управления. При скорости полета, равной круговой (п = 0),
все четыре луча (см. рис. 2.17) сливаются (q2 = 0), при этом у* = 0. С
уменьшением скорости полета области, соответствующие режимам
A^opt= 7СП1пд и yopt = у*, сужаются. Режим /Copt = А^пД возможен только при
qi> т.е. при граничных значениях оптимального угла крена (см.
рис. 2.17). По траектории полета возможно не более одного переключе-
ния аэродинамического качества, причем только с Л?т;пД на Л?тах [111].
2.8. Оптимальное пространственное движение
105
Рис. 2.17. Области возможных оптимальных режимов управления
при квазистационарном планировании
На участках полета, где управление по углу крена не является гра-
ничным, оптимальные значения управляющих переменных определя-
ются условиями
^opt ^Чпах •> tgy0pt И Q1 А?2 • (2.118)
Сравнение выражений (2.118) с выражениями (2.113) и (2.114) по-
казывает, что на участках полета, где оптимальные значения управляю-
щих перменных не лимитируются своими предельными значениями,
приближенно оптимальное управление тождественно совпадает со
средним управлением, соответствующим точному решению. Следова-
тельно, при малых углах наклона траектории приближенно оптималь-
ное управление, полученное с использованием гипотезы квазистацио-
нарности, может быть достаточно хорошим приближением к точному
закону оптимального управления.
Условия оптимальности (2.117) позволяют сделать некоторые каче-
ственные выводы о поведении экстремали, если принять во внимание
геометрическую интерпретацию функций q\ и q2 • Плоскость 17 разбива-
ет земную сферу на две полусферы, в одной из которых sinS = q\ > 0, а в
другой sinS = q\ <0. Из рис. 2.17 видно, что знак оптимального угла
крена совпадает со знаком qx. Таким образом, знак оптимального угла
крена сохраняется неизменным до тех пор, пока ЛА остается по одну
сторону от плоскости /7; при переходе через плоскость П знак крена
меняется на противоположный.
Управление углом крена всегда является граничным при q2 > 0.
Принимая во внимание равенство q2 = cos8, получаем, что управление
всегда находится на границе при 8 < к/2, причем выход на ограничение
и сход с него происходят в точках траектории, отвечающих условию
106 Глава 2. Общие положения динамики полета
^COS£=-|n^1/tgYmaxfl|.
Если величина утахд близка к к/2, то в этих точках угол £ также бу-
дет близок к л/2.
Сведение системы уравнений (2.98) или (2.101) к одному диффе-
ренциальному уравнению возможно также в случае пространственного
движения с ВРД (при V = const). Такая задача также была подробно
решена в работе [111]. Правые части уравнений движения в этом случае
формально совпадают с правыми частями уравнений (2.115), описы-
вающих пассивное планирование. Вследствие этого условия оптималь-
ности совпадают с (2.117) за исключением того, что режим A?opt= АГт,пД
отсутствует. В результате решения задачи с использованием дополни-
тельных упрощений были получены аналитические зависимости фазо-
вых координат от аргумента 5 и начальных условий.
Система вида (2.101) сводится к одному уравнению расхода массы
при решении задачи об оптимальном повороте плоскости круговой
орбиты спутника с использованием силы тяги ЖРД, направленной по
нормали к плоскости орбиты [48].
Гипотеза квазистационарности должна использоваться только для
нахождения структуры управления. Построение фазовой траектории
должно проводиться на основании интегрирования полной системы
уравнений движения. Точность построения траектории с использовани-
ем приближенно оптимального управления достаточна для практиче-
ских целей. Так, численные расчеты на ЭВМ показали, что боковая
дальность спуска при наличии ограничения на температуру в носовой
точке аппарата, определяемая с использованием приближенно опти-
мального управления, отличается от оптимального решения не более
чем на 0,1 % [111].
2.9. Оптимальное плоское движение на
квазистационарных режимах
Рассмотрим частный случай, когда движение описывается двумя
дифференциальными уравнениями вида
dxx/dx=f(xbx2, щ, иъ мг); П9)
dx2/dx =^(хьх2, w2, ..., иг).
Пусть фазовые переменные изменяются во времени монотонно
(этими переменными могут быть дальность полета и текущая масса
ЛА), тогда функции f и f2 не будут изменять своего знака по траекто-
рии. Система является автономной, время на правом конце не зафикси-
ровано. Управляющие переменные в общем случае являются ограни-
ченными:
пмпД — — Uj тахД ? Z — 1, ..., Г.
2.9. Оптимальное плоское движение
107
Пусть необходимо максимизировать фазовую переменную xj при
заданном конечном значении х2 • Как известно, в данном случае интег-
рирование сопряженной системы не требуется: управляющие перемен-
ные и, (z = 1, г) в каждой точке траектории выражаются через фазо-
вые переменные. Это обстоятельство широко использовалось во многих
известных работах при оптимизации траекторий на основе упрощенных
уравнений движения (см., например, работы [30], [46], [63], [71], [87]-
[89], [94]—[97], [124]). Одно из возможных доказательств того, что
управляющие переменные в данном случае выражаются через фазовые
переменные, было сделано И.О. Мельцем в работе [30].
Действительно, в соответствии с принципом максимума в каждой
точке траектории оптимальное значение и, определяется из условия
абсолютного максимума функции Гамильтона
Н= Р\ f + Рэ fi max,
где Р\ и Р2 - сопряженные переменные, причем на правом конце траек-
тории Р\(Т) = 1.
Так как функции f wf2 не меняют своего знака, то на всей траекто-
рии Р[ > 0. Кроме того, в данном случае
Н = Л/;+Р2/2=0. (2.120)
Пусть решение U* приводит к максимуму Н , причем оптимальное
управление может находиться как внутри заданного диапазона, так и
быть граничным. Тогда из (2.120) получим
P2/P1=-/|(U’)//2(U’).
При любом 5U имеет место неравенство
Р\ fy (U* + 5U) + Л /2 (U’ + 8U) <Pyfy (U‘) + Р2 ,/2 (U*),
или с учетом (2.120)
fy (U* + 5U) -/2 (U* + 5U) /i(U*) //2(U’) < 0.
Пусть/, > 0, тогда
fy (if + 5U) If (if + 8U) < /1(U*) //2(lf),
то есть максимуму функции Гамильтона однозначно соответствует
максимум функции, равной отношению правых частей исходных урав-
нений (2.119):
/(Xj, х2, щ , и2, ..., иг) = +f lf2 птах .
Сформулируем правило определения знака функции f:
- при максимизации конечного значения Х]
108
Гпава 2. Общие положения динамики полета
при/2>0; (2.121)
/=-/i//2 -> max при/2<0; (2.122)
- при минимизации конечного значения х,
/= f Ifi max при f2 < 0; (2.123)
f=-f\lfi -> max при/2>0. (2.124)
Пусть теперь вместе с дифференциальными уравнениями (2.119)
задано условие типа равенства
G(xi, х2, Щ , и2, ..., wr) = 0, (2.125)
причем dG/du, Ф 0.
Разрешив это уравнение относительно щ и исключив их из системы
(2.119), получим новую систему уравнений, зависящих от г - 1 управ-
ляющих переменных:
dx\ /dx -f\(x\ ,х2, «i, м2, ..., wr-i);
dx2Idx =f2 (xi, x2, W|, w2, ..., wr_i).
Как и в предыдущем случае, оптимальное управление будет нахо-
диться из условия экстремума функции
/*(Х] , х2, щ , и2, ..., Wr_j ) =/|* //2*
или, что то же самое, как и в случае определения экстремума функции
f-f/fi при условии (2.125).
В общем случае при наличии нескольких условий типа (2.125) за-
дача оптимального управления сводится к задаче определения условно-
го экстремума функции f в каждой точке траектории (при фиксирован-
ных значениях Х| и х2):
f (Х|, х2, щ , ib , ..., их) = flf2 extr;
Gf (xi, х2, щ , и2, ..., иТ) = 0, j < г.
Перейдем к рассмотрению плоского движения - одного из наибо-
лее важных случаев движения ЛА. Обычно под плоским движением
понимается полет в вертикальной плоскости (полет в плоскости боль-
шого круга Земли) без крена и скольжения. Однако, строго говоря,
траектория движения с нулевым углом крена не всегда лежит в верти-
кальной плоскости. Для случая вращающейся Земли плоскими являют-
ся только траектории, лежащие в экваториальной плоскости. Все ос-
тальные траектории отклоняются от плоскости большого круга
2.9. Оптимальное плоское движение
109
вследствие действия сил инерции, вызванных вращением Земли. При-
чем отклонение тем больше, чем больше скорость полета ЛА.
Будем понимать под плоским такое движение, когда в функционал
(2.91) не входят фазовые координаты ф, ф и X. Т.е. фактически будем
рассматривать движение в плоскости развертки. При этом угол крена не
будем полностью исключать из рассмотрения, так как в некоторых
задачах использование угла крена в качестве дополнительной управ-
ляющей переменной может привести к улучшению функционала. В том
случае, когда оптимальный угол крена не равен нулю, а движение
должно осуществляться в вертикальной плоскости, будем полагать, что
угол крена совершает знакопеременные перекладки, т.е.
cosy < 1 при siny = 0.
Угол крена может быть задан в виде функции фазовых координат или
быть постоянным (в том числе и равным нулю). В каждом отдельном
случае об угле крена будет говориться особо.
Возьмем за основу систему уравнений движения (2.89), (2.90) и ис-
ключим из рассмотрения уравнения для фазовых переменных ф, ф и X.
В результате остаются пять уравнений, описывающих движение в
вертикальной плоскости. Для дальнейшего уменьшения числа диффе-
ренциальных уравнений существуют различные способы. Одни из них
позволяют отделить уравнение для массы ЛА: масса ЛА считается
постоянной или приближенно зависимой от высоты и скорости полета
[96]. Другие допущения позволяют силу лобового сопротивления X в
первом уравнении движения считать известной функцией от высоты и
скорости, для чего пренебрегают индуктивным сопротивлением [71].
При малых скоростях полета полагают, что движение является квазиу-
становившимся, при этом в процессе изменения удельной энергии
пренебрегают изменением кинетической энергии.
В работе Л.П. Федорова [96] показано, что большинство прибли-
женных методов ("энергетический” метод Остославского - Лебедева,
метод Миеле, различные графические методы и т.д.) связаны между
собой и дают одинаковое решение задачи. Наиболее удобным методом
построения приближенно оптимальной траектории (близкой к опти-
мальной траектории по структуре управления и по величине функцио-
нала) является "энергетический". Этот метод (см., например, работы
[87], [96], [124]) основан на использовании удельной энергии и гипоте-
зы квазистационарности.
В случае квазистационарного движения, как было показано в раз-
деле 2.8, второе уравнение движения превращается в конечное соотно-
шение вида (2.111) или (2.112).
Получим еще одно конечное соотношение - для угла наклона тра-
ектории. С этой целью запишем первое и третье уравнения системы
dVIch = gonx- gT sin0; dH/dx = HsinG (2.126)
но
Глава 2. Общие положения динамики полета
и введем в рассмотрение удельную энергию ЛА
Е = Н + V2/(2gT). (2.127)
При малых (дозвуковых) скоростях полета удельная энергия опре-
деляется главным образом высотой полета, при больших (гиперзвуко-
вых) скоростях - скоростью полета. По траектории ускорение gT изме-
няется незначительно, поэтому для упрощения будем полагать, что при
дифференцировании выражения (2.127) величина gT является постоян-
ной, т.е.
dE = dH + VdV/gT.
При пх = 0 и 0= 0, как это следует из уравнений (2.126), имеет ме-
сто установившийся горизонтальный полет (V = const, Н = const),
который соответствует движению с постоянной удельной энергией.
Исследуем случай пх = 0; 0 0. Исключив из (2.126) время, полу-
чим
= dH/dV = -V/gj при пх = 0. (2.128)
Продифференцировав по Н выражение (2.127) при Е = const, полу-
чим также соотношение (2.128). Таким образом, случай пх = 0 всегда
соответствует движению с постоянной удельной энергией. Угол накло-
на траектории при этом может быть как нулевым, так и отличным от
нулевого.
Пусть теперь пх^0 и, следовательно, grH'y + И^О. Исключив из
(2.126) время, получим
sinG = при пх * 0. (2.129)
gT#v +У
При пх = 0 полученное выражение не определено, так как знамена-
тель равен нулю в соответствии с соотношением (2.128). Случай
Ну = 0 соответствует горизонтальному полету (0 = 0). При Рн = 0
имеет место либо набор высоты, либо снижение с постоянной скоро-
стью. В этом случае (2.129) превращается в соотношение
sin0 = nxgo/gT при И'н=0, (2.130)
которое также охватывает случай установившегося горизонтального
полета (пх = 0; 0 = 0).
Определим связь между производными Н'у и q'y. Для этого про-
дифференцируем по скорости выражение для скоростного напора
q'y = р'нН'у V2/ 2 + pV= q (2 IV- p/Z'v),
откуда получим
7/'v=(2/r-^'v/^)/p.
Здесь Р = - р н/р - параметр атмосферы.
При движении с постоянным скоростным напором имеем
2.9. Оптимальное плоское движение
111
Яу=2/(РР) при q = const. (2.131)
Характерно, что в выражении (2.131) производная Н’у не зависит
от скоростного напора и монотонно уменьшается по мере увеличения
скорости полета.
При больших скоростях траектории полета являются довольно по-
логими (0 « 0). В этом случае изменение удельной энергии происходит
главным образом за счет изменения скорости (dH« VdVIgx). Это озна-
чает, что
dE* VdV/gT,
то есть вместо условия Е = const можно использовать условие V= const.
Полагая, что их^0, перепишем первое уравнение (2.126) с учетом
(2.129):
JK/JT=go«x/(l +gT//'v/n.
В это уравнение входит производная Н'v, которая в общем случае
является неизвестной. Для ее исключения сделаем замену фазовой
переменной (вместо скорости будем интегрировать удельную энергию):
dE= — (1 +gyH\i!V)dV. (2.132)
ёт
Тогда система дифференциальных уравнений, описывающих плос-
кое движение, примет следующий вид
dE/di = go Vnx /gT; dm/dt = -Qt ; dL/dt=V cos0 Ro/r. (2.133)
Пусть на ЛА установлен ВРД. Запишем компоненты вектора пере-
грузки и секундный расход массы топлива в следующем виде:
пх= c^qS/(m go); пу= c^yqS/(т g0); Q^c^qF/J. (2.134)
Здесь cSx и cZy - безразмерные коэффициенты результирующей силы
ЛА: cLx = R^JtqS); cZy = R^y/(qS);
cR- коэффициент тяги ВРД: cR= R/(qF);
R- тяга ВРД, вычисленная с учетом потерь в тракте силовой уста-
новки;
J- удельный импульс ВРД: J= R/Q?.
Вместо массы введем в рассмотрение новую фазовую переменную
М ("логарифмическую" массу), как это было сделано в работе [114]:
М= In (т/то). тогда
т = тоехр(М); dm = mdM. (2.135)
В начальной точке траектории (при т = то) М= 0, по траектории пере-
менная Л/монотонно уменьшается.
Перепишем систему уравнений (2.133) с учетом (2.134) и (2.135),
исключив скоростной напор при помощи конечного соотношения
112
Гпава 2. Общие положения динамики полета
(2.111). В результате получим систему трех дифференциальных уравне-
ний
ж/л , .
cZygTcosy
dMldx=-^y.^Fl^.
c£ycosyJ
(2.136)
dL /dx = V cos0 Rq/г ,
которые в общем случае необходимо интегрировать с использованием
нескольких конечных соотношений, основными из которых являются:
Е = Н + K2/(2gT); <7 = рГ2/2;
r = RQ + H-, g=\i/r2-, gT = g0(R0/r)2;
с^у qS cosy = mgy cos0 ;
sin0 = ^-v при nx Ф 0.
(2.137)
Здесь с целью сокращения записи принято
gv = g[l - ^\2/(g^)] •
Плотность атмосферы р связана с высотой Н в соответствии с со-
отношениями СА-81 (см. раздел 2.3). Величина Н\, входящая в по-
следнее выражение (2.137), определяется численно в результате интег-
рирования системы уравнений (2.136):
H\ = \EI\V-Vlg^.
Проведем анализ полученной системы дифференциальных уравне-
ний (2.136). Правые части уравнений в общем случае зависят от управ-
ляющих переменных, скорости К и от других фазовых переменных.
Так как при у = ±л/2 и с^у = 0 правые части уравнений (2.136) раз-
рывны, будем полагать, что эти величины ограничены:
I У I — УтахД < ТС/2, > 0.
Покажем, что зависимость от угла 0 является несущественной. С
этой целью введем вместо времени новую независимую переменную t
следующим образом:
dt = cos0^T .
Переменная г, как и время, не входит в функционал и свободна на
правом конце траектории. После замены переменных cos0 исключится
из правых частей уравнений (2.136). Из двух последних соотношений
2.9. Оптимальное плоское движение
113
(2.137) угол 0 также можно исключить, в результате останется конечное
соотношение, связывающее угол атаки и высоту полета.
Зависимость правых частей (2.136) от переменных ср и ц/ (через аб-
солютную скорость ИА) является также несущественной. Действитель-
но, выше было получено приближенное равенство
g[l - HA2/(gr)>gT(l - V2 1 + 2oVcos; /V } , (2138)
8тг
где z* — угол наклона плоскости ортодромии в характерной точке траек-
тории.
В первом приближении можно положить, что cosz * = cos(p0cos\|Jo
Для определения в каждой точке траектории абсолютной скорости ИА
можно также проинтегрировать уравнения (2.90) для фазовых перемен-
ных ц/ и (р одновременно с уравнениями (2.136). При малых скоростях
полета имеет место приближенное равенство
g[l-KA2/(gr)]«gT. (2.139)
Величины г, g и gT, зависящие от высоты, в процессе движения
изменяются незначительно. В некоторых случаях для упрощения задачи
можно использовать их средние значения.
От фазовой переменной L правые части уравнений не зависят.
Удельная энергия Е входит в правые части через скорость полета. Лога-
рифмическая масса Л/ прямо не входит в правые части уравнений,
однако при этом необходимо отметить следующее. При малых скоро-
стях полета, когда вместо скорости интегрируется удельная энергия,
правые части уравнений (2.136) зависят от скорости, а значит, и от
высоты, так как
V=j2gT(E-H) .
Следовательно, с учетом уравнения равенства вертикальных сил правые
части будут зависеть от массы ЛА.
При увеличении скорости полета зависимость от массы будет ос-
лабевать и в том случае, когда удельная энергия станет определяться
главным образом скоростью полета, можно заключить, что правые
части уравнений движения не зависят от массы ЛА, что является важ-
ным обстоятельством.
Проанализируем возможные случаи движения ЛА, когда система
(2.136) сводится к двум дифференциальным уравнениям и управляю-
щие переменные могут быть выражены через фазовые переменные.
Будем рассматривать скорости полета, меньшие круговых, т.е. ИА2 <gr.
Планирование ЛА с неработающим двигателем (т = const). В
данном случае (при М= const) второе уравнение системы (2.136) ис-
ключается из рассмотрения, и остаются дифференциальные уравнения
для фазовых переменных EnL.
114 Глава 2. Общие положения динамики полета
Пусть необходимо максимизировать конечную дальность планиро-
вания при уменьшении скорости от Ко до Гк (т.е. при уменьшении
удельной энергии от Ео до £к)« С учетом того, что при неработающем
двигателе имеет место равенство К = -с\у /^zx, запишем функцию,
подлежащую максимизации в каждой точке траектории, используя
правые части первого и третьего уравнений (2.136):
/пл = - dL/dE = ATcosy —> max при Е = fix.
rgv
Знак функции/Пд выбран в соответствии с (2.122), так как при пла-
нировании dE < 0. Наибольший прирост дальности планирования имеет
место при больших скоростях, где условия Е = fix и V= fix практически
совпадают. При малых скоростях полета с учетом (2.139) максимизи-
руемая функция упрощается:
/пл= — ATcosy.
Г
Определим оптимальное управление углом крена и коэффициентом
подъемной силы в общем случае. Если движение происходит в верти-
кальной плоскости, а угол крена используется в качестве управления, то
очевидно, что максимуму/пл будет соответствовать у = 0.
Если зависимостью аэродинамических коэффициентов от высоты
можно пренебречь, то получается известное решение (см., например,
работу [71]):
^opt — -^чпах И Су Opt — СуКт >
где АГтах есть максимум аэродинамического качества по углу атаки.
Однако известно, что при увеличении высоты (при К= fix) аэроди-
намические характеристики ухудшаются вследствие влияния трения и
вязкого взаимодействия. Главным образом это касается аэродинамиче-
ского коэффициента сх inin. Будем полагать, что остальные аэродинами-
ческие коэффициенты не зависят от высоты.
Аппроксимируем зависимость cxmin от высоты (при V= fix) линей-
ной функцией следующего вида (рис. 2.18):
Сх min * ш С* min Г '' ! »’ н Рис. 2.18. Аппроксимация зависимости коэффици- ента cxmin от высоты полета при Г= fix Cxmin = Cx‘min +b(H-rf). (2.140) Здесь коэффициент cx*min и производная b = дсх inin /дН соответствуют опорной высо- те /7*. Определим оптимальное управление приближенно. С этой целью пренебрежем изменением по высоте величин г, gT и gv. Тогда максимум функции /Пл будет одно- значно определяться максимумом аэроди- намического качества К при условии
2.9. Оптимальное плоское движение
115
cyqS = mgy cos0, (2.141)
где cosG « 1.
Пусть поляра является квадратичной и симметричной:
Сх min + АСу .
При переходе на оптимальный режим полета высота увеличивается
по сравнению с опорной на величину
ЛЯ = 77opt - Я* = 1п(су opt /су*)/р,
где Су - коэффициент подъемной силы, соответствующий высоте поле-
та Я*; р - параметр атмосферы.
Введем безразмерный параметр 5, характеризующий относитель-
ный прирост коэффициента cxmin по высоте:
5 = Z)/(pcx*min),
и запишем функцию, подлежащую минимизации, исключив в выраже-
нии (2.140) высоту при помощи равенства вертикальных сил (2.141):
Сх/Су [СХ min + ^Сх min 1п(Су/Су ) “Ь АСу ]/Су > ГШП .
Из необходимого условия экстремума аэродинамического качества
ПО Су
получим
Суор< = V^xmin (1 - 5) - 5c‘mm 1П(С* / Cyopt)] / J .
Подберем высоту 27*, при которой вычисляются аэродинамические
коэффициенты, так, чтобы она совпала с высотой полета на режиме
су opt • Тогда
СУ opt— V^xminO “ 5)/Я .
Пусть при Я= /7* коэффициент подъемной силы суКт является из-
вестным. В соответствии с формулами (2.66) имеем
£yKm ~ min / А .
Исключив из двух последних соотношений коэффициент отвала
поляры, получим
Су opt /£уКт >/1 б < 1,
откуда видно, что оптимальный угол атаки всегда меньше, чем угол аКт
на этой же высоте.
116
Глава 2. Общие положения динамики полета
Определим выигрыш в аэродинамическом качестве при полете на
режиме су opt по сравнению с режимом суКт. Будем по-прежнему счи-
тать, что 7/cyoPt= Н\ Тогда коэффициент лобового сопротивления на
оптимальном режиме будет равен
(<?у opt) — Сх min(2 — 6).
При переходе с режима cyopt на режим суКт высота полета
увеличивается на величину
Д7/ — ln(cyKm /Су opt) /Р •
Коэффициент лобового сопротивления при этом равен
Сх (СуКт) “ 2 Сх min + Ь&Н — Сх min[2 + 5 ln(cyKm /Су opt)] •
Относительный прирост аэродинамического качества при полете
на режиме су opt равен
jy. цу. _ ^У opt ^xmin + $ ln(VyKm Су opt )] _ Г\ 2 — 5 1П \/1 — 8
ЛСу opt /^СуКш ; — ~ V1 - о - - .
СуКш Схт.п(2- 3) 2-S
Из полученного выражения видно, что выигрыш в аэродинамиче-
ском качестве зависит только от параметра 5 (рис. 2.19).
Проведем оценку возможного значения 5. Известно, что при увели-
чении высоты и уменьшении размеров ЛА зависимость cxmin от Н
становится все более выраженной. При спуске с орбиты квазистацио-
нарный полет начинается на высотах ~ 80 км. В этом диапазоне высот
при увеличении Н на 10 км увеличение cxmin составляет -30%, т.е.
й/Cxmin = 0,3-1 (Нм’1. Тогда при Р = Ьб-Ю^м’1 получим 6~ 0,2. При этом
Cyopt/cyKm = 0,89, а выигрыш в увеличении аэродинамического качества
составляет 0,05 %.
В процессе планирования (при
Рис. 2.19. Выигрыш в аэро-
динамическом качестве в
зависимости от параметра 5
уменьшении высоты и скорости поле-
та) производная b уменьшается, в
результате чего коэффициент cyopt
приближается к суКт, а выигрыш в
аэродинамическом качестве уменьша-
ется вплоть до нуля. Таким образом,
можно заключить, что использование
режима cyopt при проведении практи-
ческих расчетов на максимальную
дальность не дает ощутимого выигры-
ша по сравнению с режимом суКт.
Кроме того, следует иметь в виду, что
уменьшение летного значения су (при
K=fix) приводит к отрицательному
эффекту - к увеличению аэродинами-
ческого нагревания.
2.9. Оптимальное плоское движение
117
Более подробно вопросы оптимизации траекторий планирования
рассмотрены в гл. 9.
Разгон ЛА с ВРД со свободной дальностью полета L. Так как пу-
тевая дальность L не входит в правые части уравнений движения и в
функционал, то в данном случае третье уравнение системы (2.136)
можно исключить из рассмотрения, в результате чего остаются диффе-
ренциальные уравнения относительно Ем М. При увеличении удельной
энергии от Eq до Ек, как правило, требуется максимизировать конечную
массу ЛА тк или, что то же самое, необходимо максимизировать конеч-
ную удельную энергию Ек при уменьшении массы от mQ до . Исполь-
зуя правые части первого и второго уравнений (2.136), запишем функ-
цию, подлежащую максимизации в каждой точке траектории (т. е. при
£ = fix):
fnv =-dE/dM= —> max, гдеУЭФ=^^-- (2.142)
gj crf
Решение (2.142) является известным и было получено в несколько
иной форме, например, в работе [71]. Знак функции /р3р выбран в соот-
ветствии с (2.122), так как в данном случае dM< 0.
Величина /Эф называется эффективным удельным импульсом ЛА
(далее для простоты будет называться эффективным импульсом ЛА).
При разгоне /эф является положительной величиной. Воспользовав-
шись приближенным равенством
С£х Cr(F/5) ,
запишем
Лф = ^(1-^4), (2.143)
откуда следует, что при уменьшении лобового сопротивления ЛА по
сравнению с тягой ВРД эффективный импульс ЛА приближается в
пределе к удельному импульсу ВРД.
При больших скоростях полета условия Е = fix и V= fix близки. В
этом случае максимуму функции /РЗГ будет однозначно соответствовать
максимум эффективного импульса ЛА:
/эф —> max при V = fix. (2.144)
Покажем, что экстремаль, соответствующая максимуму конечной
массы тик, не зависит от того, значение какой фазовой переменной
фиксируется на концах траектории: удельной энергии или скорости
(при условии, что остальные фазовые переменные свободны). С этой
целью введем переменные
Ф= 1//эФ; 4/ = 0gT/K
118
Глава 2. Общие положения динамики полета
В процессе разгона при изменении удельной энергии от Eq до Ек в
каждой точке траектории функция Г) в соответствии с (2.142)
должна минимизироваться. Необходимым условием экстремума являет-
ся равенство нулю полной производной Т по скорости при Е = const:
cFV/dV = (d^/dH) (dH/dV) + d'¥/dV= (дФ/дН) £уН\1У+ дЧ/5У= О,
где
Н\ = -У/&.
Таким образом, в данном случае в каждой точке траектории долж-
но выполняться условие
дФ1дН=дхУ1дУ. (2.145)
Условие (2.145) было получено в работе [71] при решении задачи
оптимального разгона от скорости Vq до Ук. Действительно, в этом
случае необходимо максимизировать функционал
Ч 41+ я' IV
] f(H, Ну ,V)dV= J — dV max,
/эф
который получается из (2.142) после замены переменных при помощи
соотношения (2.132). Здесь Н(У) является управляющей функцией.
Для решения вариационной задачи составим уравнение Эйлера:
df/dH- d(df/dH'f) /dV = О,
где
df/dH = dФ/dH + Н'у d^/dH;
df/dH'y = T; dW/dV = (&¥/dH)HN + 3W.
В результате приходим к уравнению (2.145). Аналогично можно
показать, что к уравнению (2.145) сводится задача оптимального набора
высоты от Hq j\q Нк .
Таким образом, при максимизации конечной массы оптимальная
траектория является единой вне зависимости от того, какая фазовая
переменная фиксируется на концах траектории - скорость, высота или
удельная энергия (при условии, что остальные фазовые переменные
являются свободными).
Вопросы максимизации функции /рзг и оптимизации траекторий
разгона более подробно рассмотрены в гл. 7.
Крейсерский полет ЛА с ВРД (V= ККр = const). Пусть масса ЛА
уменьшается от ти0 ДО т^. Вследствие уменьшения массы высота полета
увеличивается. Как показано в разделе 8.2, угол наклона траектории в
крейсерском полете практически постоянен и не превышает 0,01°.
Рассмотрим вместо уравнения для Е два исходных уравнения (2.126)
для скорости и высоты полета. Из первого уравнения следует, что при
2.9. Оптимальное плоское движение
119
V = const имеет место равенство лх = gTsin0/go. Так как угол 0 мал, то в
практических расчетах можно считать, что пх « 0.
Исключим время из второго уравнения (2.126) при помощи третье-
го уравнения (2.136), в результате получим
dH= (r/R^QdL.
Так как угол 0 » const, то проинтегрируем данное уравнение анали-
тически, приняв г = гСр:
H=Ho+(rM}QL.
Здесь высота Но определяется из уравнения равенства вертикальных сил
при т = то.
Таким образом, в системе (2.136) остаются два дифференциальных
уравнения для фазовых переменных Ми L.
Рассмотрим вначале задачу максимизации времени полета тк при
свободной дальности. Используя второе уравнение (2.136), запишем
функцию, подлежащую максимизации в каждой точке траектории:
fx=-dx!dM=
/CsyCOSY
gycR(F / S)cosQ
-> max.
(2.146)
Знак функции fx выбран в соответствии с (2.122). Функция fx максими-
зируется при условии V= fix.
Запишем коэффициенты результирующей силы Rv в соответствии с
выражением (2.58), т.е. при условии, когда ось двигателя параллельна
вектору выходного импульса, а разворот вектора входного импульса и
сопротивление по жидкому контуру учтены в аэродинамических
коэффициентах сх и су:
с^х = cr cos(a + Sjip)F/S - сх ; с^у = cR sin(a + 8ДВ) F/S + су.
Тогда с учетом условия cZx = 0 имеем
cR = сх S7[Fcos(a + 8ДВ)]; cZy = сх tg(a + 8ДВ) + су.
Подставив эти соотношения в (2.146), получим
fx = Jcosy[sin(a + 8ДВ) + Xros(a + 8ДВ)] /gv.
При малых (дозвуковых) скоростях полета летные углы атаки ма-
лы, т.е. sin(a +8ДВ)» 0. Тогда при нулевом угле крена и с учетом соот-
ношения (2.139) последнее выражение преобразуется к виду
Л =KJIgT. (2.147)
120
Глава 2. Общие положения динамики полета
Если скорость полета задана, то оптимальное управление опреде-
ляется из условия KJ -> max при K=fix. В качестве начального при-
ближения обычно используют решение
К=Ктаг,
max •
(2.148)
Если скорость полета является свободной, то очевидно, что макси-
мум произведения KJ достигается при дозвуковой скорости, т.е. в том
диапазоне скоростей, где максимальны аэродинамическое качество и
удельный импульс ВРД.
Пусть теперь необходимо максимизировать конечную дальность
при уменьшении массы от до тк. Крейсерская скорость является
заданной. Используя выражение (2.146) и третье уравнение (2.136),
запишем функцию, подлежащую максимизации в каждой точке траек-
тории:
/кр~ №/г)Икр^
или
/кр~
(Vr)KKPJcSycosY
gyCR(F/S)
-> max.
(2.149)
Функция /кр называется коэффициентом крейсерской дальности.
Если коэффициенты результирующей силы Rz записаны в соответствии
с выражениями (2.58), то
/кр = Wr) ИКр Jcosy [sin(a + 5ДВ) + Axos(a + 5ДВ)] /gv • (2-150)
При малых (дозвуковых) скоростях полета летные углы атаки ма-
лы, т.е. sin(a +8ДВ)« 0, высота полета также мала: Тогда при
нулевом угле крена и с учетом соотношения (2.139) выражение (2.149)
преобразуется в известную формулу для коэффициента крейсерской
дальности (см., например, [71]):
fxp= KVKPJ/gj.
Сравнение с формулой (2.147) показывает, что при И=Пх опти-
мальное управление одновременно обеспечивает максимум дальности и
времени полета.
В качестве начального приближения обычно используют решение
(2.148). Непосредственная максимизация функции (2.150) показывает,
что в общем случае оптимальный угол атаки отличается от aKm, а
оптимальный режим работы ВРД отличается от режима Jmax.
На крейсерском режиме высота полета увеличивается вследствие
уменьшения массы ЛА. В результате функция /кр изменяется по траек-
тории полета. В некоторых случаях пренебрегают изменением этой
величины и используют среднее значение/<Р. Тогда, проинтегрировав
уравнение
dr —Укр dM,
2.9. Оптимальное плоское движение
121
получим известную формулу для определения крейсерской дальности
ZKp=/Kpln(mo/mK). (2.151)
Вопросы максимизации функции fa более подробно рассмотрены
в гл. 8.
Общий случай движения ЛА при больших скоростях полета с
изменением удельной энергии. Пусть скорость полета является доста-
точно большой (т.е. можно считать, что правые части уравнений (2.136)
не зависят от массы); удельная энергия ЛА изменяется от начального
значения Eq j\q конечного Ек . В конечной точке траектории необходимо
обеспечить максимум некоторой функции конечных значений фазовых
переменных М, L и т :
F(MK, LK, тк) -> max. (2.152)
При этом имеет место либо разгон, либо планирование ЛА с работаю-
щим двигателем.
Возьмем в качестве независимой переменной угловое расстояние s,
отсчитываемое по длине большого круга, и перепишем систему уравне-
ний (2.136), введя дифференциальное уравнение для времени полета:
dElds- ; dMtds . _^FIS}g, .
czy^TcosY FcLycosyJ
dLIds = Rq\ dxIds = г/VcosO .
(2.153)
Так как правые части уравнений (2.153) не зависят от фазовых
переменных М9 L и т, то вместо второго, третьего и четвертого уравне-
ний можно ввести в рассмотрение дифференциальное уравнение отно-
сительно максимизируемой функции:
dF/ds = (5F/5M) (dM/ds) + (dF/dL) (dL Ids) + (dF/dx) (dx Ids).
Таким образом, система уравнений (2.153) сводится к двум диффе-
ренциальным уравнениям относительно Е и F. Оптимальное управле-
ние в каждой точке траектории определяется из условия экстремума
функции dF/dE при Е = fix.
Частная задача максимизации дальности планирования ЛА с вы-
ключенным двигателем вытекает из общей задачи при F = L. При F = М
имеет место задача оптимизации траекторий разгона ЛА с ВРД со
свободной дальностью полета. Из общей задачи также вытекает частная
задача оптимизации траекторий на участках разгона и планирования
ЛА с ВРД при условии, что суммарная дальность полета является за-
данной (см. гл. 8).
122
Глава 2. Общие положения динамики полета
2.10. Расчет траектории движения ЛА с ВРД в режиме
отслеживания заданной программной траектории
Будем рассматривать движение ЛА с ВРД в плоскости развертки.
Предположим, что задача оптимального управления решена с использо-
ванием гипотезы квазистационарности (см. раздел 2.9), т.е. в результате
интегрирования системы уравнений вида (2.136) определены изменения
фазового вектора Хкв и вектора управления UKB по траектории полета.
Практика расчетов показывает, что точность определения с использова-
нием квазистационарной системы уравнений таких величин, как ско-
рость, высота, дальность, масса ЛА во многих случаях является вполне
приемлемой. Поэтому, если в задаче необходимо оценить только массу
топлива или дальность полета, то ее можно считать решенной.
В большинстве задач помимо конечных значений фазовых пере-
менных требуется определить изменение по траектории не только
фазового вектора, но и других траекторных переменных. При этом
действительные значения таких величин, как нормальная перегрузка иу,
угол атаки а, угол наклона траектории 0 и др., могут существенно
отличаться от расчетных значений, полученных с использованием
квазистационарных уравнений движения. В особенности это относится
к случаю движения вдоль фазового ограничения, имеющего изломы в
координатах "высота-скорость”. Так как угол 0Кв пропорционален
производной Н'у в соответствии с формулой (2.129), то в точке излома
функции /7(Т) функция 0кв(Ю терпит разрыв, в то время как в действи-
тельности, функция 0(И) является непрерывной. Кроме того, так как
перегрузка луКв определяется с помощью конечного соотношения
(2.111), то в этом случае имеет место неравенство иуквСО5у<1; для
реальной же траектории возможно противоположное: пу cosy > 1.
Пусть для определенности рассматривается задача разгона ЛА и
определены функции UkB(F), 7/кв(П и 9кв (И- Назовем эти зависимости
программными. С использованием этих зависимостей будем интегри-
ровать полную систему уравнений вида (2.71). При этом возможны
различные способы решения данной задачи.
Например, когда движение осуществляется внутри ограничений,
заданных в плоскости "высота-скорость", систему вида (2.71) можно
проинтегрировать, сделав прямую подстановку вектора UKB(F) в правые
части уравнений. Однако практика расчетов показывает, что в этом
случае возникают колебания с большой амплитудой в плоскости "высо-
та-скорость". При этом выдержать заданные ограничения в координа-
тах "высота - скорость" не удается - они будут нарушаться. Объясняет-
ся это тем, что высота и угол наклона траектории в полной системе
уравнений интегрируются, а в квазистационарной системе уравнений
определяются при помощи конечных соотношений. Поэтому выдержи-
вание ограничений при интегрировании квазистационарной системы
2.10. Расчет траектории движения ЛА с ВРД в режиме отслеживания 123
еще не гарантирует, что они будут выдержаны при интегрировании
полной системы уравнений движения.
Одним из эффективных способов расчета траекторий движения ЛА
с ВРД при наличии ограничений в фазовой плоскости "высота - ско-
рость" является применение математической модели автопилота. В этом
случае при интегрировании полной системы уравнений в качестве
исходных данных используются программные зависимости /7Кв(Ю?
0кв(Юиикв(Ю.
Задача формирования закона управления углом атаки, обеспечи-
вающего отслеживание программной траектории полета самолета в
плоскости развертки, решена в работе [76]. Решим аналогичную задачу,
приняв в качестве управляющей переменной не угол атаки, а проекцию
нормальной перегрузки на вертикальную плоскость:
ив = иу cosy, (2.154)
так как она непосредственно входит в уравнения движения.
Рассмотрим вначале случай, когда программная траектория не име-
ет изломов в плоскости "77- И". Пусть в некоторый момент времени
при т = 0 известны скорость И(0), высота /7(0) и угол наклона траекто-
рии 0(0). Значению V соответствуют программные величины 7/Кв(0) и
6кв(0). Запишем функцию ив в следующем виде:
Ив(т) = Ив.кв(т) + Див(т) (2.155)
и назовем (2.155) уравнением автопилота. Здесь ив.Кв определяется с
использованием уравнения (2.111):
ив.кв = gvCOS0KB /go • (2.156)
Так как угол 0 мал, то cosO « cos0Kb и с учетом (2.155) и (2.111)
второе уравнение движения (2.89) можно переписать как
б70/б/т« Див£о/К (2.157)
Решим следующую задачу: найдем такую зависимость Див от т,
чтобы через некоторый заданный отрезок времени Дт, который является
параметром автопилота, были выполнены три условия:
лв(Дт) = «в.кв(Дт); 0(Дт) = 0кв(Дт); Я(Дт) = /7кв(Дт). (2.158)
Для выполнения указанных условий необходимо, чтобы функция
Див(т) имела три свободных параметра. Воспользуемся квадратичной
зависимостью
Див = ат2 + Ьт + с. (2.159)
Очевидно, что в данном случае параметр с соответствует значению
Длв в начальный момент времени.
Проинтегрировав приближенно по времени уравнение (2.157) на
отрезке [0, т] с учетом (2.159), получим
124
Глава 2. Общие положения динамики полета
0(т) = 0(0) + (ат3/3 + Z>t2/2 + ст) go/^cp (2.160)
Здесь ГСр- среднее значения скорости на отрезке [0, т].
Запишем дифференциальное уравнение для высоты полета в пред-
положении малости угла 0:
dHldx=VQ (2.161)
и также проинтегрируем его по времени на отрезке [0, т] с использова-
нием (2.160):
Дт) = ДО) + ИСР 0(0) т + (ат4/12 + Ьт3/6 + ст2/2) g0. (2.162)
Подставив в (2.158) соотношения (2.159), (2.160) и (2.162) при
т = Дт, получим систему трех линейных уравнений относительно неиз-
вестнььх а, b и с
яДт2 + Ь\х + с = 0 ;
аДт3/3 + Мт2/2 + сАт = ГСР [0кв(Ат) - 0(O)]/go;
аДт4/12 + Мт3/6 + сДг/2 = [Д®(Дт) - ДО) - ГСР 0(0) Ax]/g0.
Решением этой системы является
с = Дпв(0) = {12[Дв(Дт) - Д0)]/Дт -
- 6Гср [0Кв(Ат) + 0(О)]}/(Дт go). (2.163)
Запишем уравнение (2.161) для квазистационарной траектории и
проинтегрируем его приближенно по времени на отрезке от 0 до Дт:
//кв(Ат) = Якв(0) + Дт ГСр [0кв(Ат) 4- 0кв(0)]/2.
Подставив полученное выражение в (2.163), будем иметь
Длв(0) = {12[/7кв(0) - //(0)]/Дт + 6ГСР [0Кв(0) - 0(0)]}/(Дт g0).
При малых Дт можно принять, что ИСР = И(0). В результате полу-
чим выражение
Див = [ 12(ЯКв - Н) /Дт 4- 6 V (0кв - ©)]/(Ат go), (2.164)
где все траекторные величины соответствуют текущей точке полета.
Структура выражения (2.164) с точностью до коэффициентов сов-
падает со структурой закона управления углом атаки, полученного в
работе [76]. Выражение (2.164) справедливо как при отрицательных
значениях их (при планировании), так и при положительных их (т.е. при
разгоне аппарата). Если программная высота задана при помощи скоро-
стного напора #кв, то в этом случае разность высот в (2.164) можно
переписать с использованием параметра атмосферы
//кв - Н = - 1п(ркв/р)/Р = 1п(^кв)/р, (2.165)
где величина р = - р'н/р соответствует программной высоте.
2.10. Расчет траектории движения ЛА с ВРД в режиме отслеживания 125
Окончательно угол атаки в каждой точке траектории определяется
в результате решения следующего уравнения с учетом конкретной
формы записи нормальной перегрузки:
ф(а) = Иу(а) - П- кв-+ -в- = о, (2.166)
cosy
здесь у - программный угол крена; иВкв и Див определяются по форму-
лам (2.156) и (2.164).
Уравнение (2.166) относительно угла атаки в общем случае являет-
ся нелинейным и решается любым известным способом, например
методом Ньютона. От итерационной процедуры можно избавиться,
если аппроксимировать функцию лу(а) квадратичной зависимостью
Иу(а) = А а2 + Ва + С.
В данном случае такой подход является оправданным, так как ве-
личина Див, входящая в (2.166), в свою очередь, определена прибли-
женно. Заметим, что всегда В > 0, а коэффициент А может быть любым,
в том числе и равным нулю. В связи с этим решение уравнения (2.166)
должно записываться в следующем виде:
-2Су
а=-------. ..
В + у]В2 - 4АСХ
Здесь Q = С - (ив.кв + ДивУсозу. Коэффициент всегда меньше нуля.
При А = 0 выражение (2.167) упрощается:
(2.167)
ot — Су/В.
Сделаем некоторые замечания по выбору величины параметра ав-
топилота Дт. С этой целью перепишем выражение (2.164) следующим
образом:
Длв = Див (/7) + Див (0), (2.168)
где Лив (Н) = 12(ЯКв - Н) /(Дт2 go);
Д«в (9) = 6 И (0КВ - 0)/(Дт go).
Порядок величин и Див(0) в (2.168) должен быть примерно
одинаков. Исходя из этого можно сформулировать следующий алгоритм
выбора Дт: если на текущем шаге интегрирования Див(/7) меньше по
модулю, чем Длв(0)/2, то параметр Дт уменьшается на следующем шаге
интегрирования на 54-10%. И, наоборот, если Див(0) меньше по моду-
лю, чем Див(//)/2, то параметр Дт увеличивается на 54-10%. В результа-
те по траектории параметр автопилота Дт будет меняться в соответст-
вии с изменением величин Дяв(/7) и Длв(0), причем зависимость будет
близка к монотонной. На величину Дт имеет смысл наложить ограниче-
ние снизу. Начальное значение Дт является параметром.
126
Гпаба 2. Общие положения динамики полета
программная траектория
расчетная траектория
Рис. 2.20. Программная траектория с
одним изломом
Рассмотрим случай, когда
на программной траектории в
координатах "Я- V" имеется
излом, т.е. траектория состоит
из двух участков: ЯКв1(Ю и
#кв2(Ю- Очевидно, что этим
двум участкам соответствуют
функции иКВ1(Ю> 6кв1(Ю и
иКВ2(И)> 0КВ2(Ю- Для опреде-
ленности будем по-прежнему
рассматривать разгон ЛА.
Если программная траек-
тория в координатах "Я- И”
лежит ’’далеко” от ограничений
(рис. 2.20), то можно использо-
вать следующий простой алго-
ритм: до точки излома в качестве программной принимается участок
#кв1(П> после излома - участок ЯквгСЮ- При таком алгоритме справа от
излома будет иметь место некоторое отклонение расчетной траектории
от программной (см. рис. 2.20). Однако в данном случае это несущест-
венно, так как ограничения не нарушаются, а влияние на функционал
является незначительным.
Пусть программная траектория соответствует движению вдоль ог-
раничения Яттд(Ю- Рассмотрим вначале выпуклый излом (рис. 2.21а).
В этом случае используется такой же алгоритм, как и в предыдущем
случае. Возникающий заброс расчетной траектории справа от излома
направлен в сторону, противоположную ограничению ЯКв2(Ю (см. рис.
2.21а).
Перейдем к рассмотрению вогнутого излома (рис. 2.216). Слева от
излома в качестве программной траектории будем принимать тот ее
участок, который обеспечивает наибольшее значение переменной
Рис. 2.21. Программная траектория является ограничением с выпуклым
изломом (а), ограничением с вогнутым изломом (6)
2.10. Расчет траектории движения ЛА с ВРД в режиме отслеживания 127
Ив = Ив.кв + Лив(О) + Д«в(^О-
При этом уравнение автопилота необходимо последовательно ре-
шить для каждого участка программной траектории при одинаковом
значении Дт. Следует отметить, что в данном случае Okbi^kb? и в
рассматриваемом диапазоне скоростей будет иметь место неравенство
Див1(9)< Див2(0). Слева от излома выполняется неравенство
ДлВ1(7/) > ДивгС^О, справа: ДиВ1(#) < ДивгС^О- В соответствии с указан-
ными неравенствами очевидно, что справа от точки излома программ-
ным будет участок //квгСЮ-
При скорости полета меньшей, чем ГА, имеет место
Дл7В1(//) >> Див2</0, поэтому программным является участок Якв|(П-
Начиная со скорости ИА (см. рис. 2.216), разность слагаемых ДлВ2(6) и
ДлгВ1(0) начинает превышать разность ДиВ](#) - ДиВ2(#), поэтому в
диапазоне скоростей от ИЛ до Ив программным будет участок ЯквгСЮ?
несмотря на высоту, меньшую чем 7/кв1(П- При таком алгоритме обес-
печивается плавный переход от одного ограничения к другому без
забросов траектории (см. рис. 2.21 б).
При увеличении числа изломов на программном профиле алгоритм
принципиально остается тем же, увеличивается только число переборов
исходных участков программной траектории.
Рассмотрим случай, когда в качестве программной величины зада-
на не высота, а угол атаки аКв, т.е. задана программная зависимость
оскв(Р) или сеукв(И)-
Для простоты будем полагать, что угол крена равен нулю. В этом
случае выражение (2.165) перепишется в виде
Якв - Я = (IncsyKB - 1псЕу)/р. (2.169)
Уравнение автопилота принимает следующий вид:
<р(а) = (р|(а) - лукв - Д«у= 0, (2.170)
где (р](а) =иу+ 121псЕу/(рДт2£0);
Дпу = [12 lncLyKB /(РДт) + 6И(0КВ - 0)]/(Дт go).
Угол 0квопределяется по формуле (2.129). Для определения произ-
водной Н\ продифференцируем по скорости конечное соотношение
(2.111), записанное для случая полета с программным углом атаки аКв •
?(<Ъукв) v + С£укв(р^- P#'v<7) + 2cZyKBqV/(gr - Г2) = 0.
Здесь принято, что ГА« V. Изменение g и г по скорости не учитывается.
В результате получим
H'v = | [2/К + (cZyKB)'v/cZyKB + 2K/(gr- Г2)].
128
Гпава 2. Общие положения динамики полета
Для определения тангенциальной перегрузки ихКв, входящей в
(2.129), достаточно решить уравнение их(иу) при пу=«укв- Здесь для
построения зависимости лх от пу можно воспользоваться квадратичной
аппроксимацией.
Уравнение (2.170) решается аналитически, если функцию (pi(a) ап-
проксимировать квадратичной зависимостью
<pi(a) = Ла2 + Ва + С.
В этом случае угол атаки будет определяться по формуле (2.167),
где
С^ = С — Пукв — Длу.
Таким образом, задача отслеживания заданной программной траек-
тории решена. Следует отметить, что при ее решении расчетные зави-
симости угла атаки, высоты и наклона траектории от времени полета
имеют колебательный характер. Колебания совершаются с некоторой
амплитудой вокруг программной траектории. Поэтому, если программ-
ная траектория одновременно представляет собой ограничение в коор-
динатах "Я- Г’, то, строго говоря, при интегрировании полной систе-
мы уравнений фазовые ограничения будут выдерживаться с некоторой
точностью, которая определяется характером программной траектории,
величиной параметра автопилота Дт, а также характеристиками ЛА и в
первую очередь его тяговооруженностью. При увеличении тяговоору-
жен ности ЛА качество отслеживания программной траектории ухудша-
ется. Поэтому данная методика применима только для расчета траекто-
рий пассивного полета ЛА и траекторий разгона ЛА с ВРД умеренной
тяговооруженности. При решении задачи оптимизации траекторий
движения аппаратов с ЖРД используются другие подходы.
ГЛАВА 3
РАЗГОН И ВЫВЕДЕНИЕ НА ОРБИТУ
ЛА С ИСПОЛЬЗОВАНИЕМ ЖРД
Участок полета с ЖРД присущ любой системе выведения на орби-
ту, включая одноступенчатый ВКС с ВРД. Применительно к другим
типам аэрокосмических ЛА, которые не выходят на орбиту, ЖРД может
использоваться для разгона до боль-
ших чисел М полета в атмосфере.
Примером служат различные проекты
экспериментальных ЛА и демонстра-
торов, предназначенных для отработ-
ки гиперзвуковых технологий и но-
вых типов гиперзвуковых ВРД в
полете.
Типичный пример крылатого ап-
парата, на котором установлены
только ЖРД, представлен на рис. 3.1.
Рис. 3.1. Воздушно-космический
самолет с ЖРД
На рис. 3.2 в координатах "вы-
сота-скорость” показаны воз-
можные траектории полета
летательных аппаратов с ЖРД.
Вопросы оптимизации таких
траекторий в настоящее время
хорошо изучены. Так, еще в
50-х годах Д.Е.Охоцимский и
Т.М. Энеев впервые решили
модельную задачу об оптималь-
ном выведении космического
аппарата на орбиту [73]. Было
показано, что в случае выведе-
ния ЛА со свободной путевой
дальностью в плоскопараллель-
ном гравитационном поле в
отсутствии атмосферы опти-
мальной является линейная
зависимость тангенса угла
тангажа от времени полета.
Рис. 3.2. Возможные траектории
полета ЛА с ЖРД в координатах
’’высота - скорость”:
1 - при дозвуковом старте;
2 - при гиперзвуковом старте;
3 - участки полета ВКС с ВРД и ЖРД;
4 - траектория экспериментального ЛА
130 Глава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
Аналогичное решение было получено за рубежом Лоуденом [59]. Об-
щие подходы к расчету траекторий ракет-носителей вертикального
старта подробно рассмотрены в работах [7], [70], [71], [86].
Значительный вклад в разработку теории ракетного движения в ат-
мосфере внесли ученые ЦАГИ. Так, в работе [44] В.А. Ильин дал сис-
тематическое изложение элементарной теории ступенчатых ракет.
Рассмотрены ракеты с последовательной и параллельной работой сту-
пеней. На основе обобщенных весовых соотношений и выражений,
определяющих скорость ракеты в конце активного участка, решена
задача об оптимальной ступенчатой ракете.
В работах [16], [38], [74] задача оптимального выведения крылато-
го ЛА горизонтального старта с ЖРД решена численно с использовани-
ем принципа максимума, причем в [16] рассмотрено не только плоское,
но и пространственное выведение.
В работах А.С. Филатьева [43], [100]—[102], [126]—[128] показана
возможность широкого практического использования оптимальных
решений, основанных на использовании принципа максимума, в том
числе при многодисциплинарной оптимизации параметров ЛА. При
исследовании траекторий выведения с использованием аэродинамиче-
ских сил А.С. Филатьевым был выявлен новый класс оптимальных
решений, характеризующихся колебаниями угла тангажа при полете в
плотных слоях атмосферы; такие решения позволили увеличить массу
полезного груза.
Как известо, основная трудность решения задачи в точной поста-
новке, с использованием принципа максимума, заключается в выборе
начальных значений сопряженных переменных, которые заранее неиз-
вестны. В связи с этим в настоящей главе разрабатывается приближен-
ный метод оптимизации траекторий выведения аэрокосмических ЛА с
ЖРД, основанный на склейке известного оптимального решения для
внеатмосферного участка с программой, настройка параметров которой
позволяет учесть влияние атмосферы, что практически обеспечивает
достижение значения функционала, полученного при строгом исполь-
зовании принципа максимума.
3.1. Исходные данные
Рассмотрим крылатый ЛА, на котором установлены п двигателей,
имеющих различные тягу и удельный импульс. Запишем тангенциаль-
ную и нормальную перегрузки, а также суммарный расход массы топ-
лива ЖРД, непосредственно входящие в уравнения движения:
их =[Z7?/ cosp/ cos(a + 5/)-cx^5]/(wg0); > @
пу = [ E7?/cosp/sin(a + 5,) + су ^S]/(m g0); £>г=
Здесь суммирование производится от 1 до и; Ri и Ji- модуль тяги и
удельный импульс z-ro ЖРД; р/-угол между вектором тяги z-ro двига-
3.1. Исходные данные
131
теля и плоскостью симметрии ЛА (рис. 3.3); 8,-угол заклинения
вектора тяги z-ro двигателя на виде сбоку относительно связанной оси
Ох\ (см. рис. 3.3), положительный угол 8 соответствует положительной
проекции вектора тяги на ось Оу\.
При задании коэффициентов сх и су учитывается вся внешняя по-
верхность ЛА за исключением среза сопел ЖРД.
Аэродинамические характеристики ЛА. Примем, что для ЛА с
работающими ЖРД зависимость су(а) является квадратичной, поляра -
квадратичная и несимметричная:
су = суо + су а + В а2;
Сх = сх min + А (су - Су) 2 + Сх.д (5д - FCz) / 5. (3.2)
Здесь cxmin - минимальное значение коэф-
фициента лобового сопротивления (без
учета донного сопротивления);
сх.д -коэффициент донного сопро-
тивления (по отношению к площади дна,
не занятого соплами ЖРД);
5Д - площадь донного среза аппа-
рата;
Fez - суммарная площадь среза
сопел ЖРД.
Донное сопротивление является до-
вольно значительным в общем балансе сил,
действующих на ЛА с ЖРД. Выделение
этого сопротивления в (3.2) в виде отдель-
ного слагаемого способствует более точно-
му учету внешних сил.
Принятые зависимости су и сх от угла атаки позволяют аналитиче-
ски определить первую и вторую производные по а (при фиксирован-
ных значениях чисел М и Re), которые будут необходимы при нахожде-
нии оптимального управления:
dcy/da = Су + 2Ва;
dcjda = 2А (су - су*) dcy!da,
Рис. 3.3. Углы заклинения
вектора тяги ЖРД на виде
сбоку и относительно
плоскости симметрии ЛА
(3.3)
d2cy/da2=lB\
d2cJdu2=2A [(dcy/da)2 + (cy-cy*)d2cy/da2]. J (3’4)
Аэродинамические коэффициенты cy, cx и их производные по углу
атаки являются непрерывными функциями угла а.
Чтобы упростить задание исходных зависимостей коэффициентов
Су и сх от чисел М и Re, будем полагать, что переменные Н и М связаны
между собой, т.е. в координатах "Н- М” или "я - Г’ (см. рис. 3.2) задан
132 Глава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
профиль полета, полученный с использованием предыдущей итерации
расчетов траектории. Это значит, что аэродинамические коэффициенты
суо, Су , В, cxmin, Л, су* и схД будут зависеть только от одной переменной
М и для полного задания аэродинамических характеристик требуется
семь табличных зависимостей.
Типичные зависимости аэродинамических коэффициентов от числа
М полета для ЛА с ЖРД представлены на рис. 3.4 и 3.5. На рис. 3.5
пунктиром показано максимально возможное значение коэффициента
донного сопротивления (при нулевом давлении в донной области). В
каждой точке траектории значения вышеназванных коэффициентов
определяются путем интерполяции.
Рис. 3.4. Зависимости аэродинамических коэффициентов ВКС с ЖРД
от числа М полета
Рис. 3.5. Зависимость коэффициента
донного сопротивления от числа М
полета
Тягово-экономические ха-
рактеристики ЖРД. Будем
полагать, что на ЛА установлены
ЖРД с соплом Лаваля. Основны-
ми параметрами единичного ЖРД
являются максимальная тяга 2?п и
удельный импульс Jn в пустоте.
Эти величины связаны между
собой следующим образом:
= / бттах • (3.5)
Здесь (Зттах- максимально возможный расход массы топлива в единицу
времени.
Все величины, входящие в соотношение (3.5), не зависят от фазо-
вых переменных. Воздействие окружающей среды всегда уменьшает
3.1. Исходные данные
133
максимальную тягу двигателя; на текущей высоте тяга двигателя /?н
зависит только от давления атмосферы рн '
^н=^п~ Рн^с (3.6)
Здесь Fc- площадь среза сопла.
Зависимость (3.6) называется высотной характеристикой тяги. При
записи выражения (3.6) предполагается, что течение в сопле двигателя
является безотрывным. Характер течения (безотрывное или с отрывом
потока) определяется степенью нерасчетности сопла т=р^!рс. Тече-
ние в сопле является безотрывным при тп < ~ 20 [5]. Как правило,
параметры ЖРД (давление в камере сгорания и геометрическая степень
расширения сопла) подбираются таким образом, чтобы обеспечить
безотрывное течение в сопле.
В реальных условиях распределение давления по наружной по-
верхности двигателя не соответствует принятой модели, когда оно
постоянно и равно рн • Конкретное распределение давления по наруж-
ной поверхности ЖРД зависит от компоновки двигателей на ЛА, формы
хвостовой части аппарата, условий полета (скорости, высоты, угла
атаки) и ряда других факторов. Требование определять тягу с учетом
всех этих особенностей сделало бы тягу одного и того же двигателя
неоднозначной, зависящей от большого числа внешних факторов.
Поэтому для определения текущей тяги используется выражение (3.6),
а все отличия реального значения тяги от расчетного должны учиты-
ваться при определении аэродинамического коэффициента сх.д.
Для задания площади среза сопла ЖРД удобно использовать удель-
ную лобовую пустотную тягу
^Fn~ Rn/Fc .
С помощью этой величины соотношение между значениями тяги
на уровне моря и в пустоте запишется следующим образом:
Мп = 1 — Po/^Fn •
Здесь Rq иро~ тяга двигателя и давление атмосферы при Н=0.
Если известно соотношение /?о/Яп, то удельную лобовую пустот-
ную тягу можно определить как
^Fn = Ро / (1 - Rq/Rn)-
Дросселирование тяги ЖРД осуществляется за счет уменьшения
давления в камере сгорания, в результате чего текущий расход массы
топлива Qx уменьшается практически пропорционально. Поэтому под
коэффициентом дросселирования будем понимать отношение текущего
секундного расхода топлива к максимально возможному:
v - Q^/ Qrmax
134 Глава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
Зависимости тяги и удельного импульса от v называются дрос-
сельными характеристиками. Дроссельная характеристика для тяги
ЖРД записывается следующим образом:
= ^п v- FcРн = Jn 0Tmax (v - ри/Rm) . (3.7)
Характерно, что производная текущей тяги по рн не зависит от v:
97?н / дрн --Fq.
Поделив выражение (3.7) на 0т=£?ттахУ, получим дроссельную
характеристику для удельного импульса:
Jh = [1 -/?н/(уЯрп)] •
Теоретически Jn не зависит от коэффициента дросселирования. В
этом случае зависимость 7?H(v) является линейной, JH(v) - дробно-
линейной, коэффициент дросселирования секундного расхода топлива
совпадает с аналогичным коэффициентом для пустотной тяги :
V @Т / C?Tmax R / -^max •
В реальных ЖРД при глубоком дросселировании удельный им-
пульс Ju уменьшается. В связи с этим будем полагать, что в числе ис-
ходных данных (помимо величин 7?п и T?Fn) имеется зависимость Jn(v).
В том случае, когда ЖРД должен работать в широком диапазоне
высот, вместо обычного сопла Лаваля может использоваться двухпози-
ционное сопло. В таком двигателе на малых высотах работает сопло с
меньшей площадью среза с целью уменьшения "противодавления”
Fcpu ~ см. выражение (3.6). На больших высотах используется сопло с
большей площадью среза с тем, чтобы увеличить удельный импульс
двигателя Ju за счет большей геометрической степени расширения
сопла. Для задания тягово-экономических характеристик ЖРД с двух-
позиционным соплом в дополнение к вышеуказанным величинам необ-
ходимы соотношение площадей^! = FC2//?ci и дроссельная характери-
стика удельного импульса Jui(y) для второй позиции сопла.
Определим оптимальную высоту переключения ЖРД с меньшей
площади среза сопла на большую из условия максимума эффективной
тяги ЖРД (с учетом донного сопротивления). Будем полагать, что при
переключении сопла коэффициент донного сопротивления схД и се-
кундный расход топлива не изменяются. Для первой и второй позиций
сопла эффективная тяга ЖРД записывается следующим образом:
Rc\ = V0TrnaxЛи — Fc\Ри — CX J\C[ (5дн~ Fq\)\
Rci = У^ТтахЛи ~ ^С2/?Н “ сх.Д # (ЗдН “ Rd)-
Разность эффективных тяг равна
Л7?С= RC2 ~ Rc\ = V0Tmax (Л12 “ Л11) “ (^С2 “ ^С1)(РН“ ^х.Д^)- (3.8)
3.1. Исходные данные
135
При отрицательном значении А7?с должно использоваться сопло с
меньшим срезом, при положительном - сопло с большим срезом. Из
условия Д2?с=0 и с учетом того, что ^ = 0,7рнМ1 2, из уравнения (3.8)
получим давление атмосферы, соответствующее точке переключения
сопла ЖРД:
Рн= v0Tmax (Jm-/пО / [(^С2-Fci)(l - сх.д 0,7М2)]. (3.9)
Здесь полагается, что зависимость М отрн является известной.
Следует отметить, что в формулы (3.8) и (3.9) площадь донного
среза ЛА не входит; коэффициент донного сопротивления сх.д всегда
меньше, чем 1/(0,7М2).
Типичная зависимость удель-
ного импульса от давления атмо-
сферы для ЖРД с двухпозицион-
ным соплом показана на рис. 3.6.
Переключение осуществляется на
высоте ~15 км. Скачок в удельном
импульсе вызван соответствующим
скачкообразным изменением силы
донного сопротивления. Зависи-
мость эффективного удельного
импульса (с учетом донного сопро-
тивления) от высоты при этом
является непрерывной.
Важным параметром двухком-
Рис. 3.6. Зависимость удельного
импульса ЖРД с двухпозиционным
соплом от давления атмосферы
понентного топлива является соотношение секундных расходов окис-
лителя и горючего кт = т0К/тг . Если по траектории полета величина
кт не изменяется, то плотность топлива будет равна
Рт ~ Рок
1 + £
________т___
Рок / Рг +
где рок и рг- плотности окислителя и горючего.
Задача определения оптимальной выработки компонентов топлива
ЛА с ЖРД по траектории полета рассмотрена в гл. 4.
Перейдем к рассмотрению характеристик двигательной установ-
ки-см. выражения (3.1). Покажем, что систему из п двигателей можно
заменить одним эквивалентным ЖРД. Такая замена значительно упро-
щает решение задачи оптимального управления. Учтем, что двигатели
устанавливаются на ЛА симметрично относительно плоскости симмет-
рии аппарата. Углы р, в общем случае являются ненулевыми и задают-
ся, например, из условия прохождения вектора тяги каждого ЖРД через
центр масс ЛА. Будем полагать эти величины постоянными (в действи-
тельности углы р/ могут изменяться по траектории вследствие управле-
ния вектором тяги). Определим параметры эквивалентного ЖРД из
136 Глава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
условий равенства проекций вектора тяги на оси связанной системы
координат и равенства секундных расходов массы топлива эквивалент-
ного ЖРД и системы из п двигателей:
7?cos5= S2?/Cosp/Cos5,
R sin5 = S Ri cosp, sin5z; R U= Z (7?z / Jz).
В результате получим
7?2 = (L Ri cosp, cos5z)2 + (Z Rt cospz sin8z)2;
J =RI^{RilJ^
(З.Ю)
tg 8 = (Z Rj cosp, sin8z)/(Z Rt cosp, cos8z).
Здесь R, J-тяга и удельный импульс эквивалентного ЖРД; 8-угол
заклинения вектора тяги эквивалентного ЖРД на виде сбоку относи-
тельно связанной оси Ох\.
Из соотношений (3.10) следует, что при увеличении углов pz тяга и
удельный импульс эквивалентного ЖРД будут уменьшаться. В случае
установки одинаковых ЖРД с ненулевыми углами pz удельный импульс
эквивалентного ЖРД всегда будет меньше, чем удельный импульс
единичного ЖРД.
С использованием параметров эквивалентного ЖРД компоненты
вектора перегрузки в общем случае можно записать так, как если бы на
ЛА был установлен один двигатель:
пх = [Я cos(a + 8) - сх qS]/(m g0);
пу =[Rsin(a + 8) + су qS]Kjn g0);
Qy = RU.
(З.П)
3.2. Постановка задачи
Будем рассматривать плоское движение (у = 0) крылатого ЛА с
ЖРД. Двигатели могут иметь различные тягу и удельный импульс,
однако тип используемого топлива полагается одинаковым (по траекто-
рии полета кт = const).
В начальный момент времени т0 известны масса аппарата mQ, ско-
рость Ко, высота Hq, угол наклона траектории 0О и геоцентрические
широта фо и долгота Хо. Диапазон задания величин Ко, Но и 0О может
быть достаточно широким, чтобы охватить как наземный, так и воз-
душный (до-, сверх- и гиперзвуковой) способы старта. В качестве
основного варианта будем рассматривать горизонтальный (наклонный)
старт: 0О < 90°. Вертикальный старт (0О= 90°) будет рассмотрен отдель-
но.
3.2. Постановка задачи
137
В конечный момент времени тк, который является свободным, за-
даны конечные скорость Кк, высота Нк и угол наклона траектории 0К.
Геоцентрические координаты срк и являются свободными, т.е. рас-
сматривается движение со свободной путевой дальностью • Величи-
ны Гк, Нк и 0К в общем случае могут быть как близкими к орбиталь-
ным, так и существенно отличаться от них, чтобы охватить траектории
разгона ЛА различных типов.
Угол курса \|/ может быть задан либо в начальной точке, либо в ко-
нечной. При этом на противоположном конце траектории величина у
является свободной. Вместо угла курса на правом конце может быть
задано наклонение орбиты, что эквивалентно. Для случая невращаю-
щейся Земли движение с нулевым углом крена будет осуществляться по
дуге большого круга и задание величин у, ср и X становится несущест-
венным.
Задача заключается в определении допустимого управления U(t),
обеспечивающего максимум конечной массы ЛА тк или, что то же
самое - минимум массы топлива ЖРД. Так как по условию все ЖРД
используют один тип топлива, то в этом случае будет одновременно
достигаться и максимум массы полезного груза ЛА. Координатами
вектора управления U при движении ЛА с ЖРД являются угол атаки а
и режим работы двигателей, который будем задавать при помощи коэф-
фициента дросселирования секундного расхода топлива v. Если двига-
тельная установка состоит из нескольких двигателей, то будем полагать,
что каждый двигатель дросселируется одинаково, т.е.
V Qti / max ,
где 0т/, 0т/тах - текущий секундный расход топлива через z-ый ЖРД и
его максимально возможный расход.
В качестве дополнительной управляющей переменной может быть
задан угол заклинения вектора тяги эквивалентного ЖРД 8.
Будем решать задачу с учетом ограничений, наложенных на управ-
ляющие переменные:
С^ггцпД — (X — СХ-тахД > 0 — V < УщахД — 1 (3.1 2)
и с учетом других ограничений, которые могут быть заданы при выве-
дении на орбиту.
Для пилотируемых ЛА, как правило, задается ограничение на мак-
симальное значение перегрузки (не более 34-4). Такая перегрузка реали-
зуется на конечном участке полета, где нормальные силы малы. На-
правление силы тяги (практически единственной силы, создающей
перегрузку) близко к направлению оси Ох\ в связанной системе коорди-
нат. Это означает, что вместо ограничения на суммарную перегрузку
можно задать ограничение на продольную перегрузку в связанных осях:
«х1 — ^хЬпахД •
138 Гпава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
При горизонтальном старте на крылатый аппарат в процессе его
выведения действует значительная нормальная сила Y\, которая может
быть ограничена из условия обеспечения прочности ЛА:
Fl ^1тахД •
Здесь Ki = Kcosa + Jfsina. Силу У|1пахд удобнее задавать в относительном
виде (по отношению к стартовому весу аппарата mogo)-
3.3. Оптимальная программа выведения в
плоскопараллельном поле тяготения в отсутствии атмосферы
Воспользуемся результатами решения модельной задачи об опти-
мальном выведении на орбиту в отсутствии аэродинамических сил.
Такая задача впервые была поставлена и решена в работе [73] с исполь-
зованием методов вариационного исчисления. В работе [86] приводится
решение аналогичной задачи с использованием принципа максимума,
позволяющего более просто учесть ограничения на управляющие пере-
менные. Повторим вывод этого решения, чтобы более обосновано
подойти к формированию приближенно оптимального закона управле-
ния.
Вначале в работах [73] и [86] задача решена для случая выведения
одноступенчатого ЛА в плоскопараллельном гравитационном поле
невращающейся Земли (при g = gT = const). Схема выведения на орбиту
показана на рис. 3.7. Двигатель с тягой Я установлен вдоль продоль-
ной оси ЛА и допускает дросселирование. Удельный импульс РД по-
стоянен и равен J. Координатами вектора управления U являются угол
тангажа 9 и коэффициент дросселирования секундного расхода топлива
V = £?т/£?ттах • Область допустимого управления задана условием
0 — УггнпД — — УщахД — 1 •
В начальной точке траектории (при т = 0) известны масса т0, вы-
сота у0, скорость Ко и угол наклона траектории 0О. В конечной точке
(при т = Т) заданы ук, Кк и 0К;
Рис. 3.7. Схема выведения ЛА на
орбиту в модельной задаче
дальность полета и время движения Т
являются свободными. В [73] и [86]
считалось, что в конечной точке
задано условие 0К = О, однако дан-
ную задачу можно обобщить на
случай, когда 0К^ 0.
В задаче требуется определить
оптимальную программу изменения
управляющих переменных 9 и v во
времени из условия максимума
конечной массы ЛА. Искомое
управление будет также обеспечи-
вать максимум скорости при задан-
3.3. Оптимальная программа выведения
139
ных значениях тк, ук и 0К и максимум высоты при заданных конечных
значениях тк, Гк и 0К.
В данном случае уравнения движения ЛА имеют следующий вид:
dVJdx = Rcos&lm ; dVy/dx = 7?sin9/w-g;
dy/dx = Vy; dm Idx = - v £>Ттах •
Здесь Kx, Vy - горизонтальная и вертикальная составляющие скорости;
у - текущая вертикальная координата (высота полета).
Тягу двигателя в каждой точке траектории можно записать как
R ~ V f^Tinax J>
В соответствии с принципом максимума составим функцию Га-
мильтона:
W = Pvx /teos9 /т + Р\у Rsin9 /т - PVy g + Ру Гу - Ртv £>Tmax
или
W = Wi + W2,
где
(X, Р, U) = v0Ттах [J(PVx cos9 + PVy sin») /т - Рт]; (3.13)
Н2(Х, P) = PyVy-PNyg.
Необходимым условием оптимальности управления является дос-
тижение абсолютного максимума функции Н\.
Запишем сопряженную систему:
б/Pvx Idx = 0; dPyy Idx =-Ру; dPy/dx = 0;
dPxJdx = cos9 + PVysin9) Im1
и проинтегрируем первые три уравнения:
Pvx = Ci; РУ = С2; PVy = -C2T + C3. (3.14)
В силу взаимности задачи можно полагать, что в конечной точке
максимизируется горизонтальная составляющая скорости при фиксиро-
ванном значении тик, тогда в соответствии с [79] Cj = 1.
Из выражения (3.13) следует, что максимуму Н\ при любом значе-
нии v>0 соответствует максимум функции Д9) = PVxCos9 + Р^51п9.
Введем вспомогательный угол А следующим образом:
cosA = PVx /; sinA = P^,/PI, где = ^PV2X + Pv2y .
Тогда функцию Д9) можно записать как Pscos(A - 9) и ее макси-
мум будет достигаться при cos(A - 9) = 1. А это значит, что 9 = А, и в
результате получим
140 Глава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
cos& = PVx / Л ; sinS = PVy / Л • (3.15)
При v = 0 угол & может быть любым. Однако для определенности
будем полагать, что в этом случае решение (3.15) также является иско-
мым (как если бы v являлась бесконечно малой положительной величи-
ной).
Без ограничения общности можно считать, что на всей траектории
выведения &^л/2 (участок полета с & = к/2 реализуется только при
вертикальном старте в начале движения). С учетом этого замечания из
соотношений (3.15) и (3.14) получим оптимальную программу измене-
ния угла тангажа - "закон линейного тангенса" [73]:
tg& = PVy = -C2T + С3.
Из физических соображений ясно, что угол тангажа должен
уменьшаться по траектории. Поэтому перепишем полученное выраже-
ние в виде
tg& = tg&o-G т, (3.16)
где &о - начальный угол тангажа; Ст - величина, характеризующая темп
уменьшения тангенса угла тангажа по времени. Параметры 90 и Ст
являются положительными и выбираются из условия обеспечения
заданных конечных значений высоты и угла наклона траектории.
Если в конечной точке траектории дальность полета задана, то в
этом случае оптимальным является "закон дробно-линейного тангенса"
[73]:
tg& = (tg&0 - Стт)/(1 - Clt). (3.17)
Здесь параметры &0, Ст и CL должны выбираться из условия обеспече-
ния заданных конечных значений высоты, угла наклона траектории и
дальности полета.
В работе [73] показано, что в конечной точке траектории опти-
мальный угол тангажа совпадает с углом наклона траектории, т.е.
ак = 0. Если в начальной точке угол наклона траектории свободный, то
его оптимальное значение совпадает с углом тангажа, т.е. а0 = 0.
Характерно, что оптимальные программы изменения ориентации
вектора тяги (3.16) и (3.17) не зависят от режима работы двигателя (от
глубины дросселирования). Коэффициент v входит в функцию TYi
линейно. Это значит, что оптимальное значение v будет достигать
своего максимального или минимального значения в зависимости от
знака функции переключения фп, которую можно найти, подставив
выражения (3.15) в (3.13):
Г ИпахД При фп > 0, (з । g)
V~ t и™пД прифп<0,
где
фп = JPe/w-Лп-
3.3. Оптимальная программа выведения 141
Если функция (рп тождественно обращается в нуль на некотором
интервале времени, то имеет место особое управление. В работе [86]
показано, что особое управление в задаче оптимального выведения не
может возникнуть, так как такой режим реализуется только при & = О,
т.е. когда тяга направлена горизонтально и высота полета не может
увеличиваться.
Порядок чередования участков полета с минимальной и макси-
мальной тягой, а также число этих участков в соответствии с условиями
(3.18) определяется характером смены знаков функции переключения.
В работе [86] показано, что sign <рп = sign[C2(C2x - Сз)]. В соответствии
с этим возможны только шесть вариантов смены режимов работы дви-
гателя (рис. 3.8).
Очевидно, что варианты А, Б и В, когда в начале движения тяга
минимальна (или даже равна нулю при vmil^ = 0), при выведении ЛА на
орбиту реализоваться не могут. Практическое значение имеют варианты
Г, Д и Е, когда в начале движения двигатель работает на максимальном
режиме (v = утахд). Реализация той или иной программы работы двига-
теля зависит главным образом от конечной высоты выведения 7/к. При
малых значениях Нк реализуется вариант Г, когда двигатель все время
работает на режиме максимальной тяги. В случае больших значений Нк
при выведении, например, в апогей эллиптической орбиты, может
реализоваться вариант Д. Вариант Е характерен для случая выведения
на круговую орбиту большой высоты.
В качестве основной программы, определяющей режим работы
двигателя, примем вариант Е, когда двигатель работает сначала на
максимальном режиме, затем на минимальном и снова на максималь-
ном. Будем полагать, что вариант Д получается из варианта Е как част-
Т Т
УщахД
^ттД
УттД
УттД
Т
0
0 Тп, ТП2 Т Т
Рис. 3.8. Возможные режимы работы ракетного двигателя в задаче
оптимального выведения на орбиту
о
142 Гпава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
ный случай при тП2=Л вариант Г - как частный случай при
Тп1 = ^П2 = Т. Численные расчеты траекторий выведения на орбиту с
использованием принципа максимума в более полной постановке (с
учетом влияния атмосферы) [38] подтверждают правильность принятой
программы изменения режима работы двигателя.
В работе [73] задача оптимального выведения решена также в бо-
лее точной постановке, когда вместо плоскопараллельного поля рас-
сматривается центральное поле земного притяжения. При этом показа-
но, что учет вращения Земли практически не влияет на структуру
оптимального управления углом тангажа и в уточненной задаче враще-
ние Земли можно не принимать во внимание. Для центрального поля
земного притяжения определена оптимальная программа управления
углом тангажа как функция времени. Эта программа отличается от
"закона линейного тангенса". Однако в [73] показано, что в предельном
случае, когда время выведения не превышает ЗООч-5ОО с, обе программы
совпадают.
Таким образом, все результаты решения задачи, найденные в пред-
положении плоскопараллельного поля притяжения, оказываются спра-
ведливыми и для центрального поля, если малы протяженность в про-
странстве и промежуток времени активного полета ЛА. Кроме того, как
показано в работе [73], все результаты данной модельной задачи можно
распространить и на многоступенчатые ЛА.
3.4. Основные участки выведения. Довыведение на орбиту
В соответствии с принятой в разделе 3.3 программой изменения
режима работы двигателя в момент времени тП1 коэффициент дроссе-
лирования уменьшается с утахД до vmil^, а затем в момент времени тП2
снова становится равным утахД. В случае, когда уттд > 0, полная траек-
тория выведения может быть определена только в результате численно-
го интегрирования уравнений движения от начальной точки до конеч-
ной. Подробное рассмотрение такого варианта траектории выходит за
рамки данной книги.
Рассмотрим частный случай цП1Пд = 0, как обеспечивающий наи-
большую конечную массу ЛА, в отличие от варианта ут1Пд > 0 (вследст-
вие расширения допустимой области управления). В соответствии с
принятой программой изменения режима работы двигателя разделим
траекторию выведения на три участка.
1. Активный участок (т<тП1), на котором работают маршевые
ЖРД.
2. Пассивный участок (тП1<т<тП2), на котором двигатели полно-
стью выключены.
3. Активный участок довыведения на заданную круговую орбиту
или в заданную точку некруговой орбиты (тП2^ т < Т). На этом участке
3.4. Основные участки выведения. Довыведение на орбиту
143
работают либо маршевые ЖРД (повторно включенные), либо двигатели
орбитального маневрирования.
В соответствии с этими участками исходную задачу можно разде-
лить на две части: на задачу расчета активного участка и задачу совме-
стного расчета пассивного полета и импульса довыведения. Такое
разделение задачи значительно облегчает ее решение, так как протя-
женность активного участка оказывается сравнительно небольшой и
это позволяет применить при его расчете результаты решения модель-
ной задачи для случая плоскопараллельного поля притяжения Земли.
Рассмотрим вначале вторую часть общей задачи. Обозначим пара-
метры траектории в конечной точке активного участка (при т = тП1)
через Z7nI, Гт, 9пi, wni- При этом будем полагать, что скорость и угол
наклона траектории вычислены в инерциальной геоцентрической сис-
теме координат (см. раздел 2.4). Пусть в конечной точке траектории
заданы //к, Рк, 9К. Для определенности будем полагать, что 9К > 9. По
условию задачи максимизируется конечная масса тк.
Предварительные расчеты траекторий выведения показали, что вы-
сота 7/п1 превышает 894-109 км, т.е. пассивный полет проходит в разре-
женных слоях атмосферы. Это значит, что для расчета пассивного
участка траектории можно воспользоваться теорией орбитального
движения, и это облегчает решение задачи. Аэродинамические потери
характеристической скорости ДКА, которые в действительности имеют
место при движении на пассивном участке полета, будем учитывать при
вычислении потребного приращения скорости ДГд на заключительном
активном участке довыведения.
Величина А Кд, как показали предварительные расчеты, оказывает-
ся относительно небольшой по сравнению с суммарной характеристи-
ческой скоростью выведения. Это означает, что можно пренебречь
продолжительностью последнего участка выведения и решать задачу в
импульсной постановке, используя приближенный расчет траектории:
активный участок довыведения аппроксимируется скачкообразным
(импульсным) изменением скорости, а изменение координат при этом
не учитывается. Таким образом, данная частная задача сводится к
определению параметров переходной орбиты и величины импульса
характеристической скорости довыведения, прикладываемого в конеч-
ной точке траектории.
Рассмотрим движение на пассивном участке более подробно. В ка-
честве модели Земли примем шар с радиусом RQ, вместо высоты полета
воспользуемся расстоянием от центра Земли г = RQ + Н. Гравитацион-
ное поле Земли будем полагать центральным. В этом случае в соответ-
ствии с 1-ым законом Кеплера орбитальное движение ЛА всегда совер-
шается по коническому сечению (окружности, эллипсу, параболе,
гиперболе), в одном из фокусов которого находится притягивающее
тело (на рис. 3.9 показано движение по эллиптической орбите). Уравне-
ние траектории орбитального движения имеет вид
144 Гпава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
r=p/(\ + ecos%), (3.19)
где р - параметр орбиты, определяющий ее линейные размеры;
е -эксцентриситет орбиты (определяет форму орбиты);
% -истинная аномалия (угол, отсчитываемый от линии, соеди-
няющей центр Земли с перигеем) - см. рис. 3.9.
Расстояние от центра Земли до перигея (до точки траектории,
соответствующей минимальному радиусу) находим из (3.19) при % = 0:
1\=р/(\ + е).
Параметры траектории гПь Ии, От в начальной точке пассивного
полета однозначно определяют параметры переходной орбиты [86]:
е = 71 “ uni (2 - )cos2Gni ; Р = ''ni t>m cos2 Gm .
Здесь обозначено uni = Ин2гп1 / Ц-
При движении по орбите справедливы следующие два уравнения:
V2 - 2ц/г = £ = const; r^cosO =С = const, (3.20)
где
£ = )л(е2 - 1)/р; С= Jpp .
Первое уравнение (3.20) выражает закон сохранения энергии. Вто-
рое уравнение (3.20) отражает закон площадей (скорость изменения
площади, ’’ометаемой” радиус-вектором г при движении по орбите,
остается постоянной). Величина £, входящая в (3.20), характеризует
форму орбиты. При е = 0 (£ = - ц/r) орбита является круговой, скорость
движения по круговой орбите (первая космическая скорость) равна
^кр=л/ц77.
3.4. Основные участки выведения. Довыведение на орбиту
145
При е < 1 (£ < 0) орбита является эллиптической. При е = 1 (£ = 0)
реализуется движение по параболе, скорость полета (вторая космиче-
ская скорость) равна Г2к = л/2 ИКР. При е> 1 (£> 0) движение осущест-
вляется по гиперболе.
Рассмотрим вначале случай выведения, когда в конечной точке
0к>О, т.е. орбита не является круговой. Из уравнений (3.20) получим
выражения для скорости:
КП1 = #к2-2И(1/гк-1/гП1) (3.21)
и для угла наклона траектории в начале пассивного участка:
cos6ni =rK KkCOsOk/(rm^ni). (3.22)
В данном случае при расчете активного участка в его конечной
точке из трех величин ЯП1, Ил, Ош независимой остается одна, напри-
мер //П1, которая должна выбираться из условия максимума конечной
массы тк. При достижении высоты //П1 скорость полета должна удов-
летворять условию (3.21), а угол наклона траектории - условию (3.22).
Конечный импульс довыведения не нужен. Необходимо только учесть
аэродинамические потери характеристической скорости. В данном
случае реализуется вариант выведения Д (рис 3.9). Оптимизируемый
параметр //П1 эквивалентен времени переключения режимов работы
двигателя тп •
Перейдем к рассмотрению выведения на круговую орбиту с высо-
той Нк (см. рис 3.9). В этом случае в соответствии с теорией компла-
нарных межорбитальных переходов [86] переходная орбита должна
быть эллиптической и касаться заданной круговой орбиты в своем
апогее (в точке, максимально удаленной от притягивающего центра).
Расстояние от центра Земли до апогея получается из (3.19) при % = л:
га=/?/(1 -е).
Заключительный импульс довыведения должен прикладываться в
апогее переходной орбиты (гк=^а). Определим соотношение между
параметрами траектории в апогее и в начальной точке пассивного
участка. Используя уравнения (3.20), можно записать:
Ни2 - 2ц/гП1 = Ка2 - 2ц/гк J Пи Ии cosOni = гк Их. (3.23)
Исключив скорость Их , получим
Кп 12 = -3^-----Гк~^П| 2----. (3.24)
ГП1 ГК 1 ~ (ГП1 / Гк) C0S 0П1
При расчете активного участка в его конечной точке из трех вели-
чин Иц 1, Ии, Ош независимыми являются две величины, например,
146
Глава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
и 0П1, значения которых должны выбираться из условия максимума
конечной массы тк. Скорость полета в конечной точке активного уча-
стка должна удовлетворять условию (3.24). В данном случае реализует-
ся вариант выведения Е (см. рис 3.8). Оптимизируемые параметры Нщ
и Ош эквивалентны двум значениям времени переключения тП1 и тП2 •
Потребная величина импульса довыведения в апогее переходной
орбиты равна
АГд = ГКР(гк)-Га. (3.25)
Скорость в апогее переходной орбиты определим, исключив из
(3.23):
или
JZ 2 -
к а
ГП1 ГК
К 'П1
1 (ГП1 / гк) cos ®ni
0*п1/гк)2 cosQni2
Иа = Km Оп 1 / Гк) cosQni.
Продолжительность импульса довыведения т = Т-тП2 в действи-
тельности является конечной величиной, и вследствие этого на заклю-
чительном активном участке будут иметь место гравитационные потери
характеристической скорости, которые по определению равны
ДГг= JgsinGrfT. (3.26)
О
Получим аналитическое выражение для АИГ. При выведении на
круговую орбиту и при сходе с нее гравитационные потери одинаковы.
Пусть для определенности в момент времени т = 0 начинается переход
ЛА с круговой орбиты высотой ЯКр на более высокую орбиту. Обозна-
чим скорость движения на исходной орбите через ИКр. Двигатель с
начальной тяговооруженностью = 7?/(wogo) обеспечивает прираще-
ние скорости v = А Ид по отношению к круговой (К= Икр + v). В резуль-
тате высота ЛА увеличивается на величину А, угол наклона траектории
увеличивается от 0 до 0. Будем считать величины v и h малыми:
v « Икр ; h « гКр • Пренебрежем изменением массы ЛА. Такое допуще-
ние правомочно, если учесть, что, например, у орбитального корабля
’’Space Shuttile” общий запас топлива орбитального маневрирования
составляет примерно 10% от орбитальной массы.
Запишем уравнения свободного движения ЛА (при т = const и
Л = const), воспользовавшись малостью угла наклона траектории, и с
учетом того, что dV = dv и dH = dh:
</v/rfT = g093; <&/<ft = -g[l-r2/(gr)]/K; dh/ch=VQ. (3.27)
Исключим из системы (3.27) время при помощи первого уравне-
ния, учитывая, что g= ц/г2:
de/rfv=-n(l - Г2г/р.)/(g0*RPr2); dh/dv = K0/(go9i). (3.28)
3.4. Основные участки выведения. Довыведение на орбиту
147
Проинтегрируем второе уравнение (3.28) в предположении, что
И ~ Икр и 0 ~ 0ср:
Л = ГКР 0cpV/(go*). (3.29)
Перепишем произведение К2 г, входящее в первое уравнение (3.28),
пренебрегая членами второго порядка малости:
V2r « (ГК2Р + 2 rKPv) (гКР + Л) « Кк2р гКР + 2 KkpVZ-kp + И2Р h.
Упростим первое уравнение (3.28) с учетом последнего выражения,
приняв во внимание, что И^р гКр = Ц:
dQ/dv = rKP(2wKP + Икр/г) /(go^Hr2)
и подставим в него выражение (3.29) для h :
dWdv = nKp2vrKP [1 +gKp9cp/(2go«)] Kg^Vr2). (3.30)
Здесь gKp = V^? I rKp - ускорение гравитационного притяжения на высо-
те ЯКР.
Будем далее полагать, что
gKpOCp/(2go93) «1, (3.31)
т.е., по существу, пренебрежем изменением высоты полета в уравнении
(3.30). Проинтегрируем уравнение (3.30), считая, что V® ИКр и г ~ гКР:
e = v2/(g093rKp) (3.32)
и определим условие, при котором выполняется неравенство (3.31).
Пусть угол 0Ср не превышает малую величину 5 от 2g0*/gKp • Тогда
с учетом найденного решения (3.32) имеем
ДИд2 <3(go9i)2гкр/gKP.
Для не очень высоких орбит искомое условие будет иметь вид:
ДГд < £0* , (3.33)
где kQ - некоторая величина, значение которой будет определено ниже.
Проинтегрировав выражение (3.26) с учетом (3.32) и первого урав-
нения (3.27), получим искомую зависимость
ДГг = цДГд3/(3£2932 гк3р). (3.34)
Отсюда следует, что гравитационные потери характеристической
скорости пропорциональны кубу А Кд и обратно пропорциональны
квадрату *. Численное интегрирование уравнений движения подтвер-
ждает найденную зависимость. В качестве примера был рассмотрен
сход космического аппарата с круговой орбиты высотой 200 км; удель-
148 Глава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
ный импульс ЖРД принят равным 4,5 км/с. Начальная тяговооружен-
ность Л задавалась параметрически в диапазоне 0,024-1,0. На рис. 3.10
показана зависимость погрешности
е аналитического определения
Рис. 3.10. Зависимость погрешности
аналитического определения гравита-
ционных потерь характеристической
скорости от величины импульса довы-
ведения ДКд и тяговооруженности Л
высоты в (3.30). Из рис. 3.10 можно
гравитационных потерь харак-
теристической скорости ДИГ в
зависимости от 9? и Д Кд.
При больших значениях тя-
говооруженности (Л = 0,24-1,0)
формула (3.34) дает несколько
завышенный результат по срав-
нению с величиной,полученной
численным интегрированием
уравнений движения. Это объ-
ясняется тем, что при выводе
формулы (3.34) не учитывалось
изменение массы ЛА. Как видно
из рис. 3.10, при ДРд<300 м/с
погрешность определения ДКГ
не превышает 10%.
При малых значениях тяго-
вооруженности (91 = 0,024-0,05)
формула (3.34) дает несколько
заниженный результат вследст-
вие пренебрежения изменением
определить условие, при котором
погрешность определения ДИГ (при 9? = 0,024-0,05) не будет превышать
10%. В этом случае величина коэффициента к0 в (3.33) должна быть
равна~3000.
Величина потерь ДКГ составляет небольшую долю от ДКд. Так,
при Л = 0,05 и ДРд=200 м/с гравитационные потери характеристиче-
ской скорости составляют примерно 9% от ДКд. При увеличении
тяговооруженности эта доля уменьшается.
Определим аэродинамические потери характеристической скоро-
сти на пассивном участке, которые по определению равны
ДКА = j(cx qS/m)dT,
о
(3.35)
где т - время пассивного полета.
Заметим, что в пассивном полете масса ЛА постоянна. Значение
коэффициента лобового сопротивления также можно считать постоян-
ным. Приняв во внимание, что KcosOdx = г б7%, с учетом второго уравне-
ния (3.20) запишем
q di = [р Г2г 2/(2rm Km cos0m)] d^.
3.4. Основные участки выведения. Довыведение на орбиту
149
В результате выражение (3.35) можно записать следующим обра-
зом:
Хк
ЛГА = сх5/(2тгп|ИП|созеП1) JpK2r2rfX. (3.36)
Xni
Интеграл (3.36) вычисляется численно. Углы %П1 и Хк определяются
из уравнения (3.19) в соответствии со значениями гП1 и гк. При каждом
значении % величина г вычисляется при помощи (3.19); скорость опре-
деляется из первого уравнения (3.20); а плотность - в зависимости от
высоты Н= г-Rq .
Конечная масса JIA (в конце участка довыведения) определяется с
использованием формулы Циолковского:
где /Яш-масса аппарата в начале пассивного участка; /д-удельный
импульс двигателя на участке довыведения; ЛИЕ- суммарное потребное
увеличение характеристической скорости на пассивном участке полета
и на заключительном активном участке (в случае его наличия):
ДГЕ = ДГд+ДГг+ДГА.
Слагаемые, входящие в АК. вычисляются по формулам (3.25),
(3.34) и (3.36).
Для времени движения по переходной орбите имеется аналитиче-
ское решение [86]. При движении по эллиптической орбите
Тк - Tni = а*2 [Лк- Ex - е (shiEk- sin£ni)] /^/ц ’
где а = р / (1 - е2) - большая полуось эллипса; Е - эксцентрическая
аномалия, связанная с истинной аномалией следующим образом:
tg(E/2)= tg(X/2).
V 1 + е
Таким образом, выписаны все соотношения для определения пара-
метров траектории (т, г, V, д, т) при движении на пассивном и заклю-
чительном активном участках выведения на орбиту. Интегрировать
уравнения движения на этих двух участках полета не требуется, что
упрощает решение задачи.
3.5. Формирование приближенно оптимального
управления на активном участке полета
Время полета на активном участке составляет примерно 3004-400 с.
Это означает, что можно воспользоваться результатами работы [73] (см.
150 Глава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
раздел 3.3). В соответствии с алгоритмом, изложенным в разделе3.4, на
каждой итерации расчета траектории выведения на орбиту в конечной
точке активного участка значения фазовых переменных ЯПь ^гн и бш
являются заданными. При фиксированных значениях этих параметров
максимуму конечной массы тк будет однозначно соответствовать мак-
симум массы ЛА в конце активного участка, поэтому будем решать
задачу максимизации массы •
Учет вращения Земли, как было показано в работе [73], практиче-
ски не влияет на структуру оптимального управления. Это позволяет
воспользоваться приближенными уравнениями движения
dV/dx = go nx-g sin0;
dQ/dx = g0ny/V-g [1 - V2/(gr)] cosG/K;
dH/dx = KsinO; dm/dx = - v 0Tmax •
(3.37)
По условию задачи заданы два ограничения типа неравенства:
4Л — 72Х1 Т2Х 1 тахд 0, \|>2 — ^1 К1тахД — 0>
где функции и \|/2 зависят от управляющих переменных.
В соответствии с принципом максимума необходимым условием
оптимальности управления является достижение абсолютного макси-
мума функции
Н = Ру dV/dx + Pq dQ/dx + Рн dH/dx + Pm dm/dx + Xi 4/1 + X2 44 -> max,
где Pi - сопряженные переменные; Ху - неизвестные функции.
В конечной точке Рт> 0. При < 0 соответствующая функция Ху
равна нулю.
Определим вначале оптимальное управление коэффициентом
дросселирования v. Пусть на ЛА установлены п ЖРД с фиксирован-
ными углами 5, и р,. В общем случае двигатели могут иметь различные
характеристики. Заметим, что функция 4/2 от v не зависит. Отсюда
следует, что на участках траектории, лежащих внутри области 4/1 < 0,
оптимальное значение коэффициента v в соответствии с решением
модельной задачи (см. раздел 3.3) равно максимально возможному:
vopt= ^тахд • На остальной части траектории оптимальное значение
коэффициента v является решением уравнения
Vi(v) = 0. (3.38)
При дросселировании ЖРД продольная перегрузка в связанной
системе координат в соответствии с (3.7) и рис. 3.3 записывается сле-
дующим образом:
п я
Их1 = (V £ ЯП/ cos8/ cos₽/ - PH X FCi cos8* cos₽* “ 1 (w£o).
/=1 /=1
3.5. Формирование приближенно оптимального управления
151
Здесь первое слагаемое в числителе представляет собой суммарную
пустотную тягу всех ЖРД в проекции на ось Ох\; второе слагаемое -
суммарное противодавление в проекции на ось Охх; Х\ - продольная
аэродинамическая сила (в связанной системе координат):
Х\ = (сх cosa - су sina) q S.
Решение уравнения (3.38) относительно коэффициента дроссели-
рования
И п
V1 = (Их1тахд^ g0 +Хх + cos8z cospz) /(£ДП/ cos8z cos₽z) (3.39)
/=1 /=1
в общем случае зависит от угла атаки через величину Xi, но эта зави-
симость является слабой. Объясняется это тем, что продольная пере-
грузка достигает своего максимально допустимого значения на боль-
ших высотах, где аэродинамические, силы малы. Поэтому при
вычислении продольной силы сопротивления Xi в выражении (3.39)
можно использовать численные данные с предыдущего шага интегри-
рования. Если вовсе пренебречь влиянием атмосферы, то выражение
для коэффициента дросселирования упрощается:
Ч = Их1тахД ™ COS8Z COS₽Z).
/=1
В конечном виде оптимальное значение коэффициента дроссели-
рования определяется выражением
vopt = min (утахД, V0
и должно отыскиваться первым.
Перейдем к определению оптимального угла заклинения вектора
тяги 8. Пусть управляющими переменными являются коэффициент v и
углы а и 8. Для упрощения будем полагать, что на ЛА установлен один
двигатель, ограничения на величины и Ki не заданы. Вместо угла 8
введем в рассмотрение угол заклинения вектора тяги по отношению к
вектору скорости: 82 = a + 8. Необходимым условием оптимальности
угла 8^ будет являться достижение абсолютного максимума функции Н\
(слагаемого функции Гамильтона, зависящего от угла 8^):
Н\ = Im + P07?sin8E /(т V) -> max .
Здесь использованы выражения (3.11) для компонентов перегрузки.
Для упрощения математических преобразований введем в рассмот-
рение вспомогательную переменную U= Pq /(РуР). Из необходимого
условия экстремума функции Hi получим
tgSzopt = и. (3.40)
152 Глава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
Определим оптимальную программу управления углом атаки при
8v= Szopt • Необходимым условием оптимальности угла а является
достижение абсолютного максимума функции W2 (слагаемого функции
Гамильтона, зависящего от угла атаки):
TC2=-P\CxqSlm + Pq су qS /(т Г) -> max.
Отсюда
(dcx /da) / (dcy /da) = U. (3.41)
Из соотношений (3.40) и (3.41) следует
tgSzopt= (dcx /da) / (dcy /da). (3.42)
Рассмотрим простейший случай задания аэродинамических харак-
теристик (су= <?у а и сх = cxmin + А су). Используя выражения (3.3), полу-
чим
(dcx /da) / (dcy /da) = 2Acy.
Если учесть, что А « \/ су , то
(dcx /da) / (dcy /da) » 2a. (3.43)
Из выражений (3.42) и (3.43) с учетом малости угла 8Z следует из-
вестное решение
8Zopt*2aOpt или 8Opt«aOpt. (3.44)
Данное решение является чисто теоретическим, так как на реаль-
ном ЛА управление вектором тяги обычно используется для баланси-
ровки. Более правильной является такая постановка задачи, когда на
этапе формирования облика ЛА оптимальное значение угла 5 отыскива-
ется в классе констант. При этом естественно полагать, что для каждого
нового значения угла 8 двигательная установка соответствующим
образом перекомпоновывается, обеспечивая прохождение вектора тяги
через центр масс ЛА. В этом случае решение (3.44) можно трактовать
следующим образом: оптимальный угол заклинения ЖРД 80pt равен
некоторому среднему по траектории углу атаки. Так как на тех участках
полета, где аэродинамические силы существенны, угол атаки положи-
телен, то 80pt > 0.
Далее будем полагать углы установки ЖРД фиксированными:
8/ = fix. Определим оптимальную программу изменения угла атаки при
vgi < 0 и vg2 < 0- В этом случае оптимальное управление углом атаки
определяется из условия достижения абсолютного максимума функции
Нз (слагаемого функции Гамильтона, зависящего от угла атаки):
Нз = Ру пх + Pq пу/V -> max.
3.5. Формирование приближенно оптимального управления
153
(3.46)
При фиксированных значениях v и 8, необходимое условие экстре-
мума функции 7Y3 определяется решением уравнения
ф(ос) = dnx /da + U dny /da = 0. (3.45)
Следует отметить, что уравнение (3.45) не связано с типом двига-
теля в явном виде. Это значит, что при решении аналогичной по поста-
новке задачи оно будет справедливым для любого типа двигателя,
секундный расход которого не зависит от угла атаки.
Входящие в (3.45) производные компонентов перегрузки запишем с
использованием формул (3.1):
dnjda = - [ERj cos0, sin(a + 8,) + q S dcx/da]/(m g0);
dny/da = [ZRj cospz cos(a + 8/) + q S dcy/da\/(rn g0).
В общем случае уравнение (3.45) является нелинейным. При из-
вестном значении переменной U его можно решить любым способом,
например методом Ньютона:
az+i= а,- - ф(а,У[<^ф(а/)Д/а],
где а, и аж соответствуют z-ой и i +1-ой итерациям;
dy/da = d2nx/da2 + U d2ny/da?\
Вторые производные компонентов перегрузки по углу атаки равны
d2nx /da2 = - [ZRicos0, cos(a + 8Z) + qSd2cx/da2]/(m g0);
d2ny /da} = - [SRi cosP, sin(a + 8Z) - q S d2cy /da2]/(m g0).
В выражениях (3.46) и (3.47) первые и вторые производные коэф-
фициентов су и сх по углу атаки описываются формулами (3.3) и (3.4).
Проанализируем уравнение (3.45). Рассмотрим простейший слу-
чай, когда на ЛА установлен один двигатель. Для случая полета вне
атмосферы (q « 0) из (3.45) следует решение
tg(a + 8) = U, (3.48)
совпадающее по форме с выражением (3.40). Если в (3.46) пренебречь
силой тяги по сравнению с аэродинамическими силами, то из (3.45)
получается уравнение:
(dcx /da) / (dcy /da) = U, (3.49)
совпадающее с (3.41). С учетом (3.43) из уравнения (3.49) получим
a * U/ 2.
Таким образом, можно заключить, что примерный диапазон изме-
нения угла атаки по траектории полета составляет mU/2 до U- 8.
154 Глава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
Найдем приближенное аналитическое решение уравнения (3.45)
для случая линейной зависимости су (а). При этом поставим условие,
чтобы при q = 0 полученное решение совпадало с (3.48). Вначале отме-
тим, что второе выражение (3.3) для производной сх по а с учетом
малости углов а и 8 можно переписать следующим образом:
dcx /da = 2А(су - су) суа = 2А (су0 - су’) суа + 2Л(суа)2 (а + 8) - 2А(суа)2 8 «
» [2А (су0- су‘)суа- 2Л(суа)2 8] cos(a + 8) + 2/4(cy“)2sin(a + 8). (3.50)
Подставим в уравнение (3.45) выражения для производных (3.46) с
учетом (3.50):
и cos(a + 8) (Я + qScya) - sin(a + 8) [Я + qS 2А (су°)2] -
- cos(a + 8)qS 2Acya(cyo - cy - cya 8) = 0.
После преобразований получим
tg(a + 8) =
U(R + qSc“)-qS 2Ac^ (cy0 -c'y- cya8)
R + qS2A(c“)2
(3.51)
причем при q = 0 решение совпадает с (3.48).
В случае установки на ЛА нескольких ЖРД величины R и 8 в (3.51)
соответствуют эквивалентному двигателю и определяются по формулам
(3.10).
Перейдем к рассмотрению ограничений. Выше было отмечено, что
зависимостью vgj от а можно пренебречь. Поэтому остается только
решить уравнение
\|/2(а) = (су cosa + ск sina)#5 - У1тахД = 0. (3.52)
Для этого можно воспользоваться методом Ньютона:
az+i = az - ц/2 (az)/ [<Л|/2 (az)/ rfa],
где
бЛ|/2 / da = [(dcy Ida + cx) cosa - (cy - dcx Ida) sina] q S.
В итоге угол атаки выбирается как наименьший в результате реше-
ния уравнений (3.45) и (3.52) с учетом ограничений (3.12).
Для определения оптимального угла атаки в каждой точке траекто-
рии необходимо иметь значение переменной U. В случае точного реше-
ния с использованием принципа максимума значение U получается в
результате интегрирования сопряженной системы уравнений. Пример
решения такой задачи будет рассмотрен в разделе 3.6. Изложим при-
ближенный метод определения переменной U, основанный на исполь-
зовании результатов решения модельной задачи Д.Е. Охоцимского и
Т.М. Энеева (в соответствии с работой [20]).
Перепишем выражение (3.16) для ’’линейного тангенса” угла тан-
гажа следующим образом:
3.5. Формирование приближенно оптимального управления
155
tg(a + 8 + 0) = tg90 - Ст (т - то). (3.53)
Исключив сумму углов a+ 8 в (3.48) при помощи выражения (3.53),
получим
U= tg{arctg [tgS0-Ст (т-то)]-6}. (3.54)
Здесь Эо и Ст - неизвестные параметры, значения которых выбираются
из условия попадания в заданную конечную точку (/ni, Hni, 0ni)«
При решении краевой задачи вместо параметра Ст удобнее задавать
время полета Дт = т - т0, при котором угол тангажа становится равным
нулю; тогда из (3.53) получим Сх= tg90 / Дт. Параметры Эо и Дт явля-
ются положительными и, в отличие от сопряженных переменных,
имеют вполне определенный физический смысл. Как показали расчеты,
в зависимости от условий задачи численные значения этих величин
примерно равны Эо= 404-60°; Дт = 2004-400 с.
Если заканчивать интегрирование уравнений движения по дости-
жении конечной скорости (К= КП1), то система уравнений, соответст-
вующая краевой задаче, будет иметь следующий вид:
Я(КП1, Эо, Дт) - ЯП1 =0; 0 (КП1, Эо, Дт) - 0Ш = 0 (3.55)
и может быть решена любым известным способом, например с исполь-
зованием стандартной процедуры, основанной на методе Ньютона.
После решения краевой задачи к активному участку полета при-
стыковывается участок пассивного полета и определяется импульс
довыведения в соответствии с алгоритмом, изложенным в разделе 3.4.
На конечном участке полета, где скоростной напор мал, управле-
ние, определяемое с помощью соотношения (3.54), будет практически
совпадать с оптимальным. Однако на начальных участках полета, из-за
влияния атмосферы, расчетный угол атаки может существенно отли-
чаться от оптимального. Проанализируем поведение переменной U по
траектории полета. Из (3.54) следует, что переменная U максимальна в
начальной точке и равна tg0o (при 0О = 0), далее U практически моно-
тонно убывает по траектории полета, так как Ст> 0 и 0 >0.
В разделе3.7 решена задача расчета траектории выведения на ор-
биту с использованием выражения (3.54). На рис. 3.11 пунктиром пока-
заны расчетные зависимости £7(т) и а(т), соответствующие выведению
в случае дозвукового воздушного старта. Рис. 3.11 подтверждает пред-
варительный анализ: переменная U максимальна в начальной точке.
Кроме того, характер зависимостей U(r) и а(т) примерно одинаков. В
результате этого в начальной точке траектории угол атаки существенно
больше, чем на остальных участках полета, и достигает значений
304-40°. Непосредственное использование "закона линейного тангенса"
вместо (3.54) приводит к еще большим значениям угла атаки в началь-
ной точке траектории.
156 Глава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
Рис. 3.11. Типичные зависимости угла
атаки а и переменной U от времени
полета при выведении на орбиту
В разделе 3.6 решена мо-
дельная задача с использовани-
ем принципа максимума. Зави-
симости Цт) и а(т), соответ-
ствующие решению этой задачи,
показаны на рис. 3.11 сплошны-
ми линиями. Видно, что на
начальном участке полета (при-
мерно 20 с) оптимальные значе-
ния а и U существенно меньше,
чем в случае использования
выражения (3.54).
Определим, как на значение
угла атаки ос0 (в начальной точке
траектории) влияют условия
старта. Расчетные зависимости
осо от стартового угла наклона
траектории 0О показаны на рис. 3.12 для вариантов дозвукового и гипер-
звукового воздушного старта. Пунктирные линии соответствуют при-
ближенному решению с использованием выражения (3.54), сплошные -
оптимальному решению. При увеличении 0О начальный угол атаки
уменьшается. Сравнение зависимостей показывает, что при использо-
вании выражения (3.54) начальный угол атаки завышается наиболее
сильно при малых значениях 0О при дозвуковом старте. Дополнитель-
ные расчеты показали, что начальная высота практически не влияет на
взаимное расположение зависимостей.
Таким образом, можно заключить, что основным недостатком при-
ближенного решения с использо-
ванием выражения (3.54) являет-
ся завышение переменной U на
начальном участке полета. При-
чем наиболее критичным являет-
ся вариант дозвукового воздуш-
Рис. 3.12. Зависимость начального
угла атаки от стартового угла накло-
на траектории при выведении на
орбиту в случае дозвукового (а) и
гиперзвукового (б) вариантов старта
ного старта с 0о=О° (т.е. случай,
когда осо завышается наиболее
сильно). С учетом вышесказанно-
го модифицируем выражение
(3.54) путем введения поправоч-
ного слагаемого, которое макси-
мально по модулю в начальный
момент времени и стремится к
нулю по мере увеличения време-
ни полета. Для этой цели подхо-
дящей является функция вида
3.5. Формирование приближенно оптимального управления
157
/х) = d , (3.56)
которая при х = хт имеет максимум (при d > 0) и монотонно стремится к
нулю при увеличении х. Функция (3.56) зависит от трех параметров: d,
b ихт.
Запишем модифицированную формулу для определения перемен-
ной U:
U= tg{arctg[tg90+ Сх(т - То)] - 0} -d е"л2(т’т°"т,п)2 (3.57)
и сформулируем алгоритм расчета траектории на активном участке
полета.
Параметры d, b и т1П, входящие в (3.57), оптимизируются из усло-
вия максимума конечной массы. При каждом изменении этих парамет-
ров система уравнений (3.55) относительно Эо и Дт решается заново. На
каждом шаге интегрирования системы уравнений движения (2.71)
после определения переменной U по формуле (3.57) определяется
приближенно оптимальный угол атаки из выражения (3.51) с учетом
заданных ограничений.
Оптимизацию параметров d, b и тт удобнее проводить в два этапа.
Вначале оптимизируются d и Ь при т1П=0, затем - параметр тт. Как
правило, достаточно определить оптимальные значения dub. Оптими-
зация величины тт приводит к незначительному улучшению функцио-
нала.
Модифицированное выражение (3.57) можно использовать также
для расчета траекторий разгона крылатых ЛА с ЖРД в атмосфере.
Управление углом атаки при вертикальном старте. В данном
случае за основу можно взять структуру управления, которая применя-
ется для расчета траекторий выведения ракет-носителей [86]. Траекто-
рия активного полета разделяется на четыре участка, на каждом из
которых используется свой закон управления (рис. 3.13).
1. На первом участке осуществляется вертикальное движение
(0 = 90°). Интегрируются первое, третье и четвертое уравнения движе-
ния системы (2.71). Угол атаки выбирается из условия обеспечения
w = 0 и в общем случае (при су0 ф 0) может отличаться от нулевого.
Конец участка соответствует достижению заданной дозвуковой скоро-
сти V= V\.
2. На втором участке управление углом атаки используется для ис-
кривления траектории. Угол наклона траектории при этом уменьшается
от 90° до заданного значения 0 = 02. Интегрируются первые четыре
уравнения (2.71). Угол атаки является отрицательным и выбирается из
условия обеспечения заданной нормальной силы Y\ =-|^тахД|.
3. На третьем участке осуществляется гравитационный разворот.
Угол наклона траектории уменьшается за счет действия силы гравита-
ционного притяжения. Интегрируются все уравнения системы (2.71).
Угол атаки выбирается из условия обеспечения иу = 0. Скоростной
158 Глава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
Рис. 3.13. Основные участки полета ЛА вертикального старта
напор вначале увеличивается, а затем начинает уменьшаться (см.
рис. 3.13). Конец участка соответствует достижению заданной скорости
V= Vy.
4. На последнем участке угол атаки является решением уравнения
(3.45). В зависимости от решаемой задачи для переменной U может
использоваться выражение (3.54) или (3.57). Интегрируются все урав-
нения системы (2.71).
Краевая задача решается, как при горизонтальном старте. Это от-
носится и к учету ограничения, наложенного на максимальное значение
иХ1, к расчету пассивного участка и импульса довыведения на заданную
орбиту. Величины V\, У1тахД, 02 и являются оптимизируемыми пара-
метрами и выбираются из условия обеспечения максимума . В неко-
тором смысле эти параметры эквивалентны параметрам Д b и тт, ис-
пользуемым при оптимизации траектории выведения горизонтально
стартующего ЛА.
Анализ траекторий выведения ЛА с вертикальным стартом показы-
вает, что параметры V\ и 02, по сути, определяют некоторый фиктивный
начальный угол 0О, близкий к 90° (см. рис. 3.13), как если бы гравита-
ционный разворот начинался сразу в точке старта. В связи с этим одну
величину можно зафиксировать, например принять V\ = 50 м/с. А вторая
величина - угол 02, будет являться оптимизируемым параметром. Оче-
видно, что при заданных характеристиках ЛА угол 02 можно подобрать
таким образом, что в конце гравитационного разворота при V= будет
обеспечено условие Н= Нк . При этом угол 0(Рк) будет отличаться от
заданного, однако на всей траектории будет выполнено условие пу = 0.
Таким образом, угол 02, являясь основным оптимизируемым парамет-
ром, определяет характер начальной части траектории, а параметры Эо и
Ат характеризуют искривление траектории на заключительном участке
при выполнении заданных краевых условий. При оптимальном значе-
нии 02, как правило, реализуется достаточно большая скорость в конце
гравитационного разворота: И3 = 20004-3000 м/с, причем ее влияние на
функционал незначительно. Угол атаки по модулю на четвертом участке
является небольшим. При существенном отклонении угла 02 от своего
3.5. Формирование приближенно оптимального управления 159
оптимального значения решение краевой задачи перестает сходиться. В
связи с этим при выборе начальных значений 90 и Дт необходимо также
подобрать значение угла 02, достаточно близкое к оптимальному.
При рассмотрении многоступенчатого ЛА (как с вертикальным, так
и горизонтальным стартом) в дополнение к изложенному выше алго-
ритму предусматривается дискретное уменьшение (сброс) "сухой”
массы в соответствующих точках траектории. Для и-ступенчатого ЛА
число таких сбросов равно п -1. В этом случае задача решается совме-
стно с задачей формирования облика ЛА. При очередном расчете траек-
тории в качестве исходных данных необходимо задать ’’сухие” массы
сбрасываемых ступеней и соответствующие запасы маршевого топлива
каждой ступени. Очередной сброс ’’сухой” массы должен осуществ-
ляться по мере выработки заданной массы топлива. При необходимости
запасы топлива и "сухие” массы ступеней уточняются. В зависимости
от решаемой задачи условия сброса "сухой” массы могут изменяться.
Например, таким условием может быть достижение заданной скорости
полета.
3.6. Решение модельной задачи с использованием
принципа максимума
Чтобы определить, насколько приближенное решение отличается
от точного, решим задачу, сформулированную в разделе 3.2 с использо-
ванием принципа максимума в упрощенной постановке.
Пусть на ЛА установлен один двигатель (8 = fix). Рассматривается
активный участок полета. В начальной точке значения фазовых пере-
менных Ко, Hq, 0о и т0 известны, в конечной точке активного участка
заданы Кк, Нк и 0К, конечная масса тк максимизируется. Ограничения
отсутствуют, т.е. vopt = утахД и QT = (Зттах • Управление осуществляется
только углом атаки, который определяется из условия максимума функ-
ции Гамильтона.
Воспользуемся системой уравнений движения (3.37). Соответст-
вующая сопряженная система имеет вид
dP^/dx =-Ру go дпхIdV-Рнsin0 -
-Ре [go(Vdny/dV-ny)/V2 + cose(glV2 + 1/г)];
dPe Idx = Pvg cos0 - Р0 sinO (g/V- V/r) - PH VcosQ;
(3.58)
dPH Idx = -PN [go dnx IdH + 2 g sin6/r] -
-Pe [go dny IdH + cos0 (2g/r - V 2/r2)]/ V\
dPm Idx = Pv go nx !m + P0 g0 ny l(m V).
160 Глава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
Так как максимальный секундный расход топлива ЖРД не зависит
от фазовых переменных, то будем учитывать, что производные (?ттах по
Vи Нв системе (3.58) равны нулю.
При записи компонентов вектора перегрузки будем использовать
первые степени разложения в ряд тригонометрических функций
пу= [7?(а + 8) + cyq S]/(m g0);
пх = [7?- R(a + 8)2/2 - cxqS]/(mgQ).
Атмосферу будем полагать экспоненциальной:
Р = Ро е~^н ; Pw = p^e~^H .
Полагаем, что скорость звука не зависит от высоты: <7=300 м/с.
Производные плотности, давления и скоростного напора по высоте
равны
t7p/tZZZ=-рр; фн/б/Я = -ррн; dq/dH=—$q.
Производные перегрузок по скорости и высоте
дпу IdV = (q S дсу /dV + сур VS)/(т go);
dnx /dV=-(q S dcx /dV+ схр VS) /{т g0);
дпу /дН= [(а + 8) dR/dH-су р q 5] /(т g0);
дпх /дН = \dRJdH- (dR/dH) (а + 8)2/2 + ск р q 5] /(т go).
Здесь в соответствии с положениями раздела 3.1 учтено, что аэродина-
мические коэффициенты зависят только от скорости полета, а тяга
ЖРД - только от высоты.
Пусть аэродинамическая поляра аппарата - симметричная и квад-
ратичная (сх = ск min + А с2), а коэффициент су зависит от угла атаки
линейно (су = с" а). Тогда
дсх IdV = (dcx min /dM + c2 dA/dM) /a + 2 Acy dcy /дV;
dCy/dV = (d cy/dM) a/a; dR/dH =$pHFc.
Производные перегрузок по углу атаки
dnjda = - [7? (а + 8) + 2 А су су q S\/(m go);
dny /da = [7? + cy q S]/(m go).
С учетом принятых допущений уравнение (3.45) решается анали-
тически:
3.6. Решение модельной задачи с использованием принципа максимума 161
£/(Я + с“о5) + 2Л(с“) qSb
<*= —------ < ч2--------------5- (3-59)
Я + 2Л(с“) qS
При малых углах а и 8 полученное выражение совпадает с (3.51),
если в последнем положить су0 = су*.
Будем интегрировать основную (3.37) и сопряженную (3.58) систе-
мы уравнений от начальной точки до момента достижения конечной
скорости Кк. Сформируем алгоритм определения сопряженных пере-
менных в начальной точке (PVo, Рно, Роо и Рт0). Будем выбирать значе-
ние Руо так, чтобы в соответствии с принципом максимума обеспечить
на правом конце условие PmK > 1 (в данном случае было принято
Руо= 1). Вместо значения сопряженной переменной Р0О будем задавать
в начальной точке угол атаки а0, значение которого спрогнозировать
значительно легче. Тогда из выражения (3.59) определяется переменная
Uq , а сопряженная перменная Р0О равна
Роо = Uq Vo.
Зная угол атаки, можно вычислить в начальной точке правые части
уравнений (3.37). Сопряженная переменная Рт в начальной точке опре-
деляется из условия равенства нулю функции Гамильтона:
Pm0 = (dV/dT + Р0О <70 /<7т + Рно dH /dx) ,
где РНо является неизвестным параметром.
Система уравнений, соответствующая двухпараметрической крае-
вой задаче, будет иметь следующий вид:
Н (Кк , осо, Рно) - Як = 0; 0( , а0, РНо) - 0к = 0.
3.7. Примеры расчетов. Сравнение приближенного
решения с оптимальным
Рассмотрим гипотетический ВКС со стартовой массой mQ = 500 т и
характерной площадью S = 600 м2. Стартовая тяговооруженность (по
пустотной тяге) равна 1,3. Удельный импульс ЖРД в пустоте
<7П = 4,6 км/с, удельная лобовая тяга PFn= 300 кН/м2, что примерно
соответствует отношению Рп/Ро =1,5.
Решим вначале модельную задачу, сформулированную в разделе
3.6, с использованием принципа максимума. При решении таких задач
используется двойная точность вычислений.
Для задания зависимостей аэродинамических коэффициентов ,
cxmin и А от числа М полета воспользуемся аналитической функцией
вида
162 Глава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
2 2
f(x)=fo + de~h , (3.60)
где/), d, b и хт - некоторые коэффициенты.
Функция (3.60) непрерывна и имеет один экстремум при х = хт, т.е.
качественно ведет себя так же, как и зависимости аэродинамических
коэффициентов от числа М полета. Производная функции (3.60) также
непрерывна и равна
df/dx = - 2 b2 (х - xm) d e~h {х~Хт} .
Рис. 3.14. Исходная и аппроксима-
ционная зависимости производной
< от числа М полета
Таблица 3.1
Коэффициенты аппроксимации
аэродинамических характеристик
/о d b
суа, рад’1 0,6 1,16 0,48655 1,0
Сх min 0,021 0,0209 0,3735 1,2
А 2,0 -1,45 0,20875 0,5
На рис. 3.14 в качестве при-
мера показаны исходная зависи-
мость производной от числа М
полета и соответствующая ап-
проксимационная зависимость.
Видно, что зависимости качест-
венно ведут себя одинаково, что
вполне достаточно для решения
модельной задачи. Расчетные
коэффициенты аппроксимации,
используемые для задания аэроди-
намических коэффициентов в
данном примере, приведены в
табл. 3.1.
Рассмотрим вариант вы-
ведения с дозвуковым воздуш-
ным стартом, как наиболее
критичный с точки зрения
применимости разработанного
приближенно оптимального
управления. Пусть в началь-
ной точке даны: 77о=8км;
Ко = 180 м/с (Мо = 0,6); угол
наклона траектории 0О либо
оптимизируется, либо задает-
ся. В конечной точке активно-
го участка заданы: 77к= 100 км; = 7580 м/с; 0К = 0°.
Оптимизация стартового угла наклона траектории показала, что
0oOpt=38,3°. Изменение угла атаки а и переменной U по траектории
полета при 0О= 0oopt и 0О= 0° показано на рис. 3.15. Видно, что угол 00
влияет на характер зависимости переменных а и U наиболее сильно на
начальном участке полета.
Результаты расчетов оптимальной траектории при 0О= 0° представ-
лены на рис. 3.16 и 3.17 сплошными линиями. На рис. 3.16 показан
профиль полета в координатах "высота-скорость”; на рис. 3.17я -
зависимость скоростного напора q от времени полета т; на рис. 3.176 -
3.7. Примеры расчетов. Сравнение решений
163
зависимость а(т). Время полета
равно 299,6 с; относительный
запас топлива составляет
84,6726 % стартовой массы, что
на 0,114% больше, чем в случае
Оо = Ooopt • Этим подтверждается
важность оптимизации пред-
стартового маневра самолета-
носителя.
Далее модельная задача
была решена с применением
разработанного приближенно
оптимального управления. При
этом использовалось модифи-
цированное соотношение (3.57)
для переменной U с оптимиза-
Рис. 3.15. Зависимости угла атаки
и переменной U от времени полета
(оптимальное решение)
цией параметров d, b и тт. Результаты расчетов при 0О = 0° показаны на
рис. 3.16 и 3.17 пунктирными линиями.
Профиль полета в координатах "Н- И" в случаях приближенного и
оптимального решений практически одинаков (см. рис. 3.16). Прибли-
женное решение для угла атаки и скоростного напора отличается от
оптимального решения незначительно (см. рис. 3.17). Относительный
запас топлива превышает аналогичную величину, соответствующую
оптимальной траектории, всего на 0,0023 %. Для аппарата с mQ = 500 т
разница в абсолютной массе топлива составляет ~10 кг.
Для варианта старта с оптимальным углом наклона траектории
(00 = Ooopt = 38,3°) в случае приближенного решения относительный
запас топлива на 0,0014% (на 7 кг) больше, чем в случае точного реше-
ния.
Проведем сравнение точно-
го и приближенного решений с
точки зрения величины возмож-
ного отклонения начальных
значений параметров краевой
задачи от своих искомых значе-
ний. Пусть а0* и Рно* соответст-
вуют искомому решению опти-
мальной задачи (см. раздел 3.6).
Расчетные исследования показа-
ли, что при отклонении а0 от а0*
более чем на 3-^4% при
Рно = Рно*, решение краевой
задачи перестает сходиться с
использованием стандартной
процедуры решения системы
Рис. 3.16. Профиль полета в коор-
динатах ’’высота - скорость”: при-
ближенное решение практически
совпадает с оптимальным решением
164 Глава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
------оптимальное решение;
а) -----------приближенное решение
Рис. 3.17. Зависимости скоростного напора (а) и угла атаки (б) от
времени полета
нелинейных уравнений. Аналогично, при отклонении РНо от РНо* более
чем на 5-6%, краевая задача также перестает сходиться. Таким обра-
зом, подтверждается известный факт, что основная сложность решения
задачи с использованием принципа максимума заключается в первона-
чальном выборе параметров ос0 и РНо, достаточно близких к искомым
значениям. При этом незначительное изменение исходных данных
приводит к необходимости проводить заново трудоемкую процедуру
выбора начального приближения параметров краевой задачи.
В случае использования разработанного приближенного решения
допустимый диапазон отклонения параметров краевой задачи от иско-
мых значений существенно возрастает: для Эо допустимое отклонение
составляет от минус 20% до 40%, для Ат - от минус 10% до 20%. Т.е.
переход от точного решения к приближенному позволяет существенно
расширить диапазон возможного отклонения начальных значений
параметров краевой задачи от своих искомых значений. Причем ис-
пользование модифицированного выражения (3.57) обеспечивает зна-
чение функционала, практически равное точному решению с использо-
ванием принципа максимума. Таким образом, разработанный алгоритм
расчета траектории выведения на орбиту может быть рекомендован для
проведения расчетов на этапе формирования облика ЛА.
Проведем сравнение исходного (3.54) и модифицированного (3.57)
выражений на примере решения типовой задачи выведения на орбиту в
полной постановке (см. раздел 3.2). В отличие от модельной задачи
вращение Земли учитывается, атмосфера - стандартная, задаются
реальные аэродинамические характеристики ВКС (см. рис. 3.4 и 3.5).
Учитываются ограничения: иХ1тахд=3,5; Y\ тахд/(^о£о)= 1,2. Рассматри-
3.7. Примеры расчетов. Сравнение решений
165
вается выведение на круговую орбиту высотой 200 км и наклонением
51°.
Для удобства сравнения вначале зафиксируем конечную точку ак-
тивного участка: /7™ =100 км; 0П| = О°. Значение скорости в конце
активного участка в данном случае будет составлять ИП| = 7583 м/с (в
геоцентрической вращающейся с.к.), величина импульса довыведения
равна Д = 30 м/с. Рассмотрим два варианта.
Горизонтальный старт (0о=О°). При переходе от выражения
(3.54) к (3.57) угол атаки в начальной точке уменьшается с 39° до 16°.
Суммарные потери характеристической скорости уменьшаются на
22 м/с. Вследствие этого относительный запас топлива выведения
уменьшается на 0,084% стартовой массы ЛА. При т$ = 500 т выигрыш
в абсолютной массе топлива будет составлять - 420 кг. Оптимальные
параметры, входящие в поправочное слагаемое формулы (3.57), равны
б/=0,26; 6 = 0,039; т1П = -2с. Параметры краевой задачи: 90 = 43,2°;
Дт = 287 с.
Оптимальный угол наклона траектории в начальной точке
(0о = 0ooPt = 38,3°). При переходе от выражения (3.54) к (3.57) начальный
угол атаки уменьшается на 8°. Относительный запас топлива выведения
при этом уменьшается на- 0,02% стартовой массы ВКС. По сравнению
с 0о=О° выигрыш от использования модифицированного выражения
уменьшается примерно в четыре раза. Тем не менее, в абсолютной
массе топлива величина выигрыша составляет -100 кг.
Из сопоставления двух рассмотренных примеров можно заклю-
чить, что использование модифицированного выражения (с оптимиза-
цией трех параметров d, b и тт) дает тем больший эффект, чем больше
начальный угол наклона траектории отличается от оптимального.
Определим эффект от оптимизации параметров полета в конце ак-
тивного участка. Пусть задано 0о=О°. По сравнению с вариантом
ЯП1= 100 км; 0ni = O° оптимизация параметров траектории в конечной
точке активного участка позволяет уменьшить относительный запас
топлива на 0,07% от mQ (на -350 кг). Оптимальные значения высоты и
угла наклона траектории в конце активного участка равны /411 = 90 км и
0П1=1,5°. Значение скорости в конце активного участка однозначно
определяется в соответствии с параметрами переходной орбиты (см.
раздел 3.4) и составляет 7520 м/с; величина импульса довыведения
равна АИД = 106 м/с. Таким образом, полученные численные результаты
подтверждают исходные предположения, используемые в разделе 3.4
при разработке приближенного метода оптимизации траекторий выве-
дения на орбиту.
Расчеты траекторий выведения ЛА с вертикальным стартом пока-
зали, что примерные диапазоны изменения оптимизируемых парамет-
ров равны И| = 304-100 м/с; 02= 884-89,9°; У|1пахд/(^о go) = 0,014-0,1;
Из = 5004-3000 м/с. В качестве примера проведен расчет траектории
выведения на низкую околоземную орбиту гипотетического ВКС с
166 Глава 3. Разгон и выведение на орбиту ЛА с использованием ЖРД
Рис. 3.18. Траектория выведения на орбиту ЛА с вертикальным стартом.
Зависимости угла атаки, угла наклона траектории (а) и скоростного
напора (б) от времени полета
тяговооруженностью 1,3 (по земной тяге). Параметры краевой задачи
равны 30 = 37,5°; Ат = 268,6 сек. Параметры траектории: К1 = 90м/с;
02=88°; У1тахд/(^оgo) = ОД; =1100 м/с. Время полета составляет
321 с. На рис. 3.1 Sa показано изменение углов атаки и наклона траекто-
рии, на рис. 3.186 - изменение скоростного напора в зависимости от
времени полета.
При вертикальном старте реализуется меньшее значение ^тах по
сравнению с горизонтальным стартом (ср. рис. 3.17я и 3.186); нормаль-
ные силы (величины Ki и qa) также меньше. Однако относительный
запас топлива на ~ 2 % больше по сравнению с воздушным стартом.
ГЛАВА 4
ПРОГРАММА ВЫРАБОТКИ КОМПОНЕНТОВ
ТОПЛИВА ПРИ РАЗГОНЕ ЛА С ЖРД
В предыдущей главе задача оптимизации траекторий движения ЛА
с ЖРД решалась для случая постоянной плотности топлива, т.е. в пред-
положении неизменного по траектории соотношения секундных расхо-
дов компонентов топлива. В данной главе решается задача оптимизации
выработки топлива, т.е. программы изменения секундных расходов
топливных компонентов в процессе движения ЛА с ЖРД.
Топливо влияет на облик ЛА главным образом через свою плот-
ность и удельный импульс двигателя. Увеличение удельного импульса
двигателя (за счет соответствующего выбора компонентов топлива), как
правило, сопровождается уменьшением плотности топлива. В результа-
те масса топлива уменьшается, а объем топлива и масса конструкции
увеличиваются. Масса полезного груза при этом может как увеличи-
ваться, так и уменьшаться. Одним из способов устранения противоре-
чия между плотностью и удельным импульсом является последователь-
ное применение на аппарате 2-х типов топлива.
В ряду первых исследователей данного вопроса применительно к
одноступенчатым воздушно-космическим аппаратам с ЖРД следует
отметить Р. Солкелда. В его работе [139] было получено аналитическое
выражение для определения момента смены типов топлива. Разгон ЛА
с двумя типами топлива на борту рассматривался в предположении
отсутствия внешних сил. Суммарный объем топлива ГГр, масса полез-
ного груза типг и "сухая” масса аппарата т^сух считались фиксирован-
ными. Максимизировалась располагаемая характеристическая скорость
ЛА Гхар- Было показано, что оптимальный объем первого типа топлива
равен
W = nPz^T +7У7пг +^СУХ (л п
где pi, р2 - плотности первого и второго типов топлива;
Ji,J2 -удельные импульсы, соответствующие первому и второму
типам топлива.
168 Глава 4. Программа выработки компонентов топлива ЛА с ЖРД
На основании полученного решения Р. Солкелд сформулировал
принцип последовательного использования двух типов топлива: внача-
ле должно использоваться более плотное топливо, затем - топливо,
обеспечивающее более высокий удельный импульс ЖРД. При этом
должны выполняться следующие условия:
р!/р2>Л/^1- (4.2)
Возникающий эффект увеличения располагаемой характеристиче-
ской скорости, например, по сравнению с вариантом использования
второго типа топлива, объясняется следующим. За счет добавления
энергетически менее выгодного топлива средний удельный импульс
ЖРД по траектории полета уменьшается. Однако вследствие увеличе-
ния средней плотности топлива его располагаемая масса возрастает, что
и приводит к увеличению ИХАР.
В современных экологически чистых ЖРД в основном применяют-
ся два типа топлива: керосин + О2 и Н2 + О2. Удельный импульс ЖРД
при использовании водородно-кислородного топлива на ~25% больше,
чем при использовании керосиново-кислородного топлива, однако
плотность топлива в первом случае почти в 3 раза меньше. Таким обра-
зом, эти топливные пары удовлетворяют условиям (4.2), если первым
будет использоваться топливо керосин + О2.
Задача максимизации ИХАР, решенная в работе [139], эквивалентна
задаче минимизации относительной ’’сухой” массы ЛА Wyx/^пг при
фиксированном значении ИХАР. Величина ^Сух/^пг характеризует
удельную стоимость выведения на орбиту и является одним из основ-
ных технических показателей ЛА. Возможны и другие критерии опти-
мальности, например отношение массы ПГ к стартовой массе ЛА
/лпг/^о.
Задача определения оптимальной скорости переключения двух ти-
пов топлива с использованием различных критериев решена в работе
[125]. Помимо теоретических исследований по определению эффектив-
ности применения двух типов топлива известны и различные проработ-
ки ЛА с двумя типами топлива (см. работы [67], [82]).
Наряду с дискретным переходом от одного типа топлива к другому
возможно и непрерывное изменение соотношения £т между секундны-
ми расходами окислителя и горючего в двухкомпонентном топливе. Так,
например, для водородно-кислородного топлива изменение этого пара-
метра с 6 до 7 позволяет увеличить плотность на 9,5 % при уменьшении
удельного импульса ЖРД всего на 0,6%. Поэтому изменение соотноше-
ния £т по траектории полета для двухкомпонентного топлива качест-
венно дает такой же эффект, как и последовательное использование
двух типов топлива. В работе [26] задача оптимального управления
была решена в предположении линейной зависимости от скорости
полета. В работе [17] аналогичная задача решена автором совместно с
В.Ф. Илларионовым для случая многокомпонентного топлива с исполь-
зованием принципа максимума.
4.1. Постановка задачи
169
В данной главе задача определения оптимальной программы выра-
ботки компонентов многокомпонентного топлива ЖРД по траектории
полета решается с использованием принципа максимума [79] в более
общей постановке с целью исследовать варианты как непрерывного, так
и дискретного изменения секундных расходов компонентов топлива.
4.1. Постановка задачи
При выведении на орбиту ЛА с ЖРД потери характеристической
скорости не превышают 10-И 5 % от суммарных затрат ГХар- Поэтому в
первом приближении вместо процесса выведения ЛА на орбиту можно
рассмотреть его движение в пустоте (т.е. в предположении отсутствия
аэродинамических сил и сил гравитационного притяжения). Такое
упрощение значительно облегчает дальнейшее исследование.
Пусть аппарат разгоняется от скорости Г() до скорости при по-
мощи ЖРД с суммарной тягой R. Топливо ЛА по своему составу явля-
ется и-компонентным. Теоретически возможен вариант, когда на ЛА
установлен один двигатель, работающий на п компонентах топлива.
Возможен также вариант установки нескольких различных двухкомпо-
нентных ЖРД. Будем решать задачу, не ограничиваясь конкретным
вариантом двигательной установки.
Обозначим текущие секундный расход z-го компонента топлива и
его израсходованную массу через Qi и т,. Здесь под секундным расхо-
дом компонента или топлива понимается расход его массы за 1 с. В
процессе движения масса ЛА уменьшается от до 7ик, а массы компо-
нентов израсходованного топлива увеличиваются от 0 до miK. Заданны-
ми величинами являются Ио, и Кк. В конечной точке значения масс
компонентов израсходованного топлива не фиксируются. В качестве
управляющих переменных используются п относительных секундных
расходов:
Ui = Qi/Q^ ; / = 1.гц (4.3)
где - суммарный секундный расход топлива.
На управляющие переменные наложены естественные ограниче-
ния:
О < Ui < 1; Sw/=1; /=1,..., п. (4.4)
Удельный импульс двигательной установки J= R/считается из-
вестной функцией управляющих переменных и,.
В задаче требуется определить оптимальное изменение по траекто-
рии управляющих переменных и, из условия максимума некоторой
функции масс компонентов бортового топлива ЛА:
Ф(Ш|К, Ш2К, И7пк) шах.
170 Глава 4. Программа выработки компонентов топлива ЛА с ЖРД
4.2. Решение задачи в общем виде
Запишем уравнения движения ЛА с ЖРД в соответствии с поста-
новкой задачи:
dV/dT = R/m\ dmjdx = u,R/J; (4.5)
где m = m0 - E m,.
Здесь и далее суммирование производится от 1 до п. Исключив в
(4.5) время, перепишем фазовую систему уравнений, имеющую раз-
мерность п\
dmildV=Ujml J\ (4.6)
Дифференциальное уравнение для массы ЛА можно получить,
просуммировав п уравнений (4.6):
dm /dV=-mU. (4.7)
Следует отметить, что правые части уравнений движения (4.6) и
(4.7) не зависят от тяги R.
Функция Гамильтона и сопряженная система в данном случае бу-
дут иметь вид
Н = (/я / J) ДР/^/); (4.8)
dPj/dV=- dH /dmj= "L{Pj Uj)/(4.9)
где Pj~ сопряженные переменные.
В соответствии с принципом максимума необходимым условием
оптимальности управления является абсолютный максимум функции
7Y. В конечной точке траектории должны выполняться следующие
условия:
Р,к =^5Ф(ГК)Ш; i= 1,...,и, (4.10)
где £> - неизвестная постоянная величина.
Так как функционал Ф максимизируется, то в соответствии с [79]
> 0. Вследствие свойства линейности сопряженной системы относи-
тельно Pi можно положить £ = 1.
Из (4.9) видно, что дифференциальные уравнения для всех сопря-
женных переменных Р/ одинаковы, поэтому можно записать:
d(Pi -P\)/dV=^ i = 2,...,n.
Интегрируя, получим п - 1 независимых интегралов:
Pi-P{=\Pi\ i = 2,...,n, (4.11)
где ДР, - некоторые постоянные, причем
ДР/= Лк-Лк; z = 2, ...,и; ДР1=0. (4.12)
4.2. Решение задачи в общем виде
171
Покажем, что можно найти еще один интеграл, содержащий пере-
менную Р\. Действительно, перепишем уравнение (4.9) для Р\ с учетом
соотношений (4.11):
dPJdV=lL[(P^ \Pl)ul\U
и исключим из него dV и J при помощи уравнения (4.7):
т dP\ = -Ц(Р| + ДР/) ui\dm.
Преобразуем это уравнение с учетом того, что Zw, = 1 и
dmj = - Ujdm\
d(mP\) =£(&Pj dmi). (4.13)
Проинтегрировав уравнение (4.13), получим искомый интеграл в
виде
wP|-Z(AP/W/) = C, (4.14)
где константу интегрирования найдем, используя значения фазовых и
сопряженных переменных на правом конце:
с = тк Р]К - £(&PimlK).
В итоге получим выражение для сопряженной переменной Р\
Pi =Р\ктк/т- lL[\Pi(miK - mi)] Im. (4.15)
С учетом найденных интегралов (4.11) и (4.15) функцию Гамильто-
на (4.8) можно записать следующим образом:
Н = (ml J)12(Pi + = (m/J)(P} + ZAPj щ) =
= (m/J){P}KmK/m + Z(P/K - PiK)[ui - (m/K - т,)/т]} =
= (m I J) { ЛЛ Im - P1K + PIK (w0 - m^/m - Лк Oo - m)/m\ +
+ ZP/K[wz - (m,K - т,)/т]].
После сокращения получим:
H = (тЦ)^{Р/к[щ-(т^-т^1т]}. (4.16)
Приняв во внимание соотношения (4.10), можно отметить, что
функция Гамильтона (4.16) зависит только от конечных значений масс
компонентов израсходованного топлива. Следовательно, численное
интегрирование сопряженной системы не требуется. Оптимальная
траектория может быть получена в результате интегрирования системы
уравнений (4.6). Краевая задача имеет размерность п и заключается в
решении следующей системы уравнений:
^/(Ик)-^/К = 0; z = l,..., и, (4.17)
где тк - неизвестные параметры.
1 72 Глава 4. Программа выработки компонентов топлива ЛА с ЖРД
Оптимальное управление в каждой точке траектории находится из
•условия максимума функции Гамильтона (4.16) по п переменным w, с
учетом ограничений (4.4).
4.3. Решение краевой задачи в частных случаях
Рассмотрим два частных случая зависимости функционала от масс
компонентов топлива ЛА.
А. Линейная зависимость Ф от Пусть функционал имеет вид
Ф=Л0 +ДЛ^/к), (4.18)
где Ао и A, (i = 1...., п) - некоторые коэффициенты, зависящие от пара-
метров аппарата.
Ниже будет показано, что структуру вида (4.18) имеет выражение
для относительной массы полезного груза тЦГ/то.
С учетом соотношений (4.10) имеем
Лк=Л; 7=1,..., И, (4.19)
причем значения Р/К не зависят от mlK.
Максимуму функции Гамильтона (4.16) соответствует максимум
функции
[и, - mj)/m\} / J. (4.20)
Характерно, что в (4.20) коэффициент Ао не входит.
Введем в рассмотрение дополнительные фазовые переменные ана-
логично тому, как это было сделано в работе [17]:
с/, = (т,к-т,)/тк; 7=1,...,и. (4.21)
Текущая масса ЛА связана с переменными q, следующим образом:
т = тк + Д/л/к- 777,) = тк (1 + ). (4.22)
Дифференциальные уравнения для переменных qf имеют вид
dqi/dV =-(1 +^qi)uiU\ 7=1,..., и (4.23)
и полностью описывают движение ЛА.
С учетом соотношений (4.21) и (4.22) перепишем функцию (4.20),
подлежащую максимизации в каждой точке траектории:
WA = L {Л, [и, - q, /(1 + Z?,)]} / J. (4.24)
Отметим, что в уравнения движения (4.23) и в функцию Т1\ неиз-
вестные параметры не входят. В конечной точке траектории g/f< = 0.
Конечные значения масс компонентов израсходованного топлива, необ-
4.3. Решение краевой задачи в частных случаях
173
ходимые для вычисления функционала, определяются через значения ср
на левом конце траектории следующим образом:
777/К = 777О^о/(1 + ^/о); 1 = 1, П.
Таким образом, если проинтегрировать систему уравнений (4.23)
справа налево, то можно получить оптимальную траекторию, удовле-
творяющую граничным условиям.
Характерно, что искомое решение является инвариантным по от-
ношению к конечной скорости Кк, т.е. при изменении Гк на величину
ДК каждая кривая w/opt(K) в плоскости (w/Opt, И будет сдвигаться парал-
лельно самой себе в том же направлении на такую же величину. Таким
образом, зависимости w/opt(H) будут иметь вид w/opt где -
универсальные функции, характер которых определяется только исход-
ной зависимостью J(wz).
Б. Дробно-линейная зависимость Ф от вида
Ф = [А(} + Y(Ai, где тк = - XmiK. (4.25)
Здесь Ао и Aj (/=],.,.,п) - некоторые коэффициенты, зависящие от
параметров аппарата.
Ниже будет показано, что структуру вида (4.25) имеет выражение
для массы полезного груза, отнесенной к "сухой" массе ЛА. Т.е. данный
случай соответствует минимизации относительной "сухой" массы ЛА
/Исух/^пг •
Воспользовавшись соотношениями (4.10), получим
Лк = (Л, + Ф)/777К. (4.26)
После подстановки (4.26) в (4.16) запишем функцию Гамильтона
как
7Y = Е[(Л/ + Ф) (W/W -^/к+ w/)]
откуда после преобразований получим функцию, подлежащую макси-
мизации в каждой точке траектории:
Н б = [т £(А/и,) + Ф (т + Ъп, - Етт7/К) - ЦЛ + Е(Л/ ] / J =
= [mYlAjUj) + Л0 +ЦЛ/777,)] /^[(A^lmo+Ai) (ipm + 777/)]/./, (4.27)
где 777 = 777о - UlTlj.
В полученное выражение не входят неизвестные параметры. Это
означает, что в данном случае краевая задача также решается в резуль-
тате однократного решения задачи Коши. Для этого достаточно проин-
тегрировать исходную систему уравнений (4.6) слева направо с началь-
ными условиями 777/ = 0. Оптимальное управление определяется из
условия максимума выражения (4.27) по п переменным w, с учетом
ограничений (4.4).
174 Глава 4. Программа выработки компонентов топлива ЛА с ЖРД
В данном случае решение будет инвариантным по отношению к
начальной скорости Ко. При изменении Го на величину ЛК каждая
кривая w/opt(H) в плоскости (w/opt, И) сдвигается параллельно самой себе
в том же направлении на такую же величину. Зависимости w/opt (И) будут
иметь вид W/oPt = Ф/(И- Ио), где ср, -универсальные функции, характер
которых определяется только исходной зависимостью
4.4. Оптимальные условия переключения двух типов
топлива
Рассмотрим вариант последовательного применения двух типов
топлива, являющийся одним из важнейших с точки зрения практиче-
ского применения на ЛА. Вначале исследуем вариант двухдвигательной
силовой установки, в которой каждый двигатель работает на своем типе
топлива (номер двигателя соответствует типу топлива). Будем полагать,
что секундные расходы Q\ и Q2 каждого двигателя могут изменяться от
нулевого до максимально возможного значения, а удельные импульсы
Ji, J2 и плотности топлива pi , р2 неизменны. Обозначим через / долю
секундного расхода первого типа топлива в общем расходе топлива:
l=Qy/Q^ (4.28)
где Qi=Qi + Q2. Величина / является единственной управляющей
переменной, диапазон ее изменения от 0 до 1.
Удельный импульс комбинации двух двигателей зависит от / ли-
нейно:
J={QxJx^QiJ2)IQ^ = l 71+(1-/)Л. (4.29)
Так как плотности каждого типа топлива приняты фиксированны-
ми, то в соответствии с разделом 4.1 можно ввести в рассмотрение два
относительных секундных расхода:
Щ = 01 /& = I; u2=Q2/Qt=l-l. (4.30)
Приняв во внимание линейные соотношения (4.29) и (4.30), прихо-
дим к выводу, что функция Гамильтона (4.8) является дробно-линейной
функцией /. Это означает, что по траектории полета максимуму
Н соответствует либо I = 0, либо I = 1, т.е. переключение типов топлива
(если оно есть) должно осуществляться дискретно.
Перейдем к варианту, когда на ЛА установлен один многокомпо-
нентный двигатель. В качестве примера рассмотрим трехкомпонентный
(керосин + Н2 + О2) ЖРД. Такой тип двигателя представляет наиболь-
ший интерес с точки зрения практического применения на ЛА. В дан-
ном случае первым типом топлива является пара керосин + О2, вторым
типом - пара Н2 + О2. Будем полагать, что соотношение компонентов в
каждом типе топлива является неизменным. На рис. 4.1 показана зави-
симость теоретического удельного импульса трехкомпонентного ЖРД
4.4. Оптимальные условия переключения двух типов топлива
175
от параметра / для двух значений
суммарного коэффициента избытка
окислителя, который вычисляется
следующим образом:
ССкСТ = 002 /(£?Н2 ^Н2 + 0KEP ^КЕр)>
где ZH2 = 7,94 и £Кер = 3,41 - сте-
хиометрические коэффициенты.
График построен по данным
термогазодинамического расчета
удельного импульса ЖРД с геомет-
рической степенью расширения
сопла, равной 80. Видно, что зави-
симость J(Z) является практически
линейной, т.е. в данном случае, как и
Рис. 4.1. Зависимость удельного
импульса двухтопливного ЖРД
от относительного расхода 1-го
типа топлива
в предыдущем, переключение типов
топлива должно осуществляться дискретно.
Таким образом, доказано, что переключение двух типов топлива с
фиксированными плотностями pi и р2 должно происходить только
дискретно.
Определим оптимальную скорость переключения с первого типа
топлива на второй из условия непрерывности функции Гамильтона.
Заметим, что в точке переключения справедливы соотношения
^1=/И1к; w2 = 0; w = w0-wik. Слева от точки переключения «| = 1;
и2 = 0; J = J\ , справа: щ = 0;и2 = \\J=J2 •
А. Линейная зависимость Ф от Записав значения функции
(4.20) слева и справа от точки переключения, получим уравнение
(Д| -A2m2^/m)/J\ = А2(1 - т2^/т)/ J2,
решив которое, найдем оптимальное значение относительной конечной
массы ЛА, соответствующей второму участку:
H2opt =----------
+ ^2К
]-А}/А2
(4.31)
Воспользовавшись формулой Циолковского (1.1), определим
характеристическую скорость, соответствующую второму участку
полета:
H2opt = J2ln|~/' . (4.32)
AJ А2
В данном случае найденное решение описывает протяженность
второго участка полета и является инвариантным относительно конеч-
ной скорости Ик, как это было показано в разделе 4.3. Из анализа вы-
ражений (4.31) и (4.32) можно сделать следующие выводы:
176 Глава 4. Программа выработки компонентов топлива ЛА с ЖРД
- применять два типа топлива на ЛА имеет смысл только при
О < ^2opt < Ухар •> где Гхдр = - Ио;
- при И2оР( < 0 (|i2opt > 1) на всей траектории должен использоваться
первый тип топлива;
- при K2opt > Ихар на всей траектории полета должен использо-
ваться второй тип топлива.
Б. Дробно-линейная зависимость Ф от tnlK вида (4.25). Используя
функцию (4.27), запишем ее значения слева и справа от точки переклю-
чения. В результате получим уравнение
(Ло//Ио + Al) (т + Ш|К)/^1 = [(Л0/т0 + Л1) + (Л0/т770 + Л2) w]/J2,
решив которое, найдем оптимальное значение относительной конечной
массы, соответствующей первому участку:
_777О-7И1К _ (J2 IJX - 1)(4 hnQ + )
ЦI opt---------------------------------• (4.33)
777O A2 - A}
Используя формулу Циолковского, определим характеристическую
скорость, соответствующую первому участку полета:
V\ opt = «Л 1П----=---*-------.
(Л/У,-1X4/7770 + 4)
(4.34)
В данном случае, в отличие от варианта А, найденное решение
описывает протяженность первого участка полета и является инвари-
антным относительно начальной скорости Ко, как это было показано в
разделе 4.3. Из анализа выражений (4.33) и (4.34) можно сделать сле-
дующие выводы:
- применять два типа топлива на ЛА имеет смысл только при
0 < VI opt < Ухар \
- при K|Opt > Ухар на всей траектории полета должен использо-
ваться первый тип топлива;
- при И|ор| < 0 (jiiopt >1) на всей траектории должен использоваться
второй тип топлива.
В обоих вариантах (А и Б) оптимальное решение не зависит от
Гхар- Применять два типа топлива имеет смысл только при достаточно
большой суммарной характеристической скорости ЛА.
4.5. Связь функционала с удельными весовыми
параметрами ЛА
Для численного решения задачи необходимо связать функционал с
основными параметрами ЛА. В качестве объекта исследования выберем
одноступенчатый воздушно-космический самолет с ЖРД. Относитель-
ный запас топлива такого аппарата в зависимости от типа старта со-
4.5. Связь функционала с удельными весовыми параметрами ЛА 177
ставляет 0,854-0,9 от стартовой массы . Очевидно, что одноступенча-
тый ЛА с таким запасом топлива может быть создан только при усло-
вии достижения высокого технического уровня конструкции. Поэтому
будем предполагать наличие такого технического уровня, при котором
масса полезного груза является положительной, в противном случае
задача не имеет смысла.
В работе [140] в результате исследования различных вариантов од-
ноступенчатых ВКС с ЖРД было показано, что в перспективе положи-
тельную массу ПГ могут иметь:
- ВКС воздушного старта с дозвукового самолета-носителя;
- ВКС наземного горизонтального старта с разгонного устройства;
- ВКС с наземным вертикальным стартом.
Примем эти варианты для дальнейшего рассмотрения, отметив, что
названные концепции ВКС имеют характерную особенность: расчет-
ным случаем для выбора шасси и крыла является не взлет, а посадка.
Будем полагать, что все топливо ЛА размещается в фюзеляже (в крыле
топлива нет). Примем следующую типовую операцию. ВКС выводит на
орбиту полезный груз массой тиПг- На орбите аппарат расходует задан-
ный запас характеристической скорости, используя топливо орбиталь-
ного маневрирования, массу которого обозначим через wt.om- Затем
ВКС вместе с ПГ возвращается на Землю.
При изменении программы выработки компонентов топлива в об-
щем случае могут изменяться следующие параметры аппарата:
- суммарная масса топлива wT = SwzK и его объем WT = Sw/K/pi;
- масса аппарата при спуске с орбиты (посадочная масса)
WnoC “Wo — Шт — Штом '>
- масса полезного груза wnr и объем грузового отсека
И?о = wnr/рпг, где рПг - плотность ПГ.
Используя эти параметры, запишем стартовую массу ВКС как сум-
му основных весовых составляющих:
Wo = Wnr + WT + Wt.om + a w0 + p wnoc + Y + Yro Wro, (4.35)
где a, p, у и yro - удельные весовые параметры ВКС.
Стартовую массу w0 будем считать фиксированной. Масса топлива
wtom связана с относительной конечной массой, соответствующей
участку орбитального полета, следующим образом:
Wt.om = (1 “ Pom)(w0 - wT),
где ром будем считать заданной величиной.
Слагаемое a w0 в (4.35) представляет собой массу маршевых двига-
телей, некоторых элементов оборудования и т.д., т.е. параметр а харак-
теризует те элементы ЛА, масса которых пропорциональна w0. Пара-
метр р характеризует элементы, масса которых пропорциональна
посадочной массе аппарата (бортовое оборудование, системы орби-
тального маневрирования и реактивного управления, шасси, крыло,
178 Глава 4. Программа выработки компонентов топлива ЛА с ЖРД
оперение, теплозащитное покрытие и т.д.). Параметр у характеризует
элементы, масса которых пропорциональна объему топлива (топливные
баки, оболочка фюзеляжа, некоторые элементы двигательной установки
и т.д.). Следует отметить, что удельная масса конструкции, отнесенная
к объему топлива, широко используется в ракетной технике. Так, по
данным работы [65] в зависимости от класса ракеты у = 174-27 кг/м3.
Параметр уго характеризует массу конструкции грузоотсека. В первом
приближении можно принять уго = у.
Из уравнения (4.35) найдем относительную массу полезного груза:
(m0-Sm..)gOM(l-p)-a/n0-yS(»i. /р.)
wnr/wo =------------------------------. (4.36)
^оО "* Уго /рпг)
Анализ полученного выражения показывает, что относительная
масса ПГ линейно зависит от miK, т.е. реализуется вариант А функцио-
нала. В знаменатель (4.36) входят только постоянные величины. С
учетом этого можно записать значения сопряженных переменных Л в
конечной точке в соответствии с соотношениями (4.10):
Лк = А, = -цом (1 - Р) - у /р/; i = 1,п. (4.37)
В данном случае оптимальное решение зависит от удельных весо-
вых параметров р и у и не зависит от а, причем в максимизируемую
функцию На (4.24) параметры Р и у входят линейно.
Запишем "сухую” массу ВКС следующим образом:
™сух = - тТ) Цом - ^пг •
Здесь следует оговориться, что определенная таким образом ’’сухая”
масса не вполне соответствует общепринятой весовой классификации,
так как включает в себя, например, массу рабочих жидкостей и газов.
Однако в данном случае этим можно пренебречь.
Относительная "сухая” масса равна
/Исух/^пг “
(т0-£т/к)цом
wnr
(4.38)
Исключив из правой части (4.38) массу ПГ при помощи соотноше-
ния (4.36), получим, что минимуму относительной "сухой” массы соот-
ветствует максимум выражения
ф = <w° ~ Swzk>Hom(1 ~ Р) ~ - У^(т/К /Р/)
™0-LW/K
4.5. Связь функционала с удельными весовыми параметрами ЛА 179
Анализ (4.39) показывает, что в данном случае реализуется вариант
Б функционала. Коэффициенты, входящие в функционал (4.25), нахо-
дятся в результате его сравнения с выражением (4.39):
Ао = т0 Цом (1 -р)-ат0; Л = -Цом(1 — р) — у/р, -
В максимизируемую функцию TYb (4.27) коэффициенты Ао и
At входят в следующей комбинации:
AqIitiq +Ai=-(а + у/p/); z = 1,..., п. (4.40)
Из полученных соотношений следует, что оптимальное решение
зависит от удельных весовых параметров а и у и не зависит от р.
Определим диапазоны возможного изменения удельных весовых
параметров ВКС. На рис.4.2 в координатах а-у и в координатах р-у
точками показаны удельные весовые параметры, соответствующие
нескольким системам выведения на орбиту, отличающимся стартовой
массой (от 120 до 1200 т), кратностью использования (полностью и
частично многоразовые), типом старта (вертикальный и воздушный), а
также другими характеристиками. Представленные данные отражают
как созданные системы [80], так и проектные разработки [67], [82],
[136]. Для систем с внешним топливным баком параметр у соответству-
ет ВТБ, параметр р - орбитальному самолету, а параметр а - системе
ОС + ВТБ.
Основываясь на данных, приведенных на рис. 4.2, примем следую-
щие диапазоны изменения удельных весовых параметров ВКС:
а = 0,025-5-0,04; 0 = 0,15-0,3; у = 15-25 кг/м3.
Рис. 4.2. Удельные весовые параметры различных систем выведения на орбиту
4.6. Определение эффективности последовательного
применения двух типов топлива
Вначале определим оптимальную скорость Kiopt переключения с
первого типа топлива на второй. Для этого выразим оптимальные зна-
чения Ц] и ц2 через удельные весовые параметры ЛА.
180 Глава 4. Программа выработки компонентов топлива ЛА с ЖРД
А. Максимум относительной массы полезного груза диПг/^о- Из
формулы (4.31) с учетом соотношений (4.37) получим
у(1/р2-1/р,)
И2ор* (l-Jl/J2)[pOM(l-p) + Y/p2]
(4.41)
Так как ц>0, то из (4.41) вытекают два условия: pi >р2 и Ji> J\
(противоположные условия pi<р2 и Jz<J\ соответствуют не максиму-
му, а минимуму относительной массы полезного груза). Оптимальное
значение ц2 зависит только от удельных весовых параметров р, у и не
зависит от параметра а. Оптимальная скорость переключения в данном
случае равна
Hlopt = ТхАР-Л ln(l/|12opt),
где Гхар - суммарная характеристическая скорость ВКС, соответст-
вующая участку выведения.
Б. Минимум относительной "сухой" массы шСух/^пг- Из фор-
мулы (4.33) с учетом соотношений (4.40) получим
М”! opt
(q/Y + l/p,)(J2/J,-l)
1/р2-1/р,
(4.42)
откуда следует, что pi >р2 и J2> J\. Оптимальное значение pi зависит
только от соотношения a/у и не зависит от параметра р. Оптимальная
скорость переключения равна
^lopt- 1п( 1/piopt )•
В частном случае при а = 0 выражение (4.42) упрощается:
Мл opt
J2Ux-\
Р1 /р2-1
(4.43)
Можно показать, что формула (4.43) является видоизмененной
формулой Солкелда (4.1). Условия, аналогичные (4.2), вытекают из
(4.43), если принять во внимание, что 0 < ц < 1.
В качестве примера рассмотрим топливные пары керосин + О2 и
Н2 + О2. Для проведения численных расчетов примем следующие
исходные данные: цоМ = 0,95; рпг= 100 кг/м , pi = 1040 кг/м3;
р2= 360 кг/м3; J2 = 4,5 км/с; J\/J2 = 0,8 (здесь принято £mi = 3,5; km2 = 6).
Для упрощения положим уГо = У-
На рис. 4.3 показаны результаты расчетов оптимальных значений
ц2, соответствующих максимуму wnr/^o (здесь и далее выделенная
область соответствует принятому диапазону изменения удельных весо-
вых параметров а, Р и у). В рассматриваемой области изменения Р и у
величина p2opt изменяется от 0,16 до 0,31.
4.6. Определение эффективности применения двух типов топлива 181
На рис. 4.4 в зависимости от
соотношения a/у показано изме-
нение оптимальных значений pi и
V[, соответствующих минимуму
относительной "сухой” массы
ВКС. В рассматриваемой области
изменения а и у величина p,Iopt
изменяется от 0,27 до 0,51.
На рис. 4.5 показано измене-
ние оптимальной скорости пере-
ключения в зависимости от
удельных весовых параметров для
каждого из рассматриваемых
критериев оптимальности. При
этом использовалось значение
Кхар= 8,5 км/с, что примерно
соответствует ВКС воздушного
старта с дозвукового самолета-
носителя. В рассматриваемой
Рис. 4.3. Зависимость оптимальной
относительной массы, соответст-
вующей второму участку, от удель-
ных весовых параметров ВКС
области изменения а, Р и у всегда имеет место переключение с первого
типа топлива на второй. При увеличении параметра у оптимальная
скорость V\ монотонно увеличивается. Оптимальная скорость переклю-
чения, соответствующая минимуму ^сух/^пг, на 1,54-2 км/с больше,
чем соответствующая величина, вычисленная из условия максимума
^пг/^о- При малых значениях у и р скорость переключения, оптималь-
Рис. 4.4. Зависимости оптимальных
скорости переключения и относи-
тельной массы, соответствующей
первому участку, от удельных
весовых параметров ВКС
Рис. 4.5. Зависимости оптимальных
скоростей переключения от удель-
ных весовых параметров ВКС для
двух вариантов функционала
182 Глава 4. Программа выработки компонентов топлива ЛА с ЖРД
ная по первому критерию, приближается к нулю. Это означает, что при
высоком техническом уровне конструкции практически на всей траек-
тории полета должно использоваться топливо Н2 + О2.
Перейдем к определению выигрыша в функционале от последова-
тельного применения двух типов топлива (сначала керосин + О2, затем
Н2 + О2) по сравнению с вариантом применения одного типа топлива
(Н2 + О2). Заметим, что формулы (4.36) и (4.38) соответствуют однотоп-
ливному ВКС при i = 1. На рис. 4.6 показана зависимость относитель-
ной массы ПГ однотопливного ВКС с ГХАР = 8,5 км/с от у и р. При
увеличении этих параметров критерий zwnr/^o монотонно уменьшается;
при увеличении параметра а на величину Да относительная масса ПГ
уменьшается в соответствии с (4.36) на Да/(1 + уго/рпг)-
При переходе от однотопливного ВКС к двухтопливному удельные
весовые параметры в общем случае могут изменять свои значения.
Однако для выявления качественных закономерностей примем, что
параметры а, Р и у являются одинаковыми для сравниваемых вариантов
ВКС. Значения а, Р и у будем задавать параметрически. Сравнение
проводится при одинаковом значении ГХАр.
На рис. 4.7 для ВКС с ГХАР = 8,5 км/с показан выигрыш в функцио-
нале в случае максимизации ^пг/^о- При малых у и р выигрыша прак-
тически нет. При больших величинах у и Р выигрыш в относительной
массе ПГ увеличивается до 0,006, однако в этом диапазоне изменения у
и р сама величина относительной массы ПГ уменьшается (см. рис. 4.6).
Минимизация относительной "сухой" массы приводит к значитель-
но большему выигрышу в функционале (см. рис. 4.8, где через е2 обо-
значена относительная "сухая" масса ^сух/^пг двухтопливного ВКС,
через £| - соответствующий
показатель однотопливного
ВКС). При малых у и р выиг-
рыш в ^сух/^пг составляет
104-15%. При больших у и р
выигрыш увеличивается до
4(Н60% (однако при этом ос-
новной показатель ВКС тПг/то
уменьшается).
Зависимость двух вариан-
тов функционала от скорости
ВКС V\ в момент смены типов
топлива показана на рис. 4.9.
Значения удельных весовых
параметров при этом примерно
Рис. 4.6. Зависимость относитель-
ной массы ПГ однотопливного
(Н2 + О2) ВКС от удельных весовых
параметров
соответствуют середине рас-
сматриваемого диапазона изме-
нения а, Р и у. Из рисунка
видно, что при минимизации
4.6. Определение эффективности применения двух типов топлива 183
Рис. 4.7. Выигрыш в относительной
массе ПГ двухтопливного ВКС по
сравнению с однотопливным
Рис. 4.8. Выигрыш в относительной
"сухой" массе двухтопливного ВКС
по сравнению с однотопливным
относительной "сухой" массы ЛА оптимальная скорость переключения
на ~ 1,7 км/с больше, чем при максимизации относительной массы ПГ.
В результате последовательного применения двух типов топлива отно-
сительная масса ПГ может быть увеличена на ~ 10%, относительная
"сухая" масса - уменьшена на ~ 25%. Характерно, что величина zwnr/^o,
соответствующая минимуму ^сух/^пг, не меньше, чем величина
^пг/^о, соответствующая однотопливному ВКС.
Таким образом, в результате последовательного применения на ЛА
двух типов топлива можно добиться ощутимого выигрыша в уменьше-
нии его "сухой" массы без умень-
шения массы ПГ.
Последовательное использо-
вание двух типов топлива может
быть осуществлено не только на
воздушно-космических, но и на
других типах летательных аппара-
тов, в частности, на межорби-
тальных или межпланетных КА.
В отличие от ВКС у космических
аппаратов отсутствуют аэродина-
мические потери характеристиче-
ской скорости, потери на проти-
водавление атмосферы и т. д. Для
Рис. 4.9. Зависимости двух вариан-
тов функционала от скорости
переключения двух типов топлива
(а = 0,035; р = 0,2; у = 20 кг/м3)
такого класса аппаратов исполь-
зование формулы Циолковского
является более правомерным, чем
для ВКС. Вышеприведенные
184 Глава 4. Программа выработки компонентов топлива ЛА с ЖРД
формулы остаются справедливыми для космических аппаратов, однако
численные значения удельных весовых параметров а, Р и у могут быть
несколько другими, чем у ВКС.
Принцип последовательного использования двух типов топлива
(горючего), например керосина и водорода, может быть также применен
к ЛА с ВРД. Однако для определения эффективности применения
такого технического решения необходимы более детальные расчеты.
Это связано с тем, что на самолете керосин размещается в крыле, и в
результате параметр у будет существенно изменяться в зависимости от
доли водорода. При этом будут также изменяться аэродинамические
характеристики самолета.
4.7. Определение эффективности оптимальной выработки
горючего и окислителя двухкомпонентного топлива
В предыдущем разделе задача решена в предположении, что плот-
ность каждого топлива в процессе движения является неизменной, т.е.
при фиксированных соотношениях кт секундных расходов окислителя
и горючего. Исследуем вариант непрерывного изменения km.
Будем по-прежнему рассматривать в качестве основных компонен-
тов топлива ЛА керосин, водород и кислород. Заметим, что плотности
керосина и жидкого кислорода отличаются на ~ 25 %, а плотности
жидкого кислорода и жидкого водорода - в 16 раз. В связи с этим оче-
видно, что выигрыш в функционале можно ожидать в случае непрерыв-
ного изменения соотношения компонентов водородно-кислородного
топлива, а не керосиново-кислородного.
Будем полагать, что первым компонентом является горючее, вто-
рым - окислитель. Обозначим через I относительную долю секундного
расхода водорода в общем секундном расходе топлива. Тогда щ = I;
Ы2=\-Ц и, используя функцию Гамильтона (4.16), можно записать
функцию, экстремум которой должен отыскиваться в каждой точке
траектории:
+ D)U, (4.44)
где D - некоторая функция фазовых переменных и удельных весовых
параметров ЛА.
Величина I связана с соотношением кт секундных расходов окис-
лителя и горючего следующим образом:
Z=l/(£m+l). (4.45)
Заметим, что I входит линейно в числитель Удельный импульс
J, являющийся известной функцией Z, входит линейно в знаменатель
Н\. В связи с этим, если аппроксимировать зависимость </(Z) при помо-
щи квадратичной функции
4.7. Определение эффективности оптимальной выработки горючего и окислителя 185
J=Лах [ 1 - (/ - 6,п)2 В]; В>0, (4.46)
то можно получить аналитическое решение, соответствующее экстре-
муму по /:
/opt = J(Jlm+D)2-UB -D. (4.47)
Коэффициенты, входящие в (4.46), имеют следующий смысл: 7,пах-
максимальное значение удельного импульса; /Jm - величина /, соответ-
ствующая Jmax; В - коэффициент, характеризующий темп уменьшения
удельного импульса при отклонении I Из выражения (4.47) сле-
дует, что оптимальное управление не зависит от Jmax. При резко выра-
женном максимуме J по I (т.е. при В» 1) из (4.47) получим Zopt® Zjm,
что согласуется с физическим смыслом задачи.
Определим функцию Z), входящую в выражение (4.47), для двух
рассматриваемых вариантов функционала.
А. Максимум относительной массы полезного груза /иПг/*Ио« В
данном случае уравнения движения должны интегрироваться справа
налево (см. раздел 4.3). Из выражения (4.24) с учетом (4.37) получим
D=-----------------------------=
(Л1 - Л2)(1 + ^1+^2) 1 + Я]+Я1
= МомС-Р) + у/Р2<h , (4 48)
(у/pl-у/р2)(1 + ?|+?2) 1 + 91+92 ’
где фазовые переменные qt вычисляются при помощи соотношений
(4.21).
Оптимальное управление зависит от р и у, но не зависит от а (как и
в случае оптимизации скорости переключения двух типов топлива - см.
раздел 4.6).
Б. Минимум относительной ’’сухой” массы шСух/^пг- Из выра-
жения (4.27) с учетом (4.40) получим
D = mx{Ai-A2) + A0+m0A2 = т, _ т0(а/у + 1/р2) Д9)
т(А}-А2) т w(l/p2 - 1/pJ ’
откуда следует, что в данном случае оптимальное управление зависит
только от соотношения удельных весовых параметров a/у и не зависит
от параметра р (как и в случае оптимизации скорости переключения
двух типов топлива - см. раздел 4.6).
Перейдем к численным расчетам. Примем в качестве исходной за-
висимость удельного импульса от £1П, показанную на рис. 4.10; а также
Рн2~70кг/м3 и ро2= 1135 кг/м3. Практический интерес представляет
диапазон £т>6,1, где удельный импульс уменьшается, а плотность
топлива возрастает (см. рис. 4.10). Аппроксимируем исходную зависи-
186 Глава 4. Программа выработки компонентов топлива ЛА с ЖРД
Рис. 4.10. Зависимости удельного
импульса водородно-кислородного
ЖРД и плотности его топлива от
соотношения компонентов
мость J от km при помощи функ-
ции (4.46), где Jmax = 4,6 км/с;
/jm= 0,14; В = 43,7. Как следует из
рис. 4.10, степень приближения
аппроксимационной зависимости
J(km) к исходной зависимости
является приемлемой.
В результате интегрирования
уравнений движения с использо-
ванием формулы (4.47) для каж-
дого варианта функционала была
получена оптимальная программа
изменения кт по скорости полета.
На рис. 4.11(7 показана программа
изменения £inopt для варианта
максимизации mur/mQ при не-
скольких значениях удельных
весовых параметров Р и у. В
конечной точке полета значение
fcmopt составляет 6,3-ь6,4. По мере убывания скорости полета Armopt увели-
чивается до 8^-9 (при Гхар = 9^-10 км/с) в зависимости от удельных
весовых параметров. Параметр у влияет более существенно на зависи-
мость Armopt от V, чем параметр р. Результаты расчетов качественно
согласуются с работой [26], в которой показано, что при линейной
зависимости Armopt от V величина Arinopt должна уменьшаться по траекто-
рии полета ВКС от 8 до 7.
а)
Рис. 4.11. Оптимальная программа выработки топлива Н2+ О2 при максими-
зации относительной массы ПГ ВКС (а) и при минимизации относительной
"сухой” массы ВКС (б)
б)
4.7. Определение эффективности оптимальной выработки горючего и окислителя 187
Программа изменения fcmopt по скорости полета для варианта ми-
нимизации а^сух/^пг приведена на рис. 4.116. В начальной точке траек-
тории Armopt составляет 8,24-9,1. По мере увеличения скорости Armopt у-
меньшается и в конечной точке (при ИХЛР = 9-ь 10 км/с) составляет
6,44-6,5. При увеличении параметра а оптимальная программа смеща-
ется вниз (см. рис. 4.115). Так как оптимальное управление зависит от
соотношения а/у, то при увеличении у оптимальная программа будет
смещаться вверх.
Для дальнейших расчетов зададим следующие значения удельных
весовых параметров ВКС: а = 0,035; р = 0,2; у = 20 кг/м3, что примерно
соответствует середине принятого диапазона их изменения. Для опре-
деления выигрыша в функционале исходный функционал будем вычис-
лять при km = const. При этом рассмотрим два варианта.
1. кт соответствует Jmax (т.е кт = 6,1).
2. кт определяется из условия максимума тПГ/то (или минимума
^сух/^пг)- Такое управление будем называть приближенно оптималь-
ным.
Проанализируем вначале, как соотносятся между собой оптималь-
ное и приближенно оптимальное управления. На рис. 4.12# показано
сравнение для варианта максимизации д^пг/^о- При увеличении харак-
теристической скорости ВКС от 0 до 10 км/с приближенно оптимальное
значение кт увеличивается от 6,3 до 6,9. При фиксированном КХАР
приближенно оптимальное значение кт примерно равно среднему по
траектории значению £mopt. Аналогичные зависимости для варианта
минимизации ^сух/^пг показаны на рис. 4.125. При увеличении ИХАР от
Рис. 4.12. Сравнение оптимального и приближенно оптимального законов
управления при максимизации относительной массы ПГ (а) и при
минимизации относительной "сухой" массы ВКС (б)
188 Глава 4. Программа выработки компонентов топлива ЛА с ЖРД
О до 10 км/с приближенно оптимальное значение кт уменьшается от 8,6
до 6,9.
Сравнение программ управления, соответствующих максимуму
/И|1Г//Ло и минимуму тсух/тцг, для ГХАР = 8,5 км/с показано на рис. 4.13.
На этом же рисунке показана программа управления, соответствующая
максимуму удельного импульса (£]П = 6,1). Видно, что в варианте мини-
мизации относительной "сухой" массы ЛА величина Armopt больше, чем
в варианте максимизации относительной массы ПГ. Для приближенно
оптимального управления разница в кт составляет 0,3.
Анализируя характер полученных программ управления, можно
сделать вывод, что £mopt монотонно уменьшается по траектории, при-
ближаясь в конце полета при КХАр=9-Н0 км/с к величине кт, соответ-
ствующей Jma4.
Оптимальная программа £mopt(r) с достаточной степенью точности
может быть аппроксимирована квадратичной функцией (см. рис. 4.13,
где аппроксимационная зависимость показана маркерами). Аппрокси-
мационную зависимость можно задать при помощи начального Arm0,
конечного £тК значений соотношения компонентов и производной
(dkm ldV)(} в начальной точке траектории. В этом случае зависимость
^тоР1(Ю будет иметь вид
oPt = Ar.nO + v2(£.nK - Ar.no) + (dkm !dV)Q (Ик - Го) v (1 - v),
где v = (К- Ио)/(ГК- Го); 0 < v < 1; (dkm IdV)» < 0.
Рис. 4.13. Сравнение законов управления,
соответствующих максимуму относительной
массы ПГ (а) и минимуму относительной
''сухой" массы ВКС (6):
------ оптимальное управление km opt;
------приближенно оптимальное управление к^
Перейдем к опреде-
лению выигрыша в
функционале. На
рис. 4.14df для варианта
максимизации относи-
тельной массы ПГ пока-
зана величина функцио-
нала и выигрыш в
функционале (в виде
приращения) в зависи-
мости от характеристи-
ческой скорости ВКС.
При увеличении ИХАР
выигрыш в функционале
увеличивается, однако
величина функционала
при этом уменьшается.
При ИХАР = 8,5 км/с
(ВКС воздушного стар-
та) выигрыш в массе ПГ
составляет 0,13 % от
стартовой массы аппара-
4.7. Определение эффективности оптимальной выработки горючего и окислителя 1 89
0 2 4 6 ИХАР,
а)
Рис. 4.14. Выигрыш в относительной массе ПГ (а) и в относительной "сухой"
массе (б) в зависимости от характеристической скорости ВКС:
1 - по сравнению с вариантом Jmax; 2 - по сравнению с вариантом использования
приближенно оптимального управления
та по сравнению с вариантом J = Jm^ и 0,03% от т0 по сравнению с
вариантом использования приближенно оптимального управления
(£1П = const).
В варианте минимизации относительной "сухой" массы имеет ме-
сто такая же картина. При увеличении ИХАР выигрыш в функционале
увеличивается, однако величина самого функционала ухудшается
(см. рис. 4.146, где относительная "сухая" масса ЛА обозначена через
е). В данном случае для определения выигрыша использовалось отно-
шение функционала, соответствующего £mopt, к величине исходного
функционала. При КХАР = 8,5 км/с оптимизация Аг1П позволяет уменьшить
^сух/^пг по сравнению с вариантом j;nax на 7,5 % ; по сравнению с
вариантом приближенно оптимального управления (при km = const) - на
1,5%. Объем топлива в первом случае уменьшается на 10%, во вто-
ром - на 2,5 %.
Таким образом, выигрыш в функционале по сравнению с вариан-
том использования приближенно оптимального управления является
незначительным. Кроме того, выигрыш определялся в предположении
независимости удельных весовых параметров ВКС от параметра кт.
Для реального ЖРД изменение параметра £1П в широком диапазоне
будет приводить к увеличению удельной массы двигателя и к его ус-
ложнению. Это означает, что в случае переменной по траектории про-
граммы управления величиной £1П выигрыш в функционале может
оказаться существенно меньшим, или даже нулевым. Отсюда следует,
что практически более значимым является применение в ЖРД постоян-
ного соотношения кт, оптимального из условия максимума заданной
целевой функции.
190 Глава 4. Программа выработки компонентов топлива ЛА с ЖРД
Задача определения оптимального соотношения компонентов водо-
родно-кислородного топлива ВКС воздушного старта с ЖРД в более
полной постановке была решена в работе [19]. При этом вместе с кт
оптимизировались несколько параметров ЖРД: тяговооруженность,
степень расширения сопла, давление в камере сгорания и др.
По результатам данной главы можно сделать вывод, что в случае
максимизации относительной массы полезного груза значения управ-
ляющих переменных при заданных удельных весовых параметрах ВКС
однозначно определяются на правом конце траектории и не зависят от
суммарной характеристической скорости КХАР. При минимизации
относительной "сухой” массы ЛА значения управляющих переменных
однозначно определяются на левом конце и не зависят от КХАР.
Исследование однотопливного (Н2+О2) ВКС воздушного старта
показало, что в случае использования оптимальной программы выра-
ботки компонентов топлива выигрыш в функционале является несуще-
ственным по сравнению с вариантом, когда соотношение компонентов
кт оптимизировано в предположении его неизменности по траектории.
Таким образом, для однотопливного ЛА с ЖРД наиболее значимым
является оптимизация соотношения компонентов топлива в классе
констант, а не применение переменного по траектории соотношения £1В.
Использование на ВКС двух типов топлива (вначале керосин + О2,
затем Н2 + О2) обеспечивает более существенный выигрыш в функцио-
нале. Задача оптимизации программы выработки топлива в данном
случае сводится к максимизации функции трех переменных. Оптимизи-
руемыми величинами являются:
- скорость переключения с первого типа топлива на второй;
- соотношение компонентов (в классе констант) первого топлива;
- соотношение компонентов (в классе констант) второго топлива.
Наибольший выигрыш реализуется в случае минимизации относи-
тельной "сухой” массы. При этом в зависимости от технического уров-
ня совершенства конструкции "сухая" масса ЛА может быть уменьшена
на Юн-40 % (при т0 = const) за счет применения более плотного топлива
(керосин + О2). Суммарная масса топлива увеличивается, а масса по-
лезного груза изменяется незначительно.
Дальнейшая оптимизация управления будет приводить к незначи-
тельному улучшению функционала.
ГЛАВА 5
ТРАЕКТОРИЯ ДВИЖЕНИЯ ДОЗВУКОВОГО
САМОЛЕТА-НОСИТЕЛЯ ПЕРЕД СТАРТОМ
ВОЗДУШНО-КОСМИЧЕСКОГО АППАРАТА С ЖРД
Одной из возможных концепций МКТС горизонтального старта
Рис. 5.1. Схема АКС с
дозвуковым самолетом-
носителем
является авиационно-космическая система, состоящая из дозвукового
самолета-носителя и воздушно-космического аппарата с ЖРД (рис. 5.1).
В общем случае в качестве ракетно-космических систем, стартующих с
ДСН, могут использоваться как одноступенчатый ВКС, так и многосту-
пенчатые системы (одноразовые или частично многоразовые). Так,
например, в концепции МАКС предполагается создание нескольких
вариантов ракетно-космической системы, стартующей с дозвукового
самолета Ан-225 Мр1я [82], [115]. Это:
- малоразмерный орбитальный самолет
с одноразовым внешним топливным баком
(МАКС-ОС);
- одноразовая двухступенчатая ракетно-
космическая система (МАКС-Т);
- полностью многоразовый воздушно-
космический самолет (МАКС-М).
Поэтому, говоря о ВКА, будем подразу-
мевать широкий спектр ракетных систем,
стартующих с самолета-носителя.
В авиационно-космической системе доз-
вуковой самолет-носитель обеспечивает:
- уменьшение массы крыла и шасси ВКА, что особенно важно
для одноступенчатого ВКС;
- выведение со значительным параллаксом;
- облегчение требований к энергетике выведения ВКА на орбиту
за счет увеличения его начальной энергии и уменьшения потерь удель-
ного импульса ЖРД на противодавление. Кроме того, самолет-носитель
может выполнить маневр "горку”, позволяющий увеличить стартовый
угол наклона траектории ВКА, что также облегчает требования к энер-
гетике выведения на орбиту.
192 Глава 5. Траектория движения ДСН перед стартом ВКА с ЖРД
По данным работы [140], воздушный старт позволяет увеличить
массу выводимого на орбиту полезного груза примерно на 0,9% от
массы ВКА по сравнению с наземным горизонтальным стартом. Оче-
видно, что чем больше скорость, высота и угол наклона траектории
(вплоть до 304-40°) в момент старта ВКА, тем больше масса ПГ. На
этапе формирования облика суммарную массу ВКА и топлива ДСН
можно считать фиксированной. В этом случае экономия массы топлива
ДСН, расходуемого к моменту старта ВКА, также будет приводить к
увеличению массы ПГ. Таким образом, с точки зрения увеличения
массы ПГ желательно, чтобы все четыре фазовые переменные (Г, Н, 0,
т) в точке старта ВКА были как можно больше.
В предыдущих главах задача оптимизации траекторий движения
ЛА с ЖРД решалась при фиксированных начальных условиях полета. В
данной главе будем полагать, что фазовые координаты в точке старта
ВКА с ЖРД оптимизируются с учетом энергетических возможностей
ДСН. При этом возникает задача оптимизации траектории движения
ДСН перед стартом ВКА.
Такая задача в той или иной постановке решалась во многих рабо-
тах в ЦАГИ с использованием как приближенно оптимального, так и
строго оптимального управления. Так, в работах В.П. Плохих вопросы
определения маневренных характеристик перспективных аэрокосмиче-
ских аппаратов и систем при их движении в атмосфере и космическом
пространстве исследованы вместе с вопросами формирования концеп-
ций и облика таких аппаратов [77], [78], [111], [132], [140]. В 1980-х
годах цикл работ по оптимизации траекторий ДСН при выведении на
орбиту ВКА воздушного старта был проведен К.А. Червоненко [106]. В
его работах расчеты траекторий проводились с использованием при-
ближенно оптимальных законов управления. Была исследована эффек-
тивность применения ЖРД при выполнении маневра ’’горка”. Показана
необходимость предварительного ’’заныривания" перед ’’горкой”. В
работе В.Т. Пашинцева и О.В. Балабанова [75] маневр "горка” рассмат-
ривался применительно к одноступенчатому ВКС на участке перехода
от режима работы ГПВРД к режиму работы ЖРД. Управляющие пере-
менные при этом оптимизировались в классе констант. В работах
А.С. Филатьева [101], [102], [126]—[128], О.В. Яновой, А.А. Голикова
[117], [126] задача выведения на орбиту решалась с использованием
принципа максимума путем сквозной оптимизации траектории от
начала предстартового маневра ДСН до момента выхода на орбиту с
учетом различных ограничений. При этом учитывалось обеспечение
безопасного разделения и возвращения самолета-носителя после старта
ВКА. Б.X. Давидсон в работе [31] решил задачу выведения на орбиту
ракетно-космической системы, стартующей со сверхзвукового самоле-
та-носителя. При этом также использовалась сквозная оптимизация с
использованием принципа максимума.
5.1. Постановка общей задачи. Выделение частной задачи
193
Значительный вклад в исследование движения АКС с ДСН внесли
ученые НПО ’’Молния": Е.А. Самсонов, В.М. Сумачев, Э.Н. Дудар [34],
[57].
В настоящей главе задача оптимизации траектории на участке со-
вместного полета ДСН и ВКА решается с использованием подходов,
предложенных в работе [40]. Разрабатывается приближенный метод
решения, основанный на разделении общей задачи на несколько част-
ных задач. Рассматривается влияние характеристик ВКА на оптималь-
ную траекторию предстартового маневра ДСН.
5.1. Постановка общей задачи.
Выделение частной задачи оптимизации траектории на
участке совместного полета ДСН и ВКА
В качестве объекта исследования примем АКС, состоящую из доз-
вукового самолета-носителя с ТРД и воздушно-космического аппарата с
ЖРД. Основная типовая операция заключается в следующем: АКС
взлетает с аэродрома и выходит в точку старта ВКА (рис. 5.2). При этом
используются топливо и устрой-
ства (шасси, крыло, двигатели)
только ДСН. Стартовая масса __у
АКС и масса снаряженного ДСН
приняты фиксированными. Это \
означает, что фиксированной /
является суммарная масса ВКА и / )
топлива ДСН, т.е. полная нагрузка у
ДСН. /=7
Рассматривается движение рис 5 2. Типовая схема полета АКС
АКС в вертикальной плоскости
(без крена). Дальность полета
ДСН не фиксируется. Длительность процесса разделения считается
бесконечно малой. Дальнейший полет ДСН после старта ВКА не рас-
сматривается, предполагается, что он возвращается на стартовый аэро-
дром, используя некоторую (фиксированную) массу топлива.
После отделения от самолета-носителя воздушно-космический ап-
парат начинает активное движение и выводит полезный груз на низкую
околоземную орбиту (см. рис. 5.2). В качестве функционала при опти-
мизации траектории ДСН используется масса выводимого на орбиту
полезного груза (в целях упрощения записи наряду с обозначением wnr
будет использоваться обозначение М).
Пусть на участке совместного полета ДСН и ВКА режим работы
ТРД является известным. Для определенности будем полагать, что он
соответствует максимальной тяге двигателей. Управление осуществля-
ется углом атаки самолета-носителя а. Учтем ограничения, наложен-
ные на управляющую переменную:
194
Глава 5. Траектория движения ДСН перед стартом ВКА с ЖРД
О^пмпД — — С^тахД (5.1)
и на максимальную нормальную перегрузку:
Ну < Пу тахД • (5*2)
Задача формулируется следующим образом: необходимо опреде-
лить оптимальное управление углом атаки на участке совместного
полета ДСН и ВКА, а также оптимальные параметры траектории, соот-
ветствующие точке разделения АКС: скорость И0ВКА, высоту ЯВКА,
угол наклона траектории ОоВКА и массу ВКА из условия максиму-
ма массы полезного груза ВКА.
Разделим траекторию выведения на две части.
1. На первом участке совершается совместный полет ДСН и ВКА с
использованием ТРД (от некоторой начальной точки до точки старта
ВКА).
2. На втором участке совершается самостоятельный разгон и выве-
дение на орбиту ВКА с ЖРД.
В соответствии с этим общая задача разделяется на две частных.
Вначале в результате серии расчетов траектории выведения ВКА на
орбиту и решения объемно-весовых уравнений ВКА определяется
зависимость массы ПГ от четырех аргументов: Л/(К0ВКА, ЯВКА, ОоВКА,
тВКА). При этом траектория выведения ВКА может быть рассчитана с
использованием приближенно оптимального управления (см. гл. 3). В
случае линеаризации функции М по четырем аргументам достаточно
выполнить пять циклов таких расчетов.
Затем функция М рассматривается как промежуточный функцио-
нал, с ее использованием оптимизируется управление на участке совме-
стного полета ДСН и ВКА. Определяются оптимальные значения фазо-
вых переменных в точке старта ВКА.
Общая задача является итерационной. При необходимости функ-
ция Муточняется.
5.2. Линеаризация функционала для различных типов ВКА
Будем полагать, что начальное приближение параметров траекто-
рии в точке разделения АКС является известным. Запишем функционал
в линеаризованном виде относительно некоторого опорного значения
вектора фазовых координат в точке старта ВКА:
М= М* + + My(yQ- Го*) +
+ Л/н(77о-Яо*) + Л/е(0о-0о*). (5.3)
Здесь М -масса ПГ, соответствующая начальным значениям фазовых
переменных ВКА т0, Го, HQ и Оо;
5.2. Линеаризация функционала для различных типов ВКА
195
Af* -масса ПГ, соответствующая опорным значениям фазовых пе-
ременных ВКА mQ\ VQ\ #о* и 0о*, которые будут уточняться в процессе
итерационных расчетов.
Частные производные массы ПГ по фазовым переменным в опор-
ной точке равны:
Мт=дМ/дт0’ Mv=dM/dVQ; MH=dM/dHQ; MQ=dM/5Q0.
Перепишем выражение (5.3) в универсальном виде:
М= М* + Мт (тпп - тп$) +
+ mJ [pv(Ио - Ио*) + цн (Яо - Яо*) + Це (0О - Go*)]. (5.4)
Здесь ц - относительная масса ПГ (ц = тиПг / т™); Цу = 5ц /5И0;
цн= 5ц /дНо; Це = 5ц /50о • Запись (5.4) характерна тем, что все величи-
ны, входящие в квадратные скобки, практически не зависят от старто-
вой массы ВКА.
Как будет показано ниже, структура оптимального управления
ДСН зависит от производных Мт, цу, Цн и Це и не зависит от Л/*. Оп-
ределим частные производные для различных типов ВКА. При этом
будем исследовать наиболее характерные: одно- и двухступенчатую
схемы ВКА. Каждую из схем будем рассматривать в двух вариантах:
полностью многоразовый крылатый ВКА и ракетная схема ВКА (JIA с
малой несущей способностью с одноразовыми элементами).
Для предварительной оценки величины Мт и для определения ее
физического смысла запишем уравнение весового баланса одноступен-
чатого ВКА в следующем виде:
^0= ^пг + И7СУХ1+ ^СУХ2, (5.5)
где тт - масса топлива выведения;
^cyxi - "сухая" масса ВКА, пропорциональная его стартовой массе
(топливные баки, двигательная установка и т.д.);
^сух2 - "сухая" масса ВКА, не зависящая от т0 (кабина экипажа,
системы жизнеобеспечения и т.д.).
Перепишем уравнение (5.5) в следующем виде:
Юпг = WO(1 - WT - 7ЙСУХ1)- ™СУХ2, (5.6)
откуда получим, что частная производная Мт = 1 - тТ - т Cyxi с
учетом (5.6) равна:
Мт = (типг + ^сухгУ^о. (5.7)
Как следует из формулы (5.7), при тиСух2 = 0 производная Мт сов-
падает с относительной массой ПГ. При тиСух2 > 0 имеем Мт > тиг.
Ниже будет показано, что величина Мт равна 0,04-Ю,07.
196 Глава 5. Траектория движения ДСН перед стартом ВКА с ЖРД
Определим физический смысл производных pv, Цн и Це. Очевидно,
что при изменении Ко, Но и Оо будут изменяться масса топлива и его
объем Ит- Кроме того, будет изменяться масса конструкции. Запишем
уравнение весового баланса одноступенчатого ВКА в следующем виде:
w0= wnr + wT + wro + wCyx w + Aw, (5.8)
где wro - "сухая" масса ВКА, пропорциональная объему грузового
отсека (Wo = У^Гго = ywnr/pnrJ рпг - плотность ПГ);
wCyxw-"сухая” масса ВКА, пропорциональная объему топлива
(wCyxw= у^т= ywT/pT; У - коэффициент пропорциональности; рт -
плотность топлива);
Aw - масса ВКА, не зависящая от массы и объема топлива (шасси,
оборудование и др.).
Перепишем (5.8) в следующем виде:
wnr С1 + у/рпг) = 1 - wT (1 + у/рт) - Aw /w0
и определим частную производную jiv •
"''-~>Г±Т£з- <5”
ак0 1+у/рпг
Так как для ВКА с ЖРД у = 30-5-40 кг/м3; рт= 350^-390 кг/м3;
Рпг = 70-И00 кг/м3; то из (5.9) следует, что pv«-(O,714-O,83)5wT/5Fo.
Аналогичные соотношения можно вывести для частных производных
Цн ице. __
Проведем оценку производной SmT/9K0 с использованием форму-
лы Циолковского:
wT= 1 - е’(Ик+ДИп’,/|,)/-/; а?йт/аГо = -(1 - wT)/J. (5.10)
Здесь Кк- конечная скорость ВКА; АКП-потери характеристической
скорости при выведении на орбиту; J-средний по траектории удель-
ный импульс ЖРД (для водородно-кислородных двигателей
4,4 км/с).
Относительный запас топлива выведения ВКА воздушного старта
составляет примерно 85% от w0, тогда из (5.10) следует, что
3wT/9Po«-3710'6 с/м. Для более точного определения частных произ-
водных wT по Vo, Но и 0О были проведены соответствующие расчеты
траекторий выведения на орбиту (см. гл. 3). Для определенности пола-
галось, что стартовая масса ВКА составляет 250 т. На ВКА установлены
водородно-кислородные ЖРД. В качестве опорных были приняты
следующие начальные значения фазовых переменных: Ко=18Ом/с;
//о =8 км и 00= 15°. Рассматривалось выведение на орбиту высотой
200 км. Основные параметры крылатого ВКА, его аэродинамические
5.2. Линеаризация функционала для различных типов ВКА
197
характеристики и характеристики ЖРД приняты в соответствии с рабо-
той [140]. При переходе от крылатой схемы к ракетной полагалось, что
производная уменьшается в два раза.
Для получения частных производных Мт, pv? Цн и Це были по-
строены графики изменения массы ПГ в зависимости от Го, Но, 0О и т{)
(рис. 5.3) для различных конфигураций ВКА. Расчеты проводились с
использованием методики формирования облика ВКА [140]. Для удоб-
ства сравнения частных производных, соответствующих четырем типам
ВКА, расчетные зависимости построены в виде приращений массы
полезного груза Л/^пг (см. рис. 5.3г), и относительной массы полезного
груза Дй7пг (см. рис. 5.3а, б, в). Нулевые значения приращений соответ-
ствуют опорной точке (Ко*, /То*, 6о* и ти0*)-
Анализ полученных результатов показывает, что в рассмотренном
диапазоне изменения стартовых параметров траектории зависимости
Дт77пг от Ко (см. рис. 5.3а) и ДшПгОТ т0 (см. рис. 5.3г) являются практи-
чески линейными. Зависимость Дт77пг от 0О (см. рис. 5.Зе) существенно
нелинейная. Величина Атпг достигает своего максимума при
0о >404-50°.
Расчетные значения частных производных Мт, jiv, Цн и це и част-
ных производных относительного запаса топлива по Ко, Но и 0О (в
опорной точке) приведены в табл. 5.1. Полученные данные качественно
согласуются с проведенными выше оценками.
Таблица 5.1
Частные производные относительной массы топлива и относительной
массы ПГ ВКА по фазовым переменным в точке его старта
(Vo= 180 м/с; Но= 8 км; 0О= 15°)
Производная Одноступенчатый ВКА Двухступенчатый ВКА
Многоразовый ВКС ОС + ВТБ Многоразовый (крылатая схема) Одноразовый (ракетная схема)
мт 0,059 0,0412 0,057 0,071
дтТ /д Ко, с/м -46-10^ -49-10"6 -47,5-Ю"6 -50-10’6
Цу , с/м 36-Ю-6 ЗОЮ-6 22-10"6 28-Ю’6
дт^/дНо, 1/м -1,18 кг6 -1,1810"^ -1,6-1 (Г6 -1,66 10^
Цн, 1/м 0,93-Ю”6 0,72-10"6 0,74-10’6 0,93 10"6
5/пт/<Э0о, 1/рад -2,1 10’3 -4,3-10~3 -7,7-10~3 -14,8-Ю'3
Me, 1/рад 1,6-10’3 2,6-10’3 3,6-10’3 8,5-10’3
198 Глава 5. Траектория движения ДСН перед стартом ВКА с ЖРД
а) б)
в) г)
одноступенчатый ВКС — — двухступенчатый
крылатый ВКА
ОС + ВТБ —Q двухступенчатый
ракетный ВКА
Рис. 5.3. Изменение массы ПГ в зависимости от фазовых переменных в точке
старта ВКА: зависимость относительной массы ПГ от стартовой скорости (а),
высоты старта (б) и стартового угла наклона траектории (в); зависимость
абсолютной массы ПГ от стартовой массы ВКА (г)
5.2. Линеаризация функционала для различных типов ВКА
199
Из табл. 5.1 видно, что цн слабо зависит от типа ВКА, Мп и цу из-
меняются не более чем на 70%. Наиболее сильно (в 5 раз) в зависимо-
сти от типа ВКА изменяется частная производная Це- Исследования
показали, что частные производные и 3wr/d0o(no модулю) увеличи-
ваются при увеличении тяговооруженности ВКА и при ухудшении его
аэродинамических характеристик, т.е. при переходе от крылатой схемы
к ракетной. Для дальнейших расчетов были выбраны два варианта
ВКА: одноступенчатый ВКС (наибольшее значение цу и наименьшее
значение ре) и двухступенчатый ВКА ракетной схемы (наибольшее
значение Це).
Перейдем от фазовых переменных ВКА к фазовым переменным
АКС в сборе. Так как процесс разделения ступеней по условию задачи
не рассматривается, то начальные значения Ко, HQ и Оо ВКА будут
совпадать с конечными значениями соответствующих фазовых пере-
менных АКС:
т/ _ т/ВКА . тт _ ггВКА . а _ а ВКА
?К~ ? о ’ ^К ~ Г7о ’ - Uo
Масса АКС в конечной точке совместного полета связана со стар-
товой массой ВКА следующим образом:
mK ~ + тит.взв + ^снр •
Здесь тит.взв-масса топлива, необходимого для возвращения ДСН на
аэродром; Whp - масса снаряженного ДСН.
Величины /ит.взв и тиСнр по условию задачи являются постоянны-
ми. Отсюда следует, что частные производные функционала по mfКА и
по тк в опорной точке будут совпадать.
Таким образом, выражение для функционала (5.4) можно перепи-
сать с использованием фазовых переменных АКС следующим образом:
М=М + Мт (тик - тк) +
+ ^овка [Ну(Ик-Гк*) + цн(Як-Як*) + ре(0к-Ок*)]. (5.11)
5.3. Оптимизация траектории
от взлета ДСН до точки старта ВКА
Будем решать данную задачу с использованием принципа макси-
мума [79]. С этой целью воспользуемся приближенными уравнениями
движения (2.98) с учетом малой скорости полета:
dV/dx = go^x-gTsinO; dH/dx = TsinO;
dQ/dx = (gony - gT cos0)/ V; dm/dx = -Qt • (5.12)
200 Глава 5. Траектория движения ДСН перед стартом ВКА с ЖРД
Здесь V, Н, 0 и т - фазовые переменные АКС в сборе; Qx - секундный
расход топлива ТРД.
С целью упрощения задачи будем полагать, что атмосфера Земли -
изотермическая (см. раздел 2.3); Земля - шарообразная; gT- постоянная
величина:
gT = go7?o2/(7?o + W, (5.13)
где ЯСр - средняя высота полета.
По условию задачи начальные значения фазовых переменных Го,
Но, 0о и т0 (при т = 0) являются известными (соответствуют старту
АКС с аэродрома). Конечные значения фазовых переменных Кк, Нк, 0К
и (при т = Т) свободны и выбираются из условия максимума проме-
жуточного функционала М. Время полета Т также свободно. Ограниче-
ния наложены на угол атаки и задано одно ограничение типа неравенст-
ва, зависящее от управления:
] = Пу Пу шахД — 0. (5.14)
Функция Гамильтона для системы уравнений (5.12) с учетом (5.14)
имеет вид
H = Pv (go«x - gT sin0 ) + P0 (go^y- gT cos0)/K +
+ Рн Vsin0 - Pm 2т + A,(ny - ny тахД). (5.15)
Здесь X - неизвестная функция, равная нулю при 14/1 < 0.
Запишем сопряженную систему уравнений:
дп дп„ ,
dPy/dT=- Pvgo-^т -(^ego/K+X)—+Pogony/V2-
dV dV
- P0gTcos0/K2 - PH sin0 + Pm^~;
dV
dPQ /dx = cos0 (PvgT - Рн К) - Р0 gT sin0/K;
dP^/dz=- (PegdV+V + pJ^-;
дН дН дН
dPJdx = [Pv go + ny (Pogo/V + X)]/m.
(5.16)
В соответствии с принципом максимума и с учетом принятой фор-
мы записи функционала (5.11) на правом конце должно выполняться
условие Нк = 0 и условия для сопряженных переменных:
Pvk = ^v; Pok^Wo; РНк = ^ин; РтК = ^л/т, (5.17)
где £ - неизвестная постоянная величина. Так как функционал макси-
мизируется, то > 0.
5.3. Оптимизация траектории от взлета ДСН до точки старта ВКА 201
Из соотношений (5.17) следует, что оптимальное управление на
участке совместного полета ДСН и ВКА зависит от частных производ-
ных Л/у, Mq , Мн и Мт. Кроме того, полная производная dM/dx в конеч-
ной точке должна быть равна нулю. Сравнив выражения (5.3) и (5.11),
можно записать:
Л/у — ^ОВКА M'V ? ^Н_ ^оВКаМ'Н? Mq — /77ОВКД Цо •
Частные производные Л/т, jiv, Цн и Цо были определены в разде-
ле 5.2. Так как эти величины больше нуля (см. табл. 5.1), то в конечной
точке все сопряженные переменные также должны быть больше нуля,
как это следует из соотношений (5.17).
Исключив из (5.17) неизвестную величину получим три условия,
которые должны выполняться на правом конце:
Ф1 = Р\к~ Рек Цу/Це - 0;
ф2 = T’vk-Т’нк P-v/Цн ~ 0;
фз — РVK — ВКА PV — 0«
(5.18)
На левом конце траектории значения сопряженных переменных
неизвестны. Для их определения будем использовать следующий алго-
ритм. Примем |PV0 I = 1, а знак PVo будем выбирать так, чтобы в ко-
нечной точке величина Pv была положительной. Сопряженную пере-
менную Рт0 будем вычислять из условия равенства нулю функции
Гамильтона (5.15) в начальной точке:
Лпо = [Pvo (go«x - gT sinO ) + Pqq (gony - gT cosO)/ Г + Рно Гыn0] / 0T •
Заметим, что здесь Qx больше нуля. Кроме того, как показали рас-
четы, в начальной точке фц < 0, т.е. X = 0. Неизвестные значения двух
оставшихся сопряженных переменных Pqq и РНо будем определять в
результате решения двух уравнений (например первых) системы (5.18):
Ф1(Рео, Рно) ~ 0; фг(Рео, Рно) = 0.
В данном случае порядок краевой задачи равен двум. Оставшееся
третье уравнение системы (5.18) фз = О должно использоваться для
определения конечной точки траектории. Однако, как показали предва-
рительные расчеты, каждая из функций ф1, ф2 и ф3 может иметь не-
сколько нулей на траектории полета АКС. В связи с этим наиболее
рациональным способом определения конечной точки траектории будет
являться параметрическое задание конечной массы тк. Искомому
значению тк соответствует максимум функционала М, причем равенст-
во нулю функции фз в этой точке выполняется автоматически.
Определим оптимальное управление углом атаки с учетом того, что
тяга и секундный расход ТРД не зависят от а. Запишем компоненты
202 Глава 5. Траектория движения ДСН перед стартом ВКА с ЖРД
вектора перегрузки, используя первые степени разложения в ряд триго-
нометрических функций:
пу = (Ла 4- су q S)/(mgo); пх = [Л(1 - а2/2)-cxq S\/(mgo). (5.19)
Здесь R- сила тяги ТРД самолета-носителя; су и сх- аэродинамические
коэффициенты АКС, отнесенные к площади крыла самолета-
носителя S.
Будем полагать, что поляра АКС является квадратичной и симмет-
ричной:
Су — суо “I” Су а, сх сх mjn + т4(Су) ,
тогда в каждой точке траектории (при фиксированных значениях фазо-
вых переменных)
dcy Ida = суа; dcx Ida = 2Асу суа;
7 7 7 7 „7 (5.20
d2cy Ida2 = 0; d2cx Ida2 = 2Л(суа)2.
С учетом (5.20) первые и вторые производные перегрузок пу и пх по
углу атаки будут равны
dny Ida = (R + cyaqS)l (rngv); dnxIda = - (Ra + 2Acy cyaqS)/(mgoy, (5.21)
d2ny/da2 = 0- d2nJda2 = -[R + 2A(Cya)2qS]/(mg0). (5.22)
Сформируем алгоритм определения угла атаки, состоящий из двух
этапов.
1. Пусть ограничение, наложенное на нормальную перегрузку, не
нарушается, то есть \|/i <0. В этом случае А, = 0 и оптимальный угол
атаки определяется из условия максимума функции
7Y] = Р\пх + Р$пу1У,
т.е. необходимо решить уравнение
Р\ dnx Ida + (Pq IV) dny Ida = 0.
С учетом (5.21) получим выражение для угла атаки в точке экстре-
мума:
_ /ЦЯ + с“75)/(КРу)-2>
аэ т 5
R + 2A{CyYqS
(5.23)
Характерно, что (5.23) совпадает с формулой (3.51), полученной
при рассмотрении оптимального разгона с ЖРД (при 8 = 0 и су = 0).
Определим, когда решение (5.23) будет соответствовать максимуму
функции Гамильтона. С этой целью проанализируем знак второй произ-
водной Н\ по а. С учетом (5.22) получим
5.3. Оптимизация траектории от взлета ДСН до точки старта ВКА 203
d2H{/dci2 = PNd2nJda2.
Так как вторая производная их по углу атаки всегда отрицательная,
то решение (5.23) будет соответствовать максимуму функции Гамиль-
тона при Pv> 0. При Р\< 0 максимум Н\ будет находиться на одной из
границ отрезка (атй1Д, атахД).
Таким образом,
приРу>0 a0pt = ao;
При Ру < 0 CCOpt — 0СтахД , еСЛИ &э < (ОСщахД + С^ттД)/2,
O^opt С^ттД ? еСЛИ (Хэ> (О^тахД + ^-1птд)/2-
2. Если при a = aopt ограничение (5.14) нарушается, то оптималь-
ное управление должно определяться из условия полета по ограниче-
нию \|/i = 0:
z ^утахД^О-СуО^5
a°p' R + c“qS
Неизвестная функция X определяется из условия dH /da. = 0:
. _р Ra + 2AcycyqS pQ
vS° R + c°qS
Таким образом, алгоритм расчета оптимальной траектории совме-
стного полета ДСН и ВКА сформирован.
Для проведения численных расчетов рассмотрим гипотетическую
АКС со стартовой массой 600 т и площадью крыла ДСН 5= 1000 м2.
Стартовая тяговооруженность равна -0,25. В качестве ВКА примем
одноступенчатый ВКС (см. табл. 5.1) со стартовой массой 250 т (опор-
ное значение). Заданы ограничения: атахД= 18°; иутахД = 2,0. Ограни-
чение на минимальную высоту не учитывается.
Пусть в начальной точке параметры траектории АКС имеют сле-
дующие значения: Ко = 100 м/с; 00 = 0; HQ = 0; mQ = 600 т.
Примем, что коэффициент cxmin при увеличении скорости полета
увеличивается с нарастающим темпом, остальные аэродинамические
коэффициенты являются постоянными:
Схmin = 0,022 + 2,2/(V — 260)2; Суо = -0,3; с/= 5,16 рад’1; Л = 0,05.
Удельный часовой расход ТРД является постоянным и равным
0,6 час' (J-60 км/с). Суммарная сила тяги всех ТРД на высоте 8 км
равна 7?н=8=500 кН. По высоте тяга изменяется пропорционально
плотности атмосферы, от скорости тяга не зависит.
Принятая форма задания аэродинамических и тягово-
экономических характеристик, с одной стороны, является упрощенной,
204 Глава 5. Траектория движения ДСН перед стартом ВКА с ЖРД
с другой стороны, она обеспечивает качественную зависимость компо-
нентов перегрузки от скорости и высоты полета. В летном диапазоне
максимальное аэродинамическое качество АКС в сборе составляет
14-15.
Запишем производные пу, пх и Qx по V и Я, входящие в сопряжен-
ную систему уравнений (5.16), с учетом принятых допущений:
ТпуIcV = су рyS/(mgo); дпх/дУ -- [(<7схldV)qS + сх рVS\l(mgo)\
dnv /дН = \{dR/dH)a. + су {dp/dH) V2Sll]l(mg^,
/дН = [{dR/dH) (1 - а2/2) - сх {dp/dH)V2S/2]/(mg0);
8Qr/дГ= 0; oQT/дН = {dR/dH) U,
где
dcJdV = dc^JdV = - 4,4/ (V- 260)3;
dR IdH = /?н =8 {dp/dH)/pH^; dp/dH= -0p.
Решим вначале задачу, несколько отличающуюся от поставленной.
Пусть в конечной точке угол наклона траектории фиксирован и равен
15°; дальность полета АКС - свободная. Для останова интегрирования
траектории будем использовать условие достижения конечной массы
, задаваемой параметрически, начиная от и уменьшаемое с шагом
0,1 т. При каждом значении будем решать частную вариационную
задачу со свободными значениями Ук и Нк. Неизвестные начальные
значения сопряженных переменных Рео и РНо будем определять из
условия выполнения второго условия (5.18) и условия 0К=15°. При
каждом следующем значении тк в качестве нулевого приближения для
Рис. 5.4. Зависимость порядковых
номеров значащих цифр сопря-
женных переменных Р0О и РНо,
которые необходимо изменять при
решении краевой задачи, от
конечной высоты полета АКС
Рео и Рно будем использовать реше-
ние, соответствующее предыдуще-
му значению тк.
Таким образом, протяженность
траектории и конечная высота
полета будут постепенно увели-
чиваться и теоретически можно
достичь оптимального значения тк,
соответствующего максимуму фун-
кционала (5.11) при 0К= 15°.
Однако, как показали числен-
ные расчеты, при увеличении Нк
чувствительность конечных значе-
ний фазовых и сопряженных пере-
менных к изменению значений Р0О и
Рно уменьшается. Иллюстрацией
этому служит рис. 5.4, из которого
видно, что при Як = 5 км для реше-
5.3. Оптимизация траектории от взлета ДСН до точки старта ВКА 205
ния краевой задачи необходимо изменять 12-14-ю значащие цифры
сопряженных переменных Рео и РНо- При Нк> 5 км все значащие циф-
ры переменных Р0О и РНо остаются неизменными и, таким образом,
несмотря на использование двойной точности вычислений, достичь
оптимальной траектории с применением принципа максимума в клас-
сической постановке невозможно вследствие ограниченности разряд-
ной сетки ЭВМ (не более 15-16-ти значащих цифр).
Исследуем траекторию, соответствующую наибольшей протяжен-
ности, достигнутой в расчетах (правая точка на рис. 5.4). Такая траек-
тория показана в координатах "Н- Г" на рис. 5.5 сплошной линией.
Изменение угла наклона траектории по времени полета представлено на
рис. 5.6. На траектории совместного полета ДСН и ВКА можно выде-
лить три характерных участка:
АВ - разгон с промежуточным снижением высоты (в конце уча-
стка 0 > 0);
ВС - набор высоты (0 > 0);
CF - предстартовый маневр АКС, в свою очередь состоящий из
участка разгона со снижением высоты CD и маневра ’’горка" DF.
Участки АВ и CF являются относительно короткими по времени и
характеризуются высоким темпом изменения 0, V и Н. Так как участок
CF непродолжительный, то расходом массы на этом участке можно
пренебречь и, следовательно, слагаемое Pm Qx исключится из функции
Гамильтона (5.15). В результате останутся только слагаемые, линейно
зависящие от тяги. Отсюда следует, что на предстартовом маневре тяга
ТРД должна быть максимальной.
Участок ВС, наоборот, является самым продолжительным по вре-
мени, причем его продолжительность увеличивается при увеличении
Рис. 5.5. Траектория полета АКС в
координатах ’’высота - скорость”
Рис. 5.6. Изменение угла наклона
траектории АКС в зависимости от
времени полета
206 Глава 5. Траектория движения ДСН перед стартом ВКА с ЖРД
высоты Нк. Участок ВС характеризуется незначительным изменением
скорости и угла наклона траектории, то есть здесь реализуется квази-
стационарный режим dto/dx « 0. Именно наличием протяженного квази-
стационарного участка объясняется невозможность численного реше-
ния вариационной задачи на обычной ЭВМ. Для решения таких задач
существуют специальные методы, например метод сингулярных воз-
мущений [30], [58]. Однако дальнейшее исследование оптимального
решения применительно к участку набора высоты выходит за рамки
данной работы.
5.4. Расчет траектории разгона - набора высоты ДСН с
использованием приближенно оптимального управления
Как показано в разделе 2.9, приближенно оптимальная траектория
набора высоты в координатах "высота - скорость" (участок ВС на
рис. 5.5) определяется в результате максимизации функции в каж-
дой точке при £' = fix. В данном случае максимизируемую функцию
можно записать в следующем виде:
/РЗГ- —----•
Qx St
Текущая масса АКС определяется в результате интегрирования
уравнения
dm/dE =- 1//рзг-
Угол наклона траектории определяется приближенно в процессе
построения профиля полета H(V) из соотношения (2.129)
gT&H-l-V&V
В каждой точке траектории должны выполняться конечные
соотношения
Ну = gT cos0/go; Е = Н+ V2/(2gT).
Численные расчеты с использованием исходных данных и упроще-
ний раздела 5.3 показали, что приближенно оптимальная траектория
набора высоты представляет собой гладкую кривую в координатах
"Я- И" (пунктир на рис. 5.5). В процессе увеличения высоты от 0 до
10 км скорость увеличивается от ~ 190 м/с до ~ 230 м/с.
Предельная точка на профиле набора высоты соответствует усло-
вию их = 0 и практически недостижима. Для останова процесса интег-
рирования можно использовать условие достижения максимума частно-
го функционала
Мкв = М* + Мт (тк - + тя*ВКА [pv(KK - Кк*) + цн(Як - //к*)], (5.24)
5.4. Расчет траектории разгона - набора высоты ДСН
207
который совпадает с функционалом (5.11) при це= 0.
В процессе набора высоты величины Кк и Нк увеличиваются, а ко-
нечная масса уменьшается, поэтому максимум функции Л/кв всегда
существует.
Сравнение приближенного решения с оптимальной траекторией,
полученной с использованием принципа максимума, показывает, что на
участке набора высоты скорость определяется с точностью до 0,2 м/с,
текущая масса - с точностью до 0,02 % от стартовой массы АКС.
Таким образом, применение гипотезы квазистационарности позво-
ляет построить траекторию набора высоты с достаточной для практиче-
ских целей точностью, что согласуется с известными многочисленными
работами в данной области [94]—[97], [109], [НО], [124]. При этом, в
отличие от задачи раздела 5.3, не возникает никаких трудностей, свя-
занных с ограниченностью разрядной сетки ЭВМ. Кроме того, не тре-
буется вводить упрощения при задании аэродинамических и тягово-
экономических характеристик, как это было сделано в разделе 5.3.
Сформулируем алгоритм построения приближенно оптимальной
траектории совместного полета АКС: вначале с использованием гипоте-
зы квазистационарности в координатах "Я- Г’ строится программный
профиль разгона - набора высоты от точки взлета АКС до точки, соот-
ветствующей максимуму частного функционала (5.24). Очевидно, что
программная траектория должна состоять из двух участков: участка
разгона при Н= и участка оптимального набора высоты
В общем случае режим работы ТРД на этих двух участках может
оптимизироваться. При движении по границе Я = Я^пд оптимальный
режим работы ТРД определяется из условия максимума эффективного
импульса ЛА. При построении траектории набора высоты оптимальный
режим работы ТРД и оптимальный угол атаки определяются в результа-
те максимизации функции /рзг в каждой точке траектории при Е = fix:
/рзг= * -» max.
0TgT ui
При движении АКС от взлета до точки, соответствующей макси-
муму Л/кв на оптимальном профиле набора высоты, прирост функцио-
нала по сравнению с вариантом, когда старт ВКА осуществляется с
аэродрома, является довольно значительным. Оценка на основе данных
табл. 5.1 (в предположении неизменности частных производных) дает
прирост массы ПГ 0,8-ь0,9 % от стартовой массы ВКА, что согласуется с
результатами работы [140].
После построения программного профиля полета в координатах
’’высота-скорость” проводится расчет траектории на основе полной
системы уравнений в режиме отслеживания программного профиля
(см. раздел 2.10).
К полученной траектории разгона - набора высоты пристыковыва-
ется предстартовый участок (см. разделы 5.5 и 5.6). Положение началь-
208 Глава 5. Траектория движения ДСН перед стартом ВКА с ЖРД
ной точки предстартового маневра на профиле оптимального набора
высоты можно определить параметрически из условия максимума
функционала М. В этом случае на участке предстартового маневра
вариационная задача будет решаться с фиксированным левым концом.
5.5. Исследование предстартового маневра ДСН с
использованием принципа максимума
Пусть в начальной точке предстартового маневра АКС фазовые пе-
ременные равны К) = 224 м/с; 0о = О; //0 = 9,13 км; w0 = 550 t. Примем
режим максимальной тяги ТРД. Решим задачу в начальной постановке,
т.е. со свободными координатами , Нк, 0ки тк. Будем использовать
исходные данные и алгоритм, приведенные в разделе 5.3.
Результаты расчетов, в том числе оптимальные значения фазовых
переменных в точке старта ВКА для двух вариантов АКС (с односту-
пенчатым ВКС и с двухступенчатым ВКА), приведены в табл. 5.2.
Выигрыш в массе ПГ определялся относительно случая, когда пред-
стартовый маневр отсутствует. В процессе вычислений для варианта
АКС с двухступенчатым ВКА было проведено несколько итераций по
уточнению частных производных в точке разделения. В частности,
окончательное значение частной производной функционала по углу
наклона траектории ре в точке старта двухступенчатого ВКА (при
0ОВКА = 38,3°) меньше, чем начальное приближение (при 0ОВКА= 15°).
Таблица 5.2
Фазовые переменные АКС в конечной точке предстартового маневра
Переменная Одноступен- чатый ВКС Двухступен- чатый ВКА (ракетная схема)
Время Г, с 37,8 38,6
Скорость К, м/с 229,9 190,5
Высота //, км 8,857 9,476
Угол наклона траектории 0, град 18,01 38,31
Уменьшение массы АКС Aw, кг 279 288
Выигрыш в массе ПГ Awnr (при к* = 250 т), кг / % от т0ВКА 173/0,07 1128/0,45
На основании данных табл. 5.2 можно заключить, что предстарто-
вый маневр является более значимым для ВКА с малой несущей спо-
собностью, у которого величина частной производной ре в несколько
раз больше по сравнению с крылатым ВКС. С ростом ре увеличиваются
оптимальный угол наклона траектории в точке старта ВКА и выигрыш
в функционале (относительно случая, когда предстартовый маневр
отсутствует).
5.5. Исследование предстартового маневра ДСН
209
Таким образом, конечные значения фазовых переменных и величи-
на выигрыша в массе полезного груза определяются главным образом
частной производной Це- Увеличение функционала на предстартовом
участке меньше, чем на всех предыдущих участках полета АКС
(см. раздел 5.4).
Траектория предстартового маневра в координатах ”Я- V" для рас-
сматриваемых вариантов АКС приведена на рис. 5.7. Из рисунка видно,
что в обоих случаях траекторию можно разделить на два участка:
CD - участок доразгона со снижением (в конце участка 0 = 0);
DF - маневр ’’горка”, в процессе которого угол наклона траекто-
рии увеличивается, а скорость уменьшается.
Оказалось, что в слу-
чае АКС с одноступенча-
тым ВКС на максимальное
ограничение выходит
только нормальная пере-
грузка (на конечном участ-
ке траектории). В случае
АКС с двухступенчатым
ВКА на свои максималь-
ные ограничения выходят
как нормальная перегруз-
ка, так и угол атаки. В
связи с этим для более
подробной иллюстрации
была выбрана траектория
Рис. 5.7. Траектория оптимального пред-
стартового маневра в координатах "высо-
та - скорость"
предстартового маневра
АКС с двухступенчатым
ВКА.
На рис. 5.8 в зависи-
мости от времени т пока-
зано изменение высоты, скорости полета, нормальной перегрузки, углов
атаки и наклона траектории. Видно, что в конце маневра самолет-
носитель выходит сначала на ограничение иу = иутахд, затем - на огра-
ничение а = атахД. Все сопряженные переменные, в том числе и Ру, не
меняют своего знака по траектории (рис. 5.9).
Исследуем физический смысл первого участка полета, на котором
осуществляется доразгон со снижением. С этой целью запишем выра-
жение (5.11) для функционала в следующем виде:
ф = М' + W;BKA [Иу(Кк - Гк’) + Цн (Як - Як*)].
Здесь полагается, что 0О = 0к = 0 и рассматриваемый промежуток вре-
мени мал, т.е. изменением массы АКС можно пренебречь.
210 Глава 5. Траектория движения ДСН перед стартом ВКА с ЖРД
Рис. 5.9. Траектория оптимального предстартового маневра. Зависимости
сопряженных переменных от времени полета
а) б)
Рис. 5.8. Траектория оптимального предстартового маневра. Зависимости
скорости, высоты (а), нормальной перегрузки, углов атаки и наклона
траектории (б) от времени полета
Наклону линий Ф = const в координатах "77- V" соответствует про-
изводная dH/dV=- Цу/Цн- На рис. 5.7 линии Ф = const показаны для
варианта АКС с одноступенчатым ВКС (цу/Цн = 38 с).
В рассматриваемой области полета (на больших высотах) продоль-
ная перегрузка близка к нулю, т.е. полет осуществляется с примерно
постоянным уровнем энергии. При Е = const модуль производной
dH/dV, равный К/g, не превышает 22^-24 с. В результате такого взаимно-
го расположения уровней Е = const и Ф = const (см. рис. 5.7) для рас-
5.5. Исследование предстартового маневра ДСН
211
сматриваемых типов АКС на участке доразгона со снижением достига-
ется некоторое увеличение Ф и, следовательно, функционала М.
Можно заключить, что условием существования участка доразгона
со снижением является выполнение неравенства
G = pv/|iH- K/g>0,
причем с увеличением G эффективность использования этого участка
будет увеличиваться.
Представляет интерес проведение расчета предстартового маневра
с доразгоном без выполнения "горки” (при 0К = 0). Сравнение такой
траектории с оптимальной позволит определить выигрыш от использо-
вания маневра ’’горка”.
Результаты расчетов сведены в табл. 5.3 (выигрыш в массе ПГ оп-
ределялся относительно случая, когда предстартовый маневр отсутству-
ет). Значения производных pv и цн несколько отличаются от предыду-
щего варианта расчета (при наличии маневра "горка”).
Таблица 5.3
Фазовые переменные АКС в конечной точке предстартового маневра без
выполнения ’’горки” (при 0К = 0)
Переменная Одноступен- чатый ВКС Двухступен- чатый ВКА (ракетная схема)
Время Т, с 31,3 25,1
Скорость И, м/с 247,4 249,0
Высота Н, км 8,565 8,484
Pv/Цн,с 32,5 23,7
Уменьшение массы АКС Ат, кг 230 186
Выигрыш в массе ПГ Адипг (при = 250 т), кг / % от КА 53 / 0,02 6 / 0,002
Сопоставление данных табл. 5.2 и 5.3 показывает, что для АКС с
одноступенчатым ВКС участок "разгон со снижением” обеспечивает
некоторый прирост функционала (примерно 30% от общего прироста
на предстартовом участке). Для АКС с двухступенчатым ВКА участок
"разгон со снижением” практически не обеспечивает прироста функ-
ционала. Это объясняется тем, что в варианте двухступенчатого ВКА
величина G практически равна нулю. Таким образом, можно заключить,
что на предстартовом участке основным, с точки зрения увеличения
функционала, является маневр "горка”.
Следует отметить, что рассмотренная выше задача решена без уче-
та реального процесса разделения и без учета ограничений на движение
ДСН после отделения ВКА. В процессе разделения АКС самолет-
носитель движется некоторый промежуток времени с отрицательной
212 Глава 5. Траектория движения ДСН перед стартом ВКА с ЖРД
нормальной перегрузкой, что приводит к резкому уменьшению угла
наклона траектории и может привести к нарушению ограничений,
наложенных на максимальное число М полета и скоростной напор,
которые имеют место для реального ДСН. В связи с этим потребное
конечное значение угла наклона траектории может оказаться значитель-
но больше полученного, в частности, для варианта с одноступенчатым
ВКС. Однако такие большие значения 0К будут являться следствием
учета ограничений, связанных с движением ДСН, а не энергетических
потребностей выведения на орбиту ВКА.
5.6. Формирование приближенно оптимального управления
на траектории предстартового маневра ДСН
Как показали расчеты, проведенные в разделе 5.5, предстартовый
участок является непродолжительным по времени. Изменение скорости
и сопряженных переменных по времени является относительно глад-
ким. На протяжении всего участка Pv > 0, это означает, что оптималь-
ный угол атаки определяется при помощи выражения (5.23). Перепи-
шем это выражение в следующем виде:
_U(R + c;qS)/V-2AcyOc^qS
^opt
(5.25)
R + 2A(c*)2qS
где U = Pq /Pyj.
Изменение переменной U в зависимости от времени полета для
двух вариантов АКС показано на рис. 5.10я сплошной линией. На тех
участках траектории, где ограничения отсутствуют, характер изменения
а и U примерно одинаков (см. рис. 5.1 Об/ и б). В случае АКС с односту-
пенчатым ВКС функция U(x) имеет минимум, который объясняется
наличием участка полета с малыми углами атаки при разгоне со сниже-
нием. В конечной точке переменная U всегда положительна и равна
Цо /pv •
Для формирования приближенно оптимального управления ап-
проксимируем зависимость Цт) при помощи степенной функции:
U= Umin+A (T-TUmin)n,
где l/min, А, тц min, и - четыре неизвестных параметра, значения которых
выбираются из условия максимума функции М.
Конечная точка предстартового маневра также определяется из это-
го условия. Угол атаки в каждой точке траектории определяется по
формуле (5.25) с учетом заданных ограничений (5.1) и (5.2).
В соответствии с данным алгоритмом были проведены численные
расчеты для варианта АКС с двухступенчатым ВКА. В результате оп-
тимизации показано, что функция £/(т) имеет следующий вид:
5.6. Формирование приближенно оптимального управления
213
приближенное решение
Рис. 5.10. Траектория предстартового маневра. Зависимости переменной U (а)
и угла атаки (б) от времени полета
С/= 10,6+ 3,22-10’4 (т-7,6)3'5.
Изменение переменной U и угла атаки по времени в сравнении с
оптимальным решением показано на рис. 5.10я и б соответственно.
Значения фазовых переменных в конечной точке предстартового манев-
ра приведены в табл. 5.4 в сравнении с оптимальным решением, полу-
ченным в разделе 5.5 (см. табл. 5.2). Выигрыш в массе ПГ определялся
относительно случая, когда предстартовый маневр отсутствует.
Как видно из табл. 5.4, при использовании приближенно оптималь-
ного управления конечные значения фазовых переменных определяют-
ся с точностью до 3 %, а выигрыш в массе ПГ - с точностью до
0,0016% от стартовой массы ВКА.
Таким образом, при расчете траектории полета АКС (от взлета до
точки отделения ВКА) ее рационально разделить на несколько участ-
ков, основными из которых являются:
- участок разгона вдоль минимально допустимой высоты;
- участок оптимального набора высоты;
- предстартовый участок, включающий в себя маневр ’’горку".
Основной вклад в увеличение функционала достигается на первых
двух участках полета АКС - до 0,9 % от стартовой массы ВКА.
Использование гипотезы квазистационарности при построении
программной зависимости Я(Г) на участке набора высоты самолета-
носителя обеспечивает приемлемую для практических расчетов точ-
ность.
214 Глава 5. Траектория движения ДСН перед стартом ВКА с ЖРД
Таблица 5.4
Фазовые переменные АКС с двухступенчатым ВКА
в конечной точке предстартового маневра
Переменная Приближенное решение Оптимальное решение
Время Г, с 43,3 38,6
Скорость К, м/с 192,5 190,5
Высота Я, км 9,498 9,476
Угол наклона траектории 0, град 37,07 38,31
Уменьшение массы АКС A/и, кг 320 288
Выигрыш в массе ПГ АдиПг (при mf = 250 т), кг / % от 1124/0,4496 1128/0,4512
Величина выигрыша в массе полезного груза при использовании
предстартового участка полета определяется главным образом частной
производной функционала по углу наклона траектории в точке старта
ВКА Це. С ростом Це увеличиваются оптимальный угол наклона траек-
тории в точке старта ВКА и выигрыш в функционале (относительно
случая, когда предстартовый маневр отсутствует).
Разработанный метод может быть рекомендован для проведения
расчетов на этапе формирования облика, так как определение максиму-
ма функции нескольких переменных является менее трудоемким про-
цессом, чем решение краевой вариационной задачи.
ГЛАВА 6
ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТА ТРАЕКТОРИЙ
ПОЛЕТА АЭРОКОСМИЧЕСКИХ ЛА С ВРД
Задание исходных данных для расчета траекторий ЛА с ВРД пред-
ставляет собой самостоятельную трудоемкую задачу, что связано как с
большим объемом исходной информации, так и с необходимостью
правильного согласования характеристик планера и всех элементов
комбинированной силовой установки. Пусть на ЛА установлена КСУ,
включающая в себя турбокомпрессорные и прямоточные двигатели.
Кроме того, на ЛА могут быть установлены маршевые ЖРД (либо как
отдельные двигатели, либо встроенные внутрь прямоточных двигате-
лей). Типовой пример одноступенчатого ВКС с комбинированной
силовой установкой показан на рис. 1.10. Схема КСУ, состоящей из
ТРДФ, двухрежимного ГПВРД и ЖРД линейной схемы приведена на
рис. 6.1. Основные геометрические характеристики тракта КСУ счита-
ются заданными.
Рассмотрим основные способы задания компонентов результи-
рующей силы ЛА с ВРД.
Рис. 6.1. Схема комбинированной силовой установки, состоящей
из трех типов двигателей
216 Глава 6. Исходные данные для расчета траекторий полета ЛА с ВРД
6.1. Два способа задания компонентов результирующей силы.
Аэродинамические характеристики планера
Силовое воздействие на ЛА с работающими прямоточными двига-
телями может быть определено путем прямого расчета с использовани-
ем соответствующих вычислительных методик. В этом случае интеграл
сил давления и трения определяется по всей смачиваемой поверхности
ЛА, включая внутренний тракт ВРД (см. раздел 2.5), что предполагает
наличие подробной геометрической модели внешней поверхности ЛА и
внутреннего тракта ВРД. Результаты расчета представляют собой зави-
симости коэффициентов результирующей силы и коэффициента расхо-
да воздуха от числа М полета, высоты, угла атаки и коэффициента
избытка воздуха двигателя:
сЕх (М, Я, а, акс); cZy (М, Я, а, акс); /вз(М, Я, а). (6.1)
Здесь/вз = Ко IF, где - площадь поперечного сечения невозмущенной
струи воздуха (на бесконечности); F- площадь входа в воздухозабор-
ник.
Компоненты вектора Ri и секундный расход бортового топлива в
данном случае равны
Кх = qS\ R^y = с^у qS; QT = Qb /(<*ксД))- (6.2)
Здесь 5 - характерная площадь ЛА; Lo- стехиометрический коэффици-
ент; аКс~ коэффициент избытка воздуха в камере сгорания.
Секундный расход воздуха в камере сгорания равен
eB=pKF/n=2/ri<7F/r,
где fw - коэффициент расхода прямоточного двигателя, который, как
правило, отличается от fB3 на величину Д/Ьтб , учитывающую отбор
воздуха из тракта КСУ:
/п-/вз~ А/оТБ •
Высоту полета можно исклю-
чить из зависимостей (6.1), если
известен предварительный профиль
полета ЛА в координатах "Н-М".
Характер зависимости cSx (сеу) для
ЛА с ГПВРД показан на рис. 6.2.
Задание исходных данных в виде
(6.1) является достаточно простым и
удобным, так как коэффициенты
результирующей силы непосредст-
венно входят в уравнения движения.
Однако такая форма задания не
всегда возможна, так как, например,
Рис. 6.2. Характер взаимосвязи
между коэффициентами резуль-
тирующей силы ЛА с ГПВРД
6.1. Два способа задания компонентов результирующей силы
217
исходные характеристики турбокомпрессорных ВРД обычно представ-
ляются в виде проспектных тяги и удельного импульса. Кроме того,
форма задания вида (6.1) не позволяет определить, как на траекторию
ЛА влияют характеристики двигателя и как влияют аэродинамические
характеристики. Поэтому более широко используется традиционный
способ задания исходных данных, предполагающий разделение резуль-
тирующей силы на аэродинамическую и силу тяги ВРД.
Запишем компоненты результирующей силы в предположении, что
вектор тяги ВРД выделен из Rv в соответствии с ее стандартным опре-
делением (см. раздел 2.5):
^х = /?врдх-сх^-схЖ^+АЯ|х +АЯ2х; 1
Г (6.3)
R^y — 7?врду + су qS + Cy-^qF + А7?|у + Д/?2у • J
Секундный расход топлива
2т = ^врд/^врд • (6.4)
Здесь величина 7?Врд представляет собой эффективную тягу ВРД, опре-
деленную с учетом всех видов потерь во внутреннем тракте КСУ и с
учетом отбора воздуха. Эффективный удельный импульс ВРД УВрд
соответствует эффективной тяге 7?Врд- Поправки Д7?| и ДТ?2 учитывают
разворот векторов входного и выходного импульсов.
Будем полагать, что в данном случае при вычислении аэродинами-
ческой силы учтена нижняя поверхность носовой части фюзеляжа до
первого клина воздухозаборника (в соответствии с рис. 2.146). Тогда
третьи слагаемые в (6.3) будут соответствовать силе, действующей на
жидкий контур воздухозаборника на участке от первого клина до кром-
ки обечайки.
Перейдем к рассмотрению каждой составляющей в соотношениях
(6.3).
Аэродинамические характеристики планера. Форма задания аэ-
родинамических характеристик ЛА с работающим ВРД такая же, как и
ЛА с ЖРД (см. раздел 3.1). Как правило, задаются линейная или квадра-
тичная зависимость су(а):
Су = суо + Су а + В а2
и квадратичная поляра
Сх ~ Сх min + Л (Су — Су ) + СхдВд/В. (6.5)
Слагаемое, учитывающее донное сопротивление (при наличии
донного среза), может быть записано отдельно, как это сделано в выра-
жении (6.5), или учтено непосредственно в коэффициенте cXmin- Здесь
5д - площадь донного среза; сх д- коэффициент донного сопротивления.
При вычислении аэродинамических характеристик ЛА с работаю-
щим ВРД не учитываются участки поверхности, относящиеся к тракту
ВРД (см. раздел 2.5). Вследствие этого при прочих равных условиях
218 1 лава 6. Исходные данные для расчета траекторий полета ЛА с ВРД
аэродинамический коэффициент cxmin у ЛА с ВРД всегда меньше, чем у
ЛА с ЖРД. По этой же причине при выключении ВРД коэффициент
т|П всегда увеличивается.
Будем полагать, что в координатах "77-М" или "77- Г' задан про-
филь полета, полученный с использованием предыдущей итерации
расчетов траектории. Это значит, что аэродинамические коэффициенты
суо, с™ , В, с\ |П|П, Л, Су и схд будут зависеть только от числа М полета и
для полного задания аэродинамических характеристик требуются семь
табличных зависимостей. В каждой точке траектории значения аэроди-
намических коэффициентов определяются путем интерполяции.
6.2. Проспектные характеристики ВРД
Рис. 6.3. Стандартная зависи-
мость коэффициента полного
давления от числа М полета
Перейдем к рассмотрению тягово-экономических характеристик
ВРД, которые обычно задаются в виде проспектных характеристик и
потерь тяги во входном и выходном устройствах КСУ. Под проспект-
ными понимаются характеристики ВРД, рассчитанные в некоторой
идеализированной постановке. При этом, как правило, используется
теория одномерных течений. Предполагается, что входной и выходной
импульсы потока параллельны оси
двигателя. В качестве исходных дан-
ных используются стандартные пара-
метры атмосферы и стандартная
зависимость коэффициента полного
давления = от числа М
полета (рис. 6.3). Коэффициент с
соответствует участку течения от
сечения "оо", где параметры потока
являются невозмущенными, до входа
в двигатель (до сечения за горлом ВЗ).
Для каждого типа
(внешнего сжатия, смешанного сжа-
тия и т.д.) используется своя стан-
дартная зависимость сСт(М).
При расчете проспектных характеристик обычно не учитывается
отбор воздуха на самолетные нужды. Предполагается полное расшире-
ние газа в реактивном сопле (рс =р^. Считается, что потери тяги реак-
тивного сопла являются постоянными по траектории полета и состав-
ляют, например, 2 %.
Возможны различные способы задания исходных данных ВРД в за-
висимости от решаемой задачи, типа двигателя и т.д. Рассмотрим наи-
более характерные формы задания проспектных тягово-экономических
характеристик турбокомпрессорных и прямоточных ВРД.
Турбокомпрессорные ВРД. Высотно-скоростные характеристики
(ВСХ) турбокомпрессорных ВРД задаются в виде проспектных зависи-
6.2. Проспектные характеристики ВРД
219
мостей тяги и удельного импульса от числа М полета для нескольких
значений высоты для каждого из возможных режимов работы двигате-
ля. Практика расчетов показала, что на участке разгона ЛА с турбоком-
прессорными ВРД оптимальным является режим максимальной тяги.
Поэтому ВСХ таких двигателей должны быть заданы в первую очередь
для режима максимальной (максимальной форсажной) тяги. С целью
упрощения оптимизации взлетной тяги ВРД 7?0 тяговые характеристики
удобнее задавать в относительном виде: R = R/Rq.
Таким образом, исходные ВСХ турбокомпрессорных ВРД имеют
вид _
Я(М,Я);
Удельный импульс турбокомпрессорных ВРД зависит главным об-
разом от числа М полета; зависимость от высоты является менее выра-
женной. Тяга ВРД одинаково сильно зависит как от числа М полета, так
и от высоты.
В процессе расчета траекторий обычно возникает задача интерпо-
ляции ВСХ. Что касается зависимости тяги от высоты, то правильнее
интерполировать не саму тягу, а аналог коэффициента тяги, т.е. величи-
ну R/q. Эта величина зависит от высоты существенно слабее, чем абсо-
лютная тяга, а в диапазоне высот 114-25 км является практически посто-
янной (так же как и удельный импульс).
На рис. 6.4-6.6 в качестве примера показаны высотно-скоростные
характеристики РТДп для нескольких значений степени сжатия ком-
прессора 7ск* [14]. В текущей точке полета проспектная тяга в данном
случае равна
Япр = Ro (Rh,o/Rq) (Ян,м /Ян,о).
Из рис. 6.5 видно, что задание тяги в зависимости от числа М поле-
та при Н= fix не является рациональным, так как тяга между крайними
точками изменяется в десятки раз. Более рациональным является зада-
ние тяги вдоль некоторого профиля полета, заданного в координатах
"Я-М", который совпадает с программным профилем или близок к
нему. На рис. 6.7 в качестве примера показана зависимость относитель-
ной проспектной тяги вдоль профиля полета, состоящего из двух участ-
ков: Н= 0 и q = 70 кН/м2. В данном случае изменение тяги по числу М
полета не превышает 204-30%. Таким образом, при задании ВСХ турбо-
компрессорных ВРД вместо аргументов М и Я правильнее использовать
аргументы М и д, что обеспечивает большую точность вычислений.
Реальное значение коэффициента полного давления о отличается
от своего стандартного значения Ост- Учет влияния потерь полного
давления в ВЗ на проспектные характеристики турбокомпрессорных
ВРД осуществляется с использованием метода малых отклонений.
Полагается, что относительное изменение расхода воздуха по отноше-
нию к проспектному примерно равно относительному изменению
коэффициента полного давления:
220 Гпава 6. Исходные данные для расчета траектории полета ЛА с ВРД
Рис. 6.4. Зависимость проспект-
ного удельного импульса РТДп
от числа М полета и тгк*
Рис. 6.5. Зависимость относи-
тельной проспектной тяги РТДп
от числа М и высоты полета
Рис. 6.6. Зависимость относи-
тельной проспектной тяги РТДп
от высоты полета при М = 0
Рис. 6.7. Изменение относитель-
ной проспектной тяги ВРД вдоль
заданного профиля полета
« (п- Ост) /пет ~ Ас.
Тяга, соответствующая действительному значению о, рассчитыва-
ется через проспектную тягу с использованием коэффициента влияния
полного давления на тягу двигателя kG:
R = 2?пр(1 + ^До). (6.6)
Аналогичное выражение для удельного импульса имеет вид
J = JnP[l + (£а-1)До]. (6.7)
Типичная зависимость коэффициента kG от числа М полета приве-
дена на рис. 6.8. Относительное изменение коэффициента полного
давления До является одной из характеристик воздухозаборного уст-
ройства и зависит от двух аргументов - и otv (см. раздел 6.3).
6.2. Проспектные характеристики ВРД
221
В состав проспектных характеристик турбокомпрессорных ВРД
входит зависимость приведенного расхода воздуха QB Пр от температуры
торможения ГВх*- Эту зависимость, как и тягу, удобнее задавать в отно-
сительном виде - по отношению к расходу воздуха 0в.о на взлете
(рис. 6.9), который однозначно связан со взлетной тягой.
Приведенный расход воздуха служит для определения потребной
площади невозмущенной струи воздуха и необходим для согласования
характеристик ВРД и ВЗ. Приведенный и текущий расходы воздуха
связаны следующим образом:
бв.ПР = Qb • (6-8)
Рвх N Т0
Здесь pq и То - стандартные давление и температура воздуха на уровне
моря (см. табл. 2.1).
При небольших сверхзвуковых числах М полета можно в первом
приближении пренебречь зависимостью свойств воздуха (к, $НГ и др.) от
температуры и воспользоваться газодинамическими функциями [1]. В
этом случае температура торможения равна
Твх' = Та' = Тм [1 + (к - 1) М«2/2].
Здесь к - отношение теплоемкостей для воздуха.
Расход воздуха связан с параметрами торможения следующим об-
разом:
QB = m ' (6,9)
Аг* °#вх
Здесь m - функция к и SHr; X - приведенная скорость; <?(Х) - газодина-
мическая функция (см. приложение 2).
Рис. 6.8. Зависимость коэф-
фициента влияния ка от числа
М полета
Рис. 6.9. Зависимость относительно-
го приведенного расхода воздуха от
температуры торможения
222 Глава 6. Исходные данные для расчета траекторий полета ЛА с ВРД
Исключив из выражений (6.8) и (6.9) отношение ^вх*/7^вх , полу-
чим потребную для турбокомпрессорного ВРД площадь поперечного
сечения невозмущенной струи воздуха
F^ = nQb.np где п = /(тро) = 0,004145 м2с/кг.
Если на ЛА установлены только турбокомпрессорные ВРД, то по-
требный коэффициент расхода воздуха через ВЗ в каждой точке траек-
тории равен
/вз = F^/F + А/отб •
Здесь коэффициент А/отб учитывает отбор воздуха из ВЗ (самолетные
нужды, отсос пограничного слоя для обеспечения заданного уровня
коэффициента полного давления и т.д.).
Площадь входа ВЗ в данном случае должна выбираться из условия
обеспечения воздухом двигателя в наиболее критичной по траектории
полета точке с учетом летного угла атаки. Обычно такая точка соответ-
ствует максимальному числу Мтах работы данного ВРД. Таким образом,
потребная площадь входа в ВЗ равна
F=n ев.прс / [ (/вз- А/отб) <?(^)], (6.10)
где величины 2в.пр, си /Вз соответствуют расчетной точке.
Очевидно, что для выбранного турбокомпрессорного ВРД увеличе-
ние расчетной площади входа воздухозаборника является нежелатель-
ным, так как это влечет за собой увеличение сопротивления по жидкому
контуру в соответствии с формулой (6.3) и увеличение массы конструк-
ции. Основным способом уменьшения площади входа ВЗ является
увеличение коэффициента расхода воздуха/Ьз, что может быть сделано,
например, за счет улучшения свойств поджатия носовой части фюзеля-
жа. Из формулы (6.10) следует, что, на первый взгляд, уменьшение
коэффициента давления о будет также приводить к уменьшению пло-
щади входа ВЗ. Однако вместе с этим, в соответствии с формулами (6.6)
и (6.7), будут уменьшаться тяга и удельный импульс ВРД, причем от-
ношение расчетной площади входа в ВЗ к тяге двигателя F/R может
увеличиться. В результате возврата к прежнему уровню тяги площадь
входа в ВЗ не уменьшится, а увеличится.
Выбор оптимальных параметров турбокомпрессорных ВРД пред-
ставляет собой самостоятельную важную задачу формирования облика
ЛА, которая должна решаться совместно с задачей оптимизации траек-
торий движения (см., например, работу [14]).
Если на ЛА установлены турбокомпрессорные и прямоточные ВРД
с общим воздухозаборником, то при выборе оптимальной площади
входа в ВЗ определяющим, как правило, является участок работы ПВРД
(ГПВРД). Это означает, что на участке работы турбокомпрессорных
6.2. Проспектные характеристики ВРД
223
ВРД воздухозаборник может быть максимально раскрыт, а избыточный
воздух будет перепускаться через прямоточный контур, т.е.
/п = УвЗтах “ Д/оТВ” 7% IF ,
где 7% соответствует турбокомпрессорным ВРД. В соответствии с вели-
чиной /п должно быть учтено сопротивление неработающего
прямоточного тракта.
При больших числах М полета, когда зависимость параметров воз-
духа (к, 9?в и др.) от температуры становится существенной, согласова-
ние характеристик двигателя и воздухозаборника должно проводиться
вместе со специалистами по ВРД, причем этот процесс, как правило,
является итерационным.
Прямоточные ВРД. На участке работы ПВРД (ГПВРД) в качестве
основных исходных данных используется зависимость проспектного
удельного импульса от числа М полета, коэффициента избытка воздуха,
угла атаки и высоты
J(M, оскс, а, 77). (6.11)
В данном случае (как и для турбокомпрессорных ВРД) зависимость
от высоты является слабой. То же самое относится к зависимости J от
угла атаки. В связи с этим при задании зависимости (6.11) рационально
использовать две связи - 77(М) и а(М), которые в процессе проведения
траекторных расчетов могут уточняться. При расчете характеристик
прямоточных двигателей, как правило, используется реальная зависи-
мость о(М), которая для конкретного воздухозаборного устройства
однозначно соответствует зависимости а(М).
Типичная зависимость J(aKc) для ГПВРД при нескольких числах М
полета показана на рис. 6.10 (расчеты характеристик выполнены в
ЦАГИ А.А. Семеновым и А.П. Маркеловым). Ограничения по аКс
слева при М = 6-Г7 связаны с ’’тепловым запиранием” двигателя. Вопро-
сы расчета тягово-экономических характеристик прямоточных ВРД
изложены, например, в работе [53].
Удельный импульс двигателя является основной величиной, опре-
деляющей потребную массу топлива ЛА. На рис. 6.11 показаны зависи-
мости проспектного удельного импульса от числа М полета для различ-
ных типов ВРД, работающих на водороде. На этом же рисунке показан
удельный импульс водородно-кислородного ЖРД. Видно, что у ВРД
удельный импульс в несколько раз больше, чем у ЖРД. Однако при
установке ВРД на летательном аппарате вследствие потерь в тракте
КСУ эффективный удельный импульс уменьшается на десятки процен-
тов по сравнению с проспектным значением. В связи с этим одной из
важнейших задач формирования облика аэрокосмического ЛА с ВРД
является выбор аэродинамической компоновки и параметров КСУ,
обеспечивающих минимум потерь удельного импульса ВРД. Для опре-
деления эффективных значений тяги и удельного импульса ВРД необ-
ходимо задать характеристики воздухозаборника и реактивного сопла.
224 Глава 6. Исходные данные для расчета траекторий полета ЛА с ВРД
Рис. 6.10. Проспектный удель-
ный импульс ГПВРД
Рис. 6.11. Зависимости проспект-
ного удельного импульса различ-
ных типов ВРД от числа М полета
6.3. Входной импульс потока.
Характеристики воздухозаборника
Рассмотрим плоский воздухозаборник с многоскачковой системой
торможения сверхзвукового потока, полагая, что он установлен на
нижней поверхности фюзеляжа. Пример такого воздухозаборника
(единичной ширины с тремя клиньями) показан на виде сбоку на
рис. 6.12. Основными геометрическими параметрами ВЗ являются
площадь входа F; угол выноса кромки обечайки Э; угол заклинения ВЗ
освз (угол заклинения нижней поверхности носовой части фюзеляжа по
отношению к связанной оси ЛА xj; число и углы клиньев (см.
рис. 6.12). Как правило, в ВЗ регулируются углы последнего и предпо-
следнего клина, площадь горла и др. Проходные сечения воздухозабор-
ника (как и всего тракта ВРД) должны обеспечивать работу всех двига-
телей, входящих в состав КСУ.
Возможны два основных способа задания характеристик ВЗ.
1. Характеристики ВЗ и носовой части задаются раздельно.
2. Задаются интегральные характеристики системы ”ВЗ + носовая
часть фюзеляжа" в зависимости от числа М полета и угла атаки ЛА.
Рассмотрим первый способ, когда в качестве исходных данных за-
даются характеристики изолированного ВЗ и характеристики носовой
части фюзеляжа (при ее обтекании внешним потоком). Под характери-
стиками изолированного ВЗ понимаются такие характеристики, кото-
рые получены в предположении, что воздухозаборник обтекается мест-
ным потоком под нулевым углом атаки. При этом полагается, что скос
потока и боковое растекание в сечении 1 (см. рис. 6.12) отсутствуют, т.е.
вектор скорости параллелен нижней поверхности носовой части фюзе-
ляжа (Да=0). Основное достоинство такого способа задания заключа-
6.3. Входной импульс потока. Характеристики воздухозаборника 225
Рис. 6.12. Схема плоского воздухозаборника, расположенного
на нижней поверхности фюзеляжа
ется в том, что характеристики изолированного ВЗ не зависят от угла
атаки, что значительно их упрощает.
Для вычисления слагаемых A7?ix и AFiy в формулах (6.3) необходи-
мо знать модуль и направление вектора входного импульса Ii в началь-
ном сечении 1 воздухозаборника (см. рис. 6.12). С этой целью рассмот-
рим обтекание носовой части ЛА. Предположим вначале, что течение в
сечении 1 является плоскопараллельным и вектор скорости параллелен
нижней поверхности фюзеляжа. Такое предположение позволяет вос-
пользоваться теорией одномерных течений. Входной импульс потока в
сечении 1 и импульс невозмущенного потока равны
71 = pjKi2Fi +(pi -p^Fx;
/оо = рооКо2 Foo = k= 2/вз ^оо F. (6.12)
Здесь и далее индекс ”1” соответствует параметрам потока в сечении 1.
Площадь Foo соответствует расходу воздуха через все тракты КСУ,
включая отбор воздуха.
С использованием уравнения неразрывности (pVF= const), газоди-
намических функций (см. приложение 2) и учитывая, что рК -£рМ2,
получим
/| //, = X) + —Ы ---------------— J =
кП)
= Xi /Хоо +
____^оо)! ^(Х,) 1 j
£М2 nJ’
226 Глава 6. Исходные данные для расчета траекторий полета ЛА с ВРД
где X - приведенная скорость; д(Х), Х^)» л(Х) ~ газодинамические функ-
ции (см. приложение 2); Л*п = Fw/F\ - коэффициент поджатия входной
струи воздуха нижней поверхностью носовой части фюзеляжа на уча-
стке до первого клина ВЗ; си =р\1р* - коэффициент полного давление
при обтекании носовой части фюзеляжа.
Таким образом, отношение импульсов ЦЩ в каждой точке траекто-
рии зависит непосредственно от двух переменных: от Xi и ТД] или от Xi
и G], С точки зрения упрощения вычислительного процесса удобнее
задавать величины Mj и Кп или Mi и си. Наибольшую долю в выраже-
нии (6.13) составляет первое слагаемое, второе слагаемое с ростом
скорости полета уменьшается.
Величины Кп, Mi и oj связаны между собой уравнением расхода
(6.14)
и в общем случае зависят от числа Моо и суммарного угла атаки
ocl= а + аВз (см. рис. 6.12).
Следует отметить высокую чувствительность импульса 1\ к изме-
нению входящих в формулу (6.13) величин. Незначительное отклонение
и Mi или Qi и Mi от своих истинных значений может привести к
некорректному результату: Д > До (при Моо> 1).
Проанализируем взаимосвязь между входным импульсом Д и пара-
метрами потока в сечении 1. Вначале рассмотрим режим дозвуковых
скоростей (Моо< 1). В этом случае коэффициент c>i равен 1. Из выраже-
ния (6.14) следует, что коэффициент поджатия будет однозначно связан
с Xi (т.е. с Mi). Это означает, что отношение Д/До будет также однознач-
но определяться величиной Mi при каждом значении М«. Таким обра-
зом, в дозвуковом диапазоне скоростей для определения всех парамет-
ров потока в сечении 1 и импульса Д при каждом значении Мда
достаточно иметь одну величину, например, Mi.
Исследуем диапазон малых дозвуковых скоростей (Моо< 0,2-ь0,3),
когда газ является практически несжимаемым и можно воспользоваться
уравнением Бернулли для струйки жидкости:
Pi-p^p^-Vi2)/!. (6.15)
В этом случае выражение (6.13) с учетом уравнения неразрывности
существенно упрощается:
Д//00 = (Г1/К0+ Гда/Г1)/2.
Из полученного выражения следует, что величина Д/До однозначно
определяется отношением скоростей Ki/K». Кроме того, при У», в
отличие от режима сверхзвуковых скоростей, имеет место строгое
неравенство Д/До > 1.
6.3. Входной импульс потока. Характеристики воздухозаборника 227
При малых дозвуковых скоростях справедливо соотношение
<7(Xi)/<7(Xoo) -Xi/Xoo. С учетом этого из уравнения (6.14) получим связь
между и Mi
Это означает, что при торможении потока коэффициент поджатия
меньше 1, при ускорении - больше 1. Относительное изменение скоро-
сти однозначно связано со средним коэффициентом давления р на
нижней поверхности фюзеляжа в сечении 1. Действительно, используя
уравнение Бернулли (6.15), при малых углах атаки можно получить
(V„ - К,) /К»= 1 - *4^?? = 4 •
2 рИ^/2 2
Таким образом, в диапазоне чисел Моо < 0,2-ь0,3 для полного опре-
деления всех параметров потокаи входного импульса достаточно задать
единственную зависимость ДМ = (Moo-Mi)/Moo от суммарного угла
атаки «,£. При больших дозвуковых скоростях для определения пара-
метров потока необходима зависимость ДМ от двух переменных: и
Моо. Следует отметить, что в случае установки турбокомпрессорных
двигателей при малых скоростях полета величина ДМ и другие пара-
метры потока в сечении 1 будут определяться характеристиками ВРД,
так как компрессор фактически засасывает воздух из окружающей
среды.
Перейдем к диапазону трансзвуковых скоростей. Из уравнения
расхода (6.14) следует, что при Моо=1 коэффициент поджатия равен
#(*ч), т.е.
Л‘п = ^1)<1.
Из уравнения прямого скачка следует, что производная си по Моо
равна нулю при Моо = 1- Это означает, что до чисел Моо = 1,1-s-l ,2 в пер-
вом приближении можно считать, что си » 1. Тогда из уравнения (6.14)
следует, что Кп = 1 при q(\\) ® ^(А^), то есть
Ки = 1 при Моо« 1 +(Моо-М!)/2.
Таким образом, в диапазоне изменения чисел Моо от 1 до 1 + (Моо-
Mi)/2 коэффициент поджатия меньше 1.
Перейдем к рассмотрению режима сверхзвуковых скоростей
(Моо> 1,5-ь2,0). Известно, что при обтекании клина бесконечной шири-
ны сверхзвуковым потоком идеального газа справедливо соотношение
Л = До cosa, (6.16)
которое можно получить из условия равенства сил, действующих на
контрольный объем ABCDEA, в проекции на направление Z (рис. 6.13).
228 Глава 6. Исходные данные для расчета траекторий полета ЛА с ВРД
Характерно, что отношение Ц Щ в (6.16) не зависит от числа Маха.
Коэффициент поджатия в данном случае равен
7<n = sinp /sin(p-a).
Очевидно, что при обтекании реальной носовой части ЛА отноше-
ние импульсов Д//оо не должно сильно отличаться от аналогичной
величины для клина. С другой стороны, вследствие наличия потерь в
головной волне при М*>> 1 имеет место неравенство Ц <Ц (рис. 6.14). В
связи с этим при оперировании с импульсом Ц удобно использовать
следующую относительную величину:
L II- cosav
• _ 1 00 L,
1\---------------- ,
1 - cosaL
которая в сверхзвуковой области изменяется в диапазоне 0-ь1 (в том
случае, когда боковое растекание потока является незначительным).
Входной импульс определяется через величину i\ по формуле
1\ = Ш(1 ~ cosaL) + cosas].
Таким образом, в сверхзвуковом диапазоне скоростей в случае
плоскопараллельного потока для задания входного импульса Ц и других
параметров в сечении 1 можно использовать величины i\ и, например,
Кп, которые, в свою очередь, задаются в зависимости от Мда и az .
После определения входного импульса Ц вычисляются слагаемые,
учитывающие разворот вектора входного импульса в соответствии с
формулами (2.55):
ДЯ1х= /оо cos(a + бдв) - /iCosocl ;
A7?iy=/ooSin(a+Здв) -/isinaL,
где Здв-угол заклинения оси двигателя; До вычисляется по формуле
(6.12).
Рис. 6.13. Обтекание клина
сверхзвуковым потоком
Рис. 6.14. К определению входного
импульса Ц при > 1
6.3. Входной импульс потока. Характеристики воздухозаборника 229
В общем случае течение под нижней поверхностью фюзеляжа яв-
ляется трехмерным. Характер зависимостей tfn, Mi и Qi от Мда и аЕ
определяется геометрической формой носовой части фюзеляжа. Часто
при задании характеристик ВЗ используются зависимости, соответст-
вующие обтеканию модельной носовой части фюзеляжа, задаваемой,
например, в виде треугольной пластины с углом стреловидности 80° (в
ЦАГИ такие характеристики были получены В.П. Старухиным). Харак-
теристики модельной носовой части фюзеляжа близки к реальным.
Изменение коэффициента поджатия в сверхзвуковом диапазоне скоро-
стей показано на рис. 6.15а. При малых углах атаки зависимость Кп от
as (при M00 = fix) близка к линейной. Изменение Mi рационально зада-
вать в виде уменьшения по отношению к Моо. На рис. 6.156 показана
типичная зависимость ДМ1 от Моо иа?, на рис. 6.15в - изменение Qj.
Расчеты трехмерного обтекания реальных конфигураций носовой
части фюзеляжа, проведенные в ЦАГИ (автор расчетов А.А. Губанов),
показали, что поток в сечении 1 является сходящимся на виде сбоку и
расходящимся на виде снизу. Кроме того, средний вектор скорости не
а)
Рис. 6.15. Зависимости коэффициен-
та поджатия (а), уменьшения числа
Маха (б) и коэффициента полного
давления (в) от числа М полета и
суммарного угла атаки ocz при
обтекании модельной носовой части
фюзеляжа
230 Глава 6. Исходные данные для расчета траекторий полета ЛА с ВРД
параллелен нижней поверхности фюзеляжа, угол скоса потока может
достигать 1° и более. Соотношения теории одномерных течений в
общем случае не выполняются.
В этом случае в сечении 1 можно определить средние значения па-
раметров потока; обозначим их верхним символом Так, например,
средний импульс потока представляет собой геометрическую сумму
импульсов единичных струек, проходящих через контрольное сечение с
площадью F\. Таким же образом в сечении 1 определяются средние
скорость, число маха , скоростной напор и другие параметры. Сред-
ние коэффициенты поджатия и полного давления определяются сле-
дующим образом:
£п = fptfdFS, = fndF/CpiF,).
F, F,
Проверочные расчеты показали, что среднее число Mj меньше,
чем величина Mi, определенная из уравнения расхода (6.14) с исполь-
зованием величин АГП и Gj. Модуль среднего импульса Ц меньше, чем
величина 1\, вычисленная по формуле (6.13) с использованием величин
Mj и АГП или АГпи Sp Это различие объясняется боковым растекани-
ем потока в сечении 1. Причем различие тем больше, чем больше рас-
текание потока.
В том случае, когда проспектная тяга определена с использованием
теории одномерных течений, для согласования характеристик двигателя
и ВЗ из набора характеристик обтекания носовой части ЛА необходимы
всего две величины. В качестве таких величин наиболее правильно
использовать Ц и АГП, полагая при этом, что вектор Ij параллелен
нижней поверхности носовой части фюзеляжа (Да=0). Выбор этих
величин объясняется тем, что Ц входит непосредственно в результи-
рующую силу, а коэффициент поджатия в виде сомножителя входит в
формулу для определения тяги ВРД.
Обычно средние величины АГП, Mj, Sj и т.д. определяются с
некоторой погрешностью, поэтому в процессе подготовки исходных
данных функции Ц и А?п должны быть сглажены по своим аргументам
Моо и аЕ. На рис. 6.16 показана сглаженная зависимость ц от и ocz.
При известных величинах и АГП остальные параметры (Mi, Qi, и
т.д.) в сечении 1 определяются с использованием формул (6.13), (6.14) и
других соотношений теории одномерных течений. При этом для опре-
деления Aq необходимо решить нелинейное уравнение
I M^i)
= о.
6.3. Входной импульс потока. Характеристики воздухозаборника 231
Рис. 6.16. Изменение величины
i] , характеризующей входной
импульс, в зависимости от числа
М полета и суммарного угла
атаки az
Для того, чтобы избавиться от
решения этого уравнения в каждой
точке траектории, необходимо в
процессе задания исходных данных
провести подготовительные расчеты.
С использованием исходных функ-
ций Ц (Moo, az) и £п (Moo, az) вна-
чале определяется величина Xi, а
затем число Mi как функции двух
переменных - М* и as.
Таким образом, в сверхзвуковом
диапазоне скоростей в качестве
исходных данных для расчета траек-
торий должны задаваться величины
Mi (или ДМ) и АГП в зависимости от
Моо и as. Расчетное значение коэф-
фициента полного давления при этом
будет меньше, чем о,. В данном
случае именно таким образом учитывается боковое растекание потока
под носовой частью фюзеляжа.
В том случае, когда боковое растекание невелико, можно рекомен-
довать простой способ приближенного определения параметров потока
в начальном сечении ВЗ при М^ > 1. Для этого необходима гладкая
исходная зависимость 1ХЩ от МЛ и осЕ. Пусть такая зависимость из-
вестна (например изменение i\, представленное на рис. 6.16). Требуется
определить соответствующие зависимости Mi, Кц и aj от М* и осЕ.
Рассмотрим эквивалентный клин, при обтекании которого отноше-
ние импульсов Л//» равно заданному. Угол такого клина в соответствии
с соотношением (6.16) равен
аэ= arccos(/i//ao).
При малых углах атаки угол эквивалентного клина связан с сум-
марным углом атаки следующим образом:
аэ~ Jl-i az.
Основное предположение заключается в том, что искомые величи-
ны Mi, 7СП и (Ji равны соответствующим величинам при обтекании
эквивалентного клина. В результате задача сводится к решению уравне-
ния косого скачка:
tga3= ctg р
M2sin2p-1
i х <2Г+ 1 • 2п
1 4- М[1 —-Sin Р
232 Глава 6. Исходные данные для расчета траекторий полета ЛА с ВРД
где Р - угол наклона скачка к вектору скорости невозмущенного потока.
При таком подходе к решению задачи гладкость и выполнение фи-
зических ограничений гарантируются автоматически. Расчетные зави-
симости Mi, Кп и (Ji от Моо и ot£ качественно ведут себя так же, как и
действительные зависимости. Проверочные расчеты на примере конфи-
гурации носовой части фюзеляжа в виде плоской треугольной пластины
с углом стреловидности 80° показали, что приближенные значения Mi,
A*n и Qi в пределах углов атаки до 10° отличаются от своих действи-
тельных значений не более чем на 5%. Так как в области "М - а” суще-
ствует граница, ниже которой косой скачок на клине становится отсо-
единенным, то данный алгоритм работает, начиная с чисел М« 1,5 при
ос< 12°.
Итак, для проведения траекторных расчетов после соответствую-
щей обработки исходных данных_в дозвуковой области задается вели-
чина ДМ, в сверхзвуковой - ДМ и А?п в зависимости от аргументов
Моо и ot£. При подготовке исходных данных необходимо обеспечить их
корректность, т.е. выполнение физических ограничений типа Ц < !*>
(при Моо > 1) и Qi < 1.
Тяга ВРД, по определению, представляет собой разность между
входным и выходным импульсами и уменьшается по мере увеличения
скорости полета. В связи с этим очевидна важность точного определе-
ния импульсов потока (входного и выходного), особенно при больших
скоростях полета. Определим погрешность расчета тяги двигателя в
предельном случае, полагая, что модули векторов Ii и 1да равны. Расчет-
ная тяга ВРД при этом будет занижаться по сравнению с действитель-
ной. Так, например, при осЕ = 5° максимальное завышение входного
импульса Л по сравнению с действительным значением составляет
1 - cosocl = 0,0038. Тяга ВРД при больших скоростях составляет при-
мерно 10% от /со (верхняя оценка). В результате погрешность в опреде-
лении тяги будет составлять ~ 4 %.
Перейдем к рассмотрению характеристик изолированного ВЗ, ко-
торые, как правило, определяются экспериментально. Основным пара-
метром изолированного ВЗ является расчетное число Mi = MP, при
котором скачки от всех клиньев проходят через кромку обечайки. Зави-
симость коэффициента расхода воздуха изолированного ВЗ /из = F\IF
от числа Mj показана на рис. 6.17a. При Mi« 1 коэффициент расхода
равен относительной площади горла ВЗ Fr/F. До чисел Mi = МР всегда
имеет место неравенство /из < 1; при Mi > МР коэффициент/^ равен 1.
Зависимость коэффициента полного давления изолированного ВЗ
Пиз= £>вх/А от числа Ml качественно ведет себя так же, как и
Ост(М)-см. рис. 6.3. Однако в зависимости от типа и параметров ВЗ
уровень аИз может быть как выше, так и ниже аСт-
Главный вектор сил, действующих на жидкий контур изолирован-
ного ВЗ, задается при помощи коэффициентов cxi и cyi в проекции на
6.3. Входной импульс потока. Характеристики воздухозаборника 233
а) б)
Рис. 6.17. Зависимости коэффициента расхода воздуха/Из коэффи-
циентов сопротивления сх1 и подъемной силы су] (б) изолированного
воздухозаборника от местного числа Маха Mj
оси местной системы координат ВЗ. Часто в этих коэффициентах учи-
тываются силы, действующие на обечайку и другие элементы ВЗ (в
этом случае данные силы должны быть исключены из коэффициентов
сх и су планера). Типичная зависимость сх1 и cyi от числа М| показана на
рис. 6.176. Максимум коэффициентов cxJ и сУ| реализуется при
Mi = 1,24-1,4. В этом диапазоне при увеличении конечного угла клина
ВЗ и уменьшении относительной площади его горла коэффициент /из
уменьшается, а коэффициент сх\ увеличивается.
В общем случае регулируемому ВЗ соответствует серия зависимо-
стей 7из, Сх\ и сУ1 от М|, например, в соответствии с углом конечного
клина Ок. Если на ЛА установлены только турбокомпрессорные ВРД, то
в каждой точке траектории угол Ок должен выбираться из условия
обеспечения двигателей потребным расходом воздуха. При этом, как
правило, для ВРД требуется меньший расход воздуха, чем его может
обеспечить ВЗ (т.е./врд^вз.тах), что приводит к увеличению коэффици-
ента сх\ (при М| < МР). Здесь величина М| является известной по ре-
зультатам расчета характеристик обтекания носовой части ЛА.
В случае параллельного расположения турбокомпрессорных и
прямоточных ВРД проходные сечения ВЗ могут быть раскрыты полно-
стью, а избыточный расход воздуха будет пропускаться через тракт
ПВРД (ГПВРД). При этом достаточно задать по одной зависимости /из,
Сх\ И Cyl ОТ Ml .
Определим интегральные характеристики ВЗ с учетом обтекания
носовой части фюзеляжа. Суммарный коэффициент расхода воздуха /вз
всегда увеличивается по сравнению с fa вследствие предварительного
поджатия потока носовой частью фюзеляжа (при нижнем расположении
ВЗ):
/вз = FJF = (Foo IF^F.IF) = Fn /из •
234 Глава 6. Исходные данные для расчета траекторий полета ЛА с ВРД
Коэффициент полного давления ВЗ, интегрированного с планером,
равен
а= ai Сиз •
Здесь величины Кп и с?] являются известными по результатам расчета
характеристик обтекания носовой части ЛА.
Определив действительные значения с, можно рассчитать зависи-
мость относительного отклонения_коэффициента полного давления ВЗ
от своего стандартного значения Ас (М*, а£), необходимую для расче-
та эффективной тяги ВРД:
Ас = (а - ест) /стет •
Определим силы, действующие на жидкий контур воздухозаборни-
ка. В случае изолированного ВЗ эти силы определены с использованием
избыточного давления р-р\. Перейдем к избыточному давлению
р-р^ . Заметим, что силы, вычисленные с использованием абсолютно-
го давления, остаются неизменными, а меняются только слагаемые,
учитывающие давление невозмущенного потока. Так, для продольной
силы можно записать (см. рис. 6.12)
Лр-р|)= cxi7iF=Ap-7?i (F-F1);
-^Хр-р00) схо© 7°° F А’р у?оо (F FI),
где сила Л'р соответствует интегралу абсолютного давления на жидкий
контур изолированного воздухозаборника.
Исключив эту силу, имеем
Схоо= Cxi q 1 /<?« + (Р1 -Р»)(1 -/изЖ •
Аналогичные соотношения можно записать для нормальной силы,
в результате получим
cXoo=cxi7i/7oo+2(pi/;?00- 1)(1 -/Из) /(Ж2);
<?уоо = су । lq^ + 2Q?i /^оо - 1) / (tgS АгМоо2),
где
7i /7оо = ^п =Pi м12/(^оо Моо2); Р\Ip* = Qi лО-О/т^Хоо).
Здесь 7оо = ^ооМоо2/2; S - угол выноса кромки обечайки. Величины М|,
Ci и Х| являются известными по результатам расчета характеристик
обтекания носовой части ЛА.
Коэффициенты схо0 и суо0 вычислены в системе координат ВЗ (ось х
совпадает с нижней поверхностью носовой части фюзеляжа). В скоро-
стной системе координат искомые коэффициенты равны
СХЖ СХоо COS Ct£ “I” Суоо Sin 01 £ , Су ж Суоо COS Otj СХоо sin ot^.
6.3. Входной импульс потока. Характеристики воздухозаборника 235
Таким образом, все величины, необходимые для вычисления
третьего и четвертого слагаемых в формулах (6.3), определены.
Следует отметить, что раздельное задание характеристик изолиро-
ванного ВЗ и характеристик носовой части ЛА является наиболее при-
емлемым на этапе формирования облика ЛА, когда приходится переби-
рать различные варианты тех или иных элементов компоновки.
При втором способе задания характеристик ВЗ величины
с, схЖ и суж сразу представляются в виде зависимостей от Мда и а. В
этом случае величины , М| и др. для расчета траекторий не нужны.
6.4. Выходной импульс потока. Характеристики
реактивного сопла. Эффективная тяга ВРД
Рассмотрим плоское реактивное сопло с косым срезом, интегриро-
ванное с хвостовой частью фюзеляжа. На рис. 6.18 в качестве примера
показана схема реактивного сопла ГПВРД (PC единичной ширины, вид
сбоку); при этом тракт турбокомпрессорных двигателей закрыт или
отсутствует. Одним из основных параметров PC является относитель-
ная площадь среза сопла Fq/F. С точки зрения обеспечения высоких
значений удельного импульса ПВРД (ГПВРД) эта величина должна
составлять 34-5.
В разделе 2.5 был введен вектор тяги PC (Rc = - Ic), который, как и
выходной импульс, приложен к контрольному сечению (см. рис. 6.18).
Эффективная тяга реактивного сопла Rc всегда меньше, чем идеальная
тяга Rc и, определенная в предположении полного расширения потока
(^с=Роо) с использованием теории одномерных течений. Основные
виды потерь тяги PC связаны с трением, недорасширением, неравно-
мерностью и непараллельностью выходного потока, с диссоциацией
газа и т.д.
Характеристики PC (потери идеальной тяги, модуль и направление
вектора эффективной тяги и т.д.) определяются с использованием рас-
четных и экспериментальных методов. Тяга прямоточного двигателя и
тяга его PC обычно определяются сразу как эффективные (т.е. с учетом
всех видов потерь). Вектор эффективной тяги PC приложен к косому
срезу, угол заклинения 5 может
быть как положительным, так и {7 / / / /~> /________
отрицательным (на рис. 6.18 угол \/' ////
Если в каждой точке траекто-
рии модуль и направление вектора
эффективной тяги Rc известны, то
этого достаточно для определения
результирующей силы, действую-
щей на ЛА:
Рис. 6.18. Схема плоского
реактивного сопла ГПВРД
236 Глава 6. Исходные данные для расчета траекторий полета ЛА с ВРД
Rz ~ Ra + Кж + Ii + R<? •
Здесь следует помнить, что при расчете входного импульса использует-
ся коэффициент расхода воздуха воздухозаборника /вз, при расчете
тяги PC - коэффициент /п, который вследствие отбора воздуха может
быть меньше, чем/33, на величину Д/отб (т.е. часть входного воздуха,
соответствующая коэффициенту Д/Ьтб , тормозится до нулевой скорости
относительно ЛА).
Тягу PC удобнее задавать с использованием соответствующего ко-
эффициента Crc = Rc/(qF). В качестве исходных данных достаточно
задать две зависимости
crc(M«, , а , секс); 5(Моо, а, акс)
или
Crc(Moo ,/п , О-кс); 8(Мда, Jn, акс)-
Секундный расход топлива прямоточного контура определяется по
третьей формуле (6.2).
В случае выделения тяги двигателя из результирующей силы ее
вектор определяется следующим образом:
Rвpд = (Rc - Z» ) Пдв,
где Rc-модуль эффективной тяги PC; пдв-единичный вектор, направ-
ленный вдоль оси двигателя (см. рис. 6.18).
В этом случае для полного задания тягово-экономических характе-
ристик ПВРД (ГПВРД) достаточно задать две зависимости:
J (Моо, а, акс); 8(Мда, а, акс)-
Здесь J- эффективный удельный импульс, вычисленный с учетом всех
потерь в PC; 8 - угол отклонения вектора тяги PC.
Коэффициент тяги прямоточного ВРД связан с удельным импуль-
сом следующим образом:
ск = 2//п/(акс1оИ), (6.17)
эффективная тяга двигателя и секундный расход топлива равны
R = Cr qF; Q? - 2/п qF /(секс У).
В данном случае эффективная тяга ВРД направлена вдоль вектора
пдв, компоненты вектора тяги, входящие в формулы (*6.3), записываются
в виде
^врдх = R cos(a + 8дВ); 1
г (6-18)
^врду = R sin (a + 8дВ). J
Слагаемые в (6.3), учитывающие разворот вектора выходного им-
пульса, в соответствии с формулами (2.56) равны
6.4. Выходной импульс потока. Характеристики реактивного сопла 237
ДТ?2х = Rc cos(oc + 8) - Rc cos (a + 8ДВ);
ДТ?2у= Rc sin (a + 8) - Rc sin (a + 8ДВ).
(6.19)
Здесь модуль эффективной тяги PC связан с эффективной тягой двига-
теля в соответствии с определением тяги ВРД:
Rc — R + 'Zfvi qF.
Таким образом, все составляющие соотношений (6.3), соответст-
вующие режиму работы прямоточных ВРД, рассмотрены.
Перейдем к рассмотрению PC с косым срезом в варианте, когда
КСУ работает на режиме турбокомпрессорных ВРД, а прямоточный
тракт открыт (схема PC представлена на рис. 6.19).
Схема приложения векторов тяги PC и внешних сил, действующих
на PC, зависит от положения контрольных сечений. На рис. 6.19 кон-
трольные сечения проведены таким образом, чтобы тягу сопла каждого
из двух контуров можно было в наибольшей степени считать независи-
мо (индекс ”ТК” соответствует контуру турбокомпрессорных ВРД,
"П" - прямоточных ВРД).
Для задания вектора тяги PC каждого контура необходимы две ве-
личины. Например, для каждого контура можно задавать коэффициент
тяги PC и угол заклинения по отношению к связанной оси
Crc(Moo , ос, секс);
8(Моо, а, секс).
В этом случае тяга PC каждого контура равна Rc = c^cqF.
В прямоточный контур подавать топливо имеет смысл только в том
случае, если это обеспечит прирост эффективного импульса ЛА. Фак-
тически возможны два режима: либо топливо не подается (акс —> оо),
либо коэффициент избытка воздуха соответствует ограничению, свя-
занному с тепловым запиранием в КС. В первом случае разность
/?с.п-Лп всегда отрицательна и представляет собой сопротивление
Рис. 6.19. Схема плоского реактивного сопла КСУ, состоящей из тур-
бокомпрессорного и прямоточного трактов
238 Глава 6. Исходные данные для расчета траекторий полета ЛА с ВРД
прямоточного тракта. При сверхзвуковой скорости эта величина прак-
тически линейно зависит от коэффициента расхода воздуха прямоточ-
ного контура/п • Во втором случае тяга PC прямоточного контура может
быть как положительной, так и отрицательной величиной (при большой
площади среза сопла прямоточного контура).
Внешняя сила, действующая на сопло с косым срезом, по сути,
представляет собой донное сопротивление %д (см. рис. 6.19). Коэффи-
циент донного сопротивления зависит не только от числа М полета, но
и от режима работы ВРД. Силы, действующие на PC, могут быть опре-
делены либо путем прямого расчета, либо экспериментально. Часто
вместо раздельных составляющих используется эффективная суммар-
ная сила тяги PC:
Rc = Rc.tk + Rc.n + Хд
Направление вектора Rc задается при помощи угла 8. Одна из ха-
рактерных особенностей PC с косым срезом заключается в том, что в
трансзвуковом диапазоне скоростей угол 8 отрицателен и может дости-
гать по модулю 40° и более (см. рис. 6.19). Модуль эффективной тяги
PC задается при помощи потерь идеальной тяги PC, задаваемых в
относительном виде: ___
ДЛс = (7?с-^с.и)/^с.и. (6.20)
Здесь в качестве характерной используется идеальная проспектная тяга
турбокомпрессорного контура 7?с.и • ___
Типичная зависимость А/?с от
числа М полета для комбинирован-
ного PC с косым срезом представ-
лена на рис. 6.20 (расчеты выпол-
нены А.П. Мазуровым, ЦАГИ).
Видно, что в трансзвуковом диапа-
зоне скоростей потери тяги PC
могут составлять 20 % и более, что
связано с большой силой донного
сопротивления PC с косым срезом
Лд. Причем эта сила тем больше,
чем больше степень расширения PC
на режиме прямоточных двигате-
лей. Поэтому одним из основных
вопросов формирования КСУ явля-
ется правильный выбор степени
расширения сопла с тем, чтобы
обеспечить приемлемые тягово-
Рис. 6.20. Зависимость относи-
тельных потерь тяги PC от числа
М и высоты полета
экономические характеристики КСУ как в трансзвуковом диапазоне
скоростей, так и при больших гиперзвуковых скоростях.
Используя выражение (6.20), запишем эффективную тягу PC:
6.4. Выходной импульс потока. Характеристики реактивного сопла 239
Rc — Rc и (1 “ ARc )•
Аналогичное выражение для эффективной тяги двигателя (без уче-
та потерь тяги в ВЗ) имеет вид
R = 7?пр (1 ~ £ус А7?с ).
Здесь 7?Пр - проспектная тяга ВРД; куС - коэффициент усиления потерь
тяги PC.
Определим коэффициент усиления в общем случае, когда в про-
спектной тяге ВРД учтены проспектные потери тяги PC Д7?пр . Исполь-
зуя определение тяги, запишем проспектную и эффективную тяги
двигателя:
7?пр = Яси (1 — ДЯпр ) — Ло;
Япр(1 — kyc&Rc ) = 7?с.и (1 — ДЯс ) — /оо •
Здесь входной импульс соответствует рассматриваемому ВРД.
Исключив из этих соотношений величину Rc и, после преобразова-
ний получим
> — /1 _L г /d ч1-ДЯпр/ДЯс
кус = (1 + /оо/^пр)——=-----•
1 - Д7?пр
В частном случае при АКпр = 0 данное соотношение превращается
в известную формулу
кус = 1 + Л7ЯПР = 1 + Vcl^cLqUyxp ,
где <7пр - проспектный удельный импульс ВРД.
При V= 0 коэффициент усиления равен 1, с ростом скорости поле-
та - монотонно увеличивается. На рис. 6.21 показана типовая зависи-
мость коэффициента куС от числа М полета для РТДп с тгк* = 3 (по
данным работы [14]).
Выразим эффективные тягу и удельный импульс турбокомпрессор-
ного ВРД через соответствующие проспектные значения в общем слу-
чае (при наличии потерь в ВЗ и PC):
R = 7?пр(1 + ^Д^)(1 -kyc^Rc);
«7 = Л1р[1 +Л- 1)ДЙ](1 -kyc^Rc ).
Компоненты эффективной тяги турбокомпрессорного ВРД, входя-
щие в соотношения (6.3), определяются по формулам (6.18), как и в
случае прямоточных двигателей. В общем случае угол заклинения 5ДВ
для каждого типа ВРД может быть своим. Слагаемые в (6.3), учиты-
вающие разворот вектора выходного импульса, определяются по фор-
240 Глава 6. Исходные данные для расчета траекторий полета ЛА с ВРД
Рис. 6.21. Зависимость коэф-
фициента усиления потерь
тяги PC от числа М полета
мулам (6.19). В данном случае модуль
эффективной тяги PC связан с эффек-
тивной тягой двигателя следующим
образом:
Rc = R + 2/гк
где коэффициент расхода воздуха /гК
соответствует турбокомпрессорному
топлива Q\ при этом остается
тракту.
В случае отбора воздуха из тракта
КСУ тяга ВРД в соотношении (6.3)
уменьшается на величину
Д/оо = 2Д/отб^^- Секундный расход
неизменным.
Таким образом, на режиме работы турбокомпрессорных ВРД все
составляющие соотношений (6.3) также рассмотрены. Если на каком-то
участке полета параллельно с ВРД работают ЖРД с тягой 7?Жрд и углом
установки 8Жрд, то в соотношения (6.3) необходимо добавить слагаемые
Лкрдх _ ЯЖрд cos(a + 8Жрд); ^жрду ~ Лкрд sin(a + 8Жрд).
Суммарный расход топлива при этом будет равен
Qx = 7?врд /-^врд + ^жрд /Лсрд ,
где Лсрд - удельный импульс ЖРД.
Если ЖРД установлены в виде самостоятельного агрегата в торце-
вом срезе ЛА, то при определении донного сопротивления из площади
донного среза ЛА должна быть исключена суммарная площадь среза
сопел ЖРД Fc .
ГЛАВА 7
РАЗГОН ЛА С ВРД СО СВОБОДНОЙ
ДАЛЬНОСТЬЮ ПОЛЕТА
Вопросы оптимизации траекторий движения самолетов с ВРД, в
том числе на участке разгона, в настоящее время хорошо изучены.
Большой вклад в разработку методов расчета траекторий полета с ВРД
был внесен учеными ЦАГИ. Так, задача определения оптимальной
траектории подъема самолета с ВРД в общем виде решена
И.В. Остославским с использованием энергетического метода [71]. В
работе [114] Л.М. Шкадов с использованием принципа максимума
подробно исследовал оптимальные режимы управления самолетом при
полете на дальность, в крейсерском полете, на режимах разгона, подъе-
ма и спуска самолета. В.Е. Денисов в своей диссертационной работе
[32] широко использовал гипотезу квазистационарности и проводил
оптимизацию управления при полете с ГПВРД путем максимизации
эффективного импульса ЛА. В работе Р.Д. Иродова [45] исследованы
неустановившиеся режимы полета самолета с большой тяговооружен-
ностью. Работы Л.П. Федорова посвящены анализу, обобщению и
обоснованию практического использования приближенных методов
оптимизации, основанных на упрощенной системе уравнений движения
[92]—[97]. В работах [109], [110] В.А. Широкопояс исследовал опти-
мальные режимы полета самолетов методом динамического програм-
мирования. Большой вклад в разработку теории полета с ВРД внесли,
ГС. Бюшгенс, Р.В. Студнев [22], И.О. Мельц [30], [55], В.Ф. Илларио-
нов, В.П. Плохих [111], В.Т. Пашинцев, О.В. Балабанов [75], [76],
Б.Х. Давидсон [85] и др.
За рубежом большой вклад в разработку различных методов расче-
та траекторий полета крылатых аппаратов внесли А. Миеле [63],
А.Е. Брайсон [11], [122]—[124], Р. Беллман [9], В.Ф. Денхем, С. Дрейфус
[123] и др. Так, еще в 60-х годах решены задача подъема сверхзвукового
самолета в кратчайшее время на заданную высоту, задача подъема на
максимальную высоту [122]. В работе [124] решен ряд задач оптимиза-
ции характеристик сверхзвукового самолета с использованием энерге-
тического метода, в частности, проведена максимизация полной даль-
ности при заданной массе топлива. В работе [46] приведены результаты
исследований оптимальных режимов ракет и ракетных самолетов,
полученные различными авторами (Г. Лейтман, А. Миеле, Д. Лоуден и
ДР).
242 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
По мере увеличения максимальной скорости полета все большая
часть располагаемого запаса топлива аэрокосмических ЛА должна
тратиться на его разгон. Так, масса топлива одноступенчатого ВКС
составляет более половины его стартовой массы, что приводит к боль-
шой напряженности весовой сводки аппарата. В связи с этим при ис-
следовании различных типов аэрокосмических ЛА в качестве одной из
основных возникает задача оптимизации траекторий разгона ЛА и
определения массы и объема маршевого топлива. Такой расчет может
быть проведен, как правило, только путем интегрирования уравнений
движения.
В отличие от современных до- и сверхзвуковых самолетов для аэ-
рокосмических систем выведения на орбиту наиболее характерным
является режим разгона со свободной дальностью полета. Задачу опти-
мизации траектории разгона можно условно разделить на две части: на
задачу формирования программной траектории в координатах "высота -
скорость" и задачу отслеживания программной траектории полета при
интегрировании полной системы уравнений. Первая задача была час-
тично рассмотрена в разделе 2.9, вторая - в разделе 2.10.
В данной главе разрабатывается приближенный метод оптимиза-
ции траекторий выведения аэрокосмического ЛА с комбинированной
силовой установкой, состоящей из разнотипных ВРД и ЖРД. Рассмат-
риваются основные участки полета: взлет, разгон с турбокомпрессор-
ными ВРД, разгон с ГПВРД. Сформулированы оптимальные условия
переключения различных типов двигателей. Разрабатывается подход,
позволяющий свести задачу оптимального управления к определению
экстремума функции нескольких переменных без использования со-
пряженной системы уравнений.
На рис. 7.1 в координатах "высота-скорость" показана примерная
область полета при разгоне ЛА с ВРД. При больших скоростях разгон
осуществляется на режиме, близком к q = const. В этом случае произ-
водная Н'у обратно пропорциональна скорости полета: Н'у = 2/(0 И) и
выражение (2.129) для угла наклона траектории преобразуется следую-
щим образом:
И qmn = 30-50 кН/м2 sin0 = nxg0
а производную угла 0 по времени мож-
но записать в виде
= 100*120 кН/м2 = 0 dv/dx * _4(g0»x)2 ,
\LL__________________ Г
Рис. 7.1. Возможная область
полета при разгоне ЛА с ВРД
откуда следует, что доля этой величины
от первого слагаемого второго уравне-
ния движения будет составлять
7.1. Постановка задач
243
ёи 4g0nx
gony~ рг2к'
При увеличении скорости полета модуль полученного отношения
монотонно убывает, а это значит, что траектория разгона с ВРД при
больших скоростях полета будет приближаться к квазистационарной.
Вместе с этим приближенное решение, полученное с использованием
гипотезы квазистационарности, будет приближаться к строго опти-
мальному. Поэтому в данной главе приближенно оптимальное управле-
ние и соответствующие траектории будем называть оптимальными.
7.1. Постановка задачи
Постановка задачи оптимального управления может формулиро-
ваться по-разному в зависимости от назначения и типа ЛА (выходит на
орбиту, разгоняется до максимально возможной скорости и т.д.). В
качестве основной рассмотрим задачу оптимизации траектории разгона
применительно к одноступенчатому воздушно-космическому самолету.
Пусть задан ВКС, в состав КСУ которого входят двигатели различ-
ных типов, например ракетно-турбинные, ГПВРД и ЖРД. В общем
случае в каждом типе двигателя используется свой тип топлива, напри-
мер, в ГПВРД - водород, в РТД и ЖРД - водород и кислород со своим
соотношением компонентов. Полагается, что соотношение компонентов
топлива при работе соответствующего двигателя является неизменным:
£mJ = const. Следовательно, неизменной будет плотность топлива, рас-
ходуемого каждым типом двигателя: pTj = const. Рассматривается дви-
жение ЛА в вертикальной плоскости.
В начальный момент времени т0 известны масса аппарата то, ско-
рость Го, высота Но, угол наклона траектории 0О. Диапазон задания
величин Ко, Но и 0О может быть достаточно широким с тем, чтобы
охватить как наземный, так и воздушный способы старта. В конечный
момент времени тк> который является свободным, ВРД выключаются. В
этой точке задана конечная скорость Кк, которая может быть как близ-
кой к орбитальной, так и существенно отличаться от нее. Вместо Кк
может задаваться конечная удельная энергия Ек- Остальные фазовые
переменные (в том числе и массы компонентов израсходованного топ-
лива) в конечной точке являются свободными. В частности, это означа-
ет, что рассматривается движение со свободной путевой дально-
стью •
Задача заключается в определении вектора управления U(t) или
U(P) на участке работы ВРД. Будем полагать, что метод оптимизации
траектории на участке работы ЖРД известен (см. гл. 3). Стартовую
массу т0 примем заданной, как это обычно делается при проектирова-
нии аэрокосмических ЛА. В качестве критериев оптимальности будем
244 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
использовать максимум относительной массы полезного груза или
минимум относительной "сухой” массы:
7иПг//Яо —> max или ^сух/^пг —> min .
Примем, что координатами вектора управления U при движении
ЛА с ВРД являются угол атаки а, режимы работы и диапазоны работы
различных типов ВРД. Для задания диапазонов работы двигателей
используется скорость или число М полета. Режим работы прямоточ-
ных ВРД задается при помощи коэффициента избытка воздуха акс - В
качестве дополнительной управляющей переменной для каждого типа
ВРД может быть задан угол заклинения вектора тяги реактивного со-
пла 8.
Задачу будем решать с учетом ограничений, наложенных на управ-
ляющие переменные:
С^1тппД — — С^тахД i ^КСттД — ^КС — ^КСтахД
и с учетом других ограничений, которые могут быть заданы при выве-
дении на орбиту. Такими ограничениями, как правило, являются мини-
мально допустимая высота полета Я^пд, максимально допустимые
скоростной напор ^„ахд, нормальная перегрузка иу1тахД (не более 2н-3) и
нормальная сила К1П1ахд, которую удобнее задавать в относительном
виде (по отношению к mQgo). Ограничения могут быть переменными по
траектории полета.
Для упрощения задачи полагается, что отбор воздуха из тракта
ВРД отсутствует.
При рассмотрении аэрокосмического ЛА, не выходящего на орби-
ту, например экспериментального аппарата, задача заключается в мак-
симизации конечной скорости полета при фиксированных значениях
суммарных массы и объема топлива. В качестве полезного груза такого
аппарата можно принять целевое оборудование. В силу обратимости
данная задача сводится к предыдущей, если зафиксировать конечную
скорость полета.
7.2. Упрощение задачи в случае фиксированных
диапазонов работы двигателей
В отличие от задачи, рассмотренной в гл. 3, в данном случае мак-
симум 77?пг/^о или минимум 77?Сух/^пг не соответствует максимуму
массы ЛА в точке выключения ВРД или на орбите, что связано с раз-
ными плотностями используемых типов топлива. Проанализируем
весовое уравнение ЛА с целью возможности перехода к более простому
критерию оптимальности.
Пусть диапазоны работы двигателей являются известными. Пред-
положим, что на ВКС последовательно используются три типа двигате-
лей: турбокомпрессорные ВРД, ГПВРД и ЖРД. Обозначим массу топ-
7.2. Упрощение задачи
245
лива, расходуемого в каждом типе двигателя, через , тТ2 и 7лТз соот-
ветственно. Линеаризуем стартовую массу ВКС по аргументам ], тТ2
и я?тзследующим образом:
mQ = тиПг + S(wTj + YjmTj/prj) + Атт?; j = 1,2, 3. (7.1)
Здесь каждое слагаемое у, /Г7Т) /рТ) представляет собой массу, пропор-
циональную объему топлива j-ro типа двигателя (топливные баки, часть
внешней оболочки и т.д.); pTj - соответствующие плотности топлива (по
условию задачи постоянные величины); - постоянные коэффициенты
(удельная масса конструкции); величина &т не связана с массой и
объемом топлива (шасси, оборудование и т.д.), т.е. является постоянной.
Рассмотрим первый участок полета, на котором расходуется масса
топлива тт?Т| • Запишем массу топлива, расходуемого во втором и треть-
ем типах двигателей, следующим образом:
wT2=(wo-wTi)(l -Ц2); 7T?T3 = (w0-wTi - wT2)(l - Цз) • (7.2)
Здесь = лт7Кj /wOj - относительная конечная масса, соответствующая
участку работы j-ro типа двигателя.
При фиксированных диапазонах работы двигателей величины ц2 и
цз можно считать постоянными, что подтверждает практика численных
расчетов траекторий полета. Уравнения (7.1) и (7.2) - линейные. Это
значит, что если в (7.1) исключить величины 7т?Т2 и лт?Тз при помощи
соотношений (7.2), то полученная зависимость лт?пг от тт?Т1 будет также
линейной. Отсюда следует, что максимуму тттпг при т{) = fix однозначно
соответствует минимум массы mTi •
Запишем выражение для относительной "сухой" массы ВКС:
wCyx /^ПГ = [Д Yj wTj /PTj) + Ати]/[ т0 - + Yj wTj /pTj) - Ати]. (7.3)
С учетом соотношений (7.2) можно заключить, что относительная
"сухая" масса ВКС является дробно-линейной функцией . Из физи-
ческих соображений очевидно, что минимуму mCyx/wnr будет одно-
значно соответствовать минимум тт?Т1 . Таким образом, в обоих случаях
задача сводится к минимуму массы tttti.
Данные рассуждения можно распространить на любое число типов
двигателей, причем последовательность использования различных
типов двигателей не имеет значения. Кроме того, эти рассуждения
справедливы и для многоступенчатых систем выведения в случае фик-
сированных скоростей разделения ступеней. Таким образом, чтобы
решить поставленную в данной главе задачу, необходимо последова-
тельно перебрать все участки траектории в соответствии с заданными
типами двигателей и для каждого из них решить задачу минимизации
массы топлива tt?Tj при фиксированных диапазонах работы двигателей.
Задача оптимизации скоростей включения и выключения ВРД решена в
разд. 7.6.
246 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
7.3. Взлетные характеристики
Возможны три основных способа горизонтального взлета
аэрокосмических ЛА:
- воздушный с самолета-носителя;
- наземный с использованием специального взлетного устройства-
’’разгонной тележки";
- автономный с использованием собственных средств ЛА.
В первых двух способах взлета бортовое топливо ЛА не расходует-
ся и в начале самостоятельного движения масса ЛА равна стартовой
массе 7т?о •
В случае автономного взлета с взлетно-посадочной полосы (ВПП)
масса ЛА в начале маршевого полета уменьшается на величину 7Т7Т.взп
относительно т^. Эта величина, а также ряд других траекторных пара-
метров, определяются в результате расчета взлетных характеристик. В
зависимости от характера работы двигателей, используемых в процессе
взлета, может быть [3]:
- нормальный взлет;
- продолженный взлет (до момента отказа одного наиболее крити-
ческого двигателя взлет является нормальным, после чего взлет завер-
шается с отказавшим двигателем);
- прерванный взлет (до момента отказа двигателя взлет является
нормальным, после чего начинается торможение самолета до полной
его остановки на взлетной полосе).
Вопросы расчета взлетных характеристик самолетов хорошо изу-
чены (см. например, [71], [83], [84], [91], [114]). В работах [47], [93]
проведена оптимизация взлетных характеристик. Наиболее полно
алгоритм расчета взлетных характеристик с учетом отказа критического
двигателя изложен в РДК [84]; этот алгоритм предполагает численное
интегрирование уравнений движения на всех основных участках взле-
та.
Что касается аэрокосмических ЛА, то в случае отказа двигателя
выведение на орбиту, скорее всего, будет прервано, поэтому на этапе
формирования облика основной задачей является определение массы
топлива, расходуемого при нормальном взлете. Однако при этом длина
разбега и взлетная дистанция должны определяться из условия взлета с
отказавшим двигателем. Поэтому необходимо рассмотрение всех слу-
чаев взлета: нормального, продолженного и прерванного.
В данной работе за основу взяты РДК [84] и основные нормативы
для самолетов транспортной категории [3]. Разработан алгоритм при-
ближенного расчета взлетных характеристик, основанный на использо-
вании аналитических формул с учетом особенностей, присущих аэро-
космическим ЛА.
Рассмотрен взлет с аэродрома самолета с трехопорным шасси с но-
совой опорой. Траектория взлета состоит из двух участков (рис. 7.2):
наземного (разбега по взлетной полосе) и воздушного (разгона с набо-
7.3. Взлетные характеристики
247
ром высоты). Такой взлет называется взлетом с разбегом. Траектория
взлета начинается с момента трогания с места и заканчивается на высо-
тах 400-^450 м, где полностью осуществляется переход от взлетной
конфигурации к маршевой.
Длина разбега ЛР определяется протяженностью первого (наземно-
го) участка. Воздушный участок включает в себя две части:
- участок разгона от скорости отрыва /Отр до скорости Г2 с набо-
ром безопасной высоты //без (в конце участка должны выполняться два
условия V> И2 и Н> //Без);
- траекторию начального набора высоты (участок выхода в конеч-
ную точку траектории взлета с одновременным разгоном от скорости И2
ДО Ик).
Взлетная дистанция /,Взл определяется как суммарная длина пер-
вых двух участков (до точки набора безопасной высоты) - см. рис 7.2.
Обычная методика взлета с аэродрома такова. В точке старта дви-
гатели переводятся на взлетный режим, затем отпускаются колесные
тормоза и самолет начинает движение с максимальным ускорением.
Конфигурация самолета является взлетной (шасси выпущено, механи-
зация крыла установлена во взлетное положение). На скорости V\ (см.
рис. 7.2) принимается решение о дальнейшем продолжении взлета или
о его прерывании. На скорости Кп.ст» при которой органы аэродинами-
ческого управления становятся достаточно эффективными, передняя
стойка шасси плавно поднимается и угол атаки увеличивается. При
дальнейшем росте скорости аэродинамическая подъемная сила вместе с
вертикальной составляющей тяги двигателей уравновешивает силу
тяжести и самолет отрывается от поверхности аэродрома.
Далее самолет переводится на набор высоты с одновременным раз-
гоном от скорости отрыва до скорости К2 на безопасной высоте //Без ,
равной 10,7 м. Шасси обычно убирается через несколько секунд после
отрыва, что примерно соответствует точке выхода на безопасную высо-
248 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
ту. До высоты 120 м двигатели работают на взлетном режиме. После
этого начинается уборка взлетной механизации. В любой точке траек-
тории взлета скорость самолета должна увеличиваться [3].
При расчете взлетных характеристик полагается, что разбег осуще-
ствляется по гладкой твердой сухой горизонтальной поверхности при
отсутствии ветра. Траектория взлета лежит в вертикальной плоскости.
Плотность, температура и влажность воздуха задаются в соответствии с
нормативами. Согласно [3] траектория взлета рассчитывается с учетом
отказа одного (наиболее критического) двигателя.
В основу номенклатуры скоростей, используемых при расчете
взлетных характеристик, заложены минимальные критерии, которые
должны обеспечить соответствующие безопасность и управляемость в
случае отказа двигателя. Минимальная скорость установившегося
полета, на которой самолет еще управляем, называется скоростью
сваливания Vc.
Если до скорости принятия решения V\ отказ двигателя не произо-
шел, то взлет всегда продолжается. При отказе двигателя до достиже-
ния скорости V\ имеет место прерванный взлет. Скорость V\ должна
быть меньше Кп.ст [3].
В качестве расчетной скорости отказа двигателя выбирается такое
значение, при котором дистанции прерванного и продолженного взлета
являются максимально близкими. Расчетный случай отказа двигателя
выбирается как самый неблагоприятный, взлетная дистанция при этом
будет максимально возможной, соответствуя сбалансированной длине
ВПП. Согласно [3] скорость V} должна быть больше расчетной скоро-
сти отказа двигателя на величину, которая соответствует времени между
моментом отказа критического двигателя и моментом распознавания
отказа и реагирования на него, после чего вводятся в действие средства
торможения.
Минимальная скорость отрыва РЬтртад - наименьшая скорость,
выше которой самолет может безопасно произвести отрыв и затем
продолжить взлет. Эта скорость обычно близка к Кс. С другой стороны,
^отрпнпд может быть определена с учетом геометрических данных само-
лета как скорость, при которой хвостовая часть фюзеляжа касается
ВПП перед отрывом самолета.
Еотр- скорость самолета в момент отрыва основных опор шасси от
ВПП. Эта скорость определяется величиной Кп.ст и техникой пилотиро-
вания во время отрыва передней стойки. При скорости ИОтр У самолета
должна быть возможность создания положительного градиента набора
высоты без учета влияния земли.
Ипст-скорость, при которой передняя стойка шасси отрывается от
ВПП и угол тангажа самолета начинает увеличиваться. Если при этом
реализуется максимальная практически достижимая угловая скорость
вращения самолета coz, то скорость отрыва КОтр должна быть больше,
чем 1J Котрттд при работе всех двигателей и больше 1,05КОтрттд при
отказе одного двигателя. Т.е. скорость Ип.ст ограничена снизу. Эта
7.3. Взлетные характеристики
249
величина должна быть единой для любого сочетания условий (таких
как масса самолета, конфигурация и др.) как при всех работающих
двигателях, так и при одном неработающем двигателе.
Безопасная скорость взлета К2 - это скорость самолета, достигае-
мая на высоте //без- Общие требования предусматривают, чтобы вы-
полнялось условие И2> Г2п1Н1Д, где минимальная безопасная скорость
^21тпд должна быть не менее 1,2 Ес для самолетов с ТРД, которые не
имеют средств для значительного уменьшения скорости сваливания при
одном неработающем двигателе и не менее 1,15 Ес для самолетов,
которые имеют средства для уменьшения Ис [3].
Оптимизация управления на участке разбега. В отличие от по-
лета в воздухе, при движении по аэродрому на ЛА действуют две до-
полнительные силы, приложенные к опорам шасси: сила реакции N и
сила трения F=fN (рис. 7.3), где f- коэффициент трения качения. Если
коэффициент трения качения для носовой опоры и для главных опор
шасси разный, то можно ввести в
рассмотрение приведенный коэффи-
циент, равный
+/2WW + M),
где индекс "1" относится к носовой
опоре, а индекс "2" - к главным
опорам шасси.
Уравнения движения в данном
случае имеют следующий вид:
dV/dx = (7?Zx ;
dL/dx = Г;
Здесь gT- ускорение силы тяжести, соответствующее геоцентрической
широте старта. Для определенности будем полагать, что взлет осущест-
вляется на средних широтах, т.е. gT = go
Исключив из уравнений (7.4) силу N, получим систему трех диф-
ференциальных уравнений
dV/dx = (/?Sx ; dm/dx =-RU\ dL/dx^V, (7.5)
численное интегрирование которых позволяет определить траекторию
разбега.
В отличие от разгона в воздухе, при разбеге критерием оптималь-
ности управления служит минимум длины разбега, а не массы топлива.
Масса ЛА изменяется незначительно, в связи с чем второе уравнение
(7.5) можно исключить из рассмотрения, положив, что масса ЛА равна
т$. Тогда минимуму длины разбега будет однозначно соответствовать
максимум выражения
Ф = 7?Sx +//?Ly.
mgT
Рис. 7.3. Схема приложения сил,
действующих на ЛА при разбеге
dm/dx = - RU\
R^y + N = mgy.
(7-4)
250 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
Тяга двигателей входит в это выражение линейно. Это значит, что
на взлете должен использоваться режим максимальной (максимальной
форсажной) тяги ВРД, что согласуется с требованиями [3]. В некоторых
случаях такое управление может одновременно обеспечить и минимум
массы топлива.
Определим оптимальный угол атаки. С этой целью воспользуемся
записью компонентов вектора Re, характерной для обычных самолетов
с ТРД:
7?ух = 7?cos(a + 8дв) - cxqS\ R^y = 7?sin(a + 8ДВ) + cyqS.
Здесь коэффициенты с\ и су определены с учетом сил, действующих на
жидкий контур входной струи воздуха и с учетом разворота вектора
входного импульса. На взлете эффективная тяга двигателей R обычно
на 154-20 % меньше стартовой (стендовой) тяги 7?0, вычисленной при
стандартных условиях, Н= 0 и М = 0.
Для симметричной квадратичной поляры ЛА (cx=cxmjn + Лсу2,
су = с\ а) оптимальный угол атаки будет определяться из условия
d<b/dcL = - 7?sin(oc + 5ДВ) - 2Лсу qS + /[7?cos(a + 5ДВ) + gS] = 0.
Воспользовавшись малостью углов а и 8ДВ, положим, что
siп(сх + 8ДВ) = а + 8ДВ и cos(a + 8ДВ) = 1. В результате получим
(/-5дв)7? + /с^
R + 2A(c“)2qS
(7.6)
Относительно скоростного напора функция (7.6) является дробно-
линейной. Отсюда следует, что при малых скоростях (q » 0) оптималь-
ный угол атаки равен /-8ДВ. При больших скоростях оптимальный
угол атаки стремится к величине f /2 (здесь принято, что А » 1/с“ ).
Таким образом, при разбеге aopt изменяется в диапазоне от /-8ДВ
до //2. При аор| = /72 имеет место равенство
сч-Лу = Сх.п1„-/2/(4^).
Коэффициент трения качения при движении по бетонной полосе
составляет 0,024-0,04. Это значит, что при разбеге оптимальный угол
атаки не превышает 14-3°, причем уменьшение коэффициента трения
приводит к соответствующему уменьшению оптимального угла атаки.
Как показывает практика пилотирования, на начальном этапе разбега
(до скорости подъема передней стойки шасси Рп.ст, равной 0,74-0,9 от
Котр) угол атаки равен стояночному углу аст, который обычно близок к
нулю. С учетом пологости экстремума можно заключить, что исполь-
зуемый на разбеге угол атаки близок к оптимальному.
7.3. Взлетные характеристики
251
Скорость отрыва. При достиже-
нии скорости Рп.ст угол атаки начинает
увеличиваться (рис. 7.4). Затем, после
достижения скорости Pqtp< при выпол-
нении равенства вертикальных сил,
действующих в полете:
^Ly“^OTPgO, (7.7)
происходит отрыв самолета от ВПП.
Массу ЛА в точке отрыва можно
считать равной стартовой. Основными
Рис. 7.4. Характер изменения
угла атаки в зависимости от
скорости разбега:
---- нормальный взлет;
слагаемыми R^y являются аэродинами- ------взлет с отказом двигателя
ческая подъемная сила ЛА и верти-
кальная проекция эффективной тяги двигателей, вычисленные при угле
атаки осотр в точке отрыва. С учетом этого можно получить общеприня-
тую формулу для определения скорости отрыва
т/ _ 9?sin(a0Tp + $дв)] ,7 ох
готр - U(/-о)
У РСуОТР
где G/S = m^ge/S - удельная нагрузка на крыло; М = 7?/(mogo) - текущая
тяговооруженность ЛА; р - расчетная плотность атмосферного воздуха.
Здесь предполагается, что разворот вектора входного импульса ВРД
учтен в аэродинамических характеристиках.
Если аэродинамические коэффициенты определены без учета раз-
ворота вектора входного импульса, то формула для определения скоро-
сти отрыва будет иметь вид
И0ТР= l2mQgo-^sin(aQTP+5) _ (7 9)
V РСуОТР S
Здесь - эффективная тяга реактивного сопла, равная 7? + /да, где
величина на взлете может достигать 10% от тяги ВРД; 5-угол за-
клинения вектора тяги PC.
Из зависимостей (7.8) и (7.9) следует, что скорость И0ТР уменьша-
ется при увеличении коэффициента су в точке отрыва. В связи с этим на
самолетах используется механизация крыла (предкрылки, закрылки и
т.д.), позволяющая увеличить суОтр • Однако вместе с коэффициентом су
увеличивается также и коэффициент лобового сопротивления с\, что
приводит к необходимости увеличения стартовой тяги двигателей.
У аэрокосмических ЛА скорость отрыва составляет
Ротр = 350н-400 км/ч, что существенно выше, чем у современных дозву-
ковых самолетов. Это связано с тем, что аэродинамическая компоновка
аэрокосмических ЛА не позволяет в полной мере использовать взлет-
252 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
ную механизацию, и это приводит к уменьшению максимально дости-
жимого значения су в точке отрыва.
Следует отметить особенность, присущую компоновкам ЛА с ко-
сым срезом PC. Из-за большого донного сопротивления угол 8 в форму-
ле (7.9) может оказаться существенно отрицательным, что, при прочих
равных условиях, будет приводить к увеличению скорости отрыва.
Согласно [3] скорость самолета в момент отрыва передней стойки
является единой для всех случаев взлета. Также единой можно полагать
у1ловую скорость вращения со7 при увеличении угла тангажа самолета.
Эта угловая скорость определяется характеристиками самолета и прак-
тикой пилотирования и не должна зависеть от возможного отказа двига-
теля. При одинаковой величине cdz темп нарастания угла атаки по ско-
рости будет больше в случае отказа критического двигателя
(см. рис. 7.4). Скорость отрыва в этом случае равна
v _ s’n(aoTP(-i) +$дв)] п
у PcvOtp(-d
Здесь и далее величина с индексом (-1) будет соответствовать взлету с
одним отказавшим наиболее критическим двигателем.
При нормальном взлете, т.е. при наибольшем темпе нарастания
скорости, отрыв происходит на угле атаки меньшем, чем аотрмь (см.
рис. 7.4). В результате справедливы соотношения
OCOTP < CCoTP(-l) \ Ротр > КэТР(-1) •
С точки зрения уменьшения скорости отрыва угол атаки в этой
точке должен быть максимально возможным, причем это относится к
случаю отказа критического двигателя:
<*ОТР(-1) = ССотРтахД •
Основные условия выбора угла атаки а0ТРтахд заключаются в сле-
дующем:
- должен обеспечиваться заданный запас (~ 2°) по предельному уг-
лу касания хвостовой опорой взлетной полосы при стояночном обжатии
амортизаторов и пневматиков колес шасси, т.е. угол аотршахд определя-
ется компоновкой самолета;
- должен обеспечиваться заданный запас по углу атаки, например,
не менее 1° до а1Пахд, или должно обеспечиваться аналогичное условие
для коэффициента су, например, суОтр 0,8сутахд;
- в случае отказа критического двигателя в точке отрыва и далее по
траектории должны обеспечиваться гарантированные разгон и набор
высоты с заданным углом наклона траектории в соответствии с норма-
тивами.
7.3. Взлетные характеристики
253
Из последнего условия следует, что на воздушном участке взлета
должно выполняться неравенство
пХ(.|)> sinOnTP (7.11)
Согласно [3] в точке отрыва для самолетов с двумя двигателями
0птр>О; при наличии трех двигателей 0Птр> 0,003; при наличии четы-
рех двигателей 0Птр> 0,005. При скорости И2 и при убранном шасси
аналогичные ограничения, соответственно, равны 0,024; 0,027 и 0,03.
Определим минимально допустимую тяговооруженность ЛА из ус-
ловия обеспечения заданного градиента набора высоты в точке отрыва
при взлете с отказавшим двигателем. Вначале отметим, что сразу после
отрыва ЛА от ВПП углы атаки и тангажа продолжают учеличиваться с
прежним темпом, чтобы обеспечить условие пу> 1, необходимое для
подъема на безопасную высоту. Примем, что характер изменения нор-
мальной перегрузки на первом воздушном участке (при наборе безо-
пасной высоты //без) имеет вид, как показано на рис. 7.5. Согласно
работе [91] величина АпУ| при нормальном взлете составляет 0,1, при
взлете с отказавшим двигателем
ДпУ| = 0,05. Угловая скорость вра-
щения ЛА в процессе увеличения
угла тангажа составляет coz = 3-е4 с.
В этом случае величина Т| (см.
рис. 7.5) не превышает 0,3-н0,5 с,
что на порядок меньше, чем отре-
зок времени т2. Пренебрежем
величиной Xi и будем полагать
переменную пу разрывной: слева от
точки отрыва пу = 1, справа
пу = 1 + Апу ].
Запишем условие (7.11) справа
от точки отрыва, обозначив пара-
метры траектории индексом "1":
Рис. 7.5. Зависимость нормаль-
ной перегрузки от времени на
первом воздушном участке - от
момента отрыва до момента
набора безопасной высоты
7?(.i)C0s((i| + 8дв)— cX| goTpS' ^ogo sin0nTP •
Коэффициент подъемной силы в этой точке равен
Cyi = [wogoO + Апу।) - /?(.|)Sin(ai + 8дв)]/^отр5 .
Если в последнем выражении пренебречь вертикальной проекцией
силы тяги, то потребная тяга будет определяться с некоторым запасом.
В итоге получим минимально допустимую тяговооруженность ЛА в
точке отрыва
^плпД = лдв/(идв-1)[(1 + ^пу\)/К\ + sin0nTp]. (7.12)
Здесь идВ- число используемых на взлете двигателей; потребный угол
наклона траектории 0ПТР определяется в соответствии с нормативами в
254 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
зависмости от пдВ; К\- аэродинамическое качество ЛА, соответствую-
щее режиму полета с нормальной перегрузкой 1 + Апу].
Взлет со всеми работающими двигателями. Как было показано
выше, потребную массу топлива, расходуемого на взлете, необходимо
определять для нормального взлета, но с учетом того, что скорость Ип.ст
(единая для всех ситуаций) определяется для взлета с отказом двигате-
ля. Для этого необходимо сначала выбрать угол аОтр(-1), а затем опреде-
лить скорость И0Тр(-1) по формуле (7.10).
При определении скоростей Ип.ст и ^отр воспользуемся прибли-
женным аналитическим решением. Пренебрежем изменением массы
ЛА в числителе первого уравнения (7.5) и запишем его в следующем
виде:
dV/dx = (7?х - cKqS + fcyqS -fmogo)hn, (7.13)
где /?х =/?[cos(oc + 8дв)+/sin(a + 8дв)]. Здесь слагаемым /з1п(а + 8дв)
можно пренебречь.
Воспользуемся средними по траектории величинами R, J, cxmin, А,
с\о и су(1. Величины R и / усредним по скорости полета, а коэффициенты
аэродинамических сил - по скоростному напору. В действительности
при малых дозвуковых скоростях эти величины изменяются незначи-
тельно.
Определим скорость Ип.ст- Будем полагать, что при разгоне с од-
ним отказавшим двигателем от скорости Кп.ст до ^otp(-i) тангенциаль-
ная перегрузка является постоянной и вычисляется через средние зна-
чения угла атаки и скоростного напора. Этот участок является
сравнительно коротким, так как на угол тангажа -12° самолет с угловой
скоростью вращения coz = 2-ь4 град/с может повернуться за Зн-6 с. Ис-
пользуя числитель правой части уравнения (7.13), запишем
ИхСР(-1)= ^х(.|) <7ср(^хср -fcycp)l(GIS).
Здесь Wx(-i)= №(.i)Cos(aCp + 8ДВ);
qcp = (<7п ст + <7отр(- । ))/2; ссср = (ссст + ccqtpc- i ))/2,
аэродинамические коэффициенты схСр и суСр соответствуют углу атаки
СССР •
Будем полагать, что после достижения скорости Ип.ст самолет на-
чинает увеличивать угол тангажа, вращаясь с угловой скоростью coz,
которая является постоянной и единой для нормального и продолжен-
ного взлета [3]. Тогда время увеличения угла атаки от аСт до а0тр(-о
будет равно
АТ(.|)= (CCOTP(-I) - ССст)/<*>z •
Из условия увеличения скорости от Ип.ст до KOtp(-d за время At(.i)
получим квадратное уравнение относительно Ипст •
7.3. Взлетные характеристики
255
^otp(-i)- ^п.ст-ДТ(-|)£оПИх(-1)-/- Р 011(1) (6>хСр _у^уСр)/((7/Х)] ,
(7-14)
2с
откуда Рп.ст = I -----------,
\1Ь2 -4ас — Ь
где а = Дт(. ।> g0 Р(схср -/cyCP)/(4G/S); b = - 1;
с = Hqtp(-i) - AT(.|)go [^x(-i) —f~ ^otp(-i) (<\cp -ycycp)/(2G/*S')].
Для определения скорости и угла атаки в точке отрыва при нор-
мальном взлете необходимо решить уравнение баланса вертикальных
сил
ф(Дт) = суотр Р (^отр)2/(2G/S) + 9? sin(aoTP + 5дв) — 1 — 0 , (7.15)
где ccqtp — ссст+ Дт wz \ Ротр — ^п. ст+ Дт ^хср •
Здесь средняя тангенциальная перегрузка на участке движения от
Ип.ст ДО Ротр равна
^хср= 9^ cos(aCp + бдв) -f- -fcycp)l(GIS\ (7.16)
где 7cp = (<7п.ст + <7otp)/2; otcp = (ccct + ccotp)/2;
<7otp = (G/5)[ 1 — 9? sin(otoTP + 5дв)]/^уотр •
Уравнение (7.15) является нелинейным относительно времени раз-
бега Дт от скорости Ип.ст ДО Ротр , и для его решения можно воспользо-
ваться, например, методом Ньютона:
Дт/+1 = Дт, - ф(Дт, )/ф’(ДТ/),
где в качестве начального приближения принимается Дт = Дт(.|).
В общем случае при известных значениях скоростей Гп.стя Ио гр и
при известном законе а(т) уравнения (7.5) интегрируются численно.
Проинтегрируем эти уравнения аналитически с использованием неко-
торых упрощений.
Разбег до скорости Уп.ст- Определим потребную массу топлива,
расходуемого на данном участке, приняв во внимание, что а = а(Т.
Используя уравнение (7.13) и второе уравнение (7.5), запишем
dm R dV
----=---------------------;---------------, (7.17)
т J ^-.fmaga-pSV-(cxCT-fcyCJ)/2
ИЛИ
^ПСТ ^Р^(СхСТ fcyCv) ое
256 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
где
Ж-,/W()gu) _ 2(9?x-/)G/5 . , ,х .
6 — ~ ~ ~ ~ . Лх - 9? cos(aCT + Здв).
P^(C‘vCT Р(СхСТ
Приняв во внимание, что интеграл в правой части (7.18) - таблич-
ный:
получим выражение для определения массы ЛА в точке отрыва перед-
ней стойки шасси:
। / S । е + Гц
In—— = —. . .. . In----. (7.19)
'"nci ./72[-Hcos(aCT+5дв)-ЛР(схСт- Act) е-^пст
Скорость отрыва и величина е соотносятся как
Котр/е ~ СхСТ = 0,24-0,4-
\ СуОТР-^
Получим еще одно выражение для определения массы топлива,
расходуемого при разбеге ЛА до скорости Гп.ст- С этой целью проин-
тегрируем правую часть уравнения (7.17), полагая скоростной напор
равным некоторому среднему значению #ср- В результате получается
привычная формула для определения относительного запаса топлива
ттпст“ 1 - ехР(~^п.ст/Лф.ср)- (7.20)
Здесь Лф.ср ~ среднее значение эффективного импульса ЛА, равное
Лф ср = <7[cos(acT + $дв) ~f /$Л - (схст “У^уст)7ср/(^ G/S)]. (7.21)
Сравнительные расчеты, проведенные по формулам (7.19) и (7.20)
при Котр = 300-400 км/ч; ХЛ = 0,34-1 и G/S = 34-6 кН/м2, показали, что в
качестве qCP в соотношении (7.21) необходимо использовать ^7п.ст-
Этот результат можно также получить, воспользовавшись разложением
1 4- X
в ряд функции In------ в правой части (7.19):
1 - х
, 1 + х 2х
In----- «-------—.
1-х 1—х2/3
Здесь х = ст/е.
7.3. Взлетные характеристики
257
Определим длину разбега до скорости ИПСт с использованием
третьего уравнения (7.5) и уравнения (7.13), приняв т = mQ:
Rx-fm0g0-pSV\cK-fcy)/2'
После интегрирования получим
_r"/ m.dV1
2>П СТ — I ------------------------1--
о 2(RK-fmogo)-pS(cK-fcy)V2
=G/S in ।^пст(схст ~Луст) (7 23)
«^оРС^хст — fcycv) _ cos(aCT + 8дВ) — f ]G / S
Проинтегрировав уравнение (7.22) при некотором среднем значе-
нии скоростного напора дСр, получим
V2
£п.ст = (7.24)
А£(ЛсР
где
^хср = Я cos(aCT + 8дв) ~f~ qcv(.c^ -fcycj)l{GIS). (7.25)
Сравнительные расчеты, поведенные по формулам (7.23) и (7.24),
показали, что в качестве дСр в соотношении (7.25) необходимо исполь-
зовать дп.ст • Этот результат можно также получить, воспользовав-
шись разложением в ряд функции ln( 1 -х) в правой части (7.23):
ln( 1 -х) « -(х + х2/2) « - Х .
1 -х/2
3 = ст (СхСТ У^уСТ)
ДеСЬХ [9?cos(aCT+5да)-/]С/5
Наибольшую долю в продольной перегрузке составляет тяга двига-
телей, остальные слагаемые обычно на порядок меньше.
Время движения на данном участке можно определить, используя
соответствующую массу топлива:
Тп.ст~ т т.п. ст JIR •
Разбег от скорости Уп.стбо У0ТР. Рассмотрим вторую заключи-
тельную часть разбега. Время движения Лт на данном участке было
определено при решении нелинейного уравнения (7.15). Средняя тан-
генциальная перегрузка определяется по формуле (7.16). Расходуемая
масса топлива и длина участка равны
258 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
\my=\xRIJ\ Д£ = Дт(Гп.ст + Г0Тр)/2. (7.26)
В итоге время разбега, масса топлива разбега и длина разбега рав-
ны
Тр — Тп.ст + Ат ; и?тр = ^т. п.ст + А^т ?
Lp = Ап.ст+ ATL. (7.27)
Участок взлета от момента отрыва до момента достижения
безопасной высоты. При рассмотрении воздушного участка взлета
уравнения движения записываются в обычном для полетных условий
виде (см. раздел 2.6) и в общем случае интегрируются численно; в
начальной точке (при т = 0) V= ИОтр, в конечной точке Н= /7БЕЗ.
Получим приближенное аналитическое решение с учетом того, что
данный участок полета является сравнительно коротким, а характер
зависимости иу(т) имеет вид, как показано на рис. 7.5, т.е.
Диу= Anyi (1 -т/т2),
где т изменяется от 0 до т2.
Запишем второе уравнение движения в виде
dQ/dx = g0(l + А^у - cos0)/H
и проинтегрируем его с учетом того, что cosO « 1, и в предположении,
что V= ГСр. В результате получим
о = (go/Иср) Длу1 [г - т2/(2т2)], (7.28)
где время т2 соответствует моменту достижения безопасной высоты.
Запишем уравнение для высоты полета, воспользовавшись реше-
нием (7.28), и с учетом того, что И» ГСр и sinO « 0,
dH/dx = go Диу । [т - т2/(2т2)].
Проинтегрировав его:
H = g0 А«у, [т2/2 -т3/(6т2)],
получим
т2 = I 3//без (7.29)
У
Величине ЛиУ| = 0,1 соответствует т2 = 5,7с, при ДиУ| = 0,05 имеем
т2 = 8,1 с.
Угол наклона траектории при достижении безопасной высоты ра-
вен ___________
0Н6 = 73£0Аиу1ЯБЕЗ /(2Кср). (7.30)
7.3. Взлетные характеристики
259
Определим скорость ИНб в момент достижения безопасной высоты.
Эта величина в первом приближении равна
^Нб~ Иотр + gO^xl Т2 ,
где Л7Х1 соответствует точке, лежащей справа от точки отрыва.
Для уточнения ИНб необходимо определить тангенциальную пере-
грузку Пх2 В ЭТОЙ точке при условии, ЧТО Пу = 1.
В итоге получим
Инб = Ротр + gO^xCP ^2 , (7.31)
где пхСр = (Л7х1 + ^х2) /2 .
Масса топлива при наборе безопасной высоты и соответствующая
длина участка равны
mT2 = x2R/J- L2 = T2(Vm?+V^I2. (7.32)
В итоге масса топлива, расходуемого на взлетной дистанции, время
движения и длина взлетной дистанции равны
^твзл = тт.р + ^т.2 \ 'Свзл = Тр + т2;
^взл = Lp + L2. (7.33)
Таким образом, все основные характеристики нормального взлета
определены. Следует остановиться на выборе величины Anyi, по сути,
являющейся проектным параметром. Если расчетным случаем для
выбора тяговооруженности ЛА является обеспечение взлета с одним
отказавшим двигателем, то как следует из формулы (7.12), для умень-
шения стартовой тяговооруженности величину \пу\ необходимо прини-
мать как можно меньшей, вплоть до 0,044-0,06. При этом взлетная дис-
танция будет возрастать вследствие увеличения отрезка времени т2 •
Если тяговооруженность ЛА выбрана из других соображений, то с
целью улучшения взлетных характеристик величину ДиУ] можно увели-
чить до 0,24-0,3, вплоть до величины, соответствующей максимально
допустимому коэффициенту су. В этом случае протяженность воздуш-
ного участка и взлетная дистанция могут быть уменьшены до мини-
мально возможных.
Прерванный взлет и продолженный взлет с отказавшим кри-
тическим двигателем. Вопросы расчета взлетных характеристик с
учетом отказа двигателя изложены, например, в работе [91]. Рассмот-
рим упрощенный вариант определения взлетной дистанции. Запишем
приближенную формулу для дистанции прерванного взлета
V2
^прер = L\ + V\ Atvi +-!--г. (2.34)
2£0|”хт|
Здесь Ц - длина разбега со всеми работающими двигателями до скоро-
сти И; AtVi - время движения с постоянной скоростью (примерно
260 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
3-н4 с); ихТ- средняя тангенциальная перегрузка на участке торможения,
записывается так же, как и при разбеге:
nxT = Wcos(aCT + Здв) -/т - 4ср(схт -/т CydKGlS), (7.35)
где индекс "т" соответствует режиму торможения.
Тяга двигателей в формуле (7.35) может быть как положительной
(режим малого газа), так и отрицательной (в случае использования
реверса тяги). Приведенный коэффициент трения fa существенно
больше, чем при разбеге, и составляет 0,24-0,3 в зависимости от типа
покрытия ВПП, интенсивности торможения и т.д. Угол атаки равен
стояночному, однако, в отличие от разбега, при торможении могут
использоваться специальные средства (тормозные щитки, тормозные
парашюты, интерцепторы и т.д.), которые одновременно уменьшают
коэффициент подъемной силы и увеличивают коэффициент лобового
сопротивления.
Согласно работе [91] в зависимости от типа самолета средняя тан-
генциальная перегрузка на участке торможения равна по моду-
лю 0,34-0,6. В первом приближении можно принять | ихТ I = 0,35.
Запишем приближенную формулу для дистанции продолженного
взлета
V2 - V2
£прод~£|+ п ст------— + Д£(-])+ £2(-i), (7.36)
2&<Лср(-1)
или
V2
£прод = L\ + £взл(-1) - --*--• (7.37)
2&Лср(-1)
Здесь дистанция £Взл(-1) является условной величиной и вычисляется в
предположении, что критический двигатель отключен на всей траекто-
рии взлета, начиная от точки старта. Дистанция £Взл(-1) не зависит от
скорости V\. Перегрузка л?хср(-1) вычисляется по формуле (7.25) при
тяговооруженности 9?(.|) с использованием среднего скоростного напо-
ра, равного 7п.ст/2, дистанции и Z2(-i)- по формулам (7.26) и (7.32)
с использованием изложенного выше алгоритма.
Приравняв правые части (7.34) и (7.37), получим квадратное урав-
нение относительно V\
V2 V2
—----*----+-----1---г + К| Дту1 - £взл(-1)= 0- (7.38)
2&0ЛхСР(-1) ^^ol^x'rl
В итоге скорость V\ должна выбираться с учетом условия
V\ Ип.ст [3]. Зная величину V\, можно определить дистанцию продол-
женного взлета по формуле (7.36). При этом длина L\ вычисляется по
формуле (7.24) с учетом (7.25), где qCP = qx/2 .
7.3. Взлетные характеристики
261
Потребные взлетная дистанция и длина разбега. Согласно [3]
потребной дистанцией взлета является наибольшая из двух величин:
^взл.птр - тах(£Прод; 1,15£Взл), (7.39)
где £взл определяется по формуле (7.33) для случая взлета со всеми
работающими двигателями.
Потребной длиной разбега является большая из двух величин:
£рптр = гпах[(£РПрод + £прод)/2; 1,15(£р + £взл)/2], (7.40)
где длина разбега £рпрод соответствует продолженному взлету и опре-
деляется первыми тремя слагаемыми в выражении (7.36). Длина разбега
LP и взлетная дистанция £Взл соответствуют взлету со всеми работаю-
щими двигателями и вычисляются по формулам (7.27) и (7.33).
Примеры расчета. Определим характеристики взлета с использо-
ванием полученных аналитических зависимостей. Пусть на самолете
установлены два двигателя. Основные исходные данные:
аст = 8дв = су0 = О; аотртахд = 15°; Суа = 0,057 град’1; cxmi„=0,03;
А = 0,242; сог=3град/с; /=0,03; J= 18 км/с; //БЕЗ= 10,7 м. При нор-
мальном взлете Да2У1 = 0,1; при продолженном взлете с одним отказав-
шим двигателем \пуi = 0,05.
Предварительный анализ показывает, что основные характеристи-
ки взлета (длина разбега и взлетная дистанция) зависят главным обра-
зом от двух параметров: от стартовой тяговооруженности и скорости
отрыва.
Вначале рассмотрим, как влияет стартовая тяговооруженность на
характеристики взлета со всеми работающими двигателями (при
G/S= 3,6 кН/м2). Результаты расчетов представлены на рис. 7.6 для
диапазона изменения 9? от 9?т,пД до 0,8. В данном случае минимально
допустимая тяговооруженность из условия взлета с одним отказавшим
двигателем составляет 9?тй1Д = 0,515 (см. формулу (7.12)).
При продолженном взлете увеличение тяговооруженности приво-
дит к увеличению вертикальной составляющей тяги двигателей, так как
угол атаки в момент отрыва постоянен и равен аотртахд- В результате
скорость отрыва Ротр(-1) незначительно уменьшается (см. рис. 7.6/). При
нормальном взлете увеличение 9? приводит к сокращению времени от
момента начала подъема передней стойки до момента отрыва. В резуль-
тате угол атаки в момент отрыва ccqtp уменьшается (см. рис. 7.66), а
скорость отрыва И0Тр несколько увеличивается (см. рис. 7.6а). Скорость
Рнб в момент достижения безопасной высоты увеличивается в соответ-
ствии с формулой (7.31), а угол наклона траектории 6Нб - уменьшается
вследствие увеличения средней скорости на первом воздушном участ-
ке - см. формулу (7.30).
262 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
а)
аОТР , 9нб°
- ОСОТР
-
9 Но
0,5 0,6 0,7 91
б)
в)
г)
Рис. 7.6. Влияние стартовой тяговооруженности на взлетные характеристики:
изменение скоростей отрыва и скорости в момент достижения безопасной
высоты (а), угла атаки в момент отрыва и угла наклона траектории в момент
достижения безопасной высоты (б), среднего эффективного импульса ЛА (в),
потребного запаса топлива (г), длины разбега и взлетной дистанции (б),
времени разбега и взлета (е)
----А------разбег; -----------разбег и набор безопасной высоты
7.3. Взлетные характеристики
263
Рис. 7.7. Влияние удельной нагрузки на крыло на взлетные характери-
стики: изменение скоростей отрыва и скорости в момент достижения
безопасной высоты (я); угла атаки в момент отрыва и угла наклона
траектории в момент достижения безопасной высоты (б), среднего
эффективного импульса ЛА (в), потребного запаса топлива (г), длины
разбега и взлетной дистанции (д), времени разбега и взлета (е)
Д
разбег;
разбег и набор безопасной высоты
264 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
При увеличении тяговооруженности средний эффективный им-
пульс ЛА по отношению к среднему удельному импульсу двигателей
увеличивается (см. рис. 7.6в), что связано с уменьшением доли всех
видов сопротивления по сравнению с силой тяги, как это следует из
формул (7.16) и (7.21). При этом потребный относительный запас топ-
лива на разбеге уменьшается, а на взлетной дистанции увеличивается
(см. рис. 7.6г), что связано с увеличением скорости КНб.
Увеличение тяговооруженности приводит к увеличению тангенци-
альной перегрузки на всех участках взлета, в результате длина разбега,
взлетная дистанция, и соответствующие отрезки времени уменьшаются
(см. рис. 7.66 и е).
Скорость отрыва, как следует из формулы (7.8), зависит от удель-
ной нагрузки на крыло G/S, от коэффициента суотр(т.е. от коэффициен-
тов суо, суа, угла атаки аОтр) и, в незначительной степени, от тяговоору-
женности Л. Если предположить, что величина суОтр уже выбрана как
максимально возможная, то единственным параметром, от которого
зависит скорость отрыва, остается удельная нагрузка на крыло. Резуль-
таты расчетов влияния этой величины на характеристики взлета при
постоянной тяговооруженности Л = 0,6 представлены на рис. 7.7.
Увеличение G/S приводит к увеличению скорости отрыва как при
взлете с отказом двигателя, так и при нормальном взлете (см. рис. 7 Ла).
Приращение скорости на воздушном участке (от ГОтр до ИНб) практиче-
ски не зависит от удельной нагрузки, в результате скорость Кнб также
увеличивается.
Угол атаки в момент отрыва при нормальном взлете практически
не зависит от G/S, оставаясь на ~ 3° меньшим по сравнению с аотртахд;
угол наклона траектории 9Нб уменьшается вследствие увеличения сред-
ней скорости на первом воздушном участке (см. рис. 7.76).
Средний эффективный импульс ЛА на участке разбега практически
не зависит от удельной нагрузки на крыло; на взлетной дистанции эта
величина несколько увеличивается из-за уменьшения потерь на лобовое
сопротивление (см. рис. 7.7в). Потребный запас топлива на разбеге и на
взлетной дистанции увеличивается вследствие увеличения скоростей
Иотр и Кнб (СМ. рис. 7.7г). По этой же причине увеличиваются длина
разбега, взлетная дистанция и соответствующее время движения (см.
рис. 7.7 д и е).
Как следует из проведенных расчетов, средний эффективный им-
пульс ЛА на взлете зависит от проектных параметров Л и G/S намного
слабее, чем длина разбега. В связи с этим на этапе формирования обли-
ка запас топлива можно определять с помощью приведенных аналити-
ческих зависимостей.
Очевидно, что существует такое сочетание тяговооруженности са-
молета и удельной нагрузки на крыло, при котором потребная длина
разбега (или потребная взлетная дистанция) будет равна заданной и
одновременно масса ПГ будет достигать максимума. Для упрощения
7.3. Взлетные характеристики
265
задачи в качестве критерия оптимальности будем использовать не
максимум массы ПГ, а минимум суммарной массы крыла и двигателей:
= ткр + /иТрд • Пусть удельная масса ТРД и соответствующих элемен-
тов двигательного тракта (по отношению к тяге ТРД) равна
уТрд = 0,01 кг/Н; удельная масса крыла (по отношению к площади крыла
в плане) составляет 40 кг/м2. Тогда минимизируемая функция будет
иметь вид
40
m^/m0 = g0(---+ 0,019?).
G / S
На рис. 7.8я показана расчетная связь между величинами G/S и 9?,
построенная при условии, что потребная длина разбега равна 1,8; 2.2 и
2,5 км. Видно, что при увеличении тяговооруженности удельная на-
грузка на крыло увеличивается практически линейно. На рис. 7.86
результаты расчетов показаны в виде зависимости от тяговоору-
женности при нескольких значениях LP. Оптимальная тяговооружен-
ность составляет 0,55-Ю,7 в зависимости от располагаемой длины
разбега. Удельная нагрузка при этом равна 64-7,5 кН/м2 (см. рис. 7.8б/).
Увеличение располагаемой длины разбега приводит к уменьшению
суммарной массы крыла и двигателей. При этом оптимальная тягово-
оруженность уменьшается (см. рис. 7.85), а оптимальная удельная
нагрузка на крыло увеличивается (см. рис. 7.8а). Вследствие увеличе-
ния G/S скорость отрыва также увеличивается (см. рис. 7.7а).
Следует отметить, что чувствительность ’’сухой" массы к измене-
нию проектных параметров 91 и G/S существенно больше, чем чувстви-
тельность массы топлива, расходуемого на взлете. Так, при увеличении
длины разбега от 1,8 до 2,5 км суммарная масса крыла и двигателей
уменьшается на ~ 3 % от что соизмеримо с массой ПГ. Масса топли-
а) б)
Рис. 7.8. Зависимости удельной нагрузки на крыло (а) и относительной
суммарной массы крыла и ТРД (б) от тяговооруженности самолета при
фиксированной длине разбега
266 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
Рис. 7.9. Зависимость дистан-
ции продолженного взлета от
стартовой тяговооруженности
и числа двигателей
ва, расходуемого на взлете, при этом
увеличивается всего на 0,1 % от т$.
В общем случае оптимальные
значения тяговооруженности и
удельной нагрузки должны выби-
раться не только из условия взлета,
но и с учетом других этапов полета и
ограничений. В частности, ограни-
чение накладывается на скорость
отрыва (не более 1004-120 м/с).
Рассмотрим влияние числа дви-
гателей идв на характеристики взле-
та. При взлете со всеми работающи-
ми двигателями длина разбега LP и
взлетная дистанция ЛВзл не зависят
от идв . Влияние числа идв на взлет-
ную дистанцию продолженного
взлета показано на рис. 7.9. Очевид-
но, что при идв = 2 величина Апрод максимальна. При увеличении идВ до
4 дистанция продолженного взлета резко уменьшается. Дальнейшее
увеличение числа двигателей приводит к незначительному уменьше-
нию Z/прод. Сравнение величин /,Взл и /,Прод показало, что при пдВ = 2
потребная взлетная дистанция равна взлетной дистанции продолженно-
го взлета. При идв > 34-4 потребная взлетная дистанция равна 1,15£Взл •
Траектория начального набора высоты. Если маршевая кон-
фигурация отличается от взлетной конфигурации незначительно, то
расчет дальнейшей траектории разгона ЛА можно проводить в соответ-
ствии с постановкой задачи, начиная от точки достижения высоты //без,
полагая, что к этому моменту шасси убрано. Если имеется потребность
в более точном расчете траектории начального набора высоты (до
Як = 450 м) в соответствии с [3], то можно предложить следующий
способ оптимизации траектории.
В координатах ”Я- V" строится программ-
ный профиль в виде отрезка прямой от высоты
ЯБез До высоты Як (рис. 7.10). В начальной точке
скорость ИНб и угол наклона траектории 9Нб
определяются по формулам (7.31) и (7.30). В
конечной точке скорость Ик является параметром
и определяется из условия максимума прираще-
ния удельной энергии, отнесенной к расходуемой
на данном участке массе топлива Дя?т:
(Як - Яо)/Ая?т max,
где
Ео = //без + ИН62/(2^о); Ек = Нк + KK2/(2g0)-
Рис. 7.10. Про-
граммный профиль
полета для расчета
участка начального
набора высоты
7.3. Взлетные характеристики
267
Режим работы ВРД и точка перехода от взлетной конфигурации к
маршевой задаются в соответствии с требованиями [3]; угол атаки
определяется из условия отслеживания заданного профиля полета (см.
раздел 2.10).
7.4. Оптимизация траекторий на участке работы
турбокомпрессорных ВРД
В большинстве известных работ оптимизация траекторий разгона и
набора высоты самолетов с ВРД проводится с использованием прибли-
женных методов. Подробный анализ и обобщение различных прибли-
женных методов оптимизации траекторий самолетов применительно к
участку набора высоты проведен Л.П. Федоровым в работе [96].
С исползованием [96] дадим краткий обзор этих методов. В 1946 г.
И.В. Остославским и А.А. Лебедевым был создан метод, предназначен-
ный для расчета участка набора высоты самолета, получивший назва-
ние энергетического [71]. Позднее появился метод Миеле [46], с помо-
щью которого был решен ряд задач механики полета с учетом
удовлетворения краевых условий. В 1963 г. в работе [51] был предло-
жен метод расчета подъема самолета, основанный на теории разрывных
решений задач, разработанный В.Ф. Кротовым. В работах
С.Ю. Скрипниченко [87]—[89] для расчета подъема самолета с учетом
изменения кинетической энергии был применен способ, аналогичный
тому, который использовался без учета изменения кинетической энер-
гии.
Л.П. Федоров показал [96], что все рассмотренные приближенные
методы оптимизации характеристик набора высоты представляют
собой методы решения одной и той же задачи, заключающейся в опре-
делении экстремального значения функционала
1
F= \f(y,H,R)dx
О
при упрощенной системе уравнений движения, в которой управляющи-
ми переменными являются угол наклона траектории и тяга. Все методы
связаны между собой, дают одинаковое решение задачи и дополняют
друг друга. Наиболее удобным методом построения оптимальной тра-
ектории набора высоты является энергетический, заключающийся в
максимизации подынтегральной функции при фиксированной удельной
энергии. Показано, что при разгоне и наборе высоты самолетов с ВРД в
координатах "высота-скорость" реализуется оптимальный профиль
набора высоты, который не зависит от начальных и конечных значений
параметров траектории.
Сравнение приближенного решения задачи оптимального набора
высоты с точным решением на основе метода динамического програм-
мирования, полученным в работе [110], показало, что минимальное
268 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
время набора высоты и конечная скорость в обоих случаях практически
одинаковы [96]. Это подтверждает правильность подходов, основанных
на приближенном решении задачи.
Расчеты характеристик набора высоты обычно проводятся при по-
стоянном (номинальном) режиме работы двигателей. В работе [95]
Л.П. Федоровым предложен метод оптимизации тяги, позволяющий
путем соответствующего перестроения характеристик двигателей найти
оптимальную тягу в зависимости от скорости и высоты полета. После
этого расчеты характеристик набора высоты проводятся так же, как и
при заданном режиме работы двигателей, когда тяга считается извест-
ной функцией Ни V.
В большинстве известных работ задача оптимального набора высо-
ты решалась в общем случае, когда конечная точка полета в координа-
тах ’’высота-скорость" не находится на траектории оптимального
набора высоты. При этом масса самолета задавалась либо постоянной,
либо известной функцией фазовых координат. В качестве критерия
оптимальности, помимо минимума массы топлива, рассматривались и
другие: максимум высоты подъема, минимум времени подъема на
заданную высоту и т.д.
В отличие от этого, в данной работе решается частная более про-
стая задача минимизации массы топлива, когда на правом конце (при
выключении турбокомпрессорных ВРД) фиксируется конечная удельная
энергия. Для определенности полагается, что в начальной точке фазо-
вые переменные соответствуют окончанию взлета с аэродрома. Рас-
сматривается движение без крена (у = 0). По условию задачи в конечной
точке время полета и все фазовые переменные, кроме удельной энергии,
являются свободными. В разделе 7.2 было показано, что в данном
случае максимуму общего функционала соответствует минимум массы
топлива, т.е. максимум текущей массы ЛА. Управляющими перемен-
ными являются угол атаки (или, что то же самое, профиль полета в
координатах "Я- И") и режим работы двигателей. Будем полагать, что
во всех точках траектории может быть обеспечено условие пх>0
(удельная энергия ЛА возрастает).
Чтобы провести окончательный расчет траектории с использовани-
ем полной системы уравнений, нужно сначала решить задачу формиро-
вания управления:
-определить оптимальный профиль полета в координатах "Я- И",
который будет являться программным при интегрировании полной
системы уравнений;
- определить оптимальный режим работы двигателей.
Как показано в разделе 2.9, в случае квазистационарного движения
дифференциальные уравнения сводятся к двум (относительно удельной
энергии и массы):
dE/dx = VR%K /(rngx); dm/dx = - R/J, (7.41)
7.4. Оптимизация траектории на участке работы турбокомпрессорных ВРД 269
и оптимальное управление однозначно определяется в результате мак-
симизации функции /рзг в каждой точке траектории при Е = fix :
VI R
/рзг = - dE/dM= —— _> max, где .7Эф = J— • (7.42)
gT R
Здесь /эф-эффективный импульс ЛА; 7?1х-тангенциальная состав-
ляющая результирующей силы ЛА.
Если предположить, что сила лобового сопротивления Х± вычисле-
на с учетом сопротивления по жидкому контуру и с учетом разворота
векторов входного и выходного импульсов ВРД, то можно воспользо-
ваться первой формулой (2.58):
= 7?cos(cc + 8дВ) -Xz-R-Xz,
и выражение для эффективного импульса ЛА примет вид
/эф = /(1-Ае/7?). (7.43)
Максимум /рзг определяется с условиями (2.137). В процессе оп-
тимизации текущее время обычно не требуется, поэтому его можно
исключить из системы уравнений (7.41). В результате остается одно
дифференциальное уравнение для текущей массы ЛА:
dm IdE = -т //РЗГ. (7.44)
Таким образом, в данной работе (в отличие от вышеназванных ра-
бот) при построении оптимального профиля полета масса ЛА опреде-
ляется в результате интегрирования уравнений движения.
Если оптимальный профиль полета известен, или движение осуще-
ствляется вдоль ограничения, заданного в координатах "77- Е", то
оптимальное управление можно определять из условия .7ЭФ—> шах.
Следует отметить, что при больших тяговооруженностях ЛА не
всякий профиль полета может быть реализован. Из условия sinO < 1
(0 < 90°) с использованием соотношения (2.129) получим
Ятя; + v = gT + rr' _ кг'
g0 g0
Отсюда видно, что заданный профиль полета (Я^>0) не может
быть реализован со сколь угодно большой тяговооруженностью ЛА. В
предельном случае при К„ = 0 должно выполняться условие пк < 1. При
движении с постоянным скоростным напором в дозвуковой области
(при V® 300 м/с)
пх< 1 + « 1,6.
2g0
270 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
Рис. 7.11. Характер зависимости
эффективного импульса ЛА и
функции /рЗГ дозвукового самоле-
та от числа Маха при постоянной
высоте
Рассмотрим вначале оптимиза-
цию траектории движения дозвуко-
вого самолета. Такая задача была
решена численно в гл. 5. У любого
дозвукового самолета зависимость
эффективного импульса от числа
Маха (при фиксированном режиме
работы двигателей и при Н= const)
ведет себя, как показано на
рис. 7.11.
Для объяснения характера та-
кой зависимости воспользуемся
формулой (7.43). В первом прибли-
жении зависимостью тяги и удель-
ного импульса дозвукового ТРД от
числа М при Н= const можно пре-
небречь. Наиболее сильно от числа
М полета зависит сила лобового
сопротивления = JV0 + X,. При движении влево от точки максимума (в
сторону уменьшения скоростного напора) эффективный импульс ЛА
уменьшается вследствие роста индуктивного сопротивления, так как
X^A(cJqS*A^-d-.
При движении вправо от точки максимума (при М —> 1) эффектив-
ный импульс ЛА уменьшается вследствие роста скоростного напора и
коэффициента волнового сопротивления - основной составляющей
коэффициента сх min, так как
•^Ч) — Сх min •
Произведение скорости на эффективный импульс ЛА в зависимо-
сти от числа М ведет себя аналогично ЛЭФ . При этом максимум по
числу Маха сдвигается вправо (см. рис. 7.11).
Если теперь рассмотреть увеличение скорости не при Н = const, а
при Е = const (т.е. с одновременным уменьшением высоты), то, очевид-
но, что при приближении числа Маха к 1 эффективный импульс ЛА
всегда будет уменьшаться, что связано с резким увеличением коэффи-
циента волнового сопротивления. Таким образом, зависимость функции
/рзг скорости при Е = const будет также иметь максимум в дозвуковой
области. Т.е. для дозвукового самолета всегда существует оптимальный
профиль набора высоты ЯорГ(И, обеспечивающий минимум топливных
затрат (рис. 7.12). Для каждого режима работы двигателя можно по-
строить свой профиль набора высоты и окончательно выбрать траекто-
рию, обеспечивающую в каждой точке максимум функции у^зг.
7.4. Оптимизация траекторий на участке работы турбокомпрессорных ВРД 271
При увеличении высоты оптимальная ско-
рость возрастает, а эффективный импульс ЛА и
значение функции/РЗГ уменьшаются вследствие
уменьшения тяги и увеличения индуктивного
сопротивления . Теоретически можно опре-
делить конечную точку оптимального профиля
набора высоты, где /рзг=Лф = 0 (см. рис. 7.12).
Практически эта точка недостижима вследст-
Рис. 7.12. Оптималь-
ная траектория разго-
на - набора высоты
дозвукового самолета
вие ограниченности запаса топлива самолета.
При взлете с аэродрома оптимальная тра-
ектория разгона - набора высоты в координатах
"Н- И” будет состоять из двух участков (см.
рис. 7.12):
-участка движения на минимально допус-
тимой высоте Н= ЯттД
- участка оптимального набора высоты Н=
Как было показано в гл. 5, гипотеза квазистационарности примени-
тельно к дозвуковому самолету позволяет определять оптимальную
траекторию 7/Орс(Ю с высокой точностью, что связано с небольшим
уровнем тангенциальной перегрузки.
Перейдем к оптимизации траектории разгона сверх- и гиперзвуко-
вых самолетов. Отметим, что у таких ЛА тангенциальная перегрузка
должна быть существенно больше, чем у дозвуковых самолетов, что
вызвано необходимостью преодоления трансзвукового диапазона. Так
как аэродинамические характеристики ЛА и тягово-экономические
характеристики ВРД непосредственно зависят от числа Маха, а не от
скорости, то оптимальный профиль полета удобнее строить в координа-
тах "Н- М", а не "Н- 7". Для упрощения задачи пренебрежем зависи-
мостью коэффициентов аэродинамических сил от высоты. Будем пола-
гать, что поляра самолета является квадратичной:
Су СуО Су ОС, Сх Сх min + Л(Су Су ) .
Здесь в коэффициенте сх учитываются сопротивление по жидкому
контуру и разворот векторов входного и выходного импульсов ВРД.
В качестве исходных данных примем зависимости аэродинамиче-
ских коэффициентов от числа Маха для сверхзвукового самолета с
ТРДДФ (рис. 7.13). Определим оптимальный профиль набора высоты
для вариантов упрощенных и действительных тягово-экономических
характеристик турбокомпрессорных ВРД.
А. Вариант упрощенных высотно-скоростных характеристик
ВРД. Пренебрежем зависимостью удельного импульса двигателя от
высоты и числа Маха. Будем полагать, что двигатель работает на керо-
сине: J- 18 км/с. Зависимость тяги двигателя от высоты является
существенной, поэтому будем полагать, что при V = const тяга пропор-
циональна плотности атмосферы:
Т12 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
Рис. 7.13. Зависимости аэродинамических коэффициентов от
числа Маха для сверхзвукового самолета с ТРДДФ
/? = р/р0 - (7.45)
Здесь /?о и р0 - тяга ВРД и плотность воздуха на уровне моря. Эта про-
стейшая аппроксимация качественно отражает действительную зависи-
мость тяги ВРД от высоты. Что касается зависимости тяги ВРД от числа
Маха, то рассмотрим два характерных случая.
AL Постоянный коэффициент тяги: cR = const. При таком усло-
вии тяга ВРД будет пропорциональна скоростному напору:
R = cRFpV2/2,
что наиболее характерно для прямоточных двигателей. При V= const
выполняется условие (7.45).
В данном случае выражение для эффективного импульса ЛА при-
мет вид
с F
УэфЛУ(1__х.. ).
cR S
7.4. Оптимизация траектории на участке работы турбокомпрессорных ВРД 273
Рис. 7.14. Зависимости эффективного импульса ЛА и максимизируе-
мой функции /рзг от числа Маха при Н= const (а) и при Е = const (б) в
случае постоянного коэффициента тяги
Расчетные зависимости 7Эф и /рзг от числа М при Н= const пока-
заны на рис. 7.14df. В качестве примера взята высота 8 км. Видно, что в
сверхзвуковом диапазоне скоростей эффективный импульс ЛА моно-
тонно возрастает. Это связано с тем, что при увеличении скорости
(скоростного напора) одновременно уменьшаются коэффициент cxlnin
(см. рис. 7.13) и коэффициент индуктивного сопротивления
'mg-x Y
А
Функция /рзг является возрастающей по числу Маха вследствие
возрастания скорости.
Расчетные зависимости 7Эф и /рзг от числа Маха при Е = const по-
казаны на рис. 7.146. Эффективный импульс ЛА имеет слабо выражен-
ный максимум. Функция/рзг является возрастающей во всем диапазоне
чисел М, вследствие чего оптимальный профиль набора высоты не
существует.
274 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
Рис. 7.15. Возможные ограничения
в координатах "Н - М"
Следует оговориться, что в
действительности зависимость
cR = const может иметь место толь-
ко в некотором диапазоне скоро-
стей. Для любого ВРД существует
скорость, начиная с которой коэф-
фициент тяги будет уменьшаться.
Это значит, что при больших ско-
ростях полета эффективный им-
пульс ЛА будет также уменьшаться.
В результате теоретически можно
построить оптимальный профиль
набора высоты, однако он будет
находиться в сверхзвуковой облас-
ти и не может быть реализован
вследствие наличия ограничений.
Пример таких ограничений, заданных в координатах ”Я-М”, показан
на рис. 7.15 (здесь Н\ соответствует минимально допустимой высоте
прохождения трансзвуковых скоростей).
Таким образом, при cR = const оптимальная траектория разгона -
набора высоты будет соответствовать движению вдоль ограничений,
заданных в координатах "Я- М".
А2. Тяга не зависит от числа Маха: Rip = const. Условие (7.45)
выполняется. Расчетные зависимости </Эф и Урзг от числа М при
Н= const показаны на рис. 7.16. В качестве примера взята высота 8 км
(как в варианте А1). Эффективный импульс ЛА имеет выраженный
максимум в дозвуковой области, а функция /РЗГ , в отличие от варианта
cR = const, имеет два максимума: в до- и в сверхзвуковой области.
Поведение функции /РЗГ при Е = const показано на рис. 7.17 для не-
скольких уровней удельной энергии. Видно, что при небольшом уровне
удельной энергии (на рис. 7.17 при £ = 6,5 км) максимум/РЗГ достигает-
ся в дозвуковом диапазоне скоростей. При увеличении удельной энер-
гии (в данном случае при Е= 11 км) появляется второй максимум - в
сверхзвуковой области. При дальнейшем увеличении удельной энергии
(на рис. 7.17 при Е= 15,5 км) имеет место один максимум в сверхзвуко-
вой области.
Таким образом, в данном случае, в отличие от варианта А1, опти-
мальный профиль разгона - набора высоты существует. На рис. 7.18 в
качестве примера показаны три таких траектории в зависимости от
тяговооруженности самолета.
Характер траектории оптимального набора высоты согласуется с
известными работами в данной области (см., например, [96], [97], [ПО],
[124]).
При $Л = 0,4 вначале осуществляется набор высоты с практически
постоянным числом М ® 0,9; затем число Маха несколько увеличивает-
ся. При достижении высоты И ~ 8,5 км локальные максимумы функции
7.4. Оптимизация траекторий на участке работы турбокомпрессорных ВРД 275
Рис. 7.16. Зависимости эффективного импульса ЛА и
максимизируемой функции /РЗГ от числа Маха при
Н = const в случае, когда тяга не зависит от числа Маха
Рис. 7.17. Зависимость максимизируемой функции /РЗГ от числа Маха
при Е = const в случае, когда тяга не зависит от числа Маха
/рзг в до- и сверхзвуковой областях становятся равными. Дальнейшее
оптимальное движение будет соответствовать переходу из дозвуковой
области в сверхзвуковую при Е « const. Затем осуществляется разгон в
сверхзвуковой области. Максимально достижимое число М полета
равно ~ 1,5.
При увеличении тяговооруженности оптимальный профиль в коор-
динатах "/7-М” опускается вниз по высоте. Максимально достижимое
число М полета при этом возрастает. Характерно, что при достижении
больших скоростей (в данном случае при М= 1,94-2,1) оптимальный
разгон соответствует движению на постоянной высоте Н~ 11 км. Объ-
ясняется это тем, что в соответствии с [29] параметры стандартной
атмосферы при И км терпят излом. Зависимость плотности атмо-
сферного воздуха от высоты в районе Н* 11 км показана на рис. 7.19:
при Н> 11 км падение плотности воздуха по высоте является более
276 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
Рис. 7.18. Оптимальный профиль разгона - набора высоты в случае,
когда тяга не зависит от числа Маха
интенсивным, что при определенных условиях делает невыгодным
подъем ЛА на высоты больше 11 км.
Увеличение тяговооруженности до = 0,8 приводит к увеличению
максимально достижимого числа Маха до ~2,5. В диапазоне чисел
М = 2,14-2,4 реализуется участок постоянной высоты ТУ— 11 км. При
М > 2,4 оптимальный разгон осуществляется с одновременным увели-
чением высоты (см. рис. 7.18).
Б. Траектория разгона сверхзвукового самолета с ТРДДФ. Для
реального ВРД его тяга и удельный импульс являются сложными функ-
циями высоты и числа Маха. В качестве примера рассмотрим типовой
ТРДДФ. Для простоты будем
Рис. 7.19. Зависимость плотно-
сти атмосферного воздуха от
высоты в районе 11 км
ь, что двигатель имеет два основ-
ных режима работы: режим
максимального удельного им-
пульса и режим максимальной
форсажной тяги; топливо - керо-
син. При переходе от первого
режима ко второму тяга увеличи-
вается в ~ 2 раза, а удельный
импульс уменьшается в ~ 2 раза.
Основные высотно-скорост-
ные характеристики ТРДДФ на
режиме максимальной форсаж-
ной тяги представлены на
рис. 7.20 и 7.21. На рис. 7.20<я
показано изменение тяги, а на
7.4. Оптимизация траекторий на участке работы турбокомпрессорных ВРД 277
рис. 7.206 - коэффициента тяги в
зависимости от числа Маха при
Н = const (здесь 7?0 и qQ - тяга и
скоростной напор при взлете).
Видно, что тяга двигателя увели-
чивается по числу Маха, а коэф-
фициент тяги - монотонно
уменьшается. Таким образом,
зависимость тяги от числа Маха
носит некоторый промежуточный
характер между рассмотренными
выше вариантами А1 и А2.
Удельный импульс двигателя при
увеличении числа Маха (при
Н= const) уменьшается (см.
рис. 7.20в).
Зависимость удельного им-
пульса и коэффициента тяги от
высоты (при М » const), как пра-
вило, для всех типов турбоком-
прессорных ВРД имеет вид, как
показано на рис. 7.21. При увели-
чении высоты вплоть до Н= 11 км
удельный импульс J и отношение
тяги к плотности атмосферного
воздуха 7?/р увеличиваются вслед-
ствие уменьшения температуры
атмосферного воздуха (индекс
"И” на рис. 7.21 соответствует
высоте 11 км). Так как следующий
атмосферный слой является
изотермическим, то в диапазоне
Н= 114-25 км эти величины прак-
тически постоянны.
В результате максимизации
функции /рзг (7.42) был получен
оптимальный профиль разгона -
набора высоты сверхзвукового
самолета с ТРДДФ (рис. 7.22);
здесь принято, что стартовая
тяговооруженность ЛА на макси-
мальном форсажном режиме
составляет Л 0,5. На режиме
максимального удельного им-
пульса оптимальная траектория
целиком лежит в дозвуковой
Рис. 7.20. Зависимости относи-
тельной тяги (а), относительного
коэффициента тяги (6) и удельно-
го импульса ТРДДФ (в) от числа
Маха при Н = const
278 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
Рис. 7.21. Зависимость тяги и
удельного импульса ТРДДФ (в
относительном виде) от высоты
полета при М = 2
области. Максимальная высота
подъема составляет ~ 9 км, число
Маха увеличивается от 0,75 до 0,95.
Здесь же пунктиром показан про-
филь полета, соответствующий
условию Тэф -> гпах при Е = const.
Видно, что эта траектория в коор-
динатах "Н- М" лежит левее.
При переходе на режим макси-
мальной форсажной тяги траекто-
рия набора высоты в дозвуковой
области сдвигается в сторону
больших чисел Маха. На высоте
//«9 км траектория терпит излом:
переход в сверхзвуковую область
осуществляется при Е « const (т.е. с
уменьшением высоты до Н~6 км).
Далее осуществляется разгон - набор высоты до Н ~ 11 км. При М > 1,6
оптимальный разгон соответствует движению на постоянной высоте
Н« 11 км. В данном случае наличие участка Н= const объясняется
изломом не только функции р(77), но и изломами функций J(H) и
7?/р(//), как это видно из рис. 7.21.
Таким образом, при наличии основных ограничений //>//1пй1д и
q ^q^xj\ оптимальная траектория на режиме максимальной форсажной
тяги состоит из четырех участков (см. рис. 7.22):
Рис. 7.22. Оптимальный профиль разгона - набора высоты сверх-
звукового самолета с ТРДДФ, полученный с использованием
гипотезы квазистационарности
7.4. Оптимизация траекторий на участке работы турбокомпрессорных ВРД 279
- разгон вдоль минимально допустимой высоты Н= Я,^пд;
- оптимальный разгон - набор высоты с двумя изломами в коорди-
натах "Н- М”;
- разгон на высоте Н= 11 км;
- разгон с максимально допустимым скоростным напором #тахД •
Ограничение на максимальный скоростной напор обычно состав-
ляет 504-75 кН/м2, что соответствует числам Маха 1,754-2,15 на высоте
Н= 11 км. В зависимости от характера аэродинамических характери-
стик самолета и характеристик его двигателя участок Н = И км может
отсутствовать.
Из рис. 7.22 видно, что оптимальный профиль разгона, построен-
ный с использованием гипотезы квазистационарности, не является
гладким в координатах "Я- М", а содержит участок полета со снижени-
ем высоты. На участке уменьшения высоты при Е = const угол наклона
траектории может быть любым в диапазоне -л/2 < 0 < 0. В точках изло-
ма профиля в координатах ’’высота - скорость” угол наклона траектории
претерпевает разрыв. Все эти обстоятельства связаны с упрощением
системы дифференциальных уравнений. Здесь следует отметить, что
расчет траекторий оптимального набора высоты с использованием
полной системы уравнений в работе [НО] показал, что участок умень-
шения высоты на режиме Е « const может отсутствовать. При дискрет-
ном изменении режима работы двигателя (например при включении
форсажного режима) траектория оптимального набора высоты в коор-
динатах ”Я- И” имеет разрыв (см. рис. 7.22). Все это указывает на то,
что не следует непосредственно применять полученный оптимальный
профиль полета в качестве программного для последующего численно-
го интегрирования полной системы
уравнений движения.
Методически правильнее ис-
пользовать полученный профиль в
качестве начального приближения
для построения программного про-
филя полета. Для этого его необхо-
димо сгладить и аппроксимировать
кусочно-линейной зависимостью с п
узлами. На рис. 7.23 показан пример
такого исходного профиля в коорди-
натах "Я- М".
В итоге, оптимальный про-
граммный профиль полета получает-
ся в результате минимизации массы
топлива как функции нескольких
переменных:
т«т (М,, Я,, Мп)-> min; /=1,...,и.
Рис. 7.23. Программный про-
филь полета, заданный в виде
кусочно-линейной зависимости
280 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
Здесь М/, Ht - координаты узлов профиля; Мп- число М переключения
режимов работы ВРД.
В начальной точке скорость и высота обычно являются заданными,
конечная точка соответствует выходу на режим #тахД. Масса топлива
шт определяется в результате численного интегрирования полной сис-
темы уравнений.
Практика расчетов показала, что при формировании программного
профиля, как правило, достаточно использовать 4-5 узлов. Оптимиза-
цию можно проводить, последовательно перебирая координаты точек
излома.
Оптимальный режим работы ВРД в каждой точке траектории (при
K=fix и //=fix) определяется из условия максимума эффективного
импульса:
</эф -> max.
Как следует из выражения (7.43), на тех участках полета, где
X^/R « 1, максимум эффективного импульса ЛА однозначно определя-
ется максимумом удельного импульса ВРД. Такой режим работы двига-
теля реализуется на умеренных дозвуковых скоростях полета. В тех
случаях, когда величина /R близка к 1, оптимальным является режим
максимальной тяги (максимальной форсажной тяги) ВРД. Такой режим
реализуется в трансзвуковом диапазоне скоростей, вплоть до скорости
отключения турбокомпрессорных ВРД. На остальных участках полета
возможны и другие (промежуточные) режимы работы ВРД.
На рис. 7.24 в качестве примера представлена расчетная траектория
разгона сверхзвукового самолета с ТРДДФ (стартовая тяговооружен-
Рис. 7.24. Оптимальная траектория разгона - набора высоты ЛА с ТРДДФ:
а) влияние отклонения программного профиля от оптимального на относи-
тельный запас топлива; б) изменение угла наклона траектории и
числа Маха в зависимости от времени полета
7.4. Оптимизация траектории на участке работы турбокомпрессорных ВРД 28 I
ность~0,5; характеристики двигателя представлены на рис. 7.20 и
7.21). В данном случае учтено одно ограничение: НПП11Д = О. Сплошной
линией показана траектория, полученная с использованием изложенно-
го выше алгоритма. Видно, что участок оптимального набора высоты
постепенно переходит в участок разгона на высоте Н= 11 км. Реализо-
валось одно переключение с режима максимального удельного импуль-
са на режим максимальной форсажной тяги (при М =0,9). Относитель-
ный запас топлива при разгоне вдоль оптимального профиля составляет
0,09. Сдвиг профиля набора высоты влево или вправо на ДМ = 0,2
(пунктирные кривые на рис. 7.24а) приводит к увеличению относитель-
ного запаса топлива с 0,09 до 0,1.
На рис. 7.246 показано изменение во времени угла наклона траек-
тории и числа Маха. Обычно максимум угла наклона траектории реали-
зуется на участке набора высоты; величина максимума может достигать
Отах= 30° и более. Увеличение тяговооруженности ЛА приводит к
увеличению 01пах. Характерно, что в данном случае таких максимумов
два: на каждом из двух режимов работы двигателя. Видно, что на уча-
стках с интенсивным изменением угла наклона траектории во времени
гипотеза квазистационарности нарушается (dQ/dx»0). При этом
реальное значение нормальной перегрузки может достигать 2-ьЗ, что
существенно больше квазистационарной перегрузки (л?укв< !)•
Таким образом, при малых скоростях полета гипотеза квазиста-
ционарности должна использоваться только для получения программ-
ного профиля первого приближения.
Одним из важнейших вопросов проектирования аэрокосмических
ЛА является выбор оптимальной тяговооруженности ВРД. Причем
основным условием правильного выбора этой величины является обес-
печение гарантированного прохождения
скоростей. Особенно остро этот вопрос
стоит применительно к ЛА с комбиниро-
ванной силовой установкой с большой
степенью расширения сопла. На
рис. 7.25 в качестве примера показано
соотношение сил тяги и лобового сопро-
тивления при разгоне ЛА с РТД и
ГПВРД. Видно, что наиболее критичным
является диапазон чисел М = 1,14-1,5, где
избыточная сила тяги двигателя мини-
мальна. Эту особенность необходимо
учитывать в процессе оптимизации
траекторий разгона ЛА. Если в трансзву-
ковом диапазоне, или на другом участке
разгона имеет место /эф «Ад, то это
означает, что параметры ЛА или его
программная траектория выбраны нера-
ционально и необходимо переопределе-
трансзвукового диапазона
Рис. 7.25. Соотношение
между силой тяги ВРД и
лобовым сопротивлени-
ем ЛА в трансзвуковой
области
282 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
ние основных проектных параметров и в первую очередь тяги двигате-
лей.
Как следует из приведенного выше, оптимальный профиль полета
прямо не зависит от конечной удельной энергии (от скорости отключе-
ния ВРД). Это значит, что все сказанное можно обобщить на случай,
когда скорость отключения ВРД является переменной и оптимизируется
по какому-либо критерию.
В частных случаях уравнение (7.44) интегрируется аналитически.
При /рЗГ = const имеем:
/ик/ото= ехр[(£0-£к)//рзг]. (7.46)
В случае линейной зависимости /Рзг от удельной энергии получим
,п^ = 1|пАзп<., где Ь= ^зг.к-Лзг.о (7.47)
тК Ь /рзг.о Д< ~ *0
При необходимости траекторию можно разделить на несколько
участков с соответствующим законом изменения функции УрЗГ (£).
7.5. Оптимизация траекторий на участке работы
прямоточных ВРД
В начале главы было показано, что при увеличении скорости поле-
та угол 0 и его производная по времени монотонно уменьшаются по
модулю. Отсюда следует, что на участке работы прямоточных двигате-
лей применение гипотезы квазистационарности является более право-
мерным, чем на участке работы турбокомпрессорных ВРД. При боль-
ших скоростях полета в соотношении (2.132) можно пренебречь
слагаемым gjH'v /V по сравнению с единицей, в результате получим
dE= VdV/gT, (7.48)
что означает эквивалентность условий Е = fix и V= fix.
С учетом (7.48) перепишем квазистационарную систему уравнений
(2.133):
dV/dx = Rlx /т; dm/dx = - R/J. (7.49)
В данном случае, как показано в разделе 2.9, оптимальное управ-
ление в каждой точке траектории определяется из условия максимума
эффективного импульса ЛА:
</эф= J——> max при V= fix, (7.50)
R
то есть задача оптимизации управления сводится к задаче отыскания
условного максимума функции нескольких переменных </эф(^ь w2,
wn).
Основным условием является неравенство
7.5. Оптимизация траекторий на участке работы прямоточных ВРД 283
q^qm^(y), (7.51)
где текущий скоростной напор определяется в результате решения
уравнения равенства вертикальных сил:
ср = R^y cosy - wgv cos0 = 0 . (7.52)
В процессе оптимизации управления текущее время обычно не
требуется, поэтому его можно исключить из системы уравнений (7.49).
В результате остается одно дифференциальное уравнение для текущей
массы ЛА:
dmldV=-mlJw. (7.53)
Так как при больших скоростях угол наклона траектории мал, то в
уравнении (7.52) можно положить cos0 = 1. При необходимости угол 0
определяется с использованием соотношения (2.129), где производная
Н'\ вычисляется в процессе интегрирования уравнения (7.53) с учетом
(7.51) и (7.52).
На участке работы прямоточных ВРД управляющими переменны-
ми, как правило, являются угол атаки а и режим работы двигателя
(коэффициент избытка воздуха аКс)- Будем полагать, что в качестве
дополнительных управляющих переменных могут использоваться угол
отклонения вектора тяги реактивного сопла 5 и угол крена у. При этом
пространственное движение не будем рассматривать, т.е. при cosy < 1
будем считать, что siny = 0.
Проведем предварительный анализ функции />ф и уравнения
(7.52). Эффективный импульс ЛА определяется главным образом
удельным импульсом двигателя J, который в общем случае зависит от
коэффициента избытка воздуха аКс, числа Маха, угла атаки а и высоты
полета Н. Так как диапазон углов атаки, обеспечивающих максимум
близок к летному, то в первом приближении зависимостью 7(a) можно
пренебречь.
Тяга прямоточного двигателя связана с его удельным импульсом
следующим образом:
R = cKqF~, c^=2f J . (7.54)
<W(/
Здесь У7-площадь входа в двигатель;
f - коэффициент расхода воздуха через двигатель;
/о -стехиометрический коэффициент (для водорода 34,3).
При нижнем (подфюзеляжном) расположении воздухозаборника
/~/из Ап,
где /из~ коэффициент расхода воздуха изолированного ВЗ;
Ап- коэффициент поджатия потока нижней поверхностью носовой
части фюзеляжа (см. раздел 6.3).
284 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
При лобовом воздухозаборнике/=/из •
Из (7.54) следует, что коэффициент тяги двигателя cR обратно про-
порционален скорости. В интегральной компоновке ЛА (при нижнем
расположении ВРД) тяга двигателя практически линейно зависит от
угла атаки. От коэффициента избытка воздуха аКс тяга зависит прямо и
косвенно (через удельный импульс). В диапазоне аКс> 1 увеличение
аКс приводит к уменьшению тяги двигателя.
Компоненты результирующей силы 7?^х и 7?Sy, входящие в (7.50) и
(7.52), в общем случае определяются по формулам (2.54). Запишем эти
компоненты в следующем виде:
sin(a + 8) + су qS; = 7?с cos(a + 8) - Ц - ск qS. (7.55)
Здесь /?( - тяга реактивного сопла. Силы, действующие на жидкий
контур входной струи воздуха, учтены в коэффициентах су и с\.
Будем полагать, что тяга PC и тяга двигателя связаны следующим
образом:
RC = R + L, (7.56)
где /« = 2fqF- входной импульс ВРД.
При нижнем расположении воздухозаборника входной импульс
ВРД и тяга PC практически линейно зависят от угла атаки.
Аэродинамические коэффициенты су и сх зависят от числа Маха,
угла атаки и высоты.
Таким образом, эффективный импульс ЛА в каждой точке траекто-
рии (при V= fix) зависит от 4-х переменных:
•/эф = •/эф(7/, ос, секс, 5).
В уравнение (7.52) входят 5 переменных:
ср(//, а, аКс, 8, у) = 0.
Эффективный импульс ЛА не зависит от угла крена. Если в задаче
разрешается использовать угол крена в качестве управляющей пере-
менной, то он однозначно определяется из уравнения (7.52), а высота
полета становится независимой величиной при максимизации эффек-
тивного импульса ЛА. Вместо высоты иногда удобнее использовать
скоростной напор.
Если в задаче задано у = fix, то высота полета будет однозначно оп-
ределяться из уравнения (7.52), а число независимых переменных
функции ,/Эф уменьшается на единицу. Из уравнения (7.52) вместо
высоты иногда удобнее определять угол атаки а или угол 8, тогда высо-
та становится независимым аргументом функции /Эф-
В случае, когда угол крена и угол отклонения вектора тяги PC не
используются в качестве управляющих переменных, они должны быть
заданы в виде функций фазовых координат и управляющих переменных
а и акс • Чаще всего задано у = 0.
7.5. Оптимизация траектории на участке работы прямоточных ВРД 285
Рассмотрим влияние высоты на эффективный импульс ЛА и на
слагаемые уравнения (7.52). Пусть высота полета увеличивается на
5 км (при V = const), что примерно соответствует уменьшению плотно-
сти атмосферного воздуха в два раза. В соответствии с увеличением
радиуса г ускорение gv уменьшается на ~ 0,2%. В первом приближении
этим изменением можно пренебречь.
В диапазоне высот Hv = 20-ь47 км, где преимущественно использу-
ются прямоточные ВРД, в соответствии с СА-81 увеличение высоты
сопровождается увеличением скорости звука. В результате при увели-
чении высоты на 5 км (при V= fix) число Маха уменьшается на 0,2н-0,4,
что приводит к соответствующему изменению характеристик ЛА.
Кроме того, число Re при этом уменьшается в ~ 2 раза. Вследствие
уменьшения числа Re коэффициент cxmin увеличивается, а удельный
импульс двигателя J уменьшается. Изменение этих величин может
достигать 10-е-20 %, что существенно больше по сравнению с изменени-
ем других безразмерных коэффициентов (суа, /из, Au), входящих в
соотношения (7.50) и (7.52).
В общем случае задача максимизации эффективного импульса ЛА
решается численно с использованием стандартных процедур. При этом
используются исходные зависимости без всяких упрощений. После
решения задачи формирования управления определяются функции
Якв(П и Окв(К), которые затем используются при интегрировании
полной системы уравнений движения (см. раздел 2.10).
Определим оптимальное управление для различных вариантов за-
дачи. Там, где это возможно, будем находить аналитические решения с
использованием некоторых упрощений.
Оптимальные угол атаки, угол крена, угол отклонения вектора
тяги реактивного сопла и скоростной напор.
Пусть режим работы двигателя является известным. Будем рас-
сматривать два основных варианта зависимости аэродинамических
характеристик ЛА и характеристик ВРД от высоты. В первом случае
будем полагать, что при увеличении высоты (при М = fix) характери-
стики ЛА ухудшаются: коэффициент сХ1П1П увеличивается, а удельный
импульс ./уменьшается. Во втором (частном) случае будем считать, что
эти величины не зависят от высоты.
Перепишем выражение для эффективного импульса ЛА (7.50) и
уравнение равенства вертикальных сил (7.52) с использованием соот-
ношений (7.55) и (7.54):
_ 7?cCos(a + 5)-4-cxqS
«'ЭФ — О ------------------ \
c^qF
(р = [2?с sin(a + 5) + CygSJcosy - mgy = 0 .
Здесь принято cosO = 1.
(7.57)
(7.58)
286 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
С учетом малости углов а и 5 и с учетом соотношения (7.56) полу-
чим
Лф«У(1_£^.£). (7.59)
cR F
Эта формула становится точной при 5 = -а.
Так как зависимость J от а является не столь существенной, как
с\(а), то в первом приближении оптимальный угол атаки можно найти
из условия
cx/cR--»min при V= fix. (7.60)
Рассмотрим два характерных случая зависимости коэффициента
тяги двигателя от угла атаки.
7. Коэффициент тяги cR не зависит от угла атаки. Такой слу-
чай реализуется при лобовом воздухозаборнике. Из (7.60) имеем
тривиальное решение с\ —> min, т.е. су -> min. С учетом (7.58) получим
су ~--------> min ,
qS cosy
Рис. 7.26. Зависимость эффективного
импульса ЛА от скоростного напора
на участке работы ГПВРД
откуда следует, что оптималь-
ные скоростной напор и cosy
должны быть максимальными,
т.е.
У opt — 0 И 7opt — <7тахД • (7.61)
Решение (7.61) является
справедливым как в случае,
когда величины J и cxmin зави-
сят от высоты, так и в случае,
когда эти величины не зависят
от высоты. На рис. 7.26 для ЛА
с ГПВРД показана расчетная
зависимость эффективного
импульса аппарата от скорост-
ного напора для нескольких
значений скорости полета
(остальные управляющие
переменные при этом являются оптимальными). При увеличении ско-
ростного напора эффективный импульс ЛА монотонно увеличивается,
что иллюстрирует полученное решение. Очевидно, что решение
7opt = <7тахд будет также справедливым при у = fix * 0.
Используя решение (7.61), определим оптимальный угол 5 для ва-
рианта симметричной поляры ЛА (сх = с\ min + Асу2). Так как удельный
импульс и модуль тяги ВРД не зависят от угла 5, то, как следует из
(7.50), максимуму эффективного импульса будет однозначно соответст-
7.5. Оптимизация траектории на участке работы прямоточных ВРД 287
вовать максимум по 5. В данном случае из двух управляющих пере-
менных а и 5 независимой является одна, а вторая определяется из
уравнения (7.58) при у = 0 и q= <7тахд. Выразим из (7.58) коэффициент
аэродинамической подъемной силы:
_ wgv - Лс sin(a + 5)
Cyq (7.6^)
<7тахД^
откуда
дсу /дЬ = - Rq cos(a + 8)/(^тахД5).
Из необходимого условия экстремума функции 7?vx по углу 8
dR^x /58 = - Rc sin(a + 8) - 2Асу qmaKj]S дсу /58 =
= - Rc sin(a + 8) + 2Лсу Rc cos(a + 8) = 0
получим tg(a + 8) = 2Лсу, или
8opt = arctg(2^cy) - a .
В частном случае (при су=суаа) с учетом приближенного равенст-
ва^/» 1 имеем
8opt»a. (7.63)
Физический смысл полученного решения заключается в том, что
дополнительная составляющая подъемной силы за счет тяги двигателя
позволяет уменьшить потребный коэффициент су и, соответственно,
уменьшить индуктивное сопротивление. При этом, несмотря на незна-
чительное уменьшение тангенциальной составляющей силы тяги,
величина R^x увеличивается. Характерно, что приближенное равенство
(7.63) совпадает с аналогичным соотношением для ЛА с ЖРД
(см. раздел 3.5). В обоих случаях модуль тяги двигателя не зависит от
угла атаки.
С учетом найденного решения (7.63) из выражения (7.62) получим
оптимальный угол атаки, соответствующий движению с максимально
допустимым скоростным напором:
C^opt
Су ^шахД^ +
(7.64)
В качестве примера на рис. 7.27 показана зависимость угла атаки
aopt от числа Маха для ЛА с ГПВРД (при дП1ахд = 75 кН/м2). Видно, что
при увеличении удельной нагрузки на крыло G/S угол атаки aopt увели-
чивается. Аналогичное влияние на угол aopt оказывает уменьшение
<7тахд- При числах М > 10-И2 оптимальный угол атаки начинает умень-
шаться, что связано с соответствующим уменьшением ускорения gv за
счет роста слагаемого HA2/(gr).
288 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
Рис. 7.27. Зависимость опти-
мального угла атаки от числа
Маха в случае, когда тяга ВРД
не зависит от угла атаки
U/тахД = 75 КН/М2)
части фюзеляжа используется в
случае зависимость коэффицие
линейной (см. раздел 6.3):
В выражениях (7.62) и (7.64) угол
атаки зависит от режима работы
двигателя через величину тяги PC. В
первом приближении можно пренеб-
речь вертикальной составляющей
силы тяги PC, тогда
Су q ~ ^^у/С^тахД4^) >
т.е. угол атаки можно определять вне
зависимости от режима работы двига-
теля, а затем проводить оптимизацию
коэффициента акс при сх q.
2. Коэффициент тяги cR линей-
но зависит от угла атаки. Такая
зависимость имеет место в инте-
гральной компоновке ЛА с нижним
расположением прямоточных ВРД,
когда нижняя поверхность носовой
качестве первого клина сжатия. В этом
нта поджатия от угла атаки близка к
7<п “ 1 + 7<па (сс + аВз),
где аВз-угол заклинения нижней поверхности носовой части фюзеля-
жа относительно линии отсчета угла атаки.
Представим зависимость cR(a) в следующем виде:
Cr = £ro + ИЛИ Cr — CRa(Xo + ос), (7.65)
где Х<) = cRo/cRa.
Коэффициент расхода воздуха изолированного воздухозаборника
зависит от угла атаки через местное число Маха в начальном сечении
ВЗ (см. раздел 6.3). В первом приближении этой зависимостью можно
пренебречь, тогда из формулы (7.54) получим, что производная cRa
пропорциональна производной А*па, и можно записать
Хо = А'п|^о/А'псх = 1/7<па + авз. (7.66)
Полагая, что в выражении (7.57) для эффективного импульса ЛА
cos(a 5)« 1, определим оптимальный угол атаки. С учетом соотноше-
ния (7.65) минимизируемая функция (7.60) примет вид
сх / (Хо + a)-> min при V= fix. (7.67)
Пусть аэродинамическая поляра является квадратичной:
Су — Су() + Су Сх Сх min + Л(Су — Су ) ,
7.5. Оптимизация траектории на участке работы прямоточных ВРД 289
тогда оптимальный угол атаки, соответствующий минимуму функции
(7.67), будет равен
aopt= + А - V
(7.68)
где А = (суо - су*)(су0 - су* - 2cyaAo)/(cya)2.
Аналогичное выражение получено в работе [25]. Для симметрич-
ной поляры имеем суо=су* = О и, кроме того, cxinin = Я(суа аКт)“, где угол
акт соответствует максимальному аэродинамическому качеству. Тогда
выражение для оптимального угла атаки упрощается:
/2 2
O^opt — у ^Кт + ^0 —
(7-69)
Таким образом, оптимальный угол атаки зависит от aKm, от произ-
водной 7<па и от угла заклинения нижней поверхности носовой части
фюзеляжа авз •
Рассмотрим в качестве примера разгон ЛА с ГПВРД в диапазоне
чисел М = 6^-16, приняв следующие исходные данные: производная /Спа
увеличивается от 5,7 до 19; максимальное аэродинамическое качество
уменьшается от 4 до 3,5. Эти исходные данные будут использоваться в
дальнейших примерах расчетов.
На рис. 7.28 показано изменение угла атаки, соответствующего
Тчпах • При увеличении числа М вели-
чина 7<тах уменьшается, а угол aKm
увеличивается, как это следует из
соотношения (2.67). Оптимальный угол
атаки, вычисленный по формуле (7.69),
показан на рис. 7.28 для двух значений
угла заклинения ВЗ: 0 и 2°. Видно, что
O^opt < ОСкш •
При уменьшении угла заклинения
(хВз и при увеличении скорости полета
оптимальный угол атаки увеличивает-
ся, приближаясь к акт • Действительно,
анализ формулы (7.69) с учетом (7.66)
показывает, что при уменьшении
Хо (т.е. при уменьшении угла авз и при
увеличении производной Л*па) имеет
Рис. 7.28. Зависимости опти-
мального угла атаки и угла
aKm от числа Маха в случае,
когда тяга ВРД линейно
зависит от угла атаки
место aopt->aKln.
Следует отметить, что оптимальный угол атаки не зависит от ре-
жима работы двигателя, поэтому его необходимо определять первым.
290 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
Окончательно оптимальный угол атаки должен определяться с ус-
ловием q < д|Пахд • Как будет показано ниже, траектория разгона в общем
случае состоит из двух характерных участков. В зависимости от того,
используются углы у и 8 в качестве управляющих переменных или не
используются, возможны несколько вариантов. Рассмотрим каждый из
них.
2А. Углы крена и отклонения вектора тяги PC используются в ка-
честве управляющих переменных. В этом случае из условия (7.58)
определяется угол крена или угол отклонения вектора тяги PC (при
у = fix), а высота становится независимым аргументом максимизируе-
мой функции (7.57). Для определения оптимальной высоты запишем
выражение (7.59) для эффективного импульса ЛА с использованием
формулы (7.54):
(сх min + ^су
2/F
/эф ~ /
аксЛ0К
Рассмотрим вначале основной случай, когда величины cxmin и J за-
висят от высоты. При любом значении угла атаки увеличение q (умень-
шение Н) будет приводить к увеличению эффективного импульса ЛА
вследствие увеличения удельного импульса двигателя J и уменьшения
коэффициента cxmin. То есть на всей траектории полета с прямоточными
ВРД оптимальным является максимально допустимый скоростной
напор, который в общем случае может зависеть от скорости:
(/opt — 9Гтахд(Р)’
Зависимость эффективного импульса ЛА от скоростного напора
аналогична зависимости, представленной на рис. 7.26. В данном случае
при задании аэродинамических характеристик ЛА и характеристик ВРД
должна использоваться высота, соответствующая 7тахд, что упрощает
вычисления. В примерах используется величина д1пахд = 75 кН/м2.
В общем случае расчетная траектория полета состоит из двух уча-
стков (рис. 7.2967). На первом участке yopt = 0; угол 8 определяется из
уравнения (7.58):
о . , у/ С ор^тзхД*^ х
8q = arcsin(------—--------) - aopt. (7.70)
Ac
Так как в данном случае 8q ^-a, то значение угла атаки, опреде-
ленное по формуле (7.68), будет отличаться от оптимального (так, при
М = 6 отличие достигает 15%). Точное значение оптимального угла
атаки может быть найдено в результате численной максимизации функ-
ции (7.57) с условием (7.70).
На втором участке полета (при больших скоростях) угол крена оп-
ределяется из уравнения (7.58), угол 8 становится независимым аргу-
7.5. Оптимизация траектории на участке работы прямоточных ВРД 291
Рис. 7.29. Оптимальная траектория разгона ЛА с ГПВРД:
а) характеристики ЛА ухудшаются при увеличении высоты;
б) характеристики ЛА не зависят от высоты
ментом при максимизации эффективного импульса ЛА. Как следует из
выражения (7.57), максимум 7Эф по 8 достигается при cos(a + 8) = 1, т.е.
8opt &opt • (7.71)
При этом оптимальный угол крена определяется из выражения
cosyop, = "*gv . (7.72)
S opt^max Д4^
Оптимальный угол атаки вычисляется по формуле (7.68), которая в
данном случае становится точной. Скорость начала 2-го участка опре-
деляется из условия
£у opt (/тахД S mgN •
При уменьшении G/S и при увеличении д1пахД протяженность пер-
вого участка уменьшается и, соответственно, угол крена на втором
участке увеличивается. При увеличении протяженности первого участ-
ка оптимальный угол 8 в начале траектории увеличивается и может
стать положительным.
При разгоне ЛА с ПВРД, как правило, реализуется только первый
участок полета. Второй участок полета реализуется только при больших
скоростях полета (при разгоне с ГПВРД), когда поджатие носовой части
фюзеляжа становится существенным. На рис. 7.29я показаны опти-
мальные значения управляющих переменных в зависимости от числа М
полета для случая, когда величины J и cxlnin зависят от высоты. В дан-
ном случае второй участок начинается при М « 7,8. На 2-ом участке
зависимость aopt(M) совпадает с аналогичной зависимостью, представ-
292 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
ленной на рис. 7.28 (при аВз = 0°). Угол крена увеличивается и достига-
ет величин 60° и более.
Рассмотрим случай, когда величины cxinin и <7 не зависят от высоты
(при М = fix). На первом участке полета имеет место равенство
7орг = 7тахд и все управляющие переменные определяются так же, как и
в предыдущем случае. На втором участке ^opt * 7таХд , поэтому формулы
(7.68) и (7.71) могут служить только для приближенного определения
углов а и 5 (эти формулы становятся точными для изотермической
атмосферы). Для определения оптимальной высоты на втором участке
исключим скоростной напор из выражения (7.57):
A„^C'Rcl:°S(at5b2/~^,J7. (7.73)
CR
Здесь коэффициенты тяги PC и двигателя связаны между собой сле-
дующим образом:
Crc = Cr + 2/.
В частном случае, при а = const, условия V= fix и М = fix совпа-
дают, и из выражения (7.73) видно, что эффективный импульс ЛА не
зависит от высоты. Это значит, что из условия (7.58) будет однозначно
определяться произведение
gcosy = mgy/(cyopiS),
а угол крена может быть любым в диапазоне (Ну1пах, где у1пах вычисляет-
ся по формуле (7.72). При этом скоростной напор может быть любым в
диапазоне ?т1п-^1пахд, где ^min соответствует утах.
Очевидно, что с целью уменьшения аэродинамического нагревания
можно положить у = 0, тогда на втором участке полета вследствие
увеличения оптимального угла атаки скоростной напор будет монотон-
но уменьшаться:
q^ = mg\l(cyop{S). (7.74)
В действительности, в диапазоне высот Ну = 20-ь47 км увеличение
высоты при K=fix приводит к уменьшению числа Маха. Поэтому
точное значение оптимальной высоты может быть определено только в
результате численной максимизации функции (7.73) при условии (7.70).
Расчетные значения оптимального скоростного напора представлены на
рис. 7.296. В данном случае второй участок начинается при М = 7,4.
2Б. Угол отклонения вектора тяги PC является заданным:
Ъ = 8(М). Как и в варианте 2А, траектория состоит из двух участков. На
первом участке yopt = 0 и gopt = <?тахд • Угол атаки определяется в резуль-
тате решения нелинейного уравнения (7.58). Приближенная формула
для коэффициента аэродинамической подъемной силы имеет вид
Cyq ~ ^^у/(^тахдУ) .
7.5. Оптимизация траекторий на участке работы прямоточных ВРД 293
В основном случае, когда величины J и cxmin зависят от высоты, на
втором участке полета, как и в варианте 2А, оптимальным является
максимально допустимый скоростной напор
<7opt — <7тахД •
Оптимальный угол крена определяется из уравнения (7.58):
₽‘ ^sin(a + 5) + Cyopt^5 ’
Условие для определения начала 2-го участка полета получается из
(7.75):
Rc sin(a + S) + су „pt ?тахд5 = mgv .
Приближенное решение для оптимального угла атаки на 2-ом уча-
стке можно найти по формуле (7.68). Точное значение aopt может быть
найдено только в результате численной максимизации (7.57) при
Я ~ <7тахД •
Расчетные зависимости оптимальных углов атаки и крена от числа
Маха показаны на рис. 7.30я при двух значениях угла 8 (минус 4° и 4°).
Зависимости качественно ведут себя так же, как и в варианте 2А. При
переходе от 8 = -4° к 8 = 4° угол атаки уменьшается, а угол крена уве-
личивается. При этом уменьшается протяженность первого участка и
эффективный импульс ЛА по траектории разгона, так как угол 8 суще-
ственно отклоняется от своего оптимального значения.
6
10
а)
14 М
Рис. 7.30. Оптимальная траектория разгона ЛА с ГПВРД при фикси-
рованном угле отклонения вектора тяги PC:
а) характеристики ЛА ухудшаются при увеличении высоты;
б) характеристики ЛА не зависят от высоты
294 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
Рис.7.31. Приращение эффективного импульса ЛА с
ГПВРД в зависимости от угла крена
Расчетное приращение эффективного импульса ЛА в зависимости
от угла крена при 8 =-4° показано на рис. 7.31. Видно, что при боль-
ших скоростях полета использование угла крена в качестве управляю-
щей переменной может привести к увеличению <7Эф на 130 м/с и более
по сравнению с вариантом у = 0. Появление такого решения объясняет-
ся тем, что использование управления углом крена позволяет одновре-
менно обеспечить движение с минимально возможной высотой и с
оптимальным углом атаки (что дает возможность увеличить тягу ВРД за
счет поджатия входной струи воздуха). При отклонении угла 8 от своего
оптимального значения выигрыш от использования угла крена увеличи-
вается.
В частном случае, когда величины cxmin и <7 не зависят от высоты
(при М = fix), по аналогии с вариантом 2А необходимо принять на 2-ом
участке yopt = 0. Тогда скоростной напор будет определяться из уравне-
ния (7.58):
=_______________________
CRcFsin(aOpt+8) + Cyopt5
(7.76)
Здесь коэффициент тяги PC вычислен при aopt.
Приближенное значение оптимального угла атаки можно найти по
формуле (7.68) в предположении, что высота соответствует 7,пахД. Точ-
ные значения aopt и 7opt могут быть найдены в результате численной
максимизации эффективного импульса ЛА при условии (7.76). Расчет-
ные зависимости aopt и gopt от числа Маха показаны на рис. 7.306 при
8 = -4°. Качественно зависимости такие же, как и в варианте 2А.
7.5. Оптимизация траекторий на участке работы прямоточных ВРД 295
2В. Угол крена задан фиксированным: у = 0. На первом участке по-
лета управляющие переменные определяются так же, как и в варианте
2А:
(/opt ~ <7тахД ,
угол 8 - по формуле (7.70); угол а - в результате численной максимиза-
ции функции (7.57) при условии (7.70).
На втором участке полета в общем случае, когда величины cxmin и J
зависят от высоты, оптимальные значения а, 8 и q определяются только
в результате численной максимизации эффективного импульса ЛА при
условии (7.58). При этом имеет место неравенство q < ^,пахд • Прибли-
женное значение aopt может быть найдено по формуле (7.68) при
Q ~ ^шахД •
В частном случае, когда величины cxmin и Уне зависят от высоты, а
атмосфера является изотермической, на втором участке полета
^opt СХ-opt •
Оптимальный угол атаки определяется по формуле (7.68), которая в
данном случае становится точной. Скоростной напор определяется по
формуле (7.74). Скорость начала 2-го участка определяется из условия
opt ^шахД $ mgN •
Следует отметить, что при уменьшении поджатия носовой части
ЛА решение 8opt = -aoptH решение 8opt = aopt, полученное в варианте 1
(когда тяга ВРД не зависит от угла атаки), сближаются при #тахд -> °0-
Действительно, в этом случае в варианте 1 получаем су —> 0 и
^opt ~ O^opt — 0 •
В варианте 2 при Киа —> 0 из формулы (7.69) имеем aopt = 0 и, следова-
тельно, также получаем
6Opt O^opt — 0*
Оптимальные значения управляющих переменных в зависимости
от числа Маха представлены на рис. 7.32. В варианте, когда величины
Cxmin и У зависят от высоты, реализовался только первый участок полета
<7oPt= #тахд (см. рис. 7.32я). Отрицательные значения угла 8 приводят к
тому же эффекту, что и использование угла крена в вариантах 2А и 2Б:
без уменьшения вертикальной составляющей результирующей силы
невозможно одновременно обеспечить оптимальные большие значения
скоростного напора и угла атаки.
В случае, когда величины сх min и У не зависят от высоты, второй
участок начинается при числе М « 7 (см. рис. 7.326). Из рисунка видно,
что 8opt^- aopt. В данном случае это связано с изменением скорости
звука по высоте.
296 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
Рис. 7.32. Оптимальная траектория разгона ЛА с ГПВРД
при нулевом угле крена:
а) характеристики ЛА ухудшаются при увеличении высоты;
б) характеристики ЛА не зависят от высоты
На реальном аппарате управление вектором тяги PC может быть
реализовано с помощью соответствующего изменения геометрии реак-
тивного сопла (например, при помощи отклоняющейся или выдвижной
обечайки). Если угол отклонения вектора тяги PC не используется в
качестве управления, то расчетная зависимость двигателя 5opt(M) мо-
жет оказаться полезной для специалистов по реактивному соплу. Кон-
фигурацию PC желательно выбирать таким образом, чтобы протекание
угла 8 по числу М полета было наиболее близким к расчетной зависи-
мости 8opt(M).
2Г Углы крена и отклонения вектора тяги PC заданы фиксиро-
ванными: у = 0; 8 = 8(М). На первом участке
^opt <7тахД ?
угол атаки определяется численно в результате решения нелинейного
уравнения (7.58).
На втором участке (при qopi<qmaxp) оптимальные угол атаки и ско-
ростной напор определяются численно в результате максимизации
функции (7.57) при условии (7.58).
В частном случае, когда величины cxmin и Уне зависят от высоты,
приближенное значение оптимального угла атаки может быть найдено
по формуле (7.68), при этом скоростной напор определяется по формуле
(7.76).
Расчетные оптимальные значения управляющих переменных в за-
висимости от числа Маха показаны на рис. 7.33 (при 8 = у = 0). В ос-
7.5. Оптимизация траекторий на участке работы прямоточных ВРД 297
новном случае, когда величи-
ны J и cxniin зависят от высоты,
реализовался только первый
участок полета ^opt = ?тахд (как
в варианте 2В). В частном
случае, когда характеристики
ЛА не зависят от высоты,
характер функций аО|Я(М) и
^opt(M) качественно такой же,
как и в предыдущих вариантах
(см. рис. 7.296; 7.306 и 7.326).
Оптимальный режим
работы двигателя.
Типичная зависимость
удельного импульса ГПВРД от
коэффициента избытка возду-
ха показана на рис. 7.34. Ха-
рактер зависимости является
разным при акс< 1 и аКс> 1,
Рис. 7.33. Оптимальная траектория
разгона ЛА с ГПВРД при нулевых углах
крена и отклонения вектора тяги PC:
а) характеристики ЛА ухудшаются при
увеличении высоты; б) характеристики ЛА
не зависят от высоты
что связано с термогазодина-
микой ГПВРД.
Пусть оптимальный угол атаки из-
вестен. С использованием формул
(7.59) и (7.54) запишем эффективный
импульс ЛА в виде
«/эф ~ J —
^ссксАоГ,
2./ F
откуда получим необходимое условие
оптимальности по аКс •
а//5акс =
2fF
Рис. 7.34. Характер зави-
симости удельного им-
пульса ГПВРД от коэффи-
циента избытка воздуха
(топливо - водород)
Это условие имеет простой гео-
метрический смысл: при оптимальном
значении акс тангенс угла наклона
касательной к графику функции «/(аКс)
с S
равен LqV. Отсюда следует, что по
мере увеличения скорости угол наклона касательной увеличивается и в
соответствии с характером зависимости «/(аКс) касательная будет "обка-
тывать" график функции «/(аКс) справа налево. При этом оптимальный
коэффициент аКс будет уменьшаться.
298 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
Аппроксимируем зависимость удельного импульса двигателя от
коэффициента избытка воздуха степенной функцией
j = *Znax - £(ССКС - ССКС Jm)n- (7.77)
Здесь Jmax и aKcjm- максимальное значение удельного импульса и соот-
ветствующее ему значение коэффициента избытка воздуха; В и п -
коэффициенты.
В соответствии с характером зависимости J(aKc) выделяются две
ветви: левая и правая. Каждая ветвь аппроксимируется функцией (7.77)
со своими коэффициентами Jmax, акс jm , В и п.
Принятая аппроксимация позволяет определить оптимальное зна-
чение коэффициента избытка воздуха аналитически:
акс - <*кс jm -
CkS LqV
2nBfF
п-1
(7.78)
При /7 = 2 (квадратичная функция (7.77)) имеем
* _ f т?
акг - аКо.п- •
45/F
Алгоритм определения оптимального значения аКс заключается в
следующем. Сначала уравнение (7.78) решается для левой ветви и
определяется значение аКс - При аКс* 1 решение является искомым.
При аКс* > 1 уравнение (7.78) решается для правой ветви. При aKc* 1
решение является искомым. При аКс* < 1 решением является аКс* = 1. В
итоге оптимальное решение определяется с учетом ограничения на
минимально допустимое значение аКс-
aKcoPt = тах(аКс\ акс ™пд). (7.79)
На участке работы ПВРД оптимальным, как правило, является сте-
хиометрический режим: aKcoPt = 1- Для ГПВРД, работающего на водо-
роде, расчетная зависимость aKcOpt от числа Маха показана на рис. 7.35.
На начальном участке работы ГПВРД решение соответствует ограниче-
нию аксттд (при меньших значениях аКс работа ГПВРД невозможна).
В средней части диапазона работы ГПВРД оптимальным является
стехиометрическое соотношение воздуха и топлива: aKcopt= 1- На за-
ключительном участке полета коэффициент aKcOpt монотонно уменьша-
ется, чтобы предотвратить резкое уменьшение коэффициента тяги
двигателя.
Таким образом, процедура определения оптимального управления
завершена. На рис. 7.36 показано протекание по числу М полета удель-
ного импульса ГПВРД и эффективного импульса ЛА, соответствующего
оптимальной траектории. Видно, что потери удельного импульса за
счет внешнего сопротивления ЛА могут достигать 50% и более. Так как
7.5. Оптимизация траектории на участке работы прямоточных ВРД 299
Рис. 7.35. Зависимость опти-
мального коэффициента избытка
воздуха ГПВРД, работающего на
водороде, от числа Маха
Рис. 7.36. Зависимости удельного
импульса ГПВРД и эффективного
импульса ЛА от числа Маха для
оптимальной траектории разгона
при увеличении скорости удельный импульс ГПВРД и эффективный
импульс ЛА уменьшаются, то очевидно, что при некотором значении
скорости ВРД становится неэффективным и далее необходимо исполь-
зовать ЖРД.
Дифференциальное уравнение (7.53) имеет такой же вид, как и
уравнение (7.44), только вместо удельной энергии используется ско-
рость, а вместо функции /РЗГ - эффективный импульс ЛА ./Эф • Поэтому
в частных случаях можно получить аналитические решения, аналогич-
ные (7.46) и (7.47). При 7эф= const имеем
тк/т^ = ехр[(Г0-РкУЛф]. (7.80)
В случае линейной зависимости 7Эф от скорости получим
1 w0 L ^ЭФ К и ^ЭФ.К-^ЭФ.о иоп
In—= —In J к , где Ь=----------------------. (7.81)
тк b .7ЭФ 0 Гк - Го
При необходимости траекторию можно разделить на несколько
участков с соответствующим законом изменения функции «7эф(Ю-
7.6. Условия включения и выключения ВРД
Определение диапазона работы ВРД по скорости полета является
одной из важнейших задач формирования облика аэрокосмических ЛА.
С одной стороны, при расширении этого диапазона суммарный запас
топлива уменьшается. С другой стороны, увеличение доли водородного
топлива приводит к увеличению суммарного объема топливных баков,
что, в свою очередь, вызывает увеличение ’’сухой” массы аппарата.
300 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
Рис. 7.37. Характер измене-
ния массы аэрокосмическо-
го ЛА с КСУ в зависимости
от скорости полета
Использование простых условий включе-
ния и выключения ВРД позволяет облег-
чить процесс формирования облика ЛА.
Пусть комбинированная силовая ус-
тановка ЛА состоит из трех типов двига-
телей. Каждому типу двигателя соответ-
ствует свой участок полета (рис. 7.37).
Аппарат разгоняется от скорости Ио до
Кк, в процессе разгона его масса умень-
шается от 7я0 ДО тк. Здесь , Ко и Гк -
заданные величины. Будем исследовать
второй участок полета, на котором, как
правило, используются прямоточные
ВРД. На первом участке могут использо-
ваться либо ВРД (например турбоком-
прессорные), либо ЖРД, на третьем участке - ЖРД. Плотность топлива,
расходуемого на каждом участке полета, является постоянной.
В общем случае задача определения скоростей включения и
выключения ВРД является итерационной и сводится к определению
экстремума функции двух переменных:
Ф(И, И2) —> extr.
Здесь по условию задачи функция Ф представляет собой относитель-
ную массу полезного груза типг/^о или относительную "сухую" массу
ЛА /ясух/^пг.
На каждой итерации (при фиксированных значениях V\ и И2) для
вычисления функции Ф необходимо численно проинтегрировать массу
топлива, расходуемого каждым типом двигателя, и определить основ-
ные составляющие "сухой" массы ЛА.
Определим приближенные условия включения и выключения ВРД,
полагая, что скорость И| достаточно большая. Это значит, что можно
воспользоваться гипотезой квазистационарности. Запишем функционал
в виде
Ф (Ц|, ц2, Цз) -> extr, (7.82)
где ц, - относительная конечная масса, соответствующая j-му участку:
Ц1 = т\1т$; ц2 = тДт। ; Цз = тДт^.
Пусть относительная конечная масса Ц] есть известная функция
скорости выключения первого типа двигателя V\, а относительная
конечная масса ц3-известная функция относительной скорости v,
соответствующей третьему участку (рис. 7.38). Здесь v = Ик - И2 и
dN = -dV2. (7.83)
7.6. Условия включения и выключения ВРД
301
Необходимое условие экстремума функции Ф по скорости У\ (при
V2 = fix) заключается в следующем:
б/Ф _
---= 0, или
5Ф б/ц, 5Ф б/ц2
<3ц, dV{ Зц2 dV\
(7.84)
Здесь полагается, что не
зависит от V\ . Частные производ-
ные Ф ПО Ц| и ц2 вычисляются в
соответствии с видом функции
(7.82).
Производная d\x\/dV\ в точке
выключения первого типа двига-
теля однозначно определяется
видом функции Ц|(Г|). Если на
первом участке полета использу-
ются ЖРД, то с помощью
формулы Циолковского можно
записать
Ц| = ехр(- И|/,7|СР),
Рис. 7.38. Заданное изменение
относительных конечных масс,
соответствующих первому и
третьему участкам, в зависимости
от скорости полета
где Jicp - средний эффективный импульс ЛА на первом участке полета.
Тогда
d\i\!dV । — — pt|A/|fp.
Рассмотрим участок полета с ВРД и свяжем производную dyJdV с
эффективным импульсом ЛА. Запишем уравнение (7.53):
dm/dV = - m!J3^. (7.85)
Если вместо текущей массы т воспользоваться относительной ко-
нечной массой ц = 777/7720, где 7Т7О- некоторая начальная масса, то уравне-
ние (7.85) преобразуется следующим образом:
dy\JdV = - ц/Уэф при ц = т/т{}. (7.86)
Если под относительной конечной массой понимать величину
£, = тДт, где тк- некоторая фиксированная конечная масса, то
dtjdm - - тДт1
и из (7.85) получим
dydV= ц/Уэф при 5, = тДт, (7.87)
где эффективный импульс ЛА и производная dtJdV соответствуют
текущей точке, масса аппарата в которой равна т.
Таким образом, если на первом участке используется ВРД, то
d\i\/dV\ - - Ц|//|эф(Е|),
302 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
где <7|эф(^|) - эффективный импульс ЛА в конечной точке первого
участка.
Определим полную производную dy^JdVy , входящую в (7.84), с
учетом того, что р? в общем случае зависит от двух переменных: от т\
и И:
d\i2/dV\ = (Эр12/Эт771) dm\/dV\ + Эр2/ЭИ| .
Обычно зависимость р2 от т\ является более слабой, чем от У\, и
ею можно пренебречь. Тогда
dycJdVi « Эр2/дУ\ ,
т.е. производная dycddV^ определяется при некотором фиксированном
значении начальной массы. А так как экстремум по У\ вычисляется при
К2 = fix, то это означает, что можно полагать = fix, т.е. в данном
случае является справедливой формула (7.87):
d^ldV^^IJ^V.).
Здесь Лэф(У\) - эффективный импульс ЛА в начальной точке второго
участка полета.
После исключения производной <7р2/<7Е| из (7.84) получим условие
включения ВРД, работающих на втором участке полета:
(7.88)
аф/ф,
Если на первом участке используются ВРД, то
ц, 5Ф/ф,
Если на первом участке используются ЖРД, то
Лэф(И)~Лср^-^У2 .
р, ЭФ/Эр,
Запишем необходимое условие экстремума функции Ф по скорости
У-> (при У\ = fix):
^ = 0,
dy2
С учетом соотношения (7.83) получим
ЭФ d\x2 ЭФ <7р3
Эр2 dV2 Эрз dv
ЭФ du,? ЭФ du. _
или----------— +----------- = 0.
Эр2 dV2 Эр3 dV2
(7.89)
7.6. Условия включения и выключения ВРД
303
Здесь полагается, что Ц| не зависит от И2. Частные производные Ф по
ц2 и цз вычисляются в соответствии с видом функции (7.82).
Производная d^/d\ однозначно определяется видом функции Цз(у) и
вычисляется при v = Ик - К2.
Так как на третьем участке полета используются ЖРД, то при
помощи формулы Циолковского можно записать
Цз = ехр(- у/Лср),
где Лер - средний эффективный импульс ЛА на третьем участке полета.
Тогда
б/Цз/dv = - Цз/Лср •
Производная ц2 по И2 связана с эффективным импульсом ЛА в точ-
ке выключения ВРД 72Эф(И2) в соответствии с формулой (7.86):
ф2т=-ц2/ЛЭФ(Г2).
После исключения производной б/ц2/б/И2 из (7.89) получим условие
выключения ВРД:
Лэф(И2) =---------дыду-г (7.90)
d^/dv дФ1д\х3
ИЛИ
Лэф(И2)=ЛсР-^-|^|^ •
ц3 ЗФ/5ц3
Данное условие, в отличие от условия включения ВРД (7.88), явля-
ется строгим. Очевидно, что это условие является справедливым в
случае отсутствия первого участка, например, когда на ЛА установлены
только РТД и ЖРД.
Рассмотрим основные варианты функции Ф. При изменении ско-
ростей включения и выключения ВРД в общем случае изменяются
суммарная масса топлива ЛА DnTj, объем каждого типа топлива
конечная масса аппарата тк, масса полезного груза и7Пг и объем грузо-
вого отсека Иго- С учетом этого запишем стартовую массу ЛА как
линейную функцию этих параметров:
т0 = EmTj + ат0 + PmK + Ly, И^ + тПг + Уго^го- (7.91)
Здесь а, Р и ^-удельные весовые параметры ЛА - имеют такой же
смысл, как и в разделе 4.5.
В первом приближении будем полагать, что эти параметры не зави-
сят от скорости выключения ВРД И2. Из уравнения (7.91) получим
выражение для относительной массы ПГ:
304 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
т п г/то-----------------------,
1 + У го /рпг
где
Ху( Wrj = (1 - Ц|)У|/рТ1 + Ц|( 1 - Ц2)?2 /рТ2 + Ц1Ц2О - Цз)Уз/ртз.
Здесь и’!j - объем j-ro типа топлива, отнесенный к стартовой массе ЛА.
Максимуму /ицг/wo однозначно соответствует максимум функции
Фпг = PiЦ2Цз( 1 - Р) - Syj wTj. (7.92)
Частные производные ФПг по Ц|, ц2 и Цз равны
с/ФПГ /4l| = Ц2Цз( 1 - р) + у I/ртI - (1 - Ц2) У2/рТ2 - Ц2 (1 - Цз)Уз/ртз;
с/Фпг/^ь = Ц|Цз( 1 - р) + Ц1У2/РТ2 - Ц| (1 - Цз)Уз/ртз;
б/Ф|П /б/Цз - Ц| ц2( 1 - р) + Ц1Ц2Уз/ртз.
Подставив полученные выражения в (7.88) и (7.90), получим усло-
вия включения и выключения ВРД, работающих на втором участке
полета:
Л')ф( У\) ~ «Л эф( У \) Ц2 х
х Мз(1-Р) + У2/Рт2-(]-|-Г)Уз/РтЗ. (793)
Ц,|.1,(1-Р) + у|/Рт| -(1 -Ц2)у2/Рт2-МзО-Рз)Уз/ртз ’
•Z’xiX Г2) — ./зср
(1 - р) + у2 / Рт2 - - Из )Уз1 Ртз
Рз(1-Р) + ЦзУз/Ртз
(7.94)
Здесь полагается, что на первом участке полета используются ВРД.
В выражения (7.93) и (7.94) не входит удельный весовой параметр
а, в (7.93) не входит р.|. Это означает, что соотношение
./2ЭФ( У\)/-/|эф(^i) не зависит прямо от эффективного импульса ЛА перво-
го участка полета. В (7.94) не входят Ц| и ц2. Это означает, что соотно-
шение Лэф^УЛср не зависит прямо от эффективного импульса ЛА
первого и второго участков полета. Можно показать, что если на первом
и втором участках полета используется одинаковое топливо (т.е. при
Yi/pi । = У2/Р12), то
Лэф(И)«^1Эф(Г|),
что было показано ранее в работе [114].
Выражение (7.94) можно упростить, учтя, что плотность топлива
ЖРД существенно больше плотности водородного топлива
(у2/Р'Г2 >:> Узфтз)’
7.6. Условия включения и выключения ВРД
305
Лэф(^) ~ Лср
| + У2 /Рт2
Щ(1 -Р)
Численные расчеты с использованием прогнозных значений удель-
ных весовых параметров ЛА показывают, что
Лэф(Г2)«(1,6^1,7)/3ср.
Это означает, что при </зср = 4,4 км/с эффективный импульс ЛА в
точке выключения ВРД должен быть не менее 7,04-7,5 км/с.
Рассмотрим вариант минимизации относительной "сухой” массы
ЛА. Для упрощения под "сухой” массой аппарата будем понимать его
массу без топлива и полезного груза, тогда
1 - / т0
/Ясух/^ПГ = (^0 - - ^ПгУ^ПГ ~ ~------1 •
wnr//?7o
Отсюда следует, что минимуму относительной "сухой” массы од-
нозначно соответствует минимум функции
Фсух= (а + Syj wTj) / (Ц1Ц2Ц3). (7.95)
Частные производные Фсух по щ , ц2 и равны
б/ФСух/б/Ц1 —
а + у,/рТ1
<^ФсУх/^Ц2----
а + О-ц^у^Рт, +ц1у2/рТ2 .
ШМ^Рз
б/Фсух/^Цз----
<* + (1 - /рТ1 + ИЛ1 - И2)у2/рТ2 + /рТз
PiP2P32
Подставив полученные выражения в (7.88) и (7.90), получим усло-
вия включения и выключения ВРД, работающих на втором участке
полета:
Лэф(^) «Лэф(Г1)
1 . ,. Y2 /pT2 Y1 / Рт1
1 “Г гЧ ,
а + у,/рТ|
(7-96)
Лэф(^2) — /5СР---------------7----------------7------
I_______М-1 Р-2 (Y2 / Ртг Уз / Ртз )_
ос + у,/рТ| + p.,(y2/рт2 — У,/рТ|)
(7.97)
306 Глава 7. Разгон ЛА с использованием ВРД со свободной дальностью
Следует отметить, что в выражения (7.96) и (7.97) не входит удель-
ный весовой параметр р, в (7.97) не входит , а в (7.96) не входят
ц2 и .
Если на первом и втором участках полета используется одинаковое
топливо (при у|/рт1 = Y2/PT2), то, как и в случае максимизации относи-
тельной массы ПГ, из (7.96) имеем
Лэф(И|) « </|эф(Г|).
Численные расчеты показывают, что при минимизации относи-
тельной "сухой" массы эффективный импульс ЛА в конце второго
участка несколько больше, чем при максимизации относительной мас-
сы ПГ. При прогнозных значениях удельных весовых параметров ЛА
Лэф(Г2) = ( 1,6^1,9Узср. (7.98)
Если на первом и третьем участках полета используется одинако-
вый тип ЖРД, то, как показывают расчеты, для обоих вариантов функ-
ционала
Лэф(И)«1,2Лэф(К2).
На рис. 7.39 показано характерное протекание эффективного им-
пульса ЛА по скорости полета для аппарата с КСУ.
В данном случае оптимальное число М переключения с РТДп на
ГПВРД равно ~6,1. Скачок в эффективном импульсе ЛА отсутствует,
так как оба типа двигателя используют один тип топлива. Оптимальное
число М переключения с ГПВРД на ЖРД равно ~ 14. В этой точке в
соответствии с соотношением (7.98) имеет место скачкообразное
уменьшение эффективного импульса ЛА (примерно на 3 км/с). При
ухудшении удельных весовых характеристик ЛА разрыв эффективного
импульса ЛА в точке выключения ГПВРД увеличивается.
Рис. 7.39. Зависимость эффективного импульса одноступенчатого
ВКС с КСУ от числа Маха при выведении на орбиту
ГЛАВА 8
ПОЛЕТ ЛА С ВРД НА ЗАДАННУЮ ДАЛЬНОСТЬ
Дальность дозвуковых самолетов определяется главным образом
протяженностью крейсерского полета, вопросы оптимизации которого
подробно освещены в работах [63], [71], [83], [85], [87]-[89], [91], [94],
[114], [124] и др. В инженерной практике траектория полета дозвуково-
го самолета обычно рассчитывается путем разделения ее на отдельные
участки: разгон и набор высоты, крейсерский участок, участок сниже-
ния и торможения. При оптимизации каждого участка делаются допол-
нительные допущения. Например, при расчете участков набора и сни-
жения высоты масса самолета принимается постоянной или ее
изменение учитывается приближенно, крейсерский участок рассчиты-
вается без учета изменения удельной механической энергии [96]. Как
показано в РДК по расчету летных характеристик неманевренных само-
летов [83], значения дальности и массы топлива при выходе на крейсер-
ский режим полета по оптимальным программам и по программе по-
стоянного скоростного напора мало отличаются друг от друга, поэтому
для предварительных приближенных оценок можно полагать, что тра-
ектория разгона соответствует режиму q = const. Расчет крейсерской
дальности в [83] предлагается проводить приближенно по средним
значениям высоты, массы и т.д.
Увеличение скорости полета от дозвуковой до сверх- и гиперзвуко-
вой позволяет уменьшить время полета в несколько раз, однако по мере
увеличения крейсерской скорости вклад участков разгона и планирова-
ния в общую дальность увеличивается. Также увеличивается доля
топлива, расходуемого на разгон ЛА до крейсерской скорости. В ре-
зультате эти участки нельзя рассматривать как независимые, и вместо
задачи максимизации дальности крейсерского участка должна решаться
задача максимизации суммарной дальности полета ЛА при заданной
массе полезного груза. В силу взаимности задачи можно максимизиро-
вать массу ПГ при фиксированной суммарной дальности полета.
В данной главе рассматриваются вопросы оптимизации траекторий
крейсерского полета, разгона и планирования. Масса топлива определя-
ется в результате интегрирования полной системы уравнений. Как и в
гл. 7, в данной главе рассматриваются траектории, близкие к квазиста-
308
Глава 8. Полет ЛА с ВРД на заданную дальность
ционарным. В связи с этим приближенно оптимальное управление и
соответствующие траектории будут называться оптимальными.
8.1. Постановка задачи
Пусть суммарная дальность полета является заданной (рис. 8.1),
стартовая масса аэрокосмического ЛА равна т^. Рассматривается плос-
кое движение (движение в плоскости развертки). Как и в традиционном
подходе, полагается, что траектория полета состоит из трех участков.
Такое решение, в частности, получено в работе [114] при оптимизации
управления движением самолетов с ВРД при полете на дальность (ис-
следовалась квазистационарная система уравнений). На первом участке
ЛА разгоняется от скорости Ко до крейсерской скорости Икр. На втором
Рис. 8.1. Схема полета ЛА на задан-
ную дальность
участке ЛА осуществляет крей-
серский полет со скоростью ИКР.
На третьем участке ЛА с рабо-
тающими или выключенными
двигателями планирует от скоро-
сти ККр до конечной скорости Ик.
В процессе полета на каждом из
рассматриваемых участков дости-
гается соответствующая даль-
ность! Zp3r, Zkp и //пл (см
рис. 8.1).
Задача формулируется сле-
дующим образом: необходимо определить оптимальное управление на
каждом из трех участков из условия максимума массы полезного груза
при фиксированной суммарной дальности L^ = £РзГ + £кр + £пл • Полага-
ется, что на всех участках полета используется единое топливо. При
этом максимуму массы ПГ будет однозначно соответствовать максимум
массы ЛА в конечной точке полета. Крейсерская скорость ИКр является
заданной (в общем случае эта величина оптимизируется как параметр).
В задаче могут быть заданы ограничения, наложенные как на управ-
ляющие, так и на фазовые переменные.
8.2. Максимизация коэффициента крейсерской дальности
Как показано в разделе 2.9, коэффициент крейсерской дальности
записывается следующим образом:
(^/Q^pJc^cosy
g^(F/S)
и должен максимизироваться при E=fix вместе с условиями (2.137), к
которым добавляется условие с^х=0. При больших скоростях полета
вместо условия Е = fix можно использовать условие V = fix.
8.2. Максимизация коэффициента крейсерской дальности
309
Проведем ось двигателя так, чтобы она была параллельна вектору
тяги PC (вектору выходного импульса): 5ДВ=8. Пусть разворот вектора
входного импульса и силы, действующие на жидкий контур входной
струи воздуха, учтены в аэродинамических коэффициентах с\ и су,
тогда выражение для коэффициента крейсерской дальности примет вид
(см. раздел 2.9)
/кр= (/?о/г)ГКр Jcosy [sin(a + 8дВ) + A?cos(a + 8ДВ)] /gv, (8.2)
а условия равенства сил относительно скоростных осей Ох и Оу можно
записать в виде
cR (775) cos(a + 8дВ) - сх = 0; (8.3)
cZy qS cosy - mg\ cos0 = 0, (8.4)
где
= cR (F/S) sin(a + 8дВ) + cy.
В крейсерском полете вследствие уменьшения текущей массы ЛА
увеличение высоты не превышает 5-^6 км (при дальности в несколько
тысяч километров). Поэтому можно считать, что 0 = 0 и cos0 = 1.
Вначале определим характер зависимости /КР от крейсерского чис-
ла Маха, полагая движение плоским: у = 0. При фиксированной скоро-
сти полета коэффициент /Кр определяется в основном двумя показате-
лями: летным аэродинамическим качеством и удельным импульсом
ВРД. Максимуму/<р соответствуют оптимальное значение угла атаки a
и оптимальный режим работы ВРД, причем в общем случае aopt aKm и
оптимальный режим работы ВРД не соответствует максимуму J, что
связано с наличием условий (8.3) и (8.4). Однако с целью проведения
качественного анализа будем полагать, что при каждом значении М
летное значение аэродинамического качества соответствует Х^,пах, а
режим работы двигателя соответствует Jmax. В этом случае с использо-
ванием условий (8.3), (8.4) и с учетом малости углов а и8дв соотноше-
ние (8.1) можно записать следующим образом:
/кР~ ------------— ГКР7<тах Jniax . (8.5)
rg[l-r /(rg)]
Воспользуемся усредненной зависимостью АГ1пах от числа М полета
(рис. 8.2) и данными по удельному импульсу наиболее характерных
типов двигателей (рис. 8.3). Здесь зависимость 7<тах(М) представляет
собой верхнюю границу достижимого аэродинамического качества и
построена с использованием имеющихся данных по различным проек-
там J1A. В первом приближении принято, что аэродинамическое качест-
во не зависит от типа топлива. Зависимость Jmax(M) определена по
данным работ [39], [53], [68], [90] и соответствует трем типам ВРД
(ГТД, ПВРД, ГПВРД) и двум типам топлива (керосин, водород).
310
Глава 8. Полет ЛА с ВРД на заданную дальность
Рис. 8.2. Усредненная зависимость максимального аэродинамическо-
го качества Armax и зависимость величины, учитывающей кривизну
Земли, от числа М полета
Рис. 8.3. Зависимость максимального удельного импульса
основных типов ВРД от числа М полета
Рис. 8.4. Зависимость коэффициента крейсерской дальности ЛА
от числа М полета
8.2. Максимизация коэффициента крейсерской дальности
311
Для ПВРД и ГПВРД, работающих на водороде, зависимость пред-
ставлена в виде "дорожки” с верхней и нижней границами. На рис. 8.2
также показано изменение коэффициента, учитывающего кривизну
Земли; зависимость от числа М полета является практически квадра-
тичной.
Результирующая зависимость/кр(М) представлена на рис. 8.4. При
переходе от керосинового топлива к водородному коэффициент /КР
увеличивается в ~2,7 раза в соответствии с изменением удельного
импульса ВРД. Абсолютный максимум /КР реализуется при дозвуковых
скоростях. При М > 1 по мере увеличения скорости коэффициент/Кр в
целом уменьшается, однако при этом реализуется несколько локальных
максимумов в соответствии с характером зависимости Jmax(M): при
числе М ~ 2; на участке работы ПВРД (при М = 4,54-5 для керосинового
двигателя, при М = 5,54-6 для водородного двигателя) и на участке
работы ГПВРД при М»7,5. В случае оптимистического прогноза
удельного импульса ГПВРД при М> 134-14 коэффициент крейсерской
дальности начинает увеличиваться, однако при числе М = 20 его значе-
ние меньше, чем дозвуковое значение/Кр при том же типе топлива.
Таким образом, можно заключить, что переход к большим скоро-
стям позволяет уменьшить время полета, но не приводит к увеличению
располагаемой крейсерской дальности ЛА. При рассматриваемых
исходных данных для JIA с керосиновым ПВРД рациональное крейсер-
ское число М полета равно ~4,5; для ЛА с водородным ПВРД
МКР « 5,5; для ЛА с водородным ГПВРД МКР « 7,5.
Перейдем к определению оптимального управления движением. В
функцию/кр (8.2) входят 4 управляющих переменных: углы а, 8дв,у и
режим работы ВРД. Очевидно, что если угол крена используется в
качестве управляющей переменной, то его оптимальное значение равно
нулю. При полете с заданным углом крена коэффициент/Кр уменьшает-
ся пропорционально cosy. Таким образом, задача оптимизации траекто-
рии заключается в максимизации функции/Кр при V= fix по трем аргу-
ментам при наличии 2-х условий типа равенства (8.3) и (8.4). В общем
случае такая задача решается численно с использованием стандартных
процедур. Рассмотрим основные варианты задачи оптимизации управ-
ления. Там, где это возможно, будем находить аналитические решения с
использованием некоторых упрощений.
Оптимизация угла отклонения вектора тяги PC. Будем оптими-
зировать угол 8 при некотором фиксированном значении скорости
полета. В первом приближении можно считать, что функция /Кр не
зависит от высоты (здесь и далее будем использовать это допущение).
Тогда условие (8.4) становится несущественным и остается одно усло-
вие (8.3). Условие (8.4) служит для определения скоростного напора
(высоты), который не входит в (8.2) и (8.3). Будем полагать, что коэф-
фициент тяги двигателя cR не зависит от угла отклонения вектора тяги
312
Глава 8. Полет ЛА с ВРД на заданную дальность
PC 5. Рассмотрим два варианта характера зависимости тяги ВРД от угла
атаки.
1. Тяга ВРД не зависит от угла атаки. В этом случае, как следует
из выражения (8.2), оптимум по углу 8 определяется из необходимого
условия максимума функции
Л(8) = sin(a + 8) + (су /cx)cos(a + 8) (8.6)
с условием (8.3).
Пусть аэродинамическая поляра является квадратичной и симмет-
ричной: сх= с\ П11П +J(c‘y)2. Из условия (8.3) определим коэффициент
подъемной силы
с = /gR(^^)cos(a + 8)-cxmin
У V А
и подставим в функцию Л, из которой исключим сх при помощи (8.3). В
результате получим
JcR (F/S)cos(a + 8) - с n
Л(3) = sin(a + 5) + ------——.
jAc^F/S)
Из необходимого условия экстремума функции Л(8) имеем
/ sin(a + 8)
cos(a +8)----г--,----- = О,
2 (f 1 5)cos(a + 5) - cxmui
откуда после преобразований и с использованием условия (8.3) полу-
чим
tg(a+8opt) = 2Лсу.
С учетом малости углов а, 8 и с учетом соотношения Лсуа « 1 в
итоге получается приближенное равенство
6opt« а. (8.7)
Характерно, что решение (8.7) является таким же, как при рассмот-
рении разгона ЛА с ЖРД (см. раздел 3.5) и при рассмотрении разгона
J1А с ВРД, тяга которого не зависит от угла атаки (см. раздел 7.5).
2. Коэффициент тяги ВРД cR зависит от угла атаки. Пусть оп-
тимальное управление углом атаки близко к режиму Л^тах. Примем в
первом приближении, что в условии (8.3) cos(a+8)«l. Тогда, как
следует из выражения (8.2), оптимум по углу 8 будет определяться в
результате безусловной максимизации функции А (8.6). В итоге полу-
чим
tg(^Kin + ^opt) — 2акт ?
откуда
^opt ® СК'Кт •
(8.8)
8.2. Максимизация коэффициента крейсерской дальности 313
Численная оптимизация угла 8 была проведена применительно к
ЛА с ПВРД, работающим на керосине, при МКР = 4,5 (рис. 8.5). В соот-
ветствии с данными рис. 8.2 было принято /С1пач = 6,3. Результаты опти-
мизации представлены в относительном виде (по отношению к углу
атаки оск1п=4,5°) в зависимости от относительной площади входа в
ПВРД F/S (где S - площадь ЛА в плане). Рассмотрены два варианта:
1) тяга двигателя не зависит от угла атаки;
2) тяга двигателя зависит от угла атаки линейно (в соответствии с
данными, представленными на рис. 6.15а, было принято = 3,4).
В первом варианте углы aopt и 80nt практически совпадают, что под-
тверждает аналитическое решение (8.7). Во втором варианте зависимо-
сти aopt(F/5) и 8opt (F/S) пересекаются при аор|=аКт. что подтверждает
аналитическое решение (8.8). Из рис. 8.5 видно, что в обоих случаях
при увеличении относительной площади входа в двигатель оптималь-
ные значения углов а и 8 увеличиваются практически линейно. Во
втором случае темп увеличения угла 8 примерно в 1,4 раза больше, чем
угла атаки. В первом случае оптимальный режим, соответствующий
А^тах, реализуется при F= 0,01255, во втором случае - при F= 0,0095.
Таким образом, если площадь входа в двигатель выбирается из ус-
ловия максимизации крейсерской дальности, то интегральная компо-
новка ЛА с нижним расположением ПВРД позволяет уменьшить по-
требную площадь входа в двигатель примерно в 1,4 раза. Однако если
площадь входа является избыточной для крейсерского полета, то в
результате компенсации избыточной располагаемой тяги потери даль-
ности во втором случае могут оказаться больше.
Определим выигрыш в крейсерской дальности полета при переходе
от 8 = 0 к 8opt. Пусть оптимальный угол атаки соответствует режиму
А^шах • Тогда при 8 = 0 функцию (8.6) можно записать в виде
Рис. 8.5. Изменение оптимальных углов атаки и отклонения вектора тяги
PC в зависимости от относительной площади входа в ПВРД (МК1» = 4,5):
1 - тяга двигателя не зависит от угла атаки; 2 - тяга двигателя зависит от
угла атаки (Апа = 3,4)
314
Глава 8. Полет ЛА с ВРД на заданную дальность
Ло « аАт + Кпулх (1 - аАт2 /2) « ATmax (1 + ЗаК)П2 /2) « Ктлк [ 1 + 3/(8ATmax2)].
Здесь использовано приближенное равенство aAin~ 1 /(2А71Пах).
При 8opt = аА'1П имеем
До opt ~ 2аЛт + ^)пах (1 - 2оск1П2) « A?inax (1 + 2осА'1П2) « £тах [1 + 1 /(2А71пах2)].
В результате получаем
Л8ор|/Л0« 1 + 1/(8ЛГ1Пах2).
При £|Пах = 4+6 выигрыш в крейсерской дальности составляет
0,3+0,8 %. При уменьшении А?1ШХ выигрыш от оптимизации угла 5 уве-
личивается.
Если угол 8 не может использоваться в качестве управления, а яв-
ляется проектным параметром ЛА, выполняющего длительный крей-
серский полет, то полученные решения рационально использовать при
проектировании реактивного сопла ВРД.
Совместная оптимизация управления и площади входа в дви-
гатель. Пусть относительная площадь входа в двигатель F/S является
проектным параметром ЛА. Определим оптимальное значение этой
величины из условия максимума крейсерской дальности при E=fix.
Так как величина F/S входит в условие (8.3) и не входит в функцию
(8.2), то это значит, что ее оптимальное значение (F/S)opt будет одно-
значно определяться из соотношения (8.3), а оптимальное управление
должно определяться в результате безусловной максимизации функции
(8.2).
Анализ функции /КР (8.2) показывает, что оптимальный режим ра-
боты двигателя соответствует максимуму удельного импульса ВРД. Что
касается угла атаки, то обычно полагается, что его оптимальное значе-
ние соответствует режиму А?П1ах, хотя в действительности точное реше-
ние является несколько иным. Определим погрешность приближенного
решения для двух основных случаев.
1. Если угол 8 используется в качестве управления, то оптимальные
значения углов а и 8 будут определяться в результате безусловной
максимизации функции А (8.6). В данном случае, как было показано
выше, справедливо решение (8.8): 80pt~a/;m. Тогда в результате макси-
мизации функции
А = sin(a + aAin) + (су /cx)cos(a + a^)
для случая квадратичной поляры с использованием некоторых упроще-
ний можно показать, что оптимальный угол атаки практически равен
aAm. Как показали численные расчеты, при Fniax = 3 разность (aA'm- aopt)
не превышает 0,3 %. При увеличении Fmax значения aopt и осА'т сближа-
ются. Так как в районе максимума функция А является пологой, то ее
значения при aopt и aAni практически совпадают.
8.2. Максимизация коэффициента крейсерской дальности
315
2. В случае, когда угол 5 задан нулевым (вектор выходного импуль-
са параллелен продольной оси ЛА), оптимальный угол атаки определя-
ется в результате максимизации функции
А = sina + (cy/cx)cosa .
В районе А?|пах зависимость А^(а) для квадратичной симметричной
поляры можно представить в виде
К= Ктах(1 -82/2), (8.9)
ГДе £ — (Су — СуКтУ^уКт — (& — СС-КтУоЦчт •
Действительно, с учетом соотношения су = суктО + е) имеем
к_ СУ __________gyKn.0 + £)_________=
+ Ас} 2скт1П[1/2 + Лс}Кт(1 + г)2 /(2сх|П1П)]
== <1 -—-)*(1 -е2/2)-
1/2 + (1 + 2е + е-)/2 2(1+£) + е'
Из необходимого условия экстремума функции А с использованием
формулы (8.9) получается уравнение:
cosa - cosa А?1Пах 8 /aKm - sina А?тах (1 - 82/2) = О,
или с учетом малости угла атаки и соотношения 82/2 « I:
1 — ^Мпах (^ ^'КтУ(^'К|п)_ & ^Мпах — О*
Решим это уравнение, воспользовавшись соотношением
^inax ® 1/(2акт).
Of-opt ® 1 ) •
Численные расчеты подтверждают полученное решение. Если при-
нять aopt=aKin, то при £тах = 3 погрешность определения /КР будет не
выше 0,04%. При увеличении /С1пах оптимальное решение приближается
к режиму /С1пах. Таким образом, с достаточной для практики точностью
можно считать, что в обоих рассматриваемых случаях оптимальный
угол атаки равен аЛш
С использованием полученного решения определим оптимальное
значение F/S из условия (8.3):
(F/S%pl=-----Ь-----(8.10)
cR cos(aopt+5)
С учетом соотношений
316
Глава 8. Полет ЛА с ВРД на заданную дальность
_ 2Jf . _ 1
’ Сх £\Кт min _ о
«кс4/ 2КтахЛ
в итоге получим:
(F/5)0|„ =---------------------
4/„ax./^a^cos(aKm+8)
(8-11)
где aKc jm соответствует режиму Jinax, a aKin - режиму А?1пах.
Расчетная зависимость относительной площади входа в двигатель
от крейсерского числа Маха представлена на рис. 8.6. В расчетах были
использованы данные, проиллюстрированные на рис. 8.2 и 8.3. Коэф-
фициент расхода воздуха определялся в предположении, что ВРД уста-
новлен снизу (см. раздел 6.3). Из рис. 8.6 видно, что характер измене-
ния (F/S\^ отражает характер функции Jmax(M). Для водородного и
керосинового ПВРД оптимальные значения F/S примерно одинаковы,
что связано с близостью соотношений Jmax/£(). При увеличении числа
МКр , несмотря на увеличение коэффициента расхода воздуха, величина
(/*7Л’)0Р| увеличивается.
Значения (F/S)^, представленные на рис. 8.6, необходимо рассмат-
ривать как минимально возможные. Из соотношения (8.11) видно, что
при уменьшении удельного импульса и аэродинамического качества
величина (F/S)^x увеличивается. Если учесть, что ухудшение аэродина-
мических характеристик связано главным образом с А?шах (коэффициент
отвала поляры при этом изменяется незначительно), то из формулы
(8.11) видно, что влияние А?П1ах на величину (F/S)o?{ является более силь-
ным по сравнению с Jinax.
Варианты задачи, когда одна из управляющих переменных оп-
ределяется заданным режимом полета.
1. Режим работы двигателя соответствует Jmax. В качестве
управляющей переменной будем использовать коэффициент подъемной
Рис. 8.6. Зависимость оптимальной относительной
площади входа в двигатель от крейсерского числа Маха
8.2. Максимизация коэффициента крейсерской дальности
317
силы, который в данном случае однозначно определяется из условия
(8.3). Будем полагать, что тяга двигателя не зависит от угла атаки:
3/75а = 0; углы атаки и заклинения двигателя малы: cos(a + 8) = 1;
аэродинамическая поляра является квадратичной и симметричной:
~ min ( 1 У )>
ГДе у Су /СуКт •
С учетом этого перепишем соотношение (8.3) следующим образом:
Сх mi„ (I + г) = - 2J|pax/rz (F/S). (8.12)
Пусть полет совершается с некоторой скоростью ККР. Если пло-
щадь входа F является оптимальной из условия максимума коэффици-
ента крейсерской дальности при скорости Икр (см. решение (8.11)), то
условие (8.3) запишется в виде
2сх„„„ = ~.^FavjS_ (8.|3)
«КСЛпД/
Исключив одинаковые величины из (8.12) и (8.13), получим
1 + y = 2F/Fopt,
или
СУ FyKin ~ ^2F/ Fopt — 1 .
При небольших отклонениях Fot Fopt имеем
Cy/CyKm « Ж>р1, (8.14)
где величины су,сукт и Fopt соответствуют скорости ИКР .
2. Угол атаки соответствует режиму Ктах. В этом случае коэф-
фициент избытка воздуха однозначно определяется из условия (8.3),
которое записывается в следующем виде:
Cxk,.,= -^-(W (8.15)
аКСД/
Для упрощения задачи аппроксимируем зависимость .7(аКс) при
помощи элементарной функции. Пример исходной зависимости ./(аКс)
представлен на рис. 8.7 для ПВРД, работающего на керосине (М = 4,5).
При других числах М характер зависимости является качественно
таким же. В качестве аппроксимирующей функции примем квадратную
параболу вида
J ~ Л1ах[ 1 “ 5(аКС “ аКС Jm)2],
(8.16)
318
Глава 8. Полет ЛА с ВРД на заданную дальность
Рис. 8.7. Зависимость удельного импульса ПВРД от коэффициента избытка
воздуха (М = 4,5):
------- исходная зависимость; ООО аппроксимация
где максимальное по осКс значение удельного импульса; aKCjm -
соответствующее значение коэффициента aKci 2?-коэффициент ап-
проксимации.
Аппроксимационная зависимость представлена на рис. 8.7 в виде
маркеров. Значения коэффициента В являются разными для левой
(aKc < ockv im) и правой (аКс aKcjm) ветвей. Видно хорошее совпадение
с исходной зависимостью.
Исключив одинаковые величины из соотношений (8.15) и (8.13), с
учетом (8.16) получим квадратное уравнение относительно аКс
акс /секс jm = [ 1 - 2?(аКс - секс jm)‘]2*7Fopt. (8.17)
Введем вспомогательную переменную £ = акс- аКс Jm и решим
уравнение (8.17) относительно этой переменной:
71 + 45a2KCJ,n(F/Fopl-1)F/Fopt-1
8 = —-------------------------------.
25акс
При небольших отклонениях Fot Fopt имеем
s ~ аКс jin(27Fopt О»
или
О-КС/секс Jm ~ 2^/Fopt, (8.18)
что совпадает с решением (8.14). Здесь величины аКс, акслп и Fopt
также соответствуют скорости ИКр .
Таким образом, в обоих случаях имеется пропорциональная зави-
симость между отклонением потребного управления от оптимального и
отклонением площади входа в двигатель от своей оптимальной величи-
ны.
8.2. Максимизация коэффициента крейсерской дальности 3 19
Оптимизация коэффициента подъемной силы и коэффициента
избытка воздуха прямоточного ВРД. Перейдем к рассмотрению вари-
анта, когда управляющими переменными являются су и акс, а площадь
входа является заданной величиной. Будем по-прежнему полагать, что
задана некоторая фиксированная скорость полета ИКР. С учетом реше-
ний (8.14) и (8.18) можно заключить, что в данном случае справедливы
следующие неравенства:
ССкС /ОСкС Jin < FIFQ^ , Су /СуКт < F/Fo^ .
Пусть для определенности угол отклонения вектора тяги PC явля-
ется заданной величиной: 5=аАт. Проведем предварительный анализ
ожидаемого решения. Пусть аэродинамическая поляра является квадра-
тичной и симметричной, а зависимость J(aKc) аппроксимируется квад-
ратной параболой (8.16). Введем обозначения
у = Су /суК1П и Z = акс /акс Jm •
Запишем условие (8.3) с учетом малости углов а и 5. Тогда при
F* Fopt имеем
Cx,ni„(l+r)= ^F/S. (819)
аКсА>^
а при F= Fopt
2 J f
2cx„„„ = ,nax /rK" /%,/£ (8.20)
Исключив из (8.19) и (8.20) одинаковые величины, получим
(1 + /)/2 = [ 1 - B{z - 1 )2акс j,„2] 77— F/Fopl. (8.21)
"К in
где f=fn +/1(а + авз) =/> +./аСаКт + аВз);
/кт =/о +/‘(акт + авз); (8.22)
авз-угол заклинения воздухозаборника (нижней поверхности носовой
части фюзеляжа, см. раздел 6.3).
В первом приближении можно считать, что максимум коэффициен-
та крейсерской дальности определяется максимумом произведения KJ.
Используя соотношение (8.19), представим максимизируемую функцию
как
KJ= су акс LnVSIQfFY
откуда видно, что задача сводится к максимизации функции
Л =yz/f. (8.23)
320
Глава 8. Полет ЛА с ВРД на заданную дальность
Анализ соотношений (8.21) и (8.23) показывает, что результаты оп-
тимизации удобно представить в виде зависимости величин у и z от
относительной площади входа F/Fopt. Характер решения определяется
параметрами аппроксимации В и aKcjm, а также параметрами, влияю-
щими на эффект поджатия:/),/*, аВз, «-кт - Напротив, такие параметры,
как скорость, число Маха, аэродинамические коэффициенты cya, cxniin,
характеристики двигателя Jmax, £0 и др., прямо не влияют на оптималь-
ное решение.
Рассмотрим далее два варианта зависимости тяги ВРД от угла ата-
ки.
1. Тяга ВРД не зависит от угла атаки (f=fix). В этом случае
максимизируемая функция упрощается: Л = yz. Выразим из соотноше-
ния (8.21) переменную;/:
(8.24)
V z
и подставим в максимизируемую функцию:
Л =72[l-5(z-l)2a2KCJm]zF/Fopl-z2 .
Из необходимого условия экстремума функции A(z) получим квад-
ратное уравнение относительно z. Его решением является
(8,5)
2а
где а = ЗВ(аКс .im)2F/Fopt; b = 1 - 45(aKC im)~F/Fo^;
с = [5(aKCJm)2- l]F/FOpt-
При известном значении z коэффициент подъемной силы опреде-
ляется при помощи формулы (8.24). Таким образом, задача решена
аналитически.
2, Тяга ВРД зависит от угла атаки (dflda > 0). В этом случае не
удается получить простое аналитическое решение, и задача может быть
решена только численно. Результаты расчетов с использованием точных
соотношений представлены на рис. 8.8 и 8.9 в зависимости от относи-
тельной площади входа F/Fopx. Рассмотрен диапазон изменения чисел
МКР от 4,5 до 10. При увеличении МКр оптимальное значение Fopt уве-
личивается в соответствии с зависимостью (8.11).
На рис. 8.8 показано изменение оптимальных значений управляю-
щих переменных = су/сукт и z = оскс/оскс jm • Левая точка каждой зави-
симости соответствует условию aKc = 1. Пунктирные линии соответст-
вуют варианту, когда тяга не зависит от угла атаки. Зависимости y(F)
8.2. Максимизация коэффициента крейсерской дальности
321
Рис. 8.8. Изменение управляющих переменных cyopt и aKCopt (в относитель-
ном виде) в зависимости от относительной площади входа в двигатель для
нескольких значений крейсерского числа М полета:
------тяга ВРД зависит от угла атаки;----тяга ВРД нс зависим от угла атаки
близки к линейным. При МКр = 4,54-7,5 оптимальное решение можно
приближенно записать как
j/opt« 1 + d(FIFQ^— 1), где <7= 0,34-0,35.
Зависимости zopt(F) существенно нелинейные. Расчеты подтвер-
ждают тот факт, что решение прямо не зависит от величин, не входящих
в выражения (8.21) и (8.22). Влияние крейсерского числа Маха сказыва-
ется на решении только через изменение величин, входящих в (8.21) и
(8.22). Увеличение числа Маха, как известно, приводит к увеличению
эффекта поджатия и к уменьшению коэффициента (Хкслп- Расчеты
показали, что каждый из этих факторов приводит к увеличению опти-
мального значения z (при F IF^> 1); к этому же результату приводит
уменьшение коэффициента В. При увеличении zopt оптимальное значе-
ние^ уменьшается, и наоборот. В результате при увеличении числа МКр
до 10 зависимость zopt(F) становится более крутой, а зависимость
322
Глава 8. Полет ЛА с ВРД на заданную дальность
Рис. 8.9. Зависимость относительного значения коэффициента крейсерской
дальности от относительной площади входа в двигатель
^от(^) - более пологой. К такому же результату приводит использование
эффекта поджатия (см. рис. 8.8).
На рис. 8.9 показано изменение коэффициента крейсерской даль-
ности в зависимости от площади входа в двигатель для различных
чисел МКР. Видно, что коэффициент крейсерской дальности максима-
лен при F=FO^. К уменьшению коэффициента /Кр приводит как
уменьшение площади входа, так и ее увеличение относительно Fo^. Так,
увеличение площади F по сравнению с оптимальной в 2 раза приводит
к уменьшению крейсерской дальности на 6-н10% в зависимости от
числа МКр.
Определение влияния высоты полета на коэффициент крей-
серской дальности. Высота полета связана с текущей массой при
помощи соотношения (8.4), из которого следует, что на постоянном
режиме управления (а = fix; акс~ fix; V= fix) высота всегда увеличива-
ется вследствие уменьшения текущей массы ЛА. Выразим из (8.4)
плотность атмосферы:
р = 2mgv/(ciy V2S)
и определим производную высоты по массе:
dH/dm = (dHIdp^dpIdm) = р/(р 'н т) = - 1/(0,и).
В результате получим простую формулу для определения прира-
щения высоты:
А// = - Атл /(0/л).
Так, при изменении массы ЛА на 10% высота полета увеличивается на
0,624-0,73 км в зависимости от параметра атмосферы 0.
При уменьшении массы аппарата в 2 раза, что соответствует верх-
ней оценке для ЛА, совершающего длительный крейсерский полет,
изменение высоты равно
8.2. Максимизация коэффициента крейсерской дальности
323
\Н2 = 1п2/р « 0,693/р,
что составляет 4,3-5,1 км в зависимости от параметра р.
Таким образом, если при определении коэффициента /Кр в качестве
расчетной принять среднюю по высоте точку, то наибольшее отличие
текущей высоты от расчетной будет составлять ~ 2,5 км.
Определим изменение основных сомножителей, входящих в коэф-
фициент /Кр, при увеличении высоты полета на 1 км и сделаем оценку
максимально возможного отклонения /крот своего среднего значения.
Как следует из формулы (8.1), непосредственно от высоты зависит
сомножитель/ = l/(rgv). Его производная по высоте равна
1 £ V2
dfx/dH= —[^(2---------)-1].
r~gy gy gr
Относительное изменение величины/ равно
1 £ V2
\fx/fx=\H-[^-(2-------)-1],
Г gy gr
что при МКр = 4,5-ь 10 и ЛЯ = 1 км составляет 1,6-10'4-1,8-10’4.
Диапазон высот, на которых может осуществляться крейсерский
полет при МКр = 4,5-10, составляет 25-47 км. В случае изотермической
атмосферы полученные выше решения не зависят от высоты полета и,
соответственно, не зависит от Н коэффициент крейсерской дальности.
Однако согласно ГОСТу [29] на указанных высотах атмосфера является
неизотермической. Изменение скорости звука и параметра Р для двух
соответствующих слоев стандартной атмосферы приведено в табл. 8.1.
Таблица 8.1
Изменение скорости звука и параметра Р
в 5-ом и 6-ом слоях стандартной атмосферы
Геопотенциаль- ная высота Нг, км Скорость звука а, м/с Производная скорости звука по высоте а'н, с"1 Параметр атмосферы р, м"1
20,0-32,0 32,0-47,0 295,1-303,0 303,0-329,8 (0,676+0,656)-10’3 (0,183+0,168)-10"2 (1,62+1, 54)-10’4 (1,61+1,37)10 4
Как следует из этих данных, увеличение высоты при V= const при-
водит к уменьшению числа Маха.
Далее для упрощения положим, что F= Fopt и коэффициент/Кр оп-
ределяется через максимальные значения удельного импульса и аэро-
динамического качества. Вначале определим изменение удельного
импульса в зависимости от высоты. Его полная производная по Н при
V= const равна
324
Глава 8. Полет ЛА с ВРД на заданную дальность
dJ/dH= дЛдН+ (dJ7dM) = дЛдН-М(а'н/л)(а//5М),
dH
где дЛоН- частная производная J по //при М = const; 5J75M - частная
производная ./по М при Я = const.
Относительное приращение удельного импульса равно
А7/./ = ДнДЯ+ДМДЯ,
где Дн = (дЛдНуЩ Дм = - М(я н/я)(5/75М)/</. Здесь первое слагаемое
определяет относительное изменение J за счет высоты, второе слагае-
мое - за счет числа Маха.
В качестве расчетных чисел Маха примем значения 4,5; 5,5 и 7,5,
что соответствует локальным максимумам /Кр (см. рис. 8.4), а также
число МКР= 10. Расчеты ВСХ ПВРД, работающего на керосине, прове-
денные в ЦАГИ (автор расчетов Е.В. Пиотрович), показывают, что в
рассмотренной области изменения Н и М величина дЛдН является
отрицательной и, соответственно, отрицательным является слагаемое
Дн ЛЯ (табл. 8.2).
Таблица 8.2
К определению влияния высоты на
коэффициент крейсерской дальности (при Д// = 1 км)
Мкр 11кр , км 1 1 4’5 30 5,5 32 7,5 36 10 41
j 9,9-10"6 33-1 О’6 43-10’6 56-10"6
Удельный импульс
(дЛдН)и, м 4 -210’6 - 2,5-Ю”6 -610-6 -810’6
дндя - 0,002 - 0,0025 - 0,006 -0,008
(а//ам)/./ -0,11 -0,14 - 0,096 -0,14
дм д// 0,0011 0,0046 0,0041 0,0078
(Дн + ДМ)ДЯ j -0,0009 0,0021 -0,0019 - 0,0002
Аэродинамическое качество
Дн Л// -0,0057 -0,0072 -0,012 -0,018
(дК/дМ)/К -0,106 -0,085 -0,08 - 0,063
ДмД// 0,001 0,0028 0,0034 0,0036
(Дн + Дм)Д// - 0,0047 - 0,0044 -0,0086 -0,014
AvA/7 -0,0055 -0,0021 -0,01 -0,014
Производная дЛдМ в окрестности расчетных точек является отри-
цательной (см. табл. 8.2 и рис. 8.3). При увеличении высоты число М
8.2. Максимизация коэффициента крейсерской дальности
325
уменьшается, так как я'н>0. В результате слагаемое ДМДЯ является
положительным, что ослабляет эффект уменьшения J по высоте полета
(см. табл. 8.2).
Аналогичные оценки были проведены для аэродинамического ка-
чества. При этом величина ДНД// определена на основе данных, пред-
ставленных на рис. 9.7 (см. гл. 9), а частная производная сЭАУоМ - на
основании рис. 8.2. Характер изменения величин Дн и Дм в зависимости
от МКр для удельного импульса и аэродинамического качества является
одинаковым. Изменение коэффициента /КР за счет аэродинамического
качества на 1-2 порядка больше, чем за счет соотношения l/(rgv) •
Из табл. 8.2 следует, что при увеличении МКР влияние высоты по-
лета на /кр усиливается и изменение коэффициента крейсерской даль-
ности может достигать 1-?1,4%(при Д/У = 1 км). Максимальное измене-
ние коэффициента /КР относительно своего среднего значения (при
АН = 2,5 км и МКр= 10) составляет 3,5 %.
В общем случае процедура расчета траектории крейсерского поле-
та заключается в следующем. Вначале для нескольких значений массы
ЛА (и, соответственно, высот полета) оптимизируются координаты
вектора управления и определяются максимальные значения коэффици-
ента крейсерской дальности. При этом используются, например, на-
чальная, средняя по высоте и конечная точки. Затем строится функция
/кр(/7?) и осуществляется интегрирование основного уравнения движе-
ния
did dm = -/кр /т. (8.26)
Если воспользоваться средним по высоте значением коэффициента
/крср, то можно получить известное приближенное аналитическое
решение для крейсерской дальности полета:
Lkp =/крср In (тло//«к) • (8.27)
Здесь и далее индексы "0” и "К" соответствуют начальной и конечной
точкам крейсерского полета.
Сделаем оценку точности решения (8.27). Так как в крейсерском
полете высота меняется не более чем на 5 км, то можно считать, что
коэффициент/кр изменяется по высоте линейно. Для этого случая урав-
нение (8.26) интегрируется аналитически. Вначале покажем, что высота
и дальность полета связаны зависимостью, близкой к линейной. Дейст-
вительно, с использованием соотношений (8.27) и (8.4) можно записать
£кр -/кр.ср In (тя01т) =/крср In (ро / р) =/кр.ср Рср(77- Яо), (8.28)
где параметр рСр соответствует средней высоте полета ЯСр- Зависи-
мость (8.28) является линейной с точностью до постоянства сомножи-
телей /крср и Рср .
Из формулы (8.28), в частности, следует, что угол наклона траекто-
рии примерно постоянен и равен
326
Глава 8. Полет ЛА с ВРД на заданную дальность
0кр ~ (//к- Hq)/l/кр- 1/(/кр.срРср) ,
что при/кр.ср= 354-40 тыс. км составляет 0,0094-0,01°.
Представим зависимость /Кр от высоты в следующем виде:
(8.29)
Hq
где в соответствии с данными табл. 8.2 величина коэффициента b со-
ставляет 0,074-0,57.
Исключив разность высот в формуле (8.29) при помощи соотноше-
ния (8.28), получим
./кр =/кр.о (1 -Ь —--—— ).
Укр.срРср^о
Используя это выражение, запишем дифференциальное уравнение
крейсерского полета (8.26):
dL _ dm
г г nL т ’
Ткро Ткр.о г
Укр.ср
где /7 = /?/(РсрЯ0), и проинтегрируем его от начальной до конечной точ-
ки:
/КРСР ln( 1 - иАкр//крср) = 1п(/ик/ото).
/kpow
После преобразований получим более точную формулу для расчета
крейсерской дальности:
( т (J f*P СР
AkpVkpcp[1-P4 ]/и, (8.30)
I'M
где/кр.ср/./кр.о = 1 — Ь(Нср— Но)/Но.
Расчеты показывают, что при МКр = 10 формула (8.27) дает заниже-
ние крейсерской дальности на 0,44% по сравнению с (8.30). При
уменьшении МКр точность определения дальности по формуле (8.27)
увеличивается.
8.3. Оптимизация траекторий на участке разгона
Обычно при оптимизации управления на участке разгона в качест-
ве функционала используется потерянная дальность, а максимизируе-
мая в каждой точке траектории функция записывается через километ-
ровый расход топлива [87]-[89], [96]:
8.3. Оптимизация траектории на участке разгона 327
А - r(gL/gLKp ~ 1),
где и gLKp - километровый расход топлива на участке набора высо-
ты и в крейсерском полете.
Так как километровый расход топлива пропорционален текущей
массе самолета, которая заранее неизвестна и может меняться на десят-
ки процентов, то при таком подходе точность расчетов снижается.
Получим более точное выражение для максимизируемой функции.
Предположим вначале, что на участке планирования от заданной
крейсерской скорости ГКр до конечной скорости Кк оптимальное управ-
ление известно и, соответственно, известна дальность планирования
АПл (см. рис. 8.1). Это значит, что суммарную дальность первых двух
участков А|.2 = АРЗГ+АКр можно считать фиксированной. При этом
максимуму конечной массы ЛА (т.е. максимуму массы ПГ) будет соот-
ветствовать максимум массы ЛА в конечной точке крейсерского полета
/Икр• Пусть коэффициент крейсерской дальности/Кр является известным
(определен как среднее значение на втором участке полета). Это означа-
ет, что дальность крейсерского участка АКр связана с массой ЛА сле-
дующим образом:
Lkp 1 п (т рзг//Икр).
Здесь /ИрзГ и /иКр- значения массы ЛА в конце участка разгона и в конце
крейсерского участка.
Определим оптимальное управление на участке разгона ЛА. С этой
целью запишем выражение для массы /иКр с использованием логариф-
мической массы ЛАрзГ в конечной точке разгона:
/иКр= /ИрзГехр(-АКр//кр) = /и0ехр(ЛАрзг)ехр(-АКр//кр) =
= /иоехр(Л/|>зг+ Арзг//кр- А|.2//кр)«
Здесь учтено, что АКр= А|.2-АРЗГ.
Так как Aj.2 и /Кр - постоянные величины, то из последнего выра-
жения следует, что максимуму /иКр однозначно соответствует максимум
промежуточного функционала
Ф =/кр А/рзг + АрзГ . (8.31)
Если учесть, что ЛАРзг = - 1п(/и0//ирзг), то вместо максимизации Ф
можно минимизировать величину ДА = - Ф, которая представляет собой
потерянную дальность:
ДА — Акр — Арзг ,
где АКр* =/кр1п(/л0//Ярзг)-условная дальность крейсерского полета,
соответствующая уменьшению массы от до /ирЗГ.
Функционал Ф представляет собой линейную комбинацию фазо-
вых переменных ЛА и А. Как показано в разделе 2.9, при больших скоро-
стях полета в каждой точке траектории оптимальное управление опре-
деляется из условия экстремума d<$/dE. Будем использовать это
328
Глава 8. Полет ЛА с ВРД на заданную дальность
решение не только при больших, но и при малых скоростях (в качестве
начального приближения). Запишем минимизируемую функцию:
/ J Г? ./кр dhd (1L
(Ррзг= - d<&/dE = —-------------
fKf-(-dL/dM)
-dE/dM
= fKP-(-dLldM)^m.n
при E = fix. (8.32)
Знак безразмерной функции (рРзг взят в соответствии с неравенством
dE>Q. Знаменатель в (8.32) представляет собой функцию jp3r (2.142),
полученную в задаче разгона со свободной дальностью полета.
Запишем выражение для производной (-dL/dM) с использованием
правых частей второго и третьего уравнений системы (2.136), введя
следующую величину:
(RJr)VJc.
fa = -dL ldM= . (8.33)
Сравнение полученного выражения с (8.1) показывает, что функция
/v имеет такой же вид, как и коэффициент крейсерской дальности.
Разница заключается в том, что все переменные величины, входящие в
(8.1), соответствуют крейсерской скорости полета, а переменные, вхо-
дящие в выражение (8.33), соответствуют текущей точке разгона.
С учетом введенных обозначений перепишем выражение (8.32)
следующим образом:
/кр ./у — ./кр ./у _ ,/кр£т -п
/ц Т йс ' 111 111
f / V 1 J V
./рзг ,7ЭФК
(8.34)
где
В данном случае минимизируемая функция, в отличие от традици-
онного подхода, не зависит от массы ЛА и километрового расхода
топлива.
Так как коэффициентпропорционален скорости, то это означает,
что при малых скоростях полета имеет место неравенство /v«./i<p и,
как следует из (8.34), оптимальное управление будет однозначно опре-
деляться максимумом функции /рЗГ, т.е. соответствовать задаче разгона
со свободной дальностью полета. Используя соотношения (8.31) и
(8.33), получим
d(^ = dM(fKP-fv).
Так как dM< 0, то при малых скоростях разгона справедливо неравен-
ство б/Ф < 0.
8.3. Оптимизация траектории на участке разгона
329
В общем случае величина Д может превышать ДР. поэтому диф-
ференциал б/Ф может быть как отрицательной, так и положительной
величиной. В связи с этим функция (рРЗГ записана в виде (8.32), гак как
у функции с1Ф/с1Е знаменатель при разгоне не меняет своего знака, в
отличие от функции dE/d<b.
По мере увеличения скорости коэффициент Д приближается к ДР.
а оптимальное управление - к крейсерскому. При выходе на крейсер-
ский режим (при Ж«0) задача разгона трансформируется в задач)
оптимизации крейсерского режима полета. Очевидно, что в этом случае
необходимо максимизировать величину Д. Таким образом, алгоритм
оптимизации можно записать в следующем виде:
(ррзг-^min при dE>0;
Дmax при dE^Q.
В общем случае данная задача решается только численно. Однако с
использованием некоторых упрощений можно получить аналитическое
решение. Рассмотрим частный случай, когда тяга ВРД и его удельный
импульс не зависят от угла атаки. Будем максимизировать функцию
Дф* при V= fix, записав ее в виде
| _ . ^хКт^ . -А'СКт)
Cykm /кр
Здесь функция Д(кт) вычислена не через текущие значения с\ и
cr , соответствующие разгону, а через аэродинамические коэффициен-
ты су и сх, соответствующие режиму Дпах.
Будем полагать, что поляра квадратичная, т.е. с\ = с\|М1П( 1 + у2);
^xKm = mjn; ^ = су/сукт. Тогда формулу (8.35) можно переписать в
виде
г 1-сх „„„(! +у2 )S/(CrF)
Дэф — J----------------------
Оптимум по у определяется в результате решение
квадратного уравнения:
Уг-У
CR /кр
Сх min1^ ,/v(Km)
<\т1Л
(8.36)
следующего
(8.37)
Анализ коэффициентов уравнения (8.37) показывает, что искомым
решением является корень
330
Глава 8. Полет ЛА с ВРД на заданную дальность
Рис. 8.10. Зависимость коэф-
фициента крейсерской даль-
ности от крейсерского числа
Mazxa для гипотетического ЛА
тельной площади входа на
I 6>r F ./кр
\ 2с S f
у у СХ1П1П ' J V(Km) j
Далее задача оптимизации управ-
ления на участке разгона была решена
численно. Рассмотрен гипотетический
ЛА с относительной площадью входа
F/S = 0$], у которого зависимость
коэффициента крейсерской дальности
от крейсерского числа Маха имеет
максимум при МКр=6 (рис. 8.10).
Рассматривается случай, когда коэффи-
циент расхода воздуха двигателя ЛА
увеличивается при увеличении скоро-
сти полета и угла атаки. Для опреде-
ленности принято, что угол отклонения
вектора тяги PC равен оск1П.
Вначале была проведена оптими-
зация управления при разгоне до числа
МКр= 6. В этом случае/кр= 38,1 тыс. км.
С целью определения влияния относи-
оптимальное управление расчеты были
проведены также при F/S = 0,015 и 0,02. При увеличении F/S коэффи-
циент крейсерской дальности уменьшается и становится в данном
случае равным, соответственно, 36,45 и 33,8 тыс. км. Результаты расче-
тов представлены на рис. 8.11 и 8.12 в зависимости от числа М полета
(М = 34-6).
При разгоне оптимальный угол атаки увеличивается от 14-2° до
54-7,5°, причем вблизи числа МКР зависимость становится более поло-
гой (см. рис. 8.1 It/). В конечной точке разгона оптимальный угол атаки
совпадает с углом, полученным в результате оптимизации крейсерского
режима полета при МКр= 6.
Зависимости Cyopt/^уКт и //Opt от числа Маха носят аналогичный ха-
рактер (см. рис. 8.116 и в). При F/S = 0,01 в начале разгона оптимальная
высота оказалась меньше, чем минимально допустимая высота, опреде-
ленная из условия q < еу.пахд. Таким образом, при малых скоростях
полета программная высота полета должна определяться так же, как и в
задаче со свободной дальностью разгона.
Величина aKcoPt при разгоне вначале равно 1,0, а затем увеличива-
ется практически линейно вплоть до своего крейсерского значения при
МКр= 6 (см. рис. 8.11г). Характерно, что при увеличении F/S оптималь-
ные значения коэффициента избытка воздуха, а также угла атаки и
высоты увеличиваются (см. рис. 8.1 It/, в, г). Это показывает, что избы-
точная площадь входа в двигатель частично компенсируется уменьше-
8.3. Оптимизация траекторий на участке разгона
33 I
Рис. 8.11. Траектория разгона до числа МКР= 6: изменение оптимальною угла
атаки (а), оптимального коэффициента подъемной силы (по отношению к
cvKin) (6), оптимальной высоты (б) и оптимального коэффициента избытка
воздуха (?) в зависимости от числа Маха
нием коэффициента тяги за счет
большего значения аКс и частично -
увеличением коэффициента лобового
сопротивления за счет большего угла
атаки.
Зависимость эффективного им-
пульса ЛА от числа Маха вначале
ведет себя так же, как и при разгоне со
свободной дальностью полета. При
увеличении F/S эффективный импульс
увеличивается. По мере приближения
к МКр эффективный импульс резко
уменьшается и становится практиче-
ски нулевым при М = 6 (см. рис. 8.12).
Далее оптимизация управления
была проведена для случая разгона до
Рис. 8.12. Траектория раз! она
до числа Мкр =6. Изменение
эффективного импульса ЛА в
зависимости от числа Маха
числа МКр = 7. Коэффициент
крейсерской дальности при МКр = 7 составляет /j<p = 35,5 тыс. км, что на
6,5 % меньше, чем при МКр-6 (см. рис. 8.10). Результаты расчетов
приведены на рис. 8.13 и 8.14 при F/S = 0,01.
Глава 8. Полет ЛА с ВРД на заданную дальность
Рис. 8.13. Траектория разгона
до числа МКР = 7. Изменение
эффективного импульса ЛА в
зависимости от числа Маха
Изменение эффективного им-
пульса ЛА представлено на рис. 8.13,
из которого видно, что до числа М = 5
разгон осуществляется так же, как и в
предыдущем случае, а затем эффек-
тивный импульс ЛА скачкообразно
уменьшается до нуля и остается нуле-
вым до числа М = 7. В данном случае
число М = 5 характерно тем, что в
этой точке коэффициент крейсерской
дальности имеет такое же значение,
как при М = 7 (см. рис. 8.10).
Остальные переменные до числа
М = 5 ведут себя качественно так же,
как и при разгоне до числа МКр = 6
(см. рис. 8.14л, б и я). Зависимость с\,ор(/сукт от числа Маха является
пракз ически линейной. Коэффициент избытка воздуха вначале равен 1;
начинает увеличиваться практически линейно
зачем
Рис. 8.14. Траектория разгона до числа МКр=7: изменение оптимального
коэффициента подъемной силы (по отношению к суКт) (я), оптимальной высо-
ты (о). оптимального коэффициента избытка воздуха (в) и функции /v (по
отношению к коэффициенту /Кр при МКр= 7) (г) в зависимости от числа Маха
при М = 4,74-5
8.3. Оптимизация траекторий на участке разгона
(см. рис. 8.14в). При числе М = 5 все указанные величины скачкообраз-
но изменяются до крейсерских значений, соответствующих этой точке.
Так, высота увеличивается на ~ 1 км (см. рис. 8.146); коэффициент
избытка воздуха увеличивается с 1,18 до 1,43 (см. рис. 8.14г;).
Изменение коэффициента/v (по отношению к/кр при МКр = 7) но
числу Маха представлено на рис. 8.14г. В диапазоне М = 34-5 величина
fy/fa увеличивается от 0,22 до 0,75. Так как при М >5 продольная
перегрузка равна нулю, то в этом диапазоне коэффициент Д , по сути,
представляет собой текущее значение коэффициента крейсерской
дальности.
Очевидно, что в данном случае в диапазоне чисел М = 54-7 опти-
мальная программа управления не может быть строго реализована.
Объясняется это тем, что полет при МКр = 7 является менее выгодным,
чем, например, при МКр-6. Отсюда, в частности, следует, что при
выборе крейсерской скорости полета необходимо стремиться к тому,
чтобы крейсерское число М находилось левее или соответствовало
максимуму функции/кр(МКр).
Обеспечить разгон на участке М = 54-7 можно за счет некоторого
отклонения программного управления от оптимального. Например,
коэффициент избытка воздуха можно уменьшить на 0,14-0,2 по сравне-
нию со значениями, приведенными на рис. 8.14б\ При формировании
программного профиля полета в координатах ’’высота-число Маха" за
основу можно взять зависимость, представленную на рис. 8.146. сгла-
див скачок при числе М = 5.
Вернемся к задаче разгона до числа МКР = 6, т.е. рассмотрим слу-
чай, когда коэффициент крейсерской дальности является максимальным
по числу Маха (см. рис. 8.10). Проинтегрируем уравнения движения на
участке разгона от М = 3 до Мкр - 6. В качестве критерия оптимально-
сти будем для определенности использовать суммарную дальность
разгона и крейсерского полета £|.2, соответствующую относительному
запасу топлива 30 %:
L\.2= />рзг + ^кр—шах,
где Акр=/кр1п . Здесь то - начальная масса (при М = 3); и
0,7шо
Арзг~ масса и дальность в конечной точке разгона. Максимум L|.2 соот-
ветствует максимуму промежуточного функционала (8.31).
Пусть 775=0,01. При интегрировании уравнений движения будем
использовать результаты оптимизации, представленные на рис. 8.11с/ и
в. Так как полученную программу управления нельзя считать строго
оптимальной, то за основу возьмем качественное изменение управляю-
щих переменных. Для простоты будем полагать, что угол атаки есть
линейная функция, а коэффициент избытка воздуха - кусочно-линейная
функция числа Маха (рис. 8.15). В конечной точке при М = 6 значения
управляющих переменных соответствуют крейсерскому режиму. Так
как в данном случае непосредственно задается программа ос(М). а ие
334
Глава 8. Полет ЛА с ВРД на заданную дальность
профиль полета в координатах "Н- М",
то уравнение автопилота используется
в виде (2.170). Расчеты показали, что
суммарная дальность Л|.2 равна
11130 км.
Проведем оптимизацию програм-
мы управления а(М). С этой целью
введем дополнительные промежуточ-
ные узлы в программу управления
а(М) (рис. 8.16) и будем оптимизиро-
вать их положение. В данном случае,
как и в разделе 7.4, задача сводится к
поиску максимума функции нескольких
Рис. X. I 5. Исходная программа
изменения угла атаки и коэф-
фициента избытка воздуха
Мо Мк
Рис. 8.16. Введение допол-
нительных узлов в програм-
му изменения угла атаки для
ее оптимизации
Рис. 8.17. Оптимизация про-
граммной зависимости угла
атаки от числа Маха
и тангенциальная перегрузка
переменных:
Zj.2 (а/9 М/) —> max; i = 1,..., n,
где а,, М, - координаты промежуточ-
ных узлов.
Решение задачи при п = 2 (М] =4,
М2 = 5) показало, что сдвиг узлов
вправо и вниз (рис. 8.17) позволяет
увеличить дальность L\.2 на 63 км, что
составляет примерно 0,6% от Ь].2 .
Дальнейшая оптимизация путем увели-
чения числа узлов не привела к ощути-
мому увеличению функционала.
Результаты расчетов траектории
разгона после оптимизации программы
управления а(М) приведены на
рис. 8.18. Время разгона составляет
3290 с, дальность разгона - 5360 км.
Относительный запас топлива разгона
равен 18,4 % от что соизмеримо с
общим запасом топлива. Видно, что
вторая часть разгона (при т > 2000 с)
осуществляется в условиях, близких к
крейсерскому режиму: высота, число
Маха и управляющие переменные
практически постоянны (см. рис. 8.186
и в), а эффективный импульс ЛА бли-
зок к нулю (см. рис. 8.18я).
Так как эффективный импульс ЛА
вблизи числа М = 6 практически равны
нулю, то положение точки перехода на крейсерский режим не является
строго определенным. Небольшое отклонение управляющих перемен-
8.3. Оптимизация траектории на участке разгона
335
ных а и аКс в конечной точке в
сторону увеличения может привести
к невозможности разгона до заданно-
го числа МКр . В связи с этим рас-
смотрим, как влияет на траекторию
разгона увеличение коэффициента
тяги cR на заключительном участке
разгона. С этой целью будем умень-
шать наклон конечного участка
программы оскс(М) (см. рис. 8.15),
приняв в качестве параметра значе-
ние акс при М = 6.
На рис. 8.19 показано изменение
дальности разгона в зависимости от
акс(м = б)- Видно, что уменьшение
этой величины от 1,5 до 1,4 приводит
к уменьшению дальности разгона в
~ 2 раза. Дальнейшее уменьшение
(Хкс(м = б) До 1,0 приводит к незначи-
тельному сокращению дальности
разгона. При этом суммарная даль-
ность Zi-2 уменьшается не более чем
на 0,1 %. Примем в качестве рацио-
нального значения аКс(м = б)= 1,4. На
рис. 8.20 представлено соответст-
вующее изменение эффективного
импульса ЛА по траектории, откуда
видно, что разгон стал более интен-
сивным (ср. с рис. 8.18я).
Таким образом, для обеспечения
гарантированного разгона до крей-
серского числа Маха рекомендуется
Рис. 8.18. Траектория опти-
мального разгона до числа
Мкр = 6. Изменение дальности
£РЗГ и эффективного импульса
ЛА УЭф (а), числа Маха М и
высоты Н (б), угла атаки а и
коэффициента избытка возду-
ха ПВРД акс (в) в зависимости
от времени полета
задавать конечное значение аКс на
54-10% меньше по сравнению с его
крейсерским значением.
Рассмотрим ситуацию, когда ко-
нечная точка разгона лежит правее
точки максимума, показанной на
рис. 8.10, т.е. на заключительном
участке разгона величина функции
/v больше, чем/КР. Пусть, например,
Мкр = 7. Тогда, как было показано
выше (см. рис. 8.13), на участке изменения М от 5 до 7 эффективный
импульс ЛА и тангенциальная перегрузка равны нулю. Это значит, что
на данном участке cRF = cKS и
336
Глава 8. Полет ЛЛ с ВРД на заданную дальность
1,0 1,2 1,4 «кс(м = б)
Рис. 8.19. Зависимость дальности
разгона от значения коэффициента
избытка воздуха в конечной точке
Рис. 8.20. Изменение во
времени эффективного им-
пульса ЛА при aR-c(M=6) = 1,4
KVJ
,/v------------
'' gy
*KVJ/gN
Пусть тангенциальная перегрузка является близкой к нулю величи-
ной. тогда
R R
Функция (8.34) запишется следующим образом:
Фрзг ~
./КР ./у _ /кр fy . <?т
/vnx gv
(8.38)
Так как ,/v >./кр -» то при —> 0 можно получить сколь угодно ’’глу-
бокий" минимум функции фрзг, т.е. однозначного решения в данном
случае нет. Для практических расчетов траектории разгона можно
рекомендовать задание коэффициента избытка воздуха с несколько
меньшим значением, чем aKcjm, и угла атаки с несколько меньшим
значением, чем акт- Пусть относительное отклонение аКс от aKcjm
составляет 5| > 0:
О-КС= секс JmO - 5|).
Аналогичное отклонение для угла атаки составляет 8?>0. Тогда
тангенциальная перегрузка будет равна
А\Ч51 + 52Жпах,
а эффективный импульс ЛА
./эф «Л51 + §2)-
8.3. Оптимизация траектории на участке разгона
337
Отсюда видно, что при задании 8] и 32 в диапазоне 0,054-0,1 можно
обеспечить разгон с пх« 0,024-0,04, что является вполне приемлемым.
При этом режим полета будет близким к крейсерскому.
8.4. Оптимизация траекторий на участке планирования
Предположим, что задача оптимизации траектории на участке раз-
гона JIA решена. Это означает, что известны масса /лРЗГ в начальной
точке крейсерского полета и суммарная дальность £2.3 крейсерского
участка и участка планирования. Запишем конечную массу ЛА с ис-
пользованием значения переменной Л/Пл в конце участка планирования:
wK= 7лКрехр(М1л) = Мрзгехр(-Лкр//кр) ехр(Л/Пл) =
= трзг ехр(Л/пл + ^пл//кр- ^2-з//кр)-
Здесь учтено, что ZKp = ^2-з- ^пл •
Так как в данном случае величины wp3r и Z2.3 постоянные, то из
полученного выражения следует, что максимуму /ик однозначно соот-
ветствует максимум промежуточного функционала
Ф =/кр М1Л + £пл -> max. (8.39)
Как и в случае разгона, функционал представляет собой линейную
комбинацию фазовых переменных Мм L. Запишем функцию, подлежа-
щую максимизации в каждой точке траектории, с учетом того, что
dE<0:
f\rpdM + dL
фпл ~ - d<&/dE = —----------> max при Е = fix.
-dE
В общем случае планирование может осуществляться как с выклю-
ченными, так и с работающими двигателями. В первом случае (dM= 0)
функция фпл принимает такой же вид, как и в задаче максимизации
продольной дальности (см. раздел 2.9):
R 2
фпл “/пл ~ max. (8.40)
Здесь аэродинамическое качество соответствует конфигурации ЛА с
выключенным двигателем.
При умеренных скоростях полета у^л « К, откуда следует, что по
физическому смыслу функция фпл - это аэродинамическое качество с
некоторым сомножителем.
Во втором случае (при работающем двигателе) имеем
338
Глава 8. Полет ЛА с ВРД на заданную дальность
Фпл = yy-gT-»max.
•'эф'7
(8.41)
Сравнение выражений (8.41) и (8.34) показывает, что функция (рПл
имеет такой же вид, что и фРЗГ, однако в отличие от фРЗГ, функция (рПл
максимизируется. Функция (рпл должна быть больше нуля, в противном
случае более выгодным является планирование с выключенным двига-
телем. Так как /Эф < 0, то отсюда следует, что должно выполняться
условие f\ >/кр •
Вначале исследуем вариант, когда начальное число М планирова-
ния лежит правее точки максимума (см. рис. 8.10). Рассмотрим участок
планирования в диапазоне уменьшения числа М от 7 до 5. В этом слу-
чае по аналогии с формулой (8.38)
Фпл=/ (8.42)
А”х Sn
где/у>/кр •
Очевидно, что при пх -» -0 можно получить сколь угодно большое
значение фпл- Для проведения практических расчетов, в отличие от
участка разгона, коэффициент избытка воздуха должен задаваться с
несколько большим значением, чем aKcjm, а угол атаки - с несколько
большим значением, чем aK1n •
ОСкС- акс JmO + 8|);
В этом случае имеет место
Их«-(8| + б2)/Кпах;
a=aKm(l + 32).
(8.43)
/эф ~ ~/(81 + 32).
Как и в разделе 8.3, рекомендуется задавать 8j и 82 в диапазоне 0,05-е-0,1.
Теперь рассмотрим вариант, когда начальное число М планирова-
ния лежит левее точки максимума. В этом случае обеспечить условие
_ (^/г)К/с£
А--------/г/сч А'
gvcR(F/5)
можно только за счет уменьшения коэффициента тяги cR, т.е. за счет
увеличения коэффициента избытка воздуха по сравнению с режимом
/шах •
аКС > aKC Jin •
Сделаем оценку функции фПл в случае небольшого отклонения
летного числа М от МКР. Пусть a = aKin и относительное отклонение
аКс от aKcjm составляет 8]; тогда можно записать
/v _/крО + 8|),
8.4. Оптимизация траектории на участке планирования
339
и с учетом первой формулы
(8.43) при малом значении 8|
формула (8.41) преобразуется
к виду
фпл-----Атах,
где аэродинамическое качест-
во соответствует конфигура-
ции ЛА с работающими двига-
телями.
Сравнение с формулой
(8.40) показывает, что в точке
схода с крейсерского режима
функция фпл имеет одинако-
вый вид как при работающих,
так и при неработающих
двигателях. Отличие заключа-
Рис. 8.21. Траектория планирования
ЛА с работающим двигателем. Изме-
нение оптимальных значений управ-
ляющих переменных и соотношения
fxf I/кр в зависимости от числа Маха
ется только в величине аэро-
динамического качества.
Определим поведение
функции фпл по траектории
планирования. С этой целью
решим задачу численно на
участке М = 3^-6. Примем, что
/75 = 0,01. На рис. 8.21 пока-
зано изменение оптимальных
значений управляющих пере-
менных и соотношения /v//kp
в зависимости от числа Маха
для варианта планирования с
работающими двигателями.
При уменьшении числа М
полета aKcoPt практически
линейно увеличивается от 1,5
до 3,0. Величина cyopt/cyKm
монотонно увеличивается от 1 до
ется от 1 до 2,9.
Рис. 8.22. Зависимость максимизи-
руемой функции фпл от числа Маха
для двух вариантов планирования
1,32. Соотношение /у//кр увеличива-
Изменение функции фпл(М) по числу Маха показано на рис. 8.22.
Там же представлено изменение функции фпл(М) в случае выключен-
ных двигателей. В первом случае величина фПл резко уменьшается по
траектории, а затем несколько увеличивается. Во втором случае (с
неработающими двигателями) характер функции фпл(М) соответствует
зависимости Л^пах(М). Таким образом, из полученных данных следует,
340
Глава 8. Полет ЛА с ВРД на заданную дальность
что двигатели выгоднее выключать практически сразу после схода с
крейсерского режима, что согласуется с результатами работы [114].
Далее траектория планирования была проинтегрирована численно
в диапазоне чисел М = 3-^6. В качестве критерия оптимальности ис-
пользовалась суммарная дальность крейсерского полета и планирова-
ния Л2.з, соответствующая относительному запасу топлива 20 % (по
отношению к массе в начальной точке крейсерского полета)
Z/2-з ~ ^кр + -^пл —max,
где ЛКр = /кр1п———(тк~ конечная масса (при М = 3), 77?Кр-масса в
0,8/77Кр
конечной точке крейсерского участка). Максимум Л2.3 соответствует
максимуму промежуточного функционала (8.39).
Суммарная дальность £2.3 при планировании с работающими дви-
гателями составляет 9120 км. Дальность участка планирования равна
3550 км; время 2250 с; относительный запас топлива составляет 7,4%
ОТ 777К|> •
В случае планирования с неработающими двигателями для просто-
ты полагалось, что аэродинамическое качество не ухудшается при
выключении ВРД. Расчеты показали, что суммарная дальность £2.3 при
этом на 210 км больше. Дальность участка планирования уменьшается
до 840 км, время - до 640 с. Очевидно, что если при выключении ВРД
аэродинамическое качество ухудшается значительно, то точка выклю-
чения ВРД должна сместиться в сторону уменьшения числа Маха.
ГЛАВА 9
ВОЗВРАЩЕНИЕ ЛА С ОРБИТЫ.
ПЛАНИРОВАНИЕ В АТМОСФЕРЕ
Завершающим этапом полета аэрокосмических летательных аппа-
ратов является пассивное планирование в атмосфере Земли. Траектории
возвращения с орбиты и планирования основательно исследованы во
многих работах, например, в [6], [34]—[36], [60], [61], [63], [69], [86],
[98], [103]-[105], [107], [108], [111], [118]-[120], [122], [124], [128].
Большой вклад в разработку теории планирующего полета внесли
ученые ЦАГИ. Так, в работе Л.М. Шкадова, Р.С. Бухановой,
В.Ф. Илларионова, В.П. Плохих [111] подробно исследованы вопросы
определения оптимального управления летательными аппаратами при
их пространственном движении в атмосфере. При этом задача решена
как в точной постановке, с использованием принципа максимума, так и
приближенно. В работе В.А. Ярошевского [119] сопоставляются анали-
тические и полуаналитические методы расчета траеторий входа в атмо-
сферу; определяются области применимости полученных приближен-
ных решений; исследуются задачи об оптимизации траекторий входа;
анализируются методы навигации и управления. Работы А.А. Шилова и
Ю.Н. Желнина [36], [108] посвящены исследованию вопросов входа в
атмосферу со сверхкруговой скоростью космических аппаратов с ма-
лым аэродинамическим качеством; исследования проведены с исполь-
зованием принципа максимума. В работе [108] рассмотрена задача
минимизации максимальной по траектории перегрузки. Получены
качественные выводы, касающиеся структуры оптимального управле-
ния. Работа [36] посвящена минимизации продольной дальности. Зада-
ча решена с учетом ограничения на максимальную перегрузку. Опреде-
лено оптимальное управление для различных типов траекторий. В
работах А.С. Филатьева [98], [99], [103]—[105], [128] траектории плани-
рования исследованы с использованием приближенных методов. Так, в
работе [103] разработана приближенная методика определения мини-
мально удаленного от начальной точки участка границы области земной
поверхности, достижимой летательным аппаратом. Работа [104] посвя-
щена приближенному аналитическому синтезу оптимального управле-
ния движением гиперзвуковых летательных аппаратов (ГЛА); при этом
рассмотрена задача минимизации максимальных динамических и теп-
ловых нагрузок на аппарат.
342
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
За рубежом большой вклад в разработку различных методов расче-
та траекторий спуска с орбиты и планирования в атмосфере внесли
А. Миеле [63], Д.Р. Чепмен [107], У. Лох [60], Дж. Мартин [61],
А.Е. Брайсон, В.Ф. Денхем [122], [124] и др.
В большинстве известных работ указывается на необходимость
разработки таких законов управления, которые не требуют решения
краевой задачи.
Возможна различная классификация траекторий входа. В соответ-
ствии с работой [86] одним из главных факторов, определяющих траек-
торию полета в атмосфере (условная граница которой принимается на
высоте 1004-120 км), является начальная скорость входа. По ее величине
можно классифицировать следующие случаи:
- вход с околокруговой скоростью при спуске с низких орбит;
- вход с околопараболической скоростью при возвращении от Лу-
ны и с высоких эллиптических орбит;
- вход с гиперболическими скоростями при возвращении от планет
Солнечной системы.
В зависимости от величины располагаемого аэродинамического
качества К можно выделить следующие типы траекторий входа:
- баллистическая траектория (при К= 0);
- траектория "скользящего” типа для аппаратов с малым аэродина-
мическим качеством (К= 0,24-0,3);
-траектория ’’планирующего" типа для аппаратов с большим
аэродинамическим качеством (К> 1).
Баллистический спуск с орбиты наиболее прост в реализации и ис-
пользовался при возвращении первых космических кораблей "Восток"
(СССР) и "Меркурий" (США). К недостаткам такого способа спуска
относятся большие перегрузки (не менее восьми) и большой разброс
точек посадки (сотни километров). Баллистическая траектория может
быть только плоской.
При увеличении аэродинамического качества перегрузки при входе
в атмосферу уменьшаются, а точность посадки увеличивается. В на-
стоящее время освоен не только "планирующий" спуск крылатого ЛА,
но и бездвигательная посадка на аэродром. Подтверждением тому
служат многолетняя эксплуатация МКТС "Space Shuttle" с возвращае-
мым орбитальным самолетом (США) и посадка в беспилотном режиме
ОС "Буран" (СССР).
При К> 0 управление углом крена позволяет ЛА выполнять боко-
вой маневр. Вследствие этого траектории планирования, как правило,
являются пространственными. Определение достижимой области
земной поверхности (определение маневренных характеристик ЛА)
представляет одну из основных задач формирования облика аэрокосми-
ческих аппаратов.
Обычно полагается, что аэрокосмические ЛА обладают достаточно
большим аэродинамическим качеством. В связи с этим в данной работе
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере 343
наибольшее внимание уделено траекториям ’’планирующего" типа.
Рассмотрен сход с низких и высоких орбит.
При проведении практических расчетов траекторий планирования,
как правило, стараются сгладить профиль полета в координатах "высо-
та-скорость". Одной из причин нежелательности колебательного
характера траекторий являются соответствующие колебания темпера-
турного поля конструкции аппарата. Возможны различные способы
гашения колебаний. Так, в работе [69] разработан алгоритм, хорошо
зарекомендовавший себя при исследовании траекторий спуска ОС
"Буран". В соответствии с этим алгоритмом колебания гасятся путем
введения переходного участка полета с постоянным углом крена у .
Переходный участок начинается после первого отражения от плотных
слоев атмосферы; величина у* выбирается таким образом, чтобы в
конце этого участка текущие высота и угол наклона траектории равня-
лись квазистационарным значениям. Однако такой алгоритм не гаран-
тирует гладкости траектории на последующих ее участках, в случае
резкого изменения внешних воздействий или управляющих перемен-
ных (например, при перебалансировке по углу атаки или при выходе на
ограничение). Кроме того, процедура выбора угла у* предполагает
неоднократное интегрирование траектории на переходном участке
полета, что несколько усложняет расчет траекторий.
В данной работе для гашения колебаний предлагается использовать
уравнение автопилота (см. раздел 2.10). В этом случае интегрируется
полная система уравнений движения, а в качестве исходных данных
задаются "гладкие" программные зависимости //Кв(Ю и 0Кв(П> соответ-
ствующие квазистационарной траектории. В результате определенная
"гладкость" расчетной траектории обеспечивается на всей ее протяжен-
ности.
9.1. Уравнения движения в ортодромической системе
координат. Продольная и боковая дальности планирования
При рассмотрении схода ЛА с полярной орбиты (/ = ± 90°) траек-
тория проходит вблизи геоцентрического полюса. Анализ уравнений
движения, записанных в траекторной системе координат (см. раздел
2.6), показывает, что при ф = ± тс/2 в дифференциальных уравнениях для
угла курса и долготы возникает деление на ноль. Чтобы избежать вы-
числительных трудностей при расчете траекторий, проходящих через
геоцентрический полюс или вблизи него, предлагается использовать
ортодромическую систему координат, жестко связанную с вращающей-
ся Землей (см. раздел 2.4). Этот способ широко распространен и ис-
пользуется, например, в работе [35].
Пусть в начальный момент времени аппарат находится в точке с
геоцентрическими координатами ф0, Хо и имеет угол курса ф0 • Распо-
ложим ортодромическую систему координат таким образом, чтобы в
344
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Рис. 9.1. Определение положения ортодромической системы координат отно-
сительно геоцентрической вращающейся с.к. в начальной точке траектории
начальной точке вектор относительной (воздушной) скорости лежал в
плоскости ортодромического экватора (рис. 9.1). Относительно геоцен-
трической вращающейся системы координат плоскость ортодромии
задается при помощи двух величин: наклонения /Орт и долготы Ху бли-
жайшего к начальной точке восходящего (нисходящего) узла.
Наклонение плоскости ортодромии связано с начальными геоцен-
трическими координатами следующим образом:
COS /ОРТ = COS(p0 COSYJJo. (9.1)
Для определенности будем полагать, что знаки /Орт и <|/0 совпадают.
Долгота ближайшего к начальной точке восходящего (или нисходящего)
узла равна Ху = Хо - ДХ, где
sinAX = cosiyo sincpo /sin /Орт- (9.2)
В ортодромической системе координат положение аппарата и на-
правление вектора скорости задается при помощи трех величин: широ-
ты Ф, долготы Л и угла курса Т (см. раздел 2.4). В соответствии с
установленным положением ортодромического экватора в начальный
момент времени ортодромические широта и угол курса равны нулю (см.
рис. 9.1). Диапазон их изменения такой же, как у соответствующих
геоцентрических величин. Ортодромическая долгота отсчитывается от
восходящего (нисходящего) узла с геоцентрической долготой Ху. Так
как % = 0, то в начальный момент времени ортодромическая долгота
всегда является возрастающей величиной.
При переходе из экваториальной в ортодромическую систему коор-
динат широта, долгота и угол курса определяются по формулам (2.40).
При переходе от ортодромических к обычным геоцентрическим
координатам - по формулам (2.41).
При расчете на ЭВМ функции arctg(x/y), входящей в выражения
(2.40) и (2.41), используется встроенная в компилятор алгоритмическо-
9.1. Уравнения движения в ортодромической системе координат 345
го языка функция Z = ATAN2(X I7)- где Х = sinZ и Y = cosZ. Такая функ-
ция определена при любых значениях Л' и Y, кроме Х= Y= 0.
Использование ортодромической системы координат позволяет
легко вычислять продольную и боковую дальности полета. По опреде-
лению продольная дальность спуска с орбиты равна
Дх — Ro (А — Ао).
Здесь Ао - начальная ортодромическая долгота; Ro-средний радиус
Земли.
Так как переменная А интегрируется, то ее значение может быть
любым, в том числе и больше 2л. Это упрощает вычисление продоль-
ной дальности полета, когда протяженность траектории больше одного
витка вокруг Земли.
Боковая дальность спуска L/ может определяться различными спо-
собами. Наиболее просто ее вычислить, если начальная точка отсчета
лежит в плоскости ортодромического экватора:
Zz = Ro Ф.
При левом (отрицательном) крене боковая дальность считается по-
ложительной (Л/л>0), при правом - отрицательной (Z/n<0). При
/'орт?5 0 значения L7j\ и ZZn в конечной точке траектории существенно
отличаются по модулю вследствие действия кориолисовых сил. Наи-
меньшая разница между этими величинами имеет место в случае, когда
боковая дальность отсчитывается от трассы - проекции траектории
ИСЗ на земную поверхность.
Запишем уравнения движения в ортодромической системе коорди-
нат. Очевидно, что для этого достаточно в исходных уравнениях (2.71)
заменить геоцентрические координаты \|/, (р и X на соответствующие
ортодромические координаты Т, Ф и Л:
dV/dT = gonx-g, sinO + gpcos0 simp + Av;
dQ/dx = g0nycosy/K-gr[1 - K2/(grr)] cos0/K-
-g(psin0 sinvp + A0;
dH/dx = Ksin0;
dW/dT = -gonysiny/(Vcos0) - Hcos0 tgФ cosT/r
+ gp cosvp + AM,;
б/Ф Idx- Vcos0 sinT lr;
dA Idi = V cos0 cosT /(г созФ);
dL Idx = V cos0 7?з lr.
Здесь принято, что в качестве модели Земли используется общий зем-
ной эллипсоид. Слагаемые Av, До и Дт, учитывающие силы инерции,
по-прежнему записываются через геоцентрические переменные \|/. ср, Z,
(9.3)
346
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
и вычисляются по формулам (2.72). То же самое относится к слагае-
мым. учитывающим нецентральность поля тяготения Земли.
Для шарообразной Земли в уравнениях (9.3) g, = g, g(p = 0. Уравне-
ние для массы не записывается, так как полагается, что при планирова-
нии тяга двигателя не используется (т = const). Уравнение для путевой
дальности L интегрируется для справки. В плоском движении (при
движении по дуге большого круга) имеет место Zx= L.
Выражения для тангенциальной и нормальной перегрузок, входя-
щих в правые части (9.3), в данном случае имеют следующий вид:
пх = - с\ q S /(т go); пу = су q S /(т g0). (9.4)
В случае большого аэродинамического качества планирующий ЛА
может достигнуть любой точки земной поверхности, и теоретически
возможны траектории с боковой дальностью более 10 тыс. км. Однако в
целях упрощения будем полагать, что на рассматриваемом участке
траектории имеет место < 10 тыс. км, т.е. |ф|<л/2. При таком до-
пущении использование ортодромических переменных Т, Ф и А вместо
геоцентрических координат позволяет проинтегрировать любую траек-
торию движения.
9.2. Начальные и конечные условия
Начальные условия могут задаваться различным способом в зави-
симости от решаемой задачи. Рассмотрим наиболее характерные слу-
чаи.
Задание начальных условий в геоцентрической вращающейся
системе координат. При расчете траекторий планирования гиперзвуко-
вых самолетов и других летательных аппаратов, полет которых проис-
ходит в плотных слоях атмосферы, начальные условия (Ко , Но, 0О, фо,
фо и Ло) задаются в геоцентрической вращающейся с.к. Обычно начало
планирования соответствует точке окончания крейсерского полета или
участка разгона ЛА. Пересчет в ортодромическую систему координат
осуществляется по формулам (9.1), (9.2), (2.40).
Задание начальных условий в абсолютной системе координат.
При расчете траекторий ЛА, возвращающихся с орбиты, могут зада-
ваться наклонение орбиты /, скорость ИА и угол наклона траектории 0А
в геоцентрической инерциальной (абсолютной) системе координат.
Начальный угол курса определяется из соотношения
COSk|JA = COS 7 /С05ф .
Будем полагать, что в начальной точке знаки углов курса и накло-
нения орбиты совпадают. При со5ф = 0 примем фА= /. Для перехода из
абсолютной системы координат в геоцентрическую вращающуюся с.к.
используются формулы (2.37). Пересчет в ортодромическую систему
координат осуществляется так же, как и в предыдущем случае.
9.2. Начальные и конечные условия
347
Задание начальных условий при наличии импульса торможе-
ния на орбите. В задачах максимизации достижимой области земной
поверхности одновременно может минимизироваться характеристиче-
ская скорость, потребная для схода с орбиты. При определении энерге-
тических затрат на выполнение различных маневров в космическом
пространстве широко используется приближенный расчет, основанный
на том, что длительность активных участков пренебрежимо мала по
сравнению с длительностью пассивных участков. Это позволяет ап-
проксимировать активный участок скачкообразным (импульсным)
изменением скорости и не учитывать изменение остальных фазовых
координат на этом участке. Импульсное управление не только удобно с
точки зрения упрощения расчетов, но оказывается, что именно на таких
траекториях в ряде задач достигается абсолютный минимум характери-
стической скорости, потребной для маневра.
При изменении высоты орбиты обычно применяются компланар-
ные маневры, когда на протяжении всего рассматриваемого времени
космический аппарат остается в одной и той же плоскости. Наибольшее
практическое применение имеет компланарный маневр по увеличению
(уменьшению) высоты круговой орбиты.
Пусть радиус орбиты необходимо увеличить от г<} до гк. Известно,
что при r\JrQ< 11,94 оптимальным является гомановский двухимпульс -
ный маневр. В предложенной Гоманом программе управления импуль-
сы тяги прикладываются вдоль вектора скорости на начальной и конеч-
ной орбитах. Переходная траектория представляет собой полуэллипс
Гомана, перигей которого находится на начальной орбите, а апогей - на
конечной орбите (рис. 9.2). Величины импульсов скорости равны [86]
АН = КкР(го)
(9.5)
Рис. 9.2. Двухимпульсный маневр
увеличения высоты круговой орбиты
АГ2=Гкр(/к) 1-
Рис. 9.3. Зависимость круговой
скорости от радиуса орбиты
348
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Здесь 17кр = у1^/г - круговая скорость (зависимость ГКр от радиуса
круговой орбиты г приведена на рис. 9.3).
Суммарные затраты на увеличение высоты круговой орбиты (в до-
лях начальной круговой скорости) равны [86]
ЛКк/Гкр(го) -
где А Г = А К| + А И2; 7 = //'о •
Зависимости АК|, АИ2 и АКЕ (в долях ККр(г0)) от соотношения гк/г0
пред с гавлены на рис. 9.4. Из графика видно, что зависимость AJ4 имеет
максимум при гк/го « 15,58. Максимальное значение АИу/ГКр(го) со-
ставляет 0,536 (при маневре с круговой орбиты 200 км
AJA^ = 4.2 км/с). Имея такой запас характеристической скорости,
космический аппарат может подняться на орбиту любой высоты.
При подъеме на очень большую высоту (гк/^о °°) величина им-
пульса AJA стремится к нулю. Это объясняется соответствующим
уменьшением круговой скорости (см. рис. 9.3). Величины AKj и APV
при /’к//’о —> 00 в пределе равны (V2 - 1)ККр(г0), что соответствует
разнос гн между второй и первой космическими скоростями.
Продолжительность маневра увеличения высоты круговой орбиты
равна времени движения по переходному эллипсу, то есть
т= 772; 7’=2ли3/2/л/ц; а = (гк + г(|)/2.
Здесь Г— период обращения по эллиптической орбите;
а-большая полуось эллипса.
Рис. 9.4. Характеристическая скорость гомановского двухимпульсного маневра
9.2. Начальные и конечные условия
349
Одним из важнейших является маневр перехода на геостационар-
ную орбиту (ГСО). По определению орбитой стационарного спутника
Земли называется круговая экваториальная орбита, обеспечивающая
неподвижное положение спутника относительно поверхности Земли.
Радиус геостационарной орбиты равен 7Тсо~ 42164 км. Круговая ско-
рость на этой высоте составляет 3074,7 м/с. Энергозатраты, необходи-
мые для компланарного перехода на геостационарную орбиту, близки к
максимально возможным (см. рис. 9.4) - величина ДИ£ отличается от
максимальной всего на 265 м/с. Маневр увеличения высоты орбиты с
//=200 км до г=1усо (в данном случае гк Л-о = 6,42) характеризуется
следующими энергозатратами:
ДЕ, =2457 м/с; ДГ2= 1478 м/с; ДЕХ= 3935 м/с; (9.6)
время выведения равно 5,3 часа. Скорость в апогее 1597 м/с.
Если разница между радиусами начальной и конечной орбит явля-
ется большой (при гк/го> 15,56), то более экономичным становится
трехимпульсный маневр с уходом на промежуточную орбиту, пересе-
кающую внешнюю орбиту [86]. Переходную траекторию иногда назы-
вают биэллиптической, так как она состоит из двух сопряженных полу-
эллипсов Гомана.
При небольшом изменении высоты круговой орбиты формулы (9.5)
можно упростить, оставив первые члены разложения в ряд по
/\H=rK-rQ-.
ДЕ, * ДЕ2* Д///(4г0). (9.7)
Так, при увеличении высоты от 100 до 200 км ДЕ, « ДЕ2 « 30 м/с.
Задачи разгона и торможения КА являются обратимыми, поэтому
все соотношения справедливы также для случая уменьшения высоты
круговой орбиты. При этом импульсы прикладываются против скорости
движения - сначала А Е2, затем ДЕ| .
Рассмотрим два варианта задания координат начальной точки в за-
висимости от высоты орбиты.
А. Сход с низких круговых орбит. Чтобы более точно учесть влия-
ние атмосферы в ее разреженных слоях интегрирование траектории
удобнее начинать с высоты круговой орбиты: //() = //КР. Пусть в началь-
ной точке известны координаты ф(), Хо и наклонение орбиты / .Для
схода с низкой круговой орбиты, например с высоты //КР = 200 км,
достаточно приложить один импульс ДЕСх = ДЕ2. При этом перигей
переходного эллипса должен находиться в плотных слоях атмосферы
(/Л = 50^-70 км) с тем, чтобы спускаемый с орбиты ЛА смог осущест-
вить вход в атмосферу с первого витка. При таком входе в атмосферу
экономия характеристической скорости составляет примерно AЕ,.
Следует отметить, что скорость входа в плотные слои атмосферы,
строго говоря, всегда является сверхкруговой, превышая круговую
скорость на величину, близкую к ДЕ|.
350
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Рис. 9.5. Схема приложения
импульса скорости для схода
с орбиты
Будем полагать, что импульс скоро-
сти схода ДУсх в общем случае может
быть направлен под углом 3 к вектору
VKp (рис. 9.5). Угол наклона траектории
становится отрицательным при 3 < 0.
После приложения импульса ДИсх значе-
ния модуля скорости и угла наклона
траектории в абсолютной системе коор-
динат будут равны
= Ккрл/1 + 2Д//СХ cos9/rKP + (ДКСХ /ИКР)2 ;
0Л = arctg[ArCxsin3/(KKp + АИСх cos3)].
Здесь Икр - круговая скорость, соответствующая начальной высоте.
Угол 3 в общем случае может оптимизироваться, например, из ус-
ловия максимума при фиксированном значении ДИСх- Пересчет в
ортодромическую систему координат осуществляется так же, как и в
предыдущем случае.
Б. Сход с высоких круговых орбит. Если при сходе с высокой ор-
биты используется промежуточный заход на низкую круговую орбиту,
то. по сути, реализуется вариант А.
Рассмотрим вариант прямого входа в атмосферу, например, с гео-
стационарной орбиты. В этом случае экономия характеристической
скорости составляет АИХар~ 2440 м/с по сравнению с вариантом захода
на низкую круговую орбиту [33]. Однако вместе с этим скорость входа в
атмосферу становится существенно сверхкруговой, превышая круговую
на величину ДКХдр. что приводит к значительно большему нагреванию
ЛА.
Можно полагать, что до высот Яо = 120-е-150 км движение осущест-
вляется по переходному эллипсу. Траектория описывается следующим
уравнением (см. рис. 3.9):
r = p/(\ + ecos%).
Радиус апогея переходной орбиты rtt равен радиусу круговой орби-
ты, радиус перигея гк можно задавать в качестве параметра, обычно
ГП = 304-70 км. При //л= 30 км величина импульса схода с ГСО состав-
ляет А Ис х= 1496 м/с, что на 18 м/с больше, чем соответствующий
импульс АГ2 в (9.6).
В данном случае в качестве начальных условий задаются начальная
высота Я(), параметры переходной орбиты z, гаи гк, а также координаты
Фо и ?io. При сходе с экваториальной орбиты (р0 = <Ио = 0.
Эксцентриситет и параметр эллиптической орбиты равны
9.2. Начальные и конечные условия
351
Скорость в апогее переходной орбиты
где г = ru h\.
Кх ~ (1 -е)- HKp(ra)J——- - ККр(Гд) —.
\ р V г + 1 \ г(г + 1)
Начальная скорость в абсолютной системе координат определяется
с помощью уравнения энергии К2/2 - ц / г = const:
Ид =
Здесь го = Но + 7?3.
Начальный угол наклона траектории в абсолютной системе коор-
динат определяется с помощью интеграла площадей Ргсосб = const:
0А = - arccos .
I 10 VА >
Пересчет в ортодромическую систему координат осуществляется
так же, как и в предыдущих случаях.
На правом конце траектории, вне зависимости от начальных усло-
вий, обычно задается конечная высота Як или скорость полета Ик в
геоцентрической вращающейся с.к.
9.3. Аэродинамические характеристики планирующего ЛА
Задание исходных аэродинамических данных при решении задач
планирования ЛА с большими скоростями имеет свои отличительные
особенности. В компоненты вектора перегрузки (9.4) в качестве исход-
ных входят две величины: параметр планирования <jy = cyl(GIS) и бал-
листический коэффициент ах = cJ(G/S).
Примерный диапазон изменения удельной нагрузки GIS составля-
ет 1-н5 кН/м2 (здесь под характерной площадью S понимается площадь
аппарата в плане или площадь базовой трапеции крыла).
Аэродинамические коэффициенты су и сч в общем случае зависят
от угла атаки а и от траекторных параметров V и Н (от чисел М и Re).
Рассмотрим вначале зависимость от угла атаки.
При малых скоростях полета (М<3-н4) аэродинамическая поляра
обычно полагается квадратичной, а зависимость су(а) - линейной:
Су СуО Су CL, Сх С х mu, “Ь Л (с у Су )~.
352 Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
При этом на коэффициент подъемной силы накладывается ограни-
чение с\ <сУ1Ш|Хд. Для задания зависимости аэродинамических коэффи-
циентов от угла атаки достаточно пяти величин. Так как при планиро-
вании наиболее важным является режим максимального
аэродинамического качества, то правильнее задать величины АГ1пах, сукт,
аКт . с>() и сХ1П1П. Тогда с использованием соотношений (2.64) можно
записать
~ (^уКт“ СуО У^Кт ,
\ ~ ^та\ )njn — С‘уХ|П/Лтач), А — 1/[2Л^П1ах (Cyj<ni — Су )].
В отличие от активного движения при спуске с орбиты угол атаки
может изменяться в существенно большем диапазоне - вплоть до углов,
cooi ветствующих режиму максимального значения коэффициента
подъемной силы сутах. Поэтому при больших скоростях полета
(М > 3-ь4) задание аэродинамических коэффициентов в виде квадратич-
ной поляры не всегда является приемлемым. В данной работе предло-
жен другой способ задания аналитических зависимостей су(а)и сх(а).
Представим зависимость аэродинамического коэффициента су от
угла атаки в следующем виде:
cv = В(} + В\ siп/ + В2 siп/ |sin/| . (9.8)
Здесь До, В\ и В2 - некоторые коэффициенты; / -условный угол, свя-
занный с углом атаки следующим образом:
а л
х=--------
«Супах 2
где а(Ч ,шх - угол атаки, соответствующий су 1пах.
При изменении угла атаки в диапазоне от 0 до смутах величина /
изменяется от 0 до л/2, коэффициент су - от До до су|пах, т.е. формула
(9.8) отражает реальную зависимость су(а).
Производная су по углу атаки (при фиксированных значениях фа-
зовых координат) равна
t/су Ida = cos/ (Д। + 2Д2 |sin/|) л /(2аСу max) (9.9)
и является четной функцией относительно а.
Для задания зависимости су от а правильнее задать следующие
ПЯ1 Ь ВеЛИЧИН. ССкП1, Су Кт , Су u К-т * max И Су тах . ЗдеСЬ Су а Кт dCy Ida.
при осКт. После решения системы трех уравнений
СуКт ~ В. + Д| Sin/кт + В2 $Ш~Хкт , Су 1пах — До “Ь Д| “1“ В2 ,
Су и Кт— cos/Km (Д| + 2Д2 sin/Kin) л /(2ctcy |Пах)
получим
9.3. Аэродинамические характеристики планирующего ЛА
353
D ^"у max ^*уКт ^^Су тах^*у а Кт
П2-----------------------------------;
O-SinXKm) ЛСОЗХктО-З'ПХкт)
с — с
о у max yKm г* /1 • \
= -Т—.----- в2 (1 + sin хКт);
O-siiUkJ
Bq Су max В\ В2 , Су В\ 7t /(2&Су max),
(9-Ю)
где - производная су по а при а = 0.
Коэффициент В\ всегда больше нуля. Коэффициент В2, как прави-
ло, является положительным. В этом случае обеспечивается S'-образный
характер зависимости су(а).
Из (9.9) следует, что функция (9.8) имеет экстремум при угле атаки
ссэ, определяемом из условия sin%3 = -Bi /(22?2)- Очевидно, что для
обеспечения монотонности функции су(а) в наиболее важном диапазоне
углов атаки (от аКт до асутах) должно выполняться неравенство
- 5, /(2В2) < sinxKm или - Bt /(2Вг) > 1.
Зависимость (9.8) позволяет при необходимости определять угол
атаки по известному значению су:
sin% = 2 (су - 5o)/(#i + + 4В2 |су - Во|); а = 2аСу max Х^- (9-11)
Зависимость аэродинамического коэффициента сх от угла атаки
представим в следующем виде:
сх = Ао + А2 sin2a + А31sin3a|, (9.12)
где Ао, А2 и А3 - коэффициенты.
Зависимость (9.12) является четной относительно а и при соответ-
ствующих значениях А2 и А3 имеет минимум при а = 0 и максимум при
а = ±к/2, то есть качественно ведет себя так же, как и реальная зависи-
мость сх от а.
Производная аэродинамического коэффициента сх по углу атаки
равна
dcx /da = cosa sina (2A2 + 3A31sina|) (9.13)
и является нечетной функцией относительно a.
Будем полагать, что помимо величин, необходимых для построения
зависимости су(а), в каждой точке траектории известны А?,пах и Хсутах
(аэродинамическое качество при сутах). Этих величин достаточно для
построения зависимости сх(а). Для определения коэффициентов Ао, А2
и А3 решим систему трех уравнений
354
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
^x(^Km) £yKin/-^max» ^хаКт £у а Кт/7Стах , 1
' . ' (9.14)
^ху&Су max) £у max ' -^Су max •
Решение системы (9.14) имеет следующий вид :
А2 = - [3?d - с2 (S3 - ?)]/ Z; А3 = [2$й - с2 (52 - ?)]/ Z;
Aq CyKm/^Чпах (А2 "Г А3$),
где 5 = sinaKm; S = sinaCy max;
С| ~• Су
max /А<у max £уКгп /^Чпах » ^2 Су а Кт / С^Чпах COSClKm),
Z= s[s3 + S2(2S- 35)].
Из (9.13) следует, что функция (9.12) имеет экстремум при угле
атаки осэ, определяемом из условия sina3 = - 2А2 /(ЗА3). Очевидно, что
для обеспечения монотонности функции сх(а) в диапазоне углов атаки
от aKm до aCy шах должно выполняться неравенство
- 2А2 /(ЗЛ3) < sinaKm или - 2А2 /(ЗА3) > sinaCy тах • (9.15)
Таким образом, для задания зависимостей аэродинамических ко-
эффициентов су и сх от угла атаки необходимы семь параметров. На
рис. 9.6 показан пример построения зависимостей су(а) и К(а) с ис-
пользованием предлагаемого алгоритма. Видно, что точность аппрок-
симации является вполне приемлемой. Наиболее точно аэродинамиче-
ские характеристики аппроксимируются в диапазоне от aKm до асутах,
который является основным при планировании ЛА в атмосфере с
большими скоростями.
Аэродинамические коэффициенты Су и сх в общем случае зависят
от чисел М и Re. При этом от числа Re (т.е. от высоты полета при
М = fix) зависит главным образом коэффициент лобового сопротивле-
ния сх. Зададим в координатах "Н-М" предварительный профиль
полета, близкий к полетному, в виде 7/*(М) и аппроксимируем зависи-
мость сх от Н (при М = fix) линейной функцией (см. раздел 2.9):
сх = cf + b (Н - if), где b = дсх /дН.
При таком способе учета зависимости от высоты задание аэроди-
намических характеристик значительно упрощается, так как достаточно
задать 9 табличных зависимостей (в том числе Ь и if) от числа Маха в
соответствии с предварительным профилем полета 77*(М).
Все сказанное в данном параграфе о зависимостях су(а) и сх(а) от-
носится к высоте /7*. При изменении высоты на АЯ зависимость су(а)
не изменяется, а график зависимости сх(а) сдвигается на величину 5АН.
9.3. Аэродинамические характеристики планирующего ЛА
355
Рис. 9.6. Пример построения аналитических зависимостей коэф-
фициента подъемной силы су и аэродинамического качества
К от угла атаки по семи исходным величинам:
□ □ □ исходные зависимости; ------------ аппроксимация
Часто на гиперзвуковых_режимах полета вместо чисел М и Re ис-
пользуется параметр M/vRe , характеризующий разреженность атмо-
сферы. Пример зависимостей максимального аэродинамического каче-
ства 7€П1ах и соответствующих значений угла атаки аКт и коэффициента
подъемной силы сукт от параметра М />/Re для летательного аппарата
конической формы представлен на рис. 9.7 [33]. Здесь в качестве харак-
терной использована площадь донного среза, число Re вычислено через
характерную длину аппарата: Re = рИ/ц. Видно, что в данном случае
при увеличении высоты и скорости полета величина 7€тах уменьшается
в несколько раз.
Основной величиной, необходимой для расчета максимальной
дальности планирования, является максимальное аэродинамическое
качество ЛГтах. Часто возникает задача проведения параметрических
расчетов, когда /Стах изменяется в широком диапазоне. Рассмотрим
случай, когда исходные данные заданы не полностью. Пусть в каждой
точке предварительного профиля /7*(М) известна величина А?тах и,
кроме того, могут быть заданы аКт и сукт- Построим аналитические
зависимости су(а) и сх(а), воспользовавшись упрощенным способом
задания недостающих величин.
При малых скоростях полета (М < 3-ь4) будем полагать, что аэро-
динамическая поляра является симметричной, то есть су0 = су* = 0. Тогда
Су ^уКщ/^Кт» А 1/(2/ктах СуКт )» min— -^(руКт) ?
356
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Рис. 9.7. Зависимость аэродинамических характеристик от
параметра, характеризующего разреженность атмосферы
откуда
^Чпах- 1/(2Лсукт)-
Если величина аК1П не задана, то учтя, что А сукт/акт » 1 и а» tga,
получим
tgaKm«l/№ax). (9.16)
При больших скоростях полета (М » 1) в аэродинамике использу-
ется ’’корпускулярная" модель обтекания, предложенная Ньютоном.
Согласно этой теории на плоскую пластину площадью S, обтекаемую
гиперзвуковым потоком идеального газа под углом атаки а, действует
сила R= 2<75sin2a . Аэродинамические коэффициенты и аэродинамиче-
ское качество пластины равны, соответственно,
Супл = 2sin2a cosa ; схПл = 2sin3a ; Af Пл = ctga,
причем А^пл представляет собой верхнюю грань возможного аэродина-
мического качества.
Максимум коэффициента суПл равен 0,77 и достигается при угле
атаки 54,74° (sinaCy тах = >/2/3 ). Будем полагать, что для ЛА максимум
коэффициента су реализуется на угле атаки аСу шах = 55°.
Максимальный коэффициент лобового сопротивления пластины
равен 2 и достигается при a = 90°. При поперечном обтекании цилинд-
ра сх = 4/3 «1,33. Для сферы сх = 32/(9л) «1,13. Реальное значение коэф-
фициента давления при гиперзвуковых скоростях меньше 2, поэтому
соответствующие аэродинамические коэффициенты отличаются от
указанных выше.
9.3. Аэродинамические характеристики планирующего ЛА
357
Для определения величины аКт примем за основу выражение
(9.16), из которого видно, что при уменьшении /С1пах угол атаки аКп1
будет увеличиваться. Однако очевидно, что этот угол не может превы-
шать угол acymax- С учетом этого обстоятельства модифицируем фому-
лу (9.16) следующим образом:
^max+0,9
В результате при сколь угодно малом Л?,пах угол атаки аК1П не будет
превышать 48°.
Построим зависимость су(а). Будем полагать, что су0 = В(} = 0. В от-
личие от пластины, для которой производная коэффициента су по а при
а = 0 равна нулю, для реального ЛА с® > 0. Свяжем производную с“ с
величиной су тах следующим образом:
уО ® — 7л» / (У
су 4Ьу max ' ^Су max •
Как показывает анализ аэродинамических характеристик различных
типов ЛА, I = 0,24-0,6. Примем / = 0,4.
С использованием двух последних соотношений системы (9.10)
получим
ТС 7С
Сутах=51—; в2=В^ — -\). (9.17)
Рассмотрим далее два варианта.
Значение СуКш задано. При этом характерная площадь может быть
любой. Используя соотношения (9.8) и (9.17), определим коэффициент
By.
sinXKm+[7t/(2/)-l]sin2xKra ’
где Хкт = актЛ/(2аСутах)- Коэффициенты В2 и сутах определяются из
выражений (9.17).
Значение сукт не задано. Здесь возможны два варианта:
- большое аэродинамическое качество;
- малое аэродинамическое качество.
Первый случай присущ для крылатых ЛА, поэтому в качестве ха-
рактерной будем использовать площадь плановой проекции аппарата.
Примем значение максимума коэффициента су равным 0,6. Тогда из
первого выражения (9.17) получим
В\ сутах2//тс.
358
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Коэффициент В2 определяется из второго выражения (9.17). Аэро-
динамический коэффициент СуКт вычисляется по формуле (9.8) при
а = аКш •
При уменьшении А?тах коэффициенты сукт и схкт увеличиваются и,
как показали расчеты с использованием данного алгоритма, при
Л?тах = 0,385 имеет место равенство сукт = ^тах, т.е. схК1П = 1. Дальней-
шее уменьшение /С1пах будет приводить к некорректному результату:
CxKm > 1 •
Чтобы алгоритм был работоспособным при любом значении /Стах,
будем полагать, что область малых значений аэродинамического каче-
ства соответствует условию А?тах < 0,385. В этом случае аппарат имеет
форму, близкую к сферической, и в качестве характерной используется
площадь миделя. Так как для сферы сх~ 1, то примем, что сукт ~ А?тах • В
этом случае
cvI<m - В, sinyKm
р — УКт________Л,Кт . — D 1 D
&2 .2 > Су max & 1 ' &2 •>
Sln XKm
где коэффициент вычисляется по формуле (9.18).
Таким образом, зависимость су(а) может быть построена при лю-
бом значении /С1пах.
При формировании алгоритма построения зависимости сх(а) также
будем учитывать величину /С1пах. Положим, что при большом аэродина-
мическом качестве коэффициент сх определяется по формуле (9.12) и
для вычисления коэффициентов Ао, А2 и А3 необходимо задать аэроди-
намическое качество при сутах. Для плоской пластины при а = 55°
имеем А?пл = 0,7. Для реального ЛА эта величина будет меньше, причем
очевидно, что при уменьшении A?lnax величина Акутах должна также
уменьшаться. Примем следующую эмпирическую зависимость:
А*су max = 0,7 - 0,15/А*тах при А*тах > 0,43;
А*су max 0,81666А*тах при л;пах < 0,43.
Здесь коэффициент 0,81666 выбран из условия сопряжения отрезка
прямой с гиперболой при А‘тах = 0,43.
При малом аэродинамическом качестве (при /стах < 0,2) будем ис-
пользовать упрощенную зависимость для коэффициента сх:
сх =А0 + X3sin3a,
где 3 2
^0 ~ CxKm -A3S , А3 — с2 /(3s ),
^2 — Су a Кт / (Атах GOSa^m)» $ ~ Sina^m •
9.3. Аэродинамические характеристики планирующего ЛА
359
Таким образом, все необхо-
димые величины определены. На
рис. 9.8 показаны результирую-
щие зависимости АГ(а), соответ-
ствующие изменению ЛГтах в
диапазоне 0,14-4,0 (величины aKm
и СуКт вычислялись в соответст-
вии с изложенным алгоритмом).
9.4. Постановка задачи
Рассмотрим ЛА с большим
аэродинамическим качеством.
Пусть в начальный момент вре-
мени То известны фазовые коор-
динаты: скорость Ко, высота Яо,
угол наклона траектории 0О,
ортодромические угол курса То,
Рис. 9.8. Пример построения при-
ближенной зависимости аэродина-
мического качества от угла атаки
(по заданной величине £тач)
широта Фо и долгота Ао. В конечной
точке задана скорость Кк , при этом время тк, высота Нк , угол наклона
траектории 0К и угол курса Тк являются свободными.
Задача заключается в определении допустимого управления U(t),
обеспечивающего максимум достижимой области земной поверхности:
Я(Фк , Ак) -> max.
Координатами вектора управления U являются углы атаки а и кре-
на у. Задача решается с учетом ограничений, наложенных на управ-
ляющие переменные:
С^ггппД — — С^тахД » I У I — УтахД
и с учетом других ограничений, которые обычно задаются:
сутахд -максимально допустимый аэродинамический коэффици-
ент подъемной силы;
«у! тахд - максимально допустимая нормальная перегрузка в свя-
занной системе координат;
<7тахд - максимально допустимый скоростной напор;
Аутахд - максимально допустимая температура в критической точ-
ке аппарата.
Последние три ограничения могут быть заданы в виде кусочно не-
прерывной функции /Тпнпд(Р)- Из двух ограничений а1пахд и су1пахд
можно выбрать одно наиболее сильное. Для определенности будем
полагать, что таким ограничением является атахд, причем в общем
случае эта величина может изменяться по траектории.
360
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
9.5. Приближенно оптимальное управление углом крена
и аэродинамическим качеством в отсутствии
ограничений на фазовые переменные
Как показано в работе [111], при решении задачи оптимального
пространственного движения дифференциальные уравнения для со-
пряженных переменных Рх, РЦ), и интегрируются аналитически
(см. раздел 2.7). Наличие первых интегралов облегчает решение задачи
и позволяет устранить дополнительные трудности, вызванные про-
странственностью движения. Однако краевая задача в данном случае
является трехпараметрической. Прямое решение такой задачи на ЭВМ
связано с известными трудностями, так как необходимо иметь доста-
точно хорошее нулевое приближение, которое заранее неизвестно.
При большом аэродинамическом качестве и в случае движения с
докруговыми скоростями (KA<A/g^) оптимальное управление аппара-
том при спуске с орбиты может формироваться на основе гипотезы
квазистационарности [111]. В этом случае дифференциальное уравне-
ние для угла наклона траектории превращается в конечное соотноше-
ние, и его наиболее рационально записать в виде
go «у cosy = gv cosQ, (9.19)
где gv = g[l - ^/(g'*)]; Ра - скорость в абсолютной системе координат.
Это уравнение позволяет достаточно полно учесть силы инерции (см.
раздел 2.8).
С использованием гипотезы квазистационарности в работе [111]
получены условия оптимальности управления пространственным
планированием, что существенно упрощает решение задачи. В качестве
управляющих переменных были выбраны аэродинамическое качество К
и угол крена у. Задача решена с учетом естественных ограничений на
управляющие переменные:
I У I — УтахД < ТС/2, 0 < 7С1П;ПД < К < А^тах.
Полагалось, что аэродинамические коэффициенты не зависят от
числа Маха и высоты. В отличие от исходной задачи семейство экстре-
малей при любых граничных условиях становится не более чем двух-
параметрическим. При построении достижимой области земной по-
верхности задача сводится к серии однопараметрических задач. В том
случае, когда время полета и путевая дальность не зафиксированы,
структура управления описывается соотношениями (2.117). Однако в
данном случае по-прежнему необходимо решать краевую задачу. В
связи с этим представляется важным поиск таких приближенных зако-
нов управления, для реализации которых решение краевой задачи не
требуется.
Для определенности будем рассматривать спуск в северное орто-
дромическое полушарие (Zz> 0). На рис. 9.9а показана граница дости-
9.5. Приближенно оптимальное управление в отсутствии ограничении 361
жимой области при спуске с орбиты и на ней выделены три характер-
ные точки, соответствующие полету с максимальной продольной даль-
ностью Zxmax, с максимальной боковой дальностью ZZmax и с минималь-
ной продольной дальностью ZXmin (при ZZK = 0). Будем полагать, что
конечная точка траектории с ZZmax делит граничную линию достижимой
области на две части: переднюю границу и заднюю границу.
В работе [111] сформированы приближенно оптимальные законы
управления углами атаки и крена, позволяющие построить практически
максимальную достижимую область при спуске с орбиты. Однако при
увеличении аэродинамического качества свыше 2-?2,5 эффективность
закона управления углом крена [111] при планировании ЛА к передней
границе достижимой области начинает ухудшаться. Задняя граница
достижимой области в работе [111] построена не полностью. В связи с
этим сформируем программу управления углами атаки и крена, выпол-
нив соответствующую модификацию законов управления работы [111].
1. Передняя граница получается из условия Lx -> шах при фикси-
рованном значении ZZK в конечной точке планирования (в работе [111]
использовалось условие £z -> max при АХк = fix, что приводит к анало-
гичному результату).
Как следует из [111], в данном случае на всей траектории полета
должно использоваться максимальное аэродинамическое качество:
X^pt = /Стах, что является вполне очевидным (см. также раздел 2.9).
Рис. 9.9. Приближенно оптимальная программа управления углом крена и
аэродинамическим качеством:
а) достижимая область земной поверхности; 6) программа управления, обеспечи-
вающая достижение задней границы; в) программа управления, обеспечивающая
достижение передней границы
362
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Будем полагать, что закон управления углом крена, в отличие от
работы [111], предполагает наличие участка с нулевым углом и, в об-
щем случае, состоит из трех участков (см. рис. 9.9в):
1)7=0;
2) Y УтахД ,
3)Y = YoPt(T).
Обоснуем рациональность использования первого участка. При
планировании с большим аэродинамическим качеством дальность
полета может превысить 20 тыс. км. В этом случае траектория ЛА будет
пересекать плоскость 77 (см. рис. 2.16) один или более раз, и каждый раз
в соответствии с условиями оптимальности (2.117) знак угла крена
должен меняться на противоположный. Для определения точек пере-
ключения угла крена необходимо знать положение плоскости 77, что
усложняет решение задачи. Если выбрать протяженность первого уча-
стка так, чтобы дальность полета на 2-м и 3-м участках была менее
20 тыс. км, то знак угла крена на этих двух участках меняться не дол-
жен. Необходимость в использовании плоскости 77 отпадает, что приво-
дит к существенному упрощению задачи. Для задания протяженности
первого участка должна использоваться величина, изменяющаяся по
траектории монотонно, например путевая дальность. Будем использо-
вать для этой цели дальность £Вкл.у-
Подтверждением принятого режима управления у = 0 на 1-м участ-
ке полета служат также следующие доводы. Как показывают численные
расчеты, проведенные в работе [111] с использованием принципа мак-
симума, в зависимости от потребного положения конечной точки в
начальной точке планирования возможно либо у = утах> либо у = 0,
причем второе решение реализуется при полете к передней части дос-
тижимой области (при небольших значениях 7,Zk)- Анализ 1-го соотно-
шения (2.117)
tgyOpt = - Hsi пб /cose (9.20)
также показывает, что при околокруговых скоростях, т.е. при п -> 0, на
начальном участке планирования угол крена должен быть близок к
нулю.
Из выражения (9.20) следует, что на заключительном участке поле-
та при приближении к плоскости 77 угол 5 (см. рис. 2.16), а следова-
тельно и угол крена по модулю, монотонно уменьшаются вплоть до
нуля. Как показано в работе [111], хорошим приближением к оптималь-
ному закону управления углом крена является закон вида
У^-Ук, (9.21)
где параметр характеризует угол конечного курса в ортодромиче-
ской системе координат: « Тк.
9.5. Приближенно оптимальное управление в отсутствии ограничений 363
В соответствии с (9.21) модуль угла крена монотонно уменьшается
по траектории и в конечной точке траектории приближается к нулю, т.е.
качественно ведет себя так же, как и величина yopt закона (9.20). В связи
с этим примем закон управления (9.21) для 3-го участка полета (см.
рис. 9.9в).
В результате программа приближенно оптимального управления
углами атаки и крена будет иметь следующий вид:
O^opt — ,
Yopt= 0 при L < Ьъкп у; 22)
Yopt УтахД ПрИ L > Z/BKJI.y И | Ч^ — Ч*к | > УшахД ?
Yopt = 4х-Ч'к при/, >£вкл.т и |'Р-'Рк|<У|Пахд,
где величины /,Вкл у и Тк- оптимизируемые параметры.
Так как задача решается при условии ZZK = fix, то из двух парамет-
ров Ч/к и АВклу свободным является один. Если в точке окончания пер-
вого участка закона управления углом крена имеет место V < Ио и далее
по траектории скорость полета уменьшается монотонно, то вместо
величины Авкл.у можно использовать скорость Рвкл.у
С целью обеспечения "гладкости" траектории после окончания
первого участка (у = 0) рационально переходить на режим утахД не
дискретно, а, например, линейно по дальности на протяжении некото-
рого переходного участка с дальностью ААВкл у •
Первый и второй участки закона управления углом крена могут от-
сутствовать. Так, при небольших дальностях планирования отсутствует
первый участок (у = 0). При небольших значениях угла конечного курса
(при | Ч'к I < Утахд) отсутствует второй участок.
Если в задаче ставится требование, чтобы в конце планирования
ЛА попал в заданную точку с ортодромическими координатами Фк и
Ак или максимально приблизился к ней, то в соотнгошениях (9.21) и
(9.22) вместо угла конечного курса Ч'к используется угол визирования
Ч'виз, определяемый из соотношения
tgOKcos<I)-sin(I)cos(AK - А)
sin(AK - А)
где Ф и А - текущие ортодромические координаты; числитель равен
зтЧ'виз, а знаменатель равен собЧ'виз •
Угол Ч'виз изменяется в диапазоне от минус к до л. Соотношение
(9.23) получено в результате решения сферического треугольника, две
стороны которого - это меридианы с долготами А и Ак, третья сторо-
на-дуга большого круга, соединяющая текущую и конечную точки.
2. Задняя граница достижимой области получается из условия
L\ -> min при фиксированном значении ZZK в конечной точке планиро-
364
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
вания (см. разделы 9.9 и 9.10). Здесь следует отметить, что условие
£z шах при Лхк = Ах не позволяет построить заднюю границу полно-
стью.
В соответствии с результатами работы [111] закон управления аэ-
родинамическим качеством в общем случае состоит из двух участков
(см. рис. 9.96):
1 ) ^opt — ^ЧтппД ,
2 ) A*Opt = A*max.
Первый участок полета может отсутствовать. Второй участок при-
сутствует всегда.
Закон управления углом крена в общем случае состоит из трех уча-
стков (см. рис. 9.96):
1 ) У — +утахД ?
2)у = -у.ПахД;
3)Y = Yopt(T),
причем первый участок (или первые два участка) могут отсутствовать.
На 3-м участке, как и при построении передней границы, будем исполь-
зовать закон вида (9.21).
Переключения между участками осуществляются в следующей по-
следовательности (см. рис. 9.96):
- по углу крена - с утахД на минус утахД при достижении
дальности Лп.у;
- по аэродинамическому качеству (по углу атаки) - с АГпмпд на /Стах
при достижении дальности 2П. а 5
- по углу крена - с минус утахД на yopt.
При проведении численных расчетов вместо аэродинамического
качества удобнее использовать угол атаки или аэродинамический коэф-
фициент су. Например, режим Л^пД можно задать при помощи относи-
тельной величины СуКттд/Сутах- Величине /Стад соответствуют два
значения угла атаки оскттд- В зависимости от решаемой задачи угол
атаки акпипд может находиться как слева, так и справа от аКт • С целью
уменьшения аэродинамического нагревания ЛА целесообразно исполь-
зовать аК1шпд > аКт • В этом случае угол аКттд, по сути, есть атахД.
С учетом отмеченного программа приближенно оптимального
управления углами атаки и крена примет следующий вид:
^opt С^КштД
^opt OtKin
Yopt — УтахД
Yopt УтахД
YoPt = T —Тк
при L <Ап.а;
при L > Ln а;
при L < Ln Т;
при L > Ln.y И | Т - ТК | > УтахД
при L > Ln у И | Т - Тк I < Утахд ,
(9.24)
9.5. Приближенно оптимальное управление в отсутствии ограничений 365
где величины , Ап. а и у - оптимизируемые параметры, причем
^П.у < ^П. а •
Так как продольная дальность минимизируется с условием
Lzk = fix, то свободными являются фактически два параметра. Если в
точках переключения аэродинамического качества и угла крена имеет
место V < Ро и далее по траектории скорость полета уменьшается моно-
тонно, то вместо величин Zn.a и ЛПу можно использовать соответствую-
щие скорости Рп. а И Рп.у .
С целью обеспечения "гладкости" траектории рационально пере-
ключаться с режима а/<^пд на режим a/<m не дискретно, а, например,
линейно по дальности на протяжении некоторого переходного участка с
дальностью Д£п. a •
В общем случае, когда аэродинамические коэффициенты зависят от
скорости и высоты полета, будем полагать, что они заданы в соответст-
вии с изложенным в разделе 9.3. То есть в координатах "Я - М" имеется
предварительный профиль Я(М), вдоль которого заданы зависимости
^тах(М), акт(М), су тах(М) и др. Программную высоту полета //Пр будем
вычислять при помощи соотношения (9.19), где управляющие перемен-
ные а и у соответствуют условиям (9.22) или (9.24). То есть будем
полагать, что программный угол атаки ап₽ равен aopt и* не зависит от
того, насколько программная высота ЯПр отличается от Н*.
Очевидно, что на режиме аКттд в случае //Пр * Н* программное
значение будет несколько отличаться (в большую или меньшую
сторону) от значения А71Тьпд на высоте Н\ однако это не является суще-
ственным.
При полете на угле атаки aKm в случае //Пр * Н* будут иметь место
потери аэродинамического качества. Однако, как показано в разделе 2.9,
эти потери являются незначительными. Тем не менее при задании
предварительного профиля Я*(М) необходимо стараться обеспечить его
максимальную близость к программному профилю ЯПр(М). В первую
очередь это относится к режиму полета aopt = aKm •
9.6. Оптимизация траекторий планирования при
наличии фазовых ограничений
При интегрировании траекторий будем использовать уравнение ав-
топилота, полученное в разделе 2.10:
Ив.птрСО = Ив.прСО + Див(т),
где
Ив.ПР - gv COS0np/go ;
I2in(g/gnp) + бГ(0ПР-е)
Р(Дт)2£0 Дт£о
(9.25)
(9.26)
(9.27)
366 Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Здесь ив.птр- проекция нормальной перегрузки на вертикальную плос-
кость, потребная из условия обеспечения полета по заданному про-
граммному профилю; q и 0 - текущие скоростной напор и угол наклона
траектории, которые определяются в результате интегрирования полной
системы уравнений. Индекс ”пр” соответствует программной квазиста-
ционарной траектории.
В соотношения (9.25)-(9.27) непосредственно входят программные
скоростной напор #Пр и угол наклона траектории 0Пр. Выразим эти
величины через программные управляющие переменные, воспользо-
вавшись гипотезой квазистационарности. В общем случае искомая
экстремаль может состоять из участков двух типов:
- участка движения внутри ограниченной области (движение осу-
ществляется с приближенно оптимальными углами крена и атаки - см.
раздел 9.5);
- участка движения по ограничению в координатах "Н- V".
Рассмотрим общий случай, когда аэродинамические коэффициенты
зависят от числа Маха и высоты полета.
1. Движение в свободной области фазового пространства или
при отсутствии ограничений на фазовые переменные.
В этом случае в каждой точке траектории программные углы крена
уПр и атаки аПр соответствуют условиям (9.22) или (9.24). Углу атаки
аПр соответствуют коэффициент подъемной силы суПр и аэродинамиче-
ское качество Ацр . Программный скоростной напор находится из урав-
нения (9.19):
_ mgvcos0np
#ПР-------------,
£ynp^C0SYnp
(9.28)
после чего определяется программная высота полета 7/Пр-
В формуле (9.28) программный угол наклона траектории 0Пр соот-
ветствует квазистационарному движению. Угол 0Пр является слабо
меняющейся по траектории величиной (в большинстве случаев 0Пр« 0).
С целью упрощения алгоритма вычислений при использовании форму-
лы (9.28) можно задавать значение 0пр с предыдущего шага интегриро-
вания. Этот прием будет использоваться в дальнейшем при вычислении
формул, в которые входит cos0np.
Выразим угол 0Пр через программные управляющие переменные.
Как показано в разделе 2.9, при пх * 0 для угла наклона траектории
справедливо следующее соотношение:
sine = -П-*ЩНУ-- , (9.29)
gT#v +У
где
Н'у = (2/V-q'v/q)/&.
(9.30)
9.6. Оптимизация траекторий при наличии фазовых ограничений 367
В случае пассивного планирования на всей траектории полета име-
ет место неравенство пх < 0 - см. формулы (9.4).
Продифференцируем уравнение (9.19) по скорости с учетом перво-
го соотношения (2.38) и найдем производную q'y. При этом пренебре-
жем изменением по скорости величин су, g, г, 6 и у (в действительно-
сти эти величины изменяются по скорости существенно слабее, чем
скоростной напор). В результате
f _ 2mcosQ(7 + ИЕ cosOcosy)
Я v--------------------------,
rScy cosy
или с учетом (9.19)
, _ 2#(K + KEcos0cosk|/)
Подставив полученное выражение в (9.30), после преобразований
получим
Н' - 2 *-Ауе
v pr l-rA2/(gr)’
(9.31)
где Ave= (Ие2 + We cosOnp cosy)/(gr); VE - переносная скорость. Макси-
мум величины AVe равен ~ 0,06 и достигается при движении с круговой
скоростью на экваториальной орбите.
Из выражения (9.31) следует, что производная Ну не зависит от
параметров ЛА и угла крена. При малых скоростях полета из (9.31)
получим /Гу~2/(РГ), т.е. квазистационарное движение происходит с
постоянным скоростным напором - см. формулу (2.131).
Выразим тангенциальную перегрузку через аэродинамическое ка-
чество, воспользовавшись соотношением (9.19):
пх = - gv cos0/(go^npcosy).
Подставив полученные выражения для Ну и пх в (9.29), получим
итоговое выражение для программного угла наклона траектории:
КПР cosУпр [Р V2 [1 - V2 /(gr)] + 2gT (1 - Ave )}
Здесь ускорения g и gT определяются по формулам (2.8) и (2.88). Аэро-
динамическое качество 7СПр определяется на программной высоте /7Пр
при а = aopt в соответствии с условиями (9.22) или (9.24).
В работе [60] аналогичное выражение для угла наклона траектории
имеет следующий вид:
0 = - 2g/(pK2A'cosy), (9.33)
368
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
причем эта формула справедлива только при больших скоростях, в
противном случае может оказаться, что 10 I > л/2.
Анализ выражения (9.32) показывает, что при больших скоростях
слагаемым 2gT в знаменателе можно пренебречь ввиду существенно
меньшей его величины по сравнению с РИ . В результате с учетом
малости величины AVe формула (9.32) будет совпадать с (9.33).
При малых дозвуковых скоростях (gv-Ят) величина AVe мала и,
кроме того, слагаемым РИ2 в знаменателе (9.32) можно пренебречь
ввиду существенно меньшей его величины по сравнению с 2gT. В этом
случае выражение (9.32) превращается в общеизвестную формулу
tg6 =-l/(ATcosy),
которая получается из уравнений движения при малых скоростях поле-
та при Г = в = 0.
Таким образом, выражение (9.32) для угла наклона траектории яв-
ляется обобщением формулы (9.33) на весь диапазон скоростей плани-
рования.
Потребный коэффициент подъемной силы находится в результате
решения уравнения автопилота (9.25) с использованием соотношений
(9.26)49.28) и (9.32):
А7г» ПР ^^^R /г» л л \
Суптр = mgo . (9.34)
4nPScosy
Здесь полагается, что действительный угол крена, как и программный
угол крена, равен приближенно оптимальному в соответствии с усло-
виями (9.22) или (9.24):
Y-Ynp-Yopt- (9.35)
При вычислении потребного значения су используется не действи-
тельный, а программный скоростной напор. Это объясняется следую-
щим. Уравнение автопилота было получено в разделе 2.10 в предполо-
жении, что действительная и программная траектории близки между
собой, т.е. q «дПр. При входе J1A в атмосферу реальная траектория
может существенно отличаться по высоте от программной и действи-
тельный скоростной напор в этом случае будет совершать колебания
относительно #Пр. Чтобы избежать влияния этих колебаний на потреб-
ное значение су, в знаменателе (9.34) целесообразно использовать
программное значение скоростного напора #Пр.
В результате решения уравнения (9.34) потребное значение коэф-
фициента су может существенно отличаться от его программного зна-
чения суПр. Такой случай имеет место, например, на начальном участке
спуска с орбиты, когда действительная высота полета намного больше
программной. Чтобы уменьшить потери дальности полета, целесооб-
разно наложить ограничение на максимальное отклонение потребного
значения су от программного:
9.6. Оптимизация траекторий при наличии фазовых ограничений 369
5 — б1пахд < 1,
где 3 I Су Супр I /Супр •
Пусть аэродинамические коэффициенты не зависят от высоты. В
случае квадратичной поляры аэродинамическое качество связано с Ятах
и с коэффициентом су следующим образом (см. раздел 2.5):
К=2КтяхуЦ\+уг\
ГДе у — Су /СуКт •
Отсюда следует, что на режиме, близком к Я1пах, справедливо
соотношение
ГДе 3 ~ I Су — CyKm I /£уК.т •
Например, если задать ограничение 8тахд = 0,1, то в процессе пла-
нирования текущее аэродинамическое качество будет уменьшаться по
сравнению с А?тах не более чем на 0,5% (для случая неквадратичной
поляры отклонение от Ятах будет иным). При уменьшении Зтахд потери
аэродинамического качества уменьшаются, а амплитуда колебаний
действительной траектории относительно программной увеличивается.
Из этого следует, что при выборе величины ЗтахД имеется разумный
компромисс между двумя указанными факторами.
2. Движение по ограничению в координатах ”Н- И”.
Предположим вначале, что в текущей точке программный скорост-
ной напор равен максимально допустимому:
#ПР “ #тахд(Ю-
Здесь функция дтахд(Ю однозначно связана с функцией Я1П1Пд(И)> пред-
ставляющей собой верхнюю огибающую всех ограничений, заданных в
координатах "Я- F" (рис. 9.10). Функция ЯП11пД(И) должна быть сфор-
мирована перед началом интегрирования траектории движения. Ее
можно задать в виде массива точек.
Программный угол наклона
траектории вычисляется с исполь-
зованием следующего соотноше-
ния:
sinGnp = Ихп^°я; <9-36)
+ V
Здесь производная Н\ соответст-
вует заданному ограничению
ятпД(Ю.
Чтобы исключить резкое скач-
кообразное изменение угла 0Пр по
траектории движения, желательно
задавать ограничение Ятшд(И)
таким образом, чтобы эта функция
Рис. 9.10. Задание ограничения
на траекторию движения в виде
массива точек в координатах
"высота - скорость"
370
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
была как можно ближе к "гладкой". Коэффициент сх, необходимый для
вычисления тангенциальной перегрузки ихПр, входящей в (9.36), опре-
деляется с учетом зависимости от высоты. Программный коэффициент
подъемной силы суПр, от которого зависит перегрузка ихПр, вычисляется
как наименьшее значение из трех величин:
£уПР min(cy q , Су щахД ? ^yNyl)?
где су q определяется из условия квазистационарного полета по ограни-
чению ЯПипд(К) с программным углом крена уПр = Yopt •
^vcosen, . (9J7)
?тахд£С03упр
коэффициент сутахд определен с учетом ограничения на угол атаки
(а < а1пахд); коэффициент cyNyi соответствует ограничению иУ| = л?у 1,Пахд •
Таким образом, все программные величины, необходимые для оп-
ределения перегрузки л?в птр, определены. Очевидно, что при
wgy cosenp
— су 1пахд
^7тахД^
аэродинамических сил недостаточно для квазистационарного полета, и
в этом случае необходимо увеличить су1Пахд или дтахд • При решении
уравнения автопилота (9.25) целесообразно использовать ограничение
«в.птр>0- В этом случае вертикальная составляющая подъемной силы
всегда будет направлена вверх.
Если функция Дптд(Ю имеет вогнутость (т.е. при увеличении V
производная Н’у увеличивается), то может оказаться, что в текущей
точке траектории при скорости V программными величинами будут дПр*
и 0Пр*, соответствующие скорости V < У (см. раздел 2.10).
Представим ограничение ДПтд(Ю в виде ломаной непрерывной ли-
нии (изломы находятся в исходном массиве точек). Пусть текущая точка
соответствует участку с номером i (рис. 9.11). Для определения номера
к программного участка необходимо перебрать все последующие уча-
стки (в сторону уменьшения скорости), для которых выполняется усло-
вие
(Н'у\<(Н\^.
Для каждого из рассматриваемых участков процедура определения
программных параметров (дПр, 0пр и др.) повторяется заново. В качест-
ве программного выбирается участок с номером к, обеспечивающий
«в.птр-^ max.
На рис. 9.11 показан случай, когда программным является участок
к ф i. При этом программный скоростной напор дПр больше, чем значе-
ние функции д1пахД в текущей точке, а производная Н’у меньше.
9.6. Оптимизация траекторий при наличии фазовых ограничений 371
После итогового выбора ве-
личин дПр и 0Пр потребное зна-
чение коэффициента подъемной
силы определяется так же, как и
в 1-ом варианте программной
траектории, по формуле (9.34) с
учетом (9.35).
Следует отметить, что уве-
личение программного угла
крена приводит к увеличению
коэффициента суПр и к умень-
шению тангенциальной пере-
грузки и программного угла
наклона 0Пр - см. формулы
Рис. 9.11. Определение программно-
го участка при наличии вогнутости
функции //т1Пд(О
(9.37), (9.4) и (9.36). В результате величины Див и ив.птр уменьшаются,
как это следует из формул (9.27) и (9.25).
Как было отмечено выше, уравнение автопилота (9.25) обеспечива-
ет полет по ограничению ^тахд с некоторой точностью. При этом воз-
можно кратковременное нарушение ограничения: q > д1пахд • В данном
случае с целью ускорения выхода на режим q < д|пахД предлагается
увеличивать потребное значение перегрузки ив путем уменьшения
модуля программного угла 0 следующим образом:
sin0np= sin0*--------—----------,
#пр + ~ (7пр)
где kQ > 0 - параметр, увеличение которого приводит к более интенсив-
ному увеличению иВ Птр; угол 0* вычислен по формуле (9.36).
Таким образом, в соответствии с изложенным алгоритмом в коор-
динатах ’’высота - скорость" формируются две программные траекто-
рии.
1. Траектория движения при отсутствии ограничений в координа-
тах "Н- Г". Этот программный профиль строится в процессе интегри-
рования уравнений движения.
2. Траектория полета по ограничению И1П1Пд(И) - строится до начала
интегрирования.
Каждой траектории в текущей точке соответствует свое потребное
значение коэффициента подъемной силы, полученное в результате
решения уравнения автопилота (9.25): суптр1 и суПтР2- На рис. 9.12 в
координатах ”Я- F” показано наиболее характерное расположение двух
типов программных траекторий при спуске с орбиты. В начале и в
конце траектории наибольшую высоту имеет программный профиль 1,
в средней части траектории - программный профиль 2.
Условием выбора программного профиля в текущей точке полета
является максимум потребного коэффициента подъемной силы:
372
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
су птр - тах(су птр1 , су птр?),
где коэффициент суПтр1 вычис-
лен с учетом ограничения на
максимальное отклонение лет-
ного коэффициента подъемной
силы от своего программного
значения (8 < бтахД).
Перейдем к определению
действительных значений управ-
Рис. 9.12. Типичное расположение
программных траекторий при
спуске с орбиты:
1 - траектория, обеспечивающая макси-
мум функционала без учета фазовых
ограничениий; 2 - ограничение //т,пд(Р)
ляющих переменных, которые
будут использоваться при интег-
рировании уравнений движения.
Действительный угол крена
вначале принимается равным
приближенно оптимальному. Это
значение угла крена использова-
но при вычислении су птр- см. формулы (9.34) и (9.35).
Действительный угол атаки в соответствии с постановкой задачи
определяется с учетом ограничений:
сС]п1пд — а < сс1пахд , (9.38)
77у| ^ЯуЦпахД’ (9.39)
Здесь угол атаки, соответствующий движению с максимально допусти-
мой перегрузкой, определяется в результате решения нелинейного
уравнения
С
ср(а) = —---(cosa + sina/Л) - иУ| тахд = 0.
^go
Кроме того, может быть наложено ограничение на максимальную
скорость изменения модуля угла атаки по времени:
I doddi I < (da/dx) тахД.
Для первого типа программной траектории при наличии ограниче-
ния 8 < 81пахД потребный коэффициент подъемной силы близок к своему
программному значению. При этом ограничения (9.38), (9.39), как
правило, являются несущественными.
Для второго типа программной траектории (при полете по ограни-
чению Я|Птд) потребное значение су может оказаться существенно
больше суПр. Если в результате учета ограничений (9.38) и (9.39) ока-
жется, что действительное значение су не равно потребному, то в этом
случае действительный угол крена необходимо изменить следующим
образом:
cosy = cosyopt су птр/Су, где 0 < I у I < I yopt I.
9.6. Оптимизация траекторий при наличии фазовых ограничений 373
Остановимся подробнее на обосновании правильности выбора
действительного угла крена у = yopt. В самом деле, в результате решения
уравнения автопилота (9.25) получается взаимосвязь между управляю-
щими переменными су и у в виде
(су COSy)nTP= Ив.ПТР Wgo/G/nP'S),
и далее возникает вопрос, как выбирать действительные управляющие
переменные в соответствии с соотношениями (9.22) и (9.24)? В частно-
сти, можно принять су = сукт, а угол крена определять из уравнения
автопилота.
Рассмотрим вначале задачу, когда угол атаки является заданным,
например, из условия балансировки (а = а*). Будем решать задачу с
ограничением на температуру в критической точке ЛА. Пусть радиус
сферического затупления равен = м. На рис. 9.13 показано про-
текание угла крена по скорости при полете с максимальной боковой
дальностью ЛА, имеющего постоянное аэродинамическое качество
К = 2,5. Видно, что при отсутствии ограничений зависимость у(Т)
является монотонной. В этом случае в критической точке реализуется
максимальная температура Twmax = 3120 К. При наличии ограничения
Tw < Гуутахд= 2800 К в диапазоне скоростей 5,14-7,3 км/с угол крена
уменьшается по модулю до ~33°. При 7\утахд= 2740 К угол крена
уменьшается примерно до 7° (см. рис. 9.13). Здесь в квазистационарном
полете по ограничению gTW угол крена определяется из следующего
соотношения:
mgv cosO
cosy = —7х-----.
Cy^TW
При 7\утахд<2700К несущих свойств ЛА не хватает для обеспече-
ния полета с заданным ограничением:
CyStfTW < wgvcos0.
Теперь рассмотрим случай одновременного управления углами
атаки и крена. Такая задача была решена в работе [111] для случая,
когда угол атаки входит в уравнение границы непосредственно:
G(a, Н, V) = 0. Очевидно, что здесь движение по ограничению вначале
должно обеспечиваться за счет угла атаки, а затем (в случае нехватки
управления углом атаки) - при помощи угла крена. Перейдем к случаю,
когда управляющие переменные а и у не входят явно в фазовое ограни-
чение:
G(H, V) = 0. (9.40)
Именно такой случай реализуется при задании ограничения
#1пахд(П- Вначале вернемся к исходной задаче оптимального управления
(без использования гипотезы квазистационарности) - см. раздел 2.7.
374 Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Рис. 9.13. Изменение характера протекания угла крена по скорости
планирования в зависимости от максимально допустимой температуры
в критической точке ЛА (при а = fix)
Рис. 9.14. Изменение характера протекания углов крена и атаки
по скорости планирования в зависимости от максимально
допустимой температуры в критической точке ЛА
Согласно принципу максимума определение закона управления,
обеспечивающего движение по ограничению, следует производить из
условия равенства нулю старшей производной от G по времени, в
которую управляющая переменная впервые войдет в явном виде. При
этом все предыдущие производные, как и сама функция G, должны
быть также равны нулю. Дифференцируя уравнение (9.40) по времени,
получим
G н KsinO + G v(- сх qS /т -g sinO) = 0. (9.41)
В уравнение (9.41) входит угол атаки (через аэродинамический ко-
эффициент сх), но не входит угол крена. Кроме того, в уравнение (9.41)
9.6. Оптимизация траекторий при наличии фазовых ограничений 375
не входят фазовые переменные Ф и Л, т.е. это уравнение соответст-
вует фазовому ограничению вида (2.109). Как показано в работе [111], в
этом случае первые интегралы (2.99) уравнений оптимального про-
странственного движения сохраняют свой вид. Отсюда следует вывод,
что движение по ограничению в координатах "Я- Г” должно обеспечи-
ваться сначала за счет угла атаки. Если управления углом атаки не
хватает, то движение по ограничению должно обеспечиваться за счет
надлежащего выбора угла крена. Т.е. задача решается так же, как и в
случае задания фазового ограничения вида G(a, Н, V) = 0.
На рис. 9.14 показано протекание углов атаки и крена по скорости
при полете с максимальной боковой дальностью ЛА, имеющего макси-
мальное аэродинамическое качество А?тах = 2,5 (7?w = 0,1 м). Здесь при-
нято, что максимально допустимый угол атаки равен атахд = 25°. При
отсутствии ограничений в плоскости "Я- Е” закон управления углом
крена у(Е) имеет такой же характер, как и в предыдущем случае (см.
рис. 9.13). При наличии ограничения Tw< 2800 К в диапазоне скоростей
5,54-7,1 км/с угол атаки увеличивается до ~ 15°. Ограничение на макси-
мальный угол атаки не нарушается. Изменение угла крена соответству-
ет закону (9.21). При 7w<2500K в диапазоне скоростей 5,54-7,1 км/с
угол атаки выходит на свое ограничение a = а1пахД и полет по ограниче-
нию 7\у=2500К обеспечивается за счет уменьшения угла крена (см.
рис. 9.14). Сравнение рис. 9.13 и 9.14 показывает, что одновременное
управление углами атаки и крена позволяет уменьшить ограничение
Тмпахд по сравнению с вариантом управления только углом крена. Если
сравнить два варианта управления при равных значениях 7\у1пахд, то во
втором случае можно увеличить боковую дальность планирования. Так,
при 7\утахД = 2800 К это увеличение достигает 5 %.
Таким образом, приведенные рассуждения и расчеты подтвержда-
ют правильность исходных предпосылок, заложенных в закон управле-
ния: вначале угол крена принимается равным приближенно оптималь-
ному значению в соответствии с условиями (9.22) или (9.24), а угол
атаки определяется в результате решения уравнения автопилота (9.25).
В случае нехватки управления углом атаки начинает уменьшаться
модуль угла крена вплоть до нулевого значения.
Перейдем к рассмотрению наиболее характерных случаев спуска с
орбиты и планирования в атмосфере.
9.7. Планирование с максимальной продольной дальностью
Вначале рассмотрим планирование в предположении, что ограни-
чения на фазовые переменные отсутствуют. Аэродинамическое качест-
во не зависит от числа Маха и высоты полета.
Часто требуется оценить дальность планирования, не интегрируя
уравнения движения. Когда начальная скорость Vo невелика, то проин-
376
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
тегрировав уравнение квазистационарного планирования (см. раздел
2.9)
dLldE = -
rgy
получим
Е = К(Е0-Ек), где Е = Н+ K2/(2gT), (9-42)
т.е. дальность планирования пропорциональна разности начального и
конечного значений удельной энергии
В данном случае использована модель плоской Земли. Формула
(9.42) справедлива как для вращающейся, так и для невращающейся
Земли. Погрешность расчета не превышает 5%, если Ио < 1,54-2 км/с.
При увеличении Ко сверх указанного диапазона расчетная дальность
начинает существенно занижаться по сравнению с ее действительным
значением.
При задании Ио в диапазоне до 34-3,5 км/с справедлива следующая
формула [81]:
Ь = К(Н0-Нд+^\п-Л^. (9.43)
Z 1 V п
Здесь V= V/VKP; ГКР = ^/(Rq + Яо) ~ круговая скорость на начальной
высоте.
Формула (9.43) получена из упрощенных уравнений движения, за-
писанных с учетом кривизны Земли. Нетрудно показать, воспользовав-
шись первыми членами разложения в ряд функции 1п(1 - И2), что при
малых Ио формула (9.43) превращается в (9.42).
Так как в общем случае аэродинамическое качество переменно по
скорости полета, то траекторию планирования всегда можно разбить на
отдельные участки с К= const и пользоваться формулами (9.42) и (9.43)
последовательно для каждого из них.
При Ио > 34-3,5 км/с в зависимости от направления движения по
формуле (9.43) можно получить как заниженный, так и завышенный
результат. Так, при Ио= 7 км/с погрешность расчета достигает 25 %. Это
указывает на то, что при больших скоростях полета необходимо учиты-
вать вращение Земли.
Получим формулу, аналогичную (9.43), для случая вращающейся
Земли. Пусть в начальной точке известны параметры траектории Ио,
Ио, 0о, ЧЛ) и фо (в геоцентрической вращающейся с.к.). Здесь полагает-
ся, что Но и 0О близки к своим соответствующим квазистационарным
значениям. Запишем дифференциальное уравнение для дальности
полета в следующем виде:
dL = -KR^
gydE
gr[l-KA2/(gr)]'
(9.44)
9.7. Планирование с максимальной продольной дальностью 377
Используем дифференциальную связь (2.38) между скоростями V и
ИА:
гаГ=(ГА-Ду)б/ГА, (9.45)
где Ду ~ (Озг coscp cos\pAcos0A; углы \рА и 0А вычислены в абсолютной
системе координат.
Пренебрежем изменением Av по траектории:
Av « (Оз г coszA = const, где coszA = coscp0 cosv|/A().
Здесь принято, что cos0A~ 1; zA- наклонение плоскости движения в
начальной точке, вычисленное в абсолютной системе координат. Угол
курса срА0 вычисляется через \р0 при помощи 3-й формулы (2.36).
С учетом соотношения (9.45) запишем
dE = dH + (VA- Av) e/KA/gT•
Здесь с целью упрощения полагается, что при дифференцировании
удельной энергии величина gT является постоянной.
Проинтегрируем уравнение (9.44) с учетом последнего соотноше-
ния:
L = -KR* (--------------KR f---------------+
gr [1 - Vl /{gr)] I gr [1 - Гд /(gr)]
+ ^Av,Jgr[l-K2/(gr)]’
Наибольшее изменение высоты полета происходит при КЛ« ККР.
В связи с этим пренебрежем разгрузкой в знаменателе первого слагае-
мого и учтем, что 7?ogT~ rg. В результате получим
L = K(H.-H^ +
+ ^1п1-Пк ДУ[п
2 1-Йо 2 Ккр
Здесь обозначено V А = VA/VKP.
В данном случае, как и в формуле (9.43), круговая скорость вычис-
ляется на начальной высоте, так как это дает наилучшее приближение к
действительному значению L . В отличие от (9.43) в формулу (9.46)
входит не относительная, а абсолютная скорость ИА. В начальной точке
скорость KA0 вычисляется через Ко при помощи 1-й формулы (2.36). В
конечной точке при проведении практических расчетов обычно задает-
ся относительная скорость Ик, которая составляет 1 ОО-е-200 м/с. При
таких скоростях абсолютная скорость ИА может оказаться неоднознач-
. (9.46)
378
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
ной функцией относительной скорости V. Так, например, в процессе
планирования в экваториальной плоскости в западном направлении
модуль скорости КА проходит через ноль, а вектор скорости меняет
направление на 180°.
В связи с этим предлагается следующий способ расчета дальности.
Траектория планирования разделяется на два участка. На первом участ-
ке абсолютная скорость изменяется от КА0 до КА|, где
ИА| = 8004-1000 м/с > ИЕ (наибольшее значение переносной скорости VE
достигается на экваторе и на высоте 50 км для шарообразной Земли
составляет 468,15 м/с). В этом случае ИЛ всегда будет изменяться моно-
тонно по скорости V. Дальность планирования L] определяется по
формуле (9.46). В точке 1 необходимо сделать пересчет параметров
траектории из абсолютной системы координат в геоцентрическую
вращающуюся с.к. с использованием формул (2.37). Для этого помимо
абсолютной скорости нужны две величины: (pi и \|/Ai (полагается, что
cos0A®l). Для их определения пренебрежем вращением Земли, т.е.
будем полагать, что движение происходит в плоскости большого круга
в абсолютной системе координат. Используя формулы сферической
тригонометрии, запишем
sincpi = sinAi sinzA.
Здесь Л। - ортодромическая долгота точки 1, связана с начальной орто-
дромической долготой следующим образом:
Л । = Ао + L । /7?о,
где sinA0= sincpo /sinzA.
Наклонение плоскости движения zA связано с текущими значения-
ми широты и угла курса, в том числе с их начальными значениями,
следующим образом:
COSZA= COSCpo COS\]/Ao = COS(p[ COSV|/A1 ,
откуда определяется угол курса v|/A।.
Таким образом, в точке 1 можно определить относительную ско-
рость И|. На втором участке относительная (воздушная) скорость
изменяется от V\ j\q заданной величины Гк. Дальность планирования Т2
определяется по формуле (9.43). Суммарная дальность полета равна
L = L\ + L2.
При необходимости расстояние между двумя точками с координа-
тами (ф|, Х|) и (<р2, ^2) вычисляется следующим образом:
£ = Я0АЛ,
где угол АЛ определяется с помощью теоремы косинусов сторон
сферического треугольника:
cos АА = sincpi sincp2 + coscp 1 coscp2 cos(Xi - X2) .
9.7. Планирование с максимальной продольной дальностью 379
Рис. 9.15. Взаимосвязь началь-
ных условий квазистационарного
планирования
Здесь две стороны треугольника - меридианы с долготами Х| и Х2,
третья сторона - дуга большого круга, вдоль которой вычисляется
искомое расстояние.
Аналитическое решение (9.46) для дальности полета соответствует
квазистационарному планированию. Зависимости начальных условий
квазистационарного планирования HQ и 0О от представлены на
рис. 9.15 (при А* = 3): высота определялась с использованием формулы
(9.28), угол наклона траектории - с использованием формулы (9.32) при
у = 0. Здесь и далее полагается G/S = 2 кН/м2. При больших скоростях
полета угол 0О асимптотически приближается к нулю. Профиль полета в
координатах "Н- Г” в общем случае зависит от параметра планирова-
ния сгу и, кроме того, при больших
скоростях - от наклонения орбиты
(см. рис. 9.15).
На рис. 9.16 показана зависи-
мость дальности планирования от
начальной скорости для двух зна-
чений наклонения орбиты при
К=3. Начальные высота и угол
наклона траектории соответствуют
рис. 9.15. Сравнение с решением,
полученным путем интегрирования
уравнений движения, показало, что
при К=3 погрешность аналитиче-
ского расчета L не превышает 2 %,
причем с увеличением Ио погреш-
ность уменьшается.
Определим зависимость даль-
ности планирования от аэродина-
Рис. 9.16. Зависимость дальности
планирования от начальной скорости
L, тыс. км
4
2
------1------1---
Численное
интегрирование
уравнении *
движения
Аналитический
расчет
/7о = 7 км/с
/70 = 76 км
О 0,4 0,8 К
Рис. 9.17. Зависимость дальности
планирования от аэродинамического
качества
380
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
мического качества. Анализ
формулы (9.46) показывает, что
величина L пропорциональна
аэродинамическому качеству.
Сравнение аналитического и
численного решений пред-
ставлено на рис. 9.17 (при
Ко = 7 км/с). Видно, что при
К < 0,44-0,5 аналитическое
решение существенно занижа-
ется по сравнению с числен-
ным решением. Это указывает
на то, что аналитическое реше-
ние для дальности планирова-
ния справедливо только при
больших значениях аэродина-
мического качества (при
К> 1,0-И, 5).
Исследуем влияние на-
чальных условий на дальность
планирования. На рис. 9.18
показана зависимость L от 0О
при различных значениях HQ и
Ио (численное интегрирование
наклона траектории варьировал-
Рис. 9.18. Влияние начальных условий
на дальность планирования при К= 3
уравнений движения). Начальный
ся в диапазоне от минус 6° до 6°. На максимальное значение нормаль-
ной перегрузки было наложено ограничение: иУ1<3. Результаты расче-
тов показали, что по мере возрастания Но дальность планирования
монотонно возрастает. Зависимость L от 0О является аналогичной при
малых скоростях полета (И« ИКр). При суборбитальных скоростях
существует оптимальный угол наклона траектории 0О= Н3°, обеспечи-
вающий максимум L (см. график при Ко = 7,3 км/с на рис. 9.18). По мере
увеличения Яо и Ко этот угол уменьшается.
Как следует из рис. 9.18, при отклонении Яо и 0О от своих квази-
стационарных значений расчетная дальность планирования может
существенно отличаться от соответствующей дальности квазистацио-
нарного планирования. Так, например, при изменении 0О от минус 6° до
2° (Ко = 7,3 км/с и 7/0= 100 км) дальность изменяется от 21 до
40,8 тыс. км, в то время как дальность квазистационарного планирова-
ния составляет ~ 36 тыс. км. Это указывает на то, что аналитическое
решение может использоваться только в случае незначительного откло-
нения начальных значений высоты и угла наклона траектории от своих
квазистационарных значений.
9.7. Планирование с максимальной продольной дальностью
381
Будем далее проводить расчет траектории путем численного интег-
рирования уравнений движения (Земля вращается, параметры атмосфе-
ры соответствуют СА-81).
Рассмотрим суборбитальный ЛА и определим условия, необходи-
мые для обеспечения дальности полета, близкой к длине экватора
Земли. Пусть Н$ = 100 км; i = 0. Круговая скорость ИКр на этой высоте
равна 7849 м/с в абсолютной системе координат (7377 м/с в геоцентри-
ческой вращающейся с.к.). Определим зависимость потребного аэроди-
намического качества К от Ио, соответствующую L = const. При этом
будем по-прежнему полагать, что аэродинамическое качество не зави-
сит от высоты и числа Маха. Для каждого сочетания К и И() начальный
угол наклона траектории 0О будем оптимизировать из условия L -> шах.
На рис. 9.19 показана расчетная зависимость аэродинамического
качества от ДИ, где аргумент ДИ=Икр-Ио характеризует близость
начальной скорости планирования к круговой скорости. На этом же
рисунке показано соответствующее изменение Ooopt- В расчетах допус-
калось отклонение летного значения су от сук,п не оолее 5 %. Из рисунка
видно, что если, например, аэродинамическое качество ЛА равно 2,5, го
для обеспечения дальности полета 34-40 тыс. км начальная скорость
планирования должна отличаться от круговой не более чем на
50-90 м/с. Диапазон изменения 0Oopt составляет 1,1-=-2,1°. При увеличе-
нии К с 2,5 до 3,0 соответствующая величина ДИ увеличивается до
80-155 м/с.
При уменьшении начальной скорости (т.е. при увеличении ДИ) оп-
тимальный угол 0О увеличивается, что приводит к уменьшению высоты
первого погружения в атмосферу и к соответствующему увеличению
Рис. 9.19. Зависимости аэродинамического качества К и оптимального угла
наклона траектории 00opt от начальной скорости Ио, соответствующие заданной
дальности планирования L
382
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
аэродинамического нагревания. Если аналогичную задачу решать с
учетом ограничения на Tw, то зависимости на рис. 9.19 сдвинутся в
сторону меньших значений ДИ Таким образом, можно заключить, что
для обеспечения посадки суборбитального ЛА в точке его старта ско-
рость аппарата в начальной точке планирования должна быть близкой к
круговой.
Рассмотрим траекторию спуска с орбиты летательного аппарата с
максимальным аэродинамическим качеством 7<тах=2. Пусть ограниче-
ния на фазовые координаты отсутствуют, а начальные условия сущест-
венно отличаются от квазистационарных (/То = 100 км; 0о = -1°). Иссле-
дуем зависимость дальности планирования L от параметра 8тахД,
характеризующего максимально допустимое отклонение летного значе-
ния коэффициента су от суКт, т.е. при наличии ограничения
| Су — CyKin I /^уКт — ^тахД •
При 8тахд= 0 гашение колебаний не осуществляется и траектория
имеет колебательный характер (рис. 9.20). При увеличении 8тахД ампли-
туда колебаний и их количество начинают уменьшаться, и при
8|пачД>0,15 остаются два отражения от плотных слоев атмосферы (см.
рис. 9.20). Кроме того, увеличение 81пахД сопровождается некоторым
увеличением высоты первого отражения.
На рис. 9.21 показана зависимость относительной дальности пла-
нирования (по отношению к максимальной возможной) от параметра
8,пахд. Максимум L достигается при 81ПахД»0,15. При 8тахД = 0 и 0,3
Рис. 9.20. Влияние параметра 8тахд на характер траектории планирова-
ния: зависимости высоты от времени полета
9.7. Планирование с максимальной продольной дальностью
383
Рис. 9.21. Зависимость дально-
сти планирования от парамет-
ра, характеризующего степень
гашения колебаний
Рис. 9.22. Зависимость дальности
планирования от максимально
допустимой температуры в
критической точке ЛА
дальности планирования одинаковы. В общем случае рациональное
значение 8тахД зависит от начальных условий и других исходных дан-
ных.
Рассмотрим влияние фазовых ограничений на траекторию плани-
рования при у = 0. Пусть условия входа в атмосферу близки к квазиста-
ционарным: HQ = 100км; 0о = -О,16°. Влияние величины TWmaxji на
дальность планирования при 7?w = 0,1m и атахД=45° показано на
рис. 9.22. При 7\утахД> 2700 К дальность планирования от 7\утахД не
зависит. При уменьшении 7\у1ПахД от значения -2400 К дальность пла-
нирования начинает резко уменьшаться. При Г^тахд < 2190 К аэродина-
мических сил недостаточно для того, чтобы строго выдержать ограни-
чение при рассматриваемых исходных данных.
Пусть теперь одновременно заданы ограничения на максимальные
температуру в критической точке аппарата и скоростной напор:
^тахд=2200К и <7тахд= 15 кН/м2. Расчетная траектория планирования
показана на рис. 9.23. При F® 7400 м/с траектория выходит на профиль
полета, соответствующий ограничению 7\утахд (см. рис. 9.236). Полет
по ограничению Г>у1Пахд обеспечивается за счет соответствующего уве-
личения угла атаки, максимум которого достигает 41° (при
V« 6250 м/с). При V« 3800 м/с осуществляется переход с ограничения
^тахд на д,пахд- Перед выходом на очередное ограничение происходит
кратковременное увеличение перегрузки (см. рис. 9.23а), которое и
обеспечивает плавное изменение траектории. Таким образом демонст-
рируется алгоритм отслеживания программного профиля полета с
использованием уравнения автопилота (см. раздел 2.10).
384
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Рис. 9.23. Траектория спуска с орбиты с ограничениями на максималь-
но допустимые температуру в критической точке и скоростной напор
(7W < 2200К, </< 15 кН/м2):
а) зависимость высоты Н и нормальной перегрузки пу от скорости полета;
б) зависимость температуры в критической точке Tw, скоростного напора q и
угла атаки а от скорости полета
9.8. Планирование с максимальной боковой дальностью
Вначале рассмотрим вариант, когда ограничения на фазовые пере-
менные отсутствуют. В этом случае оптимальным является режим
максимального аэродинамического качества на всей траектории. В
зависимости от величины у1пахД реализуются либо два участка закона
управления углом крена: утахД и yopt(т), либо только один участок yopt(т)
(см. раздел 9.5). Могут быть применимы как условия (9.22) при
АВКл /= 0, так и условия (9.24) при £11у=£п а = 0. Пусть ограничение на
9.8. Планирование с максимальной боковой дальностью
385
угол крена равно Утахд = 90°. Аэродинамические характеристики не
зависят от высоты и числа Маха.
Вместо закона (9.21) будем использовать модифицированный закон
управления углом крена:
yopt = />(Ч' - Ч'к), (9.47)
где Ь- дополнительный оптимизируемый параметр.
Определим влияние параметров импульса скорости схода с орбиты
на боковую и продольную дальности планирования. В качестве примера
рассмотрим сход с круговой орбиты высотой /7Кр = 200 км и наклонени-
ем i = 0. На исходной орбите прикладывается импульс AVCx (см.
рис. 9.5). Летательный аппарат имеет максимальное аэродинамическое
качество ^тах = 2,5.
Вначале расчеты были проведены для случая, когда вектор AVCx
противоположен вектору начальной скорости VKp: 3 =-180°; парамет-
ры b и Ч'к при этом оптимальны. Как видно из рис. 9.24, существует
оптимальное значение импульса схода, обеспечивающее максимум
боковой дальности. В данном случае AKCxopt“ 42 м/с. При принятом
законе управления нижняя граница по скорости схода составляет 34 м/с
(возможная наименьшая величина ДКСх реализуется, если на первом
участке входа в атмосферу использовать управление у =180° и
& ~ С^тахд)’
При AVCx< 34 м/с (Нк> 86 км) вход в атмосферу с первого витка
невозможен, так как плотность атмосферы в перигее переходной орби-
ты является недостаточной. При ДГСх> 42 м/с боковая дальность спус-
ка уменьшается вследствие уменьшения скорости входа в плотные слои
атмосферы. Оптимум Lz по
ДИсх является пологим. В
диапазоне ДКСХ = 37ч-55 м/с
боковая дальность изменяется
на 25 км (0,5 % от Zz). Про-
дольная дальность зависит от
ДИсх более существенно. Так,
в рассмотренном диапазоне
при увеличении импульса
схода Lx уменьшается от 34
до 22 тыс. км. В связи с этим
величину ДИсх можно ис-
пользовать как средство
достижения заданной про-
дольной дальности при
Lz « max.
Далее расчеты были про-
ведены для случая, когда
вместе с величиной ДИСх
Рис. 9.24. Зависимости боковой и про-
дольной дальностей планирования от
импульса скорости при сходе с орбиты
386
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Рис. 9.25. Зависимости боковой (а) и продольной (б) дальностей
спуска от модуля и направления импульса скорости при сходе с орбиты
оптимизируется угол 9. Расчетные зависимости конечных значений £z
и L\ от ДЙех и угла 9 приведены на рис. 9.25.
При небольшом отклонении угла 9 от минус 180° боковая даль-
ность практически не изменяется (см. рис. 9.25я). При ДИСх = 4(Н50 м/с
увеличение угла 9 приводит к уменьшению боковой дальности. При
ДРсх= 60 м/с, наоборот, увеличение угла 9 приводит к увеличению
боковой дальности, максимум Az реализуется при Э = - 130°. В районе
9.8. Планирование с максимальной боковой дальностью
387
максимума £z увеличение угла 9 приводит к резкому увеличению про-
дольной дальности (см. рис. 9.256), что связано с соответствующим
приближением скорости входа к ИКр. При ДИСх- 80 м/с и более зависи-
мости £z и Lx от угла 9 ведут себя аналогично (см. рис. 9.25а и б). При
этом максимум £z сдвигается в диапазон 9 =-(1054-115°). Однако, как
видно из рис. 9.25а, увеличение импульса скорости от 40 до 120 м/с
позволяет увеличить максимальную боковую дальность всего на
~ 40 км (-0,8%). Кроме того, увеличение угла 9 приводит к более
"крутому" входу в атмосферу. Так, при 9 =-105° на высоте Н= 100 км
угол наклона траектории составляет минус 0,67°. В свою очередь, это
приводит к увеличению аэродинамического нагревания. Таким образом,
можно заключить, что увеличение импульса схода свыше
ATcxopt® 42 м/с с одновременной оптимизацией угла 9 не является
оправданным, так как не позволяет существенно улучшить маневрен-
ные характеристики планирования, но требует дополнительных энерге-
тических затрат. В дальнейших расчетах было принято 9 = -180°.
Результаты оптимизации импульса схода Д/сх и параметров и Ь
для различных значений максимального аэродинамического качества
при сходе с экваториальной орбиты (//кр = 200 км, i = 0°) представлены
на рис. 9.26. Оптимальный импульс скорости AFcxopt увеличивается от
25 м/с (при /Стах = 0,1) до 42 м/с (при Л?1Пах = 2,54-3). Это увеличение
объясняется тем, что при увеличении Л?тах, т.е. при уменьшении схКщ
для обеспечения входа в атмосферу требуется меньшая высота перигея
переходной орбиты Нк. В диапазоне А7тах <3,1 значение 6ор1 равно 1.
Оптимальный угол конечного курса изменяется в диапазоне 594-90°.
При Л?тах = 0,4 реализовался минимум TKopt; увеличение TKopt при
АГтах<0,4, по-видимому, объясняется нарушением гипотезы квазиста-
ционарности. При Л?тах > 3,1 оптимальный угол конечного курса равен
90°, а параметр 6opt увеличивается от 1 до 1,11 (при А?тах = 3,8).
По результатам расчетов предлагается следующий алгоритм опти-
мизации. Вначале при b= 1 необходимо определить оптимальный угол
конечного курса Тк. Если при этом окажется 4/Kopt> 90°, то это значит,
что ^Kopt^ 90° и необходимо оптимизировать параметр Ь.
Зависимости Lz(Kmax) и Lx(Kmax), соответствующие оптимальным
значениям ДРсх, Ь и представлены на рис. 9.27. Для гашения коле-
баний было задано 81пахд = 0,05. При малых значениях Л?1пах зависимость
^z(^max) практически квадратичная; при /Стах> 1,54-2 функция Zz(/Cmax)
близка к линейной; при /Стах > 3,9 и i = 0° боковая дальность превышает
10 тыс. км. По мере увеличения Ктях продольная дальность увеличива-
ется. На рис. 9.27 также показаны зависимости Lz(Kmax) и Лх(^П1ах) при
спуске с экваториальной орбиты с наклонением i= 180°. Видно, что в
этом случае при равных значениях АГтах достигаются большие боковая и
продольная дальности в связи с существенно большей (на - 930 м/с)
начальной скоростью входа в геоцентрической вращающейся с.к.
388
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Рис. 9.26. Изменение оптимальных
импульса схода и параметров
закона управления углом крена в
зависимости от аэродинамического
качества
Лх, тыс. км £z, тыс. км
0 12 3 /Стах
Рис. 9.27. Зависимости максималь-
ной боковой дальности спуска и
соответствующей продольной даль-
ности от аэродинамического качества
и наклонения орбиты
Для предварительных оценок боковой дальности спуска с низкой
орбиты удобно использовать аналитическую зависимость £z от
аэродинамического качества, полученную в работе [111]:
Т п •
Zz = Rq -sin у cos у
6К2 cos2 у
тс2 [к2 cos2 у + 4)
(9.48)
Здесь у - постоянный по траектории угол крена, равный 45°.
Зависимость соответствующая формуле (9.48), приведена на
рис. 9.27. Так как при выводе формулы вращение Земли не учитыва-
лось, то аналитический расчет боковой дальности применим главным
образом к случаю схода с полярных орбит.
Рассмотрение влияния различных параметров на боковую даль-
ность спуска при ЛГ1Пах=2,5 показало следующее. На величину £z наи-
более сильно влияет угол конечного курса. При отклонении на
±10% от оптимального значения боковая дальность уменьшается на
2,74-3,1%. При аналогичном отклонении тормозного импульса Zz
уменьшается на 0,064-0,24%. Увеличение удельной нагрузки G/S в два
раза приводит к уменьшению Zz на 20 км (-0,36%). Однако в случае
учета ухудшения аэродинамических характеристик по высоте увеличе-
ние G/S, наоборот, приводит к улучшению маневренных характеристик
ЛА.
9.8. Планирование с максимальной боковой дальностью
389
На рис. 9.28 представлены расчетные траектории спуска с орбиты в
координатах ’’высота-скорость” (при G/S = 2 кН/м2). Увеличение /Стах
приводит к уменьшению соответствующего значения коэффициента
подъемной силы суК1П, вследствие чего высота траектории снижается.
Сравнение с траекторией продольного планирования (см. рис. 9.15)
показывает, что качественно зависимости H(V) ведут себя одинаково,
однако при полете с максимальной боковой дальностью вследствие
наличия крена при больших скоростях высота полета снижается на
10^-15 км.
Влияние начальной скорости планирования на максимальную бо-
ковую дальность показано на рис. 9.29. При задании начальных значе-
ний высоты и угла наклона траектории использовались данные, соот-
ветствующие рис. 9.28. Зависимость Zz(K0) близка к квадратичной. Как
видно из рис. 9.29, боковая дальность при V> ИКр является конечной
величиной, в отличие от продольной дальности, которая при этом мо-
жет быть сколь угодно большой, см. формулы (9.43) и (9.46).
Влияние начального угла наклона траектории на боковую и про-
дольную дальности при Ко = fix показано на рис. 9.30. Здесь принято,
что Но = 100 км; начальная скорость превышает круговую скорость на
~17 м/с. Расчетные зависимости качественно ведут себя так же, как и
зависимости от ДКСх (см. рис. 9.24). При 0О = -0,8° имеет место макси-
мум Lz . Уменьшение угла 0О до минус 2° приводит к уменьшению £z на
~ 1 %. При этом Lx уменьшается с 17 до 11 тыс. км. Увеличение ’’кру-
тизны" входа (при уменьшении угла 0О) приводит к увеличению ампли-
туды колебаний высоты полета.
Влияние параметра 5тахД на траекторию является качественно та-
ким же, как и при планировании с максимальной продольной дально-
стью (ср. рис. 9.31 и 9.20). Расчеты проводились для ЛА с максималь-
Рис. 9.28. Профиль полета с мак-
симальной боковой дальностью в
координатах "высота - скорость"
Рис. 9.29. Зависимость боковой
дальности от начальной скорости
планирования при различных
значениях /Стах
390 Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Рис. 9.30. Зависимости боковой и
продольной дальностей от на-
чального угла наклона траектории
при Hq = 100 км и Ио = 7394 м/с
ным аэродинамическим качеством
2,5 для случая входа в атмосферу
с углом 0о = - 2° при Но = 100 км и
К)» ^кр- На рис. 9.32 показана
зависимость относительной боко-
вой дальности планирования (по
отношению к максимально воз-
можной величине Zz) от 8тахД.
Максимум Zz достигается при
8тахД = 0,03. При 81пахД=0,25 на
участке после первого погружения
в атмосферу траектория становит-
ся практически гладкой (см.
рис. 9.31). Уменьшение боковой
дальности при этом составляет
-1,1% по сравнению с макси-
мально возможной.
Изменение текущих значе-
ний угла крена, боковой дальности, продольной дальности и скоростно-
го напора по скорости для типовой траектории планирования при сходе
с низкой круговой орбиты для ЛА с ЛГтах = 2,5 представлено на
рис. 9.33. Модуль угла крена монотонно уменьшается по траектории от
значения Тк до 0 (см. рис. 9.33я) в соответствии с формулой (9.47).
Наибольший темп прироста текущей боковой дальности по скорости
полета имеет место в диапазоне V= 4-Нэ км/с (М = 13н-20). В сверхзву-
ковом диапазоне скоростей (при М < 5) прирост текущей боковой даль-
ности составляет менее 7 %, в дозвуковом диапазоне - менее 0,3%.
Отсюда следует, что аэродинамические характеристики ЛА должны
Рис. 9.31. Влияние параметра 5тахД на характер траектории планирования с
максимальной боковой дальностью: зависимости высоты от времени полета
9.8. Планирование с максимальной боковой дальностью
391
задаваться наиболее точно в гиперзву-
ковом диапазоне скоростей. Скорост-
ной напор максимален при малых
скоростях полета (см. рис. 9.336). Такой
характер зависимости q(V) присущ ЛА
с большим аэродинамическим качест-
вом. В данном случае величина д1пах
составляет 25 кН/м2 и не зависит от
предыстории: спускается ЛА с орбиты
или начальная точка планирования
лежит в области сверхзвуковых скоро-
стей. Максимальная величина нормаль-
ной перегрузки пу не превышает 1,0 и
так же, как и gmax, не является критич-
ной при спуске с орбиты.
Из рис. 9.336 видно, что прирост
Рис. 9.32. Зависимость отно-
сительной боковой дальности
спуска от параметра 5тахД
продольной дальности планирования с
креном в плотных слоях атмосферы (при V < 7200 м/с) не превышает
15 тыс. км, несмотря на то, что суммарная продольная дальность спуска
с орбиты составляет 26 тыс. км (существенно больше 20 тыс. км). В
результате, задание параметра £Вкл.у в диапазоне от 0 до ~ 10 тыс. км не
оказывает влияния на траекторию полета. То же самое относится к
предыдущим расчетам (см. рис. 9.24, 9.25 и 9.27), которые проводились
при £Вкл.у=0. Таким образом, можно считать, что правило выбора
параметра Лвкл.у, сформулированное в разделе 9.5, не нарушается.
Определим взаимосвязь между основными параметрами ЛА,
управляющими переменными и температурой в критической точке Tw.
В работе [111] получено аналитическое выражение критической
скорости KTw, при которой реализуется максимум температуры для
случая невращающейся Земли:
M-2N
М
Икр « 6,5 км/с.
ЗдесьМ= 3,25; 7V=O,5 - показатели степеней при V и р в формуле
(2.83).
Получим аналогичную формулу для вращающейся Земли. С этой
целью исключим скоростной напор из уравнения равенства вертикаль-
ных сил (2.112) при помощи условия (2.84):
mgj Г _ К2 + ГАГ = 0,5 Aw(£g)27^
суПР5со5УД gTr J (0,2595 1 О^С, )2Г45 ’
(9.49)
где АИ= 2co3rcoszw, z’w-наклонение плоскости, в которой лежит теку-
щий вектор скорости.
392
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Рис. 9.33. Изменение угла крена, текущей боковой дальности (а), теку-
щей продольной дальности и скоростного напора (б) в зависимости от
скорости при планировании с максимальной боковой дальностью
Пренебрежем зависимостью параметра С\, величин gT и г, а также
управляющих переменных су и у от скорости полета. Тогда максимум
температуры будет однозначно определяться максимумом функции
У~ +У-кУ'
,
Записав необходимое условие экстремума
4,5 Г3'5-6,5 r5 5/(gTr)- 5,5 И4’5Д И/(gTr) = О,
после сокращения на У3'5 получим квадратное уравнение относительно
скорости:
У3 + У Д V 5,5/6,5 - gTr 4,5/6,5 = 0.
АУ)= У4,5
В результате
9.8. Планирование с максимальной боковой дальностью
393
Ptw -
4,5 (5,5. V 5,5 л__ 4,5 5,5 д
---£тг+ ----ДИ-------ДИ « ------gr-------ДИ~
6,5 т U3 ) 13 \6,5 т 13
« 0,8327?о - уу соз г cosz„ -6546-397 cos/,,. (9.50)
Здесь принято, что в критической точке (при V= HTW) высота полета
составляет 60 км, вектор скорости еще не развернулся относительно
первоначальной плоскости движения: zTw~ /0.
Из формулы (9.50) видно, что критическая скорость не зависит от
управляющих переменных и параметров ЛА, а зависит только от на-
клонения орбиты.
Получим приближенное аналитическое выражение для максималь-
ной температуры Т^тях при квазистационарном планировании с орби-
ты. С этой целью разрешим уравнение (9.49) относительно 7\v при
V= HTw’
Т Г Д С + Hrw Л V Vo,2595-10 4 С,)2 1"
cv5cosy7?w gyr ) 0,5(еа)‘
В полученном выражении величины HTw и ДИ зависят от наклонения
орбиты. Величина Ci = 1 -Ду/Дл где
/w = 1 2407\v - 161000; /0 = 1000Гн + И2/2,
зависит от скорости полета и температуры .
В диапазоне температур Т^= 2000^-3000 К при V= 6546 м/с вели-
чина Ci уменьшается от 0,902 до 0,835. Положим, что Ci = const и при-
мем степень черноты 8 = 0,8. Аппроксимируем зависимость от накло-
нения орбиты линейной функцией cosz. В результате получим
_ 1-0,043 cos/
Twmax ~ 630 -------- .
(сту cosy/?w)
(9.51)
График зависимости Twmax от параметра crycosy/?w для наклонений
орбиты 0 и 180° представлен на рис. 9.34. В формуле (9.51) коэффици-
ент планирования су задается в м2/Н, радиус Rw - в метрах. Программ-
ный угол крена, как видно из рис. 9.33, при И=6,5 км/с равен 65°, что
составляет примерно 0,79 от величины TKopt, зависимость которой от
А^пах представлена на рис. 9.26.
Формула (9.51) является удобной для пересчета 7wmax. Так, напри-
мер, при переходе от траектории с максимальной продольной дально-
стью (у = 0) к траектории с максимальной боковой дальностью TWmax
увеличивается в (cosy)’,/8 раз. При у = 60° это увеличение составляет
~9%. Увеличение удельной нагрузки на крыло, уменьшение коэффици-
394
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Рис. 9.34. Изменение максимальной температуры 7W, которая
реализуется при квазистационарном планировании ЛА с орбиты,
в зависимости от параметра crycosy/?w и наклонения орбиты
ента подъемной силы или уменьшение радиуса затупления 7?w в 2 раза
также приводит к увеличению Twmax на ~9%. Формула (9.51) характе-
ризует максимум температуры в квазистационарном планировании.
При "пологом" входе в атмосферу эта температура одновременно будет
максимальной на всей траектории планирования. Однако необходимо
иметь ввиду, что при "крутом" входе локальный максимум 7"Winaxi,
соответствующий первому погружению в атмосферу, может оказаться
одновременно абсолютным максимумом. Как показано в [111], мини-
мальное значение 7wmaxi реализуется при yopt = О (на участке полета до
первого отражения).
Проверочные расчеты, проведенные путем интегрирования урав-
нений движения, показали, что действительная критическая скорость,
при которой реализуется Twmax в квазистационарном полете, не является
постоянной при i = const. Так, например, при увеличении АГ1Пах от 0,5 до
2,5 скорость KTW увеличивается от 6,3 до 6,8 км/с (рис. 9.35). Это объ-
ясняется характером траектории в координатах "Н- Г7" при И>6км/с
(см. рис. 9.28). Увеличение удельной нагрузки на крыло (уменьшение
параметра планирования ау) также приводит к увеличению скорости
KTW. Несмотря на это, формула (9.51) позволяет проводить оценку
Avma.x с приемлемой для практических целей точностью.
Рассмотрим траекторию спуска с низкой круговой орбиты
(Якр = 200 км; i= 0) при наличии фазовых ограничений.
Влияние величины 7\утахД на боковую дальность планирования при
7?w = 0,1 м показано на рис. 9.36. При 7\утаХд> 3160 К боковая дальность
планирования составляет 5525 км и не зависит от 7\утахд- При
уменьшении Г\утахд, начиная с 2600 К, боковая дальность планирования
9.8. Планирование с максимальной боковой дальностью
395
Рис. 9.35. Зависимость температуры
в критической точке ЛА от скорости
полета при планировании с макси-
мальной боковой дальностью при
различных значениях Ктах
2000 3000 Avinax/b К
Рис. 9.36. Зависимости боковой
дальности планирования и
конечного угла курса от макси-
мально допустимой температуры
в критической точке ЛА
резко уменьшается. При Г\утаХд<2180К аэродинамических сил
недостаточно, чтобы строго выдержать ограничение при
рассматриваемых исходных данных. Уменьшение 7\у1пачД приводит
также к уменьшению оптимального угла конечного курса (см.
рис. 9.36).
Пусть теперь одновременно заданы 7\\1пахД = 2200 К;
<7тахд= 15 кН/м2 (такие же величины, как и при исследовании продоль-
ного планирования) и атахД = 45°. Расчетная траектория представлена
на рис. 9.37. Видно, что в координатах "высота-скорость" реализуется
точно такой же профиль полета, как при планировании с максимальной
продольной дальностью (ср. рис. 9.37я и 9.23я).
То же самое касается зависимостей 7w(K) и д(К) (ср. рис. 9.376 и
9.236). Переход с одного ограничения на другое осуществляется плав-
но, без забросов траектории.
Оптимальный угол конечного курса уменьшился по сравнению с
вариантом, когда ограничения отсутствуют, поэтому в начальной точке
траектории I у I = Тк = 50° (см. рис. 9.37в).
В диапазоне скоростей 55004-7000 м/с (т.е. при движении вдоль ог-
раничения 7\утахд) угол атаки достигает своего максимально допусти-
мого значения, а модуль угла крена значительно уменьшается, что
объясняется необходимостью увеличения вертикальной составляющей
подъемной силы. Зависимость текущей перегрузки пу от скорости
полета (см. рис. 9.37я) является качественно такой же, как и при плани-
ровании с максимальной продольной дальностью. Перед выходом на
очередное ограничение происходит кратковременное увеличение пере-
грузки, которое обеспечивает плавное изменение траектории.
396
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Рис. 9.37. Траектория планирования с максимальной боковой дальностью с
ограничениями на температуру в критической точке (Tw<2200K), на
скоростной напор (^<15 кН/м") и на угол атаки (сс < 45°). Зависимости
высоты и нормальной перегрузки (а\ температуры в критической точке и
скоростного напора (б), углов атаки и крена (в) от скорости полета
В результате уменьшения летного аэродинамического качества и
изменения программы у(К) по сравнению с вариантом планирования
9.8. Планирование с максимальной боковой дальностью
397
при отсутствии фазовых ограничений боковая дальность уменьшилась
с 5525 до 1734 км.
9.9. Планирование с минимальной продольной
дальностью
Пусть дано: ЯКр = 200 км; i = 0; Э = 180°; А Исх = 45 м/с. Аэродина-
мические характеристики ЛА не зависят от числа Маха и высоты,
максимальное аэродинамическое качество равно А?,пах = 2,5. Модуль угла
крена ограничен величиной утахд = 70°; максимальное отклонение
летного коэффициента су от своего программного значения соответст-
вует величине 5,пачД = 0,05.
Вначале проведем расчет траектории, обеспечивающей минималь-
ную продольную дальность при условии, что в конечной точке £/к = 0.
Простейший способ реализации такой траектории заключается в пла-
нировании с нулевым углом крена на режиме Я|П1пД. Примем, что мини-
мальное аэродинамическое качество достигается при угле атаки, близ-
ком к асутах и составляет Х’,тпд= 0,56. Основное преимущество полета с
максимальным углом атаки заключается в достижении минимально
возможной температуры в критической точке ЛА при его спуске с
орбиты. Расчетная траектория такого полета в координатах "Я- Г'
показана на рис. 9.38; продольная дальность составляет
Lx = 18,26 тыс. км.
Проведем расчет пространственной траектории. В общем случае в
распоряжении имеются четыре параметра: £Пу Япа.^ки b (см. разде-
лы 9.5 и 9.8). Предварительные расчеты показали, что при переходе с
режима ЯП11Пд (а -45°) на режим А?П1ах (а«9,5°) резко уменьшается
высота полета, в результате чего
максимум скоростного напора
достигает величин 100 кН/м2 и
более, а нормальная перегрузка при
этом равна 6-?8. Это указывает на
то, что при расчете таких траекто-
рий необходимо учитывать ограни-
чения на максимальные скоростной
напор и нормальную перегрузку.
Примем для дальнейших расче-
тов {/тахД КН/М" И ^у|тахД 3. В
этом случае %<opt= 180°;
^nYopt~ 14960 км (Ип.у = 5,12 км/с);
Lw «opt ~ 15467 км (Кп. а = 1,6 км/с).
Оптимизация параметра b приводит
к увеличению функционала по
сравнению с вариантом b= 1, одна-
ко выигрыш является незначитель-
Рис. 9.38. Профиль полета в
координатах "высота-скорость”
при планировании с минимальной
продольной дальностью
398
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
2000 2200 2400 2600 т,с
Рис. 9.39. Траектория планирования с минимальной продольной
дальностью. Зависимости аэродинамического качества и угла крена
(<7), угла атаки и скоростного напора (б), скорости и нормальной
перегрузки (в) от времени полета
ным, поэтому в расчетах было принято Ь=\. Из рис. 9.38 видно, что
при скорости Кп а = 1,6 км/с происходит резкое уменьшение высоты.
9.9. Планирование с минимальной продольной дальностью 399
Изменение летного аэродинамического качества, управляющих пе-
ременных у и а, скоростного напора, скорости и нормальной перегруз-
ки во времени (на участке полета Н < 70 км) представлено на рис. 9.39.
Изменение аэродинамического качества и угла крена по траектории
(см. рис. 9.39я) является качественно таким же, как на рис. 9.96
(см. раздел 9.5). Ограничения на скоростной напор и нормальную пере-
грузку (см. рис. 9.396 и в) выдерживаются строго. Движение по ограни-
чению обеспечивается в первую очередь за счет угла атаки, а затем - за
счет угла крена. Так, на отрезке времени т = 2300^-2310 с угол крена
уменьшается практически до нуля (см. рис. 9.39я) с тем, чтобы обеспе-
чить потребное значение вертикальной составляющей нормальной
перегрузки (иусо5у)Птр ; угол атаки на этом отрезке времени не увеличи-
вается более 15°, так как однозначно определяется из условия
Иу1 — Иу НпахД •
Проекция траектории на земную поверхность лежит по правую
сторону от плоскости ортодромии (рис. 9.40). Практически вся про-
дольная дальность реализуется при больших скоростях полета:
И>4^-5 км/с. В точке переключения угла атаки с режима А?1П;11Д на ре-
жим Хтах текущий угол курса равен 32°. (см. рис. 9.40). Максимальное
боковое удаление в процессе планирования составляет 171 км, даль-
ность полета в обратном направлении - 100 км. В конечной точке про-
дольная дальность равна Lxmin= 15,42 тыс. км, что на ~ 2,8 тыс. км
меньше по сравнению с плоским планированием на режиме ЛГ1П111д.
Время планирования меньше на-4,4 мин.
Сокращение дальности по сравнению с плоским движением про-
исходит вследствие двух факторов. Основной вклад в сокращение
Рис. 9.40. Проекция на земную поверхность траекторий планирования с
минимальной продольной дальностью
400
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
дальности (-2500 км) дает уменьшение высоты полета (см. рис. 9.38)
за счет крена, что приводит к более интенсивному торможению. Ис-
кривление траектории в проекции на земную поверхность приводит к
уменьшению дальности примерно на 300 км. Вследствие движения в
более плотных слоях атмосферы пространственное планирование
приводит к увеличению максимальной температуры в критической
точке 7\vmax на - 13% по сравнению с планированием с нулевым углом
крена.
Перейдем к минимизации продольной дальности при условии, что
боковая дальность является свободной. Расчеты показали, что в данном
случае на всей траектории у<0 (£n.yOpt=0) и в координатах "Lz-Zx"
траектория целиком лежит по левую сторону от плоскости ортодромии
(см. рис. 9.40). При этом Ч'кор! = 169°. В точке переключения аэродина-
мического качества (Z,ri.aopt= 15260 км) скорость существенно больше
по сравнению с предыдущим вариантом (Z,ZK=0) и составляет
Ип.а = 3,58 км/с, а текущий угол курса уменьшается до 24,6°. В конеч-
ной точке боковая дальность составляет £zk=860 km, а продольная
дальность сокращается на 170 км. Граница достижимой области при
AZk = 0^-860 км показана на рис. 9.40 пунктиром. В точке ZZK = 0 произ-
водная dLx\JdL/K< 0.
9.10. Упрощенный расчет достижимой области земной
поверхности
Построим достижимую область при планировании ЛА с низкой
орбиты, воспользовавшись исходными данными раздела 9.9. Передняя
граница этой области соответствует полету на режиме А^1пах (см. раздел
9.5). Вначале проведем расчеты траекторий, соответствующих крайним
точкам передней границы, соответствующим достижению £Х1пах и ZzZinax.
Максимум продольной дальности реализуется при у = 0 и, как было
отмечено в разделе 9.7, существенным образом зависит от условий
входа, в частности, от величины ДГСХ. При принятых исходных данных
АХ1пах = 58,48 тыс. км.
Максимуму боковой дальности соответствуют b=\\ L^j\y = ^ и
Ч'к’ = 82,2°. При этом AZmax = 5,46 тыс. км, а соответствующая продоль-
ная дальность равна ZX(Zinax)= 28,03 тыс. км. Введение ограничения на
Утах (70° вместо 90°) привело к уменьшению Z,Zinax на - 60 км по срав-
нению с аналогичным примером раздела 9.8. При рассматриваемых
условиях входа (/7Кр= 200 км) протяженность полета в разреженных
слоях атмосферы (Н> 110^-120 км) составляет -10 тыс. км, поэтому
задание величины ЛВкл,у в диапазоне 04-10 тыс. км не влияет на траекто-
рию планирования и на конечную дальность.
В общем случае для построения передней границы необходимо при
каждом конечном значении ZZK в диапазоне 04-ZZmax определить опти-
9.10. Упрощенный расчет достижимой области земной поверхности 401
мальные значения ЛВКл.у, Д^вкл.у, Ь и Ч'к из условия Z,x—>тах. Для
упрощения задачи было принято Д^Вкл.у= 3 тыс. км и b = 1.
Результаты расчетов оптимальных значений £Вклу иТкв зависимо-
сти от ZZK представлены на рис. 9.41. Видно, что угол конечного курса
^ изменяется в зависимости от ZZK практически линейно. При увели-
чении ZzZK скорость, при которой включается угол крена, увеличивается
от ~6,7 км/с до круговой (см. рис. 9.41). Разность между £хк и £Вкл.у
составляет 12,34-15,5 тыс. км, то есть продольная дальность полета с
креном не превышает 16 тыс. км. При построении передней границы
принятые ограничения на gmax и т?У1тах оказались несущественными.
Ограничение на утах является существенным только при кРк>70°.
Вследствие этого при 70° зависимость Tk^zk) имеет излом.
На рис. 9.42 показаны расчетная граница, а также несколько траек-
торий с различными значениями Тк и £ВКл.у в координатах "боковая
дальность - продольная дальность". Видно, что передняя граница по
форме близка к дуге эллипса, в передней точке dLy^/dL^^ 0, а в точке,
соответствующей максимуму боковой дальности, dL^ldLXK = 0.
Сформируем упрощенный алгоритм максимизации достижимой
области при построении передней границы. Пусть являются известны-
ми величины ZXmax, ^zmax, ^х(ZniaX) и Введем следующие обозначе-
ния. X — Z/Xk — Lx (Zmax), Z 7/ZK > L\max~ L\ (ZmaX) > P L^maK . ПрОВвДвМ
касательную к промежуточной точке М границы и запишем для нее
нормированное уравнение (рис. 9.43):
х cosS + z sinS - Р = 0,
где Р - расстояние от начала координат до касательной.
Очевидно, что максимум Р будет определять максимально возмож-
ную достижимую область. Воспользуемся результатами численных
Рис. 9.41. Передняя граница достижимой области. Изменение опти-
мальных параметров траектории в зависимости от боковой дальности
402 Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
20 30 40 50 £х, тыс. км
Рис. 9.42. Передняя граница достижимой области земной поверхности
при спуске ЛА с низкой околоземной орбиты
Рис. 9.43. К формированию упро-
щенного алгоритма максимизации
достижимой области
расчетов, представленных на
рис. 9.41 и 9.42, а именно, примем,
что угол , соответствующий
промежуточной точке передней
границы линейно связан с ZZK :
47=vPk/vFk* = z/5;
Угол наклона касательной бу-
дем определять, используя уравне-
ние эллипса (А - большая полуось,
совпадающая с плоскостью орто-
дромии; В - малая полуось). Тогда
tg£, = z'K =
(9-52)
зависит от величины ? ине зависит от координатх и z.
Выразив cosS и sin3 через tg£, запишем расстояние до касательной:
z + x\zxj
y/l+(zx)2
> max,
АЧ
Р =
откуда получим максимизируемую функцию:
или
F = I ZZK I + Лхк I ^'x I -> max
при 0 <4/ < 1
F = I £ZK/ z'x | + ZXK -> max
при 0 <Ч/< 1,
где z x определяется по формуле (9.52) при T = fix.
Таким образом, исходная задача на условный экстремум (Ах-> max
при Lzk = fix) сводится к задаче на безусловный экстремум функции F
по аргументу £Вкл.у при 4/K=fix, где угол Тк изменяется параметриче-
9.10. Упрощенный расчет достижимой области земной поверхности 403
ски от 0 до Т/. При этом точность построения достижимой области
является вполне приемлемой.
Перейдем к построению задней границы достижимой области, ко-
торая определяется в результате минимизации Лх в конечной точке
траектории по аргументам Лп.у, £п.а и ^к при LZk = fix, где ZZK изменя-
ется параметрически от 0 до ZZmax. Расчеты траекторий, соответствую-
щих Zxmin при LZk = 0 и Lxmin при свободном значении Lzk , были прове-
дены в разделе 9.9.
Результаты оптимизации параметров траектории представлены на
рис. 9.44. В диапазоне £2К=0-ь500 км оптимальное значение угла ко-
нечного курса составляет 180°, дальность точки переключения аэроди-
намического качества равна 15,47 тыс. км. Боковая дальность однознач-
но определяется величиной Zn.y, которая монотонно уменьшается от 15
до 10 тыс. км (при этом скорость переключения угла крена ИПу увели-
чивается от 5,12 км/с до круговой). При дальнейшем увеличении £ZK
дальность точки переключения аэродинамического качества монотонно
уменьшается до ~ 10 тыс. км (при этом соответствующая скорость Кп а
увеличивается от 1,6 км/с до круговой). Угол Ч'к уменьшается практи-
чески линейно от 180° до Ч'к*.
На рис. 9.45 показаны расчетная граница, а также несколько траек-
торий с различными значениями Ч'к и £П а в координатах "боковая
0 2 4 LZK , тыс. км
Рис. 9.44. Задняя граница достижимой области. Изменение
оптимальных параметров траектории и продольной дальности
в зависимости от боковой дальности в конечной точке
404
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Рис. 9.45. Задняя граница достижимой области земной поверхности
при спуске ЛА с низкой околоземной орбиты
дальность - продольная дальность". Видно, что задняя граница по
форме близка к дуге эллипса. В точке, соответствующей максимуму
боковой дальности, dLzKldLXK = 0; в точке, соответствующей минимуму
продольной дальности, dLxK/dLzK= 0. Заданное ограничение на угол
крена является существенным для всех траекторий; ограничения на
максимальные скоростной напор и нормальную перегрузку являются
существенными только для тех траекторий, кривизна которых в коор-
динатах "ZzZ-Zx" достигает соответствующей величины, в данном
случае при kPK> 1304-135° (Zz< 3 тыс. км).
Сформируем упрощенный алгоритм максимизации достижимой
области при построении задней границы. Пусть являются известными
ВеЛИЧИНЫ Z/Xmin (Z=0) > -^Xmin > ZzZ (Xmin) ? ^K(Xmin)? Z,Zmax , ^X (Zmax) И к • ВввДвМ
обозначения: X = Zx(Zmax)- ^ХК '> Z = £ZK — Z,z (Xmin) ; = Z'X(Zmax)- Z,Xmin '>
^ = ^zinax-Z,Z(X1nin)- Примем, что на участке изменения ZZK от Лг(Хтт)ДО
£zmax угол линейно связан с ZZK :
Ч7 = RFk - Ук (X.nin)]/[4V - Тк (Xmin)] = z/B, 0 < Т < 1,
а производная z х вычисляется как для эллипса с полуосями А и В по
формуле (9.52), где полуось А параллельна плоскости ортодромии.
Тогда минимизируемую функцию можно записать следующим образом:
F = Ахк~ I LzkIz\ I min при 0 <¥ < 1
или __
F = Ахк I z х I - I ZZk I -> min при 0 < Т < 1.
Таким образом, на участке изменения ZZK от £Z(Xmin) ДО Z,Zmax исход-
ная задача сводится к задаче на безусловный экстремум функции F по
аргументу Ап. а при fix, где угол изменяется от Ч'к(Хтт) до ^к*-
На участке изменения ZZK от 0 до Zz(Xmin) границу можно аппроксими-
ровать квадратной параболой с вершиной в точке, соответствующей
Z/Xmm • При этом точность построения достижимой области является
вполне приемлемой.
9.10. Упрощенный расчет достижимой области земной поверхности 405
Рис. 9.46. Граница достижимой области земной поверхности при спуске ЛА с
низкой околоземной орбиты (//КР = 200 км; / = 0). Изменение максимальной
по траектории температуры в критической точке 7wmax
Задняя и передняя границы достижимой области стыкуются в точ-
ке LZmax (при ЬХк= 28 тыс. км), образуя непрерывную линию (рис. 9.46).
Разность между АХ1пах и ZXlnin в данном случае составляет около
43 тыс. км, что больше длины экватора. Площадь передней части дос-
тижимой области, как правило, в несколько раз больше площади задней
части.
Изменение максимальной температуры TWmax, которая реализуется
в процессе планирования к различным граничным точкам достижимой
области, показано на рис. 9.46 и 9.47. Наименьшая возможная темпера-
тура (Twmax)min имеет место при планировании к заднему участку грани-
цы достижимой области (Тк = 1654-180°) - см. рис. 9.47. В этом диапа-
зоне изменения Тк критическая скорость KTW , при которой реализуется
максимум Ты, соответствует полету с максимально допустимыми
углами атаки и крена.
При планировании к задней границе после переключения с режима
ATminn на режим Ктях достигается второй максимум температуры 7winax,
который становится гло-
бальным при Тк<165°. В
результате при Тк~165°
зависимость Тытях (Тк)
имеет излом. Наибольшая
температура (TWm3X)mm имеет
место при планировании к
задней границе при
Тк~130°. Излом зависимо-
сти rWmax(TK) при Тк=Тк*
является следствием разных
законов управления при
планировании к передней и
задней границам достижи-
мой области. При полете с
максимальной продольной
дальностью температура
Рис. 9.47. Зависимость максимальной по
траектории температуры в критической
точке ЛА от конечного угла курса
406
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
имеет большее значение, чем при планировании с ZXmin, так как в
ЭТОМ Случае СуКт < Су тахД СО8утахД •
9.11. Спуск с геостационарной орбиты гиперзвукового
летательного аппарата с большим аэродинамическим
качеством
При спуске космических аппаратов с высоких орбит, а также при
возвращении от других планет скорость входа в атмосферу Земли су-
щественно больше круговой, поэтому для таких аппаратов необходимы
специальные законы управления, обеспечивающие "удержание" воз-
вращаемого КА атмосферой Земли. Как известно, выведение на геоста-
ционарную орбиту требует энергозатрат, близких к максимально воз-
можным (при рассмотрении движения в околоземном пространстве) -
см. рис. 9.4. В связи с этим в качестве наиболее характерного рассмот-
рим прямое возвращение космического аппарата с ГСО. В случае по-
садки на широтах 454-50° ЛА должен обладать достаточно большим
гиперзвуковым аэродинамическим качеством Кг. Одним из способов
обеспечения высокого значения Кг является придание возвращаемому
гиперзвуковому летательному аппарату конической формы.
Будем полагать, что в качестве ГЛА рассматривается "конус" с уг-
лом полураствора 5°. Аэродинамические характеристики ГЛА заданы в
зависимости от параметра M/VRe (см. рис. 9.7 [33]). Примем, что
удельная нагрузка G/S составляет 10 кН/м2 (в качестве характерной
используется площадь донного среза с диаметром 2 м), радиус носка
равен 7?w = 0,1m. Максимально допустимый угол атаки составляет
остахд = 45°. Другие ограничения не заданы. В качестве основной будем
решать задачу максимизации боковой дальности (конечная точка пла-
нирования соответствует числу М = 2).
После схода с ГСО космический аппарат движется по переходной
эллиптической орбите, лежащей в экваториальной плоскости. Пусть
интегрирование траектории начинается с высоты Но = 150 км. Началь-
ные скорость Го и угол наклона траектории 0О однозначно определяются
высотой перигея переходной орбиты Нл (см. раздел 9.2), которая должна
задаваться из условия гарантированного входа в атмосферу Земли.
Проведем оценочные расчеты высоты Нл. Будем полагать, что при
Н> Нк влияние атмосферы отсутствует, а ее воздействие начинается
при достижении перигея. Очевидно, что для обеспечения гарантиро-
ванного "захвата" ГЛА атмосферой подъемная сила в перигее должна
быть отрицательной: cycosy < 0. Пусть су > 0, тогда | у | > 90°.
Покажем, что оптимальным с точки зрения уменьшения скоростно-
го напора, нормальной перегрузки и аэродинамического нагревания
аппарата является угол крена |у |= 180°. При этом критичным является
только аэродинамическое нагревание ЛА, а величины пу и q не превы-
9.11. Спуск с геостационарной орбиты
407
шают значений, соответствующих горизонтальному дозвуковому поле-
ту. Действительно, при условии квазистационарного полета с |у| = 180°
из второго уравнения движения (9.3) получим:
«У = (g/go)[l - ^A2/(gr)]/cosy «(ГА/ГкР)2 - 1, (9.53)
откуда следует, что пу тах зависит только от скорости входа.
При возвращении с любой околоземной орбиты (т.е. при
V< Г2К = V2 ИКр) всегда имеет место nymax < 1- Как следует из выраже-
ния (2.84), температура в критической точке ГЛА связана со скорост-
ным напором следующим образом:
T^-qV45/^ , (9.54)
где
q = nymgblCyS. (9.55)
Из (9.54) и (9.55) видно, что при фиксированной скорости входа
уменьшить скоростной напор и аэродинамическое нагревание аппарата
можно только путем увеличения угла атаки вплоть до атахД и путем
уменьшения удельной нагрузки G/S. Из соотношений (9.53)-(9.55)
также следует, что при отклонении модуля угла крена от 180° величины
пу, q и Tw увеличиваются.
Определим высоту перигея переходной орбиты из условия гори-
зонтального полета с углом крена у = 180°:
су5р(^А - Ие)2/2 = mg[V^I(gr) - 1].
Здесь ИЕ-переносная скорость; ИкА - скорость в перигее, вычисленная
в абсолютной системе координат.
Расчетная зависимость максимально возможной высоты Як от па-
раметра планирования оу представлена на рис. 9.48я, из которого вид-
но, что в возможном диапазоне изменения оу высота Нп изменяется от
46 до 78 км. На рис. 9.486 в зависимости от показано изменение
абсолютной скорости в перигее ГяА, а также потребного импульса
скорости схода с ГСО ДИсх- Видно, что обе зависимости являются
практически линейными. При изменении Нк на 10 км скорость ИлА
изменяется на 9,1 м/с, а потребное изменение ДГСх составляет 1,07 м/с.
Отсюда следует, что для обеспечения заданной величины точность
выполнения маневра на сход с ГСО должна быть достаточно высокой.
Расчетная зависимость Twmax от Яя(при 7?w= 0,1 м и принятых допуще-
ниях) близка к линейной (рис. 9.49).
Приближенно оптимальное управление движением. При фор-
мировании приближенно оптимальных законов управления за основу
была принята программа управления, предложенная А.А. Шиловым
(ЦАГИ). Ее суть заключается в том, что траектория входа в атмосферу
разделяется на три участка и торможение до круговой скорости осуще-
ствляется на постоянной высоте. В соответствии с этим разобьем траек-
408
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Рис. 9.48. Сход с геостационарной орбиты: зависимость максимально
возможной высоты перигея переходной орбиты от параметра планирования
(я), зависимости скорости в перигее и потребного импульса схода с ГСО
от высоты перигея переходной орбиты (б)
Рис. 9.49. Сход с ГСО. Зависи-
мость максимальной температуры
в критической точке ЛА от высоты
перигея переходной орбиты
точке рассматриваемого участка,
ния (9.3) в упрощенном виде
dV/dx = -сх qS/m;
торию на участки и сформируем
приближенно оптимальные законы
управления углами атаки и крена
для каждого из них.
1-й участок - полет со сверх-
круговой скоростью до точки
первого отражения в плотных
слоях атмосферы на высоте //ют-
Очевидно, что использование
боковой силы сразу при входе в
атмосферу будет способствовать
достижению максимальной боко-
вой дальности. При движении
вблизи плоскости ортодромии в
качестве частного критерия опти-
мальности можно использовать
максимум угла курса в конечной
Запишем 1-е и 4-е уравнения движе-
dWldx=-cyqSs\ny/(mV). (9.56)
Здесь принято: cosO = 1, Ф « 0, Земля - шарообразная и не вращается.
Широта и долгота не входят в правые части уравнений (9.56). Бу-
дем полагать, что уравнения для высоты и угла наклона траектории
несущественны (движение происходит по траектории, близкой к пере-
ходному эллипсу). Тогда максимуму угла курса в конце 1-го участка
9.11. Спуск с геостационарной орбиты
409
будет однозначно соответствовать максимум производной cCV/dV в
каждой точке траектории, и с учетом (9.56) можно записать
ATsiny —> max, (9.57)
откуда получим
A'opt= АГ,„ах; 1уоР|1 = 90°.
Так как при таком управлении вертикальная составляющая подъ-
емной силы отсутствует, то в расчетном диапазоне задания Нп возвра-
щаемый ГЛА будет гарантированно достигать точки 0 = 0. При этом
высота первого отражения практически равна высоте перигея, которая
однозначно определяет условия входа в атмосферу (Яют~ Нл).
В случае минимизации температуры Twmax вместо угла атаки осКш
следует использовать угол а,пахДс тем, чтобы максимально затормозить-
ся уже при подходе к плотным слоям атмосферы.
2-й участок - горизонтальный полет со сверхкруговой скоростью
на постоянной высоте Н= Яют-
В этом случае программные углы крена и атаки связаны между со-
бой конечным соотношением
cycosy = CB, где Св = mg[\ - V^/{gry\/(qS). (9.58)
Как и на первом участке, движение описывается двумя дифферен-
циальными уравнениями (9.56). Это значит, что в данном случае опти-
мальное управление должно находиться из условия (9.57) с учетом
связи (9.58) и ограничений, наложенных на управления:
Су opt — Су щахД •> I COSy 1^1,
где Суп1ахдсоответствует а111ахД.
Приняв, что аэродинамическая поляра является квадратичной и
симметричной (сх = cxmm + Лсу2), получим аналитическое выражение
для коэффициента подъемной силы:
cyopt— ~ ^суКт + 2СВ , (9.59)
откуда видно, что равенство cyOpt = cyKm справедливо только при круго-
вой скорости (Св= 0).
При V> ИКР имеет место строгое неравенство суор1>сукт- Таким
образом, на втором участке коэффициент cyopt уменьшается от некото-
рого наибольшего значения до суК|П . При больших высотах НЮ1 наи-
большее значение су Opt будет ограничиваться величиной су1ШхД.
Выражение для оптимального угла крена получим из (9.58):
cosyopt—Св/суOpt — ....^ .. . -, (9.60)
у]СуКт + 2СВ yjCyiZm / в + 2
410
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
откуда видно, что при больших скоростях полета (I Св I»суКт)
cosyopl—> -1/V2 ; при Св = 0 cosyopt= 0.
Таким образом, на втором участке модуль оптимального угла крена
уменьшается от - 135° до 90°.
При увеличении ЯЮт до высот, при которых оптимальное значение
с\ начинает ограничиваться величиной су|ПахД, модуль угла крена в
начальной точке данного участка будет увеличиваться вплоть до 180°.
При I Св I > с\ шахД аэродинамических сил недостаточно для "удержания”
ЛА в горизонтальном полете и необходимо уменьшить высоту Я от-
Наибольшая высота Я| оттах, ПРИ которой еще можно обеспечить
горизонтальный полет с предельным управлением у = 180° и су = сутахд,
определяет верхнюю границу "коридора входа”. В этом случае, как
было отмечено выше, достигается наименьшее возможное значение
7\vmax • Вместе с тем очевидно, что такой режим управления нельзя
использовать на практике, так как в результате незначительного внеш-
него воздействия спускаемый аппарат покинет атмосферу Земли и
вновь уйдет на переходную орбиту (с уменьшенной высотой апогея по
сравнению с исходной орбитой).
Для гарантированного "захвата” ГЛА атмосферой Земли расчетное
значение Дот должно быть меньше максимально возможного. Если
высоту //ют выбрать так, что равенство cyopt= суп1ахд выполняется толь-
ко в начальной точке второго участка, то запас по управлению углом
крена будет составлять примерно 45°. Численные расчеты показали, что
при выборе высоты Яют из условия максимума боковой дальности
неравенство Яют< Я оттах выполняется.
Скорость окончания участка Г2, близкая к круговой, задается в за-
висимости от потребной продольной дальности полета ЛХк и может
использоваться в качестве оптимизируемого параметра.
Знак угла крена на 1-ом и 2-ом участках задается в зависимости от
общей протяженности траектории планирования.
3-й участок- динамическое увеличение высоты с последующим
входом в атмосферу с околокруговой скоростью.
По своему физическому смыслу данный участок совпадает с 1-ым
участком на рис. 9.9в (раздел 9.5). Поэтому примем
^opt- 7Cmax, yopt — 0.
Далее используется управление, обеспечивающее максимум боко-
вой дальности: 7Copt = Л^11ах, угол крена определяется по формуле (9.47).
В частном случае протяженность 3-го участка может быть равна нулю.
Результаты расчетов. Для выбора рациональной высоты первого
отражения ЯЮт были проведены параметрические расчеты, имеющие
целью установление границ "коридора входа”. На рис. 9.50 представле-
ны три такие траектории, отличающиеся высотой Яют- Высота
#1 от max= 69 км соответствует верхней границе "коридора входа". При
ЯюТ > 69 км аэродинамических сил ГЛА не хватает для его удержания в
9.11. Спуск с геостационарной орбиты
41 I
4 6
Г, км/с
Рис. 9.50. Сход с ГСО. Вход в атмосферу с различной высотой
первого отражения:
а) траектории в координатах "высота - скорость"; б) зависимое п>
температуры в критической точке от скорости полета
атмосфере. При НЮ1- = 50 км достигается максимум боковой дальности.
Эту высоту можно принять в качестве условной нижней границы "ко-
ридора входа", так как при уменьшении высоты ЯЮт ниже 50 км аэро-
динамический нагрев ГЛА продолжает увеличиваться, а боковая даль-
ность начинает уменьшаться. Траектория с высотой Яюг=64,4км
занимает промежуточное положение в "коридоре входа" и характерна
тем, что ограничение а1пахД достигается только в точке первого отраже-
ния (рис. 9.51).
Как показали расчеты, при больших высотах Я101 разность
Нп- Я10т не превышает 0,1 км. При уменьшении высоты НЮ[ до 50 км
эта разность увеличивается до 0,5 км, что связано с более сильным
торможением на участке входа до точки первого отражения.
Из рис. 9.506 видно, что максимум температуры 7\v по траектории
реализуется вблизи точки первого отражения. Для траектории с
Яют= 50 км этот максимум является абсолютным, так как при сверх- и
412
Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
Рис. 9.51. Сход с ГСО. Измене-
ние углов атаки и крена при
движении со сверхкруговой
скоростью для двух траекторий с
различной высотой первого
отражения:
АВ - 1-ый участок: аКп1> у = - 90°;
ВС - 2-ой участок (/7 = А/ют):
су opt- по ф. (9.59); yopt- по ф. (9.60)
докруговой скоростях используется режим £тах. Для траекторий с
/7Ю'1 = 69км и 64,4 км при V> ГКР используется режим атахД, при
К < Ккр угол атаки уменьшается до aKin(cM. рис. 9.51). В результате
этого на участке полета с докруговой скоростью реализуется второй
максимум температуры 7ф. Чтобы второй максимум не превысил пер-
вого, при полете с докруговыми скоростями было введено ограничение
7\УтахД« равное величине первого максимума. Для траектории с
//io! = 69 км реализуется возможное наименьшее значение 7wmax, рав-
ное 3500 К.
На рис. 9.51 представлены зависимости а и у от скорости при
Г > ГКР для траекторий с Яют = 69 км и 64,4 км. Эти зависимости иллю-
стрируют сформированные выше законы управления для 1-го и 2-го
участков полета. Видно, что первый участок полета (АВ на рис. 9.51)
является довольно коротким по скорости. Основное торможение осу-
ществляется на втором участке (ВС на рис. 9.51) - при движении на
постоянной высоте Яют- Вначале второго участка при Яют = 69 км
модуль угла крена равен 180°, при Яют =64,4 км - 145°. Таким обра-
зом, для промежуточной траектории входа в наиболее критической
точке запас по высоте составляет 4,6 км, запас по углу крена - 35°.
Вследствие этого высота ЯЮт = 64,4 км была принята в качестве основ-
ной для проведения дальнейших расчетов. На большей части второго
участка угол крена уменьшается по модулю от 130° до 125°.
Параметры траекторий, представленных на рис. 9.50, оптимизиро-
вались из условия максимума боковой дальности планирования (при
Я|ОТ=Г1х), протяженность 3-го участка (у = 0) была принята равной
нулю. При Я]от=50км боковая дальность планирования превышает
10 тыс. км (практически на всей траектории полета летное аэродинами-
ческое качество равно максимальному). Увеличение высоты Яют при-
водит к уменьшению боковой дальности вследствие того, что на участ-
ке полета со сверхкруговой скоростью угол атаки увеличивается вплоть
до максимально допустимого (см. рис. 9.51).
9. II. Спуск с геостационарной орбиты
413
Взаимосвязь между Twmax,
Zzk и Яют представлена на
рис. 9.52. Зависимости близки к
линейным. Увеличение потреб-
ной величины ZZK всегда сопро-
вождается увеличением темпера-
туры Zwmax. При уменьшении
высоты первого отражения от
Фотшах до 64,4 км температура
Twmax увеличивается по сравне-
нию с минимально возможной на
270 К и составляет 3770 К. Ана-
логичная величина при спуске с
низкой орбиты ЯКР = 200 км ГЛА
Рис. 9.52. Сход с ГСО. Изменение
максимальной температуры в
критической точке и высоты перво-
го отражения в зависимости от
потребной боковой дальности
с максимальным аэродинамиче-
ским качеством Я1ШХ = 2,5 состав-
ляет 3500 К (см. раздел 9.9).
На рис. 9.53 представлены
три траектории с ЯЮт = 64,4 км в
проекции на земную поверхность, отличающиеся скоростью И2 оконча-
ния 2-го участка и протяженностью 3-го участка полета (у = 0). Пара-
метры каждой траектории оптимизировались из условия максимума
боковой дальности. Для траектории 1: V2 = 0,982ИКР, участок полета с
нулевым углом крена отсутствует (эта траектория представлена также
на рис. 9.50 и 9.51). Для траектории 2: V2 - 1,011 ИКР, путевая дальность
Рис. 9.53. Траектории схода с геостационарной орбиты в проекции на
земную поверхность:
АВ - 1-й участок: осКп1; I у I = 90°;
ВС - 2-й участок (//= //|От = 64,4 км): cvopl- но ф. (9.59): yopt- по ф. (9.60):
CD - 3-й участок: аК|П ; у = 0;
DE -участок полета с докруговой скоростью: aKm : yopt- ио ф. (9.47)
414 Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
точки окончания 3-го участка составляет £Вкл.у = 23 тыс. км; для траек-
тории 3: И2 = 1,02ГКр, £вкл.у= 37 тыс. км. Для траекторий 1 и 3 имеет
место у < 0. Для траектории 2 на 1-м и 2-м участках полета угол крена
положителен, при V< ГКр - отрицателен. Из рис. 9.53 видно, что траек-
тории 1-3 определяют боковую границу достижимой области земной
поверхности. Боковую дальность более 8 тыс. км можно обеспечить как
с первого, так и со второго витка. Таким образом, ГЛА с рассматривае-
мыми характеристиками способен достичь широт 604-70° при прямом
возвращении с геостационарной орбиты.
Наибольшая боковая дальность реализуется для траектории 2, в
связи с чем эта траектория представлена ниже более подробно. Опти-
мальные параметры последнего участка равны: ^opt = 90°; Z>opt = 1,05.
Время планирования составляет - 1 час, суммарная продолжительность
Рис. 9.54. Сход с ГСО. Траектория с максимальной боковой дальностью
при //ют = 64,4 км. Изменение угла атаки (я), угла крена и аэродинами-
ческого качества (б), ортодромического угла курса (в) по скорости полета
9. //. Спуск с геостационарной орбиты 415
спуска с ГСО (с учетом времени движения по переходной эллиптиче-
ской орбите) - около 6 часов.
Изменение углов атаки и крена, аэродинамического качества и ор-
тодромического угла курса по скорости полета представлено на
рис. 9.54. Вклад участка полета со сверхкруговой скоростью в разворот
вектора скорости довольно значителен: при И = И2 модуль угла курса
составляет 14° (см. точку при И = 7400 м/с на рис. 9.54«).
На рис. 9.55 показано изменение высоты, скоростного напора и
нормальной перегрузки (в связанной с.к.) в зависимости от скорости
планирования. При Г~ ГКР ГЛА совершает динамическое увеличение
высоты до 174 км (см. рис. 9.55# и участок CD на рис. 9.53). Дальность
0 2 4
6 8 Г, км/с
Рис. 9.55. Сход с ГСО. Траектория с максимальной боковой даль-
ностью при /Уют= 64,4 км. Изменение высоты (#), скоростного
напора (б) и нормальной перегрузки (в) по скорости полета
416 Глава 9. Возвращение ЛА с орбиты. Планирование в атмосфере
этого участка полета составляет ~ 15 тыс. км. Далее ГЛА входит в
плотные слои атмосферы с околокруговой скоростью с углом наклона
траектории минус 1,26°. Угол ортодромического курса составляет 17,7°
(см. точку при V — 7300 м/с на рис. 9.54в). На последнем участке плани-
рования (DE на рис. 9.53) включается закон управления углом крена
(9.47) и осуществляется планирование, как при сходе с низких орбит
(см. раздел 9.8).
Из рис. 9.556 видно, что максимум скоростного напора достигается
на конечном участке планирования. Максимум нормальной перегрузки
достигается в точке первого отражения и составляет иу|1ШХ= 1,83
(см. рис. 9.55в), что является вполне приемлемым для спускаемых с
орбиты ЛА.
Проведенные расчеты позволяют заключить, что при сходе с высо-
ких орбит силовое воздействие на ЛА не увеличивается по сравнению с
вариантами схода с низких орбит. Основной проблемой является увели-
чение аэродинамического нагревания. Применение режима управления
а = схшачд в точке первого отражения позволяет уменьшить максималь-
ную температуру в критической точке ЛА до минимально возможной.
ГЛАВА 10
ВОЗВРАТ КРЫЛАТЫХ СТУПЕНЕЙ
К ТОЧКЕ СТАРТА МКТС
Одной из перспективных концепций систем выведения вертикаль-
ного старта является МКТС с многоразовой крылатой первой ступенью,
возвращаемой к точке старта. В качестве примера такой МКТС можно
назвать многоразовую всеазимутальную ракету-носитель [121] (см.
рис. 1.7). Вне зависимости от аэродинамической компоновки возвра-
щаемого ракетного ускорителя (ВРУ) возникает задача его оптимально-
го возврата к точке старта МКТС. ВРУ, используя свои несущие свойст-
ва, сначала совершает маневр разворота вектора скорости на -180°, а
затем, при необходимости, выполняет крейсерский дозвуковой полет с
использованием ВРД. При этом критерием оптимальности маневра
является минимум расстояния от точки окончания пассивного планиро-
вания до посадочного аэродрома, находящегося вблизи точки старта
МКТС.
По вопросам оптимизации траекторий возврата крылатых ступеней
к точке старта МКТС в настоящее время имеется значительный науч-
ный задел. Так, в работах [41] и [111] задача об оптимальном простран-
ственном движении в заданную точку земной поверхности решена с
использованием гипотезы квазистационарности. Полагается, что огра-
ничение на максимальный угол крена не превышает 90°, ограничение
на нормальную перегрузку не учитывается. В работе [111] определена
структура управления углом крена и аэродинамическим качеством (см.
также раздел 2.8). Показано, что полет должен совершаться вначале на
режиме минимального, а затем максимального аэродинамического
качества. Значение угла крена вначале равно максимально допустимо-
му, а затем по траектории монотонно уменьшается до нуля. В работе
[41] задача пространственного возврата решена в предположении, что
управляющей переменной является только угол крена. При этом разра-
ботано управление с обратной связью, обеспечивающее гашение коле-
баний высоты полета.
В работе [98] задача о максимальном приближении возвращаемого
летательного аппарата к заданной точке земной поверхности рассмот-
рена вначале в точной постановке. Затем на основе анализа оптималь-
418
Глава К). Возврат крылатых ступеней к точке старта МКТС
ного решения предложена приближенно оптимальная программа
управления углом атаки в виде функции текущих фазовых координат.
При этом учитывается, что на начальном участке движения летатель-
ный аппарат вылетает из плотных слоев атмосферы. По условию задачи
ограничение на максимальный угол крена не превышает 90°, ограниче-
ние на нормальную перегрузку не учитывается. Показано, что переклю-
чение угла атаки с максимально допустимого на значение, соответст-
вующее режиму £|пах, должно производиться в точке, где разность
углов курса и визирования на конечную точку равно -90°.
В работе [42], исходя из эвристических соображений, сформирован
приближенно оптимальный закон управления углами атаки и крена.
Траектория возвращения и соответствующая программа управления
условно разбиваются на три участка, граничные точки которых задают-
ся достижением характерных значений текущего угла курса. На первом
участке угол крена задается постоянным (больше 90°), на втором участ-
ке угол крена также задается постоянным (меньше 90°). Угол атаки на
этих участках равняется максимально допустимому. На третьем участке
угол крена монотонно уменьшается, обеспечивая в конечной точке
заданное направление полета, а угол атаки выбирается из условия
максимума аэродинамического качества.
В работе [37] задача оптимального возврата решена численно с ис-
пользованием принципа максимума для варианта, когда в точке отделе-
ния ступени скорость равна 500 м/с (М « 1,5), угол наклона траектории
равен 43,5°. Получена траектория возврата, практически полностью
лежащая в вертикальной плоскости. При этом маневр разворота вектора
скорости осуществляется через верхнюю полусферу (с уходом в разре-
женные слои атмосферы).
В данной главе, в отличие от названных работ, задача возврата к
точке старта решается в более общей постановке. Целью исследований
является разработка приближенно оптимального закона управления
углами атаки и крена, который обеспечивает значение функционала,
близкое к точному решению. Для получения структуры формируемого
закона вначале решается модельная задача с использованием принципа
максимума. Так как в работе [37] показано, что оптимальная траектория
возврата может лежать в вертикальной плоскости, то модельная задача
решается для вариантов как плоского, так и пространственного движе-
ния.
10.1. Постановка задачи
В качестве объекта исследования рассматривается крылатая первая
ступень (возвращаемый ракетный ускоритель) вертикально стартующей
системы выведения. После отделения от МКТС крылатая ступень
должна вернуться на аэродром, находящийся вблизи точки старта
(рис. 10.1). В большинстве рассматриваемых проектов МКТС верти-
кального старта скорость отделения ВРУ составляет 1500^-2200 м/с.
10.1. Постановка задачи
419
Рис. 10.1. Траектория возврата первой ступени МКТС к точке старта
При таких скоростях скоростной напор становится уже небольшим, а
угол наклона траектории еще существенно больше нуля. В связи с этим
отделившийся ВРУ вначале продолжает свое движение по баллистиче-
ской траектории, удаляясь от точки старта. Изменить направление
вектора скорости за счет своих несущих свойств аппарат может только
после входа в плотные слои атмосферы. В процессе маневра разворота
вектора скорости ВРУ интенсивно тормозится и в конце разворота
скорость становится дозвуковой. На заключительном этапе движения
аппарат при необходимости осуществляет крейсерский дозвуковой
полет с включенными ВРД.
Очевидно, что несущие свойства ВРУ должны быть достаточно
высокими. В частности, при больших сверхзвуковых скоростях аппарат
должен быть способным летать на больших углах атаки, чтобы обеспе-
чить интенсивное торможение и уменьшить удаление от точки старта.
При дозвуковых скоростях аппарат должен иметь высокое аэродинами-
ческое качество с тем, чтобы движение в сторону конечной точки как в
пассивном полете, так и с включенными ВРД было наиболее эффектив-
ным.
420
Iлава 10. Возврат крылатых ступеней к точке старта МКТС
Итак, будем полагать, что ВРУ обладает необходимыми несущими
свойствами. Параметры траектории в начале пассивного полета ВРУ
(при т = 0) являются известными:
- скорость полета ;
- угол наклона траектории Оо;
- высота полета HQ;
- путевая дальность .
Для простоты будем полагать, что выведение на орбиту осуществ-
ляется в экваториальной плоскости. В этом случае начальные значения
угла курса ф0 и геоцентрической широты ф0 равны нулю. Начальная
долгота равна X(} = L(}/Rq. Масса аппарата т в пассивном движении
является постоянной.
В конечной точке пассивного движения время т = Т не фиксирует-
ся. Для указания момента окончания интегрирования наиболее удобно
использовать удельную энергию аппарата Е = Н+ K2/(2gT), где можно
принять £Т = go • В отличие от фазовых переменных V, 0 и //удельная
энергия в пассивном движении всегда уменьшается монотонно.
В качестве основного варианта функционала примем удаление ВРУ
отточки старта МКТС в конце пассивного движения (см. рис. 10.1):
91 = Rq yjkK2 +<pK“ —> min.
При минимуме 91 будут минимальны затраты топлива на крейсер-
ский дозвуковой полет. Если необходимо построить заднюю границу
достижимой области земной поверхности, то в качестве функционала
будем принимать конечную долготу , которая должна минимизиро-
ваться при фиксированном значении фк- Угол курса в конечной точке
планирования должен быть равен углу визирования на точку старта
МКТС (см. формулу (9.23)).
В дозвуковом полете затраты энергии на разворот вектора скорости
являются незначительными, поэтому точное задание конечных значе-
ний высоты и угла наклона траектории является несущественным.
Будем полагать, что эти параметры соответствуют квазистационарному
планированию (dQ/dx « 0) на режиме максимального аэродинамическо-
го качества Л?П1ах. В этом случае 0к «-1/АГ,пах. При таких траекторных
параметрах аппарат сможет выйти на крейсерский режим полета с ВРД
без ’’забросов" траектории.
Управляющими переменными в пассивном движении являются
угол крена у и коэффициент подъемной силы су. Будем полагать, что в
общем случае угол крена не имеет ограничений (-180° < у < 180°).
Коэффициент подъемной силы ограничен сверху.
Известно, что при интенсивном развороте вектора скорости реали-
зуются большие значения нормальной перегрузки иу, поэтому будем
полагать, что задано ограничение пу< иутахД.
10.1. Постановка задачи
421
При решении задачи возврата рассмотрим два варианта. В первом
варианте траектория лежит в вертикальной плоскости. При этом угол
крена может принимать два значения: 0 и 180°. Во втором варианте
траектория возврата является пространственной, угол крена может быть
любым. При этом конечная широта либо является свободной, либо
фиксируется: срк > 0.
Задание аэродинамических характеристик в модельных зада-
чах, решаемых с использованием принципа максимума. Зависи-
мость коэффициента су от угла атаки а является несущественной и угол
атаки необходим только для справки. Вместо коэффициента аэродина-
мической подъемной силы су удобнее использовать относительный
коэффициент у = су/су^т. Анализ аэродинамических характеристик
крылатых летательных аппаратов показывает, что на режиме макси-
мально допустимого коэффициента су коэффициенту равен 4-?6. В связи
с этим будем полагать, что
0<у<утахД,
гдеутахд = 5 вне зависимости от скорости полета.
Пусть аэродинамическая поляра является квадратичной и симмет-
ричной:
Сх — сх П11П (1 + У~\
Будем полагать, что аэродинамические характеристики не зависят
от числа Re (от высоты). Для задания зависимости коэффициентов c\min
и А от числа Маха воспользуемся функцией
/(x)=f0 + d с-1’2^, (10.1)
где принято с = 2; f0 , d, b, xm- некоторые параметры. Аналогичная
функция использовалась в разделе 3.7 - см. формулу (3.60).
Экстремум fix) достигается при х = х1П и равен fi + d. При х —> оо
значение функции асимптотически приближается к fi. Будем полагать,
что левой и правой ветвям функции (10.1) соответствуют свои значения
fi , d и b. Вместо параметра b удобнее задавать значение f\ при некото-
ром значении хь Левая и правая ветви стыкуются между собой при
х = хт . Производная функции (10.1) равна
df/dx = -2b2 (х - хт) d ch2(л"? Inc. (10.2)
Значения параметров, определяющих зависимость коэффициентов
сх min и Л от числа Маха, сведены в табл. 10.1 (получены с использова-
нием аэродинамических данных работы [42]). На рис. 10.2а представ-
лены зависимости cxmin(M) и Л(М), а на рис. 10.26 - зависимости
СуКт(М) и АГтах(М), которые определялись при помощи соотношений
(2.66).
Производные коэффициентов су и сх по скорости:
422
Глава 10. Возврат крылатых ступеней к точке старта МКТС
(^y)v JV(^yKm) V, (CX)v (^xmin)v(l + У ), (10.3)
где
z v _ 1 (Cxmm)v^~Cxmm^ V
(CyKin) V - --------------2--------;
2cVKm A
(Cx min) V (<\ min) M , (A) V (^) •
Производные коэффициентов cxmin и А по числу Маха вычисляются
при помощи соотношения (10.2).
Таблица 10.1
Значения параметров, определяющих зависимость
коэффициентов сх min и А от числа Маха
Параметр функции Коэффициент лобового сопротивления сх т1П Коэффициент отвала поляры А
/о 0,013 0,78
Левая ветвь Х| 1,0 0,8
,/Ui) 0,024 0,74
л 0,02 7,0
Правая Х| 3,0 4,0
ветвь
АхО 0,03 4,0
Экстремум 1,4 1,2
функции Ахт) 0,04 0,7
а) б)
Рис. 10.2. Зависимости коэффициента лобового сопротивления схт1П и
отвала поляры А (я), максимального аэродинамического качества Ктзх и
соответствующего коэффициента подъемной силы суКт (б) возвращаемого
ракетного ускорителя от числа Маха
10.2. Решение модельной задачи оптимизации плоской траектории 423
10.2. Решение модельной задачи оптимизации
траектории возврата, лежащей в вертикальной
плоскости, с использованием принципа максимума
Воспользуемся упрощенными уравнениями плоского движения:
dV/dx = - cKqS/m - gsin0;
dO Idx = cyqScvl(mV)-CQsO{g/V-VlrY > (10 4)
dH/dx = Ksin0;
dL tdx =- Rq VcosO lr.
Здесь cr - управляющая переменная, принимающая два значения: 1 при
у = 0 и минус 1 при у = ±180°.
При записи (10.4) полагается, что Земля не вращается. Ускорение
гравитационного притяжения зависит от высоты следующим образом:
g = go(/?o/r)2. (10.5)
Производная g по высоте равна
g'H = -2g/r. (10.6)
Для плотности воздуха р примем экспоненциальную зависимость
от высоты:
р = Ро ехр(-рЯ), (10.7)
тогда
р'н = -рр; 9н = -рд. (10.8)
Скорость звука не зависит от высоты и равна а = 300 м/с.
В данном случае величина L характеризует удаление от точки стар-
та МКТС. Чтобы упростить вычислительные трудности при переходе
через точку, соответствующую строго вертикальному движению
(9 = -90°), полагается, что расчетный угол наклона траектории 0 явля-
ется неограниченной величиной. Пусть в конце движения аппарат
занимает нормальное положение (подъемная сила направлена вверх) и
угол наклона траектории совпадает с общепринятым: 0 = 9. Тогда в
начальной точке аппарат должен занимать перевернутое положение
(подъемная сила направлена вниз), а расчетный угол наклона траекто-
рии будет равен
0о = -189°-9о.
В начале движения cos0 <9 и dL ldx> 9; после разворота (при
полете в сторону конечной точки) cos0 > 9 и dL Idx < 9.
424
Глава 10. Возврат крылатых ступеней к точке старта МКТС
По условию задачи задано одно ограничение - на нормальную пе-
регрузку, то есть, задано условие типа неравенства, зависящее от фазо-
вых и управляющих переменных:
<|/1 (а) = cyqS/m - gQny 111ахД <0. (10.9)
В соответствии с принципом максимума запишем функцию Га-
мильтона
TL = - Р\ (cxqShn + gsin0) + Ро[су^5cyl(mV) - cos© (g/K- VI г)} +
+ Рн Ksin0 - PL Po Pcos0 lr + \(cyqSlm - gQny |11ахД)
и уравнения для сопряженных переменных
dP\j Idx = P\j(c*'q + c*pV)S/m - Pq [(cy'pK + сур)5 Су I(2m) +
+ cos0(g/K2 + I/r)] - PH sin0 + PLPocos0 lr - \(cyq + cypF) Sim;
dP^ldx = Pvgcos0 -P©sin0(g/r- Vtr) - PH Kcos0 - PL^oKsin0/r;
dPyJdx = P\j(cKq'^S/m + g'H sin0) - Pq [cy qrHS Cy/(mV) -
- cos© (g'n IV + K/r2)] - PL/?o^cos© /r2 - \cyq'nS/m.
Здесь Л - неизвестная переменная. Производные аэродинамических
коэффициентов сх и су по скорости определяются с помощью
выражений (10.3). Так как дальность не входит в правые части
уравнений (10.4), то dPy/dx = 0 и PL = const. Во всех точках траектории
функция Гамильтона равна нулю: Н = 0.
Для определения оптимальных значений управляющих перемен-
ных выпишем слагаемые функции Гамильтона, зависящие от су иу:
TYi =- Русх + Pq су су IV + Лсу. (10.10)
Анализ (10.10) показывает, что управляющая переменная сг входит
линейно и только во второе слагаемое TYj . Как будет показано ниже,
всегда имеет место неравенство cyopt > 0. Это значит, что второе слагае-
мое 7Y| будет максимально при Р©сг > 0. Отсюда следует
су = +1 при Pq > 0;
Су = - 1 при Pq < 0.
Теперь выражение (10.10) можно переписать следующим образом:
Н\ =-Pvcx+ \p@\cy/V +Лсу. (10.11)
10.2. Решение модельной задачи оптимизации плоской траектории 425
Сформируем алгоритм определения оптимального управления, со-
стоящий из двух этапов.
1. Пусть ограничение на нормальную перегрузку не нарушается, то
есть пу< пу 1пахД, тогда переменная Л = 0. В соответствии с принятой
формой задания аэродинамических характеристик функция Н\ является
квадратичной относительно у
Н\ =-/’VCx,nin(l +^2)+ |/’©|сук,„^/К.
Оптимальное управление определяется из условия достижения
наибольшего значения Н\ в каждой точке траектории. В зависимости от
знака Pv возможны два случая.
При Pv>0 функция Н\ является выпуклой. Записав необходимое
условие экстремума Н\ по у
&Н\1ду = -Ру сх min 2у+ I Лэ I суКп,IV = 0,
получим
|р0|
= ^К.пах, (10.12)
причем всегдауэ > 0.
В итоге оптимальное значение коэффициента у находится с учетом
заданного ограничения
yopt = гтпОэ. Утахд). (10.13)
При Pv< 0 функция Hi является вогнутой, а при Ру = 0 - линейной
относительно у. Так как |Р©|сукт/^> 0, то наибольшее значение
Н\ достигается на правой границе:
То pt — ТтахД • (10.14)
2. При нарушении ограничения (10.9) принимается, что пу = пу 1Ш1хД ,
откуда
Topt — «у шах д7И£о/(СуКт Я$).
Неизвестная переменная Л определяется из условия дН]/бу = 0:
\ = Руу/К,тк- 1Лэ1/Л
Во всех случаях yopt > 0.
Краевые условия. В начальной точке (при т = 0) параметры траек-
тории заданы: Ио, 6о, #о и Ц. В конечной точке (при т = Г, где время Т
является свободным) удаление LK минимизируется. Условием оконча-
ния интегрирования уравнений движения является достижение задан-
426
Глава 10. Возврат крылатых ступеней к точке старта МКТС
ной конечной удельной энергии Е(Т) = Ек. Таким образом, на правом
конце задана одна связь между фазовыми переменными Н и К:
Н+ V~l(2g{})-EK = Q. (10.15)
Это значит, что сопряженные переменные Pv и Рн на правом конце
равны
Pv(n = ^/g0; =
и после исключения неизвестной переменной £ получим первое
условие
f^P^T)-P^T)V/g.= Q, (10.16)
В качестве второго условия на правом конце примем
/2^0(Г)-0к = О, (10.17)
где конечный угол наклона траектории Окявляется заданным.
Значения сопряженных переменных на левом конце траектории не-
известны, однако в соответствии с принципом максимума PL<0- При-
мем для определенности Р^ = - 1/7?о. Значение сопряженной перемен-
ной Р\\ на левом конце определим из условия Н = 0:
Рно= ~ (P\odVIdx + P^dd/dx + PydL
Здесь знаменатель выражения отличен от нуля, так как по условию
задачи 0() 0.
Значения сопряженных переменных Р\ и Р® на левом конце явля-
ются неизвестными и определяются в результате решения двух уравне-
ний (10.16) и (10.17). Таким образом, в данном случае краевая задача
является двухпараметрической.
Следует отметить, что задача минимизации удаления при задан-
ном значении Ек эквивалентна задаче максимизации конечной удельной
энергии при заданном значении .
Численное решение задачи. Расчеты проводились с двойной точ-
ностью. Было принято, что удельная нагрузка на крыло равна
m /S = 300 кг/м2. В начальной точке параметры траектории равны
Яо -47,45 км; Со = 2076 м/с (Мо = 6,92);
£о = 84 км; 0О = 14,26° (0О = - 194,26°).
Заданные ограничения равны: утахд = 5; иу111ахД= 3. В конечной точ-
ке заданы условия
Ек = 0; 0к = - 10,5° (0к= - Ю,5°).
Основная сложность решения краевой задачи, как известно, заклю-
чается в выборе начальных значений сопряженных переменных (в
данном случае PVo и Р©0), достаточно близких к их искомым значениям.
10.2. Решение модельной задачи оптимизации плоской траектории 427
В противном случае стандартная процедура решения системы нелиней-
ных уравнений не обеспечивает сходимость краевой задачи. Объясняет-
ся это тем, что траектория или заканчивается достижением недопусти-
мо высоких значений скоростного напора, или начинает интенсивно
’’закручиваться” на последних участках полета. Угол наклона траекто-
рии при этом достигает сотни градусов, а управляющая переменная сг
начинает осуществлять знакопеременные перекладки. Были испробова-
ны различные способы решения краевой задачи, в том числе рассмат-
ривались различные варианты задания краевых условий. Наиболее
рациональным оказался способ постепенного удлинения траектории,
заключающийся в следующем.
Решение задачи начиналось с рассмотрения более короткой траек-
тории (на правом конце было задано Ек = 16 км, что примерно соответ-
ствует Нк~ И км; Мк« 1,2). Значения сопряженных переменных PV() и
Pqq выбирались "вручную” из условия обеспечения приемлемого вида
траектории, в частности, не допускались большие значения скоростного
напора. При выборе начальных значений PVo и Лэ» можно учесть сле-
дующие рассуждения. Так как вначале траектории подъемная сила
аппарата должна быть направлена вниз, то Р0о > 0. Очевидно, что в
начале движения подъемная сила должна быть максимальной (у = у1ПП\д)
с тем, чтобы как можно быстрее попасть в плотные слои атмосферы.
Это означает, что в соответствии с соотношениями (10.12)—(10.14)
должно выполняться условие
^пзхСИ,,). (10.18)
Ч)ТтахД
В процессе решения краевой задачи на правом конце траектории
обеспечивалось выполнение условия (10.16) и примерное выполнение
условия (10.17) для угла наклона траектории. Затем конечная удельная
энергия Ек уменьшалась на величину 14-2 км, а в качестве начальных
значений PVo и Р©0 использовались данные, соответствующие преды-
дущему значению Ек. После того, как вектор скорости осуществил
практически полный разворот, задача решалась в исходной постановке,
т.е. с учетом выполнения условия (10.17) с заданной точностью. В
процессе удлинения траектории (при уменьшении Ек от 16 км до нуля)
относительное приращение аргументов, используемое при решении
краевой задачи, уменьшалось от 10“9 до 10~н; начальный шаг интегри-
рования уменьшался от 0,01 до 0,005 с. В окрестности точек выхода на
ограничение иу = иуп1ахД, точек схода с этого ограничения, а также в
окрестности точек переключения управляющей переменной ст осуще-
ствлялся останов процесса интегрирования. После этого процедура
интегрирования запускалась несколько раз в обратном и прямом на-
правлениях с постепенным уменьшением шага интегрирования. В
конечном прогоне траектории в окрестности указанных точек шаг
428
Глава 10. Возврат крылатых ступеней к точке старта МКТС
интегрирования уменьшался в 1О10 раз. Аналогично завершался про-
цесс интегрирования в конечной точке траектории.
При £к = 0 значения невязок были вполне приемлемыми. Так, на-
пример, значение /| на семь порядков меньше, чем величина каждого из
двух слагаемых в (10.16). Функция Гамильтона по траектории не пре-
вышала по модулю 10 Л что соответствует достаточной точности
оптимального решения.
Задача решалась в двух вариантах - без учета и с учетом ограниче-
ния на нормальную перегрузку.
Задача 1 (без учета ограничения на нормальную перегрузку). Ис-
комые значения сопряженных переменных на левом конце траектории
равны:
Pv<>=-3,169-Ю’5; Р0О = 0,118. (10.19)
Здесь выписаны только первые значащие цифры. Время движения
составляет 471с. На всей траектории сг=1, т.е. у = 0°. Результаты
расчетов представлены на рис. 10.3 и 10.4.
На рис. 10.Зя показано изменение числа Маха, высоты Н и нор-
мальной перегрузки пу в зависимости от времени полета т. Вначале
осуществляется движение по баллистической траектории с незначи-
тельным торможением аппарата. Затем после входа в плотные слои
атмосферы (при т > 110 с) высота и число Маха начинают резко умень-
шаться. Максимумы нормальной перегрузки и скоростного напора
достигаются практически одновременно на режиме у)11ахд перед выходом
в точку вертикального движения. Максимум q реализуется при числе
М 3,7. Характерно, что величина максимума является вполне прием-
лемой для крылатых ЛА и составляет 32,4 кПа. Максимум пу реализу-
ется через 8 с при М»2,1 и равен 6,54. В этой точке 0 = -76°. После
выхода на дозвуковой режим полета (при т > 200 с) движение является
практически квазистационарным. При этом иу« 1; 0 ~-10°. Характерно,
что колебания траектории здесь отсутствуют. Конечная скорость равна
171 м/с (Мк = 0,57). Конечная высота при Ек = 0 всегда меньше нуля. В
данном случае это не принципиально, так как конечную точку всегда
можно сдвинуть в сторону Як 0- Протяженность траектории между
точками, в которых Нк = 0 и Ек = 0, в данном случае составляет
~ 8,1 км.
На рис. 10.36 показано изменение управляющей переменной у и
угла наклона траектории 0 в зависимости от числа Маха (здесь и далее
на рисунках угол наклона траектории представлен в обычном понима-
нии: |0| <90°). Точка, соответствующая вертикальному движению
(0 = -9О°), реализуется при числе М» 1,79 после схода с ограничения
Т = Уп,ахд. С точки зрения характера изменения управления траекторию
возврата можно разделить на три участка. На начальном участке значе-
ние коэффициента у равно максимально допустимому: у =утахД. Конец
этого участка практически совпадает с точкой достижения максимума
10.2. Решение модельной задачи оптимизации плоской траектории 429
Рис. 10.3. Зависимости высоты А/, числа Маха и нормальной перегрузки
от времени полета (а)\ зависимости управляющей переменной у и угла
наклона траектории 0 от числа Маха (б)
Рис. 10.4. Зависимости управляющей переменной у и сопряженной
переменной PQ (я), сопряженных переменных Pv и (б) от времени
полета
нормальной перегрузки (М ~ 2,1). Второй участок является переходным
и заканчивается при М » 0,85. Здесь зависимость у(П является близкой
к квадратичной. Минимум этой функции достигается при М « 1 и равен
0,96. Третий участок соответствует квазистационарному планированию.
Известно, что оптимальное решение, полученное с использованием
гипотезы квазистационарности, соответствует yopt= 1 [111]. Однако в
данном случае коэффициент у уменьшается практически линейно по
числу Маха (по скорости) от 1,22 до 0,99.
Изменение управляющей переменной у по времени показано на
рис. 10.4я. Самым протяженным по времени является квазистационар-
430
Глава 10. Возврат крылатых ступеней к точке старта МКТС
ный участок полета. Здесь же представлено изменение сопряженной
переменной Р® . Величина Р® монотонно уменьшается по траектории,
оставаясь положительной величиной, в связи с чем на всей траектории
С = I.
Изменение сопряженных переменных Pv и Рн представлено на
рис. 10.46. Эти переменные меняют свой знак один раз - с минуса на
плюс перед точкой схода с ограничения j’opt = Л’шахд • На правом конце
траектории их значения соответствуют условию 10.16.
Задача 2 (при пу < пу ,пахд). Искомые значения сопряженных пере-
менных Руо и Роо совпадают с решением задачи 1 в первой значащей
цифре. Время движения на 15 с больше, чем в указанном решении.
Реализовалось переключение управляющей переменной сг с 1 на ми-
нус 1 и обратно, что отложило соответствующий отпечаток на траекто-
рию движения. Результаты расчетов представлены на рис. 10.5-10.8.
Характер изменения высоты Н и числа Маха во времени такой же,
как и в задаче 1 (см. рис. 10.3(7). Характер траектории на дозвуковом
участке и значения фазовых переменных Г, 6 и Н на правом конце
практически не изменились по сравнению с задачей 1.
Изменение угла наклона траектории 0 и скоростного напора q в за-
висимости от времени полета показано на рис. 10.5б/. Максимум q
реализуется при числе М~4,3 перед выходом на ограничение
Иу=Иута\д и равен 23 кПа, что несколько меньше, чем в предыдущей
задаче. В этой точке 0 = - 18,3°.
На рис. 10.56 показано изменение произведения управляющих пе-
ременных усу и изменение угла наклона траектории 0 в зависимости от
числа Маха. Точка, соответствующая вертикальному движению
(0 =-90°), реализуется при числе М « 1,33 после схода с ограничений
Рис. 10.5. Зависимости угла наклона траектории 0 и скоростного напора q
от времени полета (а), зависимости произведения усг и угла наклона
траектории 0 от числа Маха (6)
10.2. Решение модельной задачи оптимизации плоской траектории 431
У = Утахд и пу = пу тахД. Участок полета с сг = - 1 (у = 180°) соответствует
диапазону уменьшения числа М от 5,6 до 3,0. Появление такого участка
объясняется тем, что при сг = -1 угол 0 начинает увеличиваться и аппа-
рат уходит в область меньших скоростных напоров (см. рис. 10.5а). где
разворот вектора скорости происходит с большим аэродинамическим
качеством. Дополнительные расчеты варианта задачи, когда на всей
траектории су = 1, показали, что учет ограничения на нормальную
перегрузку, в отличие от задачи 1, приводит к увеличению максималь-
ного скоростного напора до 420 кПа. При этом аппарат не успевает
развернуть вектор скорости и попадает в область отрицательных высот.
Вследствие наличия ограничения иу=иутахд при больших скоростных
напорах полет проходит с очень малыми значениями коэффициента
подъемной силы, в результате чего летное значение аэродинамического
качества уменьшается, что приводит к значительному ухудшению
функционала.
С точки зрения характера изменения величины у траекторию воз-
врата можно разделить на три участка (как и в задаче 1). На первом
участке значение^ равно максимально допустимому: yopt= Утахд- При
переходе от первого участка ко второму величина^ уменьшается вслед-
ствие наличия ограничения на нормальную перегрузку (см. диапазон
уменьшения числа М от 3,0 до 1,4 на рис. 10.56). На третьем (квазиста-
ционарном) участке (при М <0,83) значение у уменьшается линейно по
скорости от 1,19 до 0,99.
На рис. 10.6# показано изменение нормальной перегрузки /?у, а на
рис. 10.66 - изменение высоты Н в зависимости от скорости полета и в
сравнении с аналогичными зависимостями предыдущей задачи. Нор-
мальная перегрузка выходит на заданное ограничение в диапазоне
а) б)
Рис. 10.6. Зависимости нормальной перегрузки пу (а) и высоты // (б) от
скорости полета:
1 - без учета ограничения на нормальную перегрузку; 2 - при ограничении < 3
Рис. 10.7. Зависимости произведения усг и сопряженной переменной
Pq (с/), сопряженных переменных Ру и Ри (б) от времени полета
уменьшения скорости от 1040 до 420 м/с. Вследствие ограничения на
в этом диапазоне высота полета увеличивается на 5-^6 км.
Изменение произведения усг в зависимости от времени показано на
рис. 10.7<7. Видно, что самым протяженным является квазистационар-
пый участок полета.
Изменение сопряженной переменной Pq представлено на
рис. 10.7(7; изменение Ру и Рн - на рис. 10.76. Сопряженная переменная
Л-) меняет по траектории свой знак с плюса на минус и обратно. В этих
точка/Х меняет свой знак управляющая переменная сг . Сопряженные
переменные Ру и меняют свой знак один раз с минуса на плюс перед
точкой, где 0 = -90°. На правом конце траектории их значения соответ-
ствуют условию (10.16).
Траектория движения в координатах "высота-дальность” показана
на рис. 10.8 в сравнении с траекторией задачи 1. Баллистический уча-
сток в обоих случаях практически одинаков. Дальность вначале увели-
чивается. Вследствие наличия ограничения на пу максимальное значе-
Рис. 10.8. Траектория плоского возврата в координатах "высота - дальность":
1 - без учета ограничения на нормальную перегрузку; 2 - при ограничении пу < 3
10.2. Решение модельной задачи оптимизации плоской траектории 433
ние дальности на 16 км больше, чем в задаче 1, и достигает величины
346 км. В результате в конечной точке (при Як = 0) дальность на ~ 19 км
больше: 9} = 264,4 км в случае отсутствия ограничения; 91 = 283,2 км
ПрИ Пу шахД 3.
10.3. Решение модельной задачи оптимизации
пространственной траектории возврата с использованием
принципа максимума
Воспользуемся упрощенными уравнениями пространственного
движения:
dV/dx = - cxqS/m - gsinO;
dQ /dx = cyqScosy /(m V) - cos0(g/P- Г/г);
dH /dx = PsinO;
d\\f/dx = - cyqS siny /(m PcosO) - Feos© tgcp cos\p/r; (0.20)
dy/dx = TcosO sin\p/r;
d)Jdx = PcosO cos\p/(r coscp).
Здесь, в отличие от уравнений (10.4), в качестве управляющей пе-
ременной вместо сг используется угол крена у; фазовая переменная 0 -
угол наклона траектории в обычном понимании (I 0 I < 90°). Так же, как
и в разделе 10.2, полагается, что Земля - шарообразная и не вращается.
Ускорение g и ее производная по высоте определяются с помощью
соотношений (10.5) и (10.6). Атмосфера является экспоненциальной -
см. формулы (10.7) и (10.8) для плотности воздуха и ее производной по
высоте. По условию задачи задано одно ограничение типа неравенства
(10.9).
Запишем функцию Гамильтона:
Н = -Р\ (cxqS/m + gsinO) + Pq [cyqS cosy /(m P) - cosO (g/P- P/r)] +
+ PsinO - P4I [cyqS siny /(wKcosO) + PcosO tgcp cos\|//r] +
+ P(pPcos0 simp/r + Px PcosO cos\p/(r coscp) + X(cyqSlm - gQny тахд),
которая, как и в разделе 10.2, равна нулю в каждой точке траектории.
Запишем уравнения для сопряженных переменных по скорости,
углу наклона траектории и высоте:
dPy /dx = P\(cPq + cxpP)S/m - Pq [(cy'pP+ cyp)S cosy /(2m) +
+ cosO (g/P2 + 1/r)] -PH sinO + Pk|/ [(cy'pP+ cyp)5 siny/(2mcos0) +
+ cosO tgcp cos\p/r] - P(px cosO !r - \(cy'q + cypK) S/m ;
434
Глава 10. Возврат крылатых ступеней к точке старта МКТС
dPQ Idx = Py/gcosQ - Ре sinO (g/V- V/r) - PH Kcos0 +
+ Лг [cyq sin0 S siny /(zrzPcos2©) - KsinO tgcp cosvp^] + /^KsinO/r;
dPy\/dT = Py(cKqfHS/m + g 'H sin0) - PQ [cy q ’^S cosy /(mV) -
- cos0 (g'H/V + Г/г2)] + Лр [cyq'H5 siny/^KcosO) -
- PcosO tgcp cos\p/r2] + Ap/KcosO /г2 - X^q'^SIm.
Здесь для сокращения записи введено обозначение
ЛРх = Ар sinvg + Р\ COSY|//COS(p.
Производные коэффициентов сх и су по скорости определяются с
помощью выражений (10.3).
Сопряженные переменные Au, Ар и Ас проинтегрированы в работе
[111]:
А = С2; Ар = С3 sinA, - С4 cosA,; (10.21)
Ар = (С3 cos А. + С4 sinA.)cos(p + С2 sincp, (10.22)
где С2, Сз и С4 - неизвестные константы.
С целью определения оптимального угла крена выпишем слагае-
мые функции Гамильтона, зависящие от у:
Н2 = су(А cosy - Ар siny/cos0). (10.23)
Здесь cosO Ф 0.
Как далее будет показано, всегда имеет место неравенство су > 0,
поэтому максимуму Н2 будет соответствовать максимум функции
siп(5 - у), равный 1, откуда получим
5 - у = тг/2,
где
Ру /COS0
sinyopt = - cosS =-г-—- - ; (10.24)
A/pe2+(Pv/cose)2
p
cosyopi = sin§ = .. 9 . (10.25)
7P02+(PV|;/cose)2
С учетом полученного решения функцию Ti2 перепишем в виде
= су ^/е2 +(Pv/cosO)2 ,
причем при любом значении угла крена ГС2 > 0.
10.3. Решение модельной задачи оптимизации пространственной траектории 435
Для определения оптимального коэффициента у запишем соответ-
ствующие слагаемые функции Гамильтона:
= - Pvcx + + (PV|//cos0)2 cy/V + Лсу. (10.26)
Так же как и в предыдущем разделе, сформируем алгоритм опреде-
ления оптимального управления, состоящий из двух этапов.
1. На тех участках полета, где ограничение на нормальную пере-
грузку не нарушается, то есть при иу<иутахД, переменная Л = 0. В
соответствии с принятой формой задания аэродинамических характери-
стик функция Н\является квадратичной относительно^:
Н\ = - Pv Сх min (1 + у2) + ^Pq + (РХ|, / cosО)2 сук,п уIV.
Оптимальное значение у определяется из условия достижения
наибольшего значения Н\ в каждой точке траектории. Как и в разделе
10.2, возможны два случая в зависимости от знака Ру
При Ру>0 функция Н\ является выпуклой. Записав необходимое
условие экстремума Н\ noj^:
дН|/ду = - PV Сх min 2у + Pq + (Рч, / cos0)2 СуКт / V = 0,
получим
Уэ = 7p62+(PV|;/cos0)2 Ктт VPy), (10.27)
причем всегда у3 > 0.
В итоге оптимальное значение у должно находиться с учетом
заданного ограничения
У opt = ПМП(уэ , .Утахд). (10.28)
При Ру< 0 функция Н\ является вогнутой, а при Pv= 0 - линейной
относительно^. Так как <^Pq + (Рф / cosO)2 cyKin /К > 0, то наибольшее
значение 7Y] достигается на правой границе:
.У opt = УтахД • ( 1 0.29)
2. При нарушении ограничения (10.9) принимается, что пу = иутахд ,
откуда
.Уopt — тахД ^^o/(^yKm
Неизвестная переменная Л определяется из условия &Н\!ду = 0:
436
Глава 10. Возврат крылатых ступеней к точке старта МКТС
Л = Руу/Ктж - 5//’e2+(Pv/cos0)2 /И (10.30)
Во всех случаях yopt > 0. Сравнение с разделом 10.2 показывает, что
алгоритм определения управляющей переменной у в обоих случаях
практически одинаков, причем выражения (10.26), (10.27) и (10.30)
совпадают с аналогичными выражениями раздела 10.2 при РЦ1 = 0.
Краевые условия. В начальной точке (при т = 0) параметры траек-
тории заданы: Ко, 0О, Яо, Фо= Фо = 0 и Хо. В конечной точке (при т = Г,
где время Т является свободной величиной) минимизируется либо
расстояние 9? до точки старта, либо продольная дальность LXk = Ro^k.
Как и в задаче раздела 10.2, примем, что условием окончания интегри-
рования уравнений движения является достижение заданной конечной
удельной энергии Е = Е^. Отметим, что движение на последнем этапе
носит квазистационарный характер. С учетом этого запишем первые
два условия на правом конце:
f^P^T)-P^T)V/g.= ^ (10.31)
/2-е(П-6к = 0. (10.32)
Здесь конечный угол наклона траектории 0Кявляется заданным.
Что касается конечных значений широты и угла курса, то возмож-
ны варианты. В том случае, когда отыскивается траектория, соответст-
вующая минимуму расстояния до точки старта, минимизируемую
функцию можно записать в виде
Фк2 + Хк2 min,
откуда получим третье условие на правом конце
/з -Лр(П - Л(Пфк/Хк = о. (10.33)
Реализуемые при этом значения фки Хк можно назвать оптимальными.
В том случае, когда необходимо построить заднюю границу дости-
жимой области, задача решается при фиксированном значении фк и
третье условие на правом конце принимает вид
/з = ф(Т) — фк = 0. (10.34)
Это условие можно использовать на начальных этапах решения задачи,
чтобы пространственная траектория не вырождалась в плоскую.
По условию задачи конечный угол курса должен совпадать с углом
визирования на точку старта МКТС. В этом случае четвертое условие
на правом конце будет иметь вид
/4 = \|/(Т) - л - arctg[s^(T)/tgX(T)] = 0. (10.35)
10.3. Решение модельной задачи оптимизации пространственной траектории 437
Однако на определенных этапах решения задачи удобно, чтобы
траектория заканчивалась полетом с нулевым углом крена. В этом
случае, как следует из выражения (10.24), должно выполняться условие
f^P^T) = 0. (10.36)
Предварительный анализ результатов расчета показал, что для ва-
рианта задачи, когда минимизируется расстояние 91, при достаточно
малых значениях Ек условия (10.35) и (10.36) выполняются одновре-
менно. Если задача решается при фк^Фкорн то из двух условий (10.35)
и (10.36) может выполняться только одно. Расчеты показали, что при
использовании условия (10.35) на конечном участке полета траектория
начинает поворачиваться по углу курса вправо при фк<Фк0Р1 или влево
при фк> фКоР1, что приводит к усложнению процесса, связанного с
удлинением расчетной траектории. Если учесть, что при малых скоро-
стях полета энергетические затраты на изменение угла курса являются
незначительными, то в качестве основного можно принять условие
(10.36), а условие (10.35) при этом будет выполняться приближенно.
Значения сопряженных переменных на левом конце траектории не-
известны, однако в соответствии с принципом максимума Р\ < 0. Чтобы
порядок сопряженных переменных был примерно такой же, как и в
разделе 10.2, примем Р\ = - 1. Значение сопряженной переменной Рн на
левом конце определим из условия ТС = 0:
Рно = - (P\vdV Idx + P^dS/dx + P^d\\fldx + P^dq/dx + P\dX /<Ут)/( KosinOo)-
Значения сопряженных переменных Ру , P§, P^t и Рф на левом конце
являются неизвестными и определяются в результате решения четырех
уравнений (10.31), (10.32) и (10.33), (10.35) или (10.34), (10.36). Таким
образом, в данном случае краевая задача является четырехпараметриче-
ской. Задача минимизации расстояния 9] при заданном значении Ек
эквивалентна задаче максимизации конечной удельной энергии при
заданном значении 9?.
Численное решение задачи. В качестве исходных данных задава-
лись такие же данные, как и в случае расчета траекторий плоского
возврата (см. раздел 10.2).
Вследствие увеличения числа неизвестных параметров сложность
решения данной краевой задачи по сравнению с задачей раздела 10.2
существенно увеличивается. При неудачном задании начальных значе-
ний сопряженных переменных траектория начинает ’’закручиваться" не
только по углу наклона траектории, но и по углу курса. В работе были
испробованы различные способы решения краевой задачи, в том числе
рассматривались различные варианты задания краевых условий. Как и в
разделе 10.2, наиболее рациональным оказался способ постепенного
удлинения траектории.
438
Глава 10. Возврат крылатых ступеней к точке старта МКТС
При выборе начальных значений сопряженных переменных были
учтены следующие рассуждения. Предполагалось, что в начале движе-
ния угол крена должен быть близок к минус 180°, а коэффициент у
равен максимально допустимому. В этом случае, как следует из выра-
жений (10.24) и (10.25), должны выполняться условия
1Лио1« l/’eol; />ео<О; Л„о> 0. (10.37)
В соответствии с соотношениями (10.27)—(10.29) и с учетом
первого неравенства (10.37) должно выполняться условие, аналогичное
(10.18):
Pvo<JPe°l ктт(^.
Ч)ТтахД
В отличие от задачи, рассмотренной в разделе 10.2, где в начале
движения имеет место сг = cosy = 1, в данной задаче в начале движения
cosy~-l. В связи с этим в предыдущем случае Pqq> 0, а в данном
варианте задачи Ре0<0. В остальном задачи близки между собой и
начальный участок движения в обоих случаях практически одинаков.
Поэтому полагалось, что PVo ~ 0,3-1 О'4 и Рео®-0,1.
Оценка возможных значений Рф0 и Рф0 проводилась для основного
варианта функционала, когда минимизируется расстояние 9L С этой
целью выражения (10.21) и (10.22) были записаны с учетом того, что
углы ср и X являются малыми на всей траектории движения, и с учетом
того, что Р\ = С2 = -1 :
ЛР^С3А-С4; (10.38)
Лр«С3 +С4Л.-(р. (10.39)
Очевидно, что на последнем дозвуковом участке планирования
угол крена должен быть близок к нулю, а угол курса должен совпадать с
углом визирования на точку старта МКТС. Это значит, что в соответст-
вии с (10.24) и условием задачи на конечном участке полета должны
выполняться приближенные равенства Рф« 0 и ср/Л,«tg\|/K • С учетом
этого выражение (10.39) принимает вид
С3 + С4 А, - Xtg\pK = С3 + А(С4 - tg\|/K) « 0,
откуда видно, что равенство РЦ1«0 может выполняться в некотором
диапазоне изменения переменной Столько при условии, что
С4 «tgvj/к « фк/Ак > 0 и | С31« С4. (10.40)
Запишем условия (10.33) и (10.36) на правом конце с учетом соот-
ношений (10.38) и (10.39):
Сз Ак - С4 + фк/А-к ~ 0; С3 + С4 Ак — ф к ~ 0.
10.3. Решение модельной задачи оптимизации пространственной траектории 439
Исключив отсюда коэффициент С4, получим
С3 (1 + Хк2) » О,
или
с4 » фкАк; I Сз I« с4,
что также совпадает с (10.40).
Таким образом, можно записать:
Лро ~ Сз Ао — С4 ~ — фк/Ак; РМ/о ~ Сз + С4 Ао ® Аофк/Ак.
Предварительные оценочные расчеты показали, что
фк/Ак « 0,11-Н), 13. В этом случае получаем ЛРо ~ - 0,12; ЛРо « 1,6-10-3,
причем значение Л|/0 на два порядка меньше, чем |Рео|, что согласуется
с первым условием (10.37).
В процессе удлинения траектории начальный шаг интегрирования
уменьшался от 0,01 до 0,002 с. В окрестности точек выхода на ограни-
чение Иу=иутахд и точек схода с этого ограничения осуществлялся
останов процесса интегрирования. После этого процедура интегриро-
вания запускалась несколько раз в обратном и прямом направлениях с
постепенным уменьшением шага интегрирования. В конечном прогоне
траектории в окрестности указанных точек шаг интегрирования
уменьшался в 1010 раз. Аналогично завершался процесс интегрирова-
ния в конечной точке траектории.
Точность расчетов была вполне приемлемой. Так, например, значе-
ние невязки f\ для всех рассматриваемых вариантов задачи при Ек = 0
было на 54-6 порядков меньше, чем величина каждого слагаемого в
(10.31).
При построении задней границы достижимой области (при
Фк^ФкорО условие (10.34) использовалось следующим образом. В каче-
стве начальной принималась траектория с Ек = 74-10 км, соответствую-
щая минимуму SH. Затем проводилась процедура изменения фк • При
этом конечное значение боковой дальности (А7к=^офк) изменялось с
шагом 2 км. Для каждого заданного значения фк погрешность опреде-
ления ZZK была не выше 0,001 м, в противном случае точность осталь-
ных трех невязок оказывалась недостаточно высокой. Затем, после
достижения траектории с необходимым прогнозным значением фк,
начиналось удлинение траектории (постепенное уменьшение Ек до 0).
При этом полагалось, что f3 = 0. В результате при Ек = 0 получалось
некоторое заранее не известное значение фк. Однако такой подход
оказался вполне приемлемым для построения задней границы дости-
жимой области и, кроме того, суммарное расчетное время существенно
сократилось. Объясняется это тем, что изменять фк при Ек = 0 оказыва-
ется значительно труднее, так как в этом случае для успешного решения
краевой задачи шаг изменения ZZK должен быть на несколько порядков
меньше.
440
Глава 10. Возврат крылатых ступеней к точке старта МКТС
Для всех вариантов задачи значение функции Гамильтона по траек-
тории не превышало по модулю 10-14.
Как и в разделе 10.2, задача решалась в двух вариантах - без учета
и с учетом ограничения на нормальную перегрузку.
Задача 1 (без учета ограничения на нормальную перегрузку). Вна-
чале был рассмотрен вариант минимизации ЭГ В этом случае искомые
значения сопряженных переменных на левом конце траектории равны
Pvo = -3,089 10’5; Лю= -0,118;
Л„о = 1,208-10’3; Рфо = -0,0917.
Сопряженная переменная PVo совпадает с аналогичной величиной
задачи 1 раздела 10.2 (при рассмотрении плоского возврата) в первой
значащей цифре, Р0О - в первых трех цифрах. Значения PV(/0 и Р(ро при-
мерно соответствуют сделанному выше прогнозу.
Время движения равно 529 с (на 58 с больше, чем в задаче 1 плос-
кого возврата). Результаты расчетов представлены на рис. 10.9-10.12.
На рис. 10.9# показано изменение числа Маха, высоты Н и нор-
мальной перегрузки пу в зависимости от времени полета. Характер
изменения этих величин примерно такой же, как и в задаче 1 плоского
возврата. Однако максимальное значение пу составляет 4,9 (на 1,6
меньше), а максимальное значение q составляет 29 кПа (на 3 кПа
меньше, чем в указанной задаче).
На рис. 10.96 показано изменение управляющих переменных^ и у
в зависимости от числа Маха. Характер изменения коэффициента^ при
движении по траектории примерно такой же, как и в задаче 1 плоского
возврата. Здесь также можно выделить три участка. На начальном
Рис. 10.9. Зависимости высоты Н, числа Маха и нормальной перегрузки пу
от времени полета (я); зависимости управляющих переменных у и у от
числа Маха (6)
10.3. Решение модельной задачи оптимизации пространственной траектории 441
участке значение коэффициента у равно максимально допустимому:
Vopt= Упахд • Конец этого участка практически совпадает с точкой дости-
жения максимума нормальной перегрузки (М ~ 2,9). На втором (пере-
ходном) участке (М = 0,974-2,8) зависимость ХИ близка к квадратич-
ной. Минимум функции достигается при М = 1,1 и равен 1,19.
Последний участок (М < 0,97) соответствует квазистационарному
движению. Здесь коэффициент у уменьшается практически линейно по
скорости от 1,27 до 0,99. Характерно, что, в отличие от работ [42], [98].
[111], переход с режима yopt =_уП1ахд на режим ^opt« 1 (режим Х1ш1х) осу-
ществляется не дискретно, а на протяжении некоторого участка, на
котором число Маха уменьшается от ~ 3 до ~ 1.
Угол крена в начале движения (при М = 6,44-6,9) практически по-
стоянен и равен по модулю 178,54-179,4°. На следующем участке полета
(М = 2,54-6,3) его зависимость от числа М близка к квадратичной. В
конце планирования (при М < 0,8) угол крена практически равен нулю.
Изменение у в зависимости от времени показано на рис. 10.10с/.
Как и в задаче 1 плоского возврата, последний (квазистационарный)
участок является самым протяженным по времени. На этом же рисунке
представлено изменение сопряженной переменной Ро.
Изменение сопряженных переменных и Рп представлено на
рис. 10.106. Все сопряженные переменные меняют свой знак один раз с
минуса на плюс. В точке смены знака угол крена равен минус 90°.
Точки смены знака Pv и Рн практически совпадают с точкой смены
знака Pq . На правом конце траектории значения Pv и Рн соответствуют
условию (10.31).
Изменение угла крена и сопряженной переменной в зависимо-
сти от времени представлено на рис. 10.11. В начале движения темп
а) б)
Рис. 10.10. Зависимости управляющей переменной^ и сопряженной перемен-
ной Pq (а), сопряженных переменных Pv и РИ (б) от времени полета
442 Глава 10. Возврат крылатых ступеней к точке старта МКТС
Рис. 10.11. Зависимости угла крена
и сопряженной переменной Pw от
времени полета
изменения угла у является
незначительным, затем угол
крена с высокой скоростью
уменьшается по модулю от
-160° до -60°. Сопряженная
переменная на всей траек-
тории положительна и дости-
гает максимума при у~-120°.
На заключительном участке
планирования (при т > 300 с)
и у близки к нулю. Сопря-
женная переменная Р(р изме-
няется по траектории только в
третьей значащей цифре.
На рис. 10.12 представле-
на зависимость угла крена у,
коэффициента у и числа Маха от угла курса у. Наибольшее приращение
угла курса имеет место при | у | < 90°. При развороте траектории по
курсу на 90° число Маха уменьшается до 1,65, а коэффициенту - до 2.
При развороте на 180° скорость становится дозвуковой (М = 0,92).
Можно отметить, что зависимость у от у близка к линейной в диапазо-
нах изменения = 304-150° и 1504-185°.
Для построения задней границы достижимой области были прове-
дены дополнительные расчеты траекторий с фк^фкорг- На рис. 10.13
представлены три траектории пространственного возврата в проекции
на земную поверхность, отличающиеся конечной боковой дальностью
£/к. Оптимальная величина Z,ZK равна 23 км (траектория 1). В этом
случае реализуется минимум расстояния до точки старта МКТС:
Рис. 10.12. Зависимости управляющих переменных у, у и числа Маха
от угла курса
10.3. Решение модельной задачи оптимизации пространственной траектории 443
Рис. 10.13. Траектории пространственного возврата в координатах
"боковая дальность - продольная дальность" (при = 0):
1 - траектория, обеспечивающая минимум удаления отточки старта
МКТС ; 2 - траектория с LZK = 0; 3 - траектория с LZK = 80 км
9? = 251,85 км. В конечной точке планирования одновременно выпол-
няются условия (10.35) и (10.36). Дальность заключительного участка
планирования, когда текущий угол курса примерно равен углу визиро-
вания на точку старта МКТС, составляет ~60 км. Траектория является
гладкой, без каких либо изломов, причем участки прямого и обратного
движения примерно симметричны относительно некоторой средней
прямой.
На рис. 10.13 также показаны траектории, соответствующие конеч-
ному значению боковой дальности L/K=Q и ZZK = 80 км. Эти траекто-
рии сначала были рассчитаны с использованием условия (10.36). При
этом рассогласование по углу курса в конечной точке составило 16° и
41° соответственно. Затем траектории были пересчитаны с использова-
нием условия (10.35). При этом величина в каждом случае несколько
увеличилась, а траектория на заключительном участке несколько изо-
гнулась, в результате чего обеспечивается условие \у(Т) = ц/виз • При
£zk=0 дальность до точки старта равна SJ] =255,3 км; при £ZK = 80 км
SR = 273,73 км. При увеличении ZZK траектория в координатах "L/- L*"
распрямляется, при этом величина ZXmax и время полета увеличиваются,
а #тах И Иу1пах уменьшаются. Так, при LZK = 80 км тк = 585 с; иу1пах= 3,18;
#тах= 27,2 кПа.
Зависимость угла крена от числа Маха для варианта возврата с
Z/zk-0 представлена на рис. 10.14а. В начале движения угол крена
положителен и увеличивается от 176° до 180°, в результате чего траек-
тория в координатах ”Zz-Zx" несколько отклоняется вправо (см.
рис. 10.13). Затем угол крена меняет знак и начинает уменьшаться по
модулю до нуля, как и в основном варианте. Однако на заключительном
участке угол крена снова меняет знак и увеличивается до 16° с тем.
444
Глава 10. Возврат крылатых ступеней к точке старта МКТС
чтобы обеспечивалось условие (10.35) по углу курса в конечной точке
полета. На рис. 10.146 представлена аналогичная зависимость для
траектории с Ь7^ = 80 км. В начальной точке у = -167,5° и на всей траек-
тории угол крена меньше нуля. На заключительном участке угол крена
увеличивается по модулю до 34,4° с тем, чтобы обеспечивалось условие
(10.35).
Задача 2 (при пу < пу тахД). Вначале был проведен расчет траекто-
рии. соответствующей минимуму SJL Значения сопряженных перемен-
ных на левом конце траектории совпадают с решением задачи 1 в пер-
вой значащей цифре. Время движения на 34 с больше, чем в задаче 1 и
на 77 с больше, чем в задаче 2 плоского возврата. Результаты расчетов
67) б)
Рис. 10.15. Зависимости угла наклона траектории 0 и скоростного напора
q от времени полета (я); зависимости управляющих переменных у и у от
числа Маха (б)
10.3. Решение модельной задачи оптимизации пространственной траектории 445
Характер изменения высоты Н и числа Маха во времени такой же,
как и в задаче 1 (см. рис. 10.9я). Дозвуковой участок полета и значения
фазовых переменных V. 0 и Н на правом конце траектории являются
такими же, как и в предыдущих задачах.
Изменение угла наклона траектории 0 и скоростного напора q в за-
висимости от времени полета представлено на рис. 10.15а. Минимум
угла наклона траектории равен минус 25° и реализуется практически
одновременно с ^1пах. Далее по траектории достигается локальный
максимум угла 0, равный минус 3°, и затем угол 0 выходит на свое
квазистационарное значение, равное примерно минус 10°. Вследствие
ограничения на пу максимум скоростного напора по сравнению с зада-
чей 1 уменьшился с 29 до 26,2 кПа.
На рис. 10.156 показано изменение управляющих переменных у и у
в зависимости от числа Маха. С точки зрения характера изменения
управляющей переменной у траекторию возврата можно разделить на
три участка (как и в предыдущих вариантах задачи). При переходе от
начального участка ко второму величина у уменьшается вследствие
наличия ограничения на нормальную перегрузку (см. диапазон умень-
шения числа М от 4,2 до 1,9). В конечной точке >>Opt~ ••
Характер зависимости угла крена от числа М такой же, как и в за-
даче 1. В начале движения (при М = 6,4=6,9) угол крена практически
постоянен и равен по модулю 176,5-И 79,2°. При М =44-6,3 зависимость
угла крена является близкой к квадратичной. На дозвуковом участке
(М < 0,9) у « 0.
На рис. 10.16а показано изменение нормальной перегрузки , а на
рис. 10.166- изменение высоты Н в зависимости от скорости полета и в
сравнении с аналогичными зависимостями задачи 1. Нормальная пере-
Рис. 10.16. Зависимости нормальной перегрузки nv (а) и высоты II (б) от
скорости полета:
1 - без учета ограничения на нормальную перегрузку; 2 - при ограничении пу < 3
446 Iлава 10. Возврат крылатых ступеней к точке старта МКТС
грузка выходит на заданное ограничение в диапазоне уменьшения
скорости от 1260 до 580 м/с. Несмотря на существенную разницу в
величинах пу. отличие траекторий в координатах "высота-скорость"
является незначительным.
Характер изменения сопряженных переменных во времени при-
мерно такой же, как и в задаче 1.
На рис. 10.17 представлены зависимости угла крена у, коэффици-
ента у и числа Маха от угла курса у. Видно, что в начале траектории
(при < 10°) угол крена с высоким темпом уменьшается по модулю до
~ 73°. При развороте траектории по курсу на 90° число Маха и управ-
ляющая переменная у уменьшаются до 1,8, а при развороте на 180°
скорость становится дозвуковой (М = 0,98). Коэффициент у принимает
близкое к режиму АГтах значение (у = 1,3) при \|/> 1104-120°. Как и в
предыдущей задаче, можно отметить, что на конечном участке полета
зависимость у от у близка к линейной в двух диапазонах: у = 304-140° и
к|/= 1404-185°.
На рис. 10.18 показан заключительный участок траектории в коор-
динатах "высота-продольная дальность" в сравнении с траекториями
задачи 1, решенной для вариантов плоского и пространственного воз-
врата. Во всех случаях квазистационарный участок полета практически
одинаков, колебания траектории отсутствуют. При отсутствии ограни-
чения на в случае пространственного разворота максимальная даль-
ность на ~ 5 км больше, чем в случае разворота в вертикальной плоско-
сти (кривые 2 и 1). Однако в конечной точке минимум расстояния до
точки старта достигается в случае пространственного разворота:
Ч.К = 259,9 км при Як = 0- Выигрыш в значении функционала составляет
4,5 км. Объясняется это тем, что плоское движение (у = 0) можно рас-
сматривать как частный случай пространственного движения, когда на
угол крена наложено ограничение (у = 0 или 0 и 180°). А, как известно,
введение дополнительных ограничений всегда приводит к ухудшению
функционала.
Рис. 10.17. Зависимости управляющих переменных у, у и
числа Маха от угла курса
10.3. Решение модельной задачи оптимизации пространственной траектории 447
Рис. 10.18. Траектории возврата в координатах "высота - продольная
дальность":
1 - плоская траектория без учета ограничения на нормальную перегрузку;
2 - пространственная траектория без учета ограничения на нормальную
перегрузку; 3 - пространственная траектория при ограничении a?v < 3
Наличие ограничения на пу приводит к увеличению как макси-
мального удаления (на ~10км), так и дальности в конечной точке
планирования (кривые 3 и 2 на рис. 10.18). Расстояние 9? на 4,6 км
больше, чем при отсутствии ограничения на пу, и практически совпа-
дает с аналогичной величиной, полученной в задаче 1 плоского возвра-
та.
Как и в задаче 1, был произведен расчет траекторий с Z,ZK * и
построена задняя граница достижимой области земной поверхности -
см. рис. 10.19, где также нанесена соответствующая граница для случая.
Lzk , км
80
60
40
20
0
-20
240
200
Точки, соответствующие
минимуму расстояния до
точки старта МКТС
Рис. 10.19. Задняя граница достижи-
мой области в координатах "боковая
дальность - продольная дальность"
(при Ек = 0):
1 - без учета ограничения на нормальную
перегрузку; 2 - при ограничении пу < 3
280 £Хк •> км
448
Глава 10. Возврат крылатых ступеней к точке старта МКТС
когда ограничение на пу не задано. Вследствие наличия ограничения на
/?v проекция траектории на земную поверхность несколько разгибается,
в результате чего величины Z,ZK и 91 увеличиваются. Оптимальная вели-
чина А/к равна 32,4 км (на 9,4 км больше, чем в задаче 1). Как было
отмечено при решении задачи 1, увеличение AZK сопровождается
уменьшением иуП1ах. Вследствие этого при увеличении AZK линии 1 и 2
на рис. 10.19 начинают сближаться и при Azk>88km они полностью
совпадают. В данном случае точка £ZK ~ 88 км соответствует иу1пах=3.
Характер задней границы такой же, как и в случае возвращения ЛА с
орбиты (см. рис. 9.40 и 9.45).
10.4. Формирование приближенно оптимального
управления движением. Сравнение приближенного
решения с точным решением
С учетом полученных в разделах 10.2 и 10.3 результатов сформиру-
ем программу приближенно оптимального управления движением.
Плоское движение. Угол крена может принимать два значения: 0 и
180° (ст=± 1). Коэффициенту ограничен сверху: у<у1пахд, где утахД в
общем случае может быть переменной по скорости величиной. Если
переворот аппарата на 180° по крену не допускается, то равенство
с*] — — 1 будет означать переход на режим у1П1пД, где величинаутнД может
быть как отрицательной, так и положительной.
Программа изменения управляющей переменной сг состоит из трех
участков (рис. 10.20^): в начале и в конце движения всегда сг= 1. До
выхода в точку 0 = -9О° может включаться режим сг = - 1. Обозначим
скорости включения и выключения этого режима через и Ег2- Если
скорость не является монотонной величиной, то можно использовать
удельную энергию или дальность. Параметры Кп и ЕГ2 оптимизируют-
ся из условия минимума удаления от точки старта МКТС в конечной
точке планирования.
Программа изменения коэффициента у также состоит из трех уча-
стков. Аргументом является скорость полета (см. рис. 10.206). Участки
пронумерованы по мере возрастания скорости. На первом участке
используется линейная зависимость у(К), на втором - квадратичная, на
третьем участке у =ута\д(Ю- Всего необходимы пять параметров:
ИУ| -скорость, при которой у= 1;
KY2,y2 - скорость и значение коэффициента у в начале второго
участка;
ЕуП1 - скорость, соответствующая вершине параболы второго
участка (задается при помощи параметра АГУт= KYni - KY2);
Иуз - скорость начала третьего участка.
Необходимо выполнение условия KY|<PY2<EY3. Значение KYin
должно быть таковым, чтобы значение функции на втором участке
10.4. Формирование приближенно оптимального управления движением 449
Рис. 10.20. Программа приближенно оптимального управления движением:
а) зависимость косинуса угла крена сг от скорости полета при плоском возврате;
б) зависимость относительного коэффициента подъемной силы у от скорости
полета при плоском и пространственном возврате; в) зависимость угла крена у от
скорости полета и от угла рассогласования при пространственном возврате
находилось внутри диапазона [у)Птд, Л’тахд]- Запишем алгоритм
определения коэффициента у:
у = 1 + (V- ГУ| )(У2- 1)/(HV2- Kyi) при V< ГУ2;
у = С + А(У - ГУ1П)2 при rY2 < V < rY3;
У = Л’шахдС Г) при rY2 > Иуз ,
450
Глава 10. Возврат крылатых ступеней к точке старта МКТС
где коэффициенты квадратной параболы равны
А = (у.лахд- у2)/[( Иу3 - Иу2)( Иу3 + Иу2 - 2 Гут)]; С=у2 - А (KY2 - KYin)2.
Коэффициент у определяется с учетом ограничения на нормальную
перегрузку.
Таким образом, вариационная задача сводится к минимизации ко-
нечной дальности ZK как функции семи переменных.
Пространственное движение. Сравнение задач разделов 10.2 и
10.3 показывает, что как в плоском, так и в пространственном движении
характер изменения коэффициента у по траектории примерно одинако-
вый. В связи с этим примем программу управления с пятью параметра-
ми, представленную на рис. 10.206.
При формировании программы изменения угла крена будем ориен-
тироваться на основной вариант, когда минимизируется расстояние 9?, а
^zK=^zKoPt- Анализ результатов решения задач раздела 10.3 позволяет
сделать следующие выводы. На всей траектории угол крена не меняет
свой знак. В связи с этим будем здесь оперировать модулем угла крена.
Всего можно выделить четыре участка. На начальном участке по-
лета угол крена практически постоянен (см. рис. 10.96 и 10.156). Затем
осуществляется переход на режим у < 90°. Здесь можно считать, что
угол крена изменяется квадратично по скорости. Далее по траектории
угол крена изменяется практически линейно по углу курса, а на заклю-
чительном участке угол крена пропорционален углу курса (см.
рис. 10.12 и 10.17). В конечной точке угол крена всегда равен нулю. В
связи с этим на двух начальных участках полета в качестве аргумента
будем использовать скорость И, а на заключительных участках в качест-
ве аргумента примем рассогласование углов курса и визирования на
точку старта МКТС (как в работе [41]). Этот угол равен
5 = \|/-\|/Виз,
где
\|/виз = arctg[sincp/tgX] + л.
Здесь углы ср и X отсчитываются от точки старта МКТС. В общем
случае угол визирования определяется при помощи соотношения (9.23).
Для удобства будем оперировать модулем угла 5. По траектории
функция arctg[sincp/tgX] изменяется от 0 до 6-^7°, а угол 8 уменьшается
от 180° до 0.
Принятая программа приближенно оптимального управления уг-
лом крена приведена на рис. 10.20в. Всего используются семь парамет-
ров; участки пронумерованы в соответствии с возрастанием скорости:
8| ,yi/8| - угол рассогласования и отношение углов у и 8 в конце
первого участка;
Кг2, У2 - скорость и угол крена в конце второго участка;
ИГт -скорость, соответствующая вершине параболы третьего
участка (задается при помощи параметра ДКГ,П= ИГ1П - Рг2);
10.4. Формирование приближенно оптимального управления движением 451
Игз, Уз - скорость и угол крена в конце третьего участка.
В начале движения угол крена равен у3, затем после достижения
скорости Ргз угол крена квадратично уменьшается до у2. То есть
у= Уз при V> Игз;
у = С + А(V- ИГт)2 при ^Г2 < v < Кгз,
где коэффициенты квадратной параболы равны
А = (уз - у2)/[( Игз - ГГ2)(Игз + КГ2 - 2 ИГ1П)]; С = у2- А( ГГ2 - КГп,)2.
При скорости ИГ2 реализуется угол 82, и далее по траектории:
y=yi + (8-8J)(y2-y1)/(82-81) при 8j <8<82;
у = 8(yi/8|) при 8 < 8|.
Здесь должны выполняться условия 0 < КГ2 < Игз, 0 < 81 < 82 и
0<у<у3. Знак угла крена совпадает со знаком угла 8. При развороте
через северное ортодромическое полушарие угол крена отрицательный,
при развороте через южное полушарие - положительный.
Таким образом, вариационная задача сводится к минимизации рас-
стояния 9? как функции 12 переменных. Для проверки сформированных
приближенно оптимальных законов управления была создана вычисли-
тельная программа и решена модельная задача 2 пространственного
возврата. При этом использовались те же самые исходные данные,
допущения и соотношения, что и в разделе 10.3. Начальное приближе-
ние оптимизируемых параметров представлено в табл. 10.2.
При задании начальных значений не ставилась задача специально
приблизиться к известному решению задачи 2, решенной в разделе 10.3.
Удаление 91 в начальном приближении на 21,1 км больше по сравнению
с оптимальным решением (см. табл. 10.2).
Оптимизация проводилась с использованием стандартной проце-
дуры безусловной минимизации функции нескольких переменных из
математической библиотеки MS1MSL. Результаты оптимизации приве-
дены в табл. 10.2. В процессе оптимизации значения некоторых пара-
метров изменились в 1,54-2 раза.
Полученное решение является вполне приемлемым. На рис. 10.2\а
показано сравнение приближенного решения ХМ) с точным решением,
на рис. 10.216 - сравнение аналогичного решения для зависимости
у(М), а на рис. 10.22-для зависимости у(8). На рисунках указаны
точки переключения участков. Из графиков видно, что приближенно
оптимальное управление практически совпадает с оптимальным. Вер-
шина параболической зависимости ХМ) находится вблизи левой грани-
цы второго участка: ДКУт = 58 м/с (см. табл. 10.2 и рис. 10.21 я). Анало-
гичная величина для зависимости у(И) равна ДКГт=28м/с (см.
табл. 10.2 и рис. 10.216).
452
Глава 10. Возврат крылатых ступеней к точке старта МКТС
Таблица 10.2
Результаты оптимизации параметров
разработанного закона управления
Параметр Начальное приближение Оптимальное решение
Управление коэффициентом у
Kyi , м/с 100 167,01
Гу2,м/с 300 304,36
ДИУт, м/с 0 58,09
ИуЗ, м/ С 500 820,45
Уг 1,3 1,295
Управление углом крена у
6,° 20 41,68
Y. /5, 0,7 0,899
Р гз » М/С 1800 1504,0
$2° 176 171,53
72° 65 75,57
ДГГт, м/с 0 28,12
Р'гз, м/с 2000 1921,85
Ъ° 180 178,63
Сравнение с точным решением
Тк ^Kopt , С 32,7 -0,4
/-ZK _ /-ZKopt , КМ 14 -0,11
91 - 91Ор,, км 21,1 (7,6%) 0,07 (0,028%)
Конечный угол наклона траектории равен минус 9,92°, что соответ-
ствует его квазистационарному значению (в разделах 10.2 и 10.3 вариа-
ционная задача решалась при 0К =- 10,5°). По боковой дальности £7К
полученная траектория отличается от оптимальной на 0,36%, по време-
ни полета - на 0,07%. По величине функционала отличие приближен-
ного решения от точного составляет всего A^R = 70 м (0,028%) - см.
табл. 10.2.
Проверка отклонения параметров приближенно оптимального за-
кона управления от своих оптимальных значений показала следующее.
Увеличение параметра yi /51 до 1 (то есть использование на заключи-
тельном участке полета закона управления у = - у виз) приводит к
ухудшению функционала на 0,13 км. Уменьшение параметра^ до 1 (то
есть переход к закону управления у = 1 на квазистационарном участке
полета) приводит к ухудшению функционала на 1,4 км.
10.4. Формирование приближенно оптимального управления движением 453
а)
б)
О 30 60 90 120 150 5°
мши» приближенное решение; ------ точное решение
Рис. 10.21. Сравнение приближенного решения с оптимальным (на
основе принципа максимума). Зависимости относительного коэффици-
ента подъемной силы (а) и угла крена (б) от числа Маха; зависимость
угла крена от угла рассогласования (в)
Таким образом, можно заключить, что сформированная структура
приближенно оптимального управления движением и разработанный
алгоритм сведения вариационной задачи к минимизации функции
нескольких переменных могут использоваться на этапе формирования
454
Глава 10. Возврат крылатых ступеней к точке старта МКТС
облика МКТС вертикального старта, когда требуется проведение массо-
вых расчетов траекторий возврата первых ступеней к точке старта с
использованием реальных характеристик аппарата, атмосферы и грави-
тационного поля Земли.
10.5. Примеры расчетов для различных скоростей
отделения от МКТС
Параметрические расчеты траекторий возврата были выполнены с
использованием приближенно оптимального управления применитель-
но к гипотетическому ВРУ. При этом использовалась полная система
уравнений движения (2.71), записанная для вращающейся шарообраз-
ной Земли; атмосфера полагалась стандартной.
Взаимосвязь между параметрами траектории Ио, Но, 0О и Lo в точке
отделения ВРУ (рис. 10.22) соответствует двухступенчатой МКТС со
стартовой тяговооруженностью 1,37. Изменение Ио задавалось в диапа-
зоне 10004-2076 м/с. При Ко = 2076 м/с параметры траектории совпада-
ют с исходными данными задач, решенных в разделах 10.2 и 10.3.
Однако в отличие от разделов 10.2 и 10.3, где использовались аэроди-
намические характеристики гипотетического ЛА (в соответствии с
работой [42]), в данном случае используются расчетные аэродинамиче-
ские характеристики одного из возможных вариантов ВРУ Баллистиче-
ский коэффициент сгх и параметр планирования оу на летных режимах
примерно в 2,5 раза больше, чем в предыдущих задачах. Максимум
аэродинамического качества при дозвуковых скоростях (М < 0,6) равен
5,5; при гиперзвуковых скоростях (М = 6) А^тах = 2, что несколько
больше, чем в предыдущих задачах. Максимально допустимый угол
атаки принят равным 50° при
М > 3 и 30° при М < 2. Конечная
точка планирования соответствует
Нк = 2 км.
Были решены четыре вариан-
та задачи: для плоского и про-
странственного возврата; без
ограничения на нормальную
перегрузку и при иУ1<3, где
перегрузка иУ1 вычислена в свя-
занной системе координат.
Для вариантов задачи, когда
ограничение на пу\ не задано,
была определена зависимость
«у1 max ОТ И0 (рИС. 10.23). При
малых Ио скоростной напор в
начальной точке является сущест-
венным, поэтому иу|тах достига-
Рис. 10.22. Зависимости началь-
ных значений высоты Но, угла
наклона траектории 90 и дально-
сти Lq от начальной скорости ВРУ
10.5. Примеры расчетов для различных скоростей отделения от МКТС 455
Рис. 10.23. Зависимость максималь-
ной перегрузки лу1 от начальной
скорости ВРУ:
1 - плоский возврат: 2 -
пространственный возврат
ется в начальной точке. По мере
увеличения Ио скоростной напор
в начале движения уменьшается,
что приводит к уменьшению
Hylmax- При Ко > 1400-И 600 м/с
максимум q достигается в сере-
дине траектории при входе в
плотные слои атмосферы. В этой
же части траектории достигается
и Hyimax • Дальнейшее увеличение
Vo вновь приводит к увеличению
Hyimax, причем в плоском движе-
нии Иу|таХ на 1,5н-2,0 больше. Так
как уровень иУ1тах является до-
вольно значительным, то задачу
возврата необходимо решать с
учетом ограничения на нормаль-
ную перегрузку.
Результаты минимизации удаления 9? для рассматриваемых вари-
антов задачи представлены в зависимости от начальной скорости Vo
(рис. 10.24). Зависимости близки к квадратичным. В случае отсутствия
ограничения на иУ| конечное удаление от точки старта МКТС для обоих
типов возврата практически одинаково (с разницей до ±3,5 км) как в
1000 1200 1400 1600 1800 Ио, м/с
Рис. 10.24. Зависимость удаления конечной точки планирования
ВРУ от точки старта МКТС для различных вариантов задачи
456
Глава 10. Возврат крылатых ступеней к точке старта МКТС
указывает на важность всестороннего рассмотрения задачи, так как
решение более простой задачи плоского возврата может быть использо-
вано в качестве контрольного при оптимизации параметров управления
пространственным движением.
Учет ограничения на нормальную перегрузку в плоском движении
сопровождается значительным ухудшением функционала: на 15-ь70км
в зависимости от Ио, причем при увеличении Ио разница в 9? увеличи-
вается. В отличие от этого для варианта пространственного движения
учет ограничения на иУ| приводит к меньшему ухудшению функциона-
ла: на 4н-15 км в зависимости от Ио. Сравнение траекторий при nyi<3
однозначно указывает на то, что пространственный возврат является
более выгодным по сравнению с плоским: в зависимости от Ио выиг-
рыш в величине функционала составляет 154-48 км. В связи с этим
далее более подробно рассмотрен вариант пространственного возврата
с ограничением пУ| < 3.
Результаты расчетов при Vo = 2076 м/с представлены на рис. 10.25-
10.27. Характер зависимостей примерно такой же, как и в задачах,
решенных в разделе 10.3, однако протяженность траектории отличается
вследствие различия аэродинамических характеристик. Так, время
полета увеличилось с 563 до 725 с, расстояние 9? уменьшилось на
77 км.
Колебания траектории после входа ВРУ в плотные слои атмосферы
практически отсутствуют (см. рис. 10.25). Максимум скоростного
напора достигается при М = 2,8 и равен 17,2 кПа (см. рис. 10.26я), что в
1,5 раза меньше, чем в задаче 2 раздела 10.3. Здесь следует отметить,
что во всех вариантах расчета величина д1пах не являлась критичной. Это
значит, что в расчетах необходимо учитывать ограничение только на
нормальную перегрузку.
Рис. 10.25. Зависимости скорости V и высоты Н от времени полета
10.5. Примеры расчетов Оля различных скоростей отделения от МКТС 457
Рис. 10.26. Зависимости нормальной перегрузки лУ| и скоростного
напора q (а), коэффициента у и угла крена у (6) от числа Маха
Уменьшение угла крена по модулю до величин, меньших 90°, осу-
ществляется перед выходом на ограничение H>f = 3 (см. рис. 10.266).
Полет вдоль ограничения иУ1 = 3 происходит при уменьшении числа М
от 4,6 до 2. На этом участке коэффициенту соответственно уменьшает-
ся. На дозвуковом участке планирования коэффициент у уменьшается
от 1,22 до 1,1.
Проекция траектории на земную поверхность показана на
рис. 10.27. Основное торможение осуществляется при гиперзвуковых
скоростях (М > 5). Максимальная продольная дальность в прямом
движении составляет 206 км (на 55 км меньше, чем в задаче 2 раздела
10.3, за счет большего значения ох). Участок полета по ограничению
иУ1 = 3 заканчивается примерно в точке достижения угла курса ~ 90°.
При развороте по углу курса на 180° скорость становится дозвуковой. В
обратном движении продольная дальность равна 115 км, что на 25 км
больше, чем в задаче 2 раздела 10.3. Объясняется это тем, что за счет
большего значения параметра планирования сгу ВРУ после выхода на
дозвуковой режим имеет большую высоту полета и, соответственно.
458
Глава 10. Возврат крылатых ступеней к точке старта МКТС
Рис. 10.27. Траектория пространственного возврата в координатах
"боковая дальность - продольная дальность"
больший запас удельной энергии. Вследствие больших значений сгх и сгу
дальность S.K уменьшилась по сравнению с задачей 2 раздела 10.3 с
264,5 до 179,5 км. Увеличение удельной нагрузки в два раза при прочих
равных условиях приводит к увеличению дальности на 94 км.
Путевая дальность дозвукового полета (при М < 0,7) составляет
ДА ~ 60 км. Этот участок примерно одинаков для всех четырех вариан-
тов задачи. Для рассматриваемой МКТС скорость отделения ВРУ, при
которой он может вернуться к точке старта в пассивном движении без
использования ВРД, равна -1350 м/с (Мо ~ 4,5) - см. рис. 10.24. Оче-
видно, что если максимум дозвукового аэродинамического качества
увеличится на , то удаление от точки старта уменьшится примерно
на и кривые на рис. 10.24 сдвинутся вниз на эту величину. Изме-
нение А?1пах при гиперзвуковых скоростях практически не влияет на
величину W, так как торможение происходит на больших углах атаки.
Здесь наиболее важным является увеличение баллистического коэффи-
циента сгх до возможно больших значений.
В заключение следует отметить, что суммарные затраты времени
на проведение расчетов траекторий с использованием приближенно
оптимального управления уменьшаются в десятки раз по сравнению с
вариантом использования оптимального управления.
ПРИЛОЖЕНИЯ
1. Алгоритм определения параметров
стандартной атмосферы
Данный алгоритм позволяет определять параметры атмосферы:
давление р, плотность р, температуру Г, скорость звука а и динамиче-
скую вязкость ц по заданной высоте Н, обеспечивая их непрерывное
изменение с точностью до 15-16-й значащей цифры при вычислении на
ЭВМ с двойной точностью. При вычислении с одинарной точностью в
исходных данных из приведенных таблиц достаточно использовать
первые 8 значащих цифр. Алгоритм также позволяет определять высоту
по заданной плотности или давлению.
Отличие расчетных значений давления и плотности от табличных
значений СА-81 (ГОСТ4401-81) в зависимости от диапазона изменения
высоты составляет: при 77<80км - не более 0,001 %, при
80 < Н < 120 км - не более 0,009 %, при Н > 120 км - не более 24-3 %.
В соответствии с СА-81 [21] атмосфера делится по высоте на два
диапазона: до 120 км и от 120 км и выше. Для каждого диапазона в
качестве исходных данных задаются табличные зависимости основных
параметров атмосферы от геометрической или геопотенциальной высо-
ты. Основные физические константы СА-81 приведены в табл. П.1.1 и
2.1 (см. раздел 2.3).
Таблица 7/. /. /
Основные константы стандартной атмосферы
Наименование Обозначе- ние Значение
Универсальная газовая постоянная Показатель адиабаты Эмпирические коэффициенты Сатер- лэнда для определения динамической вязкости Условный радиус Земли 91 к = Cp/cv 5 Ps Яу 8314,32 Дж-К ‘ кмоль’1 1,4 110,4 К 1,458 10 ° кгс'м'К’12 6356,767 км
Диапазон Н < 120 км
В табл. П.1.2 приведена кусочно-линейная зависимость молярной
массы Мот геометрической высоты Н. Эта зависимость, за исключени-
ем диапазона 77=944-97 км, полностью соответствует СА-81. В диапа-
зоне высот 944-97 км вместо предлагаемой в СА-81 нелинейной зависи-
мости используется кусочно-линейная зависимость (как и в остальных
460
Приложения
диапазонах). В узловых точках значения молярной массы соответству-
ют СА-81. Градиент у = dMIdH определен с двойной точностью. Здесь и
далее запись D-n означает, что число умножено на 10 , символ D ха-
рактеризует двойную точность числа.
Таблица П. 1.2
Зависимость молярной массы от геометрической высоты
Номер узла. слоя Геометрическая высота /7, км Молярная масса кг/кмоль Градиент у, кг/(кмоль м)
1 0 28,96442 0
э 94,0 28,96442 -0,84D-6
3 94,5 28,964 -0,80D-5
4 95,0 28,96 -0J5D-4
5 96,0 28,945 -0,35D-4
6 97,0 28,91 -0J2D-3
7 97,5 28,85 -0,1511111111111112D-3
8 120,0 25,45
Таблица П.1.3
Зависимость молярной температуры от геопотенциальной высоты
Номер узла, слоя Геопотенци- альная высота //[, км Молярная температура Гм, К Градиент осм, К/м
1 -2,0 301,15 -6,5D-3
2 0 288,15 -6,5D-3
3( изотерм.) 11,0 216,65 0
4 20,0 216,65 l,0D-3
5 32,0 228,65 2,8D-3
6( изотерм.) 47,0 270,65 0
7 51,0 270,65 -2,8D-3
8 71,0 214,65 -2,0D-3
9( изотерм.) 85,0 186,65 0
10 94,0 186,65 3,0D-3
1 1 102,45 212,0 1,10004627089383 ID-2
12 // = 120 км 380,600445438114
Приложения
461
Таблица И. 1 4
Давление в узловых точках
Номер узла, слоя Геопотенциальная высота Нг, км Давление р, Па Параметр слоя P, 1/м
1 -2,0 1,27774D5 -5,255927677553125
2 0 1,0132505 -5,255886024559558
3 (изотерм.) 11,0 2,2632D4 l,576884780967599D-4
4 20,0 5,47487D3 34,16323159488196
5 32,0 8,68014D2 12,201 12531015995
6 (изотерм.) 47,0 1J0906D2 l,262275505480996D-4
7 51,0 6,69384D1 -12,201 14366420981
8 71,0 3,95639D0 - 17,0816129309231 I
9 (изотерм.) 85,0 3,63409D-l 1,830335874671486D-4
10 94,0 6,99812D-2 1 1,38771932201187
11 102,45 1,64116D-2 3,105697086067708
12 Н = 120 км 2,66618D-3
Таблица П.Т5
Плотность в узловых точках
Номер узла Геопотенциальная высота /7Г, км Плотность р, кг/м
1 -2,0 1,478079263048531
2 0 1,225000001753089
3 11,0 3,639169985202466 D-1
4 20,0 8,803456423155455 D-2
5 32,0 1,322493739974550 D-2
6 47,0 1,427529564820696 D-3
7 51,0 8,615994177212568 D-4
8 71,0 6,421053722367223 D-5
9 85,0 6,782749611702112 D-6
10 94,0 1,306145299446210 D-6
11 102,45 2,696827469887370 D-7
12 Н = 120 км 2,440384595331594 D-8
В табл. П. 1.3 приведена кусочно-линейная зависимость молярной
температуры от геопотенциальной высоты Нг (полностью соответст-
вует СА-81). В соответствии с изломами этой зависимости в данном
диапазоне высот атмосфера состоит из 11 слоев, причем 3, 6 и 9-й слои
462
Приложения
являются изотермическими. Градиент молярной температуры ам опре-
делен с двойной точностью. В 12-м слое (при Н= 120 км) молярная
температура вычислена через термодинамическую температуру. Узло-
вые точки зависимостей Гм(Яг) и М(Н) совпадают только при Я=0 и
Н= 120 км.
В табл. П.1.4 приведена табличная зависимость давления от геопо-
тенциальной высоты. В 9, 10 и 11-м узлах давление определено при
помощи интерполяции табличных данных СА-81, в остальных узлах
давление соответствует СА-81. Параметр слоя р вычислен с двойной
точностью.
В табл. П.1.5 приведены значения плотности р в узловых точках;
плотность вычислена с двойной точностью при помощи уравнения
состояния идеального газа. Эти данные необходимы для решения об-
ратной задачи: определения высоты по заданной плотности.
Определение параметров атмосферы по заданной высоте Н
1. Молярная масса определяется с использованием табл. П.1.2:
Л/=Л/* + у(Я-Я*).
Здесь и далее индекс * соответствует нижней границе рассматриваемо-
го слоя.
г- тт ^уЯ
2. Геопотенциальная высота: Яг-—-----.
Ry +Н
3. Молярная температура определяется с использованием
табл. П. 1.3:
Гм = Тм + ам (Яг - Яг ).
4. Давление в изотермических слоях определяется с использовани-
ем табл. П. 1.4:
р =т/ехр[-ри (Яг - Яг*)] ;
в остальных слоях-с использованием табл. П.1.4 и П.1.3:
р=р^/Тм/.
5. Плотность: р = р M)/(S.KTM).
6. Термодинамическая температура: Т= М1\д/Мц.
7. Скорость звука (в СА-81 табличные значения указаны только до
высоты Я < 80 км):
а = jkp/p .
8. Динамическая вязкость (в соответствии с указанием в СА-81
пользоваться в диапазоне Я< 90 км):
Приложения
463
ц = ps Т'-5/(Г + S).
9. Кинематическая вязкость (Н < 90 км): v = ц/р.
Определение высоты Н по заданному давлению р или плотности р
1. Номер слоя определяется по табл. П. 1.4 или П. 1.5.
2. Геопотенциальная высота в изотермическом слое определяется с
использованием табл. П. 1.4: Нг = Нг - In (р //?*)/ри
или - табл. П.1.4 и П.1.5: Ну = Ну - In (р /р*)/ри •
В неизотермическом слое вначале определяется молярная темпера-
тура с использованием табл. П.1.3 и П.1.4: Тм = Тм* (р* /р)1ф
или-табл. П.1.3 и П.1.5: Тм = Тм*(р*/р)17(0+1 >,
затем определяется геопотенциальная высота с использованием
табл. П. 1.3:
Ну = Ну + (Тм-7м )/осм.
R Н
3. Геометрическая высота: Н= —-—— .
/?У-ЯГ
Диапазон Н > 120 км
В качестве определяющей задается кусочно-линейная зависимость
термодинамической температуры Гот геометрической высоты Н. Пред-
ставленная в табл. П.1.6 зависимость полностью соответствует СА-81.
В соответствии с изломами этой зависимости в данном диапазоне высот
атмосфера делится на 9 слоев. Градиент температуры а вычислен с
двойной точностью.
В табл. П.1.7 приведено давление в узловых точках (в соответствии
с СА-81). Параметры р и Но , необходимые для вычисления давления,
определены с двойной точностью (табл. П.1.8). В табл. П.1.9 приведена
плотность в узловых точках (в соответствии с СА-81). Параметры Р и
Но , необходимые для вычисления плотности, определены с двойной
точностью (табл. П. 1.10).
Определение параметров атмосферы по заданной высоте Н
1. Термодинамическая температура определяется в соответствии с
табл. П.1.6:
Т = Т* + а(Я-Я*).
2. Давление определяется в соответствии с табл. П. 1.7 и П. 1.8:
464
Приложения
3. Плотность определяется в соответствии с табл. П.1.9 и П.1.10:
* < аН~Н\
р"рю1р<“|5н7й;>'
Таблица П. 1.6
Зависимость термодинамической температуры
от геометрической высоты
Номер узла, слоя Геометрическая высота //, км Термодина- мическая темпера- тура Т, К Градиент а, К/м
12 120 334,42 11,259 D-3
13 140 559,6 6,8 D-3
14 160 695,6 3,97 D-3
15 200 854,4 1,75 D-3
16 250 941,9 0,57 D-3
17 325 984,65 0,15 D-3
18 400 995,9 0,02 D-3
19 600 999,9 0,5 D-6
20 800 1000,0 0
21 1200 1000,0
Таблица П.1.7
Давление в узловых точках
Номер узла Геометрическая высота Н, км Давление р, Па
12 120 2,66618 D-3
13 140 8,26375 D-4
14 160 3,03620 D-4
15 200 8,53026 D-5
16 250 2,47564 D-5
17 325 5,24406 D-6
18 400 1,45265 D-6
19 600 8,21535 D-8
20 800 1,70593 D-8
21 1200 4,43149 D-9
Приложения
465
Таблица П.1.8
Параметры слоя для вычисления давления
Номер слоя р //о*, м
12 22,00655962398671 235,7458777047127 03
13 2,802773519274416 -104,015727397608 D3
14 6,690930405104232 10,80901233274964 D3
15 8,646375256057025 99,45555051556521 D3
16 31,16295146372413 1180,953208809561 D3
17 1,200938671099512 03 69764,32340859188 D3
18 16,61672666605679 556,9299735909109 D3
19 4,65357310961568 -207,9024043336526 D3
20 3,776285422623049 -79,40697524967592 D3
Таблица П.1.9
Плотность в узловых точках
Номер узла Геометрическая высота Н, км Плотность р, кг/м3
12 120 2,440384595331594 D-8
13 140 4,24614 D-9
14 160 1,19204 D-9
15 200 2,51904 D-10
16 250 6,05679 D-11
17 325 1,10192 D-11
18 400 2,79396 D-12
19 600 1,13960 D-13
20 800 1,14006 D-14
21 1200 1,95503 D-15
Определение высоты Н по заданному давлению р или плотности р
Я* + Я0*1п(///?)/р
1-1п(//Г)/р
в соответствии с табл. П.1.7 и П.1.8 или
табл. П.1.9 и П.1.10.
Я* + /70,1п(р,/р)/р
1-1п(р’/р)/р
в соответствии с
Н =
Н =
466
Приложения
Таблица П.1.10
Параметры слоя для вычисления плотности
Номер слоя ₽ Но*, м
12 16,0893342329255 44,0116026805006 D3
13 4,1 11713581522323 -95,2661499184306 D3
14 8,850928814221856 27,76841515671727 D3
15 11,64982921853066 158,6847704636391 D3
16 28,647797454253 935,8134643877558 D3
17 233,2110882694398 12346,75409500959 D3
18 33,47756731095902 1492,76146456588 D3
19 9,375351320689388 14,4754201880754 D3
20 3,639066851005604 -374,468670879756 D3
2. Газодинамические функции
1. Приведенная скорость:
, (Аг + 1)/2
Л - Ишкр — М /----------—
у1+(£-1)М2/2
где <2Кр - скорость звука в критическом сечении потока; к = сР1с\'- от-
ношение теплоемкостей (для воздуха к= 1,4).
2. Число Маха:
М = Via = Л.
2 /(£ + 1)
l-(jl-l) V/(£ + l)
где а - местная скорость звука.
3. Функции, связывающие параметры потока с параметрами тор-
можения (обозначены *):
к
т(Х) = Т/Т* = 1-^-Л.2; ъ(Х)=р/р' = (1-^—U2!*"1 ;
£+1 V £+1 J
1
( к — \ \к-\
£(Х) = р/р = 7Г(Х)/т(Х) = 1---X2
к £ + 1 )
Приложения
467
4. Безразмерная плотность тока:
^(Х) - рИ/(рКр^кр) -FKP/F- —-— XI 1 — —----X
V 2 ) v к +1 )
где индекс "кр" соответствует критическому сечению, или
k+]
2(А-1)
2 ( к— \ п
?(М) = м ч 1+-у-м2
5. Функция, характеризующая расход газа:
1
y(k)=p,FK?l(pF) = q(X')ln(X)= р-22-Y '--Д-j—•
к + \
6. Расход газа:
е = ргл = „£^в>
Vz” Vr*
| Гй~
I к f 2 1 q-j j—j 7 1/1
где т=л------ ---- ; sJir-газовая постоянная. При к = 1,4
y9irU + lJ
и Э1Г = 287,05 Дж/(кг-К), что соответствует сухому воздуху в нормаль-
ных условиях, имеем т = 0,040415.
ЛИТЕРАТУРА
1. Абрамович ГН. Прикладная газовая динамика. - М.: Наука, 1991.
2. Авиационно-космические системы: Сб. статей под ред. Г.Е. Лозино-
Лозинского и А.Г. Братухина - М.: Изд-во МАИ, 1997.
3. Авиационные правила. Часть 25. Нормы летной годности самолетов
транспортной категории, 1994.
4. Авиация: Энциклопедия / Гл. редактор Г.П. Свищев. - М.: Большая Рос-
сийская энциклопедия, 1994.
5. Алемасов В.Е., Дрегалин А.Ф., Тишин А. П. Теория ракетных двигателей /
Под ред. акад. В.П. Глушко - М.: Машиностроение, 1980.
6. Андреевский В.В. Динамика спуска космических аппаратов на Землю. -
М.: Машиностроение, 1970.
7. Аппазов Р.Ф., Сытин О.Г. Методы проектирования траекторий носителей
и спутников Земли. - М.: Наука, 1987.
8. Аржанников Н.С., Садекова ГС. Аэродинамика больших скоростей. - М.:
Высшая школа, 1965.
9. Веллман Р, Дрейфус С. Прикладные задачи динамического программиро-
вания. - М.: Наука, 1965.
10. Беляев А.Я., Борисов Н.Н., Пршпуманов С.Н., Смоляров В.А., Уваров И.М.,
Бузулук В.И., Володин С.В., Губанов А.А., Коваленко В.В., Червоненко К.А.
Особенности определения облика одноступенчатого ВКС с ракетным дви-
гателем, использующим сжиженный атмосферный воздух // Первый меж-
дународный аэрокосмический конгресс 1АС'94. Москва, 1994.
11. Брайсон А., Хо Ю-Ши. Прикладная теория оптимального управления. -
М.: Мир, 1972.
12. Бузулук В.И., Володин С.В., Гурылев В.Г. Некоторые проблемы формиро-
вания облика силовой установки ВКС с гиперзвуковыми ВРД // Первый
международный аэрокосмический конгресс IAC94. Москва, 1994.
13. Бузулук В.И., Володин С.В. О применении ГРПД в силовой установке
одноступенчатого ВКС // Международная конференция "Аэрогазодинами-
ка силовых установок летательных аппаратов”. ЦАГИ, г. Жуковский,
1993.
14. Бузулук В.И., Володин С.В., Семенов А.А., ДулеповН.П., ЛаншинА.И.
Сравнительный анализ различных схем ракетно-турбинного двигателя для
одноступенчатого ВКС // Авиакосмическая техника и технология, 1997,
№ 1.
15. Бузулук В.И., Гурылев В.Г, Зеленко Ю.И. Исследование теплового состоя-
ния конструкции ГПВРД и возможности ее охлаждения криогенным топ-
ливом // Международная конференция ’’Исследование гиперзвуковых те-
чений и гиперзвуковые технологии”. Секц. 7. ЦАГИ, г. Жуковский, 1994.
16. Бузулук В.И., Давидсон Б.Х., Забалуев В.Ф., Илларионов В.Ф., Плохих В.П.,
Скипенко В.В., Сонин В,В. О пространственном движении летательного
аппарата с ракетным двигателем в атмосфере // Первый международный
аэрокосмический конгресс IAC94. Москва, 1994.
Литература
469
17. Бузулук В.И., Илларионов В.Ф. Об оптимизации соотношения компонен-
тов топлива в процессе движения аппарата с ЖРД // ТВФ, 1995, т. LXIX,
№ 3-4.
18. Бузулук В.И., Лазарев В.В., Плохих В.П. Концепция летающей
лаборатории-демонстратора гиперзвуковых технологий // Сб. статей
"Проблемы создания перспективной авиационно-космической техники". -
М.: Физматлит, 2005.
19. Бузулук В.И., Ланшин А.И., Тюриков В. Е., Червоненко К.А. Влияние пара-
метров двигательной установки воздушно-космического самолета типа
"Interim HOTOL" на массу полезной нагрузки // Труды первой междуна-
родной авиакосмической конференции. Москва, 1992. - М.: Российская
инженерная академия, 1995, т. 2.
20. Бузулук В.И., Червоненко КА. О расчете траекторий выведения на орбиту
крылатых ЛА с ЖРД с использованием приближенно оптимального
управления // Авиакосмическая техника и технология, 2003, № 3.
21. Бюшгенс Г.С., Бедржицкий Е.Л. ЦАГИ - центр авиационной науки.-
М.: Наука, 1993.
22. Бюшгенс ГС., Студнев Р В. Динамика самолета. Пространственное
движение. - М.: Машиностроение, 1983.
23. Ваганов А. В., Задонский С. М., Киреев А.Ю., Падерин Л.Я., Пляшеч-
ник В.И., Скуратов А.С, Степанов Э.А., Кобзев В.И., Ярошевский В. А.,
Лаврухин ГН., Юдин В. М. Формирование облика и определение аэроди-
намических характеристик перспективного крылатого возвращаемого ап-
парата // 4-я международная конференция "Авиация и космонавтика-
2005". МАИ, Москва, 2005.
24. Водород. Свойства, получение, хранение, транспортирование, примене-
ние: Справ, изд. / Д.Ю. Гамбург, В.П. Семенов, Н.Ф. Дубовкин,
Л.Н. Смирнова; Под ред. Д.Ю. Гамбурга, Н.Ф. Дубовкина - М.: Химия.
1989.
25. Володин С.В., Бузулук В.И. Взаимосвязь параметров управления траекто-
рией и аэродинамической компоновки воздушно-космического самолета
при использовании гиперзвукового ВРД // Труды первой международной
авиакосмической конференции. Москва, 1992. - М.: Российская инженер-
ная академия, 1995, т. 3.
26. Володин С.В. О применении линейных ЖРД в силовой установке одно-
ступенчатого орбитального самолета, стартующего с дозвукового самоле-
та-носителя // Труды первой международной авиакосмической конферен-
ции. Москва, 1992. - М.: Российская инженерная академия, 1995, т. 2.
27. Горбатенко С.А., Макашов Э.М., Полушкин Ю.Ф., ШефтельЛ.В. Меха-
ника полета (Общие сведения. Уравнения движения): Инженерный спра-
вочник. - М.: Машиностроение, 1969.
28. ГОСТ 20058-80. Динамика летательных аппаратов в атмосфере. Термины,
определения и обозначения. - М.: Изд-во стандартов, 1989.
29. ГОСТ4401-81. Атмосфера стандартная. Параметры. - М.: Изд-во стан-
дартов, 1981.
30. Гревцов Н.М., Ефимов О.Е., Мельц П О., Трубецкой А.Б. Соотношение
условий оптимальности стационарного и нестационарного режимов поле-
470
Литература
та в методе сингулярных возмущений // Ученые записки ЦАГИ, 1995,
т. XXVI, № 1-2.
31. Давидсон Б.Х. Терминальное управление с использованием семейства
попадающих траекторий в пространстве оскулирующих элементов орби-
ты // Сб. статей "Проблемы создания перспективной авиационно-
космической техники". - М.: Физматлит, 2005.
32. Денисов В. Е. Исследование оптимальных режимов разгона в атмосфере
гиперзвуковых аппаратов с ВРД: Диссертация на соискание ученой степе-
ни кандидата технических наук. - ЦАГИ, г. Жуковский, 1967.
33. Дмитриев В.Г, Ермак Ю Н., Жирников Б.Л., Плохих В.П., Бузулук В. И.
Предварительное формирование облика гиперзвукового летательного ап-
парата для обслуживания спутников на геостационарной орбите // Меж-
дународная конференция МНТЦ "Системы и технологии будущего изуче-
ния и освоения космического пространства". Москва, 2003.
34. Дудар Э.Н. Многоразовый орбитальный самолет вертикального и гори-
зонтального старта // Четвертый международный аэрокосмический кон-
гресс 1АС’2ООЗ. Москва, 2003.
35. Дудар Э.Н., Ярошевский В.А. Управление боковым траекторным движени-
ем космического аппарата в атмосфере // Космические исследования,
1984, т. 22, вып. 2.
36. Желнин Ю.Н., Шилов А.А. Траектории минимальной дальности при входе
космического аппарата в атмосферу Земли со сверхкруговой скоростью //
Ученые записки ЦАГИ, 1970, т. I, № 1.
37. Забалуев В.Ф., Илларионов В.Ф., Скипенко В.В., Сонин В.В. Пространст-
венная задача о возврате отработавшей ступени // Сб. статей "Динамика и
характеристики заметности летательных аппаратов". Труды ЦАГИ, 2002,
вып. 2657.
38. Забалуев В.Ф., Илларионов В.Ф., Сонин В.В. Решение задачи оптимально-
го выведения летательного аппарата // Международная конференция
"Авиационные технологии 2000". ЦАГИ, г. Жуковский, 1997.
39. Зуев В.С, Макарон В.С. Теория прямоточных и ракетно-прямоточных
двигателей. -М.: Машиностроение, 1971.
40. Илларионов В.Ф., Бузулук В. И. Оптимизация траектории полета дозвуко-
вого самолета-носителя перед стартом воздушно-космического аппарата с
ЖРД // Авиакосмическая техника и технология, 1998, № 1.
41. Илларионов В.Ф., Пашшщев В Т. Анализ траекторий полета и законов
управления движением возвращаемых ступеней разгонных систем // Тру-
ды ЦАГИ, 1972, вып. 1438.
42. Илларионов В.Ф., Скипенко В.В., Сонин В.В. Анализ управления углами
крена и атаки при возвращении первой ступени воздушно-космического
самолета к месту старта // Труды первой международной авиакосмиче-
ской конференции. Москва, 1992. - М.: Российская инженерная академия,
1995, т. 3.
43. Ильин В.А., Филатьев А С. Синтез оптимальных траекторий выведения на
орбиту, с любой точки которых возможен спуск в атмосфере с выполнени-
ем заданных ограничений // Космические исследования, 1985, т. 23,
вып. 1.
Литература
471
44. Ильин В.А. Элементарная теория ступенчатых ракет // Труды ЦАГИ, 1960.
45. Иродов Р.Д. Расчет оптимальных неустановившихся виражей самолета в
горизонтальной плоскости // Труды ЦАГИ, 1958, вып. 727.
46. Исследование оптимальных режимов движения ракет: Сб. статей под ред.
И.Н. Садовского-М.: Оборонгиз, 1959.
47. Козин Р.В., Лосева Г.М., Федоров Л И. Расчет характеристик полного
взлета самолета // Труды ЦАГИ, 1994, вып. 2547.
48. Копнин Ю.М. К задаче о повороте плоскости орбиты спутника И Космиче-
ские исследования, 1965, т. 111, вып. 4.
49. Космонавтика: Энциклопедия / Гл. редактор В.П. Глушко. - М.: Сов.
энциклопедия, 1985.
50. Краснов И. Ф. Основы аэродинамического расчета. - М.: Высшая школа,
1981.
51. Кротов В. Ф., Саргин В.И. Об оптимальных траекториях подъема самоле-
та // Кн.: Вопросы аналитической и прикладной механики / Под ред.
В.В. Добронравова - М.: Оборонгиз, 1963.
52. Кротов В. Ф., Хрусталев М М. Оптимальное управление тягой и углом
атаки летательного аппарата при маневре подъем - разгон // Кн.: Пробле-
мы аналитической механики, теория устойчивости и управляемости. -
М.: Наука, 1975.
53. Курзинер Р.И. Реактивные двигатели для больших сверхзвуковых скоро-
стей полета. - М.: Машиностроение, 1989.
54. Ланшин А.И., Нечаев Ю.А., Скороделов В.А., Шведов А.Г. Применение
криогенных топлив как основа становления гиперзвуковой авиации и аэ-
рокосмических систем // Авиакосмическая техника и технология, 1998,
№ 1.
55. Лапин М.С., Мельц И.О. Применение прямого метода для оптимизации
управляющих функций динамической системы и их ограничений // Труды
ЦАГИ, 1970, вып. 1190.
56. Лебедев А.А., Чернобровкин Л.С. Динамика полета беспилотных лета-
тельных аппаратов. - М.: Машиностроение, 1973.
57. Лозино-Лозинский Г.Е., ДударЭ.Н. Сравнительный анализ многоразовых
космических транспортных систем // Проблемы машиностроения и на-
дежности машин. М.: Наука, 1995, № 4.
58. Ломов С.А. Введение в общую теорию сингулярных возмущений. - М.:
Наука, 1981.
59. Лоуден Д.Ф. Оптимальные траектории для космической навигации: Пер. с
англ.-М.: Мир, 1966.
60. Лох У. Динамика и термодинамика спуска в атмосфере планет: Пер. с
англ. - М.: Мир, 1966.
61. Мартин Дж. Вход в атмосферу. Введение в теорию и практику: Пер. с
англ. - М.: Мир, 1969.
62. Методы оптимизации с приложениями к механике космического полета /
Под ред. Дж. Лейтмана. - М.: Наука, 1965.
63. Миеле А. Механика полета, т. 1. Теория траекторий полета: Пер. с англ. -
М.: Наука, 1965.
472
Литература
64. Микеладзе В.Г., Титов В. М. Основные геометрические и аэродинамиче-
ские характеристики самолетов и ракет: Справочник. -
М.: Машиностроение, 1990.
65. Москаленко ГМ. Инженерные методы проектирования в ракетодинами-
ке. - М.: Машиностроение, 1974.
66. Нейланд В.Я., Тулин А. М. Аэротермодинамика воздушно-космических
самолетов: Конспект лекций. - ФАЛТ МФТИ, г. Жуковский, 1991.
67. Некоторые результаты исследований перспективных одноступенчатых
воздушно-космических аппаратов в США // ТИ ЦАГИ, 1981, № 1-2.
68. Нечаев Ю.Н. Силовые установки гиперзвуковых и воздушно-космических
летательных аппаратов. - М.: Изд-во Российской академии космонавтики
им. К.Э. Циолковского, 1996.
69. Одиненко НА., Плохих В.П., Ширанов Ю.В., ШкадовЛ.М. Построение
программы управления углом крена орбитального самолета при спуске в
атмосфере // Ученые записки ЦАГИ, 1978, т. 9, № 2.
70. Основы проектирования летательных аппаратов (транспортные системы) /
Под ред. В.П. Мишина - М.: Машиностроение, 1985.
71. Остославский И.В., Стражева И. В. Динамика полета. Траектории лета-
тельных аппаратов. - М.: Машиностроение, 1969.
72. Охоцимскии Д.Е., Сихарулидзе Ю.Г Основы механики космического
полета. - М.: Наука, 1990.
73. ОхоцимскииД.Е., Энеев ТМ. Некоторые вариационные задачи, связанные
с запуском искусственного спутника Земли // Успехи физических наук,
1957, т. LXI1I, вып. 1а.
74. Паишнцев ВТ, Балабанов О. В. Оптимизация траекторий полета самолета
с ЖРД на заключительном этапе разгона до околокруговых скоростей //
Труды ЦАГИ, 1990, вып. 2468.
75. Пашинцев В.Т., Балабанов О.В. Оптимизация управления движением
крылатого одноступенчатого ВКС с комбинированной двигательной уста-
новкой // Труды первой международной авиакосмической конференции.
Москва, 1992. - М.: Российская инженерная академия, 1995, т. 3.
76. Паишнцев В Т, Балабанов О.В. Управление углом атаки самолета с ком-
бинированной силовой установкой в режиме отслеживания программной
траектории // Труды ЦАГИ, 1990, вып. 2468.
77. Плохих В.П., Бузулук В.П. О перспективах развития многоразовых систем
выведения горизонтального старта // Сб. статей "Проблемы создания пер-
спективной авиационно-космической техники". - М.: Физматлит, 2005.
78. Плохих В.П., Лазарев В.В., Бузулук В.П. Исследования в области авиаци-
онно-космических систем // Сб. статей "ЦАГИ - основные этапы научной
деятельности. 1993-2003". -М.: Физматлит, 2003.
79. Понтрягин Л.С, Болтянский В.Г, Гамкрелидзе Р.В., Мищенко Е.Ф. Мате-
матическая теория оптимальных процессов. - М.: Наука, 1961.
80. Программа МВКА "Спейс Шаттл"//ТИ ЦАГИ, 1976,№ 17-18.
81. Проектирование самолетов / Под ред. С.М. Егера - М.: Машиностроение,
1983.
82. Проспект НПО "Молния" по многоцелевой авиационно-космической
системе МАКС, 1997.
Литература
473
83. Руководство для конструкторов по проектированию самолетов. Т. I. кн. 3.
вып. 4. Приближенные методы расчета летных характеристик дозвуковых
неманевренных самолетов. - 1981.
84. Руководство для конструкторов по проектированию самолетов. Т. 5. кн. 3,
вып. 1. Расчет взлетно-посадочных характеристик самолета. - 1978.
85. Руководство для конструкторов по проектированию самолетов. Т. 5, кн. 3.
вып. 2. Алгоритмы и программы расчета характеристик траектории само-
лета при заданном профиле полета. - 1978.
86. Сихарулидзе ЮГ. Баллистика летательных аппаратов. - М.: Наука, 1982.
87. Скрипниченко С.Ю. Модифицированный энергетический метод определе-
ния оптимальных режимов набора высоты и снижения самолета. - М.:
ОНТЭИ Гос.НИИ гражданской авиации, 1969.
88. Скрипниченко С.Ю. Оптимизация режимов полета по экономическим
критериям. - М.: Машиностроение, 1988.
89. Скрипниченко С.Ю. Оптимизация режимов полета самолета. - М.: Маши-
ностроение, 1975.
90. Теория и расчет воздушно-реактивных двигателей / Под ред.
С.М. Шляхтенко - М.: Машиностроение, 1987.
91. Торенбик Э. Проектирование дозвуковых самолетов: Пер. с англ. / Пер.
Е.П. Голубков. - М.: Машиностроение, 1983.
92. Федоров Л.П., Козин Р.В., Литвиненко П.В. Об использовании энергети-
ческого метода в механике полета // Труды ЦАГИ, 1981, вып. 2102.
93. Федоров Л.П., Козин Р.В. Оптимизация взлетной дистанции самолета //
Труды ЦАГИ, 1976, вып. 1767.
94. ФедоровЛ.П. Некоторые вопросы оптимизации траектории полета даль-
них самолетов // Труды ЦАГИ, 1973, вып. 1488.
95. ФедоровЛ.П. Определение оптимального режима работы двигателей при
выборе наивыгоднейшей траектории набора высоты самолета // Труды
ЦАГИ, 1969, вып. 1132.
96. ФедоровЛ.П. Приближенные методы оптимизации характеристик участка
набора высоты самолета // Труды ЦАГИ, 1987, вып. 2366.
97. Федоров Л.П. Расчетное исследование траектории самолета с учетом
оптимизации тяги и изменения его массы //Труды ЦАГИ. 1981, вып. 2102.
98. Филатъев А С. Анализ оптимального закона управления возвращением
гиперзвуковых летательных аппаратов // Ученые записки ЦАГИ, 1976.
т. VII, №5.
99. Филатьев А.С. Исследования оптимальных траекторий крылатого носи-
теля МВКС на участке возвращения // Труды ЦАГИ, 1977, вып. 1838.
100. Филатьев А.С. Оптимальный запуск искусственного спутника Земли с
использованием аэродинамических сил // Космические исследования,
1991, т. 29, вып. 2.
101. ФилатъевА С. Оптимизация ветвящихся траекторий авиакосмических
систем // Труды первой международной авиакосмической конференции.
Москва, 1992. - М.: Российская инженерная академия, 1995, т. 3.
102. ФилатъевА С. Практический путь повышения эффективности космиче-
ских транспортных систем на основе внедрения строгих методов сквоз-
ной оптимизации // Авиакосмическая техника и технология, 1999, № 1.
474
Литература
103. ФилатьевАС. Приближенное построение замкнутой границы области
земной поверхности, достижимой летательным аппаратом // Ученые за-
писки ЦАГИ, 1980, т. XI, № 6.
104. Филатьев А.С. Приближенный аналитический синтез оптимального
управления гиперзвуковыми летательными аппаратами при движении в
атмосфере с докруговой скоростью // Ученые записки ЦАГИ, 1980, т. XI,
№1,2.
105. Филатьев АС Снижение с помощью малых управляющих воздействий
максимальных динамических и тепловых нагрузок при пассивном движе-
нии гиперзвуковых аппаратов // Ученые записки ЦАГИ, 1978, т. IX, № 2.
106. ЦАГИ - основные этапы научной деятельности. 1968-1993. - М.: Наука.
Физматлит, 1996.
107. Чепмен Д Р. Приближенный аналитический метод исследования входа тел
в атмосферы планет. - М.: ИЛ, 1962.
108. Шилов А.А., Желнин Ю Н. О минимуме максимальной перегрузки //
Космические исследования, 1996, т. IV, вып. 4.
109. Широкопояс В.А. Исследование оптимальных режимов полета самолетов
методом динамического программирования с использованием в качестве
первого приближения опорной траектории // Труды ЦАГИ, 1973,
вып. 1460.
110. Широкопояс В.А. О возможности упрощения дифференциальных уравне-
ний движения в задаче о максимальной скороподъемности самолета //
Ученые записки ЦАГИ, 1980, т. XI, № 1.
111. Шкадов Л.М., Буханова Р.С, Илларионов В.Ф., Плохих В.П. Механика
оптимального пространственного движения летательных аппаратов в ат-
мосфере. - М.: Машиностроение, 1972.
1 12. Шкадов Л.М., Глушков П.И., Кажан В. Г, Ски пен ко В. В., Чернышев С.Л.
Возможные концепции гиперзвукового пассажирского самолета // ТВФ,
1994, том LXVIIl,№4-6.
113. Шкадов Л. М., Лазарев В.В., Плохих В.П., Бузулук В.И. Летные исследова-
ния гиперзвуковых технологий И 5-й международный научно-технический
симпозиум "Авиационные технологии 21 века". - ЦАГИ, г. Жуковский,
1999.
114. Шкадов Л.М. Лекции по оптимизации режимов полета и параметров
самолета. - ЦАГИ, г. Жуковский, 1970.
115. Шкадов Л. М., Плохих В. П., Бузулук В. И., Лозино-Лозинский Г.Е., Андре-
ев 10.В., Казаков М.И. Многоразовые космические транспортные системы
горизонтального старта // Авиакосмическая техника и технология, 1999,
№ 1.
1 16. Штехер М.С. Топлива и рабочие тела ракетных двигателей. - М.: Маши-
ностроение, 1976.
1 17. Янова О.В. Оптимизация выведения авиакосмической системы с учетом
ограничений на участке возвращения самолета-носителя // Труды первой
международной авиакосмической конференции. Москва, 1992.-М.: Рос-
сийская инженерная академия, 1995, т. 3.
Литература
475
118. Ярошевский В.А. Алгоритмы управления траекторным движением косми-
ческих летательных аппаратов на этапе входа в атмосферу // Авиакосми-
ческая техника и технология, 1999, № 1.
119. Ярошевский В.А. Вход в атмосферу космических летательных аппара-
тов. - М.: Наука, 1988.
120. Ярошевский В.А. К определению ширины входа в атмосферу для задачи
выведения космического летательного аппарата на околопланетную орби-
ту после торможения в атмосфере // Сб. статей "Проблемы создания пер-
спективной авиационно-космической техники". - М.: Физматлит, 2005.
121. Anfimov N.A. Russian "Oryol" Program. Overview (TSNHMASH, Russia) //
Presented at the AIAA 8-th International Space Planes and Hypersonic Tech-
nologies and Systems Conference, Norfolk, VA, 1998.
122. Bryson A . E., Denham W.F. A steepest-ascent method for solving optimum
programming problems // Journal of Applied Mechanics, 1962, No 2. (Брай-
сон A.E., Денхем В.Ф. Метод наискорейшего подъема для решения задач
оптимального программирования: Пер. с англ. - Министерство радиопро-
мышленности СССР, 1965, № 2377.)
123. Bryson А. Е., Denham W.F., Dreyfus S.E. Optimal programming problems with
inequality constraints // AIAA Journal, 1964, Vol. 1, No 11.
124. Bryson A.E., Dessai M.N., Hoffman W.C. The energy state approximation in
performance optimization of supersonic aircraft // AIAA Paper, 1968, No 877.
(См. также Экспресс-информацию "Воздушный транспорт", М.:
ВИНИТИ, 1969, №20).
125. Buzuluk V, Volodin S., Chervonenko К. On the efficiency of using dual-fuel
rocket engine for the single stage-to orbit vehicle // Research in hypersonic
flows and hypersonic technologies. Sec. 1. TsAGI, 1994.
126. Filatyev A., Golikov A. and Yanova O. Optimization of Aerospace System
Control with Constraints on Return Trajectories of Spent Elements // Proceed-
ings of the 4-th ESA International Conference on Spacecraft Guidance, Navi-
gation and Control Systems, ESTEC, Noordwijk, The Netherlands, 18-21 Oc-
tober 1999.
127. Filatyev AS. Optimization of Branched Trajectories for Aerospace Transport
Systems // ICAS-94-5.2.3, 19-th ICAS Congress, 18-23 September 1994, Ana-
heim CA, USA.
128. Filatyev A S. "Paradoxes" of optimal solutions in problems of space vehicle
injection and reentry // Acta Astronautica, 2000, Vol. 47, issue 1. (см. также
IAF-97-A.6.09, 48-th IAF Congress, Turin, Italy, October 6-10, 1997.)
129. Heppenheimer 7. A. The National Aerospace Plane / Published by Pasha Publi-
cations, 1987.
130. Kemp N.M. and Riddell F.R. Heat Transfer to Satellite Vehicles Re-entering the
Atmosphere // "Jet Propulsion", 1957, Vol. 27, No 2.
131. Kuczera H, Hauck H, Krammer P, Sacher P.W. The German Hypersonics
Technology Programme. Status and Perspectives // 44-th IAF Congress, 1993.
132. Lozino-Lozinsky G.E., Skorodelow V.A., Plokhikh VP. International Reusable
Aerospace System MAKS. Present State of the Art and Perspectives //
A1AA/DGLR 5-th International Aerospace Planes Hypersonics Technologies
Conference, Germany, 1993.
476
Литература
133. Malta М., Kobauashi S. Japanese Spaceplane and Hypersonic Technology
Program Overview. Progress of 1995-1996 // Int. Workshop on Space-
plane/RLV Technology Demonstrators, Tokyo, 1997.
134. Miva^i H., Monji T, Kishi K. Combined Cycle Engine Research in Japanese
HYPR Project /7 Al A A 95-2751, San Diego, 1995.
135. Orton G. Hypersonic Aircraft Studies: the AGV Project (Avion a Grande
Vitesse) /7 Toward Mach 5: Hypersonic Flight, London, 1997.
136. Parkinson R. The An-225/1 nterim HOTOL Launch Vechicle // AIAA-91-5006.
137. PoukhovA. Russian Aerospace Plane Tu-2000 // A1AA-93-5055, Munich,
1993.
138. Rausch V, Hunt J. NASA Hyper-X Program //AIAA 7-th Int. Space Planes and
I lypersonic System & Technologies Conference, Norfolk, USA, 1996.
139. Salkeld R Contribution to the Discussion of Mixed-Mode Propulsion and
Reusable One-Stage-To-Orbit Vehicles // Presented at the 23-rd International
Astronautical Congress. SP-3677, Vienna, Austria, 1972.
140. Shkadov L.M.. Denisov VEu., Lazarev VV, Plokhikh VP, Buzuluk V.I., Vo-
lodin S.V., Chervonenko K.A., SkipenkoVV Comparative analysis of various
concepts for reusable aerospace systems // Acta Astronautica, 1995, Vol. 35,
No 1.
141. Shkadov L.M., Lazarev VV, Plokhikh VP, Buzuluk VI. Flight Test for Hyper-
sonic Technologies Development and Launching to Orbit of Small Payloads //
1AF-96-V.4.07. 47-th 1AF Congress, Beijing, China, October 7-11, 1996.
Научное издание
Бузулук Валентин Иванович
О11ТИМИЗА1 (ИЯ ТРАЕКТОРИЙ ДВИЖЕНИЯ АЭРОКОСМИЧЕСКИХ
ЛЕТАТЕЛЬНЫХ АППАРАТОВ
Редактор А.П. Дьячевский
Компьютерная верстка и макет обложки: В.И. Бузулук
11одписано в печать 28.03.2008. Формат 60x90/16. Печать офсетная.
Бумага офсетная. Печ. л. 30. Тираж 1000 экз. Заказ №161
Изготовлено в ООО ’’Марийское рекламно-издательское
полиграфическое предприятие"
424020. г. Йошкар-Ола. ул. Машиностроителей. 8Г