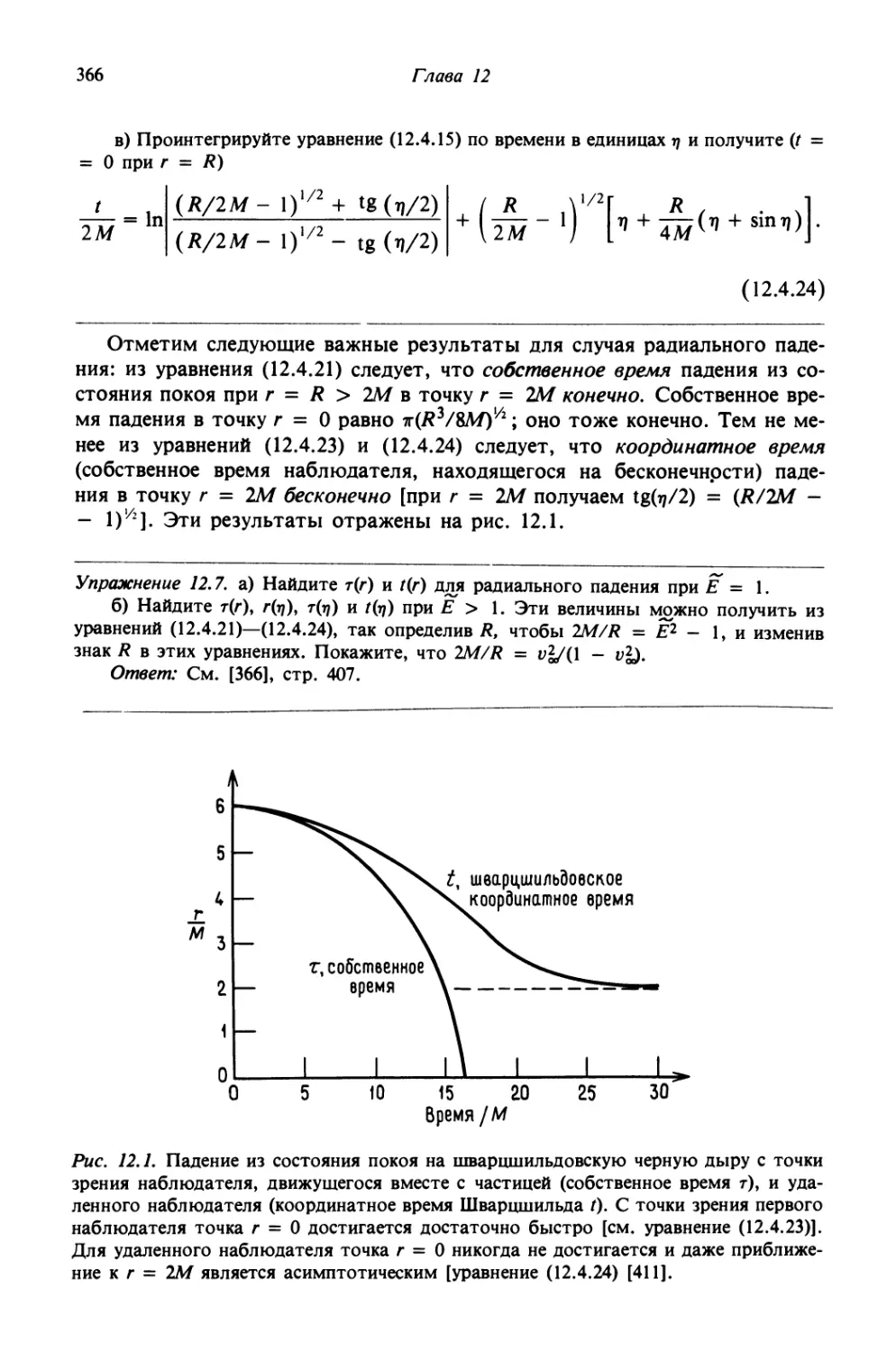
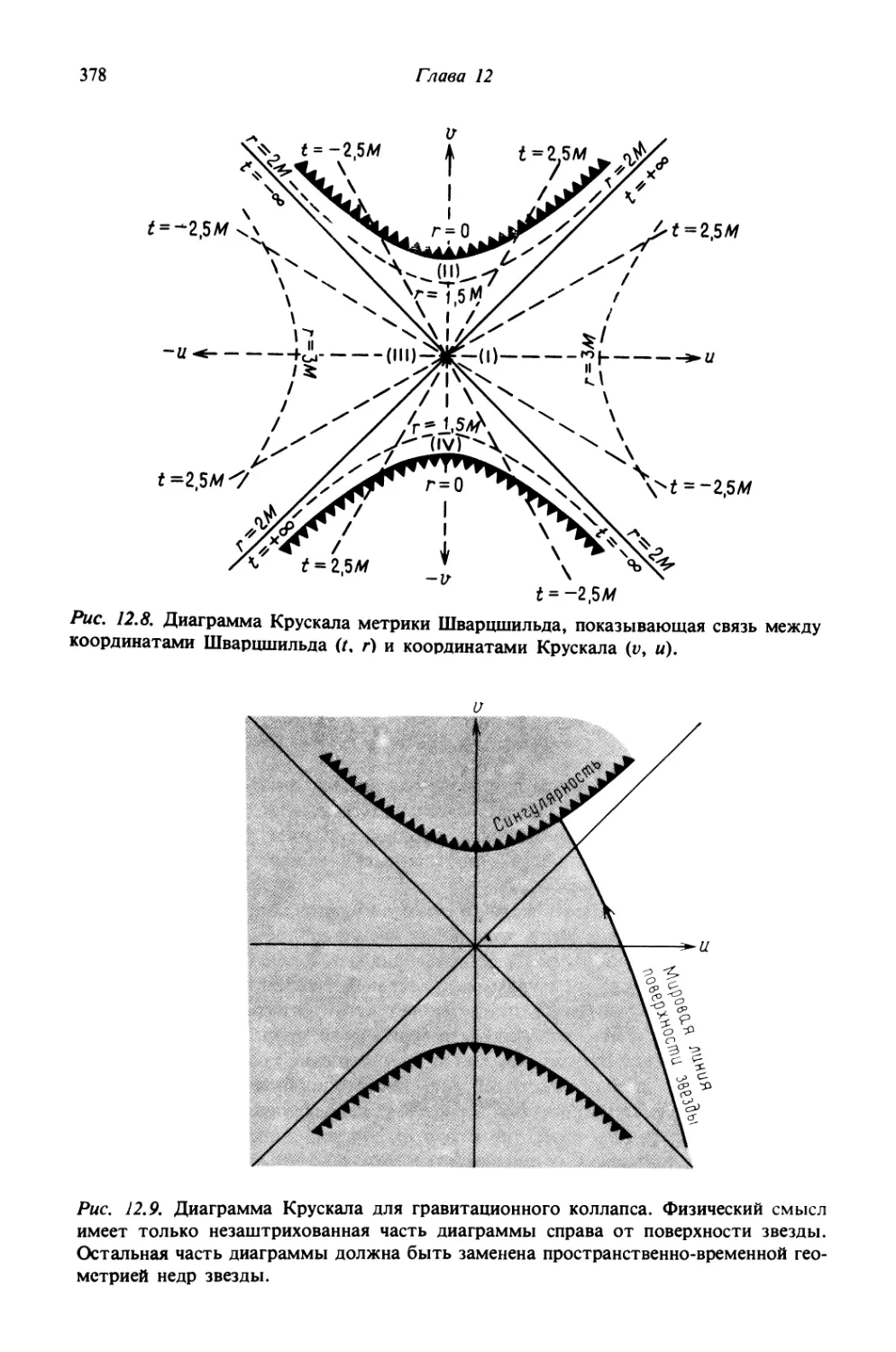
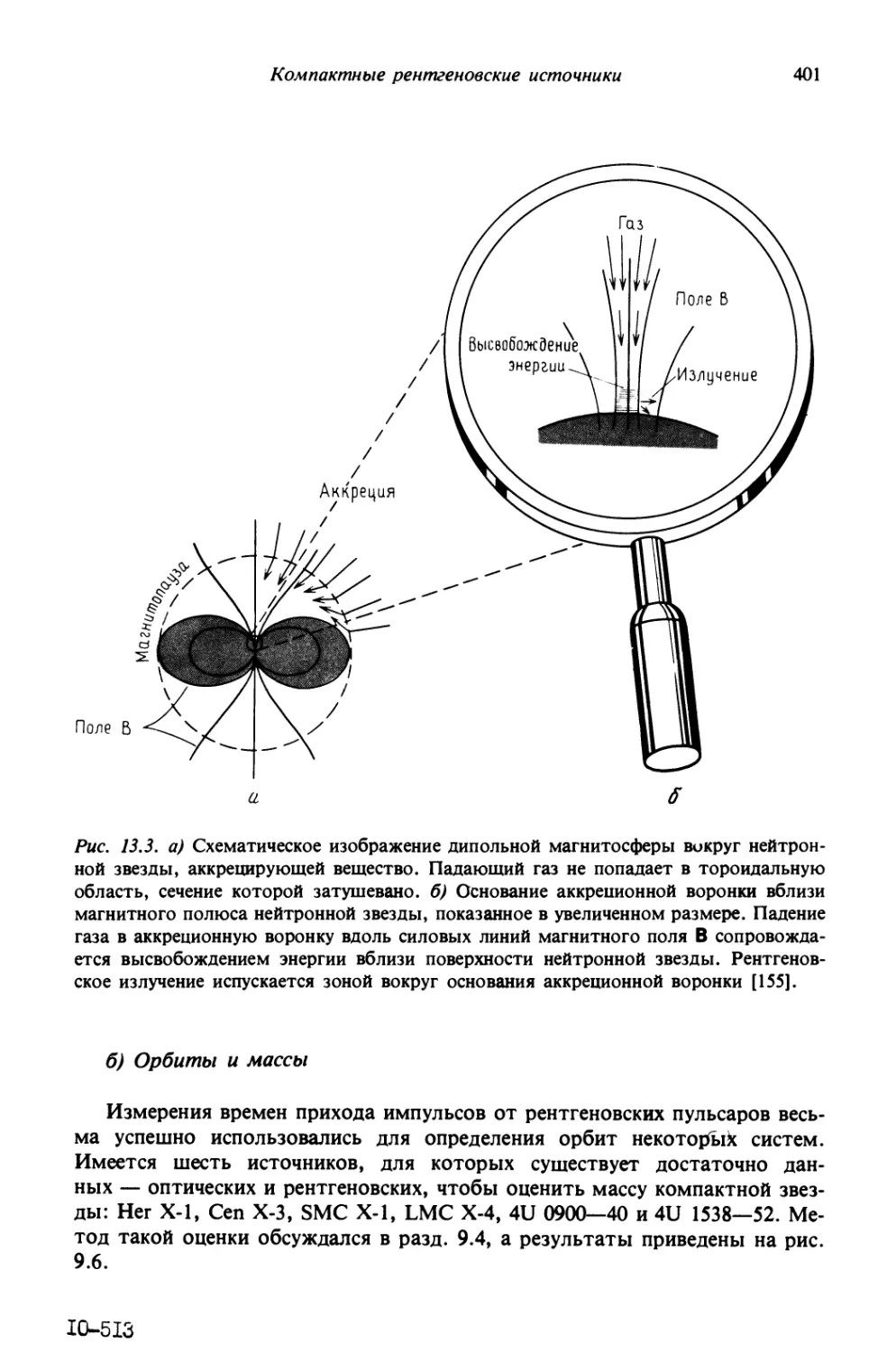
Автор: Шапиро С.Л. Тьюколски С.А.
Теги: астрономия астрофизика исследование космического пространства геодезия звезды
Год: 1985
Текст
Black Holes,
White Dwarfs,
and Neutron Stars
The Physics of
Compact Objects
Stuart L. Shapiro
Saul A. Teukolsky
Cornell University, Ithaca, New York
A Wiley-Interscience Publication
John Wiley & Sons
New York · Chichester · Brisbane · Toronto · Singapore
СШапиро, С.Тьюколски
ЧЕРНЫЕ ЛЫРЫ
БЫЫЕ тттА и
НЕЙТРОННЫЕ ЗВЕЗЛЫ
ФИЗИКА
КОМПАКТНЫХ ОБЪЕКТОВ
? в двух частях
Перевод с английского
д-ра физ.-мат. наук
А. Д. Долгова
под редакцией
д-ра физ.-мат. наук
Я. А. Смородинского
Москва «Мир» 1985
ББК 22.632
Ш24
УДК 52 + 53
Шапиро С. Л., Тьюколски С. А.
Ш24 Черные дыры, белые карлики и нейтронные звезды: В
2-х ч. Ч. 1. Пер. с англ. — М.: Мир, 1985, 256 с, ил.
В книге, написанной известными американскими астрофизиками, изложены основы физики
компактных космических объектов, представляющих собой конечные продукты звездной эволюции, — уже
открытых белых карликов и нейтронных звезд, а также предсказанных теоретиками «черных дыр»
Изложение дополняется многочисленными упражнениями В русском переводе книга разделена на две
части В части 1 последовательно обсуждаются уравнения состояния и модели сверхплотных объектов, в
том числе с учетом эффектов обшей теории относительности, остывания, врашения и магнитных
полей
Для астрофизиков и физиков, как специалистов, так и студентов Может служить учебным
пособием по релятивистской астрофизике
1704020000—317 к^^ ^^ ,^^
Ш 60—85, ч. 1 ББК 22.632
041@1)-85 524
Редакция литературы по космическим исследованиям,
астрономии и геофизике
© 1983 by John Wiley & Sons, Inc.
All Rights Reserved. Authorized
translation from English language edition
published, by John Wiley & Sons, Inc.
© Перевод на русский язык, «Мир»,
1985
От редактора перевода
Название предлагаемой вниманию читателя книги — «Черные дыры,
белые карлики и нейтронные звезды» — как бы открывает нам мир
неведомой восточной сказки. И в самом деле, компактные объекты, физике
которых посвящена книга профессоров Корнеллского университета (США)
Стюарта Шапиро и Саула Тьюколски — мир поистине сказочный, в котором
все представляется иначе, чем в наших лабораториях. Фундаментальное
отличие этого сказочного мира от привычного нам земного состоит в
том, что главный герой книги — вещество, находящееся в сверхплотном
состоянии, недостижимом (пока?) в земных условиях.
Первые указания на существование в космосе вещества, находящегося в
экстремальном состоянии, было получено еще в 1914 г. Именно тогда
американский астроном Адаме, анализируя спектр Сириуса В, слабого
спутника (с абсолютной величиной всего 11,3'") самой яркой звезды нашего неба,
пришел к заключению, что Сириус В имеет высокую температуру, близкую
тс температуре самого Сириуса, и, следовательно, должен иметь малый
радиус (меньше радиуса Земли) при массе, почти равной солнечной. До того
времени Сириус В относили к красным звездам и малую светимость
связывали с низкой температурой. Поверить в существование «белых карликов»
9 то время было трудно; но с их реальностью пришлось примириться.
Первым слово «черная дыра» произнес Джон Уилер в 1968 г., но
история идеи об абсолютно неустойчивом небесном теле — сингулярности в
космосе — уходит в давние времена. О ней впервые заговорил даже не
Лаплас в конце XVIII в., как это было общепринято считать, а еще
раньше, в 1776 г., ученик Кавендиша Майкл, который размышлял о том, что
скорость света должна уменьшаться, когда свет совершает работу против
сил поля тяготения. Он считал, что, измеряя скорость света от далекой
звезды, можно оценить ее массу. В записках Кавендиша, изданных
Максвеллом, имеется также краткое замечание о возможности существования
небесных тел, «запирающих» в своих недрах свет. Но все эти идеи были
прочно забыты и возродились лишь в наши дни.
Открытие нейтронных звезд — в виде пульсаров — относится к 1967 г.,
но их существование предсказывалось теоретиками еще в начале 30-х годов
нашего века. Так что лишь в случае белых карликов наблюдения поставили
теорию в тупик — Эддингтон писал, что современники должны были
считать соображения о белых карликах абсурдными; в двух же остальных
случаях компактных объектов теория намного опередила наблюдения.
6 От редактора перевода
История открытий всегда интересна, и, нарушая порядок страниц,
полезно начать читать книгу, которую сейчас открыл читатель, с
исторических введений — первых параграфов глав 3, 9, 10, 12; они окрашивают
изложение драматизмом развития новых идей в науке.
Приведенные выше слова Эддингтона взяты из его книги «Внутреннее
строение звезд»^\ изданной в 1926 г. и переизданной с некоторыми
дополнениями в 1930 г. С появлением этой книги теория звезд превратилась в
физическую науку. Новым в книге Эддингтона было признание ядерной
энергии (субатомной, как тогда говорили) источником, определяющим
эволюцию звезды. Эта гипотеза (тогда еще только гипотеза) унесла в небытие
критику Нернстом и Джинсом ранних попыток объяснить излучение звезд.
Следует напомнить и о предшественниках Эддингтона, которым он
отдает должное. Первым из них был Лейн, опубликовавший в 1870 г. работу
с длинным названием: «О теоретической температуре Солнца на основе
гипотезы о массе газа, объем которого поддерживается его внутренним
теплом, и описываемого газовыми законами, известными по земным
экспериментам »^\
Ньютон в свое время перенес закон всемирного тяготения из космоса на
Землю; физики прошлого века перенесли в космос земную термодинамику.
Второй важной работой, развивающей теорию звезд, стала книга Эмде-
на, вышедшая в 1907 г.^^
Около 1913 г. произошло важное событие — Герцшпрунг и Рессел
высказали смелую гипотезу о том, что звезды, которые мы видим, находятся
на разных ступенях эволюции. На диаграмме спектральный
класс — абсолютная звездная величина (носящей теперь их имя) звезды
выстроились по своему «возрасту» от гигантов до карликов.
К этим работам, ставшим классическими, полезно добавить еще работу
К. Шварпшильда"^^ о радиационном равновесии солнечной атмосферы.
Заканчивая свою книгу, Эддингтон писал, что одна из туч,закрывающих
путь развития теории, — это непонимание законов высвобождения ядерной
энергии. Тем не менее Эддингтон был полон надежд: «... недалеко то
будущее, когда мы будем достаточно знать, чтобы понять такую простую
вещь, как звезда».
Сейчас это время пришло, хотя объект нашего познания оказался
совсем не таким уж простым.
Теория компактных небесных тел возникла только потому, что
придирчивые естествоиспытатели не прошли мимо парадоксального явления, а на-
'^ Eddington А. S. The Internal Constitution of Stars. Dover Publ., N. Y., 1959
(reprinted).
^^ American Journal of Science and Arts, Ser. 2, 4, 57, 1870.
^^ Emden K. Gaskugeln: Anwendungen der mechanischen Warmetheorie. Leipzig und
Beilin, 1907.
"^^ Schwarzschi/d K. Ueber des Gleichgewicht der Sonnenatmosphare. Gottingen Nach.,
No. 41, 1906.
От редактора перевода 7
стойчиво искали его объяснения. Раскрытие загадок Сириуса В и
импульсных радиоисточников уже кажется сейчас далекими событиями, описание
которых занимает всего несколько строк. Но недаром говорят, что
озарение в начале пути стоит больше многих идей в середине. Полезно
понимать, какие преграды стояли на пути исследователей и как рассеялись тучи,
закрывавшие горизонты науки. Это помогает увидеть красоту и оценить
скрытую сложность путей познания.
Теория компактных объектов замечательна еще и тем, что такое
состояние вещества неизвестно на Земле. Когда-тр в конце прошлого века учег
ный мир был взволнован открытием «солнечного вещества»^^ — линий не
известного тогда гелия в спектре Солнца. Однако вскоре гелий был
получен в лаборатории.
Со звездным веществом дело обстоит не столь просто. Есть
популярный рассказ об изобретателе, придумавшем универсальный растворитель,
который растворяет любое вещество. Но этот растворитель, к несчастью,
не в чем было хранить.
Природа хитроумно обошла это препятствие. Сосудом для
сверхплотного вещества служит собственное гравитационное поле звезды, которое
удерживает ее от разлета. В земной лаборатории аналогом служат
современные токамаки, в которых физики рассчитывают реализовать
термоядерные процессы. В токамаках горячая плазма удерживается магнитным
полем. Внутренность токамака — первая, хотя еще очень приближенная
модель звезды.
В земных лабораториях физики стремятся создать условия, при
которых возникли хотя бы ничтожные количества сверхплотного вещества.
Задача состоит в том, чтобы сжать каким-то способом ядро атома и узнать,
нет ли у ядерной материи более плотной устойчивой фазы? Пока
единственный способ для достижения такой цели — это столкновение тяжелых
ионов друг с другом. Однако во всех известных опытах сталкивающиеся
ядра — от легких до ядер урана — разбивались на части, и большая часть
их энергии расходовалась на кинетическую энергию осколков. Но хотя
звездное вещество пока нельзя изучать в лаборатории, физики уже знают,
что при малых расстояниях между частицами, при больших плотностях, в
сотни и тысячи раз превышающих плотности, характерные для ядер, в
игру должны вступить кварки и глюоны; за пределами расстояний порядка
миллиферми A0~^^ см) начинается, как мы сейчас уверены, новая физика.
В ее изучении ускорители и телескопы будут помогать друг другу, физики
и астрофизики пойдут рука об руку.
И для тех, кто захочет пойти по этой дороге или хотя бы
познакомиться с теми удивительными перспективами, которые открываются по пути,
предназначена эта книга.
^^ Так назвал свою научно-популярную книгу, опубликованную в конце 30-х годов,
советский физик-теоретик М. П. Бронштейн. В 1960 г. книга «Солнечное вещество»
была переиздана издательством «Детская литература».
8 От редактора перевоОа
Книге предпослано авторское предисловие, где рассмотрены цели,
которые преследовали авторы, принципы отбора материала и характер
изложения, а также раздел «Рекомендации к использованию книги». Все это
несомненно окажет помощь читателю — как специалисту и преподавателю, так
и студенту или начинающему исследователю. Ввиду этого здесь можно
ограничиться лишь несколькими замечаниями.
Новая физика развивается очень быстро, поскольку здесь действительно
проходит «линия фронта» развития науки. Поэтому читателю, желающему
быть в курсе последних известий с поля этой незримой битвы, мы
рекомендуем регулярно следить за новой литературой. В частности, хорошим
дополнением к книге Шапиро и Тьюколски будет выпускаемая
издательством «Мир» в 1986 г. монография С. Чандрасекара «Математическая теория
черных дыр», в которой читатель найдет богатый теоретический
материал, в том числе по методам исследования сингулярностей в пространстве-
времени.
Далее, к настоящему времени получен новый богатый материал по
вспышкам сверхновых звезд, которым посвящены заключительные главы
книги. Большой вклад здесь внесен советскими астрофизиками.
Информацию об этих гигантских катастрофах содержат данные о
распространенности химических элементов, которые можно попытаться расшифровать на
основе теоретических представлений о процессах нуклеосинтеза.
Наконец, в гл. 8 приводится вывод уравнения состояния плотного
вещества на основе теории ядерных сил. Этой цели вполне удовлетворяют
методы и формулы, использованные в книге. Читателю, пожелавшему
расширить применение описанных приемов для иного круга задач, мы
рекомендуем обратиться к последним обзорам по физике ядра.
Следует указать, что с любезного разрешения издательства «Джон Уай-
ли энд Санз» в русском переводе книга по техническим причинам разбита
на две части. В первую часть вошли гл. 1—8 оригинального издания, во
вторую — гл. 9—16 и приложения.
И завершая наше изложение, отметим, что авторы книги написали ее
на основе курса лекций, который они читают в Корнеллском университете.
Тем самым они выполнили долг ученого — передавать новому научному
поколению последние достижения бурно развивающейся науки нашего
времени. Читатель должен узнать из книги, которая у него перед глазами, не
только об успехах науки, но и попытаться распознать на горизонте те
новые тучи, которые не позволяют завершить счастливым концом рассказ о
необычайных явлениях природы.
Л. Смородинский
Предисловие
в основу этого учебного пособия был положен курс физики компактных
объектов, который преподавался авторами в Корнеллском университете
начиная с 1975 г. Компактные объекты включают белые карлики,
нейтронные звезды и черные дыры. Они представляют собой конечные стадии
эволюции звезд и являются, таким образом, одной из основных
составляющих физической Вселенной.
Данная книга, как и предшествовавший ей курс лекций, появилась в
результате резкого подъема научных исследований компактных объектов,
начавшегося в 60-х годах. В течение этого периода в нашей Галактике были
открыты пульсары и двойные рентгеновские источники, и эти открытия
стали важными вехами в развитии астрофизики. Существование
нейтронных звезд, которые прежде существовали лишь в умах нескольких
теоретиков, было с определенностью доказано. Стала вполне реальной
возможность существования черных дыр, и даже обнаружилось несколько
кандидатов на эту роль на звездном небе. Однако еще более важно, пожалуй, то,
что эти открытия послужили толчком к новым теоретическим
исследованиям и программам наблюдений, направленным на изучение физической
природы компактных звезд. Выросло целое поколение физиков, как
экспериментаторов, так и теоретиков, а также астрономов, принимающих
участие в этой увлекательной исследовательской работе, которая
продолжается по сей день.
Изучение компактных объектов, ставшее предметом большого
внимания со стороны общественности, еще очень далеко от своего завершения.
Далеко не все вопросы, относящиеся к структуре и эволюции компактных
объектов, разрешены полностью, и тем не менее ответы на эти вопросы
вовсе не кажутся недосягаемыми. В настоящее время наука о компактных
объектах вполне сформировалась как отрасль физики, в которой
проводятся как наблюдения, так и строгие теоретические исследования. Новые
данные и новые идеи возникают здесь постоянно. Более того, некоторые из
этих идей должны оказывать большое влияние на другие отрасли физики,
поскольку в компактных объектах происходят взаимодействия всех четырех
типов. Кто, например, мог предвидеть, что вопрос о том, претерпевает ли
ядерная материя фазовый переход в кварковое состояние при высокой
плотности, будет решаться путем наблюдений с рентгеновского спутника!
Настоящая книга предназначена для аспирантов первого года или
студентов старших курсов, изучающих физику и астрономию. Для ее чтения
не требуется никаких предварительных знаний в астрофизике или в общей
10 Предисловие
теории относительности. Все необходимые понятия и математические
методы вводятся по мере надобности. Предполагается, однако, что читатель
знаком с теорией электромагнетизма, статистической физикой и
термодинамикой, классической и квантовой механикой и специальной теорией
относительности в пределах университетского курса.
Поскольку здесь даны лишь элементы общей теории относительности,
необходимые для нашего изложения, подготовленные читатели могут
обратиться к одному из прекрасных курсов общей теории относительности,
вышедших в последние годы, чтобы углубить и расширить свои знания.
Мы рекомендуем для этой цели «Гравитацию» Мизнера, Торна и Уилера
[411] или «Гравитацию и космологию» Вейнберга [606]. Читатели, у
которых возникнет желание изучить физику «обычных» звезд, горение в
которых поддерживается ядерными реакциями и которые еще не сжаты силами
тяготения до состояния компактных объектов, могут воспользоваться
монографиями Клейтона [135] или Кокса и Джули [152]. Подчеркнем, однако,
что мы пытались сделать нашу книгу полностью независимой от других
источников.
Изложенный в ней материал располагается в естественном порядке.
Для компактных объектов каждого типа (белых карликов, нейтронных
звезд или черных дыр) вначале анализируются физические свойства в
«основном» состоянии. Например, прежде всего рассматривается сферически-
симметричная неврашаюитаяся конфигурация при нулевой температуре.
Затем анализируется действие на эти объекты различных «возмущений»,
например вращения, магнитных полей, тепловых потоков, аккреции и т.п.
Как и для большинства физических систем, структура компактных звезд
лучше всего проявляется в том случае, когда они подвергаются
воздействию каких-либо возмущающих факторов. (В самом деле, невозмушенные
компактные звезды в космосе просто ненаблюдаемы!) Где это возможно,
мы привлекаем данные наблюдений, чтобы обосновать и пояснить
теоретическое обсуждение.
Авторы попытались предложить простые (например, «одномерные»)
модели аналитических вычислений вместо слишком сложных выводов или
не всегда доступных численных расчетов. Такие аналитические модели
служат для выявления основных физических принципов, хотя, может быть, и
не обеспечивают высокой точности. В случаях когда такого рода оценки
предлагаются вместо более точных вычислений, результаты последних
всегда четко сформулированы, разумеется, если они существуют вообще.
Чтобы удержать объем книги в разумных пределах, авторам пришлось
придирчиво отбирать материал. Кое в чем этот выбор произволен и
основан на субъективных симпатиях. В других случаях при отборе материала
авторы руководствовались стремлением, чтобы книга не слишком скоро
устарела. Например, политропные модели звезд или уравнение состояния
идеального ферми-газа, по-видимому, никогда не утратят своей ценности.
Другой пример: хотя точная теория остывания нейтронной звезды еще не
построена, уже теперь ясно, каковы ее основные физические принципы и
как будет проведен расчет. Поэтому мы предлагаем подробный «типич-
Предисловие 11
ный» расчет; в нем можно изменить числа, но идеи останутся
неизменными. С другой стороны, мы еще не знаем детального механизма излучения
пульсара. До сих пор остается неясным, какие физические концепции,
лежащие в основе современных моделей, окажутся правильными. Исходя из
этого, авторы ограничились в указанном случае более коротким
обсуждением. Лет через десять читатель сможет увидеть, насколько оправданным
оказался подход, избранный авторами.
Чтобы сделать книгу полезной в качестве учебника, авторы включили в
нее свыше 250 упражнений, предназначенных для проработки студентами.
Эти упражнения разбросаны по всему тексту. В некоторых из них
предлагается довести до конца выводы, начатые или намеченные в тексте; другие
представляют собой несколько более сложные задачи. Ко многим
упражнениям даны ответы. Поскольку большинство результатов, содержащихся в
>?paжнeнияx, является неотъемлемой частью изложения и используется в
дальнейшем, студенту рекомендуется по крайней мере прочитать
упражнение, даже если он не собирается era решать. Разумеется, как и в любом
разделе физики, по-настоящему овладеть предметом можно, только
основательно поработав с ним, а в данном случае работа — это решение задач.
Чтобы придать этому делу больший интерес, в книгу включен ряд
«вычислительных упражнений». Это несколько более длинные числовые
примеры, которые можно решить на настольном программируемом
калькуляторе или на любой малой ЭВМ. Такие упражнения полезны не только для
пояснения физических аспектов, но и для обучения численным методам.
Имеется немало прекрасных книг и обзорных статей, в которых
обсуждается целый ряд вопросов, затронутых в настоящей книге. Мы часто
ссылаемся на эти источники. Наряду с другими книгами, упомянутыми в
данном предисловии, для изучающих предмет исключительно полезна книга
Я. Б. Зельдовича и И. Д. Новикова «Релятивистская астрофизика», т. 1
[636].
Не удивительно, что в подготовку этой книги внесли вклад многие
люди, работающие в самых различных учреждениях. Мы просто не в
состоянии перечислить все случаи, когда студенты и наши коллеги оказывали нам
неоценимую помощь своими критическими замечаниями, советами и
указаниями. Однако мы особенно благодарны некоторым из своих коллег за
внимательное чтение отдельных разделов предварительного варианта этой
книги и за столь важные для нас отзывы. Благодарим за внимание,
бескорыстную трату времени и многочисленные советы К. Олкока, Дж. Аронса,
Дж. Бакала, Дж. Бардина, Г. Бете, Р. Бландфорда, С. Чандрасекара,
Дж. Кордеса, Т. Голда, К. Готтфрида, П. Джосса, Д. Лэмба, Ф. Лэмба,
А. Лайтмана, Ч. Мизнера, Дж. Острайкера, Ф. Пачини, Д. Пайнса, С. Рап-
папорта, Э. Солпитера, С. Сталера, Дж. Тейлора, И. Терзиана, К. Торна,
X. Ван Хорна, Р. Вагонера и И. Вассермана. Кроме того, многие коллеги
помогали нам во время работы над книгой своим ободрением и
поддержкой. Среди прочих нам хотелось бы выразить свою признательность
У. Арнетту, Дж. Бейму, Дж. Кларку, Д. Эрдли, У. Фаулеру, Р. Джиакко-
ни, Дж. Хартлу, С. Хокингу, М. Милгрому, К. Петику, У. Прессу,
12 Предисловие
P. Прайсу, ?. Рису, ?. Рудерману, Д. Шрамму, Б. Шутцу, Д. Шаме,
П. Шапиро, Л. Смарру, С. Вейнбергу и Дж. Уилеру. Мы благодарим
Р. Дункана, П. Шиндера, X. Скотта и Дж. Уонга за тщательную проверку
окончательного варианта рукописи, включая упражнения. Наконец, мы
бесконечно признательны Д. Стюарт и Дж. Уитакр за перепечатку рукописи
и внесение бесчисленных исправлений, предшествовавших окончательному
тексту.
Благодарим Национальный научный фонд за помощь в проведении
исследовательских работ, которые представлены в этой книге, и за финансов
вую поддержку Корнеллского университета. Авторы выражают
признательность за предоставление им стипендий от Фонда А. П. Слоана
(С.Л.Ш) и Фонда Дж. С. Гуггенгейма (С. А. Т.).
Стюарт Л. Шапиро
Саул А. Тьюколски
Итака, шт. Нью-Йорк
Январь 1983 г.
Рекомендации по использованию книги
Стараясь сделать книгу достаточно полной и независимой от других
источников, авторы включили в нее больше материала, чем можно изложить в
обзорном курсе в течение одного семестра. Поэтому ниже приводится
таблица, которая поможет преподавателям в отборе разумного количества
наиболее существенного материала, доступного для изложения в таком
курсе. Разумеется, любой читатель, время которого ограниченно, может
также воспользоваться этой таблицей как примерным указанием для
самостоятельного изучения предмета.
Материал, знание которого необходимо для понимания данной главы,
указан во втором столбце таблицы. В третьем столбце приводятся
разделы, наиболее важные в данной главе и доступные для изложения на
лекциях. Указания по дополнительному чтению для студентов содержатся в
четвертом столбце. Вообще говоря, для понимания данной главы необходим
только тот материал, который отобран для изложения на лекциях и
дополнительного чтения в главах, указанных во втором столбце.
Порядок изложения может быть изменен, однако мы рекомендуем тот,
который дается в таблице, чтобы не утрачивались не всегда ясные «нити
повествования», которые проходят через всю книгу.
Преподаватель может счесть необходимым уменьшить объем
предлагаемого материала еще на 10—204?, чтобы изучить его более глубоко. С
другой стороны, некоторые из читателей, возможно, захотят ознакомиться с
теми разделами, которые не рекомендованы в нашей таблице, но
представляют для них особый интерес. Например, опущенные разделы из гл. 3 и 4
могут быть интересны студентам, изучающим физику твердого тела, а из
гл. 8 и И — студентам, изучающим физику ядра и элементарных частиц, и
т.д. В таких случаях, как правило, достаточно взглянуть на название
раздела или быстро просмотреть несколько первых абзацев, чтобы составить
представление о его содержании и понять, насколько он интересен.
Разделы книги, опущенные согласно таблице, а также приложения
могут быть полностью изложены в курсе, рассчитанном на два семестра. При
этом преподаватель вполне может дополнить приведенное здесь общее
обсуждение каким-либо дополнительным и более конкретным материалом,
который можно позаимствовать из цитированной литератур л.
14
Рекомено.^.;ии по использованию книги
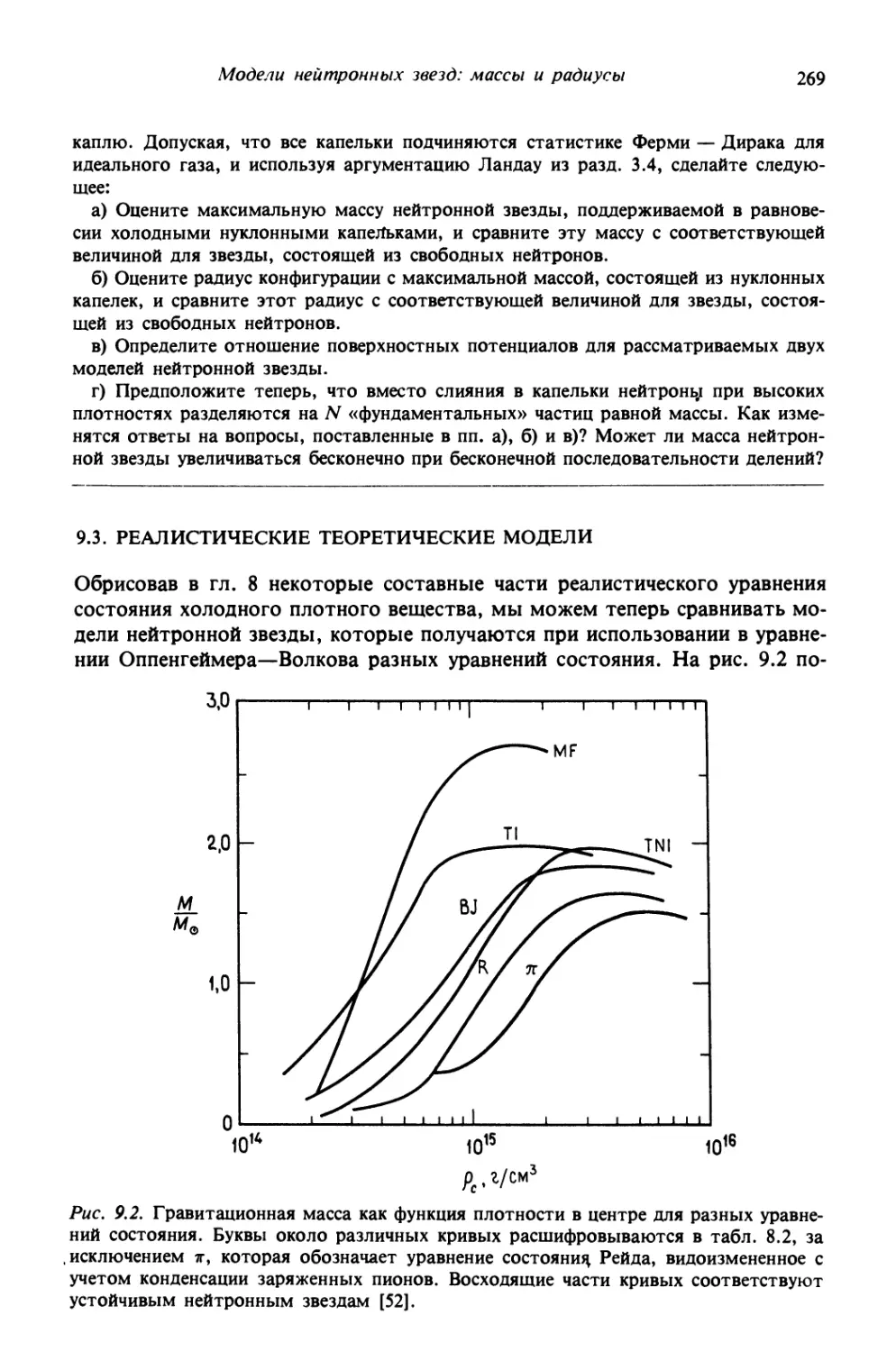
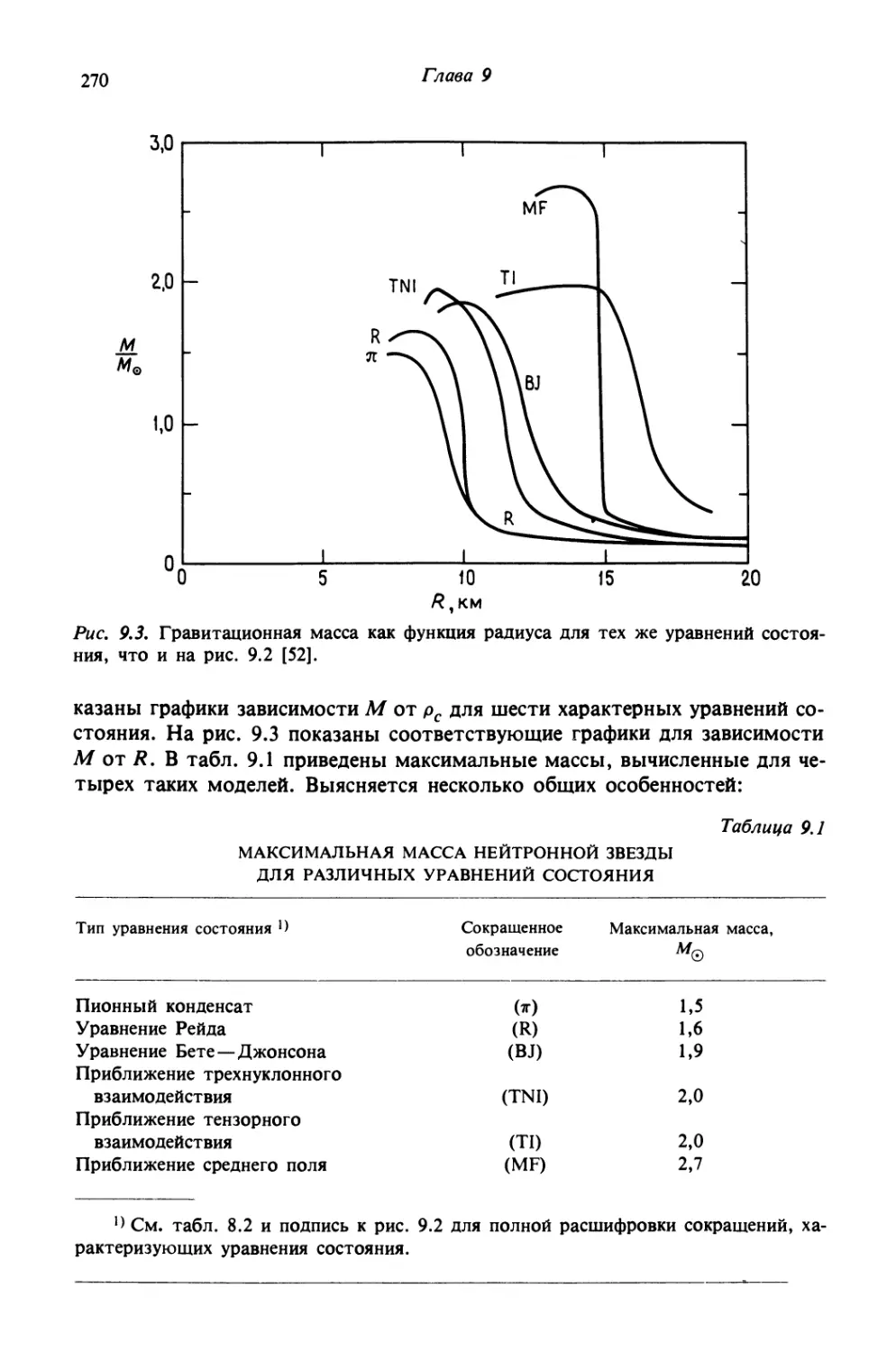
ТАБЛИЦА К РЕКОМЕНДАЦИЯМ ПО ИСПОЛЬЗОВАНИЮ КНИГИ
(КУРС, РАССЧИТАННЫЙ НА ОДИН СЕМЕСТР)
Глава
Необходимые
сведения
Лекции
Дополнительное
чтение
2
2,3
Целиком
2.1—2.6, резюме 2.1
3.2—3.6
4.1, 4.2, 4.5, 4.6
Целиком
6.1, резюме 6.1, в.9^\
6.10
7.1, 7.4^^
Приложение А
2.7
3.1
4.3, 4.4
7.3
8
9
10
11
12
13
14
15
16
17
18
2
8
—
—
5
—
13
13
5
5,
2,
6
8,
11
8.1, 8.5, 8.6, резюме 8.1
9.2—9.4
10.2, 10.3, 10.5, 10.8
11.1—11.4, 11.8—11.9
12.1, 12.3, 12.4, 12.6
13.2, 13.3, 13.5, 13.7,
резюме 13.1
14.3^>
15.1, рис. 15.1
16.3, 16.5, резюме 16.1
Опустить
18.1, 18.5, 18.7
' Только краткое содержание.
8.2, 8.4, 8.10, 8.12, 8.14
9.1
10.1, 10.7, 10.9—10.11
11.5—11.7
12.2, 12.5, 12.7, 12.8
13.1, 13.4, 13.6
14.1, 14.5^\
приложение И^^
15.2
16.1, 16.2, 16.4, 16.7
Опустить
18.2, 18.4, 18.6
Посвящается нашим семьям
Глава 1
Гибель звезд
и образование компактных объектов
1.1. что ТАКОЕ КОМПАКТНЫЕ ОБЪЕКТЫ?
Рассказ о компактных объектах логично начать с того места, где
заканчивается история нормальной звездной эволюции. Компактные
объекты — белые карлики, нейтронные звезды и черные дыры —
«рождаются», когда «гибнут» нормальные звезды, т.е. когда оказывается
израсходованной большая часть ядерного горючего звезды.
Все три типа компактных объектов отличаются от нормальных звеш
двумя фундаментальными признаками. Во-первых, израсходовав ядерное
горючее, они перестают сопротивляться гравитационному коллапсу за счет
термодинамического давления. Белые карлики удерживает от коллапса
давление вырожденных электронов, а нейтронные звезды — главным образом
давление вырожденных нейтронов. Черные же дыры — звезды полностью
сколлапсированные, т.е. это звезды, которые уже не могут противостоять
собственной силе тяготения и, следовательно, сжимаются вплоть до
сингулярности. Исключая спонтанно излучающие черные «мини»-дыры с
массами менее 10^^ г и радиусом не более 1 ферми, все три типа компактных
объектов являются по существу статическими в течение периода порядка
времени жизни Вселенной. Они представляют собой конечную стадию
звездной эволюпии.
Вторая характерная черта компактных объектов, отличающая их от
нормальных звезд, — чрезвычайно малый размер. Компактные объекты
имеют намного меньший радиус, чем нормальные звезды сравнимой
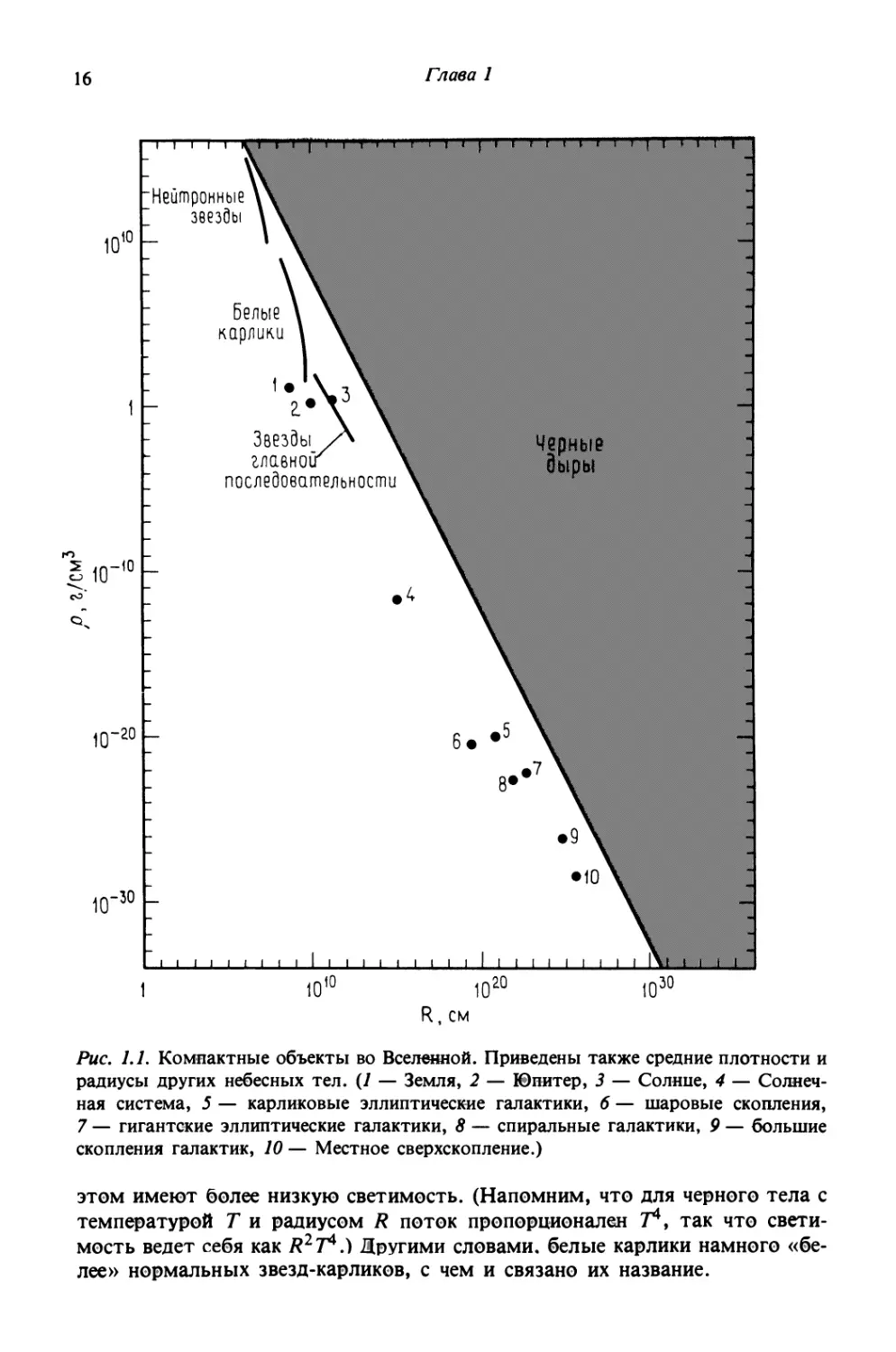
массы. Этот факт наглядно иллюстрируется табл. 1.1. и рис. 1.1.
Из-за громадного диапазона, в котором может меняться плотность
компактных объектов, их изучение требует глубокого физического
понимания структуры материи и природы сил, действующих между частицами, в
чрезвычайно широкой области изменения параметров. Все четыре типа
фундаментальных взаимодействий (сильные и слабые ядерные силы,
электромагнетизм и гравитация) играют роль в компактных объектах.
Особенно примечательна большая величина гравитационного потенциала на
поверхности компактных объектов, которая приводит к тому, что при
определении их внутреннего строения существенными оказываются эффекты
общей теории относительности. Даже для белых карликов, для которых
ньютоновская теория тяготения адекватно описывает равновесное состоя
ние, общая теория относительности оказывается необходимой при
изучении вопроса об их устойчивости.
Из-за малой величины радиуса светящиеся белые карлики, которые
излучают остатки своей тепловой энергии, характеризуются существенно
более высокой эффективной температурой, чем нормальные звезды, хотя при
16
Глава 1
10^^
5 10-^°
10'
-20
10'
¦30
I I I I I i^H''"'"'T'""^"'"""^" '"Ч' ' ' » ' I У > У г ' » ^ ' ' I Г \ ?"
Нейтронные
зеезОы
Белые
карлики
Черные
дыры
' « ' ' '
Рис. 1.1. Компактные объекты во Вселенной. Приведены также средние плотности и
радиусы других небесных тел. G — Земля, 2 — Юпитер, 3 — Солнпе, 4 — Со;шеч-
ная система, 5 — карликовые эллиптические галактики, 6 — шаровые скопления,
7 — гигантские эллиптические галактики, 8 — спиральные галактики, 9 — большие
скопления галактик, 10 — Местное сверхскопление.)
этом имеют §0лее низкую светим©сть. (Нап©мним, что для черн©г© тела с
температур©й ? и радиус©м R ????? пр©п©рци©нален 7^, так чт©
светимость ведет себя как R^T^.) Другими словами, ёелые карлики намного «ёе-
лее» нормальных звезд-карликов, с чем и связано их название.
Гибель звезд и образование компактных объектов
17
ХАРАКТЕРНЫЕ ЧЕРТЫ КОМПАКТНЫХ ОБЪЕКТОВ
Объект
Солнце^ ^
Белый карлик
Нейтронная звезда
Черная дыра
^^Mq = 1,989· 10^^ г,
Масса, ? Радиус, R
Произвольна ЮМ/с?
Rq = 6,9599· 10^® см.
Средняя
плотность,
г/см^
1
:S10'^
^10^^
Таблица 1.1
Поверхностный
потенциал,
GM/Rc^
10"^
-10-^
^10-^
~1
Черную дыру вообще никакой свет (и ничто другое) покинуть не может.
Поэтому изолированная черная дыра будет выглядеть «черной» для
любого наблюдателя. (Это утверждение нуждается в некоторых оговорках, если
принимать во внимание квантовомеханические эффекты, которые мы
обсудим в гл. 12.)
Нейтронные звезды получили свое название из-за того что они
состоят в основном из нейтронов, образовавшихся вследствие взаимного
уничтожения электронов и протонов в процессе обратного бета-распада. Так как
плотность нейтронных звезд сравнима с ядерной, то фактически они
представляют собой «гигантские ядра» {\(fi^ барионов), удерживаемые
собственным тяготением.
Белые карлики можно наблюдать непосредственно в оптические
телескопы в течение длительного периода их охлаждения. Нейтронные звезды
можно наблюдать как импульсные радиоисточники (пульсары) и косвенно
как периодические источники рентгеновского излучения, возникающего в
результате аккреции газа на нейтронную звезду (рентгеновские пульсары),
^^^рные дыры можно наблюдать только косвенно, благодаря тому
влиянию, которое они оказывают на свое окружение. Например, в некоторых
условиях они могут проявлять себя как апериодические источники
рентгеновского излучения, возникающего вследствие аккреции газа. В
последующих главах мы обсудим как эти, так и другие наблюдаемые явления,
связанные с компактными звездами.
1.2. ОБРАЗОВАНИЕ КОМПАКТНЫХ ОБЪЕКТОВ
Компактные объекты представляют собой конечные продукты звездной
эволюции. Считается, что основным фактором, определяющим, закончит
ли звезда свою жизнь как белый карлик, нейтронная звезда или черная
дыра, является ее масса.
2-353
18 Глава 1
Полагают, что белые карлики образуются из легких звезд с массами
Л/ S 4Л/0. Как мы увидим в гл. 3, для белых карликов существует
максимальное значение массы, которое составляет около 1,4Л/0.
Звезды — предшественники белых карликов, — по всей видимости,
выбрасывают некоторую часть своей массы в конце эволюции, образуя при этом
планетарные туманности.
Нейтронные звезды и черные дыры, как полагают, происходят от более
массивных звезд. Однако линия раздела между звездами, которые
превращаются в нейтронные звезды и черные дыры, весьма неопределенна, так
как конечные стадии эволюции массивных звезд мы понимаем довольно
плохо. Для нейтронных звезд также существует максимальное значение
массы (в диапазоне 1,4—SMq), но численные расчеты, в которых делаются
попытки описать медленную стационарную потерю массы звездой или
катастрофический выброс массы со взрывом сверхновой, находятся на весьма
примитивном уровне. Таким образом, судьба звезды с массой Л/ ^ 4Л/0 в
настоящее время нам неясна.
Табл. 1.2 отражает современный уровень нйшего неведения
относительно судьбы звезд в конце их эволюции. Некоторая дополнительная
неопределенность вносится тем, что при вычислениях, лежащих в основе табл.
1.2, обычно предполагают, что для судьбы звезды другие факторы
(например, магнитные поля, вращение, эффекты в двойных звездах) менее
существенны, чем масса.
Полный гравитационный коллапс, ведущий к черной дыре, в принципе
может произойти иначе, чем прямой коллапс далеко проэволюционировав-
шей массивной звезды. Например, поскольку существует определенное
максимальное значение массы, выше которого белый карлик или нейтронная
Таблица 1.2
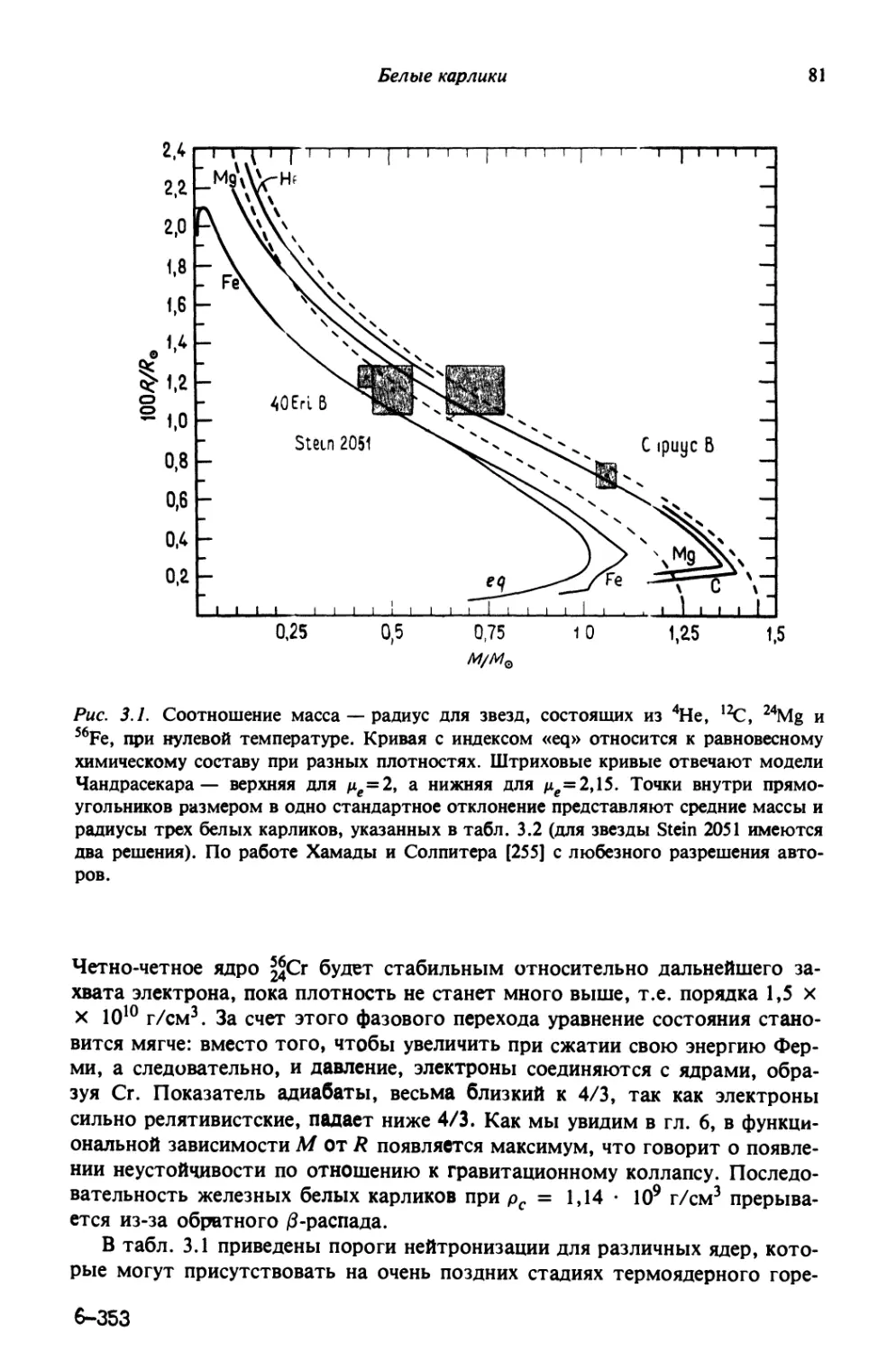
РЕЗУЛЬТАТ ЗВЕЗДНОЙ ЭВОЛЮЦИИ В ЗАВИСИМОСТИ ОТ МАССЫ [19]
Диапазон масс Ожидаемый результат
^Mq Время жизни превышает возраст Вселенной
1 :^ M/Mq S C-?-6) Белый карлик 4· планетарная туманность.
Потеря массы
(Зч-б) S M/Mq :? E + 8) а) Возгорание углерода ^? + '^С
1) «кипение» -^ сжатие ядра, либо
2) взрыв и распыление ядра, либо
3) быстрое ядерное горение и (??)
6) Пульсационная потеря массы и переход к
белому карлику
E-?-8) :^ M/Mq :? F0-5-100) Сжатие ядра + сверхновая -^ нейтронная
звезда, иногда — черная дыра (?)
F04-100) S M/Mq Неустойчивость
Гибель звезд и образование ^((омпактных объектов 19
звезда не могут противостоять коллапсу, аккреция газа на любой из этих
объектов (например, в двойной системе) может привести к образованию
черной дыры.
По крайней мере еще два процесса образования черных дыр. были
предложены теоретиками (хотя и не подтверждены пока наблюдателями!).
Первый представляет собой коллапс «сверхмассивной звезды», который
приводит к образованию «сверхмассивной черной дыры». Мы более
подробно обсудим этот процесс в гл. 17, а пока просто отметим, что такие
сверхмассивные звезды оказываются неустойчивыми, когда их плотность
достигает определенного критического значения, зависящего от величины
массы. Соответственно когда сверхмассивная звезда в своем развитии
доходит до этой плотности, испытывая лучистое охлаждение и сжатие, она
может катастрофическим путем перейти в черную дыру. Таким может
быть происхождение сверхмассивных черных дыр с массами М/М^ -
~ 10^ — 10^, которые предлагаются для объяснения сильнейшей
активности, наблюдаемой в квазарах и активных галактических ядрах.
Второй механизм представляет собой образование первичных черных
дыр в ранней Вселенной вследствие возмущений в однородном поле
фоновой плотности [265, 635]. Так как все черные «мини-дыры» с Л/ < 10^^ г
должны были излучить свою массу вследствие процесса Хокинга (см.
разд. 12.8) за время меньшее, чем возраст Вселенной, то в настоящее
время могут существовать только черные дыры с Л/ ^ 10^^ г.
В принципе астрономические наблюдения могли бы подтвердить идею,
что компактные объекты являются конечными продуктами эволюции
звезд. Подсчитав число «погибших» звезд в нашей Галактике с момента
начала звездообразования, мы можем оценить с той или иной степенью
достоверности количество (и плотность) компактных объектов, имеющихся в
Галактике в настоящее время. Затем мы можем сравнить это число с
наблюдениями.
Такие вычисления наиболее надежны в случае белых карликов. По
белым карликам и планетарным туманностям имеются богатые данные
наблюдений, поэтому могут быть проверены любые оценки их
пространственной плотности, основанные на скорости гибели звезд.
Подобные же оценки для нейтронных звезд или черных дыр являются
гораздо менее уверенными. Помимо большей неопределенности в
диапазоне масс звезд — предшественников, имеется дополнительная сложность,
связанная с тем, что нейтронные звезды и черные дыры можно наблюдать
лишь в течение весьма короткого по астрономическим масштабам
«активного» периода их существования, когда они проявляются в виде пульсаров
или компактных рентгеновских источников.
Несмотря на эти неопределенности, имеющиеся данные уже позволяют
сделать некоторые интересные заключения. Как мы увидим, компактные
объекты так же широко распространены в Галактике, как и другие звезды.
Наблюдаемая доля распределенной плотности общей массы, приходящаяся
на белые карлики, составляет заметную часть плотности массы,
заключенной в обычных звездах. Множество белых карликов и нейтронных звезд
20 Глава 1
(т.е.пульсаров) уже обнаружено, и имеется по крайней мере один хороший
кандидат на роль черной дыры (Лебедь Х-1)^) .
В оставшейся части этой главы мы обсудим, как можно оценить
частоту встречаемости компактных объектов в окрестности Солнца на
основании статистики рождения и гибели звезд. Значения, которые мы приводим,
неточны, однако при лучшем понимании поздних стадий звездной
эволюции можно будет получить более надежные оценки. К счастью,
большинство свойств компактных объектов не зависит от плохо известной истории
их предшественников. В следующей главе мы приступим к изучению
физических процессов, определяющих эти свойства^\
1.3. СТАТИСТИКА РОЖДЕНИЯ И ГИБЕЛИ ЗВЕЗД
Количественное определение скорости рождения и гибели звезд
выполняется следующим образом [26, 39, 408, 435].
Определим
ф{М^) S функция светимости звезд поля, A.3.1)
т.е. число звезд всех типов (не только звезд главной последовательности) с
данной абсолютной визуальной звездной величиной, содержащихся в
кубическом парсеке галактического диска исключая звезды скоплений. [См.
приложение А, в котором определены применяемые в астрономии единицы
«абсолютная звездная величина» (мощность) и «парсек» (длина), а также
кратко обсуждается эволюция звезд и описана главная
последовательность.]
Далее определим
<^j^g(lg ?) s современная функция масс (СФМ) звезд
главной последовательности в окрестности Солнца,
A.3.2)
т.е. число звезд главной последовательности в единичном
логарифмическом интервале массы на квадратный парсек. Заметим, что все массы в
этом разделе [такие, как Л/ в равенстве A.3.2)] выражаются в единицах
солнечных масс и что все логарифмы — десятичные. Величины ф^^ и ф(М^^)
связаны соотношением:
Фм5A8 М) = ф{М^
d\% ?
2Я(М,)/м5(М,). A.3.3)
'^ Другой объект — кандидат в черные дыры — открыт в Большом
Магеллановом облаке. — Прим. ред.
^^ Возможно, при первом чтении многие читатели захотят пропустить
относящиеся к астрономии технические детали в оставшейся части этой главы. Тем не менее,
прежде чем двигаться дальше, им следует взглянуть на табл. 1.4 , имея, однако, в
виду, что приведенные там данные содержат большие неопределенности.
Гибель звезд и образование компактных объектов
21
Здесь множитель с производной переводит функцию светимости в функцию
масс. Множитель 2Н(М^) возникает от интегрирования функции
светимости по расстоянию ?» измеряемому перпендикулярно к плоскости
Галактики в предположении, что звезды распределены по закону ехр(- \?\/?), где
Н{М^) — характерная высота. Множитель/j^s(M^) дает долю звезд данной
величины, находящихся на главной последовательности.
Основная получаемая из наблюдений величина в равенстве A.3.3) — это
Ф(М^). Результаты многочисленных определений этой функции находятся в
прекрасном согласии между собой [39, 398, 408]. В табл. 1.3 приведены
значения, принятые в работе [39]. В этой таблице также указано соотноше-
Таблица 1.3
ВЕЛИЧИНЫ, ОПРЕДЕЛЯЮЩИЕ СОВРЕМЕННУЮ ФУНКЦИЮ МАСС (СФМ)
/
J
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ФШ,^^
звезд/(пс^ · зв.вел.)
1,49(-8)
7,67(-8)
3,82(-7)
1,80(-6)
7,86(-6)
3,07(-5)
1.04(-4)
2,95(-4)
6,94(-4)
1.36(-3)
2.26(-3)
3,31(-3)
4.41(-3)
5.48(-3)
6,52(-3)
7.53(-3)
8.52(-3)
9.54(-3)
1.06(-2)
1.17(-2)
1.29(-2)
1.41(-2)
1.41(-2)
IgM/M^^^
2.07
1,80
1.53
1,26
0,99
0.72
0.45
0.36
0,26
0,17
0.08
-0.02
-0.11
-0.20
-0.29
-0.39
-0,48
-0.57
-0.67
-0,76
-0.85
-0,94
-1,04
rfM^2)
d\gM
3,7
3,7
3,7
3,7
3.7
3,7
10,8
10,8
10,8
10,8
10,8
10,8
10,8
10,8
10,8
10,8
10,8
10,8
10,8
10,8
10,8
10,8
10,8
2Я,3)
180
180
180
180
180
180
180
180
180
300
465
630
650
650
650
650
650
650
650
650
650
650
650
1? ? ^^
6,42
6,50
6,58
6,84
7,19
7,68
8,36
8,62
8,93
9,24
9,60
9,83
10,28
—
—
—
—
—
—
—
—
—
—
f ^^
0,40
0,40
0,41
0,42
0,43
0,46
0,50
0,56
0,64
0,78
0,98
1,00
1,00
1.00
1,00
1,00
1,00
1,00
1,00
1,00
1,00
1,00
1,00
<^Ms(i«^)'
звезд/(пс^ · Ig ?)
3,97(-6)
2,04(-5)
1.04(-4)
5.03(-4)
2,25(-3)
9,41(-3)
1.01(-1)
3,21(-1)
8,63(-1)
3,44( + 0)
1.11(+1)
2,25(+1)
3.10(+1)
3,85(+1)
4,58(+1)
5,29(+1)
5,98(+1)
6,70(+1)
7,44(+1)
8,21(+1)
9,06(+1)
9,90(+1)
9,90(+1)
^^ По работе Бакала и Сонейры [39], равенство A).
^ По работе Бакала и Сонейры [39], равенство A7).
^ По работе Бакала и Сонейры [39], рис. 2.
^^ По работе Миллера и Скало [408]. Мы интерполировали их результаты таким образом,
чтобы они согласовывались с результатами Бакала и Сонейры при совпадающих значениях Л/, но
не Л/у, так как в теоретических расчетах Т^^ обычно выражают как функцию Л/.
' По работе Бакала и Сонейры [40], равенство A).
22 Глава 1
ние масса— светимость, т.е. Л/^ в зависимости от Ig Л/, для главной
последовательности, которое довольно хорошо определено как в результате
наблюдений, так и теоретически. Изменение характерной высоты ? в
зависимости от Л/^ (и, следовательно, от М) определено не столь хорошо, кроме
случая самых ярких звезд. Однако из табл. 1.3 ясно, что звезды с большой
массой и большой светимостью сильнее сконцентрированы в плоскости
диска, чем звезды малой массы. Поправочный множитель /j^g обусловлен
присутствием звезд, эволюция которых зашла достаточно далеко, так что
горение происходит в них не только за счет водорода. Как правило, /j^g ~
~ 1 для слабых звезд с Л/,, > 3 (Л/ S 1,4 Mq), а для ярких звезд с Л/^ ^ О
(М > 3,5 A^0)/ms падает примерно до 1/2. Поправочный множитель ^j^g
для ярких звезд известен не очень хорошо. Полученная в результате
согласно равенству A.3.3) СФМ также приведена в табл. 1.3. Для звезд малой
массы неопределенность в этом выражении в основном связана с Н(М); для
звезд большой массы она обусловлена главным образом соотношением
между Л/ и М^, а также Ф(М^^).
Теперь определим начальную функцию масс (НФМ) для звезд поля:
f(lgM) = полное число звезд,
которые когда-либо образовались на единице площади
в единичном логарифмическом интервале масс. A.3.4)
В предположении о постоянстве темпа рождения^^ скорость
образования звезд поля в единичном интервале Ig Л/ равна просто f(lg M)/Tq. Здесь
Tq — возраст Галактики (фактически равный возрасту Вселенной), который
мы примем равным 12 · 10^ лет.
Теперь мы можем связать ф^^ с ?, введя время пребывания звезды на
главной последовательности Т^^. Большинство массивных звезд,
появившихся после начала звездообразования, уже давно ушли с главной
последовательности (Tj^g < Tq) и, следовательно, не вносят вклада в ф^^.
Поэтому
<i>Ms( Ig Ю = ?( Ig М)^, r^s < Го. A.3.5)
Менее массивные звезды все еще находятся на главной
последовательности, и потому
Фм5( Ig Ю = а Ig М), Jms > То. A.3.6)
Величина Т^^ в зависимости от ? приведена в табл. 1.3; эту
зависимость можно представить в приближенной аналитической форме:
r„s-^^4^, A.3.7)
^^ Миллер и Скало [408] приводят данные в пользу приемлемости этого
приближения.
Гибель звезд и образование компактных объектов 23
где A^MS — доля массы водорода, сожженного, пока звезда находилась на
главной последовательности, ^Х^<^ » 0,13, а ?** — энерговыделение на 1 г
массы при реакции ядерного слияния ? в Не, т.е. Е* » 0,007 с^ » 6,4 х
X 10^^ эрг/г. Из теории внутреннего строения известна грубая оценка
(соотношение «масса — светимость» для главной последовательности).
Равенства A.3.7) и A.3.8) теперь дают
/ W \-2.5
Tms - 13 X ??? ^ ^^-^^ ^ ^ 10Ме. A.3.9)
Упражнение 1.1. Определите степень надежности приближенных равенств A.3.8) и
A.3.9), сравнивая их с более точной зависимостью L и T^s от (M/Mq),
полученной с помощью табл. 1.3 и выражения (А.6).
Используя равенства A.3.5) и A.3.6) и значения ф^^, приведенные в
табл. 1.3, мы вычислим i(lgM). Результаты можно представить
аналитически с помощью следующей подгоночной функции:
Ig Ше М) = ^0 + ^1 Ig ? + ^2( Ig ^)\
^0=1,41, ^, = -0,90, ^2=-0,28, lgM>-l.
A.3.10)
Здесь Л/ измеряется в единицах М^. Наклон начальной функции масс
приближенно равен
1М =. - @,9 + 0,6 Ig ?). A.3.11)
dig ?
Эти значения не слишком отличаются от приведенных Миллером и Скало
[408], если принять во внимание существующие неопределенности.
Современные определения ? обычно сравнивают с функцией скорости
рождения звезд, введенной Солпитером [495]. В своей пионерской работе,
посвященной этой проблеме, Солпитер рассматривал концентрацию звезд в
галактическом диске, пренебрегая множителем Я(Л/^) и используя
«старые» значения Т^^. Введенная Солпитером функция скорости
звездообразования равна
в диапазоне 0,4 ^ М/М^ ^ 10.
24 Глава 1
Упражнение 1.2. Покажите, что НФМ ^^, соответствующая ^^, определяется
выражением
Из равенств A.3.12) и A.3.13) в пренебрежении зависимостью ? от ?
получим
^- -1,35, A.3.14)
d \g ?
В диапазоне масс 2+10 Л/0 такая зависимость вполне согласуется с более
поздним результатом A.3.11). Выше ЮЛ/ф наклон НФМ более крутой,
чем показывает это равенство, в то время как ниже 2 Л/0 — более
пологий. Эти различия связаны с пренебрежением Н(М) и устаревшими
значениями r^s.
Проверкой согласованности СФМ служит сравнение с пределом Оорта,
Изучая динамику движения звезд нашей Галактики в окрестности Солнца,
Оорт [424] нашел полное количество вещества, ответственного за
наблюдаемые ускорения. Недавнее определение предела Оорта приводит к
плотности @,14 ± О,ООЗ)Л/0 · пс"^ [319]. Используя СФМ, можно подсчитать
полную массу звезд главной последовательности в окрестности Солнца. Ба-
кал и Сонейра [39] получили оценку 0,040 Л/0 · пс"^. В какой форме
находится остальное вещество? Межзвездный газ дает 0,045 Л/0 · пс"^ [549].
Наблюдаемые белые карлики ответственны еще за 0,005 Л/0 · пс"^ ^\ В
итоге остается примерно 0,05 Л/0 · пс~^ «недостающей массы» в
окрестности Солнца. Существует немало предположений относительно природы
этой недостающей массы (астероиды, планеты, «медленные» карлики
класса М, черные карлики, черные дыры и т.п.). В настоящее время мы не
знаем ответа на этот вопрос.
Используя предел Оорта, можно прийти к выводу, что примерно
половина массы 1 алактики уже заключена в звездах, закончивших свою
эволюцию. Для Л/ > 0,9 Л/0 время жизни звезды на главной
последовательности, Tj^g, короче возраста Галактики Tq = 12 · 10^ лет. (Это значение
получено интерполяцией данных, приведенных в табл. 1.3.) Используя функ-
^^ Мы привели значение, данное Бакалом и Сонейрой [39]. Они предположили, что
резкое падение количества очень слабых белых карликов, отмеченное Либертом и
др. [361], является реально существующим эффектом, и таким образом определили,
что концентрация белых карликов в окрестности Соднца равна 0,008 пс "^.
Умножение на среднюю массу «наблюдаемого» белого карлика 0,65 Л/^ (см. сноску на
стр. 115 в гл. 4) дает значение 0,005 Л/^-пс~^. Это в 4 раза меньше, чем оценка,
приведенная в [605].
Гибель звезд и образование компактных объектов 25
цию скорости звездообразования по Солпитеру в качестве приближенного
выражения, найдем
/J^,M</(^j = 5 X 10-'^Ме · пс-з · год-^ A.3.15)
Умножение на Т^ дает полную массу, прошедшую через яркие звезды.
Таким образом, мы получим 0,06 Mq пс~^, т.е. примерно половину предела
Оорта.
Теперь можно подсчитать скорость гибели массивных звезд и,
следовательно, скорость рождения компактных объектов. Для звезд с массами
7t 0,9 Л/0 имеем Т^^ < Tq, и потому естественно предположить, что
звездное население стационарно — средний темп гибели находится в
примерном равновесии с темпом рождения. При упрощенном рассмотрении
можно использовать аналитическую функщ1ю скорости звездообразования,
введенную Солпитером, которая не приводит к большим ошибкам в том
диапазоне масс, который нас интересует.
Примем с иллюстративной целью, что массы звезд—предшественников
белых карликов составляет 1—4Л/0 (см. табл. 1.2). Диапазон масс
звезд—предшественников нейтронных звезд известен еще хуже, однако
примем его равным 4—10 Mq и будем считать, что все звезды с массой
больше 10 Mq заканчивают свою жизнь как черные дыры.
Функция скорости звездообразования по Солпитеру не учитывает
зависимости от высоты ? над плоскостью Галактики. Преобразуем скорость
образования звезд в единице объема в полную скорость, умножая на
эффективный объем Галактики:
i^disk = '^???) = 1,3 ? W' псЗ, A.3.16)
где мы приняли 2 ? = 180 пс, что справедливо для звезд с массами
больше 2 Л/0 (см. табл. 1.3), и характерный радиус галактического диска взяли
равным г = 15 кпс^^
Скорость образования ( = скорости гибели) для звезд с массами в
диапазоне от Л/j до Л/2 равна
--0-^(^)=-(^)-
Л/,/Л/о
ГОД \ A.3.17)
^ Эта оценка является весьма грубой, так как мы приняли, что темп рождения
звезд во всей Галактике такой же, как в окрестности Солнца. Кроме того,
«характерный» радиус диска — вовсе не четко определенная величина. (Солнце находится
на расстоянии примерно 10 кпс от центра Галактики.)
26 Глава 1
Концентрация ? компактных объектов, образовавшихся из звезд-
предшественников с массами в диапазоне от Mj до Mj, составляет
Л/,/Л/о
пс-3 . A.3.18)
л/г/л/о
Для определения массовой концентрации ? этих компактных объектов^)
нельзя просто проинтегрировать произведение Мф^. Интегрирование было
бы возможным, если бы не существовало потери массы и вся масса
звезды-предшественника оставалась в компактном объекте. Мы знаем, что
для белых карликов и нейтронных звезд, которые имеют максимальные
массы порядка 1,4 М^ и 2—3 Mq соответственно, это вовсе не так.
Потому определим р, умножая ? на среднюю массу < Л/ >, причем для белых
карликов и нейтронных звезд соответственно примем <А/>^^ = 0,65 М^ и
{M)ns = Ь4 М0. О черных дырах мы знаем еще меньше и в этом случае
просто пренебрежем потерей массы. Рассматривая отношение ? к полной
плотности массы ?? = 0,14 Mq пс"^ (предел Оорта), получим для белых
карликов или нейтронных звезд
A.3.19)
A.3.20)
Среднее расстояние между компактными объектами данного типа в
окрестности Солнца равно
(j>= L·— A.3.21)
D7гл/3) ^
Используя вышеприведенные формулы, мы можем заполнить табл. 1.4.
Некоторые из результатов, приведенных в таблице, можно сравнить с
наблюдениями. Бакал и Сонейра определили, что местная концентрация
белых карликов равна 0,008 пс"^ (см. сноску на стр. 24), что с точностью
до множителя 2 совпадает с нашей теоретической оценкой. Разделив эту
величину на Tq, получим оценку для скорости рождения белых карликов:
10"^^ пс"^ · год"^
_Р_
Рт
в то время как для черных дыр
Рт ??-'?,/?? \^о1
п(М)
Рт
М^)
-0^5
Л/,/Л/о
Л/г/Л/о
^^ Массовая концентрация объектов — это величина массы, «размазанной» по
полному объему и отнесенной затем к единице объема. — Прим. ред.
Гибель звезд и образование компактных объектов 27
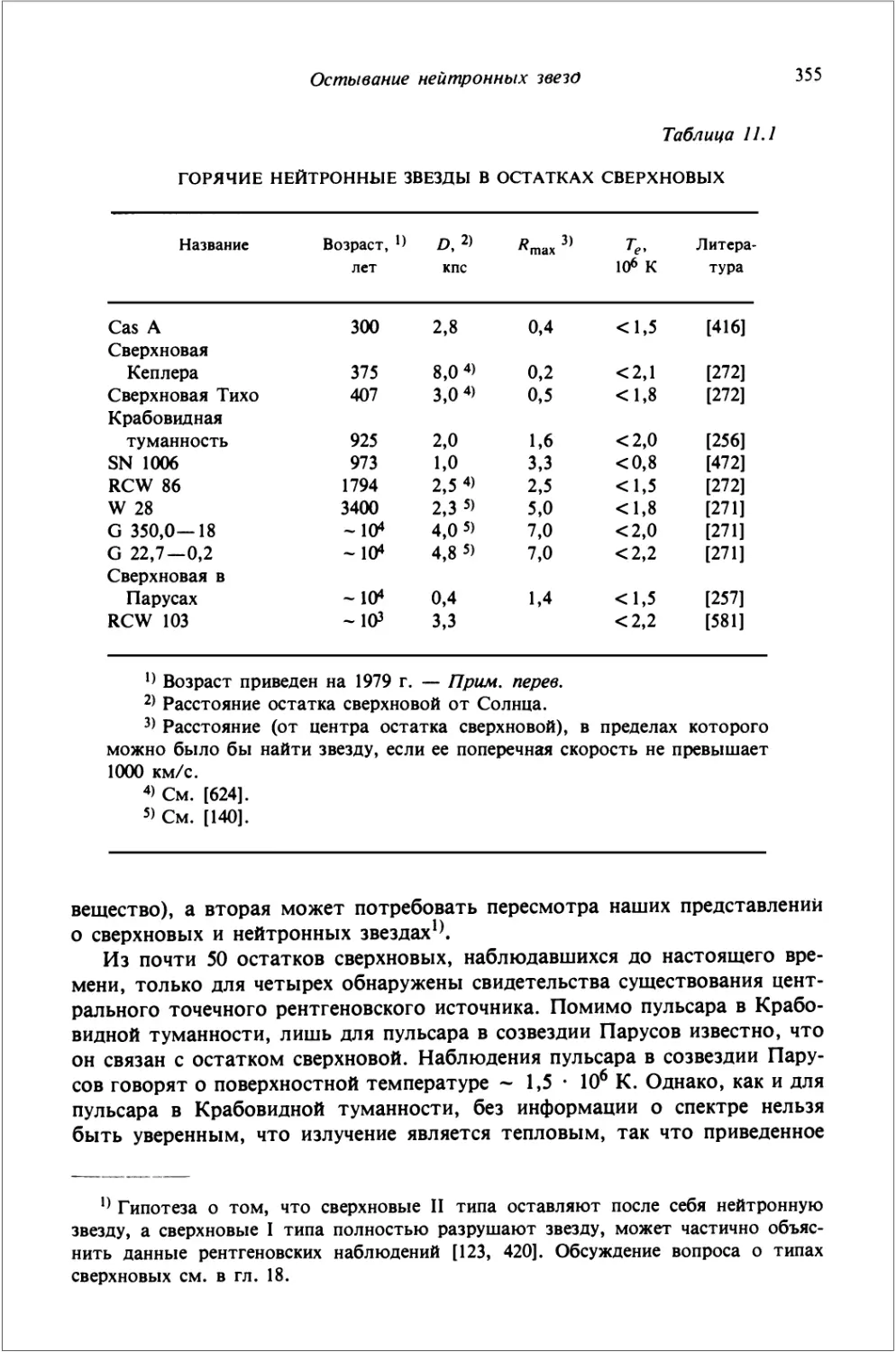
Таблица 1.4
КОМПАКТНЫЕ ОБЪЕКТЫ В СОЛНЕЧНОЙ ОКРЕСТНОСТИ^^
Объект
Белые карлики
Нейтронные звезды
Черные дыры
Диапазон
значений мае
сы звезды-
предшественника, Mq
1—4
4—10
>10
Интегральная
галактическая
скорость
рождения, год" ^
0,16
0,021
0,0085
Концентрация,
пс~^
1,5· 10-2
2,0· 10"^
8,0· 10"^
?
—
Рт
0,070
0,020
0,22
id), ПС
2,5
4,9
6,7
^^ Эти значения получены с помощью равенств A.3.17)-A.3.21).
Примечание. Ближайший известный белый карлик, Сириус В, находится на расстоянии 2,7 пс,
ближайшая известная нейтронная звезда, PSR 1929 ·? 10, удалена на 50 пс, ближайший кандидат
в черные дыры. Лебедь Х-1, ·— около 2 кпс.
Неопределенности в шкале расстояний до планетарных туманностей
затрудняют определение их скорости рождения, но большинство оценок [9,
99, 428] согласуются со скоростью рождения белых карликов.
Эти результаты, по-видимому, подтверждают гипотезу, что звезды с
массами 1—4 Mq в конце своей жизни проходят через стадию планетарной
туманности и что все белые карлики образовались в ходе такого процесса.
Данные по нейтронным звездам более неопределенные. По оценкам
Ариетта [19] скорость образования пульсаров в Галактике составляет
1
^^^^ 35 X 10^^
год"
A.3.22)
apsR -" 4 X 10"^^^^ пс-2 · год-1 A.3.23)
Тейлор и Манчестер [561] приводят оценку
^PSR - C-10) X 10-^^ пс-2 . год-1, A.3.24)
в то время как первоначальное значение, данное Ганном и Острайкером
[252], составляет
apsR = 5 X lO-^Vc-2 . год-l A.3.25)
Эти оценки чувствительны к шкале расстояний до пульсаров; определяемой
по их мере дисперсии (см. разд. 10.4).
Приведенные выше данные о пульсарах можно грубо сравнить с табл.
1.4, если разделить соотношение A.3.24) на 2// = 180 пс и умножить на
Tq = 12 · 10^ лет. В результате получим
''PSR- B-6) X 10--^пс-з,
A.3.26)
28 Глава 1
что свидетельствует о хорошем согласии данных. Более аккуратный анализ
выполнен Шипманом и Грином [537].
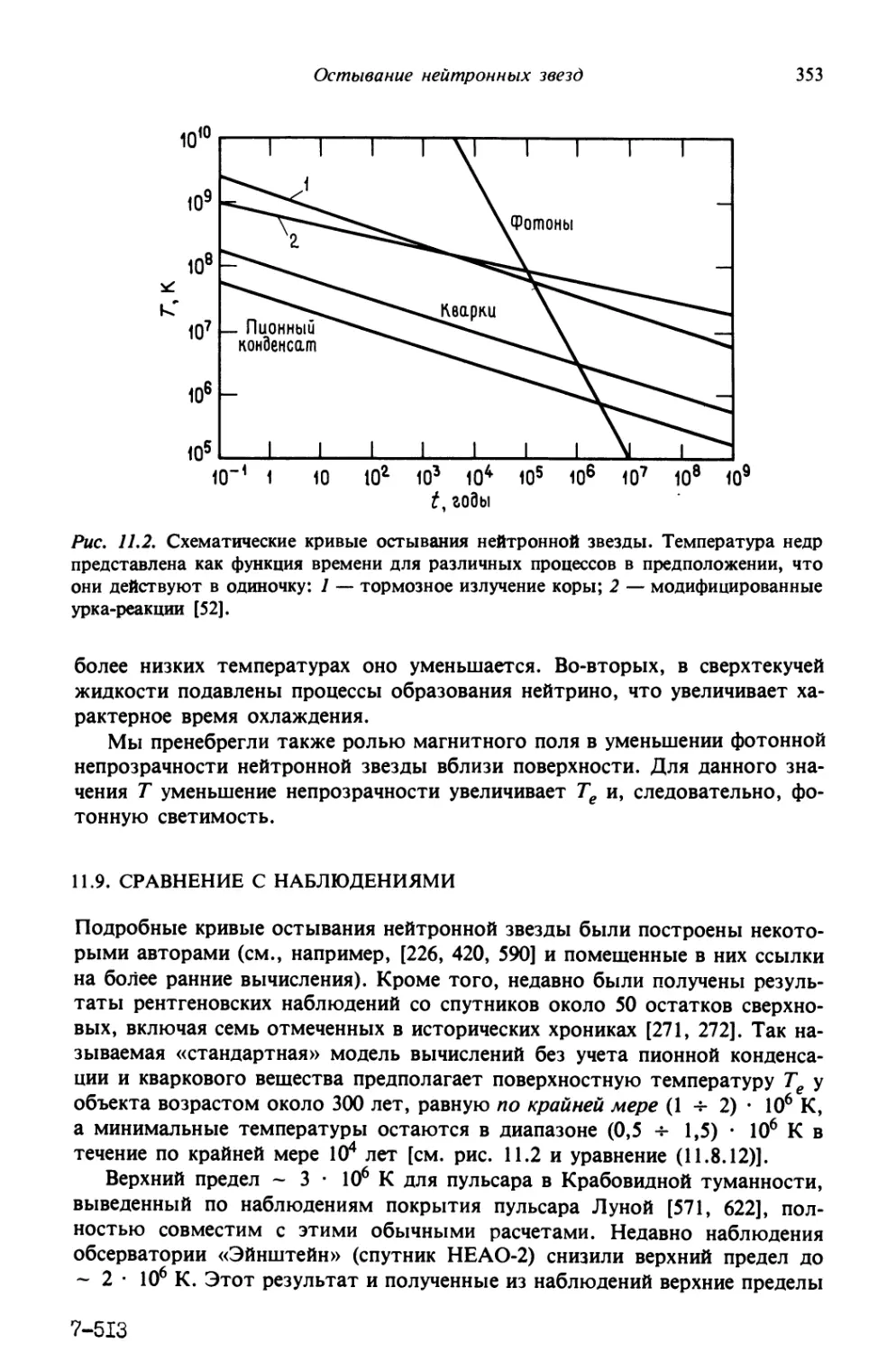
Интересно сравнить скорости рождения пульсаров и сверхновых.
Теоретики считают, что большинство пульсаров, если не все, возникают при
вспышках сверхновых. (Сверхновая 1054 г., остаток которой
отождествляется с Крабовидной туманностью, несомненно привела к рождению
пульсара.) Тамманн [556] на основании исторических источников оценил
скорость рождения сверхновых в Галактике как
^sN.hist = 7?7 " ^^^^^ ""^^^ A.3.27)
где число зарегистрированных в истории сверхновых N = 6 за время ?/ =
= 10^ лет. Величина ./' = 60®/360® — часть галактического диска, в
которой наблюдались сверхновые: по всей видимости, в других направлениях
от Солнца сверхновые невидимы из-за поглощения света в Галактике.
Приведенное значение скорости при делении на площадь галактического
диска ? · A5 кпс)^ дает
^SN
~5Х 10-^» пс-2· год-1 A.3.28)
Типичная скорость образования сверхновых в других галактиках [556] равна
/?SN ^ 1/C00 лет) на 1 галактику. A.3.29)
Если установленный на основе исторических хроник темп рождения
сверхновых в нашей Галактике является тит1чным, то, по всей видимости,
большинство внегалактических сверхновых не видно наблюдателям.
Тамманн считает, что выражение A.3.27) является хорошей оценкой для
истинной скорости образования сверхновых в нашей Галактике, в то время как
Ван ден Берг [582] получил оценку
/?SN ^ 1/F0 лет) для нашей Галактики, A.3.30)
что вдвое ниже оценки Тамманна. Заметим, что 6^^ - ^psr» ^'^^
подтверждает наши теоретические идеи.
Сравнение вычисленной теоретической скорости рождения различных
компактных объектов со статистикой галактических источников
рентгеновского излучения было бы в принципе весьма показательным. Однако,
поскольку эти источники, по всей видимости, являются компактными
объектами в двойнь/дг системах (см. гл. 13), фундаментальные трудности в
изучении их эволюции (касающиеся, например, потери массы и момента
количества движения) в настоящее время затрудняют сколько-нибудь надежное
сравнение.
Упражнение 1.3. Используя функцию скорости рождения по Солпитеру и
предполагая, что все звезды с массами > 10 Mq образуют черные дыры, оцените среднюю
массу черной дыры, образовавшейся в результате звездного коллапса. Потерей
массы пренебречь.
Гибель звезд и образование компактных объектов 29
Упражнение 1.4. Как изменятся числовые результаты в табл. 1.4 для нейтронных
звезд-и черных дыр, если Го = 18 · 10^ лет? Го = 9 · 10^ лет?
Упражнение 1.5. Главная последовательность для скопления Плеяды
представлена звездами с Л/ :S 6 Mq ; более массивные звезды уже сошли с главной
последовательности (см. приложение А.2). Открытие, что это скопление может содержать
какой-нибудь белый карлик, вынуждает сделать вывод, что в конце концов белые
карлики образуются из звезд с массами вплоть до 6 МG) (почему?), а не только с
массой, не превосходящей 4 Mq, как предполагалось при составлении табл. 1.4.
Используя функцию скорости рождения по Солпитеру, переопределите данные,
содержащиеся в табл. 1.4, с учетом этого результата. Сравните ваши теоретические
предсказания с наблюдаемой звездной статистикой для белых карликов,
планетарных туманностей, сверхновых и пульсаров. {Замечение: Романишин и Ангел [485]
изучили четыре других звездных скопления, содержащие белые карлики, и в порядке
рабочей гипотезы предположили, что звезды с массами вплоть до 7 Mq образуют
белые карлики.)
Упражнение 1.6 (основанное на работе [435]). Предположим, что звезды большой
массы (М > 8 Mq) создают пульсары, в то время как звезды промежуточной массы
D—8 Mq) взрываются полностью [22], причем при каждом взрыве из ядра
выбрасывается масса, равная примерно 1,4 Mq, в виде элементов, близких по атомному
номеру к железу.
а) Используя функцию скорости рождения по Солпитеру и Го = 12 · 10^ лет,
вычислите полную плотность железа, выброшенного в межзвездную среду такими
вз1)»>^вами.
Oweem: 2 · 10"^ Mq nc"^.
б) Используйте предел Оорта, чтобы предсказать обилие железа (долю по массе)
R га глиптическом диске, предполагая, что большая часть железа возникла в
результате таких взрывов. Сравните с наблюдаемым обилием 1,4 · 10"^ [621].
Otneem: Предсказывается 1,7 · 10" ^.
Упражнение 1.7. Пересчитайте числа, приведенные в упр. 1.4, используя функцию
скорости рождения, основанную на СФМ Бакала и Сонейры. Заметьте, что интегралы,
Шзникающие при использовании равенств A.3.10), выражаются через функцию
ошибок. В качестве альтернативы можно использовать приближенное аналитическое
выражение:
?( ig M) = DoM^·,
Do = 33, D, = -0,5, 0,\ ^ ? ^ 1,
Do = 35, D, = -1,5, 1 < Л/< 10,
Do= 163, D, = -1,9, 10 < Л/,
где ? выражается в единицах Mq . Заметьте, что в этом случае cugM =
= ??/{?\?\0).
30 Глава 1
На этом этапе следует сделать предостерегающее замечание. Помимо
неопределенностей в наблюдениях, мы сделали еще ряд теоретических
предположений, которые могут оказаться несправедливыми. В дополнение
к тем, что упоминалось выше, мы пренебрегли эффектами медленной ста-
щюнарной потери массы на поздних стадиях эволюции массивных звезд.
Так, например, в сверхгигантах типа ? Лебедя скорость потери массы
близка к ? - 1О~^Л/0 · год~^; для вращающихся эмиссионных В-звезд
? - 10-6 — 10-^0 Л/0 · год-^ Никто не знает в настоящее время, какие
звезды проходят фазу потери массы и сколько такая фаза длится.
Известны три двойные системы, содержащие белые карлики, обращающиеся
вокруг нормальных звезд, для которых возможно точное определение массы
(см. разд. 3.6). Во всех трех случаях масса белого карлика меньше массы
главного компонента, хотя белый карлик эволюционировал быстрее [ср. с
равенством A.3.9)]. Поскольку белый карлик достиг конечного пункта
своей термоядерной эволюции, звезда-предшественник должна была потерять
существенную часть своей массы. Так как расстояние между звездами в
этих системах довольно велико, кажется правдоподобным, что потеря
массы не зависит от того, что эти системы являются двойными.
Упражнение 1.8. Грубую оценку числа внегалактических случаев звездного коллапса
в заданном объеме с центром на Земле можно сделать следующим образом [19].
Светимость нашей Галактики равна Lq = Ю^^'^ Lq . Предположим, что темп этих
событий в нашей Галактике равен темпу образования сверхновых, установленному
по историческим хроникам, Rq = C0 лет)" ^.
а) Используя эти числовые значения и предположение, что R ос L· в любой
большой области вокруг Земли, определите темп внегалактических событий как
функцию объемной светимости L. Дайте обоснование предположению о линейной
зависимости.
б) Оцените «космическую излучательную способность» ? в единицах Lq Мпс~^
по величине Lq и средней концентрации галактик Hq « 0,02 Мпс~^. Определите
R{D)j где D — радиус рассматриваемой области (в Мпс). Вычислите R для
скопления Девы {D - Ю Мпс).
в) Найдите типичное значение L>obs» если типичная видимая звездная величина
наблюдавшихся сверхновых равна М'", а абсолютная величина —IS'" (вблизи
максимума). Вычислите /?(Z)obs) и сравните с наблюдаемым темпом образования
внегалактических сверхновых /?obs " C00 лет)" ^ в спиральной галактике.
Упражнение 1.9. (основанное на работах [34, 36]).
а) При типичной вспышке сверхновой должна излучиться энергия - 0,1 Mq с^ в
форме нейтрино со средней энергией ? - Ю МэВ (см. гл. 18). Если бы сверхновая
возникла на расстоянии R от Земли, она могла бы генерировать ядерные переходы в
эксперименте Дэвиса по поискам солнечных нейтрино (на ^^ci). Интервал времени
между последовательными сбо^^^^ми продуктов захвата нейтрино в установке Дэвиса
составляет около одного месяца. Чему равен эффективный поток нейтрино ф^^^ в
течение этого периода как функция /? (в с~^ · см)?
б) Примите условие Фегг о{Е) ^ 3<??> в качестве критерия регистрации нейтрино.
Здесь ?{?) — сечение захвата ( = 2,7 · 10""^^ q^2 д^ атом З'^С! при 10 МэВ), а
Гибель звезд и образование компактных объектов 31
{фа) — средняя скорость захвата солнечных нейтрино, для обнаружения которых
предназначен эксперимент. Для этой величины можно использовать измеренное
значение {фа), которое равно - 2 SNU A SNU = 10"^^ захватов на один атом в
секунду). До каких значений R установка способна обнаруживать сверхновую?
Ответ: /? - 4 кпс.
Замечание: До сегодняшнего дня из всех промеров в эксперименте Дэвиса только
в одном была обнаружена скорость захвата, достигавшая 6 SNU. Отсюда мы делаем
вывод, что за последние 10 лет в ближайших областях нашей Галактики,
составляющих " 304? ее объема, произошло не более одного звездного коллапса.
Глава 2
Уравнение состояния холодного вещества
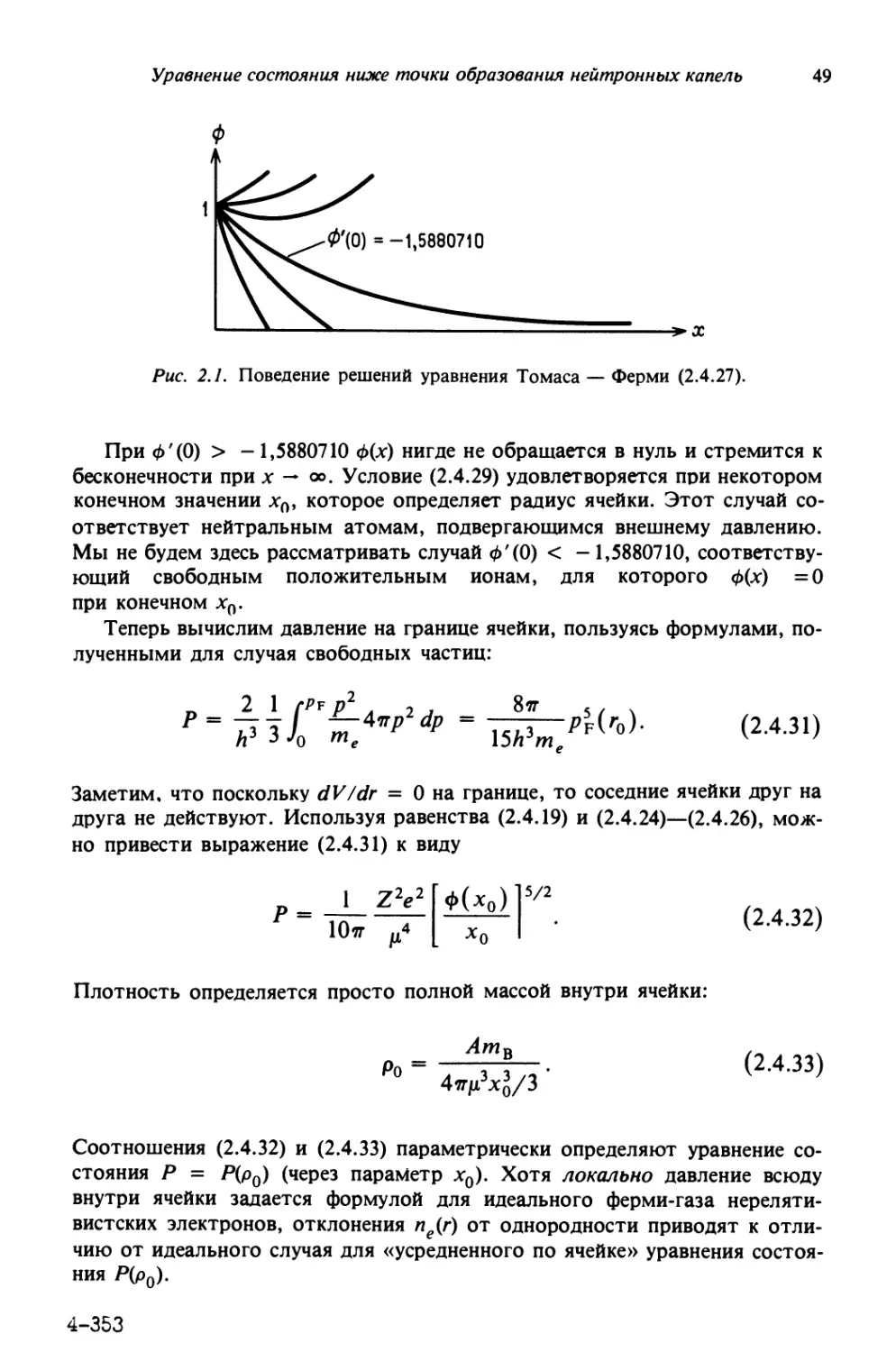
ниже точки образования
нейтронных капель
в основе теории компактных объектов лежат физические категории двух
различных типов. Эти категории в широком смысле можно
охарактеризовать как «глобальные» и «локальные». Глобальные свойства описывают
крупномасштабный динамический отклик материи на воздействие
гравитации, электромагнитных полей, вращения и т.д. Эти глобальные свойства
определяются уравнениями движения материи. В дополнение к членам,
описывающим гравитацию, электромагнитные поля и т.п., уравнения
движения включают эффекты внутренних натяжений, таких, как, например,
градиент давления и потери энергии из-за вязкости или излучения.
Величины, подобные давлению, вязкости или излучательной способности, обычно
выражают локальные свойства вещества, которые определяются
локальным термодинамическим состоянием отдельного элемента вещества.
В последующих главах мы рассмотрим как локальные, так и
глобальные свойства компактных объектов. Начнем с микрофизики, которая
необходима для изучения белых карликов, а именно с уравнения состояния
(соотношения между плотностью и давлением) до режима образования
нейтронных капель (плотность меньше - 4 · 10^^ г/см^). При подходящей
модификации часть этого рассмотрения может быть перенесена на случай
нейтронной звезды.
Прежде всего мы сделаем обзор основных термодинамических
соотношений, которые будут широко использованы в последующем изложении.
2.1. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕРМОДИНАМИКИ
Обычно термодинамические величины относят к некоторому
определенному числу частиц N в объеме К Релятивистская инвариантность
термодинамики выглядит более прозрачной, если все величины описывают
измерения, сделанные в локально сопутствующей инерциональной системе,
движущейся вместе с веществом. Таким образом, мы представим себе локальную
лоренцеву систему, движущуюся с той же скоростью, что и данный
элемент среды. Пусть ? — концентрация барионов, измеренная в этой
системе, а ? — полная плотность энергии (включающая энергию покоя). Тогда
?/? — энергия, приходящаяся на один барион. Различные величины удобно
определять в расчете на один барион, так как барионное число
Уравнение состояния ниже точки образования нейтронных капель 33
сохраняется ^^ Первый закон термодинамики имеет следующую общую
форму:
где dQ — количество теплоты, полученное в пересчете на один барион,
? ^ давление, а 1/а2 — объем, приходящийся на один барион. Черточка в
dQ напоминает, что эта величина не есть полный дифференциал.
Если в элементе среды, который все время находится в равновесии,
протекает какой-либо процесс, то
dQ= Tds, B.1.2)
где 5 — энтропия на один барион, а Г — температура. Объединяя
уравнения B.1.1) и B.1.2), получим в равновесии
''(f) =-4^) + ^^^- B.1.3)
При написании уравнения B.1.3) молчаливо предполагалось, что ?/?
является функцией только ? и s, т.е. ? = ?(?, s). Вообще говоря, плотность
энергии системы, содержащей различные типы частиц, зависит от
относительности количества этих частиц, а также от объема 1/п и значения s.
Если определить относительную концентрацию частиц /-го сорта как
1^-7' B.1.4)
где А2· — концентрация частиц сорта /, то
? = ?(?2,5^·). B.1.5)
Следовательно, в общем случае следует написать
d(j|)--pd(^'j + ?? + ??idY,, B.1.6)
где
-д{е/п) _ 2^(в/и) .-17^
Т^^^, B.1.8)
OS
^^ Мы пренебрежем реакциями с несохранением барионов и лептонов, которые
могли бы происходить при сверхвысоких энергиях (>10^^ГэВ) в некоторых теориях
«великого объединения» (см., например, [607]). В этом случае было бы необходимо
явно ввести объем данного элемента жидкости.
3-353
34 Глава 2
__ д{е/п) _ де . .
?, = -^^-^4- B.1.9)
Величина ?· называется химическим потенциалом частиц сорта /. Ее
можно интерпретировать как изменение плотности энергии при изменении
на единицу концентрации частиц сорта / при постоянных давлении,
энтропии и концентрации частиц остальных типов. Заметим, что поскольку ? по
определению включает в себя энергию покоя, то же самое справедливо и
для ?·.
В равновесии реакции между частицами приводят к состоянию с
детальным равновесием, когда каждая реакция уравновешивается ей обратной и
относительная концентрация частиц каждого сорта остается постоянной.
Таким образом, в равновесии не все относительные концентрации У·
независимы от других термодинамических величин. Равновесные соотношения
можно определить следующим образом.
Рассмотрим сначала специальный случай, когда система бесконечно
близка к равновесию. Разрешены реакции, которые приводят систему к
равновесию, но система теплоизолирована (?/? = 0) и объем ее
фиксирован, так что над ней не производится никакой работы. В этом случае
уравнение B.1.1) дает ?(?/?) = О, т.е. энергия системы остается постоянной.
Реакции порождают энтропию, но так как в равновесии энтропия
максимальна (согласно второму закону термодинамики), то в первом
приближении ds = 0. Таким образом, в равновесии уравнение B.1.6) дает
??,^>: = ?. B.1.10)
Допустим, например, что рассматривается равновесие относительно
реакции
е~+ ? *^ ? -l· ?^. B.1.11)
Тогда dY^ = dYp = -dV^ = -dY,,^ и, следовательно,
Ме + ?/. = М« + ?.,· B.1.12)
Подобные же соотношения между химическими потенциалами
справедливы для любой реакции, которая приводит к равновесию. Если химические
потенциалы известны (например, из статистической механики) как функции
состава при соответствующих значениях ? и s или ? и ?, тогда уравнение
B.1.10) определяет равновесные относительные концентрации.
Даже когда начальное состояние очень далеко от равновесия, но
система приближается к равновесию с <tO = О и dn = О, то ее энергия по-
прежнему остается постоянной. В конце концов она будет бесконечно
близка к равновесию и приведенные выше соображения станут применимы.
Таким образом, можно снова определить состав, если известны химические
потенциалы при фиксированных значениях ? и ?.
Уравнение состояния ниже точки образования нейтронных капель 35
Теперь рассмотрим общий случай, когда система не обязательно
теплоизолирована и над ней может производиться работа. Если система
достигает равновесия за счет квазистатических реакций, то Tds = </?. Однако в
общем случае второй закон термодинамики требует
dQ^ Tds. B.1.13)
В силу сохранения энергии уравнение B.1.1) приводит к результату:
d[^] + Pd[\^^Tds. B.1.14)
Если равновесие достигается при постоянных а? и 5, то уравнение B.1.14)
дает
Je<0. B.1.15)
Равновесное состояние соответствует отсутствию какого-либо изменения ?
(т.е. ?? = 0), и, очевидно, в равновесии значение ? минимально при
фиксированных ? и S. Используя уравнение B.1.6), с помощью этого принципа
можно восстановить уравнение B.1.10).
Аналогично, если Тип сохраняются постоянными, уравнение B.1.14)
дает
#<0, B.1.16)
где
f^-„-Ts B.1.17)
есть свободная энергия в расчете на один барион.
Если ? и ? постоянны (это наиболее частая ситуация, встречающаяся на
практике), то
^g<0, B.1.18)
где
g = ^^^- Ts B.1.19)
— термодинамический потенциал Гиббса в расчете на один барион.
Равновесие соответствует минимуму g при постоянных ? и Р. Последнее
выражение для условия равновесия особенно удобно, когда происходят фазовые
переходы, сопровождаемые скачком в ? при непрерывных ? и ? (см. разд.
2.7).
Используя уравнение B.1.6), из B.1.19) найдем
dg = -dP ^sdT^Zy^idYi^ B.1.20)
36 Глава 2
Таким образом, требование, чтобы g было минимальным при постоянных
? и Р, снова приводит к уравнению B.1.10).
Величины, подобные энергии, объему, энтропии и числу частиц,
называются экстенсивными величинами: при делении некоторого объема пополам
энергия, энтропия и число частиц в каждой части равны половине своего
значения для целого объема. Величины типа давления и температуры,
которые при этом не меняются, называются интенсивными величинами.
Требование, чтобы все экстенсивные величины данной системы изменялись
при изменении объема одинаково, приводит к соотношению^^
^ = Ем/>;. B.1.21)
Теперь уточним количество независимых термодинамических величин,
необходимых для описания равновесного состояния. Рассмотрим для
наглядности взаимодействующую смесь барионов (включающих, например,
нейтроны и протоны) и лептонов (включающих электроны, мюоны и
соответствующие нейтрино). Все реакции в заданном объеме сохраняют
плотность барионного числа п, электронного лептонного числа ^^Ai^e " мюонно-
го лептонного числа п^^, а также плотность электрического заряда Hq.
Выберем четыре основных химических потенциала, соответствующие этим
четырем сохраняющимся величинам, например, следующим образом: ?
(связанный с А2), ?^ (связанный с п^^), ?^ (связанный с п^^) и ц^ (связанный
с Пр). Тогда в равновесии все остальные химические потенциалы будут
линейными комбинациями этих четырех. Так, например, уравибине. B.1.12)
определяет ?^^ из реакции B.1.11).
Получаем, что все термодинамические величины, связанные с частицами
сорта /, в равновесии являются функциями только Г и ?^. (В следующем
разделе это будет показано явно для случая идеальных газов.) Итак, в
общем случае для полного описания равновесного состояния необходимо
задать ? и четыре величины ?·. Эквивалентно можно задать любые пять
независимых термодинамических величин. Обычно Hq = О, так что
требуются только четыре величины.
Ниже в этой главе мы рассмотрим идеальный газ при Г = О и условии,
что нейтрино могут уходить из системы. Это эквивалентно такому выбору
aIlc и '^La' ^'^^ химические потенциалы всех нейтрино равны нулю.
Поскольку /, Hq, А2^е " ^Lu заданы, все термодинамические величины этой си-
^^ Вывод (с использованием иных обозначений) см., например, в книге [479,
с. 314].
^^ Здесь и далее по всей книге предполагается, что нейтрино — это безмассовые
фермионы со спином 1/2 и определенной спиральностью, причем соответствующие
антинейтрино имеют противоположную спиральность. Если нейтрино не являются
безмассовыми частицами, то возможны в принципе нейтринные о^'цилляции,
вследствие чего физические нейтрино будут смесью электронного, мюонного и тау-
нейтрино. В этом случае электронное, мюонное и тау лептонные числа по
отдельности не сохраняются.
Уравнение состояния ниже точки образования нейтронных капель 37
стемы зависят только от одного параметра, например от плотности бари-
онного числа.
В ряде случаев можно использовать понятие ограниченного равновесия.
Это означает, что некоторые реакции, необходимые для достижения
полного равновесия, являются слишком медленными в представляющем
интерес временном масштабе. Это приводит к тому, что возникает более
четырех сохраняющихся величин и нужно задать большее количество п- для
описания системы. Например, характерное динамическое время для звезды
обычно много меньше, чем время, которое необходимо для изменения
состава звезды вследствие ядерных реакций. Чтобы определить давление,
внутреннюю энергию и т.п. в звезде, необходимо явно задать
относительные концентрации Н, Не и т.д., а не только просто барионную
концентрацию п. Подобная ситуация, как правило, возникает и при исследовании
химических реакций в земных лабораториях.
2.2. СВЕДЕНИЯ ИЗ КИНЕТИЧЕСКОЙ ТЕОРИИ
В кинетической теории плотности распределения частиц каждого типа в
фазовом пространстве dVUcfix d^p полностью описывают систему.
Эквивалентно можно задать безразмерную функцию распределения в фазовом
пространстве /(х, р, t), определенную согласно равенству
Здесь h} —объем ячейки в фазовом пространстве (Л — постоянная Планка),
а g — статистический вес, т.е. число состояний частицы с заданной
величиной импульса р. Для массивных частиц ^=25+ 1 (S — спин), для
фотонов g = 2, для нейтрино g = 1. Функция / определяет среднее число
заполнения ячейки в фазовом пространстве ^^
Упражнение 2.1. Покажите, что d^xcPp есть лоренц-инвариант (т.е. скаляр относи
тельно преобразований Лоренца) и, следовательно, f также лоренц-инвариант.
Концентрация частиц каждого липа задается выражением
"=1:7^^'^' B.2.2)
где интеграл берется по всем импульсам. Плотность энергии равна
d'%
=/'
d^xd^p
d'p, B.2.3)
'^ Из контекста нетрудно понять, когда символы / или g используются для
обозначения свободной энергии, как в разд. 2.1.
38 Глава 2
где
? = (р^с^ + m'^c^Y^'^y т — масса покоя частицы. B.2.4)
Заметим, что ? включает в себя энергию покоя частиц. Давление в системе
с изотропным распределением по импульсам равно
1 Г ^91 ,3 / ч
где скорость ? равна ? = рс^/Е, Это соотношение отражает просто тот
факт, что давление представляет собой поток импульса, а множитель 1/3
появляется вследствие изотропии.
Для равновесного идеального газа функция / имеет простой вид:
^'^'-«?[(?-?)????|· ?"»
где верхний знак относится к фермионам (статистика Ферми — Дирака), а
нижний — к бозонам (статистика Бозе — Эйнштейна). Здесь к —
постоянная Больцмана, г, ? — химический потенциал.
При достаточно низкой концентрации частиц и высокой температуре
f(E) сводится к распределению Максвелла—Больцмана:
/(?)«ехр(^^). B.2.7)
В этом случае/(?¦) < 1.
Для полностью вырожденных фермионов (Г — О, т.е. ?/кТ — оо) ?
называется энергией Ферми ?'р и
2.3.УРАВНЕНИЕ СОСТОЯНИЯ ПОЛНОСТЬЮ ВЫРОЖДЕННОГО
ИДЕАЛЬНОГО ФЕРМИ—ГАЗА
Изолированный белый карлик или нейтронная звезда в конце концов
охлаждаются до нулевой температуры, и только давление, присущее
материи при Г = О, удерживает их от гравитационного коллапса. Простейшее
уравнение состояния холодного вырожденного вещества — это уравнение
состояния отдельных типов идеальных (невзаимодействующих) фермионов.
Ниже мы продолжим обзор этого случая^^ В следующих разделах будут
рассмотрены более реалистичные, но и более сложные уравнения
состояния, описывающие вырожденное вещество в компактных звездах.
Более подробное обсуждение см. в книгах [114] или [135].
Уравнение состояния ниже точки образования нейтронных капель 39
Если определить импульс Ферми р^ согласно равенству
Е^^{р%с^ + тУ)''\ B.3.1)
ТО уравнения B.2.2) и B.2.8) дадут
"e = i,r^-p'dp = ^pl B.3.2)
Удобно ввести безразмерный импульс Ферми или «релятивистский
параметр» а: выражением
Тогда
х = -^^. B.з:з)
"'-17^/- ^"*^
где ?^ = h/m^c — комптоновская длина волны электрона.
Давление определяется равенством B.2.5V
^^ 3/,3^0 {?? + тУУ'' ЗЛ' ^A+х^)'/^
W^C^
У1 с
-?-?(?) = 1,42180 X Ю^Щх) дин/см2, B.3.5)
где
ф{х) = -^{хA + х^У^\2х^/3 - 1) + ln[jc + A+ Jc^)^^']}. B.3.6)
Аналогично равенство B.2.3) дает
'^ 'ЬГ^Р"'" + '"'.-')"'4^Ф= ^х(х), B.3.7)
где
Х(^) = ^{^A + ??\\ + 2х')- 1п[х + A + ??'\). B.3.8)
Даже в ситуации, когда вырожденные электроны вносят основной вклад
в давление, в плотности обычно преобладает масса покоя ионов. Эта
плотность равна
??^?,?^??^, B.3.9)
40 Глава 2
где т^ — масса ионов сорта /. Если мы определим среднюю массу бариона
как
тв ^-1^,^/ = 1^, B.3.10)
где А- — барионное число (целая часть атомного веса) ионов /-го сорта, то
Ро-пт^^^. B.3.11)
Здесь ?^ — среднее число электронов на один барион, как в равенстве
B.1.4). Например, для полностью ионизованного чистого ^^С т^ = т^ =^
= 1,66057 · 10~^ г (атомная единица массы) и У^ = Z/A = 0,5. Поэтому
Ро = 1,9479 X Ю^х^ г/смЗ. B.3.12)
Иногда используют величину
м, = ;^ B.3.13)
(средний молекулярный вес на один электрон), так что
Ро = ?em^n, = 0,97395 X 10^^^^ t/cmI B.3.14)
или
х= 1,0088 X ??-^?-^^) , B.3.15)
где Pq выражается в г/см^. Часто в равенстве B.3.13) можно пренебречь
различием между т^и m^^, Например, для полностью ионизованного
элемента с атомным весом А и номером ? можно записать ?^ = А/? с
точностью примерно 10~^.
Аналогично для определения плотности иногда используется средний
молекулярный вес ?. Тогда выражение для плотности выглядит так:
Ро= (''е + Е''/)м'^и· B.3.16)
Отсюда с помощью равенства B.3.11) получим
Здесь снова можно положить т^^/т^ = 1. Отличие этого отношения от 1
существенно только в случае очень точных вычислений. Понятие среднего
Уравнение состояния ниже точки образования нейтронных капель 41
молекулярного веса оказывается особенно полезным при отсутствии
вырождения, когда давление определяется выражением, справедливым для
классического идеального газа:
/> = («е + Е«,>Г=^/сГ. B.3.18)
Выражения B.3.5) и B.3.14) определяют параметрически через ?
уравнение состояния идеального вырожденного газа ? = P{Pq). (Заметим, что
? = Pq 4· ?/c^ — полная плотность энергии и обычно член е/с^
пренебрежимо мал.)
Упражнение 2.2. Покажите, что в пределе ? < 1 (нерелятивистские электроны)
справедливы разложения
В ТО время как для ? > 1 (релятивистские электроны)
?(.?) ^-^[х* + х^ - \\a2x ¦ ¦-^. B.3.20)
Уравнение состояния можно записать в форме политропы
? = ???, B.3.21)
TRt К TiT являются постоянными в двух предельных случаях:
1. Нерелятивистские электроны, Pq < 10* г/см', ? < \, ф{х) — ?^/15?^,
„ 5 „ 3^/?^^ h^ 1,0036 ? 10'^
^^= 3' ^= 5 .XV/3=-^;yi СГС. B.3.22)
2. Ультрарелятивистские электроны, ? > 10* г/см', ? > \, ф(х) —
4 З'/У^/' he 1.2435 X 10'^ _^
Вышеприведенные результаты можно легко перенести на случай частиц с
массой mi и статистическим весом g^, получив в результате уравнение со-
42 Глава 2
стояния идеальных фермионов произвольного сорта /. Например, для
чистых нейтронов уравнения B.3.7), B.3.14) и B.3.21)-B.3.23) превращаются
соответственно в
?„ = ^?(^„)= 1,6250 X lO^'xixJ эрг/см^ , [^п = -^) B-3.24)
Ро = '"««^ = ТГ ТЧ^" = 6,1067 X 10'^ г/смз, B.3.25)
? = ???, B.3.26)
где два предельных режима, указанные выше, суть
1. Нерелятивистские нейтроны, р^ < 6 - 10^^ г/см^,
Г = 4, К = ^-^ ^ = 5,3802 X Ю^СГС. B.3.27)
3 5 д^уз
2. Ультрарелятивистские нейтроны, р^ > 5 - 10^^ г/см^,
? = :?, /^ = ^-? ^= 1,2293? Ю^^СГС. B.3.28)
3' 4 ,„4/3 ^ ^
В этом случае плотность массы ? = е„/с^ целиком обусловлена
нейтронами и сильно превосходит р^^, если нейтроны являются
ультрарелятивистскими (Ро > 6 · 10^^ г/смЗ).
Упражнение 2.3. В равновесии можно вычислить давление по известной плотности
энергии с помощью соотношения B.1.7). Предполагая, что имеются только
электроны (т.е. ? - Eg, ? — Пе)у покажите, что равенство B.3.5) может быть выведено из
равенств B.3.4) и B.3.7).
Упражнение 2.4. Покажите, что
?,
и сравните с равенством B.1.21).
= ?
Ту
B.3.29)
Упражнение 2.5. Рассмотрите полностью ионизированное вещество, состоящее из
водорода, гелия и более тяжелых атомных ядер, / > 2. Пусть X и ? обозначают
долю по массе соответственно водорода и гелия. Покажите, что
2
^e^JZ^Tx' B.3.30)
Подставьте приближенно т, = Л/т^ для всех / и возьмите Z/A, * 1/2 при / ^ 2.
Упражнение 2.6. Покажите, что средняя кинетическая энергия электронов в
вырожденном газе равна 3/5 Яр в нерелятивистском пределе и 3/4 ?? в релятивистском
пределе. Здесь Е^' = Е^ - т^с^ =^ p^/lnig.
Уравнение состояния ниже точки образования нейтронных капель 43
Упражнение 2.7.
а) Покажите с помощью равенства B.2.7), что для нерелятивистского газа
Максвелла—Больцмана
? = пкТ, B.3.32)
? = птс^ + \пкТ. B.3.33)
б) Используя равенство B.1.21) (для одного сорта частиц), покажите, что
gimkTY'^
B.3.34)
Упражнение 2.8, Предположим, что частицы газа в упр. 2.7 имеют внутренние
степени свободы (например, отвечающие возбуждению атома или ядра). Тогда для их
энергии можно написать ? = Е^^ + Ej, где энергия центра масс ??^. определяется
равенством B.2.4), а относительно Ej предположим, что она не зависит от Я и равна
нулю в основном состоянии. Покажите, что равенство B.3.31) следует изменить,
сделав подстановку
^-* Egy^"^^^^^ B.3.35)
J
где gj — степень вырождения у-го возбужденного состояния. Как изменятся
выражения для Я, ? и 5?
Упражнение 2.9, Покажите с помощью интегрирования по частям равенства B.2.2),
что выражение ? = пкТ справедливо для газа Максвелла—Больцмана в общем
случае независимо от того, является ли он релятивистским или нет.
2.4. ЭЛЕКТРОСТАТИЧЕСКИЕ ПОПРАВКИ К УРАВНЕНИЮ СОСТОЯНИЯ
Рассмотренное в предыдущем разделе уравнение состояния идеального
вырожденного ферми-газа было использовано Чандрасекаром в его
пионерских работах [111, 112] по изучению равновесия белых карликов (см. гл. 3).
На практике к этому уравнению состояния имеются две существенные
поправки. Одна из них, обратный ?-распад, обсуждается в разд. 2.5—2.7.
Предметом этого раздела являются поправки, связанные с
электростатическим взаимодействием между электронами и ионами.
Основная часть электростатических поправок возникает из-за того, что
положительные заряды не распределены однородно по газу, а
сосредоточены в отдельных ядрах с зарядом ?. Это приводит к уменьшению энергии и
давления окружающих их электронов, так как pacctoяниe между
отталкивающимися друг от друга электронами в среднем больше расстояния
между ядрами и электронами, и потому отталкивание оказывается слабее, чем
притяжение.
44 Глава 2
В невырожденном газе роль кулоновских эффектов возрастает с
увеличением плотности. Действительно, отношение кулоновской энергии к
тепловой приближенно равно
кТ кТ ^ кТ
AАЛ)
Это отношение растет с ростом п^. Здесь {г) -^ п^ ^^^ — характерное
расстояние между электронами и ионами. Напротив, для вырожденного гдз а
имеем
^-?^. B.4.2)
Используя выражение B.3.2) для Рр, преобразуем это равенство
следующим образом:
?F \Ъ-пЧ вой'/' lz'x6xlO^^CM-3 / ^-^
где Qq = f?-/m^e^ — боровский радиус. Таким образом, Е^ < Е^ для
большинства рассматриваемых в астрофизике вырожденных газов.
Можно вывести приближенное выражение для поправки к уравнению
состояния идеального вырожденного газа, используя условие
[подразумеваемое в уравнении B.4.3)], что концентрация п^ в первом приближении
однородна.
При Г — О ионы образуют решетку, максимизирующую расстояние
между ионами. Рассмотрим «сферическую» ячейку этой решетки с объемом
4??^3 = 1/А2уу, где rij^ — концентрация ядер. В этом приближении,
называемом приближением Вигнера — Зейтца^\ газ можно представить себе
разделенным на нейтральные сферы радиусом Tq вокруг каждого ядра, причем
каждая сфера содержит ? электронов, ближайших к ядру.
Полная электростатическая энергия любой такой с(Ьеоы равна сумме
потенциальных энергий электрон-электронного (е — е) и электрон-ионного
{е — О взаимодействий. Чтобы собрать однородную сферу из ?
электронов, необходимо затратить энергию
.= f^, B.4.4)
^^ Приближение Вигнера — Зейтца гораздо лучше применимо для белых карликов,
чем для обычных (земных) твердых тел, для которых концентрация п^ заметно
более неоднородна.
Уравнение состояния ниже точки образования нейтронных капель 45
где
иЗ
q=-Ze'- B.4.5)
представляет собой шряд внутри сферы радиусом г. Выполнив
интегрирование, получим
Наличие электронной сферы вокруг центрального ядра с зарядом Ze
приводит к уменьшению энергии на
''odq ^ _ 3^ZV
''о г 2 Го
^., = Zeff --\?. НАЛ)
Таким образом, полная кулоновская энергия такой ячейки равна
Е^Е +?.= - —-^ B.4.8)
В силу того что ячейки нейтральны, можно пренебречь
взаимодействием между электронами и ядрами, находящимися в различных ячейках.
Электростатическая энергия, приходящаяся на один электрон, равна
здесь было использовано выражение
?
л. =
Атг1/Ъ
B.4.10)
Численный коэффициент в равенстве B.4.9) равен 1,45079, что очень близко
к точному значению 1,44423 для объемноцентрированной кубической
решетки [140]. Соответствующее давление отрицательно и определяется
уравнением B.1.7):
Сначала рассмотрим это выражение в ультрарелятивистском пределе. В
этом случае результат Чандрасекара для идеального газа имеет вид
Ро - йсC^2)'/'-^ B.4.12)
46 Глава 2
[ср. с равенствами B.3.5), B.3.20) и B.3.4)], и потому
где а = e'^/hc = 1/137 — постоянная тонкой структуры. Следующий член в
этом разложении по степеням aZ^^"^ возникает из-за неоднородности
распределения электронной концентрации (поправки Томаса—Ферми; ср. с
излагаемым ниже и работой Солпитера [496]).
Хотя вышеприведенные кулоновские поправки относительно малы, они
все же существенны для белых карликов с высокой плотностью вещества и
нейтронных звезд малой плотности.
В нерелятивистском пределе
л5/3
P,^h\Ъ'n?''^^ B.4.14)
[ср. с равенствами B.3.5), B.3.19) и B.3.4)], и потому
? ?2/3
T^^^W^ ???- B.4.15)
Отсюда следует, что Я = О, когда
Z2
л. =
??^??
B.4.16)
Это, согласно равенству B.3.11) при А - 2?, отвечает плотности
Ро ^0,47^ г/смЗ. B.4.17)
Равенство B.4.17) дает для железа р^ « 250 г/см^ вместо лабораторного
значения 7,86 г/см^. Причина этого расхождения состоит в том, что при
малой плотности приближение однородного газа уже неприменимо.
Точное уравнение состояния, справедливое при лабораторных
плотностях, получить весьма трудно, так как эффекты, связанные с
существованием электронных оболочек, маскируют более простые статистические
эффекты. Однако статистический подход к уравнению состояния хорошо
работает уже при плотностях, в несколько раз превышающих лабораторные,
и оказывается вполне адекватным при рассмотрении белых карликов с
малыми массами (и даже при рассмотрении глобальной структуры больших
планет).
Простейшим статистическим подходом к исследованию атомной
структуры является метод Томаса—Ферми, Предполагается, что внутри
каждой ячейки Вигнеоа—Зейтца электроны движутся в поле медленно
меняющегося сферически-симметричного потенциала V(r). Так как в любой
Уравнение состояния ниже точки образования нейтронных капель 47
точке этот потенциал является примерно постоянным, то для электронов
можно использовать статистику Ферми—Дирака свободных частиц. Это
означает, что энергия взаимодействия между электронами принимается
малой по сравнению с кинетической или потенциальной энергией отдельного
электрона. В силу этого при любом г все состояния вплоть до ?* = ^р
оказываются занятыми. Энергия Е^ не зависит от г, в противном случае
электроны перемещались бы в области с меньшим значением Е^. Таким
образом,
?р = -eV{r) + ^Щ^ = const, B.4.18)
где /7р — максимальное значение импульса электронов в точке г. Выбирая
подходящим образом произвольную постоянную в V(r)y можно придать
?'р любое удобное значение. Однако здесь мы не будем использовать эту
возможность.
Упражнение 2.10. Покажите, что утверждение о постоянстве ? можно получить из
условия, что электронное облако удерживается в гидростатическом равновесии за
счет давления идеального ферми-газа.
Аналогично равенству B.3.2) получим
"' ' 1^^'^ = |^Bш.[?, + eV{r)]Y^\ B.4.19)
Потенциал V{r) определяется уравнением Пуассона:
V^F = Airen^ -\- вклад ядра. B.4.20)
Вклад ядра представляет собой ?-функцию в начале координат, так что при
г > О его можно опустить, налагая граничные условия
lim rF(r) = Ze. B.4.21)
r-O
На границе ячейки г^ электрическое поле должно исчезать (ячейка
электронейтральна):
dr
= 0. B.4.22)
Го
Из соотношений B.4.19) и B.4.20) следует уравнение
-г^М)='^[2тХЕ,^еУ)Г^\ B.4.23)
48 Глава 2
решение которого должно удовлетворять граничным условиям B.4.21) и
B.4.22).
Удобно перейти к безразмерным величинам, положив
г = ??, B.4.24)
?p + .F(r )=^^, B.4.25)
где
,2 \1/3
'* = 1?28?) "о- ^2.4.26)
После некоторого упоощения уравнение B.4.23) превращается в уравнение
Томаса—Ферми
d^ Ф'/^
B.4.27)
С граничными условиями
Ф@) = 1, B.4.28)
Ф'(хо) = ^· B.4.29)
Упражнение 2.11. Убедитесь, что уравнение B.4.29) также можно получить, если
потребовать выполнения условия электронейтральности в форме
Z= (\??^?,??. B.4.30)
Уравнение B.4.27) нелинейно, и потому его приходится решать
численно; такое численное интегрирование было проведено в работе [196]. Если в
качестве исходного взять значение ф@) = 1 в начале координат, то
существует выделенное значение [316] ф'@) (= -1,5880710), для которого решение
асимптотически прижимается к оси ? при больших х, а соотношение
B.4.29) удовлетворяется при 04?) -^ О, ??^?) "^ ^» когда ?-? -^ оо (рис. 2.1).
Как мы увидим ниже, это случай нулевого давления, соответствующего
нулевой плотности и бесконечному радиусу (Xq — оо). Указанный недостаток
модели Томаса—Ферми, а именно, тот результат, что свободные атомы
имеют бесконечный радиус, устраняется, если учесть обменные эффекты
(модель Томаса—Ферми—Дирака).
Уравнение состояния ниже точки образования нейтронных капель
49
^х
Рис. 2.1. Поведение решений уравнения Томаса — Ферми B.4.27).
При ф'@) > - 1,5880710 ф{х) нигде не обращается в нуль и стремится к
бесконечности при дг — оо. Условие B.4.29) удовлетворяется при некотором
конечном значении дг^, которое определяет радиус ячейки. Этот случай
соответствует нейтральным атомам, подвергающимся внешнему давлению.
Мы не будем здесь рассматривать случай ф'@) < -1,5880710,
соответствующий свободным положительным ионам, для которого ф{х) =0
при конечном х^.
Теперь вычислим давление на границе ячейки, пользуясь формулами,
полученными для случая свободных частиц:
^^ Тъ^ ^"^^^^^ = ???^—^??'-?)· B.4.31)
Заметим, что поскольку dV/dr = О на границе, то соседние ячейки друг на
друга не действуют. Используя равенства B.4.19) и B.4.24)-B.4.26),
можно привести выражение B.4.31) к виду
Р =
1 7?
2^2
ЮТГ ?4
?(?)
5/2
B.4.32)
Плотность определяется просто полной массой внутри ячейки:
Агпг.
Ро =
4V^^/3
B.4.33)
Соотношения B.4.32) и B.4.33) параметрически определяют уравнение
состояния ? - P(pq) (через параметр Xq). Хотя локально давление всюду
внутри ячейки задается формулой для идеального ферми-газа
нерелятивистских электронов, отклонения п^(г) от однородности приводят к
отличию от идеального случая для «усредненного по ячейке» уравнения
состояния P(pq),
4-353
50 Глава 2
При малой плотности х^ -* оо. Асимптотика решения уравнения B.4.27)
в этом случае имеет вид
144
ф(х) г-, JC^ 00. B.4.34)
Упражнение 2.12. Покажите, что выражение B.4.34) удовлетворяет уравнению
B.4.27), однако нарушает условие B.4.28).
Таким образом,
Р~Хо''~рТ- B.4.35)
Это соотношение демонстрирует характерное увеличение «жесткости»^^
уравнения состояния с показателем адиабаты -3,3 при уменьшении
плотности^^ Следствия этого результата для белых карликов малой массы
обсуждаются в гл. 3.
В пределе высоких плотностей результат B.4.32), полученный в модели
Томаса—Ферми, как и следовало ожидать, сводится к равенству B.4.15)
(ср. с упр. 2.18).
Более полное исследование поправок к уравнению состояния в
обсуждаемом здесь режиме было проведено в работах [496, 500]. В большинстве
приложений результаты работы [196] для модели Томаса—Ферми—Дирака
являются адекватными при малых плотностях вплоть до значений
10^ г/см^. При больших плотностях обычно используется результат Чан-
драсекара для идеального газа с кулоновскими поправками B.4.11).
Упражнение 2.13.
а) Покажите, что кинетическая энергия электронов в модели Томаса-Ферми равна
dp
5 ? -?
?/4-'/^dx. B.4.36)
6) Покажите, что потенциальная энергия электронов в поле ядра равна
?,.„= -Z.^/JVr^rfA= -^ly/^^-Wiax. B.4.37)
^ «Жесткость» (и «мягкость») — качественная характеристика уравнения
состояния. Для заданной плотности более жесткому уравнению состояния соответствует
большее давление. — Прим. перев.
^^ Зельдович и Новиков [636] привели простой, но не вполне строгий вывод
значения показателя степени 10/3 в соотношении B.4.35).
Уравнение состояния ниже точки образования нейтронных капель 51
в) Покажите, что потенциальная энергия взаимодействия электронов в
сферической ячейке равна
^-' ° r'L''''''^^')//'''''''^'')^" ''I"' ^2-^^-^^)
1 Z^^ r^o ,
1 ? Jo [? Jo ^ ^^ '
+ 1Ух'^^\х%хГ'''\ B.4.39)
Упражнение 2.14. Выведите уравнение Томаса—Ферми B.4.27), минимизируя
полную энергию ? при ограничении B.4.30). Величину ? следует варьировать при
фиксированной граничной точке Xq.
Указания. 1) Это ограничение соблюдается, если варьировать функцию
•?
где ? = const — множитель Лагранжа.
2) Из-за симметрии выражения B.4.38) вариация Eg_g равна удвоенному
значению, полученному при вариации по ? первого подынтегрального выражения в
равенстве B.4.39).
Упражнение 2.15.
а) Покажите, что
dE _ 2 ф'^Чхр) Z^e^ .2440)
dxo S ??2 ? ¦
Заметим, что из-за граничного условия B.4.29) функция ф(х) неявно зависит от Xq, и,
следовательно, ее следует дифференцировать по Xq под знаком интеграла. Полезное
соотношение можно получить с помошью дифференцирования условия B.4.30) по
Xq.
б) Выведите равенство B.4.32), повторно исходя из первого закона
термодинамики.
Упражнение 2.16.
а) Исходя из равенства B.4.36), покажите, что
?к ? = 1 ^ [???????) - Ф'@)]. B.4.41)
52 Глава 2
Указание^\ Интеграл / = [?^^'^?'^^'^?? можно оценить, записав ф^^^ = Ф^^^Ф,
о
подставив для фЗ/2 выражение из уравнения B.4.27), дважды проинтегрировав по
частям, повторив подстановку для ф^^^ и снова проинтегрировав по частям.
б) Оцените внутренний интеграл в выражении B.4.39) для Eg _ g^ подставляя ф^^^
из уравнения B.4.27). На основании этого покажите, что
?р ? = Е,.„ + Е,., = - I ^ [14/^ф(;со)'/' - ф'@)]. B.4.42)
Упражнение 2.17. Проверьте, что в приближении Томаса—Ферми справедливо вири-
альное соотношение:
^??+????=|?'^.
где У - Уз тгг^.
Упражнение 2.18 (основанное на работе [500]).
Решите уравнение Томаса—Ферми в пределе высокой плотности {xq — 0)
следующим образом. Положите у - x/xq и
Xq
Покажите, что граничному условию B.4.29) можно удовлетворить при
/?A)=/?A). /,40=/,A), и т.д.,
а граничному условию B.4.28) — при
/,@)=1, /,@)=/,@)=-=0.
Покажите, что таким образом можно воспроизвести полученный ранее результат
B.4.15), т.е.
(Почему для того, чтобы найти Р{ро) при высокой плотности, нельзя просто
положить л· = хо = О и воспользоваться выражениями B.4.32) и B.4.33), подставив в
первое из них равенство B.4.28)?)
'^ Описанная здесь процедура впервые приведена Милном [409], которому было
известно аналогичное вычисление Эмденом [183] гравитационной потенциальной
энергии политропы; см. гл. 3.
Уравнение состояния ниже точки образования нейтронных капель 53
2.5. ОБРАТНЫЙ |б-РАСПАД: ХОЛОДНЫЙ ИДЕАЛЬНЫЙ п—р—е-ГАЗ
При высоких плотностях наиболее существенная поправка к уравнению
состояния обусловлена обратным ]3-распадом^^:
е-+ ? ^ ? + р. B.5.1)
Обычно протоны и нейтроны связаны в ядрах. Однако в этом разделе мы
обсудим эффекты обратного ]3-распада, рассматривая случай газа
свободных электронов, протонов и нейтронов. При этом будем полагать, что
нейтрино, образованные в реакции B.5.1), свободно покидают систему.
В разд. 2.6 и 2.7 рассмотрен более интересный случай связанных нуклонов.
Реакция B.5.1) может идти только в том случае, если энергия электрона
достаточно высока, чтобы скомпенсировать разность масс протона и
нейтрона; (т^ - гПр) ' с^ = 1,29 МэВ. Этот процесс эффективно
перерабатывает протоны в нейтроны, если не происходит ^-распад:
п-* ? ^ е^ V. B.5.2)
Реакция B.5.2) запрещена, если плотность вещества настолько высока, что
все уровни энергии электронов заняты, вплоть до того, который должен
был бы занять испускаемый в этой реакции электрон. Таким образом,
существует критическое значение плотности, ниже которой начинается
реакция B.5.2).
Можно рассчитать свойства такой смеси электронов, протонов и
нейтронов, полагая, что они находятся в равновесии. В этом случае равенство
B.1.12) дает
Ме + Мр = М«· B.5.3)
Химический потенциал нейтрино здесь положен равным нулю; иными
словами, предполагается, что концентрация нейтрино равна нулю. Введем по
аналогии с равенством B.3.3) следующие величины:
^е = —, ^„ = —, ^. = -. B-5.4)
Тогда в силу того что ?^ = [(p^cY + mjc^Y^^- и т.д., уравнение B.5.3)
принимает вид
т,{1 + х^У^' + т^{1 + xj)'/'· = т„{1 + х^„У'\ B.5.5)
'^ Там, где из контекста ясно, что речь идет только об электронных нейтрино, мы
будем вместо v^ использовать обозначение v.
54 Глава 2
Условие зарядовой нейтральности п^ = ? приводит к соотношению [ср. с
равенством B.3.4)]:
^ ^????4 B-5.6)
З^^Х', ' 3^% "
или, иначе,
т^х^ = т„х
е-'^е "·/>·"-/>· B.5.7)
Теперь уравнение состояния можно записать параметрически, например
рез параметр х^: при заданном х^ уравне
нение B.5.5) — х^. Ъ результате получим
через параметр х^: при заданном х^ уравнение B.5.7) определяет л^, а урав-
тх^ , ^ f^nC . , mjp-
? = ^?-?(^.) + -^?(^.) + -^?(^ J. B.5.8)
?', ^^ "' ??
m^c^ , , гПрС ^ ^ т„с^
? = -f-x{xe) + -f-xi^p) + -^ХМ, B.5.9)
?
"'l^f^^l^f- ^'-'''^
Упражнение 2.19. Выведите соотношение B.5.5), минимизируя ? при фиксированном
? и используя условие электронейтральности.
Минимальную плотность, при которой появляются нейтроны, можно
ЙТИ, ПОЛОЖИ!
эй плотности
B.5.6) следует
найти, положив дг^ = О в равенстве B.5.5). Поскольку оказывается, что при
этой плотности протоны будут нерелятивистскими, ?? ? < 1, и потому из
mX\+xl)'^^ = Q, B.5.11)
где Q = т^ - гПр. Разрешая это уравнение относительно х^у из выражений
B.5.6) и B.5.10) получим
13/2
1
? =
2
1
е I
= 7,37Х 103°см-з B.5.12)
и, следовательно,
Ро = пт. » 1,2 X 10^ г/см'. B.5.13)
Уравнение состояния ниже точки образования нейтронных капель 55
Упражнение 2.20. Удовлетворяется ли уравнение B.5.5) при р^ < 1,2 · 10^ г/см^?
При плотности выше указанной равновесная смесь содержит все
возрастающую долю нейтронов. Ее состав можно определить, подставив
равенство B.5.7) в соотношение B.5.5):
{т\ + mlxlY' + т^Х + xj)''' = т„{\ + x\f\ B.5.14)
Дважды возводя равенство B.5.14) в квадрат и упрощая, получим
^т\т\х\{\ + х1) = (?^ - ml)[im„ + т/ - т]] +
+ 2mlxl{ml -ml- т\) + m^x^ B.5.15)
Таким образом,
Пр _ ? ГПрХр ?
'^ ^ 2{ml-ml-ml) , JQ'- т1)[{т„ + m^f - т]]
3/2
2 2
А 4
1+-
xt
Теперь, поскольку и ?, и w^ много меньше, чем т^,
";> _ 1 ? 1 + ^Q/m„xl + 4(е^ - ml)/mlxt
«„ 8 \ 1 + 1/^2
3/2
B.5.16)
B.5.17;
Следовательно, протон-нейтронное отношение сначала убывает с ростом
л·^, т.е. с ростом плотности. Оно достигает своего минимального значения,
равного
V ч / nun
при
т„ т„
3/2
0,0026
B.5.18)
«"^^????^-^? ' Ро «'"Л » 7,8 X 10" г/смз, B.5.19)
56 Глава 2
а затем монотонно растет, стремясь к V% при дг^ — оо, или р^ — оо.
Заметим, что найденное здесь равновесное состояние является
устойчивым, так как соответствует минимуму ?.
Упражнение 2.21. Проверьте равенства B.5.18) и B.5.19).
Упражнение 2.22. Покажите, что результат п^ : Пр : п„ = 1 : 1 : 8 в пределе очень
большой плотности является тривиальным следствием электронейтральности, ?-
равновесия и ультрарелятивистского вырождения.
Упражнение 2.23. Вычислите максимальный импульс электрона, испускаемого в
реакции B.5.2). Покажите, что/т^ больше этой величины при всех плотностях,
превышающих значение B.5.12). Отсюда следует, что равновесное состояние является
устойчивым.
Результаты этого раздела, строго говоря, неприменимы к случаю гравита-
Щ10НН0Г0 коллапса с испусканием нейтрино, даже если коллапс происходит
квазистатически и при нулевой температуре. В открытой системе
термодинамическое равновесие не достигается и состав а?—р—е-смеси приходится
определять, реитая соответствующие кинетические уравнения для разных
реакций.
Приведенные выше уравнения точно описывают равновесную систему с
фиксированными зарядом (нулевым), барионным числом и лептонным
числом. При этом для лептонного числа выбрано минимально возможное
значение, т.е. рассмотрен предел ?2^ — () (?^ — 0) при сохранении условия
детального равновесия.
2.6. БЕТА-РАВНОВЕСИЕ МЕЖДУ РЕЛЯТИВИСТСКИМИ ЭЛЕКТРОНАМИ
И ЯДРАМИ. УРАВНЕНИЕ СОСТОЯНИЯ ГАРРИСОНА-УИЛЕРА
Перейдем теперь к количественному рассмотрению обратного бет^-распада
и попытаемся получить более точное уравнение состояния в диапазоне
плотности 10^ ^ ? ^ 4 · 10^^ г/см^. Мы хотим найти низшее
энергетическое состояние системы А -^ 10^'^ барионов (масса -IMq), состоящей из
отдельных ядер, которые находятся в бета-равновесии с релятивистским
электронным газом. Нужно будет определить: 1) какие ядра находятся в
этой системе, т.е. какие значения А и ? минимизируют энергию; 2)
соответствующее давление.
В этом разделе мы предположим, что по прошествии достаточного
времени после ядерного горения образовавшееся холодное вещество достигает
полного термодинамического равновесия. Тогда наинизшее по энергии
состояние определяет как состав, так и уравнение состояния материи.
Возможность того, что вырожденное вещество звезд-карликов в природе
действительно достигает минимальной энергии, обсуждается в гл. 3.
Как хорошо известно, для системы барионов с А -^ 90 состояние с
наинизшей энергией представляет собой единственное ядро; при этом
наиболее сильно связанным ядром является 26^^· ^Р** А ^ 90 состоянию с паи-
уравнение состояния ниже точки образования нейтронных капель 57
низшей энергией соответствует система, состоящая из двух и более ядер;
наиболее сильная связь имеет место для значений Л, являющихся целыми
кратными 56. Таким образом, по мере увеличения А появляется все больше
оснований рассматривать состояние вещества с минимальной энергией как
чистое I^Fe. Однако положение меняется, когда А начинает превосходить
lO^'' и становятся существенными эффекты самогравитащш. Для барионов в
гидростатическом равновесии величина плотности превосходит ? -
^ \0р г/см^. Следовательно, электроны являются релятивистскими; они
соединяются со связанными в ядрах протонами, образуя нейтроны
(обратный ]3-распад), что постепенно изменяет равновесный ядерный состав от
^е в сторону вещества, все более богатого нейтронами.
Физическая картина в общем выглядит следующим образом. Если бы
равновесная структура ядра определялась только ядерными силами,
нуклоны собирались бы в ядра неограниченного размера. Однако силы кулонов-
ского отталкивания при этом стали бы настолько значительными, что
привели бы к делению таких больших ядер. При низких плотностях эти два
противоположных эффекта взаимно уравновешиваются при А = 56.
Однако, когда в игру входят релятивистские электроны, баланс смещается.
Доля нейтронов по отношению к протонам в ядре увеличивается (из-за
обратного ]3-распада), и кулоновские силы начинают играть менее заметную
роль. Отсюда возникает тенденция к образованию больших ядер. Когда
плотность возрастает до -4 · 10^^ г/см^, отношение п/р достигает
критической величины. Любое дальнейшее увеличение плотности ведет к
образованию нейтронных капель, т.е. к появлению двухфазной системы, где
сосуществуют электроны, ядра и свободные нейтроны, которые совместно
определяют состояние с наинизшей энергией. Повышение плотности сверх
4 10^^ г/см^ ведет к увеличению отношения нейтроны —
протоны и появлению все большего количества свободных нейтронов.
Наконец, когда плотность превышает примерно 4 · 10^^ г/см^,
нейтроны создают большее давление, чем электроны. Таким образом,
нейтроны начинают играть главную роль, и среду можно рассматривать как одно
громадное ядро с плотностью несколько ниже нормальной ядерной.
Количественное рассмотрение начнем, выписав выражение для
плотности энергии смеси ядер, свободных электронов и свободных нейтронов в
борме
? = п^М{Л, ?) + ?;(/? J + ?,{?„), B.6.1)
Здесь Л/(Л, ?) — энергия ядра (Л, ?), включающая в себя массу покоя
нуклонов. В ядерной физике принято также включать в М(А, ?) массу покоя
электронов. Следовательно, из выражения B.3.7) для ?^ нужно вычесть
п^т^ср- и обозначить остаток, входящий в равенство B.6.1),через ?'.
Величина А2уу — концентрация атомных ядер, а а?^ — концентрация свободных
нейтронов. Концентрации барионов и электронов определяются
выражениями
? ^ rij^A + п„, n^=-nj^Z, B.6.2)
58
Глава 2
т.е.
1=ЛУ^ +
\>
?^?.
B.6.3)
Таким образом, вместо того чтобы рассматривать ? при Г = О как
функцию (а2, Гдг. Уе> ^п^у равным образом в качестве независимых переменных
можно выбрать (п, Л, ?, ?^). Равновесные относительные концентрации и
уравнение состояния определяются минимизированием ? по Л, ? и У^ при
фиксированном п.
Заметим, что, хотя в этой главе мы номинально интересуемся лишь
уравнением состояния до процесса образования нейтронных капель, в
уравнении B.6.1) следует предусмотреть наличие свободных нейтронов, чтобы
можно было определить начало этого процесса. Оказывается, что
уравнение состояния Гаррисона—Уилера можно легко продолжить за точку
образования нейтронных капель, что и будет сделано в данном разделе.
Величина М(Л, ?) для очень богатых нейтронами ядер, рождающихся
при плотностях выше 10^^ г/см^, экспериментально не определена, и
поэтому ее приходится выводить теоретически. По крайней мере вплоть до
образования нейтронных капель это обычно делается с помощью
полуэмпирической массовой формулы.
Весьма простой вариант уравнения состояния был получен Гаррисоном
и Уилером в 1958 г.^^ Они использовали полуэмпирическую массовую
формулу Грина [236]:
?{?, А) = [(А - Z)m„c^ + Z{m^ + т,)с^ - АЕ,] =
= т..с'
Ь^А + Ь^А^/^ - bjZ + Ь^а(^ - ^^ +
А'/'
, B.6.4)
где Ej, — средняя энергия связи, приходящаяся на один барион^\
6, = 0,991749, 6з = 0,000840, Ь^ = 0,000763,
^2 = 0,01911, ^4 = 0.10175.
B.6.5)
Это выражение основано на капельной модели ядра, причем его члены
интерпретируются следующим образом. Основной вклад в ?^
пропорционален объему ядра, как в случае капли жидкости. Отличие Ь^ от единицы
'^ Гаррисон и Уилер [259]. См. также Гаррисон и др. [261], гл. 10, где приведено
более подробное обсуждение и даны удобные приближенные выражения для
уравнения состояния.
^^ Мы умножили все величины Ь^ . .by использованные Грином, на 0,999682,
чтобы перейти от нормировки на '^ к современной нормировке на '^'
С.
Уравнение состояния ниже точки образования нейтронных капель 59
обусловлено главным образом энергией связи этого объема (радиусы адер
приближенно пропорциональны Л^^^). Слагаемое, пропорциональное bj,
представляет собой поверхностную энергию, а ^4 — симметричный член
(ядра с равным числом протонов и нейтронов имеют меньшую энергию), в
то время как Ь^ дает кулоновскую энергию. Величина Ь^ равна просто
{т^ — nijj — m^)/m^^, Оболочечными эффектами и эффектами спаривания
мы пренебрегаем ^\
Упражнение 2.24. Предположим, что ядро состоит из смеси двух идеальных
нерелятивистских ферми-газов; в одном находится ? протонов, а в другом N ·=¦ А — ?
нейтронов. Покажите, что энергия ядра (за вычетом энергии покоя) равна
-1Ч(^^Г-(?Г4
Здесь ?р — энергия Ферми за вычетом энергии покоя, определенная для А нуклонов,
находящихся в объеме К, так что в каждом состоянии с данным импульсом
находятся четыре нуклона. Найдите ?? по известной концентрации ядер л = 1,72 · 1(Я^ ча-
стиц/см^. Рассматривая отклонения от случая N = ? (минимум ?), определите
симметричный член и покажите, что примерно половина величины Ь^ может быть
объяснена в этой простой модели, использующей принцип Паули.
Упражнение 2.25. В модели ферми-газа вычислите поверхностную энергию ядра
следующим образом. Плотность состояний в фазовом пространстве без учета
спиновых эффектов равна
-^^ = -^, Е<Е,.
Отсюда число состояний с импульсами между ? ир + dp в ячейке объемом V равно
Это выражение можно также получить, решая уравнение Шредингера для свободной
частицы внутри кубической ячейки. В этом решении, однако, не следует учитывать
состояния, для которых компоненты Рху Ру или р^ равны нулю, так как они
соответствуют нулевой волновой функции. Покажите, что такое уточнение приводит к
выражению
^) Обсуждение этих эффектов можно найти в любом учебнике по ядерной физике.
60 Глава 2
где S — поверхность ячейки. Используя это выражение, получите среднюю энергию
связи, приходящуюся на одну частицу в форме разложения
? S
где flfQ = ????:. Используя выражение rjs/ = ГоА^^^ ил = A/V = ^irrj
соответственно для радиуса ядра и концентрации частиц в ядре, найдите связь между Л] и ^2 и
покажите, что рассматриваемая модель близка к реальности.
Упражнение 2.26. Выведите приближенное выражение для кулоновского члена в
равенстве B.6.4), соответствующим образом интерпретируя равенство B.4.6) и
используя значение Гд^ = 1,5 · \0~^^А^^^ см.
Упражнение 2.27. Предполагая равное количество нейтронов и протонов в ядре и
используя выражение B.6.4), изобразите график зависимости Е^ (МэВ) от А для
стабильных ядер при Л^ меньше 130. Найдите А^^^, т.е. ядро с максимальной энергией
связи. Чему равно ^'ь'тах? Для каких А > А^^ энергетически выгодно деление на
два ядра?
Уравнение B.6.1) теперь принимает вид
? = «A - yj^^^ + ?;(«J + ?„(«„), B.6.6)
где
и, = иA - yjj,
п„ = ??„. B.6.7)
Заметим, что
d^'e ^ ^'е + Ре _ „ _ _ ^2
Ej:^-m,c%
pL ^ hL±b. = ?, . B.6.8)
[Сравните с выражениями B.1.7) и B.3.29).] Гаррисон и Уилер
приближенно рассматривали ? и Л как непрерывные переменные, учитывая
полуэмпирическую массовую формулу. Таким образом, условие de/dz = О приводит
к соотношению
11 = -(^.--Л B-6-9)
Уравнение состояния нилсе точки образования нейтронных капель 61
которое можно считать непрерывным пределом условия ]3-стабильности:
M(Z - I, А) находится в равновесии с M(Z, А), причем свободный
электрон находится на поверхности моря Ферми.
Аналогичным образом условие де/дА = О приводит к равенству
^'Й(т) = ^(^·^.-'"^^')· B.6.10)
Это непрерывный предел условия равновесия (А - I) атомов типа (Z, А) с
А атомами типа (Z, А - I), Дополнительно должны возникать ?
свободных электронов с энергией на поверхности моря Ферми, когда ядерный
заряд увеличивается от (А - 1) до ??. Комбинируя уравнения B.6.9) и
B.6.10), можно получить
Из условия де/д?^ = О, пользуясь уравнением B.6.10), получим
if =^,, B.6.12)
ЧТО представляет собой непрерывный вариант условия равновесия ?/(?, А)
с ?(?, А - I) и свободным нейтроном.
Уравнение B.6.9) дает
b. + b,(l - f) -2^5^ = [A -Ь.,^)'/^- l]^, B.6.13)
где параметр х^ определен равенством B.5.4). Уравнение B.6.11) приводит
к условию
Z=?^j'^'л^/^ = 3.54^^/^ B.6.14)
а из уравнения B.6.12) вытекает
где х^ также определен равенством B.5.4). Заметим, что в
рассматриваемых условиях высоких плотностей хотя ? и возрастает с ростом А,
отношение ?/? падает, как А~^^^.
Чтооы вывести уравнение состояния из полученных выше соотношений,
выберем сначала А > 56. Тогда равенство B.6.14) определит ?. Далее
проверим, достигнута ли при этом точка образования нейтронных капель, т.е.
62
Глава 2
35 h
30
25
20
15
ID
Lg/) (г/см^)
15
Рис. 2.2. Различные уравнения состояния ниже точки образования нейтронных
капель. Буквенные индексы у различных кривых поясняются в табл. 2.2. Уравнение
состояния Чандрасекара (Ch) приведено для ?^ = 56/26. Уравнения состояния
Гаррисона — Уилера (HW) и Бейма — Петика — Сазерленда (BPS) гладко
сшиваются с уравнением состояния Фейнмана — Метрополиса — I еллеоа (FM Г) при
/0= 1(У* г/см^. Заметим, что выше точки образования нейтронных капель {р^. «
* 3,2· 10^'г/см^ показана вертикальной стрелкой) уравнение состояния
Гаррисона — Уилера гладко переходит в уравнение состояния идеального п—р—е~-
газа, а уравнение состояния BPS ??^??*^'^· Ю'' г/см^) переходит в уравнение
состояния Бейма — Бете — Петика (ВВР) (см. гл. 8).
приводит ли уравнение B.6.15) к положительным х^. Если да, то вычислим
?„, Р^ и п^ из уравнений B.3.4), B.3.5) и B.3.7), заменив в них т^ на w„. В
противном случае положим эти величины равными нулю. Уравнение
B.6.13) определяет х^ и, следовательно, ?^, Р^ и п^. Тогда
Р =
/?,?(^,?)/? + ?; + ?,
B.6.16)
Уравнение состояния ниже точки образования нейтронных капель 63
Р-Ре + Рп, B-6.17)
п^п,^+ п„. B.6.18)
Полученная в результате зависимость (уравнение состояния) ? = Р(р)
изображена на рис. 2.2. Отклонения от уравнения состояния идеального
газа электронов и ^Fe становятся заметными при ? ^ 10^ г/см^. Образование
нейтронных капель начинается при ? - 3,18 · 10^^ г/см^, где (А, Z) - A22;
39,1), т.е. в районе элемента иттоия, при этом ?? - 23,6 МэВ. При
плотностях выше указанного значения свободные нейтроны вносят все больший
вклад в полное давление и плотность. При ? - 4,54 · 10^^ г/см^, когда
{А, ?) - A87; 48,4), нейтроны обеспечивают бО^о давления и плотности;
ядра быстро становятся все менее существенными. Выше этой плотности
Гаррисон и Уилер просто использовали уравнение состояния идеального
А2—/7—^-газа, которое приведено у нас в разд. 2.5; при этом происходит
гладкое сшивание результатов как для Р, так и для dP/dp. К уточнению
этого уравнения состояния при плотностях выше точки образования
нейтронных капель мы обратимся в гл. 8. В следующем разделе обсуждаются
уточнения для плотностей от 10^ г/см^ до этой точки.
2.7. УРАВНЕНИЕ СОСТОЯНИЯ БЕЙМА—ПЕТИКА—САЗЕРЛЕНДА
Уравнение состояния Гаррисона—Уилера имеет то преимущество, что
М{А, Z) представляется довольно простой функцией. Однако для реальных
ядер А и ? принимают дискретные значения, и, кроме того, при
определении связи ядра важную роль играют оболочечные эффекты. Эти эффекты
были учтены Солпитером [496], который определил химический состав и
уравнение состояния при плотностях от 10^ до 3,4 · 10^^ г/см^, т.е. до
образования нейтронных капель.
Бейм, Петик и Сазерленд (BPS) [56] улучшили результаты Солпитера,
используя более точную полуэмпирическую массовую формулу [417].
Кроме того, они заметили, что решеточная энергия, определяемая равенством
B.4.9), существенна при определении химического состава, хотя дает лишь
небольшую поправку к электронному давлению. Причина состоит в том,
что тип находящегося в равновесии изотопа определяется главным
образом соотношением между поверхностной энергией ядра и кулоновской
энергией. При плотности 10^^ г/см^ решеточная энергия уменьшает
положительную кулоновскую энергию ядра примерно на 15%, и это оказывает
заметное влияние на состав.
Чтобы вывести уравнение состояния BPS, добавим энергию решетки к
выражению B.6.6):
? = «A - rj^^^;^^ + ?;(«J + ?„(«„) + ?,. B.7.1)
64 Глава 2
Здесь из равенства B.4.9) в предположении объемноцентрированной
кубической решетки имеем
?^= -1,44472/3^2^4/3, B.7.2)
Условие de/dY^ = О теперь дает (при использовании уравнения B.6.7)
Ч = А · ^^-^-^^
Образование нейтронных капель происходит, когда правая часть
выражения B.7.3) становится равной т^с^. (Строго говоря, нужно учесть еще
энергию взаимодействия высвобожденных нейтронов с ядрами, но этот
эффект незначителен.)
При последующем обсуждении будем считать, что плотность ниже
точки образования нейтронных капель, определяемой уравнением B.7.3), и
положим ?^ = 0.
Состав равновесной смеси можно определить следующим образом.
Зафиксируем значение п. Далее возьмем пару пробных значений (А, ?).
Поскольку М(А, ?) протабулировано и п^ = п/А, п^ = ??/?, то мы можем
вычислить ?. Испробуем все возможные значения (А, ?). Те значения,
которые минимизируют ?, определяют вид находящихся в равновесии ядер.
Давление определяется равенством
дп
= Р, + Р^, B.7.4)
А,?
где Р^ — давление идеального ферми-газа B.3.5) и
Pl = -гЧ B.7.5)
[ср. с равенством B.4.11)].
Фазовый переход от одного стабильного изотопа к другому
сопровождается скачком в величинах ? и ? = ?/c^, так как давление внутри звезды
должно быть непрерывной функцией радиуса. Величину скачка можно
оценить так. Поскольку Р^ < Р^, а Р^ зависит только от а?^, концентрация п^
фактически должна быть непрерывной на границе фаз. Но п^ = ??/?, и
потому
?? _ ?? _ ^{Z/A)
? ? ?/?
B.7.6)
Например, фазовый переход от %е (?/? = 0,4643) к ^^Ni (?/? = 0,4516)
приводит к росту плотности на 2,9%.
Из-за этих разрывов для определения давления, при котором в
действительности происходит фазовый переход, приходится использовать извест-
Уравнение состояния ниже точки образования нейтронных капель 65
Таблица 2.1
ЯДРА, НАХОДЯЩИЕСЯ Б РАВНОВЕСИИ НИЖЕ ТОЧКИ ОБРАЗОВАНИЯ
НЕЙТРОННЫХ КАПЦЛЬ
Ядро
56рс
"Ni
"Ni
<^Ni
«^Кг
«^Sc
"Ge
»«Zn
^^ Массы
^тах'
(а) BPS
8,1 X 10*^
2,7 X 10*
1,2 X 10'
—
—
8,2 X 10'
2,2 X 10'°
4,8 X 10'°
первых шести ядер
совой формулы Йенеке — Гарви
г/см^
(б) JGK 1)
8,1 X 10^
2,8 X 10*
1,3 X 10'
1,5 X 10'
3.1 X 10'
7,6 X 10'
2,6 X 10'°
Ядро
^«Ni
76рс
'26RU
'2^Мо
'"??
'2°Sr
'"Sr
^max'
(a) BPS
1.6 X 10"
1,8 X 10"
—
1,9 X 10"
2,7 X 10"
3,7 X 10"
—
6,0 X 10'° "*Кг 4,3 X 10"
известны из эксперимента. Остальные получен!
— Кельсона (JGK) (сравните
с работой [598]).
г/см^
(б) JGK 1)
8,4 ? 10'°
—
1,2 ? 10"
1,7 ? 10"
2,5 ? 10"
3,6 ? 10"
3,8 ? 10"
4,4 ? 10"
>? на основе мае-
ный критерий равенства площадей Ma?cвeллa^^ что является недостатком
обсуждавшейся выше процедуры. Гораздо удобнее найти минимум
термодинамического потенциала g при постоянном ? [ср. с уравнением B.1.18)].
При Г = О из уравнения B.1.19) следует
_ ? + f _ М{А, ?) + Z?p^ -f ???^/^?,
Теперь зафиксируем значение Р. Выберем пробные величины А и ? и
разрешим трансцендентное уравнение B.7.4) относительно п^ = jc^/Btt^X^.
Затем, пользуясь равенством B.7.7), вычислим g. Будем повторять эту
процедуру, пока не определим значения {А, Z), отвечающие минимуму g.
Полученная в результате последовательность ядер, согласно BPS, приведена
в табл. 2.1, а уравнение состояния представлено на рис. 2.2.
Теперь видна важность оболочечных эффектов: ядра от ^Se до ^^Fe
имеют замкнутые оболочки, содержащие 50 нейтронов, а ядра от ^^Мо до
'^^Кг — замкнутые оболочки из 80 нейтронов. Образование нейтронных
капель происходит при ? « 4,3 · 10^^ г/cм^ когда отношение ?/А для ^^^Кт
равно 0,3051.
Мы повторили вычисления, сделанные Беймом, Петиком и Сазерлен-
дом, используя экспериментальные данные для М(А, ?), затабулированные
в [599] для условий, доступных при измерениях, а также теоретическую
экстраполяцию Йенеке, Гарви и Кельсона, приведенную в [598] для нейтроно-
избыточных ядер. Получающаяся I результате последовательность ядер
приведена в столбце «б» табл. 2.1. Это уравнение состояния не отличается
от уравнения BPS, за исключением точек в непосредственной близости к
^^ См., например, разд. 8.6 книги [479], где обсуждаются эти вопросы.
5-353
66
Глава 2
фазовому переходу, где при заданном ? соответствующие значения ? могут
различаться примерно на 5Щ. Мы приходим к выводу, что уравнение
состояния довольно хорошо установлено вплоть до точки образования
нейтронных капель.
Вычислительное упражнение 2.28. Повторите процедуру BPS, используя другую
формулу для М{Л, ?), например, описанную в работе [598]. Как ваше уравнение
состояния соотносится с уравнением BPS?
Вычислительное упражнение 2.29. Покажите, что в предположении справедливости
уравнения состояния BPS при заданном давлении действительно имеется только
один тип атомных ядер. Перепишите уравнение B.7.1), допуская, что имеется доля/
ядер {??, Zi) и доля A - У) ядер (^2, Zi). Покажите, что, за исключением
случаев разрывной плотности, / = О или / = 1.
2.0 h
1.5 h
1.0 Г
0.5 h
0.0
—I—
?
? __
?
?
г
г
V-
L
u
L
1 1
¦r-i—1—1—1—г
BPS
\
\
«a.1 V
*\
>^
Л
Thp-e'\
¦ 1 . 1 ¦ .
—1 1 1 1 1 1 1
li
at
? ·
1 /HW/
с 1 г ··*'
>—I L ' -·
1
? / :
* 1 *
?
:|i
• If
:|:
:1:
V
/ ''"'
L/ ^_L^
7—^
/bbp
Ch
1 1
1 1
?
J
¦]
^ "H
?
-1
л
-I
-A
?
1
-J
J
Ч
15
5 10
Igp (г/см^)
Рис. 2.3. Показатель адиабаты Т = {с1\пР)/{а\пр) как функция р для уравнений
состояния, представленных на рис. 2.2.
Глава 2 67
РЕЗЮМЕ 2.1.
Уравнение состояния холодного вещества
при плотностях ниже точки образования нейтронных капель
1. Уравнение состояния вещества при нулевой температуре можно
считать хорошо известным для плотностей ниже точки образования
нейтронных капель, р^^- » 4 · 10^^ г/см^. Преобладающий вклад в давление
обеспечивают вырожденные электроны, которые становятся релятивистскими
при плотностях выше --10^ г/см^. Положительные заряды
сконцентрированы в отдельных ядрах, которые образуют регулярную решетку с куло-
новским взаимодействием, погруженную в электронный газ.
2. Если вещество находится в основном состоянии, то можно
предположить, что между ядрами имеется равновесие, т.е. энергию системы нельзя
понизить, меняя ее состав с помощью сильных, слабых или
электромагнитных взаимодействий. Можно найти отвечающий равновесию изотоп в
зависимости от плотности. При плотностях ниже - Ю'' г/см^ в основном
состоянии находятся ядра j^e. При больших плотностях равновесию
соответствуют ядра, все более обогащенные нейтронами. Все ядра
стабилизированы относительно ]3-распада заполненным ферми-морем электронов.
3. Уравнение состояния для плотностей ниже точки образования
нейтронных капель определяет структуру планет и устойчивых белых карликов.
В белых карликах полное равновесие, по-видимому, не достигается.
Следовательно, применимо уравнение состояния Чандрасекара с кулоновскими
поправками [496]. Химический состав зависит от эволюционной истории
звезды и определяет средний молекулярный вес, приходящийся на один
электрон, ?^ (ср. с гл. 3). В нейтронных звездах вещество при
рассматриваемых плотностях находится в полном равновесии, и потому применимо
равновесное уравнение состояния (например, уравнение BPS).
4. Результаты применения различных моделей для уравнения состояния
холодного вещества при плотностях ниже точки образования нейтронных
капель суммированы на рис. 2.2 и 2.3 и в табл. 2.2.
68 Уравнение состояния ниже точки образования нейтронных капель
Таблица 2.2
ПРИМЕРЫ УРАВНЕНИЙ СОСТОЯНИЯ НИЖЕ ПЛОТНОСТИ ОБРАЗОВАНИЯ
НЕЙТРОННЫХ КАПЕЛЬ
Уравнение
состояния
Чандрасекар
[111, 112],
идеальный электронный
газ (Ch)
Идеальный
п-р-е~-тг.ъ
Фейнман —
Метрополис —
Теллер [196]
(FMT)
Гаррисон —
Уилер [259] (HW)
Выше точ
ки
образования
нейтронных капель
Бейм — Пе-
тик — Сазерленд
[56] (BPS)
Диапазон значений
плотности, г/см^
0 < ? < 00
0 < ? < 1,2-10^
1,2· lO'' < ? < 00
7,9 < ? < 10^
7,9 ^ ? < 10*
10* < ? < 10^
10^ < ? < 3-10^^
Г 3-10^^ < ? < 4-10^2
L 4,5-10^2 < ? ^ 00
7,9 < ? < 10*
10* < ? < 8-10^
8-10^ < ? < 4,3-10^^
Химический
состав
е~ (ядра.
определяемые ?^)
е~, ?
л. Р. е
е-, ^Fe
Так
е- и ^бре
е~ и
равновесные
изотопы
е", ? и
равновесные
изотопы
Так же,
п-р
Так
е~ и
равновесные
изотопы
Теория
Невзаимодействующие
электроны
Равновесное
вещество
Атомная модель
Томаса — Ферми-
Дирака
же, как FMT
Невзаимодей-
ствуюище
электроны
Полуэмпирическая массоьая
формула;
равновесное вещество
как в идеальном
-е~-газе
же, как FMT
Идеальные
электроны с учетом
поправок от куло-
новской решетки
Ядерные потен-
Ш1алы, известные
из опыта (с экстра-
поляш1ей); кулонов-
ская энергия
решетки; равновесное
вещество
Глава 3
Белые карлики
3.1.РАЗВИТИЕ ТЕОРИИ БЕЛЫХ КАРЛИКОВ
Белые карлики — это звезды, масса которых примерно равна массе
Солнца, радиус — порядка 5000 км. а средняя плотность — около 10^ г/см^.
Эти звезды уже сожгли свое ядерное горючее и медленно охлаждаются,
теряя остатки своей тепловой энергии.
Теперь нам известно, что в белых карликах гравитации противостоит
давление вырожденных электронов. Однако это не всегда было ясно
астрономам, хотя компактная природа белых карликов была очевидной уже при
самых ранних наблюдениях. Например, масса наиболее хорошо изученного
белого карлика Сириус В в двойной системе Сириуса была определена с
помощью третьего закона Кеплера, примененного к орбите двойной звезды.
Ранние оценки его массы давали значения в диапазоне 0,75—0,95 Mq . Его
светимость была оценена по наблюдаемому потоку излучения и известному
расстоянию и оказалась равной примерно 1/360 светимости Солнца. В
1914 г. У. С. Адаме [4] сделал поразительное открытие, что Сириус В
представляет собой белую звезду, которая по спектру не очень сильно
отличается от своего «нормального» компаньона — Сириуса А. Приписывая
Сириусу В на основе этих спектральных измерений эффективную
температуру 8000 К и используя известное выражение для светимости черного
тела: L = A-kR^oT^^^, можно было сделать вывод, что радиус R этой звезды
составляет 18 800 км.
Упоминая о Сириусе В в своей книге «Внутреннее строение звезд», вы-
11ающийся астрофизик Артур Эддингтон [179] заключил, что «мы име-
€м звезду с массой, равной массе Солнца и радиусом намного меньше, чем
радиус Урана». Он также сообщил в своей книге о выполненных Адамсом
15} измерениях необычного красного смещения нескольких линий в спектре
излучения Сириуса В. Используя общую теорию относительности, можно
было по измеренному красному смещению сделать вывод о величине
отношения M/R, Тем самым определялся радиус Сириуса В, так как масса уже
была известна по измерениям орбиты двойной системы. Красные
смещения, полученные Адамсом (хотя и довольно грубо), подтвердили
предшествующие оценки R и компактную природу белых карликов. Эддингтон писал
в своей книге [179], что «профессор Адаме убил двух птиц одним камнем:
он осуществил новую проверку общей теории относительности Эйнштейна
и подтвердил наше подозрение, что вещество в 2000 раз более плотное, чем
70 Глава 3
платина, не только возможно, но и действительно присутствует во Вселен-
ной»^\
Эддингтон далее утверждал, что белые карлики должны встречаться
весьма часто во Вселенной, ибо хотя в то время было твердо установлено
существование только трех белых карликов, все три находились очень
близко от Солнца. Однако относительно механизма, удерживающего бе-
jibie карлики от схлопывания, Эддингтон смог только утверждать:
«Кажется вероятным, что при столь высоких плотностях обычные газовые
законы нарушаются из-за конечных размеров молекул, и я не думаю, что
белые карлики ведут себя как идеальный газ».
В августе 1926 г. Дирак [165] сформулировал статистику
Ферми—Дирака, основываясь на результатах, полученных Ферми лишь
несколькими месяцами раньше. В декабре 1926 г. Фаулер в пионерской работе
[202], посвященной компактным звездам, применил статистику
Ферми—Дирака для объяснения загадочной природы белых карликов: он
отождествил давление, которое удерживало эти звезды от гравитационного
коллапса, с давлением вырожденных электронов.
Адекватные модели белых карликов, в которых учитывались эффекты
специальной теории относительности для уравнения состояния
вырожденных электронов, были построены в 1930 г. Чандрасекаром [111, 112]. При
этом Чандрасекар сделал важное открытие, что масса 'белых карликов не
может превышать максимального значения около 1,4 Mq . Точная
величина последнего зависит от химического состава звезды. В честь автора
открытия этот максимум называется чандрасекаровским пределом,
Чандрасекар [113] сразу же осознал важность своего результата. Он писал в 1934 г.:
«История звезды малой массы должна существенно отличаться от
эволюции звезды большой массы. Для звезды малой массы естественная стадия
белого карлика является первым шагом к полному угасанию. Звезда
большой массы не может пройти через стадию белого карлика, и приходится
искать другие возможности».
В 1932 г. Ландау [337] объяснил существование чандрасекаровского
предела. Несколькими месяцами позже, узнав об открытии нейтрона, он
применил свои аргументы к нейтронным звездам (разд. 9.1).
Роль общей теории относительности в изменении соотношения между
массой и радиусом для белых карликов с массами выше 1 Mq впервые
обсуждалась Капланом [303]. Он сделал вывод, что эффекты общей теории
относительности, по-видимому, приводят к динамической неустойчивости,
когда радиус становится меньше 1,1 · 10^ км. Общерелятивистская
неустойчивость белых карликов была независимо обнаружена также
Чандрасекаром в 1964 г. [119].
^^ Результат Адамса для величины красного смещения, а также независимое
значение, полученное Муром, согласовались с обшей теорией относительности, хотя
при этом и было использовано неверное значение радиуса, полученное из
наблюдений. Современное положение дел описано в разд. 3.6.
Белые карлики 71
После открытия нейтрона стало ясно [216, 338, 425], что при очень
высоких плотностях электроны должны взаимодействовать с протонами,
образуя нейтроны вследствие обратного бета-распада. Побудительным
стимулом указанных работ послужила идея, что источником энергии
нормальных массивных звезд мог бы быть обратный бета-распад в нейтронном
ядре. Много позже Шацман [508—510] и независимо Гаррисон и Уилер [259]
учли обратный бета-распад в уравнении состояния вещества внутри белых
карликов. Шацман, а также Гаррисон, Вакано и Уилер [260] показали, что
обратный бета-распад также вызывает динамическую неустойчивость
наиболее массивных белых карликов с массой выше - 1 Mq и радиусом
меньше 4 · 10^ км. Устойчивость не восстанавливается до тех пор, пока
фактически все электроны и протоны не будут тесно сжаты вместе. При таких
высоких плотностях газ должен состоять почти полностью из нейтронов.
В этом состоянии рассматриваемый объект будет иметь массу порядка'Л/0
и радиус около 10 км. Таким образом, должен существовать новый класс
стабильных компактных звезд — это нейтронные звезды, которые были
предсказаны в 30-х годах.
На этом мы заканчиваем обзор раннего этапа разработки теории белых
карликов. Мы вернемся к этому рассказу в разд. 9.1, где проследим за
развитием гипотезы нейтронных звезд.
3.2. НАЧАЛЬНАЯ СТАДИЯ ВЫРОЖДЕНИЯ
В гл. 1 мы представили довольно убедительные данные в пользу того, что
конечным состоянием звезды, которая израсходовала свое ядерное
горючее, должен быть белый карлик, при условии что эта звезда не очень
массивна. Если учесть условия гидростатического равновесия, то можно
надежнее проследить судьбу звезды, исчерпавшей ядерное горючее.
Для сферически-симметричного распределения вещества масса внутри
сферы радиуса г определяется выражением
/ ч С" . о . dm(r) ^ J /^^,4
т{г) = / pATTr^dr, или —j-^ = 4??^. C.2.1)
•'о "''
Здесь ? « Ро "" плотность массы покоя, так как рассматривается
нерелятивистское вещество. Если звезда находится в устойчивом состоянии,
гравитационные силы в каждой точке уравновешиваются силами давления.
Чтобы вывести уравнение, описывающее гидростатическое равновесие,
рассмотрим бесконечно малый элемент жидкости, лежащий между г и г + dr
и имеющий площадь поверхности, перпендикулярной радиусу, равную dA.
Гравитационное притяжение межйу т(г) и массой dm = pdAdr такое же,
как если бы т(г) была сосредоточена в центре, наружная же масса не
оказывает никакого воздействия на dm. Действующая на dm суммарная сила
давления, направленная наружу, равна -[Р(г -I- dr) - P{r)]dA, так что в
равновесии
dP ^ ,, Gm{r)
- -j-drdA = \-^dm
dr r^
72 Глава 3
или
dP___Gm{r)p C.2.2)
dr /.2
в общем случае гидростатическое равновесие выражается условием VP =
= -рУФ, где ? — гравитационный потенциал (ср. с разд. 6.1).
Следствием уравнения гидростатического равновесия C.2.2) является
теорема вириала: гравитационная потенциальная энергия звезды равна
^RGm{r)
о
cRdP
Jq г
Jq dr
= ^зГр^^гЧг, C.2.3)
•'о
где при переходе от первого равенства ко второму было использовано
уравнение C.2.2), после чего выполнено интегрирование по частям.
Если газ описывается адиабатическим уравнением состояния
? ^ Кр1 {К,Т — постоянные), C.2.4)
то плотность энергии газа (исключая энергию, соответствующую массе
покоя) равна
e' = jr^. C.2.5)
Этот результат является следствием первого закона термодинамики в
предположении адиабатического изменения:
Интегрирование этого выражения с использованием уравнения C.2.4)
приводит к соотношению
2 ?
е = ??€^-\-???[^ C.2.7)
которое и дает желаемый результат для ?' s е - PqC^^
Таким образом, равенство C.2.3) можно переписать в виде
Ж= -3(Г- ?)?/, C.2.8)
где _ .ji
^
— полная внутренняя энергия звезды
Белые карлики 73
[/= i^e'47rr^dr C.2.9)
Упражнение 3.1. Пусть ?7" — кинетическая энергия поступательного движения
частиц, не включающая в себя энергию, связанную с внутренними степенями свободы
(например, вращательными или колебательными). Покажите, что для идеального
газа Максвелла—Больцмана, характеризуемого постоянным показателем адиабаты
Г, величина ?? связана с U соотношением ?? = Vz (Г - 1)С/. Далее покажите, что
вириальное соотношение C.2.3) для такого газа может быть записано в виде
-\w.
Полная энергия звезды ? = W + U равна
^^(f^'^'' C.2.10)
где W GM^/R.
Упражнение 3.2. Покажите, что если уравнение C.2.4) справедливо всюду внутри
звезды, то гравитационная потенциальная энергия равна
f2
--"^? (-")
Указание: перепишите уравнение C.2.3) в форме
^ ?
Проинтегрируйте это выражение по частям и воспользуйтесь равенством
.(i)-V«„,.Hi).
Проинтегрируйте по частям еще раз.
Без ядерного горючего ? убывает благодаря излучению. Согласно
выражениям C.2.10) и C.2.11), из условия ?? < О при Г ^ 4/3 следует ?/? < О,
т.е. звезда сжимается. Может ли звезда сжиматься непрерывно, черпая
энергию из бесконечных запасов гравитационной потенциальной энергии до
тех пор, пока R не обратится в нуль (или пока звезда не скол лансирует в
черную дыру)? Как мы сейчас покажем для звезд с Л/ - Mq , ответ
оказывается отрицательным.
Предположим, что давление во время такого квазистатического
коллапса определятся законом идеального газа Максвелла—Больцмана.
? = ^^^. C.2.12)
74 Глава 3
где, например, для чистого ионизированного углерода ? = 12/7 [ср. с
уравнением B.3.17)]. Тогда, согласно вириальному соотношению C.2.3):
- Ж = 3 ??4??' dr ^^^ Гро^^г^ dr = ^^kf, C.2.13)
где f—средняя температура звезды. Таким образом, ? ос м//?, т.е. ?
возрастает при уменьшении /?. Однако ? ос M/R^, так что плотность
растет еще быстрее. Мы теперь покажем, что это приводит к нарушению
соотношения Максвелла—Больцмана C.2.12); электронный газ становится
вырожденным, что приводит к ненулевому давлению даже при нулевой
температуре.
Типичный (т.е. среднеквадратичный) разброс по импульсам электронов
в газе Максвелла—Больцмана равен
^P.-{Ьm^kTr-['^"'^^^^"'"'У\ {Ъ2ЛА)
-у/2 ????????,??^^
где мы положили Г = 5/3 и использовали уравнения C.2.13) и C.2.11).
Упражнение 3.3. Проверьте первое соотношение в выражении C.2.14). Для двух
электронов
2\·/2
^Рг^'{(р.-Рг)Т-ШУ''.
Заметим, что в выражениях C.2.13) и C.2.14) ? имеет слегка различный
смысл.
Типичное расстояние между электронами равно
Таким образом, объем, занимаемый электроном в фазовом пространстве,
равен
уЗ/2г
-40
см^ · с ^
1/2/ D чЗ/2
—(^)liV'.
Белые карлики 75
Поэтому, когда звезда с массой 1 М^ сжимается до /? -- 3 · 1О~^/?0,
фазовый объем, приходящийся на один электрон, будет порядка Л^. В этих
условиях принцип запрета Паули становится существенным и приходится
пользоваться статистикой Ферми—Дирака. Как мы видели в предыдущей
главе, давление в таком газе не исчезает даже при нулевой температуре.
Поэтому теперь надо рассмотреть свойства равновесных систем, а именно
белых карликов, поддерживаемых давлением вырожденных электронов.
3.3. ПОЛИТРОПЫ
Уравнение состояния идеального ферми-газа сводится к простой политроп-
ной форме C.2.4) в предельных случаях нерелятивистских (Г = 5/3) и
ультрарелятивистских (Г = 4/3) электронов [см. уравнения B.3.21)-B.3.23)].
Равновесные системы с таким уравнением состояния называются по-
питропами; их анализ выполняется относительно просто. Сначала мы
обсудим свойства белых карликов, рассматривая их как политропы в
предельных случаях низкой (Г = 5/3) и высокой (Г = 4/3) плотности. Затем
опишем промежуточный режим и поправки к политропной картине.
Условия гидростатического равновесия C.2.1) и C.2.2),
скомбинированные вместе, дают
Подставим сюда уравнение состояния C.2.4) и запишем
rsl+i, C.3.2)
?
где ? называется индексом политропы. Полученное уравнение можно
переписать в безразмерной форме, введя величины
? = ??\ C.3.3)
г = ai, C.3.4)
'^ C.3.5)
а =
47гС
где р. = р(г = 0) — плотность в центре звезды. Тогда
1 d .2^0
ёж^'тг-'"· ^'-''^
76 Глава 3
Это уравнение называется уравнением Лейна^Эмдена для системы с
индексом политропы л. Граничные условия в центре звезды, описыв|1емой
политропным уравнением состояния, имеют вид
?@)-1, C.3.7)
вЩ - 0. C.3.8)
Условие C.3.7) непосредственно следует из уравнения C.3.3). Условие
C.3.8) следует из того факта, что вблизи центра т{г) « 4??^?^/3, так что,
согласно уравнению C.2.2), в центре dPioVdr = О = dp/dr.
Уравнение C.3.6) легко проинтегрировать численно, начиная с точки
{ = О с граничными условиями C.3.7) и C.3.8). Таким образом, найдем,
что при л < 5 (Г > 6/5) решение монотонно убывает и обращается в нуль
при конечном значении { = {р т.е. ^({i) = 0. Эта точка отвечает
поверхности звезды, где ? = ? = 0. Таким образом, радиус звезды равен
Л = ??, =
?IL^Ж?\i^-n)/2n^^^ C.3.9)
а масса равна
•? '?
= -^'^('^PcP'jtii^^]^^ [согласно C.3.6)]
= 4.а%фШ= 4.\^^^^\?-^^^"ФШ. C.3.10)
Исключая р^ из равенств C.3.9) и C.3.10), получим соотношение между
массой и радиусом для политропы:
М = 4nR^^-"^^'-"^[^^^j^]"^"~\?-"'^'-mi^)\. C.3.11)
Упражнение 3.4. Покажите, что отношение средней плотности к плотности в центре
для политропы равно рУр^ = 31 ^ 411)' /? ? ·
Белые карлики 77
Для нас особый интерес представляют следующие решения^^:
Г = 1, /1 = 1, ?, = 3,65375, (\\ви,)\ = 2,71406,
Г = !, /1 = 3, ?, = 6,89685, ex\eUx)\ = 2,01824. C.3.12)
Таким образом, для белых карликов с малой плотностью (Г = 5/3)
получим
''-'''^^'<"''(l5rSs;r)"l^)"""· <"¦''>
Упражнение 3.5. Выведите результат Л/ ~ R-^ из уравнений C.2.1), C.2.2) и C.2.4)
с помощью анализа размерности.
Для случая высокой плотности (Г = 4/3) получим
M-I,457|^j ???. (З.З.П)
Заметим, что в ультрарелятивистском пределе ? не зависит от р^ и,
следовательно, от R. Отсюда можно заключить, что при р^ — оо электроны в
звезде становятся все более и более релятивистскими, а масса
асимптотически стремится к значению C.3.17), когда /? — 0.
Предельное значение массы C.3.17) называется пределом Чандрасекара
(часто обозначается Mq^) и представляет собой максимально возможную
массу белого карлика. В случае холодного идеального газа зависимость
Mq^^ от химического состава целиком определяется ?^.
*^ Подробную таблицу параметров политропы можно найти в работе
Чандрасекара [114].
78 Глава 3
Интегрирование уравнений, описывающих внутреннее строение белых
карликов, с использованием точного уравнения состояния ферми-газа было
проделано Чандрасекаром [114] (см. рис. 3.1 и 3.2 ниже). Они, как и
следовало ожидать, согласуются с приближением политропы в
соответствующих областях.
3.4. ПРЕДЕЛ ЧАНДРАСЕКАРА
Существование ограничения на массу вырожденной звезды является
настолько важным результатом, что полезно попытаться получить его
наиболее простым способом. Мы сделаем это, следуя рассуждениям
Ландау [337], которые применимы как к белым карликам, так и к нейтронным
звездам.
Предположим, что звезда радиусом R содержит N фермионов, так что
концентрация этих фермионов равна ? - N/R^, Объем, приходящийся на
один фермион, равен - 1/л (принцип Паули), поэтому вследствие
соотношения неопределенности Гейзенберга импульс фермиона имеет порядок
hn^^^. Отсюда релятивистская энергия Ферми частиц газа равна
Е^^Нп^^'с-^. C.4.1)
Гравитационная энергия, приходящаяся на один фермион, равна
^G ^. C-4.2)
где Л/ = Nwg. (Заметим, что даже если давление создается электронами,
основная часть массы содержится в барионах.) Как будет подробно
показано в гл. 6, равновесие достигается при минимальном значении полной
энергии Еу где
...,..„.??^-5?. ,3.4.3)
Заметим, что оба слагаемых меняются как 1//?. Когда величина ?
положительна (т.е. когда N мало), ? убывает при увеличении /?. Одновременно
убывает ?'р, и электроны становятся все менее релятивистскими, причем
^? ^ Pf '^ 1/^^· Следовательно, при увеличении R в конце концов Eq
начинает превосходить по абсолютной величине ?'р и, значит, полная энергия
? становится отрицательной, причем при /? ^ оо величина ? растет,
стремясь к нулю. Таким образом, при конечном значении R должно
существовать положение устойчивого равновесия.
С другой стороны, если полная энергия ? отрицательна (т.е. если N
велико), то при уменьшении R величина ? может уменьшаться без предела. В
этом случае равновесия нет и происходит гравитационный коллапс.
Белые карлики 79
Следовательно, максимальное количество барионов, при котором еще
возможно равновесие, определяется условием ?* = О в равенстве C.4.3).
Отсюда
^.«-(?7р-2х10- C.4.4)
М^ах - ^max'^iB - Ь5Ме. C.4.5>
Таким образом, если отвлечься от числовых множителей, зависящих от
химического состава, то максимальная масса вырожденной звезды
определяется только фундаментальными постоянными.
Равновесный радиус, отвечающий массе М, близкой к М^^,
определяется началом релятивистского вырождения:
?р > тс\ C-4.6)
где т — масса либо электрона, либо нейтрона. Применяя соотношения
C.4.1) и C.4.4), с помощью этого условия получим
л<-^
h 1 he ^'''
тс \ Gm\,
5 X 10^ см, т = т^
3 X 10^см , т = т„.
C.4.7)
Таким образом, существуют два различных режима сжатия: один — при
плотностях, превосходящих плотность белого карлика, а другой — при
плотностях выше ядерной. В обоих случаях М^^^ - Mq .
Упражнение 3,6, Допустим, что мы построили последовательность различных
состояний белых карликов, состоящих из чистого 26^^» ДЛя различных значений
центральной плотности. Рассмотрите другой набор белых карликов, состоящих из
чистого ^^С.
а) Как соотносятся физические параметры Р(г), р(г), т{г) иль углеродной и
железной последовательностях?
б) Определите отношение Л/тах('^С)/Л/тах(^^Ре). Воспользуйтесь при этом немо-
дифицированным уравнением состояния Чандрасекара.
80 Глава 3
3.5. УСОВЕРШЕНСТВОВАНИЕ ЧАНДРАСЕКАРОВСКОЙ МОДЕЛИ
БЕЛЫХ КАРЛИКОВ
Полный анализ моделей белых карликов, включающий в себя поправки к
уравнению состояния Чандрасекара, которые обсуждались в гл. 2, был
выполнен Хамадой и Солпитером в 1961 г. [255]. Их результаты приведены
на рис. 3.1 и 3.2.
Основной эффект электростатических поправок состоит в том, что при
той же массе они дают меньший радиус и более высокое значение
центральной плотности, чем следует из модели Чандрасекара. Хотя кулонов-
ские поправки малы при тех высоких плотностях, которые возникают в
белых карликах с массой порядка 1 Mq , однако в этой области Г - 4/3 и,
следовательно, E/(GM^/R) < 1 [ср. с выражением C.2.10)]. Поэтому
небольшие изменения давления или энергии приводят к относительно
большим изменениям радиуса.
Один из важных эффектов, учтенных Хамадой и Солпитером,— это
влияние нейтронизации (обратного 18-распада) на однородный белый
карлик. Вполне возможно, что в реальных белых карликах никогда не
достигается равновесный химический состав, указанный Солпитером, и уравнение
состояния EPS их не описывает. Во-первых, современные расчеты
эволюции звезд — предшественников белых карликов предсказывают, что их
температура никогда не поднимается настолько высоко, чтобы в них
происходило сгорание ядер заметно тяжелее углерода. Поэтому массивные
белые карлики, по всей видимости, состоят в основном из углерода и
кислорода^\ Во-вторых, даже если горение идет вплоть до железа при
постепенном сжатии белого карлика, так что поддерживается
гидростатическое равновесие, время, необходимое для завершения соответствующих
ядерных реакций, может быть слишком велико. В соответствии с BPS при
плотностях выше р^ = 8,1 · 10^ г/см^ ядра ^^^е должны превратиться в
^^Ni. Это не может быть простым следствием 18-распадов, изменяющих ?
от 26 до 28; необходимы также реакции, изменяющие А от 56 до 62, и
такой переход от Fe к Ni, возможно, в действительности никогда не
происходит.
Что происходит, когда плотность становится выше 8,1 · 10^ г/см^?
При плотности 1,14 · 10^ г/см^ энергия Ферми для электронов равна
т^с^ ·? 3,695 МэВ. Это совпадает с порогом реакции обратного /3-
распада.
^^Fe + е--*^^Мп + V,
Нечетно-четное ядро ^^Мп немедленно захватывает еще один электрон:
') Обсуждение расчетов звездной эволюции содержится в работе Либерта [360].
Однако эти расчеты не вполне точны, главным образом из-за наличия существенной
потери массы во время эволюции.
Белые карлики
81
2?
2,г
2,0
<,8
1.6
1Л
^1.2
о
°1.0
0,8
0,6
ОЛ
о,г
гтп-т-гу-гт-п--гу-т
LMoxVv-Hf
г \п\
к v\^
1—\ \^ \ \
Г\ v\^
г \ v\^
1— \ л. Х.*^
Гг\ \Хч
1 \ ^\>^
Г ч ^ \ Х>
1— X nW"*»
N. ""^ >s?>v'
Г" ^V ЛД^У^Жм^
[— ^>№чИ|1в
V ^0Ег16 ??
L_ ^
V Stetn 2051
?
L
U
H
1. 1 1 1 1 \ \ 1 1 i
—I—r—T—I—\—1—\—??—\—1 1—1 1 1 1—??
—J
1
—J
J
4.N ¦маачдд.д'.^ ?
Г\ ? ШжЩШШ I
1*4. Ря^вИпИ "?
? "*^ ТчйэЯи ?
""^^?^ ^ ?^***'?^ "^ ?
^^??^ ^^^"""^^ ? с ipuyc ? j
^^vV^ ч ^??? ? J
^•^ч/" ^ ^ "^^ X
N^S. ^ ч ^^^ч ?
Чу 4? ч ^^^Ч^
J у j^a^- j
Л^-^^-^У^^ ¦^=?^\'?
I I .1 I I I I I I I I ¦' 1 1 1 1 11
0,25
0.5
0,75
10
угъ
1.5
Рис. 3.1. Соотношение масса ~ радиус для звезд, состоящих из ^Не, ^, ^^Mg и
^^Fe, при нулевой температуре. Кривая с индексом «eq» относится к равновесному
химическому составу при разных плотностях. Штриховые кривые отвечают модели
Чандрасекара — верхняя для ?^=2, а нижняя для ^^=2,15. Точки внутри
прямоугольников размером в одно стандартное отклонение представляют средние массы и
радиусы трех белых карликов, указанных в табл. 3.2 (для звезды Stein 2051 имеются
два решения). По работе Хамады и Солпитера [255] с любезного разрешения
авторов.
Четно-четное ядро ^Сг будет стабильным относительно дальнейшего
захвата электрона, пока плотность не станет много выше, т.е. порядка 1,5 х
X 10^^ г/см^. За счет этого фазового перехода уравнение состояния
становится мягче: вместо того, чтобы увеличить при сжатии свою энергию
Ферми, а следовательно, и давление, электроны соединяются с ядрами,
образуя Сг. Показатель адиабаты, весьма близкий к 4/3, так как электроны
сильно релятивистские, падает ниже 4/3. Как мы увидим в гл. 6, в
функциональной зависимости ? от R появляется максимум, что говорит о
появлении неустойчивости по отношению к гравитационному коллапсу.
Последовательность железных белых карликов при р^ = 1,14 · 10^ г/см^
прерывается из-за обратного ]3-распада.
В табл. 3.1 приведены пороги нейтронизации для различных ядер,
которые могут присутствовать на очень поздних стадиях термоядерного горе-
е-353
6.5 7,0 7,5 8,0 8.5 9,0 5,5 10,0 10,5 11,0
Рис. 3.2. Соотношение между массой и плотностью в центре р^ (г/см^) для звезд,
состоящих из ^^, ^^Mg, ^i, ^? и ^^е, и для равновесного химического состава при
нулевой температуре. Штриховая кривая отвечает модели Чандрасекара при ?^=2.
По работе Хамады ? Солпитера [255] с любезного разрешения авторов.
ПОРОГИ НЕЙТРОНИЗАЦИИ
Таблица 3.1
Порог нейтро-
низации, МэВ '>
pQy
г/см^
|Н-п
•^С-'^В-'^Ве
?SNe-^SF-20o
?^Mg-?iNa-?jNe
^Fe-^Mn-iJCr
0.782
20,596
13.370
10,419
7.026
5.513
4.643
1.710
3.695
1.22 X 10^
1.37 X 10"
3.90 X 10'°
1,90 X 10'°
6.21 X 10'
3.16 X 10'
1.97 X 10'
1.47 X 10'
1.14 X 10'
I)
Ha основании работы Вапстры и Боса [599]; здесь вычтена энергия массы покоя электрона
т с"- =0,511 МэВ.
Белые карлики 83
ния звезды. Кроме того, в таблице даны значения плотностей, при
которых происходит соответствующий переход. Порог обратного ]3-распада
для ^^С, который достигается при р^ = 3,90 · 10^^ г/см^, по-видимому,
представляет для нас наибольший интерес, если верны современные
расчеты звездной эволюции.
Упражнение 3.7. Проверьте значения pq в табл. 3.1, отвечающие приведенным
там порогам нейтронизаиии.
Заметим, что при ??; ^ 20 МэВ энергетически более выгодно испустить
свободный нейтрон (нейтронизация), чем захватить электрон. Так, процесс
jHe — ^Н имеет порог примерно 22,7 МэВ, в то время как порог реакции
jHe — Jh -f- А2 составляет 20,6 МэВ.
Прежде чем решить, какова будет судьба белых карликов с большой
плотностью, состоящих из легких элементов, нужно рассмотреть еще один
процесс, а именно пикноядерные реакции (от греческого «пик-
нос» — плотный). При термоядерной реакции кулоновское отталкивание
реагирующих ядер преодолевается за счет их тепловой энергии, благодаря
чему эти реакции и происходят. Однако если плотность достаточно велика,
то даже при нулевой температуре энергия нулевых колебаний ядер в
решетке может привести к значительной скорости ядерных реакций. Мы
рассмотрим эти реакции приближенно в разд. 3.7.
Хамада и Солпитер получили, что за 10^ лет пикноядерные реакции
преобразуют ? в ^Не при плотности выше 5 · 10^ г/см^, ^Не в ^? при
плотности выше 8 · 10^ г/см^ и ^? в ^Mg при плотности выше 6 · 10^ г/см^.
Эти оценки основываются на вычислениях скорости пикноядерных
реакций, выполненных Камероном [101]. Улучшенные расчеты Солпитера и
Ван Хорна [499] заставляют считать результаты Камерона завышенными.
Критическая плотность для ? оказывается порядка 1 · 10^ г/см^, а для
углерода 1 · 10^^ г/см^. Однако эти значения плотности все еще весьма
ненадежны^^ Помимо трудностей, непосредственно связанных с
вычислениями, учет конечной температуры и наличия кристаллических дефектов
может привести к заметному увеличению скорости реакций.
Загиб на Л/-/?-диаграмме Хамады—Солпитера при малых плотностях
вызван тем, что в этой области уравнение состояния становится более
жестким. Как было показано в разд. 2.4, при малой плотности Г - 10/3
(очень грубо), и поэтому, согласно уравнению C.3.11), ? - R^^^ в
противоположность соотношению ? - R~^ при Г - 5/3. Из более точного анали-
При нулевой температуре превращение "^Не в ^^С не осуществляется
посредством известного резонансного процесса, а требует редких трехчастичных соударений,
вероятность которых, по-видимому, ничтожно мала.
84 Глава 3
за Запольского и Солпитера [629] следует, что максимальное значение
радиуса белого карлика для холодных углеродных звезд составляет Rj^ax -
= 3,9 · 10-2/?0 при ? = 2,2 · 10"^ М^.
3.6. СРАВНЕНИЕ С НАБЛЮДЕНИЯМИ: МАССЫ И РАДИУСЫ
Как мы увидим в гл. 4, время охлаждения белого карлика достаточно
велико, так что множество вырожденных карликов остаются видимыми в
течение значительного времени благодаря излучению с их поверхности. Это
удачное для нас обстоятельство позволяет в «нулевом приближении»
проверить теорию белых карликов, изучая их расположение на диаграмме
Герцшпрунга—Рессела (Г—Р). Г—Р-диаграмма представляет собой
зависимость логарифма светимости L от логарифма эффективной температуры
Г^, которая определяется равенством
L = 47rR^aT,\ C.6.1)
где ? — постоянная Стефана—Больцмана^\ Белые карлики с
определенным значением массы (порядка 1 М^) имеют определенный радиус (около
10^ см), и, следовательно, согласно равенству C.6.1), они занимают
определенную линию на Г—Р-диаграмме: L - Т^. Поскольку, как мы считаем,
массы карликов составляют около 1 М^, они должны занимать узкую
полосу на Г—Р-диаграмме заметно левее и ниже главной последовательности
нулевого возраста. Сравнение теоретических оценок с наблюдениями
свидетельствует об удовлетворительном согласии (рис. 3.3).
Лучший способ определения радиуса белых карликов состоит в лодгонке
параметров модели их атмосферы по наблюдаемому остаточному
излучению. Поток F^, эрг/(с · см^ · Гц), измеряемый на Земле, равен
^ R^F^ (на поверхности) /^ ^ ^<
где R — радиус белого карлика, а D - расстояние до Земли. Величина D
для близлежащих белых карликов определяется по измерению их
параллакса. Далее строится модель атмосферы белого карлика, зависящая от
эффективной температуры и поверхностной силы тяжести, таким образом,
чтобы воспроизвести наблюдаемый поток на различных длинах волн.
Отсюда определяется значение R. Обширная сводка данных по этому вопросу
с типичной неопределенностью 5—10<?^? представлена Шипманом [536].
Найти массу белого карлика гораздо труднее, так как для этого нужно,
чтобы звезда входила в двойную или тройную систему, что позволяет
определить массу по ее динамике. В настоящее время известны три белых
карлика, для которых как масса, так и радиус известны с довольно хоро-
^^ См. приложение А, где Г—Р-диаграмма обсуждается более подробно.
Белые карлики
85
Oh
-1
AJ
-г
-ъ
-4
?—^—\—"—л—??—г
М/Мо = 1Д5 1,05 0,65 0,25
±
±
_L
±
4.6
4.4
3.8
J-.
3.6
4Д 4.0
Рис. 5.5. Положения белых карликов, расстояния до которых известны, на
диаграмме Гердшпрунга — Рессела. Наклонные линии отвечают постоянному значению
радиуса; нриписанное им значение массы получено из уравнения состояния Чандрасека-
ра при ?_-=2. (Данные собраны Суини [554].)
шей точностью. Они перечислены в табл. 3.2 и указаны на графиках
зависимости ? от R (рис. 3.1), полученных Хамадой и Солпитером. Для Про-
циона В, который обычно изображают на таких диаграммах,
неопределенности в значениях ? и R заметно больше.
Весьма обнадеживающим является то обстоятельство, что все три
белых карлика с наиболее хорошо известными значениями ? и R лежат
точно на кривых Хамады—Солпитера. Действительно, наблюдения
свидетельствуют в пользу предположения, что Сириус В и 40 Эридана В вовсе
не состоят из одного чистого железа. Поскольку интервал ошибок отвечает
одному стандартному отклонению A?), наблюдения не противоречат
утверждению, что белые карлики состоят из углерода и кислорода, как и
получается на основании современных расчетов эволюции их
предшественников.
Еще одна проверка соотношения между массами и радиусами белых
карликов может быть выполнена посредством измерения эйнштейновского
гравитационного красного смещения^
??
.1).
GM
C.6.3)
'^ Мы выведем эту формулу в разд. 5.3.
86 Глава 3
Таблица 3.2
ЗНАЧЕНИЯ МАСС И РАДИУСОВ БЕЛЫХ КАРЛИКОВ,
ПОЛУЧЕННЫЕ НА ОСНОВАНИИ ОПТИЧЕСКИХ НАБЛЮДЕНИЙ
Сириус в
40 Эридана В
Stein 2051
Масса ^\
^0
1,053 ±0,028
0,48 ±0,02
0,50±0,05
или
0,72 ±0,08
Радиус^),
^0
0,0074 ±0,0006
0,0124 ±0,0005
0,0115±0,0012
Красное смеще-
ние^^ км/с
89±1,6
23,9±1,3
7
1) Масса Сириуса — по [217]; 40 Эридана В — по [270] (см., однако, [603]); Stein 2051
[552].
2) Радиусы — по [536].
3) Красное смешение Сириуса В — по [244]; 40 Эридана В — по [603].
Наблюдаемое гравитационное красное смещение обычно выражают как
эквивалентное доплеровское смещение ??/? = v/c, т.е.
V = 0,6362^^^ км/с . C.6.4)
/<//<о
Это дает 91 ± 8 км/с для Сириуса В и 22 ± 1,4 км/с для 40 Эридана В в
прекрасном согласии с наблюдениями.
Упражнение 3.8. В литературе приведены следующие данные о красных смещениях:
Ван Маанен 2:14 ± 18 км/с [273J и 33 ± 16 км/с [218]; EG 64: 131 км/с;
EG 113:52 км/с; последние два результата получены Гринстейном и Тримбл [243],
которые отмечают, что ошибки приведенных значений могут Ьыть велики.
Согласно Шипману [536], радиусы этих звезд равны соответственно 0,0138 Rq, 0,0182 Rq
и 0,0094 /?0. Согласуются ли эти значения с соотношением масса—радиус
Хамады и Солпитера?
3.7. ПИКНОЯДЕРНЫЕ РЕАКЦИИ
В плотном веществе ядерные реакции могут идти даже при нулевой
температуре. Эти реакции происходят в силу того, что нулевые колебания ионов
с энергией Eq ~ ??^ около узла решетки позволяют им преодолевать куло-
новский барьер соседних ионов. В этом разделе мы грубо приближенно
Белые карлики 87
оценим скорость таких реакций. Наша задача будет состоять в том, чтобы
вычислить коэффициент Г, характеризующий проницаемость ионов сквозь
электростатический потенциальный барьер, препятствующий их
сближению. Величина ? зависит от детальной структуры потенциала. Она
различна для идеального газа практически свободных ионов и твердого
кристаллического тела, характеризуемого регулярной ионной решеткой. Первый
случай реализуется внутри нормальных горячих звезд главной
последовательности, второй описывает холодное вырожденное вещество в белых
карликах. Когда два иона пройдут сквозь электростатический
потенциальный барьер и соприкоснутся, вероятность дальнейшего взаимодействия
практически не зависит от их начального состояния. Этот эффект будет
использован в нашем дальнейшем анализе.
Сначала рассмотрим, как вычисляется скорость таких реакций, когда
два иона являются, по существу, свободными и находятся первоначально
на большом расстоянии (как в термоядерных реакциях или в реакциях на
ускорителе)^\ Напомним, что при малых энергиях сечение взаимодействия
двух частиц пропорционально ??^ - \/Е, где ? = h/p — характерная для
данной реакции длина волны де Бройля, а ?* — энергия пары ионов в
системе их центра масс. Напомним далее, что вероятность прохождения куло-
новского барьера для двух ионов с зарядами Zj и Zj, относительная
скорость которых на большом расстоянии друг от друга равна у,
пропорциональна проницаемости (гамовскому фактору):
Исходя из этих соображений, запишем сечение в форме
?(?) = ^???(-2^?), E = W, C-7-2)
причем мы ожидаем, что величина S(?'), описывающая вклад в сечение
чисто ядерного взаимодействия, должна быть медленно меняющейся
функцией ? (здесь ? — приведенная масса). Для определения S{E) можно
использовать лабораторные измерения ?(?), а в некоторых случаях S{E) можно
найти чисто теоретически. Например, величина S{E) для реакции
p^p^D + e^-^v C.7.3)
определяется по известной скорости слабого процесса превращения
протона в нейтрон в /7/7-рассеянии с испусканием позитрона и нейтрино и
образованием связанной А2/7-системы (дейтрона).
^ Более детальное обсуждение термоядерных реакций можно найти, например, в
гл. 4 книги Клейтона [135].
88 Глава 3
Гамовский фактоо можно найти из решения уравнения Шредингеоа вне
ядер. Волновая функция относительного движения зарядов Zj и Zj при
г > Rn(R„ — сумма радиусов ядер) равна
^,(г,в,ф)^^У,„{в,ф). C.7.4)
Мы предполагаем, что система находится в состоянии с определенным
угловым моментом и пренебрегаем спиновыми эффектами. Функция х/(г)
есть решение радиального уравнения Шредингера
^ + ^[E-V,{r)]x, = 0, C.7.5)
где ? — приведенная масса, а
У,(г) - ^^??^ + Kir), r>R„,
Kir)-^. C.7.6)
При низких энергиях рассеяние в основном идет в сферически-
симметричной 5-волне. В соответствии с этим положим 1=0.
Поведение V(r) показано на рис. 3.4, где при г > R„ изображен КДг), а
при г < R^ схематически представлен короткодействующий
притягивающий ядерный потенциал.
Проницаемость можно определить, не зная детального поведения
ядерного потенциала при г < R^. Для потенциала, изображенного на рис. 3.4,
в одномерном ВКБ-приближении проницаемость, согласно [349, гл. 4],
равна
гр _ |ХtransI ^^trans __ 3 ('I ? ?\
~ lx»cl^i„c B<?+1/2<?)^'
Здесь ? определяется как отношение потока прошедших (trans) частиц к
потоку падающих (inc), а
e = sxp(f\kix)\dxy C.7.8)
kix) = [^[Е - Пх)]у\ C.7.9)
При ? > 1
?=?· C.7.10)
Белые карлики
89
Рис. 5.?. Эффективный потенциал, описывающий относительное движение атомных
ядер. При r<R^ ядра фактически находятся в непосредственном контакте и в
потенциале главную роль играет притяжение, связанное с короткодействующими
ядерными силами. При r>R^ ядерные силы пренебрежимо малы и в потенциале
преобладает кулоновская часть. При г=^ показана классическая точка поворота,
соответствующая движению с энергией ? в системе центра масс.
В нашем примере а^ = /?^ — О, а Ь определяется выражением
? =
???2€
b
C.7.11)
Таким образом.
/>)i^-fifi/;(f-f*
? = ???(-2???).
C.7.12)
90 Глава 3
Одномерное ВКБ-приближение правильно воспроизводит существенную
экспоненту в гамовском факторе. Однако точное решение уравнения Шре-
дингера в кулоновском потенциале дает
^^jP^ = 27??6??(-27??), ? » 1. C.7.13)
??(??)?
Одномерное ВКБ-приближение дает неверный предэкспоненциальный
множитель. Мы здесь пренебрегаем этим различием.
Теперь можно найти связь между S(E) и Р^ — вероятностью ядерной
реакции, когда частицы проникли на расстояние г = R^. Пусть
W — скорость реакции (вероятность в секунду) падающего иона Zj с ядром
(ионом Zj). Тогда
W = { прошедший поток приЛ„) X ЛтгК^ X Р^
= (падающий поток) ? 6??(-27??) ? 4????„. C.7.14)
Но по определению ?(?)
W ^ о (?) ? (падающий поток)
S(E)
= —7г-^ 6??(-27??) ? (падающий поток ). C.7.15)
Сравнение выражений C.7.14) и C.7.15) дает
S{E) = 47гК1Р„Е. C.7.16)
Таким образом, неизвестная вероятность Р^ выражается через
поддающуюся измерению (в принципе) величину S(E).
Перейдем теперь к реакциям в кристаллической решетке. Скорость
реакции для одной пары ионов равна
W= (падающий поток) X Г X 47гК1Р„ = u|i//iJ^—^-^, C.7.17)
где l^inc'^ и ? при г > R^ теперь нужно вычислять в решеточном
потенциале, а ядерный фактор S(E) остается таким же, как и раньше.
Представим приближенно решеточный потенциал, рассматривая^^
одномерное движение иона между двумя фиксированными тождественными
ионами, находящимися на расстоянии 2 Rq. Более подробно мы изучим эту
^^ Изложенные здесь рассуждения представлены согласно Зельдовичу [631].
Белые карлики
91
^х
„Закрепленный"
ион 2
Рис. 3.5. Потенциал, описывающий движение отдельного «падающего» ядра
относительно «закрепленных» ядер в одномерной решетке. Ионы (ядра) находятся на
расстоянии Rq. Нулевые колебания с энергией Eq в осцилляторном потенциале вблизи
места нахождения «падающего» иона могут привести к прохождению кулоновского
барьера и ядерным реакциям.
одномерную решетку в следующей главе, а сейчас только заметим, что
такой решеточный потенциал можно записать в виде
72р2 72р2 2Z^2
Rq-x
Rq + x
Re
\x\<Rq-R„. C.7.18)
На рис. 3.5 показан вид этого потенциала, объединенного с
короткодействующим ядерным потенциалом вблизи каждого узла, где находится
неподвижный ион. Мы предположили, что все ионы имеют заряд Ze и массу т^
и что точка ? = О отвечает положению равновесия. Для ? < Rq получим
V{x)-^\Kx\ К-^^. C.7.19)
Таким образом, при малых отклонениях от положения равновесия
движение оказывается просто гармоническим с энергией нулевых колебаний,
равной
^0 = ^??^ =
Ы1)
3\»/2·
C.7.20)
92
Глава 3
Упражнение 3.9. Покажите, что ?^ фактически совпадает с плазменной частотой
ионов ? = {4TrZ^e^n./m.Y^^, где ? л —средняя концентрация ионов.
Классическая точка поворота Tq для иона с энергией ? = Eq
определяется уравнением
Ео - У{го).
C.7.21)
Приближенно заменяя K(jf) потенциалом гармонического осциллятора
C.7.19), получим
-D)'1f)"'
C.7.22)
В рассматриваемом приближении \|/^^J^^ можно считать волновой
функцией основного состояния простого гармонического осциллятора (SHO). В
трехмерном пространстве она равна
где
2 т^
C.7.23)
C.7.24)
(т.е. ион локализован в объеме ^rj в окрестности каждого узла решетки).
Полагая экспоненциальный множитель в выражении C.7.23) равным
единице, получим
????
C.7.25)
Коэффициент пропускания для падающего иона с энергией Eq снова
можно вычислить в ВКБ-приближении:
r=exp[-2/V(^)l^^]
C.7.26)
где к(х) определяется выражением C.7.9). Полагая и = x/Rq, получим
г2^2п \1/2 ., „ _ / 1 \1/2
Г= ехр
C.7.27)
Белые карлики
93
где
а =
Безразмерный интеграл в выражении для ? можно записать в виде
C.7.28)
'=/;
|-л,/«(
{u-?){u + ?)
[A-«)(! + «) J
1/2
du.
где
C.7.29)
C.7.30)
Устремляя R„ к нулю, можно взять этот интеграл с помощью таблиц
интегралов [98, равенство B56.18)]:
/=A + ?)?-2??,
тае ? и К — полные эллиптические интегралы с модулем
\-?
к =
\+?·
В пределе ? < 1 имеем
/.l-i'ln(i)"'.
Комбинируя равенства C.7.27), C.7.30) и C.7.33), получим
Г=4^ехр(-241
C.7.31)
C.7.32)
C.7.33)
C.7.34)
Отсюда после некоторых упрощений преобразуем выражение C.7.17) к
виду
W
-ш
2\·/%(????
— ' S 7-7 ехр
-AZe
(???)
1/2
C.7.35)
Упражнение 3.10. Покажите, что при плотностях < 10'" г/см' справедливо
соотношение ?о '* ^coui ~ Z'^s^/Rq, т.е. решетка фактически не существует, несмотря на
наличие нулевых колебаний.
94 Глава 3
Следуя Солпитеру и Ван Хорну [499], введем безразмерный параметр
длины:
где концентрация ионов п^ оценена в предположении, что в сфере
радиусом Rq/2 находится один ион. Число реакций на кубический сантиметр в
секунду равно
Ро = Па^ = ( Jj^'Z^YXV^expi-eX-'/^), C.7.38)
где мы приняли, что ? = y4w„w^. В этой формуле ? выражается в г/см^,
S — в МэВ · барн A барн = 10~^ см^) и
? =1,1X10^, ? = 2,85. C.7.39)
Мы умножим 7 на 4, так как каждый ион в объемно центрированной
кубической решетке имеет 8 ближайших соседей, а if — вероятность реакции
при парном соударении.
Наилучшее к настоящему времени вычисление скорости пикноядерных
реакций принадлежит Солпитеру и Ван Хорну [499]. Они использовали
более реалистическую форму потенциала решетки с учетом анизотропии и
эффекта электронной экранировки и получили следующий результат:
р^ ^ (^^A'Z'Sy\'/'^xp{-e\-'/')c-' · cм-^ C.7.40)
? = 3,90 ? 10^, ? = 2,638, C.7.41)
? = 4,76 ? 10^, ? = 2,516. C.7.42)
где
Эти два набора численных значений отвечают двум различным
приближенным потенциалам, которые огрубленно ограничивают истинный потенциал
сверху и снизу. Интересно отметить, насколько грубая формула C.7.38)
близка к выражению C.7.40), особенно если учесть, что зависимость от ?
появляется в экспоненте. Однако мы еще раз повторим сделанное выше
предостережение, что учет дефектов решетки может привести к
существенному увеличению полученных скоростей реакций.
Белые карлики 95
При конечных температурах нельзя более считать, что ядро находится в
основном состоянии решеточного потенциала. При еще более высоких
температурах решетка исчезает и система переходит в термоядерный режим.
Скорости реакций во всех этих режимах обсуждались Солпитером и Ван
Хорном [499].
Упражнение 3.11. Покажите, что выражение C.7.36) можно переписать в виде
?- ^п 1 · 0-7-43)
\А 1,36 X 10" г/смЗ /
Упражнение 3.12. Используя равенство C.7.40), получите пределы концентраций ? и
С , приведенные в разд. 3.5, доказав, что полное ядерное превращение происходит
за характерное время, определяемое условием
^0^ = «^· C.7.44)
Разрешите уравнение C.7.44) относительно р, положив г = 10^ лет и
Spp = 5,38 X 10"^^МэВ · барн,
S,,^ 8,83 X 10'^ МэВ · барн.
Значение S^c взято из работы [203], и его неопределенность, по-видимому,
определяется множителем не меньше трех.
Глава 4
Остывание белых карликов
в гл. 3 мы обсудили, как проверить наблюдениями соотношение между
массой и радиусом для белых карликов. Другой важный способ проверки
теории белых карликов основан на изучении их остывания. Как будет
описано ниже, эта проверка состоит в сравнении светимости с возрастом
белого карлика, т.е. в сопоставлении величин, связь между которыми
определяется скоростью остывания. Теория остывания белых карликов
представляет интерес не только с астрофизической точки зрения, но и как красивое
приложение физики твердого тела в весьма необычных условиях.
4.1. СТРУКТУРА ПОВЕРХНОСТНЫХ СЛОЕВ
Для нахождения скорости остывания нам надо определить, каковы условия
вблизи поверхности белого карлика.
Недра белого карлика являются полностью вырожденными. Поскольку
море Ферми заполнено, электроны имеют большую длину свободного
пробега, что приводит к высокой теплопроводности и, следовательно, к
постоянной по объему температуре. Эта изотермическая внутренняя часть
покрыта невырожденными поверхностными слоями, которые находятся в
лучистом равновесии: вещество практически находится в локальном
термодинамическом равновесии, но при этом существует направленный наоужу
поток энергии, уносимой диффундирующими фотонами. Уравнение диффузии
фотонов имеет вид
Это уравнение выведено и более подробно обсуждается в приложении И.
Здесь L — светимость (эрг/с), аГ* — плотность энергии черного тела и
к — непрозрачность (см^/г) звездного вещества. Длина свободного
пробега фотона оценивается величиной \/кр. Уравнение D.1.1) приводит к
соотношению
dr 4ас т^ 47гг^ ? · · /
Для определения непрозрачности применимо приближение Крамерса:
? = Kop7'-'·^ D.1.3)
dr 7?- D-1.4)
Остывание белых карликов 97
которое получается, если учитывать процессы фотоионизации атомов и
обратного тормозного излучения свободных электронов (связанно-свободный
и свободно-связанный переходы) ^^ Разделив условие гидростатического
равновесия
dP ^ Gm{r)p
г
на уравнение D.1.2), получим
dP^ __ 4ас 47гСт{г) Т^^^
dT' 3 ^?^ Г* ^^^-^-^)
В поверхностных слоях, которые, как мы увидим ниже, тонки по
сравнению с радиусом белого карлика, можно считать, что m(Z) = Л/. Если
исключить плотность р, используя уравнение состояния B.3.18) для
невырожденного вещества в поверхностном слое, то получим
p^p^4^^^J^j,rs^T D.1.6)
Уравнение D.1.6) с граничным условием ? = О при Г = О легко
интегрируется. Теперь, выражая ? через ? с помощью уравнения состояния, найдем
Для Kq можно использовать выражение, приведенное в книге Шварцшильда
[516, с. 237]:
Ко = 4,34 X 10^^7A + X) cMVr, D.1.8)
где X — доля водорода по массе, а ? — доля тяжелых элементов (т.е. всех
элементов, кроме водорода и гелия). Теперь с помощью уравнения D.1.8)
мы можем описывать поведение ? в зависимости от Г в наружных слоях
белых карликов.
В некоторой точке под поверхностью, где электроны становятся
вырожденными, уравнение D.1.7) становится неприменимым. Оценим
значения плотности р· и температуры Г·, при которых это происходит,
приравнивая давление невырожденных электронов давлению вырожденных. При
этом используем равенства B.3.22):
= 1,0 X lO^^i^j^'. D.1.9)
'^ См. приложение И.
98 Глава 4
Отсюда следует
р^ = B,4 X 10-« ?/cы^)?eTV\ D.1.10)
где Г· измеряется в Кельвинах. Температуру в этом переходном слое
можно выразить через светимость, сопоставляя уравнения D.1.7) и D.1.10). Это
дает
i.E.7x,0',pr.c)i^^^r=.=. D.1.11)
Таким образом, зная L, химический состав и массу белого карлика, можно
определить его внутреннюю температуру.
Для примера положим Л' = О, У = 0,9 (доля гелия по массе), ? = 0,1
и Л/ = Mq. Отсюда найдем ?^ « 2, ? » 1,4 и, следовательно,
L=BX10^ эрг/с )^П^. D.1.12)
Характерные значения L составляют 10~^ — 10~^ Lq, что отвечает Г· «
* 10^ -ь laP К и, следовательно, р· ^ 10^ г/см^ < р^. Столь низкая
плотность в переходном слое подтверждает предположение, что поверхностный
слой является относительно тонким и что он не меняет соотношение
между массой и радиусом, полученное для холодных звезд. Заметим, также,
что кТ* много меньше энергии Ферми электронов в ядре белого карлика.
Упражнение 4.L С помощью уравнений D.1.3) и D.1.7) исключите ? из уравнения
D.1.2). Затем, проинтегрировав его, получите соотношение
где г* — значение радиуса, при котором ? = Т*. Покажите, что при Г, = 10^ -ь
-?- 10^ К отсюда следует
^^—^< 10-^ D.1.14)
4.2. ЭЛЕМЕНТАРНЫЙ АНАЛИЗ ОСТЫВАНИЯ БЕЛЫХ КАРЛИКОВ [400, 516]
Когда звезда доходит до стадии белого карлика, единственным
источником излучаемой энергии является остаточная тепловая энергия ионов. При
дальнейшем гравитационном сжатии высвобождается очень мало энергии,
так как звезда уже достигла вырожденного состояния. Энергия,
выделяемая при испускании нейтрино, существенна только на очень ранней
высокотемпературной стадии. Высвобождение тепловой энергии электронов за-
Остывание белых карликов 99
труднено, поскольку в вырожденном газе большинство состояний с более
низкой энергией оказываются занятыми. Если удельная теплоемкость
ионов в расчете на один ион равна с^, то тепловая энергия, приходящаяся на
один ион (рассматриваемая только как функция температуры),
определяется равенством
Тепловая энергия = [c^dT. (^-2.1)
Полагая для невырожденного одноатомного газа, что
с^ = I* D.2.2)
получим, что полная тепловая энергия белого карлика равна
U^LkT^. D.2.3)
Здесь ? — однородная температура внутри белого карлика, которая в разд.
4.1 обозначалась Г·. Мы предположили, что в состав белого карлика
входят только ионы с барионным числом Л\ в общем случае \/Л следует
заменить на 1/? - 1/?^. Запас энергии, определяемый равенством D.2.3),
весьма значителен. При Г. - 10^ К он достигает -10^^ эрг, что сравнимо
с энерговыделением сверхновой в видимой части спектра. Скорость
охлаждения равна -dU/dt, Приравнивая эту величину выражению D.1.12) для L,
записанную в форме
L = СМТ'/'', D.2.4)
где CMq * 2 ' ^^^ эрг/с, получим уравнение
-К^?)—. (-3)
интегрирование которого дает
3 к
5 Am,
EП-5/2 _ 7--5/2) = с(/-/о). D.2.6)
где Tq — начальная температура. Полагая, что 7^ > Т, мы можем
пренебречь зависимостью от Tq в соотношении D.2.6) и написать для времени
охлаждения ? = t - tQ выражение
^^1ШМ-, D.2.7)
5 Am^L
Заметим, что из равенства D.2.4) следует
-5/7
? ?
[W <^·^·''
100 Глава 4
Для L - 10~^ Lq имеем ? - 10^ лет. Получается такой порядок величины,
какого следовало ожидать: с одной стороны, ? достаточно велико, так
что белые карлики не успели стать ненаблюдаемыми, а с
другой — достаточно мало, так что типичные светимости белых карликов
стали теперь весьма низкими. Как можно заметить, из уравнения D.2.6)
следует, что большую часть времени белый карлик имеет температуру,
близкую к современной.
В конце 60-х и начале 70-х годов рассмотренная выше теория
остывания приближенно согласовалась с наблюдениями для горячих и ярких
белых карликов A0"^ ^ ^^^О ^ Ю"^). Однако для слабых белых карликов
(L ^ 10" ^Lq) теоретические оценки времени остывания казались
завышенными более чем на порядок. Это противоречие проявлялось лля слабых
белых карликов в звездных скоплениях, где возраст белого карлика,
вычисленный на основе формулы D.2.7), оказывался выше возраста скапления^\
Кроме того, поскольку ? увеличивается по мере уменьшения L, тл должно
наблюдаться большое количество белых карликов с малыми светимостями.
Однако, например, функция светимости Вейдеманна указывает на яедиста-
ток белых карликов с L <> 10"^ L^ .
Как мы теперь знаем, это противоречие было в сущности кажущимся и
появилось из-за недооценки неточностей в наблюдениях скоплений и в
определении их возраста. Интенсивные поиски привели к обнаружению
большого количества не входящих в скопления белых карликов со
светимостью вплоть до L < 10" ^Lq. Однако упомянутое кажущееся
противоречие стимулировало попытки теоретиков «сократить» время остывания.
В следующих разделах описаны наиболее важные поправки к
элементарной теории остывания. Это сделано по следующим двум причинам. Во-
первых, по мере улучшения данных наблюдений требуется и более точная
теория, с которой эти данные можно было бы сравнить. Во-вторых, новые
наблюдения свидетельствуют о неожиданном отсутствии белых карликов с
очень малой светимостью L < \0~^ L^ [301]. Если этот дефицит
действительно имеет место, то какой физический эффект может быть
ответственным за сокращение времени остывания?
Наиболее важный эффект, которым мы пренебрегли, — это
кристаллизация ионной решетки [401, 496, 585]. Для достаточно низких температур
(и, следовательно, светимостей) удельная теплоемкость в большей степени
связана с колебаниями ионов решетки, чем со свободным движением. Де-
баевская температура {?^ - 10^ К) является критической температурой,
ниже которой с^ быстро падает, что ведет к Ьолее быстрому остыванию.
Учет этого обстоятельства должен обеспечивать улучшение согласия
теории с наблюдениями. В следующих разделах мы в основных чертах
построим теорию кристаллизации и теплоемкости ионной решетки и применим
результаты к белым карликам.
'^ Возраст скопления по существу совпадает со временем жизни на главной
последовательности наиболее ярких звезд скопления в предположении, что все звезды
образовались в одно и то же время; см. приложение А.
Остывание белых карликов 101
4.3. КРИСТАЛЛИЗАЦИЯ И ТЕМПЕРАТУРА ПЛАВЛЕНИЯ
Ионная решетка кристаллизуется, когда безразмерный параметр
{ZeY __ кулоновская энергия
г-кТ тепловая энергия
становится достаточно большим. Здесь г- определяется уравнением
D.3.1)
3
= 1, D.3.2)
где tij — концентрация ионов. При Г < 1 отклонение плазмы за счет
электростатических поправок от идеальной картины Максвелла—Больцмана
незначительно. При Г > 1 кулоновские силы преобладают и плазма
кристаллизуется, образуя периодическую решетку, которая минимизирует кулонов-
скую энергию.
Можно оценить критическое значение Г и соответствующую
температуру плавления Г^, пользуясь эмпирическим правилом Линдеманна [369]:
ионная решетка плавится, когда средний квадрат тепловых флуктуации
положения иона {{br^Y) удовлетворяет условию
((»'.)^>
1
г2 16
D.3.3)
Упражнение 4.2. Рассмотрим малое смещение иона от положения равновесия в
решетке Вигнера—Зейтца. Считая, что окружающее ион электронное облако
однородно распределено в пространстве, покажите, что возвращающая сила, которая
возникает от взаимодействия с этим облаком, представляет собой силу трехмерного
гармонического осциллятора. Вычислите величину коэффициента упругости К и
покажите, что частота колебаний равна
где ??? — плазменная частота ионов:
Заметим, что для одномерной модели решетки, использованной в разделе C.7),
также справедливо соотношение D.3.4) (ср. с упр. 3.9).
Упражнение 4,3, (основано на работе Солпитера [496]). Пусть г^а^ — радиус сферы,
внутри которой в среднем находится один электрон; здесь а^ =
= h/am^c — боровский радиус, а * 1/137. Таким образом, г, = Z^^^t^Oq.
102 Глава 4
а) Покажите, что полная кулоновская энергия ячейки решетки Вигнера—Зейтца
[равенство B.4.8)] может быть записана в виде
9 Z^/^
а энергия нулевых колебаний — в виде
^0-1^-0 = 3(^) ,-3/^ Ry.
Сравните эти величины с аналогичными величинами для объемноцентрированной
кубической (ОЦК) решетки.
Ответ: Для ОЦК решетки коэффициент в выражении Е^. вместо 9/5 становится
равным 1,804, а коэффициент 3 в выражении Eq превращается в 2,66.
б) Покажите, что отношение/ s \Eq/Ec\ в решетке Вигнера-Зейтца
удовлетворяет условию
где X — безразмерный параметр, введенный в равенстве B.3.3), который
определяет, насколько релятивистскими являются электроны. Очевидно, чтобы ионы
оставались в решетке при нулевой температуре, необходимо условие/ < 1 (почему?).
Какой величины достигает / для устойчивых карликов, состоящих из '^ с с
плотностью ? -^ \ ' 10^0 г/смЗ?
Ответ: f - 0,05.
Согласно классическим представлениям, каждая степень свободы
гармонического осциллятора вносит в среднюю энергию вклад кТ/2:
??({8??) ~ ^,кТ. D.3.6)
Соотношения D.3.4) и D.3.6) теперь дают
Более точную оценку числового коэффициента в D.3.7) можно получить
следующим образом [401]. Каждая нормальная мода колебаний иона в
решетке описывается волновым числом к и состоянием поляризации ?. Двум
поперечным состояниям поляризации припишем ? = 1, 2, а продольной
моде — ? = 3. В области применимости классической теории
Остывание белых карликов 103
где К (к, ? ) — коэффициент упругости для данной моды, а
??(?) — соответствующая частота. Чтобы определить <(ог^)^>, нужно
просуммировать равенство D.3.8) по нормальным модам колебаний иона.
Вспоминая, что плотность в фазовом пространстве для каждого
поляризованного состояния равна 1/Л^, получим, что число мод в элементе
фазового объема d^x (?? равно
d^xd^p ,? ?^ dK
Г"^ = d^x г^
= ^^дс——, D.3.9)
так как ? = Л/с. Поскольку объем, приходящийся на один ион, равен
= 1//1,, то
{(«.)>i;/^^E((«.)·).,
= / -—? ? 2/ ч · D.3.10)
Интеграл обрезается на дебаевской моде /с^, величину которой можно
найти, принимая полное число нормальных мод N ионов в объеме V равным
3?:
3
3 кЧк ЗКк^
3iV= Zfd'x^ =^, D.3.11)
или
icd = {в7г^п,У^\ D.3.12)
Чтобы дальше использовать уравнение D.3.10), нам понадобится
дисперсионное соотношение для ??(?). Спектр возбуждения решетки мы обсудим
более подробно в разд. 4.4, а здесь заметим только, что с хорошей
точностью можно принять
?3 = 0,7?^. D.3.13)
Подставляя эти результаты в равенство D.3.10), получим
{E,)>i^, D.3.14)
104 Глава 4
что МОЖНО сравнить с первоначальным выражением D.3.7).
Равенство D.3.14) и правило Линдеманна D.3.3) в точке плавления дают
Г = 75, D.3.15)
что в предположении ?^ « 2 соответствует температуре плавления
? =
zV/4^ " ^'/^
[tiL·] =2x10V/'ZV3k. D.3.16)
г* 3 2Zm
Эти значения находятся в разумном согласии с результатами, полученными
при расчетах методом Монте-Карло для однокомпонентной кулоновской
«жидкости» (Г = 126) [91], а также при учете квантовых эффектов для
ионов (Г = 160) [331]. Недавно в работе [543] было найдено значение Г =
= 171 ± 3.
Мы определили дебаевскую температуру ?^ посредством равенства
???^??^, D.3.17)
отсюда
во = 4х lOV^^K. D.3.18)
Для белых карликов с ? > 2, как правило, Т^ > ^^, так что применим
классический вывод <ог^)^>. В противном случае при вычислении <(бг^)^>
следовало бы учесть нулевые колебания. Однако оказывается, что даже для
Не с Т^ < ??^ выражение D.3.10) лучше согласуется с экспериментом, чем
результаты некоторых попыток учесть нулевые колебания.
Когда жидкость кристаллизуется при Г - Г^, выделяется скрытая
теплота, количество которой в пересчете на один ион составляет
-Я- кТ^' D.3.19)
Скрытую теплоту, выделяющуюся в процессе кристаллизации, следует
включить в полный запас энергии звезды. Как обсуждается в разд. 4.5, это
приводит к увеличению времени остывания.
Третья существенная температурная характеристика — это температура
Tg, при которой кинетическая энергия ионов начинает превышать их
колебательную энергию. При температурах выше Tg кристаллическая решетка
разрушается, образуя плотный неидеальный газ.
Это происходит, когда
({8п)')~г^ D.3.20)
или ? ~ 16 7"„ [ср. с выражением D.3.3)]. Отсюда
Г - 3 X lOV'/'Z^/' К. D.3.21)
Остывание белых карликов 105
Заметим, что для ^^С справедливо неравенство ??^ < Т^ < Т^ при условии,
что о ^ 10^ г/см.
4.4. ТЕПЛОЕМКОСТЬ КУЛОНОВСКОЙ РЕШЕТКИ
При ? > Т^ ионы можно рассматривать как идеальный газ
Максвелла—Больцмана и, следовательно, теплоемкость, приходящаяся на один
ион, равна
с„ -\к, г» Г,. D.4.1)
Это значение было использовано в разд. 4.2 при элементарном обсуждении
остывания белых карликов.
Когда температура опускается ниже Г^, начинается формирование
решетки. При этом теплоемкость увеличивается вдвое из-за дополнительного
вклада потенциальной энергии решетки, равного кТ/1 на каждую моду
колебаний. Таким образом,
с, -- 3/с, во <г Г <1с Г^. D.4.2)
При дальнейшем охлаждении ло ? <> ??^ становятся существенными
квантовые эффекты и с^^ падает много ниже значений D.4.1) и D.4.2).
Когда Г — О, то с^ ^ Г^. Поскольку этот режим может играть существенную
роль при сопоставлении данных наблюдений с теоретическими оценками
скорости остывания белых карликов и непосредственно свидетельствовать
об их кристаллизации, мы обсудим его более подробно.
Средняя энергия иона в решетке при температуре ? равна^^
где /3 = \/кТ, Теплоемкость определяется выражением
V^^^ ?,? {6??[)8??,(?)] - 1}^
С>мму по к можно заменить интегралом, что дает
_ _ к г-окЧк ' &??[???^{?)][???^{?)?
" «,-^? 2^2 xtr, (ехр[)8Л«х(к)] - 1)'
«Обычное» дебаевское приближение, которое здесь неприменимо,
состоит в следующем^\·
'^ Ср., например, с разд. 10.1 книги [479].
^^ См., например, [479], разд. 10.2.
106 Глава 4
1. Предположим, что нормальные моды колебаний в твердом теле
можно приближенно представить как распространение звуковых волн в
непрерывной упругой среде. Отсюда получим дисперсионное соотношение в
виде
??(?) = КС, ?, D.4.6)
где скорости поперечных с^ ? = с^ 2 ** продольных с^ з звуковых волн
можно выразить через параметры упругости среды.
2. Определим «среднюю эффективную» скорость звука с^:
3 2^1
3. Дебаевская граничная частота, отвечающая выражению D.4.6),
должна быть равна
??,? = '«?^?,?» D.4.8)
и, следовательно, зависит от поляризации ?. Вместо этого пренебрежем
зависимостью от поляризации и определим общую дебаевскую частоту для
всех ? в виде
где было использовано выражение D.3.12).
Тогда равенство D.4.5) принимает вид
c.-3/c/d|-^J, D.4.10)
где «функция Дебая»/р(у) определяется выражением
а «обычная» дебаевская температура ?? определена условием
D.4.12)
горое отличается от
Поскольку
fviy)
Uy)
kh
условия
^1,
^ 4^"
^ 5
» A«D,
D.3.17).
>'^0,
J_
3 '
У
00, D.4.13)
Остывание белых карликов
107
Пробольная
мода
Рис. 4.1. Спектр возбуждений объемноцентрированной кубической решетки с куло-
новским взаимодействием при учете экранировки согласно вычислениям Кларка
[129] и обзору Пайнса [457]. Штриховая линия отвечает идеализированному случаю
отсутствия экранировки. (По работе [401].)
то для «обычной» дебаевской теплоемкости получим
Ък,
Г»
'D'
12И, / ?
T<^L
D.4 л 4)
К сожалению, «обычное» дебаевское рассмотрение недостаточно для
наших целей. Основанное на грубой аналогии между твердыми телами и
упругими средами, оно неправильно описывает кулоновскую природу
ионной решетки. Наиболее существенно, что дебаевская граничная частота для
ионной решетки равна ?^, а не ?^, так как наивысшая частота в спектре
нормальных мод связана с колебаниями одного иона вокруг своего
положения равновесия.
Правильное вычисление интеграла D.4.5), определяющего с^, требует
детального анализа спектра нормальных мод (фононов) ?? (/с) ионной
решетки вблизи Г = 0. Такой анализ был проделан для
объемноцентрированной кубической решетки Кларком [129], Карром [107] и другими. Моды
колебаний такой решетки состоят из двух поперечных фононов и
продольного «плазмона». Их типичный спектр представлен на рис. 4.1.
Некоторые особенности колебательного спектра можно понять на
основе анализа нормальных мод одномерной ионной решетки, рассмотренной в
108 Глава 4
разд. 3.7. Напомним, что мы рассматриваем ионы в виде цепочки из N
частиц с массами т^, которые в положении равновесия находятся на
расстоянии /?Q(=2ry) друг от друга. Кулоновские силы действуют как «пружинки»,
связывающие ионы друг с другом, с коэффициентом упругости
?^???^ {??^?? = ^???] , D.4.15)
где ? = w,/2 — приведенная масса. Полная длина решетки равна {N +
+ \)Rq\ предполагается, что крайние ионы закреплены. Мы предположим,
что только ближайшие соседи взаимодействуют друг с другом, игнорируя
таким образом экранировку, связанную с дальнодействующим характером
кулоновского поля^\
Если смещение у-го иона от положения равновесия равно Qj, то для
малых смещений суммарная сила, возвращающая этот ион к положению
равновесия, равна
Fj = -K{qj - qj_,) + K{qj^^ - qj). D.4.16)
Уравнение движения имеет вид
rriiilj = K{qj_, - Iqj + ^^.^,), j = 1,..., iV. D.4.17)
Отыскивая нормальные моды, положим
qj{t) = fl^e'"', D.4.18)
где постоянные О: удовлетворяют уравнению
-Kaj_, + {2К- m,w')aj - ???^.^, = О, ; = 1,..., iV, D.4.19)
причем граничные условия выполняются, если наложить требования:
До = о, D.4.20)
*N+\
= 0. D.4.21)
Уравнение D.4.19) является линейным разностным уравнением второго
порядка с постоянными, т.е. не зависящими от у, коэффициентами. Его
можно решить с помощью подстановки
Qj = a,e'^Jy-^\ D.4.22)
ческий смысл имеет действительная часть Oj.
?2 = 4—sin^^. D.4.23)
где подразумевается, что физический смысл имеет действительная часть Oj
Далее найдем
ГП:
Эта экранировка будет учтена ниже в данном разделе.
Остывание белых карликов 109
Граничное условие D.4.20) требует, чтобы
? = I ' D.4.24)
так что действительная часть а^ исчезает, а условие D.4.21) приводит к
соотношению
8???(??+ 1) = 0, D.4.25)
или
^'°????' '·=1'··.,?^. D.4.26)
Здесь г нумерует N независимых решений уравнения D.4.19). Таким
образом, имеется N независимых собственных частот:
„=2(AV''sin-7-^-.. D.4.27)
т,] "(iV+l)·
Для соответствующих нормальных мод смещение у'-й частицы
пропорционально величине
Дисперсионное соотношение D.4.27) можно переписать через волновое
число /с^, определенное равенством
Тогда
Qj,- uri{K,Xj), D.4.30)
где Xj = / /?о» а дисперсионное соотношение принимает вид
?, = ?„„8??^, D.4.31)
где
= (?)?,· D.4.32)
Вышеприведенное дисперсионное соотношение, полученное для
продольных мод одномерной решетки, обладает следующими общими для
любых систем с большим N свойствами:
по Глава 4
1. При низких частотах и больших длинах волн (?^ < ^ах» '^г^о "^ ^)
линейная акустическая зависимость
?, ОС к, D.4.33)
такая же, как для упругой среды [ср. с формулой D.4.6)].
2. При высоких частотах и малых длинах волн дисперсионное
соотношение уже не является линейным. Частота ?^ достигает максимума
вблизи ? , что отвечает волновому числу к^ - ^//?q, т.е. границе «зоны Брил-
люэна» решетки.
3. Число независимых мод равно N х (размерность решетки).
Мы видим, что спектр поперечных фононов, представленный на рис. 4.1
для объемноцентрированной кубической решетки, который приближенно
выражается равенством D.3.13), качественно подобен спектру одномерной
решетки, определяемому формулой D.3.31).
Исходя из результата упражнения 4.2, можно было бы ожидать, что
спектр продольных возбуждений в плазме определяется соотношением
ыз ^ ?^. Это справедливо для высоких частот и коротких длин волн.
Однако в низкочастотном длинноволновом пределе плазмой ведет себя как
нормальный фонон с ыд - /с, что связано с кулоновской экранировкой
ионов окружающим их вырожденным электронным газом.
Чтобы показать это, предположим, что локальная плотность заряда
ионов представляет собой малое возмущение однородного нейтрального
статического фона. Допустим, что подвижный электронный газ быстро
перемещается, чтобы нейтрализовать это возмущение. Запишем
?, = Z/io + w;, D.4.34)
где Aij и л^' — малые отклонения от статических значений п^ и Zn^,
Электростатический потенциал, порожденный этим возмущением, определяется
уравнением
у2ф = -47?/?,?? + 47??/?;. D.4.35)
Далее в приближении Томаса—Ферми имеем (разд. 2.4)
^ = ^ф^ - еф(г) = const D.4.36)
МО-^ -|T(^-.)-(-^i)" D.4.37)
Разлагая выражение D.4.37) до первого порядка по еф/?? (фон почти
однороден), получим
„;.|2g*. D.4.38)
Остывание белых карликов 111
В итоге уравнение D.4.35) принимает вид
(?'~4)?= -47?/?,??, D.4.39)
где длина экранирования k~J определена выражением
4 = ? -' D.4.40)
Упражнение 4.4. Мотивируйте использование термина «длина экранирования» для
?~^ вычислив электростатический потенциал одиночного иона, покоящегося в
начале координат, который находится в вырожденной нейтральной плазме.
Указание: ? удовлетворяет такому же уравнению, как D.4.39) с -4vZed{r) в
правой части.
Ответ: ^ ^ ^ ^ ,
^>(г)^ Zeexp(-ic^r)/r].
В длинноволновом пределе ионы можно рассматривать как
«жидкость». Необходимые нам динамические уравнения, описывающие
поведение жидкости^\ это, во-первых, уравнение неразрывности:
^+?·(''<?) = 0. D.4.41)
И, во-вторых, уравнение движения:
ду ^ . Ze ,^
_+(v.V)v=- —??. D.4.42)
Линеаризация этих уравнений вблизи статического однородного фона, в
котором V = ? = О, дает
-^t + „„V-v = 0, D.4.43)
5=- —??. D.4.44)
at ^i
Рассмотрим один фурье-компонент, пропорциональный ехр(/к · г - ???).
Для него
-?/?, + /???·? = О, D.4.45)
-?? =-^^, D.4.46)
(?2 + 4)? = 47?/?,??, D.4.47)
'^ См. гл. 6.
112 Глава 4
где последнее уравнение следует из уравнения D.4.39). Умножим скалярно
уравнение D.4.46) на к и исключим к · ? из уравнения D.4.45). Далее с
помощью уравнения D.4.47) исключим ф. В результате получим
К
^2 ^ (продольная) , D.4.48)
1 + к1/к^
где
^.^^jrZ^eh^ D.4.49)
Заметим, что это относится только к продольной моде, так как,
согласно D.4.46), векторы ? и к параллельны. Из выражения D.4.48) видно, что
? - к при малых /с и ? — ? при больших к.
Экранировка не оказывает значительного влияния на поперечные моды.
Упражнение 4.5. Покажите, что в низкочастотном пределе формула D.4.48)
сводится к акустическому дисперсионному соотношению: ? — СуК, где с^ = dP/dp, а
? и ? определяются выражениями, отвечающими случаю идеального ферми-газа.
Теперь мы готовы вычислить с^ с помощью формулы D.4.5), используя
спектр возбуждений объемноцентрированной кубической решетки,
представленный на рис. 4.1. В общем случае вычисления приходится делать
численно. Однако можно легко найти вид с^ в двух предельных случаях. В
режиме высокотемпературной решетки имеем
с, ^3/:, ?^^?<^?^, D.4.50)
независимо от деталей дисперсионного соотношения и в согласии с
предыдущим рассмотрением.
В низкотемпературном режиме, ? < ??^, главный вклад в интеграл
D.4.5) дает низкочастотная, длинноволновая область. Приближенно
записав
?? = «?^?? , D.4.51)
где ?? — постоянная (ср. с рис. 4.1), получим
c„^2kfoiy^) + kf^{ys), D.4.52)
где
3? = .Уг = -?-. Уз = -?- ¦ D.4.53)
Остывание белых карликов
113
Ионная решетка
Идеальный
^Г
Рис. 4.2. Удельная теплоемкость как функция температуры (рисунок схематический;
учтен лишь вклад ионов). При низких температурах ?^<?<? . когда газ
кристаллизуется, колебания решетки увеличивают с^ по сравнению со значением Зк /2 для
идеального газа Максвелла— Больцмана. При очень низких температурах, Т<В^, с^
ведет себя как Т^.
В пределе Г ^ О, >' ^ оо с помощью выражения D.4.13) получим
На рис. 4.1 видно, что при малых к имеем а] » 0,8; аз > 1.
Следовательно, продольные моды не вносят никакого вклада и
Ионная теплоемкость при всех ? показана на рис. 4.2.
D.4.54)
4.5. УТОЧНЕННЫЙ АНАЛИЗ ОСТЫВАНИЯ БЕЛЫХ КАРЛИКОВ
В общем случае уравнение D.2.5), описывающее остывание белых
карликов, принимает вид
jJc,dT-CAmjy\
или
dt
dT САт..Т'/'
D.5.1)
D.5.2)
Если ??^ < ? < Г^, то Cj^ « ЗА: и из уравнения D.5.2) для времени
остывания следует
6 кТМ ? гг. гг. / Ч
^=5:?;^' ^D«r«r,. D.5.3)
8-353
114 Глава 4
Этот результат в два раза выше определяемого уравнением D.2.7) из-за
учета потенциальной энергии решетки.
При ? < ?^ подставим в уравнение D.5.2) выражение D.4.54) и в
результате получим
327г^/ ??
^I(
г-
МкТ ^ ^ /л ^ л\
-^-j, ?^?,, D.5.4)
где Tq — начальная температура, с которой началось остывание, Tq ?? ??^.
Как впервые было указано Местелом и Рудерманом [401], полученное время
остывания короче, чем следует из классического результата D.5.3), если ?
меньше примерно 0,1 ??^. Высказывалась надежда, что этим можно
объяснить противоречие между теорией и наблюдениями, о котором шла речь в
разд.. 4.2.
Упражнение 4.6. а) Оцените Г^ и L^, при которых происходит переход от
«классического» режима остывания к дебаевскому для белого карлика с массой 1 Mq с
углеродным ядром и со следующим составом атмосферы: X = О, У = 0,9 и ? = 0,1.
Получите приближенный критерий перехода, приравнивая выражение D.4.54) Ък.
Определите соответствующую плотность с помощью рис. 3.2.
б) Оцените г^ — время, за которое белый карлик достигнет этого перехода.
Ответы: Т^ - 4,8 · 10^ К, L^ ~ 1,3 · ??"* Lq, г^ ~ 5 · 10^ лет.
Упражнение 4.7. Используя формулу D.5.3) и аналитические выражения, полученные
в разд. 4.1 и гл. 3, оцените зависимость г и L^ от Л/ для звезд с заданным
химическим составом.
Ответы: ? - Л/-2.5, t^. - Л/^'^. В зависимости от сделанных предположений
возможны и другие ответы.
В проведенном выше аналитическом рассмотрении мы опустили в левой
части уравнения D.5.1) скрытую теплоту кристаллизации -д ^ кТ, Лэмб
и Ван Хорн [331] учли этот эффект в своем детальном расчете остывания
белого карлика, состоящего из чистого ^^С, с массой, равной 1 Mq . Это
привело к увеличению классического времени остывания на множитель
-1,6 в дополнение к мноз^^ителю 2, связанному с потенциальной энергией
ионов. Причина этого увеличения состоит в том, что энерговыделение за
счет кристаллизации равно
так
что
в
целом
?-Сскрыт. тепл ^
-^тепл
в'Греш + ^'^q
''^ класс
-Я
ЗкТ/2
5
2
^ 3'
?
3 ^ ?
¦^ ' класс
D.5.5)
~ 3. D.5.6)
Остывание белых карликов 115
Однако, поскольку кристаллизация начинается в центре звезды и по мере ее
охлаждения постепенно распространяется к наружным слоям, вклад q в
энерговыделение не приводит к возникновению пика в функции светимости.
Этот вклад не приводит к следствиям, явно свидетельствующим о
кристаллизации и не объясняет резкого убывания функции светимости.
В правой части уравнения D.5.1) мы также опустили член, связанный с
излучением нейтрино. Тепловое излучение нейтрино^^ превосходит
излучение фотонов, когда фотонная светимость L ;г 10~^'^ Lq, а температура
? ^ \(!р'^ К. Добавление L^ в левую часть уравнения D.5.1) вызовет
уменьшение времени остывания и соответствующее падение теоретической
функции светимости выше lg(L/L0) = —0,5 по сравнению с кривой остывания
Местела. Такое падение заметно на кривой Лэмба и Ван Хорна,
приведенной на рис. 4.3, которая более подробно обсуждается ниже.
Наконец, конвекция может привести к более эффективному переносу
энергии и уменьшению времени остывания. Однако тщательный анализ,
проделанный Фонтеном и Ван Хорном [199], а также Лэмбом и Ван
Хорном [331], указывает, что в первом приближении конвекция, по всей
видимости, несущественна.
Детальные расчеты охлаждения были выполнены также Суини [554], а
также Шавивом и Ковецем [535]. Результат Шавива и Ковеца для звезды с
массой 0,6 Mq часто цитируется, так как существует мнение, что средняя
масса белых карликов, найденная по радиусу, близка к этому значению^^
Результаты упр. 4.7 показывают, что дебаевское охлаждение для звезды с
массой 0,6 Mq начинается при столь низкой светимости, что оно не влияет
на функцию светимости в интересующем нас диапазоне, доступном
наблюдениям, нижняя граница которого в настоящее время опустилась до
-10~^ L0. Таким образом, результаты Шавива и Ковеца гораздо ближе
к первоначальной кривой охлаждения Местела, чем результаты Лэмба
и Ван Хорна.
4.6. СРАВНЕНИЕ С НАБЛЮДЕНИЯМИ
Детальное сравнение теории с наблюдениями можно делать двумя
способами: либо рассматривая функцию светимости белых карликов, либо
оценивая возраст белых карликов в звездных скоплениях. В принципе оба
способа позволяют выяснить, насколько хорошо мы понимаем твердотельные
свойства самогравитирующих астрономических объектов.
а) Сравнение с возрастом скоплений
Используя данные о светимости белых карликов в звездных скоплениях,
Лэмб и Ban Хорн [331] теоретически оценили их возраст, полагая, что все
'^ Процессы теплового излучения нейтрино описаны ц.разд. 18.
^^ См., например, работу [317].
116 Глава 4
белые карлики подобны чисто углеродным карликам с массой 1 Mq . Они
сравнили найденный теоретически возраст с возрастом скоплений;
очевидно, возраст любого скопления должен быть больше, чем возраст любого
находящегося в нем белого карлика, так как мы полагаем, что все звезды в
скоплении образовались одновременно. В результате было обнаружено
удовлетворительное согласие оценок (табл. 4.1). Похожее сравнение было
сделано также Суини [554].
В принципе эта процедура является очень мощным методом
наблюдательной проверки теорий, однако в настоящее время ее применение
тормозится малым числом хорошо наблюдаемых белых карликов в скоплениях и
неопределенностями в определении возраста скоплений.
б) Сравнение с функцией светимости
Напомним наше определение функции светимости, данное в гл. 1.
переписав его в виде
<i)(L/L^)d Ig (L/L0)—пространственная плотность белых карликов
в единичном интервале lg(L/L0). D.6.1)
Если скорость рождения белых карликов однородна по пространству и
постоянна во времени в течение всей жизни Вселенной, то можно ожидать,
что для белых карликов с определенным возрастом и химическим составом
величина ? удовлетворяет соотношению
d\g{L/L^)
dr
*|^|oc
D.6.2)
Это просто означает, что правая часть выражения D.6.1) пропорциональна
dr — временному интервалу, в течение которого белый карлик смещается
на единичный логарифмический интервал по шкале светимости.
Запишем raL"", где при L > L^ имеем ? = 5/7 из уравнений D.2.4) и
D.5.3), а при L < L^ из уравнения D.5.4) получаем - 1/7 :s ? < 0. Тогд^
Ig ?
-? Ig — ?- const. D.6.3)
Таблица 4.1
СРАВНЕНИЕ ТЕОРЕТИЧЕСКИХ ВОЗРАСТОВ БЕЛЫХ КАРЛИКОВ
С ВОЗРАСТОМ СКОПЛЕНИЙ [31]
Скопление
Гиады
Ясли
Диапазон
светимости,
(-1)-(-2,4)
(-2,3)-(-2,8)
Теоретический
возраст, лет
4· 10^ —5· 10^
4· 10^ —9· 10^
Возраст скопления,
лет
D - 5) · 10^
9· 10«
Остывание белых карликов
117
12 13 14 15 16 17
Рис. 4,3. Сравнение эмпирической функции светимости ? (в единицах пс~^ Л/^~'),
полученной Либертом [360] на основании данных Сиона [542], с теоретическими
функциями светимости. Черные кружки нанесены в предположении, что имеющиеся
данные относительно полны вплоть до предельного значения ?/^~13,5 (L-IO" ' Lq);
светлые кружки — до ?^~ 14,5 {L- \0~^Lq). Наклон данных определен лучще, чем
общая нормировка. Эмпирическая функция светимости Грина [238, 239], которая
имеет более надежную абсолютную щкалу, но определена только до - 10~ Lq,
показана отрезками, соответствующими одному стандартному отклонению. Сплощ-
ной линией представлена теоретическая функция Лэмба и Ван Хор на [331] для
звезды с массой 1Л/0. Штриховая кривая, представляющая закон остывания Местела
[а=5/7 в уравнении D.6.3)], близка по форме к результатам расчетов Шавива и Ко-
веца [535] для М=0,6М^, (По статье Либерта [360].)
Эмпирическая функция светимости, найденная Либертом [360] на
основании данных Сиона [542], в диапазоне от L - 10"^ L0 до - 10""* Lq
приведена на рис. 4.3. Там же изображена эмпирическая функция
светимости 1*рина [238, 239], которая известна в диапазоне от - 10"^ L^ до
- 10"^ L0. Налицо вполне хорошее по астрофизическим меркам согласие
с предсказаниями Местела, Шавива—Ковеца и Лэмба—Ван Хорна,
которые в этом диапазоне светимости близки друг к другу.
Едва ли удастся накопить достаточно статистики по горячим белым
карликам (L > 10"^ ^0)» чтобы проверить наличие провала, вызванного
нейтринным охлаждением согласно вычислениям Лэмба—Ван Хорна, так
как белые карлики проводят в этом интервале светимости сравнительно
мало времени.
Лэмб и Ван Хорн предсказывают, что дебаевский режим в охлаждении
начинается при L - \0~^ L^ и приводит к широкому максимуму с
шириной около 2 в единицах \%{L/L^). Как отмечалось выше, согласно Шавиву
и Ковецу, этот эффект должен проявляться при заметно меньших светимо-
стях из-за предположения о более низком значении массы.
118 Глава 4
Согласно сводке данных, приведенной Либертом и др. [361], белых
карликов с очень низкой светимостью (L <> 10"^'^ Lq) действительно
оказывается слишком мало. Если ещё более тщательные поиски не изменят
этого результата, то он будет иметь важные последствия. Существующие
теории остывания по-прежнему предсказывают заметное число белых
карликов с такими светимостями, и ни один известный физический эффект не
может вызвать столь резкий излом в функции светимости. В этой связи
Либерт и др. [361] высказали предположение, что звезды в диске
Галактики, которые вносят главный вклад в обсуждаемую выборку, образовались
не так давно по сравнению с принимаемым в настоящее время возрастом
галактического гало (- 10^^ лет).
Глава 5
Общая теория относительности
Те изменения гравитационного поля, которые вносятся общей теорией
относительности, оказываются весьма важными как в задачах об
устойчивости белых карликов, так и в задачах о равновесии и стабильности
нейтронных звезд и черных дыр. Это обстоятельство и вызывает столь большой
теоретический интерес к компактным объектам, наделяя эти объекты
удивительными и неповторимыми свойствами. Хотя последовательное
детальное обсуждение общей теории относительности выходит за рамки этой
книги, нам все же нужно остановиться кратко на основных идеях и
уравнениях этой теории. Такого краткого изложения будет вполне достаточно
для приложений, обсуждаемых в следующих главах. Но читатель не
должен огорчаться, если ему не удастся сразу усвоить новые для него
понятия, которые он может здесь встретить. Недоумения проясняются при
рассмотрении приложений. Интересующийся же читатель может продолжить
изучение общей теории относительности, выбрав одну или несколько из
существующих прекрасных книг на эту тему^\ Для начала будет достаточно,
если читатель познакомится с идеями и основными уравнениями,
отличающими общую теорию относительности от теории Ньютона. Это дает нам
право использовать теорию относительности в следующих главах, когда
это станет необходимым.
5.1. ЧТО ТАКОЕ ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ?
Общая теория относительности является релятивистской теорией
гравитации. Чтобы понять это немного лучше, зададим себе вопрос: какие могут
возникнуть трудности при попытке сделать релятивистской теорию
гравитации Ньютона?
Ньютоновскую теорию гравитации можно представить как теорию
скалярного поля Ф, удовлетворяющего уравнению Пуассона:
у'Ф = 47гСро. E.1.1)
Гравитационное ускорение любого объекта в этом поле равно -??.
^^ Например, по книгам Мизнера, Торна и Уилера [411], Вейнберга [606] или, как
введение, Ландау и Лифшица [341].
120 Глава 5
Согласно теории относительности, энергия в любой форме
эквивалентна массе, так что в релятивистской теории гравитации источник
гравитационного поля определяется не только pq, но и плотностью энергии. В
частности, плотность энергии гравитационного поля в ньютоновском пределе
сама пропорциональна (??)^. Если внести этот член в левую часть
уравнения E.1.1), то мы должны получить нелинейное дифференциальное
уравнение, описывающее гравитационное поле в релятивистской теории.
Символически можно написать
F{g)~GT, E-1 ·2)
где g представляет собой гравитационное поле или поля, которые сводятся
к ? в пределе слабого поля; F — нелинейный дифференциальный оператор,
сводящийся к V^ в том же пределе, а Г — некоторая величина,
описывающая все негравитационные формы энергии. При этом в нерелятивистском
пределе основным остается вклад от pq-
Великая идея Эйнштейна состояла в том, что он построил общую
теорию относительности как геометрическую теорию гравитации. Мы не
будем здесь говорить об основании этой идеи, а начнем с описания геометрии
специальной теории относительности.
В специальной теории относительности пространство-время является
сценой, на которой разыгрываются физические явления. Пространство-
время состоит из событий, для описания которых необходимо задать
четыре числа: из них три числа определяют, пространственное расположение
события относительно некоторой выбранной координатной системы и
одно'число определяет время. Геометрически пространство-время
представляет собой четырехмерное многообразие. Каждая точка в этом
многообразии отвечает событию в пространстве-времени.
Наблюдатель делает измерения в пространстве-времени, т.е.
сопоставляет координаты событиям. Таким образом, наблюдателю в пространстве-
времени соответствует некоторый выбор координат на многообразии. В
специальной теории относительности существует выделенное семейство
наблюдателей — это инерциальные наблюдатели, для которых свободная
частица движется с постоянной скоростью, bee инерциальные наблюдатели
связаны преобразованиями Лоренца, координатная система инерциального
наблюдателя называется инерциальной координатной системой, или
лоренцевой системой.
Интервал (расстояние) между двумя близко расположенными
событиями в пространстве-времени задается выражением
А^ = -c^dt^ + dx^ + dy^ + dz^, E.1.3)
где dt, dx, dy, dz — разности координат событий, вычисленные в любой
лоренцевой системе. Интервал ds не зависит от того, в какой инерциальной
системе он вычисляется, — это лоренц-инвариант. Записав х^ = ct, х^ = х,
х^ — у, х^ = Z, можно переписать равенство E.3.1) в виде
ds^-^j),pdx''dx^, E.1.4)
Общая теория относительности 121
где ?^? — диагональная матрица 4 ? 4:
T,,^ = diag(-1,1,1,1). E.1.5)
По повторяющимся индексам в выражении E.1.4) производится
суммирование от О до 3. Матрица ?^^? в специальной теории относительности
называется метрическим тензором пространства-времени; последний
описывает геометрически все свойства пространства-времени. Таким образом,
пространство-время является псевдоевклидовым метрическим
пространством, от евклидова пространства оно отличается знаком минус в равенстве
E.1.5), и его называют пространством Минковского.
Для описания пространства-времени можно было бы пользоваться не-
лоренцевыми (неинерциальными) координатными системами. Например,
для пространственной части метрики можно было бы взять полярные
координаты или же использовать координатную систему, связанную с
ускоренным наблюдателем. Если соотношение между инерциальными
координатами А^ и неинерциальными координатами >'" имеет вид
х-' = х'ЧуУ), E.1.6)
ТО выражение E.1.4) переходит в
ds' = g„p{y'')dy-'dy^ E.1.7)
где не обычным правилам дифференцирования
Метрика в форме E.1.7) может выглядеть весьма сложной, так как ее
коэффициенты могут быть недиагональными и зависеть от координат. Однако
и в 3tOM случае пространство все же остается плоским, поскольку
существует преобразование координат [обратное преобразованию E.1.6)],
приводящее метрику к псевдоевклидовой форме E.1.5) во всем пространстве.
В общей теории относительности пространство-время по-прежнему
является четырехмерным многообразием, но теперь интервал между
ближайшими событиями определяется выражением
ds^=-g,p{x'^)dx''dxP. E.1.9)
Если никаким выбором координят нельзя свести метрику к форме E.1.5) во
всех точках, то пространство-время искривлено. Гравитационное
поле,выражают через функции g^^; иными словами, гравитационное поле
определяет геометрию. Интервал ds по-прежнему является инвариантом, так что
при переходе от координат ? к координатам х^ компоненты метрического
тензора g^? преобразуются по закону
— ^"^ - (S \ 10^
122 Глава 5
Как и в специальной теории относительности, величина ds, вычисленная
вдоль мировой линии частицы, измеряет собственное время dr вдоль этой
линии: ds^ = —c^dr^.
Метрика позволяет определить скалярное произведение векторов.
Выражение E.1.9) можно переписать как
ds^^dx-dx, E.1.11)
где dfC —- вектор бесконечно малого смещения с компонентами dx". В
общем случае скалярное произведение двух векторов А и В с компонентами
Л" и 5" равно ^ ^ « /^ , ,^\
A-B^g«^^«5^. E.1.12)
Такие векторы с четырьмя компонентами называются 4-векторы; чтобы
отличить их от трехмерных векторов, будем обозначать их буквами со
стрелкой сверху. Иногда мы будем записывать ^^
^?^???^^ E.1.13)
ИЛИ
А"-8"% E.1.14)
где Н^"'^!! — матрица, обратная матрице Н^^к/з"·
Тогда А -В = А^В'' = AW^ = A^Bag^^. E.1.15)
В специальной теории относительности координаты всегда отвечают
результатам какого-то физического измерения. Даже для неинерциальных
координат можно найти интерпретацию, определив их соотношение с
инерциальной координатной системой, в которой t, х, у и ? обычным
образом связаны с измерениями, выполненными с помощью идеальных часов
и стержней. В общей теории относительности, вообще говоря, не
существует выделенных (предпочтительных) координатных систем; в принципе
здесь приемлем любой набор координат, которые гладко нумеруют все
события в пространстве-времени. (Разумеется, в одних случаях выбор может
быть более удобным, чем в других.)^^ В силу этого нам следует поближе
рассмотреть вопрос о физических измерениях.
•^ Мы не будем использовать геометрическую интерпретацию Л" как контравари-
антных компонент вектора (т.е. базисных векторов, касательных к координатным
линиям) и /4^ как ковариантных компонент (т.е. базисных векторов, ортогональных
координатным поверхностям). Нам также не понадобится явное введение
дифференциальных форм.
^^ Заметим, что общая теория относительности не запрещает существования
предпочтительных координатных систем, если в задаче имеется какая-то симметрия.
Например, в простой космологии «горячей» Вселенной выделена система, в которой
микроволновое фоновое излучение изотропно. Однако, во-первых, гравитационное
? ^ле в общем случае не имеет никаких симметрии, во-вторых, даже если симметрии
имеются, глобальных инерциальных систем в присутствии гравитационного поля не
существует.
Общая теория относительности 123
Физическая интерпретация общей теории относительности опирается на
понятие локальной инерциальной системы. Хотя в общем случае ^^^ в
формуле E.1.9) никаким преобразованием координат нельзя привести к т/^^ во
всех точках пространства-времени, однако любое событие в пространстве-
времени можно выбрать за начало координат и затем в этой точке диаго-
нализовать g^? (в фиксированной точке это просто вещественная
симметричная матрица). Можно продвинуться даже дальше, найдя
преобразование координат, в результате которого первые производные g^^ в начале
координат обращаются в нуль. Другими словами, разложение метрики в
ряд Тейлора вокруг выбранного начала координат приобретает в этом
случае вид
(Читатель может убедиться в правдоподобности данного утверждения,
подсчитав число степеней свободы при преобразовании координат. Строгое
доказательство его справедливости можно найти в стандартных учебниках
по общей теории относительности.) Любая малая координатная
окрестность, в которой метрика имеет форму E.1.16), называется локально
инерциальной системой.
Чтобы понять, почему она так называется, рассмотрим в пространстве-
времени локально инерциальную систему какого-нибудь наблюдателя.
Представим наблюдателя мировой линией всех событий, которые он
пересекает. Выберем какое-либо событие на этой мировой линии в качестве
начала координат, используемых в равенстве E.1.16). Направим единичный
4-вектор в^ по касательной к координатной линии t. Аналогично построим
в^, i^ и?^. Поосольку gA.^ = т/^, эти векторы образуют ортонормальную
тетраду, т.е. е^ * ?/- = -1, е!^ · ?^ = 1, ?/¦ · ?^ = О и т. д. Для
обозначения ортонормальных тетрад мы используем «крышки». Вплоть до
членов первого порядка по \х\ геометрия оказывается такой же, как в
специальной теории относительности. Наблюдатель может производить
измерения точно так же, как в специальной теории относительности, при
условии, что протяженность его измерительного устройства как в
пространстве, так и во времени достаточно мала. Отклонения от специальной
теории относительности определяется масштабом, задаваемым вторыми
производными g^^^ — чем сильнее гравитационное поле, тем больше
искривлено пространство и тем меньше этот масштаб.
Наблюдатель, связанный с локально ортонормальной тетрадой, как
описано выше, называется локально инерциальным, или локально лоренце-
вым наблюдателем^^ Общая теория относительности идет дальше просто-
'^ Любой наблюдатель может построить ортонормальную тетраду,
удовлетворяющую условию ^ = 0-^^ = ^7^C ^ произвольной точке пространства-времени.
Однако только в специальном случае локально инерциального наблюдателя (свободно
падающий наблюдатель, движущийся с нулевым ускорением и без вращения)
метрика удовлетворяет условию E.1.16) с точностью до ^\х\ ^, т.е. справедливо равенство
124 Глава 5
ГО условия, что измерения в локально инерциальной системе проводятся
так же, как в специальной теории относительности. Сверх того, она
утверждает, что все негравитационные законы физики в локально
инерциальной системе такие же, как в специальной теории относительности. Это
утверждение называется принципом эквивалентности. В его основе лежит
идея эквивалентности гравитационной и инертной масс,
продемонстрированная Эйнштейном в его знаменитом мысленном эксперименте с лифтом.
Если рассмотреть наблюдателя, который ставит какие-то опыты в
закрытом помещении, движущемся вверх с постоянным ускорением, его
экспериментальные результаты должны быть неотличимы от результатов,
полученных наблюдателем внутри покоящейся лаборатории, находящейся в
однородном гравитационном поле. Напротив, в системе, которая свободно
падает в однородном гравитационном поле, не должно наблюдаться
эффектов, связанных с этим полем. (Вспомните изображения космонавтов на
спутнике, движущемся по орбите вокруг Земли.)^^
Последний пример дает физическое описание локально инерциальной
системы — это система, связанная с наблюдателем, который свободно
падает в гравитационном поле. Реальные гравитационные поля, разумеется,
не являются однородными, и эта неоднородность нарушает инерциальные
свойства любой системы, потенциально являющейся глобально
инерциальной. Однако чем более «локальной» является система, тем ближе она к
инерциальной.
Упражнение 5.1. Рассмотрим две частицы с равными массами т, находящиеся на
одной вертикальной линии на расстояниях г vi г -^ h {h < г) от центра Земли. В
момент / = О эти ранее покоившиеся частицы начинают свободно падать к
поверхности Земли. Покажите, что наблюдатель, падающий вместе с одной из частиц,
увидит, что расстояние между частицами постепенно возрастает. Сформулируйте это
как количественное утверждение относительно локально инерциальной системы,
связанной с наблюдателем. В частности, найдите время, по прошествии которого
станут заметными эффекты кривизны пространства-времени, если точность измерений
составляет ??^?? ·
Принцип эквивалентности является обобщением утверждения, согласно
которому законы механики не позволяют локально обнаруживать
гравитационное поле, на утверждение, что никакие законы физики не позволяют
этого сЯ1елать. Эффекты гравитации всегда исчезают в свободно падающей
(т. е. локально инерциальной) системе отсчета.
'^ Следует учитывать, что сказанное верно только для локальных законов, таких,
как законы динамики Ньютона. Однако, наприд1ер, для силы Кориолиса, эффектов,
связанных с электромагнитным излучением, и других подобных эффектов,
определяемых полями в конечных областях пространства, такое утверждение, очевидно, не
справедливо. — Прим. ред.
Общая теория относительности 125
Принцип эквивалентности говорит нам, как нужно формулировать
негравитационные законы физики в присутствии гравитационного поля.
Начнем с любого закона теории относительности, например с закона
сохранения энергии-импульса:
?«?«^ = 0, E.1.17)
?„^-^. E.1.18)
Здесь Г"^ — тензор энергии-импульса. Как показывает уравнение E.1.17),
его 4-дивергенция равна нулю. Согласно принципу эквивалентности,
равенство E.1.17) должно быть справедливо в любой локально инерциальной
системе, где метрика имеет вид E.1.16). Мы хотим теперь переписать
выражение E.1.17) в форме, которая справедлива в произвольной системе
координат с метрикой E.1.9). Раздел математики, который занимается этими
вопросами, называется тензорным исчислением (или дифференциальной
геометрией). В данной книге нам не понадобится развивать этот формализм.
Достаточно только сказать, что нужно определить более общий, чем
E.1.18), оператор дифференцирования (ковариантную производную). Как
известно читателю, даже в плоском пространстве в правой части
выражения E.1.18) при дифференцировании векторов в криволинейных координа-
ха*н10являются дополнительные члены. Например, если в сферической си-
сгетие координат вектор имеет компоненты
А = А^е, + А'ео + А\, E.1.19^
его дивергенция не будет просто равна
д,А'+деА'+д^А\ E.1.20)
При вычислении дивергенции возникают слагаемые, связанные с
производными от е^, е^, ??. Эти базисные векторы не постоянны в
пространстве, как видно из того обстоятельства, что в указанной координатной
системе компоненты g^^ не постоянны.
Аналогично в искривленном пространстве в ковариантной
производной V^ появляются дополнительные члены, связанные с непостоянством
g^^. Однако здесь эти члены нельзя устранить сразу во всем пространстве
никаким преобразованием координат, так что производные g^^ описывают
эффекты гравитационного поля.
Это математическое выражение принципа эквивалентности иногда
называют принципом общей ковариантности: требуется, чтобы ковариант-
ные уравнения специальной теории относительности оставались ковариант-
ными не только при преобразованиях Лоренца, но и при общих
преобразованиях координат.
126 Глава 5
В общей теории относительности нет аналога ньютоновскому понятию
«гравитационного ускорения в данной точке». Такое локальное ускорение
устраняется переходом в свободно падающую систему координат. Однако
разность ускорений двух близко расположенных пробных тел устранить,
вообще говоря, не удается (ср. с упр. 5.1). Таким образом, истинное
гравитационное поле в общей теории относительности аналогично
ньютоновскому полю приливных сил Э^Ф/Эдг'с^х?', где ? — ньютоновский потенциал.
Объясняется это тем, что ньютоновское относительное ускорение двух
пробных тел равно
fl'oTH = ?\? + ??) - fl'(x)
.A,>J^(U). E.1.21)
dxJ \дхЧ ^^
До сих пор мы обсуждали, как гравитация влияет на другие физические
явления и как геометрия связана с физическими измерениями в локально
инерциальной системе. Чтобы завершить картину, нужно, пользуясь
уравнением вида E.1.2), понять, каким образом распределение массы-энергии
определяет геометрию g^?, Хотя мы и не будем явно использовать это
уравнение в его общем виде, тем не менее выпишем его, так как оно
представляет собой вершину эйнштейновской теории:
в^^^Ъчг-Т-^, E.1.22)
Здесь G^^ — тензор Эйнштейна, т. е. нелинейный дифференциальный
оператор второго порядка, действующий на g^?. В качестве источника в
уравнении Эйнштейна стоит тензор энергии-импульса материи (без
гравитационной части). Это сложное уравнение сводится к уравнению Пуассона
E.1.1) в ньютоновском пределе. Оно также гарантирует сохранение
энергии-импульса [ср. с равенством E.1.17)], так как V^C"'^ = 0.
5.2. ДВИЖЕНИЕ ПРОБНЫХ ЧАСТИЦ
Пробная частица представляет собой идеализацию материального объекта.
Предполагается, что она мала (не возмущает пространство-время вокруг
себя), не заряжена (не взаимодействует с электромагнитным полем),
сферически-симметрична (отсутствуют моменты сил вращения) и т. п. Она
просто свободно движется в гравитационном поле. В специальной теории
относительности (в отсутствие гравитационного поля) пробные частицы
движутся с постоянной скоростью. Уравнение их движения можно
получить из вариационного принципа, находя экстремум расстояния
(интервала) вдоль мировой линии:
"ijds = 0.
E.2.1)
Общая теория относительности 127
Чтобы убедиться в этом, перепишем подынтегральное выражение в форме
ds^{-ri,^x^x^)'^^d\, E.2.2)
где
^-ж- E.2.3)
Здесь ? — любой параметр вдоль мировой линии. Выражение E.2.2) для ds
инвариантно при замене параметра ? -* ?(?'). Лагранжиан для выражения
E.2.1) равен
И/2
1-{-?^??^??\ E.2.4)
Уравнения движения Эйлера—Лагранжа, получаемые из выражения E.2.1),
имеют вид
А1Щ=1к E 2 5)
Правая часть здесь равна нулю, так как L не зависит от дг". Поскольку
dL _ ,_,
дх«~ ^ Ч„/,
|?=-^-^V^ E.2.6)
ТО получим
?^,?'-?^?.??'-?. E.2.7)
Изменяя выбор параметра ? -* ?(?'), можно сделать L постоянным вдоль
траектории^^ В частности, в качестве параметра на мировой линии всегда
можно выбрать длину вдоль кривой, т. е. собственное время частицы,
которое обычно обозначают г. (Фактически 5 = ст.) В этом случае вдоль
кривой ? = 5 и L = 1 и, следовательно, уравнение E.2.7) принимает вид
?,??^ = 0. E.2.8)
Умножая это равенство на матрицу ?'^'^; обратную к ?^?, получим
;сг = 0 = ^. E.2.9)
dr^
Это — условие постоянства скорости вдоль прямой линии.
Геометрические кривые, имеющие экстремальную длину, называются
геодезическими. Геодезические в пространстве Минковского (т. е. в специ-
'^ Параметр ? в этом случае называется аффинным параметром.
128 Глава 5
альной теории относительности) представляют собой четырехмерные пря^
мые. Рассмотренный выше случай ds^ < О отвечает времениподобным,
геодезическим — мировым линиям массивных частиц. Фотоны или другие
безмассовые частицы движутся со скоростью света, так что для них ds^ =
= 0.По этой причине говорят, что свободные фотоны движутся по
нулевым геодезическим. В этом случае нельзя выбирать в качестве параметра ?
собственное время. Этот параметр удобно выбрать так, чтобы
ir=.-, E.2.10)
где ? — 4-импульс фотона. Поскольку для фотона ?^? р^р^ = О независимо
от времени, то такой выбор ? согласуется с условием ds^ = 0.
Аналогичным образом можно было бы выбрать параметр и для частиц с массой т,
т. е. ? = ?/т. Уравнение E.2.9) теперь сводится к следующему:
^ = 0; т.е. /7« = const. E.2.11)
Можно также рассмотреть пространственноподобные геодезические,
для которых ds^ > 0. Они соответствуют, например, прямым линиям в
трехмерном евклидовом пространстве в некоторый фиксированный момент
времени х^. [Приведенный выше вывод непосредственно переносится на
этот случай после изменения знака в подкоренном выражении E.2.4).]
Для нас важно, что вся методика, использованная выше для
рассмотрения простой задачи специальной теории относительности, без изменения
переносится и на общую теорию относительности. Согласно принципу
эквивалентности, вариационный принцип E.2.1) должен описывать движение
пробных частиц и в общей теории относительности: свободные частицы
движутся вдоль геодезических пространства-времени. Однако выражение
E.2.4) теперь принимает вид
L=[-g„p{xy)x''x^Y'\ E.2.12)
так что уравнение E.2.5) превращается в
???^^ + ???.,^'^^ - Igyfi,»^'^ = 0. E.2.13)
Здесь второе слагаемое происходит от выражения
Как обычно, мы использовали сокращенное обозначение:
^"^''"д^· E.2.15)
Общая теория относительности 129
Мы примем аффинную параметризацию, такую, что L = const. Далее
запишем
gafi,yX^X'' = l{gafi,y + gay,fi)x^X\ E.2.16)
так что уравнение E.2.13) примет вид
8??^^ + ?,/???^?' = О, E.2.17)
ГД1
??^? ^ ?????,? + ^??,^ ~ Syfi,a)· E.2.18)
Умножая это уравнение на матрицу, обратную метрическому тензору
и обозначаемую g^^, и переобозначая ? ^ а, получим
х" + Гр^х^х-' = О, E.2.19)
где
% ^ g"'r,^,. E.2.20)
Величины Г называются символами Кристоффеля.
Уравнение E.2.19) представляет собой окончательную форму уравнения
геодезической в общей теории относительности. Отметим, как
выполняется принцип эквивалентности. В локально инерциальной системе можно
выбрать координаты таким образом, что g^?^ ^ = О и, следовательно,
символы Кристоффеля исчезают. Таким образом, в локально инерциальной
системе пробная частица движется по прямой линии с постоянной
скоростью. Требование, чтобы это утверждение было справедливым в любой
инерциальной системе и в любой точке пространства-времени приводит к
уравнению E.2.19), где величины Г описывают действие гравитационного
поля.
Отметим различие между использованным здесь принципом общей
ковариантности и принципом лоренцевой ковариантности в специальной
теории относительности. В последнем случае требуется, чтобы переход от
одной инерциальной системы координат к другой не изменял форму
физических законов. Скорость, входящая в закон преобразования, должна
выпасть из окончательного результата. Это требование налагает весьма
сильные ограничения на возможную форму законов физики. Принцип общей
ковариантности не приводит ни к каким ограничениям на физические законы.
Можно в принципе постулировать любой закон в локально инерциальной
системе, преобразовать его к общей системе координат и утверждать, что
возникшие дополнительные члены описывают эффекты гравитационного
поля. Только эксперимент может сказать, справедлив ли закон.
Упражнение 5.2. Покажите, что если ? — аффинный параметр, то лагранжиан
L'hafiX"^ E.2.21)
9-353
130 Глава 5
на геодезических эквивалентен лагранжиану E.2.12), т. е. покажите, что уравнение
Эйлера—Лагранжа для выражения E.2.21) приводят к таким же уравнениям
геодезических с той лишь разницей, что ? более не является произвольным параметром и
условие L = const автоматически учтено в вариационном принципе.
Как обычно, определим импульс, канонически сопряженный координате
дг", условием
? ^—. ?5.2.22)
Из равенств E.2.21) и E.2.10) следует
Ра = ????^ = ????^
или
?" = «"%, E.2.23)
где g°^^ — матрица, обратная g^?. Заметим, что если L не зависит,
например, от дг^, то /?! — интеграл движения.
Упражнение 5.3. Метрика двумерного евклидова пространства может быть записана
в форме
^2^^г2 + г2^/ф2, E.2.24)
что приводит к лагранжиану
l^li^?^r?). E.2.25)
Покажите, что уравнения движения пробной частицы имеют вид
г-гф2=:0, E.2.26)
г^ = const.
E.2.27)
(Полагая ? = /, мы увидим, что это обычные уравнения Ньютона в пустом
пространстве.)
Постоянная в уравнении E.2.27) представляет собой момент количества
движения, приходящийся на единицу массы, т. е. ? ? согласно определению
E.2.22). Поскольку ^"^"^ = \/g?? = 1/г^, то выражение E.2.23) дает хорошо
известный результат р^ = ф. Физически измеряемой величиной ф-
компоненты момента является проекция вектора ? на единичный вектор в
направлении ф. С другой стороны, координатные базисные векторы ё^ и в^
удовлетворяют условиям:
ё, · ё, = g,, = 1, ё, · ёф = g,? = 0, ёф · ёф = g^^ = г^. E.2.28)
Общая теория относительности
131
^=const
0= const
Рис. 5.1. Координатный базисный вектор ?^ в точке А в г^/г, раз длиннее, чем такой
же вектор в точке В. Предполагается, что линии ? = const бесконечно близки друг к
другу.
Смысл последнего, например, равенства можно понять, если вспомнить,
что вектор вф является касательным к координатной линии ф. Это
означает (рис. 5.1), что он связывает две радиальные линии ? = const. Как видно
из рисунка, длины векторов е^ для радиусов г^ и Г2 относятся как /^//^2,
р-у где коэффициент пропорциональности зависит от мас-
т. е. ?
'?
% -
штаба по координате ф. Всегда можно сделать простой выбор е
= г^, как в равенстве E.2.28). В общем случае справедливо равенство
?
е^ =
ea-e^ = g«^.
E.2.29)
Оно следует из выражений E.1.9) и E.1.11), если заметить, что dx =
= dx" е^. Специальными случаями равенства E.2.29) являются:
Су · Су = 8^J (трехмерные декартовы),
^ * ^ ^ ^?? (четырехмерные ортонормированные). E.2.30)
132 Глава 5
Упражнение 5.4, Покажите, что р^^ = ^ - е^^.
Указание. Разложите ? = p^t^.
Теперь мы можем выбрать ортонормированный набор базисных
векторов в виде
ё, = ё„ E.2.31)
4---4^ E.2.32)
так что из равенств E.2.28) следует
ёф · ёф = -ёф · % = —g^^ == 1, и т.д. E.2.33)
Тогда
/?* = /?? == ? · ёф == -/?ф = гф. E.2.34)
Результат представляет собой знакомое выражение для компоненты
импульса, приходящегося на единицу массы (т. е. для скорости), вдоль векто-
Рае;.
Иногда мы будем использовать «крышки» также для обозначения
бесконечно малых смещений. Например, смещение в направлении ? при г =
= const равно
^Ф ^ ^^(.=const) = гаф, E.2.35)
Отсюда длина окружности радиуса г равна пути вдоль таких
последовательных смещений
? ds^??? ^фгаф^ 2??. E.2.36)
5.3. ГРАВИТАЦИОННОЕ КРАСНОЕ СМЕЩЕНИЕ
В простейшем случае гравитационное красное смещение можно
рассмотреть на примере источника и детектора электромагнитных волн (т. е.
фотонов), находящихся в фиксированном положении в статическом
гравитационном поле. Частота излучения ? в месте расположения источника (em)
равна величине, обратной интервалу собственного времени между
прохождениями двух гребней волны, измеренному в системе, связанной с
источником, т.е.
1 с
"'." {-t.,d^'d.<-)'Z' <'¦'"
Общая теория относительности
133
?«
^,,??/
^. I
¦¦ .Л'
?°
-^х^
Излучатель
ripuQMHU^
Рис. 5.2. Пространственно-временная диаграмма, изображающая гравитационное
красное смешение. Вертикальные линии представляют собой мировые линии
излучателя и приемника. Пунктирные кривые — мировые линии двух световых лучей,
испущенных с запаздыванием dx^ по координатному временному интервалу. Обратите
внимание, что координаты неинерциальны (в присутствии гравитационного поля
глобально инерциальной системы не существует).
Очевидно, dx^ = dx^^ = dx^ = О, так как источник находится в покое во
время излучения. Выражение, аналогичное E.3.1), можно написать и для
приемника (гее), и потому
[(-goo)'/'^-1.
E.3.2)
Коорбинатное время dx^, прошедшее между двумя прохождениями
гребней волны, одно и то же как для источника, так и для приемника, в силу
того, что гравитационное поле является статическим, и поэтому от х^
ничего не зависит. Какова бы ни была мировая линия одного фотона,
приходящего от источника к приемнику, очередной фотон следует по подобной
же линии, лишь сдвинутой на dx^ во всех точках (см. рис. 5.2.). Отсюда
(-goo)
(-goo)
1/2
em
1/2
rec
E.3.3)
134 Глава 5
5.4. ПРЕДЕЛ СЛАБОГО ПОЛЯ
Один из способов перехода к пределу слабого поля в общей теории
относительности состоит в альтернативном выводе формулы для красного
смещения на основе закона сохранения энергии. Фотон с частотой ? имеет
эффективную массу:
т = ^. E.4.1)
С
Его полная энергия в ньютоновском гравитационном поле с потенциалом
Ф(л·) равна hv -\- тФ(х). Приравнивая полные энергии фотона в точках
расположения источника и приемника, получим
^ ^ (^ + ФА')еш /5 4 2)
^е. A+Ф/с^),ес'
Поскольку для ньютоновского ПОЛЯ Ф/с^ < 1, это соотношение обычно
записывают в виде
А!1=_М, E.4.3)
"em С^ '
Сравнивая выражения E.3.3) и (S.4.2), получим в ньютоновском пределе
goo—(l-bf). E.4.4)
К равенству E.4.4) можно прийти и иначе, если рассмотреть движение
медленной (? < с) пробной частицы в слабом гравитационном поле
(Ф < с^). Так как поле является слабым, то можно выбрать систему
координат, которая будет всюду почти лоренцевой:
8??==??? + ^,?, |Л«^|« 1. E.4.5)
Поскольку скорость частицы ? J мала по сравнению с с и к тому же g^Q «
^ ^??* '^^ ^ главном порядке координатное время / совпадает с
собственным временем т. Поэтому ускорение частицы равно
где было использовано уравнение геодезической E.2.19). Главный вклад в
сумму по ? и jS вносит член с ? = j3 = 0; остальные меньше по крайней
мере на одну степень отношения ?/с:
^00 — ^/00
BЛо,.о-V,) " "^?- E.4.7)
Общая теория относительности 135
поскольку g^^ « ?^? и Л^· q = //q- уУ •'/с. Таким образом,
Л^ " 2
Но в ньютоновском пределе
= ^Лоо.,· E.4.8)
? ,. E.4.9)
Сравнивая уравнения E.4.8) и E.4.9), получим, как и выше^^:
и __2Ф
С
^00
>-(l.f). E.4..0)
5.5. ГЕОМЕТРИЧЕСКАЯ СИСТЕМА ЕДИНИЦ
В общей теории относительности весьма удобно выбрать такую систему
единиц, в которой с = G = 1. Другими словами, время и масса
измеряются в см, причем 1 с = 3 · 10^^ см и 1 г = 0,7425 · 10~^^ см. Последний
числовой множитель представляет собой просто значение отношения G/c^ в
системе СГС. Более удобным для астрономических приложений
переводным коэффициентом является Mq = 1,4766 км.
Интересно отметить, что в небесной механике измеряется именно
величина GMf^. Величина Mq в граммах получается из измерения С в
эксперименте Кавендиша. Значение GM^ известно с точностью порядка 10"^, а
гравитационная постоянная лишь с точностью 10"^. Масса Солнца в
километрах известна более точно, чем в граммах!
5.6. СФЕРИЧЕСКИ-СИММЕТРИЧНЫЕ ГРАВИТАЦИОННЫЕ ПОЛЯ
Предположим, что сферически-симметричная метрика может зависеть от
времени / и радиальной координаты г. Зависимость от углов должна иметь
вид
dU^^de^ ^un^edi^^. E.6.1)
Таким образом, в наиболее общем виде сферически-симметричную метрику
можно записать как
ds^ = -A{t, г) dt^ + B{t, г) dr"" + 2C(r, г) dt dr + D{t, r) dQ\ E.6.2)
^^ Постоянная интегрирования, возникающая при приравнивании выражений
E.4.8) и E.4.9) и последующем интегрировании, может быть выбрана равной нулю
в силу требования ?^?-???^ ^??~^~^ "?** г =00.
136 Глава 5
Введем новую радиальную координату
r' = Z)»/2(r,r). E.6.3)
Подставляя это в выражение E.6.2) и опуская штрих, получим
ds^ == -E{t, г) dt^ + F{t, г) dr^ + 2G(r, г) dtdr + r^dU^, E.6.4)
где ?, F и G определенным образом связаны с А, В и С, однако мы не
будем выписывать эту связь явно. Можно обратить в нуль коэффициент
перед dt dr, введя новую временную координату /'. Вид выражения E.6.4)
побуждает испробовать подстановку
dt' = E{t, г) dt - G{t, г) dr, E.6.5)
Однако в общем случае правая часть равенства E.6.5) не является полным
дифференциалом. В силу того что независимых переменных всего две (/ и
г), должен существовать интегрирующий множитель, т. е. функция H(t, г),
такая, что
Л' = Я(г, r)[E{t, г) dt - G{t, г) dr] E.6.6)
будет полным дифференциалом. Эта подстановка в выражение E.6.4)
оставляет в метрике всего две произвольные функции: коэффициенты перед
(dt')^ и dr^. Опуская штрих, запишем окончательно
ds^ = -e^'^dt^ + е^Чг^ + r4Q\ E.6.7)
где ? и ? — функции /иг. Мы используем экспоненциальную форму
коэффициентов из соображений удобства в дальнейшем.
Важный результат ньютоновской теории гравитации состоит в том, что
в любой точке вне сферически-симметричного распределения масс
гравитационное поле зависит только от внутренней массы. Более того, даже если
масса внутри движется сферически-симметричным образом, поле снаружи
не зависит от времени. Мы просто имеем ? = -?/г.
Этот результат справедлив и в общей теории относительности, где он
носит название теоремы Биркгофа и формулируется следующим образом:
сферически-симметричное гравитационное поле в вакууме обязательно
является статическим. Соответствующая метрика называется метрикой
Шварцшильда:
^,2 = _ |? _ 2^j ^,2 + |i _ ??'^??' + r4Q\ E.6.8)
Слово «вакуум» здесь означает область пространства-времени, где
гравитационные эффекты находящейся там материи пренебрежимо малы.
Постоянная Л/, появившаяся в выражении E.6.8), представляет собой массу
источника. В этом можно убедиться, например рассмотрев в этом
выражении предел слабого поля, г > М. Тогда равенство E.4.4) показывает, что
ньютоновский потенциал равен —М/г, т. е. Л/ — действительно масса.
Общая теория относительности 137
Определенную таким образом массу можно измерить, скажем, изучая
движение спутников, находящихся на удаленных орбитах, и используя законы
Кеплера, как в обычной небесной механике. Метрика Шварцшильда
определена всюду вне сферической звезды непосредственно вплоть до ее
поверхности.
Из-за относительно простой формы выражения E.6.8) координаты
имеют непосредственную физическую интерпретацию. Для любого радиуса г
существует 2-сфера эквивалентных точек ^>, а ^ и ? являются полярными
координатами на этой 2-сфере. Величина г определяется таким образом,
чтобы длина соответствующей окружности на этой 2-сфере равнялась 2??
или чтобы площадь ее поверхности равнялась 4??^. В этом можно
убедиться, положив в выражении E.6.8) / = const и г = const. Тогда метрика на
2-сфере примет вид
B)?2 = ?·2^?2. E.6.9)
Вспоминая, что ds^ описывает результаты физических измерений, получим,
что, например, длина большого круга на 2-сфере равна
? ^5=/%^ф = 27гг, E.6.10)
как и утверждалось. Заметим, что расстояние между двумя точками г^ и г-^
на радиальной линии равно
pigrrY^^dr^r^-r,. E.6.11)
Временная координата / была выбрана так, чтобы явно проявлялась
статическая природа решения, т. е. чтобы поле было инвариантно при
замене / — / + ?? Нормировка координаты / такова, что она совпадает с
временной координатой пространства Минковского при г > М, где
метрика E.6.8) сводится к метрике специальной теории относительности.
^ 7. СФЕРИЧЕСКИЕ ЗВЕЗДЫ
Метрика E.6.7) описывает также гравитационное поле внутри сферической
звезды. Для звезды, находящейся в гидростатическом равновесии, можно
взять ? и ? не зависящими от /. Предположим, что вещество звезды
можно считать идеальной жидкостью, и установим далее вид уравнения
состояния
p = p{n,s). E.7.1)
(Так как с = 1, мы не будем проводить различия между плотностью
энергии ? и плотностью массы ? = ?/c^.) Давление можно найти, используя
'^ Это двумерная сферическая поверхность с центром в точке г=0.
138 Глава 5
первый закон термодинамики, согласно соотношению B.1.7):
P = P{n,s). E.7.2)
Хотя идеальная жидкость ведет себя адиабатически (энтропия s
элемента жидкости остается постоянной), она не обязательно является изоэнтро-
пийной E может и не иметь всюду одно и то же значение). Однако в случае
холодных белых карликов и нейтронных звезд температура фактически
всюду равна нулю (точнее, кТ < Ер ) и, следовательно, всюду 5 = 0.
Позже мы обсудим сверхмассивные звезды, в которых s однородна вследствие
конвекции. В силу этого уравнение состояния можно взять в виде
Р = Р{р). E.7.3)
Уравнения, описывающие внутреннее строение в общей теории
относительности, выведены в стандартных учебниках. Мы запишем их в форме,
которая подчеркивает сходство с ньютоновской динамикой. Прежде всего
определим новую метрическую функцию т{г) с помощью равенства
,2Х
¦(-?^?
E.7.4)
Тогда уравнения Эйнштейна дают
^ = 4^rV, E.7.5)
?--^(-Я(-^)('-"Г' <"¦'>
Ньютоновский предел достигается при ? < ? и т < г.
Уравнение E.7.6) называется уравнением гидростатического равновесия
Оппенгеймера— Волкова.
Величину т(г) можно интерпретировать как массу внутри сферы
радиусом г. Уравнение E.7.5) дает для полной массы звезды величину^^
М= (^A^rr^pdr E.7.8)
•'о
Заметим, что сюда включены все возможные вклады в массу, включая
гравитационную потенциальную энергию. Это обстоятельство иногда
маскируется простым видом равенства E.7.8), однако напомним, что элемент
объема здесь равен не А-кг^аг, а величине
j^=(g^J»/2j,.x47rr2 = il -^j '^\,TrUr. E.7.9)
•^ Величина m{R) должна быть равной Л/, чтобы коэффициент внутренней
метрики Шварцшильда E.7.4) гладко сшивался с внешней метрикой E.6.8).
Общая теория относительности 139
Таким образом, равенство E.7.8) не просто суммирует ? аУ, ?, е.
локальные вклады в полную массу-энергию, но и включает глобальный вклад
отрицательной потенциальной энергии звезды.
Уравнения E.7.5) — E.7.7) нетрудно решить численно, построив тем
самым общерелятивистскую модель звезды:
1. Выберем значение плотности в центре звезды р^. Уравнение
состояния позволит найти Р^. Кроме того, имеется граничное условие т(г = 0)=
= 0.
2. Проинтегрируем уравнения E.7.5) и E.7.6), начав с г = О и используя
в качестве начальных условий значения, взятые в п. 1. При этом величина
? устанавливается с помощью уравнения состояния по изменяющейся
величине р.
3. Значение г = R, для которого ? = О, представляет собой радиус
звезды, а m(R) = Л/.
4. Метрическая функция ? имеет граничное значение
?(? = ?) = ^1?(?-^?), E.7.10)
так что она гладко сшивается с метрикой Шварцшильда E.6.8) на
поверхности. При численном расчете удобно выбрать произвольное значение
Ф(г = 0) и проинтегрировать уравнение E.7.7), начав с г = О, совместно
с уравнениями E.7.5) и E.7.6). Поскольку уравнение E.7.7) линейно по Ф,
к ? можно прибавить произвольную постоянную, с тем чтобы
удовлетворить условию E.7.10).
Упражнение 5.5. Покажите, что внутри звезды с однородной плотностью
справедливы соотношения:
E.7.11)
? _ A - IMr^/R^y^^ -A- 2M//?)'^'
? ~ 3A - 2?//?)'/' -A- 2Л/г7Л')'^' '
-1('-?Г4(-^)'"
Покажите, что условие Р^ < оо приводит к ограничению
2Л/ 8
Л 9
E.7.13)
Предел, выражаемый неравенством E.7.13), для максимального сжатия равновесной
однородной сферы, справедлив в действительности для произвольного профиля
плотности, если только плотность не растет с увеличением расстояния от центра^).
'^ См., например, книгу Вейнберга [606], разд. 11.6.
Глава 6
Равновесие и устойчивость жидких тел
в этой главе мы выведем некоторые основные свойства равновесных и
устойчивых состояний звезд. В разд. 6.1 приводятся фундаментальные
уравнения движения жидкости (сплошной среды); на эти сведения мы
будем неоднократно ссылаться далее в этой книге. В разд. 6.2—6.8
развивается ньютоновская теория равновесия и устойчивости для неврашающихся
звезд, которая включает исследование возмущений жидких тел. Основные
результаты указанных разделов суммированы в резюме 6.1. Эти
результаты обобщаются с учетом эффектов общей теории относительности в разд.
6.9, причем сводка результатов приводится в начале этого раздела.
Наконец, в разд. 6.10 полученные результаты применяются к белым карликам.
Вычисления, приведенные в этом последнем разделе, являются прототипом
аналогичных вычислений, представленных далее в книге.
6.1. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СПЛОШНОЙ СРЕДЫ
Начнем со сводки уравнений, определяющих движение нерелятивистской
однородной сплошной среды ^^.
Сохранение массы описывается уравнением неразрывности, которое
связывает плотность среды ? и ее скорость ?:
¦|^+?·(??) = 0. F.1.1)
Уравнение, описывающее сохранение импульса (второй закон Ньютона,
a = F/w, в применении к сплошной среде), имеет вид
^= -IvP- ??, F.1.2)
dt ?
где ? — давление, ? — гравитационный потенциал.
Здесь
4 = |- + ?·? F.1.3)
at dt
— полная производная по времени для индивидуального объема жидкости
(называемая также субстанциональной, или лагранжевой, производной), а
d/dt — обыкновенная частная производная по времени в фиксированной
•^ См., например, книгу Ландау и Лифшица [339].
Равновесие и устойчивость жидких тел 141
точке пространства (эйлерова производная). Если включить в правую часть
уравнения F.1.2) диссипативные члены, описывающие вязкость, то
получим уравнение Навье — Стокса (см. приложение 3).
Гравитационный потенциал определяется уравнением Пуассона
?^? = 4???. F.1.4)
Уравнение, описывающее возрастание энтропии, имеет вид
ds/dt = сумма источников энтропии. F.1.5)
Обычно правую часть выражают через функцию температуры и
плотности; она отвечает возрастанию энтропии, связанному с такими диссипатив-
ными процессами, как теплопроводность, вязкость при сдвигах и
расширении, испускание и поглощение лучистой энергии и т.д. В этой главе мы
ограничимся изучением адиабатических потоков, для которых
1 = 0. F.1.6)
Иными словами, мы считаем, что для каждого элемента жидкости
энтропия сохраняется. Заметим, что в нерелятивистском случае такие
термодинамические величины, как например энтропию, обычно относят к единице
массы, а не к одному бариону. Эти два определения различаются просто
множителем т^.
В общем (не обязательно адиаЬатическом) случае соотношения F.1.1),
F.1.2) и F.1.5) представляют сооой пять динамических уравнений,
описывающих изменения во времени величин р, ? и 5 от соответствующих
начальных значений. В каждый момент времени потенциал ? определяется по
? из уравнения F.1.4), а давление ? и температура ? определяются из
уравнения состояния. Уравнение состояния удобно найти, задав внутреннюю
энергию на единицу массы:
м = и(р,5). F.1.7)
Из первого закона термодинамики
du== -Pdl-\-l·Tds, F.1.8)
и формулы F.1.7) получаем
F.1.9)
F.1.10)
Таким образом, заложена основа для полного описания движения
сплошной среды.
0 ди
ds
?
142 Глава б
Использование первого закона термодинамики в виде F.1.8) при
рассмотрении неравновесных процессов, которые подразумеваются в
уравнении F.1.5), могло бы вызвать возражения. Ведь обычно предполагается,
что уравнение F.1.8) справедливо лишь для квазистатических изменений,
которые представляются в виде последовательности равновесных
состояний. На самом деле мы неявно предполагаем, что отклонения от
равновесия малы. Так как при равновесии энтропия максимальна, то ее
приращение — эффект второго порядка по отклонениям от равновесия. Таким
образом ошибка, связанная с использованием соотношений F.1.7), F.1.9) и
F.1.10), которые справедливы лишь при равновесии, также второго
порядка, и ею можно пренебречь^\
Упражнение 6.1. Уравнение теплопроводности
Я= -KVr, F.1.11)
где q — поток тепла и к ~ коэффициент теплопроводности, можно рассматривать
как первый член в разложении вблизи равновесного состояния, для которого
Vr = 0. Изменение энтропии определяется уравнением
p7-J=-Vq. F.1.12)
Вывести формулу
|(р5)+У-(рУ5 + -а)=к(^)'. F.1.13)
Интегрируя по объему жидкости, проверить, что приращение энтропии есть
величина второго порядка по VT. Какова физическая интерпретация члена pV5 + q/77
Задача существенно упрощается, если s не только не меняется со
временем в каждом элементе объема жидкости, но и постоянна по объему.
Другими словами, 5=const всюду; при этом поток называется изоэнтропичес-
ким. В этом случае достаточно задать одно параметрическое уравнение
состояния, например:
w = «(p), F.1.14)
которое, согласно F.1.9), эквивалентно условию
Р^Р{р). F.1.15)
Заметим, что условие гидростатического равновесия получается из
F.1.2.), если положить v = 0,
VP + ??? = 0. F.1.16)
' Для определения поведения сплошной среды вдали от равновесия нужно
использовать полное уравнение переноса Больцмана (см. [479], разд. 14.5.)
Равновесие и устойчивость жидких тел 143
Мощным методом анализа условий равновесия и устойчивости жидких
тел является исследование возмущений. Будет показано, что равновесные
состояния могут быть найдены из вариационного принципа: в равновесии
энергия достигает экстремума. Частоты колебаний вблизи равновесного
состояния могут быть найдены из рассмотрения малых отклонений от
равновесия. Синусоидальные колебания соответствуют устойчивому
равновесию (минимум энергии), а экспоненциальный рост свидетельствует о
неустойчивости (максимум энергии). Ниже мы разработаем формализм,
необходимый для доказательства и использования этих принципов. Конечной
целью будет определение критериев глобального равновесия и
устойчивости для белых карликов и нейтронных звезд.
6.2. ЛАГРАНЖЕВЫ И ЭЙЛЕРОВЫ ВОЗМУЩЕНИЯ
Укажем прежде всего различие между двумя возможными описаниями
возмущений в сплошной среде. В первом случае мы стоим на
«макроскопической» точке зрения: рассматриваются просто изменения описывающих
сплошную среду переменнььх в данной точке пространства. Такие
возмущения мы будем называть эйлеровыми, для них используются обозначения
5/7, бР, оу'.Точнее говоря, если б(х, О — некоторая величина,
характеризующая возмущенный поток жидкости, а 6?(^? — ее значение для
невозмущенного потока, то
8Q^Q{x,t)-Q^{\,t). F.2.1)
При «микроскопическом» подходе определяется лагранжево смещение
?(?, t)y которое связывает элементы сплошной среды в невозмущенном
состоянии с соответствующими элементами в возмущенном состоянии. При
этом лагранжево изменение ? ? величины Q определяется как
^Q = ?[? + ?(?, О,'] - <2?(?. 0· F-2-2)
Иными словами, элемент сплошной среды перемещается из точки х в
точку ?+?, и мы сравниваем значения Q для данного элемента. Сопоставляя
формулы F.2.1) и F.2.2), приходим к операторному соотношению
? = ? + ?· V, F.2.3)
которое применимо для скалярных величин Q, Это же соотношение мы
будем использовать и для векторов. Вероятно, полезным обобщением этого
соотношения является производная Ли^\ однако это усовершенствование
нам здесь не понадобится.
^ См., например, [209].
144 Глава 6
Лагранжево изменение скорости элемента сплошной среды ?? — это
скорость возмущенного потока в точке ? + ?(?, О относительно скорости
того же элемента в точке ? для невозмущенного потока, т.е.
Упражнение 6.2. Доказать следующие коммутационные соотношения, которые
будут использованы далее в этой главе:
F.2.5)
F.2.6)
F.2.7)
F.2.8)
F.2.9)
F.2.10)
6.3. ВОЗМУЩЕНИЯ ИНТЕГРАЛЬНЫХ ВЕЛИЧИН
Рассмотрим интеграл
1= JQ^{x,t)d'x. F.3.1)
Тот же интеграл, определенный по отношению к возмущенному потоку,
имеет вид
( ?(?, О d^x, F.3.2)
где V+AV — объем, возникающий из V при смещении точек границы,
соответствующем вектору ?. По определению первая вариация интеграла /,
возникающая при возмущении, равна^^
??^ f ?(?, О d'x - [ Qoix, t) d'x. F.3.3)
^^y+^y •'K
При замене переменных в первом интеграле, ?'=?-?(?. О» объемы инте-
а)
^)
в)
г)
д)
е)
с д д ,
'?, = ?'
с д д ^
8— 8
дх' дх'
. д д , di
?— ^ —? - ^ · V
dt dt dt
. д д , d^J
?-^ = ? ^?,
дx^ дх' дх' '
?^^^?
dt dt
d d . . d
'jt'Jt^-^^"'^7t
'^ Обозначение Ы не следует путать с обозначением эйлерова возмущения
локальной величины в жидкости.
Равновесие и устойчивость жидких тел 145
грирования в обоих членах совпадают. В низшем порядке по возмущению
якобиан преобразования равен
y.|M = i(|l±i).,,v-i F.3.4)
при бесконечно малом ?. Таким образом,
81^ ( ?(?' + ?, t)Jd\' - f ??(?, О d'x. F.3.5)
*fy Jy
Заменяя обозначение переменной интегрирования в первом члене, х'—х,
получим окончательно
?/= ?(?? + ??·?)^'?. F.3.6)
Jy
Формулу F.3.6) можно использовать при выводе выражения для ??.
Масса в произвольном объеме жидкости V сохраняется, поэтому
?? pd^x^O. F.3.7)
Jy
Таким образом,
?? = -pV ·?, F.3.8)
и, следовательно,
??= -?·(??). F-3.9)
Упражнение 6.3. Вывести формулу F.3.8), рассматривая возмущение уравнения
неразрывности в дифференциальной форме:
^+??·? = 0. F.3.10)
at
Упражнение 6.4. Показать, что
8fQpd'x^ (^Qpd'x. F.3.11)
Jy Jy
Для уравнения состояния вида
P = P{p,s) F.3.12)
мы ограничимся рассмотрением адиабатических возмущений,
?5 = 0. F.3.13)
10-353
146 Глава 6
Это значит, что
где
?
г,=
-^'т
_ дЫР
д\лр
F.3.14)
F.3.15)
— показатель адиабаты для возмущений. Заметим, что в принципе
показатель Г J не обязательно должен быть равным показателю Г,
определяющему соотношение между давлением и плотностью в равновесном состоянии.
Например, это может быть связано с тем, что некоторые реакции,
необходимые для достижения полного термодинамического равновесия, не
успевают протекать за времена, характерные для возмущения, или же просто с
тем, что равновесное соотношение между давлением и плотностью
моделируется определенным образом (например, в виде политропы с
постоянным Г), а локальное значение показателя Tj не совпадает с модельным
значением.
Возмущение внутренней ньютоновской энергии на единицу массы и для
адиабатических возмущений может быть найдено из уравнения состояния
F.3.12) и первого закона термодинамики F.1.8):
^"-(^)/^-^^)^-7""-^^^-5'"· <"¦"*
Возмущение гравитационного потенциала находится из возмущенной
формы уравнения F.1.4):
?^?? = 47????. F.3.17)
Из формул F.3.17) и F.3.9) следует
- -g/pT · V·^^^'*'. F.3.19)
Чтобы получить последнее равенство, мы проинтегрировали по частям и
отбросили поверхностный член, так как ? = О на поверхности. (Если на
поверхности р^О, например, в случае несжимаемой жидкости, то последнее
равенство справедливо только для возмущений ?, касательных к
поверхности.)
Равновесие и устойчивость жидких тел 147
Упражнение 6.5. Показать, что для радиальных возмущений сферической звезды из
формулы F.3.18а) следует
?,?? = -47rGpi'. F.3.20)
Указание. Можно воспользоваться разложением функции 1х - х'1~^ в
сферических координатах.
6.4. РАВНОВЕСИЕ КАК УСЛОВИЕ ЭКСТРЕМУМА ЭНЕРГИИ
В этом разделе мы выведем вариационный принцип для уравнения
гидростатического равновесия. Будет показано, что равновесие отвечает
экстремуму энергии данной конфигурации.
Полная энергия имеет вид
?= Г+ 17+ Ж, F.4.1)
где
F.4.2)
— кинетическая энергия,
— внутренняя энергия и
7=^ f^v'pdh
?/= fupdh
W^ ?^???^
F.4.3)
F.4.4)
— гравитационная потенциальная энергия.
Ограничимся случаем статического равновесия (?=0). При этом оГ=0 в
первом порядке по всем возмущениям, и можно исключить кинетическую
энергию из выражения вариационного принципа. Для внутренней энергии
имеем
8U=^ fi^upd'x = - jp^.i^d'x,
F.4.5)
причем мы использовали формулы F.3.И), F.3.16) и F.3.8).
Интегрирование по частям дает (так как на поверхности Я=0)
??== fvP^id'x, F.4.6)
Вариация W дает
?^= ||[??? + ?(?· ?)?]^^?, F.4.7)
148 Глава б
где были использованы равенства F.3.11) и F.2.3). Из F.3.18) следует
Таким образом,
?^?= |(???)·?^^^. F.4.8)
Окончательно из F.4.6) и F.4.8) получаем
??= J{VP + ???)·?^^^. F.4.9)
Следовательно, условие 6^=0 приводит к уравнению гидростатического
равновесия F.1.16).
Упражнение 6.6. Показать, что при наличии сферической симметрии
ф(^)= _Gm{!:)^ ^GfA^prdr, F.4.10)
г Jq
где
w(r)= Глтгрг^аг F.4.11)
•?
— масса, заключенная^ внутри сферы радиуса г, и Ф@)= ?' @)=0.
Упражнение 6.7. Показать, что при наличии сферической симметрии
W= -f^^dm +const. F.4.12)
Указать элементарный способ получения первого члена в этой формуле и найти
зависимость константы от граничного значения потенциала Ф.
Упражнение 6.8. а) Показать, что условие гидростатического равновесия может
быть получено также из другого вариационного принципа, основанного на
эйлеровых вариациях величин, характеризующих жидкость: найти экстремум ? при
условии, что полное число барионов N остается постоянным.
Указания. 1. Следует искать экстремум величины
r=E-\N, F.4.13)
Равновесие и устойчивость жидких тел 149
где множитель Лагранжа ? считается постоянным.
2. Используйте формулу F.3.3) в виде
5/=( bQd'x, F.4.14)
Это вполне оправдано, так как в объеме ? К величина ?^ равна нулю.
3. Учтите, что
?«= -^. F.4.15)
б) Каков физический смысл величины ??
в) Показать, что ? и N достигают экстремальных значений в одной и той же точке
при варьировании вдоль однопараметрической последовательности равновесных
моделей.
Замечание. При лагранжевом подходе не было необходимости налагать условие
постоянства N в явном виде. Оно автоматически следует из формулы F.3.8).
6.5. ВОЗМУЩЕНИЯ ВБЛИЗИ СОСТОЯНИЯ РАВНОВЕСИЯ
В этом разделе выводятся уравнения, которым удовлетворяют малые
возмущения статической равновесной конфигурации. Эти уравнения полезны
по двум причинам: а) они позволяют вычислить частоты и нормальные
моды колебаний вблизи положения равновесия, б) они дают возможность
выяснить вопрос об устойчивости равновесного состояния.
Динамика описывается возмущенным уравнением Эйлера:
?(^^ + ^?,?+?,?) = 0. F.5.1)
Умножая это уравнение на ? и используя формулы F.2.8), F.2.9), F.1.16) и
F.2.4), получаем
dt^ ?
Так как невозмущенная конфигурация является статической, d/dt можно
заменить Had/dt^dj. Используя формулы F.3.8), F.2.3), F.3.14) и F.1.16),
приводим это уравнение к виду
pdfe = LJJ, F.5.3)
где
-??^?,?,? - ??,??. F.5.4)
150 Глава б
Все величины здесь выражены через ?' и невозмущенные переменные, так
как ?^^? можно найти из формул F.3.19) или F.3.20).
Уравнение F.5.3) является уравнением движения для возмущений. Для
?', зависящих от времени по закону ехр(-/ыО, получим уравнение
-?Ы^-L,^e. F.5.5)
Это уравнение, дополненное соответствующими граничными условиями
для ?', представляет собой линейную задачу на собственные значения для
нормальных мод колебаний в звездах.
Упражнение 6.9. Показать, что уравнение на собственные значения для радиальных
колебаний в сферической звезде имеет вид
l(r.'^l<''i))-7fi-''«-«· <"«
где ? означает радиальную составляющую вектора ^.
Указание. Для исключения производных потенциала ? используйте формулы
F.1.4) и F.1.16).
Граничные условия для уравнения F.5.6) записываются в виде
? = О при г = О, F.5.7)
?? = 0 при г = Л. F.5.8)
В сферически-симметричном случае условие F.5.7) очевидно, а формула
F.5.8) означает, что элемент жидкости у невозмущенной поверхности
смещается к возмущенной поверхности. Так как в силу формул F.3.14) и
F.3.«) имеем
причем ? обращается в нуль при /*=/?, то в общем случае достаточно
потребовать выполнения условия
? конечно при /·=/?, F.5.10)
Уравнение F.5.6) с граничными условиями F.5.7) и F.5.10) является
задачей Штурма — Лиувидля^^ на собственные значения ?^. Укажем
некоторые результаты, следующие из теории таких уравнений.
1. Все собственные значения ?^ вещественны.
'^ См., например, книгу [414], разд. 6.3.
Равновесие и устойчивость жидких тел 151
2. Эти собственные значения образуют бесконечную дискретную
последовательность
(^1< ?\ < ?\· · · .
3. Собственная функция ^q» соответствующая минимальному
собственному значению ??, не имеет узлов на интервале 0<r<R. Вообще говоря,
собственная функция ?^ имеет на этом интервале ? узлов.
4. Собственные функции ?„ ортогональны с весом рг^
rUmPr^dr^O, т*п. F.5.11)
5. Функции ?„ образуют полный базис для разложения любой функции,
удовлетворяющей граничным условиям F.5.7) и F.5.10).
Из п.2 вытекает важное следствие: если низшая радиальная мода для
звезды является устойчивой (?1>0), то устойчивы все радиальные моды. И
наоборот, если звезда радиально леустойчива, то быстрее всего
развивается неустойчивость в низшей моде (среди отрицательных собственных
значений ?? имеет наибольшую абсолютную величину).
Рассмотрим в качестве простого примера, допускающего аналитическое
решение, развитие возмущений в однородной звезде, т.е. при постоянных ?
и Tj. Для однородной звезды в состоянии равновесия адиабатический
показатель Г = 00 (несжимаемый газ), а показатель политропы п = 0.
Упражнение 6.10. Показать, что для однородной звезды в состоянии равновесия
/>>^^(Л^-г^). F.5.12)
Подставляя формулу F.5.12) в уравнение F.5.6) и производя упрощения,
получим
A - x^)i" + ?'(^ - 4х) + (л - -^Jl = 0. F.5.13)
Здесь x=r/R, штрих означает производную по х, и
Л= 3?1^ 8_2 F.5.14)
27rGpl, li
Как обычно, ищем решение в виде ряда
л-О
152
Глава б
^Х
Рис, б. 1. Амплитуды радиальных колебаний для первых пяти мод в однородной
модели.
Коэффициент при х^"^ дает нам уравнение для показателя степени:
E + 2)E- 0 = 0.
F.5.16)
Естественно, следует выбрать 5= 1, чтобы удовлетворить граничному
условию F.5.7). Далее находим а^ = ат^ = а^=, . . = 0, и
а„^^ л^ + 5/1 + 4 - ^
^w + 2
/1^ + 7w + 10
/1==0,2,4,...,
F.5.17)
Ряд расходится, и поэтому он должен обрываться, если ? удовлетворяет
граничному условию F.5.10). Таким образом, получаем требование
^ = /1^ + 5/1 + 4, /2 = 0,2,4,...
и в силу формулы F.5.14)
2 _ I'jrGp
F.5.18)
?
[Т,{п^ + 5/1 + 6) - 8], /1 = 0,2,4... . F.5.19)
Заметим, что звезда неустойчива при условии Г|<4/3. Это общий
результат, и мы будем обсуждать и использовать его в разд. 6.7. Характерные
времена устойчивых колебаний — порядка {Gp)~ ^^^, как и следовало
ожидать из соображений размерности. На рис. 6.1 показаны амплитуды коле-
Равновесие и устойчивость жидких тел 153
баний, нормированные на одинаковое значение при /*=/?. Заметим, что при
Г| = 4/3 решение для низшей моды ? «г и соответствует ?^=0. Как будет
показано в разд. 6.7, этот результат также имеет общий характер.
Упражнение 6.11 (с использованием ЭВМ). Найти частоты нескольких низших
устойчивых пульсаций для политропы с каким-нибудь показателем ? при rj = 5/3.
Указания, а) Сделать безразмерным уравнение на собственные значения.
б) Найти функцию Лейна — Эмдена путем одновременного интегрирования
уравнения Лейна ~ Эмдена C.3.6) или использовать результаты, представленные в
работе Сервиса [519].
в) Исследовать аналитически поведение решения вблизи г=0 и r=R.
г) Возможный метод вычисления состоит в численном интегрировании уравнения
отг=Оиг=/?к какому-нибудь подходящему значению г внутри звезды с
выбранным наугад значением ?^ и граничными условиями, определенными в п.в). Так как
относительная величина этих двух решений заранее неизвестна, то можно начать
каждое из них с единицы. Если значение ?^ случайно угадано правильно, то
вронскиан двух решений в точке сшивания г обратится в нуль (почему?). Вообще говоря, он
отличен от нуля. Выберите другое ?^, проинтегрируйте от границ к г и вновь
найдите вронскиан. Теперь надо путем интерполяции или экстраполяции найти значение
?^, при котором вронскиан обратится в нуль. Продолжайте итерацию до тех пор,
пока ?2 не будет найдено с заданной точностью.
6.6. ФУНКЦИЯ ЛАГРАНЖА ДЛЯ ВОЗМУЩЕНИЙ
Мы покажем в этом разделе, что уравнение F.5.3), которому
удовлетворяет возмущение, может быть выведено из вариационного принципа.
Вариационный принцип полезен для приближенного решения уравнений для
возмущений. Однако для нас более важно, что вариационный принцип
приводит к критериям устойчивости, которые будут использоваться далее в этой
книге.
Покажем прежде всего, что оператор L^j в уравнении F.5.4)
симметричен, т.е.
fv'LJJdh = ji%jri'd'x, F.6.1)
где ?' и ?/' — произвольные лагранжевы смещения. Так как
?'?,(?,??,?^) = ?,(?,?,??,?>) - ?,?(?,?)(?,?^), F.6.2)
И
(?,'?,???/ = vXii^VjP) - ( ?,?')?'?/ - ii^V,VjP, F.6.3)
TO из F.5.4) следует
/W^</'x= -/[r,i>(v,T,')(v,i^)+ (?^>)?,'?,? +
+ (V,r()VVjP + r(iJ{V.VjP + ??,?,?) +??'V,??] dh. FД4)
154 Глава 6
Поверхностные члены от первых слагаемых в правых частях формул F.6.2)
и F.6.3) обращаются в нуль, так как на поверхности Я=0 и V^ Я=0. (Из
формулы F.1.16) следует, что V^ Я=0, если р = 0 на поверхности. Если же
pq^O, например, для несжимаемой жидкости, то мы требуем ?^?^ Я=0, т.е.
возмущение в радиальном направлении должно быть равно нулю.) Из
формулы F.6.4) видно, что оператор L^j симметричен. Заметим, что, согласно
F.3.19), последний член в правой части равен
fpiV,8<S>d'x^ -GJjpp'r{V,eVj.,^^^d'xd'x', F.6.5)
и, очевидно, симметричен.
Естественно ожидать, что лагранжиан для уравнений движения
возмущений имеет вид
L^T^-V^, F.6.6)
где Т^ — кинетическая энергия, а Kj — потенциальная энергия возмущения.
Индекс 2 означает, что выражение квадратично по ?'. Левая часть в
уравнении F.5.3) имеет вид плотности массы, умноженной на ускорение, а правая
часть L^{^ — плотности силы. Чтобы перейти от плотности силы к
потенциальной энергии, следует построить скалярное произведение i^L^P и
проинтегрировать его по объему звезды. При этом получается выражение
F.6.4) с заменой т/' на ?'. Таким образом, мы приходим к следующим
определениям:
T^^\jp{d,i'fd'x, F.6.7)
Fj= -\fi%jiJd'x = F.6.8)
= |/[r,p(v,|'f+ 2(?,?>)?'?,? +
+ i'i^{ ViVjP + ??,?,?) + pi'Vi ??] d^x. F.6.9)
Проверим теперь, что функция F.6.6) действительно является лагран-
¦аном для уравнен
ция действия равна
жианом для уравнения F.5.3). Так как оператор L-j симметричен, то вариа-
bS = SJLdt - 8\j[p{d.ef + i'V] ^^^^^^^ =
j[p{d,e){dM') + «^V] ^^^^^^^ = /(-?^??' + L,jiJ)8i4'xdt.
F.6.10)
Равновесие и устойчивость жидких тел 155
Чтобы получить последнее равенство, мы проинтегрировали по частям
первый член. Таким образом, условие 65 = 0 для произвольного 6?!
эквивалентно уравнению движения F.5.3). Отметим, что символ ? в указанном
вариационном принципе относится к обычной вариации функции между
соседними траекториями движения, связывающими фиксированные
начальную и конечную точки^\
Упражнение б. 12. Показать, что энергия колебаний на фоне первоначально
статической конфигурации
постоянна во времени. Использовать равенство dL.j/dt = 0.
^2 = 7^2+ V2 F.6.11)
овать равенство Ы../Ы = 0,
Замечание, Фридман и Шутц [209] показали непосредственным вычислением, что
Е^^Ь'^Е, т.е. энергия колебаний равна вариации второго порядка для функционала
энергии, данного в формуле F.4.1).
Упражнение 6,13, Используя формулу F.6.9), показать, что для радиальных
возмущений сферической звезды
Указания, Исключить производные Ф, используя формулы F.1.4) и F.1.16).
Подставить выражение F.3.20) для ?^^? и проинтегрировать по частям член с d^P/dP·,
Упражнение 6.14, По определению
I^]^jpiVd'x. F.6.13)
Доказать теорему вириала для возмущений, т.е.
l^=7i-K2. F.6.14)
6.7. КРИТЕРИИ УСТОЙЧИВОСТИ
Для малых отклонений от равновесия имеем
Е^Е^ + Е^, F.7.1)
где Eq — энергия равновесного состояния, а первая вариация ЬЕтЕ^
обращается в нуль, так как в равновесном состоянии энергия экстремальна.
Вторая вариация равна
^2 = 8^Е = Г2 + ^2 = ?^? + 8^{и + W), F,1,2)
где Tj и Kj даны в формулах F.6.7) и F.6.8).
^ См., например, книгу Голдстейна [232], гл. 2.
156 Глава 6
Неустойчивость соответствует неограниченному росту малого
начального возмущения (?', ?^?'). (Заметим, что начальными данными,
определяющими эволюцию возмущения, которая описывается дифференциальным
уравнением второго порядка F.5.3), являются обе величины, ?' и dfi\) В
качестве другого критерия неустойчивости можно принять также
неограниченный рост кинетической энергии Tj.
Поскольку мы рассматриваем динамическую устойчивость (т.е.
пренебрегаем всеми эффектами, обусловленными диссипативными силами), то
? — сохраняющаяся величина (см. упражнение 6.12). Предположим
теперь, что функция ^2@ положительна для всех возмущений. Так как
?^2= 72+ К2 и 7^2 "" положительно определенная функция, она не может
неограниченно возрастать. Таким образом, устойчивость обеспечена, если
К2@ — положительно определенная функция для всех ^Ч^» О·
Обратное утверждение доказано в приложении Б: если для некоторого
?^?» О величина V2 отрицательна, то возникает неустойчивость.
Так как в любой момент времени возмущение ?!{?, t) определяет
начальные данные для последующей эволюции, то критерий устойчивости
можно сформулировать следующим образом. Необходимым и
достаточным условием устойчивости является положительная определенность
потенциальной энергии К^ для всех начальных данных.
Критерий устойчивости можно выразить также на языке энергии. Если
величина ?, которая сохраняется и потому может быть задана, например,
в момент / = 0, положительна при всех начальных данных ({', Э^{'), то она
положительна, в частности, при Э^{'=0 и любых значениях {'. Таким
образом, потенциальная энергия V2 положительна и система устойчива.
Обратно, если ? при каких-то начальных данных ({', Э^{') отрицательна, то
потенциальная энергия V2 может стать отрицательной и возникает
неустойчивость. Таким образом, 6?^ О — необходимое и достаточное условие
устойчивости.
Критерий устойчивости можно связать также с разложением по
нормальным модам колебаний. Временная зависимость нормальной моды
имеет вид
И неустойчивость возникает при ?^<0. Уравнение движения для
нормальной моды имеет вид F.5.5). Умножая это уравнение на ^Ч^)» интегрируя по
всему объему звезды и используя формулы F.6.8) и F.6.13), получаем
?
2_У2
F.7.4)
Поскольку величина / всегда положительна, то положительность V2
эквивалентна условию ?^^? и гарантирует устойчивость. Появление
неустойчивости определяется условием ?^= О (соответствующая мода называется
нейтральной). Это происходит при ^2=0, т.е. при обращении в нуль ?2·
Равновесие и устойчивость жидких тел 157
Мы получили важный результат: формула F.7.4) содержит в себе
вариационный принцип для нормальных мод:
/??^ = 8V2 - у ?/ == 8V2 - оР- 81
= -j8i\L,Jij + ?'pe)d'x. F.7.5)
Таким образом, из условия ??^=0 следует уравнение движения для
нормальной моды F.5.5). Следовательно, мы пришли к новой процедуре
определения нормальных мод колебаний звезды: следует искать смещения ^Ч^)»
которые соответствуют экстремуму функционала в F.7.5). При этом
собственные частоты находятся из формулы F.7.4).
Важное приложение полученных результатов относится к радиальным
смещениям в сферической звезде. Используя формулу F.6.12) для К2,
получаем
?^
/о>.'М1''^«
к^егЧг
-^^1-. F.1.6)
Покажем теперь, что звезда устойчива, если усредненное с учетом давления
значение Гр которое мы обозначаем Гр превышает 4/3, и неустойчива,
если Г|<4/3. Границе устойчивости отвечает Г| = 4/3, при этом ?^=0.
Рассмотрим прежде всего звезду, для которой Г| = 4/3 по всему объему.
Уравнение F.5.6) имеет решение без узлов (основная мода) следующего
вида:
?^ = О, ? = const ? г. F.7.7)
Упражнение 6.15. Проверить, что формула F.7.7) дает решение уравнения F.5.6)
при Г| = 4/3.
Другими словами, звезда с Г| = 4/3 находится на границе устойчивости
относительно гомологической (т.е. автомодельной) деформации.
Предположим теперь, что Г| несколько отличается от 4/3 в различных точках
звезды. Тогда решение уравнения F.5.6), отвечающее границе устойчивости,
имеет вид
^(л) = г[1+е(Г,-!)]. F.7.8)
Таким образом, если подставить в F.7.6) пробную функцию ?(/*)=г, то
ошибка в определении ?^ будет иметь порядок величины (Г|-4/3)^.
(Напомним, что функционал в F.7.6) связан с вариационным принципом, и по-
?"
158 Глава б
тому ошибка в собственном значении пропорциональна квадрату ошибки в
собственной функции.) Таким образом, числитель в F.7.6) дает
? 9 i\Pr^ dr - 12 Грг^ dr, F.7.9)
•'о •'о
где второй член получен интегрированием по частям. Итак,
?^ ? ЗГ, - 4, F.7.10)
где
^ f^Pr^ dr
— показатель адиабаты, усредненный с учетом давления. Из формулы
F.7.10) виден характер перехода от устойчивого к неустойчивому
состоянию при падении Г, ниже граничного значения 4/3.
Можно непосредственно убедиться, что для политропы с Г = 4/3 = Г|
гомологическое расширение или сжатие звезды не выводит ее из состояния
равновесия. Применим гомологическое преобразование
Р' = АР, р' == Вр, г' = Сг, F.7.12)
к уравнению гидростатического равновесия
И в качестве дополнительного условия учтем постоянство полной массы т.
При этом мы получим два условия, касающиеся масштабных множителей,
^С==5, 5С^==1. F.7.14)
Исключая отсюда С, имеем
А = -?"''' F.7.15)
ИЛИ, согласно уравнению F.7.12),
т.е. ? = 4/3 при Г = 4/3.
Упражнение 6.16.
а) Показать, что частота радиальных колебаний ? может быть выражена через
момент инерции звезды / и полную гравитационную потенциальную энергию W
следующим образом:
.-TCr,-4(i)/(if), (елл,)
Равновесие и устойчивость жидких тел 159
где
Указание. Использовать формулу C.2.3).
б) Показать, что если Tj близко к 4/3, то определенные выше средние значения
{??/rY примерно равны друг другу, и потому
^2^т(зГ,-4). F.7.18)
6.8. ТОЧКИ ПОВОРОТА И ВОЗНИКНОВЕНИЕ НЕУСТОЙЧИВОСТИ
Предположим, что имеется однопараметрическая последовательность
равновесных звезд с одним и тем же уравнением состояния, но различными
центральными плотностями. Каков смысл максимума или минимума на
кривой зависимости ? от р^ (т.е. критических точек или точек поворота,
в которых dE^^/dp^=0)l
Ясно, что наличие такой критической точки означает, что существуют
близкие равновесные конфигурации, для которых
?eq(Pc + %) = ?cq(Pc) F8-1)
С точностью до членов первого порядка. Соседние конфигурации
получаются из первоначальной при некотором лагранжевом смещении ?, вызванном
изменением центральной плотности^^ ??^. В общем случае
?[?]=?^ + ?,[?] + ???? F.8.2)
где ?^[?] — вклад членов порядка ?" в увеличение энергии при отходе от
Eq=E^^p^. Так как Eq отвечает равновесному состоянию, то ?^[?] = 0 (см.,
например, формулу F.4.9)). Энергия ?(?) также отвечает равновесной
конфигурации, если энергия конфигурации стационарна относительно возму-
^ Заметим, что поскольку смещения ^ переводят одну равновесную конфигурацию
в другую, то в этом случае Г|=Г. Выводы этого раздела зависят от указанного
равенства. Обсуждение поведения системы вблизи точек поворота при Г,:/:Г см. в
работе Торна [567].
160 Глава 6
щений второго порядка^ т.е. ?@=0 для указанных смещений ?. Но как
следует из предыдущего параграфа, это условие означает наличие моды с
нулевой частотой, ?^=0, что соответствует границе устойчивости.
Простейший спосоь использовать этот критерий на практике состоит в
том. чтобы установить устойчивость звезд на одном из концов
последовательности (оЬычно в области малых плотностей). Тогда критическая точка
указывает значение плотности, при котором возникает неустойчивость.
Далее в этом разделе будет показано, как обобщается этот метод при
наличии нескольких критических точек.
Метод критических точек можно применять также к кривой
зависимости равновесной массы от р^. Один из способов убедиться в этом состоит в
нахождении зависимости Л/ от р^ с помощью вариационного принципа,
6^=0, где
Е^ judm- j^^dm, F.8.3)
Обозначая различные произведения числовых множителей через aj,a2»···»
получаем из соображений размерности
Е^{и)М-а,^.
Полагая Г| = Г в адиабатическом уравнении состояния
? = кр"".
получаем
V-'
так что
{и) = а^Кр^,-\
Также из соображений размерности
так что
? = ?^????'^ - afiM^^'^pY\
F.8.4)
F.8.5)
F.8.6)
F.8.7)
^6.8.8)
F.8.9)
Равновесие определяется условием dE/dp^=0 при постоянном М; отсюда
следует
М ? p<r-V3)C/2) (gglQ)
Равновесие и устойчивость жидких тел
161
Рис. 6.2. График, показывающий критические точки в зависимости массы звезды от
плотности в ее центре для равновесных конфигураций холодного вещества.
Таким образом,
dM ^ А
? Г — —
dp. 3 ·
F.8.11)
Если в семействе звездных конфигураций есть только одна критическая
точка и конфигурации устойчивы при малых плотностях, то из формул
F.7.10) и F.8.11) следует, что при dM/dp^>0 равновесные конфигурации
устойчивы, а конфигурации с dM/dp^<0 — неустойчивы^^
Выбор величины р^ в качестве параметра, описывающего
последовательность равновесных моделей, в данном случае несуществен; также
удобно представлять Л/ как функцию R. При этом мы можем рассмотреть
случай кратных критических точек. Как было указано выше, интерес
представляет прежде всего устойчивость основной радиальной моды, которая не
имеет узлов внутри звезды. В этом случае собственная функция в
критической точке — это просто лагранжево смещение ?, которое переводит
равновесную конфигурацию при плотности ниже критической в равновесную
конфигурацию при плотности выше критической. При таком движении р^
возрастает, так что вблизи центра звезды ? отрицательно. Так как
величина ? не имеет узлов, то она должна быть отрицательна и вблизи
поверхности. Таким образом, R падает при увеличении р^ в критической точке, где
основная мода изменяет устойчивость. (Вообще, dR/dp^KO при изменении
устойчивости моды с четным числом узлов и dR/dp^>0 для моды с
нечетным числом узлов.)
' Более строгое доказательство этого результата приводится Тассулем [559], с.
149.
11-353
162
Глава б
R.KfA
Рис. 6.3. График, показывающий точки поворота в зависимости массы звезды от ее
радиуса для равновесных конфигураций холодного вещества.
Диаграмма зависимости Л/ от р^ с кратными критическими точками
показана на рис. 6.2, зависимость ? от R показана на рис. 6.3. При малой
плотности (большом радиусе) все моды устойчивы. Первой появляется
критическая точка А, соответствующая максимальной массе белого
карлика. Так как R падает с ростом р^, то четная мода изменяет устойчивость.
Поскольку ?0<??<?2<... и ??>0 при малой плотности, то единственная
возможность состоит в том, что величина ?^ становится отрицательной. В
точке В четная мода изменяет устойчивость (dR/dp^<0). Величина ?? не
может стать отрицательной, так как ?\ не изменила знак. Поэтому
величина ?? должна опять стать положительной: точка В соответствует
минимальной массе нейтронной звезды. Критическая точка С аналогична А, и
?? вновь становится отрицательной: эта точка соответствует
максимальной массе нейтронной звезды. В точке D устойчивость изменяет нечетная
мода. Единственная возможность состоит в том, что ?\ становится
отрицательной. В точке ? устойчивость изменяет четная мода. Величина ?^ не
может стать положительной, так как ?^ все еще отрицательна, поэтому ?2
становится отрицательной.
Упражнение 6.17. Используя рассуждение, аналогичное приведенному выше,
убедитесь, что для любого вида зависимости ? от R при условии, что все моды
устойчивы при низкой плотности, справедливо следующее утверждение: изгиб диаграммы в
критической точке против часовой стрелки указывает на появление неустойчивости
при возрастании р^, изгиб диаграммы по часовой стрелке указывает на переход
неустойчивой моды в устойчивую.
Равновесие и устойчивость жидких тел 163
Отметим, что критерий dM/dp^>0(<0) для определения устойчивости
(неустойчивости) имеет ограниченную применимость: например, отрезок
D-E неустойчив, хотя dM/dp^>0. Однако для типичных уравнений
состояния холодного вещества наинизшая плотность, при которой dM/dp^-0 и
d^M/dpl<0, соответствует максимальной массе и плотности устойчивого
белого карлика (например, точка А на рис. 6.2). Следующая точка, в
которой dM/dp^=0 и d^M/dpl<Oy соответствует максимальной массе и
плотности устойчивой нейтронной звезды (например, точка С на рис. 6.2). Эти
результаты будут часто использоваться в дальнейшем.
РЕЗЮМЕ 6.1
Ньютоновское равновесие и устойчивость невращающихся звезд
1. Вариационный принцип для гидростатического равновесия: ??'=0 [см.
формулу F.4.9)]. Вариация производится при фиксированной массе покоя и
постоянной энтропии.
2. Поведение малых возмущений относительно равновесного состояния
определяется уравнением F.5.3) или F.5.5) (для нормальных мод).
Радиальные моды колебаний в сферической звезде являются решением задачи
Штурма—Лиувилля на собственные значения F.5.6).
3. Динамика возмущений выводится из вариационного принципа с
лагранжианом L = T2- V2 [формулы F.6.7) и F.6.8)].
4. Следующие критерии устойчивости эквивалентны:
а) Kj^ О для всех возмущений;
б) 6^^=^2^0 для всех возмущений;
в) ?^^ О для всех мод колебаний;
г) ??^4/3 только для радиальной устойчивости F.7.11).
5. Некоторые нормальные моды нарушают устойчивость, если
dE^^/dp^=0 или dM/dp^=0 (разд. 6.8).
6.9. АНАЛИЗ УСТОЙЧИВОСТИ С УЧЕТОМ ЭФФЕКТОВ
ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Почти все результаты предыдущих разделов сохраняются и в общей
теории относительности, если заменить ? на Мс^ — полную энергию,
заключенную в массе звезды [261]. В частности:
1. Среди всех конфигураций с данным полным числом барионов N
равновесию отвечает экстремум Л/ (о постоянстве N см. замечание в конце
упражнения 6.8). Можно показать, что в данном однопараметрическом
семействе равновесных состояний величины Л/ и N имеют экстремум в одной
и той же точке (см. упражнение 6.8в), поэтому эквивалентная задача
сводится к отысканию экстремума величины
Е = Мс^- m^N. F.9.1)
164 Глава б
2. Поведение малых радиальных отклонений от равновесия
определяется задачей Штурма—Лиувилля, аналогичной формуле F.6.6).
3. Для устойчивости необходима положительность второй вариации Л/.
Эквивалентное условие: ??>0.
4. Состояние устойчивости меняется в критических точках зависимости
Mgq от /?, или Mgq ОТ р^. Анализ проводится так же, как в конце разд. 6.8.
5. Поскольку уравнение для ?^ отличается от выведенного в случае
ньютоновской механики, то критерий ??>4/3 уже неприменим для
установления устойчивости. Но если релятивистские поправки малы (GM/Rc^< 1), то
новый критерий имеет вид
Г,-з>к—. F.9.2)
где к — число порядка единицы, зависящее от внутреннего строения
звезды. В целом эффект общей теории относительности сводится к нарушению
устойчивости, так как сила тяготения становится больше, облегчая
переход к коллапсу.
Оставшаяся часть этой главы будет посвящена выводу величины к для
важного случая, когда звездная конфигурация близка к политропе с л = 3,
так что Г = ?? = 4/3. Мы найдем также соответствующую плотность
звездного вещества в критической точке^\ Запишем полную энергию в виде
? = ^New, + A^GTR. F-9-3)
где ^Newt "" ньютоновская энергия звезды, а AEqjr — поправка,
обусловленная общей теорией относительности. Минимум энергии отвечает
равновесной конфигурации, а вторая производная дает возможность решить
вопрос об устойчивости.
Окончательное выражение для AEqjr дано в F.9.32); читатель,
согласный принять его на веру, может сразу переходить к этой формуле В этом
разделе мы принимаем с=С= 1.
Для сферического распределения материи, находящейся в покое в
данный момент, полная масса имеет вид [см. E.7.8)]
М= ГрАтгг^аг. F.9.4)
•?
Здесь
р = РоA + «). F.9.5)
Полное число барионов в звезде равно
•?
F.9.6)
Наш вывод следует книге Зельдовича и Новикова [636].
Равновесие и устойчивость жидких тел
165
где
d^^ |l - 2^J"'^'^47rr2jr F.9.7)
— элемент собственного объема в геометрии Шварцшильда [см. формулу
E.7.9)]. Энергия звезды (за вычетом энергии, связанной с массой покоя)
определяется согласно формуле F.9.1):
-/:И-?Г-.]
^%
F.9.8)
где мы использовали обозначение р^=т^п. Подставляя сюда выражение
F.9.5) и считая и и т/г малыми, получим с точностью до членов второго
порядка
Отметим, что величина pq^/У инвариантна и расширение на нее не влияет.
Ньютоновская энергия имеет вид
F.9.10)
где
•? -? '
F.9.11)
F.9.12)
Заметим, что в силу формул F.9.5) и F.9.7) функции т' {У) и г' (У)
отличаются от соответствующих релятивистских выражений. Попробуем
вычислить энергию звезды вначале по общей теории относительности, а
затем согласно теории Ньютона, а разность этих двух выражений обозначим
AEqj^. Как мы можем удостовериться, учитывая неоднозначность выбора
координат в общей теории относительности, в том, что в обоих случаях
имеем дело с одной и той же величиной? Иными словами, если даны две
совершенно одинаковые звезды и нужно вычислить для одной из них ?*, а
для другой — ^Newt» '^^ ^^^ установить, что эти звезды действительно
тождественны?
Ответ состоит в том, что тождественные звезды содержат одинаковые
числа барионов в данном собственном объеме (это утверждение не зависит
от выбора координат). Следовательно, Pq( У) — это одна и та же функция
и в теории относительности и теории Ньютона.
Вычитая формулу F.9.10) из F.9.9), получаем
F.9.13)
166 Глава 6
Упражнение 6.18. Используя формулу F.9.7), показать, что с точностью до членов
первого порядка
Из формул F.9.12) и F.9.14) следует
г' -r^X-fmrdr. F.9.15)
Также с точностью до членов первого порядка получаем
.'(T)-.(T)=/V[po-p(l-2^p]
= -f\d^[u-^). F.9.16)
Теперь в формуле F.9.13) можно написать
w' т т' - т т{г' - г)
г г г гг
F.9.17)
и подставить сюда выражения F.9.15) и F.9.16). Мы последовательно
сохраняли все члены второго порядка, поэтому, вычисляя теперь интегралы с
ньютоновскими выражениями для pq» /*, ^и т.д., мы получим результат с
погрешностью лишь в членах третьего порядка. Итак,
?^??? = /1 + /2 + /3 + ^4 + /5» F.9.18)
где
/1 = - / u-dm, F.9.19)
,,.-i"^rudm. F.9.21)
Jq г Jq
Г ? dm r^
— / ?
о '' •'о
г ? dm r^m
I^^r^r^dm. F.9.22)
_ fMmdm с''
Po
и =
dP
dr
?
?—
Po
m
~7^
Равновесие и устойчивость жидких тел 167
Эти выражения можно упростить, полагая, что распределение по массе
соответствует политропе с показателем л, т.е.
F.9.24)
F.9.25)
Упражнение 6.19.
а) Показать, что при выполнении условий F.9.24) и F.9.25)
/5 = -/,. F.9.26)
^ ?
Указание. Подставить —тат/г^=4жс1Р и проинтегрировать по частям,
б) При тех же условиях показать, что
/4 = 2/^ - ^/, - |/з. F.9.27)
Указание. Подставить mdm/r= -???^??, проинтегрировать по частям, чтобы
получить два члена, затем первый член вновь проинтегрировать по частям и
исключить Р, используя формулу F.9.24).
в) Показать также, что
^з = Л-;;^(/2 + /4)· F-9-28)
Указание. Проинтегрировать udm по частям, показать, что
du^ ? dP/[po(n + 1)] = пт d(\/r)/(n + 1) ,
и затем проинтегрировать по частям еще раз.
Комбинируя формулы F.9.26)—гF.9.28), получаем
Интегралы /j и /2 можно привести к безразмерному виду с помощью
соответствующих подстановок для политропы, как в разд. 3.3. В результате
?^??? = -кМ'^/у/\ F.9.30)
168 Глава 6
где
E - n)[i\\e-{i,)^
7/3
5 + 2п- п^ ^ /·{,
(и + 1) Jo
^'
^{п - \)p'i^H^di
F.9.31)
Упражнение 6.20. Проверить формулы F.9.30) и F.9.31).
Интегралы в F.9.31) вычисляются численно, политропные функции при
этом находятся либо путем одновременного решения уравнения Лейна —
Эмдена, либо из результатов Сервиса [519]. Для случая п = 3 имеем
?^??? = -0,918294 ?'/?/^ F.9.32)
6.10. УСТОЙЧИВОСТЬ БЕЛЫХ КАРЛИКОВ В ОБЩЕЙ ТЕОРИИ
ОТНОСИТЕЛЬНОСТИ
Чтобы исследовать устойчивость белого карлика с учетом эффектов общей
теории относительности, запишем полную энергию в виде
? = ?i„, + ?g,av + ???„. + Д^отя- F.10.1)
В первом приближении присутствуют только два первых члена. Их можно
найти для политропного распределения плотности.
E,,,^judm^j^dm = KpY-M-^jh'e-^'di. F.10.2)
^.av = -Gj'^dm = D.?,)'/^|^/;-?3,,,.,?. F.10.3)
Последний интеграл преобразуется к виду
И может быть вычислен с помощью интегрирования по частям. В
сущности это уже было сделано при выводе формулы C.2.11), где для
политропы было получено
^-v —5^-?- F.10.5)
Равновесие и устойчивость жидких тел 169
Из результата, приведенного в упражнении 3.4, получаем
следовательно,
1/3
F.10.7)
?.rav=-5^GMV3pl/3
47гв'
Сравнивая этот результат с формулами F.10.3) и F.10.4), получаем
Таким образом.
где
ree"^'di = ^i\\ef. F.10.8)
?;„, = k,KpY"M, F.10.9)
^grav = -kfipY'M'/\ F.10.10)
ф^М) Ml =1,75579, F.10.11)
5 - w ??
3 KTT^fgy/^
^2 =-^t^'f' = 0,639001. F.10.12)
Численные значения /Tj и /Tj даны здесь для а2 = 3.
Член AEjj^j обусловлен отличием уравнения состояния от политропы с
А2 = 3, которое связано с тем, что электроны не полностью релятивистские.
Внутренняя энергия на единицу массы равна
u^'s^^, F.10.13)
где
Р = РО^ ^е^и^е- F.10.14)
Используя формулу B.3.20), получаем
"=IS?('-I4—)¦ <^'"''>
где х>1 — релятивистский параметр.
170 Глава 6
Пропорциональный ? член в формуле F.10.15) равен просто ЗР/р, это
выражение было использовано выше при вычислении ?^^1- Следующий
член — постоянный; его можно опустить при использовании
вариационного принципа, так что поправка равна
Согласно формулам F.10.14) и B.3.4),
Интеграл в F.10.16) можно вычислить с распределением плотности,
отвечающим политропе с А2 = 3; вносимая при этом ошибка имеет более
высокий порядок. Таким образом.
wV
A^int = к, - ,2/з^Рс-'^\ F.10.18)
где
При А2 = 3 ЭТОТ интеграл равен 4,32670, так что
/Гз= 0,519723. F.10.20)
Поправка, обусловленная общей теорией относительности, по формуле
F.9.32) равна
?????= -k,^^M'/V/\ F.10.21)
^4 = 0,918294. F.10.22)
Таким образом, полная энергия, определенная в F.10.1), имеет вид
? = {AM - ВМ^/')рУ' + СМр;'/' - DM'/y/\ F.10.23)
где
А=к,К, B^kfi, С = к,^^ ' ^^3' D^k,^-. F.10.24)
Равновесие и устойчивость жидких тел 171
Равновесие достигается при дЕ/др^=0. Отсюда следует
{AM - ВМ'/'Цр;^/' - \СМр;'/' - |/)М^Зр-1/з = 0. F.10.25)
Основное приближение соответствует отбрасыванию членов,
пропорциональных С и D. При этом для массы получается формула Чандрасекара:
^=(|Г = *»^5''(^)"'^о, F.10.26)
где для К мы воспользовались формулой B.3.23). Члены с С hD дают
зависящие от р^ малые поправки к Л/.
Устойчивость нарушается при д^Е/др^, т.е. при
-И(^М - ВМ'/')р-'/' + ИСМр,-'/' + ЦПМ'/\-^/' = 0. F.10,27)
Решим уравнение F.10.25) относительно АМ—ВМ^^^ и подставим
результат в F.10.27). Поскольку теперь все величины одного порядка малости,
можно заменить Л/ на (?/??^^. В результате
^ СВ^ 16^3^2 ^We
^' DA" C^2J/3^^^^^2 ?>^
= 2,646 ? ??^^?^j' г/смЗ. F.10.28)
Это критическая плотность, при которой белый карлик теряет
устойчивость из-за эффектов общей теории относительности. Заметим, что для
^^е (?^= 2,154) получается р^=3,07· 10^^ г/см^. Это значение выше порога
обратного ]3-распада, 1,14· 10^ г/см^ (см. табл. 3.1), так что общая теория
относительности не нужна для железных белых карликов. Для ^Не или ^?
плотность р^ принимает значение 2,65· 10^^ г/см^, которое ниже порогов
нейтронизации, 1,37· 10^^ и 3,90· 10^^ г/см^ соответственно. В этих случаях
плотность в центре ограничена именно эффектами общей теории
относительности^ \
Упражнение 6.21. Энергия звезды со значением Г вблизи 4/3 также записывается в
виде [ср. формулу F.8.9)]
? = аМр^-' - k^GM'/'pY' - k,^^M'^V/\ F.10.29)
^^ Ядерные реакции при высокой плотности (см. разд. 3.5) ограничивают
плотность в углеродных белых карликах, р^<: 1· 10^^ г/см^, но точное значение этой
границы неизвестно. (См. разд. 3.7.)
172 Глава 6
Здесь ? — некоторая постоянная. Показать, что критическое значение Г, при
котором нарушается устойчивость, благодаря эффектам общей теории относительности
увеличивается так, что
г-1-1,125(^). F.10.30)
Указание. Исключить а, используя условие дЕ/др^=0.
Упражнение 6.22. Какое максимальное гравитационное красное смещение
предсказывается для сферического белого карлика, состоящего из ^Не, ^^, ^^^е? Сравните
ваши результаты с работой Шапиро и Тьюколски [532].
Упражнение 6.23. Вычислить ^М/М^^, относительную разность масс белого
карлика и звезды в пределе Чандрасекара при критической плотности F.10.28).
Результаты, приведенные в формулах F.7.18) и F.10.30), можно
объединить, записав приближенную формулу:
.2 = Ш
(ЗГ,-4)-)8^^
F.10.31)
где jS — числовой множитель. В случае белых карликов с малой массой
преобладает первый член. Основная частота колебаний возрастает при
увеличении массы (?^-Cp). Период колебаний падает от значений порядка
20 с при Л/= О,4Л/0 до 6 с при Л/= IMq .
Упражнение 6.24. Показать, что для ультрарелятивистского вырожденного
электронного газа
Г,-|-^. F.10.32)
Из этой формулы вытекает, что первый член в скобках в F.10.31) ведет
себя как р~^^^, т.е. как /?^, при M-^Mqy^. Однако I Ж1//-/?~^, поэтому ?^
продолжает расти при M-^Mq^, ньютоновские белые карлики устойчивы.
Член, обусловленный общей теорией относительности в F.10.31), меняется
как \/R\ из-за него ?^ проходит через максимум и затем меняет
знак — звезда теряет устойчивость. Соответствующий минимальный
период колебаний составляет около 2 с (см., например, [139]). Это значение
очень важно, ибо позволяет исключить возможность интерпретации
пульсаров как пульсирующих белых карликов: известны пульсары с весьма
малыми периодами — вплоть до 1,56 мс.
Глава 7
Вращение и магнитные поля
7.1. УРАВНЕНИЯ МАГНИТНОЙ ГИДРОДИНАМИКИ
Мы дадим здесь сводку уравнений магнитной гидродинамики (см.,
например, книгу Джексона [297]).
Если вещество находится под действием электромагнитных сил, то
уравнение Эйлера F.1.2) принимает вид
р^= -??-??? + -^???. G.1.1)
Здесь J — плотность тока и В — напряженность магнитного поля. В
астрофизике вещество редко обладает ненулевым полным зарядом. Поэтому,
вообще говоря, в уравнение следует добавить член р^Е, где р^ — плотность
заряда, которым мы пренебрегли. Если скорость движения вещества ?
намного меньше, чем скорость света (в астрофизике чаще всего так и
бывает), то в уравнении Максвелла:
с ot с
можно пренебречь током смещения. Тогда
-J X В = -^-(V X В) X В. G.1.3)
с Лтг
Исполыуя векторное тождество
^V(B · В) = (В'· V)B - (V X В) X В, G.1.4)
уравнение G.1.1) можно переписать в виде
?^=_??-???-^??^ + ^(?.?)?. G.1.5)
Электрическое поле ? обычно связано с током J и магнитным полем В
законом Ома:
Л = а(Е + ^Хв). G.1.6)
Здесь ? — проводимость, которая считается постоянной. Формула G.1.6)
обобщает соотношение ? = ??, справедливое в покоящейся системе отсчета,
и учитывает член первого порядка по ?/с.
174 Глава 7
Изменение поля В во времени определяется законом Фарадея:
if--VXE, G.,.7)
который, с учетом формул G.1.6) и G.1.2), а также уравнения VB = 0,
приводится к виду
^=^^(,><B) + ^V^B. G.1.8)
Нередко проводимость можно принимать бесконечно большой, так как
времена, характерные для омических потерь, велики по сравнению с
временами процессов, которые мы сейчас рассматриваем. Такая среда
называется «идеально проводящей»; в этом случае из G.1.6) следует
Е + -ХВ = 0, G.1.9)
и формула G.1.8) приводится к виду
-^= V X (? X В). G.1.10)
Это уравнение интерпретируется следующим образом: магнитный поток
через любой контур, движущийся вместе с идеально проводящей средой, не
меняется со временем — силовые линии «вморожены» в вещество^\
При рассмотрении эффектов магнитного поля в белых карликах
оказалась полезной скалярная теорема вириала. Умножим скалярно уравнение
G.1.5) на радиус-вектор ? и проинтегрируем по всему объему звезды V.
Поскольку ? = ???/??, то
Следовательно, левая часть уравнения G.1.5) принимает вид
1 d^I
2^,.-27-, G.1.12)
где /= [px^d^x — обобщенный момент инерции, а
T = ^Jpv4h G.1.13)
''^ Точнее говоря, из G.1.10) следует, что магнитный поток ф^^\^Ва8 через
любую замкнутую поверхность S, движущуюся вместе с веществом, постоянен. При
этом элемент среды, который вначале был нанизан на магнитную силовую линию,
остается на ней навсегда.
Вращение и магнитные поля 175
— кинетическая энергия. Мы воспользовались здесь тем фактом, что
для любой величины Q в сплошной среде.
Член, содержащий давление, приводится к виду
- fx · vPdh = - /? · i^P) d^x + /^V · X ^^дс = 0 + ЗП, G.1.15)
где
U^fpd'x. G.1.16)
Здесь мы учли, что на границе объема V давление ? обращается в нуль.
Гравитационный член записывается в виде
-fpx · ???^? = Gffd^xd^x'pix)x · Vt^^
-^-^ |x - \?
= ^/^'^?(?)?(?)= W. G.1.17)
Это гравитационная потенциальная энергия.
Аналогично формуле G.1.15) можно показать, что член,
пропорциональный ЧВ^, приводится к виду 3 Ш , где
Ж = :У[вЧ'х G.1.18)
—- магнитная энергия. Мы устремили границу объема V к бесконечности,
чтобы оправдать отбрасывание поверхностного члена.
Так как V · В = О, то
х-(В· V)B = (В· ?)(?·?)-?·(?· v)x
= ? [В(х · В)] - 5\ G.1.19)
При интегрировании по всему пространству содержащий дивергенцию пер-
176 Глава 7
вый член обращается в нуль, поэтому интеграл от выражения вида G.1.19)
дает вклад - 2 2)? . В итоге получаем
|^ = 2Г+ Ж+ ЗП + дЦ. G.1.20)
Отметим, что величина ? равна 2/3 тепловой энергии нерелятивистских
частиц плюс 1/3 тепловой энергии релятивистских частиц.
Предполагая, что звезда находится в равновесии, мы приходим к
скалярной формуле вириала
2Г+ ff^+ ЗП +911 = 0. G.1.21)
7.2. МАГНИТНЫЕ БЕЛЫЕ КАРЛИКИ
Ограничимся вначале невращающимися белыми карликами. В этом случае
кинетическая энергия Г=0, и теорема вириала G.1.21) принимает вид
Ж+ ЗП + 911 = 0, G.2.1)
т.е.
где угловые скобки означают усреднение. В пределе высокой проводимости
магнитный поток
Фл/ - <«>Л^ G.2.3)
сохраняется при изменении радиуса звезды. В случае нерелятивистского
вырождения Я-р^^^, а при ультрарелятивистском вырождении Р=р^^^.
Соответственно по соображениям размерности из G.2.2) в первом случае
следует
О = -«з/2-?- + ^3/2-^ + Уз/2^' G·2·^)·
а при ультрарелятивистском вырождении
где нижний индекс у безразмерных положительных констант а, ? и ?
указывает показатель политропы, а? = 3/2 или а2 = 3, описывающий каждый из
этих двух режимов.
В обоих случаях эффект магнитного поля состоит в некотором
растяжении звезды. Грубо говоря, добавление магнитного потока эквивалентно
Вращение и магнитные поля 177
«уменьшению» гравитационной постоянной С до величины
0' = в-Щ^с{\-^\. G.2.6)
Для белых карликов с нерелятивистским вырождением можно решить
уравнение G.2.4) относительно радиуса R равновесного состояния:
^ ^3/2 ^ ^0 ?? 2 ?\
«з/гС'М'/з l-91l/|iF|' ^-^
где Rq — радиус при В = 0. При малых отношениях
радиус звезды возрастает незначительно.
Для белых карликов с ультрарелятивистским выpoждeниe^! следует
прежде всего отметить, что при Ь< 1 предельная масса возрастает лишь на
небольшую величину. Решая уравнение G.2.5) относительно Л/, находим при
Ь<\
и, следовательно,
М^^ = М,{\+Щ G.2.10)
где Л/о=(/Зз /oL-pY^^ — предельная масса Чандрасекара при В=0 (см.
формулу C.3.17)).
Однако радиус звезды в случае ультрарелятивистского вырождения для
масс вблизи М^^^ может существенно возрастать даже при малых
значениях ?. Причина этого состоит просто в том, что при Ь<\ состояние звезды
весьма близко к политропе с а2 = 3, так что, согласно формуле C.2.10),
полная энергия имеет вид
Е^ -^-Y^\W\^\W\. G.2.11)
Поэтому даже небольшое изменение ? может оказывать значительное
влияние на /?:
^^-^. G.2.12)
? R
Полагая здесь ??'=? 9Ji, получаем
?? 3 ?911 3
R 3- ? \W\ 3 - я
12-353
??. G.2.13)
178
Глава 7
-1,95
-2.00 h
Ос:
5> -2,05
-2,10 К
-2J5
\-^
' I
— 5
1 1
1 1
.4
1 1
' 1
"-^^^
1 1
1 1
^3 ^
1 1
1 ' —
·1
1
0,00
0,02
O.OA 0,06
m./\w\
0.08
0.10
Рис. 7.1. Радиус белого карлика как функция магнитной энергии и углового
момента. Для звезды с массой 1,05 М^ (типа Сириуса В) показана зависимость радиуса R
от отношения магнитной и гравитационной энергии, \Ш/\У\\ R — большая из двух
величин, представляющих расстояния от центра до экватора и до полюса. Кривые,
обозначенные цифрами 7, 2» 3, 4, 5, отвечают последовательностям звезд, имеющих
угловые моменты (О, 1, 2, 3, 4)· 1,92· 10'*^ г-см^/с соответственно. (По работе [433].)
Интегрируя и считая ? постоянным при росте ?, получим
Л = ^оехр(у4^в).
G.2.14)
Таким образом, радиус существенно возрастает даже при малых ?.
Численная модель однородно вращающихся белых карликов с
магнитным полем была построена в работе Острикера и Хартвика [433]. Было
обнаружено, что для невращающейся звезды с массой 1,05 Mq (типа Сириуса
В) увеличение радиуса может описываться множителем expC,5?) (рис. 7.1).
В предельных случаях, когда ?-0,1 и радиус возрастает на 40<?^?, поле в
центре достигает 10^^'^ Гс, хотя на поверхности звезды поле на несколько
порядков ниже.
Разумно ли говорить о столь сильных полях? Поскольку при сжатии
звезды в ходе эволюции к стадии белого карлика магнитный поток
сохраняется, то и звезды — предшественники таких белых карликов должны
иметь сильные магнитные поля; из соотношения
л?Д = л^Д
wd •*'wd 4
G.2.15)
где индекс «/» соответствует звезде-предшественнику, «wd» — белому
карлику, следует, что в центре звезды-предшественника напряженность поля
должна составлять
В; ~ 10
10"
10
и
10" Гс,
G.2.16)
Вращение и магнитные поля 179
в предположении, что К^-^к^. Следовательно,
91L, 91L.
^wd
1^1 l^wdl
G.2.17)
и величина этого отношения не превосходит нескольких процентов.
Хотя и нет данных, которые бы свидетельствовали в пользу
существования таких полей^\ они не исключаются проведенными наблюдениями.
Более того, сжатие «типичного» межзвездного облака с радиусом -0,1 пс,
массой - 1Л/0 и вмороженным полем В величиной 3· 10~^ Гс при
образовании звезды из этого вещества должно приводить к магнитным полям
порядка 10^ Гс (см. [549], разд. 13.Зе).
Результаты Острикера и Хартвика показывают, что с увеличением поля
радиус возрастает, а р^. падает. В принципе магнитные поля умеренной
величины могут существенным образом влиять на зависимость радиуса от
массы, особенно для более массивных белых карликов.
Однако до сих пор наблюдения не давали свидетельств в пользу столь
сильных внутренних магнитных полей. Радиус звезды Сириус В в точности
соответствует кривой Хамады — Солпитера для звезд с нулевым полем
(см. разд. 3.6). Приблизительно 5Щ из числа наблюдаемых белых карликов
обладают поверхностными магнитными полями в диапазоне 10^—10^ Гс
(см., например, [13, 343]). Величина соответствующего внутреннего
магнитного поля зависит от модели; вероятно, она должна лежать в пределах
10^—10^^ Гс. Такие поля слишком слабы, чтобы существенно влиять на
динамику при MisMq.
7.3. ВРАЩАЮЩИЕСЯ СИСТЕМЫ: СФЕРОИДЫ МАКЛОРЕНА
Наши представления о вращающихся гравитирующих телах основаны
главным образом на изучении эллипсоидов с однородной плотностью,
динамика которых анализируется сравнительно просто (подробное изложение
можно найти в книге Чандрасекара [116]). Простейшие однородные
эллипсоиды такого типа — сфероиды Маклорена, вращающиеся с однородной
угловой скоростью.
В произвольной точке (х, у, ?) внутри однородного эллипсоида
гравитационный потенциал является квадратичной функцией координат:
? = -7гОр[А - А,х^ - А^у^ - ?,?^], G.3.1)
где постоянные Л зависят только от формы эллипсоида, иА^-\-А2-\-А2=2.
Это следует из уравнения Пуассона,
?^? = 47rGp, G.3.2)
^^ Магнитные А-звезды имеют поля < 10^ Гс на поверхности.
180 Глава 7
где плотность ? постоянна. Коэффициенты Л можно найти изящным
геометрическим методом (см., например, [116]). В случае сфероида потенциал
? можно найти также с помощью функции Грина для уравнения G.3.2):
Функция Грина разлагается в сферических полярных координатах так:
1 °° r^
= ? —^Pi{cose)Pi{cose') + [члены, зависящие от 0], G.3.4)
где ? ? — полином Лежандра, '*<('*>) — меньшая (большая) из величин г и
г'. В силу азимутальной симметрии зависящие от ? члены не дают вклада
в интеграл в G.3.3). В полярных координатах поверхность сфероида
описывается уравнением Р = Р(в), где
где вис — большая и малая полуоси соответственно. Таким образом,
Ф= -2irGpEP,(cose)/ &???'??'?,{??5?') ?
/-0 •'о
Заметим преже всего, что все члены с нечетным / выпадают, так как Я,
является здесь нечетной функцией cos^', в то время как Я(в) — четная
функция. Среди интегралов отличны от нуля только те, в которых /=0 или
1=2: для членов с /^4 степени cos^', обусловленные зависимостью Я(в)у
никогда не превосходят /-2, так что из-за соотношения ортогональности
эти члены обращаются в нуль при интегрировании. Итак, мы имеем
Ф= -27rG,o(-|r2+ Г-—I—
I 3 Jo \/а^ +
dx
\/а^+ {\/с^- \/а^)х^
- (Зсоз^в - \)!^{^?{3?' - 1) Ig [^+(^- ^'^У'])' ^^'^'^^
где дг=со5^'. Эти интегралы вычисляются в элементарных функциях, и
после некоторых выкладок мы приходим к окончательному ответу:
Л1 = 7^2 = -^^ т^— arcsin е ,
Вращение и магнитные поля 181
, 2 2A-г^)'/' . ^
Л, = ^^ — arcsin в,
^ = i L— arcsm е, G.3.8)
где эксцентриситет, по определению, равен
В гидростатическом равновесии для однородно вращающегося
сфероида справедливо уравнение
dy 1
^=-^VP- ??, G.3.10)
где
? = ???. G.3.11)
Левая часть уравнения G.3.10) преобразуется к виду
= {Kfiim - КЛЖ^^т = ?,(?.?.) - ?'?,. G.3.12)
Считая, что угловая скорость направлена по оси ?, перепишем эту формулу
в виде
^= -a2(jce,+>;е^) = ах (?? г). G.3.13)
Легко видеть, что это просто центростремительное ускорение жидкости.
Итак, проекция уравнения G.3.10) на ось ? дает
а проекция на ось ? дает
-?2?= ---?--^-. G.3.15)
Так как ? — квадратичная функция координат, ? также должно быть
квадратичной функцией. Поскольку ? обращается в нуль на границе сфероида,
получаем
P^pU-L·J^.L·\ G.3.16)
2 2 Г
182 Глава 7
где Р^ — давление в центре сфероида. Используя формулу G.3.1), из
уравнения G.3.14) получаем
G.3.17)
?, = TtGpVA^
Из уравнения G.3.15) следует
fl2 = 2irGpM, -^г\
= 2-nGp
е
3A - е')
е^
G.3.18)
Момент инерции сфероида относительно оси вращения равен
/ = fMaS G.3.19)
где
M = V(l-e2)'/V G.3.20)
Соответственно момент количества движения
J = /?, G.3.21)
И кинетическая энергия
т={т\ G.3.22)
Упражнение 7.1. Показать, что гравитационная потенциальная энергия сфероида Ма-
клорена имеет вид
= -|(^^fGpV = ^l-e^). аз.23)
Отметим одно соотношение, полезное для параметризации сфероидов Ма-
клорена:
Х = _3_(,_?0Л?!Г)_, G324)
Устойчивость сфероидов Маклорена можно исследовать, вводя
нормальные моды или используя метод тензорного вириала [116]. Наиболее
интересное нарушение устойчивости возникает из-за двух нерадиальных «то-
Вращение и магнитные поля
183
Рис. 7.2. Квадрат угловой скорости (в единицах ???) для последовательностей
сфероидов Маклорена и эллипсоидов Якоби. По оси абсцисс отложен эксцентриситет,
определенный по формуле G.3.9). (По книге Чандрасекара [П6].)
роидальных» мод, содержащих зависимость от азимутального угла,
ехр(±2/ф). Эта пара мод становится динамически неустойчивой (?^<0) при
е> 0,952887, что соответствует Г/1 W^l > 0,2738. Вековая неустойчивость
возникает на последовательности сфероидов Маклорена при меньших
эксцентриситетах, ?=0,812670, Г/1 W^l =0,1375. Частота одной из мод
обращается в нуль в этой точке, однако по обе стороны от нее ?^ остается
положительным. При ?^=0 наряду со сфероидом Маклорена существует и
другая равновесная конфигурация. В действительности Г/1 W^l =0,1375
является точкой бифуркации у в которой от последовательности Маклорена
ответвляется другая последовательность равновесных конфигураций. Эта
новая последовательность состоит из эллипсоидов Якоби ^ вращающихся
однородных тел с эллипсоидальной поверхностью. Угловые скорости и
моменты количества движения сфероидов Маклорена и эллипсоидов Якоби
показаны на рис. 7.2 и 7.3.
При заданных моменте количества движения, массе и объеме эллипсоид
Якоби имеет более низкую энергию, чем соответствующий сфероид
Маклорена (рис. 7.4). Отсюда следует, что выше точки бифуркации сфероиды
Маклорена должны быть неустойчивыми и переходить в эллипсоиды
Якоби. Однако в системе, описываемой динамическими уравнениями, энергия
184
Глава 7
Рис. 7.3. Момент количества движения [в единицах {??4?^^] для
последовательностей сфероидов^аклорена и эллипсоидов Якоби [параметрит связан с тремя
главными полуосями, a-{abcY^^y причем для сфероида а = Ь]. В обоих случаях по оси
абсцисс отложен эксцентриситет, определенный по формуле G.3.9). (По книге Чандра-
секара [116].)
сохраняется, если только в них не введены диссипативные члены.
Неустойчивость, для развития которой необходима диссипация энергии, называется
вековой в отличие от динамической неустойчивости. Добавление диссипа-.
тивных членов в динамических уравнениях, описывающих развитие
возмущений, приводит к тому, что при прохождении точки бифуркации ?
приобретает мнимую часть, пропорциональную масштабу диссипации, т.е.
коэффициенту вязкости. В противоположность этому время нарастания
динамической неустойчивости целиком определяется динамикой, оно порядка
{Gp)-'^l
Поскольку на самом деле ?^=0 является кратным корнем при
Г/1 W\ =0,1375, то в той же точке от последовательности Маклорена
помимо эллипсоидов Якоби ответвляется еще одна последовательность
равновесных конфигураций: эллипсоиды Дедекинда. Они имеют ту же форму,
что и эллипсоиды Якоби, но их форма стационарна: эллиптическая
поверхность поддерживается циркуляцией жидкости внутри тела.
Вращение и магнитные поля
185
0.2
ОЛ
-Г"
0.6 _18^ 1^
?
1Л
1.6
^-0,99920 J
^=0
? = 0,81267
J L
±
Рис, 7,4. Полная энергия E=T+IV как функция момента количества движения для
сфероидов Маклорена и эллипсоидов Якоби. Величина а связана с тремя главными
полуосями, а = {аЬсУ^^у причем для сфероида а = Ь, Для некоторых конфигураций
указана величина эксцентриситета, определенного по формуле G.3.9); показана точка
бифуркации (? = 0,81267) и точка возникновения динамической неустойчивости
(? = 0,95289).
Выше точки бифуркации сфероиды Маклорена обладают вековой
неустойчивостью и по отношению к эллипсоидам Дедекинда. Однако
благодаря вязкости дифференциальное вращение затухает, так что эллипсоиды
Дедекинда при наличии вязкости не являются равновесными. Необходимая
для перехода в другое состояние диссипация связана в этом случае с
потерями энергии на гравитационное излучение (см. работу Чандра-
секара [117]).
Если существенны и вязкость, и гравитационное излучение, то ситуация
становится более сложной [160]. Мода Якоби, которая деформирует
сфероид Маклорена, превращая его в эллипсоид Якоби, и которая неустойчива
при наличии вязкости, стабилизируется гравитационным излучением. Мода
Дедекинда, неустойчивость которой связана с гравитационным излучением,
стабилизируется вязкостью. Можно так подобрать соотношение между
вязкостью и гравитационным излучением, что все состояния на
последовательности Маклорена будут устойчивыми вплоть до точки динамической
неустойчивости. Возможно, что в астрофизических приложениях вязкость
186 Глава 7
недостаточно велика, чтобы быть существенной, но этот вопрос остается
неясным.
Как будет показано в следующем разделе, сжимаемые конфигурации с
твердотельным (однородным) вращением не представляют особого
интереса. При рассмотрении объектов, плотность которых возрастает к центру,
можно видеть, что допустимая скорость вращения, мерой которой
является, например, отношение T/\IV\, строго ограничена условием, чтобы в
области вблизи экватора не происходило истечения вещества. При
твердотельном вращении объекты, конденсированные к центру, начинают терять
массу еще до того, как скорость их вращения достигает величины, при
которой появляются «интересные» неустойчивости.
Однако при рассмотрении объектов, скорость вращения которых
неоднородна ^ отношение T/\W\ в равновесном состоянии может существенно
выходить за рамки, определяемые теоремой вириала, О^Г/1 W\ ^ 1/2 [см.
формулу G.1.21)]. При этом вновь возникает вопрос о неустойчивых
конфигурациях, не обладающих осевой симметрией. Для грубой оценки мы
примем следующие значения: Т/\\?\^ОуЫ для вековой неустойчивости
и T/\W\'^0,2b для динамической неустойчивости. Эти значения близки к
полученным для сфероидов Маклорена, и, по-видимому, на них можно
ориентироваться при самых различных распределениях момента количества
движения и уравнениях состояния. Далее этот вопрос обсуждается в
разд. 7.5.
7.4. ВРАЩАЮЩИЕСЯ БЕЛЫЕ КАРЛИКИ
Рассмотрим теперь конфигурации типа белых карликов, в которых нет
магнитного поля, но есть вращение. Кинетическая энергия вращения —
порядка
T-MQ^R"-^, G.4.1)
где J — (сохраняющийся) момент количества движения. Уравнение вириала
G.1.21) для вращающихся звезд принимает теперь вид [ср. формулы G.2.4)
и G.2.5)]
О = -«3/2-^ + 'Сз/,^^ + ^3/2^^ G.4.2)
для нерелятивистского вырождения и
0=-«3-^+K3^j^ + ft-^ G.4.3)
ДЛЯ ультрарелятивистского вырождения. То обстоятельство, что энергия
вращения в релятивистском пределе более круто зависит от радиуса, чем
внутренняя энергия, весьма существенно. При любой массе всегда может быть
Вращение и магнитные поля 187
достигнуто равновесие, если уменьшить радиус тела. Таким образом, при
любой массе можно построить равновесную модель, если момент
количества движения отличен от нуля. Разумеется, такие модели могут
оказаться нефизическими, например если приходится уменьшить радиус до
таких размеров, что плотность возрастает до 10^^ г/см^ и принятое нами
уравнение состояния неприменимо. Кроме того, такие модели становятся
неустойчивыми относительно обратного ]3-распада, слияния ядер, быстрой
эволюции, обусловленной вязким переносом импульса, и других процессов.
Используя численный метод, Джеймс [298] построил модель твердо-
тельно вращающегося белого карлика, в которой удовлетворяется
уравнение состояния Чандрасекара. Для таких тел структура моделей в целом не
очень отличается от случаев, когда вращение отсутствует. В частности,
предельная масса может возрасти не более чем на 3,5^о при заданном ?^.
Это вполне естественно, ибо, как будет показано ниже, для тел с
повышением плотности к центру твердотельное вращение возможно лишь при
условии T/\W\ < 0,007, а при этом структура тела не претерпевает серьезных
изменений по сравнению со случаем, когда вращения нет. Действительно,
из формул G.4.3) и G.1.21) следует
Разрешая это уравнение относительно М, получаем
М =
)8з
afi{\ - 2T/\W\)
= Mo[l+ij^) = b02Mo, G.4.5)
где Mq — предельная масса Чандрасекара при отсутствии вращения. Эта
оценка в целом согласуется с результатами Джеймса.
Рассмотрим теперь вывод ограничения O^T/\W\ ^0,00744 для
твердотельного вращения тела, состояние которого описывается политропой с
А2 = 3. Будем следовать книге Зельдовича и Новикова [636]. Заметим, что
для политропы с А2 = 3 ПЛОТНОСТЬ в центре в 54 раза превосходит среднюю
плотность (упражнение 3.4), так что этот объект действительно сильно
сжат к центру.
Рассмотрим прежде всего сферическую звезду, вращающуюся со
скоростью, соответствующей отрыву вещества на экваторе,
C2 = ?2^J2^^ G.4.6)
к
Для политропы С А2 = 3 (см. формулу C.2.11)]
' ' 5-п R 1 R ^ '
188 Глава 7
Кинетическая энергия равна
?=^/?2, G.4.8)
где
Значение этого интеграла равно 10,851, так что
<г2> = 0;11303Л^ G.4.10)
Используя формулу G.4.6) для ?^, получим, что на пределе разрушения
звезды
_7^^1|М<г^ G.4.11)
\W\ \Gk^/R
В противоположность этому для несжимаемой жидкости (а2—0) имеем
И, следовательно, на пределе разрушения звезды
Щ-\. G.4.13)
Сопоставление этих результатов демонстрирует роль повышения
плотности в центре звезды как фактора, понижающего верхний предел скорости
вращения для политропных конфигураций.
В этом выводе мы пренебрегли тем, что в действительности
вращающиеся тела имеют сфероидальную форму, т.е. радиус на экваторе
превосходит среднее значение, R^>R, Приближенный анализ равновесной формы
можно провести на основе модели Роша. В этой модели предполагается,
что распределение массы в основном не меняется при вращении; это
разумное приближение, так как плотность к центру звезды повышается.
Поэтому в наружных слоях гравитационный потенциал имеет обычный вид,
Ф=—см/г. При постоянной угловой скорости вращения вокруг оси ?
можно ввести центробежный потенциал:
ф^= _^?2(^2^^2)^ -{й'г^ппЧ, G.4.14)
При этом
f = ??. G.4.15)
Вращение и магнитные поля
189
^г
Рис, 7,5. Форма потенциала Ф + Ф^ вдоль радиального направления в экваториальной
плоскости (сплошная линия) и вдоль полярной оси ? (штриховая линия).
Горизонтальные прямые Xj и К^ соответствуют различным значениям константы К в
формуле G.4.17) (Зельдович и Новиков [636].)
[см. формулу G.3.13)], и уравнение гидростатического равновесия G.3.10)
принимает вид
О = -VP+ ?(? + Ф^,
G.4.16)
Л + ? + ?, = /:,
G.4.17)
где К — константа, а
J ? Г- 1
?
G.4.18)
— удельная энтальпия. Будем предполагать, что константа К в формуле
G.4.17) та же, что и в отсутствие вращения. Поскольку Л(/?)=0, то
^=--^- G.4.19)
Эффективный потенциал, ?^^^=? + ?^, показан на рис. 7.5. В плоскости
экватора Ф^^^ имеет максимум при значении радиуса r^=(GM/Q^Y^·^, причем
максимальное значение Фтах= -ViGM/r^,
Уравнение G.4.17) имеет разумное решение лишь при условии, что h
обращается в нуль на некотором расстоянии от центра, r=/?j, т.е. на
поверхности тела. Поскольку Л (г) — расстояние от точки на кривой *eff('*) ^^ ^^'
НИИ *eff=^ (^^· Р**^· ^-^?» "^^ ^^^ видим, что К ДОЛЖНО быть меньше, чем
? . Если А'=Фтах» '^^ ^1 принимает максимальное значение, равное
190 Глава 7
r^=V2R, Таким образом, твердотельно вращающаяся звезда растягивается в
плоскости экватора максимум в полтора раза. Соответствующее
максимальное значение угловой скорости равно
И отличается множителем (^)^^^^=0,544 от максимального значения для
сферического случая [см. G.4.6)]. Отсюда следует
(Г/1 И^1)тах= (-)^^^х (значение для сферы) =0,00744. G.4.21)
Ситуация здесь существенно отличается от случая сфероидов Маклорена,
которые существуют (хотя и теряя устойчивость) вплоть до T/\W\ =0,5.
Джеймс [298] показал, что для политропы с индексом а? > 0,808
истечение вещества с экватора для твердотельно вращающихся звезд начинается
ниже точки бифуркации. Однако этот предел на скорость вращения едва ли
имеет физический смысл. По-видимому, реальные звезды вращаются не
как твердое тело, по крайней мере в своих наружных слоях, так что
приведенный выше анализ просто показывает, что твердотельно вращающиеся
конфигурации не подходят в качестве моделей для быстро вращак»щихся
звезд.
При потере момента количества движения звезды сжимаются, и
отношение T/\W\ должно расти как 1//?, поэтому вращение, вероятно, более
существенно для компактных объектов, чем для звезд главной
последовательности, от которых они происходят. Детальные модели
дифференциально вращающихся белых карликов были построены Острайкером и Боден-
хеймером [430] для звезд с массами в интервале от 0,5 до 4,1 Mq . (Модели
с T/\W\ :^0,41 соответствуют массам М-^ 2,4 Mq .) Каждая модель
определяется средним молекулярным весом ?^(=2), полной массой Л/, полным
моментом количества движения J и удельным распределением момента
Для рассмотренных моделей разность угловых скоростей разных слоев
не очень велика, во всех случаях ? (на экваторе)/й (в центре)^ 0,2. Радиусы
равновесных конфигураций равны 10^ см, с точностью до множителя
порядка 2, так что в этом рассмотренные модели не отличаются существенно
от моделей невращающихся звезд с массами в интервале @,4—0,9) М^.
Поскольку плотность в центре намного меньше 10^ г/см^, вещество
устойчиво относительно обратного ]3-распада, и принятое нами уравнение
состояния Чандрасекара остается справедливым. Для моделей с массами,
превышающими 1,4 Л/0, поверхностные скорости лежат в интервале 3000 —
7000 км/с. Линии водорода, наблюдаемые в спектрах большинства белых
карликов, имеют узкие ядра, поэтому подобные быстро вращающиеся
объекты должны быть весьма редкими.
По-видимому, звезды такого типа (если только они вообще
существуют) обладают высокой светимостью. Дюрисен [171] показал, что диссипа-
Вращение и магнитные поля 191
ция энергии, связанная с вязкостью (характерное время свыше 10^ лет), в
массивных моделях приводит к высоким внутренним температурам и све-
тимостям, превышающим 10~ ^ Lq. Хотя в спектрах белых карликов типа
DC нет отдельных линий (см. приложение А) и потому они могли бы быть
быстро вращающимися, их светимости лежат существенно ниже этого
значения.
Быстро вращающиеся белые карлики устойчивы относительно схлопы-
вания, вызванного обратным ]3-распадом, если ?^<^' 10^ г/см^ (точное
значение пороговой плотности зависит от состава звезды; см. табл. 3.1).
Будем считать, что они не имеют вековой неустойчивости при Г/1 W^l <0,14 и
динамически устойчивы при T/\W\<0,26 (см. разд. 7.5). Найдем теперь
примерный предел для массы таких звезд.
Вновь воспользуемся вариационным принципом для энергии, который
обобщает выражение F.10.23) с учетом вращения (см. книгу Зельдовича и
Новикова [636]). Сделаем два упрощающих предположения: а) на подобных
сфероидальных поверхностях плотности постоянны, б) вращение преобра,-
зует сферическую поверхность постоянной плотности в сфероидальную
поверхность, ограничивающую такой же объем. Строго говоря, второе
предположение справедливо лишь для несжимаемой жидкости, однако оно
неплохо выполняется в центральных областях сжимаемой звезды, где
сосредоточена большая часть ее массы. Если уравнение состояния имеет вид
Р=Р(р), то предположение (а) также выполняется лишь для несжимаемой
жидкости (см. разд. 4.4 в книге Тассуля [559]). И снова это предположение
приводит, как мы увидим ниже, к разумной числовой оценке, если большая
часть массы звезды заключена в ее ядре.
Из указанных предположений следует, что плотность как функция
массы, заключенной внутри данного слоя сфероидальной звезды, совпадает с
плотностью для сферической звезды, имеющей ту же плотность в центре.
Поэтому, как и в формуле F.10.9), имеем
Einx^ judm
= k.KpY'M, G.4.22)
Гравитационная потенциальная энeJpгия для шара с постоянной
плотностью (политропа с А2 = 0) равна
^=_3GMi_3J^y/3^^3/3^,/3. G.4.23)
Соответствующее выражение для сфероида постоянной плотности G.3.23)
" ид
3 GM4rcsing ^ _1 (:1^ V'^^i^f5/3.1/aarcsine ^, ^2?/^
G.4.24)
имеет вид
f2
^= -f ^^^ = -|(t)"'^^^'V/'^' о - ^')
192 Глава 7
Для сферического тела в состоянии политропы с а2 = 3 формула F.10.10)
дает
W^ ^k^GM'^r/\ G.4.25)
Покажем теперь, что для политропы с а2 = 3 при наших предположениях
вращение модифицирует W так же, как и для однородной звезды:
W = -ifc,GMV3p'/3 аг^е ^^ _ ^^у/б G.4.26)
Этот результат следует из теоремы Ньютона, согласно которой потенциал
внутри эллипсоидальной оболочки с постоянной плотностью постоянен.
[Это можно показать^\ вычитая друг из друга два выражения вида G.3.1).]
Будем строить сфероидальную звезду, начиная с внешнего
сфероидального слоя с постоянной плотностью. Внутри этого слоя поместим
следующий, с постоянной, но несколько более высокой плотностью, и т.д.
Каждый слой помещается в полость, в которой потенциал постоянен. Полная
потенциальная энергия будет меньше, чем потенциальная энергия
сферической звезды, во столько же раз, во сколько потенциал внутри
сфероидальной полости меньше потенциала в сферической-полости того объема и с
той же внешней массой. Их отношение определяется множителем
^????(?-,2)./6 G.4.27)
Отсюда следует формула G.4.26). Удобно ввести параметр,
характеризующий сплюснутость:
?-(^) -{\-е^' G.4.28)
и обозначить выражение в G.4.27)
g(X) ^ \'/\\ - Х'У'^^ arccos (?^/'). G.4.29)
При этом
W= -k^GM^/'pY'giX), G.4.30)
Вычислим теперь энергию вращательного движения:
T-J-J. G.4.31)
^^ Простое геометрическое доказательство приводится в разд. 17 книги Чандрасе-
кара [116].
Вращение и магнитные поля
193
Для сфероида locMa^ отношение моментов инерции сфероида и сферы
одного и того же объема равно
1
Sphere {a^cY^' ?*
Из формул G.4.9) и G.4.31) получаем
? ^ ks\J^M-'/y/\
где
*5 = -^—\?, = 1.2042.
G.4.32)
G.4.33)
G.4.34)
Таким образом,
? = к.КМрУ - k^GM^/y/'giX) + k^\J^M-^/y/\ G.4.35)
Членами AEj^^^ и AEqjj^ можно пренебречь, так как они малы и играют
роль только при исследовании радиальной устойчивости.
Равновесие определяется условием дЕ/др^=0=дЕ/д\ при
фиксированных Л/ и У. Из условия дЕ/д\ = 0 следует
^^ ' k^fiM''^/' \W\ ? ¦
Используя формулу G.4.29), получаем
\W\ 2
1 +
3?3
3XV2
1 - ?^ A - X')'/^arccos ?'/2
G.4.36)
G.4.37)
Эта формула аналогична соотношению G.3.24) между эксцентриситетом е
и отношением T/\W\ для сфероида Маклорена.
Из условия дЕ/дрс=0 следует
\к,КМр;'/' - \kfiM'/hWp7'^' + \к,\РМ-'/\''' = о, G.4.38)
Т.е.
13-353
\к,КМр:'/' - i/:,GMV3g(X)p-V3|i - |f|) = 0. G.4.39)
194 Глава 7
Следовательно,
kfig{X){\ - 2T/\W\) ] [^(?)(? _ ??/\\?\)?^' ' ^''¦'*'*^^
где Mo=Mch= l,457B/ii^JMQ .
Максимальная равновесная масса для вращающейся конфигурации, не
подверженной вековой неустойчивости, получается, если подставить в
формулы G.4.37) и G.4.40) значение Г/1 Wl «0,14. В результате
? = 0,693, g(X) = 0^974,
? = i^TOMo = 2,5G) ^°' ^'^¦^¦^^'^
Эта величина в точности совпадает со значением, полученным в работах
Дюрисена [172] и Дюрисена и Имамуры [173] путем детальных вычислений
для предельной массы, не подверженной вековой неустойчивости. Столь
хорошее согласие, скорее всего, связано с тем, что в моделях Дюрисена
дифференциальное вращение выражено не очень сильно.
Масса, соответствующая пределу динамической устойчивости,
находится подстановкой в формулы G.4.37) и G.4.40) отношения T/\W\»0,16. В
результате получаем
? = 0,475, g(X) = 0,902,
M=3,51Mo = 5,l(^J Mo G.4.42)
в разумном согласии с полученным Дюрисеном значением Л/= 4,6 Mq .
При Г/1 W^l ;г0,14 диссипация происходит путем гравитационного
излучения. В этом случае характерные времена порядка 10^—10^ лет ([208]; см.
упражнение 17.7), в то время как характерные времена для вязкой
диссипации порядка 10^ лет [117, 172].
Согласно данным Гринстейна и др. [245], белые карлики типа DA
вращаются медленно (линейная скорость вращения не превосходит 40 км/с, а
возможно, даже ниже 10—20 км/с), а быстро вращающиеся массивные
белые карлики не наблюдаются. Очевидно, что момент количества движения
теряется звездой-предшественником, находящейся в стадии красного
гиганта, еще до образования белого карлика.
Упражнение 7,2. Решить задачу, предложенную в упражнении 6.21, добавив
вращательные члены, как в формуле G,4.35), Показать, что критическое значение Г —4/3
понижается на величину 2(Уз—Г)Г/1 И^1, Отсюда следует, что вращение стремится
стабилизировать радиальные моды.
Вращение и магнитные поля 195
Упражнение 7,3, а) Распределение плотности внутри Солнца приблизительно
соответствует политропе с /7 = 3. Найти момент инерции Солнца. (Расчеты по детальной
модели Солнца дают 5,7· 10^^ гсм^.)
б) Угловая скорость вращения поверхности Солнца равна 2,9· 10~^с~^ Считая,
что Солнце вращается как твердое тело, найти его момент количества движения.
в) Чему равно отношение T/\W\ для Солнца?
г) Предположим, что Солнце внезапно сжимается и становится белым карликом,
причем 7 и Л/ не меняются. Чему в этом случае будет равно отношение T/\W\1
д) Согласно Аллену [8], типичная звезда спектрального типа В5, принадлежащая
главной последовательности, имеет массу М-6М^, радиус/?~ 3,8/?q и угловую
скорость на поверхности -9· 10~^ с~ ^. Полагая снова л = 3 в политропном
распределении плотности, повторить выкладки пп. (а)—(г). Показать с учетом указанных
предположений, что такая звезда должна при переходе в состояние белого карлика
потерять как массу, так и момент количества движения.
7.5. КРИТЕРИИ устойчивости ДЛЯ ВРАЩАЮЩИХСЯ ЗВЕЗД
В данной книге мы не сможем подробно обсудить этот, в сущности,
технический вопрос. Мы приведем лишь сводку результатов, уделяя основное
внимание вековой неустойчивости, играющей наиболее важную роль для
компактных объектов.
Важным первым шагом к выработке критерия вековой устойчивости
для сжимаемых вращающихся звезд был вариационный принцип Линден-
Белла и Острайкера [376]. Малые возмущения в звезде описывались
вектором лагранжева смещения ? (см. разд. 6.2). Предполагалось, что
конфигурация звезды обладает вековой устойчивостью в том и только в том
случае, когда некоторый оператор С (аналогичный оператору Kj в разд. 6.7)
положительно определен. Считалось, что это условие эквивалентно
положительности полной энергии возмущения для всех начальных данных.
Позднее, в период с 1968 по 1973 г., для исследования устойчивости
звезд с дифференциальным вращением использовался метод тензорного ви-
риала [431, 434, 560]. В этом методе рассматриваются моменты уравнений,
по которым развиваются возмущения. Вычисление второго момента
эквивалентно вычислению оператора С для пробного смещения ?, линейного по
координатам. В случае сфероидов Маклорена метод тензорного вириала
дает точное решение проблемы устойчивости, так как неустойчивая
собственная функция в этом случае действительно линейно зависит от
координат. Согласно этому методу, для сжимаемых звезд вековая неустойчивость
также возникает при Г/1 W^l «0,14 в широком диапазоне распределений
момента количества движения и уравнений состояния. Нечувствительность
критического значения T/\W\ к этим условиям — результат, весьма
примечательный.
Поскольку метод тензорного вириала эквивалентен выбору
определенной пробной функции в вариационном принципе
Линден-Белла—Острайкера, то, казалось бы, его можно рассматривать как достаточное условие
неустойчивости. К сожалению, это было бы неправильно: причина в том, что
196 Глава 7
критерий Линден-Белла—Острайкера в его первоначальной формулировке
не вполне верен [46, 209, 210, 289]. Существуют «тривиальные» лагранже-
вы смещения ?, не меняющие физической конфигурации звезды. Такие
смещения соответствуют переобозначению частиц, в то время как физические
эйлеровы возмущения ??, &s и ?? остаются равными нулю. Можно выбрать
такие «тривиальные» ?, при которых оператор С принимает
отрицательные значения; разумеется, это не имеет никакого отношения к
неустойчивости.
Исправленный критерий устойчивости был сформулирован в работе
Бардина и др. [46] (см. также [209, 210]). Следует ограничиться
смещениями ?, которые «ортогональны» тривиальным смещениям в некотором
математически точном смысле, и рассматривать действие оператора С
только на такие «разрешенные» смещения. Вообще, значение оператора С
оказалось равным не полной энергии возмущения, а «канонической» энергии
Е^, т.е. величине гамильтониана возмущения. Если тривиальные смещения
не исключены, то каноническая энергия не равна полной.
Другая проблема, связанная с критерием Линден-Белла—Острайкера,
состояла в том, что диссипативный механизм не был четко отождествлен.
В случае сфероидов Маклорена вековые неустойчивости относительно
вязких и радиационных потерь возникают одновременно. Это совпадение
оказалось случайным: его нет в аналогичных моделях сжимаемых звезд.
Вообще говоря, природу диссипации можно установить прямо в ходе анализа
устойчивости (ссылки на соответствующую работу Джинса и Литлтона
можно найти в цитированных статьях [46, 208, 209, 289]). Условие
положительной определенности Е^, для всех нетривиальных смещений обеспечивает
устойчивость относительно гравитационного излучения, но не
относительно вязкой диссипации. Тензорная вириальная пробная функция не
ортогональна тривиальным смещениям и потому не позволяет проанализировать
этот случай.
По-видимому, невозможно строго сформулировать критерий вязкой
неустойчивости для звезд с дифференциальным вращением, поскольку такая
звезда находится в неравновесном состоянии. Время нарастания внесенного
возмущения должно быть того же порядка, что и время установления для
невозмущенной звезды при наличии вязкости. (Вероятно, это не относится
к аккреционным дискам, имеющим малые радиальные скорости, однако
этот вопрос строго не рассматривался.)
Критерий устойчивости относительно вязкости для твердотельно
вращающихся звезд формулируется следующим образом. Каноническая
энергия во вращающейся системе координат, Е^^, должна быть положительно
определенной. (В этом случае тривиальные смещения несущественны.)
Метод тензорного вириала эквивалентен некоторому утверждению
относительно Е^ и потому также неприменим в общем случае.
Фридман и Шутц [210] сделали примечательное открытие: все
вращающиеся звезды обладают вековой неустойчивостью относительно
гравитационного излучения. Однако для медленно вращающихся звезд
неустойчивость возникает лишь в моде с очень высоким номером w, в которой ази-
Вращение и магнитные поля 197
мутальная зависимость ? определяется множителем ехр(/тф). При этом
время нарастания неустойчивости намного больше возраста Вселенной.
Неустойчивость, существенная с физической точки зрения, развивается в моде
с /я = 2.
Дюрисен и Имамура [173] рассмотрели возникновение неустойчивости в
моде с т = 2 для вращающихся белых карликов и вращающихся политроп-
ных конфигураций, используя пробную функщ1ю, ортогональную к
тривиальным смещениям. Было обнаружено, что неустойчивость относительно
гравитационного излучения по-прежнему появляется при T/\IV\ »0,14.
Найденные ими значения всего лишь на 1—7% превосходят оценки,
полученные методом тензорного вириала. ьыла показана возможность
существования устойчивых быстро вращающихся белых карликов с массами
вплоть до 2,5 М^ .
Отметим в заключение, что при грубых оценках величину Г/IWI «0,14
можно использовать в качестве критерия возникновения вековой
неустойчивости для широкого многообразия распределений углового момента и
уравнений состояния.
Глава 8
Уравнение состояния холодного вещества
выше точки образования нейтронных капель
8.1.ВВЕДЕНИЕ
В этой главе мы завершим.начатый в гл. 2 анализ уравнения состояния
холодного плотного вещества. Здесь будут рассмотрены свойства
конденсированного вещества при плотностях, превышающих р^,^ «4,3* 10^^ г/см^,
при которых образуются нейтронные капли^\ Именно такие высокие
плотности, p^Pdrip» существуют в недрах нейтронных звезд.
Нам придется ограничиться введением в существо вопроса, так как
полное обсуждение потреоовало бы привлечения всего аппарата квантовой
теории многих тел. Тем не менее мы сможем обсудить большинство
наиболее важных физических принципов и пояснить их таким же образом, как
это было сделано в гл. 2 при анализе уравнения состояния при более
низких плотностях, P^Pdrip·
Вывод уравнения состояния при pJ^Pdrip будет состоять из двух частей.
В первой части (разд. 8.2) мы рассмотрим область промежуточных
плотностей, от Pdrip до ядерной плотности Pj^y^=2,8· 10^^ г/см^, при которой
ядра начинают распадаться и сливаться. В этой области мы достаточно
хорошо понимаем свойства плотного вещества и соответствующее уравнение
состояния. Во второй части нашего изложения мы обращаемся к высоким
плотностям, P>Pnuc» "?** которых физические свойства материи еще плохо
известны. Основная часть этой главы (разд. 8.3—8.14) будет посвящена
обсуждению этой области высоких плотностей.
С самого начала следует иметь в виду, что, несмотря на значительный
прогресс, достигнутый за последние годы, наши представления о
конденсированном веществе (их сводка дана в резюме 8.1) далеко не полны,
особенно выше Pnuc· Правильная форма ядерного потенциала пока неизвестна.
Более того, даже если оы этот потенциал был установлен, предстояло бы
еще построить достаточно удовлетворительный метод, позволяющий
проводить вычисления на основе многочастичного уравнения Шредингера.
Кроме того, почти совсем нет лабораторных данных о конденсированном
веществе при плотностях, превышающих ядерную. Поскольку
предполагаемые свойства нейтронных звезд оказываются чувствительными к
принятому уравнению состояния^\ возможно, что тщательные наблюдения за
нейтронными звездами позволят выполнить наилучшие, хотя и косвенные
измерения свойств материи при сверхвысоких плотностях.
^^ См. раздел 2.7.
^^ Эти свойства обсуждаются в гл. 9—11.
Уравнение состояния выше точки образования нейтронных капель 199
8.2. УРАВНЕНИЕ СОСТОЯНИЯ БЕЙМА — БЕТЕ — ПЕТИКА
При плотностях от Pdrip до Ршс вещество состоит из ядер, электронов и
свободных нейтронов. По мере приближения к р^ис *^^P становится все
меньше, так как энергия связи падает с увеличением плотности. Это
отчасти можно понять, поскольку действующий между нетождественными
нуклонами «тензорный» потенциал, который дает сильное притяжение в
состоянии ^1 и играет важную роль в существовании дейтрона (см. разд.
8.3), не действует между нейтронами из-за принципа Паули. В сущности,
система, состоящая из одних нейтронов, не становится связанной ни при
каких плотностях. Поскольку по мере возрастания плотности содержание
нейтронов в ядрах повышается, их стабильность падает, пока нейтронное
число не достигает критического значения, при котором ядра
разрушаются, сливаясь воедино.
Мы уделим основное внимание уравнению состояния Бейма, Бете и Пе-
тика [55] (ВВР) в указанном диапазоне значений плотности, а в конце
данного раздела наметим некоторые другие возможные подходы. Этот
метод является существенным улучшением подходов, основанных лишь на
полуэмпирических массовых формулах, таких, как метод Гаррисона — Уи-
лера (см. разд. 2.6). Массовая формула используется и при выводе
уравнения ВВР, но в нее включаются и результаты, полученные путем детальных
многочастичных расчетов.
Во-первых, поскольку присутствующие в звезде ядра содержат большое
число нейтронов, ядерное вещество по своим свойствам очень похоже на
газ свободных нейтронов, окружающий ядра. Однако в первоначальных
работах на эту тему использовались полуэмпирические массовые формулы, в
которых энергия связи нуклонов в ядре вычислялась по формулам,
относящимся к ядерному веществу, т.е. к «обычным» ядрам с ??4 =:0,5, в то
время как энергия нейтронного газа находилась с помощью вычислений,
основанных на нейтрон-нейтронном взаимодействии. Не удивительно, что
в предельном случае, когда вещество представляет собой нейтронный газ с
примесью протонов, указанные подходы приводили к разным результатам.
Во-вторых, раньше предполагалось, что поверхностная энергия ядра
определена для ядер, помещенных в пустоту. Однако наличие извне
нейтронного газа заметно понижает поверхностную энергию. Этого и следует
ожидать: если состав вещества внутри и вне ядра становится одинаковым,
поверхностная энергия должна исчезать.
В-третьих, уравнение ВВР более аккуратно учитывает эффект кулоновс-
кой энергии ядерной решетки.
Подход ВВР [55] основан на модели ядра в виде «сжимаемой жидкой
капли». Полная плотность энергии записывается следующим образом:
? = ?(.4,?,/?^,/?„,?^)
= n^{W^ + W^) + ?,(/?J(l - V^n^) + ?,(/?J. (8.2.1)
200 Глава 8
Здесь А2уу — концентрация ядер, п^ — концентрация нейтронов вне ядер
(«нейтронный газ»). Новым моментом является зависимость от объема
ядра Куу. Величина К^у уменьшается при повышении внешнего давления и
потому должна рассматриваться как переменная. Величина Wj^ — это энергия
ядра, включающая его массу покоя; она зависит от Л, Z, п^и К^у. Энергия
решетки обозначается Ff^; ?^ и ?^ — плотности энергии нейтронного газа и
электронного газа соответственно. Отметим, что Vj^rij^ — доля полного
объема, занятая ядрами, а 1 — У^^п^^ — доля объема, занятая нейтронным
газом. Условие нейтральности вещества в этих обозначениях имеет вид
и, = Zn^, (8.2.2)
а концентрация барионов
n^Anf, + {\-V^n^)n„. (8.2.3)
Заметим, что величина п^ определяется через число свободных нейтронов
N^ в объеме К^, не занятом ядрами,
где V — объем, содержащий N^ нейтронов и л^уК ядер.
Равновесие определяется условием минимума ? при фиксированном п.
Поскольку ? зависит от пяти переменных, это приводит к четырем
независимым условиям.
Первое условие возникает при рассмотрении единичного объема,
содержащего фиксированное число протонов ??^^?, фиксированное число
нейтронов в ядрах A2yy(/1-Z), фиксированное число нейтронов вне ядер
^п(^~ ^n^n)* причем доля объема, занятая ядрами, rij^Vj^, также
фиксирована. Каково оптимальное число Л для этих ядер? Оно определяется
минимизацией ? как функции Л при фиксированных Ai^yZ, п^^Л, rij^Vjsj и п^.
Отсюда следует, что ?^ фиксировано, как и ?^ (так как п^ фиксировано).
Введем обозначение
x = f. (8.2.5)
Тогда, поскольку при этой вариации А2уу= constЛ4, формула (8.2.1) дает
_9(ib±iti) .„. (8.2.6)
с физической точки зрения это означает, что энергия на нуклон внутри
ядра должна быть минимальна.
Второе условие состоит в том, что ядра должны быть устойчивы
относительно ]3-распада, т.е. изменения Z. Иными словами, энергия ? должна
Уравнение состояния выше точки образования нейтронных капель
201
иметь минимум по ? при фиксированных А, п^, V^ и п„. Заметим, что
dZ
dn^ dZ
(8.2.7)
согласно формулам B.6.8) и (8.2.2), где ?^ — химический потенциал
электрона. Таким образом, из (8.2.1) следует
^е - dZ^^^ "*" ^^^^'^л^'^л^'"'.
(8.2.8)
Эту формулу можно следующим образом переписать через химические
потенциалы ядер. Химический потенциал нейтронов в ядрах ?^^^ — это
минимальная энергия, необходимая, чтобы добавить нейтрон к ядру, т.е.
мГ = -з7(»^'^+»^1)г,„..и,.„,.
(8.2.9)
Аналогично химический потенциал протонов вычисляется при
фиксированном числе нейтронов ?—?:
-49{iys+W,),,„,,y,,„^ + ^{W^+W^)z,„^,y^,„^, (8.2.10)
dz'
дА
поскольку дЛ /??= 1''. Таким образом, условие стабильности относительно
|3-распада (8.2.8) можно записать в привычной форме:
^e-^T-l^r-
(8.2.11)
Согласно третьему условию, газ свободных нейтронов должен быть в
равновесии с нейтронами в ядрах. Иными словами, можно перенести нейтрон
из гаэа в ядро без затраты энергии. Таким образом, ? имеет минимум как
функция А при фиксированных ?, п^, У^, п. Дифференцируя формулу
(8.2.3) по А при этих условиях, получаем
дл
i-V^ns'
(8.2.12)
При дифференцировании суммы fVf^+ ff^ в формуле (8.2.1) можно
использовать равенство
_д_
дА
г,пц,Ум,п
_д_
дА
г.п^,Уц,п„
dn^j_
дА дп.
(8.2.13)
Z,nf^,VN,A
^^ Отметим, что у нас все химические потенциалы включают массы покоя. В
работе Бейма, Бете и Петика массы покоя нуклонов вычитаются из соответствующих
выражений.
202
Глава 8
так как W^^ не зависит от а2„, то с учетом (8.2.9) получаем
^??^?
(Ю _ ^^
1 - VNrtj,
dW^
^^ дп„
Z,A,ns,Vs
+ A - V.n,)^
= 0 (8.2.14
ИЛИ
?? = ?*'^^,
(S.2.15)
где, по определению, химический потенциал свободных нейтронов равен
*"" l-V^n^ дп„
Z,A,nfj,VN
dn^
(8.2.16)
Член de^/dn^y как обычно, соответствует изменению объемной энергии
нейтронного газа. Первый член в формуле (8.2.16) соответствует
изменению поверхностной энергии ядер, связанному с добавлением в газ одного
нейтрона. Действительно, энергия ядер на единицу объема, занятого
нейтронным газом, равна [см. формулу (8.2.4)]
{гьЮ^ ^
1 - Vn^n
W^.
(8.2.17)
Производная этого выражения входит в (8.2.16).
Четвертое условие равновесия состоит в том, что давление нейтронного
газа должно быть равно давлению ядер:
p{G) ^ р{Ы)
(8.2.18)
Это условие следует из минимизации ? как функции Куу при фиксированных
?, Л, д|дг и N^/V=n„(l-V^nj^). Поскольку A2„ = const/(l - КдгА2дг), то
дп^ __ п„п^
дУ^ 1 - F^/i^
Используем равенство
dV^
дп„ д
Z,A,n,,n„ ^Vs 9П„
2,А,Пк.Уы
(8.2.19)
(8.2.20)
Подставляя в (8.2.1) 1- K^w^=/i„(l- V,^n,^)/1 ^ а «ифференцируя, получаем
д , ч ^п„ dWff\
'? ^'^n
Z,A,n^,Vf^
¦«„(?-^^.«.)^^(-)
(8.2.21)
?,?,?^.?^
Уравнение состояния выше точки образования нейтронных капель 203
Очевидно,
Р'"' =-^^(^^^+ Югжп.^п,^ (8.2.22)
С учетом формул (8.2.16) и (8.2.19) из (8.2.21) следует (8.2.18), где
?<«) = «„?<«)-?„. (8.2.23)
Заметим, что определение давления в этой формуле следует из B.1.21) (см.
также упражнение 2.4).
Упражнение 8.1. Показать, что полное давление равно
где
Z....... («-2-25)
Чтобы найти уравнение состояния, надо теперь задать функциональные
зависимости И^^, if^, е^ и е^. В работе Бейма, Бете и Петика для ядерного
вещества использовалась модель сжимаемой жидкой капли. В этой модели
Wj, = ^[A - х)тУ + хт^с^ + W{k, ?)] + Же + W^, (8.2.26)
где IVq — кулоновская энергия, W^ — поверхностная энергия, а lV(k^) —
объемная энергия ядерного вещества на один нуклон при концентрации
нуклонов
2к^
п^—,. (8.2.27)
Объемная ядерная энергия W(k,x) включает эффекты нуклон-нуклонных
взаимодействий, но не включает поверхностные эффекты и кулоновское
взаимодействие. Внутри ядра n=A/Vj^. Для самосогласованного описания
ту же функцию W(k,x) следует использовать и для нейтрального газа,
положив ?·=0. Таким образом.
e„-n„[w{k„,0) + m„c'], (8.2.28)
204 Глава 8
где'^
«„-7^· (8.2.29)
Величина W(k,x) находится путем плавной интерполяции результатов
многочастичных вычислений, сделанных в различных предельных случаях
по А: и дг. Параметры в функции W(k,x) определяются с помощью подгонки
ядерных данных, как в полуэмпирической массовой формуле^\ Однако в
отличие от такой формулы функция W(k,x) зависит от плотности из-за
наличия переменной А:, в то время как полуэмпирические массовые формулы
неявно предполагают, что плотность ядерного вещества совпадает с
плотностью ядер при нормальных условиях. Определение функции W по
заданному ядерному потенциалу будет рассмотрено в разд. 8.5—8.11.
Поверхностная энергия ^^§; **спользуемая в методе ВВР, обращается в
нуль, когда плотность нейтронного газа равна плотности ядер.
Главный член в Wq равен 37^^/5гуу; это кулоновская энергия
однородно заряженной сферы радиуса г^у, причем ?^^»4??^^/3. К этому члену
добавляются различные небольшие поправки. В результате энергия
заряженной сферы вместе с энергией решетки W^^ равна
где
4я·
?
и;,г/ S 1. (8.2.31)
Упражнение 8.2. Вьшести результат (8.2.30) и обсудить предел г^./гдг-^ 1. Рассмотреть
ядерную решетку в приближении ячейки Вигнера — Зейтца, предполагая, что каждое
ядро — однородно заряженная сфера радиуса г^^ и проницаемость ядра для
электронов однородна.
Электроны прекрасно описываются как идеальный вырожденный
ферми-газ. Ведущая поправка к этому описанию уже включена в член W^,
поэтому для е^ можно принять обычное ультрарелятивистское выражение
^e = -r-A^-'nS''. (8.2.32)
^^ Отметим, что принятое в работе Бейма, Бете и Петика определение величины
к^ отличается множителем 2^^^ от обычного определения плотности через волновое
число Ферми Агр.
^^ Полуэмпирическая массовая формула для ядерного вещества обсуждается в
разд. 2.6.
Уравнение состояния выше точки образования нейтронных капель 205
Рис, 8.1. Уравнение состояния Бейма — Бете — Петика (ВВР). Для сравнения
показано уравнение состояния Гаррисона и Уилера (HW). (По работе [55].)
При известных функциях W^ и УУ{,к^) уравнение состояния может быть
построено с помощью условий равновесия (8.2.6), (8.2.11), (8.2.15) и
(8.2.18), причем давление определяется из формулы (8.2.24). Заметим, что
условие образования нейтронных капель (т.е. существования нейтронного
газа) имеет вид д^^^^ш^с^. Получаемое в конечном счете уравнение
состояния ВВР показано на рисунках 2.2, 8.1 и 8.5а, а показатель адиабаты
Г-на рисунках 2.3 и 8.2.
Основные свойства полученных методом ВВР результатов
формулируются следующим образом. Во-первых, относительный вклад свободных
нейтронов в полное давление возрастает с увеличением плотности. При об-
206
Глава 8
14
5-10
Рис, 8,2, Показатель адиабаты T = d InP/d Inp как функция ? для уравнения Бейма —
Бете — Петика. (По работе [55].)
разовании нейтронных капель давление почти полностью определяется
электронами, однако при р= 1,5· 10^^ г/см^ ^п^^ = ^»^^» ^ "Р** ^ =
= 1,5· 10^3 г/смЗр^/Р= 0,80.
Во-вторых, вблизи точки образования нейтронных капель Г ^4/3
(ультрарелятивистский вырожденный электронный газ). При плотностях
несколько выше точки образования нейтронных капель Г резко падает, как
показано на рис. 8.2. В работе ВВР получен закон этого падения:
Г = |[1-а(р-р,,рУ/^],
(8.2.33)
где а — положительная постоянная. Причина падения Г в том, что при
низкой плотности нейтронный газ вносит заметный вклад в р, но мало
меняет давление Р. Показатель адиабаты не поднимается выше 4/3, пока
плотность не станет выше ?-7· 10^^ г/см^. Как мы увидим в гл. 9, этот
результат приводит к важному следствию: плотности порядка величин,
рассмотренных в этом разделе, не могут существовать в центральных
областях устойчивых звезд^\
В-третьих, в работе ВВР [55] обнаружено, что ядра сохраняются в
веществе вплоть до плотностей около ?-2,4· 10^^ г/см^. Когда плотность
достигает этого значения, ядра начинают соприкасаться, а при более высоких
плотностях решетка разрушается и образуется ядерная жидкость.
'^ Плотности такого порядка вполне могут существовать в поверхностных слоях:
в критерий устойчивости входит среднее значение Г [см. формулу F.7.11)].
Уравнение состояния выше точки образования нейтронных капель 207
В-четвертых, при плотностях выше 2,4· 10^"^ г/см^ химический
потенциал электронов удовлетворяет условию ?^'^ 104 МэВ«т^с^, где т^ — масса
покоя мюона. При этом следует включить в уравнение состояния вклад
мюонов. В работе ВВР вычисления проводятся до плотностей порядка
5· 10^"^ г/см^; при более высоких плотностях обычная теория ядерной
материи неприменима.
Уравнение состояния ВВР подвергалось критике по некоторым пунктам
(обсуждение и обзор можно найти в работе Кануто [104J). В частности,
при этом подходе предсказывается монотонное возрастание ? с
увеличением Л, в то время как другие авторы предполагают, что при более
аккуратном учете поверхностной энергии ? останется примерно постоянным на
уровне -40. Тогда зависимость Р{р) изменится мало, а Г меняется
несколько более заметно.
8.3. НУКЛОН-НУКЛОННОЕ ВЗАИМОДЕЙСТВИЕ
В ОДНОЙ обзорной статье Бете заметил, что за предшествовавшую четверть
столетия на изучение проблемы нуклон-нуклонного взаимодействия было
затрачено больше рабочих человеко-часов, чем на какую бы то ни было
научную задачу в истории человечества. А ведь эта оценка была сделана в
1953 году [62]!
Мы начнем изложение этого вопроса с общего обсуждения зависимости
потенциала от спина и изоспина. В следующем разделе будет дан обзор
некоторых общих свойств, которые должны быть присущи потенциалу,
чтобы он позволил воспроизвести экспериментальные данные. Затем в
разд. 8.5 и 8.6 мы обсудим зависимость потенциала от расстояния между
нуклонами. Мы остановимся на одной частной модели потенциала,
потенциале Юкавы, которая может рассматриваться как прототип
потенциалов, используемых при более детальном анализе. Потенциал Юкавы будет
использоваться как в классическом подходе (в разд. 8.6), так и в квантовом
многочастичном уравнении (в разд. 8.7 и 8.8), чтобы показать, как можно
получить уравнение состояния, исходя из ядерного потенциала. В ходе
этого анализа будет показано, как потенциал используется для вычисления
объемной энергии. Наконец, результаты более детальных исследований
суммированы в разд. 8.9 и 8.10. Некоторые нерешенные проблемы
рассмотрены в разд. 8.11—8.14. В последующих главах будет показано, как
микрофизические свойства конденсированного вещества влияют на
внутреннее строение нейтронных звезд, находящихся в равновесном состоянии.
Упражнение 8.3. Используя результаты разд. 2.5, оценить долю нейтронов в
ядерной материи при плотности Рпис~^*^' ^^^^ г/см^.
В нерелятивистском пределе можно считать, как и в
электромагнетизме, что ядерные силы консервативны и не зависят от скорости ядра и по-
208 Глава 8
тому выводятся из статического потенциала. Однако в отличие от
электростатических сил ядерные силы не удовлетворяют принципу суперпозиции.
Полное взаимодействие в многочастичной ядерной системе не сводится к
сумме парных взаимодействий. Тем не менее при плотностях порядка р^^^
и более низких трехчастичные силы и другие взаимодействия более
высокого порядка менее существенны, чем двухчастичные силы, и для начала ими
можно пренебречь^\
Потенциальная энергия взаимодействия между двумя нуклонами
зависит не только от расстояния между ними г, но также и от их спинов. Вид
спиновой зависимости следует из простых соображений симметрии и
соотношений для оператора спина (см., например, книгу Ландау и Лифшица
[342], § 116 и 117). Статический потенциал может зависеть только от трех
векторов: п, единичного вектора, направленного вдоль прямой,
соединяющей частицы, и векторов спинов обоих нуклонов, Sj и Sj. Мы
предполагаем, что ядерные силы инвариантны относительно вращений, отражений и
обращения времени. (Наблюдается небольшое несохранение четности, но
оно относится к «слабым» ядерным силам, которые ответственны за ?-
распад и несущественны для предмета нашего обсуждения.) Таким
образом, потенциал должен быть скалярным относительно вращений, но не
псевдоскалярным. Он не может также включать вектора градиента, так как
присутствие градиента эквивалентно зависимости силы от скорости.
Любая функция оператора спина 1/2 сводится к его линейной функции
(см.. например, § 55 в книге Ландау и Лифшица [342]). Можно построить
только два скаляра, линейные по Sj и Sj и зависящие от указанных трех
векторов ? и Sj, Sj. Это Sj-Sj и (n-Sj)(n-S2). (Заметим, что n-Sj —
псевдоскаляр.) Если допустить силы, зависящие от скорости, то можно ввести
также члены вида L · S и (L · S)^, где L — полный орбитальный момент,
S = Sj-i-S2 — полный спин.
Итак, наиболее общий потенциал, зависящий от спина, имеет вид
Уш = V,{r) + V^{r){o, -0^)+ Кз(г)[3(о, · п)(о2 · п) - ?, · ?^]. (8.3.
Здесь мы использовали обозначение Sy=ay/2, где ?^ — спиновые операторы
Паули. Третий член записан в таком виде, что он обращается в нуль при
усреднении по направлениям вектора п; он соответствует так называемым
тензорным силам, и зависимость от ? указывает на то, что это
нецентральные силы.
Потенциал в (8.3.1) не меняет зарядового состояния нуклона и потому
назван «обычным». На опыте надежно установлено, что если пренебречь
небольшими электромагнитными эффектами и требованиями, связанными
с антис1»^лметрией, то ядерные силы, действующие между двумя
протонами, двумя нейтронами или протоном и нейтроном, в сущности,
одинаковы. Эта зарядовая симметрия называется изотопической
инвариантностью. Формально можно рассматривать протон и нейтрон как пару различ-
^^ Впрочем, ниже будет дано обсуждение решающей роли трехчастичных сил в
механизме насыщения в ядерной материи.
Уравнение состояния выше точки образования нейтронных капель 209
ных состояний одной и той же частицы-нуклона. Эта симметрия
относительно перестановки протонов и нейтронов математически описывается с
помощью формализма, полностью аналогичного используемому для
описания группы вращений. Нуклон изображается двухкомпонентным спинором
в абстрактном групповом пространстве. Свойство, аналогичное обычному
спину, называется изотопическим спином, или изоспином, и обозначается
как вектор t. Проекция изоспина для протона равна +1/2, а для нейтрона
-1/2. Оператор r=2t — та же спиновая матрица Паули, но действующая
на спиноры в изоспиновом пространстве. Полный изоспин системы
нуклонов равен T = tj + t2+..., а его проекция на ось ? — 7'з=(^1)з''"(^2)з''"··· -^^'
скольку собственное значение оператора t^ равно + 1/2 для протона и - 1/2
для нейтрона, то для системы, состоящей из ? протонов и А—?
нейтронов, Гз = 7— ViA.
Полная волновая функция системы двух фермионов, т.е. произведение
^(Г|, Sj; Г2, 82)?(?|, t2), где ? — изоспиновая часть волновой функции,
должна быть антисимметрична относительно одновременной перестановки
переменных г, S и Л Абсолютная величина полного изоспина, T = tj + t2,
определяет симметрию функции ?, так же как полный спин S = Sj + S2
определяет симметрию спиновой части волновой функции. Для двух нуклонов ?
принимает два значения, О и 1. Триплетное состояние Г= 1 симметрично,
и 7^3= 1, О или - 1, так что оно описывает систему рр, рп или пп. Для син-
глетного состояния Г=0 функция ? антисимметрична и Т2=0, что
соответствует только состоянию рп.
Поскольку величина ? определяет симметрию функции ? и в силу
антисимметрии полной функции также симметрию функции ф, то сохранение
оператора ? эквивалентно определенной симметрии волновой функции ф.
По-видимому, это соответствует строгой симметрии в сильном
взаимодействии (т.е. в пренебрежении электромагнитными силами). Заметим, что
сохранение оператора Т^ эквивалентно сохранению заряда при
фиксированном числе нуклонов и потому справедливо даже при наличии кулоновских
сил.
Операторы изоспина можно использовать для построения обменного
оператора Р^ (который иногда называется оператором Гейзенберга),
переставляющего переменные (fj, ?^) и (Г2, ?^) в системе двух частиц. Так как
(?^?=1^ то собственные значения оператора ?'' равны ±1 в зависимости
от того, на какую волновую функцию ?(?^,?^; ?2,?2) действует Р^, —
симметричную или антисимметричную. Поскольку ? соответствует
антисимметричной функции ?, то в этом состоянии Т=6. Аналогично ^^т
отвечает состоянию с Т= 1. Таким образом, оператор Р^ можно представлять
его действием на изоспиновые переменные волновой функции:
РЧ = -^^0» ^'^1 = -^1' (8.3.2)
где индекс при ? определяет значение Т. Так как Т^ имеет собственные
значения Т(Т-\-1), можно написать
Р- = 1 - Т^ = 1 - (t,.+ t2)' = - Ь 2t, · t2, (8.3.3)
14-353
210 Глава 8
где мы использовали тот факт, что t^ и tl имеют одинаковые значения,
/(/+1)=3/4. Окончательно запишем
?^=-??+?,·?2). (8.3.4)
Оператор, переставляющий спины фермионов и не действующий на их
координаты (оператор Бартлетта), также имеет собственные значения,
равные ± 1:
?'^??-? = -?5-?, P\s-x=+^s-x· (8-3.5)
Сравнивая эти формулы с (8.3.2), мы видим, что
pB = s2-l=Kl+e.-?). (8.3.6)
Оператор, переставляющий только координаты частиц и не
затрагивающий их спинов (оператор Майорана), записывается так:
рм = рьрг ^ _1A + „^ . ^)A + ^_ . ^^) (8.3.7)
Заметим теперь, что потенциал ^j-d ® формуле (8.3.1) в
действительности содержит некий член обменного типа, так как (aj ?^ можно переписать
через Р^. Обменные взаимодействия, по-видимому, необходимы для
объяснения «насыщения» ядерных сил. Более подробно этот вопрос обсуждается
в разд. 8.4. С учетом обменных сил наиболее общий потенциал, не
зависящий от скорости, имеет вид
V{r) = F„,(r) + K,J,r), (8.3.8)
где
V,Ur) = {V,{r) + F5(r)(o, · ?,) + Кб(г)[3(о, · n){o^ · ?) - ?, · ?]}^>^
Упражнение 8.4. Выражая спиновые части в формуле (8.3.8) через полный спин S,
показать, что с оператором V коммутирует S^, но не S. Поэтому в процессе
взаимодействия сохраняется лишь величина, но не направление оператора S.
Из результата, полученного в упражнении 8.4, следует, что, хотя
оператор J = L-|-S сохраняется^\ L, вообще говоря, не сохраняется. Причина
этого в присутствии тензорных сил.
Разрешенные состояния двухнуклонной системы классифицируются
заданием величин ? и S. Например, при Г= 1 и 5= 1 координатная часть
волновой функции должна быть антисимметричной относительно
перестановки частиц (четность отрицательна), так что L должно быть нечетным.
При L= 1 возможны следующие значения полного момента: У=0, 1, 2. Та-
'^ По этой причине мы считаем, что И зависят лишь от г.
Уравнение состояния выше точки образования нейтронных капель 211
Таблица 8.1
СОСТОЯНИЯ ДВУХНУКЛОННОЙ СИСТЕМЫ
S Четность Возможные состояния Нуклоны
1
1
0
0
1
0
1
0
/о
, 'D,. 'G,, ... j
(^5, + 3/),), ^D^, Cd^ + ^з), ... ]
nn, pp, np
np
КИМ образом, возможны состояния^^ ^Pq» ^Л» ^^2· Если L = 3, то У =2, 3 или
4; соответствующие состояния будут ^Fj, ^Fj, ^^4 и т.д. Как отмечалось,
вообще говоря, сохраняется только J, но не L, поэтому состояния ^2 ^ ^^2
могут смешиваться. Не существует состояний, с которыми могли бы
смешиваться ^0 и ^Pj, и в этих случаях в силу сохранения четности L также
сохраняется. В табл. 8.1 приведено несколько низших состояний двухну-
клонной системы.
Эти результаты используются для описания дейтрона — единственной
связанной двухнуклонной системы (энергия связи 2,225 МэВ). В основном
состоянии У=1, Г=0, S=l. Согласно табл. 8.1, при низшем значении L
основное состояние представляет собой смесь состояний ^| и ^D^.
Поскольку магнитный момент дейтрона близок к сумме магнитных моментов
протона и нейтрона, то S-состояние в дейтроне должно играть главную
роль. Однако у дейтрона есть электрический квадрупольный момент,
который указывает на отклонение от сферически-симметричного основного
состояния и хорошо объясняется небольшой примесью Л-состояния. Это
прямое свидетельство существования тензорных сил. (Векторное
взаимодействие, дающее правило отбора AL = 0, ±1, не позволяет объяснить
смешивание состояний с L = 0 и L = 2.)
Упражнение 8.5. Рассматривая действие оператора V^ir)+ V^irXa^a^) на состояния с
5 = 0 и 5= 1, показать, что если К^ дает достаточно большое притяжение, то
связанное состояние может существовать в триплете, но отсутствовать в синглете. Как
этот вывод соотносится с тем фактом, что в л/?-системе связанное состояние есть, а
в лл-системе нет?
'^ Мы пользуемся обычными спектроскопическими обозначениями ^^^Lj, где
значениям L = 0, 1, 2, 3, 4 и т.д. соответствуют символы 5, Р, D, F, G, ... Четность
двухчастичной системы равна (-1)^.
212 Глава 8
8.4. НАСЫЩЕНИЕ ЯДЕРНЫХ СИЛ
Как следует из экспериментальных данных, за вычетом кулоновских и
поверхностных эффектов энергия и объем ядер возрастают прямо
пропорционально числу нуклонов Л. Это свойство ядерных сил,, уже принятое во
внимание в полуэмпирической массовой формуле B.6.4), называется
насыщением по причине, которая объяснена в настоящем разделе.
Насыщение налагает жесткие ограничения на характер ядерных сил.
Например, сравнительно простой потенциал притяжения вида
V{r) = V^{r) + Кз(г)[3(о, · 0)(? · ?) - ?, · ?^] (8.4.1)
ДОВОЛЬНО хорошо описывает все данные о нуклон-нуклонных системах в
состояниях с L = 0. Однако мы сейчас покажем, что столь простые
потенциалы не могут быть положены в основу теории ядерных сил.
Полная энергия ядра имеет вид
?=Г+ Ж, (8.4.2)
где ? — кинетическая энергия, а FT — потенциальная энергия.
Потенциальную энергию можно считать суммой парных нуклон-нуклонных
потенциалов V(\x.-Xj\), т.е. суммой А(А-\)/2 отрицательных величин. В силу
принципа запрета кинетическая энергия ? определяется в основном
статистикой Ферми,
Т~АЕ^~ Ап^/' ~ ^D) = A'/'R-J, -4«·4.3)
где R — радиус ядра.
Значение R в основном состоянии определяется из условия минимума Е.
При больших А потенциальная энергия много больше кинетической,
??-?^>?, так что основное состояние определяется, по существу, из
условия минимума W. Следовательно, значение R определяется радиусом
действия ядерных сил и не должно зависеть от А. (Ниже этот довод
обсуждается более детально.) Более того, энергия связи Е^ должна быть при этом
пропорциональна А^. Оба предсказания явно противоречат
экспериментальным данным. На самом деле R^-A^^^ (т.е. ядерная плотность
постоянна, не зависит от А) и ?^-?.
Ядерные силы должны обладать каким-то свойством, которое
приводит к «насыщению», т.е. к закону ?'^-Л. Это происходит при достаточно
высоких плотностях в атомных ядрах, как и в любых системах, состоящих
из нуклонов. Особенностью ядерных сил должно быть притяжение при
небольшом числе нуклонов и отталкивание, когда нуклонов становится
много. Насыщаются и химические силы: два атома водорода образуют
молекулу, но третий атом не может к ним присоединиться. В ядерных силах
насыщение возникает в результате влияния нескольких эффектов. Мы имеем
в виду, в частности, принцип Паули, так называемые обменные силы,
возникающие от членов, пропорциональных операторам Р^ и Р^, и отталки-
Уравнение состояния выше точки образования нейтронных капель
213
вательный кор, потенциал, обеспечивающий сильное отталкивание на
малых расстояниях.
Простое модельное вычисление дает количественную иллюстрацию
того, как ядерный потенциал с чистым притяжением приводит к ядерному
коллапсу с ростом Л, в то время как наличие отталкивательного кора
способствует насыщению.
Средняя кинетическая энергия системы, состоящей из Л нуклонов и
рассматриваемой как нерелятивистский газ, равна (см. упражнение 2.6)
-2\2/3,
^'/' (8.4.4)
Мы считаем здесь нуклоны тождественными частицами, так что каждому
импульсу соответствует B/-I-1)Bя-1)=4 состояния по спину и изоспину.
Взаимодействие между двумя нуклонами будем аппроксимировать
прямоугольной ямой шириной b и глубиной Vq, Пусть ? — вероятность того,
что расстояние между любыми двумя нуклонами не превышает Ь, тогда
полная потенциальная энергия равна
W
^ А{А-\)
pv,.
(8.4.5)
Если нуклоны находятся внутри сферического ядра радиусом R с
однородным и некоррелированным пространственным распределением, то
где ? — ступенчатая функция.
"W = {J;
X > О
X <0,
(8.4.7)
? = ??\
"'?-
(8.4.8)
Интеграл (8.4.6) вычислен в приложении В. Очевидно, что при Ь>Ъ'
подынтегральное выражение всюду равно единице, и ? = 1. В общем случае
'•^•"'-(Dl'-^l^^r
R>\.
- 1.
-f
(8.4.9)
Упражнение 8.6. Вывести формулу (8.4.9) при R>b из простых соображений.
214 Глава 8
Упражнение 8.7. Оценить величину К^^^, рассматривая основное состояние
дейтрона и предполагая, что нуклон-нуклонный потенциал в дейтроне имеет вид
трехмерной сферически-симметричной ямы глубиной V^ и радиусом Ь. При г>Ь потенциал
равен нулю. Найти основное состояние в таком потенциале и, предполагая, что это
основное состояние удовлетворяет условию \Е\<У^, показать, что
???J ^ ^^ ^ 100 МэВ· Фм^, (8.4.10)
o/i
где ? — приведенная масса. (Здесь ^~1,4Фм, что соответствует комптоновской
длине волны пиона, и это приближение оправдано, поскольку энергия связи
дейтрона ?=2,225 МэВ.)
Полная энергия E=T-\-W изображена на рис. 8.3 как функция /?. При
R<b/1 она не имеет минимума, а при R>b/1 можно записать
^ R' R' ^°* 2R
16\r) 32\r)
(8.4.11)
где
-1 / Q_ \2/3 ь2
Так как квадратная скобка в формуле (8.4.11) множится на величину,
которая много больше ? даже при умеренных значениях А, то энергия ?
минимальна при значениях /?, лишь не намного больших, чем Ь/2.
Действительно, полагая dE/dR = 0, получим при Л- 1«Л
Это уравнение можно решить численно относительно R. Помимо
минимума вблизи Ь/2 (где выражение в скобках много меньше единицы), энергия
имеет максимум при R = R^>b, где отношение b/R мало.
Вывод очевиден: если потенциальная энергия имеет вид (8.4.5), то ядра,
сжатые до концентраций свыше п = ЗА /4?/? j, коллапсируют к стабильному
состоянию с радиусом R-^b/l, где b — радиус ядерного взаимодействия. В
этом состоянии энергия связи должна быть Ef^= —?<??{? — \)-?^, что
противоречит экспериментальным данным.
Предположим теперь, что на малых расстояниях существует
отталкивание. Это приводит к появлению «запретной зоны» вокруг каждого
нуклона, где волновая функция относительного движения должна исчезать. Так
как при данной плотности объем, занимаемый нуклонами, при этом
уменьшается, то импульсы нуклонов и кинетическая энергия ядра возрастают.
При увеличении ? по сравнению с W положение минимума полной энергии
сдвигается к более разумным значениям.
Уравнение состояния выше точки образования нейтронных капель 215
-6^-
-0,010'
Рис, 8.3, Графики потенциальной энергии W, кинетической энергии ? и полной
энергии ?= W-^ ? в зависимости от радиуса ядра R для системы тождественных
нейтронов, взаимодействующих при наличии потенциала чистого притяжения. Точка R^ —
радиус, при котором энергия ? максимальна. (По книге Блатта и Вайскопфа [75].)
Переходя к формулам, запишем
R = г^Л'^\ (8.4.14)
где 2го — среднее расстояние между нуклонами. Вводя параметр г^ —
радиус отталкивательного кора, выражение для кинетической энергии можно
переписать следующим образом:
"^''' "^ «^ (8.4.15)
т= ^ «^
R'
('о - '•с)
216 Глава 8
Усредненное значение W меняется не очень сильно, если /о>г^. Минимум
модифицированного таким образом выражения (8.4.11) для полной
энергии, как функции Tq, определяется уравнением
4?
.??-^-^ + ^-^1(?-^?'=1. (8.4.16)
Численно решая это уравнение для Tq, получим при Ь= 1,8 Фм и г^=0,4 Фм
(это значение не противоречит данным о рассеянии при высоких энергиях):
0,9 < 'о (Фм) < 1;5 для 4 < ^ < 216. (8.4.17)
Эту величину Tq следует сравнить с экспериментальным значением^\
-1,2 Фм. Однако более важно то, что Tq слабо зависит от А: из-за
отталкивания на малых расстояниях возникает насыщение^\
Итак, какова бы ни была форма потенциала ядерного взаимодействия,
выбранная для вычисления уравнения состояния, основное требование,
вытекающее из эксперимента, состоит в том, чтобы этот потенциал
приводил к насыщению в ядерной материи. В первую очередь следует
воспроизвести следующие четыре параметра:
1. Концентрация, при которой наступает насыщение,
л о* 0,16 нуклон/Фм^ (8.4.18)
2 и 3. Энергия и сжимаемость симметричной ядерной материи. Эти
величины выражаются через функцию lV(k,x), которая была введена в разд.
8.2 как объемная энергия ядерной материи на один нуклон. В
симметричной ядерной материи (Z=A/2) х=\/2. При плотности вблизи насыщения
можно написать
W{k,{)--Wy + \K{\-j-^, (8.4.19)
где, как можно получить из опыта,
d^w{kA)
= Ь2
Ж^ « 16 МэВ , К^к
дк'
« 240 МэВ (8.4.20)
Как следует из формул (8.2.27) и (8.4.18), kQ= 1,33 Фм~^ Отметим, что
величина АГ, называемая модулем сжатия, была определена из опыта лишь
недавно [68, 374, 627, 628]. Ранее в различных расчетах уравнений
состояния часто использовалась величина 300 МэВ.
^^ См., например, книгу [159] и приведенные там ссылки.
^ Количественное обсуждение роли обменных сил, способствующих
возникновению насыщения в ядерной материи, для этой простой модели дано в книге [75],
гл. 3.
Уравнение состояния выше точки образования нейтронных капель 1\1
4. Наконец, коэффициент объемной симметрии^^ Sy, определяющий
«кривизну» функции lV(k,x)y связанную с изменением х:
_ 1 d^Wjko.x)
'-^ а.
У Q ? 2
«ЗОМэВ. (8.4.21)
Соответственно, npn.k^kQ и дг« 1/2 можно написать
W{k,x)= ^Wy-^^Kll^-^] +4Syi^x^^]\ (8.4.22)
Упражнение 8,8, Используя тот факт, что чистый нейтронный газ не образует
связанных состояний ни при какой плотности, рассмотреть применимость выражения
(8.4.22) при х-*0. Изобразить возможную кривую зависимости lV{k,0) от к.
Указание. К какому пределу должно стремиться W, когда к (и соответственно ?)
стремится к нулю?
Используемые в настоящее время ядерные потенциалы обычно
приводят к плотности насыщения, примерно вдвое превосходящей наблюдаемое
значение. Отталкивательный кор находится из подгонки данных о фазах
рассеяния при энергиях свыше 300 МэВ: г^*0,4 Фм, и эту величину нельзя
изменить, чтобы добиться совпадения предсказываемой плотности
насыщения с наблюдаемой. Помимо упомянутых выше есть еще один эффект,
учет которого мог бы улучшить согласие данных — ?-резонанс в ???-
системе при 1236 МэВ. Однако до сих пор не было выполнено надежных
расчетов в этом направлении.
Проведенные недавно вариационные расчеты [207, 351] показали^\ что,
используя только двухнуклонные потенциалы, достаточно хорошо
описывающие лабораторные данные по рассеянию, нельзя получить правильные
величины энергии основного состояния Wy, равновесной концентрации aiq и
сжимаемости К для ядерной материи, однако теорию можно хорошо
согласовать с экспериментом, если ввести добавочное трехнуклонное
взаимодействие. Необходимый вклад трехнуклонного взаимодействия
феноменологически добавляется к энергии ядерной материи, причем вид этого
вклада определяется из физических соображений.
^^ Иногда для описания поверхностной энергии в модели жидкой капли вводят
коэффициент поверхностной симметрии S^, причем \?^=?^?'^^^ и вблизи ? =1/2
?^{?)-?^{??)-?8^{?-???. Сравнение массовых формул с экспериментальными
данными дает ?^('/2)*20 МэВ, но не позволяет найти S^ с определенностью.
^^ В этих вариационных расчетах одни только двухнуклонные взаимодействия с
реалистическим потенциалом дают равновесное значение А:^=1,7Фм~^ и -Wy =
= 17,5 МэВ, что превышает эмпирические оценки. Вклад трехнуклонных
взаимодействий можно подобрать таким образом, чтобы устранить это противоречие.
218 Глава 8
8.5. ЗАВИСИМОСТЬ НУКЛОН-НУКЛОННОГО ПОТЕНЦИАЛА
ОТ РАССТОЯНИЯ
Рассмотрим теперь важный и нерешенный пока вопрос о зависимости
основного члена в нуклон-нуклонном (NN) потенциале от расстояния между
нуклонами. Поскольку этот потенциал нельзя вывести из теории, то, исходя из
разумной формы потенциала, подбирают ее так, чтобы описать
экспериментальные данные, касающиеся MV-рассеяния при низких энергиях (от О
до - 350 МэВ), а также известные из опыта свойства ядерной материи
(энергия насыщения, плотность насыщения, энергия и сжимаемость
симметричной ядерной материи, свойства дейтрона и т.д.).
К числу потенциалов, наиболее хорошо описывающих данные о фазах
рассеяния, относится потенциал Рейда [478]. Он представляет собой
суперпозицию членов типа потенциала Юкава (см. в следующем разделе) и носит
чисто феноменологический характер. Этот потенциал не записывается в
общем виде (8.3.8) и выражается как совокупность независимых частей,
соответствующих различным парциальным волнам. Потенциал Рейда приводит
к сравнительно «мягкому» уравнению состояния, так как при ядерных
плотностях энергия системы в среднем соответствует притяжению.
Более поздний и детальный анализ MV-взаимодействия, выполненный в
ряде работ [64, 444, 445, 595], показал, что уравнение состояния
конденсированного вещества при плотностях 10^^—10^^ г/см^ должно быть гораздо
более «жестким», чем то, которое получается с применением потенциала
Рейда. Такие «жесткие» уравнения состояния получаются с потенциалами,
для которых средняя энергия системы при ядерных плотностях
определяется в основном областью притяжения, а при больших плотностях —
областью отталкивания. Уравнение состояния, выведенное в работах [207, 351] с
учетом двух- и трехнуклонных взаимодействий, соответствует большей,
жесткости, чем в теории, основанной на потенциале Рейда, хотя и мягче,
чем в более ранних моделях [444, 445], использующих только двухнуклон-
ное взаимодействие.
Уравнения состояния с более высокой жесткостью приводят к важным
изменениям наших представлений о внутреннем строении и массах
тяжелых нейтронных звезд. В частности, поскольку энергия взаимодействия при
плотностях, превышающих ядерные, определяется отталкиванием,
соответствующее давление способствует повышению устойчивости звездного
вещества против гравитационного коллапса. В результате при более
«жестких» уравнениях состояния максимальные массы звезд получаются больше,
чем при «мягких» уравнениях состояния. Кроме того, при большей
жесткости плотность в центре звезды ниже, ее радиус больше, а кора толще. Эти
различия существенны для определения предельной массы нейтронных
звезд, их поверхностных потенциалов, моментов инерции, частот
прецессии и других величин, которые могут быть косвенно связаны с данными
наблюдений.
Эти вопросы будут рассмотрены в гл. 9 и 10, но прежде мы дадим
простое количественное описание того, как можно выбрать нуклон-нуклонный
потенциал, чтобы использовать его затем в многочастичных вычислениях
Уравнение состояния выше точки образования нейтронных капель 219
и получить уравнение состояния. И выбор потенциала, и метод его
использования в достаточно точном многочастичном расчете — проблемы пока
еще не решенные. Предлагаемое нами обсуждение, в лучшем случае,
можно рассматривать как иллюстративный пример. Мы возьмем простую
форму K(r)=Kj(r), пренебрегая взаимодействиями, зависящими от спина и
изоспина. Вместо точного вычисления функции W{k,x) будет предложено
вычисление плотности энергии взаимодействия e = (W-\-mc^)n для системы
тождественных нуклонов с массой т и концентрацией ? без учета
зависимости W от лг.
8.6. ПОТЕНЦИАЛ ЮКАВЫ
В 1935 г. Юкава выдвинул смелую гипотезу, согласно которой ядерные
силы могут возникать вследствие обмена виртуальными частицами,
названными мезонами, подобно тому как электромагнитные силы возникают
вследствие обмена виртуальными фотонами. Конечный радиус действия
ядерных сил можно объяснить, если полагать, что мезон имеет ненулевую
массу покоя в отличие от безмассового фотона, который переносит даль-
нодействующие электромагнитные силы.
В приложении Г рассмотрен классический вариант теории массивных
скалярных и векторных полей. Скалярное (однокомпонентное) поле
соответствует квантам со спином О, а векторное поле (с тремя независимыми
компонентами) — квантам со спином 1. В пределе медленно движущихся
частиц с «зарядом» g, взаимодействующих благодаря скалярным или
векторным полям, мы показываем, что энергия взаимодействия равна
-??
где ? — обратная комптоновская длина волны квантов поля. Эта энергия
соответствует члену V^{r) в формуле (8.3.8), причем J^(r)=0 при 2</^6.
Здесь знак плюс (сила отталкивания) отвечает векторному полю, а минус
(притяжение) — скалярному полю. Заметим, что для получения радиуса
действия 1/?- 1,4 Фм необходима масса квантов - 140 МэВ (если считать,
что радиус действия сил сравним с комптоновской длиной волны мезона).
Эта величина как раз совпадает с массой пиона. Пионы обладают нулевым
спином, и потому пионный обмен обусловливает основную часть силы
ядерного притяжения. Применяя выражение (8.6.1) для описания
экспериментальных данных при низких энергиях^\ можно показать, что g^/he-- 10.
Поэтому ядерные взаимодействия называются сильными (в
электромагнетизме e^/hc^ 1/137).
'^ Например, данные об упругом рр- и тгУУ-рассеянии при низких энергиях
(~ 100 МэВ) можно описать с помощью потенциала однопионного обмена при
g^/hc^\5 (см., например, книгу Перкинса [454]).
220 Глава 8
Покажем теперь, как потенциал Юкавы,
е
-??
Ф= ±S—;r- (8.6.2)
можно использовать для вывода уравнения состояния ядерной материи в
различных приближениях. Разумеется, формула (8.6.2) представляется
чрезмерно упрощенной исходной посылкой, но мы будем использовать ее,
показывая, что при заданном потенциале для решения многочастичной задачи
необходимы еще различные приближения.
Начнем с простого классического анализа, основанного на работе
Зельдовича [632]. Классическая энергия системы частиц вычисляется путем
суммирования всех парных межчастичных взаимодействий. Чтобы упростить
вычисление, предположим, что макроскопическое распределение
однородно, пренебрегая, таким образом, влиянием взаимодействия на среднее
расстояние между частицами. Иными словами, мы не учитываем
«корреляций» между положениями частиц, связанных с их взаимодействием. Кроме
того, мы будем считать, что число частиц достаточно велико, и потому
суммы можно заменить интегралами, а также что размер системы R
удовлетворяет условию ?>1/?.
При указанных условиях энергия взаимодействия в объеме У равна
E^=\Lyu'±rVii^^%^%· (8.6.3)
Вычислим этот интеграл, считая, что частица, расположенная в точке /у,
соответствует началу координат, и интегрируя по сферам радиуса r=^j.
Так как /?>1/?, с хорошей точностью можно пренебречь поверхностными
эффектами и продолжить интеграл до бесконечности:
г ?^:^^, = ^. (8.6.4)
Интегрируя затем по ?, получаем
?^'±^?^?. (8.6.5)
Таким образом, полная плотность энергии равна
2irnY
?
($.6.6)
Для плотности кинетической энергии можно использовать приближение
идеального ферми-газа в пределе нерелятивистского (первая строка
формулы) и ультрарелятивистского вырождения:
e^„ = «mc^ + ^C^^)^/^^«V3
= ^hcn^y^ (8.6.7)
Уравнение состояния выше точки образования нейтронных капель
221
(см. разд. 2.3). Эта модель дает грубую оценку объемной энергии ядерной
материи, W=e/n-mc^, где мы использовали обозначения разд. 8.2 и 8.4.
Уравнение состояния вычисляется по формуле
В результате
-(f)-
? = Pv.. ±
где
причем
Рш = ^^"^
(8.6.8)
(8.6.9)
(8.6.10)
Г = 1 (нерелятивистский)
~ ? (ультрарелятивистский) (8.6.11)
соответственно в нерелятивистском и ультрарелятивистском случаях [см.
формулу B.3.26)].
Таким образом, мы видим, что при низких плотностях (p:^Pnuc)» когда
можно ожидать, что ядерная сила дает притяжение, взаимодействие
несколько уменьшает давление. Однако при высоких плотностях преобладает
отталкивание, также описываемое потенциалом Юкавы, отвечающим
обменом векторными частицами, и уравнение состояния в присутствии
взаимодействия становится более «жестким». В пределе р = е/с^—оо (т.е. при
п^оо) уравнение состояния имеет вид
При этом скорость звука стремится к скорости света.
='f)
1/2
С,
В отличие от идеального релятивистского газа, для которого
Мы вернемся к обсуждению этих результатов в гл. 9.
(8.6.12)
(8.6.13)
(8.6.14)
8.7. МЕТОД ХАРТРИ
Простейшее квантовое обобщение описанного в предыдущем разделе
классического вычисления в нерелятивистском пределе получается с помощью
222 Глава S
уравнений Хартри^\ В этом приближении многонуклонная система
описывается с помощью произведения одночастичных волновых функций,
? = ?,(?,)?2(?2)···?^(?;,), (8.7.1)
где состояние каждого нуклона полностью определяется его собственной
нормированной волновой функцией мДг^) (/=1, 2,... ?). В этом выражении
для функции ? полностью отброшены спиновые эффекты, а также
корреляции между частицами, так как волновая функция /-й частицы равна и^
независимо от положения других частиц.
Спиновые эффекты можно включить дополнительно с помощью метода
Хартри — Фока, описанного в следующем разделе. Корреляции
учитываются путем введения в волновую функцию Хартри — Фока ?
«корреляционных функций», причем полученное волновое уравнение решается в
рамках некоторой приближенной схемы (см. разд. 8.9).
В приближении Хартри энергия основного состояния системы равна
где ? — полный гамильтониан, и мы будем рассматривать случай, когда
потенциал V^2 имеет вид (8.6.1). Заметим, что в методе Хартри
/|«,(?)|^^?=1, (8.7.3)
НО различные функции и^ не обязаны быть ортогональными друг другу.
Уравнение Хартри можно вывести, используя формулу (8.7.2) для
формулировки вариационного принципа и допуская произвольные вариации
функций щ и м;при выполнении условия (8.7.3). Это уравнение имеет вид
-^?'«,+ ^;.и, = е,м,, ,= l,2,...,iV, (8.7.4)
2т
где эффективный потенциал /-й частицы равен
V,{t,)-ZJd\V,,{r,,)\Uj{r^)\\ (8.7.5)
Вместо того чтобы решать уравнение (8.7.4) для функций щ
самосогласованным образом (это слишком трудная задача), мы будем искать
энергию основного состояния системы методом теории возмущений. Предпо-
'^ Подробное изложение метода Хартри можно найти, например, в книге [63],
гл. 4.
Уравнение состояния выше точки образования нейтронных капель 223
ложим, что в низшем порядке функции и^ соответствуют свободным
плоским волнам с импульсом р = Лк,
и.==—^е^^'^\ (8.7.6)
Волновые функции нормированы здесь на объем >=L^, где 1>?~^ —
линейный размер системы.
В соответствии со статистикой Ферми мы предположим, что низшие
уровни энергии заполнены (каждый — двумя частицами) вплоть до ?=??
(или А: = А:р). Таким образом, сумма по / соответствует интегралу по к до
Агр. При этом волновая функция ? в формуле (8.7.1) описывает
вырожденную систему с однородной плотностью, и функции Uj можно рассматривать
как некоторую весьма ограниченную систему пробных функций в уравнении
(8.7.2), использование которой имеет смысл только для слабых
потенциалов взаимодействия. Это простейший квантовый аналог приближения
Зельдовича.
Используя выражение (8.7.6), представим формулу (8.7.2) в виде
Присутствующий здесь двойной интеграл вычисляется точно так же, как в
(8.6.3), и в результате
_ п2 _ 1„^2
(8.7.8)
Теперь,
так что
как
обычно.
2 „
<Я> =
, 2т
к
заменим
гГ^^л
^Z"'-
) 1 rtr
у 2wg2
?' ? ¦
^ B^)'
(8.7.9)
к h" Jo
В результате получаем полную плотность энергии,
e.if^ + «.c^ = e,„±^, (8.7.11)
ТОЧНО совпадающую в нерелятивистском пределе с классическим
результатом [см. формулы (8.6.6) и (8.6.7)].
224
Глава 8
8.8. МЕТОД ХАРТРИ — ФОКА
Волновая функция системы, состоящей из N фермионов, должна быть
антисимметричной при перестановке любой пары частиц. Это требование
можно выполнить, записав волновую функцию в виде детерминанта Слэте-
ра:
? =
(iV!)
1/2
м,A) «,B)
A)
Ml)
M,GV)
»??)
(8.8.1)
Функция ? является суммой членов, каждый из которых — произведение
одночастичных функций вида
W/(y) = W/(r,)X/(^,),
(8.8.2)
где спинор ?(?) равен либо Xj (спин направлен «вверх»), либо ?2 (спин
направлен «вниз»).
^^"(J)' >^^"(?)·
(8.8.3)
Здесь ? — аргумент ? в спиновом пространстве, принимающий два
значения, 1 или 2. Если ? = ??, то хA)= 1, ?B)=0; соответственно,если ? = ?2, то
хA)=0, хB)= 1. В отличие от метода Хартри здесь требуется
ортогональность волновых функций:
Zjd\ur{\)uj{\) = 8,j.
Из вариационного принципа
8{^\Н\^) =0
(8.8.4)
(8.8.5)
следуют обычные уравнения Хартри — Фока, которые мы не станем
выписывать ^\ Вместо этого подставим в выражение для энергии основного
состояния плоские волны, рассматривая их как пробные функции. При
вычислении энергии заметим, что функция ? нормирована, так что для всякого
оператора вида
F^Zfi (8-8-6)
^^ См. указанную книгу [63], гл. 4; мы используем те же обозначения
Уравнение состояния выше точки образования нейтронных капель 225
(/; — однофермионный оператор) среднее значение равно
(*|F|Y>=E<'I/I'>. (8-8.7)
где 1/> =М/. Для оператора вида
F-?gu^ (8.8.8)
где gij — симметричный двухфермионный оператор, имеем
<*1Л*> = I[<i/1gli/> - <'7lg|yO] =^?[<?/?^??/·> - <i/1g|yO]· (8.8.9)
Для данного гамильтониана
Комбинация членов типа/и первой части суммы в (8.8.9) (так называемый
«прямой» член) равна энергии в методе Хартри, которая была вычислена в
разд. 8.7. Кроме того, имеется еще «обменный» член,
/= -\L(u\g\ji)
= -^? ? fd%d%u*ir,)u*ir,)V,,u,it,)uj{t,) ?
??*(?,)??(?2)?,(?2)?/?,). (8.8.11)
Поскольку
Exf(«)Xy(<') = «('".,''".,). (8.8.12)
?
где w^= ± 1/2 — проекция спина на ось ?, то
I = -^?Hm,^,m,J)fd%d%ur{r,)u*ir,)V,,u,i?,)uJ{r,)
= -^2fd%d%V,Mh,r2)\\ (8.8.13)
где по определению
Р(Г1,Г2)= ?";(?2)">(??), (8.8.14)
15-353
226 Глава 8
и множитель 2 возникает от двух возможных значений m^i^ni^j.
Для плоских волн (8.7.6) получаем
р(г„г,) = ^Р"'-<'--''> ^•^А"""'^'*· (8.8.15)
Отметим, что здесь нет множителя 2, обусловленного суммированием по
спиновым состояниям, так как он уже включен в формулу (8.8.13).
Записывая к-Г|2=А^/*|2С08^ и с1^к=1жс1(соъв)к^ак, получаем
Pi^x^^i) =^—:^-r{UTik^r^2 -/:рА-,2С08/:рГ|2). (8.8.16)
?? ^2
Упражнение 8.9. Показать, что р(г^, г^)=:л/2, где п^к^/Зтг^, и объяснить, почему
этот результат представляется разумным.
Подставляя в формулу (8.8.13) выражение (8.6.1) для Kj2 и обозначая
R = Иг, + Гг),
г = г - г = г (8·«·*''^
Г ?? Г2 — ??2,
получаем
I=Tg'fd'Rd'rpHr)^. (8.8.18)
Интеграл по R дает множитель У. Интеграл по г можно записать в
безразмерном виде, вводя новые обозначения
При этом
дс = /:рг, «=-^· (8.8.19)
/=Tg2T4/(«), (8.8.20)
где
r^dx . . ч2 _
1{а)= f ^(sinx-xcosx)'e-«\ (8.8.21)
•'о х^
Уравнение состояния выше точки образования нейтронных капель 111
Этот интеграл можно вычислить путем последовательного интегрирования
по частям и сведения к табличным интегралам. В результате
Предельные значения равны
/(а)"*-, а-* О, (8.8.23)
1
« "* 00. (8.8.24)
Упражнение 8.10. Вывести предел (8.8.24), заменяя функцию sin л:—л: cos л: ее
значением при малых л:.
Заметим, что параметр ? пропорционален отношению среднего
расстояния между частицами к радиусу взаимодействия, поэтому теория
возмущений, в рамках которой мы работаем, применима, строго говоря, лишь в
пределе ol>\. Таким образом, получается
^ 97г' ?2 ^ 9,г' ?^ ?^ '
Это выражение противоположно по знаку «прямому» члену в формуле
(8.7.11) и по величине точно равно его половине. Физический смысл этого
соотношения в том, что в силу принципа Паули лишь частицы с
противоположными спинами могут сблизиться на достаточно малое расстояние и
взаимодействовать, так что учет спиновых эффектов понижает энергию
взаимодействия в два раза.
Обменный член понижает роль взаимодействий между частицами,
уменьшая энергию отталкивания и увеличивая энергию притяжения.
Поэтому обменный член дает эффективное притяжение (^ехсь*^^) ^^^ ^^^
отталкивания и эффективное отталкивание (^ехсь^^) ^^^ ^^^ притяжения.
Поскольку р = е/с^, в пределе а> 1 получаем
р = пт+ А(з^2J/з_й1^з/з i ЕП!^^ (8,8.26)
Р = Кп'/'± ^^^. (8.8.27)
Итак, мы вывели уравнение состояния для потенциала типа Юкавы в
приближении Хартри — Фока.
228 Глава 8
Упражнение 8.11. В пределе сх< 1 потенциал Юкавы переходит в кулоновский
потенциал. Используя результаты, полученные в этом разделе, найдите обменную
поправку к уравнению состояния холодного нерелятивистского газа электронов (см.
разд. 2.4 и работу Солпитера [496]).
8.9. КОРРЕЛЯЦИОННЫЕ ЭФФЕКТЫ
Изложенный в предыдущем разделе метод Хартри — Фока не позволяет
надлежащим образом учесть корреляции между нуклонами. Двухчастичные
корреляции можно включить в многочастичную волновую функцию,
записав ее в виде
^ = ^Ф, (8.9.1)
где ? — детерминант Слэтера, построенный из волновых функций,
отвечающих плоским волнам, как в формуле (8.8.1), а F— симметризованное
произведение двухчастичных корреляционных функций:
F-Y\fij (8.9.2)
Таким образом, волновая функция записывается в виде
?(?„..., г^) =^ПУ;7(|г, - г>1)ПФ.(г.), (8.9.3)
где Л — оператор антисимметризации, действующий на спины, изоспины
и координаты, а ф^ — волновые функции плоских волн с учетом спинов и
изоспинов:
Волновая функция вида (8.9.3) называется пробной функцией Джастроу, она
может быть использована для вариационного вычисления энергии
основного состояния системы. Множители f^j отражают препятствие сближению
пар частиц на малые расстояния при наличии отталкивательного кора и
потому выбираются таким образом, что равны единице на больших
расстояниях и падают почти до нуля, когда величина 1Г/-г^1 становится
порядка радиуса кора г^. Дополнительные корреляции могут возникнуть от
других компонент силы, действующей между частицами (например,
тензорных членов).
Общий метод вариационного расчета состоит в определении минимума
среднего значения гамильтониана при варьировании функций /:
5<Я>=0, где (Н)-^Щ^. (8.9.5)
Уравнение состояния выше точки образования нейтронных капель 229
Обычно такие вариационные вычисления проводятся путем разложения
величины <Я> по кластерам:
<Я> = ? Е„. (8.9.6)
Вклад А2-частичного кластера Е^ включает в себя ЗА2-кратные интегралы (по
пространству координат частиц) от матричных элементов,
присутствующих в формуле (8.9.5). Если плотность системы не слишком велика и
корреляционные длины малы, то среднее значение <Я> может быть найдено
через вклады кластеров низкого порядка.
Существует много схем построения, усечения и суммирования
кластерного разложения^\ Как правило, определение детального выражения для
энергии основного состояния требует вычисления сложных многократных
интегралов, зависящих от ф^ и f^j. Мы не будем выписывать здесь эти
интегралы, а ограничимся тем, что в следующем разделе приведем сводку
результатов одного из таких вариационных расчетов (в методе Бете —
Джонсона).
Помимо вариационного метода системы сильно взаимодействующих
фермионов можно анализировать также с помощью другого метода,
основанного на теории ядерной материи Брюкнера, Бете и Голдстоуна (общее
обсуждение этой теории можно найти, например, в книге [159]). В низшем
порядке эта теория использует сумму вкладов от процессов двухчастичного
рассеяния. В этом порядке она дает выражение, получаемое для энергии
основного состояния в методе Хартри — Фока, но «исходный» потенциал
V(r) заменяется «одетым» потенциалом V(r), который включает в себя
поправки, связанные с многочастичным обменом. В целом этот подход
можно рассматривать как разложение по параметру пг^, где ? — концентрация
нуклонов и г^ — радиус «твердого кора» (см. разд. 8.4). При малых
значениях 3fForo параметра справедливо приближение независимых пар частиц^\
на котором основана рассматриваемая теория; при больших значениях
параметра приближение неприменимо.
Теория Брюкнера, Бете и Голдстоуна считается приемлемой при
плотностях <2р„и^.. При более высоких плотностях повышается роль
многочастичных кластеров и следует применять вариационный метод. Отметим,
что в последнее время были достигнуты значительные успехи в
вариационных расчетах, учитывающих как двух-, так и трехнуклонные
взаимодействия [207,351]. Эти расчеты позволяют пол>чить результаты,
соответствующие теории Брюкнера, Бете и Голдстоуна в низшем порядке для той обла-
'^См. обзоры Кларка [134] и Дэя [158], недавние работы Пандхарипанде,
например [207] и [351], и приведенные там ссылки.
^^ В приближении независимых пар рассматривается движение двух
взаимодействующих фермионов в присутствии других фермионов, играющих роль
«наблюдателей» и влияющих на движение этих частиц только в силу принципа Паули.
230 Глава 8
сти, где можно ожидать, что оба подхода применимы. Кроме того, как
уже было сказано, появляется возможность количественно
проанализировать насыщение.
8.10. УРАВНЕНИЕ СОСТОЯНИЯ БЕТЕ ~ ДЖОНСОНА
В качестве примера мы приведем результаты Бете и Джонсона [64],
которые использовали «ограниченный вариационный метод» Пандхарипанде
[443] в низшем порядке. Были найдены уравнения состояния как для чистой
ядерной материи, так и для материи, содержащей гипероны с массами, не
превышающими массу ?-резонанса A236 МэВ). Принятый потенциал
ядерного взаимодействия был подобен потенциалу, использованному ранее
Рейдом [478], т.е. представлялся в виде суммы функций Юкавы с различными
силами и радиусами взаимодействия. Коэффициенты в этом потенциале
подбирались в каждой парциальной волне по отдельности, чтобы описать
экспериментальные данные о нуклон-нуклонном рассеянии.
Как мы видели ранее, обмен векторными мезонами приводит к
появлению отталкивания между нуклонами, в то время как обмен скалярными
мезонами приводит к притяжению. Три векторных мезона с наименьшей
массой — это ? G69 МэВ), ? G83 МэВ) и ? A019 МэВ). Из них наиболее
сильная связь с нуклонами у ?: как следует из экспериментальных данных
при высоких энергиях, gl^/hc= \0±2. Поэтому Бете и Джонсон включили
только обмен ?-мезонами: радиус действия соответствующих сил
~mJ^ = ^/w^,c=0,25 Фм. Поскольку ? — изоскаляр, то отталкивательный
кор не зависит от полного изоспина ? нуклон-нуклонной системы. Одно из
основных различий между потенциалами Рейда и Бете — Джонсона
обусловлено именно наличием в последнем случае отталкивания, связанного с
обменом ?-мезоном.
Таким образом, потенциал Бете — Джонсона берется в виде
V^Ar)-Zc;-^+Vr{r), (8.10.1)
j
где
т„с ,
X = ??, ? = —г- = 0,7 Фм
(8.10.2)
Коэффициенты Cj при j ?1 выбираются из сравнения с
экспериментальными данными, а С| и тензорный потенциал (см. разд 8.3) берутся в
соответствии с моделью однопионного обмена [см. [159], гл. 1, формула C.5)].
Обмен (псевдо)скалярными пионами использован для получения в
потенциале (8.10.1) дальнодействующего притяжения (радиус действия
соответствующих сил равен 1//?^, где 1/?^=5,5/?^, причем наиболее сильное
притяжение связано с обменом двумя пионами, т.е. представляется членом су = 2).
Уравнение состояния выше точки образования нейтронных капель 231
Притяжению отвечают отрицательные коэффициенты при функциях Юка-
вы, Cj. Отталкивание связано, в основном, с членом
У.^п—^^ (8.10.3)
где ^^/Лс= 29,6. Поразительно большая величина ^^, примерно втрое
превышающая значение, следующее из данных о рассеянии при высоких
энергиях, получается в результате подгонки данных о рассеянии при низких
энергиях и фиксированном радиусе потенциала отталкивания, который
брался равным в точности 1/?^^. Отметим, что в отличие от потенциала
Рейда не во всех членах j — целое: например, потенциалу К^ отвечает
у=5,5 в формуле (8.10.1).
Потенциалы Бете — Джонсона воспроизводят следующие из
эксперимента фазы рассеяния, энергию связи ядерной материи и квадрупольный
момент дейтрона столь же точно, как потенциал Рейда. Для простейшего
случая чисто нейтронной материи вычисление этим методом (так
называемая «Модель I») дает результаты, типичные для общего случая, хотя в
указанной модели радиус потенциала отталкивания такой же, как в
потенциале Рейда и соответствуету=7 в (8.10.1). Уравнение состояния
записывается в следующем виде (концентрация ? выражена в Фм"^):
^=Ж(^:,0) + m„c^
Ж(Л,0) = гЗби" МэВ/частица (8.10.4)
? ^ ^2^(^/") ^ 364/»°-" МэВ/Фм^
dn
= 5,83 X Ю^и""" дин/см2, (8.10.5)
где
а = 1^54, 0,\ <п<3 Фм-з или 1,7 X 10^^ < ? < 1^1 X Ю^^ г/см^
Упражнение 8,12. Использовать потенциал (8.10.3) в методе Хартри — Фока с
плоскими волнами (разд. 8.8) и получить уравнение состояния для чистой нейтронной
«жидкости». Сравнить полученные таким образом результаты с уравнением
состояния Бете — Джонсона в области 0,l:S/z:s3 Фм~^.
Упражнение 8.13. Использовать выражение (8.10.6) для скорости звука с , чтобы
найти предельную плотность, выше которой уравнение состояния Бете — Джонсона
заведомо неприменимо.
232 Глава 8
Наиболее важная черта уравнения состояния Бете — Джонсона — это
его сравнительно высокая жесткость, соответствующая адиабатическому
показателю Г = 2,54. При этом жесткость значительно выше, чем для
уравнений состояния, получаемых с потенциалом Рейда, так как в данном
случае отталкивание на малых расстояниях описывается более реалистически.
Чем больше жесткость, тем выше максимальные массы нейтронных звезд
(см. гл. 9).
Бете и Джонсон использовали свою многочастичную технику также для
исследования гиперонной жидкости, состоящей из л, р. Л, ? и ?-частиц.
Оказалось, что легкие гипероны с массами < 1250 МэВ действительно
появляются при типичных для нейтронных звезд плотностях (ni^l Фм"^,
точное значение зависит от модели). Однако, как и в более ранних работах,
полученное уравнение состояния не очень отличается от уравнения
состояния для чистой нейтронной материи. Из-за появления новых незанятых
ячеек в фазовом пространстве и соответствующего понижения уровня моря
Ферми — Дирака уравнение состояния становится несколько более мягким.
С другой стороны, в этих расчетах присутствует большая
неопределенность. Потенциал взаимодействия между гиперонами почти неизвестен и
обычно считается равным потенциалу взаимодействия между нуклонами.
Чтобы показать, как появление новых частиц включается в уравнение
состояния, рассмотрим прежде всего задачу о появлении мюонов в
идеальном газе, состоящем из нейтронов, протонов и электронов. При
нормальных условиях мюоны распадаются на электроны с испусканием нейтрино:
?-^?'?^ ?^?- ?^. (8.10.7)
Если энергия Ферми для электронов становится достаточно высокой, то
переход электронов в мюоны становится энергетически выгодным, так что
возникает равновесие между мюонами и электронами:
?'^?-. (8.10.8)
Здесь, как обычно, предполагается, что нейтрино излучаются из системы.
Хотя для доказательства того, что за интересующее нас характерное время
в мюон-электронных переходах успевает установиться равновесие,
необходим детальный расчет скоростей реакций, коль скоро мы знаем, что
равновесие достигнуто, термодинамика не требует от нас знания всех деталей
процесса. Мы просто пишем уравнение химического равновесия
М^ = Ме» (8.10.9)
и требуем сохранения некоторых величин (в данном случае — заряда).
Равновесие между нейтронами, протонами и электронами приводит к
уравнению
М« = Мр + Ме» (8.10.10)
а из электрической нейтральности следует
Пр = n^-l· п^. (8.10.11)
Уравнение состояния выше точки образования нейтронных капель 233
При известных выражениях для химических потенциалов и концентраций
частиц через плотность материи формулы (8.10.9)-(8.10.11) вместе с
уравнением для плотности представляют собой систему уравнений,
достаточную для вычисления всех свойств газа. Например, для идеального газа
получим
т^с'{\ + ???' = т,г{\ + х1У'\ (8.10.12)
т„с'{1 + х'„У'' = т^с'(\ + х^У'' + т,с'{\ + х1У'\ (8.10.13)
(т^х^У - {т,х,У + {т^х.У, (8.10.14)
? ' ^Xixn) + ^Xi^p) + ^х(Хе) + ^?(?,), (810.15)
^П ^р ^е ^?
(ср. разд. 2.3). Здесь величины ? — обычные безразмерные импульсы
Ферми. Пороговое условие, соответствующее появлению мюонов, имеет вид
А2 =0, т.е. X =0, Поскольку при этом электроны ультрарелятивистские, то
мо^но считать, чтол^>1. Формулы (8.10.12) — (8.10.14) принимают вид
т^ = т^х^, (8.10.16)
т„{\ + х^У^^ = т,{\ + х^У^^ + т,х„ (8.10.17)
^рХр = f^e^e- (8.10.18)
/ J 9\V2
и тогдал'^ = 0,1126, л· =206,8 ир=8,2М0^^ г/см^
Упражнение 8.14. Показать, что ниже плотности 8,21 · Ю'^ г/см^ существует область
значений плотности, при которых мюоны, впрыснутые в идеальный газ, состоящий
из нейтронов, протонов и электронов, будут стабильными относительно распада
(8.10.7), даже если газ не находится в равновесном состоянии.
Указание. Рассмотрите законы сохранения энерг11и и импульса для распада мюона.
Упражнение 8.15. Написать соотношения между химическими потенциалами в
равновесном идеальном газе, состоящем из п, р, е, ? ~, Л®, ? ~, ?® и ? "·". Объяснить,
почему ? "-гипероны появляются при наиболее низкой плотности, хотя и имеют
наибольшую массу. Чему равна эта плотность? Массы приведены в табл. Д. 1.
234
Глава 8
О 0,2 ?,? 0,6 0.8 1.0 \? \А 1.6 1,8
Рис, 8.4. Относительные концентрации л^ в газе свободных гиперонов в зависимости
от полной концентрации барионов л. (По работе Кануто [105].)
Вычислительное упражнение 8,16, Построить уравнение состо5Шия для газа,
описанного в упражнении 8.15, и изобразить график зависимости от ? концентраций всех
частиц, содержащихся в газе, в интервале 0<л< 10 Фм'^. Проверить таким
образом результаты Амбарцумяна и Саакяна [12], представленные на рис. 8.4. Сравнить
полученное уравнение состояния с уравнением для идеального газа, состоящего из
нейтронов, протонов и электронов.
Уравнение состояния выше точки образования нейтронных капель 235
Результат упражнения 8.16, согласно которому нейтроны преобладают
и в недрах нейтронных звезд, объясняет, почему уравнение состояния
Бете — Джонсона при наличии гиперонов мало отличается от уравнения
состояния для чисто нейтронного вещества.
Как и все многочастичные вычисления уравнения состояния, результаты
Бете и Джонсона вовсе не являются окончательными. Укажем некоторые
недостатки этого метода.
1. Использованная многочастичная техника не позволяет воспроизвести
полученные методом Монте-Карло «точные» результаты [136] для
гипотетического потенциала отталкивания типа Рейда.
2. Ни один из феноменологических нуклон-нуклонных потенциалов не
дает насыщения даже при использовании улучшенного метода вычислений.
3. Константа связи для ?-мезонов, которая получается из подгонки
данных об MV-рассеянии, g^/hc^lO, противоречит значению, которое
получается из опыта, g^/hc= 10±2.
4. Силы взаимодействия гиперонов описаны простейшим и не совсем
правильным образом; «массовые сдвиги» гиперонов, обусловленные
плотной окружающей средой, не учитываются. Указанные массовые сдвиги
могут, например, приводить к тому, что ?-резонансы появляются лишь при
плотностях, превышающих 10^^ г/см^.
5. Нарушение причинности, Р>рс^, при высоких плотностях (ср.
упражнение 8.13).
6. А-резонансы упрощенно описываются как независимые «голые»
стабильные элементарные частицы. Пионная конденсация не принимается во
внимание (см. разд. 8.11 и 8.12).
Несмотря на эти нетривиальные проблемы, уравнение состояния
Бете — Джонсона остается одним из лучших, известных до настоящего
времени. Учет отталкивания в ядерных силах на малых расстояниях приводит
к ряду жестких уравнений состояния, которые, по-видимому, несколько
лучше согласуются с существующими в настоящее время данными о
наблюдаемых нейтронных звездах. (См. гл. 9.)
Интересно, что полученное недавно в работах Пандхарипанде и его
сотрудников уравнение состояния, использующее как двух-, так и трехнуклон-
ные взаимодействия и приводящее к хорошему согласию теории с
экспериментом, весьма близко к уравнению состояния Бете — Джонсона. Оба этих
уравнения более жесткие, чем то, которое получается с потенциалами типа
Рейда, но менее жесткие, чем в модели с тензорными силами [444, 445] или
в теории «релятивистского среднего поля» [595]. Сравнение различных
моделей проводится в резюме 8.1, табл. 8.2, а также на рис. 8.5а и 8.56.
236 Глава 8
РЕЗЮМЕ 8.1.
Уравнение состояния холодного вещества
выше точки образования нейтронных капель
1. Уравнение состояния холодного вещества выше точки образования
нейтронных капель (Pdrip*^* ^^^^ г/см^) удобно рассматривать для двух
областей. Область Pdrip<?^Pnuc*-^'^'^^^^ ^/^^^ сравнительно хорошо
изучена (см., например, работу [55]). Равновесная материя состоит из
обогащенных нейтронами ядер, образующих кулоновскую решетку, электронов и
свободных нейтронов. При возрастании плотности свободные нейтроны
обеспечивают все большую долю полного давления. При ? - ?^^^
начинается деформация и разрушение ядер.
При более высоких плотностях, м>Рпис» ситуация менее ясная. В этой
области давление определяется главным образом нуклонами
(преимущественно нейтронами), вступающими в сильные взаимодействия. Помимо
нейтронов и небольшой примеси протонов и электронов, возможно,
появляются другие элементарные частицы и резонансные состояния.
2. Расчет уравнения состояния в нерелятивистской области от р^^^ до
р^ 10^^ г/см^ связан с двумя трудностями, а) определением ядерного
потенциала для нуклон-нуклонного взаимодействия, б) построением метода,
подходящего для решения многочастичной задачи. Выбор потенциала
несколько ограничен данными о нуклон-нуклонном рассеянии и свойствах ядерной
материи.
3. При сверхвысоких плотностях, р>10^^г/см^, в материи появляется
заметное количество гиперонов, и взаимодействие между нуклонами
должно рассматриваться с учетом релятивистских эффектов. К сожалению,
техника решения релятивистской многочастичной задачи для сильно
взаимодействующей материи недостаточно хорошо разработана.
4. Уравнения состояния ядерной материи, полученные до настоящего
времени» содержат множество неопределенностей. Среди них возможность
нейтронной и протонной сверхтекучести, пионной конденсации, отвердения
нейтронной материи, фазовых переходов в состояние «кварковой
материи», а также эффекты, связанные с образованием ?-резонансов.
5. Свойства нейтронных звезд чувствительны к разновесному
уравнению состояния при плотностях, превышающих р^^·^^ (см. гл. 9).
6. Типичные модели для уравнения состояния выше точки образования
нейтронных капель приводятся на рис. 8.5а и 8.56 и в табл. 8.2.
Уравнение состояния выше точки образования нейтронных капель 237
10
Lgp (г/смЗ)
15
Рис, 8.5&, Равновесное уравнение состояния для холодного вырожденного вещества.
Сплошная кривая показывает результат Бейма и др. [56] для области P^p^j^j *
*4,3· 10^ ^ г/см^, плавно переходящий в уравнение Бейма — Бете — Петика в оола-
^'^^ f^drip^f^^Pnuc^^·'^' ^^^^ ^^^^^· ^^^ сравнения штриховой линией изображено
уравнение Оппенгеймера — Волкова [427] для свободного нейтронного газа.
Типичные уравнения состояния для области выше р^^^ расположены в прямоугольнике в
правом верхнем углу графика и показаны в увеличенном виде на рис. 8.56. G —
свободные е~, решетка ^б^^е; 2 — релятивистские е~; 3 — нейтронизация; 4 —
свободные е~ у решетка из ядер, обогащенных нейтронами; 5 — нейтронные капли; б —
решетка из ядер, обогащенных нейтронами, свободные нейтроны; 7 — нейтроны,
протоны, е~; 8 — гиперонизация.)
238
37,0
36,5
s
о
1*36,0
?
?>
35,5 ?
35.0 h
?
?
?
?
Lljl
? ? ? ? ? ? ? ? J ? ? 11
??? / r/^ ?
/ /4j ?? 1
/// ]
fflv ? ? ? ? ? J_ ? ? ? ? 1
Глава 8
37,0
? 36,5
Ч 1 36.0
? 35,5
? 35.0
' ' ' Ч ' ' ' Ч
1111
34,51 ? ? МГ1ГМ ? ? ? ? ? ? ? ? ? 34,5
?,5 15,0 15,5 16,0 14,5
Igj3(i/CM^
15,0 15,5 16,0
Рис. 8.56. Типичные уравнения состояния для холодного вырожденного вещества
при плотностях выше Pnuc~^»^' ^^^^ г/см^. Обозначения даны в табл. 8.2. (По
работе Арнетта и Бауэрса [20].)
8.11. НЕРЕШЕННЫЕ ВОПРОСЫ: ?-РЕЗОНАНС
Существует целый ряд неприятных вопросов, требующих для своего
ответа сложных вычислений, которые следовало бы решить, чтобы понять,
каково уравнение состояния, например, при плотностях около 2?„^?.
Некоторые из них (например, схемы многочастичных вычислений) уже были
упомянуты выше. Хотя в данной книге едва ли уместно входить в детали этой
проблемы, мы хотели бы все же сформулировать некоторые вопросы и
указать, в какую сторону могут изменить уравнение состояния различные
неучтенные эффекты.
Один из нерешенных вопросов относится к ?-резонансу, возбужденному
состоянию нуклона, которое имеет массу 1236 МэВ и квантовые числа
/=3/2, У =3/2. В результате пионного обмена между двумя нуклонами
могут возникнуть виртуальные промежуточные состояния, такие, как NN, ??
Таблица 8.2
ТИПИЧНЫЕ УРАВНЕНИЯ СОСТОЯНИЯ ВЫШЕ ТОЧКИ ОБРАЗОВАНИЯ
НЕЙТРОННЫХ КАПЕЛЬ
Уравнение
состояния
Идеальный
нейтронный газ;
Оппенгей-
мер — Волков
[427] (OV)
Бейм, Бете
и Петик
[55] (ВВР)
Рейд [443]
(R)
Бете и
Джонсон [64]
(BJ)
Тензорное
взаимодействие
[444] (TI)
Диапазон
плотностей,
г/см^
0 ^ ? ^ 00
4,3· 10^1 <
< ? ^
^ 5 X 10^^
? > 7-10^^
1,7· 10^"^ ^
^ ? ^
< 3,2 X 10'^
? > 8,4· 10'^
Состав
?
е~, ? и
равновесные
ядра
?
?, ?. Л, ?=^'<^
?
Взаимодействия
Отсутствуют
Потенциал
Рейда с мягким
кором
Потенциал
Рейда с мягким
кором,
приспособленный к
ядерной
материи
Модифицированный
потенциал Рейда
Ядерное
притяжение,
связанное с
тензорными силами от
пионного
обмена
Многочастичная
теория
Невзаимодействующие
нейтроны
Массовая
формула для ядер,
построенная по
модели
сжимаемой жидкой
капли
Вариационный принцип,
применяемый к
корреляционным
функциям
Ограниченный
вариационный метод
Ограниченный
вариационный метод
Трехнуклон-
ное
взаимодействие [207] (???)
? > 1,7· 10^'
Среднее поле ? > 4,4· 10^^ ?
[445] (MF)
Релятивист- ? > 1,7-10^^ ?
ское среднее
поле [595]
(RMF)
Двух- и трех- Ограничен-
нуклонные взаи- ный вариацион-
модействия ный метод
Ядерное при- Приближение
тяжение, выз- среднего поля,
ванное скаляр- вариационный
ным обменом метод
Релятивист- Приближение
ское среднее релятивистского
скалярное поле среднего поля
и векторный
обмен,
описывающий ядерную
материю
240 Глава 8
или ??. Как указано в работе [237], процессы, в которых обмен пионами
вызывает притяжение, будут подавляться в плотной ядерной среде из-за
изменения энергии промежуточного состояния, а также вследствие
принципа Паули (так как многие из этих состояний уже заняты). Соответственно
следует уменьшить некоторые из дающих притяжение составляющих в
обычных двухчастичных феноменологических потенциалах, которые
подбираются для описания данных о нуклон-нуклонном рассеянии в свободном
пространстве. Поэтому уравнения состояния будут жестче, чем то, которое
получается со свободными потенциалами.
В работе [506] дано иное объяснение этого эффекта. Наличие плотной
окружающей среды меняет собственную энергию ?-резонанса и приводит к
возрастанию этой энергии на величину ^ 2(Ю МэВ. Соответствующий
химический потенциал можно записать в виде
Н = {р%с^ + тУ)'^^ + ?/(??) ^ {р%с^ + miV)'/', (8.11.1)
где ?{??:) включает поправки к собственной энергии ит'^>т^ —
эффективная масса. Возрастание эффективной массы ?-резонанса понижает
концентрацию и потому делает уравнение состояния при высоких плотностях более
жестким.
В чисто нейтронной материи этот эффект выражен более ярко, чем в
симметричной ядерной материи. Причина состоит в том, что а2А2-системы
имеют изоспин Г= 1, а А2/7-системы — изоспин Т= 1 или О (см. табл. 8.1).
Однако в преобладающем процессе, в котором рождается система ??,
изоспин может принимать только значения 1 или 2 (поскольку изоспин ? равен
3/2), так что этот процесс может происходить только в канале с Т= 1.
Учет ?-резонанса помогает понизить плотность насыщения для
симметричной ядерной материи, так как при этом возникает отталкивание в
состоянии с Г=1, если р;грпи^. Увеличение жесткости уравнения состояния
для нейтронных звезд приводит к понижению плотности и увеличению
радиуса при данной массе.
8.12. НЕРЕШЕННЫЕ ВОПРОСЫ! ПИОННАЯ КОНДЕНСАЦИЯ
Если пренебречь эффектами сильных взаимодействий между пионами и
нуклонами, то отрицательно заряженные пионы могут образовываться в
плотной ядерной материи в результате реакции
n^p-l·^- (8.12.1)
лишь при условии, что разность ?^-?^ = ?^ превосходит массу покоя ?"-
мезона, w^= 139,6 МэВ. Как было показано, ?^-100 МэВ при p-Ppuc» '^^^
что появления ? "-мезонов можно ожидать при несколько более высоких
плотностях. Это должно приводить по меньшей мере к двум важным
следствиям: уравнение состояния станет более мягким и скорость
остывания нейтронной звезды, вызванного излучением нейтрино, увеличится^^
^^ Остывание нейтронных звезд рассматривается в гл. 11.
Уравнение состояния выше точки образования нейтронных капель 241
Так как пионы — это адроны, т.е. частицы, которым присуще сильное
взаимодействие, то их свойства существенно меняются внутри ядерной
материи. Хотя взаимодействия пионов с нуклонами ядерной материи в самом
низком порядке E-волна) приводят к увеличению эффективной массы
пиона, взаимодействия более высокого порядка (р-волна) имеют
противоположный знак. Вычисления, проведенные до настоящего времени [405],
показывают, что ?"-мезоны действительно появляются при ?-2?„^^, однако
эти результаты следует рассматривать как весьма предварительные.
Интересное и важное следствие возможного появления пионов, которые
имеют спин О, состоит в том, что при достаточно низких температурах
они могут образовывать бозе-эйнштейновский конденсат. Идеальный
конденсат состоит из большого числа бозонов в состоянии с нулевой
кинетической энергией. Чтобы найти критическую температуру Г^, вспомним, что
максимальное значение химического потенциала для бозонов с массой т
равно ? = ??€^. При более высоких значениях числа заполнения для
некоторых состояний с заданным импульсом стали бы отрицательными. При
данной концентрации частиц ? температура Т^ определяется условием
? = ??€^. Отсюда следует (ср. разд. 2.2)
/1 = 4 ? ^- ^V· (8.12.2)
h ^ ^(Е-тс^)/кТ, _ ?
При низких температурах можно использовать нерелятивистское
приближение
2
Вводя безразмерную переменную
^ = 2^7;' ('-''-'^
получаем
п^—^—(ткТ)'^'Г^^^-^ (8.12.5)
Интеграл здесь равен -?^^^{·C/2), где f — дзета-функция Римана. Оконча-
0
тельно
2
' тк
/ \ 2/3
(-g) h'- (8.12.6)
При Т< ? частицы с положительной кинетической энергией имеют
распределение, соответствующее формуле вида (8.12.2) (с заменой Т^ на Т),
16-353
242 Глава 8
Согласно формуле (8.12.5), п^-Т^^^, так что
/ j^ N3/2
/i(z> 0) =/1^—1 . (8.12.7)
Все остальные частицы находятся в низшем состоянии с z = 0.
n{z = 0) = /I
-'Г
(8.12.8)
Частицы с z = 0 не имеют импульса (конденсация происходит не в
физическом, а в импульсном пространстве) и потому не вносят вклада в давление.
При Г—О практически все бозоны оказываются в этом состоянии. Таким
образом, ясно, почему пионная конденсация приводит к смягчению
уравнения состояния. Детальный, хотя и весьма предварительный расчет [25]
предсказывает уменьшение полного давления на 75 ^о при р-^'^р^ис
Отдельные свойства механизма, благодаря которому пионный конденсат делает
уравнение состояния более мягким, весьма сильно зависят от нуклон-
нуклонного взаимодействия в целом. Вполне надежное вычисление
уравнения состояния, которое учитывало бы и эффекты изобары, повышающие
давление (см. разд. 8.11), и смягчающий эффект пионного конденсата, еще
не было проведено.
Чтобы разобраться в эффектах пионной конденсации, рассмотрим
идеальный газ, состоящий из нейтронов, протонов и электронов, при Г=0 и
допустим, что выше порога возможно рождение ?~-мезонов. Условие
равновесия
дает
М„-Мр = Ме = М^» (8.12.9)
т„{\ + х^У' - т^{\ + х^У' = тД1 + х',У'\ (8.12.10)
т.
{\ -l· х^У'- т„. (8.12.11)
В уравнении (8.12.11) использован тот факт, что при Т=0 все пионы в
конденсате имеют нулевую кинетическую энергию. Из условия
электронейтральности следует
^е-^^'п^Пр^ (8.12.12)
так что
1 3^ 1 3
3?^?\ ' "" 3?^?\ '' (8.12.13)
Уравнение состояния выше точки образования нейтронных капель ТАЗ
Концентрация барионов, плотность массы и давление могут быть найдены
по формулам (ср. B.5.8) — B.5.10)]:
^ ?? + ????? (812.14)
3?% " 3^41
? = ^ХМ + ^xUp) + ^ХМ + '"."- (812.15)
л^ л^, л„
? = ^ФМ -Ь ^Ф(-р) -Ь ^HxJ. (8.12.16)
^е ^р ^п
Если, например, задана плотность, то формулы (8.12.10), (8.12.11),
(8.12.13) и (8.12.15) представляют собой четыре уравнения, из которых
можно найти х^, Хр, х^ и п^, так что все величины будут определены.
Формула (8.12.11) при х^>1 показывает, что порог образования ?"-
мезонов соответствует
^е =-^ = 273,2. (8.12.17)
На пороге «^=0, и из (8.12.13) следует
^р = ^ = 0,1488. (8.12.18)
При этом формула (8.12.10) дает
х„ = 0,5843, (8.12.19)
и из (8.12.15) получаем
Р^р,= 1^6 X 10^^ г/смЗ . (8.12.20)
При р<р^ уравнение состояния получается точно таким же, как в разд. 2.5.
При р>р^ величина х^ остается постоянной, так что п^ и Р^ также не
меняются с ростом р. Возрастающая доля отрицательного заряда связана с
пионами, которые вносят вклад в плотность массы покоя, но не в давление.
Вычислительное упражнение 8.17. Сравните равновесное уравнение состояния для
холодного идеального газа, состоящего из п, р, е и ?, с уравнением для газа,
состоящего из п,р ие без пионной конденсации. Нанесите обе кривые на график
зависимости IgP (дин/см^) от Ig р(г/см^). Кроме того, изобразите график зависимости
адиабатического показателя Т^сИпР/сИпр от \пр (г/см^) для этих двух случаев (ср.
рис.2.2 и 2.3). Поясните различие в жесткости для этих уравнений состояния выше
порога.
244 Глава 8
Заметим, что в равновесном состоянии существуют переходы
1г¦'^-7г-·«2?«1г^ (8.12.21)
так что
?.» = О, (8.12.22)
?,^= -?. = -?. < о. (8.12.23)
Таким образом и для ?^, и для ?"^ функция распределения удовлетворяет
условию/= [Q\xi[(E-?)/kT]- 11"^^0 при Г^О и всех/7^0. (Напомним, что
? включает энергию, связанную с массой покоя частиц.) Таким образом,
при Г=0 идеальный газ не содержит ?^- и ? "^-мезонов. По той же причине
существование ? "-мезонов препятствует образованию А'"-мезонов и всех
других мезонов, положительных и отрицательных. (Среди всех
отрицательно заряженных бозонов ?~-мезон имеет наименьшую массу.)
Аналогично исключается образование позитронов и антибарионов. Однако, если
принять во внимание взаимодействия между частицами, эти выводы не
вполне справедливы. В частности, рассматривалась возможность
конденсации ?^-мeзoнoв^\
Возможно, что пионная конденсация делает более вероятным
отвердение нейтронной материи при достаточно высокой плотности. Не
исключено, что отталкивание на малых расстояниях в нуклон-нуклонном
потенциале может быть достаточно сильным, чтобы удерживать нейтроны в узлах
регулярной решетки^\ Отсюда следует, что нейтронные звезды могут
иметь твердые ядра, а также твердые наружные оболочки. Предваряя
приведенное ниже обсуждение нейтронных звезд, отметим, что подобная
структура должна приводить к некоторым следствиям, доступным
непосредственным наблюдениям.
1. Высвобождение упругой энергии в сейсмически активных ядрах
нейтронных звезд должно вызывать «звездотрясения», приводящие к
временным ускорениям вращения пульсаров [489]. Явления такого типа
наблюдались, например, у пульсара в Парусах.
2. Гравитационное излучение из когерентно колеблющегося твердого
ядра [179].
3. Прецессия нейтронной звезды, вызванная сплюснутостью твердой
коры или ядра. Такая прецессия может быть причиной «включения» и
«выключения» рентгеновского излучения от аккрецируемого газа через
регулярные промежутки времени, как это наблюдается в 35-дневном цикле
двойного рентгеновского источника Геркулес Х-1 [333].
Теперь ясно, что бесконечный отталкивательный потенциал «твердого
кора» по своей сути должен приводить к образованию твердотельной
^^ См., например, работу Бейма и Петика [52] и приведенные там ссылки.
^^ Напомним рассмотренное в разд. 4.3 отвердение белых карликов, обусловленное
кулоновским отталкиванием между ядрами.
Уравнение состояния выше точки образования нейтронных капель 245
структуры, когда расстояния между частицами приближаются к радиусу
кора г^. При соответствующих плотностях бесконечно сильное
отталкивание «запирает» каждый нейтрон в отдельном узле кристаллической
решетки. Для нас, однако, важнее вопрос: может ли привести к отвердению
более реалистический потенциал с мягкой отталкивательной сердцевиной
типа Юкавы (например, потенциал Бете — Джонсона)? В этом случае еще не
выяснено, не слишком ли «мягок» потенциальный барьер и не могут ли
частицы туннелировать сквозь него. Тогда требуемая для образования
кристаллической структуры локализация частиц может оказаться
невозможной, за исключением лишь области крайне высоких плотностей^\
При решении вопроса об отвердении возникают те же трудности, что и
при построении уравнения состояния для ядерной материи: надо выбрать
форму потенциала и провести многочастичные вычисления. Результаты
нескольких работ'^^ указывают, хотя и не вполне определенно, что без пионной
конденсации ядерная материя не может отвердеть. Однако, как показано в
работе [444], механизмом, который обеспечивает отвердение, может
оказаться ?^-мезонная конденсация. Нейтральное пионное поле усиливает
эффективные тензорные силы в плотной материи, которые приводят к
пространственному упорядочиванию. К моменту написания этой книги вопрос о
том. является плотная ядерная материя твердой или жидкой, еще не решен.
8.13. НЕРЕШЕННЫЕ ВОПРОСЫ.' СВЕРХВЫСОКИЕ ПЛОТНОСТИ
При плотностях, значительно превосходящих ядерную (нап^
;^ l(V>nuc)» ядерную материю нельзя описывать с помощью нереля ^
ского многочасуичного уравнения Шредингера или использовать п.
взаимодействия. «Мезонные облака», окружающие нуклоны, перекрыла*,
ся, и систему нельзя рассматривать как совокупность отдельных
локализованных частиц, взаимодействующих через двухчастичные силы. Еще до
того как теряет смысл само понятие потенциала, различные потенциалы,
одинаково хорошо воспроизводящие данные о фазовых сдвигах в рассеянии
при низких энергиях, приводят к совершенно различным уравнениям
состояния. Причина состоит в том, что при р- 10^^ г/см^ становится весьма
существенной область действия отталкивания на малых расстояниях, к
которой нечувствительно рассеяние при низких энергиях.
Типичный подход к уравнению состояния в этой области [595] состоит в
том, чтобы построить релятивистский лагранжиан, описывающий
взаимодействие «голых» нуклонов, причем обмен скалярными мезонами
обеспечивает притяжение, а обмен более массивными векторными ?-мезонами —
отталкивание. В нерелятивистском пределе и классическая, и квантовая
теории приводят к потенциалам типа Юкавы^^ С помощью некоторого
^^ Обзор и ссылки можно найти в работе [145],
^ См., например, обзор [51] и приведенные там ссылки.
^^ См. результаты разд. 8.6 и 8.7.
246 Глава 8
«приближения среднего поля» было обнаружено [595], что при самых
высоких плотностях главную роль играет обмен векторными мезонами и
справедлив результат Зельдовича:
Р-^рс\ с^-^с. (8.13.1)
Подобные вычисления кажутся весьма многообещающими, однако пока
это не более чем пробные рейды в область сверхвысоких плотностей. Не
известно, возможно ли вообще создание какой бы то ни было
удовлетворительной теории, основанной на рассмотрении взаимодействующих
нуклонов и мезонов, или же необходима теория, основанная непосредственно на
анализе взаимодействий между кварками.
Другой подход к построению уравнения состояния при сверхвысоких
плотностях основан на предположении, что в этой области возникает
целый сонм барионных резонансов. В ряде работ были построены
статистические модели адронов [204, 254, 352]. Типичным примером является
наиболее ранняя работа Хагедорна [254]. Предполагается, что спектр масс
барионных резонансов представляется формулой
N{m)dm -^ т'^е'^^'^Ыт, (8.13.2)
где N{m)clm — число резонансов в интервале масс между т и m-\-dm.
Существующие данные о барионных резонансах можно описать формулой
(8.13.2) при Wq* 160 МэВ и -1/l^a^-S/l,
В равновесном состоянии резонансы с массой т начинают возникать
при условии ??€^=?^, так что химический потенциал нейтронов определяет
предельное значение масс резонансов при любой плотности. При
асимптотически высоких плотностях из формулы (8.13.3) следует
? == Г>(т) dm - m^le^"/'^^ (8.13.3)
Поскольку количество вновь возникающих резонансов экспоненциально
велико, наиболее массивные состояния являются нерелятивистскими. Таким
образом, асимптотика плотности имеет вид
р-^ ( "mN{m) dm - тф^-'^е^-/'^^ (8.13.4)
•?
-??^, (8.13.5)
Давление равно
'=Ж-"^'^^-^· <-")
Уравнение состояния выше точки образования нейтронных капель 247
Формула (8.13.3) дает в асимптотике
и из формулы (8.13.4) следует
Inp-;^. (8.13.8)
Таким образом, используя формулы (8.13.7) и (8.13.8), получаем из (8.13.6)
Р~^. (813.9)
ш ?
в действительности, согласно Хагедорну,
-- ^^' (8.13.10)
1п(р/ро)'
где Ро=2,5-10^^г/см^
Как и следует ожидать для системы, в которой с возрастанием
плотности рождаются все новые частицы, а не расширяется море Ферми для
какого-то одного элемента, уравнение состояния Хагедорна отвечает
весьма «мягкому» веществу. Кроме того, в модель не были включены силы
отталкивания. Скорость звука для такой материи имеет вид
2 dP с^
с:
dp 1п(р/ро)
1
1п(р/ро)
(8.13.11)
Заметим, что при р/р^-^со получается Су-*0 в противоположность
результату применения метода среднего поля, где с^^с.
До сих пор не существует определенного теоретического или
экспериментального указания на то, какая из этих двух крайних возможностей
реализуется в действительности. Отметим, однако, следующие два
обстоятельства. Во-первых, использование данных о «свободно» распадающихся
барионах с целью определения массовой формулы типа (8.13.2) для резо-
нансов почти наверняка недопустимо. В принципе массовый сдвиг,
обусловленный наличием плотной среды [ср. (8.11.1)], может стать достаточно
большим, чтобы практически полностью уничтожить высшие барионные
резонансы [105, 506]. В результате уравнение состояния Хагедорна станет
значительно более жестким. Во-вторых, предварительные оценки масс ней-
248 Глава 8
тронных звезд, основанные на данных наблюдений, по-видимому,
исключают мягкие уравнения состояния типа Хагедорна для плотностей,
превышающих р^ц^ не более чем в несколько раз. Эти уравнения предсказывают
верхний предел масс нейтронных звезд :$О,7Л/0, что гораздо ниже
«наблюдаемых» величин (см. гл. 9). Разумеется, такие наблюдения не дают
никакой информации о применимости уравнения состояния Хагедорна при
очень высоких плотностях p>Pnuc» которые едва ли существуют в
стабильных нейтронных звездах.
8.14. НЕРЕШЕННЫЕ ВОПРОСЫ:
КВАРКОВАЯ МАТЕРИЯ
Появляется все больше указаний на то, что фундаментальными
элементами всех сильно взаимодействующих частиц (например, N, ?, ?, ?, ...)
являются кварки. Если это верно, то теория кварков должна быть положена в
основу любого фундаментального описания ядерной материи при высокой
плотности. Нуклоны начинают «соприкасаться» при концентрации барио-
нов порядка D??^/3)~ ^ что соответствует плотности, которая в несколько
раз превосходит р^^^; здесь г^^ 1 Фм — характерный радиус нуклона.
Можно представить себе, что при более высоких плотностях в материи должен
происходить фазовый переход, при котором кварки начинают
«выдавливаться» из нуклонов. В результате получится кварковая материя —
вырожденная ферми-жидкость.
Кварки никогда еще не наблюдались в свободном состоянии, поэтому
полагают, что они постоянно связаны внутри адронов силами, которые
возрастают при удалении кварков друг от друга. Однако современная
теория кварковых взаимодействий («квантовая хромодинамика») указывает,
что при сближении кварков действующие между ними силы становятся
сколь угодно малыми («асимптотическая свобода»). В связи с этим было
высказано предположение [145], что при достаточно высоких плотностях
кварковую материю можно в первом приближении рассматривать как
идеальный релятивистский ферми-газ. Если это правильно, то какова должна
быть асимптотика уравнения состояния? Этим вопросом мы сейчас и
займемся.
Слабые взаимодействия могут преобразовывать одни кварки в другие,
отличающиеся «ароматом». В нейтронных звездах пороговый уровень, по-
видимому, может быть превышен только для трех наиболее легких кварков
и, d и S (см. приложение Д). Распады кварков имеют вид
s-^ и-^1+?, (8.14.1)
Уравнение состояния выше точки образования нейтронных капель 249
Здесь / означает е~ или ?~, 2i ? — соответствующее антинейтрино.
Предполагая, что вещество находится в равновесии относительно ]3-распада и,
как обычно, пренебрегая нейтрино, получаем
Mj = Mu + M/, (8.14.2)
М5 = Mu + ?/. (8.14.3)
Для ультрарелятивистского вырожденного ферми-газа имеем
Пг ? g/M?, (8.14.4)
где
g, = 6, / = ?, ^,или Sj
g/==2, / = /. (8.14.5)
Множитель 6 для кварков возникает как произведение двух спиновых
состояний на три «цветных» состояния для каждого кварка^^ Таким образом,
формулы (8.14.2)-(8.14.4) дают
Mj = Mj and ^d^^s' (8.14.6)
Равновесие между ?" и е" приводит к уравнениям ^^
?? = Me = ?/»
?,-?,^?,, (8.14.7)
Условие электронейтральности имеет вид
!«»-i«rf-^-"^-«^ = 0 (8.14.8)
^^ Краткая сводка сведений о кварках и элементарных частицах дана в
приложении Д.
^^ При ?^<m^<?^ мюонов нет, и формула (8.14.7) заведомо неверна. Однако
равновесное распределение (8.14.14) при этом не меняется.
250 Глава 8
и приводится к следующему:
и„-и,-Зи, = 0. (8.14.9)
Используя формулы (8.14.3) и (8.14.4), получаем
/«л'/^ /««\'/^ /«/\'/'
Вводя параметры
находим из формул (8.14.9) и (8.14.10)
у-\^Ъх, (8.14.12)
1=//3+ (Зх)'/\ (8.14.13)
Единственное вещественное решение этих уравнений: У=1, ?·=0. Итак, в
асимптотике имеем
f^u'^^s^'^d^ «е = '^м = 0. (8.14.14)
Основная черта этой модели состоит в том, что при высокой плотности
применимы результаты, относящиеся к свободным ультрарелятивистским
частицам, т.е.
P-^ipc^ ?-^00. (8.14.15)
Это сравнительно мягкое уравнение состояния.
При конечных плотностях следует учитывать взаимодействия между
кварками. При умеренно высоких плотностях можно использовать
разложение по константе сильного взаимодействия а^, так как кварки
асимптотически свободны. Однако при более низких плотностях вступает в силу
удержание кварков. Одной из популярных феноменологических моделей
является модель «мешка», предложенная в Массачусетском технологическом
институте [128]. В этой модели составляющие нуклон кварки заключены в
конечной области пространства, «мешке», объем которого поддерживается
некоторым удерживающим давлением 5>0, называемым «константой
мешка» (иными словами, В — плотность энергии, необходимая, чтобы
держать мешок «надутым»). Наблюдаемые массы адронов получаются в
Уравнение состояния выше точки образования нейтронных капель 251
этой модели с разумной точностью, если w^^ = w^-0, 5« 55 МэВ/Фм^,
?^^^^/16???«0,55, где ^ — константа связи глюона с кварками.
Плотность энергии кварковой материи определяется при этом вкладом
невзаимодействующих фермионов («А2^^^), который складывается с величиной В.
Вычисления, относящиеся к фазовому переходу, при котором чисто
нейтронная материя переходит в кварковую, были выполнены в ряде работ
[50, 121, 308]. Для всех рассмотренных уравнений состояния нейтронной
материи этот фазовый переход происходит при плотностях, превышающих
максимальную плотность устойчивой нейтронной звезды ^\ Однако модель
мешка — всего лишь феноменология, и пока наше понимание сильных
взаимодействий носит довольно предварительный характер. Вопрос о том,
существуют ли «кварковые звезды», пока не решен.
'^ Другая модель дана, например, в работе [192].
Содержание
ЧАСТЬ 1
От редактора перевода » 5
Предисловие 9
Рекомендации по использованию книги ,..v.... 13
Глава 1. ГИБЕЛЬ ЗВЕЗД И ОБРАЗОВАНИЕ КОМПАКТНЫХ ОБЪ^
ТОВ >. Г5
1. 1. Что такое компактные объекты 15
1. 2. Образование компактных объектов 17
1. 3. Статистика рождения и гибели звезд 20
Глава 2. УРАВНЕНИЕ СОСТОЯНИЯ ХОЛОДНОГО ВЕЩЕСТВА
НИЖЕ ТОЧКИ ОБРАЗОВАНИЯ НЕЙТРОННЫХ КАПЕЛЬ 32
2. 1. Предварительные сведения из термодинамики 32
2. 2. Сведения из кинетической теории 37
2. 3. Уравнение состояния полностью вырожденного идеального
ферми-газа 38
2. 4. Электростатические поправки к уравнению состояния 43
2. 5. Обратный )б-распад: холодный идеальный п-р-е — газ 53
2. 6. Бета-равновесие между релятивистскими электронами и
ядрами. Уравнение состояния Гаррисона — Уилера 56
2. 7. Уравнение состояния Бейма — Петика — Сазерленда 63
Глава 3. БЕЛЫЕ КАРЛИКИ 69
3. 1. Развитие теории белых карликов 69
3. 2. Начальная стадия вырождения 71
3. 3. Политропы ,. 75
3. 4. Предел Чандрасекара 78
3. 5. Усовершенствование чандрасекаровской модели белых
карликов 80
3. 6. Сравнение с наблюдениями; массы и радиусы 84
3. 7. Пикноядерные реакции 86
Содержание 253
Глава 4. ОСТЫВАНИЕ БЕЛЫХ КАРЛИКОВ 95
4. 1. Структура поверхностных слоев 95
4. 2. Элементарный анализ остывания белых карликов 98
4. 3. Кристаллизация и температура плавления 101
4. 4. Теплоемкость кулоновской решетки 105
4. 5. Уточненный анализ остывания белых карликов 113
4. 6. Сравнение с наблюдениями 115
Глава 5. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ 119
5. 1. Что такое общая теория относительности? 119
5. 2. Движение пробных частиц 126
5. 3. Гравитационное красное смещение 132
5. 4. Предел слабого поля 134
5. 5. Геометрическая система единиц 135
5. 6. Сферически-симметричные гравитационные поля 135
5. 7. Сферические звезды 137
Глава 6. РАВНОВЕСИЕ И УСТОЙЧИВОСТЬ ЖИДКИХ ТЕЛ 140
6. 1. Основные уравнения движения сплошной среды .- 141
6. 2. Лагранжевы и эйлеровы возмущения 143
6. 3. Возмущения интегральных величин 144
6. 4. Равновесие как условие экстремума энергии 147
6 5. Возмущения вблизи состояния равновесия 149
6 6. Функция Лагранжа для возмущений 153
<у 7. Критерии устойчивости 155
бг ^. Тош'ч поворота и возникновение неустойчивости 159
6 Э. Анализ устойчивости с учетом эффектов общей теории
относительности 163
d Ю. Устойчивость белых карликов в общей теории
относительности 168
Глава 1. ВРАЩЕНИЕ И МАГНИТНЫЕ ПОЛЯ 173
7. 1. Уравнения магнитной гидродинамики 173
7. 2. Магнитные белые карлики ; 176
7. 3. Вращающиеся системы: сфероиды Маклорена 179
7. 4. Вращающиеся белые карлики 186
7. 5. Критерии устойчивости для вращающихся звезд 195
Глава 8. УРАВНЕНИЕ СОСТОЯНИЯ ХОЛОДНОГО ВЕЩЕСТВА
ВЫШЕ ТОЧКИ ОБРАЗОВАНИЯ НЕЙТРОННЫХ КАПЕЛЬ 198
8. 1. Введение 198
8. 2. Уравнение состояния Бейма — Бете — Петика 199
254 Содержание
8. 3. Нуклон-нуклонное взаимодействие 207
8. 4. Насыщение ядерных сил 212
8. 5. Зависимость нуклон-нуклонного потенциала от расстояния 218
8. 6. Потенциал Юкавы 219
8. 7. Метод Хартри 221
8. 8. Метод Хартри ~ Фока 224
8. 9. Корреляционные эффекты 228
8.10. Уравнение состояния Бете — Джонсона 230
8.11. Нерешенные вопросы: ?-резонанс 238
8.12. Нерешенные вопросы: пионная конденсация 240
8.13. Нерешенные вопросы: сверхвысокие плотности 245
8.14. Нерешенные вопросы: кварковая материя 248
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании книги, ее оформлении,
качестве перевода и др. просим присылать по адресу:
129820, Москва, И-110, ГСП, 1-й Рижский пер., д. 2,
изд-во «Мир».
Стюарт Л. Шапиро, Саул А. Тьюколски
ЧЕРНЫЕ ДЫРЫ, БЕЛЫЕ КАРЛИКИ И НЕЙТРОННЫЕ ЗВЕЗДЫ
Физика компактных объектов
В дву;^ частях
1
Научный редактор М. Ф. Путов
Мл. научный редактор В. Н. Соколова
Художник А. М. Драговой
Художественный редактор М. Н. Кузьмина
Технические редакторы: Н.Б.Панфилова и Л.С.Тимофеева
Корректор Р. Л. Вибке
ИБ № 5191
Подписано к печати 15.04.85. Формат 60 ? 90'/?6.
Бумага офсетная № 1. Гарнитура тайме. Печать офсетная.
Объем 8,00 бум. л. Усл. печ. л. 16,00.
Усл. кр.-отт. 16,00. Уч. изд. л. 15,00.
Изд. № 27/3427. Тираж 4000 экз. Зак.353. Цена 2 р. 60 к.
Набрано в издательстве «Мир»
на фотонаборном комплексе «Компьюграфик»
129820, ГСП Москва, 1-й Рижский пер., 2.
Отпечатано в Тульской типографии Союзполиграфпрома
при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли
г. Тула, проспект им. В. И. Ленина, 109.
Black Holes,
White Dwarfs,
and Neutron Stars
The Physics of
Compact Objects
Stuart L. Shapiro
Saul A. Teukolsky
Cornell University, Ithaca, New York
A Wiley-Interscience Publication
John Wiley & Sons
New York · Chichester · Brisbane · Toronto · Singapore
СШапиро, СТьюколски
ЧЕРНЫЕ ЛЫРЫ
БЫЫЕ ттшА и
НЕЙТРОННЫЕ ЗВЕЗДЫ
ФИЗИКА
КОМПАКТНЫХ ОБЪЕКТОВ
^\ В двух частях
Перевод с английского
канд. физ.-мат. наук
С. Н. Родионова
под редакцией
д-ра физ.-мат. наук
Я. А. Смородинского
Москва «Мир» 1985
ББК 22.632
Ш24
УДК 52 + 53
Шапиро С. ?., Тьюколски С. А.
Ш24 Черные дыры, белые карлики и нейтронные звезды: В 2-х ч.
Ч. 2. Пер. с англ. — М.: Мир, 1985, 257—656 с, ил.
В книге, написанной известными американскими астрофизиками, изложены основы физики
компактных космических объектов, представляющих собой конечные продукты звездной эволюции,— уже
открытых белых карликов и нейтронных звезд, а также предсказанных теоретиками черных дыр.
Изложение дополняется многочисленными упражнениями. В русском переводе книга разделена на две части. В
части 2 обсуждаются современные представления о нейтронных звездах и черных дырах, пульсары,
компактные рентгеновские источники, аккреция на компактные объекты, гравитационное излучение и
коллапс обычных и сверхмассивных звезд.
Для астрофизиков и физиков — как специалистов, так и студентов. Может служить учебным
пособием по релятивистской астрофизике.
1704020000—393 ББК 22.632
Ш 60—85, ч. 1
041@1)-85 524
Редакция литературы по космическим исследованиям,
астрономии и геофизике
© 1983 by John Wiley & Sons, Inc. All
Rights Reserved. Authorized translation
from English language edition published
by John Wiley & Sons, Inc.
© Перевод с английского, «Мир», 1985
Глава 9
Модели нейтронных звезд: массы и радиусы
в этой главе мы обсудим равновесные модели нейтронных звезд.
«Холодные» модели без учета вращения получаются на основе уравнения
гидростатического равновесия Оппенгеймера — Волкова, т.е. уравнения E.7.6)
для конкретного уравнения состояния ? = Р{р), Можно создать
последовательность моделей с параметром р^; модели, для которых dM/dp^ > О,
устойчивы в данном диапазоне плотностей, а модели с dM/dp^ < О
неустойчивы (сравните с разд. 6.8 и 6.9).
Основная неопределенность в моделях нейтронных звезд связана с
уравнением состояния ядерного вещества, особенно при плотностях выше
ядерной (напоминаем, что р^^^ = 2,8 · 10^"* г/см·'). Как отмечалось в гл. 8,
несмотря на достигнутый в последние годы значительный прогресс, еще
остается несколько вопросов, ждущих своего решения. Тем не менее
интересно, что наше современное понимание природы конденсированного
вещества, как мы увидим позднее, достаточно для того, чтобы наложить
довольно строгие ограничения на массы устойчивых нейтронных звезд.
Результаты оценок масс и радиусов белых карликов из наблюдений
используются для подтверждения астрофизических моделей (см. разд. 3.6). В
то же время наблюдательные данные о массах и радиусах нейтронных
звезд с учетом неопределенностей в уравнении состояния применяются
даже для проверки теорий ядерной физики.
9.1. НЕЙТРОННЫЕ ЗВЕЗДЫ: ИСТОРИЯ ИДЕИ И ОТКРЫТИЯ
В 1934 г. Бааде и Цвикки предложили идею нейтронных звезд — объектов
с очень высокой плотностью и малыми радиусами, для которых гравита-
щюнная связь выражена гораздо сильнее, нежели для обычных звезд.
Бааде и Цвикки высказали также поистине пророческую мысль, что
нейтронные звезды образуются при взрывах сверхновых^\
^^ Бааде и Цвикки [31] в 1934 г. писали: «Со всеми соответствующими
оговорками мы выдвигаем точку зрения, что сверхновые представляют собой переходную
стадию от обычных звезд к нейтронным звездам, которые в конечной стадии
состоят из исключительно плотно упакованных нейтронов».
Как вспоминает Розенфельд [487], еще раньше, в 1932 г., когда в Копенгаген
пришло из Кембриджа сообщение об открытии Чедвиком нейтрона, он вместе с
Бором и Ландау провели вечер, обсуждая возможные следствия этого открытия.
Именно тогда Ландау предположил возможность существования холодных,
плотных звезд, состоящих преимущественно из нейтронов. Единственная публикация
Ландау по этому вопросу была посвящена нейтронным ядрам звезд [338].
262 Глава 9
Первые вычисления моделей нейтронных звезд были выполнены Оппен-
геймером и Волковым [427], которые предположили, что вещество должно
состоять из идеального газа свободных нейтронов с высокой плотностью.
Большинство работ по нейтронным звездам в то время основывалось на
идее, что нейтронные ядра нормальных массивных звезд являются
источниками звездной энергии. Когда стали понятными детали процесса
термоядерного синтеза, от этой идеи пришлось отказаться и нейтронные звезды
в течение последующих тридцати лет в основном игнорировались
астрономами. Правда, такое отношение к ним было отнюдь не всеобщим.
Например, в работах [12, 100, 255, 260] подробно рассматривались уравнения
состояния и модели нейтронных звезд, а в книге [261] приводилось
пространное обсуждение этого вопроса. Пренебрежение идеей нейтронных
звезд нередко объяснялось тем, что из-за малой площади поверхности
нейтронных звезд их остаточное тепловое излучение должно быть слишком
слабым для наблюдений на астрономических расстояниях с помощью
оптических телескопов.
Однако открытие в 1962 г. космических рентгеновских источников вне-
солнечного происхождения [223] вызвало резкий подъем интереса к
нейтронным звездам. Многие теоретики независимо друг от друга
предположили, что рентгеновский телескоп наблюдал молодую, теплую нейтронную
звезду, и поспешно начали расчеты остывания нейтронных звезд^\
Отождествление первого «квазизвездного объекта» (квазара) Шмидтом в Пало-
марской обсерватории в 1963 г. стимулировало дальнейший интерес к
нейтронным звездам. Этот интерес порождался предположением, что большие
красные смешения, наблюдаемые в спектрах квазаров^\ могут быть
вызваны гравитационным красным смещением на поверхности компактного
объекта. Аргументы, показывающие^^ что наибольшее красное смещение,
наблюдаемое у квазаров, превосходит максимально возможное красное
смещение в спектре устойчивой нейтронной звезды, вскоре рассеяли всякую
предполагаемую связь между квазарами и (изолированными) нейтронными
звездами.
Во всяком случае, после открытия рентгеновских источников и квазаров
десятки теоретиков сосредоточили свое внимание на равновесных
свойствах компактных звезд и на звездном коллапсе. Однако, несмотря на
растущие теоретические успехи, большинство физиков и астрономов не
принимали всерьез возможности существования нейтронных звезд (не говоря уже о
черных дырах!). Возможно, необходимость столь огромной экстраполяции
от хорошо знакомой физики была наиболее важным фактором,
определившим их позицию!
^^ Этому вопросу посвящена гл. 11.
^^ Первый квазар, отождествленный Шмидтом ~ ЗС 273, имел беспрецедентное
для нормальной звезды красное смещение ??/? = 0,158.
^^ В дополнение к этому аргументу имелись серьезные свидетельства, что
красные смещения квазаров по своей природе являются космологическими [498].
Модели нейтронных звезд: массы и радиусы 263
Положение резко изменилось, когда в конце 1967 г. были открыты
пульсары [274]. Голд высказал предположение [227], что они представляют
собой вращающиеся нейтронные звезды, и сейчас эта интерпретация
общепринята (см. гл. 10).
С 1968 г. было опубликовано много теоретических работ по свойствам
нейтронных звезд. Еще больше стимулировало исследования открытие
спутником «Ухуру» в 1971 г. пульсирующих компактных рентгеновских
источников («рентгеновских пульсаров»). Как полагают, эти источники
представляют собой нейтронные звезды, входящие в тесную двойную систему
и аккрецирующие газ от своего нормального звездного компаньона. Хотя
идея двойных систем с аккрецией предлагалась и ранее для объяснения
природы рентгеновских источников, первое убедительное доказательство
периодичности было найдено в источниках Центавр Х-3 и Геркулес Х-1 [312,
537].
Почти одновременное открытие поздней осенью 1968 г. пульсаров в
Крабовидной туманности [137, 481, 550] и в созвездии Парусов [345],
которые оба расположены в остатках сверхновых, послужило свидетельством
образования нейтронных звезд при взрывах сверхновых. Крабовидная
туманность, например, является остатком сверхновой, наблюдавшейся
китайскими астрономами в 1054 г. н.э.^\
Оптические и рентгеновские наблюдения рентгеновских источников,
входящих в двойные системы, позволили определить массы нейтронных звезд
в некоторых из этих систем. Открытие Халсом и Тейлором [287] первого
пульсара в двойной системе также дает возможность измерения массы
нейтронной звезды и, как мы увидим позднее, проверки существования
гравитационного излучения.
Когда писалась эта книга, было известно около 350 пульсаров, три из
которых входят в двойные системы. Известно свыше 300 компактных
рентгеновских источников, примерно 19 из которых показывают
периодичность и, по-видимому, входят в двойные системы.
9.2. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
В ЯДЕРНОЙ ОБЛАСТИ
Первое приближение в исследовании внутреннего строения нейтронной
звезды обеспечивается предположением, что вырожденный газ состоит из
невзаимодействующих частиц. В самом деле, аргументация Ландау,
приведенная в разд. 3.4, предполагает идеальный вырожденный газ нейтронов и
дает значение М^^ - 1,5 Mq при /? - 3 км для максимальной массы
нейтронной звезды и соответствующего радиуса. В этом разделе мы
рассмотрим свойства нейтронного газа, основанные на последовательно усложняе-
^^ Бааде [30], Минковский [410] и другие [174, 391] отождествили «южную
звезду» вблизи центра Крабовидной туманности как вероятный (сколлапсировавший)
остаток звезды, взорвавшейся в 1054 г.
264
Глава 9
1 1 1 1 1 1 1 1 1 1 \ 1 г
i_j I I ?..,?-"?
J I 1 L
10^
10^
10«
10"
? , г/см'
10'·
10'·
10''
10'·
Рис, 9.1. гравитационная масса как функция плотности в центре для уравнений
состояния Гаррисона — Уилера (HW) [259] и Оппенгеймера — Волкова (OV) [427].
Устойчивые ветви графика уравнения HW для белых карликов и нейтронных звезд
выделены сплошной жирной линией.
мых уравнениях состояния идеального газа. В следующем разделе мы
обсудим модели, основанные на более реалистических уравнениях состояния.
Сначала можно рассмотреть случай чистого идеального нейтронного
газа. Уравнение состояния для этого случая было выведено в гл. 2. При
первом численном рассмотрении структуры нейтронной звезды Оппенгеймер и
Волков принимали это уравнение состояния в сочетании с
общерелятивистским уравнением гидростатического равновесия [уравнение
Оппенгеймера—Волкова, или уравнение E.7.6)]. Они получили равновесные
конфигурации, показанные на рис. 9.1. Отметим, что
М^
0,7 Mq ; R = 9,6 км; р^ = 5 · 10^^ г/см^
(9.2.1)
являются параметрами конфигурации с максимальной массой. Как
обсуждалось в разд. 6.8, конфигурации с р^ > 5 · 10^^ г/см^ неустойчивы по
отношению к гравитационному коллапсу. Предел Чандрасекара для массы
нейтронной звезды (т.е. ньютоновская политропа с ? = 3 при
бесконечной плотности) равен 5,73 М^. Теория относительности снижает эту
величину по двум основным причинам: а) максимальная масса приходится
на конечное значение р^, когда нейтроны становятся уже релятивистскими, но
еще не предельно релятивистскими; б) 5,73 Mq — это масса покоя
нейтронов, а полная масса меньше этой величины из-за энергии гравитационной
сЕязи звезды.
Упражнение 9.1. Используя уравнение E.5.3), покажите, что максимальное красное
смещение ? спектральной линии, излучаемой с поверхности устойчивой нейтронной
звезды, равно
^ = -^- = 0,13 (9.2.2)
Модели нейтронных звезд: массы и радиусы 265
в предположении уравнения состояния идеального нейтронного газа. Используйте
результаты Оппенгеймера и Волкова для ? и R,
Нейтронные звезды низкой плотности с уравнением состояния
идеального нейтронного газа можно аппроксимировать ньютоновскими
политропами с А2 = 3/2 [уравнение B.3.27)]. Используя формулы для политроп,
приведенные в разд. 3.3, находим
R = 14,64 ? ,^ ^' , ) км, (9.2.3)
. (Щ^)'>^о. ('.2.5)
Таким образом, в расчетах Оппенгеймера и Волкова нет минимальной
массы для нейтронной звезды: Л/ — О и /? — оо , когда р^ — 0. В
действительности, конечно, нейтроны становятся неустойчивыми по отношению к
бета-распаду при достаточно низкой плотности.
Можно дать приближенный вывод результатов Оппенгеймера и Волкова
с использованием вариационного энергетического принципа, изложенного в
гл. 6. Поскольку р^ при М^^ находится в переходной области от
нерелятивистских к релятивистским нейтронам, неясно, какой тип политропы
является наилучшим приближением нейтронной звезды вблизи М^^.
Упражнение 9.2 покажет, что использование значения л = 3 несовместимо с
вариационным принципом, поэтому примем ? = 3/2. Результаты точно
описывают нейтронные звезды с низкой плотностью и дают оценку М^^.
Из уравнений F.10.9) и F.10.11) имеем
Е,^, = к.КрУ'М, к, = 0,795873. (9.2.6)
Значение К определяется соотношением B.3.27). Уравнения F.10.10) и
F.10.12) дают
^grav = -k2GpY^M^/\ к^ = OjeOlll, (9.2.7)
Чтобы вычислить AEjj^j, вычислим сначала
Ро
где
(9.2.8)
w_x'
^''''""""'J^' (9.2.9)
266 Глава 9
г. ? < \ —релятивистский параметр. Используя уравнение B.3.19),
находим
Первый член в уравнении (9.2.10) дает ^^^t, а второй член дает ^E^^^^
AE,„,--j^c^fx'dm. (9.2.11)
Заменив ? на Pq из выражения (9.2.9) и сделав затем обычную подстановку
политропной зависимости в подынтегральное выражение, получим
Д?ы=-А^з-1^МрУ\ (9.2.12)
где
.C^2L/3 1 ?^'?^?^?
= 1Д651. (9.2.13)
Наконец, уравнения F.9.30) и F.9.31) дают общерелятивистскую поправку
^Еотк- -K^^MУV/\ (9.2.14)
где
к^ = 0,6807. (9.2.15)
Тогда полная энергия звезды равна
? = АМрУ^ - ВМ'/'рУ - СМрУ - ОМ'/у/\ (9.2.16)
где
А-к,К, B = k,G, ^ = -?^^ ^ = ^4-^. (9.2.17)
т];^ с с
Равновесие достигается при условии дЕ/др^ = О, которое упрощается,
приобретая вид
2Ар-'/' - ВМ^/'р;^/' - 4СрУ' - IDM'/'p;'/' = 0. (9.2.18)
Оставляя только первые два члена, получаем результат (9.2.4) для
политропы с л = 3/2. Учет всех членов дает лучшее приближение к зависимо-
Модели нейтронных звезд: массы и радиусы 267
стй ? от р^, полученной Оппенгеймером и Волковым. Неустойчивость
начинается, когда д^Е/др^ = 0. Это условие после упрощения принимает вид
-2Ар;'/' + 25M2/V'/' - ^СрУ + 2DM^/'p-'/' = 0. (9.2.19)
Сложив уравнения (9.2.18) и (9.2.19), получим
Рс^ g^ ' (9.2.20)
Подставим это выражение в уравнение (9.2.18) и произведем замену
у = М^/\ (9.2.21)
Получается кубическое уравнение для у:
2А - гВ^/^С^/^у - IDy^ = 0. (9.2.22)
Положительный корень этого уравнения равен у = 6,605 · 10^^ единиц
СГС, так что
? = 1,11 Mq ; р^ = 7,43 · 10^^ г/см^ (9.2.23)
Отметим, что масса М, определяемая соотношением (9.2.23), — это в
действительности масса покоя нейтронов (в политропных формулах
используется соотношение dm = А-кг^р^ат). Если подставить значения ? и р^ из
соотношений (9.2.23) в (9.2.16), то находим
4== -0,08Ме, (9.2.24)
так что максимальная полная масса нейтронной звезды, как
предсказывается, должна быть равной 1,03 Mq , т.е. почти на 40^о выше, чем при
численном расчете.
Упражнение 9.2. а) Повторите вычисление ?/^^^?, используя политропные
соотношения с А7 = 3, как в разд. 6.10. В результате должно получиться ? =
= 0,741 Л/0 и /0^ = 3,46 · 10^7 г/см^.
б) Вспомните, что в этом случае при вычислении АЯ}^^ постоянный член
опускался [сравнить с уравнением F.10.15)]. Опущенный член равен как раз - m„c^N, т.е.
отрицательной массе покоя звезды. Следовательно, Е/с^ представляет теперь
полную массу звезды. Вычислите эту величину, используя результаты части а), и
покажите, что она больше, чем 0,741 Mq . Это означает, что звезда не связана и схема
приближения привела к неудаче. Чтобы получить какое-то представление, почему
так могло оказаться, вычислите отношение AEQj^f^/E^j^y при значениях Л/ и р^,
найденных в части б).
Упражнение 9,3. Рассмотрите нейтронную звезду, удерживаемую в равновесии
идеальным вырожденным нейтронным газом, который предполагается
нерелятивистским при всех плотностях, т.е. ? = Кр^^^ для всех pq.
268 Глава 9
а) Используйте постньютоновский вариационный метод, чтобы вывести
зависимость Л/ от Рс для равновесных конфигураций, и покажите, что она согласуется с
уравнением (9.2.4) в ньютоновской области низкой плотности.
б) Покажите, что в постньютоновском приближении все равновесные
конфигурации радиально устойчивы и что Л/ — 3,38 Mq при /о^ -* «>.
в) Численное интегрирование уравнения Оппенгеймера—Волкова при этом
уравнении состояния дает значение ?^^^? = 0,84 Mq для максимальной полной массы
при плотности в центре р^ р^^ч = 5,4 · 10^^ г/см^ и при dM/dpc < О для всех
Рс > ? с, max· Обсудите происхождение этого противоречия.
Указание: Рассмотрите Е/с^ и M/R для больших р^ в постньютоновском
приближении.
Более реалистическое уравнение состояния идеального газа
учитывает равновесную смесь невзаимодействующих нейтронов, протонов и
электронов. Это уравнение состояния анализировалось в разд. 2.5.
Напомним, что нейтроны присутствуют только при плотностях, превышающих
1,2 · 10^ г/см^. Отношение числа нейтронов к числу протонов достигает
максимума примерно при 7,8 · 10^^ г/см^, а затем уменьшается до 8, когда
? — 00. Как и всегда для идеального газа, ? — р/3, когда ? — оо.
Звездные модели, построенные с использованием этого уравнения
состояния, ненамного отличаются от полученных Оппенгеймером и
Волковым, поскольку зависимость Р(р) почти такая же, как в случае чистых
нейтронов. Например,
^тах = ^''72 М^; R = 8,8 км; р^ = 5,8 · 10^^ г/см^. (9.2.25)
Звезды с р^ ^ 7,8 · 10^^ г/см^ фактически принадлежат к ветви белых
карликов с высокой плотностью и потому они неустойчивы. Таким образом,
вблизи этого значения р^ можно ожидать локального минимума на графике
зависимости ? от р^. Соответствующая минимальная масса нейтронной
звезды, согласно уравнению (9.2.4), равна
M^i„ ^ 0,03 М^ ; /? - 48 км. (9.2.26)
Напомним, что уравнение состояния Гаррисона — У ил ера (разд. 2.6)
хорошо передает уравнение состояния для белого карлика (включая режим
образования нейтронных капель) с зависимостью для идеального
п-р-е — газа при ? = 4,5 · 10^^ т/см^. Получившийся график зависимости
? от р^ показан на рис. 9.1. Минимальная масса нейтронной звезды в
соответствии с уравнением Гаррисона—Уилера равна
M^j„ = 0,18 Mq ; /? = 300 км; р^ = 2,6 · 10»^ г/см^.
Аналогичные результаты были бы применимы и для уравнения состояния
Бейма — Петика — Сазерленда (разд. 2.7), подогнанному под идеальный
п-р-е — газ. В разд. 9.3 и 9.4 будут даны уточненные оценки минимальной
и максимальной масс нейтронной звезды, основанные на более
реалистичных уравнениях состояния.
Упражнение 9.4. Предположим, что при плотностях выше ядерной плотности
( > \0^^ г/смЗ) нейтроны объединяются в капельки, содержащие N нейтронов на
Модели нейтронных звезд: массы и радиусы
269
каплю. Допуская, что все капельки подчиняются статистике Ферми ~ Дирака для
идеального газа, и используя аргументацию Ландау из разд. 3.4, сделайте
следующее:
а) Оцените максимальную массу нейтронной звезды, поддерживаемой в
равновесии холодными нуклонными капельками, и сравните эту массу с соответствующей
величиной для звезды, состоящей из свободных нейтронов.
б) Оцените радиус конфигурации с максимальной массой, состоящей из нуклонных
капелек, и сравните этот радиус с соответствующей величиной для звезды,
состоящей из свободных нейтронов.
в) Определите отношение поверхностных потенциалов для рассматриваемых двух
моделей нейтронной звезды.
г) Предположите теперь, что вместо слияния в капельки нейтрону при высоких
плотностях разделяются на N «фундаментальных» частиц равной массы. Как
изменятся ответы на вопросы, поставленные в пп. а), б) и в)? Может ли масса
нейтронной звезды увеличиваться бесконечно при бесконечной последовательности делений?
9.3. РЕАЛИСТИЧЕСКИЕ ТЕОРЕТИЧЕСКИЕ МОДЕЛИ
Обрисовав в гл. 8 некоторые составные части реалистического уравнения
состояния холодного плотного вещества, мы можем теперь сравнивать
модели нейтронной звезды, которые получаются при использовании в
уравнении Оппенгеймера—Волкова разных уравнений состояния. На рис. 9.2 по-
р^,г/см^
Рис. 9.2. Гравитационная масса как функция плотности в центре для разных
уравнений состояния. Буквы около различных кривых расшифровываются в табл. 8.2, за
.исключением ?, которая обозначает уравнение состояни}^ Рейда, видоизмененное с
учетом конденсации заряженных пионов. Восходящие части кривых соответствуют
устойчивым нейтронным звездам [52].
270
Глава 9
Рис. 9.3. Гравитационная масса как функция радиуса для тех же уравнений
состояния, что и на рис. 9.2 [52].
казаны графики зависимости Л/ от р^ для шести характерных уравнений
состояния. На рис. 9.3 показаны соответствующие графики для зависимости
Л/ от /?. В табл. 9.1 приведены максимальные массы, вычисленные для
четырех таких моделей. Выясняется несколько общих особенностей:
МАКСИМАЛЬНАЯ МАССА НЕЙТРОННОЙ ЗВЕЗДЫ
для РАЗЛИЧНЫХ УРАВНЕНИЙ СОСТОЯНИЯ
Таблица 9.1
Тип уравнения состояния О
Сокращенное
обозначение
Максимальная масса,
Пионный конденсат
Уравнение Рейда
Уравнение Бете—Джонсона
Приближение трехнуклонного
взаимодействия
Приближение тензорного
взаимодействия
Приближение среднего поля
(R)
(BJ)
(TNI)
(TI)
(MF)
1,5
1,6
1,9
2,0
2,0
2,7
^) См. табл. 8.2 и подпись к рис. 9.2 для полной расшифровки сокращений,
характеризующих уравнения состояния.
Модели нейтронных звезд: массы и радиусы 271
1. Модели звезд, рассчитанные на основе жестких уравнений состояния
(например, указанные на рис. 9.2 BJ, TNI, TI и MF), характеризуются
более высокими массами, чем модели, полученные из мягких уравнений
состояния (например, R и ?).
2. Модели, полученные на основе жестких уравнений состояния,
характеризуются меньшей плотностью в центре, большим радиусом и
значительно более толстой корой (сравните с рис. 9.4 и приведенным ниже
обсуждением), чем модели той же массы, выведенные из мягких уравнений
состояния.
3. Пионная конденсация, если она происходит, стремится сжать
нейтронную звезду данной массы, а также уменьшить М^^^,
На рис. 9.4 показаны поперечные сечения двух звезд с массой 1,4 Mq
каждая, рассчитанных на основе мягкого (уравнение Рейда) и жесткого
(приближение тензорного взаимодействия) уравнений состояния.
«Расслоение» конфигураций является просто следствием включения в уравнение
состояния различных режимов по мере перехода к более высоким
плотностям. Можно выделить следующие слои [446]:
1. Поверхность (р ^ 10^ г/см·*) — область, где температуры и
магнитные поля, ожидаемые для большинства нейтронных звезд, могут
значительно влиять на уравнение состояния.
2. Внешняя кора A0^ г/см^ ^ ? ^ 4,3 · 10^^ г/см^) — область твердого
вещества, где кулоновская решетка тяжелых ядер сосуществует в бета-
равновесии с релятивистским вырожденным электронным газом (сравните
с уравнениями состояния для белых карликов).
3. Внутренняя кора [4,3 · 10^^ г/см^ ^ ? ^ B 4- 2,4) · 10^"^ г/см^],
состоящая из решетки обогащенных нейтронами ядер вместе со сверхтекучим
нейтронным газом и электронным газом^^
4. Нейтронная жидкость [B ^ 2,4) · 10^^ г/см^ ^ ? ^ /^согеЬ
состоящая главным образом из сверхтекучих нейтронов с малой примесью
сверхтекучих протонов и нормальных электронов.
5. Область ядра (р > Рсоге)» которая может существовать или не
существовать в некоторых звездах в зависимости от того, происходит ли
там пионная конденсация либо переход к твердому нейтронному веществу
или к кварковому веществу, или же к любой другой фазе, физически
отличающейся от нейтронной жидкости, при плотностях выше некоторого
критического значения Рсоге·
Если уравнение состояния жесткое, то центральная плотность
относительно массивной A,4 Mq) нейтронной звезды не превышает 10^^ г/см^;
фактически даже самые массивные устойчивые нейтронные звезды имеют
плотность в центре лишь в несколько раз выше 10^^ г/см^ (рис. 9.2). Таким
образом, как отмечалось ранее, вероятность перехода к кварковому
веществу или к какой-то другой экзотической форме материи кажется неправдо-
^^ См. разд. 10.9 для краткого обсуждения сверхтекучих свойств вещества
нейтронной звезды.
Рис. 9.4. Поперечные сечения моделей звезд с массой 1,4 iV/^ , построенных в соответствии с уравнениями состояния
Рейда (R) и трехнуклонного взаимодействия (THI). Показаны различные области, обсуждающиеся в тексте. Приведены
значения моментов инерции коры 1^ и сверхтекучих недр /^ [458]
Модели нейтронных звезд: массы и радиусы 273
подобной. Тем не менее, существование третьей стабильной ветви «кварко-
вых звезд» на диаграмме зависимости Л/ от р^, помимо белых карликов и
нейтронных звезд, остается возможным.
Природа может благоприятствовать нейтронным звездам с массами
вблизи предела Чандрасекара 1,4 М^^? Маловероятно, чтобы в таких
звездах с умеренно жесткими уравнениями состояния (например, TNI)
образовывались пионные конденсаты, для чего, по-видимому, требуется
? ^ 2р„ц^, если это вообще возможно. Однако с учетом
неопределенностей в уравнении состояния, описанных в предыдущих главах, можно
отметить, что такие заключения являются, в лучшем случае,
предварительными.
Минимальная масса нейтронной звезды определяется
приравниванием среднего значения показателя адиабаты Г критической величине -4/3,
определяющей радиальную устойчивость против коллапса. Как
обсуждалось в разд. 8.2, Г (р) для уравнения состояния Бейма—Бете—Петика
быстро падает ниже 4/3 при плотности, соответствующей режиму образования
нейтронных «капель», p^j^ = 4,3 · 10^^ г/см^ и затем не поднимается
выше 4/3, пока ? не превысит 7 · 10^^ г/см^. В результате минимальная масса
нейтронной звезды, вычисленная с использованием уравнения состояния
Бейма—Бете—Петика, «сшитого» с уравнением состояния Бейма—
Петика—Сазерленда ниже точки образования нейтронных капель, равна
M^j„ = 0,0925 Л/0 ; р^ = 1,55 · Ю^^г/см^; R = 164 км. (9.3.1)
Итак, р^ для конфигурации с минимальной массой гораздо больше 7 · ю^^
г/см^. Причина заключается, во-первых, в том, что к устойчивости имеет
отношение среднее значение Г, а, во-вторых, это среднее значение должно
быть больше 4/3 для устойчивости в общей теории относительности
[сравните с уравнением F.9.2)]. Поскольку уравнение состояния достаточно
хорошо известно для всех ? ^ р^, можно рассматривать приведенные выше
параметры для конфигуращ1и с минимальной массой как довольно хорошо
установленные.
Этого пока еще нельзя сказать о равновесной конфигурации с
максимальной массой из-за неопределенностей в уравнении состояния выше
/^nuc = 2»^ ' 10^^ г/см^ (вспомните рис. 9.2 и табл. 9.1). Заметим, однако,
что все современные «микроскопические» вычисления уравнения состояния
приводят к нейтронным звездам с М^^^ ^ 3 Mq . Этот результат будет,
иметь важное значение для отождествления черных дыр (разд. 13.5). В
разд. 9.5 мы еще вернемся к решающему вопросу о максимальной массе
нейтронной звезды.
9.4. ИЗМЕРЕНИЯ МАСС НЕЙТРОННЫХ ЗВЕЗД
Как мы увидели, глобальные параметры нейтронной звезды, такие как
массы, радиусы, моменты инерции и т.п., чувствительны к принятой
См., например, разд. 9.4 и гл. 18.
2-513
274
Глава 9
«микроскопической» модели нуклон-нуклонного взаимодействия. Таким
образом, изучение этих параметров на основе астрономических наблюдений
может пролить свет на проблемы адронной физики. Решающее значение
имеет определение масс нейтронных звезд из прямых наблюдений. При
недавних наблюдениях массы нескольких нейтронных звезд были определены
методами, которые описаны ниже.
а) Рентгеновские источники в двойных системах
Наиболее надежные методы определения масс астрономических
объектов основаны на третьем законе Кеплера, и нейтронные звезды не
являются исключением. Рассмотрим два сферических объекта с массами Л/| и Л/2,
движущиеся по круговым орбитам относительно общего центра масс^\ На
рис. 9.5 показана такая система (вид в орбитальной плоскости). Расстояние
между объектами равно а, а соответствующие расстояния до центра масс
равны ??] и ^2·'
« = «1 +«2» (9.4.1)
???, - М^а^ = 0. (9.4.2)
Угол / называется наклонением орбитальной плоскости относительно луча
зрения. Из диаграммы ясно, что любая деталь в спектре излучения ? ?
будет подвержена доплеровскому смещению. Амплитуда вариаций равна
?; J — проекции орбитальной скорости Mj на луч зрения:
?, =—a,sini, (9.4.3)
Рис, 9.5. Параметры двойной системы (вид в орбитальной плоскости).
'^ Случай эллиптических орбит рассматривается в разд. 16.5.
Модели нейтронных звезд: массы и радиусы 275
где ? — орбитальный период. Таким образом, если в спектре Mj видны
периодические вариации, то можно измерить Я и Ур и отсюда находится
a^mi, С другой стороны, для рентгеновских импульсов можно измерять
периодические вариации времени прихода импульсов. Амплитуда этих
вариаций равна времени прохождения света по диаметру орбиты,
спроецированному на луч зрения, т.е. {а^ sin/)/c.
Согласно закону Кеплера,
(9.4.4)
(9.4.5)
уравнений (9.4.1) и
G{M
, + ?
а'
(9.4.2) имеем
а
= ??
?.(-
+ М2
и тогда
(9.4.6)
Величина/ называется «функцией масс» и зависит только от наблюдаемых
величин ? и ?? (или ajsinO.
Если можно измерить только одну функцию масс двойной системы, то
без дополнительных предположений нельзя проследовать далее того, что
позволяет уравнение (9.4.6). Для шести двойных систем, содержащих
рентгеновские источники, удалрсь измерить как функцию масс
оптического компонента, так и функцию масс рентгеновского источника. В этом
случае имеем
где индекс «Л'» относится к рентгеновскому источнику, а индекс «О» — к
оптическому компоненту. Отношение этих двух выражений дает
отношение масс
,.?. (9.4.8)
И тогда с учетом (9.4.7) можно записать
^^^4i(l_Li)!. (9.4.9)
Для нахождения значения ? ? необходимо еще знать sin/. На практике
регистрация длительности рентгеновского затмения и/или вариаций
оптической кривой блеска используется (см., например, [33]) для установления
геометрических ограничений на значение sin/. Таким методом были вы пол не-
276
Глава 9
Ди 0900-АО
Hau 1538-52
Ц SMCX-1
СепХ-3
LMC Х-А
-]НегХ-1
И PSR 1913+16
0 12 3 4 5
Масса нейтронной звезбы, Мо
Рис. 9.6. Определение масс нейтронных звезд на основе наблюдений. Первые шесть
значений массы получены при наблюдениях рентгеновских пульсаров, входящих в
двойные системы. PSR 1913 + 16 — радиопульсар, входящий в двойную систему.
Наиболее вероятное значение массы каждого пульсара отмечено зачерненным
кружком; чертой показана оценка ошибок. Затушеванная часть рисунка представляет
диапазон значений массы нейтронной звезды, совместимых со всеми данными
A,2 — 1,6 Mq). Существование такого диапазона можно ожидать на основе
современных теоретических представлений об образовании нейтронной звезды (см. текст)
[474].
ны определения масс, показанные на рис. 9.6. Рис. 9.6 содержит также
оценки степени неопределенности этих значений.
б) Пульсары в двойных системах
Для пульсара Халса-Тейлора (PSR 1913 -ь 16), входящего в двойную
систему, из радиоизмерений получена лишь одна функция масс. Другой
компонент представляет собой какой-то компактный объект и непосредственно
Модели нейтронных звезд: массы и радиусы 277
не наблюдается. Однако высокая точность наблюдений за пульсаром в
сочетании с относительно высокой орбитальной скоростью позволили
выполнить измерения релятивистского смещения периастра и доплеровского
сдвига второго порядка. Они дали еще два соотношения между Mj, Mj, а ?
и sin/ дополнительно к уравнениям (9.4.3) и (9.4.6) и позволили получить
полные решения для всех параметров. Наилучшие значения масс пульсара и
его компаньона таковы [562] ^\·
А^пульс= Ь41 ±0.06Мо,
Мкомп = 1.41±0,06Ме. (9.4.10)
С тех пор обнаружено еще два пульсара, входящих в двойные системы.
Однако наблюдения говорят о том, что для них релятивистские эффекты
не имеют особой важности, и потому из данных наблюдений, по-
видимому, будет определена только функция масс.
Были сделаны оценки пределов масс двух непульсирующих
рентгеновских источников, входящих в двойные системы (Cyg Х-1: 9 < M/Mq < 15;
Зи 17(Ю — 37: 0,6 < М/М^ ). Однако, как будет обсуждаться в разд.
13.5, похоже, что по крайней мере один из этих объектов — Cyg
Х-1 — должен быть черной дырой.
Рассмотренные выше определения масс приводят к некоторым важным
заключениям [33, 302, 458]. Во-первых, современные данные наблюдений
совместимы со стандартными теориями гравитации и адронного
вещества. Хотя данные еще не настолько точны, чтобы обеспечить выбор
определенной модели, уже нижний предел массы пульсара PSR 1913 + 16, равный
? ^ 1,35 Mq, весьма важен, так как он исключает из рассмотрения
многие мягкие уравнения состояния (например, идеальный вырожденный
нейтронный газ, уравнения Гаррисона—Уилера, Хагедорна и др.). Одно-
единственное надежное определение массы выше 1,6 Mq позволило бы
отбросить все уравнения состояния, показанные на рис. 9.2, за исключением
самых жестких.
Во-вторых, все современные определения масс нейтронных звезд
совместимы с предположениями, основанными на теории звездной эволюции
(см., например, [13, 290]), согласно которым вырожденные ядра всех про-
эволюционировавших звезд (включая и все нейтронные звезды) должны
иметь массы порядка предела Чандрасекара — 1,4 М^ . В этом
отношении особенно интригующими выглядят результаты для PSR 1913 + 16.
Как показано на рис. 9.6, если потребовать одну и ту же массу для всех
нейтронных звезд, то это подразумевает 1,2 ^ М/М^ ^ 1,8, что опять-
таки исключает очень мягкие уравнения состояния.
Прямых измерений радиусов нейтронных звезд не существует. Однако
данные наблюдений в сочетании со специальными теоретическими предпо-
•^ См. разд. 13.5; там обсуждается наблюдение эффекта гравитационного
излучения от этой системы.
278 Глава 9
ложениями дают кое-какую информацию. Например, предположения о
том, что десять хорошо наблюдаемых барстеров а) излучают как черное
тело, б) имеют пиковую светимость, близкую к «эддингтоновскому
пределу» (Lg = 1,3 · 10^^ M/Mq эрг/с для звезды массой - 1,4 mJ^, и в)
расположены симметрично относительно центра Галактики на расстоянии
- 9 кпс, привели Ван Парадийса к заключению [586], что излучающая
поверхность имеет радиус - 8,5 км. При этом упрощенном анализе не
учитывался ряд эффектов, например сильные магнитные поля, рассеяние на
электронах и т.п. Это могло привести к занижению полученной оценки
примерно в два раза.
Упражнение 9,5, Изучите следствия вывода, что нейтронные звезды могли бы иметь
массу 1,4 Л/0 и радиус - 8,5 км в свете данных рис. 9.3.
9.5. МАКСИМАЛЬНАЯ МАССА
Возможность отождествления какого-либо компактного объекта с черной
дырой зависит, в частности, от того, позволяют ли имеющиеся данные
категорически утверждать, что масса наблюдаемого объекта больше
максимально допустимой массы нейтронной звезды (или белого карлика).
Однако, как мы видели в разд. 9.3, максимальная масса нейтронной
звезды — это чувствительная функция пока еще неизвестного уравнения
состояния ядерного вещества. Существуют ли какие-нибудь верхние пределы,
которые можно наложить на массу нейтронной звезды и которые не
зависят от деталей уравнения состояния в неизвестном режиме высокой
плотности? Как ни удивительно, ответ на этот вопрос положительный.
Обсуждая предел массы в этом разделе, мы не учитываем эффект
вращения. В следующем разделе будет показано, что он, вероятно, не играет
важной роли. В отличие от случая белых карликов вращение не может
существенно увеличить максимальную массу нейтронной звезды.
Общий анализ проблемы максимальной массы устойчивой нейтронной
звезды был выполнен Родсом и Руффини [480], которые исходили из
следующих предположений:
1. Общая теория относительности является точной теорией гравитации.
В частности, это означает, что уравнение Оппенгеймера—Волкова
определяет равновесную структуру.
2. Уравнение состояния удовлетворяет условию «микроскопической
устойчивости»
^>0. (9.5.1)
Нарушение этого условия приводило бы к спонтанному коллапсу малых
элементов вещества.
'^ Эддингтоновский предел обсуждается в разд. 13.7.
Модели нейтронных звезд: массы и радиусы 279
3. Уравнение состояния удовлетворяет условию причинности
dP
Тр ^ ''^ (9.5.2)
Т.е. скорость звука меньше скорости света.
4. Известно уравнение состояния ниже некоторой «сшивающей»
плотности Pq.
Роде и Руффини выполнили вариащюнные вычисления, чтобы
определить, какое уравнение состояния при плотности вышеро» удовлетворяющее
неравенствам (9.5.1) и (9.5.2), максимизирует величину массы. Согласно их
вполне правдоподобному результату, такому уравнению соответствует
знак равенства в (9.5.2); оно имеет вид
? = Ро + (Р - Ро)<^'' ? > ??· (9.5.3)
Они выбрали Pq = 4,6 · 10^^ г/см^ и приняли уравнение состояния
Гаррисона—Уилера для ? < Pq. Этот выбор не играет решающей роли.
Результат можно приблизительно оценить, считая значение A/j^^^^
пропорциональным (ро)~^^^ . Лишь несколько процентов массы вносится из области с
? < Pq. Уравнение состояния Гаррисона—Уилера находится в приемлемом
согласии с более реалистичными уравнениями состояния — во всяком
случае, реалистичные уравнения более жесткие.
Численное интегрирование уравнения Оппенгеймера—Волкова при
уравнении состояния типа Гаррисона—Уилера ниже pq и уравнении (9.5.3) выше
Pq дает
^тах = 3,2( ^ —] Мо. (9.5.4)
1 4,6 X 10^^ г/смЗ /о
Этот результат можно получить заново с помощью приближенных
аналитических вычислений при рассмотрении сфер с однородной плотностью в
рамках общей теории относительности [418]. Предположим, что рил
постоянны внутри звезды. Уравнение состояния определяется плотностью
р(л), а давление дается первым законом термодинамики
dn ? ^^'^'^^
Масса звезды равна
? = 47Г f V' dr = ^тгЛ^, (9.5.6)
в то время как полное число барионов (при с = G = 1) составляет
[сравните с уравнением E.7.9)]
rR пг^ dr
[1 - 2m(r)/r]'/'
/ 3 ?^^
2T«lg^l (x-sinxcosx). (9.5.7)
280 Глава 9
Величину ? определим соотношением
sin ?
= (^^)"'л. (9-5-8)
так что
2М
R
sm^X = ^. (9.5.9)
Теперь в соответствии с энергетическим вариационным принципом
(разд. 6.9) в равновесной конфигурации энергия должна быть
экстремальной при заданном числе барионов
дМ
дх
= 0. (9.5.10)
А
Здесь мы рассматриваем ? как независимый вариационный параметр.
Подставляя уравнения (9.5.5) — (9.5.8) в уравнение (9.5.10), находим
~ = ПХ), (9-5.11)
где
^(^) - -. . -з'^;^ · 7 - 1- (9-5.12)
9cosx - zsin^'x/^x - sinxcosx)
Отметим, что этот результат отличается от решения упражнения 5.3. Там
мы находили точное решение уравнения Оппенгеймера—Волкова для
простого уравнения состояния ? = const. Здесь же находится приближенное
решение для любого уравнения состояния с использованием ограниченного
класса пробных функций ? = const, ? = const (и, следовательно, ? =
= const). Для данного уравнения состояния р(п) соотношения (9.5.5),
(9.5.11), (9.5.8), (9.5.6) и (9.5.7) определяют Р, ?, /?, Л/ и Л как функции л.
Упражнение 9.6. Выведите уравнение (9.5.11).
Упражнение 9.7. Покажите, что условие О ^ Р/р ^ 1 требует О < ? ^ 72,94** и что
Р/р - 00 при ? - 80,03 **.
Упражнение 9.8. Обсудите ньютоновский предел приведенных выше уравнений. В
частности, покажите, что уравнение (9.5.11) сводится к виду
??=?, (9.5.13)
где \IV\ — гравитационная потенциальная энергия сферы с однородной плотностью
ц с объемом У [сравните с уравнениями G.3.17), G.3.8) и G.3.23) в сферическом
пределе е = 0].
Модели нейтронных звезд: массы и радиусы
281
Упражнение 9,9, Покажите, что в ньютоновском пределе ? « Р^^^/р^ и,
следовательно, ? растет с ростом w, если ? увеличивается быстрее, чем р^^^. Покажите,
что в пределе высокой плотности, где Р/р - const, вместо этого получается
? ос р-1/2.
Упражнение 9.9 демонстрирует поведение Л/, о котором говорилось
ранее: Л/-р~^^^. Оно показывает также, что Л/ достигает максимума при
каком-то промежуточном значении п. Как обычно, наличие максимума
связано с условием устойчивости, которое требует, чтобы
З^М
дх'
>0.
(9.5.14)
После довольно громоздких вычислений это условие можно записать в
виде условия, налагаемого на показатель адиабаты:
г > ГДх), (9.5.15)
(9.5.16)
где
дЫп \ Pjdp'
а критический показатель адиабаты равен
C? + ?)??+?
Гс(х) = а + 1){1 +
6?
tg^ ? - 1
J. (9.5.17)
Упражнение 9.10. Покажите, что в ньютоновском пределе
Г =1 + -??-^
' 3 105 Л '
(9.5.18)
и сравните этот результат для постоянной плотности с уравнением F.10.30) для
политропы с W = 3.
Зависимость Г^ от f = Р/р показана на рис. 9.7. Здесь можно нанести
также показатель адиабаты для любого заданного уравнения состояния.
Пересечение этой кривой с графиком Г^ определяет точку начала
неустойчивости. На рисунке показано релятивистское ограничение cfP/cfp ^ с^,
вытекающее из условия причинности. Оно требует ? ^ 0,364, ? ^ 64,19°, так что
M/R < 0,405 (причинность + устойчивость).
(9.5.19)
Это соотношение можно сравнить с более слабым пределом, вытекающим
из результатов упражнения 9.7.
282
Глава 9
^ 'г ^
\ Скорость звука
^¦^(скорость сеета)
Неустойчивость
0.1
о.г
Р/рс^
0.3
ол
0,5
Л/с. Р. 7. Область устойчивости в приближении однородной плотности. Кривая,
разделяющая области устойчивости и неустойчивости — это функция Г^, определенная
в уравнении (9.5.17). Для иллюстрации штриховой линией показан показатель
адиабаты Г для газа свободных нейтронов [418].
Упражнение 9,11. Каково максимальное гравитационное красное смещение для
излучения с поверхности устойчивой нейтронной звезды в соответствии с уравнением
(9.5.19)?
Теперь мы готовы определить максимальную массу нейтронной звезды.
Поскольку мы предположили, что знаем уравнение состояния при ? < Ро> ^
также Pq = P{pq), релятивистское ограничение dP/dp < с^ позволяет нам
записать
? < Ро + «^(Р - Ро)» ? > Ро» (9.5.20)
где t; < 1 — максимальная скорость звука выше pq. Теперь при
фиксированном значении ? величина ? увеличивается с увеличением ? и,
следовательно, с увеличением ? [соотношения (9.5.6), (9.5.8), (9.5.11) и (9.5.20)].
Максимум достигается, когда Р/р достигнет критического значения,
обозначаемого f^: в этой точке Г = ?^(?^), т.е.
ktl^2 = г^, (9.5.21)
как следует из уравнения (9.5.16). Подстановка предельного значения Р/р
из уравнения (9.5.21) в уравнение (9.5.20) устанавливает верхний предел на
среднюю плотность звезды
Ро - Л)А^
9с >
1-а,+ 1)/Г,
(9.5.22)
Модели нейтронных звезд: массы и радиусы 283
Это в свою очередь определяет верхний предел массы с использованием
соотношений (9.5.6) и (9.5.8)
„ ¦C)"=fizikL!)Zu]'^„,,. (,.5.23)
Окончательный предел массы был определен Науенбергом и Чаплином
в виде функции от ?. Они использовали уравнение состояния
Бейма—Бете—Петика, чтобы установить наиболее надежное значение
(Ро - Pq/v^). Их значение р^ = 5 · 10^^ г/см^ близко к «сшивочной»
плотности Родса и Руффини, и, что не удивительно, предсказываемая ими
максимальная масса при ? = I
^max "^ 3,6л/0 (полуаналитический результат) (9.5.24)
близка к значениям Родса—Руффини (табл. 9.2). Обратите внимание, что
а) максимальная масса увеличивается с ростом ? и б) М^^^^^ - pq ^^^ ,
поскольку (ро - P(/v^) -^ Ро вблизи V = I.
Наконец, отметим, что отказ от релятивистского ограничения
приводит к строгому пределу на массу, если допустить, что общая теория
относительности остается в силе. Предполагая ?; — оо в проведенном выше
анализе, мы увидим, что Г^ ^ оо. Из соотношения (9.5.17) видно, что в
этом предельном случае Г^ - f^ и f - оо, когда ? - 80,03° (упражнение
9.7). Таким образом, из (9.5.23) следует
= 6,05(М_ХЛ^_1.^|*'^Л,^. (9.5.25)
Таблица 9.2
МАКСИМАЛЬНАЯ МАССА УСТОЙЧИВОЙ НЕЙТРОННОЙ ЗВЕЗДЫ *^
v/c
Pq = 5-1014 г/смЗ pq = 1-1015 г/смЗ
Pq = ?· 1033 дин/см2 Pq = S- 1034 дин/см2
1,00 3,6 2,6
0,75 3,0 2,2
0,50 2,0 1,6
0,25 0,68 Неустойчивая
1) Параметры сшивания из уравнений состояния Бейма—Бете—Пе-
тика (второй столбец) и Рейда (третий столбец) (см. табл. 8.2).
284 Глава 9
Точный предел в общей теории относительности достигается для
несжимаемой звезды. Из уравнения E.7.13) следует 1)
(
IL-f <--)
Тогда из (9.5.6) следует (в отсутствие релятивистских ограничений)
Более тщательный расчет^\ в котором допускается существование
оболочки с ? < pq» Д^^ значение 5,2 Mq.
Подводя итоги, можно сказать, что жесткие уравнения состояния
предсказывают в настоящее время М^^ в интервале A,5 ^ 2,1)М^. В
зависимости от предположений, касающихся ограничений на возможные
уравнения состояния, общая теория относительности предсказывает абсолютный
верхний предел в диапазоне C -г- 5) М^ . Более высокие значения
возможны только в том случае, если отказаться от релятивистского ограничения
dP/dp < с^ 3).
9.6. ВЛИЯНИЕ ВРАЩЕНИЯ
Устанавливая пределы максимальной массы нейтронной звезды, мы
предполагали, что конфигураш1и невращающиеся и сферические. Вообще
говоря, это неверно; мы знаем, что пульсары вращаются. Более того, нам
известно, что в случае белых карликов вращение в принш1пе можно
значительно увеличить максимальную массу (разд. 7.4). В этом разделе мы
покажем, что в отличие от белых карликов, как свидетельствуют имеющиеся
расчеты, вращение не может заметно увеличить максимальную массу
нейтронной звезды (:S 20Vo). Кроме того, даже это увеличение возможно
лишь при таких частотах вращения, которые много выше всех
наблюдаемых частот пульсаров.
^^ Доказательство того, что это действительно максимум, см., например, в [606].
Можно добиться более высоких значений, если допустить, чтобы плотность
возрастала при удалении от центра; см., например, [79].
^^ См. [263] и помещенные там ссылки.
^^ Акустические сигналы распространяются в среде со скоростью (cfP/fifp),''^',
которая, вообще говоря, является функцией частоты. Уравнение состояния для
равновесной звезды дает по существу низкочастотный (? — 0) предел этой функции, так
как допускается достаточно большое время достижения равновесия. Если
предположить dP/dp>c'^ при сохранении условия причинности, то среда спонтанно
становится неустойчивой. См., например, [76].
Модели нейтронных звезд: массы и радиусы 285
Быстро вращающиеся конфигуращ1и в общей теории относительности
построить технически трудно. Кроме того, для этого случая неизвестен
простой критерий устойчивости. Существующие расчеты предполагают а)
медленное вращение [2, 262, 264], или б) твердотельное вращение и
однородные конфигураш1и [95, 96], или в) постньютоновскую гравитащ1Ю и
уравнение состояния идеального газа Ферми [530]. Численные расчеты Бат-
теруорта и Ипсера [95, 96] являются единственным экскурсом в область
сильной гравитащ1И и быстрого вращения. Ради простоты мы будем
следовать аналитическому рассмотрению Лайтмана и 111апиро [530] и придем
фактически к тем же выводам, что и при анализе случая сильных полей.
Начнем с энергетического вариащ!Онного принш1па, так изменив
уравнение (9.2.16), чтобы учесть вращение, как в уравнении G.4.35)
? = АМрУ' - Bg{X)M'/'pY' - СМрУ' - DM'/y/' + k,\PM-'^V/\
(9.6.1)
Здесь ? — энергия вращающейся нейтронной звезды, которая, как
предполагается, должна быть близкой к политропе с л = 3/2 в
постньютоновском пределе. Влияние вращения учитывается посредством приближения,
описанного в разд. 7.4. Величины А, В, С т D определены в уравнении
(9.2.17), а параметр сплюснутости ? и функция g(k) — в уравнениях G.4.28)
и G.4.29). Величина к^ [уравнение G.4.34)] имеет значение 1,926 для ? =
= 3/2.
Условие равновесия дЕ/д\ = О при фиксированных значениях Л/ и 7
дает обычное соотношение между T/\W\ и эксцентриситетом [уравнения
G.4.36) и G.4.37)]. Второе условие равновесия — это ЪЕ/Ър^ = О (значения
Л/ и 7 фиксированы). Решение двух этих уравнений одновременно дает
равновесное соотношение между ? vl р^ для различных значений J [530].
Максимальная масса определяется приравниванием нулю второй
производной ?^?·/??^=0 (это условие возникновения радиальной
неустойчивости).
Упражнение 9.12. Покажите, что определение T/\W\ и два уравнения ЪЕ/Ър =
= Ъ'^Е/Ър^ = О можно переписать в виде
МЧ^_Л1(А) (9 6.2)
дл/'»/з \w\ ? '
BgMlH (9.6.3)
'^^ %С '
286 Глава 9
Таблица 9.3
МАКСИМАЛЬНЫЕ МАССЫ ДЛЯ НЬЮТОНОВСКИХ
ВРАЩАЮЩИХСЯ НЕЙТРОННЫХ ЗВЕЗД ^^
Л
lQ49rcMVc
0,00
0,21
0,32
0,42
0,53
0,64
0,76
0,89
1,03
1,19
1,37
1,56
1,72
2,02
7/1^1
0,00
0,02
0,04
0,06
0,08
0,10
0,12
0,14
0,16
0,18
0,20
0,22
0,24
0,26
^max» ^?
1,03
1,06
1,09
1,12
1,15
1,18
1,21
1,24
1,27
1,31
1,34
1,38
1,40
1,44
Рс
10^^ г/см^
7,41
7,57
7,73
7,88
8,04
8,19
8,34
8,48
8,61
8,74
8,85
8,%
9,02
9,11
^) Значения М^^^ не совсем такие, как в работе [530], где
приводятся массы покоя.
Уравнения (9.6.2) — (9.6.4) можно решить следующим образом: выбрать
значение ? и, следовательно, найти g(\) и T/\IV\. Затем решить уравнение
(9.6.4), которое является кубическим относительно Л/*^^, для нахождения
Л/. Уравнение (9.6.3) далее даст значение р^, а (9.6.2) — значение 7.
Результаты приведены в табл. 9.3.
Вычислительное упражнение 9.13. Проверьте данные табл. 9.3. Обратите внимание,
что вам придется добавить Е/с^ к Л/, чтобы получить полную массу [см.
обсуждение после уравнения (9.2.23)].
Поскольку простые результаты, касающиеся возникновения неосесим-
метричных неустойчивостей в общей теории относительности, неизвестны,
предположим, что сохраняют силу приближенные ньютоновские критерии
T/\W\ < 0,14 для вековой устойчивости hT/\W\ ^ 0,26 для динамической
устойчивости. Фридман и Шутц [208] показали, что типичный временной
масштаб гравитационного излучения при T/\IV\ - 0,14 не превышает года
(сравните с упражнением 16.7). Очевидно, что такие нейтронные звезды не
Модели нейтронных звезд: массы и радиусы 287
проживут долго. Из табл. 9.3 видно, что максимальное возрастание Л/^^^,
обусловленное вращением (используем T/\WV = 0,14), составляет
U24- 1,03 ^^„
Однако следует ясно представлять, что приведенное выше рассмотрение
равновесных моделей вращающихся нейтронных зеезд, по-видимому,
надежна только для конфигураций с малой массой: ? < М^. Приближение
с л = 3/2 нельзя считать достаточно хорошим при значениях р^,
приведенных в табл. 9.3 [сравните с уравнением B.3.25)]. Кроме того GM/Rc^ > 0,2
для всех значений [R получается из уравнения C.3.9)], так что
постньютоновское приближение также неприменимо. Тем не менее, качественный
результат, согласно которому вызванное вращением увеличение М^^ равно
-^ 20Vo (сравните с 70Vo для белых карликов), совместим с более
детальными численными расчетами Баттеруорта и Ипсера.
Это различие между нейтронными звездами и белыми карликами
подчеркивается, если уравнение (9.6.4) переписать в виде
-(^
1
^2/3A _ 4Г/3|Ж|)
9/4
. (9.6.6)
Член в квадратных скобках представляет собой увеличение массы Л/,
связанное с вращением, и он одинаково эффективен для белых карликов и
нейтронных звезд. Член, пропорциональный Д представляет собой
уменьшение М, связанное с релятивистской теорией гравитации. Отношение этого
члена к ньютоновскому члену 1А равно GM/Rc^, так что им можно
пренебречь для белых карликов, но не для нейтронных звезд.
Более точное определение М^^ требует детального численного анализа
быстро вращающихся полностью релятивистских нейтронных звезд и
критериев их устойчивости.
Глава 10
Пульсары
10.1. ИСТОРИЯ и ОТКРЫТИЕ
в 1967 г. группа астрономов из Кембриджа во главе с Энтони Хьюишем
обнаружила^^ астрономические объекты, излучающие периодические
импульсы радиоволн. Это открытие оказало глубокое воздействие на
последующие астрофизические исследования. Его большое значение было
подчеркнуто присуждением Хьюишу в 1974 г. Нобелевской премии.
Существование устойчиво равновесных звезд, более плотных,
нежели белые карлики, предсказывалось многими теоретиками, (например,
работы [31, 427]; см. сноску на с. 261 данной книги). Бааде и Цвикки [31],
Колгейт и Уайт [144] и другие предположили, что такие объекты могут
образовываться при взрывах сверхновых. Высказывались даже догадки,
что в начальной стадии они должны быть быстро вращающимися
объектами [285, 578] с сильными магнитными полями [285, 623] и что источником
энергии Крабовидной туманности может быть вращающаяся нейтронная
звезда [610]. Предварительные характеристики простой магнитно-
дипольной модели, способной объяснить преобразование энергии вращения
нейтронной звезды в электромагнитное излучение, а затем и в энергию
движущихся частиц, во время открытия были уже в печати [437].
Таким образом, нельзя сказать, что сообщение Хьюиша и других [274]
об открытии радиопульсара с периодом 1,377 с на частоте 81,5 МГц
произошло в теоретическом вакууме. Однако отождествление пульсаров с
Нейтронными звездами для большинства астрофизиков не было
непосредственно очевидным. Первый аргумент в пользу того, что
наблюдаемые пульсары представляют собой быстро вращающие нейтронные
звезды с магнитными полями на поверхности около 10^^ Гс, был
выдвинут Голдом [227]. Он указал, что отождествление с такими объектами
объясняет многие наблюдаемые особенности пульсаров, например,
удивительную стабильность периода следования импульсов. Голд предсказал
небольшое увеличение периода по мере того, как пульсар медленно теряет
энергию вращательного движения. Вскоре после этого было открыто
замедление пульсара в Крабовидной туманности. Голд [228] показал, что
предполагаемые потери энергии примерно соответствуют количеству энергии,
выделяющейся внутри Крабовидной туманности. Этот успех наряду с неуда-
^^ См. [274]. Для ознакомления читателю можно рекомендовать рассказ Джослин
Белл^Бернелл о ее участии в открытии [93].
Пульсары 289
нами альтернативных моделей привел к всеобщему признанию модели
нейтронной звезды.
Несколько переработанный вариант цепочки рассуждений, приведших к
этому историческому объяснению, бегло обрисован в следующем разделе.
10.2. ДЕЙСТВИТЕЛЬНО ЛИ ПУЛЬСАРЫ ЯВЛЯЮТСЯ
ВРАЩАЮЩИМИСЯ НЕЙТРОННЫМИ ЗВЕЗДАМИ?
Основные наблюдательные факты, которые исключают все другие
возможности, таковы:
1. Пульсары имеют периоды в интервале 1,6 мс — 4,3 с.
2. Периоды пульсаров очень медленно увеличиваются и никогда не
уменьшаются (если не считать эпизодических «сбоев», см. разд. 10.10).
3. Пульсары являются исключительно хорошими часами. Периоды
нескольких пульсаров измерены с точностью до 13 значащих цифр.
За время 1,6 мс свет проходит 500 км. Это налагает верхний предел на
размеры излучающей области. Не было предложено ни одной
последовательной модели, согласно которой излучающая область была бы частью
гораздо большего «источника». Трудно представить такие хорошие часы
как пульсар, если излучающая область не будет тесно связана со всем
«источником» в целом. Поэтому максимальный размер источника можно принять
равным 500 км, т.е. мы имеем дело с компактным объектом. Но с каким
именно — с белым карликом, нейтронной звездой или же с черной дырой?
Сначала рассмотрим модели белых карликов. В этом случае в качестве
основного «часового» механизма сразу напрашиваются три варианта:
вращение, пульсации или двойная система. Самый короткий период вращения
для белого карлика возможен, когда он вращается со скоростью,
соответствующей началу его разрушения
?^?-^, A0.2.1)
где ? — угловая частота вращения. Будучи переписанным в терминах
средней плотности р, уравнение A0.2.1) переходит в
?^ - Gp, A0.2.2)
т.е. в универсальное соотношение между динамическим временным
масштабом и плотностью самогравитирующей системы. Взяв максимальную
плотность, равную 10^ г/см^, получим
Р = ^^> 1с. A0.2.3)
Этот результат исключает вращающиеся белые карлики.
Сходная с соотношением A0.2.3) оценка сохраняется и для
пульсирующих белых карликов. Действительно, точные расчеты показывают, что
самый короткий период для основной моды пульсаций равен - 2 с (сравните
с разд. 6.10). Высшие гармоники имеют более короткие периоды, но они
3-513
290 Глава 10
исключаются по двум причинам. Во-первых, для возбуждения гармоник без
возбуждения основной моды требуются особые условия. При этом любая
небольшая нелинейность приводит к смешиванию мод и нарушению
четкости периода. Во-вторых, потеря энергии в колебательной системе обычно
приводит к уменьшению периода.
Белые карлики в двойных системах удовлетворяют соотношению
Q'r~^^, A0.2.4)
где г — радиус орбиты. Поскольку г ^ Ry мы опять возвращаемся к
результату A0.2.3).
Пульсирующая нейтронная звезда имеет плотность примерно в 10^ раз
выше, чем у белого карлика. Поэтому основной период пульсаций равен
-- 10" ^ с, т.е. слишком короток для типичных случаев.
Подходящим выбором радиуса можно добиться.чтобы орбитальный
период двойной системы, содержащей нейтронную звезду, соответствовал
наблюдаемому диапазону 10"^ — 4 с. Однако, как мы увидим в
упражнении 16.9, такая система будет обильно излучать гравитационные волны, а
время ее жизни составит
\8/3
- 10-3 [y^J лет. A0.2.5)
Временной масштаб, в пределах которого, судя по наблюдениям,
изменяются периоды пульсаров, составляет в типичных случаях Р/Р ~ 10^ лет;
более того, гравитационное излучение заставляет период уменьшаться, а не
увеличиваться.
Как мы увидим в гл. 12, изолированная черная дыра не обладает
структурой, с которой можно связать периодический излучатель. В частности,
вращающиеся черные дыры осесимметричны. Любой механизм, связанный
с аккрецией, не может быть периодичным с такой фантастической
точностью.
Только вращающаяся нейтронная звезда удовлетворяет всем
приведенным выше ограничениям. Кроме того, как мы обнаружим, на основе такой
интерпретации хорошо объясняются и некоторые другие факты,
следующие из наблюдений.
10.3. НАБЛЮДАЕМЫЕ СВОЙСТВА ПУЛЬСАРОВ
Недостаток места не позволяет нам дать полный обзор всех удивительных
свойств пульсаров. Ограничимся кратким рассмотрением наиболее
характерных свойств (более полное обсуждение см., например, в [148, 248, 380,
404, 540]).
Пульсары 291
\^H^%f»^Jp^,.im4^tXit^tS .^.AA» ^.^JL^yirfV^'Miw^^i^AAA^^A л Щ^К^ ¦¦
1 \ \ 1 1 \ 1 1
0 2 4 6 8
Время,С
Рис, 10,1, Запись отдельных импульсов пульсара PSR 0329 + 54, открытого одним
из первых. Импульсы записаны на частоте 410 МГц при инструментальной
постоянной времени 20 мс. Период повторения импульсов составляет около 0,714 с [380].
а) Формы и спектры импульсов
В настоящее время известно окало 350 пульсаров. У всех наблюдается
широкополосное радиоизлучение в форме периодических импульсов (рис.
10.1). Интенсивности импульсов меняются в широких пределах, иногда
импульсы вообще пропадают. Тем не менее, основная запись импульсов
периодическая. Скважность (доля периода, в течение которой излучение
поддается обнаружению) обычно мала A—5Vo). При временных масштабах
< 1 мс форма импульса довольно сложна. В типичном случае импульс
состоит из двух или более субимпульсов. У субимпульсов проявляется
сложная микроструктура, которая может иметь малые характерные времена
порядка 10 МКС. Однако найдено, что средняя форма нескольких сотен
импульсов исключительно стабильна (рис. 10.2). Измеряя времена прихода
для одной и той же детали в последовательности усредняемых импульсов,
можно показать, что вращающаяся нейтронная звезда является отличными
часами. Периоды некоторых пульсаров известны с точностью до 10~^^.
Удельная интенсивность^^ радиосигналов изменяется по крутому
степенному закону /^ - v^ у где значение ? - -1,5 для ? < 1 ГГц, и еще ниже
при более высоких частотах. Типичная интенсивность (усредненная по
периоду и проинтегрированная по телесному углу) на 400 МГц
составляет -0,1 Ян [1 Ян = 10~^^ эрг/(с · см^ · Гц)]. Многие пульсары
демонстрируют высокую степень линейной поляризации — в некоторых
случаях до 100%. Величина линейной поляризации и позиционный угол
часто изменяются со временем в пределах импульса. Круговая поляризация
встречается не так часто и если присутствует, то бывает не столь сильной
как линейная.
^^ Удельная интенсивность 1^ излучения светящегося объекта определяется в
приложении И и измеряется в эрг/(с · см^ · Гц · стерад) [сравните с уравнениями
(И.1)-(И.З)].
292
Глава 10
О
Время, мс
Рис. 10.2. Последовательность ста импульсов пульсара PSR 1133 + 16, записанная
на 600 МГц. Средний профиль 500 импульсов приведен сверху. Последовательные
импульсы откладываются по вертикали, чтобы продемонстрировать изменения
формы отдельных импульсов и моментов прихода; поведение усредненного импульса
тем не менее совершенно устойчиво и периодично [148].
б) Периоды
Наблюдаемые периоды пульсаров составляют от 1,558 мс для
PSR 1937 -к 214 [32] до 4,308 с для PSR 1845 - 19. Второй по
кратковременности период у пульсара в Крабовидной туманности PSR 0531 + 21
@,0331 с), третий — у пульсара Халса—Тейлора PSR 1913 + 16, входящего
в двойную систему @,059 с), а четвертый — у пульсара в созвездии
Парусов PSR 0833 — 45 @,089 с)^\ Медиана периода — 0,67 с.
^^ В 1983 г. был открыт пульсар PSR 1953 + 29 с периодом 6,13317 мс, входяидий
в двойную систему. [См. Boriakoff К., Buccheri /?., Fauci F. Nature, 304, № 5925, 417,
1983.)—Яр^ш. ред.
Пульсары
293
1970
1975
1980
0,08925
\
PSR 0833-45
1000 2000 3000 4000
Юлианский 9eHb-Z440000,5
Рис. 10.3. Изменение периода пульсара PSR 0833 — 45 (пульсар в созвездии Парусов)
за время от конца 1%8 г. до середины 1980 г. Пронумеровано четыре больших
скачка и отмечены промежутки времени (в годах) между скачками [168].
Во всех случаях, когда проводились точные наблюдения, было найдено,
что периоды пульсаров равномерно увеличиваются (но ниже мы будем
обсуждать «сбои»). Типичные значения производной периода ? - 10"^^ с/с.
Из моделей пульсаров вытекает, что их возраст, по-видимому, меньше,
чем характерное время ? = ?/? -- 10^ лет. У пульсаров с более короткими
периодами есть тенденция к большим скоростям замедления и к меньшим
характерным временам. Для пульсара в Крабовидной туманности ? = 2486
лет. Однако у пульсара Халса — Тейлора, входящего в двойную систему,
? = 2,17 · 10^ лет.
Наиболее заметные нерегулярные изменения периодов у
пульсаров — это внезапные возрастания скорости вращения, или сбои,
наблюдавшиеся у пульсаров в Крабовидной туманности (????/?- 10"^)ив
созвездии Парусов (????? -- 2 · 10 ~^). В каждом из четырех
«гигантских» сбоев пульсара в созвездии Парусов, наблюдавшихся до сего времени
(рис. 10.3), уменьшение периода сопровождалось увеличением производной
периода (АР/Р ^ 0,01), которое затухало примерно через 50 дней. Более
мелкие скачкообразные увеличения частоты у пульсара в Крабовидной
туманности (два из которых зарегистрированы вполне надежно) разнятся
294 Глава 10
ПО величине в четыре раза. Они также сопровождались увеличением произ*
водной периода (АР/? - 2 · 10~^), которое затухало примерно за 10
дней. Мы вернемся к этим данным в разд. 10.10, где будем обсуждать
теоретические модели, позволяющие объяснить природу сбоев.
В дополнение к большим скачкам частоты, или «макросбоям»,
наблюдавшимся у нескольких пульсаров, у значительного числа пульсаров
были обнаружены также меньшие по амплитуде нерегулярные флуктуации
периодов. Это нерегулярное «дрожание» частоты пульсарных «часов«
называют шумами синхронизации^^. Шумы синхронизации представляют собой
слабые флуктуации частоты повторения импульсов. Они могут возникать
при небольших случайных событиях, когда ????/? по крайней мере на два
порядка величины ниже, чем амплитуда флуктуации при макросбое. Для
пульсара в Крабовидной туманности было показано, что спектр этих
шумов по форме не сравним со спектром «гигантских» сбоев, так что они
могут представлять совершенно разные явления [82, 249].
в) Пространственное распределение и связь
с остатками сверхновых
Мы знаем, что пульсары рождаются в нашей Галактике, поскольку, во-
первых, они сконцентрированы к плоскости Галактики (рис. 10.4 и 10.5) и,
во-вторых, у них обнаружена дисперсия, характерная для прохождения
сигналами галактических расстояний (более подробно этот вопрос будет
обсуждаться ниже).
Угловое распределение пульсаров в плоскости Галактики похоже на
угловое распределение остатков сверхновых и их предполагаемых
предшественников — ОВ-звезд, хотя средняя шкала высот распределения
над галактической плоскостью несколько выше и составляет - 300 пс. Это
совместимо с гипотезой, согласно которой пульсары возникают при
взрывах сверхновых, приобретая при этом, вероятно, относительно большую
скорость. Более впечатляющий аргумент—связь отдельных пульсаров с
известными остатками сверхновых. Пульсары PSR 0531 4· 21 и PSR 0833 -
- 45 связаны соответственно с Крабовидной туманностью и с остатком
сверхновой в созвездии Парусов. Крабовидная туманность — это остаток
сверхновой, наблюдавшейся древнекитайскими астрономами летом 1054 г.
н.э. Туманность удалена от нас примерно на 2 кпс и состоит из
расширяющихся наружу нитей, излучающих в линиях оптического диапазона, и
аморфной среды, испускающей синхротронное излучение. Открытие факта,
что пульсар в Крабовидной туманности является неизвестным до того
источником энергии туманности и что теоретический возраст пульсара
находится в хорошем согласии с фактическим возрастом 926 лет (на 1980 год).
•^ См. [83]. Для детального обсуждения наблюдения шумов синхронизации см.
[150] и помещенные там ссылки. Критика различных теоретических моделей,
предложенных для объяснения шумов синхронизации, дана в [149] и указанной там
литературе.
Рис. 10.4. Распределение пульсаров в Галактике. В принятой системе координат широта 0° соответствует
плоскости Галактики, а начало координат — направлению на центр Галактики.
296
Глава 10
1
S
1
S
о
со
1
о
ю
1
1
^ ^ о о CD о о
ГО Я <^ -^ СЧ1 го
I I I
Галактическая широта (°)
8
Л^с. 10.5. Распределение пульсаров по галактической широте. Широта 0°
соответствует плоскости Галактики.
надежно подтвердило модель вращающейся нейтронной звезды для
пульсаров (количественное обсуждение см. в разд. 10.5).
Остаток сверхновой в созвездии Парусов имее;г возраст, составляющий
по оценкам 30 000 — 50 000 лет, т.е. по порядку величины равный
характеристическому возрасту PSR 0833 — 45 (Г = 22 000 лет). Наряду с
согласием в положении и расстоянии (а ~ 500 пс) это совпадение служит
основным свидетельством в пользу связи пульсара с остатком сверхновой.
В дополнение к двум случаям явной связи пульсара с остатком
сверхновой можно отметить еще один пример вероятной и два — возможной
связи. Эти примеры относятся к молодым {<> 10^ лет) пульсарам, так что не
удивительно, что больше связей такого рода не было найдено^^ Тем не ме-
'^ Относительно недавно в остатках сверхновых были открыты два
пульсирующих рентгеновских источника. Один из них ~ быстрый рентгеновский пульсар
(Р = 0,15 с), похожий на пульсар в Крабовидной туманности [520], а второй ~
гораздо более медленный (Р = 3,5 с) [191]. Сообщалось об обнаружении
радиоизлучения от первого из этих источников [382]. Как полагают, оба они представляют
собой вращающиеся нейтронные звезды.
Пульсары 297
нее может показаться странным, что из полдюжины (или около того)
галактических сверхновых, зарегистрированных за последние 2000 лет,
только в Крабовидной туманности содержится пульсар. Возможно, механизм
излучения является сильно направленным или может оказаться, что не все
сверхновые образуют пульсары (см. гл. 1 и 11).
10.4. МЕРА ДИСПЕРСИИ
Оценка расстояния до каждого из пульсаров получается на основании его
меры дисперсии DM, определяемой как
DM = f^n^ dl = (/i,>L, A0.4.1)
•?
где L—расстояние до пульсара, w^—электронная концентрация, а /—длина
пути вдоль луча зрения. Мера дисперсии обычно выражается в пс/см^.
Само название «мера дисперсии» возникло по той причине, что
электромагнитные волны претерпевают дисперсию под действием проводящей
межзвездной среды. При этом широкополосный импульс на более низких
частотах достигает Земли позднее, чем на более высоких.
Для количественного рассмотрения вспомним, что ускорение электрона
с зарядом -ев разреженной плазме под действием распространяющейся
электромагнитной волны с частотой ? определяется выражением
тх = -еЕ, A0.4.2)
где электрическое поле можно записать в виде
? = Eoe'"^ A0.4.3)
Таким образом,
х = -^Е, A0.4.4)
???
так что поляризация среды равна
P = /i,(-e)x= -^Е. A0.4.5)
???
Однако
? = ^ГЕ> A0.4.6)
4??
где ? — диэлектрическая постоянная. Следовательно,
a=l--f,
?
A0.4.7)
^^Z—e^ A0.4.8)
298 Глава ??
где
^Р^ т
— плазменная частота.
Для распространения электромагнитной волны с волновым числом к
фазовая скорость равна
V = f = ·^· A0.4.9)
Подставив выражение A0.4.7) в A0.4.9), получим дисперсионное
соотношение
?^ = ?^ + kV. A0.4.10)
Отметим, что для распространения волны величина ? должна быть
больше, чем ??.
Групповая скорость равна
? \ '/2 / ...2
М1й = Ах-Щ" =c(i-^
•^» dk «2 2?2
^.^^^^Чг-^Л^-п] =^1-ТзЬ "»"/>· 00.4.11)
Время прихода импульса, прошедшего расстояние L и обладающего
полосой частот с центром на частоте ?. равно
,»=/-^ =1^,+41^/ -^^^DM, A0.4.12)
где мы использовали определение A0.4.1). Измеряемой величиной
является ??^(?) — временная задержка компонентов импульса с разной частотой,
а соотношение
^= -^DM A0.4.13)
дает меру дисперсии DM,
Если известна величина <а2^> (например, мера дисперсии источников,
расположенных на известных расстояниях, дает {п^) = 0,03 см~^ для
межзвездной среды в окрестностях Солнечной системы [549]), то можно
получить расстояние L до отдельных пульсаров на основании меры
дисперсии. Полученные таким путем расстояния лежат в диапазоне от - 100 пс
(PSR 0950 -Н 08) до 18 кпс (PSR 1648 - 42). Неопределенности,
обусловленные отличием средней электронной концентрации <а2^> от фактической в
разных местах Галактики, приводят к тому, что оценки расстояний до
отдельных пульсаров могут быть ошибочными примерно в два раза, но
статистически эти оценки являются, вероятно, достаточно точными.
Один из пульсаров — PSR 1929+10 — расположен достаточно близко
для того, чтобы на основе измерений в течение года его параллакса опреде-
Пульсары 299
лить расстояние до него с приемлемой точностью. Полученное таким
образом значение составляет около 50 пс [501].
Упражнение 10.1. Покажите, что предположение о ненулевой массе фотона т^ ? О
приводит в низшем приближении к дисперсионному закону с той же зависимостью
от частоты, что и в уравнении A0.4.13)^).
10.5. МОДЕЛЬ МАГНИТНОГО ДИПОЛЯ ДЛЯ ПУЛЬСАРОВ
В этом разделе мы обсудим очень простую модель пульсара, которая
объясняет многие из наблюдаемых свойств этих объектов. Модель
магнитного диполя [251, 437, 438] ясно показывает, как кинетическая энергия
вращающейся нейтронной звезды преобразуется в излучение пульсара. В этом
модельном варианте наклонного ротатора предполагается, что
нейтронная звезда равномерно вращается с частотой ? в вакууме и обладает
магнитным моментом т, ориентированным под углом ? к оси вращения.
Ниже этой модели будут противопоставлены невакуумные модели (например,
соосный ротатор)^^ Предполагается, что вращение является достаточно
медленным, чтобы в первом приближении можно было пренебречь
отклонениями от сферичности, связанными с вращением.
Упражнение 10.2. Оцените отношение центробежного и гравитационного ускорений
«а экваторе пульсара в Крабовидной туманности.
Независимо от геометрии внутреннего поля чисто дипольное магнитное
поле на магнитном полюсе звезды В ? связано с m соотношением
где R — радиус звезды. (Сравните с уравнением E.56) работы [297].)
Такая конфигурация обладает переменным во времени дипольным моментом,
если смотреть из бесконечности, и поэтому она излучает энергию со
скоростью
?= -^|т|'. A0.5.2)
Если записать
m = {BpR}{e^^co^a + е^ sin ? cos ?/ + e'^ sin ? sin ?/), A0.5.3)
•^ Допустив, что вся дисперсия пульсара в Крабовидной туманности вызвана тем,
что фотоны обладают ненулевой массой, Фейнберг [193] наложил предел
т^ < 10""*^ г на массу фотона!
^^ У такого ротатора магнитная ось параллельна оси вращения. ~ Прим. перев.
300 Глава 10
где ?| — единичный вектор, параллельный оси вращения, а ? ^ и
? ^'—фиксированные взаимно ортогональные единичные векторы,
перпендикулярные вц, то найдем
^=--^--1 . A0.5.4)
Отметим, что это излучение испускается на частоте ?.
Уравнение A0.5.4) приводит к нескольким важным следствиям. Во-
первых, уносимая излучением энергия порождается кинетической энергией
вращения нейтронной звезды:
Е={т\ A0.5.5)
где / — момент инерщ1и. Таким образом,
Е^тй, A0.5.6)
Поскольку ?¦ < о, то и ? < о, т.е. пульсар замедляется. Если определить
характеристическое время на данный момент как
(ft)o
^^'^^ A0.5.7)
?/?«8??^??'
то уравнения A0.5.4) и A0.5.6) можно проинтегрировать, что дает
^ = 4^ ^-7±^\ ' A0-5-8)
где ?^ — начальная угловая скорость при t = 0. Положив ? = ?? в
уравнении A0.5.8), получим современный возраст пульсара
/=|il-0j=f ДляЙо<;Й,. A0.5.9)
В работах [249, 250] приводится значение ? для пульсара в Крабовидной
туманности, равное 2486 лет по состоянию на 1972 г., что предполагает
возраст этого пульсара 1243 года. Этот результат сравнительно хорошо
согласуется с фактическим возрастом 918 лет A972 — 1054). Обратите
внимание, что эта оценка, впервые полученная таким образом Ганном и Ост-
райкером [251], не зависит от деталей рассматриваемой модели
нейтронной звезды. Она зависит только от общего характера поведения функции
?(/), связанного с излучением магнитного диполя. Согласие можно
улучшить, если допустить существование других механизмов потери энергии,
например гравитационного излучения (что будет описано ниже).
Пульсары 301
Модель магнитного диполя может быть использована также для
количественного расчета энергетики пульсара в Крабовидной туманности.
Следуя Ганну и Острайкеру, предположим, что пульсар в Крабовидной
туманности — это сферическая нейтронная звезда с массой Л/ = 1,4 Л/^ ,
радиусом R = 12 км и моментом инерции / = 1,4 · 10^^ г · см^. Тогда
уравнения A0.5.5) и A0.5.6) дают
? = 2,5 · 10^9 эрг; i = 6,4 · 10^» эрг/с. A0.5.10)
(Чтобы получить эти величины, достаточно знать лишь значение /.) В
нашем случае уравнения A0.5.5) и A0.5.6) не зависят от деталей механизма
потерь энергии, а вытекают из предположения, что пульсар — это
вращающаяся нейтронная звезда, вращение которой служит источником энергии.
Поэтому примечательно, что величина ? сравнима с вытекающими из
наблюдений оценками энергии (кинетической и радиационной) Крабовидной
туманности, которые соответствуют значению 5 · 10^^ эрг/с [380]. На это
согласие впервые указал Голд [228], который отметил также, что
достаточно эффективный механизм ускорения излучающих релятивистских
электронов в окружающей туманности позволяет объяснить, каким образом
высокая энергия электронов поддерживается в течение более чем 900 лет
после взрыва сверхновой.
Заметим, что значение Ё в A0.5.10) много больше, чем энергия
наблюдаемого излучения в радиоимпульсе, составляющая для пульсара в
Крабовидной туманности около 10^^ эрг/с.
Используя значение ?¦ для пульсара в Крабовидной туманности A0.5.10)
и принимая модель магнитного диполя, т.е. уравнение A0.5.4), получим
Вр = 5,2 · 10^2 Гс (sina = 1). A0.5.11)
Такое значение естественно получается при анализе коллапса звезд
главной последовательности с типичным «вмороженным» магнитным полем на
поверхности порядка 100 Гс. Уменьшение радиуса примерно в 10^ раз
приводит к увеличению В ? в 10^^ раз. Большинство полученных теоретических
значений напряженности поверхностного магнитного поля для других
пульсаров имеет такую же величину, что и в A0.5.11).
Примечательно, что недавние наблюдения за рентгеновскими
пульсарами в двойных системах (гл. 13) дают сравнимые значения
напряженности поверхностного магнитного поля. Трюмпер и др. [574] наблюдали
заметную деталь в пульсирующем жестком рентгеновском спектре Her Х-1,
а У ИТОН и др. [609] наблюдали подобную деталь в спектре источника 4U
0115 — 63. Интерпретация этих деталей как циклотронных линий приводит
к значениям
? -- D ^ 6) · 10^2 Гс в Her Х-1,
5--2- 10^2 ?^ в 4U 0115 - 63. A0.5.12)
302 Глава 10
Характерные для пульсаров сильные магнитные поля, по-видимому,
возникают при образовании пульсаров. Может ли такое поле затухнуть?
Время затухания /^ приблизительно равно
?,-^, A0.5.13)
где L — характерная длина, а ? — проводимость [сравните с уравнением
G.1.8)]. Исходя из соображений размерности, электрическую проводимость
можно выразить через т^, с ? е:
'"'^ - 10« с-'. A0J.14)
Используя это значение ? и положив L = R в соотношении A0.5.13),
оценим, что для «типичной» (однородной) нейтронной звезды t^ ^ 10^ лет,
что много больше возраста пульсара в Крабовидной туманности.
Фактическое значение ? зависит от детального характера
взаимодействия электронов с веществом звезды и может сильно отличаться от значения
A0.5.14). Однако в любом случае затухание магнитных полей пульсаров за
время их жизни должно быть мало^\
Как упоминалось выше, один из путей согласования теоретического и
фактического возрастов пульсара в Крабовидной туманности состоит в
привлечении механизма гравитационного излучения. Самый низкий
порядок гравитационного излучения — квадрупольный (см. гл. 16), поэтому,
чтобы излучать, нейтронная звезда должна обладать переменным во
времени квадрупольным моментом. Модель нейтронной звезды в виде слегка
деформированного однородного эллипсоида с моментом инерции / и
эллиптичностью ?, где
_ разность экваториальных радиусов _ а — b
средний экваториальный радиус (а + Ь)/2 *
дает [сравните с уравнением A6.6.9)]
5 с^
= A,4 · Ю^Чрг/с) ( -^^ Л (— )
\1,4 · 10^5 г · см^ / \0,0331 с /
?'
10-^ 'A0.5.16)
'^ См. [188], где подчеркивается, что затухание магнитного поля, если оно
вообще есть, происходит только в самых внешних областях звезды. Длительное
существование сильных магнитных полей в пульсирующих рентгеновских источниках
(гл. 13 и 15) наводит на мысль о длительном времени затухания магнитного поля в
нейтронных звездах, превышающем, по-видимому, несколько миллионов лет даже
около поверхности.
Пульсары 303
Согласно уравнению A0.5.16), небольшая эллиптичность может приводить
к излучению, требуемому для объяснения замедления пульсара в Крабовид-
ной туманности, соответствующего A0.5.10). Такая эллиптичность^^ может
быть вызвана внутренними анизотропными магнитными полями с
напряженностью 10^^ Гс, которым соответствуют внутренние поля звезд
главной последовательности порядка 10^ Гс непосредственно перед коллапсом.
Отметим также, что в случае постоянной эллиптичности ? закон
замедления выглядит так:
Е^^^тйо: Q\ A0.5.17)
Определив
^°" " " (l)o' ^^^-^-^^)
можно проинтегрировать уравнение A0.5.17) и получить
где ? — начальная угловая скорость при г = 0. Подстановка ? = Qq в
уравнение A0.5.19) дает выражение для современного возраста пульсара
^ = Zbw (? _ ^) < 2486 ^ ^21 год. A0.5.20)
Таким образом, одно лишь гравитационное излучение не позволяет
объяснить замедление пульсара в Крабовидной туманности. Тем не менее,
можно найти такую комбинацию гравитационного и магнитно-дипольного
излучения, которая дает как правильный возраст, так и наблюдаемые темпы
замедления пульсара [432].
Упражнение 10.3. В рамках комбинированной модели
/ЙЙ= -i8?^-??^ A0.5.21)
где |б и 7 определяются уравнениями A0.5.4) и A0.5.16). Тогда
?
?^? + ???
A0.5.22)
a) Проинтегрируйте уравнение A0.5.21) и найдите возраст
A + ?)(? - ? + Alog ?^^ = у, A0.5.23)
'^ Вопрос об эллиптичности нейтронной звезды обсуждается подробнее в разд.
10.11 и 16.6.
304 Глава 10
?.??, ,.|. (,0.5.,4)
б) Используя значения / = 918 лет, ? = 2486 лет, покажите, что решением
уравнения A0.5.23) является ? = 0,271 и что оно нечувствительно к ? для ? ^ 0,01.
в) Отсюда покажите, что
? = 2,9 · 10-^ BpSmoL = 4,6 · 10>2 Гс. A0.5.25)
г) Покажите, что гравитационное излучение преобладает в потерях энергии в
течение первых 130 лет жизни пульсара.
д) Полная энергия, излучаемая в виде электромагнитных волн, равна
А^с» - l^dQ. A0.5.26)
Выберите для определенности ?, = 10*с~· и покажите, что
Д?ет = 5,9· 1050 эрг, A0.5.27)
в то время как
A^Gw = ?/(?? - ??) - А?еш ^ i/?? = 7 X 10^' эрг. A0.5.28)
е) Покажите, что в настоящее время
?gw = 1,4 · 1038 эрг/с, ?ет = 5,1 · 1038 эрг/с
в то время как при ?^ = 10^ с ~·
?gw = 2,9 · 10^ эрг/с, ?em = 3,9 · 1045 эрг/с
в начальный момент.
Упражнение 10.4. Каково значение эксцентричности е и отношения T/\W\ для
пульсара в Крабовидной туманности в начальный момент, если ?, = 10^ с~ · ? Устойчива
ли эта конфигурация? (Примите соотношения для сфероидов Маклорена; сравните с
разд. 7.3.)
10.6. ПОКАЗАТЕЛЬ ТОРМОЖЕНИЯ
Для любой степенной модели замедления типа модели магнитного диполя
можно записать
й= - (const) ·?\ A0.6.1)
где параметр ? называется показателем торможения. Для модели
магнитного диполя А2 = 3. В общем случае можно определить
«--^, A0.6.2)
Пульсары 305
куда входит и случай A0.6.1). Таким образом, показатель торможения
может в принципе быть измерен непосредственно по значениям частоты
пульсара и ее производных. В настоящее время надежные определения
существуют только для пульсара в Крабовидной туманности, для которого
получено [249]:
? = 2,515 ± 0,005. A0.6.3)
Целый ряд факторов может нести ответственность за отклонение ? от
«канонического» значения 3^^ Например, приводились доводы [378] в
пользу того, что установление магнитной оси пульсара параллельно
(«выравнивание») или перпендикулярно («противовыравнивание») оси его симметрии
(которая не обязательно должна быть осью вращения) может происходить,
если магнитная ось блуждает по звезде (сравните с «блужданием»
магнитных полюсов на Земле). В моделях с «противовыравниванием» ? может
снизиться до 2 во время процесса установления магнитной оси, даже с
учетом того, что торможение обусловлено магнитно-дипольным излучением.
Но когда «противовыравнивание» завершается, то а? = 3.
Заметим, что если бы гравитационное излучение являлось основной
причиной торможения, то ? было бы равно 5. В комбинированной модели
Ганна-Острайкера для пульсара в Крабовидной туманности, которая
обсуждалась в предыдущем разделе.
? =
= 3,43 (в настоящее время). A0.6.4)
1 + л V · · /
10.7. НЕВАКУУМНЫЕ МОДЕЛИ ПУЛЬСАРОВ.
СООСНЫЙ РОТАТОР
Существенно, что уравнение A0.5.4)
? ^-7-, A0.7.1)
может сохранять силу также в моделях, отличных от вакуумной модели
наклонного магнитного диполя. В действительности, как впервые указали
Голдрайх и Джулиан [230] и как мы увидим ниже, сильные электрические
поля, параллельные магнитным полям на поверхности пульсара,
неизбежно должны «отрывать» заряженные частицы от звезды. Следовательно,
пульсар должен обладать плотной магнитосферой. Изучая случай, когда
магнитный дипольный момент параллелен оси вращения звезды, Голдрайх
и Джулиан доказали, что те заряженные частицы в магнитосфере, которые
«нанизаны» на магнитные силовые линии, замыкающиеся внутри светового
цилиндра, должны вращаться синхронно с пульсаром. Световой
'^ Более полное обсуждение см. в книге Манчестера и Тейлора «Пульсары» [380].
4-513
306
Глава 10
Рис. 10.6. Схема модели Голдрайха — Джулиана [230] для магнитосферы пульсара с
параллельными магнитной осью и осью вращения. Частицы, связанные с
замкнутыми магнитными силовыми линиями, вращаются синхронно с звездой и образуют
вращающуюся синхронно магнитосферу. Незамкнутые силовые линии пересекают
световой цилиндр (где линейная скорость синхронного вращения равна скорости
света) и отклоняются назад, образуя компонент тороидального поля. Вдоль этих линий
вытекают заряженные частицы. Критическая силовая линия находится при том же
электрическом потенциале, что и окружающая межзвездная среда. Эта линия
разделяет области течения положительных и отрицательных зарядов от звезды, а знаки
плюс и минус указывают на заряд в отдельных областях пространства. Штриховая
диагональная линия является геометрическим местом точек с ^, = О, где
пространственный заряд меняет знак. Угол, охватываемый областью полярной шапки,
которая содержит все незамкнутые силовые линии, равен ?^ [380].
цилиндр — это воображаемый цилиндр, ось которого совпадает с осью
вращения пульсара, а радиус простирается до такого расстояния, на
котором скорость синхронного вращения достигает скорости света (рис. 10.6).
Этот радиус области синхронного вращения выражается таким образом:
^с-
?
= 5 · 10^ ? см.
A0.7.2)
где ? — период пульсара в секундах. Когда частицы приближаются к /?^ в
экваториальной плоскости, они становятся сильно релятивистскими. Голд
[227] и другие предположили, что наблюдаемое высокочастотное излучение
пульсаров может порождаться релятивистскими частицами вблизи
светового цилиндра.
В модели Голдрайха и Джулиана и фактически во всех остальных
моделях пульсаров магнитное поле в ближней зоне (т.е. на расстояниях, мень-
Пульсары 307
ших вакуумной длины волны испускаемого излучения: л < ? = c/? = R^) в
значительной степени является дипольным. Соответственно
в-^-в,[^)', ,<«„ 00.7.3)
где В — напряженность поля на магнитном полюсе, а /? — радиус звезды.
На больших расстояниях магнитное поле выглядит как поле уходящей
волны, связанное с перпендикулярным электрическим полем той же величины
? - В и с направленным наружу вектором Пойнтинга 5 ~ сВ^/^-к. Таким
образом, полная мощность электромагнитного излучения, полученная
«сшивкой» полей при г ~ ? ~/?^, определяется выражением
Е- -{A^r^S)r^R^-
2q\ <-?"? '^P'
которое полностью совпадает с A0.7.1).
Следовательно, независимо от того, устанавливается ли дипольное поле
вдоль оси вращения или нет, плазма вблизи· пульсара может в принципе
уносить значительный момент количества движения и энергию,
обеспечивая необходимый тормозящий момент. Воспользовавшись результатами
решения уравнения A0.7.1), мы опять получим для показателя торможения
значение а? = 3. Однако детали этой картины (например, соотношение
между потоками энергии через /?^, уносимой частицами и полем,
геометрия поля и картина течения и т.д.) являются в настоящее время предметом
широкой дискуссии^\
Невакуумные модели могут также дать естественное объяснение
магнитных полей в окружающей Крабовидной туманности, наличие которых
следует из наблюдаемого синхротронного излучения. Хотя надежные
расчеты потоков полей или частиц за пределами светового цилиндра
отсутствуют, очевидно, что плотность энергии там больше не связана сильно с
вращающейся нейтронной звездой. Если в этой внешней области энергия
поля превышает энергию частиц, т.е. В^ > Втге , то из условия сохранения
энергии следует
|47ГА·^ - const, не зависит от г. A0.7.4)
В нашем случае В - 10^ Гс на расстоянии л - /?^ - 10^ см. Тогда
10'^ Гс
В - - г> R^. A0.7.5)
/- (см)
Отсюда следует, что В - 10""* Гс на расстоянии г - 1 пс в согласии с
оценками поля в туманности [490].
^^ Последние обсуждения и ссылки см., например, в статьях сборника [540] и в
отличном обзоре [404].
€)
308 Глава 10
Упражнение 10.5. Предположим, напротив, что Ер > B^/Stt для г > /?^. В этом
случае поток частиц может «причесать» магнитное поле по радиусу вдали от звезды.
Какой будет в этом случае зависимость В от г и каково значение В на расстоянии
^ I ПС?
Ответ: Условие V · В = О требует зависимости В ^ \/г^.
Как упоминалось выше, вращение нейтронной звезды, обладающей
магнитным полем, генерирует мощные электрические поля в окружающем
звезду пространстве. Рассмотрим теперь доводы Голдрайха и Джулиана
[230] в пользу того, что пространство благодаря таким электрическим
полям не может быть пустым, а должно содержать плазму.
В модели Голдрайха и Джулиана вращающаяся нейтронная звезда
имеет внешнее магнитное поле в виде диполя, параллельного оси врашения^^:
B.«.B,«>(S^...fi^-). (,0.7.6)
Предполагается, что звездное вещество является отличным проводником,
так что внутри звезды будет присутствовать электрическое поле Е^'"^ в
согласии с уравнением G.1.9):
E(in) + ??? ? B(in) ^ 0. A0.7.7)
Если предположить, что поверхностных токов нет, то нормальный и
тангенциальный компоненты В непрерывны при переходе через поверхность
звезды. Таким образом, сразу же под поверхностью
В<-) = дДсо8(?е^+^ег). A0-7.8)
Уравнение A0.7.7) дает в таком случае электрическое поле под
поверхностью
??5„8??? / sine \
?(-)= ^ Jli^e^-costfei). A0.7.9)
Тангенциальный компонент ? непрерывен при переходе через поверхность,
поэтому из уравнения A0.7.9) следует, что непосредственно вне звезды
?(out) = _ JL
д I RQBpSin^ \ э
дв\ 1с ] дв
????„
A0.7.10)
" Поскольку такая осесимметричная конфигурация не будет пульсировать,
следует допустить какое-то небольшое отклонение от строгой соосности, чтобы
объяснить импульсное излучение.
Пульсары 309
Предположим на мгновение, что внешняя среда — вакуум. Тогда
Е(-^>= -??, A0.7.11)
где
f2^ -
?'? = 0. A0.7.12)
Чтобы удовлетворить граничному условию A0.7.10) при г = R, решение
уравнения A0.7.12) должно иметь вид
ф= -^—Р2(со8в), A0.7.13)
т.е. внешнее электрическое поле является квадрупольным.
Упражнение 10.6. а) Принимая, что диэлектрическая постоянная везде равна
единице, покажите, что разрыв нормального компонента ? на поверхности звезды связан
с плотностью поверхностного заряда
???
?= -^ cos^^. A0.7.14)
6) Пренебрегая всеми макроскопическими токами вблизи поверхности (V ?
X ?(·") = О вблизи поверхности), покажите, что внутреннее электрическое поле ?
связано с внутренней плотностью заряда
?.= 4?^?·?=-2^?.?, A0.7.15)
что соответствует
?, = ?' 10-2 В, · Р-^ см-3, A0.7.16)
где В^ — это г-компонент В (Гс), а ? — период пульсара (с).
Теперь из уравнения A0.7.7) следует, что внутри звезды ? · В = 0.
Однако для области вне звезды уравнения A0.7.6), A0.7.11) и A0.7.13) дают
E.B=-^"-(f)^cos3(?. A0.7.17)
Таким образом, величина электрического поля, параллельного В, на
поверхности равна приблизительно
^„ - ^^Вр ^ 2 X 10«р-^5,2 ^/^^' A0.7.18)
где 512 — напряженность магнитного поля в единицах 10^^ Гс. Столь
сильное поле будет воздействовать на электроны и ионы, находящиеся на
поверхности, с силой, значительно превосходящей силу тяготения. Для
протонов
электрическая сила eRQB /с
сила тяготения GMm/R^
^ 109> 1 A0.7.19)
310 Глава 10
Поэтому частицы будут вырваны с поверхности и образуют плазменную
область вокруг звезды — магнитосферу. Таким образом, вакуумное
решение для области, окружающей вращающуюся нейтронную звезду,
является неустойчивым.
Внутри светового цилиндра плазма будет вращаться синхронно со
звездой благодаря сильному магнитному полю. Магнитосфера действует как
продолжение полностью проводящей внутренней области, так что условие
? · В = О и уравнения A0.7.7), A0.7.15) и A0.7.16) остаются
справедливыми. Область, где магнитные силовые линии выходят за пределы
светового цилиндра («открытая магнитосфера»), содержит частицы, которые
непрерывно теряются звездой, и удовлетворяет условию ? · В ? О (см.
рис. 10.6).
10.8. МЕХАНИЗМЫ ИЗЛУЧЕНИЯ ПУЛЬСАРОВ
Подлинный механизм, посредством которого пульсар преобразует энергию
вращения нейтронной звезды в наблюдаемые импульсы у понят
недостаточно. Было предложено много теоретических моделей, но ни одну из них
нельзя считать убедительной^^ В то же время характеристики
радиоизлучения от разных пульсаров кажутся универсальными и, по-видимому, ко всем
пульсарам приложима единая основная модель.
С другой стороны, наблюдаемая в радиоимпульсах энергия — это лишь
небольшая часть^^ диссипируемой энергии вращения, так что незнание
истинных процессов импульсного излучения может и не мешать решению
вопроса об общей энергетике излучающих нейтронных звезд.
Каковы же фундаментальные наблюдательные требования к механизму
импульсного излучения? Вот некоторые из них:
1. Излучение должно испускаться в виде сравнительно узкого пучка,
ориентация которого относительно нейтронной звезды фиксирована. Пучок
должен иметь размер по долготе не более 10° с точки зрения удаленного
наблюдателя, и такая ширина должна сохраняться в диапазоне нескольких
порядков значений частоты. Более того, форма пучка и долгота должны
оставаться стабильными в течение многих периодов вращения.
2. Механизм излучения должен создавать довольно широкополосное
излучение как на радио-, так и на оптических частотах. Ширина полосы
радиоимпульсов составляет не менее 100 МГц.
3. Процесс излучения должен обеспечивать наблюдаемые светимости
и яркостные температуры в радио-, оптическом и рентгеновском
диапазонах.
4. Излучение на радиоволнах должно проявлять сильную линейную
поляризацию, которая почти не зависит от частоты и стабильна в течение
длительных промежутков времени.
^^ Обзор и критику некоторых из моделей см. в [380, 404, 492, 540].
^^ Эта доля не превышает 10~^ для пульсара в Крабовидной туманности и 10~^
для некоторых старых пульсаров.
Пульсары 311
Яркостная температура Г^ излучающей области определяется
соотношением
^^ВЛТь). A0.8.1)
где / — удельная интенсивность [эрг/(с · см^ · Гц · стерад), а 5^ —
функция Планка (см. приложение И). Для hu < кТ^^ имеем хорошо
знакомый закон Рэлея—Джинса:
I.-^kT, {hv^kn). A0.8.2)
Радиосветимости пульсаров в предположении конусообразной формы
пучков и разумных значений расстояний лежат в диапазоне 1(Я^ - 1(Я^ эрг/с.
Если предположить, что размер излучающей площади источника по
порядку величины составляет - {ctf - 10^^ см^, где Г ^ 10"^ с — типичная
длительность импульса, получим
/^ - 10"^ - \0р эрг/(с · см^ · Гц · стерад);
Г^ ^ 10^^ - 10^^ К;
kTf^ - 10^7- 10^2 эВ. A0.8.3)
Для некогерентного излучения из термодинамики следует, что кТ^^ ^ Ер,
где Ер — энергия частицы. (Это просто переформулировка того факта, что
черное тело является наиболее эффективным излучателем.) Однако энергии
частиц, следующие из A0.8.3), абсурдно велики. Если бы даже частицы
таких высоких энергий и существовали, они излучали бы значительную часть
своей энергии на очень высоких частотах, а не в радиодиапазоне. Мы
приходим к заключению, что требуется когерентный механизм излучения, где
полная интенсивность в - N^ раз превышает интенсивность излучения
отдельной частицы (N — полное число частиц, излучающих когерентно).
Такая когерентность не требуется для наблюдаемого рентгеновского
или оптического импульсного излучения.
Упражнение 10.7. Покажите, что яркостная температура рентгеновского
излучения пульсара в Крабовидной туманности (светимость 1(р5 эрг/с) равна --10^^ К, и
докажите, что для частиц в магнитосфере приемлемое значение энергии составляет
Ер ^ 10 МэВ.
В большинстве моделей излучение сконцентрировано в конусообразный
пучок, который вращается синхронно с нейтронной звездой. В моделях с
«полярной шапкой» конус излучения направлен по оси магнитного диполя
звезды и лежит внутри синхронно вращающейся магнитосферы. В моделях
«светового цилиндра» ось конуса направлена по касательной к световому
цилиндру и перпендикулярна оси вращения звезды; в этом случае излучение
возникает вблизи R^. Были предложены и другие модели с расположением
излучающей области за пределами светового цилиндра. Поскольку
соответствующие теоретические проблемы еще далеко не разрешены, мы не
будем обсуждать эти модели более подробно.
312 Глава 10
10.9. СВЕРХТЕКУЧЕСТЬ В НЕЙТРОННЫХ ЗВЕЗДАХ
Системы многих фермионов, характер взаимодействия в которых
благоприятствует образованию пар частиц в двухчастичных состояниях, могут
претерпевать фазовый переход в состояние сверхтекучести. Если частицы
заряжены, то состояние будет сверхпроводящим. Такое состояние
представлено, например, в теории сверхпроводимости БКШ
(Бардина—Купера—Шриффера). Согласно этой теории, в металле электроны с импульсом
к и спином S спариваются с электронами, имеющими импульс -к и спин
-S. Эта связь осуществляется посредством электрон—фононных
взаимодействий в решетке (элементарное обсуждение см. в [608]).
Поскольку основное ядерное взаимодействие на больших расстояниях
имеет характер притяжения, совершенно аналогичный механизм БКШ-
спаривания может реализоваться в плотном адронном веществе, например
при лабораторных экспериментах или в веществе нейтронной звезды. Хотя
две нейтрона не могут быть связанными в вакууме, они могут оказаться
связанными, находясь в поле других нуклонов. В сильно вырожденных
системах Ферми спаривание происходит главным образом между
состояниями, лежащими вблизи поверхности Ферми. В тяжелых ядрах или в
нейтронных звездах, где отношение ? ^/? ? велико, достаточно рассматривать
лишь спаривание ? — ? и ? — р\ состояния с противоположными
импульсами для нейтронов и протонов находятся на разных поверхностях Ферми.
Нейтронные пары являются бозонами, так что их поведение, по-
видимому, аналогично поведению атомов ^Не в жидком гелии. ^Не
представляет собой сверхтекучую жидкость при температурах ниже 2,19 К. В
частности, у нее наблюдается безвязкостное течение; кинетическая энергия
чистой сверхтекучей жидкости не диссипирует из-за трения о стенки сосуда
или из-за внутреннего трения в самой жидкости.
В нейтронных звездах аналогичное поведение возможно только в том
случае, если тепловая энергия кТ меньше скрытой теплоты ?, связанной с
фазовым переходом к спаренному состоянию («энергетическая щель
сверхтекучести»). Этот параметр щели ? зависит от силы парного
взаимодействия и затем от плотности. При ядерных плотностях (р ^ 2,8 · 10^^ г/см^),
как мы знаем из лабораторных экспериментов, протоны и нейтроны
претерпевают переход к спариванию в холодном ядерном веществе с ? - 1—2
МэВ. Следовательно, при относительно низких температурах (не более
1 кэВ), ожидаемых для всех нейтронных звезд, за исключением самых
молодых (сравните с гл. 11), можно рассчитывать на обнаружение
нейтронной сверхтекучести в коре и недрах нейтронной звезды.
Можно ожидать также, что оставшиеся в недрах протоны должны
быть спаренными и, следовательно, сверхпроводящими. Однако
маловероятно, чтобы сверхпроводящими стали и электроны: в случае нейтронной
звезды электрон-фононная связь слишком слаба.
Проведенные недавно вычисления (см. обзор в [458]) свидетельствуют о
там, что внутри нейтронной звезды могут существовать по крайней мере
три различных адронных сверхтекучих жидкости:
Пульсары 313
1. Во внутренней коре D,3 · 10^^ г/см^ < ? < 2 · 10^"^ г/см^) свободные
нейтроны могут спариваться в состоянии ^Sq, образуя сверхтекучую
жидкость среди обогащенных нейтронами ядер.
2. В режиме квантовой жидкости (р ;г 2 · 10^"^ г/см^), когда ядра
растворяются в вырожденной жидкости нейтронов и протонов, для
нейтронной жидкости спаривание, вероятно, должно происходить в состоянии ^^2-
3. Протоны в квантовой жидкости, как ожидается, должны быть
сверхпроводящими в состоянии ^Sq.
Существует ряд важных следствий адронной сверхтекучести и
сверхпроводимости, которые могут привести к некоторым эффектам, поддающимся
наблюдениям. Важно отметить, что сверхтекучесть мало влияет на такие
макроскопические свойства нейтронных звезд, как их массы, радиусы и т.п.
Причина в том, что энергия спаривания не превышает \Щ от полной
энергии взаимодействия в зоне нейтронной жидкости, так что спаривание
приводит к очень незначительному изменению зависимости Я от р,
обсуждавшейся ранее для «нормального» вещества. В числе важных физических
следствий сверхтекучести можно отметить следующие эффекты:
а) Тепловые эффекты
Теплоемкость сверхтекучей жидкости или сверхпроводника значительно
ниже, чем у обычного вырожденного газа при достаточно низких
температурах. Действительно, теплоемкость изменяется как ехр( —?//??),
поскольку для возбуждения бариона сначала надо разорвать БКШ-пару. Для этого
надо затратить энергию ?. (См. «Статистическую физику» Ландау и Лиф-
шица [340], § 66.)
Это уменьшение теплоемкости сокращает характерное время
охлаждения пульсаров. Тем не менее нормальные компоненты жидкости
(например, электроны) дают полный вклад в теплоемкость, так что эффект,
обусловленный сверхтекучестью, отчасти уменьшается.
В противоположность этим эффектам фрикционное взаимодействие
между нормальным и сверхтекучим компонентами может привести к
тепловой диссипации вращательной энергии и, следовательно, к возрастанию
времени остывания пульсаров'^ Этот вопрос еще не разрешен.
Сверхтекучесть понижает также скорость излучения нейтрино по сравнению со
значениями, характерными для «нормального» вещества.
б) Магнитные эффекты
У сверхпроводников в лабораториях обычно проявляется эффект Мей-
снера: магнитное поле вытесняется из любой области, которая
становится сверхпроводящей. Однако в веществе нейтронной звезды присутствуют
^^См. [241] и гл. 11.
314 Глава 10
свободные электроны и поэтому, как ожидается, магнитное поле
пронизывает всю конфигурацию. В результате заряженные компоненты коры и
ядра объединяются магнитным полем и вращаются синхронно.
Однако сверхтекучие нейтроны очень слабо соединены с корой и
заряженными компонентами. Заряженные частицы непрерывно замедляются
тормозящим моментом реакции излучения, передаваемым магнитным
полем [уравнение A0.5.4)]. Сверхтекучая жидкость должна поэтому в среднем
вращаться быстрее пульсара. Слабые силы трения между нормальной
внешней корой и сверхтекучими нейтронными недрами связывают два этих
компонента и преобразуют часть вращательной энергии во фрикционный
нагрев.
Упражнение 10.8. Установите верхний предел на температуру ? поверхности
пульсара в Крабовидной туманности, предполагая, что вся энергия вращения диссипирует,
преобразуясь в тепловое чернотельное излучение с поверхности.
Ответ: ? :? 3 - 10^ К.
Релаксация заряженного и сверхтекучего компонентов к твердотельному
(т.е. синхронному) вращению может продолжаться в течение многих дней
или даже лет после любого внезапного изменения периода пульсара (т.е.
периода вращения заряженного компонента). Этот динамический эффект
является основой для некоторых моделей сбоев пульсаров в Крабовидной
туманности и в созвездии Парусов (разд. 10.10).
в) Гидродинамические эффекты
Уникальное следствие нейтронной сверхтекучести состоит в том, что
из-за вращения нейтронной звезды жидкость должна содержать
дискретный набор вихрей. Вихри параллельны оси вращения, и каждый из них
обладает квантованной циркуляцией
vd/ = x^, A0.9.1)
?
где V — скорость жидкости, а 2w„ — масса нейтронной пары^\
С микроскопической точки зрения жидкость движется без вращения
(V X V = 0) повсюду, за исключением сердцевины каждой вихревой линии.
При усреднении по многим вихревым линиям средняя скорость жидкости
<v> может удовлетворять обычному уравнению однородного вращения
V X <v> = 2?. A0.9.2)
^^ См. главу 11 известной книги Фейнмана [195], где обсуждается, почему
вращающаяся сверхтекучая жидкость образует вихри, подчиняющиеся уравнению A0.9.1).
Пульсары 315
Из уравнений A0.9.1), A0.9.2) и теоремы Стокса находим, что число
квантованных вихревых линий на единицу площади для пульсара в Крабовид-
ной туманности равно
;,^ = 1?^=1,9Х 10^см-2. A0.9.3)
Среднее расстояние между вихревыми линиями составляет а?" - 10~
см, что много меньше радиуса звезды. Это оправдывает макроскопический
подход: если рассматривать <v>, то со сверхтекучей жидкостью можно
обращаться как с вращающимся твердым телом. Момент инерции звезды
также имеет свое классическое значение.
Вопрос о том, «приколоты» ли сердцевины вихревых линий к ядрам в
коре или же они проникают в пространство между ядрами, пока является
предметом исследований и споров. Ответ на этот вопрос важен для
некоторых моделей сбоев пульсаров.
10.10. СБОИ ПУЛЬСАРОВ И АДРОННАЯ СВЕРХТЕКУЧЕСТЬ
Примечательно, что данные наблюдений моментов прихода импульсов от
пульсаров в Крабовидной туманности и в созвездии Парусов после
внезапных скачков частоты у них могут послужить свидетельством
существования сверхтекучести в нейтронных звездах.
При первом сбое пульсара в созвездии Парусов, для которого было
характерным резкое изменение ft (??/? - 10~^) наряду с более слабым
возрастанием ? (??/? - 2 · 10"^), Бейм, Пайнс, Петик и Рудерман [54]
предложили простую «двухкомпонентную» модель нейтронной звезды для
объяснения скачка частоты. Мы рассмотрим эту модель, которая в основном
является феноменологической, в качестве образца, чтобы показать, как в
принципе данные по наблюдениям сбоев могут быть включены в
теоретическую картину. Ниже мы сравним некоторые конкретные предсказания
модели с наблюдениями.
Согласно этой модели, нейтронная звезда состоит из нормального
компонента — коры и заряженных частиц — с моментом инерции /^ и
слабо связанной с ним сверхтекучей нейтронной жидкости, обладающей
моментом инерции /„. Предполагается, что заряженный компонент
вращается с наблюдаемой частотой пульсара ?@, поскольку считается, что все
заряженные частицы сильно связаны с магнитным полем. Вращение
сверхтекучей нейтронной жидкости, как предполагается, должно быть
квазиоднородным в том смысле, как об этом говорилось в разд. 10.9, со средней
угловой частотой ?^@. Связь между двумя компонентами описывается
одним параметром т^ — временем релаксации для диссипации энергии
вследствие трения.
В модели предполагается, что возрастание частоты вращения
вызывается «звездотрясением», происходящим в коре. Детали механизма звездо-
трясения сейчас несущественны (см. следующий раздел, где дано описание
316 Глава 10
модели). Достаточно исходить из следующих предположений: а)
увеличение скорости вращения коры быстро передается заряженным частицам в
недрах звезды посредством сильного магнитного поля (характерное время
- 100 с); б) реакция нейтронной сверхтекучей жидкости на увеличение
скорости вращения системы кора — заряженные частицы является значительно
более медленной (годы) из-за гораздо более слабой фрикционной связи
между нормальным и сверхтекучим компонентами.
Упражнение 10.9. Скачок частоты вращения коры передается заряженным частицам
в недрах звезды магнитным полем, на которое они «нанизаны». Любое возмущение
магнитного поля, вызванное, например, дифференциальным вращением, генерирует
магнитные «звуковые волны», или альвеновские волны, распространяющиеся со
скоростью
Пусть дифференциальное вращение компонента кора — заряженные частицы
сглаживается за время т^, которое требуется альвеновским волнам, чтобы пересечь
нейтронную звезду. Оцените т^ для типичного пульсара.
Ответ: т^ - 50 с.
В отсутствие сбоев взаимодействие между двумя компонентами после
звездотрясения регулируется двумя линейными уравнениями
/,?=-?-^-^""""\ A0.10.2)
j^^lM^iSbl
A0.10.3)
Здесь а — внешний тормозящий момент, действующий на кору в связи,
например, с реакцией излучения магнитного диполя. Если считать, что а и т^
постоянны на интересующих нас интервалах времени, то уравнения
A0.10.2) и A0.10.3) могут быть решены, что дает
? = -yi + ^?,?-'/^ + Й2, A0.10.4)
/?/г
?„ = ?-?,6-'/" + -^, A0.10.5)
где
/^/, + /„, т^тЛ//, A0.10.6)
а ?| и Й2 — произвольные константы, зависящие от начальных условий.
Пульсары 317
Обратите внимание, что стационарное решение {t/? -* оо) имеет вид
где соотношение
1=. _;^= « A0.10.8)
дает характеристическое время, определенное выражением A0.5.7).
Проводимые после сбоев наблюдения показывают, что для пульсара в
созвездии Парусов ? имеет значение порядка нескольких месяцев, а для
пульсара в Крабовидной туманности ? порядка нескольких недель (см.
приводимое ниже обсуждение). Итак, если грубо предположить /„ - /^, что
справедливо для массивной A,4 Mq) звезды, построенной на основе
жесткого уравнения состояния типа TI или TNI (см. рис. 9.4), то уравнения
A0.10.6) и A0.10.7) предсказывают (?„ - ?)/? порядка 10"^ для пульсаров
в созвездии Парусов и в Крабовидной туманности.
Уравнение A0.10.4) использовалось для согласования данных о
моментах прихода импульсов от пульсаров в Крабовидной туманности и в
созвездии Парусов, поступивших уже после сбоев. Допустим, что сбой
наблюдаемой угловой скорости (коры) произошел мгновенно в момент времени t =
= 0: ?@ -* QQ(t) -\- AQq. Заменим ? и ?2 в уравнении A0.10.4)
постоянными величинами ??? и «параметром восстановления» Q, так что уравнение
примет вид
?(/) = ??(/) + ???[??-'? + 1 - ?]. A0.10.9)
Параметр восстановления Q определяет степень релаксации угловой
скорости к ее экстраполированной величине: если Q = 1, то Q(t) — QQ(t)
при Г — 00. В данном случае ?Q(r) = Q^ — at/I — это частота пульсара в
отсутствие сбоя и Qq — постоянная.
Предсказываемое уравнением A0.10.9) поведение пульсара
иллюстрируется на рис. 10.7. Это описание удовлетворительно согласуется со всеми
крупными сбоями, наблюдавшимися до настоящего времени. На рис. 10.3
показаны имеющиеся данные для пульсара в созвездии Парусов, которые
ясно демонстрируют наличие сбоев. В табл. 10.1 приведены результаты
исследования девяти сбоев пульсаров, для которых был выполнен детальный
анализ.
Несомненно, решающая проверка этой феноменологической двухкомпо-
нентной модели сводится к выяснению того, дают ли аппроксимирующие
функции, которые характеризуют поведение пульсара после сбоя,
одинаковые значения Q и ? для всех сбоев одного и того же пульсара. Хотя данные
наблюдений приводят к очевидным расхождениям, примечательно, что в
самом низшем приближении указанные значения постоянны с приемлемой
точностью. Причиной видимых расхождений могут быть как трудности
318
Глава 10
^
ь
о
1=
о
??
к
????
?
???
_1_^
\"?
\ ?^?^?
\.
\ \
Ч ?
\ ^4 \
^ ? \
"¦¦?
\
—^
Время
Рис. 10.7. Зависимость угловой частоты вращения пульсара от времени после
скачкообразного увеличения скорости вращения [см. уравнение A0.10.9)] [380].
анализа данных о моментах прихода импульсов, так и слишком большое
упрощение, свойственное двухкомпонентной модели. Однако
предположение о наличии по крайней мере двух различных компонентов, которые
имеют характерные времена релаксации, сравнимые с предсказаниями теории.
Таблица 10.1
НАБЛЮДЕНИЯ СБОЕВ И ПОВЕДЕНИЯ ПОСЛЕ СБОЕВ
ДЛЯ ТРЕХ ПУЛЬСАРОВ
Дата
Пульсар
Ссылка
???/??
Q(xlOO)
г, сут
III/69
VIII/71
XII/71
Х/75
VII/78
Х/81
IX/69
Х/71
11/75
~ IX/77
0833-45 »)
0833-45
0833-45
0833-45
0833-45
0833-45
0531+21 2)
0531+21
0531+21
1641-45
[168]
[168]
[168]
[168]
[168]
[397]
[83]
[371]
[371]
[381]
2,34-10-6
1,96-10-6
1,17-10-8
2,01-10-6
3,05-10-6
1,14-10-6
-10-8
2-10-^
3,7-10-8
1,9-10-7
3,4±1,0
3,5±0,1
55"^^^
^^-12
8,8±0,8
2,4 ±0,5
7
--93
--96
-96
7
75 ±20
60±10
80 ±20
40±5
55±5
7
-4,1
15
15
31 000
^) Пульсар в созвездии Парусов.
2) Пульсар в Крабовидной туманности.
Пульсары 319
рассматривающей связь между корой и сверхтекучей жидкостью, вообще
говоря, поддерживается этими данными.
Могут ли указанные данные обеспечить улучшение нашего понимания
физической природы нейтронной звезды, если допустить, что используемая
модель корректна? Как утверждают многие исследователи, на этот вопрос,
несомненно, можно ответить положительно.^^
Рассмотрим параметры ? и т. Определив
??@ = ?@-??@, A0.10.10)
найдем из уравнения A0.10.9), что
??(? = 0)
?= ШГ^' A0.10.11)
"о
^ ??(/ = 0)
??(/ = 0)
A0.10.12)
Таким образом, Q ит могут быть в принципе определены непосредственно
из данных наблюдений после сбоя.
Параметр Q может быть связан с моментами инерции разных
компонентов. Предположим, что ответственное за сбой «звездотрясение» приводит
к изменениям ?/^, ??, ?/„, ??„ и т.д., но оставляет т^ и ? примерно
постоянными. Тогда во временных масштабах звездотрясения момент
количества движения каждого компонента по отдельности сохраняется, откуда
следует
At=-f, (,0.10.,3)
?/ ??
? ?
Дифференцирование уравнения A0.10.2) дает
A0.10.14)
.л ? ?/, ??-??„
?? = ^?^ ^. A0.10.15)
Но уравнения A0.10.13) и A0.10.8) приводят к
аМ^ ??? /?? .,^ ,· .,,
Типичным является соотношение
1
? г.
^-»1, A0.10.17)
'' См., например, [11), где приведены ссылки на более ранние работы.
320 Глава 10
так что первым членом в уравнении A0.10.15) можно пренебречь по
сравнению со вторым.
Упражнение 10.10, Проверьте, что для пульсара в созвездии Парусов неравенство
A0.10.17) удовлетворяется при разумных оценках 1/1 (например, ^ 0,01).
Таким образом, уравнение A0.10.15) с учетом A0.10.8) принимает вид
Упражнение 10.11, Покажите, что двухкомпонентная модель предсказывает для ?
большее относительное изменение вслед за сбоем, чем для ?.
Уравнение A0.10.11) с учетом A0.10.18) и A0.10.8) дает при ?? = ??^
? / ??„ \
Вспомнив соотношения A0.10.6), A0.10.13) и A0.10.14), получим
^ = 7['-?Ш¦i]¦ A010-20)
Поскольку ?^ - ? << о, в типичных случаях можно ожидать
? = ^. A0.10.21)
Таким образом, табл. 10.1 дает определенные значения моментов инерции
нормального и сверхтекучего компонентов нейтронной звезды.
Всякое сравнение между наблюдаемыми значениями Q и
теоретическими значениями 1^/1 усложняется тем, что, даже если двухкомпонентная
модель верна, отношение /„// зависит как от принятого уравнения состояния,
так и от массы нейтронной звезды. Значения /„// приведены в табл. 10.2
для разных уравнений состояния, рассмотренных ранее в разд. 9.3: мягкого
уравнения Рейда, умеренно жесткого уравнения Бете — Джонсона и очень
жестких уравнений в приближениях среднего поля и тензорного
взаимодействия^\ В типичных случаях более жесткие уравнения состояния
и меньшие массы означают относительно более толстую кору и,
следовательно, меньшие значения /^//. Одна из возможных интерпретаций
данных, полученных после сбоя, заключается в том (если допустить
правильность модели взаимодействия Рейда), что пульсар в Крабовидной туманно-
^^ Вспомните, что уравнение состояния TNI (приближение трехнуклонного
взаимодействия) сравнимо с уравнением Бете—Джонсона.
Пульсары
321
Таблица 10.2
СВОЙСТВА НЕЙТРОННЫХ ЗВЕЗД, ЧУВСТВИТЕЛЬНЫЕ К
АДРОННОМУ УРАВНЕНИЮ СОСТОЯНИЯ И К МАССЕ D
Модель взаимодействия
Масса,
М,
?
Ч^''
Жесткость
Рейд (R)
Бете—Джонсон (BJ)
Среднее поле (MF)
Тензорное взаимодействие
(TI)
Тензорное взаимодействие
(TI)
Масса
1,33
1,33
1,33
1,33
0,10
0,29
0,73
1,08
1,33
1,85
1,93
0,96
0,77
0,66
0,44
2100
130
25
10
0,0
0,0
0,06
0,29
0,44
0,70
0,66 3)
3-10-3
0,16
0,92
3;.i
*L-
71
600
») Из работы [446] с /о^ора = 2· 10»^ г/смЗ.
2) Для пульсара в Крабовидной туманности: /^ = ?(?|/?2) I?/: I [сравните с
уравнением A0.11.24)]; Г = ?/? = 2260 лет, ? = 190 С"», ?? = 0,9· 10"^ ?^ = IA^/BIq
[446].
3) В этой модели предполагается твердое ядро.
сти является довольно массивной нейтронной звездой (М/М^ ^ 1,3), а
пульсар в созвездии Парусов — сравнительно легкой (M/Mq is 0,15). Во
всяком случае, поверхностное сравнение результатов с двухкомпонентной
моделью наводит на мысль, что массы пульсаров в Крабовидной
туманности и в созвездии Парусов сильно различаются.
С другой стороны, можно привести доводы в пользу умеренно
жесткого уравнения состояния (например, уравнения с приближением трехнуклон-
ного взаимодействия), позволяющего объяснить результаты лабораторных
экспериментов, а также в пользу предположения, что все нейтронные
звезды имеют примерно одинаковую массу (- 1,4 Mq, для которой трехну-
клонное взаимодействие дает Q - 1^/1 = 0,90). Если обратить внимание на
расхождение этой гипотезы с наблюдаемыми значениями Q для пульсара в
созвездии Парусов, нетрудно прийти к заключению [458], что разные
значения Q, полученные на основе данных о моментах прихода импульсов после
сбоя, могут быть связаны с различным происхождением сбоев и/или с
более сложным динамическим поведением системы после сбоя. Поэтому
возможно, что двухкомпонентная модель оказалась слишком простой для на-
5-513
322 Глава 10
дежного объяснения связи между корой и сверхтекучими нейтронными
недрами. Действительно, Дауне [168] показал, что поведение пульсара в
созвездии Парусов после сбоя значительно отличается от предсказанного на
основе простой двухкомпонентной модели, описывающей слабо связанные
кору и сверхтекучее ядро. Очевидно, необходим дальнейший анализ (см.,
например, [11]). Тем не менее указанная модель иллюстрирует, как данные
о моментах прихода импульсов пульсаров можно использовать в качестве
мощного инструмента для исследования структуры нейтронной звезды и
физики адронов.
10.11. ПРОИСХОЖДЕНИЕ СБОЕВ ПУЛЬСАРОВ:
ЗВЕЗДОТРЯСЕНИЯ
Было предложено много моделей для объяснения внезапных скачков
частоты у пульсаров с тех пор, как они впервые наблюдались в 1969 г. (см.
обзоры [380, 462]). В их числе модели звездотрясения (происходящего в коре
и/или в ядре), «прикалывания» вихрей, магнитосферной неустойчивости и
неустойчивости в движении сверхтекучей нейтронной жидкости. В качестве
примера вычисления взаимосвязи между микроскопическими свойствами
вещества нейтронных звезд и наблюдаемыми макроскопическими
характеристиками изучим подробно модель звездотрясения [53, 489]. Согласно
этой модели, внезапное растрескивание коры нейтронной звезды
уменьшает момент инерции и, следовательно, увеличивает ?. Мы увидим, что эта
модель «коротрясения» удовлетворительно объясняет скачки частоты
пульсара в Крабовидной туманности, но не может быть применена без
модификации к пульсару в созвездии Парусов.
Упражнение 10.12 (основано на [482, 507]). Создание моделей скачков частоты,
основанных на магнитосферных неустойчивостях, стимулировалось бросающейся в глаза
корреляцией между некоторыми случаями сбоя пульсара в Крабовидной туманности
и вспышки активности «жгутов» Крабовидной туманности. Предположите, что
магнитное поле в области замкнутых силовых линий вокруг пульсара может
удерживать заряженные частицы, пока момент инерции плазмы не достигнет
максимальной величины
/-:^ A0.11.1)
([490]; попробуйте вывести соотношение A0.11.1) на энергетической основе).
Рассчитайте ??/?, если вся плазма внезапно освободилась без создания момента,
тормозящего звезду. Получите оценки для пульсаров в Крабовидной туманности и в
созвездии Парусов, предположив разумные значения для Вр, ? и R.
, -- для пульсара в созвездии Парусов,
Ответ:
?? f 10-6
V <
? (.10-7
для пульсара в Крабовидной туманности.
Картина звездотрясения основана на идее, что ядра коры нейтронной
звезды [р < B -?- 2,4) · 10^^ г/см^] образуют твердую кулоновскую решет-
Пульсары 323
ку (сравните с разд. 8.2). Из-за вращения звезды кора имеет сплюснутую
форму (сравните с разд. 9.6). При замедлении вращения звезды
действующие на кору центробежные силы уменьшаются и возникает напряжение,
стремящееся перевести кору в равновесное состояние с меньшей
сплюснутостью. Однако жесткая кора сопротивляется этому напряжению и
остается более сплюснутой по форме, нежели в равновесном состоянии. Наконец,
когда напряжения в коре достигнут критической величины, кора
трескается. Часть напряжения снимается, и избыток сплюснутости сокращается. В
результате резко уменьшается момент инерции коры и благодаря
сохранению момента количества движения внезапно увеличивается частота. Это и
приводит к наблюдаемому скачку частоты пульсара.
Для получения количественных оценок определим зависящий от времени
параметр сплюснутости ? в соответствии с выражением
/ = /оA + ?), A0.11.2)
где / — момент инерции, а /q — значение момента инерции для невращаю-
щейся сферической звезды. Параметр ? связан с параметром деформации ?
и эксцентричностью е, определенными в уравнениях G.4.28) и G.4.32),
следующим образом:
1 + ? = ?-^ =A -е^У'^\ A0.11.3)
Для малых отклонений от сферичности имеем
в=у. A0.11.4)
Рассмотрим теперь полную энергию вращающейся ньютоновской
нейтронной звезды
?-?;„.+ ir+r+?,^,i„. A0.11.5)
Здесь в дополнение к обычным членам [сравните с уравнением G.4.35) мы
ввели новый член ^'strain ^^^ учета энергии упругой деформации коры.
Разлагая выражение G.4.29) с учетом того, что ? близко к единице,
найдем
^(х)=.1_(ЦА)!=.1_^. A0.11.6)
5
Таким образом
Еы +W+T^ ?;„. + W^ + At" + /'Дгг^, A0.11.7)
где Wq — гравитационная потенциальная энергия невращающейся
нейтронной звезды, Л S I W^qI/5, а Ej^j, как мы предположили ранее, не зависит
от е.
Энергия упругой деформации появляется при сжатии твердой объемно-
центрированной кубической кулоновской решетки. Согласно расчетам
324 Глава 10
Бейма—Бете—Петика (см. разд. 8.2), кора нейтронной звезды состоит из
обогащенных нейтронами ядер, образующих такую решетчатую структуру.
Энергию деформации можно грубо оценить следующим образом.
Представим, что у звезды есть некая начальная несферичность Cq. При этой
«опорной» сплюснутости звезда свободна от напряжений. При уменьшении ?
сплюснутость ? становится меньше Cq, что вызывает деформацию коры.
Рассмотрим одномерную кулоновскую решетку, обсуждавшуюся в разд.
3.7. Сжатие решетки по мере того, как звезда изменяет свою форму,
приводит к появлению энергии упругой деформации
^strain - ? 2^^')» A0.11.8)
где
N-n^R^ A0.11.9)
— это полное число узлов решетки (ядер) в коре; а2д- l/R^ — средняя
концентрация ионов; Rq ~ R/N'^^ — расстояние между ионами; К —
«постоянная жесткости» решетки [уравнение C.7.19)] и
— среднеквадратичное отклонение иона от его равновесного положения
вследствие сжатия. Таким образом, соотношение A0.11.8) принимает вид
zV
E.,^~^n^R'{e-e,f. (Ю.И.И)
Более точное рассмотрение Бейма и Пайнса [53] дает для неэкранирован-
ной объемноцентрированной кубической кулоновской решетки
^strain = ^(? - ?o)^ A0.11.12)
где
-ш-
3 " /-^ а
1/3
A0.11.13)
Упражнение 10.13. Покажите, что для типичных параметров пульсара В < А ^ коре.
Предположите, что в коре /о :S 2 · 10^^ г/см^, ? - 10 и /7д ^ 5 х
X 1034 см-3.
Среднее напряжение о в коре определяется соотношением
1 ^^strain
к де
о =
= ]??(??-?), A0.11.14)
где Vc — объем коры, а
Пульсары 325
?=^ A0.11.15)
— средний модуль сдвига.
Уравнение A0.11.5) с учетом A0.11.12) и A0.11.7) принимает вид
?'-?, + ??' + /'Д^т^ + В{е - е,)\ A0.11.16)
где Eq — энергия невращающейся звезды, не зависящая от е. Минимизируя
уравнение A0.11.16) по отношению к ? при фиксированных значениях Л/, J
и Рс» ^Ь1 получим выражение для равновесной деформации
Поскольку ?^ - ??? и А > В, в уравнении A0.11.17) главную роль играет
первый член, а жесткость коры проявляется только в небольшом
отклонении ? от того значения, которое она имела бы, если бы звезда была
идеальным жидким телом. Таким образом,
^=^ "ti"· A0.11.18)
Упражнение 10.14. Выведите уравнение A0.10.18) для несжимаемого сфероида прямо
из уравнения G.3.18) в предельном случае малого J.
Когда среднее напряжение в коре достигает некоторого критического
значения ?^, кора трескается и результирующие напряжение, деформация и
сплюснутость внезапно уменьшаются. Коротрясение поэтому приводит к
резкому уменьшению ?^? «опорной» сплюснутости и к соответствующему
уменьшению ?? фактической сплюснутости. Уравнение A0.11.17) дает
?? =-^^??? = ^??? « ???. A0.11.19)
Это изменение может наблюдаться непосредственно, так как, согласно
уравнению A0.11.12),
Де=^ = -a = -n-0^ia^
= - (» - ^А^\- A0·1»·20)
Здесь мы использовали определение «параметра восстановления» Q: ?? во
втором равенстве — это разность между стабильной угловой частотой
перед сбоем и установившейся после полной релаксации частотой после сбоя.
Для пульсара в созвездии Парусов из уравнения A0.11.18) следует, что
равновесная сплюснутость ? - 10"^, а уравнение A0.11.20) дает ?? - 10"^
при скачке частоты. Соответствующие значения для пульсара в Крабовид-
ной туманности составляют: ? - 10~^, ?? - 10~^ - 10~^. Доступный
326 Глава 10
наблюдению эффект возникает от сжатия коры пульсара всего лишь на
долю миллиметра!
После звездотрясения пульсар продолжает замедляться обычным
образом, пока напряжение не возрастает опять до критической величины.
Промежуток времени t^ между звездотрясениями определяется в этом случае
выражением
?,-^. A0.11.21)
Снимаемое при звездотрясении напряжение с учетом уравнений A0.11.14) и
A0.11.19) описывается выражением
?? = ]??(??? - ??) = ??^. A0.11.22)
Последующее нарастание напряжения происходит с постоянной
скоростью
?=-?=-^/„?? = ^?!, A0.11.23)
где для ? использовано выражение A0.11.18). Тогда уравнение A0.11.21)
принимает вид
а
A0.11.24)
где
',==
ч
^?^'?·
2А^
A0.11.25)
В нашем случае параметр ?^ и, следовательно, г , является
чувствительной функцией массы звезды и адронного уравнения состояния (среди
прочих причин величина В пропорциональна объему коры К^). Эта
зависимость иллюстрируется в табл. 10.2, где приведены значения t^ для
нескольких различных уравнений состояния. В соответствии с этой таблицей
предположение о том, что пульсар в Крабовидной туманности — это звезда с
массой 1,3 Л/0 (структура определяется уравнением состояния TI)
приводит к предсказанию примерно десятилетнего интервала между
звездотрясениями. Это удовлетворительно согласуется с наблюдавшимися скачками
частоты (сравните с табл. 10.1) при учете неопределенностей в вычислениях
/4 и 5. В то же время при десятилетнем интервале между звездотрясениями
для пульсара в Крабовидной туманности требуется масса не более 0,5 Mq
при потенциале Бете—Джонсона и много меньшая масса при потенциале
Рейда.
Тем не менее модель коротрясения неспособна объяснить относительно
кратковременные интервалы между скачками частоты пульсара в созвездии
Парусов. Даже при самом благоприятном выборе параметров (например,
пульсар в виде легкой нейтронной звезды с массой 0,3 A/q , построенной на
Пульсары Ъ11
основе уравнения состояния с тензорным взаимодействием) /^- 10^ лет по
сравнению с наблюдаемым характерным временем порядка нескольких лет.
BonpQc о том, способны ли ядротрясения, которые могли бы
происходить, если у нейтронной звезды есть твердое ядро, объяснить
относительно большие и частые скачки частоты пульсара в созвездии Парусов, в
настоящее время остается открытым [46, 461]. В числе основных трудностей,
сопряженных с этой моделью, можно отметить а) недостаток свидетельств
в пользу существования твердых ядер у нейтронных звезд, б) отсутствие
наблюдений рентгеновского излучения, связанного с выделяющейся
энергией упругих деформаций.
Были предприняты также попытки понять сбои пульсара в созвездии
Парусов на основе детализированной модели системы «приколотых»
вихрей [11]. В этой модели гигантские сбои пульсара в созвездии Парусов и
других пульсаров представляют собой скачки в системе вихрей, которые
следуют за катастрофическим «откалыванием» вихревых линий
«приколотой» нейтронной сверхтекучей жидкости в коре. Особенности поведения
пульсара после сбоя приписываются более слабому «сползанию» вихрей,
вызванному сбоем. Хотя на основе этой модели не удалось правильно
предсказать время сбоя пульсара в созвездии Парусов в октябре 1981 г.,
модель системы «приколотых» вихрей может содержать основные
составные части более реалистичного теоретического описания гигантских сбоев.
Упражнение 10.15. а) Начав с уравнения A0.11.16), подсчитайте выделение энергии
упругих деформаций ?? при звездотрясении. Используйте соотношения A0.11.17) и
A0.11.19), чтобы записать ?? в виде
^E=^1{A + 5)(??'-?)??. A0.11.26)
Не предполагайте, что В < А.
6) Величина ?? чувствительна к значению {Eq - ?) во время звездотрясения.
Оцените ?? для ядротрясения пульсара в созвездии Парусов в предположении {Eq -
- ?) - 2 · 10-3. Для звезды с массой 1,93 Mq (уравнение состояния с тензорным
взаимодействием) и твердым ядром в работе [446] даются значения А = 17,8 · 10^2
эрг и ^ядро = 14,4 · 10« эрг.
Ответ: ?? ~ 1 · 10*5 эрг.
Глава 11
Остывание нейтронных звезд
11.1. ВВЕДЕНИЕ
Определение поверхностной температуры нейтронных звезд путем
регистрации теплового чернотельного излучения может в принципе дать
существенную информацию о внутреннем адронном веществе и о структуре
нейтронной звезды. (Мы изучали аналогичную ситуацию для белых карликов в
гл. 4.) Например, современный верхний предел 2 · 10^ К для
поверхностной температуры пульсара в Крабовидной туманности налагает строгое
ограничение на историю тепловой эволюции нейтронной звезды в первые
930 лет после ее образования. Знание тепловой эволюции нейтронной
звезды дает также информацию о таких чувствительных к температуре
свойствах, как коэффициенты переноса, переход к сверхтекучему состоянию,
затвердевание коры, о внутренних механизмах нагрева пульсара, таких как
фрикционная диссипация в местах сопряжения коры со сверхтекучей
жидкостью и т.д.
Обычно считается, что нейтронные звезды образуются при очень
высоких внутренних температурах (Т ^ 10^^ К) в ядре взрыва сверхновой (ср.
с гл. 1 и 18). Преобладающий механизм охлаждения сразу же после
образования состоит в испускании нейтрино, причем вначале характерное
время остывания имеет величину порядка секунд. Примерно через сутки
внутренняя температура падает до 10^ — 10^^ К. Излучение фотонов начинает
превосходить по интенсивности излучение нейтрино, лишь когда
внутренняя температура упадет до -10^ К, а соответствующая температура
поверхности будет при этом приблизительно на два порядка меньше.
Охлаждение путем испускания нейтрино преобладает по крайней мере первые 10^
лет, а согласно выполненным недавно стандартным расчетам остывания, и
гораздо дольше. Эти теоретические расчеты (см., например, [226, 420, 590])
дают кривые поверхнрстной температуры нейтронной звезды в
зависимости от времени, которые в принципе поддаются наблюдательной проверке.
Расчеты тепловой эволюции чувствительны к принятому ядерному
уравнению состояния, массе нейтронной звезды, предполагаемой
напряженности магнитного поля, возможному существованию сверхтекучести,
пионной конденсации, кваркового вещества и т.д. Если рассматривать все
эти ВОЗМОЖНОСТИ, возникает широкий диапазон сценариев тепловой
эволюции.
В типичных случаях находят, что поверхностная температура падает до
нескольких миллионов Кельвинов для объектов с возрастом около 300 лет и
остается вблизи @,5 -ь 2) ¦ 10^ К в течение по крайней мере 10"* лет. Такие
температуры свидетельствуют о потенциальной возможности обнаружения
Остывание нейтронных звезд 329
излучения фотонов в мягком рентгеновском диапазоне @,2—3 кэВ).
Действительно, еще до открытия пульсаров считалось, что среди первых
обнаруженных дискретных рентгеновских источников могут быть молодые
нейтронные звезды (см., например [126, 127]). Поэтому в ожидании таких
наблюдений были составлены детальные кривые остывания [577] и подробно
вычислены скорости остывания [44].
Источники рентгеновского излучения, связанные с нейтронными
звездами, стали наблюдаться только после открытия пульсаров. Однако эти
источники были не изолированными нейтронными звездами, остывающими
после образования, а нейтронными звездами в двойных системах,
аккрецирующими газ от своих компаньонов (сравните с гл. 13). В таких системах
именно падающий газ служит источником рентгеновского излучения.
Многие годы единственным наблюдательным ограничением, касающимся
процесса охлаждения изолированной нейтронной звезды посредством
рентгеновского излучения, был верхний предел порядка 3 · 10^ К для
поверхностной температуры пульсара в Крабовидной туманности, полученный при
измерениях, которые проводились во время покрытия пульсара Луной
(пульсар в Крабовидной туманности излучает рентгеновские импульсы с той же
частотой, что и радиоимпульсы, но они не имеют ничего общего с
тепловыми свойствами пульсара).
Недавно появилась возможность значительно расширить пределы
наблюдений благодаря тысячекратному увеличению чувствительности и
отличному угловому разрешению, обеспеченными выводом на орбиту
обсерватории «Эйнштейн» (спутник НЕАО-2). Характеристики такого спутника
позволяют при изучении близлежащих остатков сверхновых либо обнаружить
точечные источники, либо получить верхние пределы поверхностных
температур почти на порядок величины ниже, чем при прежних измерениях
[271]. В результате данные, поступающие от обсерватории «Эйнштейн» и
от ее преемников, возможно, позволят определить, существуют ли
действительно в недрах нейтронных звезд пионные конденсаты или свободные
кварки. (Как мы увидим, эти состояния заметно ускоряют остывание.)
Вдохновленные этой перспективой и накопленными к настоящему времени
данными, мы обсудим ниже физику остывания нейтронной звезды.
11.2. РЕАКЦИИ С ИЗЛУЧЕНИЕМ НЕЙТРИНО
В НЕЙТРОННЫХ ЗВЕЗДАХ (Г <. 10^ К)
Здесь нас интересует история тепловой эволюции нейтронной звезды после
того, как она уже остыла до температуры недр ниже нескольких
миллиардов Кельвинов. Относительно короткую эпоху, в течение которой
температура падает от - 10^^ К до - 10^ К, мы обсудим э гл. 18. Эта более
ранняя эпоха, начинающаяся коллапсом звездного ядра и взрывом сверхновой,
значительно короче, чем длительный период остывания при температурах
ниже 10^ К.
330 Глава И
При температуре недр ниже нескольких миллиардов Кельвинов любые
нейтрино, излученные в процессе остывания, свободно покидают
нейтронную звезду без взаимодействия с ее веществом, что подтверждается в разд.
11.7. Этот процесс, отличающий низкотемпературную эпоху остывания
нейтронной звезды от предыдущей высокотемпературной эпохи ее
образования, значительно упрощает изучение поздней тепловой эволюции.
При очень высоких температурах (Г ^ \0р К), существующих в ядрах
проэволюционировавших массивных звезд, основные потери энергии через
посредство нейтрино связаны с так называемыми урка-реакциями^^:
? -^/7 + ^-+ v^, е-+р-^п + v^, A1.2.1)
Эти реакции преобладают также во время коллапса ядра. В обоих случаях
нуклоны в горячих недрах не вырождены. Однако, когда нуклоны
становятся вырожденными, как например, в нейтронной звезде, ортывшей ниже
10^ К, эти реакции сильно подавляются. Ниже мы проиллюстрируем этот
важный результат.
Вспомним приведенное в разд. 2.5 обсуждение: вещество в
вырожденных недрах звезды удовлетворяет условию бета-равновесия
?„ = ?, + ?^, A1-2-2)
где с хорошим приближением [(кТ/?^? < 1] химические потенциалы
равны энергиям Ферми. Поэтому
?р(и) = ?р(/7) + ?р(е), A1.2.3)
где при ядерных плотностях
г ( \ i.pUhI
ЕАп)^т„с +^^^
Ef{e)=-Pp{e)c. A1.2.4)
Зарядовая нейтральность требует, чтобы [сравните с уравнением B.5.7)]
???)'=??«)^ A1.2.5)
так что уравнение A1.2.3) принимает вид
где Q = (т^ - Щр) с^ = 1,293 МэВ, что мало по сравнению с остальными
членами в уравнении A1.2.6) (сравните с упражнением 11.1). Уравнение
'^ Подобно тому, как казино УРКА в Рио-де-Жанейро является идеальным
стоком для денег, эти реакции служат идеальным стоком для звездной энергии.
Остывание нейтронных звезд 331
A1.2.6) показывает, что энергия Ферми нейтронов (минус масса покоя)
почти равна энергии Ферми электронов
Е',{п)^Щ^=р,{е)с = Е,{е), A1.2.7)
и поэтому
??{«)=??{?)^??{?), A1.2.8)
Е^{р)«Е^{п). A1.2.9)
Рассмотрим теперь возможность такой реакции, как распад нейтрона
[уравнение A1.2.1)] Распасться могут лишь те нейтроны, которые лежат в
пределах - кТ от поверхности Ферми. Следовательно, по закону
сохранения энергии появляющиеся протон и электрон также должны находиться в
пределах - /гГ от своих поверхностей Ферми; энергия высвобождающегося
нейтрино также должна быть порядка кТ, Ъ соответствии с неравенством
A1.2.8) протон и электрон должны иметь меньшие импульсы по сравнению
с нейтроном. Однако это невозможно: при распаде не может сохраняться
импульс, если сохраняется энергия.
Чтобы процесс осуществлялся, должна присутствовать посторонняя
частица, уносящая импульс. Поэтому в работе [127] было высказано
предположение, что в охлаждении нейтронной звезды важную роль играют
«модифицированные» урка-реакции
п^ п-^ п^ ? ^ е'^ V,, ' A1.2.10)
/I +/? + е~-^ п + ? + ?^. A1.2.11)
Этим реакциям сопутствуют реакции с излучением мюонного нейтрино
/1 + /1-^/1+/7 + ?-?- ?^, A1.2.12)
/I + /? + ?"-* ?^ ? ^- ?^, A1.2.13)
которые протекают, если ?^ > т^с^, ? г 8 · 10^"* г/см^ (сравните с разд.
8.10). Соответствующие реакции с г-нейтрино не осуществляется при
типичных плотностях недр нейтронной звезды, поскольку т^с^ =
= 1784 МэВ > ?^.
В последующих разделах мы вычислим скорость охлаждения,
обусловленного этими модифицированными урка-реакциями. Читатель,
интересующийся только результатами, может перейти прямо к уравнению A1.5.22).
Упражнение 11.1. Покажите, что в приближении идеального газа Ферми (см. разд.
2.5) приблизительно сохраняют силу следующие соотношения при ? < 2pnuc (^^-^- Для
нерелятивистских нуклонов):
332 Глава И
см ^,
«,= 1,7 X 10^^(-^-)
\ rnuc /
w, = w^ = 9,6 X 10^^(-^-) см-3,
? Pnuc /
?И«)=?р@ = 6о(-^) МэВ,
? Pnuc /
fH/') =1.9(-^) МэВ/с,
? Pnuc /
??(?) = 340(-^) МэВ/с.
? Pnuc /
rnuc >
/'f@=/'f(/') = 60(^) МэВ/с.
Здесь Pnuc = 2,8 · 10^^ г/см^.
11.3. ТЕОРИЯ СЛАБОГО ВЗАИМОДЕЙСТВИЯ
Наше современное понимание слабых взаимодействий, например ?-
распада, представлено теорией Вейнберга — Салама — Глэшоу (ВСГ)^^
Согласно этой теории, слабые силы, действующие между фермионами,
обусловлены обменом массивными векторными бозонами во многом так же,
как электромагнитное взаимодействие обусловлено обменом фотонами
(безмассовыми векторными бозонами; см. приложение Г).
В стандартной модели ВСГ существуют два заряженных
«промежуточных» бозона W^ и W~, а также один нейтральный промежуточный бозон
Z^. Как предсказывается теорией, они должны обладать следующими
массами:
^ 2^!!!ж?!^889±1,4ГэВ,2) A1.3.1)
'^ Отличное историческое введение в теорию слабого взаимодействия дано в
работе [141].
^^ В экспериментах на протон-антипротонном коллайдере Европейского центра
ядерных исследований (ЦЕРН) удалось наблюдать рождение промежуточных
бозонов и определить их массы, значения которых находятся в отличном согласии с
лредсказаниями теории. ~ Прим. перев.
Остывание нейтронных звезд 333
где угол Вейнберга ? ? определен экспериментально:
sin^e^ = 0^28 ± 0,010. A1.3.2)
При малых энергиях взаимодействия {Е^/с^ < f^i^^ aw|), которые
характеризуют все процессы, протекающие в недрах нейтронной звезды,
гамильтониан ВСГ включает в себя старый V — А-гамильтониан, предложенный
Фейнманом и Гелл-Маном в 1958 г. Здесь V обозначает векторную часть
взаимодействия, а А — аксиально-векторную часть. В обеих теориях
эффективная плотность гамильтониана имеет вид
?:w? = ^·C·^^ A1-3.3)
где J — плотность 4-тока взаимодействующих фермионов. Универсальная
постоянная связи Ферми Ср, появляющаяся в эффективном гамильтониане
для низких энергий, следующим образом связана с параметрами ВСГ (Л =
- с = 1):
Gp = -??? , "^ ,^ = 1,16632 ±0,00004 ? 10-5 ГэВ-2
40 1 1,0 ? 10-5
= 1,43582 ± 0,00005 ? 10-^Ьрг · см^^ -^ . A1.3.4)
Здесь ?? = e^/hc = 1/137 — постоянная тонкой структуры.
Важное различие между старой и новой теориями при малых энергиях
заключается в том, что в старой теории разрешены только реакции с
заряженными токами. Это такие реакции, в которых, согласно новой теории,
связующим звеном являются заряженные векторные бозоны W^ или IV~.
В модели ВСГ могут существовать добавочные реакции с нейтральными
токами, где связующим звеном служит Z^. Экспериментальное
подтверждение реакций с нейтральными токами в 1974 г. сыграло свою роль в
присуждении в 1979 г. Нобелевской премии Вейнбергу, Саламу и Глэшоу.
Реакции A1.2.1) протекают с взаимодействиями через посредство
заряженных токов (нейтрон превращается в заряженный протон), а процессы
рассеяния
? + ? -^ ? -l· п, ? -l· ? -^ ? -l· ? A1.3.5)
протекают через посредство нейтральных токов. Некоторые процессы,
например рассеяние нейтрино на лептонах
р^-\-е'--^ р^ +е-, ?'?-^ ?~-^ ^?-^ ?~. A1.3.6)
происходят как через заряженные, так и через нейтральные токи (рис.
11.1).
Поперечные сечения в старой V — А-теории обычно растут, как G^E^,
где ? — энергия двух взаимодействующих тел в системе отсчета, связанной
с центром масс. Таким образом, при ?* — оо выражение для сечения
быстро расходится. В теории ВСГ сечения сходятся быстрее, чем ? « (InEf,
334 Глава И
? 'О »е е
Рис. И. 1 Диаграммы Фейнмана для рассеяния е — ?^ : а — реакция с заряженным
током; б — реакция с нейтральным током.
где л ^ 2. Модель ВСГ, как и квантовая электродинамика, допускает
перенормировки: расходящиеся интегралы, которые возникают в членах
высокого порядка при разложении возмущений по константе взаимодействия,
можно удалить хорошо известными методами [350, 564, 565, 566].
Наконец, отметим, что модель ВСГ объединяет в одном гамильтониане
как слабое, так и электромагнитное взаимодействия. Точнее, полученные
из лагранжиана уравнения поля устанавливают такую же связь между
электромагнитными и слабыми полями, как уравнения Максвелла соотносят
между собой поля ? и В. Этот успех привел к новым попыткам «великого
объединения» описаний всех известных взаимодействий в единую теорию.
Однако здесь нам следует остановиться, поскольку обсуждение этого
вопроса завело бы нас слишком далеко.
11.4. РАСПАД СВОБОДНОГО НЕЙТРОНА
Модифицированные урка-реакции включают в себя как сильные, так и
слабые взаимодействия. Например, в реакции A1.2.10) сталкивающиеся
нейтроны обмениваются пионами, пока один из нейтронов не распадется,
превращаясь в протон. Поэтому до вычисления скоростей этих процессов
рассмотрим более простую реакцию — чистый нейтронный распад в
вакууме, т.е. реакцию A1.2.1), где эффекты сильного взаимодействия малы.
Приведенное в данном разделе обсуждение в значительной степени
применимо также к бета-распаду в ядрах.
Выделяемая при типичном бета-распаде энергия мала {Q - МэВ) по
сравнению с энергией покоя нуклонов. Следовательно, можно
воспользоваться «золотым правилом» теории возмущений, зависящих от времени, в
нерелятивистском приближении и получить скорость распада
<^'^-т[\ Z\HAp,p,dE,dE,8{E,+E,-Q). A1.4.1)
\ Spins /
Здесь Pg и Р- —плотности конечных состояний е~ и v^ соответственно,
приходящиеся на единичный интервал значений энергии, а ?^ — энергия
Остывание нейтронных звезд 335
электрона. Величина ?? является матричным элементом слабого
взаимодействия в нерелятивистском пределе
Hf, = ??/?;?,</?= G^frpi*ei*^n d% A1.4.2)
где фр, ф^, ф-и ф^ ^ волновые функции протона, электрона, антинейтрино
и нейтрона соответственно. Представим, что распадающийся нейтрон
заключен в ^щик единичного объема и соответственно пронормируем все
волновые функции.
Отметим, что интеграл в уравнении A1.4.2) — это амплитуда
вероятности найти все четыре частицы в одной и той же точке пространства.
Соответственно, слабое взаимодействие в этой области низких энергий можно'
описать с помощью «контактного потенциала»
Я/, =/*;(г)КЛг,гО*ДгО ????\ A1.4.3)
где
Если пренебречь кулоновским возмущением электрона со стороны
протона, можно записать ф^ и ?^, в виде плоских волн.Заметим, кроме того,
что длины волн этих состояний гораздо больше радиуса ядра
? = - = F'^IO "см
к ? ?
для энергий порядка МэВ. Поэтому можно разложить пространственную
часть волновой функции лептонов
урЖ = ехр[-/(к,+ к,.)т] = 1 -/(к,+ к,.)т+ ··· A1.4.5)
и оставить в интеграле A1.4.2) только первый член разложения A1.4.5).
Если оставшийся интеграл перекрытия нуклонов отличен от нуля, то
говорят, что он описывает разрешенный переход; члены высшего порядка в
разложении A1.4.5) приводят к запрещенным переходам. Ясно, что при
разрешенных переходах орбитальный угловой момент не уносится.
Спиновая часть комбинированной лептонной волновой функции может
быть либо в синглетном (полный спин нуль), либо в триплетном (полный
спин единица) состояниях. При синглетных переходах волновая функция
ядра не изменяет спин или полный момент количества движения 7, так что
AJ = 0. Триплетные переходы требуют изменения ориентации спина, и
полный момент количества движения может сохраниться, если AJ = ±1 или
0. Правило отбора для синглетного перехода (ДУ = 0) называется
правилом отбора Ферми, а триплетные переходы подчиняются правилу отбора
Гамова—Теллера^К Изменение ориентации спина осуществляется псевдо-
^^ В ядрах, испытывающих бета-распад, переходы с бесспиновыми начальными и
конечными состояниями G=0 — 7 = 0) могут протекать только как переходы
Ферми, поскольку переходы Гамова — Теллера типа О — О строго запрещены.
336 Глава 11
векторной, или аксиальной, частью слабого взаимодействия, а синглетные
переходы — чисто векторной частью.
Теперь можно написать
\ ? |Я„.р = Gl[cl\My\' + 3Ci|M,|^]. A1.4.6)
spins
Здесь My и М^ — соответственно векторный и аксиально-векторный
матричные элементы нуклона, которые определяются интегралом перекрытия
начального и конечного ядерных состояний; Су и С^ — константы связи,
каждая из которых будет равна единице, если сильные взаимодействия не
влияют на процесс, а множитель 3 появляется благодаря статистическому
весу трип летного состояния. Экспериментально найдено, что
\Су\ = 0,9737 ± 0,0025
= а= 1,253 ±0,007. A1.4.7)
Са
Су
Для распада нейтрона возьмем в качестве хорошего приближения
Му^М^^ 1, A1.4.8)
поскольку волновые функции нейтрона и протона очень похожи (изоспино-
вая симметрия). Тогда уравнение A1.4.6) примет вид
^ 1|Я/,1' = С|СМ1 + За^). A1.4.9)
Spins
При интегрировании по dE- с использованием ?-функции уравнение A1.4.1)
принимает вид
dT = ^G|C^A + 3a')p^p,dE,. A1.4.10)
Для электрона с определенной ориентацией спина имеем
^ ^^IpUl^^IEL· A1.4.11)
где
,-'^'-f·)'". (И.4.,2,
Поскольку у нейтрино нет массы покоя^\ с учетом сохранения энергии
получим
E, = Q-E, = p,c, A1.4.13)
•^ Даже если у нейтрино будет найдена небольшая масса покоя, не превышающая
несколько эВ, выведенные в этой главе скорости процессов существенно не изменятся.
Остывание нейтронных звезд 337
так что
(Q - ? J
Таким образом,
р'-'^Ътгг- (^-^-14)
^j, = ?MiLl^i^E^ _ ;„^с^)'/^?Де - E,f dE,. A1.4.15)
Определив безразмерные энергии
? О
? ^-^, ^0 ^ "-^ = 2,5312, A1.4.16)
получим
^^ = WITTi ^/' A1.4.17)
где энергетический спектр электронов распада возникает из-за фазового
множителя
J/= (?^ - 1)^/'?(?? - ?)'^?. A1.4.18)
Интегрирование по всему разрешенному диапазону ? от 1 до Eq дает
/= ^D - ?)"'B?^ - 9el -8) + 1??1?[?? + (?? - ?^'] =
= 1,6369, A1.4.19)
a отсюда скорость распада нейтрону составляет
Наблюдаемая скорость равна 1/(925 ± 11) с; расхождение возникает из-за
того, что не были учтены кулоновские эффекты при вычислении /
(значение / увеличивается примерно до 1,70) и, кроме того, существуют
эффекты квантовой электродинамики («радиационные поправки»), дающие
еще 2%,
11.5. СКОРОСТЬ МОДИФИЦИРОВАННЫХ УРКА-ПРОЦЕССОВ
Получив оценку матричного элемента слабого взаимодействия для распада
свободного нейтрона, мы имеем теперь возможность вычислить скорость
модифицированной урка-реакции A1.2.10). При этом последуем
оригинальному подходу Бакала и Вольфа [41].
6-513
338 Глава И
Пусть нижние индексы 1, 2, Г, /7, ^ и ? означают два начальных
нейтрона, конечный нейтрон, протон, электрон и антинейтрино соответственно.
Скорость реакции для заданных начальных состояний 1 и 2 равна
dV ^^8{Ef- E.)\Hf,\\p,p,dEj,dE,dE,, A1.3.I)
где выражения \??\^ надо просуммировать по конечным спинам и
усреднить по начальным спинам. Мы явно сохраним нормированный объем У
во всех фазовых множителях и в волновых функциях, так что в пустом
пространстве для каждого вида частицу будем иметь
PjdEj^d% = ^^. A1.5.2)
Однако реакция происходит в плотном газе, где большинство ячеек
фазового пространства с малой энергией занято. Следовательно, каждый
множитель d^iij надо умножить на A - У}), где
^ = ехр[(?,-м,)ДГ]-Ы ^''-'-^^
часть фазового пространства, занятая при энергии Ej (распределение
Ферми-Дирака; см. гл. 2). Множители A - fj) уменьшают скорость
реакции и называются блокирующими множителями.
Обратите внимание, что в использованном в уравнении A1.5.1)
«золотом правиле» число фазовых множителей меньше числа конечных частиц
на единицу из-за сохранения импульса. Можно получить более
симметричное выражение, если добавить множитель
«ЧР/ - Р,) d'v, = Ь\9, - р,) d'ny^ = «^(к, - к,) d^y^.
При интегрировании по Pj/ этот множитель дает единицу.
Полная светимость, связанная с выходом антинейтрино в объеме Уу
получается после интегрирования скорости реакции A1.5.1) по всем
начальным состояниям, умноженным на Е~:
L, - ^jd'n, d'n, d\.d\ d'n, d\S{E, - ?,) X
ХвЧк/-к,M|Я/,|Ч- A1.5.4)
Здесь
5 =/,/2A-/,-)A-/;,)(!-Л). A1.5.5)
а множители /, и /j отвечают за распределение начальных состояний.
Остывание нейтронных звезд 339
Упражнение 11.2. Почему в уравнении A1.5.5) нет блокирующего множителя
A - /?)? При каких обстоятельствах следовало бы включить такой множитель?
Важнейший матричный элемент взаимодействия можно записать в виде
H^i = (n,p,e,p\VJ ?, ?), A1.5.6)
где V^ — это «контактный» гамильтониан слабого взаимодействия,
приводившийся ранее для распада свободного нейтрона [уравнение A1.4.4)].
Теперь он снова подходит для представления лептонов в виде состояний
свободных частиц в уравнении A1.5.6). Однако такой способ неприменим в
случае нуклонов. Причина в том, что полный гамильтониан нуклона равен
Япис = Я,^ + я, + F, = Яо + F,, A1.5.7)
где //free — вклад свободных частиц (кинетическая энергия каждой
частицы), а Яу — гамильтониан сильного взаимодействия. Поэтому ургниение
A1.5.6) дает лишь самое низшее приближение скорости перехода, если
появляющиеся в нем волновые функции нуклонов уже являются
собственными функциями Hq. Как уже обсуждалось выше, решение уравнения Шре-
дингера для многих тел, содержащего //у, далеко не тривиально и пока еще
не получено теоретически. Последуем просто за Бакалом и Вольфом и
попытаемся оценить влияние Н^ на нуклонную волновую функция двух тел.
Запишем поэтому
Я/, = /</?^?'?„%(?)?*(?)??(?)??(?,?')?„„(··')
= ^fd^r„pirH„„ir). A1.5.8)
Мы использовали здесь уравнение A1.4.4) и положили
?» = 7^-'"'" - ^ ' 01.5.9)
сделав то же самое для ?-, как и в уравнении A1.4.5).
Предположим, что при взаимодействии в начальном л-л-состоянии
доминирует рассеяние 5-волны (т.е., L = ??? Тогда л-л-состояние должно
иметь полный спин 5 = 0 (сравните с табл. 8.1). Векторная часть (V)
слабого взаимодействия связывает это состояние с л-р-состоянием, имеющим
'^ Такое предположение справедливо при низкой плотности ? ^ /^nuc* ^ этом
предельном случае радиус твердого кора ядерного потенциала г^ много меньше h/рЛп).
Поскольку отклонение волновых функций от состояния, описываемого плоскими
волнами, определяется главным образом твердым кором, связанный с актом
рассеяния момент количества движения равен -р/^, < Л, что означает рассеяние 5-волны.
340 Глава И
S = О, а аксиально-векторная часть (А) связывает его с А2-/7-состоянием,
имеющим S = 1. Поэтому [сравните с уравнением A1.4.6)]
:2
? |я,,1^ = Шс1\мА' + 3Ci|Mj^), ^''''''^
spins
где
?^
?^=/^?(?',)*?°„. A1.5.11)
Множитель 4 появляется в уравнении A1.5.10), потому что любой из
нейтронов пары п-п может стать протоном, что дает множитель 2 для
амплитуды и 4 для вероятности.
Поскольку диапазон, в котором проявляется сильное взаимодействие,
порядка ?^ = h/m^c, ожидается, что относительные волновые функции в
уравнении A1.5.11) будут перекрываться в сравнительно небольшом объеме
порядка Xj. Таким образом, ожидается, что ? - ?^/ У. Определяя
безразмерные матричные элементы
й^.^, й,.^, (П.5..2)
получим для уравнения A1.5.4)
L, = 647гП^|А-^Х;9(С^|М^|2 + ЗС^\М^\^)Р, A1.5.13)
где безразмерный фазовый множитель ? равен
P-'r-'vHnd\SE,8\k^-k,)8{E^-E,). A1.5.14)
Отметим, что, поскольку каждый множитель d^rij пропорционален У, ? не
зависит от У и поэтому величина L- пропорциональна У. Для
антинейтринной излучательной способности ?- имеем следующее выражение:
?,.= ^ = 5,1 · 10^^Р{\Му\^ + 4,7|М^|2) эргДсм^ · с). A1.5.15)
Фазовый множитель подсчитан в приложении Е; там показано, что он
равен
,2
?-2,1 · 10-^^(-^) ГД A1.5.16)
где р^ц^. = 2,8 · 10^"* г/см^, а Г9 — температура, выраженная в единицах
10^ К. Заметим, что температурная зависимость Cj; целиком связана с
фазовым множителем; такой результат, как правило, справедлив для реакций
Остывание нейтронных звезд 341
охлаждения с участием нейтрино. Восьмая степень температуры ?
возникает следующим образом: для каждого вида вырожденных частиц только
доля порядка кТ/Ер может вносить эффективный вклад в скорость
охлаждения. Есть два таких начальных вида и три конечных. Фазовый объем
антинейтрино пропорционален Е\, а скорость потерь энергии дает еще один
множитель ?¦-. Поскольку Е- -- кТ, имеем всего восемь степеней Г.
Оценка безразмерного матричного элемента не столь проста. Можно
определить фундаментальный масштаб длины из импульса Ферми
доминирующих нейтронов с помощью выражения
/--7-?-?,4?„(/-) '^'. A1.5.17)
Бакал и Вольф предположили, что матричные элементы My и М^, как
можно ожидать, пропорциональны A/?^?, т.е. должны быть порядка
единицы при ? ~ Pnug и медленно уменьшаться, как 1/р. Во всяком случае, они
использовали некоторые результаты расчетов, выполненных для ядерного
вещества, чтобы формально вычислить
\4/3
|М/ = |М,|^ = 1,0(^) . A1.5.18)
.11) принимает вид
/ ? \2/3
?,-= 6,1 · 10^9 М^ Тд^ эрг/(смЗ · с). A1.5.19)
\ Pnuc /
Тогда уравнение A1.5.11) принимает вид
\2/3
К выражению A1.5.19) нам надо теперь добавить скорость потерь
энергии нейтрино, обусловленных «обратной» реакцией A1.2.11).
Благодаря инвариантности относительно изменения направления времени
матричные элементы Л/^ и My для реакции A1.2.11) являются комплексно-
сопряженными элементами М^ и My для реакции A1.2.10). Поскольку
фазовые множители одни и те же для обеих реакций (с учетом сделанного
предположения о пренебрежении всеми импульсами лептонов), обе реакции
дают одну и ту же скорость потерь энергии.
Реакции с излучением мюонного нейтрино A1.2.12) и A1.2.13) должны
рассматриваться, когда ?^ > т^с^ (т.е. ? > 2,9?„„? в модели свободных
частиц; сравните с разд. 8.10). Реакции с и^ отличаются от реакций с ?^
только фазовым множителем Р, где вместо p^dp^ появляется p^dp^. Поэтому
отношение скорости потерь энергии для мюонных и электронных нейтрино
равно
^ = ^ГГ. A1.5.20)
Каждый из членов уравнения A1.5.20) следует вычислять на поверхности
Ферми, поскольку только эта область фазового объема обеспечивает вклад
в скорость реакции.
342 Глава И
Упражнение 11,3. Используйте уравнение равновесия ??(?) = ?р(е) и покажите, что
???? = РеФе н^ соответствующих поверхностях Ферми, так что
2 \ 2
О, ? < 2,9р„„,
1/2
, P>2,9p„uc A1.5.21)
?р@
Умножение уравнения A1.5.19) на 2A + F) дает в конечном итоге полную
скорость потерь энергии благодаря модифицированным урка-реакциям ^ ^-
\2/3
URCA
1,2 · 1020 (-^-) Г/A + F)эpг/(cмЗ · с). A1.5.22)
\ Pnuc /
Это дает светимость нейтронной звезды с массой ? и однородной
плотностью ?
Ly^^A = 8.5 · 1038 ^|P^j'^V/(l + F) эрг/с. (И.5.23)
Недавно Фримен и Максвелл [211] повторили приведенные выше
расчеты, использовав более реалистичное выражение для сильного NN-
взаимодействия. Они получили такую же зависимость от плотности, но
численный коэффициент в уравнении A1.5.22) у них равен 7,4 · 10^^, что
почти на порядок величины больше. Для звезды с однородной плотностью
без учета мюонов это дает
^URCA = 5,3 · 10''-^[^'^'ц' эрг/с. A1.5.24)
11.6. СКОРОСТИ ДРУГИХ РЕАКЦИЙ
Обрисовав ВЫВОД соотношения A1.5.22), обсудим теперь кратко скорости
других возможных реакций охлаждения.
а) Тормозное излучение нуклонной пары
Наиболее существенный из других механизмов охлаждения, который
становится возможным при учете нейтральных токов, — это тормозное
излучение нуклонной пары
??-?-^? + ? + ? + ?, ?-\-?-^?-\-?-\-?-\-?. (?1.6.?)
'^ Наши численные результаты слегка отличаются от полученных Бакалом и
Вольфом [41] из-за разных значений для р^^^ и для константы связи бета-распада.
Остывание нейтронных звезд 343
Эти реакции изучались Флауерсом [198], а позднее Фрименом и
Максвеллом [211], которые нашли, что, хотя скорость также пропорциональна 7*,
она все же меньше скорости модифицированных урка-реакций в 30 раз.
б) Тормозное излучение нейтринных пар
Если нейтроны «заперты» в сверхтекучем состоянии (см. разд. 10.9),
скорости всех описанных до сих пор реакций «обрезаются» множителем
expi — й/кТ), где ? — энергетическая шель сверхтекучести. В этом случае
может оказаться существенным охлаждение посредством тормозного
излучения нейтринных пар ядрами коры.
Скорость процесса
е-+ (?, А) -^ е-+ (Z,A)^v^v A1.6.2)
по оценкам составляет
^ьгеш ^ 5 · 10^9 {MJMq)T^ эрг/с, A1.6.3)
где M^j. — масса коры [389]. Поскольку скорость этого процесса
пропорциональна 7|, его эффективность уменьшается по мере остывания звезды
не так быстро, как для реакции A1.5.22).
в) Пионные реакции
Бакал и Вольф первыми отметили, что конденсация пионов может
заметно увеличить скорость охлаждения недр нейтронной звезды. Если
существуют пионные конденсаты (см. разд. 8.12), то возможны бета-распад
«квазичастиц» посредством реакции
ЛГ-^ЛГ' + е-+ v^ A1.6.4)
и обратная реакция. Здесь квазичастицы N и N' представляют собой
линейную комбинацию состояний нейтрона и протона в пионном море. Пион-
ный конденсат позволяет сохранять как энергию, так и импульс в этой
реакции, которая является аналогом обычного урка-процесса A1.2.1).
Бакал и Вольф рассмотрели более простой вариант реакции A1.6.4) —
охлаждение благодаря распаду свободного пиона
тгЧ- ? -^ n-l· e~-l· v^, A1.6.4а)
тгЧ- ? -^ n-l· ?~+ ?^, A1.6.46)
и «обратным» процессам
? + е~-^ ? -I- ??~+ Vg, A1.6.4в)
п + ?~-^?-^?--\- ?^, A1.6.4Г)
344 Глава 11
Как и для модифицированных урка-реакций, полная скорость всех четырех
процессов оказывается фактически в четыре раза больше скорости одной
реакции A1.6.4а). (Вспомним, что мюоны уже присутствуют, когда
появляются пионы.)
Грубую оценку скорости реакции можно получить следующим образом.
Поскольку в этих реакциях принимают участие на два фермиона меньше,
чем в модифицированных урка-реакциях, фазовый множитель
пропорционален 7^, а не 7*. Поэтому можно ожидать, что выражение для полной
скорости реакции имеет вид
L-L--.(^^)'^, A1.6.5)
где л^/л„ — отношение концентраций пионов и нейтронов. Поскольку
??{?) - 60(p/pnuc) ^^ МэВ, из уравнений A1.5.23) и A1.6.5) получаем
L- ^ 8 · 10^ -^ -В-Г/^ эрг/с . (И.6.6)
Бакал и Вольф получили, что в действительности численный множитель
равен 1 · 10^, а зависимость от плотности отсутствует. Более поздние
вычисления Максвелла и др. [390] дают
?, - 1.5 · 10« ^'^^Т^эрт/с, A1.6.7)
где ^ - 0,3 — угол, измеряющий степень пионной конденсации (он
заменяет множитель п^/п„). Поскольку L^ очень сильно превышает lJ/*^^^, пион-
ное охлаждение будет определять скорость остывания при всех
рассматриваемых нами температурах, если только пионная конденсация имеет место.
Упражнение 11.4, Оцените верхний предел скорости охлаждения нейтронной звезды
радиусом 10 км тепловыми нейтрино [77]. Предположите, что звезда излучает
электронные нейтрино и антинейтрино как «черное тело» Ферми — Дирака при
температуре ? и химическом потенциале ?^ = ?- = 0. При достаточно высоких ? все
подсчитанные выше светимости превышают эту скорость. Объясните это расхождение.
Указание: Закон Кирхгофа.
« 6 · 10^ · 7? эрг/с.
г) Бета-распад кварков
Если ядро нейтронной звезды состоит в основном из кваркового
вещества, существует возможность значительного излучения нейтрино за
счет бета-распада вырожденных релятивистских кварков [94, 296]. В
отличие от обычного вещества нейтронной звезды, где процессы простого бета-
распада (т.е. урка-процессы) подавлены, соответствующие процессы могут
реализоваться для кварков.
Остывание нейтронных звезд 345
Вспомним наше более раннее обсуждение в разд. 8.14 трехкомпонентного
(м, d vis) кваркового вещества, находящегося в бета-равновесии. Там было
показано, что, если пренебречь массами кварков и их взаимодействиями
между собой, равновесный состав описывается соотношением
^u^^d^^s^ ^^ ^? = ^? = О, A1.6.8)
где ? = (rij^ + п^ + л^)/3 — концентрация барионов. В соответствии с
уравнением A1.6.8) каждый тип кварков имеет один и тот же импульс
Ферми, определяемый соотношением^^
p^i,) = 235(^Г ^, A1.6.9)
\ ^ nuc / ^
где Лдис ¦ Ршс^^в = 0,17 Ф"^
Похоже, что наличие конечных масс кварков и взаимодействий кварк-
кварк приводит к изменению указанного выше состава. Например, как
полагают, 5-кварк должен быть достаточно тяжелым (т^ ^ 1(Ю — ЗОО МэВ),
и если он присутствует в нейтронной звезде, то вряд ли будет
релятивистским. С другой стороны, м- и б^-кварки скорее всего являются очень
легкими (Wy - w^ -- 5—10 МэВ), т.е. они будут сильно релятивистскими и их
массами еще можно пренебрегать. Получившиеся в итоге видоизменения
равновесного состава сводятся к появлению лептонов, несущих некоторую
долю отрицательного заряда, чтобы сохранить общую зарядовую
нейтральность. В действительности, поскольку характерные энергии Ферми
кварков много больше т^с^, любое малое отличие ?^ от ?^^ (или ?^ от ?^^)
неизбежно приводит к электронам с релятивистской энергией Ферми
[сравните с уравнениями (8.14.2) и (8.14.3)].
Простейшие процессы с излучением нейтрино, протекающие в кварко-
вом веществе, — это реакции бета-распада релятивистских кварков
d-^u + е"+ v^, A1.6.10)
u + e--^d+v,, A1.6.11)
Детальный анализ этих реакций дан Ивамото [296]. Он указал, например,
что если пренебречь массами частиц и взаимодействиями типа
кварк — кварк, то сохранение энергии и импульса требует, чтобы
импульсы всех частиц в реакции A1.6.10), если она вообще имеет место, были
коллинеарными (почему?). Однако в этом случае вычисленный в рамках
теории ВСГ матричный элемент реакции оказывается тождественно равным
нулю^^ Ивамото затем показывает, что, если принять во внимание взаи-
'^ Уравнение A1.6.9) показывает, что энергии Ферми в нейтронных звездах
значительно ниже порога образования тяжелых (с, b vi t) кварков.
^^ Этот результат неприменим к реакции A1.6.11), если учитывать небольшой
импульс "кТ/с испущенного нейтрино. В этом случае импульсы частиц могут и не
быть строго коллинеарными и матричный элемент не обращается в нуль [94].
Однако скорость реакции A1.6.11), не учитывающей взаимодействия, будет в кТ/рЛе)с
раз меньше скорости, вычисленной для A1.6.10), когда взаимодействия учитываются.
346 Глава И
модействие между кварками, импульсам не требуется быть коллинеарными
для сохранения энергии и импульса и матричный элемент не обращается в
нуль. Он особо отметил, что участвующие в реакции кварки должны
располагаться вблизи своих поверхностей Ферми. В первом приближении по
константе сильного взаимодействия «^ (квантовая хромодинамика)
соотношение между химическим потенциалом кварка и ферми-импульсом
таково [49]:
M„,.= (i+^)/^f(",^)c. A1-6.12)
Легко проверить, что это видоизменение обычного для идеального газа
релятивистских фермионов соотношения ? = рр<: позволяет сохраняться
энергии и импульсу при конечном угле между импульсами
взаимодействующих частиц для реакции A1.6.10).
Когда учтены взаимодействия (но пренебрегается малым импульсом
нейтрино), излучательные способности реакций A1.6.10) и A1.6.11)
одинаковы; Ивамото рассчитал, что их сумма должна быть равной
^quark « g g . ^Qie^^JL^yy^jb ^^^/^^y,Ъ . ^)^ A1.6.13)
'*nuc
где ? ? = ? ^/? — число электронов на барион. Величина ?^ зависит от
импульса и не очень точно определена экспериментально. Как обсуждалось в
разд. 8.14, модель, разработанная Ходосом и др. [128], предполагает, что
oLg « 0,55. Однако анализ распада чармония^^ дает а^ « 0,065. Ивамото
принял в уравнении A1.6.13) значение а^ = 0,1. Он положил
также ? ? = 0,01—это значение типично для вещества нормальной
нейтронной звезды^^ В результате излучательная способность равна
.quark ^ 19 · 1025 -^Г/эрг/(смЗ · с). A1.6.14)
''nuc
Соответствующая светимость для звезды с однородной плотностью, cot
стоящей из кваркового вещества, равна
Ц-^^ « 1,3 · 10^ -^тбэрг/с. A1.6.15)
Присутствие 5-кварков приведет к дополнительному излучению
нейтрино посредством реакций бета-распада типа
S -^u-l· e--l· v^, A1.6.16)
м + е'-^ s-l· р^. A1.6.17)
'^ Чармоний — это связанное состояние ее; анализ его распада см. в [14].
^^ Сравните с упражнением 8.3; обратите внимание, что такое большое значение
Yg подходит только в том случае, если 5-кварк является тяжелым [вспомните
уравнения A1.6.8) и A1.6.9)]; полное обсуждение см. в [170].
Остывание нейтронных звезд 347
Поскольку 5-кварк обладает большой массой, импульсы
взаимодействующих частиц могут в значительной степени быть неколлинеарными, что
обеспечивает неравенство нулю матричных элементов. Однако слабое
взаимодействие между 5- и м-кварками [например, реакции A1.6.16) и A1.6.17)] в
теории ВСГ «подавлено по Каббибо» относительно взаимодействия,
связывающего d- и w-кварки [например, реакции A1.6.10) и A1.6.11)]. Точнее,
первое взаимодействие пропорционально sin^^^, а второе — cos^^^·» ^^^ ^с
называется углом Каббибо. Экспериментально обнаружено, что Bq
удовлетворяет соотношению cos^^^ « 0,974. По этой причине Ивамото
заключает, что нейтринные процессы с 5-кварком не влияют заметно на полную
светимость A1.6.14).
Вопрос о том, существует ли в ядрах нейтронных звезд кварковое
вещество, еще никак нельзя считать решенным. Однако сравнение уравнений
A1.5.24), A1.6.7) и A1.6.15) показывает, что звезда с кварковым веществом
будет остывать с гораздо большей скоростью, чем обычная нейтронная
звезда, сравнимой со скоростью остывания звезды, имеющей в ядре пион-
ный конденсат.
11.7. ПРОНИКАЮЩАЯ СПОСОБНОСТЬ НЕЙТРИНО
Если нейтринные светимости известны, можно рассчитать характерные
времена охлаждения. Основным для последующего обсуждения является
предположение, что все нейтрино, рожденные в нейтронной звезде,
ускользают из нее без дальнейших взаимодействий или потерь энергии. Сейчас
мы покажем, что для ? <> \0Р это предположение справедливо.
До открытия нейтральных токов в 1974 г. предлагалась следующая
аргументация [41]. Реакции типа
?^ + ? -^ ? -\- е~, Vg + ? -^ ? + е^,
и т.д. запрещены в недрах нейтронных звезд законами сохранения энергии
и импульса. Наиболее важным для потерь энергии нейтрино
взаимодействием будет неупругое рассеяние на электронах (для ?^^ и ?^) и мюонах (для
V и V ). В вырожденном газе сечение рассеяния ?^ — е~ равно (с учетом
лишь взаимодействия через заряженные токи)
'^'^^''"wji;;^' ^''-'-'^
где
7г \ т^с I
-4/ Q \2
-^ = 1,76· 10-^см2, A17.3)
тх"
348 Глава И
причем X « 0,1 в рамках V — А-теории (взаимодействие только через
заряженные токи) их* 0,06 в теории ВСГ (взаимодействие через заряженные
и нейтральные токи).
Поперечные сечения для остальных трех дроцессов рассеяния сравнимы
с этим значением.
Тогда средний пробег электронного нейтрино равен
?^= (?ewJ"^ A1.7.4)
Используя результаты упражнения 11.1 и старое значение ?^, основанное на
V—А-теории, получим
кэБ '^
Поскольку ?^ > 10 км, звезда прозрачна для нейтрино.
С учетом нейтральных токов эффективная длина свободного пробега
для поглощения значительно сокращается из-за реакций упругого
рассеяния ? — ?^\ например,
?-^?^-^?-^?^, ? + ?^-^?-^?^, A1.7.6)
которые протекают только через нейтральные токи. Хотя упругое
рассеяние не уменьшает энергию нейтрино, оно мешает нейтрино ускользать
сразу же после излучения. Нейтрино многократно рассеивается нейтронами в
недрах звезды пока, наконец, не столкнется с электроном (или мюоном) и
не рассеется неупруго или в процессе случайного блуждания не подойдет к
поверхности и не освободится с неизменившейся энергией.
Поперечное сечение упругого рассеяния нейтронами равно [579]
1
4 'Uec'/' A1-7.7)
а соответствующая длина свободного пробега составляет
?^ = _L·.300^(i^?^f?м. A1.7.8)
Мы использовали приведенное в упражнении 11.1 значение п^.
Эффективная длина свободного пробега для неупругого рассеяния электронами (с
'^ Термин упругое означает, что в очень хорошем приближении энергия нейтрино
Е^ < т^с^ до рассеяния равна энергии нейтрино после рассеяния в системе
координат звезды (т.е. нейтрона).
Остывание нейтронных звезд 349
учетом возросшей вероятности соударения с электронами в недрах звезды
благодаря зигзагообразному пути нейтрино) равна^^
?eff - (?„? J'/' A1.7.9)
.2xl03(?-p(i0^pKM, A1.7.10)
где мы использовали ВСГ-значение ?^. Итак, хотя эффективная длина \^^
значительно меньше ?^, она все же гораздо больше радиуса нейтронной
звезды. Следовательно, «старый» вывод о прозрачности нейтронной
звезды для нейтрино малых энергий (Т <, \0Р К, кТ % 100 кэБ) все еще верен.
11.8. КРИВЫЕ ОСТЫВАНИЯ
Теперь можно подсчитать температуру нейтронной звезды как функцию
времени. Тепловая энергия звезды заключена почти полностью в
вырожденных фермионах (нейтронах или кварках). Если пренебречь
взаимодействиями, то теплоемкость N таких частиц с массой т и параметром
релятивизма дг = Pf/mc равна [114]
dU
?,? Х^
-^к[—Х A1.8.1)
где с^ — удельная теплоемкость (на частицу).
Упражнение 11.5.
а) Проинтегрируйте уравнение A1.8.1) и найдите полную тепловую энергию U (в
первом приближении величина ? остается постоянной).
б) Каково значение U для нормальной нейтронной звезды с массой М,
плотностью ? и температурой Г?
Указание: Предположите, что ? < \ и воспользуйтесь результатами упражнения
11.1.
Ответ:
?/„ » 6 · 10*МЛ//Л/е)(р/р„„с)"'^'7^ эрг. A1.8.2)
в) Каково значение U для релятивистского кваркового вещества с л^ = п^ =
= А2^ = А2?
'^Уравнение A1.7.9) случайного блуждания фактически выводится в разд. 14.5
для аналогичного случая диффузии фотонов через горячую плазму. В этом примере
представляющий интерес процесс поглощения энергии — это обратное тормозное
излучение, а процесс упругого рассеяния — томсоновское рассеяние на свободных
электронах.
350 Глава И
Указание: Воспользуйтесь уравнением A1.6.9).
Ответ:
t/, - 9 ¦ 10^??//?4)(«?„„,)-'/?,^ эрг. A1.8.3)
Появляющаяся в уравнениях A1.8.1)-A1.8.3) температура Г— это
температура недр. Недра нейтронных звезд в хорошем приближении являются
изотермическими благодаря высокой теплопроводности вырожденного
электронного газа^^ Как и для горячих белых карликов (см. гл. 4),
заметный градиент температуры имеется только в самом наружном
невырожденном слое с малой плотностью^\
Уравнение остывания имеет вид
где L^-^ полная нейтринная светимость, а L^ — фотонная светимость.
Предполагая, что излучение фотонов с поверхности подобно излучению
черного тела с эффективной температурой Г^, получим
L, = AnR^oT* = 7 ¦ lO^(-fo^) Г,% эрг/с. A1-8-5)
где ? — постоянная Стефана-Больцмана, а Г^ ^ температура в единицах
10^ К.
Подставляя соответствующие светимости в уравнение A1.8.4) и
интегрируя, получим время, необходимое звезде, чтобы охладиться от
начальной температуры T{i) до конечной температуры T{f).
Упражнение П.б.
а) Рассчитайте время остывания, предполагая, что в нем главную роль играет
модифицированный урка-процесс. Используйте уравнения A1.5.24) и A1.8.2).
Ответ:
A/(URCA) - (^~'^'?-^(/)?? - ?
ТЛП
МО
лет. A1.8.6)
') Фактически при тепловом равновесии постоянна величина Ti-gQ^Y^^; для
тепловой энергии необходимо учитывать гравитационное красное смещение. См. [366],
задачу 14.2.
^^ Но в [420] найдено, что для нейтронных звезд с жестким (TI) уравнением
состояния отклонения от изотермичности в недрах звезды могут продолжать
существовать по крайней мере несколько тысяч лет после ее образования.
Остывание нейтронных звезд
351
б) Повторите поочередно вычисления для пионной конденсации [уравнение
A1.6.7)], кварков [уравнение A1.6.15)] и тормозного излучения нейтрино в коре
[уравнение A1.6.3)].
Ответ:
Дг(пион) - 20^-2(-5-| ^ Ti\f)l\
Аг(кварк) J^y'^'ri'inil
ТэО)
Ш1
ТэО)
ч.
''^^-'¦Ш^Г"'М'
МП
МО
с, (И-8-7)
A1.8.8)
лет. A1.8.9)
Детальные вычисления [379, 575, 576] указывают, что в общем случае
поверхностная температура и температура недр связаны соотношением
Т/Т ^ Ю-^а, 0,1 ^ ? ^ 1.
A1.8.10)
Этот результат можно понять достаточно просто, если применить анализ
области перехода от невырожденного к вырожденному состоянию,
выполненный в разд. 4.1 для белых карликов, к соответствующей области
нейтронной звезды. Как можно заметить, это та область, где электроны
становятся невырожденными, что в данном случае немаловажно; по
отношению к этой области все внутренние части нейтронной звезды, грубо
говоря, изотермичны. Предположим снова, что непрозрачность определяется
главным образом связанно-свободными и свободно-свободными
процессами и поэтому соотношения D.1.1)-D.1.11) остаются справедливыми. (В
действительности непрозрачность в основном определяется томсоновским
рассеянием при Г ^ 2 · 10^ К [127]). Принимая, что поверхность состоит
56 56
— и U = —.
26 27
нивая соотношение D.1.11) для L в единицах ? выражению A1.8.5) для L в
единицах Г^, получим
10-2 7Г^«|-^1 ("???-? . A1.8.11)
из чистого железа (It^o), имеем: Л'=0, Z= 1,?^ = ^?? = ^. Прирав-
?
Уравнение A1.8.11) согласуется с более детальным численным
рассмотрением и показывает относительную нечувствительность к температуре
коэффициента ? из соотношения A1.8.10).
Упражнение 11.7. Выполните заново анализ, приведший к уравнению A1.8.11), для
Г ^ 2 · 108 К. Замените D.1.3) на к = к^ = 0,40/?^ CMVr.
352
Глава 11
Ответ:
L=l,6· 10^''(l^)^'^'эрг/с.
-1/2
Если же теперь доминирующим механизмом потерь энергии станет
излучение фотонов, уравнения A1.8.2), A1.8.5) и A1.8.10) дают
?/(?????)=2.103«^(^)"?-(/){?-[?/
)
лет,
A1.8Л2)
где для исключения R использовано соотношение Л/ = 4??/?^/3 и
предполагается, что для коротких промежутков времени ? = const.
Упражнение 11.8. Приблизительное согласие с расчетами Цуруты [576]
обеспечивается при
2/3
т; =: (югг'.
A1.8.13)
где ? и Tg измерены в Кельвинах. Получите заново ?/ (фотон), используя это
соотношение.
Ответ:
??(?????) = 6 ¦ 10*(^) 7;:7'(/)|? -
Те.ЛО
лет.
Полученные выше результаты представлены на рис. 11.2, где
относительная важность различных процессов охлаждения показана как функция
времени для нейтронной звезды с массой Л/ = Mq , ? = р^^^ и ?^ = 0,1.
Каждая кривая на рис. 11.2 дает ?(?) для каждого процесса в отдельности в
предположении, что все остальные процессы отсутствуют. Наиболее
эффективным процессом охлаждения в данный момент времени будет тот,
для которого значение T(t) наименьшее; температура недр в этот период
будет приблизительно равна Т.
Эти характерные времена охлаждения были определены в
предположении, что нейтроны и протоны образуют нормальную жидкость.
Сверхтекучесть изменяет эти результаты посредством двух разных механизмов. Во-
первых, удельная теплоемкость скачкообразно возрастает при падении
температуры ниже точки перехода, а затем экспоненциально
уменьшается при более низких температурах. Поэтому непосредственно над
температурой перехода характерное время охлаждения увеличивается, а при
Остывание нейтронных звезд
353
10^
г>8
10** h
1 ' ' '
[ V*"^^
L Пионньш **¦—.
конйенсат
1 1 L
1 \ 1 1 I 1
Чфотоны
* ^„Кварки \ ^^^*'**·*^^
J \ \ L....-\,
1 1
^"¦"^^-J
L·^
10^
ш^
10"^ 1 10 10^ 10^ 10^ 105 10^ 10^ 10® iO^
t, гоЭы
Рис. 11.2. Схематические кривые остывания нейтронной звезды. Температура недр
представлена как функция времени для различных процессов в предположении, что
они действуют в одиночку: 1 — тормозное излучение коры; 2 — модифицированные
урка-реакции [52].
более низких температурах оно уменьшается. Во-вторых, в сверхтекучей
жидкости подавлены процессы образования нейтрино, что увеличивает
характерное время охлаждения.
Мы пренебрегли также ролью магнитного поля в уменьшении фотонной
непрозрачности нейтронной звезды вблизи поверхности. Для данного
значения ? уменьшение непрозрачности увеличивает Т^ и, следовательно,
фотонную светимость.
11.9. СРАВНЕНИЕ С НАБЛЮДЕНИЯМИ
Подробные кривые остывания нейтронной звезды были построены
некоторыми авторами (см., например, [226, 420, 590] и помешенные в них ссылки
на более ранние вычисления). Кроме того, недавно были получены
результаты рентгеновских наблюдений со спутников около 50 остатков
сверхновых, включая семь отмеченных в исторических хрониках [271, 272]. Так
называемая «стандартная» модель вычислений без учета пионной
конденсации и кваркового вещества предполагает поверхностную температуру Т^ у
объекта возрастом около 300 лет, равную по крайней мере A 4- 2) · 10^ К,
а минимальные температуры остаются в диапазоне @,5 4- 1,5) · 10^ К в
течение по крайней мере 10^ лет [см. рис. 11.2 и уравнение A1.8.12)].
Верхний предел - 3 · 10^ К для пульсара в Крабовидной туманности,
выведенный по наблюдениям покрытия пульсара Луной [571, 622],
полностью совместим с этими обычными расчетами. Недавно наблюдения
обсерватории «Эйнштейн» (спутник НЕАО-2) снизили верхний предел до
- 2 · 10^ К. Этот результат и полученные из наблюдений верхние пределы
7-513
354
Глава 11
5.8
36
1,5 2.0 г.5 3,0 3,5
4,»
-J 32
^.5
Рис. 11.3. Остывание нейтронной звезды: сравнение данных наблюдений
обсерватории «Эйнштейн» и типичных теоретических кривых остывания. Согласно принятой
модели, нейтронная звезда имеет массу Л/ = 1,3 Л/^, радиус R = 16 км и ее
структура в основном определяется уравнением состояния в приближении тензорного
взаимодействия. Измеряемые величины Т^ и L*j^ (измеренные на бесконечности)
отложены как функция времени для четырех случаев: сверхтекучие нейтроны E) и
несверхтекучие (нормальные) нуклоны (?) в отсутствие магнитного поля, а также
сверхтекучесть (Л/5) и несверхтекучесть (?/?) при магнитном поле 4,4· 10^^ Гс.
Цифры относятся к данным наблюдений: A) Cas А, B) звезда Кеплера, C) звезда Тихо,
D) Крабовидная туманность, E) SN 1006, F) RCW 103, G) RCW 86, (8) W 28,
(9) G 350,0 — 18, A0) G 22,7 — 0,2. Крестиками обозначен измеренный верхний
предел, кружки относятся к возможному «открытию» точечных источников.
Оцененные ошибки наблюдений связаны с неточностями определения межзвездного
поглощения и расстояния до источника [420].
поверхностных температур для ряда других молодых остатков сверхновых
показаны на рис. 11.3 и приведены в табл. 11.1. На рис. 11.3 данные
наблюдений сравниваются с предсказаниями теории. Из семи остатков
сверхновых, отмеченных в исторических хрониках (первые семь строк в табл.
11.1), только для Крабовидной туманности определенно известно, что она
содержит нейтронную звезду. Исторические сверхновые очень важны,
потому что их возраст точно известен. Наблюдаемые верхние пределы для Т^
близки к теоретическим пределам. Некоторые из наблюдавшихся верхних
пределов (для Gas А, остатка сверхновой Тихо и особенно для SN 1(ХN) даже
опускаются ниже самого низкого теоретического предела; это говорит
либо о том, что нейтронная звезда охлаждается быстрее, чем предсказывают
стандартные расчеты, либо о том, что после взрыва сверхновой
нейтронной звезды не осталось. Первую возможность можно объяснить более
экзотическими механизмами охлаждения (пионный конденсат или кварковое
Остывание нейтронных звезб
355
Таблица 11.1
ГОРЯЧИЕ НЕЙТРОННЫЕ ЗВЕЗДЫ В ОСТАТКАХ СВЕРХНОВЫХ
Название
Cas А
Сверхновая
Кеплера
Сверхновая Тихо
Крабовидная
туманность
SN 1006
RCW 86
W 28
G 350,0—18
G 22,7—0,2
Сверхновая в
Парусах
RCW 103
Возраст, ^)
лет
300
375
407
925
973
1794
3400
^10*
^10*
^10*
^103
/5,2)
кпс
2,8
8,0^)
3,0 4)
2,0
1,0
2,5 4)
2,3 5)
4,0 5)
4,8 5)
0,4
3,3
^тах ^^
0,4
0,2
0,5
1,6
3,3
2,5
5,0
7,0
7,0
1,4
Те^
\Ф К
<1,5
<2,1
<1,8
<2,0
<0,8
<1,5
<1,8
<2,0
<2,2
<1,5
<2,2
Литература
[416]
[272]
[272]
[256]
[472]
[272]
[271]
[271]
[271]
[257]
[581]
^) Возраст приведен на 1979 г. — Прим. перев.
2) Расстояние остатка сверхновой от Солнца.
3) Расстояние (от центра остатка сверхновой), в пределах которого
можно было бы найти звезду, если ее поперечная скорость не превышает
1000 км/с.
4) См. [624].
5) См. [140].
вещество), а вторая может потребовать пересмотра наших представлений
о сверхновых и нейтронных звездах^\
Из почти 50 остатков сверхновых, наблюдавшихся до настоящего
времени, только для четырех обнаружены свидетельства существования
центрального точечного рентгеновского источника. Помимо пульсара в Крабо-
видной туманности, лишь для пульсара в созвездии Парусов известно, что
он связан с остатком сверхновой. Наблюдения пульсара в созвездии
Парусов говорят о поверхностной температуре - 1,5 · 10^ К. Однако, как и для
пульсара в Крабовидной туманности, без информации о спектре нельзя
быть уверенным, что излучение является тепловым, так что приведенное
^^ Гипотеза о том, что сверхновые II типа оставляют после себя нейтронную
звезду, а сверхновые I типа полностью разрушают звезду, может частично
объяснить данные рентгеновских наблюдений [123, 420]. Обсуждение вопроса о типах
сверхновых см. в гл. 18.
356 Глава 11
значение лучше интерпретировать как верхний предел. Два других
точечных источника находятся в остатке RCW 103 и в ЗС 58 — возможном
остатке SN 1185. Для RCW 103 имеются указания на температуру 2,2 х
X 10^ К, а для ЗС 58 не получено надежного предельного значения. Неудача
попыток регистрации точечных источников в других остатках сверхновых
при переменных верхних пределах снова говорит либо о быстром
остывании, либо об отсутствии нейтронных звезд в большинстве остатков
сверхновых. На данном этапе можно только строить предположения о конечных
результатах этого важного исследования. Со всей очевидностью требуются
дальнейшие наблюдения и улучшенные теоретические расчеты.
Упражнение 11.9. Координатночувствительный пропорциональный счетчик на
обсерватории «Эйнштейн» имеет чувствительность 2,5 · 10~^ фотон/(см2 · с) в области
энергий 0,2—3,0 кэВ. Какой верхний предел для Tg может установить спутник, если
предположить, что нейтронная звезда имеет радиус 10 км и расположена на
расстоянии 100 ПС от нас?
Ответ: Т^ ^ 0,2 · 10^ К.
Упражнение 11.10. Используйте формулы для гравитационного красного смешения и
замедления времени и покажите, что сфера массой Л/ и радиусом /?, излучаюшая как
черное тело с температурой ? и светимостью L, при измерениях удаленным
наблюдателем проявляется как излучаюшая при температуре Т^ со светимостью Lc»> где
и
2М
-goo= ^ -
R
(Можно использовать тот факт, что удаленный наблюдатель видит также
распределение фотонов чернотельного излучения.)
Глава 12
Черные дыры
12.1. ВВЕДЕНИЕ
Мы видели в предыдущих главах, что для белых карликов, как и для
нейтронных звезд, существует максимальное возможное значение массы. Что
произойдет с нейтронной звездой, если она аккрецирует столько вещества,
что ее масса станет больше предельной? Какова судьба коллапсирующего
ядра массивной звезды, если масса ядра слишком велика, чтобы
образовать нейтронную звезду? Согласно общей теории относительности, в этом
случае никакая сила не может задержать коллапс. По мере углубления
коллапса гравитационные силы вблизи объекта становятся все сильнее. В
конце концов ничто не может вырваться из объекта во внешний мир, даже
свет. Черная дыра родилась.
Черная дыра определяется, как область пространства-времени, которая
не может сообщаться с внешней Вселенной. Граница этой области
называется поверхностью черной дыры, или горизонтом событий^К
Судьба коллапсирующего вещества после того, как оно пересечет
поверхность черной дыры, не известна. Плотность объекта с массой 1 М^
при образовании черной дыры должна составлять около 10^'^ г/см^, а для
больших масс она меньше. Можем ли мы утверждать, что при столь
экстремальных плотностях не существует каких-либо до сих пор неизвестных
источников давления, способных задержать коллапс? Ответ заключается в
том, что во время образования черной дыры уже слишком поздно
препятствовать коллапсу: вещество должно двигаться по мировым линиям
внутрь местного светового конуса, а геометрия пространства-времени
деформируется настолько, что не может ускользнуть даже «идущий наружу»
световой луч. В действительности, поскольку в теории относительности
гравитируют все формы энергии, увеличение давления только ускоряет
конечные стадии коллапса.
Если экстраполировать уравнения Эйнштейна внутрь черной дыры, то в
конце концов они нарушатся: развивается сингулярность. Квантовой
теории гравитации пока не существует, и некоторые полагают, что в такой
теории сингулярности не будет. Ее заменят конечные, хотя и невероятно
экстремальные условия.
^^ Строго говоря, горизонт событий — это трехмерная гиперповерхность в
пространстве-времени B-поверхность, существующая в течение некоторого
интервала времени). Однако мы будем свободно говорить о горизонте событий или о
поверхности черной дыры как о 2-поверхности в данный момент времени.
358 Глава 12
Упражнение 12.1. Постройте выражение для плотности на основе анализа
размерностей из с, G и И. Оцените численно эту «планковскую плотность», при которой
становятся важными квантовые гравитационные эффекты.
Ответ: ? - \0^ г/см^.
Пока сингулярность скрыта внутри горизонта событий, она не может
влиять на внешний мир. Как говорят, сингулярность «причинно
отключена» от окружающего мира. Мы, можем продолжать использовать общую
теорию относительности для описания наблюдаемой части Вселенной, хотя
и эта теория нарушается внутри черной дыры.
Можно ожидать, что решения уравнений Эйнштейна, описывающих
равновесные черные дыры, окажутся чрезвычайно сложными. В конце
концов черные дыры могут образовываться из звезд с самыми различными
распределениями масс, форм (мультипольные моменты), магнитных полей,
моментов количества движения и т.д. Любопытно, однако, что самое
общее решение для стационарной черной дыры известно в аналитической
форме. Оно зависит только от трех параметров: массы М, момента
количества движения J и заряда Q черной дыры. Вся остальная информация о
начальном состоянии теряется, излучаясь в виде электромагнитных и
гравитационных волн во время коллапса. Оставшиеся три параметра — это
независимые и наблюдаемые величины, которые полностью
характеризуют стационарную черную дыру^\ Эта ситуация отражена в афоризме
Уилера: «У черной дыры нет волос».
Масса черной дыры поддается определению, например, посредством
использования третьего закона Кеплера для спутников, находящихся в
гравитационном поле вдали от черной дыры. Заряд можно наблюдать по куло-
новским силам, действующим на пробный удаленный заряд. Момент
количества движения доступен для наблюдения по неньютоновским
гравитационным эффектам. Например, гироскоп, свободный от внешних
воздействий, будет прецессировать относительно инерциальной системы на
бесконечности (эффект Лензе-Тирринга).
12.2. ИСТОРИЯ ИДЕИ ЧЕРНОЙ ДЫРЫ
Еще в 1795 г. Лаплас [344] обратил внимание на следствие закона
тяготения Ньютона и ньютоновской корпускулярной теории света, согласно
которому свет не может покинуть объект, обладающий достаточно большой
массой и малым радиусом. Несмотря на столь раннее предсказание
возможности существования черных дыр, эта идея не нашла много
приверженцев даже после того, как была сформулирована общая теория
относительности.
^^ Полное обсуждение вопроса см. в [109].
Черные дыры 359
В декабре 1915 г. почти одновременно с опубликованием Эйнштейном
серии из четырех статей, где излагалась общая теория относительности,
Карл Шварцшильд [515] вывел общее релятивистское решение для
гравитационного поля, окружающего сферическую массу. Шварцшильд послал
статью Эйнштейну, чтобы тот пе^^дал ее в Берлинскую академию. В ответе
Шварцшильду Эйнштейн писал: «Я не ожидал, что можно было бы
сформулировать точное решение проблемы. Ваше аналитическое рассмотрение
проблемы представляется мне великолепным». Хотя значимость
результата представлялась очевидной для обоих, ни Эйнштейн, ни Шварцшильд и
никто другой в то время еще не осознавали, что решение Шварцшильда
содержит полное описание внешнего поля сферической электрически
нейтральной невращающейся черной дыры. Теперь мы называем такие черные
дыры шварцшильдовскими черными дырами, в честь Шварцшильда.
К^к мы указывали в гл. 3, Чандрасекар [112] открыл в 1930 г.
существование верхнего предела массы полностью вырожденной конфигурации. Как
почти сразу же понял Эддингтон [180], анализ Чандрасекара означал, что
образование черных дыр — это неизбежный итог эволюции массивных
звезд. Поэтому Эддингтон писал в январе 1935 г.: «Звезда, по-видимому,
должна очень долго излучать и сжиматься, пока не достигнет радиуса в
несколько километров, при котором тяготение станет достаточно сильным,
чтобы удержать излучение, и звезда сможет, наконец, обрести покой».
Однако, продолжая, он заявлял: «Я пришел к заключению, что это почти
доведение до абсурда формулы релятивистского вырождения. Различные
факторы могут сыграть свою роль, спасая звезду, но я хочу думать, что для
нее имеется более надежная защита. Я полагаю, что должны существовать
законы природы, не допускающие такого абсурдного поведения звезды».
Как видно из его заключительных замечаний, Эддингтон никогда не
принимал результаты Чандрасекара о существовании верхнего предела
массы холодной вырожденной звезды. И это несмотря на то, что Эддингтон
одним из первых понял и оценил общую теорию относительности
Эйнштейна! (Его книга [178] была первым учебником по общей теории
относительности, появившимся на английском языке.) Действительно, Эддингтон
в дальнейшем продолжал модифицировать уравнение состояния
вырожденного релятивистского газа таким образом, чтобы существовали конечные
равновесные состояния для звезд с произвольной массой^^
Правда, не один лишь Эддингтон не верил в неизбежность коллапса как
результата эволюции массивных звезд. Ландау в той же статье [337], где
приводится простой вывод предела массы (см. разд. 3.4), признавал, что
для звезд, превосходящих этот предел, «во всей квантовой теории не
существует причины, которая предотвратила бы коллапс системы в точку».
^^ Недавно Чандрасекар [118] высказал сожаление по поводу недальновидности
Эддингтона в отношении черных дыр, заявив: «Высочайший авторитет Эддингтона
в те годы задержал развитие плодотворных идей в этих направлениях почти на
тридцать лет».
360 Глава 12
Но вместо того, чтобы следовать трезвому совету, высказанному в начале
его статьи («Представляется разумной попытка подойти к проблеме
структуры звезд при помощи методов теоретической физики»), в конце ее
Ландау отступает и заявляет: «Поскольку в действительности такие массы
мирно существуют в виде [нормальных] з1езд и отнюдь не проявляют
таких абсурдных тенденций, приходится заключить, что все звезды тяжелее,
чем 1,5 Л/0, содержат область, в которой нарушаются законы квантовой
механики (и тем самым квантовой статистики)».
В 1939 г. Оппенгеймер и Снайдер [426] придали новый импульс
дискуссии, рассчитав коллапс однородной сферы с газом при нулевом давлении в
рамках общей теории относительности. Они нашли, что любая связь такой
сферы с остальной частью Вселенной в конечном счете нарушается. Это
был первый строгий расчет, продемонстрировавший образование черной
дыры.
Черные дыры и проблема гравитационного коллапса, как правило,
игнорировались до 60-х годов, даже дольше, чем нейтронные звезды. Однако
в конце 50-х годов Уилер и его сотрудники начали серьезное изучение
проблемы коллапса^^ В 1968 г. Уилер ввел термин «черная дыра» [611].
В 1963 г. Керр [311] нашел семейство точных беззарядовых решений
вакуумных уравнений поля Эйнштейна. Обобщение на случай заряда было
получено в дальнейшем Ньюменом и др. [419] как решение уравнений поля
Эйнштейна — Максвелла. Связь этих результатов с черными дырами была
понята позднее. Теперь мы знаем, что геометрия Керра — Ньюмена,
описываемая этими решениями, дает единственное и полное описание внешних
электромагнитного и гравитационного полей стационарной черной дыры.
В течение этого периода было открыто несколько важных свойств
черных дыр и доказано несколько существенных теорем, имеющих к ним
прямое отношение. Открытия квазаров в 1963 г., пульсаров в 1968 г. и
компактных рентгеновских источников в 1962 г. стимулировали интенсивное
теоретическое изучение черных дыр. Наблюдения за рентгеновским
источником Cyg Х-1, входящим в двойную систему, в начале 70-х годов (см.
разд. 13.5) дали первое правдоподобное свидетельство в пользу реального
существования черных дыр в космосе.
Перейдем теперь от истории к обсуждению физики черных дыр. Начнем
наше рассмотрение с обсуждения простейшей черной дыры с J = Q = 0.
12.3. ШВАРЦШИЛЬДОВСКИЕ ЧЕРНЫЕ ДЫРЫ
Повторим решение Шварцшильда, приведенное в уравнении E.6.8):
ds2=-{\-Ш\ dt^ + |i - ^y'dr' + гЧв' + r4in4d<t>\
A2.3.1)
I)
Результаты этих исследований приведены в книге [261].
Черные дыры 361
При этом используем геометризованные единицы {с = G =^ 1), введенные
в разд. 5.5.
Статический наблюдатель в этом гравитационном поле находится в
точке с фиксированными значениями л, ^, ?. Интервал собственного
времени для такого наблюдателя определяется уравнением A2.3.1) и
записывается в виде
j^2= _^^2 = |?_ 2^1^^2^ A2.3.2)
или
dr
= (,-?)",, (аз.3)
Это выражение для обычного гравитационного «растяжения» времени
(красное смещение), т.е. замедления часов в гравитационном поле по
сравнению с часами на бесконечности (?? < dt). Заметим, что уравнение A2.3.3)
нарушается при г = 2М. Этот радиус и есть горизонт событий (что
тождественно терминам поверхность черной дыры и радиус Шварцшильда),
По-другому его называют статическим пределом, поскольку внутри г =
= 2М никакой наблюдатель не может быть статическим, как мы увидим
позднее, он неумолимо затягивается в центральную сингулярность.
Статический наблюдатель выполняет измерения при помощи локальной
ортонормальной четверки координатных осей (см. разд. 5.1). Используя
«крышки» для обозначения величин в локальной ортонормальной системе,
получим из уравнения A2.3.1)
1/2
г
} '-
ei =
> rsL·^^- (»2.3.4)
Очевидно, что эта система координат ортонормальная, так как'*
?;·?;=(?-^) «'·«' = (?-^) «»=-1ит.д.A2.з.5)
^^Читатель может заново просмотреть конец разд. 5.2, где обсуждается
соотношение между ортонормальной и общей системами координат.
362 Глава 12
ПА. ДВИЖЕНИЕ ПРОБНОЙ ЧАСТИЦЫ
Чтобы исследовать геометрию Шварцшильда дальше, рассмотрим
движение свободно движущейся пробной частицы. Вспомним [см. уравнение
E.2.21)], что такие частицы движутся вдоль геодезических пространства-
времени, а уравнение геодезических можно вывести из лагранжиана
2L = - ?? - ^у + ?? - ^)" V + гЧ'^ + гЧтЧ^?, A2.4.
1)
где t S dt/dK - р^ — /-компонента 4-импульса и т.д. Мы выбрали
параметр ? таким образом, чтобы удовлетворить соотношению ? = т/т для
частицы с массой т.
Уравнения Эйлера—Лагранжа имеют вид
Для ?, ? и / они выглядят соответственно
''-(r2?) = /·^sin?cos??^ A2.4.3)
-^(r2sin2i?«i,) = 0, A2.4.4)
d_
d\
(¦-^)']-0. 02.4.5)
Вместо того, чтобы непосредственно использовать уравнение для г-
координаты, проще воспользоваться тем фактом, что
^???'^?^- -т\ A2.4.6)
Итак, величина L в уравнении A2.4.1) равна -т^/1.
Теперь уравнение A2.4.3) показывает, что если ориентировать систему
координат таким образом, чтобы вначале частица двигалась в
экваториальной плоскости (т.е. ? = ?/2, ? = 0), то частица останется в
экваториальной плоскости. Этот результат следует из теоремы единственности
решения таких дифференциальных уравнений, поскольку ? = ?/2 для всех
значений ? удовлетворяет уравнению. Физически этот результат очевиден,
если учесть соображения сферической симметрии.
При ? = ?/2 уравнения A2.4.4) и A2.4.5) принимают вид
/?Ф = ^^Ф = const = /^ A2.4.7)
/, 2Л/\.
-Pt^y- —у = const = ?. A2.4.8)
Черные дыры 363
Это просто интегралы движения, соответствующие циклическим
координатам уравнения A2.4.1) (см. разд. 5.2). Чтобы понять их физический смысл,
рассмотрим измерение энергии частицы, выполняемое статическим
наблюдателем в экваториальной плоскости. Эта локально измеряемая энергия
представляет собой временной компонент 4-импульса, измеренного в
локальной ортонормальной системе, т.е. проекцию 4-импульса на базисный
временной вектор:
/. 2М\-^/2
— A-—) Р^^
т.е.
?=(l-^)oca.· A2.4.9)
При А· — 00 получаем ^locai ¦" ^» поэтому сохраняющаяся величина ?
называется «энергией на бесконечности». Она связана с ^????? множителем,
определяющим красное смещение.
Упражнение 12.2. Для альтернативного вывода формулы красного смещения
используйте тот факт, что энергия ? постоянна вдоль траектории фотона, и покажите, что
^=(.-^)"'^ (.2.4.10)
для статического излучателя при г = г^^ и приемника, расположенного на
бесконечности. Объясните, почему горизонт событий для шварцшильдовской черной дыры
иногда называют «поверхностью бесконечного красного смещения».
Физическая интерпретация / следует из рассмотрения локально
измеряемой величины v^ — тангенциального компонента скорости
?
^ _ /?Ф _ ? * ёф ^ ? * У^ _ Рф/^
г;' р' ^local ^local ^local
И поэтому
/ = ?w.n)f A2.4.11)
Сравнивая с ньютоновским выражением mv^r, видим, что / — это
сохраняющийся момент количества движения частицы.
364 Глава 12
Рассмотрим теперь отдельно случаи: т ? О и т = О, Для частиц с
ненулевой массой покоя удобно перенормировать ? и I к величинам,
отнесенным к единице массы. Определим
Ё = -, / = -. A2.4.12)
т т
Затем, вспомнив, что ? = т/т, найдем из уравнений A2.4.6)-A2.4.8)
(^F=^'-(--^)(-Я· <'"¦"'
A2.4.14)
dt
dr \-2M/r'
A2.4.15)
Уравнение A2.4.13) можно решить в виде г = г(т) (в общем виде это
эллиптический интеграл), затем уравнение A2.4.14) дает ф(т), а
уравнение A2.4.15)—/(г).
Интересно рассмотреть орбиты, лежащие^ слегка над горизонтом
событий. Локально измеряемая величина v^ — радиального компонента
скорости — определяется выражением
t^' = ^ = -- = ^ = — ? = 7г, A2.4.16)
-^^ ''^ local ''^ local
вытекающим из уравнений A2.3.4) и A2.4.9). Вспоминая, что р'' = mdr/dr
и принимая во внимание уравнение A2.4.13), получим
11/2
, dr
?' = -:
Edr
-F(-^)l·;
A2.4.17)
Таким образом, при г -^ 2М находим у'^ — 1, т.е. частица с точки зрения
локального статического наблюдателя, расположенного в точке с
координатой А·, приближается к горизонту событий вдоль радиальной
геодезической со скоростью света (независимо от значений /).
Упражнение 12,3. Покажите, что тот же самый наблюдатель (находящийся в
точке с координатой г) обнаружит, что тангенциальная скорость частицы
удовлетворяет соотношению
2Л/\^/2 /
v^ = \\ -
так что i;^ — О при г — 2Л/.
('-?)'!·
Черные дыры 365
Упражнение 12.4. а) Покажите из уравнения A2.4.17), что локальный наблюдатель,
находящийся в точке с координатой г, обнаружит у частицы, свободно падающей
радиально из состояния покоя на бесконечности, скорость
J/2
v'-[^) , A2.4.19)
которая имеет точно такой же вид, что и ньютоновская скорость.
б) Получите такой же результат из уравнения A2.4.9), отметив, что Е^^^^^ s ут.
Упражнение 12.5. Частица перемещается вдоль геодезической от точки (г, ф) до
(г -^ dr, ? ¦? ??) за время dt. Локальный статический наблюдатель, находящийся в
(г, ф\ измеряет собственную длину траектории частицы, которую приходится
умножить на ?/5(/, 0, ? = const) = gi$dr{= dr) и ds{t, г, В = const) = g'^d?{- d?)
соответственно для направлений перемещения по г и 0 за это время; собственное время
этого движения, измеренное по часам наблюдателя, составляет [— ds'^{r, ?, ? =
= const]'/^ = i-^Q^Y'^^dti^dt). [Обратите внимание, что di для наблюдателя не
равно величине ?/?, появляющейся, например, в уравнениях A2.4.13)—A2.4.15) для
частицы!] Используйте выражения для этих измерений совместно с уравнениями
A2.4.13)-A2.4.15), чтобы вывести заново уравнения A2.4.17) и A2.4.18).
Простейшими геодезическими являются те, которые соответствуют
радиальному падению, т.е. ? = const. Это соотношение выполняется, если
/ = О и уравнение A2.4.13) принимает вид
^=-(?^-1+—) . A2.4.20)
Рассматривая для уравнения A2.4.20) предел л ^ оо, мы видим, что
возможны три случая: а) ? < 1, частица падает из состояния покоя при,
скажем, г =^ R; 6) ? = 1, частица падает из состояния покоя на
бесконечности; в) ? > 1, падающая частица на бесконечности имела конечную,
направленную внутрь скорость V = ?^.
Упражнение 12.6. а) Проинтегрируйте уравнение A2.4.20) для случая ? < 1, т.е. 1 -
- Е^ = 2M/R, и получите (т = О при г = /?)
-{та-^г-'Н^-')
A2.4.21)
б) Введите «параметр циклоиды» ?, исходя из уравнения
R
2
г = уA + cos ?), A2.4.22)
и покажите, что
(ш) (^ + ^i"^)· A2.4.23)
366
Глава 12
в) Проинтегрируйте уравнение A2.4.15) по времени в единицах ? и получите (/ =
= О при г = /?)
2Л/
= In
1/2
(R/2M - \У -l· tg(?/2)
1/2
(Л/2Л/-1)'/^- tg(v/2)
(R \^^ Г Л 1
2?-? [^ + 4a7^^^'^"^)J·
A2.4.24)
Отметим следующие важные результаты для случая радиального
падения: из уравнения A2.4.21) следует, что собственное время падения из
состояния покоя при г = R > 2М в точку г = 2Л/ конечно. Собственное
время падения в точку г = О равно ?(/?^/8?/)''^^; оно тоже конечно. Тем не
менее из уравнений A2.4.23) и A2.4.24) следует, что координатное время
(собственное время наблюдателя, находящегося на бесконечности)
падения в точку г = 1М бесконечно [при г = 1М получаем tg(T//2) = (R/2M -
- ?)'""']. Эти результаты отражены на рис. 12.1.
Упражнение 12.7. а) Найдите т(г) и /(г) для радиального падения при ? = \.
6) Найдите т(г), ?{?), ?{?) и ?{?) при ? > \. Эти величины можно получить из
уравнений A2.4.21)-A2.4.24), так определив R, чтобы 2M/R = Е^ - 1, и изменив
знак R в этих уравнениях. Покажите, что 2M/R = ??/(\ - у^.
Ответ: См. [366], стр. 407.
^, шварц,шильдовское
координатное время
15 20
Время/М
Рис. 12.1. Падение из состояния покоя на шварцшильдовскую черную дыру с точки
зрения наблюдателя, движущегося вместе с частицей (собственное время т), и
удаленного наблюдателя (координатное время Шварцшильда /)· С точки зрения первого
наблюдателя точка г = О достигается достаточно быстро [см. уравнение A2.4.23)].
Для удаленного наблюдателя точка г = О никогда не достигается и даже
приближение к г = 2М является асимптотическим [уравнение A2.4.24) [411].
Черные дыры
367
Перейдем теперь к нерадиальному движению. Получаемые из уравнений
A2.4.13)-A2.4.15) эллиптические интегралы трудно интерпретировать, но
мы можем получить общую картину орбит, рассматривая «эффективный
потенциал»
y(r).[^-Щ^Л\ (.2.4.25,
Тогда уравнение A2.4.13) принимает вид
(
^? = ?2 - V{r).
?? I
A2.4.26)
Для фиксированного значения Г потенциал V изображен схематически на
рис. 12.2. На диаграмме приведены^также три горизонтальные линии,
соответствующие разным значениям Е^. Из уравнения A2.4.26) следует, что
расстояние между горизонтальной линией и графиком V дает значение
{dr/dTY. Рассмотрим орбиту 7: горизонтальная линия с меткой 1
соответствует частице, пришедшей из бесконечности с энергией Е^. Когда
частица достигает радиуса, соответствующего точке Л, dr/dr проходит через
нуль и изменяет знак, т.е. частица возвращается на бесконечность. Такая
орбита называется несвязанной, а точка А называется точкой
поворота. Орбита 2 соответствует захвату: частица погружается в черную дыру.
Орбита 5 — это связанная орбита с двумя точками поворота Л| и А^-
Рис. 12.2. Профиль эффективного потенциала для частицы с ненулевой массой
покоя, движущейся по орбите относительно шварцшильдовской черной дыры с массой
Л/. Три горизонтальные линии с разными значениями Ё^ соответствуют
несвязанным орбитам (/), орбитам захвата B) и связанным орбитам C). Детали поясняются
в тексте.
368 Глава 12
Точка В соответствует устойчивой круговой орбите. Если движение
частицы будет слегка возмущено, орбита останется близкой к точке В, Точка С
соответствует неустойчивой круговой орбите: помещенная на такую
орбиту частица, получив малейшее возмущение, направленное внутрь по
радиусу, будет захвачена черной дырой. Если она получит возмущение,
направленное наружу, то улетит на бесконечность. Орбиты, похожие на / и 5,
рассматриваются и в ньютоновском случае движения в центральном
гравитационном поле, однако орбиты захвата существуют лишь в общей теории
относительности.
Упражнение 12.8. Покажите, что уравнение A2.4.26) сводится к привычному
ньютоновскому выражению для движения частицы в центральном гравитационном поле,
когда IM/r < 1.
Упражнение 12.9. а) Покажите, что dV/dr = О, когда
Л/г2 -/2^ + ЗЛ//^ = О, A2.4.27)
и, следовательно, для V нет ни максимума, ни минимума при / < 2\[3 М.
6) Покажите, что К^ах = 1 при ? = 4Л/.
Зависимость К от г для разных / показана на рис. 12.3.
Круговые орбиты существуют, если дУ/дг = О и dr/dr = 0. Уравнения
A2.4.26) и A2.4.27) дают
g-<r\">'. A2.4.29)
r{r - ЗМ)
Поэтому круговые орбиты существуют только до г = ЗМ — предельного
случая, соответствующего фотонной орбите (Е = Е/т — оо). Круговые
орбиты устойчивы, если график V вогнут, т.е. д^У/дР- > О, и неустойчивы,
если д^У/дг^- < 0. (Почему?)
Упражнение 12.10. Покажите, что круговые шварцшильдовские орбиты устойчивы,
если г > 6Л/, и неустойчивы, если г < в М.
Упражнение 12.11. а) Покажите, что в ньютоновской теории удаленная
нерелятивистская пробная частица может быть захвачена звездой с массой Л/ и радиусом R,
если только
'cnt "~
/-</,„, = BЛ/Л)'
б) Принимая во внимание эффекты общей теории относительности, ответьте,
могут ли частицы с гораздо большими значениями момента количества движения
захватываться нейтронными звездами? Белыми карликами?
Черные дыры
369
Рис. 12.3. Профиль эффективного потенциала для частиц с ненулевой массой покоя и
различными значениями момента количества движения Г, движущихся по орбите
относительно шварцшильдовской черной дьфы с массой М. Точки локальных
минимумов соответствуют радиусам устойчивых круговых орбит. Такие орбиты
существуют только для Г> bib ? [411].
8-513
370 Глава 12
Энергия связи, приходящаяся на единицу массы частицы, которая
находится на крайней устойчивой орбите с г = 6 Л/, в соответствии с
уравнением A2.4.29) составляет
I =5,72%. A2.4.30)
¦'binding щ
Это ДОЛЯ энергии покоя, выделяющаяся, скажем, когда покоившаяся на
бесконечности частица медленно приближается по спирали к самой
внутренней устойчивой круговой орбите, а затем круто падает на черную дыру.
Таким образом, преобразование массы покоя в другие формы энергии при
аккреции на черную дыру оказывается потенциально гораздо более
эффективным, чем при ядерном «сгорании», когда высвобождается максимум
0,9^0 энергии—массы покоя (Н — Fe). Это обстоятельство будет важным
для обсуждения аккреционных дисков вокруг черных дыр (см. разд. 14.5).
Высокая эффективность механизма аккреции служит основой для
привлечения черных дыр в качестве источников энергии в многочисленных моделях,
объясняющих астрономические наблюдения огромного энерговыделения из
компактных областей (например, Cyg Х-1, квазары, двойные
радиогалактики и т.п.).
Упражнение 12.12. а) Используйте уравнение A2.4.18) и покажите, что скорость
частицы на самой внутренней устойчивой круговой орбите, измеренная локальным
статическим наблюдателем, равна у<^ = 1/2 (с = 1).
б) Предположим, что эта частица испускает монохроматический свет, частота
которого в системе координат, связанной с частицей, равна ?'?^· Покажите, что
измеряемая на бесконечности частота периодически изменяется в пределах
Указание: Запишете р^/и,^ = (»'cx>/^tat)(^tat/»'em)» где
^stat частота, измеряемая
локальным статическим наблюдателем и связанная с и^^^ формулой Доплера из
специальной теории относительности.
в) Вычислите орбитальный период частицы, измеряемый локальным
статическим наблюдателем и наблюдателем на бесконечности.
Указание: Поскольку с1ф = гаф, собственная длина окружности орбиты равна
просто 1ш.
Ответ: Г,,,, = 247гЛ/, 7^ = Т,,Л1/ЪУ^^ = 4,5 · 10 " V Л//Л/о)с.
Упражнение 12.13. а) Покажите, что измеряемая на бесконечности угловая скорость
? S ??/? имеет такой же вид в геометрии Шварцшильда, как и для круговых орбит
в ньютоновской геометрии, а именно
J/2
? = (^) . A2.4.31)
б) Используйте этот результат для подтверждения значения Г^, найденного в
упражнении 12.12.
Черные дыры 371
Для последующего обсуждения аккреции на черную дыру нам
понадобится знать сечение захвата частиц, падающих на дыру из бесконечности.
Оно просто равно
^capt = ^^ах» A2.4.32)
где Ь^^ максимальный прицельный параметр захватываемой частицы.
Чтобы выразить b в единицах ?* и /, рассмотрим определение прицельного
параметра (рис. 12.4):
г-»оо
При А· — 00 уравнения A2.4.13) и A2.4.14) дают
^2 тг2
Ь= lim г sin ?. A2.4.33)
3) и A2.4.14) дают
li^f.^^zi. A2.4.34)
A2.4.35)
Подстановкой г = Ь/ф определяется соотношение
1 ?- 1
ИЛИ в единицах скорости на бесконечности ? = A - ??)~'^?
/ = ^oc(l - ^ly'^^ -^ ^00 ДЛЯ v^ « 1. A2.4.36)
Рассмотрим теперь нерелятивистскую частицу, движущуюся к черной
дыре (Е =^ 1, v^ < 1). Из упражнения 12.9 известно, что она
захватывается, если I < 4 М. Таким образом,
A2.4.37)
что дает сечение захвата
A2.4.38)
^capt ~~
??{2??
.,2
Частица
Рис. 12.4. Прицельный параметр b частицы с траекторией г = г{ф) движения
относительно массы М.
372 Глава 12
Эту величину следует сравнить с сечением захвата частиц сферой радиусом
R в ньютоновской теории:
^Newt = 'ГЛЧ 1 + -^ |. A2.4.39)
Итак, черная дыра захватывает нерелятивистские частицы как
ньютоновская сфера радиусом R = %М.
12.5. ОРБИТЫ БЕЗМАССОВЫХ ЧАСТИЦ
В ГЕОМЕТРИИ ШВАРЦШИЛЬДА
При WJ = О (например, для фотона) уравнения A2.4.6)-A2.4.8) принимают
вид
dt ?
dX 1-2Л//Г'
d± ^ J_
dX r^'
A2.5.1)
A2.5.2)
(dry ^, 1^(, 1M\
Согласно принципу эквивалентности, мировые линии частиц не должны
зависеть от их энергии. Это можно увидеть, если ввести новый параметр
A2.5.4)
Записав
[ A2.5.5)
И опустив индекс «new», найдем
^new - 1^-
b
, найдем
dt
dX
dX ~
U\2
b{\-
1
1
/
~ ?
1
• IM/r) '
1 /
A2.5.6)
A2.5.7)
Мировая линия зависит только от параметра Ь, представляющего собой
прицельный параметр частицы, а не от / и ?" по отдельности. Переходя в
уравнении A2.4.35) к пределу w — О, видим, что величина b в выражении
Черные дыры
373
A2.5.5) аналогична такой же величине, выведенной в предыдущем разделе
для частиц с массой.
Представление об орбитах фотонов можно получить, если исходить из
эффективного потенциала
так что уравнение A2.5.8) примет вид
.2
\^?) ~ ь^ ^phot@.
A2.5.9)
A2.5.10)
Ясно, что расстояние от горизонтальной линии высотой \/Ь^ до кривой
^phot Д^^т idr/d\Y. Величина Кр^о^ имеет максимум 1/B7 Л/^) при г = 3 М.
Это показано на рис. 12.5. Видно, что критический прицельный параметр,
разделяющий орбиты захвата и рассеяния, определяется выражением
1/Ь^ = 1/B7 М^), или
h = З/З ?.
A2.5.11)
Таким образом, сечение захвата падающих из бесконечности фотонов
равно
Vo. = ^ь! = пш\
A2.5.12)
Рис. 12.5. Профиль эффективного потенциала для частицы с нулевой массой покоя,
движущейся по орбите относительно шварцшильдовской черной дыры с массой М.
Если частица падает с расстояния г = оо с прицельным параметром b > З^ЗМ, она
рассеивается назад в бесконечность. Однако если b < З^ЗМ, частица захватывается
черной дырой.
374
Глава 12
Чтобы рассчитать наблюдаемое излучение газа вблизи черной дыры,
надо знать те направления движения, измеряемые статическим
наблиздателем, для которых фотон, излученный при радиусе г, может ускользнуть на
бесконечность. Обратившись к рис. 12.5, мы видим, что при г ^ 3 ?
фотон выйдет наружу, если только ?'' > О или же ?'^ < О и b > 3V3 ?, Если
ввести угол ? между направлением движения и радиусом (рис. 12.6), то
имеем (поскольку ??? = 1)
?"^ = sin ?, ?^ = cos ?.
Но уравнения A2.4.12) и A2.4.18) дают при b = 1/Е
»-^('-?)
1/2
A2.5.13)
A2.5.14)
Таким образом, движущийся в направлении черной дыры фотон ускользнет
от нее, если
sm
?>???(?_2?)
1/2
A2.5.15)
^?;^
-€—*
r/M
Рис. 12.6. a) Угол ? между направлением распространения фотона и радиальным
направлением в данной точке Р. б) Гравитационный захват излучения шварцшильдов-
ской черной дырой. Лучи, испускаемые из каждой точки внутрь затушеванной
конической полости, захватываются. Показаны полости захвата, измеренные в ортонор-
мальной системе отсчета локальным статическим наблюдателем.
Черные дыры 375
При г = 6М для ускользания требуется ур < 135°, при г = Ъ ? получаем
^ < 90°, так что все распространяющиеся внутрь фотоны будут захвачены
(т.е. 50^0 излучения стационарного изотропного излучателя,
расположенного при г = 3 Л/, захватывается черной дырой).
Упражнение 12.14, Покажите, что вылетевший наружу фотон, излученный между
г= 2Л/иг= ЗЛ/, ускользнет от захвата при условии
, З/ЗМЛ 2??
Когда источник приближается к г = 2М, ускользают только те фотоны,
которые испускаются наружу строго по радиусу. (См. рис. 12.6, где
показана диаграмма этих эффектов.)
12.6. «НЕСИНГУЛЯРНОСТЬ» РАДИУСА ШВАРЦШИЛЬДА
Метрика A2.3.1) кажется сингулярной при г = 2М: коэффициент при dt^
стремится к нулю, а коэффициент при dP- становится бесконечным. Однако
нельзя сразу же заключать, что такое поведение представляет собой
истинную физическую сингулярность. Действительно, коэффициент при d?^
обращается в нуль при ^ = О, но мы знаем, что это происходит просто
потому, что сама система полярных координат имеет здесь особенность.
Координатную особенность при ^ = О можно исключить выбором новой
системы координат (например, стереографических координат на 2-сфере).
Мы уже догадывались о том, что радиус Шварцшильда г = 2М является
лишь координатной сингулярностью. Вспомним, что при радиальном
падении частицы не отмечается ничего странного в точке г = 2 М; нет ничего
особого и в поведении г{т) в этой точке. Однако координатное время t
становится бесконечным при г = 2 Л/. Это дает веские основания
предполагать наличие координатной, а не физической сингулярности.
Есть много разных преобразований координат, которые можно
использовать для убедительного доказательства, что г = 2 Л/ не является
физической сингулярностью. Мы продемонстрируем одно из них — систему
координат Крускала [320, 555]. Она определяется преобразованием
^-[ш-'] ^''^"^•^?· A2.6.2)
Обратное преобразование задается формулами
( 2? "^)''^'''° "'"'"'' ^^^-^-^^
— = ?
4М ~ и
th^^ = -. A2.6.4)
376
Глава 12
Метрика A2.3.1) принимает вид
^2 = 32^^_,/2л,(_^^2 ^ ^^2) ^ ^2^^2 ^ гЧт'ваф\ A2.6.5)
где величина г неявно связана с м и ?; посредством уравнения A2.6.3). Ясно,
что при г = 2М метрика A2.6.5) не является сингулярной. Тем не менее
при г = О сингулярность все же существует. Можно показать, что это
реальная физическая сингулярность метрики, где напряженность
гравитационного поля становится бесконечной.
Заметим, что, согласно уравнению A2.6.3), г = О при ?^ — и^ = 1, или
V = ±A + и^У^^. Оказывается, существуют две сингулярности! Заметим
также, что г ^ 2Л/ — это область с м^ ^ ?^, т.е. м ^ \?\ или и ^ - \?\.
Другими словами, условию г ^ 2 Л/ соответствуют две области!
Начальная система координат Шварцшильда покрывает только часть
многообразия пространства-времени. Координаты Крускала дают
аналитическое продолжение тех же решений уравнений поля на все многообразие
пространства-времени. Эта ситуация отражена на диаграмме Крускала
(рис. 12.7). Координаты Крускала обладают одним замечательным
свойством: лучи света, идущие вдоль радиуса, изображаются прямыми линиями,
наклоненными под углом 45° к координатным осям [см. уравнение A2.6.5)
при ds^- = 0]. Диаграмма Крускала является пространственно-временной
диаграммой, где «временная» координата ? отложена вертикально, а
«пространственная» координата и — горизонтально. Ее можно рассматривать
? = 2?,?/ = ?;
Световой
конус
г = 0,1/ = -/1 +и^
Рис, 12,7, Диаграмма Крускала метрики Шварцшильда.
Черные дыры 377
как пространственно-временную диаграмму специальной теории
относительности, потому что в каждой точке световые конусы ограничены
прямыми линиями, наклоненными под углами ±45° к координатным осям, а
мировые линии частиц должны лежать внутри световых конусов.
Область I — это «наша вселенная», начальная область с г > 2 Л/.
Область II — это «недра черной дыры» с г < 1М. Области III и IV — это
«другие вселенные»: причем при г > 1М область III является
асимптотически плоской, а области IV соответствует г < 2Л/.
Если проверить знаки м и ?; в разных квадрантах, то обнаружится связь
между координатами Крускала и Шварцшильда в разных областях
[сравните с уравнениями A2.6.1) и A2.6.2)]:
и
Aim-') ^''^"^"ш' 02.6.6)
= ^{-
(г \V2 /
"=±BM-V ^'"'"^^?' ('•>2Л/), A2.6.7)
И
Здесь верхний знак относится к «нашей вселенной», а нижний — к «другой
вселенной». Уравнение A2.6.3) сохраняет силу всюду, в то время как
правая часть уравнения A2.6.4) становится равной и/? при г ^ 2М. Уравнение
A2.6.4) показывает, что линии с постоянным t являются прямыми. Эти
взаимосвязи видны на рис. 12.8.
Сингулярность в верхней части диаграммы Крускала при г = О
находится внутри черной дыры. Ясно, что любая времениподобная мировая линия
при г ^ 2М (т.е. в области II) должна попадать в сингулярность.
Сингулярность в нижней части диаграммы представляет собой «белую дыру», из
которой с формальной точки зрения может что-то извергаться.
Важно представлять, что полная аналитически продолженная метрика
Шварцшильда — это просто математическое решение уравнений
Эйнштейна. Для черной дыры, возникшей при гравитационном коллапсе, часть
пространства-времени должна содержать коллапсирующее вещество. Из
теоремы Биркгофа (см. разд. 5.6) известно, что вне коллапсируюшей
звезды геометрия по-прежнему описывается метрикой Шварцшильда. Таким
образом, мировая линия точки, находящейся на поверхности звезды, будет
границей части диаграммы Крускала, имеющей физический смысл (рис.
12.9). В реальных черных дырах никаких «белых дыр» и «других
вселенных» не существует.
378
Глава 12
^?=2,5?
V"i = -2,5M
i = -2.5A/
Рис. 12.8. Диаграмма Крускала метрики Шварцшильда, показывающая связь между
координатами Шварцшильда (/, г) и координатами Крускала (у, и).
Рис. J2.9. Диаграмма Крускала для гравитационного коллапса. Физический смысл
имеет только незаштрихованная часть диаграммы справа от поверхности звезды.
Остальная часть диаграммы должна быть заменена пространственно-временной
геометрией недр звезды.
Черные дыры 379
Диаграмма Крускала проясняет два основных свойства черных дыр: как
только объект пересечет г = 2 Л/, он обязательно должен попасть в
сингулярность при г = 0; находясь внутри г = 2 Л/, объект не может посылать
сигналы на бесконечность. Однако для этого горизонта нет никакого
локального метода проверки. Наблюдатель не замечает около себя ничего
существенно нового при переходе от г = 2Л/ +?кг=2Л/— ?.
12.7. ЧЕРНЫЕ ДЫРЫ КЕРРА
Наиболее общая метрика стационарной черной дыры с параметром Л/, У и
Q называется метрикой Керра—Ньюмена (см., например, [411]).
Специальными случаями ее являются метрика Керра (Q = 0), метрика Рейснера—
Нордстрема (У = 0) и метрика Шварцшильда (Q = О, У = 0).
Заряженный астрофизический объект обычно быстро нейтрализуется
окружающей плазмой. Соответственно мы упростим наше обсуждение,
предположив, что заряженные черные дыры вряд ли окажутся важными с
астрофизической точки зрения. В то же время все астрофизические объекты
вращаются и потому ожидается, что образовавшиеся при гравитационном
коллапсе черные дыры должны быть в общем случае вращающимися.
Примечательно, что, когда прекращается испускание разного рода излучений,
возникших при коллапсе, гравитационное поле асимптотически
подстраивается к метрике Керра.
Это решение уравнений Эйнштейна, найденное Керром в 1963 году,
сначала не интерпретировалось как решение, относящееся к черной дыре. Его
свойства более понятны в координатах Бойера—Линдквиста [81], где
ds
= -(^--2-) ^^ ? ^^^^ ^ ?^^ ^
^Ide^ + (г^ ^а^^ ^^^^^jsin^^^ф^ A2.7.1)
Здесь черная дыра вращается в направлении ? и
? =^, Д^г^-2Mr-l·?^ ? = г^ -l· а^соз^в. A2.7.2)
?
Эта метрика стационарна (не зависит от t) и осесимметрична
относительно полярной оси (не зависит от ф). Отметим, что а — момент количества
движения, приходящийся на единицу массы, измеряется в сантиметрах,
если принять систему единиц, в которой с = G = 1. Подстановка в
уравнение A2.7.1) значения а = О дает метрику Шварцшильда.
Упражнение 12,15. Момент количества движения Солнца (если предположить
твердотельное вращение) равен У = 1,63 · 1(У*^ г · см^/с. Каково значение а/? для
Солнца?
Ответ: 0,185.
380 Глава 12
Горизонт появляется там, где обращается в нуль функция метрики ?.
Это происходит прежде всего при большем корне квадратного уравнения
? = О,
?·^=?+(?2-?2)?/2 A2.7.3)
Заметим, что а должно быть меньше Л/, чтобы черная дыра существовала.
Если а превышает Л/, то будем иметь гравитационное поле с «голой»
сингулярностью (т.е. не «прикрытой» горизонтом событий). Крупной
нерешенной проблемой в общей теории относительности остается
предположение Пенроуза о «космической цензуре», согласно которому
гравитационный коллапс при свободных от особенностей начальных условиях никогда
не приводит к появлению «голой» сингулярности. Конечно, неизвестны
никакие механизмы, посредством которых исходная черная дыра Керра с
а < ? раскручивается так, чтобы а стало больше Л/ (см. разд. 12.8).
Черная дыра с а = ? вращается с максимальной скоростью.
Для обсуждения метрики Шварцшильда было полезно понятие
статического наблюдателя. Это обсуждение можно обобщить на случай
вращающихся черных дыр, если ввести в употребление понятие стационарного
наблюдателя, который находится в точке с фиксированными значениями г
и ^, но вращается с постоянной угловой скоростью
Условие U · U = -1 (т.е. наблюдатели движутся по времениподобной
мировой линии) имеет вид
-l = ("')'[g„ + 2S2g„ + S^,J, A2.7.5)
где уравнение A2.7.4) было использовано для замены м^. Поэтому член
уравнения A2.7.5), находящийся в квадратных скобках, должен быть
отрицательным. Поскольку ^фф в уравнении A2.7.1) — величина положительная,
так может быть, если только значение ? лежит между корнями
квадратного уравнения, полученного приравниванием нулю выражения в квадратных
скобках. Таким образом,
где
"min < ? < "шах» A2.7.6)
о = ^^^ ^^^^ ^??8??) (]2??)
min офф
Упражнение 12.16. Обсудите ограничение A2.7.6) в пределе слабого поля.
Ответ: -с/{гппв) < ? < с/(г sin^); стационарные наблюдатели должны
вращаться относительно оси ? с ? < с.
Черные дыры 381
Bu9 сверху Bu9 с5оку
Рис. 12.10. Эргосфера черной дыры Керра: область между статическим пределом
[уплощенная внешняя поверхность г = Л/ + (Л/^ - а^ cos^^)^^^] и горизонтом
событий [внутренняя сфера г = Л/ + (Л/^ - (?'?^\
Обратите внимание, что Q^^jn = О, когда g^^ = О, т.е. когда г^ - 2Мг +
+ a^cos^-? = 0. Это происходит при
Го = ? + (М^ - a^cos^eY^\ A2.7.8)
Находящиеся между г^ и Tq наблюдатели должны иметь ? > 0; в
диапазоне г^ < г < Tq нет статических наблюдателей (? = 0). Поэтому
поверхность г = Го называется статическим пределом. Она называется также
«границей эргосферы» по причинам, которые станут ясными позднее.
Обратите внимание, что для а ? О понятия горизонта г^ и
статического предела Го различны. Это отражено на рис. 12.10. Уравнение A2.7.7)
показывает, что стационарные наблюдатели не могут существовать, когда
8}ф - 8п8фф < О, т.е. когда ? < О, это возможно лишь при г < г^ . Таким
образом, мы приходим к обобщению предыдущего вывода, что
статические наблюдатели не существуют внутри горизонта для шварцшильдовской
черной дыры.
Метрику Керра можно аналитически продолжить внутрь г = г,^,
способами, аналогичными крускаловскому продолжению метрики Шварцшильда.
Однако это внутреннее решение не имеет физического смысла по двум
причинам. Во-первых, часть его надо заменить недрами коллапсирующего
объекта, образующего черную дыру. Во-вторых, что более важно, для
коллапса с вращением нет теоремы Биркгофа. Метрика Керра — это не
метрика внешнего пространства в процессе коллапса, это только
асимптотическая форма метрики, соответствующая прекращению всех динамических
процессов. Ее математическое продолжение внутрь г^ фактически не имеет
смысла. Поэтому ограничимся обсуждением области г ^ г^ и примем
точку зрения, что все, попадающее внутрь этой области, становится причинно
разобщенным с остальной частью Вселенной.
Полное описание геодезических черной дыры Керра весьма сложно из-за
отсутствия сферической симметрии. Тем не менее существует «скрытая»
симметрия, которую можно использовать для аналитического решения
задачи о геодезических [108, 411]. Чтобы хотя бы немного понять влияние
вращения на геодезические, ограничимся рассмотрением пробной частицы в
382 Глава 12
экваториальной плоскости. Это можно сделать непосредственно без
привлечения скрытой симметрии.
Положив ? = ?/1 в уравнении A2.7.1), получим лагранжиан
2L = - (l - —? —t^ ^ ?"^ "^ ('¦ ^'^^ ~~?? '
A2.7.9)
где i = dt/d\ и т.д. Для циклических координат ? и ? получаем два первых
интеграла движения
р, = -^ = const = -?, A2.7.10)
Рф =-^= const =/. A2.7.11)
Вычислив производные из уравнения A2.7.9) и решив два уравнения для / и
ф, получим
(г^ + flV + 2Ма^)Е - laMl П2 7 12)
. ^ (г~2М)/+2аМ? A2.7.13)
^ гД
Третий интеграл движения получим как обычно, приравняв ga?P°^P^ =
= -w^, т.е. L = -wV2. После подстановки уравнений A2.7.12) и
A2.7.13) и некоторых упрощений имеем
r^[^f = R{EJ,r), A2.7.14)
где
R = ?2(,.3 + д2^ + 2Mfl2) - 4flM?/ - (г - 2М)/2 - ш^Д. A2.7.15)
Можно рассматривать R как эффективный потенциал радиального
движения в экваториальной плоскости^^ Например, круговые орбиты
существуют там, где dr/d\ остается равной нулю (точка бесконечных поворотов).
Это требует
л = о, -^7 = ^- A2.7.16)
^^ Некоторые авторы определяют эффективный потенциал как величину ?,
приводящую к соотношению R = 0; мы поступали так для шварцшильдовского случая
в уравнении A2.4.26).
Черные дыры 383
После громоздких алгебраических выкладок уравнения A2.7.16) могут быть
решены по отношению к ? и I, что дает
? = r'-2Mr±a{Mr _ ^^^.?.??)
r{r^ - ЗMr±2a^/M?У^^
r{r^- ЪМг±1а{МгУ^"
В данном случае верхний знак относится к прямым орбитам (т.е. момент
количества движения частицы параллелен моменту количества движения
черной дыры), а нижний знак — к обратным орбитам. Эти формулы
обобщают уравнения A2.4.28)-A2.4.29) для метрики Шварцшильда.
Упражнение 12.17. Покажите, что третий закон Кеплера принимает вид
?= ±— — A2.7.19)
для круговых экваториальных орбит в метрике Керра (? = — = o/t)
dt
Круговые орбиты существуют повсюду, начиная от г = оо вплоть до
предельной круговой фотонной орбиты, где обращается в нуль
знаменатель формулы A2.7.17). Решив получившееся кубическое по отношению к
г^^ уравнение, найдем условие, определяющее фотонную орбиту [45]:
Грь = 2МA + cos[| arccos {??/?)]), A2.7.20)
Для flf = О получаем г^^^ = Ъ М, г, при а = ? находим г^^ = Л/ (для
прямых орбит) или 4 Л/ (для обратных орбит).
При г > г^ не все круговые орбиты оказываются связанными. У
несвязанной круговой орбиты Е/т > 1. Под воздействием бесконечно малых
возмущений, направленных наружу, частица с такой орбитой уходит на
бесконечность по асимптотически гиперболической траектории. Связанные
круговые орбиты существуют при г > г^^^, :де г^^^,—предельный
радиус связанной орбиты, соответствующий Е/т = 1:
г^ь = 2М ? А + 2М'^ЦМ + аУ^\ A2.7.21)
Отметим также, что г^^ — это минимальный периастр всех
параболических (Е/т = 1) орбит. В астрофизических задачах падающие из
бесконечности частицы движутся по орбитам, очень близким к параболическим,
поскольку ?^ < с. Любая параболическая траектория, проникающая до
384 Глава 12
г < Tjj^jj, должна приводить в черную дыру. При ? = О получается г^^ =
= 4М, при а = ? находим г^^ = Л/ (прямые орбиты) или г^^ = 5,83 Л/
(обратные орбиты).
Далеко не все связанные круговые орбиты оказываются устойчивыми.
Для устойчивости требуется, чтобы
< 0. A2.7.22)
Из уравнения A2.7.15) получаем
1-(?)^>|у. A2.7.23)
Подставив это в уравнение A2.7.17), получим уравнение четвертой степени
для г'^^ в предельном случае равенства. Решение для г^^^^—предельного
радиуса устойчивости круговой орбиты дано Бардином и др. [45]:
г^ = МC + Z2 ? [C - Z,)C + ?, + 2Z,)]'/'},
,'/3r
?, = 1 +
-я?^^rн^-m¦
\·/^
^2-^3- +Zfj . A2.7.24)
При ? = 0 получается r^^ = 6 Л/, при а = ? находим г^^ = Л/ (прямые
орбиты) или 9 Л/ (обратные орбиты). Большой интерес для оценки
потенциальной эффективности аккреционного диска черной дыры в качестве
источника энергии представляет энергия связи предельной устойчивой
круговой орбиты. Если исключить г из уравнения A2.7.17) при помощи
уравнения A2.7.23), получим
А^ 3/3A-?2)
Величина ? уменьшается от yiS79 (а = 0) до \??/3 (а = Af) для прямых
орбит, но в то же время возрастает от V8/9 до V25/27 для обратных
орбит. Максимальная энергия связи A - Е) черной дыры, вращающейся с
максимальной скоростью, равна 1 - 1/V3, или 42,3^о всей энергии покоя.
Это количество энергии, высвобождаемое веществом, которое движется по
спирали к черной дыре'и проходит последовательность почти круговых
экваториальных орбит. На конечном этапе погружения с г^^^^ в черную дыру
выделяется ничтожно мало энергии.
Обратите внимание, что система координат Бойера—Линдквиста
сводит Tj^g, Tj^b» '*ph ** '*+ к '* = А^ при ? — Л/. Как отмечается в [45], этот эф-
Черные дыры 385
фект кажущийся и зависит от выбора системы координат. В
действительности же радиусы относятся к различным областям пространства-времени.
Исключительно интересное свойство вращающихся черных дыр
заключается в том, что существуют траектории пробных частиц с
отрицательной энергией. Если решать уравнение A2.7.14) относительно ?, находим
^ 2аМ1 + (/?^? + mVA + r^'r")'^^
^ = 1 1 ??7~2 ' A2.7.26)
(Знак квадратного корня определяется, если положить г — оо.) Чтобы
получить ?¦ < О, требуется орбита с обратным движением (/ < 0),
удовлетворяющая соотношению
/?^? + wVA + ?? < ??^??. A2.7.27)
Граница области с орбитами, имеющими отрицательную энергию,
находится, если сделать левую часть неравенства A2.7.27) настолько малой,
насколько это возможно. Для этого положим т ^ О (ультрарелятивистская
частица) и г ^ 0. Тогда найдем, что граница лежит при г = 2Л/ = Tq (^ =
= ?/2). Можно показать, что статический предел Tq является границей
области, содержащей орбиты с отрицательной энергией, при всех значениях
?. Частица может быть только инжектирована на такую орбиту внутри
статического предела, а затем она опускается в черную дыру.
Пенроуз [453] использовал это свойство черных дыр Керра в
замечательном мысленном эксперименте для демонстрации того, что
вращающиеся черные дыры являются потенциально громадными хранилищами
энергии. Представим, что из бесконечности направляется частица с энергией
Е^. Ее траектория подобрана так, чтобы она попадала внутрь
статического предела. «Проинструктируем» частицу (или заранее запрограммируем
ее), чтобы она после этого разделилась надвое. Тогда один из кусочков
идет на траекторию с отрицательной энергией и опускается в черную дыру
с энергией ^'^own ^ ^- ДРУгой возвращается на бесконечность с энергией
^Ouj. Законы сохранения энергии требуют
?in =-Бои. + ^down, т.е. E^,>EJ A2.7.28)
Хотя при этом какая-то масса покоя теряется в дыре, есть энергетический
выигрыш на бесконечности. Энергия извлекается из энергии вращения
дыры, которая слегка замедляется при захвате частицы с отрицательной
энергией и обратным вращением.
Область, лежащая в пределах г^ < г < Tq, где возможно извлечение
энергии, называется эргосферой (от греческого слова, означающего
работу).
К сожалению, маловероятно, чтобы оригинальный процесс Пенроуза
был важным с астрофизической точки зрения. Бардин и др. [45] показали,
что развал частицы надвое внутри эргосферы должен происходить с
относительной скоростью, равной по крайней мере с/2; трудно представить
астрофизические процессы, приводящие к столь большим относительным
скоростям.
9-513
386 Глава 12
Прирост энергии происходит также при рассеянии волн
(электромагнитных или гравитационных) соответствующей частоты вращающейся
черной дырой. Волна частично поглощается, но рассеиваемая часть может при
соответствующих условиях получить больше энергии, чем имела падающая
волна. Важно ли рассматриваемое сверхизлучение с астрофизической точки
зрения, это открытый вопрос. Механизм сверхизлучения привлекается и в
качестве основы идеи «чернодырной бомбы» и как средство решения
высокоразвитыми цивилизациями своих энергетических проблем [465]. Между
прочим, было показано, что вращающиеся черные дыры являются
динамически устойчивыми объектами в том смысле, что они не могут спонтанно
«взрываться», выделяя энергию [466, 563] (см. также разд. 12.8).
Упражнение 12.18. Рассмотрите частицу с / = О, выведенную из состояния покоя на
большом расстоянии от черной дыры Керра. Покажите, что частица «вращается
синхронно с геометрией» по мере того, как она приближается по спирали к черной
дыре вдоль конической поверхности с постоянным значением ?. Другими словами,
покажите, что частица, если смотреть из бесконечности, набирает угловую скорость
??/? = ?(?, ?), где
?(?, ?)
Указание: Наблюдатели, находящиеся при фиксированных г и ^ с нулевым
моментом количества движения, также «вращаются синхронно с геометрией» с угловой
скоростью ?(?, ?). Такие наблюдатели определяют так называемую «локально не-
вращающуюся систему координат» (см. [45]); таким наблюдателям освободившаяся
ча'^'^ица, описанная выше, представляется движущейся в радиальном направлении.
Процедура определения углов испускания, приводящих к захвату фотона
или к освобождению фотонов из излучающего источника, расположенного
вблизи черной дыры Керра, была обрисована Бардином [44]. Захват
следует рассматривать всякий раз, когда требуется определить природу
фактически наблюдаемого на бесконечности излучения, испускаемого локальным
источником вблизи черной дыры. Для вращающейся черной дыры в
локально невращающейся системе координат преимущественно
освобождаются на бесконечность те фотоны, которые излучаются с у^ > 0. В
приложениях общего характера расчет углов выхода должен проводиться численно
[153, 527].
12.8. ТЕОРЕМА О ПЛОЩАДЯХ И ИСПАРЕНИЕ ЧЕРНОЙ ДЫРЫ
Хокинг [268] доказал замечательную теорему о черных дырах: при любом
взаимодействии площадь поверхности черной дыры никогда не может
уменьшиться. Если присутствует несколько черных дыр, сумма площадей
поверхности также никогда не может уменьшиться.
Черные дыры 387
Площадь поверхности черной дыры Керра можно совсем просто
вычислить из метрики A2.7.1). Положив / = const, г = г^ = const и использовав
уравнение A2.7.3), найдем метрику на поверхности
ds^ = (?·2+ a\os4) ??^ + -^~^sin4d^>\ A2.8.1)
Площадь горизонта равна
А = (jy[gdBd<i> = j J2Mr^uneded<i>
= 87гМ[м+ (M2-a2y/2j^ A2.8.2)
где g — детерминант коэффициентов метрики, появившихся в уравнении
A2.8.1). Обратите внимание, что для ? = О получается А = 4?B?)^, как и
ожидалось.
Упражнение 12.19. Используйте теорему площадей Хокинга и найдите
минимальную массу ^2 черной дыры Шварцшильда, возникающей при столкновении двух
черных дыр Керра с одинаковой массой Л/, но противоположно направленными
моментами количества движения а. Покажите, что если \а\ — Л/, может быть
излучено 50^0 массы покоя. Покажите, что ни при какой другой комбинации масс и
моментов количества движения не достигается более высокая эффективность.
Покажите, что, если ?7 = О, максимальная эффективность равна 19Щ.
Замечание. Фактическое количество энергии, генерируемое при таком
столкновении, поддается численному расчету. В общем виде результат еще неизвестен, но для
flf = О он составляет 0,1 <7о [544]. См. также гл. 16.
Теорему площадей можно использовать для доказательства, что нельзя
получить «голую» сингулярность, добавляя частицы к черной дыре,
вращающейся с максимальной скоростью, чтобы заставить ее «раскрутиться»
еще сильнее. Из уравнения A2.8.2) находим, что условие ЬА > О
подразумевает
[lM{M^ - ?^?^^ + 2М^ - а^] 8М > ????. A2.8.3)
Когда а ^ М, это соотношение принимает вид
?8?>???. A2.8.4)
Таким образом, М^ всегда остается больше а^ и горизонт не исчезает
[сравните с уравнением A2.7.3)]. Сечение захвата частиц, увеличивающих
значение а/М, падает до нуля при а ^ М.
Закон увеличения площадей выглядит очень похожим на второй закон
термодинамики. Бикенстейн [59] пытался разработать термодинамику
взаимодействия черных дыр. Однако в классической общей теории
относительности нет равновесного состояния, включающего черные дыры. Если
поместить черную дыру в термостат, она будет непрерывно поглощать
излучение, не приближаясь к равновесию.
388 Глава 12
Ситуация изменилась благодаря замечательному открытию Хокинга
[266, 267], который обнаружил, что, если принять во внимание квантовые
эффекты, черные дыры должны испускать излучение с тепловым спектром.
Ожидаемое число частиц данного вида, излучаемое в режиме с частотой ?,
равно
<^> = ,, ^,^4 -г , > A2.8.5)
где Г — коэффициент поглощения для этой моды излучения, падающего на
дыру. Коэффициент поглощения Г является медленно меняющейся
функцией ?, зависящей от типа излучаемых частиц, и близок к единице для длин
волн, сильно превышающих М; для простоты мы примем его равным
единице. Температура черной дыры обратно пропорциональна ее массе
^= siu/= ^^-^^^(^)- 02-В.6)
Заметим, что «планковская масса», «планковский радиус» составляют
h'^' = 2,2 · 10"^ г = 1,6 · 10"" см A2.8.7)
в системе единиц, где с = G = 1.
Упражнение 12.20. Проверьте соотношение чисел в уравнениях A2.8.6) и A2.8.7).
Приведем формулы Хокинга для шварцшильдовской черной дыры. Их
можно легко обобщить, учитывая заряд и вращение. Из соображений
размерности ? получается путем приравнивания длины волны теплового
излучения^^ hc/kT радиусу Шварщпильда. Из-за тепловой природы спектра
образуются главным образом безмассовые частицы (фотоны, нейтрино и
гравитоны). Для создани? значительного количества частиц с массой т
требуется, чтобы кТ - wc^, т.е. радиус Шварцшильда должен быть
порядка комптоновской длины волны ?^ - h/mc частицы.
Теперь можно вычислить энтропию черной дыры. Поскольку площадь
равна (при восстановлении значений с и G)
]Ш.^ A2.8.8)
= 4^(^
с^ I
имеем
если определить энтропию S в виде
кс^ 1
Gn 4
^) Эта длина приблизительно соответствует среднему расстоянию между
фотонами в равновесии при температуре Т.
Черные дыры
389
Отношение макроскопической величины И) к микроскопической (Л)
гарантирует, что черные дыры обладают высокой энтропией. Это согласуется с
идеями об «отсутствии волос», утверждающими многообразие внутренних
состояний черной дыры, соответствующих данному внешнему
гравитационному полю, а также с утверждением, что при образовании черной дыры
информащ1я теряется для внешнего мира [60].
Отметим, что во время «испарения» черной дыры (излучение тепловых
квантов) вследствие закона сохранения энергии Л/, а также Л (н S)
уменьшаются. Это нарушает теорему Хокинга о площадях. Однако один из
постулатов теоремы о площадях заключается в том, что вещество
подчиняется «сильным» энергетическим условиям, в любом случае требующим от
локального наблюдателя измерений положительных плотностей энергии и
отсутствия п^)остранственно-подобных потоков энергии. Испарение черной
дыры можно представить как образование пар частиц в ее гравитационном
поле, причем один из членов этой пары падает на черную дыру, а второй
улетает на бесконечность. При образовании пары две частицы
материализуются с пространственно-подобным разделением — в сущности это и
есть пространственно-подобный поток энергии.
Теорема о площадях, полученная в рамках классической общей теории
относительности, заменяется обобщенным вторым законом
термодинамики: в любом взаимодействии сумма энтропии всех черных дыр и энтропии
вещества вне черной дыры никогда не уменьшается. Таким образом,
черные дыры не просто подчиняются законам, аналогичным законам
термодинамики; они на самом деле очень естественно входят в расширенные
рамки термодинамики.
Процесс Хокинга можно качественно понять, рассматривая вначале
образование пар частиц в сильном электрическом поле?' (рис. 12. И). В
квантовой механике вакуум непрерывно флуктуирует с образованием и последу-
-\с-^
е~
Рис. 12.11. Образование пар частиц в сильном электрическом поле.
390 Глава 12
ющей аннигиляцией пар «виртуальных» частиц. Электрическое поле
стремится разделить заряды. Если поле достаточно сильное, частицы «тунне-
лируют» под квантовым барьером и материализуются в виде реальных
частиц. Критическая напряженность поля достигается тогда, когда работа по
разведению частиц на расстояние порядка комптоновского радиуса равна
энергии, необходимой для образования частиц
еЕХ^- 1тс^. A2.8.11)
В случае черной дыры приливное воздействие гравитационного поля
на расстоянии ?^ по порядку величины равно
GmM.
г'
-?,. A2.8.12)
Произведенная работа равна произведению этой силы на ?^. Положив г -
- GM/c^, поскольку напряженность поля максимальна около горизонта, и
приравняв эту работу энергии 2 тс^, получим
X.~^^. A2.8.13)
Таким образом, частицы создаются, когда их комптоновская длина волны
порядка радиуса Шварцшильда, как мы упоминали ранее. [В случае
безмассовых частиц, которым не требуется преодолевать барьер, приведенную
аргументацию придется несколько видоизменить. Скорость их образования
определяется доступным фазовым объемом. Если приравнять среднюю
длину волны фотона чернотельного излучения hc/kT единственной
масштабной длине, связанной с черной дырой, ОМ/с^, получим размерную
оценку температуры черной дыры, т.е. уравнение A2.8.6)].
Скорость потери энергии испаряющейся черной дырой определяется
формулой для черного тела
^ - площадь X Г^ ^ М^ X Л/-^ - Л/-^ A2.8.14)
at
Соответствующее характерное время равно
Чтобы получить правильную размерность (с учетом с = С = 1), надо
вернуть множитель h:
Для черных дыр с массой порядка солнечной испарение посредством
процесса Хокинга совершенно незначительно, что очевидно из уравнений
A2.8.6) и A2.8.16). Лишь когда Л/ <> 10^^ г, характерное время становится
Черные дыры 391
меньше возраста Вселенной. По-видимому, такие черные «мини-дыры»
могли бы образоваться лишь благодаря флуктуациям плотности во время
Большого Взрыва. Шварцшильдовский радиус такой черной дыры
составляет около одного ферми. Если действительно в ранней Вселенной
образовалось множество черных «мини-дыр», то те из них, у которых ? < 10^^ г,
уже давно должны были бы взорваться, а дыры с массой Л/ - 10^^ г
должны взрываться как раз в наше время с темпом энерговыделения
[см. уравнение A2.8.14)], образуя кванты с энергией
??- 100 I-^1 МэВ A2.8.18)
[см. уравнение A2.8.6)]. Рис [476] и Блендфорд [70] обсудили возможность
регистрации таких событий, а в работе Пейджа [441] приводятся
результаты детальных расчетов спектров энергии, излучаемой черными дырами с
массой 10^^ г.
Наблюдаемая плотность энергии гамма-лучей с энергией около 100 МэВ
равна -10"^^ г/см^ [197]. Вычисления Пейджа говорят о том, что около
10^0 энергии взрывающейся черной дыры испускается в виде фотонов (в
отличие от нейтрино, гравитонов или частиц, обладающих массой). Тогда
плотность черных дыр с массой 10^^ г должна быть меньше, чем \0~^^
г/см^, что составляет около 10~^ критической плотности, необходимой,
чтобы Вселенная была замкнутой [106, 120, 442].
Упражнение 12.21. а) Вычислите энтропию черной дыры с массой 1 Mq в единицах
постоянной Больцмана к.
Ответ: S = 1,0 · 10^7 А:.
б) Оцените энтропию Солнца. Предположите, что оно состоит из полностью
ионизованного водорода со средней плотностью 1 г/см^ и со средней температурой
106 К.
Ответ: S - 2 · 10^8 к.
в) Оцените энтропию железного белого карлика с массой 1 Mq и нейтронной
звезды с массой 1 Mq . Возьмите среднюю температуру порядка 10^ К, а средние
плотности порядка 10^ г/см~з и 10*"* г/см^ соответственно. Обратите внимание, что
выражение A1.8.1) для теплоемкости Су вырожденного идеального газа
эквивалентно также S, поскольку Су = TdS/dT. (Очень высокая энтропия черных дыр
с информационно-теоретической точки зрения обсуждается в [60]).
Глава 13
Компактные рентгеновские источники
13.1. ОТКРЫТИЕ и ОТОЖДЕСТВЛЕНИЕ
Новая эпоха в развитии астрономии началась 18 июня 1962 г., когда Джи-
аккони и его сотрудники [223] запустили с полигона Уайт-Сэндс в штате
Нью-Мексико ракету «Аэроби», на борту которой находились три счетчика
Гейгера. Они вскоре обнаружили, что в нашей Галактике имеются
дискретные рентгеновские источники. Например, они открыли объект Скорпион
Х-1—самый яркий источник на небе в диапазоне энергий 1—10 кэВ. (Его
название, которое сокращенно записывается как Sco Х-1, означает, что это
первый рентгеновский источник, открытый в созвездии Скорпиона.) Вскоре
последовали дальнейшие ракетные и баллонные наблюдения, которые
подтвердили данные, полученные на «Аэроби» и привели к уточнению
координат открытых объектов, а также к отождествлению новых источников.
К концу десятилетия было отождествлено около 20 рентгеновских
источников. Было найдено, что один из самых сильных источников —
Лебедь (Cyg) Х-1, является переменным во времени [97, 436]. Многие из
источников оказались расположенными вблизи плоскости Галактики, что
дало основание отнести большинство из них к галактическим объектам [413].
В 1966 г. в месте нахождения источника Sco Х-1 был обнаружен его
оптический двойник; оптическим источником оказалась старая звезда 12—13-й
звездной величины. В следующем году Шкловский [538] предложил
забавную (по тем временам!) теоретическую модель для Sco Х-1, согласно
которой рентгеновское излучение испускается высокотемпературным газом,
перетекающим на нейтронную звезду от оптического компонента в тесной
двойной системе. Оптический компонент представляет собой обычную
остывшую карликовую звезду, ответственную за наблюдаемое оптическое
излучение. Эта модель развивала оригинальную идею Хаякавы и Мацуоки
[269] о том, что газовая аккреция в тесных двойных системах может
оказаться источником рентгеновского излучения. (Они имели в виду
необычные условия в нормальных в остальных отношениях двойных системах.)
Камерон и Мок [102] критиковали модель Шкловского, утверждая, что
наблюдающееся мягкое рентгеновское излучение от Sco Х-1, вероятнее
всего, возникает от аккреции на белый карлик, а не на нейтронную звезду.
Были обрисованы некоторые детали механизма сферической аккреции на
белый карлик в двойной системе.
Вслед за этим Прендергаст и Бербидж [464] прказали, что газ,
перетекающий на компактную звезду от другого компонента двойной системы,
обладает слишком большим моментом количества движения, чтобы течение
было радиальным. Поэтому газ должен образовывать вокруг компактной
Компактные рентгеновские источники 393
звезды тонкий аккреционный диск с приблизительно кеплеровскими
скоростями вращения и с небольшой направленной внутрь скоростью дрейфа.
Детали этой модели были проработаны для случая аккреции на белый
карлик.
Еще в 1965 г. Зельдович и Гусейнов [634] отметили, что открытие
рентгеновского или гамма-излучения от спектрально-двойных звезд с
неразделенными линиями послужило бы сильным свидетельством присутствия
либо черной дыры, либо нейтронной звезды. (Термин «спектрально-
двойная» означает, что вывод об орбитальном движении в двойной
системе делается на основании доплеровского сдвига спектральных линий.
«Неразделенные линии» означают, что видны спектральные линии только от
одного объекта). Ясно, что черная дыра или нейтронная звезда не могут
дать оптические спектральные линии, так что в этом случае будет виден
только один набор линий.
Еще раньше Зельдович [633] и Солцитер [497] высказывали
предположение, что аккреция на черные дыры может быть эффективным способом
преобразования гравитационной потенциальной энергии в излучение.
Однако в то время они рассматривали аккрецию на сверхмассивные черные
дыры (Л/ > 10* ^0) Д^^я объяснения громадных светимостей незадолго до
того открытых квазаров.
В 1969 г. Тримбл и Торн [572] пришли к заключению, что массивные
невидимые компоненты, могущие быть только черными дырами или
нейтронными звездами, если и существуют, то лишь в немногих известных к
тому времени спектрально-двойных системах с неразделенными линиями.
Вдобавок ни одна из этих систем не совпадала в то время с
опубликованными координатами рентгеновских источников.
Итак, несмотря на растущие усилия теоретиков объяснить природу
только что открытых галактических рентгеновских источников, в то время
еще не было надежных наблюдательных свидетельств, что эти источники
имеют какое-то отношение к тесным двойным системам или к
компактным объектам. Однако идея уже пустила свои корни. С открытием
пульсаров в 1967 г. (см. гл. 10) понятие нейтронной звезды стало внушать больше
доверия.
12 декабря 1970 г. Национальным управлением по аэронавтике и
космическим исследованиям (НАСА) США с побережья в Кении был запушен
первый астрономический спутник «Ухуру»^^ Этот спутник, полностью
предназначенный для рентгеновских наблюдений в диапазоне 2—20 кэВ,
произвел революцию в наших представлениях о природе космических
рентгеновских источников и компактных объектов. Прежде чем он прекратил
функционировать (в марте 1973 г., гораздо позднее, чем следовало из
проектного времени жизни), было отождествлено свыше 300 дискретных
рентгеновских источников [200]. Особенно важным было надежное обнаруже-
^^ Слово «ухуру» на языке суахили означает «свобода»; запуск был приурочен к
празднованию независимости Кении.
394 Глава 13
ние рентгеновского излучения от двойных звездных систем^^ и открытие
рентгеновских пульсаров в двойных системах^^ Большинство
галактических рентгеновских источников, по-видимому, представляют собой
компактные объекты, которые аккрещ1руют газ, притекающий от соседних
нормальных звезд—компонентов двойных систем. Такая интерпретация
данных наблюдений вытекает из следующих фактов:
1. Переменность рентгеновского излучения с малыми характерными
временами говорит о малых размерах излучающих областей.
2. Для многих источников подтверждено, что они входят в состав
двойной системы, где оптический компонент обращается вокруг невидимого. *
3. Аккреция вещества на компактный объект, особенно нейтронную
звезду или черную дыру, является исключительно эффективным средством
преобразования высвобождающейся гравитационной потенциальной
энергии в рентгеновское излучение.
Вообще говоря, в списке кандидатов в рентгеновские источники есть все
три типа компактных объектов: белые карлики, нейтронные звезды и
черные дыры. Но в отдельных случаях конкретная природа компактного
объекта может быть отождествлена с высокой вероятностью. Рассмотрим,
например, источник Геркулес (Her) Х-1, демонстрирующий очень короткие
регулярные импульсы с периодом 1,24 с, или источник SMC Х-1, лежащий
в Малом Магеллановом Облаке (период 0,71 с). Постоянство периода
наводит на мысль о регулярном движении в гравитационном поле. Такое
движение—вращение, пульсации или орбитальное движение, характеризуется
периодами
P>{Gpy'^\ A3.1.1)
где ? — средняя плотность вещества в объеме, в пределах которого
происходит движение (сравните с разд. 10.2). Для этих источников наблюдаемые
периоды требуют ? ^ 10^ г/см^, что подразумевает присутствие
компактного объекта. В нашем случае белые карлики маловероятны (хотя такие
короткие периоды возможны для массивных быстро вращающихся холодных
карликов), поскольку горячие карлики с температурами поверхности
порядка кэВ должны иметь довольно обширные атмосферы и более длинные
периоды. Орбитальное движение, либо непосредственно модулирующее
некоторый механизм излучения, либо возбуждающее короткопериодические
пульсации, должно очень быстро затухать благодаря гравитационному
излучению. Вращающиеся черные дыры исключаются из рассмотрения,
поскольку не существует стационарных неосесимметричных черных дыр (см.
гл. 12), которые потребовались бы для создания регулярной переменности.
Поэтому с неизбежностью мы приходим к отождествлению этих (а
возможно, и всех) импульсных рентгеновских источников с нейтронными
звездами.
^^ Было отождествлено около 100 оптических компонентов [84].
^^ На 1982 г. приблизительно 19 известных рентгеновских источников
отождествлено с рентгеновскими пульсарами, входящими в двойные системы.
Компактные рентгеновские источники 395
Мы наблюдаем импульсы, по-видимому, оттого, что диаграмма на
правленности рентгеновского пучка не совмещена с осью вращения
аккрецирующей намагниченной нейтронной звезды. Измерение в спектре
излучения Her Х-1 детали, которую можно интерпретировать как циклотронную
линию, приводит к значению напряженности магнитного поля 5 - 5 · 10^^
Гс вблизи поверхности (см. упражнение 13.2). Такие сильные магнитные
поля совместимы с магнитными полями пульсаров (см. гл. 10), но не
обнаружены на поверхности белых карликов.
С другой стороны, рассмотрение непериодического быстропеременного
рентгеновского источника Cyg Х-1, входящего в двойную систему,
приводит к совершенно иному заключению, что мы подтвердим в разд. 13.5.
Большое значение массы, получаемое для этого источника на основе
комбинации оптических и рентгеновских данных (определенно М/М^ ;г 3 и,
возможно, 9 ^ M/Mq^ ^ 15), исключает из рассмотрения белый карлик
или нейтронную звезду. Именно это заключение наряду с компактностью
источника приводит к предварительному отождествлению Cyg Х-1 с черной
дырой. Если оно окажется правильным, эта находка будет, несомненно,
одним из самых замечательных открытий в истории науки.
По следам триумфального эксперимента «Ухуру» в течение 70-х годов
было запущено еще около десяти спутников, полностью или частично
посвященных рентгеновским наблюдениям. Они известны под названиями
«Коперник», «Ариэль-5», ANS, SAS-3, OSO-7 и OSO-8, COS-B, НЕАО-1 и
НЕАО-2 (обсерватория «Эйнштейн»), «Хакучо». Эти спутники оказались
полезными для подтверждения и повторного анализа наблюдений «Ухуру»,
для получения спектральной информации об избранных источниках, для
точного определения положения некоторых из них и расширения списка
известных источников посредством регистрации более слабых и более
удаленных объектов. Кроме того, за это десятилетие были обнаружены
совершенно новые классы рентгеновских источников. Самыми замечательными
из них оказались около 30 рентгеновских барстеров, первые из которых
были открыты на основании данных спутника ANS [247]. Эти
галактические источники испускают непериодические вспышки рентгеновского
излучения с характерными временами порядка минут и дней. По крайней мере
девять из них лежат в шаровых скоплениях. Хотя ни для одного из этих
источников не наблюдалось затмений, обычно считается, что в большинстве
они представляют собой нейтронные звезды, принадлежащие к двойным
системам с малой массой (см. разд. 13.6).
В нескольких следующих разделах мы дадим обзор некоторых
особенностей галактических рентгеновских источников. Наше обсуждение ни в
коей степени не будет полным; мы лишь попытаемся передать «дух» этой
относительно новой отрасли астрономии и подчеркнуть, какое
революционное воздействие она оказала на теорию компактных объектов^^ Чтобы
'^ Более детальные обзоры можно найти в [222, 253] (наблюдения компактных
рентгеновских источников), [33, 473] (рентгеновские пульсары), [355] (источники в
шаровых скоплениях и барстеры). В качестве нового каталога объектов
рентгеновского неба можно рекомендовать четвертый каталог данных спутника «Ухуру»
[200].
396 Глава 13
читатель в полной мере мог оценить приведенные ниже данные
наблюдений, мы рекомендуем ему просмотреть приложение А, в котором описаны
свойства обычных светящихся звезд. Такие звезды и служат спутниками
компактных звезд в двойных рентгеновских системах.
В гл. 14 будет обсуждаться физика аккреш1и на компактные объекты.
13.2. ОБЩИЕ ХАРАКТЕРИСТИКИ ГАЛАКТИЧЕСКИХ
РЕНТГЕНОВСКИХ ИСТОЧНИКОВ
Распределение всех 339 рентгеновских источников, помещенных в
четвертый каталог «Ухуру», показано на рис. 13.1, где представлены положения
источников в галактических координатах. Совершенно очевидна
концентрация сильных источников вдоль Млечного Пути, особенно на низких
галактических широтах (плоскость Галактики соответствует галактической
широте, тождественно равной нулю; центр Галактики лежит на галактической
долготе, тождественно равной нулю). Источники на высоких галактических
широтах значительно слабее, и многие из них можно отождествить с
конкретными внегалактическими объектами. Исключениями являются Her Х-1
и Sco Х-1, которые оба относятся к галактическим источникам. Нас здесь в
основном интересуют сильные источники, которые составляют
большинство отождествленных галактических источников.
В типичных случаях отождествленные источники расположены на
расстояниях от Солнца в диапазоне 0,5—10 кис. Значения светимостей лежат в
интервале 10^^ — 10^^ эрг/с, начиная с энергий порядка 2—6 кэВ.
Известные двойные рентгеновские источники относятся по крайней мере
к двум сильно различающимся типам звездных систем. Одна группа
источников с отождествленными оптическими компонентами связана с поздними
О- или ранними В-сверхгигантами — звездами, обладающими очень
большими массами и светимостями (см. приложение А). Эти звезды
сравнительно немногочисленны, время их жизни не превышает 10'^ лет. Такие
молодые системы, относящиеся к населению I типа, связаны со спиральными
рукавами и областями активного звездообразования вблизи плоскости
Галактики. Примерами рентгеновских источников, относящихся к населению
I типа и образующих двойные системы со сверхгигантами класса ВО,
являются Cyg Х-1, Сеп Х-3 и 2U 0900—40.
Другая группа источников связана со звездами более поздних
спектральных классов. Такие звезды по светимости, температуре и массе больше
походят на Солнце. Эти звезды населения II типа с малой массой имеют
большее время жизни, чем массивные О- и В-звезды; поэтому, как правило,
они старше и распространены более широко. Рентгеновские источники,
относящиеся к населению II типа, включают Her Х-1, Sco Х-1, Cyg Х-2 и
Cyg Х-3 ^^
'^ Двойная природа Sco Х-1 — первого открытого источника такого типа, была
доказана лишь в 1975 г. [151, 233].
Рис, 13,1, Рентгеновское небо. Источники представлены в галактических координатах. Плоскость Галактики
соответствует широте 0°, Центр Галактики лежит в начале координат. Размер кружка, изображающего источник, пропорционален
логариф\1у максимальной интенсивности источника [200].
398 Глава 13
Похоже, что большинство из 50 рентгеновских источников,
расположенных в пределах 30° от центра Галактики, представляет собой
определенный класс старых источников населения II типа с высокой светимостью. В
эту группу входят и 11 известных источников, находящихся в шаровых
скоплениях (по крайней мере девять из них дают рентгеновские всплески).
Обычно эти объекты называют источниками «центральной
галактической подсистемы»^^ из-за их концентрации вблизи центра Галактики; они
описываются ниже.
Найдено, что рентгеновское излучение всех источников является сильно
переменным с характерными временами от миллисекунд до нескольких
лет. Наблюдается как случайная, так и периодическая переменность.
Возможный кандидат в черные дыры — Cyg Х-1 — обладает сильной
переменностью с характерными временами вплоть до миллисекунд.
13.3. РЕНТГЕНОВСКИЕ ПУЛЬСАРЫ В ДВОЙНЫХ СИСТЕМАХ
Рентгеновские источники, входящие в двойные системы и
демонстрирующие периодическую переменность, называются рентгеновскими пульсарами
в двойных системах (например. Her Х-1). Они отличаются от
непериодических переменных источников, например Cyg Х-1.
Большая часть информации о галактических рентгеновских источниках
была получена при изучении рентгеновских пульсаров, входящих в двойные
системы. Знание профилей импульсов, периодов повторения импульсов и
параметров орбит для таких систем обеспечило важнейшую информацию о
физике аккрецирующих компактных звезд, особенно нейтронных звезд.
а) Профили и периоды повторения импульсов
Периоды повторения импульсов 19 известных рентгеновских пульсаров,
входящих в двойные системы, лежат в диапазоне, перекрывающем три
порядка величины: от 0,7 до 835 с (табл. 13.1). Профили импульсов
характеризуются следующими особенностями [473]: 1) большая скважность — не
менее 50^о (сравните с З^о для типичных радиопульсаров); 2) переменность
амплитуды в пределах 25—90^о; 3) широкий диапазон форм от
симметричных до сильно асимметричных; 4) отсутствие видимой зависимости
морфологии импульса от периода. У некоторых источников (например, 4U
1626—67, 4U 0900—40) профили импульса существенно зависят от энергии,
а у других (например. Her Х-1, Сеп Х-3) базовый профиль импульса
сохраняется в большом диапазоне энергий. Характерные профили импульсов 14
рентгеновских пульсаров показаны на рис. 13.2.
^^ В тексте оригинала использован термин «Galactic bulge». — Прим. перев.
Компактные рентгеновские источники
399
Таблица 13.1
РЕНТГЕНОВСКИЕ ПУЛЬСАРЫ В ДВОЙНЫХ СИСТЕМАХ
Источник
SMC Х-1
Her Х-1
4U 0115 + 63
Сеп Х-3
4U 1626-67
LMC Х-4
2S 1417-62
ОАО 1653-40
А 0535 + 26
GX 1 + 4
4U 1320-6ll
А 1239-59 J
GX 304-1
4U 0900-40
4U 1145-61
IE 1145, 1-6141
A 1118-61
4U 1538-52
GX 301 -2
4U 0352 + 30
Период
повторения импульсов, с
0,714
1,24
3,61
4,84
7,68
13,5
17,6
38,2
104
122
191
272
283
292
297
405
529
696
835
Открытие импульсной природы
источника
Люк и др. [373]
Таненбаум и др. [557]
Комински и др. [146]
Джиаккони и др. [224]
Раппапорт и др. [475]
Келли и др. [310]
Келли и др. [309]
Уайт и Прэвдо [612]
Розенберг и др. [486]
Льюин и др. [356]; Уайт и др. [614]
Хакл и др. [286]
МакКлинток и др. [396]; Хакл и др. [286]
МакКлинток и др. [395]
Уайт и др. [616]
Уайт и др. [616]; Лэмб и др. [336]
Айве, Сэнфорд и Белл-Барнелл [295]
Дэйвисон [157]; Беккер и др. [57]
Уайт и др. [614]
Уайт и др. [615]
В настоящее время никакие теоретические расчеты не позволяют
воспроизвести наблюдаемые формы профилей, показанные на рис. 13.2. Тем
не менее обычно принимается, что профили импульсов появляются
вследствие несовпадения диаграммы направленности рентгеновского пучка
с осью вращения аккрецирующей намагниченной нейтронной звезды. Этот
пучок, ориентированный, например, вдоль оси дипольного магнитного
поля звезды, по мере ее вращения становится видным последовательно с
разных направлений [155, 170, 332]. Форма профиля рентгеновского импульса
определяется сложным процессом переноса рентгеновских фотонов с
поверхности нейтронной звезды через области с намагниченной аккрецируе-
мой плазмой (рис. 13.3).
Зависимость периода повторения импульсов от времени для ряда
рентгеновских пульсаров достаточно надежно регистрировалась в течение
почти десяти лет. Если отложить периода! восьми наиболее хорошо
изученных пульсаров в виде функции времени, то становится очевидным, что
400
Глава 13
3-6 кэВ fl0535*26 104 0
О 0,5 1.0 1,5 2,0 О 0,5 1,0 1,5 2,0
Фаза импульса
Рис. 13.2. Образцы профилей импульсов 14 рентгеновских пульсаров, которые, как
полагают, находятся в двойных системах. В каждом случае данные согласуются с
учетом периода (указан в секундах) и откладываются в виде функции фазы импульса
для двух полных циклов [473].
по крайней мере у шести из них происходит «ускорение вращения» (рис.
13.4). Хотя и у этих шести источников изменение периода пульсара в
малых временных масштабах не всегда оказывается монотонным, тенденция
к вековому уменьшению периодов повторения импульсов очевидна. Такое
поведение можно объяснить воздействием моментов, приложенных к
нейтронной звезде через посредство аккрецируемого вещества, как будет
обсуждаться в разд. 15.2. Действительно, данные наблюдений обеспечивают
дальнейшие свидетельства в пользу присутствия нейтронных звезд, а не
белых карликов в двойных системах рентгеновских пульсаров.
Компактные рентгеновские источники
401
Рис. 13.3. а) Схематическое изображение дипольной магнитосферы вокруг
нейтронной звезды, аккрецирующей вещество. Падающий газ не попадает в тороидальную
область, сечение которой затушевано, б) Основание аккреционной воронки вблизи
магнитного полюса нейтронной звезды, показанное в увеличенном размере. Падение
газа в аккреционную воронку вдоль силовых линий магнитного поля В
сопровождается высвобождением энергии вблизи поверхности нейтронной звезды.
Рентгеновское излучение испускается зоной вокруг основания аккреционной воронки [155].
б) Орбиты и массы
Измерения времен прихода импульсов от рентгеновских пульсаров
весьма успешно использовались для определения орбит некотор^1к систем.
Имеется шесть источников, для которых существует достаточно
данных — оптических и рентгеновских, чтобы оценить массу компактной
звезды: Her Х-1, Сеп Х-3, SMC Х-1, LMC Х-4, 4U 0900—40 и 4U 1538—52.
Метод такой оценки обсуждался в разд. 9.4, а результаты приведены на рис.
9.6.
10-513
0,718
0,717
0716
0,715
0,714
0,713
1
;·4.
-
971
SMC ?-?
¦--¦.,
¦'>*..
""«ч^·
^.
1973 1975 1977 1979
г——?
j
\
\
1981
1,237825
1,237820
1,237815l·
1,237810l·
1,237805b
1,237800[
1,237795'
1,237790
1.237785
4,846
4,844
4,842
4,840
4.838
4,836
4,834
4,832
4,830
4,828
-I 1 1
>
-J 1 1
? 1 1 1 1 1 1^
Cen X-3 :
^
'"·*.
• ·¦·¦··.. · 1
^^
i 1 1 1 1 1 U
1971
1973 1975 1977
1979
1975 197S 1977 1978 1979 1980 1981
140
130
120
110
100
:-f-
""¦••4-..
GXl + 4
-
'^*·^.
""'*·,
• · · 1 i.._ 1 lI
1970 1972 1974 1976 1978 1980
282,95
282,90
282.85
282,80
282,751-
282,70
i 4U0900-40
1975 1976 1977 1978 1979 1980 1981 1982
1975
1976
1977 1978
1979
1972 1973 1974 1975 1976 1977 1978
Время
Рис, 13.4. Зависимость периодов повторения импульсов от времени для восьми
двойных рентгеновских пульсаров. Точками обозначены результаты отдельных
измерений периода повторения импульсов, вертикальные отрезки дают представление об
ошибках A?) измерения периода. Данные получены со спутников «Ухуру»,
«Коперник», «Ариэль-5», SAS-3, OSO-8, НЕАО-1, во время выполнения
советско-американской программы «Союз» — «Аполлон» и в экспериментах на баллонах и высотных
ракетах. Штриховые линии — это наилучшая аппроксимация данных прямой линией
по методу максимального правдоподобия [474].
Компактные рентгеновские источники
403
13.4. ГЕРКУЛЕС Х-1: ОБРАЗЕЦ РЕНТГЕНОВСКОГО
ПУЛЬСАРА В СОСТАВЕ ДВОЙНОЙ СИСТЕМЫ
После открытия рентгеновского источника Her Х-1 по данным спутника
«Ухуру» в 1972 г. [557], он стал наиболее хорошо изученным
рентгеновским пульсаром в двойной системе. По свойствам в рентгеновском
диапазоне он во многом подобен импульсному рентгеновскому источнику
Сеп Х-3, который был открыт первым [224, 542]. В обоих случаях
результаты наблюдений интерпретируются на основе модели двойной
системы с переносом массы, в которой вращающаяся нейтронная звезда ак-
крецирует вещество от другого компонента.
Особенность источника Her Х-1 состоит в том, что данные его
рентгеновских наблюдений свидетельствуют о наличии трех периодичностей:
период повторения импульсов 1,24 с, орбитальный период 1,7 сут и
приблизительно 35-дневный цикл «включено — выключено». Оценки массы
нейтронной зве^пы составляют 0,4 ^ М/М^^ ^ 2,2, а масса другого
компонента системы — звезды HZ Her равна 1,4 ^ М/М^^ ^2,8 [37]. У этой
звезды проявляются оптические импульсы с периодом 1,24 с; их
интерпретируют как результат поглощения, термализации и переизлучения в атмосфере
HZ Her импульсного рентгеновского излучения Her Х-1. Небольшая масса
HZ Her совместима с ее спектральным типом — поздний А или ранний F.
Уникальная особенность Her Х-1 — 35-дневный цикл, состоит из 12 сут
состояния с высоким уровнем интенсивности излучения, за которыми
следуют 23 сут состояния с низкой интенсивностью (рис. 13.5). В ряде
теоретических моделей [305, 456, 483] эта 35-дневная модуляция интенсивности
объясняется прецессией аккреционного диска относительно рентгеновского
источника. Прецессия вызывает «затенение» рентгеновского источника для
земного наблюдателя на продолжительное время «спокойного» состояния.
? \ Г
? \ Г
? \ Г
со
1
c\i
о
^^
?
zr
F
о
120
100
80
60
40
го
J I V—^ ^'^ I L
0,2 0.3 ОЛ 0,5 0,6 0,7
Фаза
0.8
Рис. 13.5. Результаты наблюдений 35-дневного цикла источника Her Х-1 со спутника
«Ухуру». Показана огибающая рентгеновской «кривой блеска» Her Х-1,
охватывающая полный 35-дневный цикл. В той части кривой блеска, которая представлена
прерывистой линией, наблюдения были невозможны. Скорость счета (отсчет «Ухуру» в
секунду) соответствует потоку энергии 1,7 · 10~^^ эрг/(см^ · с) [300].
404
Глава 13
10
Энергия, кэВ
Рис. 13.6. Усредненный во времени рентгеновский спектр источника Her Х-1. Спектр
отличается избытком мягкого {Е < 1 кэВ) рентгеновского излучения, непрерывным
спектром, изменяющимся почти по степенному закону в диапазоне энергий
1 < ? < 10 кэВ, эмиссионной линией железа при ? - 1 кэБ, резким падением при
? ^ 10 кэВ и деталью при ? - 50 кэВ, которая может быть связанной с
циклотронной линией [277].
Эта модель заслуживает внимания, потому что оптическая модуляция с
периодом 1,7 сут, которая явно определяется рентгеновским нагревом,
продолжает существовать в течение всего 35-дневного цикла.
Средний рентгеновский спектр Her Х-1 в диапазоне 1—40 кэБ показан на
рис. 13.6. Непрерывный спектр относительно плоский ниже -24 кэВ
[dL(E)/dE - const, где L — светимость, а ?* — энергия], но выше этого
значения энергии спектр резко падает. Если принять приближенное, но
вполне разумное значение расстояния до источника порядка 4 кпс [154],
полная светимость Her Х-1 в интервале энергий 2—24 кэБ составит около
10^^ эрг/с.
Компактные рентгеновские источники 405
Упражнение 13.1. Покажите, что указанная выше светимость слишком высока,
чтобы ее можно было обеспечить потерями кинетической энергии вращения нейтронной
звезды.
Недавно были получены данные о наличии спектральной линии в
импульсном жестком рентгеновском спектре Her Х-1 вблизи 58 кэВ [574].
Наиболее правдоподобное объяснение ее происхождения состоит в том, что
эта деталь спектра связана с электронным циклотронным поглощением
или эмиссией и говорит о наличии поверхностного магнитного поля В -
~ D—6) · 10^^ Гс. Если это наблюдение окажется верным, оно подкрепит
отождествление Her Х-1 с нейтронной звездой. Похожая деталь
наблюдалась [669] в импульсном высокоэнергетическом спектре источника
4U 0115—63 (период 3,6 с) вблизи 20 кэВ, что свидетельствует о
существовании поля В - 1 ' 10^^ Гс у этого источника.
Упражнение 13.2. а) Оцените магнитное поле В в предположении, что
наблюдавшаяся при 58 кэВ линия в спектре Her Х-1 порождается излучением электрона, который
переходит с первого возбужденного уровня Ландау в основное состояние.
Указание: Е„ ^ = ^д Bл + 1) + q'^/brigy где ?? — магнетон Бора, /? = О, 1, 2, ...,
а G — импульс, направленный вдоль В.
б) Предположив, что наблюдаемая ширина линии - 12 кэБ возникает вследствие
теплового уширения, оцените температуру газа ? в области излучения линии.
Предположите «типичный» угол наблюдения источника относительно магнитного поля.
13.5. ЛЕБЕДЬ Х-1: КАНДИДАТ В ЧЕРНЫЕ ДЫРЫ
Источник Лебедь Х-1 (Cyg Х-1) занимает центральное место среди
изучаемых компактных рентгеновских объектов. Этот источник с широчайшим
диапазоном временной переменности, первый из обнаруженных в
оптических двойных системах, вероятнее всего, представляет собой черную
дыру. Именно быстрая рентгеновская переменность этого источника положила
начало поиску по данным «Ухуру» других переменных источников, что
привело к открытию рентгеновских пульсаров в двойных системах^\
Лебедь Х-1 обладает переменностью во всех временных
масштабах — от месяцев и лет до миллисекунд. Наиболее ярко его переменность
проявляется во всплесках длительностью - 1 мс [488], которые
свидетельствуют о максимальном размере рентгеновского источника R ^ ct -
-- 300 км и доказывают, что объект является весьма компактным (рис.
13.7).
^^ Всестороннее обсуждение источника Cyg Х-1 и соответствующие ссылки см. в
[423].
406
Глава 13
318,451
318,471 318,491 318,511
СекунЭы после запуска
318,531
Рис. 13.7. Переменность источника Лебедь Х-1. Показаны несколько «всплесков»
миллисекундной длительности. Приведенные результаты, полученные при ракетных
наблюдениях примерно через 318 с после запуска, содержат экспозицию Cyg Х-1
продолжительностью 80 мс. Скорость счета интегрируется каждые 0,64 мс.
Заштрихованы всплески, для которых число импульсов за 1,28 мс превышает 12 [488].
Оптический компонент в системе Cyg Х-1 — это
спектрально-двойная звезда с неразделенными линиями, которая имеет период 5,6 сут.
Она представляет собой сверхгигант 9-й звездной величины и носит
название HDE 226868. Отождествить HDE 226868 с Cyg Х-1 впервые удалось,
когда в марте 1971 г. в направлении на Cyg Х-1 внезапно появился новый
радиоисточник и одновременно была зарегистрирована переменность
рентгеновского излучения [275, 558]. В маленьком квадрате ошибок
положения радиоисточника (не более угловой секунды) находилась оптическая
звезда HDE 226868 — двойная система с невидимым компонентом. Позже
была обнаружена модуляция рентгеновской интенсивности с периодом
5,6 сут, что подтвердило отождествление [278].
К сожалению, рентгеновские данные о Cyg Х-1 недостаточны для
определения орбитальных параметров в отличие от аналогичных данных для
рентгеновских пульсаров, входящих в двойные системы. Регулярные
рентгеновские импульсы не наблюдались и не было обнаружено четких
затмений.
Тем не менее нижний предел массы Cyg Х-1, превышающий 3 Mq ,
можно получить двумя независимыми методами^^ Для обоих методов тре-
^^ Внимательное обсуждение и ссылки см. в [35].
Компактные рентгеновские источники 407
буется надежное определение расстояния. Оно достигается на основе
оценки межзвездного поглощения, наблюдаемого в спектре HDE 226868. Если
знать абсолютную звездную величину звезды, то сравнение с видимой
звездной величиной (с поправкой на поглощение) позволяет получить
расстояние до нее [см. уравнение (А.4)]. Хотя обычно у ОВ-сверхгигантов
типа HDE 226868 абсолютная звездная величина М^^ — - 6, существуют
звезды с очень похожими спектрами, но с гораздо меньшими массой и
светимостью [573].
Вместо того, чтобы высказывать предположения о светимости HDE
226868, можно провести обзор большого числа звезд в том же направлении
и сопоставить поглощение с расстоянием для каждой из них, считая, что
спектр дает истинную светимость. Хотя любое индивидуальное
определение расстояния может быть ошибочным, при учете большого числа проб
получается достаточно верная калибровка поглощения в зависимости от
расстояния для данного направления. Два независимых обзора [86, 386], в
каждом из которых было использовано около 50 звезд, лежащих в
пределах 1° от направления на HDE 226868, привели к оценке расстояния до
HDE 226868 порядка 2,5 кпс (абсолютный минимум расстояния 2 кпс),
соответствующей наблюдаемому поглощению.
Доплеровские кривые спектра HDE 226868 дают информацию об
элементах орбиты (см. разд. 9.4). Джиз и Болтон [225] получили: ? =
= 5,60 сут (с ошибкой, пренебрежимо малой для наших целей); a^smi =
= E,28 ± 0,08) · 10^ км; f = @,252 ± О,О1О)М0 и малый эксцентриситет
(по-видимому, меньше 0,02).
Принимая теперь во внимание, что у типичного ОВ-сверхгиганта масса
превышает 20 Mq, на основе расчетов звездных моделей (см., например,
[312]) можно показать, что для получения нужной светимости при
расстоянии d - 1 кпс требуется масса по крайней мере 8,5 М^. Поскольку
(MjSini) ,
/=7-^ ??' A3.5.1
(?, + ?,?
где индекс 1 относится к оптической звезде, а 2 — к рентгеновскому
источнику, минимальное значение для ?2 получается, если положить sin/ = 1.
Это дает
М2>3,ЗМо. A3.5.2)
Еще более убедительна такая аргументация [440] (см. также [35, 387],
приводящая к нижнему пределу массы, которая использует только факт
отсутствия заметного рентгеновского затмения без каких-либо
предположений о массе оптического компонента. Отсутствие затмений подразумевает
(рис. 13.8), что
cos/>—, A3.5.3)
408
Глава 13
Рис. 13.8. Условия отсутствия затмения для Cyg Х-1.
где R — радиус оптической звезды (которая принимается сферической) и
а — расстояние между двумя объектами. Используя уравнение (9.4.5), это
неравенство можно записать
cos / >
Следовательно,
MjSin/cos^/ >
R ?2 sin i
flj sin i ? J + Mj
fR'
'\2
(ajsin/)
A3.5.4)
A3.5.5)
Величина sin/cos^/ имеет максимальное значение 2/3^3, когда sin/ = 1/V3,
и поэтому
3yf3fR^
?2 >
A3.5.6)
2(a,sin/)
Величину R^ можно найти, зная светимость и эффективную температуру:
2_ L
R^ =
АчгаТ*
С учетом уравнений (А.4), (А.5) и (А.8) получим
v2
0,4D,72-ш„-ЙС+у4„)
л2 = -^(-г^1 10^-«.^
47гаГ/ \ 1 кпс /
A3.5.7)
A3.5.8)
Здесь Wy — видимая звездная величина в диапазоне V (видимом),
ВС — болометрическая поправка, Л^ — поглощение в диапазоне V. Брег-
ман и др. [86] нашли, что V(^m^) = 8,87, а показатель цвета B—V = 0,81.
Согласно точной спектральной классификации HDE 226868^^ (см., напри-
' Она классифицируется как звезда типа 09,7 lab [594].
Компактные рентгеновские источники 409
мер, [258]), ее собственный цвет с поправкой на поглощение равен
{В— F)o = - 0,30. «Цветовой избыток», обусловленный предпочтительным
поглощением межзвездным газом коротковолнового оптического
излучения, составляет
E{B-V)^B-V-{B-V\=\,\\. A3.5.9)
Тогда полное поглощение в диапазоне V, т.е. А^, определяется формулой
А, = 3,0?(Д - F) = 3,3. A3.5.10)
Множитель 3,0 в выражении A3.5.10) — это эмпирический результат
детального изучения межзвездного поглощения [549}, представляющий собой
достаточно надежный нижний предел [518], т.е. как раз то, что нам
требуется.
Значения ВС и Т^ для звезд-сверхгигантов довольно неопределенны,
поскольку они получались в основном из теоретических расчетов и редко
проходили прямую наблюдательную проверку, пока не появилась работа Коу-
да и др. [138]. Конти [147] включил результаты Коуда и для нашего
случая дает Т^ = 30 000 К, ВС = -2,9. К счастью, поскольку величина —ВС
уменьшается при уменьшении Г^, радиус звезды R в уравнении A3.5.8)
оказывается не особенно чувствительным к неточностям ? и ВС. Из
результатов Конти вытекает:
^2=F,62- loVi-r^l км2 A3.5.11)
\ 1 кпс /
и, следовательно, из уравнения A3.5.6) получаем^^
Л/2 > 3.4Мо (у^) . A3.5.12)
Упражнение 13.3. На основе расчетов [27] модели атмосферы в работе [387]
получены оценки гравитационного ускорения на поверхности HDE 226868:
g S ^ = 1^6 X юЗ см/с2. A3.5.13)
К
Используйте/ и R из уравнений A3.5.1) и A3.5.11) для того, чтобы установить
нижний предел Л/2.
Ответ: Mj ^ 5,7 Mq.
'^ Значения Т^ и ВС, приводимые Пачинским [440], дали бы в уравнении A3.5.12)
коэффициент 3,7.
410 Глава 13
Упражнение 13.4 [440]. Еще одно ограничение, которое можно было бы наложить
на двойную систему, заключается в том, чтобы оптическая звезда не переполняла
свою полость Роша (сравните с разд. 13.7). Иными словами,
R < /^Roche- A3.5.14)
В том диапазоне масс, который нас интересует, хорошим приближением будет
выражение [439]
^ Roche
0,38 + 0,2 Ig ( ^
A3.5.15)
где а определяется (9.4.5).
а) Покажите, что минимум Mj определяется нахождением минимума функции
^2 -^, (,3.5.16)
с учетом ограничений A3.5.14) и A3.5.4):
/. = ^^@.38 + 0,2 Ig q) > ?, A3.5.17)
/2 = -^cos'>*' A3.5.18)
?/, R
^^W,' '^^;^i- A3-5.19)
б) Путем варьирования q и sin/ покажите, что минимум достигается, когда в
выражениях A3.5.17) и A3.5.18) неравенство превращается в равенство. Оцените
минимум для d = 2 кпс и б/ = 2,5 кпс.
в) Покажите, что при этом также устанавливается минимум Mj, и получите
численную оценку Л/1.
Ответ: Mj ^ 6,5 Mq (d = 2 кпс); Mj ^ 9,5 Mq (d = 2,5 кпс).
В итоге можно констатировать, что нижний предел A3.5.12), равный
3,4 Л/0, очень надежен. Если принять более разумное значение d -
- 2,5 кпс, он возрастает до 5,3 М^. Другие, менее точные, но более
реалистичные аргументы приводят к еще большим значениям массы.
Вращающийся с максимальной скоростью устойчивый белый карлик
обладает максимальной массой лишь около 2,5 Mq [см. уравнение G.4.41)].
Максимальное значение массы устойчивой нейтронной звезды около 3 М^
(см. гл. 9) зависит только от справедливости общей теории
относительности, а не от предполагаемого уравнения состояния. Наиболее вероятные
максимальные массы нейтронных звезд ближе к 2 М^ при модных в
настоящее время жестких уравнениях состояния. Поэтому мы приходим к за-
Компактные рентгеновские источники 411
ключению, имеющему глубокий смысл: вероятнее всего, Cyg Х-1 является
черной дырой. Итоги нашего обсуждения подведены в резюме 13.1.
РЕЗЮМЕ 13.1
Доводы в пользу отождествления Cyg Х-1 с черной дырой
1. Cyg Х-1—компактный объект (характерное время переменности ?/ -
- 1—10 мс, что соответствует размеру излучающей зоны R ^ ??^? ^
^ 10^ см).
2. Cyg Х-1—невидимый спутник звезды HDE 226868 (одновременная
нестационарность интенсивности радио- и рентгеновского излучения, а также
соответствие периода 5,6 сут двойной системы периоду переменности в
мягком рентгене).
3. Cyg Х-1 обладает массой М^ > 3,4 Mq (оптическая функция масс -I-
-I- спектральный тип -I- отсутствие затмений -I- расстояние).
Гипотеза черной дыры подкрепляется дополнительными
ограничениями, следующими из наблюдаемой переменности оптического излучения.
Эвни и Бакал [28, 29] пришли к выводу, что масса Cyg Х-1, вероятно,
должна быть в интервале 9—15 М^. Эти значения существенно выше
любого верхнего предела, выведенного нами для белых карликов и нейтронных
звезд.
Однако завзятые спорщики предложили для Cyg Х-1 альтернативные
модели, не содержащие черных дыр. Одна из таких моделей [43, 189]
требует присутствия третьего тела в системе, так что испускающая
рентгеновские лучи нейтронная звезда должна находиться на орбите вокруг
одного или двух членов массивной двойной системы нормальных звезд. В
другой модели [42] постулируется экзотический источник энергии,
отличающийся от аккреции газа на компактную звезду.
Третье тело должно было бы приводить к возмущению оптической
кривой блеска HDE 226868. Верхние пределы [3] таких возмущений, следующие
из наблюдений, налагают сильные ограничения на модели тройных систем,
но в принципе они остаются возможными^^
В пользу модели черной дыры свидетельствует и анализ деталей
рентгеновского спектра. Источник претерпевает частые переходы из
«спокойного» состояния, где он проводит около 90^0 всего времени, в
«возбужденное» состояние (см. [166]), где дан итог наблюдений). В «спокойном»
состоянии источник излучает в основном жесткий рентгеновский компонент,
Солпитер, когда его попросили принять участие в обсуждении положения с
Cyg Х-1, пришел к выводу: «Черная дыра в Cyg Х-1 — это наиболее консервативная
гипотеза».
412 Глава 13
характеризуемый единым степенным спектром во всем диапазоне энергий
1—250 кэВ:
-±-^^АЕ-\ A3.5.20)
477^2 dE
Здесь L — светимость, ? — энергия, d — расстояние, г, А и а —
постоянные величины. Значения ? лежит в пределах 0,5—1 при временах
интегрирования, превышающих несколько секунд.
«Возбужденное» состояние устанавливается за время порядка
нескольких дней и продолжается около месяца. Новый, интенсивный и очень
мягкий спектральный компонент появляется в полосе 3—6 кэВ. Спектральная
интенсивность выше 10 кэВ слегка падает^ сохраняя степенную зависимость
A3.5.20) с ? = 1,2 (рис. 13.9). Полная светимость в «возбужденном»
состоянии возрастает примерно в два раза и достигает 6 · Ю^'' эрг/с.
Наблюдаемый рентгеновский спектр Cyg Х-1 достаточно хорошо
моделируется излучением от газового аккреционного диска, находящегося
вокруг центральной черной дыры (см. разд. 14.5 и 14.6). Большой успех таких
моделей связан с тем, что они могут вопроизвести как мягкий, так и
жесткий компоненты спектра либо в «возбужденном», либо в «спокойном»
состоянии. Однако ни одна из моделей до настоящего времени не может
надежно объяснить необычные переходы между этими состояниями.
Длительные характерные времена таких переходов позволяют предположить,
что они связаны с изменениями скорости передачи массы от главного
компонента системы к вторичному.
Упражнение 13.5. Используйте степенную аппроксимацию данных о мягком и
жестком рентгене для Cyg Х-1, показанную на рис. 13.9, и вычислите:
а) светимость в мягком рентгене A—20 кэВ) в единицах эрг/с, когда Cyg Х-1
находится соответственно в «возбужденном» и «спокойном» состояниях;
б) светимость в жестком рентгене B0—250 кэВ) для «возбужденного» и
«спокойного» состояний;
в) полную светимость в диапазоне 1—250 кэВ для обоих состояний.
Предположите расстояние 2,5 кпс.
Замечание: Предварительные результаты рентгеновских баллонных наблюдений
говорят о том, что степенной спад спектра в диапазоне жесткого рентгена может
продолжаться по крайней мере до 3 МэВ в «спокойном» состоянии [383].
Рис. 13.9. а) Усредненный спектр мягких {2 <, ? <, 20 кэВ) рентгеновских фотонов
Cyg Х-1 до и после перехода из «возбужденного» в «спокойное» состояние в
марте — апреле 1971 г. (кружки — период с 21 декабря 1970 г. по 14 марта 1971 г.;
точки — период с 31 декабря 1971 г. по 21 января 1972 г.). Показана степенная
аппроксимация соответствующих спектров [см. уравнение A3.5.20), где ? выражено в
кэВ, б/ — в см, dUdE — в кэВ/(с · кэВ)] [588].
б) Усредненный спектр жестких {\5 ^ ? % 250 кэВ) рентгеновских фотонов Cyg Х-1.
Слева отложен спектр «спокойного» состояния (определяемый по меньшим
энергиям), а справа — спектр «возбужденного» состояния. Штриховая линия на рисунке
справа — это степенной закон, соответствующий спектру «спокойного» состояния,
приведенного слева. Приведены параметры степенной аппроксимации (в тех же
единицах, как и на рис. 13.9,?7) [166].
10^
10
-г
"I 1—I—г~г-
-!—I I I I I.
10°
0(=2,6
,^^ = 77,7
««0,6
a» 0,45
A «1.25
' ' I I ?
102
10" с—?—? ? 11111Ц—?—?
10 F
? ? II III ?^
10 20 50 100 300
Е,к.эВ
? ?
R „Возбужденное"
L \ состояние
? ?^
10"
?3
? . Ill
. ?
10 20 50 100 300
?, кэВ
414 Глава 13
Помимо Cyg Х-1, есть и другие объекты, которые можно считать
подающими надежды кандидатами в черные дыры. Из них в настоящее время
больше всего заслуживают внимания Циркуль (Cir) Х-1 и ОАО 1653—40.
Cir Х-1 — это рентгеновский источник в двойной системе из каталога
«Ухуру», обладающий быстрой переменностью, во многом похожей на
поведение Cyg Х-1 ^^ Слабость нормального красного компонента системы
делает до сих пор невозможными наблюдение спектральных линий и
определение параметров орбиты. Затменный рентгеновский источник ОАО
1653—40, обнаруженный спутником «Коперник», был отождествлен со
спектральной двойной звездой с неразделенными линиями V861 Скорпиона.
Орбитальные параметры свидетельствуют о большой массе G—11 Mq),
связанной с рентгеновским источником [469].
13.6. ИСТОЧНИКИ ЦЕНТРАЛЬНОЙ ГАЛАКТИЧЕСКОЙ ПОДСИСТЕМЫ:
БАРСТЕРЫ
Большинство из 50 (или около того) рентгеновских источников, лежащих в
пределах 30° от направления на центр Галактики, имеют одинаковые
свойства [353], такие, как 1) мягкие рентгеновские спектры, 2)
рентгеновская переменность с характерными временами от минут до дней, Ъ) L^ ^
^ 10^^ эрг/с, 4) отсутствие периодических импульсов, 5) отсутствие
затмений. Примерно у половины из этих источников наблюдаются
рентгеновские всплески. Все они называются источниками центральной
галактической подсистемы, потому что распределены как старое звездное население,
входящее в центральную галактическую подсистему (население II типа). По
меньшей мере 11 источников с такими же свойствами 1—5 входят в состав
(старых) шаровых скоплений и по крайней мере девять из них испускают
рентгеновские всплески ^^ Это сходство говорит о том, что источники
скоплений и центральной подсистемы составляют класс рентгеновских
источников старого населения II типа, отличающийся от рентгеновских ис-
^^ Обзор и обсуждение наблюдений Cir Х-1 см. в [167].
^^ См. [246]. Проведенный недавно анализ данных обсерватории «Эйнштейн»
указывает на наличие в шаровых скоплениях рентгеновских источников второго класса
с меньшими светимостями A0^"^ ^ ^^ ^ 10^^ эрг/с). В отличие от источников
высокой светимости эти объекты не сконцентрированы вблизи ядер скоплений.
Возможная интерпретация заключается в том, что источники малой светимости — это
двойные системы малой массы с белыми карликами, а источники высокой
светимости — более массивные двойные системы, содержащие нейтронные
звезды.
Компактные рентгеновские источники 415
точников, связанных с молодыми массивными звездами населения I типа.
Источники рентгеновского излучения, расположенные в центральной
подсистеме и в скоплениях, можно отождествить со старым,
«сфероидальным» компонентом Галактики, а источники, находящиеся на орбитах
около молодых массивных звезд, можно отождествить с более молодым,
«дисковым» компонентом.
Начиная с открытия в 1975 г. [61, 247] барстеров — объектов,
испускающих всплески рентгеновского излучения — их зарегистрировано более 25.
Наиболее часто встречающиеся всплески, называемые [276] «всплесками I
типа», появляются с интервалами от нескольких часов до нескольких дней.
Обычно по мере затухания такого всплеска его спектр становится более
«мягким». Характерные профили импульсов показаны на рис. 13.10.
Более своеобразны так называемые «всплески II типа», возникающие у
«быстрого барстера» МХВ 1730—335. Эти всплески наблюдаются в виде
быстрой последовательности отдельных событий с временными
масштабами от секунд до минут и проявляют очень малое «смягчение» спектра.
Энергия каждого всплеска примерно пропорциональна времени ожидания
следующего всплеска. Вдобавок «быстрый барстер» создает также
всплески I типа с интервалами 3—4 ч.
Для объяснения всплесков было предложено много моделей. Все они
привлекают аккрецию газа на компактный объект. Компактный объект
выполняет по крайней мере одну из двух функций: глубокая гравитационная
потенциальная яма обеспечивает запас энергии для эффективного
преобразования ее в излучение, а малый размер согласуется с наблюдаемой
быстрой переменностью.
Предлагаемые модели делятся на две категории [355]. В одних в
качестве основного механизма рассматриваются неустойчивости аккреционного
потока, а в других — термоядерные вспышки в поверхностных слоях
аккрецирующей нейтронной звезды. Сейчас можно отождествлять источники
центральной галактической подсистемы с компактными объектами,
имеющими массу порядка солнечной, предположительно с нейтронными
звездами, аккрецирующими вещество маломассивного компонента двойной
системы. Всплески I типа, вероятно, возникают в результате термоядерных
вспышек, а всплески II типа быстрого барстера могут оказаться
следствием неустойчивостей аккреционного потока.
Отсутствие рентгеновских импульсов и затмений позволяет усомниться
в правильности отождествления барстеров с аккрецирующими
нейтронными звездами. Можно ожидать, что такие объекты должны испускать
импульсы, если только у них есть магнитные поля, достаточно сильные для
управления аккреционным потоком и не совмещенные с осью вращения,
такие, как у рентгеновских пульсаров в двойных системах, связанных со
звездным населением I типа. Возможно, что барстеры являются более
старыми нейтронными звездами и их магнитные поля затухли (см.
упражнение 10.3) или сориентировались параллельно оси вращения. Не исключено
также, что канализирование газа сильными магнитными полями в моло-
Рис. 13.10. Профили всплесков I типа пяти разных источников в пяти различных диапазонах. Профиль всплеска достаточно xapaKTepei
для каждого конкретного источника. Обратите внимание, что во всех случаях постепенный спад (хвост) существует дольше при боле(
низких энергиях, нежели при более высоких [354].
\ ?
? ?
(эУо/шэьэшо)
?—?
? CD ?
CD >i· <^
(эуо/шэьэшо) (эе'О/шэьэшо) (э8'о/шэьэшо)
ge^<9-e gev^i-9 g€^<6l-8
CD CVl
(эд'О/шэьэшо)
ge^ZZ-6l
Компактные рентгеновские источники 417
дых нейтронных звездах может подавлять термоядерные вспышки, что
объясняет, почему рентгеновские пульсары в двойных системах не
проявляются как барстеры.
Отсутствие затмений^^ у всех хорошо изученных источников создает
большие затруднения для теоретиков. Однако в некоторых моделях с
аккреционным диском (например, [407]) предусматривается возможность су-
шествования «рентгеновского призрака» в орбитальной плоскости двойной
системы малой массы и тем самым исключается обнаруживаемое в ином
случае затмение.
Учитывая очень высокую частоту появления и связь с самым старым
звездным населением, рентгеновские источники шаровых скоплений, по-
видимому, можно выделить в совершенно особый класс [306]. Из 150 (или
около того) известных галактических рентгеновских источников 1Щ
находятся в шаровых скоплениях. Однако полная масса звезд шаровых
скоплений составляет лишь окбло ?,?^? всей массы Галактики.
Глубокая потенциальная яма скопления, сгущающегося к центру,
способна удерживать газ, выбрасываемый старыми звездами. Это породило
идею, что сверхмассивная центральная черная дыра A00—1000 Mq) могла
бы аккрецировать газ и подпитывать наблюдаемый источник [38, 541]. На
эту идею повлияли также результаты теоретических исследований,
согласно которым ядра шаровых скоплений испытывают вековой «коллапс» к
состоянию с высокой звездной плотностью. Такой процесс мог бы повлечь за
собой столкновения и слияние звезд, а в конечном итоге — образование
сверхмассивной черной дыры^\
Тенденция к равнораспределению энергии в звездных скоплениях (путем
гравитационного рассеяния) означает, что массивные звезды приобретают
меньшие скорости и потому остаются в самых центральных областях
скопления. Данные [246] рентгеновской обсерватории «Эйнштейн» позволили
определить положение восьми рентгеновских источников в шаровых
скоплениях с точностью 1—3". Результаты, показывающие, что некоторые
источники видны на расстоянии более \" от центров скоплений,
свидетельствуют против гипотезы сверхмассивных черных дыр и совместимы с
предположением об объектах, имеющих массу порядка 2М^ [368]. Вопрос этот
еще нельзя считать полностью решенным.
Сравнительно недавно у барстера 4U 1916—05 [596, 597, 613]
наблюдались понижения поглощения с периодом 50 ± 0,5 мин. Кроме того,
обнаружены модуляции с периодом 4,3 ч оптического потока барстера МХВ
1735—44 [394] и 4-часовые модуляции у барстера МХВ 1636—53 [451]. Хотя
полученные данные следует считать предварительными, эти периодические
вариации могут оказаться первым прямым аргументом в пользу двойной
природы рентгеновских барстеров.
^^ См., однако, обсуждение в конце разд. 13.6.
^^ Более подробное обсуждение см., например, в [365, 548].
II-5I3
418 Глава 13
13.7. СТАНДАРТНАЯ МОДЕЛЬ; АККРЕЦИЯ В ТЕСНОЙ
ДВОЙНОЙ СИСТЕМЕ
а) Простые оценки
Выше мы рассмотрели некоторые наблюдательные свидетельства в пользу
того, что галактические рентгеновские источники представляют собой,
компактные объекты, аккрецирующие газ в двойных системах. Согласно таким
представлениям, падающее на компактный объект вещество высвобождает
гравитационную потециальную энергию, которая нагревает газ и
генерирует излучение. Примечательно, что даже самое упрощенное описание такого
процесса показывает, насколько естествен и эффективен этот механизм для
генерации наблюдаемого рентгеновского излучения.
Рассмотрим стационарную аккрецию газа с темпом Л/ на нейтронную
звезду массой Л/^ и радиусом R^, Пренебрежем магнитными полями и
предположим сферическое течение, когда газ движется со скоростью свО'
бодного падения у^р пока не достигнет «твердой» поверхности звезды. Газ
резко тормозится на поверхности, и кинетическая энергия его падения
преобразуется в тепло и излучение. В равновесном состоянии возникшая
светимость L^ составит
GMM^
L^-{Mvl--—^, A3.7.1)
Тогда эффективность излучения (в единицах энергии покоя) падающей на
нейтронную звезду массы равна
Итак, для типичных нейтронных звезд эффективность достаточно велика:
? ^ 0,1.
Предположим теперь, что основная часть излучения испускается в виде
чернотельного теплового излучения с поверхности при температуре Т^^\
L, = 4^Я2аГь\. A3.7.3)
Для наблюдаемых источников мягкого рентгена со светимостями порядка
\0^^ эрг/с уравнение A3.7.3) приводит к Т^^ - \0р К при типичных
радиусах нейтронных звезд. Таким образом, аккрецирующие нейтронные звезды
со светимостями 10^^ эрг/с — это естественные источники рентгеновских
лучей A0^ К ~ 1 кэВ).
Уравнение A3.7.1) показывает, что средний темп аккреции, требуемый
для создания такой светимости, равен ? - 10" ^Mq год~^ Такой темп
аккреции вполне может достигаться в тесных двойных системах (см. разД.
13.76).
Упражнение 13.6. Повторите приведенные выше упрощенные вычисления для случая
сферической аккреции на белый карлик и прокомментируйте различия.
Компактные рентгеновские источники 419
Наконец, рассмотрим, почему стационарные рентгеновские светимости
наблюдаемых галактических источников обычно составляют - 10^^ эрг/с и
не превышают более чем в несколько раз 10^^ эрг/с^\ Исходя по-прежнему
из нашей простой модели, подсчитаем выталкивающую силу потока
излучения с поверхности, которая действует на падающее веществЪ, скажем,
ионизованный водород. Предположим, что эта сила обусловлена томсо-
новским рассеянием на электронах, которые затем передают воздействие
протонам через посредство взаимной электростатической связи. Допустим
также, что средний импульс излученного фотона равен/?. Поскольку том-
соновское сечение симметрично для рассеяния вперед и назад, фотон с
импульсом ? в среднем при столкновении передает электрону импульс р.
Энергия типичного фотона равна рс, и при излучении в радиальном
направлении число фотонов, пересекающих в единицу времени единичную
площадку на радиусе г, равно Ь^/^^-кг^рс). Число столкновений, приходящееся
на электрон в единицу времени, получим путем умножения на томсонов-
ское сечение oj = 0,66 · 10"^ см^. Сила, действующая на электрон, — это
просто скорость передачи импульса, так что, умножая на р, получим
?. = ?^· A3.7.4)
Заметим, что выведенное нами выражение сохраняет силу, даже если не все
фотоны излучаются в радиальном направлении; при столкновении
передается радиально лишь компонент р^ импульса, но поскольку поток энергии
??/^??^ направлен по радиусу, число фотонов, пересекающих единичную
площадку за единицу времени, равно Ь^/^-кР-р^с.
Чтобы происходила аккреция, сила тяготения должна превосходить
силу давления фотонов A3.7.4). Сила тяготения, действующая на электрон,
передается через посредство протона
F = ^^-^. A3.7.5)
Поскольку как A3.7.4), так и A3.7.5) пропорциональны 1/г^, существует
критическая светимость — эддингтоновский предел [179], выше которого
радиационное давление превосходит силу тяжести:
,^.1^.,,3.,0..(?).... 03.«,
^^ Из тех галактических источников, расстояние до которых можно оценить
надежно, наивысшая средняя рентгеновская светимость L^ « 5 · 1(Я^ эрг/с
зарегистрирована у рентгеновского пульсара SMC Х-1, находящегося в Малом Магеллановом
Облаке [467].
420 Глава 13
Упражнение 13.7 Покажите, что тот же самый предел A3.7.6) применим для
массивных звезд, поддерживаемых в гидростатическом равновесии радиационным
давлением. Допустите, что оптическая толщина достаточно велика, лучистый поток
можно вычислить в диффузионном приближении [см. уравнение D.1.1)] и томсоновское
рассеяние служит основным источником непрозрачности.
Несмотря на значительные упрощения, допущенные в приведенном
выше рассмотрении (сферическая симметрия, стационарное состояние,
томсоновское рассеяние, чистый ионизованный водород, ньютоновское
тяготение^^), интересно отметить, что у 36 источников из каталога «Уху-
ру» с известными или оцененными расстояниями светимость в диапазоне
2—10 кэВ «обрезается» при - 10^''''' эрг/с, что согласуется с уравнением
A3.7.6) для звезды с массой 1 Mq [385]. Это еще один аргумент в пользу
модели газовой аккреции на компактную звезду для галактических
рентгеновских источников. Меньшие светимости означают просто, что источнику
не хватает топлива.
В следующих двух главах мы еще вернемся к подробному обсуждению
механизма аккреции и рассмотрим белые карлики и черные дыры, а также
нейтронные звезды.
Аналогичные простые соображения облегчают отождествление бар-
стеров. Хвосты наблюдаемых спектров всплесков достаточно хорошо
аппроксимируются кривой излучения черного тела. Если измеряемый поток
равен F^y а температура — ?^,^,, то, поскольку F^ = L^^-KdP- (в
предположении изотропности излучения и расстояния d)^ уравнение A3.7.3) дает
Для одного конкретного барстера при предполагаемом [553] расстоянии
10 кпс были получены значения радиуса около 100 км для первых 10 с и
около 15 км для более поздней стадии всплеска.
Ван Парадийс [586] исследовал 10 барстеров, открытых спутником
SAS-3 и имеющих хорошие спектральные данные. Он предположил, что
^^ Обратите внимание, что в сильном гравитационном поле F^^^^ больше на
релятивистский поправочный множитель A - IGMJrc'^Y'^K В связи с этим докадьный
эддингтоновский предел L^^^ больше на тот же множитель. В случае сферической
аккреции радиационное давление будет превосходить силу тяготения и при больших
значениях г, если только L превосходит величину, данную в A3.7.6), так что эта
величина остается максимальной наблюдаемой светимостью в стационарном
состоянии. В альтернативном случае излучения тонкой атмосферы, нагреваемой снизу
поверхностью горячей звезды, измеряемая локально критическая светимость больше
A3.7.6) на множитель A - 2GM^//?^c^)"'^', где /?^ — (шварцшильдовский) радиус
звезды. Это означает, что максимальная наблюдаемая светимость на бесконечности
меньше A3.7.6) на множитель A - 2GM /R с^)~'^' (см. упражнение 11.10).
Компактные рентгеновские источники 421
максимальная светимость обеспечивает «стандартную свечу»^^ для барсте-
ров (т.е. предполагается, что она должна быть одинаковой для всех
источников и потому d ос F~g|^). Тогда из уравнения A3.7.7) вытекает
/ F \'/' 1
Л.аЬ^ -Г- A3.7.8)
\ -^ max / i bb
Для каждого источника комбинация наблюдаемых величин в выражении
A3.7.8) в течение всплеска значительно не изменяется. Это дает высокие
основания предполагать, что в хвосте всплеска наблюдается остывающая
поверхность постоянного размера R^. Более того, само значение выражения
A3.7.8) оказывается примерно одинаковым для различных источников со
стандартным отклонением около 20^о. Это говорит о том, что все
компактные объекты, порождающие всплески, имеют приблизительно
одинаковые размеры.
Предположив, что максимальная светимость соответствует эддингто-
новскому пределу A3.7.6) при М^ = 1,4 Mq , Ван Парадийс нашел среднее
значение Rx - 7 км с разбросом 20^о. Релятивистские поправки и учет
отклонений от спектра черного тела, вызванных рассеянием, могут в какой-
то степени изменить выводы, к которым мы пришли^\ Однако, даже если
приведенные выше значения содержат большие ошибки, они четко
указывают, что речь идет о нейтронных звездах, а не о белых карликах или
сверхмассивных черных дырах с Л/ ;г 1(Ю М^.
Упражнение 13.8.
а) Покажите, что «наблюдаемый чернотельный радиус» барстера должен быть
равным
Лос-^^;^) · A3.7.9)
Используйте упражнение 11.10 и уравнение A3.7.3) и покажите, что (с = G = 1)
^00=^A-^) . A3.7.10)
где R — фактический радиус в координатах Шварцшильда.
б) Предположите теперь, что 2М < R < Ъ М. При этдм фотоны могут
ускользать на бесконечность только в пределах угла ^ к радиальному направлению (см.
упражнение 12.14). Покажите, что для изотропного излучения доля ускользающего
потока составляет sin^ ^ и, следовательно,
Л^ = 3>/ЗЛ/, 2Л/<Л<ЗЛ/. A3.7.11)
^^ Т.е. эталон яркости. — Прим. перев.
^^ См. приведенное выше обсуждение, а также работы [229, 587, 588]; обратите
внимание, что 2GM/Rc^ =^ 0,6(Л//1,4 Л/^) {R/1 км)-^.
422 Глава 13
Могут ли нейтронные звезды иметь радиусы в таком интервале?
Указание: См. упражнение 5.5.
Интересно также, что отношение а усредненной по времени энергии
непрерывного (хотя и переменного) рентгеновского потока к энергии,
излучаемой в типичных всплесках I типа, составляет не менее 100. Это значение
совместимо с идеей, что всплески I типа вызываются вспышками
термоядерных реакций, например, гелия или более тяжелых элементов на
поверхностях нейтронных звезд. Из уравнения A3.7.2) следует, что гравитационная
потенциальная энергия, высвобождающаяся на поверхности нейтронной
звезды в виде непрерывного излучения, должна быть порядка etrigc^ - 100
МэВ на каждый аккрецируемый нуклон. Выделяющаяся в ядерных реакциях
с участием гелия и более тяжелых элементов энергия, кото1?ая затем
высвобождается в виде излучения при всплеске, равна - ?,?^? w^c^ - 1 МэВ
на аккрецируемый нуклон. Таким образом, модель термоядерной вспышки
предсказывает
«==^^^Ж1Т0^) · A3.7.12)
Упражнение 13.9. Средняя энергия всплесков II типа быстрого барстера примерно в
130 раз больще энергии всплесков I типа у того же источника. Какое значение это
имеет для выбора между неустойчивостями аккреционных потоков и
термоядерными вспыщками в качестве механизма, порождающего всплески II типа? (Сравните с
[276].)
Однако, подчеркивая сложность проблемы, отметим, что у некоторых
источников всплесков I типа значения а существенно меньше 100
(например, у барстера 4U 1608—52, который испускает два всплеска с
интервалом менее 10 мин, имеющих а <, 2,5). В числе правдоподобных объяснений
упомянем анизотропную светимость, вызываемую аккрецией, но эта
проблема далека от решения.
Рис. 13.11. Два возможных механизма переноса массы в двойном рентгеновском
источнике. Сплошная кривая указывает полость Роша, вне которой нормальный
главный компонент начинает сбрасывать газ на компактный компонент. В случае а
главный компонент лежит внутри полости Роша, но теряет массу посредством
звездного ветра. Вращающаяся по орбите компактная звезда является препятствием для
ветра, и около нее под действием гравитационного поля формируется изогнутый
ударный фронт. Некоторая часть вещества, переработанного ударной волной,
захватывается компактной звездой. В случае б синхронно вращающийся главный
компонент расширяется до границ своей полости Роша и начинает переполнять ее. Газ,
текущий через внутреннюю точку Лагранжа Lj, обладает значительным моментом
количества движения. Некоторая часть этого газа захватывается компактной
звездой и течет к ней, образуя аккреционный диск.
^owuuL^mH^u 3eej^^
\ Ah киецаонньй
\\ IZK
I w мпактная
I звезЗа
424 Глава 13
б) Двойная система
Мы изложили некоторые прямые наблюдательные аргументы в пользу
двойной природы компактных рентгеновских источников. Среди этих
свидетельств периодические затмения рентгеновских источников нормальными
компонентами двойных систем, периодические доплеровские сдвиги
оптических-линий в спектре нормального компонента, вариации периодов
рентгеновских импульсов и в ряде случаев нагрев одной стороны звезды —
главного компонента рентгеновским источником. Типичные периоды двойных
систем измеряются сутками.
Важный во многих отношениях перенос массы от главного компонента
двойной системы к компактному вторичному компоненту может
осуществляться посредством двух различных механизмов: вытеканием из
переполненной полости Роша или же звездным ветром (рис. 13.11). В случае
переполнения полости Роша вещество медленно вытекает через седловую точку
гравитационного потенциала двух звезд и быстро захватывается
компактным объектом. В системе координат, вращающейся синхронно с двойной
системой, эквипотенциальные поверхности вблизи каждой из звезд
представляют собой сферы. По мере увеличения в размере они деформируются,
пока не приходят в соприкосновение во «внутренней точке Лагранжа» Lj
(рис. 13.12). Первая общая эквипотенциальная поверхность ограничивает
«пояость Роша», если вращение главного компонента синхронно вращению
двойной системы, или «приливную полость», если главный компонент
заметно не вращается. Обычно предполагается, что главный компонент
расширяется, «заполняя свою полость Роша», и таким образом облегчает
утечку вещества через точку L j. При таких процессах возможны темпы
потери массы от 3 · 10""* до 3 · 10"^ М^/тол [155, 583]. Согласно моделям
перетекания, захваченная плазма обладает достаточным моментом
количества движения, чтобы образовать аккреционный диск вокруг компактной
звезды.
В случае аккреции от звездного ветра лишь малая часть (не более ?,?^?)
плазмы, выбрасываемой главным компонентом, захватывается
гравитационным полем компактной звезды. Захваченный газ обладает некоторым
моментом количества движения относительно компактной звезды, но он
может оказаться недостаточным для образования аккреционного диска. В
этом случае аккреция более или менее близка к сферической. Теория
звездного ветра и наблюдения говорят о том, что заметные ветры
порождаются достаточно массивными звездами, расположенными в верхней части
главной последовательности; для таких звезд разумно предположить
темпы потери массы 10"'^ - \0~^ М^/тоя [147].
в) Происхождение и эволюция
Происхождение и эволюция компактных рентгеновских источников в
конечном счете связаны с эволюцией тесных двойных систем, которые бы-
Компактные рентгеновские источники ^25
ли предметом интенсивного исследования еще до открытия двойных
рентгеновских систем (обзор работ см. в [439]). В настоящее время
построены (например, [584]) сценарии эволюции специально для двойных
рентгеновских систем.
Такая система берет свое начало от массивной тесной двойной системы.
Более массивная звезда эволюционирует быстрее и расширяется, заполняя
свою полость Роша за 10^ — \0Р лет, т.е. еще до того, как начнется
сгорание гелия в ее недрах. Вскоре (примерно через 10"* лет) большая часть
массы перетекает к другому компоненту. Таким образом, менее массивный
компонент становится теперь более сильно проэволюционировавшей
звездой и ее эволюция в конечном счете определяет природу системы. При
малых значениях массы звезда становится, по-видимому, белым карликом.
При больших значениях ? она через -10^ лет, вероятно, претерпевает
гравитационный коллапс, который приводит к взрыву сверхновой и
образованию нейтронной звезды или черной дыры. Тем временем более массивная
звезда продолжает эволюционировать, и, если двойная система не была
разрушена взрывом сверхновой, эта звезда через 10^ — 10^ лет достигает
границы своей полости Роша. С этого момента она начинает возвращать
вещество компактному компоненту, что приводит к испусканию
рентгеновского излучения.
Упражнение 13.10. Рассмотрите двойную звездную систему, где один из компонентов
взрывается как сверхновая и выбрасывает значительную часть своей массы.
Предположите, что масса теряется за время, много меньшее орбитального периода.
Предполагая орбиту круговой, вычислите, какая доля массы может быть потеряна без
разрушения двойной системы. Каков будет критерий для эллиптической орбиты?
Ответ: ^М/М < 1/2 для круговой орбиты, где Л/ — полная масса системы.
В обрисованной выше картине решающим фактором оказывается масса
системы. В системах с малой массой, где можно ожидать образования
белых карликов или нейтронных звезд, характерные времена эволюции
велики и оптические звезды будут представителями «более старого» звездного
населения (например, Sco Х-1, Cyg Х-2, Cyg Х-3, Her Х-1). В системах с
большой массой характерные времена эволюции сравнительно малы и
звезды будут принадлежать к «более молодому» звездному населению. Если
потеря примерно половины всей массы приводит к разрушению двойной
системы, оставшаяся после взрыва масса по-прежнему будет достаточно
большой и это отождествление сохранится (например, Cyg Х-1, Сеп Х-3,
Зи 0900—40, SMC Х-1).
Из хорошо изученных двойных систем Her Х-1 (эксцентриситет е <
< 0,002), Сеп Х-3 {е = 0,0008) и SMC Х-1 (е < 0,0007) имеют почти
круговые орбиты [473], как и Cyg Х-1 (е < 0,02) [225]. Только у 4U 0900—40 (е =
= 0,092), GX 301—2 te = 0,44) и 4U 0115 -l· 63 (е = 0,340) орбиты имеют
доступный измерению эксцентриситет, как и у двойного радиопульсара
426
Глава 13
-1.781
-1,781
Рис. 13.12. Эквипотенциали ф^^, = const для ньютоновского гравитационного и
центробежного потенциалов в орбитальной плоскости двойной звездной системы с
круговой орбитой. В показанном здесь случае отношение масс составляет
Л/д^:Л/, = 10:1, причем нормальная звезда Mj^ находится слева, а компактная звезда
Л/.
• справа. Эквипотенциали характеризуются значениями ? , измеренными в
единицах G{M^ + М^)/а, где а — расстояние между центрами масс двух звезд. Самая
внутренняя из представленных эквипотенциалей ограничивает полость Роша для
каждой из звезд. Внутри полости Роша, но вне поверхности звезды потенциал
определяется в основном «кулоновским» A/г) полем звезды, так что эквипотенциали
имеют почти сферическую форму. Потенциал имеет локальные точки устойчивости
(У?gc = 0), называемые «точками Лагранжа»; их положение указано буквами L· с
численными индексами [422].
(е = 0,617) [562]. Эволюционная история эксцентриситетов двойных систем
теоретически еще недостаточно разработана.
В то же время, вопреки обрисованной выше картине, имеющиеся
данные противоречат интерпретации рентгеновских источников в скоплениях
как продуктов эволюции двойных систем. Шаровые скопления — это очень
старые объекты, имеющие возраст около 10^^ лет, и большинство
входящих в них звезд с большими и промежуточными массами уже проэволюци-
онировали. Кроме того, до сих пор не получены наблюдательные
свидетельства присутствия в скоплениях нормальных двойных звезд.
Компактные рентгеновские источники 427
Если рентгеновские источники шаровых скоплений действительно
представляют собой компактные объекты звездного типа, а не сверхмассивные
черные дыры, то весьма вероятно, что их образование связано со
специфическими условиями, которые существуют в плотных ядрах шаровых
скоплений. Одна из возможностей состоит в том, что массивные звезды
скопления, имеющие короткое время жизни, порождают компактные объекты
вблизи его центра. Эти компактные объекты могут затем претерпевать
тесные неупругие сближения с нормальными звездами малой массы,
приводящие к их захвату и к образованию двойных систем. Если гипотеза
захвата справедлива, эволюция рентгеновских источников шаровых скоплений
должна, вероятно, отличаться от эволюции остальных источников
центральной галактической подсистемы. Если последние — это двойные
системы с малой массой, содержащие нейтронные звезды, то они, по-видимому,
являются первичными двойными системами.
Глава 14
Аккреция на черные дыры
14.1. ВВЕДЕНИЕ
Процесс, посредством которого компактные звезды захватывают
окружающее вещество, называется аккрецией. Как уже говорилось в гл.
13,'аккреция газа на компактные объекты с массой ? - ?q , по-видимому,
подпитывает энергией наблюдаемые в двойных системах рентгеновские
источники. Этот же процесс в гораздо больших масштабах может действовать в
квазарах и ядрах активных галактик, где наблюдается быстропеременное
излучение при высокой светимости от относительно компактных областей.
В этом случае возможный источник энергии — аккреция на сверхмассивные
черные дыры с массой ? ^ 10^ — 10^ Mq . Изолированные компактные
звезды с ? - ?0 также могут аккрецировать газ, странствуя в
межзвездной среде нашей Галактики. Число таких объектов может быть весьма
значительным^^
Все эти объекты не случайно привлекают внимание исследователей.
Дело в том, что при падении в сильном гравитационном поле, скажем
нейтронной звезды или черной дыры, примерно Ю^о энергии, соответствующей
массе покоя аккрецируемого вещества, может быть преобразовано в
излучение. Таким образом, процесс аккреции оказывается значительно более
эффективным источником космической энергии, чем многие другие
астрофизические механизмы (например, ядерный синтез).
Расчет аккреционного течения на компактную звезду и картины
испускаемого излучения, вообще говоря, очень сложен. Выясним, с чем это
связано. Предположим, что эффективная длина свободного пробега частиц газа
между столкновениями достаточно мала, чтобы течение по своей природе
было гидродинамическим. Во-первых, надо определить геометрию течения:
в общем случае, если газ обладает собственным моментом количества
движения, течение будет двухмерным или трехмерным в зависимости от
характера симметрии. В простых случаях течение может оказаться
сферически симметричным (таким, например, будет случай, когда вдали от
стационарной компактной звезды среднее движение газа отсутствует) или
дискообразным (как в случае осесимметричного течения газа, имеющего
собственный момент количества движения). Такие виды течения значительно
упрощают анализ. Во-вторых, следует качественно оценить
преобладающие механизмы нагрева и охлаждения, характерные для аккрецируемой
плазмы. Если оптическая толщина газа дяя испускаемого излучения велика
Грубый «подсчет» см. в разд. 1.3.
Аккреция на черные дыры 429
(т.е. фотоны рассеиваются или поглощаются газом, прежде чем смогут
ускользнуть на бесконечность), то результирующие скорости нагрева и
охлаждения будут сами по себе зависеть от поля излучения, которое
следует определять самосогласованно. В-третьих, необходимо оценить
возможную роль магнитных полей в плазме. Магнитные поля могут пронизывать
плазму уже вдали от компактной звезды, либо они могут порождаться
самой звездой (либо и то, и другое вместе!). В любом случае вклад
магнитного поля в давление и в скорости нагрева и охлаждения должен быть
правильно учтен. В-четвертых, надо правильно учесть эффект давления
излучения, сдерживающего аккреционное течение. В-пятых, надо иметь
представление о граничных условиях течения как на больших расстояниях, где газ
«сливается» с внешней средой, так и на поверхности звезды, где газ плавно
поглощается звездой. Итак, в общем случае аккреции требуются решать
зависящие от времени многомерные релятивистские, магнитогидродинами-
ческие уравнения и связанные с ними задачи переноса излучения!
Поэтому неудивительно, что проблема газовой аккреции на компактные
звезды решена только для отдельных идеализированных случаев. Даже при
самых простых предположениях (например, стационарный поток со
сферической или дисковой геометрией) анализ усложняется требованием
самосогласованности. Например, подлежащее вычислению поле излучения
обычно определяется процессами нагрева и охлаждения, предполагаемыми для
расчета температур газа, а последние в свою очередь определяют поле
излучения!
Несмотря на все эти трудности, в последние годы достигнут прогресс в
развитии теории аккреционных течений и приложении этой теории к
компактным рентгеновским звездам. Действительно, как мы видели в разд.
13.7, даже самые простые предположения, касающиеся светимостей и
спектров, дают результаты, которые качественно согласуются с многими
данными рентгеновских наблюдений.
В нескольких следующих разделах мы обсудим идеализированные
модели, иллюстрирующие физическую суть рассматриваемого процесса.
Вначале мы уделим внимание аккреции на черные дыры. В этом случае
трудности, связанные с учетом картины течения на поверхности звезды,
несколько меньше благодаря отсутствию магнитного поля^^ и наличию горизонта
событий («пылесосные» граничные условия). В гл. 15 мы вернемся к
рассмотрению аккреции на нейтронные звезды и белые карлики. Во всех
случаях будем считать, что гравитационное поле центральной компактной
звезды преобладает над полем падающего вещества. Соответственно мы
пренебрегаем собственной гравитацией аккрецируемого газа, как и очень
медленным увеличением массы центрального объекта вследствие
аккреции^^.
^^ Вспомните теорему об «отсутствии волос» у черных дыр, разд. 12.1.
^^ Аккреция на компактные объекты обсуждалась в ряде книг и обзорных статей,
например [636] (до результатов «Ухуру»), [321, 330, 367, 422, 459]. В них читатель
может найти дополнительные сведения и ссылки на интересующую его литературу.
430 Глава 14
Введение в проблему переноса излучения дано в приложении И.
Рекомендуем читателю, не знакомому с основами теории переноса излучения,
прочитать это приложение, прежде чем переходить к следующему разделу.
14.2. БЕССТОЛКНОВИТЕЛЬНАЯ СФЕРИЧЕСКИ СИММЕТРИЧНАЯ
АККРЕЦИЯ
В ЭТОМ разделе будет рассмотрена аккреция бесстолкновительного газа
идентичных частиц с массой т на центральную звезду массой ? и
радиусом R. Этот процесс впервые был исследован Зельдовичем и Новиковым
[636]. Общее рассмотрение будет ньютоновским, но темп аккреции,
полученный для центральной шварцшильдовской черной дыры, окажется
правильным и в релятивистском случае.
Вся информация об аккрецируемом газе содержится в функции
распределения частиц/(г, ?,?, определяемой как
Дг, V, t)(fi r(fi ? — число частиц, находящихся в элементе фазового объема
(firifiv с центром в точке (г, ?), в момент времени t.
A4.2.1)
Величина/называется также «плотностью в фазовом пространстве»,
потому что для нерелятивистских частиц d^v и d^p пропорциональны.
Плотность частиц в координатном пространстве определяется выражением
/i(r,0=/ /(r,v,0^^t;, A4.2.2)
а дисперсия скоростей (т.е. «температура») — выражением
<?^(?,0> = ·;^/ v'f{r,y,t)d\ A4.2.3)
И так далее (интегрирование по всем ?).
Функция распределения / бесстолкновительного газа определяется бес-
столкновительным уравнением Больцмана, или уравнением Власова
ftfi^^^^ о = I7 + V · V,/ + * · V,/= о, A4.2.4)
где V ? г — скорость частицы вдоль координаты г, а ? — ускорение.
Уравнение A4.2.4) — это просто уравнение неразрывности потока частиц в
шестимерном фазовом объеме (вывод и обсуждение см., например, в [479]).
Уравнение A4.2.4) представляет собой теорему Лиувилля: функция
распределения сохраняется вдоль траектории каждой частицы. Для
интересующей нас задачи ? = — ??, где ? — гравитационный потенциал
Ф=——-+Фсг, A4.2.5)
Аккреция на черные дыры 431
и для самогравитации
У^Фсг ^^'ггОр, A4.2.6)
где плотность массы ? = пт получается из уравнения A4.2.2). В
дальнейшем будем пренебрегать caмo?paви?aциeй частиц и поэтому положим ? =
= -GM/Гу где г — расстояние до центральной звезды.
В случае стационарного течения, когда функция распределения / не
зависит от времени, она зависит только от интегралов движения^^ Для
сферически симметричной системы таких интегралов два: энергия ? и
абсолютная величина момента количества движения У, значения которых (в
пересчете на единицу массы) даются выражениями
E^\,^^^ir)^y^Yy^^^^^ A4.2.7)
/ = п;,. A4.2.8)
Здесь v^viVf — радиальная и поперечная скорость частиц. При заданных ?
и J траектория частицы в сферическом потенциале полностью определена
и, следовательно, / = ??, J), Если, кроме того, распределение по
скоростям повсюду изотропно, то функция / упрощается еще больше, так как
она не зависит от J. В этом случае/ = /(?"), где в соответствии с
уравнением A4.2.7) ? ^ ф{г) [т.е. частицы с ?" < Ф(г) отсутствуют]. Для
стационарного сферического распределения с изотропными скоростями уравнение
A4.2.2) сводится к виду
п{г) = 4???^/?? = 4?? [2{Е - Ф)]^/'/(^) dE, A4.2.9)
а уравнение A4.2.3) — к виду
^'('¦)> = ????? t2(^ - ^)ГЧ{Е) dE. A4.2.10)
Упражнение 14.1. Докажите что при/ = /(?") справедливы соотношения <у2(г)> =
= 3<?;2(?)> ?{?}{? = {v}{r))/l.
Рассмотрим теперь аккрецию невзаимодействующих частиц на звезду.
Частицы, имеющие момент количества движения, меньший критического
значения J^^^(E), будут захвачены звездой, когда достигнут перицентра.
Для нерелятивистских частиц, обращающихся вокруг ньютоновской звезды
с радиусом /?, имеем
У^„(?)= [2(^^ + ^1'^^/? (нерелятивистские частицы; ^^^.2.11)
L \ ^ / J ньютоновская звезда).
'^ Этот результат часто называют «теоремой Джинса» [299].
432 Глава 14
Упражнение 14.2. Проверьте уравнение A4.2.11).
Для нерелятивистских частиц, обращающихся вокруг черной дыры (или
очень компактной нейтронной звезды), имеем
ЮМ (нерелятивистские частицы; ..^^.^.
•^min(^) = , A4.2.12)
с черная дыра).
Этот результат следует из упражнения 12.9, поскольку условие для
захвата имеет вид Е^ > V^^ и ?^ = 1 для нерелятивистских частиц. Поэтому
величина ^п^п^^ определяет «конус потерь» в пространстве скоростей, в
пределах которого частицы поглощаются звездой вблизи перицентра.
Благодаря наличию конуса потерь [J < J^j^(E)] удобно определить плотность
частиц как функцию от ?* и У. Уравнения A4.2.7) и A4.2.8) позволяют
переписать элемент d^v скорости в виде
d^v = iTTv.dv.dv^ = ; , A4.2.13)
где «дополнительный» множитель 2 появляется по той причине, что при
заданной энергии ? величина ?^ может быть как положительной, так и
отрицательной. Теперь можно определить ?~ (г, Е, J) -^ число частиц с
направленной внутрь радиальной скоростью, приходящееся на единичный
интервал значений г, ? и J:
ЛГ-(г, Е, J) drdEdJ = \f{E, J) d^rd\
= S^^/-fdrdEd/. A4.2.14)
Полный темп захвата частиц центральной массой равен
N,,, = Г dEi'-'''^^^d/\v,\N-{r, ?, J)\ = Stt'T dE(''-''^^^dJfJ,
A4.2.15)
a соответствующий темп аккреции массы составляет М^^^ = mN^^^.
Рассмотрим теперь конкретный пример, анализируя захват
несвязанных нерелятивистских частиц с энергиями ? > 0. Предположим, что всегда
существует бесконечный резервуар таких частиц, окружающий звезду, и
что распределение частиц изотропное и моноэнергетическое. Вдали от
звезды концентрация частиц постоянна и равна п^, а скорость частиц равна
?^ < с. Таким образом.
/ = /(^) = ^. ^^^"У,, A4.2.16)
4'гB?„)
Аккреция на черные дыры 433
где
^00=^, t)^«c. A4.2.17)
Нормировка дельта-функции в формуле A4.12.16) может быть проверена
сравнением с уравнением A4.2.9), поскольку ? = О при г = оо. На больших
расстояниях/ -* n^b(v - ?^)/???\^, но выражение A4.2.16) справедливо
всюду согласно теореме Лиувилля. Из выражения A4.2.15) сразу же под-
считывается темп захвата несвязанных частиц
ЩЕ > 0) - Sn'fdEf{E)f'-d/J = 4n4"dEf{E)J^iE).
•? •'о •'о
A4.2.18)
Этот результат применим даже в случае аккреции на черную дыру,
поскольку при стационарном поглощении несвязанных частиц первое
интегрирование в уравнении A4.2.15) может быть оценено для произвольно
большого г. Тогда формулы A4.2.11), A4.2.12) и A4.2.16)-A4.2.18) дают
М{Е>0) = mN{E>0)
= / (нерелятивистские частицы; ньютоновская звезда),
\\67r{GMfp^v-'c-^
\ (нерелятивистские частицы; черная дыра), A4.2.20 )
где р^ = тп^.
Упражнение 14.3. Выведите заново уравнения A4.2.19) и A4.2.20), обратив
внимание, что масса, пересекающая в единицу времени сферу большого радиуса г > R по
направлению внутрь равна (для частиц, находящихся на орбитах захвата)
М{Е > 0) = (???^??/4?L7??2??<,» где телесный угол захвата равен ??<, = ас/г^, а
сечение захвата ?^ дается уравнениями A2.4.38) или A2.4.39). Поэтому ЩЕ > 0) =
= Роо^оо^с·
Упражнение 14.4. а) Вычислите темп аккреции массы на шварцшильдовскую черную
дыру, помещенную в изотропный резервуар фотонов с плотностью энергии ?»
вдали от звезды.
Указание: Используйте метод предыдущего упражнения и уравнение A2.5.12)
для аз-
Ответ: ? = 11жСР-Ь^^^/(^,
б) Какова минимальная масса черной дыры, которая может удвоить свою массу
за время, меньшее возраста Вселенной / = 10^^* лет, если ее поместить в фоновое
космическое микроволновое излучение с температурой 3 К? Примите, что
температура микроволнового фона за этот период не изменялась со временем.
12-513
434 Глава 14
Обратите внимание, что вместо уравнения A4.2.19) надо использовать
уравнение A4.2.20), когда Rc^/GM < 8, как, например, в случае очень
компактных нейтронных звезд. Выполняя оценку выражения A4.2.20) для
условий, присущих ионизованному компоненту межзвездной среды нашей
Галактики, получаем темп аккреции на черную дыру
Л/(?> 0)=1,56 . \Q-M :^^—т-\{чг\( ^^^—) ' ^0/^^^-
^ ^ ' I 10-24 г/смЗ /\Мо/ I 10 км/с '
A4.2.21)
Нетрудно вывести дисперсию скоростей несвязанных частиц и их
плотность в виде функций расстояния от звезды для функции распределения,
задаваемой уравнением A4.2.16). Потребуем выполнения условия г > R,
чтобы можно было пренебречь исчезновением частиц из-за соударения со
звездной поверхностью и релятивистскими поправками вблизи горизонта
событий черной дыры. В соответствии с этим выражение A4.2.9),
рассчитанное для ?¦ > О, дает
1/2
«?>?('·) = «»(?+^) , A4.2.22)
а уравнение A4.2.10) дает
{Лг))е>о - Лг) = vi[\ + ^j. A4.2.23)
Уравнение A4.2.23) может быть также получено из A4.2.7) и A4.2.17). Его
можно использовать для определения «температуры» частиц в
соответствии с
Те>Лг) = 7;o(i + ^). \кТ - {mv\ A4.2.24)
В нашем случае уравнения A4.2.22)-A4.2.24) иллюстрируют весьма
общую особенность сферически симметричной аккреции на центральную
массу. Определим радиус «аккреции», или «захвата» г^ как такой радиус, при
котором кинетическая энергия частицы равна ее потенциальной энергии
1GM
Га^—Г' A4.2.25)
Тогда очевидно, что при г > г^ профили плотности и температуры мало
отличаются от их асимптотических значений на бесконечности. Однако при
г < Гд гравитационный потенциал центральной массы влияет на
распределение, фокусирует частицы и увеличивает их плотность и температуру.
Качественно аналогичное поведение характерно также для гидродинамической
Аккреция на черные дыры 435
аккреции (см. разд. 14.3), но в этом случае плотность увеличивается
гораздо сильнее, чем по формуле A4.2.22), благодаря столкновениям.
Упражнение 14.5. Рассмотрите аккрецию несвязанных частиц, подчиняющихся
вдалеке от центральной звезды распределению Максвелла—Больцмана (MB) для
скоростей и ^ имеющих концентрацию /7^ и среднеквадратичную скорость ?^?.
Подсчитайте Л/(Е > 0), /7(г), {v'^{r)) и Т{г) для такого распределения; изучите как случай
ньютоновской звезды, так и случай черной дыры (но только для г > К).
Ответ: М^^{Е > 0) = %B????^^0^?^?^?-^€-^ A4.2.26)
(нерелятивистские частицы; черная дыра).
Как подчеркивается Зельдовичем и Новиковым [636], приведенные выше
уравнения для Л/, п(г) и других параметров могут применяться только к
несвязанным частицам, достигающим центральной звезды из бесконечности с
? > О, Число связанных частиц неограниченно, если полностью пренебречь
столкновениями. В этом случае распределение связанных частиц,
движущихся по эллиптическим орбитам вокруг центральной звезды, является
начальным условием, которое может быть задано произвольно и независимо
от уравнения A4.2.16). При строгом отсутствии столкновений семейство
связанных частиц на орбитах захвата не пополняется за счет распределения
несвязанных частиц. Лишь при наличии столкновений частица с энергией
? > О может случайно в результате рассеяния перейти на связанную
орбиту с is < 0. Поэтому влияние любого вклада связанных частиц в ?
непродолжительно и исчезает со временем, когда достигается стационарное
состояние.
Пожалуй, более интересен случай, когда столкновения все же
происходят. Если длина свободного пробега между столкновениями много меньше
характерного размера, т.е. \ < г (большие сечения рассеяния), то течение
становится гидродинамическим и его можно определить путем анализа
движения жидкости. Этот важный режим обсуждается подробнее в
следующем разделе. Если же оо > ?^ > г (так что сечения рассеяния малы, но
конечны), режим течения описывается уравнением Больцмана с учетом
столкновений:
fA^Y- <·^·""
В данном случае правая часть уравнения A4.2.27) не обращается в нуль,
потому что столкновения могут изменить распределение частиц в фазовом
объеме.
В общем случае уравнение A4.2.27) чрезвычайно сложно для решения.
Упрощение возможно, когда неравенство ?^. > г оказывается очень
сильным. Тогда в нулевом приближении функция распределения
удовлетворяет условию Df/Dt « О, а столкновительный член рассматривается как
возмущение первого порядка. В этом режиме характерное «динамическое
время пересечения», соответствующее периоду орбитального движения ча-
436 Глава 14
стицы, t^ - г/?, гораздо меньше характерного времени релаксации
вследствие столкновений t^ - \/v, т.е. /^ < t^. Таким образом, на интервалах,
сравнимых с динамическим временем, функция/в первом приближении
должна удовлетворять уравнению Власова A4.2.4); она с высокой степенью
точности подчиняется теореме Лиувилля и для сферически симметричных
систем должна иметь вид/ = f(E, У). Однако из-за столкновений функция
распределения / должна также испытывать медленные вековые изменения
на интервалах, сравнимых с характерным временем релаксации.
Действительно, при t > t^ столкновения фактически определяют вид функции
распределения, выбирая среди многих возможных решений уравнения Власова
именно те, которые удовлетворяют «столкновительным» ограничениям.
Здесь напрашивается аналогия с динамическим равновесием
эволюционирующих звезд, которые с высокой степенью точности удовлетворяют
условию гидростатического равновесия, но испытывают вековое расширение
или сжатие во временных масштабах, определяемых процессом
термоядерного синтеза.
Дальнейшее упрощение возможно, если основные эффекты
столкновений порождаются рассеянием на малые углы, В этом случае итоговое
отклонение частиц определяется накапливающимся эффектом многократных
рассеяний на малые углы, а не небольшим числом соударений, приводящих
к рассеянию на большие уГлы (- 90°). Тогда можно представить правую
часть уравнения A4.2.7) в виде следующего приближения разложения по
возмущениям, называемого уравнением Фоккера—Планка. Такое
разложение удобно, когда столкновения имеют кулоновский характер (т.е. когда
силы между частицами изменяются как 1/г^), как, например, при кулонов-
ском рассеянии заряженных частиц в плазме или при гравитационном
рассеянии тел в звездном скоплении.
Предполагается, что в типичных случаях течение плазмы на
компактную звезду по своей природе является гидродинамическим с ?^ < г^\ С
другой стороны, динамическое поведение звезд в шаровом звездном
скоплении описывается уравнением Фоккера—Планка. В этом случае величина
?^, связанная с гравитационными «столкновениями» (т.е. рассеянием)
между звездами, удовлетворяет условию оо > ?^. > г или t^ < t^.
Динамическая эволюция шаровых звездных скоплений в последнее время привлекает
большой интерес теоретиков. Это связано с разработкой новых численных
методов решения уравнения Фоккера—Планка, появлением хороших
наблюдательных данных для шаровых скоплений и открытием рентгеновского
излучения от шаровых скоплений (см. гл. ??\ Отметим, наконец, что
динамическое поведение нормальных галактик описывается бесстолкнови-
^^ См., однако, анализ случая с ?^ > г в [58].
^^ Для ознакомления с общим обсуждением динамической эволюции шаровых
звездных скоплений рекомендуем читателю обзоры [365, 548] и помещенные там
ссылки на литературу.
Аккреция на черные дыры 437
тельным уравнением Больцмана, поскольку t^ < ty^ < /^, где /// ~ 1/Я ~
- 10^^ лет [Н " 100 км/(с · Мпс)] — возраст Вселенной, а Я —
постоянная Хаббла.
Упражнение 14,6, Подсчитайте скорость, с которой несвязанные звезды с
распределением Максвелла—Больцмана будут поглощаться массивной черной дырой Л/,
расположенной в центре очень плотного активного галактического ядра.
Предположите, что звездная плотность равна п^о = Ю^пс~^, а дисперсия скоростей составляет
{viiY'^^ = 250 км/с вдали от дыры. Предположите далее, что звезды поглощаются
вслед за приливным возмущением дырой на расстоянии приливного разрушения
Гр = R{M/mY', где т — масса, а /? — радиус звезды.
Указание: J^^(E) = [2(Е + GA/A^)]'/^^,.
14.3. ГИДРОДИНАМИЧЕСКАЯ СФЕРИЧЕСКИ СИММЕТРИЧНАЯ АККРЕЦИЯ
Учитывая существующие типичные условия газовой динамики в
межзвездной среде и при обмене веществом между звездами двойных систем,
можно полагать, что аккреционное течение на компактные объекты по своему
характеру должно быть гидродинамическим. Иногда одних лишь
столкновений может оказаться недостаточно, чтобы эффективно связать частицы,
как в случае кулоновских столкновений в межзвездной плазме, аккрецируе-
мой на компактную звезду с массой порядка солнечной. Однако обычно
влияние макроскопически слабых магнитных полей или двухпотоковых
плазменных неустойчивостей (либо другие коллективные плазменные
эффекты) сокращает эффективную длину свободного пробега частицы, делая
ее малой (т.е. \^^ < г), и тем самым обеспечивает гидродинамический
характер течения. Такова, например, ситуация, наблюдаемая в солнечном
ветре, где магнитные поля и плазменные неустойчивости приводят к
сильной связи между заряженными частицами разного типа и сохраняют
гидродинамический характер истечения ветра ^^
Рассмотрим теперь стационарную сферически симметричную аккрецию
окружающего газа на стационарную невращающуюся черную дыру с
массой Л/ в предельном случае сплошной среды. Предположим, что течение
газа в первом приближении адиабатическое, рассматривая потери энтропии
из-за излучения как малое возмущение. При этих предположениях газ будет
характеризоваться показателем адиабаты Г, а давление повсюду будет
связано с плотностью массы покоя соотношением
Р = Кр^ К,Т^ const, A4.3.1)
^^ Истечение звездного ветра фактически представляет собой аккрецию,
«обращенную во времени»; см. ниже.
438 Глава 14
Скорость звука ? определяется выражением ? s {dP/dpY^ = (^?/??^,
справедливым повсюду. Предположим, что на бесконечности газ покоится и
имеет плотность р^, давление Р^ и скорость звука а^.
Основные характеристики течения достаточно хорошо описываются,
если использовать ньютоновскую гравитацию, особенно на больших
расстояниях от дыры г > GM/c^, Отличительная особенность аккреции на черную
дыру по сравнению с аккрецией на несколлапсированную звезду с
«твердой» поверхностью заключается в том, что черная дыра налагает
уникальные условия регулярности на течение при малых радиусах вблизи г =
= 2MG/c^, Эти условия находятся с учетом релятивистских
гравитационных эффектов^^. Условия регулярности для черных дыр служат для
однозначного определения темпа аккреции массы М. При аккреции на звезду,
обладающую поверхностью, темп аккреции зависит от граничных условий
вблизи поверхности. Решение для черной дыры оказывается единственно
возможным решением задачи аккреционного течения над звездой. Как
будет показано ниже, это решение дает максимальный темп аккреции.
В дополнение к уравнению A4.3.1), которое заменяет уравнение
энтропии, течение полностью описывается уравнением неразрывности
1 d
V · pu =
и уравнением Эйлера
V.pu = -^|(r^p«) = 0, A4.3.2)
Z), = ^^>-^^A\ A4.3.3)
[сравните с уравнениями F.1.1) и F.1.2)]. Написанные выше уравнения
приведены для стационарного сферически симметричного течения; при этом
и < О соответствует радиальной скорости, направленной внутрь.
Уравнение A4.3.2) можно проинтегрировать, что дает уравнение для М,
которое, как будет видно ниже, определяет набор собственных значений:
47гг^рм = Л/ = const (не зависит от г). A4.3.4)
Уравнение A4.3.3) также можно проинтегрировать, использовав A4.3.1), и
получить обычное уравнение Бернулли
12.^2^^ 1 ,
где для определения постоянной интегрирования использованы граничные
условия на бесконечности. Течение определено, как только известны Л/ и
распределения Р(г) и м(г).
'^ См. приложение Ж, где релятивистское рассмотрение сопоставляется с
ньютоновским.
Аккреция на черные дыры 439
Как было показано Бонди [78], различные значения ? ведут к физически
разным классам решений при одних и тех же граничных условиях на
бесконечности. Здесь нас интересует только то единственное решение, при
котором скорость монотонно возрастает от нуля при г = оо до скорости
свободного падения при малых радиусах: и -* BСМ/гУ^\ когда г ^ 0. В
действительности, релятивистские уравнения при г = 2GM/c^ требуют
выбора именно этого решения, чтобы избежать появления особенностей течения
вне горизонта событий (сравните с приложением Ж). Для вычисления
требуемого темпа аккреции М, перепишем уравнение A4.3.2) в виде
+ - + - = 0 A4.3.6)
р' м' 2
— + — + -
риг
(штрихом обозначена производная d/dr), а уравнение A4.3.3) в виде
Решив уравнения A4.3.6) и A4.3.7) относительно и' и /о',получаем
"'==^, Р'=--^, A4.3.8)
где
2a^/r-GM/r^ A4.3.9)
J,,.'"'/r-f"/'\ (,4.3..0)
И
Z) = i^—^ A4.3.11)
up
Как показывают соотношения A4.3.8), чтобы обеспечивать гладкое
монотонное увеличение и с уменьшением г и одновременно исключить
появление особенностей в течении, решение должно проходить через
«критическую точку», в которой
Z), == ZJ = ^ = О at г = г,. A4.3.12)
Из уравнений A4.3.9)-A4.3.12) находим, что при критическом радиусе
2 2 1 ?^^ / ч
""s^^-J-T^ A4.3.13)
так что критический радиус соответствует радиусу области околозвукового
течения, при котором скорость течения сравнивается со скоростью звука.
440 Глава 14
Комбинируя уравнение A4.3.13) с уравнением A4.3.5), можно связать а^, и^
и г, с известной скоростью звука на бесконечности:
5 - ЗГ \ GM
а' = и'
I 2 \ 5 / 5 - ЗГ \ GM
[jzrj^yi^ ^. = (-4-)^- A4.3.14)
Таким образом, видно, что в области околозвукового течения
гравитационный потенциал GM/r^ сравним с внутренней тепловой энергией
окружающего вещества, приходящейся на единицу массы, а^.
Теперь можно вычислить темп аккреции из уравнения A4.3.4),
используя зависимость
?
Получаем
?/ = 4^???«?'(^) =4^?,|^|?^?^, A4.3.16)
где безразмерное собственное значение ?^ для околозвукового течения
дается соотношением
^^ = BJ (^-) 0^-3-17)
Значения ?^ как функции Г приведены в табл. 14.1.
Таблица 14.1
СОБСТВЕННЫЕ ЗНАЧЕНИЯ ?^
1 1,120
4/3 0,707
7/5 0,625
3/2 0,500
5/3 0,250
Упражнение 14.7. Докажите, что для Г = 1 \ - e^/V4 и что для Г = 5/3
\ = 1/4.
Выражения для темпа околозвуковой аккреции можно переписать в виде
Л
M = 4^X,(GM)'p^a-'c-2-^. A4.3.18)
Аккреция на черные дыры 441
Как показывает сравнение A4.3.18) с A4.2.20), приближенное равенство
скорости звука а^ средней скорости частицы ?^ подразумевает, что темп
гидродинамической аккреции больше темпа бесстолкновительной аккреции
на большой множитель (c/a^Y (порядка 10^ для типичного межзвездного
ионизованного газа с ??» ^ ^0 км/с). Физическая причина такого
несоответствия проста: столкновения между частицами ограничивают их
поперечное движение и направляют частицы в радиальном направлении,
обеспечивая эффективный захват. Для идеального газа Максвелла—Больцмана со
средним молекулярным весом ? имеем
ркТ 2 _ r^tr
?^== , Г=Г
???^ ???^
[??- <"¦'¦">
Применение уравнения A4.3.19) для расчета ? ионизованного компонента
межзвездной среды (предполагается, что это чистый водород: ? = 1/2)
дает для Г = 5/3
? =8.77 · 10-'*
(^)(lO--°°r/cM3 ??^^) ^^0^^°^
MYi 9^ \l T^
I ?/?/ Ьо-^Ч/смЗ /I 10" К.
- '·» ¦ '"?^? ..-^:,^., ?^?" '"¦ 04.3.20)
Упражнение 14.8. Докажите, что темп околозвуковой аккреции — это
максимально возможный темп стационарной аккреции для данного значения Г [78].
Указание: а) Запишите уравнение Бернулли A4.3.5) в безразмерном виде
где
и где л· = r/{GM/al,), ? s и/а, ? = /о//ооо = {а/а„)^^(^ - ^). Используйте уравнение
A4.3.4), чтобы исключить ?.
б) Покажите, что как /, так и g проходят через минимальные значения, равные
соответственно /^ и ^,, где
/ 1 Г+ 1
^'^2Т^ ???? = ?, = 1,
1 Г + 1 Г 1 т-сз-згмг+о 1
442 Глава 14
в) Докажите на основе результатов а) и б), что наибольшее значение, которого
может достичь ?, равно
ч(Г+1)/2(Г-1) , J ч(Г+1)/2(Г-1)/з _ зр\-E-ЗГ)/2(Г-1)
= ?^? = (? 7^-згу
Упражнение 14.9. Докажите, что при Г > 5/3 не существует стационарных
околозвуковых политропных решений.
Указание: Уравнения A4.3.8) должны дать действительные значения и' и /о',
когда правые части вычисляются с использованием правила Лопиталя при г = г^.
Обратите внимание, что благодаря A4.3.6) правило Лопиталя следует применять
только к одному из уравнений.
Профили околозвукового течения выводятся просто. На больших
расстояниях от области околозвукового течения (т.е. г t> г^)
гравитационный потенциал центральной массы едва ощутим, так что температура и
плотность остаются близкими к асимптотическим значениям на
бесконечности:
? «Рос» Т^Т^, а^а^, 7^^' A4.3.21)
Из A4.3.4), A4.3.16) и A4.3.21) следует, что скорость течения уменьшается
с возрастанием г в соответствии с соотношением
f-^i^f.-, f»l. A4.3.22)
Ниже околозвуковой области на течение существенно влияет
гравитационное поле центральной массы. Для г/г^ < 1 член GM/r преобладает над
членом ufV(r - 1) в уравнении A4.3.5). Скорость течения достигает скорости
свободного падения, а замедление, вызванное давлением газа, становится
пренебрежимо малым:
Согласно A4.3.4), A4.3.16) и A4.3,23), плотность растет с уменьшением г
следующим образом:
Этот рост значительно больше найденного для случая бесстолкновительно-
го течения [уравнение A4.2.22)], даже если характерные скорости частиц
такие же. Причина снова связана со способностью столкновений
эффективно «канализировать» течение, направляя его по радиусу в
гидродинамическом пределе. Оценка уравнения A4.3.24) при г = IGM/c^ показывает, что
Аккреция на черные дыры
443
у горизонта событий увеличение плотности в гидродинамическом случае
больше, чем для бесстол кновительного газа, приблизительно в (с^/а^
раз. Увеличение температуры при малых значениях г можно оценить,
комбинируя уравнения A4.3.19) и A4.3.24):
?^?
[2'/2
IGMY''
\al] \
Г-1
-3(Г-1)/2
г
rs
<к 1
(,<г<|).
A4.3.25)
Если сравнивать уравнения A4.3.23)-A4.3.25) с (Ж.34)—(Ж.36), то видно,
что первые оказываются релятивистски «правильными», если
отождествить г с шварцшильдовской радиальной координатой, м — с радиальной 4-
скоростью, а ? — с плотностью массы покоя.
Уравнения A4.3.23)-A4.3.25) слегка изменяются в особом случае: Г =
= 5/3, для которого в ньютоновском приближении г^ = 0. В этом случае
находим, что для r(GM/al) < 1 критическое решение удовлетворяет
соотношениям
\ 2г I GM/ai
Соответствующие профили плотности и температуры при малых г
определяются при этом уравнениями A4.3.4), A4.3.16), A4.3.17) и A4.3.19):
у 3/2 \
(-!)¦
A4.3.26)
21/2
~4~
Рос ·* \ а,
? 1 GM
gm\
.-3/2
GM/al
«: 1
(-1)·
A4.3.27)
Уравнения A4.3.26) и A4.3.27) изменяются в результате умножения на
численные коэффициенты порядка единицы, когда используются
релятивистские уравнения течения. В приложении Ж показано, что на горизонте г =
= IGM/c^ радиальная 4-скорость и^ = 0,782, и подсчитаны
соответствующие увеличения плотности и температуры [см. уравнение (Ж.38)].
Получены точные численные значения этих отношений для нерелятивистских ба-
рионов, аккрецируемых из типичного межзвездного газа.
Упражнение 14.10. Рассмотрите околозвуковую аккрецию с Г = 1
(изотермическое течение).
а) Как изменится уравнение A4.3.5)?
б) Объясните, почему в этом случае все еще справедливы уравнения
A4.3.21)-A4.3.25).
444
Глава 14
и/а 1,0 \-
Рис. 14.1. Схема некоторых возможных решений уравнений Бонди для
стационарного адиабатического сферически симметричного течения около точечной гравитирую-
щей массы. Зависимость числа Маха (¦ и/а) от расстояния показана для трех
значений безразмерного параметра ?. Стрелки, указывающие налево, означают
аккреционное течение, а направо — истечение ветра. Жирная сплошная линия соответствует
околозвуковой аккреции.
Граничные условия на бесконечности (т.е. и = О, а = а^, ? = р^)
неоднозначно определяют и решение ньютоновских уравнений A4.3.2) и A4.3.3)
или уравнений A4.3.4) и A4.3.5) для аккреции. Действительно, как указал
Бонди, существует второй класс аккреционных решений, удовлетворяющий
тем же самым граничным условиям. Этот класс характеризуется
дозвуковым течением в любом месте. Дозвуковое решение существует для
каждого значения ? в диапазоне О ^ \ < \ (рис. 14.1). Определим г^-в
соответствии с уравнением A4.3.14). Дозвуковые решения продолжают
удовлетворять уравнению A4.3.21) для г/г^ > 1. Однако при г < г^ течение
значительно отличается от околозвукового. В дозвуковом случае второй член
в левой части уравнения A4.3.5) преобладает над первым членом по мере
уменьшения л, что для 1 < Г < 5/3 приводит к соотношению
1
Г- 1
[в-
GM
г «: л
1 < Г < —; дозвуковое |.
течение
A4.3.28)
Уравнение A4.3.28) представляет собой уравнение гидростатического
равновесия при политропном уравнении состояния.
Упражнение 14Л. Выведите уравнение A4.3.28) непосредственно путем
интегрирования уравнения гидростатического равновесия при политропном уравнении
состояния, т.е. уравнении A4.3.1).
Аккреция на черные дыры
445
Таким образом, течение в дозвуковом режиме «закупоривается»
обратным давлением. Это обратное давление возникает благодаря большому
градиенту плотности, создаваемому по мере того, как вещество
накапливается вблизи центральной массы. Из уравнения A4.3.28) находим
^2ДГ-1)
Рос \ 0« /
1 +
(Г - l)GM
а^г
1ДГ-1)
(Г - \)GM
1ДГ-1)
Г «: Л
(?<?<|;
A4.3.29)
дозвуковое I.
течение '
Упражнение 14.12. Рассчитайте профиль дозвуковой плотности для Г = 1 и Г =
= 5/3 при малых г.
Увеличение плотности, даваемое уравнением A4.3.29) для дозвукового
течения, явно больше соответствующего эффекта для околозвукового
течения [уравнение A4.3.24)]. Этот общий результат справедлив для всех
1 ^ Г ^ 5/3.
Упражнение 14.13. Подсчитайте скорость дозвукового течения при малых г
Ответ:
? Igm\
BГ-3)ДГ-
"(¦
1, дозвуковое 1
течение /
A4.3.30)
В предельном случае, соответствующем ? = О = м (т.е. аккреции нет),
дозвуковой режим сводится к гидростатической «протяженной атмосфере».
В общем случае граничные условия на поверхности аккрецирующей
звезды определяют, какой режим — околозвуковой или дозвуковой —
приложим к данной физической ситуации. Для звезд с «твердой» поверхностью
(например, белый карлик или нейтронная звезда) допустимо стационарное
дозвуковое течение. Для черных дыр течение должно быть околозвуковым
(см. приложение Ж).
Отметим, попутно, что дополнительные типы течения,
соответствующие разным граничным условиям, описываются уравнениями Бонди
A4.3.4) и A4.3.5). Согласно одному из решений, движение соответствует
стационарному истечению вещества из центральной звезды. Во внутренних
областях при г < г^ газ движется наружу с дозвуковыми скоростями,
пересекает звуковую точку при г = г^ и со сверхзвуковой скоростью уходит на
бесконечность. Скорость истечения определяется уравнением A4.3.16) при
? = ?^ (см. рис. 14.1). Это решение можно использовать для звезд, генери-
446 Глава 14
рующих звездный ветер [447]. Второй тип истечения соответствует
сверхзвуковому течению во всех местах с ? > ?^ (см. рис. 14.1). Физической
причиной такого истечения может быть воздействие некоторого
негидродинамического механизма ускорения частиц, не учитываемого в приведенных
здесь уравнениях [636].
Наконец, заметим, что решение Бонди применимо с некоторыми
изменениями для случая аккреции на черную дыру, движущуюся через
однородную среду. Если движение черной дыры в окружающей среде сильно
дозвуковое со скоростью V < а^, ?? эти изменения малы. Если же дыра
движется с произвольной (но нерелятивистской) скоростью У > а^,
эффекты движения черной дыры более значительны. По порядку величины член
?7^, появляющийся в уравнении Бонди для темпа аккреции, профиля
температуры и плотности, следует заменить множителем (К^ -Ь а^. Таким
образом, темп аккреции становится равным
к = АтЦ0М)\а1 + V^y^^%^, A4.3.31)
где ? — постоянная порядку единицы. Уравнение A4.3.31) было впервые
предложено (без множителя ?) Бонди [78]. Тем самым он объединил в одной
формуле темп сферически симметричной аккреции, соответствующий
дозвуковому течению вдали от гравитирующей массы, с темпом аккреции,
рассчитанным в [80, 284] для сверхзвукового течения.
Если У > а^, можно ожидать формирования ударной волны за черной
дырой [497] (рис. 14.2). После сжатия в ударной волне температура газа
возрастает до кТ - ШдУ^. Для любого значения У частицы газа,
находящиеся в пределах расстояния г^ - СМ(У^ + а^ от черной дыры, будут
захвачены. За пределами г^ кинетическая энергия направленного движения
частиц газа относительно дыры {У^/2 на единицу массы) будет больше
гравитационной потенциальной энергии (СМ/г), так что гравитационное при-
Убарньш фронт
??? 14.2. Линии тока частиц газа, падаюшич со сверхзвчковой скоростью на грави-
тирующую точечную массу, в системе координат, где эта масса покоится.
Аккреция на черные дыры 447
тяжение черной дырой будет пренебрежимо малым. Газовое давление
приводит к симметризации течения в пределах расстояния г^, так что при г <
< г^ движение газа становится квазирадиальным. В этой внутренней
области уравнение Бонди снова применимо. Эти качественные представления
были проверены подробными двухмерными гидродинамическими
расчетами Ханта [288].
Аккреция на черную дыру, движущуюся через окружающую среду со
сверхзвуковой скоростью, вероятно, характерна для двойной системы, в
которой нормальный главный компонент находится внутри своей полости
Роша, но испускает звездный ветер. В этом случае дырой будет захвачен
только газ, лежащий внутри аккреционного цилиндра радиусом г^ =
= ????/?^^^, где ? — масса черной дыры, V^^^ — скорость ветра
относительно дыры, а ? — постоянная порядка единицы (см. ра^д. 13.76 и рис.
13.11). В этом случае темп аккреции определяется уравнением A4.3.31) с
заменой V^ на K^gj.
Упражнение 14.14. а) Оцените темп газовой аккреции на компактный вторичный
компонент ? ? (черная дыра) в источнике Cyg Х-1. Предположите, что аккреция
вызвана звездным ветром от нормальной звезды, который имеет постоянную
скорость, сравнимую со скоростью убегания с поверхности звезды:
Здесь Л/, > Л/, и /?, — масса и радиус нормального главного компонента.
Покажите, что темп аккреции определяется выражением [529]
^ [ik)[5j-S[ 10-^М:/год)'^<^^^°^· A4.3.32)
В уравнении A4.3:32) М^ — темп истечения стационарного сферически
симметричного ветра (Mjv = Ажг^ V^ = const), а — расстояние между компонентами двойной
системы, ? — орбитальный период (орбита предполагается круговой).
Указание: F?ei « Vj + Vj,, где К^ — скорость вторичного компонента
относительно главного. Обратите внимание, что нормировка множителей в уравнении
A4.3.32) выбрана в согласии с результатами наблюдений двойной системы Cyg Х-1
(см. разд. 13.5).
б) Покажите, что нормировка параметров в уравнении A4.3.32) соответствует
наблюдаемой рентгеновской светимости - 5 · 10^^ эрг/с, если предположить
эффективность преобразования массы покоя в излучение около \04q.
в) Вычислите долю массы М/М^ испускаемого газа, аккрецируемого на
компактный вторичный компонент.
448 Глава 14
14.4. ИЗЛУЧЕНИЕ ПРИ СФЕРИЧЕСКИ СИММЕТРИЧНОЙ АККРЕЦИИ
НА ЧЕРНЫЕ ДЫРЫ
В этом разделе будет оценено количество излучения, испускаемого во
время стационарной сферически симметричной аккреции на стационарную
черную дыру. В общем случае такие вычисления нетривиальны, поскольку
требуется самосогласованное рассмотрение гидродинамических уравнений
движения, связанных с уравнениями переноса излучения. Более того, результат
сильно зависит от предполагаемых физических (граничных) условий,
существующих вдали от черной дыры (г > г^). В процессе последующего
обсуждения будет рассмотрен простой случай, когда гидродинамическое
течение является в первом приближении адиабатическим, а потери энергии на
излучение представляют собой малое возмущение. Итак, можно
воспользоваться адиабатическими уравнениями Бонди для определения течения и
использовать результирующий профиль течения для расчета темпа
испускания излучения. Если этот темп излучения меньше темпа аккреции
тепловой энергии, течение будет почти адиабатическим, а проведенный
анализ — целиком самосогласованным. По окончании анализа докажем
важное обстоятельство: сферически симметричная- аккреция на черную
дыру может и не быть эффективным механизмом преобразования энергии,
соответствующей массе покоя, в излучение. Разумеется, этот важный
результат очень сильно зависит от «режима», но справедлив по крайней мере
для одного астрофизического процесса — аккреции межзвездного газа на
черную дыру [525, 526, 527, 539].
Для определенности предположим, что шварцшильдовская черная дыра
находится в состоянии покоя среди однородного ионизованного газа,
состоящего из чистого водорода. Предположим, что покоящийся на
бесконечности газ, имеющий температуру Т^ и концентрацию частиц ?^,
стационарно аккрецируется на черную дыру. Такая ситуация соответствует
случаю аккреции в типичных межзвезгных областях НИ (т.е. областях
ионизованного водорода), где п^ - \ см~^ и Т^ - \0^ К.
В адиабатическом пределе течение описывается уравнениями Бонди с
одним важным исключением: показатель адиабаты Г = ГG) будет
изменяться в зависимости от температуры ? и, следовательно, от расстояния
до дыры г. Конкретно, по мере того как г уменьшается, а кТ увеличивается
выше т^с^у электроны становятся релятивистскими, что приводит к
падению Г до значений ниже 5/3. По существу имеются два разных режима
адиабатического течения, различающихся величиной температуры: кТ <
< т^с^ или кТ > т^с^ (но всегда кТ < т с^). В обоих режимах Г
фактически является постоянной. Для адиабатических изменений имеем (помня,
что здесь ? = тп означает плотность массы покоя)
Здесь ? — плотность полной энергии, ? = рс^ + ?'. Используя уравнение
Аккреция на черные дыры 449
A4.3.1) и выполнив интегрирование, получаем выражение для плотности
тепловой энергии в любом режиме
?
?' = ?-—[^ Г = ^0^^^ A4.4.2)
В режиме кТ < т^с^ (т.е. ? < d · 10^ К) водородная плазма является
нерелятивистской, так что
?' = ЪпкТ, ? = InkT. A4.4.3)
Вклад протонов и электронов одинаков, так как ? — концентрация
протонов, равная концентрации электронов.
Плотность полной энергии равна
? = п{тр + т,)с^ + ЪпкТ. A4.4.4)
Сравнение выражений A4.4.2) и A4.4.3) дает знакомый результат:
Г = |, кТ<^т,с\ A4.4.5)
Для области ближе к черной дыре найдем, что т^с^ < кТ < т^с^ (т.е.
6 · 10^ К < Г < 1 · 10^^ К). Электроны становятся релятивистскими, а
протоны остаются нерелятивистскими. Поэтому
?' = C + i)nkT, ? = 2пкТ,
? = ^пкТ + птрс\ Г = -^, т.с^ <^ кТ <^ т/. A4.4.6)
Здесь для релятивистских электронов использовано соотношение ? = ?' =
= ЪпкТ.
Упражнение 14.15. Покажите, что для полностью ионизованной смеси водорода
и гелия получается
х+Н^-х)
вместо A4.4.6). Здесь X — относительное содержание водородных ионов,
следовательно, A -- Л^ — относительное содержание ионов гелия.
Упражнение 14.16. Покажите, что для релятивистских электронов и протонов
(т.е. кТ > тр(Р·) Г = 4/3. Объясните, почему точно такое значение Г
получается для чисто протонного газа.
Поскольку ? и Я подобраны так, чтобы быть непрерывными при кТ =
= 2/3 т^с^, имеет смысл определить «эффективный показатель адиабаты»
Г* посредством соотношений
г* = ^
3'
13
9 '
кТ 2
2^1
т. кТ 2
—?- » > —
A4.4.7)
13-513
450 Глава 14
Разумеется, переход от нерелятивисткого режима к релятивистскому на
самом деле не резкий, а гладкий и постепенный; однако соотношений
A4.4.7) вполне достаточно для наших целей.
Теперь нетрудно получить решение для течения. Как обсуждалось в
разд. 14.3, темп аккреции определяется параметрами газа на больших
расстояниях от черной дыры, где электроны еще не стали релятивистскими. В
этой области Г* = 5/3 и
IV2
«^ =
2Х ?
5кТ
3 гпр
A4.4.8)
Темп аккреции ? определяется уравнением A4.3.16), которое выражено
численно в A4.3.20) для рассматриваемого сейчас случая (?^ = 1/4). При
больших г > г^ = CM/flf^уравнения A4.3.21) и A4.3.22) описывают
параметры течения. При малых г < г^ существуют два режима в зависимости
от того, являются электроны релятивистскими или нет. Определим пере-
2 ^
ходный радиус г,, при котором кТ = кТ* = —т^с^. Параметры течения в
этом случае следуют из A4.3.26) и A4.3.27) для нерелятивистской области
г, < г < г^, где скорость еще дозвуковая ^^
Упражнение 14.17. а) Покажите, что г, определяется выражением
'.-?^4^- 04.4.9)
С
6) Найдите численные значения радиусов г^ = IGM/c^, г, и г^ в единицах M/Mq
и Гоо/10^ К.
'^ Как показано в приложении Ж, течение для Г = 5/3 становится
околозвуковым при радиусе г^ = 3GM/4a^ с > О, если принимать во внимание общую теорию
относительности. Соответствующий темп аккреции, определяемый при г^, все еще
дается уравнением A4.3.16), а параметры газа повсюду остаются сравнимыми с
ньютоновскими значениями. Для Г s Г* темп аккреции остается таким же, если
только г^ > г^, т.е. если — {т^/тр)с/а^ > 1 или Т^ < 1 · 10^ К [см. A4.4.9) и
A4.3.19)]. Тот факт, что Г изменяется приг^, не имеет отношения к определению Л/,
поскольку это изменение не может «передаваться» против сверхзвукового течения. В
другом случае уравнение A4.3.16) также дает достаточно точное значение Л/, если
9
только выполняется соотношение 1 > 5/3 - Г > — {а^/сУШр/т^ для г > г^ . Это
условие гарантирует, что, хотя Г* близко к 5/3 выше по течению, оно отклоняется от
5/3 настолько, чтобы сделать возможным неравенство г^ > г^ [см. A4.3.14)].
Аккреция на черные дыры
451
В области релятивистских электронов IGM/c^ < г < г* и течение
оказывается сверхзвуковым, так что уравнения A4.3.23) и A4.3.24) применимы
для определения мир соответственно. Температура дается общим соотно
шением ?
- р^* ^ которое в сочетании с уравнениями A4.3.24) и A4.4.7)
дает
i-A^r
A4.4.10)
Упражнение 14.18. а) Подсчитайте температуру Т^ на горизонте событий и
Сравните ее с температурой адиабатического течения с постоянным значением Г =
*= 5/3 (см. уравнение (Ж.46)].
Ответ:
^2/3/
иш
« 1,4 · 10^^ К < Г(Г = |)
б) Подсчитайте р{г)/роо = п{г)/По, на горизонте событий.
Ответ:
A4.4.11)
A4.4.12)
Отметим, что точное интегрирование релятивистских уравнений Эйлера
с использованием соотношения A4.4.7) дает на горизонте Г = 1,0 · 10^^ К
и р/р^ = 3,9 · 10" {TJ\(f К)~з/2 [525]. Замена A4.4.7) реальной,
зависящей от температуры непрерывной функцией Г = ГG) дает вместо этого
? = 0,76 · Ю" К, но значение р/р^ на горизонте сохраняется прежним
[87].
Теперь, когда параметры течения известны в виде функций координат,
можно вычислить интенсивность излучения. Большая часть излучения
возникает в области, расположенной вблизи горизонта событий с внешней
стороны, где температура и плотность газа достигают максимальных
значений. В интересующем нас диапазоне температур и плотностей
преобладающим механизмом излучения будет тепловое тормозное излучение, или
свободно-свободное излучение. Релятивистское тормозное излучение
генерируется вследствие неупругого рассеяния релятивистских тепловых
электронов (нерелятивистскими) ионами и другими электронами. Излучатель-
ная способность (интенсивность излучения на единицу объема) в предельно
релятивистском случае определяется выражением
Aff = (Л,,.+ Л,^эрг/(смЗ · с),
A4.4.13)
где
Л^^ = llaZ^r^n^riiCkT
Л^^ = 1Ааг^п]скТ
-г + In
4
^)-0,577
т,с^
A4.4.14)
452 Глава 14
В уравнении A4.4.14) ? = е^/Лс—постоянная тонкой структуры, а г^ =
= е^/т^с^ — классический радиус электрона^^ Для рассматриваемого здесь
газа, состоящего из чистого водорода, ? = 1 и а?^ = а?, s а2.
Упражнение 14.19. а) Объясните, почему Л^^/Л« * 2 в предельно
релятивистском случае для чистого водорода.
б) Каково приближенное значение отношения Л^^/Л^, для нерелятивистского
газа, состоящего из водорода?
Ответ: --^ ~ -^^-f- (нерслятивистский газ).
Если пренебречь эффектами специальной теории относительности,
связанными с движением падающего газа, и эффектами общей теории
относительности, проявляющимися в сильном гравитащюнном поле черной
дыры, полная светимость газа равна
-'•'""(?????^)"^)'-- (—"
При получении выражения A4.4.15) были использованы параметры течения
на горизонте, выведенные в некотором приближении в упражнении 14.18.
Поскольку подынтегральное выражение резко растет при уменьшении г,
основной вклад в излучение дает область, расположенная с внешней
стороны горизонта. Точное релятивистское интегрирование испускаемого
излучения дает [525, 527]
В этом выражении соответствующим образом учтены релятивизм течения,
доплеровское и гравитационное красные смещения, захват фотонов черной
дырой и т.п. Соответствующий спектр оказывается умеренно плоским
при энергиях ниже
hv - кТ^ -^ 10 МэВ, A4.4.17)
и экспоненциально спадает при более высоких энергиях. Таким образом,
излучение состоит в значительной степени из очень жестких рентгеновских
лучей и гамма-лучей. При характерных межзвездных плотностях аккреци-
^^ См. [388]. Читатель может приближенно скомпоновать выражения A4.4.14) на
основе уравнений и обсуждения, приведенных в разд. 15.3 монографии [297].
Аккреция на черные дыры 453
руемое вещество остается «оптически тонким» для этих фотонов и они
уходят наружу на бесконечность, не задерживаясь рассеянием или
поглощением.
Упражнение 14.20. Преобладающим источником непрозрачности для типичных
фотонов с энергией ? - 10 МэВ является комптоновское рассеяние на
релятивистских электронах; сечение этого процесса равно ?(?) = aj(mgC^/E), где ?? —
томсоновское сечение. Покажите, что соответствующая оптическая толщина для
рассеяния ? = 1 origdr гораздо меньше единицы при типичных межзвездных
плотностях (т.е. п^а ~ 1 см"^). Дайте интерпретацию полученного результата.
Примечательно, что выражение A4.4.16) дает очень малую
эффективность преобразования энергии массы покоя в излучение
Мс^
Даже если вращающаяся черная дыра обладает максимально возможным
моментом количества движения, эффективность сферически симметричной
аккреции возрастает всего лишь на 15^о по сравнению со значением,
следующим из A4.4.18) [527].
Присутствие «запутанного» магнитного поля, приводящего к синхро-
тронному излучению в дополнение к тормозному излучению, может в
какой-то мере увеличить эффективность ([293, 402, 422, 526, 539], см. также
упражнение 14.21). Однако в общем случае сферически симметричная
аккреция межзвездного газа черными дырами оказывается неэффективным
механизмом излучения. Таким образом, в этом случае положение совершенно
иное по сравнению со сферической аккрецией на нейтронную звезду, где
? - 0,1, или с дисковой аккрецией на черную дыру, где ? =
= 0,05—0,42 в зависимости от величины момента количества движения
дыры а/М и от направления вращения газового диска относительно дыры
(см. разд. 14.5). При иных граничных условиях для газа вместо
предполагавшихся типичных межзвездных параметров или при учете
турбулентности эффективность может оказаться совсем другой. Однако для таких
режимов в настоящее время нет надежных релятивистских расчетов.
Упражнение 14.21. Предположите, что аккрецируемый газ обладает равномерно
распределенным магнитным полем
Такое поле может образоваться, если в любом месте рост вмороженного
хаотического поля, с которым сцеплена падающая плазма, ограничен пересоединением про-
454 Глава 14
тивоположно направленных радиальных силовых линий магнитного поля [526, 539].
Характерное время пересоединения определяется соотношением /^???? ~ ''/^а» ^^'^
Уд " {ВУ^жрУ"^^ — альвеновская скорость, или магнитная «звуковая скорость».
Усиление поля В ограничено условием /гесоп ~ ^ff» где /ff - r/{GM/rY^ — время падения.
Это условие и приводит к уравнению A4.4.19).
а) Подсчитайте синхротронную светимость L^y^, возникающую от вращения
релятивистских электронов вокруг равномерно распределенных силовых линий.
у™.. Л.у„=|^(-?|)^(-^)^эрг/(см3.с)
Ответ: L^^ ~ 10^^(^^/1 см-^)^G^/10^ ?.?\?/?^? эрг/с
Замечание: Расчеты в рамках общей теории относительности дают значения
светимости, которые ниже более чем в десять раз.
б) Получите оценку характеристической частоты испускаемого излучения.
(еВ^^\
Указание: hv - ??? ^ h ? ? , где ын — синхротронная частота и где ? =
\т,с /
? Eg/mgC^ удовлетворяет условию <7^> = ИкТ/т^с^ для теплового
релятивистского электронного газа.
Ответ: ? - 10^^ Гц, или ? - 30 мкм (инфракрасный диапазон).
14.5. ДИСКОВАЯ МОДЕЛЬ АККРЕЦИИ НА КОМПАКТНУЮ ЗВЕЗДУ
Аккреция на компактную звезду в двойной системе может сильно
отличаться от сферически симметричной, поскольку аккрецируемый газ
обладает моментом количества движения. Рассмотрим случай, когда компактный
объект^^— это черная дыра. Если момент количества движения на единицу
массы / превосходит rjC, где rj — радиус самой внутренней устойчивой
круговой орбиты (см. гл. 12), центробежные силы становятся значительными
еще до того, как газ опустится под горизонт событий. В этом случае газ
будет выброшен на круговые орбиты вокруг черной дыры. Движение газа
внутрь возможно только после того, как вязкостные напряжения унесут
лишний момент количества движения. Сопутствующий нагрев, вызванный
силами трения, и более длительное пребывание газа вне горизонта
событий приводят к значительному увеличению светимости по сравнению с
величинами, рассчитанными в предыдущем разделе для сферически
симметричной аккреции. Фактически полная энергия, излученная единицей массы
по мере ее дрейфа через диск внутрь по направлению к черной дыре,
должна быть равна гравитационной энергии связи единицы массы на
внутреннем крае диска при г = rj (если предположить, что дополнительная
энергия, излучаемая позже, когда масса быстро опускается с расстояния
г = rj к горизонту событий, сравнительно невелика). Таким образом, га-
Аккреция на черные дыры 455
рантируется, что эффективность излучения в случае дисковой аккреции на
черную дыру должна быть равной по меньшей мере^^
? — Ej = 0,057 для невращающейся дыры,
= 0,42 для дыры, вращающейся с
максимальной скоростью и
вращения диска в прямом
направлении.
A4.5.1)
При дисковой аккреции на белый карлик или на нейтронную звезду
внутренний край диска tj может быть близок к поверхности звезды^^ В
этом случае максимальные эффективности излучения диска сравнимы со
значениями
? - 10"^ для белого карлика, A4.5.2)
2 Re - 10"^ для нейтронной
звезды.
Итак, по порядку величины полная светимость аккреционного диска
должна равняться
~ \0-^Мс^ -
^ \0~^Мс^ -
10^^ (
10^7 /
? \
^ Ю-^Мф/год^
^ ? ^
^ Ю-^М^/год ^
1 эрг/с для белого кар
J эрг/с для нейтронной
' звезды или
черной дыры.
A4.5.3)
Помимо светимости диска при аккреции на белый карлик или
нейтронную звезду, следует учитывать светимость сравнимого порядка величины,
возникающую при столкновении газа с поверхностью звезды (или с
поверхностными магнитными полями), замедлении и диссипации его
кинетической энергии. Следовательно, порядок величины полной светимости в
случае аккреции на нейтронную звезду или белый карлик зависит от характера
аккреции (дисковая или сферически симметричная). В любом случае вся
гравитационная энергия связи выделяется на поверхности в виде излучения по
мере того, как газ падает в потенциальном поле звезды и останавливается
на ее поверхности. Полная светимость, таким образом, всегда равна L =
= GMM/R (если пренебречь поправками на эффекты общей теории
относительности^^). Однако при аккреции на черную дыру ситуация может
^^ См. уравнение A2.4.30) и обсуждение, следующее за уравнением A2.7.25).
^^ Здесь предполагается, что на их поверхностях имеются только очень слабые
магнитные поля; другие варианты рассматриваются в гл. 15.
^^ В общей теории относительности светимость при стационарной аккреции
вещества, падающего на сферическую звезду из состояния покоя на бесконечности,
определяется выражением L = [1 — A — 2GM//?c2)^]Mc2 в предположении, что
вещество полностью останавливается на поверхности [см. уравнение [12.4.9)].
456 Глава 14
зависеть весьма чувствительно от геометрии течения. По крайней мере для
дисковой аккреции эффективность неизменно высока.
Дисковая аккреция всегда должна происходить в двойных системах, где
нормальный главный компонент, заполняющий свою полость Роша,
подпитывает газом компактный вторичный компонент. В этом случае
характерный момент количества движения газа значительно превышает г^с, что
очевидно из рис. 13.11,6. Когда подпитка газом происходит благодаря
звездному ветру, ситуация не столь очевидна (см. рис. 13.11,uf). Превышает
ли / величину rjC или нет, это чувствительно зависит от параметров ветра
и двойной системы [291, 529] (см. упражнение 14.22).
Упражнение 14.22. Вернемся к упражнению 14.14, где рассматривается
аккреция звездного ветра на компактную вторичную звезду. Для той же самой системы:
а) Покажите, что момент количества движения на единицу массы, переносимый
аккрецируемым газом, равен
^'\^?^T ^^^-5·^)
б) Оцените отношение значений / для случаев аккреции звездного ветра и
аккреции, вызванной заполнением полости Роша.
Ответ: {rJaY - 10"^ — 10"^.
в) Предположите, что наружный край диска имеет радиус г/), при котором
значение выражения A4.5.4) равно моменту количества движения на единицу массы для
элемента газа, находящегося на круговой орбите вокруг черной дыры: / = {СМгрУ .
Подсчитайте Гр/г/ для параметров, соответствующих двойной системе Cyg Х-1 и
прокомментируйте результат.
Ответ:
^ « 1601^-«
\VJ\ \\0Mo)\30Mol [s'.el \20Ro)
Дисковая аккреция возможна также при течении турбулентного газа на
сверхмассивную черную дыру в плотном галактическом ядре или в
квазарах, или же в центре нашей Галактики.
В этом разделе будет обсуждаться строение кеплеровского
аккреционного диска вокруг центральной точечной массы. Первым обратил внимание
на важность момента количества движения для аккреции в двойной системе
Прендергаст [464]. Он построил модели дисковой аккреции на белые
карлики в двойных системах. Позже в работах [422, 470, 521, 522] были
построены модели ньютоновского аккреционного диска для течения на нейтронные
звезды и черные дыры. В работе [422] рассматривались эффекты обшей
теории относительности для внутренних частей аккреционного диска.
Аккреция на черные дыры 457
Линден-Белл [375] первым предположил, что в ядрах галактик могут
содержаться сверхмассивные черные дыры, окруженные газовыми
аккреционными дисками ^^
Начнем с качественного обзора дисковой аккреции. Рассмотрим, что
происходит в двойной системе по мере того, как газ переносится от
нормальной звезды к компактному компоненту. Если этот процесс возникает в
результате перетекания из заполненной звездой полости Роша, газ
переносится через критическую точку Лагранжа Lj, после чего совместное
действие гравитационных и кориолисовых сил удерживает его на
приблизительно круговой орбите вокруг компактной звезды (см. рис. 13.12).
Некоторая часть газа, сброшенная ранее, вращается по орбите вокруг
компактной звезды в виде аккреционного диска. Падающий газ взаимодействует с
газом в диске через посредство вязкостных напряжений. Некоторая часть
падающего газа воспринимает момент количества движения от диска и
затем выбрасывается из области диска; часть этого газа падает обратно на
нормальную звезду, а часть вообще выбрасывается из системы через ла-
гранжеву точку L2- Если рассматриваемый процесс протекает в виде
аккреции звездного ветра, внешняя граница диска, по-видимому, располагается
гораздо ближе к компактной звезде. За пределами этой границы аккреция
будет почти сферически симметричной. Режим аккреции изменяется на
таком расстоянии, где характерные значения момента количества движения
на единицу массы для газа, аккрецируемого из звездного ветра, и для
элемента газа, находящегося на круговой кеплеровской орбите вокруг
компактной звезды, оказываются равными (см. рис. 13.11,6 и упражнение
14.22).
Независимо от того, как образовался аккреционный диск, большая
часть гравитационной энергии выделяется в самых внутренних его частях,
наиболее близких к компактной звезде (отсюда же испускается большая
часть излучения). Приток газа и «сброс» момента количества движения
почти полностью происходят во внешних частях. Поскольку нас интересует
испускаемое при аккреции излучение, мы сосредоточим внимание на
внутренних областях диска.
При вращении вокруг компактной звезды примерно в круговом режиме
каждый элемент газа в диске совершает медленное движение по радиусу
внутрь, поскольку торможение, связанное с силами трения, приводит к
уменьшению момента количества движения. Таким образом, газ дрейфует
к компактной звезде по очень пологой спиральной траектории по мере
того, как его момент количества движения передается наружу — из
внутренних областей диска во внешние. Одновременно вязкостные напряжения,
возникающие вследствие относительного сдвига элементов газа при
орбитальном движении, приводят к выделению «фрикционного» тепла. В ста-
^^ Обзоры и ссылки на свежие работы по дисковой аккреции даны в [367, 469].
Приведенное ниже в разд. 14.5 рассмотрение ньютоновской дисковой аккреции во
многрм аналогично представленному в [422].
458 Глава 14
ционарном состоянии большая часть этого тепла затем излучается с
верхней и нижней поверхностей диска.
Изучим теперь количественно структуру внутренних областей
ньютоновского аккреционного диска вокруг компактной звезды массой М,
Предположим, что газ вносится в диск с постоянным темпом ? и аккрециру-
ет на компактную звезду с таким же темпом. Пренебрежем всеми
приливными гравитационными силами, действующими на диск со стороны
нормального компонента. Предположим, что центральная плоскость диска
совпадает с экваториальной плоскостью компактной звезды, определяемой
условием ? = 0.
При кеплеровском круговом движении каждый элемент обладает
удельным моментом количества движения /, равным
l={GMrY^\ A4.5.5)
Вблизи звездной поверхности при малых значениях г величина / гораздо
меньше, чем на наружном крае диске. Поэтому скорость, с которой
момент количества движения должен удаляться из диска проходящим газом,
в стационарном случае должна составлять
/ = М/(^) - M{GMr^y^\ A4.5.6)
Пусть толщина диска будет 2/?, а его поверхностная плотность при радиусе
г будет ?. Тогда можно записать
pdz^lhp, A4.5.7)
где ? измеряется высотой перпендикуляра к средней плоскости диска, а
значение ? в правой части уравнения A4.5.7) вычисляется для ? = 0. В данном
случае и в дальнейшем будет проводиться усреднение по вертикали всех
величин, зависящих от ?, с заменой интегралов от произведений
произведением усредненных величин. Пусть ?^ — величина направленной внутрь
радиальной скорости газа (у^ > 0), а у^ и ? — соответственно^^ кеплеровская
орбитальная скорость и угловая скорость:
„..,й.(^)'" 04.5.8)
При характерных для данного случая значениях вязкости ?^ всегда будет
гораздо меньше, чем v..
^^ В гл. 14 и 15 все пространственные векторные и тензорные компоненты
связаны с «обычными» ортонормальными базисными векторами (например, ? = у-в- +
+ у^е^ + y-?- в цилиндрической геометрии). Однако в дальнейшем договоримся
опускать «крышку» в индексах компонентов. Такое упрощение не должно вызывать
недоразумений.
Аккреция на черные дыры
459
Рис. 14.3. Разрез тонкого кеплеровского аккреционного диска, расположенного
вокруг центральной черной дыры.
Предположим, что диск тонкий, т.е. что h повсюду удовлетворяет
неравенству
h{r) «: г. A4.5.9)
Как будет показано ниже, уравнение A4.5.9) требует, чтобы температура
была «умеренной», т.е. кТ < GMm /г. Такие низкие температуры будут
достигаться, если генерируемое вязкостными напряжениями тепло
эффективно излучается наружу и не накапливается в диске. Таким образом, в
отличие от случая сферически симметричной аккреции тонкий аккреционный
диск должен быть в высокой степени неадиабатическим [см. уравнение
A4.3.27), т.е. кТ - GMm /г для сферически симметричной аккреции с Г =
= 5/3]. В предельном случае, когда уравнение A4.5.9) справедливо,
связанные двухмерные уравнения осесимметричного течения распадаются
на отдельные уравнения для радиального и вертикального движений. Этот
распад в значительной мере упрощает гидродинамические уравнения.
Обозначим через Д вязкостное напряжение (сила на единицу площади),
которое характеризует воздействие в направлении ? элемента жидкости
при радиусе г на соседние элементы, находящиеся при г -\- ?^? (рис. 14.3).
460 Глава 14
Это напряжение связано с тензором напряжений уравнением
и^ ~^Ф' A4.5.10)
где для кеплеровского диска
/,?=-2?)?=-24( —j · A4.5.11)
Здесь ? — коэффициент динамической вязкости [г/(см · с)]. [Краткое
обсуждение гидродинамических уравнений движения вязкой жидкости см. в
приложении 3, где выводятся уравнения A4.5.10) и A4.5.11).] Пока
отложим обсуждение природы вязкости. Наконец, обозначим через F полный
поток излучения, испускаемый верхней (или нижней) поверхностью диска.
В стационарном состоянии структура диска определяется путем
одновременного решения четырех уравнений сохранения (массы, момента
количества движения, энергии и вертикального импульса). Кроме того, должны
быть заданы вязкость ? (например, выраженная через локальные
термодинамические параметры), а также зависимость, описывающая перенос
излучения от центра к поверхности. Эти уравнения обсуждаются ниже.
а) Сохранение массы покоя
Интегрирование стационарного уравнения неразрывности массового
течения V · (pv) = О приводит к следующему результату:
? = ??????, = const . A4.5.12)
Уравнение A4.5.12) показывает, что скорость переноса массы к центру в
цилиндре радиусом г не зависит от г.
б) Сохранение момента количества движения
Пусть У+ = M{GMrY^ — скорость связанного с притоком газа переноса
момента количества движения в направлении к звезде через радиус г диска
(см. рис. 14.3). Пусть J~ — скорость, с которой момент количества
движения поглощается компактной звездой. Поскольку удельный момент
количества движения, накапливаемый компактной звездой, не может
превосходить величину /(г,) на внутреннем крае диска, можно записать
/-= ??{0???^^, где \?\ < 1. A4.5.13)
(Например, при аккреции на черную дыру ? « 1)^^ Сохранение момента
количества движения требует, чтобы результирующая скорость изменения
'^ Заметим, что условие ? = 1 для черной дыры является всего лишь
приближением. Оно эквивалентно условию отсутствия напряжений на границе при г^ [см.
уравнение A4.5.14)] и приводит ?? — оои/о — оо при этом радиусе [см. A4.5.37)].
Соотношение ? = 1 требует, чтобы при радиусах, меньших г,, газ быстро опускался
по спирали на черную дыру без излучения. Строго говоря, это неверно, но подобная
идеализация, по-видимому, оправдана; см. [554].
Аккреция на черные дыры 461
момента количества движения в пределах г была равна вращающему
моменту, обусловленному вязкостным напряжением. В соответствии с этим
Момент сил = (сила вдоль е^/площадь) ? (площадь) ? (г)
= У"·" — J~ у или
(Д)B^г · 2Л)(г) = Л/[(СМг)·/' - )S(GMr,)'/']. A4.5.14)
Заметим, что в стационарном состоянии требуемое напряжение Д
определяется однозначно величинами ? и М.
в) Сохранение энергии
Из уравнения C.6) известно, что энтропия (тепло) порождается
действием вязкости со скоростью
? ? п75 = ^-- « —^— = . A4.5.15)
Подставив в уравнение A4.5.15) уравнения A4.5.11) и A4.5.14), найдем
. 1/21
2hQ = ^^ ^^
Airr^
-^т
A4.5.16)
Предположим, что это тепло не накапливается, а полностью излучается
наружу. Тогда уравнение A4.5.16) непосредственно дает интегральный
поток, испускаемый с верхней и нижней поверхностей диска при радиусе г:
(Поскольку диск тонкий, излучение направлено в основном в вертикальном,
а не в радиальном направлении.)
Важная особенность уравнения A4.5.17) состоит в том, что радиальное
распределение испускаемого потока совершенно не зависит от закона
вязкости, который еще предстоит задать.
Полная светимость диска равна
L=fyx2.rdr^(l-?)^?. A4.5.18)
Именно такая светимость следует из сохранения энергии. Ньютоновская
энергия гравитационной связи на грамм массы при г, равна Е^ = GM/lr^, а
кинетическая энергия вращения, получаемая от компактной звезды, равна
(упражнение* 14.23) ?^ = A - ?)??/?^, В соответствии с этим уравнение
A4.15.18) правильно дает L = (Е^ -\- Ej^)M.
Упражнение 14.23. Проверьте приведенное выражение для Ej^, используя
уравнение A4.5.13).
Указание: Подсчитайте работу, произведенную вращательным моментом,
который воздействует со стороны звезды на диск при Г/.
462 Глава 14
Упражнение 14.24. Рассчитайте эффективность излучения тонкого
ньютоновского аккреционного диска, простирающегося вокруг центральной черной дыры до Г/ =
= 6GM/c^. Сравните полученный результат с эффективностью релятивистского
диска вокруг неврашающейся черной дыры.
Ответ: ? = 1/12, или 8,3<^) против 5J%.
г) Сохранение вертикального импульса
Поскольку нет результирующего движения газа в вертикальном
направлении, сохранение импульса вдоль оси е^^ сводится к условию
гидростатического равновесия. Приравнивание компонента силы тяготения компактной
звезды вдоль е^ вертикальному градиенту давления в диске дает
\ dP GM ? t . /,. . ,^4
--:^ = ;-- {z<^r). A4.5.19)
Замена в уравнении A4.5.19) дифференциалов конечными разностями (т.е.
замена ?? на « Р, где ? — давление, вычисленное при ? = О, и замена
?? ~ Л) дает для полутолщины диска
В уравнении A4.5.20) с — скорость звука в центральной плоскости диска.
Упражнение 14.25. Рассмотрите условие тонкого диска A4.5.9), которое вместе
с уравнением A4.5.20) требует
А « -^ « 1. A4.5.21)
Какие ограничения налагает уравнение A4.5.21) на внутреннюю температуру диска ?
в областях, где давление газа преобладает [сравните с первым членом уравнения
A4.5.29)]?
д) Закон вязкости
Ни один физический процесс не понят так плохо в теории дисковой
аккреции, как природа вязкости. Похоже, что источником вязкости должна
быть мелкомасштабная турбулентность газодинамического течения.
Хаотические магнитные поля, тянущиеся вместе с аккрецируемой плазмой,
перемешиваемые благодаря дифференциальному вращению диска и
испытывающие пересоединение на границах между хаотическими ячейками, также
должны вносить значительный вклад в вязкость [176, 422, 465]. К счастью,
интегральный профиль потока, даваемый уравнением A4.5.17), и полная
светимость не зависят от неопределенного закона вязкости. В то же время,
к сожалению, детали строения диска и спектр испускаемого излучения
зависят от вязкости.
Аккреция на черные дыры 463
Чтобы продвинуться вперед, воспользуемся результатами Шакуры и
Сюняева [522] и составим основанное на динамических соображениях
правдоподобное соотношение между турбулентной вязкостью и сдвиговым
напряжением. В теории турбулентного движения коэффициент динамической
вязкости дается выражением
? * Pt^turb^urb' A4.5.22)
где i;jyj.jj — скорость турбулентных ячеек относительно среднего движения
газа, а 1^^^^ — размер наибольшей турбулентной ячейки (см., например,
[339], разд. 31). При сверхзвуковом движении ударные волны будут
приводить к диссипации кинетической энергии турбулентности, преобразуя ее
в тепло, поэтому потребуем v^^^^^ ^ с^. Размеры ячеек ограничены
толщиной диска, так что 1^^^^^ ^ Л. Используя уравнения A4.5.10), A4.5.11),
A4.5.12) и A4.5.20), найдем ограничения, касающиеся напряжения
и = -V ^ {pc,h)il » рс^ - Р. A4.5.23)
Тогда можно записать в общем виде
/ф = «^» A4.5.24)
где вводится безразмерный параметр вязкости а, который не поддается
сколько-нибудь точному вычислению, но удовлетворяет ограничению
? < 1. A4.5.25)
Модели, построенные с использованием уравнения A4.5.24), называются
«?-дисками». В таких моделях а остается обычно свободным постоянным
параметром в уравнениях строения диска. Интересно, что значение ?
может быть прокалибровано эмпирически при помощи зависящих от времени
спектров, полученных при наблюдении вспышек в двойных системах с
переносом массы, содержащих карликовые новые. Сравнение наблюдений
таких «катаклизматических переменных» с зависящим от времени потоком,
ожидаемым от тонкого аккреционного диска в системе, дает а в интервале
от 0,1 до 1^К Эти значения совпадают с оценками из работы [176], где
рассматривалась вязкость, возникающая вследствие сдвигового усиления и
пересоединения силовых линий хаотического магнитного поля. Для этого
случая получены значения 0,01 < ? < 1^^
'^ См. [48, 377]; в настоящее время не ясно, остается ли а на этом уровне или же
уменьшается во время спокойного периода между вспышками.
^^ Совершенно иной подход к роли магнитных полей в механизме уноса момента
количества движения изложен в работах [69, 74, 372]. Авторы этих работ
обнаружили, что если в диске имеется упорядоченное магнитное поле с большой
перпендикулярной составляющей, то как энергия, так и момент количества движения могут
уноситься посредством намагниченного релятивистского ветра.
Электродинамическая «импульсноподобная» модель предусматривает возможность появления
спаренных «струй» релятивистской плазмы, движущихся перпендикулярно плоскости
диска. В экстремальных условиях магнитное торможение может заменить вязкостное
торможение, рассмотренное в уравнении A4.5.24).
464 Глава 14
е) Непрозрачность
При типичных параметрах аккреции на компактные звезды с ? -
~ Л/0 господствующим источником поглощения фотонов в диске
оказывается нерелятивистское тепловое тормозное излучение, или «свободно-
свободные» переходы. Сравнимую (но все же меньшую) роль могут играть
«связанно-связанные» переходы в линиях и «связанно-свободные»
ионизационные переходы. Таким образом, усредненная по частоте средняя по
Росселанду непрозрачность, связанная с поглощением, равна (сравните с
приложением И)
i^abs - % ^ 0.64 X 1023(р[ г/смЗ ])(Г[К])"^^' cMVr. A4.5.26)
Главный источник рассеяния фотонов — томсоновское рассеяние, для
которого
i^scatt - i^es = 0,40 CMVr. A4.5.27)
в типичных случаях поглощение преобладает над рассеянием в более
холодных внешних областях диска при больших радиусах, в то время как
рассеяние преобладает над поглощением в горячих внутренних областях.
Полная усредненная по Росселанду непрозрачность (росселандово среднее)
удовлетворяет следующему приблизительному соотношению [см. уравнение (И.30)]
. \. « J- + ^. A4.5.28)
?^??» ^ / '^scatt '^abs
ж) Давление
Полное давление в диске представляет собой по существу сумму
теплового давления газа и давления излучения. Для ионизованного водорода это
дает
Р(р,Г)=^+Р,^, A4.5.29)
где в случае локального термодинамического равновесия
^ad - ???\ A4.5.30)
В типичных случаях газовое давление преобладает над давлением излучения
по всему диску, за исключением (в зависимости от параметров) самых
внутренних областей, где высокая температура.
з) Перенос излучения
При типичных параметрах перенос к поверхности тепла,
выделяющегося внутри диска из-за вязкости, осуществляется в основном посредством
излучения, а не проводимостью или конвекцией. В общем случае возможны
несколько режимов переноса излучения, которые применимы в различных
Аккреция на черные дыры 465
областях диска и (в зависимости от темпа аккреции, массы компактной
звезды и т.п.) в разных моделях диска.
Если полная оптическая толщина диска г (измеренная в вертикальном
направлении) превосходит единицу, фотоны переносятся к поверхности
путем диффузии [уравнение (И.34)].
nr,z)=-|^^p, т>1. A4.5.31)
Здесь F{r, ?) — вертикальный поток фотонов; принято локальное
термодинамическое равновесие между газом фотонов и веществом^\ Величина
? — оптическая толщина, вычисленная на основе полной усредненной по
Росселанду непрозрачности:
= ???^?«?(?,?)? A4.5.32)
•?
(см. приложение И). Заменив дифференциал на конечные разности, можно
приближенно проинтегрировать уравнение A4.5.31), чтобы получить
величину потока через поверхность
F(r)»^«^^, г(г)>1. A4.5.33)
Появившиеся в уравнении A4.5.33) величины ? и F определяются
уравнениями A4.5.7) и A4.5.17) соответственно, а значения Тир следует вычислять
вблизи центра диска при ? = 0. Этот «оптически толстый» режим
применим во внешних областях диска фактически для всех его моделей, а также
во внутренних областях диска для всех моделей, за исключением самых
горячих.
Если ? меньше единицы, диск становится «оптически тонким» для
уходящих фотонов. В этом случае фотоны могут свободно покидать систему
после излучения, не испытывая ни поглощения, ни рассеяния. Тогда
пригодное только для случая диффузии уравнение A4.5.33) должно быть
заменено новым
F{r) « Гл(р, Т) dz « АЛ(р, Г), т(г) < 1, A4.5.34)
•?
где Л(р, 7) — средняя излучательная способность [эрг/(с*см^I вещества
диска. Обычно величина Л определяется тепловым тормозным излучением
(свободно-свободное излучение) и/или комптонизацией, которые
обсуждаются в приложении И.
^) Фактически маловероятно, чтобы уравнение A4.5.31) было применимо в
глубоких ие1фах диска, где, по-видимому, важен турбулентный перенос. Однако диффузия
фотонов возможна во внешней атмосфере диска, где формируется испускаемый
спектр, если только ? > 1.
?4-5?;3
466 Глава 14
Упражнение 14.26. Покажите (приблизительно), что уравнения A4.5.33) и
A4.5.34) эквивалентны, когда ? - 1, если непрозрачность определяется
преимущественно процессами истинного теплового поглощения.
Указание: Используйте закон Кирхгофа.
и) Решение: структура «стандартной» модели диска
Уравнения A4.5.7), A4.5.12), A4.5.14), A4.5.17), A4.5.20), A4.5.24),
A4.5.28), A4.5.29) и A4.5.33) или A4.5.34) дают девять алгебраических
соотношений для девяти величин: ? (г), Л(г), ?(?), v^(r), P(r), T(r), f^(r), к(г) и
F(r) — в виде функций г. Л/ и М. Хотя алгебраическое решение довольно
трудоемкое, оно было получено в работах [422, 543]. Обнаружено, что при
фиксированных значениях Л/ и ? удобно разделить диск на три разные
области в зависимости от г. Эти области таковы:
1. Внешняя область (большие значения г), где давление газа преобладает
над давлением излучения и непрозрачность определяется свободно-
свободным поглощением.
2. Средняя область (меньшие значения г), где давление газа преобладает
над давлением излучения, но непрозрачность обусловлена в основном
рассеянием электронов.
3. Внутренняя область (очень малые значения г), где давление излучения
преобладает над газовым давлением, а рассеяние как источник
непрозрачности преобладает над поглощением.
(При определенном выборе ? внутренняя и средняя области могут вообще
отсутствовать.) Обычно переход от внешней области к средней (г^^)
происходит, когда /Г^^ - к^^, что справедливо при
— = 4 X ??^???^?? ?'/'. A4.5.35)
Здесь Гу ? СМ/с^;^^ величина ? определена в упражнении 14.28, аЛ/^
выражается в единицах Ю^'' г/с. (Вспомним, что 10^'^ г/с - 10~^ М^/гол — это
то значение Л/, которое дает полную светимость L = еЛ/с^ - Ю^'' эрг/с
при эффективности ? - Ю^о; такая светимость характерна для сильных
галактических рентгеновских источников.) Переход от средней области к
внутренней (г^^) происходит, когда Я^ - Pj.ad» '^'^^ справедливо при^^
^=80?2/2??^| ^^'М}^/Щ''/^К A4.5.36)
Из уравнения A4.5.17) следует, что излучение от диска имеет максимум
при малых радиусах г - Юг^. Итак, для черных дыр с массой порядка
Эту величину не следует путать с использовавшимся выше критическим
радиусом околозвукового течения, который также обозначался г .
Уравнение A4.5.36) может быть подтверждено результатами упражнения
A4.28).
Аккреция на черные дыры 467
звездной большая часть излучения (и фактически все рентгеновское
излучение) возникает во «внутренней области» диска.
Упражнение 14.27. Рассмотрим типичный двойной рентгеновский источник с
Л//Л/0 = лУп = 1 = а.
а) Предположив, что компактный компонент — это черная дыра, подсчитайте
доли полной светимости диска, испускаемые внутренней, средней и внешней
областями диска (радиус полости Роша принят равным г/j - 3 · 10^^ см).
б) Оцените отношение полной светимости диска у белого карлика к светимости
диска у черной дыры или нейтронной звезды.
Упражнение 14.28. Решите уравнения, определяющие строение внутренней
области аккреционного диска вокруг черной дыры. Предположите, что ? = Prad =
= — ?/?*, а Г = iTes. Покажите (и сравните с [422, 523]), что
3
F- E X 10'Ьрг/(см2-с))(Л/-2Л/,7)г-^?,
? « G т/см^){а-'МЩ,')г^/Ц-\
Л = A X 10Чм)(Л/,7)?,
? = C X 10-^ T/CM^){a-'MM;i')r^/^r^,
Г=EХ 10^?)(??/)"'?-?8,
г,,-Ъ{а-'МЩ;)г'/Ц-\ A4.5.37)
где
Здесь ? измеряется в единицах Mq , а г ~ в единицах г^.
к) Решение: спектр излучения в «стандартной» модели диска
Температура Г, которая фигурирует в уравнениях, определяющих
строение диска, например в уравнении A4.5.37), представляет собой типичную
температуру внутренней части диска при ? « 0. В общем случае ? > Т^,
где Гу — характерная температура поверхности, на которой формируется
спектр испускаемых фотонов. Приведенное неравенство следует из
уравнения диффузии излучения A4.5.31), которое показывает, что поток
фотонов возникает вследствие градиента температуры в диске. Величины ? и Т^
468 Глава 14
становятся сравнимыми, если диск оптически тонкий в отношении
поглощения; к этому случаю применимо уравнение A4.5.34). Таким образом, для
определения спектра фотонов в общем случае требуется тщательный
анализ профилей температуры и плотности на поверхности диска.
Если диск оптически толстый и поглощение превосходит рассеяние,
локальное излучение имеет вид излучения черного тела. В таких областях
спектр описывается функцией Планка с температурой Г^, равной локальной
эффективной температуре. В соответствии со сказанным
Tsir)-
4/-(/-)
1/4 I ? \~'^^ I г \"'/''
A4.5.38)
Эта температура характеризует вещество под поверхностью на глубине,
соответствующей оптической толщине 7\^ - 1. В основном именно на этой
глубине рождаются типичные фотоны, покидающие диск; такие фотоны с
частотой V рождаются при r^J -- 1, где
T,«^icfpAz^ 1, A4.5.39)
(предполагается, что поверхность однородная и изотермичная). Фотоны,
излученные при больших значениях rj^ поглощаются до того, как смогут
уйти с поверхности. Поэтому интенсивность возникающего излучения
определяется сложением излучений от слоев, начиная cz = Оидог = ??,
лежащих под поверхностью:
h-jl'^z- \-???^), A4.5.40)
где fj — излучательная способность от свободно-свободных переходов,
В^ — функция Планка, а отношение j^J/k^Jp вычислено с использованием
закона Кирхгофа. Уравнение A4.5.40) выводится более точно в приложении
И [см. уравнение И. 19)]. Поток, пересекающий поверхность и
направленный наружу, связан при этом с интенсивностью / соотношениями
F,= Г I^cosedQ-lTTB^T,),
•'о
F = f^F, dv - аТ; (% » к J, A4.5.41)
которые дают знакомый результат для излучения черного тела.
Большой успех теории дисковой аккреции связан с тем, что даже самые
простые предположения позволяют получить эффективные поверхностные
температуры в мягкой рентгеновской области при разумных параметрах
двойных систем, содержащих компактные объекты. Это еще раз
свидетельствует в пользу отождествления наблюдаемых рентгеновских
источников в двойных системах с аккрецией на компактные звезды.
Аккреция на черные дыры 469
Согласно результатам обсуждения, приведенного в разд. 14.5,
поглощение превосходит рассеяние только во внешней области аккреционного
диска. Таким образом, уравнение A4.5.38) применимо только при г > г^^ [см.
уравнение A4.5.35)]. Переписав уравнение A4.5.38) в форме
3/4
Г, ^A . 105К)Л/г/( —)' ?^/^ A4.5.42)
\ 'от /
ВИДИМ, ЧТО внешняя область испускает чернотельное излучение с
температурой Т^ < 10^К. В более глубоких областях, как будет показано ниже,
температура несколько превышает значение, следующее из уравнения
A4.5.38).
Рассмотрим изменение спектра в средней и внутренней областях
диска, где для типичных фотонов рассеяние на электронах преобладает над
поглощением. Для простоты вновь допустим, что поверхность является
однородной и изотермической. Излученные фотоны могут многократно
испытывать (почти) упругое рассеяние, прежде чем покинут поверхность.
Вследствие этого типичный фотон «случайно блуждает» по
зигзагообразной траектории внутри диска, прежде чем достигнет поверхности. Пусть
Az* — глубина (расстояние от поверхности по вертикали), на которой при
свободно-свободном переходе родился фотон с частотой и, покидающий
диск. Пусть As — полная длина пробега фотона при зигзагообразном дви-
. жении до ухода из диска. Соответственно
т/^- 1 - kI^pAs. A4.5.43)
Интенсивность излучения из области О ^ ? ^ Az* равна
/.-???*. A4.5.44)
Величина Az* меньше, чем ??, которая была найдена ранее, когда прене-
брегалось рассеянием. Теперь зигзагообразное блуждание фотона
увеличивает вероятность его захвата·до выхода из диска и тем самым уменьшает
глубину, излучение с которой вносит вклад в возникающий поток. В
частности, если ?^^ — полное число рассеяний до выхода из диска, то
Ks=r'r ?,,--—, A4.5.45)
где \^ — средняя длина пробега на рассеяние. Поскольку рассеяние
приводит к случайному блужданию фотонов, результирующее расстояние,
пройденное в вертикальном направлении, равно при этом ?'^^\$·
Следовательно,
??* = KV%^. A4.5.46)
Комбинируя уравнения A4.5.43), A4.5.45) и A4.5.46), получаем
^- ~ -^ A4.5.47)
470 Глава 14
и
^"*~ ( ^/2 ~^^lir) · A4.5.48)
Подстановка соотношения A4.5.48) в A4.5.46) дает интенсивность
которая отличается от A4.5.40).
В рассматриваемом случае непрозрачность при свободно-свободном
поглощении в ионизованном водороде определяется выражением
icf - 1,5 · io25p7'-V2g^^llL?Z cmVf, A4.5.50)
[уравнение (И.43)], где ^^^—медленно меняющийся «множитель Гаунта»
порядка единицы, 2i ? = hv/кТ. На достаточно высоких частотах ?
рассеяние преобладает над поглощением. Соответственно,
F, = r^b^cosedQ - 2??,{??^] , A4.5.51)
•'о \ l^es I
ИЛИ
дс^/^ехр(-дс/2) / „ ч
^^ ^ , /\,1/2 > ('^? ^ '^es), A4.5.52)
(^- 1)
Это «модифицированное» чернотельное спектральное распределение.
Интегрирование по всем частотам дает полный поток, если предположить, что
рассеяние превосходит поглощение даже при малых значениях ?,
удовлетворяющих условию X < I:
F ~ 6,2 · 10"р'/'7;'/'эрг/(см2 · с). (% « к„).'> A4.5.53)
Грубое приближение интеграла в уравнении A4.5.51) можно записать в
виде соотношения
/ ?? \1/8
7;ff«7;(^J , (?,,»?,,), A4.5.54)
где использовано тождество F = ??^^^ и где применяется средняя по Россе-
ланду непрозрачность для соотношения в скобках. Уравнение A4.5.54) по-
^^ Условие Kff ^ «es ^^^ средних по Росселанду непрозрачностей эквивалентно
требованию, чтобы k^J < к^^ для всех ? ^ 6 [сравните с уравнениями (И.43) и
(И.44)].
Аккреция на черные дыры 471
называет, что в результате рассеяния средняя энергия излучаемых
поверхностью фотонов -- кТ^ увеличивается по сравнению со значением,
характерным для излучения в термодинамическом равновесии. Заметим, что
уравнение A4.5.54) можно вывести (с точностью до численного множителя
порядка единицы) и непосредственно из (И.38) и (И.39), если отождествить
величину г = Tgg в этих уравнениях с оптической толщиной, при которой
рождаются выходящие фотоны. В этом случае
(к \^/2
A4.5.55)
в соответствии с уравнением A4.5.48). Отсюда и следует уравнение
A4.5.54).
Упражнение 14.29. Покажите, что результат приведенного выше анализа
интенсивности излучения от изотермической однородной оптически толстой пластины с
рассеянием и свободно-свободным поглощением можно выразить в следующем
виде:
1/2
, т*>1, A4.5.56)
для произвольной частоты Vy если эффективная оптическая толщина на поглощение
т* превосходит единицу. Здесь
Tff, % > i^cs·
Если г* < 1, фотоны никогда не перепоглощаются, так что они не
могут термализоваться. Следовательно, излучающая область оказывается
оптически тонкой и
/,«л(р,Г)Л, т*<1. A4.5.58)
Если поверхностные области нельзя считать однородными и
изотермичными, чего можно ожидать для релятивистской атмосферы в
гидростатическом равновесии, то спектр приобретает несколько иной вид (сравните с
[522]). Пренебрегая такими отклонениями и предполагая, что
поверхностная плотность сравнима с плотностью внутри, можно использовать
уравнение A4.5.53) вместе с A4.5.17) и A4.5.37) для оценки Т^ в оптически
толстых внутренних областях:
?, = B?10'?)?2/' -^ ^пдЯ ^*^'· (*4·5·59)
Основная особенность этой «модифицированной» чернотельной
температуры состоит в том, что она заметно выше эффективной температуры
472 Глава 14
A4.5.38) во внутренней области. Соответственно, излученные из этой
области фотоны будут иметь более высокую энергию (т.е. будут «жестче»),
чем при излучении диска как абсолютно черного тела. В самом деле,
поскольку излучение черного тела термодинамически представляет собой
наиболее эффективный механизм излучения, любой другой процесс излучения,
создающий такой же поток, должен протекать при более высоких
температурах.
В самых внутренних областях диска, которые в зависимости от
параметров являются оптически тонкими (т.е. г* < 1 от ? = О до ? = Л),
излучение связано со свободно-свободными переходами и комптонизацией.
Комптонизация — это механизм, посредством которого фотоны могут
обмениваться эйергией с электронами, когда энергия фотона испытывает
доплеровский сдвиг второго порядка (т.е. v^/c^ - кТ/т^с^) вследствие
томсоновского рассеяния^^ Эти области могут иметь температуры,
несколько выше определяемых уравнением A4.5.59), вплоть до максимальных
значений Т^^ ^ 4 · 10^ К для ? - 1, ? -- 6 М^ и ЛУ^ г 10 [364].
Составной спектр излучения можно получить, если определить
локальный поток и спектр для каждой области диска, а затем сложить вклады
всех областей. Результаты таких подсчетов показаны на рис. 14.4 для
случая аккреции на черную дыру с массой порядка солнечной. Этот рисунок
наглядно иллюстрирует способность дисковой аккреции генерировать
мощный поток мягкого рентгеновского излучения.
14.6. ДРУГИЕ МОДЕЛИ
Рассмотренная выше модель аккреционного диска в принципе представляет
собой самое простое решение гидродинамических уравнений для тонкого
аккреционного диска. Однако это решение вовсе не единственное. Более
того, было показано^^ что внутренней области этого «стандартного» диска,
где давление излучения преобладает над давлением газа, должна быть
свойственна вековая неустойчивость, приводящая к дроблению на кольца.
К тому же модель «стандартного» диска, предложенная для описания
аккреции на черную дыру в тесной двойной системе, не позволяет объяснить
^^ Краткое рассмотрение эффекта комптонизации приведено в разд. И.З
приложения И. Общее обсуждение см., налрим^?, в [318, 452, 493]. Обсуждение
комптонизации мягких рентгеновских лучей, образовавшихся при свободно-свободных
переходах, дано, например, в [194, 231]. Приложение к аккреционным дискам содержится в
работах [522, 534]. Эффекты, зависящие от времени, рассмотрены в [363, 449].
^^ В работах [1, 362] показано, что с учетом эффектов общей теории
относительности все аккрецисжные диски — «стандартные» или любые другие, вблизи своих
внутренних краев должны обладать тепловой и вековой динамической
устойчивостью. Однако стабилизирующее влияние эффектов общей теории относительности не
может простираться достаточно mnsmo во внутреннюю область, которая
продолжается вплоть до рад»уса г^^ > г^, га^ релятивистские эффекты уже не столь важны.
Аккреция на черные дыры
473
ih
0.1 h
0.01 h
0,001
u
г~
—?— ?—
? — .1
? ?
модифициробанный
-.^0 ^4
Модифицироеанный
-txfi-hu/iT)
1 .._L.
?
\
1-
Ч
"?
0,01
0,1
10
too
?..
Рис. 14.4. Схема спектра излучаемой энергии для двух моделей диска вокруг че1ЖОй
дыры по расчетам Шакуры и Сюняева [522] без учета релятивистских поправок и
захвата излучения дырой. В обеих моделях предполагается, что дыра не вращается и
внутренний край диска расположен щж rj = 6Л/. Модель а соответствует ? ~ 10"^,
? = Mq, ? = 1О~^Л/0/год, L = Lg^^ * 10^* эрг/с; модель б соответствует
? - 10~^ -5- 1 (спектр нечувствителен к величине а), ? = Mq, ? = 10~^ Л/^/год,
L « 10^ эрг/с. Часть спектра, отмеченная как черное тело у в основном излучается
внешне холодной областью, где рассеяние электронами не существенно. Часть
спектра, обозначенная термином модифшфированный, излучается средней и
внутренней областями, где рассеяние на электронах является оснош1ым источником нехфо-
зрачнрсти. Температура жспонешщальиого «хвоста» — это поверхностная ?e^шepa-
тура самой внутреш1ей области [422].
жесткое рентгеновское излучение (- 100 кэБ), наблюдамое от Cyg Х-1
(см. разд. 13.5 и рис. 13.9).
Торн и Прайс впервые предположили [570], что внутренняя часть
аккреционного диска оптически тонкая и находится при высокой температуре
(- 10^ К). Такое предположение в отличие от «стандартной» модели диска
с оптически толстой и низкотемпературной внутренней областью
позволяет объяснить природу наблюдаемой жесткой составляющей в спектре
Cyg Х-1 вблизи 100 кэБ. По мнению Торна и Прайса, вековая
неустойчивость внутренней области стандартного «холодного диска» может
«раздувать» эту оптически толстую область, где преобладает давление излучения,
преобразуя ее в более горячую оптически тонкую область, где давление
определяется газом (рис. 14.5). Согласованная модель «горячего диска» с
такими свойствами была построена в работе [534]. Когда ее применили к
Cyg Х-1, модель совершенно естественно дала требуемую температуру теп-
474 Глава 14
\ I
Дыра
Рис, 14,5, Строение области «горячего» аккреционного диска, испускающей
рентгеновские лучи. Оптически тонкая область G) испускает комптонизированные фотоны
(высокие энергии), оптически толстая область B) — тепловые фотоны (низкие
энергии). Типичные размеры: радиус черной дыры ~ 12 км, радиус «утоньшения»
г^ - 30 — 300 км, радиус всей области, излучающей рентген, - 300 км [570].
лового излучения 10^ К. В этой «двухтемпературной» модели электроны
находятся при температуре 10^ К во всей внутренней области, а температура
ионов в 3—300 раз выше. Жесткий рентгеновский спектр для энергий выше
- 8 кэВ создается комптонизацией мягких рентгеновских фотонов,
излучаемых в оптически толстых частях диска; спектральная кривая имеет
степенной характер в диапазоне от 8 до - 500 кэВ, а выше она экспоненциально
падает. Показатель степени зависит от безразмерного параметра компто-
низации
Акт
у - ^тЛ. A4.6.1)
имеющего обычно значение >' « 1 во всей внутренней области. В этом
случае интенсивность определяется выражением (см. приложение И, разд.
И.З)
?,?:?^^^^???{--?)^ A4.6.2)
т
--|-(?*7?· <"¦"'
так что в типичных случаях интенсивность излучения от диска
пропорциональна /^ - л'~^ехр(—Л"). Этот результат вполне выдерживает сравнение с
наблюдаемым жестким спектром Cyg Х-1 (сравните с разд. 13.5 и рис. 13.9
и И.1). Однако данные наблюдений спектра при энергиях выше
-200 кэВ еще остаются неясными. Отсутствие «завала» спектра при
высоких энергиях вплоть до ^ 100 кэВ указывает на то, что электронная
температура области, излучающей жесткий рентген, составляет более 10^ К, но
Аккреция на черные дыры 475
проведенные до настоящего времени наблюдения позволяют это значение
рассматривать в качестве нижнего предела^^
Были предложены и другие модели «горячего диска», способные
объяснить жесткое рентгеновское излучение. Некоторые из таких моделей
основаны на наблюдениях Cyg Х-1; другие на наблюдениях жестких
рентгеновских (обычно степенных) спектров квазаров и ядер активных галактик.
Модель, вперв1?1е предложенная в работах [67, 358, 429], предполагает
существование горячей короны, в центре которой находится оптически толстый
аккреционный диск. Высокая температура короны создается акустическими
и альвеновскими волнами, а также диссипацией магнитных полей в верхней
атмосфере диска. Жесткое рентгеновское излучение испускается короной,
где происходит комптонизация мягких фотонов горячими тепловыми
электронами^^.
Еще один класс самосогласованных моделей «горячего диска» был
предложен в работах [450, 471]. Там предполагалось, что диск, оптически
тонкий как для излучения, так и для поглощения, удерживается давлением газа
и что в нем преобладает охлаждение тормозным излучением. При
подходящих параметрах модели (Мр ^ 0,1 М/М^) спектр имеет «тормозную»
форму, т.е. dL/dEoie~^, причем температура излучения % 10 кэВ. Таким
образом, модель не позволяет получить степенной профиль для энергий
выше 10 кэВ. Как двухтемпературная модель, так и оптически тонкая
модель с тормозным излучением не исключают возникновения тепловых неу^
стойчивостей, которые ведут к образованию конденсаций [468]. Однако
даже в этом случае диск может быть устойчивым в смысле среднего по
времени, хотя и испытывать большие флуктуации [523].
Упражнение 14.30, а) Решите взаимосвязанные уравнения строения диска для
оптически тонкой модели с тормозным излучением. Предположите, что ? « Р^^,
? * 1 и Л = Aff = 1,43 · Ю'^^ {p/nipYT^'g^^ [gff - 1; см. уравнение (И.46)].
Покажите, что [450]
Г=A,1 Х10»К)(^) К-^/Ц]/\
? = B,7 X Ю-» )l·^ Л/з" 'Л- ''^ЧУ* т/см^,
^^ Обзор данных, касающихся наблюдения жесткого рентгена от Cyg Х-1 и
состояния модели комптонизации,см., например, в [357].
^^ Сравнение оптически тонкой двухтемпературной модели и модели диска с
короной см. в [359].
476 Глава 14
где
Л/з^-^. А/.= ^
1/2
Ю^Л/о ' 10^^ г/с
Заметим, что строение диска зависит от ?17 и Л/3 только через отношение ?^?/?-^ -
-- L/A0-^Lej1ji), где L — полная светимость диска, а Lg^jji — предельная эддингто-
новская светимость черной дыры [см. уравнение A3.7.6)].
б) Сравните температуру излучения оптически тонкого диска с тормозным
излучением и «стандартного» аккреционного диска при значении радиуса,
соответствующем максимальному потоку (/? -- 1). Представьте полученные результаты в виде
графика зависимости от Л/A ^ М/М^^ < 10^) для L/Ledd = 0,1. Прокомментируйте
применимость этих двух моделей диска к мягкому рентгеновскому излучению от
галактических черных дыр в двойных системах (Л/ -- Mq ) и от сверхмассивных
черных дыр в плотных ядрах галактик и квазарах {M/Mq - 10^I).
^) Детальное обсуждение спектров излучения от аккреционных дисков различного
типа, образующихся вокруг массивных черных дыр, см. в [177].
Глава 15
Аккреция на нейтронные звезды
и белые карлики
в первых трех разделах этой главы рассматриваются некоторые
особенности аккреции на нейтронные звезды. Наше обсуждение основано на
общепринятом представлении, что импульсные рентгеновские источники — это
магнитные нейтронные звезды, которые аккрецируют газ, перетекающий
от главного компонента в двойной системе (см. гл. 13). Будет показано,
что для моделей аккреции на нейтронные звезды существуют строгие
ограничения, вытекающие из наблюдений. В частности, ати модели должны
объяснять изменения периода, наблюдаемые у многих рентгеновских
пульсаров. В последнем разделе кратко обсуждаются основные особенности ак-
круеции на белые карлики.
15.1. АККРЕЦИЯ НА НЕЙТРОННЫЕ ЗВЕЗДЫ: МАГНИТОСФЕРА
Наше понимание теории аккреции на нейтронные звезды и интерпретация
результатов наблюдений значительно углубились за последние десять лет.
Однако существующая картина еще дает немало поводов для сомнений.
Очень важная особенность аккреции на нейтронные звезды, усложняющая
рассмотрение, состоит в присутствии сильного магнитного поля, которое
от поверхности звезды простирается наружу, образуя звездную
магнитосферу. Это поле может управлять характером течения газа на поверхность
звезды, определять действующие на звезду вращающие моменты, форму
среднего импульса и спектр испускаемого излучения и т.п. Поэтому
вначале обсудим роль, которую играет магнитное поле нейтронной звезды при
аккреции^^
Вдали от нейтронной звезды магнитное поле слабо влияет на характер
аккреционного течения, и поэтому на больших расстояниях остаются в
силе приведенные в предыдущей главе решения для сферически симметричной
и дисковой аккреции. Однако вблизи звездной поверхности течение
плазмы, по-видимому, полностью определяется магнитным полем.
'^ Строение магнитосферы вращающейся нейтронной звезды и ее влияние на
течение аккрецируемого газа впервые обсуждались в [155, 332, 470]. Более поздний
обзор приведен в [324].
478 Глава 15
Рассмотрим влияние дипольного магнитного поля, имеющего за
пределами звезды величину
5«-^=10'^зоЛб-'G)'гс. A5.1.1)
В уравнении A5.1.1) величина ? — магнитный момент, а Дзо означает
момент в единицах 10^^ Гс · см^, R — радиус звезды, а /?^ — радиус в
единицах 10^ см. Предположим вначале, что на больших расстояниях от звезды
течение носит сферически симметричный характер. Тогда интуитивно
можно ожидать, что магнитное поле начнет сильно влиять на течение, когда
плотность магнитной энергии окажется сравнимой с плотностью
кинетической энергии аккрецируемого газа. Это условие определяет характерный
радиус поверхности в магнитосфере Гд, называемый альвеновским
радиусом:
^^^ = |р('л)«.^('л). A5.1.2)
На основании уравнений A4.3.23) и A4.3.4) для стационарного
околозвукового течения со скоростью, близкой к скорости свободного падения, можно
записать следующие соотношения:
»('·)*% = ^—;r-J -
47Г%Г^
Подстановка уравнения A5.1.1), которое, строго говоря, справедливо
только в экваториальной плоскости, и уравнения A5.1.3) в A5.1.2) приводит к
результату
Соотношение A5.1.4) можно переписать в единицах полной светимости,
возникающей вследствие аккреции, которая определяется формулой
= Л/(
?). A5.1.5)
Подстановка A5.1.5) в A5.1.4) дает
где ^37 — светимость в единицах 10^^ эрг/с. Поэтому в типичных для
нейтронных звезд случаях Гд > /?.
Аккреция на нейтронные звезды и белые карлики 419
Магнитное поле не проникает в падающую плазму на расстояния,
существенно превышающие Гд. На альвеновской поверхности магнитное по'ле
будет индуцировать токи в падающей плазме. Эти поверхностные токи
экранируют магнитное поле звезды при г >
г< г 1).
Упражнение 15.1. Пусть нейтральный пучок холодной плазмы, которая движется со
скоростью ? в свободной от магнитного поля области, падает перпендикулярно на
плоскую поверхность, за которой имеется однородное поле ?, параллельное
плоскости [332]. Столкновениями между частицами можно пренебречь.
а) Опишите движение электронов и ионов после того, как они пересекли
плоскую поверхность. Покажите, в частности, что в этом случае возникает ток,
параллельный рассматриваемой поверхности, и оцените глубину проникновения ионов.
б) Оцените вклад ионов и электронов в плотность поверхностного тока g и
соответствующий скачок магнитного поля, вызываемый этим током.
Ответ: ^B - 47г(^,. -Ь ^J/c = ????^/?
в) Используя полученный ответ и уравнение A5.1.2), докажите, что эти
экранирующие токи, индуцируемые на альвеновской поверхности, должны
скомпенсировать магнитное поле звезды на расстояниях г > гд.
Задача о пересечении падающей плазмой магнитных силовых линий или
о проникновении плазмы вдоль силовых линий к поверхности звезды
исключительно сложна для решения. По-видимому, вблизи альвеновской
поверхности образуется стоячая ударная волна, которая служит препятствием
на пути аккреционного потока. Температура газа непосредственно за
ударной волной, которая преобразует кинетическую энергию потока в
тепловую энергию хаотически движущихся частиц, приближенно определяется
выражением
kT~mУ~^^^ A5.1.7)
ИЛИ
Рассматривая течение плазмы при /* < /"д, естественно предположить,
что плазма может достигать поверхности звезды, просачиваясь на
магнитные полюса в виде узкого аккреционного столба [155, 332, 470].
Представим, что эта область ограничена теми силовыми линиями, которые в от-
^^ Если пользоваться привычной геофизической терминологией, то поверхность,
по которой протекают экранирующие токи, можно назвать «магнитопаузой». Мы
не проводим различия между магнитопаузой и альвеновской поверхностью,
которые, вообще говоря, в зависимости от характера течения могут и не совпадать; см.
[24].
480 Глава 15
сутствие аккреции проникали бы за альвеновский радиус (сравните с рис.
13.3). В нашем случае форма силовых линий дипольного поля определена
соотношением (sin^^)/r = const, так что последняя невозмущенная силовая
линия, которая замкнется внутри альвеновской поверхности, выходит с
поверхности на магнитной широте ^^, где угол ?^ определяется выражением
sin4 = -«3x 10-^
/u'^vi.'"!^)
-1/7
A5.1.9)
если для оценки Гд использовать уравнение A5.1.6). Итак, площадь
поперечного речения аккреционного столба вблизи каждого полюса на
поверхности звезды приближенно будет равна
А « ???^??\ « Ю^^см^, A5.1.10)
что составляет малую часть площади всей сферической поверхности.
При заданной концентрации плазмы вблизи полярных шапок диаграмма
испускаемого излучения будет характеризоваться значительной угловой
анизотропией, зависящей от детальной природы аккреционного течения.
Таким образом, имеется правдоподобное объяснение механизма генерации
импульсного рентгеновского излучения для наклонного ротатора (т.е. для
звезды, у которой направления магнитной оси и оси вращения не
совпадают).
Упражнение 15.2. Используйте уравнение A5.1.10) для оценки эффективной чер-
нотельной температуры излучения, испускаемого с одной из магнитных полярных
шапок в предположении, что L37 " 1.
Однако сравнительно недавно было высказано предположение [23, 24,
181, 182], что в широком диапазоне условий наиболее важным процессом,
посредством которого плазма попадает в магнитосферу, должна быть
«обменная» неустойчивость Рэлея—Тейлора. В принципе эта неустойчивость
позволяет плазменным каплям или нитям проникать в магнитосферу
«между силовыми линиями» и падать на поверхность звезды в любом месте без
«зацепления» за силовые линии. При этом вещество выпадает на
поверхность в основном вблизи магнитных полюсов, но эффективная площадь
нагреваемых полярных шапок значительно превосходит значение,
определяемое A5.1.10). Эти вопросы еще далеки от полного решения.
15.2. ДИСКОВАЯ АККРЕЦИЯ И ИЗМЕНЕНИЯ ПЕРИОДА
ИМПУЛЬСНЫХ РЕНТГЕНОВСКИХ ИСТОЧНИКОВ
Обратимся теперь к случаю, когда вещество вдали от звезды втекает в кеп-
леровский аккреционный диск. Определение альвеновского радиуса при
дисковой аккреции оказывается гораздо более трудной задачей. Наиболее де-
Аккреция на нейтронные звезды и белые карлики 481
тальная модель дисковой аккреции разработана в настоящее время Гошем
и Лэмбом [219, 220, 221], которые принимали во внимание сильную
магнитную связь между звездой и аккрецируемой плазмой в диске. Авторы
рассматривали частный (но нетривиальный) случай аккреции осесиммет-
ричного диска ротатором, у которого ось вращения параллельна
магнитному полю. Характер течения анализировался при помощи приближенных
методов с использованием двухмерных гидродинамических уравнений.
«Проскальзывание» силовых линий звездного магнитного поля сквозь
плазму диска учитывалось введением эффективной проводимости. Такая
модель позволяет учесть проницаемость внутренней части диска как
следствие плазменных неустойчивостей (в частности, неустойчивости
Кельвина— Гельмгольца), турбулентной диффузии и пересоединения
магнитных силовых линий. Однако величина проводимости определяется
исключительно условиями стационарного течения.
Гош и Лэмб нашли, что такое проникновение магнитного поля
приводит к образованию широкой переходной области, соединяющей нево:1му-
щенное течение в диске вдали от звезды с течением в магнитосфере вблизи
звезды. Можно достаточно просто оценить характерный радиус г^
границы, отделяющей внешнюю часть переходной зоны с кеплеровским
движением, от внутренней части, где скорость уже отличается от кеплеровской.
Начнем с магнитогидродинамического уравнения Эйлера G.1.1).
Используя уравнение G.1.2) и положив для стационарного состояния все
производные по времени равными нулю, находим
?(?· v)v= -VP- ??? + 4^(V ? В) ? В. A5.2.1)
Используя векторные тождества, перепишем левую часть уравнения в виде
?(? · V)v = p[{W + (? ? ?) ? ?]. A5.2.2)
Мы собираемся вывести уравнение сохранения момента количества
движения относительно оси ?. Обратимся для этого к рассмотрению ф·
компонента уравнения баланса сил A5.2.1). Вследствие осевой симметрии
все градиентные члены равны нулю и потому в цилиндрических
координатах имеем
[(V X в) X В]ф = \вХгВ^)^ + В,В^,. A5.2.3)
После использования уравнения Максвелла
0 = vB = -^(rB,)., + 5,,„ A5.2.4)
уравнение A5.2.3) принимает вид
[( V X В) X В]ф = -^(гЧ^ф),, + E.5*).,· A5.2.5)
15-513
482 Глава 15
Выражение, аналогичное A5.2.3), содержится в последнем члене уравнения
A5.2.2), если В заменяется на ?; кроме того, можно положить ?^ = 0.
Тогда уравнение A5.2.1) дает
P^rr{rv,)^-^[{r%B,)^ + r^{B,B,)]. A5.2.6)
Рассмотрим теперь конфигурацию магнитного поля в диске. В
отсутствие диска силовые линии дипольного поля не имеют ф-компонента (т.е.
они полоидальны), а вблизи экваториальной плоскости преобладает
компонент В^. Однако, если вокруг звезды имеется диск, силовые линии,
«вмороженные» вначале во вращающуюся плазму, испытывают сдвиг в
направлении ф. Этот сдвиг приводит к появлению отличного от нуля компонента
5ф. Предположим, что силовые линии, будучи сдвинутыми, остаются
непрерывными при пересечении поверхности диска. Тогда компоненты В.
должны быть одинаковыми по величине, но противоположными по
направлению сверху и снизу от плоскости диска. В результате магнитное поле
внутри диска будет гораздо сильнее меняться по высоте ?, чем по радиусу г
(например, В^ изменяется от -\-B^ до -В^ при изменении ? от -Л до + Л,
где h <t г -— толщина диска). Кроме того, предполагается, что В^ < Вф, В^,
поскольку диск расположен вблизи экваториальной плоскости, а газ
движется почти по круговым орбитам. Таким образом, первым членом в
правой части уравнения A5.2.6) можно пренебречь.
Вспомним, что из уравнения неразрывности V · (pv) = О следует
rpv,= const. A5.2.7)
Интегрирование уравнения A5.2.7) по ? в интервале от -Л до Л с учетом
A4.5.7) дает уравнение A4.5.12):
A^rhv^p = ?. A5.2.8)
Таким образом, если проинтегрировать уравнение A5.2.6) в пределах от
-Л до Л и пренебречь изменением ?^ по ?, то получим
Л/(го,)^ = гЧ«Ф· A5.2.9)
Следуя Гошу и Лэмбу, можно приближенно оценить уравнение A5.2.9),
чтобы получить переходной радиус Tq. Предположим, что переходная
область имеет конечную толщину вдоль радиуса ? < г, в пределах которой
вращающий магнитный момент, действующий на плазму диска, тормозит
азимутальную составляющую ее движения. Тогда уравнение A5.2.9) неявно
определяет г^ посредством соотношения
M[^)v^«r%B^. A5.2.10)
Теперь предположим, что там, где магнитное поле звезды начинает
определять азимутальную составляющую движения, справедливо приближенное
соотношение В^ « 5^, где компонент В^ сравним с невозмущенным ди-
Аккреция на нейтронные звезды и белые карлики 483
польным полем в экваториальной плоскости. Используя это приближение
наряду с соотношением ?^ « ?^^ для кеплеровского движения, а также
предполагая, что неравенство h s ? s г ограничивает диапазон
возможных значений ширины переходного слоя (Гош и Лэмб нашли, что ? - 4/?
при Tq), можно решить уравнение A5.2.10) относительно Tq:
[^)^ Аа<Го<Аа. A5.2.11)
Здесь Гд — альвеновский радиус, определенный для случая радиальной
аккреции выражением A5.1.4). Вблизи Tq невозмущенный диск будет иметь
полутолщину Л, соответствующую «средней области» стандартного
аккреционного диска. Это значает, что
^ « 9 X 10-V>/20a-'/'°i-j^j"'^'°(A/,,)'/'i'/5, A5.2.12)
где член г в правой части выражен в единицах GM/c^.
Уравнение A5.2.12) может быть выведено на основе результатов,
полученных в разд. 14.5^^ Подстановка A5.2.12) с ? « 1 « м^^ « A/ZA/q в
A5.2.11) дает в конечном итоге
0,3гд % г^< Гр^ (грубая оценка). A5.2.13)
При несколько более точной оценке Гош и Лэмб нашли, что
А-о « 0,5гд. A5.2.14)
Значение оценки A5.2.14) и модели дисковой аккреции, где она
используется, состоит в том, что из этой модели следует особенно простое
соотношение между увеличением скорости вращения ? аккрецирующей
нейтронной звезды и произведением PL·^^'^ для данной звезды (здесь ? — период
вращения звезды). Вспомним, что одно из весьма немногих точных средств
наблюдений за импульсными рентгеновскими источниками состоит в
определении скорости, с которой изменяется период следования импульсов
(сравните с разд. 13.3 и с рис. 13.4). В отличие от радиопульсаров,
вращение которых, как следует из наблюдений, замедляется, у рентгеновских
пульсаров проявляется вековое возрастание частоты вращения. Поэтому
можно рассчитывать, что эта скорость увеличения частоты отражает
характер переноса момента количества движения от падающей плазмы на
аккрецирующую звезду. В свою очередь этот характер зависит от вида
течения вне магнитосферы.
Рассмотрим теперь перенос момента количества движения при дисковой
аккреции на вращающуюся нейтронную звезду, у которой направление
магнитного поля совпадает с осью вращения. Представим, что звезда вместе с
магнитосферой заключены внутри поверхности Sq, слегка выходящей за
1)
См., например, [422], уравнение E.9.8).
484
Глава 15
пределы Tq. Скорость изменения момента количества движения системы
звезда — магнитосфера определяется выражением
^(/fl,) = M/(ro) + iV,
A5.2.15)
где / — момент инерции всей системы (практически он равен моменту
инерции одной лишь звезды), Q^ — угловая скорость вращения звезды,
/ — удельный момент количества движения аккрецируемой плазмы, а
N — магнитный и вязкостный вращающие моменты, действующие сразу
же за пределами Sq. Записав соотнощение
dt </М^'
z^ ^
получим [332]
?
?
?
? dl
I dM
dt
Ы
I
N
/?/
A5.2 Л 6)
A5.2.17)
где I,
ют, что
^ — Rl^/M. Типичные уравнения состояния ядерной материи показыва-
М dl
I dM" '
A5.2.18)
если исключить случай самых легких нейтронных звезд. Поэтому первым
членом в правой части уравнения A5.2.17), малым по сравнению со
вторым, можно пренебречь. Для кеплеровского орбитального движения
справедливо соотношение
7(го) = (СМго)
1/2
A5.2.19)
так что обычно /(??) > /^.
Предположим, что вязкостным и магнитным вращающими моментами
можно пренебречь (N = 0), и определим скорость убыстрения вращения,
которая соответствует одному лишь второму члену в уравнении A5.2.7).
Комбинация соотношений A5.1.5), A5.1.6), A5.2.14), A5.2.17) и A5.2.18)
приводит к следующему результату:
-Р«5.8 X 10"^
^Мж)
hV
{РЦ^'^У с/год. A5.2.20)
Таким образом, мы приходим к выводу (по крайней мере в предельном
случае N = 0), что величина ? для звезды с данной массой (а
следовательно, и радиусом) и с данным магнитным моментом зависит только от
PL^^^. Гош и Лэмб показали, что это заключение остается справедливым,
даже когда важными становятся вращающие моменты, которые
возникают из-за магнитной связи при /* > /? (вязкостные вращающие моменты в
диске обычно играют меньшую роль). Такие магнитные вращающие мо-
Аккреция на нейтронные звезды и белые карлики 485
менты особенно важны для «быстрых ротаторов». По определению
быстрые ротаторы имеют высокие значения безразмерного «параметра
быстроты» ?^, определяемого выражением
где йк(го) — кеплеровская угловая скорость, соответствующая радиусу г^
[182]. Например, Her Х-1, для которого ?^ « 0,4, очевидно, можно считать
«быстрым ротатором», а GX 1 + 4, для которого ?^ « 3 · 10~^,
вероятно, можно назвать «медленным ротатором». Для медленных ротаторов
магнитная связь приводит к умеренному возрастанию момента сил,
ускоряющего вращение, примерно на 404?. Следовательно, уравнение A5.2.20)
остается справедливым как по величине, так и по знаку. Для «быстрых
ротаторов» вращающие магнитные моменты во внешней части диска
отличаются по знаку от моментов сил, связанных с магнитным полем на
внутреннем крае диска и с моментом количества движения потока вещества,
уменьшая тем самым скорость возрастания частоты. При достаточно
высоких угловых скоростях звезды, или, что эквивалентно, при достаточно
низких темпах аккреции, звезда будет даже замедлять вращение, хотя
аккреция и испускание рентгеновского излучения продолжаются.
Упралснение 15,3, Почему низкий темп аккреции эквивалентен большой угловой
скорости вращения звезды, как отмечалось выше?
Ответ:
-5/7
a,,= l,2P-4W3^^(]^)" . A5.2.22)
Учитывая рассмотренные выше соображения, Гош и Лэмб объяснили
существование большого числа долгопериодических (Я ^ 100 с) источников
с коротким характерным временем возрастания частоты (-50 — 100 лет).
По их предположению, источники неоднократно проходили состояние с
низкой активность^), когда темп аккреции падает и на звезду действуют
значительные моменты сил, приводящие к замедлению вращения.
Модель Гоша и Лэмба обеспечивает количественное обоснование
выдвинутых ранее идей [155, 332, 470], согласно которым величина ?^ должна
стабилизироваться при значениях порядка 0^(/^), в результате чего ?^
приближается к единице. Эта модель свидетельствует о невозможности
стационарной аккреции при ?^ > ^k('*o)· ^ ^^^ случае центробежная сила,
действующая на плазму при Tq, оказывается слишком большой, чтобы
допустить твердотельное вращение. Результирующая радиальная сила
(центробежная + гравитационная + магнитная) достаточно велика и направлена
наружу, так что скорость втекания вещества быстро падает до нуля.
Отдельные авторы [155, 232] предположили, что для достаточно быстрых
ротаторов на систему звезда — магнитосфера должен действовать замедляю-
486 Глава 15
щий вращающий момент, вызванный выбросом массы. По очевидным
причинам этот механизм называется «эффектом пропеллера».
Пожалуй, наиболее веский аргумент в пользу аккреции на нейтронную
звезду как механизма, объясняющего импульсное рентгеновское излучение
и подтверждающего общую правильность магнитосферных моделей,
вытекает из сравнения наблюдаемых изменений периодов следования импульсов
с теоретически предсказанными. Модель дисковой аккреции Гоша и Лэмба
предсказывает, что вся совокупность импульсных рентгеновских
источников должна ложиться на одну кривую -Я = f(PL^^^) [сравните с
уравнением A5.2.20)], если все они имеют одинаковую массу ? и одинаковый
магнитный момент ?. (Вспомните, что / и /? однозначно определяются массой
? при заданном уравнении состояния.) Разумеется, трудно предполагать,
что у всех импульсных рентгеновских источников будут одинаковые
значения Л/ и ?. Однако корреляция между ? и PL^^^ все же должна
существовать, если изменения ? и ? при переходе от источника к источнику будут
не слишком велики. На рис. 15.1 наблюдаемые величины отложены в
зависимости от PL^^^ для девяти источников. Приведены также теоретические
кривые возрастания частоты вращения для нейтронных звезд с Дзо - ^»^^ ^
M/Mq = 0,5; 1,3 и 1,9 (в предположении «жесткого» уравнения состояния
с тензорным взаимодействием [444]; сравните с разд. 8.5 и табл. 8.2).
Отметим, что линейный участок теоретической кривой при больших
значениях PL^^^ (что соответствует малым значениями ?^, согласно упражнению
15.3) приближенно описывается уравнением A5.2.20). Загиб теоретической
кривой вниз при малых значениях PL^^^ возникает из-за магнитной связи
между диском и звездой при г -- г^. Рассматривая этот график, можно
прийти к выводу, что все источники, за исключением объекта Паруса Х-1,
лежат в затененной области, перекрываемой кривыми, которые
соответствуют массам нейтронных звезд в интервале 0,5 ^ M/Mq ^ 1,9. Согласие
с наблюдениями источника Паруса Х-1 может быть получено, если этот
источник обладает гораздо большим магнитным моментом, чем
остальные (например, Дзо "* ^^)» ^^^ ^^» ^'^^ более вероятно, в этом случае
происходит не дисковая, а сферически симметричная аккреция, вызванная
звездным ветром (сравните с упражнением 14.14)^^
^^ Начиная с 1975 г. вплоть до 1978 г. период импульсов от источника Паруса Х-1
{= 4U 0900 — 40) уменьшался со средним значением - Р/Р « 1,5 · 10~^ год~^ (за
исключением возрастания периода в конце 1975 г.). Однако с 1979 года период стал
увеличиваться со средней скоростью Р/Р «« 3 · 10~^ год"' (см. рис. 13.4). Такие
флуктуации можно понять, если Паруса Х-1 — это рентгеновский пульсар,
аккрецирующий звездный ветер, а параметры ветра испытывают небольшие изменения. В
качестве альтернативы наблюдения можно объяснить флуктуациями темпа
аккреции, если Паруса Х-1 —- это «быстрый ротатор» с дисковой аккрецией и большим
значением ?. Будущие рентгеновские наблюдения, если они покажут корреляцию
между периодом и светимостью, помогут решить этот вопрос [221].
Аккреция на нейтронные звезды и белые карлики
487
^h
-А V-
А 0535-^2
г\~ М/М. -0,5 >#|gfc>^l,9 VeLo. Х-1
4U0115+63
Рис. 15 1 Теоретическое соотношение между скоростью увеличения частоты
вращения — ? и величиной PL^^^ в сравнении с результатами наблюдений (до 1976 г.) для
девяти импульсных рентгеновских источников. Единицы измерения -Д ? и
L — секунда в год, секунда и \&^ эрг/с соответственно. Показан эффект изменения
массы нейтронной звезды в предположении, что магнитный момент звезды равен
?^^ = 0,48 и что для всех звезд справедливо уравнение состояния с тензорным
взаимодействием. Затушеванная часть рисунка представляет область, перекрываемую
теоретическими кривыми для 0,5 ^ М/М^ ^ 1,9. Штриховая линия —
теоретическая кривая для отношения М/М^ = 1,3, обеспечивает наилучшее согласие с
данными наблюдений. Поскольку кривые, соответствующие разным звездным массам,
пересекаются, верхняя граница затушеванной области определяется огибающей кривых
[221].
Упражнение 15.4. а) Определите скорость возрастания частоты вращения при
аккреции звездного ветра по аналогии с уравнением A5.2.20), справедливым для дисковой
аккреции [221].
Ответ:
-Р« 3.8 X 10
hV
L
W СМ2/С
P^Un с/год.
488 Глава 15
Обратите внимание, что ? не зависит от ? (почему?).
б) Используйте результаты упражнения 14.22 для /^ — удельного момента
количества движения аккрецируемого газа, чтобы оценить —Р.
Явное согласие между теоретическими предсказаниями для дисковой
аккреции и результатами наблюдений восьми из девяти тщательно
исследованных источников подтверждает картину дисковой аккреции на
магнитную нейтронную звезду^^.
15.3. ИЗЛУЧЕНИЕ ОТ АККРЕЦИРУЮЩИХ НЕЙТРОННЫХ ЗВЕЗД
Если выполняется неравенство /? < Гд, подавляющая часть излучения
возникает достаточно глубоко под альвеновской поверхностью, вблизи
поверхности звезды. В это излучение вносят вклад ряд физических процессов
и радиационных механизмов. Ожидаемые спектр излучения и характер его
пространственного распределения сложным образом зависят от геометрии
течения и от характера замедления падающей плазмы вблизи поверхности
нейтронной звезды. Хотя этим вопросам было посвящено несколько
работ^\ уверенное предсказание спектра излучения пока еще не достигнуто.
Конечно, полная светимость четко определяется параметрами М, R и ? в
соотбетствии с формулой
GM
R
L=^-^M. A5.3.1)
Однако и в этом случае спектральный анализ усложняется присутствием
магнитных полей на поверхности. Они вынуждают плазму течь вдоль
силовых линий, вызывают очень быструю потерю энергии поперечного
движения электронов на циклотронное излучение и приводят к анизотропиям
тепловых скоростей, излучательных способностей, непрозрачностей и, в
конечном итоге, интенсивностей рентгеновского излучения. Однако не одни
только магнитные поля приносят осложнения. На самом деле диапазон
правдоподобных спектров излучения достаточно велик даже для
сферически симметричной аккреции на ненамагниченную нейтронную звезду в
зависимости от поведения плазмы вблизи поверхности.
Рассмотрим, например, случай, когда падающий пучок ионов
постепенно замедляется в сравнительно протяженном слое атмосферы нейтронной
звезды благодаря обычным кулоновским столкновениям с электронами.
Этот сценарий впервые был предложен Зельдовичем и Шакурой [638] (см.
также [10]). Если падающая плазма останавливается благодаря кулонов-
^^ См., однако, работу [24], где приведена альтернативная модель скачка частоты
для источников с малой светимостью; она основана на механизме сферически
симметричной аккреции звездного ветра и предполагает проникновение плазмы внутрь
магнитосферы вследствие неустойчивости Рэлея — Тейлора.
^^ Обзор проблемы и ссылки на литературу см. в [367].
Аккреция на нейтронные звезды и белые карлики 489
ским соударениям с веществом звезды, то большая часть энергии
выделяется под поверхностью на пути в несколько длин свободного пробега
фотонов. Излучение поэтому термализуется до выхода на поверхность. В
данном случае энергия фотонов сравнима с эффективной поверхностной
температурой черного тела, что дает для сферически симметричного течения
Процессы, приводящие к увеличению ? выше минимального значения
Tjjjj, включают в себя томсоновское рассеяние фотонов электронами в
низких слоях атмосферы или фотосфере [см. уравнение A4.5.54)], комптонов-
ское рассеяние горячих (^ 10^ К) электронов на тепловых фотонах в
верхних слоях атмосферы, канализирование вещества к полярным шапкам
«воронкой» магнитного поля — при этом излучающая поверхность имеет
площадь меньше 4?/?^ [см. уравнение A5.1.10)]. Тем не менее, когда
замедление вещества происходит вследствие одних лишь кулоновских
столкновений, возникающее излучение по своему характеру относится к мягкому
тепловому рентгену.
Рассмотрим, однако, альтернативную возможность, когда
коллективные плазменные эффекты, которые, кстати, наблюдались в солнечном
ветре, приводят к более резкому замедлению падающего потока плазмы,
нежели кулоновские столкновения. Примером подобного эффекта может
служить «двухпотоковая» неустойчивость, при которой сильные электрические
поля, возникающие в результате флуктуации плотности заряда, могут
замедлять один плазменный пучок, движущийся сквозь другой. В предельном
случае, когда бесстолкновительная неустойчивость особенно сильна и
эффективное замедление происходит чрезвычайно быстро, непосредственно
над поверхностью звезды может возникнуть стоячая ударная волна. Такую
возможную картину впервые исследовал^! Шапиро и Солпитер [531] (см.
также [315, 580]. В этом случае ударная волна способствует
преобразованию кинетической энергии падающего потока в тепловую энергию, так что
Г^Г„«1^, A5.3.3)
?
где y^f « {IGM/RY^ — скорость свободного падения вблизи поверхности.
Нетрудно показать, что кулоновские столкновения не способны
привести к такой «хаотизации» кинетической энергии вблизи нейтронной звезды.
Оценим сечение ион-ионЦого кулоновского рассеяния в потоке. С
точностью до логарифмического множителя это можно сделать, исходя из
формулы
?, « ^^e^ff» A5.3.4)
где r^ff — расстояние, на которое расходятся ионы, когда ион-ионная
потенциальная энергия становится сравнимой с кинетической энергией. Это
490 Глава 15
такое расхождение, при котором ионы отклоняются от своих
невозмущенных траекторий приблизительно на 90°. Таким образом.
^r-hm,v\ A5.3.5)
'eff
где принято ? - \ и где ? ^ ^ff — скорость падающего ионного пучка, а
также ионная тепловая скорость в области за ударной волной. Средняя
длина пробега на ион-ионное кулоновское столкновение с учетом A5.1.3) и
A5.1.5) составляет
?,« —-^, A5.3.6)
где и, — концентрация ионов, ар — массовая плотность, определяемая
выражением
р^—^ ^, A5.3.7)
Комбинация уравнений A5.3.4)—A5.3.7) приводит к следующему
результату:
Итак, соотношение A5.3.8) показывает, что расстояние ?^, необходимое
для термализации падающего потока, намного превосходит R.
Логарифмические поправки [297, 547], связанные с далекими соударениями, которые
приводят к накапливающимся рассеяниям на малые углы, уменьшают
отношение A5.3.8) всего лишь примерно в 10 раз. Следовательно, тонкий
фронт ударной волны над звездой оказывается возможным только в том
случае, если предположить действие других, бесстолкновительных
механизмов.
Если подобный бесстолкновительный механизм задан, соотношение
A5.3.3) предсказывает очень высокие температуры газа вблизи
поверхности:
Т<Т,,^{ или X—Лб'. A5.3.9)
I 100 МэВ ) ^о
Тогда ускоренные в ударной волне электроны должны излучать, помимо
мягкого рентгена, и гамма-лучи. Примерно половина всей кинетической
энергии падающей плазмы преобразуется в тепловую энергию
релятивистских электронов сразу за фронтом ударной волны (другая половина
переходит в тепловую энергию ионов). Эти релятивистские электроны испускают
поток гамма-излучения с энергией 10—100 МэВ, половина которого
направляется вниз к звезде и приобретает тепловой спектр, а оставшаяся часть
Аккреция на нейтронные звезды и белые карлики 491
испускается наружу, не испытывая возмущений. Итак, приблизительно 1/4
A/2 ¦ 1/2) всей светимости будет наблюдаться в виде обильного потока
гамма-излучения, а остальное — в виде мягкого рентгена.
Упражнение 15.5. Процесс, в результате которого ускоренные в ударной волне
электроны испускают фотоны, согласно рассмотренной выше картине, — это
релятивистский комптон-эффект. Покажите, что фотоны со средней энергией Е,,
рассеиваемые релятивистскими электронами с энергией Е^ > /w^c^, приобретают среднюю
энергию Ef - {4/3)iEg/mgC^)^Ei (в предположении, что распределения электронов и
фотонов изотропны). Пользуясь этим результатом, покажите, почему мягкие
рентгеновские лучи, испускаемые звездной поверхностью, могут покидать фронт
ударной волны с энергиями, лежащими в гамма-диапазоне.
Существуют ли достаточно сильные бесстолкновительные процессы,
приводящие к образованию тонкого фронта ударной волны, высокой
температуре газа и излучению жестких фотонов, в настоящее время
неизвестно. Наблюдения не дают убедительных оснований для предположения, что
нейтронные звезды со стационарной аккрецией излучают интенсивные
потоки гамма-лучей. Однако и в этом случае трудности обнаружения
фотонов в диапазоне 10—100 МэВ не позволяют прийти к определенному
15.4. АККРЕЦИЯ НА БЕЛЫЕ КАРЛИКИ
Недостаток места не позволяет нам обсудить теорию аккреции на белые
карлики сколько-нибудь подробно^\ Тем не менее этот процесс важен по
нескольким причинам.
1) Согласно общему мнению, мягкое и жесткое рентгеновское
излучение, которое наблюдается от известных двойных систем, включающих
белые карлики типа ДМ Her, DQ Her и SS Cyg, вызвано аккрецией на
магнитные белые карлики [322]. Рентгеновский источник ДМ Her и ему
подобные обладают сильной круговой поляризацией (^ 10%) в оптическом
диапазоне. Отсюда делается вывод, что на поверхности этих источников су-
^^ Сообщение о всплесках космического гамма-излучения в диапазоне энергий
0,2—1,5 МэВ появилось в 1973 г. [313], и с этого времени они подтверждались
многочисленными последующими наблюдениями (обзор работ и ссылки на литературу
даны в [314]). Короткие временные масштабы всплесков @,1 с ^ ?? ^ 100 с)
послужили основанием для применения к этим источникам моделей компактной звезды
(особенно нейтронной звезды). Обзоры этих и других моделей, объясняющих
наблюдаемые гамма-всплески, приведены в [326, 491].
2) Читателям, интересующимся этим вопросом, рекомендуем ознакомиться с
работами, упоминающимися в разд. 14.1 и 15.4, которые содержат более подробное
обсуждение и дополнительные ссылки на литературу.
492 Глава 15
шествуют сильные магнитные поля с напряженностью 5 < \0Р — 10^ Гс.
Источники типа DQ Her вспыхивают как новые звезды, и у них
проявляются когерентные пульсации малой амплитуды (с периодом 71 с для DQ
Her). Данные оптических наблюдений четко свидетельствуют о
существовании крупных аккреционных дисков вокруг таких белых карликов. Это
говорит о том, что магнитные поля в системах типа DQ Her слабее
предполагаемых у AM Her. (Сильное магнитное поле может разрушить диск и
привести к радиальному течению вешества на звезду.) Источники типа SS Cyg
(в том числе такие, как U Gem и АК Per) — это катаклизматические
переменные, для которых характерны частые вспышки, как и у объектов типа
AM Her, но в то же время оптические наблюдения доказывают
существование у них аккреционного диска.
2) Многие из отождествленных двойных рентгеновских систем с малой
массой, подобные Cyg Х-2 и Sco Х-1, а также некоторые источники
центральной галактической подсистемы (см. гл. 13) могут также оказаться
немагнитными белыми карликами с умеренной светимостью.
Аккреция на белые карлики в некоторых отношениях отличается от
аккреции на нейтронные звезды. Если падающий газ имеет типичный для
космических условий химический состав (например, 70% водорода по
массе, 25% гелия и несколько процентов более тяжелых элементов), то в
результате ядерных реакций под поверхностью звезды выделяется
приблизительно 8 МэВ ядерной энергии на нуклон. После усреднения во времени эта
избыточная энергия в случае аккреции белыми карликами будет превышать
гравитационную потенциальную энергию, выделяющуюся при падении
газа. Однако ядерная энергия может выделяться во взрывных вспышках, так
что большую часть времени преобладает квазистационарный
гравитационный механизм выделения энергии.
Далее отметим, что температура оптически толстой фотосферы белых
карликов, испускающей чернотельное излучение, не достаточно высока для
создания заметной светимости в рентгеновском даиапазоне. Согласно
соотношению A5.3.2), при /?g * 5(Ю имеем Т^^^ « 44 эВ, так что в излучении
фотосферы преобладает жесткий ультрафиолет.
Однако похоже, что аккреция на белый карлик приводит к образованию
стоячей волны над поверхностью звезды. В отличие от аккреции на
нейтронную звезду в данном случае одни лишь кулоновские столкновения
способны приводить к образованию тонкого фронта ударной волны над
поверхностью [?//? < 1, согласно уравнению A5.3.8)]. Как следует из
A5.3.9), электронная температура за фронтом ударной волны может
достигать значений Т^^ ^ 1(Ю кэВ. Таким образом, область, расположенная
за ударной волной над фотосферой, может испускать рентгеновские лучи,
образованные в результате тормозного излучения из оптически тонкого
слоя [6, 190, 279, 307]. Кроме того, если присутствует магнитное поле, в
этой области появится также циклотронное излучение.
В соответствии с детальными расчетами Лэмба и Мастерса [328]
приблизительно половина потока тормозного излучения испускается от
поверхности наружу в жестком рентгеновском диапазоне A0—100 кэВ). Прибли-
Аккреция на нейтронные звезды и белые карлики 493
зительно половина потока высоких гармоник циклотронного излучения
также испускается наружу, на этот раз в ультрафиолетовом диапазоне.
Остальное тормозное и циклотронное излучение испускается внутрь и либо
отражается от поверхности, либо поглощается ею. Результирующий поток
термализованного чернотельного излучения с поверхности испускается в
ультрафиолетовой или ближней рентгеновской области, причем L^^ «
* L^y^ + L^^^^, где L^b» ^сус ^ ^brem — чернотельная, циклотронная и
тормозная светимости соответственно. Лэмб и Мастере предсказывает, что
магнитные белые карлики могут оказаться очень мощными
ультрафиолетовыми (:S 10 эВ) источниками и что ультрафиолетовый поток может
сильно превосходить рентгеновский поток.
Спектры излучения, возникающего при аккреции на немагнитные или
слабо намагниченные вырожденные белые карлики, отличаются от
спектров карликов с сильными магнитными полями отсутствием
ультрафиолетового циклотронного излучения (т.е. L^^^ < ^Ьгет ^^^ ^ "^ ^^^ ^^ [321]).
Если полная светимость превосходит максимальное значение L^^ =
= 10^^ эрг/с (< L^^^), холодное падающее вещество над ударной волной
оказывается достаточно непрозрачным, чтобы рассеивать большую часть
рентгеновского излучения и понижать энергию фотонов (посредством ком-
птон-эффекта). В результате для немагнитных карликов должна
существовать заметная корреляция между рентгеновской спектральной
температурой и светимостью.
Интересно, что наблюдения источника Cyg Х-2 с рентгеновского
спутника «Коперник» показывают подобную зависимость светимости от
спектра. Если теория верна, наблюдения [85] свидетельствуют, что
Cyg Х-2 — это аккрецирующий вырожденный карлик с массой - 0,4 Mq ,
расположенный от Солнца на расстоянии 250 ± 50 пс. В работе [325]
выдвинуто также предположение, что многие до сих пор не отождествленные
источники центральной галактической подсистемы (см. гл. 13) с малой
светимостью — это вероятные кандидаты на отождествление с
аккрецирующими немагнитными белыми карликами, поскольку у них также
проявляется ожидаемая корреляция между рентгеновской спектральной
температурой и светимостью. Действительно, подсчитано, что полное число таких
объектов в Галактике может быть порядка 10^. Интересно сравнить это
число с ожидаемым количеством аккрецирующих магнитных карликов
(- 10^), а также сильных (L ^ 10^^ эрг/с) рентгеновских источников —
аккрецирующих нейтронных звезд (около 100).
Глава 16
Гравитационное излучение
16.1. что ТАКОЕ ГРАВИТАЦИОННАЯ ВОЛНА?
В общей теории относительности гравитационные волны описываются в
виде «ряби» на кривизне пространства-времени, распространяющейся со
скоростью света. Представление о гравитационных волнах, как и о волнах
на поверхности океана, связано с введением идеализированного понятия
однородного невозмущенного «фона», в котором распространяются волны.
Однако в отличие от океанских волн гравитационные волны не
сопровождаются движением материальной среды — они представляют собой
«рябь» на фоне геометрии пространства-времени.
Покинув источник («ближнюю зону»), волны обычно попадают в
область, где их длина ? оказывается малой по сравнению с радиусом
кривизны R окружающего пространства-времени, через которое они
распространяются.
Упражнение 16.1. а) Покажите, что для самогравитирующих источников,
характерное время колебаний которых определяется динамическими процессами, длина
волны ? меняется от нескольких километров до нескольких астрономических единиц
по мере того, как плотность меняется от значений, свойственных черным дырам, до
значений, характерных для звезд.
Указание: вспомните уравнение A0.2.2).
б) Напряженность фонового гравитационного поля измеряется приливным
гравитационным полем [см. уравнение E.1.21)]
ilid-^. (c=G=l). A6.1.1)
Здесь ? — масса источника гравитации, а L — характерный размер. Выражая эту
мысль иначе, можно сказать, что радиус кривизны фонового поля равен
«-(ilid)"'^'- A6.1.2)
Покажите, что радиус кривизны в межгалактическом пространстве, в галактиках и
Солнечной системе по порядку величины равен соответственно 10^^ 10^ и 0,1
световых лет.
Большое значение R, полученное для Солнечной системы, — это просто
иная формулировка утверждения, что гравитация в ней слабая. В
Солнечной системе можно ввести координаты, почти совпадающие с
координатами Минковского, так что
gM. = v + ^.' 1^.1« ?· A6-1-3)
Гравитационное излучение 495
Члены h содержат квазистатические вклады от Солнца, планет и т.п.
(см. гл. 5), а также любые возможные гравитационные волны от
астрономических источников. В нашем обсуждении мы не станем касаться
квазистатических вкладов, а сосредоточим внимание на волновых составляющих
h . Как правило, мы будем прийодить лишь конечные результаты, уделяя
?|??0 места их выводам ^\
Гравитационные волны полностью описываются двумя безразмерными
амплитудами, скажем, Л^ и Л^. Выберем направление распространения
вдоль оси ?. Тогда h^ и Л^ будут зависеть только от величины (t -
— ?/с). Если ввести тензоры поляризации е"^ и е^ , обладающие
свойствами
е^ = -е^у = 1, е^ = е^ = 1, остальные компоненты
равны нулю, A6.1.4)
то можно записать выражение для гравитационной волны в виде
Это симметричный пространственный тензор со следом, равным нулю,
поперечный к направлению распространения (z-компонент отсутствует).
Тензор Лд^ оказывается аналогом векторного потенциала в
электродинамике с лоренцевской калибровкой. В электродинамике для вакуума
справедливы соотношения
^0 = 0, ^,,, = 0, D^, = 0, A6.1.6)
последнее уравнение вытекает из максвелловских уравнений поля в данной
калибровке. Здесь же получается
hll = ^, hJlu-O, D/iJ,^ = 0, A6.1.7)
В сочетании с условием, что след тензора равен нулю. Последнее
уравнение — это уравнение поля Эйнштейна в данной калибровке. Система
координат, в которой справедливы уравнения A6.1.7), называется в общей
теории относительности ТТ-калибровкой (ТТ от transverse-traceless —
поперечная, со следом, равным нулю. — Перев.).
Когда электромагнитная волна взаимодействует с заряженной частицей,
она вызывает ее ускорение, перпендикулярное к направлению
распространения волны (поперечное ускорение) и пропорциональное е/т —
отношению заряда частицы к ее массе. Аналогично, когда гравитационная волна
попадает на свободную частицу, она сообщает ей поперечное ускорение.
Однако «гравитационный заряд» частицы (ее реакция на гравитационную
силу) равен ее инертной массе (принцип эквивалентности). Таким образом.
^^ Детальное рассмотрение теории гравитационных волн приведено, например, в
[411].
4% Глава 16
в общей теории относительности у всех частиц оказывается одно и то же
гравитационное «е/т». Поэтому все свободные частицы, расположенные в
одном и том же месте, испытывают одинаковое поперечное ускорение.
Поскольку локальные инерциальные системы координат определяются
свободно движущимися частицами, то и сами локальные инерциальные
системы координат испытывают такое же ускорение. Поэтому в данном случае
ускорение нельзя обнаружить локально. С другой стороны, ускорение
различно в разных точках пространства-времени и это дает возможность
регистрировать гравитационные волны. (Здесь мы просто высказали в иной
форме утверждение, что «истинное» гравитационное поле — это поле
приливных сил, которое может быть измерено только при нелокальном
сравнении.)
Рассмотрим локальную инерциальную систему координат, связанную с
пробной свободной частицей. Пусть в этой системе координат ?. — вектор,
которым измеряется отклонение второй пробной частицы от опорной.
Тогда проходящая гравитационная волна будет вызывать малое
относительное ускорение частиц
ij-WjIik^ A6.1.8)
которое в свою очередь вызовет небольшое изменение расстояния между
ними, равное
«^ = ^Л;Д, A6.1.9)
По порядку величины относительная деформация, вызванная
гравитационной волной, равна
у-Л, A6.1.10)
Этот результат очень полезен для грубых оценок.
Отметим, что относительное ускорение A6.1.8) поперечно как в том
смысле, что оно ортогонально к направлению распространения волны, так
и потому, что оно равно нулю, если вектор {у параллелен направлению
распространения.
Упражнение 16.2. а) Рассмотрите плоскую волну, распространяющуюся в
направлении оси zc/i+ #0, ?? =0. Покажите, что поле относительных ускорений
имеет дивергенцию, равную нулю, и поэтому может быть представлено «силовыми
линиями» подобно электрическому полю в вакууме.
б) Нарисуйте картину силовых линий и покажите, что она имеет квадрупольный
характер, а расстояние между линиями уменьшается при удалении от начала
координат.
Когда гравитационная волна попадает на объект, внутри которого
действуют силы, разные части объекта не могут двигаться как свободные
частицы. Вместо этого объект начинает колебаться в соответствии е обыч-
Гравитационное излучение 497
ными законами движения, причем колебания возбуждаются движущей
силой гравиташюнной волны
Fj = {m^, A6.1.11)
действующей на каждый элемент с массой т. Здесь ?^ — смещение
элемента массы относительно центра масс.
Фактически выражения A6.1.8)-A6.1.11) справедливы только в том
случае, когда величина смещения частиц ??? мала по сравнению с длиной
волны ?. Если это не так, эффекты запаздывания изменяют линейную
зависимость от ij на синусоидальную (см. [411], упражнение 37.6),
приблизительно имеющую вид sin B????/?).
Поскольку гравитационные волны могут возбуждать силы и
производить работу, они должны нести энергию и импульс. Плотности энергии и
импульсов не могут быть локализованы в точке (в точке нет
гравитационных сил!), но могут быть локализованы в области размером порядка
нескольких длин волн. Тензор энергии-импульса гравитационной волны,
распространяющейся в направлении оси ?, имеет отличные от нуля
компоненты
где угловые скобки означают усреднение по нескольким длинам волн. Здесь
7^ — плотность энергии, Т^ — поток энергии (равный плотности
импульса, умноженной на с^), а 7^^ — поток импульса.
16.2. ОБРАЗОВАНИЕ ГРАВИТАЦИОННЫХ ВОЛН
В случае электромагнетизма основная мода мультипольного излучения от
нерелятивистской системы зарядов — дипольное излучение. Векторный
потенциал в волновой зоне при лоренцевской калибровке имеет вид
^.(^.^^) = i:4('-7)' A^-2-0
где г ? 1x1, а d — электрический дипольный момент. Электрические и
магнитные поля (с пространственной зависимостью типа 1/г),
вычисленные на основе уравнения A6.2.1), зависят только от компонентов d,
поперечных направлению распространения ? ? ?/r, так что член dj в уравнении
A6.2.1) можно заменить его поперечной составляющей
dJ^Pj.d,, A6.2.2)
где Рд — проекционный оператор
Pjk^^k-'ijnk- A6.2.3)
16-513
498 Глава 16
Подставляя в вектор Пойнтинга выражения для полей ? и В, полученные
из A6.2.1), получаем угловое распределение потока
d^E 1 ..^^т^
'dUU^'^^dj ^^ A6.2.4а)
1
Ачтс
[djdj- [пАУ]. A6.2.4Ь)
Величину dj следует вычислять с учетом времени запаздывания / - г/с.
Выбирая направление оси ? вдоль п, можно легко проинтегрировать
уравнение A6.2.46) по телесному углу, что дает
Z^e^-f—44- A6.2.5)
Записав dj = exj для точечного заряда, видим, что полученное
выражение — это просто формула Лармора.
Теперь на основе соображений размерности можно было бы ожидать,
что основной модой гравитационного излучения от источника с малыми
внутренними скоростями также будет дипольное излучение
с^
где гравитационный дипольный момент равен
dj^Lf^A^f A6.2.7)
А
И В уравнении A6.2.5) член е^ заменен на Gm^. Однако уравнение A6.2.7)
дает
dj = Lm^Xj'* = ?/^, A6.2.8)
А А
где р^ — импульс А-й частицы. Поскольку полный импульс системы
сохраняется, dj = 0. В общей теории относительности дипольное излучение
отсутствует.
Следующие моды мультипольного излу1ения — это магнитное
дипольное и электрическое квадрупольное. Магнитный дипольный момент масс
равен
?^]:?^'?{???')-^?}\ A6.2.9)
^ А ^ А
где j^ — момент количества движения А-й частицы. Ввиду сохранения
момента количества движения Д = 0. Таким образом, в общей теории
относительности нет магнитно-дипольного излучения. Низшая мода
излучения — электрическое квадрупольное.
Гравитационное излучение 499
Аналогом уравнения A6.2.1) служит
2 G
с
где -f — квадрупольный момент масс
S момент масс
^j.^Zm^fxt-U^^^^f]. A6.2.11)
Как и в монографии Мизнера, Торна и Уилера [411], здесь используется
перечеркивание символов, чтобы отличить принятое нами определение ква-
друпольного момента от других, имеющихся в литературе. Верхний индекс
«7T>J означает поперечную часть со следом, равным нулю:
?7 = Pj,Pkn,f,m - kPjkiP.JiJ- A6.2.12)
Отметим, что по порядку величины
Л-^4^ A6.2.13)
г
с
где г^^^ — это «радиус Шварцшильда» для массы, участвующей в квадру-
польном движении, а ?; — характерная скорость.
Поток энергии дается тензором энергии-импульса
'Por = ^'-^{h]loh]L) A6.2.14)
[сравните с уравнением A6.1.12)]. Подстановкой выражения A6.2.10)
получим
d^E \ G "Vx-Vx
^'8^'^yj'^J'' ~ 2"'^'^"* "·" 2\"j">^J4 )' A6-2.15b)
[сравните с уравнениями A6.2.4а,бI. Интегрируя по п, получаем
^0^^^--^^(^^^- A6.2.16)
Аналогичная электромагнитная формула имеет множитель 1/30 вместо
1/5, потому что там волны описываются векторными, а не тензорными
полями.
Квадрупольная формула A6.2.16) с определением A6.2.11) справедлива
для медленно движущихся источников (? < с) со слабым внутренним
гравитационным полем (ньютоновский потенциал ? < с^). Другие случаи.
500 Глава 16
для которых можно рассчитать гравитационное излучение, обсуждаются в
[568].
Отметим, что отсутствие гравитационной «светимости» L^y^y
сферически симметричных источников — это общий результат, следующий из
теоремы Биркгофа (гл. 5).
Сила реакции излучения, соответствующая потерям энергии A6.2.16),
может быть выражена в виде градиента потенциала ньютоновского типа
F<^<^^^t) = ^mV^^''^^'\ Ф<^^^^'> = \ —ffx X,. A6.2.17)
Здесь заключенный в скобки индекс «5» означает пятую производную по
времени. Это выражение легко поддается проверке:
dt
= ??,·?<-'"
л
А ^
= -|5^/», A6.2.18)
где в последней строке использовано соотношение ^^6д = 0. Усреднение
по нескольким циклам (для периодического источника) или на интервале
времени, достаточно большом по сравнению с характерным динамическим
временем (для источника с ограниченным движением), позволяет дважды
выполнить интегрирование по частям и превратить -^^)^^) в ?^^?^^
возвратившись таким образом к уравнению A6.2.16).
Упражнение 16.3. Момент количества движения, уносимый гравитационными
волнами, дается выражением
^^Z^.jkxfFi;^"-'"'- A6.2.19)
"' А
Покажите, что отсюда следует
dJ, 1 G
с
^=-5-^.>*<?*'">· A6.2.20)
Обратите внимание, что момент количества движения не уносится, если источник
осесимметричный; это результат, имеющий общий характер.
Гравитационное излучение 501
16.3. ОЦЕНКИ ПО ПОРЯДКУ ВЕЛИЧИНЫ
Оценка амплитуды h гравитационной волны приведена выше [см.
соотношение A6.2.13)]. Вычисляя dE/dty заметим, что
где Л/, /?, Г и ?; — соответственно характерные значения массы, размера,
масштаба времени и скорости источника. Таким образом, из уравнения
A6.2.16) следует
dE GIM^^
dt с
где
с'
-ШЬ'-^^Ш- (-3.2)
Lo = 7^ = 3.6 X 1059 эрг/с. A6.3.3)
Упражнение 16.4. Стальной стержень массой 10^ кг и длиной 20 м вращается со
скоростью, соответствующей пределу механической прочности C0 рад/с). Оцените
Ответ: - 10~23 эрг/с.
Упражнение 16.5. Покажите, что
? ? ^int
^Gw ^ ^????-? A6.3.4)
где Lint ^ ??^/? — внутренняя мощность, связанная с квадрупольным движением.
Из уравнения A6.3.2) следует, что максимальная мощность
гравитационного излучения достигается, когда г^^^ - R и ? - с. Поэтому
компактные объекты — это важные потенциальные источники гравитационных
волн.
Астрофизические системы обычно гравитационно связаны, поэтому,
согласно теореме вириала.
MR^ I потенциальная
Кинетическая энергия ^ | энергия
или
?3 \1/2
-?—1
\gm]
^ A6.3.5)
A6.3.6)
502 Глава 16
Уравнение A6.3.6)—это соотношение между характерным временем и
средней плотностью, с которыми нам неоднократно приходилось сталкиваться
раньше. Исключая из уравнения A6.3.2) ?/с, получаем
^GW
- Ь,[Щ\ A6.3.7)
Упражнение 16.6. Покажите, что энергия гравитационных волн, излучаемых
несферической самогравитирующей системой, равна
Ь.Е - L^^T - МсЧ'-?] . A6.3.8)
-GW^ -- ^ j^ I
Уравнения A6.3.7) и A6.3.8) еще раз подчеркивают важность
компактных объектов как потенциальных источников гравитационных волн.
Эффективность излучения гравитационных волн можно
параметризовать
Тогда соотношения A6.2.13), A6.3.5) и A6.3.8) дают
? ^ е^^^ ^ 3 X 10-Ч-^Г/^{^<^\. A6.3.10)
г 10,1/ (г/Юкпс) ^ '
В соотношении A6.3.10) в качестве единицы измерения г взято расстояние
до центра Галактики, и для нормировки ? выбрано оптимистическое
значение 10^0. Если при оценках используется полная масса системы, то в ?
входят как степень несферичности, так и степень компактности.
Приведенные выше оценки относятся к энергии, излученной за
характерное динамическое время Т. Если система эволюционирует дальше, ? и
?? будут соответственно большими, но h останется без изменения.
Упражнение 16.7. Покажите, что время затухания гравитационного излучения
? - E/{dE/dt) приблизительно равно
^ \ '•Sch /
A6.3.11)
Оцените ? для несферических белых карликов и нейтронных звезд. (Аналогичные
соображения использовались в разд. 7.4 и 9.6, где доказывалось, что белым карликам
и нейтронным звездам qT/\W\ ^ 0,14 должна быть свойственна вековая
неустойчивость, вызванная гравитационным излучением.)
Ответ: Для белых карликов ? < \Ф лет; для нейтронных звезд ? ^ 300 с.
Каковы шансы обнаружить гравитационные волны от
астрофизического источника? Рассмотрим сильно асимметричный взрыв сверхновой в
Гравитационное излучение 503
центре нашей Галактики, приводящий к образованию нейтронной звезды
или черной дыры. Принимая ? - \0Щ и Л/ - ^0» из соотношений
A6.1.10) и A6.3.10) находим, что смещение конца полутораметрового
стержня на Земле составит всего лишь
??-5 X 10"'"^ см,. A6.3.12)
или 1/200 ферми! Хотя и эта оценка не вселяет большого оптимизма, надо
еще вспомнить [см. уравнение A.3.27)], что события такого рода случаются
примерно раз в 30 лет! Чтобы достичь более «сносной» скорости счета,
скажем одного события в месяц, надо рассматривать все более удаленные
галактики вплоть до скопления галактик в Деве (--20 Мпс), пока скорость
вспышек сверхновых не станет достаточно высокой. Как следует из
A6.3.10), это означает, что h ^ 10~^Ч
Начало гравитационной астрономии положено работами Вебера [602].
Детектор Вебера в виде цилиндра изготовлен из материалов с высоким
значением добротности Q, таких, как алюминий, сапфир, ниобий, и
изолирован от всех возможных возмущений земного происхождения. Падающая
гравитационная волна приводит к возбуждению в цилиндре основной
моды колебаний, соответствующих резонансной частоте, и смещение цилиндра
регистрируется соответствующим датчиком. (Вебер сначала использовал
пьезоэлектрические кристаллы, размещенные на поверхности цилиндра.)
Сигнал усиливается электронной схемой и анализируется в поисках
свидетельства всплеска гравитационного излучения. Сравнивая сигналы от двух
цилиндров, разнесенных на большие расстояния, можно более достоверно
отождествить события внеземного происхождения.
Первые детекторы Вебера имели резонансную частоту в диапазоне
нескольких килогерц, что соответствовало излучению от компактных
объектов с массой порядка солнечной [см. уравнение A6.3.6)]. Чувствительность
детекторов «первого поколения», изготовленных Вебером и другими
исследователями, достигала h -- 10~^^. Хотя Вебер и сообщал о регистрации
заметного числа событий при такой чувствительности, ни одна из других
групп не смогла подтвердить его данные, и сейчас общепринято считать,
что эти события не были вызваны гравитационными волнами.
В настоящее время входят в строй детекторы «второго поколения»,
охлаждаемые до температур жидкого гелия и рассчитанные на
чувствительность порядка h - 10"^^. Чтобы достичь чувствительности
h - 10" ^\ потребуется создать «третье поколение» детекторов,
возможно, с охлаждением до температур порядка 0,001 К.
Другой перспективный путь разработки детекторов связан с
использованием лазерных интерферометров. Проходящая гравитационная волна
изменяет относительную длину оптических путей в плечах интерферометра,
что возможно зафиксировать по возникающему сдвигу интерференционных
полос. Форвард [201] создал прототип подобного прибора, имеющий
чувствительность h - 10~^^. В настоящее время в ряде мест сооружаются
более чувствительные детекторы и не исключено, что можно будет
достичь чувствительности h - 10~^^. Интерферометры обладают определен-
504 Глава 16
ным преимуществом перед резонансными системами, поскольку они
регистрируют полный сигнал Л (О, а резонансная система фактически
измеряет только фурье-компонент сигнала, соответствующий резонансной
частоте.
Третий метод обнаружения гравитащ!Онных волн связан с очень
точным доплеровским слежением с Земли за космическими аппаратами. Для
этого случая интересны низкочастотные гравитащюнные волны в
диапазоне 10~^ — 10~^ Гц. (Эти пределы определяются тем, что, с одной
стороны, требуется около 100 с для точного считывания показаний атомных
часов, а с другой стороны, вращение Земли не дает возможности проводить
непрерывное слежение за аппаратом из одной точки.) Такие
низкочастотные волны могли бы возникать при катастрофических событиях,
например, излучаться сверхмассивными компактными объектами ^\
16.4. ГРАВИТАЦИОННОЕ ИЗЛУЧЕНИЕ ОТ ДВОЙНЫХ СИСТЕМ
Рассмотрим прежде всего случай, когда две точечные массы Mj и Mj
находятся на круговой орбите радиусом а относительно друг друга. Если а^ и
^2 — соответствующие расстояния до центра масс, то
М^а^ = Mjflj = М^» A6.4.1)
где
— приведенная масса.
Если ось ? совпадает с осью вращения, аф — азимутальный угол между
осью X и прямой, соединяющей массы, то
f,^ = (M,af + M2al)cos^it> + const. A6.4.3)
Здесь использовано то обстоятельство, что величины M^af/3 (/ = 1, 2)
для каждой частицы постоянны. Уравнение A6.4.3) может быть
переписано в виде
Аналогично
^хх = 2Ма^со8 2ф -I- const. A6.4.4)
fyy = -???^08 2? -I- const,
^xy = fyx = ???^8??2?. A6.4.5)
^^ Дальнейшие подробности, касающиеся детектирования гравитационных волн,
изложены в работе [568], где содержатся ссылки на дополнительную литературу.
Гравитационное излучение 505
Поскольку ? = Шу где ? — орбитальная угловая скорость, находим
= ?? ——7^. A6.4.6
Здесь учитывался третий закон Кеплера
GM
а
Потеря энергии приводит к сокращению расстояния а между массами и,
следовательно, к уменьшению орбитального периода ? s 2?/?. Поскольку
энергия равна
2 а '
имеем
1^ = 11^ = -11^ 96 G^ му
? ? 2 ? ? 2 ? ? ^ с^ ?^ '
Q2^^ ?^?, + ?^. A6.4.7)
A6.4.8)
A6.4.9)
Упражнение 16.8. Предположив, что приведенные выше выражения остаются
справедливыми при ?7 — О, покажите, что время /q» необходимое для уменьшения а от
начального значения а^^^ до нуля, равно
Упражнение 16.9. Покажите, что по порядку величины /q [или P/{dP/dt)]
определяется соотношением
^-Ю'(^)''' A6.4.11)
ДЛЯ Ml - М2 - л/0. [Этот результат был использован в уравнении A0.2.5), чтобы
исключить интерпретацию пульсаров как двойных систем, состоящих из нейтронных
звезд.]
Упражнение 16.10. Используя уравнение A6.2.20), покажите, что для круговых
орбит
df _ 32 GV^ ?^?/?^ A6.4.12)
dt 5 с' ?'/^ '
506 Глава 16
Покажите, что
dE ^<и , ,
^ = ?^^ A6.4.13)
и, следовательно, круговая орбита остается круговой.
Если две массы находятся на эллиптической орбите с эксцентриситетом
е, то [366, 455]
dE dE
dt dt
dJ dJ\
dt dt\
0-A +
f{e).
g{e),
e-0
f.e' + ^e*)
A-e^)-
-7/2
>
A6.4.14)
A6.4.15)
A6.4.16)
'^:^iJl7i' ('^-^i^)
g{e) ^ {\ + ie'){\ - e')-\ A6.4 17)
Здесь dE/dt и dJ/dt усреднены no орбите. Поскольку выражения A6.4.7) и
A6.4.8) справедливы и для эллиптических орбит, уравнение A6.4.9) примет
вид
1 dP 96 G^ ?V ., ^^
Упражнение 16.11, Используя соотношение для эллиптической орбиты
2EJ^
gYm
получите оценку изменения эксцентриситета de/dty связанного с гравитационным
излучением, и покажите, что de/dt < 0: реакция гравитационного излучения стремится
округлить эллиптическую орбиту.
16.5. ПУЛЬСАР PSR 1913 + 16, ВХОДЯЩИЙ
В ДВОЙНУЮ СИСТЕМУ
В настоящее время наиболее убедительное свидетельство существования
гравитационных волн следует из изучения орбиты первого пульсара,
открытого в составе двойной системы. Учитывая важность этого объекта,
опишем его свойства подробнее.
Пульсар PSR 1913 + 16, входящий в двойную систему, был открыт
Халсом и Тейлором в 1974 г. [287]. Авторы быстро поняли, что
наблюдаемые изменения частоты пульсара можно объяснить эффектом Доплера,
Гравитационное излучение 507
вызванным орбитальным движением нейтронной звезды вокруг
невидимого компонента двойной системы с периодом около 8 ч. Сообщение об
открытии высокоточных часов — пульсара, движущегося со скоростью
- 300 км/с в гравитационном поле другого компонента, вызвало бурю
активности среди специалистов, занимающихся теорией относительности.
Природа предоставила нам полигон для проверки различных
релятивистских эффектов. На практике эти эффекты обнаруживаются на основе
изучения моментов прихода импульсов от пульсара [72, 184]. Ниже будет дано
упрощенное описание, основанное на периоде повторения импульсов.
Пусть масса пульсара равна Mj, а масса другого компонента
системы — Mj. Если предположить, что объекты сферически
симметричны, то в первом приближении (ньютоновский закон тяготения) они
движутся по эллиптическим орбитам вокруг общего центра масс. Пусть
/ — наклонение орбитальной плоскости к лучу зрения (рис. 16.1). Выберем
направление оси ? вдоль «линии узлов», т.е. вдоль проходящей через
начало координат прямой, по которой орбитальная плоскость пересекается с
плоскостью, перпендикулярной лучу зрения. Пусть ? — угловое расстояние
перйастра от узла, измеренное в плоскости орбиты. Тогда положение
пульсара в любой момент времени задается соотношениями
? = ?·,008?, >^ = ?·,8???, A6.5.1)
где
¦ = "**· "-TTTJ^· <'"¦«
Угол ? (измеряемый от перйастра) в небесной механике называется
истинной аномалией.
Отношение периодов следования импульсов, принимаемых на Земле
F/)j.g^ и испускаемых пульсаром (^Оет» может быть записано в виде
(gprec ._ (gprec (^Ostat ,,^,,,
где индекс «stat» означает наблюдателя, неподвижного относительно
центра масс и находящегося вблизи пульсара. Предположим на мгновение, что
приемник (на Земле) тоже неподвижен относительно центра масс. Тогда,
если г — расстояние между Mj и Mj, то
согласно формуле гравитационного красного смещения E.4.2). Формула
Доплера дает
(«Os.a, ^ [j f
(.-^)- A.^), „«.3,
(«Ое
где ? — единичный вектор, направленный с Земли на излучающий пульсар.
508
Глава 16
Пульсар
К Земле
Рис. 16.1. Орбита пульсара в двойной системе. Точка О лежит в центре масс
двойной системы, а точка ? — в периастре пульсара. «Линия узлов» Ох проходит через
точку О вдоль пересечения орбитальной плоскости с плоскостью, перпендикулярной
лучу зрения (см. текст).
Итак, уравнение A6.5.3) с точностью до членов порядка ?'^ и М/г
принимает вид
(gprec^ ^ I Vl-n , 1 t)^ GM^
Теперь запишем
(SOem ^- 2 ,2
? = е,' = cos /е, -I- sin /e,
re
(cm. рис. 16.1). Таким образом, выражения A6.5.1) дают
V| · ? = (r|Sin ? -l· r|i//cos i//)sin /.
A6.5.6)
A6.5.7)
A6.5.8)
Гравитационное излучение 509
Используя выражения A6.5.2) и второй закон Кеплера, записанный в виде
РA - ?2K/2
после простых алгебраических преобразований найдем, что
V| ·? = ?[??^{? + ?) + ???8?], A6.5.10)
27ra,sin/
^--^ . 1/0' A6.5.11)
До сих пор наш анализ был аналогичным рассмотрению спектрально-
двойных звезд с неразделяющимися спектральными линиями. Важное
отличие состоит здесь в том, что величина {bt)^^, которую нельзя получить
из наблюдений спектральных линий, остается неизвестной. Поэтому любой
постоянный член в правой части уравнения A6.5.6) не может быть
измерен: он просто «поглощается» членом E/)g^. В частности, невозможно
определить постоянную скорость центра масс Солнечной системы
относительно центра масс системы пульсара. (Движение Земли по
околосолнечной орбите приводит к эффекту Доплера, который исключается учетом
известной скорости этого движения.)
Из доплеровского члена первого порядка можно найти параметры е и ?
посредством уравнения A6.5.9), которое после интегрирования дает ф@.
Кроме того, используя независимые, переменные во времени члены
уравнения A6.5.10), пропорциональные cos ? и sin ?, можно определить К и ?.
Зная К, получаем а^ sin/, а из Я и aj sin/ обычным путем выводится
функция масс
.\3
(МЛ. ?.? G \ ? I ^
Высокая точность измерения моментов прихода импульсов от пульсара
позволяет оценить также члены уравнения A6.5.6), представляюпще
поперечный доплеровский сдвиг и гравитационное красное смещение. Найдем
?? = г2 ^ г,У
= (^)'?^(? + 2есо8ф + .2), A6.5.13)
GM. GM^
2
(М, + М,)г,
A6.5.14)
510 Глава 16
Таким образом, с учетом третьего закона Кеплера
у2 ПАА'^
получим
где
-Б- = ^-Г-. A6.5.15)
1 ?~*\?
-??\ + ^ = )8со8ф + const, A6.5.16)
GMHM. + 2МЛе
? ^- ' 2 . ..· A6.5.17)
(?,+ М2) ?,(? -е^)
Как можно было предвидеть исходя из теоремы вириала, доплеровский
сдвиг второго порядка и гравитационное красное смещение дают величину,
доступную измерению. Отметим, однако, что зависимость от времени в
уравнении A6.5.16) имеет тот же самый вид, что для члена первого
порядка ??cos? cos0 в уравнении A6.5.10). Для чисто эллиптического движения
величину ? измерить нельзя [71, 90].
К счастью, нас спасает общая теория относительности. Орбита
пульсара несколько отличается ot точного эллипса. Существует смещение пери-
астра, даваемое выражением ^^
?= /"^^^ ,. A6.5.18)
Измеренное значение ? для пульсара в двойной системе составляет около
4,2° в год (сравните со смещением 43" в столетие для Меркурия!). Таким
образом, если положить ? = wq -\- ?? в уравнении A6.5.10), то теперь
появятся четыре независимые, изменяющиеся со временем
тригонометрические комбинации фи ??. Следовательно, на интервалах времени порядка
нескольких лет можно разделить К, ?Q, ? и ?. В частности, в ? и jS входят
иве разные комбинации четырех параметров Л/р Mj, а^ и sin/ из функции
масс, а также а^ sin/. Итак, измерения ? и ? позволяют получить полное
решение для параметров двойной системы.
Вспомним теперь уравнение A6.4.18) для скорости изменения периода ?
двойной системы. Зная все параметры системы, можно предсказать
величину Р. Если это предсказание согласуется с измерениями, то
существование гравитационных волн подтверждается!
Тут у читателя могут возникнуть сомнения. В конце концов можно
предсказать и другие эффекты типа потери массы системой или, наоборот.
^^ Это выражение, выведенное впервые Робертсоном [484], справедливо
независимо от того, сравнима пробная масса Mj с массой Л/2, как в случае Меркурия и
Солнца, или нет.
Гравитационное излучение 511
аккреции вещества, которые будут приводить к увеличению или
уменьшению орбитального периода. Аналогично и смещение периастра не
обязательно следует полностью приписывать эффектам общей теории
относительности. Если звезда — компаньон пульсара окажется несферической
вследствие вращения или же приливного воздействия пульсара, то квадру-
польное гравитационное поле этого компонента двойной системы также
может вызывать смещение периастра.
Предположим, однако, что величина ? измерена и что она согласуется с
предсказанным значением, полученным при учете одних лишь эффектов
общей теории относительности. Было бы чудом, если бы общая теория
относительности давала неверное предсказание Р, но существовал другой
источник ? и/или А влияние которого компенсировало бы ошибку таким
образом, чтобы дать точно измеренную величину. Поскольку физики не
верят в чудеса, мы приходим к заключению, что предсказания общей теории
относительности подтверждаются и что мы наблюдаем реальный эффект
гравитационного излучения.
По мере повышения точности при наблюдении моментов прихода
импульсов появится возможность измерять другие релятивистские эффекты.
Один из них состоит в изменении временной задержки сигналов, которые
на своем пути к Земле пересекают орбиту в различных точках; такой
эффект уже измерялся [524] для космических аппаратов в Солнечной системе.
Кроме того, существует ряд различных постньютоновских периодических
отклонений от эллиптического движения, еще не проверенных в Солнечной
системе. В общей теории относительности каждый из этих членов
содержит определенную известную комбинацию параметров Mj, Mj, а^ и sin/.
По мере измерений все большего числа таких членов (а похоже, что скоро
такие измерения будут возможны), дающих результаты, совпадающие с
предсказаниями общей теории относительности, доказательства
справедливости общей теории относительности и существования гравитационных
волн будут все более обос^юванными.
Пульсар, входящий в двойную систему, наблюдается Тейлором и его
сотрудниками со времени открытия в 1974 г., причем точность измерений все
увеличивалась. Последние значения параметров системы приведены в табл.
16.1. Величина ? связана с ? соотношением
?.???^. A6.5.19)
???
2
Эффект временной задержки и постньютоновские орбитальные эффекты
находятся сейчас почти на пределе обнаружения. Никаких параметров,
соответствующих этим эффектам, в табл. 16.1 не приведено.
Отметим, что выражение A6.5.18) может быть переписано с учетом
A6.5.12) в виде
6^GM,sin/ 3GV3(MjJJ^/2^\V3
a,sin/(l-e^)Pc^ = A-,2),2 [т] ' ^^^'^-^^^
512 Глава 16
Таблица 16.1
ПАРАМЕТРЫ ПУЛЬСАРА
В ДВОЙНОЙ СИСТЕМЕ О
Параметр Значение
Рр, С
Pp. 10-»8
Рр, 10-30 с-1
{?? sin /)/с, с
е
Л с
? (град/год)
7Ь, Ю. Д.
? (град/год)
7» с
А 10-12
0,0590299952709B0)
8,628B0)
-58A200)
2,34186B4)
0,617139E)
27906,98161C)
178,8656A5)
2442321,4332092A5)
4,2261G)
0,00438B4)
-2,30B2)
1) Взято из работы [562]. Рр — период
пульсара, ? — орбитальный период. Го —
эпоха, или начало отсчета времени измерений.
Числа в скобках соответствуют оценкам
неопределенностей последних значащих цифр.
Используя измеренное значение ? из табл. 16.1 вместе со значениями Я и е,
находим
М, + М2 = 2.8278G) Me. A6.5.21)
Подчеркнем, что здесь не следует употреблять раздельно величины С и
Mq в единицах СГС^\ Гравитационная постоянная известна с точностью
хуже четырех значащих цифр. Величина GMq/c^ = 4,925490 · 10"^ с
известна гораздо более точно, так что значение (Mj + Mj) можно намного
точнее выразить в солнечных массах, нежели в граммах!
Перепишем теперь менее точно измеренные параметры ?, sin/ и Я,
подставляя численные значения Я, е, а^ sin/ и Mj + Mj. Выражение A6.5.19)
принимает вид
^" (?,+ M2)'/V '2^'
= @,0007344 s)M2B,8278 + М^), A6.5.22)
^^ По этой причине значения, которые следуют из табл. 16.1, слегка отличаются
от приведенных в [562].
Гравитационное излучение 513
где величина Mj измерена в солнечных массах. Уравнение A6.5.15) дает
а из уравнения A6.4.18) следует
Р =
(?)
5 с'{М, + М^)^/'
= -1,202 X 10"^^МзB,8278 - Мз). A6.5.24)
Отметим, что по порядку величины ?? - 10"^ с/год. Учитывая, что
пульсар в двойной системе находится от нас на расстоянии около 5 кпс,
приходится поражаться, что точность синхронизации времени прихода
импульсов позволяет планировать измерения столь малого эффекта!
Принимая 7 = @,00438 ± 0,00024) с, из выражения A6.5.22) находим,
что Mj = A,41 ± О,О6)Л/0 и, следовательно, согласно A6.5.21), Mj имеет
такое же значение. Тогда уравнение A6.5.24) предсказывает ? = -2,40х
X 10"^^ в отличном согласии с измеренной величиной (-2,30 ± 0,22) ?
X 10-^2
Пока что представляется, что общая теория относительности вполне
позволяет объяснить поведение пульсара в двойной системе и что квад-
рупольная формула излучения гравитационных волн подтверждается в
пределах ошибок измерений - \0%. Эти ошибки должны в значительной
степени уменьшаться по мере продолжения измерений орбитального
периода. Итоги нашего обсуждения приводятся в резюме 16.1.
Эта демонстрация существования гравитационных волн в случае
подтверждения будет иметь такое же значение, что и опыт Герца,
подтвердивший предсказание электромагнитных волн Максвеллом. Правда, в отличие
от опыта Герца условия данного эксперимента мы контролировать не
можем. Просто нам повезло, что природа снабдила нас подходящей
лабораторией.
РЕЗЮМЕ 16.1
Пульсар PSR 1913 + 16 в двойной системе — гравитационные волны существуют!
1. Двойная система состоит из пульсара, движущегося по эллиптической
орбите, и ненаблюдаемого главного компонента. Пульсар обладает
орбитальной скоростью около 300 км/с. Изменения моментов прихода
импульсов на Землю обеспечивают информацию об орбите.
2. Систему характеризуют четыре основных параметра: массы Mj и Л/2;
flfj — главная полуось орбиты пульсара относительно центра масс (причем
M2Uf2 = Mjufi) и / — наклонение плоскости орбиты к лучу зрения.
17-513
514 Глава 16
3. Две комбинации этих параметров, а^ sin/ и функция масс,
измеряются по ньютоновским эффектам в пренебрежении членами порядка v/c,
4. Общая теория относительности в настоящее время дает возможность
измерить еще три комбинации параметров: одну по смещению периастра,
одну из комбинации доплеровского сдвига второго порядка и
гравитационного красного смещения и одну по затуханию орбитального движения,
вызванному излучением гравитационных волн.
5. Указанные пять соотношений между четырьмя параметрами хорошо
согласуются между собой, что подтверждает существование
гравитационных волн и говорит об отсутствии возможных возмущающих влияний на
систему, которые могли бы усложнить интерпретацию данных. В
частности, квадрупольная формула излучения гравитационных волн, основанная
на общей теории относительности, подтверждается с точностью на уровне
ошибок современных измерений порядка Ю^о.
6. С повышением точности наблюдений прихода импульсов
измерениям станут доступны другие релятивистские эффекты и могут быть
подтверждены дополнительные соотношения между указанными четырьмя
параметрами.
16.6. ИЗЛУЧЕНИЕ ОТ ВРАЩАЮЩИХСЯ МАСС:
ЗАМЕДЛЕНИЕ ПУЛЬСАРОВ
Осесимметричный объект, вращающийся как твердое тело вокруг оси
симметрии, не обладает переменным во времени квадрупольным (или более
высокого порядка) моментом и потому не должен излучать
гравитационные волны.
Пусть главные моменты инерции объекта равны /j, /j и /3. Тогда
излучение возникнет, если объект вращается вокруг главной оси 63 и
оказывается неосесимметричным (/j q^ /j). Однако он может излучать и будучи осе-
симметричным объектом при условии, что ось вращения не совпадает о
осью симметрии 63. В общем случае излучать может несимметричный
объект, вращающийся вокруг произвольной оси.
Рассмотрим вначале случай /j nt /2 с вращением вокруг 63. Возможным
физическим аналогом будет пульсар, жесткая кора которого способна
выдержать «гору». Система координат х'·, вращающаяся вместе с объектом,
связана с инерциальной системой координат вращательной матрицей (обе
системы обладают общим началом координат, совпадающим с центром
масс):
х' = Rx. A6.6.1)
где
I cos ? sin ? о]
Л/у= -8??? С08ф о , A6.6.2)
?? О ij
Гравитационное излучение 515
и ? = ?/, ? = const (вращательные моменты отсутствуют). Тензор
инерции в инерциальной системе координат имеет компоненты,
определяемые соотношением
I^R^I'R, A6.6.3)
где /' —диагональная матрица с диагональными элементами /р /j и /3.
Будем использовать индексы 1, 2, 3 для обозначения компонентов в
системе отсчета, связанной с объектом, г х, у, ? — для инерциальной системы
координат. Уравнения A6.6.2) и A6.6.3) дают
4^ = С08^/| -I- 8??^?/2 = 1С08 2ф(/| - /j) + const. A6.6.4)
Аналогично
^?^ = /?? = ????2?(/, -/2).
^уу = I COS2ф(/2 - /?) -I- const,
/,, = const, /^, = ly, = 0. A6.6.5)
Поскольку
Tr/' = Tr/ = /| -I- /2 -I- /з = const, A6.6.6)
можно использовать 1^ вместо i-^ в формуле потерь энергии A6.2.16)
(вспомните, 4To^.j = -I-j -\- ~ ?-???), Таким образом,
= _ ^^1B?)^(/^ - /2)'<со822ф + 25??22? + со822ф>
= -f ^(/,-/2)V. A6.6.7)
Если объект может быть аппроксимирован однородным эллипсоидом с
полуосями а, Ь, с, тогда
/, = ^Л/(Ь2 + с2), /2= iM(fl2 + c2), /3 = ^?(?2 + ^2). A6.6.8)
В случае малой асимметрии (т.е. а ^ Ь) можно записать
f.-f^/.va'. (,6.6.9)
где эллиптичность ? определяется соотношением
Эта формула приводилась ранее как выражение A0.5.15).
516 Глава 16
Теперь обратимся к случаю твердотельного вращения вокруг неглавной
оси, но для простоты предположим, что /| = /j. Выберем фиксированное
направление момента количества движения, так чтобы вектор J в инерци-
альной системе координат был направлен вдоль е^. Преобразование к
координатам, связанным с объектом, выполняется при помощи углов Эйлера
(см. [232], уравнение 4.46):
«и =
cos ? COS ? - COS ? sin ? sin ? cos ? sin ? + cos ? cos ? sin ? sin ? sin ?
- sin ? cos ? - cos ? sin ? cos ? - sin ? sin ? + cos ? cos ? cos ? sin ? cos ?
sin ^ sin ? - sin ? cos ? cos ?
A6.6.11)
При свободной прецессии ось симметрии 63 и вектор угловой скорости
вращаются вокруг в^ с постоянной угловой скоростью ? = У//|, причем угол ?
между вз и в^ сохраняется постоянным. Кроме того, вектор угл1^вой
скорости прецессирует относительно е^ с угловой скоростью ? =
= (/| - /з)Фсо8^//з, которая оказывается постоянной в системе
координат, связанной с телом.
Уравнения A6.6.3) и A6.6.11) дают
4х ^ /?(??8^? -I- ??^^???^?) + ?'^??^???^?
= Ил - 1г?^^^0со^'^1ф + const. A6.6.12)
Аналогично
Л, = ^,х=И/1-/з)8ш'^81п2ф,
?? = hx = ~(Л ~ /з)81пвС08в81пф,
Jyy^ ^l{j\^ /з)81п^вС08 2ф + С0П81,
^yz = hy = (л ~ /з)81п ?008^008 ?,
/,, = /з + (/, - I^)s\n4 = соп81. A6.6.13)
полагая ? = ?/, ? = ? = const, найдем
— = --^П^ + 7^ + 2/^ + 2/^ + 2/^
= - ? "т(Л - Л)'<^ 8??^?B?)'B??8^2? + 28??22?)+
^ с
+ 2 8??^??08^??^(8??^? + С08^ф)>
= -|^(Л-/з)^81п^вAб81п^в + со8^в). A6.6.14)
Гравитационное излучение 517
Для малого «угла качания» ? получаем
f = -f|(/,-/3)V0^ A6.6.15)
Отметим, что при вращении вокруг главной оси [уравнение A6.6.7) или
A6.6.9)] частота излучения составляет 2? , что ясно из уравнений A6.6.4) и
A6.6.5). Однако в случае, описываемом уравнением A6.6.15), преобладает
излучение на частоте ?, поскольку учет 1^^ и 1у^ приводит к появлению
члена cos^^ в уравнении A6.6.14).
Для обнаружения гравитационных волн от пульсара (например, от
пульсара в Крабовидной туманности или в созвездии Парусов)
предлагалось построить резонансный детектор, тщательно настроенный на
соответствующую частоту, которая хорошо известна из радионаблюдений.
Если излучение вызвано существованием «горы» на поверхности пульсара и
ось вращения совпадает с главной осью, то эту идею можно реализовать,
выбрав резонансную частоту равной 2?. Если же излучение связано
главным образом с «качанием», то частота появления пятна, фиксированного
на поверхности пульсара, равна
(О, «? + ?. A6.6.16)
По-видимому, ?^ и будет частотой электромагнитного излучения, но она
будет отличаться от частоты гравитационных волн ? = ? на небольшую
неизвестную частоту прецессии ф.
В общем случае, когда излучение порождается и «горой», и «качанием»,
величина dE/dt определяется сумг^ой уравнений A6.6.7) и A6.6.15), если
эффекты «горы» и «качания» достаточно малы^^
Если излучение пульсара вызвано существованием «горы»,
максимальная эллиптичность, определенная формулой A6.6.10), по порядку величины
должна быть равна безразмерной деформации, соответствующей пределу
прочности коры. Это очень неопределенная величина. Для идеально чистых
кристаллов в лаборатории она порядка 10"^ — 10"^, но, если в кристаллах
имеются примеси или дефекты, она снижается до - 10"^. Модель звездо-
трясений (разд. 10.11) не позволяет достаточно точно определить эту
величину для пульсаров, но обычно считается, что в лучшем случае она должна
быть порядка 5 · 10""*. «Горы» на пульсаре имеют высоту не более
нескольких метров!
Для излучения пульсаров, связанного с «качанием»
/з - /, = е/з,
где ? теперь означает параметр сплюснутости, как в уравнении A0.11.2).
Его значения в диапазоне 10"^—10""* кажутся правдоподобными (см.
^^ Детальное рассмотрение общего случая, включая возмущения метрики Л, см. в
[639].
518 Глава 16
разд. 10.11). Эффект «качания» учитывался при объяснении
«микротрясений» пульсаров в Крабовидной туманности и в созвездии Парусов. Верхняя
оценка ? порядка 10"^; вероятно [460], ? < 10"^— 10"^.
Упражнение 16.12. Оцените dE/dt по отдельности для излучения, порождаемого
«горой» и «качанием», на примере пульсаров в Крабовидной туманности и в созвездии
Парусов. Оцените также амплитуду волны h на Земле, предполагая, что расстояние
до пульсара в Крабовидной туманности 2000 пс и до пульсара в созвездии Парусов
500 ПС. Каково максимальное значение Л, согласующееся с замедлением пульсаров?
Упражнение 16.13. а) Покажите, что
? dt
для излучения, вызванного «качанием». (В данном случае J = J^; нет
необходимости предполагать угол ? малым.)
б) Покажите, что гравитационное излучение приводит к экспоненциал^эному
уменьшению угла ? со временем, а составляющая момента количества движения
вдоль оси симметрии У cos^ остается постоянной.
16.7. ГРАВИТАЦИОННЫЕ ВОЛНЫ ПРИ СТОЛКНОВЕНИЯХ
Другим потенциальным источником гравитационного излучения могут
быть столкновения или тесные сближения астрофизических объектов.
Рассмотрим идеализированную ситуацию, когда две точечные массы Wj
и ^2 падают навстречу друг другу из состояния покоя на бесконечности.
Предположим, что они испытывают лобовое столкновение, так что
движение направлено вдоль оси х. Выберем положение покоящегося центра масс
в точке X = 0. Тогда
W|X| = -^2^2 = М·^' A6.7.1)
где
jc = jCj-X2' ^^ Л/ ' ? ? ш,+ ^2. A6.7.2)
Поскольку
получаем
m,xf + W2X2 = M·^^ A6.7.3)
fxx = IM^'' fyy = bz- -^ IM^ · A6.7.4)
Используя уравнение движения
GM
x= Г' A6.7.5)
?
Гравитационное излучение 519
или, что эквивалентно
х^ ^ GM
2 X '
A6.7.6)
находим
Таким образом.
^=-\???^^. A6.7.7)
^ = 1?//2 +f2 +/2Ч
8 GVM^ / jc^
Полная энергия, излученная при столкновении, равна
dE ^ cdE \
A6.7.8)
^-/f-Zfi
dx
8 б^УМ\^^,^^|/2/-«^ Jx
15 ^5
{IGMY^'f -^. A6.7.9)
Интеграл в уравнении A6.7.9) расходится при х^^^ -^ 0. Однако и наше
ньютоновское рассмотрение становится неприменимым по мере того, как
•^min ¦" ^- Поэтому МЫ «обрежем» интеграл на «горизонте» дг^^4„ =
= 2GM/c^; результаты соответствующего релятивистского рассмотрения
приводятся ниже. При х^^^ = IGM/c^ уравнение A6.7.9) дает
Можно сравнить этот результат с точными релятивистскими
вычислениями [156] излучения пробной частицы, падающей по радиусу из
состояния покоя на бесконечности в шварцшильдовскую черную дыру. В этом
случае приведенная масса совпадает с массой пробной частицы, а полная
масса — это масса черной дыры. В работе [156] получено
?? = 0,0104^, A6.7.11)
?
что вполне согласуется с уравнением A6.7.10), если учитывать
произвольность сделанного обрезания интеграла.
В работе [544] приводятся результаты численного решения на ЭВМ
полных уравнений Эйнштейна и рассчитано излучение, возникающее при
лобовом столкновении двух шварцшильдовских черных дыр одинаковой
массы. При этом найдено
?? = 0,001Mc^ A6.7.12)
520 Глава 16
где неопределенность численного решения, вероятно, оценивается
множителем, не превышающим 2.
Положив в выражении A6.7.10) Wj = Wj, получим
^E = ^,Мс^ = 0,0012Мс2, A6.7.13)
что близко к результату, полученному численным методом. Можно
предполагать, что большая энергия излучается, если соударение оказывается не
точно лобовым [161].
Упражнение 16.14. Вычислите форму волны hjij{t), наблюдаемую удаленным
наблюдателем по направлению, составляющему угол ? с осью х, для лобового
столкновения, проанализированного в этом разделе.
Рассматривая идеализированные столкновения, можно вывести важный
результат, касающийся низкочастотного спектра энергии гравитационных
волн, связанных с коллапсом. Определим преобразование Фурье ?^1^{?)
величины tji^ следующим образом:
^)*'(?) = --^???;*@^'"'^'. A6.7.14)
B7Г) •'-оо
Обратное преобразование имеет вид:
1Л') --^гГ ff^{-)e—d<.. A6.7.15)
B7Г) •'-оо
Поскольку "tji^it) — действительная величина,
?^(?) = ?)?4-?), A6.7.16)
где звездочка обозначает комплексно-сопряженную величину.
Выведем теперь теорему Парсеваля для спектра энергии ??/??.
Поскольку ijl\t) — действительная величина, можно записать
-¦?--,? ""Г ''"Г .<"¦*;."(")*;;'·("¦)«'"--'"¦ Aбл.п)
ШТГ с^ У_оо •'-оо •'-ос
1 G^ г^
Интегрирование по / дает о-функцию, так что
где использовано соотношение A6.7.16). Таким образом,
г^ dE
^E
Гравитационное излучение 521
где
Рассмотрим теперь низкочастотный предел уравнения A6.7.20). Когда
? — О, выражение A6.7.14) дает
(???)
A6.7.21)
где fji({t) не равно нулю только в интервале /^ ^ / ^ tr. Для столкновения
при свободном падении, описанного выше, t^ = -оо, /^ = г^^^. Из
уравнений A6.7.20) и A6.7.21) следует, что ??/?? не обращается в нуль при ? =
= О, если "^^@ не равно нулю при t^ или tf [предполагается, что i^(//) ^?^
? ·?^(/?)]. Итак, движение из состояния покоя при конечном значении
радиуса, или гиперболическое соударение (конечная скорость на бесконечности),
приводят к ненулевому значению ??/?? при ? ^ 0. Однако, как будет
показано ниже, параболическое соударение (свободное падение с нулевой
скоростью на бесконечности) дает ??/?? - ?^^^ — О, когда ? — 0.
Если подставить выражения A6.7.4) прямо в A6.7.14), переходя в
дальнейшем в пределу ? — О, мы получим расходящийся интеграл. Поэтому
сначала перепишем уравнение A6.7.14), выполнив интегрирование по
частям:
т-) = '
^''^' ii.y^^
dt
A6.7.22)
Теперь уравнения A6.7.4) — A6.7.6) дают
у / ч 4 ???
???@= з~7~' A6.7.23)
где
X = {??^\20??^\-??^\ JC ^ 00 при Г ^ -00. A6.7.24)
«Обрежем» уравнение A6.7.24) на л-^^^^ = 2GM/c^ при / = t^^^.
Для / > t^^ положим все производные "^^@ равными нулю. Таким
образом, первый член в правой части уравнения A6.7.22) равен нулю и мы
имеем
''^ ^ B.)-/^-^-00 3V3(-,)^/' ^^^-^-^^^
Положив у = -?/, получим
-^""^ B.)'/^з Ij //3- ^''-'-''^
522 Глава 16
Когда ? — О, можно положить нижний предел интегрирования равным
нулю. Тогда интеграл равен Г('/з)ехр( —/?/6). Подставляя это значение в
уравнение A6.7.20) и используя выражения A6.7.4) для -l· и ^^^, находим
^ - ^^^^^Щl^-?GM^r^^\ ? - 0. A6.7.27)
^^ 577C)'/' С^
Степенной закон ?^^^ в пределе ? — О следует из поведения ¦f'jk(t) при
Г — —00. В этом режиме источник оказывается ньютоновским и
использованная выше квадрупольная формула должна быть отличным
приближением. Итак, даже если в результате коллапса или столкновений образуется
черная дыра, низкочастотный спектр гравитационных волн формируется на
самой ранней стадии и может быть вычислен с использованием квадруполь-
ной формулы. В частности, свободное падение из состояния покоя на
бесконечности в общем случае приводит к степенному закону ?^^"^ при ? —
- О [5931.
Гравитационное излучение, вызванное лобовым столкновением двух
нейтронных звезд с одинаковой массой, должно быть, вероятно, гораздо
сильнее, чем предсказывает уравнение A6.7.12), если нейтронные звезды
достаточно массивны и компактны. В этой ситуации распространение от точки
контакта наружу двух ударных волн отдачи приводит к замедлению
движения сталкивающихся масс, что служит причиной резкого изменения квадру-
польного момента. Предварительные расчеты [132, 528, 618]
свидетельствуют о типичной эффективности излучения порядка LE/Mc^ - 0,01, что
соответствует амплитудам волн h - 10"^^ при расстояниях 10 Мпс
(скопление галактик в Деве). Таким событием, хотя они случаются не так уж
часто, вполне может отмечаться конечный этап эволюции двойных
пульсаров. Оценки [131, 133] показывают, что в пределах 40 Мпс от Земли может
происходить примерно одно такое событи/ в год. Чтобы обнаружить
подобное столкновение, требуется чувствительность детекторов порядка
h - 10-22.
16.8. ГРАВИТАЦИОННЫЕ ВОЛНЫ ПРИ КОЛЛАПСЕ С ОТКЛОНЕНИЯМИ
ОТ СФЕРИЧЕСКОЙ СИММЕТРИИ
Одним из наиболее вероятных источников гравитационного излучения
кажется гравитационный коллапс массивной звезды, приводящий к
образованию нейтронной звезды или черной дыры. Размерные оценки разд.46.3
говорят о том, что звезда может излучить значительную долю энергии Мс^,
если коллапс достаточно отличается от сферически симметричного.
Детальные расчеты такого коллапса начали появляться только теперь. Для
них необходимо применение двух- или трехмерных гидродинамических
представлений с полным учетом эффектов общей теории относительности.
При этом требуется аккуратное рассмотрение уравнения состояния коллап-
Гравитационное излучение 523
сирующего вещества, а также геометрии пространства-времени, чтобы
подсчитать поток гравитационных волн (обсуждение этих работ приведено
в [544]).
Некоторое представление об этих сложных расчетах можно получить из
более простых вычислений сфероидальной или эллипсоидальной модели
[494]. В этом случае рассматривается ньютоновский коллапс однородного
сфероида или эллипсоида. Чтобы форма объекта оставалась
эллипсоидальной, закон изменения давления должен быть квадратичным по
координатам:
F-?M[^-'i-'i-^\ A6 8.1)
где а, b и с — полуоси, а Р^ — давление в центре. Уравнение состояния
можно промоделировать, если принять
Рс = Рс{р)^ A6.8.2)
A6.8.3)
где однородная плотность ? дается выражением
?
^ АчтаЬс/г '
Трехмерные гидродинамические уравнения движения для такой
конфигурации сводятся к обыкновенным дифференциальным уравнениям для
величин а, b и с, являющихся функциями времени.
Для получения больших потоков гравитационных волн необходимы
значительные отклонения от сферической симметрии. Начав с почти
сферической конфигурации при больших радиусах, можно ввести эллиптичность,
если объект обладает моментом количества движения. Для сфероида с
малым моментом количества движения J имеем У ос е, где эксцентриситет е
определяется выражением
^2=1-4 A6.8.4)
а'
(сравните с разд. 7.3).
Упражнение 16.15. Используйте результат, полученный в разд. 7.3, чтобы показать
vV2
J=[?) {GaY'^e A6.8.5)
ДЛЯ сфероида Маклорена в пределе е ^ 0.
Уравнение A6.8.5) показывает, что в ходе осесимметричного коллапса с
сохраняющимися значениями J и ? эксцентриситет е должен расти. Это
вытекает из детальных расчетов. Момент количества движения обеспечива-
524
Глава 16
ет центробежную поддержку экваториальной оси uf, в то время как коллапс
полярной оси с не связан с вращением.
Упражнение 16.16. Покажите, что для сфероидального коллапса
Для доказательства может оказаться полезным уравнение A6.6.8).
A6.8.6)
Рьс
10-^
10-6
10-8
^0-10
10-^^
<п-1^
—
—
-
297
1
0,001
1
•
и
,_
29,7
0.01
1
^ >
•
и
•
и
и
и
•
и
•
•
•
•
•
•
и
и
^
!
Пульсар ? „ Крабе"
1 . I
2,97
1
0.1
1
1.61
0,3
1
-J
\ ~?
—j
PSR 1937+214
,
_j 1
10^6 10^7 10^8 10^^
J, эрг· с
Рис. 75.2. Эффективность гравитационного излучения как функция момента
количества движения для сферически несимметричного коллапса звездного ядра.
Показаны результаты численных расчетов, в которых для моделирования коллапса
вырожденного гомологичного ядра массой Л/ = 0,8 Mq принимаются однородные
сфероиды. Начальная плотность равна р, = 4 · 10^ г/см^, эксцентриситет е,,
период вращения Р,. Коллапс начинается из состояния покоя и описывается
реалистичным «горячим» ядерным уравнением состояния [уравнение A6.8.2)], причем
предусматривается возникновение «отдачи» (см. гл. 18). Эффективность излучения,
вызванного первоначальным падением вещества и последующим «отскоком» (при
'^отскок "" ^0^^ г/см^), показана щтриховой линией [см. уравнение A6.8.8)]. Полная
эффективность после того, как затухнут все колебания звездного ядра, показана
сплощной кривой. Стрелками отмечены оценки моментов количества движения
пульсара в Крабовидной туманности и пульсара PSR 1937 -1-214, которые обладают
самыми короткими периодами среди известных пульсаров C3 мс и 1,6 мс
соответственно) [494].
Гравитационное излучение 525
Из уравнений A6.8.4)-A6.8.6) следует, что для малых значений J
^aj"^ (малый У). A6.8.7)
dt ^ ^
При больших значениях J конфигурация не коллапсирует к малым
радиусам и высоким плотностям из-за больших центробежных сил,
действующих в экваториальной плоскости. Таким образом, dE/dt стремится к нулю
как при больших, так и при малых моментах количества движения У.
Максимум достигается при некотором промежуточном значении У^, которое
обычно на порядок выше момента количества движения Солнца для
объекта с массой порядка Mq , коллапсирующего в нейтронную звезду. При J -
~ J^ энергия вращения коллапсирующей звезды становится сравнимой с
гравитационной потенциальной энергией и, следовательно, эксцентриситет
становится большим при плотностях несколько выше ядерной.
Максимальная эффективность излучения ??/?/c^ составляет, самое большее, 1^о в
предельных случаях, а типичные эффективности могут быть на несколько
порядков величины ниже.
Эффективное излучение возможно также, если магнитные поля
достаточно сильны, чтобы вызвать отклонения от сферы. Другая
возможность обедпечивается появлением (по любой причине) небольшого
начального эксцентриситета, который возрастает в процессе коллапса. Если
коллапс протекает в виде нескольких последовательных стадий, то во время
каждой из них эксцентриситет может увеличиваться, что приводит к
высокой эффективности излучения. Подобный сценарий отражен на рис. 16.2
и основан на расчетах коллапса сфероида [494]. Вопрос о том, какая из
этих возможностей реализуется в природе, остается открытым, пока не
будут выполнены крупномасштабные расчеты на ЭВМ или созданы
детекторы гравитационных волн с достаточной чувствительностью.
Упражнение 16,7. а) Используйте анализ размерностей и соотношение A6.8.7),
чтобы показать, что при коллапсе медленно вращающегося звездного ядра с
образованием черной дыры выделяется энергия в виде гравитационных волн, равная
6) Оцените численно эффективность излучения ^Е/Мс^ для коллапса звездного
ядра с таким же моментом количества движения, какой имеет пульсар в Крабовид-
ной туманности.
Глава 17
Сверхмассивные звезды и черные дыры
17.1. ВВЕДЕНИЕ
Сверхмассивные звезды — это гипотетические равновесные конфигурации с
массами в диапазоне 10^ — 10^ М^. Как мы увидим, они могут быть
довольно компактными с потенциалами на поверхности, составляющими
небольшую, но не пренебрежимо малую долю с^. В ходе квазистатической
эволюции они могут претерпевать катастрофический гравитационный
коллапс. Следовательно, возможные предшественники сверхмассивных черных
дыр — это сверхмассивные звезды. Обе категории объектов —
сверхмассивные звезды и сверхмассивные черные дыры — часто привлекаются в
качестве источника энергии, ответственного за интенсивную активность,
которая наблюдается в квазарах и ядрах активных галактик. По этим
причинам обсуждение свойств сверхмассивных звезд выглядит вполне
естественным в книге о компактных объектах. Как мы увидим, общие свойства
равновесия и устойчивости сверхмассивных звезд можно без труда
проанализировать на основе математического аппарата, уже разработанного для
белых карликов и нейтронных звезд (используя, например, энергетический
вариационный принцип; см. гл. 6).
По мере увеличения массы рассматриваемой звезды вклад излучения в
давление, удерживающее систему в равновесии, становится все больше, а
доля газового давления все уменьшается. Этот факт будет показан ниже. В
соответствии с теоретическими расчетами [51-7] «нормальные» звезды
главной последовательности имеют максимальную массу около 60 Mq . Выше
этого значения массы сочетание давления излучения и ядерной энергии,
выделяющейся в центральных областях звезды, приводит к сильной пульсаци-
онной неустойчивости. Это теоретическое предсказание подтверждается
отсутствием наблюдаемых звезд с массами более 60 Mq .
Несмотря на существование этого предела, давно предполагается, что в
природе могут образовываться сверхмассивные звезды с массами гораздо
выше 1000 ?0. Такой объект будет поддерживаться в гидростатическом
равновесии почти полностью за счет давления излучения
P = P, = ifl?^ A7.1.1)
dP ^ Gm{r)p .j^ J 2)
Сверхмассивные звезды и черные дыры 527
В поверхностных слоях поток энергии переносится наружу путем диффузии
фотонов. Светимость определяется выражением
Зкр ал
где принятая непрозрачность обусловлена томсоновским рассеянием в
ионизованной водородной плазме
к =-^ = 0,40 cmVf. A7.1.4)
Здесь Oj — томсоновское сечение рассеяния, а w^ — масса протона
[сравните с уравнениями (И.31) и (И.41)]. Подставив уравнения A7.1.1) и A7.1.2) в
A7.1.3) и положив т(г) = Л/, получим
L = Lndd = = 1>3 X 10^«т^ эрг/с. A7.1.5)
Опт -'^О
Итак, звезда излучает на эддингтоновском пределе (см. разд. 13.7).
Хойл и Фаулер [282, 283] были первыми, кто предложил
сверхмассивные звезды в качестве источников энергии для квазаров и ядер активных
галактик. Типичная светимость квазара порядка Ю'^ эрг/с A0^^ ^©·)
естественно приводит к идее излучения на эддингтоновском пределе
объектом с массой ? - 10^ Mq. Начиная с 1963 г. возможность высвобождения
больших количеств ядерной и гравитационной энергии в таких объектах
исследовалась неоднократно ^\
Зельдович [633] и Солпитер [497] в качестве альтернативы высказали
предположение, что объектами, ответственными за энергетическую
активность квазаров и ядер активных галактик, могут быть сверхмассивные
черные дыры. С тех пор модели черной дыры как источника наблюдаемого
оптического, радио- и рентгеновского излучения этих объектов стали
предметом интенсивных теоретических исследований^^ В большинстве из
предложенных моделей в качестве механизма, обеспечивающего энергию
излучения, предполагается аккреция газа на сверхмассивные черные дыры (см.
гл. 14). Как уже отмечалось в разд. 13.7, максимальная светимость,
порождаемая аккрецией, должна быть, вероятнее всего, сравнимой с L^^^, Как
сверхмассивные звезды, так и черные дыры могут излучать на
эддингтоновском пределе, и это объясняет, в частности, почему и те, и другие
объекты занимают видное место в моделях квазаров и ядер активных
галактик.
Сравнительно недавно Торн и Брагинский [569] предположили, что
гравитационный коллапс сверхмассивных звезд и столкновения
сверхмассивных черных дыр в квазарах и ядрах активных галактик могут вызывать
всплески длинноволнового гравитационного излучения с \ ^ 10^ (М/
/10^ М^) км.
^^ Обзор и ссылки на ранние работы см. в [522]; ссылки на более поздние работы
приведены в [421].
^^ Ссылки приведены в [73, 477].
528 Глава 17
Некоторые данные наблюдений свидетельствуют о существовании в
центрах галактик несветящихся компактных объектов. Например, звезды
вблизи центра гигантской эллиптической галактики М87 в скоплении Девы
обладают большими скоростями, которые можно объяснить,
предположив, что они движутся в гравитационном поле центральной черной дыры,
имеющей массу 5 · 10^ М^ [162, 503, 626] ^\ В нашей Галактике высокие
скорости газовых облаков вблизи центра могут служить аргументом в
пользу существования там компактной массы с Л/ - 10^ М^^ [323].
Упражнение 17.1. Центральный объект туманности 30 Золотой Рыбы в Большом
Магеллановом Облаке предварительно отождествлен со сверхмассивной звездой
[ПО]. Уверенное отождествление затрудняется по меньшей мере двумя факторами:
а) наблюдаемый спектр «загрязнен» другими звездами, и не исключено, что он
создается скоплением очень горячих, но в других отношениях нормальных звезд; б)
отмечается заметное пекулярное поглощение света пылью. Однако наблюдения со
спутника ШЕ показывают, что очень яркий голубой источник излучения в центре
этой гигантской области ионизованного водорода представляет собой пекулярный
горячий объект с мощным звездным ветром. Наблюденные спектры позволяют
оценить, что скорость истечения ветра V^ должна составлять 3500 км/с, а цветовая
температура — около 60 000 К. По оценкам с учетом расстояния, потока излучения
(с поправками на поглощение) и цветовой температуры светимость должна быть
порядка 0,7 · 10^ Lq.
а) Предполагая, что источник представляет собой отдельную светящуюся
звезду, используйте выражение A7.1.5) для оценки ее массы.
Ответ: M/Mq « 2000.
б) Предполагая, что звезда излучает как черное тело с температурой Г,
подсчитайте ее радиус.
Ответ: R/Rq « 80.
в) Совместима ли гипотеза сверхмассивной звезды со скоростью ветра,
подчиняющейся очевидному ограничению V^ > V^^^, где Kgsc = {IGM/RY^ —скорость
убегания?
г) Что можно сказать по поводу пульсационной неустойчивости сверхмассивной
звезды, учитывая наблюдения заметного звездного ветра {М^ « 10"^·^ Л/0/год)?
В последующих разделах мы будем рассматривать свойства
сверхмассивных звезд, пренебрегая поначалу эффектами общей теории
относительности, выгоранием ядерного горючего и другими усложняющими
факторами. Поскольку предполагается, что давление целиком обусловлено
излучением, значение показателя адиабаты для сверхмассивной звезды D/3)
находится на грани динамической неустойчивости. Поэтому далее мы обсудим,
как эффекты общей теории относительности влияют на устойчивость.
Затем обсуждаются дополнительные эффекты, связанные с ядерными
реакциями, вращением и т.д. Наконец, описываются результаты численных
расчетов коллапса сверхмассивных звезд в сверхмассивные черные дыры.
•^ Альтернативная интерпретация без предположения о черной дыре изложена в
[169].
Сверхмассивные звезды и черные дыры 529
17.2. ОСНОВНЫЕ СВОЙСТВА СВЕРХМАССИВНЫХ ЗВЕЗД
Рассмотрим идеализированный случай сферического облака полностью
ионизованного водорода. В нулевом приближении пренебрежем давлением
водородного газа. Давление и плотность энергии излучения равны
Р,^\аТ\ е^^аТ\ A7.2.1)
Используя первый закон термодинамики — уравнение B.1.3), находим
величину энтропии фотонов, приходящуюся на барион
Предположим, что энтропия постоянна по всей звезде^^ Плотность равна
Р^гп^п, A7.2.3)
где гпу^ — масса водородного атома; плотностью энергии излучения ?/c^
здесь можно пренебречь.
Выражения A7.2.2) и A7.2.3) дают
и уравнение A7.1.1) можно записать в виде
Р^Р^^Кр^^\ A7.2.5)
где
Таким образом, структура звезды соответствует политропной
конфигурации с А2 = 3.
В первом приближении энергию такой конфигурации можно записать в
эиде
? = ?,,, + ?^,, = k.KMpV' - kfiM'/'pV\ A7.2.7)
где k^ = 1,75579, Atj = 0,639(Ю1 [см. уравнения F.10.9) и F.10.10)].
Равновесие наступает, когда дЕ/др^ = О, что дает соотношение между энтропией и
массой [см. уравнение C.3.10)]:
к Ък
НЩ-"'-АШ- <"-'>
^^ Вероятно, это предположение справедливо из-за наличия конвекции. См. снос|ку
в разд, 18.2 и [135], где обсуждается конвекция.
18-5X3
530
Глава 17
?,???
1,005
1,000
0,995
^ 0,990
^ 0,985
0.980
0,975
0.970
1—1
-
-
1
1 1 1 1 1 1 1|
J 1 1 1 и |1
1—1—гт
Рр=0
ото
л...
1 1 М|
mil
1—г-
А
1 1_
1 1 1 1 III
-]
ч
-j
-^
-^
1 II 1 ?
10-
10
-3
? , г/см^
10-
10-
Рис. 17.1. Зависимость равновесной массы от плотности в центре сверхмассивной
звезды при постоянной энтропии. Энтропия задается значением ? [см. уравнение
A7.3.5)]; в данном случае ? = 8,494 · 10"^. Штриховая кривая показывает
равновесную массу ньютоновской конфигурации, удерживаемой в равновесии
исключительно давлением излучения [см. уравнение A7.2.8)]. Сплошная кривая показывает
равновесную массу звезды, удерживаемой в равновесии как давлением излучения,
так и давлением газа в соответствии с общей теорией относительности. Штриховая
кривая повсюду удовлетворяет условию dM/dp^ = О, так что все равновесные
конфигурации устойчивы к радиальным колебаниям. Снлошная кривая имеет максимум
при р^ = p^^jj, где dM/dp^ = 0. При р^ < р^^^ стабилизирующее влияние давления
газа на радиальные возмущения преобладает над дестабилизирующим влиянием
нелинейного тяготения, так что эти конфигурации устойчивы. При р^ > р^^-^ справедливо
обратное утверждение. Следовательно, точка А находится на ветви равновесной
кривой, соответствующей неустойчивости [533].
Здесь
A7.2.4):
к — постоянная Больцмана. Температура дается уравнением
Г= 1,98 X 10
-(¦
¦U)
1/6
A7.2.9)
1 г/см^
Поэтому в первом приближении масса ньютоновской равновесной
конфигурации зависит только от удельной энтропии и не зависит от плотности в
центре. В этом случае при заданном значении s^ график зависимости ? от
р^ является просто горизонтальной линией, как показано на рис. 17.1.
Сверхмассивные звезды и черные дыры 531
17.3. ВЛИЯНИЕ ПЛАЗМЫ
Газовое давление водородной плазмы
Pg=2nkT, A7.3.1)
вдвое превышает давление протонов или электронов по отдельности.
Плотность энергии равна
eg = m^nc^+ ЪпкТ, A7.3.2)
где мы принимаем, что газ нерелятивистский (кТ < fn^c^). Таким образом,
первый закон термодинамики дает следующее выражение для энтропии:
s^ = 2к\п[^^\ + const. A7.3.3)
Оказывается, что постоянный член не связан с нашим последующим
рассмотрением, но его численное значение представляет интерес. Для нашего
случая найдено, что он равен [см. уравнение B.3.34)]
Т = ^"(^ЬТ' A7-3.4)
?
Sq ^B7тк\ 3 . 7 ,
т. + 5 + 21п2 = -21,0,
где температура ? выражена в Кельвинах, а плотность ? — в г/см ^.
Заметим, что уравнения A7.2.1), A7.2.2) и A7.3.1) дают
^ = ^ = ^- A7-3-5)
Поэтому, когда ? > ^0» так что s/k > 1 [уравнение A7.2.8)], и jS < 1,
давление газа становится всего лишь малым возмущением.
Упражнение 17.2. Сравните 5^ и 5^ для ? = 10^ -^0» ? = \0^ г/см^ и для ? =
= IO^Mq, ? = 1 г/см^. Температура дается выражением A7.2.9).
Ответ: Sg < s^.
Упражнение 17.3. а) Покажите, что, когда учитываются как давление, излучения, так
и давление газа, сверхмассивная звезда описывается ньютоновской политропой с
? = Кр^, где К дается уравнением A7.2.6), а Г определяется выражением
г-1+4 = | + т+ е(/8').
? 3 О
Где ?' — плотность полной внутренней энергии, за исключением энергии,
соответствующей массе покоя.
532 Глава 17
б) Используя результат, полученный в части а), докажите, что при строго
ньютоновской гравитации равновесия сверхмассивная звезда, безусловно, устойчива к
радиальным адиабатическим возмущениям при произвольных значениях плотности в
центре.
Указание: См. разд. 6.7.
в) Зафиксируйте энтропию, положив ? = 8,494 · 10~^, и вычислите
соответствующие значения А^ и Г.
Ответ: К = 3,839 · Ю·» (в единицах СГС), Г = 1,3347.
г) Постройте на рис. 17.1 равновесную кривую М{р) для ньютоновских политроп,
соответствующих этому значению энтропии [можно аппроксимировать требуемые
величины Лейна—Эмдена ^j и ^fl^'(^i)l, используя уравнение C.3.12)]. Сравните
ващу кривую с графиком ньютоновской политропы, поддерживаемой одним
давлением излучения, и прокомментируйте результат.
Указание: Оцените, каков знак dM/dpc в этих двух случаях.
Мы хотим вычислить поправки к ?^^^^, связанные с влиянием
водородной плазмы. Полная внутренняя энергия, приходящаяся на единицу массы,
равна
Сг + «е аТ^ ЪкТ
^^—. A7.3.6)
? ? ^н
где отброшен постоянный член, представляющий массу покоя. Требуется
выразить ? через плотность ? и полную энтропию
^ = 5, + 5^ = j^ + k\n — -l· Sq. A7.3.7)
Выражение ? через 5 в нулевом приближении получается, если пренебречь
5^, и дается уравнением A7.2.4) с заменой s^ на s. Подставим это
выражение в малый член 5 , так что
^-н«ГЗ^ / _?o_^j„ 3^]_ A7.3.8)
Таким образом,
Зр \ 5 5 4т^ар]'
r.(J?^)'''(,-io_|,„ 3^1 A7.3.9)
\4m^al \ 3s 3s 4т^ар J
Для простоты будем рассматривать Sq/s как малую величину, что верно
при M/Mq > 10^ [см. соотношения A7.2.8) и A7.3.4)], но не существенно
для доказательства. Теперь подставим выражение A7.3.9) в A7.3,6). В
малом члене ЪкТ/т^ достаточно оставить только нулевое приближение для
Т. Находим
и « ЗКр^/^ + ??'/^ + ??^/?? ?, A7.3.10)
Сверхмассивные звезды и черные дыры 533
где
4^^0 / 35 \'/'
35 \ 4w_
\4/3
5 ?' ^ък1 Ъ8 \
1/3
4Ь/ 3^\-J 3^\ (j,3.11)
35 \4тна/ \4тна/ ^ '
-^D^.) С"-)
Теперь выражение для полной внутренней энергии принимает вид
E,„, + AEi,,==fudm, A7.3.13)
где интегрирование выполняется по распределению массы для политропы с
л =й 3. Первый член в уравнении A7.3.10) дает Е-^^^ [см. уравнение A7.2.7)].
Подставляя ? = ?^?^ [уравнение C.3.3)], получаем
?i„^ + ??;„, = А:,(л: + I + ????' + ?,?????? ?„ A7.3.14)
где
^-^^/^In^^Jm. A7.3.15)
17.4. УСТОЙЧИВОСТЬ СВЕРХМАССИВНЫХ ЗВЕЗД
Как и в случае белых карликов (гл. 6), для изучения устойчивости
сверхмассивных звезд следует учесть эффекты общей теории
относительности — уравнения F.10.21). Поэтому запишем
= АМрУ - ??'/?' + CMpY'ln ?, - DM'/y/\ A7.4.1)
где
^=/:,(^ +^ +?), B^k,G,
С--^, /) = ^, А:4 = 0,918294. A7.4.2)
Для равновесия требуется выполнение условия ЪЕ/Ър^ = О при постоянных
А/ и S. Это приводит к уравнению
О = j(^M - ДЛ/5/3 + CA/ln р^)р: 2/3 + сщ- 2/3 _ 2?,д^7/3р- i/з
A7.4.3)
534 Глава 17
Члены, пропорциональные С иО, дают небольшие поправки, зависящие от
р^, к соотношению A7.2.8) между s и ? ъ равновесном состоянии. В
результате равновесная масса ? теперь изменяется в зависимости от р^ при
фиксированном значении 5, как показано на рис. 17.1.
Неустойчивость возникает, когда д^Е/др^ = 0; в этой точке dM/dp^ =
= О, как видно на рис. 17.1. Дифференцирование уравнения A7.4.3) дает
О = -^{ам- вм'/^ + CMinpJp;^/^ - \смр;'/^ + \вм'/^р;^/\
A7.4.4)
Умножив уравнение A7.4.4) на C/2) р^ и сложив с уравнением A7.4.3),
получаем
О = \СМр;^/^ - \DM'/^p;'/\ A7.4.5)
или, записав р^ = p^j.^ для точки появления неустойчивости, приходим к
результату
'' ' A7.4.6)
(ЪСУ 1
\2d] л/""
Подставляя значения С и Z) из выражений A7.4.2), ? из A7.3.12) и s из
A7.2.8), получаем
k^kc'¦ X^jikfiY^* 1
= 1,996 X ??^? ^ г/смЗ. A7.4.7)
Используя уравнение A7.4.3) в A7.4.1), получим выражение для энергии в
равновесном состоянии
Е^^ = -ЪСМрУ^ + DM'/^py\ A7.4.8)
Равновесная энергия при появлении неустойчивости, согласно уравнениям
A7.4.5) и A7.4.7), равна
Е,^, = -DM'/V,Q = -3,583 X 10^^ эрг, A7.4.9)
и не зависит от М.
Упражнение 17.4. а) Найдите температуру в центре при появлении неустойчивости.
6) Найдите фактор красного смещения GM/Rc^ при появлении неустойчивости.
Ответы:
?;„, = B,49X10" К) ^, A7.4.10)
1/2
(f).„,-°H^)
Сверхмассивные звезды и черные дыры 535
Отметим, что, как следует из уравнения A7.4.11), максимальное
гравитационное красное смещение для устойчивой сверхмассивной звезды очень
мало — в интервале 10"^ — 10""*. Тем не менее, как и для белых карликов,
небольшие поправки за счет эффектов общей теории относительности
оказываются решающими при определении устойчивости системы, близкой к
ньютоновской.
17.5. ЭВОЛЮЦИЯ СВЕРХМАССИВНЫХ ЗВЕЗД
Попытаемся теперь проследить эволюцию сверхмассивной звезды, начиная
со сжатия большого диффузного водородного облака. Как показывает
уравнение A7.2.8), для равновесия сферической сверхмассивной звезды
требуется, чтобы значение энтропии на барион лежало в интервале 10^ — 10"*.
Это гораздо больше энтропии водородного газа в типичных примерах
астрофизической плазмы [см. уравнение A7.3.4)]. Поэтому начальный лциа-
мический коллапс должен быть диссипативным (столкновение фрагменюв
облака, турбулентность, ударные волны), чтобы возникла равновесная кон-
4я!гурация, которую мы обсуждали. Вагонер [592] рассматривал
альтернативную возможность, что еще до того, как энтропия возрастает,
становятся важными центробежные силы, обусловленные начальным моментом
количества движения, которые приводят к образованию сверхмассивного
диска.
Мы предполагаем, что температура в центре никогда не становится
настолько высокой, чтобы ядерное сгорание приобрело важное значение.
Простое сравнение скорости генерации ядерной энергии с фотонной
светимостью — уравнение A7.1.5) — показывает [636], что это допущение
обосновано при ? ^ 6 · \(f Л/0. В этом режиме можно также пренебречь
эффектом образования электрон-позитронных пар.
Как только сверхмассивная звезда возникла, ее эволюция сводится к
квазистатическому продвижению через последовательность равновесных
состояний с возрастающей центральной плотностью. Звезда излучает на
эддингтоновском пределе, масса ее по существу остается постоянной, а
энтропия и энергия уменьшаются. Когда энергия уменьшается от нуля до
^crit» плотность становится достаточно высокой для появления
неустойчивости, определяемой общей теорией относительности. Звезда претерпевает
катастрофический коллапс.
Описанную картину можно считать обоснованной, если характерное
время тепловой эволюции больше характерного гидродинамического
времени. Тогда звезда успевает перестраивать свою структуру, чтобы в
процессе эволюции всегда находиться в равновесии. Оценивая характерное
время тепловой эволюции, имеем
-1
i^ = 2,8xlO'*i-^j с. A7.5.1)
536 Глава 17
где использованы уравнения A7.1.5) и A7.4.9). Для гидродинамического
времени получаем
'hydro - (Gp.)"'^' = 2,7 ? lO-^j^j'^' с. A7.5.2)
где мы использовали уравнение A7.4.7). Два характерных времени
сравниваются при ? - 10^ ^0» вь1ше этого значения массы равновесная фаза
эволюции сверхмассивных объектов отсутствует. Отметим, что
равновесная фаза длится только 10 — 10^ лет при значениях массы в интервале
10^ — 10^ М^ .
Какова судьба сверхмассивной звезды, которая в процессе эволюции
достигла плотности, критической в отношении коллапса? Одна возможность
состоит в том, что с повышением температуры и плотности ядерные
реакции начинают протекать с высокой скоростью, приводя звезду к сильному
взрыву. Похоже [206], что это происходит со звездами, имеющими массу
? ^ 3 · 10^ Mq . Однако при больших значениях массы уже ничто не
может задержать коллапс: образуется черная дыра. На рис. 17.2 показано
образование такой черной дыры, согласно расчету на ЭВМ коллапса
сверхмассивной звезды с Л/ = 10^ М^^, выполненному Шапиро и Тьюколски
[533]. Представлена пространственно-временная диаграмма, где время от
ложено по вертикали в единицах времени пролета фотоном расстояния,
равного шварцшильдовскому радиусу GM/c^, а радиус отложен по
горизонтали в единицах шварцшильдовского радиуса. В качестве радиальной
координаты принят так называемый «изотропный» радиус, использованный для
упрощения расчетов на ЭВМ. В верхней части рисунка указана
эквивалентная шварцшильдовская радиальная координата Гу, соответствующая
окончанию вычислений. Координата г^ определена таким образом, чтобы
площадь сферической поверхности радиусом г^ равнялась s^ = 4??^. При
больших значениях г/М разница между г, г^ и обычной ньютоновской
радиальной координатой исчезает.
Пунктиром представлены мировые линии сферических оболочек
вещества, испытывающих сжатие к меньшему радиусу. Цифры около каждой
мировой линии указывают долю массы, находящейся внутри данной
оболочки. Сплошные линии обозначают выходящие радиальные световые лучи.
Штриховая линия — это горизонт событий (поверхность черной дыры; см.
гл. 12). Ему соответствует пара световых лучей, испущенных в разное
время при одном и том же значении радиуса, один из которых уходит на
бесконечность, а второй не уходит. Затененная часть рисунка внутри границы
черной дыры — это область «ловушечных поверхностей». В этой области
площадь сферической световой вспышки немедленно уменьшается из-за
влияния сильного гравитационного поля. Прямые линии со стрелками
показывают мировые линии радиально входящих и выходящих световых
лучей в отсутствие гравитационного поля. Траектории фотонов, излученных
вблизи черной дыры и внутри ее, отличаются от этих прямых, что
отражает йЛияние сильного гравитационного поля. Отметим, что горизонт
движется наружу к г^ = 2GM/c^ по мере того, как все больше вещества падает
Сверхмассивные звезды и черные дыры
2ЭЗ
162910
162900
162890
t/M
162880
162870 h
162В60
Рис. 17.2. Пространственно-временная диаграмма коллапса сверхмассивной звезды с
? = 10^Mq , ведущего к образованию черной дыры. Коллапс начинается с
неустойчивой равновесной конфигуращ1И Л, показанной на рис. 17.1. (Подробности
обсуждаются в тексте.) [533].
в черную дыру. Вертикальные асимптоты мировых линий частиц и
фотонов при г = О — это ложный эффект, связанный с координатной системой.
Основная особенность этого и других расчетов в том, что коллапс
гомологичен. По существу скорость изменяется линейно с радиусом, а
мгновенные фотографии профиля плотности в разные моменты времени
аналогичны друг другу по форме, хотя величина плотности возрастаете^
Вследствие гомологичной природы коллапса вся масса движется внутрь
когерентно, пересекая горизонт событий всего лишь за несколько пролетных
единиц времени, т.е. за несколько GM/c^. Такое когерентное движение при
столь коротком характерном времени может привести к заметному всплес-
^^ Решения такого типа называются также автомодельными. — Прим. перев.
538 Глава 17
ку гравитационного излучения, если коллапс сопровождается
несферическими возмущениями (вызванными, например, влиянием вращения или
магнитных полей). Формула квадрупольного излучения A6.2.16) как раз
показывает, насколько чувствительно испускаемое излучение к характерному
времени коллапса: АЕ ос т~^. Время пролета фотоном отрезка, равного
шварцшильдовскому радиусу для массы Af, представляет собой кратчайшее
характерное время, в течение которого возможны значительные изменения
в крупномасштабном распределении массы. Только при гомологичном
коллапсе г может приближаться к этому пределу. Если же вместо этого
вначале прокол лансирует центральная часть звезды, а далее последует
относительно медленная аккреция основной массы на центральную черную дыру,
то время коллапса г окажется намного более продолжительным и
гравитационное излучение будет значительно слабее.
Глава 18
Звездный коллапс и взрывы сверхновых
18.1. ВВЕДЕНИЕ И ПРЕДУПРЕЖДЕНИЕ
Наше обсуждение компактных объектов было бы неполным без
рассмотрения сверхновых. Как уже описывалось в разд. 9.1 и 10.1, для некоторых
астрофизиков не стало сюрпризом, когда пульсары в Крабовидной
туманности и в созвездии Парусов были обнаружены в остатках сверхновых. Еще в
1934 г. Бааде и Цвикки [31] показали, что гравитационной энергии,
высвобождаемой при коллапсе эволюционирующего звездного ядра в
нейтронную звезду, более чем достаточно, чтобы обеспечить энергией
наблюдаемые вспышки сверхновых. С тех пор многие исследователи рассматривали
коллапс и взрывы сверхновых как события, тесно связанные с
образованием нейтронных звезд (и, возможно, черных дыр).
В настоящее время имеется немало· косвенных свидетельств,
позволяющих считать рождение нейтронных звезд следствием коллапса и взрывов
сверхновых. Все расчеты эволюции невращающихся звезд с массами в
диапазоне 10 IS M/Mq is 70 показывают, что у таких звезд развивается
неустойчивое ядро, которое содержит примерно 1,5 Mq железа и
претерпевает динамический коллапс [16, 47, 601]. Оптические, радио- и рентгеновские
наблюдения расширяющегося газа, который имеется в остатках
сверхновых II типа, хорошо согласуются с предположением, что эти массивные
звезды разрушаются вслед за взрывом в ядре^\ Например, взрывной
ядерный синтез в массивной звезде позволяет объяснить относительное
содержание элементов между кислородом и элементами «железного максимума»
[18, 600], а также обогащенных нейтронами изотопов («г-процесс»).
Относительное содержание элементов в остатках сверхновых Кассиопея А [125]
и Корма А [103] свидетельствует, что составляющее их вещество
образовалось из оболочки массивной звезды. Кривые блеска сверхновых II типа
хорошо согласуются с моделью, предусматривающей импульсное выделение
энергии порядка 10^^ эрг внутри внешней оболочки проэволюционировав-
шей массивной звезды, достигшей стадии красного гиганта [21, 122, 124,
235, 346]. Энергия взрыва гораздо меньше энергии гравитационной связи,
высвобождающейся при коллапсе ядра в нейтронную звезду:
^в.-^^
'x'o'l^Kio^) '''¦ <"¦'¦"
^^ Наблюдатели делят сверхновые на два типа. В этой главе будут
рассматриваться только сверхновые II типа, возникающие, как считают, в результате
коллапса массивных звезд (Л/ > 8Л/^). Сейчас полагают, что сверхновые I типа возникают
при полном взрыве вырожденного ядра звезды с массой 4 ^ М/М^ ^ 8, который
не образует заметного остатка.
540 Глава 18
Однако самый важный аргумент — это отождествление пульсаров,
которое явно свидетельствует, что внутри молодых остатков сверхновых
находятся нейтронные звезды.
Существует, правда, одна деталь, вносящая дисгармонию в эту
последовательную во всех других отношениях картину: ни один из современных
численных расчетов, моделирующи?^ гравитационный коллапс звездного
ядра, не приводит к взрыву! Некоторые теоретические модели,
разработанные в течение многих лет исследования этой проблемы, предсказывали
взрывы, следующие за коллапсом ядра [15, 89, 144, 294, 513, 617, 619].
Однако последние результаты моделирования, основанные на более ясном
понимании привлекаемых сложных физических процессов, не позволяют
прийти к выводу об одновременном образовании газового остатка и
нейтронной звезды.
Если принять во внимание достаточно сложную физику коллапсирую-
щего звездного ядра и трудность численных расчетов, то не удивительно,
что определение конечного этапа эволюции массивных звезд оказалось
одной из самых сложных проблем теоретической астрофизики. Один из
источников затруднений связан со сложным глобальным взаимодействием
гравитационных и гидродинамических сил, с одной стороны, и процессом
переноса нейтрино — с другой. Кроме того, существуют еще не вполне
ясные детали в наших представлениях о микрофизике горячего и плотного
вещества. Поэтому понятно, почему вплоть до настоящего времени
практически всем расчетам моделей коллапса ядра и взрыва сверхновых присущи
те или иные известные недостатки, которые потенциально могут влиять
на конечный результат моделирования.
Если вспомнить бурную историю исследования коллапса и
противоречивые результаты его расчетов за последние 15 лет, то очевидно, что
рассматривать несовершенные современные модели как точные было бы
крайне преждевременным. Их предварительный характер становится
совершенно ясным, если вспомнить, что в этих вычислениях мы имеем дело с
веществом, плотность которого близка к ядерной, и что они обычно
ограничиваются сферическими невращающимися немагнитными конфигурациями.
По этой причине, а также из-за общего недостатка места наше обсуждение
коллапса сверхновых будет достаточно кратким. Мы сосредоточим
внимание на нескольких важнейших физических идеях, лежащих в основе наших
представлений о коллапсе звездного ядра, а не на конкретных моделях.
Поскольку не исключено, что даже это обсуждение в самом ближайшем
будущем станет устаревшим, мы рекомендуем читателю ознакомиться с
текущей литературой по проблеме коллапса и сверхновых ^\
^^ Исторический обзор ранних (до 1970 г.) моделей коллапса ядра и взрыва
сверхновой с обсуждением некоторых процессов с участием нейтрино, которые
учитываются в этих моделях, имеется в книге Зельдовича и Новикова [636]. Обзор более
новых работ (до 1983 г.) с акцентом на соответствующие уравнения состояния
горячего плотного вещества дан в [19, 347]. Современный анализ проблемы
гравитационного излучения, возникающего при коллапсе звездного ядра, содержится в обзорной
статье E45); см. также гл. 16.
Звездный коллапс и взрывы сверхновых 541
18.2. НАСТУПЛЕНИЕ КОЛЛАПСА
{Сак сейчас полагают, в недрах массивных звезд (8—10 ^ M/Mq islO) в
течение - Ю'' лет эволюции происходит термоядерное сгорание все более и
более тяжелого ядерного горючего. Этот процесс начинается с синтеза
водорода в гелий (температура начала горения Т^ jg - 2 · Ю'' К), протекает
при последовательно возрастающих температурах благодаря сгоранию
^Не, ^^С, ^^О, ^е и ^^i (температура начала горения Т^^ ig ^ ^ · 10^ К) и
завершается образованием ^^Fe — ядер с максимальной энергией связи на
нуклон. Практически все расчеты этого процесса показывают, что у
эволюционирующих массивных звезд образуются центральные ядра с массой
Л/роге ^ 1,5 ?/q, которые состоят в основном из элементов группы железа
и удерживаются в равновесии прежде всего давлением вырожденных
электронов.
Арнетт [19] предложил простое объяснение того, почему все модельные
расчеты эволюции массивных звезд приводят к сходным конечным
состояниям («конвергенция ядер»). Из-за большого градиента температуры (т.е.
градиента энтропии) тепло в ядре передается в основном путем конвекции.
Если устанавливается конвективный режим, то возникают течения,
которые перемешивают вещество ядра и выравнивают температуру^^ По этой
причине ядро относительно однородно по составу.
Обратим теперь внимание на уравнение состояния, в котором главную
роль играют электроны:
? ? кТ
^^^^^^-^К^ГУ-'. A8.2.1)
? ^в
Уравнение A8.2.1) представляет собой приближенную интерполяцию
между описаниями газа Максвелла—Больцмана и вырожденного вещества.
Здесь ?? = п^/п — число электронов на барион, а /Ср — постоянная для
нерелятивистского (Г = 5/3) и крайне релятивистского (Г = 4/3) пределов
вырождения (см. разд. 2.3). Для сферической конфигурации с массой Л/ и
радиусом R уравнения гидростатического равновесия C.2.1) и C.2.2)
требуют выполнения приближенного соотношения
??^^^^???'/^??\ A8.2.2)
где индексом «с» отмечены значения величины в центре, а
/ — структурный множитель, зависящий от эффективного показателя по-
^^ В работе [135] приводится обсуждение конвекции и вывод критерия Шварц-
шильда [514] для конвекции KdT/dr)^^,^^\ > \{dT/dr),^^ I, где idT/dr)^^,^^—
фактический градиент температуры в недрах звезды, а (dT/dr),^^ = (Г/Р)A - \/T)dP/dr —
так называемый адиабатический градиент температуры; Г — показатель адиабаты.
Ясно, что, если температура изменяется с расстоянием слишком быстро, возникает
конвекция.
542 Глава 18
литропы или от зависимости плотности от радиуса. Комбинация
уравнений A8.2.1) и A8.2.2) дает
MIl^fGM'/?' - K^YeVc-'^ A8.2.3;
Рассмотрим теперь максимальную температуру, которая возможна для
конфигурации с данной массой. Результат укажет, какая масса требуется
для поджига данного вида ядерного горючего.
При больших значениях ? в правой части уравнения A8.2.3) главную
роль играет первый член, так что Т^ ос рУ^. Следовательно, в этом случае
непрерывное сжатие приводит ко все более высоким температурам, так
что со временем загорается любое горючее. Однако при малой массе и
Г > 4/3 температура Т^ снижается до нуля, когда плотность ?
увеличивается до
?,„,-=?-^ . (.8.2.4,
При р^ < p^rij имеем Т^ ос рУ^М'^^^, хотя большие значения р^ не имеют фи-
зическога смысла (Т^ < 0). Таким образом, в этом случае конфигурация в
процессе сжатия проходит через максимум Г, а затем охлаждается, когда
равновесие поддерживается давлением вырожденных электронов. Какой из
этих вариантов эволюции реализуется для данной конфигурации, зависит
от соотношения ее массы и предельной массы Чандрасекара, для которой в
уравнении A8.2.3) т; = О, а Г = 4/3:
(К \^^^
^сь = I -^) У' - 5,83У/Мо A8.2.5)
[сравните с уравнением C.3.17)]. Реакции между ядрами кремния —
последний этап сгорания ядерного топлива — начинаются при высоких
температурах кТ ^ 0,6 т^с^. Поэтому неудивительно, что для достижения столь
высоких максимальных температур и начала горения кремния требуется
масса с Mgj jg - M(^j^. Если после исчерпания более легких элементов в
ядре окажется, что Л/^оге *^ ^Si, ig» '^^ реакции с участием кремния начнутся
не раньше, пока сгорание легких элементов в оболочке не приведет к
увеличению Mcore· Поскольку В начале сгорания кремния У^ = 0,42 [сравните с
уравнением A8.2.7)], условие завершения ядерного синтеза в центре звезды
выглядит следующим образом^^:
'^ В звездах малой массы с полной массой Л/ ^ 1,2Mq ядерное горение не может
дойти до завершения, поскольку требуемые для этого высокие температуры не
достигаются. Такие звезды образуют белые карлики, недра которых состоят из несго-
ревших '^С и ^? (см. гл. 3.)
Звездный коллапс и взрывы сверхновых 543
Л/со. ^ Msi,i, « МсЛУе - 0,42) « 1,2Л/о. A8.2.6)
Если же, напротив, Л/^оге ^ ^Si, ig "^ некоторой более ранней стадии
эволюции массивной звезды, гидростатическое сжатие будет продолжаться до
достижения достаточно высоких центральных температур. Между
последовательными этапами ядерного синтеза важную роль играет нейтринное
охлаждение вблизи центра, сильно зависящее от температуры Т.
Нейтринное охлаждение уменьшает энтропию, приводя к положительному
градиенту энтропии в ядре. Влияние этого эффекта в конечном счете заключается в
подавлении роста конвективного ядра на каждой последовательной стадии
ядерного синтеза, что приводит к сокращению области, в пределах
которой происходит химическое перемешивание. Термоядерный «пепел» будет в
этом случае заключать в себе меньшую массу, чем содержалась в
начальном невыгоревшем ядре.
При любом сценарии эволюции, т.е. независимо от того, превышает ли
отношение A^core^^ch единицу до начала сгорания кремния или нет,
конечный ее результат состоит в приближении Л/^оге ^ ^сь- Этот факт
подтверждается всеми детальными расчетами эволюции. Вещество звездного
ядра («пепел» от сгорания кремния) состоит в основном из обогащенных
нейтронами ядер группы железа (т.е. ^^е, ^^, ^Fe, ^^Ni и т.п.).
Таким образом, звезда с массой 15 М^ будет иметь к началу коллапса
ядро с массой около 1,5 Mq, а значения температуры Т^ ^, плотности р^ у,
доли лептонов в центре У^ ^ и энтропии на барион s^ приближенно
определяются следующими соотношениями^^:
^^соге - 1,5Мо > Mch. A8.2.7)
Т; ,^ 8^0 X 10^ к = 0,69 Мэв/к
р, , « 3^7 X Ю^г/см^
П.-0,42
syk « 0,91 j
После сгорания кремния сочетание двух разных физических эффектов
подводит ядро звезды к состоянию динамической неустойчивости и
возникновению гравитационного коллапса. Вначале коллапс стимулируется
частичной диссоциацией ядер железа. При этом расходуется энергия связи
ядер и в результате понижается давление. По мере развития коллапса
растет плотность, увеличивая химический потенциал электронов. Это
приводит к нейтронизации ядра по мере того, как электроны захватываются
находящимися в ядрах протонами (см. разд. 2.6 и 8.2). Как диссоциация, так
и нейтронизация уменьшают показатель адиабаты для звездного вещества
до значений ниже 4/3, приводя тем самым к коллапсу.
^^ См. [17, 601]. Отметим, что чем дальше от центра ядра, тем ниже плотность и
температура, в то время как энтропия слегка выше, чем в центре, но во всем ядре
близка к единице. Поскольку величины s и ?^ изменяются в пределах ядра
незначительно, индекс «с» у этих переменных отброшен.
544 Глава 18
18.3. ФОТОДИССОЦИАЦИЯ
Частичная фотодиссоциация ядер на альфа-частицы при высоких
температурах изучена достаточно хорошо [92, 280]. При больших значениях Тир
реакции, связанные с сильными и электромагнитными взаимодействиями, идут
достаточно быстро и протекают по существу в равновесии с обратными
реакциями. Расщепление ядра 2бРе — типичный пример таких процессов:
у+^^Ре?± 13а+ 4/1. A8,3.1)
Требуемая для этого процесса энергия равна
Q == с^{\Ът^ + 4w„ - wpe) == 124,4 МэВ. A8,3.2)
В равновесии уравнение B.1.10) дает для реакции A8.3.1)
Мре= 13I1, +4?„, A8.3.3)
где ?^ — химический потенциал частиц /-го типа. При интересующих нас
температурах и плотностях ядра и нуклоны оказываются
невырожденными, так что применима статистика Максвелла—Больцмана:
кТ
A8.3.4)
[сравните с уравнением B.3.31)]. Напомним, что для систем с внутренними
степенями свободы (скажем, ядро, имеющее возбужденные состояния)
статистический вес g^ является функцией ядерного распределения по
состояниям (см. упражнение 2.8):
g, = IB/,+ l)e-^'/*^ A8.3.5)
где Ij. — спин г-го возбужденного состояния, а ?^ — энергия возбуждения.
Для температур ^ 1 МэВ можно положить g^ = 1 (основное состояние;
/ = 0), ^^ = 2 (свободный фермион; / = 1/2) и gp^ = 1,4 (основное
состояние с / = О плюс низшие возбужденные состояния) [281].
Подстановка уравнения A8.3.4) в A8.3.3) приводит к уравнению Саха
для равновесного соотношения между альфа-частицами, нейтронами и
ядрами железа:
« = Щж_\'Ча^'\-,,.г A8.3.6)
С точностью луч те \Щ можно заменить массу ядер с атомным весом Л на
Л/Г7^, так что
Звездный коллапс и взрывы сверхновых 545
n''nt 2« ??????'
*а *п
(ff) ''^'" <·'¦'¦"
'^Fe E6Г'A.4)\ 2
Если предположить, что ядро ^^е наиболее распространенное из тяжелых
ядер, то из A8.3.1) следует
? = —п A8.3.8)
13 "
Уравнения A8.3.7) и A8.3.8) позволяют вычислить степень диссоциации для
любого значения ? и Т.
Упражнение 18,1, Покажите, что вещество, состоящее из ядер ^^^е, альфа-частиц и
нейтронов, будет состоять наполовину (по массе) из ядер железа ^^^е и наполовину
из альфа-частиц и нейтронов при условии
Igp = 11/,2+ Ь5%7;-^Д, A8.3.9)
где /О — плотность в г/см^, а Г^ — температура в единицах 10^ К [281].
В соответствии с уравнениями П8.3.9) и A8.2.7) для 50<^)-ной диссоци-
ции при плотности в ядре, близкой к р^ ^, требуются температуры порядка
Тд ^ 11, ЧТО ненамного выше Т^ /. Поэтому неудивительно, что коллапс
начинается, когда ядрр с массой 1,5Л/0 вступает в этот физический режим.
При несколько более высоких температурах (но при тех же плотностях)
происходит фотодиссоциация альфа-частиц на нуклоны посредством реакции
? -Ь^^Не^^ 2р + In, A8.3.10)
Энергия, ?peбyQмaя для этого процесса, равна Q' = 28,30 МэВ. Поскольку
энергия образования каждой новой частицы, возникающей в результате
реакции A8.3.10) (??? =4-1 = 3; Q'/^N = 9,5 МэВ), больше, чем энергия
на новую частицу, созданную посредством реакции A8.3.1)
(AN = 13 + 4 - 1 = 16; Q/AN = 7,7 Мэв), для диссоциации ^Не
требуются более высокие температуры, чем для диссоциации ^^е. Таким образом,
существует область температур, где ^^е диссоциирует на ^Не, но ^Не не
диссоциирует на свободные нуклоны.
19-513
546 Глава 18
Упражнение 18.2. а) Покажите, что соответствующее уравнение Саха для
диссоциации альфа-частиц на нуклоны имеет вид
б) Вычислите температуру Т* для 50<7о-ной диссоциации:
1) ^^^е на ^Не и свободные нейтроны; 2) ^Не на нуклоны — при ? = ^0^ г/см^ и при
о — ?
Ответ: При ? = 10^ г/см^ Т*{^^е) = 9,6, Г*(^Не) = 15,2.
При любом реалистическом вычислении надо рассматривать полный
набор ядер, — устойчивых и неустойчивых, — которые при высоких
температурах и плотностях находятся в ядерном статистическом равновесии
(ЯСР). Типичные реакции имеют вид
{?, А) + ? ^ {? + \,А + 1) + ?
(Z,^) + /i^(ZM + l) + y, A8.3.12)
сюда относятся также реакции типа (а, ?), (?, ?), (?, /?), (?, ?) и т.п. При
наступлении коллапса ядра и нуклоны нередко рассматриваются
приближенно как идеальный нерелятивистский газ Максвелла—Больцмана, так
что для каждого типа частиц применимо уравнение A8.3.4). Для каждой
реакции, входящей в соответствующую цепочку, применимо условие
равновесия B.1.10). Однако, поскольку все возможные реакции типа A8.3.12)
находятся в равновесии, имеется только два независимых химических
потенциала, удовлетворяющих условиям сохранения заряда и числа барионов.
Обозначая их как ?^ и ?^, получаем соотношение
?{?, А) = ??^ + (А - ?)?„ A8.3.13)
В качестве условия ядерного статистического равновесия.
Далее уравнение A8.3.4) дает
2
«, = ?{?, А) = il|iiif^„^^-^exp
где
QiZ,A)
кТ
,A8.3.14)
Q{Z, А) = c^[Zmp + {А- Z)m„ - M{Z, А)] A8.3.15)
— это энергия связи ядра, а g(Z, Л) — ядерная функция распределения по
состояниям A8.3.5) и
Звездный коллапс и взрывы сверхновых 547
\ 2??^ I
Чтобы определить л и п„, можно воспользоваться условием
сохранения заряда и числа барионов
^„ Л, ==-2- = и, A8.3.17)
??.?^-??,, A8.3.18)
где ?^ — среднее число электронов на барион. Таким образом, из
соотношений A8.3.14) — A8.3.18) очевидно, что в ЯСР химический состав,
уравнение состояния, удельная энтропия и т.п. можно определить, если заданы
три величины: р, Г и ?^ [186]. В приложениях к описанию звездной
эволюции или расчетам коллапса величина ?^ определяется для любого момента
из предыдущей истории эволюции. На ранних стадиях эта история
включает в себя термоядерный синтез тяжелых элементов из легких,, что влияет
иа ??. Для более поздних стадий, следующих за сгоранием кремния, эта
величина определяется нейтронизацией (см. разд. 18.4).
Упражнение 18.3. Определяя состав с учетом единственной реакции, описываемой
уравнением A8.3.1), мы не задавали величину У^, а наложили ограничение
я„ = 4/13/7^. Покажите, что оно эквивалентно условию У^ = 26/56 = 0,464.
Как подчеркнул Арнетт [19], анализ полного набора реакции в
состоянии ЯСР при высоких плотностях, достигаемых во время коллапса
звездного ядра, осложняется рядом факторов. В их число входят:
1) неопределенность значений g^ и Q для экспериментально
неисследованных ядер, находящихся вдали от области бета-устойчивости;
2) необходимость внесения поправок, связанных с конечным размером
^дер и ядерной поверхности, а также с кулоновской энергией;
3) необходимость учитывать эффекты нуклонных взаимодействий и
вырождения нейтронов при высокой плотности ^\
В последних работах по уравнению состояния горячего плотного ве-
ttiecTBa, возникающего при коллапсе звездного ядра, основное внимание
выло сосредоточено именно на этих вопросах [66, 187, 334].
^^ Обсуждение этих факторов в случае плотного вещества при Г = О см. в гл. 2
И 8.
548 Глава 18
18.4. НЕЙТРОНИЗАЦИЯ И ИСПУСКАНИЕ НЕЙТРИНО
По мере того как плотность звездного ядра возрастает, высокая энергия
Ферми электронов стимулирует их захват атомными ядрами и свободными
протонами (нейтронизация). Это приводит к снижению ?^ и уменьшению
вклада вырожденных электронов в полное давление, удерживающее ядро
звезды от гравитационного коллапса. В конце концов чандрасекаровская
масса Mq^{ Y^) — максимальная масса, которая может быть поддержана
давлением вырожденного электронного газа, — становится меньше массы
звездного ядра [см. уравнение A8.2.5)]. Начиная с этого момента коллапс
звездного ядра начинает развиваться по-настоящему. По мере того как
плотность еще более возрастает, происходит все больше захватов
электронов протонами, давление (и разность Г - 4/3 < 0) падает все сильнее и
коллапс ускоряется. В процессе нейтронизации испускаются нейтрино и по
крайней мере в начале процесса многие из них уходят наружу.
Нейтрино образуются во время коллапса как вследствие
нейтронизации, так и в результате теплового излучения. Тепловые механизмы
осуществляются посредством аннигиляции реальных и виртуальных электрон-
позитронных пар с излучением пар ии. Если нейтринная пара уходит из
системы, число лептонов в звездном ядре остается неизменным. Наиболее
важны следующие процессы теплового излучения:
1. Аннигиляция пар
(И/, Z)
е^-^е- -^ p-^v, A8.4.1)
2. Распад плазмонов
3. Фотоаннигиляция
(возбуждение плазмы) — и-\- и. A8.4.2)
Ч- ? ^ е~+ V + р, A8.4.3)
4. Тормозное излучение
i^V ?)
e-^{Z,A) ^ {Z,A)^e-+v^v. A8.4.4)
Все указанные выше процессы могут осуществляться посредством
заряженных токов с обменом заряженными векторными бозонами {W"^) и
посредством нейтральных токов с обменом векторными мезонами ? (см. гл.
11). Например, в случае е"^е"-аннигиляции (реакция 1) пара электронных
нейтрино ?^?^ может быть создана путем обмена либо ?-, либо W"^-
мезонами. Однако мюонные и тау-нейтринные пары ? ? и ?^?^ (либо
нейтринные пары, связанные с «тяжелыми лептонами», если они
существуют) могут быть получены только благодаря обмену Z-мезонами. Скорости
приведенных выше реакций были рассчитаны в работах [163, 164] с
использованием теории слабых взаимодействий Вейнберга—Салама—Глэшоу.
Отметим, что «плазмой» — это квантованная электромагнитная волна,
распространяющаяся в плотной диэлектрической плазме. Он ведет себя как ре-
Звездный коллапс и взрывы сверхновых 549
лятивистская бозе-частица с массой покоя гп^^^ = Ныр/с, где ? ? —
плазменная частота. В отличие от свободного фотона плазмон энергетически
неустойчив к распаду на пару нейтрино — антинейтрино из-за этого
«избытка» энергии массы покоя.
В типичных случаях тепловые процессы с излучением нейтрино
преобладают в ядре массивной звезды до тех пор, пока коллапс не набрал полную
скорость. Они важны также во время последних стадий коллапса, когда
способствуют уносу тепловой энергии из внешних областей звездного ядра,
нагретых ударной волной. Нейтрино, образующиеся при тепловых
процессах, обладают энергиями Е{у) порядка кТ,
Среди реакций нейтронизации наиболее важны следующие:
1. Захват электронов атомными ядрами
е-+ {?,?) ^?^^{?- \,А). A8.4.5)
2. Захват электронов свободными протонами
е~+Р -^?^ + ?, A8.4.6)
Обе из приведенных выше реакций протекают посредством заряженных
токов. Матричный элемент реакции A8.4.6) хорошо известен: процесс
тесно связан с распадом свободного нейтрона, уже проанализированным нами
в разд. 11.4 [см. уравнение A1.4.9)]. Однако в процессе коллапса нуклоны и
атомные ядра образуют невырожденный нерелятивистский ферми-газ, за
исключением области самых высоких плотностей, когда нейтрино уже не
покидают ядро звезды. Таким образом, в отношении нейтронизации
коллапс отличается от более поздней и продолжительной стадии остывания
теплой нейтронной звезды, обсуждавшейся в главе 11. Для этой стадии,
следующей за коллапсом, характерны температуры, которые заметно ниже
1 МэВ, и нерелятивистский, но сильно вырожденный газ нуклонов, так что
приведенные выше реакции нейтронизации сильно подавлены.
Во время коллапса большинство нуклонов остаются связанными в
тяжелые ядра, как рассматривается ниже в разд. 18.6. Массовое число Л, число
протонов ? и число нейтронов {Л — ?) возрастают с увеличением
плотности и снижением У^. Поэтому захват электронов свободными протонами
ограничен из-за низкого содержания свободных протонов. Кроме того,
захват электронов атомными ядрами ограничивается высокими пороговыми
энергиями, которые возрастают по мере того, как ядра становятся все
более насыщенными нейтронами. К тому же только «валентные» протоны
способны испытывать переходы в «сверхразрешенные» состояния. В
соответствии с названием «сверхразрешенные» распады не только разрешены в
том смысле, что не изменяют орбитальные угловые моменты нуклонов в
атомных ядрах, но и к тому же ядерный интеграл перекрытия [сравните,
например, с уравнениями A1.4.2) или A1.5.8)] равен практически единице.
Достаточно надежные расчеты оболочечной модели захвата электронов
атомными ядрами промежуточной и большой массы только еще выполня-
550 Глава 18
ются [213, 214, 215]. В работе [213] было показано, что захват электронов
ядрами подавляется, когда число нейтронов N = А — ? превосходит 40. В
этом случае нейтронная оболочка в конечном состоянии оказывается
заполненной и разрешенные переходы Гамова—Теллера в это состояние не
происходят. Последствия этого блокирующего эффекта нейтронной оболочки
для коллапса звездного ядра еще полностью не исследованы. Однако
предварительный анализ [212, 591, 630] говорит о том, что скорость захвата
электронов атомными ядрами сначала быстро растет {р % 10^^ г/см^), но в
конечном итоге подавляется, что приводит к преобладанию реакции
A8.4.6) над реакцией A8.4.5) и к снижению общих темпов нейтронизации.
Как только коллапс набрал скорость, нейтронизация становится
наиболее важным механизмом образования нейтрино. Нейтронизация уменьшает
У^, понижает электронное давление и оказывает влияние на ядерное
статистическое равновесие. Средняя энергия нейтрино, образующихся при
электронном захвате, сравнима с электронной энергией Ферми:
(?(г)> - <?,_> - ?^ = 51,6(У,р,2)'^'мэВ. A8.4.7)
где ? 12 — плотность в единицах 10^^ г/см^. [Соотношение A8.4.7) следует
из B.3.1) и B.3.15) при ? - \, Заметим, что обозначение ?~ ^ в уравнении
B.3.15) соответствует в нашем случае ?^ и не относится к химическому
потенциалу.]
Вычислим теперь скорость захвата электронов свободными протонами,
т.е. реакцию A8.4.6). Это вычисление выполняется легче, чем для захвата
электронов атомными ядрами, и к тому же оно дает верный порядок
величины для полной скорости захвата. Воспользуемся методом возмущений и
матричным элементом слабых взаимодействий, которые применялись в
разд. 11.4 для определения скорости распада свободного нейтрона. Примем
сразу же, что нуклоны остаются нерелятивистскими и невырожденными.
Это предположение справедливо для всех стадий коллапса горячего
звездного ядра, за исключением самых последних. (В частности, это условие
удовлетворяется в начальной фазе падения вещества внутрь, когда
высвобождающиеся нейтрино могут свободно покинуть коллапсирующее
звездное ядро.) Можно вновь использовать нерелятивистское приближение
«золотого правила», чтобы получить скорость захвата при заданных
начальных состояниях протона и электрона:
?^=?[\ ? |Я/,|^]A-Л)р,./?,в(?, +?-?,).A8.4.8)
\ Spins I
Различные члены, появившиеся в уравнении A8.4.8), уже были определены
в разд. 11.5 и 11.4. В частности, матричный элемент дается уравнением
A1.4.9), а плотность конечных состояний нейтрино — посредством
уравнения A1.4.14) с использованием условия сохранения энергии в виде
К = ^е- б» A8.4.9)
Звездный коллапс и взрывы сверхновых 551
Используем снова нормировку на ящик единичного объема. Величина
(/ - Л) — нейтринный «блокирующий фактор», дающий долю незанятого
фазового объема нейтрино. Как для электронов, так и для нейтрино
примем равновесное распределение Ферми—Дирака
/ = F ^- ^ . A8.4.10)
' ехр[(?,.-д,)ДГ] + 1
Уравнение A8.4.10) неприменимо для нейтрино, пока они не будут
захвачены в ядре звезды и их плотность не вырастет. Однако, хотя вплоть до
этой стадии нейтрино легко ускользают их ядра и, следовательно, не тер-
мализованы, предполагается, что /^ < 1, так что детальный вид их более
раннего распределения не имеет значения. Подстановка различных
множителей в уравнение A8.4.8) приводит его к виду
^Г = ^GlCU^ + За'){\ -fr):r^,HE, + Q-E,) dE,.
A8.4.11)
Чтобы найти полную скорость реакции в расчете на один протон,
выполним интегрирование по всем начальным состоянием электрона и по с/Е^ с
учетом выражения A1.4.11) для плотности электронных состояний. В
результате получим
A8.4.12)
где
S^W-fJ. A8.4.13)
Используя ?-функцию для интегрирования по dE^, найдем
?=^^??1^/, A8.4.14)
где
^ - ?^?,???} - тУУ'\Е, - QYS. A8.4.15)
Вычислим интеграл / для начальных стадий коллапса, когда электроны
предельно релятивистские и вырожденные (Е^ > т^с^\ ?^> кТ), а
нейтрино свободно покидают звездное ядро (/^ < 1). Поскольку /^ « О для
^е > ?^? ЭТОМ пределе, получим
552 Глава 18
I = f'dE.E^iE, - QY = f'dE.Et = \?\. A8.4.16)
Jq Jq D
Упражнение 18.4. Оцените I в предельном случае низких температур,
соответствующем поздним стадиям коллапса, когда нейтрино оказываются захваченными в ядре
звезды. В этом режиме Е^ > т^с^у ?^> кТ и ?^ > кТ.
Ответ:
/= Г dEAE^-QYE^
¦'Q+?.
Скорость захвата электронов свободными протонами в расчете на ели
/1ножением Г
dn^ dn
ницу объема находится умножением Г на концентрацию протонов ? :
____..-„д. ,,8.4.,7)
Разделив A8.4.17) на а?, с учетом соотношений A8.4.14) и A8.4.16) получим
Упражнение 18.5. Какова средняя энергия нейтрино, испускаемых при электронном
захвате? [Предположите условия, совместимые с уравнением A8.4.16).]
Указание: <Е > = f E^dT/T.
Ответ:
где {Е^) — средняя энергия электронов в релятивистском море Ферми.
Упражнение 18.6 а) Оцените численно скорость электронного захвата A8.4.14) для
предельно релятивистских вырожденных электронов и свободно ускользающих
нейтрино.
б) Подсчитайте соответствующую нейтринную светимость на протон.
Ответ:
а) Г. = 6,29 X 10^1(-^^] с-' · протон-·.
Звездный коллапс и взрывы сверхновых 553
б) L, = 5Л5 X 10 ^^:^(-^ I эрг/(с протон),
' 6 I т,с^ 1
18.5. НЕПРОЗРАЧНОСТЬ И ЗАХВАТ НЕЙТРИНО
Для каждого процесса излучения нейтрино существует обратный процесс,
соответствующий поглощению нейтрино. Как поглощение, так и рассеяние
препятствуют ускользанию нейтрино из коллапсирующего звездного ядра.
Наиболее важные процессы таковы:
1. Рассеяние на свободных нуклонах
(Z)
(^)
v-^p^v+p, A8.5.1)
2. «Когерентное» рассеяние тяжелыми атомными ядрами (А О 1)
(Z)
v + {Z,A)^v + {Z,A), A8.5.2)
3. Поглощение нуклонами
v^-^n^ р + е , A8.5.3)
4. Рассеяние нейтрино на электронах
e'-l· ? -^ е~Л· V. A8.5.4)
Аналогичные процессы возможны и для антинейтрино. Два первых
источника непрозрачности существуют благодаря нейтральным токам и не
рассматривались всерьез до создания теории слабых взаимодействий Вейн-
берга—Салама—Глэшоу. Их полные сечения, измеренные в системе
координат покоя вещества, определяются соотношениями^^
«^««?^??;^), Е,<кт„с\ A8.5.5)
^^ Соотношения A8.5.5) и A8.5.6) наряду с сечениями для других
преобладающих источников нейтринной непрозрачности можно найти в работе [579].
554
Глава 18
для рассеяния на свободных нейтронах и
^coh i_„
тх'-
l-4 + Dsin^^,-lL
?„ «: 300^-^/^ МэВ
A8.5.6)
для когерентного рассеяния, где о^ = 1,76 · 10""*^ см^ следует из
выражения A1.7.3), а ^^^ — угол Вейнберга, измеренное значение которого
приведено в A1.3.2). Для нейтрино низких энергий (т.е. Е^ < ^rf^^ рассеяние на
нуклонах и атомных ядрах становится упругим: начальные и конечные
энергии нейтрино почти равны. Кроме того, как впервые было отмечено
Фридманом [205], нейтрино могут также когерентно рассеиваться
атомными ядрами, причем сечение рассеяния пропорционально квадрату атомной
массы Л^, как видно из A8.5.6). Такое рассеяние когерентно в том смысле,
что атомное ядро действует нелинейно как одна частица, а не просто как
группа из А отдельных нуклонов. Существование тяжелых ядер при
высоких плотностях делает когерентное рассеяние преобладающим источником
непрозрачности во время «горячего» коллапса звездного ядра.
Роль реакций с нейтральными токами состоит в том, что они
увеличивают непрозрачность для нейтрино без существенного изменения
интенсивности излучения. Таким образом, реакции с нейтральными токами
подавляют перенос нейтрино в коллапсирующих звездных ядрах и усиливают
захват нейтрино.
В отличие от рассеяния на нуклонах и атомных ядрах рассеяние
нейтрино на электронах оказывается неупругим и изменяет энергию нейтрино в
системе координат, где звезда покоится. Неупругий характер ? ^ е-
рассеяния является следствием малой энергии, соответствующей массе
покоя электрона, так как обычно Е^ > т^ср-. Столкновения между нейтрино и
вырожденными электронами могут приводить к заметным потерям
энергии нейтрино. Нейтрино высоких энергий (Е^ > ?^) могут
взаимодействовать с электронами, находящимися на большой глубине в море Ферми.
При таких взаимодействиях полная энергия, приближенно равная ?^, в
среднем делится пополам между электроном и нейтрино. Для нейтрино
малых энергий (Е^^ < ?^) эффект электронного вырождения очень важен.
Казалось бы, нейтрино могут набирать энергию при таком взаимодействии,
что должно приводить к равнораспределению энергии. Однако электрон с
энергией Е^ < ?^ не может терять энергию. В результате, чтобы в конце
концов реакция все же протекала, нейтрино малых энергий с Е^ < ?^ могут
терять даже больше половины своей энергии в каждом акте рассеяния.
Поэтому такой процесс весьма важен для термализации нейтрино и
способствует их приведению к локальному равновесию, когда они «заперты» в
Звездный коллапс и взрывы сверхновых
555
звездном ядре при высоких плотностях. Сечение рассеяния не^^трино малых
энергий на вырожденных электронах приведено в соотношении A1.7.2).
Поглощение нуклонами — процесс, обратный нейтрон и зации, также
вносит вклад в термализацию нейтрино. Сечение поглощения нейтрино
свободными нерелятивистскими нейтронами ?^^ может быть вычислено еще
раз из известного матричного элемента заряженного тока для распада
свободного нейтрона [см. уравнение A1.4.9)]. Скорость реакции A8.5.3) на
нейтрон определяется выражением
а„с = jdV = ^[GlCl{\ + 3a')]fp,dE,i\ -feLE, + Q- ?,),
A8.5.7)
где снова предполагается, что падающие частицы и и ? заключены в ящик
единичного объема. С помощью уравнений A1.4.11) и A8.4.10) уравнение
A8.5.7) может быть проинтегрировано, что дает
0« = ??
где
A + 3fl2)c
WX"
-I
-#'-
mx
2\2
1/2
1{Е, + Q)^
A8.5.8)
/(?, + ?) - 1 ^^р^^^^ ^ ^ _ ^^^^^^^ ^ J . ^jg 3.9)
Для предельно вырожденных и ультрарелятивистских электронов
ограничивающий множитель / переходит в ехр(- ?/кТ) при Е^ < ?^? в единицу
При Е^ ^ ?^, что отражает важную роль вырождения электронов в
сдерживании поглощения нейтрино при низких энергиях.
Упражнение 18.7. Покажите, что сечение поглощения антинейтрино в процессе
ifg + ? -^ ? + е'^ можно получить, положив / = 1 и заменив Q на. — Q в выражении
A8.5.8). (Предположите, что в коллапсирующем звездном ядре, где -?^+ =
= U _ > кТ, позитроны не вырождены.)
По мере увеличения плотности во время коллапса звездного ядра и
роста непрозрачности нейтрино все труднее ускользнуть из звезды [17, 329,
392, 393, 504, 505]. При плотностях выше
A8.5.10)
Ptrap- 3 X 10^^ г/смЗ,
556 Глава 18
нейтрино оказываются «захваченными», движутся вместе с веществом и
образуют полувырожденное море Ферми. По определению при ? - р^^^^
характерное время диффузии нейтрино из звездного ядра становится
сравнимым с характерным временем коллапса. Этот факт можно использовать
для оценки Pj . Гидродинамическое характерное время коллапса /^.^ц по
порядку величины соответствует времени свободного падения:
{Gp)
^ -4Х 10-?,?/2^, A8.5.11)
1/2
где ? - ?/D?/?^/3) — средняя плотность коллапсирующего звездного
ядра, а ? - Mq. Характерное время диффузии можно оценить, предполагая,
что преобладающим источником непрозрачности является когерентное
рассеяние, так что
где \^^^ — средняя длина свободного пробега типичного нейтрино в море
тяжелых атомных ядер (Z, Л), а A^scatt ^ 1 "^ число актов рассеяния,
испытываемых нейтрино до ухода из системы. Когерентное (упругое) рассеяние
приводит к траекториям нейтрино, характерным для случайного
блуждания. Нейтрино движутся зигзагообразно внутри звездного ядра, не изменяя
заметно свою энергию, пока не достигнут поверхности. Поэтому N^^^^^
определяется с помощью уравнения «случайного блуждания»^^
K'^KQ.-R- A8.5.13)
Среднюю длину свободного пробега Хд можно оценить из уравнения
A8.5.6)
(?^;^)"^=-?°^=(^)??\ A8.5.14)
где предполагается, что все нуклоны содержатся в тяжелых атомных
ядрах, и в качестве образца выбрано ядро ^^Fe.
При вычислении ?^^{?^) используются соотношения A8.4.7) и A8.4.19),
которые дают типичную энергию нейтрино, излучаемых при захвате
электрона протоном^^:
?^ = |?^ ^ 33p'f МэВ. A8.5.15)
'^ Аналогичное обсуждение фотонов, испытывающих упругое томсоновское
рассеяние, см. в разд. 14.5 (к).
^^ См., однако, упражнение A8.14), где рассматривается захват электрона
тяжелым ядром.
Звездный коллапс и взрывы сверхновых 557
Подстановка соотношения A8.5.15) в A8.5.14) дает
(?^^"')"' - 3,9 X \0-'рМ'см-\ A8.5.16)
Решив уравнение A8.5.13) относительно ?^^^^^ и подставив результат с
учетом A8.5.16) в соотношение A8.5.12), получим
W-0^08p,2C. A8.5.17)
Соотношения A8.5.11) и A8.5.17) показывают, что при достаточно высоких
плотностях /jjiff > г^.о||. Два характерных времени становятся сравнимыми,
W - ^соп - ? - Ptrap - Ь^ X 10^' г/с^'' A8.5.18)
Полученное значение меньше чем в два раза отличается от найденного при
более детальных гидродинамических расчетах [17, 619] [см. также
A8.5.10)], в которых учитывались увеличение плотности к центру, захват
электронов тяжелыми атомными ядрами и рассеяние нейтрино с
уменьшением энергии.
Упражнение 18.8. Оцените плотность /о^, при которой типичные нейтрино
испытывают однократное рассеяние, прежде чем покинуть ядро звезды, т.е. [A^scatt^^j^ ^ ^Ь
Покажите, что р^ <
/Ojзапотеет: /0^ ~ /Otrap/^^·
Захват нейтрино имеет огромное значение для коллапса звездного ядра.
При ? ^ Pjj.^p большинство нейтрино, образованных при захвате электронов,
остается в веществе и число лептонов на барион не изменяется. Распределение
нейтрино достигает равновесного ферми-дираковского вида, поэтому
физическое состояние системы барионов, лептонов и фотонов может быть
однозначно определено тремя величинами: скажем. Г, ? и У^ или s, ? и ?^.
В результате захвата нейтринные светимости сильно падают.
Рассмотрим, например, светимость звездного ядра, плотность которого в центре
достигла значения ? = 2,8 · 10^^ г/см^, характерного для ядерной материи.
При более высоких плотностях тепловое давление и ядерные силы
приводят к более жесткому уравнению состояния, что препятствует дальнейшему
коллапсу (см. разд. 8.5). Большая часть энергии гравитационной связи
звездного ядра выделится в конечном итоге в виде нейтрино. Если бы
захват нейтрино отсутствовал, вся энергия связи полностью излучалась бы в
виде нейтрино за характерное время коллапса — время, которое требуется
558 Глава 18
ДЛЯ сжатия ядра звезды от радиуса 2R^^^ до R^^^ [p^uc ~ ^/D?/??^^./3), что
дает R^^^ ~ 12 км при ? ~ A^qI- Таким образом, нейтринная светимость
достигла бы при этом своего максимально возможного значения
^..шах ~ ^^У^"" ~ 10" эрг/С. A8.5.19)
*со11
где для вычисления /^.^ц использовалось соотношение A8.5.11). В
действительности же захват нейтрино приводит к излучению высвобождаемой
гравитационной энергии за гораздо более продолжительное время диффузии,
которое при ? - р^^^ намного превышает время коллапса. В результате
фактическая нейтринная светимость близка к
1^ ^ ^^'^^""с ^ 10^2 эрг/с, A8.5.20)
^diff
где для вычисления t^^^^ использовалось соотношение A8.5.17). Значение
A8.5.20) по порядку величины совпадает с результатами более детальных
модельных вычислений ^\ которые показывают сильное неравенство
L^ < L^ ^^^. Это неравенство свидетельствует о том, что на стадии
развитого коллапса нейтрино не могут свободно покидать звездное ядро.
Поэтому основная часть высвободившейся гравитационной энергии должна
преобразовываться в другие виды внутренней энергии (например, тепловую
энергию, энергию возбужденных состояний атомных ядер, кинетическую
энергию «отскока» и т.д.), а не выделяться немедленно в форме
нейтринного излучения. Следовательно, захват нейтрино приводит к тому, что
коллапс звездного ядра на поздних стадиях (р ^ Ptrap) ^ динамических
временных масштабах очень близок к адиабатическому процессу.
Упражнение 18.9. Предположите, что нейтринная светимость A8.5.20) реализуется в
виде теплового излучения с поверхности звездного ядра. Подсчитайте эффективную
температуру излучения, предположив, что существует три типа безмассовых
нейтрино {v^, V и ?/^) и что нейтрино и антинейтрино испускаются в одинаковом
количестве. Вычислите среднюю энергию {Е^) излучаемых нейтрино.
Ответ:
L,= {iKoT,\,){AmR^), A8.5.21)
(^,(излуч)>= 3,15A:7;ff. A8.5.22)
'^ См., например, [17], где получена максимальная светимость, равная
8 · Ю" эрг/с, а также [619].
Звездный коллапс и взрывы сверхновых 559
18.6. ЭНТРОПИЯ И УРАВНЕНИЕ СОСТОЯНИЯ
ВО ВРЕМЯ ГОРЯЧЕГО КОЛЛАПСА
В своем недавнем анализе уравнения состояния горячего плотного
вещества при звездном коллапсе Бете, Браун, Эпплгейт и Латтимер [66]
подчеркнули важность подробного рассмотрения энтропии, приходящейся на ба-
рион. Тот факт, что вначале энтропия мала {s/k - 1), лишь слегка
возрастает перед захватом нейтрино (^s/k ^ 0,5), а затем остается
постоянной в течение адиабатической стадии {sJk - 1—2), имеет очень важный
смысл для уравнения состояния. В частности, малая энтропия на барион в
сочетании с большим числом лептонов, связанным с захватом нейтрино
{Yf ~ 0,3—0,4), приводит к сохранению тяжелых атомных ядер вплоть до
ядерных плотностей вещества, когда в конце концов из атомных ядер
«выдавливаются» нуклоны. Поэтому процесс частичного расщепления
атомных ядер на альфа-частицы и свободные нейтроны, происходящего в
начале коллапса при более высоких плотностях, заменяется обратным
процессом, когда альфа-частицы возвращаются в атомные ядра. Низкое значение
s/k и высокое значение У/ препятствуют появлению нейтронных капель,
которое привело бы к чрезмерному возрастанию полной энтропии. Таким
образом, горячее вещество при высоких плотностях ведет себя совершенно
иначе, чем холодное (сравните с гл. 2 и 8), для которого s/k = о, а
Yf < \. В холодном веществе нейтронные капли образуются при ? =
SS р^^. = 4,3 · 10^^ г/см^ < р^ц^., а свободные нейтроны преобладают в
составе системы при ? ^ p^jrip·
Подсчитаем начальную энтропию вблизи центра звездного ядра, когда
коллапс только начинается при Т^ · « 8 · 10^ К, а р^ ¦ ^ 3,7 · 10^ г/см^
(см. A8.2.7)]. Для грубой оценки упростим химический состав,
предположив, что все барионы находятся в идеальных невырожденных ядрах ^^Fe,
окруженных предельно вырожденным, ультрарелятивистским электронным
морем Ферми. В нашем случае начальная энтропия на атомное ядро,
связанная с поступательным движением, дается уравнением B.3.34)
(I)
(на ядро) = — + In
1 156т.ЛТЛ'/^
?±1
Fe \ 2??^
= 16,7, A8.6.1)
где A2pg = р^ ./56w^ — концентрация ядер железа. Начальная энтропия на
один барион получается делением соотношения A8.6.1) на 56:
(ю
(на барион) = 0^30. A8.6.2)
Для электронов удельную энтропию можно легко получить из
соотношения A1.8.1) в предельном случае ? s Pj/mf > 1, что дает
кТ
(на электрон) = тг^—^^ = 1^10. A8.6.3)
т
560 Глава 18
Упражнение 18.10. Выведите формулу A8.6.3) из соотношения A1.8.1).
Указание: е.. = Tds/dT.
При вычислении соотношения A8.6.3) использовалось уравнение A8.4.7)
с У^ = 26/56 = 0,464, что дает энергию Ферми ?^ = 6,2 МэВ. Умножая
A8.6.3) на У^, что дает электронную энтропию на барион, и прибавляя
результат к значению A8.6.2), получаем полную начальную энтропию на барион
^ -0^30+0,51 =0,81. A8.6.4)
Бете и др. [66] выполнили более тщательное вычисление величины s/k.
Они рассматривали частичную диссоциацию ядра ^^Fe на альфа-частицы и
нейтроны в соответствии с уравнением A8.3.6). Альфа-частицы и
нейтроны, если их рассматривать как идеальные невырожденные частицы,
увеличивают численное значение A8.6.1) на 3,6. Бете и др. оценили также вклад
в энтропию от возбужденных состояний атомных ядер, что добавляет к
значению A8.6.1) еще 4,8.
Упражнение 18.11. Используйте уравнения A8.3.7) и A8.3.8) для оценок п^, п^ и п^^
при р^ . и Г^ ^. Найдите отсюда 5^/А^.
Упражнение 18.12. Рассмотрите атомное ядро как вырожденный нерелятивистский
ферми-газ, состоящий из А идентичных нуклонов при плотности
'^nuc ~ ^'^ ' ^^'^ г/см^. Каждое состояние с заданным импульсом может содержать
четыре частицы (два спиновых состояния у протона и нейтрона).
а) Покажите, что энергия Ферми ядра (без учета массы покоя) равна
б) Используйте удавнение A1.8.1) в нерелятивистском пределе, чтобы показать,
что энтропия возбужденных ядерных состояний в этой «модели ферми-газа с
конечной температурой» равна
(?)
(на ядро)= А — ~^ - 4 9.
ехс ^ ^F,nuc
Скорректировав уравнение A8.6.3), чтобы получить электронную
энтропию реальной смеси ядер подобных железу с У^ . = 0,42 [сравните с
A8.2.7)], и добавив результат к вкладу барионов. Бете и др. получили в
Звездный коллапс и взрывы сверхновых 561
конце концов полную энтропию на нуклон:
-^ = [ -^ I (электронная) + Т") (нуклонная)
= 0,48 + 0,45 = 0,93 (полная), A8.6.5)
что близко к грубой оценке A8.6.4).
Теперь, когда мы знаем начальную энтропию, рассмотрим, как она
изменяется во время ранних стадий коллапса, предшествующих захвату
нейтрино. Возрастание энтропии проходит только через слабые
взаимодействия, поскольку вещество находится в равновесии относительно сильных и
электромагнитных взаимодействий. В соответствии с первым законом
термодинамики [см. уравнения B.1.1) и B.1.6)] скорость изменения энтропии 5
определяется выражением
?=? + ???, A8.6.6)
где q — количество поглощенного тепла в расчете на барион, а /
обозначает различные типы ядер, нуклонов и лептонов.
Рассмотрим потери тепла, связанные с ускользанием нейтрино. В этом
случае можно записать
^« -<?.>escr^, A8.6.7)
esc
где <?'^>esc ~ средняя энергия ускользающих нейтрино, а т^^^ — среднее
время ускользания из звездного ядра. Величину т^^^ можно оценить из
соотношения
^(f'^diff),
A8.6.8)
где r^jj^f определено выражением A8.5.12) и дает т^^^ при N^c^tt > ^-
Сосредоточим внимание на электронных нейтрино, поскольку они
преобладают во время коллапса. Полное изменение числа нейтрино
определяется тогда разностью между образованием нейтрино при захвате
электронов (основной механизм излучения на ранних стадиях коллапса) и потерями
нейтрино вследствие ускользания из звездного ядра. Это изменение
описывается уравнением
?=-?-^. A8.6.9)
'esc
Член ^ ?.?. в уравнении A8.6.6) можно записать в виде
??^?^? = мЛ + мП; + М.К + ?? + ??? Уг . A8.6.10)
20-513
562 Глава 18
где последний член описывает атомные ядра в реакциях типа
?-+B,+ \,Ai)^{Z„Ai) + v. A8.6.11)
Реакции нейтронизации сохраняют число барионов и заряд, так что
1ГгЛ+^/.+ ^- = о,
X:r^,z,+ r^-i; = o. A8.6.12)
Из уравнения A8.3.13) для ядерного статистического равновесия следует,
что
Z^zjz, = ?[2:,?, + {А, - ?,)?„]7?,. A8.6.13)
И, наконец, уравнения A8.6.10), A8.6.12) и A8.6.13) дают
EM/J'/ = (Ме + Мр - Mjn + ?.?. A8.6.14)
Подстановка уравнений A8.6.7), A8.6.9) и A8.6.14) в A8.6.6) дает
? = - (?, + ?, - ?„ - ?,)^ + (?, - (?,)^)^. A8.6.15)
Nssc
Первый член в уравнении A8.6.15) представляет собой изменение энтропии,
вызванное процессами слабых взаимодействий, которые не являются бета-
равновесными. Второй член — это изменение энтропии вследствие потерь
нейтрино.
Для вычисления изменения энтропии при помощи уравнения A8.6.15)
критическим оказывается связанное с ним уравнение для У^, дающее AY^ за
счет нейтронизации. Если просто обратиться к уравнению A8.4.18),
дающему скорость захвата электронов свободными протонами, и положить
?? = У^, то приходим к следующему результату:
^Ye-fKdt- [п(р)/со..(р)]р-р.„,, A8.6.16)
ИЛИ же с учетом соотношений A8.4.7) и A8.5.11)
Yej - Yej - - E,1 ? ^O^Ye'fpVlW A8.6.17)
Уравнение A8.6.17) ясно показывает, что большая часть электронных
захватов, предшествующих захвату нейтрино, происходит при ? - р^^ар-
Подстановка значения A8.5.10) для р^^^^ дает У^ j- - 0,07. Более тщательный
анализ Бете и др., в котором предполагается нейтройизация тяжелых ядер,
а не свободных протонов, дает вместо этого результата значения
Y^j ~ 0,31 и ДУ^ ~ - 0,11 для характерной доли лептонов в звездном яд-
Звездный коллапс и взрывы сверхновых 563
ре при захвате нейтрино. Недавние расчеты [202], где рассматривалось
влияние заполненных нейтронных оболочек, приводящее к уменьшению
скорости захвата электронов большими атомными ядрами, позволяют
предполагать, что доля лептонов в звездном ядре при захвате нейтрино еще
больше: Yg J - 0,34, а в работе [88] приводится значение У^ j - 0,35—0,36.
При заданном уравнении для У^ теперь можно вычислить изменение
энтропии согласно уравнению A8.6.15). В случае достаточно хс^подного
вещества, когда свободных протонов мало и нейтронизация идет в основном
через атомные ядра, первый член обычно преобладает [187]. Но тогда
химические потенциалы должны быть сильно неравновесными, чтобы
превосходить энергию возбуждения вторичного ядра ?. Итак,
Me + М;, - Мп - ?? ^ ? - 0(/сГ), A8.6.18)
где обычно ? - 3 МэВ, а ?^ - О перед захватом нейтрино. В этой
ситуации первый член уравнения A8.6.15) приводит к увеличению удельной
энтропии. Второй член может преобладать при более высоких значениях
начальной энтропии, когда больше свободных протонов и нейтронизация за
счет свободных протонов становится важной. В этом случае энергия
нейтрино имеет величину порядка - ?^, что гораздо больше, чем ?^ -\- ? - ?^.
Если эти нейтрино уходят из звездного ядра, не испытывая рассеяния с
уменьшением энергии (см. разд. 18.5), то второй член приводит к
уменьшению энтропии. В своих расчетах Бете и др. [66] нашли, что конечное
значение энтропии на барион (Sj/k) лежит в диапазоне 1—1,5. Таким образом,
до захвата нейтрино энтропия изменяется мало и потому остается низкой
и после захвата.
Адиабатический характер коллапса звездного ядра на поздних стадиях
иллюстрируется уравнением A8.6.15). Вслед за захватом нейтрино
нейтронизация протекает в бета-равновесии, так что первый член становится
малым. В то же время значение т^^^ велико (т^^^ > г^^ц), и поэтому второй
член также оказывается малым. Следовательно, изменением энтропии в
течение коллапса после захвата нейтрино можно пренебречь. (Заметим,
однако, что увеличение энтропии при диссипации энергии ударной волны,
которая следует за «отскоком» звездного ядра при плотности в центре
порядка р^ц^., в конечном итоге оказывается важным; см. разд. 18.7.)
Пожалуй, наиболее существенная особенность коллапса звездного ядра,
обнаруженная в результате последних расчетов, состоит в том, что
свойства ядра на стадии развитого коллапса (например, Y^j и s/k) почти не
зависят от многих предположений относительно микрофизики вещества,
глобальной скорости коллапса и начальных условий. В работе [187] найдено,
например, что число лептонов Yj = У^ + У^ оказывается порядка У, - 0,3,
а изменение удельной энтропии меньше ± 0,5 независимо от больших
изменений предполагаемых физических и астрономических параметров. Эта
нечувствительность переменных, определяющих состояние вещества, к
деталям картины коллапса позволяет относиться к результатам расчетов с
большим доверием и значительно упрощает вывод уравнения состояния.
A w„
^
[ f
lAm^kTY^^]
—
I 2??' 1 J
\ ?4??^ ттЧТ
I ¦·¦ "^ ??''
j Me 2?^p nuc
564 Глава 18
Поскольку энтропия очень мало изменяется до захвата нейтрино и
остается постоянной после захвата, коллапс фактически идет по адиабате с
малой и постоянной удельной энтропией. В первом приближении полная
энтропия на барион как функция У^, ? и Г равна [см. соотношения A8.6.1),
A8.6.3) и упражнение 18.12]
— « -={ -г- + In
«const, A8.6.19)
где пренебрегается вкладом от свободных барионов и альфа-частиц и
предполагается, что все нуклоны связаны в атомные ядра со средним атомным
весом А
Рассмотрим зависимость Г от ? во время коллапса. В начале коллапса
энтропия определяется в основном первыми двумя членами выражения
A8.6.19). Поскольку первый член только логарифмически зависит от ? и Г,
можно думать, что второй член (по крайней мере вначале) будет
определять направление кривой Г — ? по адиабате и, следовательно, будет
приблизительно постоянным. Учитывая это, а также соотношение A8.4.7),
можно предположить, что во время коллапса применимо соотношение
Г - р^'^^ с условием У^ - const. Поэтому имеем
r«r,i-^| E«const; y^«const), A8.6.20)
V Pc,i '
где Т^ ? и р^ I принимают значения A8.2.7). Если в центре звездного ядра в
заключительной стадии коллапса достигается ядерная плотность р^^^ =
?=: 2,8 · 10^^ г/см^, температура там дойдет до значения Т^^^^ « 29 МэВ в
соответствии с уравнением A8.6.20). Более внимательное рассмотрение
показывает, что Г^ц^., скорее всего, будет несколько ниже (Г^^^. « 10 МэВ) и что
уравнение A8.6.20) предсказывает слишком уж крутой подъем Г (рис. 18.1).
Поправки к уравнению A8.6.20) необходимы, в частности, для учета
растущего вклада возбужденных ядерных состояний в энтропию,
представленного третьим членом уравнения A8.6.19).
Вычислительное упражнение 18.13. Используйте уравнение A8.6.19) с /1 = 56 и
у = 0,464 для вычисления адиабатической зависимости Г от р. Отложите ваши
результаты на графике аналогично рис. 18.1 для значений s/k = 0,5; 1,0; 1,5; 2; 3. Для
каждой адиабаты определите Т^^^ и относительный вклад каждого члена уравнения
A8.6.19) в энтропию при ? = ? .
Детальные вычисления уравнения состояния горячего плотного
вещества [66, 187, 334, 335] основаны на предположении, что вещество состоит из
Звездный коллапс и взрывы сверхновых
CD
Г)
с;»
1
'
-
1
1 I м 1Р| 1 1 I I ! mi
л.
Абийбйгпы
. 1 1 1 1 II 1 1 1 1 II Ml 1
I 1 I II I III
: ' ' ! ! Ч i I 1 1 I ! ¦ " l·
-1
1 1 ? 1 Ml 1 1 1 1 1 1 Ml
10^
Плотность D, г, см^
10^·
10^'
Pwc. 18.1. Диапазон адиабат с низкой энтропией, найденных для коллапса звездного
ядра. Траектории коллапса были получены на основе гидродинамических расчетов
коллапса ядра с использованием уравнения состояния горячего плотного вещества
C34, 335]. (Рисунок заимствован из работы [591].)
тяжелых ядер, альфа-частиц, нейтронов, протонов, электронов и
электронных нейтрино. В приближении, когда величины 5 и К^ рассматриваются как
постоянные, вычисление локального уравнения состояния не связано с
глобальными гидродинамическими расчетами. Именно это разделение,
обусловленное захватом нейтрино, дало возможность достичь прогресса в
разработке реалистического «горячего» уравнения состояния для коллапса. С
другой стороны, согласование гидродинамических расчетов и расчетов
переноса нейтрино необходимо, чтобы определить изменения 5 и У^,
вызываемые, например, нейтронизацией, ускользанием нейтрино, диссипацией в
ударной волне и т.д. Такой согласованный расчет особенно необходим,
чтобы оценить, действительно ли выделяемая во время коллапса
гравитационная потенциальная энергия может быть источником взрыва сверхновой.
В существующих вычислениях «горячего» уравнения состояния тяжелые
ядра часто представляются одним лишь типом (Л, Z) частиц при каждой
плотности. Масса-энергия частиц этих типов оценивается по
полуэмпирической массовой формуле вида, рассмотренной в гл. 2 для вещества с
7^ = 0. Такая формула маскирует эффекты спаривания и оболочечной
структуры, но она может обеспечивать удовлетворительное приближение
при конечных температурах, с которыми приходится иметь дело во время
коллапса звездною ядра (- 1—10 МэВ). Поскольку в течение коллапса
температуры остаются низкими по сравнению с энергией Ферми,
характерной для нуклонов в ядре (- 40 МэВ; см. упражнение 18.12), при
определении равновесного состава поправками на конечную температуру часто
пренебрегают.
566 Глава 18
Концентрация нуклонов каждого типа, не находящихся в ядре,
определяется из стандартных интегралов Ферми (см. гл. 2). При этом
учитывается, что при ядерном равновесии химические потенциалы внутри атомного
ядра и вне его равны. Наконец, условия зарядовой нейтральности и
сохранения барионов используются для подсчета числа нуклонов, атомных ядер
и электронов [см. уравнения A8.3.17) и A8.3.18)].
Допустим, что принята модель ядра в виде «сжимаемой жидкой капли»
[55]. Тогда величина
? = ?„-?,, A8-6.21)
появляющаяся, например, в уравнении A8.6.15), получается
непосредственно приравниванием правых частей уравнений (8.2.8) и (8.2.11), что дает
?= -¦^(^;?+ »^'l)x,«.,k,.»„· A8.6.22)
Бете и др. [66] нашли, что производную в уравнении A8.6.22) можно
аппроксимировать выражением
? (МэВ) « 207@,45 - |)(?,32 " f ) + ?, Q^{m,- m^)c\
A8.6.23)
Пренебрегая образованием нейтронных капель, в приведенном выше
уравнении можно заменить ?/? на У^. Бете и др. нашли также, используя
модель [55], что наиболее вероятный атомный вес в том же приближении
определяется выражением
А« 194A - Y,f{\ - 0^36p'f)"' A8.6.24)
И что 90^0 нуклонов остаются связанными в атомные ядра вплоть до
ядерных плотностей.
Упражнение 18.14. При захвате электронов тяжелыми ядрами возникающие
нейтрино обладают средней энергией [66]:
(Е^)тпуч « 1(?^ - /2 - ?).
При захвате электронов свободными протонами энергия нейтрино выше:
(?у)излуч = бМе
[см. уравнение A8.4.19)]. Используйте приведенные выше результаты для численных
оценок изменения полной энтропии на барион, которое происходит (до стадии
захвата нейтрино ядром звезды) в результате захвата электронов а) тяжелыми ядрами,
б) свободными протонами. (Считать, что одновременно осуществляется только
Звездный коллапс и взрывы сверхновых 567
один из процессов: либо а), либо б).) Предположите, что большинство захватов
электронов происходит перед самым началом стадии захвата нейтрино, когда
AY, « 0,35 - 0,42 « -0,07, кТ - 1,5 Мэв, ?, « О « У,, ? ~ 3 МэВ.
Указание: Используйте соотношения A8.4.7), A8.5.10), A8.6.9), A8.6.15) и
A8.6.23).
Ответ:
а) ??5» -??[|(?,-?) + |?]>0,
б) T^s^ -?7,[?,-?-|?,]<0.
Важный вывод, что при больших плотностях продолжают
существовать тяжелые атомные ядра, следует из малой энтропии, характерной для
коллапса, и существования захвата нейтрино. Захват тормозит нейтрониза-
цию, поскольку влияние моря Ферми нейтрино направляет реакции типа
е-+ (?, ?)^{?- \,?)-^? A8.6.25)
справа налево. В результате число электронов У^ остается высоким во
время горячего коллапса, что в силу зарядовой нейтральности означает
присутствие большого числа протонов. Поскольку образование протонных
капель при низкой энтропии энергетически невыгодно, все протоны остаются
в атомных ядрах. Однако равновесное отношение ?/? в ядрах составляет
:S 0,3—0,4 при высоких плотностях, поэтому ядра должны быть очень
тяжелыми, чтобы вместить требуемое число протонов.
Упражнение 18.15. Подсчитайте Л при ? , пользуясь соотношением A8.6.24).
Окончательное уравнение состояния оказывается довольно простым.
При плотностях вплоть до Pnu^ давление определяется главным образом
релятивистскими вырожденными электронами. Таким образом, показатель
адиабаты Г при падении вещества звезды к центру близок к 4/3; небольшое
уменьшение по сравнению с 4/3 связано главным образом с захватом
электронов. В начале коллапса давление электронов повсюду в звездном ядре
близко к гидростатической равновесной величине
л * i'e, « {y.,iPY'\ 08.6.26)
профиль плотности соответствует политропе с показателем а? = 3. После
нейтронизации У^ снижается от - 0,42 до - 0,34—0,36, так что давление в
начале захвата нейтрино падает ниже равновесного значения в соответст-
568 Глава 18
ВИИ с выражением
\4/3
?>=(^| Рея - @,7-0,8)i'e<,· A8.6.27)
Как отмечалось в гл. 6, конфигуращ1я с Г = 4/3 обладает нейтральной
устойчивостью к гомологичным радиальным возмущениям. Таким
образом, коллапс протекает гомологично (как и в аналогичной ситуации для
сверхмассивных звезд, описанной в гл. 17) и соотношение A8.6.26)
справедливо (приближенно) вплоть до ядерных плотностей. В этой точке
уравнение состояния становится жестким и Г резко увеличивается. При р^^^ и
выше этой плотности атомные ядра сливаются. Как только это произойдет,
вещество можно рассматривать как однородную среду, состоящую из
отдельных протонов и нейтронов. Эти нуклоны, «выдавленные» из атомных
ядер, можно рассматривать как вырожденный газ Ферми с
взаимодействиями. При этих плотностях можно использовать результаты вычислений
для вещества с Г = О со всеми соответствующими им неопределенностями
(см. гл. 8).
Вскоре после того, как в центре звезды достигаются ядерные
плотности, движение вещества звездного ядра достаточно быстро замедляется.
Реакцией на возрастание давления ядерного вещества становится «отскок»
звездного ядра. В следующем разделе будут рассмотрены следствия этого
«отскока». Как сейчас полагают, он составляет основу взрыва сверхновой.
18.7 ГОМОЛОГИЧНЫЙ КОЛЛАПС ЗВЕЗДНОГО ЯДРА,
ОТСКОК И ЧТО ЖЕ ДАЛЬШЕ?
Голдрайх и Вебер [231] показали, что если показатель адиабаты коллапси-
рующей ньютоновской газовой сферы удовлетворяет условию Г = 4/3, то
коллапс внутренней части конфигурации будет гомологичным. Это
означает, что положение и скорость данной точечной массы в гомологичном
«внутреннем» ядре меняются по закону
?(/) = ?@'·?, ; = f, A8-7.1)
где Tq — начальное положение. Плотность тем временем изменяется
самосогласованно в соответствии с уравнением
р{г{1),1)-^а-\{г^), A8.7.2)
и профиль плотности во время коллапса сохраняется. Голдрайх и Вебер
нашли, что масса гомологичного внутреннего ядра может быть найдена из
соотношения
^hc = \;0449d'/^M, A8.7.3)
Звездный коллапс и взрывы сверхновых 569
где d = Р/Рщ < 0,971 — дефицит давления, а Л/ — масса начальной
равновесной политропы с А2 = 3 [625].
Мы уже сталкивались с гомологичным коллапсом в гл. 17, где изучался
коллапс в черную дыру сверхмассивной звезды с Г « 4/3 и б/ « 1.
Предполагается, что коллапс звездного ядра также должен быть гомологичным
во внутренних областях, поскольку основной вклад в давление вносят
вырожденные релятивистские электроны, для которых Г « 4/3. Это
предположение подтверждается детальными гидродинамическими расчетами
коллапса звездного ядра [17, 591, 619], которые свидетельствуют, что
соотношение A8.7.3) выполняется с точностью лучше 20^о. Таким образом, из
соотношений A8.2.5) и A8.2.7) следует, что ? - М^у^ - 5,83 У^ ^М^ -
- 1А/0. Поэтому с помощью выражений A8.6.27) и A8.7.3) можно
оценить, что гомологичное внутреннее ядро имеет массу ^^
Mh, - @,6-0,8)Ме. A8.7.4)
Как только в гомологичном внутреннем ядре плотность достигает
^nuc ^ ^'^ " ^^^^ г/см^, давление быстро возрастает, так как нуклонный
жомпонент вызывает «ужесточение» уравнения состояния, и поэтому Г
превышает значение 4/3. При плотностях, в несколько раз превосходящих р^^^,
давление оказывается достаточным, чтобы сдержать коллапс. Вследствие
этого гомологичное ядро «отскакивает» от центра, прежде чем в конце
концов придет к гидростатическому равновесию. «Внешняя» часть ядра
тем временем продолжает падать к центру со сверхзвуковой скоростью. В
результате «отскочившая» назад внутренняя часть ядра, действуя как
поршень, возбуждает ударную волну во внешней части ядра, падающей к
центру.
Характерная начальная энергия, сообщаемая ударной волне, в несколько
раз больше 10^^ эрг [589, 619], что соответствует начальной скорости
волны Ug ^ 5 · 10^ см/с. Этой энергии более чем достаточно, чтобы разру-
imiTb массивную звезду, при условии, что энергия передается оболочке,
окружающей железное ядро. В этом случае ударная волна по мере
прохождения через звезду должна изменять направление движения вещества к
центру на обратное, вызывая взрывное движение наружу. В результате
возникает вспышка сверхновой, а внутри остается родившаяся нейтронная
звезда. Однако на самом деле энергия постоянно «вытекает» из ударной
волны вследствие испускания нейтрино и диссоциации атомных ядер.
Компенсируется ли такая «утечка» энергии притоком кинетической энергии
падающего вещества, преобразованной в тепло, и диффузией нейтрино к
фронту ударной волны? Этот вопрос остается в настоящее время
предметом дискуссий [88, 347, 589].
^^ Обычно начальная масса ядра бывает несколько больше, Л/ ~ 1,4Л/^, что
связано с тепловым повышением давления вырожденных холодных электронов [88].
570 Глава 18
Упражнение 18.16. Оцените энергию связи Е^ вещества звезды с массой - 10 М^ и
радиусом ~ 5/?0, окружающего коллапсирующее вырожденное я1ро и сравните с
начальной энергией ударной волны.
Ответ: Е^ ~ GM^/R ~ 10^® эрг сразу после «отскока» ядра звезды.
Упражнение 18.17. Оцените характерную температуру вещества за фронтом ударной
волны. Что происходит с атомными ядрами после прохождения через ударную
волну?
Ответ: УткТ < Vim^uj ~ 13 МэВ, что выще энергии связи атомного ядра.
Выброс наружу внешних слоев массивной звезды посредством
гидродинамической ударной волны «отскока», порождаемой внутренним ядром,
остается наиболее вероятным механизмом взрыва сверхновой на основе
гравитационного коллапса. Любопытно, что аналогичная картина
предусматривалась в одной из самых первых моделей сверхновых, предложенной
Колгейтом и Джонсоном [143]. Они предположили, что спадающее к центру
ядро звезды может испытывать достаточно быстрый «отскок» при
высоких плотностях (из-за вырождения атомных ядер), который приводит к
возникновению ударной волны, передающей энергию в наружные слои
звездного вещества.
В течение ряда лет было предложено много различных моделей
сверхновых, объясняющих, каким образом энергия гравитационной связи,
выделяемая при коллапсе, может эффективно переноситься во внешние слои
звезды, обеспечивая их выброс. Кол гейт и Уайт [144] предложили модель,
согласно которой пары нейтрино-антинейтрино, образующиеся в горячем
веществе за фронтом ударной волны, переносят свою энергию в наружные
области с меньшей плотностью. Нагрев, вызванный этим переносом,
обеспечивает достаточное тепловое давление, которое «сдувает» внешние части
звезды, оставляя внутри теплую нейтронную звезду. К сожалению,
подробные гидродинамические расчеты с привлечением переноса нейтрино [15,
617] показали, что этот механизм неэффективен из-за слишком высокой
непрозрачности звездного вещества для нейтрино; он может обеспечивать
лишь образование черных дыр без всякого взрыва.
Впоследствии было высказано предположение [511], что нейтрино,
покидающие звездное ядро, могут передавать свой импульс лежащему
снаружи веществу и вызывать тем самым взрыв. Эта модель, основанная на
переносе импульса нейтрино, также оказалась несостоятельной, как только
были выполнены более тщательные численные расчеты с учетом слабых
нейтральных токов [89, 620]. Причина в том, что нейтральные токи
приводят к большим нейтринным непрозрачностям и малым потокам [см.
уравнение A8.5.20)]. Действительно, вклад импульса может быть эффективным
только в том случае, если нейтринная светимость превосходит
критическую «эддингтоновскую нейтринную светимость», при которой
направленная наружу сила, обусловленная вкладом импульса нейтрино, равна направ-
Сверхмассивные звезды и черные дыры 571
ленной к центру силе тяготения. По аналогии с уравнением A3.7.6),
дающим эддингтоновскую фотонную светимость, можно записать (пренебрегая
асимметрией вперед—назад в дифференциальном сечении рассеяния):
^???,? , A8.7.5)
где к^ — доминирующая нейтринная непрозрачность. Предположим, что
основным механизмом непрозрачности во внешних слоях является
когерентное рассеяние тяжелыми атомными ядрами и что нейтрино за
распространяющейся наружу ударной волной «отскока» обладают энергиями,
сравнимыми с ЗкТ :S 25 МэВ [см. выражение A8.5.22) и упражнение 18.17].
При таких предположениях с учетом соотношения A8.5.6) найдем
-coh
?„ «
Am,
-2,2 ? 10-^^cMVr, A8.7.6)
где принято ? « 26, Л « 56 и ?^ = 25 Мэв. Подстановка значения A8.7.6)
в выражения A8.7.5) дает
^Edd.. « 2 X lO^Spr/c > 4, A8.7.7)
где оценка L^ представлена соотношением A8.5.20). Неравенство A8.7.7)
показывает неэффективность передачи импульса как единственного
механизма, ответственного за выброс оболочки.
Хотя механизм ударной волны «отскока» кажется наиболее вероятным
средством создания взрыва, недавние детальные гидродинамические
вычисления с учетом переноса не подтвердили эффективность этого механизма
(см., например, обзор [347]). Однако ситуация может измениться, если в
численное моделирование поведения ядра после «отскока» будут внесены
необходимые уточнения. В качестве альтернативы возможны и другие,
более экзотические механизмы, приводящие (поодиночке или совместно) к
возникновению взрыва. Среди них могут быть конвекция [185],
неустойчивость Рэлея—Тейлора [142, 370, 546] или отклонения от сферической
симметрии, вызванные, например, вращением или магнитными полями [349,
415].
Один факт не вызывает сомнения: несколько нейтронных звезд,
например, пульсары в Крабовидной туманности и в Парусах, находятся сейчас
внутри остатков сверхновых. Безусловно, гравитационный коллапс может
приводить к взрыву сверхновой и образованию нейтронной звезды. Как это в
действительности происходит, еще предстоит определить.
Упраокнение 18.18. Просмотрите рефераты литературы за последние 12 месяцев,
посвященной гравитационному коллапсу звездного ядра и взрывам сверхновых. Какова
общепринятая точка зрения (если она существует) относительно вероятного
механизма взрыва и образования нейтронной звезды? Поддерживают ли детальные
расчеты эту точку зрения? Убедило ли это вас?
Приложение А
Некоторые сведения из астрономии
АЛ. ПАРСЕКИ И ЗВЕЗДНЫЕ ВЕЛИЧИНЫ^)
В качестве стандартной астрономической единицы длины выбран парсек.
Это такое расстояние, с которого отрезок длиной в одну астрономическую
единицу (среднее расстояние между Землей и Солнцем) виден под углом,
равным одной секунде дуги. Переводные множители таковы:
1 ПС = 3,086 · 10^^ см = 3,26 световых лет. (АЛ)
Во внегалактической астрономии в качестве единицы более удобен мегапар-
сек:
1 Мпс = 3,086 · 10^^ см. (А.2)
Наблюдаемый блеск звезды или галактики на небе выражается в
логарифмическом масштабе. Пусть J^ — падающий поток энергии от объекта
[выраженный в эрг/(см^ · с)] в некоторой выбранной полосе длин волн, а
/2 — поток энергии от второго объекта в той же полосе длин волн. Тогда
видимые звездные величины двух объектов связаны соотношением
т^-ш, =2,5 Igi^j, (А.З)
(подчеркнем, что логарифмы десятичные). Следует отметить, что чем
слабее объект, тем выше его видимая звездная величина. В величину
падающего потока / вносятся поправки на поглощение и рассеяние в Галактике. Во
всех случаях, когда мы используем значение w, подразумевается, что эти
поправки внесены.
Абсолютная звездная величина ? объекта — это мера его истинной
светимости, т.е. энергии, излучаемой в выбранной полосе длин волн, в
таком же логарифмическом масштабе, какой использован в соотношении
(А.З). Нормировка Л/ такова, что если поместить объект на стандартном
расстоянии 10 пс от нас, то его видимая звездная величина сравняется с
абсолютной звездной величиной М. Если истинное расстояние до звезды
равно Dy то по закону обратных квадратов падающий поток окажется
меньше, чем при опорном расстоянии, в (D/10 пс)^ раз. Поэтому видимая
звездная величина объекта, находящегося на расстоянии D, согласно уравнению
^^ Содержание разд. А.1 близко следует работе [452].
Некоторые сведения из астрономии 573
А.З, удовлетворяет соотношению
ПС
ш-М = 51е1зО^). (А.4)
Величина т — ? называется модулем расстояния.
Хотя детально измерить спектры слабых звезд затруднительно,
широкополосная фотометрия, при которой используется небольшое число
фильтров разного цвета, дает достаточную информацию для
приближенного определения температуры звездной поверхности. Синяя и В11зуа.'ъная
(желтая) видимые величины звезды обозначают^ я буквами В и V
соответственно, а их разность В—V определяет показатель цвета звезды.
Центр синей полосы В приходится на 4400 А, а визуальной К — на
5500 А. Существует однозначное соответствие между показателем цвета
звезды и положением максимума в спектре непрерывного излучения,
позволяющее определить цветовую температуру. Цвет овая температура — это
температура черного тела, имеющего такое же распределение
относительной интенсивности, или цвет, что и данная звезда. Поскольку излучение
звезд отличается от излучения черного тела, цветовая температура
меняется с длиной волны.
Если бы приемник излучения мог воспринимать весь излучаемый
звездой спектр, то его измеренная абсолютная звездная величина оказалась бы
абсолютной болометрической звездной величиной М^. Таким образом,
абсолютная визуальная звездная величина преобразуется в абсолютную
болометрическую звездную величину, если внести поправки на величину
излучаемой энергии, не попадающей в ту часть спектра, которая воспринимается
регистрирующим прибором. Если болометрическую поправку обозначить
ВС (это отрицательная величина), а абсолютную визуальную звездную
величину ? у у то абсолютная болометрическая звездная величина равна по
определению
М^^^МуЛ- ВС. (А.5)
Удобная начальная точка отсчета связана с абсолютной звездной
величиной Солнца: My = 4,79. Поэтому светимость объекта, имеющего
абсолютную звездную величину My в визуальной полосе длин волн, равна
L{My) = 10^»^^'^^-^-)Le, (^-^)
где
Lq = 3,90 ± 0,04 X 10^^ эрг/с.· (А.7)
Поскольку болометрическая поправка для Солнца равна ВС = -0,07,
можно записать следующее выражение для полной светимости объекта:
/^=10°W2-«*)Lo. (А.8)
Заметим, что наиболее яркие звезды имеют наименьшие звездные
величины.
574
Приложение А
А.2. ЗВЕЗДНЫЕ КЛАССЫ И ДИАГРАММА ГЕРЦШПРУНГА—РЕССЕЛА
Ниже приводится элементарное обсуждение диаграммы Герцшпрунга—Рес-
села — важного инструмента для классификации звезд и определения их
возраста. Более детальное обсуждение строения и эволюции звезд можно
найти во многих руководствах (например, [135]).
Одним из первых результатов применения цветовой фотометрии было
обнаружение корреляции между показателями цвета звезд и интенсивностя-
ми конкретных линий поглощения в их спектрах. Такие наблюдения
привели к классификации звезд по спектральным классам. В дополнение к
другим отличительным признакам каждый спектральный класс соответствует
определенному диапазону поверхностных цветовых температур. Основные
спектральные классы и соответствующие им диапазоны температуры
показаны в табл. А.1. Солнце — это звезда класса G.
тральный
класс
05
ВО
В5
АО
А5
F0
F5
GO
G5
КО
К5
МО
М5
Абсолют -
ная
визуальная
звездная
величина
К
-6,0
-3,7
-0,9
0,7
2,0
2,8
3,8
4,6
5,?
6,0
7,4
8,9
12,0
ГЛАВНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Показатель
цвета
В- V
-0,45
-0,31
-0,17
0,00
0,16
0,30
0,45
0,57
0,70
0,84
1,11
1,39
1,61
метрическая
поправка
ВС
-4,6
-3,0
-1,6
-0,68
-0,30
-0,10
-0,00
-0,03
-0,10
-0,20
-0,58
-1,20
-2,1
Эффективная
температура
поверх -
ности
7;,к
35,000
21,000
13,500
9,700
8,100
7,200
6,500
6,000
5,400
4,700
4,000
3,300
2,600
Цветовая
температура
7;,к
70,000
38,000
23,000
15,400
11,100
9,000
7,600
6,700
6,000
5,400
4,500
3,800
3,000
Таблица А. 1
Абсолютная
боло^метри-
ческая
звездная
величина
Мь
-10,6
-6,7
-2,5
0,0
1,7
2,7
3,8
4,6
5,1
5.8
6,8
7,<
9,8
Логарифм
светимости
\%{L/Lo)
6,13
4,56
2,88
1,88
1,20
0,80
0,37
0,05
-0,15
-0,43
-0,83
-1,15
-2,03
Белые карлики имеют цвета, которые соответствуют классам от О до
М. По характеру спектров карлики можно разбить на две
последовательности, каждая из которых перекрывает весь диапазон цветов. Карлики
последовательности DA отличаются водородными линиями в спектрах; к другой
последовательности относятся карлики прочих классов (обычно с
атмосферой, обогащенной гелием). Основные спектральные классы (в соответствии
с определением Гринстейна [242]) приведены в табл. А.2. Буква D означает
«вырожденный» (degenerate). В настоящее время, помимо DA, F, известно
много других гибридных спектров, и скоро, по-видимому потребуется
новая схема классификации.
Некоторые сведения из астрономии 575
Таблица А.2
СПЕКТРАЛЬНАЯ КЛАССИФИКАЦИЯ БЕЛЫХ КАРЛИКОВ
Название Спектральные особенности
класса
DA Присутствуют линии Н, нет линий Не
DB Сильные линии Не I, нет линий ?
DO Сильные линии Не И, есть линии Не I и/или ?
DF Присутствуют линии Са И, нет линий ?
DG Присутствуют линии Са II и Fe I, нет линий ?
DA, F Присутствуют линии ?, слабые линии Са II, нЬт Не
DC Непрерывный спектр
В начале нашего столетия датский астроном Э. Герцшпрунг и несколько
позднее американский астроном Г. Рессел сделали замечательное
открытие, что реальные звезды распределяются только по некоторым областям
диаграммы цвет—светимость. Это открытие иллюстрируется на рис. А.1.
Любая диаграмма, где сопоставляется величина, относящаяся к
светимости (например, светимость, болометрическая звездная величина,
визуальная звездная величина и т.д.), с величиной, имеющей отношение с цвету
(например, показатель цвета, цветовая температура, спектральный класс и
т.д.), называется диаграммой Герцшпрунга—Рессела, или просто
диаграммой Г—Р.
Если отложить на диаграмме Г—? большое число наблюдаемых звезд
всех классов, то обнаруживается, что более 804? звезд попадает в узкую
диагональную полосу, называемую главной последовательностью.
Следующий крупный класс звезд — белые карлики — включает около 104? всех
звезд. Основное значение диаграммы Г—? в том, что она содержит
данные об эволюционной последовательности звезд. Из теоретических
расчетов звездной эволюции найдено, что в процессе своей эволюции звезды
перемещаются по диаграмме Г—? и проводят большую часть времени в
наиболее населенных областях диаграммы. Эволюционный трек отдельной
звезды на диаграмме Г—? определяется ее начальным химическим
составом и начальной массой. Таким образом, сравнение расчетов эволюции с
наблюдаемым положением на диаграмме Г—? дает информацию о
начальных параметрах звезд, продолжительности каждой стадии их эволюции и о
возрасте.
Из теоретических расчетов вытекает следующая упрощенная
интерпретация диаграммы Г—Р: к звездам главной последовательности относятся
звезды, в недрах которых происходит превращение водорода в гелий; этот
Приложение А
Ml
-6
-2
+ 2
+ Б
0
Ac
^я>
-
Голуоой
5
"--^
! - ! .-^
ььгщгпкхШ'.ы
\ Г J р J ^О1 "·\ CI ? '^ ?? я
Ч^\ еатеь
"v^^_^ ^ y^
Сол hue ^^^^^^^^^-^..^^
\ 5елый Же. ^" ". '/ ^н-
Л,„] - ...1 1 1 „, ,1
i
Гиганшо!
.^^: '. ? ^г:
- =
—
^v J
-0,4
+ 0Л +0.8
3 -к
+ 1Д
-1,6
юосо
1000
100
10
1
0,1
0,01
Рис. A.l. Схематическое представление плотно населенных областей на диаграмме
Герцшпрунга — Рессела. Значительная часть всех звезд располагается вблизи
главной последовательности. Следующие наиболее населенные области заняты белыми
карликами и гигантами. Ветвь субгигантов и горизонтальная ветвь хорошо заметны
в таких звездных системах, имеющих большое число гигантов, как шаровые
скопления [135].
процесс составляет основу первой, самой продолжительной стадии
активной жизни Звезды. Главная последовательность не представляет собой
эволюционную кривую. Напротив, положение вновь рожденной звезды на
главной последовательности определяется ее массой и химическим
составом. При заданном химическом составе более массивные звезды имеют
более высокие температуры и светимости. Время жизни звезды на главной
последовательности является круто падающей функцией начальной массы
М, что отражает резко возрастающую зависимость светимости от массы.
Время пребывания звезды на главной последовательности приближенно
определяется уравнением A.3.9). Например, звезды с массой порядка массы
Солнца остаются на главной последовательности - 10 млрд. лет, а более
массивные звезды — всего несколько миллионов дет.
В типичных случаях 70—80^?? массы звезды в начальной стадии
эволюции составляет водород, 20—30<Уо — гелий и 0,1—3^?? — более тяжелые
элементы. Когда в центральной области активного ядерного горения
исчерпано 10—20<?^? водорода, выделение ядерной энергии в центре звезды
прекращается, но оно продолжается в тонком слое, который постепенно
смещается наружу к поверхности звезды. В результате ядро звезды, уже не
Некоторые сведения из астрономии 577
поддерживаемое давлением, несколько сжимается под действием
собственной гравитации и разогревается. Высвободившаяся гравитационная энергия
вызывает расширение внешних слоев звезды и поддерживает ее
светимость. Во воемя этой стадии эволюции звезда уходит с главной
последовательности и следует по ветви субгигантов диаграммы Г—? вверх и
направо в область красных гигантов (см. рис. А.1). В течение этого
эволюционного периода звезда сильно краснеет в связи с тем, что площадь ее
поверхности увеличивается (радиус может вырасти почти в тысячу раз).
В течение относительно быстрого перехода звезды с массой ? < Mq к
ветви гигантов ее центральная область становится достаточно плотной для
того, чтобы электроны оказались вырожденными (типичные значения
плотности и температуры ядер составляют 10^ — 10^ г/см^ и 30—70 млн.
К соответственно). Когда масса вырожденного ядра достигнет примерно
0,5 Mq , температура ядра становится достаточно высокой для того,
чтобы начался За-процесс, в ходе которого гелий быстро превращается в
углерод («гелиевая вспышка»). Выделившаяся энергия повышает
вырождение электронов, центральная область расширяется, а оболочка сжимается,
и звезда достаточно резко (например, за -10^ лет для звезды с Л/ =
= 0,65 A/q) перемещается на горизонтальную ветвь диаграммы Г—Рч
Эту ветвь нельзя считать чисто эволюционной кривой. Положение звезды
на горизонтальной ветви опять определяется массой гелиевого ядра и
водородной оболочки, а также химическим составом звезды-предшественника,
когда та находилась в верхней части области красных гигантов. Возможно,
ситуация усложняется до сих пор плохо исследованными процессами
потери массы, которую испытывает звезда, находясь на ветви гигантов.
Массивная звезда с Л/ ^ Mq не становится вырожденной на ветви субгигантов
и сжигает свой гелий постепенно без взрыва.
Последующая эволюция звезд на горизонтальной ветви понята еще
недостаточно. Звезда в процессе эволюции может несколько раз
возвращаться в область красных гигантов, где может начинаться сгорание других
видов ядерного топлива. В конечном итоге ядерное топливо звезды
истощается и она со временем прекращает излучать. Если звезда обладает
достаточной массой, она может взорваться как сверхновая и/или сколлапси-
ровать с образованием черной дыры. Сравнительно малые звездные
остатки могут сжиматься, образуя либо белый карлик (М -^ 1,4 Л/q , радиус
-- 10^ см), удерживаемый от коллапса давлением вырожденных
электронов и показанный в левом нижнем углу диаграммы Г—Р, либо
нейтронную звезду (Л/ :s 3 Mq , радиус - 10^ см), которая удерживается в
равновесии давлением вырожденных нейтронов и ядерными силами
отталкивания.
21^513
Приложение Б
Условие неустойчивости Кз < О
Приводимое доказательство того, что условие Kj < О означает
неустойчивость, основано на энергетическом принципе Л аваля, Мерсье и Пелла [348]
и справедливо для любого симметричного и не зависящего от времени
оператора L^j. Его значение состоит в том, что оно не связано ни с какими
предположениями о свойствах нормальных мод колебаний (например, об
их полноте). ^
Предположим, что К2@ < О для некоторого возмущения ^'(x» О в
произвольный момент времени /. Выберем этот момент так, чтобы t = 0.
Запишем ?' для этого момента времени в виде г/'(х» 0). Тогда, согласно
F.6.8),
1
2«'/р(т?')'^'х (Б.1)
при соответствующем выборе ? > 0.
Построим теперь новое возмущение ?'(?» О» при котором кинетическая
энергия 7^2@ неограниченно растет (если нам это удастся, мы покажем в
явном виде, что система неустойчива).
Рассмотрим начальные данные
?'(?,?) = ?(?,?), а,Г(х,0) = aV(x,0), (Б.2)
которые однозначно определяют новое возмущение. Для этой функции ?'
уравнение F.6.7) дает
TM-^OL-^jpiifd'x, (Б.З)
так что
?^ = Г2 + F2 = 0. (Б.4)
Поскольку величина Е^ сохраняется, 7^2 = ~^2 ^^^ ^^^^ ^- Поэтому из
результатов упражнения 6.14 вытекает
Условие неустойчивости V2 < 0.
579
Из неравенства Шварца следует
12
jp{d,i')i,d'x\ ^fp{d,i'Ydhfp{i-Yd'x (Б.6)
или
f )"<-=·
Комбинация выражений (Б.5) и (Б.7) дает
или
Of»»·
dt\I dtj
Ho из (Б.2.) следует
и поэтому
1 ^
/ J/
1 dl ,
2«,
r-O
ДЛЯ ? > 0.
После интегрирования получаем
/@>/@)е2<";
отсюда с учетом уравнения (Б. 5) следует
T2it)^a^l{0)e^'".
(Б.7)
(Б.8)
(Б.9)
(Б. 10)
(Б.11)
(Б. 12)
(Б. 13)
Таким образом, кинетическая энергия неограниченно растет и система
неустойчива.
Приложение В
Вычисление интеграла в уравнении (8.4.6)
Как отмечалось в тексте, требуется рассмотреть лишь случай b < 2R.
Интеграл может быть вычислен посредством трудоемкого прямого
геометрического определения области интегрирования. Мы предлагаем здесь
альтернативный метод, основанный на представлении ступенчатой функции в
виде
причем контур, по которому ведется интегрирование, проходит на
бесконечно малом расстоянии ниже начала координат вблизи ^ = 0. Уравнение
(В.1) можно проверить, замыкая контур в верхней полуплоскости для
дг > О и в нижней полуплоскости для дг < 0.
Таким образом.
1 /.00 p'f^b t t
?2?(?>,/?)^/ = ^j ^dk^^dx,dx^e-'^\'^-'^\. (B.2)
_1
?
Теперь используем разложение *^
d__
dk
в интеграл (В.2) вклад обеспечивают только члены с I = т = О, так что
D7г)' г^ ^. е'''^ d
•'О -?
(В.4)
Теперь запишем
(^2= Г^Г2+ (%. (В.5)
•'о •'о •'г,
'^ 3iu разложение получается, если взять производную d/dk от комплексно-
сопряженного выражения уравнения A6.22) из монографии Джексона [297].
Вычисление интеграла в уравнении (8.4.6)
581
В первом интеграле г^ = rj и г> = rj, а во втором эти обозначения
поменялись местами. Используя соотношения
ЛЫ=^, Л<о"*(х) =
le
(В.6)
находим
_DjrY
liri J_
/->[·'"(
2iR^ 3R^ 5
ЗЛ" 2k^ 2k''
k* 2k^ k^ 2k''
(B.7)
Поскольку b < 2R, член, пропорциональный e\p[ik(b — 2Л)], не дает
никакого вклада, что можно показать, если замкнуть контур в нижней
полуплоскости. По теореме о вычетах получим
miJ.J" к" (и-1)!'
И тогда
2??
+
32R^
(В.8)
(В.9)
что совпадает с результатом, приведенным в тексте.
Читатель может проверить, что если b > 2R, вклад второго члена
уравнения (В.7) в результат (В.9) приводит к следующему выражению:
^b>2R
т-
(В. 10)
Этот результат получается тривиально, если обратить внимание, что при
b > 1R ступенчатая функция, входящая в определение / [уравнение (В.2)],
всегда равна единице.
Приложение Г
Скалярные и векторные теории поля
Читатели, вероятно, лучше всего знакомы с теорией элек-рромагнитного
поля. Это векторная теория, поскольку основная полевая переменная в
лагранжиане — векторный потенциал А^. Уравнения поля вытекают из
принципа наименьшего действия:
?5 = 0, (Г.1)
где действие равно
ftd^x, (Г.2)
а ? — плотность лагранжиана. Величина ? должна быть лоренцевским
скаляром, так что действие S — это лоренц-инвариант.
Запишем
S = 5,„ + 5р + Si„,. (Г.З)
Здесь S^^ — действие свободного электромагнитного поля, зависящее
только от /4^, 5 — действие частиц, а S-^^^ — член, описывающий
взаимодействие.
Лагранжиан свободного поля равен
? = — F ?^? (? 4)
где тензор электромагнитного поля определен как
???^^?,?-^?,?^ (Г.5)
а запятая означает частную производную. Определение (Г.5) автоматически
гарантирует, что удовлетворяется половина уравнений Максвелла, а
именно
???, у + Руа, ? + F?y, а = 0. (Г.6)
Оставшиеся уравнения Максвелла следуют из вариационного принципа.
Уравнения Эйлера—Лагранжа для свободного поля таковы:
St _ дг ^ / ^? » ^ о (Г 7)
«Л З^а ???\9?,^?
Скалярные и векторные теории поля 583
Первый член в уравнении (Г.7) равен нулю для <?ет' ^ второй член дает
-J-F«% = 0. (Г.8)
Лагранжиан свободной частицы рассматривался в разд. 5.2. Удобнее
использовать квадрат этого лагранжиана, так что
S,
= /Ьр^т (Г.9)
= /??^'?, (Г.Ю)
где
^р = ?^^???^"""^, (Г.11)
?р = >/?«/,"""^?'[^^ - ?^{?)] dr. (Г.12)
Здесь ?" (?) — мировая линия частицы с массой w, а м" = dz^/dr —
4-скорость. Для системы из N частиц следует брать сумму N членов,
каждый из которых имеет вид (Г.9).
Если у частицы имеется заряд е, то ее 4-ток равен
Г = eju4^[x^ - ?^(?)] dr. (Г.13)
Упражнение Г. I. Сделав замену переменных интегрирования в
на /, проверьте, что это уравнение эквивалентно выражениям
7° = ??^[?-?(/)],
J = ev53[x-z(r)].
Член, описывающий взаимодействие, равен
•^int = /^int ^Т
-j^in.d'x.
где
^т\ ~ *^"^а>
^int = ^^?""·
уравнении (Г.13) с ?
(Г. 14)
(Г. 15)
(Г. 16)
(Г. 17)
(Г. 18)
(Г. 19)
584 Приложение Г
Таким образом, уравнения Максвелла при наличии источников имеют
вид
^? ^ ^^ст . ^^int ^ о (Г.20)
8А, и, ЬА, '
или с учетом уравнений (Г. 8) и (Г. 18)
F«^^ = 4w/". (Г.21)
Уравнение движения для каждой частицы принимает вид
8L _ dL d I dL\
??" ~ dz" dT [ди"}
(Г.22)
где/, = Lp + Z,j„j. Из уравнений (Г. 11) и (Г. 19) следует (поскольку>1^^
является функцией ?" вдоль мировой линии частицы)
0 = eApy--^{mv,pU^ + eA„). (Г.23)
Таким образом, получаем соотношение
= eF„y, (Г.24)
которое определяет силу Лоренца [см., например, [297], уравнение
A1.144)].
Существуют стандартные приемы, позволяющие преобразовать любую
теорию поля, заданную в лагранжевой форме, в гамильтонову форму и
построить тензор энергии-импульса поля. Знаки членов свободного поля S^^
и Sp определяются требованием, чтобы соответствующие свободные
гамильтонианы (или, лучше, плотности энергии) были положительными.
Знак Sj^j остается произвольным. Хотя изменение знака заряда изменяет
знак поля, порождаемого зарядом, в уравнении (Г.21) результирующая
сила, действующая на другой заряд, остается такой же благодаря
компенсирующему изменению знака в уравнении (Г.24).
Электромагнетизм — это векторная теория поля для безмассовых
частиц. В теории поля для частиц с массой имеется член
- 3^?'?^"> (Г.25)
добавляемый к плотности лагранжиана (Г.4). Уравнение (Г.21) принимает
вид
Скалярные и векторные теории поля ^^5
F«% + ?^^" = 47гГ. (Г.26)
Упражнение Г.2. Покажите, что условие сохранения заряда 7", ? = О автоматически
гарантирует для векторного поля частиц ненулевой массы выполнение условия
Лоренца
Л"" ^^0. (Г.27)
Подставив уравнение (Г.5) в уравнение (Г.26), получим
?^^'^? - ?^'^^? + ?^^" = 47г/«. (Г.28)
Поменяв порядок частных производных в первом члене, видим, что он
равен нулю в соответствии с уравнением (Г.27). Второй член равен просто
оператору Даламбера со знаком минус, так что
D.4" - ?^?"" = -???. (Г.29)
Упражнение Г.З. Рассмотрите решения уравнения (Г.29) при 7« = О, имеющие вид
плоских волн в вакууме :
y^« = ?«e-'"V^^*^ (Г.ЗО)
где а" — постоянная. Покажите, что
— -k^ = ?\ (Г.31)
и сделайте отсюда вывод, что кванты соответствующего квантового поля обладают
массой ??/c.
Найдем теперь статическое взаимодействие между двумя покоящимися
точечными «зарядами». Для заряда ^, покоящегося в начале координат,
можно записать [см. (Г. 14) и (Г. 15)]
/О = g8'{x), J = 0. (Г.32)
Поэтому в уравнении (Г.29) можно положить
^^ = ф, А = О, (Г.ЗЗ)
где
?^? - ?^? = -47rg8\x). (Г.34)
Уравнение (Г.34) можно решить, например, при помощи преобразования
586 Приложение Г
Фурье. В результате получается потенциал Юкавы
е~^'
<i> = g-^, (Г.35)
Обратите внимание, что в соответствии с уравнением (Г.24) сила,
действующая на другой заряд ^', равна
та = -g'V<i), (Г.36)
так что одноименные заряды взаимно отталкиваются. Энергия
взаимодействия между двумя равными зарядами положительна, и
величина ее равна
Теперь рассмотрим скалярное поле частиц с ненулевой массой.
Плотности лагранжиана равны
afield» -8^(Ф,„Ф" + МУ), (Г-38)
Cin, = -РФ, (Г.39)
а величина ? ? по-прежнему определяется уравнением (Г. 12). Здесь
о — плотность скалярного заряда
p = gjd?Ь*[x'^-z'^{^)]. {Г.40)
Варьируя ф, получим уравнение поля
Пф - ?2? = 47гр, (Г.41)
а варьирование г" дает уравнение движения частицы
Для точечного заряда, покоящегося в начале координат, получим
V^<i>-iii2<i> = 47rg6^(x), (Г.43)
так что
е~^'
Ф=-8—^· (Г.44)
Таким образом, одноименные скалярные заряды взаимно притягиваются.
Скалярные и векторные теории поля ^g^
Энергия их взаимодействия
отри14апгельна.
Отметим, что, поскольку частицы и античастицы обладают зарядами
противоположного знака, силы между частицами и античастицами носят
характер притяжения для векторных полей и отталкивания для скалярных
полей.
Приложение Д
Кварки
Элементарные частицы делятся на два класса: лептоны, которые не
участвуют в сильных взаимодействиях и не обнаруживают никакой внутренней
структуры, и сильно взаимодействующие адроны. В настоящее время
известно три типа лептонов: е, ? и г, каждый со своим нейтрино,
взаимодействующим только с данным лептоном (экспериментальные
доказательства существования ?^ пока только косвенные).
Адроны подразделяются на барионы, которые в конечном итоге
распадаются, превращаясь в протоны (т.е. имеют барионное число, равное
единице) и мезоны (барионное число равно нулю). Кварковая модель весьма
успешно объяснила многие свойства адронов. В настоящее время
считается, что существует шесть «ароматов» кварков. Они обозначаются и (up), d
(down), 5 (strange), с (charm), t (top) и b (bottom). Кварки имеют спин 1/2 и
каждый обладает тремя «цветами». Барионы состоят из трех кварков, а
мезоны из кварка и антикварка. Кварки и, с и t обладают зарядом +2/3, а
d, S и b имеют заряд -1/3. У всех кварков странность равна нулю, за
исключением 5-кварка, у которого она составляет - 1.
Предполагается, что сильное взаимодействие между кварками возникает
из-за обмена безмассовыми частицами со спином 1, называемыми «глюо-
нами», которые переносят цветовые квантовые числа. Эту теорию
называют «квантовой хромодинамикой» — сокращенно КХД.
Кварки и лептоны группируются в три семейства:
d и S с Ь t
Слабое взаимодействие отвечает за переходы между разными ароматами
кварков и между семействами лептонов. В модели Вейнберга—Салама
(которая является составной частью квантовой хромодинамики) слабое
взаимодействие и электромагнетизм объединены в одну теорию.
Электромагнитное взаимодействие возникает благодаря обмену безмассовыми
фотонами со спином 1, а слабое взаимодействие появляется вследствие обмена
частицами со спином 1 и с очень большой массой (- 80 ГэВ) —
бозонами W'^, W~ и ZP. «Нормальное» вещество состоит в
значительной мере из представителей первого семейства: нейтрон является
просто триплетом udd, а протон — триплетом uud.
В табл. Д.1 приводится перечень свойств частиц. В нее включены все
«устойчивые» частицы (с временем жизни > 10"^^ с), а также некоторые
представляющие интерес резонансы с более коротким временем жизни.
Кварки
589
СВОЙСТВА ЧАСТИЦ U
Частица t J^ Масса,
е
?-
?
?
?
?
?
?+
??
?-
VQ
'?~
МэВ
Лептоны
1/2 0,511003
1/2 105,6594
1/2 1784
Нестранные барионы
1/2 1/2+ 938,280
1/2 1/2+ 939,573
3/2 3/2+ 1232
Барионы со странностью — /
0 1/2+ 1115,60
1 1/2+ 1189,36
1 1/2+ 1192,46
1 1/2+ 1197,34
Барионы со странностью —2
1/2 1/2+ 1314,9
1/2 1/2+ 1321,3
Таблица Д.]
Среднее время
жизни, с
стабилен
2,19714-10-6
5-10-13
стабилен
925
6-10-24
2,63-10-10
8,00-10-11
6-10-20
1,48-10-10
2,9-10-10
1,64-10-10
Барион со странностью —5
О 3/2+ 1672,5
8,2-10-1
л;
тгО
V
?
?
?'
?
J/?
?
ко.
Очарованный нестранный барион
О 1/2+ 2282
Нестранные мезоны
1
1
О
1
о
о
о
о
Мезоны со странностью -/
1/2 О- 493,67
КО 1/2 О- 497,7
0-
0-
0-
1-
1-
0-
1-
1-
1-
139,567
134,963
548,8
769
782,6
957,6
1019,6
3096,9
9456
1-10-13
2,603 10-8
8,3· 10-17
8·10-l^
4,3 10-24
6,6· 10-23
2,4· 10-21
1,6· 10-^-2
1,0· 10-20
1,6· 10-20
1,237· 10-8
/^, :8,92 10-11
А:^.:5,1810-8
590
Приложение Д
Продолжение табл. Д.1
Частица
JP
Масса,
МэВ
Среднее время
жизни, с
Очарованные нестранные мезоны
D^ _ 1/2 О- 1869,4
/>о, D 1/2 О- 1864,7
9· 10-13
5 10-13
F^
Очарованный странный мезон
О О- 2021
2-10-
1^ Данная таблица заимствована из [448]. Во втором столбце
указан изоспин /, в третьем — спин и четность УЛ Как правило, массы и
времена жизни округлены. Полный перечень свойств частиц и ошибок
указанных в таблице численных значений дан в [448].
Приложение ?
Фазовый множитель в уравнении A1.5.16)
Вычисляя в этом разделе фазовый множитель ? уравнения A1.5.14), будем
следовать Бакалу и Вольфу [41]. Такие интегралы часто появляются в
нейтринной физике и физике конденсированного вещества^^ Используем
приближение, считая, что величина кТ пренебрежимо мала по сравнению
со всеми входящими в задачу кинетическими энергиями Ферми.
Используя уравнение A1.5.2), перепишем ? в виде
P = BJY\pfdpjSE,8{Ef - Ei)A, (E-D
где
В = {т^с)-'\2^)-'\ (Е.2)
6
Л=Н-'(иЩ8'{к.^к,). (Е.З)
В интеграле А достаточно рассмотреть только ту часть фазового
объема, где энергии частиц отличаются от энергий Ферми всего на несколько
кТ. Соответствующий ферми-импульс нейтрона велик по сравнению с
ферми-импульсами протона и электрона (см. упражнение 11.1); импульсом
нейтрино кТ мы полностью пренебрегаем. Учитывая, что
к,. = к,+ к2, к^=к,,+ к,, (Е.4)
где
к, = к^ + к, + к,-, (Е.5)
получим
Н^А = fdQ^dQ2dQydQpdQ,dii^-S\k^ + kj - к,, - kj. (Е.6)
Сначала выполним интегрирование по dU^, записав дельта-функцию в виде
,?(??-??^2-.)
.2
8{ку - |к, + к^ - к,|) ^ ^ ,2 ' №.7)
1)
Например, в теории гелия-3.
592 Приложение ?
Интегрирование по dQy дает единицу и остается
h'A » fdQ, dQ^ dQ, dil, dQ, ^(^1—^1^^^2-kj) ^^ ^^
^ ky
Перепишем оставшуюся дельта-функцию в виде
8[ку - [к] + |к2 - kj2 - 1к,%г - kJcosO,)'/']
8[cosg, - {kl - A:f - |к, - k,|^)/Bfe,|k, - k,|)]
A:,|k2 - kJA,, · ^ · '
Здесь мы выбрали ось ? так, чтобы она совпадала с направлением kj и
kj - к^, а также использовали тождество b\f{x)\ = 6(дг - ?)/\/'{?)\, где
Да) = 0. Выполнив интегрирование по c/fij, получаем
3. ^ J^ .dQ^dQ^dQ.dQ,
kykj |к2-к,|
(ЕЛО)
Вспомнив, что ^2 ^ *5> находим
или
^=D,?)'B;>,;»2/?-)"'· №.12)
Дифференциалы импульсов в j равнении (ЕЛ) можно упростить,
используя соотношение:
dE,
Pjdpj = Ej-^ = mjdEj, j^n,p,
?, = -^. (ЕЛЗ)
Тогда все pj (за исключением р·.) можно положить равными рр(/) и
вынести из-под интеграла. Это дает
? = 2%'c-*Bmlm^pAp)pUe)f UdEjE^SSiEf- ?,). (?.14)
Теперь выражение (ll.i.5) для статистического множителя S может быть
Фазовый множитель в уравнении A1.5.16)
593
записано в виде
где
OnF
безразмерные энергии
юделив
5=ПA + ^
У-1
Xj определяется
x^=?{E^-
хг = )8(^2 -
^3 = -?{?,
?,= -?{??
Х5 = -?{??
?,
'Г\
соотношениями
mJ>
?«).
-Me)'
-?«)'
-Мр)'
получим для уравнения (Е.14)
? = 2%'c-'Bmlm^pAp)pUe){kTYl,
где
' dyy'J,
(?. 15)
(?. 16)
(?. 17)
(?. 18)
(?. 19)
Lxj-y
(E.20)
Интеграл У не охватывает энергии меньше тс^. Однако мы не сделаем
ошибки больше expl-??'??)], если расширим область интегрирования для
каждой величины Х: от — оо до оо.
Чтобы вычислить J, начнем с представления
(Е.21)
22-513
594
Приложение ?
Тогда
1 /·«>
(E.22)
где
/•00 _ ,
f{z) = / i/xe'"(e^+ 1) '.
(E.23)
В уравнении (E.23) величина ? должна иметь небольшую отрицательную
мнимую часть, чтобы интеграл сходился.
Оценим/к) посредством интегрирования
K^(j)dwe''''{e'' + 1)"
(Е.24)
по контуру, показанному на рис. Е.1. Вклад вертикальных отрезков в
предельном случае /? — оо равен нулю. Интеграл вдоль действительной оси
дает /(?), а вклад от интеграла вдоль линии Im(w) = 2? равен
-exp(-2?^)Дz). Единственный полюс подынтегрального выражения в
уравнении (Е.24), охватываемый контуром, находится в точке w = /?;
вычет в этой точке равен -exp(-?z). Таким образом.
или
к = f{z) - e-^^'f{z) = -2те-
/ sh 41 ?
(?.25)
(?.26)
Возвращаясь к уравнению (?. 22), имеем
1
2'TnJ_^_i^ V sh ?? ?
(?.27)
Здесь мы ввели - /? в пределы интегрирования как напоминание о том, что
? имеет небольшую отрицательную мнимую часть. Постараемся вычислить
-R+Zin
у
-1
?
я
\т{ю}
i
)
i
:??
0
R+Zm
?
/
^
R
^Я^{ш)
Рис. ?. 1. Контур интегрирования для уравнения (Е.24) с /? -* оо.
Фазовый множитель в уравнении A1.5.16)
595
J путем нахождения удобного замкнутого контура. Если сделать
подстановку
(Е.28)
2 = 2—/
(Е.29)
в выражение (Е.27), то находим
Уравнения (Е.27) и (Е.29) дают
A+^^)/ = --/ +/ \dze ''У\-г
??? J \ sh 7?2 /
Здесь мы замкнули контур, как показано на рис. Е.2, где вертикальные
отрезки не дают вклада в конечный результат. Единственный полюс,
находящийся внутри контура, лежит в точке ? = 0. Таким образом.
A -I- еУK = Вычет в 2 = О от
izy[_l_\
\ Sh 7Г2 /
(Е.31)
Вычет находится посредством разложения в ряд показательной функции и
гиперболического синуса вблизи точки ? = О и сравнения коэффициентов
при члене \/?. Это дает
/1 I ?\ г ЗТГ ЗТГ 2.^4
(Е.32)
Рис. Е. 2. Контур интегрирования для уравнения (Е. 30).
596 Приложение ?.
Таким образом, уравнение (Е.19) дает
Подынтегральное выражение в уравнении (Е.ЗЗ) представляет собой
энергетический спектр антинейтрино. Сам интеграл можно найти в справочнике
Градштейна и Рыжика [234]. Он равен
/ = 11^1^. (Е.34)
^ 120960 ^
Использовав в уравнении (Е.18) результаты упражнения 11.1, наконец,
получим
? = 2,1 X 10-^^(-^) Г/, (Е.35)
\ Pnuc /
т.е. результат, использованный в уравнении A1.5.16).
Отметим, что в процессе вычисления мы пользовались массами
свободных частиц для нуклонов Wy, а не их эффективными массами т* ^ rrij.
Эффективные массы учитывают нуклон-нуклонные взаимодействия между
нуклонной системой из двух тел и окружающим нуклонным
морем — системой многих тел. Учитывая существующие неопределенности
в значениях эффективных масс, мы пренебрегали этой поправкой^^
^^ Обсуждение этого вопроса см. в [211].
Приложение Ж
Сферически симметричная аккреция
на черную дыру:
релятивистские уравнения
в этом приложении мы обсудим общие релятивистские аналоги уравнений
Бонди [78] для сферически симметричной непрерывной адиабатической
аккреции на шварцшильдовскую черную дыру с массой Л/. Мы покажем, что
релятивистские уравнения для аккреции на черную дыру требуют перехода
к сверхзвуковому течению.
Граничные условия на бесконечности остаются теми же, что и раньше:
газ покоится; концентрация барионов равна п^; плотность массы
покоя — тп^, где т — средняя масса бариона; полная плотность массы-
энергии р^. Как обычно, связь между полной плотностью массы-энергии и
плотностью энергии, соответствующей массе покоя, дается соотношением
р^тп + ?\ (Ж.1)
где ?' — плотность внутренней энергии. (В этом приложении используется
система единиц с = С = 1.) Для адиабатического течения известно, что
? = Р{п), и этого условия вполне достаточно для доказательства
околозвукового характера течения. Основными уравнениями являются следующие:
уравнение еохранения барионов
(/»««);„= о, (Ж.2)
уравнение сохранения импульса (релятивистское уравнение Эйлера)
(р + P)u,.pu^ = -Р„ - и„Р_у, (ж.З)
и уравнение сохранения массы-энергии [уравнение энтропии, см. уравнение
B.1.3I
4^)...A)-г*, о.
(Ж.4)
Читателю, незнакомому с тензорным исчислением, придется принять на
веру, что уравнения (Ж.2) и (Ж.З) — это релятивистские обобщения
уравнений F.1.1) и F.1.2) (см., например, [411]). Здесь м" означают компоненты
4-скорости жидкости. Уравнение (Ж.4) можно записать в виде
^ = ??? (Ж.5)
dn ? '
598
Приложение Ж
который окажется полезным в дальнейшем.
Уравнения (Ж.2) и (Ж.З) можно записать в шварцшильдовских
координатах в виде
/1' . W' . 2
+ — + - = О,
? и г
(Ж.6)
ии
1 dP(, , 2 2М\ ?
(ЖЛ)
где штрих означает дифференцирование по г, а м означает направленную
внутрь радиальную компоненту скорости и = I ?'? . Определим скорость
звука в соответствии с соотношением
а^^
dP dP ?
dp dn ? + ?'
(Ж.8)
где мы воспользовались уравнением (Ж.5). Теперь можно записать
уравнение (Ж.7) в виде
мм' + — + 1 + и^ ]а^— = О,
(Ж.9)
где использовано равенство Р' = (dP/dn)n'. Сразу же видно, что
уравнения (Ж.6) и (Ж.9) представляют собой релятивистские обобщения
уравнений A4.3.6) и A4.3.7).
Продолжая, как и в ньютоновском случае, стремиться к решению
относительно и' и п'у получаем
м =
^1
D '
и =
D '
где
п
D,
_ 2и^/г - М/г^
(Ж. 10)
(Ж. 11)
(Ж. 12)
?) =
и^-{\ -2М/г + и^)а^
ип
(Ж. 13)
Теперь докажем, что при любом уравнении состояния,
удовлетворяющем релятивистскому условию а^ < 1 (см. разд. 9.5), течение должно прохо-
Сферически симметричная аккреция на черную дыру 599
дить через критическую точку, расположенную вне горизонта событий
(г = 2Л/). При больших значениях г, как мы знаем, течение удовлетворяет
условию и^ < \ и является дозвуковым: и^ < а^ (например, при г—оо, м— О,
а -^ а^), поэтому из уравнения (Ж. 13) следует
D=-- —<0. (Ж.14)
ип
Однако при г = 2Л/ получаем
D = -(\ -?^)>0, (Ж.15)
?
поскольку а^ < 1. Таким образом, величина D должна пройти лерез нуль в
некоторой точке г = г^ вне г = 2Л/. Чтобы избежать особенностей в
течении, необходимо с учетом (Ж. 10) потребовать выполнения соотношений
?), = ?J = ^ = О при г = г,.
Из уравнений (Ж.И)—(Ж. 13) находим, что при г = г^
„2 = _^ = |1. (Ж.17)
Заметим, что собственная скорость жидкости у'', измеряемая локальным
неподвижным наблюдателем, связана с и отношением
«'= -^ = ^^-^ = -^1 ТЮГТ (Ж.18)
(см. разд. 12.2 и 12.4). Используя равенство -1 = и · и, которое дает
--<"'I'-?^)*?4^?· <'^">
находим, что уравнение (Ж.18) принимает вид
\v'\ = -; ~?7? · (Ж.20)
A -2М/Г+ ^2I/2
Итак, в соответствии с уравнением (Ж.20) при больших значениях г > 2Л/,
где и < 1^ имеем \?? = м; по мере того как г — оо, собственная скорость
течения ?;'' — О, оставаясь дозвуковой. При г=2М получаем \?''\ ? 1 > uf
и собственная скорость, равная скорости света, оказывается
сверхзвуковой. Существенно, что li;*l = 1 при г = 2М независимо от величины и.
Таким образом, одно лишь требование, чтобы собственная скорость равня-
600 Приложение Ж
лась скорости света на горизонте, само по себе вовсе не гарантирует
прохождение течения через критическую точку вне г = 2Л/ вопреки тому, как
иногда утверждается.
Чтобы продвинуться дальше, придадим уравнениям (Ж.6) и (Ж.9) вид
уравнений сохранения [403]. Это дает
4жтпиг^ = Л/ = const (не зависит от г) (Ж.21)
mi'-^-i-"
р^ + Р.''
(Ж.22)
Уравнение (Ж.21) дает темп аккреции массы покоя, а уравнение (Ж.22)
является релятивистским уравнением Бернулли.
Чтобы подсчитать точное значение Л/, нам необходимо принять
уравнение состояния. Вслед за Бонди [78] предположим политропное уравнение
состояния
? = Кп^, К, Г const. (Ж.23)
Подстановка уравнения (Ж.23) в уравнение (Ж.4) дает
j(j) = A:/i^-2jn. (Ж.24)
Интегрирование приводит к следующему результату:
p = m/i+ jA^, (Ж.25)
где постоянная интегрирования т вычисляется посредством сравнения с
уравнением (Ж.1). Следовательно,
P±L^ni + .^Kn^-\ (Ж.26)
? Г - 1
и, согласно выражению (Ж.8),
д2 = и^}__ ^ (Ж 27)
или
,2
1 - aV(r - 1)
(Ж.28)
Сферически симметричная аккреция на черную дыру 601
Подстановка уравнений (Ж.26) и (Ж.28) в уравнение (Ж.22) дает
Преобразуя обе части уравнения (Ж.29) и производя вычисления в
«звуковой» точке при помощи уравнения (Ж. 17), получаем
A + 3??)(? - j^j-1' = (l - j^l'. (Ж.ЗО)
Теперь можно ожидать, что при больших г ^ г^ барионы должны быть
нерелятивистскими са ?, а^ < 1 (т.е. ? < тс^/к = 10^^ К), если они были
нерелятивистскими на бесконечности (т.е. а^ < 1). Разлагая уравнение
(Ж.ЗО) по степеням а^ и а^ до первых неисчезающих членов, находим
.7 2
^s
»
SS
5
1«
2
-ЗГ
'00'
ai.
Г
=
1
3
г
?
1
i»
(Ж.31)
Уравнение (Ж.31) подтверждает наши ожидания, что из условия а^ <^ 1
следует а^ < I.
Упражнение Ж.1. Получите критический радиус в единицах ? и а^^ для 1 ^ Г < 5/3
и сравните с результатом в ньютоновском приближении — уравнением A4.3.14).
Ответ:
г
Л'
Г
Л'
iSi
«
5
3
—
4
-ЗГ
4
Л/
—
в^'
м
2 *
Г =
г =*
5
= —
3
5
—
3*
Теперь уравнение (Ж.28) для аУ(Г - 1) < 1 дает
?2??-1)
«00 ~ Uoo/
(Ж.32)
Следовательно, темп аккреции равен
? = Ачттп.и.г^ = 4^Л,Л/^и„а-\ (Ж.ЗЗ)
602 Приложение Ж
где мы использовали уравнения (Ж.21), (Ж. 17), (Ж.31) и (Ж.32).
Безразмерный параметр аккреции \ в уравнении (Ж.33) определен для
1 ^ Г ^ 5/3 уравнением A4.3.17). Таким образом, мы нашли, что темп
аккреции в первом приближении с учетом релятивистских поправок равен
результату Бонди [78] для ньютоновского околозвукового течения.
Эквивалентность ньютоновского выражения результату, полученному в
рамках обшей теории относительности, вполне объяснима с физической
точки зрения: критический темп аккреции определяется условиями в одной
и той же звуковой точке г = г^, которая лежит вне горизонта (Гу > 2М) и
не подвержена влиянию нелинейной гравитации. С другой стороны,
условие регулярности, налагаемое на решение с релятивистским течением
вне горизонта, делает необходимым определить в первую очередь
околозвуковое течение!
Для оценок параметров течения при малых радиусах г <t г^ заметим
прежде всего, что, поскольку течение является околозвуковым с и > а,
уравнение (Ж.29) требует, чтобы при Г ? 5/3
2 2М /т- 5\
(Ж.34)
Из соотношений (Ж.21), (Ж.33) и (Ж.34) можно подсчитать степень сжатия
газа
-^-^ «-^1 ^-I . (Ж.35)
yf2
az^r
Предположив, что газ подчиняется распределению Максвелла — Больцма-
на с давлением ? = пкТ, где ? — температура, с учетом (Ж.23) для
адиабатического температурного профиля^ имеем следующее выражение:
?
-т"'Ы'шг"-'-
На горизонте событий (индекс «Л») в этом случае находим независимо от
массы ? черной дыры
I?IL^h(^? II^ \Ы—\
Г-1
(Ж.37)
где мы ввели скорость света с.
Числовые коэффициенты в приведенных выше выражениях для особого
случая Г = 5/3 несколько иные. В этом случае а остается сравнимой с и
внутри околозвуковой области. Поскольку в Соответствии с уравнением
Сферически симметричная аккреция на черную дыру 603
(Ж.31) а^ ^ А^даДля г < г^, в уравнении (Ж.29) можно положить правую
часть равной единице при г = 2М, что дает
а
С использованием уравнения (Ж.27) это соотношение принимает вид
Теперь уравнения (Ж.21) и (Ж.33) дают при \ = 1/4
Поскольку в соответствии с уравнением (Ж.27)
^" * Зт '
(Ж.41)
уравнение (Ж.39) принимает вид
2
211/3
"* + 7IT7I"i''-»*0· (Ж.42)
Численное решение уравнения (Ж.42) дает следующий результат:
Мл «0,782 (r = i). (Ж.43)
Теперь из уравнения (Ж.40) следует
^._1_[^Г IlJAY'\^\\ (Ж.44)
Проведем численные оценки соотношений (Ж.44) в случае
нерелятивистских барионов, аккрецируемых из межзвездной среды. Скорость звука в
окружающей среде равна
°. - (Iff)" ""-'(т^)"*-^=- "^¦«>
Подстановка уравнений (Ж.43) и (Ж.45) в (Ж.44) дает
504 Приложение Ж
-^« 1,ЗЗХ 10>2|-^
г \"^/^
Таким образом, температура Tf^ не зависит от ?^^. Причина в том, что при
Г = 5/3 значительная доля гравитационной потенциальной энергии,
сравнимая с энергией массы покоя на горизонте, неизбежно преобразуется в
тепловую энергию (оба вида энергии изменяются пропорционально \/г
внутри ГуГ кТ - GMm^/r). Адиабатическое течение в предельном случае
Г = 5/3 приводит к максимально достижимой температуре газа на
горизонте. При Г < 5/3 тепловые энергии меньше.
Вычислительное упражнение Ж.2. Решите численно уравнения (Ж.21), (Ж.22) и
(Ж.36) для аккреции нерелятивистских барионов при Т^ = 10^ К (Г = 5/3).
Определите безразмерные профили концентрации п{г)/п„, скорости и{г)/с и температуры
Д'")/^'» в виде функций от г/Л/. Изобразите ваши результаты графически (на бумаге
с двойной логарифмической сеткой) в области значений 2М ^
^ г ^ 10г^, где г^ = GM/al,.
Устойчивость стационарной сферической аккреции на шварцшильдов-
скую черную дыру изучалась несколькими группами авторов. Наиболее
общий анализ принадлежит Монкрайфу (см. [412] и приведенные там ссылки
на более ранние работы). Монкрайф выполнил в рамках общей теории
относительности анализ нормальных мод решения, соответствующего
околозвуковому течению. Он нашел, что не существует неустойчивых мод ни в
дозвуковой, ни в сверхзвуковой областях — течение устойчиво.
Приложение 3
Гидродинамика течения вязкой жидкости
Уравнение движения нерелятивистской вязкой жидкости имеет вид
""^^ "^^"^^'-i· C.1)
где тензор вязких напряжений J, имеет компоненты
^7 ^ hi ^ '? ( ^/. J + ^У, / - 3 «/у t);t, к ); C.2)
а его след равен нулю. Здесь ?{? > 0) — коэффициент динамической, или
сдвиговой, вязкости; объемной вязкостью мы пренебрегаем^\ Когда ? = О,
уравнение C.1) переходит в уравнение Эйлера для идеальной жидкости.
Чтобы найти скорость нагрева жидкости в результате вязкостной
диссипации, рассмотрим скорость изменения энергии единицы массы
жидкости (измеряемой при совместном движении с жидкостью):
Ш^^ + и]^У'^ + ^. C.3)
dt\2 I dt dt
Здесь и — внутренняя энергия на единицу массы, а du/dt дается первым
законом термодинамики F.1.8). Выражая d?/dt при помощи уравнения C.1),
а dp/dt — при помощи уравнения неразрывности F.1.1), находим
4(it;2 + «)= --vVP + -v.(vt)--Vv+r^
dt\2 j ? ? ^ -' ? at
._iv.(Pv-t.v) + rf-^i,,o,,. C.4)
Находящийся в правой части уравнения C.4) член типа дивергенции
представляет собой скорость, с которой производится работа над единичной
массой жидкости, так что, если проинтегрировать по массе элемента
жидкости объемом У, получим
J - ? (Pv - t · v)p ?/? = |(?? - t · ?) · dA
•^ Cm. книгу Ландау и Лифшица [339], гл. 2, для выяснения всех деталей.
606 Приложение 3
где
f = Рп - t · ? C.5)
— внешняя сила (на единицу площади), действующая на поверхность,
нормаль к которой определяется единичным вектором п.
Таким образом, два оставшихся члена в уравнении C.4), связанные с
внутренним нагревом, должны полностью сбалансироваться:
= li^i,) -^ ^jj)^ij (?· к. tjj симметричен)
= i(i''>^f*'>^^'^)''>
= —ГГ.. C.6)
поскольку след I = t^jb^j = 0. Уравнение C.6) показывает, что возрастание
энтропии зависит от квадрата отклонения от равновесия (т.е. от квадрата
градиента скорости). Этого и следовало ожидать, так как энтропия имеет
максимум в равновесном состоянии.
Ограничимся теперь кеплеровским аккреционным диском, где у
скорости в сущности имеется только ф-компонент (т.е. ?^ < ?,. < ? ?):
^? =^^^-[-^} · C.7)
? циклических координатах единственным компонентом ^, которым нельзя
пренебрегать, оказывается [см. [339], уравнение A5.15)]
^. = ^ = ^^(^^ + ^^--7^)- (^-^^
Используя выражение C.7), находим
Вязкостная сила в направлении 0, вызываемая трением между соседними
элементами жидкости, приводит к тормозящему моменту, который уносит
момент количества движения наружу за пределы системы. Нормаль к
поверхности, разделяющей соседние элементы жидкости, в данном случае
направлена радиально, так что описываемая уравнением C.5) сила должна
иметь вид
L = -V· C·>0)
Приложение И
Перенос излучения
в этом разделе собраны основные соображения о переносе излучения в
газовой среде. Для более подробного ознакомления отсылаем читателя к
отличным книгам Чандрасекара [115] (где особое внимание уделяется
форме и решению уравнения переноса), Михаласа [406] (приложения к
атмосферам звезд) или Рыбицкого и Лайтмана [493] (процессы излучения).
Отличные обсуждения, касающиеся переноса излучения, можно найти в книгах
Клейтона [135] (приложения к недрам звезд) и Зельдовича и Райзера [637]
(приложения к явлению ударных волн).
И.1. УРАВНЕНИЕ ПЕРЕНОСА
Напомним, что фундаментальной величиной, описывающей
термодинамическое состояние ансамбля частиц — в данном случае фотонов, — служит
функция распределения/(г, р, t) (см. гл. 2). Число фотонов в единице
фазового объема d^rd^p с координатами г и ? в момент времени t связано с /
соотношением
d% = l-fd^rd'p = 4/^' dp dQ d'r, (И.1)
где h — постоянная Планка, с — скорость света, а и — частота, связанная
с импульсом соотношением ? = hu/c. Направление распространения
определяется единичным вектором п, которому соответствует элемент
телесного угла dQ. Энергия, которую несут фотоны в этом объеме, выражается
как
dE ^hvd% = ^dv dQ d^r, (И.2)
с
Выражение (И.2) в таком виде определяет величину /Дг, п. О, связанную с
/ соотношением
/Дг,п,/) = ^/('',г,п,/). (И.З)
с^
Величина /^, называемая удельной интенсивностью, определена таким
образом, что /^(г, п, tyJudQ описывает энергию фотонов в интервале частот
от ?^ до ?' + dv, пересекающих в единицу времени единичный элемент
поверхности с нормалью ? в пределах телесного угла dQ, ориентированного в
608 Приложение И
направлении п. Итак, поле излучения полностью описывается любой из
функций как /^, так и /.
С функцией /^ связаны ее моменты. Так, величина
^ Mir
дает удельную плотность энергии в точке г, а векторная функция
ГДг,0= / /.?^? (И.5)
Mir
определяет удельный поток по направлению п^\ Поэтому удельный поток
через поверхность с единичным нормальным вектором m равен
F^r, Mn)sF,-in= f /.costfja, (И.6)
Mir
где ? — угол между направлением распространения фотонов ? и нормалью
к поверхности т. Заметим, что если поле излучения изотропно, т.е. /^ не
зависит от п, то из уравнений (И.4) и (И.5) следует
в.[ = (изотропия),
^ (И.7)
Полные интенсивность, плотность энергии и поток получаются
интегрированием соответствующих монохроматических величин по частоте
J/.00 /.00 /.00
^ I^dv, e,^\e[dv, ?^??,??. (И.8)
о •'о •'О
в особом случае, когда преобладает локальное термодинамическое
равновесие (ЛТР), характеризуемое температурой Г, величина /^ описывается
функцией Планка
а ?^ и ?^ определяются выражениями
с с^ cxp{hv/kT) - 1
е. S ?
?
??^ (И. 10)
^^ Термин «удельный» используется здесь для обозначения понятия
«рассчитанный на единичный интервал частот»; в литературе употребляются и другие
названия.
Перенос излучения 609
где а = 7,56 · 10" ^^ эрг/(см^ · град"*) — постоянная плотности излучения,
а индекс «Р» означает «планковский».
При строгом термодинамическом равновесии F = О (никакого потока
ни в каком направлении). Однако при ЛТР уравнения (И.9) и (И. 10) можно
использовать с высокой точностью даже в присутствии небольшого
отличного от нуля потока F, если градиент интенсивности (связанный,
например, с градиентом температуры) мал.
Рассмотрим теперь излучение и поглощение фотонов в газовой среде.
Определим коэффициент излучения, излучательную способность j^(r, ?, t),
так, чтобы величина j^dvdO. представляла собой скорость спонтанного
излучения энеогии, приходящегося на единичный объем в интервале частот
{у, V -\- dv) и направленного в пределах телесного угла ? вдоль вектора ? в
момент времени t. Аналогичным образом определим коэффициент
поглощения, или непрозрачность /с^(г, п. О» так, чтобы величина K^pI^dvdQ
представляла собой соответствующую энергию, поглощенную в единице
объема в единицу времени из пучка данной интенсивности /^ (таким
образом, /с^ измеряется в cMVr). Если допустить, что фотоны распространяются в
среде прямолинейно, то полное изменение /^ на расстоянии rfs, измеряемом
вдоль светового пути в направлении п, равно
где учитываются локальные изменения со временем и с расстоянием.
Уравнение (И. 11)—это уравнение переноса излучения, В типичных приложениях
можно рассматривать газ в состоянии ЛТР в любой точке пространства и
в любой момент времени. При таких условиях термодинамическое
состояние газа можно описать двумя параметрами, например температурой и
плотностью. Соответственно те функции, которые зависят от локального
состояния вещества, например непрозрачность к^, будут зависеть только
от ? и Г.
Во многих случаях, включая ЛТР, j^ и к^ принимают относительные
значения, характерные для строгого термодинамического равновесия, когда
1^ ш В^ ^ const. В этих случаях левая часть уравнения (И. 11) обращается в
нуль, что дает
где Г — локальная температура. Уравнение (И. 12) известно как закон
Кирхгофа; оно отображает детальное равновесие, которое должно
существовать между поглощением и излучением в термодинамическом
равновесии. Отметим, что стимулированное излучение может рассматриваться как
процесс с «отрицательным поглощением», поскольку оно тоже
пропорционально /^. Таким образом, мы подразумеваем, что величина к^ описывает
также эффекты стимулированного излучения. В законе Кирхгофа к,, явно
включает в себя стимулированное излучение, как этого требует детальное
равновесие.
23-513
610 Приложение И
Подстановка соотношения (И. 12) в уравнение (И.П) дает следующий
результат:
1 г9/
--^ + ? · V/, = к,р{В, - /J. (И.13)
Иногда полезно рассмотреть первый момент уравнения (И.13),
получаемый интегрированием по dO. с использованием выражений (И.4), (И.5) и
(И. 10):
-^ + ? F, = €?,?{?? - ??). (И.14)
Здесь предполагается, что непрозрачность к^ изотропна. Уравнение (И.14) в
сущности представляет собой «уравнение неразрывности» для излучения
данной частоты, включающее источники и стоки излучения.
Формальное решение уравнения переноса излучения можно получить в
предположении, что те функции, которые зависят от локального
термодинамического состояния газа [например, В^(Т), к^(р, Г)], — это известные
функции пространственных координат и времени. Для простоты
предположим, что имеется стационарное состояние, и пренебрежем производными
по времени в уравнении (И.П). В этом случае уравнение (И.13) можно
рассматривать как обычное линейное дифференциальное уравнение для /^
вдоль направления распространения:
^^кАВ.-h). (И.15)
Если определить оптическую толщину т^ вдоль направления
распространения выражением
??^^?^??, (И. 16)
то можно проинтегрировать уравнение (И.15), чтобы получить
интенсивность излучения из области, имеющей полную оптическую толщину т/.
I, = /ДО)ехр(-т,) + ГЧ(Г)ехр[- (т, - <)] dr;. (И.П)
•?
Здесь /^@) — интенсивность излучения, падающего на заднюю сторону
области, где по определению оптическая толщина г^ должна быть равна
нулю. В общем случае температура среды может быть переменной, т.е. ? =
= Т{т^), Для особого случая, когда температура ? постоянна, уравнение
(И.П) дает
4 = /ДО)ехр(-т,) + ВЛТ)[\ - exp(-Tj] (Г = const). («-?»)
Следовательно, для «оптически толстой» области, в которой т^ > 1,
?,^?^?), ?, »1. (И.19)
Перенос излучения 611
Сооотношение (И. 19) отражает тот факт, что излучение от
изотермического, оптически толстого газового слоя не отличается от излучения черного
тела, имеющего температуру газа. Для «оптически тонкого» слоя, у
которого г^ <^ 1, в отсутствие падающего излучения [т.е. /^@) = 0]
интенсивность равна
h= ? Л ds
•?
«ВДГ)т, (Г = const), (И.20)
где L — полная геометрическая толщина слоя вдоль луча света. Таким
образом, в оптически тонком слое поглощение испущенного излучения
незначительно. Уравнение (И.20) справедливо независимо от того, изменяется
ли Г в пространстве или нет [сравните с уравнением (И. 11)]. Заметим, что
в зависимости от изменения непрозрачности с частотой область может
быть оптически толстой на одних частотах и оптически тонкой на других.
И.2. ДИФФУЗИОННОЕ ПРИБЛИЖЕНИЕ
Уравнение переноса излучения значительно упрощается, когда поле
излучения оказывается лишь слегка анизотропным. Умножим уравнение (И. 13) на
? и проинтегрируем по всем углам. Заметив, что к^р5^ не зависит от
направления и потому не вносит вклада в интеграл, и вспомнив определение
(И.5) потока, получаем
--^F, + |n(n· ?/,)^?= -K,pF,. (И.21)
Предположим далее, что излучение можно рассматривать как
квазистационарное в каждый момент времени, в результате чего уравнение (И.21)
сводится к виду
|?(? · v/J ?/? = -ic.pF,. (И.22)
Уравнение (И.22) остается справедливым, даже если поле излучения
меняется со временем при условии, что эти изменения достаточно медленны и
их можно описать посредством соответствующих изменений темпфатуры
и плотности газа со временем *\
Теперь вспомним, что в строго изотропном поле излучения удельный
поток ?^ равняется нулю. Для слегка анизотропного поля излучения можно
оценить левую часть уравнения (И.22), если оставить только наиболее
значащую изотропную часть Т^. Тогда /-компонент равен
fn,n,d,I,dil = {d,Ofn,n,dQ = C,/,)^5,, = f 5,??, (И.23)
'^ Обсуждение этого вопроса см. в [637], разд. 11.6.
612 Приложение И
где использовалось уравнение (И.7). Таким образом, уравнение (И.23)
принимает вид
^'=-^7р^< (И.24)
И вместе с уравнением (И. 14) в квазистационарном пределе дает
VF, = CK,p(er-6;), (И.25)
Взятые вместе, уравнения (И.24) и (И.25) составляют диффузионное
приближение уравнений переноса излучения. Это приближение справедливо,
если поле излучения изотропно на расстояниях, сравнимых со средней
длиной свободного пробега фотонов:
?, S -L (И.26)
или малых по сравнению с ней. Заметим, что для применения
диффузионного приближения ЛТР, вообще говоря, не требуется, т.е. ЛТР является
достаточным, но не необходимым условием использования диффузионного
приближения.
Предположим теперь, что ЛТР существует, и рассмотрим
проинтегрированный по частотам вариант уравнения (И.24). При заданном ЛТР
можно положить ?^ = ?^, так что после интегрирования по ? получаем
F= --^?-?????, (И.27)
Определив усредненную непрозрачность, или росселандово среднее,
выражением
\_JS'{\/KMdt^/dT)dv
к= ?^{dг?/dT)dv ' ^-''^
МОЖНО переписать уравнение (И.27) в следующем виде:
в дальнейшем иногда мы будем ставить черточку над /с, подчеркивая, что
речь идет о росселандовом среднем.
Упражнение И, L Покажите, что росселандов весовой множитель ???/?? имеет
максимум при hv ^ 3,8 кТ, так что главную роль в процессе переноса играют фотоны
относительно высоких энергий.
Хотя все наше обсуждение до сих пор было сосредоточено на
источниках непрозрачности, связанной с истинным поглощением [уравнение
(И. 12)], а не на источниках рассеяния, полученные результаты можно
легко обобщить с учетом рассеяния. Если существует более одного источника
Перенос излучения 613
непрозрачности, уравнение (И.29) все еще применимо, но со средней по
Росселанду непрозрачностью, определяемой соотношением
1 / 1
С| -I- «2 "·¦
(И.ЗО)
Усреднение в уравнении (И.ЗО) выполняется с учетом росселандова
весового множителя. Непрозрачность, связанная с рассеянием, может быть
включена в сумму, фигурирующую в уравнении (И.ЗО), но, поскольку рассеяние
не подчиняется закону Кирхгофа, поправка на стимулированное излучение в
членах, описывающих рассеяние, отсутствует.
Для переноса излучения в сферических звездах уравнение (И.29) часто
записывается в виде
L{r)^4.r^F^ j;^^-^, (И.31)
где L(r) — светимость (выражаемая в эрг/с) на расстоянии г. Для таких
систем результирующий поток фотонов определяется температурным
градиентом в недрах звезды.
Тепловая структура атмосферы излучающей области довольно просто
может быть определена в диффузионном приближении. Предположим, что
атмосфера рассматривается как полубесконечное, плоскопараллельное
полупространство при Л ТР. Представим, что поток через атмосферу
постоянный:
(И.32)
F = const. ^ '
Уравнение (И.32) применимо с достаточной точностью к самым внешним
слоям оптически толстой излучающей области, поскольку большая часть
излучения испускается массой газа, расположенной значительно ниже
поверхности. Уравнение (И.32) также следует непосредственно из уравнения
(И.25), если предположить существование Л ТР. В этом случае V · F^ =
= dF^/dz = О, где ? — расстояние, измеренное в направлении внешней
нормали к поверхности атмосферы. Если заменить ? средней оптической
толщиной г, причем
Jt= -Kpdz (И.ЗЗ)
(знак минус означает, что оптическая толщина г, равная нулю на
поверхности, увеличивается по мере продвижения в глубину атмосферы), то можно
переписать уравнение (И.29) в виде
j:,^c dEp с djaT'^)
~ 3 ?/? 3 dr (И.34)
Интегрирование уравнения (И.34) по г дает
Ер = аТ"^ = Зт- + const. (И.35)
с
614 Приложение И
Постоянную интегрирования в уравнении (И.35) можно определить,
налагая граничные условия на поле излучения при г = 0. Если предположить,
что поле излучения на поверхности изотропно в пределах внешней
полусферы, но исчезает в пределах внутренней (т.е. ни один фотон не падает на
поверхность из вакуума), то из уравнений (И.4) и (И.5) легко получить
соотношение
/V = ^, т, = 0, (И.36)
или при ЛТР
2
X' '^ = ^· (И.37)
Подставив уравнение (И.37) в уравнении (И.35), получим профиль
температуры вещества в единицах оптической толщины:
г" =70-A+у). (И.38)
В уравнении (И.38) Tq — температура поверхности, т.е. ??(? = 0) = аТ^.
Она следующим образом связана с эффективной температурой,
определяемой соотношением F = ??^^^, где ? ? ас/4:
?,„ = 2'/?. (И.39)
Уравнение (И.39) часто называют «эддингтоновским приближением»
атмосферного профиля. В соответствии с уравнениями (И.38) и (И.39)
эффективная температура совпадает с температурой вещества при г = 2/3.
Если в непрозрачности основную роль играют процессы истинного
поглощения, то выходящие на поверхность фотоны возникают вблизи и выше
слоя, для которого г « 2/3 [сравните с уравнением (И. 17)]. Таким образом,
характерная спектральная температура фотонов («цветовая температура»)
будет сравнима с эффективной температурой. Если в непрозрачности
преобладают процессы рассеяния, уравнение (И.38) по-прежнему описывает
(правда, приближенно) профиль температуры. Однако выходящие на
поверхность фотоны будут образовываться в типичных случаях гораздо
глубже, скажем, при ? ^ т^ > 1. Появляясь под поверхностью на большой
оптической глубине г^, фотоны многократно испытывают рассеяние, прежде
чем выйдут на поверхность. Если рассеяние упругое, то фотоны выходят
на поверхность с цветовой температурой, которая сравнима с
температурой вещества в точке их образования при г^; следовательно, цветовая
температура r^Qi « Г(г^) > T^ff ^К Итак, упругое рассеяние приводит к
увеличению характерной энергии выходящих на поверхность фотонов выше
значения, соответствующего тепловому излучению черного тела.
^^ Более детальное обсуждение см. в разд. 14.5 (к).
Перенос излучения 615
И.З. ИСТОЧНИКИ НЕПРОЗРАЧНОСТИ
Перенос излучения в астрофизической плазме зависит от нескольких
различных источников непрозрачности. Какой из них играет главную роль,
зависит от термодинамического состояния газа, т.е. от ? и Г. Для многих
обсуждающихся в этой книге приложений (например, исследование
рентгеновских источников) могут оказаться важными нерелятивистские (hv <
< tn^c^, кТ < т^с^) источники непрозрачности, которые рассматриваются
ниже.
Рассеяние на свободных электронах
Сечение рассеяния фотонов на свободных электронах представляется
формулой Томсона
?? = ^ ( -^ I = 0,665 X 10-2^ см2. (И.40)
^ 3 1 т,с'
Это сечение не зависит от частоты фотона, и рассеяние является упругим.
Соответствующая непрозрачность дается выражением
iCes = -^ = 0,40/, cNiVr, (И.41)
где п^ = feP/rrip — концентрация свободных электронов, а/^ — число
свободных электронов, приходящееся на барион^^ Поскольку рассеяние
электронов не зависит от частоты, росселандово среднее для рассеяния к^
также определяется выражением (И.41).
Свободно-свободное поглощение (обратное тормозное излучение)
Непрозрачность для свободно-свободного поглощения (т.е. поглощения
фотонов свободными электронами в присутствии положительных ионов с
зарядом ? и атомным весом Л) дается выражением^^
1 — ехр
(i^)], (И.42,
где п^ = fjp/mpA — концентрация ионов, /^ — доля атомов, ионизованных
до заданного состояния, а g^^ — множитель Гаунта для свободно-
свободных переходов, слегка меняющийся с частотой и. Приведенное выше
выражение для непрозрачности основано на предположении, что электро-
^^ Ранее число электронов, приходящихся на барион в полностью ионизованной
плазме, обозначалось У^ =/^.
^^См., например, [422, 549]; заметим, что величина к^, определенная в [549],
соответствует введенной нами величине рк .
616 Приложение И
ны обладают максвелловским распределением по скоростям относительно
фотонов. Таблицы усредненных по максвелловскому распределению
множителей Гаунта приведены в [240, 304]; для hv/kT <>\ и кТ ^ Z^Ry
gff ^ 1. Определенная уравнением (И.42) непрозрачность при свободно-
свободных переходах может быть переписана в виде
к« = A,50 X \0'')l^f-]pT-'''gJ ^ ~ ^^P^'^^McMVr. (И.43)
где X = hv/kT. Соответствующее росселандово среднее можно подсчитать
из уравнений (И.28) и (И.43), что дает
к„ = @,645 X 10^' )(^ Jg„pr-3^ сиУт, (И.44)
где iff ~ 1 — усредненный по частоте множитель Гаунта.
Отметим, что усредненная непрозрачность изменяется пропорционально
рТ~^'^, как впервые было показано Крамерсом. Любая непрозрачность,
которая так же зависит от ? и Г, называется непрозрачностью Крамерса.
Излучательная способность при свободно-свободных переходах может
быть вычислена на основе закона Кирхгофа, т.е. из уравнений (И. 12) и
(И.42). Результат равен
'' ^3It) -;;;уШ ^^^^'^^'^^^^тг)
= 5,44 X 10-39^1??|^ ехр(^) эргДсм^ · с · стер · Гц). (И.45)
Полное количество энергии, излученное при свободно-свободных переходах
в единице объема за единицу времени, получается путем интегрирования
уравнения (И.45) по всем частотам и умножения на 4?:
Л^^ = 1,42 X 10-2^2/1^/1.7^/? эрг/(смЗ · с), (И.46)
где соответствующий средний множитель Гаунта g^f снова оказывается слабо
изменяющейся функцией (порядка единицы).
Поглощение при связанно-свободных переходах (фотоионизация)
Поглощение при связанно-свободных переходах происходит, когда атом
со связанными электронами поглощает фотоны с энергией, достаточной
для ионизации атома. Обратный процесс называется излучением при
свободно-связанных переходах и является следствием захвата свободного
электрона в связанное состояние, сопровождаемого излучением фотона,
необходимость которого вытекает из условия сохранения энергии.
Перенос излучения 617
Поперечное сечение фотоионизации водородоподобного атома,
находящегося в состоянии с главным квантовым числом п, можно записать в
виде^^
'bf
= B,82xlO^')-fj«bfCM2. (И.47)
Из выражения (И.47) можно получить непрозрачность при связанно-
свободных переходах и соответствующее росселандово среднее.
Приближенное выражение этого среднего для смеси частично ионизованных
атомов разных видов приведено в [516]:
iCbf « D.34 X 10^5)^^7A + Х)рТ-^'^см^/т, (И.48)
где X и ? представляют соответственно относительную долю водорода и
тяжелых элементов (т.е. всех других элементов, кроме водорода и гелия) в
смеси. Заметим, что уравнение (И.48) также имеет вид закона
непрозрачности Крамерса.
Хотя преобладающий источник непрозрачности в любом диапазоне
параметров определяется детальным поведением ? и Г, общая картина
выглядит следующим образом. При низких температурах Г, когда
значительная часть атомов может быть лишь частично ионизована, важную роль
играет поглощение при связанно-свободных переходах (при еще более
низких температурах может доминировать непрозрачность, возникающая из-
за дискретных «связанно-связанных» переходов^\ При больших значениях
температуры Г, когда ионизация уже почти завершена, будет преобладать
поглощение при свободно-свободных переходах. Наконец, при дальнейшем
увеличении ? ведущая роль переходит к рассеянию на электронах,
поскольку к^ уменьшается с увеличением ? [см. уравнение (И.44)]. При
релятивистских энергиях фотонов (И? ^ пг^с^) и температурах электронов (кТ ^ ^е^^)
становятся важными другие процессы. В этом случае приведенные выше
уравнения для тормозного излучения и рассеяния на электронах должны
быть изменены^^
Комптониза14ия
Комптонизация — это такой процесс, при котором фотоны могут
набирать или терять энергию в результате комптоновского рассеяния на
тепловых электронах. Было доказано, что этот процесс должен быть важным
^^ См. [135], уравнение C.151).
^^ Этот процесс называется также «поглощением в линиях». — Прим. перев.
^^ Более подробное рассмотрение и ссылки см., например, в [65, 493].
618 Приложение И
для испускания рентгеновских лучей, которые излучаются газом при
аккреции на компактные объекты. Ниже коротко рассматриваются основные
особенности комптонизации^^
Рассмотрим бесконечный и однородный максвелловский газ
нерелятивистских электронов с температурой ? и концентрацией п. Изменение во
времени функции распределения фотонов/, связанное с многократным
нерелятивистским обратным комптоновским рассеянием на этих электронах,
определяется уравнением Компанейца [318]. Оно представляет собой
приближение Фоккера—Планка к столкновительному уравнению Больцмана для
фотонов и справедливо с точностью до квадрата передаваемой при
столкновении энергии (эта величина мала, т.е. ?? < кТ). Уравнение имеет вид
Э/
а
Н"-<ШЩ<у^*''")]¦ '"^'^
где X = hv/kT. Как и следует ожидать, стационарное состояние
достигается при
^^expUf-^Wl-r (7 = ^)' (И.50)
где ? — постоянная. При ? ^ О уравнение (И.50) описывает общую
равновесную функцию распределения газа Бозе—Эйнштейна, т.е. равновесие с
сохраняемым числом частиц. Поскольку при комптонизации сохраняется
число фотонов, уравнение (И.50) вполне применимо. Когда в результате
многократных рассеяний фотонное распределение достигает бозе-
эйнштейновского вида, соответствующего уравнению (И.50), процесс
«насыщается» и дальнейший эффективный обмен энергии с электронами
прекращается. В этом случае спектр фотонов принимает знакомую форму,
определяемую законом Вина, когда/ < 1:
/^ ? jcYa jc^xp(-jc). (И.51)
Эффективная скорость передачи энергии от электронов фотонам в единице
объема A(^Qj^p находится умножением уравнения (И.49) на hv и
интегрированием по фазовому пространству. После выполнения интегрирования по
частям результат принимает вид [452]
Лсошр = J ^"§7
Э/ Uv'^dv
сЗ
Г кТ 2ж(кТУ
'Т"е-^г\—-2
т с^ {hcYmc^e
(И.52)
- [ dxx*f(\ + /I,
•^ Более подробное обсуждение содержится в работах, указанных в разд. 14.5 (к).
Перенос излучения 619
где е^ — плотность энергии фотонов, определяемая соотношением
e,.iI^Uta./. (И.53)
8?(?:?)^
*?
Если предположить, что распределение фотонов можно аппроксимировать
равновесным планковским распределением, но при температуре ?^?^ ? Г,
уравнение (И.52) даст
Лсотр = ^Т^е^г-^^ (^ ^ ^ph) (^-54)
Уравнение (И.54) показывает, что комптонизация приводит к
охлаждению вещества, когда ? > ?^?^, и нагреву, когд ? < Т^^.
Рассмотрим видоизменение уравнения (И.49) в том случае, когда
выходящие фотоны испускаются в среде с конечной глубиной рассеяния т^^
(например, в однородном диске с полутолщиной Л, где т^^ « ???^? отсчиты-
вается от средней плоскости диска). Предположим, что фотоны
стационарно образуются при относительно низкой энергии в диске (х < 1),
диффундируют наружу к поверхности, испытывая многократное рассеяние и
покидают диск. Вероятность ускользания типичного фотона на одно компто-
новское рассеяние приближенно можно считать обратно пропорциональной
среднему числу столкновений ?^.
В нашем случае
A^,«max(T,3,T,2s)» (И.55)
поскольку Tgg <> 1 приводит к свободному уходу, а при Tgg ^ 1 фотон до
ухода испытывает случайное блуждание в среде. В стационарном
состоянии можно записать «модифицированное» уравнение Компанейца,
описывающее рождение, комптонизацию и уход фотонов из среды [534]:
где функция б(дг) описывает скорость рождения фотонов. Предположим,
что фотоны рождаются с какой-то низкой энергией л·^ <^ 1, выше которой
величина Q пренебрежимо мала («источник мягких фотонов»).
Сконцентрируем внимание на таких выходящих комптонизированных фотонах с ? >
> Xgy для которых в уравнении (И.56) можно пренебречь членами/^ < 1 и
Q, В этом случае получающееся уравнение дает следующее приближенное
решение:
/а jc'", jc, «: jc «: 1, (И.57)
"--^/!^^ у^л. «-'
620
Припожение И
Cglv
ос J/
ccv^expi"^)
^?
Рис. И.1. Спектр, излучаемый при комптонизации фотонов низких энергий
высокоэнергичными тепловыми электронами [493]
/а ехр(-дс),
дс » 1.
(И.59)
Интенсивность выходящего излучения в этой области х^ < ? < 1 имеет
степенной вид
•¦-¦i^r-
(И.60)
Таким образом, при у ^ 1 или w ^ - 4 в результате комптонизации
может происходить значительное усиление «жесткого спектрального»
компонента (с энергией выше v^); выходящего из среды излучения. Этот эффект
возникает вследствие многократного «рассеяния с набором энергии»
мягких фотонов на электронах с более высокой температурой. Спектр
выходящего из среды излучения проиллюстрирован на рис. И.1.
Литература
1. Abramomcz ?. ?. Innermost Parts of Accretion Discs are Thermally and Secularly
Stable. Nature, 294, 235, 1981.
2. Abramomcz M. ?., Wagoner R. V. Variational Analysis of Rotating Neutron Stars.
Astrophys. J., 204, 896, 1976.
3. Abt H. ?., Hintzen P., Levy S. G. A Search for a Third Star in Cygnus X-1 System.
Astrophys. J., 213, 815, 1977.
4. Adams W. S. The Spectrum of the Companion of Sirius. Pub. Astron. Soc. Рас,
27, 236, 1915.
5. Adams W. S. The Relativity Displacement of the Spectral Lines in the Companion of
Sirius. Proc. Nat. Acad. Sci. USA, 11, 382, 1925. Erratum: Observatory, 49, 8a,
1925.
6. Aizu K. X-Ray Emission Region of a White Dwarf with Accretion.Progr. Theor.
Phys., 49, 1184, 1973.
7. Allen С W. Astrophysical Quantities. 2nd ed.. University of London, London,
England, 1963. (Имеется перевод: К. У. Аллен Астрофизические величины. —
М.: ИЛ, 1960.)
8. Allen С. W. Astrophysical Quantities. 3rd ed., Athlone, London, England, 1973.
(Имеется перевод: К. У. Аллен. Астрофизические величины. — М.: Мир, 1977.)
9. Alloin D., Cruz-Gonzalez С, Peimbert ?. On the Number of Planetary Nebulae in
our Galaxy. Astrophys. J., 205, 74, 1976.
10. Alme M. L., Wilson J. R. X-Ray Emission from a Neutron Star Accreting Material.
Astrophys. J., 186, 1015, 1973.
11. Alpar M. ?., Anderson P. W., Pines D., Shaham J., Giant Glitches and Pinned
Vorticity in the Vela and Other Pulsafs. Astrophys. J. Lett., 249, L29, 1981.
12. Амбарцумян В. ?., Саакян Г. С. Вырожденный сверхплотный газ
элементарных частиц. Астрон. ж., 37, 193, 1960.
13. Angel J. P. R. Magnetic White Dwarfs. Ann. Rev. Astron. Astrophys. 16, 487,
1978.
14. Applequist Г., Politzer H. D. Heavy Quarks and e^e— Annihilation. Phys. Rev.
Lett., 34, 43, 1975.
15. Arnett W. D. Mass Dependence in Gravitational Collapse of Stellar Cores. Can. J.
Phys., 45, 1621, 1967.
16. Arnett W. D., Advanced Evolution of Massive Stars: VII. Silicon Burning.
Astrophys. J. Suppl., 35, 145, 1977.
17. Arnett W. D., Neutrino Trapping During Gravitational Collapse of Stars. Astrophys.
J., 218, 815, 1977.
18. Arnett W. D. On the Bulk Yields of Nucleosynthesis from Massive Stars. Astrophys.
J., 219, 1008, 1978.
19. Arnett W. D. Gravitational Collapse of Evolved Stars as a Problem in Physics. In
Sources of Gravitational Radiation, L. L. Smarr, editor, Cambridge University
Press, Cambridge, England, 1979.
622 Литература
20. Arnett W. D., Bowers R. L. A Microscopic Interpretation of Neutron Star Structure.
Astrophys. J. Suppl., 33, 415, 1977.
21. Arnett W. D., Falk S. W. Some Comparisons of Theoretical Supernova Light Curves
and with Supernova 1961 (Type II). Astrophys. J., 210, 733, 1976.
22. Arnett W. D., Schramm D. N. Origin of Cosmic Rays, Atomic Nuclei and Pulsars in
Explosions of Massive Stars. Astrophys. J. Lett., 184, L47, 1973.
23. Arons y.. Lea S. M. Accretion onto Magnetized Neutron Stars: Structure and
Interchange Instability of a Model Magnetosphere. Astrophys. J., 207, 914, 1976.
24. Arons J., Lea S. M. Accretion onto Magnetized Neutron Stars: The Fate of Sinking
Filaments. Astrophys. J., 235, 1016, 1980.
25. Au C. K. Equation of State for Pion Condensation Neutron Star Matter. Phys.
Lett. B, 61, 300, 1976.
26. Audouze У., Tinsley B. M. Chemical Evolution of Galaxies. Ann. Rev. Astron.
Astrophys., 14, 43, 1976.
27. Auer L. H., Mihalas D. Non-LTE Model Atmospheres. VII. The Hydrogen and
Helium Spectra of the О Stars. Astrophys. J. Suppl., 24, 193, 1972.
28. Avni y., Bahcall J. N. Ellipsoidal Light Variations and Masses of X-Ray Binaries.
Astrophys. J., 197, 675, 1975.
29. Avni y., Bahcall J. N. Masses for Vela X-1 and Other X-Ray Binaries. Astrophys. J.
Lett., 202, L131, 1975.
30. Baade W. The Crab Nebula. Astrophys. J., 96, 188, 1942.
31. Baade W., Zwicky F. Supernovae and Cosmic Rays. Phys. Rev., 45, 138, 1934.
32. Backer D. C, Kulkarni S. R., Heiles C, Davis M. M., Goss W. M. A Millisecond
Pulsar. Nature, 300, 615, 1982.
33. Bahcall J. N Masses of Neutron Stars and Black Holes in X-Ray Binaries. Ann.
Rev. Astron. Astrophys., 16, 241, 1978.
34. Bahcall J. N. Solar Neutrino Experiments. Rev. Mod. Phys., 50, 881, 1978.
35. Bahcall J. N. Optical Properties of Binary X-Ray Sources. In Physics and
Astrophysics of Neutron Stars and Black Holes, R. Giacconi and R. Ruffini, editors.
North Holland, Amsterdam, Holland, 1978.
36. Bahcall J. N. Solar Neutrinos: Rapporteur Talk. In Neutrino-81, R. J. Cence, E. Ma
and A. Roberts, editors. Department of Physics and Astronomy, University of
Hawaii, Honolulu, Hawaii, 1981.
37. Bahcall J. N., Chester T. J. On the Mass Determination of Hercules X-1. Astrophys.
J. Lett., 215, L21, 1977.
38. Bahcall J. N, Ostriker J. P. Massive Black Holes in Globular Clusters. Nature, 256,
23, 1975.
39. Bahcall J. N, Soneira R. M., The Universe at Faint Magnitudes. I. Models for the
Galaxy and the Predicted Star Counts. Astrophys. J. Suppl., 44, 73, 1980.
40. Bahcall J. N., Soneira R. M. The Distribution of Stars to V= 16th Magnitude Near
the North Galactic Pole: Normalization, Clustering Properties and Counts in Various
Bands. Astrophys. J., 246, 122, 1981.
41. Bahcall J. N.. Wolf R. A. Neutron Stars. II. Neutrino-Cooling and Observability.
Phys. Rev. B, 140, 1452, 1965.
42. Bahcall J. N, Rosenbluth M. N, Kulsrud R. M. Model for X-Ray Sources Based on
Magnetic Field Twisting. Nature Phys. Sci., 243, 27, 1973.
43. Bahcall J. N., Dyson F. У., Katz J. L, Paczynski B. Multiple Star System and X-Ray
Sources. Astrophys. J. Lett., 189, L17, 1974.
44. Bardeen J. M. Timelike and Null Geodesies in the Kerr Metric. In Black Holes,
C. DeWitt and B. S. DeWitt, editors, Gordon and Breach, New York, New York,
1973.
Литература 623
45. Bardeen J. Л/., Press W. Я., Teukolsky S. A. Rotating Black Holes: Locally
Nonrotating Frames, Energy Extraction and Scalar Synchrotron Radiation.
Astrophys. J., 178, 347, 1972.
46. Bardeen J. M., Friedman J. L., Schutz B. F., Sorkin R. A New Criterion for Secular
Instability of Rotating Stars. Astrophys. J. Lett., 217, L49, 1977.
47. Barkat Z. Evolution of Supernova Progenitors. In Supernovae, D. ? Schramm у
editor, Reidel, Dordrecht, Holland, 1977.
48. Bath G. Т., Pringle J. E. The Evolution of Viscous Discs.—L Mass Transfer
Variations. Mon. Not. Roy. Astron. Soc, 194, 967, 1981.
49. Baym G., Chin S. A. Landau Theory of Relativistic Fermi Liquids. Nud. Phys. A^
262, 527, 1976.
50. Baym G., Chin S. A. Can a Neutron Star be a Giant MIT Bag? Phys. Lett. B, 62,
241, 1976.
51. Baym G., Pethick С Neutron Stars. Ann. Rev. Nucl. Sci., 25, 27, 1975.
52. Baym G., Pethick C. Physics of Neutron Stars. Ann. Rev. Astron. Astrophys., 17,
415, 1979.
53. Baym G., Pines D. Neutron Starquakes and Pulsar Speedup. Ann. Phys., 66, 816,
1971.
54. Baym G., Pethick C, Pines D., Ruderman M. Spin Up in Neutron Stars: The Future
of the Vela Pulsar. Nature, 224, 872, 1969.
55. Baym G., Bethe H. ?., Pethick C. J. (BBP). Neutron Star Matter. Nucl. Phys. A,
175, 225, 1971.
56. Baym G., Pethick C, Sutherland P. (BPS). The Ground State of Matter at High
Densities: Equation of State ans Stellar Models. Astrophys. J., 170, 299, 1971.
57. Becker R. H. et al. A1540-53, an Eclipsing X-Ray Binary Pulsator. Astrophys. J.
Lett., 216, Lll, 1977.
58. Begelman M. C. Nearly Collisionless Spherical Accretion. Mon. Not. Roy. Astron.
Soc, 181, 347, 1977.
59. Beckenstein J, D. Black Holes and Entropy. Phys. Rev. D, 7, 2333, 1973.
60. Bekenstein J. D. Statistical Black-Hole Thermodynamics. Phys. Rev. D, 12, 3077,
1975.
61. Belian R. D., Conner J. P., Evans W.D. The Discovery of X-Ray Bursts from a
Region in the Constellation Norma, Astrophys. J. Lett., 206, L135, 1976.
62. Bethe H. A. What Holds the Nucleus Together? Sci. Am., 189, No. 3, 58, 1953.
63. Bethe H. ?., Jackiw R. W. Intermediate Quantum Mechanics. 2nd ed., Benjamin,
New York, New York, 1968.
64. Bethe H. ?., Johnson M. B. Dense Baryon Matter Calculations with Realistic
Potentials. Nucl. Phys. A, 230, 1, 1974.
65. Bethe H. ?., Salpeter E. E. Quantum Mechanics of One- and Two-Electron Atoms,
Academic Press, New York, New York, 1957. (Имеется перевод: Г. Бете,
Э. Солпитер. Квантовая механика атомов с одним и двумя электронами. —
М.: ИЛ, 1960.)
66. Bethe Я. ?., Brown G. ?., Applegate У., Lattimer J, ?. (BBAL). Equation of State
in the Gravitational Collapse of Stars. Nucl. Phys. A, 324, 487, 1979.
67. Бисноватый-Коган Г. С, Блинников С. И. Disc Accretion onto а Black Hole at
Subcritical Luminosity. Astron. Astrophys., 59, 111, 1977.
68. Blaizot J. P., Gogny D., Grammaticos B. Nuclear Compressibility and Monopole
Resonances. Nucl. Phys. A, 265, 315, 1976.
69. Blandford R. D. Accretion Disc Electrodynamics—A Model for Double Radio
Sources. Mon. Not. Roy. Astron. Soc, 176, 465, 1976.
70. Blandford R. D. Spectrum of a Radio Pulse from an Exploding Black Hole. Mon.
Not. Roy. Astron. Soc, 181, 489, 1977.
624 Литература
71. Blandford R. D., Teukolsky S. A. On the Measurement of the Mass of PSR 1913 +
+ 16. Astrophys. J. Lett., 198, L27, 1975.
72. Blandford R. D., Teukolsky S. A. Arrival Time Analysis for a Pulsar in Binary
System. Astrophys. J., 205, 580, 1976.
73. Blandford R. D., Thorne K. S. Black Hole Astrophysics. In General Relativity. An
Einstein Centenary Survey, S. W. Hawking and W. Israel^ editors, Cambridge
University Press, Cambridge, England, 1979. (Имеется перевод: P. Блэндфорд и
К. Торн. Астрофизика черных дыр. В сб.: Общая теория относительности (ред.
С. Хокинг и В. Израэль). — М.: Мир, 1983, стр. 163.)
74. Blandford R. D., Znajek R. L., Electromagnetic Extraction of Energy from Kerr
Black Holes. Mon. Not. Roy. Astron. Soc, 179, 433, 1977.
75. Blatt J. Л/., Weisskopf V. F. Theoretical Nuclear Physics, Wiley, New York, New
York, 1952. (Имеется перевод: Дж. Блатт и В. Вайскопф. Теоретическая
ядерная физика. — М.: ИЛ, 1954.)
76. Bludman S. ?., Ruderman ?. ?. Noncausality and Instability in Ultradense Matter.
Phys. Rev. D, 1, 3243, 1970.
77. Bludman S. ?., Ruderman M. A. Bounds on Neutrino Burst Intensity Imposed l?y
the Exclusion Principle and Causality. Astrophys. J. Lett., 195, L19, 1975.
78. Bondi H. On Spherical Symmetrical Accretion. Mon. Not. Roy. Astron. Soc, 112,
195, 1952.
79. Bondi H. Massive Spheres in General Relativity. Proc. Roy. Soc. London Ser. A,
282, 303, 1964.
80. Bondi H., Hoyle F. On the Mechanism of Accretion by Stars. Mon. Not. Roy.
Astron. Soc, 104, 273, 1944.
81. Boyer R. Я., Lindquist R. W. Maximal Analytic Extension of the Kerr Metric. J.
Math. Phys., 8, 265, 1967.
82. Boynton P. E. Pulse Timing and Neutron Star Structure. In lAU Symposium No. 95
Pulsars, W. Sieber and R. Wielebinski, editors, Reidel, Dordrecht, Holland, 1981,
p. 279.
83. Boynton P. E. et al. Optical Timing of the Crab Pulsar NP 0532. Astrophys. J., 175,
217, 1975.
84. Bradt H. V. D., McClintock J. E. The Optical Counterparts of Compact Galactic
X-Ray Sources. Ann. Rev. Astron Astrophys., 21, 13, 1983.
85. Branduardi G., Kylafis N. D., Lamb D. ?.. Mason K. O. Evidence for the
Degenerate Dwarf Nature of Cygnus X-2. Astrophys. J. Lett., 235, L153, 1980.
86. Bregman J. et al. On the Distance to Cygnus X-1 (HDE 226868). Astrophys. J.
Lett., 185, LI 17, 1973.
87. Brinkmann W. Adiabatic Accretion onto a Schwarzschild Black Hole. Astron.
Astrophys., 85, 146, 1980.
88. Вгоу^п G. E., Bethe H. ?., Baym G. Supernova Theory. Nucl. Phys. A, 375, 481,
1982.
89. Bruenn S. W. Neutrino Interactions and Supernovae. Ann. N. Y. Acad. Sci., 262,
80, 1975 (Seventh Texas Symposium).
90^ Брумберг В. ?., Зельдович Я. Б., Новиков И. Д., Шакура Н. И. Определение
массы компонентов и наклона двойной системы, содержащей пульсар, по
релятивистским эффектам. Письма АЖ, № 1, 5, 1975.
91. Brush S. G., Sahlin ?. L., Teller ?. Monte Carlo Study of a One-Component
Plasma. I. J. Chem. Phys., 45, 2102, 1966.
92. Burbidge E. M., Burbidge G. R., Fowler W. ?., Hoyle F. Synthesis of the Elements
in Stars. Rev. Mod. Phys., 29, 547, 1957.
93. Burnell S. J. B. Petit Four. Ann. N.Y. Acad. Sci., 302, 685, 1977 (Eighth Texas
Symposium).
Литература 625
94. Burrows ?. Beta Decay in Quark Stars. Phys. Rev. Lett., 44, 1640, 1980.
95. Butterworth E. M., Ipser J. R. Rapidly Rotating Fluid Bodies in General Relativity.
Astrophys. J. Lett., 200, L103, 1975.
96. Butterworth E. ?/., Ipser J. R. On the Structure and Stability of Rapidly Rotating
Fluid Bodies in General Relativity. L The Numerical Method for Computing
Structure and its Application to Uniformly Rotating Homogeneous Bodies. Astrophys. J.,
204, 200, 1976.
97. By ram E. Г., Chubb T. ?., Friedman H. Cosmic X-Ray Sources, Galactic and Ex-
tragalactic. Science, 152, 66, 1966.
98. Byrd P. F., Friedman M. D. Handbook of Elliptic Integrals for Engineers and
Scientists. 2nd ed.. Springer-Verlag, New York, New York, 1971.
99. Cahn J. H., Wyatt S. P. The Birthrate of Planetary Nebulae. Astrophys. J., 210,
508, 1976.
100. Cameron A. G. W. Neutron Star Models. Astrophys. J., 130, 884, 1959.
101. Cameron A. G. W. Pyconuclear Reactions and Nova Explosions. Astrophys. J.,
130, 916, 1959.
102. Cameron A. G. W., Mock M. Stellar Accretion and X-Ray Emission. Nature, 215,
464, 1967.
103. Canizares C. R., Winkler P. F. Evidence for Elemental Enrichment of Puppis A by
a Type II Supernova. Astrophys. J. Lett., 246, L33, 1981.
104. Canuto V. Equation of State at Ultrahigh Densities, Part I. Ann. Rev. Astron.
Astrophys., 12, 167, 1974.
105. Canuto V. Equation of State at Ultrahigh Densities, Part II. Ann. Rev. Astron.
Astrophys., 13, 335, 1975.
106. Carr B. J. Some Cosmological Consequences of Primordial Black-Hole
Evaporation. Astrophys. J., 206, 8, 1976.
107. Carr W. J. Energy, Specific Heat, and Magnetic Properties of the Low-Density
Electron Gas. Phys. Rev., 122, 1437, 1961.
108. Carter B. Global Structure of the Kerr Family of Gravitational Fields. Phys. Rev.,
174, 1559, 1968.
109. Carter B. The General Theory of the Mechanical, Electromagnetic and
Thermodynamic Properties of Black Holes. In General Relativity: An Einstein
Centenary Survey. Eds. 5. W. Hawking, W. Israel, Cambridge University Press,
Cambridge, England, 1979.
110. Cassinelli J. P., Mathis J. 5., Savage B. D. Central Object of the 30 Doradus
Nebula, a Supermassive Star. Science, 212, 1497, 1981.
111. Chandrasekhar S. The Density of White Dwarf Stars, Phil. Mag., 11, 592, 1931.
112. Chandrasekhar S. The Maximum Mass of Ideal White Dwarfs. Astrophys. J., 74,
81, 1931.
113. Chandrasekhar S. Stellar Configurations with Degenerate Cores. Observatory, 57,
373, 1934.
114. Chandrasekhar S. An Introduction to the Study of Stellar Structure. University of
Chicago Press, Chicago, Illinois, 1939. (Имеется перевод: С. Чандрасекар.
Введение в учение о строении звезд. — М.: ИЛ, 1954.)
115. Chandrasekhar S. Radiative Transfer. Dover, New York, New York, 1960.
(Имеется перевод: С. Чандрасекар. Перенос лучистой энергии. — М.: ИЛ, 1953.)
116. Chandrasekhar S. Ellipsoidal Figures of Equlibrium. Yale University Press, New
Haven, Connecticut, 1969. (Имеется перевод: С. Чандрасекар.
Эллипсоидальные фигуры вращения. — М.: Мир. 1973.)
117. Chandrasekhar S. The Effect of Gravitational Radiation on the Secular Stability of
the Maclaurin Spheroid. Astrophys. J., 161, 561, 1970.
24-513
626 Литература
118. Chandrasekhar S. The Role of General Relativity in Astronomy: Retrospect and
Prospect. In Highlights of Astronomy, vol. 5. Ed. P. A. Wayman, Reidel,
Dordrecht, Holland, 1980.
119. Chandrasekhar S., Tooper R. F. The Dynamical Instability of the White-Dwarf
Configurations Approaching the Limiting Mass. Astrophys. J., 139, 1396, 1964.
120. Chapline G. F. Cosmological Effects of Primordial Black Holes. Nature, 253, 251,
1975.
121. Chapline G. F., Nauenberg M. Phase Transition from Barion to Quark Matter.
Nature, 264, 235, 1976.
122. Chevalier R. A. The Hydrodynamics of Type II Supernovae. Astrophys. J., 207,
872, 1976.
123. Chevalier R. A. Exploding White Dwarf Models for Type I Supernovae.
Astrophys. J., 246, 267, 1981.
124. Chevalier R. A. The Interaction of the Radiation from a Type II Supernova with a
Circumstellar Shell. Astrophys. J., 251, 259, 1981.
125. Chevalier R. ?., Kirshner R. P. Spectra of Cassiopea A. II. Interpretation.
Astrophys. J., 219, 931, 1978.
126. Chiu H.-Y. Supernovae, Neutrinos and Neutron Stars. Ann. Phys., 26, 364, 1964.
127. Chiu H.-Y., Salpeter E. E. Surface X-Ray Emission from Neutron Stars. Phys.
Rev. Lett., 12, 413, 1964.
128. Chodos ?., Jaffe R. L., Johnson K., Thorn С В., Weisskopf V. F. New Extended
Model of Hadrons. Phys. Rev. D, 9, 3471, 1974.
129. Clark С В. Coulomb Interactions in the Uniform-Background Lattice Model.
Phys. Rev., 109, 1133, 1958.
130. Clark D. H., Caswell J. L. A Study of Galactic Supernova Remnants, Based on
Molongolo-Parkes Observational Data. Mon. Not. Roy. Astron. Soc, 174, 267,
1976.
131. Clark J. P. A. The Role of Binaries in Gravitational Wave Production. In Sources
of Gravitational Radiation. Ed. L. Smarr, Cambridge University Press, Cambridge,
England, 1979, p. 447.
132. Clark J. P. ?., Eardley D. M. Evolution of Close Neutron Star Binaries.
Astrophys. J., 215, 311, 1977.
133. Clark J. P. ?., Van den Heuvel E. P. У., Sutantyo W. Formation of Neutron Star
Binaries and Their Importance for Gravitational Radiation. Astron. Astrophys.,
72, 120, 1979.
134. Clark J. W. Variational Theory of Nuclear Matter. In Progr. Part. Nucl. Phys.,
vol. 2, Pergamon, Oxford, England, 1979, p. 89.
135. Clayton D. B. Principles of Stellar Evolution and Nucleosynthesis, McGrow-Hill,
New York, New York, 1968.
136. Cochran S. G., Chester G. V. Неопубликованная работа 1973 г., цитированная
в [105]. См. также Cochran S. G. Неопубликованная диссертация, Cornell
University, и Ceperley D. Л/., Chester G. V., Kalos ?. ?. Exact Calculations of
the Ground State of Model Neutron Matter. Phys. Rev. D, 13, 3208, 1976.
137. Cocke W. У., Disney H. У., Taylor D. J. Discovery of Optical Signals from Pulsar
NP 0532. Nature, 221, 525, 1969. (Имеется перевод: У. ???, Г. Дисней,
Дж. Тейлор. Открытие оптических сигналов от пульсара ?? 0532. В сб.
статей: Пульсары. — М.: Мир, 1971, стр. 137.)
138. Code А. D., Davis J., Bless R. С, Hanbury-Brown R. Empirical Effective
Temperatures and Bolometric Corrections for Early-Type Stars. Astrophys. J., 203,
417, 1976.
139. Cohen J. M., Lapidus ?., Cameron A. G. W. Treatment of Pulsating White
Dwarfs Including General Relativistic Effects. Astrophys. Space Sci., 5, 113, 1969.
Литература 627
140. .Coldwell-Horsfall R. ?., Maradudin ?. ?. Zero-Point Energy of an Electron
Lattice. J. Math. Phys., 1, 395, 1960.
141. Coleman S. The 1979 Nobel Prize in Physics. Science, 206, 1290, 1979.
142. Colgate S. A. Supernova Mass Ejection and Core Hydrodynamics. Mem. Del. Soc.
Astron. Ital., 49, 399, 1978.
143. Colgate S. ?., Johnson M. H. Hydrodynamic Origin of Cosmic Rays. Phys. Rev.
Lett., 5, 235, 1960.
144. Colgate S. ?., White R. H. The Hydrodynamic Behavior of Supernovae
Explosions. Astrophys. J., 143, 626, 1966.
145. Collins J. C, Perry M. J. Superdense Matter: Neutrons or Asymptotically Free
Quarks? Phys. Rev. Lett., 34, 1353, 1975.
146. Cominsky L., Clark G. W., Li R, Mayer W., Rappaport S. Discovery of 3,6-s
X-Ray Pulsations from 4U 0115 + 63. Nature, 273, 367, 1978.
147. Conti P. S. Stellar Parameters of Five Early Type Companions of X-Ray Sources.
Astron. Astrophys., 63, 225, 1978.
148. Cordes J. M. Coherent Radio Emission from Pulsars. Space Sci. Rev., 24, 567,
1979.
149. Cordes J. M., Greenstein G. Pulsar Timing. IV. Physical Models for Timing Noise
Processes. Astrophys. J., 245, 1060, 1981.
150. Cordes J. M., Helfand D. J. Pulsar Timing. III. Timing Noise of 50 Pulsars.
Astrophys. J., 239, 640, 1980.
151. Cowley A. P., Crampton D. The Spectroscopic Binary Scorpius X-1. Astrophys. J.
Lett., 201, L65, 1975.
152. Cox J. P., Giuli R. T. Principles of Stellar Structure. Vols. I—II. Gordon and
Breach, New York, New York, 1968.
153. Cunningham С Т., Bardeen J. M. The Optical Appearance of a Star Orbiting an
Extreme Kerr Black Hole. Astrophys. J. Lett., 173, L137, 1972.
154. Davidson K., Henry J. P. A Physical Model of HZ Her. Bull. Am. Astron. Soc,
4, 411, 1972.
155. Davidson K., Ostriker J. P. Neutron-Star Accretion in a Stellar Wind: Model for a
Pulsed X-Ray Source. Astrophys. J., 179, 585, 1973.
156. Davis Л/., Ruffini /?., Press W. Я., Price R. H. Gravitational Radiation from a
Particle Falling Radially into a Schwarzschild Black Hole. Phys. Rev. Lett., 27,
1466, 1971.
157. Davison P. J. N. A Regular Pulsation in the X-Ray Flux from A1540-53. Mon.
Not. Roy. Astron. Soc, 179, 35F, 1977.
158. Day B. D. Current State of Nuclear Matter Calculations. Rev. Mod. Phys., 50,
495, 1978.
159. De Shalit ?., Feshbach H. Theoretical Nuclear Physics. Wiley, New York, New
York, 1974.
160. Detweiler S. L., Lindholm L. On the Evolution of the Homogeneous Ellipsoidal
Figures. Astrophys. J., 213, 193, 1977.
161. Detweiler S. L., Szedenits E. Black Holes and Gravitational Waves. II. Trajectories
Plunging into a Nonrotating Hole. Astrophys. J., 231, 211, 1979.
162. de Vaucouleurs. G., Nieto J.-L. Luminosity Distribution in the Central Regions of
Messier 87: Isothermal Core, Point Source or Black Hole? Astrophys. J., 230, 697,
1979.
163. Dicus D. A. Stellar Energy-Loss Rates in a Convergent Theory of Weak and
Electromagnetic Interactions. Phys. Rev. D, 6, 941, 1972.
164. Dicus D. ?., Kolb E. W., Schramm D. M, Tubbs D. L. Neutrino Pair
Brehmsstrahlung Including Neutral Current Effects. Astrophys. J., 210, 481, 1976.
628 Литература
165. Dirac P. ?. ?. On the Theory of Quantum Mechanics. Proc. Roy. Soc. London
Ser. ?., 112, 661, 1926.
166. Dolan J. F. et al. High-Energy X-Ray Spectra of Cygnus XR-1 Observed from
OSO-8. Astrophys. J., 230, 551, 1979.
167. Dower R. G., Bradi H. V., Morgan E. H. Circinus X-1: X-Ray Observation with
SAS-3. Astrophys. J., 261, 228, 1982.
168. Downs G. S. JPL Pulsar Timing Observations. I. The Vela Pulsar. Astrophys. J.,
249, 687, 1981.
169. Duncan M. J., Wheeler J. С Anisotropic Velocity Distributions in M87: Is a
Supermassive Black Hole Necessary? Astrophys. J. Lett., 237, L27, 1980.
170. Duncan R. C, Shapiro S. L., Wasserman I. Equilibrium Composition and
Neutrino Emissivity of Interacting Quark Matter in Neutron Stars. Astrophys. J.,
267, 358, 1983.
171. Durisen R. H. Viscous Effects in Rapidly Rotating Stars with Application to
White-Dwarf Mode.ls. II. Numerical Results. Astrophys. J., 183, 215, 1973.
172. Durisen R. H. Upper Mass Limits for Stable Rotating White Dwarfs. Astrophys.
J., 199, 179, 1975.
173. Durisen R. H., Imamura J. N. Improved Secular Stability Limits for Differentially
Rotating Polytropes and Degenerate Dwarfs. Astrophys. J., 243, 612, 1981.
174. Duyvendak J. J. L. Further Data Bearing on the Identification of the Crab Nebula
with the Supernova of A.D. 1054. Part I: The Ancient Oriental Chronicles. Proc.
Astron. Soc. Pacific, 54, 91, 1942.
175. Dyson F. G. Seismic Response of the Earth to a Gravitational Wave in 1-Hz Band.
Astrophys. J., 156, 529, 1969.
176. Eardley D. M., Lightman A. P. Magnetic Viscosity in Relativistic Accretion Discs.
Astrophys. J., 200, 187, 1975.
177. Eardley D. Л/., Lightman A. P., Payne D. G., Shapiro S. L. Accretion Discs
around Massive Black Holes: Persistent Emission Spectra. Astrophys: J., 234, 53,
1978.
178. Eddington A. S. The Mathematical Theory of Relativity. Cambridge University
Press, Cambridge, England, 1922. (Имеется перевод: ?. С. Эддингтон. Теория
относительности.—? —Л.: Гостехиздат, 1934.)
179. Eddington А. S. The Internal Constitution of the Stars. Cambridge University
Press, Cambridge, England, 1926.
180. Eddington A. S. In Minutes of a Meeting of the Royal Astronomical Society.
Observatory, 58, 37, 1935.
181. Eisner R. F., Lamb F. K. Accretion Flows in the Magnetospheres of Vela X-1,
A0535 + 26 and Her X-1. Nature, 262, 356, 1976.
182. Eisner R. F., Lamb F. K. Accretion by Magnetic Neutron Stars. I. Magnetospheric
Structure and Stability. Astrophys. J., 215, 897, 1977.
183. Emden R. Gaskugeln. B.C. Teubner, Leipzig, Germany, 1907.
184. Epstein R. The Binary Pulsar: Post-Newtonian Timing Effects. Astrophys. J., 216,
92, 1977. Errata: ibid., 231, 644, 1979.
185. Epstein R. I. Lepton-Driven Convection in Supernovae. Mon. Not. Roy. Astron.
Soc, 188, 305, 1979.
186. Epstein R. /., Arnett W. D. Neutronization and Thermal Disintegration of Dense
Stellar Matter. Astrophys. J., 201, 202, 1975.
187. Epstein R. /., Pethick C. J. Lepton Loss and Entropy Generation in Stellar
Collapse. Astrophys. J., 243, 1003, 1981.
188. Ewart G. Л/., Guyer R. ?., Greenstein G. Electrical Conductivity and Magnetic
Field Decay in Neutron Stars. Astrophys. J., 202, 238, 1975.
Литература 629
189. Fabian ?. С, Pringle J. ?., Whelan J. A. J. Is Cyg X-1 a Neutron Star? Nature,
247, 351, 1974.
190. Fabian A. C, Pringle J. E., Rees ?/. J. X-Ray Emission from Accretion onto
White Dwarfs. Mon. Not. Roy. Astron. Soc, 175, 43, 1976.
191. Fahlman G. G., Gregory P. C. An X-Ray Pulsar in SNR G109. 1—1.0. Nature,
293, 202, 1981.
192. Fechner W. В., Joss P. C. Quark Stars with "Realistic" Equations of State.
Nature, 274, 347, 1978.
193. Feinberg G. Pulsar Test of a Variation of the Speed of Light with Frequency.
Science, 166, 879, 1969.
194. Felten J. E., Rees M. J. Continuum Radiative Transfer in a Hot Plasma with
Application to Scorpius X-1. Astron. Astrophys., 17, 226, 1972.
195. Feynman R. P. Statistical Mechanics: A Set of Lectures, Benjamin, Reading,
Massachusetts, 1972. (Имеется перевод: P. Фейнман. Статистическая механика.
Курс лекций. 2-е изд.—М.: Мир, 1978.)
196. Feynman R. Р., Metropolis ?., Teller ?. Equations of State of Elements Based on
the Generalized Fermi-Thomas Theory. Phys. Rev., 75, 1561, 1949.
197. Fichtel C. E. et al. High-Energy Gamma-Ray Results from the Second Small
Astronomy Sattelite. Astrophys. J., 198, 163, 1975.
198. Flowers E. G., Sutherland P. G., Bond J. R. Neutrina Pair Bremsstrahlung by
Nucleons in Neutron-Star Matter. Phys. Rev. D, 12, 315, 1975.
199. Fontaine G., Van Horn H. M. Convective White-Dwarf Envelope Model Grids for
H-, He-, and C-Rich Compositions. Astrophys. J. Suppl., 31, 467, 1976.
200. Forman W. et al. The Fourth Uhuru Catalog of X-Ray Sources. Astrophys., J.
Suppl., 38, 357, 1978.
201. Forward R. L. Wideband Laser-Interferometer Gravitational-Radiation
Experiment. Phys. Rev. D, 17, 379, 1978.
202. Fowler R. H. Dense Matter. Mon. Not. Roy. Astron. Soc, 87, 114, 1926.
203. Fowler W. ?., Caughlan G. R., Zimmerman B. A. Thermonuclear Reaction Rates,
II. Ann. Rev. Astron. Astrophys., 13, 69, 1975.
204. Frautschi 5., Bahcall J. N., Steigman G., Wheeler J. С Ultradense Matter.
Comments Astrophys. Space Phys., 13, 69, 1971.
205. Freedman D. Z. Coherent Effects of a Weak Neutral Current. Phys. Rev. D, 9,
1389, 1974.
206. Fricke K. J. Dynamical Phases of Supermassive Stars. Astrophys. J., 183, 941,
1973.
207. Friedman В., Pandharipande V. R. Hot and Gold, Nuclear and Neutron Matter,
Nucl. Phys. A, 361, 502, 1981.
208. Friedman J. L., Schutz B. F. Gravitational Radiation Instability in Rotating Stars.
Astrophys. J. Lett., 199, L157, 1975. Erratum: ibid., 221, L91, 1978.
209. Friedman J. L., Schutz B. F. Lagrangian Perturbation Theory of Nonrelativistic
Fluids. Astrophys. J., 221, 937, 1978.
210. Friedman J. L., Schutz B. F. Secular Instability of Rotating Newtonian Stars.
Astrophys. J., 222, 281, 1978.
211. Friman B. L., Maxwell O. V. Neutrino Emissivities of Neutron Stars. Astrophys.
J., 232, 541, 1979.
212. Fuller G. M. Neutron Shell Blocking of Electron Capture During Gravitational
Collapse. Astrophys. J., 252, 741, 1982.
213. Fuller G. Л/., Fowler W. ?., Newman M. J. Stellar Weak-Interaciion Rates for
sd-Shell Nuclei. I. Nuclear Matrix Element Systematics with Application to 26a1
and Selected Nuclei of Importance to the Supernova Problem. Astrophys. J.
Suppl., 42, 447, 1980.
630 Литература
214. Fuller G. ?., Fowler W. ?., Newman ?. J. Stellar Weak Interaction Rates for
Intermediate-Mass Nuclei. II. A = 21 to A = 60. Astrophys. J., 252, 715, 1982.
215. Fuller G. M., Fowler W. ?., Newman M. J. Stellar Weak-Interaction Rates for
Intermediate-Mass Nuclei. III. Rate Tables for the Free Nucleons and Nuclei with
A = 21 to A = 60. Astrophys. J. Suppl., 48, 279, 1982.
216. Gamov G. Structure of Atomic Nuclei and Nuclear Transformations. Clarendon,
Oxford, England, 1937.
217. Gatewood G. D., Gatewood C. V. A Study of Sirius. Astrophys. J., 225, 191,
1978.
218. Gatewood G., Russell J. Astrometric Determination of the Gravitational Redshift
of Van Maanen 2(EG 5). Astron. J., 79, 815, 1974.
219. Ghosh P., Lamb F. K. Disk Accretion by Magnetic Neutron Stars. Astrophys. J.
Lett., 223, L83, 1978.
220. Ghosh P., Lamb F. K. Accretion by Rotating Magnetic Neutron Stars. II. Radial
and Vertical Structure of the Transition Zone in Disk Accretion. Xstrophys. i.,
232, 259, 1979.
221. Ghosh P., Lamb F. K. Accretion by Rotating Magnetic Neutron Stars. III.
Accretion Torques and Period Changes in Pulsating X-Ray Sources. Astrophys. J., 234,
296, 1979.
222. Giacconi /?., Ruffini /?., Eds., Physics and Astrophysics of Neutron Stars and
Black Holes. North Holland, Amsterdam, Holland, 1978.
223. Giacconi /?., Gursky H., Paolini F. /?., Rossi B. B. Evidence for X-Rays from
Sources outside the Solar System. Phys. Rev. Lett., 9, 439, 1962.
224. Giacconi R. et al. Discovery of Periodic X-Ray Pulsations in Centaurus X-3 from
UHURU. Astrophys. J. Lett., 167, L67, 1971.
225. Gies D. R., Bolton C. T. The Optical Spectrum of HDE 226868 = Cygnus X-1.
Radial Velocities and Orbital Elements. Astrophys. J., 260, 240, 1982.
226. Glen G., Sutherland P. On the Cooling of Neutron Stars. Astrophys. J., 239, 671,
1980.
227. Gold T. Rotating Neutron Stars as the Origin of the Pulsating Radio Sources.
Nature, 218, 731, 1968. (Имеется перевод: Т. Голд. Вращающиеся нейтронные
звезды как источники пульсирующих^ радиоисточников. В сб. статей:
Пульсары.—М.: Мир, 1971, стр. 163).
228. Gold Т. Rotating Neutron Stars and the Nature of Pulsars. Nature, 221, 25, 1969.
229. Goldman I. General Relativistic Effects and the Radius and Mass of X-Ray
Bursters. Astron. Astrophys., 78, L15, 1979.
230. Goldreich P., Julian W. H. Pulsar Electrodynamics. Astrophys. J., 157, 869, 1969.
231. Goldreich P., Weber S. V. Homologously Collapsing Stellar Cores. Astrophys. J.,
238, 991, 1980.
232. Goldstein H. Classical Mechanics. 2nd ed, Addison-Wesley, Reading,
Massachusetts, 1981. (Имеется перевод: Г. Голдстейн. Классическая механика,
2-е изд.—М.: Наука, 1975.)
233. Gottlieb ?. W., Wright ?. L., Liller W. Optical Studies of Uhuru Sources. XI. A
Probable Period for Scorpius X-1 = V818 Scorpii. Astophys. J. Lett., 195, L33,
1975.
234. Градштейн И. С, Рыжик И. В. Таблицы интегралов, сумм, рядов и
произведений. — М.: Наука, 1971.
235. Грассберг Е. К., Имшенник В. С, Надежин Д. К. On the Theory of the Light
Curves of Supernovae. Astrophys. Space Sci., 10, 28, 1971.
236. Green A. E. S. Nuclear Physics. McGraw-Hill, New York, N.Y., 1955.
237. Green A. M., Haapakoski P. The Effect of the ? A236) in the Two-Nucleon
Problem and in Neutron Matter. Nucl. Phys. A, 221, 429, 1974.
Литература 631
238. Green R. F. Неопубликованная диссертация. California Institute of Technology,
Pasadena, California, 1977.
239. Green R. F. The Luminosity Function of Hot White Dwarfs. Astrophys. J., 238,
685, 1980.
240. Greene J. Bremsstrahlung from a Maxwellian Gas. Astrophys. J., 130, 693, 1959.
241. Greenstein G. Pulsar Timing Observations, X-Ray Transients and the
Thermal/Timing Instability in Neutron Stars. Astrophys. J., 231, 880, 1979.
242. Gree',istein J. L. Spectra of Stars Below the Main Sequence. In Stars and Stellar
Systems. Vol. 6. Ed. J. L. Greenstein. Univ. of Chicago Press, Chicago, Illinois.
1960, p. 676.
243. Greenstein J. L., Trimble V. L. The Einstein Redshift in White Dwarfs. Astrophys.
J., 149, 283, 1967.
244. Greenstein J. L.; Оке J. В., Shipman H. L. Effective Temperature, Radius and
Gravitational Redshift of Sirius B. Astrophys. J., 169, 563, 1971.
245. Greenstein J. L., Boksenberg ?., Carswell /?., Shortridge K. The Rotation and
Gravitational Redshift of White Dwarfs. Astrophys. J., 212, 186, 1977.
246. Grindlay J. E. X-Ray Sources in Globular Clusters. In X-Ray Astronomy with the
Einstein Satellite. Ed. R. Giacconi. Reidel, Dordrecht, Holland, 1981.
247. Grindlay J. et al. Discovery of Intense X-Ray Bursts from the Globular Cluster
NGC 6624. Astrophys. J. Lett., 205, L127, 1976.
248. Groth E. J. Observational Properties of Pulsars. In Neutron Stars, Black Holes
and Binary X-Ray Sources. Eds. H. Gursky and R. Ruffiniy Reidel, Dordrecht,
Holland, 1975.
249. Groth E. J. Timing of the Crab Pulsar. III. The Slowing Down and the Nature of
the Random Process. Astrophys. J. Suppl., 29, 453, 1975.
250. Gullahorn G. E., Isaacman R., Rankin J. M., Payne R. R. The Crab Nebula
Pulsar: Six Years of Radio-Frequency Arrival Times. Astron. J., 82, 309, 1977.
251. Gunn J. E., Ostriker J. P. Magnetic Dipole Radiation from Pulsars. Nature, 221,
454, 1969.
252. Gunn J. E., Ostriker J. P. On the Nature of Pulsars. III. Analysis of Observations.
Astrophys. J., 160, 979, 1970.
253. Gursky H., Ruffini /?., Eds. Neutron Stars, Black Holes and Binary X-Ray
Sources, Reidel, Dordrecht, Holland, 1975.
254. Hagedorn R. Remarks on the Thermodynamical Model of Strong Interactions.
Nucl. Phys. B, 24, 231, 1970.
255. Hamada Г., Salpeter E. E, Models for Zero-Temperature Stars. Astrophys. J.,
134, 683, 1961.
256. Harnden F. R. et al. X-Ray Observations of the Crab Nebula with the Einstein
Observatory. Bull. Amer. Astron. Soc, 11, 789, 1979.
257. Harnden F. R. et al. Observations of the Vela Pulsar from the Einstein
Observatory. Bull. Amer. Astron. Soc, 11, 424, 1979.
258. Harris D. L. The Stellar Temperature Scale and Bolometric Corrections. In Basic
Astronomical Data, Vol. III. Ed. K. A. Strand, Univ. of Chicago Press, Chicago,
Illinois, 1963.
259. Harrison B. K., Wheeler J. A. (HW), 1958. См. [260, 261].
260. Harrison B. K., Wakano M., Wheeler J. A. Matter-Energy at High Density; End
Point of Thermonuclear Evolution. In La Structure et revolution de I'univers. On-
zieme Conseil de Physique Solvay, Stoops, Brussels, Belgium, 1958, p. 124.
261. Harrison B. K., Thorne K. 5., Wakano M., Wheeler J. A. (HTWW). Gravitation
Theory and Gravitational Collapse. Univ. of Chicago Press, Chicago, Illinois,
1965. (Имеется перевод: Дж. Уидер, Б. Гаррисон, М. Вакано, К. Торн.
Теория гравитации и гравитационный коллапс. — М.: Мир, 1967.)
632 Литература
262. Hartle J. В. Slowly Rotating Relativistic Stars. I. Equations of Structure.
Astrophys. J., 150, 1005, 1967.
263. Hartle J. В., Sabbadini A. G. The Equation of State and Bounds on the Mass of
Nonrotating Neutron Stars. Astrophys. J., 213, 831, 1977.
264. Hartle J. В., Thorne K. S. Slowly Rotating Relativistic Stars. II. Models for
Neutron Stars and Supermassive Stars. Astrophys. J., 153, 807, 1968.
265. Hawking S. W. Gravitationally Collapsed Objects of Very Low Mass. Mon. Not.
Roy. Astron. Soc, 152, 75, 1971.
266. Hawking S. W. Black Hole Explosions? Nature, 248, 30, 1974.
267. Hawking S. W. Particle Creation by Black Hole. Commun. Math. Phys., 43, 199,
1975.
268. Hawking S. W., Ellis G. F. R. The Large Scale Structure of Space-Time.
Cambridge Univ. Press, Cambridge, England, 1973. (Имеется перевод: С. Хокинг,
Дж. Эллис. Крупномасштабная структура пространства-времени. — М.:
Мир, 1977.)
269. Hayakawa 5., Matsuoka Л/. Origin of Cosmic X-Rays. Progr. Theor. Phys.
Suppl., No. 30, 204, 1964.
270. Heintz W. D. Astrometric Study of Four Visual Binaries. Astron. J., 79, 819,
1974.
271. Helfand D. J. Unpulsed X-Rays from Pulsars. In lAU Symposium 95, Pulsars.
Eds. W. Sieber and R. Wielebinski, Reidel, Dordrecht, Holland, 1981.
272. Helfand D. У., Chanan G. ?., Novick R. Thermal X-Ray Emission from Neutron
Stars. Nature, 283, 337, 1980.
273. Hershey J. Astrometric Study of the Sproul Plate Series on Van Maanen's Star,
Including Gravitational Redshift. Astron. J., 83, 197, 1978.
274. Hewish ?., Bell S. J., Pilkington J. D. H., Scott P. R, Collins R. A. Observation
of a Rapidly Pulsating Radio Source. Nature, 217, 709, 1968. (Имеется перевод:
?. Хьюиш и др. Наблюдение быстро пульсирующего радиоисточника. В сб.
статей: Пульсары. — М.: Мир, 1971, стр. 27.)
275. Hjellming R. Л/. Radio Variability of HDE 226868 (Cygnus X-1). Astrophys. J.
Lett., 182, L29, 1973.
276. Hoffman J. ?., Marshall H. L., Lewin W. H. G. Dual Character of the Rapid
Burster and a Classification of X-Ray Bursts. Nature, 271, 630, 1978.
277. Holt S. 5., McCray R. Spectra of-Cosmic X-Ray Sources. Ann. Rev. Astron.
Astrophys., 20, 323, 1982.
278. Holt S. 5., Boldt E. Л., Serlemitsos P. У., Kaluzienski L. J. New Results from
Long-Term Observations of Cygnus X-1. Astrophys. J. Lett., 203, L63, 1976.
279. Hoshi R. X-Ray Emission from White Dwarfs in Close Binary Systems. Progr.
Theor. Phys., 49, 776, 1973.
280. Hoyle F. The Synthesis of the Elements from Hydrogen. Mon. Not. Roy. Astron.
Soc, 106, 343, 1946.
281. Hoyle F., Fowler W. A. Nucleosynthesis in Supernovae. Astrophys. J., 132, 565,
1960.
282. Hoyle F., Fowler W. A. On the Nature of Strong Radio Sources. Mon. Not. Roy.
Astron. Soc, 125, 169, 1963.
283. Hoyle F., Flowler W. A. Nature of Strong Radio Sources. Nature, 197, 533, 1963.
284. Hoyle F., Lyttleton R. A. Evolution of Stars. Proc Camb. Phil. Soc, 35, 592,
1939.
285. Hoyle F., Narlikar J. V., Wheeler J, A, Electromagnetic Waves from Very Dense
Stars. Nature, 203, 914, 1964.
Литература 633
286. Huckle ?. ?. et ??. Discovery of Two-Periodic X-Ray Pulsators. Mon. Not. Roy.
Astron. Soc, 180, 21P, 1977.
287. Hulse R. A, Taylor J. H. Discovery of a Pulsar in a Binary System. Astrophys. J.
Lett., 195, L51, 1975.
288. Hunt R. A Fluid Dynamical Study of the Accretion Process. Mon. Not. Roy.
Astron. Sbc, 154, 141, 1971.
289. Hunter С On Secular Stability, Secular Instability and Points of Bifurcation of
Rotating Gaseous Masses. Astrophys. J., 213, 497, 1977.
290. Iben I. Post Main Sequence Evolution of Single Stars. Ann. Rev. Astron.
Astrophys., 12, 215, 1974.
291. Илларионов A. Ф., Сюняев P. A. Комптоновское рассеяние тепловыми
электронами в рентгеновских источниках. Астрон. ж., 49, 58, 1972.
292. Илларионов А. Ф., Сюняев Р. А. Why the Number of Galactic X-Ray Stars is so
Small? Astron. Astrophys., 39, 185, 1975.
293. Ipser J. /?., Price R. H. Accretion onto Pregalactic Black Holes. Astrophys. J.,
216, 578, 1977.
294. Иванова Л. ?., Имшенник В. С, Надежин Д. К. Научные информации
Астрономического совета АН СССР, 13, 3, 1969.
295. Ives J. С, Sanford P. W, Bell Burnell S. J. Observations of a Transient X-Ray
Source with Regular Periodicity of 6,75 min. Nature, 254, 578, 1975.
296. Iwamoto N. Quark Beta Decay and the Cooling of Neutron Stars. Phys. Rev.
Lett., 44, 1637, 1980.
297. Jackson J. D. Classical Electrodynamics, 2nd ed, Wiley, New York, New York,
1975. (Имеется перевод: Дж. Джексон. Классическая электродинамика. — М.:
Мир, 1965.)
298. James R. А. The Structure and Stability of Rotating Gas Masses. Astrophys. J.,
140, 552, 1964.
299. Jeans J. H. Problems of Cosmogony and Stellar Dynamics. Cambridge Univ.
Press, Cambridge, England, 1919.
300. Jones C, Forman W. UHURU Observations of Hercules X-1 During the Low
State of the 35-Day Cycle. Astrophys. J. Lett, 209, L131, 1976.
301. Joss P. С X-Ray Bursts and Neutron-Star Thermonuclear Flashes. Nature, 270,
310, 1977.
302. Joss P. C, Rappaport S. Observational Constraints on the Masses of Neutron
Stars. Nature, 264, 219, 1976.
303. Каплан С ?. Сверхплотные звезды. Научные записки Львовского
университета, 15, 109, 1949.
304. Karzas W. У., Latter R. Electron Radiative Transitions in a Coulomb Field.
Astrophys. J. Suppl., 6, 167, 1961.
305. Katz J. L. Thirty-Five-Day Periodicity in Her X-1. Nature Phys. Sci., 246, 87,
1973.
306. Katz J. L. Two Kinds of Stellar Collapse. Nature, 253, 698, 1975.
307. Katz J. L. X-Rays from Spherical Accretion onto Degenerate Dwarfs. Astrophys.
J., 215, 265, 1977.
308. Keister B. D., Kisslinger L. S. Free-Quark Phases in Dense Stars. Phys. Lett. B,
64, 117, 1976.
309. Kelley R. L. et al. Discovery of X-Ray Pulsations from 2S 1417-624. Astrophys. J.,
243, 251, 1981.
310. Kelley R. L. et al. Discovery of 13,5-s X-Ray Pulsations from LMC X-4 and an
Orbital Determination. Astrophys. J., 264, 568, 1983.
311. Kerr R. P. Gravitational Field of a Spinning Mass as an Example of Algebraical'/^
Special Metrics. Phys. Rev. Lett., 11, 237, 1963.
634 Литература
312. Kippenhahn R. Mass Exchange in a Massive Close Binary System. Astron.
Astrophys., 3, 83, 1969.
313. Klebesadel R. W., Strong I. В., Olson R. A. Observations of Gamma-Ray Bursts
of Cosmic Origin. Astrophys. J. Lett., 182, L85, 1973.
314. Klebesadel R. W., Fenimore E. E., Laros J. G., Terrel J. Gamma-Ray Burst
Systematics. In Gamma-Ray Transients and Related Astrophysical Phenomena.
Eds. R. E. Lingenfelter, H. 5. Hudson and D. M. Worrall, American Institute of
Physics, New York, New York, 1982.
315. Klein R. /., Stockman H. 5., Chevalier R. A. Supercritical Time-Dependent
Accretion onto Compact Objects. I. Neutron Stars. Astrophys. J., 237, 912, 1980.
316. Kobayashi 5., Matsukuma Г., Nagai 5., Umeda K. Accurate Value of the Initial
Slope of the Ordinary TF Functions. J. Phys. Soc. Jap., 10, 759, 1955.
317. Koester D., Schulz H., Weidemann V. Atmospheric Parameters and Mass
Distribution of DA White Dwarfs. Astron. Astrophys., 76, 262, 1979.
318. Компанеец A. C. Установление теплового равновесия между квантами и
электронами. ЖЭТФ, 31, 876, 1956.
319. Krisciunas К. Toward the Resolution of the Local Missing Mass Problem. Astron.
J., 82, 195, 1977.
320. Kruskal M. D. Maximal Extension of Schwarzschild Metric. Phys. Rev., 119, 1743,
1960.
321. Kylafis N. D., Lamb D. Q. X-Ray and UV Radiation from Accreting Nonmagnetic
Degenerate Dwarfs. Astrophys. J. Lett., 228, L105, 1979.
322. Kylafis N. D., Lamb D. Q., Masters A. R., Weast G. J. X-Ray Spectra of
Accreting Degenerate Stars. Ann. N. Y. Acad. Sci.,336, 520, 1980 (Ninth Texas
Symposium).
323. Lacy J. Я., Baas F., Townes С ?., Geballe Т. R. Observations of the Motion and
Distribution of the Ionized Ga, in the Central Parsec of the Galaxy. Astrophys. J.
Lett., 227, L17, 1979.
324. Lamb F. K. Structure of the Magnetospheres of Accreting Neutron Stars. In
Proceedings of the Sydney Chapman Conference on Magnetospheric Boundary Layers.
Ed. B. Battrick, 1979 (ESA SP Series).
325. Lamb D. Q. Degenerate Dwarf X-Ray Sources. In Compact Galactic X-Ray
Sources: Current Status and Future Prospects. Eds. F. K. Lamb and D. Pines.
Physics Dept., Univ. of Illinois, Urbana, Illinois, 1979.
326. Lamb D. Q. Surface and Magnetospheric Physics of Neutron Stars and Gamma
Ray Bursts. In Gamma Ray Transients and Related Astrophysical Phenomena.
Eds. R. E. Lingenfelter, H. 5. Hudson and D. M. Worrall. American Institute of
Physics, New York, New York, 1982.
327. Lamb D. Q., Lamb F. K. Nuclear Burning in Accreting Neutron Stars and X-Ray
Bursts. Astrophys. J., 220, 291, 1978.
328. Lamb D. Q., Masters A. R. M. Radiation from Accreting Magnetic Degenerate
Dwarfs. Astrophys. J. Lett., 234, LI 17, 1979.
329. Lamb D. Q., Pethick C. J. Effects of Neutrino Degeneracy in Supernovae Models.
Astrophys. J. Lett., 209, L77, 1976.
330. Lamb F. A'., Pines D., eds. Compact Galactic X-Ray Sources: Current Status and
Future Prospects. Physics Dept., Univ. of Illinois, Urbana, Illinois, 1979.
331. Lamb D, Q,. Van Horn H. M. Evolution of Crystallizing Pure ^^C White Dwarfs.
Astrophys. J., 200, 306, 1975.
332. Lamb F. K., Pethick С У., Pines D. A Model for Compact X-Ray Sources:
Accretion by Rotating Magnetic Stars. Astrophys. J., 184, 271, 1973.
333. Lamb D. Q., Lamb F. K., Pines D., Shaham J. Neutron Star Wobble in Binary
X-Ray Sources. Astrophys. J. Lett., 198, L21, 1975.
Литература 635
334. Lamb D. Q., Lattimer J. M., Pethick С У., Ravenhall D. G. Hot Dense Matter
and Stellar Collapse. Phys. Rev. Lett., 41, 1623, 1978.
335. Lamb D. Q., Lattimer J. M., Pethick C. У., Ravenhall D. G. Physical Properties
of Hot, Dense Matter: The Bulk Equilibrium Approximation. Nucl. Phys. A, 360,
459, 1981.
336. Lamb R. C. et al. Two X-Ray Pulsars: 2S 1145—619 and IE 1145,1—6141.
Asrophys. J., 239, 651, 1980.
337. Ландау Л. Д. On the Theory of Stars. Phys. Z. Sowjetunion, 1, 285, 1932.
338. Ландау Л. Д. Origin of Stellar Energy. Nature, 141, 333, 1938.
339. Ландау Л. Д., Лифшиц ?. ?. Механика сплошных сред. — ?.—Л.: ГИТТЛ,
1953.
340. Ландау Л. Д., Лифшиц Е. Л/. Статистическая физика. 2-е изд. — М.: Наука,
1964.
341. Ландау Л. Д., Лифшиц Е. Л/. Теория поля. 6-е изд. — М.: Наука, 1973.
342. Ландау Л. Д., Лифшиц Е. Л/. Квантовая механика: нерелятивистская теория.
3-е изд. — М.: Наука, 1974.
343. Landstreet J. D. The Magnetic Fields of Single White Dwarfs. In White Dwarfs
and Variable Degenerate Stars (lAU Colloq. No. 53). Eds. H. M. Van Horn and
V. Weidemann. Univ. of Rochester Press, Rochester, New York, 1979.
344. Laplace P. S. Le Systeme du Monde. Vol. II. Paris, 1975. (Имеется перевод:
П. Лаплас. Изложение системы мира, т. 1—2. СПБ, 1861.)
345. Large Л/. /., Vaughan А. ?*., Mills В. Y. А Pulsar Supernova Association? Nature,
220, 340, 1968.
346. Lasher G. A Simple Model for the Early Part of Type I Supernova Light Curves.
Astrophys. J., 201, 194, 1975.
347. Lattimer J. M. The Equation of State of Hot Dense Matter and Supernovae. Ann.
Rev. Nucl. Part. Sci., 31, 337, 1981.
348. Laval G., Mercier C, Pellat R. Necessity of the Energy Principles for
Magnetostatic Stability. Nuclear Fusion, 5, 156, 1965.
349. LeBlanc J. Л/., Wilson J. R. A Numerical Example of the Collapse of a Rotating
Magnetized Star. Astrophys. J., 161, 541, 1970.
350. Lee B. W., Zinn-Justin J. Spontaneously Broken Gauge Symmetries. I.
Preliminaries. Phys. Rev. D, 5, 3121, 1972.
351. Legaris I. E., Pandharipande V. R. Variational Calculations of Realistic Models of
Nuclear Matter. Nucl. Phys. A, 359, 349, 1981.
352. Leung Y. C, Wang C. G. Equation of State of Matter at Supernuclear Densities.
Astrophys. J., 181, 895, 1973.
353. Lewin W. H. G., Clark G. W. Galactic Bulge Sources, What Are They? Ann. N.Y.
Acad. Sci., 336, 451, 1980 (Ninth Texas Symposium).
354. Lewin W. H. G., Joss P. C. X-Ray Burst Sources. Nature, 270, 211, 1977.
355. Lewin W. H. G., Joss P. С X-Ray Bursters and the X-Ray Sources of the Galactic
Bulge. Space Sci. Rev., 28, 3, 1981.
356. Lewin W. H. G., Ricker G. /?., McClintock J. E. X-Rays from a New Variable
Source GX 1 +4. Astrophys. J. Lett., 169, L17, 1971.
357. Liang E. P. T. Test of the Inverse Compton Model for Cygnus X-1. Nature, 283,
642, 1980.
358. Liang E. P. Г., Price R. H. Accretion Disc Coronae and Cygnus X-1. Astrophys.
J., 218, 247, 1977.
359. Liang E. P. Т., Thompson K. A. Transonic Disc Accretion onto Black Holes.
Astrophys. J., 240, 271, 1980.
360. Liebert J. White Dwarf Stars. Ann. Rev. Astron. Astrophys., 18, 363, 1980.
636 Литература
361. Liebert J.» Dahn С. С, Gresham Л/., Strittmatter P. A. New Results from Survey
of Faint Proper-Motion Stars: A Probable Deficiency of Very Low Luminosity
Degenerates. Astrophys. J., 233, 226, 1979.
362. Lightman A. P., Eardley D. M. Black Holes in Binary Systems: Instability of Disk
Accretion. Astrophys. J. Lett., 187. LI, 1974.
363. Lightman A. P., Rybicki G. B. X-Rays from Active Galactic Nuclei: Inverse Com-
pton Reflection. Astrophys. J. Lett., 229, L15, 1979.
364. Lightman A. P., Shapiro S. L. Spectrum and Polarization of X-Rays from
Accretion Disks around Black Holes. Astrophys. J. Lett., 198, L73, 1975.
365. Lightman A. P., Shapiro S. L. The Dynamical Evolution of Globular Clusters.
Rev. Mod. Phys., 50, 437, 1978.
366. Lightman A. P., Press W. Я., Price R. Я., Teukolsky S. A. Problem Book in
Relativity and Gravitation. Princeton Univ. Press, Princeton, New Jersey, 1975.
(Имеется перевод: ?. Лайтман, В. Пресс, Р. Прайс и С. Тьюколски. .Сборник
задач по теории относительности и гравитации. — М.: Мир, 1979.)
367. Lightman А. Р., Shapiro 5. L., Rees ?. J. Accretion onto Compact Objects. In
Physics and Astrophysics on Neutron Stars and Black Holes. Eds. R. Giacconi and
R. Ruffini. North Holland, Amsterdam, Holland, 1978.
368. Lightman A. P., Hertz P., Grindlay J. E. A New Statistical Test with Application
to Globular Cluster X-Ray Source Masses. Astrophys. J., 241, 367, 1980.
369. Lindemann F. A. Molecular Frequencies. Phys. Z., 11, 609, 1910.
370. Livio M., Buchler J. R., Colgate S. A. Rayleigh — Taylor Driven Supernova
Explosions: A Two-Dimensional Nimerical Study. Astrophys. J. Lett., 238, LI39,
1980.
371. Lohsen E. Third Speed-up of the Crab Pulsar. Nature, 258, 688, 1975.
372. Lovelace R. V. E. Dynamo Model of Double Radio Sources. Nature, 262, 649,
1976.
373. Lucke R. et al. Discovery of X-Ray Pulsation in SMC X-1. Astrophys. J. Lett.,
206, L25, 1976.
374. Lui Y. W. et al. Observation of the Giant Monopole Resonance in ^^^^Zn. Phys.
Lett. B, 93, 31, 1980.
375. Lynden-Bell D. Galactic Nuclei as Collapsed Old Quasars. Nature, 223, 690, 1969.
376. Lynden-Bell D., Ostriker J. P. On the Stability of Differentially Rotating Bodies.
Mon. Not. Roy. Astron. Soc, 136, 293, 1967.
377. Lynden-Bell D., Pringle J. E. The Evolution of Viscous Discs and the Origin of the
Nebular Variables. Mon. Not. Roy. Astron. Soc, 168, 603, 1974.
378. Macy W. W. Pulsar Magnetic Axis Alignment and Counteralignment. Astrophys.
J., 190, 153, 1974.
379. Malone R. C. Неопубликованная диссертация. Cornell Univ., Ithaca, New York,
1974.
380. Manchester R. M, Taylor J. Я Pulsars. Freeman, San Francisco, California, 1977.
(Имеется перевод: P. Манчестер и Дж. Тейлор. Пульсары. — М.: Мир, 1980.)
381. Manchester R. ?., Newton L. ?., Goss W. ?/., Hamilton P. A. Detection of a
Large Period Discontinuity in the Longest Period Pulsar PSR 1641-45. Mon. Not.
Roy. Astron. Soc, 184, 35P, 1978.
382. Manchester R. M, Tuohy I. R., D*Amico N. Discovery of Radio Pulsations from
X-Ray Pulsar in the Supernova Remnant G32,4—1,2. Astrophys. J. Lett., 262,
L31, 1982.
383. Mandrou P., Niel ?/., Vedrenne G., Dupont ?., Hurley K. Observation of Cygnus
X-1 in the Energy Range 100 keV—3 MeV. Astrophys. J., 219, 288, 1978.
384. Maraschi L., Cavaliere A. X-Ray Bursts of Nuclear Origin? In Highlights of
Литература 637
Astronomy, Vol. 4, Part 1. Ed. E. A. Miiller. Reidel, Dordrecht, Holland, 1977, p.
127
385. Margon В., Ostriker J. P. The Luminosity Function of Galactic X-Ray Sources: A
Cutoff and a "Standard Candle"? Astrophys. J., 186, 91, 1973.
386. Margon В., Bowyer 5., Stone R. P. S. On the Distance to Cygnus X-1. Astrophys.
J. Lett., 185, LI 13, 1973.
387. Mauder H. On the Mass Limit of the X-Ray Source in Cygnus X-1. Astron.
Astrophys., 28, 473, 1973.
388. Maxon S. Bremsstrahlung Rate and Spectra from a Hot Gas (Z = 1). Phys. Rev.
A, 5, 1630, 1972.
389. Maxwell O. V. Neutron Star Cooling. Astrophys. J., 231, 201, 1979.
390. Maxwell O., Brown G. E., Campbell D. K., Dashen R. F., Manassah J. T. Beta
Decay of Pion Condensates as a Cooling Mechanism for Neutron Stars. Astrophys.
J., 216, 77, 1977.
391. Mayall N. t/., Oort J. H. Further Data Bearing on the Identification of the Crab
Nebula with the Supernova of 1054 A. D., Part II: The Astronomical Aspects.
Proc. Astron. Soc. Pacific, 54, 95, 1942.
392. Mazurek T. J. Chemical Potential Effects on Neutrino Diffusion in Supernovae.
Astrophys. Space Sci., 35, 117, 1975.
393. Mazurek T. J. Pauli Constriction of the Low-Energy Window in Neutrino
Supernova Models. Astrophys. J. Lett., 207, L87, 1976.
394. McClintock J. E., Petro L. D. lAU Circular No. 3615, 1981.
395. McClintock J. E. et al. Discovery of a 283-Second Periodic Variation in the X-Ray
Source 3U 0900—40. Astrophys. J. Lett., 206, L99, 1976.
396. McClintock J. E.» Rappaport S. ?., Nugent J. J., Li F. K. Discovery of a
272-Second Periodic Variation in the X-Ray Source GX 304—1. Astrophys. J.
Lett., 216, L15, 1977.
397. McCulloch P. M., Hamilton P. ?., Royle G. W. R., Manchester R. N. lAU
Circular No. 3644, 1981.
398. McCuskey S. W. The Stellar Luminosity Function. In Vistas in Astronomy, Vol. 7.
Ed. A. Beer. Pergamon, Oxford, England, 1966, p. 141.
399. Merzbacher E. Quantum Mechanics. Wiley, New York, New York, 1970.
400. Mestel L. On the Theory of White Dwarf Stars. I. The Energy Sources of White
Dwarfs. Mon. Not. Roy. Astron. Soc, 112, 583, 1952.
401. Mestel L., Ruderman M. A. The Energy Content of a White Dwarf and its Rate of
Cooling. Mon. Not. Roy. Astron. Soc, 136, 27, 1967.
402. Meszaros P. Radiation from Spherical Accretion onto Black Holes. Astron.
Astrophys., 44, 59, 1975.
403. Michel F. С Accretion of Matter by Condensed Objects. Astrophys. Space Sci.,
15, 153, 1972.
404. Michel F. C. Theory of Pulsar Magnetospheres. Rev. Mod. Phys., 54, 1, 1982.
405. Мигдал A. Б. Pion Fields in Nuclear Matter. Rev. Mod. Phys., 50, 107, 1978.
406. Mihalas D. Stellar Atmospheres. 2nd ed. Freeman, San Francisco, California,
1978. (Имеется перевод: Д. Михалас Звездные атмосферы, ч. 1—2. — М.:
Мир, 1982.)
407. Milgrom ?. On the Nature of the Galactic Bulge X-Ray Sources. Astron.
Astrophys., 67, L25, 1978,
408. Miller G. E., Scalo J. M. The Initial Mass Function and Stellar Birthrate in the
Solar Neighborhood. Astrophys. J. Suppl., 41, 513, 1979.
409. Milne E. A. The Total Energy of Binding of a Heavy Atom. Proc. Camb. Phil.
Soc, 23, 794, 1927.
410. Minkowski R. The Crab Nebula. Astrophys. J., 96, 199, 1942.
638 Литература
411. Misner С. W., Thorne К. 5., Wheeler J. A. Gravitation. Freeman, San Francisco,
California, 1973. (Имеется перевод: С. Мизнер, К. Торн, Дж. Уилер.
Гравитация, т. 1—3. М.: Мир, 1976—77.)
412.· Moncnef V. Stability of Stationary, Spherical Accretion onto a Schwarzschild
Black Hole. Astrophys. J., 235, 1038, 1980.
413. Morrison P. Extrasolar X-Ray Sources. Ann. Rev. Astron. Astrophys., 5, 325,
1967.
414. Morse P. Л/., Feshbach H. Methods of Theoretical Physics, Vol. 1. McGrow-Hill,
New York, New York, 1953. (Имеется перевод: ?. Морс, Г. Фешбах. Методы
теоретической физики, т. 1 — М.: ИЛ, 1958.)
415. Miiller ?., Hillebrandt W. A Magnetohydrodynamical Supernova Model. Astron.
Astrophys., 80, 147, 1979.
416. Murray S. S. et al. High-Resolution X-Ray Observations of the Cassiopeia A
Supernova Remnant with the Einstein Observatory. Astrophys. J. Lett., 234, L69,
1979.
417. Myers W. D., Swiatecki W. J. Nuclear Masses and Deformations. Nucl. Phys., 81,
1, 1966.
418. Nauenberg M., Chapline G. Determination of Properties of Cold Stars in General
Relativity by a Variational Method, Astrophys. J., 179, 277, 1973.
419. Newman E. T. et al. Metric of a Rotating, Charged Mass. J. Math. Phys., 6, 918,
1965.
420. Nomoto K., Tsuruta S. Cooling of Young Neutron Stars and the Einstein X-Ray
Observations. Astrophys. J. Lett., 250, LI9, 1981.
421. Norgaard H., Fricke K. J. "^Li Production in Bouncing Supermassive Stars. Astron.
Astrophys., 49, 337, 1976.
422. Новиков И. Д., Thorne К. S. Black Hole Astrophysics. In Black Holes, Eds.
С DeWitt and B. DeW'itt. Gordon and Breach, New York, New York, 1973.
423. Oda M. Cyg X-l/A Candidate of the Black Hole. Space Sci. Rev., 20, 757, 1977.
424. Oort J. H. Note on the Determination of K^ and on the Mass Density Near the
Sun. Bull. Astron. Inst. Neth., 15, 45, 1960.
425. Oppenheimer J. R., Serber R. On the Stability of Stellar Neutron Cores. Phys.
Rev., 56, 540, 1938.
426. Oppenheimer J. R., Snyder H. On Continued Gravitational Contraction. Phys.
Rev., 56, 455, 1939.
427. Oppenheimer J. R., Volkoff G. M. (OV). On Massive Neutron Cores. Phys. Rev.,
55, 374, 1939.
428. Osterbrock D. E. The Origin and Evolution of Planetary Nebulae. Mem. Soc. Roy.
Sci. Liege, 5, 391, 1973.
429. Ostriker J. P. Работа 1976 г., цитированная в статье: Liang ?. P. Т., Price
R. ?. Connective Accretion Discs and X-Ray Bursters. Astrophys. J., 218, 243,
1977.
430. Ostriker J. P., Bodenheimer P. Rapidly Rotating Stars. И. Massive White Dwarfs.
Astrophys. J., 151, 1089, 1968.
431. Ostriker J. P., Bodenheimer P. On the Oscillations and Stability of Rapidly
Rotating Stellar Models. IIL Zero-Viscosity Poiytropic Sequences. Astrophys, J.,
180, 171, 1973. Erratum: ibid., 182, 1037, 1973.
432. Ostriker J. P., Gunn J. E. On the Nature of Pulsars. L Theory. Astrophys. J.,
157, 1395, 1969.
433. Ostriker J. P., Hartwick F. D. A. Rapidly Rotating Stars. IV. Magnetic White
Dwarfs. Astrophys. J., 153, 797, 1968.
434. Ostriker J. P., Tassoul J. L. On the Oscillations and Stability of Rotating Stellar
Models. II. Rapidly Rotating White Dwarfs. Astrophys. J., 155, 987, 1969.
Литература 639
435. Ostriker J. P., Richstone D. O., Thuan T. X. On the Numbers, Birthrates and
Final States of Moderate- and High-Mass Stars. Astrophys. J. Lett., 188, L87,
1974.
436. Overbeck J. W., Tananbaum H. D. Twofold Increase of the High-Energy X-Ray
Flux from Cygnus XR-1. Phys. Rev. Lett., 20, 24, 1968.
437. Pacini F. Energy Emission from a Neutron Star. Nature, 216, 567, 1967.
438. Pacini F. Rotating Neutron Stars, Pulsars and Supernova Remnants. Nature, 219,
145, 1968. (Имеется перевод: ?. Пачини. Вращающиеся нейтронные звезды,
пульсары и остатки сверхновых. В сб. статей: Пульсары. — М.: Мир, 1971, с.
167.)
439. Paczynski В. Evolutionary Processes in Close Binary Systems. Ann. Rev. Astron.
Astrophys., 9, 183, 1971.
440. Paczynski B. Mass of Cygnus X-1. Astron. Astrophys., 34, 161, 1974.
441. Page D. N. Particle Emission Rates from a Black Hole: Massive Particles from an
Uncharged, Nonrotating Hole. Phys. Rev. D, 13, 198, 1976.
442. Page D. N., Hawking S. W. Gamma Rays from Primordial Black Holes.
Astrophys. J., 206, 1, 1976.
443. Pandharipande V. R. Hyperonic Matter. Nucl. Phys. A, 178, 123, 1971.
444. Pandharipande V. R., Smith R. A. к Model Neutron Solid with ?° Condensate.
Nucl. Phys. A, 237, 507, 1975.
445. Pandharipande V. P., Smith R. A. Nuclear Matter Calculations with Mean Scalar
Fields. Phys. Lett. B, 59, 15, 1975.
446. Pandharipande К /?., Pines D., Smith R. A. Neutron Star Structure: Theory,
Observation and Speculation. Astrophys. J., 208, 550, 1976.
447. Parker E. N. Dynamical Properties of Stellar Coronas and Stellar Winds. IV. The
Separate Existence of Subsonic and Supersonic Solutions. Astrophys. J., 141, 1463,
1965.
448. Particle Data Group. Review of Particle Properties. Phys. Lett. B, 111, 1, 1982.
449. Payne D. G. Time-Dependent Comptonization: X-Ray Reverberations. Astrophys.
J., 237, 951, 1980.
450. Payne D. G., Eardley D. M. X-Ray Spectrum from Disk Accretion onto Massive
Black Holes. Astrophys. Lett., 19, 39, 1977.
451. Pedersen H. У., van Paradijs У., Lemn W. H. G. Evidence for a Four Hour
Orbital Period of 4U/MXB 1636—53. Nature, 294, 725, 1981.
452. Peebles P. J. E. Physical Cosmology. Princeton Univ. Press, Princeton, New
Jersey, 1971. (Имеется перевод: П. Пиблс. Физическая космология. — М.:
Мир, 1975.)
453. Penrose R. Gravitational Collapse: The Role of General Relativity. Riv. Nuovo
Cim., 1, 252, 1969.
454. Perkins D. H. Introduction to High-Energy Physics. Addison-Wesley, Reading,
Massachusetts, 1972. (Имеется перевод: Д. Перкинс. Введение в физику
высоких энергий. — М.: Мир, 1975.)
455. Peters Р. С. Gravitational Radiation and the Motion of Two Point Masses. Phys.
Rev., 136, 1224, 1964.
456. Petterson J. A. Hercules X-1: A Neutron Star with a Twisted Accretion Disk?
Astrophys. J. Lett., 201, L61, 1975.
457. Pines D. Elementary Excitations in Solids. Benjamin, New York, New York, 1963.
(Имеется перевод: Д. Пайнс. Элементарные возбуждения в твердых телах. —
М.: Мир, 1965.)
458. Pines D. Pulsars and Compact X-Ray Sources: Cosmic Laboratories for the Study
of Neutron Stars and Hadron Matter. J. Phys. Colloq., 41, p. C2/111, 1980.
640 Литература
(Имеется перевод: Д. Пайнс. Пульсары и компактные рентгеновские
источники: лаборатории для изучения нейтронных звезд и адронного вещества.
УФН, 131, 479, 1980.)
459. Pines D. Accreting Neutron Stars, Black Holes and Degenerate Dwarf Stars.
Science, 207, 597, 1980.
460. Pines D., Shaham J. Free Precession of Neutron Stars: Some Plain Truths,
Cautionary Remarks and Assorted Speculations. Comments Astrophys. Space Phys., 6,
37, 1974.
461. Pines D., Shaham J., Ruderman M. Corequakes and the Vela Pulsar. Nature Phys.
Sci., 237, 83, 1972.
462. Pines D., Shaham У., Ruderman M. A. Neutron Star Structure from Pulsar
Observations. In lAU Symposium No. 53: Physics of Dense Matter. Ed. С J. Hansen.
Reidel, Dordrecht, Holland, 1974.
463. Polidan R. 5., Pollard G. 5. G., Sanford P. W., Locke M. C. X-Ray Emission
from the Companion to V861 Sco. Nautre, 275, 296, 1978.
464. Prendergast K. H., Burbidge G. R. On the Nature of Some Galactic X-Rsiy
Sources. Astrophys. J. Lett., 151, L83, 1968.
465. Press W. H., Teukolsky 5. A. Floating Orbits, Superradiant Scattering and the
Black Hole Bomb. Nature, 238, 211, 1972.
466. Press W, H., Teukolsky 5. A. Perturbations of a Rotating Black Hole. II.
Dynamical Stability of the Kerr Metric. Astrophys. J., 185, 649, 1973.
467. Primini F. et al. Orbital Elements and Masses for the SMC X-1/Sanduleak 160
Binary System. Astrophys. J. Lett., 210, L71, 1976.
468. Pringle J. E. Thermal Instabilities in Accretion Discs. Mon. Not. Roy. Astron.
Soc, 177, 65, 1976.
469. Pringle J, E. Accretion Discs in Astrophysics. Ann. Rev. Astron. Astrophys., 19,
137, 1981.
470. Pringle J. E., Rees M. J. Accretion Disc Models for Compact X-Ray Sources.
Astron. Astrophys., 21, 1, 1972.
471. Pringle J, E., Rees M. У., Pacholczyk A. G. Accretion onto Massive Black Holes.
Astron. Astrophys., 29, 179, 1973.
472. Pye J, ? et al. An X-Ray Map of SN 1006 from the Einstein Observatory. Mon.
Not. Roy. Astron. Soc, 194, 569, 1981.
473. Rappaport 5., Joss P. С Binary X-Ray Pulsars. In X-Ray Astronomy with the
Einstein Satellite. Ed. R. Giacconi. Reidel, Dordrecht, Holland, 1981.
474. Rappaport 5., Joss P. C. X-Ray Pulsars in Massive Binary Systems. In Accretion
Driven Stellar X-Ray Sources. Eds. W. H. G. Lewin and E. P. J. Van Heuvel.
Cambridge Univ. Press, Cambridge, England, 1983.
475. Rappaport 5. et al. Discovery of a 7,68 Second X-Ray Periodicity in 3U 1626—67.
Astrophys. J. Lett., 217, L29, 1977.
476. Rees M. J. A Better Way of Searching for Black Hole Explosions? Nature, 266,
333, 1977.
477. Rees M. J. Sources of Gravitational Waves at Low Frequencies. In Proc. Internat.
Symp. Experimental Gravitation. Academia Nazionale dei Lincei, Rome, Italy,
1977, p. 423.
478. Reid R. V. Local Phenomenological Nucleon-Nucleon Potentials. Ann. of Phys.,
50, 411, 1968.
479. ReifF. Fundamentals of Statistical and Thermal Physics. McGrow-Hill, New York,
New York, 1965.
480. Rhoades С ?., Ruffini R. Maximum Mass of a Neutron Star. Phys. Rev. Lett.,
32, 324, 1974.
Литература 641
481. Richards D. W., Comella J. W. The Period of Pulsar NP 0532. Nature, 222, 551,
1969.
482. Roberts D. H., Sturrock P. A. The Structure of Pulsar Magnetospheres.
Astrophys. J. Lett., 173, L33, 1972.
483. Roberts W. J. A Slaved Disk Model for Hercules X-1. Astrophys. J., 187, 575,
1974.
484. Robertson H. P. Note on the Preceding Paper: The Two-Body Problem in General
Relativity. Ann. of Math., 39, 101, 1938.
485. Romanishin W., Angel J. R. P. Determination of the Upper Mass Limit for Stars
Producing White-Dwarf Remnants. Astrophys. J., 235, 992, 1980.
486. Rosenberg F. D., Eyles C. J., Skinner G. K., Willmore A. P. Observations of a
Transient X-Ray Source with a Period of 104 s. Nature, 256, 628, 1975.
487. Rosenfeld L. In Astrophysics and Gravitation. Proc. 16th Solvay Conference on
Physics, Editions de TUniversite de Bruxelles, Brussels, Belgium, 1974, p. 174.
488. Rothschild R. E., Boldt E. ?., Holt S. 5., Serlemitos P. J, Millisecond Temporal
Structure in Cygnus X-1. Astrophys. J. Lett., 189, L13, 1974.
489. Ruderman M. Neutron Starquakes and Pulsar Periods. Nature, 223, 597, 1969.
490. Ruderman M. Pulsars: Structure and Dynamics. Ann. Rev. Astron. Astrophys., 10,
427, 1972.
491. Ruderman M. Theories of Gamma Ray Bursts. Ann. N.Y. Acad. Sci., 262, 164,
1975 (Seventh Texas Symposium).
492. Ruderman M. Pulsar Radiation Mechanisms. Ann.N.Y. Acad. Sci., 336, 409, 1980
(Ninth Texas Symposium)
493. Rybicki G. В., Lightman A. P. Radiative Processes in Astrophysics. Wiley, New
York, New York, 1979.
494. Saenz /?. ?., Shapiro S. L. Gravitational Radiation from Stellar Core Collapse.
III. Damped Ellipsoidal Oscillations. Astrophys. J., 244, 1033, 1981.
495. Salpeter E. E. The Luminosity Function and Stellar Evolution. Astrophys. J., 121,
161, 1955.
4%. Salpeter E. E. Energy and Pressure of a Zero-Temperature Plasma. Astrophys. J.,
134, 669, 1961.
497. Salpeter E. E. Accretion on Interstellar Matter by Massive Objects. Astrophys. J.,
140, 796, 1964.
498. Salpeter E. E. Superdense Equilibrium Stars. In Quasi-Stellar Sources and
Gravitational Collapse. Eds. /. Robinson, A. Schild and E. L. Schucking. Univ. of
Chicago Press, Chicago, Illinois, 1965.
499. Salpeter E. E., Van Horn H. M. Nuclear Reaction Rates at High Densities.
Astrophys. J., 155, 183, 1969.
500. Salpeter E. E., Zapolsky H. S. Theoretical High-Pressure Equations of State
Including Correlation Energy. Phys. Rev., 158, 876, 1967.
501. Salter M. J., Lyne A. G., Anderson B. Measurements of the Trigonometric
Parallax of Pulsars. Nature, 280, 477, 1979.
502. Sandage A. et al. On the Optical Identification of Sco X-1. Astrophys. J., 146,
316, 1966.
503. Sargent W. L. et al. Dynamical Evidence for a Central Mass Concentration in the
Galaxy M87. Astrophys. J., 221, 731, 1978.
504. Sato K. Neutrino Degeneracy in Supernova Cores and Neutral Current of Weak
Interaction. Progr. Theor. Phys., 53, 595, 1975.
505. Sato K. Supernova Explosion and Neutral Current of Weak Interaction. Progr.
Theor. Phys., 54,*1325, 1975.
506. Sawyer R. F. Energy Shifts of Excited Nucleons in Neutron-Star Matter.
Astrophys. J., 176, 205, 1972. Erratum: ibid., 178, 279, 1972.
5-513
642 Литература
507. Scargle J. A, Pacini F. On the Mechanism of the Glitches in the Crab Nebula
Pulsar. Nature Phys. Sci., 232, 144, 1971.
508. Шацман Э. Влияние равновесия «электрон—ядро» на внутреннее строение
белых карликов. Астрон. ж., 33, 800, 1956.
509. Schatzman ?. White Dwarfs. Interscience, New York, New York, 1958.
510. Schatzman E. Theory of White Dwarfs. In Hdb. d. Phys., Vol. 51. Ed. S. Flugge.
Springer-Verlag, Berlin, Germany, 1958.
511. Schramm D. N., Arnett W. D. The Weak Interaction and Gravitational Collapse.
Astrophys. J., 198, 629, 1975.
512. Schreier E. et al. Evidence for the Binary Nature of Centaurus X-3 from Uhuru
X-Ray Observations. Astrophys. J. Lett., 172, L79, 1972. Errata: ibid., 173, L51,
1972.
513. Schwartz R. A. Gravitational Collapse, Neutrinos and Supernovae. Ann. Phys., 43,
42, 1967.
514. Schwarzschild K. Equilibrium of the Sun Atmosphere. Nachr. Ges. Wiss. Got-
tingen Math. Phys. Kl., 1, 41, 1906.
515. Schwarzschild K. On the Gravitational Field of a Point Mass in Einstein's Theory.
Sitzungsber. Dtsch. Akad. Wiss. Berlin, Kl. Math. Phys. Tech., 1916, p. 189.
516. Schwarzschild M. Structure and Evolution of the Stars. Princeton Univ. Press,
Princeton, New Jersey, 1958.— (Имеется перевод: ?. Шварцшильд. Строение и
эволюция звезд. — М.: ИЛ, 1961.)
517. Schwarzschild Л/., Harm R. On the Maximum Mass of Stable Stars. Astrophys. J.,
129, 637, 1959.
518. Seaton M. J. Extinction of NGC 7027. Mon. Not. Roy. Astron. Soc, 187, 785,
1979.
519. Service A. T. Concise Approximation Formulae for the Lane-Emden Functions.
Astrophys. J., 211, 908, 1977.
520. Seward F. A, Harnden F. R. A New, Fast X-Ray Pulsar in the Supernova
Remnant MSH 15—52. Astrophys. J. Lett., 256, L45, 1982.
521. Шакура ?. И. Дисковая модель газовой аккреции на релятивистскую звезду в
тесной двойной системе. Астрон. ж., 49, 921, 1972.
522. Шакура Н. Я., Сюняев Р. А. Black Holes in Binary Systems. Observational
Appearance. Astron. Astrophys., 24, 337, 1973.
523. Шакура ?. И., Сюняев P. ?. К Theory of the Instability of Disk Accretion onto
Black Holes and the Variability of Binary X-Ray Sources, Galactic Nuclei and
Quasars. Mon. Not. Roy. Astron. Soc, 175, 613, 1976.
524. Shapiro I. I. Fourth Test of General Relativity. Phys. Rev. Lett., 13, 789, 1964.
525. Shapiro S. L. Accretion onto Black Holes: The Emergent Radiation Spectrum.
Astrophys. J., 180, 531, 1973.
526. Shapiro S.L. Accretion onto Black Holes: The Emergent Radiation Spectrum. II.
Magnetic Effects. Astrophys. J., 185, 69, 1973.
527. Shapiro S. L. Accretion onto Black Holes: The Emergent Radiation Spectrum. III.
Rotating (Kerr) Black Holes. Astrophys. J., 189, 343, 1974.
528. Shapiro S. L. Gravitational Radiation from Colliding, Compact Stars:
Hydrodynamic Calculations in One Dimension. Astrophys. J., 240, 246, 1980.
529. Shapiro S. L., Lightman A. P. Black Holes in X-Ray Binaries: Marginal Existence
and Rotation Reversals of Accretion Disks. Astrophys. J., 204, 555, 1976.
530. Shapiro S. L., Lightman A. P. Rapidly Rotating, Post-Newtonian Neutron Stars.
Astrophys. J., 207, 263, 1976.
531. Shapiro S. L., Salpeter E. E. Accretion onto Neutron Stars under Adiabatic Shock
Conditions. Astrophys. J., 198, 671, 1975.
Литература 643
532. Shapiro S. L., Teukolsky S. A. On the Maximum Gravitational Redshift of White
Dwarfs. Astrophys. J., 203, 697, 1976.
533. Shapiro S. L., Teukolsky S. A. Gravitational Collapse of Supermassive Stars to
Black Holes: Numericaf Solution of the Einstein Equations. Astrophys. J. Lett.,
234, L177, 1979.
534. Shapiro S. L., Lightman A. P., Eardley D. M. A Two-Temperature Accretion Disk
Model for Cygnus X-1: Structure and Spectrum. Astrophys. J., 204, 187, 1976.
535. Shaviv G., Kovetz A. The Cooling of Carbon-Oxigen White Dwarfs. Astron.
Astrophys., 51, 383, 1976.
536. Shipman H. L. Masses and Radii of White-Dwarf Stars. III. Results for 110
Hydrogen-Rich and 28 Helium-Rich Stars. Astrophys. J., 228, 240, 1979.
537. Shipman H. L., Green R. F. Revised Stellar Birthrates and the Genesis of Pulsars.
Astrophys. J. Lett., 239, LI 11, 1980.
538. Шкловский И. С. Природа рентгеновского источника Sco Х-1. Астрон. ж., 44,
930, 1967.
539. Шварцман В. Ф. Гало вокруг черных дыр. Астрон. ж., 48, 479, 1971.
540. Sieber W., Wielebinski R. {Eds). lAU Symposium No. 95: Pulsars. Reidel,
Dordrecht, Holland, 1981.
541. Silk y., Arons J. On the Nature of the Globular Cluster X-Ray Sources. Astrophys.
J. Lett., 200, L131, 1975.
542. Sion E. M. Statistical Investigations of the Luminosity Distribution of the
Spectroscopic White Dwarf Sample. In White Dwarfs and Variable Degenerate Stars,
lAU Colloq. No. 53. Eds. H. M. Van Horn and V. Weidemann, Univ. of
Rochester Press, Rochester, New York, 1979.
543. Slattery W. L., Doolen G. D., DeWitt H. E. Improved Equation of State for the
Classical One-Component Plasma. Phys. Rev. A, 21, 2087, 1980.
544. Smarr L. L. Gauge Conditions, Radiation Formulae and the Two Black Hole Colli
sion. In [545], 1979.
545. Smarr L. L. {Ed.) Sources of Gravitational Radiation. Cambridge Univ. Press,
Cambridge, England, 1979.
546. Smarr L. L., Wilson J. /?., Barton R. Г., Bowers R. L. Rayleigh-Taylor Overturn
in Supernova Core Collapse. Astrophys. J., 246, 515, 1981.
547. Spitzer L. Physics of Fully Ionized Gases. 2nd ed. Interscience, New York, New
York, 1962. (Имеется перевод: Л. Спитцер. Физика полностью ионизованного
газа. — М.: ИЛ, 1957.)
548. Spitzer L. Dynamical Theory of Spherical Stellar Systems with Large N. In lAU
Symposium No. 69: Dynamics of Stellar Systems. Ed. A. Hayli. Reidel, Dordrecht,
Holland, 1975.
549. Spitzer L. Physical Processes in the Interstellar Medium. Wiley, New York, New
York. 1978. (Имеется перевод: Л. Спитцер. Физические процессы в
межзвездной среде. — М.: Мир, 1981.)
550. Staelin D. Я., Reifenstein ?. С. Pulsating Radio Sources near the Crab Nebula.
Science, 162, 1481, 1968.
551. Stoeger W. R. Boundary-Layer Behavior of the Flow at the Inner Edge of Black
Hole Accretion Disks. Astrophys. J., 235, 216, 1980.
552. Strand K. A. Triple System Stein 2051 (G175—34). Astron. J. 82, 745, 1977.
553. Swank J. H. et al. Spectral Evolution of a Long X-Ray Burst. Astrophys. .1. Lett.,
212, L73, 1977.
554. Sweeney M. A. Cooling Times, Luminosity Functions and Progenitor Masses of
Degenerate Dwarfs. Astron. Astrophys., 49, 375, 1976.
555. Szekeres G. On the Singularities of a Riemannian Manifold. Publ. Mat. Debrecen,
7, 285, 1960.
644 Литература
556. Таттапп G. Supernova Rates. In Supernovae and Supernova Remnants. Eds. J.
Danziger and A. Renzini. Mem. Soc. Astron. Italiana, 49, 299, 1978.
557. Tananbaum H. et al. Discovery of a Periodic Pulsating Binary X-Ray Source in
Hercules from Uhuru. Astrophys. J. Lett., 174, L143, 1972.
558. Tananbaum H., Gursky H., Kellogg E., Giacconi R., Jones C. Observation of a
Correlated X-Ray — Radio Transition in Cygnus X-1. Astrophys. J. Lett., 177,
L5, 1972.
559. Tassoul J. L. Theory of Rotating Stars. Princeton Univ. Press, Princeton, New
Jersey, 1978. (Имеется перевод: Ж-Л. Тассуль. Теория вращающихся звезд. —
М.: Мир, 1982.
560. Tassoul J. L., Ostriker J. P. On the Oscillations and Stability of a Rotating Stellar
Models. L Mathematical Techniques. Astrophys. J., 154, 613, 1968.
561. Taylor J. H., Manchester R. N. Galactic Distribution and Evolution of Pulsars.
Astrophys. J., 215, 885, 1977.
562. Taylor J. H., Weisberg J. M. A New Test of General Relativity: Gravitational
Radiation and the Binary Pulsar PSR 1913 + 16. Astrophys. J., 253, 908, 1982.
563. Teukolsky S. ?., Press W. H. Perturbations of a Rotating Black Hole. ??.
Interaction of the Hole with Electromagnetic and Gravitational Radiation. Astrophys. J.,
193, 443, 1974.
564. 7 Hooft G. Renormalizable Lagrangians for Massive Yang—Mills Fields. Nucl.
Phys. B, 35, 167, 1971.
565. 7 Hooft G., Veltman M. Regularization and Renormalization of Gauge Fields.
Nucl. Phys. В., 44, 189, 1972.
566. 7 Hooft G., Veltman M. Combinatorics of Gauge Fields. Nucl. Phys. B, 50, 318,
1972.
567'. Thorne K. S. The General Relativistic Theory of Stellar Structure and Dynamics.
In High-Energy Astrophysics, vol. 3. Eds. С DelVitt, E. Schatzman and P. Veron.
Gordon and Breach, New York, New York, 1967.
568. Thorne K. S. Gravitational-Wave Research: Current Status and Future Prospects.
Rev. Mod. Phys., 52, 285, 1980.
569. Thorne K. S., Braginsky V. B. Gravitational-Wave Bursts from the Nuclei of
Distant Galaxies and Quasars: Proposal for Detection Using Doppler Tracking of
Interplanetary Spacecraft. Astrophys. J. Lett., 204, LI, 1976.
570. Thorne K. 5., Price R. H. Cygnus X-1: An Interpretation of the Spectrum and Its
Variability. Astrophys. J. Lett., 195, LlOl, 1975.
571. Toor ?., Seward F. D. Observation of X-Ray from the Crab Pulsar. Astrophys.
J., 216, 560, 1977.
572. Trimble V. L., Thorne K. S. Spectroscopic Binaries and Collapsed Stars.
Astrophys. J., 156, 1013, 1969.
573. Trimble V., Rose W. K., Weber J. A Low-Mass Primary for Cygnus X-1? Mon.
Not. Roy. Astron. Soc, 162, IP, 1973.
574. Trumper J. et al. Evidence for Strong Cyclotron Line Emission in the Hard X-Ray
Spectrum of Hercules X-1. Astrophys. J. Lett., 219, L105, 1978.
575. Tsuruta S. Cooling of Dense Stars. In lAU Symposium No. 53: Physics of Dense
Matter. Ed. C. J. Hansen. Reidel, Dordrecht, Holland, 1974, p. 456.
576. Tsuruta S. Thermal Properties and Detectability of Neutron Stars — I. Cooling
and Heating of Neutron Stars. Phys. Rept., 56, 237, 1979.
577. Tsuruta S., Cameron A. G. W. Cooling of Neutron Stars. Nature, 207, 364, 1965.
578. Tsuruta S., Cameron A. G. W. Rotation of Neutron Stars. Nature, 211, 356, 1966.
579. Tubbs D. L., Schramm D. N. Neutrino Opacities at High Temperatures and
Densities. Astrophys. J., 201, 467, 1975.
Литература 645
580. Tuchman ?., Yahel R. ?. Accretion onto Neutron Star: The X-Ray Spectra and
Luminosity. Astrophys. Space Sci., 50, 473, 1977.·
581. Tuohy /., Garmire G. Discovery of a Compact X-Ray Source at the Center of the
Supernova Remnant RCW 103. Astrophys. J. Lett., 239, L107, 1980.
582. Van den Bergh S. Comment on Supernova Rates. In Supernovae and Supernova
Remnants. Eds. J. Danziger and A. Renzini. Mem. Soc. Astron. Italiana, 49, 299,
1978.
583. Van den Heuvel E. P. J. Modes of Mass Transfer and Classes of Binary X-Ray
Sources. Astrophys. J. Lett., 198, L109, 1974.
584. Van den Heuvel E. P. J., Heise J. Centraurus X-3, Possible Reactivation of an Old
Neutron Star by Mass Exchange in a Close Binary. Nature Phys. Sci., 239, 67,
1972.
585. Van Horn ? ?/. Crystallization of White Dwarfs. Astrophys. J., 151, 277, 1968.
586. Van Paradijs J. Average Properties of X-Ray Burst Sources. Nature, 274, 650,
1978.
587. Van Paradijs J. Possible Observational Constraints on the Mass-Radius Relation of
Neutron Stars. Astrophys. J., 234, 609, 1979.
588. Van Paradijs J. On the Maximum Luminosity in X-Ray Bursts. Astron.
Astrophys., 101, 174, 1980.
589. Van Riper K. A. Stellar Core Collapse. IL Inner Core Bounce and Shock
Propagation. Astrophys. J., 257, 793, 1982.
590. Van Riper K. ?., Lamb D. Q. Neutron Star Evolution and Results from the
Einstein X-Ray Observatory. Astrophys. J. Lett., 244, L13, 1981.
591. Van Riper K. ?., Lattimer J. M. Stellar Core Collapse. L Infall Epoch. Astrophys.
J., 249, 270, 1981.
592. Wagoner R. V. Physics of Massive Objects. Ann. Rev. Astron. Astrophys., 7, 553,
1969.
593. Wagoner R. V. Low-Frequency Gravitational Radiation from Collapsing Systems.
Phys. Rev. D, 19, 2897, 1979.
594. Walborn N. R. The Spectrum of HDE 226868 (Cygnus X-1). Astrophys. J. Lett.,
179, L123, 1973.
595. Walecka J. D. A Theory of Highly Condensed Matter. Ann. Phys. 83, 491, 1974.
5%. Walter F. M., White N. E., Swank J. H. lAU Circular No. 3611, 1981.
597. Walter F. M. et al. Discovery of 50 Minute Binary Period and a Likely 22
Magnitude Optical Counterpart for the X-Ray Burster 4U 1915—05. Astrophys. J.
Lett., 253, L67, 1982.
598. Wapstra A. H., Bos K. A 1975 Midstream Atomic Mass Evaluation. Atomic Data
and Nuclear Data Tables, 17, 474, 1976.
599. Wapstra A. H', Bos K. The 1977 Atomic Mass Evaluation. Atomic Data and
Nuclear Data Tables, 19, 175, 1977.
600. Weaver T. ?., Woosley S. E. Evolution and Explosion of Massive Stars. Ann.
N.Y. Acad. Sci., 336, 335, 1980 (Ninth Texas Symposium).
601. Weaver T. ?., Zimmerman G. В., Woosley S. E. Presupernova Evolution of
Massive Stars. Astrophys. J., 225, 1021, 1978.
602. Weber J. Detection and Generation of Gravitational Waves. Phys. Rev., 117, 306,
1960.
603. Wegner G. A New Gravitational Redshift for the White Dwarf ?^ Eri B. Astron.
J., 85, 1255, 1980.
604. Weidemann V. Luminosity Function and Space Density of White Dwarfs. Z.
Astrophys.» 67, 286, 1967.
605. Weidemann V. Mass Loss towards the White Dwarf Stage. Astron. Astrophys., 59,
411, 1977.
546 Литература
606. Weinberg S. Gravitation and Cosmology. Wiley, New York, New York, 1972.
(Имеется перевод: С. Вейнберг. Гравитация и космология. — М.: Мир, 1975.)
607. Weinberg S. Cosmological Production of Barions. Phys. Rev. Lett., 42, 850, 1979.
608. Weisskopf V. F. The Formation of Cooper Pairs and the Nature of
Superconducting Currents. Contemp. Phys., 22, 375, 1981.
609. Wheaton W. A. et al. An Absorption Feature in the Spectrum of the Pulsed Hard
X-Ray Flux from 4U 0115 + 63. Nature, 282, 240, 1979.
610. Wheeler J. A. Superdense Stais. Ann. Rev. Astron. Astrophys., 4, 393, 1966.
611. Wheeler J. A. Our Universe: The Known and the Unknown. American Scientist,
56, 1, 1968.
612. White N. E., Pravdo S. H. The Discovery of 38,22 Second X-Ray Pulsations from
the Vicinity of ОАО 1653—40. Astrophys. J. Lett., 233, L121, 1979.
613. White N. E., Swank J. H. The Discovery of 50 Minute Periodic Absorption
Events from 4U 1915—05. Astrophys. J. Lett., 253, L61, 1982.
614. White N. E., Mason K. O., Huckle H. E., Charles P. ?., Sanford P. W. Periodic
Modulation of Three Galactic X-Ray Sources. Astrophys. J. Lett., 209, LI 19,
1976.
615. White N. E., Mason K. O., Sanford P. W. The X-Ray Behaviour of 3U 0352 + 30
(X Per). Mon. Not. Roy. Astron. Soc, 176, 201, 1976.
616. White N. E., Parkes G. E., Sanford P. W., Mason K. O., Murdin P. G. Two
X-Ray Periodicities from the Vicinity of 4U 1145—61. Nature, 274, 665, 1978.
617. Wilson J. R. A Numerical Study of Gravitational Stellar Collapse. Astrophys. J.,
163, 209, 1971.
618. Wilson J. R. A Numerical Method for Relativistic Hydrodynamics. In [545], 1979,
p. 423.
619. Wilson J. R. Neutrino Flow and Stellar Core Collapse. Ann. N.Y. Acad. Sci., 336,
358, 1980 (Ninth Texas Symposium).
620. Wilson J. R., Couch R., Cochran S., LeBlanc J., Barkat Z. Neutrino Flow and the
Collapse of Stellar Cores. Ann. N.Y. Acad. Sci., 262, 54, 1975 (Seventh Texas
Symposium).
621. Withbroe G. L. The Chemical Composition of the Photosphere and the Corona. In
The Menzel Symposium (NBS Special Pub. 353). Ed. K. B. Gebbie. Government
Printing Office, Washington, D.C., 1971.
622. Wolff R. S., Kestenbaum H. L., Ku W., Novick R. Search for Continuous X-Ray
Emission from NP 0532. Astrophys. J. Lett., 202, L77, 1975.
623. Woltjer L. X-Rays from Type I Supernova Remnants. Astrophys. J., 140, 1309,
1964.
624. Woltjer L. Supernova Remnants. Ann. Rev. Astron. Astrophys., 10, 129, 1972.
625. Yahil ?., Lattimer J. M. Supernovae for Pedestrians. In Supernovae: A Survey of
Current Research. Eds. M. J. Rees and R. J. Stoneham. Reidel, Dordrecht,
Holland, 1982.
626. Young P. J., Westphal J. ?., Kristian J., Wilson С P., Landauer F. P. Evidence
for a Supermassive Object in the Nucleus of the Galaxy M87 from SIT and CCD
Area Photometry. Astrophys. J., 221, 721, 1978.
627. Youngblood D. H., Rosza С ?., Moss J. M., Brown D. R., Bronson J. D.
Isoscalar Breathing-Mode State in ^^Sm and 208рь. phys. Rev. Lett., 39, 1188,
1977.
628. Youngblood D. H., Rosza C. M., Moss J. M., Brown D. R., Bronson J. D. The
Breathing Mode State in •'WSm and ^ospb. /^ Proceedings of the International
Conference on Nuclear Structure. J. Phys. Soc. Japan (Suppl), 44, 197, 1978.
629. Zapolsky H. 5., Salpeter E. E. Mass-Radius Relation for Cold Spheres of Low
Mass. Astrophys. J., 158, 809, 1969.
Литература 647
630. Zaringhalam ?. Работа 1982 г., цитированная в [88].
631. Зельдович Я. Б. О ядерных реакциях в сверхплотном холодном водороде.
ЖЭТФ, 33, 991, 1957.
632. Зельдович Я. Б. Уравнение состояния при сверхвысокой плотности и
релятивистские ограничения. ЖЭТФ, 41, 1609, 1962.
633. Зельдович Я. Б. Судьба звезды и выделение энергии при аккреции. ДАН, 155,
67, 1964.
634. Зельдович Я. Б., Гусейнов О. X. Collapsed Stars in Binaries. Astrophys. J., 144,
840, 1965.
635. Зельдович Я. Б., Новиков И. Д. Гипотеза задержавшихся в расширении ядер
и горячая космологическая модель. Астрон., ж., 43, 758, 1966.
636. Зельдович Я. Б., Новиков И. Д. Релятивистская астрофизика. М.: Наука,
1%7.
637. Зельдович Я. Б., Райзер Ю. П. Физика ударных волн и высокотемпературных
гидродинамических явлений.—М.: Наука, 1966.
638. Зельдович Я. Б., Шакура ? И. Рентгеновское излучение при аккреции газа на
нейтронную звезду. Астрон. ж., 46, 225, 1969.
639. Zimmerman ?. Gravitational Waves from Rotating and Precessing Rigid Bodies.
II. General Solutions and Computationally Useful Formulas. Phys. Rev. D, 21,
891, 1980.
Предметный указатель
Адроны 588
Аккреционная воронка 401
Аккреционный диск 412, 484, 486
кеплеровский 456, 459, 480, 606
, прецессия 403
Аккреционный столб 479
Аккреция дисковая 370, 454, 480
— на белые карлики 392, 455, 477, 491
— на нейтронные звезды 392, 415, 418,
455, 477
— на черные дыры 370, 384, 393, 428,
437, 448, 455, 599
— околозвуковая 441, 443, 444
— , радиус 434
— сферически симметричная 370, 418,
430, 437, 448, 488, 599. См. такэюе
Течение аккреционное
Активные галактики 526, 527
Альвеновские волны 316, 454
Альвеновский радиус 478, 480, 483
Аромат кварков 249, 588
Аффинный параметр 129
Барионы 588
Барстеры 278, 395, 414, 420
— , рентгеновские всплески 414, 416,
420, 422
Бартлетта оператор 210
Белые дыры 377
Бернулли уравнение 438, 441
релятивистское 600
Бета-распад 53, 334, 341
— кварков 344
— обратный 43, 53, 71, 80, 171, 191
Биркгофа теорема 136, 377, 381, 500
Бифуркации точка 187
Бозе-эйнштейновский конденсат 241
Бойера — Линдквиста система
координат 379, 384
Болометрическая поправка 573
Больцмана уравнение 430, 436
с учетом столкновений 435
Большой Взрыв 391
Бонды решение для сферически
симметричной аккреции 432, 444, 448, 587
«Быстрый ротатор» 485
Вебера детектор 503
Вейнберга — Салама — Глэшоу теория
332, 553
Вейнберга угол 333, 553
«Великого объединения» теории 33, 334
Вигнера — Зейтца приближение 44,
101, 204
Вириала теорема 72, 174, 176, 182, 186,
195, 501, 510
Власова уравнение 430, 436
Возраст пульсара 294, 2%, 300
Вращение белых карликов 186, 289,
290, 394
— нейтронных звезд 284, 289
— черных дыр 379, 394
Вязкость 458, 462, 605
— , параметр 463
— , влияние на устойчивость 184, 190,
196
Гамовский фактор 87
Гаунта множитель 470, 615
Гейзенберга оператор 209
Гелиевая вспышка 577
Геодезическая 127, 128, 362, 381
Геометрическа#х:истема единиц 135
Геркулес (Her) Х-1 244, 263, 394, 395,
396, 399, 401, 403, 425
Герцшпрунга — Рессела диаграмма 84,
85» 574
, горизонтальная ветвь 576, 577
Гиббса термодинамический потенциал
35, 65
Гидростатическое равновесие 71, 75, 96,
140, 163, 444, 541
в общей теории относительности
137
Гипероны 232, 233, 234, 236, 238
Главная последовательность 575
Глюоны 250
Голдрайха — Джулиана модель 306
Горизонт событий 357, 361, 380, 436,
443, 451
Гравитационное излучение 185, 194,
244, 289, 302, 494
вращающихся масс 514
двойной системы 504
при коллапсе 522, 538, 540
при столкновениях 518
Гравитационное красное смещение 85,
132, 350, 353, 363, 452
в двойной системе 507
Предметный указатель
649
максимальное 172, 262, 281,535
Гравитационные волны 494
, детекторы 503, 517
Двойная система 274, 284, 392, 394,
406, 422, 491, 506. См. также
Спектрально-двойные звезды
Дебаевская температура 104
Дедекинда эллипсоид 184
Джаспц)оу пробная функция 228
Джинса теорема 431
Дисперсионное соотношение 109, 298
Дисперсия 291, 294. См. такэюе Мера
дисперсии
Диссоциация ядер 543, 560
Доплера эффект 506, 509
Дэвиса эксперимент 30, 31
«Железный максимум» 539
Жесткость уравнения состояния 50, 232
Заряженные токи 333, 334, 347, 348,
548
Звездная величина 408, 572
абсолютная 20, 407, 572
болометрическая 573
видимая 572
Звездный ветер 424, 437, 446, 456, 486,
528
«Звездотрясение» 244, 315, 319, 322, 5\%
Звука скорость в ядерной материи 221,
231, 247, 279
при аккреции на черную дыру
438, 440, 441, 598
«Золотое правило» теории возмущений
334, 338, 339, 550
Излучательная способность 609
Изотопическая инвариантность 208
Изоспин 209, 240, 336, 590
Интенсивные величины 36
Интервал пространственновременной
120
«Испарение» черной дыры 19, 389, 390
Истинная аномалия 507
Карликовые новые 464
«Катаклизматическая» переменная 463,
492
Квазары 19, 262, 360, 370, 475, 526
Квантовая хромо динамика 248, 346, 588
Кварки 248, 344, 588
Кварковое вещество 248, 347, 349, 354
Кварковые звезды 250, 276
Кеплера закон второй 509
третий 383, 505, 510
Кирхгофа закон 466, 468, 609
Кластеры 229
Классификация звезд спектральная 574
Коллапс сверхмассивной звезды 18,
535, 541
гомологичный 537, 568
Компанейца уравнение 618, 619
Комптонизация 472, 474, 617
Конвекция 115, 529, 543
Конус потерь 432
«Коротрясение» 322, 325, 326
«Космическая цензура» 380
Крабовидная туманность 263, 288, 294,
322, 354. См. также Пульсар в
Крабовидной туманности
Кривая блеска 403, 411, 539
Кристоффеля символ 129
Крускала диаграмма 375, 376, 378
Лагранжа точка 424, 426, 457
Лагранжева производная 140
Лазерный интерферометр 503
Лармора формула 498
Лебедь (Cyg) Х-1 20, 27, 357, 392, 395,
396, 398, 405, 425
— отождествление с черной дырой 411,
473
— , переменность 405
— , рентгеновский спектр 405, 473
Лейна — Эмдена уравнение 76, 153, 168
Лензе — Тирринга эффект 358
Лептоны 588
Лиувилля теорема 430, 433, 436
Локальное термодинамическое
равновесие 608
Магнитный диполь 288, 299
Магнитосфера 305, 401, 479
Магнитопауза 479
Маклорена сфероид 179, 182, 523
Максвелла — Больцмана идеальный газ
73, 105, 113, 441, 546
Максвелла уравнения 173, 481, 582
Масс функция для двойной системы
275, 407, 509, 514
для звездообразования 20, 21, 22
Масса недостающая 24
«Масса — светимость» соотношение 23
Массовая формула полуэмпирическая
58, 63, 199, 204
Маха число 444
Межзвездное поглощение 407, 409
Мезоны 588
Мейснера эффект 313
Мера дисперсии 27, 297
Метрика 121, 135
— Керра 359, 379
— Керра — Ньюмена 359, 379
— Рейснера — Нордстрема 379
— Шварцшильда 136, 139, 359, 375,
376, 379
650
Предметный указатель
«Мешка» модель 250
Микротрясение 518
Минковского пространство 121, 137
Наблюдатель инерциальный 120
— статический 361, 363, 380
— стационарный 380
Навье — Стокса уравнение 141
Население звездное I типа 396
II типа 396, 397, 414
Насыщение ядерных сил 212, 216
Нейтральные токи 330, 342, 347, 348,
553, 570
Нейтронизация 80, 82, 236, 543, 548,
549
Нейтронные капли 32, 198, 206, 237,
273, 559, 566
Непрозрачность 95, 464, 609
— , источники 615
— Крамерса 95, 616, 617
— нейтринная 553, 571
— средняя по Росселанду см. Росселан-
дово среднее
Неразрывности уравнение 140, 145, 438,
460, 482
Неустойчивость аккреционного потока
415, 422
— вековая 183, 196, 472, 502
— двухпотоковая 489
— динамическая 183, 185, 528
— Кельвина — Гельмгольца 481
— магнитосферная 322
— пульсационная 526, 528
— Рэлея — Тейлора 480, 488
Область НП 448
Обсерватория «Эйнштейн» 329, 353,
356, 395, 414, 417
Ома закон 173
Оорта предел 24, 26
Оппенгеймера — Волкова уравнение
138, 236, 261, 275
Оптическая толщина 610
Ортонормальная система координат
123, 361
Остаток сверхновой 294, 296, 353. См.
также Крабовидная туманность
«Отскок» ядра 524, 558, 568, 569
Отталкивательный кор 213, 215, 217,
229, 244
Параметр быстроты 485
— восстановления 317, 325
Парсеваля теорема 520
Паули принцип 78, 199, 277, 240
Пикноядерные реакции 83, 86
Пионный конденсат 240, 245, 271, 272,
343, 356
Плазмоны 548
Планетарная туманность 27
Планка функция 608
Планковская масса 388
— плотность 358
Показатель торможения пульсара 304,
307
Покрытие пульсара Луной 329, 350
Полярная шапка 306, 311
Потенциал Бете — Джонсона 230
— Рейда 218, 231
— Юкавы 207, 219, 220, 227, 596
Правило отбора Гамова — Теллера 355
Ферми 335
Прицельный параметр 371, 372, 373
«Пропеллера» эффект 486
Пространство — время 120
Процион В 85
Пуассона уравнение 47, 119, 141
Пульсар в Крабовидной туманности
263, 292, 294, 298, 303, 315, 318, 321,
326, 353, 355, 539
— в Парусах 263, 291, 294, 315, 321,
326, 355, 532
— Халса — Тейлора 260, 273, 292, 293,
506
Резонансы 588
Рентгеновские барстеры см. Барстеры
Рентгеновские источники 274, 277, 297,
392, 396
«Рентгеновский призрак» 417
Росселандово среднее 464, 612
Ротатор быстрый 485, 486
— медленный 486
— наклонный 299, 480
— соосный 299
Саха уравнение 547
«Сбой» пульсара 289, 293, 314, 315, 317
«гигантский» 294, 327
«Сверхизлучение» 387
Сверхмассивные звезды 19, 138, 526
Сверхновые 28, 30, 261, 288, 354, 355,
539
— в двойных системах 425. См. также
Остаток сверхновой
Сверхпроводимость 312
Сверхтекучесть 312, 340, 343, 349
Светимости функция 20, 116, 117
Световой цилиндр 305, 306, 311
Свободная энергия 35
Сингулярность 357, 375, 380
— «голая» 380, 387
Синхротронное излучение 453
Крабовидной туманности 307
Сириус В 27, 69, 81, 85, 86, 178, 179
Скважность импульса 291, 398
Предметный указатель
651
Скорпион (SCO) Х-1 392, 396, 425
Случайное блуждание 349, 469, 519
Слэтера детерминант 227, 228
Смещение периастра 510, 514
Спектральная классификация звезд 574
белых карликов 575
Спектрально-двойные звезды 393, 406
Солпитера функция 23
Статический предел 361, 381, 385
Субгиганты 576, 577
Субимпульс пульсара 294
Тензор поляризации 495
Теорема о площадях черных дыр 386,
389
Термодинамика черной дыры 365
— , I закон 33, 72, 141, 279
— , II закон, 35, 387, 389
Течение аккреционное дозвуковое 444,
445, 599
околозвуковое 439, 444, 450
сверхзвуковое 446, 450
Томаса — Ферми метод 46
Тормозное излучение 342, 343, 451, 453,
464, 475, 492, 548, 615
обратное 615
ТТ-калибровка 495
Ударная волна 422, 446, 479, 489
в сверхновой 569
Удельная интенсивность 607
Урка-реакции 330
модифицированные 331, 342, 350
Устойчивость вековая 183, 289
— , критерии 155, 195, 289
— нейтронной звезды 281
— орбиты 384
— с учетом эффектов ОТО 163
— сверхмассивных звезд 533
«Ухуру» 253, 393, 395, 396, 401, 403,
405, 414
Фарадея закон 174
Фейнмана диаграмма 334
Ферми импульс 39
— энергия 38, 78, 560, 565
Фоккера — Планка уравнение 436
Фотодиссоциация 544
Фотоионизация 616
Фотонная орбита 373, 383
Хартри приближение 221, 222
Хартри — Фока метод 222, 224
Химический потенциал 34, 36, 53, 201,
241
Хокинга процесс 19, 389
Цвет кварка 249, 588
Цвета показатель 573, 574
Цветовая температура 573
Центавр (Сеп) Х-3 263, 396, 399, 400,
401, 402, 403, 425
Циклотронная линия 301, 395, 404
Чандрасекара формула 171
Чандрасекаровский предел массы 70,
77, 78, 172, 177, 187, 273, 359, 542
Чармоний 346
Черная дыра Керра 360, 381, 387
первичная 19, 391
сверхмассивная 19, 393, 417, 428,
456, 526
шварцшильдовская 359, 360, 388,
430
Черные «мини-дыры» 15, 19, 390, 391
Черные карлики 24
Четырехвектор 122
Шаровые скопления 395, 398, 414, 417,
436
Шварцшильдовский радиус 361, 375,
388, 420, 536
Штурма — Лиувилля задача 150, 164
Эддингтоновский предел светимости
278, 419, 421
для нейтринного излучения 571
для сверхмассивных звезд 527
Эддингтоновское приближение для
атмосферы 614
Эйлера уравнение 174, 438, 451, 481
релятивистское 587
Эйлерова производная 141
«Эйнштейн» см. Обсерватория
«Эйнштейн»
Эйнштейна уравнение 126, 138
Эквивалентности принцип 124, 372. 495
Экстенсивные величины 36
Эксцентриситет орбиты 425, 506
Энтропия 34, 138
— при гравитационном коллапсе 559,
561
— сверхмассивной звезды 530
— черной дыры 388, 391
Эргосфера 381, 385
Эффективная температура 614
Эффективный потенциал 367, 369, 373,
382
Юкавы потенциал 207, 219, 220, 227,
586
Ядерное статистическое равновесие (ЯСР)
546, 562
«Ядротрясение» 527
Якоби эллипсоид 183
Янский 291
Яркостная температура 311
Содержание
ЧАСТЬ 1
От редактора перевода 5
Предисловие 9
Рекомендации по использованию книги 13
Главах. ГИБЕЛЬ ЗВЕЗД И ОБРАЗОВАНИЕ КОМПАКТНЫХ
ОБЪЕКТОВ 15
1.1. Что такое компактные объекты? 15
1.2. Образование компактных объектов 17
1.3. Статистика рождения и гибели звезд 20
Глава!. УРАВНЕНИЕ СОСТОЯНИЯ ХОЛОДНОГО ВЕЩЕСТВА
НИЖЕ ТОЧКИ ОБРАЗОВАНИЯ НЕЙТРОННЫХ КАПЕЛЬ .... 32
2.1. Предварительные сведения из термодинамики 32
2.2. Сведения из кинетической теории 37
2.3. Уравнение состояния полностью вырожденного идеального
ферми-газа 38
2.4. Электростатические поправки к уравнению состояния 43
2.5. Обратный )8-распад: холодный идеальный л-/?-е-газ 53
2.6. Бета-равновесие между релятивистскими электронами и ядрами.
Уравнение состояния Гаррисона—Уилера 56
2.7. Уравнение состояния Бейма—Петика—Сазерленда 63
Глава 3. БЕЛЫЕ КАРЛИКИ 69
3.1. Развитие теории белых карликов 69
3.2. Начальная стадия вырождения 71
3.3. Политропы 75
3.4. Предел Чандрасекара 78
3.5. Усовершенствование чандрасекаровской модели белых карликов . 80
3.6. Сравнение с наблюдениями: массы и радиусы 84
3.7. Пикноядерные реакции 86
Глава 4. ОСТЫВАНИЕ БЕЛЫХ КАРЛИКОВ 95
4.1. Структура поверхностных слоев 95
4.2. Элементарный анализ остывания белых карликов 98
4.3. Кристаллизация и температура плавления 101
4.4. Теплоемкость кулоновской решетки 105
4.5. Уточненный анализ остывания белых карликов ИЗ
4.6. Сравнение с наблюдениями 115
Глава 5. ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ 119
5.1. Что такое общая теория относительности? 119
5.2. Движение пробных частиц 126
5.3. Гравитационное красное смещение 132
5.4. Предел слабого поля 134
5.5. Геометрическая система единиц 135
5.6. Сферически-симметричные гравитационные поля 135
5.7. Сферические звезды 137
Содерокание
653
Глава 6. РАВНОВЕСИЕ И УСТОЙЧИВОСТЬ ЖИДКИХ ТЕЛ 140
6.1. Основные уравнения движения сплошной среды 141
6.2. Лагранжевы и эйлеровы возмущения 143
6.3. Возмущения интегральных величин 144
6.4. Рарновесие как условие экстремума энергии 147
6.5. Возмущения вблизи состояния равновесия 149
6.6. Функция Лагранжа для возмущений 153
6.7. Критерии устойчивости 155
6.8. Точки поворота и возникновение неустойчивости 159
6.9. Анализ устойчивости с учетом эффектов общей теории
относительности ^ 163
6.10. Устойчивость белых карликов в общей теории относительности . 168
Глава 7. ВРАЩЕНИЕ И МАГНИТНЫЕ ПОЛЯ 173
7.1. Уравнения магнитной гидродинамики 173
7.2. Магнитные белые карлики 176
7.3. Вращающиеся системы: сфероиды Маклорена 179
7.4. Вращающиеся белые карлики 186
7.5. Критерии устойчивости для вращающихся звезд 195
Глава 8. УРАВНЕНИЕ СОСТОЯНИЯ ХОЛОДНОГО ВЕЩЕСТВА
ВЫШЕ ТОЧКИ ОБРАЗОВАНИЯ НЕЙТРОННЫХ КАПЕЛЬ 198
8.1. Введение 198
8.2. Уравнение состояния Бейма—Бете—Петика 199
8.3. Нуклон-нуклонное взаимодействие 207
8.4. Насыщение ядерных сил 212
8.5. Зависимость нуклон-нуклонного потенциала от расстояния 218
8.6. Потенщ1ал Юкавы 219
8.7. МетодХартри 221
8.8. Метод Хартри—Фока 224
8.9. Корреляционные эффекты 228
8.10. Уравнение состояния Бете—Джонсона 230
8.11. Нерешенные вопросы. ?-резонанс 239
8.12. Нерешенные вопросы. Пионная конденсация 240
8.13. Нерешенные вопросы. Сверхвысокие плотности 245
8.14. Нерешенные вопросы. Кварковая материя 248
ЧАСТЬ 2
Глава 9.
9.1.
9.2.
9.3.
9.4.
9.5.
9.6.
Глава 10.
10.1.
10.2.
10.3.
10.4.
МОДЕЛИ НЕЙТРОННЫХ ЗВЕЗД: МАССЫ И РАДИУСЫ 261
Нейтронные звезды: история идеи и открытия 261
Уравнение состояния идеального газа в ядерной области 263
Реалистические теоретические модели 269
Измерения масс нейтронных звезд 273
Максимальная масса 278
Влияние вращения 284
ПУЛЬСАРЫ 288
История и открытие 288
Действительно ли пульсары являются вращающимися
нейтронными звездами? 289
Наблюдаемые свойства пульсаров 290
Мера дисперсии 297
654
Содержание
10.5. Модель магнитного диполя для пульсаров 299
10.6. Показатель торможения 304
10.7. Невакуумные модели пульсаров. Соосный ротатор 309
10.8. Механизмы излучения пульсаров 310
10.9. Сверхтекучесть в нейтронных звездах 312
10.10. Сбои пульсаров и адронная сверхтекучесть 315
10.11. Происхождение сбоев пульсаров: звездотрясения 322
Глава 11. ОСТЫВАНИЕ НЕЙТРОННЫХ ЗВЕЗД 328
11.1. Введение 328
11.2. Реакции с излучением нейтрино в нейтронных звездах {Т is> 10^ К) 329
11.3. Теория слабого взаимодействия 332
11.4. Распад свободного нейтрона 334
11.5. Скорость модифицированных урка-процессов 337
11.6. Скорости других реакций 342
11.7. Проникающая способность нейтрино 347
11.8. Кривые остывания 349
11.9. Сравнение с наблюдениями 353
Глава 12. ЧЕРНЫЕ ДЫРЫ 357
12.1. Введение 357
12.2. История идеи черной дыры 358
12.3. Шварцшильдовские черные дыры 360
12.4. Движение пробной частицы 362
12.5. Орбиты безмассовых частиц в геометрии Шварцшильда 372
12.6. «Несингулярность» радиуса Шварцшильда 375
12.7. Черные дыры Керра 379
12.8. Теорема о площадях и испарение черной дыры 386
Глава 13. КОМПАКТНЫЕ РЕНТГЕНОВСКИЕ ИСТОЧНИКИ 392
13.1. Открытие и отождествление 392
13.2. Общие характеристики галактических источников 396
13.3. Рентгеновские пульсары в двойных системах 398
13.4. Геркулес Х-1: образец рентгеновского пульсара в составе двойной
системы 403
13.5. Лебедь Х-1: кандидат в черные дыры 405
13.6. Источники центральной галактической подсистемы: барстеры .... 414
13.7. Стандартная модель: аккреция в тесной двойной системе 418
Глава 14. АККРЕЦИЯ НА ЧЕРНЫЕ ДЫРЫ 428
14.1. Введение 428
14.2. Бесстолкновительная сферически симметричная аккреция 430
14.3. Гидродинамическая сферически симметричная аккреция 437
14.4. Излучение при сферически симметричной аккреции на черные
дыры 448
14.5. Дисковая модель аккреции на компактную звезду ,.... 454
14.6. Другие модели 472
Глава 15. АККРЕЦИЯ НА НЕЙТРОННЫЕ ЗВЕЗДЫ И БЕЛЫЕ
КАРЛИКИ 477
15.1. Аккреция на нейтронные звезды: магнитосфера 477
15.2. Дисковая аккреция и изменения периода импульсных
рентгеновских источников 480
Содержание
655
15.3. Излучение от аккрецирующих нейтронных звезд 488
15.4. Аккреция на белые карлики 491
Глава 16. ГРАВИТАЦИОННОЕ ИЗЛУЧЕНИЕ 494
16.1. Что такое гравитационная волна? 494
16.2. Образование гравитационных волн 497
16.3. Оценки по порядку величины 501
16.4. Гравитационное излучение от двойных систем 504
16.5. Пульсар PSR 1913+16, входящий в двойную систему 506
16.6. Из пучение от вращающихся масс: замедление пульсаров 514
16.7. Гр^авитационные волны при столкновениях 518
16.8. Гравитационные волны при коллапсе с отклонениями от
сферической симметрии 522
Глава 17. СВЕРХМАССИВНЫЕ ЗВЕЗДЫ И ЧЕРНЫЕ ДЫРЫ 526
17.1. Введение 526
17.2. Основные свойства сверхмассивных звезд 529
17.3. Влияние плазмы 531
17.4. Устойчивость сверхмассивных звезд 533
17.5. Эволюция сверхмассивных звезд 535
Глава 18. ЗВЕЗДНЫЙ КОЛЛАПС И ВЗРЫВЫ СВЕРХНОВЫХ 539
18.1. Введение и предупреждение 539
18.2. Наступление коллапса 543
18.3. Фотодиссоциация 547
18.4. Нейтронизация и испускание нейтрино 548
18.5. Непрозрачность и захват нейтрино 553
18.6. Энтропия и уравнение состояния во время горячего коллапса 559
18.7. Гомологичный коллапс звездного ядра, отскок и что же дальще? . 568
Приложение/^. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ АСТРОНОМИИ 572
А.1. Парсеки и звездные величины 572
А.2. Звездные классы и диаграмма Герцщпрунга—Рессела 574
Приложение Б. УСЛОВИЕ НЕУСТОЙЧИВОСТИ Kj < О 578
Приложение В. ВЫЧИСЛЕНИЕ ИНТЕГРАЛА В УРАВНЕНИИ (8.4.6) 580
Приложение Г. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ТЕОРИИ ПОЛЯ 582
Прилоэнхние Д. КВАРКИ 588
Приложение Е. ФАЗОВЫЙ МНОЖИТЕЛЬ В УРАВНЕНИИ A1.5.16) 591
Приложение Ж. СФЕРИЧЕСКИ СИММЕТРИЧНАЯ АККРЕЦИЯ НА
ЧЕРНУЮ ДЫРУ: РЕЛЯТИВИСТСКИЕ УРАВНЕНИЯ 597
Приложение 3. ГИДРОДИНАМИКА ТЕЧЕНИЯ ВЯЗКОЙ ЖИДКОСТИ 605
Приложение И. ПЕРЕНОС ИЗЛУЧЕНИЯ 607
И.1. Уравнение переноса 607
И.2. Диффузионное приближение 611
И.З. Источники непрозрачности 615
Литература 621
Предметный указатель 648
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании книги, ее оформлении,
качестве перевода и другие просим присылать по адресу: 129820,
Москва, И-110, ГСП, 1-ый Рижский пер., д. 2,изд-во«Мир».
Стюарт Л. Шапиро , Саул А. Тьюколски
ЧЕРНЫЕ ДЫРЫ, БЕЛЫЕ КАРЛИКИ И НЕЙТРОННЫЕ ЗВЕЗДЫ
Физика компактных объектов
В двух частях
2
Научный редактор М. Ф. Путов
Мл. научные редакторы: В. Н. Соколова, И. А. Гревцова
Художник А. М. Драговой
Художественный редактор М. Н. Кузьмина
Технические редакторы: Н. Б. Панфилова, Л. С. Тимофеева
Корректор Р. Л. Вибке
ИБ№5193
Подписано к печати 11.06.85. Формат 60х90Иб.
Бумага офсетная № 1. Гарнитура тайме. Печать офсетная.
Объем 12,50 бум.л. Усл. печ. л. 25,00.
Усл. кр.-отт. 25,00. Уч. изд. л. 27,05.
Изд. № 27/3646. Тираж 4000 экз. Зак. 513 Цена 3 р. 60 к.
Набрано в издательстве «Мир»
на фотонаборном комплексе «Компьюграфик»
129820, ГСП Москва, 1-й Рижский пер., 2.
Отпечатано в Тульской типографии Союзполиграфпрома
при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли
г. Тула, проспект им. В. И. Ленина, 109.
ЧЕРНЫЕ ^ЫРЫ
БЫЫЕ1ЙВ1ИКИ И
НЕЙТРОННЫЕ ЗВЕЗДЫ
СШапирй СТьюколски
ЧЕРНЫЕ ^ЫРЫ
БИЫЕ \шмт и
НЕЙТРОННЫЕ ЗВЕЗДЫ