А.А. Гусак, Е.А. Бричикова, Г.М. Гусак
СПРАВОЧНОЕ
ПОСОБИЕ К
РЕШЕНИЮ ЗАДАЧ
/ ТЕОРИЯ ФУНКЦИИ
КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
И
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
кА. Гусак
Е.А. Бричикова
Г.М. Гусак
ТЕОРИЯ ФУНКЦИЙ
КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
И
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Справочное пособие
к решению задач
Минск
ТетраСистемс
2002
УДК 51(076.1)
ББК22.11я73
Г96
Авторы:
доктор физико-математических наук, профессор А.А. Гусак,
старший преподаватель белорусского национального технического
университета А.А. Бричикова,
кандидат физико-математических наук, доцент Г.М. Гусак
Рецензенты:
кандидат физико-математических наук, профессор А.А. Дадаян
Гусак А.А.
Г 96 Теория функций комплексной переменной и операционное
исчисление / А.А. Гусак, Е.А. Бричикова, Г.М. Гусак —
Мн.: ТетраСистемс, 2002.-208 с.
ISBN 985-470-054-2.
Пособие включает в себя следующие разделы: комплексные
числа, элементы теории функций комплексной переменной, ос-
новы операционного исчисления. Пособие содержит определе-
ния основных понятий, соответствующие формулы, примеры
решения типовых задач различной степени трудности, задачи
для самостоятельного решения, ответы и указания к ним. Помо-
жет при подготовке к практическим занятиям, зачетам и экзаме-
нам, а студентам заочных отделений - самостоятельно выпол-
нить контрольные работы.
Предназначено для студентов и преподавателей вузов.
УДК 51(076.1)
ББК 22.11я73
© Гусак А.А., Бричикова Е.А., Гусак Г.М., 2002
© Оформление. НТООО "ТетраСистемс"
ISBN 985-470-054-2	© НТООО «ТетраСистемс», 2002
Предисловие
Справочное пособие к решению задач по высшей математике из-
дается в четырех частях:
•	Аналитическая геометрия и линейная алгебра.
' • Математический анализ и дифференциальные уравнения.
•	Теория вероятностей.
•	Теория функций комплексной переменной и операционное
исчисление.
Данная книга предназначена для обучения студентов вузов по
разделу курса высшей математики «Теория функций комплексной
переменной и операционное исчисление».
В пособии рассматриваются следующие вопросы: комплексные
числа, их геометрическое изображение, действия над ними в
алгебраической и тригонометрической форме, геометрическое
истолкование этих действий; основные элементарные функции
комплексной переменной, дифференцирование и интегрирование в
комплексной области, функциональные ряды с комплексной
переменной, особые точки, вычеты; основные правила, формулы и
теоремы операционного исчисления с приложением к решению
обыкновенных дифференциальных уравнений и их систем.
Пособие имеет следующую структуру. В начале каждого пара-
графа приводятся теоретические сведения: определения основных по-
нятий, формулировка теорем, соответствующие формулы. Далее сле-
дуют примеры решения типовых задач различной степени трудности.
Затем предлагаются задачи для самостоятельного решения. Приведены
ответы к задачам, к некоторым из них даны указания. Каждый пара-
граф завершается вопросами теоретического характера, чтобы чита-
тель смог проконтролировать свои знания изучаемого материала.
Четвертая глава содержит краткий очерк истории возникновения
и развития теории функций комплексной переменной и операционного
исчисления. Книга включает биографический словарь, в котором при-
ведены краткие сведения о жизни и деятельности ученых, названных в
пособии и чьи научные исследования были посвящены теории функ-
ций комплексной переменной и операционному исчислению.
Авторы
3
Глава 1.
Комплексные числа
Известно, что действительных чисел недостаточно для того, что-
бы решить любое квадратное уравнение с действительными коэффи-
циентами. К числу квадратных уравнений, которые не имеют действи-
тельных корней, принадлежат уравнения х + I = 0, х + a = 0 (а > 0).
Решение таких уравнений приводит к необходимости рассмотрения
множества комплексных чисел, которое в качестве своего подмноже-
ства содержит множество всех действительных чисел.
§1.1. Множество комплексных чисел.
Основные понятия
Пару (а, Ь) действительных чисел а и b называют упорядоченной,
если указано, какое число считается первым, какое - вторым. Примеры
упорядоченных пар чисел: (0, 2), (5, 7), (7, 5). Отметим, что последние
две пары различны, хотя образованы одними и теми же числами.
Каждую упорядоченную пару чисел обозначим одной строчной
буквой греческого алфавита. Введем понятие равенства двух пар, оп-
ределим действия над ними.
Рассмотрим две упорядоченные пары действительных чисел
a = (a,Z>), р = (с, d).	(1.1)
Эти пары называют равными, если a = с, b = d, т.е.
(a, Ь) = (с, d)o(a = с, b = J).	(1.2)
Суммой двух пар (1.1) называют упорядоченную пару
а+ Р = (a, Z>) + (c, J) = (а + с, Z> + J)	(1.3)
а их произведением — упорядоченную пару
а + Р = (а, Ь) (с, d) = (ac-bd, bc + ad).	(1.4)
Из равенства (1.3) видно, что упорядоченная пара
0 = (0,0)	(1.5)
обладает тем свойством, что сложение ее с любой другой упорядоченной
парой не меняет последней пары: (а, Ь) + (0, 0) = (а, Ь). Упорядоченная
4
пара (1.5) играет роль нуля при сложении упорядоченных пар, назы-
вают ее нуль-парой.
Вычитание и деление упорядоченных пар определяется с помо-
щью их сложения и умножения.
Разностью а-0 двух упорядоченных пар (1.1) называют такую
упорядоченную пару у = (х, у), что у + 0 = а. Использовав равенства
(1.2) и (1.3), найдем хну. Поскольку
а = у + р,
то
(а, Ь) = (х, у) + (с, d) - (х + с, у + d),
т.е.
а-х + с, Ь =у + d,
откуда
x = a-c,y = b-d.
Таким образом, вычитание упорядоченных пар (1.1) определяется
формулой
а - Р = (а, b)- (с, d) = {а-с, b -d).	(1.6)
а
Частным — (Р*0) двух упорядоченных пар (1.1) называют та-
кую упорядоченную пару 8 = (х, у), что 8 • Р = а. Найдем х и у с помо-
щью равенств (1.2) и (1.4). Так как
а = 8 • р,
то
(а, b) = (х, у)(с, d) = {xc—yd, ус + xd),
т.е.
a = xc—yd, b = xd + yc.
Эта система имеет решение
_ (ac + bd) _ {be-ad)
(с2 + d2)’ У {с1 + d2)
5
2	2	ОС
Если ₽ * 0, т.е. с + а * 0, то частное — двух упорядоченных пар
(1.1) определяется так:
a_fac + M bc-ad\
r ”	2 , .2 ' 2	,2 •	( ’7'
p \c +a c +d J
Из этого равенства при a = 0, т.е. а = с, b = d, следует, что
i(c2+d2 de —cd
1 ~	2 j2 ’ 2 , j2 ’
y^c +d c +d J
l = (l,0).
Значит, роль единицы при делении двух упорядоченных пар вы-
полняет упорядоченная пара
1=(1,0).	(1.8)
Рассмотрим упорядоченные пары
а = (а, 0), b = (Ь, 0).	(1.9)
Арифметические действия над этими парами производятся так, как
и над действительными числами:
а + b = (а + Ь, 0), а - b = (а - Ь, 0), ab = (ab, 0), — = [ —, 0 1,
b \Ъ )
поэтому действительные числа отождествляются с упорядоченными
парами (1.9).
Комплексным числом называют упорядоченную пару (а, Ь) дейст-
вительных чисел а и Ь. Рассмотрим упорядоченную пару
/ = (0,1).	(1.Ю)
Применяя формулу (1.4), получаем
i2 =i-i = (0,1) (0,1) = (0 -1, 0 + 0) = (-1, 0).
Поскольку (-1, 0) = -1 (см. (1.9)), то
/2=-1, 1 =	(1.11)
Упорядоченную пару (1.10), удовлетворяющую соотношениям
(1.11), называют мнимой единицей. С помощью мнимой единицы мож-
но выразить любое комплексное число a = (a, b), т.е. упорядоченную
пару действительных чисел. В самом деле, так как
6
bi = (b,O)(Q, l) = (0, £),
то
(a, b) = {a, 0) + (0, b) = a + bi,
(a, b) = a + bi.
(1.12)
Поскольку (a, b) = a + bi, (a, b) = (0, b) + (a, 0) = bi + a, to a + bi = bi + a.
Значит, в правой части формулы (1.12) можно менять местами слагае-
мые. Выражение а + bi называют алгебраической формой комплексного
числа. Число а называют действительной частью, число Ь— мнимой
частью комплексного числа а + Ы. Обозначая комплексное число а + Ы
одной буквой а, записывают а = Rea b = Ima, где Re — начальные бук-
вы латинского слова realis (действительный), Im — начальные буквы
латинского слова imaginarius (мнимый). Кроме этих обозначений,
употребляют и другие, например, а = 7?(a), b = /(а), где а = а + Ы.
Отметим частные случаи формулы (1.12). Если b = 0, то {а, 0) = а -
действительное число; если a = 0, то
(G,b)=bi.	(1.13)
Число Ы называют чисто мнимым числом или просто мнимым.
Два комплексных числа а + Ы и с + di называют равными, когда а = с,
b = d;
(а + Ы = с + di) <=> (a = c,b = d).
Комплексное число равно нулю, когда равны нулю его действи-
тельная и мнимая части:
(а + Ы = 0) О (а = 0, b = 0).
Если дано комплексное число а = а + bi, то число а — bi, отли-
чающееся от а только знаком при мнимой части, называют числом,
сопряженным числу а, и обозначают a. Числом, сопряженным a,
будет очевидно а, поэтому говорят о паре сопряженных чисел. Дейст-
вительные числа, и только они, сопряжены сами себе.
Пример 1. Даны две упорядоченные пары действительных чисел
a = (4, 3), Р = (1, 2). Найти их сумму a + 0, разность a - 0, произведе-
„	a
ние ар и частное —.
7
Решен не. Принимая во внимание формулы (1.3), (1-4), (1.6) и (1.7),
соответственно находим:
а + Р = (4,3) + (1,2) = (4 + 1,3 + 2) = (5,5),
аР=(4,3) (1,2) = (4.-1 -3-2,31 +4-2) = (-2,11),
а —Р = (4,3) - (1,2) = (4 -1,3 - 2) = (3,1),
а (Ч-1 + 3-2 3-1-4-2 рО 5^
рЧ 12+22 ' 12+22 М5' 5J (
Пример 2. Доказать, что сумма двух упорядоченных пар действи-
тельных чисел не зависит от порядка слагаемых.
Решение. Если а = (а, Ь), 0 = (с, d), то в соответствии с (1.3)
а + Р = (а, b) + (с, d) = (а + с, b + d),
Р + а = (с, d) + (a, b) = (c + a, d + b) = (а + с, b + d).
Следовательно, а + р = р + а.
Пример 3. Доказать, что произведение двух упорядоченных пар
действительных чисел не зависит от порядка множителей.
Ре Ш ен и е. Когда а = (а, b), Р = (с, d), то в соответствии с формулой
(1.4)
‘ ар = (а, Ь) (с, й) = {ас-bd, be + ad),
Ра = (с, d) {a, b) = (са - db, cb + da) = {ас- bd, be + ad).
Из-этих двух равенств следует, что ар = Ра.
Пример 4. Противоположной к упорядоченной паре а называют
упорядоченную пару Р такую, что а + Р = 0.
Найти упорядоченную пару, противоположную упорядоченной
паре а=(а, Ь).
Реш ен и е. Пусть Р = (х, у), тогда
а+Р = (а, Ь) + {х, у)= (а + х,Ь + у).
Так как
а + р = 0,
&
то
(a + x,b +у) = 0.
На основании определения равенства двух упорядоченных пар и
формулы (1.5) получаем: а + х = 0, Ь+у = 0, откудах = -а,у = —Ь.
Следовательно упорядоченная пара, противоположная упорядочен-
ной паре а = (а, Ь) имеет вид -а = (-а, -Ь). В частности, для а = (4, -3)
противоположной будет -а = (—4, 3).
Пример 5. Обратной к упорядоченной паре а называют упорядо-
ченную пару у такую, что ay = 1.
Найти упорядоченную пару, обратную упорядоченной паре
а = (а, Ь), где а + Ь2 * 0.
Решение. Обозначим у=(х,у), найдем х и у. Принимая во внима-
ние формулы (1.4), (1.8) и определения равенства двух упорядоченных
пар, получаем
ау = (а, Ь) (х, у) = (ах -by,bx + ay) = 1 = (1,0),
откуда
ах - by = 1, bx + ау = 0.
Решая эту систему уравнений, находим
_ а _ -Ь
а2+Ь2’ У а2+Ь2
Обозначим упорядоченную пару, обратную упорядоченной паре
а = (а, Ь) через а’1, тогда
-I _ 1 а — А
а ~ 77 ~ „2	2 ’ 2 , .2 •
+о a +b J
В частности, если а = (1, 3), то
1 ( 1	-3 Wl -3
а ll2 + 32 ’ I2 +32) U0’ 1°
= (0,1;-0,3).
Пример 6. Указать действительную и мнимую часть чисел: а-5,
Р = 7/, у = 4 - 3/.
9
Решение. Принимая во внимание соответствующие определения и
обозначения, получаем
Rea = 5, Ima = 0; ReP = 0, Imp = 7; Rey = 4, Imy = -3.
Пример 7. Записать числа, сопряженные числам: a = 7 + 5i, р = -3,
у = 8i, 5 = -6i.
Решение. На основании определения заключаем, что
a = 7 - 5г, Р = -3, у = -8г, 8 = 6/.
Пример 8. Противоположным комплексному числу а называют чис-
ло Р такое, что a + Р = О, т.е. Р = -а; если а = а + Ы, то -а = -а - Ы.
Найти числа, противоположные комплексным числам: a = 2 + 3/,
Р=4-5г, у = -8+7г, 8 =-6-9г.
Решение. В соответствии с определением находим, что
-а = -2-Зг,-р = -4 + 5г, -у = 8-7г, -8 = 6+9г.
Задачи
Найдите сумму a + р, разность a - р, произведение ар, частное
a/р двух упорядоченных пар:
1. а = (4,2), р = (1,3).	2. а = (2,-5), р = (3,4).
Даны три упорядоченные пары действительных чисел: a = (a, b),
р = (с, d), у = (е,/). Докажите, что:
3. (а + р) + у = а + (р + у).	4. (ар)у = а(ру).
5. (а + Р)у = ау + ру.
Найдите упорядоченные пары, противоположные данным упоря-
доченным парам:
6. a = (3, 5).	7. р = (4, -3).
8. у = (-5,9).	9. 8 = (-2,-8).
Найдите упорядоченные пары, обратные данным упорядоченным
парам:
10. a = (3,1). 11. р =(4,-2). 12. у = (-1,7).	13. 8 = (-6,-2).
Запишите действительную и мнимую часть комплексных чисел:
14. а = 5 + 3г. 15. р = 6-7г.	16. у =5+2г.	17. 8 =-9-8г.
Запишите числа, сопряженные комплексным числам:
18. a =2 + 4/. 19. р = 5-6/.	20. у = 4/.	21. 8=-7г.
10
Запишите числа, противоположные комплексным числам:
22.а=6 + 2г. 23.р = 7-5/.	24.у = -8 + Зг. 25.8 = ^-9г.
Ответы
, 1. а + р = (5, 5), а - р = (3, -1), ар = (-2, 14),	= (1, -1). 6. -а = (-3, -5).
1 (3 -1А
7. — = —,— . 14. Rea = 5, Ima = 3. 18. а = 2- 4/. 22. -а =-6 - 2i.
а 110 10j
Вопросы
1.	Что называют упорядоченной парой действительных чисел?
2.	Какие упорядоченные пары чисел считаются равными?
3.	Как определяется сложение двух упорядоченных пар действи-
тельных чисел?
4.	Как определяется умножение двух упорядоченных пар дейст-
вительных чисел?
5.	Какая упорядоченная пара выполняет роль нуля при сложении
упорядоченных пар?
6.	По какой формуле находится разность двух упорядоченных пар
действительных чисел?
7.	Какая упорядоченная пара называется противоположной дан-
ной упорядоченной даре?
8.	При каком условии определено деление двух упорядоченных
пар действительных чисел?
9.	По какой формуле вычисляется частное двух упорядоченных
пар действительных чисел?
10.	Что является единицей при умножении упорядоченных пар
действительных чисел?
11.	По какой формуле находится упорядоченная пара чисел, об-
ратная упорядоченной паре a = (a, b)7
12.	Что называют комплексным числом?
13.	Как определяется мнимая единица?
14.	Какова алгебраическая форма комплексного числа?
15.	Что называют действительной частью комплексного числа?
16.	Что называют мнимой частью комплексного числа?
17.	Какое число называют чисто мнимым?
18.	Какие комплексные числа называют сопряженными?
19.	Как определяется равенство комплексных чисел?
20.	Что следует из равенства а + Ы = 0?
21.	Определено ли неравенство между комплексными числами?
И
§1.2. Геометрическое изображение комплексных
чисел. Комплексная плоскость
Как известно, действительные числа можно изображать точками пря-
мой линии. Комплексные числа можно изображать точками плоскости.
Фиксируем некоторую плоскость и выберем на ней прямоуголь-
ную декартову систему координат (рис. 1.1). Комплексному числу
(а, Ь) = а + Ы сопоставим точку М(а, Ь) этой плоскости с координатами
(а, Ь). Если b = 0, то получим действительное число (а, 0) = а, которое
изображается точкой А на оси Ох (см. рис. 1.1). Вследствие этого ось
Ох называют действительной осью (точками оси абсцисс изображают-
ся действительные числа). Если а = 0, то получаем чисто мнимое число
Ы, которое изображается точкой В(0, Ь), лежащей на оси Оу. По этой
причине ось ординат называют мнимой осью (точками этой оси изобра-
жаются чисто мнимые числа). Отметим, что мнимая единица i изобра-
жается точкой (0, 1), расположенной на положительной полуоси орди-
нат и отстоящей от начала координат на расстояние, равное единице.
Число (-/) изображается на оси ординат точкой (0, -1), симметричной
точке (0, -1). Любое комплексное число а = а + Ы, где а 0, b 0, изо-
бражается точкой плоскости, не лежащей на осях координат. Обратно,
любой точке М(а, Ь) плоскости соответствует комплексное число
а = а+Ы. Таким образом, между множеством комплексных чисел и
множеством точек плоскости установлено взаимно однозначное соот-
ветствие. Плоскость, точки которой отождествляются с комплексными
числами, называют комплексной плоскостью. На комплексной плоско-
сти комплексно сопряженные числа а = а + Ы и а=а-Ы изобража-
ются точками М(а, Ь) и <Y(a, —b), симметричными относительно оси Ох.
12
Рассматривают также комплексную переменную z = х + iy, где х,
у- действительные переменные, i — мнимая единица. Значения этой
переменной — комплексные числа, изображаемые точками комплекс-
ной плоскости. Вследствие этого комплексную плоскость называют
также плоскостью комплексной переменной.	'
Пример 1.Где на плоскости расположены точки, изображающие
комплексные числа z = х + iy, для которых Rez > О?
Решение. В соответствии с определением Rez = x для чисел
z = х + iy. Так как по условию Rez > 0, то х > 0. Последнему неравенст-
ву удовлетворяют координаты всех точек полуплоскости, расположен-
ной справа от оси Оу и точек самой этой оси.
Пример 2. Какое множество образуют точки, изображающие ком-
плексные числа z = х + iy, для которых |Rez| < 3?
Решение. Поскольку Rez = х для чисел z = х + iy и |Rez| = |х|, то не-
равенство |Rez| < 3 принимает вид jx| < 3, или —3 < х < 3. Этим неравен-
ствам удовлетворяют координаты всех точек комплексной плоскости в
полосе между прямыми х =-3, х = 3.
Пример 3. Где расположены точки, изображающие комплексные
числа z = х + iy, для которых Imz < 0?
Решение. В соответствии с определением lmz=y для z = x + iy.
Принимая во внимание условие Imz < 0, получаем у < 0. Этому нера-
венству удовлетворяют координаты всех точек полуплоскости, распо-
ложенной ниже оси Ох, и точек, лежащих на данной оси.
Пример 4. Какое множество образуют точки, изображающие ком-
плексные числа z = х + iy, для которых |Imz| < 4?
Решение. Так как Imz = у для чисел z = х + iy и |Imz| <4, то [у| < 4,
или —4 <у<4. Этим неравенствам удовлетворяют координаты всех то-
чек, принадлежащих полосе между прямыми, параллельными оси Ох и
проходящими соответственно через точки —4/ и 4z.
Пример 5. Что представляет собой множество точек, изображающие
комплексные числа z = х + iy, для которых 0 < Rez < 1, 0 < Imz < 1?
Решение. Первые неравенство определяют полосу между осью Оу
и прямой х = 1, вторые неравенства - полосу между осью Ох и прямой,
проходящей через точку, изображающую число i. Следовательно, со-
вокупность этих неравенств определяет множество точек квадрата с
вершинами в точках, изображающих числа 0, i, 1 + i, 1.
13
Задачи
1.	На комплексной плоскости постройте точки, изображающие
комплексные числа: 1). 3 + 2г; 2). 4 - 5г; 3). -6 + 7г; 4). -9 - 8z; 5). 2z;
6).-3z; 7).-5; 8). 6; 9). 1; 10). 0.
2.	Выясните геометрический смысл следующих величин:
1)	. |Rez|, 2). | Imz| (z = x + iy).
3.	Дайте геометрическое описание множеств всех точек комплекс-
ной плоскости, изображающих числа z = x + iy и удовлетворяющих
следующим неравенствам:
l)Rez<0; 2)Imz>l; 3) |Rez|<2; 4) |lmz|<l, 0< Rez <1;
5) |Rez|< 1, 0<Imz<l; 6) -l<Rez<0, -l<Imz<0.
Изобразите эти множества на чертеже.
4.	Где расположены точки, изображающие комплексные числа
z = х + iy, для которых: 1) Rez > 3; 2) Imz < 3; 3) |Rez| < 1; 4) |Imz| > 2;
5) |Rez| < 1, |Imz| < 1 ? Сделайте соответствующие рисунки.
5.	Запишите с помощью неравенств следующие множества точек
комплексной плоскости: 1) полуплоскость, расположенная слева от
мнимой оси; 2) второй квадрант; 3) полуплоскость, расположенная
выше действительной оси на расстоянии не меньше 3; 4) полоса, точки
которой отстоят от мнимой оси на расстоянии меньше 2; 5) квадрат с
вершинами в точках 0, i, 1 + /, 1; 6) прямоугольник с вершинами -1, 1,
1 - i, -1 - i.
Ответы
2.	1) Расстояние до мнимой оси от точки, изображающей комплексное
число z; 2) расстояние до действительной оси от точки, изображающей ком-
плексное число z. 3. 1) Полуплоскость, расположенная слева от мнимой оси, и
сама эта ось; 2) полуплоскость, расположенная выше горизонтальной прямой,
проходящей через точку z = i (точки этой прямой не включаются); 3) полоса,
состоящая из точек, расстояния которых до мнимой оси меньше 2; 4) мно-
жество точек внутри прямоугольника с вершинами в точках -i, 1 - г, 1 + г, i
(стороны прямоугольника не включаются). 4. 1) В полуплоскости, расположен-
ной справа от прямой х = 3 и на самой прямой; 2) в полуплоскости, располо-
женной ниже горизонтальной прямой, проходящей через точку z = Зг, и на этой
прямой; 3) в полосе между двумя прямыми х = -1, х— 1 и на этих прямых;
4) вне полосы между горизонтальными прямыми, проходящими соответственно
через точки -2/ и 2г; 5) внутри квадрата с вершинами в точках -1 - i, -1 + i,
1 + i, 1 - i и на его сторонах. 5. 1) Rez < 0; 2) Rez < 0, Imz > 0; 3) Im z > 3;
4) | Re z | < 2; 5)0<Rez<l, 0<Imz<l; 6)|Rez|<l, -l<Imz<0.
14
Вопросы
1.	Как изображаются комплексные числа?
2.	Что называют комплексной плоскостью?
3.	Что называют действительной осью?
4.	Что называют мнимой осью?
5.	Как изображаются мнимая единица i и число -i?
§1.3. Арифметические действия
над комплексными числами
Из определения комплексного числа (как упорядоченной пары дей-
ствительных чисел) и определения арифметических действий над упо-
рядоченными парами (см. формулы (1.3), (1.4), (1.6), (1.7) следует, что
(а + Ы) + (с + di) = (a + c) + (b + d)i,	(114)
(а + Ы) - (с + di) = (а - с) + (Z> - d) i,	(1-15)
(а + bi) (с + di) = (ас - bd) + (be + ad) i,	(1-16)
a + bi ac + bd be-ad . , 2
---T= 2	+ 2 j2l (c2+^2*0).
c + di c +d c +d2
(1-17)
Формула (1.14) определяет правило сложения двух комплексных
чисел: чтобы сложить два комплексных числа, необходимо сложить
соответственно их действительные и мнимые части. Формула (1.15)
означает, что при вычитании одного комплексного числа из другого
необходимо вычесть отдельно их действительные и мнимые части.
Формулу (1.16) можно получить путем умножения по правилам
алгебры и замены i его значением:
(а + Ы) (с + di) - ас + adi + bci + bdi2 - (ас - bd) + (be + ad) i.
Чтобы получить формулу (1.17), необходимо предварительно ум-
ножить числитель и знаменатель на число с - di (число, сопряженное
числу (с + di):
а + Ы _(а + bi) (с — di) _ас- adi + bci - bdi2 _ ac + bd be-ad .
c+di (c+di) (c-di) c2-d2i2 c2 + d2 c2 + d2
Полагая в этой формуле а = 1, b = 0, получаем
—^7 = ^Ат2-^4г-	<118)
c + di c2+d2 с +d2
15
Формулой (1.18) определяется число р ', обратное числу Р = с + di
(Р # 0, т.е. с +	0).
Действия над комплексными числами подчиняются тем же зако-
нам, что и действия над действительными числами. Если а = а + Ы,
р = с+ di, у = е + fi, то
а + р = р + а; (а + р) + у = а + (Р + у); аР = Ра; (ар)у = а(Ру).
Сумма и произведение сопряженных комплексных чисел являют-
ся действительными числами. Так, если а = а + Ы, z = а - Ы, то
а + а = 2а, аа = а2+Ь2.
Далее, верны следующие равенства:
а+р = а + р, а-р = а-р, ар = а-р, =
Пример 1. Найти сумму и разность двух комплексных чисел
а = —4 + 5/, р = 8 - 3/.
Решение. В соответствии с формулами (1.14) и(1.15) находим:
а + Р = (-4 + 5/)+ (8-3/) = (-4 + 8) +(5 -3)/ = 4 + 2/,
а-р = (-4 + 5/)-(8-3/) = (-4-8) + (5-(-3))/ = -12 + 8/.
Пример 2. Найти произведение комплексных чисел а = 4 + 2/,
р = 1 + 3/.
Решение. Принимая во внимание свойства умножения комплекс-
ных чисел и равенство z = -1, находим
аР = (4 + 2z) (1 + 3z) = 4 -1 + 4 - 3/ +1 - 2/ + 6z2 = 4 + 14/-6 = -2 + 14/.
Пример 3. Найти частное	комплексных чисел a = 10 + 8/, Р = 1 + /.
_	„ a
Решение. Умножая числитель и знаменатель дроби — на число
р =1 - i, сопряженное с числом р, получаем
a _ I0 + 8z _ (10 + 8/)(1 -/) _ 10-10/ + 8/-8/2 _ 18-2/ _д.
Р~ 1 + / " (! + /)(!-/) "	I-/2	2
16
Пример 4. Дано комплексное число Р = 3 -4i. Найти число р ', об-
ратное числу р.
Решение. Так как рч = —, то
Р
1_ 1 _ 1(3 + 40 _ 3 + 4/ _3+4/_ 3 _4_.
р ~ 3-4i ~ (3-40(3 + 40 ~ 9-16i2 ~ 25 “ 25 25
что соответствует формуле (1.17).
Задачи
Выполните указанные действия над комплексными числами:
1. (4 + 7/) + (3 + 2/). 3. (3-5/)+ (8-7/)- 5. (9+ 7/)-(6+2/). 7. (9-8/)-(3-4/). 9. (1 + 2/) (2-/). 11. (2-30(6+4/). 13. 1+3/ 15. 2 + 3/	2. (1-6/)+ (5+4/). 4. (7-2/)+ (-3-8/). 6. (8 + 6/) -(5 -4/). 8. (-5-7/)-(-9-8/). 10. (2-5/)(3+4/). 12. (1 +/)(2 + 3/). 14. «±*. 1 + / 16. 3 + 4/
Найдите числа, обратные следующим комплексным числам:
17. a = 3-i.	18. а = 8-6/.
19. а = 1 + 3/.	20. а = 6 + 8/.
Верны ли следующие равенства:
21. -J-a = i-Ja (д>0).	22. -Ja = i*J- а (а>0)?
Ответы
1.7 + 9/. 2.6-2/. 3.11-12/. 4.4-10/. 5.3 + 5/. 6.3 + 10/. 7.6-4/.
8.4 + Z. 9.4 + 3/. 10.26-7/. 11.24- 10/. 12.-1 +5/. 13. 1 -1. 14. 7-/. 15. 1 -/.
( ]4	7 )
16.------,---. 17. 0,3 + 0,1/. 18.0,08 + 0,06/. 19. 0,1 - 0,3/. 20.0,06 - 0,08/.
21.	Верно. 22. Неверно. Указание. Предположив, что равенство верно, за-
меним в нем V—а на i-ja, тогда -Ja = i2-Ja, или -/a = —Ja, 1 =— 1, что про-
тиворечиво.
17
Вопросы
1.	По какой формуле находится сумма двух комплексных чисел?
2.	Каково правило вычитания двух комплексных чисел?
3.	Как найти произведение двух комплексных чисел?
4.	Как найти частное двух комплексных чисел?
5.	По какой формуле находится число, обратное комплексному числу?
6.	Как производятся действия над комплексными числами?
7.	Каким числом выражается сумма двух сопряженных комплекс-
ных чисел?
8.	Каким числом является произведение двух сопряженных ком-
плексных чисел?
9.	Чему равно комплексное число, сопряженное сумме двух ком-
плексных чисел?
10.	Чему равно комплексное число, сопряженное разности двух
комплексных чисел?
11.	Чему равно комплексное число, сопряженное произведению
двух комплексных чисел?
12.	Чему равно комплексное число, сопряженное частному двух
комплексных чисел?
§1.4. Возведение в степень комплексного числа.
Извлечение квадратного корня
из комплексного числа
Рассмотрим сначала, как выражаются целые положительные сте-
пени мнимой единицы i. Принимая во внимание равенство I2 =-1, по-
лучаем: г3 —i2i 1)г =— I, г4 =г3г =(—г)г =—г2 =1,	г5=г4г=г,
г6 = г5г = г2 = -1, г7 - ibi = (“1)г - ~i, i* = i1 i = (~i)i - ~i2 = 1 и т.д.
В общем виде полученные результаты можно записать так:
/4* =1, z’4*+I=/> /4*+2=_1> ;4Ы=_(. (А =0, 1, 2, ...).	(1.19)
При возведении комплексного числа а + Ы в степень л (л — нату-
ральное число, л > 2) пользуются формулой бинома Ньютона
(а + Ы)п =ап +an-]bi + ^~^an-2(bf)2 +П('П~^~2)ап-3(Ы)3 + ...
... + »(»-!)ап-к (ЬГ)к + +	(1 20)
1 *2'3 ’к
18
В правой части этого равенства заменяют степени мнимой едини-
цы по формулам (1.19) и приводят подобные члены, в результате по-
лучают некоторое комплексное число с + di.
Квадратным корнем из комплексного числа называют комплекс-
ное число, квадрат которого равен данному числу. Обозначим квад-
ратный корень из комплексного числа а + Ы через и + vi, тогда по оп-
ределению
yja+bi—u+vi', (u+vi)2 =а+Ы.
Из второго равенства следует, что
и2— v2 =а, 2uv=b.	(1.21)
Возведем в квадрат каждое из этих равенств и сложим:
(и2 -v2)2 +4w2v2 =а2 +Ь2, (и2 +v2)2 = а2 +Ь2,
откуда и2 + v2 = уа2 + Ь2.
Это равенство и первое из равенств (1.21) дают возможность оп-
2	2
ределить и и v :
и2 =-^а + у]а2 +Z>2^, v2 =-^-а + у]а2 +Ь2	(1-22)
Из этих уравнений находят два значения м, которые отличаются
только знаком, а также два значения v. Все найденные значения будут
действительными, потому что выражения а + а2 +Ь2 и - а + у/а2 + Ь2
при любых а и b являются положительными. Знаки и и v надлежит вы-
брать так, чтобы эти числа удовлетворяли второму из равенств (1.21).
В итоге получают два комплексных числа щ + v1/, и2 + v2i, которые
имеют противоположные знаки и являются значениями квадратного
корня из комплексного числа а + bi.
Итак, извлечение квадратного корня из комплексного числа все-
гда возможно и дает два значения, которые отличаются только знаком.
Пример 1. Возвести в квадрат комплексное число а = 4 + 3/.
Решение. Применив формулу (а+Ь)2 = а2 + 2ab+b2 и равенство
i2 =-1, получим
(4+3/)2 = 42 +2-4-Зг+(Зг)2 = 16+24/~9 =7+24/.
19
Пример 2. Найти третью степень комплексного числа а = 2 - 4/.
Решение. Применяя формулу (а+i)3 = а3 + 3a2b+3ab2 +Ь3 и со-
2	-3
отношения г —1, i —-1, находим
(2-4/)3 =23 +3-22(-4/) + 3-2(-4/)2 + (-4/)3 =
= 8 - 48/ 4- 96/2 - 64= 8 - 48/ - 96 + 64/ = -88 +16/.
Пример 3. Найти действительную и мнимую части комплексного
числа ОС = (1+2/)4.
Решение. Формула бинома Ньютона при п = 4 принимает вид
(n+i)4 =п4 + 4п36+6п262 +4п63 + 64.
На основании этой формулы получаем
(1 + 2/)4 = 1 + 4-2/ + 6(2/)2+4(2/)3) + (2/)4 =
= 1 + 8/ + 24Z2 +32/3 +16/4 = 1 + 8/ —24 - 32/ +16 = —7 — 24/.
Значит,
Rea = -7, Ima = -24.
Пример 4. Извлечь квадратный корень из числа a = 5 + 12/.
Решение. Обозначим квадратный корень из числа а через и + vi,
тогда (u+vi)2 =5+12/. Принимая во внимание формулы (1.22) и ус-
ловие а = 5, b = 12, находим:
2 _ (5 + Vs2 +122 ) _ (5 +13) _	2	_	_
U — —~~~~~—	— у к — у Ц, — J.	— j
2	2
2	-2	12
Найдено два значения квадратного корня из числа
a = 5 + 12/: щ + v(/ = 3 + 2/, и2+v2/ = -3-2/.
Пример 5. Извлечь квадратный корень из мнимого числа a = 2/.
Решение. В данном случае а = О, b = 2. По формулам (1.22) находим:
2 _(O + Vo2+22)_,	,
U — ~~~~~’ — 1, И\ — 1» Wn — —1»
2	1	2
20
Следовательно, и, + vti = 1 + i, и2 + v2i = -1 -i.
Пример 6. Решить квадратное уравнение z2 - 6z + 25 = 0.
fp2
Решение. Пользуясь формулой z12=-—±J——q для корней
2 V 4
квадратного уравнения х2 + рх +q — 0, находим
z, 2 =3 + 7з2 -25 =3 + 7^16 = 3 + 4/, raei = ^4.
Это уравнение имеет комплексные корни.
Пример 7. Решить квадратное уравнение
z2-(4+6/)z-5+ 10/= 0
с комплексными коэффициентами.
Решение. Принимая во внимание результаты примера 5, получаем
z, 2 = (2 + 3/)±7(2+ 3/)2-(-5 + 10/) = (2 + 3/) + V4 + 12/ + 9/2 +5-10/ =
= (2 + 3/) ± 5/2? = (2 + 3/) ± (1 + /'); z, = 3 + 4/, z2 = 1 + 2/.
Пример 8. Найти значение выражения z3 - 2z2 + 5z при z = 1 - /.
Решение. Так как (I-/)2 = 1-2/ + /2 =1-2/-1 = -2/,
(1 - /)3 = (1 - /)2 (1 - /) = (-2/) (1 - /) = -2/ + 2/2 = -2 - 2/,
то
Z3 -2z2 + 5z = (-2 - 2/) - 2(-2/) + 5(1 -/) = -2 - 2/ + 4/ + 5 -5/ = 3 - 3/.
Пример 9. Доказать, что комплексное число z = 1 - / является кор-
нем уравнения z3+2z2-6z + 8 = 0.
Решение. Действительно,
z2 =(1~/)2 =-2/, z3 =(1-/)3 =-2-2/,
21
поэтому
z3 +2z2 ~6z+8 -
= (-2-2/) + 2(-2/)-6(l-/) + 8 = -2-2/-4/-6 + 6/ + 8 = 0.
Задачи
Возведите в указанные степени данные комплексные числа:
1. (1+02.	2. (1-4/)2.	3. (2-/)2.	4. (1+2/)2.
5. (2+5/)3.	6. (1+/)3.	7. (1-2/)3.	8. (1 + /V3)3
9. (2+3/)4.	10. (1+/)4.	11. (I-/)4.	12. (1-2/)4.
13. (1+/)5.	14. (1+/)6.	15. (I-/)6.	16. (1+/)7.
Найдите действительную и мнимую части каждого комплексного
числа:			
17. (I-/)2.	18. (-3-2/)2.	19. (4+3/)2.	20. (3-4/)2
21. (5 - 4/)2.	22. (4+5/)2.	23. (3+2/)3.	24. (4+3/)3
25. (2+4/)3.	26. (3-6/)3.	27. (2-3/)4.	28. (3+4/)4
Найдите значения квадратного корня из комплексного числа:
29. 3-4/.	30. -5 + 12/.	31. 5-12/.	32. 7-24/.
33.-7 + 24/.	34. -3-4/.	35.9 + 40/.	36.11 + 60/.
Решите квадратные уравнения:
37.	z2-4z + 13 = 0.	38. z2-(4-2/)z+ll+6/=0.
Вычислите значения данных выражений при указанных значениях z:
39.	z3 - 2z2 + 3z при z = 1 + /.
40.	z4 + 2z3 - 3z2 + 4z при z = 1 - /.
Проверьте, являются ли указанные комплексные числа z корнями
следующих уравнений:
41.	z3-2z2 + 2z = 0, z = l + /.
42.	z4 — 5z3 + 4z2 + 2z - 8 = 0, z = 1 - /.
Вычислите:
43.	44.
(I-/)3	(I-/)5
45.
(l + /)2,,+l
(I-/)2"-1
(n — натуральное число).
22
Ответы
1.	2/. 2. -15 - 81. 3. 3 - 41. 4. -3 + 4/. 5. -142 + 65/. 6. -2 + 21. 7. -11 + 21.
8. -8.9. -119 - 120/. 10. -4.11. -4.12. -7 + 24/. 13. -4 - 41. 14. -81. 15. 81.16. 8 - 81.
17.—2/. 18. Rea = 5, Ima =12. 19. Rea = 7, Ima = 24. 21. Rea =9, Ima = —40.
23. Rea = -9, Ima = 46. 24. Rea = -44, Ima =117. 25. Rea = -88, Ima = -16.
27. Rea = -119, Ima = 120. 28. Rea =-527, Ima = -336. 29. ±(2 +/).
30. ±(2 + 31). 31. +(3 - 21). 32. ±(4 - 31). 33. ±(3 + 41). 34. ±(1 - 21). 35. ±(5 + 41).
36. ±(6 + 5/). 37.2 + 3/, 2-3/. 38.Z! = l+2/, z2 = 3-41. 39.1+1. 40.2-3/.
41.Является корнем. 42. Является корнем. 43.2. 44.-2. 45.(-1)"2. Указа-
(l + /)2n+I fl + iV"	1 + 1
ние. +----'-z—г= = -----------г-
(i-o2"-1 U-/J (i-о
Вопросы
1.	Сколько значений могут принимать целые положительные сте-
пени мнимой единицы 1?
2.	Запишите значения первых восьми степеней 1.
3.	Как в общем виде записываются натуральные степени 1?
4.	Как возвести комплексное число в степень п?
5.	Что называют квадратным корнем из комплексного числа?
6.	Как извлечь квадратный корень из комплексного числа?
§1	.5. Модуль и аргумент комплексного числа.
Тригонометрическая форма
комплексного числа
Как уже отмечалось (см. §1.2), комплексному числу a = а + Ы со-
ответствует точка М(а, Ь) комплексной плоскости (рис. 1.2). Модулем
комплексного числа a = а + Ы называют длину г отрезка ОМ, где О -
начало координат, М(а, Ь) - точка, изображающая это комплексное чис-
ло. Модуль комплексного числа a = а + Ы обозначают символом |а|:
г = \ОМ\, г = |а| (|а|>0).	(1.23)
Поскольку | ОМ | = уа2 + Ь2 (см. рис. 1.2), то
jaj = Va2 + 62, | а + h/1 = Va2 + h2, r = Ja2 +b2,	(1.24)
т.е. модуль комплексного числа равен арифметическому значению
квадратного корня из суммы квадратов его действительной и мнимой
части. Если 6 = 0, т.е. число а является действительным, причем a = а,
то формула | а | = 4а2 + Ь2 принимает вид |а| = 4а2.
23
Аргументом комплексного числа а = а + bi называют величину
угла <р наклона отрезка ОМ к оси Ох. Аргумент комплексного числа а
обозначают через Arga. Аргумент комплексного числа а имеет беско-
нечное множество значений, отличающихся друг от друга на число,
кратное 2л. Аргумент не определен лишь для числа 0, модуль которого
равен нулю. Среди значений аргумента комплексного числа
a * Осуществует одно и только одно значение, заключенное между -л
и л, включая последнее. Его называют главным значением аргумента и
обозначают arga. Итак, аргумент комплексного числа удовлетворяет
соотношениям
Arga = arga + 2to (к = 0, + 1, + 2,...), -л<а^а;£л.
С помощью модуля и аргумента комплексное число a — а + Ы
можно представить и в другой форме. Поскольку
« = гсозф, /> = г5Шф,	(1-25)
то
a + bi = г (cos ф + i sin ф) (г>0),	(1.26)
где
г = Va2 + b2, со5ф = —г- а , sin ф = —г	(1-27)
7a2 + b2	4 а1 +Ь2
Выражение в правой части равенства (1.26) называют тригоно-
метрической формой комплексного числа. Отметим особенности
24
тригонометрической формы комплексного числа: 1) первый множитель -
неотрицательное число, г > 0; 2) записаны косинус и синус одного и
того же аргумента; 3) мнимая единица умножена на синус угла.
Два комплексных числа, заданных в тригонометрической форме,
равны тогда и только тогда, когда их модули равны, а аргументы отли-
чаются на величину, кратную 2л.
Следовательно, если
^(costp] +/sin(p]) = r2(cos(p2 + /sincp2),	(1.28)
то
П=г2’ Ф2=Ф1+2£л (к = 0, +1, +2,...).	(1-29)
Обратно, из равенств (1.29) следует равенство (1.28).
Если комплексное число а = а + Ы записывается в тригонометри-
ческой форме а = г(созф +/51пф), то комплексно-сопряженное число
а = а-Ы записывается в форме а - г (cos (-ф) + гз1п(-ф)). Значит,
а =|а|, arga =-arga (рис. 1.3).
Замечание. Комплексное число a = а + Ы = r(cosip + /sin<p) можно
представить в показательной форме. Принимая во внимание формулу Эйлера
е'9 = cos<p + Zsi п<р, получаем
r(cos<p + Zs i n<p) = re'9.	(1.30)
Правую часть этого равенства называют показательной формой комплекс-
ного числа.
25
Пример 1. Заданы ли в тригонометрической форме следующие
комплексные числа:
л . . л 1 /г ( л) . . ( л
z. =3 cos— + /sin— , z, =V2 cos-----+ /sm-----
I 4	4J 2 I I 3J I 3
л . . д')	. Зл . Зл]
z, = -2 cos—+ /sin — L z. =7 sin — + /cos— ,
I 5	5 J 4 I 5	5 J
,( л . л ]„
z, = 5 cos— + /sm — ?
I 6 4j
Решение. Сравнивая запись каждого из этих чисел с формулой
(1.26), заключаем, что числа z, и z2 заданы в тригонометрической
форме. Остальные числа даны не в тригонометрической форме: число
z3 содержит отрицательный множитель (~2<0), число z4 имеет вид
r(sin<p + icos<p) [а не r(cos(p + /sincp)], число z5 содержит косинус и
синус разных аргументов (а не одного и того же аргумента).
Пример 2. Найти модуль и аргумент комплексного числа а = 2 + 2/.
Решение. В данном случае а = 2, Ь = 2. По формуле (1.24) вычис-
ляем модуль этого комплексного числа: j а | = 7з2 + 22 =78 =2>/2. С
помощью формул (1.27) находим:
а
cos <р = —
г
2 _ 1
2V2 71
b
Sin ф = —
2 _ V2
272	2 ’
л	л _,
Ф = arga = —, Arga = — + 2£л, к = 0, ±1, ±2, ... .
4	4
Пример 3. Записать в тригонометрической форме комплексное
5 + i
число----.
2+3/
Решение. Найдем сначала действительную и мнимую части этого
комплексного числа:
5 + i _ 5 + i 2-3/ _ 10-15/' +2/' —З/2 _
2 + 3/~ 2 + 3/ 2-3/~	22-(3/)2
26
10-15/ + 2/ + 3 13-13/ , .
4 + 9	13
Применяя формулы (1.27), находим модуль и аргумент комплекс-
ного числа 1 —i (а = 1, b = -1):
г = Ji2 +(-1)2 = V2; соэф = — =	sin ср = — = -^-,
У 2	г 42	2	г 2
Л	л
<p = arga = —, Arga = — + 2Ал, к = 0,± 1,± 2,....
4	4
Число 1 - i в тригонометрической форме имеет вид
, •	( п}  ( Л У)
1 -1 = у2 cos — +sin — .
V 4J V 4j)
n	-	10 + 8/	„
Пример 4. Комплексное число ——— записать в показательной
форме.
Решение. Сначала найдем действительную и мнимую части данно-
го комплексного числа:
10+8/ _ (10+8Q(9+i) _ 90+10/+72/+8/2 _ 90+82/-8 _ 82+82/
9-/ " (9-/)(9+/) ~	92-/2	” 81+1	“ 82	+ *'
С помощью формул (1.27) находим модуль и аргумент комплекс-
ного числа 1 + / (а = 1, b = 1): г = л/12 +12 = з/2;
а 1	4~2	b	4~2	л
г	^2	2	г 2	4
В соответствии с формулой (1.30) записываем данное число в по-
л/
казательной форме: 1 + / = 42 е4 .
Пример 5. Доказать, что ет = -1.
Решение. Воспользуемся формулой е,<₽ =cos<p + /sin<p.
При <р = л эта формула принимает вид ет = cos л + / sin л.
Поскольку созл = -1, sin л = 0, то ет =-1.
27
Задачи
1.	Заданы ли в тригонометрической форме следующие комплекс-
ные числа:
Л	л	. . л^	Л	(	л^	. . (	лП
z, =4 cos— + isin — , z2 =2 cos----+ isin---L
I	3	3/	I	k	6j V	6JJ
f	л . . л^	Л Л . , л^
Z1 = -5 cos— + isin — , z, =6 cos----«sin— ,
I	8	8/	4V5	5)
r-( . Зл . Эл')	rr( . 2л . 7л
z, = v2 sin — + icos— , Zf. = —y3 sin — + icos— ,
5	(	4	4 )	6	(3	6 )
Л я . . л Y
z7 = 7 cos— + isin— ?
7	V 12	12j
Найдите модуль и аргумент каждого из комплексных чисел:
2.5.	3.-6. 4. i.	5.—i.	6.4-41.	7.-2-2L
8.-1+1.	9. -cos— + isin —.	10. 1 + cos—+isin—.
7	7	7	7
Запишите в тригонометрической форме следующие числа:
11.3.	12.-5. 13.21. 14.-7Л 15.3+3/.	16.-5+ 5/.
,„l + i 5-/ ,п Л 2л . . 2л
17. --.	18. --.	19. 5 cos-г sin— .
1-/	2-3/	L 3	3 J
Запишите в показательной форме следующие комплексные числа:
20. 1 + /17. 21. -1 + /V3.	22. (1+/7з)3. 23. I-/25.
24. (1-1)3.	25. 4| sin—+ICOS—|.	26. -2 + /2з/з.
V 4	4 J
Докажите следующие равенства:
7U	Ki
27. е2” =1.	28. Л = /.	29.	= -/.
30. Точки Мх, Мг, М3, изображающие соответственно комплекс-
ные числа z,, z2, z3, лежат на одной прямой. Докажите, что отноше-
z2-zl
ние —------ является действительным числом.
г3 -z2
Ответы
1. В тригонометрической форме заданы числа zt,z2,z7. 2. |а| = 5,
arga = 0. 3. |а| = 6, arga = n. 4. |а| = 1, arga = —.	5. |а| = 1, arga=-—.
28
6. |а| = 4л/2, arga = —\ 7. |а| = 2-J2, arga = -
„II,	6л
9.	| а | = 1, arga = —.
10.	|a| = 2cos—.
1 1	14
11.	3(cos0 + zsin0).
л
12.
5 (cos л + i sin л).	13.
{ 7t . 7t |	< л -| f Я I . f Л
2 cos—+ zsin — .	14. 7 cos---+ /sin-----
2 J I I 2 J I 2
2
IS.
„ IZ	Л	. Л )
3V2 cos—+ z sin— .
I	4	4 1
,. . /тГ	Зл	Зл 1
16.	5V2 cos---ь/sin— .
I	4	4 J
17.	cos—+ z'sin—.
2	2
18.
f 2л ]	. \ 2л
19. 5 cos--------+ i sin--------
I ( 3 ) I 3
Я/
2m	-m	3m	-m	-2m
21.	2e~. 22. 8e”. 23 -/2e~. 24. 2^2e”T. 25. 4eV. 26. 4e~.
Вопросы
1.	Что называют модулем комплексного числа?
2.	Что называют аргументом комплексного числа?
3.	Что называют главным значением аргумента комплексного
числа?
4.	Как обозначаются модуль и аргумент комплексного числа?
5.	Как найти модуль комплексного числа а + bi?
6.	Как найти аргумент комплексного числа а + bi?
7.	Что называют тригонометрической формой комплексного
числа?
8.	Каковы особенности тригонометрической формы комплексного
числа?
9.	Чему равны главные значения аргументов чисел: а) действи-
тельных положительных; б) действительных отрицательных; в) мни-
мых Ы (Ь > 0); г) мнимых -bi (b > 0)?
10.	Каковы условия равенства двух комплексных чисел в триго-
нометрической форме?
11.	Как записать тригонометрическую форму числа a = a-bi,
сопряженного числу a = а + bi, если известна тригонометрическая
форма числа а?
12.	Как связаны модули и аргументы двух сопряженных комп-
лексных чисел?
13.	Что называют показательной формой комплексного числа?
14.	Как получена показательная форма комплексного числа?
29
§1.6. Действия над комплексными числами,
заданными в тригонометрической форме
Рассмотрим два комплексных аир, заданных в тригонометриче-
ской форме
а = r(coscp + zsincp), р = р(сояф + /sin\р).	(1.31)
Найдем произведение и частное этих комплексных чисел. Выпол-
няя умножение, получаем
ар = г (cos ср + i sin ср)-р (cosvp + /sin ф) = гр (cos ср cos ф + i cos ср sin ф +
+ i sin ср cos ф - sin ф sin ф) = r p ((coscp cos ф - sin ф sin ф) +
+ i (cos ф sin ф + sin ф cos ф)),
ар = r p (cos (cp + ф) + i sin (ф + ф)).	(1.32)
Получено произведение комплексных чисел а и р в тригонометриче-
ской форме. Из равенства (1.32) следует, что
|ар| = гр, ф + \р = Arg(aP),
т.е. модуль произведения комплексных чисел равен произведению мо-
дулей множителей, а сумма аргументов является аргументом произве-
дения этих чисел.
Предполагая, что Р*0, т.е. р*0, находим частное двух ком-
плексных чисел (1.31):
a _ г (cos ф + / sin ф) _ г (созф + z sin ф)(соз ф — z sin ф) _
Р р(сояф + zsin ф) р(созф +/sin ф)(созф - zsin ф)
г ((созф cos ф + sin ф sin ф) + /(зшф сояф -сояф sin ф)^|
_	-	‘	-	I
COS \|/ + Sin \|/	J
^- = -(cos (ф-ф) + гып(ф-ф)).	(1.33)
₽ Р
Из этой тригонометрической формы частного следует, что
a |«|	. fa'l
— =т—г, ф-ф = Аге — ,
р |р|’ v v Чр/
т.е. модуль частного комплексных чисел равен частному модулей чис-
лителя и знаменателя, а разность аргументов является аргументом ча-
стного этих чисел.
30
Если а = 1 = l(cos O + /sin 0), р = p(cosy + zsin у) и р*0, то фор-
мула (1.33) принимает вид
— = —(cos (0-у) + /sin(0-у)),
Р Р
Р-1 =-j^ = p-1(cos(-y) + /sin(-\p)),	(1.34)
откуда
|р-1| = |р|-1, argP-1 =-argP,
т.е. модуль комплексного числа р ', обратного числу р, равен обратной
величине модуля числа р, а его главное значение аргумента отличается
от главного значения аргумента р только знаком.
Переходим к вопросу о возведении в степень комплексного числа
a = r(cos<p + /sin<p), заданного в тригонометрической форме. Если п-
натуральное число, то с помощью формулы (1.32) получаем формулу
(r(cosq> + /sinq)))” = г” (cos nq> +isinnqj).	(1.35)
Следовательно, при возведении комплексного числа в степень
модуль возводится в ту же степень, а аргумент умножается на показа-
тель степени.
Формула (1.35) верна и для целых отрицательных показателей: по-
скольку а-" = (а-1)”, то достаточно использовать эту формулу для числа
а-1, тригонометрическая форма которого определена формулой (1.34).
Формулу (1.35) называют формулой Муавра. Отметим частный
случай этой формулы: при г = 1 получим
(cosqj + /sin<p)" =cosnqj + /sinnq).
Пусть требуется извлечь корень степени п из комплексного числа а,
т.е. найти такое комплексное число р, что р” = а. Запишем числа аир
в тригонометрической форме a =r(cosq> + /sinq)), р = p(cos0+ /sin0)
и обозначим корень степени п из числа а через Va :
i(/r(cosq) + zsin ф) = р (cos 0 + i sin 0),	(1.36)
r (cos q> + i sin q>) = (p (cos 0 + i sin 0))"
31
В соответствии с формулой (1.35) получаем
r(cosq> + /sinq)) = р" (cos пв + isinn0),
откуда
р"=г, «0 = ф + 2Лл (к = 0,±1,±2,...)
или
г = ц[р, 0= Ф + 2Н (£ = 0, ±1,±2,...).
п
(1-37)
Таким образом, определены модуль р и аргумент 0 числа 0 - корня
и-ой степени из числа а. Следовательно, формула (1.36) принимает вид
г—---------—г пг( Ф + 2&Т1 . . ср + 2АтсЛ
wr(cosф +1sinф) =>/г cos--------+ isin------- ,	(1-38)
( п	п )
где у[г - арифметическое значение корня, к - любое целое число.
Придавая к значения к = 0, 1,2,..., п - 1 получаем п значений корня:
(1-39)
г, пг( ф + 2(и-1)л . . ф + 2(и-1)л')
Р„_] =vr COS-!----i----—-l-lSin —--i----L—
<	П	П J
Докажем, что среди этих значений корня нет одинаковых. Пусть р
и q- любые разные числа из системы чисел 0, 1,2, ...,w- 1, тогда
Ф + 2рт1 ф + 2<з л p-q „
—---------------=-------2 л.
п	п п
Поскольку ——— не является целым числом, то число ——— 2л
п	п
не будет кратным 2л, т.е. комплексные числа
( ф + 2»л	. ф + 2»л^ „г-f ф + 2«л . . ф + 2«л'1
-V г cos —--+1 sm  ---- , vr cos —---+1 sin  --—
In	n )	\ n	n )
32
являются различными, ибо разность их аргументов не является числом
кратным 2л (см. формулы (1.28) и (1.29)).
Предположим, что к - любое целое число; пусть к = nq + s, где
О < s < п -1, тогда
Ф + 2£л _ ф + 2(л<7 + .у)7г _ ф + 2.У7г
п	п	п
т.е. при этом к значение аргумента отличается от значения аргумента
при к = s на число, кратное 2л. Следовательно, при этом значении к
получаем такое значение корня, как и при к- s.
Итак, извлечение корня л-ой степени из комплексного числа все-
гда возможно и дает п разных значений по формулам (1.38). Из этих
формул следует, что все п значений корня л-ой степени из числа а
расположены на окружности радиуса | а | с центром в начале коор-
динат и делят эту окружность на л равных частей.
Отметим, что корень л-ой степени из действительного числа а
также имеет л различных значений; действительных среди этих значе-
ний будет два, одно или ни одного, в зависимости от знака а и четно-
сти числа л. Корень л-ой степени из нуля имеет только одно значение
равное нулю: >/о = 0.
Пример 1. Найти значения квадратного корня из числа
.( л . . л
а = 4 cos— +1 sin —
I 4	4
Решение. В соответствии с формулами (1.39) находим
л . . лЛ t—(	id 4 +7. к и . . л/4+2£лЛ
4 cos— + isin — = V4 cos—---+ isin —----- , к = 0,1.
I 4 4J I 2	2 J
При к = 0 получаем
Р„ = 2| cos— + /sin —
I 8	8
при к - 1 - второе значение корня
n J 9л . . 9л)
Pi =2 cos—— + isin ——— = — Pq
о	о J
2 Зак. 1816
33
Пример 2. Найти значения квадратного корня из числа а = I.
Решение. Сначала представим это число в тригонометрической
Л л
форме: / = cos—+/sin —. На основании формул (1.39) получаем
г I	л	. . л	л/2+2кл	. л/2+2кл
Ji =, cos— + /sin— = cos-----+ /sin--------, к = 0,1.
V	2	2	2	2
Следовательно,
„ л . . л Л .Л „	5л. .5л
Вп = cos—+ /sin —=-+ /—, В, =cos— + /sin — = -p0.
po 4	4	2	2	1	4	4
Пример 3. Найти значения кубического корня из числа
Зл . Зл)
а = 27 cos— +1 sin — .
14	4 J
Решение. В соответствии с формулами (1.39) получаем
Г ( Зл . Зл') -./—ГсозЗл/4 + 2Лл .sin3n/4 + 2fat'|
з 27 cos— + /sin— =v27 ---------------+ /------------ ,
V к 4	4 J V 3	3	)
A = 0,1,2.
Придавая к значения 0, 1,2, находим три значения корня кубиче-
ского из данного числа:
„	( Л . я) „	Пл . . 11 л Л
Вп = 3 cos— + /sin— ; В, = 3 cos-+ /sin-- ;
но V 4	4/ V 12	12 J
„	„(	19л . . 19л^
В? = 3 cos--+/sin-- .
H2 I 12	12 J
Пример 4. Найти значения корня кубического из числа-8.
Решение. Представим это число в тригонометрической форме
-8 = 8(cos л + /sin л) и применим формулы (1.39):
-------------------—г л+2кл . . л + гЛлА , „ , „
V-8 =у18 (cos л + i sin л) =21 cos—-— + /sin—-—I, к =0,1,2;
| Л Л ] Г"
Ро =21 cos—F/sin— =1 + /V3; Р] =2(созл + /5тл) = -2;
34
р2 =21 cos— + zsin — | = 1-/л/з.
I 3	3 J
Пример 5. Найти значения корня 6-й степени из числа -64.
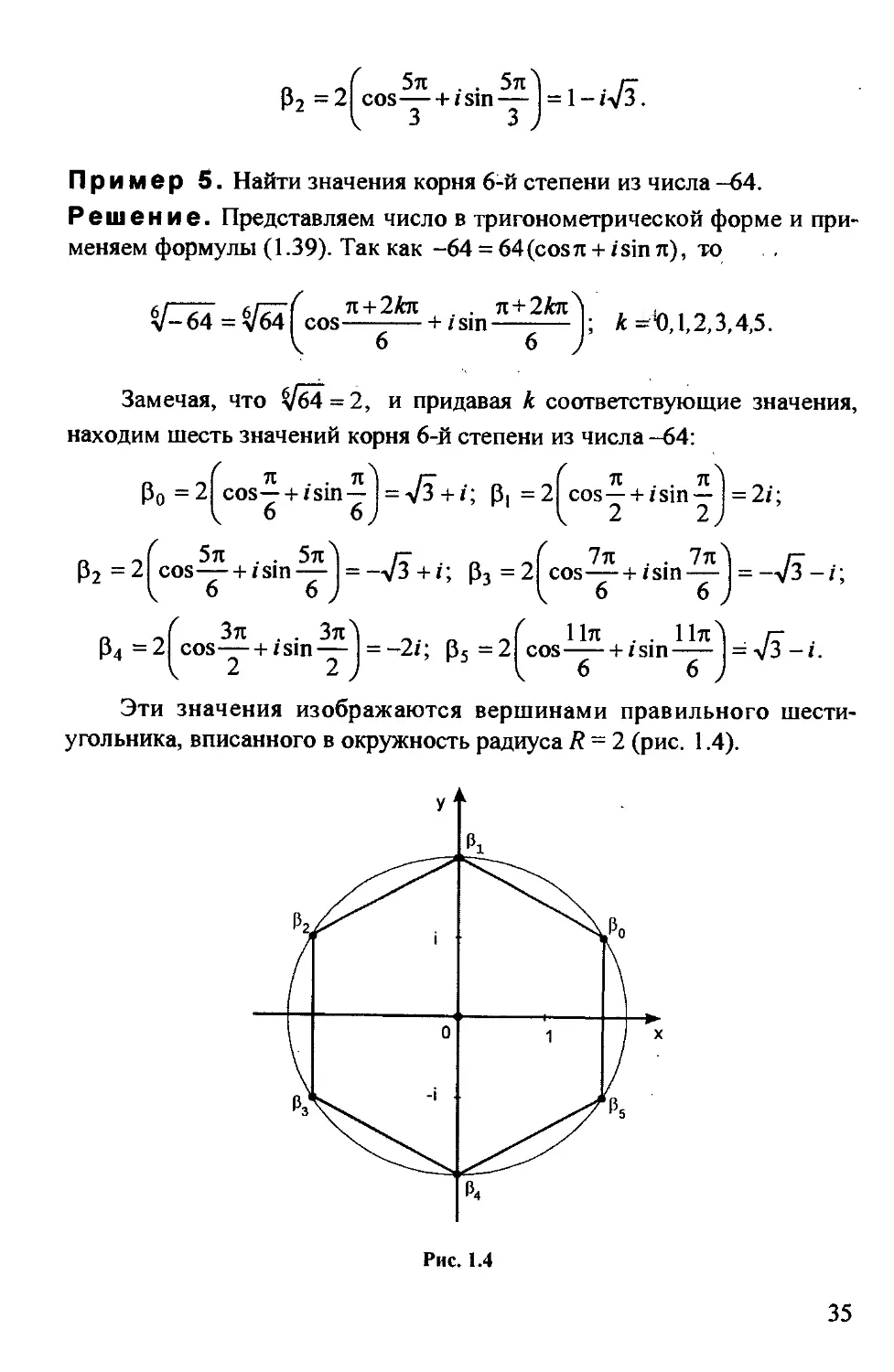
Решение. Представляем число в тригонометрической форме и при-
меняем формулы (1.39). Так как -64 = 64(cosл+zsin л), то
л/	।	л + 2Лл	. Л"Ь 2/ciz ।	«а.
V-64 = V64 cos--+ zsin----- ; к -'0,1,2,3,4,5.
<6	6 )
Замечая, что ^64 = 2, и придавая к соответствующие значения,
находим шесть значений корня 6-й степени из числа -64:
Во = 2 cos— + zsin — = л/з +z; В. = 2 cos — + zsin — = 2z;
°	<	6 6J HI<2 2 J
B2 =2| cos— + zsin— | = —Уз +z; B3 =2| cos— + zsin—1 = —Уз-z;
H2<6	6 J	H3 V 6	6 J
( Зл . . 3л)	( Пл . . Пл) . /- .
В4 =2 cos—+zsin— =-2z; В, =2 cos-+ zsin- = V3 -z.
<2	2 )	H5<6	6 )
Эти значения изображаются вершинами правильного шести-
угольника, вписанного в окружность радиуса R = 2 (рис. 1.4).
35
Пример 6. Доказать, что cos2q> = cos2q> - sin2cp, sin2cp = 2sinqjcosq).
Решение. В формуле (1.35) положим г = 1, п = 2, тогда
(coscp + sincp)2 = cos2q> + /sin2q).
Так как
(cosф + isin ф)2 = cos2 ф + 2г'5!пфС05ф + /2 sin2 ф =
= cos2 ф-sin2 ф +2/5тфС05ф,
то
соз2ф + isin2ф = (cos2 ф-sin2 ф) + /251'пфсо5ф,
откуда
соз2ф = cos2 ф-sin2 ф, зт2ф = 2sinфсозф.
Пример 7. Доказать, что верны следующие равенства:
1) созЗф = cos3 ф-Зсозфзт2 ф, sinЗф = 3cos2 sin ф — sin3 ф;
2) созЗф = 4cos3 ф —Зсозф, зтЗф = Ззтф-Дзт3 ф.
Решение. Полагая г = 1, и = 3 в формуле (1.35), получаем
(созф + i sin ф)3 = созЗф + i sin Зф.
Поскольку
(сО5ф + Zsin ф)3 = cos3 Ф + /ЗСО52 ф5Щф + г2ЗС05ф5Щ2 ф +
+ z3 sin3 ф = cos3 ф-3со5ф5т2ф + i(3cos2 фзт ф-sin3 ф),
то
созЗф + zsinЗф = cos3 ф — Зсозф sin2ф + z(3cos2 фвтф-эт3 ф),
откуда
созЗф = cos3 ф —Зсозф sin2 ф, зтЗф = 3cos2 фзт ф-sin3 ф.
Первые два равенства доказаны. Преобразуя эти равенства, полу-
чаем
созЗф = cos3 ф —Зсозф (1 - cos2 ф) = cos3 ф -Зсозф + 3cos3 ф,
sinЗф = 3sin ф (1-sin2 ф)-sin3 ф = 3sin ф-Ззт3 ф-sin3 ф.
Таким образом, получены следующие равенства:
со53ф = 4со53 ф-Зсозф, sinЗф = 3sinф — 4sin3 ф.
36
Задачи
Найдите произведение двух комплексных чисел:
Г~( Л . Л | „ rzl Л . . л
1.	a=V2 cos—-t-zsin— , B = 3V2 cos—+zsin —
I 15	15/	{5е
~	.( Л . . Л^ _ „ Г Л , . . Л
2.	a = 4 cos—+ ism — , В = 2 cos—+ism—
I 7	7 J I 21	21
Найдите частное — двух комплексных чисел:
„	л	..	лУ	„	-(	л . .л
3.	a = 15 cos—Hsin— , В = 3 cos—i-isin—
I	3	3)	I	4	4
(	Л	.	лА	„	. (	Л	. . Л
4.	a = 12 cos— + isin — , B = 4 cos—+isin—
I	4	4)	{.	12	12
Возведите а указанную степень каждое из данных комплексных
чисел:
Z ,	ч хЗ
- J 71 • • Л ]
5.	4 cos—+ z sin —
3	3 J J
Z ,	4x5
_ I f- (	Л ..ЛИ
7. у2 cos— + zsin—
I I	5	5))
z ,	x.	\-3
„ I „ ( Л . . Л I )
9. 2 cos— + zsm —
ll 5	5)
Z z	W4
z „ I - | Л . Л
10. 3 cos— + z sin—
I I 8	8J J
Найдите значения корня указанной степени из данных комплекс-
ных чисел:
И. J9|cos—+ zsin—|. 12. з18| cos—+ /sin—|. 13. l/-2 + 2i.
v V 4	4J V I 4	4 )
14.	V7.	15.	16. tfl + l. 17. tf-i.
Докажите, что верны следующие равенства:
18.	cos4<p = cos4 <p +sin4 <p-6sin2 <pcos2 <p;
sin 4<p = 4 cos3 <p sin <p - 4 cos ф sin3 ф.
19.	соз4ф = 8со54ф-8со52ф + 1;
Sin 4ф = 45ЩфСО5ф-85П13 фСО5ф.
20.	(a2 +b2)(c2 +d2) = (ac-bd)2 +(ad + bc)2 для комплексных
чисел a = a + bi, fi = c + di.
37
Ответы
Г	4тг	4тг ।	Г	4л	4л 1	(	л	л I
1. 6 cos—+i'sin— . 2. 8 cos— + isin— . 3. 5 cos—+ zsin— .
I	15	15 J	I	21	21J	I	12	12j
4. 3|cos—+z'sin—|. 5.-64. 6.-25. 8.-27. 9. — I cos(-— | + zsin|- — |
( 6	6 J	5 }	{ 5 )
i it	it ।	। Oir	Oir i	i it	it
11.	3 cos—+ zsin— ,	3 cos— + zsin— .	12. 2 cos—+ z sin—
18	8 J I 8	8 J	14	4
~ |	11л . . 11л ]
2 cos-----+ zsin---- ,
V 12	12 J
„ (	19л . . 19л]
2 cos--+ zsin- .
112	12 J
Зл/4+2Лл . Зл/4 + 2Ы^	, n , _
---------+1 sin--------- , к = 0, 1, 2.
4	4 J
15. ±^-(l + z),
Вопросы
1.	Запишите формулу для произведения двух комплексных чисел,
заданных в тригонометрической форме.
2.	Чему равен модуль произведения двух комплексных чисел?
3.	Что является аргументом произведения двух комплексных
чисел?
4.	Запишите формулу для частного двух комплексных чисел, за-
данных в тригонометрической форме.
5.	Чему равен модуль частного двух комплексных чисел?
6.	Что является аргументом частного двух комплексных чисел?
7.	Запишите тригонометрическую форму для числа 0 ', обратного
числу 0 = р (cosy + zsin у).
8.	Каковы соотношения между модулем и аргументом двух вза-
имно обратных комплексных чисел 0 и 01?
9.	Запишите формулу Муавра.
10.	Какой вид имеет формула Муавра при г = 1?
11.	Как извлекается корень л-ой степени из комплексного числа в
тригонометрической форме?
12.	Сколько значений имеет корень л-ой степени из комплексного
числа?
13.	Запишите п различных значений корня л-ой степени из ком-
плексного числа в тригонометрической форме.
14.	Как геометрически изображаются различные значения корня
л-ой степени из комплексного числа в тригонометрической форме?
38
§1.7. Корни из единицы
Рассмотрим важный случай извлечения корня, а именно извлечения
корня л-ой степени из числа 1. Как уже отмечалось (см. §1.6), корень
л-ой степени из действительного числа а имеет л различных значений.
Представляя число 1 в тригонометрической форме 1 =cosO + zsinO и
применяя формулу (1.38), получаем л значений корня из единицы
„г~ 2кп . . 2кп ,, „ . „	,,
a/1=cos----+ zsin---, (к = 0,1,2,...,л —1).	(1-40)
л	л
На комплексной плоскости корни л-ой степени из единицы изо-
бражаются точками, расположенными на окружности радиуса R = 1 и
делящими ее на л равных дуг; одной из таких точек будет точка, изо-
бражающая число 1. Точки, изображающие комплексные корни л-ой
степени из единицы, расположены симметрично относительно дейст-
вительной оси, т.е. попарно сопряжены.
Теорема 1.1. Все значения корня л-ой степени из комплексного
числа а можно получить умножением одного из этих значений на все
значения корня л-ой степени из единицы.
Корни л-ой степени из единицы обладают следующими свойствами.
1.	Произведение двух корней л-ой степени из единицы также яв-
ляется корнем л-ой степени из единицы.
2.	Число, обратное корню л-ой степени из единицы, является кор-
нем л-ой степени из единицы.
3.	Любая степень корня л-ой степени из единицы есть также ко-
рень л-ой степени из единицы.
4.	Всякий корень Л-ой степени из единицы является также корнем
/-ой степени из единицы для любого /, кратного к.
Корень степени л из единицы называется первообразным, если
все его степени от первой до (л - 1 )-ой отличны от единицы.
Теорема 1.2. Корень л-ой степени из единицы тогда и только то-
гда будет первообразным, если его к-е степени, где к = 0, 1, 2, ..., л - 1
различны.
Теорема 1.3. Если е- первообразный корень л-ой степени из еди-
ницы, то число е тогда и только тогда будет первообразным корнем,
когда числа Аил взаимно просты.
Число первообразных корней л-ой степени из единицы равно
числу целых положительных чисел к, меньших л и взаимно простых с
ним. Если р - простое число, то первообразными корнями р-ой степе-
ни из единицы будут все эти корни, кроме самой единицы.
39
Пример Т. Найти все значения кубического корня из единицы. Ка-
кие из этих корней являются первообразными?
Решение. В соответствии с формулой (1.40) получаем .
з /7”	2Ал . . 2Ал . л 1 о
Vl = cos---+zsm-----, к = 0,1,2.
3	3
Придавая к указанные значения, находим:
_	. „ ,	2л	. 2л 1 .л/з
£n = cos0 +zsin 0 = 1; в, = cos— + zsin—=— + z —;
°	1	3	3	2	2
4л . . 4л
е7 = cos— + zsin—=
2	3	3
.л/з
z----.
2
2
2
Поскольку р - простое число, то корни Е] и е2 являются первооб-
разными.
Пример 2. Найти все значения V--8, если известно одно из них,
равное -2.
Решение. Принимая во внимание теорему 1.1 и результаты приме-
ра I, получаем два других значения:
-2Е] = 1-/>/з, -2е2 = 1 + z'a/з.
Пример 3. Найти все значения корня четвертой степени из едини-
цы. Какие из этих корней являются первообразными?
Решение. На основании формулы (1.40) получаем
!Лл . 2Лл ,	„ , „ „
— + zsm—, к =0,1,2,3.
4	4
Придавая к указанные значения, находим:
2тт 7Т 71
Ел =cosO + zsmO = l; е, =cos— + zsin— = cos— + zsin— = z;
0	1	4	4	2	2
6л . . 6л Зл . . Зл
£-> =СО5Л + г51НЛ=-1; е-. =cos— + zsin — = cos — -i-zsin — = —z.
2	4	4	2	2
Принимая во внимание теорему 1.2, заключаем, что первообраз-
ными корнями будут корни Е] = z и е2 = -z (так как только их к-е сте-
пени, где Л = 0,1,2,3, различны).
40
Задачи
1.	Докажите, что первые три степени каждого из чисел
1	• ^3	1	2	3 /	2	3 \
Е] =-—+ z-^-, е2 =	те- числа £, , £, , £, (ие2, е2, е2)
исчерпывают все множество значений V?.
2.	Докажите, что первые четыре степени каждого из чисел в, = i
.	2 Ч 4 z	23 4ч
и е2 = -I, т.е. числа , £j , е,,	(иб2, £2» £г> £г) исчерпыва-
ют все множество значений д/1 •
Найдите все значения корня указанной степени из единицы:
3.	V1.	4, V1- 5. VF. 6. V1. 7. VI. 8. ’V1.
Найдите все значения корня указанной степени из данного числа,
если известно одно из них:
9. V-27, е = -3. 10. ^^64, е = -4.	11. ^^32, е = -2.
12.	V-243, е = -3.
Решите уравнения и изобразите на чертеже их корни:
13.	z2+4 = 0.	14. z3+8 = 0. 15. z4+64 = 0.
16.	z5+32 = 0.	17. z6+1 = 0.	18. z6+64 = 0.
19.	z7 +128 = 0.	20. z8+l = 0.
Ответы
>. vl = COS---+isin ,
5	5
к =0,1,2,3,4;
Eq = cos0 + zsin0=l;
2л . . 2л e, =cos—+isin—, 1	5	5	4л . . 4л в, =cos—+zsin	,	E, 5	5	3.	6л . . 6л = cos—+zsin—, 5	5
8л . . 8л e4 = cos— + I sin—, 5	5	6r	2fcn . 2fai 4. vl =cos	+zsin	, 6	6	k = 0,1,2,3,4.5,
£0 = cosO + zsinO = l;	л . . л	1 з/з e, =cos— + zsin—=—+—t, 3	3	2	2	2л e2 =cos—+ 3
. . 2л	1 -A + isin— =	+	z, 3	2	2	£3 = cos л+z'sin л =—1,	e4 =	4л . . 4л cos—+zsin— = 3	3
1 -Л.	5л 2 2s	3	. 5л 1	_ 4-ZSin—=	1. 9. E=-3, 3 2	2	3(1-,УЗ) 1	2
41
е2 = 3О+и/з) 13	= 2j; z_,=_2. 14 Z( = _2< Z2=\-i4i, z, = i+14/3,
л/з 1 . . л/з 1 .	>/з 1 . . л/з 1 .
17- Т+Г’ ’’ ~^+ 21’	-2~2г-
Вопросы
1.	Сколько различных значений имеет корень и-ой степени из
единицы?
2.	Запишите формулы для п различных значений корня и-ой сте-
пени из единицы.
3.	Как геометрически изображаются различные значения корня п-
ой степени из единицы?
4.	Как можно получить все значения корня и-ой степени из комп-
лексного числа посредством значений корня и-ой степени из единицы?
5.	Каковы свойства корней и-ой степени из единицы?
6.	Какие корни н-ой степени из единицы называются первообраз-
ными?
7.	Каково необходимое и достаточное условие того, что корень и-ой
степени из единицы является первообразным?
8.	Чему равно число к первообразных корней и-ой степени из
единицы?
9.	Сколько будет первообразных корней р-ой степени из единицы,
если р - простое число?
§1.8. Геометрическое истолкование
арифметических действий
над комплексными числами
Обратимся снова к комплексной плоскости, каждая точка z кото-
рой изображает комплексное число z=x+ iy. Отметим, что число -z,
противоположное числу z, изображается точкой, симметричной точке z
относительно начала координат. Ведем в рассмотрение радиус-вектор
Oz, точки z и выясним геометрический смысл сложения, вычитания,
умножения и деления комплексных чисел.
Теорема 1.4. При сложении комплексных чисел радиус-векторы
соответствующих точек складываются.
Действительно, если комплексное число Z] = X] + /у], изображает-
ся точкой с координатами (х„ у}), а число z2 = х2 +iy2 - точкой с
42
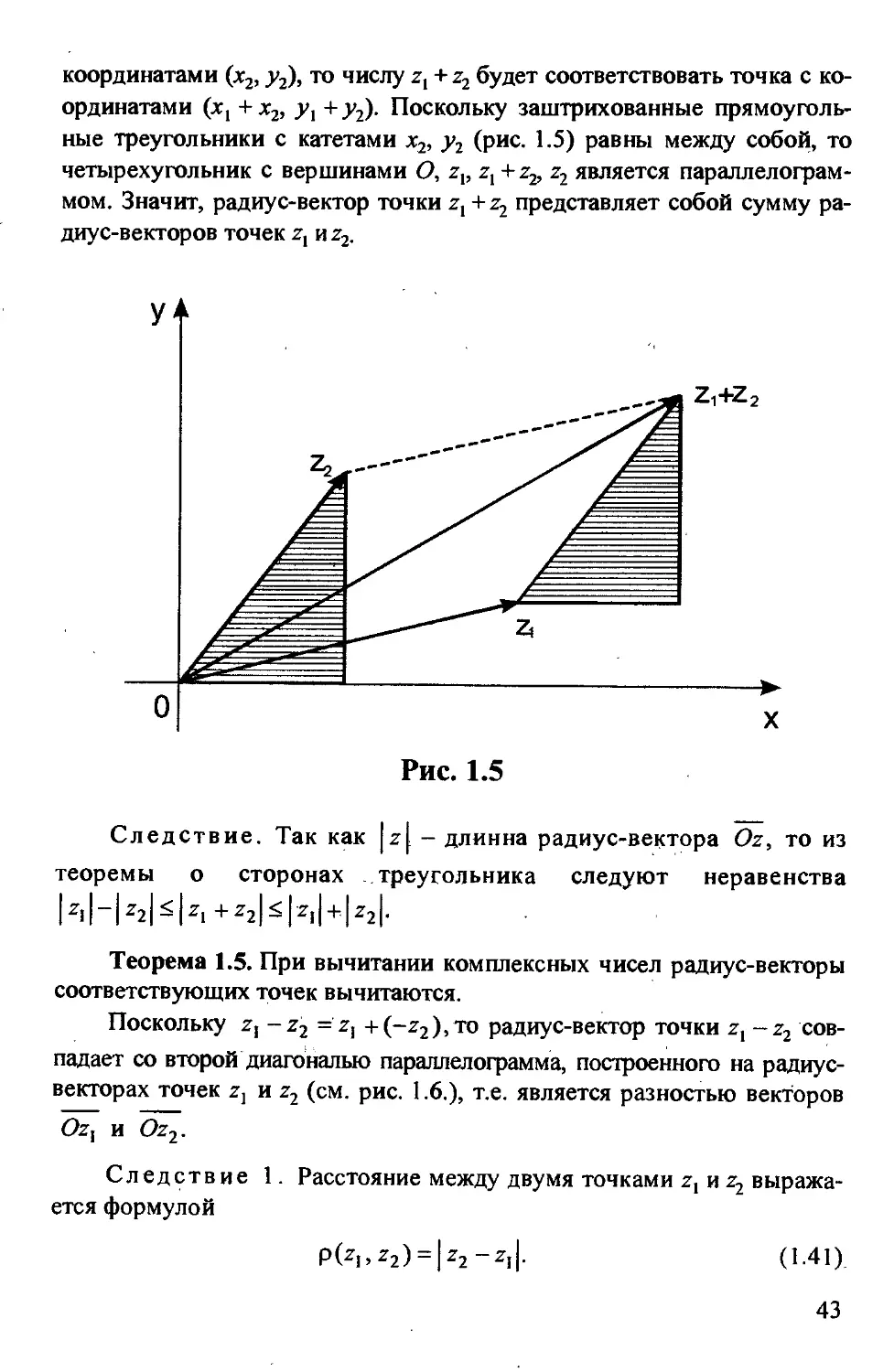
координатами (х2, у2), то числу z1 + z2 будет соответствовать точка с ко-
ординатами (Xj + х2, yt +у2). Поскольку заштрихованные прямоуголь-
ные треугольники с катетами х2, у2 (рис. 1.5) равны между собой, то
четырехугольник с вершинами О, z1; z1 + z2, Z2 является параллелограм-
мом. Значит, радиус-вектор точки z, + z2 представляет собой сумму ра-
диус-векторов точек z1 иг2.
Следствие. Так как |z| - длинна радиус-вектора Oz, то из
теоремы о сторонах треугольника следуют неравенства
Ы-ЫФ1+г2|ф1| + Ы-
Теорема 1.5. При вычитании комплексных чисел радиус-векторы
соответствующих точек вычитаются.
Поскольку Z] -z2 = Z] +(-z2),to радиус-вектор точки z1 — z2 сов-
падает со второй диагональю параллелограмма, построенного на радиус-
векторах точек Zj и z2 (см. рис. 1.6.), т.е. является разностью векторов
Ozt и Oz2.
Следствие 1. Расстояние между двумя точками z{ и z2 выража-
ется формулой
p(z,,z2) = |z2-z,|.	(1.41)
43
Следствие 2. Поскольку |-z2| = |z2| и z}-z2 = z} + (-z2), то
ki|-k2|^k,-г2|<|г|| + |г2|.
Выясним геометрический смысл умножения и деления комплекс-
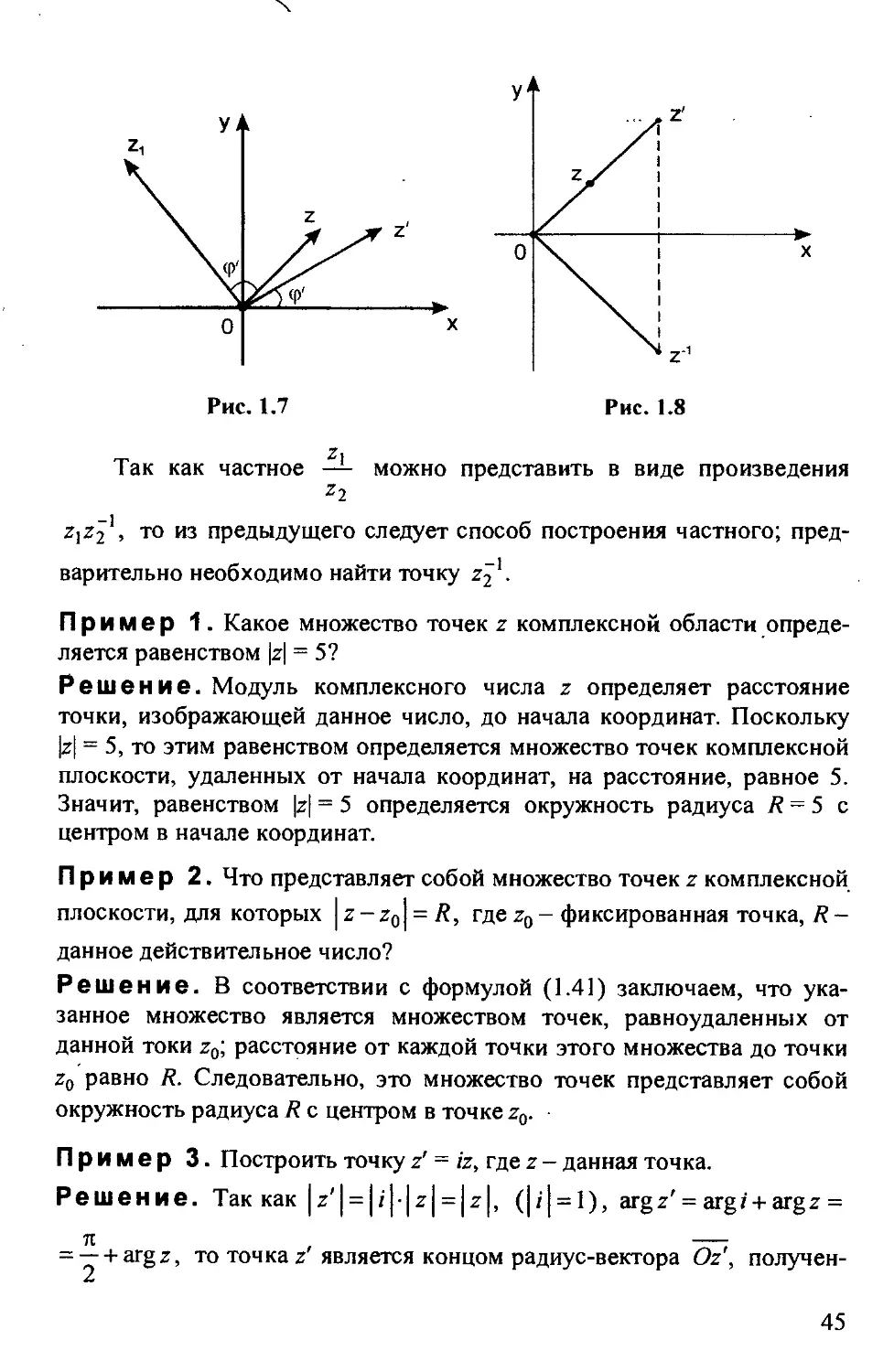
ных чисел. Модуль и аргумент произведения комплексных чисел
z = r(cos(p + /sinq>), z' = r'(cos(p'+zsin(p') определяются соответст-
венно формулами Jzz'l = rr', ф + ф' = Arg(zz'). Пусть точки z и z', изо-
бражающие эти числа, Оги Oz — соответствующие радиус-векторы
(рис. 1.7). Направленный отрезок Oz повернем вокруг точки О против
движения часовой стрелки на угол q>' = argz', а затем растянем его в
г' - |z'| раз (при 0 < г' < 1 это будет сжатие, а не растяжение); получим
направленный отрезок Ozx. Конечная точка z} этого отрезка будет
служить изображением произведенияzz' комплексных чисел z иг'.
Формулы |z*'| = |z| ’, argz'1 = -argz (см. §1.6) позволяют по-
строить точку z-1, изображающую число, обратное числу г. Эту точку
можно построить следующим образом. От точки z перейдем к точке г',
лежащей на расстоянии г-1 (г=|г|)от нуля на том же луче, выходя-
-1
щим из точки О, что и точка г, а затем перейдем к точке z , симмет-
ричной точке z' относительно действительной оси (рис. 1.8).
44
„ z\
Так как частное — можно представить в виде произведения
*2
Z]Z2*, то из предыдущего следует способ построения частного; пред-
варительно необходимо найти точку z^} 
Пример 1. Какое множество точек z комплексной области опреде-
ляется равенством |z| = 5?
Решение. Модуль комплексного числа z определяет расстояние
точки, изображающей данное число, до начала координат. Поскольку
|z| = 5, то этим равенством определяется множество точек комплексной
плоскости, удаленных от начала координат, на расстояние, равное 5.
Значит, равенством |z| = 5 определяется окружность радиуса R = 5 с
центром в начале координат.
Пример 2. Что представляет собой множество точек z комплексной
плоскости, для которых | z -z0| = R, где z0 - фиксированная точка, R -
данное действительное число?
Решение. В соответствии с формулой (1.41) заключаем, что ука-
занное множество является множеством точек, равноудаленных от
данной токи z0; расстояние от каждой точки этого множества до точки
z0 равно R. Следовательно, это множество точек представляет собой
окружность радиуса R с центром в точке z0.
Пример 3. Построить точку z' = к, где z — данная точка.
Решение. Так как |z'| = |z|-|z| = |z|, (|z| = l), argz' = argz + argz =
л	—
= y + argz, то точкам является концом радиус-вектора Oz , получен-
45
ного вращением Oz вокруг точки О на прямой угол в направлении
против движения часовой стрелки (рис. 1.9).
Задачи
Приведите геометрическое описание всех точек z комплексной
плоскости, удовлетворяющих соответствующему соотношению:
1. |z| = 3.	2. |z|<7.	3. |z|>5.	4. |z-2| = 3.
5. |z-l-z| = 8.	6. |z-z0| = 5.	7. |z-z0|</{. 8. |z-z0|</J.
9. |z-z0|>/?.	10. |z-z0|>7?. 11. 3 <|z—ij < 5.
12. Л] <|z-z0|< R2.	13. /?, <|z-z0|<tf2.
14. |z-z|<2.	15. |z-z| = |z-l|.
16. | z-Zj | = | z-z2|.	17. 11+z | <| l-z|.
1	1	z—2	z—1
18.	Re- = -.	19. Re—= 0.	20. Im—= 0.
z 3	z+2	z+1
21.	Постройте точку z' = -zz, где z - данная точка.
22.	Докажите, что для произвольных комплексных чисел zx и z2
выполняется тождество |zj +z2|2 +|zj -z2|2 = 2(jz]|2 + |z2|2 j. Выясните
геометрический смысл этого тождества.
23.	Даны три вершины параллелограмма z,, z2, z3. Найдите четвер-
тую вершину z4, противоположную вершине z2.
46
Ответы
1.	Окружность радиуса R = 3 с центром в начале координат. 2. Круг ра-
диуса R = 7 с центром в начале координат. 3. Множество точек, лежащих вне
круга радиуса R = 5 с центром в начале координат (точки окружности - грани-
цы этого круга - данному множеству не принадлежат). 4. Окружность радиуса
R - 3 с центром в точке z0 = 2. 5. Окружность радиуса R = 8 с центром в точке
z0 = 1 + I. 8. Круг радиуса R с центром в точке z0. 11. Кольцо между двумя ок-
ружностями радиусов R{ = 3, R2 = 5 с центром в точке z0 = 1 (точки этих ок-
ружностей исключаются). 15. Прямая, перпендикулярная к отрезку с концами
в точках z, = i, z2 = 1 и проходящая через его середину. 16. Прямая, перпенди-
кулярная к отрезку с концами в точках z,, z2 и проходящая через его середину.
17. Полуплоскость, лежащая слева от мнимой оси. 18. Окружность, построен-
ная на отрезке [0; 3] как на диаметре. 19. Окружность радиуса R = 2 с центром
в точке z = 0. 20. Действительная ось. 23. z4 = zl+z3- z2.
Вопросы
1.	Как изображается геометрически комплексное число z = x+ iyl
2.	Как геометрически изображается число -z, противоположное
числу z?
3.	Что называют радиус-вектором точки z?
4.	Что геометрически означает сумма двух комплексных чисел z1
и z2?
5.	Докажите неравенства | Z] |—| z21 < | Z] -ь z21 < | zj 14-1 z21.
6.	Что геометрически означает разность двух комплексных чисел
Zj и z2?
7.	По какой формуле определяется расстояние между двумя точ-
ками Zj и z2?
8.	Докажите неравенства | z} | -1 z21 < | z} - z21 < | z} | +1 z21.
9.	Как построить точку, изображающую произведение двух ком-
плексных чисел?
10.	Как построить точку z ’, изображающую число, обратное чис-
лу z (z 10)?
11.	Как построить точку, изображающую частное — двух ком-
г2
плексных чисел?
47
Гпава 2.
Элементы теории функций
комплексной переменной
Методы теории функций комплексной переменной находят ши-
рокое применение при решении важных практических проблем. Сред-
ствами этой теории, в частности, доказана теорема о подъемной силе
крыла самолета.
§2.1. Понятие функции комплексной переменной.
Предел и непрерывность
Комплексное число z = x + iy, где х, у - действительные числа, i -
мнимая единица (/ = з/-Г) изображается на комплексной плоскости
точкой с координатами (х, у).
Множество называется связным, если две любые его точки можно
соединить непрерывной кривой, все точки которой принадлежат этому
множеству. Связное открытое (не содержащее границу) множество
называется областью.
Пусть D— область комплексной плоскости С. Если каждой точке
z е D по определенному правилу f поставлено в соответствие единст-
венное комплексное число w = и + iv, то говорят, что в области D оп-
ределена однозначная функция комплексной переменной z = x+ iy, и
пишут w =J(z), z е D. Функцию w =J{z) =J[x + iy), можно рассматри-
вать как комплексную функцию двух действительных переменных х и
у, определенную в области D. Задание такой функции равносильно за-
данию двух действительных функций и= и(х,у), v = v(x,y), (х,у) е D,
w = и + iv. Таким образом, если z = х + iy, w = и + iv, то
w =fiz) = и(х, у) + /г(х, у).	(2.1)
Комплексное число с называется пределом однозначной функции
w =fiz), при z —> а, если для всякого числа е > О существует такое чис-
ло 8 > О, что из неравенства |z - а| < е следует неравенство
]/(z)-c|<£.	(2.2)
В этом случае пишут lim f (z) = с.
z—>a
Функция w =fiz) называется непрерывной в точке z0, если
lim/(z) = /(z0).	(2.3)
48
Функция, непрерывная в каждой точке некоторой области D на-
зывается непрерывной в этой области.
Область D называется односвязной, когда она ограничена замкну-
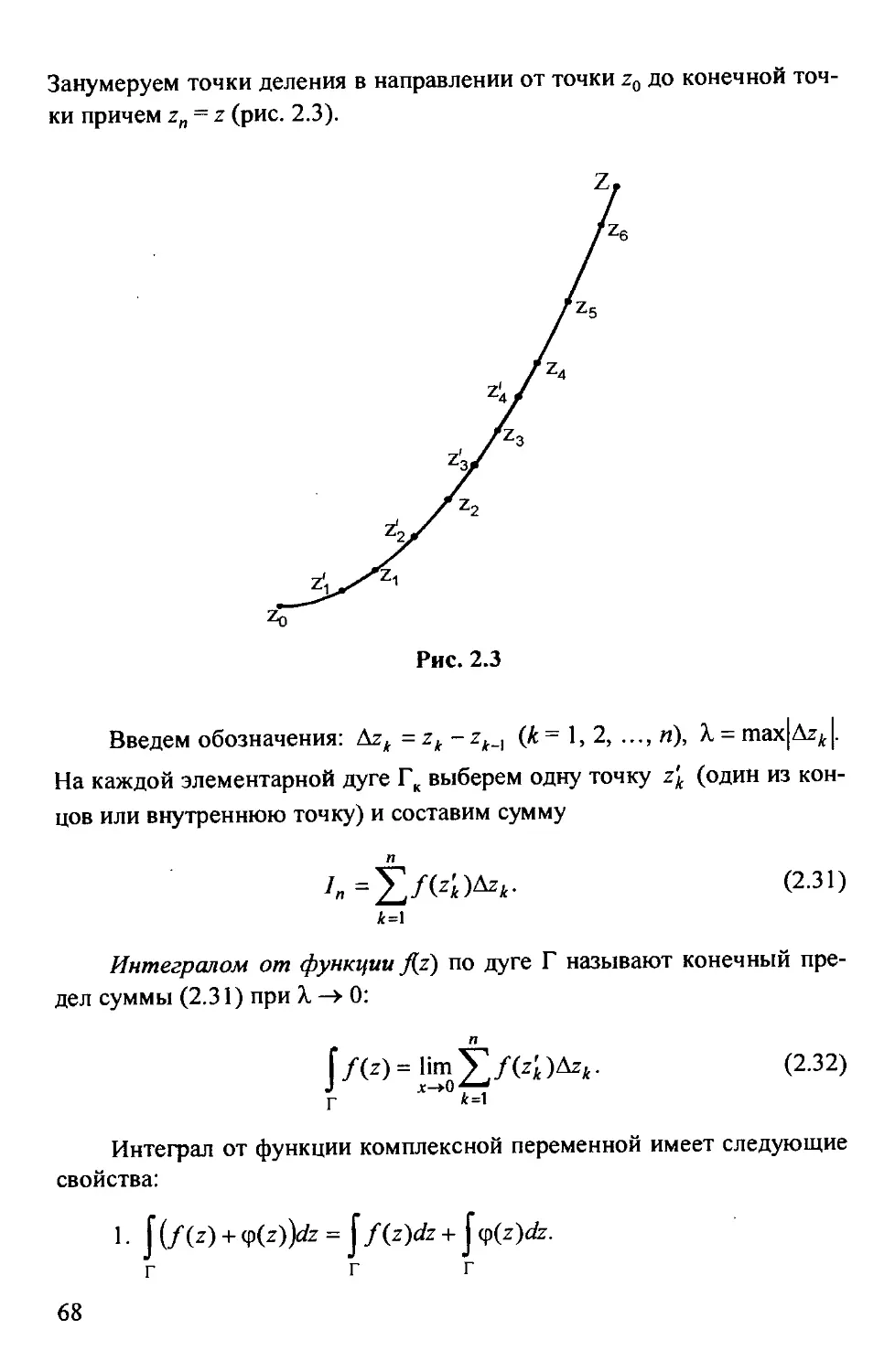
той линией Г, не пересекающей себя (рис. 2.1). Область D называется
двусвязной, когда она ограничена двумя замкнутыми линиями Г, и Г2,
которые не пересекаются и каждая не пересекает себя (рис. 2.2); внут-
ренняя линия Г2, в частности, может вырождаться в точку или в дугу
непрерывной линии. Аналогично определяются трехсвязная, четырех-
связная и т.д. области.
Рис. 2.1	Рис. 2.2
Замечание. Если существуют значения z е D, каждому из которых
поставлено в соответствие несколько значений w, то функция w ~flz) называ-
ется многозначной.
Пример 1. Найти значение функции^) = z + 3z2 - 5z + 9 при z = 1 - i.
Решение. Поскольку (1 -z)2 = 1 - 2z + z2 = 1 — 2z — 1 = —2/,
(1 - 0’ = О - 02 О - 0 = -21 (1 - i) = -2z + 2z2 = -2 - 21, to
/(l-z) = -2-2z+3(-2z)-5(l-z)+9 = -2-2z-6z-5 + 5z+9 = 2-3z.
Пример 2. Доказать, что число z= 1-z является корнем уравнения
z3 + 3z2 -8z + 10 = 0.
Решение. Так как (1 -z)2 = -2z, (1 -z)3 = -2 -2z (см. пример 1), то
(1-z)3+3(l-z)2-8(l-z) + 10 =-2-2z+3(-2z)-8(l-z) + 10 =
= -2-2z-6z-8 + 8z +10 = 0 + Oz = 0.
Это означает, что число z = 1 - z есть корень данного уравнения.
49
Пример 3. Найти значения функции fiz) = z -2z + 5z при сле-
дующих значениях аргумента: 1) z = z; 2) z = 1 - z; 3) z - 2 + i.
Решение. Принимая во внимание значения степеней мнимой еди-
ницы (см. формулы (1.19)) получаем:
f (j) = i3 - 2i2 + 5z = -i + 2 + 5i = 2 + 4/.
Поскольку
(1 - z)2 = -2z, (1 - z)3 = -2 - i (см. пример 1),
то
/(1 - z) = (1 - z)3 - 2 (1 - z)2 + 5 (1 - z) = -2 -2z - 2(-2z) + 5 - 5/ =
= -2-2z + 4z + 5-5z =3-3z.
Далее
7(2 + z) = (2 + z)3 -2(2 + z)2 + 5(2 + /) =
= 23 +3-22z+3-2z2+z3 - 2(4 + 2z+z2) + 5(2 + z) =
= 8 + 12z+6z2+z3-8-8z-2z2+10 + 5z =
= 8 + 12z* —6 — z — 8 — 8/ + 2 + 10 + 5/ = 6 + 8z.
Пример 4. Дана функция f{z) =-----------, где z = x + iy. Найти ее
(x-zy)
значения при z = 1 + z, z = z, z = 3 - 2/.
Решение. Сначала придадим функции вид (2.1):
x-iy (x-zy)(x + zy) х -Гу2
. X . у
fkz) = —2—2+‘——г
x +y X +y
Если Z = 1 + Z, TOX = l,y - 1, поэтому
Л 1 .1 1 .1 1+
f (1 + z) r-z- + Z —-Z  HZ —-
P+12	P+12 2	2	2
50
При z = i, это значит х = 0, у = 1, получим XD ~ > В случае z = 3 - 2/,
т.е. х = 3, у = -2, находим:
3	-2	3	21 3-2/
f (3 - 2z) = —----- +1 —------- =------=------.
32+(-2)2	З2+(-2)2	13 13	.13
Замечание. Данную функцию можно записать и в таком виде:
/(z) = ——- С учетом этой формулы находим:
X + у
/0 + 0 =-у-, /(«) = /, /(3-20 = ^-.
Пример 5. Доказать, что функция fiz) = z является непрерывной
при любом значении z.
Решение. Зафиксируем значение z0 и рассмотрим разность
z2—Zq = (z — z0)(z + z0). Когда z—>z0, то существует такое положи-
тельное число М, при котором выполняются неравенства |z| < М,
|z0| < М, поэтому
р2 -*о2| = |г-г0||z + z0|<|z-z0|-(jz| + |z0 |)<2Л/|z-z0|.
g
В качестве 8 выберем число 8 = -^^-, где е > 0. Из неравенства
|z - z0| < 8 следует, Что
|z2-z2|<2M8=2M^- = e, |z2-z2|<e.
Поскольку выполнено неравенство (2.2), то lim z2 = Zq. Так как вы-
z->z„
полняется равенство (2.3), то функция fiz) = z непрерывна в точке z0.
Точка z0 была зафиксирована произвольно; значит функция fiz) -z2
непрерывна в любой точке.
Задачи
1.	Дана функция fiz) = z + z. Найдите ее значения при значениях
аргумента: 1) z = 1 + i; 2) z = 2 - z; 3) z = z; 4) z = -1.
2.	Дана функция fiz) = x + zy2, где z = x + iy. Найдите ее значения
при значениях аргумента: 1) z = 1 + 3z; 2) z = 4 - 2i; 3) z = z.
3.	При каких значениях z функция y(z) = z - 2z + 2z равна нулю?
51
4.	Является ли число z = 1 + i корнем уравнения
z3 + 3z2 - 8z + 10 = О?
5.	Найдите значение функции^)= z - z + z - z приz = 1 + i.
6.	Докажите, что число z = 1 + i является корнем уравнения
z4 + 2z3 — 3z2 + 2z + 6 = 0.
7.	Найдите значения функцииДг) = z + 2z - 3z - 4z при z = z,
z = 2 + i, z = 2 - i.
В задачах 8-10 докажите, что при любом значении z непрерывны
следующие функции:
8.	y(z) = |z|.	9.flz) = az + b.	10./(z)==z3.
Ответы
1.	1) 1 +3z; 2)5(1 -z); 3)-1 + i; 4)0. 2. 1) 1 + 10»; 2) 16 + 4»; 3) Z. 3.z = 0;
z = 1 - i, z = 1 + i. 4. Является. 5. -3 - i. 7./(z) = 4 - 6z.
Вопросы
1.	Как изображается геометрически комплексное число z = а + z’6?
2.	Что называют комплексной переменной?
3.	Что называют комплексной плоскостью?
4.	Какое множество точек плоскости называют областью?
5.	Что понимают под функцией комплексной переменной?
6.	Чему равносильно задание функции комплексной переменной
fiz) = и + zv?
7.	Как определяется предел функции w =/(z) ПРИ z —> zz?
8.	Каково определение непрерывности функции/(г) в точке z0?
9.	Какая функция называется непрерывной в области?
10.	Что называют односвязной областью?
11.	Приведите пример односвязной области?
12.	Что называют двусвязной областью?
13.	Приведите пример двусвязной области.
14.	Что понимают под многозначной функцией?
15.	Приведите пример многозначной функции.
§2.	2. Основные элементарные функции
комплексной переменной
Функции комплексной переменной е, sinz, cosz, определяются как
суммы соответствующих степенных рядов, сходящихся на всей ком-
плексной плоскости:
z z2 Z3
ez =1 + — + — + — + ....	(2.4)
1! 2!	3!
52
sinz = z- — + -— — + ....	(2.5)
3!	5!	7!
z2 z4 z6
cosz = l ——— + -— — + ....	(2.6)
2!	4!	6!
Показательная функция e имеет следующие свойства:
1) z21+22 = е2'е2г, где zb z2 - произвольные числа; 2) е2-2*"' = е2, (А = 0,
±1, ±2, ...), т.е. е является периодической функцией с периодом 2л/.
Тригонометрические функции sinz, cosz- периодические с дейст-
вительным периодом 2л; они имеют только действительные нули
Л
z = h и z = — + кп соответственно, где к = 0, ±1, ±2, ...
2
Для функций е2, sinz, cosz, справедливы следующие формулы
Эйлера
еа = cos z + / sin z, е-'2 = cos z - i sin z,	(2.7)
откуда
Jz . ~-iz	~iz -iz
& + &	•	6	6	-
cos z _-------, sin z =-------.	(2.8)
2	2/
Если z = x + iy, to ez = ex+ly = exe'y, поэтому
ez = ex(cosy + isiny).	(2.9)
Тригонометрические функции tgz, tgz определяются формулами
sinz	cosz
tgz=------, ctgz = —;—.	(2.10)
cosz	sinz
Все формулы тригонометрии остаются справедливыми и для три-
гонометрических функций комплексной переменной.
Гиперболические функции shz, chz, thz, cthz, определяются фор-
мулами
shz = -----—, chz= 6- +-e...	(2.Ц)
2	2	J
thz = —, cthz = —.	(2.12)
chz	chz
53
Функции shz, chz можно рассматривать как суммы степенных ря-
дов, сходящихся на всей комплексной плоскости:
3	5	7
shz = z + — + — + — + ...,	(2.13)
3!	5!	7!
2	4	6
chz = 1 + —+ — + — + ....	(2.14)
2!	4!	6!
Тригонометрические и гиперболические функции связаны между
собой следующими равенствами:
sinz = -i sh iz,
cosz = ch iz,
tgz = -i thiz,
ctgz = zcthzz,
sh z = -z sin iz.
chz = cos iz,
thz = -ztgzz,
cthz = zctgzz.
(2-15)
Логарифмическая функция Lnz, где z * О, определяется как функ-
ция, обратная показательной, причем
Lnz = ln|z| + zArgz = ln|z| + zargz + 2A7tz, к = 0, ±1, ±2,...	(2.16)
Эта функция является многозначной. Главным значением Lnz на-
зывают также значение, которое получается при к = 0; оно обозначает-
ся через lnz:
lnz = ln|z| + zargz.
(2.17)
Очевидно, что
Ln z = In z + 2kni, к = 0, ±1, ±2,...	(2.18)
Справедливы следующие равенства:
Ln (Z|Z2) = Ln Zj + Ln z2,
= Lnz| - Lnz2,
Ln(z”) = «Lnz, Ln Vz =	-,
n
Обратные тригонометрические функции Arcsinz, Arccosz, Arctgz,
Arcctgz определяются как функции, обратные соответственно функци-
ям sinw, cosw, tgw, ctgw. Например, когда z = sinw, то w называют арк-
синусом числа z и обозначают w = Arcsinz.
54
Все эти функции являются многозначными; они выражаются че-
рез логарифмические функции следующими формулами:
Arcsinz = -zLn^zz+Vl-z2 J,	(2.19)
Arccos z = - z Ln ^z + Vz2 -1	(2.20)
.	z , 1+zz
Arctgz =—Ln-------,	(2.21)
2 1-zz
.	z _ z+z
Arcctg z = — Ln----.	(2.22)
2 z-z
Главные значения обратных тригонометрических функций arcsinz,
arccosz, arctgz, arcctgz получают, когда рассматривают главные значе-
ния соответствующих логарифмических функций.
Общая степенная функция w = z°, где а = а + zfJ - любое ком-
плексное число, определяется формулой
za=eOLnz,	(2 23)
ее главное значение равно
z°=eolnz.	(2.24)
Общая показательная функция w = a, (а#0, а # 1) определяется
формулой
„z ~zLna
а -е ,	(2.25)
главное значение этой многозначной функции равно
az=ezlno.	(2.26)
Пример 1. Доказать, что sinz2 +cos z2 = 1.
Решение. Принимая во внимание формулы (2.8), получаем:
55
Пример 2. Доказать, что
sin (Z| + z2) = sin Z|  cos z2 + cos Z|  sin z2.
Решение. Пользуясь формулами (2.8), находим:
sinz1-cosz2+cosz|-sinz2 =
ei2'- е~‘2' e'22 + e~'22 , e12' + e~‘2' <F2 - e~'22
2i ’	2	+	2	’	2/
е'(‘,+г2) + g/(Z|-z2) _ e/(z2-Zi) _ g-i(z,+z2)
= -------------------------------—-------+
41
g<(Z|+Z2)_ el(Z!-Z2)+ gl(Z2-Z1)_ e-l(z,+z2)
+ ------------------------------------------ =
4i
g'tn+Zl) _ g-'(Z|+Z2)
=--------------------= sin (Z| + z2).
Пример 3. Доказать, что
ch(Z| + z2)=chz, chz2 + shz| • shz2.
Решение. Принимая во внимание формулы (2.11), получаем
ch Z| • ch z2 + sh Z|  sh z2 =
_ e2' + e~2' e22 + e~22	e2' - e~2' e22 - e~22 _
~	2	2	+	2	2
e2l+Z2 + e2i~22 + eZ2~2' + e~2'~22
=---------------------------+
4
56
eZl + Z2 _ gZl“Z2 _ eZ2"zl + g"Zl-Z2
+ ---------------------------------
4
2е 1 2 + 2е
4
= ch(z, +z2).
2
Следовательно,
ch(z| + z2 )=chz, • ch z2 + sh z,  sh z2.
Пример 4. Найти 1) cos/; 2) sin(l + 2z).
Решение. По первой из формул (2.8) находим
—+—- = е '+е = ch 1«1,5431.
2	2
е + ।
cos / =-----
2
В соответствии co второй из формул (2.8) получаем:
е/(1+20 _е-К1+20	е-^-^е
sm( 1 + 2z) =------------=------------=-------------
2/	2/	2z
е 2(cos 1 + zsin 1)-е2(cos 1- zsin 1) _
cos 1(е 2 - е2) + zsinl(e2 +е 2)	е2+е~2 . ,	.е2-е2
--------i------------------------------------------sln 1 + ।-------cos 1 =
2/	2	2
= ch2sinl + zsh2cosl »3,7622 x 0,8415 + /3,6269 x 0,5403 =
= 3,1650+ 1,9596/.
Пример 5. Найти: 1) ln(—1); 2) Ln(—1); 3) lnz; 4) Lnz; 5) ln(3 + 4z),
Ln(3+4z").
Решение. Поскольку |-1|= 1, а главное значение аргумента равно
л, то в соответствии с формулой (2.17) получим ln(-l) = lnl +nz = nz;
по формуле (2.18) найдем
Ln(-l) = 7tz + 2fatz = (2& + l)7tz, А = 0, ±1, ±2,...
57
На основании тех же формул и с учетом того, что |z| - 1, argz - —,
находим:
Ini = In 1 + — z = — z, Lnz = — z + 2kni, к = 0, ±1, ±2,...
2	2	2
Так как
[3 + 4zj = т/з2 + 42 =5, arg(3 + 4z) =arctgy,
TO
4
ln(3 + 4z) = In 5 + z arctg—,
Ln(3 + 4z) = In 5 + z arctg— + 2/citi,
A = 0,±l,±2,...
Пример 6. Найти 1) z2; 2) 21 >l.
Решение. В соответствии с формулой (2.23) или (2.25) при a = i,
71
z = i и с учетом того, что Ln z = — z + 2кт (см. пример 4) получаем
=e'Ln' =е'(’''/2 + 2Ы) =e-n/2-2fat,	= о, ±1, ±2,...
_	J	-я/2
Главное значение z равно е
На основании формулы (2.25) при а - 2, z = 1 + z, находим:
21+( _ е(1+')Ьп2 _ (1+ <)(ln2+2fau) _ е(1п2-2*я) + /(1п2+2*я) _
= eln2 2fcl(cosln2 + zsinln2).
Замечание. Здесь использована формула (2.9).
Пример 7. Найти 1) Arcsin2, 2) Arctg2z.
Решение. С помощью формул (2.16) и (2.19) находим:
Arcsin 2 = -zLn(2z±z73) = -z'Lnl(2±73)zj=
=-z ln(2±>/3) + zy + 2A7rz =у-Лп(2±з/3) + 2Ал7, к =0,±1,±2,....
2
58
В соответствии с формулами (2.16) и (2.21) получаем
Arctg(2z) = -^Ln(-|
I In—+ ш' + 2Ати
21 3
= —+ *^3 + fa =0,±l, + 2,....
2	2
Пример 8. Найти [±| и argz для числаz = sin2z.
Решение. Так как sin2z = zsh2 (см. формулы (2.15)), то Rez = О,
2	-2
в —Q
Imz = sh2. Поскольку sh2 = —-— > 0, то Imz > 0. Следовательно,
. .	. _ я
|z| = shz, argz - у.
Пример 9. Найти Re/(z) и Im/(z), еслиУ(г) = sinz.
Решение. Принимая во внимание результаты примера 2 и равенст-
во z = х + у, получаем y(z)= sinz — sin(x + zy) - sinx x coszy + sin/y x cosx.
Так как coszy = chy, sinzy = zshy (см. формулы (2.15)), то
/(z) = sin x • chy + zshy • cos x.
Отсюда следует, что
Re f(z) = sin x • chy, Im f(z) = shy • cos x.
Пример 10. Найти модуль и аргумент числа/(/), если
о
У(г) = (1 - /)ctgz .
Решение. Число У(') = (1 ~ Octgz2 представим в виде произведения
двух чисел: flj) = z1 • z2, z, = 1 - i, z2 = cth(-l); найдем модуль и аргу-
мент каждого из них.
Для числа z( = 1 - i, имеем [z|[ = -Jl, argZ| = Число z2 явля-
ется действительным, причем отрицательным, поскольку
cth(-l) =
ch(-l) _ chi
sh(-l) shl
e' + e 1
<0.
e -e
59
Значит,
2
I I 11	£ +1
|z2| = cthl = ——argz2 = л.
Используя правило умножения комплексных чисел в тригономет-
рической форме (см. гл. 1, §1.6), получаем
/(Q = |z1| |z2| = V2cthl, arg/(Z) = argZ] +argz2 =
Пример 11. Найти мнимую часть числа cha, где а - тот корень
уравнения z4 + 4 = 0, который расположен в третьей четверти.
Решение. Корнями уравнения z + 4 = 0, или z - -4, являются четы-
ре комплексных числа, которые можно найти по формуле (см. гл. 1, §1.6)
V-4 = ^4(cosu + /sin л) =
г-( л + 2Лл . .
V 2 cos---------+ zsm
I 4
л + 2Ал
4
£ = 0, 1,2,3.
Подставляя значения к. в эту формулу, находим:
Ы Л . . л
an =V2 cos — + zsin —
0 I 4	4
z—(	5л . . 5л
a2 = >/2 cos— + isin —
2 I 4	4
/—(	7л . . 7л
a, = v2 cos— + isin —
3 I 4	4
В третьей четверти находится корень a2 = -l - i. Вычисляем те-
перь ch(-l -i) = ch(l + i). Поскольку
ch( 1 + i) = chi • chz + shl • shz = chi • cosl + zshl sinl,
TO
Im cha2 = shl • sinl.
60
Замечание. Здесь использованы формулы:
ch(Z] + z2) = chZ] • chz2 + shz] • shz2 (см. пример 3)
shz = -i sin iz (см. формулы (2.15)).
Задачи
Докажите, что верны следующие равенства:
1.	ch2z-sh2z = l.
2.	cos(Z] + z2) = cos Z] cos z2 - sin Z] sin z2.
3.	sh(Z] +z2) = shz] -chz2 +chZ] shz2.
4.	sin2z = 2sinz-cosz.
Вычислите следующие значения:
iit	। л ।	(л ।
5.	sin(m). 6. shZ. 7. ch2z. 8. cos—. 9. sinl—+ zl. 10. tgl — zl
Найдите все значения следующих логарифмов:
11. In е; Ln е. 12. ln( 1 + z); Ln(l + z).	13. In i; Ln i.
Найдите все значения обратных тригонометрических функций:
14. Arccosl. 15. Arctgl. 16. Arcctg(l + z).	17. Arcsinz.
2 1
18.	Найдите |z| и argz, если z = zsin -.
i
19.	Найдите Re/(z) и Im/(z), если/(г) = chz.
20.	Найдите модуль и аргумент числа/(0, если/(г) = tgz.
Ответы
5.	ishTt. 6. zsin 1. 7. cos2. 8. ch-^-. 9. ^-(chl+ zshl). 10. ch~- IL 1; 1 + 2kni.
12. —ln2+z—; —Jn2+/~+ 2fct |. 13. z—; zf—+ 2Ati|. 14. 2kn. 15. — + kn.
2	4	2	(4	)	2 U J	4
16. ar^g2_^]n5 + to 17. to-zln[V2+(-l/+1j. 18.|z| = sh2l, argz=-y.
e2 — 1	л
19.	Rey(z) = cosy • chx, Im/(z) = shx • siny. 20. |/(z)| = thl = —-, arg/(z) = —.
e +1	2
Вопросы
1.	Как определяется функция/(z) = /?
2.	Каковы свойства функции/(г) = /?
61
3.	Как определяется функция fiz) = sinz?
4.	Каковы свойства функции^) = sinz?
5.	Как определяется функция fiz) = cosz?
6.	Каковы свойства функции//2)= cosz?
7.	Запишите формулу Эйлера.
8.	Запишите выражение для е, где z = х + iy.
9.	Как определяются функции/(г) = tgz,/(z) = ctgz?
10.	Как определяются гиперболические функции?
11.	Запишите разложение в степенной ряд функции/(г) = shz.
12.	Запишите разложение в степенной ряд функции/(г) = chz.
13.	Запишите формулы, связывающие тригонометрические и гипер-
болические функции.
14.	Как определяется логарифмическая функция fiz) = Lnz?
15.	Запишите формулу для функции/(г) = Lnz.
16.	Что называют главным значением Lnz?
17.	Запишите формулы для Ln(z,z2), Ln — , Ln(z"), Ln y[z .
18.	Как определяются обратные тригонометрические функции?
19.	Как определяются обратные тригонометрические функции че-
рез логарифмические?
20.	Как определяется общая степенная функция /(z) = za, где
а = а + ф?
21.	Как определяется общая показательная функция fiz) = а (а-
комплексное число, а * 0, а * 1)?
§2.3. Дифференцирование функций
комплексной переменной
Рассмотрим функцию w =fiz), определенную в некоторой области
D комплексной плоскости, и точки z е D, (z + Az)eD. Обозначим:
Aw =fiz + Az) -fiz), Az = Дх + /Ду.
Производной функции w =fiz) в точке z называют конечный предел
отношения Aw/Az, когда Az произвольным образом стремится к нулю:
= lim = lim	(2.27)
Az->0 Az	Az—>0	Az
Функция, имеющая производную в точке z, называется дифферен-
цируемой в этой точке.
62
Если z = х + iy, w =fiz) = w(x, y) + rv(x, у), то в каждой точке диффе-
ренцируемости функции^) выполняются равенства
= (228)
дх ду ду дх
которые называют условиями Д'Аламбера-Эйлера (или условиями Ко-
ши-Римана).
Обратно, если в некоторой точке (х, у) функции и=и(х,у),
v = v(x, у) дифференцируемы как функции действительных перемен-
ных х,у и, кроме того, удовлетворяют равенствам (2.28), то функция
y(z) = и + iv является дифференцируемой в этой точке z = х + iy как
функция комплексной переменной z.
Функция w ~fiz) называется аналитической в точке z е D, если
она дифференцируема в ией и некоторой ее окрестности. Функция fiz)
называется аналитической в области D, если она дифференцируема в
каждой точке этой области.
Для всякой аналитической функции fiz) производная f\z) выража-
ется через частные производные функций и = и(х, у), v = v(x, у):
,, ди . dv dv	. ди	ди	. ди dv . dv
f(z) =— + i— =-------1— =-------1— = — + i—.	(2.29)
дх дх ду	ду	дх	ду ду dx
Геометрический смысл модуля и аргумента производной. Ес-
ли функция fiz) - аналитическая в точке z0 и /tzo) * т0 1Д2о)1 равен
коэффициенту растяжения в точке z0 при отображении w =fiz) плоско-
сти z на плоскость w, точнее: при ]/*(z0)| > 1 будет растяжение, а при
|f(z0)| < 1 - сжатие. Аргумент производной f'(z0) равен углу, на который
необходимо повернуть касательную в точке z0 к любой гладкой кривой
на плоскости, которая проходит через точку z0, чтобы получить на-
правление касательной в точке w0 -fiz0) к образу этой кривой на плос-
кости w при отображении w =fiz). Отметим, что при ср = arg/lz) > 0 по-
ворот осуществляется в направлении против движения часовой стрел-
ки, а при q> < 0 - по часовой стрелке.
Отображение с помощью аналитической функции w=fiz) назы-
вают конформным отображением.
Дифференцирование элементарных функций. Производные
элементарных функций z", lnz, е, sinz, cosz, tgz, arcsinz, arccosz, arctgz,
shz, chz находят по формулам:
63
(zny = nzn-1, (lnz)' = -, (ezy = ez,
z
(sin z)' = cosz, (cosz)'=-sin z, (tgz)' = —,
cos z
(arcsinz)' = . 1	, (arccos z)' = - V- , (arctgz)' = —3_,
7i3?	ViZ?	i+z2
(shz)' = chz, (chz)' = shz.
Гармоническая функция. Функция <p(x, у) называется гармони-
ческой в области D, если она имеет в ней непрерывные частные произ-
водные второго порядка и удовлетворяет в этой области уравнению
Лапласа
^ + ^ = 0.	(2.30)
дх2 ду2
Если функция fiz) = и + iv w — аналитическая в области D, то ее
действительная часть и=и(х, у) и мнимая часть v = v(x, у) являются
гармоническими функциями в этой области.
Однако, если их(х,у), v,(x, у) - две произвольные гармонические
функции, то функция/](z) = их(х,у) + zv/x, у) вовсе не обязана быть
аналитической функцией: для аналитичности/j(z) нужно, чтобы функ-
ции W] = w/x, у), V] = v,(x, у) удовлетворяли условиям Д'Аламбера-
Эйлера.
Пример 1. Выяснить, является ли аналитической функция w = ?.
Решение. Поскольку z = х + iy, то w = (х + (у)2 = х + 2ixy + 12у2,
xv = (х2 — у2) + 2ixy, и(х,у) = х -у2, v(x,у) = 2ху. Находим частные про-
изводные функций и = и(х, у), v = v(x, у):
ди _	ди	_	dv	_	dv	_
— = 2х,	— = -2у;	—	= 2у,	— = 2х.
дх	ду	дх	ду
Следовательно, и'х =v'y,	и'у	= -v'x;	условия (2.28) выполнены для
всех точек плоскости Оху. Значит, функция w = z является аналитиче-
ской на всей плоскости.
64
Пример 2. Выяснить, является ли аналитической функция w = z .
Решение. Если w = z И z = х - iy, то и + iv = х - iy, и = х, v = -у, от-
куда
ди	, ди	Л dv	п dv	, ди	dv
дх ду дх ду дх	ду
Следовательно, первое из условий (2.28) не выполняется. Функ-
ция w = z не имеет производной ни в одной точке плоскости и поэто-
му не является аналитической.
Пример 3. Выяснить, является ли аналитической функция w = zRez.
Решение. Если w = zRez, где z = х + iy, то w = (х + iy)x = х2 + ixy,
2
и — х , v = ху, откуда
ди „ ди . dv dv
— = 2х, — = 0; — = у, — = х.
дх ду дх ду
Равенства (2.28) выполняются только для х = 0 му = 0.
Таким образом, функция w = zRez дифференцируема только в
точке z = v и нигде не является аналитической.
Пример 4. Найти аналитическую функцию fiz), если известна ее
мнимая часть v(x, у) = 2х2 - 2у2 + х.
dv	dv
Решение. Поскольку — = 4х + 1, — = -4у, то из равенств (2.28)
дх	ду
получаем
Эи	ди	.
— = -4у, — = -4х -1.
дх	ду
Из первого уравнения находим и= J-4ytZr = -4ху + ф(у), где
ф(у) - произвольная функция. Для определения функции ф(у) продиф-
ференцируем по у функцию и = -4х + ф(у) и подставим полученную
производную во второе уравнение: -4х + ф(у) = -4х - 1, откуда ф'(у) = -1,
ф(у) = -у + С. Следовательно, и = -4ху -у+ С, поэтому
w = и + iv = -4ху -у + С + z(2x2 - 2у2 + х) =
= 2/(х2 — у2 + 2 ixy) + i(x + iy) + С;
w =flz) = 2iz2 + iz + C,
где z = x + iy.
3 Зак.1816
65
Пример 5. Найти аналитическую функцию Дг), если ее действи-
.	.	2	2
тельная часть и(х,у)=х — у -х.
Решение. Так как — = 2х-1, — = -2>>, то из равенств (2.28)
дх	ду
следует, что
dv _	, dv _
— = 2х -1, — = 2 у.
ду	дх
Из первого уравнения находим
v= Г(2х-1)«7у = 2ху - у + ср(х),
где ср(х) - произвольная функция.
Для определения функции ф(х) находим v'x = 2у+ф'(х) и подстав-
ляем во второе уравнение: 2у + ф'(х) = 2у, откуда ф'(х) = 0, ф(х) = С.
Значит, v = 2ху —у + С, поэтому
Дг) = и + iv = х -у -х + i(2xy - у + С) =
= х - у + 2ixy - (х + iy) + С = (х + iy)2 - (х + iy) + Ci,
или
fiz) = z - z + Ci.
Пример 6. При каком условии трехчлен и = ах + 2Ьху + су2 является
гармонической функцией?
Решение. Находим частные производные первого и второго по-
рядка: u'x = 2ax + 2by, u'y=2bx + 2cy; w^ = 2a, w'y= 2с. Вторые част-
ные производные удовлетворяют уравнению (2.30), т.е. 2а + 2с = 0, ко-
гда а + с = 0. При этом условии данный трехчлен будет гармонической
функцией, которая имеет вид и = ах + 2Ьху - ау .
Задачи
1. Исходя из определения, найдите производную функции
fiz) = z - 3z + 2.
В задачах 2-5 найдите производные функций
2. fiz) = z — 4z2 + 5z + 1.
4. /(z) = ^|.
z + 1
3. /(z) = e3,z+2.
cz + a
66
В задачах 6-9 выясните, является ли аналитической функция/^).
f>.fa) = z\	7./(z) = Rez. 8./(z) = e2. Mz) = |z|.
В задачах 10-14 найдите аналитическую функцию для которой
заданы указанные условия
10.	и(х, у) = Re/(z) = х - у2 + Зх + у, 7(0) = I.
11.	Reflz) = х - Зху2 + 2,/(0) = 2 + i.
12.	v(x,у) = Im/(z) = 2ecosj,/(0) = 2(1 + i).
13.	lm/(z) = x3 + 6x2_y - 3j/x - 2j>3,y(0) - 0.
14.	Re/(z) = x2 -y + xy,7(0) = 0.
Ответы
l./(z) = 2z- 3. 2. 3z - 8z + 5. 3. 3/e3'z+2. 6. Аналитическая. 7. He является
аналитической. 8. Аналитическая. 9. He является аналитической.
10. fa) = z + (3 - i)z + i. 11. z + 2+ i. 12. lie + 2. 13. (2 + t)z . 14. -1(2 - z)z2.
Вопросы
1.	Что называют производной функции/^) в точке z?
2.	Каков геометрический смысл модуля производной?
3.	Каков геометрический смысл аргумента производной?
4.	Что называют конформным отображением?
5.	Какую функцию называют дифференцируемой в точке?
6.	Какую функцию называют аналитической в точке?
7.	Какую функцию называют аналитической в области?
8.	Запишите условия Д'Аламбера-Эйлера.
9.	По каким формулам находят производные функций z", lnz, е*?
10.	По каким формулам находят производные тригонометриче-
ских и обратных тригонометрических функций?
11.	По каким формулам находят производные гиперболических
функций?
12.	Какая функция называется гармонической?
§2.4. Интегрирование функций
комплексной переменной
Рассмотрим однозначную функцию fa), определенную и непре-
рывную в области D. Пусть Г - кусочно-гладкая дуга линии, которая
целиком принадлежит области О; дуга Г ограничена точками z0 (на-
чальная) и Z (конечная). Разделим дугу Г на и элементарных дуг Гк.
67
Занумеруем точки деления в направлении от точки z0 до конечной точ-
ки причем zn = z (рис. 2.3).
Рис. 2.3
Введем обозначения: Az* = z* -z*_, (к = 1, 2, ..., ri), А. = max|Az*|.
На каждой элементарной дуге Гк выберем одну точку z'k (один из кон-
цов или внутреннюю точку) и составим сумму
п
4=1
Интегралом от функции fiz) по дуге Г называют конечный пре-
дел суммы (2.31) при А. —> 0:
п
j/(z)=lim^/(z;)Az*.	(2.32)
р	Л=1
Интеграл от функции комплексной переменной имеет следующие
свойства:
1-	J(/(z) + <p(z))cfe = f/(z)dz + Jcp(z)tfe.
Г	г	г
68
2.	J af(z)dz = aj f(z)dz (а - постоянная),
г	г
3.	Если дуга Г геометрически совпадает с дугой Г, но имеет на-
правление, противоположное направлению дуги Г (для Г начальная
точка Z, конечная z0), то
г
г
4.	Если дуга Г состоит из дуг Г], Г2,..., Г„ (см. рис. 2.3, п = 7), то
г
Г|
Г2
5.	J dz - z-Zq.
г
6.	Если |/(z)| < М во всех точках дуги Г и длина дуги Г равна /, то
г
п
7.
*=1
г
г
Вычисление интеграла от однозначной функции/(z) = w(x, у) +
+ Zv(x, у) комплексной переменной z = х + iy сводится к вычислению
криволинейных интегралов:
(2.33)
г
г
Интеграл J f (z)dz, вообще говоря, зависит от пути интегрирова-
ния Г.
Если/(2)- аналитическая функция в односвязной области D, то
значение интеграла J f (z)dz не зависит от линии Г, а только от на-
г
чальной и конечной точки этой линии.
69
Теорема Коши. Для всякой функции fiz), аналитической в некото-
рой односвязной области D, интеграл J f (z)dz по любому замкнутому
г
кусочно-гладкому контуру Г, целиком принадлежащему области D,
равен нулю:
J/(z)<fc = O.
г
Если кривая Г задана параметрическими уравнениями х = x(t),
У ~ У(?У a.<t<^,ro
₽
jf(z)dz = jf[z(t)]z'(t)dt,	(2.34)
Г	а
где z(r) = x(t) + iy(t).
Если функция fiz) является аналитической в односвязной области
D, содержащей точки z0 и zt, то справедлива формула Ньютона-Лейб-
ница
Z|
J f(z)dz = F(z}) - F(z0 ) = F(z)\^,	(2.35)
где F(z) - первообразная для функции/^), т.е. F(z) =fiz) в области D.
Если функции fiz) и (p(z) - аналитические в односвязной области
D, a z0 и Z] - произвольные точки этой области, то справедлива форму-
ла интегрирования по частям:
Z|	Z1
J j\z)q'(z)dz = [/(z)<p(z)]"' - Jq(z)f\z)dz.	(2.36)
Z0	z0
Замена переменной в интегралах от функций комплексной пере-
менной проводится аналогично случаю функции действительной пе-
ременной. Если аналитическая функция z = <р(и>) отображает взаимно
однозначно линию Г] в w - плоскости на линию Г в z - плоскости, то
J f&)dz = J /[tp(w)]cp'(w)rfw.	(2.37)
г г,
70
Если путь интегрирования является лучом, исходящим из точки z0,
или окружностью с центром в точке z0, то целесообразна подстановка
z-z0=pe'v.	(2.38)
В первом случае <р - const, р - действительная переменная интег-
рирования; во втором случае р = const, <р - действительная переменная
интегрирования.
Пример 1. Вычислить интеграл Jzdz, где Г - линия, соединяю-
г
щая точки z =-1, z = 1, причем: 1) Г - отрезок действительной оси от
точки z = -1 до точки z = 1; 2) Г - верхняя полуокружность Jzj = 1.
Решение. Поскольку для комплексного числа z = x + iy сопряжен-
ными является число z = х - iy, то на действительной оси (у = 0) z = х,
dz = dx и z=x. В первом случае получаем
1	2 ’
J zdz = J xdx = — = 0.
г -1	-1
Верхнюю полуокружность |z| = 1 можно задать так: z = е'9, где
0 < <р < л, причем <р убывает от л до 0, когда точка пробегает полуокруж-
ность от z = -1 до z = 1. Так как z = е^, dz = ie*dty, то во втором случае
о	о
J zdz = J е~'ч>/е'<|><йр = zj zftp = -л/.
Г	тс	тс
Замечание. Функция w = z не является аналитической (см. пример 2,
§2.3). Значение интеграла от этой функции зависит от пути интегрирования,
соединяющего указанные точки.
Пример 2. Вычислить интеграл J(l + z-2z)zfc, где Г- отрезок
г
прямой между точками z, = 0, z2 = 1 + i.
Решение. Перепишем подынтегральную функцию в виде
fiz) = и(х,у) + iv(x,y~): 1 +i-2z= 1 + z-2(x-zy) = 1 -2x+z(l +2у).
Здесь и(х, у)= } - 2х, v(x, у) = 1 + 2у.
71
На основании формулы (2.33) получаем
J(I + i - 2z)dz = J(1 - 2x)dx - (1 + 2y)dy + iJ (1 + 2y)dx + (1 - 2x)dy.
г	г	г
Отрезок прямой между точками z} = 0, z2 = 1 + i имеет уравнение
у = х (0<х< 1), поэтому dy=dx-, пределы интегрирования соответст-
венно равны: а = 0, b = 1. Следовательно,
।	।
| (1 + i - 2z)dz = j [(1 - 2х) - (1 + 2x)}ix + i j [(I + 2x) + (1 - 2x)]dx =
г	0	0
1	1
= -4 J xdx + 2/J dx = -2 + 2i = 2(/ -1).
о	о
r dz
Пример 3. Вычислить интеграл ------------, где Г-окружность радиу-
J z-a
г
са г с центром в точке а.
Решение. Переходим к новой переменной в соответствии с фор-
мулой (2.38): z = а + ге'ф, 0 < <р < 2л. На основании формулы (2.37) по-
лучаем
Г, Г,	г.
Поскольку Г, - отрезок действительной оси от точки 0 до точки
2 л, то
2я
| сЛр = | сАр = 2л.
г, г,
Таким образом,
J	= i Jc/<p = 2 л/.
гZ ° г,
72
2+i
Пример 4. Вычислить интеграл J (3z2 + 2z)dz.
i-i
Решение. Так как подынтегральная функция f{z) = 3z + 2z являет-
ся аналитической при всех z, то с помощью формулы Ньютона-Лейб-
ница находим:
2+<	2+.
j(3z2 + 2z)<fc = (z3 + z2 )||_+' = (2 + /)3 + (2 + 02 - (1 ~ 03 - (1 - 02 =
1-/
= 23 + 3 • 22i + 3 • 2? + i3 + 4 + 4i + 2 - (1 - 3i + 32 -3) - (1 - 2i + 2) =
= 8 + 12/ - 6 - i + 4 + 4i — 1 — 1 + 3i + 3 - i - 1 +2i+ 1 = 7 + 19/.
I
Пример 5. Вычислить интеграл J z sin zdz.
о
Решение. Функция Xх)= ^sinz является аналитической на всей
плоскости z, поэтому интеграл от нее не зависит от пути интегрирова-
ния, соединяющего точки z = О и z = /. На основании формулы интег-
рирования по частям (2.36) и формулы Ньютона-Лейбница получаем
J z sin dz = J z(— cos z)’dz = - z cos z^ + J cos zdz = -z cosz]^ +
0	0	0
+ sinz|'o = -/cos/ +sin/ = /(shl - chi) = /(1,1752-1,5431) = -0,3679/.
Замечание. Здесь использованы равенства shz = -/sin/z, chz = cos/z при
z= 1 (см. формулы (2.15), §2.2): shl = -/sin/, chi = cos/, поэтому-/cos/=-/ch 1,
sin/ = /shl.
Пример 6. Вычислить интеграл ^Rezdz, где дугой Г является:
а) прямолинейный отрезок, соединяющий точку 0 с точкой 1 + /; б) ло-
маная, состоящая из прямолинейного отрезка, соединяющего точку 0 с
точкой 1, и прямолинейного отрезка, соединяющего точку 1 с точкой
1 +/.
Решение. Уравнения отрезка, соединяющего точки 0 и 1 + /, в па-
раметрической форме имеют вид
х = /, у = /,
73
а в комплексной форме z = (1 + f)t, где действительная переменная t
изменяется от 0 до 1. Поскольку dz = (1 + i)dt, то в соответствии с фор-
мулой (2.34) находим:
1 1 1
J Re zdz = J Re[(l + z)f](l + i)dt = J/(l + i)dt - (1 + z) J tdt =
г о	о	о
1 + f
2
Переходим ко второму случаю. Уравнение отрезка, соединяюще-
го точки 0 и 1 в комплексной форме z = t, где t изменяется от 0 до 1;
уравнение отрезка, соединяющего точки 1 и 1 + i в комплексной форме
z = 1 + it, где 0 < t < 1. Следовательно,
1
J Re zdz = J Re tdt +
г о
2
Пример 7. Вычислить интеграл j(z-a)ndz, где п- натуральное
г
число, Г - окружность радиуса R с центром в точке а.
Решение. Перейдем к новой переменной <р по формуле z = а + Re,<₽,
где 0 < <р < 2л. Поскольку dz = iRevdtp, то
2к	2я
[(z-a)ndz= [ RneimpiRe"fd(p = i j Rn+i e'(n+l )ф dtp =
г	о	0
l(n+l)q>
= iRn+'---------
/(И+1)
2n
0
prt+l /	\	Drt+1
e'2(-lA_e0 =*_(1_1) = O.
П+1'	' « + 1
Здесь принято во внимание (см. формулы (2.4)), что
J2tn+ 1)к _ COS2(W + 1)д + zsin2(n + 1)Л = 1.
Итак,
j(z-a)ndz = 0.
г
74
Пример 8. Вычислить интеграл J-----------—, где п- натуральное
число, Г - окружность радиуса R с центром в точке а.
Решение. Уравнение окружности в комплексной форме имеет вид
z - а = Re'4’, где 0 < <р < 2л. Так как dz = Rie'vdq>, то на основании фор-
мулы (2.34) получим:
г dz
{(*-«)"
(I)
Рассмотрим два случая: 1) п 1 (и = 2, 3,...); 2) п = 1.
В первом случае находим:


Г dz _ i
J (z-aY1 Rn
о (1
= 0,
2я/(1-л)	. О»
так как е = 1 и е = 1.
Если же п = 1, то из (I) следует, что
Здесь предполагается, что контур Г точка обходит в положитель-
ном направлении (т.е. против часовой стрелки). Когда контур Г точка
обходит в отрицательном направлении, то
J z-а
Из (II) следует, что если контур Г точка обходит к раз в положи-
тельном направлении, то
-------= 2Лтсг;
если в отрицательном направлении, то
[ & = -2kni.
J z-a
75
Пример 9. Вычислить интеграл j(iz2-2z)dz, где Г- отрезок
г
прямой с началом в точке z} = 1 и концом в точке z2 = i.
Решение. Параметрические уравнения прямой, проходящей через
данные точки запишутся так: х = t, у = -t + 1, поэтому уравнение дан-
ного отрезка в комплексной форме имеет вид z(t) = t + j(l -t), где
1 > t > 0; при Z] = 1 получаем точку zt = 1, при z2 = 0 - точку z2 = i.
Преобразуем подынтегральную функцию:
iz - 2z = r[Z + z(l - Z)]2 - 2[Z + z(l - Z)] =
= /[Z2 + 2 iZ( 1 - Z) + ?(1 - Z)2] - 2Z- 2i + 2it =
— i\? + 2it — 2/Z2 - (1 - 2z + Z2)] — 2z — 2i + 2it =
= Z(Z2 + 2it - 2/Z2 - 1 + 2z - Z2) - 2Z - 2 i + 2it =
= /(2Z + 2 it — 2ZZ2 — 1) - 2z - 2i + 2 it =
= 2it + 2i2t- 22?-i-2t- 2i + 2it =
= 2it - 2Z + 2Z2 - z - 2z -2i + 2it = (2Z2 - 4z) + i(4z - 3).
Поскольку z = t + i(\ -1), dz = dt- idt, iz2 -2z = (2Z2 - 4Z) + z(4Z- 3),
Z( = 1, Z2 = 0, то по формуле (2.34) находим:
о
J (Zz2 - 2z)dz = J[(2z2 - 4z) + i(4t - 3)](dt - idt) =
Г	1
= J {[(2Z2 - 4Z) + 4Z - 3] + i[(4t - 3) - (2Z2 - 4t)] }dt =*
1
0
= j[(2Z2 - 3) + f(8z - 2Z2 - 3)]dt =
1
0
4z2--z3-3z
3
i
( 2 f 2 У
= — + 3+Z1-4 + — + 3
MM 3 J
Z_i
3 3’
Итак,
76
^(iz2 -2z)dz = ^-^.
г
Задачи
Вычислите интегралы:
i+i	i
1. Jzc7z.	2. Jsin2 zdz.
о	о
3.	j zdz, Г - ломаная ОВА, где 0(0,0), В(1,0), Л(1,1).
г
4.	J zdz, Г - нижняя полуокружность |z| = 2 от zx = -2 до z2 = 2.
Г
5.	J|z|zfife, Г - верхняя полуокружность |z| = 1 от z, = 1 до z2 = -1.
г
6.	^zezdz, Г - произвольная линия, соединяющая точки z} = О,
г
ni
z,= —.
2 2
г dz
7.	I —, Г - верхняя полуокружность |z| = 1 от zt = 1 до z2 = -1.
г Z
8.	J \mzdz по двум путям: 1) Г, - отрезок действительной оси от
г
z} = 3 до z2 = -3; 2) Г2 - верхняя полуокружность |z| = 3 от zt = 3 до
z2 = -3.
9.	J Re zdz , Г - дуга параболы у = 2х2 от z, = 0 до z2 = 1 + 2i.
г
10.	| (2х - 3iy)dz, Г - нижняя полуокружность |z| = 2 от z} = -2 до
г
z2 = 2.
11.	J(2z + Y)zdz, Г - единичная окружность |z| = 1.
г
12.	J |z|fife , Г - нижняя полуокружность |z| = 2 от z, = -2 до z2 = 2.
г
77
Ответы
l.i. 2. (2 — sh2). 3.1+i. 4.2m. 5. ni. 6. -j + l-i. 7. m. 8.1)0;
2)	—!2 9. —+ A|. 10. 10m'. Указание. x = -+--, y = -—11.2m'.
’	2	2 3	2	2i
12.	8.
Вопросы
1.	Что называют интегралом от функции w -fiz) комплексной пе-
ременной z по дуге Г?
2.	Каковы свойства интеграла от функции комплексной переменной?
3.	По какой формуле вычисляют интеграл от однозначной функ-
ции fiz) = и(х, у) + iv(x, у) комплексной переменной z - х + iy?
4.	Зависит ли значение интеграла J f (z)dz от линии ГsD, если fiz) -
г
аналитическая функция в области D?
5.	Сформулируйте теорему Коши.
6.	Запишите формулу для вычисления интеграла J f(z)dz, если
г
линия Г задана параметрическими уравнениями х = x(t), у = y(t), где
а < t < р.
7.	Запишите формулу Ньютона-Лейбница.
8.	Какой вид имеет формула интегрирования по частям?
9.	Запишите формулу замены переменной в интеграле J f(z)dz .
г
10.	В каких случаях при вычислении интеграла целесообразна под-
становка z = z0 + ре41?
§2.5. Интегральная формула Коши
Если функция fiz) является аналитической в области D, ограни-
ченной кусочно-гладким контуром Г, и на самом контуре, то верна ин-
тегральная формула Коши
Я^о) ~ • ((239)
2тп J z-zn
г и
где контур Г обходят так, чтобы область D все время оставалась слева
(обход контура против движения часовой стрелки).
78
Если функция j[z) является аналитической в области D и на ее
границе Г, то для любого натурального п верна формула
/(n)(z0) = —.[	(2.40)
2™ Jr(z-z0)"+1
где zoeD, геГ,/"^) - значение и-ой производной функции^) в точке z0.
Формулы (2.39) и (2.40) дают возможность вычислить следующие
интегралы:
[^-dz = 2nif(z0),	(2.41)
•> z-z0
г и
Г /(z)tfc= 2ш (п)
]г(^оГ «!
Г ^7
Пример 1. Вычислить интеграл I —---------, где Г - окружность ра-
+1
диуса R = 1 с центром в точке z = 1, причем обход контура осуществ-
ляется против часовой стрелки.
Решение. Чтобы воспользоваться формулой (2.41), преобразуем
подынтегральную функцию следующим образом:
z +1 (z-i)(z + i)	z-i- z-i	z + i
Функция y(z) = l/(z + i) является аналитической внутри рассмат-
риваемого круга и на его границе, поэтому справедливы формулы (2.39)
и (2.41). В соответствии с последней формулой получаем
( ~ = fdz = 2ni f (i) = 2ni— = n.
f?+l [z-i	2i
Пример 2. Вычислить интеграл	где Г-любой замкну-
г z
тый контур, который не проходит через точку z = 0. Обход контура со-
вершается против часовой стрелки.
79
Решение. Если точка z = О находится вне контура Г, то функция
sinz _	„	,
—— будет аналитической на контуре и в области, ограниченной этим
Z
контуром, поэтому в соответствии с теоремой Коши (см. §2.4) инте-
Г sin z
грал равен нулю: —— dz = 0.
г z
Если точка z = 0 принадлежит области, ограниченной контуром Г,
то справедливым будут формулы (2.40) и (2.42) для функции^2) = sinz,
z0 = 0, п = 1. На основании формулы (2.42) для этого случая получим
г sin z _ .	. „ .
—— az = 2 л/ cos 0 = 2 л/,
поскольку/(z) = (sinz)' = cosz.
Г ez dz
Пример 3. Вычислить интеграл I—----------, где Г - окружность
J z2 —6z
|z-2| = 5.
Решение. В области, ограниченной окружностью |z — 2| = 5, име-
ются две точки z = 0, z = 6, в которых знаменатель дроби равен нулю.
Формулой (2.39) непосредственно пользоваться нельзя. В этом случае
вычислить интеграл можно следующим образом. Разложим дробь
1
—----- на элементарные дроби:
z2 — 6z
1
z2 — 6z
1 ( 1
6 ^z -6
z
С учетом этого равенства и в соответствии с формулой (2.39) по-
лучим (при z0 = 6 и z0 = 0 соответственно):
г ez ,	1 f ez dz
j z2 - 6z 6Jz-6
Ц . e36-l .
---2л/ =------л/.
6	3
1 f e , I _ . зл
---I---dz = —2л/ eib
63 z 6
г
Пример 4. Вычислить интеграл —-----------— dz, где Г - окружность
Jr(z2-1)2
|z-l|=l.
Решение. Подынтегральная функция sinnz/(z2- I)2 является анали-
тической в области |z — 1| < 1 везде, кроме точки z0 = 1. Выделяем под
80
знаком интеграла функцию f(z), аналитическую в круге |z - 11 < 1. Для
этого запишем подынтегральную функцию в виде
sin nz _ sin яг/(z +1)2
(z2 — I)2	(z-1)2
и в качествеДг) рассмотрим функцию sinnz/(z + I)2.
На основании формулы (2.42) при п = 1 и z0 = 1 получим
Г sinnz/(z +1)2
--- у ’ dz = 2nif (1).
Jr (z-1)2
Найдем производную функции fi^z) = sinnz/(z + I)2 и ее значение
при z =1:
ncosnz(z + l)-2sin nz , 2лсо5л л
;	~2^~=" 4 '
Следовательно,
,	[ sin яг
/(*) = ------у
г pz d7
Пример 5. Вычислить интеграл ----------, где Г - окружность |z| = 1.
г z
Решение. Функция /(z)= е является аналитической в круге |z| < 1,
точка z0 = 0 принадлежит этому кругу, поэтому в соответствии с фор-
мулой (2.41) получаем
J— dz = 2л// (0) = 2л/е° = 2ni.
г Z
г dz
Пример 6. Вычислить интеграл |	, где Г - окружность
' Z2 + 1
|z + z|=l.
Решение. Подынтегральную функцию представим в виде
1 1 1 ч ч 1
-Д—Г = 7----75--/ =----7/О), /(z) =----;.
z +1	(z-/)(z + /) z + г	z — i
81
Поскольку функция /(z) =----- является аналитической в круге
z-i
\z + г| < 1 и точка z0 = -i принадлежит этому кругу, то на основании
формулы (2.41) получаем
dz = 2лг/(-г) = 2лг—-— = 2т—— = —тг.
z + i	-i- i - 2i
Пример 7. Вычислить интеграл ------------, где Г - окружность
J z(z - 2г)
|z —Зг| = 2.
ez
Решение. Функция /(z) =— аналитична в круге, ограниченном
z
окружностью Г; точка z = 2/ принадлежит этому кругу. Применяя фор-
мулу (2.41), находим
Г —е dz— _ Г f(z)dz _	_ 2П/J!— = ле2' - ^(cos2 + isin2).
J z(z - 2г) J z - 2г	2г
_	n „	rcoszdz „
Пример о. Вычислить интеграл ----------, где Г - замкнутый кон-
Jr(z-03
тур, однократно обходящий точку г.
Решение. Применяем формулу (2.42), которая при п = 2 имеет вид
г f(z)dz _ 2т
I;—v	(о)-
*(z-z0)	2!
Функция y(z)= cosz аналитична в области, ограниченной конту-
ром Г и на самом контуре; точка z = г принадлежит указанной области.
В соответствии с записанной формулой получаем
coszdz _ 2т г/2(cosz)
(z-г)3	2! dz1
= -7ucosz|z_;. = mcosi = -m
2
(Здесь принята во внимание формула cosz =----- при z = г).
82
Пример 9. Вычислить интеграл I---------------------, где Г - окруж-
J (Z + l)3(z-l)
ность |z| = 2.
Решение. Знаменатель (z + l)3(z- 1) подынтегральной функции обра-
щается в нуль в двух точках zt = -1 и z2 = 1, лежащих внутри круга |z| < 2.
Разложим функцию f (z) =--------i----- на элементарные дроби
(z + 1) (z-1)
1	_ 1	1____j_ 1__1	1	1
(z + l)3(z —1) ” 8 z-1 8 z + 1 4 (z + 1)2 2 (z + 1)3'
Следовательно,
r chzdz _ 1 C chzdz 1 rchzdz 1 Г chzdz 1 Г chzdz
J (z+1)3(z-1) “ 8 JTT"8 j77Г" 4 J (z + 1)2 “2 j (z+1)3'
Первые два интеграла вычислим с помощью формулы (2.41);
г chzdz „ . , , Г chzdz п ,
I------= 2л/сЫ, I-------= 2тасЫ.
J z-1	J Z+1
г	г
Третий и четвертый интегралы вычисляем согласно формуле (2.42)
при п = 1 и п = 2 соответственно:
г _chz6fe _ 27П-(с|12у|	_ -2лйЫ,
Jr(* + 1)2 lz=-’
f chzdz 2 л/. . .,i	. ,,
------г- = —— (chz)	= Tuchl.
J (z + 1)3 2i ?b=-i
Подставляя найденные значения в равенство (I), получаем
f chzdz	2тисЫ 2л<сЫ 1 _ ., , 1
------5--------------------+—2л;зп1 —л/сЫ =
J(z + l)3(z-l)	8	8	4	2
shl-chl
2
Tti = -
л/
2£
83
Задачи
Вычислите интегралы
„ г z1dz	о
1.		, если: 1) Г - окружность |z| = 3;
J z-2z
г
2)	Г - окружность |z| = 1.
2.	[ Z dz, где Г - окружность |z| = 2.
J z + i
г
3.	Г е. если: 1)Г - окружность |z —2| = 1;
р +2z
2) Г - окружность |z - 2| = 3.
г sin Z	_	.	. .1 л
4.	I-----dz^ где Г - окружность |z + ?| = 3.
J Z + /
г
Г COS Z
5.	------dz, где Г - окружность \z - 11 = 1.
J z-n
г
. f ezdz „	, , _ ,
6.	I-----, где Г - окружность |z| - 1.
J z2+2z
г dz
1. —-----, если: 1) Г - окружность \z - 2/| = 2;
J z2 +9
2)	Г - окружность |z + 2/| = 2.
f zdz
8.	I —---, где Г - окружность |z + 2| = 2.
Р -1
„ f chizdz „	11-0
9.	—---------, где Г - окружность |z| - 2.
» z2 +4z + 3
ш Ге'^г Г	ill
10.	, где Г - окружность |z- z| = 1.
* z + 1
.. f sinfc ,	I I П
11.	—---------dz, где Г - окружность z = 2.
•z2-4z+3 .
12.	| c0^z dz, где Г - окружность |z| = 1.
84
rsh2z ,	...
13.	I —— az, где Г - окружность |z| = 1.
г z
, г zdz	„	.	,
14.	------------, где Г - окружность Iz - 3 = 6.
J (z-2)3(z + 4)
Ответы
1.	1) -8л/; 2) 0. 2.2л. 3.1) 0; 2) -л//3. 4. п(е-е~'). 5. 0. 6. ni. 7. 1) л/3; 2) -л/3.
8. ni. 9. л/cosl. 10. пе~1. 11. лсЫ. 12. -ni. 13. 2л/. 14. -Л//27,
Вопросы
1.	Запишите интегральную формулу Коши.
2.	Запишите формулу для значений л-ой производной от функции
Дг) в точке z0.
3.	Какие интегралы можно вычислить с помощью интегральной
формулы Коши?
4.	Какие интегралы можно вычислить с помощью формулы для
л-ой производной?
§2	.6. Ряд Тейлора
Функция/z), однозначная и аналитическая в точке z0, разлагается
в окрестности этой точки в ряд Тейлора
оо
f{z) = ^cn^-zQ)n,	(2.43)
л=0
коэффициенты сп которого определяются формулами
Сп=^_Л£)^_=/^о)>л = о,1>2,
2л/J (z-z0)"+ л!
(2-44)
где Г - окружность с центром в точке z0, расположенная в окрестности
точки z0, в которой функция У(2) является аналитической. Центр ок-
ружности круга сходимости находится в точке z0; эта окружность про-
ходит через особую точку £ функции fiz), ближайшую к точке z0, т.е.
радиус R сходимости ряда (2.43) будет равен расстоянию от точки z0 до
ближайшей особой точки £ функции^2)-
85
Для функций -----, ----, (1 +z)“, ln(l + z) ряды Тейлора имеют
l-z 1 + Z
соответственно следующий вид:
—— = l + z + z2 + z3 +... + zn +... (Л = 1),	(2.45)
1 —z
— = l-z + z2-z3+... + (-l)"z"+... (Л = 1),	(2.46)
1 + z
(Uz)»=H-azt^az^a<a-1>(a~2)?t
2!	3!
+ a(a-l)...(a-(и-!))_„ +	,R =
и!	"	k
(2-47)
-2 -3 г4	г«
ln(i + z) = z- —+ —- —^.^(-l)"-’—+ ... (Л = 1)	(2.48)
2	3	4	и
Степенной ряд (2.47) называется биномиальным. Формула (2.48)
определяет разложение в ряд Тейлора в окрестности точки z0 = 0 глав-
ного значения логарифма. Чтобы получить ряд Тейлора для других
значений многозначной функции Ln(l +z) необходимо в правой части
добавить слагаемое 2rmi, где п = ±1, ±2, ±3,... :
Z Z
Ln(l + z) = z------+------... + 2птп, и = ±1, ±2,... .
2	3
(2-49)
Пример 1. Разложить в ряд Тейлора функцию f (z) =-------- в окре-
3-z
СТНОСТИ ТОЧКИ Z = 0.
Решение. Преобразуем эту функцию следующим образом:
1 1 _ 1 1
З-z ” 3(l-z/3) - 3 l-z/3
Поскольку (см. формулу (2.45))
р- = l + z + z2 +z3 +... (|z|<l),	(2.50)
86
z
то при t = — получим
1
l-z/3
z z2 Z3
i+33 + з3
Следовательно,
1 1
З-z " 3
Z
3
1 1
1-2/3 ” 3
2	3
Z Z	Z
—I-----1---
з з2	з3
1	1	z	z2	z3	z"
	  1   "I “I т +... н--------г
3-z---------------------------------3	З2	З3	З4	3"+I
2
Полученный ряд сходится при — < 1, или |z| < 3.
Пример 2. Разложить в ряд Тейлора функцию f(z) =—-— в ок-
7 -5z
рестности точки z0 = 1.
Решение. Преобразуем данную функцию:
1 =	1	=	1	=	1	= J_ 1
7 —5z 7 —5(z-l)-5 ” 2 —5(z —1) “ 2[l-5(z-l)/2] ~ 2 ’ l-5(z-l)/2'
В соответствии с формулой (2.50) при t = 5(z- 1)/2 получаем
1	5	52	, 53 ч
-------------= l+-(z-l) +—(z-l)2+ — (z-l)3+....
l-5(z-l)/2---2	22	23
Следовательно,
з
-L-=i--------’---= 1 i+A(Z-i)+4(Z-i)2+4(Z-i)3+... ,
7-5z 2 l-5(z-l)/2 2	2	22	23
IIS	S2	S”
---= —+ —(z-l) + —(z-1)2 + ... +-r(z — 1)" + ....
7 —5z 2 22	23	2n+1
Полученный ряд сходится при ^-(z-1) <1, или
2
5
87
Пример 3. Разложить в ряд Тейлора функцию fiz) = chz в окрест-
ности точки z0 = 0.
Решение. Гиперболический косинус определяется формулой
Заменяя в формуле (2.4) z на (-z), получаем
е
(2-51)
Значит,
, 1
chz -
2
Итак,
z2m
(2ти)! +
Полученный ряд сходится при всех z, как и ряды для функций е и еz.
Пример 4. Разложить в ряд Тейлора функцию /(z) = — в окрест-
Z
ности точки z0 = -2.
Решение. Поскольку
1 _ 1 1 1 1 1
z~ (z + 2)-2~ 2-(z + 2)~ 2[l-(z + 2)/2]“ I’ l-(z + 2)/2’
то на основании формулы (2.50) при t = (z + 2)/2 получаем
1 _	1Г	, z + 2	| (z + 2)2	| (z + 2)3	|	| (z + 2)n	|
z	2	2	22	23	2"
Следовательно,
1_ 1 z + 2 (z + 2)2	(z+2)n
_	9	9З ’	->л+1
88
Этот ряд сходится, когда
< 1, т.е. при |z + 2| < 2.
Пример 5. Разложить в ряд Тейлора по степеням z функцию
/(z) = -^—+ е"г.
1 + Z
Решение. Пользуясь формулами (2.46) и (2.51), находим искомое
разложение
( z2 г3
/(z) = (l-z + z2-z3 +...)+ l-z+ —-у + ..
= 2-2z + [ 1 + —|z21 + —|z3 +...+ (-l)"-1 1 + —?—
I	2!J	I 31J	l (л-1)!
Ближайшей к точке z0 = О особой точкой данной функции являет-
ся точка z = -1, поэтому радиус сходимости полученного ряда R = 1.
Пример 6. Найти разложение в ряд Тейлора по степеням z для
функцииу(г) = z2cosz.
Решение. Принимая во внимание формулу (2.3), получаем
Итак,
,4	,6	,8
z2 COSZ = z2--------+-----------+ ... + (-1)1
2!	4!	6!
г2"+2
Т^)!
Полученный ряд сходится для всех х, как и ряд для cosz.
Пример 7. Найти разложение в ряд Тейлора по степеням z для
ez
функции /(z) = ---.
1 - z
Решение. Пользуясь формулами (2.4) и (2.45), находим:
—— = (1 + z + г3
1-z
Z Z2 Z3
---1------1---
1!	2!	3!
89
ez , „	5 2	„	1
----= l + 2z + — z + ... + anz + ..., гдеа„ =a„_,+—.
1 - z	2	n\
Точка z = 1 является особой для данной функции, поэтому радиус
сходимости полученного ряда R = 1.
Пример 8. Найти первые три члена разложения функции fiz) = eslnz
в ряд Тейлора по степеням z.
Решение*. Полагая t = sinz в равенстве (см. формулу (2.4))
получаем
gsinz _ 1 sin Z ! sin2z ! sin3 z !
1!	2!	3!
Принимая во внимание формулу (2.5), находим:
esinz
if z3
— z------
3!l	3!
sinz 1 ,	,1 2 .
в = 1 + Z4-------Z +....
2
Пример 9. Разложить в ряд Тейлора по степеням z функцию
fiz) = (1 — z + z2)e.
Решение. С учетом формулы (2.5) находим:
п °° п	«	л+1
Z	V1 2	V1 z	V-"1
л=0	л=0	*’	л=0
л=0	'	л=0	л=0
zn+2
гЛ
1 1
00	„	00	„
Z	Z
п=0	л=1 v ’
® ,п
У——
(и-1)! (л-2)!
Z".
Поскольку
_1_ _ 1	1 = 1 г _ п
и! (и-1)! +(и-2)Г (п-2)!< ti~)’
90
то
(l-z + z2)ez =1 +
Пример 10. Найта первые пять членов разложения в ряд Тейлора
функцииХг) = /cosz.
Решение. Принимая во внимание формулы (2.4) и (2.6), находим:
г f, z z1 Z3 z4 z5 z6
е cosz = 1 + —+ — + — + — + — + — +
1! 2!	3!	4!	5!	6!
2!	4!	6!
-z1
2
1	3	1	4	1	5
+ — Z + — z +-------Z
6	24	120
-J-z‘
720
| ,	1 2	1	4	1	6 I. 1 3	1
X 1----Z +----Z-------Z + ... =l + z— z —z
720 J 3
24
3	1 4	1	5
— Z--------Z +....
6	30
Итак.
z	,	.	1 3	1 4	1	5
е cosz = l + z—z —z----------z +
3	6	30
Пример 11. Разложить в ряд Тейлора функцию fiz) = tgz в окрест-
ности точки Zq = 0.
Решение. Ближайшая от начала координат особая точка функции tgz
7Г	,	2	3
есть z = —, поэтому функция tgz разлагается в ряд с0 + c,z + c3z + ... в
I I 71
круге, |z|<—,
где си (« = 0,1,2,3,...) - коэффициенты, значения кото-
рых подлежат определению.
Заметив, что tgz - нечетная функция, поэтому в разложении будут
только члены с нечетными показателями, использовав равенство sinz =
= cosz • tgz и ряды для sinz и cosz (см. формулы (2.5) и (2.6)), получим
z5 z7
z-----+---------+
3!	5!	7!

1 -2
1	4
2
z
з
2	4	6
Z Z Z
"гГ 7Г "бГ
(ctz + c3z3 +c5z5 +c7z7 +...).
91
Сравнивая коэффициенты при z, z, z , z ,в обеих частях равен-
ства, находим:
1 11 11
1 — Ci 9 ~ — — Ci — С] ,	— Сс — — С? Ч* ~“Ci ,
1	3!	2! 1	5!	2!	4! 1
1 111
---— С7-С< Ч--С-i-Ci, ....
7!	2!	4!	6!
Из этих уравнений определяем коэффициенты:
С| = Ъ Сз = |,
С5
2	17
=---, С7 =----
15	315
Следовательно,
5 , 17 ,
tgZ = Z + -JZ3
2
+ — z +----z
15	315
Задачи
Разложите в ряд Тейлора в окрестности точки Zq = 0 каждую из
функций:
1. /(Z) = -L-.	2. /(z) = —!—.	3. /(Z) = -±-.
z + 8	3 - 2z	4 + 3z
4.	y(z) = shz.	5.y(z) = cos2z.	6.y(z) = e22.
Разложите в ряд по степеням z каждую из функций:
7.	y(z) = eoz.	8.y(z) = cosaz.	9.fiz) = sinaz.
S' 1
10.	ftz) = chaz.	11. j(z) = shaz.	12. f(z) =-------—.
Разложите в ряд Тейлора в окрестности указанной точки каждую
из функций:
13.	/(z) = l, z = -3.	14./(z) = —, z = 2.
3	z-1
15.	/(z) = -J-, z = 2.	16. /(Z) = —1—, z = 3.
z + 5	3 - 2z
Разложите в степенной ряд в окрестности точки z = 0 каждую из
функций:
17.y(z) = zcosz.
2O.y(z) = sin2z.
18.Xz) = zV.
21./z)=
19. /(z) = lshz.
22. /(z) = -L + ez.
1 — z
91
Ответы
L (И<8)-
п=0	2
z2"~'
з-
л=0
4. V —---------. 5. У (-1)
<•} 2п
2_______ 2п
(2ny.Z
О"
6. y3_L_
4-1 п\
/7=0
2п
7. У —
" п\
10. У-—Z2". 11. У
/7=0
8- £(-’)
л=0
a2"+1z2,,+1
(2и + 1)! ‘
aln zi„
(2«)!Z
/7=0
13. _у (£±21
Ди -07 + 1
/7=0
(|*+ 3| < 3).
15.
/7=0	7
16.
*	-2/7 + 1
17.	г+у(-1)"£—.
£	(2«)!
18.	z2
®	„2"+1
9. У (-1)" —----------
(2« + ’)!
/7=0
/,+ 2"(z-3)
л=0
/7+2
-1)"£—
и!
(И<1).
“ 2л
19.	у —£—
•	-2//-I
20.	У (-1)" ---------г2"
£	(2”)!
. 2 l-cos2z
sin z ---------------- ]
2
*	„2/7
21-
77=0
Указание.
разложением
/7=0
Воспользоваться формулой
ряд функции fiz) = cos2z.
и
в
z
3
н
Вопросы
1.	Какой вид имеет ряд Тейлора для функции fiz), аналитической
в точке z0?
2.	Как определяются коэффициенты ряда Тейлора?
3.	Запишите разложение в степенной ряд функции /(z) = —5—;
1 - z
чему равен радиус сходимости этого ряда?
4.	Запишите разложение в ряд по степеням z для функции
/(z) = ——; чему равен радиус сходимости этого ряда?
1 + z
5.	Какой вид имеет биномиальный ряд, каков радиус его сходи-
мости?
93
6.	Запишите разложение в ряд по степеням z для функции fiz) ~
= ln(l + z); чему равен радиус сходимости этого ряда?
7.	Запишите разложение в степенной ряд функции^) = Ln(l + z).
§2	.7. Ряд Лорана
Функция^), однозначная и аналитическая в кольце г < |z-z0| < R
(не исключены случаи г-О, R = +оо), разлагается в этом кольце в ряд
Лорана
4-00	-1	оо
/(*) = ^C„(z-zo)" = ^c„(z-z0)" +^c„(z-z0)",	(2.52)
Л=—00	л=-оо	л=0
коэффициенты которого определяются формулами
cn= — [-f(z)dz м = 0,±1,±2,(2.53)
2ni)r(z-z0y+'
где Г - произвольная окружность с центром в точке zQ, расположенная
внутри этого кольца.
В формуле (2.52) ряд
-1	оо
сн(г-г0)п=У \п	(2.54)
,	n=l(z-Z0)
называют главной частью ряда Лорана, а ряд
оо
^cn(z-z0)" =Со +C1(z-zo)+c2(z-zo)2 +...	(2.55)
п=0
называют правильной частью ряда Лорана.
Пример 1. Разложить в ряд Лорана функцию f(z) = —-— в кольце
I+ Z
1 < |z| < +00.
Решение. Преобразуем данную функцию следующим образом:
1 1 1 1
1 + z z(l/z + 1) z 1 + 1/z
94
Так как |z| > 1, то l/|z| < 1, поэтому с учетом формулы (2.46) полу-
чаем разложение второго множителя в сходящийся ряд
1 ,111
-----= 1----+—------г- + ...
1+1/z Z z2 Z3
Следовательно,
1	1	1	1 f, 1 1	1
1 + z z 1 + 1/z z^ z z z
Полученное разложение содержит только главную часть ряда Ло-
рана; это ряд вида (2.54).
Пример 2. Разложить в ряд Лорана в окрестности точки z = 0 функ-
ez
цию /(z) = —.
z
Решение. Принимая во внимание разложение е в степенной ряд
(см. формулу (2.4)), находим:
Главная часть полученного ряда Лорана содержит только один
член.
Пример 3. Разложить в ряд Лорана в окрестности точки z0 = 0 функ-
... ч ez-1
цию /(z) =-----.
z
Решение. С учетом формулы (2.4) получаем
,	, Z Z Z	Z
е" -1 = —к--------------1--------1-... +-------к...
1! 2!	3! м!
95
Следовательно,
Полученное разложение не содержит главной части.
Пример 4. Разложить в ряд Лорана функцию /(z) = в окре-
стности точки z0 = 0.
Решение. Принимая во внимание формулу (2.5), находим искомое
разложение:
sinz if z3 z5 z7
i	з 5
sin z 1 z z z
~zr~~z 3!+^T 7!
Пример 5. Разложить в ряд Лорана функцию /(z) =--------— в ок-
z
рестности точки z0 = 0.
Решение. С учетом формулы (2.6) получаем:
<	2	4	6	8
1-cosz = 1- 1- — + -—— + — +
" 8!
2! 4! + 6!	8!
2!	4!	6!
Таким образом,
z2 2!	4! + 6!	8!
1 -cosz _ 1	z2	z4	z6
z2 ~ 2! 4!	6!	8!
96
-1 —- с
Пример 6. Разложить в ряд Лорана функцию f (z) =---------------в окре-
стности ТОЧКИ Zj, = 0.
Решение. С учетом формулы (2.51) получаем
Z Z2
---1--
1! 2!
1-е '
z3 z4 z5 z6
----1---------1-----
3! 4! 5! 6!
Следовательно,
l-e~z _	1	би	z2 ।	z3	z4	। z5	z6	।	?
z3	z31^1!	2! +	3!	4!	+ 5!	6!	+">
1 — е~2	1	1	1	z	z2	z3
--- — — — ---------1-------1--------F.«..
Z3	z2	2!z	3!	4!	5!	6!
Пример 7. Разложить в ряд Лорана функцию /(z) = z3 cos— в ок-
z
рестности точки z0 = 0.
Решение. Для любого комплексного t справедливо равенство (см.
формулу (2.6))
,2	,4	,6	,8
C0S/-1------+-------+----
2!	4!	6!	8!
Полагая в этом равенстве t - —, получаем
z
1,1	1	1 Z
COS— — 1	— 4-~--— 4-— —
z 2!z2 4!z4 6!z6 8!z8
Итак,
,з
з 1 з| ,	1	1	1 z
Z COS— = Z 1----------4-----------— +---
Z I 2!z2 4!z4 6!z6 8!z8
4 Зак. 1816
97
3	1	3
z cos— = z
z
z	1	1 z
2!	4!z	6!z3	8!z5
Полученное разложение справедливо для любого z * 0. В данном
случае «кольцо» представляет всю комплексную плоскость с одной вы-
брошенной точкой z = 0. Это «кольцо» можно определить с помощью
следующего соотношения: 0 < |z - z0| <+<»; здесь г = 0, /? = +», zo = 0.
Данная функция является аналитической в указанном «кольце».
£
Пример8. Разложить в ряд Лорана функцию /z)= z в окре-
стности точки z0 = 0.
Решение. Для любого комплексного t выполняется равенство (см.
формулу (2.4))
Полагая здесь t = —, получаем
z
7,11	1	1 Z 1
е - = 1 ч—।-т- ч-т- ч-— ч-г ч-т
z IXz1 З’г3 4!z4 5!z5	61 z6
Принимая во внимание это разложение, находим:
з-з!,11	1	1	1	1
z ez =z 1ч- — Ч--Г-Ч-—-+-—ч-—г +-7
z 2!z2	З!г3 4!z4	5!z5	6!z6
3-32*11	1	1
ez = z +z +—+—+-4-—x-ч-—-
2! 3! 4!z 5!z2 6!z3
Полученное разложение справедливо при любом z * 0.
Пример 9. Разложить функцию f (z) =---------- в ряд Лорана в сле-
z(l-z)
дующих кольцах: 1) 0 < |z| < 1; 2) |z| > 1; 3) 0 < \z- 11 < 1.
Решение. Во всех этих кольцах данная функция является аналити-
ческой, поэтому может быть разложена в них в соответствующий ряд
Лорана. Представим эту функцию в виде суммы элементарных дробей:
, 1 11
f(z) =-------=—ч-------.
z(l - z) z l-z
98
1.	Поскольку |z| < 1, то с учетом формулы (2.45) получим
1	111,	2	3
z(l-z) z 1-z Z
Главная часть ряда Лорана представлена здесь только одним сла-
гаемым.
2.	Если |z| > 1, то |l/z| < 1, поэтому
1	111	1	1 (,	1 1	1	А
	=		-1+ — + -у+—г+ — L
z(z-l)-------------z z 1-1/z-Z	Z^	Z	Z	z3	)
1 _ _ _1____1__1 
z(z-l) z2 z3 z4
В этом разложении отсутствует правильная часть.
3.	Если 0 < |z- 1| < 1, то функцию — нужно разложить в геомет-
Z
рический ряд со знаменателем z - 1 :
1111 , ,
—----- = -----+—-—- =---------+1 -(z-1) + (z-1)2 -(z-1) +....
z(l - z) 1-z 1 + (z -1)	z -1
Главная часть полученного ряда Лорана содержит только один
член.
Пример 10. Функцию /(z) =---------------разложить в ряд Лорана,
(z-l)(z-2)
приняв Z0 = 0.
Решение. Данная функция имеет две особые точки: z = 1, z = 2. Сле-
довательно, существуют три кольца, в каждом из которых функция яв-
ляется аналитической: 1) круг |z| < 1; 2) кольцо 1 < |z| < 2; 3) внешность
круга |z| < 2, т.е. |zj > 2.
Функцию^) разложим на элементарные дроби:
1 1____________1_. 1	1 1
(z-l)(z-2) z-2 z-Г z-2~ 2 l-z/2'
1. Поскольку |z| < 1, |z/2| < 1, то с учетом формулы (2.50) получим
	— 1-1	1—— -I—— +... -I-н
l-z/2----------------------2 22 23	2”
99
11	1	_ 1 z z2 z”
z-2	2 l-z/2	2 22 23	2"+l
--— = —J— = l + z + z2 + z3 + ... + z” +....	(II)
z—1	1—z
Сложив ряды (1) и (11), найдем, что
1	1	f,	И	Г, И	2 f, 1 L
(z-l)(z-2)	2	f	22J	I	23J I	2”+J
Полученный ряд является рядом Тейлора.
2. Если 1 < |z| <2, то ряд (I) сходится (ибо |z/2| < 1), но ряд (II)
расходится (так как |z| > 1).
Разложение (II) заменим другим:
1	11	1 f,	1	1	1	Alli	,ПП
	=	= — 1 + - + —+ — + ... =--—(III)
z-1---------------------------------z 1-1/z-zf	Z	z2	Z3	) Z z2 Z3
Ряд (III) сходится, поскольку |z| > 1 И |l/z| < 1.
Сложив ряды (I) и (III), получим ряд Лорана для данной функции
в указанном кольце:
1	1	z	z2 z” J_______________1__1_________1__
(z-l)(z-2) ~	2	22	23	” 2"+|	" z	z2	z3	z”
Коэффициенты этого ряда определяются формулами:
с„ =—Ц-, л = 0,1, 2,...; с_ =-1, л=1, 2,....
п п
3. Когда |z| > 2, то равенство (III) верно, поскольку и |z| > 1, но ряд
в правой части формулы (I) уже будет расходящимся. Разложение (I)
заменим другим:
1	1	1	1 f,	2	22	23
z-2	z	1—2/z	z^	z	z2	z3
1
z-2
1	2	22
- + T+-3
z z z
2«-i
z”
(IV)
100
Этот ряд сходится, так как |z| > 2 и, следовательно, |2/z| < 1. Сло-
жив (Ш) и (IV), получим разложение данной функции в ряд Лорана
1	1	22 -1 23 -1	2"-1—1
----------= —-- 4-------1----	1-... 4	1-
(z-l)(z-2) z2 z3 z4-----------------z"
для которого
с„ = 0,я = 0, 1,2,...;с„ = 2” *-1,л= 1,2, 3,....
Замечание. Этот пример показывает, что для одной и той же функции
flf) ряд Лорана, вообще говоря, имеет разный вид для различных колец.
z4
Пример 11. Функцию f(z) =----------
(z-2)2
разложить в ряд Лорана по
степеням z-2.
Решение. Введем новую переменную Z по формуле Z = z - 2, тогда
,, . z4 (Z + 2)4 Z4 +8Z3 +24Z2 +32Z + 16
/(z)===--------------
(Z	L
=	+ —+ 24 + 8Z + Z2,
z2 Z
т.е.
—24 + 8(z — 2) + (z —2)2.
(z-2)2 z-2
Здесь главная часть ряда Лорана имеет два члена, а правильная
часть - три члена. Поскольку полученное разложение содержит только
конечное количество членов, то оно справедливо для любого z, кроме
z=2.
Задачи
 i t ».
Разложите в ряд Лорана в окрестности точки z0 = 0 следующие
функции:
sinz cosz ez . i \z _ з . 1
1. ----•	2. ——	3. —.	4. г e .	5. zJsin—.
Z	z2 z	z
4	1 _sin2Z 1 . 2 2	„1 + cosz
6. z cos—. 7. -------.	8. —sin —.	9. ------.
Z	z	z z	z4
101
z	z2	Z
Разложите в ряд Лорана по степеням z следующие функции в ука-
занных кольцах:
ГЗ.—Ц-; 1) 0 < |z| < 1; 2)l<|z|<+oo.
z + z2
1>2<и<3; 2)3<Н<+°°-
Cz-2Xz-3)
i.----------; l<|z|<2.
(z + l)(z-2)	1 1
2z + 3
'• ~5---------
z2 +3z + 2
1 <|z| <2.
Разложите в ряд Лорана по степеням z - z0 следующие функции при
заданных zobуказанных кольцах:
17.	; Zq = -2; 1 < |z + 2| < 3.
Z “ 1
18.	2.rTj_; z0=2; 0<|z-2|<l.
z -3z + 2
19.	Z + 2—; z0 = 1; 2 < Iz -11 < +oo.
z2-4z + 3	1	1
2^—2-^; z0=l; l<|z —1|<2.
z(z-3>
Ответы
, , z2	z4	z6 3!	5!	7! 1	1	1	1	z	z2	z6 zJ	z2	2z	3!	4!	5!	6!	,1	1	z2	z4	z6 z2	2!	4!	6!	8! .2	111	1 4. Z + Z 4— 4	4	T" 4	— + .... 2 3!z 4!z2 5!zJ
- 2 1 1 1 1 5. z?	+ —T	- + —7--.... 3! 51z2	7!z4	9!z6	4_£^ 1__1_ J	 ’Z 2! + 4! 6!z2 + 8!z4
_ 2	8 j 32 5 7. —z	z3 +—z5-.... 2!	4!	6!	8 42	+		 ‘ 2!2zJ	4!2z5	6!2z7
a 2	1	1	z2 z4	2!z2	4!	6!	in	Z z1 z3 z4 2! 3! 4! 5!
102
? z5
---+ — ....
5! 7!
»=0
15.
3k z
11.-^-- — + —
z2 z 3!
jj(-i)-z'
w=0
_ -ifl-1	~n-\
w=l
16. ytr+унц
7n Аши 7/,+I
n~\	n=Q
18. -J- +£(-1)^-2)".
z »=0
y(-i)‘
Zu J"
..—л
1
z2
1	z2	z5 z5
2!z	4!	6!	8!
JS, n»-l i
//=1	«=0
1	1	A	1(1	z	z2	z3
zJ	z4	J	3(2	22	2’	24
1 ^(Z + 2)"
n-0
tr(z + 2)"	3'
19. —!—+5
z-1
20. IV <z!E
9Zu(z_iy
и= Iх z
Вопросы
1.	Какой вид имеет ряд Лорана?
2.	Какому условию должна удовлетворять функция, чтобы для нее
можно было записать ряд Лорана?
3.	По какой формуле определяются коэффициенты ряда Лорана?
4.	Что называют главной частью ряда Лорана?
5.	Что называют правильной частью ряда Лорана?
§2	.8. Нули функции. Особые точки
Нули функции. Рассмотрим функцию fiz), аналитическую в точ-
ке z0. Точка z0 называется нулем функцииfiz) порядка (или кратности)
п, когда выполняются условия:
Ж» = 0,/'(*о) = 0,O(zo) = O,/W(zo) # 0.	(2.56)
Если п = 1, то точка z0 называется простым нулем.
Значение z0 тогда и только тогда является нулем и-го порядка
функции fiz), аналитической в точке Zq, когда в некоторой ее окрестно-
сти верно равенство
F(z) = (z - z0)"(p(z),	(2.57)
где <p(z) - функция, аналитическая в точке z0 и <p(z0) # 0.
103
Особые точки. Особой точкой функции fiz) называется точка z0, в
которой эта функция не является аналитической. Точку z0 называют изо-
лированной особой точкой функции fiz), когда существует окрестность
этой точки, в которой fiz) является аналитической всюду, кроме z0.
Особую точку z0 функции fiz) называют устранимой, когда суще-
ствует конечный предел этой функции в данной точке:
lim /(z) = с.	(2.58)
Точку z0 называют полюсом функции fiz), когда
lim /(z) = oo.	(2.59)
z-»z0
Для того, чтобы точка z0 была полюсом функции fiz), необходимо
и достаточно, чтобы эта точка была нулем функции
=	(2-60)
/(г)
Точку z0 называют полюсом порядка п (n>V) функции fiz), когда
эта точка является нулем порядка п для функции <p(z) = —-—. В слу-
/(*)
чае и = 1 полюс называют простым.
Для того чтобы точка z0 являлась полюсом порядка п функции
fiz), необходимо и достаточно, чтобы функцию fiz) можно было при-
вести к виду
/(2)’Г^7’	<2'61)
где (p(z) — функция, аналитическая в точке z0 и <p(z0) * 0.
Точку z0 называют существенно особой точкой функции fiz), когда
в ней функция fiz) не имеет ни конечного, ни бесконечного предела.
Справедливы следующие утверждения.
1.	Точка z0 является устранимой особой точкой функции fiz) тогда
и. только тогда, когда ее лорановское разложение в окрестности точки
Zq не содержит главной части.
104
2.	Точка z0 является полюсом функции fiz) тогда и только тогда,
когда главная часть ее лорановского разложения в окрестности точки
z0 содержит лишь конечное число членов:
/(z) =	С-к	+ ...+	+ У с„(z-z0)" (с_** 0).
(z-z0) z-z0
Наибольший из показателей степени разности z - z0 в знаменате-
лях, т.е. число к, совпадает с порядком полюса.
3.	Точка z0 является существенно особой точкой функции fiz) то-
гда и только тогда, когда главная часть ее лорановского разложения в
окрестности точки z0 содержит бесконечное множество членов.
Пример 1. Доказать, что точка z0 = 0 является нулем второго по-
рядка для функции^?)= 1 - cosz.
Решение. Запишем разложения в ряды данной функции и ее пер-
вых двух производных:
/(z) = l-cosz = l-
z2 z4
/'(z) = l- —+ —-
2! 4!
Поскольку fiO) = 0,/'(0) = 0,/"(0) =1*0, т.е. выполняются усло-
вия (2.56) при п = 2, то z0 = 0 - нуль второго порядка для функции
fiz) = 1 - cosz.
Z1
Пример 2. Найти порядок нуля z0 = 0 для функции f(z) =------.
z-sinz
Решение. Использовав разложение функции sinz в ряд Тейлора, по-
лучим
z-sinz z-(z-z3/3!+z5/5!-...) z3/3!-z5/5!+...’
105
f (z) = z4-----5--------, fiz) = z4<p(z), <p(z) =--.
l/3!-z2/5! + ...	i/3!_z2/5! + ...
Таким образом, функция /(z) записана в виде (2.57), где <p(z) -
функция, аналитическая в точке z0 = 0, причем <р(0) = 6^0. Значит,
точка z0 — нуль четвертого порядка для данной функции.
Пример 3. Найти нули функции fiz) = (z2 + l)3sinz и определить их
порядки.
Решение. Когда Xz)= 0, или (z2+l)3sinz = o, то z2+l=0 либо
sinz = 0. Из первого равенства следует, что z = -i, z = i; второе равенст-
во выполняется при z = кл, где к = 0, ± 1, ± 2,....
Пусть z = —z, тогда функцию fiz) можно представить в виде (2.57):
fiz) = (z + z)3<p(z), <P(Z) = (z _ 03sinz является аналитической в точке z = -i,
причем <p(-i) = —8/sinz = 8shl * 0. Значит, точка z = -z есть нуль третье-
го порядка.
Аналогично доказывается, что z = z - нуль третьего порядка. Функ-
ция sinz имеет нули z = кл, к = 0, ± 1, ±2,.... Действительно,
sin z = (-1)* &'т(г-кл) = (-1)*
(г-Лл)3 , (г-^71)5
-----__ +------------
Это нули первого порядка для функции fiz) = (z + I)3sinz: film) = 0, но
/'(кл) 0, ибо f'(z) = 6z(z2 + l)2sinz + (z2 + l)3cosz.
ez -1
Пример 4. Доказать, что точка z0 = 0 для функции f(z) =-------------
z
является устранимой особой точкой.
Решение. Действительно, поскольку
z	z2 z3 ez-1 z z2
e =l + z + — + — + ..., -----= 1 +—+ — + ...,
2!	3! z 2! 3!
ez
lim f (z) = lim-----= 1,
z->0	z->0 z
to z0 - устранимая особая точка (см. формулу (2.58)).
Пример 5. Найти полюсы функции
106
/(z) = —5---Ц------7.
(z2-l)(z2+l)2
„	д.	/X (z2-l)(z2+l)2
Решение. Так как для функции <p(z) = ------- точки z, = -1,
z
z2 - 1 - нули первого порядка z3 = -i, z4 = i— нули второго порядка, то
для функции Дг) точки Zj = -1, z2 = 1 - полюсы первого порядка, точки
z3 = -i, z4 = i— полюсы второго порядка.
P(z)
Замечание. Если /(z) = где P(z) и Q(z)- многочлены, не
2(z)
имеющие общих корней, то корни многочлена Q(z) (и только они) являются
полюсами функции Дг). Порядок полюсов fiz) совпадает с кратностью соответ-
ствующих корней многочлена Q(z). Например, когда
z -1
f(z\ —	1
(z + 0(z-3)2(z + 4)3 ’
то z = —i - простой полюс, z2 = 3 полюс второго порядка, z = —4 - полюс третье-
го порядка.
Пример 6. Исследовать особые точки функции
sin z
/(Z)= з. 2
Решение. Поскольку z +z -z- 1 = z2(z + l)-(z+ l) = (z+ 1Дг2- 1) =
= (z+ i)2(z— 1), то функция имеет особые точки z= 1, z = -l. Исследу-
ем точку z = -1. Функцию Дг) приведем к виду (2.61):
=	/(г).Л<£>, ф(г) = ™£
(z + lr	(z + 1)2	z-1
где <p(z)- функция, аналитическая в окрестности точки z = -l, причем
. sin(-l) „
ф(-1) =------—*0. Следовательно, точка z = -l является полюсом
второго порядка.
a	.	„ x	,, x sinz/(z + l)2
Аналогично, записав функцию Дг) в виде f(z) =-----------—
z-1
,, х Ф1(г)	, х S*nz
J (z) =---, <pj (z) =-----, заключаем, что z = 1 - простой полюс
z-1	(z + 1)
данной функции.
107
Пример 7. Найти особые точки функции/(z) = e'/z и определить их
типы.
Решение. Принимая во внимание, что (см. формулу (2.4))
,	.	t t2 tn
е =1 +—+ — + ... + — + ...,
1! 2! и!
при t = 1/z получаем
-,11 1
l!z 2!z2	и!г”
Этот ряд сходится всюду, кроме точки z = 0. Его можно рассмат-
ривать как разложение функции е' 2 в ряд Лорана в окрестности точки
z = 0. Поскольку главная часть ряда имеет бесконечное множество
членов, то точка z = 0 является существенно особой точкой для функ-
l/z
ции е .
z4
Пример 8. Найти нули и особые точки функции /(z) =——.
1 + Z
Решение. Поскольку fiz) = z4<p(z), где <p(z) =—J-—, <р(0) =#= 0, то в
1 + z
соответствии с формулой (2.57) заключаем, что z0 = 0 - нуль четверто-
го порядка.
г.	л.	1	1 + z4
Рассмотрим функцию ------= —т—, нули которой совпадают с
/(г) z4
нулями ее числителя 1 + г4. Найдем эти нули:
z + 1 = 0, z = V-T = ^/соз(л+2л Л) + /5ш(л+2л Л) =
(2к+ )л . . (2Л + 1)л	, п , „ ,
= cos ----— + i sin	, к = 0, 1, 2, 3.
4	4
Следовательно,
Эти нули простые, поэтому функция -------— имеет в указанных
1 + Z4
точках полюсы первого порядка.
108
Пример 9. Найти особую точку функции /(z) = ^^-, указать ее
z
характер.
Решение. Особой точкой для этой функции является zo = O; при
этом значении функция не определена. Разложим данную функцию в
ряд Лорана в окрестности точки z0 = 0. Поскольку
sin
z =
то
В полученном разложении главная часть отсутствует; следова-
тельно, точка z0 = 0 является устранимой особой точкой функции
sinz
/(z) =------•
z
Замечание. Этот результат следует также из определения устранимой
особой точки (см. формулу (2.58)). Действительно, поскольку
sinz , z2 z4 z6
-----= 1	+	+ ...,
z 3!------------5!	7!
то
.. sinz
lim----= 1.
z-»0 z.
Пример 10. Найти особые точки функции /(z) = ez/(l z).
Решение. Функция определена и является аналитической всюду,
кроме точки z = 1. Разложим эту функцию в ряд Лорана по степеням
z— 1.
Поскольку
z 1-Z-1	1___1
,	1-z	1-Z	Z-1’
109
то
cz/(l-z) _ c-lg-l(z-l) _ с-1 У1 Н)”	1	. _
(z-l)"
_>	е-'	е~'	е-<
= е----------1-------т----------г- +....
z-1 2!(z-l)2 3!(z-l)3
Главная часть этого разложения - бесконечный ряд. Следователь-
но, z = 1 - существенно особая точка данной функции.
Задачи
Найдите нули функций, определите их типы
l.y(z) ~ cos2z.	2.y(z) = z-z3.
3.	=	4 z + 1
5./z) = z3(z2 + 4)2.	6. fiz) = sin33z.
7.y(z) = ctg4z.	8./(z) = (z2+2z+1)3.
9./z) = (z3+l)2.	1O.Xz) = z(1-A
Определите типы особых точек функций
11. /(z) = r z -2z + 5	1	3 12. /(z) = l + -i-- z z — 2
13./(z)=—!—.	14. /(z) = —-Ц-.
1 - cos z	z(l-e2z)
15. /(z) =	—	.	16. /(z) = sin—.
(z-2)(z-3)(z-4)	z
XX	z+1	sin z
17	1Я	—
	J	7
(z + /)(z-2)2(z-3)3	(z + n)(z2-l)
z2	2z2 -1
19- /W =	r.	20. /(z)= 7 \	.
(z~3)4	z7(z2+9)3
21. f(z) = —^—
е~г-1
„ у-z ч cosnz/2 е'
22. /(z) =--z-----+---------г.
sin2 (z-1) (z-1-л)3
ПО
Ответы
д 71
1. Простые нули zk = — + —к, к = 0, ±1, ±2,.... 2. Простые нули z, =0,
1 л/з 1 л/з
z = 1, z, =-1. 3. Простые нули z, = -1, z^=~2+i~Y’ z3= —Прос-
тые нули z, =— i, z = i; нули второго порядка z, = 1, z, = 2. 5. Нули второго по-
рядка z, = -2z, z = 2z; нуль третьего порядка z, = 0. 6. Нули третьего порядка
д	. д	.
zk -—к, к = 0, ±1, ±2, ... . 7. Нули четвертого порядка zk = — + пк, к = 0, ±1,
±2, ... . 8. Нуль шестого порядка z = -1. 9. Нули второго порядка z, =-1,
z, = —
3 2
1
V3
-у.- 10. Простые нули zk = nki, к = 0, ±1, ±2,..., z = 0 -
нуль второго порядка. 11. Простые полюсы z, = 1 + 2z, z = 1 - 2z. 12. Простые
полюсы z, =0, z =2. 13. Полюсы второго порядка zk = 2kn, к = 0, ±1, ±2, ....
14. Простые полюсы zk = nki, к = ±1, ±2, ... ; полюс второго порядка z = 0.
15. Простые полюсы z, = 2, z = 3, z, = 4. 16. Существенно особая точка z = 0.
17. Простой полюс z, =-/, полюс второго порядка z =2; полюс третьего по-
рядка z, = 3. 18. Простые полюсы z, = -1, z = 1; устранимая особая точка z = -п.
19. Полюс четвертого порядка z = 3. 20. Полюсы третьего порядка z, = —3/,
z = 3z; полюс седьмого порядка z = 0. 21. Простые полюсы z = 2nki, к = ±1, ±2,
...; устранимая особая точка z = 0. 22. Простой полюс z = 1, полюсы второго
порядка zk = 1 + пк, к * 0, к * 1; полюс третьего порядка z = 1 + п; существенно
особая точка z = 0.
Вопросы
1.	Что называют простым нулем функции Дг)?
2.	Что называют нулем кратности п функцииДг)?
3.	Каково необходимое и достаточное условие того, что точка г0
является нулем функцииДг)?
4.	Что называют особой точкой функции Дг)?
5.	Какая особая точка называется устранимой?
6.	Какая точка называется простым полюсом функцииДг)?
7.	Каково необходимое и достаточное условие того, чтобы точка
г0 была простым полюсом функцииДг)?
8.	Что называют полюсом порядка п функцииДг)?
9.	Каково необходимое и достаточное условие того, чтобы точка
г0 являлась полюсом порядка п для функцииДг)?
10.	Что называют существенно особой точкой функцииДг)?
11.	Как найти устранимую особую точку функции Дг) по ее лора-
новскому разложению?
111
12.	Как найти простой полюс функции fiz) по ее разложению в
ряд Лорана?
13.	Как найти полюс порядка п функции fiz) по ее разложению в
ряд Лорана?
14.	Как найти существенно особую точку функции fiz) по ее раз-
ложению в ряд Лорана?
§2.	9. Вычеты функций
Вычетом однозначной аналитической функции fiz) в изолирован-
ной особой точке z0 называется число, которое обозначают res f(z) 1 и
г»
определяют формулой
res/(z) = ^-|/(z)pk,	(2.62)
°	Y
где интеграл взят в положительном направлении по конуру у.
Замечание. Используются и другие обозначения: res[/(z), z0], res /(z),
z=z0
res/z.).
В качестве контура у рассматривается окружность с центром в
точке z0 достаточно малого радиуса; такого, чтобы окружность не вы-
ходила за пределы области аналитичности функции fiz) и не содержала
внутри других особых точек этой функции. Вычет функции равен коэф-
фициенту при минус первой степени в лорановском разложении функ-
ции fiz) в окрестности точки z0:
res/(z0) = c_1.	(2.63)
Вычет функции в устранимой особой точке равен нулю.
Если г0 — полюс л-ro порядка функции fiz), то
res/(Z)=-----— • lim —-[f(z)(z-z0)n).	(2.64)
z0 (л-1)! г->г° dz" 1
В случае простого полюса (л = 1)
res /(г) = lim {/(z)(z - z0 )}.	(2.65)
z0	z-»z„
1 res - сокращение французского слова residu, что обозначает вычет.
112
Если функциями) в окрестности точки z0 является частным двух
аналитических функций
4>(г)
причем <p(z0) * 0, t|/(z0)
ЛД то
= 0, a \p'(z0) 0, т.е. z0 - простой полюс функции
res/(z) = -^^-,
V (zo)
(2.66)
Если z0 - существенно особая точка функции fiz), то для нахожде-
ния resj(z0) необходимо определить коэффициент с_, в лорановском
разложении функцииДг) в окрестности точки z0; это и будет resfiz0).
Теорема 9.1. Если функция fiz) является аналитической на грани-
це Г области G и всюду внутри области, за исключением конечного
числа особых точек z„ z2.zn, то
J f(z)dz = 2 л £ res f(zk).	(2.67)
Г	k=i
Эта теорема называется теоремой Коши о вычетах. Ею пользу-
ются при вычислении определенных интегралов и нахождении сумм
рядов.
Вычет функции относительно бесконечно удаленной точки.
Говорят, что функция fiz) является аналитической в бесконечно уда-
ленной точке z = оо, если функция
ФЙ) = ^
аналитична в точке £ = 0. Например, функция /(z) = sin— аналитична
z
в точке z = оо, поскольку функция <р(£) =	= s*n £ аналитична в
точке £ = 0.
Пусть функция fiz) аналитична в некоторой окрестности беско-
нечно удаленной точки (кроме самой точки z = оо).
113
Говорят, что z = oo является устранимой особой точкой, полюсом
или существенно особой точкой функции fiz) в зависимости от того,
конечен, бесконечен или вовсе не существует предел этой функции
при z —> оо.
Критерии типа бесконечно удаленной особой точки, связанные с
рядом Лорана, изменяются в сравнении с критериями для конечных
особых точек.
Теорема 9.2. Если z = оо является устранимой особой точкой функ-
ции fiz), то ее лорановское разложение в окрестности данной точки не
содержит положительных степеней z; когда z = оо - полюс, то это раз-
ложение содержит конечное число положительных степеней z, в случае
существенно особой точки - бесконечное множество положительных
степеней z.
При этом лорановским разложением функции fiz) в окрестности
бесконечно удаленной точки называют разложение в ряд Лорана, схо-
дящийся всюду вне круга достаточно большого радиуса R с центром в
точке z = 0 (кроме, быть может, самой точки z = оо).
Рассмотрим функцию fiz), аналитическую в некоторой окрестно-
сти точки z = оо (кроме, быть может, самой этой точки).
Вычетом функции fiz) в бесконечности называется число, опре-
деляемое формулой
res/(z) = —f/(z)</z,	(2.68)
«о 2л/ J
Y-
где у_ - окружность достаточно большого радиуса |z| = р, которую точ-
ка z проходит по часовой стрелке (при этом окрестность точки z = оо
остается слева, как и в случае конечной точки z0).
Из этого определения следует, что вычет функции в бесконечно-
сти равен коэффициенту при z~' в лорановском разложении fiz) в окре-
стности точки z = оо, взятому со знаком минус:
res/oo) = -с_|.	(2.69)
Известные разложения е\ sinz, cosz, shz, chz (см §2.2) можно рас-
сматривать как лорановские ряды в окрестности точки z = оо. Посколь-
ку каждый ряд содержит бесконечное множество положительных сте-
пеней z, то указанные функции в точке z = oo имеют существенную
особенность.
114
Теорема 9.3. Если функция j[z) имеет в расширенной комплекс-
ной плоскости конечное число особых точек zt, z2,	z„, то сумма всех
ее вычетов, включая и вычет в бесконечности, равна нулю:
res f(z) + У res f(zk) = 0.	(2.70)
00	£=0
Из теорем следует, что
п
гез/(г) = -У res/(zt).	(2.71)
00
к=\
Равенство (2.71) используется при вычислении некоторых инте-
гралов.
Пример 1. Найти вычет функции /(z) = -у--
Решение. Данную функцию можно записать так: У (г) =—+-у и
Z Z
рассматривать эту сумму как разложение в ряд Лорана по степеням z,
для которого с_] = 1. В соответствии с формулой (2.63) заключаем, что
гезДО) = 1 (z0 = 0 - особая точка).
Замечание. Вычет можно найти и с помощью формулы (2.64). По-
скольку z„ = 0 - полюс второго порядка, то
1 d((z+ l)/z2)z2) cf(z + l)
res/(z) = — lim—-----—-—- = lim — ---- = 1.
о 1! г->о dz z-»o dz
Пример 2. Найти вычеты функции /(z) =-----------------.
(z-2)(z-4)
Решение. Эта функция имеет два простых полюса: z = 2, z = 4. В со-
ответствии с формулой (2.65) находим:
res f (z) = lim----------(z - 2) = lim —-— = -1;
2	z->2 (z - 2)(z - 4)	z-»2 z - 4
.. . ..	z(z-4)	.. z 4
res f (z) = lim--------— = lim-----=-------- 2.
4	z->4(z-2)(z-4) z-»4z-2 4-2
115
Пример 3. Найти вычеты функции /(z) =--------у.
(z-1)
Решение. Поскольку z0 = 1 - полюс третьего порядка, то на осно-
вании формулы (2.64) получаем
res/(2)=llim	=1.
iJ ’ 2!^I	Cfe2	2’~i dz1 2!
2	*
Пример 4. Найти вычеты функции /(z) = z cos------.
z-1
Решение.Точка z0=l является единственной конечной особой
точкой функции fiz). Чтобы найти resjV), разложим fiz) в ряд Лорана в
окрестности точки z0= 1, воспользовавшись рядом Тейлора для cosz
(см. формулу (2.6)):
При t =---- это разложение принимает вид
z -1
1,1 1
cos--- 1------ +----
z-1	2!(z —I)2 4!(z-l)4
Следовательно,
= [l + 2(z-l) + (z-l)2] 1-
1 1
2!(z—I)2 4!(z —I)4
Нас интересует только коэффициент при -------. Соответствую-
z-1
щий член ряда имеет вид 2(z -1)---5—- = ——. Значит, с, = -1, по-
2!(z-l)2	z-1
этому res /(z) -- с_, = -1.
116
Пример 5. Найти вычеты функции f(z) = z3e2.
Решение. Особыми точками ЭТОЙ функции ЯВЛЯЮТСЯ ТОЧКИ Z|=0
(существенно особая точка), z2 = oo (полюс третьего порядка). Разло-
жим функцию в ряд Лорана:
.	з(.	1	1	1	1	'I
f(z) — Z Id---1-----T- d--r- d--J- d-... ,
I	z	2!z2	3!z3	4!z4	J
f(z) = z3 d-z2 + — d- — d-—-—d-..., 0 < ]z| < 00.
2! 3! 4!z
Из этого разложения следует, что
res/(z) = c_] =1 = -1- и res/(z) = -c_1 = -1 = -А-.
о	4! 24	<»	4!	24
Пример 6. Найти вычеты функции /(z) = sin| 1 d- — |.
k z J
Решение. Функция имеет существенно особую точку z = 0. Разло-
жим функцию в ряд в окрестности этой точки:
. Г, П . ,	1	, . 1
sm Id-— = sml-cos—d-cosl sm —=
V z)	z	z
. / .	1	)	/1	1	'I
= sml 1--------d-... d-cosl-----т-d-... =
I	2!z2	J	Iz	3!z3	J
. , sin 1	1	1
= Sinl------- d-cosl-cosl----7d-....
2!z2 z 3! z3
Следовательно,
res/(z) = c_] =cosl.
i
Пример 7. Найти вычеты функции /(z) = (z-l)ez~2.
Решение. Функция имеет существенно особую точку z = 2. Разла-
гаем функцию в степенной ряд:
1 1 1 1
(z-l)ez-2 =(z-2d-l)ez-2 =(z-2)ez~2 +e2~2 =
117
„ ,	1 Г, i ] irii
— 2 + (z — 2) ч-1 ч— ч-— —I—
z—2\	2l) (z-2)2 \2! 3!
Значит, res f(z) = c_t = 1 +— = —. Поскольку нет других конечных
3
особых точек, то по формуле (2.71) находим, что res f(z) =—; точка
<ю	2
z = оо является полюсом первого порядка данной функции.
Пример 8. Найти вычеты функции f(z) = ——.
z1 -2z-3
Решение. Особыми точками этой функции являются точки zt = -l,
z2 = 3, z3 = оо. Записываем разложения функции в ряд Лорана в окрест-
ности указанных точек.
s 1	" (— пл+'
/<г>-Т7=г£^<г’3)”’
л=0
и>з.
л=1	z
Из этих разложений находим:
res/(z) = c-i = ~, res/(z) = с_, = р
res/(z) = -c_t
СО
Полученный результат иллюстрирует теорему 9.3:.
res /(z)4-res /(z)4-res /(z) = —-ч- — -1 = 0.
-i	з	to	4 4
118
Отметим, что для данной функции zt = -1, z2 = 3 — простые полю-
сы, a z3 = оо - устранимая особая точка.
Пример 9. Найти вычеты в конечных особых точках функции
/(z) =
z + 2
(z + l)2(z-3)‘
Решение. Для этой функции точка z = 3 является полюсом первого
порядка и выполняются условия применимости формулы (2.66). При
этом функцию удобно представить в виде
z-3
Применяя указанную формулу, находим
. (z + 2)/(z + 1)2
res /(z) = - — —
з J	(z-3)'
z + 2
(z + 1)2
z=3
5
16’
Точка z = -l для функции (I) является полюсом второго порядка.
Применяем формулу (2.64) при п = 2. Запишем решение согласно ал-
горитму, предлагаемому этой формулой.
1. УмножаемДг) на (z + I)2 и записываем функцию
<p(z) = /(z)-(z + l)2=^|.
г-3
2. Находим производную функции <р(г):
Ф'(г)= ----
I г-3
z-3-(z + 2)
(z-3)2
-5
(z-3)2
= V(z).
3. Применяя формулу (2.64), получаем
res/(z) = l lim---
-i l!~-i(z-3)2
5
16’
Пример 10. Найти интеграл
• li 1 L
sin 1 + — \az.
I z J
119
Решение. Единственной конечной особой точкой для функции
/(z) = sin| 1 + — I является z = 0- существенно особая точка. Точка
\ z)
z = 0 принадлежит области, ограниченной контуром интегрирования.
Так как res/(z) = cost (см. пример 6), то по формуле (2.62) по-
лучаем
cos 1 = —5— f
2ni *
|z-l|=2
• I, 1 L
sm 1+— laz,
I z J
откуда
sin|
|z~l|=2
1+— kfe = 2n/cosl.
z J
Пример 11. Найти интеграл
Решение. Функция /(z) = z3ez имеет единственную конечную
особую точку z = 0, которая является существенно особой; она при-
надлежит области, ограниченной контуром интегрирования.
Найдем вычет данной функции, для чего разложим ее в степенной
ряд:
з 7 з(,	1	1	1	1	1
z ez = z 1+ —+--+—- +----- +—-
I	z	2!z2	3!z3	4!z4	5!z5
3	2 Z 1	1	1
+ z + —+ —+----+----
2! 3! 4!z 5! z2
Следовательно,
res/(z) = — = —
о 4! 24
На основании формулы (2.62) имеем
1	1 I з
— =------- ®zJezok,
24 2 л i J
I4=i
120
откуда
14=1
„	„	Г ln(z + 2) ,
Пример 12. Вычислить интеграл -------------— dz, где у - окружность
J Z
Y
I I 1
z = —, которую точка z проходит в положительном направлении.
Решение. В круге
z
—, содержится только одна особая точка по-
дынтегральной функции - это полюс второго порядка z0 = 0. Вычет
функции Дг) в точке z0 = 0 найдем в соответствии с формулой (2.64):
res/(z) = lim z2 ——= lim[ln(z + 2)1 = lim —5— = —.
oJ 2 z—>ol	z2 J z->oL 2J z->0 2 + Z 2
На основании формулы (2.62) получаем:
f dz
Пример 13. Вычислить интеграл ф----------------- в следующих
* z(z + 2)(z + 4)
y
случаях: 1)у— окружность |z| = 1; 2)у- окружность |z| = 3; 3)у- ок-
ружность |z| = 5.
Решение. Найдем сначала вычеты функции f(z) =----------------
z(z + 2)(z + 4)
относительно простых полюсов Z| = 0, z2 = -2, z3 = -4:
res /(z) = lim z/(z) = lim-5-----= —,
о z->o2V2 z->o(z+2)(z+4) 8
res/(z)= lim (z+2)/(z) = lim—-----— = —
-2	z-t-2	z->-2z(z+4)	4
res/(-4)= lim (z+4)/(z) = lim—------— = -.
z—»-4	z->-4 z(z + 2) 8
121
Интегралы найдем с помощью формулы (2.67).
В первом случае в области, ограниченной окружностью |z| = 1,
находится только один полюс z = 0, поэтому
|/(г)<& = 2лД = -у.
т
Во втором случае окружность |z| = 3 ограничивает область, кото-
рая содержит полюсы z{ = 0, z2 = -2, тогда
В третьем случае внутри области, ограниченной контуром |z| = 5,
находятся три полюса: zx = 0, z2 = -2, z3 = —4, поэтому
Пример 14. Вычислить интеграл ®---------—-----, где у- окруж-
J(z-l)2(z2+l)
ность (х - I)2 + (у - I)2 = 2.
Решение. Подынтегральная функция имеет три особые точки:
Z] = 1 - полюс второго порядка, z2 = /, z3 = —i - простые полюса. Внутри
контура у находятся точки z{ = 1 и z2 = i. Точка z3 = -i лежит вне этого
контура (сделайте рисунок).
В соответствии с формулой (2.67) получаем:
dz
-------------= 2П‘
(z-l)2(z2+l)
res/(z) + res/(z)
1 /
где
/(Z) (z-l)2(z2+l)‘
Вычет в точке z{ = 1 находим по формуле (2.64) при п = 2:
res f(z) = lim (z-1)2--------------
i ^>idz[ (z —l)2(z2+1)
122
1-	-2z
= lim——
7—U /-Л . 1\2
2’
По формуле (2.65) найдем вычет в точке z2 = г.
res /(z) = lim
i	z-¥i
1
(z-l)2(z+z)
1 _ 1
2z(z-l)2 ~ 4'
Следовательно,
f dz
J(z-l)2(z2+l)
Пример 15. Найти интеграл ф -----------------.
X(z-2)(z2+1)
z2
Решение. Подынтегральная функция f (z) =------------z-----
(z-2Xz2+1)
быть представлена в виде
/(z) =----------------•
(z-z)(z + z)(z-2)
Эта функция имеет простые полюсы zx = i, z2 = -i, z3 = 2.
ветствии с формулой (2.65) находим вычеты:
z2	1
res/(z) = lim(z - z)/(z) = lim--—---- =
'	z-и	z-м (z - 2)(z + z) 2z(2 - z)
может
coot-
Z2
res /(z) = lim (z + i)f(z) = lim ---——
z->-/(z-z)(z-2)
1
2z(2 + z)’
res/(z)= lim(z-2)/(z)= lim—-= -.
2	z->2	«2z2+|	5
По формуле (2.67) находим искомый интеграл
1______1	! 4~
21(22i(2 + i) +5
f z2dz
ф —z----------= 2ni
J (z2+1)(z-2)
123
= л
1
2-z
1	8 .
----+—i
2 + i 5
2iti.
Задачи
Определите типы особых точек и найдите вычеты в этих точках
следующих функций
, ч sinz
1. f(z) =--------, z = 0, z = -л, z = оо.
г3(г + л)
„	„ sinz
2. f(z) = —------z = 0, z = -л, z = оо.
г2(г + л)2
z
(г-1)(г-3)
3. /(z) =
z = 1, z = 3.
Найдите вычеты в особых точках функций
5-	Ж) = 2,---г	6./(z)=iii.
z2(z-l)2	Z-l
7. /(z) = —
z - z
9- /(^)= 3/21 :ту-
z3(z2+4)2
8- /(*) =
1
z2 +4
10. /(z) =
z + 1
(z2-z-2)2’
С помощью вычетов вычислите интегралы
f z1 dz	, . „
17.	ф—----------, у - окружность z =3.
J(z2+1)(z-2)
18.	j>—j-j-, у - окружность |z| = 4.
Y Z Z
124
19.	®---------------, Y - окружность \z\ = 5.
J(z-l)(z-2)(z-3)
Y
20.	<£---, у - окружность (x - I)2 + (у - l)2 = 2.
J (z-l)2(z2+l)
f zdz	.	,
21.	<|>--, у - окружность |z - i| = 1.
J ez - i
Y
»» Г zdz	.	. * .
22.	®—---, у ~ окружность |z - 11 = 1.
J z4+l
Y
Ответы
1. z = 0 - полюс второго порядка, res f(z) = 0; z = —n - устранимая особая
о
точка, res/(z) = 0; z = оо - существенно особая точка. 2. z = 0 — полюс первого
Я
порядка, res/(z) = 1/тг2; z =-л- полюс первого порядка, res/(z) =-1/л2;
о	я
z = оо - существенно особая точка, res/(z) = 0. 3. z = 1, z = 3 - полюсы перво-
СО
го порядка; res/(z) = -1/2, res/(z) = 1/2. 4. z = 2 - полюс третьего порядка,
res/(z) = l. 5. res/(z) = 3, res/(z) = -3, res/(z) = 0.	6. res/(z) = 2i.
7. res/(z) = l, 0	0	1	»	/ res/(z) = -l/2,	res/(z) =-1/2.	8. res/(z) =-z/4, 1	1	2i
res /(z) = <74. 10. res/(z) = l/9,	9. res/(z) =	res/(z) = -^-,	res/(z) = 1/64. 0	32	2'	64	2' res/(z) =-1/9,	res/(z) = 0.	11. res/(z) = -/74, 2	co	1< 2i
res f(z) = i/4. 14. res /(z) = l /2, 0	12. res/(z) = -e '.	13. res/(z) = 1,	res/(z) = -l. 1	0	00 res/(z) = i/2nk,	£ = ±1, ±2,	z^-nik.
•72	72	-72
15. res/(z) = —(1 + 0, res/(z) = -^-(l-0,	res/(z) =—— (1 + 0,
•io	8	ъ	2
J?	J? л/2 J? л/2	л/2	л/2
res/(z) =-—(1-0, где zx = — + <—, z2= —— + /—, г3=—-—i—,
•4	2	22	22	22
z4=— -i—. 16. res/(z) = l, res/(z) = -l. 17.2m. 18.0. 19.0. 20. -—.
2	2	1»	2
21. n
125
Вопросы
1.	Что называют вычетом однозначной аналитической функции
fiz) в изолированной особой точке?
2.	Каковы обозначения вычета функции fiz) в точке z0?
3.	Чему равен вычет функции fiz) в точке z0?
4.	Чему равен вычет функции в устранимой особой точке?
5.	Как определяется вычет функции в ее простом полюсе?
6.	Как определяется вычет функции в ее полюсе и-го порядка?
7.	Как определяется вычет функции f(z) = в ее простом no-
4'0)
люсе?
8.	Как найти вычет функции fiz) в ее существенно особой точке?
9.	Сформулируйте теорему Коши о вычетах.
10.	Как определяются устранимая особая точка, полюс, сущест-
венно особая точка функции fiz) в случае z = оо?
11.	Каковы особенности лорановского разложения в окрестности
точки z = оо для устранимой особой точки, полюса, существенно осо-
бой точки?
12.	Как определяется вычет функции в бесконечности?
13.	Чему равен вычет функции^2) в бесконечности?
14.	Чему равна сумма вычетов функции fiz), имеющей конечное
множество особых точек z{, z2,..., zn?
126
Гпава 3.
Основы операционного исчисления
Операционное исчисление — раздел математического анализа, ме-
тод которого позволяет в ряде случаев посредством простых правил
решать сложные задачи. В основе метода лежит идея замены изучае-
мых функций (оригиналов) некоторыми другими функциями (изобра-
жениями), получаемыми из первых по определенным правилам. Опе-
рационное исчисление имеет важное значение в механике, автоматике,
электротехнике и других областях.
Для развития операционного исчисления большое значение имели
труды английского инженера, физика и математика Оливера Хевисай-
да (1850-1925).
§3.1. Оригинал и изображение
Функцией-оригиналом называют любую комплекснозначную1 функ-
цию fit) вещественной переменной t, удовлетворяющую следующим
условиям:
1	.Д0 интегрируема на любом конечном промежутке оси Ot (ло-
кально интегрируема).
2	. fit) = 0 для всех t < 0.
3.1/(/)| возрастает не быстрее показательной функции, т.е. сущест-
вуют такие постоянные М> 0 и s, что ]Д/)| < Ме‘ при всех t.
Нижнюю грань s0 всех чисел s, для которых выполняется это не-
равенство, называют показателем роста функции fit).
Используют и другое определение функции-оригинала.
Оригиналом называется комплекснозначная функция fit), непре-
рывная на интервале 0 < t < +оо, если существует действительное число
х0 (показатель роста функции fit)) такое, что интеграл
+оо
I =	оо
о
сходится при j > s0 и расходится при j < s0.
1 Комплекснозначные функции действительного переменного t имеют вид
fit) =f\(t) + (4(0, гДе f\(t), fi(t) ~ действительные функции, i = л/-Т. Если
f2(t) = 0, то Д/) является действительной функцией. Комплекснозначные функции
не следует смешивать с функциями fiz) комплексной переменной z = х + iy,
всегда представимыми в виде fiz) = и(х, у) + iv(x, у), где и(х, у), v(x, у) - функ-
ции двух действительных переменных х и у (см. гл. 2, формула (2.1)).
127
Если рассматриваемый интеграл сходится при всех действитель-
ных 5, то показатель роста s0 считают равным -оо; если же он расхо-
дится при всех действительных з, то полагают s0 = +оо.
Определение оригинала fit) на интервале 0 < t < +оо продолжают
на все отрицательные t, полагая fit) = 0 при t < 0.
Изображением функции fit) называют функцию F(p) комплекс-
ной переменной р = s+ i8, определяемую формулой^
+00
F(p)=fe~p,/(t)dt.	(3.2)
о
Интеграл в правой части этого равенства называют интегралом
Лапласа, а переход от оригинала к его изображению - преобразова-
нием Лапласа.
Тот факт, что F(p) является изображением fit) символически запи-
сывают так:
fit)^F(p)
и называют операционным (или операторным) равенством.
Употребляют и другие обозначения, например,
F(p) = Lfit),F(p)^fit).
Обратным преобразованием Лапласа называется преобразование,
относящее изображению F(p) его оригинал fit), что символически за-
писывается так: L~lF(p) =fit).
Теорема 1.1. Функция F(p) определена в полуплоскости Rep =
= s>s0, где з0- показатель роста fit), и является в этой полуплоскости
аналитической функцией.
Следствие. Изображение F(p)—>0 при р—> оо так, что Rep = s
неограниченно возрастает, а р находится в полуплоскости Re/? > з0:
lim F(p) = 0.
p—>00
Теорема 1.2. Преобразование Лапласа
+00
F{p)=\e-p,f{t)dt	(3.3)
о
единственно в том смысле, что две функции J\(t) wf2(t), имеющие оди-
наковые преобразования Лапласа, совпадают во всех точках непре-
рывности для всех t > 0.
128
Пример 1. Показать, что «единичная функция»
Л(0 =
1 при t > О,
О при t < 0.
(3.4)
является функцией-оригиналом. Эта функций называется функцией Хе-
висайда.
Решение.'Пользуясь первым определением функции-оригинала, за-
ключаем, что все три условия для этой функции выполнены: 1) функция
r|(z) интегрируема на любом конечном промежутке <t<t2; 2) r](7) = О
при всех t < 0; 3) |т](г)| является постоянным, равным единице, поэтому
|rj(z)| <1 • esl = esl (М= 1, s > 0 в условии ]Д/)| < Me'; нижней гранью чи-
сел s > 0 является число s0 = 0, при этом |т](г)| < 1 • ё°' = 1).
Принимая во внимание второе определение, получаем:
p-Mh(')|<*= f =	|о+°° = |
ООО
при j > 0, так как е " —> 0 при t —> +оо. Когда s < 0, то интеграл расхо-
дится.
Следовательно, функция Хевисайда является оригиналом с пока-
зателем роста s0 = 0.
Пример 2. Показать, что комплекснозначная функция flf), удовле-
творяющая при всех t неравенству ]Д7)| < Ме°', где М > 0, а > 0, являет-
ся оригиналом.
Решение. В соответствии с условием получаем оценку для инте-
грала (3.1):
+«	+со
je-v'|/(z)|z/z<A/Je4'-a)'z/z.
о	о
Интеграл в правой части неравенства сходится при s - а > 0, или
s> а, поэтому сходится и интеграл в левой части при s> а.
При s<a интеграл расходится. Функция^/) является оригиналом.
Пример 3. Установить, является ли оригиналом функция /(/) = -.
Решение. Интеграл (3.1) в данном случае принимает вид
5 Зак. 1816	129
+оо	+оо
p--V(o|^= р р
о	о
Так как при s > 0 lime-'7 i: - = 1, то на основании признака срав-
<->о t t
нения для несобственных интегралов рассматриваемый интеграл будет
+00
г dt
расходящимся, как и интеграл I —. При s < 0 интеграл также расхо-
о *
дится. Следовательно, функция f(t) = - не является оригиналом.
Пример 4. Показать, что функция
е3' sin 2/ при t > О,
/(0 =
при t < О
является функцией-оригиналом.
Решение. Убедимся в том, что все три условия, определяющие
функцию-оригинал, выполняются для данной функции^/).
Действительно, функция^/) локально интегрируема: интеграл
h
J е3' sin 2tdt
'i
существует для любых конечных t} и t2. Условие 2 выполняется в соот-
ветствии с определением функции fit) (fit) = 0 при t < 0). Наконец,
|e3sin2/| < е3/ для любых вещественных t, так что в качестве М в усло-
вии 3 можно взять число, больше или равное единице, = 3.
Пример 5. Установить, является ли оригиналом функция
ЛО = е(3 + 2°'.
Решение. Интеграл (3.1) в данном случае принимает вид
+оО	+оО	+<Ю
р-Л|/(0|<*= |е-Л'|е(3+2')р/= Je-''e3'|e2"p/.
0	0	о
130
Чтобы найти модуль функции е", воспользуемся формулой Эйле-
ра (см. гл. 2, формулу (2.7)), которая здесь принимает вид е1" = cos2/ +
+ /sin2z, и формулой для модуля комплексного числа (см. гл. 1, форму-
лу (1.24)); получим
|е2" | - a/cos2 21+sin2 It -1.
Следовательно,
+<ю	-ню	-ню
Je-''|e(3+2,),pr= р-'-'е3'|е2,'р/= р-('-3)'Л.
о	о	о
Последний интеграл сходится при (s - 3) > 0, т.е. s > 3, и расхо-
дится при s < 3, поэтому данная функция J(t) является оригиналом с
показателем роста 50 = 3.
Пример 6. Установить, является ли оригиналом функция^/) = е'2.
Решение. Рассмотрим интеграл
-ню	-ню
j е~"' |/(/)|c/Z = |е“Л'е' dt.
о	о
Поскольку при любом фиксированном s, начиная с некоторого
достаточно большого t,
то последний интеграл расходится при всех 5. Значит, fit) = е' не яв-
ляется оригиналом (,s0 = +оо).
Пример 7. Установить, является ли оригиналом функция
/(z) = sin-.
t
Решение. Оценим интеграл вида (3.1) для данного случая:
-НЮ	-НЮ	-ню
| e-''[/(Z)|rf = J e~sl sin - dt < j e~s,dt.
о	0	t 0
131
Последний интеграл сходится при всех s > 0 и расходится при s < 0.
Следовательно, данная функция является оригиналом с показателем
роста s0 = 0.
Пример 8. Установить, является ли оригиналом функция fit) = е4',
где <7 = а + /р - любое комплексное число.
Решение. Рассмотрим интеграл вида (3.1):
+со	+00	+оо
j е-" |/(Г)|Л = j e-v' \е4' |л = J e~s,eal |е,₽' |л =
О	0	0
+оо	+оо
о	о
Интеграл сходится при s - а > 0, или s > а, и расходится при
s < а. Итак, функция fit) = е4' является оригиналом с показателем роста
s0 = а = Re<y.
Пример 9. Найти изображение единичной функции Хевисайда, опре-
деляемой формулой (3.4).
Решение. В соответствии с формулой (3.2) получаем
F(p) = [le~p,dt = lim (e~p,dt = lim -— = lim--------------e~pa .
J	0-++00J	a-++oo — n a->+ool n n )
0	0	X 0	X /
Если Rep > 0, to lim e~pa = 0; в этом случае
</->+оо
+C°	1
= —,	(3.5)
о	P
F(P) = ~, n(0^~-	(3.6)
P	P
Замечание. Изображение (3.5) получено при условии Rep = s> 0. При
s < О интеграл Лапласа не существует. Однако функция — является аналити-
Р
ческой на всей плоскости комплексной переменой р, кроме р = 0, и ее значения
для Rep < 0 можно рассматривать как значения изображения F(p) при Rep < 0.
132
Для функции ДО = 1 операторное равенство 1 == — будет выполнятся при
Р
всех р*0.
Пример	10.	Найти изображение функции fit) -	еь.
Решение.	Принимая во внимание равенство^/)	^== F(p), получаем
+«	+«
е' = ^ekte-pldt= je^^dt =
о	о	Р
(3.7)
Р~к
когда Re(p- к) > 0. Поскольку функция —5— является аналитической
Р~к
п^и всех р*к, то ее можно рассматривать как изображение функции
е для таких р.
Задачи
В задачах 1-10 установите, какие из функций являются оригина-
лами и найдите показатели их роста.
1. f(t) = е(5+2<У>‘.	2. f(t) = e^‘.
3. /(r) = /sin|.	4-
5. /(/) = ch(4-3r)/.	6. Л') = 8Ш(2-0Л
7. /(/) = е'3.	8. Л') = —• г-1
9./(Г) = Г3.	10. Л0 = е1/(г1)2.
В задачах 11-14 найдите изображения F(p) оригиналов fit)	
11. /(»)-<•	12. Л0 = е<1-')'.
13.ло=С при0<,<Л [0 при t > а.	„	,	— при 0 < t < а Н. Л0= а 1 при t > а.
Ответы
1.	Оригинал, s0 = 5. 2. Оригинал, s0 = 2. 3. Оригинал, s0 = 0. 4. Оригинал,
s0 = 0. 5. Оригинал, s0 = 4. 6. Оригинал, s0 = 1. 7. Не оригинал (s0 = +оо). 8. Не
133
оригинал (s0 = +оо). 9. Оригинал, so = 0. 10. Не оригинал ($0 = +оо). И. —
Р
1	1-е4"	1 \-е~ар
12. --!--. 13. ——. 14. -	. .
р -1 + I	р	ар
Вопросы
1.	Что называют функцией-оригиналом?
2.	Что называют показателем роста функции//)?
3.	Как определяется единичная функция Хевисайда?
4.	Как определяется изображение функции//)?
5.	Что называют интегралом Лапласа?
6.	Что называют преобразованием Лапласа?
7.	Что называют операционным равенством?
8.	Как формулируется теорема 1.1?
9.	Каково следствие из теоремы 1.1?
10.	Как формулируется теорема 1.2?
11.	Чему равно изображение единичной функции Хевисайда?
12.	Чему равно изображение функции//) = eto?
§3.2. Основные правила и формулы
операционного исчисления
Свойство линейности. Если / = ^(р), / = Г2(р), а Сх, С2-
произвольные постоянные, то
С./(О + с^со = С,Г,(р) + C2F2(p).	(3.8)
В частности изображение суммы функций определяется форму-
лой
Ш + Ш^рх(р)+ f2(p).
Дифференцирование оригинала. Если функция//),/'(г), ...,/<л)(/)
являются функциями-оригиналами и//) == F(p), то
/'(/) = рГ(р)-/(0),
Г(/) = р2^(р)-р/(0)-/'(0),
=pnF(p) - pnlf(0) ~ pn‘ 7'(0)	^(O),
134
rae/w(Z) = lim f(k\t), к = 1, 2.n - 1, /(0) = lim /(/).
«->+0	+o
Если J(0) = 0, /W(0) - 0, k= 1, 2,..., w— 1, то эти формулы прини-
мают вид
Л/)=рГ(р),/'(/)=р2Г(р),...,/л)=рпЯр).	(3.10)
Интегрирование оригинала. Интегрирование оригинала сводит-
ся к делению изображения нар: еслиД/) === Ftp), то
(З.И)
Дифференцирование изображения. Дифференцирование изобра-
жения сводится к умножению оригинала на (-/): еслиу(/) = Ftp), то
Ftp)=-iftfy,
(3-12)
в общем случае
?”Хр) (-0Ж
(3.13)
Интегрирование изображения. Если интеграл
сходит-
р
ся, то он является изображением функции :
(3.14)
р
где
р
р
С помощью формулы (3.14) можно вычислить некоторые несобст-
венные интегралы. Еслиу(/) = F(p) и интеграл dt сходится, то
о t
"\^Л=\р(р)с1р.	(3.15)
о	о
135
Предельные соотношения. Если//) == F(p), то
lim pF(p) = f(0),
/7-» «
(3.16)
где р —> оо вдоль положительного направления вещественной оси.
Если/г) == F(p) и существует lim f{t) = /(оо), то
+09
lim pF(p) = /(оо).
/7~» О
(3-17)
Пример 1. Найти изображения тригонометрических функций: 1) sinar,
2) cosaZ.
Решение. На основании формулы (3.7) получаем
lai .	1 -их/ .	1
в	.. Q тт—	' ,
p-ia' ’ p + ia
В соответствии с формулой (3.8) при/(?) = e,aZ,/(Z) = е ,a/, С, = —,
2г
С2 = —- находим:
1 z lai -iai\ -If1 1	|	1 2га а
sin at = —(е -e ) f= —--------------------=-------5----7 = “5----
2г	2г\р-га p + ia.) 2г p2+a p +a
1
при C, = —, C2 = — получим:
.	1 z zaz —iai \	. 1 l 1	1 i P
cosa/ = — (e +e ) = — --------------+-------—Г-
2	2 p - га p + iaj p2 +az
Таким образом,
a	. p
smat t= — ---cosaZ =	—-.
p2 +a2	p2 +a2
(3.18)
Пример 2. Найти изображения гиперболических функций: l)sha/;
2) cha/.
136
Решен ие. Принимая во внимание формулы (3.7) и (3.8), находим:
	.	1 z а/ -az ч • 1 I 1	1 I О.
shaZ = — (е -е ) т=—---------------=	---г,
2	2\^р-а р + а.) р -от
chaZ = — (еа‘ +<’-“') Н-[—Т—
2	2^р-а р+а
Следовательно,
shaZ т=  ,а , , cha/ = 	.
р -or	р -а
Р ,
р2-а2
(3-19)
Пример 3. Найти изображение функции fif) = sin2Z с помощью диф-
ференцирования оригинала.
Решение. Используем первую из формул (3.9): /(z) = pF\p) -fifi).
Поскольку flfi) = 0, то формула принимает вид /(z) = pF(p). Так как
/V) = 2sinZcosZ = sin2z, то sin2z = pF(p). На основании первой из фор-
2
мул (3.18) получаем sm2z =—---, поэтому
р +4
= pF(p),
р +4
откуда
F(p) =----г------, sin2Z =--у---
р(р +4)	р(р2+4)
t
Пример 4. Найти изображение функции Jercfr.
О
Решение. В соответствии с формулой (3.7) при к= 1 получим
е = —-—. На основании формулы (3.11) найдем, что
р-1
jeTch =
о
; jeTch =
о
1/(р~1)
Р
1
P(P-1)‘
137
Пример 5. Найти изображение функции fit) = z", где п - натураль-
ное число.
Решение. Из операторного равенства 1 =— (см. §3.1, замечание к
Р
примеру 9), пользуясь правилом интегрирования оригинала, находим:
7	.1	'[ t2 .1 'гт2 t3 .1
J	р2 J 1-2 р3 J1-2	1-2-3 р4
О	и 0	и о	Г
7	z" ____1	____. и!
J1-2 -(и-1) "1-2-и ~ рп*х ’ ~ рп'х '
Пример 6. Найти изображения функций: 1) zsinaz; 2) ZcosaZ.
Решение. Поскольку sinaZ = ,a 2, cosaz = ——7 (см. фор-
р +а	р +а
мулы (3.18)), то с помощью правила дифференцирования изображения
(см. формулу (3.12)) получим:
. 0(р2+a2)-2pa	2pa
-ZsinaZ =	 =-----, г
(р2+а2)2	(р2+а2)2
+<*2)-2р .Р _ р2+а2~2р2	- р2 +а2
(р2+а2)2	(р2+а2)2	(р2+а2)2
Таким образом,
zsinaz = — 2^*—;zcosaZr==——^гт-	(3.20)
(p2+a2)2	(p2+a2)2
Пример 7. Найти изображение функции fit) = z"eat, где п - нату-
ральное число.
Решение. Из соотношения еа< =—-— (см. формулу (3.7)) «~крат-
р-а
ным дифференцированием изображения (см. формулу (3.13)) получаем
(-Z) е =
(-1)ип1	?	п\
(р-аГ1’	6 ’	(p-a)"+1
138
Пример 8. Найти изображение функции f(t) = ——.
Решение. На основании операторного равенства sin? = —— (см.
Р +1
первую формулу (3.18)) и правила интегрирования изображения (см. фор-
мулу (3.14), находим
+® ,
sint .Г аи , л 1+00 я
----== ------z- - arctgw =	arctgp = arcctgp,
t J 1 + w2	2
p
sin t
—— == arcctgp.
(Для многозначной функции Arctgz, Lnz и т.д. рассматривают ветви,
л
для которых arctgl = —, In 1 = 0 и т.д.).
4
+00
_  Л „	г sin / ,
Пример 9. Вычислить интеграл ------------at.
о t
Решение. Принимая во внимание соотношение sint == —5-— = F(p),
р +1
с помощью формулы (3.15) получаем
сО	сО
г sin/ , г dp	100 л
J —й = 177Т=агс,8'’1» =Г
О	о и
Пример 10. Проверить, выполняются ли предельные соотношения
для следующих функций: г|(/), sinz, е , где а - вещественное число.
Решение. Равенство (3.16) выполняется для всех этих функций.
Действительно, поскольку
,л . 1	. t .	1 а/ .	1
П(/) == —, sinz = —----, е ==------,
Р	р +1 р-а
то
lim р—= 1 = г|(0), lim —— = O = sinO, lim—-— = 1 = е°.
д-x» р	р2 +1	р->х р — а
139
Равенство (3.17) для функции sin/ не выполняется, так как limsinl
/—>00
не существует; для функции при а > 0 оно также не выполняется.
Для функции т](0 и при а < 0 это равенство будет справедливым:
lim р — = 1 = lim Л(/); lim —-— = lim = 0.
р-»о р /->+«> р~»о р — а /->+<»
Пример 11. Найти изображение F(p) функции/}/) = ст₽/ + 2е~31 + 1.
Решение. Пользуясь линейностью преобразования Лапласа, форму-
лами (3.6), (3.7) и второй формулой (3.19), находим
F(p) =
р 2	1
—+----+—.
р-4 р + 3 р
Пример 12. Найти изображение функции/}/) = sinz • sin3/.
Решение. Сначала воспользуемся тригонометрической формулой
sinasinp = ^[cos(a- ₽)- cos(a + P)] и преобразуем данную функцию
/(/) = sin / sin 3/ = ^-[cos(-2/)- cos4/] = -^-(cos2z- cos4/).
Применяя свойство линейности преобразования Лапласа, вторую
из формул (3.18), получаем
Р
<Р2+4
^(р) = |
Р
р2+16,
Задачи
В задачах 1-6, используя свойство линейности преобразования
Лапласа, найдите изображения F(p) соответствующих оригиналов ft)
2.ft)=e‘ + 2е~3' + t3.
4. ft) = cos2z cos3z.
6./(z) = sin2/.
1./С0 = ST)2r + 5е3'’ + 1.
3./}/) = sin6/ sin4/.
5. flji) = cos5/sin3/.
В задачах 7-10, применяя правило дифференцирования, найдите
изображения F(p) оригиналов/}/)
l.fit) = /shto/.	8. ft) = zchioZ.
9.ft) = t2e3'.	\Q.ft) = ?e'.
140
В задачах 11-14, используя правило интегрирования изображения,
найдите изображения F(p) оригиналов fit)
11. f(t)=^±	12. f(t) =	COS/-1 t
еа1 - е₽' 13.	=	±-.	U.f(t) =	shz t
В задачах 15-18 с помощью дифференцирования оригинала, най-
дите изображения следующих функций
15. fit) = e^'cost.	M>.fit) = e^sint
17. fit) = e^'chXz.	18. fit) = AhU
В задачах 19-22 с помощью правила интегрирования оригинала
найдите изображения следующих функций
19. f(t)= j(u-cosu)du.
о
I .
ч fsinw ,
20. /(/) = ------du.
J и
о
21. f(t)~ J(sinw + K2)dw.
о
22. f(t)= je~uu3du.
о
В задачах 23-30 найдите изображения F(p) следующих функций
23./7) = cr|3f + Зе"2* + 1. 25.//) = sin3/. 27.//) = t2cost. 1	24.//) = cost. 26.fit) = te. 28.//) =/(e + сту). 1
29. f(t)= Jsinxcft. 0	30. f(t)= Jchmcft. 0
Ответы
1. F{p)	II Ъ bJ 1 M + + ъ 1 1 рл	1,1	2	6 + —. 2.	+	+—r- P	p + 1 p+3 p
3 ’f P _	P "I 4	if p , P	c if 8	2
2fp2+4	р2 + 100/	bJ + ts) LO ъ bJ + ts bJ + Ch 1 ъ bJ +
6. 	*	. p(p2+4) .	2pco ’ (P2-®2)2	. 8.-^±<.	9.-^.	10.—^. (p2-®2)2	(p-З)3	(p-2)4
11. ln-£-.	12. In '		13. Inrf 14.11n^±l. 15. P{P+? -1.
p-1	V? + l	p-a	2 p-1	(p + a) +1
141
16. ----. 17. —р(р*д) -1. 18. ---------------19. -L----------------.
(р + о)2 + 1	(р + о)2-Х2	(р + о)2-Х2	р3 р3 + \
„„ 1 (л ) „ 2 р 1 „	6	р 3	1
20. —----arctg? . 21. — -----:--+ —. 22. --------т-23.	— +--------+ —.
Р\2	) рА рг + \ р р{р + \)	/? ~9 р + 2 р
24. 1Г1 I Р......1	25	6	26.	1	27. 2р? ~6р
2^/? p2 + 4j ’ (/?2 +1)(/?2+9)	(р-1)2'	(Р2 + 1)3'
28.	2.(Р2 + р + 1>. 29. -1. 30.  1
(Р -1) Р(Р +1) Р
Вопросы
1.	Как формулируется свойство линейности?
2.	По каким формулам осуществляется дифференцирование ори-
гинала?
3.	Какой вид принимают формулы дифференцирования оригинала
в случае, когда функция и ее производные до (и - 1)-го порядка равны
нулю?
4.	Как осуществляется интегрирование оригинала?
5.	По какой формуле осуществляется дифференцирование изобра-
жения?
6.	Как осуществляется интегрирование изображения?
7.	Какой вид имеют предельные соотношения?
8.	Запишите изображения для тригонометрических функций sina/,
cosa/.
9.	Какой вид имеют изображения для гиперболических функций
sr]a/, сца/?
10.	Запишите изображения для функций /sina/, /cosa/.
11.	Какой вид имеет изображение для функции flf) = ?е1', где п -
натуральное число?
12.	Какой вид имеет изображение для функции f (t) =	?
+00	.
г,	г Sin t , „
13.	Чему равно значение интеграла ----at ?
о '
14.	Выполняются ли предельные соотношения для функций Т](Г),
е , sin/, где а - вещественное число?
142
§3.3. Основные теоремы операционного
исчисления
Теорема 3.1. (Теорема подобия). Если/(О = F(p) и X > 0, то ум-
ножение аргумента оригинала на положительное число приводит к де-
лению изображения и его аргумента на это число:
Теорема 3.2. (Теорема смещения). Если/(/) = F(p) и а - произ-
вольное комплексное число, то изменение (смещение) аргумента изо-
бражения на величину а приводит к умножению оригинала на величи-
al
ну е :
F(p-a) = e“X0-	(3.22)
Теорема 3.3. (Теорема запаздывания). Если/(0 = F(p) и 0 > О,
то запаздывание аргумента оригинала на положительное число 0 при-
водит к умножению изображения на величину ерв:
F(z-0) = e-p0F(p).	(3.23)
Теорема 3.4. (Теорема умножения). Если Ft(p) =/(0, F/p)
то
I
Ft(p)F2(p) = j/ (t)/2(z - t)A.	(3.24)
о
Замечание. Интеграл в правой части этой формулы называют сверт-
кой или складкой функции	и обозначают/(/)*/,(/), а операцию полу-
чения складки называют свертыванием функций. В связи с этим теорему ум-
ножения можно сформулировать так: умножение изображений приводит к
свертыванию их оригиналов. Эту теорему называют также теоремой сверты-
вания и теоремой Бореля.
Свертка функций обладает переместительным свойством:
i
F\(p)F2(p) = j/2 (т)/ (г - т) А.
о
143
Поскольку функция <р(/) = J/i(t)/2(Z-t)A равна нулю при t= О,
о
то, пользуясь правилом дифференцирования оригинала, получаем сле-
дующую запись теоремы умножения:
pFSp)F2(p) [/1(т)/2(^-т)Л.	(3.25)
at J
о
Интеграл в правой части этой формулы называют интегралом
Дюамеля. Если выполнить дифференцирование в интеграле Дюамеля,
то теорема умножения примет вид
рГ,(р)Г2(р) =/Ж(0) + f/(0/2'('-0^	(3.25а)
О
или, учитывая равноправность функций/(%(/),
=/2«/i(0) + fл (T)Zi'a-т)Л.	(3.256)
о
Примененное здесь правило дифференцирования интеграла по пе-
ременной, входящей в качестве параметра в подынтегральную функ-
цию и в верхний предел интегрирования, определяется формулой
j/(x, t)dx = f(t, f) + j/, (x, t)dx.	(3.26)
)	a
Последние две записи теоремы умножения можно видоизменить,
если учесть, что
I	i
pi СОЛ (?-т)Л= р2 (т)/,(г-т)А,
О	о
I	I
[fi (0/1 (t -x)dx= р, (т)/2 (г - т)Л.
О	о
144
Теорема 3.5. Если fit) — оригинал с периодом со > 0, то его изо-
бражение выражается формулой
(3'27)
где
(0
Ф(р)=	(3.28)
о
Эту теорему называют теоремой об изображении периодического
оригинала.
Теорема 3.6. Если F(p) - аналитическая функция в окрестности
бесконечно удаленной точки, равна в ней нулю и если лорановское
разложение F(p) в окрестности бесконечно удаленной точки имеет вид
оо
= <3’29)
4=1 Р
то оригиналом F(p) служит функция
причем этот ряд сходится при всех t.
Теорему 3.6 называют первой теоремой разложения.
Пример 1. Найти изображение sinpz, зная изображение sin А
Решение. Поскольку sinz =—, то в соответствии с теоремой
р2 +1
подобия (см. (3.21)) получаем
. _	. 1	1	1 Р2	р
s,n(1'^77F
Пример 2. Найти изображения функций: 1) ea,sinpz; 2) e^cospt
Решение. Пользуясь формулами
sinpz = - ,Р , cospz = р ,
р2+р2	р2+р2
6 Зак. 1816
145
с помощью теоремы смещения (см. (3.22)) находим:
e“'sinpt =----------------------, e^cospt =------—у.
(р-а)2+02	(р-а)2+р2
Пример 3. Найти изображение функции sin(t- l)T](t- 1), где t](t)-
функция Хевисайда (см. §3.1).
Решение. Вид функции показывает, что здесь имеется запаздывание
аргумента на величину 0 = 1. С помощью теоремы запаздывания (см.
(3.23)) и формулы sinz = --^— получаем
Р +1
e~p
sin(z — l)rj(z — 1) =——.
р +1
Замечание. В случае функции sin(t- 1 )п(0 оригинал нужно искать сле-
дующим образом. Поскольку sin(t- l)r|(t) = (sin(t)cosl —cost • sinl)rj(Z), cosl,
sinl - постоянные, то по свойству линейности с учетом формул (3.18) получаем
sin(t- 1)ц(0 =cosl ------sinl ? -.
Пример 4. Найти изображение функции/(г) = |sint|.
Решение. Поскольку |sint| - периодическая функция с периодом
со = л, то изображение /-~(л)=	- (см. (3.27)), где
1-е ’’’
ф(р) = Je pl |sin t\dt = Je sin tdt.
о	0
Дважды проинтегрировав по частям, получим
ф(р) = -е р1
cos/ + psint
р2+1
e^+l
p2+l
о
Следовательно,
g-^+l
л +1
1	Дл
—Z C/T]—.
л2+1	2
146
Пример 5. Найти изображение периодического оригинала^*) с пе-
риодом со = 2л, который равен sinz при 0 < t < л и нулю при л< t < 2л.
Решение. Оригинал для t > 0 можно записать так: ft) = sinz - rj(sinz).
ф( л)
Искомое изображение имеет вид F( л) =--------jj-, где
1 - е р
2п	л
<р(р) = j*e-z" sin t r|(sin t)dt = ^e~pl sin tdt =
о	0
Итак,
----- (см. пример 4).
2 . 1
-Ttp
1
M (л1 2 +1)(1 - e~Up) (л2 + l)d - e~*p)
Пример 6. Найти оригинал/(z) по его изображению
Решение. Изображению придадим другой вид:
1 1 1
_3z 2	_4	2 1
Р (Р +1)	Р Р +1
4 ’
Будем считать, что
1	1	z3
= ~T~7	sinr =/W, F2 (p) = —	=Л(0;
p +1	p	о
здесь использовано равенство Г =  при п = 3 (см. §3.2, при-
Рп+
мер 5). С помощью теоремы умножения (см. (3.24)) получаем
1	1	. d 'f(z-x)3 .
р—.----й---= — Р---------sin тот.
р4 P2+1	<*0J 6
В соответствии с формулой (3.26) находим производную
d 'р-т)3
dt J 6
О
7 - т)3 sin т
sintrfi
о
147
1 f.	. 2 •	>
= — |u-t) siniar.
2 J
0
Дважды интегрируем по частям, получаем:
— |(/ - т)2 sin т dx = — [(/ - т)2 (- cos т) - 2(/ - т) sin т + 2 cos т
о
г2
=---+ COS/-1.
2
Следовательно,
Z2
/(/) = —+ COS/-1.
Пример 7. Найти оригинал fit) д ля изображения F(p) = In 1 н— .
I Р)
Решение. Использовав разложение функции ln( 1 + z) в ряд Тейлора
(см. гл. 2, §2.6, формула (2.48))
z2	z"
ln(l+z)= z- —+ ... + (-l)"-1—- + ... (|z| < 1),
2	п
получим
ад = ---!т+...+(-1Г,-^+... (|р|> 1).
р 2р2	пр
В соответствии с теоремой 3.6 находим оригинал
/(/) = 1—
2 1! 3 2!
(-1)"-'
.. + -— -----------+ ...=
п (п-1)!
.л-1
Г1 —
и!
t t2
= 1- —+ — -...+ (-1)‘
2! 3!
j
t
t2 t2	tn
t-—+-—...+(-1Л’—+...
2!	3!	„!
148
(	?	?	fn
1- l-f+-——+...+(-1)"’1—+ •
2! 3!	n!
Следовательно,
t
Пример 8. Найти свертку оригиналов /(0 = t, f2(f) = cost и изобра-
жение свертки.
Решение. По определению свертки
I
t*COSt = J(f-T)COST<#.
о
Интегрируя по частям, получаем
i	I
J(f-T)cosx<A = J(z-x)eZ(sinT) =
о	о
I
= (f-T)sinx|o + Jsinxrfr = -cost|o =l-cosf
о
Изображения заданных оригиналов таковы:
(частный случай операторного равенства ? = —),
Рп+
р
cost =	—
р2+1
(частный случай операторного равенства cosaz = ——— ).
р2 + а2
На основании теоремы умножения изображений находим, что
р2 р2+1	р(р2+1)
149
Замечание. Тот же результат получается непосредственно: поскольку
. - 1	 Р
Т = —, cosz = —Р—, то по свойству линейности
' Р	Р2 + !
„	' • 1 Р Р2+1~Р2	1
р р2+1	р(р 2+1) р(р +1)
Пример 9. Найти свертку оригиналов ft (z) = t, f2(t) = е и изображе-
ние свертки.
Решение. По определению свертки
I	I
1*е‘ = |(7 - т)етА = j(Z- x)dex =
о	о
I
= (Z-x)eT| + ГетА = 0-/ + ет| = е'-/-1.
Io J	1о
о
Используя свойство линейности, находим
< . ,	• 1	11	p2-{p-\)-p(p-V) _	1
p-1 p1 p рЧр-У) p (p-i)
Пример 10. Используя формулу Дюамеля, найти оригинал flf) по
его изображению F(p) =-------------.
(р — 1)(р+1)
Решение. Поскольку (см. формулу (3.7)) —-—= е, —?— = е
р-\	р + 1
(/;(/) = е, f2(f) = е '); далее (е1)' = е, е | , = 0 = 1, то по формуле Дюамеля
(3.256) находим:
р—---------— = е”'1+ [e‘Te'”Tfifr = е~' + е‘ [е-2тА =
Р-1 Р + 1	J	'
।
= е ‘ +е
о
1 -2i	1 0
"те +~е
2	2
- е ‘ +е" ~~е
150
-I 1 -2« О -t 1 -t 1 । е1 + е 1
= е +е----е +—= е-----е +—е = ------
I 2 2J 2	2	2
= ch/.
Итак, оригиналом данного изображения является функция fit) = ch/.
Задачи
1	. Применяя теорему подобия, найдите изображение cosp/, зная
изображение cos/.
2	. Используя теорему запаздывания, найдите изображение ориги-
нала
/(,)=0 "р"
[1 при t > а.
В задачах 3,4 с помощью теоремы смещения найдите изображения
функций
з	.//) = Льр/.	4.//) = Льр/.
В задачах 5-9 найдите свертки функций /(/), f2(t) и изображения
сверток
5-/1(0 = л(0 (функция Хевисайда),/(/) = sin/.
6	./1(0 = Л/2(0 = sin/.	7./(/) = е',/2(/) = е'.
8	./(/) ~ cos/,/2(/) = cos/.	9./(/) = cos/,/(/) = sin/.
В задачах 10-13, применив теорему умножения изображений, най-
дите оригиналы//) по их изображениям F(p)
10	./^)=-^—.
Р -1
12	.F(p)=-—1-----
Р Чр +1)
ll.F(p)=---------
Р(Р +0
13./^,)=	*---
P3(P-1)
Р3
В задачах 14-16, применив формулу Дюамеля, найдите оригина-
лы//) по их изображениям F(p)
U.	Г(р)= р2 -------
(Р +4)(р +9)
16	. F(p) =--------.
(Р-1ХР +1)
15. F(p) =
(р2-1)(р2+1)
17- F{p) = ——----.
Р(Р +1)
151
Ответы
p	e~“1’
1.	—-. 2.-------. Указание. График оригинала/Z) представляет собой
Р +Р Р
график единичной функции r|(Z), сдвинутый вправо на а (сделайте чертеж), по-
р-а _ ,	.1
—--------. 5. 1 - cosz =-----:----.
Р(.Р +0
Р2
(р2 + 1)2'
этомуУ(<) = T|(Z - а). 3. --Р . 4.
(p-а) -Р
Г	•	1
6. Z - Sinz 5= — 5--
P2(P2+D
„	.	р2-1
9. ZCOSZ = —----=-.
(р2+1)2
р
13. /(z) = l-z-y-e-'.
7. shz =
(р-а)2-р2
1_
р2-1
8.
sinz + zcosz.
10.y(z) = shz.	11. /(z) = 1 - cosz.
12.y(z) = t- sinz.
14. f (t) = “(chz + cosz). 15. /(z) = y(3sin3z-2sin2z).
2
1	Z2
16.	f(t) = — (е‘ + cosz + sinz). 17. /(Z) = —+ COSZ-1.
Вопросы
1.	Как формулируется теорема подобия?
2.	Какой вид имеет формула, отражающая теорему подобия?
3.	Как формулируется теорема смещения?
4.	Какой вид имеет формула, отражающая теорему смещения?
5.	Как формулируется теорема запаздывания?
6.	Какой вид имеет формула, отражающая теорему смещения?
7.	Как формулируется теорема умножения?
8.	Какой вид имеет формула, отражающая теорему умножения?
9.	Что называют складкой или сверткой функций///) и/2(Z)?
10.	Что называют свертыванием функций?
11.	Какую формулировку можно придать теореме умножения, ис-
пользуя понятие свертывания функций?
12.	Как по-другому называют теорему умножения?
13.	Что называют интегралом Дюамеля?
14.	Каково содержание теоремы об изображении периодического
оригинала?
15.	Как формулируется теорема разложения?
§3.4. Нахождение оригинала по изображению
Для отыскания оригинала fit) по известному отображению F(p) при-
меняются следующие приемы.
152
1..С помощью второй теоремы разложения, которая утверждает,
что при определенных условиях, наложенных на F(p), оригиналом для
F(p) служит функция
f{p) = Yres^p)^'],	(3.30)
л Л
где сумма вычетов берется по всем особым точкам рк функции F(p).
В частности, если F(p) =	- правильная рациональная дробь,
то оригиналом ее служит функция
л 1	1
/(') = £;----lim <3-31>
~ (г*-1)!/>->/>* фг‘ 1 г
где рк- полюсы F(p) кратности гк и сумма берется по всем полюсам
F\p) (рк - корни функции Л(р)).
Если все полюсы рк функции F(p) простые, то формула (3.31) уп-
рощается и принимает вид
=	(332)
2. Если F(p) -	- правильная рациональная дробь, то разла-
гают эту дробь на сумму простых дробей и находят оригиналы для ка-
ждой простой дроби.
В некоторых случаях для восстановления оригинала удобно при-
менять соответственно теоремы: запаздывания, смещения, об интегри-
ровании изображения и др.
Пример 1. Найти оригинал fit) по его изображению
р + р +1
(р-\)(р + \)2'
Решение. Здесь корни знаменателя R(p) = (р- 1)(р + I)2 и их крат-
ности таковы: pt = 1, г, = 1; p2 = ~i, r2 = Z. Для функции F(p) рх = \-
полюс первого порядка, р2 = -1 полюс второго порядка.
153
Формула (3.30) в данном случае принимает вид
f (t) = res F(p)epl + res F(p)epl.
Так как
resF(p)ep' - lim -	,g/*
1	(P + 1)
4
d( p2 + p + \ nt
rQsF(p)ep' = lim — — ——ep
-i	p-+-\dPy p-\
lim (2p + l)(p~l)~(p2+p + l) ep, + -P2+P + lfop<
(p-1)2	P~x
= lim
P 2p 2 CP' j P +P + ^lcPl
(P-1)2	P-!
1-/1
= — e--te
4	2
TO
/(0 = -e'+-e’'--fe-'.
4	4	2
Пример 2. Найти оригинал fit) по его изображению
Решение. Функция F(p) имеет полюсы рх = 1 и р2 = -1, каждый
второго порядка, т.е. гх = 2,г2 = 2. Воспользуемся формулой (3.31), для
чего сначала определим выражения в фигурных скобках:
F(p-)ep\p-px)r' =F(P)ep,{P-\)2 = / 2 ер'(р-1)2
(Р -1)	(Р + 1)
о/
F(P^(p-Piy‘
{р -1)	(р-1)
154
Формула (3.31) принимает вид
/(О = lim
ре”1
1 ~—Т
(Р + 0 р
реР1
-i/>
+ lim
^"’LCp-i)
Поскольку
реР*
lim —-------
,. (еР1 + ptepl)(p + l)2-2(р + \)рер1
lim ------------------------------------
+ !)4
(е‘ +te')22-2-2-k'	4/е'	1 ,
= ---:------т-------- =---= — te ,
24	16	4
lim
(е2” + pteP1 )(р -1)2 - 2(р -1)реР1
(Р-1)4
_ (е ' -/е')(-2)2 -2(-2)(-1)е" _ -4/е-' _ 1
24	" 16 " 4^
ТО
z/ Л 1 » 1	1 Г1 ,
f(t) = —te—te = —t -- = —/sh/.
4	4	2 ^2	J 2
Пример 3. Найти оригинал fit) по его изображению
(Р-1)(Р + 2)(Р-3)’
Решение. Все корни знаменателя являются простыми: р{ = 1, r{ = 1;
р2 = -2, r2 = 1; р3 = 3, r3 = 1. Функция F(p) имеет полюсы первого по-
рядка: pt = 1, р2 = -2, р3 = 3. Для нахождения оригинала fit) воспользу-
емся формулой (3.32). В данном случае Q(p)^=p+\, Л(р) = (р-1)х
х(р + 2)(р - 3), R(p) = р3 - 2р2 - 5р + 6, Л'(р) = Зр2 - 4р - 5. Произведем
необходимые вычисления и запишем их в таблице 3.1
155
Таблица 3.1
Рк	&Рк)=Рк+ 1	R'(p) = 3 pl -4р*-5	Q^Pk) гР1, R'(Pk)
1	2	3 • 1 -4-5=-6	2 .	1 , —е =—е -6	3
-2	-1	3(-2)2 - 4(—2) - 5 = 15	—е-2' =_±е-2' 15	15
3	4	3 -32-4-3-5= 10	—е3‘ =—е3' 10	5
В соответствии с формулой (3.32) находим оригинал
/(0 = --е'-—е-2'+-е3'.
3	15	5
Замечание. Этот пример можно решить и с помощью разложения
функций F(p) в сумму элементарных дробей.
Разложение дробной рациональной функции F(p) иа элементарные дроби
имеет вид
р+1	_ А В С
(р-1Хр+2)(р-3)" р-1+ р+2 + р-3’
откуда
р + 1 = Я(р + 2)(р-3) + В(р-1)(р-3) + С(р-1)(р + 2).
Полагая в этом тождестве р последовательно равным р = 1, р = -2, р = 3,
, 1
получаем А =	,
Значит,
В=-—, С=-
15	5
1
ч 11	1	1	21
F (р) -------------1-----
3 р-1 15 р + 2 5 р-3
к!
внимание операторное равенство е =
1
--- и свойство
Принимая во
Р-
лииейности, находим
156
Пример 4. Найти оригинал fit) по его изображению
1 \Н)-----------э
Р(Р-1)(Р +4)
Решение. Разлагаем F(p) в сумму элементарных дробей
1	_ А В Ср + Р
Р^Р-^ХР2 +4) Р +Р-1 р2+4’
откуда
1 = А(р - 1)(р2 + 4) + Вр(р2 + 4) + (Ср + £)(/> - \)р.
Полагая в этом тождестве последовательно р = 0, р- 1, p = 2i, на-
ходим значения коэффициентов А, В, С, D.
При р = 0 получаем
1	= А(-1 )(0 + 4); 1 = -4А, А =
4
При р = 1 тождество принимает вид
2	1
1 = В- 1(1+4), 1 =55, В = ~.
При р = 21 (тогда р2 = 42 = ~4,р2 + 4 = 0) получаем
1 = (С • 2i + £>)[(2/)2 - 2i] =
= (2Ci + Р)(~Д - 2i) = -8C7 - 4Ci2 -4D- 2Di,
1 = (4C - 4D) - (8C + 2D)i- 4C - 4D = 1, 8C + 2D = 0,
4C = -D,-D —4D = 1,—5D= 1, £) = --, C = —.
5	20
Следовательно,
4	1111	1 p	1	1
4 p 5/7-1 20 p2 4-4 5 p2 4-4
157
Так как
— = 1, —-—= е,	— = cos2z, —— == sin2z,
р ’	р-1 р2 +4	р +4
то
f(t) =	+ — е' +— cos2z——sin2z.
45	20	10
Пример 5. Найти оригиналy(z) по его изображению
F(P)~ (р-2)2(р2+1) ’
Решение. Разложение F(p) на элементарные дроби имеет вид
ч 1	А В Ср+ D
F(p) =-----z—z------=----+------т + —;--->	(1)
(р-2)2(р2+1)	р-2 (р-2)2	р2+1
откуда
1 = А(р - 2)(р2 +1) + В(р2 +1) + (Ср + D)(p - 2)2.	(II)
Определим коэффициенты А, В, С, D разложения (I).
Полагая р = 2 в тождестве (II), получаем
1 = В(22 + 1), 1 = 5В, В =
При р- i тождество (II) запишется так:
1 = (Ci + D)(i - 2)2 = (Ci + £))(? - 4i + 4) = (Ci + D)(3 - 4i) =
= 3Ci - 4Ci2 + 3D- 4Di = 3Ci + 4C+3D- 4Di.
Поскольку
1 =(4C+3D) + (3C-4D)i,
TO
4C + 3D= l,3C-4D = 0.
158
Из этих уравнений находим значения С и D:
4	4	3	4 3	4
ЗС = 4О, C = — D, 4—0 + 30 = 1, 250 = 3, О =—, С=--------= —.
3	3	25	3 25 25
При р = 0 и найденных значениях В, С, D равенство (II) принима-
ет вид
1 =А(0-2)(0 + 1)+ -(0 + 1) + | — 0 + — |(-2)2 = —2А + — + —,
5	(25	25 j	5 25
откуда
„ , 1	12 , 17-25	8	,	4
5 25	25	25	25
Подставляя найденные значения А, В, С, D в равенство (I), полу-
чаем
^.4111	4 р	3	1
25 р-2 5 (р-2)2 25 р2+1 25 р2+1
Так как
1	.21	1	.	21 р
------е , --------- т= te ,	— =
Р-2	(р-2)2	р2+1
1
cosz, —----
р2+1
sin/,
то
/(/) = -—е2'
25
1 2,	4	3 .
+ — te +—COS/ + —sin/.
5	25	25
Замечание. Значения коэффициентов А, В, С, D можно определить и
другим способом, придав тождеству (II) иной вид:
1 = Л(р3 - 2р2 + р - 2) + В(р2 +1) + С(р3 - 4р2 + 4р) + О(р2 - 4р + 4),
\ = (А+С)р3 + (В-2А-4С + D)p2 + (А + 4С - 4D)p + (В-2А + 40).
Приравнивая коэффициенты при одинаковых степенях р в обеих частях
последнего тождества, получаем систему четырех линейных уравнений отно-
сительно четырех неизвестных Л, В, С, D:
A + C = 0,B-2A-4C + D = 0,A+4C-4D = 0,B-2A+4D= 1.
Решив эту систему, найдем, что
159
Пример 6. Восстановить оригинал по его изображению

р2-2р + 3
р(/+2) ‘
Решение. Разложение F(p) на элементарные дроби имеет вид
р2-2р + 3 _ А Вр + С _ А(р2 +2) + (Вр + С)р
р{р2 +2) р + р2+1	р(р2+2)
= И + в)Р2 +с/? + 2Л) р2 - 2р + 3 = (Л + В)р2 + Ср + 2А.
Р(Р +2)
Приравнивая коэффициенты при одинаковых степенях р, получаем
А + В = 1, -2 = С, 3 = 2А,
откуда
3	1
А=—, В = -—, С = -2.
2	2
Следовательно,
„ ч 3 11
Р(Р) = ~---- 2 о
2 р 2 р2+2
1
р2 + 2
Р -2-
Поскольку
Р-- =cos>/2
Р P2+(V2)2
, Р г- , = sin -J2 t,
р2ч42)2
то
2 2
Пример 7. Найти оригинал fit) по его изображению
F(p) =
1
(P2+1)2’
160
Решение. В данном случае F(p) уже является элементарной дробью.
Чтобы найти оригинал, воспользуемся теоремой умножения и тем, что
1 . .
—----== Sint
р2+1
Применяя теорему умножения, получаем
ч 1	1	1	. г .	. .	. ,
F(p) = —------- = —-----3— = sin т s ш(г - т)Л =
(р2+1)2	р2+1 р2+1 J
— J[cos(2t-z)-cosz] eft = — Jcos(2t - t)dx— JcoszA =
О	2 О	2 о
1 .	I if 1	1
= —sin(2x-ZM „ —cosz-xl =—sinz---------ZCOSZ.
4	k=° 2	10 2	2
Итак,
f(f) = —smt~—t cos z.
в и
Пример 8. Найти оригинал fit} по его изображению F(z) =--.
р+1
Решение. Наличие множителя указывает на необходимость приме-
нения теоремы запаздывания. В данном случае
’ Р + 1 ’
поэтому
=e’(,’l)n(z-l).
р + 1
Пример 9. Найти оригиналfi(t} по его изображению

161
Решение. Поскольку р2 +6р + 10 = (р2 +6р + 9) + 1 = (р+3)2 +1, то
условие можно представить в виде
Fx (р) = F{p - (-3)) = F(p + 3) = ---L—
(Р + ЗГ+1
и воспользоваться теоремой смещения.
В соответствии с теоремой (3.2) получаем
F(p - (-3)) = e~3'f(t), fit) = F(p) =
P +1
Так как
1 . .
—— = sin/,
p2+l
то оригиналом для F,(p) является функция
Л (0 = e-3'/(z), f (z) = е”3' sin t.
Пример 10. Найти оригинал ft(p) по изображению
r(t}z Р2^
1 р3 +3р2 +5р + 2
Решение. Преобразуем правую часть этой формулы к виду
р2+2	_ (р+1)2-2(р+1)+3
р3+Зр2+5р+2	(р+1)[(р+1)2 +2]
и условие запишем так:
Л(Р)=:^(р-(-1)) = ^(р + 1) =
(Р +1)2 ~ 2(Р + 1) + 3
(р + !)[(/> +1)2 + 2]
На основании формулы (3.22) получаем
F(p-(-\)) = e-‘At),
(I)
где
At) = F(p) =
р2 -2р + 3
р(р2+2)
162
Оригиналом для последнего изображения F(p) является функция
3 1
f(f) = — -—cos-j2t--j2sm-j2t (см. пример 6). Подставляя это
выражение в правую часть формулы (I), получаем искомый оригинал
(31 г-
-/i(O = e~'l-“COSV2Z-
л/2 sin
л/2/
Задачи
Найдите оригинал fit) по его изображению F(p)
’• -1—• p +3p + 2	1 P( n\ —	1
	Г (P)	2 C p +5/> + 4
3.	. p +2/7 + 2	
5-^>v+2>+/	
гпр>-<л,‘	8- /?(p) = -vA— p (p +1)
9. F(p) =	-P + 2 	. (p + l)(p-2)(p2+4)	10. F(p)=	. p +3p +3p + l
11. F(p) =	1	. (p-l)2(p + 2)	12. F(p) = -^^	. p +4p +5p
13. F(p) = p -p -6p	14. F(p) =	J	 (p + l)(p + 3)
15. F(p) = -^-^. рЧр-Ъ2	16. F(p) = — P2^~1 p -2p2 +2p-l
Ответы
1. /(Z) = e '-е~2‘. 2. у(е-е41). 3. е-'sinz. 4. e2'sinZ. 5. 1-е~'-te1.
6. (1-Z)e-'.	7.-^-ZsinZ. 8. Z-sinZ. 9. —е2'ен——cos2z-—sin2z.
2	6	15	10	5
10. е Z(l-Z2).	11.-е'+3Ze').	12.-|+-^-(4sinZ-3cosZ).
163
13. —(8e3' + 12e~2'-5).	14. — —U~3'(2? + 2/ + 1).	15. 2 + t + Zte'-Ze'.
15	8	8
16. 2e‘ + е‘/г
§3.5. Решение дифференциальных уравнений
и их систем
Методы операционного исчисления применяются при интегрирова-
нии дифференциальных уравнений и их систем. С помощью этих мето-
дов интегрирование некоторых классов линейных дифференциальных
уравнений сводится к решению алгебраических уравнений; из алгеб-
раического уравнения находят изображение решения данного уравне-
ния, после чего по изображению восстанавливают само решение.
Пусть требуется найти решение линейного дифференциального
уравнения с постоянными коэффициентами
у(”) + а1у(”“,)+ ... +а„_1у' + алу=Ж	(3.33)
удовлетворяющее нулевым начальным данным
Я0)=У(0) = ...=/ °(0) = 0.	(3.34)
Предположим, что искомая функция у = y(t), и ее производные у',
у, ...,у™ и данная функция у( О являются оригиналами. Обозначим изо-
бражения функций y(t) и /(0 соответственно через Y(p) и F(p) или ко-
роче Y и F. Пользуясь ими и правилом дифференцирования оригинала
(см. (3.10)), находим
у = Y,y' = pY,y' = p2Y,° = р~ 'Г,у(п) = p"Y. (3.35)
Поскольку ?= F(p), то на основании свойства линейности (см.
(3.8)) получим уравнение в изображениях
pnY+ap'Y+... + a„Y=F(p),	(3.36)
которое соответствует данному дифференциальному уравнению. Из
уравнения (3.36) найдем изображение Yискомого решения
Y =------.	(3.37)
Р”+а1Рп '+... + а„
164
Найдя изображение F(p) функции fit), получим изображение У и
вопрос будет сведен к отысканию соответствующего оригинала, который
является решением данного дифференциального уравнения и удовле-
творяет условиям (3.34).
Таким образом, чтобы решить уравнение (3.33), необходимо знать,
как по оригиналу найти изображение и по данному изображению -
оригинал.
При интегрировании дифференциальных уравнений находит при-
менение интеграл Дюамеля (см. (3.25)).
Пусть необходимо найти решение дифференциального уравнения
(3.33), удовлетворяющего условиям (3.34). Запишем дифференциальное
уравнение с такой же левой частью и правой частью, равной единице:
2(я) + alz(n~ ° + ... + a„_1z' + a^z- 1.	(3.38)
Будем искать решение этого уравнения, удовлетворяющее нуле-
вым начальным данным:
z(0) = /(0) = ... = z(n ~ \0) = 0.	(3.39)
Обозначим изображение решения z(t) через Z, получим уравнение
в изображениях
pnZ+ a\p”~xZ+ ... + a„_ypZ+ a^Z =—,	(3.40)
P
откуда
p{pn+a{p” 1 + ... + a„_lp + a„)
Из этого равенства и равенства (3.37) находим, что
Y=pF(p)Z(p).	(3.42)
Пользуясь интегралом Дюамеля, получаем
У = —j/(T)z(Z-T)fift,
о
или
У = -^ р(т)/О - т) А.	(3.43)
о
165
Таким образом, когда известно решение уравнения (3.33) при
fit) = 1, удовлетворяющее нулевым начальным данным, то можно сразу
найти в квадратурах решение этого уравнения для любой функции fit)
при тех же начальных данных.
Замечание 1. Если начальные данные не являются нулевыми,
то изображения производных находят с помощью формул (3.9). Напри-
мер, еслиХО) * 0, то У	и т-Л-
Замечание 2. Если за начальный момент взято значение t0 * 0, а
не t = 0, то вводят новую переменную т по формуле т = t -t0, t = r +10,
тогда т = 0 при t = /0.
С помощью операционного исчисления можно найти решения сис-
тем дифференциальных уравнений с постоянными коэффициентами, а
в некоторых случаях - решения дифференциальных уравнений с пере-
менными коэффициентами, решения дифференциальных уравнений в
частных производных.
Пример 1. Найти решение уравнения у"-у' = 1, удовлетворяющее
условиям: у(0) = 0, у'(0) = 0.
Решение. Обозначим через Y изображение функции Х0- Ут== Y,
2	1
тогда у' = pY, у” ==pY. Поскольку 1 = —, то уравнение в изобра-
Р
жениях имеет вид p2Y - pY =—, откуда
Р
у _	1	. 1-р2+р2	-1-Р [	1	_	1	1 |	1
р(р2-р)	р2(р-1) р2 Р~1 р2 р р~х
„	ж	1	1	. ,	1	. ,
Принимая во внимание формулы —L ----------------= е,
р р р-1
получаем искомое решение у=е -f-1. Легко проверить, что эта
функция удовлетворяет данному уравнению и нулевым начальным
данным.
Пример 2. Найти решение дифференциального уравнения уи + у =
= 2cosf, удовлетворяющее условиям: Х0)= 0, у'(0) ~ -1 
Решение. Изображение функции у обозначим через У, а изо-
бражения производных найдем с помощью формул (3.9): у= У,
У =рУ-Х0)=рУ,у" =р2У-рУ(0)-г(0)=р2У+ 1.
166
Поскольку cos/==—у-—, то уравнение в изображениях прини-
Р +1
мает вид
р2у+ 1 + г=-3£_,
Р2 + 1
откуда
у = _2р_______1
(р2+1)2 р2+1’
Принимая во внимание первые из формул (3.18) и (3.20), получаем
Следовательно,
у = tsmt - sin/,
или
у = (I - l)sint
Пример 3. Проинтегрировать уравнение у” +4у = 8sin2z при на-
чальных условиях: у(0) = С„ у'(0) = С2.
Решение. Обозначим через Y изображение решения у(0- Изо-
бражения производных найдем с помощью формул (3.9): у= Y,
2	2
У = pY - С„ У' == р Y~ Cj> - С2. Так как sin2/ = —-- (см. пер-
р +4
вую из формул (3.18)), то операторное уравнение принимает вид
2	16
р2Г-С1р-С2+4У=—-------,
р +4
или
2	16
(р+4)У=—?— + Схр + С2,
р +4
откуда
,,	16	р „	1
К — ----— + С] —z— + с2 — -.
(р2+4)2	р2+4	р2+4
167
Для двух последних слагаемых имеем
11
—-—— = cos2/, — -= —sin 2/.
р2+4	р2+4	2
Что касается оригинала для первого слагаемого, то его найдем с
4 р
помощью формулы ——7^= tein2f (см. первую из формул (3.20))
(Р +4)2
и правила интегрирования оригинала (см. (3.11)) следующим образом:
16
(р2 +4)2
4р
= 4------—т- = [rsin2n/r =
Р (р2+4)2 J
„	1	о 1	 „
= 4 —rcos2r+—sin 2г
2	4
т== sin2z - 2zcos2t
о
Значит, искомое решение имеет вид
Q
у = С, cos 2t +—sin 2t + sin 2t - 2t cos 2t,
1	2
или
( C,
y = C,cos2t+Csm2t-2tcos2t, \C= — + 1
1	I 2
Пример 4. Проинтегрировать уравнение у” +у' = t при начальных
данных у(0) = У (0) = 0.
Решение. Найдем сначала решение уравнения z" + z' = 1 при нуле-
вых начальных данных. Уравнение в изображениях имеет вид
p2Z + pZ = —,
Р
откуда
z= I =P2+(1-P2)=_L+_L_1; z =
р(р2+1)	р2(р+1)	р+1 р2 р
168
На основании формулы (3.43) получаем:
y(f) = — J(e т + т - 1)(Z - т) А = [(е т + т - 1)(/ - т) j + |(е т + т - 1) А =
о	о
/2
y(t) = —-t-e-‘+l.
Пример 5. Найти решение уравнения у" -у’ -бу = 2е', удовлетво-
ряющее условиям: у(0) = 0, у' = (0).
Решение. Операторное уравнение в данном случае принимает вид
,	2
Р F(p) -pF(p) - 6F(p) =-
р-4
откуда
(р—4)(р2 - р-6) (р-4)(р-3)(р+2)'
Разлагая эту дробь на элементарные дроби, находим
ч 1	1	21	11
F(p) =--------------+--------.
15 р + 2 5 р-3 3 р-4
Следовательно, искомое решение определяется формулой
Пример 6. Найти решение задачи Коши: у” — Зу' + 2у = te31; у(Г) = 1,
у'(1)=1-
Решение. В отличие от предыдущих примеров, здесь за начальный
момент взято значение t = 1, а не t = 0. Введем новую переменную
x = f-l, откуда / = т+1. С учетом последнего равенства искомая
функция y(z) = у(т +1) = у(т). Данное уравнение и начальные данные
запишутся так:
у* - Зу' + 2у = (т + 1)е3е3т, у(0) = у'(0) = 1.
169
Найдем решение полученного уравнения:
y = Y, У =pY-\, у' = p2Y-p-A;
(т + 1)е3х = те3х + е3х
1	1	р-2
~ (р-3)2 + (р-3) ~ (р-3)2 ’
(р3-Зр + 2)У = е3-^? + р-2;
(Р-3)
(р -1 )(р - 2)Y = е3	+ (р - 2);
(Р-3)2
------+1; r = eJ-----------Г- +--
(р-3)2	(р-1)(р-3)2 р-1
Поскольку
--- == в ,
р-1
I _ 1	1	1	2
(р-1)(р-3)2 ~ 4|_р-1 + р-3+ (р-3)2
—(ех-е3х+2те3х),
у = ±е3(ех -е3х +2те3х) + ех;
£1+1Ъ+21_1ез(^)_
I4 J 4
Возвращаясь к переменной t (т = /-1), получаем решение исход-
ной задачи Коши
е3 + 4 i 2/ — 3 з/
у=--------е +-------е
4е 4
Пример 7. Найти решение уравнения у" + у = t, удовлетворяющее
условиям: у(1) = 1, У(1) = О-
170
Решение. Положим t = т+ 1, y(t) = y(t + 1) = у (т), тогда уравнение
и начальные условия примут вид
у’ + у' = т + 1, у(0) = 1, у'(0) = 0.
Составим операторное уравнение для этого дифференциального
уравнения. Пусть
ЭДНЦр),
тогда
У'(т) 7=^pY(p) ~ 1, У’(У) 7=^ р2Г(р) -р-
Операторное уравнение и его решение запишутся так:
p2Y(p')-p + pY(p)-l = -±T+—, Цр) = -у +—•
р Р	р Р
Переходя к оригиналам, получаем
у(Т)===И+^_.
Возвращаясь к переменной t (заменив т на t — 1), найдем искомое
решение исходной задачи Коши
Пример 8. Найти решение системы дифференциальных уравнений
у' + Зу + z = 0, z' —у + z =0
при начальных условиях у(0)= 1, z(0) = 1.
Решение. Введем обозначения Y = у, Z = z, тогда система в изо-
бражениях примет вид
pY- 1 + 3K+Z=0, PZ- 1 -r+Z=0,
(p + 3)K + Z= 1,-Г+(р+1)Z= 1.
Решение этой системы получим с помощью формул Крамера
Д„	Дг
Y = —, Z =—где Д- определитель системы, \z - определи-
Д	Д
171
тели, полученные из определителя системы заменой коэффициентов
при соответствующих неизвестных свободными членами. Поскольку
д = (^+ЗХ/7+1) + 1 = /72 +4/7+4,
А = (р + 2)2, Ад, = /7 + 1 — 1 — /7, Az = /7 + 3 + 1 = /7 + 4,
у _	Р	_ (/7 + 2)-2 = 1______2
(р + 2)2	(р + 2)2	Р + 2 (р + 2)2’
z_ р + 4 _(р + 2) + 2	1 t 2
(/7 + 2)2	(р + 2)2	р + 2 (р + 2)2’
1	. -21	1	• . -2'
Р+2 '	’ (р + 2)2 ’
то
у = е-2' (1-2/), z = e~2,(l + 2t).
Пример 9. Найти решение системы дифференциальных уравнений
у' - 2у - 4z = cos/, z* +у + 2z = sin/
при начальных условиях ХО) = z(0) = 0.
Решение. Система в изображениях принимает вид
(p-2)Y-4Z=-/-, Y+(р+2)Z =———.
PZ +1	/7 +1
Изображения Y и Z определяем с помощью формул Крамера. По-
скольку
А = (/7-2Хр + 2) + 4 = /72,
л __(Р + 2>)Р . 4	Р2+2/7 + 4	_ /7-2 р 2
У р2 +1 р2 +1	/72 +1	’	*	/72 +1	/72 -+1	/72 +1 ’
/>2 +2/7 + 4 _ 4/72 +4 + 2/7-3/72 _ 4	2р(/72 +1~Р2) _ 3
" /72(/72 +1)	/72(/72 +1)	7Т+ P2(P2+1)	Р2+1’
к = _4_ + 2_^£_____L_; Z- 2 - 2(1 + /?2)-/?2,
р2 р Р2 + \	/72 + Г р2(р2 +1) р\р2 +1) ’
172
7_	2	2
W+1’
1	.,	1	1	. . р
— = 1, —г = t, —— = smf, — = cosf,
Р р2 р2+1	р2+1
то
у = 4t + 2 - 2cost - 3sinf, z = -2t + 2sint.
Пример 10. Найти решение системы дифференциальных уравнений
х' - Х + у+ Z, у' = х-у + z, z' = х + у-Z
при начальных данных: х(0) = 0, Х0)= 1, z(0) = 0.
Решение. В изображениях система принимает вид
pX = X + Y + Z,	(1-р)Х + Y +Z = 0, '
pY -1 = X - Y + Z,  или X - (1 + p)Y + Z = -1, 
pZ = X + Y-Z, X + Y-(l + p)Z = 0.
Изображения X, Y, Z находим с помощью формул Крамера.
Поскольку
Д = (р+1)(р+2) + (2-р), Дх=-(р + 2), Ьу=2-р2, Ьг=-р,
ТО
-(р + 2)	_	1
(р + 1)(р + 2)(2-р) (р + 1)(р-2)’
Y =	2~Р2	=	Р1-2
(р + 1)(р + 2)(2-р) (р + \)(р+ 2)^-2)’
Z =-------~-Р-----=------Р--------.
(р + \)(р + 2)(2-р) (р + \)(р + 2)(р-2)
Разлагая полученные дроби на элементарные, находим, что
Г=1._Ь+1._Ь+1._Ц
3 р-2 3 р + 1	3 р + 1 2 р + 2 6 р-2
173
z=l._L_+1.__L_
3 р + 1 2 р + 2 6 р-2
Принимая во внимание равенство еа> = —— (см. главу 3, фор-
р-а
мулу (3.7)), получаем искомое решение данной системы дифференци-
альных уравнений при указанных начальных условиях:
1	7/	1	-/	1 -1	1	-2;	1	2t
х = —е—е , у = —е +—е	+—е
3	3	3	2	6
1 -I 1 -21	1	2/
z = —e —е +—е
3	2	6
Задачи
В задачах 1-10 найдите частные решения дифференциальных
уравнений, удовлетворяющие заданным начальным условиям:
1. у" - 2у' = е2', ХО) = 0, У(0) = 0.	2. у” +4у = sin2t,
3. у" + 2у' + 2у = 1, Х0) = 0, /(О) = 0.
5. у" + 2у' + у = sin/, Х0) - 0, У (0) = -1.
7. у' + у = cos/, Х0) = -1, У(0) = 1.
9. у" + 2у' -Зу = е ‘, у(0) = 0, у'(0) = 1.
ХО) = О,У(О) = 1.
4. у" + Зу + Зу = 0,
Х0) = 0,у(0)=1.
6. У' + у' = t2 + 2t,
Х0) = 4,У(0) = -2.
8. у" - 2у' - Зу = 2t,
Х0)=1,У(0)=1.
10. у" + 9у' = cos/,
Х0) = 0,У(0) = 0.
В задачах 11-18 решите задачу Коши для системы линейных диф-
ференциальных уравнений с постоянными коэффициентами
(х' + у = 0,
[У+х = 0,
Х°) = b
Х0) = -1.
fx' + Зх + у = 0, х(0) = 1,
[у - х + у = 0, у(0) = 1.
х' + х-у = е‘,
у' +у-х=е ,
х(0) = 1,
Х0) = 1.
(х'+4х+4у = 0, х(0) = 3,
(у'-2х + 6у = 0, у(0) = 15.
fx' — 2х — 4у = cos/, х(0)=0,
[у' + х + 2у = sin/, у(0) = 0.
х' = y + z,
16.  у' = Зх + z,
z' = Зх + у,
ХО) = о,
ХО) = 1,
z(0) = l.
174
17.
х' = 2х - у + z, х(0) = 1,
у' = х + z,	у(0) = b
z' = —3x + y-2z, z(0) = 0.
18.
х' = y + z,
у' = x + z,
z' = х +у,
х(0) = 1,
у(0) = 0,
z(0) = 0.
Ответы
2. у(0 = ~sin2f - — /cos 2/.
’ 8	2
4. ХО ~ е‘ — е 21.
1. y(t) = ±(l-e2,+2te2').
4
3. >(/) = у(1-е“' cos/ -e“'sin/).
5. y(t) = ~(е~' ~te~' ~ cos/).
7. XO = 'jls’nl_cos/ + sin/.
9. У({) ~ — (Зе' - е " - 2е').
8
11. ХО = е, у(1) = еч.
13. ХО = eZ, ХО = е‘-
15.	ХО = 2 + 4/ — 2cos/ - 3sin/, ХО = -2/ + 2sin/.
16.	x(t) = |(е3' - е-* ), y(t) = у (Зе3' + 2е~2'), z(/) = |(Зе3' + 2е~2'
17.	ХО = 2 - е', ХО = 2 - е', z(t) = 2е' - 2.
18.	x(t) = — е~' +— е2‘, y(t) = —e2'-—e~’, z(t) = — е2‘	е~‘.
3	3	3	3	3	3
6. у(1) = — + 2е~' +2.
о z ч 1 з, 4	4 2
8. y(t) = —е3 + — е-------------1.
9	9	9 3
10. Х0 = ~е 9<+~(9sin/-cos/).
12. ХО = е2‘( 1 - 2/), ХО = e"2'( 1+2/).
14. ХО = ~8е“2' + 11е“8', ХО = 4е“2' + 11Х8'.
175
Глава 4.
Из истории развития теории функций
комплексной переменной
и операционного исчисления
Теория функций комплексной переменной росла и развивалась
постепенно, вместе с ростом всего математического анализа. Основное
свойство аналитических функций - их представимость степенными ря-
дами- впервые в истории математики использовалось как системати-
ческий прием решения задач в работах И. Ньютона.
К приемам разложения в ряды, развитым Ньютоном, последую-
щее развитие математики добавило еще два, весьма существенных: ряд
Тейлора и ряд Маклорена.
§4.1. Первое появление комплексных чисел
На выражения вида a + 4~b, где b > 0, впервые обратил внима-
ние итальянский ученый Джироламо Кардано (24.09.1501-21.09.1576).
Кардано родился в Павии, окончил Павийский университет (1521),
доктор медицины (1526), был практикующим врачом. Читал лекции по
математике и медицине в Миланском университете (с 1534 г.). Про-
фессор медицины Павийского университета с 1539 г.
Кардано был одним из тех математиков, которые открыли спосо-
бы решения алгебраических уравнений третьей и четвертой степеней.
В 1545 г. вышла его книга «Великое искусство или о правилах алгеб-
ры», посвященная решению указанных уравнений. В книге рассматри-
ваются и квадратные уравнения. Он обращает внимание на то, что при
нахождении корней квадратного уравнения в некоторых случаях при-
ходят к квадратному корню из отрицательного числа. Кардано рас-
сматривал следующую задачу: найти два числа, сумма которых равна
10, а произведение равно 40. Эта задача сводится к решению системы
уравнений
х +у = 10, ху = 40
или к решению квадратного уравнения х - 10х + 40 = 0. Решая это квад-
ратное уравнение, он находит, что х, = 5 + 7-15, х2 = 5-7-15. Оче-
видно х, + х2 = 10, должно быть также (5 + 7~15)(5-7-15) = 40. Чтобы
получить этот результат, необходимо принять, что (-7-15)7-15) = 15.
176
Решения вида а + 4-b (6>0) Кардано называл «софистически от-
рицательными». Он рассматривал такие решения как курьез и старался
не пользоваться ими (считая, что в таких случаях задача не имеет ре-
шений).
Однако в дальнейшем ему снова пришлось рассматривать выра-
жения а + (Ь > 0) при изучении кубических уравнений. Решая
уравнение х3 = ах + b (а > 0, b > 0), он получал его корень по правилу,
которое соответствует формуле '
(4.1)
По формуле (4.1) невозможно было найти корень, когда
(4.2)
подкоренное выражение для квадратного корня оказывалось отрица-
тельным; этот случай назвали неприводимым. Например, уравнение
х = 15х + 4 имеет корень х = 4, но по указанной формуле получаем
х = 3^/-121 +^2-з/-121. Каким же образом из этой формулы из-
влечь число 4? Как объяснить это удивительное обстоятельство?
Чтобы ответить на подобные вопросы, математикам XVI-XVII
вв., необходимо было научиться обращаться с выражениями вида
а + у/-Ь (Ь > 0); в частности, изучить, как извлекать кубические корни
из таких выражений. Сначала математики очень неохотно приступали
к изучению этих выражений. Они называли выражения
а + ^-Ь (Ь>0) «мнимыми числами», «потайными решениями» урав-
нений. Считалось, что такие выражения не имеют реального содержа-
ния. Положение осложнялось тем, что к тому времени еще не успели
как следует освоить и отрицательные числа. Как правило, отрицатель-
ных чисел стремились избегать. Об этом свидетельствует тот факт, что
кубические уравнения, не содержащие члена с квадратом переменной,
рассматривали в следующих трех видах:
х = ах + Ь, х + b = ах, х = ах + Ь,
где а и Ь— действительные положительные числа (а не в виде
х + рх + q = 0, где р и q- действительные числа как положительные,
7 Зак. 1816
177
так и отрицательные). Поскольку коэффициенты уравнения считались
положительными, то необходимо было исследовать отдельно три ука-
занных вида кубических уравнений. Даже в более позднее время отри-
цательные числа называли «ложными» (так как они меньше, чем ни-
что, т.е. меньше нуля). При рассмотрении выражений а+4-b (Ь>0)
прибавлялась новая трудность - нужно извлекать квадратный корень
из «ложного» числа. Получить что-нибудь реальное при такой опера-
ции не рассчитывали. Результаты этих операций считали бесполезны-
ми и старались их не применять.
Пользу мнимых величин первым оценил итальянский математик
и инженер-гидравлик Бомбелли (1526-1573). Рафаэль Бомбелли ро-
дился в Болонье. Изучал математику в Болонском университете. Его
научные исследования относились к алгебре и геометрии. В 1572 г.
было опубликовано его сочинение «Алгебра». С помощью мнимых ве-
личин он объяснил, как получить действительные решения кубическо-
го уравнениях = ах + Ьв неприводимом случае.
n	Р? м3
Он отмечал, что разность 1 — 1 - I — I в этом случае является
отрицательной, поэтому квадратный корень из нее не может быть ни
положительным, ни отрицательным. Бомбелли предложил названия
для такой величины: плюс от минуса (piii di mend), когда ее прибавля-
ют и минус от минуса (тепо di mend), когда ее вычитают. Таким обра-
зом, у Бамбелли рШ di тепо R. q. 3 означает + -J-3, а тепо di тепо
R. q. 5 означает -7-5. Далее в его книге приводятся правила умно-
жения мнимых и действительных чисел. Эти правила даны в словесной
формулировке, в современных обозначениях они записываются так:
(+1Х+0 = Н (-1Х+0 = Ч (+1Х-0 = Ч (-1Х-0 « +i,
(+0(+0 = -1, (+/Х-0 = 1, (Ч(-0 = -1, НХ+О = 1.
Например, последнее правило имело такую формулировку: «Минус
от минуса на плюс от минуса дает плюс». Указанными правилами бы-
ли заложены камни фундамента теории комплексных чисел. Он провел
ряд примеров на действия над комплексными числами: 8/ + (-5/) = 3/,
^3+1710 ^3-/710 = VTo и т.п.
Бомбелли обнаружил, что кубические корни из комплексно сопря-
женных чисел являются комплексно сопряженными числами. Этим он
воспользовался для исследования неприводимого случая при решении
178
кубического уравнения x3 = ax + b. Решение (4.1) этого уравнения он
записал в виде
р-у]-д
(43)
з
тогда и —
-3uv+p, u2+v~yp2+g, откуда 4«3 = Зси + р, (с = ур2 + д). По-
следнее уравнение имеет действительный корень. Таким образом, Бом-
белли объяснил; как уравнение в неприводимом случае может иметь
действительный корень, хотя он выражается через кубические корни
из мнимых величин:
х = {и + J-v) + (w - V-v) = 2w.
Необходимо отметить, что общего решения задачи Бомбелли де
получил, поскольку для определения и он снова вынужден был рас-
сматривать неприводимый случай: уравнение 4м3 = Зси + р совпадает с
з , ,	X b а
уравнением х = ах + b при и = —, р = —, с = Путем проб он смог
решить отдельные числовые примеры.
Вопрос об извлечении корней из комплексных чисел был рас-
смотрен Муавром в начале XVIII в.
§4.2. Возникновение теории функций
комплексной переменной
Первое применение комплексных чисел к решению задач матема-
тического анализа принадлежит Лейбницу и И. Вернули. Именно в пе-
чатных работах и в научной переписке оба ученых, используя для ин-
тегрирования рациональных функций прием разложения на элемен-
с	Г d*	,
тарные дроби, пришли к интегралам вида ----, где а и Ь - ком-
J ах + Ь
плексные числа, и рассматривали их как «мнимые логарифмы».
Насколько, однако, смутными и противоречивыми были тогда сведе-
ния о комплексных числах видно, например, из того, что Лейбниц в
1702 году в одной из своих статей отзывается о мнимых числах как о
«чуде анализа, ... двойственной сущности, находящейся между бытием
и небытием». В этой же статье он ставит следующий важный вопрос:
можно ли любой многочлен с действительными коэффициентами
179
представить в виде произведения множителей первой и второй степени?
Лейбниц заявляет, что это не верно. В частности, он не заметил, что
двучлен х + а можно разложить на множители (х - V2 ах + а) и
(х2 + л/2 ах + а2), хотя и рассматривал возможность такого разложения.
Оперируя с логарифмами отрицательных и мнимых чисел, ни
И. Бернулли, ни Лейбниц не знали, что нужно понимать под логариф-
мом комплексного числа. Это видно из спора между Лейбницем и
Бернулли о логарифмах отрицательных чисел. Лейбниц утверждал, что
логарифмы отрицательных чисел мнимы, а Бернулли пытался дока-
зать, что они действительны. Хотя Лейбниц и занимал в этом споре
формально правильную позицию, однако, по существу, был весьма да-
лек от истины; он, так же как и его оппонент, и не подозревал, что ло-
гарифм многозначен. Теорию, устраняющую все затруднения, дал Эй-
лер в статье «Спор между Бернулли и Лейбницем о логарифмах отри-
цательных и мнимых чисел» (1749).
„	d(-x) dx
Бернулли утверждал следующее: поскольку ----------= —, то
- X X
1п(-х) = In х. Лейбниц возражал, что правило дифференцирования ло-
гарифмов справедливо только для положительных х. Эйлер не согла-
сился с этим возражением Лейбница и отметил, что «аргумент
И. Бернулли не доказывает того, что хочет доказать». Все дело в том,
что из равенства дифференциалов двух функций d In х и d 1п(-х) сле-
дует лишь, что эти функции 1п(-х) и In х отличаются на постоянную.
Постоянная эта равна ln(—1), так как ln(-x) = ln((— 1)  х) = 1п(—1) + In х;
утверждение Бернулли означает, что ln(—1) = 0, но это должно быть
доказано.
Эйлер показал, что ни один из его предшественников, стоявших
на противоположных позициях, не сумел обосновать свою точку зре-
ния. Выяснив это и одновременно охарактеризовав всю трудность во-
проса, он изложил правильное решение вопроса.
Леонард Эйлер сыграл важнейшую роль в развитии начал теории
аналитических функций в XVIII в. Первый этап его изысканий закан-
чивается классическим сочинением «Введение в анализ бесконечных
Т. 1» (1748). В начале этой книги автор подчеркивает, что «даже нуль
и мнимые числа не исключаются из значений переменной величины» и
далее дает множество примеров плодотворности такого широкого толко-
вания переменной. Таким образом, переменная величина у Эйлера явля-
ется комплексной переменной. Во второй главе Эйлер формулирует тео-
рему о том, что любой многочлен с действительными коэффициентами
180
может быть разложен на множители первой и второй степени. Однако
он не владеет полным доказательством этой важной теоремы. Факти-
чески оно должно было бы основываться на доказательстве существо-
вания корня любого алгебраического уравнения с действительными
коэффициентами: для такого доказательства математика XVIII в. еще
не создала почвы. В седьмой главе «Введения в анализ» сообщаются
установленные Эйлером формулы для показательной функции и лога-
рифма, которые в современной записи выглядят так:
/ \л
е2 = lim 1 + —I
л-> оо I nJ
lnz = lim п zn -1 .
В восьмой главе рассматриваются тригонометрические функции ком-
плексной переменной sinz, cosz, tgz, ctgz; формула Муавра
впервые в математической литературе появляется в явном виде
(cos z±4-У sinz)” = cos nz±4-isinnz.
Здесь же Эйлер получает знаменитые формулы
которые в настоящее время называют его именем, а также формулы
e+VzT v _ cos v+sjn v, е~^Е\ v _ CQS v _ sjn
выражающие мнимые показательные количества через синусы и коси-
нусы действительных дуг.
Итак, Эйлер в течение 30-40-х годов XVIII в. разработал теорию
элементарных функций комплексной переменной и к известным раз-
ложениям этих функций в степенные ряды добавил еще аппарат бес-
конечных произведений. В частности, он получил разложение функ-
ции sin z в бесконечное произведение
sin z = z
4]
4л2 Н
9л2
Следующий этап в развитии теории функций комплексной пере-
менной связан с открытием того фундаментального факта, что пары
сопряженных гармонических функций, т.е. решения системы диффе-
ренциальных уравнений с частными производными
ЭР 5g дР _ dQ
дх ду ’ ду дх
181
могут быть получены как действительные и мнимые части произволь-
ных аналитических функций f(x+4-\y) комплексной переменой
x+V-ly и с приложениями этого факта к решению задач механики,
картографии и интегрального исчисления. Основной предпосылкой
для указанных исследований служило истолкование уравнения
Р'х ~ Q'y как условия, при котором выражение Pdx + Qdy представляет
полный дифференциал некоторой функции от х и у. Этот результат
был получен Эйлером в 1734 г. (опубликован в 1740 г.).
В «Опыте новой теории сопротивления жидкости» (1752) Д'Алам-
бер, в связи с изучением обтекания твердого тела однородной невесо-
мой жидкостью, решает задачу отыскания двух функций р и q по их
полным дифференциалам
dq - Mdx + Ndz, dp - Ndx - Mdz.
Из сравнения этих дифференциалов он получает уравнения
дх dz dz дх
называемые обычно уравнениями Коши-Римана. Эти уравнения полу-
чил вновь (притом из весьма общих соображений) и существенно ис-
пользовал Эйлер, поэтому исторически значительно правильнее назы-
вать их уравнениями Д'Аламбера-Эйлера.
В работах Д'Аламбера и Эйлера, в последующих трудах Эйлера и
Лагранжа комплексные числа выступают как пары действительных
чисел, имеющих тот или иной конкретный смысл — геометрический,
физический или аналитический (пары функций). Опираясь на то или
иное истолкование комплексных чисел, математики рассматривают
соотношения между комплексными числами, как источник соотноше-
ний между действительными числами, как «сдвоенные» соотношения
между последними.
Эйлер в связи с задачей о построении географических карт изучал
проблему конформного отображения в общей постановке и использо-
вал для этой цели комплексную переменную.
Таким образом, в XVIII в. был накоплен обширный материал по
основам теории аналитических функций и выявлена плодотворность
изучения функций комплексной переменной. Основную роль в этой
работе играл петербургский академик Леонард Эйлер.
182
§4.3	. Уточнение концепции комплексного числа
В дальнейшей истории теории функций комплексной переменной
существенную роль играло развитие и распространение представлений
о комплексных числах как о векторах или точках плоскости. Весьма
близок к таким представлениям был Эйлер в тех работах, где он пере-
ходил от записи комплексного числа в виде х±4~\у к тригонометри-
ческой форме комплексного числа ^(cosco ±V-1 sin®), а также в
статьях, где он переходил от точек (х,у) плоскости (географической
карты) к комплексным числам х + iy, выражал последние через долготу
и широту точек сферы, а затем возвращался к координатам хи у.
Полное геометрическое истолкование комплексных чисел и ос-
новных действий над ними впервые было предложено норвежцем Кас-
паром Бесселем (08.06.1745-25.03.1818), работавшим геодезистом-
картографом Датской академии наук. Оно содержится в его единст-
венном математическом труде, представленном академии в 1797 г. и
два года спустя напечатанном в ее записках: «Опыт об аналитическом
представлении направления и его применениях, преимущественно к
решению плоских и сферических многоугольников». Целью Бесселя
было создать удобный аппарат решения геодезических задач, для чего
он систематически разработал векторное исчисление на плоскости, тут
же выступающее как геометрическая модель алгебры комплексных
чисел. Идея выразить изменение направления отрезка (слово «вектор»
введено позже) с помощью алгебраических символов формулируется
совершенно отчетливо. «Настоящий опыт предпринимается с целью
узнать, как аналитически представлять направление», и «посредством
одного только уравнения, связывающего один неизвестный отрезок и
несколько известных отрезков, получить такое выражение, которое
сразу представляло бы искомый отрезок как по величине, так и по на-
правлению». Обычные алгебраические операции позволяют изменить
направление только на противоположное, т.е. положительное на отри-
цательное и наоборот. Создание исчисления отрезков, имеющих на
плоскости произвольные направления, требует обобщения алгебры;
нужно «расширить определения алгебраических операций, но так...,
чтобы не было противоречия со старой теорией чисел...»
Применяя правило умножения к основным единицам, обозначае-
мым +1, —1, +е, —е, Бессель вывел следующие формулы:
(+1)(+1) = +1, (+1)(-1) = -1, (-1)(-1) = +1,
(+1)(+е) = +е, (+1)(-е) = -е, (-1Х+е) = -е, (-1)(-е) = +е,
183
(+е)(+е) = -1, (+E)(-E) = +1, (—e)(—e) = —1.
«Отсюда следует, - заключает Вессель, - что е равно V-T ».
Направленному отрезку ставится в соответствие комплексное
число в тригонометрической форме r(cosv + esinv) и рассматриваются
все операции над комплексными числами; формула Муавра доказыва-
ется и для дробного рационального показателя.
Таким образом, в «геометрическом анализе» Весселя нашли реаль-
ное истолкование и обоснование комплексные числа и действия над
ними. Понятия, в течение двухсот пятидесяти лет представлявшиеся
только удобными фикциями, получили ясный реальный смысл, а сам
термин «мнимое число» стал всего лишь историческим пережитком.
К сожалению, замечательный труд Весселя стал известен широким
кругам математиков только в конце XIX в., после того, как в 1897 г.
Датская академия наук опубликовала его французский перевод. В конце
XVIII вив начале XIX в. геометрическому истолкованию комплексных
чисел и операций над ними пришли и другие ученые, среди которых
живший в Париже уроженец Женевы Жан Робер Арган (18.08.1768-
13.08.1822). Его сочинение «Опыт некоторого способа представления
мнимых величин в геометрических построениях» было издано аноним-
но в Париже (1806). Оно оставалось незамеченным, пока Жозеф Диаз
Жергонн (19.06.1771-04.05.1859), основатель журнала «Анналы чис-
той и прикладной математики», не опубликовал указанную работу в
четвертом номере своего издания (1813). После этого сочинение Арга-
на получило широкую известность. Арган предложил краткое и эле-
гантное доказательство основной теоремы алгебры.
В первой четверти XIX в. многие математики были весьма близки
к геометрическому представлению комплексных чисел. Всеобщую из-
вестность и признание представления комплексных чисел в виде точек
плоскости получило с 1831 г., когда было опубликовано сочинение Гаусса
«Теория биквадратных вычетов», включавшее обоснование комплекс-
ных чисел и их геометрическую интерпретацию. Комплексные числа
использовались Гауссом почти во всех его работах по арифметике, алгеб-
ре, теории функций, теории поверхностей (конформное отображение).
Долгий и сложный путь к геометрическому истолкованию комп-
лексных чисел проделал Коши. Понимание им комплексных чисел ме-
нялось почти на протяжении всей его творческой деятельности. В
«Алгебраическом анализе» (1821) он относит «мнимые выражения»
(т.е. комплексные числа) и «мнимые уравнения» (т.е. равенства, со-
держащие комплексные числа) к разряду символических, понимая под
последними такие, которые «взятые буквально не точны или лишены
184
смысла, но из которых можно выводить точные результаты, модифи-
цируя и меняя по определенным правилам либо сами уравнения, либо
символы, в них содержащиеся». Он уточняет, что «всякое мнимое
уравнение - это только символическое представление двух уравнений
между двумя действительными количествами». Почти через четверть
века Коши вновь обращается к выяснению понятия комплексного числа.
Он снова повторяет прежнюю концепцию, ссылаясь на «Алгебраиче-
ский анализ». Вместе с тем он продолжает искать иное, содержательное
понимание комплексных чисел. Таким поискам посвящено несколько
работ, опубликованных после 1847 г. Коши останавливается на геомет-
рическом представлении комплексного числа, отдавая ему преимуще-
ство перед алгебраическим. Он предлагает «после новых и зрелых раз-
мышлений» полностью отказаться от знака V-Т и заменить теорию
мнимых выражений теорией количеств, названных «геометрическими».
При этом геометрическое количество гр является вектором с длинной г
(называемой модулем) и полярным углом р (аргумент или азимут).
Геометрическое количество приводится к виду х + iy, который называ-
ется аффиксом точки А(х, у).
В статье «О функциях геометрических количеств» Коши дал оп-
ределение функции комплексной переменой. Если z=x+iy- аффикс
подвижной точки А и Z = X + iY - аффикс движущейся точки В, то «Z
должно считаться функцией z, когда значение z определяет значение Z.
Но для этого достаточно, чтобы X и Y были определенными функция-
ми х и у. Тогда также положение движущейся точки А будет опреде-
лять всегда положение движущейся точки В». Итак, Коши узаконил
наглядное представление о функции комплексной переменной, кото-
рым он фактически (не вполне осознанно) пользовался в своих преды-
дущих исследованиях и которое вполне естественным представлялось
Гауссу еще в 1811 г.
В заключение приведем некоторые сведения, относящиеся к сим-
волике и терминологии. Знак мнимой единицы / (от слова imaginaire-
мнимый) предложил Эйлер в 1777 г. (опубликовано в 1794 г.), а в об-
щее употребление ввел Гаусс в 1801 г.; Коши стал им пользоваться с
1847 г. Термин «комплексное число» встречается у Л. Карно (1803 г.),
но в обиход вошло благодаря Гауссу (с 1831 г.). Слово «сопряженный»
впервые применил Коши в 1821 г., «модуль» - Арган, за ним Коши.
Слова «абсолютная величина» и запись |а + />/| принадлежат Вейершт-
рассу (хотя об «абсолютной величине а + bi писал Арган). Термин «нор-
ма» (V«2 + й2) для комплексного числа a + bi предложен Гауссом.
185
§4.4	. Развитие комплексного интегрирования
Наибольшее значение для построения теории функций комплекс-
ной переменной имели исследования, в которых применялись и разви-
вались эйлеровы методы вычисления определенных интегралов с ис-
пользованием комплексной переменой.
Лаплас в цикле работ, опубликованных в 1782-1786 гг., развивал
метод решения линейный разностных и дифференциальных уравне-
ний, основанный на замене неизвестной функции y(s) интегралами
вида J<p(x)x’<& или j" ср (х) e~sxdx, где <р(х) - новая неизвестная
функция. Здесь же впервые встречается знаменитое преобразование
Лапласа. Указанные интегралы берутся между пределами, удовлетво-
ряющими некоторому уравнению - уравнению пределов, вообще неал-
гебраическому. Нередко корни этого уравнения оказывались мнимы-
ми. Получив интегралы с «мнимыми пределами», Лаплас подвергал их
различным преобразованиям, основанным на замене переменной ин-
тегрирования, и приходил к интегралам от действительных функций
действительной переменной. Лаплас отмечал, что переходы от дейст-
вительного к мнимому позволили ему найти значения многих опреде-
ленных интегралов, и оценивал роль этих переходов как своего рода
индукцию, признавая необходимой дополнительную проверку резуль-
татов, полученных на этом пути. Он указывал, что Эйлер одновремен-
но с ним использовал переход от действительного к мнимому для вы-
числения интегралов, но что полученные Эйлером результаты вышли в
свет позднее соответствующих результатов Лапласа.
Проблема комплексного интегрирования в полном и совершен-
ном виде была высказана Гауссом в его письме к Бесселю от 19 декабря
1811 г., которое, к сожалению, впервые было опубликовано вместе со
всей перепиской двух ученых только в 1880 г. Гаусс писал следующее.
«Что нужно понимать под J<p (х)<& для х = а + Ы Очевидно, если
хотят исходить из ясных понятий, нужно принять, что х, отправляясь
от значения, для которого интеграл должен равняться нулю, посредст-
вом бесконечно малых приращений (каждое вида а + Ы) переходит к
х = а + Ы и тогда сложить все <р (х)с&. Так смысл вполне установлен.
Но переход может совершаться бесконечно многими способами. Так
же как совокупность всех действительных чисел можно мыслить в ви-
де бесконечной прямой линии, так и совокупность всех величин, дей-
ствительных и мнимых, можно сделать зримой посредством бесконеч-
ной плоскости, каждая точка которой, определяемая абсциссой а и ор-
динатой Ь, будет как бы представлять величину а + Ы Непрерывный
186
переход от одного значения х к другому а + Ы совершается поэтому по
линии и, следовательно, возможен бесконечно многими способами. Я
утверждаю теперь, что интеграл J <р (х) dx при двух различных пере-
ходах сохраняет одно и то же значение, если внутри части плоскости,
заключенной между двумя линиями, представляющими переход,
функция <р(х) нигде не равна ». Это прекрасная теорема, нетрудное до-
казательство которой я дам при удобном случае. Она связана с други-
ми прекрасными истинами, касающимися разложений в ряды. Переход
в каждой точке следует производить так, чтобы ни разу не затронуть
места, где <р(х) = оо. Я настаиваю на том, что такие точки следует обхо-
дить, что для них, очевидно, первоначальное основное понятие инте-
грала |<р (х) dx теряет ясность и легко приводит к противоречиям.
Вместе с тем, отсюда ясно, как функция, порожденная посредством
интеграла J <р (х) dx может иметь многие значения для одного и того
же значения х, а именно в зависимости от того, будет ли при переходе
<р(х) - оо, допущен однократный или многократный обход вокруг точ-
ки, в которой или же такого обхода совсем не будет».
Здесь же Гаусс впервые дает полное объяснение многозначности
,	Г
логарифма, определяемого как —.
J х
Результаты исследований Коши, имеющие значение для истории
теории функций комплексной переменной, первоначально изложены в
его «Мемуаре о теории определенных интегралов» (представлен в
1814 г., опубликован в 1825 г.). В этом мемуаре нет еще того отчетли-
вого понимания всей проблемы комплексного интегрирования, кото-
рое обнаруживается в цитированном письме Гаусса. Такое понимание
складывалось у него постепенно, в течение почти трех десятилетий.
Однако его труды были опубликованы в свое время (хотя и с некото-
рым опозданием), и именно они, а не идеи Гаусса, легли в фундамент
систематического построения общей теории.
В «Мемуаре об определенных интегралах, взятых между мнимыми:
пределами» Коши определяет интеграл по аналогии с интегралом от
функции действительной переменной как предел интегральной суммы.
Определенный им интеграл от комплексной функции является инте-
гралом вдоль некоторой кривой и посредством уравнений этой кривой
сводится к обыкновенному определенному интегралу. Коши формули-
рует и доказывает здесь свою основную теорему: «Если f(x + 4-\y)
187
конечна и непрерывна для х0<х<Х vt y0<y<Y ,то значение инте-
грала не зависит от природы функций х = <р(/), у ~ V(0" (т.е. не зави-
сит от кривой интегрирования, соединяющей в прямоугольнике
х0 < х < X, у0 < у <Y вершины (х, у) и (X, У)). Это и есть интеграль-
ная теорема для случая прямоугольной области.
В период с 1826 по 1829 г. Коши создает теорию вычетов. Назва-
ние вычет (буквально: остаток) объясняется тем, что Коши пришел к
этому понятию, отыскивая разность между интегралами, взятыми по
таким двум путям, имеющим общее начало и конец, между которыми
заключаются полюсы функции. В таком виде вычеты встречаются в
указанных двух его мемуарах. Во втором из них уделяется наибольшее
внимание анализу случаев, когда функция обращается в бесконечность
внутри или на сторонах прямоугольника. Здесь интегралы по разным
путям имеют вообще неравные значения, и Коши вычисляет разности
между ними, делая различные предположения.
Сам термин и определение вычета встречаются впервые в его ста-
тье «О новом роде исчисления, аналогичного исчислению бесконечно
малых» (1826). Коши вводит и определяет понятие следующим образом:
«Если, после того как найдены значения х, обращающие fix) в беско-
нечность, прибавить к одному из этих значений, обозначаемому через
X], бесконечно малое количество £ и далее разложить /(Х[+е) по воз-
растающим степеням этого количества, то первые члены разложения
будут содержать отрицательные степени е и один из них будет произ-
ведением на конечный коэффициент, который мы назовем вычетом
функции f (х), относящимся к частному значению xt переменной х".
Вслед за этой статьей Коши написал ряд других, в которых рас-
сматривал приложения теории вычетов к вычислению интегралов, раз-
ложению функций в ряды и бесконечные произведения.
§4.5	. Из истории операционного исчисления
Одним из важнейших источников современного операционного
исчисления явилось формальное символическое исчисление. Сущность
этого исчисления состояла в том, что символы операций (дифференци-
рования, интегрирования и др.) отделялись от функций и над ними
производились математические действия, как над числами или функ-
циями. В результате получалось соотношение между символами опе-
раций, которое переходило в соотношение между функциями, когда
символам операций возвращался их первоначальный смысл.
188
История символического исчисления ведет свое начало от Лейбни-
ца. В одной из статей, посвященных некоторым задачам дифференци-
ального исчисления, Лейбниц указал, что л-й дифференциал произве-
дения двух функций по форме выражения подобен n-й степени бинома:
dn(uv) = vdnu + C'ndv d"~'u + С2 d2v dn~2u + ... + udnv.
На эту аналогию Лейбниц указывал и в письмах к И. Бернулли, который
в ответ обратил внимание на то, что в определенных случаях с помощью
аналогии по заданному дифференциалу можно найти интеграл.
Замечания Лейбница о «биномиальной» аналогии Лагранж в 1772 г.
развил в стройную схему своеобразного алгоритмического исчисле-
ния. Символ дифференцирования он рассматривал как фиктивную ве-
личину, к которой можно прилагать обычные правила алгебры. Следо-
d
вало лишь в окончательном результате п-ю степень символа —, при-
dx
dnu
мененного к величине и, выражать в форме ----. Лагранж заметил,
dxn
что сам принцип аналогии, на котором основано предложенное им ис-
числение, не очевиден, хотя это не отражается на точности получае-
мых результатов. Он считал, что аналитически доказать этот принцип
очень трудно.
Несколько позже, в 1776 г., подобные результаты получил Лап-
лас. Сочинения Лагранжа и Лапласа вызвали к жизни большое количе-
ство исследований. Итальянский ученый А.М. Лорнья (18.10.1735-
28.06.1796) по образцу исчисления Лагранжа разработал «новый вид
«конечного и бесконечного исчисления», которое характеризовал сле-
дующим образом:
«Новый вид исчисления, о котором идет речь в настоящем ме-
муаре, состоит в том, что символы d, Д, Е, J, которыми пользуются в
обычном конечном или бесконечном исчислениях, рассматриваются в
двух различных аспектах, а именно: или как условные знаки, предна-
значенные для указания на изменения состояния величин, перед кото-
рыми они поставлены, или же как алгебраические количества».
Вопросами разработки символического исчисления занимались
многие французские и английские ученые.
В России символическое исчисление стало известно из книг зару-
бежных ученых, в частности, из трехтомного курса дифференциально-
го и интегрального исчисления французского математика С.Ф. Лакруа
(28.04.1765-25.05.1843).
189
В 1862 г. в Киеве была издана монография М.Е. Ващенко-Захар-
ченко «Символическое исчисление и приложение его к интегрированию
линейных дифференциальных уравнений». Эта монография представ-
ляет собой результат глубокого изучения литературы по символическим
методам, дополненный исследованиями, примерами и решениями
автора.
Символическое исчисление достигло своего апогея в конце XIX в.
в трудах английского ученого и инженера Оливера Хевисайда, давше-
го ему новые важные приложения. Хевисайд предложил формальные
правила обращения с оператором р =— и некоторыми функциями
dt
этого оператора. Пользуясь символическим исчислением, или, как его
стали называть, операционным исчислением, он решил ряд важнейших
задач электродинамики.
Научными исследованиями Хевисайд начал заниматься с первых
лет своей практической деятельности. Главной областью его исследо-
ваний была теория телеграфной и телефонной связи. Вместе с тем он
применял свои глубокие математические познания в самых различных
областях естествознания. Ему принадлежит идея распространения ре-
зультатов, полученных при изучении законов электрических цепей, на
колебательные и другие механические явления.
За плодотворные и глубокие исследования Хевисайд был избран
членом Лондонского королевского общества (Британской академии
наук). Но вскоре у него возник конфликт с математиками. Его обвиня-
ли в отсутствии систематичности при исследовании поставленных за-
дач и математической строгости. Сочинения Хевисайда не принимали
к опубликованию, потому что «их трудно читать». В ответ на это Хе-
висайд сказал, что такие сочинения «еще труднее писать».
Все положения операционного исчисления были выведены Хеви-
сайдом эмпирически и независимо от других ученых. Впервые он по-
пытался опубликовать свои результаты в серии статей «об операторах в
физической математике». Были опубликованы только две первые час-
ти - в 1892 и 1893 г., а третья часть отклонена (так как ее «трудно чи-
тать»), Все три части вошли в состав его главного трехтомного труда
«Электромагнитная теория» (1899). Хевисайду удалось создать такую
систему, которая, постоянно совершенствуясь, смогла развиться в ис-
числение, ставшее рабочим инструментом физиков и инженеров различ-
ных специальностей. Операционное исчисление Хевисайда оказалось
чрезвычайно ценным при исследовании любых переходных процессов
как в электрических, так и в механических системах, поскольку такие
системы описываются линейными дифференциальными, разностными
190
или интегральными уравнениями. Сведение к линейным задачам было
исходным предположением Хевисайда и его продолжателей.
Дальнейшее развитие операционного исчисления состояло в обос-
новании концепций Хевисайда. Вскоре в качестве основного положе-
ния исчисления было принято преобразование Лапласа, на которое
имеется ссылка и в трудах Хевисайда. Хевисайд понимал, что преоб-
разование Лапласа можно применить для обоснования операционного
исчисления, но по каким-то причинам не сделал этого.
Тем временем операционное исчисление как метод решения раз-
нообразных технических задач все более и более распространялось. В
начале XX в. его используют в своих исследованиях американские ин-
женеры, которых мало интересовали вопросы обоснования нового ис-
числения. Практическая же его направленность их вполне устраивала.
С конца 20-х годов операционное исчисление появилось в числе
обязательных курсов в некоторых высших технических школах.
В развитие операционного исчисления внесли вклад русские, ук-
раинские и белорусские математики. Академики Н.Н. Боголюбов и
Н.М. Крылов усовершенствовали операционное исчисление, обосновав
его применимость для решения задач, приводящих к дифференциаль-
ным уравнениям в частных производных. Это обобщение дало воз-
можность применять операционное исчисление к нелинейным задачам
математической физики. Во второй половине 40-х годов были опубли-
кованы исследования И.З. Штокало по операционному исчислению. В
них операционное исчисление распространено на новые классы линей-
ных дифференциальных уравнений с переменными коэффициентами.
Эти исследования имели важное значение как для дальнейшего разви-
тия самой теории операционного исчисления, так и для практических
приложений.
В 40-60-е годы выполнен ряд работ по применению операционно-
го исчисления для решения важных практических задач механики,
электротехники, теплотехники, математической физики, теории авто-
матического регулирования.
В настоящее время операционное исчисление и его многочислен-
ные приложения получили широкое распространение и стали одной из
актуальных областей прикладной математики.
191
Биографический словарь
Бернулли- семейство швейцарских математиков, родоначальником
которого был выходец из Голландии Якоб Бернулли (умер в
1583 г.). В различных поколениях Бернулли математиками были:
Якоб (1654-1705), Иоганн (1667-1748), Николай (1687-1759),
Николай (1695-1726), Даниил (1700-1782), Иоганн (1710-1790),
Иоганн (1744-1807), Якоб (1759-1789).
Бернулли Иоганн (27.07.1667-01.01.1748)- швейцарский математик,
профессор Гронингенского (с 1695) и Базельского (с 1705) уни-
верситетов, почетный иностранный член Петербургской АН (1725).
Развивал идеи Лейбница в области анализа бесконечно малых.
Дал первое систематическое изложение дифференциального и ин-
тегрального исчисления. Продвинул разработку методов решения
обыкновенных дифференциальных уравнений. Поставил класси-
ческую задачу о геодезических линиях, нашел характерное гео-
метрическое свойство этих линий, вывел их дифференциальное
уравнение. Предложил правило раскрытия неопределенностей
вида (правило Лопиталя-Бернулли), методы интегрирования
рациональных дробей, определение функции как аналитического
выражения, составленного из переменных и постоянных. Иоганну
Бернулли принадлежат также и исследования по механике: теория
удара, движения тел в сопротивляющейся среде и др.
Ващенко-Захарченко Михаил Егорович (31.10.1825-14.08.1912) -
украинский математик. Учился в Киевском университете, затем в
Париже в Сорбонне и Коллеж де Франс, где слушал лекции Ко-
ши. В 1863-1902 гг. работал в Киевском университете (с 1868 г. -
профессор). Его докторская диссертация «Риманова теория функ-
ций составного переменного» (1866) - одно из первых русских
сочинений по этой тематике. Другие исследования посвящены
теории линейных дифференциальных уравнений, символическим
методам, теории вероятностей и истории математики. В 1862 г.
издал первую на русском языке монографию о символическом
исчислении, в 1883 г. - монографию по истории геометрии в
древности и в средние века. Автор 12 учебных пособий по раз-
личным разделам математики. Оказал большое влияние на разви-
тие математического просвещения в России.
Вейерштрасс Карл Теодор Вильгельм (31.10.1815-19.02.1897)- не-
мецкий математик, профессор Берлинского университета (с 1856 г.),
член Парижской АН (с 1868 г.), почетный член Петербургской
192
АН (с 1895 г., член-корреспондент с 1868 г.). Его основные ис-
следования посвящены математическому анализу, теории функ-
ций, вариационному исчислению, дифференциальной геометрии
и линейной алгебре. Он дал строгое доказательство основных
свойств функций, непрерывных на отрезке; предложил признак
равномерной сходимости функционального ряда; построил при-
мер непрерывной функции, не имеющей производной ни в одной
точке. Центральное место в его работах занимает теория аналити-
ческих функций, в основу которой он кладет степенные ряды. Им
исследовано поведение аналитической функции в окрестности
изолированной особой точки, доказана теорема об аналитичности
суммы равномерно сходящегося ряда аналитических функций.
Гаусс Карл Фридрих (30.04.1777-23.02.1855)- немецкий математик,
астроном, геодезист, физик; почетный иностранный член Петер-
бургской АН (1824). Учился в Гёттингенском университете (1795-
1798). В 1799 г. получил доцентуру Брауншвейге, в 1807 г. - ка-
федру математики и астрономии в Геттингенском университете, с
которой была также связана должность директора Геттингенской
астрономической обсерватории. Отличительными чертами твор-
чества Гаусса являются глубокая органическая связь между теоре-
тической и прикладной математикой, необычайная широта пробле-
матики. Его труды оказали большое влияние на развитие алгебры,
теории чисел, дифференциальной геометрии, теории тяготения,
классической теории электричества и магнетизма, геодезии, целых
отраслей теоретической астрономии. Гаусс предложил несколько
вариантов доказательств основной теоремы алгебры, построил
теорию комплексных чисел.
Д'Аламбер Жан Лерон (16.11.1717-29.10.1783)- французский мате-
матик, механик, философ, член Парижской (1741), Французской
(1754) и других академий; почетный член Петербургской академии
наук (1764). Он является одним из основоположников методов
прикладной механики и математической физики. Основные мате-
матические исследования Д'Аламбера относятся к теории диффе-
ренциальных уравнений, обоснованию исчисления бесконечно
малых и теории рядов. При решении одного из уравнений гидро-
динамики впервые применил функции комплексной переменной.
Установил связь аналитических функций с гармоническими
функциями. Вместе с философом-просветителем Д. Дидро пред-
принял в 1751 г. издание «Энциклопедии наук, искусств и реме-
сел». Написал для нее вступительную статью «Очерк происхож-
дения и развития наук», в которой предложил классификацию на-
ук и ряд статей. Впервые высказал идею о времени как четвертом
193
измерении. Занимался также литературной деятельностью и был
избран членом Французской академии «Сорока бессмертных».
Дюамель Жан Мари Констан (05.02.1797-29.04.1872)- французский
математик, член Парижской АН (с 1840 г.), член-корреспондент
Петербургской АН (с 1859 г.). Окончил Политехническую школу
в Париже (1816), работал там же до 1869 г. (с 1830г.- профес-
сор). Одновременно преподавал в Сорбонне и Нормальной школе.
Основное направление его научной деятельности - математиче-
ская физика. Исследовал проблемы теории колебаний, теории уп-
ругости, теории рядов. Создал общий метод исследования вынуж-
денных колебаний упругих тел. Сформулировал принцип-аналог
метода вариации постоянных (принцип Дюамеля), ввел представ-
ление смешанной задачи с однородными граничными условиями
для неоднородного линейного уравнения с частными производ-
ными через решение соответствующей задачи для однородного
уравнения (интеграл Дюамеля). Изучал влияние температуры на
упругие деформации твердых тел. Оказал влияние на постановку
преподавания математического анализа. Изданный им в 1840 г.
курс анализа неоднократно переиздавался во Франции и был пе-
реведен на русский и немецкий языки. Такой же популярностью
пользовался и его «Курс механики» (1845).
Коши Огюстен Луи (21.08.1789-23.05.1857)- французский матема-
тик, член Парижской АН (с 1816 г.), почетный иностранный член
Петербургской АН (1831). Окончил Политехническую школу
(1807), Школу мостов и дорог (1810) в Париже. В 1810-1813 гг.
работал инженером на сооружении военного порта в Шербуре.
В 1816-1830 гг. преподавал в Политехнической школе и в Коллеж
де Франс, с 1848 г. - в Парижском университете. Труды Коши от-
носятся к различным областям математики и математической фи-
зики. Его курсы анализа, основанные на использовании понятия
предела, послужили образцом для большинства курсов позднейше-
го времени. В своих курсах он дад определение понятия непрерыв-
ной функции, осуществил четкое построение теории сходящихся
рядов (критерий Коши, признак Коши), ввел определение инте-
грала как предела сумм и др. Коши систематически развивал ос-
новы теории аналитических функций комплексной переменной;
дал выражение аналитической функции в виде интеграла (интеграл
Коши). Разработал теорию вычетов и ее приложений к различным
вопросам анализа. В теории дифференциальных уравнений ему
принадлежит заслуга постановки одной из основных задач (задача
Коши), доказательства теорем существования решений и метод
интегрирования уравнений с частными производными первого
194
порядка. Коши выполнил ряд работ по теории упругости, оптике,
алгебре, геометрии, теории чисел. Он предложил термины: «мо-
дуль комплексного числа», «сопряженные комплексные числа»,
обозначения: г - для вектора, 1g - для десятичного логарифма.
Лагранж Жозеф Луи (25.01.1736—10.04.1813) — французский матема-
тик и механик, член Берлинской АН (1759) и директор ее матема-
тического класса (1766-1787), член Парижской АН (1772), ино-
странный почетный член Петербургской АН (1776). Родился в
Турине, где Окончил университет и с 17 Лет начал преподавание
математики в Артиллерийской школе. В 1759-1787 гг. работал в
Берлине, ас 1787 г. - в Париже; профессор Нормальной школы
(1795), Политехнической школы (1797). Лагранж вместе с Эйле-
ром заложили основы вариационного исчисления. Ему принадле-
жат выдающиеся исследования по математическому анализу (его
именем названы: форма остаточного члена ряда Тейлора, форму-
ла конечных приращений, функция и множители для определения
условного экстремума, интерполяционная формула), по различным
проблемам дифференциальных уравнений (теория особых реше-
ний, метод вариации произвольных постоянных и др.), по алгебре
и теории чисел, механике, астрономии, математической картогра-
фии. Лагранж впервые ввел в рассмотрение двойные и тройные
интегралы, предложил обозначения для производной (у', /'(*)) и
для функции арксинус (arcsin). Является автором двух классиче-
ских трактатов: «Аналитическая механика» (1788), «Теория ана-
литических функций» (1797). Парижская академия наук дважды
присуждала премии Лагранжу за его научные работы.
Лаплас Пьер Симон (23.03.1749-05.03.1827)- французский астроном,
математик и физик, член Парижской АН (1785), член Француз-
ской академии (1816), почетный иностранный член Петербургской
АН (1802). Учился в школе Монашеского ордена бенедиктинцев,
из которой вышел, однако, убежденным атеистом. С 1771 г. -
профессор Военной школы в Париже. Деятельно участвовал в ре-
организации системы высшего образования во Франции, в созда-
нии Нормальной и Политехнической школ. Председатель Палаты
мер и весов (1790), руководил введением в жизнь новой метриче-
ской системы мер. Во времена Наполеона был министром внут-
ренних дел. Научное наследие Лапласа относится к области небес-
ной механики, математики и математической физики. Фундамен-
тальными являются его работы по дифференциальным уравнени-
ям, теории вероятностей. Он развил методы небесной механики и
завершил почти все то, что не удалось его предшественникам в
195
объяснении движения тел Солнечной системы на основе закона
всемирного тяготения Ньютона. Небесная механика во многом
обязана трудам Лапласа, которые подытожены им в классическом
сочинении «Трактат о небесной механике» (т. 1-5, 1798-1825).
В алгебре ему принадлежит важная теорема о представлении опре-
делителей суммой произведений дополнительных миноров (тео-
рема Лапласа). Он занимался и физикой; опубликовал ряд работ
по теории капиллярности и установил закон, носящий его имя;
вывел формулу для распространения звука в воздухе.
Лейбниц Готфрид Вильгельм (01.07.1646-14.11.1716)- немецкий ма-
тематик, философ, физик, изобретатель, юрист, историк, языковед,
член Лондонского королевского общества (1673), член Париж-
ской АН (1700). Изучал юриспруденцию и философию в Лейп-
цигском и Йенском университетах. С 1672 по 1676 г. с диплома-
тической миссией находился в Париже, где изучал математику и
естествознание. Принял участие в создании Берлинской академии
наук и был ее первым президентом (1700). Способствовал откры-
тию академий наук в Вене и Петербурге. В 1711, 1712, 1716 гг.
встречался с Петром I, работал над проектом организации образо-
вания в России. Лейбниц почти одновременно с Ньютоном и не-
зависимо от него создал основы анализа бесконечно малых. Дал
определения дифференциала и интеграла, ввел символы диффе-
ренциала d и интеграла |, разработал правила и формулы диф-
ференцирования, предложил определения экстремумов и способы
их нахождения, установил взаимно обратный характер основных
операций анализа - дифференцирования и интегрирования. Зало-
жил основы теории рядов и теории дифференциальных уравнений.
Им предложены математические термины, вошедшие во всеобщее
употребление, - функция, дифференциал, дифференциальное урав-
нение, алгоритм, абсцисса, ордината и др. Изобрел счетную маши-
ну и первый интегрирующий механизм. Начал разработку симво-
лического исчисления.
Лоран Пьер Альфонс (18.07.1813-02.09.1854)- французский матема-
тик и военный инженер. Окончил Политехническую школу в Пари-
же (1832). Его научные исследования относятся к вариационному
исчислению, теории функций, теории колебаний, математической
физике. Он доказал теорему о разложении функции комплексной
переменной, аналитической в круговом кольце, в ряд, названный
рядом Лорана. Это доказательство содержится в статье «Обобще-
ние теоремы Коши, относящейся к сходимости разложения функ-
ции по возрастающим степеням неизвестной» (1843).
196
Маклорен Колин (1698-14.06.1746)- шотландский математик, член
Лондонского королевского общества (с 1719 г.). Окончил универ-
ситет в Глазго, куда поступил в возрасте 12 лет. В 1718-1722 гг.
преподавал в Абердинском колледже. В 1722-1726 гг. жил во
Франции. Профессор Эдинбургского университета (с 1726 г.). Ос-
новные исследования посвящены математическому анализу, гео-
метрии, механике. Издал монографию «Теория флюксий» (1742),
в которой доказал ряд теорем анализа, решил многие задачи гео-
метрии, механики и астрономии. Опубликовал сочинение о раз-
ложении функций в степенные ряды и трактат по алгебре. Автор
«комментария» к «Математическим началам натуральной фило-
соф ии>>* Ньютона. Парижская академия наук дважды присуждала
ему премии: за работу о падении тел (1724) и работу по приливам
и отливам (1740); последняя была разделена между ним, Л. Эйле-
ром и Д. Бернулли.
Муавр Абрахам де (26.05.1667-27.11.1754)- английский математик, член
Лондонского королевского общества (1697), член Парижской и
Берлинской академий наук. Предложил правила возведения в п-ю
степень и извлечения корня и-й степени для комплексных чисел.
Исследовал степенные ряды, названные им возвратными; первым
пользовался возведением в степень бесконечных рядов. В теории
вероятностей доказал частный случай теоремы Лапласа.
Риман Георг Фридрих Бернхард (17.09.1826-20.07.1866)- немецкий
математик. Учился в Геттингенском и Берлинском университетах.
В 1851 г. защитил докторскую диссертацию «Основы общей тео-
рии функций одной комплексной переменной». С 1857 г. профес-
сор Геттингенского университета. Его лекции легли в основу ряда
курсов (математической физики, теории тяготения, электричества
и магнетизма, эллиптических функций), изданных после смерти
Римана его учениками. Труды Римана оказали большое влияние
на развитие математики 2-й пол. XIX в. и в XX в. В докторской
диссертации он положил начало геометрическому направлению
теории аналитических функций; им выведены римановы поверх-
ности, важные при исследовании многозначных функций. В ряде
работ он исследовал разложимость функций в тригонометрические
ряды и в связи с этим определил необходимые и достаточные ус-
ловия интегрируемости в смысле Римана (интеграл Римана), что
имело значение для теории множеств и теории функций действи-
тельной переменной. Им предложены также методы интегрирова-
ния дифференциальных уравнений с частными производными.
Тейлор Брук (18.08.1685-29.12.1731)- английский математик, член Лон-
донского королевского общества (1712). Нашел общую формулу
197
для разложения функций в степенные ряды, которую опублико-
вал в сочинении «Прямой и обратный метод приращений» (1715);
эта формула и ряды были названы позже его именем. В указанном
сочинении он положил начало математическому изучению задачи
о колебании струны. Ему принадлежат заслуги в разработке теории
конечных разностей. Тейлор предложил правило дифференциро-
вания функции, обратной данной. Впервые обратил внимание на
особые решения дифференциального уравнения. Является автором
работ о перспективе, центре качания маятника, полете снарядов,
взаимодействии магнитов, капиллярности и др. Занимался также
вопросами оптики, астрономии, философии.
Хевисайд Оливер (18.05.1850-03.02.1925)- английский физик, инже-
нер и математик, член Лондонского королевского общества (с
1891 г.), почетный доктор философии Геттингенского универси-
тета (с 1905 г.). Самостоятельно изучал математику и физику. Ра-
ботал инженером по технике слабых токов в фирмах Ньюкасла, в
Дании. С первых лет практической деятельности стал заниматься
научными исследованиями, главным образом по теории телеграф-
ной и телефонной связи. Применял математику к различным об-
ластям теоретического естествознания (определял возраст Земли,
изучал движение электронов, термоэлектрические явления, уве-
личения массы при очень высоких скоростях). Разработал метод
символического (операционного) исчисления, позволяющий дос-
таточно просто решать многие сложные математические задачи
механики, электротехники, автоматики и др. Первые его исследо-
вания по операционному исчислению опубликованы в 1892 г.,
они также вошли во второй том его главной работы «Электромаг-
нитная теория» (1899). Независимо от Дж. Гиббса и одновремен-
но с ним объединил векторные представления У. Гамильтона и
Г. Грассмана в векторное исчисление в его современном виде.
Векторные методы впервые применил в 1882 г., через три года
опубликовал полное сообщение о своих идеях по векторному
анализу. Ввел (1892) термин «орт» и название «набла» для операто-
ра Гамильтона V; предположил (1891) обозначать векторы жирны-
ми буквами. Хевисайд был избран почетным членом Американ-
ской академии искусств и наук (1899), почетным членом Инсти-
тута инженеров-электриков в Лондоне (1908), почетным членом
Американского института инженеров-электриков (1919), в 1921 г.
ему присуждена медаль Фарадея, учрежденная Институтом ин-
женеров-электриков.
Эйлер Леонард (04.04.1707-07.09.1783)- математик, механик и физик.
Родился в Базеле (Швейцария). Окончил Базельский университет
198
(1724). По приглашению Петербургской академии наук приехал в
Россию (1727). В Петербурге работал с 1727 по 1741 г. и с 1766 г.
до конца своей жизни. С 1741 по 1766 г. жил и работал в Берлине.
Круг научных занятий Эйлера охватывал все разделы современ-
ной ему математики и механики, теорию упругости, математиче-
скую физику, оптику, теорию машин, картографию баллистику,
морскую науку, страховое дело, теорию музыки и др. Свои резуль-
таты и результаты, полученные другими учеными, Эйлер систе-
матизировал в ряде классических монографий, большая часть ко-
торых вошла затем в учебные пособия для высшей и отчасти
средней школы. Трудно перечислить все теоремы и методы Эйле-
ра; только немногие фигурируют в учебной литературе под его
именем: теоремы Эйлера, тождества Эйлера, эйлеровы постоян-
ные, функции, углы, интегралы, формулы, уравнения, подстанов-
ки и т.д. В его трудах многие математические формулы и симво-
лика получили современный вид. Ему принадлежат обозначения:
е, л (постоянные), i (мнимая единица), sin х, cos х, tg х (тригоно-
метрические функции), Ах (разность, приращение), Е (знак сум-
мы),/(х) (обозначение функции) и др.
199
Некоторые оригиналы
и их изображения
	Оригиналы f (t)	Изображения 0
1	2	3
1.	1	p
2.	tn (и = 1,2,3,...)	n! pn+l
3.	ta (а>-1)	Г(а +1) Pa+I
4.	ecl (c = a + b\)	1 p-c
5.	tnecl (n = 1,2,3,...)	n! (p-c)n+1
6.	taec‘ (а>-1)	Г(а + 1) (p-c)“+1
7.	sin pt (t > 0)	P (P2+P2)
8.	cos pt	. P (P2+P2)
9.	shpt	P (P2-P2)
10.	ch pt	P (P2-P2)
11.	ect sin pt	P (p-c)2+p2
200
1	2		3
12.	ect cosP?		P-c (p-c)2+p2
13.	ecZ shp/		P (p-c)2-p2
14.	e"chp/		p-c (P-C)2-P2
15.	/sinP?		2pP (P2+P2)2
16.	/cos P?		(P2-P2) (p2+p2)2
17.	/sh p/		2pP (P2-P2)2
18.	/chp/		(P2+P2) o2 -p2)2
19.	sin(t - t) (t > 0)		e~xp p2+l
20.	cos(t - t)		pe-Tp P2 +1
21.	sint t		arcctg p
22.	f sin x , Sit = 1	dx J X 0		arcctg p P
23.	f COS X , Cit = — |	dx J X t		1 ! 1 In 	 p Jp2+1
24.	J	= -|= le~x2dx Vn J a	le-«77 P
201
1	2	3
25.	z—\ 1 1 — 1 4-	ln| 1+—I I PJ
26.	Int	—[in —- y l у = 0.57722... P\ P )
27.	bt „al e ~e t	p-b
28.	at bi e —e a-b	1 (P - a)(p - b)
29.	cosat - cosbt	P
	»2 Л b -a	{p2+a2\p2+b2)
30.	1 - cos at a2	1 P{P2 +«2)
202
Предметный указатель
А
Алгебраическая форма
комплексного числа 7
Аргумент комплексного числа 24
В
Вычет функции 112
Г
Геометрический смысл модуля и
аргумента производной f'(z) 63
Главное значение аргумента
комплексного числа 24
д
Действительная ось 12
Действительная часть
комплексного числа 7
Дифференцирование
-изображения 135
-оригинала 134
- функции комплексной
переменной 62
И
Интеграл
-Дюамеля 144
-Лапласа 128
- от функции f(z)
Интегрирование
-изображения 135
-оригинала 135
К
Комплексная плоскость 13
Комплексное число 6
М
Мнимая единица 6
Мнимая ось 12
Мнимая часть комплексного
числа 7
Мнимое число 7
Модуль комплексного числа 23
Множество связное 48
И
Непрерывность
- функции комплексной
переменной 48
Нули функции 103
О
Область 48
-двусвязная 49
-односвязная 48
Операционное (операторное)
равенство 128
П
Первообразный корень 39
Показатель роста функции 127
Показательная форма
комплексного числа 25
Предел функции комплексной
переменной 48
Преобразования Лапласа 128
Производная функции
комплексной переменной 62
Р
Ряд Лорана 94
-	Тейлора 85
С
Свертка функций 143
Сопряженные комплексные
числа 7
Т
Теорема запаздывания 143
-	Коши о вычетах 113
-	подобия 143
-смещения 143
-	умножения изображений 143
203
Точка
-особая 104
—	изолированная 104
—	полюс 104
—	существенно 104
—	устранимая 104
Тригонометрическая форма
комплексного числа 24
У
Упорядоченная пара
действительных чисел 4
Условия Д'Аламбера-Эйлера
(Коши-Римана) 63
Ф
Формула
-	Коши интегральная 78
-	Муавра 31
Формулы
-Эйлера 53
Функции
-	гиперболические комплексной
переменной 53
-	элементарные комплексной
переменной 52—55
Функция
-	аналитическая 63
-	гармоническая 64
-	дифференцируемая 62
-изображение 128
-	комплексной переменной 49
—	многозначная 49
—	однозначная 48
—	оригинал 127
-	Хевисайда 129
204
Литература
1.	Араманович И.Г., ЛунцГ.Л., Эльсгольц Л.Э. Функции комплексного пе-
ременного. Операционное исчисление. Теория устойчивости. М.: Наука,
1969.
2.	Волков И.К., Канатников А.П. Интегральные преобразования. Операци-
онное исчисление. М.: Изд-во МГТУ, 1996.
3.	Волковысский Л.И., Лунц Г.Л., Араманович И.Г. Сборник задач по теории
функций комплексного переменного. М.: Наука, 1975.
4.	Гусак А.А., Гусак Г.М., Бричикова Е.А. Справочник по высшей математи-
ке. Мн.: ТетраСистемс, 2000-2002.
5.	Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах.
Часть III. М.: Высшая школа, 1971.
6.	Диткин В.А., Прудников А.П. Интегральные преобразования и операци-
онное исчисление. М.: Наука, 1972.
7.	Диткин В. А., Прудников А.П. Справочник по операционному исчисле-
нию. М.: Высшая школа, 1965.
8.	Князев П.Н. Интегральные преобразования. Мн.: Вышэйшая школа, 1969.
9.	Краснов М.Л., Киселев А.И., Макаренко Г.И. Функции комплексного пе-
ременного. Операционное исчисление. Теория устойчивости. М.: Наука,
1981.
10.	Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного пе-
ременного. М.: Наука, 1973.
11.	ЛунцГ.Л., Эльсгольц Л.Э. Функции комплексного переменного. М.: Нау-
ка, 1965.
12.	Маркушевич А.И., Маркушевич Л.А. Введение в теорию аналитических
функций. М.: Просвещение, 1977.
13.	Маркушевич А.И. Очерки по истории теории аналитических функций. М.-
Л.: Гостехиздат., 1951.
14.	Пантелеев А.В., Якимова А.С. Теория функций комплексного переменно-
го и операционное исчисление в примерах и задачах. М.: Изд-во МАИ,
1998.
15.	Пчелин Б.К. Специальные разделы высшей математики. М.: Высшая шко-
ла, 1973.
16.	Сборник задач по теории аналитических функций /Под редакцией
М.А. Евграфова. М.: Наука, 1972.
17.	Сборник задач и упражнений по специальным главам высшей математики
/Под редакцией Г.И. Кручковича. М.: Высшая школа, 1970.
18.	Свешников А.Г., Тихонов А.Н. Теория функций комплексной перемен-
ной. М.: Наука, 1979.
19.	Шахно К.У. Элементы теории функций комплексной переменной и опе-
рационного исчисления. Мн.: Вышэйшая школа, 1975.
20.	Штокало И.З. Операционное исчисление. Киев: Наукова думка, 1972.
21.	Гусак А.А. Высшая математика: В 2 т. - Мн.: ТетраСистемс, 1998-2002.
205
Оглавление
Предисловие................................................3
Глава 1. Комплексные числа....................................4
§1.1	. Множество комплексных чисел. Основные	понятия.'...4
§1.2	. Геометрическое изображение комплексных чисел.	,,
Комплексная плоскость...............................12
§1.3	. Арифметические действия над комплексными числами.15
§1.4	. Возведение в степень комплексного числа. Извлечение
квадратного корня из комплексного числа.................18
§1.5	. Модуль и аргумент комплексного числа. Тригонометрическая
форма комплексного числа................................23
§1.6	. Действия над комплексными числами, заданными
в тригонометрической форме.............................30
§1.7	. Корни из единицы.................................39
§1.8	. Геометрическое истолкование арифметических действий
над комплексными числами...............................42
Глава 2. Элементы теории функций комплексной
переменной...............................................48
§2.1	. Понятие функции комплексной переменной. Предел и
непрерывность..........................................48
§2.2	. Основные элементарные функции комплексной переменной.52
§2.3	. Дифференцирование функций комплексной переменной.62
§2.4	. Интегрирование функций комплексной переменной....67
§2.5	. Интегральная формула Коши........................78
§2.6	. Ряд Тейлора......................................85
§2.7	. Ряд Лорана.......................................94
§2.8	. Нули функции. Особые точки......................103
§2.9	. Вычеты функций..................................112
Глава 3. Основы операционного исчисления.................127
§3.1	. Оригинал и изображение..........................127
§3.2	. Основные правила и формулы операционного исчисления ... 134
§3.3	. Основные теоремы операционного исчисления.......143
§3.4	. Нахождение оригинала по изображению.............152
§3.5	. Решение дифференциальных уравнений и их систем..164
206
Глава 4. Из истории развития теории функций комплексной
переменной и операционного исчисления........176
§4.1	. Первое появление комплексных чисел..........176
§4.2	. Возникновение теории функций комплексной переменной.179
§4.3	. Уточнение концепции комплексного числа......183
§4.4	. Развитие комплексного интегрирования........186
§4.5	. Из истории операционного исчисления.........188
Биографический словарь...............................192
Некоторые оригиналы и их изображения.................200
Предметный указатель.................................203
Литература.......................................... 205
207
По вопросам оптового приобретения книг
обращаться по тел. 219-73-88, 219-73-90
Книжный Интернет-магазин издательства "ТетраСистемс"
http://www.book.shop.by
(доступен в Минске по БЕСПЛАТНОЙ линии: тел. 210-57-87)
Справочное издание
ГУСАК Алексей Адамович
БРИЧИКОВА Елена Алексеевна
ГУСАК Галина Максимовна
Теория функций
комплексной переменной
и операционное исчисление
Справочное пособие к решению задач
Справочное пособие
Редактор С.В. Процко.
Дизайн обложки С. А. Демидовой.
Компьютерная верстка А. А. Кузей.
Ответственный за выпуск А.Ф. Мясников.
Подписано в печать с готовых диапозитивов 14.08.2002.
Формат 60x84 '/|6. Бумага для офсетной печати. Гарнитура Таймс.
Печать офсетная. Печ.л. 18,0. Усл.печ.л. 30,24. Тираж 3100 экз.
Заказ 1816
Научно-техническое общество с ограниченной ответственностью "ТетраСистемс"
(Лицензия ЛВ № 76 от 19.11.1997).
220116. г. Минск, а/я 139 (тел. 219-74-01; E-mail: books@tut.by; http://www.ts.by).
Республиканское унитарное предприятие
«Издательство "Белорусский Дом печати"».
220013, г. Минск, проспект Ф. Скорины, 79.