Текст
ПОСОБИЕ
ПО МАТЕМАТИКЕ
ДЛЯ ПОСТУПАЮЩИХ
В ВУЗЫ
Под редакцией Г. Н. ЯКОВЛЕВА
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия
для поступающих в вузы
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1981
22.1
П 62
УДК 51
Коллектив авторов:
А. Д. КУТАСОВ, Т. С. ПИГОЛКИНА,
В. И. ЧЕХЛОВ, Т. X. ЯКОВЛЕВА
ололэ лло © Издательство «Наука».
20203—002 mmmm Главная редакция
П 28-80. 1702030000 Физико-математической
053@2)-81 литературы, 1981
ОГЛАВЛЕНИЕ
Предисловие , 7
Глава I. Множества. Понятие функции и обратно"! функции 9
§ 1. Множество. Подмножество. Объединение и пересечение множены
Числовые множества . . . , 9
§ 2. Понятие функции 18
§ 3. Координатная плоскость. График функции 21
§ 4. Обратная функция 22
ЗАДАЧИ РАЗДЕЛА 1 25
ЗАДАЧИ РАЗДЕЛА II 27
Г лап а II. Элементы логики. Взаимно обратные и взаимно противопо-
противоположные теоремы. Метод математической индукции 30
§ 1. Высказывания. Операции над высказываниями , 30
§ 2. Предложения, зависящие от переменной 37
§ 3. Взаимно обратные и взаимно противоположные теоремы. Необ-
Необходимые и достаточные условия , 42
§ 4. Метод математической индукции 47
задачи раздела : 51
задачи разде.ла ii 54
Глава III Уравнения и системы уравнений 58
§ I. Урапнения с одним и несколькими переменными .......... 58
§ 2. Системы уравнений , , 63
§ 3. Системы линейных урапненим ,..,,...,..,.... 67
§ 4. Задачи на составление ураьнеинл . 72
ЗАДАЧИ РАЗДЕЛА I 75
ЗАДАЧИ РАЗДЕЛА II 75
Глава IV. Алгебраические неравенства ,. 81
§ 1. Функциональные первенства Понятие равшхнлыюсти нера-
неравенств , , 81
§ 2, Рациональные неравенства Метод интервалов 83
§ 3. Иррациональные неравенства 87
§ 4. Неравенства с модулем , 89
§ 5. Неравенства с параметрами 90
§ 6. Доказательство неравенств 94
§ 7. Приложение неравенств к задачам на наибольшие и наименьшие
значения 98
ЗАДАЧИ РАЗДЕЛА I 100
ЗАДАЧИ РАЗДЕЛА 11 .... 101
Глава V. Последовательности. Предел последовательности. Предел функ-
функции. Производная , 105
§ 1. Бесконечные последовательности. Последовательности ограничен-
ограниченные и неограниченные , 105
§ 2, Предел последовательности. Теоремы о сходящихся последова-
последовательностях 107
§ 3. Монотонные последовательности. Теорема BeiiepiuTpacc;i Ill
§ 4, Арифметическая прогрессия , 113
§ 5. Геометрическая прогрессия 115
§ 6, Предел функции. Непрерывность функции 117
§ 7. Производная, ее геометрический смысл 121
§ 8. Предел функции на бесконечности 125
§ 9. Односторонние пределы. Бесконечные пределы 126
ЗАДА ЧИ РАЗДЕЛА I , 129
ЗАДАЧИ РАЗДЕЛА II 131
Г%1 а в а VI, Исследование функций и построение их графиков 136
§ 1. Четные и меченые функции 136
§ 2. Периодические функции 138
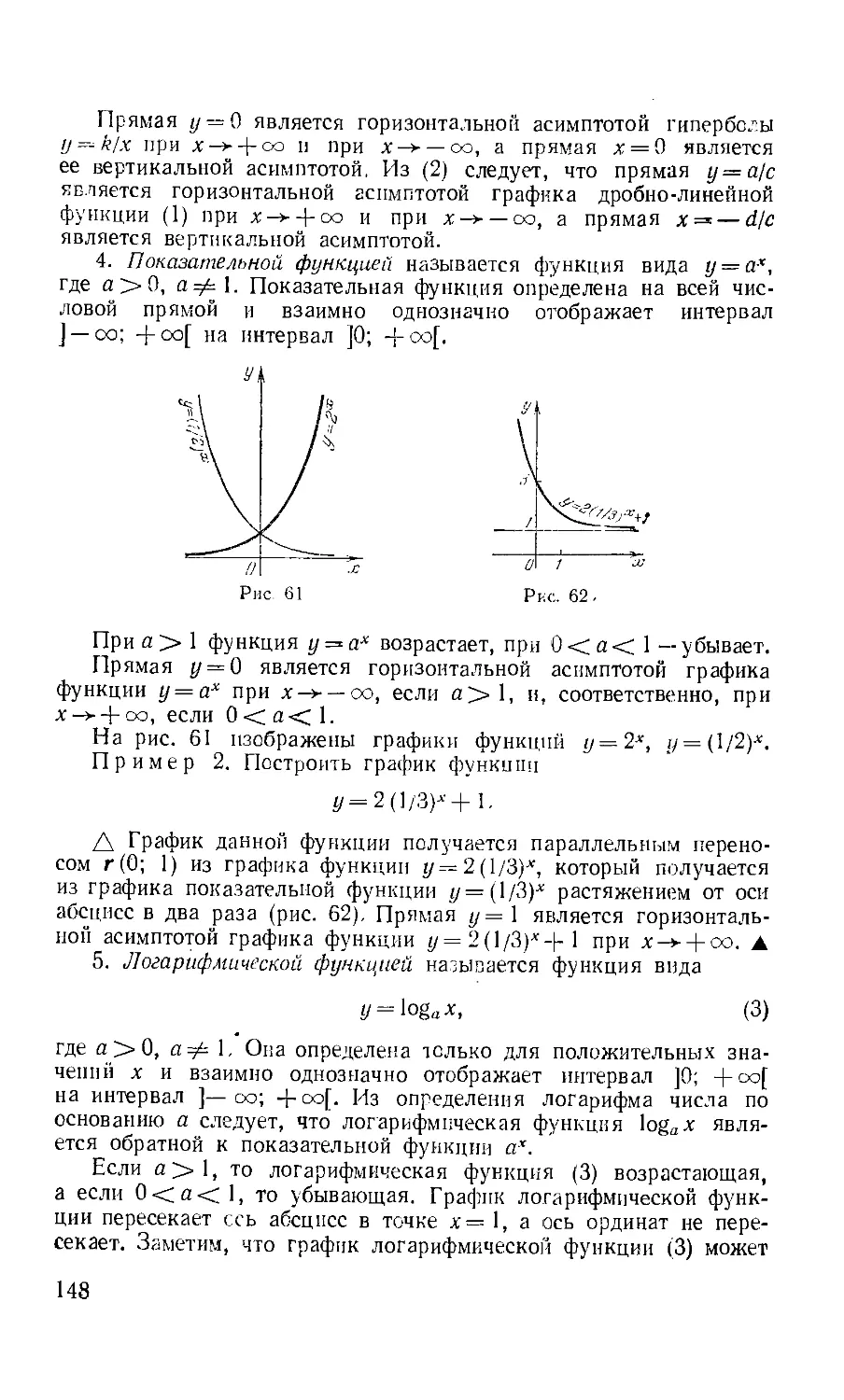
§ 3. Асимптоты , 140
§ 4, Преобразования графиков функций 143
§ 5, Элементарные функции и их графики ....,,...,, 145
§ 6. Построение графиков функций 153
§ 7. Применение производной к исследованию функций и построению
их графиков ,...,.,.,,.... 155
§ 8. Наибольшее и наименьшее значения функции 158
ЗАДАЧИ РАЗДЕЛА I 160
ЗАДАЧИ РАЗДЕЛА II 161
Глава VII. Векторы 163
§ 1. Некоторые необходимые определения п обозначения, ....... 163
§ 2. Векторы, их обозначение и изображение, Коллинеарные и ком-
компланарные векторы 165
§ 3, Сумма векторов. Противоположный вектор. Разность векторов . 167
§ 4. Умножение вектора на число. Признак коллинеарности 170
§ 5, Условие компланарности векторов. Разложение вектора по трем
некомпланарным векторам , , , 171
§ 6. Угол между векторами. Скалярное произведение векторов .... 173
§ 7, Базис. Координаты вектора. Действия над векторами, заданными
своими координатами , , 176
§ 8. Прямоугольная система координат. Уравнение плоскости. .... 178
ЗАДАЧИ РАЗДЕЛА I . 181
ЗАДАЧИ РАЗДЕЛА II • 183
Глава VIII. Комплексные числа, . 187
§ 1, Определение комплексных чисел ,...,,.,...,., 187
§ 2. Свойства операций сложения и умножения 188
§ 3, Алгебраическая форма записи комплексных чисел. Правила дей-
действий с комплексными числами, записанными в алгебраической
форме , , , 190
§ 4. Геометрическая интерпретация комплексных чисел. Модуль и
аргументы комплексного числа ..,.., , . 193
§ 5. Тригонометрическая форма записи комплексного числа. Умноже-
Умножение и деление комплексных чисел, записанных в тригонометри-
тригонометрической форме 198
§ 6. Возведение в степень и извлечение корня ,....,... 200
§ 7. Алгебраические уравнения ,,,.,, . . • 203
ЗАДАЧИ РАЗДЕЛА Г 208
ЗАДАЧИ РАЗДЕЛА II 208
F Л а в а IX, Тригонометрические уравнения, системы, неравенства .... 211 __
§ I. Тригонометрические уравнения 211
§ 2. Системы тригонометрических уравнений 225
§ 3. Тригонометрические неравенства 234
ЗАДАЧИ РАЗДЕЛА 1 239
ЗАДАЧИ РАЗДЕЛА II 240
Глава X. Показательные и логарифмические уравнения, системы и нера-
неравенства 248
§ 1. Показательные уравнения , 250
§ 2. Логарифмические уравнения 251
§ 3. Разные примеры уравнений 255
§ 4' Система показательных и логарифмических уравнений 258
§ 5. Показательные и логарифмические неравенства 2бу
ЗАДАЧИ РАЗДЕЛА I 2G5
ЗАДАЧИ РАЗДЕЛА I! 263
Глава XI. Комбинаторика. Формула Ньютона для степени бинома. Слу-
Случайные события и их вероятности 273
§ I. Размещения, перестановки, сочетания 273
§ 2. Формула Ньютона 281
§ 3. Случайные события и их вероятности 285
ЗАДАЧИ РАЗДЕЛА I 288
ЗАДАЧИ РАЗДЕЛА II 289
Глава XII. Интеграл 292
§ I. Первообразная и неопределенный интеграл 292
§ 2. Интеграл и формула Ньютона —Лейбница . , 298
§ 3. Площадь криволинейной трапеции ЗОЛ
§ 4. Применение интеграла к вычислению объемов тел 30d
§ 5. Применение интеграла при решении физических задач 312
ЗАДАЧИ РАЗДЕЛА I 314
ЗАДАЧИ РАЗДЕЛА II 310
Глава XIII. Решение планиметрических задач 319
§ I. Разные задачи 320
§ 2. Подобие треугольников. Теоремы синусов и косинусов 328
§ 3. Свойства хорд, секущих и касательных 333
§ 4. Алгебраические и тригонометрические методы решения. Приме-
Применение векторной алгебры . , , , ,,,.,.,.,.,.... 336
ЗАДАЧИ РАЗДЕЛА I 340
ЗАДАЧИ РАЗДЕЛА II 342
Глава XIV. Множества точек на плоскости и в пространстве. Задачи
на построение 348
§ I. Множества точек, обладающих заданным свойством 348
§ 2. Применение метода координат 354
§ 3. Задачи на построение 356
ЗАДАЧИ РАЗДЕЛА I 362
ЗАДАЧИ РАЗДЕЛА II 363
5
Глава XV. Стереометрия (часть I) 3CG
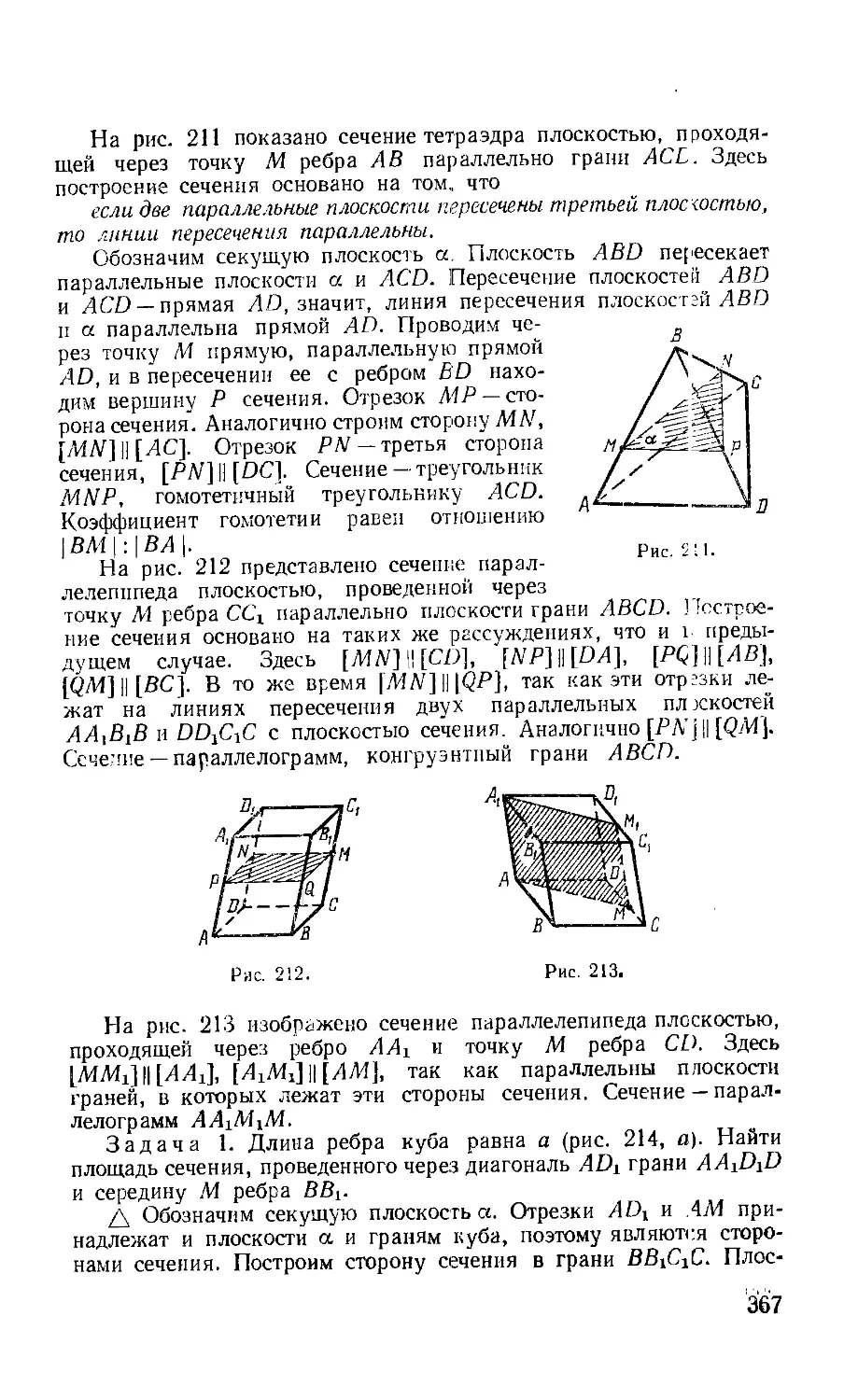
§ I. Сечении многогранников 366
§ 2. Применение критериев коллинеарности и компланарности век-
векторов в решении задач 379
§ 3. Угол между прямыми в пространстве 385
§ 4. Применение скалярного произведения векторов в решении зядач 387
ЗАДАЧИ РАЗДЕЛА I 390
ЗАДАЧИ РАЗДЕЛА II 391
Глава XVI. Стереометрия (часть II) , 399
§ I. Перпендикулярные прямые и плоскости 399
§ 2. Об изображении на рисунках перпендикулярных прямых и плос-
плоскостей. Построение сечений, перпендикулярных прямой или
плоскости 403
§ 3. Угол между прямой и плоскостью 407
§ 4. Расстояние от точки до плоскости, расстояние между прямыми
и плоскостям!.1 410
§ 5. Двугранный угол. Угол между плоскостями. Бнссектор. Трех-
Трехгранный угол 414
§ 6. О вычислении объемов многогранников и их частей 420
§ 7. Задачи па комбинации многогранников 423
ЗАДАЧИ РАЗДЕЛА I 425
ЗАДАЧИ РАЗДЕЛА II 426
Глава XVII. Фигуры вращения 434
§ 1. Цилиндр 434
§ 2. Конус 437
§ 3. Сфера 441
§ 4. Комбинации сферы, конуса и цилиндра 451
ЗАДАЧИ РАЗДЕЛА 1 455
ЗАДАЧИ РАЗДЕЛА II 456
Приложение. Образцы вариантов, предлагавшихся в 1977 — 1979 гг.
на письменных вступительных экзаменах по математике 4G4
Решения задач I раздела 474
Ответы к задачам II раздела и приложения 574
Список формул 600
ПРЕДИСЛОВИЕ
Эта книга написана для учащихся, желающих углубить и
несколько расширить свои знания, с тем чтобы лучше подгото-
подготовиться к вступительным экзаменам в вузы. Она может томочь
и тем, кто уже окончил школу, но продолжает изучать матема-
математику самостоятельно или на подготовительных курсах и отделениях.
Авторы надеются, что учителя средних школ, преподаватели
профтехучилищ и техникумов, руководители математических круж-
кружков и студенты педагогических вузов найдут в книге материал,
который смогут использовать в своей работе. Наконец, книга
может представлять интерес как сборник, содержащий более 2000
задач, из которых треть задач приведены с решениями. Значи-
Значительная часть задач предлагалась на вступительных экзаменах
в различных вузах.
Книга написана в соответствии с программой по математике
для средних школ, и в ней используются терминология и обозна-
обозначения, принятые сейчас в школе. Пособие не содержит система-
систематического изложения школьного курса математики и не может
заменить школьные учебники. Тем не менее все основные i важ-
важные, по мнению авторов, вопросы освещены достаточно подробно.
В некоторых случаях добавлен материал, несколько выходящий
за рамки ныне действующей программы для поступающих г, вузы.
Авторы считают, что изучение этого материала будет способство-
способствовать развитию математической культуры учащихся, а также при-
принесет пользу при дальнейшем обучении в вузах.
Книга состоит из 17 глав. Каждая глава содержит теорети-
теоретический материал и задачи. Изложение теории сопровождается
разбором большого числа примеров различной трудности. Задачи
в каждой главе разбиты на два раздела: задачи первого раздела
даны с решениями, задачи второго раздела — только с отЕ;етами.
Авторы настоятельно советуют учащимся обращаться к приведенным
7
в книге решениям задач 1-го раздела только после настойчивых
попыток решить задачу самостоятельно. Самостоятельное решение
одной задачи часто приносит больше пользы, чем разбор готовых
решений нескольких задач. Учащимся, которые желают посту-
поступить в вузы с повышенными требованиями по математике, следует
изучать материал более глубоко с непременным решением доста-
достаточного количества задач.
В конце книги в «Приложении» даны образцы вариантов
письменных экзаменационных работ по математике, предлагавшихся
в 1977—1979 гг. Они дают представление о степени трудности
задач на приемных экзаменах в различных вузах страны.
В заключение отметим, что пособие написано на основе опыта
заочного обучения математике школьников 8—- 10 классов в заочной
физико-технической школе при Московском физико-техническом
институте. Авторы благодарят директора ЗФТШ, заслуженного
учителя РСФСР Т. А. Чугунову за помощь в работе. Авторы
выражают также глубокую благодарность профессору Г. Н. Яков-
Яковлеву, советами и рекомендациями которого они постоянно поль-
пользовались.
Г л а в а I
МНОЖЕСТВА. ПОНЯТИЕ ФУНКЦИИ И ОБРАТНОЙ ФУНКЦИИ
§ 1. Множество. Подмножество. Объединение
и пересечение множеств.
Числовые множества
Множество. В математике понятие множество используется
для описания совокупности предметов или объектов. При этом
предполагается, что предметы (объекты) данной совокупности
можно отличить друг от друга и от предметов, не входяцих в
эту совокупность. Например, можно говорить о множестве всех
книг данной библиотеки, множестве всех вершин данного много-
многоугольника, множестве всех натуральных чисел, множестве всех
точек данной прямой. Книги данной библиотеки, вершины данного
многоугольника, натуральные числа, точки данной прямой явля-
являются элементами соответствующих множеств.
Множества обычно обозначаются большими буквами Л, В,
X, ... Тот факт, что объект а является элементом множества Л,
записывается так: а е Л и читается «а принадлежит множеству
Л», «а входит в множество Л». Запись афА (или аЦ=А) озна-
означает, что а не является элементом множества Л.
Например, если через М обозначено множество натуральных
чисел, то
3eN, 20 eN, 0 ^ IN, 3/2 ^№
Обычно множество задается указанием характеристического
свойства его элементов, т. е. такого свойства, которым обладают
все элементы данного множества и только они. Чаще всего это
свойство формулируется словами: множество учеников данного
класса, множество решений уравнения х2— 1 =0, множество точек
плоскости, равноудаленных от двух данных точек.
Может оказаться, что множество определено таким свойством,
которым не обладает вообще ни один объект. Рассмотрим, напри-
например, множество треугольников, длины сторон которых рав'ны
1 см, 2 см, 5 см. Из геометрии известно, что треугольника с
такими длинами сторон не существует, т. е. так определенное
множество не содержит ни одного элемента. Ни одного элемента
не содержит и множество рациональных чисел, квадрат которых
равен двум. Множество решений системы уравнений
также не содержит ни одного элемента. Говорят, что эти множе-
множества пустые. Пустое множество не содержит элементов, оно обоз-
обозначается знаком G).
Если множество содержит конечное число элементов, бывает
удобно задать это множество перечислением его элементов. Эле-
Элементы множества выписываются подряд и заключаются в фигурные
скобки, порядок записи при этом роли не играет. Например, множе-
множество, состоящее из трех букв а, б, в, записывается так: {а, б, в\.
Множества А и В называются равными, если они состоят из
одинх и тех же элементов. В этом случае пишут А--В.
Множество решений уравнения хг — 5х + 6 = 0 содержит те же
самые элементы (числа 2 и 3), что и множество простых чисел,
меньших пяти. Эти два множества равны.
Числовые множества. В алгебре чаще всего приходится иметь
дело с множествами, элементами которых являются числа. Такие
множества называются числовыми. Для некоторых часто встречаю-
встречающихся числовых множеств в школьном курсе математики приняты
стандартные обозначения: М —множество натуральных чисел, Z—¦
множество целых чисел, (Q — множество рациональных чисел, 'к—¦
множество действительных чисел.
Действительные числа изображаются точками координатной
прямой (числовой оси). Координатная прямая — это всякая прямая,
q E N на которой выбраны направление, при-
—l—-—-1 1 J;—»- нимаемсе за положительное, точка —на-
'' '' '"' 'г чало отсчета и единица измерения — мас-
fJ»c, 1. штабный отрезок, длина которого прини-
принимается равной единице. Координатная
прямая обычно изображается горизонтально, положительное направ-
направление указывается стрелкой, начало отсчета обозначается О (рис. 1).
Точка О разбивает координатную прямую на два луча, один из
которых имеет положительное направление и называется положи-
положительным лучом, другой — отрицательным. Число, изображением
О ? М МОЕ
о 1 з.т ^7 -tot ^v
Рис. 2. Рис. 3.
которого на координатной прямой является точка М, называется
координатой точки М. Координата начальной точки О равна
нулю. Координата любой точки М, лежащей на положительном
луче ОЕ, равна длине отрезка ОМ: х = \ОМ\ (на рис. 2 коорди-
координата точки М равна 2,5). Если же точка М лежит на отрица-
отрицательном луче, ее координата равна длине отрезка ОМ, но взятой-
10
со знаком минус: л; = — \ОМ\ (на рис. 3 координата точки М
равна — 1). Вся координатная прямая обозначается Ох.
Неравенства между действительными числами на координатной
прямой получают простое истолкование. Если xt < хг, то точка
с координатой х± лежит левее точки с координатой хг. Расстояние
между двумя точками Мх и М2 координатной прямой равно абсо-
абсолютной величине разности их координат х1 и хг: \ MlMi\ = \x1 — х%\.
Пусть а и Ъ — действительные числа и a<ib. Ниже в таблице 1
даны названия, определения и обозначения числовых множеств,
называемых числовыми промежутками, и их изображение на ко-
координатной прямой. Каждый из числовых промежутков опреде-
определяется как множество действительных чисел х, удовлетворяющих
определенным неравенствам.
Таблица 1. Числовые промежутки
Название
отрезок от а до ft (замкнутый
промежуток)
Неравенство,
определяю-
определяющее множе-
множество
X =?S
Обозначение
[a, ft]
Изображение
интервал от а до Ь (открытый
промежуток)
]а; Ь[
b се
открытый слева промежуток -от
а до Ь
]а; Ь]
открытый справа промежуток
от а до ft
а ^ х <: i
[а; ft[
b
А
числовой луч от а до +оо
[а; +сх>[
открытый числовой луч от а
ДО +СО
а <х
а; +со[
числовой луч от —со до а
]—со; о]
а, ж
открытый числовой луч от —оо
до а
х < а
] —оо; а[
а са
Открытый слева и открытый справа промежутки (см. таблицу 1)
называются также полуоткрытыми промежутками, а числовые
лучи — бесконечными промежутками. Множество действительных
чисел R обозначается также ] — оо; +оо[ и называется числовой
прямой. Всякая координатная прямая является изображением
числовой прямой.
При рассмотрении числовых множеств вместо слов «элемент»,
«число» употребляется также слово «точка». Так, например, вместо
11
«число 1 принадлежит отрезку [0; 2]» говорят: «точка 1 лежит
на отрезке [0; 2]» или «точка 1 принадлежит отрезку [0; 2]».
Подмножество. Всякое натуральное число принадлежит множе-
множеству целых чисел; любая точка интервала ]а\ Ь[ является точкой
отрезка [а, Ь]\ любой правильный треугольник является элементом
множества всех треугольников.
Если любой элемент множества А принадлежит также мно-
множеству В, то множество А называется подмножеством множества
В. Это записывается так: Л с В или Bz^A. В этом случае
говорят, что множество А содержится в множестве В или мно-
множество В содержит множество А. Таким образом, множество IN
натуральных чисел является подмножеством множества Z целых
чисел, т^ е. (N с: Z; интервал ]а; Ь[ является подмножеством отрезка
[a, b]: ]a; b[cz[a; Ъ].
Если в множестве А найдется хотя бы один элемент, не
принадлежащий мдоже?тву В, то Л _н§_ Я?_ляехся подмножеством
множества В: АфВ. Например, отрезок [а; Ь] не является под-
подмножеством промежутка ]а; Ь], так как а е [а, Ь], но а ф ]а; Ь].
Из определения подмножества следует, что любое множество
является подмножеством самого себя, т. е. справедливо утвержде-
утверждение Л с Л.
Полагают также, что пустое множество является подмножеством
любого множества. Это вполне естественно, так как пустое мно-
множество не содержит ни одного элемента и, следовательно, в нем
нет элемента, который не принадлежал бы любому другому
множеству.
Рассмотрим, например, множество учеников некоторого класса;
обозначим это множество X, и пусть К —множество учеников
того же класса, получивших за контрольную по истории оценку
«отлично». Если все ученики класса получили за эту контрольную
отличную оценку, то X и У равные множества: X — Y. Если же
ни один ученик класса не получил «отлично», то множество Y
пустое, Y = ф. Но в любом случае множество Y является под-
подмножеством множества X: КсХ.
Рассмотрим еще произвольное множество, состоящее из трех
элементов, которые обозначим а, Ъ и с, и найдем все его под-
подмножества.
Это пустое множество 0; множества, содержащие по одному
элементу: {а}, {Ь}, {с}; множества, содержащие по два элемента:
{a, b}, {b, с], {а, с}; само множество {а, Ъ, с). Число всех этих
подмножеств равно восьми. Таким образом, любое множество,
состоящее из трех элементов, имеет 8 = 28 подмножеств. В даль-
дальнейшем (см. глава XI) будет установлено, что если множество
состоит из п элементов, то число всех его подмножеств рав-
равно 2я.
Пересечение множеств. Рассмотрим два множества:
Х = {0, 1, 3, 5}, К = {1, 2, 3, 4}.
.12
Числа 1 и 3 и только они принадлежат одновременно обоим
множествам X и Y. Составленное из них множество {1, 3} содер-
содержит все общие для множеств X и Y элементы.
Множество, состоящее из всех элементов, принадлежащих и
множеству А и множеству В, называется пересечением множеств
А и В и обозначается А Л В.
Таким образом, множество {1, 3} является пересечением рас-
рассмотренных множеств X н Y:
{О, 1, 3, 5}Л{1, 2, 3, 4} = {1, 3}.
Для отрезка [—1; 1] и интервала ]0; 3[ пересечением, т. е.
множеством, состоящим из общих элементов, является промежуток
]0; 1] (рис. 4).
Пересечением множества прямоугольников и множества ромбов
является множество квадратов. Пересечение множества учеников
восьмых классов данной школы
и множества членов химического 4'//<г///////ь =»-
кружка той же школы есть мно-
множество учеников восьмых клае- <,/>//////<//<//////.•<> =»_
сов, являющихся членами хими- О 3 ^
ческого кружка. «""ч. ¦ >-
Если множества Л и В не 0 1 &
имеют общих элементов, то гово- р 4
рят, что эти множества не пересе-
пересекаются или что их пересечение —
пустое множество, и пишут А(]В = ф. Например, пересечение
множества четных чисел с множеством нечетных чисел пусто.
Пустым является и пересечение числовых промежутков ]— 1; 0]
и [2; +ос[ (рис. 5).
Пересечение любого множества А с пустым множеством есть,
очевидно, пустое множество: А(]ф ==ф-
Объединение множеств. Вновь возьмем множества Х =
= {0, 1, 3, 5} и Y — {1, 2, 3, 4} и наряду с ними рассмотрим множе-
множество {0, 1, 2, 3, 4, 5}. Это мно- i/r ,,,,,,
жество содержит все элементы j о 2 х
множества X (числа 0, 1, 3, 5) и р 5
все элементы множества Y (числа
1, 2, 3, 4) и не содержит ника-
никаких других элементов, т. е. множество {0, 1, 2, 3, 4, 5} со-
содержит те и только те элементы, которые принадлежат или
множеству X или множеству У.
Множество, состоящее из всех элементов, принадлежащих или
множеству А или множеству В, называется объединением мно-
множеств Л и В и обозначается Л IJ В.
Итак,
{0, 1, 3, 5}U{1, 2, 3, 4}=={0, 1, 2, 3, 4, 5}.
13
Объединение множества положительных четных чисел и мно-
множества положительных нечетных чисел есть, очевидно, множество
натуральных чисел. Объединением множества учеников школы
моложе 12 лет с множеством учеников той же школы старше
10 лет является множество всех учеников этой школы.
Объединением числовых промежутков [—1; 1] и ]0; 3[ явля-
является промежуток [ —1; 3[ (рис. 6).
Заметим, что не всегда объединение числовых промежутков
можно представит!) одним числовым промежутком. Например,
объединение множеств ]—1; 0J
^у////г,-,//,и, ^ и ^2; -|-оо[ числовым промежут-
ком не является (см. рис. 5).
6^//<-/,',-/'^z.-,-/////a—^ Данные определения пере-
U J м Сечения и объединения множеств
^-//^/.-//.,-.-. ,,.,-. -,,,.-,,ь ., хорошо иллюстрируются при на-
¦7 ¦гь глядном изображении множеств
на плоскости. Множества схе-
схематически изображаются круга-
кругами, прямоугольниками. Напри-
Например, на рис. 7 так изображены множества А и В, множество А
заштриховано горизонтально, множество В — вертикально. На
рис. 8 и 9 заштрихованы соответственно множества А(]В и
А\]В.
Рис. 0.
Рис, 8.
Рис. 9.
Часто приходится рассматривать объединение и пересечение
трех и более множеств. Объединение множеств А, В и С есть
множество, каждый элемент которого принадлежит хотя бы одно-
одному из множеств А, В или С (рис. 10). Пересечение множеств А,
В и С есть множество всех элементов, принадлежащих и множе-
множеству А, и множеству В, и множеству С (рис. И).
Например, объединение множеств остроугольных, тупоуголь-
тупоугольных и прямоугольных треугольников есть множество всех треу-
треугольников; объединение множеств вершин треугольников, вписанных
в данную окружность, представляет собой множество точек этой
окружности. Если А, В и С — соответственно множества учеников
класса, решивших на контрольной по математике задачу по
алгебре, задачу по геометрии, задачу по тригонометрии, то пере?
14
сечение этих множеств есть множество учеников этого класса,
решивших все три задачи.
Объединение и пересечение множеств обладают многимг свой-
свойствами, аналогичными свойствам суммы и произведения чисел,
А.
с
АПВЛС,
С
Рис. 10.
Рис. 11.
например переместительным, сочетательным и распределительным
свойствами (слева записаны равенства для множеств, справа —
для чисел):
1. А[]В = В[]А, a-\-b=b + a.
2. Af\B = B(]A, ab^ba.
3. (A\JB)\JC = A\J(B\JC), (а + Ь)+с = а + ф+с).
4. (A[\B)f]C'=A[\(B[\C), (ab)-c = a-(bc).
5. (A\]B)[\C = (A[\C)\)(B[\C), (a + b)c
Однако эта аналогия не всегда имеет место. Например, для
множеств справедливы равенства (первое из них проиллюстриро-
проиллюстрировано на рис. 12)
С
Рис. 12.
6.
7. А[}А = А.
8. АГ\А=*А.
Соответствующие равенства для чисел, очевидно, верны не всегда.
15
Для конечного множества Л через т (Л) обозначим число его
элементов. Число элементов пустого множества, очевидно, равно
нулю. Для любых конечных множеств Л и В справедливо
равенство
т{А[]В)=т(А)-{-т(В)—т{АГ\В). A)
Действительно, пусть множества Л и В не пересекаются, т. е.
т (А П В) = 0. Их объединение получается добавлением к элементам
одного множества всех элементов другого множества, поэтому
т(А[}В)=т(А) + т(В).
Если же пересечение множеств Л и В не пусто, то число их
общих элементов равно т(Л|~|В). Объединение этих множеств
образуется добавлением к элементам множества Л всех тех
элементов множества В, которые не входят в Л. Число таких
элементов равно т(В) — т(А[\В). Таким образом,
Пример 1. Экзамен по математике сдавали 250 абитуриентов,
оценку ниже пяти получили 180 человек, а выдержали этот экза-
экзамен 210 абитуриентов. Сколько человек получили оценки 3 и 4?
Д Пусть Л — множество абитуриентов, выдержавших экзамен,
В — множество абитуриентов, получивших оценки ниже 5, по
условию т(Л) = 210, m(B)=180, m (Ли В) = 250. Абитуриенты,
получившие оценки 3 и 4, образуют множество Л|"|В. По фор-
формуле A) находим
Дополнение. Часто ограничиваются рассмотрением всевоз-
всевозможных подмножеств одного и того же множества, которое в этом
случае называют основным или уни-
универсальным множеством. Обозначим
основное множество буквой Е. Для
любого множества Л, принадлежащего
основному множеству Е, справедливы
равенства
Множество элементов основного
Рис 13. множества Е, не принадлежащих
множеству Л, называется дополне-
дополнением множества Л до множества Е или просто дополнением и
обозначается А. Объединение множества Л и его дополнения А
есть основное множество: А [} А = Е. Пересечение множества со
своим дополнением пусто: A f] А — ф . Дополнение пустого мно-
множества есть основное множество: ф = Е, а дополнение основного
множества пусто: Е — ф. На рис. 13 основное множество Е схема-
16
тически изображено в виде прямоугольника, его подмножество А
заштриховано, не заштриховано дополнение множества А.
Для любых подмножеств А и В основного множества - Е
справедливы равенства
B)
A U В = А П В,
А П В = A U В.
C)
Первое из этих равенств проиллюстрировано на рис. 14, а и б.
На рис. 14, а заштриховано объединение множеств Л и В, не
АПВ
а)
Рис. 14.
заштриховано дополнение этого множества, т.е. Ли В. На рис.
14, б множество А заштриховано горизонтально, множество В —
вертикально, двойной штриховкой покрыто их пересечение А (] В.
Для числовых множеств в качестве основного множества можно
взять множество действительных чисел R. Дополнением до R
множества {Q рациональных чисел
является множество иррациональ-
иррациональных чисел, дополнением луча
[0; +оо[ является открытый луч
]-оо; 0[.
Пример 2. В школе 1400
учеников. Из них 1250 умеют
кататься на лыжах, 952 —на конь-
коньках. Ни на лыжах, ни на конь-
коньках не умеют кататься 60 учащих-
учащихся. Сколько учащихся умеют ка-
кататься и на лыжах и на конь-
коньках?
Д Множество учеников школы будем считать основным мно-
множеством Е, А и В — соответственно множества учеников, умеющих
кататься на лыжах и на коньках (рис. 15). Учащиеся, не умеющие
кататься ни на лыжах,_ ни_ на коньках, составляют множество
А[}В. По условию т (А (] В) ==60, а так как по формуле B)
¦17
Рис. 15.
Af\B = A\JB, то и in {A U В) = 60. Отсюда т (А [} В) = т{Е) —
— т (A U В) =1340. Зная т(А) и т(В), по формуле A) находим
т {А п В) = ш (Л) + /и (В) - m (Л U В) = 862. а
§ 2. Понятие функции
Пусть X — некоторое числовое множество. На множестве X
определена числовая функция, если каждому элементу множества X
поставлено в соответствие действительное число. Множество X
называется при этом областью определения функции. Произволь-
Произвольный элемент области определения обычно обозначается буквой х
и называется аргументом функции или независимой переменной.
Выражение «аргумент х пробегает множество X» понимается в том
смысле, что вместо х может быть взято любое число из области
определения функции.
Например, числовая функция определена следующим образом:
каждому числу х отрезка [0, 1] ставится в соответствие число
2х-\-\. Отрезок [0, 1] — ее область определения, закон соответ-
соответствия может быть записан так: х-+2х-\-1.
Другой пример функции; каждому рациональному числу ста-
ставится в соответствие число 1, а каждому иррациональному —
число 0. Область определения — все множество действительных
чисел (эта функция называется функцией Дирихле).
Обычно закон соответствия обозначается некоторой буквой,
например /, и говорится, что на множестве X определена функция
/ или f(x). Употребляется также запись функции в виде у~[(х),
здесь х означает аргумент, у — соответствующее ему значение
функции, /—закон соответствия. Иногда говорят, что функция
/ ставит в соответствие (сопоставляет) значению аргумента х
значение //.
Рассмотренная функция х-+2х-\-1 с областью определения
Х = [0; 1] может быть записана в виде f(x) — 2x+l, x e [0; 1],
или у — 2х-\-\, х е [0; 1], а функция Дирихле, например, так:
,, , J 1, если х—рационально,
\ 0, если х —иррационально.
Разумеется, вместо букв х, f, у можно взять другие буквы,
например, функция может быть записана в виде y = q>{t) или
Если число а принадлежит области определения функции /,
то говорят, что функция / определена в точке а. Для того чтобы
указать значение функции в фиксированной точке а, используется
такая запись: f(a), у {a), f(x)\x,a. Вот, например, значения функ-
функции y = 2x+l, x<=[0; 1J, в некоторых точках:
у@)= 1, у A/2) = 2, у C/4) = 5/2, 0A) = 3.
18
Множество всех значений функции f(x), когда аргумент х
пробегает область определения функции, называется множеством
значений функции /. Например, множество значений функции
// = 2л; -(-1, *е[0; 1], есть отрезок [1; 3J, а множество значений
функции Дирихле состоит из двух чисел 0 и 1.
Множество значений функции является подмножеством мно-
множества U действительных чисел. Поэтому иногда говорят, что
функция есть отображения одного подмножества (области опре-
определения) на другое подмножество (множество значений) множества
действительных чисел.
Две функции считаются разными, если у них одна область
определения и каждому числу из области определения они сопо-
сопоставляют одно и тоже значение. Например, функция f(x)=x — 1
с областью определения ] — 1; + 1[ и функция g(x) — {х2 — I),' (х-\- 1)
с той же областью определения равны, так как для любого х из
множества ]— 1; + 1 [ имеет место равенство
х-—\ ,
Х-)- 1
Часто функцию задают формулой, указывающей последователь-
последовательность математических операций, которые надо выполнить над
аргументом, чтобы получить ее значение. При этом ничего не
говорится об области определения. В этом случае считается, что
функция определена на множестве тех значений аргумента, для
которых указанные формулой действия выполнимы. Множество
всех таких значений аргумента называется естественной областью
определения функции, заданной формулой, или областью допусти-
допустимых значений аргумента. Естественная область определения
функции / заданной формулой обычно обозначается D (/). В слу-
случае задания функции формулой возникает задача нахождения
области определения (имеется в виду естественной области опре-
определения) функции.
Пример 1. Найти область определения функции
2-х'
Д Действия, указанные этой формулой, выполнимы для тех
значений аргумента х, для которых подкоренное выражение неот-
неотрицательно, т. е. ггз-,5=0- Решая это неравенство, находим, что
оно справедливо лишь на промежутке [—1; 2 [, который и яв-
является естественной областью определения рассматриваемой
функции, а
Пример 2. Найти область определения функций
/ (х) = h (х) + /2 (х) --= j/1^7* + JLzl.
19
Д Функция ft (х) —-У\ — х2 определена на множестве тех
значений х, для которых 1—а2^э0. Это есть отрезок [—1; 1].
Итак, О(/]) = [-1; 1].
Для функции /2 (х) = (х — 3) / Bл; + 1) естественной областью опре-
определения является множество всех значений аргумента, для кото-
которых знаменатель дроби не обращается в куль, т. е. хф —1/2.
Таким образом, D (/,) = ] —ос; — 1/2 [ U ]— 1/2; + оэ\.
Функция / (х) = /г (х) -f- f'i ix) будет определена в точке й тогда
и только тогда, когда точка а принадлежит и области определе-
определения функции f1 (x), и области определения функции /2 (х). Дру-
Другими словами, естественная область определения функции f (х)
есть пересечение областей определения функций fl и /2:
D(/) = D(/,)nfl(/s) = [-l; - 1/2 [ U]-1/2; 1]. А
Напомним определения некоторых часто встречающихся функций.
Многочленом п-й степени (п^аО) стандартного вида называется
функция
у = ао + а1х+ ... +а:1х", апф0;
числа а0, аъ ... , ап называются коэффициентами этого мно-
многочлена. Область определения многочлена — вся числовая прямая.
Многочлен n-й степени обозначается также Рп (х).
В частности, многочлен первой степени
у=Рг (х) = «о + а±х, а± Ф О,
называется линейной функцией, а многочлен второй степени
-\-а^хг, а2ф0,
называется квадратичной функцией или кводрстчым трехчленом.
Многочленом п-й степени называется функция, которая опреде-
определена на всей числовой прямой и может быть приведена к мно-
многочлену л-й степени стандартного вида. Например, квадратичными
функциями являются функции, определенные формулами
Действительно, сбе они определены на всей числовой прямой и
для любого числа х имеют место равенства
1 - х3 + (х2 - 3) (х + 1) = х2 - Ъх - 2,
' +1 = |/(л;2 + 1J = .v2 -f 1 •
Функция / (х) = .. на своей области определения совпадает
с многочленом первой степени у = х— 1. Однако функция f (х) не
является многочленом, так как ее область определения не совна-
дает с множеством R, она не определена в точке л; = — 1.
20
Рациональной функцией называется функция, которая может
быть представлена в виде отношения двух многочленов стандарт-
стандартного вида
_ Рп (х) __ _ао_Н-а1х4- ... -\-апх.п
У~ Рт (х) ~ 'b^'-j-blx-j- ... -\-bmxm'
Естественная область определения рациональной функции есть
вся числовая прямая за исключением тех точек, в которых зна-
менатель обращается в нуль. Например, функция f(x)=. , ..
является рациональной, ее область определения есть вся числовая
прямая за исключением х = —1.
§ 3. Координатная плоскость. График функции
Две взаимно перпендикулярные координатные прямые : общим
началом отсчета образуют прямоугольную систему координат на
плоскости. Масштабные отрезки обычно берутся равными, однако
иногда используются координатные прямые и с разными масштаб-
масштабными единицами. Одну из этих пря-
прямых обычно изображают горизон-
горизонтально, называют осью абсцисс и обоз-
обозначают Ох. Другую прямую рисуют
вертикально, называют осью ординат
и обозначают Оу (рис. 16). Общее
начало —точка О —называется нача-
началом координат.
Плоскость с выбранной на ней
системой координат называется коор- р ]6
динатной плоскостью. На коорди-
координатной плоскости каждой точке ста-
ставится в соответствие пара чисел, называемых координатами этой
точки относительно данной системы координат. Пусть Мх \ Му —
ортогональные проекции точки М соответственно на ось абсцисс
и на ось ординат. Точка Мх, как точка координатной прямой Ох,
имеет координату х, а точка Му, как точка координатной пря-
прямой Оу, имеет координату у. Пару чисел (х; у) (ее называют
«упорядоченной» парой в том смысле, что х на первом месте, а у
на втором) называют координатами точки М и пишут 1Л(х; у).
Координачы х и у называются соответственно абсциссой и орди-
ординатой точки М.
Каждой упорядоченной паре чисел (а; Ъ) на координатной
плоскости соответствует единственная точка М, для которой эти
числа являются координатами; х = а, у = Ь. Таким образом, между
точками координатной плоскости и упорядоченными парами действи-
действительных чисел (х; у) устанавливается взаимно однозначное соот-
соответствие. Множество пар действительных чисел иногда называют
числовой плоскостью.
21
и У,
!/
f
О
ш
-
/
I
IV
М(х;у}
1
1
1
ее ¦ as
Координатные прямые делят плоскость на четыре координат-
координатные угла (квадранта), которые нумеруются так, как показано
на рис. 16.
Расстояние между точками Мх (Хь y{j и М2 (х2\ у2) выражает-
выражается через их координаты по формуле (рис. 17)
Пусть задана функция y = f{x) с областью определения X.
Графиком функции / (х) называется множество точек координат-
координатной плоскости с координатами (х; f(x)), т. е. множество точек,
Рис. .17.
Рис. 19.
абсциссы которых принадлежат множеству X, а ординаты равны
соответствующим значениям функции. На рис. 18 и 19 изобра-
изображены графики линейной функции у = 3 — 2х и квадратичной
функции у = 2 — х — х2.
Изображение графика функции на координатной плоскости дает
наглядное представление о свойствах и поведении функции. Про-
Простейшим способом построения графика функции y = f(x) является
способ построения по точкам. Составляется таблица значений аргу-
аргумента и соответствующих значений функции:
Н I х2 х3 I...
Уг Уг \Уз ]•••
— и на координатной плоскости наносятся точки Mi (хг\ yt),
Мч(х2\ уг) и т. д. Эти точки соединяются плавной кривой, кото-
которая с некоторым приближением изображает график функции
y — f(x). Приближение это, однако, может оказаться достаточно
грубым. В связи с этим для построения графика функции, как
правило, применяют другие методы. О них будет рассказано
в главе VI.
§ 4. Обратная функция
Пусть функция y = f(x), определенная на множестве X, такова,
что двум разным значениям аргумента хг и хг ставит в соответст-
соответствие разные значения ух и уг. Например, таким свойством обла-
22
Рис. 20.
дает функция у = 2х— 1, график которой изображен на рис. 20.
Действительно, для нее, если х1фх2, то yi=f (xt) ^ f (х2) =¦¦ у2, так
как f (xi) — f (x2) = 2 (ajj. — *2). Этот факт имеет следующую геомет-
геометрическую интерпретацию: каждая прямая, параллельная оси Ох
и проходящая через точку у0, принадлежащую множеству значе-
значений функции, пересекает график функции лишь
один раз. Напротив, функция у = хг не обладает
указанным свойством. Например, значение функ-
функции у=\ соответствует двум значениям аргу-
аргумента a'i = —1 и x2=l (прямая, параллельная
оси Ох к проходящая через точку у—-1, пересе-
пересекает график этой функции в двух точках
(рис. 21)).
Функция y = f(x) с областью определе-
определения X, которая двум разным значениям аргу-
аргумента сопоставляет различные числа, устанавли-
устанавливает взаимно однозначное соответствие между
областью определения X и своим множеством значений У. Дей-
Действительно, каждой точке х из X функция ставит в соответствие
некоторое у из множества У, двум разным значениям хг и х2 со-
сопоставляются разные значения ij\~f(X\) и y2 = f(x2) и каждая
точка у eF соответствует одному из значений аргумента х. При
этом каждой точке у множества У соответ-
соответствует единственное число х такое, что
y = f(x), т. е. это соответствие однознач-
однозначное. Таким образом, на множестве
У определена функция, которая назы-
называется обратной функции / и обозначается f~l.
Областью определения обратной функции f'1
является множество значений функции /.
Функция, которая имеет обратную, называ-
называется обратимой.
Например, функция у = 2х — 1 обратима.
Множество ее значений есть вся числовая
прямая. Любому числу у соответствует
значение х =-я-(/ + '2-(это соответствие для точки у0 на р не. 20
указано стрелкой). Формула х — ~2-#+ у определяет функцию х =
Z1^f~1(y)< обратную функции y — f(x).
График функции у = f (х) = 2х¦ — 1 является и графиком обрат-
обратУ к
О
1
Рис. 21.
ной функции x =
y1 только график обратной функ-
функции расположен непривычно: ось аргумента (ось Оу) расположена
вертикально. Если, как обычно, обозначить аргумент обратной
функции через х, т. е. представить ее в виде y — f~1(x), то гра-
график обратной функции будет, вообще говоря, отличаться ст гра-
графика функции y = f(x). На рис. 22 изображены график функции
23
у
= / (л;) =f 2x — 1 и график ее обратной функции у = f-1 (х) = -„- х + ~-
Они симметричны относительно биссектрисы I и III координатных
углов.
Как правило, если функция /обратима, то ее аргумент и аргу-
аргумент обратной функции обозначаются одной буквой, т. е. зти
функции рассматриваются в виде y = f(x) и y = f~x(x).
Пусть функция y = f(x) обратима. Покажем, что графики
функции y = f(x) и ее обратной функции y = f~l(x) симметричны
относительно биссектрисы I и III координатных углов, т. е. сим-
симметричны относительно прямой у = х.
ь)
^ /
/
>
У'
/
/
/
X
Рис. 22.
Рис. 23.
? Если точка М (а; Ь) принадлежит графику функции у = /п),
то b = f(a) (рис. 23). Так как существует обратная функция,
то из этого равенства следует, что a = f~1(b) и, значит, точка
М' (Ь; а) принадлежит графику обратной функции f/ = /~] (x). Верно
и обратное: если точка М' (Ь, а) принадлежит графику обратной
функции y = f~l(x), то a = f~1(b). Следовательно, b = f(a) и точка
М (а; Ь) принадлежит графику функции y = f(x).
Установим, что точки М (а; Ь) и М'ф; а) симметричны отно-
относительно би:сектрисы I и III координатных углов. Пусть афЬ,
т. е. точки М и М' не совпадают. Легко видеть, что эти точки
равноудалены от начала координат, значит, прямая, проходящая
через начало координат и середину отрезка ММ', перпендикулярна
этому отрезку, а точки М и М' симметричны относительно этой
прямой. Поскольку середина отрезка ММ' имеет координаты
((а + Ь)/2; (а + Ь)/2), то уравнение прямой есть и = х. Д
Подчеркнем, что. функция обратима тогда и только тогда,
когда эта функция двум разным значениям аргумента ставит
в соответствие разные значения. Функция / (х) =»= х1, Х=к,
не обладает этим свойством, она не имеет обратной функции.
Рассмотрим функцию, заданную той же формулой /(*)== л;2
с областью определения Х = [0; +ос[. Если х1 и х2 принадлежат
области определения и ххфх%, то /(л;,) — f(x*) = (Xx — x2) ( )
24
Здесь ххфх» и .Гх-1-л-.2>0, поэтому f (xi) Ф\ (х*). Следовательно,
функция f(x) = x2, X = [0; +оо[, имеет обратную функцию. Для
ее нахождения разрешим уравнение у = х2 относительно х, учи-
учитывая, что лгЗаО. Получим х — ]/~у. Поменяем в этой формуле х
и у местами: у = Ух. Итак, для функции f(x) = x2, X = [0; +оо[,
обратная функция имеет вид /-1 (х) = \^х, ее область определения —
промежуток [0; +°°[- Графики этих функций изображены на рис. 24.
Рассмотрим функцию / (х) = ха. Она определена на всей число-
числовой прямой, множество ее значений также вся числовая прямая
У,
0
1
1
1*5
и
а;
Рис. 24.
Рис. 25.
рис. 25). Покажем, что эта функция имеет обратную. Пусть
Х\ ф х2. Рассмотрим разность / (xi) — f (x2):
f (*,) - / (х2) =х\-х\ = (Xl - д:2)
Первая скобка отлична от нуля, так как Xit^^. вторая также
отлична от нуля, так как содержит сумму квадратов двух сла-
слагаемых, которые в силу условия хх Ф х2 не могут обратиться
в нуль одновременно. Таким образом, разным значениям аргу-
аргумента из множества ] — сю, -|- ос[ соответствуют разные значений
функции. Значит, существует обратная функция. Она обозначается
y — -{fx. Ее область определения — вся числовая прямая. График
функции у = Ух изображен на рис. 25 штрихами.
В заключение заметим: из определения обратной функции сле-
следует, что всегда существует обратная функция к обратной и при
этом [f-xyx = f. В силу этого функцию / и ее обратную /-1 (если
она существует) называют взаимно обратными функциями.
ЗАДАЧИ РАЗДЕЛА /
1. Пусть А — множество делителей числа 15, В —множество простых чисел,
меньших Ю, С —множество четных чисел, меньших 9. Перечислить моменты
этих множеств и найти А[)В, А(]С, В[\С, {А[)С)(]В, А(]В[\С.
25
2. Пусть А = [— 1; 1J, В = ] — оо;0[, С — [0; 2[. Найти следующие множества:
Л (J С, А[\В, A U ВЦ С, (A[jB)(]C, fin С —и изобразить их на координатной
прямой.
3. Найти подмножества X и К множества ?, если для любого подмножества
А множества Е имеет место равенство Af\X = A[)Y.
Изобразить на координатной плоскости множество, координаты (х; у) точек
которого удовлетворяют условию D — 6):
4. [х| + |?/| = 1. 5. j х-\-у | sg 1 и | х—f/l^l.
6. х2 — 2х +(/гй0.
7. В группе из 100 туристов 70 человек знают английский язык, 45 знают
французский язык и 23 человека знают оба языка. Сколько туристов в группе
не знают ни английского ни французского языка?
8. В олимпиаде по математике принимало участие 40 учащихся, им было
предложено решить одну задачу по алгебре, одну по геометрии и одну по три-
тригонометрии. Результаты проверки решений представлены в таблице;
решецы задачи
по алгебре
по геометрии
по тригонометрии
по алгебре и геометр ми
по алгебре и тригонометрии
по геометрии и тригонометрии
коли честно
решивших
20
18
18
7
8
9
Ичвесяпо также, что им одной задачи не решили грое. Сколько учащихся
решили все три задачи? Сколько учащихся решили ровно две задачи?
9. Пусть А — множество решений уравнения /(х) = 0, В — множество реше-
решений уравнения g(x) = 0. Доказать, что для любых многочленов f (х) и g (x)
множество А[]В является множеством корней уравнения f (х) •§ (х) =0,
а АПВ — множеством корней уравнения (f (х))г + (g (х)J = 0.
Верно ли это же утверждение, ьели f (х) — многочлен, a g (х) — рациональ-
рациональная функция?
Найти область определения функций A0—16);
10.
12.
= у 2-<—3х.
V 11 f (Y\
1-U
-. 15. f{x)=
arccosBx—1)'
16. / (*) = lg [A,25)' - *a— @,4096I+JiJ.
Найти множество значений функций A7—18):
17. f(x) = V* + 2x+2. 18. f(X) = -i^r.
Найти обратную функцию y = f~l(x) для функции y=*f(x) A9—21);
26
19. tf = x»+l, xej-oo; 0]. 20.0=1+'-. 21. tf = -J±^.
22. Найти при каких значениях параметров а и Ь линейная функция
у = ах-\-Ь имеет обратную и совпадает с ней,
ЗАДАЧИ РАЗДЕЛА //
Записать множества А, В и С перечислением их элементов и найти А[)В,
В ПС, (Л U В) ПС, Л ЛЯЛС, если A—2):
1. А — множество делителей числа 12; В — множество /opiieii уравнения
х"—G.v + 5 = 0; С — множество нечетных чисел х таких, что 3sS*=sl2
2. А—множество четных чисел х, 3<х<10; В — множество делителей
числа 21; С — множество простых чисел, меньших 12.
3. Привести примеры числовых множеств А и В таких, что
a) A[)B=R, А[]В = ф; б)А\}В=А, А[]В = В.
Найти А[}В, А(]В, А[\С, В[}С, А[\В[\С, (А[]В)[\С и изобразить эти
мпождетва па координатной прямой, если D—G):
4. Л = [0; 3], В = \\\ 5[, C = ]—2; 0].
5. Л = [—'оо] 1], В = [1; +со[, С = ]0; 1[.
6. Л = [—3; 1], В = [2, -|-оо[, С = ]-со; —2[.
Множества Л и В — подмножества основного множества R. Найти А\]В,
А(] В, A U В, Af\B, A\JB н изобразить эги множества па координатной пря-
прямой G—10):
7. А = \— 1; 0|, В=[0; 2[.
8. Л = [0; 3[, S = J—I; +oo[.
9. Л = ]—со; 1], В = ]—оэ; —3[.
10. Л = J0; +оэ[, б=[—1; 1[.
11. Множеств А и S являются подмножествами множества Я (рис. 26).
Указать штриховкой множества:
а) Л us, А \]В; б) Л и в, Ллб;
в) ЛПЙ, Ли5; г) Л Л В, (А Л В) U (А Л 5).
12. Л — подмножество множества натуральных чисел, каждый элемент мно-.
жества Л есть число, кратное или 2, или 3, или 5. Найти число элементов
в множестве Л, если среди них имеется: 70 чисел, крат-
кратных 2; 60 чисел, кратных 3; 80 чисел, кратных 5; 32
числа, кратных 6; 35 чисел, кратных 10; 38 чисел,
кратных 15; и 20 чисел, кратных 30.
13. В штучном отделе магазина посетители обычно
покупают либо один торт, либо одну коробку конфет,
либо один торт и одну коробку конфет. В один из дней
было продано 57 тортов и 36 коробок конфет. Сколько
было покупателей, если 12 челоиек купили и торт и ко-
робку конфет?
14. В спортивном лагере 65% ребят умеют играть в футбол, 70%—в во-
волейбол и 75%—в баскетбол. Каково наименьшее число ребят, умеющих играть
И в футбол, и в волейбол, и в баскетбол?
27
15. Каждый из учеников класса в зимние каникулы ровно два раза был
в театре, при этом спектакли А, В и С видели соответственно 25, 12 и 23
ученика. Сколько учеников в классе? Сколько из них видели спектакли А
и В, А и С, В и С?
16. В течение недели в кинотеатре демонстрировались фильмы Л, В и С
Из 40 школьников, каждый из которых просмотрел либо все три фильма, либо
один из трех, фильм А видели 13, фильм В —16, фильм С—19. Найти,
сколько учеников просмотрели все три фильма.
17. В отряде из 40 ребят 30 умеют плавать, 27 умеют играть в шахматы
и только пятеро не умеют ни того ни другого. Сколько ребят умеют плавать
и играть в шахматы?
18. На уроке литературы учитель решил узнать, кто из 40 учеников класса
читал книги А, В а С. Результаты опроса оказались таковы: книгу А читало
25 учащихся, книгу В — 22, книгу С —также 22. Книгу А или В читали 33
ученика, А или С —32, В или С—31; все три книги прочли 10 учащихся.
Сколько учеников прочли только по одной книге? Сколько учащихся не читали
ни одной из этих трех книг?
19. Среди абитуриентов, выдержавших приемные экзамены в вуз, оценку
«отлично» получили: по математике — 48 абитуриентов, по физике — 37, по рус-
русскому языку —42. по математике или физике —75, по математике или русскому
языку—76, по физике или русскому языку —66, по всем трем предметам —4.
Сколько абитуриентов получили хотя бы одну пятерку? Сколько среди них
получивших только одну пятерку?
20. Найти пересечение числовых множеств А и В, если каждый элемент
множества А имеет вид 4я+2, п е IN, а каждый элемент множества В имеет
вид Зя, п е IN-
Изобразить на координатной плоскости множество, координаты (*; у) точек
которого удовлетворяют условию B1—28):
21. | х-\-у \=х-\-у. 22. у — *25г0.
23. \у\ —1*| 5=0. 24. *2 + </г — 4(/sS0.
25. х* + у*^2\х\+2\у\. 26. \х-у\ = \х-у+\ |.
27. logI/2 B-)?-}!)<0. 28. (х-\х\У* + (у-\
Найти область определения функций B9—38):
29. /(*)=J'A3 — Ъх—2*2.
30. /(*) =
34. /(*) = log3logI/2*. 35. f{x)=Vx*-\x\-2.
l/ cosx- —
36. fW = logM(#-3x + 2). 37. f (*)='___===-
38. / (*) =YlofiS.j * + (logn,2*3) (log0l2 0,0016*)+ 36.
Найти множество значений функций C9—44):
28
40. Ux) = V2x-ifl-\
41. /(*) = sin* —5cos*. 42. /(*) = lo
43. /(jr)^=(sin x + cosx"J. 44. / (x) = 4* — 2X+ 1.
45. Доказать, что четная функция не имеет обратной.
Найти обратную функцию f/ = /(.v) для функции y = f(x) D6—50):
46. s, = *3-l, X=]-oo;0]. 47. .1/=4хГ*
48. у=\Гх. 49. у = -у-р-^з. 50. s = J,
Для каждой из следующих функций установить, существует ли обратная
функция, и если существует, то найти ее E1—54):
51. (/ = 2 + х — я2, Х = [1/2, +оо[. 52. у = х3 — х.
53. </ = л-2 — 2л:—3, Х = [0; 3]. 54. ^=лг|лг| — 2л:—8.
55. Доказать, что при всех значениях параметров а и b таких, что
. , 2лг + а „
— 4, функция y = ~L——х" совпадает со своей обратной.
56. Каким условиям должны удовлетворять числа а, Ь, с и d
чтобы функция (/ = —^—у- совпадала со своей обратной?
57. При каких значениях а функция у=ха совпадает со своем обратной
функцией?
Глава II
ЭЛЕМЕНТЫ ЛОГИКИ. ВЗАИМНО ОБРАТНЫЕ
И ВЗАИМНО ПРОТИВОПОЛОЖНЫЕ ТЕОРЕМЫ.
МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
§ 1. Высказывания. Операции над высказываниями
Под высказыванием понимают всякое утверждение, о котором
имеет смысл говорить, что оно истинно или ложно. Примерами
высказываний могут служить следующие утверждения:
1. Москва — столица XXII летних Олимпийских игр.
2. Анатолий Карпов—двенадцатый чемпион мира по шахматам.
3. Число 221—простое.
4. 13< 17.
Утверждения 1, 2 и 4, как известно, истинны. Утвержде-
Утверждение 3 —ложно, так как 221 = 13-17.
Таким образом, каждое высказывание или истинно, или ложно;
одновременно быть истинным п ложным высказывание не может.
Высказывания могут быть образованы с помощью слов или
символов, однако далеко не каждый набор слов или символов
(даже осмысленный) является высказыванием.
Например, утверждения:
1. В Московский государственный университет поступить легко.
2. л->0.
высказываниями не являются, так как судить об их истинности
или ложности невозможно.
Для обозначения высказываний обычно используют заглавные
буквы латинского алфавита А, В, С и т. д. Например, пишут
А = \6<с7\, В = {число 6 простое}.
Это означает, что высказывание В заключается в утверждении,
что число 6 простое, а высказывание А в том, что 6 ¦< 7. Знак
«=» заменяет слова «есть высказывание».
Высказывания А и В являются примерами простых высказы-
высказываний. Из простых высказываний при помощи так называемых
логических связок (союзов «и», «или», слов «если..., то...», «тогда
и только тогда, когда...») можно образовывать новые высказыва-
высказывания. Например, из высказываний
Л = {6<;7} и В =i {число 6 простое},
30
используя логические связки, можно образовать следующие слож-
сложные высказывания:
С = {6<;7 или число 6 простое},
D = {6<7 и число 6 простое},
Е = {6 < 7 тогда и только тогда, когда число 6 простое},
F' = {если 6<7, то число 6 простое}.
Отметим, что новые высказывания можно образовывать и из
таких высказываний, которые никак не связаны между собой
по смыслу. Например, высказывание
б = {если слон насекомое, то Антарктида покрыта
тропическими лесами}
составлено при помощи логической связки «если..., то...» из двух
высказываний, между которыми нет никакой смысловой связи.
В математической логике истинность или ложность с/ожных
высказываний, образованных при помощи логических связок,
устанавливается независимо от смысла простых высказываний,
составляющих сложное. Истинность или ложность сложного вы-
высказывания полностью определяется, во-первых, тем, какие логи-
логические связки использованы для образования сложного высказы-
высказывания, и, во-вторых, тем, какие из простых высказываний, обра-
образующих сложное, истинны и какие ложны. Для этого в логике
вводятся операции над высказываниями, соответствующие сьязкам,
при помощи которых образуются сложные высказывание. Тем
самым, союзам «и», «или», словам «тогда и только тогда, когда...»,
«если..., то...» придается точный однозначный смысл.
Если высказывание образовано из двух высказываний при
помощи союза «или», то говорят, что оно является суммой (дизъ-
(дизъюнкцией) этих высказываний.
Высказывание, составленное из двух высказываний три по-
помощи союза «и», называют произведением (конъюнкцией) этих
высказываний.
Высказывания, образованные из двух высказываний при помощи
слов «тогда и только тогда, когда...», «если..., то...», называют
соответственно эквивалентностью и импликацией.
Из простых высказываний
Л = {6<7} и В == {число 6 простое}
при помощи логических связок выше были составлены высказы-
высказывания С, D, Е и F. Теперь можно сказать, что эти высказывания
являются соответственно суммой, произведением, эквивалентностью
и импликацией высказываний А и В.
Сумму любых высказываний А и В записывают в виде А-\-В
(или A\J В), произведение в виде АВ (или А/\В). Для эквива-
эквивалентности используют знак <=> (или ~), т. е. пишут А<=5>В
(или Аг-^В). Импликацию записывают в виде Л=}В (читается:
«из А следует В» или «если А, то В»),
31
Для любых двух высказываний истинность или ложность их
суммы, произведения, эквивалентности и импликации определяется
следующим образом:
сумма А + В высказываний является истинным высказыванием
только тогда, когда по крайней мере одно из слагаемых истинно;
произведение АВ высказываний истинно только в том случае,
если оба сомножителя истинны;
эквивалентность А <=> В представляет собой ложное высказы-
высказывание, если одно из высказываний истинно, а другое ложно;
в противном случае, т. е. если оба высказывания истинны или
оба ложны, эквивалентность является истинным высказыванием;
импликация А-=$ В есть ложное высказывание только в том
случае, если А — истинно, а В — ложно; во всех других случаях,
а именно, если
1) Л —истинно, В —истинно,
2) А — ложно, В —истинно,
3) А — ложно, В — ложно,
высказывание А =э В считается истинным.
Пример 1. Даны два высказывания
Л = {2 = 3[ и ? =
В чем заключаются высказывания А-\-В, АВ, А<=^>В,
Какие из этих высказываний истинны и какие ложны?
Д Высказывание
= {2 = 3 или 2<3}
истинно, так как одно из слагаемых является истинным выска-
высказыванием. Высказывание А-\-В можно записать в виде одного
верного нестрогого неравенства: 2=s:3, Высказывание
ЛВ = {2 = 3 и 2<3},
очевидно, ложно. Для того чтобы произведение двух высказыва-
высказываний было истинным, нужно чтобы оба высказывания были истин-
истинными .
Эквивалентность
Л<=>В = {2 = 3 тогда и только тогда, когда 2<3}
представляет собой ложное высказывание, так как Л — ложно,
а В — истинно.
Импликация
Л => В = {если 2 = 3, то 2 < 3}
является истинным высказыванием. В самом деле, импликация
А => В согласно определению ложна только тогда, когда А —
истинно, а В —ложно. ^
Итак, истинность или ложность высказывания, образованного
из каких-либо высказываний с помощью операций сложения,
32
умножения, эквивалентности и импликации, зависит только от
распределения истинности и ложности между высказываниями,
над которыми производятся логические операции. Эту зависимость
удобно описывать следующими четырьмя таблицами, которые
называют таблицами истинности логических операций (буква И
означает, что соответствующее высказывание истинно, буква Л —
соответствующее высказывание ложно):
Таблица I
Таблица II
А
И
И
Л
Л
В
и
л
и
л
А+В
и
и
и
л
А
И
и
л
л
в
и
л
и
л
АВ
и
л
л
л
A
И
И
Л
Л
Та
блица
В
И
л
и
л
111
А <
и
л
л
и
А
И
И
Л
л
т
а б л и ц г
В
И
л
и
л
IV
Л :
=>в
и
л
и
и
Таблицы истинности логических операций дают возможность
определить истинность или ложность любых высказываний, имею-
имеющих вид А-\-В, АВ, А$=$В, А=$В. В связи с этим таблицы
называют также таблицами истинности высказываний А-\-Е, АВ,
А<^>В, А=$В.
Для дальнейшего изложения из всех рассмотренных логиче-
логических операций особенно важной является импликация А =$ В.
Первый член импликации А =э В высказывание А называется
посылкой или условием, второй член В — заключением. Таблица
истинности для импликации, в отличии от таблиц I —III, изме-
изменяется при перестановке столбцов для А и В. Отметим также,
что импликация не полностью соответствует обычному пониманию
слов «если ..., то ...» и «следует». Из третьей и четвертой строк
таблицы IV вытекает, что если А ложно, то, каково бы ни било В,
высказывание А =э В считается истинным. Таким образом, из
неверного утверждения следует ясе что угодно. Например, утверж-
утверждения несли 6 простое число, то 7 < 6» или «если 7 < 6, то суще-
существуют ведьмы» являются истинными. Истинным является и рас-
рассмотренное ранее ь-ыскаэывание: «если слон — насекомое, то
Антарктида покрыта тропическими лесами».
2 п/ред. Г. Н. Яковлева 33
Помимо только что рассмотренных четырех логических опера-
операций в математике используется еще одна простая, но очень важ-
важная операция— операция отрицания. Эта операция соответствует
логической связке «не». Каждому высказыванию А можно сопо-
сопоставить утверждение, заключающееся в том, что высказывание А
лбжно. Такое утверждение либо истинно, либо ложно и, следо-
следовательно, само является высказыванием, причем истинным, если А
ложно, и ложным, если А истинно. Это новое высказывание обо-
обозначают через А и называют отрицанием А. Например, для выска-
высказывания
А ~ {число 6 простое}
отрицание может быть построено так:
Л = {число 6 не простое}
или
или
А ={неверно, что число 6 простое},
А = {число 6 составное}.
В данном случае исходное высказывание ложно, поэтому его
отрицание истинно.
Таблица истинности для отрицания имеет вид:
Таблица V
л
И
Л
А
Л
И
Рассмотрим высказывание
А = {город Нью-Йорк —столица США}.
Отрицанием этого высказывания будет высказывание
А = {город Нью-Йорк не является столицей США}.
Поскольку высказывание А — ложно, высказывание А —
истинно. Заметим, что было бы ошибкой считать отрицанием
высказывания А высказывание
В = {город Вашингтон — столица США}.
Новые высказывания могут быть образованы при помощи не-
нескольких или даже всех пяти логических операций, причем каж-
каждая из операций может применяться несколько раз. В таких слу-
случаях истинность или ложность сложного высказывания в зави-
34
симости от истинности или ложности составляющих его высказы-
высказываний можно установить, построив таблицу истинности сложного
высказывания, последовательно используя таблицы истичности
логических операций.
Составим, например, таблицу истинности для высказываний,
имеющих вид В=$ А. Псследовательно используя таблицы V и IV,
получим таблицу:
А
И
И
л
л
в
И
л
и
л
в
Л
И
л
и
А
л
л
и
и
В =) А
и
л
и
и
Третий и четвертый столбцы являются вспомогательными. Для
высказываний вида В=$А получена таким образом следующая
таблица истинности:
А
И
и
л
л
в
и
л
и
л
В—) А
и
л
и
и
Сравним полученную таблицу с таблицей IV для импликации
А=$В. Таблицы совпадают, т. е. высказывания вида А:=$В и
В=^Д имеют одинаковые таблицы истинности. Такие высказыва-
высказывания называются равносильными. Равносильные высказывания сое-
соединяют знаком равенства.
Для любых высказываний Л и б можно, следовательно,
записать
Равносильность высказываний вида Л =э В и В=$ А означает,
что каковы^ бы ни были высказывания А и В высказывания
Лг)В и В=$ А либо оба истинны, либо оба ложны. Из истин-
истинности или ложности одного из них следует соответственно истин-
истинность или ложность другого.
Важную роль в логике играют тождественно истинные и тож-
тождественно ложные высказывания. Тождественно истинные выска-
высказывания истинны всегда, независимо от того, истинны или ложны
составляющие их высказывания. Примеры тождественно истин-
истинных высказываний: Л + Л, Л <=>/!, (Л =} В) <=> (S=t> Л). Тож-
Тождественно истинные высказывания будем обозначать буквой /.
2* 35
Тождественно ложные высказывания ложны всегда, т. е. неза-
независимо от истинности или ложности высказываний, которые их
составляют. Такие высказывания будем обозначать буквой L.
Примеры тождественно ложных высказываний:
АА, (ВA) A, AL.
И в самой математике и в ее приложениях приходится иссле-
исследовать различные виды высказываний на равносильность. В слу-
случае, если высказывания составлены из небольшого числа простых,
равносильность или неравносильнссть можно установить, построив
таблицы истинности сложных высказываний и сравнив их. Но
следует иметь в виду, что таблица истинности высказывания,
образованного из п простых высказываний, содержит 2й строк.
Поэтому обычно равносильность устанавливается другим способом:
некоторое количество основных равносильностей (законов алгебры
высказываний) проверяется на основании таблиц истинности,
полученные равенства используются при доказательстве других
равенств точно так, как в элементарной алгебре в тождественных
преобразованиях используются алгебраические законы:
а + b = b -f- а (перемест ительный),
а + (Ь -}- с) = (а -\- b) -f- с (сочетательный),
а (Ь -\- с) = ab -f- ас (распределительный),
и другие.
Легко проверяются следующие равносильности:
1. А + В = В + А. 2. АВ = ВА.
3. А + (В + С) = (А + В) + С. 4. А(ВС)=(АВ)С.
5. А(В + С) = АВ+АС.
6.
7. А~УВ = АВ. 8. АВ = А + В.
9. Л = А, А + А = А, АА=А.
10. Л + Л = /, AA = L,
Л + /=/, А1 = А,
= A, AL = L.
Выписанные выше первые пять законов аналогичны законам
обычной алгебры чисел. Остальные не имеют аналогий в элемен-
элементарной алгебре.
Используя законы сложения и умножения высказываний,
решим следующую задачу.
Пример 2. Брауну, Джонсу и Смиту предъявлено обвине-
обвинение в соучастии в ограблении банка. Похитители скрылись на
поджидавшем их автомобиле. На следствии Браун показал, что
преступники были на синем «Бьюике»; Джонс сказал, что это
был черный «Крайслер», а Смит утверждал, что это был «Форд
36
Мустанг» и ни в коем случае не синий. Стало известно, что желая
запутать следствие, каждый из них указал правильно либо только
марку машины, либо ее цвет. Какого цвета был автомобиль и
какой марки?
Д Рассмотрим высказывания:
А = {машина синего цвета},
В = {машина марки «Бьюик»},
С = {машина черного цвета),
D = {машина марки «Крайслер»},
? = {машина марки «Форд Мустанг»}.
Так как либо цвет машины, либо марка каждым из соучастников
преступления названы верно, то из показаний Брауна следует,
что высказывание A -f В истинно. Из слов Джонса вытекает истин-
истинность высказывания C^-D. Утверждение Смита означает, что
истинно высказывание А + Е.
Так как высказывания А-{-В, C-\-D, A-\-E истинны, то
истинно и их произведение
Раскрывая скобки, получим
Р = (АС + AD+ ВС + BD) (А + Е) =
= АСА + АСЕ + ADA + ADE -f ВС А + ВСЕ + BDA -\- BDE.
Из условия задачи легко усматривается, что из полученных восьми
слагаемых семь (все кроме пятого) являются ложными вьсказы-
ваниями. Поэтому
т. е. высказывание ВС А истинно, а это означает, что преступ-
преступники скрылись на черном «Бьюике». А
§ 2. Предложения, зависящие от переменной
При изучении математики постоянно приходится иметь дело
с различными предложениями (утверждениями), зависящими от
одной или нескольких переменных. Например, предложение
«число 5 является делителем числа я» зависит от переменной п,
принимающей натуральные значения При каждом п = Ыг, АеМ,
оно истинно, при каждом пфЫг, А е М, — ложно. Уразнения
и неравенства также являются такого рода предложениями.
Например, неравенство х — 2>0 можно рассматривать кап пред-
предложение, зависящее от переменной х. Истинность или ложность
этого предложения зависит от того, какое именно значение пере-
переменной х берется. Если, например, х = 2>, то предложение истинно,
если л: = 0, то ложно. Уравнение х-{-у=\ является прецложе-
37
нием, зависящим от двух действительных переменных х и у. При
х — у=\/2 предложение х-\-у=\ истинно, при х=у=0 оно,
очевидно, ложно.
Предложения, зависящие от переменной, встречаются не только
в математике. Например, предложение «хоккеист команды „Спар-
„Спартак" высшей лиги забил 400 шайб» определено на множестве всех
хоккеистов команды «Спартак». Как известно, это предложение
истинно для Старшинова и ложно для каждого из остальных
членов команды.
Предложения, зависящие от переменных, обозначают через
A in), В(х), С (х\ у) и т. д. Для каждого предложения должно
быть тем или иным способом указано, на каком множестве оно
рассматривается или, как еще говорят, на каком множестве оно
определено или задано. Предложение А (х), хеУИ, не является,
вообще говоря, высказыванием, и поэтому не имеет смысла ста-
ставить вопрос о том, истинно оно или ложно. Ответа на такой воп-
вопрос не существует (за исключением того случая, когда множе-
епю М состоит из одного элемента). Но как только некоторый
элемент хп е М выбран или, как говорят, фиксирован, предпо-
предполагается, что А (х0) будет либо истинным, либо ложьым, т. е.
будет высказыванием. Множество М, на котором задано предло-
предложение А (х), можно разбить на два подмножества. Одно подмно-
подмножество содержит те и только те элементы М, для которых А (х)
истинно. Это подмножество называют множеством истинности
предложения А(х). Другое подмножество содержит те и только
те элементы М, для которых А (х) ложно. Если первое из этих
подмножеств обозначить буквой А, то второе следует обозначить
через Л, так как оно является дополнением множества А до мно-
множества М.
Например, для предложения
А (*) = {*»-5* + 6<0}, xgeR,
множеством истинности Л является интервал ]2; 3[, множеством
Л — объединение промежутков ]— со; 2] и [3; -f- °о[-
Два предложения А (х) и В (х), заданные на одном и том же
множестве, называются равносильными, если их множества истин-
истинности совпадают.
Например, предложения
равносильны, так как множеством истинности каждого из них
является интервал ]2; 3[.
На предложения, зависящие от переменных, естественным
обра юм распространяются все логические операции, введенные
в § 1.
38
Отрицанием предложения А (х), х е М, называется предложе-
предложение Л (а:), определенное на том же множестве М и обраща ощееся
в истинное высказывание для тех и только тех элементов мно-
множества М, для которых Л (х) — ложное высказывание.
Из определения следует, что если Л —множество истинности
предложения Л (а:), то множеством истинности отрицания А(х)
является дополнение А множества Л до множества М. На рис. 27, а
схематически изображены множества М, А и Л. Множество
истинности отрицания Л (х) заштриховано.
б) в)
Рис. 27.
Рассмотрим операции сложения, умножения и импликации для
предложений, заданных на одном и том же множестве М.
Сумма А(х) + В(х) обращается в истинное высказываьие для
тех и только тех элементов множества М, для которых по ь райней
мере одно из слагаемых обращается в истинное высказызание.
На рис. 27, б два круга схематически изображают множества
истинности Л и Б соответственно дли Л (х) и В (х). Множеством
истинности суммы А(х)-\-В(х) будет, очевидно, объединение Л U В
множеств Л и б. На рисунке оно заштриховано.
Произведение Л (х) В (х) обращается в истинное высказывание
для тех и только тех элементов множества М, для которых оба
сомножителя обращаются в истинные высказывания. Множеством
истинности произведения А(х) В(х) является пересечение Л|"|Б
множеств Л и б. На рис. 27, б оно заштриховано.
Импликация А(х)=$В(х) обращается в ложное высказывание
для тех и только тех элементов множества М, для которых
посылка А(х) истинна, а заключение В (х) —ложно. На p^ с. 27, г
штриховкой показано множество истинности импликации А (х) =г>
=> В (х).
Пример 1. Пусть
— два предложения, зависящие от переменной х, xeR. В чем
заключаются предложения
а) А(х) + В(х), б) А(х) В(х),
в) Л (х)=>В(х), г) В(х) => А (х),
д) Л (х) В (х), е) В (х) => Л (х)?
Каковы их множества истинности?
39
Д а) Предложение А (х) + В (х) заключается в том, что верно
по крайней мере одно из двух неравенств
Очевидно, что множеством истинности А (х) + В (х) является про-
промежуток [—2; +оо[.
б) Произведение предложений А (х) и В (х) есть предложение,
в котором утверждается, что оба неравенства х — 2>0их + 25г0
справедливы, т. е. переменная х удовлетворяет системе неравенств
/*-2>0,
Множество истинности — интервал ]2; + оо[.
в) Для импликации А (х) => В (х) («если х — 2 > 0, то х + 2 5= О»)
множество истинности состоит из всех действительных чисел.
г) Для импликации В (я) => А (х) («если х + 2 5^ 0, то х — 2 > О»)
множеством истинности является объединение двух интервалов,
а именно ]—сю; —2 [U]2; +oo[. Для каждого числа х, принад-
принадлежащего отрезку [—2; 2], импликация В (х) :г> А (х) обращается
в ложное высказывание.
д) Для произведения А (х) В (х) множеством истинности будет
множество решений системы неравенств
т. е. пустое множество.
е) Для импликации В (х) => А (х) («если х + 2 < 0, то х — 2 «? О»)
множеством истинности является множество всех действительных
чисел. А
С предложениями, зависящими от переменных, связаны два
вида часто встречающихся утверждений.
1) Предложение Л (х), хеМ, обращается в истинное выска-
высказывание для всех элементов множества М.
2) Предложение А(х), х^М, обращается в истинное выска-
высказывание хотя бы для одного элемента множества М, другими
словами, существует элемент х0 е М, для которого А (х0) — истин-
истинное высказывание.
В математике принято записывать такие утверждения кратко,
используя для этого специальные знаки: знак общности V (пере-
(перевернутая первая буква английского слова АИ — все) и знак
существования 3 (перевернутая первая буква английского слова
Exists —существует). Знак общности V заменяет в словесных
формулировках слова: все, всякий, каждый, любой. Знак суще-
существования 3 употребляется вместо слов: хотя бы один, найдется,
существует.
40
Используя знаки общности и существования, утверждения 1
и 2 можно записать следующим образом:
1) (V*) А(х), 2) (эх) А(х); х*вМ.
Заметим, что первое утверждение равносильно утверждению: мно-
множеством истинности А предложения А (х) является множество М,
т. е. А=М. Второе утверждение равносильно следующему: мно-
множество истинности А предложения А (х) не пусто, т. е. Афф.
Каждое из рассмотренных утверждений либо истинно, либо
ложно и, следовательно, является Еысказыванием.
Например, для предложения
с помощью знаков общности и существования можно построить
два утверждения:
1) (Vх) Л (я) = {для всех действительных чисел х2>0\.
2) (э*) А (х) = {существует действительное число, для кото-
которого х2>0}.
Каждое из этих утверждений является высказыванием. Первое
высказывание, очевидно, ложно, второе истинно.
Для того чтобы убедиться в истинности высказывания (\'х) А (х),
хёМ, необходимо проверить истинность предложения / (х) для
всех элементов множества М.
Если множество М содержит мало элементов, можно попы-
попытаться все их перебрать и для каждого убедиться в истинности
утверждения А(х). Если же М — бесконечное множество или, хотя
и конечное, но содержит много элементов, доказать истинность
высказывания можно лишь логическим рассуждением.
Очень важно понимать, что для того чтобы опровергнуть
высказывание (ух) А (х), достаточно указать только один элемент
ieM, для которого А (х) Ложно. Элемент х множества М, для
которого предложение А (х) неверно, называется контрпримером
для высказывания (V*) А (х).
Таким образом, чтобы убедиться в ложности высказывания
(Ух) А (х), достаточно найти (или, как еще говорят, псстроить)
один контрпример. Рассмотрим предложение
А (п) н= {число п2 + п + 41 простое},
Для высказывания
Л (n) s {при каждом натуральном п
число п2 + п + 41 простое}
элемент п = 40 является контрпримером. Действительно, число
402 + 40 + 41 =40-41+41 делится на 41 и, следовательно, А D0)—
ложное высказывание.
Замечательно, что для всех п < 40 предложение А (п) истинно.
41
§ 3. Взаимно обратные и взаимно противоположные теоремы.
Необходимые и достаточные условия
Большинство теорем, встречающихся в школьном курсе мате-
математики, формулируются (или могут быть сформулированы) следую-
следующим образом: для любого элемента х множества М из предложе-
предложения А (х) следует предложение В (х). Используя обозначения,
введенные в §§ 1, 2, каждую такую теорему можно записать
в виде (ух) А(х)=$В(х), хеМ. Рассмотрим, например, следую-
следующие четыре теоремы.
Теорема 1. Если сумма цифр натурального числа делится
на 3, то и числа делится на 3.
Теорема i. Если четырехугольник является прямоугольником,
то его диагонали конгруэнтны. J:
Теорема 3. Если хотя~Ш одно из двух чисел делится на 7,
то и их сумма делится на 7.
Теорема 4. Диагонали ромба взаимно перпендикулярны.
Каждая из этих теорем понимается как высказывание вида
(V*) А(х)=*В(х), х^М,
и, следовательно, все четыре теоремы имеют одинаковое строение.
В теореме 1 речь идет о двух предложениях:
А (п) = {сумма ш;фр числа п делится на 3},
В (п) = [число п делится на 3},
зависящих от переменной п <= N.
В теореме утверждается, что для каждого натурального числа
верно утверждение: если сумма цифр числа делится на 3, то
и число делится на 3, т. е. утверждается истинность высказывания
(Vn) A(n)=$B(n), «eN.
Из арифметики известно, что это высказывание истинно, т. е.
теорема 1 верна.
В теореме 2 рассматривается множество Q всех четырехуголь-
четырехугольников q и на этом множестве два предложения
A (q) = {четырехугольник q — прямоугольник},
В (q) = {диагонали четырехугольника q конгруэнтны}.
Теорема утверждает, что для любого четырехугольника верно
следующее: если четырехугольник является прямоугольником, то
его диагонали конгруэнтны. Таким образом, теорема 2 понимается
как высказывание
(Vq) A(q)=>B(q), q^Q.
В геометрии доказывается, что эта теорема верна.
42
В теореме 3 говорится о двух предложениях
А (п; т)э={п или т делится на 7},
В (п; т) = {п-\-т делится на 7},
заданных на множестве всех пар (п; т) натуральных чисел.
В теореме утверждается истинность высказывания
(\fn; m) А(п; т)=$В(п; т), п, шёЦ,
которое, очевидно, ложно, и, следовательно, теорема 3 неверна.
Для нас важно сейчас то, что логическое строение этой теоремы
точно такое же, как и у теорем 1 и 2.
Из-за краткости формулировки теоремы 4 о диагоналях ромба
может даже показаться, что эта теорема не имеет формы
(ух) А (х) =$В (х). На самом деле это не так. Точная формули-
формулировка этой теоремы такова (напомним, что ромбом называется
параллелограмм, у которого все стороны равны):
Теорема 4. Пусть Р — множество всех параллелограммов
и пусть
А (р) = {параллелограмм р — ромб},
В (р) = {диагонали параллелограмма р взаимно перпендикулярны}
— два предложения, заданные на множестве Р.
Тогда
(VP) Л(р)=>Я(р), реЛ
т. е. для любого параллелограмма верно утверждение: если парал-
параллелограмм—ромб, то его диагонали взаимно перпендикулярны.
В формулировке каждой теоремы, имеющей вид
(V*) А(х)=$В(х), xgeM,
можно выделить условие теоремы (предложение А (х)) и заклю-
заключение теоремы (предложение В(х)).
Теоремы, отличающиеся друг от друга условием или заклю-
заключением, являются различными теоремами.
Рассмотрим еще один пример.
Теорема 5. Пусть Q — множество всех четырехугольников
и пусть
A (q) = {четырехугольник q — ромб},
В (q) = {диагонали четырехугольника q взаимно перпендикулярны}
два предложения, заданные на множестве Q.
Тогда
(Vq)A(q)=>B(q), q GE Q,
т. е. для любого четырехугольника верно утверокдение: если четы-
четырехугольник—ромб, то его диагонали взаимно перпендикулярны.
Теорема 5 не тождественна теореме 4, — это две различные
теоремы, так как предложения A (q) и В (q) заданы в одном
43
случае на множестве всех параллелограммов, в другом — на мно-
множестве всех четырехугольников.
Четкое и однозначное выделение в каждой теореме условия
и заключения позволяет однозначно определить понятия обратной
и противоположной теорем.
Теоремы
(V*) А(х)=эВ(х), х<=М,
и
(V*) В(х)=$А(х), х<=М,
называются взаимно обратными.
Иногда одну из этих теорем называют прямой, тогда другую
называют обратной.
Ясно, что любую из двух взаимно обратных теорем можно при-
принять за прямую.
Из данного определения видно, что, поменяв местами в фор-
формулировке некоторой теоремы условие и заключение, мы полу-
получаем формулировку теоремы, обратной исходной.
Важно понимать, что для пары взаимно обратных теорем
могут осуществляться все три возможности, а именно:
1) обе теоремы верны,
2) одна из теорем верна, другая неверна,
3) обе теоремы неверны.
Для того чтобы показать, что первый случай может иметь
место, достаточно рассмотреть теорему 1 и обратную ей теорему
(если число делится на 3, то сумма цифр числа делится на 3).
Теорема 4 о диагоналях ромба и теорема, ей обратная (для
любого параллелограмма верно утверждение: если в параллело-
параллелограмме диагонали взаимно перпендикуляр-
перпендикулярны, то этот параллелограмм есть ромб)
также верны.
Для теоремы 2 обратная формулиру-
формулируется следующим образом: «если диагонали
четырехугольника конгруэнтны, то четырех-
четырехугольник является прямоугольником». Эта
теорема неверна. В качестве контрпримера
можно взять четырехугольник, изображен-
изображенный на рис. 28; таким образом, из двух
взаимно обратных теорем одна может быть
верна, другая неверна.
Аналогично взаимно обратными являются теорема 5 и следую-
следующая теорема: «если в четырехугольнике диагонали взаимно пер-
перпендикулярны, то такой четырехугольник есть ромб». Как из-
известно, теорема 5 верна, а обратная ей —неверна. В качестве
контрпримера можно опять взять четырехугольник, показанный
на рис. 28.
Третий случай, когда обе теоремы — и прямая, и обратная —
неверны, тоже может иметь место. Для теоремы 3 обратной является
44
теорема: «если сумма двух чисел делится на 7, то хотя бы одно
из слагаемых делится на 7». Эта теорема, очевидно, неверна,
так же как и обратная ей теорема 3. Обратим еще раз внима-
внимание на теоремы 4 и 5 о диагоналях ромба. Выше уже отмечалось,
что эти теоремы суть различные теоремы; если бы мы не разли-
различали их, понятие обратной теоремы потеряло бы одноз ичный
смысл: теорема имела бы две обратных, из которых одна была
бы верна (обратная для теоремы 4), а другая нет (обратная для
теоремы 5).
С понятием прямой и обратной теоремы тесно связано упо-
употребление слов «необходимо», «достаточно», «необходимо и доста-
достаточно» и им подобных.
Если теорема (Ух) А (х) =$ В (х) верна, то предложение А (х)
называется достаточным условием для В (х), а предложение В (х) —
необходимым условием для А (х).
Вернемся к теореме 2:
Dq)A(q)=>B(q), q^Q,
где
A (q) = {четырехугольник q — прямоугольник},
В (q) = {диагонали четырехугольника q конгруэнтны-
и Q — множество всех четырехугольников. Эта теорема веона, и,
следовательно, A (q) является достаточным условием дл:1 В (q),
т. е. для того чтобы диагонали четырехугольника были конгру-
конгруэнтны, достаточно, чтобы четырехугольник был прямоугольником.
Предложение В (q) является необходимым условием дли A (q),
т. е. для того чтобы четырехугольник был прямоугольником,
необходимо, чтобы диагонали четырехугольника были конгру-
конгруэнтны.
Если справедлива не только теорема
но и ей обратная
(Чх) В (х) =э А (х), хевМ,
то А (х) является необходимым и достаточным условием для В (х),
а В (х) — необходимым и достаточным условием для А(х).
Например, в начале параграфа проводилась теорема¦1: «если
сумма цифр натурального числа делится на 3, то и число делится
на 3». Эта теорема верна. Справедлива и обратная теорема. По-
Поэтому можно сказать, что для делимости числа на 3 необходимо
и достаточно, чтобы сумма цифр числа делилась на 3.
Следует помнить, что в тех случаях, когда в теореме содер-
содержатся слова «необходимо и достаточно», доказательство обяза-
обязательно должно состоять из доказательства необходимости и из
доказательства достаточности. Ведь в такой формулирсвке на
самом деле объединены формулировки двух теорем: прямой и
обратной. Каждая нуждается в доказательстве, так как из
45
справедливости одной ни в коем случае не следует справедливость
другой.
Отметим еще, что вместо слов «необходимо и достаточно»
иногда употребляют слова «тогда и только тогда'», «в том и
только в том случае» и т. п.
Например, теорема 1 и ей обратная, могут формулироваться
так: «Натуральное число п делится на 3 тогда и только тогда,
когда сумма цифр числа п делится на 3». Слово «условие» часто
заменяют словом «признак», и говорят о необходимом признаке,
или о достаточном признаке, или, наконец, о необходимом и до-
достаточном признаке.
Перейдем к понятию противоположной теоремы.
Теоремы
(Ух)А(х)=}В(х), х<=М,
называются взаимно противоположными.
Если, следовательно, в формулировке некоторой теоремы за-
заменить условие и заключение их отрицаниями, то получится фор-
формулировка теоремы, противоположной исходной.
Всякая теорема
(V*) А (х) => В (х)
порождает, таким образом, еще три теоремы:
обратную (Ух) В (х) =? А(х),
противоположную (Ух) А (х)=$ В (х),
противоположную обратной (Ух) В (x)=s> А (х).
Например, взяв в качестве исходной рассмотренную выше тео-
теорему 5, будем иметь (для произвольного четырехугольника):
1) исходная теорема: если четырехугольник — ромб, то его
диагонали взаимно перпендикулярны (теорема верна);
2) обратная теорема: если диагонали четырехугольника вза-
взаимно перпендикулярны, то четырехугольник есть ромб (теорема
неверна);
3) противоположная теорема: если четырехугольник не ромб,
то его диагонали не перпендикулярны (теорема неверна);
4) противоположная обратной: если диагонали четырехуголь-
четырехугольника не взаимно перпендикулярны, то четырехугольник не яв-
является ромбом (теорема верна).
В рассмотренном примере прямая теорема и противоположная
обратной оказались истинными, а обратная и противоположная —
ложными. Это совпадение не является случайным. Прямая тео-
теорема и теорема противоположная обратной либо обе истинны,
либо обе ложны, т. е. имеет место равносильность
(V*) А (х) =^> В (х) = (Ух) B(x)z^A (x),
46
Часто доказательство одной из этих теорем вызывает трудно-
трудности, в таком случае следует попытаться доказать другую.
Известный метод доказательства от противного как раз и со-
состоит в том, что вместо исходной теоремы доказывают п эотиво-
положную обратной.
§ 4. Метод математической индукции
Во многих разделах арифметики, алгебры, геометрии, анализа
приходится доказывать истинность предложений А (п), зависящих
от натуральной переменной, для всех значений этой переменной.
Доказательство истинности предложения А(п) для всех з^чений
переменной часто удается провести методом математической ин-
индукции, который основан на следующем принципе.
Предложение А (п) считается истинным для всех натуральных
значений переменной, если выполнены следующие два условия:
1. Предложение А (п) истинно для я=1.
2. Из предположения, что А(п) истинно для n—-k (где k —
любое натуральное число), следует, что оно истинно и для сле-
следующего значения n = k-\-l.
Этот принцип называется принципом математической индук-
индукции. Обычно он выбирается в качестве одной из аксиом, опреде-
определяющих натуральный ряд чисел, и, следовательно, принимается
без доказательства.
Под методом математической индукции понимают следующий
способ доказательства. Если требуется доказать истинность пред-
предложения А (п) для всех натуральных я, то, во-первых, ;ледует
проверить истинность высказывания /4A) и, во-вторых, тредпо-
ложив истинность высказывания A(k), попытаться доказать, что
высказывание A(k-\-\) истинно. Если это удается доказать, при-
причем доказательство остается справедливым для каждого натураль-
натурального значения k, то в соответствии с принципом математической
индукции предложение А (и) признается истинным для всех зна-
значений п.
Метод математической индукции широко применяется три до-
доказательстве теорем, тождеств, неравенств, при решении задач на
делимость, при решении некоторых геометрических и многих дру-
других задач.
Пример 1. Доказать истинность предложения
А (п) = {число 5 ¦ 23"-2 + З3*-1 кратно 19}, пеН
Д 1. Высказывание Л A) = {число 5-2 + 32 кратно 19] истинно.
2. Предположим, что для некоторого значения n = k
Л(?) = {число б-г^ + З3*-1 кратно 19}
истинно. Тогда, так как
5. 2=» <»+] )-2 -f З3 ^/;+1»-1 = 8 • 5 • 23*-2 + 27 • З3*-1 =
*= 8 E • 23''-2 + З3'; I-1) 4-1Э • З3*-1,
47
очевидно, что и A(k-\-\) истинно. Действительно, первое слагае-
слагаемое делится на 19 в силу предположения, что A (k) истинно; вто-
второе слагаемое тоже делится на 19, потому что содержит множи-
множитель 19. Оба условия принципа математической индукции вы-
выполнены, следовательно, предложение А (п) истинно при всех
значениях п. а
Пример 2. Доказать формулу
Д 1. При п=\ обе части равенства обращаются в единицу
и, следовательно, первое условие принципа математической индук-
индукции выполнено.
2. Предположим, что формула верна при n = k, т. е.
Прибавим к обеим частям этого равенства (k-\-\K и преобра-
преобразуем правую часть. Тогда получим
Таким образом, из того, что формула верна при n — k, следует,
что она верна и при n = k-\-\. Это утверждение справедливо при
любом натуральном значении 1г. Итак, второе условие принципа
математической индукции тоже выполнено. Формула доказана. ^
Пример 3. Доказать неравенство
"г „ л о ~Ь • • • 4" о„ I | ¦> 1-
п+1 ' п + 1 ~ ' " "•" Зп+1
Д 1. При п=\ неравенство справедливо, так как
2. Предположим, что неравенство верно при n = k, т. е.
'"•¦" h3%+l -> у-
Прибавим к обеим частям неравенства сумму трех дробей
3k + 2 ' Зй-1-З ^ 3/jf 4
1
и перенесем первое слагаемое левой части, т. е. г-т—г в правую
часть неравенства. Тогда получим
k + 2 + • • • + з?+Т > ! J ' ' ""
48
Правая часть этого неравенства больше единицы, так как
iiii ^
I I * 1 ' I _j L_ — i _j_
Следовательно, левая часть тем более больше единицы, т. е.
' Т ¦ • ¦ Н ^ *
(A+D + 1 ' ••• ' 3(А+1)+1 " *•
Последнее неравенство из исходного неравенства получается при
Итак, предположив истинность неравенства при n = k, мы до-
доказали его истинность при n = k-\-\. Таким образом, методом
математической индукции неравенство доказано, а
Пример 4. Пусть х1у х2, ..., х„ — произвольные положитель-
положительные числа, причем хгх2.. .хп = 1. Доказать, что
. + Xn7S П.
Д 1. Если п=\, то по условию Xi=l и, следовательно,
можно написать Xi5=l, т. е. для п—\ утверждение верно.
2. Предположим, что утверждение верно для n = k. Пу:ть xlt
хъ, ..., Xk, x,ki-i — произвольные положительные числа и
Х\Х% . . . XjiX/i+l = 1 •
Могут представиться два случая: либо все эти числа равнэ1 1, и
тогда их сумма равна k-\-\ и неравенство доказано, либо среди
этих чисел есть хотя бы одно число, не равное единице, и тогда^
обязательно есть, по крайней мере, еще одно число, не равное
единице, причем если одно из них меньше единицы, то другое
больше единицы. Не ограничивая общности, можно считать, что
хк > 1, а Хы-i < 1 • Рассмотрим теперь k чисел
Х\, Х<ь, . . • , X/f-i
Произведение их равно единице, и, следовательно, по нплуктив-
ному предположению
Xi + х2 +... + хь-! -1- зд+1 Ss k.
Прибавим к обеим частям последнего неравенства xk-\-xk+1 пере-
перенесем хкхк^ направо и преобразуем правую часть неравбнства:
Х\ + Х2 + . . . + Хк + Xft+1 >- k — XkXk^ + Xk
= k+l+xk(l -xkH) + xkll-\ =k+l+xk(l-xki.1)-(l-;:h+l) =
= k+ 1 +A -xk+1)(xk-l)^k+ 1.
Таким образом, из истинности утверждения при n = k выте-
вытекает его истинность при n = k-\-\. Утверждение доказано. Из
приведенного доказательства следует, что знак равенства в дока-
доказываемом соотношении имеет место тогда и только тогда, когда
х\ = х2 =... = хп = 1. ^
49
Пример 5. Доказать неравенство
Х}Х2 ... Хп,
где Xi, x2, ..., х„ —произвольные положительные числа.
Д Это важное неравенство между средним арифметическим и
средним геометрическим п чисел является простым следствием
соотношения, доказанного в предыдущем примере. В самом деле,
пусть Х\, х2, ..., хп — произвольные положительные числа. Рассмот-
Рассмотрим п чисел
Х\ х2 хп
п., ' п, ' • ¦ • ' п
У XX Х у ХХ Х )'
п,п
XtX2 ... Хп у ХгХ2 ... Хп )' ХХХ2 ... Хп
Очевидно, что все эти числа положительны и произведение их
равно единице. Следовательно, по доказанному в примере 4 их
сумма больше или равна га, т. е.
II, I П.
хх х у
5s п.
П.
у ххх2 ... хп у х±х2 ... хп у хгх2 ... хп
Отсюда
. . . Хп
причем знак равенства имеет место тогда и только тогда, когда
Неравенство между средним арифметическим и средним гео-
геометрическим п чисел часто оказывается полезным при доказа-
доказательстве других неравенств, при отыскании наименьших и наи-
наибольших значений функций (см. главу IV, § 6, 7).
Рассмотрим некоторые обобщения принципа математической
индукции.
Пусть р — некоторое целое число.
Предложение А (п), где п целое, истинно для всех целых
значений п~^р, если выполнены следующие два условия:
1. Предложение А (п) истинно для п = р.
2. Из предположения, что А (п) истинно для n = k (k — целое,
k следует, что оно истинно для следующего значения п =
При р = 1 получается первоначальная формулировка принципа
математической индукции.
Пример 6. Доказать, что любую сумму денег, большую 7
копеек, можно разменять только трехкопеечными и пятикопееч-
пятикопеечными монетами.
Д Пусть сумма равна п копейкам. Если п=8, то утвержде-
утверждение верно. Пусть утверждение верно для п = k. Могут предста-
представиться только два случая для размена суммы в k копеек:
а) потребовались только трехкопеечные монеты,
б) потребовалась хотя бы одна пятикопеечная монета.
50
В случае а) удаляем три трехкопеечные монеты, добавляем
две пятикопеечные м тем самым размениваем сумму в k-\-\ ко-
копеек. В случае б) удаляем одну пятикопеечную монету, добав-
добавляем две трехкопеечные монеты и тем'самым размениваем сумму
в k -f-1 копеек. А
В некоторых задачах принцип математической индукции
используется в следующей форме.
Предложение А(п), где п —целое число, истинно для всех
п^р (р — некоторое целое число), если выполнены два условия:
1. Предположение А (п) истинно для п = р и п — р-\-\.
2. Из предположения, что А (п) истинно для n-=k и п =
= k — 1, следует, что оно истинно при п = k -\-1 (для любого
k>p).
Проиллюстрируем применение этого принципа на следующем
примере.
Пример 7. Доказать, что функция Тп (х) = cos (n ¦ arccos х)
на отрезке [—1; 1] совпадает с некоторым многочленом стелени п
(п— неотрицательное целое число).
1. При п = 0 и п=\ получаем соответственно То (х) = 1 и
Ti(x)=x, т. е. утверждение верно и для п — 0 и для п=\.
2. Рассмотрим Тк^{х) и проведем преобразования
Tkn (x) = cos ((k + 1) arccos х) =
= cos (k arccos x) ¦ cos (arccos x) — sin (k arccos x) ¦ sin (arccos .:) =
= Tk (x) Tx (x) — 2 (cos ((k— 1) arccos x) — cos ((k + 1) arccos .c)) =
= Tk (x) Tt (x) - * G1*.! (x) - Tk+1 (x)).
Мы получили следующее рекуррентное соотношение.
Tkn (х) = 2Л (х) Tk (х) - 7V.! (x)
или
Сделаем индуктивное предположение: функции Tk-\ (x) и
Ttl (х) на отрезке [—1; 1] совпадают с многочленами «ответ-
«ответственно k— 1-й степени и &-й степени. Тогда из полуденной
рекуррентной формулы следует, что 7Vi (x) совпадает с много-
многочленом степени k -\-1.
Согласно принципу математической индукции утвер>кдение
доказано для всех п^О. А
ЗАДАЧИ РАЗДЕЛА I
1. Электрическая цепь между точками М и N составлена по схеме, изо-
изображенной на рис. 29. Рассмотрим следующие четыре высказывания:
А = (элемент k цепи вьшел ия строя},
В/ = {элемент /; цепи вышел из строя} (' = 1. 2, 3).
51
Замкнута ли цепь, если
а) высказывание А-\-В^В2В3 истинно,
б) высказывание А (Ву-\-В2 + Б3) истинно?
2. Докажите формулу
В
вильныл ответ: если изучал первый,
3. На вопрос, кто из трех учащихся изучал логику, был получен пра-
то изучал и второй, но неверно, что
если изучал третий, то изучал и
второй.
Кто из учащихся изучал логику?
4. «Вернувшись домой, Мегрэ по-
эвонил на набережную Орфевр.
— Говорит Мегрэ. Есть новости?
— Да, шеф. Поступили сообце-
ния от инспекторов. Торранс уста ю-
вил, что если Франсуа был пьян, то
либо Этьен убийца, либо Франсуа лжет.
Жуссье считает, что или Этьен убийда,
или Франсуа не был пьян и убийство
произошло после полуночи. Инспектор Люка просил передать Вам, что если
убийство произошло после полуночи, то либо Этьен убийца, либо Фран-уа
лжет. Затем звонила ...
— Все. Спасибо. Этого достаточно. — Комиссар положил трубку. Он знал,
что трезвый Франсуа никогда не лжет. Теперь он знал все».
Рассмотрите следующие высказывания:
А = {Франсуа был пьян},
В = {Этьен убийца},
С= {Франсуа лжет},
D = {убийство произошло после полуночи}.
Запишите, используя логические операции, высказывания инспекторов Тор-
ранса, Жуссье и Люка. Составьте произведение этих трех высказываний и
упростите его. Что следует из показаний испекторов? Какой вывод сделал
комиссар Мегрэ?
5. Для доказательства равенства
У 5 K2 + 7 —
У
— 7 = 2
ученик привел следующее рассуждение: «Возведя в куб обе части равенства,
получим
14 - 3 (VTFl+7)a VW^~1 + 3 VW^+1 (VW^Tf = 8
ИЛИ
3 У$ V 2 + 7
- 7 {У5 V'l + 7 -Yb V~2- 7) = 6;
но, так как
-V 5)^2-7 = 2,
52
1/5/2+71/5/2—7 = 1
то
{/4=1, 1 = 1,
что и требовалось Доказать».
Доказал ли ученик равенство?
6. Ученику была предложена следующая задача:
«Гипотенуза прямоугольного треугольника лежит в плоскости а, один
катет составляет с плоскостью а угол в 45°, другой — угол в 60°. Бсльший
катет равен а. Найти гипотенузу».
Ученик сделал чертеж (рис. 30), из прямоугольного треугольника АОС
нашел
i CO =a sin 45° = a /2/2,
из прямоугольного треугольника ВОС нашел
\ВС\=-
со
2 I CO
sin 60° /З У л
и по теореме Пифагора определил гипотенузу
| = /|ЛС|2+|ВС|2 =
-V4-V
Рис. 30,
. Прн каких значениях k истинны следую-
следуюВерен ли полученный результат?
7. Дано неравенство fce + /2=g
щие утверждения:
а) При любом I неравенство имеет хотя бы одно решение.
б) Существует I, при котором неравенство имеет хотя бы одно решение?
8. На множестве всех натуральных чисел заданы три предложения:
А (и) = {число /г + 48 является квадратом натурального числа},
В (п) = {число п оканчивается цифрой 4),
С (п) = {число п — 41 есть квадрат натурального числа}.
При каких значениях п нз данных трех предложений два истинны 1 одно
ложно?
9. Для теоремы «если квадратное уравнение не имеет двух различных
действительных корней, то дискриминант этого квадратного уравнения непо-
неположителен» сформулируйте обратную, противоположную и противоположную
обратной теоремы. Указать, какие из этих теорем верны.
10. Докажите или опровергните следующие утверждения:
а) Для делимости числа пг—1 (п ^5) на 24 достаточно, чтобы t. было
простым числом.
б) Для делимости числа и2—1 (п :э= 5) на 24 необходимо, чтобы t. было
простым числом.
11. Для каких натуральных значений п истинно предложение
12. На плоскости произвольным образом проведены п прямых. Доказать,
что черной и белой красками можно так закрасить плоскость, что нобые
две части, имеющие общую сторону, будут окрашены в разные цвета.
53
ЗАДАЧИ РАЗДЕЛА II
1. По мишени произведено три выстрела. Пусть
Аь = {мишень поражена при k-u выстреле}, ft=»l, 2, 3.
Что означают следующие высказывания:
а) Аг + А2 + Аз, б) АхАъА3; в) А^А^ + А^Аа + А^к^
2. Разбирается дело Брауна, Джонса и Смита. Один из них совершил пре-
преступление.
На следствии каждый из них сделал два заявления.
Браун. Я не делал этого.
Смит сделал это.
Джонс. Смит не виновен.
Браун сделал это.
Смит. Я не делал этого.
Джонс не делал этого.
Суд установил, что один из них дважды солгал, другой—дважды скгзал
правду, третий —один раз солгал, один раз сказал правду. Кто совершил пре-
преступление?
3. Для полярной экспедиции из восьми претендентов А, В, С, D, Е, F,
G и Н надо отобрать шесть специалистов: биолога, гидролога, синоптика,
радиста, механика и врача. Обязанности биолога могут выполнять Е и G, гид-
гидролога В и F, синоптика F и G, радиста С и D, механика С и Я, врача А
и D. Хотя некоторые претенденты владеют двумя специальностями, в экспе-
экспедиции каждый сможет выполнять только одну обязанность. Кого и кем сле-
следует взять в экспедицию, если F не может ехать без В, D —без Н и без С,
С не может ехать одновременно с G, а А не может ехать вместе с В?
4. Рассмотрим два определения легкой контрольной:
1. Контрольная работа называется легко, если каждую задачу решил хотя
бы один ученик.
2. Контрольная работа называется легкой, если хотя бы один ученик
решил все задачи.
а) Может ли контрольная быть легкой в смысле первого определения и
трудной (не легкой) в смысле второго?
б) Может ли работа быть легкой в смысле второго определения и трудной
в смысле первого?
5. Ученики 10 В класса хвастались тем, что онн выше ростом учеников
10 А. На вопрос учителя математики: «Что, собственно, означает, что вы выше
ростом?» — ученики 10 В дали следующие ответы:
1. Любой из нас выше любого из них.
2. Самый высокий нз нас выше самого высокого нз них.
3. Для любого ученика нашего класса найдется ученик класса А меньшего
роста.
4. Каждый ученик класса А ниже хотя бы одного ученика нашего класса.
5. Средний рост учеников нашего класса больше среднего роста учеников
класса А.
Есть ли среди этих ответов равносильные? Если есть, то какие?
54
6. На множестве всех натуральных чисел заданы три предложения
А (п) = {число п2 — 2 кратно 7),
В (п) = {число п — 2 кратно 7},
С (п) з= {4/г2 — 360/г + 8099 < 0}.
При каких значениях п из данных трех предложений два истинны и одно
ложно?
7. Даны три предложения, заданные на множестве всех действительных
чисел:
А (х) = {х— целое число},
В (х) = {х2 — Ъх—целое отрицательное число},
С (л;) = ¦!.*:-| целое положительное число>.
При каких значениях х ложно одно и только одно из этих трех предло-
предложений?
8. Дана система уравнений
где а, Ь, с — действительные числа.
При каких значениях а при любом Ь найдется такое с, при котором система
имеет хотя бы одно решение?
9. Даны две точки А @; 9), В C; 6) и система неравенств
При каких значениях параметра а решением системы будут координаты
а) хотя бы одной точки отрезка АВ,
б) каждой точки отрезка АВ?
10. Для каждой из нижеследующих теорем сформулируйте обратную, про-
противоположную и противоположную обратной. Указать, какие из теорем верны.
а) Если в четырехугольник можно вписать окружность, го этот четырех-
четырехугольник представляет собой ромб.
б) Если параллелограмм является прямоугольником, то вокруг пего можно
описать окружность.
в) Если многоугольник является четырехугольником, то сумма его bi утрен-
утренних углов равна 360°.
11. Какие из следующих шести теорем являются по отношению друг
к другу обратными, противоположными, противоположными обратным? Какие
из этих теорем верны?
Теорема 1. Если каждое из двух натуральных чисел делится нацело на 7,
то их сумма делится на 7.
Теорема 2. Если ни одно из двух чисел не делится на 7, то и их сумма
не делится на 7.
Теорема 3. Если хотя бы одно из двух чисел делится на 7, то и их сумма
делится на 7.
Теорема 4. Если сумма двух чисел делится на 7, то каждое слагаемое
делится на 7.
55
Теорема 5. Если сумма двух чисел не делится на 7, то ни одно из слагае-
слагаемых не делится на 7.
Теорема 6. Если сумма двух чисел не делится на 7, то хотя бы одно из
слагаемых не делится на 7.
12. Дана теорем?: в любом четырехугольнике, который не является пря-
прямоугольником, диагонали не конгруэнтны. Сформулировать теоремы: обрат! ую,
противоположную и противоположную обратной. Какие из этих четырех теорем
верны?
13. Для теоремы: «Если функция дифференцируема в точке, то она непре-
непрерывна в ней» — сформулировать теоремы: обратную, противоположную и противо-
противоположную обратной. Какие из этих четырех теорем верны?
14. Замените многоточия словами «необходимо и достаточно», «необходимо,
но не достаточно», «достаточно, но не необходимо» так, чтобы получились вер-
верные утверждения:
а) Для того чтобы выиграть в лотерее, ... иметь хотя бы один лотере?ный
билет.
б) Для того чтобы из трех чисел а, Ь, с хотя бы два были равны м<жду
собой, ..., чтобы
(a —ftJ + (ft—сJ + (с —аJ = 0.
в) Для того чтобы сумма двух действительных чисел была числом ргцио-
нальным, ..., чтобы каждое слагаемое было рациональным числом.
г) Для того чтобы медиана треугольника была равна половине стороны,
которую она делит, ..., чтобы треугольник был прямоугольным.
д) Для того чтобы функция у = ах2 + Ьх + с при всех целых х принимала
целые значения, ..., чтобы 2а, а-\-Ь, с были целыми числами.
15. Доказать или опровергнуть следующие утверждения:
а) Для того чтобы число л2 + 20(/г>3) было составным, достаточно, чтобы п
было простым.
б) Для того чтобы число /г2+ 20 (п > 3) было составным, необходимо,
чтобы п было простым.
16. Доказать, что при любом натуральном /г:
а) /гB/г2 —З/г+1) кратно 6;
б) lin+i+122"-1 делится нацело на 133;
в) Ф — п кратно 5; г) я' —/г кратно 7.
17. Доказать, что при любом натуральном /г > 1 число 22"+1 оканчи-
оканчивается цифрой 7.
18. Методом математической индукции доказать справедливость равенств
для каждого натурального значения п:
а) 1 -2 + 2-5 + ... + /гC/г— 1) = /г2 (/г+1);
б)
1-5 ' 5-9 ' ¦" ' D/z —?)Dn+l) 4/i+lf
56
19. Доказать, что
1 пя+1 Он i
з+зз+...+зз...з=-
(левая часть равенства содержит п слагаемых).
20. Доказать равенство
]/2 +1^2 +... + V 2 = 2 cos (Л/2Я+1), л
SIN
(в левой части содержится п корней).
21. При каких натуральных значениях п верны неравенства:
а) 3">2я + 7л; б) 2* > /г2 + 4/г + 5?
22. Методом математической индукции доказать справедливость следующих
неравенств для всех натуральных /г>1:
13 5 2/г—1 1
2 ' 4 6 ''' 2/г < У~3/г~+Т '
б)^т-' ' ' '- 13
23. На сколько частей разделится сфера п плоскостями, проходящими
через центр, если никакие три плоскости не проходят через один и тот же
диаметр.
24. Пусть хъ х2, ..., хп — произвольные неотрицательные числа, тричем
*! + х2+ ...+*„ 55 1/2.
Доказать, что
Глава III
УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ
§ 1. Уравнения с одним и несколькими переменными
Любое предложение вида
f(x)=g(x), A)
где f (х) н g(x) — некоторые функции, называется уравнением
с одной переменной х (или с одним неизвестным х). Функция f (х)
называется левой частью, a g(x) —правой частью уравнения A).
Число а называется корнем (или решением) данного уравне-
уравнения с переменной х, если при подстановке числа а вместо х в обе
части этого уравнения получаем верное числовое равенство, т. е.
если при х = а обе части уравнения определены и их значения
совпадают.
Решить данное уравнение —значит найти множество всех кор-
корней (решений) этого уравнения в области R.
Два уравнения называются равносильными {эквивалентными),
если они имеют одно и то же множество решений, т. е. если
каждое решение первого уравнения является решением второго
и, наоборот, каждое решение второго уравнения является реше-
решением первого уравнения, или если оба уравнения не имеют решений.
Например, уравнения 5л:-|-]=6 и 2х = 2 равносильны, так
как каждое из них имеет единственный корень х=1.
Уравнение вида
ах = Ь, B)
где а и Ь — некоторые заданные числа, называется линейным урав-
уравнением.
Очевидно, если а — Ь = 0, то любое число является решением
уравнения B). Если а = 0, но 6#0, то уравнение B) решений
не имеет. Если же афО, то это уравнение имеет единственное
решение х = Ь/а.
Уравнение вида
= 0, C)
где а, Ь, с —некоторые числа, причем афО, называется квадрат-
квадратным.
58
Простейшее квадратное уравнение имеет вид х2-\-с = 0. Оно
не имеет решений, если о 0, имеет одно решение х — 0, если
с = 0, и имеет два решения х — J/ — с и х-= — У— с, если с<0.
Легко проверяется, что уравнение C) равносильно уравнению
tf + lx + L^Q.
'а 'а
Преобразуем левую часть этого уравнения:
Отсюда видно, что уравнение C) не имеет решений, если D =
= b2 — 4ас<0, имеет единственное решение х = — ^-, если D=0,
и имеет два решения х =— 2а~~2а~' если D>0
Таким образом, все решения уравнения C), если они есть,
находятся по формуле
Х~
2а
Пример 1. Решить уравнение
2х+1 _ 4—х
3-х ^ х+[ '
Д Умножим обе части данного уравнения на C — х) (.<•+ !)•
Очевидно, любое решение данного уравнения является и реше-
решением полученного уравнения
Как легко видеть, оно равносильно квадратному уравнении!
Находим корни этого уравнения:
х = — 5 ± У5 + 11 = — 5 ± 6,
т. е. х = —11 и х= 1.
Следовательно, решениями данного уравнения могут быть лишь
числа —И и 1. Проверкой убеждаемся, что эти числа являются
решениями данного уравнения.
Ответ: {—И, 1}. ^
Пример 2. Решить уравнение
Зх 2х Зх — 6
х-1\ х + 2 (х—
Д Любое решение данного уравнения является решением
уравнения
59
которое получается из данного умножением на (х — \)(х-\-2).
Очевидно, это уравнение равносильно следующему квадратному
уравнению
По формуле D) находим его корни: х = —3 и х = —2.
Следовательно, решениями данного уравнения могут быть лишь
числа —3 и —2. Проверкой убеждаемся, что число —3 является
его корнем, а число —2 не является его корнем, так как при
х=—2 не определены обе части данного уравнения.
Ответ: {—3}. ^
Пусть заданы два уравнения. Тогда, если любое решение пер-
первого уравнения является решением и второго уравнения, то вто-
второе уравнение называется следствием, первого.
Если уравнение fi(x)=g1(x) является следствием уравнения
f(x)=g(x), то будем писать
Если уравнения f(x)=g(x) и h(x)=g1(x) равносильны, то,
очевидно, каждое из них является следствием другого. В этом
случае будем писать
Сформулируем несколько утверждений, широко используемых
при решении уравнений. Их доказательство предоставляется чита-
читателям в качестве легкого, но полезного упражнения.
1. Если функция ф (х) определена для всех х, для которых опре-
определены f (х) и g(x), то
(/ (х) = g (х)) <=> (/ (х) + ф (х) = g (х) + Ф (х)).
В частности,
2. Если функция ф (х) определена для всех х, для которых
определены f (х) и g(x), то
(/ (х) = g (х)) => (/ (х) Ф (х) = g (х) ф (х)).
Если, кроме того, ц>(х)фО для всех х, то
(f (х) = g (x)) <=> (/ (х) q>(x) = g (x) ф (х)).
В частности, для любого числа k Ф О
3. Для любых f(x), g(x) и
60
Очевидно, что любое решение х0 уравнения
f (х) = g (х) <р (х) E)
такое, что ц>(хд)ф(), является решением и уравнения
/(*)__.„/,л F)
Следовательно, в множестве всех чисел, для которых ц>()
уравнения E) и F) имеют одни и те же решения. В этом случае
будем говорить, что при условии ф(л:)^0 уравнения E> и F)
равносильны, и писать
i} (<р (л:) фО, f(x)=g(x) <р (а:)).
4. Каждое решение уравнения f(x)g(x)=0 является решением
по крайней мере одного из уравнений f(x)=O или g (х) = 0:
(/ (х) g (х) = 0) =5 (/ (х) = 0 или g (х) = 0).
Если функция f (х) опредемна для всех х, где g (х) = 0, а функ-
функция g (х) определена для всех х, где f (х) — 0, то
(/ (х) g (х) = 0) <=> (/ (х) = 0 млм я (х) = 0).
5. Для любых f (x) и g(x) и любого натурального п
Пример 3. Решить уравнение
Д Воспользуемся сформулированными выше утверждениями
и введенными обозначениями. Тогда
D (х + 5) = (а- + 2J) <=>
=>(л;2=16)<^(л; = 4 или х==—4).
Таким образом, решениями данного уравнения могут быть лишь
х = 4 и х = —4. Проверкой убеждаемся, что только х = 4 является
решением данного уравнения.
Ответ: {4}. А
Y
Заметим, что уравнения 2Yx-\-b =х + 2 и 4 (х + 5) = (;; + )
равносильны при условии х + 2^0. Поэтому схему решения
уравнения можно изобразить так:
4 (а: + 5) = (х + 2J) о
o(xSz-2, л:2=16)о(;: = 4).
Пример 4. Решить уравнение
|/4 + 2х--л2" = а:-2.
61
Д Имеем
2x-x2 = х - 2)
o(xis2; х = 0 или х = 3) <=> (х = 3).
Ответ: {3}. А
Любое предложение вида
/(*; y) = g(x; у), G)
где f (х\ у) и g (х; у) — некоторые функции переменных хну,
называется уравнением с двумя переменными хну или с двумя
неизвестными х и у. Функция f(x; у) называется левой частью,
a g(x; у) — праюй частью уравнения G).
Решением данного уравнения с переменными х, у называется
упорядоченная пара чисел (а; Ь), при подстановке которых соот-
соответственно вместо л; и у в обе части этого уравнения получается
верное числовое равенство.
Множество точек координатной плоскости, координаты которых
являются решениями уравнения, называется графиком этого урав-
уравнения. Так, например, графиком уравнения (х — хо)% + (у — yoJ = R2,
где R>0, является окружность радиуса R с центром в точке
(х0; у0). Графиком уравнения у = ах* + Ьх -\- с, где а, Ь, с —неко-
—некоторые числа, причем а=/=0, является парабола.
Уравнение' вида
0, (8)
где а, Ь, с —некоторые числа, называется линейным. Графиком
линейного уравнения (8), у которого хотя бы один из коэффици-
коэффициентов а или Ь не равен нулю, является прямая. Если а = Ь =
= с = 0, то любая пара чисел является решением уравнения (8),
а если а = 6 = 0, но сфО, то уравнение (8) решений не имеет.
Если каждое решение уравнения G) является и решением
уравнения
fi(x; y)=gi(x\ У), (9)
то уравнение (9) называется следствием уравнения G). В этом
случае график уравнения G) является частью графика уравнения
(9) (в частности, они могут совпадать). Если графики уравнений
совпадают, то они называются равносильными.
Легко доказать, что
1. (f(x; y)=g(x; y))<*(f(x; y)-g(x; y)==0).
2. (f(x; y) = g(x; y))o(kf(x; y)=kg(x; y))
для любого числа 1гфО.
3. (-~l^ = g(x; У))<*(<р(х; У)ФО, f(x; y) = g(x; y)<p(x\ у)).
^- (/(*; y)g(x\ if) = 0) => (/(jc; y)=0 или g(x; y)=0).
62
Пример 5. Нарисовать график уравнения у2 = 4х*.
Д Имеем
> (у2 - 4х2 = 0) <^> ((у - 2х) (у + 2х) = 0) <*
<=>(у — 2л; = 0 или г/+ 2я = 0) о (г/= 2л: или у--= — 2х).
Таким образом, график уравнения ?/2 = 4л:2 — это пара пересе-
пересекающихся прямых, заданных уравнениями у = 2х и у=--—2х
(рис. 31). ж
Наряду с уравнениями с одной переменной и с двумя перемен-
переменными в дальнейшем будут рассматриваться уравнения с тремя
и более переменными.
В общем случае решением уравнения с п переменными назы-
называется упорядоченный набор из п чисел, при подстановке которых
вместо переменных в обе части уравнения полу-
получается верное числовое равенство.
§ 2. Системы уравнений
Любое конечное множество уравнений называ
ется системой уравнений. В общем случае можно /
рассматривать систему т уравнений с п переменными '
(неизвестными), причем возможны все три случая рИс. 31.
т = п, т<Сп и т> п. Решением системы уравнений
с п переменными называется упорядоченный набор из п чисел,
являющийся решением каждого из уравнений системы. Решить
систему — значит найти все ее решения.
Сформулируем несколько правил преобразования систем урав-
уравнений.
1. Если в системе заменить какое-либо из уравнений на ему
равносильное, а остальные оставить без изменения, то вновь полу-
полученная система равносильна исходной.
2. Пусть f = g и ср = я|) — какие-нибудь два уравнения системы.
Тогда если в системе заменить уравнение f = g на уравнение
/4-ф=? + 113 (оно называется суммой уравнений f = g и ц=\р),
а остальные оставить без изменения, полученная система равно-
равносильна исходной.
3. Пусть система содержит уравнение х = ц>, где х — некоторая
переменная, а ц> — некоторая функция, не зависящая от х. Тогда
если во всех уравнениях системы, кроме уравнения х = ц>, вместо
х подставить ер, полученная система равносильна исходной.
На этом правиле основан способ решения систем, ко'орый
называется способом подстановки или способом исключения неиз-
неизвестных. Он сводит решение данной системы к решению системы
меньшего числа уравнений с меньшим числом переменных
(неизвестных).
4. Если система содержит уравнение f-g = O, то она распада-
распадается на две системы, в одной из которых уравнение f ¦ g = 0 заме-
63
нено на / = 0, а в другой—на g = 0. При этом каждое решение
данной системы является решением одной из полученных систем.
Если же функции fug определены на одном и том же множе-
множестве, то каждое решение полученных систем является решением
исходной системы. В этом случае говорят, что данная система
равносильна совокупности полученных систем.
На этом правиле основан способ решения систем, называемый
способом разложения на множители.
Пример 1. Решить систему уравнений
х — у=\.
Д Из второго уравнения системы находим х=\-\-у и под-
подставляем это выражение для х в первое уравнение. В результате
получим уравнение A -\-уJ-{-у2 = 2Ъ, содержащее только перемен-
переменную у. После преобразований получаем квадратное уравнение
у2 + у — 12 = 0. Оно имеет корни t/x = 3 и г/2= — 4. Теперь, под-
подставляя эти значения для у в уравнение л; = 1 -f-1/, находим
хг = 4 и х2= — 3. Следовательно, данная система имеет решения
D; 3) и ( — 3; —4). Заметим, что при решении этой системы был
применен метод подстановки.
Ответ: {D; 3), (-3; -4)}. А
Пример 2. Решить систему уравнений
( у2-\=4х2
\
Д Из первого уравнения системы следует, что у2 = Bх-\- IJ,
т. е. ?/ = 2л:+1 или у=— 2х— 1. Следовательно, данная система
равносильна совокупности следующих двух систем:
у=-2х-\,
Решим сначала первую систему. Подставив у = 2х+\ во вто-
второе уравнение системы, получаем
4х2 + Bх+\J-ЗхBх+\) = \,
и, наконец, хBл:+1) = 0, т. е. х = 0 или х = —1/2. Подставив
эти значения для х в уравнение у = 2х-{-1, получим соответственно
у=\ иу = 0. Следовательно, первая система имеет решения @; 1)
и (-1/2; 0).
Аналогично решается вторая система. Подставив у = — 2х — 1
во второе уравнение, получим, что л: Bл: + 1) = 0, Т. е. Х = 0 ИЛИ
х——1/2. Следовательно, вторая система имеет решения @; —1)
и (-1/2; 0).
Ответ: {@; 1), (-1/2; 0), @; -1)}. А
64
Пример 3. Решить систему уравнений
Д Умножив первое уравнение на 7, второе на —5 и сложив,
получим уравнение
12у2-2х2-5ху = 0.
Разложим его левую часть на два сомножителя. Для этого решим
его, например, относительно у как квадратное уравнение:
_ Ьх ±/25х2 + 96^ _ 5х ± 1 \к
У— 24 ~ 24 *
2 1
Следовательно, // = --х или у = — -тХ.
Данная система равносильна совокупности двух систем
2
Подставляя у = — х в первое уравнение, получаем
Следовательно, первая система имеет решения C; 2) и (—3; —2).
Аналогично получаем, что вторая система имеет решения
(/ -1/]/3) и (-4/J/3; 1/|/).
Ответ: {C; 2), (-3; _2),D/>/; -1//3), (-4//3";
Пример 4. Решить систему уравнений
Д Введем новые переменные м и и:
Тогда из данной системы относительно переменных и и v получим
систему уравнений
Легко видеть, что система уравнений A), B) равносильна
системе уравнений B), C). Следовательно, чтобы найти все решения
3 п/ред. Г. Н. Яковлева
системы A), нужно решить систему уравнений B), C). Причем,
если (%; уп их; и,)— некоторое решение этой системы, то (а:х; //х) —
решение системы A).
Система уравнений B), C) имеет специальный вид: уравне-
уравнения C) не содержат переменных х и у. Поэтому сначала решают
систему уравнений C), а затем, подставив в B) найденные значе-
значения для и и v, решают полученную систему уравнений относи-
относительно переменных х, у.
Решим систему C). Для этого обе части первого уравнения
возведем в квадрат:
— ив полученном уравнении сделаем замену а2 — и2-\-5. В резуль-
результате после некоторых преобразований получим уравнение
Это уравнение является квадратным относительно и'2. По формуле
для корней квадратного уравнения находим и2 = 4. Следовательно,
любое решение системы C) есть решение системы уравнений v~ = 4,
и2 = 9, которая имеет четыре решения: C; 2), C; —2), (—3: 2),
(—3; —2). Проверкой убеждаемся, что система C) имеет только
два решения C; 2) и (—3; —2).
Теперь из уравнений B) найдем соответствующие значения
переменных х, у. Подставив в B) значения ы = 3, v = 2, получим
х = 9, .?/= 4. При и =—3, v = —2 получим систему, не имеющую
решений. Следовательно, система A) имеет единственное решение
х = 9, у = 4.
Ответ: {(9; 4)}. а
Приведенное решение схематически можно изобразить следую-
следующим образом:
{A); B)} «{B); C)} о
¦о {B); и = 3, о = 2 или « = —3, v = — 2} о
<^{B); «--=3, и = 2}о{х = 9, у = 4, «=3, и = 2}.
Способ, который применялся при решении системы A), называ-
называется способом введения новых переменных (неизвестных). Этот спо-
способ часто применяется при решении систем. Приведем еще один
пример решения системы способом введения новых переменьых.
Пример 5. Решить систему уравнении
Д Преобразовав второе уравнение системы к виду
(х + уJ-3ху = 3,
66
видим, что удобно ввести новые переменные и=х + у, v=::y. Для
и, v получим систему уравнений
{и — и — 1,
«2-ЗО=:3.
Выразив и из первого уравнения и подставив во второе, полу-
получим квадратное уравнение
корнями которого являются числа »[ = 2и v2 = —1. Из /равне-
/равнения « = о+1 находим «! = 3 и и2 = 0.
Из предыдущего следует, что данная система равносильна
совокупности следующих двух систем:
xy = 2 \ xy = —1.
Первая система имеет два решения A; 2) и B; 1). Вторая
система имеет также два решения A; —1) и (—1; 1).
Ответ: {A; 2), B; 1), A; —1), (—1; 1)}. А
§ 3. Системы линейных уравнений
Рассмотрим систему двух линейных уравнений с двумя пере-
переменными:
Если все числа аи br,'cr, а2, b.2, с2 равны нулю, то любая
пара чисел является решением данной системы. Если же аи blt
а.2, Ъг равны нулю, а хотя бы одно из чисел сх или с2 отлично
от нуля, то система не имеет ни одного решения.
Рассмотрим случай, когда хотя бы одно нз чксел аъ a., bu b2
отлично от нуля. Пусть, например, ах ФО.
Тогда система A) равносильна системе
\Х + Ъ^1> B)
I а.гх -\- Ьгу ~-сг.
Прибавив ко второму уравнению первое уравнение, ум-южен-
ное на —а2, получим
' :-Ьл1а2)у = с,-^а,. C)
Следовательно, если Ъг—-а2ф0, т. е. аф^ — аф^Ф®, то
3*
67
Подставив это значение у в первое уравнение системы B),
находим
Таким образом, если а1Ь2 — аф1ф0, то система B), а также
и система A), имеет единственное решение, которое определяется
по формулам D), E).
Пусть теперь аф2 — a2bx = 0. Тогда если ахс2 — а2сг Ф 0, то урав-
уравнение C), а также система A), не имеет решений. Если же ахсг —
— a2ci = 0, то любая пара чисел (х; у), где
xy ye|R
ах ах *" v
является решением системы A).
Таким образом, если a1b2 — a2b1 — 0, то система A) либо
не имеет решений, либо имеет бесконечное множество решений.
Пусть, по-прежнему, Й1^0иЬа —- а2 = 0. Обозначим a2lax = k,
тогда a« = ka1 и из условия Ь2—-а^ = 0 следует, что Ьа = A^i-
В этом случае система A) имеет вид
ахх + bty = clt
axx + kbxy = Co.
Эта система имеет решение тогда и только тогда, когда съ — ксх.
Таким образом, если агФ0, а афг — сфх = 0, то система имеет
решение тогда и только тогда, когда второе уравнение получается
из первого почленным умножением на число k = a2/a1.
Выше предполагалось, что ^ФО. Если же, например, Ь2ф0,
то, поменяв местами уравнения и переменные в обоих уравнениях,
придем к уже разобранному случаю.
При нахождении решений систем в случае, когда atb2 — афх Ф 0,
можно пользовался формулами D), E), а можно проводить все
преобразования, которые мы делали при выводе формул D), E).
Пример 1. Решить систему уравнений
(
\
2
Д Второе уравнение умножим на у и вычтем почленно из
первого. В результате получим у у = 5, т. е. г/ = 3. Подставив
это значение у в первое уравнение заданной системы, получим
х= 1.
Ответ: {A; 3)}. А
68
Пример 2. Решить систему уравнений
Г 3*- «/ — 1.
[ 12л:~4г/ = 4.
Д Данная система равносильна одному уравнению Зх — у—\,
так как второе уравнение получается из этого почленным умно-
умножением на 4. Следовательно, ей удовлетворяет любая пара чисел
х, у = Зх — 1, и других решений система не имеет.
Ответ: {(х; 3*—1), хе^Щ. А
Пример 3. Решить систему уравнений
( х-\- у=--3,
Д Ни одна пара чисел не удовлетворяет этой система урав-
уравнений. Действительно, если первое уравнение почленно умножить
на 2 и Еычесть из второго, то получим уравнение 0=2, которое,
очевидно, не имеет решений.
Ответ: Система не имеет решений, а
Пример 4. При каких значениях параметра а система двух
уравнений
П
имеет бесконечнее множество решений?
Разделим первое уравнение на 8:
а-\-\ . а ,_.
-^р-* + ?/== у G)
Из второго уравнения системы F) вычтем уравнение G), умно-
умноженное на а + 3:
t+'y+q^ (8)
Очевидно, что при любом а система уравнений G), (8) равно-
равносильна данной. Следовательно, если в уравнении (8) коэффициент
при х не равен нулю, т. е. если
то система F) будет иметь единственное решение. Поэтому си-
система F) может иметь бесконечнее множество решений только
la + 1 )(а+3) „
тогда, когда а— у ^ 'v ¦ = 0, т. е. когда
Это квадратное уравнение имеет корни а = 3 и а = \.
69
При а = 3 из F) получаем систему
(
которая, очевидно, не имеет ни одного решения.
При а = 1 из F) получаем систему
равносильную одному уравнению х-\~4у = 2. Решением этого урав-
уравнения будет любая пара чисел B — 4у; у), где yeR. Следова-
Следовательно, система F) имеет бесконечное множество решений только
при а= 1.
Ответ: а= 1. а
Линейным уравнением с я переменными хь я2, ..., хп на?ы-
вается уравнение вида
ai*i + a2.v2 + • • • + ал = 6, (9)
где аь а2, ..., о„, Ь — некоторые числа. Если все числа аи ...
.,., ап, b равны нулю, то любой набор п чисел является реше-
решением этого уравнения. Если же все числа alt ..., ал равны
нулю, а ЬфО, то уравнение (9) не имеет решений. В дальнейшем
будем предполагать, что не все коэффициенты аъ ..., а„ равны
нулю.
При нахождении решений системы т линейных уравнений с а
переменными удобно пользоваться методом Гаусса. Этот метод
является частным случаем метода исключения переменных и
состоит в том, что равносильными преобразованиями данную
систему приводят к так называемой треугольной форме.
Пример 5. Решить систему уравнений
+ У+ 2 = 6,
2 = 8.
Д Прибавив почленно к первому уравнению второе, умно-
умноженное на —2, получим
— у 4-2 = 1 или у — г — — 1.
Далее, к третьему уравнению системы прибавив второе, умно-
умноженное на —3, получим уравнение —2у — 2г = —10. Наконец,
прибавив к этому уравнению уравнение y — z = — 1, умноженное
на 2, получим —4г = —12, т. е. 2 = 3.
70
В результате преобразований получили систему уравнений
+y+z= 6,
y — z = —\,
2 = 3,
которая, очевидно, равносильна данной.
Системы такого вида называются треугольными. Они легко
решаются. Действительно, из третьего, второго и первого урав-
уравнений последовательно находим 2 = 3, y = z— 1==2, x = fi — y —
— 2=1.
Ответ: {A; 2; 3)}. а
Решение системы линейных уравнений приведением к тре-
треугольной форме называется методом Гаусса.
Пример 6. Решить систему уравнений
х\ "Т" Х2 ~~ Х3 — 2|
Ч + хз = О-
Д Эту систему трех уравнений с четырьмя переменными
решим методом Гаусса.
Вычитая из второго, уравнения системы первое, получаем
Рассмотрим систему уравнений
2 + *Э =0,
I д.1.__1
( ^3+2 Л4"" 2 '
Эта система треугольной формы равносильна данной. Счдтая х4
произвольным, последовательно находим
— — * = * + ' v х —\ —
Следовательно, любой упорядоченный набор из четыре:: чисел
вида (l—t; 4" +-о ^ —Т~~Т^; 0' где ^е^' является реше-
решением данной системы уравнений, и других решений эта система
не имеет.
71
Пример 7. Решить систему уравнений
j— Хъ— Х4= 1,
¦5х3 — Зх4 = 6.
Д Вычитая из второго уравнения системы первое, получаем
уравнение
Далее, вычитая из третьего уравнения системы первое, умножен-
умноженное на 3, получаем
2х2 +8х3 = 3, *2-]-4*3 = 3/2.
Наконец, вычитая из последнего уравнения уравнение х2-|-4х3=1,
получаем уравнение 0 = 1/2, которое, очевидно, не имеет решений.
Следовательно, данная система не имеет решений.
Ответ: Система несовместна, а
Из приведенных примеров следует, что система линейных
уравнений может иметь одно решение (см. пример 5), бесконечное
множество решений (см. пример 6) и может не иметь ни одного
решения (см. пример 7).
§ 4. Задачи на составление уравнений
Пример 1. На обработку одной детали первый рабочий
затрачивает на 6 минут меньше, чем второй. Сколько деталей
обработает каждый из них за 7 часов, если первый обрабатывает
за это время на 8 деталей больше другого?
Д Обозначим через п количество деталей, которое обрабаты-
обрабатывает первый рабочий за 7 часов. Тогда одну деталь он обрабаты-
обрабатывает за 7/п часов. Второй рабочий за 7 часов обрабатывает я —8
деталей, следовательно, одну деталь он обрабатывает за 7/(я —8)
часов.
Так как на обработку одной детали первый рабочий затрачи-
затрачивает на 6 мин меньше, то
7 _ Т_ _ J_
л —8 п ~ 10 "
Решим это уравнение.
После умножения обеих частей уравнения на п(п — 8) и при-
приведения подобных членов получаем квадратное уравнение
п% - 8п - 560 = 0.
Найдем корни этого уравнения:
n = 4± j/16+560 = 4 ±24.
72
Условию задачи удовлетворяют только положительные зна1ения п,
поэтому п = 28. Следовательно, первый рабочий обрабатывает 28
деталей, второй на 8 меньше, т. е. 20 деталей.
Ответ: 28 и 20 деталей. А
Пример 2. В сосуде было 10 лшров соляной кислоты. Часть
соляной кислоты отлили и сосуд дополнили таким же количе-
количеством воды. Затем снова отлили такое же количество :меси и
дополнили сосуд таким же количеством воды. Сколько литров
отливали каждый раз, если в результате в сосуде оказался
64%-й раствор соляной кислоты?
Д Обозначим через х литров количество соляной кислоты,
которое отлили первый раз. После первого отливания и добавле-
добавления воды в смеси стало 10 — х литров соляной кислоты и х лит-
литров воды. Следовательно, в каждом литре смеси содержится
10—х
—7q— литра кислоты.
После отливания х литров смеси в сосуде остается 10 —л:
литров смеси, в которой содержится
литров соляной кислоты.
После доливания х литров воды в сосуде оказывается 10 лит-
литров смеси, из них -—; ¦¦ литров соляной кислоты. Процентное
содержание соляной кислоты равно
С другой стороны, по условию задачи это содержание равно 64%.
Поэтому для х получаем уравнение
A0-а-J = 64,
из которого следует, что х = 2.
Ответ: 2 литра. ^
Пример 3. Если двузначное число разделить на произведе-
произведение его цифр, то в частном получится 1, а в остатке 16. Если
же к квадрату разности цифр этого числа прибавить произведе-
произведение его цифр, то получится заданное число. Найти это число.
Д Обозначим первую цифру искомого двузначного число
через а, а вторую цифру через Ъ. Тогда искомое двузначное числа
равно \0а + Ь.
Из первого условия задачи следует уравнение
A)
а из второго — уравнение
B)
73
В результате для а и Ъ получили систему уравнений A), B).
Левые части в уравнениях A), B) равны, следовательно, равны
и правые, т. е. ab-\- 16 = (a — bJ + ab. Из этого уравнения следует,
что (а — бJ = 16, т. е. а — Ь = ±4.
Рассмотрим случай, когда а —6 = 4. Подставив а = 6 + 4
в уравнение A), после преобразований получим квадратное урав-
уравнение
Ьг —7& —24 = 0.
По формуле корней квадратного уравнения имеем
,_ 7 ±/49 + 96 _ 7±УН5
°^ 2 2 •
Так как ft —целое число, то в этом случае задача не имеет
решений.
Рассмотрим второй случай, когда а —6 =—4, т. е. а = 6 —4.
Подставив это выражение для а в уравнение A), получим квад-
квадратное уравнение
б2- 156 + 56 = 0.
Решая это уравнение, находим 6i = 7 и 62 = 8. Из формулы с.=
= 6 — 4 находим пх = 3 и а2 = 4.
Ответ: 37 и 48.
Пример 4. Два спортсмена бегают по одной замкнутой
дорожке стадиона. Скорость каждого постоянна, и на пробег всей
дорожки один тратит на 5 секунд меньше другого. Если они
начинают пробег с общего старта одновременно и в одном направ-
направлении, то окажутся рядом чере^ 3D секунд. Через какое время
они встретятся, если побегут одновременно с общей линии старта
в противоположных направлениях?
Д Пусть vu у., —скорости спортсменов. Для определенности
положим У2>У!. Обозначим через S длину замкнутой дорожки
стадиона- Тогда первый спортсмен пробегает се за S/Vi секунд,
а второй — за S/v2. Так как первый спортсмен затрачивает на
5 сек. больше, то получаем уравнение
А_Л=5. C)
За 30 секунд спортсмены пробегают расстояния соответственно
30ух и 30у2. Если они бегут в одном направлении, то в момент
их встречи второй пробежит на один круг больше, т. е.
S = 3Q(v2-v1). D)
Получили систему двух уравнений C), D) с тремя переменными
vu vit S.
Разделив обе часги уравнения D) на 30S, получим
Ex _ i!t - -1. ' E)
S 5 ~~ 30 * 10'
74
Введем обозначения p1 = v1fS и p2 = v2/S. Тогда из уравне-
уравнений C), E) для рх и р2 получим систему
1 Pi Рг /с\
Из второго уравнения находим
Подставив это выражение в первое уравнение системы F),
получим квадратное уравнение
Следовательно,
" —5 + 25 1
_
300 ~~ 300 "~ 15
(Здесь перед корнем взят только знак +, так как по условию
задачи pi>0). Подставив это значение рх в G), получил р2 —
= 1/10. Зная pi и р2, легко ответить на вопрос, постай леиный
в задаче: через какое время спортсмены встретятся, если тобегут
одновременно с общей линии старта в противоположных направ-
направлениях. Действительно, это время равно
S 1 1 1 _ J50 _-
vi,}h_ P1 + P2 1 , J 5
S + S 15 + 10
Следовательно, искомое время равно 6 секундам.
Ответ: 6 с. а
Заметим, что рх и р2 —зто величины скоростей споргсменоз
в случае, если за единицу длины принять длину замкнутой
дорожки стадиона.
ЗАДАЧИ РАЗДЕЛА I
Решить ураьнения A—5):
3 2 а:—1
2.
3.
5.
х+2 х+
|/ g jjj. у '.
2x* + 3x—5l
1 x*+3x+\
УЗ— х
:+1 | + 4.
л3 + 4^+9
' 2х2 -4- 3jt -|- 9 -l-i
2.
3=0.
75
Решить системы линейных уравнений методом Гаусса F—8):
6.
8.
3*+ у+
2х+
= 8, 7.
= 6,
4*t — *2 + 3*3+*4 = 4.
х + 2у—Зг=1,
2*+3//—6г = 0,
Зд: + 3// — 5г = 0,
Х-\- //+ 2=3.
( 2*2-|-3i/2 — 4j
\ 2*2 — //2 = 7.
Решить системы уравнений (9—13):
9. ( *-+2//2 — 2ху = о, 10.
\*+2//=7."
11. Г 3*«— *2 — ф =5, 12.
13.
3*22—4*1/+ — = 0,
3*2 — //2=1.
14. Найти все значения параметра с, при которых система
не имеет ни одного решения.
15. Вдоль реки расположены пункты А, В, С (В между А и С). Катер
прошел расстояние от А до С за 7 часов. На каждом из участков АВ и ВС
его собственная скорость (скорость относительно воды) была постоянна, при-
причем на участке ВС в 1 -- раза меньше, чем на участке АВ. Обратный путь
от С до Л катер прошел за 8 часов, и на всем пути его собственная скорость
была в 1 раза больше, чем при движении из А в В. Если бы на обратном
3
пути собственная скорость катера была такой же, (как и при движении из А
в В, то участок от В до А он прошел бы за 6 часов. Сколько времени катер
шел от В до О (Скорость течения реки постоянна.)
ЗАДАЧИ РАЗДЕЛА II
Решить уравнения A — 11):
2 2Hiiii^±i
2/ + 1"
2//+1 у+\
5у+4
76
7.
8. Vx~^
10.
11.
X — iVJ^\^=\. 9.
— V*2 — 2д;-Гз = о.
10.
10 = 0.
12. При каких значениях параметра а уравнения лг2 + 5л:+а=0 н'-|-
+ 2ax-\-a2—4а+25 = 0 имеют действительные корни?
Решить системы уравнений методом Гаусса A3—18):
у — 72 = 0,
3* —
13.
/— 102=— 3.
15. ( Хх— Хг — А"з + *4=1.
17.
14.
1,
2=1,
— 2=1,
/ —42=19,
5л + 3г/—Зг= 15,
од: —3(/ + 3г= 15.
cx — jfa — лг3 = — 3, 18.
^ — ^ + ^3—2^4=3,
*1 — #2 — Х3 — Д;4 = 1 >
Решить системы уравнений A9—30):
/ = 28,
19. ( *2+f/2 = 41, 20.
\ х +у = 9.
21. / х2 — Xy=G, 22.
\ ху+ i/2=4.
23. I x — xy3 = l, 24.
= 3.
I x — xi
25. | x* — xy+y2 =7,
-.1.
{
26.
¦17.
27. / x 4 28.
-- + -—= 2,
c+j/_ 10
/ — 2x— 2u=2.
29.
y^S^-^/i, 30-
I *+i/=12.
31. Сколько действительных решений имеет система уравнений
в зависимости от параметра а?
77
32. Определить, при каких значениях параметра а система уравнений
{
имеет в точности два решения.
Решить системы уравнений C3 — 38):
33. ( ху — лгг + 3</ + 6г = 0, 34. [ ху-\-2цгг — 42a =0,
I > I
j I
^ гу — г2—2х— (/ = 0. \ у3 — 7хг2—13z:i = 0.
35. ( у3 — ху + х- — г3, 38. ( xy — 5x + 6y — iz,
[ ¦''~y'i=x--\-y"-^zi. { уг =
f !/2 + г2 = ^ + 2(/2-2,
| ;!* + .*2=!,-э + 2г* —3,
ATI/
39. Если двузначное число разделить на произведение его цифр, то в част-
частном получится 3, а в остатке 9. Если же из квадрата суммы цифр этого числа
вычесть произведение его цифр, то получится данное число. Найти это число.
40. Имеется дпа растнора поваренной соли разной концентрации. Если
слить вместе 100 г первого раствора и 200 г втррого, то получится 50%-й
раствор. Если же слить 300 г первого раствора и 200 г второго, то получается
42%-й раствор. Определить концентрации данных растворов.
41. От двух кусков сплава с различным процентным содержанием меди,
весящих соответственно т. кГ и п кГ, было отрезано по куску равного веса.
Каждый из отрезанных кусков был сплавлен с остатком другого куска, после
чего процентное содержание меди в обоих сплавах стало одинаковым. Сколько
весил каждый из отрезанных кусков?
42. Бассейн, к которому подведены две трубы, через первую трубу напол-
наполняется на 5 часов быстрее, чем через вторую. Если сначала открыть вторую
трубу, а через 8 часов открыть и первую, то бассейн будет наполнен за 18 ча-
часов. Какова емкость бассейна и сколько воды птекает через каждую трубу за
1 час, если за 5 часов через первую трубу и за 4 часа через вторую прохо-
проходит в сумме 20 м3 воды?
43. Бассейн наполнялся несколькими насосами одинаковой производитель-
ностн, которые включались один за другим через рапные промежутки времени.
К моменту включения последнего насоса была заполнена 1/6 часть бассейна.
В другой раз при наполнении этого бассейна производительность каждого насоса
была уменьшена на 10%, а промежутки между включениями остались преж-
прежними. Какую часть бассейна наполнят насосы d этот раз за первую половину
всего времени работы?
44. Однотипные детали обрабатываются на двух станках. Производитель-
Производительность первого станка на 40% больше производительности второго. Сколько
деталей было обработано за смену каждым станком, если первый работал
78
б эту смену 6 часов, а второй —7 часов, причем вместе они сбработали
616 деталей?
45. Двум рабочим было поручено изготовить партию одинаковы t деталей.
После того как первый проработал 7 часов и второ.'! 4 часа, оказ;лось, что
они выполнили 6/9 всей работы. Проработав совместно еще 4 часа, они уста-
установили, что им остается выполнить 1/18 всей работы. За сколько часов каж-
каждый из рабочих, работая отдельно, мог бы выполнить всю работу?
46. Две бригады колхозников должны были закончить уборку урожая за
12 дней. После 8 дней совместной работы первая бригада получила другое
задание, поэтому вторая закончила оставшуюся часть работы зл 7 дней. За
сколько дней могла бы убрать урожай каждая бригада, работая отдельно?
47. Две организации приобрели некоторое количество разных туристиче-
туристических путевок, первая — на 300 рублей, вторая —на 270 рублен. Втсрая орга-
организация купила на 5 путевок меньше, но заплатила за каждую плевку на
3 рубля больше. Сколько путевок купила каждая организация?
48. ЭВМ должна решить две задачи. Первая состоит из 9 миллюнов опе-
операций типа Л и 16 миллионов операций типа В и требует 11 минут 40 секунд
машинного времени. Вторая задача содержит вдвое больше операций типа А
и вдвое меньше операций типа В, на ее решение машина тратит 13 минут
20 секунд. Сколько операций каждого типа может выполнить ЭВМ в секунду?
49. Пассажир метро спускается вниз по движущемуся эскалатору за
24 сек. Если пассажир идет с той же скоростью, но по неподвижному эска-
эскалатору, то он спускается за 42 сек. За сколько секунд он спустится, стоя на
ступеньке движущегося эскалатора?
50. Найти скорость и длину поезда, зная, что он проходит ми ло непод-
неподвижного наблюдателя за 7 сек и затрачивает 25 сек на то, чтобы пройти
с той же скоростью мимо платформы длиной 378 м.
51. Два автомобиля, двигаясь по кольцевой дороге с постоянны ли скоро-
скоростями в одном направлении, оказываются рядом через каждые 56 Mi-нут. При
движении с теми же скоростями в противоположных направления:: автомо-
автомобили встречаются через каждые 8 минут. За какое время проедет всю кольце-
кольцевую трассу каждый автомобиль?
52. Из пункта А выехали три велосипедиста, первый на 1 ча: раньше
двух других, стартовавших одновременно. Скорость каждого вело:ипедиста
постоянна. Через некоторое время третий иелосипедист догнал перво о, а вто-
второй догнал первого на два часа позже, чем третий. Определить стношение
скоростей первого и третьего велосипедистов, если отношение скогости вто-
второго к скорости третьего равно 2/3,
53. Пешеход и ьелосипедист отправляются из пункта А в пунк? В одно-
одновременно. В пункте В велосипедист поворачивает обратно и встречает пеше-
пешехода через 20 мин. после начала движения. Не останавливаясь, велосипедист
доезжает до пункта А, поворачивает обратно и догоняет пешехода через
10 мин. после первой встречи. За какое время пешеход пройдет г уть от А
до й?
54. Катер по реке и автобус по дороге, идущей вдоль берега реки, отрав-
отравляются одновременно из пункта А в пункт В и совершают безостановочное
движение между А к В. Первая встреча их произошла, когда автобус прошел
5/9 всего расстояния от Л до В, а вторая встреча — когда автобус иэсле пер-
79
вого захода в В проехал 1/8 всего расстояния от В до А. Первый раз в пункт
А автобус прибыл на 16 мин. позже катера. Через сколько часов после на-
начала движения автобус и катер первый раз окажутся одновременно в пункте
А, если скорость катера в неподвижной воде и скорость автобуса постоянны.
55. Из пункта А в пункт В одновременно отправились два поезда. Каж-
Каждый из них вначале двигался равноускоренно (ускорения поездов различны,
начальные скорости равны нулю), а затем, набрав некоторую скорость,—рав-
скорость,—равномерно. Пройдя треть пути от Л до В, один из поездов поравнялся с другим
поездом и с этого момента начал двигаться равномерно. Весь путь от Л до В
один из поездов прошел в 1,2 раза быстрее другого поезда. Определить отно-
отношение скоростей равномерного движения поездов.
56. Несколько самосвалов загружаются поочередно в пункте А (время
загрузки одно и то же для всех машин) и отвозят груз в пункт В, там они
мгновенно разгружаются и возвращаются в А. Скорости машин одинаковы,
скорость груженой машины составляет 6/7 скорости порожней. Первым выехал
из А водитель Петров. На обратном пути он встретил водителя Иванова,
выехавшего из А последним, и прибыл в А через 6 минут после встречи.
Здесь Петров сразу же приступил к загрузке, а по окончании ее выехал в В
и встретил Иванова второй раз через 40 минут после первой встречи. От места
второй встречи до А Иванов ехал не менее 16 минут, но не более 19 минут.
Определить время загрузки.
Глава IV
АЛГЕБРАИЧЕСКИЕ НЕРАВЕНСТВА
§ 1. Функциональные неравенства.
Понятие равносильности неравенств
Рассмотрим две функции f(x) и g(x), определенные на неко-
некотором множестве X. Часто бывает необходимо узнать, при каких
значениях х значения первой функции меньше соответствующих
значений второй. Другими словами, требуется найти вс<: значе-
значения переменкой, при которых верны числовые неравенстве! f(x)<i
<#(*)• Такого типа задачи принято называть задачами на реше-
решение неравенств.
Таким образом, решить неравенство
f(x)<g(x)
— это значит найти все значения х, при подстановке которых
в неравенство получается верное числовое неравенство. Каждое
такое значение х называется решением неравенства. Совокупность
всех решений называется множеством решений. Решить неравен-
неравенство—значит найти его множество решений. Неравенстве f(x)<i
<.g(x) называют строгим, неравенство f (х) «ё g(x) — нестрогим.
При решении неравенств, так же как и при доказательстве
неравенств (о чем речь пойдет в § 6), фундаментальное значение
имеет понятие равносильности неравенств.
Два неравенства
h (х) < gi (х) и /2 (х) < gt (x)
называют равносильными на множестве М, если каждое решение
первого неравгнетва, принадлежащее множеству М, является ре-
решением второго неравенства и, наоборот, каждое решение второго
неравенства, принадлежащее множеству М, является решением
первого неравенства.
Равносильными на множестве М считают также неразенства,
которые на этом множестве ке имеют ни одного решения
В некоторых случаях удается, последовательно преобразуя
данное неравенство, свести его к более простому неразенству,
равносильному исходному. При установлении равносильности
неравенств чаще всего используются следующие утверждения.
81
1. Неравенства
f(x)<g(x) и -f(x)>-g(x)
равносильны на любом числовом множестве.
2. Если / (х) и g (х) на множестве М принимают только поло-
положительные значения, то неравенства
f(x)<g(x) и щ>-^
равносильны на М.
3. Если функции f(x), g(x), ц>(х) определены на множестве М,
то неравенства
f(x)<g(x) И f
равносильны на множестве М.
Отсюда следует равносильность неравенств
) и f(x)-q>(x)<g(x),
т. е. правило переноса слагаемых из одной части неравенства
в другую.
4. Если функции f (x), g(x), ф (х) определены на множестве М
и ф (х) >0 на этом множестве, то неравенства
f(x)<g(x) и f(xL>(x)<g(xL(x)
равносильны на М.
5. Если функции f(x) и g(x) определены на множестве М
и принимают только положительные значения, то неравенства
f(x)<g(x) и f*(x)<g*(x)
равносильны на М.
Справедливость этих утверждений легко следует из соответст-
соответствующих свойств числовых неравенств. Аналогичные утверждения
верны и для нестрогих неравенств.
Заметим, что для доказательства неравносильности двух нера-
неравенств на некотором множестве достаточно указать один элемент
этого множества, являющийся решением одного неравенства, но
не удовлетворяющий другому неравенству.
Пример 1. Равносильны ли на множестве всех положительных
чисел следующие неравенства:
а) х2 ^ х3 и 1 «s х,
б) хя + Ух<х2 + Ух и х*<х2,
в) У'х
Д а) Неравенства равносильны в силу утверждения 4 для
нестрогих неравенств:
= **,
82
б) Равносильность неравенств следует из утверждения 3:
f(x)=xs, g(x)=x\ (p(x) = Vx-
в) Неравенства равносильны согласно утверждению 5:
Пример 2. Равносильны ли неравенства из примера 1 на
множестве всех действительных чисел?
А а) Неравенства неравносильны, так как х=- О удовлетворяет
первому неравенству и не удовлетворяет второму.
б) Неравенства неравносильны, так как х =— 1 удовлетворяет
только второму неравенству.
в) Неравенства неравносильны, так как х =—1 входит
в множество решений второго неравенства, но не принадлежит
множеству решений первого. А
Пример 3. Равносильны ли на множестве всех действитель-
действительных чисел неравенства
х-2>х2?
Д Если х3-{-х — 2^0, то решений нет ни у первого неравен-
неравенства, ни у второго. Если х3 + х — 2>0, то и х>0, и согласно
утверждению 5 неравенства равносильны. СледоЕ*ательно, данные
неравенства равносильны на везм множестве действительных
чисел, а
§ 2. Рациональные неравенства. Метод интервалом
В главе I в качестве простейших числовых функций рассмат-
рассматривались многочлены
и функции, представимые в виде отношения двух многочленов
*-«<">-¦?&
т. е. рациональные функции.
Число а называется нулем функции у = Р„(х) или корнем
многочлена Р„(х), если Рп(а) = 0.
Например, многочлен Р2 (х) = 6 -- 5х + х2 имеет два н>лях = 2
и х = 3, так как А3B)=0 и Р2C) = 0. Многочлен может вообще
не иметь нулей: например, Ро (я) = 1 или Р2 (х) = 1 + х2. Известно,
что число нулей многочлена не превышает его степени (гл. VIII, § 7).
Нули многочленов Рп (х) и Qm (x) будем называть критическими
значениями переменной или критическими точками рациональной
функции
83
Например, для функции
_ Р3(х) х3— 6л2 — л:+6 _ (л:2—!) (л —6)
У ~ QAx) = x* + 3x + 2 ~ (х+1)(х + 2)
критическими значениями переменной являются
х = — 2, х = — 1, х=1, х = 6.
Рациональным неравенством называется неравенство, которое
содержит только рациональные функции.
Рациональные неравенства часто удается решить так назы-
называемым методом интервалов. Этот метод основан на одном важном
свойстве рациональной функции, которое мы примем без доказа-
доказательства, а именно: в интервале между двумя своими соседними
критическими точками рациональная функция сохраняет знак.
Метод интервалов состоит в следующем. Рациональное нера-
неравенство приводят к стандартному виду.
"п i)\ ~>® или п"il <Q (B слУчае строгого неравенства),
**/и \Х) чт \Х)
О 1х\ ^ в или "о^Ж^^ (в случае нестрогого неравенства).
Затем находят все критические точки рациональной функции.
Эти точки отмечают на числовой оси. Вся числовая ось разбива-
разбивается критическими точками на конечное число интервалов, на
каждом из которых левая часть неравенства сохраняет знак. Чтобы
определить знак левой части на всем интервале, достаточно опре-
определить знак Рп (x)lQm (x) в одной какой-либо точке этого интервала
и тем самым установить, входит ли этот интервал в множество
решении данного неравенства.
Что касается самих критических точек, то в случае строгого
неравенства Рп (x)/Qm (x) > 0 они, очевидно, не входят в множество
решений; в случае нестрогого неравенства Рп (x)/Qm (x) э= 0 нули
многочлена Рп (х) входят в множество решений, если только они
не являются нулями и многочлена Qm(x).
Не следует думать, что методом интервалов можно решить
любое рациональное неравенство. Метод интервалов применим
только тогда, когда известны (или могут быть найдены) нули
многочленов Рп(х) и Qm(x), т. е. критические значения переменной
для рациональной функции Рп (x)/Qm (x). К сожалению, задача
отыскания нулей многочлена далеко не всегда может быть реше-
решена (см. гл. VIII, § 7).
Пример 1. Решить неравенство
Д Нули многочлена, стоящего в знаменателе: х = — 1 и х = —2.
Нули многочлена, стоящего в числителе, легко находятся.
84
В самом деле,
А-з_3*2-х + 3 = х2(х-3)-(х-3) = (х-3) (х- 1) (х-\-1).
Неравенство можно записать теперь следующим образом:
(х —3) (х— 1) (х+ 1)
Критические точки рациональной функцин суть
х = —2, х = — 1, х=1, х = 3.
Числовая ось разбирается этими точками на 5 интервалоЕ. Отме-
Отмечаем точки на числовой оси (рис. 32). Для определение знака
функции на каждом интервале можно действовать следующим
образом. Замечаем, что при х~>3 все линейные множители числи-
числителя и знаменателя рациональной функции положительны и,
следовательно, на интервале J3; +оо[ функция принимает только
положительные значения. На рнс. 32 над интервалом ]i5; -f-°°[
ставим знак «плюс».
При переходе через точку х = 3 от интервала ]3; +оо[ :< интер-
интервалу ]1; 3[ лишь один из линейных множителей, а именно х — 3,
изменяет знак и, следовательно, функ-
функция становится отрицательной. На
рис. 32 под интервалом ]1; 3[ ставим
знак «минус».
Затем, переходя к следующему Рис. 32.
интервалу ]—1; 1[, устанавливаем,
что знак изменяется только у множителя х—\. Это означает,
что при переходе через точку х~\ левая часть неравенства
изменяет знак. При переходе через точку х = — 1 знак функции,
очевидно, сохраняется, так как множитель х-\-\ присутствует
и в числителе и в знаменателе рациональной функции. Наконец,
переход к последнему интервалу ]—оо; —2[ опять сопровождается
изменением знака функции. Чередование знаков фиксиэуем на
рисунке.
Поскольку неравенство строгое, сами критические точки не
являются решениями. (Стрелки на рис. 32 как раз и указывают
на это.)
Ответ: ]-2; -1[и]-1; 1[U]3; +oo[. A
В процессе решения данного неравенства может возникнуть
соблазн заменить его с самого начала более простым нераиенстаом
(* + 2) —"'
Такое упрощение (сделанное без всяких оговорок) приведет
к ошибке. Полученное неравенство неравносильно исходному, так
как в его множество решений входит х = — 1, а это гначение
переменной не является решением данного неравенства.
85
Пример 2. Решить неравенство
(X+3)»
Д Критические точки рациональной функции:
х ——3, # = 0, х = 4.
Числовая ось разбивается на 4 интервала (рис. 33), на каждом
из которых легко определяется знак функции. При определении
знака нужно следить только за изменением знака линейных мно-
множителей знаменателя, так как квадра-
квадратичные множители числителя (лг + 3J
и x2Jrx-{-l положительны на всех
четырех интервалах. Из трех критн-
ри gg ческих точек только х = —3 входит
в множество решений неравенства.
Ответ: {—3} U ]0; 4[. А
Пример 3. Найти область определения функции
2 1 2*-1
х2—х+\ х-\-\ х3-\-\ '
Для нахождения области определения данной функции нужно
решить неравенство
2 1_ 2х-\ ^п
xz — x+l х+1 х3 + 1 ="
Приводим его к стандартному виду:
Находим критические точки х = — 1 и х — 2 и записываем нера-
неравенство следующим образом:
Так как х2 — х+1>0 для всех значений переменной, переходим
к равносильному неравенству
р 34 Критические точки разбивают чис-
числовую ось на три интервала (рис. 34).
Определяем знак левой части нера-
неравенства на каждом интервале. Исследуем сами критические точки:
точка х = 1 является нулем числителя и, так как неравенство
нестрогое, входит в множество решений. Точка х= — 1, хотя и
86
является нулем числителя, ие принадлежит множеству решений
из-за того, что обращает в нуль знаменатель.
Ответ: ]—оо; —1[и]—1; 2]. а
§ 3. Иррациональные неравенства
Перейдем к рассмотрению неравенств, содержащих переменную
под знаком корня (радикала). Обычный способ решения таких
неравенств заключается в сведении их к рациональным неравен-
неравенствам. Освободиться от радикалов иногда удается путем возведения
обеих частей неравенства в степень. К сожалению, эта операция
часто приводит к неравенству, неравносильному исходному. Поэтому
при решении иррациональных неравенств рекомендуется п юявлять
максимальную осторожность. Прежде всего следует огра учиться
рассмотрением только тех значений переменной, при которых обе
части неравенства имеют смысл. Рассмотрим типичней при-
пример.
Пример 1. Решить неравенство
! —x.
Нередко учащиеся приводят такое рассуждение: «при решении
иррациональных уравнений и неравенств необходимо прекде всего
избавиться от корня, поэтому возведем в квадрат обе части
неравенства, т. е. напишем
но отсюда следует, что 3^4 что неверно; значит предложенное
неравенство решений не имеет».
Зададимся вопросом, насколько правдоподобен порученный
результат?
В данном случае достаточно внимательно посмотреть на нера-
неравенство, чтобы увидеть, что полученный результат н<: юько
неправдоподобен, но просто невереи. При х = Ь, например, левая
часть неравенства положительна, тогда как правая отрицательна.
Таким образом, неравенство имеет решения и, следогательно,
приведенное рассуждение порочно.
Дадим правильное решение примера 1.
Д Очевидно, следует рассмотреть только те значения х, при
которых х2 — 4х + 3 2э 0. Нули многочлена х2 — Ах + 3 суть хх = 1,
дс2 = 3. Следовательно, множество решений неравенства ;:2 — 4л: -f-
+ 3^0 таково: ]—оо; I]U[3; +оо[. Ясно, что на интервале ]1; 3[
нет решений, так как левая часть неравенства при люЗом х из
этого интервала не имеет смысла.
Заметим далее, что ]/~х2 — Ах -\- 3 ^ 0 (радикал понимается
в арифметическом смысле), н так как при любом х^',\ правая
часть неравенства iwenbiiie нуля, то все хЗгЗ являются репе ни ям и.
87
Если же jcsS 1, то 2 —л;>0 и, возведя обе части неравенства
в квадрат, получим равносильное неравенство
которое не имеет решений, так как неравенство 3^4 ложно.
Ответ: [3; +оо[. А
Пример 2. Решить неравенство
1 — У'\ — 4 у» _3_
>
Д Левая часть неравенства имеет смысл тогда и только тогда,
когда \х |^1/2 и хфО.
Если —l/2ss;x<:0, то левая часть неравенства отрицательна
и, следовательно, решений на этом интервале нет.
Пусть 0 < х^ 1/2, тогда, после очевидных преобразований
получим
х
Обе части неравенства неотрицательны, поэтому, возводя обе части
в квадрат, получим равносильное неравенство
\-4х2< 1-Зл: + |-л;2.
Последовательно упрощая это нерагенство, получим
Учитывая ограничение 0<*«;l/2, приходим к окончательному
результату 12/25<a;«s 1/2.
Ответ: ] 12/25: 1/2]. А
Пример 3. Решить неравенство
Д Обе части неравенства имеют смысл для тех и только тех
значений х, которые удовлетворяют системе неравенств
2x-5
Легко видеть, что эта система имеет одно решение х = 5/2. Под-
Подстановкой в неравенство убеждаемся, что л; = 5/2 является решением.
Ответ: {5/2}. ж
88
§ 4. Неравенства с модулем
В школьном курсе математики часто встречаются неравенства,
содержащие переменную под знаком абсолютной величины (под
знаком модуля).
Для решения таких неравенств рекомендуется разбить числовую
ось на отдельные промежутки так, чтобы на каждом из нш: можно
было записать неравенство, не используя знака абсолютной
величины.
Пример 1. Решить неравенство
Д Всю числовую ось разобьем на два промежутка
j_TO; _6/5[ и [-6/5; +оо[. /
На каждом из этих промежутков неравенство может быть запи-
записано без знака модуля.
Для промежутка ]—оо; —6/5[ верно равенство |5a-J-6|—
= — Ьх — 6, и, следовательно, неравенство принимает вид
л:2 + 5л: + 6>0 или (л- + 3)(х + 2)>0,
откуда хе]—оо; —3[U] —2; +оо[. Учитывая, что переменная
принадлежит промежутку ]—оо; —6/5[, получаем решение исход-
исходного неравенства на этом промежутке:
]-оо; -3[U]-2; -6/5[.
На втором промежутке [—6/5; -J-oo[ справедливо равенство
15л: + 6 | = 5x4-6, и, следовательно, неравенство записывается так:
х2 — Ьх — 6>0, или (х+ 1) (х— 6) >0, откуда хе=\—оо; — 1[ (J
U]6; -(-°°[- Учитывая, что переменная принадлежит промежутку
[—6/5; — оо[, получаем множество решений неравенства на этом
промежутке:
[-6/5; -1[U]6; +oo[.
Ответ: ]-оо; — 3 L U ] — 2; -1[U]6; +oo[. A
Пример 2. Решить неравенство
x2 — x—2 -" 1 '
Д Для я^1/2 неравенство можно переписать без знака
абсолютной величины:
2*—1 1
Это рациональное неравенство. Приводим его к'стандартноиу виду
89
Применяя метод интервалов, получаем хе]- 1; 0[U]2;5[. Огра-
Ограничение х 5= 1/2 заставляет оставить лишь интервал ]2; 5[. Если
л;<1/2, то неравенство примет вид
x2—x—2 "^ 2 '
Приводим неравенство к стандартному виду
Применяя метод интервалов, легко получаем, что у е
е] —4;—1[U]1;2[. Ограничение х<;1/2 заставляет оставить
только интервал ]—4; — 1[.
Ответ: ]— 4;— 1[ (J ]2;5[. А
Пример 3. Решить неравенство
Д На интервале ]—оо; — 1[ по определению модуля имеем
|дс — 1 i = — х+l, \х+1\ = — х—\, и, следовательно, на атом
интервале неравенство равносильно линейному неравенству — 2х<С
<4, которое справедливо при х> — 2. Таким образом, в мно-
множество решений входит интервал ]—2; — 1[. На отрезке [— 1; 1]
исходное неравенство равносильно верному
числовому неравенству 2<4. Поэтому все
значения переменной, принадлежащие этому
отрезку, входят в множество решений.
На интервале ]1; +°°[ опять получаем
линейное неравенство 2дс<4, справедливое
при х<с2. Поэтому интервал ]1; 2[ также
входит в множество решений. Объединяя по-
лученные результаты, делаем вывод: нера-
Рис. 35. венству удовлетворяют все значения перемен-
переменной из интервала ]— 2; 2[ и только они.
Тот же результат можно получить из наглядных и в то же
время строгих геометрических соображений. На рис. 35 построены
графики функций
0 = /(*) = [*-1| + [х+1| и у = 4.
На интервале ]—2; 2[ график функции y = f{x) расположен под
графиком функции у = 4, а это и означает, что неравенство
/{х)<С4 справедливо.
Ответ: ]-2; 2[. д
§ 5. Неравенства с параметрами
Решение неравенств с одним или несколькими параметрами
представляет собой, как правило, задачу более сложную по срав-
сравнению с задачей, в которой параметры отсутствуют.
90
Например, неравенство
У а -\- х -\- ]/ а — х > а,
содержащее параметр а, естественно, требует для _своего решения
гораздо больших усилий, чем неравенство
~х> 1.
Что значит решить первое из этих неравенств? Это, по существу,
означает решить не одно неравенство, а целый класс, целое мно-
множество неравенств, которые получаются, если придавать пара-
параметру и конкретные числовые значения. Второе же из еыписэн-
ных неравенств является частным случаем первого, так как полу-
получается из него при значении а=\.
Таким образом, решить неравенство, содержащее параметры,
это значит определить, при каких значениях параметроз нера-
неравенство имеет решения и для всех таких значений параметров
найти все решения.
Подчеркнем еще раз: неравенство с параметрами долж ю быть
рассмотрено при всех значениях параметров. Если хотя бы одно
значение какого-либо параметра не исследовано, решение задачи
не может быть признано полным.
n_pji_Mj; R_„Ь_Решить линейное неравенство
Д Заметим сразу, что при а —0 неравенство решений не имеет,
так как обе части неравенства теряют смысл.
Затем преобразуем неравенство следующим образом:
Если !—„'->О, то хsg2. Решая неравенство
получаем а<0 или а>2/3. Таким образом, если а<;0 или
а>2/3, то Ж 2.
Если
т. е. 0<а<2/3, то х^2. И, наконец, если а = 2/3, то х—•
любае число.
Ответ: Если а < 0, то х е ] — со; 2],
если а = 0, то решений нет,
если 0<а<2/3, то хе[2; + оо[,
если а = 2/3, то хе] + °°; +°о[.
если а > 2/3, то х е ] — со; 2]. а
91
Пример 2. Решить неравенство \х — а\-\-\х-\-а\<Ь, а
Д Частный случай этого неравенства a—I, ft = 4 был рас-
рассмотрен в примере 3 § 4. Для решения данного неравенства
с двумя параметрами а и ft воспользуемся геометрическими сообра-
соображениями. На рис. 36 построены графики функций
y = f(x) = \x-a\ + \x + a\ и у=Ь.
Очевидно, что при ftsg2|a| прямая у — Ь проходит не выше
горизонтального отрезка кривой у = \х — а\-\-\х + а\ и, следова-
следовательно, неравенство в этом случае не имеет решений (рис. 36, а).
У
-/а/ 0
/
P.all
b \ У=Ь
! ¦¦¦
. Ш х
а)
Рис. 26.
Если же ft>2ja|, то прямая у = Ь пересекает график функции
y = f(x) в Двух точках (—ft/2; ft) и (ft/2; ft) (рис. 36, б) и нера-
неравенство в этом случае справедливо при — ft/2<.х<.ft/2, так как
при этих значениях переменной кривая у — \х-\-а\-{-\х — а\ рас-
расположена под прямой у — Ь.
Ответ: Если ftsg2|a|, то решений нет,
если ft>2|a|, то хе]— ft/2; ft/2[. A
Пример 3. Решить неравенство
Левая часть неравенства имеет смысл тогда и только тогда,
когда х и а удовлетворяют следующей системе неравенств:
с a +
\ a-
При a<0 эта система, очевидно, не имеет решений. Если а = 0,
то система имеет единственное решение х = 0. Но при а —0 зна-
значение переменной х = 0 не удовлетворяет неравенству. Если
а ,> 0, то решениями системы будут все значения переменной х,
принадлежащие отрезку [—а; а]. При условиях а>0 и \х\^а
исходное неравенстЕО можно, не нарушая равносильности, почленно
возвести в квадрат и получить
2а + 2 /a2- x2 > а\
откуда
Теперь придется рассмотреть три случая:
1°. Если а2 — 2а<сО, т. е. 0<а<2, то, так как левая часть
неравенства при |x|«g:a неотрицательна, а правая — отрицательна,
неравенство справедливо при всех \х\^а.
2°. Если а2 — 2а = 0, т. е. а = 2, то неравенство имеет вид
2 |/^4 — х2 > 0 и удовлетворяется при |х|<2.
3°. Если а2 — 2а > 0, т. е. а>2, то, возведя обе части нера-
неравенства в квадрат, приходим к равносильному неравенству
4 (а2 - х2) > а4 - 4а3 + 4а2,
упрощая которое, получаем
-4х2>а3(а-4), т. е. г»
Теперь видно, что при а ^=4 решений нет. В случае, когда
2<а<;4, решениями последнего неравенства будут все значе-
значения х, для которых
Будут ли все эти значения х давать решение исходного нера-
неравенства? Это зависит от того, будут ли значения выражения
а V а( —а) ^^ д ^ ^. ^ Превосходить а или не буДут. ^аПОМ-
ним, что мы рассматриваем лишь те значения переменной х, для
которых \х\^а. Докажем, что они не будут превосходить а,
т. е. что
Возводя в квадрат обе части неравенства, получаем
аD4~а)<1 или 4а-а2s?4,
т. е. а* — 4a + 4^U и, следовательно, приходим к верному нера<
венству (а —2J;э=0. Проведя рассуждения в обратном порядке,
убедимся в справедливости неравенства
aVa(A-a) _ Л
Ответ: Если asgO, то решений нет;
если 0<а<2, то х^[—а; а];
если а = 2, то х е ]— 2; 2[;
если 2<а<4, то ,]
если а^4, то решений нет. л
Помимо задач рассмотренного типа, в которых требуется
решить неравенство при всех значениях параметра, встречаются
93
задачи, где нужно из всех значений параметра выделить те, при
которых неравенство будет обладать некоторыми задаваемыми
свойствами; например, будет удовлетворяться при любом значе-
значении переменной, или вообще не будет иметь решений, или будет
иметь только одно положительное решение и т. д. Рассмотрим
задачу такого типа.
Пример 4. При каких значениях параметра а неравенство
2— ах—х* ^п
верно при всех значениях переменной?
Д Так как 1—х + х2>0 при всех х, то данное неравенство
равносильно квадратичному неравенству
2-ах-х?^3-Зх + Зх2 или 4ха + (а - 3) д; + 1 5гО.
Последнее неравенство справедливо при всех значениях перемен-
переменной при условии (а — ЗJ — 16 sg 0, т. е. | а — 31 ^ 4, откуда
— 4<й-3«й4 и, следовательно, — 1г^а^7.
Ответ! ае[—1; 7]. ^
§ 6. Доказательство неравенств
В предыдущих параграфах рассматривались задачи, в которых
нужно было решить неравенство, т. е. найти множество его реше-
решений. Часто встречается другая постановка задач, связанных
с неравенствами. Помимо неравенства задается некоторое множе-
множество значений переменной и требуется доказать, что все его эле-
элементы принадлежат множеству решений данного неравенства.
Такие задачи принято называть задачами на доказательство
неравенств.
Если в задаче на доказательство неравенства множество зна-
значений переменной не оговаривается— это означает, что справед-
справедливость неравенства требуется установить для всех действитель-
действительных значений переменной.
Для решения подобных задач используются самые разнообраз-
разнообразные приемы и методы. В тех случаях, когда переменная или
параметр, входящие в неравенство, принадлежат множеству
натуральных чисел, часто с успехом может быть применен метод
математической индукции, о котором рассказывалось во второй
главе.
Рассмотрим некоторые другие способы доказательства нера-
неравенств. Иногда неравенство удается доказать путем сведения его
с помощью равносильных преобразований к очевидному неравен-
неравенству.
Пример 1. Доказать справедливость неравенства
для всех положительных значений переменной.
94
Д Преобразуем неравенство следующим образом!
«¦ 1ГВ/1#1. ~ III ' ~ 1 Р
л
2У \0J ^ 40/ 10
*(/уТо*^ y J^ L
(/уТо*^ y + ^ +
\\ 2 |/10 7 40' / 10
Справедливость полученного неравенства при всех х>0 очевидна.
Но последнее неравенство равносильно исходному, которое тем
самым доказано. ^
Пример 2. Доказать неравенство
х2 + у2 - ху - х - у + 1 Ss 0.
Д Преобразуя неравенство
приходим к очевидному неравенству. Проведенные преобразования
не нарушают равносильности неравенств, поэтому данное нера-
неравенство верно при любых значениях переменных х и у. л
В следующем примере сведение к очевидному неравенству не
удается провести сразу для всех значений переменной. Однако
для каждого из трех промежутков, на которые предварительно
разбивается вся числовая ось, справедливость неравенства уста-
устанавливается элементарно.
Пример 3. Доказать неравенство
Д На промежутке ]— со; 0] неравенство верно, так как первые
четыре слагаемые левой части неотрицательны. На интервале
]0; 1[ справедливость неравенства становится очевидной после
следующей группировки слагаемых:
Если, наконец, хе]1; +оо[, то, переписав неравенство г. таком
внде
убеждаемся в его истинности.
Неравенство доказано для всех действительных значений пере-
переменной. А
Следующие два примера иллюстрируют применение метода
оценок при доказательстве неравенств.
95
Пример 4. Доказать неравенство
Д Левая часть неравенства содержит п слагаемых, каждое из
которых не меньше последнего слагаемого. Поэтому левая часть
неравенства оценивается снизу следующим образом:
1 1 1 1 _ 1 _ 1
Пример 5. Доказать неравенство
2Т + ~32 +"- + "^<1~Т> weIN- ">!•
Д Каждое слагаемое левой части неравенства допускает сле-
следующую оценку сверху:
J^ 1 _ _j l
/г2 ^ k(k — 1) ~ /г—1 ft'
и, следовательно, левая часть неравенства оценивается таким
образом:
-1-1
а именно это и требовалось доказать. А
Рассмотрим еще один распространенный способ доказательства
неравенств. Он заключается в использовании некоторых извест-
известных неравенств. В главе второй было доказано замечательное
неравенство о среднем арифметическом и среднем геометрическом
причем было подчеркнуто, что неравенство является строгим
тогда и только тогда, когда не все х{ равны между собой. Это
неравенство, которое обычно свягывают с именем великого фран-
французского математика XIX Еека О. Коши, бывает очень полезно
при доказательстве многих неравенств.
Пример 6. Доказать неравенство
х* +1/ + z* +1* S& ixijzt.
Д Положим в неравенстве Коши о среднем арифметическом и
среднем геометрическом
Xi = x*, х2 = у\ х3 = г*, я4 = /4 и 1 = 4.
96
Тогда получим
что и требовалось доказать. А
Пример 7. Доказать, что последовательность
монотонно возрастает, т. е. доказать справедливость нераиенства
Д Рассмотрим я+1 положительных чисел
ЛГ, = 1, Х2=1+ —, Х3 = 1 + —,..., Л-л
и применим к ним неравенстно Кошм.,
Получим
1+1
т. е.
или
Пример 8. Доказать, что сопротивление последовательного
соединения п проводников превышает сопротивление пар;1ллель-
ного соединения тех же проводников не менее, чем в п% раз.
Д Обозначим сопротивление данных проводников чеэез Г\,
гз, ..., гп. Пусть /? — сопротивление последовательного их соеди-
соединения, ^ — сопротивление параллельного их соединения. Тогда
+
и, следовательно,
но по теореме о среднем арифметическом можем записать
откуда получаем ~^п2, что и требовалось доказать. А
4 о/ред. Г. Н. Яковлева QJ
§ 7. Прилох.ение неравенств к задачам на наибольшие
и наименьшие значения
Задачи на отыскание наибольших и наименьших значений
функций чрезвычайно важны для математики, физики и для дру-
других наук. В математике разработан мощный аппарат (дифферен-
(дифференциальное исчисление) для решения подобных задач. Применение
дифференциального исчисления для нахождения нгибольшнх и
наименьших значений функций рассматривается в VI главе, § 8.
Тем не менее, иногда такого типа задачи элементарными средст-
средствами удается решить быстрее, проще и изящнее. Неравенства,
рассмотренные в § 6, оказываются
здесь очень полезными.
Из неравенства Коши о сред-
среднем арифметическом и среднем
геометрическом вьпекают два важ-
важных утверждения.
1. Если сумма произвольных
р 37 положительных чисел хг, хг, ...
..., х„ равна s, то их произведе-
произведение Р = хгх2...хп достигает наи-
наибольшего значения, равного {ь/и)п, при равенстве всех чи-
чисел.
2. Если произведение произвольных положительных чисел хъ
л'о, ..., х„ равно Р, то пх сумма s =х,+... + *„ принимает наи-
наименьшее значение, рав-юе и \/"Р, при равенстве всех чисел.
Пример 1. Из круглого бревна радиуса R выпилить прямо-
прямоугольную балку так, чтобы количество отходов было наименьшим
(рис. 37).
Д Количество отходов определяется площадью заштрихован-
заштрихованной части в сечении бревна, поэтому задачу можно свести к сле-
следующей: в круг радиуса R вписать прямоугольник наибольшей
площади. Если х и у~стороны прямоугольника, S—площадь
прямоугольника, то S=xy. Если прямоугольник вписан в круг,
то х2 + у2 = 4/?2. Следовательно, S = х V^4/?2 — х2. Заметим, что S
будет достигать наибольшего значения тогда, когда будет наи-
наибольшим S2 = х2 DR2 - v2).
Но сумма множителей х2 и 4#2 — х2 постоянна и равна 4R2,
следовательно, наибольшее значение их произведения равно
D#2/2J, а наибольшее значение S равно 2R2, причем оно дости-
достигается, если х% = AR2 — х2, т. е. при x=\'r2R, но тогда у = \/~2R.
Количество отходов будет наименьшим, если в сечении балки
будет квадрат, а
Пример 2. Найти наименьшее значение функции
/ (х) = х + --. а>0, на интервале ]0; +оо[.
98
Д Положим Xi = x, х2 = а/х. Произведение ххх^ = а, т. е. по-
постоянно, следовательно, сумма Хх-\-х% принимает наименьшее зна-
значение, равное 2]/а, при x = Ya-
Отметим, что отсюда следует полезное неравенство
а>0,
причем равенство достигается при х=Уа. а
Пример 3. Найти наименьшее значение рациональной функции
на интервале ]0; -fooL.
Д Представим / (х) в виде суммы шести слагаемых
произведение которых равно единице. Сумма таких слагаемых
достигает наименьшего значения при равенстве всех слагаемых,
т. е. при условии х3 = х—\/х, откуда следует, что х=1. Следо-
Следовательно, наименьшее значение f (х) и а интервале ]0: + оо[
равно 6. ^
В заключение следует сказать, что среди задач на наибольшие
и наименьшие значения функций, которые могут быть решены
элементарными средствами, т. е. без привлечения производной,
учащимся чаще всего предлагаются задачи, при
решении которых используется следующее экстре- / у
мальное свойство квадратичной функции. Из тож-
тождества
видно, что функция / (х) = ах2 + Ьх + с имеет наи-
наименьшее (если а>0) или наибольшее (если«<0)
значение, равное c — b^jAa, при а = —Ь/2а.
Пример 4. Окно имеет форму прямоуголь-
прямоугольника, дополненного полукругом (рис. 38). Пери-
Периметр окна равен Р. При каком отношении сторон прямоуголь-
прямоугольника окно будет пропускать больше света?
Д Обозначим длины сторон прямоугольника х и у; тогда пло-
щадь окна S = ху -]-у! т,) » н0 х и У связаны соотношением
Следовательно,
или
99
P72
Функция S достигает наибольшего значения при х = —-— =
1 i "^
сур р
= j-j—. Нетрудно подсчитать, что у = -т-,—•
Таким образом, высота прямоугольной части окна должна
быть в два раза меньше ширины, а
ЗАДАЧИ РАЗДЕЛА I
1. Равносильны ли неравенства = > —75— и %х > (х—7) C— х) на от-
о—х л
резке [4; 8]?
Исследовать на равносильность неравенства B — 4j на множестве всех
действительных чисел:
2. X— l^Vx и (х— ]
3. Х+1 ^Vx и
4. |Л^3+*—2<* и х'-\-х —
Решить неравенства E—6):
5 *ъ. 15 6 B-^) (^
7, Найти область опрелеления функиии
Решить неравенства (8—12):
8. V & — А
9. V&c— 4+/2л:— 13 > К13 — 2*.
10.
П.
,-1-2
1. 12.
ал:—Зл;—2а+6"л: —2'
13. Доказать неравенство
6
для всех неотрицательных значений переменных х, у, г.
14. Доказать неравенство
. _| _____ _i _| ^-^ О « ^ (И
15. Доказать неравенство
100
16. При каких значениях а система нераоенста
< ах—1 s=:0,
\ х—4а^-.О
имеет хотя бы одно решение?
17. При каких значениях а все нули функции
лежат на интервале ]—2; 1[?
18. Определить, при каких значениях переменно! многочлен
принимает наименьшее значение. Чему оно равно?
19. Спортплощадку площадью 0,9 гектара, имеющую форму прямоуголь-
прямоугольника, необходимо огородить с севера и юга деревянным забором, с юстока и
запада—проволочным. Установка 1 метра деревянного забора обходится
в 5 рублей, проволочного — в 2 рубля. На строительство выделено 1200 руб-
рублей. Достаточно ли этом суммы?
20. Через пункт В проходят две прямолинейные дороги, одна в пункт Л,
/\
другая в пункт С, причем ABC =120°. Из А в В и из В в С одновременно
выезжяют два автомобиля. Найти отношение их скоростей, если изве:тно, что
наименьшее расстояние между автомобилями было в тот момент, когд,1 автомо-
автомобиль, гышедший из пункта А, прошел седьмую часть своего пути.
21. Из квадратного листа жести со стороною а, отрезай по углам конгру-
энтиые квадраты и загибая края, составляют прямоугольную открытую ко-
коробку Чему должна быть разна сторона выбрасываемых квадратоз, чтобы
получилась коробка наибольшей вместимости?
ЗАДАЧИ РАЗДЕЛА 11
Исследовать на равносильность на множестве всех действительных чисел
неравенства A—5):
1. (* + 7)Bл:+1)>(* + 7J и '2х+\>х + 7.
2. x^-\-x-{-V'x<.2-\-Vx и хг + х<2.
3. Vx—7 2=* и х—7 22*2.
4. 1 —УЪР>Ъ и 1— К2л:>0.
5. Vx— 1 22* и
Решить неравенства F—18):
6. (Зх2— \Зх +
7. B*-5)(jcj-
*^ ' **•
х-2— Юх+20 ^ xa— G.« — 7^x — 3'
101
'•
4л-+ л.-'2
2
J
(х — 2)*'
л:2 —4
2х '
Ах
18-
1
1
XX 1 X ~-r~ 1 X
Найти область определения функций A9 — 20):
- 20-
I/ ¦* о
у о —f t-X —
Решить неравенства B1—40):
-х+\. 22.
21. У2х + 5>х+1. 22. V х"- — Ах>х — Ъ.
23. Ух"-—х—\2>х—\. 24. У~Х>~Ъх^\>х-2.
25. Ух"- — Ъх— 10<8— х. 26.
27. i!^r4lv-'JI
2—x — 2>2х + 3.
29.
31. -
33.
2ха
1
<1. 30.
:3. 32.
35. У2=х
»¦
39.
^А. 36.
:3 + Ьх + 7 — У Зл:2 + 5л: + 2 > 1.
9
Указание: сделать замену переменной Зх2 -J- 5д:-J- -у = /,
Решить неравенства с параметрами D1—46):
а?х+\ аЧ + Ъ а + 9х
41.
4Д —з 2"-^
6
"б"'
43.
2a+1
(а —3)(л-—2) -"*•—2'
а—r>0, a 2= 0.
44. ax>\jx. 45.
46. \x — a\ + ]x j
Указание: полезно построить графики функций
102
47. При каких значениях параметра а неравенство
ах*- + ?>х + А _
удовлетворяется при всех значениях переменной?
48. При каких значениях параметра а неравенство
'- + ах+\
<з
удовлетворяется при всех значениях переменной?
49. При каких значениях параметра а неравенство
справедливо при всех значениях переменной кроме одного?
50. При каких значениях параметра а неравенство
> 1 —За
справедливо при всех положительных значениях переменной?
51. При каких значениях а корни уравнения
(а — Ъ)х> — 2йх + 6й = 0
положительны?
52. При каких значениях а один из корней уравнения
Bа+\)х- — ах + а — 2 = 0
больше единицы, а другой меньше единицы'1
Доказать неравенства E3 — 55):
53. Х" + Ъ > 2, 54. {х + и + г)^ =а 27 хуг.
V х2\2
55. (A-3 + x2-(-*+lJ 2sl6x3; x е= [0; +оо[.
56. Доказать неравенство
ху уг , гх
г х ' у
для всех положительных значений переменных х, у, г.
57. Доказать неравенство
*2 + У2 + 2-=г12
для всех значений переменных, удовлетворяющих условию x-\-y-\-z= 6.
58. Доказать неравенство
для всех натуральных значений п и всех положительных значений х.
59. Найти наибольшее и наименьшее значения суммы .2л:2 —|— 3(/2 при усло-
условиях х-\-у~1, д:>0, у>0.
60. Какую наибольшую площадь может иметь прямоугольник, сумма трек
сторон которого равна ста метрам?
61. Плоская фигура состоит из прямоугольника и равностороннего тре-<
угольника, построенного на стороне прямоугольника. Как велика может быть
площадь такой фигуры при заданном периметре?
юз
62. У продавца испортились весы (плечи весов оказались неравными).
Продавец отпустил покупателю два вес,]; первый раз на одну чашку весов
положил килограммовую гирю, а на вторую — товар, во второй раз поменял
гирю и товар местами. Сколько получил покупатель: два килограмма, больше
двух килограммов или меньше двух килограммов товара?
63. Водоем имеет форму правильного треугольника. Между расположен-
расположенными на берегу пунктами А и В ходит паром. Велосипедист, которому нужно
попасть из А в В, может воспользоваться паромом или может ехать по берегу.
При каком наименьшем отношении скорости велосипедиста к скорости парсма
при любом расположении пунктов А и В переправп на пароме но дает выиг-
выигрыша во времени?
64. Две дороги пересекаются под прямым углом. По напраплению к пере-
перекрестку движутся две автомашины: по первой дороге — со скоростью 60 км/ч,
по второй—со скоростью 80 км/ч. В 12 часов обе машины находились в 10 км
от перекрестка.
В какой момент расстояние между машинами будет наименьшим? Где
будут находиться машины в этот момент?
65. Два туриста вышли из пункта А в пункт S. Первый первую половину
времени шел со скоростью vlt а вторую половину со скороаью v2; второй
турист первую половину пути шол со скоростью иь а вторую половину — со
скоростью v2. Кто из них затратил мепьшг времени на прохождение пути
из А в В?
66. Расстояние между пунктами А и В равно 100 км. Из А в В одновре-
одновременно отправляются два велосипедиста. Скорость первого на 10 км/ч больше
скорости второго. В пути первы'1 велосипедист делает остановку на 50 минут,
но в пункт В прибывает первым. В каких пределах заключена скорость пер-
первого велосипедиста?
67. Лодка плывет по реке из пункта А в пункт В и обратно. Расстояние
между пунктами Л и В равно а, скорость течения реки равна V. Какова
должна быть скорость лодки, чтобы время, затраченное на весь путь, было
меньше /?
X*-4- 1
68. При каких значениях х рациональная функция у= 0 принимает
х~~т'
наименьшее значение? Чему оно равно?
69. В турнире шахматистов II разряда 24 участника. Для выполнения
нормы I рязряда нужно набрать не менее 141/2 очков. Каково наибольшее
число шахматистов, которые могут выполнить норму I разряда? (В шахмат-
шахматных турнирах выигравший получает одно очко; если партия заканчивается
вничью, каждый из игравших получает 1/2 очка.)
70. Завод должен переслать заказчику 1100 деталей. Детали для пересылки
упаковываются в ящики. Имеются ящики трех типов. Ящик первого типа
вмещает 70 деталей, ящик второго типа — 40 деталей, ящик третьего типа —
25 деталей. Стоимость пересылки ящика первого типа 20 руб., ящика второго
типа —10 руб.. ящика третьего типа—7 руб. Какие ящики должен использо-
использовать завод, чтобы стоимость пересылки была наименьшей? Недогрузка ящиков
не допускается.
Глава V
ПОСЛЕДОВАТЕЛЬНОСТИ. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ.
ПРЕДЕЛ ФУНКЦИИ. ПРОИЗВОДНАЯ
§ 1. Бесконечные последовательности.
Последовательности ограниченные и неограниченные
Бесконечной числовой последовательностью называется чи :ловая
функция, определенная на множестве IN натуральных чисел. Аргу-
Аргумент этой функции обычно обозначается п, а сама фунщия —
буквой с индексом внизу: а„, Ь„, х„ и т. п. Таким of разом,
бесконечная последовательность задана, если указан зак )н, по
которому каждому натуральному числу п ставится в cootbi тствне
определенное число ап.
Бесконечная последовательность а„, п^Ы, запись Бается
в виде
аи а2; ...; ап; ...
пли кратко (а„). Числа аи а-2, ап называются элемента ш или
членами последовательности, ai —первым членом, а2 —в'орьш,
ап — п-м членом последовательности.
Рассмотрим примеры:
а) Каждому натуральному числу п ставится в cootbi тствие
число (п— \)/(п+ 1), тем самым определяется последовательность
„ 1 j^ з_ п—\
и' "з ' 2 : 5 ' ••• ; п+\' ••'
с п-и членом а„ = (л—1)/(/г +!)•
б) Каждому натуральному числу п сопоставляется число, равное
/г-му десятичному знаку после запятой числа 8/33 в десятичной
записи. Этот закон соответствия определяет последовател! ность,
у которой ai = 2, й2 = 4, aa = 2, a, = 4. Нетрудно показа1 ь, что
/г-й член этой последовательности можно записать в виде
Последовательности задаются различными способами. 11апри-
мер, указывается формула, связывающая значения n-го члена
последовательности с его номером для любого натураль юго п
(такова последовательность а)). Закон соответствия межд} номе-
номером члена и значением этого члена может быть задан словесно,
как, например, в последовательности б). Используется также
105
рекуррентный способ: задаются несколько первых членов после-
последовательности и формула, называемая рекуррентным соотноше-
соотношением, выражающая следующие члены последовательности через
предыдущие, например, fli = l, ал = 2ал_1 + 3 при п^2.
Пример 1. Доказать, что если fli = l и ап = 2ап-1 + 3 при
п з= 2, то я-й член последовательности имеет вид
an = 2»+i-3. A)
Д Используем метод математической индукции. При п = 1
формула A) верна. Предположим, что она серна при «=?:>= 1,
т. е. afe=2/i+1 —3. Подставляя ъто шраженне для /г-го члена
в рекуррентное соотношение aftf] = 'Jak-\-rA, получим flft+i =
= 2 B*+х — 3) + 3 = 2Л+2 - 3. Но это и есть формула (]) для п = k + !.
Из принципа математической индукции следует, что формула A)
справедлива для любого натурального числа п. а
Важным частным случаем последовательностей являются ариф-
арифметическая и геометрическая прогрессии. Они рассматриваются
в §§ 4 и 5.
Последовательность (а„) называется ограниченной, если суще-
существуют два числа а и Ь такие, что при всех п выполняются
неравенства
а<ай<Ь. B)
При этом говорят, что число а ограничивает последовательность
снизу, а число Ъ — сверху.
Последовательность ((« — 1)/(п+ 1)) ограничена, так как при
всех п имеют место неравенства Osg; (п — 1)/(и+ 1) =^ 1.
Последовательность (( —1)п) также ограничена, так как для
любого натурального п справедливы неравенства — 1 sg; ( — 1)" ss; I.
Можно показать, что данному определению ограниченной
последовательности равносильно следующее: последовательность
(а„) называется ограниченной, если существует число М такое,
что при всех п выполняется неравенство
Не всякая последовательность является ограниченной.
Л]; п мер 2. Доказать, что последовательность in) не явля-
является ограниченной.
Д Предположим противное, т. е. предположим, что последо-
последовательность (п) ограниченная. Это означает, что существует такое
число М, что при всех п справедливо неравенство | п | sg M. Однако,
например, для натурального числа п — [М]-\-1 (здесь [М] — целая
часть числа М) это неравенство не выполняется. Следовательно,
предположение неверно, т. е. последовательное,гь (а) не явля-
является ограниченной. ^
106
Последовательность, не являющаяся ограниченной, называется
неограниченной. Сформулируем определение неограниченной после-
последовательности, построив отрицание определения ограниченной
последовательности: (ап) — неограниченная последовательность,
если для любого числа М найдется такой номер п, что \а,.\>М.
О 1 я
Рис. 39.
Если изображать члены последовательности точками коорди-
координатной прямой, то все члены ограниченной последовательности
лежат на некотором отрезке. Например, у последовательности
а„ = (п — 1)/(п-\- 1), «е= IN, все члены лежат на отрезке jO; 1]
(рис. 39).
Для неограниченной последовательности вне любого отрезка
найдутся члены это;'! последовательности.
§ 2. Предел последовательности.
Теоремы о сходящихся последовательностях
Число а называется пределом последовательности (а,), если
для любого положительного числа е найдется такое натуральное
число N, что при всех n>N выполняется неравенство
| ап - а |< е.
Тот факт, что число а является пределом псследовате пыюсти
(а„), записывается в виде
Нтй„=й или ап-+а при /г->со.
л-»оо
Пример 1. Доказать, что Пт -—— =0.
Д Неравенство
(-1)"
-0
<е, т. е. — <е, выполняемся при
всех я>1/е. Таким образом, для любого е>0 можно взять,
например, УУ = [1/е]+1- Если учесть, что W > 1/е, то для любого
n>N будем иметь ¦ 0 <е. Это и означает, что (—1)"//г->-
->0 при /г->со. ^
Заметим, что неравенство |а„ —а|<е равносильно неравенст-
неравенствам
Это означает, что число ап принадлежит интервалу ]а — е; а-\-е[.
Такой интервал налывается е-окрестностью точки a (pic. 40).
107
Определение предела мсжно перефразировать следующим обра-
образом, придав ему геометрическую наглядность: число а называ-
называется пределом последовательности (ап), если в любую е-окрест-
ность числа а попадают все члены последовательности, кроме,
быть может, конечного числа их. Действительно, если а„->а
при п—у-оо, то для каждого е>0 найдется такое А/, что все
члены последовательности с номерами п > N лежат в е-окрест-
ности числа а и, значит, вне этой окрестности MorjT находиться
только первые N членов последовательности.
a ci+g
Рис. 40.
Например, для последовательности ((— 1)"/«) в е-окрестность
точки нуль при в = 1/10 попадают все члены последовательности,
кроме первых десяти, при 8=1/100 —нее члены последователь-
последовательности, кроме пергых ста, так как
Пример 2. Пусть Игл ап = а и а>0. Доказать, что начи-
пая с некоторого номера все члены последовательности (аи) по-
положительны.
Д Так как Игл ап = а>0, то для е = а/2>0 найдется нату-
ралыюе число N laicoe, что при n>N выполняется неравенство
\а„ — а|<а/2. Перепишем это неравенство в виде — а/2<а„ —
— и<;я/2, тогда ь'олучим
а„>о/2>0. а
Геометрический смысл доказанного утверждения вполне очевиден:
если число а положительно, то существует его окрестность, не
О а,
Рис. 41.
содержащая нуля, и в эту окрестность согласно определению
попадают все члены последовательности, кроме, быть может,
конечного числа (рис. 41).
Пример 3. Пусть lim а„ = а и а„^0. Доказать, что
108
Д а) а = 0. По определению предела для любого е >0 по
числу е2 найдется такое N, что при n~>N имеет место |a,i|<ea.
Так как по условию а„^0, то 0sSan<e2. Но тогда гри тех
же п>Л/ выполняется неравенство | Уа„ — 01 = Уап <е.
б) а>0. Для любого е>0 найдется такое N, что при n~>N
выполняется неравенство \а„ — а\ <е,Уа. Тогда при тех же
п> N будет справедливо неравенство
В.
\Уап-Уа | = Чг^^Г- V-mV-^—-V=
V а„+у а у ап + У а У а
В обоих случаях доказано, что lim Уап— У а, А.
Пример 4. Доказать, что limgn = 0, если |д|<1.
П-* GO
Д При <7 = 0 утверждение очевидно; если же q=?--0, то
Ч—г>1. Обозначим а = -г—г—1 (а>0), тогда
г>1- Обозначим a j
| l/q\n= A +а)п. Применяя неравенство Бернулли J), пэлучим
j \lq |п = A +а)" > 1 +от > an, откуда следует
|<7|п<1/ем. A)
Для любого ё>0 возьмем JV = [ 1 /cte J -f-1. Так как N>l/az, то
при п> N из A) будет следовать \q\n<i l/ctn< 1/afJ< е. Это
означает, что lim |g|™ = 0. ^
л—* со
Последовательность, имеющая предел, называется сходящейся,
а последовательность, не имеющая предела, — расходящейся.
Пример 5. Доказать, что последовательность с я-м чле-
членом а„=1+( —1)" является расходящейся.
Д Предположим противное, т. е. предположим, что сущест-
существует число а, являющееся пределом этой последовательности.
Тогда по определению предела для е=1/2 найдется такоз нату-
натуральное число N, что для любого «>/V выполняется неравен-
неравенство \ап — а К. 1/2.
Отсюда следует, что если /гх> W и n2~>N, то
\ап2-а\< 1. B)
Однако, если взять n1 = 2N (/tj > W) и /г2 =
то для таких номеров получим
что противоречит B). Следовательно, не существует числа а,
являющегося пределом последовательности оп = 1 + (— 11", эта
последовательность расходящаяся, а
!) См. «Алгебра и начала анализа». Учебное пособие для 9-гэ класса
средней школы под редакцией А. Н. Колмогорова, стр. 12.
юэ
Напомним теоремы о сходящихся последовательностях, кото-
которые изучаются в школьном курсе математики.
Теорема 1. Если последовательность сходится, то она
имеет только один предел.
Теорема 2, Если последовательность сходится, то она
ограничена.
Теорема 3. Если последовательности ап и Ьп сходятся, то
lim («„ + &„) = Hm an-\~ lim bn;
п-*со п-*со п—*со
lim (an — bn)— lim an— lim bn;
П-* CO П—» ОЭ П—¦ CO
lim (anbn)= lim a,r lim bn.
л —> со n —* со
, кроме того, Ьпф§ для любого п и lim Ь„
п —¦ оэ
lim ап
Из теоремы 2 следует, что любая неограниченная последова-
последовательность является расходящейся. Например, последовательности
(/г), ((п2+\)/п), B") расходящиеся, так как они неограниченные.
Из теоремы 3 следует, что постоянную можно выносить за знак
предела, т. е. если последовательность (ап) сходится, то
lim (can) = c lim an.
п —* оэ п —¦ оо
Рассмотрим примеры на вычисление пределов.
„ г- и - 1- 7nJ —Зп+12
Пример 6. Найти lim ¦ . . 0 . 9 •
f?->oo n--f-zn-f- z
Д Применяя теорему 3, получаем
, 3 , 12 .. /_ 3 12 \
7 -^ lim 7
7n2-3/j+12 ,. « я2 п-.оэ\ я я*/
llm := lim = =
99 = 799
- + 4" limfn2+2
Я Т Я2
1 / 1 \3
7 — 3 lim —+12( lim --]
n-»oo Я \л->оо n i _
1 i—v— ~~~ *
1+2 lim --+2( lim — j"
Пример 7. Найти lim (j/n2 + n — п).
п-»оэ
Д Так как
,г =
110
и lim l/ 1 -\— = 1 (см. пример 3), то по теореме 3 будем иметь
II-* СО ' П
У 1+?
4.
§ 3. Монотонные последовательности. Теорема Вейерштэасса
Последовательность (ап) называется возрастающей, если для
любого п выполнено неравенство ап+1 ;> ап. Последовательность (а„)
называется убывающей, если для любого п выполнено нергвенство
+i
Например, последовательность (и2) возрастающая, так как для
любого натурального п имеет место ап+1 = (п + 1)а > «а = fln После-
Последовательность A/п) убывающая, так как для каждого п справед-
справедливо неравенство 1/(м+1)<1/и, т. е. в„+1<а„.
Последовательность (ап) называется неубывающей, если ?я+1^а„
для любого м, и невозрастающей, если а„+1«е;а,, для любого п.
Например, последовательность с п-и членом ап = [(л+1)/2]
неубывающая: 1; 1; 2; 2; 3; 3; ...
Все такие последовательности (возрастающие, убывающие, не-
неубывающие, невозрастающие) называются монотонными.
Пример 1. Доказать монотонность последовательности, м-й
член которой имеет вид ап = Уп+1-~Уп.
Д Заметим, что
ап =
VZ+l + Vii
поэтому при любом п
_ 1
Ци.1.1 ttij
n + 2 + Vn+l Vn+\+Vn
-(VjiT2-Vn)
Таким образом, ап+1<.ап, т.е. последовательность убывающая, а
Не всякая последовательность монотонная. Примером немоно-
немонотонной последовательности является последовательность ((—1)"/«).
Каждый ее элемент с четным номером больше как предыдущего,
так и последующего:
_, 1 . _ L. !. _±. _ ' • '
•* I "о > "О ' Л • с I • • •
2 ' 3 ' 4 • .5 ' •'• 2ft-1 ' 2k' 2A+1 ' "*
Для монотонных и ограниченных последовательностей справед-
справедлива следующая теорема:
Теорема Вейерштрасса. Если последовательность моно-
монотонна и ограничена, то она имеет предел.
111
Эта очень важная в математическом анализе теорема дает
достаточные условия существования предела последовательности.
Из теоремы Вейерштрасса следует, например, что последователь-
последовательность площадей правильных n-угольников, вписанных в окруж-
окружность единичного радиуса, имеет предел, так как является воз-
возрастающей и ограниченной последовательностью. Предел этой
последовательности обозначается я.
Пример 2. Доказать, что последовательность fli = 2, an =
= («„_!+1)/2 при п:>2 имеет предел и найти его.
Д Найдем несколько первых членов последовательности:
а1 = 2; 02 = 3/2; а3 = 5/4; а4 = 9/8.
Все они принадлежат промежутку ]1; 2]. Докажем, что при всех л
выполняются неравенства
1<а„<2. A)
Применим метод математической индукции. При п = 1 неравенства A)
справедливы, так как ax = 2. Предположим, что при n — k^-X
имеет место 1<яА=^2. Так как ak+1 = (ab+ l)/2, то из ак>\
следует аА+1>1, а из ай<2 получаем акп<.2. Таким образом,
l<aft+1sg2, т. е. A) выполняется и при n = k+\. Из принципа
математической индукции следует, что неравенства A) выполняются
для любого натурального п.
Далее,
G-,-t-l 1—а,.
/у _^_ 1 п L1-
nil u/i Ь L',-I — п »
отсюда, учитывая что а„> 1 для любого м, получим anH — an<z0.
Следовательно, art+1<;a,i при всех п — последовательность убываю-
убывающая. По теореме Вейерштрасса эта последовательность имеет пре-
предел, обозначим его а: а= lim an. Очевидно, что если последова-
п-ют
тельность (ап) имеет предел, то
lim an= lim йл+1.
га—> оэ и -> со
Для рассматриваемой последовательности ал+1 = -^ + -^, поэтому
lim an+1= lim Dl +
т. e.
откуда находим, что а=1. Итак, доказано, что lim а„ = \. ^
п-»оо
112
§ 4. Арифметическая прогрессия
Последовательность (я„), у которой aL = a и при любом п
A)
где а и d — любые заданные числа, называется арифметической
прогрессией. Число d называется разностью арифметической про-
прогрессии.
Арифметическая прогрессия является монотонной последова-
последовательностью: возрастающей при d>0 (так как апп — ап =-¦ d>0),
убывающей при d<0 (так как ап+1 — an = d<z0), иевозрастаю-
щей при d = 0. Для п-го члена арифметической прогрессии спра-
справедлива формула
-l). B)
Докажем ее методом математической индукции.
? При п = 1 эта формула верна: а^ = а. Предполо» им, что
формула B) верна при n = k^l, т. е. ak = a + d(k— 1). По опре-
определению арифметической прогрессии аА+1 = аА + d- Подставляя
сюда выражение для fe-ro члена, получим
а это есть формула B) при n = k-\-l. Из принципа математиче-
математической индукции следует, что формула B) верна для любою нату-
натурального п. Щ
Из формулы B) следует, что если разность арифметической
прогрессии отлична от нуля, то арифметическая прогрессия является
неограниченной последовательностью. Доказательство этого факта
аналогично доказательству неограниченности последователь! ости (п)
(см. пример 2 § 1).
Чаще всего рассматривается арифметическая прогрессия, со-
содержащая конечное число членов, которая называется конечной
арифметической прогрессией.
Свойства арифметической прогрессии.
1. Каждый член арифметической прогрессии, начиная со вто-
второго, равен среднему арифметическому его соседних членоз, т, е.
при k^2
ap C)
2. У конечной арифметической прогрессии а^, я2; ...; а,, сумма
членоз, равноотстоящих от ее концов, равна сумме крайних чле-
членов, т. е. для k=\, 2, ..., п
я* + ал-*+1 = в1 + <1я- D)
3. Сумма членов конечной арифметической прогрессии равна
произведению полусуммы крайних членов на число членов, т. е.
113
если 8„ = аг + ал + .
Sn = a-dpi-n. E)
? При &3s2 имеем ak = ak_x-\~d и ak = akn — d. Складывая
почленно эти равенства, получим 2ай = ай-1 + а/гц, откуда сле-
следует C).
В конечной арифметической прогрессии «^ а2; ...; ап члены ak
и fln-йн равноотстоят от концов. По формуле B) ak = a^-d(k—l)
и an_A,.1 = fl + d(n —/г). Сумма этих членов afc-fan-*n — 2a + d(«— 1)
и равна сумме крайних членов a1Jran — 2aJrd(n — 1).
Если Sn = a1 + a2 + --- + a*. то 5„ = ап + ал-1 + ... + Я1- Склады-
Складывая почленно эти равенства и используя свойство 2, получаем
2Sn = (flj + an) + (Oj + a«-i) + • • • + («i + а п) = п (аг + ап),
откуда следует формула E)
Если в формулу E) подставить выражение B) для n-ro члена,
то получим
п-
Пример 1. Сумма третьего и седьмого членов арифметиче-
арифметической прогрессии равна 6, а их произведение равно 3. Найти
сумму первых шестнадцати членов этой прогрессии.
Д Обозначим первый член прогрессии а, а ее разность d.
Тогда по формуле B) имеем a3 — a + 2d и a, = a-\-6d. По усло-
условию а3 + #7 = 6, а3а7 = 8. Подставляя сюда выражения для а3 и а,,
получим систему
(
решая которую, находим я=1, d=l/2 и a = 5, d = —1/2. По
формуле F) вычисляем сумму первых 16-ти членов для каждой
из прогрессий:
S1(! = 2a+l5d. 16 = 76 при a=l, d=l/2,
S,e = 20 при a = 5, d = —1/2. a
Пример 2. Сумма первых /г членов арифметической прогрес-
прогрессии, разность которой отлична от нуля, равна половине суммы
следующих п членов. Найти отношение суммы первых Зп членов
этой прогрессии к сумме ее первых п членов.
Д Если Sft —сумма первых k членов прогрессии, то условие
можно записать следующим образом: Sn= -к-(S2n— Sn), откуда
114
следует 3Sn = S2/!. Используя формулу (G) для суммы Sft отсюда
получим
2 d( + l). G)
Искомое отношение SSn/Sn имеет вид
5Як _ о _2а-МC/?— 1)
S,, 2a-\-d (и — 1)~~*
Подставляя сюда а из G) и сокращая иа <i=H=0, находим S3n/Sn —
= 6. А
§ 5. Геометрическая прогрессия
Последовательность {<?„), у которой а^ — а и для любого п
йя+1 = йл<7, A)
где а и д —любые отличные от нуля заданные числа, называется
геометрической прогрессией. Число q называется знаменателем
геометрической прогрессии.
Если а>0 и q>\, то геометрическая прогрессия является
возрастающей последовательностью, так как для любого п имеем
йпп/ап = Ц> 1. т. е. апП>ап; если же а>0 и 0<<7<1, то
геометрическая прогрессия убывающая: ап+1 = anq< а„.
Очевидно, что при fl<0, наоборот, геометрическая прогрес-
прогрессия убывающая, если q>\, и возрастающая, если ()<cq<.\.
При q <0 каждый член прогрессии имеет знак, противопо-
противоположный знаку последующего члена, она не будет монотонной.
Формула для п-го члена геометрической прогрессии илеет вид
ая = ач"-1. B)
Докажем ее методом математической индукции.
Ц Формула B), очевидно, верна при м=1, предположим, что
она верна и при n — k^l, т. е. ak — aqk~1. Из A) следует ак+1 =
= akq. Подставляя сюда выражение для k-vo члена, получаем
<Xk+\=aql't т. е. формула B) верна и при n = k-\-\. Из тинципа
математической индукции следует, что формула B) спрг ведлива
для любого натурального п. ?|
Геометрическая прогрессия, содержащая конечное ч»:ло чле-
членов, называется конечной геометрической прогрессией.
Пусть (й„)— геометрическая прогрессия с первым членом а и
знаменателем q.
Свойства геометрической прогрессии.
1. Квадрат каждого члена геометрической прогрессии, начиная
со второго, равен произведению соседних членов, т. е. при k^2
al = ak-ictbn- C)
Если все члены геометрической прогрессии положительны, то это
свойство формулируется так: каждый член геометрической про-
115
грессии, начиная со второго, равен среднему геометрическому его
соседних членов, т. е. ak = |/ай_хайн.
2. У конечной геометрической прогрессии аи а2; ...; ап произ-
произведение членов, равноотстоящих от ее концов, равно произведению
крайних членов, т. е.
акап-к,,Л = а1ап. D)
3. Если знаменатель геометрической прогрессии q не равен
единице и Sn = a1Ji-a2 + ... + an, то
Sn^a^-. E)
Доказательства свойств 1 и 2 аналогичны доказательствам
соответствующих свойств арифметической прогрессии. Докажем
свойство 3.
Q Пусть Sn = a1-Jra2 + ... + an. Используя формулу B), можно
записать
Sn = a + aq + ... + aq*-\ F)
тогда
G)
Вычитая почленно из равенства F) равенство G), получим
откуда при цф\ следует формула E). Щ
Пример 1. Сумма первых четырех членов геометрической
прогрессии равна 30, а сумма следующих четырех членов равна
480. Найти первый член прогрессии.
Д Пусть а —первый член и q — знаменатель геометрической
прогрессии. По формуле E)
a-?f = 30. (8)
Следующие четыре члена aq*, aqb, aq*, zq1 образуют геометриче-
геометрическую прогрессию с первым членом acf и знаменателем q, поэтому
по формуле E)
^4=^ = 480. (9)
Из (8) и (9) следует ^ = 16, откуда q = 2 или q = — 2. Если
q = 2, то из (8) находим а = 2, а при q = — 2 получаем а = — 6. а
В примере 4 § 2 было доказано, что lim qn = 0, если | q \ < 1. Из
п-юо
этого следует, что если знаменатель q геометрической прогрессии
(ап) удовлетворяет условию \q\<c\, то ап—>0 при и-+оо. Дей-
Действительно, так как atl = aqn~1, то
lim an— \\maqn~1 = a lim qn~1 = 0.
n-»oo n-»oo n-voo
116
Геометрическая прогрессия, знаменатель которой удовлетво-
удовлетворяет условию |<7|<1, называется бесконечно убывающей геометри-
геометрической прогрессией.
Если (ап) — бесконечно убывающая геометрическая прогрессия,
то существует предел последовательности сумм ее первых п чле-
членов. По формула E)
и так как qn-*-Q при п—>оо, то l'im Sn = a/(\ —q).
и —- ею
Этот предел называется суммой бесконечно убывающей геомет-
геометрической прогрессии и обычно обозначается S. Итак
Пример 2. Найти сумму бесконечно убывающей геометри-
геометрической прогрессии, у которой сумма первых трех членов равна 7,
а произведение этих членов равно 8.
Д Пусть а — первый член и ^ — знаменатель геометрической
прогрессии. По условию
Из второго уравнения системы находим aq = 2, тогда, подстав-
подставляя a=2jq в первое уравнение системы, получаем квадратное
уравнение 2q2 — 5q + 2 = 0, корни которого q=\/2 и q = 2. После-
Последовательность бесконечно убывающая, jg[<;l. Следовательно,
9=1/2, н тогда a = 4. Сумму этой прогрессии находим по фор-
формуле A0): S = j2r- = 8. A
§ G. Предел функции. Непрерывность функции
Напомним, что любой интервал, содержащий точку и, назы-
называется окрестностью точки а. Симметричный интервал ]a — I; a-f6[
при любом 6>0 называется Ь-окрестностыо точки а.
Пусть функция / (х) определена в некоторой окрестности точки а
за исключением, быть может, самой точки а, т. е. никаких пред-
предположений о том, определена ли функция в точке а или нет, не
делается.
Число b называется пределом функции f(x) при х, стремя-
стремящемся к а (или в точке а), если для любого положительного чи-
числа е найдется такое положительное число 6, что при всез: хфа,
удовлетворяющих неравенству \х — а|<6, будет выполняться
неравенство
117
Для обозначения того, что число b есть предел функции /(х)
при х стремящемся к а, пишут
lim/(x) = b, или f(x)->b при х->а.
*->а
Заметим, что условия \х — а | <; 6, хфа означают, что точка х
принадлежит 6-окрестности точки а и отлична от а; эти условия
можно объединить в такой записи:
О < | х — а | < 6.
Данное определение предела можно проил-
проиллюстрировать следующим образом (рис. 42).
Возьмем число е > 0 и на оси Оу отметим
е-окрестность точки Ь, т. е. интервал
\Ь — е; 6 + е[, через концы которого проведем
прямые, параллельные оси Ох. Получим полосу
шириной 2е. Если для любого е > 0 можно
указать такое б>0, что график функции
i/ = /(x), рассмотренный для х из б-окрест-
равных а, целиком находится в этой полосе,
О\ сй-д а а*б^ ее
Рис. 42.
ности точки а и не
то число b является пределом / (х) при ^.стремящемся к а.
Пример 1. Доказать, что lim (Зх — 1) = 2.
Д Функция / (х) = Зх — 1 определена в любой окрестности
точки х=1. Неравенство |/(х) —2|<е, т.е. |Cх— 1) — 2| =
= 3|х — 1 | < е, будет выполняться для всех х, удовлетворяющих
условию | х — 1 | <с е/3. Таким образом, для любого е >> 0 можно
взять б = е/3, тогда для всех х таких, что |х— 1 |<б, будет спра-
справедливо неравенство | / (х) — 21 = 3 j х — 1 | < е. Это и означает, что
limCx— 1) = 2. a
Пример 2. Рассмотрим функцию f(x) = (x2—l)/(x—l), она
определена всюду за исключением точки х=\. Доказать, что
при х, стремящемся к 1, эта функция имеет предел, равный 2.
Д При всех х ф 1 имеем (х2 — 1 )/(х — 1) = х -f 1, следовательно,
|/ (х) — 21 = |х — 11 и неравенство | / (х) — 21 < г выполняется, если
\х— 1\<.е и хф\. Поэтому для любого е > 0 можно взять 6 = е,
тогда при всех х, удовлетворяющих условию 0<|х— 1|<б,
X*— 1
будет справедливо неравенство
X— 1
-2
= \х— 1 |<е. Таким
образом, по определению (х2 — 1)/(х— 1)->2 при х-> 1. А
Решения примеров 1 и 2, в частности, показывают, что б
зависит от е, причем зависимость эта, вообще говоря, различна
для различных функций.
Пример 3. Пусть / (х) >> 0 в некоторой окрестности точки а,
lim/(x) = b и Ь>0. Доказать, что при х, стремящемся к а,
ж-*а
существует предел функции Vf{x) и lim|//(x) —
118
Д Из определения предела следует, что для любого е>0
существует 6>0 такое, что для всех х, удовлетворяющих усло-
условию 0 ¦< | х — а|<б, выполняется неравенство |/(х)—Ь\>г/Ь.
Тогда для тех же х из неравенства
I/M-6I ^ l/W-ft|
следует
rf (х) — Уь\<.г. Это означает, что lim l/"/(x) ==УЬ. А
х-+а
Не для всякой функции, определенной в окрестности точки а,
существует предел при стремлении х к а. Рассмотрим, например,
функцию
II, если х>0,
О, если х = О,
— 1, если х<0,
график которой изображен на рис. 43. Докажем, что э-а функ-
функция не имеет предела в точке х==0. Проведем доказательство
методом от противного.
Q Предположим, что существует
число b такое, что
/
о
OS
Рис. 43.
lim sign x — b.
х-+0
По определению предела для любого
е>0 и, следовательно, для е= 1/2 най-
найдется такое б >» 0, что для всех х, удовлетворяющих условию
О < | х | < б, будет справедливо неравенство | sign x — b\< 1/2. Та-
Таким образом, если Xi и х2 такие, что 0 < j хх |< б и 0 < | х21 <
<б, то |signxi — b | <С 1/2 и | sign лг2 — b | <C 1/2 и, следовательно,
| sign *i — sign х31 = | sign Xi — b -f & — sign x21 ^
< |sign xi — 6 | -f | sign x2 — 6 |< 1.
Однако, взяв хх = 6/2 и #2 = —6/2, будем иметь | sign хг — sign x21 =
Полученное противоречие показывает, что функция signx не
имеет предела в точке х = 0. Ц]
Для функций, имеющих предел в точке, справедлива "еорема,
аналогичная теореме о сходящихся последовательностях.
Теорема. Пусть при х, стремящемся к а, существуют пре-
пределы функций / (х) и g(x). Тогда при х, стремящемся к г, суще-
существуют такэюе пределы суммы, разности и произведет я этих
функций, при этом
lim (f(x)+g(x)) = lim /(х) + limg{x),
lim (/ (x) ¦ g (x)) = lim/ (x) ¦ \img(x).
Если, кроме того, limg(x)=?O, то существует предел частного
f(x)/g(x) и
... Hm/W
,.m./M __,-,« ...
jt-effW lim ?М '
2л: — 3
Пример 4. Найти lim
Д По теореме о пределах имеем
lim B*-3) 2 lim*-3
lim 2*~3 = *-<3 ^ _2-3-Э 1
i , 3 + 7* limC + 7x) 3 + 7 lim x 3 + 7-3 8"
3 3
Пример 5. Найти li
Д При х, стремящемся к 1, предел знаменателя равен нулю,
поэтому применить теорему о пределе частного нельзя. Однако,
преобразовав дробь следующим образом:
х-\ (jc-1)(K
и сократив на х—1 (если х->1, то хф\), получим
Так как lim|/x + 3 = 2 (см. пример 3), то
х-Л
,. KjT+3-2 i-1 11
x-+i x-\ x-+i Ух + Ъ + 2 lim Ух + Ъ + 2 4
Для некоторых функций предел при х, стремящемся к а,
равен значению функции в точке а (см. примеры 1 и 4). Од-
нако это не всегда так, например для функ-
функции
Jfh при хф0'
1 при х = 0,
график которой представлен на рис. 44, пре-
предел при х->0 равен нулю, а /@)=1.
Если предел функции f(x) в точке а равен значению функции
в этой точке:
lim/(*)=/(а),
дс-»а
то функция / (х) называется непрерывной в точке а.
120
Из теоремы о пределах следует, что линейная функция непре-
непрерывна в любой точке, т. е. для любой точки х0 имеет место
lim (а0
Многочлен Рп (х) — а0 + агх -\-,,. -|- апхп также является непре-
непрерывной функцией в любой точке:
lira Рп(х) = Р
Это следует из того, что многочлен есть конечная сумма слагае-
слагаемых вида akxk, k^sO, для каждого из которых
lim akxk = ак (х0)"
Х-*Ха
(последнее устанавливается методом математической индукции).
Из непрерывности многочлена и теоремы о пределе частного
следует, что рациональная функция непрерывна в любо?! точке
области определения, так как
limzra- = (n7T- если <U*o)=*o.
Все элементарные функции, например
х", ах(а>0), sinx, tgx,logax (a>0, аф\),
непрерывны в каждой точке, в окрестности которой эти функции
определены.
Если функция непрерывна в каждой точке Е1екоторого интер-
интервала, она называется непрерывной на этом интервале. График
непрерывной на интервале функции может быть нарисовар одним
движением карандаша без отзыва от бумаги.
Каждая элементарная функция непрерывна на любом интер-
интервале, на котором она определена.
§ 7. Производная, ее геометрический смысл
Пусть функция y = f(x) определена на некотором интервале
]а; Ь[, содержащем точку х0. Для любой другой точки х интер-
интервала ]а; Ь[ разность х — х0 обозначается Ах и называется прира-
приращением аргумента; соответствующая разность значений функции
f(x) — f(x0) обозначается Д/ (х0) (или Ау(х0)) и называется прира-
приращением функции. Из равенства Ах — х — х0 следует х = хо-\-Ах и
Если х->х0, то, очевидно, Дх->0.
Производной фур1кции y = f(x) в точке х0 называется предел
отношения приращения функции к соответствующему приращению
121
аргумента, когда последнее стремится к нулю. Производная функ-
функции y=fix) в точке х0 обозначается f (х0) или у' (х0). Таким
образом, по определению
Для существования производной /' (х0) необходимо, чтобы
функция / (х) была определена в некоторой окрестности точки х0.
Покажем, что также необходимо, чтобы функция была непрерывна
в точке а'о. Пусть существует /' (л), тогда
lim (/ (х) - f (дг„)) = lim f-~E!rA " (* ~ хо) = V («о) '0 = 0.
Отсюда следует, что lim f (x) —f(x0), ьто и означает непрерыв-
Х — Ха
пасть функции f(x) в точке х0.
Функция, имеющая производную в точке х0, называется диф-
дифференцируемой в этой точке; операция нахождения производной
называется дифференцированием.
Функция, дифференцируемая в каждой точке некоторого ин-
интервала, называется дифференцируемой на этом интервале. Произ-
Производная дифференцируемой ка интервале функции y = f(x) сама
является функцией аргумента х, ее обозначают f (x) или у' (х) и
называют производной функцией.
Пример 1. Доказать, что функция f(х) = 1/х дифференци-
дифференцируема на интервале ]0; -(- оо[ и (\гх)'=—- для любого х е.
е]0; +оо[.
Д Пусть хо>О и х>0. Имеем
т. е.
А/ (х0) =
Отсюда, зная, что lim У"х0 + Ах~ Ух0 (см. пример 3 § 6), по-
поля-.о
лучаем
Г {Х) Ц™
Это означает, что функция f(x) = V~x диффе; ипцнруема в каждой
точке интервала ]0; +оо[ и {[/"х)' = —-^=. а
Z у X
Укажем основные формулы и правила дифференцирования,
с помощью которых в большинстве случаев можно при дпфферен-
122
цировании обойтись без непосредственного вычисления производ-
производной как предела отношения ,-— при Дд:-»-0.
Производные элементарных функций
1. (хп)' = пхп-\ яеМ. 5. (ех)'==ех.
2. (sinz)' = cosx. 6. (а*)'--= ах In а, а>0.
3. (cosx)'= —sinx. 7. (lnx)'=lx-.
8<1о^' = та fl>0> °^Ь
Правила дифференцирования.
Пусть с —постоянная, и(х), v(x) и щ (х) — дифференцируемые
на некотором интервале ]а; Ь[ функции, на этом же интервале
справедливы приводимые формулы:
с' = 0.
(си)' = си'.
(«1 + «2 + • • • + и„)' = U[ -I- «j +... + «^.
(uv)' =u'v-\-uv'.
u'v — uv' , r
Приведем примеры нахождения производных.
Пример 2. Найти производную функции у = х2-\—.
д ,/ = (д-2)' 4- (лг1)' = 2х — 1 • Jtr2 = 2х — ~. Формула (х ")' =
= —nx "-1, леМ, следует из правила дифференцирования
частного, если положить '/ = 1, v = xn.A
Пример 3. Найти производную функции у = л;4 — 2х3-\-Зх — 7.
Л У' = (х*)' - 2 (*у + 3 (х)' - G)' == 4л3 - 6ая + 3. а
Пример 4. Найти производную функции у = х\пх.
д ?/' = (*)'lnz + jt(lnz)' = 1 -1пх + л;-^-=1пл;+1. ^
Пример 5. Найти производную функции у= .
—Bх—1). 1 _
C+хJ
Правило дифференцирования сложной функции.
Пусть y = F(u), u = u(x) и (/(х) = 7^ (и (х)) — сложная функция.
Если функция и(х) дифференцируема в точке х0 и функция F (и)
дифференцируема в точке ии = и(х0), то сложная функция у (х) =
= F (и (х)) дифференцируема в точке х0 и
y'(xo) = F'(uo)u'(xo).
123
Пример 6. Найти производную функции у = (sin х-}-cos хK.
Д Полагаем здесь и (x) = sinx-\-cosx, y = ua. По правилу
дифференцирования сложной функции для любого х получаем
у' (х) = (ил)' и' (х) = 3и2и' (х)= 3(sinx-f cos xJ (cos x ~ sinx). a
Пример 7. Найти производную функции у(х) = ]/лх2 — 2х.
Д Полагая и(х) = х2 — 2х, получаем у(х) = \^и(х). Так как
(]/и)' =—yrz (см. пример 1), то имеем
2 V и
Геометрический смысл понятия производной становится ясным
из рассмотрения графика функции y = f(x), определенной на не-
некотором интервале ]а; Ь[.
У „I/ Для значений аргумента
Хо + Лл; и хп из интервала
]а; Ь[ соответствующие
ординаты графика функции
равны f(xo+&x) и /(*„),
разность значений этих ор-
ординат есть At/ (х0): &у (х0) =
— f(xo). Отно-
>У Wi) равк0 угЛОВО-
0
шение-
СС3
А!/
му коэффициенту прямой,
Рис_ 45, проходящей через точки
графика Af(A-0, /(.v0)) и
Л^(д;о-+ А^с. !(Ч + &х)). Прямая MN называется секущей (рис. 45).
Пусть Ax-vO, тогда точка N стремится к точке М. Если
существует производная f (хп), т. е. предел отрюшения —тт~> т0
секущая MN стремится к прямой, проходящей через точку М,
с угловым коэффициентом /' (х0). Предельное положение секущей
MN при стремлении N к М называется касательной к графику
функции y = f(x) в точке М. Угловой коэффициент касательной
равен /' (jt0), иначе tga—-f'(x0). Уравнение касательной, как
уравнение прямой, проходящей через точку М (х0, у0) с угловым
коэффициентом /' (хп), может быть записано в виде '—^ = f (х0)
или (так как г/о = /(*о))
A)
Пример 8. Найти уравнение касательной к параболе у-=х—
х2 -|- 6 в точке с абсциссой х0 = 1.
Д Находим производную функции / (х) = х — х2 + б:
124
и подставляем в уравнение касательной A) значения хо=1,
f(xo) = 6 и /' (х0) =—1, получаем уравнение касательной v-\-x =
^ 7. А.
Понятие производной является одним из основных в матема-
математическом анализе. О применении производных к исследованию
функций см. главу VI.
§ 8. Предел функции на бесконечности
Пусть функция f (х) определена вне некоторого отрезка [с; d],
как говорят, определена в окрестности бесконечности.
Число Ь называется пределом функции f(x) при х, стремящемся
к бесконечности, если для любого положительного числа е най-
найдется такое положительЕгое число М, что для всех х, удовлетво-
удовлетворяющих условию |х|>М, выполняется неравенство |/(х) — Ь | <е.
При этом пишут \imf(x) = b или f(x)-+b при х-^-оо.
1С-+О0
Пример 1. Доказать, что lim(l/x) = 0.
Д Функция f(x)—\/x определена для всех х^О. Для лгобого
е>0 неравенство \f(x) — 0| = 1/111<s будет выполняться, если
|*|>1/е. Таким образом, для любого е>0 можно взятэ М =
= 1/е, тогда при всех х таких, что \х\>М, будет справедливо
неравенство
1-0
<е. Это и означает, что 1/х-^-0 при х-
X
-»-оэ. А
Теорема о пределах, сформулироЕзанная в § 6, остается спра-
справедливой, если всюду х-*-а заменить на х-»-со.
Пример 2. Найти
lim —.,'/",¦ ¦¦
«-.00 *" + °
Д Как было отмечено, теорема о пределах останется справед-
справедливой при х-»-со, в частности, если пределы числителя и знаме-
знаменателя существуют и предел знаменателя отличен от нуля, то
существует предел отношения и равен отношению пределов,
поэтому имеем
о / 3 \ / 1 V2
-i. lim 12 + -Л 2+з( Hm -M
'2X~
^ «-со
(-1)
hra 1+-я i+5 lim -
Часто представляет интерес нахождение пределов ф/нкции
отдельно при стремлении х к -foo и к -оо. Определим эти
пределы следующим образом:
а) lim f
ХтСО
если для лЕобого е>0 найдется такое число Л1, что для зсех х,
удовлетворяющих условию х^>М, выполняется иераЕЮиство
\f(x)-b\<*.
125
6) lim f(x) = b,
X->—со
если для любого е>0 найдется такое число М, что для всех х,
удовлетворяющих условию х<С.М, выполняется неравенство
|/(*)-й|<е.
Если lim / (л:) = Ь, то, как нетрудно видеть,
lim f(x)= lim f(x)=-b.
jt->-|-co x — — со
Например, из того, что lira A/х) = 0, следует 1/л;->-0 при х->
*'—»СО
-> -f- СО И X -> ОО.
Заметим также, что теорема о пределах останется справедли-
справедливой, если всюду вместо х-уа подставить х->--|-оо или х-> — оо.
2х
Пример 3. Найти пределы функции f(x) = -r-r-,—г, когда х
' + I * \
стремится к -foo и когда х стремится к —со.
2х 2х
Л Если *>0, то __ = — „
lim —-|—¦= Jim -: = lim -. — 2.
X
2x 2x
Если же х<0, то r-j-—\~tzt> поэтому
llm llm lim 2 A
» —СО _± ]
X
§ 9. Односторонние пределы. Бесконечные пределы
Рассмотренная в § 6 функция sign x (см. рис. 43) не имеет
предела в точке х = 0. Однако, если ограничиться рассмотрением
только положительных х, то предел при х, стремящемся к 0, су-
щестгует и равен +1, Если же рассматривать только отрица-
отрицательные х, то предел при х, стремящемся к 0, также существует
и равен — 1. Говорят, что функция sign* при х, стремящемся
к нулю, имеет односторонние пределы: правый предел, равный
-j— 1, и левый определ, равный — 1.
Правой окрестностью точки а назовем любой интервал
]а; а-\~с[ при с>0. Пусть функция f (x) определена в некоторой
правой окрестности точки а. Число b называется правым пределом
(или пределом справа) функции f (х) в точке а, если для любого
положительного числа е найдется такое положительное число б,
что при всех х, удовлетворяющих условию а<х<о + б, т. е.
принадлежащих правой б-окрестности точки а, выполняется нера-
неравенство \f(x) — b|<e. При этом пишут:
lim f(x) = b.
126
Аналогично определяется предел слева. Левой окрестностью
точки а называется любой интервал }а — с; а[ при с> О Пусть
функция f (х) определена на некоторой левой окрестности точки а.
Число b называется левым пределом (или пределом слева) функ-
функции f(x) в точке а, если для любого положительного «ела е
найдется такое положительное число 6, что при всех х, удовлет-
удовлетворяющих условию а— 6«<х-<о, т. е. принадлежащих левой
б-окрестности точки о, выполняется неравенство |/(*) —Ь'<е.
Если левый предел в точке а равен Ь, то пишут
lim f(x) = b.
х-*а — О
В том частном случае, когда рассматриваются правый и левый
пределы в точке нуль, они записываются в виде
lim f(х) и lim fix).
*-.-)-О x-^ — 0
Таким образом, для функции sign л;
lim sign x =1, lim sign x = —1.
*-» + !) x-* — 0
Пример 1. Доказать, что
lim ^=1.
x-*-i-ov x + x
i/^ x
Д Функция f(x)—-r=—- определена при х>0 и при этом
Vx-x Vx(]-Vx) \-Vx
Vx-Yx Vx(\+Vx) \+V"i
Поэтому
\-Vx_ j
\+Vx
\+Vx
Для любого е>0 возьмем 6 = е2/4, тогда, если 0О<6, то
\f{x)-\ |<2j/x<2j/6=8. Это и означает, что lim У-й^-=
*-.+о Vх + х
= 1. ^
Утверждения теоремы о пределах функций, сформулированной
в § 6, останутся в силе, если всюду х-*-а заменить на х^-а-{-0
(соответственно на х-*-а — 0).
Бесконечные пределы. Пусть функция f(x) опргделена
в некоторой правой окрестности точки а и существует правый
предел функции jj^:, равный нулю:
lim 7Т
127
Например, функция f(х) = 1 /Ух — 1 определена при
Hm (l/f(x))= lim Ух-1=0.
-»l+0 *-»!+0
Если f(x)>0 в некоторой правой окрестности точки а и
lim (l//:(x)) = 0, то говорят, что функция ^(л;) стремится к плюс
бесконечности при стремлении х справа к точке а и пишут
lim
(читается: предел функции f{x) справа в точке а равен плюс
бесконечности).
Если f(x)<.0 в некоторой правой окрестности точки а и
lim (\/f(x)) = 0, то говорят, что функция f(x) стремится к минус
бесконечности при стремлении х справа к точке а и пишут
lim /(*)= —оо
(читается: предел функции f(x) справа в течке а равен минус
бесконечности).
Таким образом, lim (l/Ух— l)= + са, так как 1/Ух— 1>0
t-1+O
при х>1 и lim ]/x—1=0.
х-* 1+0
Аналогично определяются бесконечные пределы слева в точке а
для функции /(я), определенной в некоторой левой окрестности
точки а:
lim f(x)= -\-oo,
jf-»a —0
если /¦ (х) > 0 в некоторой левой окрестности точки а и
lim (l/f(*)j = O.
х-*а — 0
lim f(х)= — со,
х-»а— 0
если / (л;) < 0 в некоторой левой окрестности точки а и
lim (l/f(*)) = 0.
Х-\-1
Пример 2. Для функции f (x) = -jITf па&ТИ пределы справа
и слева в точке х= 1.
Д Функция f (х)= ¦ .- определена в окрестности точки jc = 1,
но не в самой этой точке, и
Далее, функция f(x)= _. положительна на интервале ]1; 3/2[
и отрицательна на интервале ]1/2; 1[, поэтому по определению
128
бесконечных пределов справа и слева имеем
lim f(x)=-\-oo и lim f (x)= — оо (рис. 46). А
v Г I П *-_w1 П
Если функция /(х) при х, стремящемся к а справа или слева,
имеет бесконечный предел, то при графическом изображении этой
функции проводят также прямую х = а. Это делает изображение
более наглядным.
У,
О
\
-1
Рис. 46.
О /
Рис. 47.
Рис, 48.
Для функции, определенной в правой и левой окрестностях
точки а, ее праЕый и леЕый пределы могут быть оба бесконечные
и разных знаков (рис. 46), оба бесконечные одного знака, как,
например, у функции /(л;)=1/х2 в точке х = 0 (рис. 47),
Может быть и так, что один из односторонних пределов
конечный, другой — бесконечный (рис. 48).
Бесконечные пределы определяются также при х, стремящемся
к -f-оо или —оо, например, lim /(л:)=+оо, если f (х) опреде-
дс-> — оэ
лена и положительна при всех х < М для некоторого М н
lim (!//(*)) =0.
Пример 3.
lim —
*-»-|-оэ
Л-+2
! .. 1— 2х — х- ,
¦ = — оо, lim — = + оо.
Понятие бесконечного предела широко применяется при иссле-
исследовании функции и построении их графиков (см. гл. VI).
ЗАДАЧИ РАЗДЕЛА !
«<
шя предела, доказа'
нить следующую таблицу зависимости N от е:
1. Исходя из определения предела, доказать, что lim - =1 i закол-
П-tCO П + '
6
N
1/10
1/100
1/1000
2. Доказать, что последовательность \п^ ) является неограниченно;"!.
5 n/ред. Г. Н. Яковлева 129
3. Доказать, что последовательность (—— . i ) является расходящейся,
4. Доказать, что lim A/яа)==0 для любого а > 0,
п-*со
5. Пусть последовательности (ап) и (Ьп) таковы, что | ап | г=; | bn | при
любом п и lim bn = 0. Доказать, что lim а„ = 0.
л-*со п-*со
6. Доказать, что lim (Vn+i — Vn)=0.
п-юэ
7. Найти формулу п-то члена последовательности, заданной речуррентно;
fli=2, fln+i=-Q-fln + -Q-i i e IN. Hartти предел этой последовательности.
о о
Найти пределы последовательностей:
10. Доказать, что lim yra=\ для любого а > 0.
11. Пусть последовательности (ап), (Ьп) и (хп) таковы, что lim an =
п-*са
= lim bn = a и для любого я выполняется неравенство ап-^хпг^Ьп. Доказать,
га-»от
что lim хп = а.
п~*со
12. Найти lim "'"
13. Доказать, что последовательность, заданная рекуррентпо: ai = V2,
an+i~V% + an, neIN, удовлетворяет теореме Вейерштрасса. Найти предел
етой последовательности.
14. Найти число членов арифметической прогрессии, у которой отношение
суммы первых 13 членов к сумме последних 13 членов равно 1/2, а отношение
суммы всех членов без первых трех к сумме всех членов без последних трех
равно 4/3.
15. Сумма членов арифметической прогрессии и ее первый член положи-
положительны. Если увеличить разность этой прогрессии на 3, не меняя первого
члена, то сумма ее членов увеличится в два раза. Если же первый член исход-
исходной прогрессии увеличить в четыре раза, не меняя ее разности, то сумма членов
увеличится также в два раза. Найти разность исходной прогрессии.
16. Бесконечно убывающая геометрическая прогрессия, сумма которой
равна 16/3, содержит член, равный 1/6. Отношение суммы всех членов про-
прогрессии, стоящих до него, к сумме всех членов прогрессии, стоящих после
него, равно 30. Определить порядковый номер этого члена прогрессии.
17. Найти значение произведения 0,2 G) • 0,1 F3) в виде простой дроби.
18. Исходя из определения предела функции в точке, доказать, что
lim *sin — = 0.
130
Найти пределы функций:
19. lim
20. lim
.1 х — 1
21. lim
JC-» —1
22. lim
cos 2л:
я sin л: + cos *
23. Найти пределы справа и слева в точке х = 0 функции
х—\х
/(*)=-
2х
24. Найти пределы справа и слева в точке х=\ функции
д;2_2| Ж-1 [-
25. Найти lim
26. Найти
27. Доказать, что при х-*--}-со функция f(x) = smx не имеет пи конеч-
конечного, ни бесконечного предела.
28. Найти проп.чводпую функции у= \\г
29. Нацти уравнение касательной к графику функции у=У4х—3 — >
в точке с абсциссой х = 3/2.
30. Найти уравнение общей касательной к параболам
у = х"- — 2х + Ъ и у = х- + 2х — 11.
ЗАДАЧИ РАЗДЕЛА II
1. Доказать ограниченность последовательностей:
1-я
а)
б)
в)
2. Исходя из определения предела, доказать:
» + (-')" \
а> lim 7Г+Т=2; б) lim
... sin и ,. я — а
в) hm —— = 0; г) lim ¦7r-r-r
_ i
2""
Для каждой из последовательностей заполнить таблицу зависимости Л/ от е:
в
N
1/10
1/100
1/1000
3. Доказать, что следующие последовательности являются неограниченными:
а) ап = (—I)"-n, neIN; б) а„=я'2 —я, я е IN;
в) а„ =
1-я
Уп
^-, я е IN; г) а„ = я + (—1)"-я, m
131
4. Доказать, что следующие последовательности являются расходящимися:
a)on = sin~, /ie№ б) ап=~ + (-1)п, пе=Ы;
LJ un ¦— r_ t it c= UN,
r) an= 1+- I, я <= IN (здесь [ ]—знак целой части числа).
Найти пределы последовательностей E—14):
с .. 10" я „ ,. 6я3-2я+1
5. lim .„„. , . 6. hm —r~ —.
п —> со
7. lim VJZ±L. 8.
9. lim i±2±^±».. ,0.
1
11. lim ,/ l+2«. 12. lim ¦—+'+...+- '
«-.со n^>oo\i-* •'¦o (n —l)-/
13. r,m i_±±_. и. lim ~ -.
n^oo 3« —2" n-co 217" +1
15. Доказать монотонность следующих последовательностей:
г) Начиная с какого п последовательность (п ¦ q") при 0<9<1 будет
ji! о тон на?
16. Найти, при каких соотношениях между а, Ь, с и d последовательность
(—хт) ^Удет: а) возрастающей, б) убывающей.
17. Доказать, что lim n-qn—0 при \q\<\.
18. Доказать, что последовательность имеет предел и найти его:
а)о1=1/2, о„=1/B-а„_1) при п^2;
б) а!=1/2, а„ = 2/C —а„_!) при п^2.
19. Найти формулу п-го члена для каждой из следующих последователь-
последовательностей и найти ее предел:
а) а1==3, an+1 = anJ при я>1;
5 3 1
6)fli = l, 02=2", an = yOn-i—уЯи-а ПРИ
20. Записать в виде обыкновенной несократимой дроби:
21. Найти число членов арифметической прогрессии, у которой отношение
суммы первых 23 членов к сумме последних 23 членов равно 2/5, а отношение
суммы всех членов без первых семи к сумме всех членов без последних семи
равно 10/7.
132
22. Найти число членов геометрической прогрессии, у которой о (ношение
суммы первых 11 членов к сумме последних 11 членов равно -р. , а отношение
о
суммы всех членов бгз первых деняти к сумме всех членов без последних де-
девяти равно 2.
ЯЗ. Три числа х; у; г образуют в указанном порядке геометрическую про-
прогрессию, а числа х; 2у\ Ъг образуют в указанном порядке арифметическую
прогрессию. Найти знаменатель геометрической прогрессии, отличной ог 1.
24. Второй, первый и третий члены арифметической прогрессии, разность
которой отлична от нуля, образуьэт в указанном порядке геометрическую про-
прогрессию. Найти ее знаменатель.
25. Разность арифметической прогрессии отлична от нуля. Числа, рапные
произведениям первого члена этой прогрессии на второй, второго члена на
третий и третьего на первый, образуют в указанном порядке геометрическую
прогрессию. Найти ее знаменатель.
26. Найти четыре целых числа а; Ь; с; d, первые три из которые а; Ь; с
в указанном порядке образуют геометрическую прогрессию, а последи ie три Ь;
с; d в указанном порядке образуют арифметическую прогрессию, если сумма
крайних чисел равна 21, а сумма средних чисел разна 18.
27. В арифметической прогрессии, разность которой отлична ст нуля,
сумма первых Ъп членов равна сумме следующих п членов. Налти о'чюшениа
суммы первых 2п членов к сумме следующих 2л членон.
28. Найти первый член геометрической прогрессии, у которой о-цошеиие
суммы первых пяти членов к сумме их обратных величин равно 49, а сумма
первого и третьего членов равна 35.
29. Найти знаменатель бесконечно убывающей геометрической прогрессии,
у которой отношения суммы кубоа всех члыюв к сумме квадратов scex чле-
членов равно 3, а отношение суммы всех членов к сумма квадратов все с членов
равно 3/7.
30. Три числа составляют геометрическую прогрессию. Если второй член
уменьшить па 4, то полученные три числа в том же порядке опять составляют
геометрическую прогрессию. Если третий член новой прогрессии уменьшить
на 9, то получится арифметическая прогрессия. Найти эти числа.
31. Три числа, сумма которых равна 78, образуют геометрическую про-
прогрессию. Их можно рассматривать также как первый, третий и девять,я члены
арифметической прогрессии. Найти эти числа.
32. Найти сумму бесконечно убывающей геометрической прогрессии, вто-
второй член которой равен 6, а сумма ее в 8 раз меньше суммы квадэатов ее
членов.
33. Найти сумму бесконечно убывающей геометрической прогрессии, у ко-
которой сумма квадратов первых п членов равна сумме первых 2я членов,
а сумма кубов первых п членов в три раза меньше суммы первых 3,ч членоя.
34. Найти сумму бесконечно убывающей геометрической прогреешь сумма
первого и пятого членов которой равна 34, а произведение первого и jea?,Toro
членов равно 4.
35. Найти сумму бесконечна убывающей геометрической прогрессии, все
члены которой положительны, если сумма первых трех членов это,! пр эгрессни
равна 39, а сумма обратных ьелниж э:их членов paiina 13/27.
133
36. Найти сумму S бесконечно убывающе1} геометрической мрогресгиц
если эта сумма иа 6 больше суммы периых трех ее членов, а сумма первых
трех на 1 больше суммы следующих трех членов.
37. Две арифметические прогрессии содержат одинаковое число членов.
Отношение последнего члена первой прогрессии к первому члену второй про-
прогрессии равно отношению последнего члена пторой прогрессии к периому члену
первой прогрессии и равно 4, Отношение суммы членов первой прогрессии
к сумме членов второй прогрессии равно 2, Определить отношение разностей
этих прогрессий.
38. Сумма членов и разность арифметической прогрессии положительны.
Если увеличить разность прогрессии на 2, не меняя ее первого члена, то сумма
ее членов увеличится в три раза. Если же разность исходной прогрессии уве-
увеличить в 4 раза, не меняя первого члена, го сумма членов прогрессии увели-
увеличится в 5 раз. Определить разность исходной прогрессии,
39. Две бесконечно убывающие геометрические прогрессии таковы, что
первый член первой прогрессии является знаменателем второй, а знаменатель
первой прогрессии является первым членом второй прогрессии. Сумма сумм
обеих прогрессий равна 2. Найти первый член первой прогрессии, если ее зна-
знаменатель равен 1/3.
40. Исходя из определения предела функции в точке, доказать, что:
а) Игл (**—1) = 3; б) lim -i!n|. = G; в) lim ^icos-1 =0.
*-»2 *-»3 х — •J *-»U x
Найтн пределы функций D1—51):
41. lim ' 7 ^ . 42. lira л '." . 43. lir
x-*0 * x x — l x I x.-
44. lim f—i . 3 1. 45. lim
46. lim (*-')^p. 47. li
48. lim . X + 3 . 49. lim
50. \\mt-^—-xy 5i. lim x (\
52. Найти пределы справа н слева в точке х = 0 функции
53. Найти пределы справа н слева в точке х = 0 функции
54. Найтн пределы справа н слева в точке х=\ функции
134
„ u . ... 2(x — x3)A~\x — к?\ ,
55. Для функции f(x)=?rj zh\ Г" а) наити пределы справа и сле-
2(х— х3)— \х— х3
ва в точке х = 0, б) найтн пределы справа и слева в точке х=\.
56. Доказать, что lim = 0.
*->оо х
57. В точке х = 0 найти пределы справ;а и слева функции f(x) = V,1/x.
58. В точке х=\ найтн пределы справа и слева функции f(x) = т~Г
х [х\
Найтн производную функцнн у (х) E9 — 64):
59. у = Х~Х ¦¦ 60. у={х — 2) cos х — sin x.
V х+\
в1. х = 3^-^. 62. v =
+ 1
^. 62. v = ^.
л: + 1 sin л: + cos л:
63. jr = je In (x*— 1). 64. # = 2* • (I —x).
65. Упростить выражение для f(x) и найти /' (х):
К^г jc—2
/(¦*)== .- , А
66. Найти точку х, в которой обращается в нуль производная функции
f(x)=<**-*¦ + 2ei-s* + 7x - 5.
2
67. Решить неравенство f'(x)<g'(x), если /(*) = — и g (х) — х— х3.
68. Найти уравнение касательной к параболе у = 3х2 — *+1 в точке с абс-
абсциссой х=\/2.
69. Найти, какой угол образует с осью абсцисс касательная к 1араболе
у = х2 — 5л: + 7 в точке М B; 1).
70. Найти уравнение общей касательной к параболам //=*2+1*+8 и
71. Найтн уравнение прямой, проходящей через точку A/2; 2). касаю-
Х
щуюся параболы у = 2—--, и пересекающей график функции у= VA — x2'.
а) в одной точке, б) в двух точках.
Глава VI
ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ИХ ГРАФИКОВ
§ 1. Четные к нечетные функции
Функция / (х), определенная на множестве X, называется
четной, если для любого хееХ выполняются условия:
-хеХ и/(—*) = /(*)•
Очевидно, что функции /(л:)=1 п f(x)—x2, определенные
на всей числовой оси, являются четными функциями. Однако
функция f (х) = х2, х е [1; 2], определенная лишь на отрезке [1; 2j,
не является четной, так как точка 1,5 принадлежит области опре-
определения функции, а точка —1,5 не принадлежит.
График четной функции на координатной плоскости симмет-
симметричен относительно оси ординат.
? Действительно, пусть функция/(.г), хееХ, четная и пусть
точка М с координатами х0, у0 принадлежит графику этой функ-
функции, т. е. j-jE/Y и yQ = f(xQ). Тогда согласно определению четной
функции
а это и означает, что точка М'(—х0; у0), являющаяся симметрич-
симметричной точке М (х0; у0) относительно оси Оу, принадлежит графику
данной функции. Щ
Верно и обратное утверждение: если график функции / (х)
симметричен относительно оси ординат, то эта функция f (х) четная.
Если две четные функции имеют одну и ту же область опре-
определения, то сумма, разность и произведение этих функций явля-
являются четными функциями.
Функция f(x), определенная на множестве X, называется
^счетной, если для любого х ен X выполняются условия:
—X ЕЕ X И / (—*) = — / (X).
Например, функции / (х) =¦- х3 и f (x) = sin x, определенные на всей
числовой прямой, являются нечетными функциями.
Легко показать, что график нечетной функции на координат-
координатной плоскости Оху симметричен относительно начала координат О.
Верно и обратное утверждение: если график функции / (х) на коор-
координатной плоскости Оху симметричен относительно начала коор-
координат 0, то функция f(x) является нечетной функцией.
136
Если две нечетные функции fix) и g(x) имеют одну и ту же
область определения X, то функции f(x)+g(x) и f[x)—g(x)
являются также нечетными функциями, а функция f (х) -{.'(х) явля-
является четной функцией.
Отметим, что области определения четных и нечетных функций
являются симметричными относительно точки О на координатной
прямой Ох.
Например, функция 1л х не является ни четной, ни нечетной,
так как она определена лишь для л;>0. Функция f (х) -¦¦ 1/(х — 1)
также не является ни четкой, ни нечетной, так как точка —1
принадлежит области определения функции, а точка 1 не при-
принадлежит. Функция / (х) = хг + За-, хотя и определена на всей
числовой прямой, однако не является ни четной, ни чечетной,
так как, например, /A) = 4, а /(—1)==—2, т. е, /A) =^/(—1)
" /(!)?=-/(-1).
Приведенные выше примеры показывают, что существуют
функции, которые не являются ни четными, ни нечетными. Для
любой функции f (х) можно доказать следующее утверждение.
Если функция f (х) определена на множестве X, которое явля-
является симметричным относительно точки О на координатной пря-
прямой Ох, то ее можно представить в виде суммы двух функций —
четной и нечетной, причем такое представление единственно.
? Действительно, пусть существуют четная функиия /, (х)
и нечетная функция ft(x) такие, что
/М = Л (*)+/*(*)
для любого хе.Х. Тогда для каждого ieX f(—x)=ii(—x) +
+ h(—x) = fi(x) — fi(x). Для определения функций Д (г) и /2 (х)
получаем следующую систему уравнений:
f(.-x)=h(x)-fAx),
из которой следует, что
ш = 1Щк*, ш = 1Щ±^1. A)
Следовательно, искомые функции однозначно определяются по дан-
данной функции формулами A). Из этих же формул следует, 1:то иско-
искомое представление всегда существует. Щ
Пример 1. Представить функцию
в виде суммы четной и нечетной функций.
Д Данная функция является суммой нечетной функции М*K
= Зхй и четной функции fi(x)=—4л;4 + л2 + 1. Очевидно, что
эти же функции получаются и по формулам A).
137
п
Заметим, что функция /t (x) содержит только те слагаемые,
в которых х входит в четной степени, а функция /2 (х) содержит,
слагаемые, в которых х входит в нечетной степени, а
Пример 2. Пусть на отрезке [0; 1] задана функция \{х) =
— 2х-\-\, Можно ли доопределить эту функцию во всех точках
числовой оси так, чтобы вновь полученная
функция была: а) четной, б) нечетной.
Д а) Функцию / (х) можно доопределить на
всей числовой прямой так, чтобы вновь получен-
полученная функция была четной. Одной из таких функ-
функций является функция F (х) — 1 + 2 \х |, х ен R
(рис. 49).
Очевидно, что такая функция не опреде-
определяется однозначно. Действительно, таким свой-
свойством обладает и функция b\ (х), которая рав-
Рис 49. на H~2i.v| на отрезке [—1; lj и равна нулю
для всех х, \ х | > 1.
б) Заметим, что если нечетная функция определена прия = 0,
то /@;=/(—0) = —/@) и, следовательно, /@) = 0.
Так как заданная функция f (х) при л-==0 принимает значение 1,
то доопределить ее на всей числовой прямой так, чтобы она была
нечеткой функцией, невозможно, а
§ 2. Периодические функции
Многие важные процессы в пр.чроде и технике являются перио-
периодическими. Изучение таких процессов приводит к необходимости
рассмотрения периодических функций.
Функция f{x), определенная на множестве X, называется
периодической, если существует такое число Т>0, что для любого
хе^Х выполняются условия:
х + ТееХ, х-ГеХ
Число Т называется периодом функции f (х), хееХ.
Очевидно, что если Т — период некоторой функции, то и любое
число вида пТ, где /igeM, является периодом этой функции.
Покажем, что если число То>0 является наименьшим перио-
периодом некоторой функции, то любой период этой функции имеет
вид пТ0, пеМ,
? Пусть То — наименьший период, а Т — какой-то период функ-
функции f(x), хеъХ. Найдем число п е W такое, что Т = пТ0 -{-аТ0,
где 0<а< 1. Тогда для любого хеХ имеем
/ (х) = / (х 4-Г) = / (л: + «То + аГ0) = / (х + аГ0).
А так как То — наименьший период, то отсюда следует, что а =
т. е. Г = /;Т0. Ш
138
Рассмотрим функцию sin л;. Из ее Определения следует, что
она периодическая и что число 2л является ее периодем. Пока-
Покажем, что любое положительное число Г<2я не является ее перио-
дом. Действительно, sin (я/2) = 1, но sin (-^ + Т ] < 1. Следователь-
Следовательно, 2я является наименьшим периодом функции sin*.
Не всякая периодическая функция имеет наименьший период.
Например, функция f(x) — 2, xeeR, является периодической, ее
периодом является любое положительное число. Очевидно, что
эта функция не имеет наименьшего периода.
Из самого определения следует, что если периодическая
функция f (х) не определена в точке х0, то она не определена
и во всех точках вида хо± пТ, где яенМ, а Т —период функ-
функции f(x). Поэтому любая функция, определенная во всех точ-
точках числовой прямой, кроме одной точки, не является периоди-
периодической.
Также из самого определения следует, что если функция не опре-
определена, например для всех х^са или х^а, то она не является
периодической. Так, например, функция f(x) = sin ]^x, определен-
определенная лишь для х^О, не является периодической.
Функция f (х) = хх определена на всей числовой прямой, но тем
не менее не является периодической. Действительно, если число
Г>0— период этой функции, то /@) = /(Г), т. е. 0== 74, что
невозможно.
Пример 1. Доказать, что функция cos2* периодическая,
и найти ее наименьший период.
Д Так как функция cos x периодическая с периодом 2я, то
и функция cos2л; периодическая и число 2я является ее перио-
периодом. Найдем ее наименьший период.
Легко убедиться, что число п является периодом функции
cos2х. Действительно, для любого xel\{
cos2 (х -f я) = (— cos хJ = cos2 х.
А так как cos2 0 = cos2 я = 1 и cos2 х < 1 для любого х е ]0; я[,
то число я является наименьшим периодом данной функ-
функции, а
Очевидно, что если две периодические функции Д (х) и '/3 (х),
хееХ, имеют один и тот же период Т, то их сумма, разность
и произведение тоже будут периодическими функциями и число
Т будет их периодом.
Если периодические функции Д (х) и /2 (х), х е= X, имеют соиз-
соизмеримые периоды Тг и Го, то они имеют общий период.
Действительно, так как Т\ и 1\ соизмеримы, то суцествуют
натуральные числа пит такие, что тТг = «Г2 = Т. Следонательно,
число Т — общий период функций /i (x) и/2(х). В частности, в этом
случае функции fi(x) + f2(x), h(x)—f2(x), fi(x)-f*(x) являются
периодическими с периодом Т.
139
Пример 2. Доказать, что функция
/ (х) = cos Зх + cos Ах
периодическая, и найти ее наименьший период.
Д Функция cos3x имеет период 7i = 2n/3, а функция cos Ax —
период /Г2 = 2я/4. Периоды Т\ и 7^ соизмеримы: 3711 = 4/Г2 = 2я.
Следовательно, число 2я является периодом данной функции.
Покажем, что этот период наименьший.
Наибольшее значение функции f(x) равно 2, и оно достига-
достигается в тех точках, где cos3,\;-=l и cos 4а; =1. На отрезке [0; 2л]
функция cos3x принимает значение 1 в точках 0, 2л/3, 4я/3, 2я,
а функция cos 4л; принимает значение 1в точках 0, я/2, я, Зя/2,
2л. Следовательно, функция / (х) = cos 3x + cos Ax на отрезке [0; 2я]
принимает значение 2 лишь в точках 0 и 2л. Отсюда и следует,
что число 2я — наименьший период. А
Если периоды функций fj(x) и /а(х), л;е.Х, несоизмеримы,
то функция fi(x)-}-h(x) не является периодической функцией.
§ 3. Асимптоты
При исследовании функции и построении ее графика важно
выяснить характер ее поведения в окрестности точек разрыва
и точек, где функция не определена, а также выяснить ее поведе-
поведение при х-*--\-аэ и х—»—со.
Рассмотрим функцию
Она определена для всех
поведение функции A) при х
geR, кроме # = ¦—1. Исследуем
+ оо. Так как / (х) = л; + 1 -г-г,
X ~f- 1
то разность / (а;) — (х + 1) стремится к нулю
при х-у-\-со. Заметим, что модуль разно-
разности f(x) — (лг-fl) равен расстоянию от точки
М(х; f(x)) до точки М' (х; х+1) прямой /,
заданной уравнением у — х-\-\. А так как
\MM'\ = V2\MN\ (рис. 50), где N- про-
проекция точки М на /, то отсюда следует, что
расстояние от точки М до прямой / стре-
стремится к нулю при *->--{-оо. В этом случае
прямая / называется асимптотой графика
функции y = f(x) при х-> + оо. Аналогично
показывается, что в данном случае расстоя-
расстояние от точки М графика функции до пря-
прямой / стремится к нулю при х-> — оо. Прямая /называется асим-
асимптотой графика функции y = f(x) при л'-> —оо.
Дадим соответствующие определения.
ее
Рис. 50.
140
Пусть функция / (х) определена на бесконечном интеграле
]а; +оо[. Прямая y = kx-\-b называется асимптотой графика
функции y = f(x) при x->--j-oo, если
lim (f(x)-(kx + b))=0.
Аналогично прямая у — kx + b называется асимптотой графика
функции y = f(x), хе] —00; Ь[ при х->—00, если
lim (f(x)-
Теперь изучим поведение функции A) при л:->-—1.
Так как при *-»-— 1 предел числителя равен —1, а предел
знаменателя равен 0, причем х-\-1<0 при х<.—1 и х+10
при х >—1, то
lim f (x) = +оэ и
lim / (х) = — оо.
лг—>—J-t-0
•7
i/k
Отсюда следует, что график данной функции в окрестности
точки х — — 1 имеет вид, указанный на рис. 51. Видно, jto точка
М(х; f (х)) графика функции при jc-»- — 1 прибли-
приближается к прямой х = —1: расстояние от точки М
до прямой х = — 1, равное х+1, стремится к нулю
при я-»— 1.
Прямая х = — 1 называется вертикальной асимп-
асимптотой графика функции y = f(x) при *->¦ — 1
слева и справа.
Дадим соответствующее определение.
Пусть функция / (х) определена на некотором
интервале ]а; Ь[. Если f(x)->co при *->-я + 0,
то прямая х = а наз)лвается вертикальной асимп-
асимптотой графика функции при х^-а справа, А если
/(*)->-со при х^>-Ь — 0, то прямая х = Ь называ-
называется вертикальной асимптотой графика функ-
функции y = f(x) при х^>-Ь слева.
Пусть прямая y — kx-\-b является асимптотой графика функ-
функции при х ->¦ -\- со. Рассмотрим функцию а (х) =f(x) — kx — b.
Из определения асимптоты следует, что
lim сф-) = 0.
I
Pic. 51.
Так как b = / (х) ~ кх — а(х), то
а так как
6= lim (f(x)-kx),
Х—*--\-О0
XXX
B)
141
то
k= lim i^- . C)
X-»-)-O3 X
Очевидно, что если существуют пределы B) и C), то прямая
y — kx-\-b является асимптотой графика функции при я->- + со.
Аналогично можно показать, что если функция y = f(x) опре-
определена на интервале ] — оо; а[ и если существуют пределы
lim -^L-=A, lim (f(x)-kx) = b,
*-» —оэ * x-> — оэ
то прямая y = kx-\-b является асимптотой графика функции у ==¦
= / (jc) при х —у — оо.
Прямая y = kx-\-b называется наклонной асимптотой, если
k=?0. Если й = о, то прямая у = Ь называется горизонтальной
асимптотой.
Пример 1. Найти асимптоты графика функции
Д Функция / (х) представима в таком виде:
Так как lim , . . =0, то прямая у = х — \ является асимптотой
х-»оо I х\ "г '
графика функции y = f(x) при х->- + оэ, а прямая у=— х— 1
является асимптотой графика функции y = f(x) при *-»—оо.
Так как , . . . >>0 для любого х, то график функции y — f(x)
лежит выше асимптот.
Вертикальных асимптот график функции y==f(x) не имеет. А
Пример 2. Найти асимптоты графика функции / (х) — У хг — 1.
Д Функция y = f(x) определена для \х\^\.
Вертикальных асимптот график функции f (х) ке имеет.
По формуле C)
А= lim V?^X = lim
По формуле B)
6= lim [Vx^T-x\= lim
V XZ— 1
= lim , —== lim ¦ ,
Таким образом, график функции y = f(x) имеет асимптоту # =
при x-*- + °°-
142
Найдем асимптоту графика функции y = f(x) при х-у — со
= lim -
х-* — оэ
Ъ= lim (V*=T + x)= lim
Щ
Ухг—\—Х
Х2_\_Х2 _.]
= lim -,—= lim ¦ , — = 0.
x^_m]/xi—\ — x x->-coVxli-\—x
Следовательно, график функции y = f(x) имеет асимптоту у =
= —х при х^>—оо. а
Заметим, что график функции / (х) = Ух2 — 1 имеет различные
асимптоты при х-*--\-оо и л;->—оо. График функции A) имеет
одну и ту же асимптоту при я->--|-со и *->¦ — оо.
Пример 3. Найти асимптоты графика функции j(.v) = ;e +
Д Так как lim/(л) = со, то прямая л: = 0 является верти-
х->а
кальной асимптотой графика функции y = f(x) при д;->0. Так
как НтA/л;) = 0, то прямая г/ = х является наклонной асимптотой
х->оэ
графика функции y = f(x) при х-у + со и *->¦ — со. а
Пример 4. Найти асимптоты графика функции / х) = ,
хе[я; +00).
Д Функция y = f(x) представляет собой произведение ограни-
ограниченной функции sin л; на функцию 1/х, которая стремится к О
при х ->¦ + оо . Поэтому
lim f(x) = O,
*-> + оэ
т. е. прямая г/ = 0 является горизонтальной асимптотой графика
функции y = f(x) при я->- 4-°о •
Этот пример интересен тем, что график функции / (х) пересекает
асимптоту г/ = 0 бесконечное число раз. ^
§ 4. Преобразования графиков функций
В этом параграфе покажем, как из графика функции y = f(x)
можно получить графики функций вида y=Af(ax + b)+B, где
А, В, a, b — некоторые действительные числа.
1. График функции у = / {х)-\-Ь получается из граф1 ка функ-
функции у = f (х) параллельным переносом r@; b).
143
Если Ь>0, то перенос совершается параллельно оси ординат
на расстояние Ь вверх, а если Ь<0, то вниз на расстояние |Ь|.
На рис. 52 изображены графики функций y---f(x), y = f(x)-\-\
и y = f(x)-2.
2. График функции y = f(x-\-a) получается из графика функ-
функции y=f(x) параллельным переносом г(—а; 0).
Если а > 0, то график переносится параллельно оси абсцисс
влево на расстояние а, а если а<0, то вправо на расстояние |я|.
На рис. 53 изображены графики функций y = f\x), y = f{x-\-l)
и tj = f(x-2).
Риь 52.
Рис. 53.
3. График функции y = Af(x), где Л>0, получается из гра-
графика функции y = f(x) сжатием к оси или растяжением от оси Ох
в отношении 1 : А, т. е. если 0<M<;l, то сжатием в 1/.4 раз,
а если Л>1, то растяжением в А раз.
Рис. 55.
На рис. 54 изображены графики функций y = f(x), y = 2f(x)
1
2
4. График функции г/ = — /(х) получают из графика функции
= f(x) зеркальным отражением относительно оси абсцисс.
На рис. 55 изображены графики функций y — f(x) ну — —f(x).
144
5. График функции y = f(kx), где /.'>0, получается из графика
функции y = f(x) сжатием к оси ординат или растяжением от оси
ординат в отношении \'.-г, т. е. если 0<?<1, то растяжением
в \/k раз, а если k>\, то сжатием в k раз.
На рис. 56 изображены графики функций y==f(x), y=fBx)
и y = f(x/2).
Рис. 56-
6. График функции y = f(—x) получается из графика функции
y = f(x) зеркальным отражением относительно оси ординат.
На рис. 57 изображены графики функций y = f(x) и y = f(—х).
7. Рассмотрим теперь, как
получается график функции
у = Af (ах + Ь) + 5, где Л > 0 и
а ."> О, из графика функции у =
= f(x). Так как
то сжатием к оси ординат в от- Рис. 57.
ношении 1 : - из графика функ-
функции y = f(x) получим график функции y = f(ax). Из этого i рафика
сжатием к оси абсцисс в отношении 1 : А получим график функции
у= Af(ax), из которого параллельным переносом г(—b/а; В) полу-
получим график функции у= Af (ax-\-b)-\-В.
§ 5. Элементарные функции и их графики
1. Линейной функцией называется функция вида y=kx + b,
где k и b — некоторые действительные числа. Она определена
на всей числовой прямой R. Если кфО, то ее множеством значений
является все множество R, если же fc = 0, то множество значений
состоит из одного числа Ь.
Функция y = kx-\-b является монотонной: при ?>0 oia воз-
возрастает на R, при &<0 она убывает, а при k = 0 она постэянная.
Графиком линейной функции y = kx-\-b является прямия, про-
проходящая через точку @; Ь) с угловым коэффициентом k. При k^=0
эта прямая пересекает ось абсцисс в точке х = —bjk, а при & = 0
она параллельна оси абсцисс.
145
У
X
На рис. 58 изображены графики прямых у~х, у=2, у=—2x4-1-
2. Квадратичной функцией называется функция вида
у = ах2 4- Ьх 4- с,
где а, Ь, с —некоторые действительные числа, причем афО. Она
определена на всей числовой прямой R и принимает действитель-
действительные значения.
Простейшей квадратичной функцией является функция вида
у = йх2, где а>0. Эта функция является четной, неотрицательной
и принимает любое значение из множества
[0; -f- оо[. На промежутке ] — со; 0[ она убывает,
а на промежутке [0, ~\~ оо[ возрастает. Точка
л; = 0 является точкой минимума. При любом
а > 0 график функции у = ах2 получается из
графика функции у = х2 сжатием к оси абсцисс
в отношении 1:а.
График функции у —ах2, где я<;0, полу-
получается из графика функции y = \a\xi зеркаль-
зеркальным отражением относительно оси абсцисс.
При о<0 функция у—-ах2 на промежутке
] — со; 0[ возрастает, а на ]0; -f- co[ убывает. Точка х — Q явля-
является ее точкой максимума.
На рис. 59 изображены графики функций у = х2, у — 2х2, у =
При любом афО функция у=ах2 является четной, и поэтому
ось Оу является осью симметрии графика этой функции. График
функции у = ах2 называется параболой, точка пересечения пара-
параболы с ее осью симметрии называется вершиной параболы. Оче-
Очевидно, что у параболы, заданной уравнением у = ах2, вершина
находится в точке О @; 0). Ветви параболы
при а > 0 направлены вве:рх, при а < 0 — вниз.
Покажем, что графиком любой квадратич-
квадратичной функции является парабола с вершиной
в некоторой точке Мо (х0; уп) и осью сим-
симметрии, параллельной оси ординат. Действи-
Действительно, так как
Рис. 58.
I
ах1
= й (л:2
V
Ьх + с =
Рис. 59-
то график функции у = ах2 -\- Ьх -\- с получается из графика функ-
, I b Aac — №\ ™ *
цниу = ах* параллельным переносом г 1-х-; —т— • 1аким обра-
образом, вершина параболы, заданной уравнением у = ах2 -\- Ьх -\- с,
находится в точке с координатами
хй = — Ь/2а, уй = Dас-Ь2)/4а.
146
Осью симметрии является прямая х — — Ь/2а, причем ветви
параболы направлены вверх, если а>0, и вниз, если а<0.
Пример 1. Построить график функции у = — 2х2-\-Ах-\-\.
Д Так как
у = — 2л-2 + Ах + 1 = — 2 (л-2 - 2х) + 1 = — 2 (х - 1)»+ 3
то график данной функции получается из графика функции у =
= —2л;2 параллельным переносом гA; 3). Таким образом, графи-
графиком данной функции является парабола, у которой ветви направ-
направлены вниз и вершина лежит в точке Ма(\; 3)
(рис. 60). А
3. Дробно-линейная функция задается формулой
где а, Ь, с, d — некоторые действительные числа.
Очевидно, что если c = d = 0, то формула A) не
задает никакой функции. Если же е = 0,
то получается линейная функция
Рис. @-
Поэтому будем считать, что дробно-линейная функция задается
формулой A), где сфО, и определена для всех jceR, кроме
х = — d/c В этом случае правую часть формулы A) можно пре-
преобразовать следующим образом:
/ d \ , , ad
ах + Ь а\х+^)+Ь-Т- а , bc-ad 1
±
cx + d I . d\ ~ с~*~ с* . d' {A>
C[X+c) * + 7
Отсюда видно, что функция, заданная формулой A), где bc — ad = 0,
во всех точках определения принимает постоянное значение а/с.
Эта функция отличается от постоянной функции лишь тгм, что
она не определена в точке — d/c.
Предыдущее исследование делает естественным следующее опре-
определение: дробно-линейной функцией называется функция вида A),
где с^=0 и bc — ad^=0.
Из формулы B) следует, что график дребно-лпнейной функ-
функции A) получается параллельным переносом г (—d/c; а/с) из гра-
графика функции
k , __ be—ad
У — — i гДе «— ^5 •
Как известно, графики функций вида y = k/x, где 1гф0, назы-
называются гиперболами. Из формулы B) следует, что графиком любой
дробно-линейной функции является гипербола.
147
Прямая г/ = 0 является горизонтальной асимптотой гиперболы
у=--к/х при х->~-\-оо п при х-*—оо, а прямая х = 0 является
ее вертикальной асимптотой. Из B) следует, что прямая у=а/с
является горизонтальной асимптотой графика дробно-линейной
функции A) при х->-\-сю и при х-*—оо, а прямая х = — die
является вертикальной асимптотой.
4. Показательной функцией называется функция вида у = ах,
где а>0, аф\. Показательная функция определена на всей чис-
числовой прямой и взаимно однозначно отображает интервал
J —оо; -foo[ на интервал ]0; +со[.
У,
I
Рис. 61
О 1
Ркс. 62.
При а> 1 функция у = ах возрастает, при 0<а< 1 —убывает.
Прямая у —0 является горизонтальной асимптотой графика
функции у = ах при х-*—оо, если а> 1, и, соответственно, при
х->- + со, если 0<а<1.
На рис. 61 изображены графики функций у = 2х, у = A/2)*.
Пример 2. Построить график функции
Д График данной функции получается параллельным перено-
переносом г@; I) из графика функции у = 2A/3)*, который получается
из графика показательной функции (/=A/3)* растяжением от оси
абсцисс в два раза (рис. 62), Прямая у=\ является горизонталь-
нон асимптотой графика функции г/= 2(l/3)*-f-1 при х-у-\-оо. ^
5. Логарифмической функцией называется функция вида
y = \ogax, C)
где а>¦ 0, аф 1, Она определена только для положительных зна-
значений х и взаимно однозначно отображает интервал ]0; +оо[
на интервал ]—со; + °°[. Из определения логарифма числа по
основанию а следует, что логарифмическая функция logax явля-
является обратной к показательной функции ах.
Если а>1, то логарифмическая функция C) возрастающая,
а если 0<а< 1, то убывающая. График логарифмической функ-
функции пересекает ссь абсцисс в точке х= 1, а ось ординат не пере-
пересекает. Заметим, что график логарифмической функции C) может
148
быть получен из графика функции у==ах зеркальным отражением
относительно прямой у = х.
На рис. 63 изображены графики функций y = \og2x и lagi/^x.
Пример 3. Построить график функции
у =
— 54
D)
Д Так как
у = log1/3 27 | х - 2 [ = — 3 + log,/21 х - 2 |,
то график данной функции получается параллельным переносом
г B; —3) из графика функции
i- E)
Эта функция определена для всех Jt/O и является четной. Сле-
Следовательно, часть ее графика, соответствующая х<0, получается
из графика функции y = \ogmxy где ж>0, зеркальным отражением
относительно оси ординат. На рис. 64 изображен график функции
y = \ogyjt\x\, а на рис. 65 —график функции
y = log1/3|27*-54|. a
6. Степенной функцией с показателем р на-
называется функция, задаваемая формулой
У=х", F)
где р — некоторое действительное число.
Сделаем несколько замечаний относительно
естественной области определения функции, за-
задаваемой формулой F).
Из определения степени следует, что если р — Haxyf альное
число, то формула F) определяет функцию на всей числовой пря-
прямой. В частности, при р = 1 получается линейная функция,
Рис. 63.
Рис. 64.
Рис. 65.
а при р = 2 — квадратичная функция. Если р— целое отрицатель-
отрицательное число, то функция F) определена для всех действительных
значений х, кроме х = 0. В частности, если р = — 1, то фуньция F)
является простейшей дробно-линейной функцией.
149
Если р не является целым числом, то степень хр в общем
случае определена лишь для х>0. Например, функция y = xlli
определена на бесконечном промежутке [0; +оо[, а функция у =
= хг1Н определена на бесконечном промежутке ]0; +оо[.
На рис. 66 изображены графики этих функций.
Таким образом, естественная область определения функции,
задаваемой формулой F), существенно зависит от показателя р.
Однако следует заметить, что на практике часто под областью
определения степенной функции понимается естественная область
определения соответствующей формулы.
Например, естественно считать, что
функция у = х1/л, являющаяся обратной
к функции у = х3, определена на всей
числовой прямой.
7. Основными тригонометрическими
функциями называются функции синус,
косинус, тангенс, котангенс:
sin л;, cos л;,
Рис. 66.
._sinx . cosx
cos x & sin x
Функция синус определена на мно-
множестве R всех действительных чисел,
является нечетной и периодической с наименьшим периодом 2л.
График синуса называется синусоидой (рис. 67). Функция sin.v
на отрезке [—л/2; л/2] возрастает от —1 до +1, на отрезке
[л/2; Зл/2] убывает от +1 до — 1, и т. д. Так как функция sin x
Рис. 67.
периодическая с периодом 2л, то ее график на любом отрезке
[а-\-2пп; ос + 2л(п+ 1)] длины 2л получается из ее графика на от-
отрезке [а; ос-|-2л] параллельным переносом гBлп; 0).
Функция косинус определена на множестве R всех действитель-
действительных чисел, является четной и периодической с наименьшим перио-
периодом 2л. На отрезке [0; л] она убывает от + 1 до — 1, а на отрезке
[л; 2л] она возрастает от —1 до +1. Так как cos л; = sin (х + ^)
для любого jteR, то графиком функции y = cosx является сину-
синусоида, которая получается из синусоиды y = sinx, изображенной
на рис. 67, параллельным переносом г(—л/2; 0). График функ-
функции у — cos х изображен на рис. 68.
Функция
150
определена на множестве всех действительных чисел, кроме чисел
вида ^ + л/г, где п <~ Z, т. е. кроме тех точек, в коюрых cos л;
Рис. 68.
обращается в нуль. Функция tg* является нечетной и периоди-
периодической с наименьшим периодом я. На интервале ] —я/2; я/2[
она возрастает от — оо до +оо. Прямые л; = — я/2, х = я/2 яв-
являются вертикальными
асимптотами графика
функции y = tgx. Так
как функция tg* пери-
периодическая с периодом
я, то ее график на лю-
любом интервале вида
"In. п . г
— ~п + п.п; д + ия по-
получается из ее графика на
] — я/2; я/2 [ параллель-
параллельным переносом г (ля; 0).
График функции y = tgx
изображен на рис. 69.
Функция
Рис. 69.
-2it
, a cos x У
** sin x
определена на множестве
всех действительных чи-
чисел, кроме чисел ви-
вида пп, где п е Z. Функ-
Функция ctg х является нечет-
нечетной и периодической с
наименьшим периодом я.
На интервале [0; я] она
убывает от + оо до — оо.
Прямые х = 0, х = я яв-
являются вертикальными
асимптотами графика
функции у = ctgх. Так как функция ctg* периодическая : пери-
периодом я, то ее график на любом интервале ]шх; {п+1)п[ по-
получается из ее графика на ]0; я[ параллельным переносом г (пп; 0).
График функции y = ctgx изображен на рис. 70.
Рис. 70.
151
Пример 4. Построить график функции y = 2sinBx — -~\.
Д Так как
то искомый график получается из графика функции y = s'mx пос-
последовательным применением следующих преобразований: 1) сжа-
сжатием к оси ординат в два раза из синусоиды y — sinx получается
Рис. 71.
график функции у = sin 2л:, который называется синусоидой
с периодом л (рис. 71), 2) параллельным переносом г@; я/6)
из синусоиды г/= sin 2л; получается гргфнк функции г/ =
= sin 2(х — -gj (рис. 72), 3) растяжением от оси абсцисс в два раза
из синусоиды у = sin 2 (х — ^ J получается искомый график (рис. 73).
Он также называется синусоидой. ^
152
Вообще, график функции у = A sin со (х — ее), где Л>0 и
называется синусоидой с периодом 2п/со, амплитудой А и началь-
начальной фазой а.
§ 6. Построение графиков функций
При построении графиков функций целесообразно действовать
по следующей схеме.
1. Найти область определения функции (если она не yv азана).
2. Установить, является ли функция четной илн нечет юй.
3. Установить, является ли функция периодической.
4. Найти асимптоты.
5. Найти промежутки возрастания и убывания функци-i.
6. Найти точки пересечения графика функции с осями соорди-
нат.
7. Найти экстремумы функции.
Данные исследования функций сразу же по мере их юлуче-
ния наносим на чертеж.
Пример 1. Построить график функции
Д Функция f (x) задана на всей числовой прямой и я )ляется
четной, так как /(*) = /(—х) для любого хеРч.
Функция / (х) не является периодической.
Так как
2
/ (х)= 1 — х2 -> 1 при я->-|-оо и при х-i—оо,
то прямая г/= 1 является горизонтальной асимптотой графика
функции при лг-^ + оо и при х-*- — оо.
Заметим, что /(лг)<1 для любого *e(R и, следова гельно,
график функции f(х) расположен ниже прямой у=\. Так как
2
функция на интервале ]0; +оо[ убы- „.
2 '
вает, то функция f(x)—\ j—р возрастает . —
на этом интервале. На интервале | — оо; 0[ —~vV
функция 2 возрастает, а потому функ- -/
ция /(*)=! J-—7- убывает на интервале Рис. 74
X -f- 1
]— оо; 0[.
График функции f (х) пересекает ось абсцисс в точках х= 1 и
х = — 1, а ось ординат в точке у — — 1.
2
Функция принимает наибольшее значение при х=0,
следовательно, функция f(x) при х — 0 принимает натеньшее
значение, равное — 1.
График функции A) изображен на рис. 74. А
153
Пример 2. Построить график функции
Д Функция /(х) определена для всех хфО ц является нечет-
нечетной, так как f{x) = — /(—х) для любого хфО. Функция f(x) не
является периодической. Действительно, любое число Т>0
принадлежит ее области определения, а число Т — Т = 0 не
принадлежит области определения, следовательно, никакое число
Т > О не может являться периодом функции f(x).
Построим график функции f(x) для лг>0. Так как
lim /(*)= lim x + -| = + oo.
lim (/(*)-*) = lim 1 = 0.
x—>4-°° * —»+ °°
то прямая х = 0 является вертикальной асимптотой, а прямая
y — x является наклонной асимптотой графика функции f (х) при
х-*--\-оэ.
На промежутке ]0; 1] функция f(x) убывает, а на [1; +со[
возрастает. Действительно, пусть 0 < хх < xit тогда
!
Отсюда следует, что если 0 ¦< хх ¦< я.
довательио, f (x2)<if(x1). Если же 1s^a;i<j;2, to 1 —
f(xi)>f(x1). Так как на ]0;
1, то 1--гт-<0 и, сле-
1 ^
и
ТУ at
f(i)f() ] [ функ-
функция /(л;) убывает, а на [1; +со[ воз-
возрастает, то точка х=1 является точ-
точкой минимума функции: f (x)>f(l) — 2
для любого х > 0, х Ф 1. График функ-
функции /(я) изображен на рис. 75. А
Пример 3. Построить график
функции
Рис. 75.
Функция B) определена для всех
xgR, кроме я = 0. Если х>0, то
е1>*>1 и, следовательно, f(x)<l/2.
На интервале ]0; +оо[ функция е1** убывает, и поэтому функ-
функция /(х) возрастает, причем
lim
J/X
= 0, lim
1
2"*
154
Следовательно, прямая г/=1/2 является горизонтальной гсимпто-
той графика функции B) при я-> + оо, причем график функции
B) при лг>0 лежит ниже этой прямой. Если л;<0, то el'x < 1
и, следовательно, f(x) > 1/2. Функция еМх
убывает на интервале ]— оо; 0[, и поэтому
функция f (х) возрастает, причем
lim Л77=1. lim Х—х = \-
+ е *-*-оо е ^ _
Следовательно, прямая х= 1/2 является рис 76.
горизонтальной асимптотой графика функ-
функции B) при я-> — оо, причем график функции B) при л; < О ле-
лежит над асимптотой. График функции B) изображен на рис. 76.
§ 7. Применение производной к исследованию функций
и построению их графиков
При исследовании функций и построении их графиков широко
используются производные. С их помощью у заданной пункции
находятся интервалы возрастания и убывания и точки экстрему-
экстремумов.
Справедливы следующие утверждения.
Если функция fix) со всех точках, некоторого интервала имеет
положительную производную f (x), то она возрастает на этом
интервале, а если отрицательную производную, то f (х) гбывает.
Пример 1. Найти интервалы возрастания и убывания функ-
функции
fix)=--2xi-9x2+l2x. A)
Д Данная функция определена и имеет производную на всей
числовой прямой. Так как
10 — fi / V \\ I V 0\
то /' (лг)>0 на интервалах ]—оо; 1[ и ]2; +оо[ и /'(^<0 на
интервале ]1; 2[. Следовательно, функция A) возрастает на интер-
интервалах ]—оо; 1[ и ]2; +оо[ и убывает на интервале ]1; '.:[.
Ответ: ]— оо; 1[ , ] 2; + оо[— интервалы возрастания, ]1; 2[ —
интервал убывания функции A). а
Промежутки, на которых функция возрастает или убывает,
называется ее промежутками монотонности.
Пример 2. Найти промежутки возрастания и убывания
функции
f(x) = ~-. B)
Д Функция B) определена для всех положительные хф\,
т. е. на интервалах ]0; 1[ и ]1; +оо[. Так как
155
то f (х) > 0, если х>е, и f (х) < 0, если х < е. Следовательно,
функция B) на интервалах ]0; 1[ , ] 1; е[ убывает, а на интервале
}е; +оо[ возрастает. Из непрерывности функции B) вточкел' = е
следует, что промежуток ]1; е] является промежутком убывания,
а [е; + оо[ — промежутком возрастания функции B).
Ответ: ]0; 1[ ,] 1; ё\ — промежутки убывания, [е, -(-оо[ —
промежуток возрастания функции B). ^
Точка х0 называется точкой минимума функции f {х), если
сущестзует такое 6>0, что эта функция определена в 6-окрест-
ности ]а'о — б; хо-\-8[ точки х0 и f(x)>f(xQ) для всех хфх0 из
этой 6-окрестности. Если же / (а;) < / (х0) для
всех хфх0 из ]х0 — 6; х„ + 6[, то точка х0
называется точкой максимума функции f(x).
Точки минимума и максимума функции на-
называются ее точками экстремума, а значе-
Н[]я фуШщИН ВЭГНХ ТОЧ.КЗХ — ЭКСтрвМуМпМИ
Рис 77_ данной функции.
Для функции, график которой изображен
на рис. 77, точки х}, х3 — точки максимума,
а точки #2) х4 —точки минимума. Точки а и Ь не являются точ-
точками экстремума этсн функции, тгк как у них кет окрестностей,
целиком входящих в область определения функции.
Для функции f{x)~\x\, определенной на всей числовой пря-
прямой, /@) = 0 и /(х)>0 для любого х ф 0, и поэтому точка х = 0
является точкой минимума функции f(x) = \x\.
Для функции f(x)=—(x— lJ + 3 точка х=\ является точкой
максимума, так как /(я) </A) = 3 для любого хф 1.
Функция /(*) = sii](l/je), л;>0, имеет бесконечное множество
точек экстремума. Действительно, каждая то^ка х, удовлетворяю-
удовлетворяющая условию — = -^—|-2л«, где п = 0, 1, 2, ..., является ее
точкой максимума, а каждая точка х, удовлетворяющая условию
--= — g +2л«, — ее точкой минимума. Экстремумы этой функ-
функции во всех точках максимума равны 1, а в точках минимума
равны — 1.
Для нахождения точек экстремума заданной функции важную
роль играет теорема Ферма:
Если точка xQ является точкой экстремума дифференцируемой
функции f (х), mo f'(xo) = Q.
Из теоремы Ферма следует, что точки экстремума заданной
функции следует искать среди точек, в которых производная
функции равна нулю или не существует.
Точки, в которых производная функции обращается в нуль
или не существует, называются критическими точками этой
функции.
Точки экстремума функции являются ее критическими точками.
Однако не всякая критическая точка является точкой экстремума.1
Например, точка х = 0 для функции f(x) = x3 является крити-
критической, так как /' @) = 0, но, очевидно, не является точкой
экстремума.
Пример 3. Найти точки экстремума и интервалы возраста-
возрастания и убывания функции f (х) = хе~х.
Д Данная функция определена и имеет производную для
всех xefc
/' (х) = е-х — хе-х = irx (\ —х).
Из уравнения /'(х) = 0 находим критические точки функции / (х).
У данной функции существует одна критическая точка х=\. Так
как f (х)>0 для х<\ и /'(х)<0 для х>\, то функция f (х)
возрастает на интервале ]—оо; 1[ и убывает на ин!ервале
]1; +ос[. Следовательно, точка х—1 является точкой максимума
функции f(x).
Ответ: f (х) возрастает на ]—оо; 1[, убывает на ]1; +оо[;
х=1— точка максимума. А
При исследовгнни точек экстремума \У
функции удобно пользоваться следующими
достаточными условиями для точек макси-
максимума и минимума.
Точка х0 является точкой максимума
функции f(x), если у точки х0 существует
такая окрестность, что в ней f(x) непре-
непрерывна,
-л -ю
f (х) > 0 для х<х0
Г (а) < 0 для х > xQ.
-8
Рис. 78.
Если же f (X) < 0 для х < хе и f (х) > 0
для х > л'„, то х0 — точка минимума.
В разобранных выше примерах было показано, как приме-
применяется производная к нахождению интервалов возрастания и
убывания и точек минимума и максимума у данной функции.
Если все эти исследования проведены, то, очевидно, можно
более точно изобразить график этой функции.
Пример 4. Построить график функции
У =
(х- IJ
х+1
C)
Д Функция C) определена для всех ieR, кроме л = — 1.
Она не является ни четной, ни нечетной и не является периоди-
периодической. Ее график пересекает оси координат в точках @; 1) и
A; 0). Так как у(х)—>- — оо при x-vl—0 и у(х)-*¦ + оо при
х-*-\-\-0, то прямая jc = —1 является вертикальной асимптотой.
Других вертикальных асимптот нет. Для нахождения наклонных
асимптот заметим, что
х+\
x+l
Следовательно, прямая у = х — 3 является асимптотой при х-*-\-оо
и при х-*- — оо. Найдем производную
(л:+1J
(л:+1J
Точки л: = — 3, л;=1 являются критическими для функции C):
в них производная обращается в нуль.
Легко видеть, что у'(х)>0 для х<С — 3, у'(х)<0 для х е
е ]— 3; 1[идлял;е]—1; 1[, у' (х) > О для д: > 1. Следовательно,
функция C) на промежутке ]—оо; —3] возрастает от — оо до
— 8, на промежутке [—3; — 1[ убывает от —8 до — оо, на
промежутке ]—1; 1] убывает от +оо до 0, на промежутке
[1; -|-оо[ возрастает от 0 до +оо. Отсюда следует, что функция
C) при х = — 3 имеет максимум, а при х = 1 —минимум. Состав-
Составляем таблицу.
X
У
у'
J—оо; —3[
1— оо; —8[
+
— 3
— 8
0
max
1-3; -1[
1-8; -оэ[
—
\
1
1
— 1;
+ ОЭ
—
\
И
0[
1
0
0
min
Л;
Ю;
+ со[
+ со[
+
График функции C) изображен на рис. 78. А
§ 8. Наибольшее и наименьшее значения функции
Пусть функция f (х) определена и непрерывна на отрезке [а; Ь]
и пусть Xi, ... , я* — критические точки функции / (х), т. е. точки,
в которых функция не имеет производной, и точки, в которых
производная равна нулю. Тогда на каждом из интервалов
]й; х}[ ,..., ]xh; b[ производная F (х) сохраняет знак, и, следо-
следовательно, на каждом из этих интервалов функция fix) либо
возрастает, либо убывает. Поэтому наибольшее из чисел /(а),
/(Xi), ..., f(xk), f (b) является наибольшим значением фу нкции / (х)
на отрезке [а; Ь], а наименьшее из этих чисел является наимень-
наименьшим значением функции на [а; Ь].
Заметим, что наибольшее и наименьшее значения функции
f(x), х^[а; Ь], находятся среди чисел f(a), f(xi),..., f(xk),
f(b), где хи ... , ^ — критические точки функции f (x) на la; b[.
Пример 1. Найти наибольшее и наименьшее значения функ-
функции
A)
158
а) на отрезке [0; 2]; б) на промежутке [—2; — 1[.
Д Функция A) определена и имеет производную на всем
множестве R действительных чисел, По правилам дифференциро-
дифференцирования находим
Таким образом, функция A) имеет две критические точки х = 1 и
х — Ъ. Причем f (х) на промежутке |—оо; 1] возрастает от — оо
до/A) = 5, на [1; 3] убывает от/A) = 5 до /C)= 1 и на [3 +оо[
возрастает от /C) = 1 до + оо.
На интервале }0; 2[ функция A) имеет одну критическою точ-
точку х=\. Следовательно,
min /(x) = min{/@)i /A); /B)} = min{l; 5; 3}=l,
(; 2]
max /(*) = max{/@); /A); /B)} = 5.
[0; 2|
На интервале ]—2; — 1[ функция A) не имеет критических
точек и возрастает. Следовательно, на множестве [—2; — 1[ у
функции A) наименьшее значение равно /(—2) = — 49. Однако
среди значений функции f(x), когда х е [—2; — 1[, нет наиболь-
наибольшего, так как точка х = —1 не принадлежит этому множеству.
Ответ: а) Наименьшее значение функции равно 1, нтиболь-
шее значение равно 5; б) наименьшее значение функции равно — 49,
наибольшего значения нет, а
Пример 2. Найти наибольшее значение функции
= 3x-tgx, *eE[0; п/2[.
Д Данная функция непрерывна и имеет производную
Она на интервале ]0; л/2[ обращается в нуль в точкг х0 =?
~ arccos (l/j/З), причем /' (х)>0 для х<_х0 и f'(x)<0 для
х>х0. Следовательно, точка хо = arccos(l/]/3) является точкой
максимума данной функции:
/ (arccosу=\ = 3 arccos -i= - tg /arccos J=j = 3 arccos ~-
-i= - tg /arccos J=j = 3 arccos ~
Функция f (x) на отрезке [0; arccos (l/"|/3)] возрастает, а на
промежутке [arccos (l/]/3); л/2[ убывает. Следовательно, наиболь-
наибольшее значение функции / (х) = Зх — tg x, *е[0; я/2[, равно
3 arccos A/3)-1/2. А
Пример 3. Найти наибольший объем цилиндра, вписанного
в данный конус.
159
Д Пусть задан конус с высотой Н и радиусом основания R
(рис. 79). Обозначим через h высоту цилиндра и через г радиус
основания цилиндра, вписанного в данный конус. Обозначим
ВМ = х. Тогда h = РВ = х¦ tgKML = х -к- и r = R—x. Объем
-X R И
цилиндра V равен nr2h. В нашем случае
Определим, при каком значении х объем ци-
цилиндра будет принимать наибольшее значение.
Найдем произзодиую V (х):
Рис. 79,
V'(x) = 0 при x = R/3. При x<R/3 производная V (х)>0 и
V'(x)<zO при x>R/3. Следовательно, в точке x = R/3 функция
V (х) имеет максимум. Так как х может меняться от нуля до R,
причем V @) = V (R) = 0, то число
является наибольшим значением объема вписанных цилиндров, д
ЗАДАЧИ РАЗДЕЛА I
1. Определить, какие из нижеприведенных функций являются четными,
какие нечетными, а какие не являются ни четными, ни нечетными:
/1(х) = Ул^-5.«
M*) = *3 + 3siHA",
е~х—\
/4 (х) =х* — Г) cos к,
ех+[ ' i*\~>--
2. Исследовать на периодичность следующие функции и определить наи-
наименьший период, если он существует:
1, если х — рациональное,
если х — иррациональное;
б) f{x) = cos3 х sin x — sin3 х cos x.
3. Найти все асимптоты графиков следующих функций:
V"J Х^т: в) /(*) = 1/'F+6jc + 8.
а) /(*> = { J;
4. Построить графики следующих функций (не применяя производной);
а) f1(X) =
б) Ы*)= lg(sinx); в) fa(x) =
160
5. Применяя производную, построить графики следующих функций:
6) /(*>-
6. Найти интервалы монотонности и точки экстремумов функции
) = 2 1п(х — 2) — л2 + 4л: + 1.
7. Найти наибольшее и наименьшее значения функции i(x)=-~ х3—
о
—„ х2-\-6х на отрезке [1; 4J.
8. Около данного шара описать конус наименьшего объема.
ЗАДАЧИ РАЗДЕЛА II
1. Определить, какиг из приведенных ниже функций в области, где они
определены, являются четными, какие нечетными, а какие не язляютс; ни чет-
четными, ни нечетными:
к (*) = 1 +Х"— х*, U (х)=х + х3-3*5,
h (*) = VT+I, U (х) = V\-x\
U (х) = У&-ЗХ-А, f9 (х) = In i=^,
/, (х) = 3х + 3 ~х, /в (х) = х sin 3*.
2. Представить следующие функции в виде суммы четных и нечетных
функций в области, где они определены:
h {х) = sin 3* + 2х tg *, М*) = * In |* | +~,
X-- + &+X *х + х*
h(x)
3. Доказать, что производная четной функции нечетна, а производная
нечетной функции четна.
4. Верны ли утверждения: а) если f (x) —четная функция, то /(^ — нечет-
нечетная функция, б) если f (x) — нечетная функция, то /(х) —четная функция.
5. Существуют ли всюду определенные функции, являющиеся одновземенно:
а) четными и возрастающими на U, б) нечетными и убызающимн на R, i) нечет-
HbiNm и положительным;! из R?
6. Пусть задана функция f(x) = ex, х > 0. Доопределить функмпо / (х)
в области х г? 0 так, чтобы впоьь голуче1:ная функция на м южегтве
]—со, + оо[ была: а) чгтпоч функцией, б) нгчетно."| фунхцигЧ.
7. Исследовать на периодичность следующие функции и определить наи-
наименьший период, если он существует:
fx{x) = x?+i, /2(.v-)==2tgy + 4tg|-,
8. Может ли сумма двух непериодических всюду определенных функций
быть периодической функцией?
6 п/ред Г. Н Яковлева 161
9. Пусть задана дифференцируемая периодическая функция / (х),
Доказать, что /' (х) — также периодическая функция на R.
10. Найти все асимптоты графиков следующих функций:
б) /»W-!7f=Tl 6)/вМ=:м'> где W = *-M-
11. Построить графики следующих функций (не применяя производной):
1) h(x) = el/sinx; 2) /2(x) = cos(lnx);
3) /s (*) = arc sin (sin x); 4) /4 (x) = [Y/^?^0 5!
5, /5 (jc)=>/-(jc), где /¦ (jc)—расстояние от х до ближайшего целого числа,
12. Применяя производную, построить графики следующих функций:
3) /з (*) = A + *) | *!/э; 4) и М =
б) /в (*) = sin4 х + cos4 x; 6) /„ (х) = 1 n jc//i.
13. Найти все значения а, при которых функция
возрастает на R.
14. Пусть х1 и дс2 — соответственно точка максимума и точка минимума
функции f(x) = 2x3 — 9ол:2+12а2л:+1. Прн каких а х\ = х?
15. Найти наибольшее и наименьшее значения функции
у=х"-Bх — 3)— 12 (Зх — 2)
на отрезке [ — 3; 6].
16. Найти наибольшее и наименьшее значения функции /(*) =
«= log1/3 (дса + л —2) на отрезке [3; 6].
17. Найти экстремумы функции /(*) = (* — 3)е'Л'"^1' на интервале ] — 2; 4[,
а также наибольшее и наименьшее значения на отрезке [ — 2; 4].
18. Найти наибольшее и наименьшее значения функции / (х) я= cos2* -J-
-f cosJC + 3,
19. Найти радиус основания цилиндра, имеющего при данном объеме V
наименьшую полную поверхность.
20. Найти косинус угла при вершине равнобедренного треугольника,
имеющего наибольшую площадь при данной постоянной длине / медианы,
проведенной к его боковой стороне.
Глава VII
ВЕКТОРЫ
§ 1. Некоторые необходимые определения и обозначения
Любая лежащая на прямой точка А разбивает ее па два
луча с началом в точке А. Луч с началом в точке А, на котором
лежит точка В, обозначается [АВ) (рис. 80).
Два луча, лежащие на одной прямой, называются сонаправ-
ленными, если их пересечение есть луч, и называются противо-
противоположно направленными, если их пересечение лучом не является.
Например, на рис. 81 лучи [АВ) и [ВС) сонаправлеиы, а лучи
[АВ) и [СВ) — противоположно направлены.
Рис. 80.
Рис, 81.
Если два луча лежат на параллельных несовпадающих прямых,
то они лежат в некоторой плоскости. Прямая, проходящая через
их начала, делит эту плоскость на две полуплоскости. Если эти
Рис. Р2.
Рис. 83.
лучи лежат в одной полуплоскости, они называются сонси.-равлен-
ными (рис. 82), если в разных полуплоскостях —противог,оложно
направленными (рис. 83). То, что лучи [АВ) и [CD) сонаир авлены,
обозначается так:
, [АВ) ft [CD).
6* 163
Если лучи [АВ) и [CD) противоположно направлены, то пишут
[AB)\\[CD).
Очевидно, что два луча, порознь сонаправленпые третьему,
сопаправлены друг другу.
Параллельным переносом пространства (плоскости), определяемым
упорядоченной парой (А, В) несов-
несовпадающих точек, называется такое
преобразование пространства (плоско-
(плоскости), при котором каждая точка М
отображается на такую точку N, что
луч [MN) сонаправлел лучу [АВ) и
расстояние [ MN | равно расстоянию
| АВ \. Другими словами, все точки
Рис. 84, пространства (плоскости) смещаются
в направлении луча [АВ) на расстоя-
расстояние | АВ j (рис. 84).
Тождестве иное преобразование, отображающее каждую точку на
себя, называется параллельным переносом на нулевое расстояние.
Свойства параллельного переноса
1. Параллельный перенос есть перемещение, т. е. отображе-
отображение, сохраняющее расстояния.
2. Параллельный перенос отображает прямую на параллель-
параллельную ей прямую, луч на сонаправленный ему луч.
Параллельный перенос пространства отобрао/сает плоскость
на параллельную ей плоскость.
3. Композиция двух параллельных переносов (т. е. два парал-
параллельные переноса, выполненные последовательно) есть параллельный
перенос.
4. Отображение, обратное параллельному переносу, есть
параллельный перенос.
Угол между лучами. Пусть два луча /i и /2 не сона-
правлены и не противоположно направлены (рис. 85). Из произ-
произвольной точки О выходит единственный луч [ОА), сонаправленный
Гнс. 85.
с лучом 1и и единственный луч [ОВ), сонаправленный с лучом
12- Лучи [ОА) и [ОВ) ограничивают выпуклый угол АОВ, величина
которого меньше 180°. Если же лучи h и h противоположно
направлены, то лучи [ОА) и [ОВ), им сонаправленные и имеющие
1G4
общее начало, ограничивают два выпуклых развернутых угла
(рис. 86).
Углом между лучами 1Х и /2 называется величина выпуклого
угла между любыми двумя лучами, имеющими общее начало и
сонаправленными с данными.
Так, углом между лучами /х и 12 на рис. 85 является вели-
величина угла АОВ, а угол между лучами k и 12 на рис. 86 равен 180°.
Рис. 80
Независимость угла между лучами от выбора точки сон трав-
травленных с ними лучей следует из теоремы:
Если стороны двух выпуклых углов соответственно сонапраа-
лгны, то эти углы конгруэнтны.
Угол между сонаправленными лучами полагается равным О".
Таким образом, угол между лучами может принимать значения
от 0° до 180°.
§ 2. Векторы, их обозначение и изображение.
Келлинеарные и компланарные векторы
Вектором называется параллельный перепое. Для обозначе-
обозначения векторов используются символы а, Ь, л: и т. п. Векторы
рассматриваются на плоскости (параллельный пе-
перенос плоскости) и в пространстве (параллельный
перенос пространства). И в том и в другом слу-
случае вектор определяется упорядоченной парой то
чек, т. е. заданием точки и ее образа.
Вектор й, определяемый упорядоченной па-
парой (А, В) несовпадающих точек, изображается
направленным отрезком (стрелкой) с началом в то-
точке А и концом в точке В (рис. 87). Этот вектор
а обозначается также АВ и пишется а = АВ. По определению
вектор а = АВ отображает каждую точку М на такую точеу Л',
А
Рис.
р р у у
что луч [MN) сонаправлен с лучом[АВ) и
у еу Л,
= |Л?|. Направ-
Направление луча [АВ) называется направлением вектора а = АЁ. Рас-
Расстояние \АВ\ называется длиной или модулем вектора с. = АВ
(обозначается \АВ\ или \а\). ^
Если [MN)\\[AB) и \MN\ = \AB\, то вектор а = АВ обозна-
обозначается также MN и изображается направленным отрезком <: нача-
началом в точке М и концом в точке N. Очевидно, при изобргжении
1G5
вектора направленным отрезком за его начало может быть взята
любая точка, т. е. вектор имеет бесчисленное множество изобра-
изображений. Например, на рис. 88 вектор а = АВ изображен направ-
направленными отрезками PQ, АВ, MN, OOi.
Построение направленного отрезка MN такого, что MN =а,
называется откладыванием вектора а от точки М.
Если АВ и CD являются обозначениями одного и того же век-
вектора, то пишут AB — CD и говорят, что векторы АВ и CD равны.
Подчеркнем, что равенство AB = CD означает
\AB\ = \CD\ и [AB)\\[CD).
Параллельный перенос на нулевое расстояние называется
нулевым вектором и обозначается О. Нулевой вектор отображает
каждую точку на себя, поэтому он обозначается также ~А~А, ~ВВ
и т. п. Длина нулевого вектора равна
нулю. Нулевой вектор не имеет опреде-
определенного направления.
Два ненулевых вектора АЁ и CD
называются сонаправленными (обозначается
ЛИ ff CD), если сонаправлены лучи [АВ)
и [CD), и называются противоположно на.
правленными (обозначается АВ \\~CD), если
лучи [АВ) и [CD) противоположно на-
направлены.
Два ненулевых вектора называются коллинеарными, если они
сонаправлены или противоположно направлены. Ясно, что кол-
линеарные векторы изображаются параллельными направленными
отрезками.
На рис. 89 изображена трапеция ABCD, MN —ее средняя
линия. Векторы AD, ВС, NM коллинеарны: ~AD\\B~C и A~D*\\NM.
Нулевой вектор считается коллинеарным любому вектору.
Будем говорить, что ненулевой вектор АВ параллелен плоско-
плоскости, если прямая АВ параллельна этой плоскости.
р
Рис. 88.
;L
У
А Л
Рис. 89.
Ненулевые векторы называются компланарными, если они
параллельны одной и той же плоскости. Любые два вектора
всегда компланарны, а три вектора могут не быть компланар-
166
пыми. На_рис.^90 изображена треугольная призма
Векторы АС, АВ и CiBi компланарны, а векторы АС, АВ и АА~[
компланарными не являются.
§ 3. Сумма векторов. Противоположный вектор.
Разность векторов
Композиция двух векторов а и b есть вектор (свойство 3
параллельного переноса, § 1), который называется суммой векто-
векторов а и & и обозначается а + Ь.
Сумма ненулевых векторов а и Ь находится по правшу тре-
треугольника (рис. 91): от произвольной
точки О откладывается вектор О А —а,
от конца направленного отрезка OAt
т. е. от точки А, откладывается век.
тор ~АВ = Ь, тогда ОВ = а-\-Ь. Правило
треугольника сложения векторов легко
запоминается в буквенной записи:
О А + А В = б~В
I ! I—t
(стрелочками внизу указана последовательность букв в записи
вектора суммы).
Рис. 92.
Заметим, что это правило применимо и в том случае, когда
векторы а и b коллинеарны (рис. 92).
Законы сложения векторов
1. a-\-b = b-\-a (переместительный закон).
2. (а-\-Ь)-\-с = а-\-{Ь-\-с) (сочетательный закон).
3.
Из переместительного закона следует
правило параллелограмма сложения векто-
векторов: сумма двух неколлинеарных векторов
есть вектор, изображаемый диагональю па-
параллелограмма, построенного на направлен-
направленных отрезках, изображающих данные век- Рис- 93'
торы и имеющих общее начало (рис. 93).
Сумма трех векторов а, Ь и с определяется как сумма вектора
а-\-Ь и вектора с (рис. 94). В силу сочетательного закона
167
(a-\-b)-\- c —a -\-(b-\-c), поэтому сумма трех векторов a, b и с
записывается без скобок: a + b+с. Аналогично определяется сумма
любого числа векторов, например a-\-bJrc-rd=(a-\-b-\-c)J\-d.
На рис. 95 показано, как находится сумма векторов а, Ь, с и d
гю правилу многоугольника.
>-*-?
О' л А
Рис. 96.
Если три вектора а, Ь и с некомпланарны, их сумма может
быть найдена по правилу параллелепипеда: вектор а + 6 — с изоб-
изображается диагональю параллелепипеда, построенного на направ-
направленных отрезках, изображающих векторы a, b и с и имеющих
общее начало (рис. 96). Действительно:
ОА + ОВ + ОС = ОА + A D + DDi = б15х.
Пусть вектор а определяется упорядоченной парой точек (А, В):
а = АВ. Вектор, определяемый упорядоченной парой точек (В, Л),
называется противоположным вектору а и обозначается —а:
Сумма вектора и ему противоположного вектора есть нулевой
вектор (тождественное отображение):
—а) = 0 или
Очевидно, что длины вектора а и ему противоположного век-
вектора —а равны, а направления этих векторов противоположны:
а
—а\, а\\(—а).
Разностью а — b двух векторов а и Ъ называется сумма
вектора а и вектора, противоположного вектору Ь, т. е.
а —6 = я+ (—&).
Если 0А=а и ОВ = Ь (рис. 97), то вектор а — Ь изображается
направленным отрезком В А:
61-0В = ВА
1—1
168
(стрелочки внизу указывают последовательность букв в записи
вектора разности),
Заметим, что если на векторах а и 6, отложенных от общего
начала О, можно построить параллелограмм (рис, 98), тэ длина
диагонали, имеющей то же начало О, равна длине вектора а-\-Ь,
а длина другой диагонали равна длине вектора а — Ь:
\OC\ = \a-\-b\, \ВА\ = \а-Ь .
Если с = а — Ь, то а = с-\-Ь. Действительно:
Это показывает, что слагаемые в векторных равенства): можно
переносить из одной части равенства в другую, изменив гтоящие
перед этими слагаемыми знаки на противоположные.
а-д
Рис. 97.
Пример 1. В параллелограмме ABCD диагонали пересекаются
в точке О (рис. 99). Найти сумму векторов UA + OB + GC + OD.
Д Диагонали параллелограмма, пересекаясь, делятся гюполам:
\ОА\ = \ОС\. Лучи [ОА) и [ОС) противоположно направлены,
поэтому векторы бА и СС — противополож-
противоположные, их сумма равна нулевому векто-
вектору: OA+VC = 0. Аналогично устанавли-
устанавливается, что ОБ и OD — противоположные
Еекторы. Итак, OA + OB + CC-\-OD =
= (ОА + ОС) + (OB + 0D) = 0. А
Пример 2. Доказать, что для любых
векторов а и b справедливо неравенство
\а + Ь\<\а\-\-\Ь\.
Д Если один из Еекторов а или Ь нулевой, то это неравенство,
очевидно, выполняется. Пусть а и Ь — ненулевые векторы, ОЛ= а
и AS = 6 (рис. 91), тогда по правилу треугольника бВ = а-\Ь.
По свойству расстояний для любых трех точек О, А и В выпол-
Рис. 99.
р
няется неравенство | ОБ | ==? | О А | + | АВ |, поэтому
+ IH
Заметим, что для различных точек О, А и В равенстве ]0J3j —
= |ОЛ| + \АВ\ выполняется тогда и только тогда, когда точки О,
169
А и В лежат на одной прямой, причем точка А лежит между
точками О и В. Следовательно, для ненулевых векторов а и Ь
равенство \a\b\~\a\-\-\b\ справедливо
тогда и только тогда, когда они сонаправ-
лены. А
ПримерЗ. В треугольнике ABC ме-
медианы пересекаются в точке О (рис. 100).
Найти сумму векторов
ОА + ОВ + ОС.
Д Построим параллелограмм AOCD,
По правилу параллелограмма OD = О А -\-
+ ОС. Диагонали параллелограмма, пере-
пересекаясь, делятся пополам, следовательно,
[ 0D j = 21 ON |, точка N — середина сто-
стороны AC, BN — медиана. Медианы треугольника, пересекаясь,
делятся в отношении 2:1, считая от вершины, поэтому | OB | =
¦--2\ON\. Таким образом, \OD\=\OB\, а так как лучи [OD) и
[ОВ) противоположно направлены, то OD = —OB.
Итак,
О'А-\-ОВ + ОС = (ОА + ОС) + ОВ =Ш)+~бВ = —ОВ + ОБ = 0. а
§ 4. Умножение вектора на число. Признак коллинеарности
Произведением ненулевого вектора а на чиста х^=0 называется
вектор, длина которого равна |x|-|aj и который сонаправлен
вектору а при х>0 и противоположно направлен при x<iO.
Произведение вектора а на число х обозначается х-а.
Произведение нулевого вектора на любое число и произведение
любого вектора на нуль по определению считается равным нуле-
нулевому вектору:
а:0 = 0, 0-а = 0.
Законы умножения векторов на числа
х (уа) = (ху) а (сочетательный закон).
ха-\-уа^(х + у)а,
(распределительные законы).
1.
2.
3.
4.
Из определения произведения вектора на число получается
следующий признак коллинеарности:
Вектор Ь коллинеарен ненулевому вектору а тогда и только
тогда, когда существует такое число х, что Ь = ха.
Пример 1. Найти, на какое число л; надо умножить ненуле-
ненулевой вектор а, чтобы длина вектора т = ха была равна единице
170
И а) вектор т был сонаправлен вектору д; б) вектор т был
противоположно направлен вектору д?
/; а) /и 11 д, когда х > 0; так как |х|=х и | m | =¦= # | д | при
а;>0, то из условия | m | = 1 следует я=1/|д|.
б) /nfjfl, когда Ж0; Так как |#| =—х при дг<0, тс [т|«*
*=—х\а\. Из условия |т| = 1 находим х — — \l\a\. ^
Заметим, что вектор, длина которого равна единице, называется
единичным или ортом.
Из признака коллинеарности следует, что для неколлинеарных
векторов а и b равенство xa-\-yb = 0 выполняется только тогда,
когда х = у = 0. Действительно, предположим, например, что
х Ф 0, тогда из ха + уЬ = 0 получим а = — — b, a это npoTt воречит
тому, что векторы а и b неколлннеарны. Следовательно, ^«0,
Аналогично устанавливается, что //==0.
Пример 2. Векторы а\\Ъ неколлинеарны. Найти, при какому
векторы с = (х — 2)а-\-Ь и d = Bx-\-l)a— Ъ будут коллииеариы.
Д Вектор с ненулевой, так как коэффициент при Ь отличен
от нуля, следовательно, существует такое число у, что d = ус, т. с.
Как было сказано, слагаемые в векторном равенстве можно пере-
переносить из одной части в другую, изменяя знаки
слагаемыми на противоположные, поэтому будем иметь
Векторы а и b неколлинеарны, поэтому
Решая эту систему, находим у — —1 и х =1/3. При %=1/3
5 5
векторы cud таковы: с*= —уД + й, я* = у а — Ь, Как лег-
легко видеть, они противоположные: й — — с. А-
§ 5. Условие компланарности векторов.
Разложение вектора по трем некомпланарным векторам
Пусть векторы а и b неколлинеарны, отложим их от одной
точки: ОА = а и ОВ = Ь (рис, 101). Любой ненулевой взктор с,
компланарный с векторами а и Ь, по определению naf аллелен
плоскости ОАВ,
Если построить вектор GC = c, то точка С лежит в плоскости
ОАВ, поэтому говорят, что любые три компланарные векторы
можно перенести в одну плоскость.
Теорема. Если векторы а и b неколлинеарны, то любой
компланарный с ними вектор с можно единственным образом
представить в виде с = ха-\- yb.
171
Такое представление называется разложением вектора с на
плоскости по дсум неколлинеарным векторам а и Ь.
Пример I. Дан параллелограмм ABCD (см. рис. 93). Разло-
Разложить векторы АВ i: AD по векторам АС и BD.
Д Напомним, что АС=Ад-\-АВ и BD—AD — АВ. Отсюда следует
2AD = A~C+BD и 2АВ = АС - BD. Таким образом,
AD = ~ (АС + Щ и АВ = \ (AC -BD). A
Пример 2. На стороне ВС треугольника ОВС расположена
точка N так, что | BN | : | ВС | = п (рис. 102). Разложить вектор ON
по векторам OS i: ОС.
Рис. 101 -
Рис. 102.
Д Векторы BN и ВС коллинеарны и сонаправлекы, следова-
следовательно, BN=xBC и х>0. Поскольку jfl^V|=n|BC|, то х = п
н BN = nBC~. Так как ВС = ОС -О~В и Ш = OB+~BN, то
ON = OB + n (ОС — ОВ) = пОС+ A - я) 63.
Заметим, что при /г =1/2 точка W является серединой стороны
ВС, а ОЛ/ — медианой треугольника. В этом случае
ON=lf(O~C+OB). A
Нетрудно видеть, что справедливо обратное утпе[?;зден::е: если
некоторый вектор с разложен по дзум не;;оллппеар;:ы;.1 векторг.м
а и Ь, то векторы а, Ъ \\ с компланарны. Действительно, пусть
c = xa-\-yb. Если чкела хну отличны ст нуля, то нектары ха
и уЬ также неколлякеар.чы. Отложим эти велторы от некоторой
точки О: ха = ОА \\yb==OB. Тогда вектор с = ~0С—~6А-\-0~3
изображается диагональю параллелограмма, построенного на век-
векторах ОА и ОВ. Следовательно, точки О, А, В к С лежат в одной
плоскости и векторы а, Ъ и с компланарны. Если же одно из
чисел, например х, разно нуло, то с-~у b и, следовательно,
вектор с коллинеарен вектору b и потому комплана]ги с векто-
векторами а и Ь.
172
Таким образом, справедлив следующий признак (критерий)
компланарности трех векторов:
если векторы а и Ъ неколлинеарны, то вектор с компланарен
с векторами а и Ъ тогда и только тогда,
когда имеет место разложение c = xa-{-yb.
Нулевой вектор по определению счи-
считается компланарным с любыми двумя
векторами.
Теорема. Если векторы а, Ь и с
некомпланарны, то любой вектор d можно
единственным образом представить в виде
d = xa-\-yb-\- zc.
Это представление называется разложе-
разложением вектора d по трем некомпланарньш
векторам а, Ь и с.
Пример 3. Дана треугольная призма ABC AiBxCi (рис. 103).
Разложить вектор ААХ по векторам ACU BAV и CBV
Д По правилу треугольника имеем
'АА1 = 'АВ + В~Аи БВ1=ВС+СВ1, ССХ^СА' +А(\.
Складывая левые и правые части этих векторных равенств, получаем
А\ + ВВ1 + СС1 = (АВ + ВС + С А) + В/п + СВк + AC v
Так как АВ + ВСУ+СА = АА=О и AAi = BB1 = CC\, то 371Л1 =
= BAi-{-CBi-^-ACi и, следовательно,
ТАХ = J- (ВА1 + СВ1 + ЛС,). А
§ 6. Угол между векторами.
Скалярное произведение векторов
Углом между векторами а —АВ и b = CD называется угол
между лучами [АВ) и [CD). Таким образом, если от одной точки
отложить векторы а = 0М и b = ON (рис, 104), то величина
угла M0N есть по определению угол между векторами а и Ь.
Этот угол обозначается (а, Ь).
Угол между векторами, как и угол между лучами, может при-
принимать значения от 0° до 180°. Если векторы сонаправлены, то
угол между ними равен 0°, а угол между противоположно направ-
направленными векторами равен 180°.
Если угол между векторами а и Ь равен 90° (рис. 105), то
векторы а и Ь называются перпендикулярными или ортого-
ортогональными. Перпендикулярность векторов а и Ъ обозначается
так: а±_Ь.
173
Пример 1. Пусть а и Ь — ненулевые неколлинеарные век-
торы. Доказать, что вектор с = -, \- у.-г образует равные углы
с векторами а и Ь.
А\
О
Рис. 105.
Д Векторы fli = a/|a| и bi = b[\b\ единичные: |ai| = |&i| = l
Отложим векторы fli и Ъг от одной точки: О А — ах и 05 = ?гь
построим параллелограмм ОАСВ (рис. 106), тогда OC = ax + &i ==
= -—- + Thj — C- ^ параллелограмме ОАСВ длины
сторон О А и ОВ равны, следовательно, ОАСВ —
ромб и его диагональ ОС является биссектрисой
угла АОВ. Отсюда заключаем, что вектор с=ОС
образует равные углы с векторами п\—0А [(
Ъ\ = ОВ и с коллинеарными им векторами а и Ь
и направлен по биссектрисе угла между векторами
а и Ь. а
Скалярным произведением ненулевых векторов а и b называется
число, равное произведению длин этих векторов на косинус угла
между ними. Скалярное произведение вектороЕ! аи b обозначается
а ¦ Ь. Таким образом,
Рис. 106.
= \a\
\b\cos(a, b).
Если один из векторов нулевой, то скалярное произведение
по определению равно нулю: а-0 = 0й = 0.
Подчеркнем, что скалярное произведение есть число (когда
рассматриваются векторы, числа часто называют скалярами).
Скалярное произведение вектора на самого себя равно квадрату
его длины: a-a = jaj2.
Скалярное произведение векторов положительно, если угол
между ними острый, скалярное произведение отрицательно, если
угол между векторами тупой.
Если угол между векторами равен 90°, то косинус этого угла
равен Е1улю и скалярное произведение этих векторов также равно
нулю. Верно и обратное утверждение: если скалярное произведе-
произведение ненулевых векторов равно нулю, то векторы перпендикулярны.
174
Следовательно, два ненулевые векторы перпендикулярны тогда
и только тогда, когда скалярное произведение этих акторов
равно нулю.
Свойства скалярного произведения
2. a b — b a.
3. (xa)b = x(ab).
4. (а + с) b = a b + cb.
Например, используя эти свойства, получим
(а + b) ¦ (а — b) = а (а - b) + b ¦ (а — Ь) = а ¦ а — a b + Ь а - b й =
Пример 2. Найти длину диагонали АС ромба ABCD (рис.
107), у которого длины сторон равны 1 и угол BAD разен 30°.
Д По правилу параллелограмма АС —
= АВ + AD. Из свойств скалярного проиЗЕе-
дения следует
| Л С |2 = (АВ + ADJ = | ЛВ |2 +
+2AB-AD + \AD\2. A) Рнс. Ю'.
Так как [АВ[ = [ЛЙ =1 и (АВ, AD) = 30°, то 7\L\-AD =
»= 1/3/2. Учитывая это, из A) получаем | АС|2 = 2-\-\Г3, откуда
находим [ АС \ = у 2 -f 1/3. А
Если векторы а и b ненулевые, то косинус угла между этими
векторами находится по формуле
*•"*)= Т^ПТГ- B)
Пример 3. Длины ненулевых векторов а и b равны. Найти
угол между этими векторами, если известно, что векторы р ¦-= а -\~ 1Ь
и q = 5a — 4b перпендикулярны.
Д Так как векторы р и q перпендикулярны, то их скалярное
произведение равно нулю:р-q = (a-\-2b)¦ Eа — Щ = 0. Используя
свойства скалярного произведения, получаем. (а-\~ 2Ь) ¦ Eа — Щ =
= 5\a\2 + 6a-b — 8| b\2. Таким образом,
\a\\b\cos{a, b)-8\b\2--=0,
откуда при [а| = |b | получаем
6|aj2cos(aT?)~3|a|2 = 0.
Поскольку \а\Ф0, то, сокращая на а 2, находим cos (a, ,b) = 1/2.
Следовательно, угол между векторами а и b равен 60°. ^
175
§ 7. Базис. Координаты вектора. Действия над векторами,
заданными своими координатами
Три единичных взаимно перпендикулярных вектора, взятых
в определенном порядке, называются прямоугольным базисом в про-
пространстве (рис. 108). Векторы прямоугольного базиса принято
обозначать /, J, k (читается: / — «и», j —«>ки», k —«ка»).
Каждый вектор можно единственным сбрэзом разложить по
любым трем некомплянарным векторам (§ 4), поэтому каждый
вектор а можно единственным сбразом представить
(в виде
Числа х, у, г называются координатами вектора а
в базисе (/, j, k). Если a = xi-\-yj-\-zk, то пишут
Рис ЮЗ « = (*! У'< 2)-
Рнс т Например, / = A; 0; 0), у=@; 1; 0), ft = @; 0; 1),
0 = @;0;0).
Пусть а=(лу, уг; 2Х) и Ь = (х2; ?/2; г2). Из единственности
разложения следует, что векторное равенство а = Ь равносильно
системе трех скалярных равенств:
Справедливы следующие правила действий над векторами,
заданными своими координатами.
1. При сложении векторов а=^(ху, ух; гЛ) и Ь = (х2; у/, г->) их
соответствующие координаты складываются:
2. При умножении вектора а = {х\ у\ z) на число л:г ко:-¦ .-.
паты вектора а умножаются на это число:
та = (тх\ ту; тг).
3. Скалярное произведение векторов а = (лгь ух; Zi) w Ь
— (Х2~, Уъ\ 22) равно сумме произведений соответствующих к: ;
дннат:
4. Длина вектора а = (х; у; г) равна корню квадратному и
сумм квадратов его координат:
Пример 1. Найти координаты и длину вектора 2а — ЗЬ,
если д = @; 3; 2) и й = (—2; 3; 2).
Д По правилам действий над векторами находим 2а = @; 6; 4),
3& = (—6; 9; 6), и, наконец, 2а-36 = F; —3; —2). Теперь
находим длину этого вектора: \2а — 36| = }^624-32 + 22 = 7. A.
176
Пример 2. Найти, при каких тип векторы а — (\ т;—2)
и Ъ — (—2 3; п) коллниеарны.
Д Вектор Ь колликеарен вектору а^О тогда и толькэ тогда,
когда существует число р такое, что Ъ — ра. Для данны> векто-
векторов а и Ь это векторное равенство равносильно системе —2 = р,
3 — тр, п =—2р, из которой находим р = —2, ш = —3/2, /г = 4.
Итак, а = A; —3/2; —2); & = (—2; 3; 4). а
Пример 3. Найти, при каком значении т секторы а =
= A; 3; —2) и & = (—1; т; 4) перпендикулярны.
Д Ненулевые векторы перпендикулярны тогда и только тогда
когда их скалярное прои;-:веделп:е разно нулю. Так как а-Ь —
= — 9 -f 3/п, то а ¦ b — 0 при т = 3. л
Пример 4. Найти координаты единичного вектора ,>, сона-
правленного с вектором а = B; —3; 6).
Д Ь\\а, если Ъ — та и /л>0. Из условия |&| = 1, учитывая
что \b\ — \tn\\a\ = m\a\ при т>0, заходим т=1/|д|. Вычис-
Вычисляем длину вектора а: \а\ = 7. Т:ш;м образом, /и = 1/7 и & =
= B/7; — 3/7;_С/7). д
Пример 5. ::_ л;и кг.еппусы углоз, которые образует с базис-
базисными векторами во;-: го о ¦¦:? — {3; 0; —\).
Д Вычислим c;-:j.";.л1;:» произзеденпя вектора а с каждым
из базисных векто; гл. /.-,< как / — A; 0; 0), У=@; 1; 0) и
й = @; 0; 1), то a-i -~>\ n-J—O; a-k-= — 4. Длины базисных
векторов равны 1, м-;,: члгм д;п:1'у вемтсра а: \а\ = Ъ. Теперь
по формуле B) § С .:-:..;:::л
cos (ар7) = j^.; = J , cos (О) - ]^Т = 0,
COS (а, Л) == -;'--.—^- = — "з" • А
Векторы на плоскости. Дза единичных Pic, 109.
перпендикулярных вектора, взятых в определенном
порядке, называются прямоугольным базисом на плоскости (pi;c. 109).
Базис на плоскости обозначается (/, J).
Любой вектор а плоскости, на которой выбран бази: (/, j),
единственным образом разлагается по базисным векторам: с =х/ +
4- у/- Числа х и у называются координатами вектора а, пишется
а = (х; у).
Пусть а = (хи ух), & = (а-2; уг), тогда
2. та = (тх1; mijx).
3. a b = хЛх2 -\- уф_.
4. \a\ =
Векторное равенство а = Ь равносильно системе двух скаляр-
скалярных равенств: Хх = х2, У\ = у2.
177
Пример 6. Определить угол между векторами с = 4а-{-Ь и
— ~a + ~b, если а = (— 1; 1) и Ь = A; 3).
Д Находим координаты векторов end
* = (-4+1; 4 + 3) = (-3; 7),
Вычисляем длины векторов с и d и их скалярное произзедение:
Уб8 d = V29, c-d = 29. По формуле B) § 6 находим
I с ! ! й | У'58 /29 V2 '
следовательно, угол между векторами с w d равен 45°. А
§ 8. Прямоугольная система координат. Уравнение плоскости
Если задана точка О и прямоугольный базис I, J, к, то гово-
говорят, что в пространстве задана прямоугольная система координат
(рис. ПО). Точка О называется началом координат. Начало коор-
координат и каждый из базисных векторов определяет координатную
ось: вектор О А = I определяет ось абсцисс (обозначается Ох), век-
вектор OB=jr определяет ось ординат (Оу), вектор OC = k опреде-
определяет ось аппликат (Oz). Плоскости, проходящие через каждые
две координатные оси, называются ко-
координатными плоскостями.
Для каждой точки М координаты
вектора ОМ в базисе (/, j, k) называются
координатами точки М в прямоуголь-
прямоугольной системе координат Охуг. Таким об-
образом, если
то числа х, у, z есть координаты точ-
Рис. ПО. ки М; они называются: х —абсциссой,
у — ординатой, г — аппликатой точки М.
Координаты точки М пишутся в круглых скобках рядом с
буквой: М (х\ у; г).
Если OM = xi + yj+zk, то числа х, у и г являются коорди-
координатами таких точек Mi, M2 и М3 соответственно на осях абсцисс,
ординат и аппликат, что 0Мг = xi, 0M2 =yj, 0М3 = zk (см. рис. 110).
Чтобы построить точку М (х; у; г), надо построить векторы
ii, OM2 = yj и O~M3 = zk и вектор 0M = 0Mi + dM2^dM3.
Пусть а = АВ и точки А и В заданы своими координатами:
(и у!, Zi), В(х2; у2, г2). Так как А~В='6В — 0А, то ~АВ =
= (х2 — х1\ у2 — уй z2 — z1), т. е. чтобы найти координаты вектора,
178
надо из координат его конца вычесть соответствующие координаты
начала.
Расстояние между точками А и В равно длине вектора АВ,
поэтому
\АВ\ = V(x2 - х,J + (у2 - УхJ + (г* - ztf.
Пример 1. В треугольнике с вершинами в точках А C; 2; •—3),
5E; 1; —1) и С(\; —2; 1) определить величину угла при вер-
вершине А.
Д Величина угла при вершине А равна углу между векто-
векторами АС и АВ (рис. 111). Косинус угла <р между векторами АС
и АВ находится по формуле B) § 6. Определяем координаты
векторов ~АС и АВ: АС = (—2\ — 4; 4), АВ =
= B; — 1; 2). Теперь находим длины этих векторов и их
скалярное произведение:
I AC = У 22 + 42 + 42 = 6, | AB | = ]/ 22 + I2 + 22 == 3;
• ' — • ^
Тогда cos ф = 8/F • 3) = 4/9 и, следовательно, ф =
= arccos D/9). А Рис- ш.
Прямоугольная система координат на плоскости
определяется аналогично — заданием точки О и прямо-
прямоугольного базиса (/, /). Оси координат называются соответственно
осями абсцисс и ординат. Координатами точки М называются
координаты (х; у) вектора О/И. пишется М (х; ф (рис. 11.2).
Если точки заданы своими координатами: Л (хи у{) и В (х2; у2), то
АВ\ =
Пример 2. Дана точка Л (— 1, 1) и вектор а = C; 2), Найти
координаты такой точки б, что ЛВ = а.
Д Пусть (х\ у) — координаты точки В,
тогда ЛВ = (х-\-1; у—1), и если а = ЛВ,
tojc+1=3 и у—1=2. Находим jc = 2,
г/ = 3. Тогда В имеет координаты B; 3). а
Пример 3. Дан треугольник с вер-
вершинами в точках ЛA; 1), В(—4; 3) и
С B; 2). Найти длину медианы Л/V.
Д Пусть О — начало координат, тогда Рис.112.
0В = (—4; 3) и ОС = B; 2). Если W-ce- __
редина стороны ВС, то (см. пример 2 § 5) CW = (ОВ + ОС)/2, от-
откуда следует, что координаты середины отрезка ВС равня полу-
полусумме соответствующих координат точек В и С. Находим
179
C + 2)/3), тогда N (— 1; 5/2)
Уравнение плоскости. В прямоугольной системе коор-
координат любое уравнение
ax + by + cz + d = 0, A)
в котором хотя бы один ич коэффициентов а, Ь, с отличен от нуля,
определяет плоскость. Верно и обратное; каждая плоскость может
быть задана уравнением вида A).
Пример 4. Составить уравнение плоскости, проходящей
через точки А @; 1; 5), В C; 0, 0) и С(—1; 1; 6).
Д Пусть уравнение этой плоскости ах -{• by \-cz-{• d = 0. Коор-
динаты точек А, В и С удовлетворяют ему, следовательно,
Из второго уравнения находим d — — За. Подставляя это в первое
и третье уравнения, получим систему
6 +5с = За,
b + 6с = 4а.
Почленно вычитая из первого уравнения второе, получаем с = а,
и тогда находим Ь = — 1а. Уравнение плоскости имеет вид
ах — 2ау + аг — 3a = 0 или (так как a, b и с одновременно не
равны нулю)
дс-
Ненулевой вектор я = ЛВ называется перпендикулярным плос-
плоскости, если прямая (АВ) перпендикулярна этой плоскости.
Пусть вектор п = (а\ Ь; с) перпендикулярен плоскости, прохо-
проходящей через точку М (хп; уп; га). Тогда для любой точки Мл (х; у; г)
этой плоскости векторы п и ММг перпендикулярны, следовательно,
я • MMj =0. Записывая это скалярное произведение в координатах,
получаем следующее уравнение плоскости:
а(х-хо) + Ь(у-уо) + с(г-г<)) = 0, B)
которое, если положить d== — ахо — Ьуй — сго, приводится к виду A).
Таким образом, уравнение ах-\-by-\-cz-\-d = 0 определяет плес-
кость, перпендикулярную вектору я = (а; Ь; с).
Пример 5. Найти уравнение плоскости, проходящей через
начало координат перпендикулярно вектору я = (—2; 1; 3).
Л Подставляя в уравнение B) координаты вектора я и коор-
координаты точки М @; 0; 0), получаем уравнение плоскости: —2х -\-
+ г/4-Зг = 0. А
180
Пусть две плоскости заданы уравнениями
-i = 0.
агх + Ьгу + c
C)
D)
Эти две плоскости параллельны тогда и только тогда, когда
коллинеарны перпендикулярные им векторы щ~ (йь bt: ct) и
п2(а2; Ь%, с2), т. е. существует таксе число тфО, что aj =ma.2">
bi — mbi, c1 = mc2. Плоскости, заданные уравнениями C) и D;,
перпендикулярны тогда и только тогда, когда перпендикулярны
векторы и1 = (аь &.; сх) и я2 = (а2; Ьг; сг), т. е. когда п^щ^О.
1 s-X Г\У.
Рис. 113.
Пересекаясь, две плоскости образуют четыре двугранных угля,
попарно равных по величине. Углом а между плоскостями назы-
называется величина меньшего из этих двугранных углов. Он равен
углу ф между векторами щ и Л2> если 0 sg ф ^ 90° и равен
180°-ф, если 90°^ф<180а (рис. 113). И в том и в другом
случае cosa = |cc^|. Таким образом, косинус угла а между
плоскостями, заданными уравнениями C) и D), находится по
формуле
cosa =
«1 i I «2 I
Пример 6. Найгн угол мезкду плоскостями
/ + + = 0 и
Д Векторы Лх и щ, перпендикулярные этим плоскостям, имеют
координаты й1 = @; —3; 1), w2 = @; 2; 1). Найдем длины этих
векторов и их скалярное произведение: [«хj = "|/^10, \щ\='\/гЪ',
щ-П2 = — 5. Тогда по формуле E) получаем с os a =
= 1—5i/(l/fO/5) = l/yX откуда a = 45°. А
ЗАДАЧИ РАЗДЕЛА I
1. В трапеции ABCD отношение длины основания ВС к длине основания AD
равно п. Диагонали трапеции пересекаются в точке 0. Разложить вектор АО
по векторам АВ и AD.
181
2. Даны три ненулевых вектора а, ft, с, каждые два из которых неколли-
неарны. Найти их сумму, если вектор а-\-Ь коллинеарен вектору с, а вектор
ft + c коллинеарен вектору а.
3. Медианы граней ОАВ и ОАС тетраэдра ОАВС пересекаются в точках М
и N соответственно. Доказать, что векторы M~N и ВС коллинеарны и найти
отношение [ ~MN \ : | ВС |.
4. Точки М, N, Р и Q лежат соответственно на сторонах АВ, ВС, CD и
DA параллелограмма ABCD, причем ] AM \ ! \АВ\ = \BN \:\ВС\ = | СР\: \CD\ =a
= \DQ \ I | DA \. Доказать, что MNPQ — параллелограмм.
5. Доказать, что любые два ненулевые вектора а и ft коллинеарны тогда
и только тогда, когда существуют такие числа хну, одновременно не равные
нулю, что выполняется рааенство xa+yb = 0.
6. Два ненулевые вектора а и ft таковы, что \ a-\-b \ = \ a— Ь\. Дока-
аать, что векторы а и ft перпендикулярны.
7. Зная, что ; л | = 11, | fo ; = 23 и ;a-ft[ = 30, найти \а + Ь .
8. Вектор а + ЪЪ перпендикулярен вектору 1а — ЬЬ и вектор a —4ft пер-
перпендикулярен вектору la — 2ft. Найти угол между векторами а и ft.
9. Единичные векторы а, ft и с удовлетворяют условию a-\-b-\-c = Q,
Вычислить а • ft + ft • с-\-с ¦ а.
10. Найти такое число т, чтобы векторы а = /—y' + 2ft, ft = 3/+_/ и с =•
*=m/ + 2ft стали компланарными.
11. Найти координаты вектора ft, коллинеарного вектору а — (\\ 1; —1/2),
образующего острый угол с базисным вектором ft, и такого, что jft| = 3.
12. Найти координаты единичного вектора р, перпендикулярного векто-
ряМ a = l-\-j-\-k и ft = / + 3/ — ft и образующего тупой угол с базисным век-
вектором J.
13. Найти координаты вектора ft, компланарного с векторами I и j, пер-
перпендикулярного вектору а = 4/ — 3/' + 5ft, и такого, что |a] = [ftj.
14. Найти координаты точки, принадлежащей оси ординат и одинаково
удаленной от точек А B; —!; 1) и В @; 1; 3).
15. От одной точки отложены векторы л = (—4; 0; 3) и ft "=A4; 2; —5).
Найти вектор й, который будучи отложен от той же точки делит угол между
векторами а и ft пополам и длина которого равна Кб'
16. Даны Л C; 2), В E; 1), D(l; —2). Найти длину диагонали АС парал-
параллелограмма ABCD.
17. Даны В B; —19; 16), С (—4; 29; ^-20), М A; —1; 1). Найги расстоя-
расстояние от точки М до середины отрезка ВС и расстояние от точки Ж до точки N,
принадлежащей отрезку ВС, и такой, что | BN \ i j ВС \ = 1/3.
18. Составить уравнение плоскости, проходящей через точку А A; —3; 2)
параллельно плоскости 4х—2г/ — 2 + 7 = 0.
19. Точка А (—1; —1; 2) является основанием перпендикуляра, опущен-
опущенного из начала координат на плоскость. Составить уравнение этой плоскости.
20. Найти расстояние от точки А (—2; 3; —4) до плоскости 2х-\-2у — z +
4-8 = 0.
21. Найти угол между плоскостью, проходящей через точки А @; 0; 0),
В(\\ 1) 1), С C; 2; 1), и плоскостью, проходящей через точки А @; 0; 0),
fl(lj 1; 1), DC; 1; 2).
182
ЗАДАЧИ РАЗДЕЛА II
1. ABCDEF— правильный шестиугольник. Разложить векторы ifc и BD
по векторам АВ и AF.
2. О ABC —тетраэдр, /Ш —медиана грани ABC. Разложить вегтор AM
по векторам ОА, ОВ, ОС
3. ABCD— параллелограмм, точка М — середина стороны CD. Разложить
векторы BD и AM по векторам ВМ и МС.
4. Дан параллелепипед ABCDAiBiCiPy (рис. 114). Разложить векторы
AAL, AC и Ш по векторам ОЛЬ DC1! и Ш^.
5. В треугольнике ABC точки Af и N— сере-
середины сторон ЛВ и ЛС. Разложить векторы ЛВ„
~АС и ADV по векторам ~BN и ЙИ.
6. В тетраэдре О ABC точки М и N— сере-
середины ребер ОВ и ОС. Разложить векторы AM,
BN и Ш по векторам ОА, ОВ, ОС.
7. В треугольном призме АВСАф^} диаго-
диагонали грани BBjCjC пересекаются в точке М. р ^
Разложить векторы AM и АгМ по векторам ВЛ>
ВВц В"С*.
8. Может ли длина вектора а — b быть: а) меньшз, б) равна, в) больша
суммы длин 1.ектороп а и Ь?
9. Доказать, что любые дза ненулевые сонаправленные г.екторы а и Ь
удовлетворяют условию a/, a [ = ft/| ft j.
10. Найти число л, если длина вектора Ь = ха равна 3 | « j и вгктор ft:
а) сонаправлен вектору а, б) противоположно направлен вектору а.
11. Векторы а и ft неколлинеарны. Найти числа х и: у, если векторы
xa + yft и (j/+l)a + B—jt) ft равны.
12. Векторы а и & неколлинеарны. Найти числа х и г/, если векторы
B — *)a + ft и i,'a + (« — 3) ft равны.
13. Векторы а и ft неколлинеарны. Найти число х, если векторы (л — 1)а+
-)- 2?» и 3a + A:ft коллинеарны.
14. Векторы а и ft неколлинеарны, Найти число я, если векторы
2
и A—х)а—.-ft сонаправлены.
О
15. Векторы а и ft образуют угол 120°. Найти х из условий, что | ft | =
= 2 [в | и вектор a-\-xb перпендикулярен вектору а — Ь.
16. Определить, при каких хну вектор а = — 2i-\-2,j -\-ijk коллинеарен
вектору b=xl — 6j-\-2k.
17. Найти единичный вектор, «(направленный вектору a = — 6/-J-3/ — 2ft.
18. Определить длины векторов a + ft и а—Ь, если а = C; —5; 8) и Ь =
= (-1; 1; -4).
19. Дано: |a|=13, jft |=19 и \а— й j = 22. Найти |o + ft|.
20. Дано: |a|=6, |a-fft|=ll, |а —6| = 7. Найти j ft j.
183
21. Определить длины векторов la— b и 3ft — а, если а =—2/+/ и 6 =
= -t-2j.
22. Найти угол между диагоналями параллелограмма, построенного на
секторах о = A; 2) и ft = B; —1).
23. Найти угол между векторами а = D; 0, 3) и Ь = B; —2; 1),
24. Угол между векторами а и ft равен 120°, |а| = 3 и |ft|=2. Найти:
а) a-ft, б) (a + fcJ, в) (a —ftJ, г) (а + 2ft) -Ba — ft).
25. Векторы a, ft и с удовлетворяют условию а + 6 + с = 0. Вычислить
йб + ftc + ca, если |а! = 1, !ft| = 3; |cj = 4.
26. Найти координаты вектора ft, коллинеариого вектору а = B; —3) и
удовлетворяющего условию aft =—26.
27. Вычислить скалярное произведение векторов 4а — ft и 2а + 3ft, если
| a j = 2, | ft j = 3 и угол между векторами аи Ь равен 120°.
28. В плоскости найти координаты единичного вектора е, перпендикуляр-
перпендикулярного вектору АВ, если А A; —1) и В C; 0).
29. Найти aft, если a = 4/ + 7/ + 3ft и 6 = 3/ — 5/ +ft.
30. Найти Fet + e2) • (ех —2е2), если угол между единичными векторами et
и ^2 равен 60°.
31. Найти угол между векторами аи d, если |a|=2Sft| и вектор 2a + ft
перпендикулярен вектору a — 3ft.
32. Найти координаты вектора ft, коллинеарного вектору а = (—1; 1; —2),
если, a • ft = 12.
33. Найти координаты вектора ft, коллинеарного вектору а—(—1, 2),
если | ft | = VAi6.
34. Найти, при каких тип вектор a = 3/ — 1j-\-mk коллннеарсн векгору
35. Найти, при каком т. вектор а = (т; 7; —2) перпендикулярен векгору
ft = (—3; m; -|-2).
36. Найти координаты вектора ft, перпендикулярного вектору а = (—2; 1)
если | ft 1 = 1/5.
37. Найти косинусы углов, которые образует с базисными векторами век-
вектор a = B; —1; —2).
38. Пусть ?i и е2 — единичные неколлинеарные векторы. Вычислить
Bе1-5ег)(Зе1 + е2), если | eL + e21 = ]/1.
39. Найти угол между векторами ХВ и а = A; —3; 1), если А (—5; 7; —8)
и В (-7; 9; —9).
40. Найти координаты единичного вектора, противоположно направленного
вектору АВ, если Л G; 4; —2) и ВA; 2; 1).
41. Найти угол между векторами а-\-Ь и 2а — с. если a =—/+/ —ft,
6 = 2/-/+2ft, с = _2Л-/ —3ft.
42. Найти угол между векторами АВ и CD, если Л (—5; 1); В (— 1; 4),
СA; —4); DB; 3).
184
43. Найти координаты векторов АВ и 2ВА, если А C; —1; 2) и
В(-1; 2; 1).
44. Найти координлты точек Mt и Л!2, симметричных с точко • М (\; —2; 5)
относительно оси абсцисс и относительно плоскости Qxy состветствени э.
45. Дано: А (-1; -2; 4), ?C; 2; _2); С C; -2; 1). Найти /гол при
вершине С треугольника ABC.
46. Найти длину медианы AM треугольник'! ABC, если /1 B; ;i/2; —4),
ВC; —4; 2), СA; 3; —7).
47. Найти расстояние от точки AJ (—2; 0; 1) до середины отрезка АВ,
если Л B; —1; 0) и В (—2; 3; 2),
48. Даны: А(—1; 3; —7), В B; _1; 5), С @; 1, —5). На:!ти \АВ\ и
49. Даны: Л A; —2; 2), В (\; 4; 0), С (—4; 1; 1), D (—5; —5; I:). Найти
угол между векторами АС и ВО.
50. Вычислить длины диагоналей параллелограмма, построенного ia векто-
векторах 5й+2й и а — Зй, если |й[=2]/2, |ft| = 3; (вГЬ) = 45°.
51. Найти угол между векторами p-\-q и p — q, если j0 = 8/-f4/, ^ =
52. Вектор а, у которого первая координата вдвое больше второй, обра-
образует с базисным вектором k угол 135°. Найти его координаты, если |«| =
= 5 VA2.
53. Вектор а, коллинеарнын вектору 6 = A2; —16; 15), образует с базис-
базисным вектором k остры.1 угол. Зная, что |а|=100, найти координаты век-
вектора а.
54. Найти координаты вектора а, перпендикулярного базисному 1ектору j
и вектору ft = 3/+/ —2ft, если |й| = ]Лз.
55. Найти координаты единичного вектора а, перпендикулярного векторам
i+j и / + *.
56. Найти координаты вектора а, перпендикулярного векторам i—j и
/ — ft, если j а | = ^3.
57. Найти координаты вектора а, коллинеарного вектору Ь=F; 8; —7,5)
и образующего тупой угол с базисным вектором /', если |а| = 50.
58. Найти т и я, если вектор а = C; т; —1) перпепдпкуллрен вектору
Й = B; 1; я) и |а| = |й|.
59. Напти координаты вектора а, перпендикулярного векторам I к Ь —
= 3/+У —ft, если \a\ = V'2.
60. HaviTii координаты единичного вектора в, перпендикулярного вектору
Ь — (—\\ 2; 2) и образующего равные углы с векторами ; и /.
61. Найти уравнение плоскости, проходящей через точку А (\\ 3; 1) пер-
перпендикулярно вектору rt = (—1; 2; —5).
62. Составить уравнение плоскости, проходящей через точку А A; —3; 2)
параллельно плоскости 2х-\-у-\-2г— 1 =0.
185
63. Какие из следующих пар плоскостей являются! а) параллельными,
б) перпендикулярными?
1) 2* + 3(/—г + 6 = 0, х—у — г — 7 = 0;
2) 2х — 3i/ + 5z —1=0, 2х—3(/ + 5г + 3 = 0.
64. Найти, при каком m плоскость 2х-\-ту — 3z—1=0 будет перпендику-
перпендикулярна плоскости 5х-(-1/ + Зг + 1 =0.
65. Вычислить расстояние от начала координат до плоскости х— 2(/ + 2г —
— 6=0.
66. Найти угол между плоскостью Оху и плоскостью V2x-\-y — 32-\-\7 = 0,
67. Найти угол между плоскостями л: — (/1^2 + 2 —1 =0 и x-\-yY2—z-{-
+ 3 = 0,
Глава VIII
КОМПЛЕКСНЫЕ ЧИСЛА
В этой главе вводятся и изучаются комплексные числа, являю-
являющиеся обобщением действительных чисел. Последний параграф
посвящен алгебраическим уравнениям с комплексными коэффи-
коэффициентами.
Комплексные числа и функции комплексной переменкой играют
исключительно важную роль во многих разделах математики и
физики.
§ 1. Определение комплексных чисел
Рассмотрим множество, элементами которого являются псе упо-
упорядоченные пары действительных чисел. Пара чисел я зляется
упорядоченной, если указано, какое число из пары является пер-
первым и какое — вторым. Элемент рассматриваемого множества будем
обозначать так: (а; Ь), на первом месте будем записывать первое
число, на втором — второе число пары. Элементы (а; Ь) и (Ь; а)
считаются различными, если а Ф Ъ. Элементами нашего множества
будут, например, пары @; 0); A, 0), @; 1), @; j/2), (л; 1),
(—1; 106). Элементы (аг\ Ь\) и (а2; Ь2) считаются равными тогда
и только тогда, когда
Введем теперь в множестве всех упорядоченных пар ^йстви-
тельных чисел алгебраические операции: сложение двух пар и
умножение двух пар. Сделаем это следующим образом,
Суммой элементов (аг; Ь\) и (а2! Ь2) назовем элемент
Произведением пар {ах\ Ьг) и (й2; Ь2) назовем пару
— Ьфг\ ахЪг
Для обозначения операции сложения двух элементов нашего мно-
множества будем употреблять знак «+», при записи произведения
сомножители будем писать рядом, опуская точку — знак умно-
умножения.
187
Таким образом, введенные нами операции определяются ра-
равенствами
A)
B)
I!.-.пример, сумма и произведение пар C; —7) и B; 9) вычис-
вычисляются так:
C; -7) + B; 9) = C + 2; -7+ 9) = E; 2),
C; -7) B; 9) = C- 2-(-7)9; 3-9+ (-7) 2) = F9; 13).
Теперь можно дать определение комплексного числа.
Комплексными числами называются упорядоченные пары дейст-
действительных чисел, для которых формулами A) и B) определены
операции сложения и умножения.
Комплексные числа часто обозначают одной буквой, причем
обычно используют для этого буквы z или w, иногда с индексами,
например zL, z2, wQ. Равенство z = (a\ b) как раз и означает, что
комплексное число (а; Ь) обозначено буквой z.
§ 2. Свойства операций сложения и умножения
Введенные в § 1 операции сложения и умножения обладают
следующими свойствами:
1. 21 + 22 = 22 + 2! (переместительный закон для сложения).
2. (гг + 22) + 23 = 2Х + (г2 + г3) (сочетательный закон для сло-
сложения).
3. Для любых комплексных чисел zx и г2 существует ком-
комплексное число 2 такое, что гх-\-г = гг- Это число называется раз-
разностью чисел 22 и z\ и обозначается z2 — z\.
4. 2x?2 = 222i (переместительный закон для умножения).
5. (zxz2) z-i = zx (z2z3) (сочетательный закон для умножения).
6. Для любых комплексных чисел г^Фф; 0) и г2 существует
чясло г такое, что 2i2 = 22. Зто число называется частным ком-
комплексных чисел г2 и гх и обозначается z2/zv Деление ка комплекс-
комплексное число @; 0), которое называется нулем, невозможно.
7. гх (г2 + 23) = 2X22 + 2i23 (распределительный закон).
Все перечисленные свойства операций сложения и умножения
вытекают из формул A) и B) § 1, дающих определение этих опе-
операций. Докажем свойства 3 и 6, проверку остальных свойстз
предоставим читателю.
[^Доказательство свойства 3. Пусть zl = (ai; bi),
Zi = (a2; b2) и z(x; у). Тогда равенство 2i + 2 = 22 примет вид:
(аи bi) + (x; y) = (a2; Ьг).
Сложив комплексные числа в левой части равенства, получим
188
Из определения равенства упорядоченных пар действительных
чисел следует, что . и у удорлетворяют системе двух уравнений
Эта система имеет единстпепное решение х = а.1 — аи у—Ъ« — Ь\.
Следовательно, разность г2 — гх всегда существует, причем
2 = 2/-2i=(a2; Ю-(аи bl) = (a2 — al; b2 — bi). A)
Эта формула дает правило вычитания комплексных чисел. gjg
? Доказательство свойства 6. Пусть г1-={а1\ ЬС),
?2 = (а2; Ьг) и г = (х; у). Тогда равенство г±г = г% примет вид
(аи bi)(x; y) = (a.i, Ы).
Перемножив комплексные числа в левой части равенства, пзлучнм
= (а2; hi).
Из определения равенства пар следует, что хну удовлетворяют
системе двух линейных уравнений
Умножив почленно первое уравнение на аъ второе на Ь{ и по-
почленно сложив полученные уравнения, найдем
Аналогично получим
(
Итак, наша система равносильна следующей:
Поскольку ?i = (ai; bi)=^@; 0) и, следовательно, а\-\-Ь\=?--0, си-
система имеет единственное решение
_
Таким образом, частное двух комплексных чисел при условии,
что делитель отличен от нуля, всегда существует, причем
\ а\ + ы\ • ej + ftj
Формула B) дает правило деления комплексных чисел. Щ
Введенные операции сложения и умножения позволяют рас-
рассматривать комплексные числа как обобщение действительных
чисел, а на действительные числа смотреть как на частный слу-
случай чисел комплексных. В самом деле, рассмотрим не все ком-
189
плексные числа, а только комплексные числа вида (а; 0). Из
формул сложения, умножения, вычитания а деления легко усмат-
усматривается, что в результате сложения, умножения, вычитания и
деления (афО) таких чисел всегда получаются числа такого же
вида. Кроме того, видно, что правила действий с комплексными
числами вида (а; 0) полностью совпадают с соответствующими
правилами действий с действительными числами. В связи с этим
комплексное число (а; 0) отождествляют с действительным чис-
числом а и считают, что {а; 0) = а. Например, @; 0) = 0, B; 0) ¦-•= 2,
(_7; 0) = -7.
Множество действительных чисел становится при этом подмно-
подмножеством множества комплексных чисел.
Комплексные числа вида @; Ь) назывяют мнимыми. Число
@; 1) называют мнимой единицей и для его обозначения исполь-
используют букву i, т. е. @; l) = j. Используя формулу умножения,
легко проверить, что произвольное мнимое число @; Ь) предста-
вимо в виде произведения чисел (Ь; 0) и @; 1), т. е. @; Ь) =
= (Ь; 0)@; 1). Но так как (b\ Q) — b и @; 1) = /, то мнимое
число @; Ь) записывают в виде Ы. Например, @; 2) = 2/,
@; -1) = -1\
§ 3. Алгебраическая форма записи комплексных чисел.
Правила действий с комплексными числами, записанными
в алгебраической форме
Каждое комплексное число z = (a; Ь) можно представить сле-
следующим образом:
г-(а; Ь) = (а; 0) + @; Ь) = (а; 0) + (Ь; 0)@; 1).
Учитывая, что (а; 0) = а, (Ь; 0) = Ь, @; l) = i, получаем
z = (a\ b) = a-\-bi.
Запись комплексного числа z = (a; k) в впде а-\-Ы называется
алгебраической формой записи комплексного числа.
Действительное число а называет ся действительной частью
комплексного числа а-\-Ы, действительное число b называется
мнимой частью комплексного числа a-\-bi.
Из сказанного в предыдущих параграфах вытекают следую-
следующие правила действий с комплексными числами, записанными
в алгебраической форме.
Дна комплексных числа zl = al-\-bli и za = a, + b2t равны
тогда и только тогда, когда at = a2 и bL = b2, т. е. когда равны
и действительные и мнимые части комплексных чисел. Обратим
внимание на то, что одно равенство гх = 22 комплексных чисел
равносильно двум равенствам a1 = a.i, Ьг = Ь2 действительных
чисел. Заметим еще, что понятия «больше», «меньше» для комп-
комплексных чисел не определяются. Записи i>0, l-j-i<2 и им
подобные лишены всякого смысла.
196
Формула сложения в новых обозначениях записывается так:
(а, + bLi) + (fl2 + M = а, + fl, + (Ьг + К) L A)
Она дает правило сложения комплексных чисел, записанных
в алгебраической форме.
Умножение комплексных чисел, заданных в алгебраической
форме, производится следующим образом:
{ау + V) (о, + V) = аха2 - btb2 + {афг + аД) I. B)
Эта формула не что иное, как формула B) § 1, запрсанная
в новых обозначениях.
Положив в B) fl1 = fl2 = 0, bi = b2=l, получим важное соот-
соотношение
« 1,
или, применяя для произведения и сокращенное обозначение
« = «»,
Р = -1. C)
Отметим еще, что формула B) не нуждается в запомшании,
так как получается автоматически, если формально перем.южить
двучлены flx + bxi и Oj + W по обычному правилу умножения
двучленов и затем в соответствии с формулой C) заменить I2
на — 1.
Пример 1. Найти сумму и произведение комплексные чисел
21== — 3 + 2/ И 22=13-1.
A 21 + 22 = (-3 + 2/) + A3-t)==10 + i,
2l22 = (— 3 + 2i) A3 - i) = — 39 + 3i + 26f + 2 = — 37 + 2W. A
Пример 2. Найти сумму и произведение комплексные чисел
Zi = a + bi и z2 = a — bi.
Д Zi + z2 = (a + Ы) + (а -Ы) = 2а,
Zlz2 = (а + Ы) (а - Ы) = а2 - abt + abt - (bif = а2 + b2. a
Комплексные числа а-\-Ы и a — bi, т. е. числа, отличающиеся
только знаком мнимой части, называются сопряженными. Число,
сопряженное числу z, обозначается 2. Пример 2 показывает, что
сумма z + 2 сопряженных чисел есть всегда число действитель-
действительное, а произведение zz — число действительное и, боле( того,
неотрицательное.
Прежде чем перейти к обратным операциям, отметим еще
один частный случай формулы B). Положив аг = а, bi = 0, a2 = a,
Ь2 = Ь, получим правило умножения действительного чиола на
комплексное:
= сш -\-abi.
Обратные операции, вычитание и деление комплексных чисел,
^записанных в алгебраической форме, производятся согласно
191
следующим формулам:
(а* + b2i) - (flx + hi) = a2 - a, + (bt - h) t, D)
Формулы D) и E) —это формулы A) и B) из § 2, записанные
в иных обозначениях. Положив в формуле E) а2 = а, Ь2~Ь,
fl1 = a, bi = 0, получим правило деления комплексного числа
а-\-Ы на действительное число а:
а-\-Ы _ a b .
а а ' а
Пример 3. Даны комплексные числа гл = — 3 + 2i и z2 =
»= 13 —t. Найти разность г2 — гх и частное г^г\.
Д По формуле D) находим
гг - zx = A3 - п - (— 3 + 2i) = 16 - 3t.
Используя формулу E), получаем частное
г* - JtzL - (-3I3+2(-1) (— 3)(— 1)—13 ¦ 2 _ _ 41 _ 23 .
zt" —3+2t ( —3)= + 22 '+ (—3J + 22 1 13fl Ж
Формула E) довольно громоздка и трудно запоминается.
Поэтому лучше ею не пользоваться. Проще умножить числитель
и знаменатель дроби z2/zi на zb т. е. на число, сопряженное
знаменателю. Тогда нахождение частного z2/Zi сведется к умно-
умножению числа 22 на число 2Х и к делению полученного произве-
произведения на положительное число Zi?i (см. пример 2).
Другими словами, для деления комплексных чисел рекомен-
рекомендуется пользоваться формулой
Ч
Для чисел, рассмотренных в призере 3, будем иметь
13 — i _ A3—i)(— 3 —2Л _ — 39 —2CH + 3i — 2 __ _ 41 _ 23 .
— 3+2( (—3 + 20 (—3—20 9+4 13
Пример 4. Записать комплексное число
3-Н
A+0A-20
в алгебраической форме.
Л г= 3 + ' _ 3 + '_ _3+>_
192
A+0A—20 1 —2i + t + 2 3 — i
_ C + 0C + 0 _ 9 + 6t— 1 4 3 .
" ~"9+l "" " + 5 '¦
M(a;b)
Рис. 115.
§ 4. Геометрическая интерпретация комплексных чи«л.
Модуль и аргументы комплексного числа
Хорошо известно, что между множеством всех упорядоченных
пар действительных чисел и множеством всех точек плоскости
может быть установлено взаимно однозначное соответствие. Для
этого достаточно выбрать на плоскости систему координат и каж-
каждой упорядоченной паре чисел (а; Ъ) поставить в соотвзтствие
точку М (а; Ь), т. е. точку с абсциссой л = а и ординатой tj=~-b
(рис. 115). Комплексные числа мы определили
как упорядоченные пары действительных чисел,
для которых определены операции сложения
и умножения. Следовательно, каждому комплекс-
комплексному числу (а; Ь) — а-\-Ы может быть постав-
поставлена в соответствие точка М (а; Ь) и, наоборот,
каждой точке М (а; Ь) плоскости — комплексное
число (а; Ъ) = а-\-Ы. Установленное таким об-
образом соответствие является, очевидно, взаимно
однозначным. Оно дает возможность рассматри-
рассматривать комплексные числа как точки координат-
координатной плоскости. Эту плоскость называют комплексной плоскостью.
Ось абсцисс называют действительной осью (на ней располо-
расположены точки, соответствующие числам (а; 0) = а), ось ор/шнат —
мнимой осью (на ней лежат точки, соответствующие мнимым
числам @; Ь) = Ы).
Часто удобно истолковывать комплексное число (а; Ъ) --=•• а + Ы
как вектор ОМ (рис. 115). Очевидно, что каждому вектору пло-
плоскости с началом в точке О@; 0) и с концом в точке М (а; Ь)
соответствует комплексное число
(а; Ь) = а-\-Ы и наоборот. Точке
О @; 0) соответствует нулевой
вектор.
Соответствие, установленное
между множеством комплексных
чисел с одной стороны и мно-
множествами точек или векторов
плоскости с другой стороны, поз-
позволяет комплексные числа назы-
называть точками или векторами и
говорить, например, о векторе
а-{-Ы или точке а-\-Ы.
Изображение комплексных чисел векторами позволяет дать
простое геометрическое истолкование операциям над комплекс-
комплексными числами. Остановимся пока только на сложении комплекс-
комплексных чисел.
При сложении чисел zi = a1 + bif и z2 = ci2-\-b?.i складываются
их действительные и мнимые части (рис. 116). При сложении
соответствующих им векторов OMi и ОМ2 складываются * х коор-
Ркс. 116.
7 п/ред. Г. Н. Яковлев!
193
динаты. Поэтому при установленном соответствии между комп-
комплексными числами и векторами сумме z^-\-Zt чисел гх и г2 будет
соответствовать вектор ОМ, равный сумме векторов ОМг и ОМ2.
Таким образом, сумма комплексных чисел геометрически может
быть истолкована как вектор, равный сумме векторов, соответст-
соответствующих слагаемым комплексным числам.
Определение. Модулем комплексного числа (а; Ь) = й-{-1Ь
называется длина соответствующего этому числу вектора.
Для модуля числа z используется обозначение |г]. По тео-
теореме Пифагора (рис. 115) для модуля комплексного числа г =¦«
= a-\-ib легко получается следующая важная формула:
|z| = Vfla + b«, A)
выражающая модуль комплексного числа через его действитель-
действительную и мнимую части.
Сопряженные комплексные числа имеют равные модули. Дей-
Действительно,
Заметим, что для действительного числа z = a-\-iO модуль
совпадает с абсолютной величиной числа:
Пример 1. Найтн модули комплекс-
комплексных чисел:
' ZC Z] = Z — ?, i?2 — ? у XJ ~x~ ul, iC3 — t.
Д По формуле A) находим
Рис. 117.
Кб)"+ 5» =7.
Для вычисления модуля z3 нет необходимости использовать фор-
формулу A). Длина вектора z3 = i очевидно равна единице, поэтому
Z3 | = 1• А
Комплексные числа z, имеющие один и тот же модуль |z| = r,
соответствуют, очевидно, точкам комплексной плоскости, распо-
расположенным на окружности радиуса г с центром в начале коорди-
координат (рис. 117).
Если |z |=^=0, то существует бесконечно много комплексных
чксел с данным модулем. Модуль, равный нулю, имеет только
одно комплексное число, а именно 2 = 0.
Геометрически очевидно, что комплексное число 2^=0 будет
задано, если помимо модуля числа z указать еще и направление
Ьектора г, задав, например, величину угла <р (рис. 117).
194
Определение. Аргументом комплексного числа z=/=0
называется величина угла между положительным напраьленнем
действительной оси и вектором z, причем величина угл< счита-
считается положительной, если отсчет ведется против часовой стрелки,
и отрицательной, если отсчет производится по часовой стрелке.
У
У
-t-i
Рис. 118.
Заданием модуля и аргумента комплексное число опрелеляется
однозначно. Для числа 2 = 0 аргумент не определяется но в
этом и только в этом случае число задается толькс своим
модулем.
Аргумент комплексного числа, в отличие от модуля, опреде-
определяется не однозначно. Например, аргументами числа z= I -\-i явля-
являются следующие углы: ф! = -"-, фг==-г4~ уи
= ^—2п = —^
118)
Z:
Рис. 119
и, вообще, каждый из углов <рА == - +
-f- Ink, где ? — произвольное целое число.
Любые два аргумента комплексного
числа отличаются на число, кратное 2я.
Например, разность <р2 — ф3 аргументов
щ = 9я/4 и фз = — 7я/4 числа z == 1 -\- i
равна An. Для обозначения множества
всех аргументов числа г = а-\-Ы исполь-
используется обозначение argz или arg (a-\-bi). Ьсли речь идете
либо одном из аргументов, то его обычно обозначают бу
Пример 2. Найти аргументы комплексных чисел: г
z-i~l, z3 = — 1 +1.
Д Построив векторы zu z2, z3 (рис. 119), находим i
аргументов для каждого числа: цч = — л/2, ср., = 0, «р3
Следовательно,
каком-
<вой ср.
L = —i,
дин из
= Зл/4.
где k — произвольное целое число. А
Действительная и мнимая части комплексного числа г-=а-\-Ы
выражаются через его модуль \z\ = r и аргумент ср следующим
7*
195
образом:
a = rcos(f, b = r sirup. B)
Эта связь легко устанавливается при рассмотрении рис. 117.
Таким образом, аргументы ф комплексного числа могут быть
найдены из системы уравнений
cos 4 = 77=4=?=?;' sin<P = 1-7=5=FS- C)
Пример 3. Найти аргументы комплексного числа г = — 1 —
Д В данном случае а = — 1, Ь = — У. Система C) имеет вид
cos<p = —1/2, sincp = — У 3/2.
Решив эту систему, найдем <р4 = -? + 2nk, k <=е Z. Следовательно,
arg z = ^ + 2я/>, teZ. A
Аргументы комплексного числа можно найти и иначе. Из фор-
формул C) видно, что каждый из аргументов удовлетворяет урав-
уравнению
tg ф = Ь/а.
Это уравнение не равносильно системе C), оно имеет больше
решений, но отбор нужных решений (аргументов комплексного
числа) не представляет труда, так как
из алгебраической формы записи комп-
комплексного числа всегда видно, в каком
квадранте комплексной плоскости оно
расположено.
Пример 4. Найти аргументы комп-
комплексного числа 2 = — "|/3~+t.
Д Каждый из аргументов ф числа
2 = — УЗ + i удовлетворяет уравнению
tg ф = — 1/"|/3.
Из уравнения следует, что ф* = — -*-+
я/г, fceZ. Так как число г = — "|/3-f-
Рис. 120.
+ J расположено во втором квадранте комплексной плоскости, то
его аргументами будут числа ц>ь при нечетных значениях k.
Следовательно,
arg(
~
В заключение этого параграфа рассмотрим вопрос о геометри-
геометрическом смысле модуля разности двух комплексных чисел. Построим
196
вектор z2 —Zi как сумму векторов г2 и (—гх) (рис. НО). По
определению модуля число |z2 — Zi| есть длина вектора г2 —гь
т. е. длина вектора ОМ. Из конгруэнтности треугольников OMNt
и MiM2O следует, что \ОМ\ = \М1М2\. Итак, длина 1ектора
Zv_ — Zi равна расстоянию между точками zx и z2. Таким оГразом,
модуль разности двух комплексных чисел есть расстояние между
точками комплексной плоскости, которые соответствуют этим
числам.
Это важное геометрическое истолкование (или, как еш г гово-
говорят, геометрическая интерпретация) модуля разности двух комп-
комплексных чисел позволяет при решении некоторых
задач с успехом Е;спользовать простые геометри-
геометрические факты.
Пример 5. Какие множества точек комплек-
комплексной плоскости задаются условиями:
а) |г-»| = 1, б) ;2-[-zj<!2-2!,
в) 2<[2-l+2ii<3?
Д а) Условию [г — г| = 1 удовлетворяют те и
только те точки комплексной плоскости, которые
удалены от точки i на расстояние, равное единице. Такие точки
лежат на окружности единичного радиуса с центром в "очке i
(рис. 121).
б) Используя геометрическую интерпретацию модуля р; зности
двух комплексных чисел, задачу можно переформулирова "ь так:
каково множество точек комплексной плоскости, которые распо-
расположены ближе к точке z = — 2, чем к точке г ==2? 'Ясю, что
Рис. 122.
Рис. 123-
таким свойством обладают все точки плоскости, лежащи< лзвее
мнимой оси и только они. На рис. 122 искомое множеств) точек
заштриховано.
в) Комплексные числа z, удовлетворяющие неравенстве м
удалёны от точки 1 —2t на расстояние большее или равно: двум,
НО меньшее трех. Такие точки расположены внутри и н, i внут-
197
ренней границе кольца, образованного двумя концентрическими
окружностями с центром в точке 1 — 2i и с радиусами г = 2 и
R = 3. На рис. 123 искомое множество показано штриховкой, а
§ 5. Тригонометрическая форма записи комплексного числа.
Умножение и деление комплексных чисел, записанных
в тригонометрической форме
Вернемся к формулам B) предыдущего параграфа:
Эти формулы связывают действительную и мнимую части комп-
комплексного числа z = aJrbi с его модулем г и аргументом ф.
Каждое комплексное число z = a-\-bi, отличное от нуля, может
быть, следовательно, записано в виде
.. z = r (cos <p-|-tsin cp). A)
Запись комплексного числа в виде
-i sin<p),
где /- — модуль числа, а ф —один (любой) из его аргументов,
называется тригонометрической формой записи.
Для того чтобы перейти от алгебраической формы записи
числа к тригонометрической, достаточно найти модуль комплекс-
комплексного числа и один из его аргументов.
Пример 1. Записать числа zx = —\—i, z2 = —2, zs = i
в тригонометрической форме.
Д Так как \г1\=У, а фх =— Зя/4, то
2l = у2 (cos (- Зя/4) + i sin (- Зя/4)).
Модуль г2 равен 2, а одним из аргументов г2 является угол
<р2 = я, поэтому
22 = 2 (cos я + I sin я).
Учитывая, что jzs] = l, а ф3 = я/2 —один из аргументов z3, по-
получаем тригонометрическую форму записи для га:
Пример 2. Записать числа
2Х = 2 cos Gя/4) - 2i sin (я/4), гг = — cos (я/17) + i sin (яу17)
в тригонометрической форме.
Д Для записи чисел г1 и г2 в тригонометрической форме
нет необходимости предварительно находить их модули и аргу-
аргументы (хотя сделать это совсем не трудно). Воспользуемся тем,
что
cosGra/4) = cos( — я/4), a —sin (я/4) = sin < — я/4),
198
и сразу получим тригонометрическую форму для первого числа
zt = 2 (cos (- л/4) -1- i sin (- л/4)).
Аналогично, учитывая, что
cos() cos
получаем
Тригонометрическая форма записи комплексных чисел окалы-
окалывается очень удобной при умножении и делении чисел. Прежде
чем перейти к рассмотрению этих операций, отметим, что два
комплексных числа
я . / я \ . 16я
-jy = sin f л—^) = 51П-^-,
и Z2 =
равны тогда и только тогда, когда
т. е. когда модули чисел равны, а аргументы отличаются на
2nk, где k — некоторое целое число.
Пусть теперь
zi — ri (cos 9i + f sin фх) и г2 == r2 (cos ф., -\- с siп ф.2) —
два числа, записанных в тригонометрической форме.
Представим в тригонометрической форме их произведение:
ф.2 — ЙГПф! 5Шф2 + t Sln
+ J COS ф,_ 51Пф2),
ИЛИ
г,г.2 = ггг2 (cos (фх + ф2) + i sin (фх + ф.2)). B)
Следовательно,
Таким образом, справедливо следующее утверждение: модуль
произведения двух комплексных чисел равен произведению нодулгй
этих чисел, сумма аргументов сомножителей является аргумен-
аргументом произведения.
Пример 3. Найти произведение чисел
Пя \ тГа f 3,1 . . Зл
—j и *a = y8(os + /sin
А как \Zl\ = yi, |22[ = V8T то | zxz%\ =V2 \r8 =4.
Аргументом произведения zfa данных чисел будет сумма
199
, 11л . Зя 25 ~
(Pi + Фа = -f + "F = ~8~ Я' ^леД°вательн°.
гггг = 4 (cos B5я/8) + i sin B5 л/8)),
или
Z& - 4 (cos (9л/8) +1 sin (9я/8)). ^
Перейдем к делению чисел. Запишем частное двух комплекс-
комплексных чисел
гх «= rx (cos фх +1 sin фх) и 22 = г2(со$ф2-|-1 sin фх)
в тригонометрической форме. Умножая числитель и знаменатель
частного zjz2 на coscp2 — i sin ф2, получим
г^_ _ ft (сод (fa -+-1 sin фх) (cos ф2 — t sin ф2) _
z2 fi (cos ф2 + i sin ф2) (cos ф2 — i sin ф2) ~
rx (cos ф! cos ф2 + sin ф! sin ф2 + i sin ф! cos ф2 — i cos фх sin ф2)
** r2(COS^<p2+Sin'^2) '
ИЛИ
-|- = -^- (cos (фх - фа) + i sin (ф3 - фг)). (З)
Следовательно,
IZj/zг I = ri/r2, arg(Zi/zj) = фх
Таким образом, модуль частного двух комплексных чисел равен
частному модулей этих чисел, разность аргументов делимого и
делителя является аргументом частного.
Пример 4. Записать число г — , ,О>'"Г- ¦ / ,-» в тригоно-
r r cos (л/3) -|-1 sin (я/3) г
метрической форме.
/\ Введем обозначения z1 = i~l, 2j = cos(n/3) + t sin(n/3).
Число z% записано в тригонометрической форме. Очевидно, что
|z2|=l и фа = л/3. Найдем модуль и аргумент числа z2: \zx | =
= У, <р1 = Зл/4. По формуле C) получим
т. е.
г = |/2 (cos (бя/12) +1 sin (бя/12)). А
§ 6. Возведение в степень и извлечение корня
Формула для произведения двух комплексных чисел может
быть обобщена на случай п сомножителей. Испольауя метод
математической индукции, легко получить следующий результат:
модуль произведения п комплексных чисел равен произведению
модулей Ёсех сомножителей, сумма аргументов всех сомножите-
сомножителей является аргументом их произведения.
200
Отсюда, как частный случай, получается формула
(г (cos ф + i sin ф))л = rn (cos rup + t sin щ), A)
дающая правило возведения комплексного числа г (coscp-^sincp)
в целую положительную степень:
При возведении комплексного числа в степень с натуральным
показателем его модуль возводится в степень с тем же показа-
показателем, а аргумент умножается на показатель степени.
Пример 1. Записать число г = (i — l/ЗI3 в алгебра «есной
форме.
/\ Сначала запишем данное число в тригонометрической
форме, а затем перейдем от тригонометрической формы к алге-
алгебраической. Найдем модуль и один из аргументов числа . — l/3i
r= If-"|/3"! =2, ф = 5л/6.
Представим число i —1^3 в тригонометрической форме:
i - "J/3 = 2 (cos Eл/6) + i sin Eл/6)),
Теперь, применяя формулу A), получаем
О1 -УI3 = B (cos Eя/6) +11 sin Eя/6))I3 =
= 213 (cos F5л/6) + i sin F5л/6)) = 213 (cos Eл/6) + i sin Eл/6)).
Такова тригонометрическая форма данного числа, Запишем это
число в алгебраической форме:
(i -1/3I3 = 213 (cos Eл/6) + i sin Eл/6)) =
Перейдем к извлечению корня данной степени из комплекс-
комплексного числа. Число г называется корнем степени п из числа w
(обозначается V~w), если zn = w.
Например, числа ?x = t и га = — i являются корнями степени
2 (квадратными корнями) из числа до = —1, так как i- = — 1 и
( — гJ — —1- Из определения вытекает, что каждое решение
уравнения гп = w является корнем степени п из числа w. Дру-
Другими словами, для того чтобы извлечь корень степени п \ъ числа
w, достаточно решить уравнение zn=--w.
Если о) = 0, то при любом п уравнение zn=*w имеет одно
и только одно решение г = 0. Если ы>фО, то и г^О, л следо-
следовательно, и г и w можно представить в тригонометрической
форме:
2 = г (созф + t sin(f), да = р (cos a +1 sin а).
Уравнение г" = до примет вид
г" (cos пф + i sin Пф) = р (cos a-\-J sin а).
Два комплексных числа равны тогда и только тогда, когда
равны их модули, а аргументы отличаются на 2л&, где k — неко-
некоторое целое число. Следовательно,
г" = р и п<р = си -(- 4nk
ИЛИ
г=п/р и ф—;- + -?*. ieZ.
Итак, все решения уравнения г" = и> могут быть записаны
следующим образом:
Легко видеть, что все числа zfr, получаемые при k = 0, 1, 2, ...
..., п— 1, различны. Если брать значения k^n, то других ком-
комплексных чисел, отличных от z0, zlt z2, ..., 2n-lt не получится.
Например, при k = n получаем
= Vp (cos (а/я)+ i sin
Таким образом, если ш^=0, то существует ровно п корней сте-
степени п из числа w; все они получаются из формулы
, 2я,\ . . . /а . 2д,\\ B)
+ —А)-И8ш(т + —A)), W
А = 0, 1, 2, ..., л-1.
Из формулы B) видно, что все корни степени п из числа w
имеют один и тот же модуль, но разные аргументы, отличающи-
отличающиеся друг от друга на —А, где k — некоторое целое число.
Отсюда следует, что комплексные числа, являющиеся кор-
корнями степени п из комплексного числа w, соответствуют точкам
комплексной плоскости, расположенным в вершинах правильного
/
«-угольника, вписанного в окружность радиуса j/p с центром
в точке 2 = 0.
Сделаем еще одно замечание относительно обозначения у w.
Обычно под j^w понимается множество всех корней степени п
из w. Например, под j/"-—1 понимается множество, состоящее
из двух чисел i и — i. Иногда под -\f~w понимают какой-либо
один корень степени п из числа w. В таких случаях следует
обязательно указывать о каком значении корня идет речь.
Пример 2. Найти все значения -^ — 64.
Д Запишем число до = — 64 в тригонометрической форме;
— 64 = 64 (cos я -f- i sin л).
202
Применяя формулу B), получаем
2я
2л
k = 0,
4,5.
Следовательно,
z0 = 2 (cos (л/б) +1 sin (л/6)) = Уз + ?,
гг = 2 (cos <я/2) +1 sin (я/2)) = 2t,
г2 = 2 (cos Eя/6) + i sin Eл/6)) = — Уз + i,
za=2 (cos Gл/6) + i sin Gя/6)) = — Уз -1,
г4 = 2 (cos (Зя/2) -f t sin (Зя/2)) = — 2t,
гь = 2 (cos (П л/6) + / s i n A1 л/6) = У3 - i.
Точки, соответствующие числам 2k, расположены в вершинах
У .
Z2,
Рис. 124.
правильного шестиугольника, вписанного в окружность радиуса
2 с центром в точке г = 0 (рис. 124). ^
§ 7. Алгебраические уравнения
Рассмотрим алгебраическое уравнение степени п с комплекс-
комплексными коэффициентами, т. е. уравнение вида
Число гв назьшаетх;я решением или корнем уравнения, е:ли при
подстановке г„ вместо z в уравнение получается Еернсе числовое
равенство. Следовательно, если г9 — корень уравнения A), то
апг1
= 0.
203
Например, следующие уравнения:
2+1-? = 0,
г2 -1=0,
— являются алгебраическими уравнениями соответственно первой,
второй, пятой и седьмой степеней. Корнем первого уравнения
является число го = — 1 + '. второе уравнение имеет два корня
20=1 и г1 — —1. Число zQ = i — корень третьего уравнения, так
как г° + i3 + i • i2 -+¦ i = 0. Очевидно, что го = 0 —корень четвертого
уравнения. Помимо корня z0 —0 четвертое уравнение, как это
следует из предыдущего параграфа, имеет еще шесть корней.
Решить уравнение в множестве комплексных чисел —значит
найти все корни уравнения.
Общий вид алгебраического уравнения первой степени:
Очевидно, что такое уравнение имеет одно и только одно реше-
решение 20 = — «o/ai- Уравнение второй степени (квадратное уравне-
уравнение) в общем виде записывается так:
ао = 0, а2ф0.
Для решения этого уравнения преобразуем тождественно его левую
часть
! \ ~"~ a2 г a2 У
и найдем корни
r 2a.J - Aai ' Z~ 2c, ' 2c2 '
2=- 2^—- B)
В последней формуле введено обозначение D = a\ — 4aoa., (дискри-
(дискриминант квадратного уравнения обозначен буквой D), под УD
понимаются все значения корня.
Формула B) для корней квадратного уравнения имеет такой
же вид, как и в случае, когда коэффициенты уравнения действи-
действительные числа и решения отыскиваются в множестве действитель-
действительных чисел. Но поскольку в множестве комплексных чисел операция
извлечения квадратного корня имеет смысл для любого комплекс-
¦204
ного числе, ограничение D > О становится излишним. Более того,
оно вообще теряет смысл, так как дискриминант может огазаться
числом не действительным, а для таких чисел понятия «больше»,
«меньше» не определены.
Таким образом, в множестве комплексных чисел yfaew&HHe
а2г2 + 0^ + 00 = 0
(а2, аи а0 — комплексные числа, а2ф0) всегда разрешимо
Если D = а\ — 4аоа2 = 0, уравнение имеет один корегь, если
D^O, уравнение имеет два корня. Во всех случаях корь и квад-
квадратного уравнения можно найти по формуле B),
Пример 1. Решить уравнение г2 + З + 3
Д По формуле B) находим
г~
Учитывая, что j/" — 3 = it i'V 31 получаем
2 = з Уъ з V
Пример 2. Решить уравнение
Д По формуле для корней квадратного уравнения имзем
_ 8 + 3t + /(8+3Qa —4A3+13Г) _ 8 + 3I + /3 —4i
г - j 5"
Для определения всех значений VS—4i можно было бы исполь-
использовать формулу 2 § б, но гораздо проще применить другой прием.
Положим
тогда 3 — 4» = х2 + 2xyi — у2 и, следовательно, х и у удовлетворяют
системе уравнений
(х2-у* = 3,
причем х и у — действительные числа. Система имеет два действи-
действительных решения х — 2, у*= —1 и х= —2, у=\. Поэтому
-2 + i
206
r?e;;i-fi,4t'M к рхсмотгению алгебраических уравнений более
высокой степени. Решение уравнения A) при я>2 является,
как правило, задачей неизмеримо более сложной. В 1799 г. вели-
великим математиком Карлом Гауссом была доказана теорема:
Каждое алгебраическое уравнение имеет в множестве комплекс-
комплексных чисел по крайней мере один корень.
Эту теорему принято называть основной теоремой алгебры.
Она носит имя Гаусса. Доказательство ее достаточно сложно и
в курсах элементарной математики не приводится (см. доказа-
доказательство в книге Л. С. Понтрягина «Метод координат» из серии
«Знакомство с высшей математикой»).
Опираясь на теорему Гаусса, можно доказать, что левая часть
уравнения A) всегда допускает представление в виде произведения:
где г,, г2, ... , zt/ — некоторые различные комплексные числа,
а ау, а2, ..., ak — натуральные числа, причем
ocj-f а2 -[-. .. + ак = п.
Отсюда следует, что числа zu г2, ..., zk и только они являются
корнями уравнения A). При этом говорят, что 2t является корнем
кратности alt г.2 — корнем кратности аг и т, д. Если условиться
корень уравнения считать столько раз, какова его кратность, то
можно сформулировать теорему:
Каждое алгебраическое уравнение степени п имеет в множестве
комплексных чисел ровно п корней.
И теорема Гаусса, и только что сформулированная теорема
являются типичными теоремами существования. Они дают исчер-
исчерпывающее решение вопроса о существовании корней у произволь-
произвольного алгебраического уравнения, но, к сожалению, ничего не
говорят о том, как найти эти корни. Если корень уравнения
первой степени ахг + йо = О определяется формулой г = —ajav
если корни уравнения второй степени а2г2 + агг -!- а0 = 0 всегда могут
быть легко найдены по формуле B), то уже для уравнений
третьей и четвертой степени аналогичные формулы настолько
громоздки, что ими предпочитают не пользоваться, а для уравне-
уравнений степени выше четвертой подобных формул в общем случае
вообще не существуетх). Отсутствие общего метода решения
алгебраических уравнений не мешает, конечно, в частных случаях
в зависимости от специфики уравнения, отыскать все его корни.
Например, формула B) § б позволяет найти все корни уравнения
anzn-\-a0 = Q, т. е. двучленного уравнения степени п.
Для решения уравнений с целыми коэффициентами часто
оказывается полезной следующая теорема:
1) Отметим, что в высшей математике разработаны разнообразные методы,
позволяющие находить приближенные значения корней алгебраических уравнений
с нужной точностью,
206
Целые корни любого алгебраического уравнения с целыли коэф-
коэффициентами являются делителями свободного члена.
Q Доказательство этой теоремы провести легко. Пусть z = k—
— целый корень уравнения
апгп + я„_!Z«-l +... + ахг + а0 = О
с целыми коэффициентами. Тогда
и, следовательно,
Число ankn-x + ... + ах при сделанных предположениях, очевидно,
целое, значит, k — делитель числа а0. Ц
Пример 3. Решить уравнение
Д Рассматривая делители свободного члена, убеждаемся в том,
что только г = 3 является целым корнем уравнения. Делим левую
часть уравнения на г —3:
г3 - бг - 9 |z-3
Зг2-бг
~3г2-9г
Зг-9
Зг-9
С)
и, решая квадратное уравнение
получаем остальные корни. Итак,
_ о _ з . Уъ _ з .Уъ
Z1 — о, 22 — 2 2 ' Zg — 2 ' 2 ' J
Пример 4. Найти целые корни уравнения
2га-5г2-2г-2 = 0.
Д Целыми корнями уравнения могут быть только :±1, ±2.
Подстановка в уравнение показывает, что ни одно из этих четы-
четырех чисел не удовлетворяет ему. Предложенное уравнение целых
корней не имеет. ^
Пример 5. Решить уравнение
Д Подвергая испытанию делители свободного члена, найдем,
что г = :?2 суть корни уравнения. Разделив левую часть уравне-
207
ния на г2 —4, придем к уравнению
z3-2z2-9z+18 = 0,
корнем которого является г = 2. Разделив на г —2, получим
г2 —9. Таким образом, левая часть уравнения разлагается на
множители:
Итак, уравнение имеет три однократных (простых) корня
г ——3, г ——2, г = 3 и один двукратный корень z = 2. а
ЗАДАЧИ РАЗДЕЛА I
1. Представить комплексное число
(l-j-2Q*-(l-<K
в алгебраической форме.
2. Найти модули и аргументы комплексных чисел:
а) z = -^±^- . б) z = sin Fn/5) + ! A+cos Fл/5)).
3. Представить г в алгебраической и в тригонометрической формах;
а) г = (|/3"—(I00. б) z=l+cos(IOn/9) + ismA0ir,/9).
4. Представить число z = (tgl—О4 в тригонометрической форме.
Б. Решить уравнение 22 + jzj2 = 0,
6. Какое множество точек комплексной плоскости задается условием!
а) | 2+1 | = | г — i|. б) |г,2 + 3г+3"г =0.
б) sin | г | > 0?
7. На комплексной плоскости даны точки ?1=^6-|-8i, г2 = 4 — Зг. Найти
комплексные числа, соответствующие точкам, принадлежащим биссектрисе угла,
образованного векторами zL и z2.
8. Среди комплексных чисел г, удовлетворяющих условию
найти число, имеющее наименьший положительный аргумент,
9. Решить уравнение г4-(-8 + 8!-''3 1=0.
10. Записать
У5 + 12Г + У5—12t
_
в алгебраической форме при услозии, что действительная часть комплексных
чисел У~5+12?, Уз—12i отрицательна.
И. Доказать, что остаток от деления многочлена Рп(г) на г — г0 равен
Р„ (г0) (теорема Бвэу),
ЗАДАЧИ РАЗДЕЛА II
1. Найти г!+г4, г,г2, zi—z.i.—1- , если:
Ч
а) ^ = 2 + 5;, г.г = \— 7/.
б) z^Vi-Yii, г,=.К"
208
2. Записать 2 в алгебраической форме!
_41+63* 6t + l Л /-1+^3/ у8
г)г
г+2 ' Г)г
3. Найти комплексное число 2, удовлетворяющее уравнению
(f_,)(l+20 + (l-i«) C-40=1+74,
и записать его в алгебраической и в тригонометрической формах,
4. Решить систему уравнений
( Zl + 2z2=l + (.
\ 3^ + ^=2-31,
5. При каких действительных значениях х и у комплексные числа
г! = 9(/2 — 4— Юлч и za = 8
являются сопряженными?
6. Доказать равенства:
7, Решить уравнения:
а) га + г = 0, б) г2 + |г|=0.
в) \г\ — и=1—2С. г) г2 = г3.
д) г2 + 2|г| + |2!!| = 0.
8, Решить систему уравнений
|z+l-i| = |3-z
9, Доказать, что система уравнений
решений не имеет.
10, На комплексной плоскости даны точки гь г3, г3, являющиегя верши-
вершинами треугольника, Найти точку пересечения его медиан.
11, Найти множество точек комплексной плоскости, удовлетзоряющих
условии:
a) ,z + l_f| = ;2_i + i|. б) A-О* = A+0«.
в) : г + 1+2< |й=0, г) argz = Bn+l)n, nsZ.
Д) |г+1 j^Jz + ij, е) !г + 2-г|=1/3. ж) lg | г + t1 J ==? I.
Dn+l) nsZ
з) ^
и) \г— 2;а
12. Среди комплексных чисел г, удовлетворяющих условию:
a) :z + l-/jg?l, б) |z-5t'|
найти число, имеющее наименьший положительный аргумент.
13. Записать г в тригонометрической форме:
a) z = — Уз + i. б) z = —1,
209
в), —„."-/й," Da--, 1 + 'Гз
z=-
_cos—W sin— '
14. Представить z в алгебраической форме;
a)l»J V^_
«)•-(—^ + ^Г. »>«-[-ггУГ. »ен.
Г) 2 = ^
15. Найти все значения y/~w, если;
а) и! = + 1, л = 3. б) аи = — 1, л = 4.
в) ш = —4 + K48i, л = 3. r) w=l+t, n = 8.
16, Пусть А/,(к=\, 2, ..,, л) —вершины правильного л-угольника, впи-
вписанного в окружность радиуса /?=1, Найти;
а) |Л1Л2|2 + |Л1Л3|2 + ... + ;Л1Л„|2.
б) \A1At\-\A1Aa\-...-\A1An\.
17. Решить уравнения;
a) za — 2iz — 5 = 0. б) z2 —
в) 2Ь-—I—i V = 0. г)
д) z4 —4г3+7га —16г+12 = 0.
е) z5- + 2z4 + 4z3 + 8z2+16z + 32 = 0.
18. Доказать, что если уравнение
а/гг« + an_iZ«-i +,.. + ахг + а0 = 0
с действительными коэффициентами имеет корень гу, то число zu также является
корнем этого уравнения.
19, Убедиться в том, что число 1+« является корнем уравнения
Зг4—5z3 + 3z2 + 4z — 2 = 0t
и найти остальные корни.
20, Найти общие корни уравнений:
21. При делении многочлена Рп(г) на z — i в остатке получается i, а при
делении на z + i в остатке получается 1+Л Найти остаток от деления Рп (z)
на 2^+1.
22, Может ли точка z = 0 принадлежать какому-нибудь многоугольнику,
вершины которого находятся в точках
Глава IX
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ,
СИСТЕМЫ, НЕРАВЕНСТВА
§ 1. Тригонометрические уравнения
Простейшие тригонометрические уравнения.
Вначале напомним формулы для решения простейших "ригоно-
метрическпх уравнений:
s'mx = a, х = (—1)" arcsin а-}-л/г при
1, A)
1, B)
cos x = a, x = ± arccos a -f 2я« при
tg x = a, x — arctg a -j- n/x, ueR, C)
ctgA; = a, x = arcctg a-\-nn, aeR, D)
где n = 0; ±1; ±2; ..., т. e, n ge Z.
Уравнения sin л: = а и cos x = а имеют решения для любого
ae[—1; 1], т, е, при \а\^\. Если же |а|>1, то эти уравне-
уравнения решений не имеют.
Уравнения igx = a и ctgx = a имеют решения для любого
Для записи решений простейших тригонометрических уравне-
уравнений можно использовать и обозначения из теории множеств,
например множество решений уравнения sinA: = a, ia|^l, можно
записать в виде
-nn[ne=Z}. E)
В A) —D) решения уравнений выражены через значение обрат-
обратных тригонометрических функций. Напомним некоторые свойства
этих функций.
Каждая из функций arcsina и arccos а определена на отрезка
[-1J 1] и
/2, ae[-I; 1],
, oge[—1; 1].
Функция arcsina является нечетной, т. е.
arcsin (— а) = — arcsin a.
Функция arccos а не является ни четной, ни нечетной. Каждая
из функций arctg а и arcctg а определена на всей числовой
211
прямой и
— я/2< arctgа< я/2, fleR,
0<arcctga<n, a e IR.
Функция arctg а является нечетной, т. е.
arctg (— а) = — arctg а.
Функция arcctga не является ни четной, ни нечетной.
Для решения тригонометрического уравнения, не являющегося
простейшим, его сводят теми или иными преобразованиями к одному
или нескольким простейшим.
Пример 1. Решить уравнение 2sin2х = 1.
Д Преобразуем уравнение, воспользовавшись равенством
2sin2x = I — cos 2.x:, верным для всех х, тогда получим
1 — cos 2х = 1, cos 2x = 0.
Значит, 2x = -|4J?Ctt, neZ.
Ответ: x = -J + -5p, neZ. ^
Пример 2. Решить уравнение
tg2x = 3. F)
Д Если х — решение данного уравнения, то
либо tgx = >% G)
либо tg х = —1/3 • (8)
Очевидно, верно и обратное, если х — решение одного из урав-
уравнений G), (8), то х — решение уравнения F). Таким образом,
множество решений уравнения F) есть объединение множеств
решений уравнений G) и (8). В этом случае говорят, что уравне-
уравнение F) равносильно совокупности уравнений G) и (8).
Уравнения G) и (8) имеют соответственно решения
х = -?- + пп, п е Z,
х = — -д- + пп> п
Объединение этих двух множеств и есть множество всех решений
уравнения F). Эти решения можно для краткости записать в виде
х = ±-g•
Для тригонометрических уравнений не существует единого
метода решения. В каждом конкретном случае успех определяется
в частности знанием тригонометрических формул и навыками
решения задач.
212
Многие тригонометрические формулы являются вернымк равен-
равенствами для всех значений, входящих в них переменных. Гаковы,
например, формулы двойного аргумента:
sin 2а = 2 sin а • cos а,
cos 2а = cos2 а — sin2 а = 2 cos2 а — 1 = 1 — 2 sin2 а,
формулы половинного аргумента:
sin2|-= 1A-cos a), cos»|-= у A+cos а),
формулы для суммы и разности синусов и косинусов, длг произ-
произведения синусов и косинусов, формулы для синуса и косинуса
суммы и разности.
Некоторые тригонометрические формулы являются мерными
равенствами не для всех значений переменных. Например, равенство
¦ sin 2а
tga = -
1 -f--cos 2a
верно только для аф~-\-пп, nsZ. Отметим, что и правая и
левая части этой формулы как функции а имеют одну я ту же
область определения, а именно, они определены для в:ех
ф-^-\-пп, neZ. Другим примером служат формулы
которые также являются верными равенствами для всех аф
ф-^ + пп, neZ. Но здесь в отличие от предыдущей формулы
левые и правые части имеют разные области определения. Левые
части в (9) определены для всех aeR, а правые — только для
аФ^ + пп, «sZ, Этот факт, как будет видно из примеров, сле-
следует учитывать при использовании формул (9). и аналэгичных
им, например формулы для тангенса двойного аргумента, формул
для тангенса суммы и разности и т. д.
Рассмотрим примеры решения различных уравнений.
Уравнения
sin ах + sin bx = О, smax—sinbx==O,
= (), cos ax — cos bx — 0
легко решить, используя формулы для суммы и разности синусов
и косинусов.
Пример 3. Решить уравнение sin6x + sin4x = 0.
Д Применив формулу для суммы синусов, получим
2 sin bx cos x = 0. A0)
213
Если а; —решение этого уравнения, то верно по крайней мере
одно из равенств
sin 5л: = 0 или cosx = 0. A1)
Обратно, если х решение одного из уравнений A1), то, очевид-
очевидно, х является и решением уравнения AС). Таким образом, урав-
уравнение A0) равносильно совокупности уравнений A1). Уравнения A1)
имеют соответственно решения
Все эти значения х и только они являются решениями исход-
исходного уравнения, л.
Уравнения
sina*4-cos&e = 0, sin ax — cos bx = 0
можно свести к уравнениям, указанным выше, с помощью формул
приведения.
Пример 4. Решить уравнение sin;c = cos 2х.
Д Преобразуем уравнение, используя формулу__пр_иведения
и формулу для разности синусов:
sinx— cos 2л: = 0, sinx — sin fy — 2x\ = 0,
2 sin I (ax -1) cos 1 (f - *) = 0.
Получившееся уравнение равносильно совокупности двух уравнений:
т-> Wo п \ , п , 2nk
Решаем первое уравнение: -^\Ъх — -^\ = ак, д: = "е"+~з~>
Для второго уравнения имеем
^ /eZ.
Легко видеть, что все решеаня второго уравнения содержатся
в множестве решений первого. Действительно, при k = — l — 3Z,
I е Z, имеем ж = -J + 2я(~'~эг) = - -5.- 2я/, т. е. получаем все
решения второго уравнения
Ответ: {« + J?|
{ }|}
Замечание о форме записи решений. Целочисленные
параметры в различных множествах решений одного уравнения
можно обозначать как разными буквами, так и одной буквой.
Скажем, в примере 3 была использована одна буква п.
В тех же случаях, когда элементы множеств сравниваются
между собой, следует использовать различные буквы для обозна-
обозначения целочисленных параметров. Так было сделано в примере 4.
214
Уравнения вида
asm(ax-\-bcos<*tx = c, а2 + Ьгф0. A2)
Пример б. Решить уравнение sin 2лг -\- cos 2х = —1.
Д Это уравнение является частным случаем рассматриваемых
уравнений при а = Ь = \, с = —1, со ==2. Разделив обе части урав-
уравнения на У2, получим
¦~7=- sin 2х + -7= cos 2х = — -7=-.
Учитывая, что 1/"|/~2 = cos (я/4) = sin (я/4), запишем эти урав-
уравнение в виде
sin 2xcos (я/4) 4-cos 2r sin (л/4) =—1/}^.
Воспользовавшись формулой для синуса суммы аргументов, придем
к уравнению
\
Отсюда х = ((— 1)л+1 — 1) ~ + ~, п е= Z- Эти знач;ения л; и состав-
составляют множество всех решений исходного уравнения. ^
В общем случае, для того чтобы преобразовать уравнение A2)
к простейшему введением вспомогательного угла, разделим обе его
части на УсР-\-Ьг, получим уравнение
sin сод; + Т7== cos сод; = тт=тГ'
Пусть ф — одно из решений системы
а .
rns ф = sin <р =
Используя эти равенства, запишем уравнение в
sin сод; cos ф+cos сод; sin ф = с [У а2 -\- Ь2.
Применив формулу для синуса суммы аргументов, получим урав-
уравнение
s in (сод; -f ф) = с/У a2 -f fe2,
которое, как видно из проделанных выкладок, равносильно исход-
исходному уравнению. Полученное уравнение, а значит, и исходное
имеют решения тогда и только тогда, когда \с\^~Уa2-\-f2.
Для преобразования уравнений вида A2) можно использовать
также формулы синуса разности, косинуса суммы и разности
аргументов.
215
Пример 6. Решить уравнение 12 cos я — 5 sin* = —13.
Д Разделим обе части уравнения на ]/Т2^ + 52= 13, получим
12 5 .
-tx-cosa; —j-g- sinjc = — 1.
Одним из решений системы
cos <p= 12/13, sin ср = 5/13
является cp = arccos A2/13). Учитывая это, запишем уравнение
в виде
cosх cos ф — sin* sin ф = — 1
и, применив формулу для косинуса суммы аргументов, получим
cos (я-f ф) = — 1, откуда д; + ф = я + 2яя, *=*— ф-f пBп+ 1), т. е.
х = — arccos A2/13)+ яBи+1), пе2.
Эта формула и дает все решения исходного уравнения. ^
Введение нового неизвестного. В ряде случаев урав-
уравнение удается преобразовать к виду, содержащему лишь одну
тригонометрическую функцию.
Пример 7. Решить уравнение
sin 3* +cos 2х = 1.
Д Воспользуемся формулами cos 2л: = 1 — 2 sin2.* и
sin Зл: = sinA;C — 4 sin2jc).
Вторая формула легко получается, если в равенстве sin3ji: =
*= sin (.к + Зл:) правую часть преобразовать по формуле синуса
суммы, а затем по формулам двойного аргумента.
После подстановки исходное уравнение примет вид
sinxC-4sin2x)+l-2sin2x=l.
Отсюда 4 sin3л:+ 2 sin2я — 3 sin х = 0. Обозначив / = sinx, получим
4t* -f 2f2 — 3/=0. Это уравнение имеет корни h = 0, /а = (У^З — l)/4,
/s=—A^13+1)/4. Значит, исходное уравнение равносильно сово-
совокупности уравнений
Находим последовательно решения полученных уравнений:
дс = яп, /igZ; x = (— 1)"arcsin -^—-j-nn, neZ;
третье уравнение решений не имеет, поскольку — (]/13-т- 0/4 <!
•<— 1. Найденные значения х и только они являются решениями
исходного уравнения. А
216
Если уравнение содержит лишь одно из выражений
sin* 4- cos* или sin* — cos х
и функцию sin2* (или произведение sin* cos*), то, вводя новое
неизвестное
t = sin* 4- cos* или t = sin* — cos*
и учитывая, что
sin2* = (sin*4-cos*J— 1, \
/ A3)
sin2*= 1 — (sin* — cos*J, J
придем к уравнению относительно t.
Пример 8. Решить уравнение
sin * 4- cos * = 1 — sin 2*.
Д Обозначим i = sin*4-cos* и воспользуемся первой из фор-
формул A3), получим
откуда t2 +1 — 2 = 0, t\=\, h = — 2. Исходное уравнение равно-
равносильно совокупности уравнений
= — 2.
Решаем каждое из уравнений, например, введением вспомоиггель-
нзго угла. Для первого уравнения находим * = ((— 1)"--1)-^- -f-
+ яи, neZ; второе уравнение решений не имеет, по:кольку
Ответ: * = ((— 1)"- 1)-*- + я«, neZ. ^
Пример 9. Решить уравнение
7
sin4 * + cos4 * = y sin * cos *.
Д Преобразуем выражение sin4*-f cos4*, сыделив полный
квадрат:
sin4* -f cos4 * = sin4 x -f 2 sin2 * cos2 * + cos4 * — 2 sin2 * со*2л: =
= (sin2 * + cos2 *)a — 2sine к cos2 *,
откуда
sin4 * 4- cos4 * = 1 — у sin8 2*.
Пользуясь полученной формулой, запишем уравнение в виде
1 -у sin2 2* = -^ sin 2*.
217
Обозначив siu2x = i, получим 2P-\-7t — 4 = 0, откуда /:i = l/2,
ti = — 4. Уравнение sin2x = 1/2 имеет решения * = (—\)n~-\--?t
neZ; уравнение sinA; = — 4 решений не имеет. ^
Сумму sin6 я-f-cos8 л: можно выразить через sin 2х, расклады-
раскладывая ее на множители как сумму кубов.
В предыдущих примерах для преобразования уравнений ис-
использовались формулы, правая и левая часть которых определены
для всех значений х, и сами формулы являются верными равен-
равенствами для всех х.
Рассмотрим примеры решений уравнений, в которых исполь-
используются формулы, правая и левая части которых определены не
для всех значений х.
Пример 10. Решить уравнение
6tg2x-2cos2.x; = cos2x. A4)
Д Преобразуем уравнение по формулам
2cos'*=l+cos2x, tg»* =
Заметим, что обе части второй формулы определены, хотя и не
для всех, но для одних и тех же значений х, а именно, они оп-
определены для всех хфп„--\-пп, beZ. Для таких же значений х
определена и левая часть данного уравнения. После подстановки
получим уравнение
Очевидно, что любое решение уравнения A4) является решением
уравнения A5), и обратно, каждое решение уравнения A5) явля-
является решением уравнения A4), т. е. уравнения A4) и A5) рав-
равносильны. Решаем уравнение A5). Обозначая cos2j: через t и
преобразуя A5), получим уравнение Bt2-\-9t — 5)/(l + /) = 0, откуда
/i = 0,5, 4 = — 5. Следовательно, уравнение A4) равносильно
совокупности уравнений
cos 2л; = 0,5, cos2x =— 5.
Первое из этих уравнений имеет решения л: == ± у + яя, я ge X\
второе — решений не имеет. ^
Рассмотрим теперь случай, когда для преобразования уравне-
уравнения используются формулы, правая и левая части которых имею!1
разные области определения.
Пример 11. Решить уравнение
5 sin2jc — 5 cos 2jc = tg a: + 5. A6)
Д Выразим sin 2х и cos 2x через tgx по формулам (9)!
218
Подставляя в уравнение вместо sin 2* и cos 2x правые чаоти этих
формул, получим
i_tg^_. -
Выясним, равносильны ли уравнения A6) и A7). Функции sin 2х
и cos 2х определены для всех х, а подставленные вместо них
правые части формул (9) определены лишь для хф'-^-\-пп, п е
е Z. Значит, в результате подстановки исключены из рассмотре-
рассмотрения значения х = ^--\-пп, neZ. Но ясно, что ни одно из этих
значений х не является решением исходного уравнения A6),
поскольку его правая часть для х=-^-\-яп, ле2, не опре-
определена. Отсюда следует, что каждое решение уравнения A6) яв-
является решением уравнения A7). Очевидно, верно и обратное.
Таким образом, уравнения A6) и A7) равносильны.
Решаем уравнение A7). Обозначив tgx = t, получим
1+/* "
После простых преобразованяя прядем к уравнению t3 — 9t-\-10 =
= 0, равносильному предыдущему. Один нз делителей свободного
члена, а именно, t\ = 2, является решением этого уравнения. Раз-
Разложив теперь левую часть на множители (например, с помощью
деления многочлена t3 — 9^+10 на разность^ — 2), получим
(t - 2) (t2 + It - 5) = 0. Решив квадратное уравнение Р- + It - 5 = 0,
найдем еще два решения t2 = V~G—\, h = — ]/б—1. Тгким об-
образом, исходное уравнение A6) равносильно совокупности урав-
уравнений
которые имеют соответственно решения
х = arctg 2-\-nn, neZ,
х = arctg ("|/б — 1) + пи, fie Z,
х= — arctg(yr6+
Эти значения х я составляют множество всех решений уравне-
уравнения A6). ^
В формулах (9), как уже отмечалось, левые части оп]>еделены
для всех значений х, а правые —лишь для хф -^--\-лп, n^Z.
Поэтому подстановка в уравнение правых частей этих формул
вместо левых может привести к потере решений вида х- у + ял,
йб2. При использовании такого преобразования следует либо
установить равносильность полученного уравнения исходному (так
219
было сделано в примере 11), либо подстановкой значений х =
= у4-1ш, neZ, в исходное уравнение проверить, нет ли среди
них решений. Следующий пример подтверждает необходимость
такой проверки.
Пример 12. Решить уравнение
os2.? = — 1. A8)
Д Преобразуем уравнение с помощью формул (9) (способ,
предложенный в примере 5, на наш взгляд предпочтительнее):
Уравнение A9) не равносильно исходному уравнению A8). Дей-
отвительно, значения x = ^-{-nk, /ieZ, не являются, очезидно,
решениями уравнения A9). В то же время подстановкой легко
убедиться в том, что все эти значения х являются решениями
уравнения A8).
Рассмотрим теперь значения хф к -\-nk, k e Z. Ясно, что лго-
бое решение уравнения A8), удовлетворяющее условию х Ф — ¦
является решением уравнения A9), и наоборот, любое решение
уравнения A9) является решением уравнения A8). Решаем урав-
уравнение A9). Преобразуя его, получаем
l + tg^jt ' откУДа tg*= — li
х = —-. -\-nk, feeZ. Эти значения х вместе со значениями х =
= ~--{-nk, &eZ, и составляют множестзо всех решений урав-
уравнения A8).
Ответ: -J-^—^-зт^; —r--fn&[&eZ[ (если в ответе к приме-
примеру 5 взять соответственно /: = 2&+1 и n — 2k, то получим дан-
данный ответ).
Подстановка в уравнение левой части формул (9) вместо пра-
правой может привести к появлению посторонних для исходного
уравнения значений х = -~-{-яп, /ieZ. При таких преобразова-
преобразованиях следует проверить, все ли решения полученного уравнения
являются решениями исходного.
Указанные особенности преобразований уравнения с помощью
формул (9) и связанная с ними необходимость проверки имеют
место и в других случаях, когда используются формулы, празая
и левая части которых имеют разные области определения.
Отметим еще, что уравнение, к которому приводят преобра-
преобразования по формулам (9), нередко получается сложным. Поэтому'
220
прежде чем применять эти формулы, полезно поискать иные пути
решения.
Однородные уравнения.
Пример 13. Решить уравнение
sin2 х — 3 sin x cos х-\~2 cos2 x = 0.
Д Рассмотрим такие х, что cosj<: = 0. Из уравнения следует,
что тогда и sin x = 0, а это невозможно. Следовательно, среди
этих значений х решений нет. Рассмотрим значения х, дл ч кото-
которых cos х фО. Разделив обе части данного уравнения h«i cos1*,
получим уравнение
tg2*-3tg*+2 = 0,
равносильное исходному. Решив его как квадратное уравнение отно-
относительно tg лг, найдем
tg*=l, tg* = 2.
Отсюда получаем ответ: х = -^ + я«, х = arctg 2 -f- л«, « е Z. ^
Рассмотренное уравнение является примером уравнен1Я вида
'O, B0)
которое называют однородным относительно и и v степени 2.
В предыдущем примере « = sin*, v = cos я. Как было почазано,
уравнение вида B0) делением обеих его частей на v2 сводится
к квадратному уравнению
относительно t = u/v. Такое же преобразование можно применить
для решения однородных уравнений более высокой степей \.
Некоторые уравнения, не являющиеся однородными, можно
свести к однородным, используя равенство
sin8 х + cos2 x '= 1,
верное для всех х.
Пример 14. Решить уравнение 2sin3* = cos.»,\
Д Поскольку cos^ = cos^(sina^ + cos2^) для всех х, то дан-
данное уравнение равносильно уравнению
2 sin8 х = cos x sin2 x + cos8 x,
однородному относительно sin* и cos* степени 3. В случае
cos х = 0 решений, очевидно, нет. Деля обе части уравнения на
cos8* и обозначая tg* = /, приходим к уравнению
2/8-/2-1=0.
Одним из его корней является h = l. Разложив левую часть на
221
множители, получим (/— \}BР + { + 1) = 0. Поскольку 2**-f*+ 1>
>0 для любого t, корень ^ = 1 является единственным. Отсюда
Ответ: |^- + л/г| п е Z\-
Разложение на множители. Преобразование уравнения
с целью выделения общего множителя часто представляет собой
наиболее короткий путь решения. Рассмотрим несколько примеров.
Пример 15. Решить уравнение 2sin3x + cosa2x = sin x.
Д Сгруппируем члены уравнения и преобразуем его следую-
следующим образом:
B sin3х — sinx) + cos2 2л; = О,
sin* B sin2* — 1) +cos22x = 0.
Воспользовавшись формулой 1 — 2sin2x = cos2x, получим
— sin x cos 2х + cos2 2х = О,
cos 2x (cos 2x — sin x) = 0.
Последнее уравнение равносильно исходному. В то же время оно,
очевидно, равносильно совокупности уравнений
cos 2х = 0, cos 2x — sin л: = 0.
Эти уравнения имеют соответственно решения
* — ~4" г ~2 • -^ — "о" "^ ~' "
(второе уравнение решено в примере 4), которые являются реше-
решениями и исходного уравнения. А.
Пример 16. Решить уравнение
sin lx -|-x) = s'
Д Преобразуем левую часть уравнения:
sin (х + 4) = sin л: cos-^- +cos л: sin ^- = -1- (sin j; -f cos ^)-
Правую часть разложим в произведение как сумму кубов;
sin3х + cos3x = (sinx + cosx) (sin2* — sinxcosx-f-cos2x) =
= (sinл; + cosx) A — sin*cos*).
Теперь уравнение можно записать в виде
(sinх + cosx)('—— 1 -f sin* cos л:] = 0.
Это уравнение равносильно совокупности уравнений
-у=— 1 4-sin л: cos л; = 0.
222
Первое из этих уравнений равносильно уравнению tgx =— 1,
а второе — уравнению sin2x = 2 — ]/. Следовательно,
n
Это и есть все решения исходного уравнения, а
В некоторых случаях при решении уравнения методом разло-
разложения на множители могут появиться посторонние значения неиз-
неизвестного. Они устраняются подстановкой наиденных значений
в исходное, или равносильное ему, уравнение.
Рассмотрим соответствующий пример.
Пример 17. Решить уравнение
tgx — sin.* = I — tgjcsin*.
Д Сгруппируем члены уравнения и преобразуем его (ледую->
щим образом:
A -f-sinx) tgx — A +sin*) = 0,
(l+sin*)(tg*-l) = O. B1)
Получившееся уравнение равносильно исходному. Если *--реше-
*--решение этого уравнения, то х является и решением одного \м урав-
уравнений
l+sin* = 0, tg*-l=O. B2)
Обратное в данном случае (и в отличие от того, что было в при-
примерах 15, 16) неверно. Первое уравнение в B2) имеет решения
х =—У + 2ЯЛ, «eZ. Для всех этих значений х функция tgx
не определена, поэтому эти значения не являются решениями
исходного уравнения. Второе уравнение в B2) имеет решения
х—^--{-пп, яе2. Подстановка в B1) показывает, что эги зна-
значения являются решениями этого уравнения, а значит, и ис-
исходного.
Ответ: {—+ nnjns
Использование оценок. Некоторые тригонометрические
уравнения удается решить, используя неравенства
верные для всех а.
Пример 18. Решить уравнение sin3^4-cos2ii; + 2 =
Д Поскольку sinЗлг^= — 1 и cos2x^—1, то si3
S= — 2, причем равенство здесь имеет место тогда и толькс тогда,
когда одновременно выполняются равенства
sin3* = —I, cos 2* = — 1. B3)
223
Это означает, что исходное уравнение равносильно системе B3).
Уравнения этой системы имеют соответственно решения
X =>
, !s2.
Изобразим эти решения соответствующими точками единичной
окружности (на рис. 125 решениям первого уравнения соответст-
соответствуют утолщенные точки, решениям второго уравнения—точки,
помеченные крестиком; для нахождения этих точек, достаточно
в первом случае взять fe = 0, 1, 2, а во втором — / = 0, 1). Число
х будет решением системы B3) тогда и только тогда, когда оно
является решением обоих уравнений в B3). Из рис, 125 видно.
что такими числами являются лишь числа
У,
я
*= IT
Пример 19. Решить уравнение
cos
-X-COS ¦
Ряс. 125.
Д Воспользовавшись формулой для
произведения косинусов, преобразуем урав-
уравнение к виду
cos (\^2х) 4- cos х = 2.
Это уравнение равносильно системе
cos|^2.v;=l, cosx=l. B4)
Уравнения системы имеют соответственно решения х = }/Г2пп,
«eZ; x = 2nm, meZ. Решениями системы B4) являются те
и только те значения х, для которых при некоторых целых т и п
выполняются равенства х = ~|/2 л« = 2пт. Найдем все целые тип,
для которых У2пп = 2пт. Сократив здесь на|^2п, получим, что «=я
=|/*2т. Это равенство возможно только при т = 0, « = 0. Действи-
Действительно, если т ф 0 и п=У~2т, то ]/2=«/т. Но это равенство
неверно, так как |/2 —не рациональное число, а п/т — рациональ-
рациональное. Следовательно, т = 0, но тогда и я = 0. Таким образом, си-
система B4), а значит, и исходное уравнение имеют единственное
решение х = 0. А
В заключение этого параграфа рассмотрим пример уравнения,
которое не является тригонометрическим, но при исследовании
которого используются свойства тригонометрических функций.
Пример 20. Доказать, что при а>C]/3— л)/6 уравнение
решении не имеет.
224
Пусть аХЗу^З—я)/6. Отметим, что C V — ni/6>0.
Пусть \x\~5z.2, тогда -^\х\-\-а>\, в то время как s
бначит, данное уравнение не имеет решений на множестве
На отрезке [—2; 0] имеем sinxscO, a -^-\x\-\-a^a>Q, по-
поэтому здесь также решений нет.
На интервале ]0; 2[ уравнение имеет вид
1
sinx —g-л; ==а.
Найдем на этом интервале наибольшее значение функции f(x)~
= sin л; —-туХ. Определяем критические точки: /' (х) = cosx--y=0,
х=^г (остальные решения этого уравнения не принадлежат
О
]0; 2[). Если 0<х<п/3, то /' (х) > 0, поэтому функция f(x) на
интервале ]0; п/3[ монотонно возрастает и, значит, f (x)<J(n/3).
А если п/3<х<2, то /'(х)<0, поэтому функция f(x) h;i интер-
интервале "; 21 монотонно убывает и/(х) </(п/3). Таким образом,
значение
'\3~
—я
\3~У 2 =~ G
является наибольшим на ]0; 2[, т. е. для всех х <= ]0; 2[
sin л; — yx^ (¦ ~П <-а'
Значит, и на интервале ]0; 2[ данное уравнение решений
не имеет. А
§ 2. Системы тригонометрических уравнений
В этом параграфе рассмотрим на примерах некоторые приемы,
используемые при решении тригонометрических систем. Ограни-
Ограничимся при этом лишь системами с двумя переменным!' (часто
говорят также, неизвестными) хну. Решения системы записыва-
записываются как обычно в виде упорядоченных пар (х\ у).
Системы, содержащие уравнение вида
х-\-у = <х или х—у=а,
подстановкой можно свести к одному уравнению.
Пример 1. Решить систему
sin (x — у) = 2 sin х sin у,
х + у = п/2.
8 п/ред. Г. Н. Яковлева 225
Д Сделаем подстановку У = \ — х в первое уравнение и пре-
преобразуем erot
sin Bл; — — ) = 2 sin x sin (-?- — х),
In \
— sin (-2— 2atJ = 2 sin л: cos л:,
— cos 2x = sin2x, tg2x = —1,
откуда x = — g- + ^p neZ. Теперь находим у = ~ — -—, «
r\ if я . яп 5я nn
Ответ. ^~T + _;—-_]|
В некоторых случаях прежде чем выполнять подстановку
в уравнение системы, бывает полезно его преобразовать.
Пример 2. Решить систему
sin2#= 1/2,
х — г/ = 4п/3.
Д Преобразуем первое уравнение данной системы:
~ A -cos 2bc) +у A - cos 2y) = J ,
cos 2л: + cos 2г/ = 1, 2 cos (x + у) cos (л; — у) = 1.
Ясно, что система
| cos (* +г/) cos (х-г/) =1/2,
\ х — г/ = 4п/3
имеет те же решения, что и исходная, т. е. эти системы равно-
равносильны. После подстановки х — у = 4п/3>в первое уравнение полу-
полученной системы будем иметь cos(x + y)cosDn/3) = \/'2, откуда
cos(x + y) = — 1 и, следовательно, х + У = яB/г+ 1), ieZ. Теперь
при каждом neZ из линейной системы
\ л; — у =
находим х = -?¦1 + п«, г/ = — -5-4-п«, neZ. Множество всех таких
пар значений х и у и есть множество всех решений исходной
системы, а
В предыдущих примерах получаемые соотношения между неиз-
неизвестными х и у и множество решений системы записывались
с помощью только одного целочисленного параметра. Обычно же
при решении систем с двумя переменными появляются два цело-
целочисленных параметра.
226
Пример 3. Решить систему
j sin (* + */) = О,
| sin (*-//) = О. ()
Д Из первого уравнения системы A) следует, что
х + у = пт, meZ, B)
а из второго
х — у = пп, «gZ. C)
Теперь при произвольно взятых значениях т и « из линейной
системы
^ x — y = :
находим
где meZ и neZ. Эти пары чисел и только они и составляют
множество всех решений системы A). а
Было бы ошибкой вместо систем вида D) (где тип — любые
целые числа) рассмотреть только системы
( х + у = пт,
\ х — у = лт, i«eZ
(к такой ошибке обычно приводит употребление одной буквы для
обозначения параметров в соотношениях вида B), C)). Дгйстви-
тельно, системы вида D) охватывают все возможные пары пара-
параметров т и п, в то время как в системах вида E) рассматриваются
лишь пары с равными значениями (яг = и). Это приводит к потере
решений. Из E) следует, что
х = лт, у -= О,
где т е Z, тогда как, например, все пары
х = 0, у = пп, /ieZ,
также являются решениями системы A).
Рассмотрим примеры решений более сложных систем.
Введение новых переменных можно использовать, наг ример,
в тех случаях, когда система содержит только две тригонометри-
тригонометрические функции или приводится к такому виду.
Пример 4. Решить систему
( sin ;c + cos у=\ч
\ cos 2x — cos 2y = 1.
Д Преобразуем второе уравнение:
l-2sia2x+l — 2cos2//= 1, sin2x + cos2у = 1/2.
6* 227
Ясно, что система
sin x + cos у= I,
sin2 х + cosa i) = 1/2
равносильна исходной. Обозначив для простоты и = sinx, v = cos//,
получим
Г и +v -1,
\ «2 + у2= 1/2.
Легко установить, что эта алгебраическая система имеет единст-
единственное решение и — 1/2, v = 1/2. Следовательно, исходная система
равносильна системе
' sin л: = 1/2,
COS2/= 1/2.
Эти уравнения имеют соответственно решения:
х = (— l)m~ + nm, ffieZ,
у = ±~ + 2пп, п<=Ъ.
Множество всевозможных пар, составленных из этих значений х
и у, и есть множество всех решений исходной системы. Для
краткости такие пары записывают в виде
x = (—l)mj + nm, y = ±^ + 2nn, m,n(=Z,
подразумевая, что знак в формуле для у выбирается произвольно, а
Пример 5. Решить систему
sin х +sin г/= ^2,
cos х cos у — 1/2. '
Д Первое уравнение, используя формулу для суммы синусов,
приведем к виду
х-\-у х—у 1
sin cos = —г=-
2 2 Vi
Левую часть второго уравнения преобразуем следующим образом:
cos х cos у = ~ (cos (х + у) + cos (х - у)) =
228
В результате получаем систему
cos"
.-sin"
у.
равносильную исходной. Обозначив и = sin((% + //)/2), y =
= cos((;c — //)/2), придем к системе
Г uv=l/V2,
\ w« —ы*= 1/2,
которая имеет два решения: ur=\f\f2, v1=\;ui = — lf\/, ьг =
=* —1. Таким образом, каждое решение исходной системы явля-
является решением одной из систем:
1)
sin
COS
1
х + у
х-У _¦>
о — 'i
2)
sin
?-И/
COS
Х — У
_ 1
G)
Проведя выкладки в обратном порядке, убеждаемся в тэм, что
верно и обратное: каждое решение любой из систем 1) и $') явля-
является решением исходной системы. В таких случаях говорят, что
система F) равносильна совокупности систем G).
Из системы 1) имеем
где т, п^Т,- Отсюда находим
(8)
где т, neZ.
Решаем систему 2):
x-Y-y
= я
где т, « е Z- Отсюда
, у = (-1)»+1^ + я(/п-2я-[), (9)
где m, «eZ.
Ответ: Множество всех решений системы задается фор пулами
(8), (9). А
Рассмотрим пример еще одной замены.
229
Пример 6. Решить систему
sin х 4- cos х = —¦?=¦ + sin у — cos ij,
2 sin 2* = !- +sin 2#.
Д Обозначим
и = sin*-}-cos я, у = sin у — cos//
и воспользуемся тем, что sin2х = и2— 1, sin2y = 1 —у2. Это позво-
позволяет свести данную систему к алгебраической:
Получившаяся система имеет два решения:
ы1 = —4/31^2, ох = — 7/31/2; «8 = 1/2; У2 = 1/1/2.
Таким образом, исходная система равносильна совокупности двух
систем:
sinx-f cos jc = — 4/31/2, 2) | sm^-fcosx = |/2,
sin г/ -cos # = —7/31/2; \ sin^-cos//= 1/1/2.
Первая из этих систем решений не имеет, поскольку |sin</—¦
— cos f/1 -s^l/2, a | — 7/31/2 | > 1/2. Решения уравнений систе-
системы 2) найдем введением вспомогательного угла:
sin (л: -\--д-) = 1» Л:= х+ 2яш;
у - -4) = -2-. У = (—!) -6- + 4 + яя,
где т, п е Z- Эти пары значений х и у \\ составляют множество
всех решений исходной системы. А
В ряде случаев для решения системы ее преобразуют с помощью
почленного сложения, вычитания, умножения, деления уравнений
с целью, например, исключить одно из неизвестных (переменных),
разложить полученное уравнение на множители и т. д. Рассмотрим
несколько примеров использования таких преобразований.
Пример 7, Решить систему
/ cos х cos y = 3/4,
I sin x sin у = — 1/4.
Д Складывая и вычитая почленно уравнения системы, полу-
получаем соответственно
cosxcos//+sinxsini/= 1/2, cos(x — y)= 1/2;
cosx cos у — sin xsin// = 1,
230
Система
г cos (х- у) =--1/2,
\
равносильна исходной. Решаем каждое уравнение этой системы:
¦ я
Взяв в первой из этих формул верхний знак, найдем, что
11 ? (л-т), A0)
л; = 11+я(т + 'г), 0 = _ + я(лт),
где т, neZ. Для нижнего знака получим
х = — -?- + я(т + /г), г/ = |- + л(п-яг), A1)
где т, /igZ. Формулы A0) и A1) и задают множесТЕо всех
решений исходной системы. Для краткости используют и такую
запись:
х = ±~--\-л(т + п), у=--^~ + л(п-т),
где in, n^Z, оговаривая, что в этих формулах следует одно-
одновременно брать либо верхние, либо нижние знаки. ^
Пример 8. Решить систему
tg ^
Д По формуле приведения имеем tgT?- — x) =ctgfy — ^ +-¦«
. Значит, исходная система равносильна системе
Перемножив почленно уравнения этой системы, получим уравне-
уравнение
1 =8 cos3у sin3 у,
откуда sin32t/=l, sin2t/=l, 2y= -t) -\-2лп, у='--\-лп, neZ.
Эти значения подставляем в систему A2) и, учитывая, что
cos (а + я/г) = (— l)"cosa, sin (а + я/г) = (— l)"sina,
231
получаем
tg ("-+ *) = (-
A3)
Если n = 2k, fteZ, то г/=-^-+ 2лй, а система A3) равно-
равносильна одному уравнению tg (^- + jcj= 1, откуда x = nl, /eZ.
Если n = 2k+l, *eZ, to y = ^+nBk+l), а система A3)
равносильна уравнению tg f ^ + x) =—1, откуда x = — ~ -)- л/, Ie Z.
Ответ
: {(л/; ^-
Z}- A
Пример 9. Решить систему
I, ft-
\ cos x — cos t/ = УЪ
Д Преобразуем сначала уравнения системы по формулам
суммы синусов и разности косинусов. Получим систему
sin *+М cos
равносильную исходной. Обозначим (х-{-у)/2 = и, (x — y)/2 =
тогда эта система будет иметь вид
|sin и cosy = 1/2
\sin и sin v = —
Ясно, что если (и; у) —решение системы A5), то sinu cosy =
= 1/2^=0. Поэтому для любого решения этой системы, разделив
почленно второе равенство в A5) на первое, получим, что
Отсюда находим v = — ~-{-лп, яе2. После подстановки этих
значений в A5) получим систему
fsinu«=(-l)»,
\
232
откуда и = (— 1)п-^ -\-2nm, meZ. Теперь из системы
x—у я .
находим
х = ( — 1)п~ — ^-\-лBт + п), у = (— 1)пу + у-j-яBт — л), A6)
где т, /ieZ.
Ответ: Множество всех решений системы дается форму-
формулами A6). ^
Пример 10. Решить систему
cos х=\-\- cos у\
I l/'2sin.Jt = sinу.
Д Возводя почленно уравнения системы в квадрат и скла-
складывая, получаем уравнение
Отсюда cos у — 0, (/ = -- +ял, /ieZ. Подстановка этих значений
у в исходную систему дает
{cos х =
Если n — 2k, /ieZ, то
jcosx=l/j/2,
I sinA;=l/VA2,
откуда а; = -^ + 2я/, IeZ. При этом // =
Если же n = 2k+l, fteZ, то
cos х =
sin x = —1/1/2,
откуда х = — ^--|-2я/, /eZ. При этом у = -~
Ответ: |^ + 2я/; -^- + 2я/г], [— -^ + 2я/; ^ + 2яй
Если бы в данном примере использовать для нахождения зна-
значений х, например, только первое уравнение системы, то легко
видеть, что получились бы посторонние значения переменных.
233
§ 3. Тригонометрические неравенства
При решении неравенств с тригонометрическими функциями
существенно используются периодичность этих функций и их
монотонность на соответствующих промежутках.
Простейшие тригонометрические неравенства.
Функция sin А' имеет наименьший положительный период 2я.
Поэтому неравенства вида
sin х < a, sinxsga B)
достаточно решить сначала на каком-либо отрезке длины 2я.
Множество всех решений получим, прибавив к каждому из най-
найденных ка этом отрезке решений числа вида 2я/г, п е Z-
зк
г
~2
Рис. 126.
Рис. 127.
Неравенство A) удобно решить сначала на отрезке [ — л/2; Зя/2]
(здесь график функции sinx образует «холмик», рис. 126).
Пример 1. Решить неравенство sin лг> — 1/2.
Д Решим это неравенство на отрезке [ — я/2; Зл/2]. Рассмот-
Рассмотрим его левую половину— отрезок [ — я/2; п/2\ (рис. 127). Здесь
уравнение sin* = — 1/2 имеет одно решение х= — п/6, а функция
sin л; монотонно возрастает. Значит, если -л/2<^<-п/6, то
sin я её sin (— я/6) = —1/2, т. е. эти значения х решениями нера-
неравенства не являются. Если же — я/6 < х ss п/2, то siruO-
>sin( — я/6) = —1/2. Все эти значения х являются решениями
неравенства.
На оставшемся отрезке [я/2; Зл/2] функция sinx монотонно
убывает и уравнение sinx = —1/2 имеет одно решение х = 7я/6.
Следовательно, есля л/2s?.x< 7я/6, то sin x\> sin Gя/6) = — 1/2,
т. е. все эти значения х являются решениями неравенства. Для
234
*е[7л/6; Зл/2] имеем sinjc^sin Gл/6) = —1/2, эти значения я
решениями не являются.
Таким образом, множество всех решений данного неравенства
на отрезке [ — я/6; Зя/2] есть интервал ]—я/6; 7я/6[.
В силу периодичности функции sin jc с периодом 2л значения
х из любого интервала вида
также являются решениями неравенства. Никакие другие зна-
значения х решениями этого неравенства не являются. Ответ запи-
запишем в виде
-^+2лп-
¦
+ 2лп, где л
подразумевая, что решениями исходного неравенства яиляются
те и только те значения х, каждое из которых при некотором
neZ удовлетворяет этим двум неравенствам. ^
У\
V3
г
А\
д Т
!\
~2п «\
•Ч /
-- 1
7п 5:4 Ш-
Рис. 123-
Неравенства B) удобно решить сначала на отрезке [я/2; 5я/2]
(здесь график sin* образует «впадину», рис. 128). На рис. 128
дана графическая иллюстрация к решению неравенства
sinx:s? j/3/2
(подробные рассуждения предлагается провести читатель)). Его
решениями являются те и только те значения х, каждое из кото-
которых при некотором /igZ удовлетворяет неравенствам
~
Для неравенств
cos х < a, cos х «S a
C)
удобно сначала найти решения на отрезке [0; 2я] («впадина»,
рис. 129).
Пример 2. Решить неравенство cosjesg—1/2.
Д На отрезке [0; я] функция cos x монотонно убывает
(рис. 129), а уравнение cosje = —1/2 имеет одно решение х =
= 2я/3. Рассуждая также, как и в примере 1, получаем, зто зна-
235
чення х из отрезка [2я/3; я] и только они являются решениями
данного неравенства на отрезке [0; я]. На отрезке [л; 2л] функ-
функция cos* монотонно возрастает и уравнение cosa; = —1/2 имеет
решение лг = 4я/3. Отсюда следует, что все значения х на отрезке
[я; 4л/3] и только они являются здесь решениями данного нера-
неравенства.
Рис. 129.
Таким образом, множество решений неравенства cosx^ —1/2
на отрезке [0; 2я] есть отрезок [2л/3; 4я/3]. Функция cos л:
периодична с периодом 2я, поэтому все значения х, каждое из
которых при некотором /ieZ удовлетворяет неравенствам
2я' "- s*<? + 2™,
и только они являются решениями исходного неравенства. А
Неравенства
cos х > a, cGSx^a D)
удобно решить сначала на отрезке [ — л; я] («холмик», рис. 130).
Рис. 130 является графической иллюстрацией к решению нера-
неравенства
cos х > 1/1^2
(подробных рассуждений не приводим). Все решения этого нера-
неравенства задаются неравенствами вида
где л.
236
Неравенства
tg*>a,
tgx^za, tgx<a,
E)
удобно решить сначала на интервале ] —л/2; л/2|", а неравенства
, ctgx<a F)
— на интервале ]0; л[. Функции tgjc и ctgл; имеют период л,
поэтому, прибавляя к найденным на соответствующих интерва-
интервалах решениям числа вида я/г, zie^Z, получим все решенря нера-
неравенств E) и (б).
Пример 3. Решить неравенство tg;c<:2.
Д На интервале ] —я/2; я/2[ функция tg д; монотонно воз-
возрастает (рис. 131) и уравнение tgx = 2 имеет одно решение х~
= arctg 2. Если — я/2 < х < arctg 2, то tg л; < 2, значит, :>ти зна-
значения х являются решениями данного неравенства. Если arctg 2 <
eg; л: <С я/2, то tgA;55 2. Эти значения х решениями не являются.
Следовательно, множество решений неравенства tg л: < 2 т интер-
интервале ] —я/2; я/2[ есть интервал ]—я/2; arctg 2[.
Рис. 131.
Рис. 132.
Решениями данного неравенства на всей числовой прямой
являются все те и только те значения х, каждое из которых
при некотором neZ удовлетворяет неравенствам
— у + я/г <*< arctg 2 +я/г. ^
Рис. 132 является графической иллюстрацией к решению нера-
неравенства
Его решениями являются те и только те значения х, каждое из
которых при некотором п eZ Удовлетворяет неравенствам
л/г < х s^ arcctg (— 2) -f я/г.
237
Примеры решения более сложных неравенств.
Для сведения тригонометрических неравенств к простейшим три-
тригонометрическим неравенствам можно использовать в подходящих
случаях те же преобразования (введение нового неизвестного,
разложение на множители и т. д.), которые в § 1 применялись
для решения уравнений.
Пример 4. Решить неравенство sin (—х + —}<Г7=~-
Д Обозначим t — -:X-\-^, тогда неравенство будет иметь вид
sin t< I/VI
На отрезке л/2 s-;c t-^ 5л/2 множеством решений этого неравенства
является интервал Зл/4 < t < 9л/4. Множество всех решений запи-
запишем в виде
~ + 2nn<t<-" + 2nn, где neZ- G)
Подставив в G) t = ^x-\-^r, получим
Зя . о 3 , я ^ 9л ,
-j + 2я/г <-jх + j2 <--4- +
4 4 13 4
откуда -д- л -f- о лп<; х < -<р я + --г ля , где /г е= Z. Все те и только
те значения х, каждое из которых при некотором neZ удовлет-
удовлетворяет этим неравенствам, и являются решениями исходного нера-
неравенства. ^
Пример 5. Решить неравенство cos2а; — sin 2л;5ьО.
Д Преобразуем это неравенство с помощью введения вспомо-
вспомогательного угла, в результате получим неравенство
имеющее те же решения, что и исходное. Из свойств косинуса
следует, что решениями этого неравенства являются те и только
те значения х, каждое из которых при некотором fieZ удовлет-
удовлетворяет неравенствам
- -J + 2я« < 2х + ~*Sy + 2ял,
т. е. —Д + пп <=х<,^ + яп. ^
Пример 6. Решить неравенство sin а; + cos 2a; > 1.
Д Воспользовавшись формулой cos 2а; = 1 —2 sin2 x и обозначив
f = sin л:, запишем данное неравенство в виде
238
Отсюда 0</<1/2. Таким образом, решениями исходного нера-
неравенства являются те и только те значения х, для которьх
О < sin л: < 1/2. (8)
На отрезке [— л/2; Зя/2] левое неравенство имеет эешения
(рис. 133) 0<л;<я. Среди этих значений х решениями правого
неравенства системы (8) являются
0<;е<я/6, 5п/6<л;<;п.
Это и есть множество всех решений системы (8), а з ;ачит, и
исходного неравенства на отрезке Г—л/2; Зя/2].
Рис. 133.
Теперь, используя периодичность функции sinx, легко найти
на числовой прямой все решения.
Ответ: 2лп<л:<~ + 2я«,
5я
~6~
2я/г ¦
где п (
ЗАДАЧИ РАЗДЕЛА I
Решить уравнения A—9):
1. cos Ъх cos х = cos Ьх.
2. 2 sin2 2x + sin2 4x = 5/4. 3. sin Ъх == sin x + sin 2x.
4. 4 cos x cos 2x = cos Зх. 5. A -f cos x) ctg x = sin 2л.
6. 2(/2-l)sin*+l-tg*=l/cos*.
7. tg.v-f ctg2* = 2ctg4*. 8. /l + sin.v + cos* = 0.
9. | cos x—2 sin 2x — cos 3x|= 1—2 sin x — cos 2x.
10. Доказать, что arccos a + arccos (—а) = я, |а|^1.
11. Найти все значения a(a=^=0), для которых уравнение
X
\ (/2 — 8/+ 13) d/ = *sin —
о
имеет решение. Найти это решение.
Решить системы уравнений A2—14):
sin х = cos 2y.
¦239
Г 2 sin x sin y+cos 2y — /2 = 0,
| cos 2л+2 cos дс cos 1/ + ]^2=0.
tg (</ + -| j = cos 2л.
Решить неравенства A5—17):
15. sin x ^ cos 2x. 16. 2 tg 2* ==: 3 tg x.
17. sin *<; | созх |.
ЗАДАЧИ РАЗДЕЛА II
Решить уравнения A—17):
х х
1. cos6.«-|-2cosax= i 2. sin 2x = cos4 -^ — sin1 -=-.
3. tg2AT • tg2 3* = 1. 4. sin x + cos * = K2 cos 5*.
5. cos2x + sin 2*= cos x + sin x.
6. cos x sin 7x= cos 3x sin 6x.
7. 1ё*=-^Йт- 8' ^2sin^ + ctg^ = °- 9- ctg»jc-tg»x=|-.
10. sln22x —cos2* + -j =0. 11. si
12. +
13. 6 [ sin x\ cosjc— 1 =cos4x. 14. 1 — cos 3x ¦ ctg.v=sin 3x.
13. cos | x + -.-) + cos (x —j I = -^ cos 2x.
16. sin (x + -s- J • sin (x — -5- ) = sin x.
17.
sin x
18. Найти пересечение множества {х \ cos2x + 3cos х-\-2 = 0) и множеств
{ х I ; /2 х - 5 ] < 1}.
Решить уравнения A9—22):
19. sin4x+cos4*=--. 20. 2 cos" ж — 2 sin8 x = sin 4t.
О
21. tg^ + -j)-tgjc-l. 22.
23. Найти все значения р, для которых уравнение
sin х -f- p cos л = 2р
имеет решения.
Решить уравнения B4—25):
Y
24. 2sin* + cos*.|+2 + cos*=0. 25.
2в. Вычислить sin 2а, если sin а— cos а = 1/2.
240
Решить уравнения B7—28):
27- ЖТ + -EoI7 = 2 V'2- 28' 3 cos (* + т) = П sin
ЖТ + EoI7 = 2 V2- 28' 3 cos (* + т
29. Доказать, что
Я , Я/1 _
для всех ^g+y « е Z-
Решить уравнения C0—53):
30. sin(-? + A:) + ctg(?n-A:) = 0. 31.
\ z I
32. sin 4л + 2 cos* л = 1. 33. sin2 2л — 4 cos4 л = sin 4л.
/6
34. cos 2л =-у (cos л — sin л).
35. ctg*-lg*=-I-(sin*-cosjO. 36. ап4л:
2
37. : ' , ,,. = cos л — соз (л/4).
cos л + cos (я/4)
39> cos л; + / ЗлЛ =
сса[х-т)
40. 3 (cos л — sin л) = 1 -\- cos 2х — sin '2x.
41. cos Бх — cos Зл = 3 sin ix.
42. sin 3* — sin л + соэ2л= 1.
43. sin Зл + sin 4л + sin Ъх; = 0.
44. 4 sin 3x + sin 5л — 2 sin л • cos 2x = 0.
45. sin л • ct-,' Зл = cos 5jc. 40. 1 + sec x = ctg2 —.
47. sin л ¦ sin 2л ¦ sin 3* = -.- sin 6л.
4
COS X ~~ 1 у
48. = 2 sin л. 49. cos 4л — 3 cos л = 4 sin2 ~-.
50. (sin x+Vi cos x) sin 3jc = 2.
51. sin л —sin 2л + sin 5л + sin 8л =0.
52. tg x ¦ tg A/л) = 1. 53. tg -i-^L-r = - /3.
54. Найтн все решения уравнения sin2 *+ зт22л-|-5т2 Зл = 3/2, удовлет-
удовлетворяющие неравенству cos ле > 1/к 2.
Решить уравнения E5—65):
sin I
241
55. \ ^- = 2 sin л— '
. , я \ sin л
sin л — —
56. ? )g* = sin 2л—1. 57. 1яЗл—tgл = 4sinл:.
1 -f- tg Л
9
68. sin2 2л — tg2 л = ¦- cos 2л.
59. sin3 л + cos3 л = sin 2л + sin л + cos л.
60. 2втл = 8тЗл. 61. cos Зл-|- 6 cos2 x = cos x.
62. 2 cos л—совул=1.
63. sin Зл-+ sin 5* = 2 (cos2 2л— sin2 Зл).
64. 5 sin л + 6 sin 2л + 5 sin Зл + sin 4л = О.
65. sin2 2x + sin2 Зл + sin 2 4л + sin 2 5л=2.
66. Проверить, какие из чисел множества А являются решениям
уравнения:
(
\
а) Л=Ьгссо8г7=
\ V 3
Ьгссо8г7= + —
\ V 3 2
, 1 я
1 — = 6;
2
1
sin л cos 2л
б) ^ = {nn-arctg3|neZ}, 12 tg 2л + -^-+1 =0.
Решить уравнения F7 — 76):
67. ]-Z2x
68. tg jk + 2 ctg 2л: = cos л: -|- sin 2л.
69. \~Cigi* =4cos2^ л —2. 70. 2tg2л+tgЗл = tgE
71 _L___L_ i _J , 72 sin 3* |, cos 3* 't
' sin x sin 2л sin 3x" ' cos 2x sin 2л sin
73. tg 2л r-5— = -г—: ctg 3.r.
s sin 3x sin 4л &
„. cos ж-j-cos 2д: — cos 3* — cos 4* _, x
sin 4x 4- sin 3x — sin Ix — sin x- ~~ ** 2 *
__ о ¦ r, cos ж ¦ cas Зл
¦ 75. 2 cos л — sin Зл = — :—.
I sm л I
76. sin л —2 sin 2л4-sin Зл=! 1 — 2 cos *4-cos 2x \.
77. При каких а уравнение
a sin (x
(x + t)= si" 2x + 9
имеет решение?
Решить уравнения G8—86):
78. sin* л + cos" x = a sin 4x.
79. a cos Зл + sin 2л • siii л — cos x=0.
60. sin3 2л + а sin2 2л-f sin2 л = sin- Зл.
81. ^2 sin 2* + 2 sin* = 0. 82. Vl + sin л=cos л.
83. f/cos2* — 5 sin х + 2 cos x = 0.
86. 2 cos x = V2+ sin Злг.
87. При каких а уравнение
К sin х — Vcos x -— a
Имеет решения?
88*. При каких а уравнение
У\ +sin
а) имеет решения?
б) имеет единственное решение на отрезке [—л/3; k/3J?
Решить уравнения (89—97):
89. tg 7х = 2 tg5х + tg2 Ъх Aglx.
90. ctg ( з + 3*) + ctg (^ + *) = 2 sin (-J - 2*).
91. sin * + 2 cos л: = cos 2x — sin 2x.
92. cos 3* — cos 2x = sin 3x.
no ¦ -3 4 . , x .
93. sin x — sin -.- x = — sin2 -=- • sin x.
2. о Z
94. cos12 л; + sin8 л; A + cos2 л;K = 1.
95. cos2 x — sin2 (jt Уз) = 1. 96. cos0 2jtJt — 2 sin'1 я* = 3.
97. 2 sin2 * • cos2 ix = sin2 Jt-f cos2 ix.
Решить системы уравнений (98—99):
tgJC + 3 tg y = 0, i cosjc • cosy=3 sin x sin y,
98. I ,. , n. r_ 99J .. , л 3 _
100. При каких а система
I 8 cos x ¦ cos (/ • cos (a: — (/) + 1 = 0,
имеет решения? Найти эти решения.
Решить системы уравнении A01—124):
Г sin х + sin у = sin
cos 2 +COS
/2
,05. f —•-^A 1O6.f tg,.tg2(/=1.
I sin 2^; + sin 2y = 0. l У 3 sin 2* — 3cos 2y=0.
( cosjc — sin x= 1+cosy — sin y,
j
104> j 3sin 2x —
( sin jc + sin у = 2 sin (*+y),
107. j ^ y___3
1 C0S 2"CO8'2"~4
108
' л 2sin Bx + y) cosy + cos 2y+1=0.
243
109 f 2 sin дс - cos (/
I
no
...
/ 4
2 ctg jc + ctg.//,
2 sin у ¦ cos x = ctg x + 2 ctg y.
sin 6*=sin (*+«/)—sin (*—и
sin bx = sin (/ — sin 6*.
sin *— 2 sin у = Ъ,
2 cos * — c
112
113
s'n
cos 2* sin j/+ cos * cos j/
ctg * — tg x sin 2(/ — sin у = 0.
2 sin jc sin (/ = cos 2 x + cos 2(/,
2 cos jc sin # = cos 2x — cos 2(/.
2 sin2jc =
sin D* —
/2 sin Bл:-
sin Cjc —jr) =
; —2i/)=0.
¦„{
у 1 + sin x ¦ sin у = cos x,
2 sin x- ctg у+1=0.
ein y — cos(/ =
120
f 2sin2y + sin 2(/ = cos (* + {/),
\ cos2 л; + 2 sin 2y + sin2 у = cos (*—y)
i 3tg((//2)+6sinJC=2sin((/-JC),
tgDr/2JsinJt 6sin(if + Jt)
122.
123.
124*.
sin x; + cos x = 2 sin y,
sin 2л; = /3 sin 2y — 3 cos 2</.
cos л; = cos (/ cosz,
cos у = cos л; cos z H—-^ sin x sin 2,
cos z = cos л; cos у Н—-?=r sin x sin (/.
sin л; + sin 2 = 1^2 cos (/,
cos^+cosz = 1^2 sin y,
cos 2i/ +cos 2z = sin 2x.
' , sin г , „
tg* • tg y= f-3,
ь ь cos x cos (/
, , sin л; r
tg и • tg 2 = 5,
cos у cos 2
- tg x =
sin
cos z cos *
Решить неравенства A25—138):
125. 2 cos2 * > 3/2. 128. sin x =2 cos *.
127. sin * + 2cos*<2. 128. cos 2jc+3 sin x :
244
129. sin * + sin 3*2гО. 130.
131. t
132. sin
133. sin jc + sin 3x< sin 5* +sin 7x.
134. | sin x\ > | cos* j.
136. l+cos2*^;cos*(l+j 1— 2 cos л !).
136.
137. 1/ -=—cos2a'> sin x — cos*.
138. /sin
139. Доказать тождества:
a) (sin (Y + P) — sin a) (sin (y — fl) + sin a) =
==(sin (Y + a)—sin P) (sin (y — a) + sing);
6) cosa + sin a + cos3a + sin 3a = 2 KiJcosa sin +
140. Упростить выражение
sin2 a + sin2 p + 2 sin a sin P cos (a + fi).
141. Доказать:
a)
l+cosBa + 63Q) + sinBa + 810) _
j 1 -cosBa-630°)-j-sin Bа-81(Г)" ga"
142. Доказать, что
если 5 sin a = 3 sin (a + 2J3) Ф 0.
143. Доказать:
a) ctg7,5o + tg67,5o-ctg67,5o-tg715° =
0) . я ~ . 2я + . Зя "
Sin у Sin -y- Sin -y-
144. Вычислить:
а) cos 3a cos3 a + sin 3a sin3a, если cos2a = a.
б) (sin 4a+ 2 sin 2a) cos a, если sin a =1/4.
,.. _ , sin8 ф , cosem sin4 ф , cos4 q
145. Выразить через a и b ¦—^--\ Si » если H T^' = ~
146. Найти:
a) sin (arccos (— 3/5.)). 6) cos B arcain C/4)).
d) tg (arcsin B/3)). r) cos (arcctg (— 2)).
д) cos B arctg 2) — sin D arctg 3).
147. Доказать:
а) arcsin x-\- arccos x = n/2, * i= [— 1; 1].
б) arctg x + arcctg х = л/2, xeR.
в) arctgx = arcctgA /дс), *>0,
arctg x= arcctg A/дс) — я, х<0,
245
r) arcsin *=arccos У 1 — хг,
arcsin лс = —arccos Kl — x2, —
я) arccos * = arcsinVl — х2, 0=
arccos *=я — arcsin ]/l —к1 —
148. Доказать, что функция
2x
у = 2 arctg*+ arcsin-
принимает одно и то же значение для всех *:> 1. Найти это значение,
149. Найти все значении а, при которых уравнения
4 cos2 х — cos Зх = a cos х — | а — 4 | A +cos2*)
и
2 cos х cos 2x= 1-|-cos2*+cos3x
равносильны.
Решить уравнения A50—154):
150. ctg (^ (
151.2 sin2 (-5- cosa jt j = 1 — cos (я sin 2л).
152. 2 I *—6 I cos x = x — 6. 153.
Х~Т
154. — 2/3nsiiut= 1 лг+jt | + | jc —2jt ].
155*. Доказать, что для любого а и любого натурального п > 1
cosa + cos (аН —)+ ••• +cos (а + (;г — 1) — ) = 0.
156. Ha йти сумму tg2 ~ + tg^ -??- + ... + tg2 ~.
157. Найти общие решения уравнений
5я
sin 5л* + cos 5ял- -[- 2 sin - -- = 0
YI Sin -|^ +3 cos ~ + sin Юлх = 0.
1Б8. При каких значениях а уравнение
\ sin '^ (fu = a? ^" l"-fl-a-
о
имеет решение? Найти это решение.
159. Найти наименьшее значение функции
при д
246
180. Найти все значения а, при которых квадратичная функция .:2cosa +
+ 2х sin а +~?т (cos а — s'n а) является квад]ратом линейной функции.
161. Найти все значения а, при которых квадратный трехчлен х' sin la.—
— (sin2 2а— 4 cose а) х-\ имеет два одинаковых по абсолютной Ееличина
COS ОС
корня разных знаков.
162. Найти все принадлежащие отрезку [2; 3) решения уравнение
а
¦j cos (х + a2) dx — sin а.
о
Решить уравнения A63—165);
183. ai'ccos x= 2 arcsin x.
164.
185. arctg B tg 2дг- 6 tg x) = "+д:.
166. При каких а уравнение
(arcsin x
имеет единственное решение?
167. Найти все пары чисел (х; у) такие, что
а) sin (* — (/) + sin у — sin x=4 sin (yft).
б) cos4 х 4- cos4 у г — = 1.
cos3 х cos2 у
в*) соз х +cosy — cos (л-+ у) = 3/2.
:3/2,
I sin2A--;-sm2iy>:3;
\ cos x • cos j/= 1/4.
168. Решить систему уравнений
2~Х — 2Х sin 2y — siri y=0.
169. Доказать неравенство
cos х з= 1 — -V.
170*. При каких а неравенство
tg2 (cos /4л ^Tit2) — 4а tg (cos /4яа — х") + 2 + 2а ^ 0
имеет и притом конечное число решений? Найти эти решения.
247
Глава X
ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ,
СИСТЕМЫ И НЕРАВЕНСТВА
Вначале напомним некоторые свойства показательной и лога-
логарифмической функций, часто используемые при решении уравне-
уравнений, систем уравнений и неравенств, содержащих эти функции.
Показательная функция ах рассматривается при любом поло-
положительном основании а(а>0). Ее областью определения является
множество всех действительных чисел (х е R), множество ее зна-
значений — это множество всех положительных действительных чисел
(a*>0). При любом положительном а и любых действительных х
и у верны следующие утверждения:
1. axav = ax+y. 2. -а-х--= ах~У.
а»
3. агх = ~. 4. (ах)У = ах».
5. а°=1. 6. fl1 = a. 7. 1*=1.
8. Если а> 1, то функция ах возрастает, если 0<;а< 1, то
функция ах убывает.
Логарифмическая функция \ogax рассматривается при любом
положительном н не равном единице основании а(а>0, аф\).
Ее область определения — множество всех положительных дейст-
действительных чисел (.v>0), множеством ее значений является мно-
множество всех действительных чисел (—оо < ]oga;e< + oo). При
любом положительном а, не равном единице, и любых положи-
положительных х и у верны следующие равенства:
Г а10""* =х (основное логарифмическое тождество).
2'. logaa* = *.
3'. loga xy=logn -H-log,, у (формула для логарифма произведения).
4'. \0ga(l/x)=— \0gaX.
5'. loga (x/y) -= loga x ^- loga г/ (формула для логарифма частного).
6'. loga;ea = Gt loge;e для любого а (формула для логарифма
степени).
Т. 1 oga« х = — loga х для любого а Ф 0.
8'. log,,;e = ^—~ для любого Ь>0, Ьф\ (формула перехода,
к новому основанию).
9'. logea=l. 10'. logal=0.
248
11'. Если а> 1, то функция logrtx возрастает, если же 0<
1, то функция loga* убывает,.
Функции ах и logax являются взаимно обратными, это выра-
выражено равенствами Г и 2'.
Замечание. Отметим важную особенность формул Г, 3',
5', 6'. Их правые и левые части, взятые по отдельности, опре-
определены на разных множествах значений переменных (х шм х и у
соответственно). В формуле Г левая часть определена линь при
х>0, а правая—для всех xeR. В формулах 3' и i' левые
части определены для всех пар значений х и у одного знака
(т. е. при ху>0), а правые —лишь для х>0, г/>-0. В фор-
формуле 6' при а = 2п, где п — целое, пфО, левая часть определена
для всех хфО, правая же —только для x>0.
Отмеченную разницу множеств определения следует уч^ывать,
применяя эти формулы для преобразования уравнений и нера-
неравенств. Она может привести как к потере решений, так и к по-
появлению посторонних значений неизвестных. В соответствующих
примерах на это будет обращено внимание. Отметим, что ; подоб-
подобным обстоятельством мы уже сталкивались ранее (см., например,
гл. IX).
Из свойств показательной функции следует, что при любом
а>0, аф\, уравнение
имеет и притом единственное решение для любого Ь>0. Это
решение в общем случае записывается в виде x = loga/>. Если
а=1, то уравнение Iх = 6 имеет решение только для Ь==1. Его
решением является любое действительное число.
Из свойств логарифмической функции следует, что при любом
о>0, аФ\, уравнение
\ogax = b
имеет и притом единственное решение для любого Ъ е R. Его
решение в общем случае записывается в виде х = аь.
При решении показательных и логарифмических уравнений
часто используются два преобразования: логарифмирование и
потенцирование.
Логарифмирование по основанию с>0, сф\, представляет
собой переход от равенства
а = Ъ A)
к равенству
log, a = log, Ь B)
(здесь а и b могут обозначать как числа, так и выражения,
содержащие переменные). Если A) —верное равенство и обе
его части положительны (а>0, Ь>0), то и B)-верное
равенство.
249
Потенцированием по основанию с>0, сф\, назовем переход
от равенства B) к равенству A). Если B)—верное равенство, то
и A) —верное равенство.
§ 1. Показательные уравнения
Пример 1. Решить уравнение
Д Обе части уравнения положительны. Логарифмируя по
основанию 2, получаем уравнение
которое, очевидно, имеет те же решения, что и исходное, уравне-
уравнение, т. е. равносильно ему. Преобразуя это уравнение и учиты-
учитывая, что Iog23 = ~2 Iog29, получаем
откуда л; = 3/2 (так как Iog29—1 =/=0).
Ответ: 1,5. а
Так же как и в этом примере, уравнение вида
d <х> = bg (x>,
логарифмируя по некоторому основанию с>0, сф\, можно пре-
преобразовать к равносильному уравнению
f(x)\ogca = g(x)\ogcb.
Некоторые показательные уравнения введением нового пере-
переменного удается свести к алгебраическому уравнению, например
квадратному, и т. д.
Пример 2. Решить уравнение
Д Поскольку 0,2 = 5-1, то 0,2*-2 = 52-*, и поэтому уравнение
можно записать в виде 5х-1-{-5л-х = 26. Обозначим 5х-1 -=t, тогда
откуда t2 — 26/ + 25 = 0. Получившееся квадратное уравнение
имеет решения /t = 25 и /2=1. Отсюда 5*-1 = 25, х = 3; 5Х~1=\,
х=\. Найденные значения х и являются решениями исходного
уравнения.
Ответ: {3; 1}. А
Пример 3. Решить уравнение
25* - 12-2*-6,25-0,16* = 0.
250
Д Запишем уравнение в виде
5а* -12- 2*-6,25 .0,4** = 0.
Замечая, что 2 = 5-0,4, а следовательно, 2* = 5*- 0,4-*, приходим
к уравнению
53х - 12 ¦ 5* ¦ 0,4* - 6,25 ¦ 0,43* = О,
которое является однородным степени 2 относительно 5J' и 0,4*.
Разделив его на 0,4х и обозначив / = E/0,4)*= 12,5*, получим4
квадратное уравнение t2 — 12t — 6,25 = 0. Его корни суть / = —0,5
и /-2=12,5. Уравнение 12,5* = —0,5 решений не имеет, уравнение
12,5*= 12,5 имеет решение х=\, которое является решением и
исходного уравнения, А
Некоторые показательные уравнения удается решить, исполь-
используя свойства возрастания и убывания показательной функции.
Пример 4. Решить уравнение 4*-f-9* = 25*.
Д Легко угадать н проверить, что х = 0,5 — решение данного
уравнения.
Вопрос в том, единственно ли это решение? Пока не дэказано,
что других решений нет, или пока не найдены все другие реше-
решения (если они есть), задачу нельзя считать решенной.
Ответ на поставленный вопрос вытекает из решения следую-
следующей задачи.
Пример 5. Пусть 0<а<1, 0<6<1 и пусть уравнение
имеет решение х0. Доказать, что это решение единственно.
Д Показательная функция с положительным основанием, мень-
меньшим единицы, убывает, поэтому, если х<.ха, то ах^>ах« и М>
>ЪХа. Отсюда следует, ч,то ах-\-Ьх>ах°-\-Ьх° — \. Значит, при
х<Сх0 данное уравнение решений не имеет. Если х>хй, то ах•<
<С.аХо и 6*<;&•*% откуда ах + Ъх<а*° + Ь*° = 1. Таким образом, и
при х~>хй данное уравнение решений не имеет. Тем самым дока-
доказано, что х0 — единственное решение. А
Вернемся к примеру 4. Разделив обе части данного уравнения
на 25*, запишем его в виде
D/25)* + (9/25)* =1.
Это уравнение имеет решение яо==О,5. Согласно доказанному
в примере 5 других решений быть не может. Теперь задача при-
примера 4 решена полностью.
Ответ: 0,5. А
§ 2. Логарифмические уравнения
Пример 1. Решить уравнение
l)=l. A)
Д Потенцируя по основанию 2, получаем
х(х-1) = 2. B)
Это уравнение имеет решения Xi = 2, х2 = —1. Подставляя их
в уравнение A), убеждаемся в том, что они являются решениями
и этого уравнения.
Ответ: {2; —1}. а
Как видно из решения, уравнения A) и B) оказались равно-
равносильными. И в общем случае уравнение вида
\ogaf(x) = g(x) C)
равносильно уравнению
f(x) = az<-x\ D)
Действительно, если х — решение C), то, потенцируя верное равен-
равенство C), получаем, что и D)— верное равенство. С другой стороны,
если х — решение D), то, логарифмируя верное равенство D) (обе
его части положительны), получаем, что и C) — верное равенство.
Пример 2. Решить уравнение log3 C-* — 8) = 2 — х.
Д Потенцируя по основанию 3, получаем уравнение
3*-8 = 32-\
откуда З2* — 8- 3х — 9 = 0. Это квадратное относительно 3х урав-
уравнение имеет корни 9 и —1. Уравнение 3Л'= —1 решений не имеет,
уравнение 3* = 9 имеет решение х — 2, которое является и реше-
решением исходного уравнения.
Ответ: 2. а
Пример 3. Решить уравнение
lg(*2-6* + 7) = lg(*-3).
Д Потенцируя по основанию 10, приходим к уравнению
х2-6х + 7 = х-3,
откуда х2 — 7х + 10 = 0, хх = Ь, х2 = 2. Подстановка хх = 5 в исход-
исходное уравнение приводит к верному равенству Ig2 = lg2, значит,
#! = 5 — решение исходного уравнения. При подстановке х% = 2
в уравнение появляется выражение lg(—1), которое не опреде-
определено. Значит, хг = 2 не является решением исходного уравнения.
Ответ: 5. а
Рассмотренное уравнение является примером уравнения вида
\ogag{x). E)
Такое уравнение, вообще говоря, не равносильно уравнению
F)
Решениями уравнения E), очевидно, будут все те и только те
решения уравнения F), для которых /(д;)>0 (или, что то же,
252
g(x)>0). В примере 3 из двух решений уравнения х2 —
=х — 3 только одно, а именно, хх = Ъ, удовлетворяет условию
х — 3>0. Только это значение х и является решением исходного
уравнения.
Пример 4. Решить уравнение
logaA: + log2(A;—1)= 1.
Д Преобразуем сумму логарифмов в логарифм произпедеиия
Это уравнение (см. пример 1) имеет решения *i = 2, х2=-\. Под-
Подставляя %\ =2 в исходное уравнение, получаем верное равенство
1 = 1, значит, Xi = 2 — решение исходного уравнения. При подста-
подстановке Хг = — 1 уже в первом слагаемом левой части получаем выра-
выражение log2 (—1), которое не определено. Значит, хг = — 1 не является
решением исходного уравнения.
Ответ: 2. А
Как видно из этого примера, преобразование суммы логариф-
логарифмов в логарифм произведения может привести к уравнению, нерав-
неравносильному исходному. А именно, не всякое решение получен-
полученного уравнения может быть и решением исходного. Это связано
с тем, что, как уже отмечалось ранее (замечание к формулам Г,
3', 5', 6'), логарифм произведения может быть определен и тогда,
когда логарифмы сомножителей не определены. Если при реше-
решении уравнения использовалось указанное преобразование, то Есе
найденные значения неизвестного следует проверить, подставляя
их в исходное уравнение. Либо же следует установить, для каких
из этих значений будут положительны выражения, стоящие под
знаком логарифмов в исходном уравнении.
Сказанное в полной мере относится и к случаю преобразова-
преобразования разности логарифмов в логарифм частного.
Пример 5. Решить уравнение
log3 B - х) - log3 B + х) - log3 x + 1 = 0.
Д Преобразуем данное уравнение:
iot. <2-*K -о B—*K _,
Отсюда х2 + Ъх — 6 = 0, #i = l, хг = — 6. Для Xi=\ все выраже-
выражения, стоящие под знаком логарифмов в исходном ураннении,
положительны, значит, х\= 1 — решение этого уравнения. Для
х2 = — 6 не определен уже log3 (—6), поэтому х2 = — 6 не ялляется
решением исходного уравнения.
Ответ: 1. а
Пример 6. Решить уравнение
lg(xa + 75). G)
253
Д Учитывая, что 2 lg Bx) = lg Dx2), преобразуем дан :юе урав-
уравнение к виду
lgD*2) = lg(x2-f 75). (8)
Это уравнение, как легко установить, имеет решения ^ = 5,
x-i = — 5. Обратим внимание на то, пто в уравнении (8) выраже-
выражение lg Dя2) определено для всех х Ф 0, в то время как в исход-
исходном уравнении G) соответствующее выражение 21gB;n опреде-
определено лишь при л'>0. Проверка показывает, что из двух решений
уравнения (8) лишь х± = Ь является решением уравнения G).
Ответ: 5. А
Как видно, из этого примера, замена в уравнении выражения
2flloga/(jc) на loga(/(х)Jп (п — целое, пфО) также может приво-
приводить к появлению посторонних значений неизвестного. Как и
ранее, это связано с тем, что второе выражение имеет более
«широкую» область определения, чем первое.
Замена одного из выражений, входящих в уравнение, на дру-
другое, имеющее более «узкую» область определения, естественно
может привести к потере решений. Примерами таких преобразо-
преобразований могут служить преобразование логарифма произведения
в сумму логарифмов, вынесение показателя степени из-лод знака
логарифма и т. д. В таких случаях следует рассмотреть тем или
иным способом все значения переменной, среди которых могут
быть решения уравнения. Скажем, преобразуя logo (f (х)Jп, где
л—целое, пфО, нужно рассмотреть два случая:
если f (х) > 0, то loge (/ (x)f = 2л loga/ (х),
если /(*)<(), то loga(/(x)J'! = 2nloga(—f(x)).
Пример 7. Решить уравнение
lgBx) = -|-lg(x-15)*. (9)
Д Пусть х— 15 > 0, тогда \g(x— 15L = 41g(x— 15) и, значит,
= lg(x-15). A0)
Отсюда 2х = х— 15, х = —15. Это число не является, очевидно,
решением ни уравнения A0), ни уравнения (9).
Пусть х— 15<0, тогда \g(x— 15;4 = 41g(l5 — x) и исходное
уравнение сводится к уравнению
Ig2x = lgA5-*). A1)
Его решением является х = 5. Это же значение х является и
решением исходного уравнения (9). ^
Заметим, что если бы вместо двух случаев и соответствующих
уравнений A0), A1) рассмотреть лишь тот случай, когда lg (x— 15L=
= 41g(x— 15) (уравнение A0)), то решения уравнения (9) были бы
не найдены.
254
Некоторые логарифмические уравнения в результате иреобра-
вований и введения нового переменного удается свести к алгеб-
алгебраическим уравнениям.
Пример 8. Решить уравнение
lOgjX _ l0g8 4*
log4 2x ~ logle 8л: '
Д Обозначим log2A; = ^ перейдем к основанию 2 и восполь-
воспользуемся формулой для логарифма произведения. Будем им<>ть
1о& 2х = у 1о&2х =1.A + 0.
log8 Ах = у log2 Ах = у B + 0.
\ogu8x = \\og28x==l C + 0-
В результате исходное уравнение запишется в виде
_± 2B + 0
l+t 3C + 0'
Решив это уравнение, найдем, что 2;l=l, h = — 4. Соответственно
получаем log2jc == 1, я = 2; Iog2* =— 4, х2=1/16.
Ответ: {2; 1/16}. А
§ 3. Разные примеры уравнений
Пример 1. Решить уравнение log3х = 1 + log*9.
о
Д Переходя к основанию 3, имеем 1ое*9=~-, . Обззначив
10g3 X
t = \og3x, запишем исходное уравнение в виде
Это уравнение имеет решения /i==2, ^ = — 1. Соответственно
находим Iog3* = 2, х = 9 и log3j<; = —1, х= 1/3.
Ответ: {9; 1/3}. А
Для преобразования выражения а'°в«* бывает полезна формула
где а > 0, Ь>0, с>0, с=^= 1. Вывод ее весьма прост: из зерного
равенства \ogcb\ogca = \ogca-\ogcb следует, что верно и равен-
равенство logc(alogci) = logc(blogca), а отсюда, потенцируя, приходкмк A).
Пример 2. Решить уравнение 25'sjc = 5 + 4xlg5.
Д Согласно A) имеем xIs5 = 5's-t. Учитывая это, запишем урав-
уравнение в виде521з* — 4• б'а-^ — 5 = 0. Это уравнение является квад-
квадратным относительно б'я*. Его корни суть 5 и —1. Из тс го что
51s-t = 5, следует, что lg^=l, я=10. Уравнение 5&* = —1 реше-
решений не имеет. Значит, исходное уравнение имеет одно решение
Ю
265
Рассмотрим примеры уравнений, содержащих иыражения
(/(х))*'^. Здесь мы будем рассматривать лишь такие значения х,
при которых основание f (х) положительно.
Пример 3. Решить уравнение x's2jc=.5.
Д Здесь следует, очевидно, рассматривать лишь значения х>-0.
Логарифмируя по основанию 10, получаем уравнение
IgBx)-lg* = lg5,
равносильное, как легко видеть, исходному. Полученное уравне-
уравнение преобразуется к квадратному уравнению
относительно \gx. Отсюда находим
lgх = у (- ^ 2 ±
Учитывая, что lg 5 = 1 — lg 2, получаем, что lg2 2+4 lg 5 = (lg 2 — 2)а,
следовательно, lg x = -^ (— lg 2 ± (lg 2 — 2)). Соответственно имеем
lg.< = —1, * = 0,1; lg jc = 1 — lg 2 = lg5, х = 5.
Ответ: {0,1; 5}. а
Пример 4. Решить уравнение
Д Равенство а* = 1, где а > 0, верно тогда и только тогда,
когда либо а — \ (в этом случае Ь — любое число), либо Ь = 0
(в этом случае а —любое положительное число). В соответствии
с этим рассмотрим два случая.
1) \х — 3j == 1. Отсюда х — 3 = ±1, Xi = 4, x% — 2. Для первого
значения Xi = 4 показатель левой части исходного уравнения
определен, и, следовательно, ^ = 4 —решение исходного уравне-
уравнения. Для второго значения х2 = 2 показатель не определен, это
значение не является решением исходного уравнения.
2) (д;2-8х+15)/(,г-2) = 0. Отсюда д;2-8л;+15 = 0, ^ = 5,
а-2 = 3. Из этих двух значений решением исходного уравнения
будет лишь Х\ = Ь, а значение аг = 3 — постороннее, так как для
него основание степени в левой части исходного уравнения равно
нулю. Таким образом, исходное уравнение имеет два решений1.
хх = \ и л;2 —5. А
И в общем случае уравнение вида
(/(*))*<*>= 1
сводится к совокупности двух уравнений:
1) f(x) = l,
2) <p(*)=0.
256
Решениями исходного уравнения будут все те и только т; реше-
решения этих двух уравнений, для которых выражения qi(x] и f (х)
определены и / (х) > 0.
Пример 5. Решить уравнение
Д Потенцируя по основанию 2л- — 1, приходам к уравнению
о,- 1
которое, как легко видеть, имеет следующие решения: xi = \,
х2 = — 1, хя = \^3, х4 = — ]/3. Все решения исходного уравнения
содержатся среди этих значений х. Подстановка н исходное урав-
уравнение показывает, что его решением будет лишь х=[^3. Для
х = — 1 н х = — ]/3 основание логарифма 2х— 1 отрицательно,
а для а'=1 оно равно 1. Все эти три значения не являются реше-
решениями исходного уравнения.
Ответ: ]/3. д
Рассмотренное уравнение является примером уравнения вида
Iog<p <*)/ (х) = а.
Множество всех решений этого уравнения состоит из Есех тех
и только тех решений уравнения
которые удовлетворяют условиям ф(х)>0, ф(л')-<М.
Пример 6. Решить уравнение \og3x х = logStx x.
Д Решения этого уравнения, очевидно, следует искать лишь
среди значений х, удовлетворяющих условиям г;>0, Зх=?'-1,
9хф1. Полагая еще, что хф\, перейдем к основанию х:
B)
Iog.v 9* "
Отсюда следует, что log* 9х = log* Зх, log^3 = 0, 3 = x°, 3=1.
Полученное неверное равенство показывает, что уравнение B) ре-
решений не имеет. Неверным было бы заключить отсюда, что и
исходное уравнение не имеет решений. Осталось не исслгдован-
ным еще значение х=\. Оно-то и является, очевидно, реленнем
исходного уравнения, а
Этот пример показывает, что при переходе к новому эснова-
ншо, которое является выражением, содержащим неизвестное,
может произойти потеря тех решений исходного уравнения, для
которых это выражение равно единице.
9 п/|'ед. Г. Н. Яковлева 2^7
§ 4. Системы показательных и логарифмических уравнений
Рассмотрим сначала примеры
шить методом подстановки.
Пр имер 1. Решить систему
Рассмотрим сначала примеры систем, которые удается легко
решить методом подстановки.
Д Из второго уравнения системы следует, что log4 (х/у) = 1,
откуда х — 4у. Заменив в первом уравнении системы х на 4у,
получим уравнение
с одной переменной. В первом выражении левой части этого урав-
уравнения перейдем к основанию 2, второе выражение преобразуем
по формуле логарифма степени, учитывая, что у>0, уф\- После
простых преобразований получим уравнение logijt/=l. Отсюда
logs У =1, Ч = 2, и тогда х = 8; log2 г/ ==—1, у =1/2, а х~ 2. Под-
Подставив найденные пары значений л; = 8, у =2 и х = 2, у =1/2
в исходную систему, легко проверить, что обе они являются ре-
решениями этой системы, д
Пример 2. Решить систему1)
Д Выразив из второго уравнения у = х~°^ и заменив в пер-
первом уравнении у на x~0-5, придем к уравнению
хх~х'3'7' _ ^--0,5л:-0,5л'" °'~\ (И
Учитывая, что х>0, разделим обе части этого ураЕнения на
выражение, стоящее в правой части (оно также положительно).
В результате получим уравнение
Отсюда: 1) х = \, тогда и у= 1, эта пара значений х и г/
является, очевидно, решением исходной системы; 1.1) 1,5л: —
— 0,5л-°-5 = 0, откуда х1-5=1/3, x=l/-j/9, тогда у = |/з. Убе-
Убедиться в том, что пара х=\{\Г§, у = \/~$ является решением
исходной системы, можно непосредственной проверкой. Можно
поступить и иначе. Эта пара является, очевидно, решением си-
системы, образованной уравнением A) и уравнением у = х~°-5- А эта
система равносильна исходной, что сразу видно после замены
в уравнении A) А-5 на у.
Ответ: {A; 1), AД/9; УЦ. А
*) Если основание и показатель степени зависят от переменных, то здесь,
как и ранее, рассматриваются лишь те значения переменных, при которых
основание положительно.
258
Некоторые системы показательных и логарифмических уравиг-
пий удается свести к алгебраическим системам уравнений
П р и м е р 3. Решить систему
log, х = log4 у + log4 D - .г),
Iog3 (jc -[- //) = log:, a: — log;j гу,
Д В первом уравнении приходим к основанию 2, а затем пре-
преобразуем систему к виду
1°йз (х + у) == log.i (х/у).
Отсюда следует, что
"а = "'4Г4 B)
Каждое решение исходной системы является решением и системы
B). Значения х и //, дающие решения исходной системь, удов-
удовлетворяют, очевидно, неравенствам
0<у. C)
Легко проверить, выполняя обратные преобразования, что каж-
каждое решение системы B), удовлетворяющее неравенствам C), яв-
является и решением исходной системы.
Запишем систему B) в виде
(х + у) == 4г/,
= х/у.
Подставляя х/у вместо х-\-у в первое уравнение этой с ;стемы,
найдем, что х2 = 4г/2, Если х = 2у, то из второго уравнения сле-
следует, что у ==2/3, а значит, х = 4/3. Если же х--—2//, тэ нера-
ве!'ства C), очевидно, не выполнены и в этом случае решении
исходной системы нет. Найденная пара значений л; = 4/3, (/ = 2/3
удовлетворяет неравенствам C) и является единственным реше-
решением исходной системы, д
Пример 4. Решить систему
I log,, (ху) = 3 log';, х ¦ log., //,
Д Учитывая, что х>0 н г/;>0, преобразуем левыг части
уравнений по формулам для логарифма произведения к частного
и после введения новых переменных « = log8x, v = log$y полу-
получаем систему
и 4- v = 3«и,
D)
4 (н — у) = u/v. v
9* 259
Перемножив почленно уравнения этой системы, получим u2 = 4v~,
откуда и = 2и или ы = —2а. Подставляя и — 2и в систему D),
найдем, что и = 1/2, а значит, ы=1. Отсюда Iog8.v==l, дг = 8;
logs</ = 1/2, «/ = 2"|/2. В случае ы =—2и аналогично получим, что
л; =1/2, // = "|/2. Таким образом, исходная система имегт два ре-
решения: х = 8, // = 2 V 2 и .V = 1/2, г/= 1/2". А
§ 5. Показательные и логарифмические неравенства
Некоторые показательные и логарифмические неравенства уда-
удается решить непосредственно, используя свойства возрастания и
убывания показательной и логарифмической функций (свойства 8
и 11', указанные во вводной части).
Пример 1. Решить неравенство О.б1/*^0,0625.
/\ Заметив, что 0,0625 = 0,5", запишем неравенстьо в виде
*. A)
Поскольку показательная функция с основанием, меньшим еди-
единицы, убывает, это неравенство верно тогда и только тогда, когда
верно неравенство
1/Ж4. B)
Другими словами, неравенство B) равносильно неравенству A).
Неравенству B) удовлетворяют следующие значения х; х<0,
*.>1/4. а
Пример 2. Решить неравенство
/\ Здесь следует рассматривать лишь такие значения х, при
которых
Логарифмическая функция с основанием, большим единицы, воз-
возрастает, поэтому неравенство C) верно тогда и только тогда,
когда наряду с неравенством D) верно и неравенство
1ТГ>3. E)
Очевидно, любое решение неравенства E) удовлетворяет усло-
условию D), поэтому неравенство E) равносильно неравенству C).
Неравенство E) имеет следующие решения: —3<х< — 1. А
Пример 3. Решить неравенство
log«.2(*2-4)^-1. F)
Д Следует рассматривать лишь значения х, для которых
-' DV *2-4>0. G)
260
Логарифмическая функция с основанием, меньшим единиц j, убы-
убывает, поэтому решениями неравенства F) являются те и только
те значения х, которые наряду с G) удовлетворяют неравенству
х2-4 ^0,2-'= 5.
Иначе говоря, неравенство F) равносильно системе нержнств
Эта система имеет, очевидно, следующие решения: 2< |х|'?ИЗ. а
Точно так же, как рассмотренные в примерах 1—3 неравен-
неравенства, решаются и неравенства вида
fl'W>fl?l*), lOgaf(x)>b И Т. Д.
Пример 4, Решить неравенство
Д Это неравенство равносильно системе неравенств
Эта система в свою очередь равносильна системе неравенств
Здесь мы учли, что основание логарифма меньше единицы, а также
то, что неравенство 2х — ,>>0 следует из правого неравенства
этой системы. Преобразуя полученную систему, получаем ol/16>
>2-vSsl, откуда log.231-4>л;->0. а
П р и м е р 5. Решить неравенство 2х < З1/-*.
Д Заметим, что обе части данного неравенства положительны,
следовательно, определены логарифмы этих частей, например по
основанию 2. По свойству логарифмической функции получаем,
что данное неравенство верно тогда и только тогда, когд; верно
неравенство
Il3i/
т. е. эти неравенства равносильны. Преобразуя пэлученног нера-
неравенство, имеем
.v<>g23, *=%Ь1<О.
Решив последнее неравенство, например методом интервалов,
найдем, что его решения таковы: *<; — уПоёгЗ, 0О'-<
<y4og73. а
Пример 6. Решить неравенство lg (л:2 — 16)^lgD.i— 11),
261
Д Это неравенство равносильно системе неравенств
О <х2- 16^4*-11. (8)
Множеством решений первого неравенства 0-<x2—16 является
объединение двух интервалов ]—оо; —4[ и ]4; -)- оо[. Множество
решений второго неравенства — отрезок [—1; 5]. Пересечение этих
двух множеств —промежуток ]4; 5] —является решением рассмат-
рассматриваемой системы, а значит, и исходного неравенства. ^
Как и в примере 6, при решении неравенств вида
logag(*) (9)
или нестрогих неравенств такого вида следует рассматривать
лишь такие значения х, для которых / (х) > 0 и g(x)>0. При
этом условии неравенство вида (9) равносильно системе нера-
неравенств
0<[(x)<g(x) при 1<й,
или системе неравенств
f(x)>g(x)>0 при 0<й<1.
Рассмотрим примеры более сложных неравенств.
Если неравенство содержит степень, основание и показатель
которой зависят от переменной, то здесь будут рассматриваться
лишь такие значения этой переменной, при которых основание
положительно.
Пример 7. Решить неравенство
(х-3J*2-7*> 1. A0)
Д Если х — 3>1, то данное неравенство верно тогда и только
тогда, когда 2х2 — 7л; >0. Значит, любое решение системы не-
раЕеиств
является решением исходного неравенства A0).
Если 0<л; — 3<1, то неравенство A0) верно то№ и только
тогда, когда верно и неравенство 2л;2 — 7 л; <0. Значит, любое
решение системы неравенств
2;t2-7;t<0 ( '
также является решением неравенства A0).
При х — 3=1, т. е. х — 4, неравенство A0), очевидно, неверно.
Из сказанного следует, что множество решений неравенства A0)
является объединением множеств решений систем нераиенств A1)
и A2).
Легко найти, что множество решений системы A1) есть интер-
интервал ]4; -f oo[, а системы A2) —интервал ]3; 3, 5[. Объединение
262
этих двух интервалов и есть множество решений гсход: чгэ не-
неравенства.
Ответ: ]3; 3,5[U]4; + оо[. А
Как и в этом примере, при решении неравенств вида
[ A3)
следует рассматривать два случая:
/(*)>1 и 0 </(*)< 1. A!)
В случае нестрогих неравенств вида A3) нужно учесть и случай
Пример 8. Решить неравенство (х2 — 2,5л: + I) х+1^ .
Д Это неравенство равносильно совокупности двух систем не-
неравенств:
Первая из этих систем неравенств имеет решения х^—1. Вто-
Вторая система имеет решения 0=^.t<;0,5, 2<X2=;2,5. Все гти зна-
значения х и составляют множество решений исходного неравенства.
Ответ: {— оо; —1]U[O; 0,5[U]2; 2,5]. а
При решении неравенств вида
log/u>gM>«. logf(x)g(x)<a ^ A5)
следует так же рассматривать два случая:
f{x)>\ и 0</(х)<1. A6)
Г2а->1, ГО<2
I х" -5х + 6>2х, " j 0 <х
Пример 9. Решить неравенство 1о22а-(л:2 5 )
Д Если 2х > 1, то данное неравенство верно в том п только
том случае, когда х'1 — 5х + 6 > 2х. Если же 0<2л;<1, го дан-
данное неравенство верно тогда и только тогда, когда х- — 5;'-f-6<
< 2х. Учитывая еще, что в любом случае должно выподняться
неравенство х" — 5л:+ 6 >-0, получаем, что данное нерачепстгю
равносильно совокупности двух систем неравенств
2л:<1,
5.г-Ь:1 < 2л.
Первая из этих систем имеет решения 0,5-<л-<1, о<х. Зо вто-
второй системе первое неравенство верно при 0<х<0,5, а нера-
неравенство х2 — 5х + 6 < 2х — при 1<л--<6. Сравнивая зтп д за мно-
множества, видим, что вторая система решенш'1 не имеет. Следова-
Следовательно, множество решений исходного кераоенстЕа сотад^ст
в данном случае с множеством решений персон из p;:cc.v.ot;v.::h u к
систем.
Ответ: ;о,5; 1[ U ]б; -foo[. A
2G3
При решении нестрогих неравенств вида A5) следует рассмат-
рассматривать и случай
*(*) = (/(*))». A7)
Пример 10. Решить неравенство logi/JC——y*g— 1.
Д Это неравенство равносильно совокупности двчх систем
неравенств:
/ 1/л>1, г 0
\ 2я1 ] 2л:
1 [
Решаем первую из этих систем. Неравенство 1/л;>1 имеет
решения 0<х<;1. Значит, *¦—1<0, а тогда из неравенства
Bх — 1)/(х — 1)>0 следует, что 2л;— КО, т. е. л:<0,5. Нера-
Неравенство Bx—\)l(x—\)=s^x сводится (поскольку л;—1<0) к не-
неравенству 2х— 1^х(х — \), которое имеет решения 0,5-C —"|/)-----с
*S х <; 0,5C-f-УЪ). Пересечение, этого отрезка с интервалом
0<.т<0,5 есть промежуток
0,5C-у'5)^л'<0,5, A8)
который и является множеством решений первой системы.
Вторая система решается аналогично, множество ее решении
есть промежуток
,6C +у'5). A9)
Ответ: [0,5 C-~|/5); 0,5 [ U ] 1; 0,5C +]/5I- А
Некоторые показательные и логарифмические неравенства вве-
введением нового переменного удается свести к алгебраическим не-
неравенствам, например квадратным.
Пример 11. Решить неравенство log4 x — log* 4 s^ o/2.
Д Запишем неравенство в виде
и обозначим t=log/ix. В результате получим неравенство
которое имеет решения: ^<s?—0,5, 0</^=2. Отсюда соответст-
соответственно находим, что
log4*-<— 0,5,
Ответ: ]0; 0,5]и]1; 16]. ^
Пример 12. Решить неравенство
264
Д Это неравенство равносильно системе неравенств
О < 16*-2- 12* О2**.
Запишем эту систему в виде
О < 42* - 2 ¦ 4х ¦ 3* *? 3 • 3 *.
Разделив каждую часть на 32а>0 и обозначив / = D/3)-\ полу-
получим систему алгебраических неравенств:
О < Р - 2/ < 3.
Эта система имеет решения: 2<.t^3. Отсюда находим, что
Ответ: ]log4/32; log4/3 3]. А
При решении неравенств следует учитывать те замечания по
поводу появления посторонних значений переменной или потери
решений, которые были сделаны ранее при решении уравнений.
Пример 13. Решить неравенство
2!og8(*-l)>logjE-*)+l. B0)
Д Преобразуем данное неравенство к виду
x). B1)
Всякое решение исходного неравенства B0) является, очевидно,
и решением неравенства B1). Обратное верно в том и только том
случае, когда х — 1>0, т. е. х>\.
Далее, неравенство B1) равносильно системе неравенств
(х-1J>2E-*)>0. B2)
Первое неравенство этой системы имеет решения: х<С—3, 3<Сх,
второе неравенство —решения: я<;5. Следовательно, систела B2)
имеет решения: х<С—3, 3-<л;<:5. Из них условию х> I удов-
удовлетворяют лишь значения х из интервала ]3; 5[. Этот интервал
и есть множество решений исходного неравенства.
Ответ: J3; 5[. ^
ЗАДАЧИ РАЗДЕЛА I
Решить уравнения A—6):
2. x'°^Cj:) = 16|/x*.
1
4. 1-log, (*+!)» = у l
x 2 •
265
7. При каких значениях а уравнени
log.(_i
имеет единственное решение?
Решить системы уравнений (8—13):
8 { logyx + log,-у ==2,5,
' \ 27
\у
< 4л''-!/ = 27 + 9-1'-1/,
\ 8-чi/ — 21 -2аМ^ =
Г 5=3,
10. J 11.
I №315
!) — log2 x = log2 (x + 3;/) — !,
12. | xy+ 1 x
13.1 ~ ' x ~ ' ~~ '
\ 2-x-y — 2 . 3*+У + 3 ¦ 9X = 0.
Решить неравенства A4— 19):
14l 9_<-__2 Э= З^Л"' '5' log3 (-v" + 2) >" 1о8гч2 81 ¦
,6_ log2 ,v-¦ log, Dx) __c
log, Bл-) ¦ logw (8r) ^°
17. log.v Fx-1)> log* B*).
18*. log.f ,.a x rf" 1озл x2, a > 0, а ф 1.
ЗАДАЧИ РАЗДЕЛА II
Решить уравнения A—4):
1. 25! i-2-*l=54-s*. 2. 4'v-3v-°'5
2jc
3. 5-c.2r+l =50. 4. 5|оггЛ + 2-х1о3г5= 15.
5. Вычислить бел таблиц значение выражения
),)¦/. 2-4 _ !_ogi 192
To!b72 ~~ "bg:7'2 *
С. Выразить:
л) logr, 30 через a=log.i20 и & = lg3;
(>) 1°Д|2Я 48 через a = log3 15 и b--logl224.
Решить уравнения G — 24):
7. 2;hr2Af-|-5 ¦ 2coslj: = 7. 8. 4cos2* + 4cos3a;=3
/ _J_\
9. fi-'G2* \26-5sin2j;j = 5.
10. 3-lG-v-[-36-v = 2-81-*. 11. 9!o^U-2*>=5.
266
0,5 lo,t ,-{x* — у)
12. X Vx
13. 4kj^"-*)--=B^
/ — i- -1
14. loge\3-4 *+2-9 x
15. Зл- -!- C - х) log3 2 = log3 (9 ¦ (|-j" + 2 ¦ 6*) + 1.
16. 3 log; sin x+log2 A —cos 2.v) = 2.
17. *1O&^
18 x ]°s° X ~ 3 '°g3 X =- 3~ '°S2 1^2 64 + 8
19. A — lg 2! logs л= lg 3— lg (x— 2).
20. ,og2^-1 = ,og^.
21. lgKx-5+lgl/2x-3+l = lg30.
22. log , (cos x+^j + log^ (cos x - ^) = 2.
T 3"
23. 2 log2 sin x + log2 4 ctg2 x = -j^-2.
24. 2 1og3^+l=log3^.
25. Найти вес решения уравнения
n i jii sin х
2 log,, cie x ' — lot;,! 2 -r—^ -. = 0,
00 ° ' b02 5 siiu- 4cos.v
принадлежащие отрезку [3,3; 4].
26. Найти решения урагнепия ctgx-f-Jog^ x = 2 на интервале ] 0; я[.
27. Найти:
а) сумму KopFieii уравнения
л- + 1 == 2 log2B* + 3) — 2 log4 A980 —2-л);
б) произведение корней уравнения
Решить уравнения B8 — 42):
28. ] cos* |sin2*- 1.5 5|пд;+ 0.5_ ]_
29. (tgxfnx = (dgxfmx.
80. logj:_1Bx3—10л-2+13х—1) = 3.
81. log^(x+1J=1. 32. log8cos^sinA: +
33. !cgsjn 3x (cos x— cos 2x) = 1.
34. a-2 logs -»;2 - Bл2 + 3) log9 Bx + 3) = 3 log3
35. log2 log3 Bjc + 3) +log, log,
" 3
36. logs(log,je-9) = 2 + loga(l-
37. log!^ C-*) = logs-.*(!-•»:)¦
267
ЬИ- logt_2A. Fх*_ Zx 4- 1) - log,_3A. (\\я- - 4* + 1) = 2,
39. log,, 3 - 1облг/з 3 + log e/6! 3 = 0.
41. log5 x • log3 x = log5 л- + log3 л-.
42. logaj.r = я loga^j:, где а>0, я#1, п ф 2.
43. Доказать, что logau ¦ logaSb = log,j6 —logttS'J.
Решить уравнения D4 — 54):
+^ + g1r = 21gf1
45. lg (x- 10) • Ig (.*+ 10) = lg (x-- 100)- 1.
46. lg-2 (* + l) = lg (x+ 1) • lg (*- l) + 2 Ig2(*- I)-
47. 3.2'^^-2,+2_3,og;cC.t-,,_5i6lo3,2C,
48. 1оЙ2 B )'5^I+ 5) = 1 - logo.B (л - 0,5).
49. j/"logA. !/3^.1og3x-+l=0.
50. ^4 log4 x- — 2 H- ^ 1
51. 3 log,« (V x^Tl + x) -{- log2 (|/"^+T- x) = logl0 Dл--i- 1) -
5l'. logj' tg x-j- logo sin" x . log,, cos2 х = 1.
53. lg'- cos x = lg A — sin x) • lg A -|- si» >;) ¦
54. (V^TW + A/4 + П5)' == S.
55. При каки.ч значениях а уравнений loij.v.|.rt (л — 2) =2 имсе?
Нос рсшэпис?
5й. Сколько pcmeniiii имеет уравнение e2x~x'-r'2x-i — 3 = xi'?
Решить уравнения E7 — 58):
57*. i^lУ _ ^=^_ =-.1, 0<а<1.
\ la j \ 2а )
58*. Iog
Решить системы уравнении E9 — 85):
log3x+log3i/=2-l-lot!37, (.o
= 2. ' '
3 ¦ x«-i =-- 4,
65
^+1G
66. _±_
{ 5-16stn-f-2.3COiy=2.
268
67.
— log4 *-log4 i/ = 0.
" I lg2 (*-</)+ lg*-lg</=0.
" 1 Iх — 5.
73- { log,к 2,5
=У
"¦{
75"
lg </¦ lg (* + >/) = lg * - lg (x—y).
log, A0-2») = 4-»,
6 f log2 (*-3) • lObV
' { logr,*• logs Bx-
2l/+l)-3 log3 Br/-l) +2 = 0.
( Wx-(log*y-\aexy+l)=M,
lg xy=V\ogyx ¦ j lg у j — 7.
Г
78.
Г log^x + log^g i/-log§/3 (*+#)= 1,
log3/2*-log3/2i/ + log3/2(
2-
5</-* = 3-9*. \ 2^ + 8.2^ = 8-16*+16й.
) 2-Зл'-У— 5»-* = 3 ¦ 9*.
81. I
, 2-ад —2-4-f2 + 64 = 0,
82. ' 2У<х+г> + 2 ¦ 2A''"+-?) 20 ¦2-v^ = 0
— 24 ¦ 2^г = 0.
63.
269
84. ; 1 -j- log ij = \ogy
t a-2-v+1 —2-2» = —3f/-4v'-^,
85. \ M^y 8.v+/_,
Sfi. Найти все значения а, при которых система
/ = 4,
имеет решения.
87. Найти все знамения а, при которых система
< 2"x-\-(a-\-l)by2 = a-,
{ ^-1)^+^=1
имеет хотя бы одно решение при любом Ь (a, b eR).
88. Определить без таблиц, какое из чисел больше:
а) 0 или log]ogj., 0,5; б) log, 2 пли —.
Решить неравенства (89—108);
89.
91.
90. 4 . 0,5
< 0,25м.
l. 92. log,.2r,(.v-l)<0,5.
93. logA. 7 > log.v 3. 94.
fir>. log, logj (jc-— 4x + 3
Tfi"
97. !og=*3 > 1, a > 0, с
88. ,-^\- < 4, 99. 5 ¦
2a' — 3
1 —x
96.
log:
л: 4-3
x — A
- 10*.
100. 0,8v—l,25A4l>0,25.
10!. 2-3-v'4-9'4A":> 12-*+18.
102. 0,4lg2vJr'iS6,252-Igvl.
103. log3 CX- 1) • log, (Зл|-2 — 9) > 3.
104. 3--v-[-3-v'log23 —Iog26>0. Верно .-я, что lo^;J2 — 1
нерли ir лъа?
1ЙГ>. log2(Ar-l) + lo
10,5. log.,
log,,
107. 4 lo?I6 соз 2лг + 2 log4 sin x+ log2cos x-\-3 > 0.
108. 2 logj (x + 2) — logj (? + 5) < 1.
109. На;"'ти область определения функции
У = v ' log5 лг+ 1оав"^"-лг) - logs (ж - 1).
270
Решить неравенства A10—133):
по. Mi^li^i.
ig(A--l)
111. log2 (x?-4x + 4) + 2x > 2- (x + 1) log?,,e B -a:).
113.
114. log3 * • log3 2x + log3 ж • log2
115. log0l5 (x + 2) • loga (x + 1) + log.v+1 (v + 2) > 0.
116. !ogA. 2 ¦ log2jt 2 . log2 4* > 1.
117. logaj:<61ogjea— 1, a>0, a--?\.
118. log^2 6 + 1оёл+2 6 > log.v_2 6 • log.vh;, 6.
119. 2bh"^x+xl°e'x^3Q.
r20* lo
izu .
121. x^]os^<a^, d>0, c^l.
122. ' л:— 1 }°SA4~'-)>.x_lbs,(\-yx)t
123. logl^ ^—j^fy > 1 • S24. log.M (Jt= -4x)**r. 4.
125. 1—l
126.
127.
128. V log3 (9a:+ 18) ^ log,.,
129. УУо^ + 2УЩ72^
130 IgJlif±?il?hl]ii_
Ig (sin .v + cos .к)
131. jAi_iQg(,*_J/'l+log7I' > с KJ, о > 0,
132*. log,(A- — c)>2, aeJ5.
i^=I 10
1- 1 ^~ О 0 v "
Л 1 О .—х
134. При каких значениях а пераьсиспю
Be])i;o п])н любом действительном х?
135. lhu'iiH все значения a, при которых каждое решение неравенства
log4^BA-2—5х — 3)^1
будет и решением неравенства х2-\-а2х — 2а4eg0.
136. Доказать, что log2 3 — не рациональное число.
137. Определить без таблиц, что большо:
г) log., 60 или log3 30; б) Iog375 или logj П.
138. Доказать, что для всея х~>- 1
139*. Найти среди целых чисел все решения неравенства
2а:+1 <21og2(A:
271
140. Докззать, что для любых а > 0 и Ь > 0 верно неравенство
141. Пусть 0<а<1, ф (х)~ах-\-(\ — а)*. Доказать, чт , если х>1, то
Ф (х) < 1, а если х < 1, то ф (х) > 1.
142. Пусть а>0, ф (х)=A -\-а)х—а*. Доказать, что если х~>\, то
Ф (а:) > 1, а если х < 1, то ф (х) < 1.
143. Пусть 0 < а < 1, а > 0, & > 0. Доказать:
a) aa-fti-<*<a + 6; б) аа ¦ и^~а^аа ¦ A — a)l"a (a+ 6).
144. При каких действительных х к у верно неравенство
V\ogx(n-Vy) + 2 cos (Зл cos Vy) + y\oga_v-i =S 0?
Решить системы A45—146):
B^ = ^ + 4,
I 2*-iSi/
!47. Найти множество точек плоскости, координаты (х; (/) которых удов-
удовлетворяют системе:
з« <*-</> _б • 3-2*—3"!' > 0,
148. Найти среди целых чисел нее решения системы уравнений
1,5у-2 " =1,
{ 2.V — 3^=1.
149. Найти
lira (log^ra • logn («+!)•... • log,lS_i /Is).
п-*со
Глава XI
КОМБИНАТОРИКА. ФОРМУЛА НЬЮТОНА ДЛЯ СТЕП ЕНИ
БИНОМА. СЛУЧАЙНЫЕ СОБЫТИЯ И ИХ ВЕРОЯТНОСТИ
§ 1. Размещения, перестановки, сочетания
1. Примеры простейших комбинаторных задач. Начнел с не-
нескольких примеров, типичных для комбинаторики задач.
Пример 1. В классе 30 учащихся. Сколькими способами
могут быть выбраны комсорг и староста, если каждый учнцийся
может быть избран на одну из этих должностей?
Д Так как по условию задачи каждый учащийся может быть
избран комсоргом, то, очевидно, существует 30 способов выбора
комсорга. Старостой может стать каждый из оставшихся 2Э чело-
человек. Любой из 30 способов выбора комсорга может осущест;*ляться
вместе с любым из 29 способов выбора старосты. Поэтому суще-
существует 30-29=870 способов выбора комсорга и старосты. 4
Пример 2. Для дежурства в классе в течение недели (кроме
воскресенья) выделены 6 учащихся. Сколькими способами можно
установить очередность дежурств, если каждый учащийся дежурит
один раз?
Д В понедельник может дежурить любой из выделенны с шести
человек. Во вторник может дежурить каждый из еще н<: дежу-
дежуривших пяти учащихся. Следовательно, расписание дежурств на
первые два дня недели можно составить 6-5 = 30 способами.
К среде остаются четыре человека, которые еще не дежузили, и
поэтому на среду дежурного можно будет назначить 4 спссобами.
Каждый из этих способов может комбинироваться с любым из
30 способов выбора дежурных на понедельник и вторник. Таким
образом, существует 6'5-4=120 способов установления очеред-
очередности дежурств на первую половину недели. В четверг сможет
дежурить любой из трех еще не дежуривших учащихся, в пят-
пятницу—любой из двух еще не дежуривших. К субботе выбора
не будет, так как останется один человек, который еще не дежурил.
Он и будет дежурным в субботу. Ясно, что число способов, кото-
которыми можно установить очередность дежурств учащихся, равно
6-5-4-3-2- 1 = 720. А
Пример 3. Для проведения экзамена создается komi-ссия из
двух преподавателей. Сколько различных комиссий можнэ соста-
составить из пяти преподавателей?
273
Д Обозначив для удобства преподавателей буквами А, В, С,
D, Е, нетрудно выписать все возможные варианты для состава
комиссии, а именно:
АВ, AC, AD, AE,
ВС, BD, BE,
CD, CE,
DE.
Таким образом, видно, что число различных комиссий ран.но 10. А
Пример 3 удалось решить простым перебором всех возможных
случаев. Конечно, такой метод применим только тогда, когда
число случаев невелико. Если бы в примере 3 речь шла о созда-
создании комиссии не из двух человек, а допустим, из семи, а выби-
выбирать экзаменаторов нужно было бы, например, из четырнадцати
преподавателей, то попытка перебрать все способы окончилась бы,
по всей видимости, неудачей, так как в этом случае можно обра-
образовать 3432 комиссии. Этот результат легко можно будет получить
после того, как будут выведены общие формулы, позволяющие
решать подобные задачи (см. пример 9).
Но прежде чем переходить к выводу этих формул, вернемся
к рассмотренным примерам. Посмотрим, что общего в этих при-
примерах и есть ли какая-либо существенная разница между ними.
Прежде всего отметим, что во всех трех примерах эечь идет
0 некотором конечном множестве элементов и о количестве его
подмножеств, удовлетворяющих некоторым заданным требованиям.
Так, в примере 1 рассматривалось множество всех учащихся
класса, т. е. множество, состоящее из 30 элементов, и требовалось
найти число всех различных подмножеств этого множества, состоя-
состоящих из двух элементов (двух учащихся, избранных комсоргом и
старостой). В примере 2 рассматривалось шестиэлементнее множе-
множество дежурных и определялось число шестиэлементных подмно-
подмножеств этого множества, отличающихся друг от друга только
порядком следования элементов. В примере 3 из пятиэлсментного
множества всех преподавателей выделялись различные двухэле-
двухэлементные подмножества (комиссии) и подсчитывалось их число.
Наряду с отмеченным сходством, при рассмотрении примеров
1 — 3 выявляется одно очень важное различие, существующее между
ними. Оно заключается в том, что в примерах 1—2 и в примере 3
совершенно по-разному понимаются слова «различные подмноже-
подмножества». В примере 3 различными считались подмножества, отли-
отличающиеся друг от друга по крайней мере одним элементом.
Порядок элементов не принимался во внимание. Комиссии, состоя-
состоящая из преподавателей Иванова и Петрова, ничем естественно
ве отличается ^т комиссии, состоящей из Петрова и Иванова.
В примере 1, напротив, подмножества, отличающиеся друг от
друга только порядком элементов, считались различными. Выбор
Иванова комсоргом, Петрова старостой и выбор Петрова комсор-
274
гом, а Иванова старостой—это два различных способа выбора.
В примере 2 различными считались подмножества, если oi и отли-
отличались друг от друга только порядком следования элементов.
Если подмножества, отличающиеся только порядком следова-
следования элементов, считаются различными, то говорят об упорядочен-
упорядоченных подмножествах. В противном случае прилагательное «упоря-
«упорядоченные» опускают. Например, у множества, состоящего из четырех
элементов а, Ь, с, d, имеется, очевидно, 4 трехэлементных под-
подмножества
abc, abd, acd, bed
и 24 трехэлементных упорядоченных подмножества
abc, abd, acd, bed,
acb, adb, adc, bde,
bac, bad, cad, cbd,
bca, bda, cda, cdb,
cab, dab, doc, dbc,
cba, dba, dca, deb.
В комбинаторных задачах всегда необходимо подсчитать число
всех подмножеств данного множества, удовлетворяющих опреде-
определенным условиям, но в одних задачах подмножества, стличаю-
щиеся только установленным в них порядком следования элемен-
элементов, приходится считать различными, в других порядок следования
элементов не важен, и подмножества, отличающиеся тол эко рас-
расположением элементов, не считаются различными.
2. Размещения. Пусть имеется множество, содержащее п эле-
элементов. Каждое его упорядоченное подмножество, состояпее из k
элементов, называется размещением из п элементов по k элементов.
Из определения нытекает, что n^sk^O и что размещения
из п элементов по k элементов — это все А-элементные педмноже-
ства, отличающиеся составом элементов или порядком их следо-
следования. Для множества, состоящего из 4-х элементов а, Ь, с, d,
все размещения по 3 элемента были выписаны в конце предыду-
предыдущего пункта: их оказалось 24, они отличаются друг ст друга
либо составом элементов, либо порядком их расположения,
В комбинаторных задачах необходимо уметь подстывать
число всех размещений из п элементов по k элементов. Для сбо-
значенпя этого числа применяется специальный символ /* (чита-
(читается: «число размещений из п по k» или «Л из п по Ь).
А — первая буква французского слова arrangement, ^то озна-
означает размещение, приведение в порядок. Мы уже видели, что
число размещений из 4 элементов по 3 элемента равно 24, т. е.
А\ — 24. Теперь должно быть ясно,, что в примере 1 тре5овалось
найти число размещений из 30 элементов по 2 элемента, и из
решения этого примера следует, что Л^и=870. Далее, очевидно,
275
что Ап=\, так как существует только одно подмножество «-эле-
«-элементного множества, не содержащее элементов (пустое множества).
В общем случае на вопрос о числе размещений из л. элемен-
элементов по k элементов дает ответ следующая формула:
An = n(n-\)(n-2)...(n-k+l), k>Q, A)
т. е. число размещений из п элементов по k элементов равно произ-
произведению k последовательных натуральных чисел от п до п — k + 1
включительно.
Q Число размещений из п элементов по k элементов равно
числу всех ^-элементных упорядоченных подмножеств множества,
содержащего п элементов. Первый элемент подмножества можно,
очевидно, выбрать п способами, второй элемент подмножества
можно выбрать уже только п—\ способом, так как в качестве
второго элемента можно взять любой элемент множества, кроме
уже выбранного первым. Каждый из способов выбора первого
элемента может объединяться с каждым из способов выбора вто-
второго, и следовательно, существует п(п—\) способов выбора пер-
первых двух элементов при построении /е-элементного упорядочен-
упорядоченного подмножества. После выбора первых двух элементов остаются
я — 2 возможности для выбора третьего элемента, и опять-таки
каждая из этих возможностей может комбинироваться с любой
из возможностей выбора первых двух элементов, т. е. выбор пер-
первых трех элементов может быть осуществлен п(п— \){п — 2) спо-
способами. Последний k-Vi элемент й-элементного подмножества может
быть выбран п — k-\-\ способом, так как к моменту выбора &-го
элемента осталось n — (k—\) элементов. Щ
Формулу A) удобно записывать в другом виде. Будем для
краткости произведение п (п— 1) (п — 2)... 3- 2- 1, т. е. произве-
произведение всех натуральных чисел от п до единицы, обозначать сим-
символом п\ (читается «эн факториал»). Используя знак факториала,
можно, например, записать:
11 = 1,
21 = 2-1 = 2,
3! =3-2-1=6,
4!=4-3-2-1=24,
5! = 5-4-3-2-1 = 120.
Умножим и разделим произведение, стоящее в правой части фор-
формулы A), на (п — k)\ Тогда получим
Лк_ п(п-\)(п-2)... [п-к+Щп-к)\
Ап~ (^=6I "
или
276
Формула A) была получена в предположении, что k^-О, фор-
формулой B) можно пользоваться и при k = 0, так как она \ в этом
частном случае дает правильный результат, а именно
При выводе формулы A) предполагалось также, что п=?0, т. е.
что данное множество имеет хотя Гы один элемент. Ес/н м = 0,
то это означает, что рассматривается пустое множество, а так
как пустое множество имеет только одно подмножество (само-
себя), то Л2=1. Если условиться, что 0! = 1, то формула B)
будет давать верный результат и в случае /г = 0. В самом деле
Л 1
Пример 4. Вычислить
Д Используя формулу B), получаем
20! 20!
,4-Ляо 14! + 15! 16! , 16!
Л'о ' Ш_ ~ 14! ^ 151
16!
= 16-15+16 =16-16 = 256. А
Пример 5. В седьмом классе изучается 14 предметов. Сколь-
Сколькими способами можно составить расписание занятий на субботу,
если в этот день недели должно быть 5 различных уроков?
Д Различных способов составления расписания, очевидно,
столько, сколько существует пятиэлементных упорядоченных под-
подмножеств у четырнадцатиэлементного множества.
Следовательно, число способов равно числу размещений из
14 элементов по 5, т. е. равно А\ц_. По формуле A), полагая
в ней л =14, ? = 5, находим
А]х = 14 • 13 • 12 • 11 • 10 = 240 240. а
3. Перестановки. Размещения из п элементов по п элементов
называются перестановками из п элементов.
Перестановки яеляются частным случаем размещений. Так как
каждая перестановка содержит все п элементов множества, то
различные перестановки отличаются друг от друга только поряд-
порядком элементов. Число перестановок из п элементов обозначают
через Рп. Р — первая буква французского слова permutation —
перестановка. Теперь ясно, что в примере 2 требовалось найти
число всех перестановок из 6 элементов (число всех возможных
перестановок дежурных класса). Это число оказалось равным 7zO.
Следовательно, Рй =720.
277
В общем случае число перестановок из п элементов Рп = А",
и следовательно, его можно найти по формуле A) или по форму-
формуле B), положив в каждой из них k = n.
Действительно, формула B) дает
fn-An— {п_пу - 0! -«¦',
из формулы A) находим
Р„ = А'п = п (п - 1) (п - 2)... (л - п + 1) = л!.
Итак, число перестановок из п элементов равно п\
Таким образом в множестве, содержащем п элементов, устано-
установить определенный порядок следования элементов или, как говорят,
упорядочить такое множество можно п\ способами.
Например, ашсок учеников класса, в котором 20 человек
и нет однофамильцев, можно составить
20! = 2 432 902 008 176 640 000 способами.
Пример 6. Сколько шестизначных чисел, кратных пяти,
можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что в числе
цифры не повторяются.
[\ Для того чтобы число, составленное из заданных цифр,
делилось на 5, необходимо и достаточно, чтобы цифра 5 стояла
на последнем месте. Остальные пять цифр могут стоять на остав-
оставшихся пяти местах в любом порядке. Следовательно, искомое
число шестизначных чисел, кратных пяти, равно числу переста-
перестановок из пяти элементов, т. е. 5! =5 ¦ 4-3 • 2-1 = 120. А
Пример 7. Найти п, если
/\ Применяя формулу для числа перестановок и формулу B)
для числа размещений, перепишем данное уравнение следующим
образом:
(я + БI 94П (я+ 3I
(n — k)\ ~~ (/1 + 3 —й-3)Г
Полученное уравнение равносильно квадратному уравнению
(и+ 5) (я+ 4) = 240.
Его корни п=11 и п — —20. При п = —20 и левая, и правая
части уравнения не имеют смысла. При м=11 для любого k
такого, что 0^^sg;ll, справедливо равенство-р-^— = 24ОЛi^3.
Итак, « = 11. А
Пример 8. Сколько различных перестановок можно образо-
образовать из букв слова «задача»?
278
Д Образовать какую-либо перестановку из букв слона «зада-
«задача»—это значит на шесть занумерованных мест каким-нибудь
образом поставить одну букву «з», одну букву «ц», одну букву «ч»
и три буквы «а». Если буквы «з», «д» и «ч» как-то поставлены,
то остальные места заполняются буквами «а». Но сколькими спо-
способами можно поставить три различные буквы на шесть мест?
Очевидно, что число способов равно числу всех трехэлементных
упорядоченных подмножеств шестиэлементного множестза, т. е.
равно А\ = 6-5- 4 = 120.
Можно рассуждать и иначе. Если бы все шесть букв слова
были различны, то число перестановок было бы равьо 6!. Но
буква «а» встречается в данном слове три раза, и перестановки
только этих трех букв «а» не дают новых способов расположения
букв. Поэтому число перестановок букв слова «задача» будет
не 6!, а в 3! раз меньше, т. е.
6! 6 • 5 ¦ 4 ¦ 3 • 2 ¦ 1 а с. л юл *
"зГ = зПП = 6-5-4=120. А
4. Сочетания. Пусть имеется множество, состоящее нз п эле-
элементов. Каждое его подмножество, содержащее k элементов,
называется сочетанием из п элементов по к элементов.
Таким образом, сочетания из п элементов по k элементов — это все
fe-элементные подмножества «-элементного множества, причем
различными подмножествами считаются только те, которые имеют
неодинаковый состав элементов. Подмножества, отличающиеся
друг от друга только порядком следования элементов, не считаются
различными. Например, для четырехэлементного множества а, Ь,
с, d сочетаниями по 3 элемента являются следующие подмюжества:
abc, abd, acd, bed.
Число всех сочетаний из п элементов по k элементен обозна-
обозначается символом С* (читается: «число сочетаний из п по Ь или
«це из п по Ь). С —первая буква фрунцузского слова combina-
sion — сочетание. Мы только что видели, что С| = 4. В гримере 3
было найдено число сочетаний из 5 элементов по 2 элемента,
причем оказалось, что С" = 10.
В общем случае число сочетаний из п элементов по I' элемен-
элементов определяется следующей формулой:
C C)
Ь"~ (n-k)lkl " . { >
? Сначала образуем все возможные неупорядоченные подмно-
подмножества, содержащие k элементов. Их число равно Скп. Затем из
каждого полученного подмножества перестановкой его элементов
получим все упорядоченные подмножества, которых будет, очевидно,
в k\ раз больше, так как каждое fe-элементное множество можно
упорядочить k\ способами. Итак, Aka = k\Ckn, откуда и следует
формула C). Щ
279
Формулу C) можно записать в другом, более удобном для
вычислений виде. Сократив числитель и знаменатель дроби на
(п — k)\, получим
l2
т. е. число сочетаний из п элементов no k элементов равно про-
произведению всех натуральных чисел от п до п — k -\-1 включительно,
деленному на kl.
Пример 9. Сколько экзаменационных комиссий, состоящих
из 7 членов, можно образовать из 14 преподавателей?
Д Очевидно столько, сколько существует семиэлиментных
подмножеств у четырнадцатиэлементного множества. По формуле D)
находим
П1 14-13-12-1Ы0-9-8 14-13-12-1Ы0-9-8
U= 71 = 7.6.5.4-3-2.1
Пример 10. В чемпионате страны по футболу (высшая лига)
участвуют 18 команд, причем каждые две команды встречаются
между собой 2 раза. Сколько матчей играется в течение сезон?.?
Д В первом круге состоится столько матчей, сколько суще-
существует двухэлементных подмножеств у множества, содержащего
18 элементов, т. е. их число равно С18. По формуле D) получаем
/-,2 18 • 17
Cis==—j
Во втором круге играется столько же матчей, поэтому в тече-
течение сезона состоится 306 встреч, а
Пример 11. Решить неравенство
Д Левая часть неравенства имеет смысл тогда и только тогда,
когда л; —целое число, принадлежащее отрезку [1; 11]. Правпя
часть имеет смысл в том и только в том случае, когда х — цел^е
число и х е [0; 10]. Следовательно, решениями неравенства могут
быть только целые значения х, лежащие на отрезке [1; 10].
Используя формулу C), данное неравенство запишем следую-
следующим образом:
101 9 101
(х~ 1I A0—*+1)! ^ *1A0—*)| •
Разделив обе части неравенства на ... ,.0_ -., , получим
11 —JK — X '
откуда #>22 — 2х, т. е. ^>22/3. Учитывая ограничения
и хе[1; 10], получаем множество решений данного неравенства:
{8; 9; 10}. а
280
Числа С„ обладают многими интересными и важными свойст-
свойствами, Остановимся на двух свойствах, которые часто используются.
Первое свойство: Ckn = Cnn~k.
Ц Применяя формулу C), получаем
pn—k н\ п\ pk man
" ~ (n — (n — k))l(n—k)T~~ k\(n—k)\ —^"- Ш
Пользуясь этим свойством, можно упрощать вычисление чисел С„
в тех случаях, когда k~>n/2, например
1 r 1А \'\
L.1K —Ыд —
Второе свойство:
C^i=C*+4c? (k<n). E)
Q Опять используем формулу C):
1-l | pkп\|п!
U "Г
(n—ky.kl
n\ I n — k . k + \\ _
(n+l)l
§ 2. Формула Ньютона
Хорошо известные формулы
(а + Ь)* = а3 + За2й -f 3ab2 +
можно записать так:
(а + ЬK = Qq3 +
Возникает естественная гипотеза: не будут ли справедливы
аналогичные формулы для четвертой, пятой и вообще лю€ой нату-
натуральной степени двучлена (бинома)?
Выясним сначала, будет ли справедлива аналогичная формула
для четвертой степени. Для этого обе части формулы длу (a-\-b)z
умножим на а-\-Ь. Тогда получим
(а + bf = (Qaa + Qa2b + C\ab2 + Qb3
= Qa* + QcPb + Qa2b2 + Q
- Qa* + (Q + Cl) a?b + (Cl -f Q) a2b2 + (C\ + CJ) аи3
281
Учитывая, что
Q = C\, Q + Q = Q,
убеждаемся в справедливости формулы
{а + Ь)* = Qa* + С[а% + Qa2b2 + Qab* + Qb*.
Таким образом, нам удалось, используя формулу дл?: третьей
степени бинома, получить аналогичную формулу для четвертой
степени. Проведенное рассуждение, во-первых, подтверждает гипо-
гипотезу и, во-вторых, наталкивает на мысль воспользоваться для ее
доказательства методом математической индукции.
Теорема. Для произвольных чисел а и b и произвольного
натурального числа п справедлива формула
A)
Используя знак суммы, формулу Ньютона можно записать
короче:
n-kbk. B)
Для л=1 формула Ньютона имеет вид
и, так как С? = С1=1, она, очевидно, верна.
Предположим, что формула справедлива для п ¦¦— т, т. е.
k=0
Тогда
k=0
|] b"+ |] С*
к~!
«Clam +1
Учитывая, что
CO pQ pk , pk—\ pk ptn pm-\-\
m — ^т-И) "ЯТ1 iil ^ ^ji
p
получаем
m+t
/л i »,\m+1 V1
(а-г о) = 2j
282
Таким образом, из справедливости формулы A) для п — т следует
ее справедливость для п — т-\-\, и, так как формула вер; у и при
п—1, то на основании принципа математической индупшп ее
справедливость установлена для всех натуральных значен;и п. Щ
Формула A) носнт имя великого английского физика и мате-
математика И. Ньютона. Правая часть ее называется разлсжением
натуральной степени бинома. Коэффициенты Chn называются бино-
биномиальными коэффициентами.
Отметим некоторые характерные особенности формулы Ньютона.
а) Правая часть формулы Ньютона содержит п-\-\ слагаемых.
б) Каждое слагаемое имеет вид С*а"~*Ь*.
Слагаемое Cknan~bbk, стоящее на А+1-м месте, удобно считать
/г-м членом разложения и обозначать через Tk, т. е.
При этом условии То = С"пап — нулевой член разложения, 7\=
= С1па"~гЬ — первый член разложения, Тп = С„Ьп — я-й ч/ен раз-
разложения.
в) Показатели степени при а в каждом следующем члене раз-
разложения на единицу меньше, чем в предыдущем, показатели
степени при Ь — на единицу больше. Сумма показателей степени
при а и b в каждом члене разложения равна п.
г) Коэффициенты разложения, одинаково удаленные от нулевого
и от я-го члена разложения, равны, так как Ckn~Cn~k.
Пример 1. Возвести в шестую степень двучлен
Д Положив в формуле B) а = х2, b = —y, n = 6, полечим
= x2 - 6xwy + I5xgy2 - 20xeyz + 15*Y - 6x2y5 + if. a
Пример 2. Найти четвертый член разложения степени
бинома [Ух +)
\
\ Vх I
Д Положив в формуле C) я = 9, /е = 4, а~\/~х, Ь--=1/^/'х,
получим
/1
I
Пример 3. Найти член разложения степени бинома
i не зависящий от х.
283
Д Положив в формуле C) и =12, о=1/Х b — Ух, получим
Тк = Cb A/*)I2~* (Ki)* = C'hx~U ' * \
Для того чтобы член разложения не зависел от х, необходимо
и достаточно, чтобы—1^+9 <'<: = 0, откуда k = S.
Итак, восьмой член разложения не зависит от х. Вычислим его:
т8 = Ci-2 = с и = 4321—
Пример 4. Найти сумму всех биномиальных коэффициентов
L, п —р U л -р Lj -р . . . -р О/[.
Д Положив в формуле B) а = 1, /? = i, будем иметь
Таким образом,
Смысл последнего равенства заключается в следующем. Так
к Си — это число всех подмноже
содержащих k элементов, то сумма
как Си — это число всех подмножеств n-элементного множества,
дает, очевидно, число всех подмножеств «-элементного множе-
множества. Следовательно, число ссех подмножеств множества, содер-
содержащего п элементов, равно 2п.
П р и ы е р 5. Для освещения зала может быть включена каж-
каждая из имеющихся 10 ламп. Сколько существует различных спо-
способов освещения зала?
Д Очевидно столько, сколько существует подмножеств у де-
сятиэлементного множества, т. е. 210 = 1024. При этом учитыва-
учитывается и тот способ «освещения», при котором ни одна лампа не
горит. А
Пример 6. Найти наибольший коэффициент многочлена
/ 1 , - ''10
U + з х) •
Д Обозначим коэффициент многочлена при хк через ak.
Используя формулу B), расположим данный многочлен по воз-
возрастающим степеням переменной х:
HJ 10
ъ
() () х =
к = (J k — О
Лля отыскания наибольшего коэффициента а,, решим неравенство
alt i^ak, т. е.
Разделив обе части неравенства на 2''~1/310, получим
откуда
10! „ 2-Ю!
После дальнейших очевидных сокращений будем иметь
1/A0-*+1)<2/Л:, k === 20 -2/е + 2, ?=^22/3.
Туким образом, доказано, что
Очевидно, что при /г > 22/3 имеет место противоположное нера-
неравенство Aц-\~> а,,, т. е. коэффициенты многочлена, начиная
с седьмого, убывают.
Итак, коэффициент а7 является наибольшим среди всех один-
одиннадцати коэффициентов данного многочлена. Наибольший коэф-
коэффициент равен
±Y7?_y. a
1 3 / \ 3 /
При доказательстве формулы Ньютона не предполагалось, что
а и b —действительные числа. Поэтому формулы A) —C) спра-
справедливы и в том случае, когда а и b — произвольные комплекс-
комплексные числа.
Пример 7. Записать комплексное число B + j')e в алгебраи-
алгебраической форме.
Д Полагая в формуле B) я = 6, а = 2, b = i, получше
I!
4 = 0
= С\2* + С\ 25i + Cl 2'' I' + Cl 23 ia + Cl 21 i" + Cl2i* + Ct i[ =
= 64+1921-240-I6O1 + 6O+12*-1=— 117H-44i. A
§ 3. Случайные события и их вероятности
Рассмотрим простой опыт, заключающийся в подбрасывании
монеты. Этот опыт имеет два исхода: либо монета упадет так,
что сверху окажется герб, либо она ляжет гербом вниз. Гот или
иной исход опыта зависит от многих причин, которые не под-
поддаются учету, и заранее предсказать результат опыта нельзя.
Событие, состоящее в том, что «выпал герб», является примером
285
глЬчайнс-го события. Другими примерами случайных событий
fiioryr служить: «появление единицы» при бросании игральной
гости (кубика из однородного материала с гранями, занумеро-
занумерованными цифрами от единицы до шести), выход из строя электро-
электролампы до определенного срока, несоответствие стандарту выбран-
выбранного для контроля изделия. Во всех этих случаях невозможно
предсказать заранее, до окончания опыта, произойдет или не
произойдет соответствующее событие. Поэтому такие события п
Называют случайными.
В опыта с подбрасыванием монеты оба исхода очевидно рав-
равноправны, до опыта нет никаких оснований предпочитать одна
исход другому. В таких случаях говорят, что оба исхода равно-
равновероятны, а вероятность каждого из них равна 1/2. При подбра-
подбрасывании игральной кости имеется шесть исходов. Так как кость
предполагается однородной и симметричной, то все исходы опыта
одинаково возможны пли равновероятны. Вероятность каждого
исхода равна 1/6.
Обобщением этих простых опытов будет опыт, в котором воз-
возможны п равновероятных исходов: «ь и2, ..., и„ (их назывгют
также элементарными событиями). В эгом случгс вероятность
каждого исхода принимается равной \/п. Записывают это сле-
следующим образом:
Р («j) = 1/л, Р («г) = 1/я, ..., Р (н„) = 1/л.
Первая из этих формул читается так: «вероятность U\ равна 1/«»
(Р — первая буква английского слова «probability»— вероятность).
Рассмотрим теперь опыт с п равновероятными исходами и
некоторое событие Л, которое происходит тогда, когда опыт
оканчивается какими-то k исходами, и не происходит hi том слу-
случае, если имеет место один из остальных п — k исходов. Будем
говорить, что исходы, приводящие к событию Л, благоприятст-
благоприятствуют ему. Вероятностью события Л, связанного с опытом с п
равновероятными исходами, называется отношенье числа исхо-
исходов, благоприятствующих событию А, к числу есс-х исходов, т. е.
P(--I)-*. (О
где k — число исходов, благоприятствующих событию /.
Попейим сказанное примерами. Олыт с игральной костью
имеет шесть равновероятных исходов.: щ — выпала грамь с номе-
номером i (г'=1, 2, 3, 4, 5, 6). Рассмотрим следующие события, свя-
связанные с этим опытом:
событие Аг — число выпавших очков кратно 3,
событие А2 — выпало прсспе чг.сло,
событие Ля —выпало 7 очков,
событие Лд —число Еыпавцтих очкоз меньше 7.
Событию .4i благоприятствуют два исхода н3 и и с,. Положив
в формуле A) п = 6, ft = 2, находим Р(Л1) = 2/б-= 1/3.
286
Событию Л2 благоприятствуют три исхода м2, и3, иъ- Но фор-
формуле A) получаем Р(Л2) = 3/6 = 1/2.
Событию А3 не благоприятствует ни один из возможны): нехо-
неходов. Следовательно, Р (Л3) = 0/6 = 0. Событие Л3 являетсл при-
примером невозможного события.
Событию А4 благоприятствуют все шесть исходов, поэтому
Р(Л4) = 6/6=1. Событие Л4 —пример достоверного события.
Вероятность любого события А удовлетворяет неравенствам
что непосредственно следует из формулы A), так как очевидно,
что O^k^n.
Для вычисления вероятностей событий по формуле A) прихо-
приходится находить число всех равновозможных исходов и число
исходов, благоприятствующих случайному событию. Здесь часто
оказываются полезными комбинаторные формулы, рассмотренные
в § 1.
Пример 1. Опыт заключается в подбрасывании двух монет:
медной и серебряной. Какова вероятность того, что хотя бы на
одной монете появится герб?
Д Равновероятными исходами опыта являются следующие:
iii — герб появился на обеих монетах,
ы2 — герб Еыпал только на медной монете,
и3 — герб выпал только на серебряной монете,
«4 —герб не выпал ни на одной монете.
Благоприятствуют ссбытию А (появлению герба хо:я бы на
одной монете) исходы «ь щ и и3. Полагая в формуле A) п = 4,
k = 3, получаем Р(Л) = 3/4. А
Пример 2. Набирая номер телефона, абонент забьл две
последние цифры и, помня лишь, что эти цифры различны, мабрал
их наудачу. Какова вероятность того, что номер набран пра-
правильно?
Д Две последние цифры можно набрать числом способов,
равным числу упорядоченных двухэлементных подмножеств у десяти-
элементного множества (множества всех цифр). Это число способов
равно А\{). Следовательно, всего существует А\й исходов. Благо-
Благоприятствует событию А (цифры набраны верно) только один исход.
Поэтому
Р(Л)=1/Л;0= 1/10-9= 1/90. А
Пример 3. Среди 100 электроламп 5 испорченных. Какова
вероятность того, что выбранные наудачу 3 лампы окгжутся
исправными?
Д У множества, содержащего 100 элементов, существует С\м
трехэлементных подмножеств. Поэтому 3 лампы из 100 можно
выбрать Cf00 способами. Лампы выбираются наудачу. Это означает,
что все эти способы выбора (все исходы) равновероятны.
287
Число благоприятных исходов (все три лампы оказались ис-
исправными) подсчитывается аналогично. Из 95 исправных ламп
3 лампы можно выбрать С3т способами, так как именно столько
существует трехэлементных подмножеств у 95-ти элементного мно-
множества. Полагая в формуле A) n = Ciw, k = Cl%, получаем
Р (А) = СУ CU = ?ы9ю% **
ЗАДАЧИ РАЗДЕЛА I
1. На пять сотрудников выделены три путеаки. Сколькими способами их
можно распределить, если: а) все путевки различны, б) все путевки одинаковы?
2. Сколькими способами можно расположить в ряд 5 белых и 4 черных
шара так, чтобы черные шары не лежали рядом? Рассмотреть два случая: а)
шары одного цвета не отличимы друг от друга, б) все шары разные.
8. Сколько диагоналей имеет выпуклый п-угольник?
4. На первой из двух параллельных прямых лежит 10 точек, на вто-
второй—20. Сколько существует треугольников с вершинами в этих точках?
5. Четыре автора должны написать книгу из 17 глав, причем первый и
третий должны написать по 5 глав, второй —4, а четвертый 3 главы книги.
Сколькими способами можно распределить главы между авторами'1
6. Известно, что крокодил имеет не более 68 зубов, Доказать, чго среди !617
крокодилов может не оказаться двух крокодилов с одним и тем же набором
зубов.
7. Сколько различных десятизначных чисел можно написать, используя
цифры 1 и 2?
8. Буквы азбуки Морзе представляют собой набор «точек» и «тире». Сколько
букв может быть в азбуке Морзе, если буква не должна содержать более
четырех знаков.
9. Автомобильные номера состоят из трех букв (всего используется 30 букв)
и четырех цифр (используются все 10 цифр). Сколько автомобилей можно
занумеровать таким образом, чтобы никакие два автомобиля не имели одина-
одинакового номера?
10. Сколькими способами In элементов можно разбить на пары, если раз-
биемия, отличающиеся только порядком элементов внутри пар и порядком
расположения пар, считаются одинаковыми?
11. Найти средний член разложения
12. При каких значениях х пятый член разложения Bх + 3)9 будет большэ
соседних с ним членов?
13. Найти члены разложения (^3 + ^2)", являющиеся целыми числами,
14. Найти коэффициент многочлена A +3x-f-2x3I0 при х4.
15. Найти сумму коэффициентов многочлена A3-t3 — 7х — 5I00.
п
16. Вычислить 2 Cj/r
288
17. Из десяти билетов выигрышными являются два. Определить вероятность
того, что среди наудачу взятых пяти билетов: а) один выигрышный, 5) оба
выигрышных.
18. В лифт 8-этажного дома на первом этаже вошли 5 человек. Предпо-
Предположим, что каждый из них независимо друг от друга и с равной вероятностью
может выйти на любом из этая:ей, начиная со второго. Найтн верояти.ост > того,
что все пятеро выйдут на разных этажах.
ЗАДАЧИ РАЗДЕЛА II
1. Вычислить:
a) Л. (Cj + CJ); б)
2. Найтн п, если:
а) С«+'-С«н.з=15(я + 2); б) J_ = 2, + J_:
в) 5С?=С* + 2; г) *
д)ед-5С23п +
, Ап
4 J^_.
)!<4Р' '
3. Найти множество знамений функции:
а) /(х) = И7^; 6)/W = C^+-,8.
4. В классе 30 учащихся. Сколькими способами можно выделит! двух
человек для дежурства, если: а) один из них должен быть старшим; б| стар-
старшего быть не Должно?
5. Сколько различных двузначных чисел можно образовать из цифр 1, 2,
3, 4 при условии, что в каждом числе нет одинаковых цифр?
6. Сколько различных двузначных чисел можно образовать из циф) 1, 2,
3, 4?
7. Никакие три диагонали выпуклого десятиугольника не Пересе ?а:отся
в одной точке. Определить число точек пересечения диагоналей.
8. Сколькими способами на шахматной доске можно расставить i: ладей
одного цвета, чтобы они не били друг друга и стояли только на герных
клетках?
9. Из цифр 0, 1, 2, 3 составлены всевозможные четырехзначные чис,ia так,
что в каждом числе нет одинаковых цифр. Сколько получилось чисел? Сколько
среди них четных чисел?
10. В розыгрыше первенства по футболу было сыграно 153 матча. Каждые
две команды встречались между собой один раз. Сколько команд участвовало
в розыгрыше первенства?
11. Во взводе 3 сержанта н 30 солдат. Сколькими способами можна выде-
выделить одного сержанта и трех солдат для патрулирования?
12. Сколькими способами можно составить расписание занятий н; по4едель-
ник, если в этот день должно быть пять занятий: по алгебре; геометрии, илории,
географии и литературе, причем алгебра и геометрия не должны следовать
непосредственно друг за другом?
10 п/рэд. Г. Н. Яковлева : , 289
13. Сколько различных перестановок можно образовать из букз следующих
слов: а) зебра, б) баран, в) водород, г) абракадябра?
14. Сколькими способами можно раздать 28 костей домино четырем игрокам
так, чтобы каждый получил 7 костей?
15. Хоккейная команда состоит из 2 вратарей, 7 защитников и 10 напа-
нападающих. Сколькими способами тренер может образовать стартовуо шестерку,
состоящую из вратаря, двух защитников и трех нападающих?
16. Сколько существует шестизначных чисел, все цифры которых нечетны
A, 3, 5, 7, 9)?
17. На конференции должны выступить докладчики А, В, С и D, причем В
не может выступать раньше А. Сколькими способами можно установить очеред-
очередность выступлений?
18. Сколько делителей имеет число 462?
19. На полке стоят т книг в черных переплетах и п книг н синих пере-
переплетах, причем все книги разные. Сколькими способами можно расставить книги
так, чтобы книги в черных переплетах стояли рядом?
20. Сколькими способами можно упаковать 9 разных книг в 5 бандеролей,
если 4 бандероли должны содержать по 2 книги?
21. Сколькими способами 12 одинаковых монет можно разложить по пяти
различным кошелькам так, чтобы ни один кошглек не остался пустым?
22. Сейф запирается на замок, состоящий из пяти дисков, н,ч каждом из
которых изображены цифры 0, 1, 2 9. Замок открывается, если на дисках
набрана одна определенная комбинация цифр. Хватит ли 10 дней на открытие
сейфа, если «рабочий день» продолжается 13 часов, а на набор одной комби-
комбинации цифр уходит 5 секунд?
23. Среди всех целых чисел от 1 до Ю4 каких больше: тех, для записи
которых используется цифра 9, или тех, которые записываются без нес?
24. Написать формулу Ньютона для степени бинома:
a) (-v+1O; б
25. Используя формулу Ньютона, вычислить:
a) (VA-VZf; б) (Vf+l)*+(Vi-i)*;
26. Нанти:
а) седьмой член разложения (у а—\/ ЬI3.
б) член разложения (allijra~ili) 8, не зависящий от а;
в) член разложения (Уа+Уа2I8, содержащий а:8',
г) член разложения (А6+1I9ао, содержащий хп'60.
27. Найти члены разложения, являющиеся целыми числами:
а) (Vz + y'if' б) (К'б-У^)8.
28. Сколько членов разложения (l^3-f-{/бI24 являются целыми числами?
29. Найти наибольший коэффициент многочлена:
')[{-+TXJ- б)(Г5 + |/2,Г.
30. Найти коэффициент многочлена;
б) A+*4— а:3)8 при а:8;
б) A +А-Ч--*8O ПРИ *'"•
290
31. Найти сумму коЭ'Ъфпциентов многочлена:
а) D*-5)Я; б) /зУ2\
32. Доказать равенства:
а) ftC*=nC*z;:
б) С' -'1С\-уЪС\- ... +(- l)"-inc»=0;
в) С\ + 2С2+ЗС,3+ ¦¦¦ -!-nC;j = n2"-';
33. Из урны, в которой находятся 3 белых, 4 черных, 5 крагных шароп,
наудачу вынимается один. Какова вероятность того, что вынутый шар окажется:
а) белым, б) черным, в) желтым, г) красным?
34. Бросаются две игральные кости. Какова вероятность того, чт> сумма
очков, выпавших на двух костях, окажется равной 8?
35. Куб, все грани которого окрашены, распилен на 64 кубика одш акового
размера. Полученные кубики тщательно перемешаны. Какова вероятность того,
что среди наудачу выбранных двух кубиков оба имеют ровно по две о сращен-
сращенные грани?
33. Работа каждого из четыре* учеников заочной школы может проверяться
одним из семи преподавателем'!. Какова вероятность того, что все четыре работы
проверены разными преподавателями?
37. Экзаменационная программа содержит 40 попросои. На экзамене пред-
предлагается ответить на два из них. Ученик подготовил ответы на 30 вопросов.
Какова вероятность того, что па экзамене ему предложат дпа вопроса, ia кото-
которые он подготовил ответ?
33. В лотерее па 50 билетов 8 выигрышных. Какова вероятность того, что
среди первых пяти наугад выбргнных билетов два будут выигрышным! ?
39. Первенство но баскетболу разыгрывают 18 команд, среди соторых
2 команды экстракласса. Для уменьшения общего числа игр команды путем
жеребьевки разбиваются на две равные группы. Какоза вероятность того что два
команды экстракласса окажутся: а) в разных подгруппах; б) v. одной по;грунпе?
40. Доказать, что вероятность того, что у двенадцати случайно пыпрзниых
человек дни рождения приходятся на разные месяцы, меньше 1/10000.
Глава XII
ИНТЕГРАЛ
§ 1. Первообразная и неопределенный интеграл
Во многих задачах приходится по заданной функции находить
новую функцию, производная которой в каждой точке равна зна-
значению данной функции в этой точке. В качестве примера можно
привести задачу о нахождении закона движения s(t) материаль-
материальной точки по заданному закону изменения ее скорости v (t).
В этом примере задана функция v(t), le]a; b[, и требуется
найти функцию s (t) такую, что s' (t) = v (t) для любого t e ]a; Ъ[.
Определение. Функция F(x), х е ]а; Ь[, называется пер-
первообразной для функции f(x), ,«ё]й; Ь[, если F'(x)=f(x) для
каждого х е ]а; Ь[.
Для функции )(х) = 2>х2; jceR, первообразной является функ-
функция F(x)=x^, так как (х3)'= 3х2 для любого xef!. Легко видеть,
что функция F (х) = л:3 + 2 также является первообразной для
функции / (х) = Зх'\ так как (л;3 + 2)' = Зх2 для любого j:eR.
Очевидно, что и в общем случае, если F (х) есть г ервообраз-
ная для функции f (x), то при любой постоянной С функция
F(x)-{-C также является первообразной для функции f(x). Дей-
Действительно,
для любого х из рассматриваемого интервала.
Таким образом, если функция имеет хотя бы одну первооб-
первообразную, то она имеет бесконечное множество первообразных.
Справедлива следующая теорема.
Если функция F (х) есть первообразная для функции f(x), то
любая первообразная для функции f (х) имеет вид F [х)-\-С, где
С —некоторая постоянная, т. е. множество \F (x)J-C \C e R}
является'множеством всех первообразных для функции f(x).
Из этой теоремы следует, что при любом С функция F (х) =
= х3 + С является первообразной для функции f(x) = 2>x2 и дру-
других первообразных эта функция не имеет.
Пример 1. Для функции /(х) = cosx + sinx найти перво-
первообразную F (х), удовлетворяющую условию /7@)= 1.
Д Одной из первообразных для функции / (х) — cos x + sinx
является функция sin x — cosx. Из теоремы следует, что любая
292
первообразная для данной функции имеет вид F (х) ¦-- sin x — :оз х-\-
+ С, где С —некоторая постоянная. Для определения постэяниай
С воспользуемся условием /7@)=1. Из него находим
sinO-cos
т. е. С = 1 4-cos0-— 2. Следовательно, функция F{x)—unx —
— cos x -\- 2 является искомой первообразной, а
Для нахождения первообразных справедливы следующие три
правила.
1. Если функция F (х) является первообразной для функции
f(x), а функция G(х) является первообразной для функции g(x),
то финкция F(x)-\-G(x) является первообразной для функции
f(x) + g(x).
Ц Действительно, производная от суммы функций равна сумме
производных, т. е.
(F (х) + G (л-))' = F' (х) + G' (х) = / (x)+g(x),
а это и означает, что функция F(x)-f-G(х) является первообраз-
первообразной для функции f(x)-\-g(x). Щ
2. Если функция F (х) является первообразной для функции
f{x), то функция kF (х) является первообразной для функции kf (x),
Q Действительно,
т. е. функция kF (х) является первообразной для kf(x), Q|
3. Если функция F (х) является первообразной для функции
f (x)j то функция F (у (t)) является первообразной для функции
f(y(t))y'(t)- (При этом предполагаем, что функции f(y{t)), у' (t)
и F (у (/)) определены.)
Это правило сразу же следует из правила дифференцирования
сложной функции.
В частном случае, если y(t) = atJrb, a=/=0, и если F (х\ явля-
является первообразной для функции f (х), то функция - F'at-{-b)
является первообразной для функции f(at-\-b).
Пример 2. Найти все первообразные для функция
Д Функция f (х) равна сумме двух функций. Найдем перво-
первообразную для функции Зе2дс+1. Так как первообразной для функ-
функции ех является функция ех, то первообразной для функции е2дг+1,
по правилу 3 будет функция --^+1, По правилу 2 первэобраз-
1 3
ной для функции Зе2л+1 будет функция 3- ~ е2х г, т. е. ^ е2хН-
293
Так как
то по
Найдем теперь первообразную для функции \/cos2(nx/4). Та
функция tgx является первообразной для функции l/cos2*, то по
правилу 3 функция — tg~ является первообразной для функции
l/cos2(nx/4). По правилу 1 функция ^ e2jf+1 + ~^ tg^p является
первообразной для функции f(x). Любая первообразная для функ-
функции f (х) задается формулой
где С —произвольная постоянная, д
Пример 3. Найти функцию F(x), если известно, что
F' (x) = e*inx cosx и F(n/2) = e-{-3.
Д Требуется из всех первообразных для функции esin*cosje
выделить ту, которая при л; = л/2 принимает значение е-\-3. Так
как производная от sin л: равна cos л; и так как первообразная
от ех равна ех, то по правилу 3 первообразной для e&inxzosx
является функция esin *. Действительно,
(gsin ху = gsln х (Sin ху _ gsin * cos x_
Любая первообразная для функции esin*cosx имеет вид esinx +
-\-С, где С—произвольная постоянная. Определим С из условия,
что F (л/2) = е -f- 3. Из него находим
eSinu/2)_|_c==e + 3, т. е. С = 3.
Следовательно, искомая функция имеет вид eslnJt + «^ A
Определение. Множество всех первообразных для функ-
функции f (х), х е \а; Ь[, называется неопределенным интегралом от
функции f (x) и обозначается
\f(x)dx.
Это обозначение читается: «неопределенный интеграл от функ-
функции / (х) по dxi>, или короче «интеграл от / (х) по dxi>.
Из вышесказанного следует, что если F (х) является первооб-
первообразной для функции / (х), то
R}. A)
На практике формула A) записывается более кратко:
\ B)
Функция f (x) называется подынтегральной функцией, выраже-
выражение f (x) dx называется подынтегральным выражением, а постоян-
постоянная С называется постоянной интегрирования.
294
Пример 4. Найти ^
Д Чтобы кайти неопределенный интеграл от cor; >: по dx,
достаточно найти какую-то первообразную для функции соях,
т. е. найти функцию F (х) такую, что F' (х) — cos.v. Из таблицы
производных следует, что такой функцией будет sin.v. Следова-
Следовательно,
^ cos х dx — sin х~\- С. А
Нахождение функции по ее производной назын^етсп иьтари-
иьтарированием функции. Интегрирование —действие, обратное диффе-
дифференцированию. Правильность интегрирования проверяется диффе-
дифференцированием. Из свойства дифференцирования легко получаются
следующие два свойства для неопределенных интегралов:
\ (/ (х) +ё(х)) dx =¦• \ I (х) dx + [ а (х) dx, C)
\kf(x)dx=k\f (x) dx, k ф 0. A)
Формула C) означает, что каждая первообразная фрикции
f(x)-\-g(x) является суммой некоторых первообразных для f (х) и
g(x) и, наоборот, сумма любых первообразных для f (х) и g(x)
является первообразной для f(x) + g(x). Так что из формулы C)
следует, что если F (х) — первообразная для функции f(x), a G(x) —
первообразная для g'(x), то
\ (/ (х) + g (х)) dx = F (х) А- С, (х) -|- С,
где С —произвольная постоянная. Коротко формула C) читается
так: «интеграл от суммы функции равен сумме интегралов от этих
функций».
Формула D) означает, «тс каждая первообразная для функ-
функции kf(x), где кфО, есть произведение постоянной k и некото-
некоторой первообразной для функции f (х) и что любое такое произве-
произведение есть первообразная для функции kf(x).
Из формулы D) следует, что если F (х) есть первообразная
для / (х) и k^=0, то
где С —произвольная постоянная.
Зчметим, что формула D) перестает быть верной в случае
k = 0. Действительно, в этом случае левая часть есть
где С —произвольная постоянная, а правая часть есть
0-У (х) dx ¦-= 0.
Используя таблицу производных, составляем таблицу неоп-
неопределенных интегралов.
2.
3. J -x dx =\n\x\-!-С.
В частности, jj еА' dx = e-v + С.
5. jj cos x dx = sin x + С
6. ^ sin x cfx = —
Формулы 2, 3, 7, 8 справедливы для тех интегралэв, где оп-
определены подынтегральные функции.
Докажем, например, формулу 3.
Q Подынтегральная функция определена для всех х
Если х > 0, то j х | = х и
Если же х < 0, то | х | = — х и
(ln|*|)' = (in (-*))'=
Следовательно,
Aп|х|)' = 1/«
для любого х ^= 0, н поэтому
для х>0 и для х<0. Щ|
Пример 5. Найти jj (x2 -]- 2ел) <ix.
Д Согласно формулам C) и D)
\ (х2 + 2еА') dx = J ^2 d-^ "I- 2 \ eX dx-
Интегралы, стоящие в правой части этого равенства, являются
табличными:
f х2 dx = ^- хя -1- С, С e-v й'х = e-v + С.
296
Следовательно, функция -^х3-\-2ех является первообразной для
функции хг-\-1ех, и поэтому
(х2 + 2еЛ') fix = — л:3 + 2ev -f С,
где С — произвольная постоянная, а
Пример 6. Найти [—~dx.
3-.v2
| —*---C. A
Пример 7. Найти ^s'maxdx.
Д у s\v?xdx = \ -j ах =
(* 1 , С cos 2х , 1 1 . „ , „
= V -^dx— \ —— dx = — х — 4-sin 2x ,LC. A
Лля нахождения интегралов от функций вида sin mx cos /u,
sin mx sin па; и cosmxccs/u удобно использовать следующие три-
тригонометрические формулы:
2 sin mx cos nx = sin (m — /i) x + sin (пг + п) x, E)
2 sin mx s in nx = cos (m — n) x — cos (in Jr /г) х, F)
2 cos mx cos nx = cos (m — /г) я 4- cos (m -\- /?) x. G)
Пример 8. Нгйти ^ sin x cos 3xdx.
Д По формуле E) имеем
sinxcos3x = g- (sin 4л; — sin 2x).
Поэтому
\ sin x cos3.it; d.v = „ » sin4j;djf — 0- \ si
Легко видеть, что для функции sin 4л: функция — ;,-cos4x явля-
является первообразной. Аналогично функция —х- cos 2x является
первообразной лля sin 2x. Следователь;ю,
l sin х cos Зх dx = ? (— 4" cos ^х) ~ 2Г (~~ COS
= -^- cos 2,r — -g cos 4д; ¦ f- С. А
Для вычисления неопределенных интегралов часто быв зет по-
полезна формула интегрирования по частям.
207
Пусть функции и(х) и v(x) имеют производные иг (х) и vf (х).
Тогда имеет место следующая формула, носящая название фор-
формулы интегрирования по частям:
^uv' dx = uv — \ u'v dx. (8)
Зта формула является следствием формулы производной от
произведения двух функций: (uv)' = u'v + uv'. Действительно,
$ (uv)' dx — $ u'v dx -\- $ uv' dx,
и поэтому
Jj uv' dx = uv — \ u'v dx.
Заметим, что здесь произвольная постоянная не пишется, так как
она содержится в написанных интегралах.
Пример 9. Найти \x<>mxdx.
Д Так как sin л: является производной от — cosx, то
^ х sin х dx = J x (— cos л')' dx.
Применяя формулу (8), получаем
$ х (— cos x)' dx = x (— cos x) — jj (— cos x) x' dx =
= — x cos x-|- $ cos xdx = — -v cos x-\-s\nx-{-C. A
Пример 10. Найти ^Inxdx.
Д Для нахождения интеграла воспользуемся формулой (8).
Для этого положим и = \пх и у' = 1. Тогда у==д: и и' = ]/д;, и
поэтому
Ппxdx = x\nx — ^ dx = x\nx — x-\-C. a
§ 2. Интеграл и формула Ньютона — Лейбница
Определение. Пусть задана функция f(x), определенная на
некотором интервале X, и пусть F (х), хевХ, некоторая перво-
первообразная функции f(x). Тогда число F(b)—F(а), где аеХи
6еХ, называется интегралом от а до b от функции f (x) и
обозначается
6
Таким образом, согласно определению, если F' (x)—f(x), то
d^ = FF)-F(a). A)
Функция / называется подынтегральной функцией, переменная
х называется переменной интегрирования, отрезок с концами о и
Ъ называется отрезком интегрирования, число Ъ называется верх-
верхним пределом интегрирования, число а — нижним пределом интег-
интегрирования.
Равенство A) нссит название формулы Ньютона — Лейбница.
Для удобства записи разность F (Ь) — F (а) обозначают F {х) |ь.
Пользуясь этим обозначением, формулу Ньютона — Лейбпща за-
записывают в виде
Заметим, что интеграл от а до Ь от функции f (х) не зависит
от выбора первообразной для функции [ (х). Действительно, если
Ф (х) — некоторая первообразная для [ (х), отличная от г (х), то
существует постоянная С такая, что Ф (х) = F (x) -f- С для любого
х из рассматриваемого интервала, и поэтому Ф(/;)~ф(а)= Fib) —
Пример 1. Вычислить ^2xdx.
[
Д Так как B-v/ln 2)' = Iх, то функция F (х) = 2х/\п 2 язляется
первообразной для функции f(x)=--2x, и поэтому но формуле
Ньютона — Лейбница получаем
s
2xdx=
In 2
— /92 — 91 —
In 9 V" ^ """ In 9"
Сформулируем некоторые свойства интегралов. При этом
будем предполагать, что все рассматриваемые интегралы су-
существуют.
Свойство 1.
b be
\ (/(х) +g(x))dx=\f (x)dx+\g(x)dx. B)
а а а
Свойство 2.
Ь b
\kf(x)dx=k\f(x)dx. C)
а а
2
Пример 2. Вычислить § (х + 3cosx)dx.
1
Д Воспользовавшись свойствами 1 и 2, получаем
2 2 2
(х -\- 3 cos х) dx = \ х dx + 3 jj cos x dx =
l 1
+ 3in2 —3sin 1 =|- + 3 sin 2-3sin 1. a
299
Свойство 3,
Ь с Ь
\f(x)dx=\f(x)dx + \f(x)dx, D)
a (i с
Свойства 1, 2, 3 легко доказываются, если воспользоваться
определением интеграла, Докажем, например, свойство 3.
D Пусть функция F (х) — некоторая первообразная функции
/ (х) на некотором интервале, который содержит точки a, b и с,
Тогд-]
J\f(x)dx+\f(x)dx. Ш
с а
Свойство 4. Пусть функции f (х) и ц>(t) такие, что опре-
определена и непрерывна сложная функция f (cp (t)). Тогда, если функ-
функция ф@ имеет производную ц>'(t), справедлива формула
\f(<p(t))v'(t)dt = lf(x)dx, E)
а а
где а = ф(а) и Ь = ф(Р).
D Пусть F (х) — первообразная функции f(x). Тогда, как легко
видеть, функция F (ц> (t)) является первообразной для функции
/ (ф(/))ф' (t). Поэтому
0 Ь
\ f (Ф @) Ф' @ dt = F (Ф (Р)) - F (Ф (a)) = F(b)-F(a) = \f (x) dx. Щ
а а
Формула E) называется формулой замены переменной интегри-
интегрирования. Она сводит вычисление интеграла от одной функции
к вычислению интеграла от другой функции, который в каком-то
смысле проще, Формула E) применяется как слева направо, так
и справа налево.
ь
Пусть задан интеграл \ff(x)dx. При замене х на t по формуле
а
x = cp(t) нужно вместо х подставить ф@. вместо dx подставить
ф' (t)dt, а новые пределы интегрирования а и р найти изуслозий
Ф(а)=а, ф(р) = Ь, Тогда
\ \{t)L'[t)dt. E')
Пример 3. Вычислить $ ]/а2 — х2 dx, а > 0.
о
300
Д Перейдем к новой переменной интегрирования /, положив
x = asint, где *е[0; л/2]. Когда t изменяется от 0 до --, то х
изменяется от 0 до а. В этом примере / (*) = ]/о2 — х2. Подставив
x = as'mt, получим
/ (a sin t) = У a2 —a2 sin21 = a )Л — sin2* = a cos /.
Вместо dx подставляем (a sin t)' dt = a cost dt.
По формуле E) получаем
а л/2 ат/2
-x2dx= $ a cos * ¦ a cos * = а2 \ cos* tdt.
~ , , 1 + cos It
л ак как cos2 i = ——¦- , то
я/2 л/2 л/2
j COS ¦ - 2" 3 + 2 ) cosz =
о и и
2 , ¦ й'2 . о, Л/2 ЗХЙ2
4 ' А
Пусть задан интеграл ])/(ф(*))ф'(*)d*. При замене * на /у по
формуле у—<р{х) нужно вместо ф(*) подставить у, вместо р' (*) dx
подстав[ггь dy, а за ноЕые пределы интегрирования взят3 числа
Л = ф(а), В = фF). Тогда
'(*)А«=5/D/)^. E")
Л/2
Пример 4. Вычислить \ sin2xcosxdx.
о
Д Данный интеграл можно вычислить непосредственно по
определению, найдя предварительно одну нз первообразных для
подынтегральной функции. Однако его проще вычислить, нос поль-
пользовавшись формулой замены переменной интегрированы л. Дей-
Действительно, перейдем к новой переменной интегрировании, поло-
положив y=sinx. Под знаком интеграла вместо sin2* подстлвим у2.
Так как производная от sin* равна cos*, то вместо cos*d*
подставим dy. Новые пределы интегрирования находим нз усло-
условий Л = sin 0 = 0 и ? = sin (л/2)= 1. По формуле E") получаем
я/2 I
[ sin2xcosxdx= [у2dy = ~^y^0 = -^. ^
и и
501
При вычислении интегралов часто используют формулу интегри-
интегрирования но частям:
ь ь
jj uv' d* = uv I* — ^ ti'v dx,
a a
которая, как и для неопределенного интеграла, является непо-
непосредственным следствием формулы для производной произведения
функций.
2
Пример 5. Вычислить ij xex dx.
о
Д Воспользуемся формулой интегрирования по частям. Для
этого положим и = х и v' = ex. Тогда и'—А н v=ex-\-C, где С —
произвольная постоянная. Для простоты будем считать, что С = О,
т. е. за функцию v возьмем функцию ех. Теперь по формуле
интегрирования по частям получаем
2 2
jj xex dx = хех |5 — ^ ех dx = 2е2 ~ ех ;5 — 2ег — е2 + 1 — е'г -Г 1 ¦ А
о о
Свойство 5. Если f(x)-s:.g(x) для любого х<=[а; Ь\, то
ь ь
\f(x)dx<_\g(x)dx. F)
а а
? Пусть F (х) — первообразная функции / (х), a G (х) — перво-
первообразная функции g(x) такие, что F (а) = G (а) = 0, тогда
F(x) = \f(t)dt, G(x) = \e(t)dt.
а а
Напомним, что эти первообразные называются интегралами
с переменным верхним пределом.
Рассмотрим функцию ([>(x) — G(x) — F(x). Эта функция неубы-
неубывающая и ср (а) = 0. Действительно, ф' (х) = G' (х) — F' (х) = g (x) —
— /(хMг0 для любого xei[a; b\ и ф {a) = G (a) — F(a)~-0. Следо-
Следовательно, ф (b) = G (Ь) — F(Ь) 5&0, т. е. G (b)l^F(b), что и требо-
требовалось доказать. Щ
Следствие. Ес^гы m и М — наименьшее и наибольшее значе-
значения функции f (х) на отрезке [а; Ь\, то
x^M{b-a). G)
а
Г] Действительно, так как m^f (х) ^ М, то в силу свойства 5
справедливо неравенство
ь ь ь
\ т dx < \f{x)dx^\M dx,
302
из которого и получается неравенство G), если учесть, что
b Ь
S)mdx = m(b — a), jj M dx = M (b — а). Щ
а а
Пример 6. Используя формулу G), оценить значение интег-
интеграла
Д Наименьшее значение функции е~хг на отрезке [0; 1] равно
г1, а наибольшее значение равно 1. И поэтому
i
е-1 =sc $ е- *' dx ^ 1. ^
§ 3. Площадь криволинейной трапеции
Пусть задана неотрицательная непрерывная функция /(х),
х е [а; Ь]. Множество точек плоскости, координаты ьоторых
удовлетворяют неравенствам а<х<й, 0 <//</(*), называется
криволинейной трапецией.
Криволинейная трапеция аАВЬ ограничена графиком функции
f (х), отрезками прямых х = а и х = Ь и отрезком оси Ох (рис. 134).
Выведем формулу для вычисления пло-
площади S этой криволинейной трапеции.
Разобьем отрезок [а; Ь] точками
Ъ — а
A = 0, 1, 2,..., п)
на п равных по длине отрезков [jtj_i; Xj]
(i=\, 2,..., /г). На каждом отрезке
\Xi-u xt], как на основании, построим два Рис. 134.
прямоугольника высоты т; и Mit где пц и
Mi — наименьшее и наибольшее значения функции f (х) на отрезке
[xi-il xi]. Площади этих прямоугольников соответственно равны
/н,Ах,- и MiAxj, где Ах; = xi — xi-\.
Через sn обозначим сумму площадей всех прямоугольников
высоты nil, т. е.
sn =
тп Ддся.
Аналогично через Sn — сумму площадей всех прямоугольников
ьысоты Mi, т. е.
Sn = 2 Mi Ах,- = М1Ах1 + ... + Ма Ахп.
Зоз
Очевидно, что 5Й<5<5„. Можно показать, что при га->-оо
s,, и Sn стремятся к одному и тому же пределу — к площади криво-
криволинейной трапеции аАВЬ.
В силу неравенства G) § 2 получаем п неравенств
где
А 7
i =
а к
- 1 2
как
. , п. Следовательно,
i= I
п *i
¦ s s.
/¦ (л) ^ =
ft
TO
Отсюда в пределе при n-vco следует равенство
ь
S = \f{x)dx. A)
а
Заметим, что для любого ?,• е [x,-_i; лг,-] выполняется неравен-
неравенство m,^f{ti)^Mi, и поэтому
V т, Ах,- < I] / &) A.vj < J] Л1, Ал>
Отсюда в пределе при гс-э-оо получаем формулу
lim Yinii)'^i = S=\i(x)dx.
я-оо ,- = 1 о
Пример 1. Показать, что для прямоугольного треугольника
справедлива формула A).
д Пусть задан прямоугольный треугольник с катетами длины
а и Ь. На плоскости введем систему координат так, как указан.;
на рис. 135. Данный треугольник является частным случаем
криволинейной трапеции, причем f(x) = ~x, ^e[0; а].
Отрезок [0; а] точками X; = — i (i = 0, I, 2, ..., л) разделим
304
/
на п отрезков длины а/л. Тогда т, = ^ (/— 1), &Л-,— п /, и по-
поэтому
_ "V А//- п а - аЬ i
Отсюда видно, что
hmsn= lim \ = -,-.
/l-»co n -»co
Таким образом доказано, что площадь данного треугэльника
равна -^ab, т.е. вычисляется
по известной формуле. А
о
Рис. 135.
Рис. 136.
/ e
Рис. 137.
Пример 2. Найти площадь фигуры, ограниченной частью
параболы у = х2 и отрезками прямых у = 0 и х = 2 (рис. 136).
Д Используя формулу A), имеем
2
8
5 = \ х2 dx = -s- =
J 3 |o
3 "
Пример З. Найти площадь фигуры, ограниченной линиями
у = х, ij—1/x, у = 0 и х = е.
Д Данную фигуру прямой х—1 разобьем на две части (рис.
137): криволинейную трапецию, соответствующую функщи у=^х
на отрезке [0; 1], и криволинейную трапецию, соответствующую
функции г/= \/х на отрезке [1; е]. Через 5i и 5.2 обозначим их
площади. Тогда
= lne=.l,
м, следовательно, 5 =
= у + 1 = 1, 5. А
Рассмотрим фигуру, ограниченную отрезками прямых х — а и
х = Ь (а <С Ь) и графиками неотрицательных и непрерынных на
305
\a\ b] функций /i (x) и /2 (х), причем fi(x)^f2(x) (рис. 138).
Площадь данной фигуры равна разности площадей двух криво-
криволинейных трапеций аАВЬ и аА'В'Ь, т. е.
= ](fi(x)-fi(x))dx. B)
а
В общем случае справедливо следу-
следующее утверждение.
Площадь S фигуры, координаты то-
точек которой удовлетворяют ьеравенст-
fi(x) и [2(х)~ заданные
/¦ .t;
Рис. 138.
вам a^xs^b, fi(x)
непрерывные функции, вычисляется по формуле
ь
C)
Ц Действительно, пусть т — наименьшее значение функции Д (л')
на отрезке [а; Ь]. Тогда f2(x) — mssf1(x) — m~^Q для любого
х <s [а; Ь]. Фигура, координаты которой
удовлетворяют неравенствам
получается из данной параллельным пере-
переносом вдоль оси Оу. Следовательно, их
площади равны, и поэтому (см. формулу B))
ь
S = \ (}г (х) -чп - h (х) + т) их =
а
Ъ
Пример 4, Найти площадь фигуры, ограниченной линиями
у = х2-4л; + 5 и у = х+\ (рис. 139).
Д Найдем абсциссы точек пересечения графиков функций
у = х-\-\ и у = х2— Ах + 5, для этого решим уравнение х-\-1 =
= х2 — 4х-\-5, Из квадратного уравнения х2 — 5дс + 4 = 0 находим
Х\ — 1 и х2 = 4. Искомую площадь находим по формуле C):
4 4
5 = J (х -Y 1 - (jc2 - Ах -Y 5)) d* = J (— л2 + 5* - 4) dx =
¦(¦
/ *3 ] &
I 3 * 2
= -1F4-1)+-|A6-1)-4 D-1) =-21+ 37,5-12 = 4,5. А
306
Если требуется вычислить площадь более сложной фиг/ры, то
стараются сз разбить на несколько фигур, для вычисления пло-
площади каждой из которых можно применить одну из формул A) —
-C).
Пример 5. На рис. 140 изображена фигура, ограниченная
линиями у=—х2-\-Бх — 5, у — — хг-\-Ах — 3 и у = 3х— 15. Найти
площадь этой фигуры.
Д Точки А, в, D являются точками пересечения данных
парабол с осью Ох. Найдем абсциссы ьтих точек, гсля этогс решим
дза уравнения — х2-\-6х — 5 = 0 и
— х*-\-4х — 3 = 0. Корнями первого
уравнения являются числа х=\ и
л: = 5, а корнями второго уравнения
являются числа х=\ и ж = 3. Следо-
Следовательно лсл=1| %д = 5, Хд = 3. Для
определения абсциссы точки С решим
уравнение — х2 + Ах — 3 = Зх — 15,
Решая квадратное уравнение х" —
— х— 12 = 0, находим, что Xi —-- — 3,
#., = 4, т. е. #с = 4. Разобьем данную
фигуру отрезками [DB] и [?CJ на
три фигуры и обозначим их площади
соответственно Sb S2, S3, как ука-
указано на рис. 140. Рис. 140.
Вычислим площадь 5Ь Для этого
из площади криволинейной трапеции,
ограниченной графиком функции </ = — х--\-6х — 5 и отрезком
[1; о\ оси Ох, вычтем площадь криволинейной трапеции, ограни-
ограниченной графиком функции « = — х2-\-4х — 3 и отрезком [1; 3]
оси Ох, т. е.
I
- 5) dx - \ (— х1 -\- 4х - 3) dx =
28
"'
Для вычисления площадей S2 и 53 применим формулу C):
-3)dx = (\x3-2;
Таким образом, S —
+ S:, = 73/6.
307
§ 4. Применение интеграла к вычислению объемов тел
1. Объем пирамиды. Сначала рассмотрим треугольную пира-
пирамиду ABCD, у которой ребро AD перпендикулярно плоскости ABC,
и выразим объем V этой пирамиды через высоту H = \AD\ и
площадь основания S, считая известным, что объем прямой призмы
равен произведению площади основания на высоту.
з
Рис, 141.
Рис, 142,
Отрезок DA точками NU, М2, ..., М„-г разобьем на п равных
по длине отрезков и через каждую точку Mt проведем плоскость,
параллельную основанию ABC (рис. 141). Тогда пирамида разо-
разобьется на п частей: одну пирамиду и и—1 усеченных пирамид.
Очевидно, объем пирамиды ABCD не меньше объема vn ступенча-
ступенчатой пирамиды, вписанной в ABCD (рис. 142), и не больше объема Vn
ступенчатой пирамиды, описанной около ABCD (рис. 143):
V ^ Vn,
A)
И
причем, Vn — vn = S—.
Пусть S (х) — площадь сечения пирамиды ABCD плоскостью,
проходящей параллельно основанию ABC на расстоянии х от
вершины D, и пусть хо = 0, xt = \DMi\, xn = \DA\ = H. Тогда
S (xi) — плошадь сечения, проходящего через точку Mh и
1=1
где Ах,- =Xi — xt~i ==Ii/n. Так как функция S (х), х
растающая, то
xi
8(хм)Ахг^ \ S(x)dx^S(x,)Axi
; /Л, воз-
воздля любого i=l, 2 п, и поэтому
S(x)dx<-_Vn.
308
Из A) и B) следует, что
V -
dx
н
n
при п-^оэ. Таким образом, справедлива формула
V = $ S (х) dx.
C)
Известно, что S (x)/S =х2/Н2. Учитывая это соотношение, :з фор-
формулы C) получаем
н
X2 г, , S Л3
V — \ -jp S dx — -д.2 3
Я _ 1
Таким образом, объем пирамиды вычисляется по формуле
V = ~SH, D)
где S — площадь основания, а Я —высота пирамиды.
Формула D) выведена для специального вида треугольных
пирамид. Легко доказать, что она справедлива для любой пира-
пирамиды.
2. Объем тела вращения. Пусть задана криволинейная трапе-
трапеция, ограниченная графиком неотрицательной функции i = f(x),
х €Е [а; Ь], осью абсцисс и прямыми х — а
и х = Ь (рис. 144). При вращении этой
криволинейной трапеции вокруг оси Ох
образуется геометрическое тело Ф
(рис. 144). Это геометрическое тело на-
называется телом вращения.
Выведем формулу для объема тела
вращения Ф. При этом, для простоты,
будем предполагать, что функция / (.v)
неубывающая. Пусть S (х) — площадь се-
сечения тела Ф плоскостью, проходящей
через точку с абсциссой х параллельно
плоскости Oyz. Очевидно, что любое такое
сечение тела Ф является кругом или
точкой и S (х) = я/2 (х). Отрезок [а; Ь] точками Х[ = а-\ I, где
?=0, 1 ..., п, разобъем на п равных по длине отрезков н через
каждую точку разбиения проведем плоскость, перпендикулярную
оси абсцисс. Тогда тело Ф разобьется на п тел вращения Фь
Фа, ¦¦-, Ф/1, сумма объемов которых равна объему тела &.
Рис. 144,
309
Очевидно, объем тела Ф, не меньше объема цилиндра, у кото-
которого высота равна Дх* = х,; —X;_i и радиус основания ранен //,_] =
= /(xj-i), и не больше объема цилиндра с высотой Дх* и радиусом
основания yi = f(xi) (рис. 145). Следовательно, объем V тела Ф
удовлетворяет неравенствам
V
E)
где ия =
*< — объем ступенчатого тела вращения, вписан-
ного в тело Ф, а 1/„ = ^] л//; Дл;,- —объем ступенчатого тела вра-
1
I
i
о
щения, описанного около Ф. Причем,
Vn — vn = n (у;,. — г/о) • —- ->• О
при /г-»-со. Из монотонности функ-
ции / (х) и свойств интеграла следу-
следуют неравенства
ny'i _ 1 Дх; sg ^ я/2 (дс) их sr;. nt/f Дд-,-,
Рис. 145.
где t = l, 2 п. Суммируя по i, из этих неравенств получаем
ь
vn =s= I я/2 (х) dx <: Vn- F)
а
Теперь из E) и F) следует, что
ь
V - я \ /2 (х) dx
при n—>-oc, и поэтому
V = n]f*(x)dx.
G)
Учитывая, что я/2 U) = S (д), формулу G) для объема тела вра-
вращения можно записать в виде интеграла от площади S (х) его
поперечного сеченпя:
ь
V = J S (*) dx, (8)
Пусть геометрическое тело Ф заключено между плоскостями
х = а и х = Ь и пусть 5 (х) — площадь сечения тела Ф плоскостью,
перпендикулярной оси Qx и проходящей через точку с абсциссой
310
x e [a; b]. Тогда, как и в случае тел вращения, объем V тела Ф
вычисляется по формуле (8).
Пример 1. Криволинейная трапеция, ограниченная графиком
функции y = sinx, ле[A; я], и осью абсцисс, вращается вокруг
оси Ох. Найти объем образованного вращением тела.
Д Применяя формулу G), получим
V =
Заменим sin2 а' на —=-тг—, тогдз
V
С 1—cos2.t , /лх
= я ^ 2 dx = [Т
4 sm 2xj
2 '
Пример 2. Найти объем тела, отсекаемого от цилиндра
х2-\-у2 = \ (рис. 146) плоскостью г == 2х.
Д Рассмотрим сечение этого тела плоскостями, перпендику-
перпендикулярными оси Ох. Сечение, проходящее через точку с абсциссой
х е ]0; 2[ перпендикулярно оси Ох, является прямоугольником.
Обозначим площадь такого прямоугольника через S (х). Вычис-
Вычислим S(x) для хе]0; 2[. Сторона прямо-
прямоугольника \АВ\, лежащая в основании ци-
цилиндра, равна
| = 21/|ОЛ|2-|О?|2==
Сторона прямоугольника | AD j равна отрез-
отрезку \EF\ и равна 2х. Следовательно, площадь
прямоугольника ABCD равна
S (х) = 2х 1/4-х2.
По формуле (8) объем тела равен
2
V = l\2xV4-x2dx.
Рис. 146
Сделаем замену переменного под знаком интеграла, положим
у = 4 — х2. Тогда по формуле E") § 2 получаем
V = J -1/4 - х2 (—2х) dK = — \ Vd dij =
16
3 '
§ 5. Применение интеграла при решении физических задач
1. Задача о вычислении пути. Пусть материальная точка дви-
движется прямолинейно с некоторой скоростью v = v(t), зависящей
от времени t. Требуется найти путь, который проходит точка за
промежуток времени от t—Ti до t = T2. Если скорость движения
постоянна и равна v0, то путь S равен произведению скорости
на время движения, т. е. S =--vo(T2 — 7\).
Если же скорость не п<.стоянка, то
S=\v(t)dt. A)
г,
Ц Действительно, разобьем отрезок [Ти Т2] на п равных по
длине отрезков, при этом tn = Tlt ^- = 7'i-|—- -i, где/ = 1,2...
..., п. Приближенно будем считать, что скорость v (t) на проме-
промежутке [//-3; г'/j постоянна и равна v (т,), где т, — некоторая точка,
принадлежащая отрезку \thl; /,]. Тогда путь, пройденный точкой
за время от /,_i до /,-, приближенно равен произведению
v (т,) (ti — ti-i) = v (т;) А/,-, и путь, пройденный течкой за промежуток
п
времени [7^; Г2], равен приближенно ^] v (т,) At-t. Путь S, про:1!-
дениый точкой за время от 7\ до Th равен пределу этой суммы
при и->со, т. е. интегралу A). Щ
Пример 1. Тело движется прямолинейно со скоростью у(^) =
= 3-|-3/2 м/с. Найти путь, пройденный телом за первые 5 с.
Д По формуле A) находим
= 140. А
Пример 2. Тело движется прямолинейно со скоростью v(t)~
^ + бГ2м/с. Найти путь, пройденный телом за третью секунду.
Д По формуле A) находим
2. Работа переменной силы. Пусть материальная точка дви-
движется по оси Ох под действием силы Р. Если сила Р постоянна
и / — проекция этой силы на ось Ох, то произведение f-(b-a)
называется работой силы на отрезке пути [а; Ь].
Выведем формулу для подсчета работы А силы Р в случае,
когда сила не является постоянной.
312
Пусть / (л;) — проекция силы Р на ось Ох. Пока» ем, что
работа А силы Р на отрезке пути [а; Ь] вычисляется по формуле
A = \f{x)dx. B)
а
Ц Будем предполагать, что / (х) является непрерывной функ-
функцией на отрезке [а; Ь\. Отрезок [а; Ь] точками
b^i (i = 0, 1, 2, .... я)
разобьем на п рапных по длине отрезков [x,_t; xt]. Очевьдно, что
длина каждого из этих отрезков равна Axt = (b — а)/п. и еремится
к нулю при л-^оо. Поэтому можно считать, что работа силы Р
на отрезке пути [jc,-_i; л;,-] приближен-
приближенно равна / (Xi) Ax,, а вся работа на
отрезке [а; 6] равна сумме
;) Дх,-,
которая является интегральной сум-
суммой функции / (х) на отрезке [а; Ь].
Тогда в пределе при п-+оо получаем
формулу B). Ц
Заметим, что формулу B) иногда
удобно записывать в другой форме, а
шленно
А = \{Р, e)dx,
Рис. 147.
где е — единичный вектор оси Ох, а (Р, е) — скалярное произве-
произведение векторов Р и е.
Пример 3. Сила в 2Н растягивает пружину на 4cv. Какую
работу надо произвести, чтобы растянуть пружину на 4 см?
Д По закону Гука F = kx, т. е. сила, растягивающая пру-
пружину на величину х, пропорциональна этому растяжению. Из
условия 2 = & • 0,04 находим коэффициент растяжения k: он равен 50.
По формуле B)
0,04
5ad 25ajg-w = 0,04. A
Пример 4. Вода, подаваемая с плоскости основания в кони-
конический бак через отверстие в дне, заполняет весь бак. Определить
затраченную при этом работу, если высота бака равна h, радиус
нижнего основания (дна) равен г, а радиус верхнего основания
равен R, R>r.
Д Рассмотрим сечекие конического бака, проходящее через
его ось. И выберем оси координат в этом сечении так, к;ж пока-
показано на рис. 147. Разобьем отрезок [0; /i] оси Ох точкши л^=
313
~-'^i на п равных по длине отрезков [а-,-.,, хг] (i = l, 2, ,.., п).
Образующая конуса в Еыбранной системе координг.т имеет
уравнение у = г -\- х —у-¦ Следовательно, объем 1-го слоя Vt при-
приближенно равен ny]Axi, а его потенциальная энергия прибли-
приближенно равна npgyfXjAxi, где р—плотность воды, a g — ускоре-
ускорение свободного падс-пия. Отсюда следует, что
A--- Urn y^npgtfiXiAxi,
т. е.
А =•= npg *\ у-х dx.
Очевидно, что потенциальная энер[ня равна искомой работе.
Таким образом,
ь.
4- л; —:— dx.
Вычислиа этот интеграл, получим
ЗАДАЧИ РАЗДЕЛА I
1. Найти все первообразные для следующих функцпл:
а) / (а:) = *5; б) / (х) = -^ sin C* + I);
В) / {Х) =
2, Найти все первообразные для функции f(x) = \x\.
3, HaiiTii для функции f(x)=x2 первообралную, график которой прохо-
проходит через точку М B; 3).
4. Для функции / (х) = [-2'-:х мантн первообразную F (х), удозл.:тво-
ряюасую условию F A) = 3.
5. Найти следующие неопределенные интегралы:
У1'3 ' V1'5
а) \ (P + W)dt; б) ) —-~
(' С I
в) \ sin 2х cos 4х dx; г) \ (№х -|r г
1 1
Jr - г _.
41
6. Применяя формулу нктсм¦piipoLanrii по частям, нлкти следующие не-
неопределенные интегралы:
а) \' х cos х dx; б) ^х\п к dx.
314
7. Доказать, что функция
( 1,
= 0, * = 0,
1-1, х<0
ие имеет на всей оси ни одной первообразной.
8. Вычислить следующие интегралы:
1 я A3
а) ^ х3 dx; б) | sin x dx;
И — 31/4
9 3
1
2 я/2
д) ((Зг1 + 4)'/3 х2 dx; е) ^ х sin
1 о
1
ж)
1 -2
S. Начти производный следующих функций:
а) Ф (х) = W2 sin tdt\ б) Ф(х)= \' 2; cos (sin 0 dt.
О 2х
10. В каком отношении делится площадь квадрата параболой, nf входящей
через две его соседние вершины и касающейся его стороны в ее середине?
11. Найти площадь фигуры, ограниченной линиями у = \х2 — ' \ и у =
= 5 + 1 ж j.
12. Найти площадь фигуры, ограниченно."! линиями 2j/ = *2j-x — 6 и
2i/ = — л2 + 3х + 6.
13. Доказать, что если функция f (х), хе[—а; а], где а > 0, четная, то
а а
\ f(x)dx=2 \f(x)dx.
— а о
14. Доказать, что если функция f (x), x e R, периодическая с периодом
Т>0, ю
а+Т Г
U /(.*r)d.t=\V(Jc)rfjc
а 6
ДЛЯ ЛЮбОГО « SE IR.
15. Найти объем тела, обраяовгппого врг.щенмем фигуры, ограниченной
линиями х((/ + 2) = 4, х= 1 и у=^(), вокруг оси Оу.
16. Найти объем тела, образованного вращением фигуры, ограниченной
2 .
0;
линиями 1/= — х и i/=sin«, ж ее
вокруг оси
17. С како"! силой однород1!и i стержень 0-^x^1 линейной шотности S
притягивает материальную точку Р {а} (а > /) массы т?
18. Однородное тело в форме прямого кругового цилиндра высоты Л и
с радиусом основания /? вращются вокруг своей оси с постоянной угловой
скоростью ы. Найти кинетическую энергию тела, если плотность материала,
из которого изготоилено тело, равна р,
315
-ЗАДАЧИ РАЗДЕЛА II
1. Нант вел первообразные для следующих функций:
я» / (Л) = <я#н + i- cos -^ - 3
3in 2
2. Найти для функции /{.':) первообразную, график которой проходит
через заданную точку:
а) /(*)=-!=-+sin Bх+1), М{1; 1);
Ух
3. Для функции / (х')= 2cosЗл:—3sin4x найти первообразную F(x), удовлет-
удовлетворяющую условию /7(я/2) = 1.
4. Найти функцию / (х), если известно, чго /' (х) = 5езх и /@)==4.
5. Найти все первообразные для функции f(x) = Bx — 3) | х — 2 j в проме-
промежутке ]— 3; 1[ и в промежутке ]1; 3[.
6. При каких значениях х обращается в нуль та из первообразных функ-
функции / (х) = я sin ях-]-2х —4, которая при х=1 имеет значение 3?
7. Пусть функция F (х) является первообразной для некоторой периодиче-
cko'i функции /(х). Является ли периодической функция F (х)?
8. Пусть функция F (х) является первообразной для некоторой четной функ-
функции / (х), х s R. Является ли нечетной функция F (.v)?
0. Пусть функция F (х) является первообразной для некоторой нечетной
функции I (х), х s R. Является ли четной функция F (v)?
10. Найти следующие неопределенные интегралы:
а) ^ (х2-|-2 sin 3x--f-e2x) dx;
С С л3 -1- *> V~~k -!- v l^x
б) \ sin 6/ cos tdt; в) \ ' ^ " /-_| ' f— dx;
e) \ Ix-lldx; ж) \ f"
1 H-cosx
11. Применяя формулу интегрирования по частям, найти следующие
неопределенные интегралы:
а) \ х sin х dx ; б) ^ х2 cos x dx;
в) $ (х2 + 1) ех dx; г) J x • 21* dx,
316
12. Вычислить следующие интегралы:
а я/2
а) ^ (* +1) dx; б) J cos ж dx;
2 —я
2 2
в) JBw-coe2x)dr, г)
3 2
0 о
ж) \" ж cos л- d*; s) \ I 2-* — 2~-«
1 -1
я/2
¦ 1
/
¦ 1+,Ь.2« + сое2х
j sin х + cos ж
л/6
а
13. Найти все числа а>0, для которых f B — 4x-\-3x-) dxr~ a.
о
14. Найти числа А к В такие, чтобы функция вида f (х) =--А1Х-j-В,
з
удовлетворяла условиям/'A) = 2 и \f(x)dx = 7.
15. На»ти все решения уравнения \ cos(t-|-a2)d* = sinet, принадлежащие
п
отрезку |2; 3].
Ifi. Найти производные следующих функций:
а) <l)(*) =
2 cos u
б) ф tf) = j2*'ln(l+A-2Hx; в)Ф(«)= (j e-«sin3B.v-f-5)iiJ?.
B sin (i
17. Вычислить площадь фигуры, ограниченной линиями:
а) 1/= l/cos2x, 1/ = 0, г=-0, л: = я/4;
б) у = х2; у = У х\ в) у = ех, j/ = e~v, x=\\
г) у = 2 + sin r, j/ = l +cos2 лг, д: s [0: л];
д) | i/|=l-д;2; с) I/ = A/2)', .<—2y-f-2 = 0, д: = 2;
ж) л'{/ = 7, у---=0, х = 4, х-—\1;
з) 1/ = -3^-|ж| + 3, fy = 0;
и) 3«/ = —ла + 8« —7, (у+1=4/(л- — 3);
к) 1/ = х3, 1/= 1/г, х = 2.
18. Вычислить площадь фигуры, ограниченной линиями (/ = \- , ж=1 и
касательной, проведенной в точке B; 3/2) к кривой у= \- 1.
19. При каких положительных значениях параметра а площадь фигуры,
ограниченной линиями y — cosax, у=0, х=л/6а, x~nl'2a, больше 3?
317
29, Дана криволинейная трапеция, ограниченная линиями j/ = 0, г~а(а>0)
F у — ха. Какую часть площади трапеции составляет площадь треугольника,
стсекагмого от данной трапеции касательно,"] к линии у-=х3 в точке х=2а/3?
21, В пекоторэ-i точке графика функции у — Ух касательлая накло-
наклонена к оси абсцисс под углом 45;\ Вычислить площадь фигуры, ограниченной
этой каелтельнол и прямыми у —0 и ж—1/4,
22. Доказать, что если функция /(х-), х s [—а; а], нечетная, то
23, Вычислить объем тела, образованного при вращении аокруг о;н О-л
, ограниченном линиями j/ = a'3, у—I, x="i.
24. Вычислить объем тела, образованного вращением вокруг прямо"!
у=1 фигуры, ограниченной графиком функции г/ = 1 -[-cos2 дг на промежутка
[—я/2; л/2] и этой прямом.
2G. Найти объем тела, образованного при вращении криволинейной тряпецни
i/=xa, х е [0; 1], а > 0, а) вокруг оси Gx, б) во:;руг оси Оу, в) вокруг пря-
прямой ь = 1, г) вокруг прямой х=\, }{) вокруг п;;Г,мэй г/ = л.
Глава XIII
РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ ЗАДАЧ
Решение геометрических задач часто вызывает трудности
у учащихся. Это в первую очередь связано с тем, что редко какая
задача в геометрии может быть решена только с использованием
определенной формулы. При решении большинства задач не обой-
обойтись без привлечения разнообразных фактов теории, доказательств
тех или иных утверждений, справедливых лишь при определенном
расположении элементов фигур. Можно с уверенностью сказать,
что для успешного решения геометрических задач неооходимо сво-
свободно владеть всем теоретическим материалом. Но и при хоро-
хорошем знании теории приобрести навык в решении задач можно
лишь решив достаточно много задач, начиная с простых i пере-
переходя к более сложным.
В этой главе приведено большое число задач различной труд-
трудности с решениями. Особенно подробны решения задач § 1, где
мы напоминаем формулировки многих теорем и показываем их
применение. Ряду задач предшествует обсуждение некоторых опре-
определений и теорем. Это сделано с целью подчеркнуть важные и
часто ускользающие от внимания учащихся их следствия. Неко-
Некоторые утверждения, содержащиеся в школьном учебнике лишь
в форме задач, нами сформулированы и доказаны как теоремы,
так как они часто используются в решении задач.
Одна и та же задача может быть решена, как правило,
несколькими способами. Приведенные здесь решения не всегда
самые изящные и короткие, однако мы рыбрали именно эти реше-
решения для того, чтобы показать определенные приемы решений,
продемонстрировать применение различных теорем.
Сделаем несколько общих замечаний.
О чертеже. Выполняя чертеж (рисунок), стремитесь :делать
его соответствующим условиям задачи. Так, если сказало, что
некоторый угол вдвое больше другого или отрезки перпендику-
перпендикулярны, отразите это на чертеже. Хороший чертеж —это удобный
для восприятия наглядный способ записи условий задгчи, он
может стать помощником в решении задачи, подсказать правиль-
правильный ход рассуждений. В то же время надо отчетливо понимать,
что даже самый аккуратный, выполненный с помощью циркуля
и линейки чертеж сам по себе ничего не доказывает. Все, что
319
«увидено» из чертежа, должно Сыть обосновано соответствующим
логическим выводом.
О поиске решения. Начиная решать задачу, используйте опре-
определение и свойства входящих в задачу данных и искомых эле-
элементов, ведите рассуждения: треугольник равнобедренный, сле-
следовательно, ..., две касательные проведены из одной точки,
следовательно, ..., окружность описана около прямоугольного
треугольника, следовательно, ...и т. п. Вспомните теоремы, в кото-
которых связаны данные и искомые элементы задачи, вспомните
похожие задачи.
О проверке решения. Для контроля правильности решения
задачи (особенно самоконтроля на экзаменах) полезно не только
еще раз просмотреть решение и проверить выкладки, но провести,
в некотором смысле, обратное решение: исходя из ответа, еычи-
слить известные элементы, проверить, существует ли фигура при
найденном значении искомой величины. Если задача с параметром,
выбрать для проверки такое значение параметра, при котором
решение очевидно или результат легко находится.
§ 1. Разные задачи
Задача 1. В треугольнике ABC медиана AM перпендику-
перпендикулярна медиане BN (рис. 148). Найти площадь треугольника ABC,
если \АМ\ = т и \BN\ = n,
Д Пусть медианы AM и BN пересекаются в точке О. Меди-
Медианы треугольника пересекаясь делятся в отношении 2:1, считая
2
от вершины, следовательно, \АО\ = -^\АМ\. Медиана AM пер-
перпендикулярна медиане BN, значит, от-
отрезок АО — высота треугольника ABN.
Используя формулу площади "треуголь-
|Д >& ника
S = -' aha, A)
Рис. 148. где а —основание, ha — высота к осно-
основанию о, получаем, что площадь треу-
треугольника ABN равна -2 | АО \ ¦ \ BN\ = ^пгп. Треугольники ABC
и ABN имеют общую высоту, проведенную из вершины В, осно-
основание АС вдвое больше основания AN. Из той же формулы пло-
площади следует, что площадь треугольника ABC вдвое больше пло-
2
щади треугольника ABN, т. е. равна -5 тп. а
Задача 2. Найти площадь трапеции, зная длины йг и da
ее диагоналей и длину высоты h.
Д Рассмотрим трапецию ABCD, в которой | BD | = da и | Л С | =
= d2 (рис. 149). Через точку D параллельно диагонали АС про-
320
ведем прямую, точку пересечения этой прямой с прямзй ВС
обозначим К. В четырехугольнике ACKD противоположные'сто-
противоположные'стороны попарно параллельны, следовательно, ACKD — параллелог-
параллелограмм,
\=dz и
Из последнего равенства следует, что
\ = \BC\+\CK\ =
т. е. длина отрезка ВК равна сумме длин оснований тргпеции.
Площадь трапеции, длины оснований которой равны а и b и
длина высоты равна h, находится по формуле
S=^±4 B)
поэтому площадь трапеции ABCD равна -^\BK\h. Пусть DMД_
А_ВК, тогда \DM\=h. Из прямоугольных треугольнике!; BMD
и DMK, используя теорему Пифагора, находим длины отрезков
ВМ и МК:
\МК\= Vr\DK |2 - | DM |2 = jAi'l - /i2.
Таким образом, площадь трапеции ABCD равна
В этой задаче дополнительным построением получила треу-
треугольник, площадь которого, с одной стороны, равна площади
трапеции, а с другой—легко вычисляется по данным иада^и.
Приведем еще один пример, в котором используется тот же пэием^-
построение фигуры равной площади.
а
Рис. 149.
Задача 3. Найти площадь треугольника ABC, если \АВ\==
= 3 см, |SC| = 7 см и длина медианы ВМ равна 4 см.
Д Достроим треугольник ABC до параллелограмма ABCD
(рис. 150). Диагонали параллелограмма, пересекаясь, делятся riono-
лйм, поэтому точка М лежит на диагонали BD и \BD\=='A\BM.'
11 n/ред. Г. Н. Яковлева
Ж
Площади треугольников ABC и BCD составляют половину пло-
площади параллелограмма ABCD, следовательно, площади этих
треугольников равны. В треугольнике BCD известны длины трех
его сторон:
| SC | = 7 см, ]CD| = 3 cm, |BD| = 8 см.
Площадь треугольника, длины сторон которого раЕны а, Ь и
с, находится по формуле Герона:
S = V~j(p-a)(p-b)(p-c),
где 2р = a -f- b + с.
Подставляя в эту формулу числовые значения длин сторон,
находим, что площадь треугольника BCD, как и площадь треу-
треугольника ABC, равна 6]/3 см2. ^
В следующих двух задачах напомним некоторые теоремы о пря-
прямоугольных треугольниках.
Задача 4. В прямоугольном треугольнике ABC из вершины
С прямого угла проведена высота CD (рис. 151). Точка D нахо-
находится на расстоянии т и п от катетов АС и
ВС соответственно. Найти длины катетов.
А Пусть DAi.A-.AC и DBi±BC. Если дее
прямые перпендикулярны одной и той же пря-
прямой, то они параллельны, следовательно, DAi | ВС
и DBA АС. Тогда CBxDAi — по определению
прямоугольник, поэтому \CAi\ = \DBi\ = n и
Cfit =\DAi\ = m.
В прямоугольном треугольнике CD А отре-
отрезок DAi является высотой, проведенной из вер-
вершины прямого угла. Высота прямоугольного
треугольника, проведенная из вершины прямого
угла, есть среднее пропорциональное между проекциями катетов
на гипотенузу, следовательно,
\DAl? = \CAl\-\AlA\.
Обозначив Ь==|ЛС}, это равенство перепишем в виде т2 =
= п(Ь — п), откуда находим b = (я2 + /л2)/п. Аналогично, обозна-
обозначая \ВС\ = а, из прямоугольного треугольника BCD находим а =
*=(п? + та)/т.
Таким образом, катеты равны п"+т1 и п2+т^ш А
Задача 5. Радиус окружности, вписанной в прямоугольный
треугольник, равен г. Найти площадь этого треугольника, если
длина гипотенузы равна с.
Д Пусть окружность, вписанная в прямоугольный треугольник
ABC, касается гипотенузы АВ в точке Р и касается катетов
в точках М а N (рис. 152).
322
Касательная к окружности перпендикулярна радиусу, прове-
проведенному в точку касания, поэтому, если О —центр окружности, то
ОМ _1_ ВС и ON JL АС. Отсюда следует (рассуждения аналогичны
рассуждениям задачи 4), что CMON — прямо-
прямоугольник, а так как | ОМ | = | ON \ = r, то
СМОЛ/— квадрат, площадь которого равна г2.
Прямоугольные треугольники конгруэнтны,
если гипотенуза и катет одного конгруэнтны
гипотенузе и катету другого, поэтому прямо-
прямоугольные треугольники МВО и РВО конгру-
конгруэнтны и, следовательно, имеют равные пло-
площади. Аналогично устанавливается, что равные
площади имеют прямоугольные треугольники
МАО и РАО. Таким образом,
Сумма площадей треугольников РВО и РАО равна площади
треугольника BOA, площадь которого находится по формуле A)
и равна -_-сг. Окончательно получаем S ЛВС = г2-\-cr. a
Рассмотрим задачу о делении отрезка при пересечении его
прямой. Как правило, такая задача решается дополнительным
построением — проведением параллельной
прямой и использованием теоремы о пере-
пересечении сторон угла параллельными пря-
прямыми.
Задача 6. Точка N. лежит на сторо-
стороне АС треугольника ABC (рис. 153), при-
причем \AN\:\AC\ = n. Найти, в каком от-
отношении медиана AM делит отрезок BN.
Д Пусть О — точка пересечения меди-
медианы AM и отрезка BN. Требуется найти
отношение \BO\:\ON\. Проведем прямую NК параллельно ме-
медиане AM. Параллельные прямые отсекают на сторонсх угла
пропорциональные отрезки. Параллельные прямые AM н NK
пересекают стороны угла NBC, следовательно,
\ВО\ _ _!_ВЛ4Ч / /оч
'ON | "~ , МК , * ^ '
Те же прямые пересекают и стороны угла АСВ, поэтому
\МС\ _\АС\
\MK\~ \AN\'
Заметим, что М— середина стороны ВС, значит, | ВМ j =--! МС |;
кроме того, \AC\:\AN\=\/n, таким образом,
Рис. 153.
\ВМ<
мс\
мк
\мк
и тогда из C) следует, что | ВО \: \ ON | = 1: п. А
11*
323
Используем аналогичные дополнительные построения для доказа-
доказательства следующей теоремы о свойстве биссектрисы треугольника.
Теорема. Биссектриса внутреннего угла треугольника делит
противолежащую этому углу сторону на отрезки, пропорциональ-
пропорциональные прилежащим сторонам, т. е. если A D —биссектриса треу~
гольника ABC (рис. 154), то -гугг — ¦ йГ •
Ц Проведем прямую ВК, параллельную
биссектрисе AD. Параллельные прямые ВК
и DA, пересекая стороны угла ВС К, отсе-
отсекают на них пропорциональные отрезки,
имеем
\BD\ \KA\
А
Рис. 154.
¦С
АС\
Заметим, что треугольник КАВ равнобедренный. Действительно,
если дее параллельные прямые пересечены третьей, то соответ-
соответственные, а следовательно, и накрест лежащие углы конгруэнтны,
поэтому
ВКА = DAC, КВА = BAD,
а равенство углов BAD и DAC следует из того, что A D — бис-
биссектриса угла А. Таким образом, \1(А\ =
=! АВ ], и из D) следует
\DC\
\АВ\
\АС\
Рис. 155.
Рассмотрим несколько задач, в условии
которых задана окружность.
Задача 7. Диаметр CD параллелен хор-
хорде АВ той же окружности (рис. 155). Найти
длину хорды АВ, если \АС\ = Ь и \ВС\ =
= а (а>Ь).
Д Дуги, заключенные между параллельными хордамщ конгру-
конгруэнтны, кроме того, конгруэнтные дуги стягиваются конгруэнт-
конгруэнтными хордами, поэтому \BD\ = \AC\ = b.
Вписанный угол, опирающийся на диамгтр^прямой, следовательно,
CBD = 90° и треугольник CBD — прямоугольный. По теореме Пифа-
Пифагора находим | CD \ = ]/ а2-\-Ь2.
Пусть ВК JL CD. Площадь прямоугольного треугольника CBD
равна половине произведения длин его катетов, с другой стороны,
она может быть выражена по формуле A), т. е. имеет место
\СВ\ \BD |
равенство -^\СВ\- \BD | = -9-|CD [• |ВК
из которого находим
Пусть О—центр окружности и OMj_AB. Отрезки двух
параллельных прямых, заключенные между двумя параллельными
324
прямыми, конгруэнтны между собой, следовательно, \ОМ\ = \
Диаметр, перпендикулярный хорде, делит ее пополам, поэтому
)ЛМ| = |МВ[. Из прямоугольного треугольника ОМВ, в котором
| ОВ | = | CD |/2, находим
а"- — Ьг
следовательно, АВ = (а2 — Ь2)/Уа2-\-Ь*. А
Задача 8. На основании ВС трапеции ABCD, как на диа-
диаметре, построена окружность, которая проходит через сгредины
Диагоналей трапеции и касается ос-
основания AD (рис. 156). Найти углы
трапеции.
Д Пусть окружность пересекает
диагональ BD в точке М, тогда по
условию | fi/Vf j = | Л'Ш |. Вписанный
угол ВМС прямой, так как опирается
на диаметр. Прямоугольные треуголь- Рис. 15G.
ники конгруэнтны, если катеты од-
одного конгруэнтны катетам другого, поэтому Д ВМС ^ Д DMC
(\ ВМ ! = | MD |, СМ — общий катет) и, следовательно, | ВС \ =» | CD \,
Так как окружность проходит также через середину Д1 агонали
АС, та аналогично устанавливается \АВ\ = \ВС\. Таким обра-
образом, трапеция равнобедренная и углы при основании ргвны.
Окружность касается основания AD, поэтому расстояние
между основаниями равно радиусу окружности, и если СК J_ AD,
то ! С/С | = -2-| ВС\. Отсюда следует, что в прямоугольнсм треу-
треугольнике CKD гипотенуза CD в два раза большз катета СК, сле-
следовательно, катет СК лежит против угла в 30е.
Итак, углы трапеции ABCD равны 30° и 150я. А
В решении этой задачи в частности было доказано, что если
медиана треугольника (BCD) является высотой, то треугольник
равнобедренный. Легко доказываются также следующие признаки
равнобедренного треугольника (доказательство проведите само-
самостоятельно):
если углы при основании треугольника равны, то треугольник
равнобедренный;
если высота треугольника является биссектрисой, то тре-
треугольник равнобедренный;
если медиана треугольника является биссектрисой, то тре-
треугольник равнобедренный.
В дальнейшем будем использовать эти признаки.
Задача 9. Из точки А проведены две прямые, касающиеся
окружности радиуса г в точках М и N (рис. 157). Найти длину
отрезка MN, если расстояние от точки А до центра окружности
равнб а.
325
Д Пусть О —центр окружности, тогда ОМА = ONA = 90°.
В прямоугольных треугольниках ОМА и ON А гипотенуза О А
общая и \0M\ = \0N\ = r, следовательно, ДО/ИЛ оё ДОА/Л. Из
конгруэнтности этих треугольников следует, что углы МАО и
NAO конгруэнтны и \AM\ = \AN\. Тс-
ким образом, треугольник MAN равно-
равнобедренный. В равнобедренной треуголь-
треугольнике биссектриса является медианой и
высотой, поэтому, если Е — течка пере-
пересечения О А и MN, то О А _1_ ME и
\ME\ = \EN\.
Для площади S прямоугольного тре-
треугольника ОМА имеем
Рис. 157.
= -~\ME\
\OA\= 2-\0М\\АМ'
откуда, так как J AM j = ]/а2 — г, находим \ ME
и | MN \ = 1г У~аГ^?\/а. а
В решении этой задачи доказаны два свойства касательных,
которые сформулируем следующим образом:
если из точки к окружности проведены две касательные, то
а) длины отрезков касательных от. этой точки до точек ка-
касания равны,
б) прямая, проходящая через центр окружности и эту точку,
делит угол между касательными пополам.
Первое из указанных свойств поможет нам решить следую-
следующую задачу.
Задача 10. В треугольник ABC площади S вписана окруж-
окружность радиуса г, которая касается сторон АС и ВС соответственно
в точках М и N (рис. 158). Найти длину стороны АС, если
АМ\
АС -5:6
¦ft
Рис. 158.
/ИС | = 2:3 и \BN
Д Длину стороны АС обозначим а. Из
условия | AM |: \МС | = 2 : 3 находим, что
| AM | = 2а/5 и j MC | = За/5.
По свойству касательных, проведен!!ых
из одной точки, имеем [ NC | = \МС\ = За/5,
и тогда из условия j BN | : \NC | = 5 : 6
получаем \BN \ = а/2.
Если окружность касается стзроны АВ
в точке Р, то также j АР | = | AM | = 2о/5
и
\Р\ \\ /.
Площадь треугольника через длины его сторон G, Ь, с и
радиус г вписанной окружности выражается по формуле
E)
где 2р = a -f- b -f с.
326
Находим полупериметр р треугольника АВС:р = За/2, тогда
3 2 5
по этой формуле S= 2 or и, следовательно, а = --- . д
Напомним, что:
в четырехугольник можно вписать окружность тогда и только
тогда, когда суммы длин противоположных сторон равны,
около четырехугольника можно описать окружность тогда а
только тогда, когда симма противоположных углоз четырехуголь-
четырехугольника равна 180°.
Задача 11. Прямоугольная трапеция описана около окруж-
окружности. Найти радиус окружности, если длины оснований трапе-
трапеции равны а и Ь.
Д Пусть /" — радиус окружности, которая вписана в прямо-
прямоугольную трапецию ABCD (рис. 159). Так как трапеция прямо-
прямоугольная, то \АВ\ = 2г. Пусть \ВС\ = Ь и \AD\=ta. В эту тра-
трапецию вписана окружность, следовательно,
откуда
ВС | + \AD
получаем
AB\Jr\CD\,
в
CD =a-<rb-2r. Пусть
СК'± AD, тогда \СК\ = \АВ\ = 2г и \KD\ =
= a — b. По теореме Пифагора | CD j2 =
= \CK\2-\-\KD\i, т. е. ( b2
-{-(a — bJ, откуда находим
Ряс 159
Приведем пример задачи, решение которой становятся проще
при дополнительном построении окружности.
Задача 12. В прямоугольном треугольнике ABC утол С
прямой, величина угла А равна сб(сб< я/4), точка D — середина
гипотенузы. Точка Вх симметрична точ-
точке В относительно прямой CD. Найти
величину угла AB-J2.
Д Пусть точка В1 симметрична точ-
точке В относительно прямей CD (ркс. 160),
тогда точки В и В1 лежат на одном
перпендикуляре к прямой CD и на
равном расстоянии от этой прямой,
т. е. Bfi,l CD и | OB | = | OBJ. Отре-
Отрезок OD соединяет середины сторон тре-
треугольника ВВ±А, следовательно, OD —
средняя линия треугольника BBXA, она параллельна стороне
ARi. А так как OD±_BBU то и АВХ ±_ ВВи т. е. т?еуголь-
ник ВВ^А прямоугольный.
Вершины прямоугольных треугольников с гипотенузой АВ
лежат на окружности с диаметром АВ, следовательно, точки
А, В, С и Si лежат на окружности с диаметром АВ.
Величина вписанного угла равна половине угловой величины
дуги, на которую он опирается. Вписанные углы ВАС и ВВХС
Рис. 1G0
327
опираются на одну дугу, поэтому их величинн равны: ВВЬС —
Отсюда находим, что ABLC = ^
§ 2. Подобие треугольников. Теоремы синусов и косинусов
Подобие треугольников. Напомним определения подобия фигур:
фигура Фх называется подобной фигуре Ф (записывается ФХ^Ф),
если существует отображение фигуры Ф на фигуру Фь при
котором для любых двух точек М и N фигуры Ф и их образов —
точек Mi и jVi отношение расстояний j MN j и \MiNi\ есть
величина постоянная. Число k = j MiNi\/\ MN < называется коэ4>-
фициентом подобия.
Наиболее часто в решении задач используется подобие треу-
треугольников. Если треугольник АхВуС^ подобен треугольнику
ABC и вершины Ах и Bi являются образами вершин А и В,
то коэффициент подобия этих треугольников равен j Ax3i \l\ AB |,
как говорят, равен отношению длин соответственных сторон.
Признаки подобия треугольников
1. Если три стороны одного треугольника пропорциональны
трем сторонам другого треугольника, то такие треугольники
подобны.
2. Если два угла одного треугольника равны двум углом дру-
другого треугольника, то такие треугольники подобны.
3. Если две стороны одного треугольника пропорциональны
двум сторонам другого треугольника и углы между этими сторо-
сторонами равны, то такие треугольники подобны.
Задача 1. Прямая, проходящая через точку пересечения
диагоналей трапеции параллельно ее основаниям, пересекает
боковые стороны трапеции в точках М
и N. Найти длину отрезка MN, ес-
ли Длины оснований трапеции рав-
равны а и Ь.
Д Пусть диагонали трапеции
k ABCD пересекаются в точке О, от-
¦° резок MN параллелен основаниям
р ,6] и содержит точку О (рис. 161),
\AD\=a, \BC\-b. Если две парал-
параллельные прямые пересечены третьей,
то соответственные и накрест лежащие углы равны. Основания
трапеции параллельны, следовательно, BDA —CBD и CAD =
— ВСА и по второму признаку подобия /\,ВОС^/\JX)A. Следо-
328.
вательно,
\во\ \вс\
0D\
\AD\
т. е.
ДО I 6 „
-ттгч4 = —. Отсюда находим, что
ВО]
а+Ь'
A)
Прямая MN параллельна основанию AD, поэтому ЕМО~
— BAD и BOM = BDA, треугольники МВО и ABD также по-
подобны и | МО \/\ AD | = j ВО j/j BD J. Отсюда, учитывая A), полу-
получаем | МО | = ab/(a-irb). Аналогично устанавливаем, что \NO\ =
с=- abl(a-\-b), таким образом, MN | = 2аЬ/'(а-\-Ь). ^
Сформулируем признаки подобия прямоугольных треугольни-
треугольников
1. Деа прямоугольных треугольника подобны, если они имеют
по равному острому углу.
2. Деа прямоугольных треугольника подобны, если катеты
одного пропорциональны катетам другого.
3. Два прямоугольных треугольника подобны, если катет и
гипотенуза одного пропорциональны катету и гипотенузе другого.
Задача 2. В треугольнике ABC проведены высоты AM и
BN (рис. 162). Найти углы треугольника MNC, если Л— а и
Д Прямоугольные треугольники АМС и BNC имеют равные
острые углы при вершине С, следовательно, они подсбны и
j NC |/| BC\ = \ МС |/i АС |. Отсюда заключаем, что
в треугольниках MCN и АСВ стороны, приле-
прилежащие к равному углу при вершике С, про-
пропорциональны, следовательно (по третьему при-
признаку подсбия), эти треугольники подобны.
В подобных треугольниках против соответ-
соответственных сторон лежат равные углы, поэтому
Результат этой задачи можно сформулнро- А
вать так: если соединить основания двух высот
треугольника, то образуется треугольник, по-
подобный данному, а
Из определения подобия фигур следует, что в подобных фи-
фигурах все соответственные линейные элементы пропорциональны.
Так, отношение периметров подобных многоугольников равно
отношению длин соответствующих сторон. Или, например,
в подобных треугольниках отношение радиусов вписанных окруж-
окружностей (также и описанных окружностей) равно отношение длин
соответственных сторон. Это замечание поможет нам решить сле-
следующую задачу.
Задача 3. В прямоугольном треугольнике ABC из вершины
С прямого угла проведена высота CD (рис. 163). Радиусы окруж-
окружностей, вписанных в треугольники ACD и BCD, равны соответ-
Рис. 1<>2.
329
ственно гх и г2. Найти радиус окружности, вписанной в треу-
треугольник ABC.
Д Обозначим искомый радиус г, положим \АВ\=с, \AC\-b,
| ВС \ = а. Из подобия прямоугольных треугольников ACD и
ABC (у них равные углы при вер-
вершине А) имеем -' = ? , откуда Ь =
г1 о
= — с. Прямоугольные треугольни-
треугольники CBD и ABC также подобны, по-
по, откуда а — -*с. Так
как a2-Vb2=c2, то, возводя в квад-
квадрат выражения для а и Ь и склады-
Рис. 163.
этому — =
вая их, получим (-—iV + f — JV2 = с2 или r'~y * = 1. Теперь на-
находим г = у i
Напомним, что отношение площадей подобных фигур равно
квадрату коэффициента подобия. Для треугольников это утвер-
утверждение можно сформулировать так: пло-
площади подобных треугольников относятся
как квадраты длин соответственных сторон.
Рассмотрим характерную задачу на эту
тему.
Задача 4. Через точку М, лежащую
внутри треугольника ABC, проЕ;едены три
с прямые, параллельные его сторонам. При
этом образовалось три треугольника
(рис. 164), площади которых равны Sit
S2 и S3. Найти площадь треугольника ABC.
Д Легко видеть, что треугольники ЕКМ, MQF и PMN по-
подобны треугольнику ABC. Пусть S— площадь треугольника ABC,
тогда
Si | ЕМ р Sj MF |2 S3 j PN |a
Т = ТЛСУ* ~S = | AC |2 ' "S = I AC |2 "
Отсюда находим
л/
Рис. 164.
А так как \EM\ = \AP\, \MF\ = \NC\, то
| EM \ +1PN
Таким образом,
MF | = | AP | +1 PN\ +1 NC \ = | AC |.
Отсюда следует S =
330
2- A
Теоремы косинусов и синусов. Для произвольного тргувдь-
ника, длины сторон которого обозначены а, Ь, с, а величины
противолежащих им углов—Л, В, С, справедливы две теоремы,
устанавливающие соотношения между сторонами и углами треу-
треугольника, утверждения которых можно кратко записать тж:
теорема косинусов:
теорема синусов:
а
sin A sin В sin С
Покажем на примерах, как применяются эти теоремы.
Задача 5. Найти длину медианы треугольника АВ
веденной из вершины С, если длины сторон, лежащих
вершин Л, В и С, равны соответственно
а, Ь, с.
Д Пусть СМ—медиана треугольни-
треугольника ABC (рис. 165). Обозначим т = \СМ\,
Ф = СМЛ, тогда СМВ= 180°- <р. Из тре-
треугольников АСМ и СМВ по теореме ко-
косинусов будем иметь
/•2 р
C, про-
пропротив
f »
а2 = т3 + J - 2т |- cos A80° - ц>).
Рис. 165-
и учитывая,
что
Складывая почленно два эти равенства
cosA80° —ф) = — cos ф, получаем а3-|-6а = 2/п2 + :^-, откуда нахо-
Димт2 = т + т-т-
Таким образом, | СМ I = 1/ 4" + ~г • А
Задача 6. Площадь треугольника ABC равна 16 см2. Найти
длину стороны АВ, если |ЛС| = 5 см,
| ВС | = 8 см и угол С тупой (рис. 1C6).
Д Площадь треугольника через
длины двух сторон а и b и величину
угла С между ними выргжается еле- .
дующим образом:
B)
Рис. 166.
Для данного треугольника ABC из этой формулы следует
. sinC = 2S/ab = 4/5. Так как угол С тупой, то косинус этого
угла отрицателен, и поэтому
331
Теперь по теореме косинусов находим | АВ |2 = а2 + Ьг — 2ab cos С =
=s 137. Следовательно, \АВ \=\/"l37 см. а
Задача 7. В равнобедренном треугольнике ABC длины
боковых сторон АВ и АС равны Ь, угол при вершине А равен
2а. Прямая, проходящая через вершину В и центр О описанной
около треугольника ABC окружности, пересекает сторону АС
в точке D (рис. 167). Найти длину отрезка BD.
Д Центр описанной около равнобедренного треугольника ABC
окружности лежит на его биссектрисе АК (так как АК 1. ВС и
\ВК\ = [ КС !), следовательно, ABD = OAB=a. Итак, в треуголь-
треугольнике BAD два угла известны, а так как сум-
сумма углов треугольника равна 180°, то BDA =
= 180° — За. По теореме синусов из треуголь-
треугольника BAD имеем
sin
Рпс 167.
[J
sinA80J — За)'
откуда, учитывая, что sin A80° — За) = sin За,
находим
Приведем доказательство теоремы синусов, по ходу- которого
установим одно важнее соотношение.
Q Пусть около треугольника ABC, длины сторон которого,
противолежащие вершинам А, В, С, обозначены а, Ь, с, описана
окружность радиуса R (см. рис. 168). Проведем диаметр BD.
Вписанные углы BDA и ВСА опираются на одну дугу, следова-
следовательно, BDA — C. Угол BAD прямой, так
как опирается на диаметр, значит, треуголь-
треугольник BAD прямоугольный и
с = 2R sin С. C)
Аналогично устанавливается, что а — 2/? sin A
и b ==2/? sin В. Из этих равенств следует
Рнс. 168.
sin A sin В sin С
D)
Если из C) выразить sin С и подставить в формулу B), то
получим выражение площади треугольника через длины его
сторон а, Ь, с и радиус описанной окружности R:
abc
E)
Задача 8. Точка Лг лежит на стороне АС правильного
треугольника ABC (рис. 169). Найти отношение радиусов окруж-
332
нсстей, описанных около треугольников ABN и ABC, если
\AN\i\AC\ = n. м-уг
Д Обозначим через а сторону правильного треугольниюМвС,
тогда \AN\ = па. Длину стороны BN найдем по теореме юсину-
ссв из треугольника ABN:
i Л W |а — 21 Л S | Л Л/1 cos 60°
- л'- а.
Пусть Rx и R2 — радиусы окружностей, описанных соответственно
около треугольников ABN и ABC. По фор-
формуле E) получим
в.
<-> /SRW —
п V\+п2 — па3
С другой стороны, треугольники ABN и
ABC имеют общую высоту, проведенную из
вершины В, поэтому их площади относятся
как длины оснований, т. е. Sabn==hSAbc-
Подставив сюда выражения для площадей,
получим п Y1 + «2 — «a3/4i?1 = naA/AR2, откуда находим
§ 3. Свойства хорд, секущих и касательных >:,
Углы, измеряемые с помощью дуг окружности. Угловс ^вели-
^величиной дуги называют величину соответствующего ей центрального
угла. Величина впиханного угла равна половине угловой величины
дуги, на которую он опирается. Установим, как измеряются углы
с вершинами внутри или вне круга, когда стороны эти:? углов
пересекаются с окружностью.
Теорема. Величина угла с вершиной внутри круга равна по-
полусумме угловых величин дуг, заключенных между его шеренгами
Рис. 170.
Рис. 171.
и их продолжениями. Величина угла, образованного двумя секу-
секущими с вершиной вне круга, стороны которого пересекают этот
круг, равна полуразности угловых величин большей и меньшей дуг,
заключенных между его сторонами.
333
¦ . Q Рассмотрим угол АМВ (рис. 170). Заметим, что « = ~2-
E = -„
ренних, с ним несмежных, поэтому АМВ = сс + р = -^
!. Внешний угол треугольника равен сумме двух внут-
внутBt).
Рассмотрим теперь угол АМВ, образованный двумя секу-
секущими МА и MB (рис. 171). Так как a = ~AJlu f>=~AB, to
по свойству внешнего угла треугольника получаем АМВ = $—
2
Теорема. Величина угла, образованного касательной и хор-
хордой, имеющими общую точку на окружности, равна половине угло-
угловой величины дуги, заключенной между его сторонами.
Ц Рассмотрим угол NAB, образованный касательной и хор-
хордой (рис. 172). Проведем диаметр АС. Касательная перпендику-
перпендикулярна диаметру, проведенному через точку касания, следова-
следовательно, CAN = 90° и СВА-=Ж°. Далее, а=^ВС,
— а, отсюда получаем
Лав =1 A80° - вс) = \ Ш
(случай тупого угла, на рис. 172 угол МАВ, рассматривается
аналогично). Q
м
Задача 1. Окружность проходит через вершины В, С и D
трапеции ABCD и касается стороны АВ в точке В (рис. 173).
Найти длину диагонали BD, если длины оснований трапеции
равны а и Ъ.
Д Угол между касательной АВ и хордой BD, как и вписан-
вписанный угол BCD, измеряются половиной угловой величины дуги
BnD, следовательно, ABD = BCD. Основания трапеции парал-
параллельны, поэтому CBD — BDA. Таким образом, треугольники ABD
и BCD имеют по два равных угла и, следовательно, подобны. Из
подобия получаем | BD |/| AD | = | ВС ]/| BD \, откуда следует | BD j2 =
ЯС| и \BD\ = Vab. A
334
Свойства секущих и касательных. Докажем теорему, называе-
называемую «теоремой о касательной и секущей», часто приме 1яемую
в решении задач.
Теорема. Пусть к окружности проведены из одной глочки М
касательная МА и секущая MB, пересекающая окружносп ь в точ-
точках В и С (рис. 174). Тогда справед-
справедливо равенство
\МА\2 = \МВ\\МС\,
т. е. если из точки М к окружно-
окружности проведены касательная и секущая,
то квадрат отрезка касательной от
точки М до точки касания равен Рис. 174.
произведению длин отрезков секу-
секущей от точки М до точек ее пересеченая с окружностью.
Ц По предыдущей теореме MAC =-^ АС, но также ABC =
= -кАС, следовательно, MAC-— ABC. Так как в треугольниках
АМС и ВМА угол при вершине М общий, то отсюда по
второму признаку подобия следует, что эти
треугольники подобны. Из подобия имеем
| МА \/\ MB | = | МС j/| MA |, откуда получаем
\ \\\ Н
Задача 2. Радиус окружности равен г.
Из точки М проведена секущая MB, прохо-
проходящая через центр окружности, и касатель-
касательная МА, причем \МВ\ = 2\МА\ (рис 175).
Найти, на каком расстоянии от центра ок-
окружности находится точка М.
Об \ОМ\
Рис. 17:").
Д Обозначим х = \ОМ\, тогда \ВМ\=х-\-г и \СМ =х — г,
кроме того, по условию | МА
\
= -„- (х-\-г).
2 2
По теореме о касательной и секущей имеем
= (х-\-г) (х — г), откуда, сокращая на (х-\-г),
получаем -г- (х + г) = х — г и легко находим
Задача 3. Через точку М, удаленную
от центра окружности на расстоянии Ъ, про-
проведена секущая МА так, что она делится ок-
окружностью пополам: |МВ| = |6Л| (рис. 176).
Определить длину секущей МА, если радиус
окружности равен г.
Д Проведем секущую МС через центр окружности. Из тео-
теоремы о касательной и секущей следует, что если из точки М
проведены две секущие МА и МС, пересекающие окружность
Рис. 176.
335
в точках В и D соответственно, то [ МА 11 MB [ = [ МС \ | MD [, так
кЩ! оба ¦ произведения равны квадрату длины касательной, про-
веДФнней' из точки М к той же окружности. По условию | ОМ | = Ь,
поэтому i,| МС | = Ь + /¦ и | MD | = Ь — г. Обозначим '\МА\== х, тогда
|'/Ш|=х/2 и по указанному свойству двух секущих, проведенных
из одной точки, получаем х • -*=(& + r) (Ъ — г), откуда находим
Рис. 177.
У() А
Свойство пересекающихся хорд.
Теорема. Если через точку, взятую внутри круга, проведены
две морды, то произведение длин отрезков одной хорды равно про-
произведению длин отрезков другой хорды, т. е.
(рис. 177) если через точку М проведены две
хорды АВ и CD, mo\MA\\MB\ = \MC\\ MD |.
Ц Проведем хорды АС и BD. Вписан-
Вписанные углы CAB и CDB опираются на дугу
СВ, следовательно, CAB = CDB. Аналогично
ACD = ABD. Таким образом, треугольники
АСМ и DBM подобны и | MA \/\ MD =
= | МС|/| MB |. Отсюда получаем | МЛ \ \МВ \ =
= \MC\\MD\. Щ
Задача 4. Две окружности внутренне касаются » точке Q
(рис. 178). Прямая, проходящая через центр Oi меньшей окруж-
окружности, пересекает большую окружность в точках А и D, а мень-
меньшую — в точках В и С. Найти отношение ра-
радиусов окружностей, если j АВ | : | ВС!: | CD \ =
= 2:4:3.
Д Пусть R и г — соответственно радиусы
большей и меньшей окружностей, тогда
| ВС \ = 2г и из заданной пропорции получаем
\АВ\ = г и \CD\=~r.
Проведем диаметр QP. Диаметр, проведен-
НЫи в Т0ЧКУ касания, перпендикулярен каса-
касательной, поэтому точки Oi лежат на QP.
пересекающихся хорд имеем 10$ \' OP |
j
Рис. 178.
По свойству
| А
у р р 1$ \i |
| ОцА \ | OJ) |, отсюда, учитывая, что j ОУР \ = 2R — г, | OiA | =
= \01В\ + \ВА\ = 2г и | ОхО I = j CD Н-! СОХ'[ = | г, получаем
BR — г) г — 5г2. Теперь легко находим R/r = 3. a
§ 4. Алгебраические и тригонометрические методы решения.
Применение векторной алгебры
В рассмотренных ранее задачах нам приходилось решать не-
несложные алгебраические уравнения, использовать теоремы коси-
косинусов и синусов, находить значения углов. Очевидно, что отде-
336
лить геометрию от алгебры и тригонометрии невозможно, поскольку
многие геометрические утверждения сформулированы в алгебраи-
алгебраической форме (теорема Пифагора или свойство высоты прямо-
прямоугольного треугольника) или тригонометрической (теоремы сину-
синусов и косинусов). Однако возможности применения алгебры и
тригонометрии гораздо шире. Во многих случаях решения геомет-
геометрических задач сводятся к решению соответствующих алгебраи-
алгебраических или тригонометрических уравнений и систем. Рассмотрим
в качестве примеров следующие задачи.
Задача 1. В окружность радиуса R вписан равнобедренный
треугольник, у которого сумма длин основания и высоты равна
диаметру окружности. Найти высоту этого треугольника.
Д Пусть BD — высота равнобедренного треугольника ABC
(рис. 179). Так как диаметр, перпендикулярный хорде, проходит
через ее середину, то течка D лежит на диаметре BF. Обозначим
h = \BD\ и 2Ь = \АС\. По условию 2R = h + 2b, а по свойству
пересекающихся хорд (§ 3) имеем b2 = hBR — h). Таким образом,
получили систему
\ b* = hBR-h).
Исключая 2R, находим bz = 2bk, откуда b = 2h, и тогда из пер-
2
вого уравнения получаем
2
= ~~-R. A
О
Задача 2. Центр окружности, вписанной в прямоугольный
треугольник ABC, находится на рзестоянии ]/5 см и у 10 см от
вершин А и В (рис. 180). Найти катеты. '
Д Задача решается просто, если за неизвестные принять' йе
катеты, а радиус вписанной окружности г и а = ОАК. Гак как
центр вписанной окружности лежит на пересечении биссектрис
углов Л и В, то 0ВК = ^г — а. Из прямоугольных треугольни-
треугольников OAK и ОВК находим
и r =
( -.'¦¦ — а
337
следовательно,
|/ 5since = |/l6sin(" — се). A)
Задача свелась к простому тригонометрическому уравнению.
Так как ein(~ — a) — -^- (cos а — since), то из A) получаем sin се =
«=coscc — since, откуда tga= 1/2.
Зная iga, по формуле sina = -7=J^=- находим sinoc=l/j/5
V 1Иё2«
й, следовательно, г=1 см.
Так как \АС\~-\АМ\ + \МС\ и ,'5С| = |5JV| + | ЛГС|, то легко
ваходн-л ! АС | «= 3 см и | ВС | = 4 см. А
Задача 3. Равнобедренные треугольники ЛВС (| ЛВ j = j ВС |)
а Л'В'С' (\А'В'\^\В'С'\) конгруэнтны. Вершины А', В', С
расположены соответственно на продолжениях
стороны ВС за точку С, стороны ВА за точ-
точку А, стороны АС за точку С, причем пря-
прямые ВС и В'С перпендикулярны (рис. 181).
Найти углы треугольника ABC.
Д Обозначим Ь = \АВ\ и ф = ЛВС. Пусть
прямые ВС и В'С пересекаются в точке Q.
Так как по условию А'В±В'С и ?)СС' =
-=ЛСВ = В7СМ7, то угол СС'Л'-г рямой и
отрезок CQ является высотой прямоугольного
1-ис 181. треугольника СС'А'. Следовательно,
iQC'|2 = !QC||Qi4'|. B)
Из прямоугольного треугольника B'QA' находим |Q/l'| = bsincp,
\B'q = b cos tp, и так как | QC | = | В'С | - | QB' |, то |QC'| =
= ЬA-соБф). Далее, |QC|= QB|-jBC|. Найдем \QB\ из пря-
прямоугольного треугольника B'BQ:
! ^ ' tg <p sin ф '
тогда \QC\ = b (cos ф — 1)¦ Подставляя в B) длины соответствую-
соответствующих отрезков и сокращая на Ь2, получим тригонометрическое
уравнение A — cos фJ = sin qp /"!!_?. — 1), которое приводится к виду
Бшф = 2 соБф— 1. Возводя это равенство в квадрат, выражая
sin2 ф через cos2 ф, получим 5 cos3 ф — 4 cos ф = 0, откуда находим
cos ф = 0 и cos ф = 4/5. Очевидно, что cos ф Ф 0 (в противном слу-
случае прямые В'А' и ВС не пересекались бы), поэтому cos гр = 4/5
и ф = arccos D/5). А
При сведении геометрической задачи к алгебраической или
тригонометрической приходится вводить несколько неизвестных.
Не обязательно за неизвестные величины принимать те, которые
338
требуется найти. Как показывает решение задачи 2, иногда удобно
ввести другие, относительно которых получаются более простые
соотношения и, лишь найдя их, вычислять искомые. Кроме того,
найденные решения алгебраических и тригонометрических урав-
уравнений и систем часто требуют геометрической проверки, как, на-
например, в задаче 3.
Большинство геометрических задач на максимум и минимум
также решаются с привлечением алгебры и тригонометрии. В этих
случаях задачу сводят к исследованию на максимум н минимум
некоторой алгебраической или тригонометрической фупкщ и. Заме-
Заметим, что при этом исследование надо проводить на ton множе-
множеств значений аргумента, на котором существует рассматриваемая
геометрическая фигура.
Задача 4. В прямоугольном треугольнике ABC гипотенуза
АВ имеет длину с и образует с катетом АС угол а. Точка D
расположена на гипотенузе АВ и
имеет наименьшую, по сравнению с
другими точками отрезка АВ, сумму
квадратов расстояний до прямых АС
я ВС. Найти длину отрезка АО.
Пусть DM J.. АС и DM ± ВС
(рис. 182). Обозначим х = | AD \, тогда n
| ON j = х s in се, | DM j = (с — х) cos a.
Сумму квадратов расстояний от точки D до прямых АС и ВС
обозначим /, имеем / = x2 sin2 се + (с — xJcos2a. Требуется узнать,
при каком значении х эта функция имеет наименьшее -.наченне,
если х заключено в пределах О^х^с. Преобразуем функцию/
к виду f = x2-\~c2 cos2 а — 2а: cos се. Производная этой функции
равна 2х — 2с cos с. и обращается в нуль при x = ccosa. Это зна-
значение х принадлежит отрезку [0; с], слева от этой точки произ-
производная отрицательна, справа— положительна, следовательно, при
х = с cos се функция / имеет минимум.
Таким образом, jy4Dj = ccosa. a
Применение векторной алгебры. С помощью векторное алгебры
некоторые задачи и теоремы планиметрии, требующие сложных
геометрических рассуждений, сводятся к сравнительно простым
вычислениям. Рассмотрим для примера следующую задачу.
Задача 5. В треугольнике ABC на сторонах АВ, ВС и С А
расположены точки Аи В1 и Ci так, что
\AAi\ _ IBBij = ICCxl
I =
\ АВ \ ~ \ ВС \~ \ АС \ '
Доказать, что точки пересечения медиан треугольников ABC и
.diBiCi совпадают.
Д Пусть АВ = а, АС = Ь (рис. 183). Если AM — медиана тре-
треугольника ABC, то АМ = (а-{- Ь)/2. Медианы треугольника
339
пересекаются в одной точке, каждая медиана в этой точке делится
в отношении 2:1, считая от вершины, поэтому если 0—точка
пересечения медиан треугольника ABC, то
Рассмотрим треугольник А^Сх (рис. 184). Обозначим т =
= | ААХ \I\AB\, тогда KJZX = A — m) ft — та и Афх = A — т) а +
-{¦ т(Ь — а). Если AiMx — медиана треугольника АхВхСц то
Точка
АМг = 1 (Л А + АА) = ]- F -Ь A - Зяг) а).
пересечения медиан треугольника
лежит на
**с
и |i4iO
вектор
т. е.
= /Тл; + Л]О = ша + -у F + A - 3/11) а) = -~ (а + Ь).
сов-
совСравнивая C) и D), получаем A6=AOl, т. с. точки О и
падают. А
ЗАДАЧИ РАЗДЕЛА I
1. Диагонали трапеции, пересекаясь в точке О, разбивают трапецию на
4 треугольника с вершиной в точке О. Доказать, что площади треугольников,
прилежащих к боковым сторонам трапеции, равны.
2. В треугольнике ABC через точку М, лежащую на стороне ВС, прове-
проведены прямые, параллельные сторонам АС и АВ. Площадь образзвавшегося
при этом параллелограмма составляет 5/18 площади треугольника ABC, Найти,
в каком отношении точка М делит сторону ВС.
3. Точки М, N и Р лежат на сторонах АВ, ВС н АС треугольника ABC,
причем I AM j/| АВ | = | В\' \j\ ВС\ = \СР \1\ СА | = 1/3. Прямые CM, AN и ВР,
пересекаясь, ограничивают треугольник, площадь которого равна 5, Haiim
площадь треугольника ЛВС.
4. При повороте с центром в точке С на угол а (а < л/2) треугольник
ABC переходит в треугольник А'В'С, Точка В' является образом точки В и
340
лежит на стороне АВ; точка Л'—образ точки А. Найти угли треугольника
ABC, если прямые АС и А'В' перпендикулярны.
5. Доказать, что три высоты треугольника или три прямые, ш которых
лежат высоты, пересекаются в одной точке.
6. Продолжения высот треугольника ABC делят описанную о соло тре-
треугольника ABC окружность на дуги, длины которых относятся как p:q:r.
Найти углы треугольника ABC.
7. Две окружности радиусов R и г (R ;> г) внутренне касаются в точке А.
Через точку В, лежащую на большей окружности, проведена прямая, касаю-
касающаяся меньшей окружности в точке С. Найти длину отрезка АВ, если
\ВС\=а.
8. Окружность, вписанная в треугольник ABC, делит медиану ВМ на три
конгруэнтные отрезка. Найти отношение длин сторон треугольника ABC.
9. Продолжения еысот ВМ и CN остроугольного треугольника ЛВС пере-
пересекают описанную около пего окружность в точках Р и Q. Найти радиус опи-
описанной окружности, если \ ВС =а и \PQ\ = ~~a-
э
10. Точка Е лежит на стороне АС правильного треугольника ABC, точ-
точка К —середина отрезка АЕ. Прямая, проходящая через точку Е перпендику-
перпендикулярно АВ, и прямая, проходящая через точку С перпендикулярно ЕЮ, пере-
пересекаются в точке D. Найти углы треугольника BK.D.
И. В равнобедренном треугольнике ABC (| АВ \ = \ ВС !) медиан;: AD пер-
перпендикулярна биссектрисе СЕ. Определить величину угла АСВ.
12. В треугольнике ABC величина угла при вершине А равна а. Найти
длину биссектрисы треугольника, проведенной из вершины А, если \АВ\=с
| ЛС[ = 6.
13. В треугольнике ABC величина угла при вершине В равна ф величина
угла при вершине С равна 2ф. Окружность, проходящая через точ!Ш А, С и
центр описанной около треугольника ABC окружности, пересекает сторону АВ
в точке М. Определить отношение \ AM i : | АВ |.
14. В треугольнике ABC перпендикуляр, проходящий через сергдину сто-
стороны АВ, пересекает сторону АС в точке М, при этом j MA : : МС =3. Пер-
Перпендикуляр, проходящий через середину стороны АС, пересекает сторону АВ
в точке N, так что ; AN \ : \ NB ; = 2. Определить углы треугольника ABC.
15. Доказать, что если в треугольнике ABC длины сторон АВ и ВС раз-
различны, то биссектриса угла ABC лежит между медианой и высотой, проведен-
проведенных из той же вершины.
16. В треугольнике ABC длины сторон связаны соотношением | ВС |2 -}-
+ I AC ]2 = 5 I АВ Is. Доказать, что медианы AM и BN перпендикул! рны.
17. Две окружности радиусов \г§ см и \Г2 см пересекаются ) точке А.
Расстояние между центрами окружностей равно 3 см. Через точку А проведена
прямая, пересекающая окружности в точках В и С так, что \ А1\\ — \ АС\.
Найти длину отрезка АВ.
18. В ромбе ABCD угол BAD острый. Окружность, вписанная в этот
ромб, касается сторон АВ и CD соответсгпенно в точках М и Л\ пересекут
отрезок СМ в точке Р, а отрезок BN — в точке Q. Найти отношение ! /JQj: \QN j,
если \СР\:\РМ\=9: 16.
141
19. Дана окружность с диаметром АВ. Вторая окружность с центром
в точке А пересекает первую окружность в точках С и D, а диаметр АВ
в точке Е. На дуге СЕ, не содержащей точку D, взята точка М, отличная от
точек С и Е. Прямая ВМ пересекает первую окружность в точке N. Найти
длину отрезка MN, если \CN \ = a, DN j = Ь.
20. Дан треугольник ABC. Биссектриса внешнего угла треугольника при
вершине А пересекает ггрямуго ВС в точке М. Доказать, что | MB I: j MC\ =
= \АВ\:\АС\.
21. Дан треугольник ЛВС. Точка М лежит на прямой ВС, при этом 1 MB [ 1
:\МС\— \АВ \:\ АС \. Доказать, что точка М лежит либо на биссектрисе
угла А треугольника ABC, либо на биссектрисе внешнего угла при вер-
вершине А.
22. В параллелограмме ABCD острый угол равен а. Пусть С\, О2, Оя и
04 — центры окружностей, описанных соответственно около треуголькиков DAB,
DA С, DBC и А ВС. Определить отношение площади чешрехугольника 0^0,0^0^
к площади параллелограмма ABCD.
ЗАДАЧИ РАЗДЕЛА II
1. Доказать, что в любом треугольнике сумма длин его трех медиан меньше
перимегра треугольника, но большз трех четвертей периметра.
2. В равнобедренном треугольнике длина основания равна а, длина высоты,
опущенной на основание, равна h. Найти расстояние от середины основания
до боковой стороны.
3. Определить площадь трапеции, если известно, что при последовательном
соединении серздин ее сторсн образуется квадрат, длина стороны которого
равна а.
4. В трапеции длина основания равна 2а, длины всех остальных сторон
этой трапеции равны а. Кайти расстояние от середины одной боковой стороны
трапеции до другой боковой стороны.
5. Вычислить площадь круга, вписанного в равнобедренную трапецию,
длины оонозаний которой равны а и Ь.
6. Трапеция описана около окружности. Найти отношение длины средней
линии трапеции к ее периметру.
7. В прямоугольном равнобедренном треугольнике через вершину прямого
угла проведены две прямые, которые разбивают этот угол на три конгруэнтных
угла. Найти длины отрезков, на которые эти прямые разобьют гипотенузу,
если длина ее равна а.
8. Найти площадь треугольника ABC, вписанного в окружность, если
вершины А и С отстоят от касательной, проведенной через вершину В, на
расстояниях т и я и | АС \ = Ь.
9. В треугольнике ABC проведена высота BD. Через точку D проведена
прямая параллельно стороне АВ до пересечения со стороной ВС в точке К.
Найти отношение | ВК |/1 КС \, если площадь треугольника BDK составляет 3/16
площадм треугольника ABC.
10. В равнобедренном треугольнике ABC (| АВ | = | ВС \) биссектриса АЕ
пересекает высоту BD в точке О, причем \ОВ \/\OD \ = 3. В каком отношении
высота AF делит высоту /3D?
342
11. В равнобедренном треугольнике ABC (| АВ | =; ВС I) высота IF пере-
пересекает высоту BD в точке О, причем | ВО l/| OD i =n, В каком отношении
биссектриса АЕ делит высоту BD7
12. В выпуклом четырехугольнике ABCD, площадь которого равна 24 см2,
проведены диагонали. Известно, что площадь треугольника ABC вдвое больше
площади треугольника ACD, а площадь треугольника BCD втрое больше
площади треугольника BDA. Найти площадь треугольника ABC.
13. В параллелограмме проведены биссектрисы его внутренние углов.
Площадь полученного от их пересечения четырехугольника равна 1/4 площади
параллелограмма. Найти отношение длин сторон параллелограмма.
14. В треугольнике ABC на стороне АС взята точка М, а на стороне
ВС— точка N. Отрезки AN и ВМ пересекаются в точке О. Найти площадь
треугольника CMN, если площади треугольников ОМА, ОАВ и OBN соответ-
соответственно равны Si, S2, S3.
15. В равнобедренном треугольнике ABC (,АВ\ = \ВС ;) биссектрисы BD
и AF пересекаются в точке О. Отношение площади треугольника DOA к пло-
площади треугольника ВОР равно 3/8. Найти отношение \AC\j\AB\.
18. Прямая, параллельная основаниям трапеции, делит ее на ,две части,
площади которых относятся как т: п. Найти длину отрезка этой прямой,
заключенного между боковыми сторонами трапеции, если длины оснований
трапеции равны а и Ь,
17. В равнобедренную трапецию, длины оснований которой равны а и Ь,
вписана окружность. Определить длину диагонали трапеции.
18. Доказать, что во всякой трапеции сумма квадратов длин диагоналей
рпвна сумме квадратов длин непараллельных сторон и удвоенного про «ведения
длин оснований.
19. Найти длину основания равнобедренного треугольника, если длина
высоты, опущенной на основание, равна Л и радиус вписанной окружности
равен г.
20. Дан треугольник ABC. Точки М, N и Р лежа г на продолжениях сто-
стороны АВ за точку В, стороны ВС за точку С и стороны С А за точку А, при
этом \ВМ\ = т\АВ\; \CN \—п\ ВС |; \АР\—р\АС\. Найти отношение пло-
шздей треугольников MNP и ABC.
21. Точки М и N, D и Е, К a L лежат соответственно на сторонах АВ,
АС и ВС треугольника ABC, при этом ! AM | = | MN j = | NB ;; | В К | == | KL \ =
= | LC \; | AD \ = \ DE \— | ЕС ,. Вычислить площадь четырехугольника, образо-
образованного пересечениями прямых ML, NK, BD, BE, если площадь треуголь-
треугольника ABC равна S.
22. Точки М, N и Р лежат на сторонах АВ, ВС и АС треугольника ABC,
при этом ! АМ | : | MB = I BN \:\ NC \ = \СР \:\ РА \ = т: п. Определить отно-
отношение площадей треугольников MNP и ABC.
23. Из вершины А треугольника ABC проведены биссектрисы внутреннего
и внешнего углов, пересекающие прямую ВС в точках D и Е соответственно.
Определить отношение \АВ\/\АС\, если BD |/, BE | =3/5.
24. Из вершины А треугольника ABC проведены биссектрисы внутреннего
и внешнего углов, пересекающие прямую ВС в точках D и Е соотв:тственно.
Найти радиус окружности, описанной около треугольника ADE, если j BC\=a
и \АВ\/\ АС \=2/3.
343
25. Окружность, построенная на основании AD трапеции ABCD как на
диаметре, проходит через середины боковых сторон АВ и CD трапеции и
касается основания ВС. Найти углы трапеции.
26. Окружность радиуса R, проведенная через вершины At В и G прямо-
прямоугольной трапеции ABCD (Л=В=я/2), пересекает отрезки AD и CD соответ-
соответственно в точках М и N так, что | AM \l\AD\ = 'CN;. ! CD | = 1 i 3, Найти
площадь трапеции.
27. Из точки М проведены две прямые, касающиеся окружности в точках А
и J3. Из точки А проведена прямая, перпендикулярная диаметру BD и пересе-
пересекающая его в точке jV. Доказать, что прямая MD делит отрезок AN пополам.
28. В прямоугольном треугольнике длины катетов равны а и Ь (а < Ь).
Найти радиус окружности, проходящей_ через середину меньшего катета и касаю-
касающейся гипотенузы в ее середине.
29. В окружности даны две хорды: \AB\-~a и 'АС\=Ь, Длина дуги АС
вдвое больше длины дуги АВ. Найти радиус окружности.
30. Две касательные, проведенные из одной точки к окружности радиуса R,
Образуют угол 60°, Найти радиус окружности, которая вписана в угол, обра-
образованный этими касательными, и касается данной окружности.
31. В полуокружность радиуса R вписан квадрат так, что одна его сторона
лежит (на диаметре и две вершины--на окружности. Найти длину стороны
квадрата.
32. Из точки А проведены дне прямые, касающиеся окружности рядиуса R
в точках В и С. Треугольник ABC — правильный. Найти его площадь.
33. На боковой стороне АВ равнобедренного треугольника, как па диаметре,
построена окружность. Окружность пересекает основание АС в точке М и боко-
боковую сторону ВС в точке N. Найти длину отрезков MN и JVC, если \АС\—а
и \АВ\ = Ь,
34. Окружность радиуса R проходит через вершину А равнобедренного
треугольника ABC, касается основания ВС в точке В и пересекает боковую
сторону АС в точке D. Найти длину боковой стороны АВ, если i AD ;/ DC \ = k.
35. В треугольнике ABC длина высоты AD равна 2 V 2 см, длина высоты BE
равна 3 см. Высота СК в точке пересечения высот делится б отнолешш 5:1,
считая от вершины С, Найти площадь треугольника ABC.
36. Дан равнобедренный треугольник ABC ( АВ = ВС ,). На высоте BD,
как на диаметре, построена окружность. Через точки А и С проведены к этой
окружности касательные, которые пересекаются в точке 0. Найти отношение
\AB\-.\AC\, если , АО | l j AC j=3 : 2 и BD j < ; AC ;.
37. В равнобедренном треугольнике ABC (j AB\ — ]- ВС \ на высоте BD,
как на диаметре, построена окружность. Через точку А проведена прямая,
касающаяся окружности в точке М и пересекающая прямую BD в точке О.
Найти отношение j АВ \ I | АС ;, если j ОМ , : | АС ] — 2 и \AC\<\BD\.
38. Первая из двух окружностей проходит через ценгр второй и пересекает
ее в точках А и В. Касательная к первой окружности, проходящая через
точку А, Делит вторую окружность в отношении т:п (пкп). Найти, в каком
отношении вторая окружность делит первую.
39. В треугольнике ABC угол В прямой, медианы AD и BE взаимно пер-
перпендикулярны. Определить величину угла С.
344
40. Периметр прямоугольного треугольника ABC (С = я/2) равен 72 см,
а разность между длинами медианы СК и высоты СМ равна 7 см. Найти
площадь треугольника ABC.
41. Около прямоугольного треугольника ABC описана окружнось. Рас-
Расстояния от концов гипотенузы АВ до прямой, касающейся окружности в 'очке С,
соответственно равны т и п. Найти катеты АС и ВС.
42. Дан прямоугольный треугольник ABC с катетами |ЛС| = 3 см и
| ВС |=4 см. Через точку С проведена прямая, лежащая вне треугольника и
образующая с катетами углы, равные 45°. Найти радиус окружности, прохо-
проходящей через точки А, В и касающейся этой пряной.
43. Дан прямоугольный треугольник ABC. Окружность с цен:ром на
катете АС касается гипотенузы АВ и пересекает катет ВС в точке Р гак, что
\ВР |: | PC | = 2: 3. Найти отношение радиуса окружности к длине катгта ВС,
если | АС \: \ВС 1 = 4:5.
44. Пусть О—точка пересечения медиан треугольника ABC длини сторон
которого равны а, Ь, с. Доказать, что , ОА \* + \0В \2 + ,0С ;2 = у (а2-]- &2 + с2).
45. В окружность вписан треугольник ЛВС, через точку 0 пересечения его
медиан проведены порды AAlt BBlt CCV Доказать, что
lA0\ , |ВО| , |СО] _
[Afil^ \В,0\ T Idol
46. Две окружности радиусов R и г (R> г) имеют внешнее касание
в точке Л. Через точку В, взятую на большей окружности, проведена прямая,
касающаяся меньшей окружности в точке С, Найти длину отрезка ПС, если
длина хорды АВ равна а.
47. Около треугольника ABC описана окружность. Диаметр AD пересекает
сторону ВС в точке Е, прн этом \АЕ\ = \АС\ н | BE |/| СЕ | =3/2. Найти
отношение j D? j/i Л? !.
48. В равнобедренном треугольнике ABC (AB—BC) медианы /\D н СЕ
пересекаются в точке 0. Отношение радиуса окружности, впнеаннен в тре-
треугольник АОС, к радиусу окружности, вписанной в четырех угол ыпп: CDBE,
равно 2/3. Найти отношение | AC i/J ВС |.
49. Две окружности радиусов 5 см и 3 см внутренне касаюта. Хорд
большей окружности касается меньшей окрухшости и делится точкой касания
в отношении 3 : 1. Найти длину этой хорды.
50. Две окружности радиусов 5 см и 4 см касаются внешне. Прямая,
касающаяся меньшей окружности в точке А, пересекает большую окружность
в точках В и С так, что | АВ\ = \ ВС \. Найти длину отрезка АС.
51. Две окружности радиусов \^2 см и I см пересекаются в точк: А. Рас-
Расстояние между центрами окружностей равно 2 см. Хорда АС больше,г окруж-
окружности пересекает меньшую окружность в точке В и делится в этой точке пополам.
Найти длину этой хорды.
52. Две окружности внутренне касаются. Прямая, проходящая че;>сэ центр
большей окружности, пересекает ее в точках А и D, а меньшую окружность —
в точках В и С. Найти отношение радиусов окружностей, если | АВ \ : | ВС \:
:| CDj = 3:7:2.
345
53. В трапецнн ABCD боковая сторона ВС перпендикулярна основаниям
AD и ВС. Точка Е — середина стороны CD. Найти отношение \AD\-.\BC\,
если \АЕ\ = 2\АВ\ н прямая АЕ перпендикулярна прямой CD.
54. Треугольник ABC — правильный. На продолжении стороны АС за
точку А взята точка М, н около треугольников АВМ и МВС описаны окруж-
окружности. Точка А делит дугу МАВ в отношении МА : АВ =п. Найти, в каком
отношении точка С делит дугу МСВ.
55. Точка Е лежит на стороне АС правильного треугольника ABC, точка
К —середина отрезка АЕ. Прямая, проходящая через точку Е перпендику-
перпендикулярно АВ, и прямая, проходящая через точку С псрпердикулярно ВС, пере-
пересекаются в точке D. Найти углы треугольника BKD.
56. Окружность, вписанная в трапецию ABCD, касается боковой стороны АВ
в точке F. Найти площадь трапеции, если \ AF \=m, \FB\ = n, а длина мень-
меньшего основания трапеции ВС раина Ь.
57. Через вершины А и С треугольника ABC проведена окружность К,
центр которой лежит на окружности, описанной около треугольника ABC.
Окружность К пересекает продолжение стороны ВА (за точку А) в точке М.
Найти угол ВС А, если ; МА \ : ! АВ \ = 1: 5, a ABC = arcsin C/5).
58. Около окружности описана равнобедренная трапеция ABCD. Боковая
сторона АВ касается окружности в точке М, а основание AD — в точке N.
Отрезки MN и АС пересекаются в точке Р так, что \ N Р | : | РМ | =2. Найти
отношение A D \ : . ВС \.
59. В окружность вписана трапеция ABCD (AD — большее основание). Из
вершины С проведен перпендикуляр к AD, пересекающий окружности в точке Е.
Отношение длины дуги ВС (не содержащей точки D) к длине дуги CDE равно 1/2.
Радиус окружности равен высоте трапеции. Найти отношение \AB\:iBC\.
60. В треугольнике ABC перпендикуляр, проходящий через середину сто-
стороны АВ, пересекает прямую АС в точке М, а перпендикуляр, троходящий
через середину стороны АС, пересекает прямую АВ в точке N. Известно, что
! MN 1 = 1 ВС | и прямая MN перпендикулярна прямой ВС. Определить углы
треугольника ABC.
61. В равнобедренной трапеции ABCD величина угла при основании AD
равна а, длина боковой стороны АВ равна Ь. Окружность, касающаяся сто-
сторон АВ и AD и проходящая через вершину С. пересекает стороны ВС и CD
в точках М и N соответственно. Определить i ВМ ;, если | CN \/i ND | = 3.
62. В равнобедренной трапеции ABCD величина угла при основании AD
равна arcsin B4/25). Окружность радиуса R касается основания AD, боковой
стороны АВ и проходит через вершину С. Она отсекает па сторонах ВС
и CD конгруэнтные отрезки МС и NC соответственно. Найти длину
отрезка ВМ.
63. Площадь трапеции ABCD равна s, отношение оснований | AD \: \ ВС ' = 2.
Отрезок MN расположен так, что он параллелен диагонали BD, пересекает
диагональ АС, а отрезок AM параллелен отрезку CN. Определить площадь
четырехугольника AMND, если | CN | : | AM =3, BD | : J MN | =(> (найти все
решения).
64. В ромб ABCD вписана окружность. Прямая, касающаяся этой окруж-
окружности в точке Р, пересекает стороны АВ, ВС и продолжение стороны AD соот-
346
ветствежю в точках Л/, Q и М так, что ; MN \ : | NP !' ! PQ [=7 : 1 : 2. Опре-
Определить углы ромба.
65. Диагонали четырехугольника ABCD пересекаются в точке М, и угол
между ними равен а. Пусть Оъ 0.2, О3, О4 —центры окружностей, описанных
соответственно около треугольников ABM, ВСМ, CDM, DAM. Определить
отношение площадей четырехугольников ABCD и О^О^зО^
66. В четырехугольнике ABCD острый угол между диагоналями равен а.
Через каждую вершину проведена прямая, перпендикулярная диагонали, не
содержащей эту вершину. Определить отношение площади четырехугольника,
ограниченного этими прямыми, к площади четырехугольника ABCD.
67. В параллелограмме ABCD угол BAD равен а. Пусть О— произвольная
точка внутри параллелограмма, Оь О2, О3, 04 — точки, симметричные точке О
относительно прямых АВ, ВС, CD, AD соответственно. Определить отюшеиие
площади четырехугольника OjO.2O.-jO4 к площади параллелограмма.
68. В остроугольном равнобедренном треугольнике ABC величина угла при
основании АС равна о., а длина боковой стороны равна а. Точка М располо-
расположена на отрезке ВС и имеет наименьшую по сравнению с остальными точками
отрезка ВС сумму квадратов расстоянии до прямых АС и АВ, Найти длину
отрезка МС.
69. В трапеции длина меньшего основания равна длинам боковых сторон.
При каком угле при большем основании трапеция будет иметь наибольшую
площадь?
70. В равнобедренном треугольнике ABC величина угла при основ,шин АС
равна а, длина боковой стороны равна а. Через точку М, лежащую на боковой
стороне, проведены две прямые, параллельные сторонам треугольника, отрезаю-
отрезающие от треугольника ABC параллелограмм наибольшей возможной i лощади.
Найти площадь этого параллелограмма.
71. Дана окружность радиуса R с диаметром AD, Окружность с центром
в точке А пересекает первую окружность в точке В, а диаметр AD — в точке С,
При каком значении радиуса второй окружности длина отрезка ЕС будет
наибольшей?
72. Найти углы треугольника, в котором высота, биссектриса и медиана,
проведенные из одной вершины, делят угол на четыре конгруэнтные \тла,
Глава XIV
МНОЖЕСТВА ТОЧЕК НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ.
ЗАДАЧИ НА ПОСТРОЕНИЕ
§ 1. Множества точек, обладающих заданным свойством
В геометрии часто возникает потребность выделить из всех
точек плоскости или пространства те точки, которые обладают
некоторым специальным свойством. Все точки плоскости или
пространства разбиваются при этом на два множества: одно
множество включает в себя те и только те точки, которые обла-
обладают указанным свойством; другое множество состоит из всех
остальных точек, и следовательно, ни одна точка этого второго
множества не обладает рассматриваемым свойством. Каждая зада-
задача, связанная с нахождением того или иного множества точек,
обладающих некоторым свойством, неизбежно требует доказатель-
доказательства двух утверждений, двух теорем: прямой и противоположной.
Утверждая, например, что множеством точек плоскости, равно-
равноудаленных от двух заданных точек Лий, является прямая /,
перпендикулярная к отрезку АВ и проходящая через его середину,
необходимо доказать не только то, что каждая точка прямой I
равноудалена от точек А и В, но и то, что любая точка, не
принадлежащая прямой /, не находится на одинаковом расстоянии
от заданных точек. Непонимание этого простого обстоятельства
с неизбежностью приводит к ошибкам: к логической неполно-
неполноценности решения, а в ряде случаев —к неверному результату.
Замечание. Часто вместо доказательства прямой теоремы
(Vx) (А (х) => В (х) и противоположной (Ух/ А (х) =э В (х) доказы-
доказывают прямую и обратную (V*) В (х) => А (х). Законность такого
способа действий ьытекает из того, что из истинности обратной
теоремы (Ух) В (x)z=$ А (х) следует истинность противоположной
(Vx) А (х) ==> В (х) (см. § 3 главы II).
В задачах на отыскание множества точек, обладающих задан-
заданным свойством, обычно получаются точки, прямые, отрезки,
окружности или их дуги, многоугольники, круги, плоскости,
сферы. Формулировку задачи: «найти множество точек, обладающих
заданным свойством» следует понимать в таком смысле: перечис-
перечислить точки этого множества, если их конечное число, указать,
каким прямым, отрезкам, окружностям, дугам окружностей,
плоскостям, сферам принадлежат точки заданного множества.
348
Полезно знать множества точек на плоскости и в пространстве,
обладающие простейшими и наиболее часто встречающимися свой-
свойствами. Перечислим некоторые из таких множеств.
На плоскости:
а) Множеством точек, расстояние от которых до данноь точки
О равно R, является окружность радиуса R с центром в точке О
(рис. 185).
Pnc. 18G.
Рнс. 187.
б) Множеством точек, равноудаленных от двух данньк точек
А к В, является прямая, перпендикулярная к отрезку АВ и
проходящая через его середину (рис. 186).
в) Множеством точек, равноудаленных от двух данных пере-
пересекающихся прямых, является пара взаимно перпендикулярных
прямых, делящих пополам углы между данными
прямыми (рис. 187).
г) Множеством точек, равноудаленных от
трех заданных точек, не лежащих на одной пря-
прямой, является точка — центр окружности, прохо-
проходящей через данные точки (рис. 188).
д) Множеством точек, из которых данный
отрезок АВ виден под прямым углом, т. е.
множеством точек М, для которых АМВ = л/2,
является окружность с диаметром АВ без то-
точек А и В (рис. 189).
В пространстве:
а) Множеством точек, расстояние от кото-
которых до данной точки О равно R, является сфера
радиуса R с центром в точке О.
б) Множеством точек, равноудаленных от
двух данных точек А и В, является плоскость,
перпендикулярная отрезку АВ и проходящая через его сере-
середину.
в) Множеством точек, равноудаленных от двух данных пере-
пересекающихся плоскостей, является пара взаимно перпендикулярных
плоскостей, делящих пополам двугранные углы между данными
плоскостями.
г) Множеством точек, равноудаленных от трех заданных точек,
не лежащих на одной прямой, является прямая, проводящая
Рис, 189.
349
Рис. 190.
через центр окружности, проведенной через данные точки, и пер-
перпендикулярная плоскости, содержащей данные точки.
д) Множеством точек, из которых данный отрезок АВ виден
под прямым углом, т. е. множеством точек М, для которых
ЛМВ = я/2, является сфера с диаметром АВ без точек А и В.
Рассмотрим теперь несколько задач.
Задача 1, Найти множество точек, являющихся серединами
хорд, проведенных из одной точки данной окружности.
Д Пусть точка О —центр данной окружности, точка Л—точка
окружности (рис. 190), Докажем, что множеством середин всех
хорд окружности, проходящих через точ-
точку А, является окружность с диаметром АО,
за исключением точки А. Обозначим мно-
множество всех точек окружности с диамет-
диаметром АО, кроме точки А, буквой Г,
Пусть точка М обладает заданным
свойством, т. е. является серединой некото-
некоторой хорды, исходящей из точки А. Воз-
Возможны два случая. Если точка М— сере-
середина диаметра АА', то она совпадает с
точкой 0 и, следовательно, принадлежит
множеству Г. Если точка М— середина некоторой хорды АВ, не
совпадающей с диаметром А А', то соединим ее с точкой 0 и рас-
рассмотрим угол АМО. Так как точка М — середина хорды АВ,
то [АВ\ J_[0M\, т. е. угол АМО прямой, и поэтому точка М при-
принадлежит окружности с диаметром АО (с. 349, пункт д|).
Докажем обратное утверждение: если точка УИеГ, то она
является серединой некоторой хорды, исходящей из точки Л.
Опять рассмотрим два случая. Если течка М совпадает с точкой
О, то М— середина хорды АА'. Если М ф 0, то соединим точки
М и 0. Так как УИеГ, то угол
АМО прямой и, следовательно, точ-
точка М — середина хорды АВ. А
Задача 2. Найти множество
точек, являющихся серединами от-
отрезков, концы которых лежат на
разных сторонах данного угла (дан-
(данный угол меньше развернутого).
Д Очевидно, что никакая точка
плоскости, не принадлежащая дан-
данному углу ABC (рис. 191), не мо-
может быть серединой отрезка, концы
которого лежат на разных сторонах угла. Столь же оче-
очевидно, что в искомое множество не могут входить точки, распо-
расположенные на сторонах данного угла. С другой стороны, каждая
точка, лежащая внутри угла, является серединой некоторого
отрезка, концы которого расположены на сторонах угла. Докажем
в
Рис. 191
350
это. Пусть М — произвольная точка, лежащая внутри угла. Про-
Проведем через нее прямую параллельно стороне ВА угла ABC, и
пусть Р — точка пересечения этой прямой со стороной угла ВС.
Отложим на стороне ВС отрезок РК, конгруэнтный отрезку ВР.
Через точки К и М проведем
прямую. Отрезок РМ является
средней линией треугольника KBL,
т. е.точка М —середина построен-
построенного отрезка KL. а
Задача 3. На плоскости даны
две точки А и В. Найти множество
точек М этой плоскости таких,
что | AM | /\МВ | = 2.
Д Предположим сначала, что
точка М не лежит на прямой АВ.
Пусть М обладает заданным свой-
свойством; это означает, что \АМ\ = 2\МВ\. Продолжим отрезок AM
(рис. 192) и проведем биссектрисы углов АМВ и ВМА'.
Пусть УИХ —точка пересечения биссектрисы угла АМВ с отрез-
отрезком АВ, а Л12 —точка пересечения биссектрисы угла t'MA' с
продолжением отрезка АВ. По свойству биссектрисы внутреннего
угла треугольника (§ 1 гл. XIII) имеем
Рис. 192.
\AMt\
АМ\
MB
и по свойству биссектрисы внешнего угла треугольника
ча 20 раздела I главы XIII) можем записать
\АМо
(зада-
МгВ\
- ШИ. = 9
IMS
Отсюда следует, что расположение точек Мг и М2 на прямой
АВ не зависит от того, где находится точка М. Если заметить
теперь, что угол между биссектрисами ММг и ЛШ2 пршой, то
станет ясно, что если точка М принадлежит искомому множеству,
то отрезок МгМ2 виден из нее под прямым углом. А это означает
(с. 349, пункт д)), что точка М находится на окружности,
построенной на отрезке MiM2, как на диаметре.
Проведенное рассуждение теряет смысл в том случае, когда
точка М лежит на прямой АВ (в этом случае нельзя, например,
рассматривать угол АМВ и его биссектрису). Но на прямой АВ
найти точки М, удовлетворяющие условию задачи, легко. Эю,
очевидно, уже построенные нами точки Мг и М2. Точка М, делит
отрезок АВ (считая от точки А) в отношении 2:1. Точка Л1а
удалена от точки А на расстояние вдвое большее, чем от ' очки В.
Докажем теперь обратное утверждение: каждая точка М
окружности, построенной на отрезке М1Мг, как на диаметре,
обладает свойством |ЛМ| = 2|/Ш|, т. е. принадлежит искомому
множеству. Концы диаметра MtM2, т. е. точки Мг иМ,, очевидно,
351
обладают нужным свойством. Пусть М — любая другая точка
окружности с диаметром МгМ% (рис. 193). Проведем через точку
В прямую, параллельную прямой AM и пусть K^uL— точки
пересечения этой прямой с прямыми
ЛШ2 и ММг. Из подобия треуголь-
к \ ников АММ2 и BKMt получаем
\АМ\
>ВК\
\АМ.2\
I
1 = 2.
Из подобия треугольников АММг и
BLAf имеем
Рис. 193.
Из полученных равенств следует, что \ВК\ = \АМ\/2 и |BL| =
= | AM 1/2 т е |В/(| = !В?|. Таким образом, в прямоугольном
треугольнике KML отрезок ВМ является медианой и, следова-
следовательно, \ВМ\ = \ВК\. Учитывая, что \АМ\1\ВК\ = % получаем
\АМ \I\BM | = 2.
Итак, каждая точка окружности с диаметром МгМ2 обладает
заданным свойством. А
Задача 4. Найти множество точек, являющихся основаниями
перпендикуляров, опущенных из данной точки пространства на
прямые, лежащие в заданной плоско-
плоскости и пересекающиеся в одной точке,
д Обозначим через А данную точ-
точку пространства, через В—ее проек-
проекцию на данную плоскость, через С —
точку пересечения прямых. Рассмотрим
сначала случай, когда А, В, С— раз-
различные точки пространства (рис. 194).
Пусть точка М принадлежит иско-
искомому множеству. Это означает, что
[AM]J_(CM), но отсюда следует, что
и проекция MB наклонной AM на
данную плоскость перпендикулярна прямой СМ, т.е. угол СМВ —
прямой. Следовательно, точка М лежит на окружности с диамет-
диаметром ВС.
Докажем обратное утверждение. Пусть М — произвольная точка
окружности с диаметром ВС, не совпадающая с концами диамет-
диаметра-с точками В и С. Тогда угол СМВ опирается на диаметр.
Следовательно, этот угол прямой, поэтому [ВМ] _L (CM)-_ Но если
проекция ВМ наклонной AM перпендикулярна ^прямой СМ, то
и сама наклонная перпендикулярна этой прямой, т. г. [/Ш]_]_
J_(CM). Значит, действительно, точка М обладает заданным
свойством (является основанием перпендикуляра, опущенного из
точки А на некоторую прямую, проходящую через точку С и
лежащую в плоскости). Концы диаметра ВС также обладают
Рис. 194.
352
заданным свойством. В самом деле, точка В является основанием
перпендикуляра, опущенного из точки А на прямую СВ. Течка С
язляется основанием перпендикуляра, опущенного из точки А на
прямую, проходящую через точку С перпендикулярно отрезку СВ.
Отметим теперь два частных случая расположения точек
А, В, С.
Первый случай: точка А принадлежит заданной плоскости.
В этом случае точка А совпадает с точкой В. Легко видеть, что
и в этом случае, в качестве множества оснований перпендикуля-
перпендикуляров, опущенных из точки А = В на прямые, проходящие через
точку С, получается окружность с диаметром СВ. Но доказатель-
доказательство с этом случае упрощается, так как не придется ссыпаться
на теорему о трех перпендикулярах и ей обратную. Второй слу-
случай: точка С, через которую проводятся прямые, совпадает с
точкой В —проекцией точки А на заданную плоскость. И этом
случае очевидно, что иекомым множеством
является точка, а именно, точка С=В. а
Задача 5. Даны две скрещивающиеся
прямые 1г и /2. Найти множество точек,
являющихся серединами отрезков, концы I,
которых лежат соответственно на прямых
/х и 1г.
Д Обозначим через а и Р параллель-
параллельные плоскости, содержащие соответственно
прямые 1Х и /а, длину общего перпендику-
перпендикуляра KL обозначим через h (рис. 195). Рис. 195.
Пусть точка М принадлежит искомому мно-
множеству точек, это означает, что точка М является середиюн не-
некоторого отрезка АВ, концы которого —точки А и Б-лежат
соответственно на прямых 1г и /2.
Пусть точки Вх и Мг — проекции соответственно точек В и М
на плоскость а. Отрезок ММ1 является средней линией треуголь-
треугольника ABBV Так как \BB1\ = \KL\ = h, то ММг\^к/2. Таким
образом, если точка принадлежит искомому множеству, то она
находится на одинаковом расстоянии от плоскостей а и (\ т. е.
лежит в плоскости, перпендикулярной к отрезку KL и проходя-
проходящей через его середину.
Докажем обратное утверждение: каждая точка М плоскости,
перпендикулярной отрезку KL и проходящей через его середину,
является серединой некоторого отрезка, концы которого лежат
на прямых /, и l.v Проектируем точку М на плоскость а полу-
получаем точку Мг. Через точку /Их проводим отрезок АЗУ так чтобы
концы отрезка —точки А и В1 — лежали на разных сторонгх угла
ВгКЛ и точка М1 делила бы отрезок АВ1 пополам. Как это
сделать, показано в решении задачи 2. Проектируем теперь точку
Вх на плоскость р1, получаем точку В и соединяем ее с точкой А.
Отрезок АВ будет содержать точку М. Предположив противное,
легко получим, что точка М не находится на одинаковом
12 п/ред. Г. Н, Яковлева
расстоянии от плоскостей о и 0, что противоречит исходному пред-
предположению. Из подобия треугольников АМХМ и АВгВ вытекает,
что \АМ\ = \МВ{. а
§ 2. Применение метода координат
Для нахождения множества точек плоскости, обладающих
заданным свойством, во многих случаях можно использовать метод
координат. В простейших задачах в качестве искомых множеств
получаются прямые, окружности, отрезки, дуги окружностей.
Применяя метод координат, можно получить их уравнения. Ис-
Исследуя эти уравнения, можно узнать, что представляют собой
сами множества.
Применение метода заключается в следующем. На плоскости
выбираем некоторым образом систему кооодинат и пытаемся,
прежде всего, установить, какому уравнению удовлетворяют ко-
координаты точки М (х; у), если эта точка обладает заданным
свойством. Затем обязательно проверяем, будет ли каждая точка
М (х; у), координаты которой удовлетворяют найденному уравне-
уравнению, обладать заданным свойством. Проделав все это, мы тем
самым получим уравнение, которому
удовлетворяют координаты тех и
только тех точек плоскости, которые
принадлежат искомому множеству.
По найденному уравнению определя-
определяем, что представляет собой искомое
множество.
Задача 1. Решить методом коор-
координат задачу 3 из § 1.
Д Выберем систему координат.
Начало координат поместим в точку
А (рис. 196), аа ссь абсцисс возь-
возьмем прямую (АВ), и пусть точка В в нашей системе дмеет коор-
координаты {Ь; 0), где b — длина отрезка АВ.
Пуоь точка М (х; у) обладает заданным свойством, т. е.
\АМ\/\МВ\ = 2. (!)
Рис. 196.
Так как \ АМ\ = У х2 + у2 и | MB | = ]/ (х — ЬJ
точки М удовлетворяют уравнению
то координаты
Преобразуем его следующим образом:
B)
354
Мы получили уравнение окружности радиуса R = -^-b с центром
ч b; Or Таким образом, доказано, что если точка
М(х; у) обладает заданным свойством A), то она лежгг на
окружности B).
Докажем обратное утверждение. Пусть точка М (х; у) лежит
на полученной окружности. Это означает, что ее координаты
удовлетворяют уравнению B), которое равносильно (как это видно
из уже проделанных выкладок) условию A). Следовательно, точка
М (х; у) обладает заданным свойством.
2
Итак, искомое множество —окружность радиуса R = -s b
i 4
с центром в точке С „ Ь; О
Задача 2. Концы отрезка длины а скользят по двум стс ронам
данного прямсго угла. Какую линию описывает середина отэезка?
Д Поместим начало координат в
вершину угла, оси направим по сто-
сторонам угла (рис. 197).
Пусть точка М (х\ у) обладает в(о;2ф.
заданным свойством, т. е. является
серединой отрезка длины а, концы ко-
которого принадлежат сторонам угла.
Очевидно, что точка М (х; у) может
находиться только в первом квадранте Рис. 197.
координатной плоскости, поэтому х5-О
и г/5*0. Обозначим концы отрезка через А и В. Легко шдеть,
что если М(х; у) — середина отрезка АВ, то точки А и В имеют
координаты: А Bх; 0), В @; 2у). По теореме Пифагора из тре-
треугольника АОВ получаем
Но по условию задачи \АВ\=а и, следовательно, координаты
точки М удовлетворяют уравнению
Таким образом, доказано, что точка М (х; у) принадлежит дуге
окружности
расположенной в первом квадранте: a'S^O, </5s0.
Докажем обратное утверждение. Пусть точка М (х; у) г ринад-
лежит дуге окружности радиуса R = a/2 с центром в начала
координат, расположенной в первом квадранте. Соединим точку
М(х; у) с точкой АBх; 0). Продолжим отрезок AM до пересече-
пересечения с осью ординат в точке В. Абсцисса точки В, очевидно, равна
нулю; ордината равна 2у. Следовательно, точка М (х; #) —середина
12* 355
отрезка АВ. Концы этого отрезка принадлежат сторонам угла.
Покажем, что длина этого отрезка равна а. Найдем его длину
по теореме Пифагора:
но ио предположению точка М (х; у) лежит на дуге окружности,
уравнение которой х2 -f у2 = (а/2J, и поэтому \АВ\ — а. Таким
образом, доказано, что если точка М принадлежит д^ге окруж-
окружности радиуса R = a/2 с центром в начале координат, располо-
расположенной в первом квадранте, то она является серединой некоторого
отрезка длины а, концы которого принадлежат сторонам данного
прямого угла. ^
§ 3. Задачи на построение
В задачах на построение требуется построить некоторую гео-
геометрическую фигуру (точку, прямую, окружность, треугольник)
с помощью тех или иных чертежных инструментов: линейки,
циркуля, угольника и других. Чаще всего встречаются задачи,
в которых разрешается использовать два инструмента: линейку и
циркуль. В этом параграфе; рассматриваются только такие задачи.
Под линейкой подразумевается инструмент, с помощью кото-
которого можно построить произвольную прямую, в частности прямую,
проходящую через две данные точки. Линейка считается безмас-
безмасштабной и односторонней. Безмасштабность означает, что на
линейке отсутствуют деления, и поэтому с ее помощью нельзя
откладывать отрезки, Односторонность линейки означает, что
нельзя использовать одновременно оба ее края, т, е. что с помощью
такой линейки нельзя, например, провести две параллельные
прямые, С помощью циркуля можно на данной прямой отложить
любой данный отрезок, можно провести произвольную окружность
или окружность, радиус которой равен длине заданного отрезка.
Не следует думать, что главное в задачах на построение —факти-
—фактическое выполнение построения с использованием названных ин-
инструментов, Главнее заключается в том, чтобы найти и описать
последовательность действий, ведущих к построению нужной
фигуры; доказать, что построенная фигура удовлетворяет всем
условиям задачи; выяснить, всегда ли построение можно осуще-
осуществить; сколько существует решений, нет ли частных случаев,
в которых построение упрощается, усложняется или делается
невозможным.
Напомним несколько простейших построений, которые будут
использоваться в дальнейшем в качестве отдельных составных
шагов при решении более сложных задач.
Построение 1. Построить прямую, перпендикулярную
к данному отрезку АВ и проходящую через его середину.
Д Проводим окружности радиуса г>\АВ\/2 с центрами
в точках А и В (рис. 198), Получаем точки С и Ci —точки пере-
356
сечения ' окружностей. Через С и Сх ироводим прямую, <оторая
является искомой, а
Замечание. Построение 1 используется также н для целения
отрезка пополам. Точка О —точка пересечения отрезка АВ е пря-
прямой CCi — является серединой отрезка АВ.
Построение 2. Построить точку, симметричную данной
точке М относительно данной прямой 1{Мф1).
Д Проводим окружность с центром М и радиусом, большим
расстояния от М до / (рис. 199). Из точек Л и В пересечения
А
Рис. 193.
окружности с прямой /, как из центров, проводим окружности
радиуса г—-\АМ\. Точка N пересечения этих окружностей явля-
является искомой. А.
Построение 3. Построить перпендикуляр к Данюй пря-
прямой /, проходящий через данную точку М.
Д Возможны два случая: а) М ф I, б) М е /. В первое случае
построим точку Лг, симметричную точке М относительно трямой /
(построение 2). Проведем через М и N прямую. Прямая MN
является искомой.
Во втором случае проводим произвольную окружносп с цент-
центром в точке Л1. Отмечаем точки А и В пересечения окружности
с прямой I. Проводим две окружности с центрами в точках А
и В, радиус которых г = \АВ\. Ис-
Искомая прямая проходит через точки
пересечения этих окружностей. А
Построение 4. Построить пря-
прямую, проходящую через данную точ-
точку М и параллельную данной прямой
N
М
О
А
Рис. 20С.
В
)
Д Выбираем на прямой / две точ-
точки А и В (рис. 200). Строим точку О —
середину отрезка AM (построение 1), а затем точку N—точку, сим-
симметричную точке В относительно центра О. Прямая MN — ис-
искомая. ^
Построение 5. Даны два отрезка, длины которых равны
аи b: Построить отрезок, длина которого равна 'Yah.
357
Д Проведем произвольную прямую, выберем на ней некоторую
точку А и отложим от нее на этой прямой отрезок AN, длина
которого равна а (рис. 201). Затем от точки N на той же прямой
отложим отрезок NB, длина которого равна Ъ. Находим середину О
отрезка АВ (построение 1). Проводим окружность радиуса г~
= j OA | с центром в точке О. Строим прямую, перпендикулярную
отрезку АВ и проходящую через точку N (построение 3). Отме-
Отмечаем одну из точек (точку С) пересечения
прямой и окружности. Отрезок CN — иско-
мый, так как
Рис. 201.
Построение 6. Построить окружность,
проходящую через три данные точки А, В,
С, не лежащие на одной прямой.
Д Проводим прямую /, перпендикуляр-
перпендикулярную отрезку АВ и проходящую через его
середину (построение 1). Проводим прямую р, перпендикулярную
отрезку АС и проходящую через его середину. Точка О--1(]р есть
центр искомой окружности. Проводим окружность с центром в теч-
течке О радиуса R = \OA\. Эта окружность—искомая, д
Рассмотрим несколько задач.
Задача 1. Построить окружность, проходящую через две
данные точки и касающуюся данной прямой.
Д Пусть А и В—данные точки, / — данная прямая. Очевидно,
что задача не имеет решения, если точки А и В расположены
по разные стороны от прямой
/. Столь же очевидно, что пег
решения и в том случае, когда
обе точки лежат на прямой /.
Пусть точки А и В нахо-
находятся по одну сторону от пря-
прямой /. Предположим, что задача
решена, т. е. искомая окруж-
ность построена. Обозначим че-
через Р точку касания окружно-
окружности и прямой /, через М — точку пересечения прямых (АВ) и I
(рис. 202). По теореме о касательной и секущей, проведенных из
одной точки к окружности (глава XIII § 3), будем иметь
\МР\2 = \МВ\\МА\ или \МР\ = У\МВ\\МА~\.
Теперь становится понятно, как провести построение. Проводим
прямую АВ. Отмечаем точку М = (АВ)(]1. По известным отрезкам
МА и MB строим отрезок, длина которого равна ]/|МВ|(М.4|
(построение 5). Откладываем этот отрезок на прямой / or точки М
в обе стороны. Получаем точки Р и Р'. Проводим окружности
через точки А, В, Р и через точки А, В, Р' (построение 6).
Задача имеет два решения.
"с
358
Легко видеть, что описанное построение не возможно и двух
случаях:
а) прямая АВ параллельна прямой /,
б) одна из данных точек лежит на прямой I.
Оказывается, что и в этих частных случаях задача имеет
решение.
В случае а) (рис. 203) проводим прямую р, перпендикулярную
отрезку АВ и проходящую через его середину (построение 1).
Через течку Р = р(]1 и точки А и В проводим искомую окруж-
окружность (построение 6). Задача имеет одно решение.
Рис. 203.
В случае б) (рис. 204) проводим прямую р, перпендикулярную
отрезку АВ и проходящую через его середину. Затем через точку А
проводим прямую q, перпендикулярную прямой / (построение 3).
Точка O = p(]q является центром искомой скружнести. Задача
имеет одно решение, д
Одним из методов решения задач на псстроенке являете:! метод
множеств, обладающих заданным свойством. Этот метод особенно
удобен, когда требуется псстроить течку (или точки), удовлетво-
удовлетворяющую нескольким условиям, или когда задача сводите! к та-
такому построению. Проиллюстрируем этот метод на следующей
задаче.
Задача 2. Построить окружность данного радиуса г, прохо-
проходящую через две данные течки.
Д Задача сводится к построению точки —центра окру;кности.
Отбросим условие о том, что радиус скружнести ревен г. Пусть
окружность имеет произвольный радиус, но проходит через две
заданные точки А и В. Тогда множество центров всех таких
окружностей будет представлять собей прямую, перпендикулярную
хорде АВ и проходящую через сергдину отрезка АВ. Не будем
теперь принимать во внимание требование о прохождении окруж-
окружности через точку В. Пусть окружность проходит только через
точку А и имеет данный ридиус г. Центры всех таких окружностей
лежат, очевидно, на окружности радиуса г с центром в точке А.
Таким образом, центр искомой окружности, во-первых, лежит
на прямой, перпендикулярной к отрезку АВ и проходящей через
его середину, и, во-вторых, принадлежит окружности рааиуса г
с центром в точке А, т. е. находится на пересечении прямой и
окружности (на рис. 205 они показаны пунктиром). Но прямая
359.
и окружность могут не пересекаться (рис. 205, о), могут иметь
одну общую точку (рис. 205, б), могут иметь две общие точки
(рис. 205, в).
Теперь можно сформулировать окончательный результат:
а) если г<-<г\АВ\, построение невозможно, задача не имеет
решений;
б) если г^-«\АВ\, соединяем точки А и В, делим отрезок АВ
пополам, проводим окружность радиуса г с центром в середине
отрезка АВ; задача имеет одно решение;
Рис. 205.
в) если г>-л-\АВ\, соединяем течки А и В, строим прямую,
перпендикулярную к отрезку АВ в его середине, радиусом г про-
проводим окружность с центром в течке А; получаем две точки Oi
и О2- пересечения построенных прямой и окружности; проводим
две искомые окружности радиуса г с центрами в течках Oi и О.{,
задача имеет два решения. ^
Другим распространенным методом решения задач на построе-
построение является метод подобия. Во многих задачах часто бывает
удобнее сначала построить фигуру, подобную искомой. Для этого
часть требований, предъявляемых к фигуре, отбрасывается, так
что остающимся условиям удовлетворяет бесчисленное множество
фигур, подобных искомой. Из этого множества подобных фигур
выделяется затем та фигура, которая удовлетворяет всем требова-
требованиям задачи. В этом и заключается идея метода.
Задача 3. Дан острый угол M0N и внутри него точка А.
Построить треугольник, одна вершина которого находится а точке А,
а две другие В и С —на сторонах ОМ и ON данного угла, причем
[ВС]±\ОМ)п\АС\ = \ВС\.
2\ Проведем луч О А (рис. 206). Ослабим условия задачи, не
будем требовать, чтобы вершина треугольника находилась и точке А,
потребуем лишь, чтобы она лежала на луче ОА.
36Q
м
В этой ослабленной формулировке задача легко решается.
Возьмем на луче ON произвольную точку D и опустим « нее
перпендикуляр DE на прямую ОМ, затем из точки D о шшем
окружность радиуса R = \DE\, которая пересечет луч ОА ? двух
точках К и L. Соединив каждую из этих точек с течками D и Е,
получим два треугольника DKE и DLE, которые удовлетворяют
всем условиям задачи в ослабленной формулировке. Точка D
выбиралась на луче ON про-
произвольно, и, следовательно,
можно построить сколько
угодно треугольников, подоб-
подобных треугольнику DKE, и
сколько угодно треугольни-
треугольников, подобных треугольнику
DLE. Проведем теперь через
точку А прямые, параллель-
параллельные отрезкам KD и КЕ; они
пересекут стороны угла в Pic. 20(f.
вершинах С и В искомого
треугольника. Аналогично получим второе решение: треугольник
АВ'С. Задача всегда имеет два и только два решения, а
Остановимся в заключение на методе симметрии. } ]ногда
удается существенно упростить задачу, заменив один из заданных
элементов (точку, прямую, окружность) другим, симметрично
расположенным относительно не- Л
которой прямой. Классическим при-
примером такой задачи является сле-
следующая:
Задача 4. Даны две точки,
расположенные по одну сторону
от данной прямой. Найти на пря-
прямой точку, сумма расстояний от
которой до двух заданных точек
наименьшая.
Д Рассмотрим точку Alt сим-
симметричную данной точке А отно-
относительно данной прямой (рис. 207), и пусть точка М-¦ произ-
произвольная точка этой прямой. Тогда, так как |ЛМ| = |.4М|, то
Рис. 207.
Следовательно, сумма |ЛМЦ-|ВМ| будет наименьшей, если
будет наименьшей сумма | А±М Ц- \ВМ |. Но последняя сумма,
очевидно, будет достигать своего наименьшего значения тогда,
когда точка М будет лежать на прямой ВАХ (на нашем рисунке
будет совпадать с точкой Р). Отсюда вытекает следующее построе-
построение: строим точку, симметричную одной из заданны), точек
относительно заданной прямой, проводим через нее и другую
361
заданную точку прямую; точка пересечения построенной прямой и
данной является искомой. Очевидно, что задача всегда имеет
одно н только одно решение.
ЗАДАЧИ РАЗДЕЛА I
1. Дан треугольник ABC. Найти множество точек М, расположенных
в плоскости треугольника и таких, что площади треугольников АМВ и ВМС
равны.
2. Дан треугольник ABC, В плоскости этого треугольники найти множество
точек М таких, что сумма площадей треугольников АМВ и АМС равна
3. Даны отрезок АВ и на нем точка С. Найти множество точек пересечения
двух конгруэнтных окружностей, одна из которых проходит через точки А и С,
другая—через точки С и В.
4. Точки А, В, С лежат на одной прямой (точка В располсжена между
точками А и С). Через точки А и В проподятся окружности н черзз точку С—
касательные к ним. Найти множество точек касания.
5. Найти множество точек плоскости, абсолютная величина разности квад-
квадратов расстояний которых до двух заданных точек этой плоскости постоянна
и равна «> 0.
6. Найти множество точек плоскости, сумма квадратов расстояний которых
от двух данных точек плоскости равна квадрату расстояния до третьей точки
плоскости.
7. Найти множество точек пространства, являющихся основаниями перпен-
перпендикуляров, проведенных через данную точку пространства к плоскостям, про-
проходящим через данную прямую (данная точка не лежит на данной прямой).
8. Даны трехгранный угол и точки А и В, лежащие на двух разных
ребрах трехгранного угла. Найти множество точек пересечения медиан треуголь-
треугольников ABC, где С —произвольная точка третьего ребра.
9. Отрезок не имеет общих точек с плоскостью и не параллелен ей. Через
концы отрезка проводятся сферы, касающиеся плоскости. Найти множество
точек касания.
10. Найти множество точек пространства, через которые нельзя провести
прямую, пересекающую две данные скрещивающиеся прямые.
11. На сторонах АВ и ВС остроугольного треугольника ABC построить
соответственно точки D и Е так, чтобы J AD i = ] DE \ = \ ЕС !.
12. Два пункта А и В расположены по разные стороны прямолинейного
канала, ширина которого постоянна. Где надо построить мост, чтобы путь от
одного пункта в другой был кратчайшим?
13. По разные стороны от прямой / даны точки А и В. Найти на прямой
точку С такую, чтобы разность \ АС \ — \ ВС \ была наибольшем (расстояние от
точки А до прямой I больше расстояния от точки В до прямой /).
14. Даны острый угол АОВ и две точки М и N внутри него. Как направить
луч света из точки М, чтобы он, отразившись сначала от стороны АО, а затем
от стороны ВО, прошел через точку N?
15. Даны угол и точка вне его. Провести через эту точку прямую, отсе-
отсекающую от угла треугольник данного периметра 2р,
362
ЗАДАЧИ РАЗДЕЛА II
1. Дана окружность и точка внутри ее. Найти множество середин хорд
окружности, проходящих через данную точку.
2. Найти множество середин отрезков, соединяющих данную точку лежа-
лежащую вне дайной окружности, с точками этой окружности.
3. На плоскости даны точки А и В. Начти множество проекций тзчки А
на прямые, лежащие в плоскости и проходящие через точку В.
4. На плоскости даны точки А и В. Найти множество точек плсскости,
симметричных точке А относительно прямых, лежащих в плоскости и п юходя-
щих через точку В.
5. Дан прямой угол с вершиной в точке О. Пусть ОМ — произвольная
ломаная длины I, каждог звено которой параллельно одно:! из стороч углл.
Найти множество точек М, лежащих внутри угла или на сторонах угла.
6. Прямоугольный треугольник перемещается в плоскости так, что В'-.ршпчы
его острых углов скользят но двум взаимно перпендикулярным прямым. Какую
фигуру образуют вершины прямого угла этого треугольника?
7. На окружности даны две неподвижные точки А и В. Точки С и Я
перемещаются по окружности так, что расстояние между ними не изменяется.
Доказать, что точка пересечения прямых АС и BD движется при зтоы но
некоторой окружности, проходящей через точки А и В.
8. Найти множество точек плоскости, сумма квадратов расстояний которых
до двух данных точек А и В этой плоскости равна s > 0.
9. Даны прямая и на ней точки А и В. Найти множество точек <асашщ
окружностей, одна из которых касается данной прямой в точке А, другая —
в точке В.
10. Найти множество центров прямоугольников, вписанных в данный тре-
треугольник так, что две вершины прямоугольника лежат на основании треуголь-
треугольника, а две другие вершины — на боковых сторонах,
11. На плоскости а даны три попарно пересекающиеся прямые, не прохо-
проходящие через одну точку. Найти множество точек плоскости а, равноотстоящих
от данных прямых,
12. Даны отрезок АВ и на нем точка С. Найти множество точек А таких,
что
13. Найти множество точек, сумма квадратов расстояний которых до вершин
острых углов равнобедренного прямоугольного треугольника вдвое больше
квадрата расстояния до вершины прямого угла,
14. Дан квадрат со стороной в. Найти множество точек, лежащи:; в пло-
плоскости квадрата а таиих, что сумма расстояний от каждой из которых до
прямых, содержащих стороны квадрата, равна 4а.
15. Найти множество точек пространства, равноотстоящих от всех вершин
равнобедренной трапеции,
16. Найти множество точек пространства, равноотстоящих от трех попарно
пересекающихся плоскостей, не проходящих через одну и ту же прямую и
перпендикулярных некоторой плоскости а.
17. Найти множество точек, симметричных данной точке А относительно
точек данной прямой /,
363
18. Найти множество точек пространства, симметричных данной точке А
относительно прямых, параллельных данной прямой I.
19. Найти множество точек пространства, симметричных данной точке А
отЕгосительно плоскостей, проходящих через данную прямую I,
20. Найти множество точек пространства, симметричных данной точке А
относительно прямых, проходящих через другую данную точку В
21. Найти множество точек пространства, симметричных данной точке А
относительно плоскостей, проходящих через другую данную точку В.
22. Даны шар и прямая, не имеющие общих точек, Найти множество
центров сечений шара плоскостями, проходящими через данную прямую.
23. Найти множество точех пространства, из которых к данной сфере
радиуса R можно провести три попарно перпендикулярные касательные.
24. Концы отрезка длины а скользят по двум взаимно перпендикулярным
прямым lt и 12. Какую линию описывает середина отрезка?
25. Трапецию пересечь прямой, параллельной основаниям, так, чтобы
отрезок, заключенный мажду бокозыми сторонами трапеции, дел*лея диагона-
диагоналями на три конгруэнтные части.
26. Через точку пересечения двух окружностей провести прямую так, чтобы
отрезок ее, заключенный внутри окружностей, имел данную длину а.
27. Даны две точки и окружность. Провести через данные точки две
секущие, хорды которых внутри данной окружности были бы конгруэнтны
и пересекались бы под данным углом а.
28. Построить окружность, касающуюся двух данных окружностей, причем
одной из них в данной точке.
29. Через две данные точки провести окружность, делящуюся данной
окружностью на две конгруэнтные дуги.
30. Вписать в равносторонний треугольник другой равносторонний тре-
треугольник, стороны которого были бы перпендикулярны к сторонам данного
треугольника.
31. Дана окружность и на ней три точки. Вписать в эту окружность тро-
угольник так, чтебы его биссектрисы при продолжении проходили чер-?з
данные точки.
32. Дана окружность и на ней три точки. Вписать в эту окружность тре-
треугольник так, чтобы продолжения высоты, биссектрисы и медианы, исходящих
из одной и той же вершины треугольника, пересекали окружность в данных
точках,
33» Даны центры окружностей, вневписанных в треугольник. Построить
треугольник.
Указание. Окружность называется вневписанной в треугольник, если она
касается одной стороны треугольника и продолжений двух других сторон
треугольника.
34. Даны центры вписанной, вневписанной и описанной окружностей.
Построить треугольник,
35.. Даны три параллельны? прямые. Построить квадрат, три вершины
которого лежали бы на трех данных прямых.
36. В данный треугольник вписать квадрат (на одной стороне треугольника
должны лежать две вершины квадрата, на двух других сторонах —по одной
вершине).
364
57. Построить квадрат по заданной вершине и двум точкам, которые лежат
на двух сторонах квадрата, не проходящих через данную вершину.
38. Построить параллелограмм по заданным Диагоналям dx и d2 и острому
углу а.
39. Б данную окружность вписать трапецию, зная высоту трапеции h
н разность d оснований трапеции.
40. На одной из сторон острого угла взяты две точки А и В. Найти на
другой стороне угла точку С такую, чтобы величина угла АСВ была наибольшей.
41. На плоскости длны три параллельные прямые. Отрезок АВ п?рпендн-
кулярен этим прямым, а кс;;бы его лежат на первых двух прямых. Найти на
третьей прямой точку С такую, чтобы величина угла АСВ была наибольшей.
42. Даны угол и внутри него точка М. Построить треугольник наимень-
наименьшего периметра, одна вершина которого находится в точке М, а две другие
лежат на разных сторонах данного угла.
43. Даны угол и внутри него точка М. Провести через точку М прямую
так, чтобы сумма длин отрезков, отсекаемых прямой на сторонах упа, была
наименьшей.
44- Через поле идет прямая дорога. Пешеход может передвигаться по
дороге со скоростью, не превышающей 6 км/ч, и по полю со скоростью, не
превышающей 3 км/час. Где пешеход может оказаться через час, если j началь-
начальный момент он находится на дороге?
Глава XV
СТЕРЕОМЕТРИЯ (ЧАСТЬ I)
§ 1. Сечения многогранников
Сечения многогранников плоскостью используются при реше-
решении многих стереометрических задач. В этом параграфе разобраны
некоторые способы построения сечений. Рассмотрены сечения пло-
плоскостями, проходящими через данные точку и прямую, через три
данные точки, а также сечения, способ задания которых содержит
условие параллельности сечения данной плоскости, данной прямей
или двум данным прямым. Примеры построения сечения плоскос-
плоскостями, перпендикулярными данной прямой или плоскости, приве-
приведены в гл. XVI.
На рис. 208—213 изображены некоторые сечения тетраэдра
и параллелепипеда. На ряс. 208 сечение проведено через ребро
АВ и точку М ребра CD, на рис. 209 —через вершину D и точки
М и Л' на ребрах АВ и ВС; на рис. 210 —через вершину С
Рис. 208.
Рис. 210.
и точки М и N ъ гранях ACD и АСВ. В каждом из этих слу-
случаев построение сечения основано на простом следствии :лз аксиом
стереометрии:
если две плоскости имеют две общие точки, то прямая, про-
проведенная через эти точки, является линией пересечения данных
плоскостей.
Например, на рис. 210 точки Р = (CM) f\[AD] и Q = (CN)(][AB]
принадлежат и плоскости сечения и грани ADB, поэтому отрезок
PQ — сторона сечения.
366
На рис. 211 показано сечение тетраэдра плоскостью, проходя-
проходящей через точку М ребра АВ параллельно грани ACL. Здесь
построение сечения основано на том., что
если две параллельные плоскости пересечены третьей плоскостью,
то линии пересечения параллельны.
Обозначим секущую плоскость а. Плоскость ABD пересекает
параллельные плоскости а и ACD. Пересечение плоскостей ABD
и ACD — прямая AD, значит, линия пересечения плоскостзй ABD
и а параллельна прямой AD. Проводим че-
через точку М прямую, параллельную прямой
AD, и в пересечении ее с ребром BD нахо-
находим вершину Р сечения. Отрезок МР — сто-
сторона сечения. Аналогично строям сторону MN,
[MN]\\[AC]. Отрезок ЯЛ? —третья сторона
сечения, [РЛ/]|| [DC]. Сечение —треугольник
MNP, гомотетичный треугольнику ACD.
Коэффициент гомотетии равен отношению
\ВМ\:\ВА\.
На рис. 212 представлено сечение парал-
параллелепипеда плоскостью, проведенной через
точку М ребра ССх параллельно плоскости грани ABCD. Построе-
Построение сечения основано на таких же рассуждениях, что и i преды-
предыдущем случае. Здесь [MN]\\[CD], [NP]\\[DA], [PQ)\\[AB],
\QM] || [ВС]. В то же время |MN]|| IQP], так как эти отрззки ле-
лежат на линиях пересечения двух параллельных плоскостей
AAiBxB и DD^iC с плоскостью сечения. Аналогично [РN\ \\ [QM].
Сечелие — параллелограмм, конгруэнтный грани ABCD.
Рис. 2 П.
Рис. 212.
Рис. 213.
На рис 213 изображено сечение параллелепипеда плоскостью,
проходящей через ребро ЛЛХ и точку М ребра CD. Здесь
[MMi]|| [ЛЛх], MiM^lli^TW], так как параллельны плоскости
граней, в которых лежат эти стороны сечения. Сечение — парал-
параллелограмм AAiMiM.
Задача 1. Длина ребра куба равна а (рис. 214, а). Найти
площадь сечения, проведенного через диагональ АБг грани AA±D\D
и середину М ребра ВВу.
Д Обозначим секущую плоскость а. Отрезки ADX и 4Л1 при-
принадлежат и плоскости а и граням куба, поэтому являются сторо-
сторонами сечения. Построим сторону сечения в грани BBiCiC. Плос-
367
костк ВВуСуС и AAiDyD параллельны, поэтому линия пересече-
пересечения плоскостей а и ВВ^С^С параллельна прямой ЛОХ. Поскольку
прямые SCi и AD\ параллельны, эта линия пересечения парал-
параллельна и прямой SCi- Проводим через точку М в плоскости
ВВ^СуС прямую, параллельную прямой BCt, ее пересечение с реб-
ребром SiC, дает веошину сечения (см. рис. 214, б). Сечение —тра-
—трапеция AMNDlt [Af JV] || [/4Dil
Рис. 214.
Найдем длины сторон этой трапеции. Имеем \ AD] \ — а
отрезок MN — средняя линия в треугольнике fiZ^CY поэтому
MN | = 2 \BCi\ = 4=. В прямоугольных треугольниках АВМ и
5Л1 j =
| = а/2) находим | ЛЛ1
~i!*bl-jk
D1C1N (\AB\ = \CiPi_\ = a,
=» | D[Af i = a]/5/2. Значит, трапеция ЛМЛ^О! равнобедренная.
Найдем ее высоту (рис. 214, б). Опускаем перпендикуляры МР и
NQ на основание ЛОЬ получаем j PQ \ = \ MN j = a/]/2, jDiQ| =
= -^W-- В прямоугольном треуголь-
пике DiQiV(|DiAr| = a"|//2, | DiQ | = a/2"|/) находим
= Зо/2|Л2. Определяем площадь сечения
Ответ: 9a2/8. a
На рис. 215 показано построение сечения тетраэдра пло-
плоскостью, проходящей через точки М, N, Р на ребрах тетраэдра.
Точки М и N заданы так, что прямые MN и АС не парал-
параллельны. Отрезки MN и NP являются сторонамя сечения
(рис. 215, а). Точка Р —общая для плоскостей MNP и ABC.
Вторую общую точку находим в пересечении прямых MN и АС,
S — (MN) П (АС) (ркс. 215,6). Прямая SP — линия пересечения
плоскостей MNP и ABC. Пересечение этой прямой с ребром АВ
дает вершину Q сечения, Q = (SP)(][AB]. Сечение—четырехуголь-
Сечение—четырехугольник MNPQ.
Задача 2. Определить вид сечения куба плоскостью, прове-
проведенной через середины ребер АВ, AAlt AiDi (рис. 216, а), и
найти площадь сечения, если ребро куба имеет длину а.
368
Д Обозначим секущую плоскость а. Отрезки MN и МР при-
принадлежат и плоскости а и граням куба, поэтому являются сто-
сторонами сечения (рнс. 216, а).
Строим точки SL и S2 пересечения прямой NP, принадлежащей
плоскости а, с прямыми AD и DDX (ркс. 216, б). Прямая S±M —
линия пересечения плоскостей а и A BCD. Находим точки пере-
пересечения прямой S1;M с ребром ВС (точка S3 на рис. :?16, б) и
с прямой CD (точка S4). Точки S2 и S4 —общие для плоскостей а
и CdDiD, прямая S2Si — линия пересечения этих плоскостей.
Находим точки пересечения прямой S2S4 с ребрами CCi и
CiDy (S5 и Se). Сечение—шестиугольник PNMS3SbSu.
Заметим, что противоположные стороны сечения параллельны,
так как лежат на [линиях пересечения плоскости а с попарно
параллельными плоскостями граней.
N
A
'A
i i
7
Докажем, что вершины Sa, S5, 5Й сечения являются середи-
серединами ребер, на которых они лежат. Отрезок NP — средшгя линия
в треугольнике AAiDu поэтому (NP)\\(ADi) (рис. 217) Анало-
Аналогично имеем (M^KBAj), а так как (BAX)\(CDX), то (MN)\(CDX).
Таким образом, плоскость а сечения параллельна плоскоси ADXC.
Отсюда следует, что и линии пересечения этих плоскостей с гра-
3,69
нями куба параллельны, т. е. [УИ53]|[^4С], [S5Se]|[CDi]. Точно
так же доказываем, что а \\ {ВАХСЛ) ((MN) \\ (ВЛХ), (NP) 1 (AD{) || E^)),
откуда получаем [S3S5]||[BC]], [Se^JJIAA]. Теперь из того, что
\ВМ\ = \МА\, применив три раза теорему Фалеса, получим
|fiS3j = |S3C|, |CS8| = |S8Ci!, jC1Sei = |SeD1l. Значит, точки S3,
S5, Se—-середины ребер, на которых они лежат.
Из доказанного следует, что длина каждой стороны сечения
равна а/У~2. Докажем еще, что каждый угол сечения имеет ве-
величину 120°. Рассмотрим треугольник SXMN. Легко установить,
что этот треугольник правильный. Действительно, из конгруэнт-
конгруэнтности треугольников SiAN и PAXN (по катету и острому углу)
имеем \SiA \ = \РА1\ = а/2. Тогда \S1N\='
А,
==aj\/. Учитывая, что и \MN\-
= а/)/~2, видим, что треугольник
SiMN правильный, а значит, SXMN =
==5,ЛШ = 60°. Отсюда следует, что
6'3Л1..v =MNP = 120°. Рассмотрев тре-
треугольники S3SbSb и S6S',P, получим
аналогично, что и остальные углы се-
сечения имеют величину 120°.
Таким образом, сечение — правиль-
правильный шестиугольник со стороной а/У2.
Его площадь равна C|ЛЗ/4)а2.
Ответ: Сечение — правильный шестиугольник, площадь его
равна C У3;4)а2. а
На рис. 218 показано построение сечения тетраэдра пло-
плоскостью, параллельной ребру АС и проходящей через точку М
ребра CD и точку .V в грани ABD. Построение основано на сле-
следующей теореме.
Рис. 217.
1)
Рис. 219.
Если плоскость и проходит, через прямую, параллельную другой
плоскости, и пересекает эту плоскость, то линия пересечения пло-
плоскостей параллельна данной прямой.
370
Обозначим плоскость сечения а. Плоскость ACD имеет с пло-
плоскостью а общую точку М и содержит прямую АС, параллель-
параллельную плоскости а. Следовательно, линия пересечения этих плоско-
плоскостей проходит через точку М параллельно прямой АС. В соот-
соответствии с этим построена сторона MSr сечения (рис. 218, б),
[MSi]\[AC]. Проведя прямую S^1, найдем вторую сторону сече-
сечения— S1S2. На рис. 218 течка N дана так, что точка S2 принад-
принадлежит ребру АВ. Плоскость ABC также содержит прямую АС,
параллельную плоскости сечения. Поэтому сторона сечения S:S3
проведена параллельно ребру АС (рис. 218, в). Отрезок S3M —
четвертая сторона сечения. Сечение MSiS-2Sa — трапеция
(j"J/HSi]||fi4C]|[S2S3]). В зависимости от расположения точки N от-
относительно отрезка /3Si сечение
может быть и треугольником
(рис. 219).
Задача 3. Построить сечение
треугольной призмы плоскостью,
проходящей через точки Ai и С
(рис. 220, а) параллельно пря-
прямой ВСг. Определить, в каком
отношении эта плоскость делит
ребро АВ.
Д Плоскость сечения обозна-
обозначим а. Линия пересечения пло-
плоскостей а и BBiCiC проходит че-
через точку С параллельно прямой
ВСХ (рис. 220, б), ее точку пере-
пересечения с прямой ВВХ обозначим
Sx. Точка Sj — общая для плоско-
плоскостей а и AAJi\B. Еще одна об-
общая точка А1 дана в условии.
Построив прямую AiSi, найдем
вершину S2 сечения. Сечение —
треугольник AiCS2.
О | 4S1 I SZB !
Рис. 220.
^4S21
AS2\
Из подобия треугсльников
j AA^ \: | BSX |." Так как
[ВС^Ц^С]), то BSL =
\ AS | S-2B | —
получаем \ AS2 j
у
Определим отношение I
A{AS2 и SiBS2 имеем | AS2\: j s,B
SiSC. С -параллелограмм [Jf]
== ! С,С j. Учитывая, что и | AAV \ = J СХС |
— 1 : 1. А
Задача 4. На ребре АВ тетраэдра расположена гочка Л1
так, что \АМ\:\АВ\ = 1, 0<1<1 (рис. 221, а). Построить се-
сечение тетраэдра плоскостью, проходящей через точку М и парал-
параллельной ребрам AD и ВС. При каком X это сечение будет ром-
ромбом, если \AD\:\BC\ = m?
/\ Секущую плоскость обозначим а. Линия пересечения этой
плоскости с плоскостью ABD параллельна прямой AD ({AD)\a).
Проводим [M/V]||[.4D] (рис. 221,6), Линии пересечения плоско-
плоскостей ВСА и BCD с плоскостью а параллелы.'ы прямой ВС
371
ЦВС) (а). Строим [MQ]||[BC| и [NP]l[BC]. Четвертая сторона се-
чения PQ параллельна ребру AD. Сечение — параллелограмм
MNPQ ([MN]i[AD]\\[PQ], [NP]\\[BC]\\[MQ]).
Выразим длины сторон параллелограмма MNPQ через длины
ребер AD и ВС. Из подобия треугольников AMQ и ABC имеем
j MQ \:\BC = AM | : АВ\ = 1, откуда
]MQ| = A,|BC|. Теперь находим \ВМ\ =
= \АВ\-\АМ\ = {\-Ц\АВ\, и из подо-
подобия треугольников BMN и BAD получаем
\ MN |: | AD | = | ВМ \: \ В А \ = 1 — \, т. е.
| MN \ = A — X) | AD\. Подставляя в равен-
равенство ! MN | = [ MQ | полученные выражения,
будем иметь A — к) \ AD j = X | ВС |, откуда
. _ 1.4D 1 _ от
~~ | ВС | + | AD ~ от+Г
Ответ: Сечение будет ромбом при Я=
()
Замечание. Если противоположные
ребра AD и ВС тетраэдра перпендику-
перпендикулярны, то параллельные им стороны MN
и MQ сечения также перпендикулярны.
В этом случае сечение— прямоугольник, а
при Х = тЦт-\-1) — квадрат. В частности,
если тетраэдр ABCD правильный, то сечение, проведенное через
середину ребра АВ параллельно ребрам ВС и AD, квадрат
(см. задачу 2 § 4 этой главы).
В рассмотренных до сих пор примерах, для того чтобы найти
сечение многогранника, выполнялись построения в плоскостях
a) S) г)
Рис. 222.
граней этого многогранника (или только в гранях). В некоторых
задачах для нахождения сечения приходится ряд построений про-
проводить вне плоскостей граней.
Разберем, например, построение сечения тетраэдра ABCD пло-
плоскостью MNP, где точки М, N и Р расположены соответственно
372
на ребре AD, в грани BCD и в грани ABC тетраэдра, как ука-
указано на рис. 222, а, причем (MN)%(ABCj. Здесь данные таковы,
что для каждой грани тетраэдра известна только одна общая
точка с плоскостью сечения ММР. Для того чтобы построить
линию пересечения плоскости какой-либо грани с плоскостью
MNP, необходимо найти еще одну общую точку для этих плоско-
плоскостей. Рассмотрим плоскость ABC. Точка Р — общая для плоско-
плоскостей ABC и ММР. Второй общей точкой является точка пересе-
пересечения прямой ММ с плоскостью ABC ((MN)-^(ABC)). Как по-
построить эту точку? (рис. 222, б, для
сравнения обратитесь к рис. 215, б).
Рис. 222, в содержит ответ на этот воп-
вопрос. Через точки М, N и вершину D
тетраэдра проводим плоскость, строим
ее линию пересечения Л5Х с плоско-
плоскостью ABC. Общая точка S2 прямых ММ
и ASx и является точкой пересечения
прямо» ММ с плоскостью ABC. Пря-
Прямая PS2 — линия пересечения плоско-
плоскостей MNP и ABC. Дальнейшее пост- Рис. 223.
роение сечения не вызывает затруд-
затруднений. Вершины 53 и 5.1 (рис. 223) находим как точки пере-
пересечения прямой PS2 с ребрами ВС и АВ, пересечение прямой
<Ь\А/ с ребром CD дает вершину S-a- Сечение — четырехугольник
S5
t-1,
На рис. 224, а —в показано построение сечения тетраэдра по
трем точкам: М — в грани ABC, N— в грани BCD и Р-—в грани
ACD ((MM)%(ACD)). Для нахождения точки пересечение прямой
ММ с плоскостью ACD проведена вспомогательная плоскость через
эту прямую и вершину В тетраэдра (рис. 224, б). Прямая 5ii 2 — пере-
пересечение этой плоскости с плоскостью ACD. Точка S3 = (MN) f\ (Si52)
является точкой пересечения прямой ММ с плоскостыэ ACD.
373
Дальнейшие построения (рис. 224, в) проводятся так же, как и
в предыдущем случае.
В двух последних примерах для построения точки пер'гсечения
прямой MN с плоскостью грани тетраэдра (грани ABC на рис. 222, в,
грани ACD на рис. 224, 6) была проведена вспомогательная плос-
плоскость через эту прямую и одну из вершин тетраэдра ((MDN) —
рис. 222, в, (MBN) — рис. 224, б). Такой же прием для нахож-
нахождения точки пересечения прямой и плоскости л?ожно использо-
использовать и в других случаях. В пирамиде, и в частности, в тетраэдре
вспомогательную плоскость часто удобно проводить через дан-
данную прямую и через вершину; в призме, и в том числе, :з парал-
параллелепипеде — через данную прямую параллельно боковым реб-
ребрам.
Задача 5. Построить сечение параллелепипеда плоскостью,
проходящей через середины М и N ребер AD и ВВг и точку Р
пересечения диагоналей грани А&Сфх (рис. 225, а). Определить,
в каком отношении плоскость сечения делит ребро АВ.
Д Построение сечения показано на рис. 225, б —г. Обозначим
секущую плоскость a, a = (MNP). Вначале находим точку пере-
пересечения прямой NP с плоскостью AAiDtD. Эта прямая лежит
в плоскости BBxDxD, пересекающей плоскость AA^DJ) по пря-
прямой DDi. Точка Sx пересечения прямых NP и DDX (рис. 225, б)—
искомая. Аналогично находим точку S2 пересечения прямой NP
с плоскостью ABCD, 52 = (Л/Р) ПфВ). Плоскость а пе:ресекает
плоскость AAxDJ) по прямой SXM, а плоскость ABCD — по пря-
прямой S2M. Находим две вершины сечения: S3 = (StM) f] [Di^liJ и
S4= (StM) П[АВ] (рис. 225, е). Точка S3 = (S3P) [ЦВА]- послед-
последняя вершина сечения. Заметим, что прямые S5N и S^vl пересе-
пересекают прямую ВС в одной и
той же точке S8 = (ВС) f] a.
Пятиугольник MS3S5NSi —
искомое сечение (рис. 225, г).
Стороны S3Sa и М84, а также
5
Рис. 225.
ребра
Р
следует, что \BSs
рр )
кз Р — центр симметрии параллелограмма
Sl Таким образом, (#Se f = j А^
\S
MS3 и SbN сечении парал-
параллельны, так как лекат в па-
параллельных гранях.
Найдем отношение | AS4 |:
:|S4Bj. Из подобия треуголь-
треугольников MASi и S8?!S4 (рис.
225, е) икееы | AS* |: | BS, | =
= \AM\:\BSt\. Из конгру-
конгруэнтности треугольников BSCN
и BLS&N (точка N — середина
= \BiSb\. Далее, поскольку тон-
" TolBiSsf^
Учитывая еще, что
Pl (
\AM\ = \DM\, получаем \ASi\
бия треугольников DSiМ и
f j |
BSi\ = \DM\:\D1S3\. Из подо-
подо^^ имеем | DM |: | О^ \
374
= \DS1\:\D1S1\, а из конгруэнтности треугольников S^P и
NBP (рис. 225, б) (по стороне и прилежащим углам) следует,
что \DiS1\ = \B1N \. Учитывая, что
1
и, значит, \DSl\ = -~\DD1\. Отсюда
DM \
= \DSl\:\D1S1l = 3:1,
получаем
последовательно имеем
IS4 \:\BSt\ = \DM\: j L\S3 j = 3:
Ответ: Ребро АВ разделено в отношении 3:1, считая от вер-
вершины А. А
Задача 6. На ребрах ААг и ССг параллелгпипеда
(рис. 226, а) расположены соответственно точки М и N гак, что
I = т, ! CN j : | Cd.
Построить сечение пагаллеле-
Рис
гшпеда плоскостью, прохо-
проходящей через точки М и N
параллельно диагонали BD
основания. Определить, в
каком отношении эта пло-
плоскость делит ребро ВВХ.
Д Ранее уже были рас-
рассмотрены примеры построе-
построения сечения, параллельного
дайной прямой (рис. 218 —
220). Данная задача от-
отличается от этих приме-
примеров тем, что ни одна из точек М и N сечения не лежит в пло-
плоскости грани ABCD, где расположена прямая BD, параллельная
сечению. Стороны сечения, выходящие из вершин М и N, не бу-
будут параллельны прямой BD, так как она пересекает грани, в
которых лежат эти стороны.
Обозначим плоскость сечения а;. Прямая BD расположена
в плоскости BlBxDiD (рис. 226, б), следовательно, плоскости а и
fiSiDiD пересекаются по прямой, параллельной BD. П(строим
точку пересечения прямой MN, лежащей в плоскости а, с пло-
плоскостью BBxDjD. Плоскость AA^iC, содержащая прямуо MN,
пересекает плоскость BBtDiD по прямой Od, параллельно! боко-
боковым ребрам параллелепипеда. Общая точка Е прямых MN и OOL
и есть точка пересечения прямой MN с плоскостью BBiDiD.
Теперь через точку Е в плоскости BB±DiD проводим прямую,
параллельную прямой BD, и находим ее точки пересечен.!я Р и
Q с ребрами ВВГ и DDV соответственно (рис. 226, е). Прямая PQ
есть пересечение плоскостей а и BBiDiD, следовательно, тэчки Р
и Q являются вершинами сечения. Сечение —параллелограмм
MPNQ, [MQ]\\[PN], [MP]\[QN\.
Найдем отношение | ВР \: j РВг |. Имеем \ВР\ = \ОЕ\, поскольку
ВОЕР — параллелограмм, отрезок ОЕ-средняя линия в трапеции
AMNC, значит,
\ = ~^-(\AM\
). Отсюда, учитывая, что
375
\AM\ = m\AA1\, |C/V| = n|CCi|, а
чаем | ВЛ | = \ ОЕ | = ^±L^. | ввх |.
Далее
, полу-
находим | />Bi | =
"
Ответ: Ребро Bfii разделено в отношении " —, считая
.Z — ttl — ft
от вершины В. а
Замечание. В задаче 6 вместо плоскости BBJ)iD можно
было бы взять и другую плоскость, например плоскость грани
ABCD. Соответствующие построения показаны на рис. 227 (Si =
= (MN)(](AC), (SoS3)\\(BD)).
Рис. 227.
Задача 7. На диагонали АВ± грани АВВ^ треугольной
призмы (рис. 228, а) расположена точка М так, что | AM |: | МВХ \ =
= 5:4. Построить сечение призмы плоскостью, проходящей через
точку М и параллельной диагоналям AtC и Bd двух других
граней. Определить, в каком отношении эта плоскость делит
ребро ССх.
Д В задаче 4 уже был рассмотрен пример построения сечения,
проходящего через данную точку параллельно двум данным пря-
прямым. Эта задача отличается от задачи 4 тем, что ни одна из пря-
прямых АгС и SCi, параллельных сечению, не лежит в плоскости
грани ABBiAi, где дана точка М сечения. Каждая из этих пря-
прямых пересекает плоскость ABBiA^ Поэтому нельзя сразу начать
от точки М построение сечения, как это делалось в задаче 4.
В таких случаях бывает полезно построить сначала некоторое
вспомогательное сечение, параллельное данным прямым.
Проведем плоскость через прямую AiC параллельно прямой
Ж?! (рис. 223, б, (CSi)||(CiB), см. т?,кже задачу 3, рис. 220),
треугольник AiS2C — сечение призмы этой плоскостью. Плоскость
искомого сечения обозначим а. Эта плоскость параллельна пере-
пересекающимся прямым АгС и CSi плоскости A^Si, поэтому а || (AiCSi).
Отсюда следует, что стороны искомого сечения параллельны сто-
сторонам сечения Л^С, лежащим в тех же или параллельных гра-
гранях. Теперь, исходя из этого, можно построить сечение. Через
точку М проводим прямую, параллельную прямой Л^, и нахо-
376
дим ее точки пересечения 53, 54 с ребрами (рис. 228, в), затем
как а || SCij),
сечение (отме-
(отметим, что |S,S,J|||a;,S7]).
Найдем отношение | CS6 \: \ 56Ci J. Рассмотрим грань АА^В-.В
(рис. 228, в). Из подобия треугольников Л54М и В^УИ имеем
р
строим стороны [S4S5] || [S2CL [555е] II [BCi] (так
[5e5,]|| [Cv4i]. Пятиугольник S3S4S5SaS7 — искомое
[SSJ [SS])
|/*S4|:|Bb«
тывая.что|
I
| = ] AM
tM | = 5:4.
a\AxS3 =
Обозначим
\АВ\
• = *. Учи-
УчиАВ , I ВД
| S2Sfi | и : Л^! | = | ЛВ |, имеем
л:)|ЛВ|. Получаем уразненне
. — х) = 5/4, из которого находим д: = 1/3. значит,
152541 = 3- j АВ |, откуда jS4B | = | S.2B | - |ЗД
ку [S455] || [52С], то | С55 ]; | S5B | = | S2S41: |;
что [SBS6] || [BCi], следует, что \CSR\:\SeC
= ^ ! АВ \. Посколь-
ПоскольРебро
' j = 2, а из того,
= |С56!:|55,3| = 2.
разделено в отношении 2:1, считая )т вер-
Ответ:
шины С. А
Рассмотрение примеров построения сечений завершим своего
рода «нотацией».
Как только плоскость сечения задана (тремя точками, двумя точ-
точками и параллельной сечению прямой и т. д.), так расположение
вершин сечения на ребрах многогранника, его сторон в граня:с опре-
определяется однозначно. Появиться они должны в результат* обос-
обоснованного построения, размещение их «приблизительно», «i а гла-
глазок» недопустимо. Практика приемных экзаменов показывает, что
напомнить это, в общем-то, очевидное требование не лишне.
В заключение этого параграфа покажем на при-
примерах, как используются сечения в задачах о парал-
параллельных прямых и плоскостях.
Задача 8. На диагоналях АВ± и ВС± граней
куба ABCDAiBiCiDi расположены соответственно
точки М и N так, что отрезок MN параллелен грани
ABCD. Найти отношения | AM \: | АВг \ и | BN |: |ВСГ\,
если | MN | : | АВ \ = У~5/3.
Д Пусть согласно условию (МЛ') || (ABCD). Че-
Через точку М проведем в грани AAxBJi прямую 5г52
(рис. 229), параллельную прямой АВ. Плоскость, определяемая
прямыми MN и SiS2, параллельна плоскости ABCD. Сечение;
куба этой плоскостью — квадрат S]52SaS4, конгруэнтны! гра-
грани ABCD.
Ри
Обозначим
ников MBiS2
— | B]S<j | : | BiB
AM\:\ABl\ = x, |
и ABiB имеем
. Учитывая, что
, I = *!??, I. Из
АВ\=а.
МВ1\
= A-х)
|
подобия
Из подобия трсуголь-
АВг\ = \ MS21: | АВ | ='
АВ1\, попуча^м
v\\ RR q I Ч Q I
— Xf]\ DD\ , 3 | JJ2 | =
треугольников В52Л/,
377
и ВВА имеем | S2N |: |Bi | |
Отсюда следует, что | S2N \=--ха и \BN
|| = |B52|
\ВСх\ = \АМ\
АВ1
В прямоугольном треугольнике MS2N имеем \MN\ —
Рис. 230.
= A — x) a, | S2M | = xa, следовательно, по теореме Пифагора
-' ф = A — xf a2 -j- x°-a2, 9x* - 9x + 2 = 0. Корни этого уравнения
У
суть *i = 2/3, х-2 = 1 /3. Таким образом, возможны
дза положения отрезка MN, удовлетворяющие
условию задачи. Первому соответствует рис. 229,
второму— рис. 230.
Ответ: | AM |: , АВХ \ = \ BN \: \ ВСХ | ==2/3 или
AM\:\ABl\-^\BN\:\BC1\ =1/3. А
Замечание. При решении этой задачи ча-
рез прямую MN была проведена плоскость, парал-
параллельная плоскости ABCD. Имеет место следующая
теорема:
через прямую, параллельную данной плоскости, можно провести
и притом только одну плоскость, параллельную данной.
Ц Для доказательства через какую-либо точку данной прямой
проведем вторую прямую, параллельную данной плоскости. Эти
две прямые и определяют пло-
плоскость, параллельную данной.
Единственность следует из того,
что через точку можно провести
только одну плоскость, парал-
параллельную данной плоскости. Щ
Задача 9. Точки М и N —
середины ребер AD к ВВХ па-
параллелепипеда (рис. 231, а),
j MN | = а, диагонали грани
j4ifiiCjDi пересекаются в точке Р. Прямая, проходящая через
точку Р параллельно прямой MN, пересекает плоскость AAJD^D
в точке Q. Найти длину отрезка PQ.
Для решения этой задачи можно использовать сечение парал-
параллелепипеда плоскостью MNP. А именно, построить линию пере-
пересечения плоскостей MNP и АА^^В, найти на ней точку Q, и т. д.
^построения указаны на рис. 231,6). Иногда в подобных задачах
о параллельных прямых и плоскостях удается избежать каких-либо
построений. Например, для решения этой задачи воспользуемся
двумя простыми теоремами:
1) отрезки параллельных прямых, заключенные между двумя
различными параллельными плоскостями, имеют равные длины;
2) если две пересекающиеся в точке 0 прямые пересечены двумя
параллельными плоскостями в точках А и Alt В и Вх соответст-
соответственно, то \АО\/\ОА1\ = \ВО\/\ОВ1\. Доказательства этих теорем
легко восстановить по рис. 232, 233.
Решим данную задачу.
Рис. 231.
378
Д Пусть R — точка пересечения прямой PQ с плос <остью
BBjCiC. Согласно первой из указанных теорем, отрезки QR и MN
параллельных прямых, заключенные между параллельным! плос*
костями AA^D н ВВ^хС, имеют равные длины, т. е. \QR\ —
= [MN \ = a. Отрезки QR и
заключенные между тчми же
Рис. 232.
Рис. 233.
т.
параллельными плсскостямп, пересекаются в точке
\Р | : | PBi |=1. Тогда согласно второй теореме и ] QP |
е. \QP\ = \PR =о/2. Ответ: а/2. А
В этом решении вообще не требуется
никакого рисунка.
Замечание. В дополнение к теоре-
теоремам 1) и 2) укажем еще одну теорему:
если прямые а и b пересечены тремя
параллельными плоскостями в точках АЛ,
Р, фичем
Р = 1,
А2
и Вх, В2, В., соответственно, то
IA^I/I^ihj^j/iai
Доказательство можно найти, исходя
из рис. 234. Прямые а и Ь могут быть
параллельными, пересекающимися или рИс. 234.
скрещивающимися. Используя это утвер-
утверждение, в задаче 8 (рис. 229) можно было сразу утверждать,
что \BN[:\ Bd\ = | AM |: | ABl |.
§ 2. Применение критериев коллинеарности
и компланарности векторов в решении задач
Критерии коллинеарности и компланарности (гл. VI) векторов
служат основой для применения векторной алгебры в решении
стереометрических задач. Они позволяют выразить в виде ьектор-
ных равенств различные утверждения о расположении точег, пря-
прямых и плоскостей в пространстве. Переход от векторных р; венств
к скалярным происходит на основе единственности разле жения
вектора по двум неколли неарным или трем пекомпланарньм век-
векторам. Проиллюстрируем это рядом примеров.
1°. Для того чтобы три различные точки А, В, С лежали
на одной прямой, необходимо и достаточно, чтобы вектооы А В
и АС были коллинеарны, т. е. чтобы существовало число Я такое,
что
379
Доказательство этого утверждения сразу вытекает :та опреде-
определения колликеарных векторов и из того, что векторы АВ и АС
отложены от одной точки А (рис. 235).
Задача 1. В параллелепипеде (рис. 236) через середину М
ребра ВС проведена прямая, пересекающая прямые АС^ и DDt
соответственно в точках А^ и Р. Нгйти отношение | МЛ' |: | NP \.
Д Три не компланарных вектора АВ, AD и ААх обозначим
для краткости соответственно а, Ь, с. Остальные векторы будем
раскладывать по этим трем.
Точка N лежит на прямой АС\, поэтому вектор NA колли-
неарен ненулевому вектору AClt т. е. N А=хАСъ Для вектора
ACi имеем разложение АС, —а-\-Ь-\-с, значит, ЛМ = х [а + Ь-|-с).
Р
Рнс. 235.
Рис. 23G.
Вектор NM является суммой векторов N А, АВ и ВМ: NM =
— NA~\-AB + BM. Подставляя сюда разложение вектора NA
и учитывая, что АВ = а, ВМ = ^- ВС =-9- AD —-~-bt получаем
АШ =
b +хс.
, Вектор DP коллинеарен вектору DD^, a DDt =¦¦ с, поэтому
DP = ус. Теперь из того, что N~P = AVI + AD -\- DP, находим
Согласно сформулированному выше утверждению ].°, для того
чтобы точки М, N и Р лежали на одной прямой, необходимо
и достаточно, чтобы имело место векторное равенство
Подставляя сюда разложения векторов NM и NP, получаем
380
Эго векторное равенство в силу единственности разложения рав-
равносильно системе трех скалярных:
х=к
Решив эту систему, найдем К = —1/2, х = —2/3, у = 2. Таким
образом, NM = — ~N~P, откуда I NM | = ~ \NP\.
Ответ: 1 : 2. ^
2°. Пусть А1 и Л2 — различные точки прямой а, В± и В, — раз-
различные точки прямой Ь.
Для того чтобы прямые а и b были параллельны, необходимо
и достаточно, чтобы векторы А^А2 и ВЛВ\ были коллииеарны,
т. е. чтобы существовало пшког число Я, что
Доказательство этого утверждения сразу следует из определе-
определения коллинеарных векторов и из того, что отрезок A1A? лежит
на прямой о, а отрезок BiB2 — на прямой Ь (рис. 237).
Рис. 238.
Задача 2. ABCDAXBXCXD^ — параллелепипед, АС и Dd —
диагонали его граней. Доказать, что существует и притом
единственная пара точек М е (АС) и JV e (DCi) такг я, что
(MN) || (BDi). Найти отношение | MN |: | BDt |.
Д Пусть М—точка прямой ЛС, а // — точка прямой C]D
(рис. 238). Для параллельности прямых ЛШ и BD± согласно
утверждению 2° необходимо и достаточно, чтобы существовало
такое число К, что
~ A)
Найдем разложения векторов MN и BDX по векторам (ГД_ СЁ
и CCi, которые обозначим соответственно а, Ь, с. Имеем BDX =
= B~C + CC1 + C'1Di. Здесь BC = — CB = — b, C^bx^^ZD^a,
поэтому
Ж B)
381
Вектор MN представим в виде суммы: MN = MC-{-CCi-{-C1N.
Здесь вектор МС коллинеарен вектору С А, поэтому МС = хСА.
Но СА = а + Ь, значит, МС = ха + хЬ. Вектор^ СгЫ коллинеарен
вектору C\D, a C1D = a — c, значит, C\N = yC1D = ya — yc. Отсюда
находим
~ b + (l-y)c. C)
Подставляя разложения B) и C) в A), получаем
(x-{-y)a + xh + (l—y)c = Xa — Xh
Это векторное равенство равносильно система
Решив эту систему, найдем Я =1/3, х — —1/3, // = 2/3. Значит,
существует и притом единственное положение точек М и N, при
котором (MN)\\(BDl). Это положение задается найденными зна-
ченикми х и у: СМ =—хСА = -^СА, CiN = ^-CiD. При этом
= BDJ3, и значит, | MN \ = \ BDX [/3. Ответ: 1/3. А
В двух предыдущих задачах от векторного равенства, выра-
выражающего геометрическое содержание задачи, совершался переход
к равносильной ему системе трех скалярных уравнений и реша-
решалась эта система. Подчеркнем, что векторное равенство равносильно
именно системе уравнений. Если даже для ответа требуется зна-
значение лишь одного из неизвестных (и рассмот-
рассмотренных задачах это X), нельзя ограничиваться
нахождением только этого значения. Следует
проверить, что полученная система имеет ре-
решение. Случается и так, что значение одного
неизвестного может быть найдено, а система
Рис 239. и вместе с ней задача решения не имеют.
3°. Для того чтобы различные точки А,
В, С и D лежали в одной плоскости, необхо-
необходима и достаточно, чтобы секторы АВ, АС, ЛЬ были компла-
компланарны, т. е. чтобы существовали такие числа а к р, что
Доказательство вытекает из определения компланарных век-
векторов и из того, что векторы АВ, АС и AD (а значит, и векторы
аАВ и РЛС) отложены от одной точки А (рис. 239).
382
Задача 3. Через концы трех ребер параллелепипеда,
дящих из одной вершины, проведена плоскость. Опре
в каком отношении она делит диагональ параллелепипеда,
дящую из той же вершины.
Д Возьмем произвольную вершину параллелепипеда, обо
ее А, остальные вершины обозначим, как показано на рп
Пусть М — точка прямой АС\. Для того
чтобы точки Л], В, D, М лежали в од-
одной плоскости, необходимо и достаточно,
чтобы векторы АуВ, Аф и А\М были
компланарны, т. е. чтобы существовали
числа аир такие, что
A\M = a.AlB-\-$AJ)- D)
Обозначим ~АВ = a, AD = b, AAi=--c.
Разложим Еекторы в D) по этим трем
векторам. Имеем А\В = а — с, A JJ =
= & — с. Далее, ЛГМ —- А~[А + АМ. Здесь _^
АТА = — с, а вектор AM коллинеарен вектору АСи т. е.
— x-ACi = x(a + b + c). Значит, А%М = xa + xb + (х— 1)с
ставляя найденные разложения в D), получаем
выхо-
выхоелить,
выхо-
выхозначим
:. 240.
Рис. 240.
ЛМ =
. Под-
Под— (a-|- P) с,
откуда
Решив систему, получим х= 1/3, а= 1/3, р= 1/3. Таким образом,
AM = ЛС]/3, т. е. плоскость BDA\ отсекает треть AHaronaj и Ad,
считая от вершины А. Отсюда | AM \: \ MCi | = 1 : 2.
Ответ: 1 :2. А
Из D) получим еще АгМ = ^(А~В-\-AiD). Это означает, что
М— точка пересечения медиан треугольника BAXD. Ины ш сло-
словами, диагональ АС\ пересекает треугольник BAiD вточ!<е пере-
пересечения его медиан.
Задачу 3 можно решить еще проще, используя сечения. Сде-
Сделайте это самостоятельно.
4°. Пусть а и Ъ различные прямые, Аг и Л2 —точки прямой
а, А±фА±, В] и В2 — точки прямой Ь, ВгФВ*.
Для того чтобы прямые а и b пересекались, необхсдимо и
достаточно, чтобы векторы АгВг, AiA2 и ВгВг были компланарны,
т. е. чтобы существовали такт числа аир, что
383
Q Необходимость. Если прямые а и Ь пересекаются, то
точки Аи А2, Bi, В2 лежат в одной плоскости, и, следовательно,
векторы AiBi, AiA^ и BiB2 компланарны
Достаточность. Пусть Л1В1 = аЛ1Л!!-г-рВ[Ва. Отложим от
точки Ai вектор Л1Л1 = аЛ1Л.2. Его конец, точка М, принадлежит
прямой а. От точки Вг отложим вектор ВгМ = — PBiB2, его конец,
точка N, принадлежит прямой Ь. Из векторного равенства
mn = ma,
+
выражая правую часть через векторы Л5.42 и BiB.,, получаем
MN =
= О-
Из определения нулевого вектора следует, что точки М и N сов-
совпадают, т. е. прямые а и Ь пересекаются. Щ
Задача 4. Точки М и N— середины
ребер тетраэдра (рис. 241), точки Р и Q
расположены на ребрах AD и ВС так, что
отрезки MN и PQ пересекаются, а |ЛР|:
: | AD ; = 2 : 3. Найти отношение | BQ |: | ВС ].
Д Для того чтобы прямые MJV и PQ
пересекались, необходимо и достаточно, чтобы
существовали такие числа аир, что
МР — aMN-\-$PQ. E)
Разложим векторы^ MN, PQ и МР по
векторам АВ = а, AC = b, AD = c. Имеем
MN = МА + AD + DN, и так как МА = - ~ a, DN = ^ Z)C,
D~t = 'Al: — Ab = b-c, то
MN = -l-
Обозначим |BQ|: | ВС
вая, что PQ = PA
jc. Тогда BQ = xBC = x(b-a). Учиты-
Учитыа РЛ =-|/Я = — |-с, получаем
Наконец, находим МР = МА-{-АР = —2-fl-f yf.
Подставляя полученные разложения в E), имеем
384
откуда
I-
PI 1 v\
0=2+
'
2 R
Из этой системы находим р = —1/2, ж = 2/3, а-=2/3. Следова-
Следовательно, ! BQ ! : | ВС [ = 2 : 3.
Ответ: 2 : 3. а
Таким же образом, как это сделано в предыдущих призерах,
можно выразить в виде векторных равенств услозня параллель-
параллельности прямой и плоскости, двух плоскостей и т. д.
§ 3. Угол между прямыми в пространстве
Для любых двух прямых в стереометрии введено понят! е угла
между ними.
Углом между двумя пересекающимися прямыми на:ывают
величину меньшего из углов, образованных этими прямым!. Есл-i
все четыре угла, образованные пересекающимися прямым!г, кон-
конгруэнтны, то угол между ними ранен 90е (или я/2 радиан ¦.
Если две прямые параллельны, то угол между ними сштают
равным 0°.
Углом между двумя скрещивающимися прямыми называв >т угол
между двумя пересекающимися прямыми, соответственно парал-
параллельными данны:,! скрещивающимся прямым 1).
В этом определении точка, через которую проводят:я две
пересекающиеся прямые, может быть выбрана произвол!.н<\ угол
между скрещивающимися прямыми от этого не
зависит. Это вытекает из следующей теоремы:
если пересекающиеся прямые а и b парал-
параллельны соответственно пересекающимся пря-
прямым al «_ bt, то угол между прямыми а и b
равен иглу между прямыми ах и Ь^.
Q Для доказательства выделим на каждой
паре параллельных прямых сонаправлеш'ме
лучи и воспользуемся тем, что два иьшуклых
угла с сонапоавленкымп сторонами конгру-
конгруэнтны /рис. 242): fO/Mitt[OiMi), \OPy\\iOj\},
следовательно, /_f'O.U-}^ ^РЛЛК и т. д. Щ
Из оп;1еделений угла между прямыми и из указанной теоремы
следует, что
Рис. 242
х) Термин syror!>>r обпзнэчаюти'': а этих определениях величину, употреб-
употребляется также и как название геометричесю i фигуры. Из текста быв ict яг.но,
в какоч емьиле употресляетч'я этот термин,
13
Г. Н.
335
если прямые а и Ъ параллельны соответственно прямым at и
&i, то угол между прямыми а и Ь равен углу мео/сду прямыми ах
и bi.
Задача 1. Найти угол между прямыми, на которых лежат
диагонали АВг и BCi граней куба (рис. 243, а).
Д Данные диагонали лежат па скрещивающихся прямых.
Диагональ АВг грани ADDtAx параллельна диагонали ВС\, поэтому
угол между прямыми ADi и
ABi равен углу между прямыми
ВСХ и АВЪ
Рассмотрим треугольник
~>i (рис. 243, б). Каждая его
сторона —диагональ грани куба.
Длины этих диагоналей равны,
значит, треугольник ABiD, рав-
равносторонний и B1ADL==6Q°. Мы
кс' ' нашли угол между лучами ABi
и ADi, он оказался острым,
поэтому угол между прямыми ADi и АВх имеет ту же величину.
Ответ: 60°. а
Задача 2. В правильной треугольной призме (рис. 244)
AAi\ = ~—\AB\. Найти угол между прямыми АВХ и BCi,
Д Совершим параллельный перенос ВхСг'диагонали АВЪ образ
точки А обозначим А2 (рис. 244, б). Угол между прямыми ABt
В,
Б
и ВСХ
[АА2
равен углу между
А]II[ВС], \АА,\ = \
АВСА
Рис. 244.
прямыми
,с, = \вс
ВСХ и СИ,. Имеем
Следовательно, чегы-
[2]|[]II[] \,\ \| |
рехугольник АВСАг—параллелограмм и более того, ромб, поскольку
\ВС\ = \АВ\. Точка О —центр этого ромба, поэтому SO —высота
треугольнике ABC. Обозначим \АВ\ — а, тогда \ВО\ = аУ~3/2,
\ВА2
я BBiC]
отрезка
=-- У6/5 а. Теперь в треугольнике
находим
=аУЗ. Учитывая, что | ВВХ | = а/У5, в треугольниках ВВХА
находим | ABi \ == \ BCt\ = Уё[5а. Отрезок A,,Ci~ образ
B при параллельном переносе, поэтому | A2Ci | = | АВ{; =
12 по теореме косинусов
2\BC1[\C1Ai
386
откуда BCiA., = arccos (—1/4). Угол между лучами СгВ и С1А.г
оказался тупым (я/2 <С arccos (—1/4) << я), следовательно, угол
между прямыми СгВ и CiAt является дополнительным i этому
углу: [CiB, С1Л2) = я —arccos (—1/4). Воспользопавшись тожде-
тождеством arccos x-j-arccos (—х) = л, (\х\^1), получим что
\С\В, С] А.2) — arccos A/4).
Ответ: arccos A/4). а
В двух рассмотренных задачах нахождение угла между прямыми
сводилось к нахождению угла между лучами с общей верпинон,
параллельными данным прямым. Если
с.— угол между прямыми, то угол меж-
между лучами может оказаться равным или
а или я —а. Это обстоятельство необ-
необходимо учитывать, особенно в тех за-
задачах, где по заданному углу между
прямыми требуется найти другие пара-
параметры многогранника.
Задача 3. В правильной треуголь-
треугольной призме (рис. 244, а) угол между
прямыми АВ, и SCX равен arccos A/4),
сторона основания имеет длину а. Най-
Найти длину бокового ребра.
Д Обозначим длину бокового ребра Ь. Выполним тгкне же
построения, как и при решении задачи 2. Рассмотрим дза слу-
случая: 1) ВС\А2=-- arccos A/4) (рис. 245); 2) ВС]А2 = я — arc< os A/4)
(рис. 244, б).
= аУ2.
Рис. 215.
Имеем
угольнике
За2 = 2 (а2
\ = \АВ1\ = \ВС1\ =
| В Л,
В тре-
треA^ по теореме косинусов находим в первом случае:
2) A — -А, аналогично во втором случае: За2 =
== 2(а2-\-Ь2)( 1 +хг Отсюда соответственно Ь\ — а, Ь2 = а/~\Г5. Та-
Таким образом, задача имеет два решения. Второй случай 'оответ-
ствует данным задачи 2.
Ответ: а или а/У5. а
§ 4. Применение скалярного произведения векторос
в решении задач
Скалярное произведение векторов можно использов; ть для
нахождения углов между прямыми, длин отрезков, рас:тояния
от точки до прямой и т. д.
Из формулы
a-b=\a\-\b\cos(cC'b),
13*
337
которая является определением скалярного произведения векторов
а и Ь, следует, что
COS [l
\a\-\b\'
Применим эту формулу для нахождения угла между прямыми.
Пусть Ах и А2 — некоторые: точки прямой а, АХФ А%, Вх и В2 —
точки прямой Ь, ВгфВ0. Величина ф угла между векторами
АгА2 и ВхИг лежит в пределах от 0 до л и определяется формулой
аА ¦ Ъ[в1
Угол а между прямыми а и Ь лежит в пределах от 0 до л/2.
Если 0*ёф=^л/2, то а —ф и cos а = cos ф = | cos (p |, если же
я/2 < ф «? л, то а = л — ф, a cos а = — cos ф =
«=jcos(p|. Значит,
cosVo, Ь) = ~ ' \ в в\ '
Из этой формулы следует:
для того чтобы прямые а и Ъ были пер-
перпендикулярны, необходимо и достаточно,
чтобы
АуА\ ~ Bi~B2 = 0.
Задача 1. В правильном тетраэдре точки М и N- середины
ребер АВ и CD (рис. 246), \АВ\ = а. Найти:
1) длину отрезка MN;
2) угсл между прямыми MN и ВС.
3) Доказать, что прямая MN перпендикулярна ребрам АВ
и CD.
Д Обозначим ВС —а, ЙА = Ь, BD = c. Имеем
а | = | & | = | с | = а, а Ь =
= Ь с-= а212.
Раскладываем вектор MN по векторам а, Ь, с. Поскольку
' =MB+BC + CN, a MB = — -l-b, CN = I CD,CD =¦ с-а, то
MN = ' (а -
1) Находим
\ЖМ |2 = ^ (а - *
Отсюда | MN | =
388
2) Вычисляем MN-ВС = ~(а — Ь + с) а = ^-, и учггывэя,
что \MN\=a/Y2, \BC\ = a, получаем
cos (MN, ВС) = -^~-^г = 7П
\MN . ВС, \'-2
Згичит, (MN, ВС) = я/4.
3) Находим последовательно:
= y (а-Ь + с) ¦ {с-а) = -^ ((с-fa)- (с-а) ~&(с -л)) =
Отсюда и следует, что (MN) _]_ (AB), (MN) J_ (CD).
Ответ: 1) aj\r2\ 2) я/4. А
Задача. 2. В тетраэдре ABCD имеем ] АВ'•-¦=[ ВС], AD\ =
— | DC \. Доказать, что ребра АС и BD перпендикулярно.
Д Выберем три некомпланарных вектора: ВС = а, ЗА=О,
ЁЬ = с (рис. 247). Имеем Й5 = а —с, DA = b~c. По условию
|«1 = |&! и ;а —с j = |ft —с|. Отсюда следует, что (а —сJ —
— (Ь — сJ, а? — 2ас-\-с- = Ьг — 2Ь-с + сг. Учитывая, чтоа2 = &а,
получаем а-с = Ь-с, т. е. (а — Ь)с = 0. Поскольку а— !» = ДС,
c = BD, то .4С-Ш5 = О, т. е. (ЛС) J_ (BD). ^
Следствие. 5 правильной треугольной пирамиде, в част-
частности, в правильном тетраэдре противополож-
противоположные ребра перпендикулярны.
3 задаче 1 было доказано, что прямая,
проходящая через середины скрещивающихся
ребер правильного тетраэдра, перпендикулярна
этим ребрам.
Имеет место утверждение:
для любых двух скрещивающихся прямых су-
существует и притом единственная прямая, пере-
пересекающая обе данные прямые и перпендикулярная J3"c- 'ii7-
каждой нэ них.
Отрезок, имеющий концы на двух скрещивающихся nj ямых и
перпендикулярный этим прямым, называете:! ш; общим перпен-
duiii/ляром. Среди всех отрезков, концы которых лежат ia двух
скрещивающихся прямых, общий перпендикуляр имеет гаимень-
шую длину. Поэтому расстояние между скрещивающимися пря-
прямыми равно длине их общего перпендикуляра.
Задача 3. Ребро к>ба имеет длину а. Найти расстояние
между прямыми, на которых лежат скрещивающиеся диагонали
двух смежных граней куба.
389
Д Рассмотрим, например, диагонали АС и Л,й гргней куба
(рис. 248), Пусть М — точка прямой АС, N — точка прямой АХВ.
Условие иериендикулярности отрезка MN прямым АС и АУВ
равносильно тому, что
Ш-АС = 0, MN-BA^Q. A)
Разложим векторы АС, ВА1 и MN по векторам АВ = а, AD =
= Ь, А А 1 — с. Имеем АС=а-\- Ь, В~АХ = с — а. Далее, поскольку
точка М лежит на прямой АС, а точка N —
на прямой АХВ, то АМ = хАС, a BN = уВ'Аг.
в Учитывая это, находим MN — МА -\-АВ +
BN = — хАС'+ а + уВА\ =- A —х—у] а—xb \-
Подставляем разложения векторов в урав-
уравнения A) и преобразуем эти уравнения:
(A — х — у) а — xb + ус) ¦ (aJr Ь) =-0,
(A — х — у) a — xbJryc)-(c — a) =0,
}A— х-у)а2-ха2 = 0, ( 1 — 2х — у = 0,
[уа2-(\-х-у)а2 = 0, \—1+х + 2у = 0
Отсюда находим х = у= 1/3. Значит, точки М и N лежат на от-
отрезках АС и ВАХ и \АМ\ = \АС\/Ъ, \ BN | = J BA11/3.
Теперь имеем MN = „а — -„ & + -s-c, значит,
ЗАДАЧИ РАЗДЕЛА I
1. Доказать, что
а) отрезки, соединяющие вершины тетраэдра с точками пересечения медиан
противоположных граней, пересекаются в точке (обозначим ее О), которая
делит каждый из этих отрезков в отношении 3:1, считая от вершины;
б) отрезки, соединяющие середины 1крещивающихся ребер тетраэдра, пере-
пересекаются в той же точке О, которая является серединой каждого из них.
2. Длина каждого ребра тетраэдра ABCD равна а. На ребрах DA, DC и
ВС расположены соответственно точки М, N и Р так, что | DM I = \ CN | =
= а/3, -СР,=а/5. Построить сечение тетраэдра плоскостью MNP и найти
длину отрезка BQ, где Q={MNP)[\(AB).
3. Основанием пирамиды SABCD служит параллелограмм ABCD. По-
Построить сечение пирамиды, проходящее через вершину А и середины М и Р
ребер SB и SD. Определить, в каком отношении сечение делит ребро SC.
4. Длина ребра куба ABCDAiBxCJi^ равна а. На ребрах AD и В^Сх
взяты соответствен но точки М и Q, а на ребре CD — точки Р и Л' так, что
390
\ = \DN\=a/Z. Построить сечение куб.) плоскостью, про-
проходящей через прямую МР параллельно прямо."! NQ, и найти площ; дь этого
сечения.
5. Длины ребер АС и BD тетраэдра ABCD равны соответственю а и 6,
угол между прямыми АС и BD равен ср, Найти наибольшую площадь сеченич
тетраэдра, параллельного прямым АС и ВО.
6. Даны прямая а и плоскость у, точки Ах и Аг лежат на прямой а.D1^=А2),
точки М, N и Р, не лежащие на одной прямой, принадлежат плоскости у.
Доказать: для того чтобы прямая а и плоскость у были параллельны необхо-
необходимо и достаточно, чтобы векторы А\А%, MN и МР были комплаияр ;ы, т. е.
чтоГь; существовали числа а. и fi такие, что
А^С2 = аШ + C/ИР.
7. Точки М, N к Р соответственно —середины ребер АВ, CD u 1 С тетра-
тетраэдра ABCD. Через точку Р проведена плоскость, параллельная пр?мым DM
н ЛЛЛ В каком отношении эта плоскость разделяет ребро AD}
8. В прямоугольном параллелепипеде ABCDAiBlClDl из верти! AY и Д
опущены перпендикуляры ^4tP и BQ на диагональ ЛС^ Найти длин;' отрезка
PQ, если \АВ\=а, \AD\ = b, \AA,\=c.
9. Каждое ребро правильно,') призмы АВСА^В^С] имеет длину а. На диа-
диагоналях АВ^ и BCi граней призмы озяты соответственно точки М i N так,
что (A^.V) JL (АВ), J МЛ/ J =—---. В каком отношении точки М и Л/ делят
отрезки Л Si и ВС1!?
ЗАДАЧИ РАЗДЕЛА «I
1. Доказать, что если плоскость параллельна одной из двух параллельных
прямых, то она параллельна и другой прямой.
2. Две прямые одной плоскости параллельны двум прямым Др той пло-
плоскости. Следует ли отсюда, что эти плоскости параллельны?
3. Дзе пересекающиеся прямые одно"! плоскости параллельны др год пло-
плоскости. Доказать, что эти плоскости параллельны.
4. Две плоскости параллельны. Доказать, что прямая, параллель 1ая однол
из этих плоскостей, параллельна н другой плоскости.
5. Доказать, что если прямая параллельна каждой из днух Пересе :ающихся
плоскостей, то она параллельна их линии пересечения.
С. Как следует провести плоскость у, чтобы она пересекала дг з данные
плоскости а и р по параллельным прямым?
7. Доказать, что через данную прямую можно провести плоское ь, парал-
параллельную другой данной прямой. При каком условии такая плоское ь единст-
единственная?
8. Доказать, что через любую точку можно провести плоскость и притом
только одну, параллельную двум данным скрещивающимся прямым.
9. Даны скрещивающиеся прямые а и Ь и точка М, Построить прямую,
проходящую через М и пересекающую а и Ь. Найти множество всех точек М,
для которых задача не имеет решения.
391
10. Даны три попарно скрещивающиеся прямые. Доказать, что существу-
существует прямая, пересекающая эти три данные прямые. Единственна ли такая
прямая?
11. Могут ли параллельные проекции скрещивающихся прямьх на пло-
плоскость: а) быть параллельными, б) совпадать?
12. Может ли параллельная проекция тетраэдра па плоскость быть:
а) трапецией; б) параллелограммом; в) пятиугольником?
13. Может ли параллельная проекция параллелепипеда на плоскость быть:
а) трапецией; б) пятиугольником; в) шестиугольником?
14. Доказать, что если параллельная проекция плоского четырехуголь-
четырехугольника на плоскость есть параллелограмм, то и сам четырехугольник — паралле-
лсграмм.
15*. Параллельная проекция равностороннего треугольника из плоскооь
оказалась также равносторонним треугольником. Доказать, что дл]-ны сторон
этих треугольников раЕны.
16. В четырехугольной призме одна из диагоналей пересекает три другие.
Доказать, что эта призма —параллелепипед.
17. Скрещивающиеся диагонали ABlt ВСЛ, CDlf DA^ граней параллелепи-
параллелепипеда ABCDA^BjCiDi имеют равные длины. Доказать, что гран;1 ABCD и
AiBjCiPj, — ромбы, а остальные грани —прямоугольники.
18. На ребрах SA, SB и SC пирамиды SAEC расположены соогветственно
точки Аи Bi и Cv Прямые А-^Ву, В1С1 и CxAi пересекают соответственно
прямые АВ, ВС и СА в точках М, N и Р. Доказать, что точки М, N и Р
лежат на одной прямой.
19. На ребрах АВ и CD правильного тетраэдра ABC.D расположены соот-
соответственно точки М и Р так, что | AM \ : \ АВ ] = ! DP \ : }DC , = 1 : 3. Найти
площадь сечения тетраэдра, проведенного через точки М и Р параллельно
пряной АС, если ребро тетраэдра имеет длину а.
20. На ребрах ААЪ CClt CjDi параллелепипеда ABCDA1BlCiDl располо-
расположены соответственно точки М, N и Р так, что | AM ! : АА^ ; = Cs\ | : jCiC , =
= | CjP | : | CjDi !. Построить точку Q пересечения плоскости MNP с прямо"]
ВС и найти отношение J5Q | : ! ВС \.
21. Плоскость пересекает боковые ребра ААЪ ВВи СС^ и DP, паралле-
параллелепипеда ABCDAlBiClD1 соответственно в точках М, N, Р н Q, причем
\AM\:\AAl\ = m, \BN \: \ВВ1' = п, '• СР | : j CCt ' = о. Найти отношение
DQ |: DD^ I.
22. Через вершину С тетраэдра ABCD и середины ребер AD и BD про-
проведена плоскость. В каком отношении эта плоскость разделит отрезок MN, где
М и N — соответственно середины ребер АВ и CD.
23. На ребрах А1В1, АВ и СС^ призмы ABCAiB1C1 расположены соот-
соответственно точки М, N я Р так, что \ АХМ I : ; Афу | = | ВЫ \: \ В А \ =
= | СХР | ; [ CjC | = 1 : 2. Построить точку Q пересечения плоскости М NP с пря-
прямой BiCi и найти отношение | C^Q \: \ В^С^!.
24. В Призме АВСА1В1С1 медианы основания ABC пересекаются Б точке М,
а диагонали граней AAjC^ и BBjCjC — b точках N и Р соответственно- Пло-
Плоскость MNP пересекает прямые: В^Сг и СС1 в точках К и L соответственно.
Построить сеченве призмы этой плоскостью, в найти отношения I В, К | : | 5^1
и IdLj.MCCji,
392
25. Плоскость пересекает ребра АВ, АС, СС^ и ВВХ призмы AiCA^BjC^
соответственно в точках К, L, М и N. Площади фигур AKL, CLM i CM MB
равны соответственно 1/6, 1/12 и 1/2 площади той грани, в которо! каждая
из них находится. Найти О)ношение площади треугольника BKN к площади
грани AAiBiB.
26. В тетраэдре ABCD через середину М ребра AD, вершину С и точку N
ребра BD такую, что BN ! : \ND j = 2 : 1, проведена плоскость, В ка :ом отно-
отношении эта плоскость разделяет отрезок KL, где К и L — соответстве шо сере-
середины ребер АВ a CD?
27. Основанием пирамиды SABCD служит параллелограмм AICD. На
ребре SD взята точка L так, что ! SL ] : \LD | =2, точка К — середина ] ебра SB,
Построить сечение пирамиды плоскостью AKL и определить, в какор отноше-
отношении эта плоскость Делит ребро SC,
28. Основанием пирамиды SABCD служит трапеция ABCD. Сгношение
длин оснований AD и ВС этой трапеции равно 2. Построить сечение пирамиды,
проходящее через вершину D и середины ребер SA и SB. Определ! ть, в ка-
каком отношении сечение делит ребро SC.
29. Через середины М и N соответственно ребер АА\ п C^Di п фаллеле-
пипеда ABCDAiB^iDi проведено сечение, параллельное диагонали BD осно-
основания. Построить сечение и определить, в каком отношении оно дел лт диаго-
диагональ AiC параллелепипеда.
30. Через середины М и .V ребер AD и ССУ параллелепипеда фоведена
плоскость параллельно диагонали DB1 параллелепипеда, В каком отношении
эта плоскость делит ребро BBJ
31. Точки О и Oj — центры гранен ABCD и /^B^Di куба ABCD.^B^Di
На отрезке 00^ взята точка S так, что \O-iS \ : \ OS =1 :3. Через >ту точку
проведено сечение куба, параллельное его диагонали АСХ и диагенали BD
основания, Найти площадь сечения, если ребро куба имеет длину а.
32. Среди всех сечений куба, проходящих через его диагональ указать
то, которое имеет наименьшую площадь. Найти эту площадь, если р бро куба
имеет длину а.
33. Рассматриваются сечения параллелепипеда ABCDAyBiCJ) плоско-
плоскостями, параллельными скрещивающимся диагоналям ABt и ВС1 гране! ААгВф
и BBfiiC. Указать сечение с максимальной площадью.
34. Плоскость пересекает ребра АВ, AC, DC и DB тетраэдра Соответст-
Соответственно в точках М, N, Р и Q, причем | AM \ : | MB \ = m, \AN\\ NC\ = n,
\DP\:\PC\ = p. Найти отношение \DQ\: \QB I.
35. В правильной четырехугольной пирамиде SABCD сторона кчювания
имеет длину а, а боковое ребро —длину I. Параллельно ребру SA и диаго-
диагонали BD основания проводятся сечения. Найти наибольшую плошад! сечения.
36. Все ребра правильной призмы АВСА1В1С1 имеют длину а. Рассматри-
Рассматриваются отрезки с концами на диагоналях ВС1 и СА1 боковых гран( ii, парал-
параллельные плоскости АВВХА\-
1. Один из этих отрезков проведен через точку М диагонали В^ такую,
что | ВМ |; | ВСХ | = 1:3. Найти его длину,
2. Найти наименьшую длину всех рассматриваемых отрезков.
37. В треугольной призме ABCAxBxCi точки М и N — серединп боковых
ребер tEt н CCi- Через точку 0 пересечения медиан треугольника ABC про-
393
ведепа прямая, пересекающая прямые /ИЛ/ и ABt соответственно в точках Р
и Q. Найти отношение | PQ | : [ OQ \.
38. В тетраэдре ABCD проведены медианы AM и DN граней ACD и ADB,
и на этих медианах взяты соответственно точки Е и F так, что (EF)\(BC).
Найти отношение \ EF \ : \ ВС \.
39. В призме АВСА1В1С1 медианы оснований ABC и AlBiCl пересекаются
соответственно в точках О и Ох. Через середину отрезка ООХ проведена пря-
прямая, параллельная прямой СА^. Найти длину отрезка этой прямой, лежащего
внутри призмы, если \СА1\=а.
40. Основанием пирамиды SABCD служит параллелограмм ABCD, диаго-
диагонали которого пересекаются в точке О. Через середину отрезка SO проведена
прямая, параллельная медиане ВМ грани SAB. Найти длину отрезка этой
прямой, лежащего внутри пирамиды, если \ВМ\=а.
41. На ребрах AD и BD тетраэдра ABCD взяты соответственно точки М
и N так, что j AM | : | AD =р ВЫ ] : i BD |=/п. Найти расстояние ^ежду точ-
точкам» пересечения медиан треугольников ANC и ВМС, если | АВ\ = а.
42. Ребро правильного тетраэдра имеет длину а. Через вершину тетраэдра
проведено сечение, являющееся треугольником. Доказать, что периметр р
сечения удовлетворяет неравенствам 2а < р^За.
43. Даны точки А, В, С, D. Точки М и N — середины отрезков АВ и
CD, точка О —середина отрезка MN (если отрезок вырождается в точку, то
его середину считаем совпадающей с этой точкой).
Доказать, что для любой точки S
44. Дан тетраэдр ABCD. Доказать, что существует и притом только одна
точка М такая, что
~МА + ~Ш + МС +'Ш5 = 0.
45. В параллелепипеде ABCDAiBfi^D^ точки М и N — середины ребер АВ
и AJ^. Плоскость CMN пересекает прямые BiClj^DBl соответственно^ точ-
точках Р и Q. Найти разложения векторов АР и AQ по ректорам АВ=а,
J6 = b, ~АА[=с.
46. Даны четыре различные точки А, В, С, D. На отрелках АС и BD
взяты соответственно точки М и /V так, что [ AM \—\ \ AC \, \ BN \ — Х ! BD I.
Доказать, что векторы АВ, CD и M.N компланарны, и найти разложение
вектора MN по векторам А~В и CD.
47. Даны четыре различные точки А, В, С, D. Точки М и N — середины
огрезкол ВС и AD соответственно. Доказать, что если \MN \= -^ (| АВ \ -\-
+ \CD\), то (AB)i(CD).
48. Даны скрещивающиеся прямые а и & и па них соответственно точки
Ai Аг, А3 и Въ В2, В3 (А? между Ai и А^, В2 между В^ и Вп). Известно,
что ; А\_А2 \: | А2АЯ \ — [ В^В?, \: \ S2S3 |. Доказать, что середины отре.зкоз АлВи
А2В2, А3В3 лежат на одной прямой.
49. ABCDA\BxCxD\ — параллелепипед. Проведена прямая, пересекающая пря-
прямые АА\, ВС и CjDj гоотвегсткешю в точках М, N и Р так, что \MN | ; \МР \ =
=--2. Найти отношение BN |: J ВС \ (найти все решения).
394
50. Ребро куба ABCDA^B^CJix имеет длину а. На прямой I Cj взята
точка М так, что прямые DAU АВХ и DJA параллельны одной глоскости.
Найти длину, отрезка DXM.
51. На ребре AD и диагонали А\С параллелепипеда ABCDAJijC DL взяты
соответственно точки М и N так, что прямая MN параллельна ыоскости
BDC1 и AM | : i AD | = 1 : 5. Найти отношение \CN \:\ С At !•
52. Даны четыре точки А, В, С, О, не лежащие в одной плосюсти. До-
Доказать, что для того чтобы точка М лежала в плоскости ABC, нео( ходнмо и
достаточно, чтобы существовали три числа х, у, г, удовлетворяю! ше двум
53. Основанием четырехугольной пирамиды SABCD служит п араллело-
гра.мм ABCD. Плоскость пересекает ребра SA, SB, SC и SD cooti етственно
в точках М, N, Р и Q. Пусть j SA j :\SM\ —tn, \SB\:\SN =n,\SC : j SP \ =
= p, jSD|:|5Q! = g. Доказать, что
54. Центр нижнего осисшпння куба соединен прямыми с четыры я верши-
вершина:.:;! верхнего основания. Определить углы между этими прямыми.
55. Точки К,—середина ребра АА\ куба ABCDA^BfiiP^. Нг ;itii угол
между прямыми а) ВК и ВС^, б) ВК и ADt; в) ВК и А\СЛ.
5G. Точка М — середина ребра CD правильного тетр.вдра ABCD. Найти
угол между прямыми А/А и ВС.
57. Точки М и N — середины ребер ВС и AD тетраэдра ABCD, i котором
| АС \ = [ BD , а угол между прямыми АС и BD равен а. Найти у] ол между
прямыми МЛ' и АС (найти псе решения).
58. Все ребра правильно'! четырехугольно!! пирамиды SABCD имеют
одинаковую длину. Найти угол между прямыми: a) AM и BN, где М и /V —
середины ребер SB и SC соответственно; б) SP и B.V, где Р- -середина
ребра АВ.
59. В тетраэдре ABCD известно, что \AC\ = \BD\ и (АС) ± (BD). На
ребрах AD и СВ взяты соответственно точки М и Л/ так, что j AM | : j ЛО ] =
|= j CM ! : | CB | и (ЖуГлс) = 4-(лТл/7во)- Найти отношение | Ai \! : ! AD\.
60. Ребра ЛВ и CD тетраэдра ABCD перпендикулярны и \АВ\ = CD |=
==а. На ребре ЛВ взяты точки М и Л/, а на ребре CD — точки / и Q так,
что | АМ \ = | Л/В ! = | СР ] = J QD \ =ka (I < 1/2). Найти расстояние м жду сере-
серединами отрезков УИР и Л/Q.
61. Даны три не компланарных вектора. Существует ли четвертЕ й вектор,
перпендикулярный трем данным?
62. Даны три попарно перпендикулярные прямые. Четверта i прямая
образует с данными прямыми соответственно углы а,, а.ъ а3. Доказать, чго
г cos2a2 -(- cos'-'a3 = 1 •
63. Дан параллелепипед ABCDA^Bfiip^. Доказать, чю
! ААУ ? si -^ С АВу |2+: BCt ;¦' +, CDj ;2+; l>ax ?).
S95
64. В тетраэдре ABCD известно, что D/4B = АВС = л/2, (АВ.сЪ^^я,
2 | AD | =| CD |= j ВС j. Найти угол между прямыми AD и ВС.
65. Точка М — середина ребра AtBi куба ABCDAiBlClDi, а точка W —
центр грани ABBtAi. Найти угол между прямыми MD и CN,
60. Два ребра тетраэдра перпендикулярны скрещивающимся с ними ребрам.
Доказать, что и два других скрещивающихся ребра тетраэдра перпендику-
перпендикулярны.
67. Отрезок АВ является общим перпендикуляром к скрещивающимся
прямым 11 и /2 (А е llt Be /2). На пряных /t и 12 взяты соответственно точки
С и D так, что 'АС ' = BD = АВ =-- CD , Найти угол между пря-
прямыми /t и /2.
68. Угол между скрещивающимися прямыми /, и /2 равен а, отрезок ЛВ
является их общим перпендикуляром (А е /lP Be /2). На прямых /t и /2
взяты соответственно точки С и D так, что i АС \ =: BD = а, \CD, = b.
Найти | ЛВ j (найти все решения). При каком соотношение между а и b за-
задача имеет решение при любом а?
69. Сторона основания правильной треугольной прнзмы нмеет длину а, две
непересекающиеся диагонали боковых гранен призмы перпендикуляр [Ы. Найти
длину бокового ребра призмы.
70. На диагоналях граней ОгА, AtB, BYC, CJ) куба ABCOAlBlClDl
взяты соответственно точки М, N, Р, Q так, что ' D^M \ ; > DtA , = ' BN \ : BAi =
= | BtP j : I BtC i = ; DQ j : j DCt, =>„, а прямые МЛ' и PQ перпендикулярны.
¦ Найти X.
71. Все ребра правильной призмы /IBC/liB^ имеют длину а. .Рассматри-
.Рассматриваются отрезки с концами иа пряных АВ1 и BCj, перпендикулярные прямой
ACi- Найти наименьшую длину таких отрезков.
72. Ребро куба ABCDAiBjCJii имеет длину а. На диагоналях DtA н
/^б взяты соответственно точки М н Л/ так, что DtA7 ' :: DtA i = j Л'В : j /4tB j =
= 1:3, Найти расстояние от вершины С до прямой M;V.
73. Ребро куба ABCDA^B^^D^ имеет длину а. На прямой BCi взята
точка М так, что прямые DiM, DAlt ABt параллельны одной плоскости.
Найти: а) расстояние от точки М до прямой ABt; б) площадь сечения куба
плоскостью MDiBlt
74. В прямоугольном параллелепипеде ABCDA\B^CiDi известно что,
| AD | ; [ DC \=n. В каком отношении общий перпендикуляр прямых ААХ и
SjD делит отрезки AAt и BtD?
75. В правильном тетраэдре ABCD проведены высоты DE и BF граней
ABD и BDC. В каком отношении разделены отрезки DE и BF основаниями
их общего перпендикуляра?
76. Длина каждого ребра параллелепипеда ABCDAiBlCiDl равна а, все
плоские углы при вершине А имеют величину я/3. Определить расстояние
между прямыми АС и DBY.
77. Длина ребра правильного тетраэдра ABCD равна а. Точка Е — сере-
середина ребра CD, точка F —середина высоты BL грани ABD. Отрезок МЫ
с концами на прямых AD и ВС пересекает прямую EF и перпендикулярен ей,
Найти длину этого отрезка,
39G
78. Длины ребер АВ и ВС прямоугольного параллелепипеда АВСС AiBlClDl
р.;вны соответственно а и 1а. Известно, что существует прямая, пере-екающая
прямые AAlt ВС и ClDl и образующая с ними равные углы. Hai ти длину
ребра AAi (найти все решения).
79. Сторона основания ABC правильной призмы АВСА1В1С1 расиа а.
Точки М и N — середины ребер АС и AiBt соответственно, точки /V, и Nt—
основания перпендикуляров, опущенных из точек М и N на прялую fiCt.
а
Найти длину бокового ребра призмы, если Л^А^ j =тгг~.
80. Пусть S — площадь треугольника ABC. Доказать, что
S = j У \АВ\г.\АС *-(АВ'АС)*:
81. Длина ребра правильного тетраэдра ABCD равна а. На р 'брах AD
и BD взяты соответственно точки Е и Р так, что | DE ! : ЕА 1= : BF | : | FD =
= 2. Найти площадь треугольника СЕР.
82. Даны четыре вектора a, ft, ? и d. Векторы а, ft, с компла 1ярны, по
попарно не коллинеарны, вектор d не компланарен с векторами a, ft, с.
Известно, что (а, ft) = (ft, с) = л/3, \d,a)=a, \d, б)=р. Найти уп л между
векторами d и с.
ЯЗ. Четыре луча, выходящие из одной вершины, образуют поп; рно углы
равной величины. Найти ату величину.
84. Длина ребра куба равна а. Ндйти сумму скалярных прс «ведений
векторов, начала которых находятся в центре куба, а концы в его i ершинлх.
85. Даны точки А, В, С, О, причем точки Л, В и С не лежат на одной
прямой. Известно, что для любых точек М величина у (М) = [ MA \2-[ j MB p -|-
-+- \МС ]- — 3| МО |3 имее! одно и то же значенке. Доказать, что 0 —т< чка пере-
пересечения медиан треугольника ABC.
Sii*. В пространстве даны различные точки А, В, С, D, не лс кащие на
одно;; прямой. Пусть ? — произвольная точка пространства, обозначил
; 5Л ,2+: sc г2 — [ sb ,2—| sd ?.
Доказать, что
а) у (S) имеет одно и то же значение для вс;х точек просфаи'тва тогда
и только тогда, когда точки А, В, С, D являются вершинами шраллело-
грамма;
б) если существуют четыре такие точки Sj, S.,, S3, Sit не лежа цие в од-
одной плоскости, что г/ (S г) = I/ (S2) = y (S3)—y (S4) = 0, то А, В, С, ©--вершины
прямоугольника.
Для данной величины уа найти множество точек S простри ства, для
которых у (S) = y0.
67. Основание пирамиды —правильный восьмиугольник со сторо1 ой длины
в, вершнни пирамиды удалена от центр,а основания на расстоялпа Ь. Найти
сумму квадратов длин боковых ребер.
397
88. Даны точки А, В, С и D. Найти точку М такую, что величина
| МА |2+1 MB ]2+| МС |2+| MD |2 имеет наименьшее значение.
89. Доказать, что дли любых четырех точек А, В, С, D
А~В -~CD = -2 (| AD 1^ + ; ВС |*-j АС ,2_! BD ]*).
90. В пространстве даны четыре точки А, В, С и О{АфС, ВфБ),
точки Р и Q соответственно —середины отрезков ЛС и BD. Доказать, что
| АВ |2+| ВС |2+1 CD [2+1 AD |2 = | ЛС |2 + | BD |2 + 4 | PQ \\
91. Даны точки А, В, С, D (АфВ, СфО), Доказать: для того чтобы
прямые АВ и CD были параллельны, необходимо и достаточно, чтобы
2 [ АВ \ ¦ | CD \ = \ | AD |2+1 ВС [2-1 AC j2-1 BD [2 [.
Глава XVI
СТЕРЕОМЕТРИЯ (ЧАСТЬ II)
В этой главе рассмотрим различные задачи, связаннь е с пер-
перпендикулярностью прямых и плоскостей, задачи о вышсленин
угла между прямей и плоскостью, между плоскостями, ) нахож-
нахождении объемов многогранников и их частей, задачи на комбинации
многогранников.
§ 1. Перпендикулярные прямые и плоскости
Прямая и плоскость называются сзаимно перпендикулярными,
если прямая перпендикулярна каждой прямой, лежащей в г лоскости
— таково определение перпендикулярных прямой и плоскости.
Задача 1. Основание пирамиды —правильный тре /гольпик
ABC (рис. 249), боковые ребра SA, SB, SC имеют равпье длк'.ы.
Доказать, что пирамида SABC правиль-
правильная. .7
Д Пусть SO — пысота пирамиды, тогда
из определения перпендикулярных прямой
и плоскости следует, что углы SO A, SOB,
SOC прямые. Обозначим \SA\ = \SB\ =
= | SC | = /, \SO\ = h. Из прямоугольных
треугольников SOA, SOB и SOC находим,
что \АО\ = \ВО\ = \СО\= j/T^/il Значит,
течка О —центр окружности, описанной р „ с
около правильного треугольника ABC, a
потому является центром этого треуголь-
треугольника. Таким образом вершина 5 данной пирамиды npoei тируется
в центр основания (правильного треугольника ABC), т. е. пира-
пирамида правильная, а
Совершенно аналогично доказывается, что пирамида, основа-
основание которой правильный многоугольник, а боковые реб)а имеют
равные длины, правильная. В частности, правильный тетраэдр,
т. е. тетраэдр, все ребра которого имеют равные длины, — пра-
правильная пирамида. За основание можно принять люб'Ю грань
правильного тетраэдра.
Признак перпендикулярности прямой и плоскости состоит
в следующем:
399
Рис. 250.
если прямая перпендикулярна каждой из двух пересекающихся
прямых, лежащих в плоскости, то эти прямая и плоскость взаимно
перпендикулярны.
Задача 2. Доказать, что диагональ АС основания правиль-
правильной четырехугольной призмы (рис. 250) перпендикулярна плоско-
плоскости BBtDtD.
Д Достаточно доказать, что прямая АС перпендикулярна
каким-либо двум пересекающимся прямым, лежащим з плоскости
BBtD^D. Поскольку ABCD — квадрат, то (AC) J^(BD). Докажем,
что (АС) ±_ (ВВх). Данная призма — нравиль-
с пая, поэтому (ВВг) _L (ABCD). Отсюда соглас-
' но определению перпендикулярности прямой
и плоскости следует, что (ВВ^ j (АС). Та-
Таким образом, прямая АС перпендикулярна
пересекающимся прямым BD и ВВ1 плоско-
плоскости 66,DiD. Это согласно признаку перпен-
перпендикулярности прямой и плоскости означает,
4to(AC)±(BB1D1D).a
При установлении перпендикулярности
прямых часто используется теорема о трех
перпендикулярах:
для того чтобы прямая, лежащая в плоскости, была перпен-
перпендикулярна наклонной, необходимо и достаточно чтобы эта пря-
прямая была перпендикулярна проекции наклонной на эту плоскость.
Следует тетко различать и соответствен-
соответственно использовать достаточное и необходи-
необходимое условия, выраженные в этой теореме.
Достаточное условие состоит в том, что
если прямая, лежащая в плоскости,
перпендикулярна проекции наклонной на
эту плоскость, то она перпендикулярна
и самой наклонной.
Задача 3. Доказать, что диагональ
BDX куба (рис. 251) перпендикулярна диа-
диагонали АС грани ABCD.
Д Прямая BD является проекцией наклонной BDi на пло-
плоскость ABCD, поскольку (DXD) J_ (ABCD). Грань ABCD — квадрат,
значит, (AC) ±_(BD). Отсюда в силу достаточного условия теоремы
о трех перпендикулярах следует, что (AC) _LFDx). a
Из доказанного утверждения вытекает полезное
Следствие. Диагональ куба, выходящая из некоторой его
вершины, перпендикилярна плоскости, проведенной через концы
трех ребер куба, выходящих из этой же вершины.
Q Рассмотрим, например, диагональ BDX (рис. 252). Доказано,
что (BDi) ±_(АС). Совершенно аналогично устанавливается, что
(BDL) I (ABi). Отсюда следует, что (BD) ]_ (ABiC). H:i свойств
симметрии куба ясно, что аналогичный факт имеет место и для
любой другой диагонали куба. Щ
Рис 251.
400
Необходимое условие сформулированной выше теоремы о трех
перпендикулярах заключается в следующем:
если прямая, лежащая в плоскости, перпендикулярна шклон-
ной, то она перпендикулярна и проекции наклонной на эну пло-
плоскость.
Рис. 252.
Задача 4. В тетраэдре ABCD ребро АВ перпендикулярно
ребру CD, а ребро АС — ребру BD. Доказать, что основание
высоты DO тетраэдра является точкой пересечения высот (или их
продолжений) треугольника ABC.
Д Рассмотрим сначала случай, когда ни одно из ребеэ BD и
CD не перпендикулярно плоскости ABC, т. е. каждое из этих
ребер лежит на прямой, наклонной к плоскости ABC. Пс ;кольку
(DO) _L (ABC) (рис. 253), то прямая SO —проекция прямой BD
на плоскость ABC, Прямая АС, лежащая в плоскости Ai\C, пер-
перпендикулярна по условию наклонной BD. Отсюда согласно необ-
необходимому условию теоремы о трех перпен-
перпендикулярах следует, что (AC) _L (ВО). Со-
Совершенно аналогично доказывается, что
(СО) ±_(АВ). Таким образом, точка О —
это точка пересечения высот (или их про-
продолжений) треугольника ABC.
Теперь обратимся к случаю, когда одно
из ребер, пусть это будет, например, реб-
ребро BD, перпендикулярно плоскости ABC
(рис. 254). В этом случае точка 0 совпа-
совпадает с точкой В, прямая CD является на-
наклонной к плоскости ABC, и ее проекцией на эту плоскость яв-
является прямая (ВС). Согласно необходимому условию тезремы о
трех перпендикулярах, из того, что (АВ) J_ (CD), СЛбД'6Т, ЧТО
(АВ) _\_(ВС). Значит, треугольник ЛВС прямоугольный, и точка В
является точкой пересечения его высот, а
Рассмотрим задачу, которую легко решить, применив признак
перпендикулярности двух плоскостей:
401
если плоскость проходит через перпендикуляр к другой пло-
плоскости, то она перпендикулярна это! плоскости.
Задача 5. Доказать, что в правильной четырехугольной
призме ABCDAiBiCiDi плоскости ADXC и BB-lDJ) перпендику-
перпендикулярны.
Д В задаче 2 было доказано, что (AC) J_ (BBxDxD) (рис. 255).
Отсюда согласно признаку перпендикулярности плоскостей и сле-
следует, что (AD1C)±(BB1D1D). a
Укажем еще две теоремы, полезные при установлении пер-
перпендикулярности прямой и плоскости. Первая из них состоит
в том, что
если две плоскости взаимно перпендикулярны, то прямая, про-
проведенная в одной плоскости перпендикулярно линии пересечения
этих плоскостей, перпендикулярна другой
плоскости.
Задача 6. В правильной четырех-
четырехугольной призме ABCDAiBiCiDi найти
длину перпендикуляра, опущенного из вер-
вершины Вг на плоскость AD^C, если i АВ | = а,
I ААХ ; = Ь.
в
Рис. 256.
пер-
Рис. 255.
Д В задаче 5 доказано, что плоскости
пендикулярны. Линией пересечения этих плоскостей является
прямая DO (рис. 256). Пусть ВЛМ — перпендикуляр, проведенный
в плоскости ВВф-^Р к прямой DO. Тогда по указанной выше
теореме (ВХМ) ±_ (ADXC). Пусть N = (DlO)^(BB1). В прямоуголь-
прямоугольном треугольнике NBlD1(NB1bi=-90°) имеем |Z?1D1|==a]/ и,
очевидно, | NBi | = 2Ь. Следовательно,
+ 2a2.
Отрезок ВгМ является высотой в треугольнике NB-^D-^. Тогда для
площади этого треугольника имеем, с одной стороны, 5 =
1|17П| |ПП| - - " " 1 ' "ггл ' \BiM\. Отсю-
да
NDX | =
а с другой — S = у | Л/Dj
BiDil-I^VBil, т. е.
\NDt\
402
Вторая теорема гласит:
если две пересекающиеся плоскости а и р перпендикуляр: ы пло-
плоскости у, то и линия пересечения плоскостей акр перпенди-
перпендикулярна плоскости у.
Попытайтесь самостоятельно доказать эту теорему (см, зщачу 1
из I раздела этой главы).
§ 2. Об изображении на рисунках перпендикулярных прямых
и плоскостей. Построение сечений, перпендикулярных п »ямой
или плоскости
В стереометрии основой для выполнения рисунков прэстран-
ственных фигур служит параллельное проектирование ia пло-
плоскость чертежа. Параллельные проекции обладают, как жвестно,
рядом простых свойств. Например, при параллельном пэоекти-
ровании сохраняются параллельность прямых, отношена г длин
параллельных отрезков. Но в то же время при параллельном
проектировании, вообще говоря, не сохраняются величннь углов.
На рис. 257 даны изображения куба в параллельной про-
проекции. Грань AAiBiB расположена параллельно плоскости чер-
чертежа, и поэтому ее проекция — квадрат, конгруэнтный самой
грани. Грань ABCD не параллельна плоскости чертежа. 1,е изоб-
изображение—параллелограмм, который уже не конгруэнте! самой
грани. Проекцией прямого угла ABC в зависимости от <то рас-
расположения и от направления проектирования может бьть как
острый, так и тупой угол. И в общем случае, перпенд (куляр,
—jc
Рис. 253,
проведенный в пространстве из данной точки к данной прямой,
на рисунке изображается прямой, вообще говоря, не nepi ендику-
лярной изображению данной прямой. Для того чтобы правильно
показать на рисунке такой перпендикуляр, определяют обычно
положение его основания относительно каких-либо заданных
на рисунке точек данной прямой.
Задача 1. Сторона основания правильной четырехугольной
призмы ABCDAiBiCiDi (рис. 258) имеет длину а. Построить изо-
изображение перпендикуляра, проведенного из середины М ребра A
к прямой BDi, и найти длину этого перпендикуляра.
403
Д Рассмотрим треугольник MBD,. Перпендикуляр, опущенный
из точки М на прямую В/Л, является высотой этого треуголь-
треугольника. Обозначим \AAx\~b, тогда \АМ\=\№А1\ = ЫС?.. В пря-
прямоугольных треугольниках МАВ и MAiDi находим | MB \ = | MDx | =
— "|/а2-)- '. Значит, треугольник MBDX равнобедренный, а его
высота из вершины М является и медианой, т. е. основание
этой высоты—середина отрезка BDi. Соединив точку М и сере-
днпу N диагонали BDlt получим изображение перпендикуляра,
опущенного из точки М па прямую В/Л.
1
Тетерь, учитывая, что ] BDi | — } -' 2а2 -f /г, ' В Л' | --- ---о
из прямоугольного треугольника MNB лаходим \MN
Для того чтобы изобразить на рисунке перпендикуляр, про-
проведенный в пространство из данной точки на данную плоскость,
обычно определяют положение его основания осноснтелыю задан-
заданных на рисунке точек этой плоскости.
S
Рис. 250.
Построим, например, на рисунке правильной треугольной
пирамиды SABC (рис 259, а) ее высоту SO {/_, ABC — основание
пирамиды). Основанием высоты правильной пирамиды согласно
определению является центр основания этой пирамиды. Центр
правильного треугольника ABC совпадает с точкой пересечения
его медиан. В соответствии с этим на рис. 259, а построены
медианы AM и BN. Точка О их пересечения будет изображением
основания высоты.
Основание высоты правильной четырехугольной пирамиды
(рис. 259, б) находим как точку пересечения диагоналей парал-
параллелограмма, изображающего основание этой пирамиды — квадрат
ABCD. Аналогично находится на рисунке правильной шестиуголь-
шестиугольной пирамиды (рис. 259, в) основание ее высоты.
Построение перпендикуляра к прямой или к плоскости часто
используется при построении сечения фигуры плоскостью, перпен-
перпендикулярной данной прямой или плоскости.
404
На рис. 260 а, б показано построение сечения прав! льной
треугольной пирамиды SABC плоскостью, проходящей чере i сере-
середину М ребра SA перпендикулярно высоте СМ основания пира-
пирамиды. Секущую плоскость обозначим а. Поскольку (СУ) J_oc,
то и (ABC) _Loc. Отсюда следует, что перпендикуляр, опуи.енный
нз точки М на плоскость ABC, принадлежит плоскости с. Этот
перпендикуляр параллелен высоте пирамиды нз вершины S.
На основании этого анализа делаем следующие построения: :троим
высоту SO пирамиды и проводим [МSi]||[SO] (рис. 260, fli. Сто-
Сторона сечения, лежащая в грани ABC, перпендикулярна прямой
СМ, а значит, параллельна ребру АВ. Через точку SL приводим
[РфЩЛВ] (рис. 260, б). Из параллельности PQ и АВ с 1едует,
что и сторона сечения, лежащая в грани ASB, параллельна
ребру АВ. Строим [Л//?ЩЛВ]. Сеченае —трапеция PMRQ
а)
Рис. 260.
Рассмотрим еще один пример построения сечения, не шенди-
кулярного прямой.
Задача 2, Построить сечение куба, проходящее чер«:з сере-
середину М ребра AAi (рис. 261, а) перпендикулярно диагонали
BiD куба, и определить, в каком отношении оно делит эгу диа-
диагональ.
Д Как и в задаче 1 этого параграфа легко доказать, что
перпендикуляр из точки М на прямую BiD проходит чер;з сере-
дг.ну О отрезка BiD, Точно также и перпендикуляр из с< редины
N ребра ЛЛ на прямую BLD проходит через точку О (рис. 261, б).
Значит, плоскость сечения проходит через точки М, N и О и,
в частности, делит диагональ BXD пополам. Построим само сече-
сечение. Для этого докажем, что плоскость сечения прохода через
середину S ребра АВ. Прямая SO, как и прямая МО, перпен-
перпендикулярна прямой BiD. Поэтому и плоскость M0S, как и пло-
плоскость MOM, перпендикулярна прямой BVD. Но тогда гти пло-
плоскости совпадают, т. е. S e (MOM). Теперь можно восполь; оваться
результатом задачи 2 из § 1 главы XV. Там было доказ; но, что
сечение куба плоскостью MNS — правильный шестиугольник
405
(рис. 261, в) с вершинами в серединах ребер, не пересекающих
диагональ BiD.
Ответ: 1:1. а
Рассмотрим пример построения сечения, перпендикулярного
данной плоскости.
Задача 3. Каждое ребро правильной четырехугольной пира-
пирамиды SABCD имеет длину а. Построить сечение, проходящее
через диагональ BD основания (рис. 262, а) перпендикулярно
грани SCD, и найти его площадь.
Рис. 261.
Д Сначала построим перпендикуляр из какой-либо г:очки пря-
прямой BD к плоскоаи CSD. Этот перпендикуляр принадлежит
плоскости сечения и вместе с прямой BD полностью определяет ее.
Построение удобно выполнить из центра О основания ABCD.
Действительно, плоскость SOM, где М — середина ребра CD
(рис. 262, а), перпендикулярна плоскости CSD ((CD) j_(SOM),
(CD) d (CSD)). Поэтому высота треугольника SOM, проведенная
из вершины О, будет перпендикуляром к плоскости CSD. Опре-
Опреа)
Рис. 2G2.
делим, в каком отношении основание N этой еысоты делит сторо-
сторону SM. В прямоугольном треугольнике SOM (SOM = 90°) имеем
| ОМ | = а/2, | SM | = й ]//2. По свойству прямоугольного треуголь-
ника | ОМ |а = j MN \-\SM\, откуда j MN \ = -—д. Значит,
406
== „-1 SM I и точка N — центр правильного треугольника CSD.
Проводим медиану DK треугольника CSD (рис. 262, б), N =
= (DI() f](SM)), получаем сечение —треугольник DKB.
Найдем площадь сечения. Высота h треугольника Dl'B из
вершины В вдвое больше длины перпендикуляра ON, noci ольку
точка О —середина отрезка BD. В прямоугольном треугольнике
SOM имеем \ON\=V\ MN \ ¦ \ SN\=af\/~&. Следовательно, h= laY
и площадь треугольника DKB равна -y/i| DK \ = a2f2~\f2. iL
§ 3. Угол между прямой и плоскостью
Углом между прямой, наклонной к плоскости, и этой плоскостью
называется угол между прямой и ее ортогональной проекцией на
эту плоскость.
Если прямая перпендикулярна плоскости, то угол межд { ними
равен 90°, если прямая и плоскость параллельны, то угол между
ними равен 0°.
Задача 1. Найти угол между ребром
правильного тетраэдра и плоскостью грани,
не содержащей это ребро.
Д Найдем угол между ребром АО и пло-
плоскостью ABC (рис. 263). Длину ребра тетра-
тетраэдра обозначим а. Опустим перпендикуляр DO
на плоскость ABC. Точка О — центр треуголь-
ника_ ABC (задача 1 § 1), поэтому АО\ =
fl]/3/3. Прямая АО является проекцией пря-
прямой AD на плоскость ABC, значит, угол ме-
между прямой AD и этой плоскостью равен
DAO. Имеем cos ОАО = | АО \/\ AD | = "|//3,
ОАО = arccos(l/]/3). Легко видеть, что любое ребро п )авиль-
ного тетраэдра составляет с плоскостью любой грани, не содер-
содержащей это ребро, угол такой же величины. Ответ: arccos(l/t^3). A
При определении угла между прямой и плоскостью ча(,то воз-
возникают ошибки из-за неправильного нахождения ортогш альной
проекции прямой на плоскость.
Задача 2. В правильной треугольной призме АВСА\ВхС^
\АА\\ = \АВ\. Найти угол между диагональю АВ1 и плоскостью
AAdC
Рис. 263
Д Построим проекцию прямой Л5Х на плоскость jlAxCtC
Плоскости AiB^ и АА&С перпендикулярны, поэтому перпен-
перпендикуляр ВХМ (рис. 264) к прямой ЛхС, будет и перпенди! уляром
к плоскости AAiCiC. Прямая AM является ортогональной проек-
проекцией прямой АВг на плоскость AAiCiC. Угол между пряной АВХ
и плоскостью AAiCxC равен ВХАМ., Обозначим \АВ\ = с, тогда
407
и \ААх] = а, а | ABt ] — аУ'2. Высота ВхМ правильного треуголь-
треугольника AtBxCi равна «У 3/2. В прямоугольном треугольнике В^АМ
имеем
sin В! AM = | ВХМ \,'\ АВХ | = У6/4, ВГЛМ = arcsin (V/4).
Ответ: arcsin(]/6/4). ^
Замечание. Неверно было бы принять за угол между пря-
прямой ЛВх и плоскостью АА^СХС угол ВИА (рис. 264), Прямая ЛЛ,
не является ортогональной проекцией пря-
прямой ABi на плоскость AA^CiC, а угол B^.^,
равный я/4, вовсе не является углом между
этими прямой и плоскостью.
Для нахождения угла между прямой н
плоскостью можно использовать и координат-
координатный метод.
Пусть в пространстве введена прямоуголь-
прямоугольная система координат, пусть плоскость а
задана уравнением (см. гл. VII, § 8)
Рис. 264.
и пусть на прямой а заданы ДЕе точки Ах (хх\ уй ?i] и
Уг\ z2). Угол между прямой а и плоскостью а обозначим ф.
A)
Рассмотрим два Еектора
п = (а; Ь; с) и I — А1Аг — (х2 —хг\ i
Угол ф определяется следующей формулой:
sin ш = ——
Т I П !
г2
B)
Действительно, вектор п — {а\ Ь\ с) перпендикуляр<?н плоско-
cv;i а, заданной уравнением A), поэтому, обозначив ф=(я, /),
будем иметь:
если
j, то ф= ~0- — ty (рис. 265, o)j
408
если 2- < г|з < я, то <р = г|з — ™- (рис. 265,6).
В обоих случаях имеем sin ф = | cos г|з |. Отсюда и из тох), что
cos \\> = . "' следует формула B).
В задачах при выводе уравнения плоскости часто ис юльзу-
ется то, что
уравнение всякой плоскости, проходящей через точку
М (ду, уо\ z0), можно записать в виде
а (х - х0) + Ъ{у- г/о) + с (г — г0) = 0.
C)
Задача 3, В правильной четырехугольной призме отношение
длин бокового ребра и стороны основания равно 2. Най' и угол
между диагональю BDi призмы (рис. 266) и плоскостью BC^D.
Д Введем систему координат, как показано на рис. 266х).
Длину стороны основания призмы обоз-
обозначим s, тогда длина бокового ребра
равна 2s. Находим координаты точек
В, С1у D и Eh.: B(s; s; 0), Cj@; s; 2s),
D@; 0; 0), Dx @; 0; 2s). Плоскость ВСф
Лроходит через точку D@; 0; 0), по-
поэтому согласно C) ее уравнение имеет
вид ах -f- by -f- сг = 0. Подст авл я я сюда
координаты точек В и Сь получаем си-
систему
6s + 2cs = 0,
откуда находим, что а = 2с, Ь = —2с. Значит, уравнение шоскости
BCSD имеет вид
Учитывая, что сфО (иначе все три коэффициента обр;щаются
в нуль), и сокращая, получаем уравнение
Таким образом, вектор л, перпендикулярный плоскости BCiD,
имеет координаты B; —2; 1). Находим координаты (р; q\ r) век-
вектора l = BDi. p = O~s = — s, <? = 0 — s=— s, r = 2s--0 = 2s.
Вычисляем:
l-n = (—s).2 + (—s)-(—2) + 2s- l=2s,
l =3,
2 + 4s3 =
x) Для простоты на рисунке прямоугольной системы координат не всегда
будем изображать базис (/; /'; к), указывая лишь положительное на [равленме
осей.
409
Обозначим через ср угол между прямой BDt и плоскостью
Находим по формуле B)
\l
n
¦n
•1
Ф
1
I
—
3-
arcsin
2s
Кб -s
(/6/9).
2
31^6
^
И 6
9
§ 4. Расстояние от точки до плоскости,
расстояние между прямыми и плоскостями
Напомним определение расстояния между фигурами: наимень-
наименьшее среди расстояний между точками, одна из которых принад-
принадлежит фигуре Фи а другая —фигуре Ф2, называется расстоянием
между фигурами Фх и Фг-
Если точка не принадлежит плоскости, то расстояние от этой
точки до плоскости, как известно, равно длине перпендикуляра,
опущенного из точки на плоскость. Если точка принадлежит
плоскости, то расстояние между ними равно нулю. Ранее в этой
главе уже встречалась задача о н<1хождении
расстояния от точки до плоскости (задача 6
§ 1). Укажем другие способы нахождения
этого расстояния.
Если известен объем V пирамиды и пло-
площадь Q ее основания, то высота Н пирамиды
определяется по формуле
Эта высота есть не что иное как расстояние
от вершины пирамиды до плоскости ее осно-
основания.
Задача 1. Площадь боковой поверхно-
поверхности и объем правильной четырехугольной пи-
пирамиды равны соответственно S и V. Найти расстояние от вер-
нш;ы основания пирамиды до плоскости боковой грани, не содер-
содержащей эту вершину.
Д Найдем расстояние от вершины В до плоскости SCD
(рис. 267). Рассмотрим пирамиду SBCD. Она имеет общую с пи-
пирамидой SABCD высоту из Бершины S, а площадь ее основания
BCD вдвое меньше площади квадрата ABCD. Значит, если обоз-
обозначить объем этой пирамиды Уь то Ух = У/2.
Примем за основание пирамиды SBCD грань SCD Площадь
этой грани, очевидно, равна S/4. Высота пирамиды SBCD, опу-
опущенная из вершины В, равна расстоянию от точки В до плоско-
плоскости SCD, обозначим эту высоту d. Имеем: 1/1=—.-j-S-d =
= -pj-S-d. Учитывая, что У1==--1/, находим d = 6y/S. Результат,
410
счгвидно, не зависит от Еыбора вершины основания и пл( скости
Соковой грани, не содержащей эту вершину.
Ответ: 6V/S. ^
Для того чтобы найти расстояние от точки до плоскости, можно
использовать и координатный метод, а именно,
расстояние р от точки Мп {х0; уп) г0) до плоскости, 31 данной
уравнением ах -\- by + cz + d -¦= 0, находится
но формуле
__ axo-'rbij,,-\-c2a-\-d 1 , j.
(задача 7 из раздела I этой главы).
Задача 2. В правильной треуголь-
треугольной призме (pile. 268) |ЛБ| = 4 см,
\AAx\-—Зсм. Найти расстояние от вер-
шины d до плоскости ADB, где D — се-
середина ребра Axd.
Д Введем прямоугольную систему ко-
координат, как показано на рис. 268. Ось х
этой системы и медиана ВМ треугольни-
треугольника ABC лежат в плоскости основания и
перпендикулярны прямой АС, поэтому ось х параллелы а пря-
прямой ВМ. Заметим, что заштрихованная часть плоскости ADB не
является сечением призмы. Находим координаты точек / , В, D
и С]-. Л@; 0; 0), fiBy3; 2; 0), D @; 2; 3), d @; 4; 3). По из-
известным координатам точек А, В, D найдем уравнение плзскости
ADB так же, как это сделано в задаче 3 § 3, получим
Рис. 2Gii.
Расстояние р от точки Сг @; 4; 3) до этой плоскости находим
по формуле A):
_ \УЗ ¦0-3-4 + 2-31 _ 6 = _3_
Р " Кз + 9 + 4 ~~ 4 ~~ 2 '
Ответ: 3/2 см. ^
Задачи о нахождении расстояний между прямой и параллель-
параллельной ей плоскостью, между параллельными плоскостями сводятся
к нахождению расстояния от точки до плоскости. Это вытекает
из следующих двух утверждений:
расстояние между прямой и параллельной ей плоскость о равно
расстоянию от произвольной точки прямой до данной пм скости;
расстояние между двумя параллельными плоскостями равно
расстоянию от произвольной точки одной плоскости до другой
плоскости.
Докажем первое из этих утверждений (рис. 269, а), второе
доказывается совершенно аналогично (рис. 269, б).
(П Пусть а || а, а<?а (если ас: а, то расстояние межд/ ними,
очевидно, равно нулю). Пусть А — произвольная точка п] ямой .-<,
411
[ ] J_ а (рис. 269, a). Нужно доказать, что расстояние между а
и а равно | ААХ |. Через прямую а и точку Ах пропедем пло-
плоскость р, тогда р_]_а. Пусть ai — ^{]a, тогда ai||a. Во.чьмем про-
произвольные точки /W e a, N е; а. В плоскости |3 проведем перпен-
перпендикуляр MMi к прямой с,, тогда, очевидно, | MMi | = | AAi\.
Рис. 209.
Ь)
Кроме того, [MAfi]_La (поскольку p_La), а значит, j ЛШ i 3=
> I ММХ \. Отсюда и следует, что J MN \ ^ j ЛЛ, |. Таким образом,
АА11 — наименьшее среди расстояний между точками прямой a
и плоскости а, т.е. ! Л., ; — расстояние ме-
между этими фигурами. Щ
Задача 3. Высота правильной четырех-
четырехугольной пирамиды SA8CD и сторона ее ос-
основания равны а. Найти расстояние между
прямой Ав и плоскостью SCD,
Д Проведем плоскость через першину S
пирамиды и середины М и Л' реэер ЛИ и
CD (рис. 270). Эта плоскость перпендику-
перпендикулярна плоскости SCD. Перпендикуляр МР
на прямую .S/V является также перпендику-
перпендикуляром к плоскости SCD. Его длина и равна
расстоянию между прямой АВ и плоскостью SCO. Высота SO
пирамиды и отрезок МР являются высотами треугольни-
треугольника SMN. В этом треугольнике имеем: jM;Vj = a, \SO[ = a,
\SN\ = V\ SO |2 + | ON i2 = '|/"a2 + -^- = -^|-a. Площадь треуголь-
треугольника SMN равна, с одной стороны, -w- \ MN \ ¦ \ SO |, а с другой,
Рис. 270.
| МР |. Отсюда находим
•! SO I
j SN | I' 5
найти расстояние между
Ответ: 2а/]/5. а
Задача 4. В кубе
плоскостями ABLDx и BDC1} если
Диагональ АХС (рис. 271) куба перпендикулярна плоскостям
li и BDCi (следствие из задачи 3 § i этой главы), --la резуль-
результата задачи 3 § 2 гл. XV следует, что плоскости AB\D и BDCi
делят диагональ ALC на три конгруэнтных отрезка, т. ;., если М
412
и Л7 —точки пересечения диагонали АХС с этими плоскостями,
ю \АхМ | = \MN | = | NC\ = ¦*-1 АХС\. Длина отрезка MN равна
расстоянию между плоскостями ABxDx и
Поскольку ]А\С\ = у.
то \ MN
\<ъ
п.
Ответ: а]/3/3. А
Расстояние между скрещивающимися пря-
прямыми, как известно, равно длине их общего
перпендикуляра.
Задача 5. В тетраэдре ABCD ребра АВ и ркс 2-,
CD имеют длину а, остальные ребра — длину Ь.
Найти расстояние между прямыми АВ и CD.
Д Пусть М и N — середины ребер АВ и CD (рис. 272).
В равнобедренных треугольниках ABC и ЛбО находим ] СЛ4 | =
= | DM | = l/ Ь2 — -/-• Треугольник CjWD равнобедренный, поэтому
[MN] _'{_ (CD). Аналогично устанавливаем, что
треугольник ANB равнобедренный(\АN\ = \NB ;),
поэтому [MN] J_ (/4S). Значит, MN — общий пер-
перпендикуляр прямых АВ и CD. Из треугольника
CMN У
находим \MN\= У\ СМ :2 - j CN ,2 =
Ответ:
в
Рис. 272.
Следствие. В правильном тетраэдре с реб-
ребром а отрезки, соединяющие середины скрещива-
скрещивающихся ребер, являются общими перпендикулярами к этим 1ебрам,
и длина каждого из этих отрезков равна а/У2.
Для того чтобы найти расстояние между скрещиваю цимися
прямыми, не обязательно строить их общий перпендикул; р. Две
скрещивающиеся прямые всегда можно
заключить в две параллельные плоскости.
Схема построения одной из этих плоско-
плоскостей (через прямую Ь) показана на рис.
273: В — произвольная точка прямой Ь,
Oil с, ах(]Ь = В, b<^a, axcza. Расстояние
между прямыми а и b равно расстоянию
от любой точки прямой а до плоскости а.
Через прямую а также можно провести
плоскость р, параллельную плоскости а. Расстояние мед ду пло-
плоскостями аир равно расстоянию между прямыми а и Ь.
Задача 6. В правильной треугольной призме (рис. 274, а)
В\ = 4 см, |i4i4i| = 3cM. Найти расстояние между прям лми АВ
и CiM, где М — середина ребра АС.
Рис. 273.
413
Д Через точку А в плоскости AA^CiC проведем прямую,
параллельную прямой CVW. Ясно, что она пройдет через середину D
ребра /liCi (рис. 274, б). Плоскость ADB проходит через пря-
прямую АВ и параллельна прямой С\М. Расстояние между прямыми
Рис. 274.
АВ и С±М равно расстоянию от какой-либо точки прямой СХМ
до плоскости ADB. В задаче 2 этого параграфа было найдено
расстояние от точки С\ до плоскости ADB, оно равно 3/2 см.
Ответ: 3/2 см. А
§ 5. Двугранный угол. Угол между плоскостями.
Биссектор. Трехгранный угол
Величиной двугранного угла называется величина его линейного
угла. Линейный угол — это сечение двугранного угла какой-либо
плоскостью, перпендикулярной ребру. Сто-
Стороны линейного угла перпендикулярны ре-
ребру двугранного угла. Для нахождения ве-
величины двугранного угла можно построить
его линейный угол и найти его величину.
Задача 1. Найти величину двугранного
угла при ребре правильного тетраэдра.
Д Найдем величину двугранного угл",
при ребре АВ (рис. 275). Пусть DO — вы-
высота тетраэдра, DM — высота грзни ABD,
тогда МО — проекция DM на плоскость ABC,
а потому и [AfO]j_MB]. Значит, /_ DMO—
линейный угол двугранного угла при ребре АВ. Длину ребр i
тетраэдра обозначим а, тогда \DM | = а]/3/2. Точка О —центр
грани ABC, поэтому |МО| = аУ/6. Из прямоугольного тре-
треугольника DMO находим cos DMO = | МО |/| DM | = \/Ь. Значит,
двугранный угол при ребре А В имеет величину arccos(l/3). Та-
Такую же величину имеют двугранные углы и при других ребрах
правильного тетраэдра.
Ответ: arccos(l/3). ^
414
Рис. 276.
Задача 2. Все ребра правильной четырехугольной пира-
пирамиды SABCD имеют одинаковую длину. Найти величину ДЕуграь-
ного угла между гранями SBC и SAD.
Д Плоскость SBC проходит через прямую ВС, параллельную
плоскости SAD ((BC)\\(AD), рис. 276). Поэтому линия пе >есече-
ння плоскостей SBC и SAD — прямая I,
проходит через точку S параллельно пря-
прямой ВС. Прямая I является ребром дву-
двугранного угла, величину которого нужно
найти. Пусть М и N — середины ребер
AD и ВС соответственно. Плоскость SMN
перпендикулярна ребру /. Действитель-
Действительно, (ВС) J (MN) и (BC)_\_(SN), значит,
(BC)_L(SMN). Но 1\\(ВС), поэтому и
l_L(SMN). Отсюда следует, что /_ MSN —
линейный угол двугранного угла между
гранями SBC и SAD. Длину ребра пи-
пирамиды обозначим а. Пусть SO — высота
пирамиды. Обозначим еще MSN =а. В равнобедренном треуголь-
треугольнике MSN имеем [ MN \ = a, \MS\ = \NS\=a V3/2, | ON = а/2.
Отсюда sin(a/2) = |CW|/|SW | = l/l/з. Теперь находим <osa =
= 1-2 sin2 (a/2) = 1/3, a = arccos A/3).
Ответ: arccos A/3). a
Две пересекающиеся плоскости образуют четыре двуг >анных
угла. Если эти углы конгруэнтны, то плоскости называются пер-
перпендикулярными, угол между ними равен я/2. Если же плоскости
не перпендикулярны, то углом меж-
между ними называется меньшая из ве-
величин двугранных углов, образован-
образованных ими. Таким образом, угол меж-
между плоскостями лежит в пределах от
О до я/2.
Задача 3. В правильной шести-
шестиугольной пирамиде SABCDEF отно-
шение высоты к длине стороны осно-
основания равно ]/"б : 4. Найти угол ме-
между плоскостями SBC и SDE.
Д Построим линию пересечения
плоскостей SBC и SDE — прямую
SM (рис. 277, М = (ВС) П (ED)). Будем искать величину дзугран-
иого угла с гранями BSM и ESM, для чего построим сначала
его линейный угол.
Пусть О —центр основания пирамиды. Точка О — сгредина
диагонали BE, а поскольку треугольник ВМЕ правиль шй, то
(МО) _|_ (BE). Прямая МО — проекция прямой SM на п/оскость
основания (SO — перпендикуляр к этой плоскости), по;тому и
(SM) _]_ (BE). Пусть ON — высота в треугольнике SOM, аэгда из
Рис. 277.
415
того, что (SM) J_ (OiV) и (SM) JL (BE), следует, что (SM) J_
т. e. BNE — линейный угол двугранного угла BSME, Найдем
величину угла BNE.
Длину стороны основания пирамиды обозначим а, То.'да \BE\~
--=\ВМ\ — \ЕМ[ = 2а, и, значит, \М0\ =а\' 3. Из прямоугольного
треугольника SOM находим j SM | = У [ SO \2 + \0M г ==-^-~a.
Далее находим i ON = -—, L'..,' = -4-. Из симметрии относительно
1 У О
плоскости SOM ясно, что если BNE = q>, то BNO — <р/'1. Из тре-
треугольника BON находим tg (ф/2) = BO\i\ON\ = У'3, откуда ф =
= 2л/3. Это и есть величина двугранного угла BSME. Поскольку
Ф> л/2, то угол между плоскостями BSC и ESD равен л — ф — л/3.
Ответ: л/3. а
Для нахождения угла между плоскостями можно использовать
и координатный метод.
Пусть плоскости заданы уравнениями
а.2х + Ь-iij + с2г + йг = 0.
Угол между этими плоскостями обозначим ф. Тогда (гл. VII, § 8)
COS ф — •
"l
где «i = (ab hu Ci), щ = {аг\ b«; t,).
Задача 4. В кубе (рис. 273) точки Е, F, М—середины
ребер AAU AB, CCi соответственно. Найти угол между плоско-
плоскостями EFD и A]DlM.
Д Введем прямоугольную систему координат, как показано
на рис. 278. Длину ребра куба
обозначим а и найдем координаты
точек: D @; 0; 0), Е (а; 0; а/2),
F(a\ a/2; 0), Ах{а; 0; а),
D, @; 0; а), М @; а; а/2). По из-
известным координатам этих точек
найдем уравнение плоскости EFD:
и, уразнеш-;е плоскости
(заи1трнхованная на рис. 273 часть
плоскости AiDiM не является сечением куса). Вектор nl =
= (!;— 2; —2) перпендикулярен плоскости EFD, а вектор щ —
— @; 1; 2) — плоскости Л^/И. Находим угол ф между этими
4:16
плоскостями:
i/i,-'V [1-0 — 2-1 — 2-2
COS ф ==
1 И, 1 ¦ ! Я, ; П+4+4'V I
Ф — агесоз B/|/ 5). а
Биссектором двугранного угла наъыд.ды'ся полуплоскосг>, раз-
разделяющая его на два двугранных угла равной величины.
Границей бнссектора является ребро двугранного угла.
Биссектор существует для любого двугранного угла. Построить
его можно следующим образом: строим какой-либо линснн!, ii угол
данного двугранного угла (рис. 279);
строим биссектрису этого линейного
угла; полуплоскость, определяемая реб-
ребром двугранного угла и этой биссектри-
биссектрисой, и является биссектором данного
двугранного угла, Докажем это.
Q Плоскость линейного угла аОЬ
(рис. 279) перпендикулярна общему ре-
ребру I двугранных углов aid и 6ф. Зна-
Значит, углы аОс и сОЬ — линейные углы р"с' 279'
этих двугранных углов. Но с —биссек-
—биссектриса угла аОЬ, поэтому аОс = сОЬ. Значит, двугранные углы а/б
и 6/6 равны по величине, т. е. б —биссектор двугранною угла
Легко также видеть, что биссектор пересекает каждый линей-
линейный угол двугранного угла по его биссектрисе. Иначе это можно
выразить так:
биссектриса каждого линейного угла принадлежит биагктору
данного двугранного угла.
Биссектор двугранного угла обладает рядом свойстз, анало-
аналогичных свойстэам биссектрисы плоского угла.
Задача 5. Доказать, что биссектор двугранного уг ia есть
множество точек этого угла, равноудаленных от плоскостей его
граней.
Q Множество точек двугранного угла равноудален! ых от
плоскостей его граней, обозначим X, биссектор —б.
Докажем, что каждая точка множества X принадлеж гг бис-
сектору, т. е. что Хс8. Отметим сначала, что ребро / дзугран-
г.ого угла (рис. 280 а) принадлежит и множеству X и биссе! тору S.
Вне ребра / в гранях угла нет, очевидно, точек, принадлежащих
множеству X. Рассмотрим теперь внутренние точки двуг шнного
угла. Пусть Mel Проведем через точку М плоскость у пер-
перпендикулярно ребру / (рис. 280, а). Сечением двугранно!о угла
будет его линейный угол аОЬ. Пусть ММх и АШ2 — пеэпенди-
куляры на прямые, содержащие лучи а и Ь. Тогда ММЛ и ММг
будут перпендикулярами к плоскостям граней угла, а значит,
lMMi| = |ЛШ2|, так как М & X. Значит, точка М yi ла аОЬ
D ч/род. Г. Н. Яковлева 417
равноудалена от прямых, на которых лежат его стороны. Из пла-
планиметрии известно, что в этом случае точка принадлежит биссек-
биссектрисе угла аОЬ. Но тогда вместе с биссектрисой сна принадлежит
биссектору б. Тем самым доказано, что X с: 6.
Замечание. Линейный угол двугранного угла меньше раз-
Еернутого угла. Как доказано, ОМ—биссектриса линейного угла
аСЬ, поэтому луч ОМ составляет с лучами а и b острые углы.
Отсюда следует, что основания перпендикуляров ММ1 и А4М2
лежат на лучах а и b соответственно. С учетом этого и сделан
рис. 280, а.
а)
Рис. 280.
Докажем, что каждая точка биссектора принадлежит множе-
множеству X, т. е. 6 с X. Точки ребра /, как уже отмечалось, при-
принадлежат и биссектору и множеству X. Пусть М — произвольная
точка биссектора, не принадлежащая ребру. Проведем спять череi
точку УМ плоскость у перпендикулярно ребру /, в сечении получим
линейный угол аОЬ (рис. 280, б). Биссектор, как установлено
выше, пересекает этот линейный угол по биссектрис.;. Значит,
точка М принадлежит биссектрисе угла аОЬ, а потому равноуда-
равноудалена от прямых, на которых лежат его стороны, т. е |AfMij =
= |Л4УИ2|. Перпендикуляры MMi и УМУИ2 к сторонам угли являются
и перпендикулярами к плоскостям граней
двугранного угла, поскольку плоскость у
перпендикулярна этим плоскостям. Поэтому
точка М равноудалена и от плосюстей гра-
граней, т.е. УМ е X. Отсюда следует, что 6 cz X.
Таким образом, доказано, что X cz б и
б с X. Это означает, что б = X, что и тре-
требовалось. Ц
Простейшим из многогранных углов яв-
является трехгранный угол. Для описания
трехгранного угла чаще других используются
следующие величины: величины трех его
плоских углов —граней (рис. 281) ASB, BSC и CSA н величины
трех его двугранных углов при ребрах SA, SB и SC. Эти шесть
величин связаны между собой. Например, по известным величи-
величинам плоских углов можно найти величины двугранных углов.
418
Напомним, что для существования трехгранного угла ; пло-
плоскими углами а, р и v необходимо и достаточно, чтобы г ыпол-
нялись Два условия:
Если хотя бы одно из этих условий не выполнено, то тре<граи-
ного угла с данными плоскими углами не существует (см. -л. II,
задача 6 раздела I).
Задача 6. В трехгранном угле SABC плоские углы ASB,
ASC и двугранный угол при ребре SA имеют величин г 60°.
Найти величину угла BSC.
Д На ребре SA возьмем точку М Ф S и проведем [MN]J_[SA),
[MP]J_[SA) (рис. 282). Обозначим \SM\ = a. Из прямоупльных
треугольников SMN и SMP
находим: \MN\ = \MP\ = a~[/~3,
\SN\ = \SP\ = 2a. Угол NMP-
линейный угол двугранного угла
при ребре SA, значит, NMP —
= 60°. Теперь в треугольнике
MNP находим, что | NP | = а ]/3.
Из теоремы косинусов в тре- ^
угольнике SNP имеем
cos NrSP =
!SN H-jSP i2 — 1 NP г 5
2 : SNI •' SP;
Рис. 282.
откуда JVSP = arccosE/8). A
Задача 7. Доказать, что биесектогы двугранных углоз трех-
трехгранного угла пересекаются по одному лучу.
Q Рассмотрим два биссектора, например Pi и р3 (рис. 283).
Их пересечение есть луч с вершиной S; обозначим его /. Пусть
Л— произвольная точка луча /, A^S. Опустим перпсндш уляры
AAi, АА2, АА3 на плоскости граней угла. Так как А е рь то
ААг\ = | ААУ\, кроме того, | АА3 \ == j AA^\, поскольку .1ер3.
Значит, | ЛЛ2| = | АА3\, т. е. точка А равноудалена от пло( костей
граней NSP и MSP. Отсюда следует, что точка А принаугежит
биссектору двугранного угла при ребре SP. Поскольку А — про-
произвольная точка луча /, то и весь луч принадлежит бисс< ктору.
Таким образом, все три биссектора пересекаются внутри трех-
трехгранного угла по одному лучу. Щ
Из планиметрии известно, что биссектрисы углов треугольника
пересекаются в одной точке.. Биссекторы двугранных углов тетра-
тетраэдра обладают аналогичным свойством.
Задача 8. Доказать, что биссекторы двугранных углоп тетра-
тетраэдра пересекаются в одной точке внутри тетраэдра.
Ц Пусть / — луч, по которому пересекаются биссектогп трех-
трехгранного угла при вершине А, а М— точка пересечена i этого
14*
410
луча с гранью BCD (рис. 284). Концы отрезка AM принадлежат
разным граням двугранного угла при ребре ВС, поэтому биссек-
тор этого угла пересекает отрезок AM. Точку пересечения обо-
обозначим О.
Рис. 283.
Ркс. 284.
от
Точка О принадлежит лучу /, поэтому она равноудалена
плоскостей ABC, ABD и ACD. В то же время расстояния от
точки О до плоскостей ABC и BCD равны, так как эта точка
принадлежит биссектору двугранного угла при ребре ВС, Таким
образом, точка О равноудалена от плоскостей всех граней, т. е.
принадлежит биссекторам всех двугранных углов тетраэдра. Щ
§ 6. О вычислении объемов многогранников и их частей
Задача 1. В треугольной пирамиде SABC проведено сече-
сечение Л,Sid, параллельное основанию пирамиды, так, что |S/li|:
: | SA \ = ft. Доказать, что если Vi и V соответственю объемы
пирамид SAiBiCi и SABC, то
Q Рассмотрим гомотетию с центром S и коэффициентом k.
Треугольник А^В^С^ (рис. 285) является образом треугольника ABC
при этой гомотетии, так как | SB, |: | SB| = ] SCX \:\SC\==\SA^ j:
:\SA\ = k. Следовательно, Sa^.c^^Sabc- Пусть SO —высота
пирамиды SABC, O1 = [SO](](A1B1C1), тогда SOi — высота пира-
миды SAiBiCi и \SO\\-k\SO\. Отсюда следует, что
что и требовалось.
420
Замечание. 1) Аналогичный результат, очезидно, имеет
место и для произвольной многоугольной пирамиды, поскэльку
ее можно представить как объединение нескольких треугольных
пирамид (рис. 286).
2) Используя полученный в задаче 1 результат, нетрудно
вывести формулу для объема усеченной пирамиды:
где Н — высота усеченной пирамиды, Sx и S-, — площади ее осно-
оснований.
Рис. 285.
При вычислении объема призмы наряду с формулой V =-H-Q,
где Н — F-ысота призмы, a Q —площадь основания, бывает пэлезна
и формула V = l-S, где / — длина бокового ребра, a S — шощадь
перпендикулярного сечения призмы.
Задача 2. Объем треугольной призмы
ABCAiBrCt равен V. На ребрах BBi и ССХ
расположены соответственные точки М и N
так, что | ВМ |: | BBi \~т, \ CN |: | ССг \ = п.
Найти объем многогранника ABCAiMN (усе-
(усеченной призмы).
Д Пусть АгВ.гСч, — перпендикулярное се-
чапке призмы (рис. 287), /4aD —высота этого
сечения, Обозначим |y4,4i] = /, IB2C2.'=<?,
I A..D | ••-= /j. Имеем | BM \ = tnl, \CN\ = л/,
| StM i = A - m) /, I CiiV ] = A - n) l. Найдем
объем пирамиды AiByC\NM. Ее основание —
трапеция BtCiNM. Высота этой трапеции, очезндно, равна В.,Сг\,
т. е, а. Находим площлдь трапеции:
Srp = 'a (I BiM | -
ft *>-— f- —
Рис. 287.
Заметим, что отрезок A2D перпендикулярен плоскости ЕВ\СЛС,
поэтому высота пирамиды AyBiCiNM iu вершины А\ равна
421
\A2D\ = h, Отсюда, если Vi — объем пирамиды, то Vi-= 3/i5Tp ==
= ~- B-т-п) iah.
Находим площадь перпендикулярного сечения призмы: S =s
= -0 ah. Значит, объем всей призмы выражается формулой V =
= --lah. Сравнивая выражения для Vx и V, видим, что Vi =
= -„- B — т — п) V. Находим объем У2 многогранника AbCAiMN:
Для нахождения объема многогранника часто используется
дополнение этого многогранника до пирамиды или призмы или
разбиение на такие фигуры.
Задача 3, В треугольной призме ABCAiBid проведено сече-
сечение через вершину А и середины ребер BBL и ВхСх, Найти отно-
отношение объемов частей, на которые сечеш.е
разделило призму.
/1 Строим сечение. Пусть М и JV- се-
середины ребер BBL и BLd (рис. 2Щ. Находим
точки S = (MN) П (<Х\) иР= (SA) П (ЛЛ).
Сечение — четырехугольник AMNP.
Объем призмы обозначим V, а объем
части, содержащей ребро ССи — V\. Сам
способ построения сечения подсказывает,
как можно выразить Vi черео V. Пост-
Построим точку L = (MN) П (ВС). Для того
чтобы найти Уь нужно из сбъема пи-
пирамиды SALC вычесть объемы пирамид
SPNCt и MALB. А эти объемы легко
выразить через объем призмы.
Высоту призмы обозначим И, площадь
основания — Q, объемы пирамид SALC,
SPNCi и MALB соотвеютвенио V2, V3, V\-
Поскольку М и N — середины ребер, то | BL \ = 2 \ ВС |, а | CL | -=
= -2-|ВС|. Отсюда следует, что SAlc= 2Q- Далее, имеем | SCX | =
| = -о-1 ССг |. Значит, высота пирамиды SALC равна
Рис. 288.
I
|-Я. Находим Vz=l-llI-SALC=--jHQ, т. е. V2 = |
Пира-
Пира|-Я. Находим Vz=l-llI-SALC=--j
мида SPNC'i гомотетична пирамиде S.4LC с коэффицрентом k —
= 1/3 (| SCi |: | SC | = 1 : 3;> отсюда следует, что V3 = /гэ V2 = 3',. К.
Поскольку /VJ —середина ребра ВВи то высота пирамиды /VJ/iLB
равна ,-. Н, а из того, что | BL \ = -2-1 ВС |, следует, что 5^л = 2 Q.
422
Значит, \'^^= ^•^
= -^H-Q--=-^V. Теперь находи-1 Vt -*
23
23
— V2 —V3—V4 = -gg-V. Объем отсеченной части призмы, содержа-
содержащей ребро ААи равен V — Vi= 13/36, а отношение оэъемов
частей равно 13:23. а
§ 7. Задачи на комбинации многогранникоз
Задача 1. Сторона основания правильной четырехугольном
пирамиды имеет длину а, высота пирамиды равна п. В пи)амиду
вписан куб так, что четыре его вершины принадлежат основанию
пирамиды, четыре других лежат в боковых гранях, а четыре ребра
куба параллельны диагонали основания
пирамиды. Найти длину ребра куба.
Д Пусть четыре ребра куба парал-
параллельны диагонали АС (рис. 289) основа-
основания пирамиды, обозначим эти ребра MN,
PQ, MiNi и PiQi. Искомую длину ребра
куба обозначим Ь.
Рассмотрим сечение пирамиды плоско-
плоскостью верхнего основания куба (Ai.BiCiDx
на рис. 289). Это квадрат, ребра MiNx
и P\Q\ куба параллельны его диагонали
AiCi- Следовательно, N1M1B1 = я/4, а от-
отсюда заключаем, что и ,
т. е. прямоугольный треугольник AUA^Qi
равнобедренный. Более того, треуголь-
треугольники MtBiNi и MiXiQi конгруэнтны, так как конгруэнтны их
гипотенузы, | MiAri | = |MiQi | = 6. Значит, | B\Mi \ — \ А^Мх \ Отсю-
Отсюда следует, что Ь — \ MiNi \ = | AxCi |/2.
Теперь воспользуемся тем, что расстояние между плои остями
AxBiCxDx и ABCD равно Ь. Пусть SO — высота пирамиды,
O1 = [SO](](A1B1C1D1). Имеем \OOi\ = b, \SOt\ = h-b, \SOi\:
:\SO\ = (h -b):h. Отсюда следует, что и [Aid |: | АС \ = (h - by. h.
Учитывая, что \A1C1\ = 2b, \AC\-aY2, получаем 2Ь/сУ~2 —
= (h — b)lh, откуда находим, что b ~-ha /(a + Ylih).
Заметим, что рассуждения и расчеты мы провели, предпола-
предполагая, что указанное в условии расположение пирамиды и к^ба воз-
возможно. Из решения следует, что в данную пирамиду можно
вписать куб так, как требуется. Действительно, проведем :ечениа
пирамиды, параллельное ее основанию, через точку А ре эра SA
такую, что -—— — — А . Легко показать, что середины сто-
у \SA\ a + Vih v
рон сечения и основания перпендикуляров, опущенных из них
на плоскость основания пирамиды, являются вершинами куба,
423
удовлетворяющего условиям задачи. Из приведенного решения
следует также, что существует только один такой куб.
Ответ: ahl(a + y~2h). 4
В решении этой задачи было использовано сечение одного из
данных многогранников плоскостью грани другого. Рассмотрение
таких сечений бывает полезно в некоторых задачах, где один из
многогранников вписан в другой. Рассмотрим теперь задачу, где
такие сечения вряд ли помогут делу.
3 з д а ч а 2. Сторона основания правильной треугольмои приз;, ы
ABCAiBiCi имеет длину а. Два ребра правильного тетраэдра рас-
расположены на прямых AiB и В\С. Найти длину ребра этого
тетраэдра.
Д На прямых AiB и ВгС очевидно, лежат скрещивающиеся
ребра тетраэдра. Но в правильном тетраэдре такие ребра перпен-
перпендикулярны (задача 2 § 4 главы XV), следовательно, и прямые
АгВ и ВгС должны быть перпендикулярны. Из этого условия
найдем далее длину / бокового ребра призмы.
Изесстно также, что сбш,ий перпендикуляр скрещивающихся
ребер правильного тетраэдра имеет длину bJY~2, где Ь — длина
ребра тетраэдра (след-
(следствие задачи 5 § 4). Зна-
Значит, если d— расстояние
между прямыми АгВ и
BiC, то b = d 1/2.
Найдем длину / бо-
бокового ребра призмы из
указанного выше усло-
условия. Спроектируем диа-
диагональ ВгС на плоскость
AA^BiB, ее проекцией
будет прямая В-^М- (рис.
ц) 290, а), где М — середи-
середина ребра АВ Из того,
Рис 290. что (ВД _]_ (AiB), сле-
следует, что (BiM) _]_ (А\В).
MBiB и AiBA подобны, и
откуда /2 = а2/2, 1 = а/У.
а)
Тогда прямоугольные треугольники
потому \BBi\:\AB\ = \MB : | ААЛ |, у /, /]
Определим расстояние d между прямыми А^В и ВЛС. Проведем
[Bi?)]||[j4iB] (рис. 290, б). Искомое расстояние равно расстоянию
от точки В до плоскости DB\C, т. е. высоте пирамиды BDBiC из
вершины В. Найдем объем этой пирамиды, приняв за основание
грань DBC, получим, что F = a3/4)/6. Теперь примем за осно-
основание грань DBiC. Имеем
Треугольник DBxC прямоугольный, так как
424
(А1В)±(В1С). Значит,
о i no i inn Зя
bDBtC = -J I УЙ1 I • I filC I = -4"'
Подставляя в формулу V = ~^d-SDBtc значения V и SDBtc, полу-
получим, что d = a/Yb- Наконец, находим b — d/Y2 = a/Y~3-
Легко понять, что если призма имеет такое боковое ребро,
как найдено, то можно расположить правильный тетраэдр ука-
указанным в условии образом. Диагонали AiB и В-^С будут перпен-
перпендикулярны. Отложив на каждой из прямых АгВ и В^С о г осно-
оснований их общего перпендикуляра отрезки длины &/2 = ?/2]/,
получим четыре точки, которые и будут вершинами прав1льного
тетраэдра.
Ответ. й/У~3. а
ЗАДАЧИ РАЗДЕЛА I
1. Доказать, что плоскость, перпендикулярная каждой из двух пересе-
пересекающихся плоскостей, перпендикулярна и их линии пересечения.
2. Доказать равносильность следующих утверждений:
а) боковые ребра пирамиды имеют равные длины;
-б) боковые ребра пирамиды одинаково наклонены к плоскости основания;
в) около основания пирамиды можно описать окружность, а высста пира-
пирамиды проходит через ее центр.
3. Доказать, что плоскости, перпендикулярные ребрам тетраэдра и прохо-
проходящие через их середины, пересекаются в одном точке.
4. Сторона основания правильной пирамиды SABCD имеет длину а, боко-
боковое ребро — длину /. Построить сечение пирамиды, перпендикулярное боковому
ребру SC и проходящее через его середину, и найти площадь сечет я, если:
5. В кубе ABCDAiBfixD^ проведено сечение через диагональ А 01 грани
AAiD-^D, перпендикулярное плоскости ВСЛО. Найти отношение объем* >в частей
куба, на которые он разделен сечением.
6. В правильной четырехугольной пирамиде SABCD боковое je6po SB
образует с плоскостью основания угол я/4, Найти угол между этим эебром и
плоскостью SCD.
7. Доказать, что расстояние р от точки Ма (х0; (/„; г0) до пло> кости а,
заданной уравнением ax-\-by-\-cz-\-d = 0, вычисляется по формуле
' 8. Даны координаты вершин основания правильной пирамидь SABCi
А E; 1; —1), В E; —2; 2), С B; —2; —1). Вершина S пирамиды ле;<ит в ко-
координатной плоскости Оуг. Найти расстояние между прямыми SB и 1С.
9. Прямая пересекает грани ул и Va двугранного угла еоответстве! но в точ-
точках Л и В и составляет с плоскостью грани Yi угол я/6, ас nj осностью
425
гржш у.,— угол afisin !),7. Величин;! двугранного угла разпа л/3. На;'.тп угол
между прямой АВ » ребром двугранного угла.
10. В четырехугольно! пирамиде SABCD, основанием которол служит
параллелограмм ABCD, проведено сечение через ребро АВ и середину М
ребра SC, Найти отношение объемов частей, на которые сечение разделило
пирамиду.
11. Объем тетраэдра равен V. Все вершины параллелепипеда лежат на
поверхности тетраэдра, причем трг; грани параллелепипеда принадлежат трелр
граням тетраэдра. Найти наибольший возможный объем такого параллеле-
параллелепипеда,
ЗАДАЧ!! РАЗДЕЛА II
1. В координатном пространств даны точки М (—I; 3; 2), /V (I; 1; 3) и
Л(— 1; 2; 3). На прямо'! MN взята точки В и С так, что ДЛС = 9(У\ Л5С =
— 30°. Напти координаты этих точек.
2. Доказать, что прямая и плоскость, перпендикулярные однэч прямо.!,
параллельны.
3. Доказать, что если длины диагоналей параллелепипеда равны, то этот
параллелепипед прямоугольный.
4. В прямоугольном параллелепипеде одна из его диагоналел терпендпку-
лярна плоскости, проявленной через концы трех ребер, ныходяших из Toil же
вершины, что и эта диагональ. Доказать, что этот параллелепипед — куб.
5. Доказать, что высоты правильного тетраэдра пересекаются в одной
точке — центре тетраэдра.
6. Найти величины углов между прямыми, соединяющими центр правиль-
правильного тетраэдра с его вершинами.
7. Основанием пирамиды служит ромб с острым > глом величина а. Длима
стороны основания и трех боковых ребер равна а. Найти длину четвертого
бокового ребра пирамиды, если известно, что она меньше а.
8. Основанием пирамиды SABC является правильны.'! треугольник ABC
со стороной длины а. Грань SAB перпендикулярна плоскости основания, вы-
высоты граней SAC и SBC из веришни S равны соответственно У У) а и 1^2 а.
Найти высоту пирамиды.
9. В пирамиде SABC углы ABC, SAB и SCB прямые, SH— высота пи-
пирамиды. Выразить вектор SH черс:.р векторы SA, SB и .SC.
10. Основанием пирамиды SABCD является равнобедренная трапеция
ABCD, в которой \ЛВ\ = \ВС\—-а, \АП\=9.а. Плоскости граней SAB ч
SCD перпендикулярны плоскости основания пирамиды. Найти высоту пира-
пирамиды, если высота грани SAL7 из першины S' равна 2а.
11. Доказать, что следующие утверждения равносильны:
а) высоты (или их продолжения) тетраэдра пересекаются в одной точю;
б) каждые два скрещнвающихсл ребра тетраэдра перпендикулярны;
в) основание одно!! нз высот тетраэдра есть точка пересечении высот
грани;
г) основание каждом высоты тетраэдра есть точка пересечения высот гра-
грани, на которую опущена эта высота.
426
12. Доказать: для того чтобы ортогональной проекцией прямого угла на
плоскость был прямой угол, необходимо и достаточно, чтобы одна i з сторон
данного угла была параллельна плоскости проекций, а другая не 1ерпендн-
кулярна этой плоскости.
13. Площадь правильного треугольника равна S. Нго ортогональ io.i про-
проекцией hi плоскость является равнобедренный треугольник с углом при вер-
вершине величины а. Найти площадь этой проекции, если: а) а>луЗ; б) а<я/3.
14. Длина ребра куба ABCDA^C^ равна а. Точки Р, К, L— :ередины
ребер AAU AiDi, B1C1 соответственно, точка Q— центр грани CC^D. Отре-
Отрезок MN с концами на прямых AD и KL пересекает прямую PQ и i ер^кдл-
кулярен ей. Найти длину этого отрезка.
15. В 1реугольной призме ABCAxBxCi ючки М, N и Р соотв :тствег;но
середины сторон АВ, ВС и СА основания ABC, Отрезки МСи NЛь РВУ по-
попарно перпендикулярны и длина каждого равна а. Напги объем при; мы.
16. Плоские углы при вершине пирамиды прямые, So — площад. основа-
основания, Si, S2, S3—площади боковых граней. Доказать, что S-j = Sf--S! + S*,
17. Ребро правильного тетраэдра ABCD имеет длину а. Найти площадь
ортогональной проекции тетраэдра на плоскость, проходящую через середины
ребер АВ, BD и DC.
18. Основанием призмы ABCAiBfii служит правильный треугольник ABC,
длина стороны которого равна 2а. Ортогональной проекцией призм! на пло-
плоскость основания ABC является трапеция с боковой стороной АВ и п ющадью.
в два раза большей площади основания. Ньйти высоту призмы, если [. lS1J=b-
(Найти все решения.)
19. В кубе ABCDAiB^iDi точки Е и F — середины ребер A^l х и СХ1^
соответственно. Построить перпендикуляр из точки /-" нл плоскоет, EBD и
найти его длину, если ребро куба имеег длину а.
20. В правильной четырехугольной призме ABCDA1BlC1D1 crop зна осно-
основания имеет длину а. Через точку Сх проведена прямая, перпендикулярная
плоскости BAiD. Найти длину отрезка этой прямо.;, лежащего внутр [ призмы,
если длина бокового ребра равна; а) а V 2, б) а/2 |/2.
21. Все ребра правильной призмы АВСА1В1С1 имеют длину а, Пряма:1,
перпендикулярная плоскости BAiC, пересекает прямые ВСХ и ABt :оответст-
веино в точках М и N. Найти длину отрезка MN. (Указание. Выразить
векторно условие перпендикулярности отрезка MN плоскости ВА±С.)
22. Через середину высоты правильно.! четырехугольной пирами; ы прове-
проведено сечение, перпендикулярной боковому ребру. Найти площадь этого сече-
пия если длина Сокового ребра равна а, а угол между Соковыми ребрами,
лежащими в одной ] р; ни, равен: а) 60°, б) 120".
23. Рассматриваются с чения куба плоскостями, перпег.дикулярш>ми одно/)
из его диагоналей. Определить наибольшую возможную площадь сеч<ння, если
ребро куба имеет длину а.
24. В правильной треугольно! призме АВСА-^В^Су через вершину Вг про-
проведено сечение, перпендикулярное диагонали САХ боковой грани AAiC,C.
Найти площадь сечения, если: а) \ АВ\ = \ AAi\=a; б) | АВ \ — '2а, \ ААг \ = а.
25. Основанием пирамиды SABCD служит ромб ABCD со crop зной дли-
длины а и острым углом величины а Основанием высоты иирамидь является
427
центр ромба ABCD. Плосколи граней SAB и SCD перпспдикуля эпы. Майти
объем пирамиды
26. В правильно:! шестиугольнэй пирамиде SABCDEF угол ме-кду апофе-
апофемой боковой грани и ег проекцией на плоскость основания ранги я/3. По-
Построить сечение пирамиды, проходящее через ребро АВ перпендикулярно
г р пи и SCD и определить, в каком отношении оно разделит высоту пирамиды.
27. Три непересекающиеся диагонали боковых граней треугольчой призмы
перпендикулярны и длина каждой из них равна а. Найти объем тизмы.
28. Точка М— середина бокового ребра АА{ параллелепипеда
АБСОАф^С^Р^. Прямые BD, М1\ и Afi попарно перпендикулярны. Найти
ьы-огу параллелепипеда, если \BD\-2a, \ ВС { -- •-=- а, 'А^С'^Ла
29. Три плоскости попарно перпендикулярны, прямая состазляет с ними
углы ф!., ф-2 и ф3. Доказать, что sin2 (pl + sin2 ф2 + sin2 <ра = 1.
30. Из точки А плоскости проведены по разные ее стороны отрезки AM
и АЫ, Каждый из отрезков имеет длину а и образует с плоскостью угол а.
У:ол между проекциями этих отрезкоз на плоскость равен E. Определить
длину отрезка ММ.
31. В плоскости расположен отрезок АВ длины а. Из точек А и В про-
проведены перпендикуляр AM и наклонная В Л' к плоскости (по одну ге сторону),
3 у^-
прнчем I AM | = | BN \ = ~^-а, \ММ\=2а, ЛВЛ' = С0°. Найти угол между
прямой МЫ и плоскостью.
32. Найти углы между линией пересечения плоскостей
2х — у — г~0 к х — 2(/ + г=0
и а) координатными осями; б) координатно-i плоскостью Ох:;.
33. Сторона основания правильной треугольно.! призмы A5CAlBlCl имеет
длину а. Точка О —середина ребра АВ, точка ? лежит на ребре Afi^. Пря-
Прямая DE образует углы а и (J с плоскостями ABC и AAiCfi соответственно,
Найти пысоту призмы.
34. В правильной треугольной пирамиде сторона осноааш-л и;.;;:ет длину а,
усол между апофемой и бокозол гранью равен я/4. Определить высоту пи-
рамиди.
35. В правильном тетраэдре ABCD через аершину В проведена плоскость,
параллельная ребру CD и составляющая с ребром AD угол, равный: а) я/3;
б) arcsin 5/С. В каком отношении эта плоскость делит ребро ADt
36. Основанием прямоугольного параллелепипеда ABCDAiBiC1Dl является
кв-npjr ABCD. Найти наибольшую возможную величину угла ме«ду прямой
BDV и плоскостью BDCL,
37. Плоскость пересекает отрезок. Доказать, что она делит егэ в отноше-
отношении равном отношению расстояний от его концов до этой плоскости.
38. Сколько имеется плоскостей равноудаленных от четырех точек, не ле-
лежащих в одной плоскости?
39. Вычислить расстояние от точки Л? C; 1; —1) до плоскости 22* — 4у
— 20г — 45 = 0; и от точки N D; 3, —2) до плоскости Зх—i/-f-5z-f 1 — 0.
40. На оси г найти точки равноудаленные от плоскостей x + ty — Ъг— 2 = 0
и 5х + 2 +8 = 0,
423
41. Известии координаты четырех вершин параллелепипеда ABCDA BxCiD^,
ЛA; 1; 1), В C; 2; 0), С C; 5; 0), Ct C; 7; 2). Найти координаты остальных
вершин и расстояние от вершины А до плоскости CDDXCX.
42. В пирамиде SABC ребро ЯЛ перпендикулярно плоскости ABC, \ AC \—
= \СВ\, \AS\ = \AB\=a. Через середину ребра АС проведена nj оскость,
перпендикулярная ребру SB. Найти расстояние от вершины С до згой пло-
плоскости.
43. Сторона основания ABC правильной пирамиды SABC имеет дану а,
боковое ребро — длину Ь. На каком расстоянии от прямой ВС след' ет про-
провести сечение пирамиды, параллельное ребрам ВС и SA, чтобы пломадь ею
была наибольшей из возможных?
44. Грань AAtBiB призмы ABCA^^i перпендикулярна ее основание ABC.
Высота призмы равна Н, площадь грани AA]B±B равна площади о> нования
призмы. Найти расстояние от точки В до плоскости САЛВ^.
45. В правильной пирамиде SABCD длина общего перпепдикуля >а ребер
SA и ВС равна а, а его основание делит отрезок ВС в отношении 1 : 3. Опре-
Определить объем пирамиды.
46. Даны вершины АО; 2; 3), В B; 3; 5), Ах C; 3; 4) и С± D; >; 5) па-
параллелепипеда ABCDAiBjCiDL. Найти расстояние между прямым AD^
и ВС.
47*. Объем тетраэдра ABCD равен 5 см3. Через середины ребер / D и ВС
пронедена плоскость, отстоящая от вершины А на расстоянии 1 см i пересе-
пересекающее ребро CD в точне М так, что ] DM \ : J МС , = 2 : 3. Вычислить пло-
площадь сечения тетраэдра этой плоскостью.
48*. Основанием пирамиды SABCD является ромб ABCD со :тороной
длиьы а и острым углом ВЛО = 60°. Высота пирамиды равна ^ a i SBA +
-f-SBC = 180°. На ребре SC взята точка М так, что \CS\ = 3\CM . Найти
расстояние между прямыми DM и АС.
49*. В пирамиде SABC общий перпендикуляр прямых АС и SB [роходит
через середину ребра SB. Площади граней ASB и BSC равны, площгць грани
ASC вдвое больше площади грани BSC. Внутри пирамиды есть -очка М,
сумма расстояний от которой до вершин В и S равна сумме расстояний до
плоскостей всех граней пирамиды. Найти \МВ\, если \AC\=V"b см, |SB| =
= 1 см.
50. Ребро правильного октаэдра имеет длину а. Определить кр ггчайшее
расстояние по поверхности октаэдра между серединами двух параллельных
ребер.
51*. Сторона основания правильной треугольной призмы имеет длину а,
боковое ребро —длину /. Определить кратчайшее расстояние по пОЕгрхности
призмы между вершиной одного основания и серединой противопол» жной ей
стороны другого основания,
52. Плоскость равнобедренного треугольника образует с плоек< етью а,
проходящей через его основание, угол <р. Угол при вершине треугольника
равен \|). Найти угол между боковой стороной и плоскостью а.
53. Дан прямоугольник, длины сторон которого равны 1 см и 2 см. Через
меньш}ю сторону прямоуюльннка проведена плоскость а, составл пещая с
429
диагональю прямоугольника угол ф. Найти угол между этой плоеиктыо и пло-
плоскостью прямоугольника.
54. В правильной четырехугольной пирамиде двугранный уол между
смежными боковыми гранями имеет величину а. Найти величину двугранного
угла при основании пирамиды.
55. В кубе ABCDAlBiCiDl найти угол между плоскостями: ;i) AiDM и
А^В^СО; б) AtDM и C^DN, где М и Л' — середины ребер АВ и ВС соответст-
соответственно; в) EDCi и ЕВ,С; г) AAlD1D и EFO, где Е и F соответствен!» — сере-
середины ребер ААг и CD, a 0—центр грани Аф1С{О1.
Г>6. Через вершину А куба ABCDA^B^C^Dx проведена плоскость, парал-
параллельная диагонали ВО,, куба и диагонали, В,С его грани. Найти уол между
этой плоскостью и плоскостью ABCD.
57. В правильной шестиугольной пирамиде SABCDEF плоскости граней
SAB и SCD перпендикулярны. Определить углы между плоскостями; a) SAB
и SDE; б) SAB и SBC.
58. Основанием пирамиды служит треугольник со сторонами а, а, Ь. Каж-
Каждая боковая грань наклонена к плоскости основания под углом величины а.
Найти: а) площадь боковой поверхности пирамиды; б) объем пирамиды для
случая, когда а = 5 см, й=б см, а-=45".
59. Катеты АВ и АС прямоугольного треугольника расположены соответ-
ствеЕШО в разных гранях двугранного утла и составляют с его ребром острые
углы величины ср н ф соответственно. Найти величину двугранного угла.
60. Стороны АВ и АС равностороннего треугольника расположены соот-
соответственно в гранях аир острого двугранного угла величины ф. Сторона АВ
образует с ребром двугранного угла острый угол \|). Определить угол между
плоскостью ABC и гранью fi.
61. В тетраэдре ABCD двугранные углы при ребрах АВ, АС и BD пря-
прямые. Один из отрезков, соединяющих середины противоположных ребер тет-
тетраэдра, имеет длину а, я другой —длину a V&. Найти длину наибольшего
ребра тетраэдра.
62. В гранях двугранного угла расположены точки А и В. Доказать, что
биссектор делит отрезок АВ в отношении, равном отношению расстояний от
точек Л и В до ребра двугранного угла.
63. Сторона основания правильной четырехугольно, пирамиды имеет дли-
длину а, дчуграпньш угот при основании — величину а. Проведен биссектор
одного из двугранных углов при основании пирамиды. Найти площадь полу-
получившегося сечения.
64. В пирамиде SAВС бокоаое ребро SA перпендикулярно плоскости осно-
основания ABC, \SA\=a, \ВС\—2а. Двугранные углы при ребрах SB и SO
каждый имеют величину 60°. Найти обьем пирамиды.
65. О;нованием прямого параллелепипеда ABCDAiBlClDl служит ромб
ABCD, высота параллелепипеда равна а. Плоскость АВ^М, где М — середина
ребра ВС. образует углы в 60° с плоскоегями АА,С{С и BB^jD, Определить
обьем параллелепипеда.
G6. Линейные углы ASB, BSC, CSA трехгранного угла имеют соответственно
величины л/3, я/6, агееоз О/^З). Найти величину доуграииого угла при
ребре S3.
430
67. Доказать, что, если в трехгранном угле SABC двугранные углы при
ребрах SB и SC имеют равные величины, то равны и величины проп вополож-
ных им плоских углов ASC и ASB.
68. Каждый двугранный угол трехгранного угла имеет величину а. Найти
величину плоских углов, и указать все возможные значения о.
69. Каждый плоский угол трехгранного угла имеет величину л/2. Внутри
угла расположена точка, удаленная от двух граней угла иа расстояние а,
а от третьей — на расстояние За. Найти расстояние от этой точки до верш лпы угла.
70. Каждый двугранный угол трехгранного угла имеет величину с Внутри
угла на расстоянии а от его вершины расположена точка, удаленная от пло-
плоскости каждой грани на одно и то же расстояние. Наши это расстоя :ие,
71. Каждый плоский угол четырехгранного угла имеет величи iy а, все
двугранные углы при ребрах дайкою четырехгранного угла имеют одинаковую
величину, Определить величину этих двугранных углов.
72. В правильной треугольной пирамиде длина стороны осисвани i раЕяа а,
а —величина плоского угла при вершине пирамиды, р—величина двугранного
угла между боковой гранью и основанием, у — угол между боковым ребром и
основанием, б —величина двугранного угла между боковыми граням!. Найти
объем пирамиды в каждом из следующих четырех случаев: а) о is a = 1/4;
б) tg Р = 2; в) tgy=l; г) cos6=1/5.
73. Гранями треугольной пирамиды являются равнобедренные треугольник?!.
Основание каждого из этих треугольников имеет длину а, а против элежащий
ему угол —величину а. Найти объем пирамиды.
74. Длина стороны меньшего основания правильной усеченной треугольной
пирамиды равна а, двугранный угол пирамиды при ребре меньшего основания
имеет величину 120°, высота пирамиды рапна а/2. Найтн объем пирамиды.
75. Основанием пирамиды служит прямоугольный треугольник с острым
углом а. Каждое боковое ребро составляет с плоскостью основания пирамиды
угол в 30° и имеет длину Ь. Найти объем пирамиды.
76. В пирамиде SABC каждые два скрещивающихся ребра перпенд шулярны,
| ЛВ ] = | ИС |=Ь, ЪАС = а, двугранный угол пирамиды при ребре ВС имеет
величину tp. Найтн объем пирамиды.
77. Основанием пирамиды служит равнобедренная трапеция с ост ;ым утлом
величины а и площадью S. Каждая боковая грань составляет с <слованием
угол величины р*. Найтн объем пирамиды.
78. Основание пирамиды — выпуклый многоугольник, плошдп- 6охоеых
граней равны. Доказать, что сумма расстояний от любой точки о« ог.ания до
плоскостей бокопых граней пирамиды — величина постоянная.
79. Скрещивающиеся диагонали двух параллельных гранен парал. елепипеда
служат ребрам тетраэдра. Определить отношение объемов параллелепипеда и
тетраэдра.
80. Если поверхность тетраэдра разрезать вдоль ребер AD, BD, CD, то ее
разверткой на плоскость ЛВС будет квядрат со стороной длины а. Найти
объем тетраэдра.
81. Плоскость переткнет Соковые pefipa SA, SB и SC трсугол>псы пира-
пирамиды cooTbt'TCTEeimo в точках М, N н Р так, что \SM\: SA\ — m,
\SN\:\SB' = n SP i : I SC j = p. Найти отнои.енне объемов пирамид SMNP и
SABC.
431
82. Найти отношение объемов частей, на которые призма АВСЛ^В^С^ раз-
шоскоггыо, проходящей:
а) через вершину Bt и середкт ройер AAj. и АС;
б) через середины ребер АВ, АС и БЗг,
п) через точку пересечения медиан основания ABC, середину реЗра A-fii и
точку пересечения диагоналей грани BBijCiC.
88. Доказать, что любая плоек эсть, проходящая через точку пересечения
диагоналей параллелепипеда, делит его на две части разного объем;-.
84. Доказать, что всякая плоскость, проходящая через середины даух
гкрещиаанЯцихся ребер тетраэдра, рассекает его на две части, равные по
объему,
85. Овнованиями усеченной четырехугольной пирамиды служат параллело-
граммы ABCD и A\BxC]Di, отношение длин сторон которых рапнэ 2. Через
p-j6po В fix проведено сечение, параллельное грани AA^DjD. Найти отношение
объемов частей, на которые это сечение разделило пирамиду.
88. Отношение длин двух скрещгзающихся ребер тетраэдра равпе q, Парал-
Параллельно этим ребрам проведена плоскость так, что в сечении получился ромб.
Найти отношение объемов частой, на которые эта плоскость разделила
тетраэдр.
87. В тетраэдре ABCD известно, что , АВ \—2а, \AD\=\BD — Ь, \ АС \ —
=|BCj=c (n<b<c). Прямые DM и fl.V, где М и Л' — середины ребер АВ
и CD перпендикулярны. Найтн объем тетраздра.
88. В тетраэдре ABCD грань ABC — правильный треугольник, грань DBC
перпендикулярна ей, Ь,4С = я/3, AD =6 см, угол между прямым-t AD н ВС
равен arcoos A/4). Найти объем тегсаэлра (найти в:е решения).
89. Дана треугольная призма АВСА1В1СХ объема V. Найтн сбъгм части
призмы, ограниченной ее основанием i41fl.C], бокозыми гранями и плоскостями
ABCi, ВСАи CABV
90. "координатном пространств'? фигура Ф задана как множество всех тех
и только тех точек, координаты которых удовлетворяют неравенству \х\^\-
--|(/'+ г | «G а. Найти объем фкгу;>ы Ф.
91. Боковое ребро правильной треуго.аьяои пирамиды наклоненс к плотко-
сти ее основания под углом ф. Одно oinoaaiiiie правильной треугольной прнлмы
принййлажиг основанию пирамиды, а вершины другого лем'.ат на боковых рсбрэч
пирамиды. Все ребра призмы имеют длину а. Налги оОьем пирачиды. При
каком значении <р этот объем будет наименьшим?
02. Ребро АВ тетраэдра ABCD является диагональю основан! я четырех-
четырехугольной пирамиды, а ребро CD параллельно плогкогти ее осиоваш-я и копки
его лежат на боковых ребрах пирамиды. Определить наименьший возможны.!
объем пирамиды, если объем тетраэдра равен I'.
93. Дан правильный тетраэдр ABCD. Каждая из его вершин Л, В, С, D
симметрично отражена относительно плоскости противоположной ей грани,
в результате получены соответственно точки Аи Blt Сь Dt. Найтг; от1:ошет:>
объемов тетраэдров AiB^iDi и ABCD.
94. В тетраэдре отрезки, соединяющие его вершины с точками пересечения
медиан противоположных граней, пересекаются п точке О. Второй тетраэдр
симметричен исходному относительно точки О. Найти объем обцей части этих
1етраэдроп, если объем исходного тетраэдра patteH V.
432
S3. Объем правильно! четырехугольно"; пкрамкдц SABCD равен "'. Высота
SP пирамиды является ребром правильного тетраэдра SPQR, плоское !ь грани
PQR которого перпендикулярна ребру SC. Найти объе;,? общей части гирамиды
и тетраэдра.
9о. В тетраэдре ABCD ребра АВ и CD перпендикулярны, \АВ\ = а,
\CD\-b. Отрезок, соединяющий середины ребер АВ и CD пер ленд жулярен
им. и длина его равна с. Вершины правильного тетраэдра лежат па hoi ерхяоети
тетраэдра ABCD, одно из его ребер параллельно ребру АВ, другое —р:бру CD.
Найти длину ребра этою правильного тетраэдра (найти все решения),
97. Все вершины правильной пирамиды SABCD расположены fa ребрях
правильной пирамиды QMNP с основанием МУР. Известно, что i лоскость
ABCD перпендикулярна плоскости боковой грани QMN пирамиды QMNP.
Найти отношение объемов этих пирамид.
98. Объем треугольной призмы АВСАгВ^С^ равен V, Проведенп четыре
плоскости: первая — через вершину С параллельно плоскости АВСи 1торая —
через вершину Сх параллельно плоскости A^Bfi, третья —через р« 5ро BBt
параллельно ребру АС, четвертая —через ребро AAt параллельно р :бру ВС.
Найти объем тетраэдра, ограниченного этими четырьмя плоскостями.
99. В правильной призме ABCAiBfii сторона основания имеет ;лину 2а,
боковое ребро — длину а. Проьедены три плоскости: первая — через ве)шину А
перпендикулярно прямой АВЬ вторая—через вершину В перпендикулярно
прямой SCj, третья —через вершину С перпендикулярно прямой С А . Найтя
объем тетраэдра, ограниченного этими тремя плоскостями и плоскостьк A^B^Ci.
100. Длина ребра куба ABCDAiB^CJJ^ равна а. Точка С —середина
ребра AD Одно ребро правильного тетраэдра лежит на прямой ED , другое
на прямой, проходящей через точку Лх и пересекающей npsivfyro ВС в точке /?.
Найти: а) \BR\\ б) длину ребра тетраэдра.
101. Два правильных тетраэдра ABCD и MXPQ расположены так, что
плоскости BCD и NPQ совпадают, вершина М лежит на высоте АС первого
тетраэдра, а плоскость М.К'Р проходит через центр граня ABC и середину
ребра BD. Найти отношеииг длин ребер тетраэдров.
102. Сторона основания правильной треугольной пирамиды нме т длину
2 }^6 см, а высота пирамиды равна 3 см. Вершина А куба ABCDAlB1ClDl
сходится в центре основания пирамиды, вершина С]. — на высоте п [рамиды,
а рэбро CD лежит в плтм.'остг одноП из бокояыч граней. Найти длину pe'ipa куба.
Глава XVII
ФИГУРЫ ВРАЩЕНИЯ
§ !. Цилиндр
Цилиндром называется фигура, полученная при вращении
прямоугольника вокруг оси, содержащей его сторону (рис. 291).
Круги, полученные вращением сторон прямоугольника, перпенди-
перпендикулярных оси (ОА и Oi^i на рис. 291), на-
называются основаниями ц'илиндра. Радиус ос-
основания называют также радиусом цилиндра.
Фигура, полученная вращением стороны
прямоугольника, параллельной оси, (АА1 i:a
рис. 291.) называется боковой поверхностью
цилиндра. Все точки боковой поверхности
удалены от оси цилиндра на расстояние, рав-
равное его радиусу.
Всякое сечение цилиндра плоскостью,
проходящей через ось, (осесое сеч?ние) есть
прямоугольник (BBxCiC на рис. 291). Его
стороны, параллельные оси (BBU CCi), на-
называют образующими боковой поверхности
цилиндра. Каждая образующая перпендику-
перпендикулярна плоскостям оснований цилиндра, длина образующей равна
расстоянию между этими плоскостями, т. е. высоте цилиндра.
Всякое сечение цилиндра плоскостью, перпендикулярной его
оси, есть круг, конгруэнтный основаниям цилиндра.
Ортогональной проекцией цилиндра на плоскость, перпендику-
перпендикулярную его оси, является круг радиуса, равного радиусу цилиндра,
проекцией оси является цеьтр этого круга. Проекцией боковой
поверхности является окружность, ограничивающая этот круг.
Задача 1. Вершины Л, В и Di куба ABCDA^dD! лежат
па боковой поверхности цглиндра, ось которого шраллельна
прямой DCL. Найти радиус цилиндра, если ребро куба имеет
длину а.
Д Плоскость BAiDLC перпендикулярна прямей ВС-^ (рис. 292),
а значит, и оси цилиндра. Проекции точек В и Di на плоскость
BAJ),C совпадают с самими этими точками. Проекцией точки А
является середина Аг отрезка ВАЪ Проекцией боковой поверх-
поверхности цилиндра на плоскость ВА^О^С служит окружность, про-
Рис. 291.
434
ходящая через точки В, Л,, Dt. Радиус этой окружности равен
радиусу цилиндра. Этот радиус найдем по формуле R = ai^f3,
где аи аг, а3 — длины сторон ВА2, A>DU BDi треугольника BA±DU
a S — площадь этого треугольника. Имеем о, = | А2В | =; а/\г~2,
а3 = \ BDi | =а j/З, а из треугольника A2AxDt
находим а2 = | A2DX | = а 1^3/2. Далее, S =
1 'A R i
AlDl\ =
К2
Теперь находим
«?/
Призма называется вписанной в цилиндр
(а цилиндр — описанным около призмы), если
основания призмы вписаны в основания
цилиндра. Очевидно,
для того чтобы около пршмы можно было
описать цилиндр, необходимо и достаточно,
чтобы призма была прямая и около ее осно-
основания моокно было описать окруокность.
В частности, около любой прямой треугольной призмы i около
любой правильной призмы можно описать цилиндр. Каждое
боковое ребро вписанной в цилиндр призмы является обра: ующел
боковой поверхности цилиндра.
Задача 2. Рассматриваются всевозможные правильн>ie тре-
треугольные призмы заданного объема V. Около каждой 1:з этих
призм описан цилиндр. Найти наименьшую пло-
площадь поверхности такого цилиндра.
Д Высоту призмы обозначим И, длину сто-
стороны основания а, радиус описанного цилинд-
цилиндра R (рис. 293). Этот радиус равен радиусу
окружности, описанной около основания при-
призмы, а поскольку основание — правильный тре-
треугольник, то R = a/}^3.
По условию имеем a2H = V, откуда Н =
41/
= —;-—. Учитывая
это,
находим площадь
S = 2tiR2 + 2nRH =
Рис. >93.
поверхности цилиндра:
= -^-(а2-\ ). Площадь S является функцией переменной % е 10;
о \ п /
4- оо[. Находим критическую точку этой функции: S' =
2я / 41/ \ •/¦ - -
= -j-Bfl—^-J = O,ao = j/2V. Легко видеть, что функция ¦.'> имеет
при а — а0 наименьшее значение и оно равно 2л ^4V*.
Ответ: 2n-^rAV2. A
Пусть плоскость а параллельна оси цилиндра, d — расстояние
между этой плоскостью и осью, R — радиус цилиндра, Если d>R,
435
то плоскость а. не имеет с цилиндром общих точек. Если 0 ^~ й <l R,
то сечение цилиндра плоскостью а есть прямоугольник (экс. 294)-
Если d — R, то плоскость а имеет с боковой поверхностью
цилиндра одну общую образующую {КК\ на рис. 294), эта обра-
образующая лежит на ортогональной проекции
оси цилиндра на плоскость а. В этом
случае плоскость а называется касатель-
касательной к боковой поверхности цилиндра.
Цилиндр называется вписанным в приз-
призму (а призма — описанной около цмлиндра),
если основания цилиндра вписаны в осно-
основания призмы. Легко видеть, что
для того чтобы в призму можно было
вписать цилиндр, необходимо и достаточно,
чтобы призма была прямая и в основание
ее можно было еписать окружность.
Каждая боковая грань описанной около
цилиндра призмы касается его боковой
поверхности по образующей. Эта образую-
образующая проходит через течки касания соответ-
соответствующих сторон основания призмы с окружностями оснований
цилиндра.
В любую прямую треугольную призму и в любую правильную
призму можно вписать цилиндр.
Задача 3. Радиус цилиндра равен г, а высота его равна 5г.
Около цилиндра описай параллелепипед, отношение объема кото-
Рпс. 294.
Л,
Рис. 2<>б.
находим sin a = 4/5.
рого к объему цилиндра равно 5 : л. Найти
длину отрезка большей диагонали парал-
параллелепипеда, лежащего внутри цилиндра.
Д Грани параллелепипеда, списанные
около оснований цилиндра обозначим
ABCD и AiBiCiDi (рис. 295) так, что
BAD ==а<л/2. Параллелограмм, описан-
описанный около окружности, является ромбом,
поэтому ABCD — ромб. Пусть BE — высота
этого ромба, тогда \BE.--2r и из треу-
треугольника ABE находим ; АВ 1 == 2r/sina.
Площадь ромба ABCD равна 4r2/sina.
Поскольку высота параллелепипеда равна
ьысоте цилиндра, то VИ — 20ra/sina. Учиты-
Учитывая, что Vu = 5лг!, из условия V,,: VIV = 5 : л
Отсюда следует, что cos (a/2) = i!/|/5. Hi
треугольника АОВ находим | A0\ = | AB\cos(aj2) = ]/~5 г, откуда
AC\ = 2\AO\=2V5r.
Рассмотрим сечение цилиндра плоскостью AAtCiC (ACi и АУС —
большие диагонали параллелепипеда, \ АСЛ\ = \ АХС\). Это сече-
сечение—прямоугольник PP\Q\Q. Пересечение диагонали АС\ с этим
436
прямоугольником— отрезок MN — и есть отрезок этой диагонали,
лежащий внутри цилиндра. Найдем его длину.
Из прямоугольного треугольника АСС\ имеем \АС1\ —
= V[AC!2 +!ССг |2 = 3у'Ь т. Из пропорции \MN \:\AC1\--=\PQ\:
\\АС\, учитывая, что \PQ\~2r, находим
| Ah\r \ = | Ad !-\PQ\:]AC\ = 3r.
Ответ: Зг. А
Кроме рассмотренных случаев расположения цилиндра и мно-
многогранника возможны и другие.
Задача 4. Дана правильная треугольная пирамида обьема '/.
В эту пирамиду вписан цилиндр так, что одно из его оснований
принадлежит основанию пирамиды, а
другое основание вписано в сечение
пирамиды плоскостью, параллельной ос-
основанию. Найти наибольший возмож-
возможный объем такого цилиндра.
Д Высоту пирамиды обозначим И,
длину стороны основания —а, высоту
цилиндра— h, радиус цилиндра —г. Рас-
Рассмотрим сечение ALBLCi (рис. 296) пи-
пирамиды плоскостью верхнего основания
цилиндра. Это правильный треугольник,
гомотетичный основанию ABC с коэф-
коэффициентом гомотетии, равным (Н — h)!H.
Следовательно, его сторона имеет длину
a[H — h)/H, а радиус вписанной окруж-
окружности равен УЗ а(Н — h)/5H. Это и есть
радиус цилиндра, т.е. г — \''i a(H — h)l6H. Находим объем цилин-
цилиндра как функцию Гг.
Рис. 296.
Затем ищем критическую точку най.теняой функции:
па*
И
~h){H — Щ, /ia = -p Очевидно, что при h = h0 функция
Уц имеет наибольшее значение, равное-^-,-""//. Учитывая, что по
V'i
условию —гк-а2Н=У, получаем, что наибольший воз ложный
объем рассматриваемых цилиндров равен
V.
§ 2. Конус
Конусом называется фигура, полученная вращением прямо-
прямоугольного треугольника вокруг оси, содержащей его катег. Дру-
Другой катет треугольника, вращаясь вокруг этой оси, дает круг,
437
Рис. 297.
стояние, равное
называемый основанием конуса. Фигура, образованная вращением
гипотенузы, называется боковой поверхностью конуса.
Отрезки, соединяющие вершину конуса с точками окружности
его основания, называют образующими боковой поверхности ко-
конуса (говорят также короче —образующими конуса; SA и SB на
рис. 297). Все образующие имеют одинаковую длину и состав-
составляют с осью острые углы одной и той же
величины.
Всякое сечение конуса плоскостью, про-
проходящей через ось (осевое сечение),— равно-
равнобедренный треугольник (Д ASB на рис. 297,
|S.4| = |S?|). Величина угла при вершине
этого треугольника называется углом раст-
раствора конуса. Если угол раствора равен <р,
то угол между образующей и осью равен <р/2.
Всякое сечение боковой поверхности ко-
конуса плоскостью, перпендикулярной его оси
и не проходящей через вершину, есть ок-
окружность. Все точки этой окружкости уда-
удалены от вершины конуса на одинаковое рас-
' л2 + Л2, где л —радиус окружности, a h— рас-
расстояние от вершины конуса до плоскости сечения. Верно и об-
обратное: точки боковой поверхности конуса, равноудаленные от
его вершины, лежат на одной окружно-
окружности— сечении боковой поверхности пло-
плоскостью, перпендикулярной оси. Ее. и
точки М и N боковой поверхности ко-
конуса равноудалены от его вершины, то
ось. конуса лежит в плоскости, проходя-
проходящей через середину отрезка MN и пер-
перпендикулярной ему (на рис. 297 | МР < —
= \PN, (SAB)±[MN\).
Задача 1. В правильной пирами-
пирамиде SABC сторона основания ABC имеет
длину а, боковое ребро —длину 2и.
Точки S, В ц С лежат па боковой по-
поверхности конуса, имеющего вершину в
точке А. Найти угол растиора этого
конуса.
Д На луче AS (рис. 298) возь;,:»:м
точку D, так, что | AD \ ~ а. Тогда
| AD | = | АВ | = | АС\, следовательно, точки В, С и D, принад-
принадлежащие поверхности конуса, лежат в одной плоскости, пер-
перпендикулярной его оси. Сечение боковой поверхности конуса
этой плоскостью есть окружность, описанная около треугольника
BCD. Определим радиус этой окружности, для чего найдем длины
сторон BD и CD. В треугольнике SAB iiiiej..! r_osSAB —
298.
438
= I ЛВ 1: 21 AS | = 0,25 и по теореме косинусов находим |??D| =
= УЪ11 а. Очевидно, \CD\ = \BD\. Теперь в треугольнике BCD
имеем cosDBC = | ВС |: 2 | BD | = 1/1/6, откуда sinDBC = 1/5/6.
Радиус окружности, описанной около треугольника BCD нахо-
дим по формуле R = \ CD\: 2 sin DBC = 3a/2"j/5. Обозначим угол
раствора конуса <р, имеем sin (cp/2) — R : | AD \ = 3/21/, откуда
(p = 2arcsin C/21/5).
Ответ: 2 arcsinC/21/5). А
Пирамида называется вписанной в конус (а конус — опи:анныч
около пирамиды), если ее вершина совпадает с вершиной конуса,
а основание вписано в основание конуса т
(рис. 299).
Каждое боковое ребро вписанной в конус
пирамиды является образующей конуса, (вы-
(высота конуса совпадает с высотой пирамиды.
Легко видеть, что
для того чтобы около пирамиды можно
было описать конус, необходимо и достаточно,
чтобы боковые ребра пирамиды имели равные
длины.
Задача 2. В конус вписана пирами-
пирамида SABCD, основанием которой служит тра-
трапеция ABCD. Известно, что SAD = 60°,
j ВС | = За, | /ID | = 8а (ВС и AD - основания
трапеции), длина высоты SO пирамиды равна 1а. Найт i пло-
площадь боковой поверхности конуса.
Д Основание пирамиды— трапеция ABCD (рис. 299) — i писана
в основание конуса, значит, эта трапеция равнобедренна?. Учи-
Учитывая это, находим | АВ\ = (\ AD\ — | ВСi): 2cos60° = 5а. Из тре-
треугольника ABD, применив теорему косинусов, получим \BD\ =
— la. Находим радиус окружности, описанной около трапеции
ABCD, по формуле R = | BD |: 2 sin 60° = 7a/j/~3. Затем находим
Рис. 299.
длину образующей конуса / = | AS | = j/| АО |2+ | 5О|2= 1
бй S / 93
у ру у | | j| | | |
и площадь его боковой поверхности S — я/?/ = 98яа2/3.
Ответ: 98лаа/3. а
Пусть плоскость а проходит через вершину S конуса и состав-
составляет с его осью / угол -ф. Пусть ф —угол между образующей и
осью конуса. Напомним, что -ф — это величина угла между осью
/ и ее ортогональной проекцией Г на плоскость а. Поэтому лю-
любая прямая в плоскости а, проходящая через вершину S и не
совпадающая с /', составляет с осью / угол, больший i|;. Этсюда
следует, что если г|з>ф, то плоскость а не имеет с конусом дру-
других общих точек кроме вершины S.
Если 0=<SiJ)<;ep, т° сечение конуса плоскостью а есть равно-
равно1 S
бедренный треугольник {/\SAB на рис. 300,
При
439
s
Рис. 300.
плоскость, проходящая через ось конуса и середину
отрезка АВ, перпендикулярна секущей плоскости а. При ip = 0
имеем осевое сечение конуса.
Если 1|з = ф, то плоскость а имеет с боковой поверхностью
конуса лишь одну общую образующую (SK, рис. 300), лежащую
на ортогональной проекции оси / на
плоскость а. В этом случае плоскость а
называется касательной к боковой по-
поверхности конуса. Плоскость, проходя-
проходящая через ось конуса и образующую,
по которой плоскость а касается боко-
боковой поверхности (плоскость SOK на
рис. 300), перпендикулярна касательной
плоскости. Касательная плоскость пере-
пересекает плоскость основания конуса по
прямой, касающейся окружности осно-
основания конуса (прямая k на fine. 300).
Отметим, что прямая k и образую-
образующая SK перпендикулярны.
Задача 3. Грани двугранного уг-
угла, имеющего величину а, касаются бо-
боковой поверхности конуса. Угол между ребром двугранного угла
и осью конуса равен р. Найти угол раствора конуса.
Д Очевидно, вершина S конуса принадлежит ребру данного
двугранного угла. Пусть О —центр основания конуса. Обозначим
1501 = 0, ф — угол раствора конуса.
Пусть ОМ0 — перпендикуляр к ребру
двугранного угла, а О/И, и (Ш2 —
перпендикуляры к плоскостям его
граней (рис. 301). Тогд.з SNi и
SNi — образующие, по которым грани
угла касаются боковой поверхности
конуса, и 6SM'1 = OSM2 = qj2. Далее,
угол MiM0M2 — линейный угол дву-
двугранного угла, значит, MiM0M2 = a,
рис 301 По условию дано еще, что 6SM0 = $,
Из треугольников OS Mi и 0SM%
имеем \0М1\ = ]0М2\ = asin (<p/2).
Отсюда следует, что М<Р — биссектриса угла МуМ^М2 (т. е,
ось конуса принадлежит биссектору данного двугранного угла).
Учитывая это, из треугольника ОМоМх находим |ОЛ10| =
С другой стороны, из треугольника
OSM0 имеем IОМ0 !=« sift р. Таким образом, sm ,T. ,n\ - sin 1
куда sin (ф/2) = sinP • sin (a/2).
Ответ: 2 arcsin (sin P sin (а/2)), ^
: sin 2 =
от-
440
которая в то
Пирамида называется описанной около конуса (а кону: — впи-
вписанным в пирамиду), если вершина пирамиды совпадает с верши-
вершиной конуса, а основание пирамиды описано около основа тя ко-
конуса. Очевидно,
для того чтобы в пирамиду можно было вписать конус необхо-
необходимо и достаточно, чтобы в основание пирамиды можго было
вписать окружность, а основание высоты пирамиды было центром
этой окружности.
В частности, в любую правильную пирамиду можно эписать
конус.
Каждая боковая грань пирамиды, описанной около конуса,
касается его боковой поверхности по образующей
же время является высотой этой боковой
грани и проходит через точку касания со-
соответствующей стороны основания пира-
пирамиды с окружностью основания конуса
(рис. 302, SKi — высота грани SAL/l, и т. д.).
Отметим еще, что в пирамиде, опи-
описанной около конуса, двугранные углы
при основании имеют одну и ту же вели-
величину. Она равна углу наклона образу-
образующей конуса к плоскости его основания
(S1UO и т. д., на рис. 302).
Задача 4. Около конуса описана пи-
пирамида. Доказать, что отношение объемов
пирамиды и конуса равно отношению
площадей их боковых поверхностей.
Д Обозначим радиус основания конуса г, его высоту Н, длину
образующей /, периметр основания пирамиды Р (на pic. 302
р,|С
Поскольку основание пкрамиды
конуса, то площадь осно-
ОКх\ = г, SO | = 77, |SA'i| = ,
описано около окружности основания
вания пирамиды равна 2 гР. Следовательно, объем пирамиды вы-
выражается по формуле Vn = -fr гРН. Объем конуса находим по фор-
формуле VK = -s-nr2//. Отсюда имеем Vn: УК = Р : 2л/\ Для площадей
боковых поверхностей пирамиды и конуса имеем соответственно
Еыражения: Sn= 0 IP, SK = nrl. Отсюда Sn: SK = Р : 2пг. Видно,
что отношения
и Sn: SK равны.
§ 3. Сфера
Сфера радиуса R есть множество точек пространства, удален-
удаленных от данной точки на положительное расстояние R. В коорди-
координатном пространстве сфера с центром О (а; Ь\ с) и радкусом R
441
задается уравнением
(х - af + (у -
+ (z - cf = R\
Сфера является фигурой вращения. При вращении полуокруж-
полуокружности радиуса R вокруг ее диаметра получается сфера радиуса R.
Сечение сферы радиуса R плоскостью, отстоящей от ее центрм
на расстоянии d, Q^d<.R, есть окружность радиуса г-¦
~V~R% — d2. Сечения, равноудаленные от центра сферы, имеют
равные радиусы.
Рис. 303.
Сечение сферы плоскостью, проходящей через ее центр (?1 = 0),
называется большой окружностью. Если центр сферы не лежит
в плоскости сечения @<d •</?), то прямая, проходящая через
центр сферы и центр окружности сечения, пер-
перпендикулярна плоскости сечения (рис. 303).
Если точки А и В принадлежат сфере,
то ее центр как точка, равноудаленная от
А и В, лежит в плоскости, перпендикуляр-
перпендикулярной отрезку АВ и проходящей через его
середину (плоскость а на рис. 304).
Задача 1. Доказать, что через любыг
четыре точки, не лежащие в одной плоскости,
можно провести сферу и притом только одну.
Д Центр сферы, проходящей через дан-
данные точки, должен принадлежать каждой к;
плоскостей, проведенных через середины отрезков с концами в
данных точках перпендикулярно этим отрезкам. Известие! (гл. XV!,
задача 3 раздела I), что эти плоскости пересекаются в одной то-
точке, обозначим ее О (рис. 305). Эта точка равноудалена от все1:
данных точек. Расстояние между точкой О и какой-лиОо из данных
точек обозначим R. Сфера с центром О и радиусом R проходи:
Рис. 305.
412
через все данные точки. Из проведенного рассуждения видно, что
такая сфера может быть только одна, а
Многогранник называется вписанным, в сферу (а сфера — опи-
описанной около многогранника), если все вершины многогранника
лежат на сфере.
Из результата задачи 1 следует, что около любого тетраэдра
можно описать сферу. В правильном тетраэдре его центр удален
от каждой вершины на расстояние, равное ЗЯ/4, где Я-высота
тетраэдра. Значит, центр правильного тетраэдра является цент-
центром описанной сферы. Радиус этой сферы равен ЗЯ/4 = г|/13/4,
где а —длина ребра тетраэдра.
Центр куба удален от каждой его вершины на расстояние
а "К3/2, где а —длина ребра куба. Значит, центр сферы, описан-
описанной около куба совпадает с центром
куба, а радиус этой сферы равен а У 3/2.
Задача 2. Все плоские углы при
вершине S пирамиды SABC прямые,
\SA\ = a, \SB\ = b, \SC\ = c. Найти ра-
радиус сферы, описанной около пирами-
пирамиды SABC.
Д Центр окружности, описанной
около треугольника SAB,— середина Ох
гипотенузы АВ (рис, 306). Через точ-
точку Oi проведем прямую I A_(SAB). За-
Заметим, что /1|(SC), поскольку прямые/ А
и SC перпендикулярны плоскости SAB.
Через середину М отрезка SC перпен-
перпендикулярно ему проведем плоскость а.
Точка О пересечения плоскости а и прямой / равноудалена от всех
вершин пирамиды, а следовательно, является центром сферы, зписан-
ной около пирамиды. В прямоугольном треугольнике SOO, имеем
i 1 1
){I = -1 АВ | = -„- \/ а2-{-Ь2, следовательно,
Рис. 306,
|OOi| = |AfS|=yc, |:
радиус описанной сферы равен | SO | = У | ОО± j2 -f-1 •>
l
Ответ: -^-Уa2-\-b2 + c2. a
Для пирамиды и призмы имеют место следующие утверндения:
а) Для того чтобы около пирамиды можно было описать сферу,
необходимо и достаточно, чтобы около основания пирамиды можно
было описать окружность (рис. 307).
Доказательство этого утверждения аналогично доказательству
того, что около всякого тетраэдра можно описать сферу (задача 1
этого параграфа, задача 3 раздела I гл. XVI).
б) Для того чтобы около призмы можно было описать сферу,
необходимо и достаточно, ктобы призма была прямая и чтобы
443
около ее основания можно было описать окружность (рис. 308,
см. задачу 9 раздела I).
Центр сферы, описанной около пирамиды, лежит на перпен-
перпендикуляре к плоскости основания, проведенном через центр ок-
окружности, описанной около основания. Центр сферы, описанной
о^.оло призмы, является серединой отрезка, соединяющего центры
окружностей, описанных около оснований призмы.
Рис. 307.
Рис. 308.
Из указанных утверждений следует, что около любой правиль-
правильно! пирамиды и около любой правильной призмы можно описать
сферу.
Рассмотрим понятие касательной плоскости к сфере. Если
расстояние от центра сферы до плоскости равно радиусу сферы
(d = R), то сфера и плоскость имеют одну
общую точку. Такая плоскость называется
касательной к сфере. Радиус, проведенный
в точку касания, перпендикулярен каса-
касательной плоскости.
Если сфера касается двух плоскостей,
то ее центр удален от каждой плоскости
на расстояние, равное радиусу сферы.
Если касательные плоскости параллельны,
то точки касания являются концами од-
одного диаметра сферы, перпендикулярного
обеим плоскостям (рис. 309). Если ка-
касательные плоскости пересекаются, то центр сферы принадлежит
биссектору двугранного угла между плоскостями (рис. 3!.О). Точки
касания сферы с плоскостями принадлежат граням этого угла.
Сфера называется вписанной в многогранный угол, если она
касается каждой его грани.
Задача 3. Доказать, что в любой трехгранный угол можно
вписать сферу.
Д Центр сферы, вписанной в трехгранный угол, должен при-
принадлежать биссекторам его диугранных углов. Известно (гл. XVI,
§ 3, задача 7), что эти бнесекторы пересекаются внутри трехгран-
Рис. 309.
44.4,
пого угла по лучу (луч / на рис 311). Пусть О —точк! этого
луча, не совпадающая с вершиной угла, R — расстояние от этой
точки до плоскостей граней. Сфера с центром О и ради/сом R
касается всех граней угла, т. е. вписана в данный трехпанный
угол. А
Рис. 310.
Рис. 311.
В
Заметим, что луч /, не считая его начала, есть мнсжестЕО
центров сфер, вписанных в данный трехгранный угол.
Сфера называется вписанной в многогранник (а многогран-
многогранник — описанным около сферы), если она касается всех его гранен.
Центр вписанной сферы является общей точкой биссекторов
всех внутренних двугранных углов многогранника. Отсюда сле-
следует, что если вписанная сфера существует, то только одна.
Известно (гл. XVI, § 5, задача 8), что биссекторы двугранных
углов тетраэдра пересекаются в одной точке. Сфера с центром
в этой точке и радиусом, равным рас-
расстоянию от этой точки до плоскости какой-
либо грани тетраэдра, касается всех гра-
граней тетраэдра. Значит,
в любой тетраэдр можно вписать сферу.
Задача 4. В тетраэдре ABCD | АВ | =
= 4 см, | CD |=12 см, \АС\=\ВС\=
= | AD | = | BD | = 3 J/6 см. Найти ' радиус
сферы, вписанной в этот тетраэдр.
Д Пусть М и Л/ — середины ребер
АВ и CD (рис. 312). Поскольку тре- ~
угольники АСВ и ADB равнобедренные,
то [CM] _L[АВ] и [DM]±[AB], Это оз-
означает, что «угол CMD — линейный угол
двугранного угла при ребре АВ. Из прямоугольных треуголь-
треугольников АМС и AMD находим, что | СМ \ = \ DM | = 5 ]/ 2 см.
Видно, что треугольник CMD равнобедренный, поэтому MN —
биссектриса угла CMD. Но тогда полуплоскость AN В (г гра-
Рнс. 312,
445
ницей АВ) — биссектор двугранного угла при ребре АВ. Анало-
Аналогично устанавливаем, что полуплоскость CMD (с границей CD)
является биссектором двугранного угла при ребре CD. Цгнтр впи-
вписанной в тетраэдр сферы лежит на отрезке MN — пересечении этих
двух биссекторов.
Из прямоугольного треугольника BND находим, что | BN \ —
— 3}/2 см, а из прямоугольного треугольника NMB находил
\MN\=--VU см.
Пусть О —центр вписанной сферы, г —ее радиус. Проведем
перпендикуляры ОК и 0L к граням BCD и ABD, тогда \0К —
= iOL| = r. Обозначим еще BNM = a, DMN = $. Из прямоуголь-
прямоугольных треугольников NMB и NMD находим соответственно sina^
= У 2/3 и sinP — 3 У 2/5. Из прямоугольного треугольника OKN
0N\= ^^ = -4= г. Тогда | ОМ | == | MN \ - \ ON | = ]/Т4 —
sin а К 2
имеем
sin а
-4=
К 2
— V: /', и теперь из прямоугольного треугольника OLM получаем
уравнение
i у- г) ¦ -¦ = г. Отсюда находим,
что
г =
= 3/]/7 см. А
В правильном тетраэдре его центр удален от каждой грани
на расстояние, равное Я/4, где Я —высота тетраэдра, Следова-
Следовательно, центр вписанной в правильный
тетраадр сферы совпадает с центром тет-
тетраэдра. Радиус этой сферы вычисляется по
I 1/' С
формуле г — -^ Н — -то-, где а — длина реб-
ребра тетраэдра.
В кубе центр вписанной сферы сов-
совпадает с центром куба. Радиус этой сфе-
сферы равен а/2, где а —длина ребра куба.
Не в каждом многограннике биссек-
Торы двугранных углов пересекаются в
одной точке, значит, не в каждый много-
многогранник можно вписать сферу.
Задача 5. Доказать, что е:ли в ос-
основание пирамиды можно вписать окруж-
окружность, а основание высоты пирамиды является центро\< этой ок-
окружности, то в пирамиду можно вписать сферу.
Д Пусть L\, Ln, ... — точки касания вписанной в основание
пирамиды окружности с его сторонами, Р —центр вписанной
окружности (рис. 313). Прямоугольные треугольник!! SPL ,
SPL2, ... конгруэнтны и имеют общий катет SP. Следователь!!'),
биссектрисы углов при вершинах L\, L2, ... пересекают этот кат -
в одной и той же точке О. Из точки О опустим перпендикуля|: i
О/С2, ... "а гипотенузы SL\, SL?, ... Плоскость SLtP пе -
44'
;:гед-
i\ С1Ъ
пендикулярна плоскости грани SAXA2, поэтому (O/Ci)_L(
Аналогично имеем @Д*2) .L (SA2A3), (ОКр) _1_ EЛ3Л4) и т. д. Учи-
Учитывая, что \0Р j = j 0Кл | = \OKi\-. ¦¦, видим, что точка О равно-
равноудалена от плоскостей всех граней пирамиды. Значит, сфера
с центром О и радиусом г = \ОР\ касается всех граке!, т. е.
вписана в данную пирамиду, а
Из доказанного утверждения следует, что
в любую правильную пирамиду можно вписать сферу.
Сфера может быть вписана и в пирамиды, не удовлетвори1;'. ir,ue
условия утверждения задачи 5.
Задача 6. Основание пирамиды SABCD — квадрат ЛВСЭ,
ребро SA перпендикулярно плоскости основания; \AB\---3 с»,
|5Л| = 4 см. Доказать, что в пирамиду можно вписать oV-j-.y,
и найти радиус этой сферы.
Д Вначале получим некоторые необходимые условия, лГ.<_,!0-
Е!.иеся расположения центра сферы и ее радиуса. Для это г
положим, что вписанная в пирамиду сфера суш.есчвует, \
С —ее центр, /- — радиус. Через центр О
проведем плоскость, перпендикулярную
прямой AD (плоскость KLM на рис.. 314).
Пусть / — линия пересечения плоскос-
плоскостей SAD и SBC. Поскольку (ВС) || (ЛЯ),
то и l\(AD). Проведенная плоскость
перпендикулярна каждой из прямых
АО, ВС и /, поэтому углы LKM,
KML и KLM соответственно — линейные
углы двугранных углов при ребрах AD,
ЪС и / (последний есть двугранный угол
между гранями SBC и SAD). Поскольку
сфера касается граней каждого из этих
двугранных углов, то ее сечение плоско-
плоскостью KLM (большая окружность) должка
сыть вписана в треугольник KLM.
Г-^диус этой окружности легко найти.
Х.ействителько, плоскости KLM и ASB
параллельны, а отсюда следует, что треугольники KLM и ASB
конгруэнтны и | KL\ = \AS\--=\ см, \КМ | = J AB | = 3 см. Радиус
окружности, вписанной в прямоугольный треугольник KLM, най-
найдем по формуле г = 2S/P, где 5 и Р соответственно — площадь
и периметр этого треугольника, получим г = 1 см. Это и есть
радиус вписанной сферы. Точно такой же результат будет полу-
"ен, если рассмотреть сечение пирамиды и сферы плоскостью,
проведенной через центр О перпендикулярно ребру АВ (плоскость
PQR на рис 314). Треугольник PQR конгруэнтен треугольнику
KLM(\PQ\ = 4 см, |Я/?| = 3 см), и радиус вписанной в него
окружности (большой окружности сферы) равен 1 см.
Теперь докажем, что вписанная сфера действительно сущест-
существует. Внутри трехгранного угла ASBD (с вершиной А) Еозьмем
Рис. 314.
447
точку О, отстоящую от каждой грани угла на расстоянии 1 см.
Сфера с центром О и радиусом 1 см касается граней SAD, SAB
и ABCD пирамиды. Рассмотрим опять сечение KLM, проведенное
через центр сферы. Точка О отстоит ст сторон KL и КМ треу-
треугольника i\LM на расстояни:: 1 см, а значит, совпадает с центром
вписанной в этот треугольник окружности. Поэтому, если [ОЕ] L
J.[LM\, то !ОЯ| = 1 см. Из того, что (KLM) ±(SBCi, следует,
что [ОЁ] ±_ (SBC). Значит, точка О отстоит от плоскости SBC на
р৩гояние 1 см, а сфера с центром О и радиусом 1 cfv.. касается
этой плоскости, Аналогично доказывается, что сферг касаемся
и грани SCD. Таким образом, вписанная сфера существует и ее
радиус равен 1 см.
Ответ: 1 см. а
Для призмы имеет место следующее утверждение:
фля тдро чтобы в призм,! можно было вписать сферу, необхо-
необходимо и достаточно, чтобы в перпендикулярное сечение призмы
мотно было вписать окружность и чтобы высота призмы была
равна диаметру этой окружности
(см. задачу 45 раздела \\).
Диаметр сферы, вписанной в при-
призму, равен диаметру окружности,
вписанной в перпендикулярное сече-
сечение призмы (сечение MNPQ на рис.
315). Центр сферы лежи1 на пря-
прямой (ЯР, на рис. 315), проведенной
параллельно боковым реСрзм через
центр окружности, вписанной в пер-
перпендикулярное сечение, и является
серединой отрезка, отсекаемого на
этой прямой основаниями призмы
(рис. 315, центр О —середина отрез-
отрезка PPV высота QQt призмы равна
диаметру сферы.) Точки касания сферы
призмы принадлежа? перпендикулярному
С,
Рис. 3iS.
с боковыми гранями
сечению, проведенному чере:;; центр сферы.
В правильную призму можно вписать сферу tr.oedi и только
тогда, когда вг высота равна диаметру окружности, вписанной
в основание.
Задача 7. Около сферы описан прямой параллелепипед с
диагоналями длины \ Гб см и 4 см. Найти радиус сферы.
Д Высота данного параллелепипеда равна диаметру вписанной
сферы. Обозначим радиус сферы R, тогда H = 1R.
Пусть АС и BD соответственно большая и меньшая диагонали
основания параллелепипеда (рис. 316), обозначим \AC\ — dL,
\BD\=d.2. Поскольку параллелепипед прямой, ACL и BDX будут
тогда его большей и меньшей диагоналями, т. е. \АС1\ = 4 см;
\BDl\—\rl0 см. Из прямоугольных треугольников АССХ и BDDt
448
получаем
= 10.
A)
Рассмотрим перпендикулярное сечение параллелепипеда, про-
проходящее через центр О сферы. 5>то параллелограмм /t,B2C2D.)
конгруэнтный основанию, ив
частности, | А2О | = ~dx, \ В2О | =
= yd3. Поскольку этот парал-
параллелограмм описан около окруж-
окружности, он является ромбом, и,
значит, А2ОВ2 = 90°. Пусть
[ОК]±[А,В2], тогда \OK\ = R, и
из прямоугольного треугольника
АгОВ.г имеем, что \ОК\ • \ АгВг\ =
= | А2О\ ¦ \В2О\, следовательно,
2RVd\+d$ = d1d2. Из этого ура-
уравнения, используя A), получаем
уравнение 3#4 — Ш2+ 10 = 0,
откуда #i = 10/3, Rl=l. Значе-
Значение Ri = 10/3 является, очевидно, Рг, ч^;
посторонним (dl + 4 #1 > 10), зна-
значит, R2 = l, R = l см. а
Задача 8. Около сферы радиуса R описан много!ранник
объема V и с площадью поверхности S. Доказать, что R-.= 3VlS.
Д Представим описанный многогранник как объединена пира-
пирамид, вершинами которых является центр сферы, а основаниями —
грани многогранника (заметим, что описанный мкогогран шк яз-
ляется выпуклым). Обозначим площади граней многогранника 5,,
S.2, .... Sn, по условию Sx + S2 +... + Sn = S. Радиус, провгден-
ный в точку касания /'-и грани (площади 5;) со сферой, явля-
является высотой пирамиды, для которой эта грань служит оснозанием.
Значит, объем /-й пирамиды равен R-Sj'3. Сумма объемэв всех
этих пирамид равна объему многогранника:
Отсюда получаем, что RS/3 = V, т. е. R = 3V/S. А
Прямая имеет со сферой общие точки тогда и толькс тогда,
когда расстояние d от центра сферы до этой прямой не превос-
превосходит радиуса R сферы.
Если 0^d<iR, то прямая пересекает сферу в двух точках.
Отрезок с концами в этих точках называют хордой, а прямую —
секущей (рис. 317, (SA) — секущая, [ЛВ] — хорда).
Если d = R, то прямая имеет со сферой одну общую тачку —
основание перпендикуляра, опущенного из центра сферы на эту
15 п/ред. Г. Н. Яковлева 449
ппямую. Такая прямая называется касательной к сфере (рис. 317,
(SK) — касательная). Любая касательная прямая лежит в касатель-
касательной плоскости, проведенной через точку касания прямой и сферы.
Верно и обратное: любая прямая, лежащая в касательной пло-
плоскости и проходящая через точку ка-
касания, является касательной к сфере.
Секущие и касательные прямые к
сфере обладают такими же езойствамн
как и секущие и касательные к ок-
окружности. Укажем кекоторьш из этих
свойств.
а) Перпендикуляр из центра сферы
на секущую прямую проходит через се-
середину хорды (рис. 317,| AM. | = | MB I,
\ОМ]±[АВ}).
Рис. 317. б) Плоскость, проходящая через
центр сферы и перпендикулярная хор-
хорде, проходит через середину хорды.
Это утверждение полезно сформулировать в равносильной
форме.
б') Плоскость, проведенная через середину хорды перпендикулярно
этой хорде, проходит через центр сферы.
в) Если две прямые пересекаются в точке S и касаются сферы
соответственно в точках К и L (рис. 317), то \SK\ = \SL\
(теорема о касательных).
г) Если две прямые пересекаются в точке S, и осна из них
касается сферы в точке К, а другая пересекает сферу в точках
А и В (рис. 317), то \SA\-\SB\ = \SK\2
(теорема о касательной и секущей).
д) Если две прямые пересекаются в точке
S и пересекают сферц соответственно в точ-
точках А, В и С, D (рис. 317, 318), то
\SA]r\ SB | = j SC | ¦ I SD | (точка S может
лежать как снаружи, так и внутри сферы,
в последнем случае данное утверждение иногда
называют теоремой о пересекающихся хордах).
Свойство б) (и б')) является следствием
Рис. 318. свойства а). Для доказательства свойств а),
в), г), д) можно провести плоскость соответст-
соответственно: в случае а) —через секущую прямую и центр сферы; в слу-
случае в) —через касательные SK и SL; в случае г) — через каса-
касательную и секущую; в случае д) — через прямые АВ и CD, a
затем воспользоваться соответствующими свойствами хорд, секу-
секущих и касательных к окружности.
Задача 9. Доказать, что существует сфера, касающаяся
всех ребер правильной треугольной пирамиды, и найти ее радиус,
если сторона основания пирамиды имеет длину а, боковое ребро —
длину Ь.
450
Д Если сфера касается сторон основания ABC (рис 319),
то ее сечение плоскостью основания— окружность, впи:анкая
в треугольник ABC. Эта окружность касается сторон треуголь-
треугольника (он правильный) в их серединах Л'ь Къ К3. Центр сферы
должен быть равноудален от этих точек, следовательно, должен
лежать на перпендикуляре к плос-
плоскости основания, проходящем через
его центр Р, т. е. на прямой SP.
Если сфера касается ребра AS в
точке Li, то ее центр лежит в плос-
плоскости, проведенной через точку L\
перпендикулярно ребру AS. Эта пло-
плоскость пересечет плоскость ASP по
прямой, перпендикулярной ребру AS.
Заметим еще, что по свойству каса-
касательных ! ALX | = | АК\ | = а/2, где а —
длина стороны основания.
Из проведенного анализа выте-
вытекает, что центр сферы должен быть
точкой пересечения прямой SP с пря-
прямой, проведенной в плоскости ASP
перпендикулярно ребру AS через Рис. 319.
точку Li этого ребра такую, что
\АЦ\ = а/2. Обозначим точку пересечения этих прямых О \ дока-
докажем, что сфера с центром О и радиусом г = \ОК\\ действительно
касается всех ребер пирамиды.
Во-первых, очевидно,
0Ка |, т. е. этг. сфера
касается всех сторон основания. Во-вторых, из конгруэнтности
прямоугольных треугольников ОЬгА и ОК\А (по катету i гипо-
гипотенузе) следует, что \OLi\ = \OKi\=r, значит, сфера касается
и ребра AS. Если [0L2] _L [BS], [OLZ]J_[CS], то из конгруэнтности
треугольников SOLi, SOL?,, SOLa (по гипотенузе и острому углу)
следует, что |0L2 | = |0L3| = I ОЦ | = г. Значит, сфера касается и
ребер BS и CS. Тем самым доказано, что сфера, касающаяся
всех ребер пирамиды существует.
Найдем радиус этой сферы из подобия треугольников SLXO
и SPA. Имеем г :\AP\ = \SL1\:\SP\, откуда, учитывая, чго
у о
получаем, что г =а BЬ — а)/2У'ЗЬ2— а? . А
§ 4. Комбинации сферы, конуса и цилиндра
Сфера называется описанной около цилиндра (конус?), если
окружности его оснований (окружность его основания и вгршина)
принадлежат сфере (рис. 320, 321).
IS* 451
Около любого цилиндра и около любого конуса можно описать
сферу. Центр описанной сферы совпадает с центром окружности,
описанной около осевого сечения соответственно цилиндра или
конуса. Радиус сферы равен радиусу этой окружности.
Рис. 320
Рис. 321.
Сфера называется вписанной в цилиндр (а цилиндр — описанным
около сферы), если сфера касается каждой образующей и обоих
оснований цилиндра (рис. 322).
В цилиндр можно вписать сферу тогда и только тогда, когда
его высота равна диаметру основания. Центр вписанной сферы
является серединой отрезка, соединяющего центры оснований
цилиндра. Каждой образующей сфера касается в ее середине,
5,
Рис. 322.
Рис. 323.
множество точек касания есть окружность — сечение боковой по-
поверхности цилиндра плоскостью, параллельной основаниям и про-
проходящей через середину высоты.
Сфера называется вписанной в конус (а конус — описанным
около сферы), если сфера касается основания конуса и каждой
образующей (рис. 323).
452
В любой конус можно вписать сферу. Ее центр совпадает
с центром окружности, вписанной в осевое сечение конуса радиус
сферы равен радиусу этой окружности. Множество точек касания
сферы с образующими есть окружность— сечение боковой поверх-
поверхности конуса плоскостью, параллельной основанию когуса (на
рис. 323 точка Q — центр этой окружности).
Задача 1. В конус вписана сфера. Окружность касания
сферы с боковой поверхностью конуса служит окру.кностыо
основания цилиндра, вписанного в эту
сферу. Площадь сферы составляет 4/9
площади поверхности конуса. Найти
отношение объемов цилиндра и ко-
конуса.
Д Ось конуса является в то же
время и осью цилиндра, центр сферы
лежит на этой оси. Рассмотрим сечения
трех данных фигур плоскостью, прохо-
проходящей через ось конуса (рис 324). Сече-
Сечение конуса (осевое)— треугольник ASB,
сечение сферы — окружность с центром О,
вписанная б треугольник ASB (К, L,
Р — точки касания), сечение цилиндра (осевое)— прямоутльник,
вписанный в эту окружность, отрезок LK служит стороной этого
прямоугольника.
Пусть / и гк — длина образующей и радиус основания конуса,
r — радмус сферы, гц, Л —радиус основания и сысота цилиндра.
Имеем (рис. 324): \SB\ = l, PB\ = rK, \ KB | = | РВ | ==/•„ (по
свойству касательных), \SK\ = l — rK, \SP\=yi'1 — r\,\OK\ = r.
Из подобия прямоугольных треугольников SKO и SPB заходим,
что
^ j
Рис. 321.
г = г..
l—Гд
Площади поверхностей конуса и сф|еры определяем соответственно
по формулам: SK — nrK(l-{-rK), S = Anr2 — 4nrl1:^--. По /словию
' "г''к
5:5,. = 4:9, откуда получаем уравнение Р — 7rJ-\- Юг] =0, и
находим, что либо / = 5гк, либо /==2гк.
Из подобия треугольников SQiK и SPB имеем |QiA'!=»
ISK \ ¦
^g- Учитывая, что \QiK\ = rn, получаем, чго гц =
— Гк{1 — К)/1- Из прямоугольного треугольника 0&/С оходим
| OQ11 = VI OK |2 - | QXK |2 = T-1/ lf~. Для высоты щлиндра
2/*2 f 7
имеем равенство h = 2\0Qx\, значит, h = -— 1/ -prf. Находим
453
объемы конуса и цилиндра:
1 г.
5/2
КК 3 Ш«У '«• U /3(,+/.|(I/2 '
и отношение этих объемов: Vл : VK = " "г-- Подставляя зня-
чепия 1 = Ьгк и / = 2гк, найдем соответственно, что либо KU:VK==
== 16: 125, либоУц: VK= 1:4.
Ответ: 16:125, или 1 : 4. А
Рассмотрим взаимное расположение двух сфер с центрами Ох
и О2, радиусами rt и г2. Пусть d — \ ОгО2 \ — расстояние между
центрами этих сфер.
Если d^>rt-\-r2 или d<C\r1 — Го\, то сферы не имепт- общих
точек.
Если | га. — г.г! < d< f\ + )'2. то пересечением сфер служит
окружность. Плоскость этой окружности перпендикулярна пря-
прямой О{О,:, центр окружности лежит на этой прямой (рис. 325).
уж*
Рис. 325.
Рис. 32S.
Если d = r-i_-{-r2 или d = \r1 — r2\ (в последнем случае Гхфг2),
то сферы имеют только одну общую точку и называются касаю-
касающимися. Общая течка сфер лежит на прямой ОгО2 и называется
точкой касания. Если d — г,. + г2, то говорят о внешней касании
(на рис. 326, а это сферы с центрами Ог и 02), если же d =
= \r-i_— г.2\, то —о внутреннем касании (на рис. 326, а это сферы
с центрами Ог и Ог). На рис. 326, б показано сечение касаю-
касающихся сфер плоскостью, проходящей через линию центров 0^0г.
Касающиеся сферы имеют в точке касания общую касательную
плоскость.
Задача 2. Три сферы каждая радиуса г касаются плоскости
а, и каждая из сфер касается двух других. Найти радиус чет-
454
вертой сферы, касающейся плоскости а и каждое uz трех данных
сфер.
Д Пусть Оь О2, О3 — центры данных сфер, О — центг. четвер-
i ф И OO \ ОООО ! 2 Ч ф
Toii сферы. Имеем
фр
= ! О2О31 — j О3О, ! = 2г. Четверта i сфера,
ф
фр | ^ 31 j р
очевидно, только внешне может касаться данных сфер, поэтому
| OOi | = j ОО21 = | ОО3 j = г + я, где * — радиус четвертой сферы.
Точка О равноудалена от тсче;< О,, О2, О3, поэтому лежит на
перпендикуляре к плоскости O,O.,O{i, проведенном через центр
правильного треугольника О^О2д3. От плоскости а (на эис. 327
N --___
Рис. 327.
эта плоскость задана точками касания Л'ь /(.2, Л'3) "очка О
удалена на расстояние х, \ОК\=х. Каждая из точек Ои О2, О3
удалена от плоскости а на расстояние г. Поскольку [/'/(] _1 а,
то и | РК | = г, а | РО | = | г — х |. Учитывая, что | РОг | = 2г]/3/3,
из прямоугольного треугольника ОРОг имеем | 00] |2 = | 9,Р j2+
-\-\P0\2, (r-]-xJ = Yr2 + (r — xf. Из этого уравнения >аходим,
что х — г/3. А
ЗАДАЧИ РАЗДЕЛА 1
1. Из круга вырезается сектор с углом а. при вершине и сворачивается
в коническую воронку. При каком а. получится воронка наибольше! вмести-
вместимости?
2. Правильный треугольник со стороной длины а вращается ас круг оси,
параллельной его высоте и отстоящей от нее на расстояние b~>aj2. Найти
объем фигуры вращения.
3. Сторона основания правильной треугольной призмы имеет длир у 1,6 дм,
боковое ребро—длину 1,2 дм. Четыре вершины призмы лежат на окружности
основания конуса, две другие — на его боковой поверхности. Найти объем этого
конуса.
455
4. РсСро куба AECDAiBiCiDi имеет длину а. Найти радиус сфезы, прохо-
проходящей через ьершины В, Си середину ребра AD и центр грани ССD^D.
5. В сфере радиуса г проведены хорда АВ и диаметр CD. Известно, что
| АВ ;=---г, (.46, СХ>) = я/3, АС | = |/'2г, \ВС\>\АС\. Найти длину отрезка BD.
6. Около сферы радиуса R описан усеченный конус (основания и каждая
образующая конуса касаются сферы), образующая которого имеет длину а.
Найти объем этого конуса.
7. В сферу радиуса R вписана правильная четырехугольная пирамида,
в которой двугранный угол при боковом ребре имеет величину 120°. Вторая
сфера касается первой сферы и боковых граней пирамиды. Найти j адиус вто-
второй сферы.
8. В двугранный угол величины 2а вписаны ДЕе касающиеся друг друга
сферы, каждая радиуса г. Третья сфера, вписанная в этот же угол касается
первых двух. Найти радиус третьей сферы.
9. Доказать, что для того чтобы около призмы можно было описать сферу,
необходимо и достаточно, чтобы призма была прямая, и чтобы окогго ее осно-
основания можно было описать окружность.
10. Длина бокового ребра правильной треугольной пирамиды рлвна высоте
основания пирамиды и равна а. Сфера касается плоскости основания пирамиды,
двух ее боковых ребер и продолжения третьего бокового ребра га вершину
пирамиды. Найти радиус этой сферы.
11*. В правильной пирамиде SABC сторона основания ABC имеет длину а,
боковое ребро—длину 2а/3. Сфера касается всех ребер этой пирам! ды. Найти
площадь части сферы, лежащей вне пирамиды.
12. Две сферы St и S2 касаются друг друга и каждая сфе[а касается
обеих граней а и E двугранного угла величины 2ф. Сфера St касается грани а
в точке A, a ajjepa S2 касается грани 0 в точке В. В каком отношении отре-
отрезок АВ делится сферами?
13, Высота цилиндра равна Зл. Внутри цилиндра расположены три сферы
радиуса г так, что каждая сфера касается двух других и боковой юверхности
цилиндра (т. е. имеет с этой поверхностью одну общую точку). Две сферы
касаются нижнего основания цилиндра, а третья сфера — верхнего основания,
Найти радиус цилиндра.
ЗАДАЧИ РАЗДЕЛА II
1. Требуется изготовить открытый цилиндрический бак объема V. Каковы
должны быть радиус и высота бака, чтобы площадь его повертости была
наименьшей?
2. Ребро куба имеет длину а. Две вершины куба являются цертрами осно-
оснований цилиндра, остальные вершнкы лежат на боковой поверхности цилиндра.
НаМти объем этого цилиндра.
3. Объем тетраэдра ABCD равен V, Ребра АВ и CD тетраэдга перпенди-
перпендикулярны, имеют равные длины, и отрезок MN, соединяющий и* середины,
перпендикулярен этим ребрам. Прямая MN является осью цилиндра, окруж-
окружности оснований которого имеют но одной общей точке с двумя гранями тет-
тетраэдра, Найти наибольший возможный объем такого цилиндра,
456
4. Все вершины правильной пирамиды SABCD лежат на боковой поверх-
поверхности цилиндра, ось которого перпендикулярна плоскости SAB. Hai'm радиус
цилиндра, если \АВ] = а.
5. В правильной четырехугольной пирамиде SABCD сторона о<нования
имеет длину а, боковое ребро — длину -о-о. Одно основание цилиндр) лежит
в плоскости SAB, другое — вписано в сечение пирамиды. Найти площадь боко*
вой поверхности цилиндра,
6. В правильной призме АВСАф^С^ длина каждого ребра равнг а. Вер-
Вершины А и Ах лежат на боковой поверхности цилиндра, плоскость BBfifi
касается этой поверхности. Ось цилиндра параллельна прямой В^С. Найти
радиус цилиндра.
7. Вершины прямоугольника лежат на боковой поверхности щлиндра.
Доказать, что две параллельные стороны прямоугольника перпенднкул' рны оси
цилиндра,
8. Вершина А правильной призмы ABCA^jCi совпадает с центрсм одного
из оснований цилиндра, вершины Bt и С\ лежат на окружности другого осно-
основания, а вершины Аи В, С —на боковой поверхности цилиндра. Определить
отношение объемов цилиндра и призмы.
9*. Одна вершина правильного тетраэдра расположена на оси цилиндра,
а другие вершины —на боковой поверхности этого цилиндра. На'пи длину
ребра тетраэдра, если радиус цилиндра равен R.
10. Прямая касается боковой поверхности цилиндра, если она лежит в каса-
касательной плоскости и имеет с поверхностью цилиндра одну общую точк/. Ребро
куба ABCDAiBlClDl имеет длину а. Цилиндр, ось которого параллельна
прямой BDi, расположен так, что прямые ААи ВС и C^D^ касаются егс боковой
поверхности. Найти радиус цилиндра (найти все решения).
11. Площадь сечения конуса плоскостью, составляющей угол ЗС= с осью
конуса, равна площади осевого сечения. Найтн угол раствора конуса.
12. В конус вписана правильная треугольная пирамида. Площадь боковой
грани пирамиды равна площади осевого сечения конуса. Найти отношение пло-
площадей боковых поверхностей конуса и пирамиды.
13. Угол раствора конуса равен 2а, длина образующей равна . Найти
наибольшую возможную площадь сечепня конуса плоскостью, проходящей через
вершину. Найтн величину угла между осью и плоскостью сечения наибольшей
площади.
14. Точки А A; 2; —2), В D; 2; — 2) С C; 4; —2) лежат на оюужности
основания конуса, высота которого равна 3. Найти координаты вершины конуса
и площадь сечения конуса плоскостью z = 0.
15. Точки ЛA; 2; —1), В (—2; 2; —1), С (—2; 2; 3) лежат us окруж-
окружности основания конуса, точка М {0; 6; -л) на его боковой поверхности. Найти
площадь полной поверхности конуса.
16. Конус описан около куба следующим образом: четыре вершины куба лежат
в плоскости основания конуса, а четыре другие вершины — на его боковой
поверхности. Какой наименьший объем может иметь такой конус, если ребро
куба имеет длину а?
457
17. Ребро куба ylSCD,41B1CiD1 имеет длину а, точк'.( М и N — середины
ребер /L4( и AXBV соотаегствешю. Плоскость DLMN касается бокстой поверх-
поверхности конуса, осью которого служит прямая СС\, а центром основании—точка С.
Найти объем этого конуса.
18. В тетраэдре ABCD двугранные углы при ребрах ВС и CD прямые.
Длина одного из ребер тетраэдра в три раза больше длины не пересекающегося
с ним ребра. Вершина конуса совпадает с одной из вершин тетраэдра, окруж-
окружность основания конуса описана около однол из граней, Найти угол в осевом
сечении конуса.
19. В тетраэдре ABCD двугранные углы при ребрах АВ и 1Ю прямые,
ACD—а. Вершима конуса совпадает с одной из вершин тетраэдра, окруж-
окружность основания конуса вписана в одну из граней, Найти угол в осевом сече-
сечении конуса,
20. Основание прямой призмы АВСА1ВХС1 — прямоугольный -реугольник
с катетами АВ и ВС длины 8 см и б см соответственно. Гипотенуза ЛС является
диаметром основания конуса, вершина которого лежит на ребре А^В . Ребро АВ
пересекает боковую поверхность конуса в точке М так, что ЛУИ! =5 см.
Определить объем конуса.
21. Отношение радиусов оснований усеченного конуса равно 2. Вершины А,
В, В,, Av празилыюй призмы АВСАХВ1С1 расположены па окружности боль-
шгго основания, а вершины С и Сх — на окружности меньшего основания конуса.
Найти отношение объема конуса к объему призмы.
22. Вершины Л, В и С правильного тетраэдра лежат на боконон поверх-
поверхности конуса, вершина D принадлежит его основанию, прямая АЭ перпенди-
перпендикулярна плоскости этого основания. Найти длину ребра тетраэдра, если угол
раствора конуса равен 90°, а радиус его основания R.
23. Радиус меньшего основания усеченного конуса равен 3/-, радиус боль-
большего основания—7г. Вершины S п А правильной пирамиды SABC лежат на
окружности меньшего основания конуса, вершины В к С основани? ABC пира-
пирамиды лежат на окружности большего основания конуса. Найти объем пира-
пирамиды SABC.
24. Прямая касается боковой поверхности конуса, если она лежит в каса-
касательной плоскости и имеет общую точку с образующей, не совпадающую с вер-
вершиной конуса.
Основание конуса лежит в плоскости грани ABCD куба ABCDAiBiC^D^,
а вершина S конуса лежит на луче ООи где О и О! —центры гганей ABCD
и AlBiCxDl соответственно. Диагональ АВХ касается боковой поверхности
конуса. В каком отношении точка касания делит отрезок АВЪ >:сли | SO |=
= 2 00, !?
25*. Треугольник ABC площади S расположен в одной плоскости с пря-
прямой /. Точка пересечения медиан треугольника удалена от I на расстояние d.
Доказать, что объем фигуры, полученной вращением треугольника вокруг пря-
прямой I, равен 2я dS.
26. Вершины прямоугольника лежат на боковой поверхности кжуса. Дока-
Доказать, что две параллельные стороны прямоугольника перпендикулярны оси
конуса.
458
27. В сферу радиуса R вписана правильная четырехугольная п фамида.
Каков наибольший возможный объем этой пирамиды?
28. Около шара объема V описана правильная треугольная пирамида.
Каков наименьший возможный объем этой пирамиды?
29. Около шара описана правильная усеченная треугольная п фамида,
боковое ребро которой составляет с плоскостью основания угол 60", Найти
отношение объема шара к объему этой пирамиды.
30. Ребро правильного тетраэдра имеет длину а. Высота тетраэдра шляется
диаметром сферы. Какова площадь части поверхности тетраэдра, лежащей внутри
это;'! сферы?
31. Сфера касается всех ребер куба. Найти объем части куба, кжащей
внутри сферы, если ребро куба имеет длину а.
32. Сфера касается всех боковых ребер правильной четырехугольно! призмы
и ее оснований. Найти отношение площади части сферы, лежащей вне призмы,
к площади полной поверхности призмы.
33. В пирамиде SABC все плоские углы при вершине S прямые. ]_ оказать,
что вершина S, точка пересечения медиан треугольника ABC и центр описан-
описанной около пирамиды сферы лежат на одион прямой.
34. Ребро куба имеет длину а. Найти радиус сферы, проведенной через
Еершнны A, D и середины ребер ВгСг и CtDi.
35. В тетраэдре ABCD двугранные углы при ребрах АВ, ВС и CD прямые,
ABC —BCD— а. Радиус сферы, описанной около тетраэдра равен R. Найти
объем тетраэдра.
36. Точки А а В лежат в разных гранях прямого двугранного угла,
точка А удалена от ребра этого угла на раесстояние За, точка В- на рас-
расстояние 4а. Найти наименьший радиус сферы, касающейся граней угла и пря-
прямой АВ.
37. В кубе ABCDAiBiCiDx точки Е a F — середины ребер АА и A^Di
соответственно, \АВ\=а. Найти радиусы сфер, проходящих черезточ^ Е и F
и касающихся плоскостей ВВ^С^С и DD^iC.
38. Сторона основания правильной треугольной призмы ABCAiBjCi имеет
длину а. Точка D — середина ребра АВ, точка Е лежит на ребре A\Ci. Пря-
Прямая DE образует углы а. и ^ с плоскостями ABC и АА^С^С соответственно.
Найти радиус сферы с центром на отрезке DE, касающейся плоскостей ABC
и ААЛСХС.
39. Все ребра правильной четырехугольной пирамиды имеют .(лину а.
Найти радиус сферы, проходящей через центры боковых граней и касающеься
сторон основания пирамиды.
40. В пирамиде SABC ребро SC составляет с плоскостью основания угол 6(Г.
Вершины А, В, С и середины всех боковых ребер лежат на сфере радиуса г.
Найти высоту пирамиды.
41. В тетраэдре ABCD грань ABC—прямоугольный треугольник (ВС А =90г),
ребро AD перпендикулярно плоскости ABC, | AD | = | ВС |=3 см, | AC j = 4 см.
Найти радиус сферы, вписанной в тетраэдр.
42. Основанием пирамиды SABCD является ромб с диагоналями /Си BD,
|j4C| = 8 cm, |BD|=6 cm, ребро SA перпендикулярно плоскости основания и
цлина его равна 2 см. Найти радиус сферы, вписанной в пирамиду,
459
43. В правильной шестиугольной пирамиде центры вписанной и описанной
сфер совпадают, а) Найти отношение радиусов этих сфер, б) Найти величину
плоского угла при вершине пирамиды.
44. Доказать, что для любой призмы описанной около сфера отношение
площади боковой поверхности к площади основания равно 4.
45. Доказать, что для того, чтобы в призму можно было вписать сферу,
необходимо и достаточно, чтобы в перпендикулярное сечение пр«мы можно
было вписать окружность, и чтобы высока призмы была равна диаметру этой
окружности-
46. Доказать, что для того, чтобы существовала сфера, касающаяся веек
ребер тетраэдра, необходимо и достаточно, чтобы суммы длин скрецивающихся
ребер тетраэдра были равны,
47. В прямой двугранный угол вписана сфера радиуса г. Прямая касается
сферы в точке К и пересекает грани угла в точках Л и В так, что |ЛК1:
!| KB |=3: 2, Каждая из точек А к В удалена от ребра двугран.юго угла па
расстояние Зг. Найти длину отрезка А В.
48. Ребро куба ЛВСОЛ1Д1С1О, имеет длину а. На диагоналях АС и
BiD1 граней куба взяты соответственно точки Е и F так, что впи:анная в куб
сфера делит отрезок EF на три части, отношение длин которых р ibho 3 ; 7 :1,
считая от точки Е, Найти длину отрезка EF.
49. Каждое ребро правильной четырехугольной пирамиды и\еет длину а.
Через середины боковых ребер, принадлежащих одной из боковых граней, гро-
ведена плоскость, касающаяся вписанной в пирамиду сферы. Нгйти площадь
получившегося сечения.
50. В правильной пирамиде SABCD сторона основания ABCD имеет длину я,
высота пирамиды равна а \>' 2. Сфера, вписанная в пирамиду, касается грани SAD
в точке К. Найти площадь сечения пирамиды, проведенного через ребро ЛВ и
точку К.
51. В тетраэдре ABCD длина каждого из ребер ЛВ и CD равна 4 см,
длина каждого из остальных ребер равна 3 см. В этот тетрлэдр вписана
сфера. Определить объом тетраэдра, вершинами которого являются точки каса-
касания сферы с гранями тетраэдра ABCD.
52. Ребро правильного тетраэдра ABCD имеет длину а. Сфера, вписанная
в трехгранный угол с вершиной А, касается плоскости, проверенной через
середины ребер АВ, AD а ВС. Найти радиус этой сферы.
53. В прямоугольном параллелепипеде ABCDAiBLClDl известно, что
\АВ\=Ъа, \ ВС \ = . BBi: —а. Сфера, вписанная в трехгранный угол ВАВ^С
(с вершиной В), касается диагонали ACi. Определить радиус сферы (ианти все
решения).
54. В правильной пирамиде SABCD сторона основания имеет длину 8 см,
боковое ребро — длину 9 см. Сфера касается плоскости основания пирамиды
в точкг А и прямой SB. Найти радиус этой сферы (наГпи все решения).
55. Сфера радиуса г касается всех ребер треугольной пирамиды, центр
этой сферы лежит па высоте пирамиды. Доказать, что пирамида правильная,
и найтн ее высоту, если центр сферы удален or вершины пирамиды на рас-
расстояние гУъ.
460
56. Каждый плоский угол трехгранного угла с вершиной S имеет Еедичину
60". На ребрах трехгранного угла взяты соответственно точки А, В иС так,
что \SA | = 2a, \SB\ = \ SC\=a. Найти радиус сферы, касающейся petiep угла
и плоскости ABC (найти все решения).
57. Основанием параллелепипеда ABCDA^B^^Di служит прямо} гольник
ABCD, сторона AD которого в четыре раза длиннее высоты параллелепипеда.
Сфера с центром в точке О касается реEер ВС, A\Bi и DDX соответственно
в точках В, Аг и Ог. Найти величину угла АХОВ.
58. В тетраэдре скрещивающиеся ребра имеют равные длины. Доказать,
что центры вписанной в тетраэдр и описанной около него сфер совпадают.
Верно ли обратное утверждение?
59. Сфера касается всех ребер треугольной призмы. Определить отношение
объемов сферы и призмы.
60*. В каждый из трехгранных углов тетраэдра вписана сфера. Все четыре
сферы имеют одинаковый радиус и пересекаются в одной точке. Найти радиус
этих сфер, если радиусы описанной около тетраэдра и вписанной в нгго сфер
равны соответственно /? и т.
61, В куб с ребром длины а вписана сфера. Для произвольно взятзй точки
сферы найти суммы квадратов расстояний от этой точки до: а) вершин, б) гра-
граней, в) ребер куба. Доказать, что эти суммы не зависят от выбора течки.
62. Через центр сферы проведены плоскость а и три попарно пер!ендику-
лярных радиуса. Найти сумму квадратов расстояний от концов этих >адиусов
до плоскости ос, если радиус сферы равен R.
63*. На сфере радиуса г расположены три окружности радиуса г/2 та»,
что каждая из них имеет с каждой из двух других по одной общей точкг. Найти
радиус окружности, лежащей на этой сфере и имеющей с каждой из трех дан-
данных окружностей по одной общей точке.
64. Угол между смежными боковыми гранями правильной тре /голыюй
пирамиды равен Зя/4. Сфера с центром в вершине пирамиды касаетс; основа-
основания пирамиды. Какая часть сферы находится внутри пирамиды?
65*. Ребро правильного тетраэдра ABCD имеет длину а. Сфера касается
ребер АВ, АС и AD соответственно в точках В, С и D. Найти площадь части
сферы, лежащей внутри тетраэдра.
66. Доказать, что если фигура Ф, не лежащая целиком на прямо} /, сим-
симметрична относительно любой плоскости, проходящей через прямою /, то
Ф — фигура вращения, и осью вращения япляется прямая /.
67. Найти объем фигуры, полученной вращением правильного шегт и уголь-
угольника вокруг оси, содержащей его сторону, если длина этой стороны равна а.
68. Периметр равнобедренного треугольника равен Р. Каковы долхны быть
длины его сторон, чтобы объем фигуры, полученной вращением этого •реуголь-
ника вокруг основания, был наибольшим?
69. Две сферы с центрами Oj и О2 пересечены плоскостью, перпендикуляр-
перпендикулярной отрезку OjO2 и проходящей через его середину. Эта плоскость дмлнт пер-
первую сферу на части, отношения площадей которых равно т:1, а вторую
сферу — на части, отношение площадей которых равно п:\ (т>1, л>1).
Найти отношение радиусов этих сфер.
70. Объем шара равен V. В сферу, ограничивающую этот ujaji, вписан
цилиндр. Каков наибольший возможный объем этого цилиндра?
' '461
7(. Сбгем шара равен V. Нагги им; ft линий объем конуса, вгисашюго
в сферу, ограничивающую этот шчп.
72. Площадь сферы равна 5. Около эгоп cq-еры описан конус, h акова наи-
наименьшая площадь поверхности этого конуса?
78. На высоте конуса, как на диаметре, построена сфера. Площадь
части сферы, лежащей внутри конуса, равна площади поверхности части
конуса, лежащей внутри сферы. Определить угол в осевом сечении конуса.
74. Доказать, что для того, чтобы в усеченный конус можно било вписать
сферу (касающуюсяего обоих оснований и каждой образующей), необходимо и
достаточно, чтобы длина образующей была равна сумме радиусов оснований.
75. В усеченный конус с боковой поверхностью площади Sy вписана сфера,
площадь которой равна 5,. Найта угол между образующей н плоскктью осно-
основания конуса.
76. В конус вписана сфера. Плоскость, проходящая через вершлну конуса,
делнт его боковую поверхность на части, отношение площадей которых равно
1 : 2. Сферу эта плоскость делит на части, отношение площадей которых равно
1 : 5. Найти угол раствора конуса.
77. Около сферы описан конус, угол раствора которого равен 60°. Найти
отношение объемов частей конуса, лежащих вне сферы.
78. В пирамиде SABC все плоские углы при вершине S прнмне, | АС \ =
=[SC;, \АВ =2R, угол между ребром SC и плоскостью ABC равен 45°.
На ребре АВ как на диаметре построена сфера. Найти радиус сфе]>ы, вписан-
ноii в трехгранный угол CSAB (вершина С) и касающейся данной а[«ры (найти
все решения),
79. На плоскости лежат три сферы, каждая из которых касается двух
других. Расстояния между точками касания сфер с плоскостью раины соответ-
соответственно а, Ь, с. Найти радиусы сфер.
80. Две сферы, радиуса г каждая, касаются друг друга. Прямая, обра-
образующая с линией центров угол ос, касается сфер соответственно в точках А
и В. Найти расстояния от точек А и В до линии центров сфгр и длину
отрезка АВ,
81. Две сферы равных радиусов касаются друг друга. Прямая пересекает
эти сферы последовательно в точках А, В, С и D (ВС—отрезок, лежащий вне
сфер) так, что \АВ\ = \ CD\ = a, | ВС \=па. Найти расстояние от :ггой прямой
до линии центров сфер.
82. В прямой двугранный угол вписаны две сферы равных радиусов, касаю-
касающиеся друг друга. Прямая пересекает газани угла в точках А и В составляет
с каждой гранью угол величины 30е и касается каждой нз сфер. В каком
отношении точки касания делят отрезок АВ?
83. Три сферы равных радиусов г касаются плоскости а и каждая из сфер
касается двух других. Прямая а, параллельная плоскости а, касается каждой
сферы. Найти расстояние между а и а.
84. Каждая из четырех данных сфер радиуса г касается оста пьных трех.
Найти радиусы сфер, касающихся всех данных четырех сфер.
85. Сферы St и S2 радиуса 2т к сферы S3 и Sk радиуса г расположены
так, что каждая из сфер касается трех других. Сферы Si и 1>3 касаются
в точке А, сферы S2 и S4 — в точке В. В каком отношении сф:ры Ss и Si
разделяют отрезок АВ?
462
S6. Два конуса имеют общую вершину, и образующая первого конуса
1
пвлягтся высотой второго. Уго.1 раствора первого конуса равен ;rccos -=-,
о
угот раствора второго равен 2л/3. Определить угол между образую цими, по
которым пересекаются боковые поверхности конусов.
87. Угол раствора конуса равен л/3. Внутри конуса располохены три
сферы радиуса г. Каждая сфера касается двух других сфер, основания конуса
н его боковой поверхности. Найти радиус основания конуса,
88. Внутри цилиндра расположены четыре одинаковых шара так, что
каждый из шаров касается трех других и боковой поверхности цилиндра. Два
шара касаются нижнего основания, а два других —верхнего основания 1илипдра.
HaiiTH объем цилиндра, если объем шара равен V.
89. Два конуса с равными углами раствора имеют общую вершину и
касаются друг друга (т. е. их боковые поверхности имеют одну оби ую обра-
образующую). Каждая грань двугранного угла, имеющего величину 2«, касается
боковой поверхности каждого из конусов. Найти угол раствора этих конусов.
90. Три конуса с равными углами раствора имеют общую вчршину и
каждый из конусов касается двух других. Вес три конуса касакгся одной
плоскости. Определить угол раствора этих конусов
Приложение
ОБРАЗЦЫ ВАРИАНТОВ, ПРЕДЛАГАВШИХСЯ В 1977—1979 г.
НА ПИСЬМЕННЫХ ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНАХ
ПО МАТЕМАТИКЕ
1. Московский государственный университет
а) Механико-математический ф а к у л ь т е т
1. Разность V |40^2 —57| — V 40|/ + 57 является целым числом. Най-
Найдите это целое число.
2. Найти все решения уравнения
а
cos (х -{- а2) dx = sin а,
принадлежащие отрезку [2; 3].
3. В остроугольном треугольнике ЛВС из вершим А и С огушеиы вы-
высоты АР и CQ на стороны ВС и ЛВ. Известно, что площадь треугольника ABC
равна 18, площадь треугольника BPQ равна 2. а длина отрезка PQ равна 2|/2.
Вычислить радиус окружности, описанной около треугольника ABC
4. Найти все значения параметра а, при которых система неразенств
имеет решение.
5. Объем тетраэдра ABCD равен 5. Через середины ребер AD и ВС про-
проведена плоскость, пересекающая ребро CD в точке М. При этоу отношение
длины отрезка DM к длине отрезка МС равно 2/3.
Вычислить площадь сечения тетраэдра указанной плоскостью, если рас-
расстояние от нее до вершины А равно 1.
б) Факультет вычислительной математики и киберне-
кибернетики.
6. Решить неравенство
(*—1) \гх* — х — 2 5зО.
7. Найти точки минимума функции
\Гп X . . X Х — Я
КЗ cos 2 +sin-2 j-.
8, Найти уравнение прямой, проходящей через точку с координатами
хг
A/2; 2), касающейся графика функции (/ = 2—^ и пересекающей в двух раз-
различных точках график функции y~V4 — хг.
464
9. Совокупность А состоит из различных натуральных чисел. Ко;ичество
чисол в А больше семи. Наименьшее общее кратное всех чисел из А раино 210.
Для любых двух чисел из А их наибольший общий делитель больше единицы.
Произведение всех чисел из А делится на 1920 и не является квадрате м ника-
никакого целого числа. Найти числа, из которых состоит А.
10. Основанием пирамиды ABCFJ1 служит выпуклый четырехугольник
АВСЕ, который диагональю BE делится на два 'равновеликих треугсльника.
Длина ребра АВ равна единице, длины ребер ВС и СЕ равны. Сум; га длин
ребер АН и ЕН равна V^2. Объем пирамиды равен 1/6. Найти радиус шара,
имеющего наибольший объем среди всех шаров, помещающихся i пира-
пирамиде АВСЕН.
в) Физический факультет.
11. Решить уравнение sin2 jc = 3/4.
12. Найти площадь замкнутой фигуры, ограниченной линиями:
(/ = 0, (/ = 20 — 6jc — 2jc2.
13. Найти отрицательные члены последовательности
_ An+t 143
где An+i — число размещений, а Ря+2 и Рп — числа перестановок.
14. Дана равнобедренная трапеция, в которую вписана окруя яоеть и
около которой описана окружность. Отношение высоты трапеции к радиусу
описанной окружности равно К2/3. Найти углы трапеции.
15. Длина ребра куба ABCDA^BfiyD^ ((ЛЛО |j (SSt) [(CC0 li.DDx)) равна 1.
На ребре АА\ взята точка Е так, что длина отрезка АЕ равна 1/3. На )ебре ВС
взята точка F так, что длина отрезка BF равна 1/4. Через центр куба v точки Е
и F проведена плоскость а. Найти расстояние от вершины В± до плоскости а.
г) Географический факультет.
16. Решить неравенство
17. В треугольнике ABC сторона АВ имеет длину 3 м, высота CD, опу-
опущенная на сторону АВ, имеет длину У^З м. Основание D высоты С D лежит
на стороне АВ, длина отрезка AD равна длине стороны ВС. Найги длину
стороны АС.
18. Найти промежутки возрастания и убывания, а также точки максимума
и минимума функции у=х/\пх.
19. Грузовик и гоночный автомобиль выехали одновременно из 1ункта А
и должны прибыть в пункт С. Грузовик, двигаясь с постоянной скоростью,
доехал до пункта С, проделав путь, равный 360 км. Гоночный а!томобиль
поехал по окружной дороге и сначала доехал до пункта В, распо; ожешюго
в 120 км от пункта А, двигаясь со скоростью, вдвое большей скорости грузо-
грузовика. После пункта В он увеличил свою скорость на 40 км/ч и проехал путь
от пункта В до пункта С, равный 1000 км. Он прибыл в пункт С на 1 час
15 мин. позднее грузовика. Если бы гоночный автомобиль весь сво i путь от
пункта А до пункта С ехал с той же скоростью, что и от пункта В до тункта С,
465
то в пункт С он прибыл бы на 1 час позднее грузовика. Найти скорость гру-
грузовика.
20. Решить уравнение
¦2 sin (зх-\- л \ = V 1+8 sin 2xcos22x.
П. Московский автомобильно-дорожный инстит /т
2х 1
21. Найтм экстремумы функции у = т-—jtj и указать интервалы воэрастя-
(х 1)
ния и убывания.
22. Вычислить объем тела, образованного при вращении во<руг оси Ох
фигуры, ограниченной линиями у = х3, </=1, х=Ъ.
23. Решить уравнение
1 J = 16
1 + cos2 дг "*" 1 + sin2 л; И"
24. Решить неравенство
25. Решить уравнение
5 "
HI. Московский инженерно-строительный институт
26. Для оплаты пересылки четырех бандеролей понадобились I различные
почтовые марки на общую сумму в 2 руб. 80 коп. Определить стоимость марок,
приобретенных отправителем, если эти стоимости составляют арифметическую
прогрессию, а самая дорогая марка в 2,5 раза дороже самой дешеиой.
27. Векторы а и Ь взаимно перпендикулярны, а вектор с образует с каждым
из них угол в 60°. Зная, что !aj=3, |&| = 5 и |с| = 8, вычислить скалярное
произведение (За — 2Ь) ¦ (Ь + Зс).
28. Решить уравнение
7 . 2>xV1 5-14 = 3*+4 5Л+3
29. Решить уравнение
== 6 sin х -\- 8 cos х.
cosx
30. Вычислить площадь фигуры, ограниченной линиями
IV. Московский инженерно-физический институт
31. Найдите сумму всех трехзначных натуральных чисел, которые при
делении на 3 дают остаток, равный 2.
32. В основании пирамиды SABC лежит равнобедренный треугольник ABC,
| АВ | = i AC \ = a, ABC = (f. Прямая (AS) составляет с плоскостью основания
пирамиды угол величиной а, плоскость боково» грани (BSC) составл гет с той же
466
плоскостью угол величиной fl и SAC = SAB. Найдите объем пирамиды KSLC,
если известно, что точки К и S принадлежат ребрам [AS] и [BS] соответст-
соответственно, а площадь треугольника KSL относится к площади треугольника ABS
как 4 : 25.
33. Решите систему уравнений
1оЗ 1 /з (Л'-гУ) + 1о5з (х — у) = 2.
.04. Найдите критические точки функции
координаты которых удовлетворяют неравенству хг—10 <—19,5л.
V, Московский институт инженеров геодезии, аэрофотосъемки
и картографии
35. Решигь уравнение 7lgA'==98 —xlg7.
36. Решить уравнение 2 + cos Ax = 2 sin2 х.
37. Решить неравенство
¦',<..
38. При каком значении г нектары а --=B; —3; 4) и Ь — (—3; 2 г) пер-
перпендикулярны.
39. Вычислить интеграл
— 18
\ V
VI, Московский институт народного хозяйства
40. Решить неравенство
41. Найти наибольшее и наименьшее значения функции
/ (jc) = 2 ¦ 3ЗЛ' — З2" ¦ 4 + 2 • 3-v
на отрезке [—1; 1].
42. Найти площадь фигуры, ограничением графиками функций
у=>Р — 4, у — 4 — х'2.
43. Радиус вписанной в коиус сферы равен R. Найти объем кои/са, если
центр описанной вокруг конуса сферы совпадает с центром вписашкй сферы.
44. На мебельной фабрике изготавливаются столы и стулья. На изготов-
изготовление одного стола расходуется 5 м досок и 1 м фанеры. На изготовление
одного стула расходуется 1 м досок и 2 м фанеры. Сколько было произведено
столов и стульев, если известно, что досок и фанеры было израсходовано
по 900 м?
467
VII. Московский институт стали и сплавов
45. Решить уравнение Зл—Kl8x+1+ 1 =0.
46. Решить неравенство
47. Решить уравнение
48. Найти
49. Найти угол между плоскостью, проходящей через точки А @; 0; 0),
ВA; 1; 1), С C; 2; 1), и плоскостью, проходящей через точки А @; 0; 0),
ВA; 1; 1), DC; 1; 2).
VIII. Московский институт электронного машиностроения
50. Решить уравнение
/1/14 \ /ViA \
l°g2 (^ г- cos х J + log2 ^—- cos xj = — 3.
51. Найти образ точки А B; 7) при повороте координатной плоскости вокруг
точки М B; 3) на угол — я/2. Найти образ еще одной точки (по Вашему вы-
выбору). Найти образ точки С(—4; 8) при этом повороте.
52. Проверить, какое из чисел больше: С}; нлн C^-fC^, и найти все зна-
значения га, для которых Сп<.Сп-\-Сп-
53. Наитн наибольшее и наименьшее значения функции
/ (х) = е2х -1 + 2«1 2* + 7х - 3
на отрезке [0,14; 1].
54. Назовем число а хорошим, если для всякого х выполняется неравенство
а) Доказать, что число 4 является хорошим числом.
б) Найти все хорошие числа.
IX. Московский институт электронной техники
55. Решить уравнение
sin4 х — cos4 x = cos x.
56. Решить уравнение
* + 5 х+ 17
32*-7==0,25-128*-3.
57. Вычислить площадь фигуры, ограниченной графиками фуитий
468
Г.8. В равнобедренной трапеции меньшее основание и боковая сторона
разьы а. Найти большее основание Ь, чтобы площадь трапеции были макси-
максимальной.
59. Даны три ненулевых вектора а, Ь, с, каждые два из которых некол-
линеарны. Найти иг. сумму, если вектор а-\-Ь коллннеарен вектору г, а век-
вектор Ь-\-с коллинеарен вектору а.
X. Московский областной педагогический институт
60. Вычислите площадь фигуры, ограниченной линиями
у==5/х, у—6 — х.
61. На основаниях АВ и CD трапеции ABCD построены квадрать (вне ее).
Докажите, что прямая, соединяющая центры квадратов, проходит че1ез точку
пересечения диагоналей трапеции.
62. Решите неравенство
1с^5р-2*)>1.
63. Решите уравнение
2 cos х— V 2 +sin 2x-
64. Высота правильной четырехугольной пирамиды составляет i боковой
гранью угол 30". Через стороиу основания пирамиды проведена плоскость,
перпендикулярная противолежащей грани. Найдите отношение объем>в много-
многогранников, полученных при пересечении пирамиды плоскостью.
XI. Московский физико-технический институт
65. Решить неравенство 0,1 А'н I < 0,8-f- - • Ю1'.
66. Решить систему уравнении
log* -^ — log, г. logu у =0.
67, Окружность, построенная на основании AD трапеции ABCJ как на
диаметре, проходит через середины боковых сторон АВ и CD т>апеции и
касается основания ВС. Найтн углы трапеции.
6S. Решить уравнение
3 sin За- = cos 4х — sin 9л" — cos \Qx,
00. И.1 пункта А в пункт В отправились одновременно два поездг. Каждый
из них вначале двигался равноускоренно (ускорения поездов различил, началь-
начальные скорости равны нулю), а затем, набрав некоторую скорость, — р< вномерно.
Отношение скоростей равномерного движения поездов равно 2. Пройд i четверть
пути от А до В, поезда поравнялись, причем в этот момент скоро(ть одного
была в 1,5 раза больше скорости другого. Найти отношение промеж /тков вре-
времени, за которые поезда прошли путь от А до В.
70. Найтн наибольшую возможную величину угла между плоско! тыо боко-
боковой грани и.не, принадлежащим ей боковым ребром правильной четырехуголь-
четырехугольной пирамиды,
469
XII. Москссгкий энергетический институт
71, Упростив выражение
найти его предел при х->- 1/8.
72. Решить систему уравнений
73. Сумма бесконечно убывающе'! геометрической прогрессии расна наиболь-
наибольшему значению функции / (к) = Ъх3 — х —76 на отрезке [0; 3]; первый член про-
прогрессии равен квадрату ее знаменателя. Найти знаменатель прогрессии.
74. Найти все значения х, удовлетворяющие уравнению
7л\ . 5л
и лежащие на отрезке [— л/2; 2я].
75. Через вершину Сх куба AliCDAiBlC1D1 проведена плоскAсть, пересе-
пересекающая ребра [ВС] и [CD] н образующая с гранью ABCD уюл а, при-
причем в сечении получен равнобедренный треугольник. Найти площгдь сечения,
если длина ребра куба равна а (рассмотреть возможные случаи).
ХШ. Ленинградский государственный университгт
(математико-механический факультет
и факультет прикладной математики — процессов управления)
76. Для каких а и b (a, b e R) графики функций / (дг) = 2л4—
н g(x) = 2axa—1 имеют лишь две сйщне точки?
77. Сколько шестизначных чисел содержат точно четыре различные цифры?
78. Решить уравнение (a e IR)
1 + 2 (sin2 2х — 2а cos 2х + a) tg2 x — cos 4x = 0.
79. Угол между смежными боковыми гранями правильной четырехугольной
пирамиды равен а, длина стороны основания —а. Найти радиус а)еры, касаю-
касающейся боковых граней пирамиды и описанной около пирамиды сфеэы.
80. Найти вектор а = (х; у; г), образующий равные >глы с векторами й =
= (у; —2г; Зх), c = Bz; Зд-; —у), если а перпендикулярен нектору d =
= A; —1; 2), |а| = 2КЗ и угол между вектором а и осью Оу — тупой.
XIV. Ленинградский институт точной механики и сптики
81. Упростить выражение
((l—
1 + j/ ab I
82. Решить уравнение
л — 2х , . 5л + 2х , 13л
«м—5—+SU1—j—= tg-j-
?л ?л *X
470
83. Решить неравенство 2 }гх2 3= (х— 1)Н-2.
84. Доказать равенство
т+'А /-"И
85. Число 12 разбить на два слагаемых так, чтобы сумма кубов э их сла-
слагаемых была наименьшей.
XV. Ленинградский электротехнический институт
86. Отец хочет разделить 180 яблок между пятью своими детьми. Пзловину
яблок он отдает своим сыновьям, которые делят их между собой поровну,
а другую половину отдает дочерям, которые тоже деляг их поровну. Оказалось,
что каждая дочь получила на 15 яблок больше, чем каждый сын. Сколько
у отца было сыновей и дочерей?
87. Решить уравнение sin2 2* + sin2 x= 1.
88. Решить уравнение
89. Найти наибольшее и наименьшее значения функции / (х) = 2>х% — 9х* ¦+>
+ 2 в промежутке [—1; 1].
90. Дано р арифметических прогрессий, каждая из которых содерж it n чле-
членов. Их первые члены соответственно равны 1, 2, 3, ..., р, а разнос и 1, 3,
5 2р — 1. Найти сумму членов всех прогрессий.
XVI. Новосибирский государственный университет
(механико-математический, физический, экономический факультети)
91. По дорожке, имеющей форму окружности, из двух диаметр ал ыо проти-
противоположных точек А и Б выбегают одновременно два спортсмена и бегут
с постоянными скоростями навстречу друг другу. Первая их встреча произошла
через / секунд в а метрах от Б, вторая встреча — в 2а метрах от / (о>0).
Найти скорости спортсменов, если под расстоянием понимается длина кратчай-
кратчайшего пути по дорожке.
92. Решить уравнение
cos 6х -f- tg2 x + cos (>x - tg2 л: = 1.
93. Окружности О1 и О2 касаются друг друга внешним образом в точке А,
отрезок АВ — диаметр Ov Длины отрезков, отсекаемых окружностями на неко-
некоторой прямой, проходящей через точку В, равны 2 см, 3 см, 4 см, i читая от
точки В. Найти радиусы окружностей.
94. Определить, при каких значениях параметра а уравнение \ogix^ax-\-\) =
= 1/2 имеет единственное решение.
95. В освовании треугольной призмы лежит равнобедренный прямо; гольный,
треугольник ABC, длины катетов АВ и АС которого равны а. Екняные ребра
АА', ВВ', СС образуют с плоскостью основания угол в 60°, а диагеналь ВС
боковой грани СВВ'С перпендикулярна ребру АС. Найти объем прп::мы, если
длина диагонали ВС равна a Y& •
471
XV11. Казанский государственный университет
(факультет вычислительной математики и кибернетики)
96. Решить уравнение
2 sin2 [х — -~j = 2sina*— igx.
97. Решать неравенство ; 3* — 3 | + 9* — 3 > 0.
98. В правильную четырехугольную пирамиду с высотой Н и стороной
основания а вписан прямоугольный параллелепипед, основанием которого
является квадрат со стороной Ь, так что его нижнее основание лехит на осно-
основании пирамиды, а вершины верхнего основания лежат на боковых ребрах
пирамиды. При каком Ь объем вписанного параллелепипеда будет наибольшим?
Найти объем при этом значении Ъ,
99. На дороге па расстоянии 10 м друг от друга лежит некоторое коли-
количество столбов. Начав с одного крайнего столба, рабочий перенес псе столбы
по одному к другому крайнему столбу, причем для этого ему в общей слож-
сложности пришлось пройти 1,44 км. Сколько столбов лежало на дороге?
XVIII. Киевский государственный университет
(механико-математический факультет)
100. В правильную четырехугольную пирамиду, боковые грнш которой
наклонены к плоскости основания под углом ф, вписан цилиндр (одно основа-
основание цилиндра лежит в плоскости основания пирамиды, а окружность второго
его основания имеет по одной общем точке с каждой бскошп г эаныо пира-
пирамиды). Радиус основания цилиндра и его высота равны г. Выч1 слить объем
пирамиды. При каком значении угла (р объем пирамиды наименьший?
101. Вычислить площадь фигуры, ограниченной графиками функций
¦Л — &\
у=—4— н У = 7-'-!-
102. Решить неравенство
/ **-3 > Vb (log., *'-3).
103. Сколько есть четырехзначных чисел, запись которых и десятичной
системе счисления содержит не более двух разных цифр?
XIX. Куйбышевский государственный университет
(физический факультет)
104. Дан куб ABCDAiBlCiDi. Доказать, что расстояние между плоско-
плоскостями, одна из которых проходит через вершины А, Ви Du а другая —через
вершины В, С], D, равно 1/3 диагонали куба.
105. Найти модуль разности экстремумов функции
472
106. При каких значениях а неравенство
выполняется для Есех действительных х?
107. Найти область определения функции
1
cos л:— .-
5.v — 6.Y-
XX. Ярославский государственный университет
(математический факультет)
108. Найти высоту треугольной пирамиды наибольшего объема, ви санной
в шар радиуса R.
109. Сколько различных шестизначных чисел можно составить из цифр 1,
2, 3, 4, 5, 6, 7, чтобы цифры не повторялись и крайние цифры были четными?
ПО. Решить неравенство
111. Решить уравнение
,/п 8л \ .
cos2! - - cos х 5~ 1 = ' •
РЕШЕНИЯ ЗАДАЧ РАЗДЕЛА I
ГЛАВА !
1. Имеем
А = {\; 3; 5; 15}, i?=<2; 3; 5; 7}, С =¦¦ {2; 4; 6; Ц.
Исходя из определений объединения и пересечения множеств, пол/чаем /1U#=
= {1; 2; 3; 5; 7; 15}, В(]С={2\, А[]С = {\; 2; 3; 4; 5; 6; 8; 15}, поэтому
(A U С) П В = {2; 3; 5}. Множества А и С не имеют общих элементов, следова-
следовательно, А(\С=ф и А(]В(\С=ф.
2. Легко находим, что А[}С = [—\; 2[, А(]В~[—1;0[, А\]В\]С=>
= ]-оэ;2[, (»UB)flC = [O; 1], В(]С = ф.
3. Если равенство
ЛпХ = /1иУ A)
имеет место для любого подмножества А множества Е, то оно справедливо
и в том случае, когда А совпадает с множеством Е и когда А яв/яется пустым
множеством, так как для всякого множества Е по определению Е с: Е и 0 с: Е.
При /1=? из A) следует Е(]Х=-Е U У. Так как X и К — подмюжества мно-
множества ?, то Е(]Х = Х и ?иУ=-^, таким образом, получаем Х = Е.
Если А=ф, то из (!) получаем Ф(\Х = ф\]У. Заметим, ч-о ф(\Х = ф
и ф\]У = У, следовательно, У=ф. Итак, Х = ? и У = 0.
4. Легко видеть, что если точка (х; (/) принадлежит данному множеству,
то ему принадлежат также точки (—х; —у), (—х; у), (х; —у), ¦¦. е. это мно-
множество симметрично относительно обеих координатных
осей и начала координат. Поэтому рассмотрим точки,
принадлежащие первому квадранту: }'^0, у^-0.
Координаты точек множества удовлетворяют уравне-
уравнению х-\-у=\, а так как х^О и i/=sO, то это есть
отрезок с концами в точках @; 1) и A; 0).
Все множество (рис. 328) получаем из этого от-
отрезка симметрией сначала относительно оси Ох, за-
затем симметрией полученного множества относительно
оси Оу.
5, Перепишем условие | х-\-у | ^ 1 )> виде —1 sg
!=сх + уsS 1 • Множество точек, координаты которых удовлетворяют условию
* + (/??:1, есть полуплоскость, граница которой — прямая х-\-у = 1, причем
та полуплоскость, которая содержит точку @; 0). Множество точек, опре-
определяемое неравенством *+УЗ=—1. также есть полуплоскость, содержа-
содержащая точку @; 0), граница этой полуплоскости — прямая х-\-у = —1.
474
Рис. 328.
Множество точе::, для координат которых выполняются оба неравенств;!, есть
пересечение этих полуплоскостей, т. е. есть полоса, границами которой явля-
являются параллельные прямые х-\-у = 1 и х-\-у =— 1.
Аналогично устанавливается, что условие ! х—у | =ёГ: 1 опредечяет голосу,
границами которой являются параллельные прямые х — у=\ и х — у =—1.
Если координаты точки М удовлетворяют одновременно условиям \х-\-у\^\
и | х — i/|^l, то точка М принадлежит пересечению множеств, определяемых
каждым из этих условий, т. е. искомое множество есть пересечение ука)анных
полос (рис. 329) — это квадрат с вершинами в точках @; 1), (I; 0), (--I; 0),
@; -1).
*
У
Рис. 329.
Рис. 330.
G. Так как у = —х2-\-2х есть парабола, пересекающая ось абсцисс i точках
л: = 0 и х = 2, имеющая прямую х= 1 осью симметрии, вершина которой имеет
координаты A; 1), то множество точек, ко рдинаты которых удовле"воряют
условию (/г=; — х2-\-'2х, ограничено этой параболой, точки множества л:жат на
параболе и ниже се (рис. 330).
7. Множество туристов данной группы, знающих английский язьк, обоз-
обозначим А, знающих французский язык — В, тогда туристы, знающие и тот и
другой язык, образуют множество А(] В. По условию
т(/1) = 70, тE) = 45, т (Л Л Я) = 23. По формуле A)
§ 1 находим т (/111-8) = 92. Множество А[]В есть
множество туристов, знающих хотя бы один из этих
двух языков, следовательно, не знают ни фргнцузского
пи английского 8 туристов нз группы.
8. Эта задача решается легче, если прибегнуть к
наглядному изображению множеств (рис. 331). Введем
обозначения: А — множество учащихся, решивших за-
задачу по алгебре, В — по геометрии, С — по тригоно-
тригонометрии.
Если .к; —число учащихся, решивших Есе три за-
задачи, то G — х) есть число учащихся, решивших за-
задачи по алгебре и геометрии, но не по тригонометрии, (8 —дс) —по алгебре и
тригонометрии, но не по геометрии, (9—х)--по геометрии и тригонометрии, по
не по алгебре.
475
Если а, Ь, с — количество учащихся, решивших только одну задачу соот-
соответственно по алгебре, геометрии и тригонометрии, то имеем
т(Л)=20=15 + а —лг, .
— х,
— х,
откуда находим: а = 5-{-х, Ь~1-\-х, с=\-\-х.
Всего в олимпиаде принимало участие 40 человек, три не решили ни одной
задачи, следовательно, хотя бы одну задачу решили 37 учанихся. Те, кто
решил хотя бы одну задачу, образуют множество А\]В\]С, тиким образом,
т(А\]В\]С)=Ъ7. А так как т (А[]В (JC) = a + 6 + c + 24 — 2х, то,-подставляя
выражения для a, b и с, отсюда находим х=5.
Итак, все три задачи решило пятеро. Число учащихся, реиивших розно
по две задачи, равно 24— Ъх, т. е. равно 9.
9. Пусть С — множество корней уравнения / (х) g (х) = 0. Е:ли a se С, то
/(a)g(o) = 0 и либо ае/1, либо а ?Е В, т. е. ае/lUB. Верно и обратное:
из а е А {] В следует а ?Е С. Действительно, если а ?Е А [} В, то либо а ?Е А,
либо о se В. Если, например, <к=А, то /(а) = 0. Функция g (х) —многочлен,
область ее определения — вся числовая прямая, следовательно, фужцня^ опре-
определена в точке а и /(a)g(a) = 0. Аналогично рассматривается случай oefl.
Из ска-зашюго следует, что С=А U В.
Если одна из функций, например g(x), не многочлен, а рациональная
функция, ю утверждение С = А[]В, вообще говоря, уже неверно. Например,
Х2 I 3
если g (х)= 2 ., f(x) = x— 1, то д;=1е/1 (/A) = 0). одна<о при х—\
функция g(x) не определена. Следовательно, при х—\ не определена функция
/ (х) S (•*¦) и 1 не может принадлежать множеству ее нулей.
Рассмотрим теперь уравнение /2 (х)-\-^(х) = 0, множество его корней
обозначим D. Если oeD, то /(я.) = 0, g(a) = 0, т. e. a e /iflS. Эбратно, если
a s /1A Д, то ое^ и /(a) = 0, a se В и g(^) = 0, медователыю, a se D.
Таким образом, D=A(]B.
10. Функция f (х) = Уз + х + УЗ — х определена, если 3 + л::г0 и 3 —л-^
5=0, т. е. определена на пересечении множеств, заданных неравенствами *Э=
Ss —3 и .r=ss3. Таким образом, D (/) = [ — 3; 3].
11. Функция определена при всех значениях х, кроме х=-±_ 1, Ее область
определения
j-oo; -1[IJ]-1; +1[U]1; +ооГ-
12. Функция определена при всех значениях аргумента, для которых
2-f-3J?5 0, Перепишем это неравенство в виде C/2)*sgl, откуда, логариф-
логарифмируя по основанию 3/2 (заметим, что 3/2>1), получим х-^0, Область
определения функции такова: ] — оо; 0].
13. Логарифм определен для любого положительного числа при любом
положительном не равном единице основании. Таким образом, функция опре-
определена для всех значении х, для которых х3—1>0 и 3+*>i), Ъ+хф\,
Решая совместно неравенства, находим, что
Jte]-3; -1[U]1; +<»[.
Учитывая, что хт? — 2, получаем следующую область определения функции:
1-3; -2[11]-2; — 1 ? U ] 1: +оо[.
476
. 14. Функция определена, если выполнены условия
9 — хф 1, т. е. *== — 5, *<9, х ф 8. Следовательно, D (/) = [ — 5; 8[U ]8; 9[.
15. Функция arccos/ определена на отрезке [ — 1; 1], обращается i нуль
при t = \, таким образом, функция / (х) определена при выполнении условий:
— 1г?2л: —1<1 и 2л> 0, 2хф\. Из первого неравенства следует Q ^х<
< 1, откуда, учитывая, что хф1/2 и хфО, получаем следующую оэласть
определения функции:
]0; 1/2[U11/2; 1[.
16. Функция определена для тех значений аргумента, для которых лоло-
зхительно выражение, стоящее под знаком логарифма, т, е. A,25) ~х —
— @,4096I+* > 0. Заметим, что 1,25 = 5/4, 0,4096 = E/4)~4, поэтому нера-
неравенство можно переписать в виде E/4)~(* 1) > E/4) t4+4-e>< откуда а едует,
что х удовлетворяет неравенству я2—1<4 + 4д; или х'1—4х— 5 < 0. Корни
уравнения х— 4х—5 = 0 есть —1 и 5, поэтому а2 —4л —5<0 при
— 1 <л<5, Область определения функции такова: ]— 1; 5[,
17. Квадратичную функцию ф (х) = хг-{-2х-\-'2 представим в виде i р (л:) =»
= (л-|- 1J-|- 1. Очевидно, что при х=-—1 она принимает наименьшее значение
равное 1. Множество значений функции ф (х) есть промежуток [1; +о>[, От-
Отсюда следует, что для функции V <р (х) множеством значений является также
промежуток [1; +оо[.
18. Заметим, что функция нечетная. Рассмотрим х^.0. Из неравенства
2аЬ<:а2-|-й2 следует, что 2х^1-\-х2 при всех х, причем равенство дхтига-
ется тогда и только тогда, когда x—l (a = b). Таким образом, при X&--Q
Функци нечетная, следовательно множество ее значений есть отрезок [ — 1; +1],
19. На промежутке ] — со; 0[ функци i у = хг-\-\ монотонно уэывает»
Действительно, если %<a;2^0, to
) — у (хг) = х\ — х\ = (*! —х,) (х^+Хъ)> 0
(так пак обе скобки отрицательны). Следовательно, существует обратная
функция. Разрешаем уравнение у = хг-\-\ относительно х, учитывая что х
отрицательно, получаем x=—Vy—\. Таким образом, f~^(x)=. — Vx--\.
20. Так как у {хх)—(/(%) = , то у (хх) = у (х.2) лишь при x1 = xi>
хг х2
Функция устанавливает взаимно однозначное соответствие между оиастью
определения и множеством значений и потому имеет обратную. Разрешая
i,l 1
уравнение i/=l-| относительно х, получаем х= р следовательно,
х+3 ,.
то у=——?¦ при хфЧ и не определена при
(х2 —
i — 5){x2 — 5)'
477
поэтому y(xl) = y(x2) лишь при условии xl=xi. Таким образом, эта функция
устанавливает взаимно однозначное соответствие между областью определения
к множеством значен мл и потому имеем обратную.
Разрешая уравнение ч = (х-\-Ъ)Цх — 5) относительно х, пслучаем х =
= C + 5i/)/(i/—1). Вспоминая, что хфО, исключаем значение у = — 3/5. Итак,
3
х— 1 '
22. Для существования обратной функции необходимо и достаточно, чтобы
различным значениям аргумента соответствовали разные значения функции.
Пусть Хуфх^. Так как у (х{) — у (*2) = а (*i— x2), то обратная функция будет
существовать, лишь если афО. При афО уравнение у = ах-\-Ь разрешается
относительно х: х — (у — Ь)/а, Таким образом, обратная функция существует,
если а ф О, и имеет вид
_х _ b
Функция у = ах-\-Ь будет совпадать с функцией у= , ести при любом
х будет справедливо равенство
, , х Ъ
а а
Полагая х = 0, получим Ь= — Ь/а, а полагая х=\ при условии Ъ = — Ь/а
будем иметь а=\/а. Решая систему
| Ь=-Ь/а,
\ а=\/а,
находим а = 1, & = 0 или а:= —1, .'; — любое. В первом случае функция f/ =
= принимает
вид у = х, во втором у=—х-\-Ь. Полученное нами
необходимое условие является и достаточным. Действительно, функции </ = *
и '-/= — * + &, очевидно, совпадают со своими обратными функциями. Заметим,
что прямая у = х совпадает с биссектрисой 1 и 111 координатных углов, а
любая прямая у = —х-\-Ь перпендикулярна этой биссектрисе и при симметрии
относительно нее отображается на себя.
ГЛАВА II
1. а) Цепь разорвана, так как или элемент k вышел из строя, или вышли
из строя одновременно все три элемента !;, или произошло и то и другое
б) Ток проходит по цепи, так как работают элемент k и по крайней мере
один из элементов /(.
2. Составим таблицу истинности для высказываний вида А+В
А
И
и
л
л
й
V.
л
и
л
л
л
л
и
и
А+В
и
л
и
и
478
Таблица истинности для А-\-В совпадает с таблицей истинности дтя пи-
пликации Azz^B. Формула доказана.
3. Обозначим буквами Аи Аг, А3 высказывания, состоящие соответственно
в том, что первый, второй, третий учащиеся изучали логику. Из у:ловия
задачи следует истинность
Р = (Л1==> Л2) (Л^=> Л2).
Освободимся от импликации, используя формулу
,4=>В = 1 + В,
доказанную в предыдущей задаче. Тогда получим
Для дальнейшего упрощения воспользуемся формулами 7 и 9 из § 1 с. 36:
Л + В = А В и А = А.
Получаем
откуда
т. е. логику изучал третий учащийся, а первый и второй не изучали.
4. Инспекторы комиссара Мегрэ установили истинность высказывай-ш:
Л=>(В + С), В + ЛО, D=>(B-}-C).
Произведение
этих трех высказываний истинно. Освободимся от импликации, псю.чьзуя
формулу, доказанную в задаче '2.
Получим
Р = (Л + В + С) (В + ЛЮ) (ZT+B + C).
Упростим произведение первой и третьей скобок согласно закон1 6 § 1,
с. 3G. Тогда будем иметь
р = (ad-\- в+с) (в + Id).
Еще раз применяя этот закон, получим
Р=В + СЛО.
Таким образом, из показаний инспекторов следовало лишь, что или Этьен —
убийца, или одновременно имели место три обстоятельства: Франсу лгал, <йрансуа
не был пьян, убийство произошло после полуночи. Но комиссару Мегрэ 5ыло из-
известно, что трезвый Франсуа не лжет, т. е. что AC^L, и следовательно,
Р = В + СЛО = В + ?=В, т. е. В истинно. Итак, убийство coDepiun.i Этьеи.
5. Равенство не доказано. В процессе «доказательства» дважды исполь-
использовалось соотношение
VbVt + 7 - V~5V' 2 -7 = 2,
справедливость которого как раз и требовалось установить,
479
Для доказательства равенства можно поступить так. Обозначим, левую
часть через а, т. е. положим
VWT+7 - УьУЪ—1 = а.
Возведя в куб обе части, получим
14-з(^51^ + 7)Ч/б72-7 + 3^5/2+7 (Кб/2~-г)а = аЗ!
или
3 V5 1/2 + 7УьУ2-7(Кб/2+ 7-Кб/2-7) = 14 -а».
Но, так как
КбП+7 - VbVl-1 = a,
то
3|/50 — 49а=14 — а»,
т. е. левая часть равенства равна одному из корней уравнения
—14 = 0.
Так как а = 2 единственный действительный корень этого уравнения, то равен-
равенство доказано.
6. Проведенные рассуждения и выкладки доказывают линь следующее:
если прямоугольный треугольник, о котором говорится в условии задачи, суще-
существует, то его гипотенуза равна aVbl'i. Но само существованie такого тре-
треугольника ниоткуда не следует. Легко убедиться в том, что яа самом деле
такого треугольника не существует. В противном случае велшина плоского
угла АСВ трехгранного угла CAQB была бы больше суммы величин двух
остальных плоских углов АСО к ОСВ.
7. Утверждение а) истинно при всех кфЪ.
Если 6 = 0, то, например, при 1 = 1 неравенство не имеет решений.
Если й>0, то каково бы ни было I неравенство будет кметь решения
Если й<0, то при любом I неравенство будет иметь решения х е
= [-«¦/*: +оо[.
Утверждение б) истинно при всех значениях k. Действительно, при любом
k существует I, а именно 1=0, при котором неравенство имеет решение x=Q.
8. Если число п оканчивается цифрой 4, то число л+ 48 оканчивается
цифрой 2 и, следовательно, не может быть квадратом натурального числа, так
как квадрат натурального числа обязан оканчиваться одной из следующих
цифр: 0, 1, 4, 5, 6, 9. Таким образом, А {п)В (я) при всес л—ложное
высказывание.
Высказывание С (п)В (п) также ложно при всех л, так как если л оканчи-
оканчивается цифрой 4, то л — 41 оканчивается цифрой 3 и поэтому не может быть
квадратом натурального числа.
Посмотрим, есть ли такие значения л, при которых истинно высказывание
А (п)С (п). Если Л (л) и С (л) истинны одновременно, то
480
Ёычитая почленно из первого уравнения второе, получим
89=р2-<72 = (р-<7)(р
Но-$9 — число простое, и поэтому должно быть
откуда р = 45 и я = 45э —48= 1977.
Следовательно, только значение я = 1977 может быть решением задачи.
Проверка показывает, что /1 = 1977 в самом деле есть решение.
9. Обратная теорема: если дискриминант квадратного уравнения неполо-
неположителен, то уравнение не имеет двух различных действительных коршй.
Противоположная теорема: если квадратное уравнение имеет два различных
действительных корня, то дискриминант этого уравнения положителен.
Противоположная обратной: если дискриминант уравнения положителен,
то уравнение имеет два различных действительных корпя.
Все четыре теоремы верны.
10. а) Утверждение верно. Докажем это. Пусть я(пз=5)—простс е число,
тогда я—1 и п-\-\ — два последовательных четных числа, и, следог ательно,
их произведение п- — 1 делится на 8. Помимо этого, из трех последов «тельных
чисел я—1, я, я+1 одно должно делиться на 3, но я не делится на 3,
а поэтому п-—1 обязано делиться.
б) Утверждение неверно. Для доказательства достаточно взять я — 25.
11. Легко проверить, что высказывания Л A), Л B), ..., Л (8)--ложны,
а Л (9) — истинно.
Пусть Л (я) истинно для некоторого значения я = ?. Используя )'то пред-
предположение, имеем
Далее, легко доказать, что
Следовательно,
т, е, Л(<г+1) истинно. Проведенное рассуждение верно для всех значений
k 3=9.
В силу принципа математической индукции высказывание Л (я) истинно
при любом я 3=9.
12. В случае одной прямой утверждение очевидно, Предположим, что
утверждение верно при я = А, Пусть теперь на плоскости произвольном обра-
образом проведено ft + 1 прямых, Докажем, что черной и белой краске й можно
закрасить плоскость так, что любые две части, имеющие общую сторожу, будут
окрашены в разные цвета. Для этого выберем из проведенных прямых одну
прямую и назовем ее для удобства дополнительной. Остальные k прян ых назо-
назовем основными. Закрасим плоскость нужным нам образом, учитывая только
основные прямые. По индуктивному предположению это сделать можн<. Допол-
Дополнительная прямая разбивает теперь уже раскрашенную плоскость ня две полу-
полуплоскости. В одной из них изменим цвет каждой части на противопс ложный.
Покажем, что после этого вся плоскость с учетом всех ft+1 прямьх закра-
закрашена так, как нам надо. Возьмем любые два соседних участка, Они разделя-
16 п/ред. Г. Н. Яковлева '481
ются или какой-либо из основных прямых, или дополнительной. В первом
случае эти участки были первоначально окрашены в разные цвета, а затем
либо оба поменяли свой цвет на противоположный, либо не меняли вообще
свой цвет. Таким образом, в этом первом случае они окрашены в разные цвета.
Во втором случае эти участки первоначально были окрашены одинаково,
а затем цвет одного из них был изменен на противоположный, :. е. в этом
случае они окрашены в разные цвета. Таким образом, из возможности окрасить
плоскость нужным нам способом в случае k прямых вытекает, что и в случае
k-\-\ прямых такая раскраска возможна.
ГЛАВА III
1. Умножив обе части данного уравнения на (х-\-1) (х-\-1), получим урав-
уравнение
3(*+1) —B*—1)B + *) = 2*+1,
которое, очевидно, равносильно кв;эдратному уравнению
Х- + Х — 2 = 0. A)
Следовательно, решениями данного уравнения могуг быть лишь коэни уравне-
уравнения A); л = —2 и х=1. Число —2 не является корнем данного уравнения,
так как при х = —2 не определены обе части данного уравнения. Проверкой
убеждаемся, что число 1 является решением данного уравнения.
Ответ: {1}.
2. Приведем схему решения данного уравнения;
=> (9-5,= (V^
(* — 3) — 18 = 0) <=>Bл;2 — 2>х — 27 = 0) <=>
<=}(* = —3 пли * = 9/2).
Следовательно, решениями данного уравнения могут быть лишь х = —3 и
л: = 9/2. При дс = 9/2 не определены обе части данного уравнения Проверкой
убеждаемся, что л = —3 является корнем данного уравнения.
Ответ: {—3}.
3. Возведем обе части уравнения в квадрат, получим
После преобразований имеем
*2 — 14л— 15 + 8|*+1 |=0. A)
Если х"^.— 1, то | де —{— 1 |=я-|-1 и уравнение A) равносильно квадратному
уравнению хг — 6х—7=0, корнями которого являются числа 7 и —1. Заме-
Заметим, что оба эти числа удовлетворяют условию х"^. — 1.
Если же Aisg—1, то | jc —f-1 |=—х—1 и уравнение A) равносильно урав-
уравнению л2—22л —23=0, корнями которого являются числа 23 и — 1. Условию
х^—1 удовлетворяет только число —1.
Следовательно, корнями данного уравнения могут быть толькз числа —1
и 7. Проверкой убеждаемся, что оба эти числа являются корнями данного
уравнения.
Ответ; { — 1; 7}.1
482
4. Введем новую переменную
х—Ъ
Тогда относительно и получим уравнение
И-!—2,
которое после умножения обеих частей на и сводится к квадратному у >авнению
единственным корнем которого является и=—1. Подставив найденное значе-
значение и в A), получим уравнение
Оно легко преобразуется в квадратное уравнение
корнями которого являются числа —3 и —2. Легко проаерить, что оба числа
удовлетворяют данному уравнению.
Ответ: {—2; —3}.
5. Вводем новую переменную
Тогда
xfi — Sv— 6 = 0,
5 ± K25 + 24 5 ± 7
Следовательно, ц = 6 и 2л^ + 3д: + 9 = 36. Корнями этого уравнения являются
числа 3 и —9/2. Проверкой убеждаемся, что эти числа являютс( корнями
данного уравнения.
Ответ: {3; —9/2).
6. Из второго уравнения вычтем первое, умноженное на 3, затем нз
третьего вычтем первое, умноженное на 2. В результате получим систему
| —5у —8z = — 18,
{ —3t/—4z = — 10.
Теперь к третьему уравнению прибавим почленно второе, умноженное на
— 3/5. Окончательно получим систему
8 18
5г=Т«
2 = 1.
котг.рая имеет треугольную форму и, очевидно, равносильна данной. Из нее
последовательно находим z-=\, у —2, х=-\.
Ответ: {A; 2; 1)}.
16* 483
7. Из первого, второго и третьего уравнений вычтем почлеинс четвертое,
умноженное соответственно на 1, 2 и 3. В результате получим систгму
1
„-4z = -2,
if-8z = -6,
_8г = —9.
Вычитая почленно из третьего уравнения этой системы второе, получаем урав-
уравнение — 4г =—4, которое, очевидно, противоречит последнему уравнению
системы. Следовательно, система не имеет решений.
Ответ: Система несовместна.
8. Прибавив почленно первое уравнение, умноженное на —2, <о второму
и, умноженное на —4, к третьему, получим систему
[ -5x2-x3-3xt = 0.
Второе и третье уравнения этой системы совпадают, поэтому даш ая система
равносильна системе уравнений
( *1 + *а + *э+*4=1|
\ — 5*а — х3 — Зд:4 = 0.
Из второго уравнения следует, что
1 3
Подставив это выражение для х2 в первое уравнение, получим
1 I 1 3 \ ,42
*1 = 1 — Х2 — Х3 — X* = 1 — ! — -- Х3 — - Хц I — Х3 — Хц = 1 — - Х-, — - Х4.
Следовательно, общее решение данной системы имеет вид
4 2 13
— 5 Хз—5 *4' —W Хз—5"*4' Хз'
где х3 и *4—произвольные. Таким образом, данная система имеет бесконечно
много решений.
Ответ: | A ——% — -_- X,; —^ х3—- дс4; ха; хЛ, х3 е= R, xt
V\OO 00 /
9. При решении этой системы применим метод подстановки. Из второго
уравнения системы находим х = 1 — 1у и подставляем в первое урашение:
G-20*+ 2^-2^G-2») = 5.
После преобразований этого уравнения получаем квадратное уравнение
Оно имеет корни (/j = 2 и у2=\\/5. Подставляя эти значения для i/ в уравне-
уравнение х = 7 — 2у, находим хг = Ъ и ла==13/5,
Ответ: {C; 2), A3/5; 11/5)}.
10. Прибавив почленно первое уравнение, умноженное на 7, ко второму
уравнению, умноженному на — 3, получим уравнение
14*2 + 21 г/2 — 28ху = 6*2 _ 3i/a(
которое легко приводится к уравнению
484
Решив его как квадратное уравнение относительно х, получим
х = 2у и х = Зу/2.
Данная система равносильна совокупности двух систем
х = 2у, f 2х = 3у,
И
( х = 2у, f 2х = 3у,
\ 2х*-у* = 7 И I 2х*-у* = 7,
Подставляя х = 2у во второе уравнение, получаем
8t/2_y2==7, I/a=l, У=±.\.
Следовательно, первая система имеет решения B; 1) и (—2; —1). Поставляя
x = 3yl% во второе уравнение, получаем
18 —
-4-</2-«/2 = 7, </2=2, y = ±V~2-
Следовательно, вторая система имеет решения C/У~2; \Г2) и (—3 У; —1^2).
Ответ: {B; 1), (-2; -1), (з//2~; /2), (-3/^21 ->А2)}.
11. Введем новые переменные и = ху и v = x--\-y2. Для них имеем систему
уравнений
( 3« —и = 5,
\ — ч2 + 9и2=155.
Подставляя у^3« — 5 во второе уравнение, получаем —9u2 + 30u — 2Е+9ua =
= 155. Следовательно, а = 6 и у = 13. Теперь решаем систему
Подстапляп i/ = G/a во второе уравнение, получаем
*5 + -^- = 13, х* — 13л-2 + 36 = 0.
По формуле корней биквадратного уравнения имеем
т. е. л = ;1;3 и x=;t;2. Следовательно, система имеет 4 рашенич: C; 2),
(-3; -2), B; 3) и (-2; -3).
Ответ: {C; 2), (—3; —2), B; 3), (—2; —3)}.
12. Прибавив к третьему уравнению почленно первое и второе, получим
уравнение
которое, очевидно, преобразуется к виду
(x + y + z)[x-z-\-\) = 0. A)
Теперь рассмотрим систему, которая получается из данной заменой третьего
¦уравнения уравнением A). Полученная система распадается на две системы
у которых первые два уравнения, как н у данной, а третьим у[авнением
у первой является
X + y + Z:=0, B)
а у второй—•
0. C)
485
Решим эти системы.
1) Из B) находим г = —х—у и подставляем это значение для г в первые
два уравнения. В результате относительно х и у получим систему двух урав-
уравнений
С 2ху + уЪ-х + у = 0,
0. ( '
Из второго уравнения вычтем почленно первое, умноженное на 3, и решим
полученное уравнение
как квадратное относительно переменной х. Тогда
Ъу it W+W _ % ±. 5ц
х- 4 - 4 '
т. е. х = 2у или х = —у 12. Следовательно, система D) равносилыа совокуп-
совокупности двух систем, у которых первое уравнение, как и в D), а вторым урав-
уравнением является соответственно х==2у или х = — у/2.
Если х = 2у, то из первого уравнения системы D) для у получзем уравне-
уравнение 5г/а— у = 0, которое имеет два корня </i = 0 и t/2=l/5. Следовательно,
в этом случае система D) имеет два решения @; 0) и B/5; 1/5).
Если у = —2х, то из первого уравнения следует, чтод; = 0. Следовательно,
в этом случае система D) имеет одно решение @; 0).
Из уравнения B), учитывая найденные решения системы D], получаем,
что рассматриваемая система имеет два решения @; 0; 0) и B/5; 1/5; —3/5)
2) Из C) находим г = х-\-\ и подставляем в первые два уравнения дан-
данной системы. Получим систему линейных уравнений
С Зх + у+\=0,
X 2*-3(/-1=0,
которая легко решается: х = —2/11, (/ = — 5/11. Следовательно, рассматривае-
рассматриваемая система трех уравнений имеет единственное решение
х = —2/\\, (/ = —5/11, 2 = 9/11.
Ответ: {@; 0; 0), B/5; 1/5; —3/5), (—2/11; —5/11; 9/11)}.
13. Введем новые переменные и и v по формулам
x = u\z и y = v/z. A)
Тогда относительно переменных и, v, z получим систему уравнении:
t 27us — v3 — lZuv =
\ 3ua — 4 — 4-3 = (
^ B)
Зц— v= 1.
Подставив и = 3и — 1 в первое уравнение системы B), получм квадратное
уравнение 12ц2 — 4ц—1=0, корнями которого являются числа %==l/2 и иг =
= —1/6. Подстаапяя эти числа в уравнение v—-Zu — 1, получаем v1==\/2 и
v2 — — 3/2. Из второго уравнения системы B) находим zt = 4/15 ч г2= 12/37.
Теперь, зная u, v, г, по формулам A) находим Жх=15/8, г/, = 15/8 и хг =
= —37/72,1/2=—37/8. Следовательно, данная система имеет решения:
A5/8; 15/8; 4/15) и (—37/72; —37/8; 12/37).
Ответ: {A5/8; 15/8; 4/15), (—37/72; —37/8; 12/37)},
486
14. Из второго уравнения системы определим у:
и подставим в первое уравнение системы:
После преобразований получаем уравнение
(са + 6с + 8)л = с2 + с—2.
Если (са + бс + 8) =7^0, то это уравнение имеет единственное решение
С2+6С + 8 '
Подставляя это значение х во второе уравнение системы, определим единствен-
единственное значение у. Таким образом, если t2 + 6c+8^t0, то система имеет единст-
единственное решение. Пусть теперь с такое, что г2 + бс + 8 = 0, т. е. с=—4 или
с= — 2. При е = —4 данная система принимает вид
— 4я — 4у = — 3,
Очевидно, что никакая пара чисел не удовлетворяет этой системе. Следова-
тельно, при с = —4 данная система несовместна. При с = —2 данна! система
принимает вид
Эта система имеет бесконечное множество решении.
Следовательно, только при с=—4 данная система не имеет i и одного
решения.
Ответ: с = — 4.
15. Через va обозначим скорость реки, а через v — собственную скорость
катера на пути от А до В. По условию задачи собственная скорость ;атера на
пути от В до С равна 2ti/3, а собственная скорость катера на пути ог С до А
равна iv/З. Следовательно, собственная скорость катера при движе!ии от А
до С на всех участках пути меньше, чем при движении от С до / . Однако
путь от А до С катер прошел за 7 часов, а путь от С до А — зй 8 часов.
Отсюда следует, что река течет из пункта А в пункт С По услоеию катер
прошел путь от Л до С за 7 часов, причем его скорость на участгах АВ и
ВС равна соответственно v-\-v0 и ——\-v0. Следовательно,
АВ\ \ВС\ _
г ~о7 — ' •
Из второго условия задачи следует, что путь от С до А катер г рошел за
4
8 часов со скоростью --& — &„, и поэтому
ij
487
Наконец, из третьего условия получаем
\АВ
¦6.
Введем обозначения a — \AB\/v0, b = \BC\/va и p = u/uu. Тогда для о, b, p
получаем следующую систему уравнений:
^— + " = 7
= 8,
I'-'
= 6.
Р-1
Из третьего уравнения системы следует, что а = б(р—1). Подставляя
14
выражение для а во второе уравнение этой системы, получаем ?> = -— р—2,
о
Подставляя выражение для а и Ь в первое уравнение системы, отюсительно р
получаем квадратное уравнение
4р2 — 7р—15=0,
корнями которого являются числа 3 и —5/4. Условию задачи удовлетворяет
12
только число 3. Тогда Ь= 12, и искомое время равно -= , г. е. 4 часам,
4-3+1
ГЛАВА IV
1. Не равносильны, так как, например, х = 7 входит в множество решений
второго неравенства, но не содержится в множестве решений первого.
2. Не равносильны, значение х = 0 удовлетворяет первому неравенству, но
не удовлетворяет второму.
3. Равносильны. Множество решений у данных неравенств одно и то же —
это пустое множество.
4. Не равносильны, так как х=0 принадлежит множеству решений вто-
второго неравенства, но не содержится в множестве решений первого неравенства,
5. Приводим неравенство к стандартному виду:
-'^ + 2~'5>0-
Находим критические точки х = —2, д; = —5, х = Ъ и записываем неравенство
следующим образом:
(х 4- 5) (х — 3) „
х-+2 >0>
Критические точки разбивают числовую ось на четыре интервал з (рис. 332).
Определяем знак левой части неравенства на каждом интервал*. Получаем,
что рациональная функция
.488
положительна иа двух интервалах: ]—5; — 2[ и ]3; +оо[. Сами крктйчеекие
точки в нашем случае в множество решений, очевидно, не входят.
Рис. 332. Рис. 333,
6. Неравенство уже имеет стандартный вид. Находим критические точки:
х = — У% х = — 1, * = /2, * = 3, * = 4.
Числовая ось разбивается критическими точками на шесть интервалов (рис. 333),
иа каждом из которых рациональная функция сохраняет знак. Легко усматри-
усматривается, что на интервалах ]—у Т, —1[, ]—1; У2[ и ]3; 4[ рациональная
(V2 - х) (/2 + л:) (х - ЗK ..
функция ' —-~ положительна. Исследуем критичен ие точки.
(х -\-1) (х 4)
Точки x=±V2, л; = 3 являются нулями числителя, и, так как неэавенство
нестрогое, входят в множество решений. Нули знаменателя х = —1, х — А ие
принадлежат множеству решений (стрелки на рис. 333 указывают на это).
Ответ: [—1^2; — 1[U] —I; /2~]ll[3; 4[.
7. Для нахождения области определения данной функции нуж! о решить
рациональное неравенство
2х+\ * + 4-^р
x — 2
которое легко приводится к стандартному виду
(х-2)Bх+5)'^0'
Критические точки л = 2 и х = —5/2 разбивают числовую ось на рм интер-
интервала, два из которых дают множество решении неравенства и, следовательно,
являются областью определения функции.
Ответ: ]— оо; — 5/2 [ U ] 2; +оо [.
8. Левая часть неравенства имеет смысл тогда и только то1да, когда
ха — 40л + 39>:0, т. е. если х^\ или яэ^ЗЭ. Если х<1, то пр man часть
неравенства отрицательна, тогда как левая — положительна. Следшательно,
на интервале ]—со; 1[ решений нет. Значение х=\ удовлетворяет нера-
неравенству и, следовательно, входит в множество решений неравенства. Если
х ^39, то законно возведение в квадрат обеих частей неравенства, т. е. хг —
— 40л: + ЗЭг^д:3 — 2*-|-1, — 38*^ — 38, или х3=1. Учитывая ограничение,,
получаем х 5s 39.
Ответ: {1} 1J [39; +оо[.
9, Квадратные корни, входящие в неравенство, существуют од.ювременно
для тех и только тех значений х, которые удовлетворяют системе неравенств
13л— 4 5s 0,
2л—13 5г 0,
13 — 2*550.
489
Эта система имеет решение и притом только одно: х== 13/2. Пэдстановкой
в данное неравенство убеждаемся, Что л=13/2 является решением.
10. Положим г = 9л;а — в*, тогда неравенство примет вид
Очевидно, решения могут быть только в том случае, когда
— 1/5г?2<7,
но для таких значений г можно обе части неравенства возвести в квадрат!
5г+1 <49-14г + г\
га—19г + 48>0,
2<3 и г>16.
Следовательно,
1 '5 < г < 3
Теперь осталось решить систему квадратных неравенств .
Неравенство 9х3 — в* < 3 верно при всех значениях х из интервал!
— 1/3 < л: < 1.
Неравенству
— 1/5 ;? 9*a — 6*,
удовлетворяют все лггс E — 2 \^5 )/15 и все х^ E + 2 Кб )/15. Оба неравен-
неравенства, таким образом, справедливы, если
11. Данному неравенству удовлетворяют те и только те зиа'ения пере-
переменной х, которые удовлетворяют либо неравенству
либо неравенству
4
х ~~~~
Каждое из этих рациональных неравенств легко решается методом интервалов.
Приводим первое неравенство к стандартному виду
или(ж+П(ж-4)
и
х х
Критические точки д: = —1, х = 0, x = i разбивают всю числовую ось на че-
четыре интервала, на каждом из которых определяем знак рациональной функ-
функции и получаем решение
— 1eS*<0 и *S=4.
Второе неравенство в стандартном виде записывается так:
?=?=!< о
х ~~~
или
0.
X
490
Из четырех интервалов, на которые числовая ось разбивается тремя ьритиче*
скими точками я = A— УТ7)/2, * = 0, я = A+VT7)/2, два интервала, а именно
1_]/Т7 n
х<—^ и 0<х<
входят в множество решений. Правые концы этих интервалов, очевидце, также
удовлетворяют неравенству.
'~f'7
Ответ! 1-ooj '~f'7]UH; 0 [ U I 0; ^-±~]U[4; +co[.
12. Заметим сразу, что при а = 3 неравенство решений не име<т. При
всех остальных значениях параметра а неравенство является рациональным.
Применим метод интервалов. Приведем неравенство к стандартному в^у
2а+1 — я(а-З).
или
х-2
= 0.
Критические точки я = 2 и х=Bа+1)/(а— 3) разбивают числовую ос > натри
интервала. Неравенство выполняется на среднем интервале и в т< чке х =
= Bа+ 1)/(а — 3), Определим, какая из критических точек являете i левым
концом среднего интервала. Для этого составим разность
а-Ъ Q-3"
Теперь видно, что ирн а;>3 левым концом среднего интервала бу;ет точка
х = 2; при а<3 точка х = Bа + 1)Да —3). Следовательно, если а > 3, ю нера-
неравенству удовлетворяют Есе значения х из промежутка
если а<3, то неравенству удовлетворяют все значения переменной из про-
промежутка
Ответ: Приа>3 х е j2; Ba+ 1)/(а-3)],
при а<3 «е [Bа+1)/(а-3); 2[,
при а = 3 решении нет.
13. Преобразуем неравенство следующим образом:
х + -»:</ + у -\-1/2 + z + z.v — 6 V x-.jz 5= 0,
(х. - 2 1Л*!/г+1/г) -i- (у - 2 l/".vyi-b сг) + (г — 2 KiyF+ ^
- Гх'уГ 35 0.
Справедливость последнего неравенства очевидна. На множестве всех неотри-
неотрицательных зыачениП переменных проведенные преобразования не нарушили
равносильности неравенств. Неравенство доказано.
491
14. Левая часть содержит 2я+1 слагаемых. Каждое слагаейое не пре-
превосходит 1/(я + 1). Поэтому
1 . . 1 „,„... 1
я+1 ^'
15. В неравенстве
Зя+1
'я+1 < п+1
= 2.
положим
Получим
2«—1
> 2,
... + <"-'),
2"-1з=«уА2(я~')'1/2,
16. При любом отрицательном значении а решением системы является,
например, #=1. При а = 0 система также имеет по крайней мере одно реше-
решение, так как х=1—решение системы и в этом случае. Если а>0, то система
может быть записана так
С xsC I/a,
\ х =? 4а,
и для существования решения необходимо и достаточно выполнение нера-
неравенства
4а s? 1/а,
т. е. а2^ 1/4, а=== 1/2.
Ответ; ]— со; 1/2].
17. Рассмотрим сначала случай, когда а = 2. В этом случае j (х) = 4ж + 5
и единственный нуль х = —5/4 функции / (х) принадлежит интервалу ]—2; 1[.
Следовательно, аьачение а = 2
удовлетворяет поставленному
условию.
Пусть тепер! а Ф 2. По-
Позаботимся сначала о том,
чтобы нули у функции / (х)
существовали. Для этого не-
необходимо и доста -очно, чтобы
дискриминант квадратного
трехчлена (а — 2[ *2 + 2a.v +
+ а + 3 был неотрицателен,
т. е. а2 — (а — 1!)(а+ 3)^
^0, откуда 1;?б. Об-
Обратим далее в шмание на
Ркс. 334. следующее обстоятельство.
Если 2 < а ^ 6, то для того
чтобы пули функции f (х) принадлежали интервалу ]—2, 1[, необходимо и
достаточно, чтобы выполнялись неравенства / (—2) > 0 и / A) > 0 (см. рис. 334, а).
Если же а<2, то для того чтобы нули функции f (х) лежали h.i интервале
492
б)
J—2, 1[, необходимо и достаточно, чтобы выполнялись неравенства /|—2)<;0
и/A)<0(рис.334,б).
Таким образом, помимо значения а = 2, условиям задачи будут удзвлетво-
рять те и только те значения а, которые удовлетворяют по краш ей мере
одной из следующих двух систем неравенств:
a>2, | /(-2)=a-5<0,
/<_2)=a-5>0, ' /d)
= 4a+l>0,
Первая система имеет решение 5<a«s^6, вторая система удовлетворяйся при
-1/4.
Ответ: ]-оо; —1/4[ U{2} U ]5; 6].
3
18. Положим x = t — „-, тогда
Мы получили квадратный трехчлен относительно t2. Наименьшее зна [ение до-
достигается при
9 , _1_
4 "г 4 5 3/5
/5 э\/5 М
Наименьшее значение равно [ -т Г/1*4 4)= '
Ответ: При х=(—¦i±V'5)l2 многочлен принимает наименьшее шачение,
равное —1.
19. Обозначим через х длину северной стороны, через у — длину восточ-
восточной. Тогда *r/ = 9000 (м2) и стоимость S (в рублях) строительства будет равна
S = 1 Ox -J-41/. Найдем наименьшее значение S
Воспользуемся неравенством
x+--^2Va, a>0, хе=]0
и получим, что
S^ 10 • 2 1/3600=1200,
причем знак равенства имеет место только при
х = У'а = /3600 = 60.
Ответ: Выделенной на строительство суммы будет достаточно только
в том случае, если северная сторона спортплощадки будет иметь длину
60 метров.
20. Обозначим расстояние между пунктами А и В через а, Кз &LBM
(рис. 335) по теореме косинусов найдем расстояние s(t) между автомобилями
493
в момент времени t после начала движения:
Под радикалом стоит квадратный трехчлен относительно t:
Наименьшее значение этого квадратного трехчлена, а, следовательно, и s (t)
достигается при
Но в условии задачи сказано, что в этот момент времени первый автомобиль
L А
прошел седьмую часть своего пути, следовательно, t — a/7Vlt Так™ образом,
получаем соотношение
a{2Vl-V2) a
из которого определяем искомое О7ношение скоростей:
\W\ — 7VLV.1 = 2
V± _ 5 + К25 + 96 _ 5+11 _ 2_
V2 ~ 24 ~ 24 ~ '
21. Пусть х — длина стороны выбрасываемых квадратов, V (х) -объем г;о-
лучившейся коробки, тогда
V {х) = {а — 2xfx
или
V т- (а-1х)(а-2х)Ах
V (X) .
Из последнего представления для V (х) видно, что сумма трех множителей,
стоящих в числителе, равна 2а и, следовательно, произведение ух. достигает
наибольшего значения при равенстве всех множителей, т. е. если
а — 2х = а — 2х = Ах,
то я = а/6,
Ответ: Сторона выбрасываемых квадратов должна быть равн;; а/6.
1. Заметим, что
я2— 1
ГЛАВА V
2 ' 2
<--?¦ и неравенство 2/п' <е выпол-
выполняется для всех я, удовлетворяющих условию я>1/2/е. Для лтбого е>0
494
возьмем N = [V2/e]+l (N >V2/e), тогда при всех rf> N выполняется не-
неравенство
я2 —
— 1
Учитывая
е
N
Ф-
установленную
1/10
5
-1 1
-1 <10
зависимость N от е, заполним
1/100
15
я*+1
1
"^ 100
я2-
п* +
таблицу:
1/1000
45
-р — 1 <
1
1000
2. Для любого положительного числа М возьмем я = 2 ([М\ -\-\), тогда
для элемента последовательности с этим номером, учитывая, что п четное,
получим
3. Предположим противное, т. е. предположим, что существует число а,
являющееся пределом последовательности (а„). По определению пре (ела для
е=1/3 найдется такое число N, что при всех я > N выполняется неравенство
\ап — а|<1/3. Отсюда следует, что для любых номеров я1 и я2 та сих, что
¦п1 > N и я2 > N, должно выполняться неравенство
| вЯ1 - а„з | « | аЯ1 - а |+| а„а - а | < 2/3.
Однако, взяв nl—2N и я2 = 2Л^ + 1, получим
2Л/
Л/ +
¦—О
2JV
iV + 1
1.
Полученное противоречие и доказывает, что предположение неверно, г. е. дан-
данная последовательность расходящаяся.
4. Для любого е>0 неравенство 1/яа<е выполняется для любе, го нату-
натурального п, удовлетворяющего условию «>-щ-- Таким образом, для любого
е > 0 можно взять N =
1, тогда при всех n> N будет справедливо
неравенство
я«
5. Пусть lim bn = 0, тогда для любого е>0 найдется такое N, что при
'] —> СО
всех /1 > N выполняется неравенство |6j, |<е. По условию | an | s~ | 6n | при
п=-1, 2, ... , тогда при
означает lim йи = 0.
;i -» со
6. Так как
будет выполняться и неравенство
1
<е, что
Vn+\-\-Vn Vn
495
и 1 irti (l/^n)=O (это следует из задачи 4 при а= 1/2), то, как следует из
п~*со
предыдущей задачи, lim (Vn-\-1 — Vn)=0.
П-+СО
7. Рассмотрим новую последовательность (Ьп) такую, что Ьп=гп-\-х (л —
= 1, 2, ...) и выберем х так, чтобы последовательность (Ьп) определялась воз-
возможно более просто. Подставим ап = Ьп—х в рекуррентное соотношение, опре-
определяющее ап, получим &„+1—A: = yFn —л) + у или й„+1 = у&„-|--д-+-з"-К.
Возьмем х=—1/2, тогда bn+1 — -^bn, т. е. последовательность (&,) является
геометрической прогрессией со знаменателем 9=1/3 и первым чтецом Ьх =
= 3/2. Итак,
) и an = y(yj +-2-.
Легко находим lim аге = -„-, так как lim [-«-) =0.
8. По формуле суммы первых k членов геометрической прогрессии при
й=я+1 имеем
п_ 1—а"+1
'+а 1—а '
1-й
Поэтому, учитывая, чго ]а|<1 и |й|<1, получим
A —й) A —а"+1) 1-
...+*»~Л™ A—a)(i—ь«+1)—1—а Л^тз^^-узг*
9. Под знаком квадратного корня стоит сумма первых л членог, арифмети-
арифметической прогрессии с первым членом а!=1 и разностью d = 2. Ло формуле
суммы арифметической прогрессии имеем
П0ЭТ0МУ 2яз + »+1
,. nV
lim ——
10. При a^l очевидно, что lim у а=1.
л-»оз
Пусть а>1, тогда по свойству неравенств |/~а>1. Обо;начим ft =
= уга— 1. Из неравенства Бернулли A -\-h)n 5=1 -|-rift следует (A -\-h)n — \)/п5?
~^h. Подставляя сюда ft^y^a—1, получим (а—1)/яЗ= у а—1, и так как
Ya — 1 >0, то отсюда следует у а — 1 | < (а— 1)/л. Для любого е>0 возь-
возьмем N = [(a— 1)/е] +1, тогда при всех n>N будем иметь y'a —l[sS
sg(a— l)/n< (a— 1)JN <e (так как N>(a — l)/e). Это и означает, что
lim у a=l.
П—*СО
496
ПриО<а<1 имеем 1/а>1,и из доказанного следует, что lim -|/\/а = 1.
п — 1 1
Поэтому lim j/a = lim — =
n-co п-со yi
/l-*00
11. Из определения предела следует, что для любых е > 0 найдется тгкое Nlt
что при всех n^>N-i выполняется неравенство \ап — а]<Се, т. е. а — е <а,г<
<Са + е и найдется такое N.2> что при всех л >• JV2 справедливо неравенство
|йи —а | <е, т. е. а—е<6и< а + е. Тогда, если N >Ni и N > JV2, r ри всех
n>N выполняются одновременно неравенства а — е<а„ н Ьп<:а--е. Из
условия ans^xns^bn получаем, что при n~>N имеет место а — е <ая г^л:„ «^
е5й„<а + е, т, е. |л„—а|<е. Это и означает, что lim xn — a,
П-» 00
Из доказанного в частности следует, что если для любого п выполняется
неравенство а^хп^Ьп и lim bn — a, то lim дс„ = а.
rt —> ОО Л -+ 00
12. Очевидно, что -/ 3" + 5" =5 1/ f-=-J +1 . Далее, для любого п спра-
справедливо неравенство 1 < C/5)" + 1 < 8/5, откуда следует 1 < ^C/5 п + 1 <
<у'8/5. Как следует из решения задачи 10 lirn |Л8/5 = 1, тогда из )ешения
задача 11 следует, что limy C/5)"+1 = 1, Таким образом,
lim y/'3» + 5'1=5 lim V C/5)" + 1 = 5.
n-юо П-»с»
13. Докажем, что для любых п справедливо неравенство
1<а„<2, A)
При п=\ это неравенство справедливо, так как а! = У. Пусть неравен-
неравенство A) верно при n = fe3=l. Из рекуррентной формулы а^,+1=У + а,! и усло-
условия а„>1 следует, что aft+1>K2+1 > 1, а из условия ап < 2 i олучаем
aft+i< К2 + 2 = 2. Таким образом, l<aft+1<2 и из принципа математической
индукции следует, что неравенство A) верно для любого п.
Покажем теперь, что ап+1>ап, т. е. У 2 + а„>а„. Так как ап>), то это
неравенство равносильно такому: 2+an>a^ или а^_ал_2 <;о. Квадратичная
функция /:(л:)=л:2 — л—2 обращается в нуль при х=—1 и * = 2 и fia интер-
интервале ]—1; 2[ отрицательна. Поскольку а„е]1; 2[ при любом п, то а\ — ап —
— 2<0 и, следовательно, У2 + а„>а„. Итак, последовательность (ап) ограни-
ограничена и монотонна. По теореме Вейерштрасса она имеет предел, обознач ш его а.
Из равенства а,!+1 = У + ап следует
lim an+1= lim /2 + a,j = K2+ lim
п-
т. е. а=К2 + а. Отсюда находим, что а~2 (а=—1, очевидно, не годходит,
так как 1 <ап<2).
14. Пусть а —первый член и А — разность арифметической прогрессии,
S/, — сумма первых fe членов этой прогрессии, п — число ее членов. Условия
497
задачи можно записать в виде
Sl3 = l_ Sn-Ss = 4^
$п — Sn-u 2 ' Sn_a 3
Используя формулу F) § 4 гл. V для S^, отсюда получим
Умножая первое равенство па 2 и складывая почленно со вторим, получим
60d = 3nd, откуда находим л = 20.
15. Пусть а —первый член и d — разность арифметической профессии, п —
число ее членов, Sn — ее сумма,
2a + d(n-\) _
¦->« — 2
Сумма Sn n членов арифметической прогрессии с первым члеюм а и раз-
разностью <2 + 3 такова:
я 2a+{d + 3){n-\) „
¦-> п о "•
а для арифметической прогрессии с первым членом 4а и разнос"ью d сумма
ее п членов будет равна
По условию Sre = 2Sn = Sre. Отсюда следует
Aa — d(n— 1) и 2а=(п — 1) C — d),
откуда, так как а Ф 0, находим d = 1.
16. Пусть а — первый член, 9 — знаменатель бесконечно убывающей геомет-
геометрической прогрессии и пусть а„=1/6.
Сумма всех членов прогрессии, стоящих до этого члена, равнг сумме пер-
первых л—1 членов прогрессии, по формуле E) § 5 гл. V
"-1 \-q •
Сумма всех членов, стоящих после члена ап, равна сумме бесконе жо убываю-
убывающей геометрической прогрессии с первым членом aqn и знаменателем q, т. е.
равна aqn -. , таким образом,
Кроме того, по условию а/(\ — <?)= 16;3 и ш)п'1=\/6. Из последних двух
равенств, исключая а, получаем
qn-i A _ 9)= ^ иди qn-i =.. _ + qnt
а из A) следует ЗО<7"= 1 —qn~l. Подставляя сюда выражение для q"'1, получаем
Щ"=^-0», т.е. 31,- = -^, ,- = -!-,
тогда qn~i = -^г + Цп = -г^• Теперь легко находим, что </=1/2 и г =5.
498
17. По определению
2 7 7 2 7/11 \
°'2G)=То"+ Too"+ 1ооо'+""=Т6"+ Too" I1+TF + Тбо"+"Г
Используя формулу суммы бесконечно убывающей геометрической прогрессии,
получим
О от- A A.S ! *-+-?- = I
",-\О — ш -Г ,00 1 ~ 10 "*" 90 18""
_1
Тб"
0.1F3)=-— + -JQQQ-+ 1Ооооо +'"=W + Tooo'i
Аналогично получаем
-— + -JQQQ-+ 1Ооооо
_ J_ _63_ 1 _ 1 63 9_
"" Т6Г + 1000" ' 1 ~ TO + "990' ~ 55"'
100
Таким образом,
0,2G)-0,1F3)== 1/22.
18. Так как функция sin A/л)определена для всехл=^0 и | sin A/л) ] «S 1, то
[лет A/л) —0 | = | л sin A/л) К | л|
и неравенство | л sin A/л) —0 | < е, очевидно, выполняется для всех; таких,
то 0<:#|<8. Таким образом, для любого е>0 возьмем б = е, тпгда для
всех х, удовлетворяющих условию 0 < | л | < б, будет справедливо
| д: sin A/л)—0 [е5|л j <б = е,
lim л + 2
19. lim —. —
+ 3—1 lim
20. lim — г- = lim
„, .. 2л! + л — 1 .. Bx— 1)(л+1) ,. 2л—1 3
21. lira ., ' == lim -i-'; '' hm
„, T cos 2л; (сов2л — 81п2л)
22. Так как —: : = -=-^ ; - = созл — sm л; (при условии, что
sin л + cos л sin л + cos л v 3
sin x+cosx^t 0) н, как отмечалось, функции cos .г и sin x непрерывны в любой
точке, то
lim —. 1; = lim (cosл — sin x) = cos f ) — sin [ — —( =1^2.
„„ T- , ( x при x>0,
23. 1ак как \x \=\ r „'то
1 ' \ —x при х<0,
x при
л — [л! _ / 0, при х>0,
2л ~ I. 1, при л<0.
Очевидно, что lim ^ ^0 и limJl
2x
»—о ,
24. Если *> 1, то \х — 1 \=х— 1 и
IK) x? — 2x+\ (x—l) x—\
1 . x — l
Очевидно, что /(л)>0 при л> 1 и lim -5-7^7 == "т —ГТ^ » cjе!©вательне4
lim тrr
г-»1 +0 А (X)
lim
Если же я< 1, то |ле— 1 | = — х-\-\ и
—\ (Х-\)(Х+\)
/(*) =
—3 (я—1
х+3*
поэтому
lim
1
. Так как
ветрудно видеть,
26. Так как
B+т)
и lim — = 0j то, кан
hm —
Тб"'
<го легко находим
27. Очевидно, что функция sin x не может иметь бесконечного предела,
так как jsin;t:|=sl. Покажем, что не существует и конечного предела у этой
функции при я->-+оо. Предположим противное, т. е. пусть й= lim sin x.
По определению предела на бесконечности, для любого е > 0 и, следовательно,
для е=1/2 найдется такое число М > 0, что для всех х таких, что х>УИ,
выполняется условие | sin х — 6 | <. 1/3. Откуда следует, что если х1 > М и
Л2> М, то
| sin xt — sin х2 | ^ | sin xx — b j +1 sin x.2 — b j < 2/3,
Однако, если выбрать n=[Af] + l (n>Af) и взять x1 = y,n (xt > M) и
то
| sin ^!—sin
sin
-8т(-^ + 2я/Л| = 1>2/3.
Полученное противоречие доказывает, что функция sin х при х —*--|-схэ не имеет
предела.
500
28. Функцию г (х) =—т=? можно рассматривать как сложную пункцию
_ V х _
2=iri, Где u(x)=Vx. Зная, что г'= — 1/и2 и «' = 1/B Vx), по правшу диф-
дифференцирования сложной функции получаем A/ Ух )'=г'и' =—1/BхУ х).
Производная от функции у (х) = (о (лт)M°, где v (x)=yx +—?=, такие нахо-
находится по правилу дифференцирования сложной функции: у' (дг)=50и49о'. Так как
TO
4
j
29. Если существует производная /' (д;0), то уравнение касательной к гра-
графику функции y = f(x) в точке с абсциссой х0 имеет вид </ = /' (Х'о) (.:—л:0) -f-
+ /(а:0). Так как
то подставляя в уравнение касательной л:0 = 3/2, f (хо) = Уз /2 и /' (х0) =
1
получаем i/ = —^^дг.
30. Пусть /г(л:)=л:а —2дг+5 и f2 (*) = я2 + 2* — 11, и пусть прямая i/=»
= йл:+г касается графиков функций y=fi(x) и у = B(х) соответственно в точ-
ках хг и *2, тогда уравнение этой прямой можно записать в двух ви;ах:
y = fi(x.J (x—x2)+f2(x2).
Отсюда следует, что
Для данных функций fx (x) и f2 (x) получаем систему
{V V О
Х*-*2-1б
решая которую, находим х1 — 5, х.2=3. Тогда имеем ft = 8, /=—20. Уравнение
общей касательной таково: « = 8дг—20.
5—дг| = —11—jcf.
ГЛАВА VI
1. Функция fi(x) не является ни четной, ни нечетной, так как, например,
Функция f2 (x) не является ни четной, ни нечетной, так какоиа огределеиа
только для *5й2/3.
Функция f3(x) определена на всей действительной оси и является нечетной,
как сумма двух нечетных функций х3 и 3sin*.
Функция fi(x) определена на всей действительной оси и являете.! четной
функцией, как разность двух четных функций х* и 5cos*.
; 501
Функция /в (х) определена на всей действительной оси. Функция не явля-
является ни четной, ни нечетной, так как, например, fb (In 2) = —1/6, У5 (—In 2) =^
= 2/3.
Функция /6 (х) определена для любого teR, Так как для любого х
то
h 1-х) = 1 n (-дс + VWD = - In (дс + /F+l) = -/e (*).
Следовательно, /6 (д-) является нечетной функцией.
2. а) Функция f(x) является периодической, причем ее периодсм является
любое положительное число. Действительно, пусть Т — положительное рацио-1
нальное число. Тогда, если х — рациональное, то аг + Г также рациональное,,
и тогда f(x)= I =f(x + T). Если же х — иррациональное, то и х-\-Т — ирра-
иррациональное, поэтому f (x)^=O — f (х-\-Т).
Никакое иррациональное положительное число Т не является периодом
этой функции, так как f (—Г) = 0, но / (— Т + Т) — Д0)= 1.
Покажем, что функция f (x) не имеет наименьшего периода. Предположим,
что То — наименьшее положительное рациональное число, являющее<я периодом
функции f(x). Но число Т0/2 < Го также является периодом это! функции.
Следовательно, наше предположение, что есть наименьший положительный
период, неверное.
б) Так как функции cos x и sin x являются периодическими с периодом 2л,
то функция f (x) также является периодической и число 2л является ее периодом.
Определим наименьший период функции. Имеем
/ (х) = cos х sin x (cos2 x — sin2 x) = -~- sin 2x cos 2x = - - sin Ar.
Следовательно, наименьший период функции / (х) равен л/2.
3. а) Так как /(х)->-оо при *-> — 3 и при л-> + 3, то прямые х = —3
и х = 3 являются вертикальными асимптотами. Так как
при а:->-+оо и при х-+—оо, то прямая у=\ является асимптого"! графика
функции / (х) при х-+-\-со и при х-*-—оо.
б) Прямая х=\ является вертикальной асимптотой, так как Нт / (х)=оо.
Далее, функция / (я) представима в таком виде:
f(X) С*+1
; =*+17.
\ Х—\
2
Так как lim г=0' то прямая у=х-\-1 является асимптотой при х^~ \- ~о
X ->оо X — 1
и х-> — оо.
в) Функция f(x) определена для .«2э — 2 и для х<~ — 4. В;ртикали-!).1\
асимптот график данной функции не имеет. Для нахождения асимптот при
a:-v + oo и х~> — со воспользуемся формулами B) и C) § 3 гл. VI. По i]op-
муле C)
^EI
*= lim J^±E±I- lim l/T^T-A =1.
502
По формуле B)
6= lim
«-¦+00
= lim
= Hm
Следовательно, прямая i/ = a: + 3 является асимптотой графика функции
f (х) при х->+оо. Аналогично показываете:), что прямая у=—х — 3 мвляется
асимптотой при х-*- — оо.
4. а) Функция f (х) определена на всей действительной оси и не мвляется
ни четной, ни нечетной. Она также не является периодической фуикщ ей и не
имеет асимптот. Из определения модуля следует, что
/<*Н
4 \
К-х — 2 , если
— ~-лг2, если х< 1.
2
Графиком функции 1/ = —;,-х2 является парабола, вершина которой лежит
•j
в начала координат и ветви которой направлены вниз. На бесконечно!г проме-
промежутке 1—оо; 0[ функция f(x) возрастает, а на промежутке ]0; 1[ /бывает.
Точка х = 0 является точкой максимума функции f (х). Графиком функции
/4 \
у — х — -х—2 является парабола, которая пересекает ось Ох в точках х = 0
\ J /
и х = 3/2. Следовательно, абсцисса х вершины парабо-
параболы равны 3/4, а ордината у равна —3/4. Следова-
Следовательно, при х~^\ функция f (х) возрастает. Точка
а:=1 является точкой минимума, так как в этой
точке функция f(x) непрерывна и на интервале ]0; 1[
она убывает, а на интервале ]1; +°°[ возрастает.
График функции / (х) приведен на рис. 336.
б) Функция / (лг) = lg (sin л:) определена для тех
значений х, где sin х>0, т. е. для х е ]2л«; 2лл + л[,
neZ- Рис. Зев.
Так как функция sin а:—периодическая, с перио-
периодом 2л, то функция lg (sin лг) также является периоди-
периодическом с тем же периодом. Поэтому достаточно построить график фун сции на
интервале ]0; л[, а затем достроить график функции во всех точках, гае функ-
функция определена. Прямые х=0 и х = л являются вертикальными асимптотами,
так как f(x)-y- — со при дг-v+O и при х->-п— 0. На интервале |0; л/2[
функция sin х возрастает от 0 до 1, а функция lg (sin х) возрастает от — со до 0.
На интервале )л/2; л[ функция sin х убывает от 1 до 0, а функция lg (sin x)
убывает от 0 до — оо. Точка л/2 является точкой максимума для данной
функции. График функции / (х) изображен на рис. 337.
503
У,
0
/"
/~2-
Г
1
"\| /3 СС
%/ р
в) Функция / (х) = 2соа* определена на всей действительной оси. Так кан
функция cos х четная, то и функция / (х) четная. Функция соз х является перио-
периодической с периодом 2л, поэтому и функция / (х) является периодической с тем
же самым периодом. Следовательно, достаточно построить график функции на
отрезке [0; 2л].
-2ft
Зл ев
Рис. .337.
Заметим, что график функции f (x) не имеет вертикальных асимптот.
На отрезке [0; л] функция cosx убывает от 1 до —1, поэтому функция f (x)
убывает от 2 до 1/2. На отрезке [л; 2л] функция cos х возрастает от—1 до 1,
а функция / (х) возрастает от 1/2 до 2. В точках х = 2пп, neZ, 4ункчия / (х)
имеет максимумы, равные 2, а в точках лг = 2яп + л, ле2, функция / (х)
имеет минимумы, равные 1/2. График функции / (x) = 2cosx изобранад на рис. 338.
-2л ~-jn -n
Рис. 338.
5. а) Функция /(*) = -
определена для всех хфЪ. Она не является
ни четной, ни нечетной и не является периодической. Ее графин пересекает
ось Ох в точке х = 2 и ось Оу в точке 1/=8/9.Так как f (х) -)—оэ при х-+Ъ,
то прямая л: = 3 является вертикальной асимптотой для графика функции / (х).
Заметим, что
8—12х+вха —х3 8 — Ъх
'(*' л;2 — 6л- + 9 ~ *+*2 —6л: + 9'
поэтому прямая у — —х является наклонной асимптотой графика функции при
х-*--{-со и при х-у — со. Найдем производную
3B — хJ(— 1)(х—ЗJ— B — хK2(х — 3) _ B —xJ(!i —х)
/'W=-
(х— ЗL
(х— ЗK
Точки х = 2 и х = Ъ являются критическими точками. На бескон(чном проме-
промежутке ]—оо; 2[ производная f (х) отрицагельна, следовательно, функция \ (х)
убывает от —оо до 0. На интервале ]2; 3[ производная отрицательна, следо-
следовательно, функция убывает от 0 до—оо. На интервале ]3; 5[ производная
положительна, функция f(x) возрастает от —оо до —27/4. -И, наконец, на
бесконечном промежутке ]5; + °°[ производная отрицательна, функция / (х)
убывает от —27/4 до —оо. Отсюда следует, что точка х = Ь является точкой
максимума. Заносим все данные исследования в таблицу.
X
У
У'
]-оо; 2[
]+оо; 0[
—
\
2
0
0
]2; 3[
10; -оо[
—
\
]3; 5[
+
5
27
0
max
]5; +«*
1 27- Г
--
\
График функции / (х) изображен на рис. 339.
б) Функция / (А") = х-\-е~х определена для всех «eR, Она не язляется
ни четной, ни нечетной, а также не является периодической. Ее граф ik пере-
пересекает ось ординат в точке (/=1. Ось Ох график
функции не пересекает. Вертикальных асимптот
нет. Так как lim e~x = Q, то прямая у = х явля-
является наклонно"! асимптотой при а--> + со- При
a:-v—оо наклонной асимптоты не существует,
так как
изводную
—оо при х-у- — со. Найдем про-
проТочка х=0 является критической точкой, в ней
производная обращается в нуль. Легко видеть,
что /' (а:) < 0 при х < 0 и /' (л:) >0 при х > 0.
Поэтому функция / (х) убывает на бесконечном Рис. 339.
промежутке ]—оо; 0[ и возрастает на ]0; +оо[.
Отсюда следует, что в точке х=0 функция имеет минимум. График функции
/ (а:) изображен на рис. 340.
ч , 6 sin х „
в) Функция /(*0 = -?гт—:— определена для всех *eR. Она шляется
2. —]-* COS X
нечетной функцией и периодической с периодом 2л. Поэтому до паточно
построить ее график на отрезке [0; л]. Так как 2 + cosats=1, to вертикальных
асимптот данная функция не имеет. Найдем производную
t>( _e cos х B + cos х) — sin x (—sin x) c 2cosa:+1
Точки х^2лп±-^
B +COS А"J '
neZi являются критическими точками. Отрезку [0; л]
принадлежит точка а-=2я/3. На интервале ]0; 2я/3[ производная положительна,
следовательно, функция f (х) возрастает. На интервале ]2л/3; л[ производная
отрицательна, следовательно, функция / (а:) убывает, Поэтому точка х = 2я/3
505
является точкой максимума. График функции f (х) изображен на рис.341.
Заметим, что во всех точках вида лг=2ля + -д-. neZ, функцш f (x) имеет
О
максимумы, а во всех точках вида х = 2пп —, п е Z. —минимумы.
о
-.•Уз -—,
6. Функция /(.<с) = 2 In (x — 2)— x2 + 4*+l определена для х>2. Найдем
ее производную
г. . 2
' к''~х-2 ~~ ' '~ ""л;-2"
Точка х = 3 является критической точкой данной функции. На интервале ]2; 3[
производная f (x) положительна, следовательно, на этом интервале функция
возрастает. А на бесконечном промежутке ]3; + со[ производная f (х) отри-
отрицательна, следовательно, здесь функция f (x) убывает. Точка х=-3 является
точкой максимума.
7. Функция f (х) определена и имеет производную для всех ;• е R. Нахо-
Находим производную функции / (дг):
V {уЛ —^ j^2 Cjy Ц_ Q =^ (Y О) (Y 3^
Функция f (x) имеет две критические точки х = 2 и х=3. Обе точки принад-
А лежат отрезку [1; 4]. Следовательно,
mill /(*)=mi:-i{/(l), /B), /C), /D)} =
[l; 4]
23 28 27
max
: 4]
32
23
, /B), /C),
Рис. 342.
Ответ: Наибольшее значение равно 32/6, а наименьшее
равно 23/6.
8. Пусть некоторый конус описан около данного шара ради-
радиуса R (рис. 342). Очевидно, что центр шара О лежит на высо-
высоте конуса АВ. Обозначим через г радиус основания конуса и через h его вы-
высоту. Тогда объем конуса V равм -^пгУг, Легко доказать, что | ВС | =
о
= | CD |, т. е. jCDj = r. Из подобия треугольников ABC и AOD следует, что
ВС\
\OD\
АВ\
\AD
г
т. е. — = -
R
506
Отсюда получаем
г V
и, наконец,
/1-2/?'
Следовательно,
Найдем минимум функции V (/i). Вычислим производную
1 2/i2— 4/?/i — h2 1 h(h — \R)
3 (Л — 2А?У2 3 (h—2/?J
Производная V (h) обращается в нуль при h = 4R, причем при прохождении
через точку h=4R производная меняет знак с минуса на плюс. Следов; тельно,
при /i = 4/? функция V (k) имеет минимум. Наименьшее значение объем! равно
ГЛАВА VII
| QQ ВС '
1. Л BOCcaAAOD (рис. 343), поэтому - =—-=- = п, откуда,
Аи Ли \
учитывая, что ] АС I = j АО | + j ОС I, находим 'АО =- \АС\. Далее
1 + п
~АО\\АС, поэтомуЛО= -^— АС, ВС \\ AD, \ ВС , =
— п ¦ \ AD ', следовательно, BC = nAD, а так как АС =
= AB-j-BC, то окончательно имеем
(AB+nAD).
2. Используя признак коллинеарности, можем запи- Рис. 3 13.
сать а-\-Ь = хс, и ft-j- c = ya. Векторы ft и с некол-
линеарны, следовательно, у ф 0 и а = —ЙН с. Подставляя sto в первое
равенство, получаем ( 1-| j ft = Ix )с. Векторы ft и с не нулевые и
неколлинеарные, поэтому последнее равенство может выполняться лгшь при
условии 1 -|—г = 0 и >: = 0. Тогда ц— — 1, х= — 1 и легко нахо; им
г/ У
3. Пусть D — середина ребра ОА тетраэдра ОАВС (рис. 344). Име<м ВС =
= DC — DB, MN = Ш? — DM. Так как DN \\ DC и /Ш ff DB и, кроме того,
по свойству медиан
I DAM I I DM j 1
¦ ;= .г- И
] DC j ~~ 3 |Dfl | ~ 3 '
607
. 1 . 1 .
то DN = --DC и DM = —D5. Таким образом,
О О
MN =~ DC — -1- DB = 4- ВС .
О •! О
По признаку коллинеарности вектор MN коллинеарен вектору ВС и
\ш\ :| вс |=1/з.
4. Пусть т = \ AM j/j AB |, тогда (рис. 345)
AM =tnAB, BN=тВС и МВ = (\—т) АВ.
Находим MN = MB + BN = (\— т) АВ + т'ВС. По условию такль! ~РС = тЪ~С,
QD = mAD, поэтому
D~P=(\ — m)DC и QP = A — m)DC + mAD.
ABCD — параллелограмм, поэтому DC = AS и BC = AD. Сравнивав выражения
„ для векторов MN и QP, устанавливаем, что MiV =
= QP. Из этого равенства следует, что J MN \ = \QP \
и /WN [!QP. Таки-4образом, в четырехугольнике MNPQ
противоположные стороны равны по дл ше и парал-
параллельны, и потому MNPQ — параллелограмм.
В N
Рис. 344.
5. Необходимость, Пусть а и Ь — ненулевые коллинеар ше векторы,
По признаку коллинеарности (§ 4) существует такое число а, что Ь=аа.
Тогда при х = а и у=—1 выполняется равенство
0. A)
Достаточность. Пусть аи Ь — ненулевые векторы, для ко'орых выпол-
выполняется равенство A), причем х и у и одновременно не равны нулю. Если,
например, хфй, то из A) получаем а = —Ь, откуда (по признаку кол-
коллинеарности) следует, что а и Ь коллинеарньг. Аналогично рассматривается
случай и ф 0.
6. Пусть \а + Ь\ = \а — Ь\, тогда ) а + Ь |2 = [а — Ь j2. Так как \а + Ь |2==
= (а4-й)(а + й) = ;а|2 + 2а-й + |й|2 и j а — Ь |2 = (а — й) (а- -Ъ) = \ а |2 —
— 2а • й + | й j2, то из равенства \a-\-b f = \a — b'f следует а ¦ b-- = (). Скаляр-
Скалярное произведение ненулевых векторов равно нулю тогда и только гогда, когдэ
они перпендикулярны.
508
7. Складывая почленно равенства
\а + Ь? = \а\
\а — Ь |2=(aj2 — 2afc+!fc|2,
получим
|a + e|« + |e-ft,« = 2|ai« + 2|e|».
Отсюда, зная, что |о|=11, |й|=23и \а— ft| = 30, находим |a + fc! = 20.
8. Если векторы перпендикулярны, то их скалярное произведение равно
нулю, следовательно,
(а+ 36) Ga — 5ft) = 0, (а — 4й)Gа — 2ft) = 0.
Используя свойства скалярного произведения, отсюда получим
7 | а |2+ 16а • ft- 15 | ft |2 = 0, 7 | а |2-30а • fc + 8 | ft |а = 0.
Исключая из этих равенств I a |2, находим а-й = |й|г/2, а подставлш это
в первое равенство, получаем ] a | = | ft |. Так как о • ft = | о | • | ft | cos (а.й|,то из
условия a-fc = |fc|2/2 при |o| = |ft| находим cos (a,ft) = 1/2. Следовательно,
угол между векторами а и ft равен 60".
9. Из равенства
при условии a+fc+c=0 и |oj = |ft| = |c] = l получаем
a-b + b-c + a-c= — 3/2.
10. Векторы а и ft, очевидно, не коллинеарны. Вектор с, компла! арный
с векторами а и ft, может быть разложен по этим векторам: с = ха+уЬ. Это
векторное равенство равносильно системе трех скалярных равенств:
щ = х+Ъу, 0 = — х+у, 2 = 2х.
Находим: х=\, (/=1, /я = 4.
11. Вектор ft коллинеарен вектору а, поэтому ft = ma и |ft! = |/n||a|.
—Г з
1 + 1+—= -, то |/и|=2. Если /п^2, то ft =
= B; 2; —1), а если ш = — 2, то fc = (—2; —2; 1). Пусть Ь = (х; у; г), тогда
cos (ft, ft) = z/|fc |. Если угол между векторами ft и ft острый, то косину; этого
угла положителен и координата г вектора Ь также положительна. Таким обра-
образом, ft = (— 2; —2; 1).
12. Пусть р = (х; у; г). Вектор р перпендикулярен векторам а и ft, следо-
следовательно, а-р = 0 и ft.p=0. Выражая скалярные произведения через коорди-
координаты, получим
х+у-\~г = 0 и х + Ъу—2=0,
откуда находим, что г = у и х = —2у. Вектор р единичный, следовательно,
*2 +1/3 + z2 = 6i/2 = 1. Угол между векторами р и _/ тупой, косинус этою угла
отрицательный, а так как cos (р, j) = y, то i/<0. Итак, i/=—l/j/^6 и р =
13. Вектор Ъ компланарен с векторами / и ], следовательно, может быть
разложен по этим векторам: b = xi-\-yj. Так как a J_ ft, то a-fc = 0. записы-
записывая скалярное произведение через координаты векторов, получаем 4*— 3i/=0,
х. Длина вектора а равна |^4а + За + 5а = ]/50 и равна д
509
т. е. у=-^-х. Длина вектора а равна |^4а + За + 5а = ]/0 и равна длине
о
4
вектора Ь, поэтому х2 + г/2 = 50, откуда, поскольку у~-~-х, получаем х2=18,
х = ±з/2. Таким образом, fc=:±C/2; 4/2).
14. Если точка М (х; (/; 2) принадлежит оси ординат, то х =2 = 0. Итак,
точка М имеет координаты @; !/; 0), поэтому | AM | = /22 + (i/ +1J+12 и
jfi.W j = /(i/—1J+32. Из условия \АМ\ = \ВМ\ получаем (#+1J + 5 =
= (у— 1J + 9, откуда находим i/=l и М @; 1; 0).
15. Пусть О~Л=а и ОВ=Ь. Если вектор ОС сонаправлен вектору оЗ
и)дС|=|ОЛ|, то вектор OD является диагональю ромба О ЛВС и делит
угол АОВ пополам. Так как |я|=5, [й| = 15, то, очевидно, ОС = fc/3 =
= 14/3; 2/3;—5/3), тогда OD = (L4+ОС = B/3; 2/3; 4/3). Искомый лектор dcona-
су
праплен Об, поэтому d=xOD, х > 0. Поскольку | OD |= к- /( ,а | d | = /б,
то * = 3/2. Итак, d = (l; 1; 2).
16. Если А, В, С и D — последовательные вершины параллелограмма, то,
AC = AB + AD. Зная координаты точек Л, В и D, находим, Л~В = B; —1),
Л?) = (—2; —4), тогда ЛС = @; —5) и |ЛС| = 5.
17. Пусть О —начало координат, точка N принадлежит отрезку ВС, при-
причем \BN | : | ВС\ = п. Тогда (см. пример 2 § 5) ОЛ/=я • ОС + (;—я) Ofl". Это
означает, что координаты точки N следующим образом выражаются через
координаты точек С (хс; ус; гс) и В (хв; ув; гв);
N (пхс + (\ — п)хв; пус + (\ — п)ув; ягс + A — я) г„).
Если JV —середина отрезка ВС, то и = 1/2. Координаты середины отрезка
равны полусумме координат его концов. Для данных точек В и С находим
N(— I ;5; —2), тогда
| MN \ = /A + 1J + (- 1-5J + A
В том случае, когда п=1/3, координаты точки Л' таковы: N @; —3; 4) и
18. Если плоскость а параллельна плоскости a^ + &// + cz + d = 0, то пек-
тор (а; Ь; с) перпендикулярен плоскости а. Отсюда следует, что уравнение
плоскости, проходящем через точку А A; —3; 2) параллельно плоскости 4х —
— 2у — 2 + 7 = 0, имеег вид 4 (х— 1) — 2 G/ + 3) — B — 2) = 0, т. е. Ах — 2</— г —
— 8 = 0.
19. Если О —начало координат, то вектор ОА = (—1; —1; 2) перпендику-
перпендикулярен данной плоскости и ее уравнение имеет вид —(*+ 1) —(г/+ 11 + 2 B — 2) =
= 0, т. е. х + у— 2г + 6=0.
20. Пусть точка В (х0; у0; г0) является основанием перпендикуляра из
точки А на плоскость. Точка В лежит в плоскости, следователью, ее коорди-
координаты удовлетвор яют уравнению плоскости;
г0 + 3 = 0. A)
Вектор АВ = (хо-{-2\ уа — 3; го + 4) перпендикулярен плоскости, поэтаму он
коллинеарен вектору п = B; 2; —1), т. е. координаты векторов АВ я п щю-
510
порциональны:
Отсюда получаем </о =
(/„-3
1
— 1
5, zo = — х0— 5. Подставляя эти выражение в A),
находим Atc= — 4, тогда 1/A=1 и го = —3. Итак, АВ = (—2; —2; 1) н [AJIj = 3.
21. Пусть Pi и р2 — соответственно плоскости, проходящие через точки А,
В, С и А, В, D. Составляем их уравнения (см. пример 4 § 8 гл. VII); полу-
получаем
х — 2г, + г = 0 и х + у — 2г = 0.
Векторы яг и я2. перпендикулярные этим плоскостям, таковы:
иг=A; —2; I) и «2 = A; I; —2).
Косинус угла между плоскостями рх и Р2 находим по формуле E) § 8 кт VI
i Пл ¦ Я,! 1
cos а =
I
Итак, а = 60э.
и,
I «1 I I «2 1
2
A+202-A-03
ГЛАВА VIII
i2—A—0 A —2i
2гA —0
— I+6t
C + 20 E + 120 - C + 40 - 9 + 46i - C + 40
_l+6i l — 6> A — 60B + 70 44 — 5i __ АЛ — 5:
Ответ:
— 12 + 42; 6B — 70 6B — 70B + 70 6D+49) 318
22 5 .
2. а) Находим последоьатрлыю модули и аргументы чисел:
Число
1+1
A + 013
1-(
A-07
A+/I3
A-07
Его модуль
V2
(VW3
Vi
(Vi)"
{VW 8
Один из его аргументов
л/4
13л/4
-л/4
— 7л/4
4 \ 4 ) °
Ответ: Модуль числа равен 8, аргументы B?+!)л, k e Z-
б) Находим модуль:
/• = /(sin Fл/5)J + A + cos Fл/5)J = У 2 + 2 cos (Gя/5] = 2 У (cos (Зл/5)J• = =
= 2 | cos (Зл/5) | = — 2 со; (Зл/5).
511
Аргументы ф данного комплексного числа обязаны удовлетворить уравнению
tg(p= 5шFя/5) A)
или
2 cosa (Зл/5) Зл_ / л\
g<P~ 2 sin (Зл/5) cos (Зя/5) ~ S "~5~ ~ g\ "То"/ '
откуда ф = .-.у + яй, & е Z- Данное комплексное число распс ложено в 2-м
квадранте, так как sin-,.— <0, a l+cos-p->0. Поэтому аргу\ентами будут
те и только те решения уравнения A), которые лежат во второй четверти, т, е,
Ф = — -до + я-г-глп, nel
9л
Ответ: г = —2 cos (Зл/5), ф = у^- + 2ля, я e Z.
3. а) Найдем сначала тригонометрическую форму данного комплексного
числа. Запишем в тригонометрической форме число Уъ — L Так как V 3 — i | = 2„
а один из аргументов фх=—л/6, то
1Л3 — г = 2 (cos (— л/6) + ( sin (— л/6)).
Следовательно,
(/3-0100 = 2100 (cos (— 100л/6)-Н sin (— ЮОл/6)),
или
(\ГЪ — (I00 = 2100 (cos Dя/3) + i sin Dл/3)).
Теперь легко записать данное число и в алгебраической форме:
(УЪ-1)т = 2т (cos Dл/3) + 1 sin Dл/3)) =
= 2юо ^_ _^_ _ j Lpj =— 2»*— i2«» УЗ.
Ответ: — 2" — 12м У 3 , 2V° (cos Dл/3) + 1 sin Dя/3)).
б) Данное число уже записано в алгебраической форме. Для того чтобы
записать его в тригонометрической форме, найдем сначала мо/уль данного
числа:
Юл ... Юл
= У A
Юл
1 -f-cos
~~ 5л
cos ——
=:-2с08-д-
Для определения аргумента решим уравнение
sin (Юл/9)
1+соз(Шл/9) *
Преобразуя правую часть, получим
_ sin (Юл/9) _ 2 sin Eл/9) cos Eл/У 5j:
ёф Г+соТПОл/ЭГ ~~ " 2 cos2 Eл/9) ~ g ~9~'
откуда ф = -^-+лА, fteZ. Так как 1-{-cos (Юл/9) >0, a sir (Юл/9) <0,
512
то число расположено в четвертом квадранте комплексно! плоскости ио^ним из
его аргументов является <pt=14n/9.
Ответ: 1+cos (Юл/9) -ft sin A0л/9),
— 2 cos Eл/9) (cosA4ji/9)+i sin A4л/9)).
4. Находнм модуль комплексного числа tg 1 — i:
I tg 1—t [=Ktg21 + 1= I/COS 1.
Аргументы ф числа tg 1 — i удовлетворяют уравнению
tg Ф = — 1/tg 1.
Ргшая это уравнение, получим
Число tgl —t расположено в четвертом квадранте комплексной шк скости,
поэтому
+1+
Теперь можем записать число tgl—i в тригонометрической форме;
'Зл .
Применяя формулу A) § 6, имеем окончательно
(tgl—(L=—^ (cos 4 + i sin 4).
Ответ: г = —тт- (cos 4 + i sin 4).
cos4l '
б. Запишем г в алгебраической форме:
г = х+(у.
Тогда уравнение можно переписать так:
или
х*+2xyi—У- + х
Комплексное число равно нулю тогда и только тогда, когда равны нулю и
действительная и мнимая части его, поэтому
2а:2 = 0, 2jh/= 0.
Полученная система имеет бесчисленное множество решений @; Ь), где Ь —
произвольное действительное число. Отсюда следует, что множество эешений
исходного уравнения —бесконечное множество. Оно состоит из всех комплекс-
комплексных чисел, соответствующих точкам комплексной плоскости, лежадим на
мнимой оси.
Ответ: г = Ы (Ь —произвольное действительное число).
6. а) Условию jz+I |=| г — i \ удовлетворяют те и только те точки ком-
комплексной плоскости, которые одинаково удалены от точек гг =—1 и z2 = i.
Множеством точек, равноудаленных от точек zx и г2, является прямая, пер-
перпендикулярная отрезку, соединяющему эти точки, и проходящая 'ерез его
середину. На рис. 346 изображена прямая /, дающая искомое множесво.
17 п/ред. Г. Н, Яковлева 513
б) Положим z = x-\-iy, тогда заданное условие примет сле;ующий вид:
*2+У2 + 3 (х + ((/) + 3 (х - iу) = О,
Это уравнение окружности с центром в точке (— 3; 0), радиус которой ра-
равен 3 (рис. 347).
--/ о
Рис. 346.
Рис. 347.
в) Данное неравенство равносильно неравенствам
*=0, 1, 2, ...
Искомое множество точек (на рис. 348 оно заштриховано) предст, 1вляет собой
бесконечную систему концентрических колец с центром в точке г = 0. Сама
точка z = 0 не принадлежит множеству.
7. Чтобы получить какой-нибудь вектор, идущий по биссек-рисе, доста-
достаточно сложить два любых вектора одинаковой длины, имеющих направление
векторов 2t и г2 (рис. 349). Так как длина вектора гх в два оаза больше
длины сектора г2, то векторы zj2 и г2 будут иметь одну и ту же длину,
поэтому вектор, равный их еум!\ е:
//А 1
г1 + гя = + 43,
лежит на биссектрисе угла, образованного
векторами гх и г2. Вся гопокушость
Рис. 348.
Рис. 349.
векторов, удовлетворяющих поставленному условию, дается, очевидно,
мулой < G-{-(), где < — произвольное положительное число-
Ответ; 7t-\-it, t — произвольное положительное число,
8. Комплексные числа, удовлетворяющие условию
фор-
14
расположены на окружности радиуса /3 с центром в точке z=—
(рис. 350). Чтобы найти точку окружности с наименьшим положительным
аргументом, проведем касательную [ОТ) к окружности. Точка Kacai кя»Р,
очевидно, будет обладать нужным свойством.
Из прямоугольного треугольника OP E (угол
еЪр =60°, ]ОР; = 3) найдем
|Р?; = |ОР| sin ?ОР = 3^3"/2,
\ОЕ\ = \ОР [ cos ?ОР = 3/2.
Ответ: Наименьший положительный аргу-
аргумент имеет число
— 2
3/3 .
9. Задача сводится к нахождению всех значений у —8 — &['3i. Запишем
число ш = — 8 — 8у 3 ( в тригонометрическом форме:
|ш | = Кб4 + 3-64 =16,
tgcp = V% ф, = 240°,
w = 16 (cos 240° + i sin 240°).
Применяя формулу B) § 6 для отыскания всех значений ^fw , получил
zfc = 2(cosF0° + 90c&) + isin F0э + 90°&)), ft = 0, 1, 2, 3.
Следовательно,
г„ = 2 (cos 60° + isin 60°),
z1 = 2 (cos 150°+ ( sin 150°),
г2 = 2 (cos 240° + i sin 240°),
г3 = 2 (cos 330° + ( sin 330°).
Ответ: 1 + г/з", -VJ + l, -1-(Уз", Vi-L
10. Положим К5+12( =x-\-iy, 'тогда
5+12/ = ^ + 2xy(— if-
и, следовательно, л; и у удовлетворяют системе
х- — у" = 5, ху = 6.
Решая систему, получим дна решения C; 2) и (— 3; —2). Но уело: иго дей-
действительная часть /5+12! отрицательна. Таким образом, l/5 —f- 12г = = — 3—¦
— 2i. Аналогично найдем /5— 12< =—3 + 2(. Теперь легко получаем
+/5— 12t_ -3 —2( —
3
От в ет: —^-i.
11. При делении многочлена степени п на многочлен первой степени
в частном получится многочлен степени п — 1 ив остатке многочлен нулевой
17*
515
степени. Обозначив частное от деления Р„ (г) на г — га через (?я. i(z) и оста-
остаток через и>с, можем записать тождество
Рп (г) =- Qn-i (г) (* - *о) + «"о.
Подставив в это тождество г = г0, получим
Рп (го) = Qn-i (*о) (г.) — 2о) + «"о,
т. е. wa=Pn (г0),
ГЛАВА IX
1. Так как cos 6л: = cos 5л: cos ж — sin 5л; sin х, то sin 5л; sin х — 0, и поэтому
sin5*: = 0, x = nkjb, или sin л; = 0, х = к1, где &, IeZ. Все решения второго
уравнения входят в множество решений первого (k — Ы).
Ответ: {л&/5 ! k e Z}-
2. Используя формулы 2 sin2 2jc= I — cos 4л:, sin2 4.«= 1 — cosMa, приходим
к уравнению cos2 4л:+cos 4л;—г—'®* квадратному относительно cos 4x. Решив
его, найдем, что cos4.<= —3/2, ccs4a:=1/2. Первое из этих урав)ений реше-
решений не имеет, второе имеет решения х— + -^т + -q— . * е; Z-
Ответ: |± -гя- + -тг- k e
3. Преобразуем уравнение:
sin 5л; — sin х = sin 2л;, 2 sin 2л; cos Zx — sin 2л;.
Отсюда sin 2ж = 0, x — nkj2, или <:os3a-=1/2, х = ±---\—=-, гд^ k е=',
U О
Ответ:
4. Так как cos3.t~cos Bx-\-x) =cos 2л; cos л: — sin 2x sin лг, то 3 cos л cos 2л;-f-
-f- sin л: sin 2л:=0, cos x C cos 2д:-(- 2 sin2 *)=0 и, следовательно, cosa; = 0, x=*
= v+rf, *eZ, или 3 cos 2дс + 2 sin2A; = 0, cos2x=—1/2, x= ±-~ -\-nk,
Ответ: jy-fjiu, ±-
5. Преобразуем уравнение:
A + cos л;) — 2 sin x cos x = 0,
v ' sm x '
cosx.. ¦-c_2sin2^ = 0.
.(
sin x
Отсюда cos x = 0, I+cosa;— 2 sin2A; = 0 при условии
sin* =5^0. A)
Все решения x = ---\-nk, JeZ, первого уравнения удовлетворяют A). Второе
уравнение, используя формулу sm2x= 1 — cos2*, приводим к виду 1+cosjk)x
516
XBcosx —1) = 0. Если cosx =—1, то stnx = 0 и условие A) не вытолнедо.
Если же cosx = l/2, т. е. х = ±_ -^ + 2n.k, iSgZ, to условие A) выполнено.
Ответ: •!-=- +я&, ±-я- + 2я& | & е
6. При условии
cos х ф 0 A)
данное уравнение равносильно уравнению
2 — 1) • 2 sin х cos x + cos x — sin x= 1.
Обозначим cosx — sin лг = ^, тогда 2 sin x cos At = 1 — t'1, и, следо! ательно,
= 0, откуда <=1 или / = 1/2. Уравнение cos л — sin л; = 1 введением ьспомога-
тельного угла преобразуем к уравнению coslx-| \=n——t откуда находим,
что x — 3i- j-\-2nk, k e Z. Если взять верхний знак, то х = 2к!., и усло-
условие A) выполнено, следовательно, x = 2nk — решения исходного уравнения.
Если же взять нижний знак, то х=——-\-1nk, a cosx = 0, т. е. э н значе-
значения л: посторонние. Решив аналогично уравнение cos л; — sin x—Vi, найдем,
что х = —^- + 2яй, SeZ. Эти значения удовлетворяют условию A) и, следо-
следовательно, являются решениями исходного уравнения.
Ответ: iink, — ~ + 2nk | k e z\.
7. Преобразуем уравнение:
sin х cos 2* _ cos 4x
cos x sin 2x sin Ax '
sin 2x sin x + cos 2x cos x cos 4x
cos x sin 2a: sin 2x cos 2x '
cos x cos 4x
cos x sin 2x ~~ sin 2a; cos 1x '
Сократив левую часть иа cos л: и умножив обе части получившегося уравнения
на sin 2x cos 2x, придем к уравнению
cos 2x — cos 4x = 0.
Из всех его решений решениями исходного уравнения будут лишь те, для
которых
cosx^O, 6in2x^0, cos 2x^0,
или, что то же,
sin 4а: ^0. A)
Преобразуем полученное уравнение к виду 2 sin x sin 3* = 0. Если sin x = 0, то
и sin 4аг=0, т. е. условие A) не выполнено, и такие значения х рвениями
nk
исходного уравнения не являются. Если sin Зх = 0, то я = —, 6<aZ. Для
любого целого k возможны только три случая: k = 3l, k = 3l-\-l или r==3l — I,
где leZ- Если & = 3/, то x=nl и sin4x==0; если же k = 3i ±. 1, то
517
x= it -, + л/ и sin 4*=sin (± -=- +4я/)--=Т- -у- =jt 0. Значит, решениями ис
ходного уравнения являются лишь значения х=±-Г1--\-л1.
о
Ответ: jjt -|- + я/1 / е
8. Запишем уравнение в виде
|/1 + sin х = — cos х
и возведем обе его части в квадрат:
I + sin х = cos2 At. A)
Решениями исходного уравнения будут все те и только те решения уравне-
уравнения A), для которых
cosxsgO. B)
Преобразуем A): 1 + sin * = (! + sin x) A—sin х), или A + sin x) sin х-. = 0, откуда
sin л- = — 1, х = —'о +2nk, teZ; sinx = 0, л- = я/, /eZ. Все значения х =
д
==—,-, +2я/г удовлетворяют условию B) и, следовательно, являются реше-
решениями исходного уравнения. Если x = nl, то cosn/ = (—1)' и видно, что усло-
условие B) выполнено лишь при нечетных l — 2m-\-\, meZ. Знач] т, из рас-
рассматриваемых зпаченил х решениями исходного уравнения будут лишь х —
«= Л B/7!-'г I), ШЕ?.
Ответ: |— ^+2л/1>, л B*+ 1); й е Z>.
9. Тяк как
cos х — 2 sin 2л: — cos 3.v = (соч х — cos За:) — 2 sin 2a: =
= 2 sin л: sin 2л:— 2 sin 2л: ==2 sin 2л (sin x — 1),
а
1 — 2 sin а' — cos 2х = [ 1 — cos 2,v) — 2 sin x =
— 1 sin2 a:— 2 sin x = 2 sin ;.: (sin At— 1),
то
I sin 2.v(sin a:— 1) i = sin x(sin x— 1).
Отсюда, учитыв я, что sin x—] |=—(sin x—1) (так как sin л: — 1=^0),
получаем, что
— 2 | sin л: ] ; cos х ; (sin х— 1)= sin x (sin х— 1),
и значит, fin л—1=0, х= -+2л?, /г е 2, или
2 j sin x ! - | cos a- j = — sin x.
Решим последнее уравнение. Если sin а: 5э= 0, то | sin x j = sin x, и значит,
2 sin х ! cos х | = — sin x,
sin At = 0, x = nk, k e Z, или 2!cosa'| = —1
— это уравнение решений не имеет. Если sin х < 0, то | sin х !=—sin x,
поэтому
2 sin * j cos * j = sin x,
518
Так как sin х Ф О (sin.v<0), то | cos v [ = 1 /2, откуда cosx = ~, x= + "-+
1 2л
+ 'Ink, или cos Л' — , х = ±~~- + 2яй, 4gZ. Из найденных знатеинй х
2 Л
следует отобрать лишь те, для которых sin*<;0. В первом случая имеем
sin ( +: -¦ ¦ + 2л&] = ± V3/2, значит, нужно взять лишь значения, ссответст-
вующне нижнему знаку, т. е. х = —^-\-2nk. Во втором случае таи же еле-
2л ,
дует взять лишь значения, соответствующие нижнему знаку, т. е. х=—к--г
о
+ 2 л/г.
Ответ: |у
10. Функция arccos (/ является обратной к функции // = cosx, для которой
за область определения принят отрезок [0; я]. Значит, для любого х = @; я]
arCCOS (COSAt)=At
и для любого у е [— 1; 1]
cos (arccos (/) = (/.
Обозначим arccosa = a, тогда cosa = a. Поскольку as [0; я], то и я — a = [0; я].
Учитывая, что cos (л — a) = —cosa = — а, получаем
arccos (— а) = arccos (cos (я — а)) = я — а = я — arccos а,
т. е. arrcos a -f- arccos (—а) = я, что и требовалось доказать.
11. Поскольку
х
xt a
то -.— 4х2 + 13х — х sin—. Отсюда, учитывая, что хфО (при х— ) правая
о X
часть уравнения не определена), получаем уравнение
"*-4x+13=sin -, A)
J А
равносильное исходному. В левой части выделим полный квадрат:
у- 4.«+ 13 = у (>:2- 12* + 36 + 3) = ¦'- (a:-GK+ 1.
xi
Теперь видно, что —4лг+132?1 для всех х. В то же время sin iа/х)^ 1,
О
значит, равенство (]) возможно тогда и только тогда, когда
( l(*_6f+l = l,
( sin (а/д;}= 1.
Отсюда следует, что х = 6, sin(a/6)=l. Последнее имеет место тол >ко, если
•V-= 2 Ня/г, т. е. а =3A +4*) я, где deZ. Таким образом, исходлое урав-
519
ненне имеет решение только для a--=3(l+4k)n, k e 2, и его решшием явля-
является х=6.
Ответ: а = 3A + 4?)я, fteZ; х=6.
12. Из второго уравнения получаем
sin х— sin |у — 2</j = О,
и, следовательно, sin (-?- + (/ — хЬ=0> 0ТКУДа * =-«-— 2i/+ 2лА, ;ieZ, или
cos ^--</+^-) = 0, откуда х = у
Подставляя значения л; = -=—2y-\-2nk в первое уравнение и i/читывая,
/л \
что tgf-^—2jy+2n*j = ctg2t/, получаем
ctg2(/=tg3(/.
Выразив ctg 2(/ через tg у, получим
ttf2 W— 1
Это квадратное относительно tg2 у уравнение решений не имеет.
Подстановка в первое уравнение значений х = --- + 2у + 2лк гает анало-
аналогично
-ctg2(/=tg3!/, 2tg4(/+tg2(/-l=0,
откуда ijg2i/= — 1 или lg2y=lj2. Очевидно, решения имеет только второе
уравнение, и у= ± arctg {\/У~2)-\-я1, 'eZ. Отсюда следует, что х=~±
± 2 arctg-7- + 2n {l-\-k), I, k^Z- Заметим, что каково бы ни било / сумма
К2
l-\-k в силу произвольности ft может быть равна любому целом/ числу т.
Другими словами, каждому из значений у = ±_ arctg —.—+ ni соотве гствуют все
значения х = — + 2 sretg-^ + 2л/п, meZ.
2 К2
Ответ: J—± 2 arctg ——-\-2лт; + arctg——-\-nb \ от, /е2>.
13. Сложив почленно уравнения системы, получим
2 (cos л; cos (/ + sin л; sin у) + cos 2л; -f- cos 2 (/ = О,
откуда 2 cos (At— i/) + 2 cos(a; + (/) cos(x — i/) = 0,
COS(X-(/)(l..f.COS(JC+(/)) = 0.
Это уравнение вместе с любым из уравнений исходной системы, например
с первым, составляет систему
( 2 sin х sin у + cos 2y — ]^2= О,
520.
равносильную, исходной системе. Из второго уравнения системы A) следует,
что
cos(x—1/) = 0, x = ~2Jr У+nki
или
cos (x -f- у) = —1, *=л— y-\-2nk, где te2.
Подстановка *«=-д-+у + лй в первое уравнение системы A) дает
(— l)*2cosi,' sin y + cos2y—]/r2 = Q, cos2(/-f (— ')* sin 2y = Vl.
Вводя вспомогательный угол, получим cos [2y—(—1)*-^-1 = 1, отку ia у =
(— 1)* -к- + я/, I <= Z, и значит,
о
*,
Подстановка л:=л— ?/-}-2эт/г в первое уравнение системы A) дает 2 sin2/y +
+ cos2i/ — l/2=0,
1—cos2(/ + cos2(/ —/2 = 0, 1-/2=0,
что невозможно.
Ответ: 0 +(- 1)* ?+я (ft + J); (- 1)* f + «') | *. le
14. После згмены j: + -t- = s, i/ + ^- = < система будет иметь вид
= sin2/,
Г tgs = sin2/,
\sin2s = tg^. V '
Перемножив почленно уравнения этой системы, получим
Igssin 2s = tg? sin 2t, 2 sin3s = 2 sin2/!,
1 — cos2s = l— cos2*, cos 2/—cos 2s = 0,
sin (s — t) sin (s+ /) = (),
откуда sin(s —1) = 0, s = ^ + jift, *eZ, или sin(s + 0=0, s = —
Подстановка s = / + nA в систему A) приводит к одному уравнению lg? = sin 2t,
которое имеет решения: t — nm, / = -"¦--(—^-, где mEZ. По формуле s ^=
находим соответственно s = n(/n + &), s = -,-+л I ^- + /г J, m. 4eZ,
Множество значений s = л (m + k), k e Z, соответствующее t = nm, m тем же
соображениям, что и в примере 12, можно записать в виде s = nn, n=X.
Подставив s = — t+nl в систему A), аналогично найдем, что 1=ад и,,
значит, s = {l — m) л, /, meZ. При любом т разность 1—т мо кет быть
любым целым числом в силу Произвольности /, поэтому множество зн 1чений s,
соответствуюш,их t=nm, можно записать в виде s = nn, n e Z- В):дно, что
это множество значений su/ содержится в ранее найденном. Теперь находим
т+лп, у=—j-\-nm, m, neZ;
B)
ffl , ,\ ЛОТ
Ответ: Решение системы дается формулами B),
521
15. Данное неравенство легко сводится к квадратному неравештву
2 sin2 х+sin х — 1 52 О
относительно sin x. Решив его, получим
sinj:;?—1 или sin л:52 1/2.
Первое неравенство сводится к уравнению sin * = —1 с решениями х =— -„-|-
+2лй, 4eZ. Множеством решении второго неравенства является эбъединение
, iieZ.
отрезков --- + 2nk sSх ^ —-
О О
Ответ: x = —-%
°™- + 2л*,
о
16. Выразив tg 2л через tg x, преобразуем неравенство
Ai"r --Stgx^O, -J??^(i+3tg»Jc)^0.
1 —
Поскольку l+3tg2J:>0, то
tgx
1 — tg* jk
Это неравенство, очевидно, равносильно исходному. Решив его относительно
tg л, получим — 1 <: tg д: =si0 и l<tg*. Отсюда соответственно находим, что
Ответ: — -^- + яп < * =? лп, -.- + лп < j: < ~ + лп, n
17, Построим графики функций sin х и | соз л: | (рис. 351) 1 обратимся
к ним для наглядной иллюстрации рассуждений. На отрезке [я; 2s] sin-KsgO,
а | cos х | ;г 0, причем Icosa;[ = 0 то^тько при л^Зл/2, и в этом случае sin x =
= — 1. Значит, все числа из отрезка [л; 2л] удовлетворяют данно лу неравен-
неравенству. На отрезке [л/2; л] j cos je i =—cos x, и уравнение sin jr = —:os.v имеет
одно решение *=Зл/4. Поскольку на этом отрезке sin j: mohotoiho убывает,
а | cos лг | монотонно возрастает, то все числа из промежутка [Зя/4; л] удов-
удовлетворяют неравенству sin х < I cos х \. На отрезке [2л; 5л/2] | соз* [=cos;t,
уравнение sin j: = cosj: имеет одно решение 9л/4. Здесь функция sin x возрастает,
a cos х убывает, поэтому все числа из промежутка [2л; 9л/4] уде влетворяют
неравенству sin х < j cos х \. Таким образом, на отрезке [л/2; 5л/2| длины 2л
522
все решения исходного неравенства составляют интервал }Зл/4; 9я/4[. П сколь-
скольку 2л— общий период функций sin х и | cos .t , множество всех решены:! дан-
данного неравенства является объединением интервалов Г-р + 2лп; -^ 2яя ,
Ответ: ~ + 2яп <х < ~ + 2mi, n e Z-
ГЛАВА X
1. Перейдя к основанию 2, после очевидных преобразований i олучим
уравнение
которое является однородным степени 2 относительно 2"" и 2'Разделив на
2 и обозначив t = 2x~"x, получим квадратное уравнение 1г — 3/—4 = 0,
которое имеет корни —1 и 4. Уравнение 2Х~^Х=—1 решений п: имеет.
Уравнение 2*~~ =4 сводится к уравнению х— (/jc = 2, квадратному отно-
относительно V^x. Его корни 2 и —1, но поскольку Ух>^0, то \fх=2 откуда
* = 4.
Ответ: 4.
2. Логарифмируя по основанию 5 (обе части уравнения положи ¦ельны),
получаем уравнение
4
log6(&0 • Iog5.v=log516+ g-
/ 4 \
равносильное исходному. Преобразуем его к виду log? х+ 3 log5 2 1ояг, х —
\ •-> I
— 41og52 = 0, и решив это кр,адратное относительно log5 x уравнение, накдем,
что log5 л; = 4/3, л; = 54/3; log, * = — 3 log5 2, л; =1/8.
Ответ: 54/3, 1/8.
3. Потенцируя, получаем уравнение
1 + cos х = 2 sin'2 x,
преобразуя которое, находим 1 -|-cosa; = 2 (I -|- cos л;) A—cosa;), (l-fcosA;)x
XBcosa;— 1)=0. Следовательно, cos.v=—1, л;==лBп + 1), neZ; <:o : дг= 1/2,
* = :±-_- + 2яп, nsZ. Значения х = лA-|-2п) и х — — '- +2яп не удовлет-
о о
воряют условию sin х > 0. Значения же х = -~ + 2яп, как легко г,\ оверить,
являются решениями исходного уравнения.
Ответ: — + 2лп, где п <= Z-
4. Переходим к основанию 3:
523
учитывая, что log3 (*+ \)- = 2 log3 | *+1 |, получаем уравнение
l-lo
Отсюда
(О
" к-\-\ | Л- + 3'
Поскольку левая часть этого уравнения положительна, то выполнив обратные
преобразования, получим, что уравнение A) равносильно исходному уравне-
уравнению. Решаем A). Имеем 3 (* + 3) —| *+1 j • (* + 5), и если дс+1 >0, то к? +
+ 3л; — 4 = 0, откуда л;=1, дс = —4, причем условию jc+1>0 удовлетворяет
лии/ь х— I; если л;+1<0, то х'--\-9х-\- 14 = 0, откуда дс = —2, х=—7, и
оба эти значения удовлетворяют условию х+1 < 0.
Ответ: 1; — 2; —7.
5. Перейдя к основаншо 10, получим
2_ = _1_
lg @,5 + cos2 x) ~lgsin2*'
откуда
lg sin2 2л-= lg @,5 +cos2 x), sin2 2x=0,5 + cos2 x,
1 —cos2 2к = 1 +0,5 cos :2л;, cos 2л; (cos 2л;+0,5) =0.
а) cos2a; = O, 2х — — -'глп, и в этом случае sin 2.t=(— 1)"-, т е. правая
часть исходного уравнения ие определена.
б) cos 2* = —0,5, 2х ---± ---+2лп, х=±—- + пп. Значения л; • = ^- + ni
не удовлетворяют условию sin2x>0, значения же * = -л-+ля, кас легко про-
верить, являются решениями исходного уравнения.
Ответ: -^-
6. Перейдя к основанию 2, получим
, ' _о
log sin x log cos к '
L_ + ,
log2 sin х log2 cos к log2 sin x ¦ log3 cos к
откуда log2 cos x + loga sin x + 1 = 0, log2 sin 2x = 0, sin 2x = 1, x = — + nn. Про-
Проверкой убеждаемся в том, что решениями исходного уравнения 5удут лишь
значения x = -z--\-2nn (легко видеть, что достаточно проверить зсловия 0<
< sin х < 1, 0 < cos х < 1),
Ответ: —-+2лп, neZ.
7. Обозначим /=»*— 1, тогда х = * + 1 и log, (* + l +а) = 1/2. Обозначим
еще 6=1+а, в результате исходное уравнение примет вид
tag/(/ + &) = 1/2. A)
Потенцируя по основанию <, получим
t + b = Yt. B)
524
Всякое решение A) является, очевидно, и решением B), Обратно если t
решение B) и
0 0, гф\, C)
то, логарифмируя B) по основанию /, получим, что A) — верное равештво.
Решив B) как квадратное относительно у t уравнение, найдем, чтз
1) Vt"
0+/Г46), 2) VT = 1 A -V\=Tb).
Ясно, что B) имеет решения, если только 1— 4ft S; О, т. е. 6=^1/4. При этсм
условии 1 + Kl—46:5=1, поэтому формула 1) определяет решете /j.=
= -й- (l — 2b-\-V I—4б) уравнения B). Первое из условий C) для этсго реше-
решения, очевидно, выполнено. Кроме того, из 1) видно, что равенство V h— (а зна-
значит, и tx = \) возможно только при 6 = 0. Таким образом, если isgl/4 и
6=^0, то 1) задает решение tx уравнения A). Рассмотрим формулу 2). Условие
Vi >0 (а значит, и t>0 из C)) выполнено тогда и только тог;а, когда
1 —V\ —46 >0, откуда 6>0. При этом 1 — ]Л —46 < 1, а VI < 1/2 и
t< 1/4 < 1, т. е. выполнено и второе условие из C). Значит, формула 2) задает
решение h=iy 0 —26 —Kl —46) уравнения A), если 0<й=?1/4. В итоге
получаем, что при 6 < 0 уравнение A) имеет одно решение /1( а при 0 «; 6 =ё 1/4
решениями A) являются и1,и t2% причем ?i = ?2 только при 6 = 1/4 Значит,
A) и вместе с ним и исходное уравнение имеют единственное решен! е только
при 6<с0 или 6=1/4, или что то же, при а<—1 или а = —3/4.
Ответ: а<—1, а = — 3/4.
8. В первом уравнении перейдем к основанию у:
1
log() X
После очевидных преобразований придем к уравнению log^A;—2,f \op,y x 4-
-}-1=0, откуда logyA; = 2, logyA; = 0,5, и значит, х = у2, х=Уу. Ъ первом
случае из второго уравнения системы находим i/;1 = 27, :/ = 3, и то!Да л; = 9.
Во втором случае f/'-e=27, у — 9, а л;=3.
Ответ: C; 9), (9; 3).
9. Обозначим и=^2х+У, у = 3-|:"У, тогда имеем
Из первого уравнения последней системы, учитывая, что « + и>0, «ыражаем
и — а = 27 (u-^-v)'*, подставляем во второе уравнение и преобразуем его:
27 (И2"Н«/"hi/2) = 21 (И + !/J| 2«2~5f'f-j-2i»2 = 0. Решив это уравн .-/ше как
квадратное относительно и, найдем, что u = 2v, u = v/2. Подстановк; в урав-
уравнение и2 —1>2 = 27 соответственно дает: 4и2— и2 = 27, у = 3 (поскольку v > 0),
1 3
и тогда и = 6; —i>a —1J = 27, ——у2 = 27, это уравнение решений tie имеет.
525
Таким образом, 2-*+^ = 6, 3* 4 = 3, откуда х -)-</ = Iog2 G, х — у = -Л, а л:
= 2 log:, 12 = log4 12, .v = ~log23 = log43.
Ответ: (log4 12; Iog43).
10. Логарифмируя по основанию 10, получаем систему
I ig5-u:*=ig3-igi/,
lg 5
равносильную исходной. Из первого уравнения выражаем lg У — -п,~о'1&х' под"
ставляем во второе уравнение и преобразуем его: lg 3 • (lg 3 + lg х) =
= Ig 5 • (lg5+j||lgA(lg23-!g2 5)(lg3 + lg*) = 0, откуда !g3 + !g л: ==0, по-
поскольку lg- 3 — lg2 5 Ф 0. Значит, х== 1/3, и тогдл lg ?/ = — lg 5, (/=1/5.
Ответ: A/3; 1/5).
11. Как уже отмечалось, если основание и показатель степей i содержат
переменную, то здесь всюду рассматриваются лнль такие значения геременной,
при которых основание положительна. В данном случае следует рассматривать
лишь значения л:> 0, у > 0. С учетом этого, логарифмируя по основанию 10,
получаем систему
(ylgx = xlgy,
\ x\gx=--9y\gy,
равносильную исходной. Из первого уравнения системы выражаем к y=--\gx
и подставляем во второе уравнение: j:lg* = 9i/- —- lgjc, (л;2 — 9у- lg x = 0.
Отсюда:
1) lg.v = 0, jc=1, и тогда lgy — 0, y=\;
2) л;2 —9(/2 = 0, x = 3i/ (так как *>0и(/>0) и значит, lg у = -^ lg 3(/,
4^=3.!/. ?г = 3, y = Yi, и тогда * = 3^3.
Ответ: A; 1), C^3; |лЗ).
12. Преобразуем систему:
x 2 ' ( хг — ?ixy-\-2yi=--Q, .
xy~\-\ _ x \.y2 — xii+ 2y — 2л: = 0. ^'
. 2y2 + y — x + 2~ ~2y'
Каждое решение исходной системы будет и решением системы (Г, обратное
же может быть и неверно. Все решения системы A) нужно будет проверить
подстаног.кой в исходную систему. Второе уравнение системы A) запишем
в виде {у — х) (х— 2) = 0. Если х = 2, то из первого уравнения i истемы A)
получлем, что у8 — Зу + 2 = 0, откуда у = 1, у=\. Значит, B; 2), B; ^ — реше-
решения системы A). Если у — х, то первое уравнение системы A) является верным
526
равенством: Jfi — Злг24-2*г = 0. Значит любая пара чисел вида (с; <) также
является решением системы A). Найденное ранее решение B; 2) сдержится
в этом множестве.
Проверим, какие из решени!! B: 1), (с; с), где ceR, системы 1) явля-
являются решениями исходной системы. Легко убедиться подстановкой, чтс B; 1) —
решение этой системы. Из первого уравнения исходной системы следует, что
х>0, поэтому нужно рассмотреть лишь пары {с; с), где с>0. Поел ¦ подста-
подстановки получим
По§2 Bса) - loga с = loga Dс) - 1,
{
и легко видеть, что для о0 эти равенства верны. Значит, все гпры вида
(г, с), где с>0, также являются решениями исходной системы.
Ответ: B; 1), (с; с), где с> 0.
13. Умножив почленно первое уравнение системы па 2~Х+У ¦ ЗаУ, получим
32у_2.3А'^ — 2-*-« = 0, откуда 2~^» = ЗаУ — 2 • Зл+«. Подстановка но второе
уравнение системы дает З2^ — 4 • 3Vvu-+-3 • З3* = 0, или после умножения на
3-2V; з2'!/~*)_4 .3^^ + 3 = 0. Решив это квадратное относительно 3«~ ¦' уравне-
уравнение, найдем, что ЗУ~"* = 3, 3#~*=1. Отсюда (/ — х~], y—x = Q. Если / —.*• —1,
то из первого уравнения исходной системы получим 6~2У = \/6, (/=1/!!, и тогда
*=y_l=— 1/2. Если же у — * = 0, то аналогично имеем 6« = — i, в это'л
случае решений нет.
Ответ: (—1/2; 1/2).
7 2
14. Обозначим / = 3*, тогда неравенство будет иметь вид ^—- gs .
Преобразуя его, получим -—^— ' ". =s^0. Разложив на множнтсти числи-
числитель как квадратны;! трехчлен и f- — 2 как разность квадратов, будем иметь
^=^0, откуда, учитывая, что t>0, а значит, ,' + {< 2>
7
V2){i-\/2)(t-\)
приходим к неравенству -j ^т —<°- Решив ею, напри-
(t]/2)(t\)
мер, методом интервалов, найдем, что l/2^i<l, I^2<^=g3. Otci )да 1/2<
Л<1, l/2<3Jcsg3, и соответственно, — Iog32s?jr<0, ¦j\og3'.\<x^\.
Ответ: [ — log8 2; Of U ] -^ log3 2; ll.
15. Переходим к основанию 3: log3 (x -f-2) ;> -j —r-?jri и обоз1ачив t ¦=
log (л' + ^)
= log3 (x-\-2), преобразуем неравенство к виду > 0. эешпв это
неравенство, найдем, что —2<;<0, 2<it. Отсюда получаем
9<л; + 2, 7<х,
Ответ: ]— 17/9; — l[Uj7; +oo[.
527
16. Перейдем к основанию 2 и обозначим log^x^t, в результа е получим
8(^ + 2/) _ г
3(<+i)(/ + 3) ¦"- •
Преобразуем это неравенство:
(/ + >')(<+5).л
3) "
Методом интервалов найдем, что t <. — 5, —3<?<—9/7, —1<;/. Отсюда
соответственно Iog.2 х < — 5, 0 < х < 2 5; —3 < log, х < — 9/7, 2 ^ < с < 2~9/7;
— 1 < \ogi х, 0,5 < х.
Ответ: ]0; 2 &[ U]2 3; 2-9/7[U]0,5; + оэ[.
17. Если х>\, то б* — 1 > 2*, *>1/4. Значит, все значения ) >1 явля-
являются решениями исходного неравенства. Если 0<л;<1, то 0<6с — \ <2х.
Левое неравенство 0<6х— 1 имеет решения дт>1/6, а правое нер ibchctbo —
решения *<1/4. Значит, при 0 < ,t< 1 исходное неравенство им&:т решения
1/6 < ж < 1/4.
Ответ: ]I/G; 1/4[U]1; +oo[.
18. Поскольку х > 0, то loga x"- = 2 log^ x. Переходим к основанию а и
преобразуем неравенство к виду
Пусть д>1, тогда х + я>а>1, loga (х + а) > 1 >0, 1—2 logeuc +
поэтому неравенство (I) сводится к неравенству loga*;:>0, откуда j 2s 1. Зна-
Значит, при а>1 множество решений исходного неравенства есть промежуток
[1; +оо[.
Пусть 0<а<1. Если х>\, то logax<0, loga {x+a) < 0, а 1 —
— 2 logj (х-\-а) >0, значит, неравенство A) неверно, Число х = 1 йвляется
решением A). Если 0 < л; < 1, то loga х > 0 и (I) сводится к неравенству
Решив это неравенство относительно loga(* + a), найдем, что log t {x-\-a) 5е
Э=1/2, log,, {х-\-а) < 0. Отсюда соответственио x + a-s^Va, x-^Vi — a; x +
-f- a > 1, х > ! — а.
Таким образом, при 0<а<1 неравенство A) имеет решения 0<a:s?
=SJ К а — а, I — а<л^1.
Ответ: Если а> 1, то х> 1; если 0<а<1,то0<*:ё: )/а —я, 1 — а <
<*=я:;1.
19. Полагая j: > I, преобразуем неравенство:
с , Ъ(х— 1) , 2 (л: —2) М1
2 + log, * < -^^-, log3 jc < -2~Г~* ( }
В случае 0 •< х < 1 имеем:
^! i^I. B)
Изобразим для наглядности графики функции log-, х и 2 (х — 2)/B*— 1) [рис. 352).
Пусть х>\ (неравенство A)). Если 1 <х^2, то loga*>0, а 2 (л: — 2)/Eк— l)^0t
528
значит, здесь решений нет. Если
3
, то log3A;>= I, а
2 (л: —2) _1х — \ —3
2х— 1 2х~-'А~
= 1 —
2л;—1
<1, поэтому и здесь решений нет. Пусть 2<л;<3, Здесь
, а функция 2 (л; — 2)/Bл; — 1) моно-
монотонно возрастает 1таккакЗ/2л; — 1 монотонно убы-
вает, а значит, 1 ——
— возоас
тает ], и
поэтому
-~~ I У
2 (г — 2)/B* —1)<2. C — 2)/B ¦ 3 — 1) = 2/5. Срав-
ним числа log3 2 и 2/5. Имеем -^- = Iog332/5 =
¦= log3 9|/3 < logj 321/5 = log,, 2. Отсюда следует,
что при 2<л;<3
. log3 х > log, 2 > 2/5 > 2 (х- — 2)/Bл; — 1).
Таким образом, и при 2<C.v<3, а значит, и при
всех х > 1 неравенство A) решений не имеет.
Пусть 0<л;<1 (неравенство B)). Если
0<х< 1/2, то log3A;<0, а 2 (л; — 2)/B*— 1) > 0, рИС( 352,
т. е. log3 Jr <2 (л; — 2)/Bж— 1), и все эти значе-
значения х не являются решениями неравенства B).
При1/2<л;<1 функция 2 (х— 2)/Bл;— 1) = 1 — 3/B* — 1) монотонно возра-
стает, и значит,
1)
<2A—2)/B-1 —1)=—2. В то же врем! здесь
logajc> log3A/2) =—Iog32>-1. Поэтому log3*> 2(*-2)/Bж-1), т. е.
все значения 1/2<лг<1 являются решениями неравенства B).
Ответ: ]1/2; 1[.
ГЛАВА XI
1. Из пятиэлементного множества всех сотрудников выделяем трехэлемент-
трехэлементные подмножества, состоящие из тех сотрудников, которые получают [ утевки.
В случае а) следует рассматривать упорядоченные подмножества (первый сотруд-
сотрудник получает первую путевку, второй — вторую, третий—третью), и поэтому
их число равно Л? = 5-4-3 = 60. В случае б) порядок, в котором выделяются
сотрудники, не важен, так как все путевки одинаковы, и, следовательн э, число
5 • 4
способов равно С\=С%=—у— = 10.
2. Рассмотрим сначала случай а). Пусть белые шары уложены в р;д, тогда
черные шары можно положить по одному на шесть мест: 4 места -между
пятью белыми шарами, 2 места — спереди и сзади от белых шаров. Но па шесть
мест четыре шара можно положить С\ способами, так как именно столько суще-
существует четырехэлементных подмножеств у шестиэлементного множества Следо-
Следовательно, в случае а) число способов равно Q==C§
15. В счучае б)
из каждого расположения шаров, рассмотренного в случае а), можно поду-.
чить 61-41 способов, так как белые шары можно переставить 5! егкхобамн и
529.
черные —41 способами. Поэтому в случае б) число способов paei о С\ 5! 4! =
= 43 200.
3. Соединяя каждую пару вершин многоугольника, получав!: либо диаго-
диагональ, либо сторону многоугольника. Число различных пар вершш п-угольника
равно Сп (столько существует двухэлементных подмножеств у i-злементного
множества). Так как у п-угольника п сторон, то число диагонале'1 равно
4. Треугольники могут быть двух видов. У треугольников первого вида
одна вершина на первой прямой, две вершины — на втором прямой. Вершину
на первой прямой можно выбрать 10 способами, две вершины на второй пря-
прямой можно выбрать C'ju способами. Всего, следовательно, существует 10 ¦ С~о
треугольников первого ьида. У треугольников второго вида о.шя вершина
находится на второй прямой, а две другие вершины — на первой. Число
таких треугольников подсчитывается аналогично. Оно равно 20 ¦ С'"и. Таким
образом, искомое число всех треугольников
^ 1О0A9 + 9) 2 8О0
5. Первое решение. У множества, состоящего из 17 эле(»ентов, суще-
существует С\7 пятиэлемептпых подмножеств. Поэтому первому автору можно дать
главы С\7 способами. Аналогично из оставшихся 12 глав втором автор может
получить 4 главы С}., способами. Трети)! автор получает 5 глав С\ способами,
а четвертому достаются оставшиеся 3 главы. Число способов распределения
глав равно, следовательно,
С5,С'аС; = 171531360.
Второе решение. Занумеруем для удобства главы арабски.ш цифрами,
а авторов — римскими. Представим в виде следующей таблицы одш. из способов
распределения глав;
1
2, 4, 8, 11, 14
И
1, 5, 7, 13
Ш
9, 10, 15, 16, 17
IV
3, 6, 12
Любая перестановка чисел второй строки будет приводить к новому рас-
распределению, если только она не сводится к перестановке чисел впутай столбцов.
Так как всего существует 171 способов перестановки чисел вто )o"i строки,
я любые перестановки чисел внутри столбцов (их соответственно 5 , 41, 51, 3!)
не дают новых способов, то искомое число способов распределения глаз
^r =1715'Л360.
3!
E!j- ¦ 4! ¦ 3!
6. Подсчитаем максимальное число крокодилоз с неодинаковом набором
зубов. Очевидно, что их число равно числу всех подмножеств у 68-элементного
множества, т. е. равно 263. Так как 1617 = 208, то 1617 крокодилов логут имел,
различные наборы зубов. Ясно, что если крокодилов более ]6V^ осойгй, то среди
530
ник обязательно найдутся по крайней мере два с одним и тем же н; бором
зубов,
7. Рассмотрим 10-элементное множество мест, на которые записываются
цифры числа. Возьмем любое его подмножество. На места, входящие в это под-
подмножество, поставим цифру 1; остальные места заполним цифрой 2. Число
записано. Выделив другое подмножество и проделав то же самое, получим дру-
другое число. Ясно, что чисел можно записать столько, сколько существует под-
подмножеств у 10-элементного множества, т. е. 2!0 = 1024.
8. Рассмотрим множество мест, на которые ставятся «точки» и «тире» при
записи буквы, содержащей k символов. Это множество состоит из k элементов.
Рассмотрим любое его подмножество, заполним его «точками», на остальные
места поставим «тире». Буква записана. Разных букв, в записи которых i споль-
зуется k символов, будет очевидно столько, сколько существует подмн зжеств
у fe-элементного множества, а ик, как известно, 2*. Так как по условию задачи
для записи буквы не должно использоваться более четырех символов, то всего
можно записать
4
2 2* = 2 + 2г + 2з + ^ = 30 букв.
9. На первом месте у автомобильного номера может быть любая из 3) букв.
Следовательно, первая буква может быть выбрана 30 способами. На втором
месте также может находиться любая из 30 букв, поэтому первые два буквы
номера могут быть р.ыбраны 302 способами. Ясно, что три буквы молно вы-
выбрать 303 способами. Аналогично рассуждая, получаем, что четыре цифры
можно выбрать 104 способами. Таким образом, всего может быть занумеровано
30-1 • 104^27 • Ю7 автомобилей.
10. Эту задачу можно решить, используя формулы для числа соче-анш"; и
числа перестановок. Однако результат можно получить быстрее и прои.е, если
рассуждать следующим образом. Обозначим число разбиений на пары в случае
In элементов через R2n. Выберем какой-нибудь элемент. С участием этого эле-
элемента пару можно образовать In— 1 способом. Каждый раз после образования
одной пары будет оставаться 2п—2 элементов, которые можно разбить на
пары Р2Я_2 способами, Поэтому Дгя = Bп — 1) #гя_г. Используя эту pei уррент-
ную формулу, получаем
= Bп— 1)Bл — 3) ... 3./?2 = Bл— 1)Bя — 3) ... 3-1.
Таким образом, число разбиений равно произведению веек нечетных нлтураль-
ных чисел, не превосходящих In—1.
11. Средним членом разложения является пятый. Формула для общего
члена разложения в данном случае дает
12. Составляем систему неравенств:
Используя формулу для общего члена разложения, получаем
С% BхL35 > Q Bл:M З4,
С\ BхK 3".
531
После сокращения имеем
3 ( 3 — 2л: > О,
\ х(х—\)>0.
Решив эту систему, получим
хе]— со;0[ U ]1;3/2[,
13, Запишем общий член разложения:
/3*/3 А = 0.
Числа Ть будут целыми, если степени (9—k)/2 и А/3 —целые числа. Из того
что ?/3 целое, следует, что k может принимать значения 0, 3, 6, 9. При этих
значениях k степень (9 — k)/2 будет целым числом только при ? = 2 и при k=9.
Следовательно, только третий и девятый члены разложения являотся целыми
числами, причем
14. Положив в формуле Ньютона п=10, а=\, Ь = Ъх-\-2х3, i олучим
ш
A+Зл: +2*3I0= 2 С*„ (Зх+2*3)*.
* = о
Легко видеть, что только при k = 2 и при k = \ получаются слагаемые, содер-
содержащие х*. Заменяя многоточием те слагаемые, которые заведомо одержат х не
в четвертой степени, будем иметь
Таким образом, искомый коэффициент равен 12С]О + 3*С'0 = 17 550,
15. Сумма коэффициентов любо~о многочлена
Рп М = апх" + an^xn-i + ... + ахх + а0
равна значению многочлена при х-=\. В самом деле,
Заданный многочлен при х=\ обращается в единицу, поэтому су«ма всех его
коэффициентов равна единице,
J6. Напишем разложения по формуле Ньютона дая (\-\-хJа и A-хJ"-'
Положив в этих тождествах х=1, будем иметь
Сложив почленно зти равенства, получим
17. Всего существует Q, способов взять 5 билетов из 10, Следовательно,
число всех исходов в каждом из случаев а) и б) одинаково и равно С%.
В случае а) благоприятный исход состоит в том, что из двух выигрышных
билетов берется один (это можно сделать двумя способами), а из восьми не-
невыигрышных выбираются четыре (это можно сделать С| способами). Число
532
благоприятных исходов равно 2 . С\, а вероятность в случае а) равно отноше-
отношению 2С'/Суо = 5/9,
В случае б) благоприятный исход заключается в том, что среди взятых
пяти билетов 2 выигрышных (их можно взять одним способом) и 3 невьигрыш-
ных (их можно взять С- способами). Число благоприятных способов, следова-
следовательно, равно С\, а вероятность в случае б) равна отношению СЦС\ ,=»2/9.
18. Каждый человек может выйти из лифта семью способами (на саждом
этаже, Е<ачиная со второго). Поэтому всего возможно 75. исходов. Благоприят-
Благоприятный исход состоит з том, что все пятеро выходят на разных этажах, Поэтому
первый может выйти семью способами, второй — только шестью, третий — только
пятью, четвертый — четырьмя и пятый—тремя способами. Число благоприятных
исходов равко Л} = 7 • б • 5-4 • 3, а искомая вероятность равна
A) 7-G-5-4.3 _ 360
7 "TU> ¦
ГЛАВА XII
1. а) Одной из первообразных для функции *6 является функция -q-**-
Следовательно, в силу теоремы § 1 гл. XII любая первообразная вдеет вид
F (х) = — х*-{-С, где С —произвольная постоянная.
б) Одной из первообразных для функции -^ sin (Зх+1) является пункция
^cos C* + 1). и. следовательно, любая первообразная имеет вид F (х) =¦
в) В § 1 гл. XII было доказано, что одной из первообразных дл i функ-
функции 1/х является функция 1п|*|. Легко видеть, что функция -=- In 5a;-j-G|
и
является одной из первообразных для функции l/Ej:-f-6). СледовательШ', любая
первообразная для заданной функции имеет вид
г) Дифференцированием проверяется, что функция -^ tg Bx-j-1) шляется
первообразной для функции З/cos2 Bх-\-1). Аналогично проверяется, ч:о перво-
первообразной для функции cos 6x является функция -?- sin 6*. Следовательнс, любая
первообразная для заданлюй функции имеет вид
/fW tgB+l) +
2, Пусть F (х) — первообразная данной функции. Тогда F' (х) = х д ы х>0
0 и
533
и F'(x) = — х для х<0, Следовательно, F (х) = -0- к? + Сх для с>0 и
F (л) = — 0-л2 + С, для *<0, где Сг и Сг — произвольные постояннее. По усло-
условию функция/7 {х) имеет производную в каждой точке, и поэтому он; непрерывка
на всей действительной осн. Из непрерывности функции F (x) i точке х=0
следует, что С1 = С2- Таким образом, из предположения, что у фу! кции / (х) =
«=|jf|, JteR, есть первообразная F (х), следует, что F (х) имеет в щ:
+C
где О—произвольная постоянная. Легко проверяется, что каждая такая функ-
функция действительно является первообразной для заданной функции \х\.
8. Искомая первообразная для функции f(x)~x2 имеет вид
где О —некоторая постоянная. Для определения С воспользуемс: i условием,
что график искомой первообразной проходит через точку B; 3), т. е, FB) = 3.
Отсюда получаем С=1/3, Следовательно, F (х) — (х3-\-1)/3,
4. Искомая первообразная имеет вид
93JC
2з
где С — некоторая постоянная. Из условия F(l) = 3 получаем С= 3—^-г—^«
и, следовательно, искомая первообразная есть
б. а) Неопределенный интеграл от суммы функций равен сумме неопреде-
неопределенных интегралов от этих функций, поэтому
j (P + Зе'О dt = j P dt + 3 J e? dt,
где, кроме того, постоянный множитель 3 вынесен за знак интеграла. Перво-
Первообразной для t3 является функция t'/4, а первообразной для е6' явлгется функ-
функция е6//5. Следовательно,
~ /* +
где С — произвольная постоянная,
б) Аналогично предыдущему
в) Используя соотношение
sin 1x cos 4л; == (sin 6x— sin 2л:)/2,
534
получаем
SIC 1С 1
sin 2x cos 4x dx — — \ sin6xdx—5- V sin л;йл;==—^
r) f f
1
—- cos2j +C.
6. а) Положим и — x и и' = cos х. Тогда и' = 1 и о = sin t, и по ([ ормуле
интегрирования по частям получаем:
( хcos хdx = х sin х—\ sin x dx=-x sin Jf + cosx
б) Положим u = lnx и v'=x. Тогда и' = \/х, v = x2/2 и
л; In х dx = -=- х2 In
л —i С
7. Предположим, что функция f(x) имеет первообразную F (х) на Р. Тогда
Р(д:) = 1 для д:>0 и F'(х) =—1 для х<0. Следовательно, F (х) = = х-\-Су
для л;>0 и F(jc) = — Jc + C2 для л;<0. Из непрерывности функции f (x) при
х = 0 следует, что F @) = С1 = С2. Поэтому функция F (х) имеет вид F (х) ---
— I Х\~\-С, где С — некоторая постоянная. Эта функция при х = 0 не им'«т про-
производной и в силу этого ни для одной функции не является первооэразной
на R, что противоречит предположению. Следовательно, наше предположение
неверное, и поэтому функция /(Jc) = si^n;c на U не имеет первообразно!!.
8. а) Так как функция хл/4 есть первообразная для Xх, то по (формуле
Ньютона—Лейбница получаем
1
б) Функция —cos ж является первообразной для sin х, и поэтому
Я/3
sin х dx = — cos л;
D) Имеем
я/3
-я/4
У2~\
9 58
г) Первообразной для функции 1/К2х+3 является функция /2х+3.
Поэтому
з
VlX+Ъ
Д) Перейдем к новой переменной интегрирования, положив Ъх'-\-4 = у.
Тогда (Зх3 + 4)|/3=(/|/3, (/'=9л^ и, следовательно, Cx3 + 4)l/3x2dx = (//3 ~ Ж/.
535
Найдем новые пределы интегрирования:
По формуле замены переменной получаем
2 28
/5=3- l3-f 4=7, fi = 3--2'
е) Положим и = х и и' = sin x,
интегрирования по частям имеем
я/2
тогда и' = 1 и v = — cos x.
12 ' •
1о формуле
\ xsinxdx=—xcosx
о о
ж) Положим и = \пх и г/=1/.<:2
интегрирования по частям имеем
я/2 я/2
-j- \ cosxdx=
л/2
sinA:
= 1.
тогда и
= 1/х,
О
г =— 1
1о формуле
1пх
' = In л;
1 ¦
з) Функция \х\ равна х при х>0 и равна —л; при х<0. Поз тому подын-
подынтегральная функция f (х) равна л; (л;— 2) = л;2 — 2х при л;>0 и раыа — х?-\-2х
при л;<0. Разбивая
2 0
( j(x)dx= j (
— 2 — 2
интеграл на дна интеграла, получаем
2
x-\-^ (rf — 2x)dx =
0
"Л
9. а) Пусть функция F (() — первообразная для функции/ @ = t2 s n I. По фор-
формуле Ньютона — Лейбница имеем <$(x) — F(x) — F @). Из определсиш первооб-
первообразной следует, что F'(x)=x2 sin.t. Поэтому Ф' (х) =
= {г (х) — F @))' = F' (х) = х2 sin х.
б)'Пусть функция F (/)—первообразная для функ-
функции /@ = 2' cos (sin /). Тогда Ф (x) = F C,v2)--/' Bл). Те-
перь применяя правило дифференцирован! я слояшой
функции, получаем
ф' (х),= (f (Зл:!|) — F Bл:))' = 23х~cos (sin (Зл:2)) -ix —
— 22х eos (sin Bz)) ¦ 2.
10. Обозначим длину стороны квадрата через а и
гыберем систему координат так, как показано на рис. 353,
В этой системе координат уравнение параболы имеет вид {/ = to2, причем k
определяется из условия, что парабола проходит через точку (а/2; и). Таким
образом,. k = 41a. Парабола разбивает квадрат на две части: AB0CD и ВОС,
Вычислим площадь криволинейной трапеции AB0CD:
а/2
I
-а. о\ а.'
Рис. 353.
4 л1
-а/2
-а/2
а*
У
Отсюда следует, что SB0C=a2—- =
О
площадь квадрата в отмщении 1 : 2.
536
--а2
Следовательно, пара5ола делит
11. Построив графики функций у = \хг — 1 j и д = \х\-\-5, видим, ч'о тре-
требуется найти площадь фигуры ABCDEF (рис. 354), Из системы уравнений
находим координаты точек D и F, в которых пересекаются заданные линии.
Именно DC; 8) и F (—3; 8). Из рисунка видно, что \х% — 1|<|*Ц-5 Лля
3 со
Рис. 354.
любого х е ]—3", 3| и данная фигура симметрична относительно оси Сх. Сле<
довательно, S=2SBCO? н по формуле B) § 3 гл, XII
Легко видеть, что
з
Далее,
„ „ o /39 22\ 73
Следовательно, 5 = 2--^ 5-==">
12. Линия 2{/ = х2 + л; — 6 является параболой с вершиной в точке
А(—1/2;—25/8) (рис. 355), а линия 2у——xa+3x+6—параболой с вершиной в точ-
точке С C/2; 33/8). Требуется найти площадь S фигуры ABCD, где В и D— точки
пересечения парабол. Решая систему
2у=х*+х-6,
( 2у=х*
\2г/=_
находим, что координатами точки D являются числа х=—2, у — —2, а коор-
координатами точки В — числа х = 3, у = 3, Используя формулу C) § 3 л, XII.
537
получаем
—2
125
13. Так как
а
— а
то нужно доказать, что
— а и
Для этого сделаем замену х=—/ и затем поменяем местами пред лы интегри-
интегрирования:
и о а
— а а О
Функция / — четная, поэтому / (—/) = /(/) и
Следовательно,
14. Прежде
0
0
— о
всего заметим,
а+т
а
ЧТО
ix =
а
f f i
0
Г
а
и
а
= ^ / (*
'+ \
Т
f(x)dx.
A)
Во втором интеграле сделаем замену переменной интегрирован ш х—1-{-Т
Тогда
а+Т а
\ f(x)rtx=\f(t + T)dt,
т о
а так как f(l-\-T) = f(t), то
а+Т а
\ f(x)dx = \f(t)dt. B)
В последнем интеграле переменную интегрирования снова обозна шм через х.
Теперь из A) и B) получаем
а+Т Т а Т
j /(х) dx=\ f (х)dx+\f (x) dx=\ f(x) dx.
a a 0 0
15. Пусть А и В — точки пермечения гиперболы *(у + 2) = 4 с прямыми
у —0 и х — 1, а С —точка пересечения этих прямых, тогда А B; 0), ВA; 2),
538
C(l; 0) (рис. 35G). Требуется вычислить объем V тела, образованного spame-
нием фигуры ABC вокруг оси Оу. Искомый объем равен разности V i—V2
объемов тела, образованного вращением криволинейной трапеции OABD зокруг
оси Оу, и цилиндра с радиусом основания 1 и высотой 2. Объем V1 вычис-
вычисляется по формуле для объема тела вращения:
Объем V2 цилиндра равен 2я. Следовательно,
Рис. 356.
= 4л.
о
^— У2=2л,
Рис. 357.
16. Объем V заданного тела (рис. 357) равен разности Vl — V2 >бъемов
тела, образованного вращением криволинейно"! трапеции, ограниченно;! графи-
графиком функции r/=sinx, х ¦= [0; я/2] и отрезками прямых г/ = 0 н х= л/2, и
конуса с радиусом основания 1 и высотой л/2. Объем Vt вычисляет: я с по-
помощью интеграла
л/2 я/2
1—cos 2л: л л / 1 . „ \ \п/2
sin2 л: dx = n 1
о о
л2
Объем V2 косинуса равен л2/6. Следовательно, искомый объем равс1 -j
__ л3 _ л2
~6 12""
17. Разобьем отрезок [0; /] оси Ох на п равных по длине частей (pic. 358).
Согласно закону Ньютона участок стержня
[Xi_x; X;] массы б Ах,- притягивает материальную .—• >
точку Р с силой, приближенно равнол
р
— к
тб
Рис. 358.
где к — коэффициент пропорциональности (гравитационная постоянная!. Тогда
сила F, с которой однородный стержень притягивает материальную точку Рt
приближенно равна сумме
kmb A*;
639
Переходя к пределу при я -»¦ со, получаем
Следовательно,
р
km
ff.
а—х |о а а — / а(а—/)
18. Выберем систему координат, как показано на рис. 359. Разобьем отре-
отрезок fO; R] оси Ох на п равных по длине частей. Кинетическая энергия Е;
кругового кольца, заключе-шого между
окружностями радиусов г; = д:,_1 и г =
= х;, приближенно равна rr^v'j/2, где
V
mi — масса этого кольца, а у; = аг;<ц.
Так как
т; = pta (x'l — х}_,) = р/т (х 4-xi+l) Дат,.,
1Ш
хь/2
Рис. 359.
то приближенно т; равна 2phnxi Axi и кинетическая энергия ?,• приближенно
равна phn(?t4} Ахг Тогда кинетическая энергия Е всего тела триближенно
равна сумме
Переходя к пределу при n-voo, получаем
R
ГЛАВА ХШ
1. Пусть диагонали трапеции ABCD пересекаются в точке i) (рис. 360).
Треугольники ABD и ACD имеют общее основание AD и рав.гые высоты,
проведенные к этому основанию, поэтому их площади равны. П ющади тре-
треугольников АВО и С DO меньше
площадей треугольнш оз ABD и
ACD на величину пл( щади треу-
треугольника ADO и, следовательно,
равны.
2. Пусть РМ\\АС и MQ\\AB
(рис. 361). Обозначил Ь = \ВС\,
х = j ВМ ,: | МС \, тома | ВМ \ =
)
Рис. 360.
+ ц
Легко видеть, что треугольники РВМ и Q/ИС подобны треугольнику ABC.
Поэтому, если S—площадь треугольника ABC, то
с -( * \*
SPBM ~ [Г-f-j
s
[
540
5 - I x
По условию S — SpBM — SOMC = TzS, откуда получаем 1 — (у—
5
= yg ИЛИ
5*2— 26*+5 = 0.
Решая уравнение, находим * = 5 и *==1/5, В обоих случаях точка Л! Делит
сторону ВС на отрезки, длины которых
относятся как 5:1.
3. Пусть So, Si, S2, S3 соответственно
площади треугольников ABC, PEC, AMF
и DBN (рис. 362). Нетрудно видеть, что
AMC
+ SABN + S
PBC
и так как
SFDE=S, то отсюда получаем
М>
A)
К Р
Рис, 362.
Найдем S[. Проведем Л4К [|BP, тогда Д ЛМК со А ЛВР. Из подобия следует:
\АК\=-^\АР), и так как | АР \ = ~ \ АС \, то | АК \ =~~ | АС |, Тогда
с
°АМК —
2 „
27 О
7
~27 О
Треугольники РЕС и КМС также подобны, поэтому Sx = (| PC |/| КС \'_2 S
Отсюда, учитывая, что
| PC | = -=- j АС \ и
7 1
= -д-! АС ], получаем Sj = --- So.
| КС \
Аналогично устанавливается, что S2 = S3 = „^ So,
и поэтому из A) следует S = -_- So, т. е. S0 = 7S.
4. При повороте на угол а каждая прямая повора-
поворачивается на этот угол, следовательно, АВ'А' =а (рис. 363),
Тогда из условия А'В J_ АС следует Л =-^ — а. Да-
Далее, так как |СВ' \ = \СВ\, то треугольник СВВ' равно-
равнобедренный и ВВ'С = В. С другой стороны, углы ABC и А'В'С конгруэнтны,
т. е. А'В'С = В. Углы АВ'А', А'В'С и СВ'В образуют развернутый, поэтому а +
Н-2В=я, откуда находим B = i — ~. Угол С находим из услогия, что
* 3
сумма углов треугольника равна я, получаем С = -^-<х,
5. Через вершины Л, В и С треугольника проведем прямые, паралелль-
ные противоположным сторонам (рис. 364), эти прямые в пересечении ограни-
541
чивают треугольник Л'В'С. В четырехугольниках АС ВС и ABA'В противо-
противоположные стороны попарно параллельны, следовательно, это пара ыелограммы
и С В : =| АС \, \ В А' \ — \ АС |. Таким образом, точка В является серединой
стороны А'С. Аналогично устанавл гвается, что
точки А я С являются серединами стзрон С В' и
А'В'.
Если ВК — высота треугольника /ВС, то пря-
прямая ВК есть серединный перпендикуляр к сто-
стороне А'С треугольника А'В'С. Аналогично, если
AM 1 ВС и CN 1 АВ, то прямые ЛЛ! и CN яв-
являются срединными перпендикулярам! соответст-
соответственно к сторонам С'В' и А'В'. Срединные перпен-
перпендикуляры к сторонам треугольника пе{есекаются в
Рис. 364. одной точке, следовательно, три прямые, на которых
лежат высоты треугольника, также л;ресекаются
в одной точке.
6. Пусть продолжения высот, проведенных из вершин А, В i С, пересе-
пересекают окружность в точках Л', В' и С (рис. 365) и пусть
СВА' :А^СВ' : ВгАС = р:д : г. A)
Обозначим углы, на которые высоты делят углы при вершинах, со (тнетствеяио
Л] и А-,, В1 и В2, С1 и С2. Рассмотрев вписанные углы, опирают [еся на дуги
СВА', А'СВ' я В'АС, из A) получим:
(С\ + Л2): (А1 + В2) : (В\ + С2) =* Р : Я : г. B)
Пусть О—точка пересечения высот треугольника ABC. Из подобия прямо-
прямоугольных треугольников АОК и ВОМ следует, что Ах = В2- Аналогично уста-
устанавливается, что С1 = А2 и в\ = С2. Учитывая это,
из B) получаем
откуда следует:
Рис.365.
Теперь из условия Л+В + С=2(Л1 +
легко находим Ви Clf At и вычисляем в личины уг-
углов треугольника:
д_ р+д п й__ д + г я
% _
p + q + r 2*
2'
7. Пусть Ot и О2 — центры большей и меньшей окружностей соо гветственно,
D — точка пересечения хорды ЛВ с меньшей окружностью (рис. 366), Если
О2М ]_АВ, то \АМ = -1
|, и если
1 ЛВ, то
у | ЛВ |. Из
подобия прямоугольных треугольников О2Л/И и О1ЛЛ' получаем | А0г\: | А01
AM |: | ЛЛ' |, откуда | AD \;\ АВ \ = г :Ц. По теореме о касательной и се-
542
кущей имеем
|ВС|2=; лвцво; = ! лв К] ав\ — \ad\
или а2=| АВ\*(\-Г-\. Находим | АВ \ =а V RI{R-r).
8. Пусть Р, Q и N—точки касания окружности сторон треугольника
(рис. 367). Обозначим а = ] ВС \, Зх=\ВМ\. Из теоремы о касательно! и се-
секущей следует
< ВР \ = \ BN \ = \QM , = V2x.
Но так как \СР \ = \ CQ
= \СМ\=а. Точка М — середина с ороны
АС, следовательно, \АС\=2а и АМ\ = а,
N
Рис. 366.
Рис, 367,
Далее, | AN \ = \ AQ | = | AM |+| MQ \ = a + V2x, поэтому \АВ=а +
+ 2 V2 х.
Используя выражение для медианы через длины сторон треугольш ка (см.
задачу 5 § 2 гл, XIII), можем записать:
2 |ВМ ,2=1 ВС ,»+| ЛВ,2_!^_
или
5л2 — 2 V2ax = 0. Таким образом, х=—=—а и
и
2 — 2а2. Отсюда получаем квадратное уравнение
АВ , = -" а. Итак, имеем \ ВС \: \ АС \ :\ АВ '
13
5'
= 5: 10: 13.
9. Пусть О —точка пересечения высот треуголь-
треугольника ABC (рис. 368). Прямоугольные треугольники
ВАМ и BOW содержат по равному острому углу при
вершине В, следовательно, BON =А. Угол ВАС опи-
опирается на дугу ВС, на эту же дугу опирается
угол BQC, поэтому BQC = A, треугольник BOQ равнобедренный и \ ВО \ =
— \BQ\. Обозначим х=\ВО\. Треугольники QOP и ВОС подобны (CQP —CliP
\QO
Рис. 3i.8.
и qpb=qcb),
во\
-Б7Г7 = тг. откуда следует \QO\=--x, E равно-
ZjL j О О
бедренном треугольнике высота является медианол, поэтому \NO\:= г-х и
о
cosA =¦
ВО I
3 4
. у. Тогда sin A1 = у и радиус R
описанно-i около
треугольника ABC окружности находим по формуле D) § 2 гл, XIII /? =
==_а___ 5
И 2 sin Л ~~ 8
10. Пусть D/7 i. ЛВ (рис. 369), тогда треугольник AFE прямоугольный и
FK — его медиана. Следовательно | FK [ = | ЛК |, а так как FAK = = 60а, то тре-
треугольник Л/^К —правильный. Отсюда следует, что FK\\BC h\FB\ = \KC\,
т. е. FBCK— равнобедренная трапеция, оюло которой
может быть описана окружность.
Далее, в четырехугольнике FBCD противоположные
углы BFD и BCD по условию прямые. Значит, около
четырехугольника FBCD также можно опи;ать окруж-
окружность, и BD — диаметр этой окружности.
Обе указанные окружности проходят через точки F,
В и С и потому совпадают. Отсюда следу< т, что угол
BKD опирается на диаметр и потому пря юй: BKD =
= 903 и КОВ = КС В =60°, Тогда Ь
Рис. 369.
П. Пусть медианы AD и биссектриса СЕ пересекаются в точке О
(рис. 370). В треугольнике ACD биссектриса СО является высотой, поэтому
(см. § 1 гл. XIII) треугольник ACD равнобедренный: \ АС \=*',С1) \. Тогда из
условия, что точка D — середина стороны ВС, следует \ВС\=2\АС\ и
= у|ЛС|
Таким образом, АСВ =atccos A/4).
I ар ! _
<аь i — '
b
Рис. 371.
12. Пусть AD — биссектриса угла ВАС (рис. 371). Обозначил x = \AD\.
Очевидно, что площадь треугольника ABC равна сумме площадей треугольни-
треугольников ABD и ADC, поэтому, используя формулу площади B) § 2 гл, XIII,
можно записать
1
L 1 .а 1 . . а
be sm а =у ex sin -g- + 2 6* sin у.
Отсюда, учитывая, что sin а = 2 sin (а/2) соз (а/2) и sin (а/2) Ф 0, получим
2*ccos(«/2)=*(&-f-c), откуда *=—^- cos-^-.
13. Пусть О —центр окружности, описанной около треугольника АВО
(рис, 372). Вписанный угол ABC опирается на дугу АС, на кэторую опи-
опирается, также центральный угол АОС, следовательно, АОС = 2<р. i окружно»
644
сти, описанной около треугольника АОС, иа дугу АС опираются вписанные
углы АОС и АМС, поэтому ЛМС = ЛОС = 2ф, а так как в треугольниках
ЛВС и АСМ углы при вершине А равны, то ACM = ABC = ср.
Применяем теорему синусов к треугольникам АМС и ABC, имеем
\АМ\ АС\ I ЛС АВ.
откуда получаем
sin ф
I AM j
sin 2ф
sin cp \2
sin
1
sin 2ф '
\AB' \ sin 2cp / 4 cos2 ф *
А
Ряс. 372.
14. Пусть в треугольнике ABC точка Я—середина стороны АВ и точи Q —
середина стороны АС (рис. 373). Положим а = \ВС{, b = \AC,, (= ¦ АВ \,
тогда AM ~-rb, \MC'=-'-b, ЛЛ';=-~-си j NB , =— с, Из пря.моуг)льяых
т т О О
треугольников Л/ИР и Л(>-А|' следует
I /1Q _ 3 b
4" У
соз A = .,.- = ^- -г- и cos Л = ¦ ..,
I AM; 3 & iЛЛ ,
Отсюда получаем, что с = —— й и cos А = -тр. Таким образом, А = :/4. Из
треугольника ЛВС по теореме косинусов находим
, / --
а—у biJrc2~2bc соз А = —т^ ''•
3
Теперь используем теорему синусов:
л С
sin С = — sin Л = ¦
b j 2
sm В = — sin Л = -;- и
V5
a
а V 10
Итак, Л = л/4, B=arcsin B/^5), C=arcsiri C/|/"id).
15. Пусть в треугольнике ABC длины сторо;;,
прилежащих к вершине В, различны (иначе треуголь-
треугольник ABC — равнобедренный и биссектриса угла В
является медианой и высотой) и пусть ВК — биссек-
биссектриса этого треугольника (рис. 374), Опишем около треугольника / ВС ок-
окружность и продолжим прямую ВК до пересечения с окружностью в течке К'.
Очевидно, что точка К' — середина дуги АС, поэтому, если через точку К'
провести прямую, перпендикулярную хорде АС (т, е. параллельнуо высо-
высоте BN треугольника ABC), то она разделит хорду АВ пополам, Отспда сле-
18 н/ред. Г. Н. Яковлева 545
дует, что точка К лежит между точкой М — серединой стороны ЛВ, и точкой
Л' — основанием высоты, т. е. биссектриса лежит между медианой и высотой,
16. Применим векторную алгебру. Пусть СВ = а, CA = b, B~t?-. = n, АЙ=т
(рис. 375), тогда n = -^b — a и»* = --а —ft. Найдем скалярное троизведение
векторов т и п:
m-n=-e-ft--fla* + b Щ. A)
Если АВ = с, то с = а — Ь и с ;2= а ,2 + | ft ,2 — 2а • ft, откуда, используя
2
условие задачи ' а ,2+, ft ,.2 = 5 ' с ,2, находим а ¦ ft == - (; а ,2+| ft |2), Подстав-
Подставляя это в A), получаем ;н-н = 0. ('ледонателыю, векторы AM v BN, а зна-
чнг, и медианы AM и BN, перпендикулярны.
Рис. 375.
Рис. 376.
17. Пусть О, и О2 — центры окружностей (рис. 376). О М \_ ВС и
O2/V J_ ВС, тогда, если | ЛВ ] = х, то
| В/И | = I МА : = ; Л/V ; =• | NC \ --= х/2
и
Проведем О2К )СВ, тогда 02К ± OjyM и | О,/С ,2= | 0г02 ^— Э2/( р, т. е.
Решая это уравнение, находим x = Ci/[^5, таким образом, АВ =6/^5 см.
18. Обозначим jMTj=// (рис. 377), тогда из условия ; СР \ : | .Э/И | = 9: 16
находим tCP. — y-y. По теореме о касательной
и секущей имеем | CN f = = | СЯ | | Л1 С |, откуда
3
находим j CN j = -у. Пусть О —целтр окруж-
о
мости, тогда ОЛ1 J_ AB, ON J_ DC и из условия
AB^CD следует, что точки М, О и N лежат на од-
одной прямой. Из прямоугольного треугольника CMN
4
находим ; MN \ — ^ у. Обозначим I ME | = *, тогда
о
|?)JV {=r-\MB \ = x и jBCI = !DC| = ^ + v-</. Проведем BF\MN, о'евидно, что
О
546
4 3
| BF | = | MN | = -=-(/, |Cf | = -g-(/ — .v. По теореме Пифагора имеем
О О
3 \2
-5-у-х\ -
откуда находим * = yf
4 ¦. /
Далее, из прямоугольного треугольника MBN получаем ! BN \ — - |/ -_ у,
н по теореме о касательной и секущей имеем j MB ;2 = ; BN \ ¦ i BQ j, >ткуда
2 /~ 2
|SQ|=—-|/ --(/. Теперь находим
|BQi:|QiV| = |flC|:(i8JV|-|flQ|) = l:9.
19. Пусть прямая ВМ пересекает вторую окружность в точке К (ри( . 378).
Угол ANB опирается на диаметр, он прямой, поэтому диаметр QP перпендику-
перпендикулярен хорде КМ и делит ее пополам: I KN |=| NM I. Далее, хорда CD lepneu-
дикулярна диаметру АВ, поэтому СтВ=ЪпВ и CNB = DNET. Пусть прямая
DN пересекает вторую окружность в точке F, тогда КЛ'F~DNВ =CNВ. Кроме
того, при симметрии относительно диаметра PQ вторая окружность пе| еходнт
в себя, и так как KN 1_ PQ и | KN \ —| NM |, то точка М отображаится на
точку К. Углы MNC и KNF конгруэнтны, поэтому точка С отобргжается
на точку F, Отсюда следует, что ¦ FN \-\NC \. По свойству пересека!лнихся
хорд (§ 3 гл. XIII) имеем \ KM J | NМ. I —-\FN j | ND\, откуда получаем ; ИЛ/| =
Л'
А
с
Рис. 378.
Рис. 379.
20. Пусть BF \\ AM (рис. 379); пересекая стороны угла МСА, пр;мые BF
И AM отсекают пропорциональные отрезки:
\МВ\ \AF\
мс\
лс\ •
1
Пусть AD — биссектриса треугольника ABC, тогда BAD = -„ ВАС, по МАВ =
= ' (l80° — ВЛС), поэтому МЛЬ = лТл8-Ь8ЛО = 90°, т. е. биссектрисы внеш-
внешнего и внутреннего углов при одной вершине треугольника перпендикулярны.
По построению BF\\AM, тогда BF A. AD. Таким образом, в треугольш ке ABF
биссектриса АО является высотой, следовательно, треугольник ABF равнобед-
равнобедренный: |ЛР| = |ЛВ|. Учитывая это, из A) получим
[МС\ \АС\'
18*
547
Случай, когда прямую ВС пересекает продолжение биссектрисы AM, рас-
рассматривается аналогично.
21. Возможны только два случая: либо точка М лежит внутри отрезка ВС,
либо вне отрезка ВС. В цервом случае (ряс. 380) проведем ВЬ \АМ, тогда
\КА \: ,АС\ = 'ВМ\: \МС'.
По услопию \ВМ\:\МС\ — \АВ\:\АС\, следовательно, j h А |: I АС ! =
= i AB j : ; ЛС ;, откуда следует | /С/5 = ЛВ ]. В равнобедренном треугольнике
КАВ углЫ при основании равны, но ВКА—-МАС и КВА=ВЛМ, поэтому
ВАМ — MAC, т. е. ЛМ — биссектриса треуголь-
треугольника ABC.
Во втором случае рассуждения аналогичны
(см. рис. 379).
Рис. 380.
Рис. 381-
22. Рассмотрим параллелограмм ABCD (рис. 381). Центры О, и О3 окруж-
окружностей, описанных около треугольников DAB н РВС, лежат на серединном
перпендикуляре к отрезку ВО, по разные сторопн от ВО и на рав юм расстоя-
расстоянии от BD. Аналогично центры О, и (Я, окружностей, опнеанны) около тре-
треугольников DAC и ЛВС, лежат на се-редпппом перпендикуляре к отрезку ЛС,
по разные стороны от АС и на равном расстоянии ог /1С. Отсюда следует, что
в четырехугольнике ОхО,,ОпО^ его диагонали 0,0;, и О/Л пересекаясь в точке О
(в точке пересечения диагоналей BD и АС г-аргллелогракма ЛВ('О), делятся
пополам, следовательно, О\О./}3ОЛ — параллелограмм.
Обозначим
|ЛС!==2,/2, : О,(9Г4 ' = 2.')t1 | О2О4 | = 2t 2. Так как
OiO3 J. BD и О2О4 х Лс, то угол между диагонл.-пмн S?) и ЛС параллело-
параллелограмма ABCD равен углу между диагоналями О,О3 и О2О4 параллелограмма
OiO2O/»j, поэтому
Пусть .W — середина стороны AD, тогда точки Л'/, OL и Оа лежит на одной
прямо» и, как нетрудно видеть, АОО^Ь^О^О (как \тлы с соответ:твенно пер-
перпендикулярными сторонами). Как установлено psnee,
треугольники О±ОгО и ОАО годобпы и ('С^ : СО2' = \ OD
U] : ui = d1: d.L. Отсюда следует, что
, поэтому
\ОА\, т. е.
Злметпм, что О-, — центр окружности, описанный около треугольника DAB,
поэтому вписанный угол DAB и центральный угол ВОф опираются па одну
дугу и Ш^В = 2?ШГ=2а. Далее, OtO 1 DB и | DO j = j ОБ !, следсвагелыю,
OOjB — a и d1/ui = tga. Таким образом, SABCD : SOiOuQi0t = tc>2 a.
548
ГЛАВА XIV
1. Заметим, что ии одна точка М, принадлежащая прямой АВ или фямой
ВС, не может содержаться в искомом множестве. В самом деле, если М е\ (АВ),
то треугольник АМВ не существует; если М е (ВС), то не существует тре-
треугольник ВМС.
а)
С
Рис. 382
Пусть М принадлежит искомому множеству. Это означает, что глощади
треугольников АМВ и ВМС равны (рис. 382). А так как у этих треугольников
сторона ВМ общая, то высоты А А' и СС равны, т. е. | А А' \=\СС \. Отсюда
следует, что точка М принадлежит прямой, проходящей через точку Б и оди-
одинаково удаленной от точек А и С. Таких прямых, очевидно, две: одна парал-
параллельна отрезку АС (рис. 382, а). Другая проходит через середину Л.' отрезка АС
(рис. 382, б), так как тогда из равенства \АА'\ = \СС'\ следует р; вепстао
площадей треугольников АВК к КВС, из которого вытекает, что | АК,\--=\ КС \,
Точка В, в которой эти прямые пересекаются, как уже отмечалось, не принад-
принадлежит искомому множеству. Из проведенных рассуждений ясно, что если :очка М
не принадлежит указанным прямым, то
площади треугольников АМВ и ВМС не
равны.
Таким образом, искомое множество об-
образуют две; пересекающиеся в вершине В
прямые (без точки пересечения): прямая,
параллельная стороне АС, и прямая, прохо-
проходящая через середину стороны АС.
2. Обозначим через Q площадь тре-
треугольника ABC и предположим для опре-
определенности, что s > Q. Заметим, что искомое
множество не может содержать точек, расположенных на прямых АВ и АС, так
как в этих случаях не существует либо треугольник АМВ, либо т>еуголь-
ннк АМС.
Пусть точка М принадлежит искомому множеству. Рассмотрим сначала
случаГг, когда М находится внутри угла EAF (рис. 383). По условии задачи
549
имеем
Mc — s- Принимая во внимание очевидное равенсво
S&AM В + SAAMC = SAABC + 5ДЛМО
получаем sa/jxc"-=s — Q- Следовательно, в искомое множество в::одят такие
точки М, для которых площадь треугольника ВМС постоянна и равна s — Q.
Ясно, что площадь треугольника ВМС будет постоянна, если точка М будет
находиться на прямой KL, параллельной стороне ВС данного тр ;угольнпка.
Она будет равна s —.2. если рас-
расстояние между стороной ВС и
s п
прямой KL равно 2 —,—-, Так
I ВС j
как М находится внутри угла
EAF, то в искомое множество
входят все точки шг ервала АУ_.
Если точка М расположена внут-
внутри угла F.AF, но не п эинаддежит
интервалу KL, то оч:видно, что
Перейдем к случаю, когда точка М лежит внутри угла FAE' (рис. 384).
Отложим на луче АЕ' отрезок АВ', конгруэнтный отрезку АВ, и заметим, что
saamb~s&A MB" Последнее равенство позволяет заменить треуготышк ABC
треугольником АВ'С и тем самым прийти к случаю, который уже был рас-
рассмотрен. Следовательно, искомому множеству принадлежит и интервал K'L.
Рассмотрим оставшиеся два случая (рис. 385): точка М лежит внутри угла
E'AF' или внутри угла F'AE. Получим еще два интервала K'L' и 1'К, причем
[K'L'\UKL] и [L'K\i\[LK'}.
?' К'
Рис. 384.
Рис. 385.
Таким образом, искомым множеством точек является граница параллело-
параллелограмма K'LKL', за исключением его вершин (рис. 385).
Если SsgQ, то приведенные рассуждения нуждаются в несуиественных
изменениях. В этом случае в качестве искомого множества точек мы также
получаем границу параллелограмма без вершин, но одна сторона параллело-
параллелограмма будет находиться внутри (s<Q) или на границе (s=Q)треупмн пика ABC.
550
3. Очевидно, что точка С принадлежит искомому множеству. Пусть М —
произвольная точка искомого множества, не совпадающая с точкой С (ри:. 386).
Рассмотрим углы МАВ и МВА. Эти углы опираются в конгруэнтных зкруж-
ностях на конгруэнтные дуги СМ и поэтому конг-
конгруэнтны. Следовательно, МАВ = МВА, т. о. треуголь-
треугольник АМВ равнобедренный, причем 1МЛ| = ]Л1В|.
Таким образом, если точка М принадлежит искомому
множеству и не совпадает с точкой С, то она одина-
одинаково удалена от данных точек А и В, т. е. лежит
на прямой, перпендикулярной отрезку АВ и прохо-
проходящей через его середину.
Пусть точка М принадлежит прямой, перпенди-
перпендикулярной отрезку АВ и проходящей через его середину
точку D. Если М не совпадает с D, то /VI явля-
является точкой пересечения двух конгруэнтных окружносте:"!. В само1, деле,
проведем через точки Л, С и М одну окружность и через точки В, С и /VI —
другую. Эти окружности удовлетворяют вгем условиям задачи: первая гроходит
через точки Л и С, вторая — через В и С; окружности пересекаются и яыяются
СМ
конгруэнтными, так как радиус первой по теореме синусов равен —
2 s n MAC
СМ '¦
радиус второй равен ^-. Радиусы равны из-за равенства углов:
2 sin MBC
Рис. ЗвГ
Итак, искомое множество состоит из точки С и всех точек прямой, перпен-
перпендикулярной отрезку АВ и проходящей через его середину, кроме ¦'вредины
отрезка АВ.
Легко видеть, что в случае, когда точка С является серединой отрезка АВ,
искомым множеством является прямая, пер-
перпендикулярная отрезку АВ и проходящая
через его середину.
4. Пусть точка М принадлежит искомому
множеству, т, е. является точкой касания
некоторой окружности, проходящей через
точки А и В, и прямой, проходящей через
точку С (рис. 387). Известно, что квадрат
касательной равен произведению секущей иа
ее внешнюю часть. Следовательно, j CM \- =
= I ЛС j ; ВС I, т. е. точка М находится па
окружности радиуса R — У \ АС \ \ ВС \ с цент- ""'
ром в точке С.
Я'-Но, что точка М не может лежать па данной прямой. Пусть те !ерь М —
точка указанной окружности (рис. 387), не лежащая на данной прямы.
Проведем через М прямую, перпендикулярную к отрезку СМ. Пусть О —
точка пересечения этой прямой с перпендикулярной к отрезку АВ прямой,
проходящей через его середину. Рассмотрим окружность с центром в точке О,
проходящую через точку М. Очевидно, что прямая СМ является карательной
551
К этой окружности. Остается показать, что эта окружность проходит через
точки А и В. Используя три раза теорему Пифагора, получаем
j OB Г2= i ОП ,2+ i BD ,2 = | ОС j«-1 DC ? + \ BD ;2 =
= \ОМ\*+\СМ\* — |Dr|2 + |fiDp.
Теперь преобразуем правую часть, применяя формулу для разности квадратов
двух чисел:
OB p= j ОМ !2+| СЛ1 р — (| DC | — | BD .) (| ВО \ +1 DC j)=
= |OAfi* + |CAf|»-|?C||i4C|.
Так как 1 CM ,2 = j ВС | | ЛС |, то | OB | =, ОЛ4 |. ^
Таким образом, искомое множество — окружность радиуса \ \ АС 11 ВС
с центром в точке С без двух точен, лежащих на данной прямой.
5. Пусть расстояние между данными
точками А и В равно 2а, Выберем систему
координат так, как указано i а рис. 388.
Пусть точка М (х; у) принад1е.;кит иско-
искомому множеству, тогда
\ \АМ :2—\ВМ 2(=S,
По теореме Пифагора находим
Рис. 388.
\ВМ ,3=(л —
Упро;иая это уравнение, получаем
C(c;d)
Таким образом, искомое множество содержит точки, координаты ко' орых х и у
удовлетворяют уравнению
j4.vaj = s. Следовательно, точ <а М (х; у)
принадлежит либо прямой * =-s/4a, либо
прямой х——s/4a. Так как проделан-
проделанные преобразования равносил! ны, то Еер-
по и обратное утверждение: 1аждая ioj-
ка прямых x=:S/4a и x~--s/4a прл-
надлежит искомому множеств/. На рис.
388 показано расположение п )ямых для
случая s — 6a2.
6. Обозначим первые две ючки че-
через А и й, третью '.ереэ С. Выберем
систему координат гак, чтобы точки А и
В имели координаты (— а; 0) и (а; 0)
(рис. 389). Координаты точки С в зтом
системе обозначим соответагенне через
Рис. 389.
с и d. Пусть точка М(х\ у) принадлежит искомому множеству. Тогда
или
(х+аJ + у2 + (х-аJ + у2=(х-с)г-\-(у-с
Упрощая это уравнение, получаем
г—2о2,
A)
B)
Итак, координаты точки М обязаны удовлетворять уравнению B) Верно
и обратное утверждение: если координаты точки М удовлетворяют ypaeiii ншоB),
то для точки М выполняется условие A), т. е. точка М принадлежит искомому
множеству.
Исследует уравнение B). Если
уравнением окружности радиуса
А
Рис. 300.
ю уравнение B) шлг.ется
с центром в топке Ох (—с; —d). Если c2 + d2 = a2, то уравнению B) удовлет-
удовлетворяют только координаты точки Ot (—с; ¦—d). Если с2 + ^2<о2, тс уравне-
уравнению не удовлетворяют координаты ни одной точки плоскости.
Таким образом, получаем окончательный результат. Если точка С нахо-
находится дальше от середины отрезка АВ, чем точки А и В, то искомы! множе-
множеством является окружность радиуса R — У 2с'2 + 2d- — 2a2 с центром в точке*
симметричной точке С относительно середины отречка АВ. Если то та С от
середины отрезка АВ находится па таком же расстоянии, что и точш А и В,
то искомым множеством является
точка, симметричная точке С отно-
относительно середины отрезка АВ. Если
точка С расположена ближе к сере-
середине отрезка АВ, чем точки А и В,
то искомым множеством б\дет пу-
пустое множество.
7. Пусть точка М принадлежит
искомому множеству, т. е. ; вляется
основанием перпендикуляра, проведенного через данную точку А к i^которой
плоскости а, проходя:цел через данную прямую / (рнг. 390).
Опустим из точки М перпендикуляр МР па прямую I и соединил: точку А
с точкой Р. По геореме о трех перпендикулярах [АР] J_ / и, следе (ательио,
точка М принадлежит плоскости [} таком, что р1 J_ I и А е fi. Далее гаи как
в треугольнике AMP угол AMP прямой, то точка М принадлежит окр 'жности s
с диаметром АР, лежащей в плоскости р\
Докажем обратное утверждение. Пусть М — произвольная точка окружно-
окружности s. Проведем через точку М и прямую I плоскость а. Эта плоскость перпен-
перпендикулярна плоскости Р, в которой находится окружность s (из-за того, чт
Р J- ')¦ Далее, так как АР диаметр, то [AM] 1 [МР] и, следовательно, AM] j_a,
т. е. точка М является основанием перпендикуляра, проведенного чер«ч точку А
к плоскости, проходящей через данную прямую I.
Проведенное доказательство не проходит для двух точек окру жности s:
течки А и ее проекции на прямую I точки Р.
Несмотря на это обе точки принадлежат искомому множеству. Действи-
Действительно, точка А является основанием перпендикуляра, проведенного через нее
к плоскости, проходящей через прямую I и точку А. Точка Р— основание
перпендикуляра, проведенного через точку А к плоскости, проходящей через
прямую /, перпендикулярно отрезку АР.
• Итак,, искомое, множество—окружность, расположенная в плоек )стн, про-"
ходящей через данную точку А перпендикулярно данной прямой I, тиаметром
которой является отрезок АР, где Р — проекция точки А на прямук /.
553
8. Пусть точка М принадлежит искомому множеству, т. е. является точ-
точкой пересечения медиан некоторого треугольника ЛВС (рис. 391), Проведем
медианы СК и SK треугольников ЛВС и ASB. Пусть О — точка пересечения
медиан треугольника ASB. Соединим точку М с точкой О. Так каи
i см j _ | so |
\МК\
\ОК
: = 2,
то [ОМ] jj [SCJ, т. е. точка М принадлежит прямой, параллельно! третьему
ребру трехгранного угла и ироходгщей через
точку О,
Ясно, что точки этой прямой, находящи-
находящиеся вне трехгранного угла, не принадлежат
искомому множеству. Точка О щ инадлежит
множеству, так как в ней пересекаютгя медианы
треугольника ASB (С говпадает с S)
Докажем, что все точки луча ON при-
принадлежат искомому множеству. Пуст, /И — про-
произвольная точка этого луча. Про ведем пло-
плоскость АМВ. Она пересечет третье | ебро в не-
некоторой точке С.
Рассмотрим плоскость SMC, Так как [ОМ]]] [SC\, то плоскост,, SMC пе-
пересечет отрезок АВ в его середине (в точке К). Следовательно, прямые СМ и
SO пересекаются в точке К, причем
Р.
301.
мс ¦
so \
но
so\
\ок
¦=2
/
и, следовательно, М — точка пересечения медиан треугольника Al'C, Таким
образом искомое множество—луч ON, еоиапраиленный третьему ргбру трех-
трехгранного угла с началом в точ-
точке О — точке пересечения медиан
треугольника ASB (S —вершина
трехгранного угла).
9. Пусть точка М принад-
принадлежит искомому множеству, т. е.
является точкой ка:ания не-
некоторой сферы, прохедящей че-
через концы А н В длнпого от-
отрезка, с данной глоскостью
(рис, 392). Продолжен отрезок
АВ до пересечения с i лоскостыо
и в точке О, соеди шм точку
пересечения О с точкой М. Через лучи ОВ и ОМ проведем плоек о лъ. Она
пересечет сферу по окружности, касающейся луча ОМ в точке М По тео-
теореме о касательной и секущей, проведенных из одной точки к окружности,
находим
\ОМ\ = 1/\ОВ\-\ОА\, A)
т. е. точка М находится на окружности радиуса R=l//\OB\ ¦ \ОА\ с центром
в точке О,
Рис, 392.
554
Докажем обратное утверждение. Пусть точка М находится на eaj деимой
окружности. Тогда справедливо равенство A).
Проведем через три точки А, В и М вспомогательную окружность и обо-
обозначим ее центр буквой Si. В силу условия A) отрезок ОМ являете i каса-
касательной к этой окружности и, следовательно, [ОМ] J_ [/WSj]. Проведем теперь
через точку М перпендикуляр к данной плоскости, а через точку 5t— lepncn-
дикуляр к плоскости вспомогательной окружности. Эти два перпенд1 куляра
расположены в плоскости, перпендикулярной к отрезку ОМ я про; эдяш.ей
через точку М. Легко видеть, что они не могут быть параллельны. Обозначим
буквой S точку их пересечения. Соединим точку 5 с точками А к В. Проек-
Проекциями отрезков SA, SB, SM на плоскость вспомогательной окружноетч явля-
являются соответственно ее рипусы SyA, S^B, SLM. Из этого заключ;ем, что
\SA\ —\ SB\ = \SM\. Следовательно, сфера с центром в точке S и с радиу-
радиусом | SM | касается данной плоскости в точке М и проходит через каты от-
отрезка АВ, т. е. точка М принадлежит искомому множеству,
Итак, искомое множество памдеио. Это окружность, лежащая в данной
плоскости, с центром в точке О (точке пересечения продолжения дан юго от-
отрезка с плоскостью) и с радиусом R = V , OB j • , ОА \.
10. Проведем через данную прямую lt плоскость аь параллельную прямой
2 плоскость а.2, параллельную прямой
множеством
всех точек
(рис, 393 . Дока-
Докам,
г
\
\
V
i
Т---Л
/ /
/ /
/ /
/ м
д
\—~
W
Рис, 3U3.
Рис,
12, и через прямую
жем, что искомым
является множество
плоскостей «[ и а2, не принад-
принадлежащих прямым /j и 12- Если
точка М\ принадлежит плоскости
а2) но не лежит на прямой /а,
и если через нее проходит пря-
прямая, пересекающая прямую /а,
то эта прямая лежит в плоско-
плоскости cta и, следовательно, не мо-
может пересекать прямую 1и кото-
которая лежит в плоскости aL. Точно так же показывается, что кажд: я точка
плоскости Oj, не лежащая на прямой llt принадлежит искомому мгожеству.
Докажем, что никакие другие точки пространства не обладают нуж шм нам
свойством, т. е. покажем, что через любую другую точку прострат гва мож-
можно провести прямую, пересекающую /х и 1.2. Если точка М лежит на прямых
1\ или lv то это о'гевидно. Пусть точка М не лежит ни в плоскости хь ни в
плоскости а2 (рис. 394). Проведем плоскость а через точку М и прямую
ii и плоскость р через точку М и прямую /2. Плоскости а и f> перес< кугся по
некоторой прямой f, которая непременно пересекает и прямую lt и п эям.ую 12.
В самом деле, прямая I лежит в одной плоскости а. с прямой lt. Она ie парал-
мяъяа. пршмой, 1и так как июче точка А1 лемала. бы в плоскости а«. Анало-
Аналогично прямая / лежит с прямой 1,2 в одной плоскости р и не парал.ельна 12,
так так в противном случае точка М лежала бы в плоскости с^.
11. Применим метод подобшь Отбросим условие, что точка Е лежит на
стороне ВС. Отлежим, на, стороне АВ произвольный отрезов АК (чис. 395).
На стороне ВС отложим [CL], так что |CL| = | АК\, н: через точну L »р«в€-
555
дем прямую LP, параллельную стороне АС. Из точки К, как из ц;нтра, про-
проведем окружность радиуса \КА\. Пусть Л1 —точка пересечения этом окруж-
окружности с прямой LP, лежащая внутри треугольника. Соединим точку М с точ-
точкой К и проведем через точку М прямую, параллельную \ВС]. Пусть N—•
точка пересечения этой прямой со стороной АС. Мы получим четырехугольник
AKMN, у которого три сторо-ibi равны
Продолжим теперь отрезок AM цр пере-
пересечения со сторонол ВС в точье Е, через
точку Е проведем прямую, параллельную
отрезку КМ и перетекающую сторону АВ в
точке D. Четырехугольник ADEC подобен
четырехугольнику AKMN и, еле;опательно,
;
Задача имеет одно и только с дно реше-
решеРис, ЗУ5.
12. Пусть ширина канала равна Н, Проведем через точку А пртмую, пер-
перпендикулярную каналу, и отложим на ней отрезок ААУ длины h тгк, как по-
показано на рис, 390, Соединим точку AL с точкой В. Пусть Л' —то'ка пересе-
пересечения прямой ALB с пряно* 1Х (рис.
396, а). Мост надо строить е точке К,
так как пугь ALKB является Kf атчайшим.
В самом деле, для любого др /гого пути
ALj^KiB получаем
а)
A L, L
в,
Т
1
= ! AL; + 4.R \-\-\ KB
Рис.
и
б)
306.
В I,
Рис. 397.
Знак равенства имеет ivfecro только тогда, когда пункты А и Е располо-
расположены па берегах канала: А е /2, fiel, (рис, 396. б), В этом часты )м случае
мост можно строить в любой точке, принадлежащей отрезку AtB.
13. Построим точку Sj, симметричную точке В относительно прямой I
(рис. 397), Через точки А и Bv проведем прямую р. Пусть С = 1(]р, Докажем,
что точка С искомая. Рассмотрим произвольную точку С( е /, не сов вдающую
с С. Тогда
\ACl\-\BCl\ = \ACl\- \ BLCL \ < [ АВ1J = [ AC j -1 В? \ = \ АС \ - - \ ВС |,
т. е. для любой точки С1 (С1фС) прямой / разность \ACl[ — \BC | меньше
разности \AC\-~ \ ВС \.
556
14. Построим сначала точку Мь симметричную точке М относительно сто-
стороны АО, затем точку Nlt симметричную точке N относительно сто[ оиы ВО
(рис. 398). Проведем прямую M1N1. Отметим точки К и L — точки пересечения
прямой MjA/j со сторонами угла. Из конгруэнтности треугольников МРК и
МгРК и треугольников NQL a N^QL следует, что луч света нужно н« править
из точки М в точку К.
Рис. 398.
15. Отложим от вершины А на сторонах угла отрезки АВ и АС длины р
(рис. 399). Через точки В а С проведем прямые 1г и /2, перпендш улярные
сторонам угла. Пусть О =-'id's- Построим окружность с центром у точке О
радиуса г — \ОВ\ — \ОС\. Из данной точки М проведем касател!- iyio MT
к этой окружности. Треугольник KLA, где К и L — точки переест ня каса-
касательной со сторонами угла, имеет периметр равны"! 2р, т. е. являс «[ неко-
mlim. Докажем это:
I АК : + , XL ! + | AL ; = ! AK ; -+-! ХЛ/ |+ | Л/L
ГЛАВА XV
\ AL , ==
| AB\-\-\ ЛС\=2р,
1. а) Середины ребер тетраэдра обозначим SL, S2, ..., Sn (рис, 4@), точки
пересечения медиан гранен — Л^, М», Мя, М^ Отрезки DMt и А, 12 лежат
в плоскости ЛОЯх и, очевидно, пересекаются, их точку пересечения чбозначим
О. Поскольку lMiAf2] », [DA\ и М1М2 \: \ DA ,= 1 : 3, то из подобна треуголь-
треугольников MfiM2 и DO А следует, что DO'; : | ОМг \ = \ АО \: | ОЛ12 | ==
= j DA \ : \М1М2\ — 3: 1. Аналогично (из рассмотрения треугольнике) BS,,D н
CS3D) доказывается, что и отрезки ВМ3 и СЛ14 пересекают отр> зок DA1X
в точке, делящей его в отношении 3:1, считая от вершины, т. е. в той же
точке О. Отрезки ВМ3 и СМг разделены этой точкой в таком же о ношении.
G) Докажем, что точка О является серединой отрезка S^. Рассмотрим
треугольник j4DSx (рис. 400, 401). Обозначим О'= [DMt] fl [S^j] и докажем,
что О' = 0. Отрезок SiS2—медиана в треугольнике DSj/1, и юскольку
lyWj/Vl,] i| \AD], отрезок SiS2 пересекает отрезок MjA42 в его середине К
(рис.401). Учитывая, что | К Mi \ : \ S2D | = | МХМ2 \ : \ DA |= 1 : 3, из подобия
треугольников КМУО' и S2DO' получаем, что | КО' ! : | S2O' \ = \М1О' \ : I DO' J =
= 1:3. Из последнего равенства и следует, что О' = О. Кроме того, получаем,
557
что \O'S2 =A:|/CS, I, а поскольку |/CS2 |=---g-1 StS, |, то \O'S2\= ~\ StSt\.
Таким образом, точка 0@=0') является серединой отрезка S^. Из рас-
рассмотрения треугольников CSaD и SS5D аналогично доказывается, что точка
О—середина отрезков S3S4 и S?,Sa.
л . м, s,
Рис. 401.
2. Погтроевше сечения показано на рис. 402: 1) S = (MM)(](A<?), 2) Q-
Обозначим :SQ; = A-a и проведем [QQt] J [ЛС]. Тогда i QQl | = | BiJt , ' = ха, и
4
так как ! ВР :—¦ а, то \QLP
О
4 \
с —Xja. Из подобия треугольников SPC и
QPQ, следует, что | SC \ : \ QQt) = I CP \ i j QtP |, откуда \SC\=
2
т —
;а. Прове-
дем [AWIJ I [ЛС]. Рассуждая аналогично, найдем, что \SC\==a/:\. Значит,
дс/D —5*)-=1/3. откуда х= 1/2, |SQ|=a/2.
Ответ: а/2.
Рис. 402.
3. Строим точку пересечения прямой AM с плоскостью SCD Так как
¦(¦Afl)|(CD), то (AB)(SCD), и значит, плоскости SAB и SCD пересекаются
по прямом, параллельной (АВ) (на рис. 403 1\(АВ)). Находим S1== AM)(]l =
= (AM) fl (SCD), A'=(S1P)ntSC]. Сечение-четырехугольник ЛМЛ/f .
Пусть So^^S^fl^D). Поскольку М и Р—середины отрезков S5 и SD,
то | StS 1 = 1 Л8 j, |S2D | = j 5Х5 |. А так как j CD j = ; АВ \, то J S/ |==|CD|,
558
a | S2C | = 2 | CD |. Теперь из подобия треугольников SNSy и CNS2 i о.п/чаем
\SN\:\ NC\ = | SS1\ :\CS21 = 1 :2.
Ответ: 1:2, считая от вершины.
4. Рассмотрим плоскость NQP. Она пересекает грань ВССУВУ по отрезку
CQ. Плоскость сечения пересекает плоскость NQP по прямой, пара, лельной
прямой NQ. Проводим в плоскости NQP
прямую (PT)l(NQ) (рис. 404). Точка Т =
= (PT)fl(CQ) принадлежит плоскости сече-
сечения. Отметим, что так как | СР | = [ PN j, то
и \СТ \ = \TQ\. Дальнейшие построения:
S1 = (МР) п (ВС), S^^T) n [CCjl,
S5 = (MP) п'(АВ), S9=(S4S5) П [^Sil.
S7 = (S4Sr,) П [<4/1i]. Сечение — шестиуголь-
шестиугольник MPS2S3SeS7.
Найдем площадь сечения. Легко ви-
видеть, что | StC I = | S;,A | = а/3. Поскольку
Г—середина отрезка CQ, то \QS3 ; =
^ISjC^a/Зи |S3B1j = u/3. Из подобия Рис.404,
треугольников 5Х52С и S3S4B| треуголь-
треугольнику S3S2C1 следует, что ! S2C |= ] S^By I =a/3. Таким образом, BSX i =
= j BS4 j = i BS5 | = 4a/3, а отсюда следует, что треугольник SiS,Sr, пс-эвильный
н длина его стороны равна iV2a/3, а площадь равна 8 V 31 а2/9. Каждый
из треугольников SjS^P, SiS^S^, S:,MS7 подобен треугольнику .^S^Sr, с
коэффициентом, равным 1/4. Значит, площадь каждого из этих тре> юлышков
1 8 V 3 V 3 „
равна уд—q—a2 = -j^-a2. Теперь находим площадь
16
сечей»:
М
Рис. '05.
Ответ: —~ а2.
5. Пусть MNPQ — сечение тетраэдра плоскостью,
параллельной прямым АС и BD (рис. 405, [MN]][QP]\\
\\[АС], [MQ] i [NP] § [BD]). Тогда (MW, MQ)= (ЛС, BD) =
= ф, а значит, QMN ~q> или QAliV = n —ф. В обоих
случаях sin QMN = sin ср. Обозначим | AM J : | АВ \ =х, тогда \ MQ \=> ¦] BD j =»
= х6, атак как J MB | = A — х) I ЛВ I, то j AliV | = A — х) \ АС \ = A —х) с. Находим
площадь сечения: S = | MQ | I MN \ sin ф = л: (I—л:) ab sin ф, где 0 < к •; 1. Функ-
Функция х(\ —х) (это квадратный трехчлен —х2-{-х) имеет наибольшее зн; чение при
л; = 1/2, и оно равно 1/4. Значит, наибольшую площадь имеет сечен ie, прохо-
проходящее через середины ребер АВ, ВС, CD и AD, и эта плош здь равна
— ab sin a.
4
Ответ: — ab sin a,
4
559
6. Необходимость. Пусть a J у, тогда лучи [ALAt), \fr N), [МР)
(рис. ' 400) лежат на прямых, параллельных плоскости у. Это означает, что
векторы А,А2, MN и МР компланарны. Поскольку векторы МЛ' и МР не
коллинеарпы (точки М, N и Р не лежат на одной прямой), вектор AjA3 раз-
разлагается по этим векторам: А^А% = aMN -\-$МР.
Достаточность. Пусть Aj~A3 = а'ММ + р>МР- От точки М отложпм
вектор М0= aM/V + pVWP. Если Р = 0, то /WQ = аЛШ и точка Q лежит на
прямой Л'1/V. Так как Л:Л2 = М<3, то направления этих векторов юппадают,
а это значит, что лучи [ЛхЛз) и [ЛСД, задающие эти направления, лежат на
параллельных прямых, т, е. а'-. (ММ). Отсюда следует, что а:; у. Аналогично,
если а-=0, получим, что а I] (МР), т. е. ay. Если а Ф 0 и $фО, т> согласно
правилу параллелограмма точка Q принадлежит плоскоггн Y. Значит, и (MQ) с у.
Из того, что ЛЛЛ7=М^, как и ранее, получаем, что a (<UQ), т. е. a , у-
Рис. 406.
М
Рис. 407.
7. Пусть Qs[HD], обозначим AQ , : \ АО ' — х (рис. 407). Поскольку
прямые DM и i4iV параллельны плоскости, проведенной через пря« 'ю PQ, то
векгоры D/VJ, Л,V н PQ компланарЕ!ы. Л так как векторы DM и АХ, оче-
очевидно, не коллипеарны, то вектор РЦ разлагается по этим вето зам, т. е,
существуют числа а и р такие, что
~PQ=a'DM + $AN. (I)
Разложим векторы PQ, DM и AN по пекоыпланарныи векторам /В., АС и
AD. Имеем DM =
AM = —
f-4- ж
AN = у (AD+lC , PQ =
=~РВ-\-ВА~ +~AQ=~C~B — 'A
= '- (Ли- AC) —
= ~-~ AB —
1 __ . 1 ._^
— ,,- AC -j- xAD- Подставляя эти разложения в A), получаем —¦-'-АВ —
—0- AC + xAD = ™- АВ + -«-
-|:— a) AD, откуда находим, что о; = _ 1,
Р = — 1, *= 1/2. Значит, ; /1Q = | AD>/2, а ; AQ \ : | QD | = 1 : 1,
Ответ: 1 : 1.
8. Векторы АР и AQ коллинеарны вектору ACL (рис. 408). Поэтому
J\P = xAClt AQ = yAC\. Отсюда следует, что А^Р= — AA^-^xAV^, BQ =
= — АВ-\-уАС1. Поскольку (ALP) j_ (АС^, то А[Р-А~С1 = 0, от суда х =
560
AAt ¦
-|2^-« Так как АСх — АВ-\- AD-\- ААЪ то j ACL i2 = a3-f-ft2- -с2 и
г = с2. Значит, ;c==c2/(a2-f-ft2 + c2). Аналогично находим, чи у =
т-й2 + с2). Далее, PQ = Л^ — у4?= (у — х) ACL, и значит, j DQ | =
j. |/Id | = | с2 — a2i/V/a2 + (
= | ?/ —
Ответ: j с2 — а2
Рис. 403.
/14
9. Поскольку (МЫ) А. (АВ), то A1V-B/4=O. Разложим вектор MN то не-
некомпланарным векторам В А, ВС и ВВ\ (рис. 409). Обозначим ^ MBL ¦ : ] / Вг | =
==x, j B/Vj:l Bd;=y. Имеем ЛТ/У = М31 + В73 + ВЛГ=>:Й"В1—ЙВ1 + "ВС1 =
= л: (SB l — ВЛ") — ВВ\ И- у (Вй (-|- ВС) = — д'ВЛ + у ВС + (х + у — 1) ВВХ. 1 [з того
что МЫ-ВА=0 н !/Ш,г;2==а2/3, учитывая, что j ЙЛ |= | ВС \ = | В1 j | =a,.
ВЙ-ВС = а2/2, ВД • ВВ1 = ВС • В~В1 = 0, получаем
|_ х2а2 + (/2а2 + (х + у — 1У сР — еда2 = а2/3.
Из первого уравнения следует, что у = 2х, и поэтому из второго уравнения
получаем ЗОл2—18>c-f-2 = 0, откуда %=l/3; x2=l/6. Соответственно и, ходим,
что у1 = 2/3; у2 = 1/3. Отсюда легко найти, что либо | AM \ : ] /1ВГ j =
= |B(V| : | /VCjj=2: 1, либо I AM : iMBji = 5: 1, \BN\i \NCi\ = l : 2.
Ответ: j Л
IB/V |: |А/Сц = 1
MBX ¦ = j BN | : j
| = 2 :
или
AM j
=5 :
ГЛАВА XVI
1. Пусть у J_ a, V J-P. a П P ==c.
= 6. Нужно доказать,
что
На прямой с возьмем точку М и проведем через нее в плоскости a lepnen-
дикуляр С! к а, а в плоскости р—перпендикуляр сг к Ь. Тогда ct X у, ;а X у,
и так как через одну точку М можно провести только один перпендикуляр
к v. то С! = с2. Поскольку сг cz а, а сг с р, то сг = с2 = а[\ (}=с. Значит с X Y>
что и требовалось доказать.
561
Рис.410.
2. Докажем, что из а) следует б). Пусть \ SAl\ = \ SA2\ = ... — \ SAn\ = l
(рис. 410), SO — высота пирамиды, \SO\ = H. Имеем sin SAfi^s п SA2O = ...
... = sin SAnO = H/l, откуда SAlO = SA2O—...=SAnO, т. е. боювые ребра
одинаково наклонены к плоскости основания.
Докажем, чго из б) следует в). Пусть SAfi^SA^O^...-^ 5/4иО = ф.
= ... = 1 ОАп | = Я ctg<p, значит, окружность : центром О
и радиусом R — H ctg fp описана около оснозаиия пира-
пирамиды.
Наконец, докажем, что из в) следует а). Пусть
О — ценгр окружности, описанной около основания, тогда
; О А11 = I ОА2 ] =... = ] О А п ; = R — радиус окружности.
Поскольку SO — высота пирамиды, то j SAt \-.^ SA2 J= ...
...= SAn |= VR2-}-I12, т. е. боковые р?бра имеют,
равные длины. Таким образом, доказано, что а) влечет б)
б) влечет в), а в) влечет а). Отсюда и ледует, что
любые два из этих трех утверждений равносильны.
3. Плоскость, проходящая через середину отрезка
и перпендикулярная ему, является множеством всех то-
точек, равноудаленных от концов этого отрезка.
Пусть О — центр окружности, описанной около грани АВ1 тетраэдра
(рис. 411), I — прямая, проходящая через точку О перпендикуля )но плоско-
сэи ABC. Каждая точка прямой I равноудалена от точек А, В, С. Действи-
Действительно, j О А I = ] OB i = [ ОС , и если S e; I, S фО,
то из пря?.1оугольных треугольников 50/1, SOB и
SOC получаем, что \ SA j = | SB ,= SC ;. Пусть
плоскость а проходит через середину ребра AD и
перпендикулярна ему. Докажем, что о и / пересе-
пересекаются. Предположим, что а||/. И) того, что
AD) \_а, а / || а, следует, что (AD) J /. Посколь-
Поскольку еще I J_ (AB), то / X (ABD). Почучилн, что
через точку А проведены две разные плоскости ABC
и ABD, перпендикулярные прямой /. Но это не-
невозможно, следовательно, утвержден! е, что / |[ а,
неверно, т. е. / % а. Пусть S = l()a. Тэгда ] SD \ =
= J SA !, так как Sea, и , SB \ = | SC I =, SA ], так
как S е I. Значит, точка S равноудалена от всех точек А, В, С и D, а по-
потому принадлежит каждой плоскости, проходящей через середш у ребра тет-
тетраэдра и перпендикулярной этому ребру.
4. В плоскости ASC через середину М ребра SC проведем п< рпепдикуляр
к этому ребру, он будет лежать в плоскости сечения. Точку пересечения этого
перпендикуляра с АС обозначим К и найдем \ КС \. Из треугольника SOC
(рие. 412, а, 6) имеем cos ф= [ ОС |: \CS\-a: ]/2 I, следователью, а) ссвф=
I, б) созф=1/1/'?. Теперь из треугольника КМС находил: а) | КС \ =
4-\АС „ б) \КС\= ^а
ляясь от найденной точки К, строим сечение. Плоскость а сечения и прямая BD
562
I
Рие. 411.
= -4'\АС\. Отправ-
перпендикулярны ребру SC, поэтому они параллельны. Значит, и лнни i пере-
пересечения плоскостей а и ABCD параллельна (BD). Проводим (EF) || (BD) затем
(ЕМ) и (FM). В результате получаем сечения: а) пятиугольник MMPQR;
б) четырехугольник MNPQ.
Рис. 412.
Найдем площади сечений.
а) Имеем | ТИК | = i MC I • tg гр = -
—- а, | EF \ = 2 ; КС \ = -~-
2 (•' 2
о,
= ^-|?/;l|-|MKi = —g— а2- Легко видеть, что | С? ! =-| ВС:, a !?/•; =
= 1-\СЕ\, отсюда | ?Р | = -„- | EF . Проведем [MMt] || [SB], тогда \ ЕВ [ =
= I ВМг;, и значит, | EN
1
ЕМ |. Из того, что |?Р,= • j ?7-' : и
О
1
== „- i ЕМ \, следует, что SEpN = ^ SEfM. Из симметрии всех фигур этноси-
тельио плоскости SAC следует, что SFqr = Sepn = -„¦ SEFM. Значит, i лощадь
сечення равна
о2.
б) Аналогично находим |/(М| = 1/ -^ а, \ EF \ = ./9 о, ¦S?/TAJ='--j—о2.
В APSM имеем р5м'=я-2ф, tgPSA?=— tg 2Ф=4/3, [ РЛ1 j = ! MS , • tg Р5ЛГ=
о. Значит, j PM[=y | KM |. Проведем [MMJ || [SB]. Имеем
|?C|=|-! ВС |, |?М1{ = 2; ВС |, | BMt \ = |- | ВС \, значит, j
ИЕ
= | MLB | : [ MXE |=1:4. Из того, что \ MP \ = -^ i MK |, | MN j = — | ME \,
следует, что SMNP= -^ SMBK, т. е. SMflrpo =
|Aq" 5 }'Г5
Ответ: а) -г—а3, б) —^— а'.
563
5. Диагональ A-fi куба перпендикулярна плоскости BDCX (рис. 413), поэтому
плоскость сечения параллельна прямой АгС. Исходя из этого, строим сечение
следующим образом: в плоскости A^DCB^ через ее точку О пересечения
с диагональю ADl проводим прямую, параллельную АгС, до пересечения
с ребром CD в точке К, в результате получаем сечение — треуго гьник AD^K.
Поскольку \DO \ = \ОА1\, то и \DK\ = -. КС \. Обозначим длин сребра куСа
через а. Объем пирамиды D^ADK равен -w- • -о • | AD | • | DK \ • \ LDX | = -гтг а3.
о Z IZ
Отсюда следует, что отношение объемов частей куба, на которые он разделен
сечением, равно 1:11.
Ответ: 1:11.
6. Обозначим | SB |=я (рис. 414). Найдем длину /; перпендикуляра, опу-
опущенного из точки В на плоскость SCD, т. е. расстояние От • той точки до
плоскости SCD. Так как (АВ) || (SCD), то расстояние от середины М ребра АВ
до плоскости SCD также рашо Л. Пусть
N —середина ребра CD, тогда (SMN) j_
± (SCD), и если IMP] I (SN), то [МР\ J.
1 (SCD), а значит, \ МР \ = h. Зайдем \МР]
как высоту треугольника SMN. Так как
SBO~= л/4. то SO |= | OB |= 2/]/2", и зна-
значит, ! МО \ = о/2, j MN 1 = 2, ! SN i =
= /| SO р + ! O.VT2 = Q Кз"/2. Теперь нахо-
находим /i=[MPj=SO; ¦ ;AW |; J.'7V|= K2/3q.
Отсюда, если а —угол между (SB) н (SCD),
то sin a = li/a = |/ 2 /3.
Ответ: arcsin |^2 /3.
7. Если /iloea, то и р = 0, и ахо +
-j-fcyJ + c20 + A' = 0, значит, в этом случае
формула верна. Пусть Л10 ф a, Ml(xi; y^,z{)
— основание перпендикуляра, опущенного из точии Л!о на а. Обозначим
ro = QMo= (х0; ув; г0), г^—ОМ^ =(Х\', Уй ?i). где О —начало координат. Рарен-
ство axl-\-by1_-^al + d = Q можно переписать в виде n-r,-\-d^O, где и =
= (о; Ъ; с) —вектор, перпендикулярный плоскости. Векторы M^l^ri — г„ и
564
Рис. 415.
п коллинеариы; поэтому
rl—Го =
р = |
= 0, и значит, X =— ¦
= 1X1
откуда г1 = г
• Теперь имеем
Тогда
VV
8. Пусть М —центр основания ABC (рис. 41э), тогда ОМ = -= (О/4 -\ ОВ -)-
-|-ОС) = D; —1; 0). Точка S имеет координаты S @; у; г), поэтому MS"==OS—
— ОМ = (—4; (/+1; г). Находим АВ = @; —3; 3), ЛС--=(—3; —3; 0). Пос сольку
(MS) _L (ЛВС), то MS ¦ ,4В =0, MS • ЛС = 0. Записывая эти равенства в кэорди-
натах, получаем —3 (г/ + 1) + Зг = 0, 12— 3 (г/ + 1) = 0, откуда г/ = 3, г= 4.
Пусть Р— середина ребра ЛС, PQ — перпендикуляр к (SB) в плоскост; SBP,
Так как (ЛС) 1 (SBP), то (ЛС) 1 (PQ), и значит, PQ —общий перпендикуляр
к прямым АС и SB, a ! PQ!—расстояние между этими прямыми. Имеем ОР =
= 2 (ОЛ+"ОС)= G/2; —1/2; —1), ВР = ОР—ОВ = (—3/2; 3/2; —3), BS =
= OS—ОВ=(—5; 5; 2), AfS = (—4; 4; 4). Отсюда ( ВР | = 1/2772", I BS |-. = j/54,
MS ] = 1/48, а 1 PQ I =; ВР , ¦ ¦ MS j: j BS j =2 Кз~.
9. Пусть /—ребро двугранного угла (рис. 416). Проведем шк скости
(АРМ) _]_ / и (BQN) 1 I, тогда ЛР/Vl —BQN = я/3. Проведем еще перпеадику-
ляры ААг и BBL к плоскостям
граней Ya и Yi угла. Посколь-
Поскольку двугранный угол олрьы,
точки ^i и В, лежат соответ-
соответственно на сторонах РМ и QN
линейных углов. По условию
BAB'i=^n/G, ~АВА\ =атЫп0,7.
Пусть (АС) \\ I, тогда (АС) ±
J_(SQiV), и значит, 'ВСА = л/2.
Угол В.4С — острый, его вели-
величина и равна углу между (ЛВ)
и I. Обозначим АВ = а.
Находим j BBi [=a.sin BABX =
= о/2, I QBV \ = \ BBt \ ¦ clg'BQBi=
a , ,
= TF? ' ] >->-a'Sin
Поскольку , QC | =; PA j, то i BXC : =
Х; = a • cos (л/6) = а J.A3/2, [ ЛС | =
2, [РЛ | = ! ЛЛ! I: si
i — [QB! i =9a/10|/3~, В ДЛВ^1 имеем
i /4Bi. I2 —I BiC I2 =—=—a. Следоаа-
тельно, cos В ЛС = | ЛС | : i AB j = 2 ^3 /5.
Ответ: агссозBКз"/5).
10. Строим сечение ABMN (рис. 417, [MN] \\ [АВ] \\ [CD]). Объем ш.рамиды
S.4BCD обозначим V, объем пирамиды SABMN — Vv Объем l\ paeei сумме
565
обгемов V2 и V$ пирамид SBMN и SB AN. Сравним объемы пирамид SBMN
и SBCD, Примем за основания этих пирамид грани SMN и SCD точка В —
общая вершина пирамид. Поскольку | SM
SC\, то
— --- SSCD,
сеченной части равен
значит, Уа= -д VSBCD. Очевидно, Vi;BCd = ~2~V'
1
поэтому 1/2 = —К,
о
Рассмотрим пирамиды SBAN и SBAD. За
их основания примем грани SAN и SAD, точка
В — общая вершина этих пирамид. Поскольку
N — середина ребра SD, то SSAy:=у sSad> и
= j-V. Теперь находим
объем Vt = Vt-\-Va=~ V, Объем другой от*
о
а отношение объемов частей р; вно 3:5.
значит, Уз = -п-
11. Ясно, что тетраэдр и параллелепипед имеют общую вершину, которую
обозначим D (рис. 418). Ребра параллелепипеда, выходящие из этой вершины,
лежат на ребрах тетраэдра. Грани ABC тетра-
тетраэдра может принадлежать лишь вершина парал-
параллелепипеда, не лежащая с вершиной D в одной
грани Такая вершина только однл, ее обозна-
обозначим Fx. Рассмотрим сечения тетра-дра плоско-
плоскостями DiElFiGl и DDtFxF. Обозначим
\CF-i \:\СК | = (/, \MF-i! : \MN \ = x, И — высота
тетраэдра из вер шины С, h — высота параллелепи-
параллелепипеда на основание DEFG. Высо'а тетраэдра
CDXMN из вершины С равна Н -h. Этот те-
тетраэдр гомотетичен тетраэдру CDAB с центром С
и коэффициентом у. Поэтому SDtM j=-y"- ¦ SDAB,
Н — /i = (/H, т. е. Л = A—у) Н. Треугольники
MEXFX и MDXN подобны с коэффициентом х
поэтому SMEiFi =-t*. SMDiN, а ¦•реугольники
NGlF1 и NDtM подобны с коэффициентом подобия 1— х, поэтому SA;C]fj =
= A— xf SN?>tM. Отсюда следует, что SDjE^FiGi= SDiMN —SMEiF —SNCiFi =
= 2лг A —д:) SDiMN = 2x(l— x)y*SDAB. Находим объем параллелепипеда: V„--=
= 6л:A— х) уг A— у) V, где 0<х<\, 0<у<1. Функция хЛ—х) имеет
наибольшее значение при л=1/2, и оно равно 1/4. Для фуикгии уаA — у)
легко установить, что на интервале ]0; 1[ наибольшее значение oia принимает
при у = 2/3, и оно равно 4/27. Значит, х(\ — х) у2 A — у) sc(l/4) D/27)=l/27
при 0<л<1, 0<(/<1, причем равенство имеет место при х= 1/2, (/ = 2/3.
Таким образом, наибольшее значение объема параллелепипеда равно 6 • -~~-V =
Рис. 418.
566
=s~V. Наибольший объем имеет параллелепипед, у которого верш «ш Ft
совпадает с точкой пересечения медиан грани ABC.
Ответ: -^
ГЛАВА XVII
1- Д Пусть R —радиус круга, г —радиус основания конуса, тогда 2л-=/?а,
откуда r = Ra/2n, Находим высоту конуса и его объем: H = VRi--rt =
= х, 0<л<1, и Va = nRn/3. Тогда V = VoxVl—x. Находим произ; одную
2 Зд-
V' = V0— и критическую точку л:0 = 2/3. Легко видеть, что в этой
2 V 1-х
точке функция V имеет наибольшее значение.
Ответ: При а = 2л]^2/3. А
2. Д При вращении прямоугольной трапеции
MNBC (рис. 419) получим усеченный конус с вы-
высотой // = ] BD | = о 1^3/2 и радиусами оснований
Д =| МС j = 6 + (я/2) и /- = 1 /VB | = й. Объем этого
конуса равен
М
пН
о2
Аналогично находим объем усеченного конуса, полученного вращением
прямоугольной трапеции MNBA :
Объем заданной фигуры вращения равен разности объемов этих конусов: V =
Ответ:
-6а2.
3. Д Из условия вытекает, что одна из боковых граней призмы вписана
в основание конуса (рис. 420). Эта грань—прямоугольник со сторонами дли-
длины 1,6 дм и 1,2 дм, следовательно, радиус основания конуса pasei R =
= —-}^1,6s+ 1,2* = 1 дм. Прямоугольные треугольники СОК и SOK подобны.
поэтому \SO\:\CD\=\OK\:\DK\. Отсюда, учитывая, что | CD | =0,
| ОХ |= 1 дм, \DK | = | OK I —I OD [=0,4 дм, получаем, что | SO
Теперь находим объем конуса: V = — R2 - \ SO | =2п/Кз дм3. А
ДМ,
дм.
567
4. Д Введем систему координат, как показано на рис. 421. Течки В, Си М
(середина ребра AD) и N (центр грани CCflJJ) имеют координат л В (о; а; 0),
Рис. 421.
С} @; о; а), Л/ @; а/2; о/2), М (а/2; 0; 0). Подставив эти координаты в урав-
уравнение сферы
получим систему уравнений
(а - xtf ~|- (о - {
Относительно дг0, %. го (координат центра сферы) ;\ R—ее ряциусч. Вычтя вто-
второе уравнение из первого, я четвертое из второго и третьего, noeie упрощений
будем иметь
+ го=~2 а,
Отсюда находим дго = го=Яа/4, уп = о/4. Подстэеив эти значеии! в люСое из
уравнений исходной системы, получим, что й = а К 35/4 А.
5. Д Пусть О —центр сферы (рис. 422). Из того, что \ОС \ — \ОА\ = г,
\ АС 1=1^2 г, следует, что АОС = я/2. Через точку В проведем плоскость
0 1 (CD), и пусть iV = Pf|(CD). Проведем также прямую (ЛР) | (CD), Pea.
Тогда (CD) I (P/V), и значит, (P/V) || (ИО), а потому i O;V | = | Al |. Поскольку
АРВ = л/2, fi2p = (/iflI~Cb) = n/3, то | /IP | = | /Ifl | cos (л/3) = /-/2. Значит,
плоскость E' проходит через середину одного из радиусов ОС |ли OD. Если
предположить, что плоскость § проходит через середину М.ради/са ОС, то из
568
того, что в треугольнике ОВС высота ВМ является и медиалой, следует, что
| ВС | = | ОБ [ = /¦, а это противоречит условию \ВС\>\АС\. Значит, пло-
плоскость р4 проходит через середину N радиуса OD, и тогда \BD\-=r,
Ответ: г, А
Рис. 422.
Рис.423
6. Д Сфера касается основании конуса в их центрах, значит, высота конуса
равна 2R. Обозначим радиусы оснований конуса /-ил, (г > гх). Рассмотрим
сечение данных фигур плоскостью, проходящей через ось РРг конуса (рис* 423).
Сечение сферы — большая окружность, сечение конуса — равнобедренна; трапе-
трапеция MM^N^il, описанная около этой окружности. Пусть К—точка касания,
тогда по свойству касательных имеем \МК \ — [МР \=r, M,K \ = \ M1f-l\ = rl.
Но \MK\ + \KMi\-=a, значит,
а = /¦ + /-!. A)
В прямоугольном треугольнике MM^Q имеем
Рис. 424.
Объем конуса равен -^ ¦ 1R (г2 + ггг -J- r'i)
7. Д Легко установить, что центр сферы,
касающейся боковых граней пирамиды, лежит
на луче SP (рис. 424), где Р — центр основа-
основания ABCD, Из того, что вторая сфера касается не только боковых граней,
но и сферы, описанной около пирамиды, следует, что центр второй сф;ры ле-
лежит на диаметре SQ описанноп сферы, a Q — точка касания этих сфер. Пусть
О —центр второй сферы, К—точка ее касания с гранью SBC, г — рад! ус этой
сферы. Обозначим еще OSK — <x. Имеем
\OQ=\OK\ = r, \SO =2R-r, \OK | = i SO | sin a,
t, e. r±=BR — r) sin a, откуда /- = 2# sin a/(l + sin a).
569
Найдем sin а. Пусть [BF] 1 {SQ, тогда BFD = 120е, PFB=№\ PBF=W.
Пусть [SE\ I [SCj, M = (BF)n(S?), тогда [PM] _L (SBC), поскольку
J_ (S8C), (SP?) 1 (SBC), a (PM) ={BFD) ft (SPE). Таким образом,
и из прямоугольного треугольника РМВ находим \РМ\=-^\РВ\, Учитывая,
что
получаем
что sin РЕМ = ,
V 2
Отсюда следует, что
= 45°, а значит, и a =
перь легко находим,
&J = 45°. Те-
ТеX'2 — l) R.
Рис. 425.
что г =
Ответ: 2{V5 — I) R. А
8. Д Обозначим центры ;анных сфер
(?! и O.it центр третьей сферы О, радиус этой
сферы Д (рис. 425), Точка О принадлежит
биссектору данного угла и плсскости, про-
проходящей через середину Р отрезка OtO2 и
перпендикулярной ему. Следовательно, точ-
точка О принадлежит пересечению бнссектора с
этой плоскостью—лучу QP. И:<еем | OQ \ =
= /?/sina, \PQ\ = \O1Qi\ = r/sma, | OP | =
sin a
\ОлР\ — г, \ООл 1=
ника
sin a
no теореме Пифагора получаем
Из прямоугольно го треуголь-
OP р = | 0^ |2 — | OtP j2, откуда
— lr (l + sin2a) R + /-2 =
_ 1 + sin2a + Уъ sin2 a
cos3 a
- sin4 a
A)
Ответ:/? дается формулой A). A
9. о Необходимость. Если призма вписана в сферу, го каждая ее
грань, и, в частности, основание, вписана в окружность — сечет-е сферы пло-
плоскостью этой грани. Каждая боковая грань такой призмы — параллелограмм,
вписанный в окружность, значит, боковые грани —прямоуголы ики. Отсюда
следует, что боковые ребра призмы перпендикулярны плоскостям оснований,
т. е. призма — прямая.
Достаточность. Пусть ААХ — боковое ребро призмы, Р \ Рх — центры
окружностей, описанных около оснований (рис. 308 гл. XVII, с. 444). Парал-
Параллельный перенос ААХ отображает одно основание призмы на друое, при этом
точка Pi является образом точки Р. Значит, РР^ — ААЪ а потому прямая РРг
перпендикулярна основаниям призмы. Отсюда следует, что середина Э отрезка PPt
равноудалена от всех вершин призмы, т. е. данная призма вписана в сферу
с центром О и радиусом R=\ О А [. Щ
10. Л Пусть сфера с центром О касается ребер SB и ЛС пирамиды
(рис. 426) в точках К\ и Кг, продолжения ребра SA за вершин) S в точке Q
и плоскости ABC в точке Р. Пусть [ОЦ 1 (SBC). Тогда из того что [OKil 1
1 |SB], [ОКа1 1 [SCJ, следует, что [LKJ I [SB], [LK2] 1 [SCj Из равенств
570
\0Kt |= I 0K2 l — R, где R — радиус сферы, следует, что | LKi | = 1 LK-2 \. Этсюда
и из того, что основания перпендикуляров LK\, и L/C2 к прямым SH и SO
принадлежат отрезкам SB и SC, вытекает, что точка L лежит на биссектрисе SD
угла BSC. Плоскость SAD и прямая 0L перпендикулярны плоскости SBC,
значит, точка О лежит в плоскости ASD, а точка Р—на луче AD, Из равен-
равенства | ОР | =| 0Q I, следует, что АО—биссек-
АО—биссектриса угла SAD. Треугольник SAD рапнобед-
ренный, поэтому биссектриса АО проходит
через середину стороны SD и перпендикуляр-
перпендикулярна ей. Учитывая, что @1.) _L (SD), полу-
получаем, что прямые 0L и АО совпадают, и зна-
значит, L — середина стороны SD.
Найдем \LK-i\. В треугольнике SBD
имеем
\SD i=
a,
I = I BD ;
= —%rrr . Из треуголь-
3^2
= \/Уб, \AL\=
Pll°-
\SB\
ника DAL находим sin
= K5/6a, а из треугольника АОР находим
j АО | = | OP /s\nDAL = Vf> R, тогда \L0\= V&R — /5/6 а. Теперь из т[еуголь-
ника OLKi получаем
а.
Это уравнение имеет единственное решение R = 4a/B> V&)-
Ответ: 4а/C ^5). А
11. Д Пусть 0t —центр окружности, вписанной в треугольник AS,], D и
/( — точки касания ее со сторонами АВ и SA, г — радиус ЭЮ1 окр>жности
(рис, 427). Из подобия треугольников SBD
и SOj^K находим, что r = a,B Vl)- Пусть
SP — высота пирамиды. Из треугольника
SDP находим j SP | = а/3. Радиус R сферы,
касающейся ребер пирамиды, находим, как
и в задаче 9 § 3 гл. XVII, получим ./? =
= а/B|^3). Радиус окружности, вписанной
в основание ABC пирамиды, также равен
о/B ^3), поэтому центр сферы совпадает с
центром Р основания. Вне пирамиды распо-
расположены три- сферических сегмента, отсечен-
отсеченных боковыми гранями, и полусфера, отсеченная основанием. Площа;д> этой
полусферы равна 2я/?2 = яа2/6. Площадь сегмента находим по сюрмуле
Sceru = 2nRh, где Л = R — | РОУ \ — высота сегмента. Имеем \РОУ \ = Vk~'' —гг =
671
Рис. 427.
i = т^-а,
я A^7-2)
а2. Площадь части с:реры, лежа-
паг п B Yl — 3)
щей вне пирамиды, равна 3ScelMH—т— = .,._ а3.
у=
Ответ:
31/7
12. Д Пусть Л1 и Л' —точки пересечения отрезка АВ соответственно со
сферами Sx и S2 (рпс. 428), [ AM \=х, | AW = i/, ' Wfl ; = z, j ЛЯ [=--а. Пусть
Я —точка касания сферы Si с гранью р, L —точка касания сферы S2 с гранью а.
Рис, 428.
По свойству касательных п секущих к сфере имеем (а — х) ¦ а = \ ВК ,:, (а — г) а =
= I AL |2. Обозначим радиусы сфер соответственно гх и г» и про 1едем [ОгР\ ||
| [Kfl]. В треугольнике OiO^P имеем j О,Ог | = r1 + r2, j O.ZP ; = : ra— -j , [0^ | =
. Из симметрии отно-
отно^rxrs. Та<имобразом,
аг — A
= K| 0L02 |a — | (V'"= 2 I-'r7r"a. Значит, н ]BK| = 2Krv
сительно плоскости биссектора ясно, что j AL : = j flK ;=2
(а—х)а = (а — 2)a =
откуда л = г =
= а—." — г=
Значит, х: у: г = (а2 —4г1г2) : (8г,г2 —а2): (аг —4г1г2).
Найдем а = | ЛВ | из треугольника ABC, где [SC] X [ЕС\. Имгем \ АЕ\ =
, | СЕ \ = [ BF ! = ra ctgif, и из треугольника ЛЕС получаем, что
j AC B = r; ctg2 rp + rS ctg2 ф —2r1r.2ctg2 ф cos 2ф.
Из треугольника ВКС находим | ВС \*=\ВК 2 — \ КС :2 = 4r1r2 — (r2 — r{f ctg2 ф.
Отсюда а2= ЛВ :2 = ! ЛС ,2+ '¦ ВС 2 = 4r1r2 (I +cos2 rp), Подставлят это выра-
выражение в отношения х:у:г = (а2 — Ar1i\i):{8tir2 — а1): (аа—4/'1г2) и, упрощая,
получим, что х : у : г= 1 : tg2 ф : 1. А
13. Центры сфер обозначим Оь О2, Оп (рис. 429, а), точки касания двух
сфер с нижним основанием цилиндра обозначим К\, К2. точку касания третьей
сферы с верхним основанием — К я. Имеем ¦ ОгК\ \ = ; О2К^ \ = \О3 Кз\=г,
| ОХО2 i = ; ОХО3 ; = , О2О3 ; = 2г. Из точки О3 опустим перпендикуляр O3L на
плоскость нижнего основания цилиндра, тогда \O3L |=2r. Пусть [О М\ 1 [O3L],
тогда I ML j = | 03M J ^r, n из прямоугольного треугольника O^Af находим,
что |01М;=КЗл Очевидно, и 'ЛЮ2!=КЗ/-.
Рассмотрим ортогональные проекции сфер и боковой поверхности цилиндра
на плоскость его нижнего основания. Проекциями сфер являются кр;гн радиуса г
572
с центрами Klt /С2 и L (рис. 429, б), окружности этих кругов обозначим %,
ш2, ш3. Проекцией боковой поверхности цилиндра будет окружность е о ниж-
нижнего основания, которую обозначим со. Точка касания боковой поверхности
цилиндра с первой сферой спроектируется в точку, принадлежащую и о и «о|г
причем это будет единственная общая точка этих двух окружностей. Значит,
окружности со и а»! внутренне касаются. Точно так же со касается и окруж-
окружностей со2 и со3. Таким образом, центр О окружности со удален от каждой из
Рис. 429.
точек Ki, K2, L на расстояние R — r, где R— радиус со. Значит, О—центр окруж-
окружности, описанной около треугольника K\LK^. Из треугольника K\LN i [LN] j_
= V%r, cosKiLN = ^2/3, I LO | = -'- | /CXJL | : cos ~J\LN =
1 [KxKaD находим!
=-- Зл/2 ^2. Отсюда R = | LO i + /¦ = C
+ 4) /-/4.
ОТВЕТЫ К ЗАДАЧАМ РАЗДЕЛА II И ПРИЛОЖЕНИЯ
ГЛАВА I
1. А[}В = {1; 2; 3; 4; 5; 6; 12}, SflC = {5}, (A [) В) (} С = {3; 5},
2. А[)В={1\ 3; 4; 6; 7; 8; 21}, В(]С = {3; 7}, (Л\]В)Г С = {3; 7},
= {0), В [}С = ]— 2; 0] U
6. ЛиВ = [—3; 1]U[2; +°°[, ЛПВ = ф, ЛПС==[—3; — ![,
1 —да; — 2[U]2; +оо[, (ЛиВ)ЛС = [—3; —2[, ЛГ)ВЛС=ф.
7. Л U В = 1 — 1; 2[, А(]В = {0\, А{]Б = ~\— со; 0] (J [2; + х|
]0; 2[, Л U S = 1 — со; — 1] (J [2; + оо[.
8. Л U В = ] — 1; + оо[, Л Г) В = [0; 3[, Л US = ] —оо; — 1] и [0 3
]—1; 0[ U [3;+оо[, А\]В=]— со; — 1].
9. Либ = ] — оо; 1], ЛГ)б = ]— оо; 3[, Либ = 1—оо; +со[, Л П В = ф,
3. Например; а) Л = ]—оо; а], В = ] а; + оо[, где а —любое действитель-
действительное число, б) В — подмножество любого множества А.
4. Л11В = [0; 5[, А{]В = [1; 3],
А[\В[\С = ф, {AUB) ПС={0}.
5. А[]В = ] — оо; +оо[, ЛПВ = {1), ЛПС = ]0; 1[, S|jC=|O; +oo[,
1; +оо[,
10. Л U S = |
= [—1; 0], Либ=Ч— со;
11. а)
]—оо; —1 U
+ со[,
УУ/
щ
I
т
уУ//
¦У/Уб.
ш
S
Щ
%^
i
1
У-У/
Wy
щ
ууу
574
12. 125, 13. 81. 14. 10%. 15. 30; 7; 18; 5, 16. 4. 17. 22,
18. Только книгу Л— 6, только книгу В — 5, только книгу С— 4; не про-
читали ни одной—3.
19. 94; 65. 20. 12п + 6(п = 0, 1, 2, ...).
21. U 22.
24.
О се
26. Прямая у = х-\- -_-.
27-
ж
28.
ч #**
29. -3; j . 30. [0; 1[.
31. — -S- + 2яп; 2яп [} 2яп; 2лп + -я-1 , " <
575
32. [1; 2[. 33. ]-оэ; l-VlJUJl; l + ^
34. ]0; l/2[. 35. ]— оэ; — 2] U [2; + oo[.
36. 1—1; 0[U]0; 1[U]2; + oo[.
]][J [ 88.10; 125].
39. ]—1; + 1]. 40. {1}. 41. [— ]^26; + УЩ.
42. ]—оэ; -2] U [2; -f oo[. 43. [0; 2]. 44. |~; + оэ
46. — V^+l. 47. ~j-. 48. **, ie[0;+ 00[. 49
50. — l+Vl+x при а;3=0, 1 — V 1 — х- при х<0.
51. Да, /-1W = -2L+|/ |¦-*•
2| |
52. Нет (например, {/ A) = {/ (— 1)=0).
53. Нет (например, у @) =i/ B) = — 3).
54. Нет (например, {/ @) = {/ B)=— 8).
56. d=— а. 57. + 1.
ГЛАВА (I
1. а) Есть хотя бы одно попадание, б) Все три выстрела потали в цель.
\ в) Мишень поражена одним и только одним выстрелом.
2. Смит.
3. В экспедицию следует взять Е — биологом, В — гидрологе м, С — ради-
радистом, D — врачом, /¦' — синоптиком, Н — механиком.
4. а) Да, может. Такой контрольной будет, например, контрольная, в кото-
которой количество задач равно количеству учеников, причем первый j ченнк решил
только первую задачу, второй—только вторую, третий — только т >егыо и т.д.
б) Нет, не может. Из того, что существует ученик, решивши! все задачи,
следует, что каждая задача решена хотя бы одним учеником (например, тем,
который решил все задачи).
5. Да, есть, Равносильными являются второй и четвертый отпеты.
6. п=45. 7. х=2, х = C+У5)/2. 8. [—1/2; 1/4].
9. а) [—36/5; 9], б) [—27/5; 0].
11. 1 н 4, 2 и 5 являются взаимно обратными; 2 и 3, 4 и б —взаимно
противоположными; 1 и 6, 3 и 5 являются противоположными обкггным.
Теоремы 1 и 6 верны, остальные неверны.
12. Прямая теорема и противоположная обратной неверны. Обратная и
противоположная — верны.
13. Обратная теорема: если функция непрерывна в течке х, то она
дифференцируема в этой точке.
Противоположная теорема: если функция не дифференцируема
в точке х, то она не может быть непрерывной в этой точке.
Противоположная обратной: если функция не яв, 1яется непре-
рызной в точке х, то она не дифференцируема в этой точке.
Прямая теорема и противоположная обратной верны. Обрати; я и противо-
противоположная неверны (контрпример у (#) = !# j, x = 0).
576
14. а) необходимо; б) достаточно; в) достаточно; г) необходимо и дост
tORHo; д) необходимо и достаточно
21. a) ns4; б) я2=7. 23. пг — п-(-2.
ГЛАВА Ш
1. {0.5}. 2. {1; —0,75}. 3. {—0,8}.
4. {-б; 2; - 2 - /б; _2 + /б|.
5. |о; -JJ. 6. О- 7. D).
8. *s[l; 2J. 9. {(_7+/l3)/3}. 10. {—1; 1} 11. {-3; -4}.
12. 6,25, 13. {A; 2; 1)}.
15. Система несовместна. 16. {3; 1; 1}. 17. Система несовместна.
18. {(—1—-v2 + jc4; х2; 2 — х4', *4), *2<eR, x46eR}.
19. {D; 5), E; 4)}. 20. {G; -3), (-7; 3)}.
21. {C; 1), (-3; -1), (-/2; 2/2), (/2; —2/2)}.
22. {@; 0), A; 1), ((l +/5)/6; (l ±/~5)/б)}.
23. {A/4; -3), B7/4; -1/3)}.
24. {A; 2), (-1; -2); (/2; /2), (-/2; -/§)}.
25. {(-3; -2), C; 2), (-2; -3), B; 3)}.
26. {B; 3), B3/4; -9/2)}. 27. {F; 4), C6/5; 5)}.
28. {E; 4), (-0,5; -0,4)}. 29. {D; 1)}. 30. {E; 7)}.
31. Если а= 1/2, то 4 решения, если а= 1, то 4 решения, если 1/2 < а < 1,
хо 8 решений. При остальных а нет действительных решенил.
32. 5/2. 33. {@; 0; 0), (—6/5; 8/5; —2/5), @; —4/3; 2/3)}.
34. {B; — 1; —1), (—3/2; 9/2; 3/2), (г, 0; 0), xeR).
35. {@; 0; 0), @; — 1; 1)}. 36. {@; 0; 0), G; 7; 7), E/2; 5; 15/2)}.
37. {A; -1; 2), (_ 1; 1; -2), C /2/5; 5/2/8; l/~2),
(-3/2/5, -5/2/8, -4/2)}.
38. {C/2; 2; 5/2), (—3/2; —2; —5/2)}.
39. {(—1; 0; 1/2), A; 0; — 1/2), (;/|/'з, — 2»//з, i/2/з),
(-i/|/3, 2i/l/3, -i/2/З)}.
40. G3. 41. 30% и 60%. 42. тп/(т + п) кг.
43. 60 ms; 2,4 м» и 2 м3. 44. 0,425.
45. 336 и 280. 46. 18 ч и 24 ч.
47. 28 дней и 21 день. 48. 20 и 15. 49. 3 • 104 и 4 ¦ 10*.
50. 5G с. 51. 21 м/с и 147 м. 52. 14 мин. и 56/3 мин.
53. 0,5. 54. 1 час. 55. 4 часа. 56. 1,4. 57. 13 мин.
ГЛАВА iV
1. Неравносильны. 2. Неравносильны. 3. Равносильны. 4. Неравно:ильиы.
5. Равносильны. 6. ]1/3; 4[. 7. { —2} IJ [2; 5/2].
8. ]5-/5; 3|'j]4; 5+1 5[. 9. ]-оэ; — 1L U ]3; 7[.
19 п/ред. Г. Н Я'молова 577
10. ]_oo; -3[u]-2; 0[. 11. ]-l; 0[U]l; Ч-
12. ]-4; 0[U]0; +oof. 13. ]-l; 2[U]2; 5[.
14. ]-oo; -3[u]-l; 0[U]0; 1[U]7; +сю[.
15. ]2; +oo[. 16. ]-co; _1[у]-1; 2].
17. ]-2; 2[U]2; +oo[. 18. ]-cx>; -ЦШ-1: 0[U]0; 1
19. ]-5; -3]U]3; 4]. 20. ]-l; 2[. 21. [-5/2; 2[.
22. ]-oo; 0]U]9/2; +oo[. 23. ]-oo; -3]u]13; + oo[.
24. ]-oo; -1]U]8; +co[. 25. ]-oo; -2] и [5; 74/13[.
26. ]-oo; (Кз7-13)/б[. 27. [15/8; 2[ U ]3; +oo[.
28. ]—oo; — 2/3] U [1/2; +oo[.
29. ]E-K30")/10; E-]/20"/10[u]E + K20)/l0;
30. ]2/3; 3/2[U]3/2; 4[. 31. [-1; - |Аз"/2]U[VT/2; l].
32. ]-oo; -2]U]0; + oo[. 33. [-4; (l-Kl43"T)/10]U]0; 4|.
34. [2; (_7 + КН6~)/2[. 35. {2}. 36. {-1, 1}. 37. [-2; 0[ J]0; 8/5[,
38. ]l; 2lVb]. 39. ]-2; — 1]U[—2/3; l/3[. 40. {7}.
4). При ja|>3 I — oo; - , при a|<3 ^; +co , при а= — 3
решений нет, при а = 3 ] — oo; +oo[.
42. При а < |
a2—12a —2 1 3 , .
— со; ¦—2a —i ' при а= 2" ]—со; +<х>[>
3 [а"-— 12а — 2 , Г
2 [ 2а-3 = +СО| •
НИИ ИСТ.
43. При а>3 Ъ; ^У-1, при a<3 \2й+} ; 2Г, при а = 3 реше-
J а — о J {_ а 6 L
ИСТ.
44. Приа-<0 ] —со; 0[; при а>0 | — тт^\ 0MJ |рг-", +оо .
45. Если а^О, то *е] — 1;0[, если а > 0, то д; е I j ; а I.
46. Если й <с 2 ' а |, то решений нет, если 2 ! а [ sg й^кЗ | а !, то х е
е [ — й + 2 |aj; й —2|а|], если й>3 | а |, токе [—6/3; й/3].
47. а<71/24. 48. —1<а<5. 49. а = 7/4.
50. a>=l/3. 51. 3sSasSl8/5. 52. j a | < 1/2.
59.12; 24/5. 60. 1250 м2. 61. 6+^3 р".
62. Покупатель получил больше двух кг товара. 63. 2.
64. Расстояние между автомашинами будет наименьшим через 8,4 минуты
после полудня. Первая машина в этот момент будет находиться в 1,6 км
от перекрестка. Вторая машина минует перекресток и удалите i от него на
1,2 км.
65. Первый турист.
66. Скорость первого велосипедиста больше 10 км/ч и мен >ше 40 км/ч.
67. Скорость лодки должна быть больше
578
68. При х= чг]/ |^2 —1 д принимает наименьшее значение 2^2 —2.
69. 18. 70. 4 яшика первого типа и 25 ящиков второго типа.
ГЛАВА V
б. 105, в. 6. 7. 1, 8. 2/5. 9. 1/2. 10. 1. П. 2.
12. 1 (использовать , ., , ,, = -г—, . , ). 13. 1,
\ kifi-f-1) к к —|— 1 /
14. 0 (использовать lim \fa = 1
\ Л-XXI
16. a) ad— йс>0; б) ad — йс<0.
18. а) 1 (показать, что (an) —возрастающая и ограниченная); б)
19. а) а„= 1 + о-^7 (см- заДачУ 7< раздел I), lim an = \\ б)
3 lim а„ = 4; в) а^—3-—, Нт а„ = 0.
20. a) 2; 6) 7/33; в) 5/14. 21. 40. 22. 38. 23. 1/3. 24. —2.
25. —2. 26. 3; 6; 12; 18. 27. 1/5. 28. 28. 29. 1/2.
30. 4; 2; 1 и 1; 2; 4. 31. 6; 18; 54 и 26; 26; 26. 32. 24. 33. 1/3.
34. 64; 64/3. 35. 81/2. 36. 9. 37. 26. 38. 4/3. 39. 2/3. 41. 2.
42. 3. 43. 1/2. 44. — 1. 45. 1/2. 46. 1/2.
47. 3(*"—1=(*—D(*7 + .i« + ... + l), ** — \=(x— l)(x-' + x- + x-| I
48. 2. 49. 1/2. 50. 0. 51. 1/2. 52. 1; 0. 53. —1; 1. 54. 1: 0.
55. a) 3; 1/3. 6) 1/3; 3. 57. +oo; 0. 58. +oo; 1. 59.
60. B-х) sin x. 61. * + 6^*~', 62.- 2- -.
2Vx{x+\f (smx + cosxJ
63. h,(x«-l) + jj—p 64. 2* A-х) In 2-2*. 65. -
66. A—ln2)/2. 67. ] —1; 0[Ul0; +l[. 68. y = 2x+0,25. 69. 135'
70. y = 8* + 4. 71. a) y = 2; 6) y + x = 5/2.
ГЛАВА VI
1. /г, fit /,, f8 — четные, f2, fa — нечетные, /3, fs —ни четные, ни не> етные.
2. Функции /lf /3, /4 имеют представление f,- = 9,- (х)+г|)г (х), где q,-(Jf) =
U х)п A_четная функция, г|); (х)=^-^-!—^-i —нечетная функ-
ция A = 1, 3, 4); функция /а не имеет такого представления, так как область
ее определения несимметрична относительно начала координат.
4, а) Неверно; б) неверно. 5. а) Нет; б) да; в) нет.
6, а) е'* '; б) й' * 'sign*.
7, /i., /з непериодические; h периодическая, Г=6л; ^ периодшеляя,
Г = л/2,
8, Может,
19» 573
10, 1) x=\, x = —\, y = 0; 2) x=2/3; 3) x=\, y = 0; 4) x=~ + nn, ns
e Z; 5) x=0, y = 0; 6) y = 0,
11, 1) Функция периодическая с периодом 2л; прямые х = тп, п е Z,—
вертикальные асимптоты; на 2лп—=-; 2лп\ и 2лп; 2л«Н-'.-, функ-
функция убывает, на 2jm + Tf; 2лп + л и 2лп + л; 2лп + -- воз)астает; х =
Зл л
= —+ 2лп — точки максимума, х = -^- + 2пп~точки минимума, !') Функция
определена при х > 0; х = г2ЯЛ, neZ,- точки максимума; х = вям"л—точки
минимума; /2(е2Лп)=1, ,f2 (<?л+алп) = — 1; асимптот нет. 3) ФункцИ! определена
на R, нечетная, периодическая с периодом 2л; ]3(х.) = х на ]—я/2; л/2[,
/3 (х) = п — х на ]л/2; Зл /2[; х= ", -f Inn, лё2,- точки максимума, #= ~у +
-)- 2лп, neZi — точки минимума 4) Функция определена на R, четная; х =
=-s +2пл и jc^—-„—2пл, где п = 0; 1; 2; ..., — точки мак:имума; х —
= -=~-|-2пл и дг^ =—2пя, где я = 0; 1; 2; ... ,—точки мнним/ма; прямая
(/ = 0 — горизонтальная асимптота. 5) Функция четная, периодическая с пери-
периодом 1; fb(x)=x для хе [0; 1/2J, \ь (х)= 1 — х для х е [1/2; 1].
12. 1) Функция определена для всех х ^6—1; #= — 1 и у= 1 --асимптоты;
х=—3 — точка минимума; |—со; —3[ и ] —1; +°°[ — интервалы убывания,
] — 3; —1[ — интервал возрастания. 2) Функция определена для всех хф
z^-^zYS', х = —м, х=уЗ,у = —х— асимптоты; |—со; —3[п]3;+оо[ —
интервалы убывания, ] — 3; —[3[, ]—^; \ 3[, ]v3; 3[—интервалы
возрастания; х = —3 —точка минимума, х = 3 — точка максимума. 3) Функция
1 2 Г
определена для всех х; I — со; —- и ]0; +"^1 — интервалы возрастания;
2
интервал убывания; х= — - — точка максимума; х —. 0 — точка
о
минимума; при х — 0 график функции имеет вертикальную касательную.
4) Функция определена вне интервала ]0; 4[; асимптоты: у=] П5И х-* — со
и у = —1 при х-+-\-со; функция убывающая. 5) Функция шриодическая
л к'л
с периодом л/2; x=knft, ieZ, — точки максимума, х= -- -\- —-, teZ,—
точки минимума. С) Функция определена для х>0; х=\— Тс'чка пере-
пересечения графика функции с осью абсцисс; у = 0 —асимптота щ и *-*-f-oo,
х = 0 — вертикальная асимптота; ]0; ег[ — интервал возрастания, ]е2. -|-оо[ — ин-
интервал убывания; х = е" — точка максимума.
13. При a*S —3 и аЗ= 1. 14. 2.
15. max/ = /F) =132, mln/ = /C) = —57.
16. max 1 = 1 C) = — log3 10, min/ = /F) = —log3 40.
17. x = — 1—точка, максимума, х = 2 — точка минимума; max/ = /D) = e6,.
ЬИ-
min/ = /B)=— ез.18. max/ = 5, min/ = 2,75. 19. a/V/2n. 20. 0.8.
580
ГЛАВА VII
1. BC = AB + AF, BD = AB + 2AF. 2. AM = -^- (OB + ОС — 20A)
3. BD = B~M— MC,
4. АЛ1 = ОЛ1 —DB
5. ДВ = --^Ш-|м, ЛС = --д-CM—|
6. ЛМ = 2 OB - О Л, ВЛ/ = i- ОС -OB, Ш = i- (ОС - OS) •
7. Ш=-ва+-2-вв1+~'вс, А$=-вА--2-~вв1+--2~вд.
8. а) Да, а и ft—любые неколлинеарные векторы либо одинаково направ-
направленные ненулевые; б) да, а и Ь — противоположно направлены нли котя бы
один нз них нулевой вектор; в) нет.
10. а) х = 3; б) х = — 3. 11. ж = 3/2, г/=1/2.
12. х = 4; {/ = — 2. 13. х = 3 или х = — 2. 14. —1.
15. 2/5. 16. jc = 4, (/ = —1. 17. (—6/7; 3/7; —2/7).
18. ;a + fti=6, > —Ь,= 14. 19.24. 20.7.
21. i 2a — i>!=5, i 3f>—а |=1л50. 22.90'. 23. arccos A1/15).
24. — 3, 7, 19, 1. 25. —13. 26. (—4; 6). 27. —25.
28. ±A/^5; — 21^5). 29. —20. 30. —3/2. 31. 60'.
32. (—2; 2; —4). 33. ±([r2; —2/2). 34. m = 4; n=— 3/2. 35 1.
36. ±A; 2). 37. 2/3; —1/3; —2/3. 38. —11/2.
39. arccos (—3//T1). 40. F/7; 2/7; —3/7). 41 60°. 42. 45\
43. (-4; 3; —1); (8; —6; 2). 44. Мг(\; 2; —5); M2(l; —2; —5),
45. arccos (—9/25). 46. 5/2. 47. У 5. 48. 13; —524. 49. 90э.
50. 15; /593. 51. arccos F3/65). 52. {2\%\ j/5; —5)-
53. D8; —64; 60). 54. ±B; 0; 3). 55. ± (l/^3; —1/КЗ; 1/|Аз).
56. +A; 1; 1). 57. (—24; —32; 30). 58. m = —31/12; rt = 41/12.
59. ±@; 1; 1). 60. ±B/3; 2/3; —1/3). 61. x — 2j/ + 5z = 0.
62. 2к-\-у + 2г— 3 = 0. 63. 1) Перпендикулярны, 2) параллельны,
64. —1. 65. 2. 66. 30°. 67. 60°.
ГЛАВА VIII
1. а) 21 + 2з = 3-2г-, 2l22 = 37-9i, г1-гя=1 + 12«, -J = - |?- + Я г;
j JO
{ +i^(-; в) -l + f i; r) -117
2- a) f; б) { +i^(-; в) -al + f i; r) -117 + 44,,
4 '
4. 2A= 1 —t, za = t. 5, (-2; —2); (—2; 2),
581
6. Докажите равенства для двух чисел, затем примените меч од математи-
математической индукции.
1 Уъ 1 V~3
7. а) z1 = 0, z2 = — 1, z3 = y + —/, z4 = y g— I) б) г, = 0, гг = (,
z3 = -i; в) г = 2—|«; г) г = 0, гА = cos^=* + f sin ^* , й = 0, 1, 2, 3,4;
д)г = с + /3с(, где с —произвольное действительное неположнте 1ыюе число.
11. а) Прямая, проходящая через точки г = 0 н z=l+i. б) Прямая, про-
кодящая через ючки г = 0 и г = — l+i. в) Точка г = — 1—2i. r) Действитель-
Действительная отрицательная полуось г = х, х < 0. д) Полуплоскость (вместе с границей),
ограниченная прямой, проходящей через точки г = 0 и z = l + i, и содержащая
точку 2 = —('. е) Окружность радиуса R=V^3 с центром в точю: z =—2-f-i,
ж) Круг радиуса #=10 с центром в точке z = — I без границы круга н без
центра, з) Угол (без границы) с вершиной в точке г==—/, сторсны которого
проходят через точки г = 1 и г = 0. н) Окружность радиуса ^=3 с центром
в точке г = 0.
12. а) г = «; 6) г = ^+^(.
5 5
13. а) 2 U:os y + isin ~\; б) cos я + i sin я; в) cos ~ +isin -^-;
Зя Зя 1 / Пя , . . Пя
г) cos И sin—; Д) cos И sin
2 2 Vsrin-^l 20 20
14. a) z = —V~2; б)г = -У^-+^; b)z«=(—1)«; г)г=--2'ь
15. а) 1, -^- +~2-!. -у 2~^; б) _ + _(, _-__ + !_ (>
V'2 ^2 . V2 V2 . I 2я . . 2я\ „/ 8л , 8л\
„/ Lя , . . Ня\ ч le/7i / 8fe+l , . 8й+1 \ t
2^cos-g- + isin-g-J; r) /2^cos—^-я + isin -^— jtj, й = ;0, 1,2,3,
4, 5, 6, 7.
16. a) 2n; 6) n.
17. a) Zl = 2 + i, га = -2 + (; б) г1=13-/, га = 7 + «; в) г* =
_{/2(са.^±1я + «йп^±1Я),А = 0, 1,2,3,4; r) Zft = cos ^ +1 sin ^,
*=1, 2, 3, 4, 5; д) zi=l, z2=3, z3 = 2i, z4 = —2i; e) z1 = l--^3i, гг =
= -l + /3i, z3 = -2; z4 = _l-K3i, г.=
18. Воспользуйтесь формулами задачи 6.
iq i •• /13-1
19. z2=l—i; z3 = ; z4=
20. 21 = -1r+^-i; ?l = -l_i^i. 21. j
5в2
22. Нет, не может. Указание, Докажите, что все вершины наедятся
внутри круга радиуса R-
1
1—2
с центром в точке
1
1 —z"
ГЛАВА IX »)
1. яA+2/г)/8, яA+2/г)/4. 2. яA+2/г)/2, (— l)»IL + n/i.
3. яA+2/г)/8, яA+2/г)/4. 4. я(8/г —1)/16, п(8/г+1)/24.
б. яA+4/г)/6, 2я/г. 6. я/г/2, л A+2/г)/8. 7. я A2/г—1)/12, я A2/г--5)/12.
I ] у 2 Г 1
8. я(8/г±3)/4. 9. ± arctg —т^ + п/г. 10. ± - arccos |-яг.
Vi 2 4
И. яA+2/г)/2. 12. (—1)«+1~+Я^-. 13. ±^ + 2я/г, ±5?- + ^я/г.
14. —-7Г + 2я/г, (— 1)п-- +я/г. 15. ± arccos (—1/2 У) + 2я/г.
¦s 6
16. (— 1)«+!-?- +яп. 17. i: arccos (—1/4) + 2пл. 18. я, 4я/3.
,9. ±-"- + ™. 20
21. яп, я D/г— 1)/4. 22. л/г, я (Зп — 1)/3. 23. /> | •:= 1/^3.
24. arccos C/5) + я B/г+1). 25. я B/г +1)/2. 26.3/4.
27. П+2п/г, — ± — +2я/г. 28. —Я-± arccos——-+2я/г. 30. л(
4 4 3 4 2 /2 *
31. я/г, яC/г-1)/3. 32. ^ A+2/г), (-1)*11 + ^ •
33. пA+2/г)/2, яA+2/г)/4.
34. л D/г+1)/4, я B4/г+1)/12, яB4гг
35. " +я/г, — Я- + (—1)" arcsin ^
4 4 У 2
36. - -я + я/г, (-1 )»n ."L + ?^1. 37. ± Я + 2я/г,
38. Если , а | 3= 1, то х= - +л/г, дс= + a- arccos \-пп; сслн [ « j <; 1,
то х = + я/г.
. 39. Я+я/г, (—1)ппЯ + ЯД. 40. яA+4/г)/4. 41. я/г/4.
4 о Z
х) Здесь в ответах для кратности указаны только значения пере денного,
целочисленные параметры обозначены буквами т, п, ... Например, запись
, я A+2/г) я A+2/г) ГяA+2п) я( +2/г)
«I. ' , ' ' » следует понимать так: «1, > ' , —^-j—-
/г <ее Z/»-
583
42. (—1)»—+ яп, —-5- + 2яп, яп. 43. -2?, ±-? + 2яп. 44 ля/3.
45. яA+2/г)/12, я A+2/0/2. 46. яA+2я), я Fя _t l)/3.
47 "" Я+я/г + ~arccos - + я/г
50. я A+6я)/6. 51. я/г/3, яA+2я)/7.
62. Л('? + ля± |/ (-о-+яя| -4J, я^-1, 0.
47. ~, Я+я/г, ±4-агссм4- + яя. 48. 2яCп± 1)/3. 49. яA+2п).
53. —2, — ~, 1. у (—7 ± 3 ]/5). 54. яA6n ± 1)/8.
55. яA+2п)/6. 56. яA+4п)/4. 57. ля, я Fя ± 1)/9.
58. яA+2я)/4, яCя± 1)/3. 59. яп/2. 60. яя, я Fя -+_ 1)/6.
61. яA+2я)/2, яFп±1)/3. 62. яFя±1)/3, 4яя.
63. я A +2я)/2, я A +4я)/18. 64. яп/2, 2я (Ъп -?. 1)/3.
65. я A +2п)/14, я A +2я)/4.
66. a) arccos(l/^3) + n(I+4rt)/2; б) я Bn + I) — arctg 3.
67. ян/2. 68. (-1)«~ + пп. 69. (_1)«+1-^+^.
70. яя, я (I+2п)/16. 71. яA+2я)/7, /г^7т + 3, т е Z-
72. я Fя + 1)/6. 73. я (I +2/г)/5, я ^ 5т+ 2, т е 2- 74. я ( +2я)/2.
75. яA6/г + 3 + 2)/8, я(8/г — 3)/4, я B4я —3 V2)/12.
76. 2яя, я A +2п)/2, я Fя — 1)/6. 77. | а | =s 10.
78. Если | в | 3s 1/2, то х= (arctg Dа ± 2 Via? — \) + яп)/2; если а | < 1/2,
то решений нет.
79. Если ае L-; I , то д; = я A+2я)/2; если а^1--; Г,
= я A+2/г)/2, х=±. Y
то х =
80. Если | а | > ]/5, то д; = я/г/2; если |а|^]^5, то х---пп12, х =
= — | arcsin -r=+(—I)n+1 arcsin —+ ля ].
81. яя, я(8я —3)/4. 82. 2яп, яDп—1)/2. 83. я A2я —5)/6.
84. я C/г + 1)/6. 85. я (I + 2я)/4.
86.-Я-+2я«, —arcsin ^'^~1+2яя. 87.
88. a) Ig;ags|/4 + 2)/2; б)
89. яп/3. 90. яFя+1)/18.
91. яDя—1)/2, — ±arccos
4
4 2 1/2
ПО Я1 Я1/1>Я • 1| Л. Я
92. — -. +ял, ^+(—1)" arcsin—7=-+™, 2я/г, — -,т--
4 4 2/2 2
93. 2яя/3. 94, я/г/2. 95.0. 96. 2я—,у. 97. я (I+2я)/2.
584
99. (у-л — 2лп; яга], IU- + -s- — 2га) л; ±~
л
100. Если а = 2ял, то *=±у+я (ra + m), j/ = =f---+п (и —т); если
= Bга+1)я, то * = ±^-+n^+m+-2-j, 1/ = ц; -"- + я (га — т + -^ 1;
а Ф лп, то решений нет.
101. (+0,5; ±0,5), (±1; 0), @; ±1).
102. (arctgB±0,8V) + nm; arctg B + 0,8 YD + лп).
103. (я (8m ± 1)/2; 2я Bп+ 1)), Bя Bт+ 1); я (8/г ± 1)/2).
+2и\ ± ao I 7J\
104. | — -Я ± arccos—7=+2-ит\ — — ± arccos I 7J\
\ 4 2^2 4 \ 2/2/
105. (я Bт— 1)/4; it Bт + 8л+1)/4).
,06. ((_lyHl.J+J«
107. (+ "о- + 2я (т+п); ± -„- -f 2я (т — /г) J, знаки берутся произюльно.
108. х —любое число, не равное лA+2т)/4, у = л (I -\-2п)/2.
109. (-|A+2т); 2 (l+2«)j, ( J A +2т); 2яя—?- A + 2т)
ПО. (±5+гоя;нй(-1)-5+яи), (^; яга).
111. ((—1)" arcsin G/8) +я (л + 2;п); (—1)" arcsin A/4) +лга).
112. ^ + ?™;^ + лBя-
[-т- + я«; я Bя — m)l.
\4 /
113. ((— 1)п-"-+ти; -Я+яга), ((—1)"+1 arctg/2 + ят; -"-
/ я 1/' 10 —1/2 \ /
114. — + яш; (—1)т+ч+1 ar.:sin 3 1-ял , ( ят; (—1
\ 4 4 у \
( п- + ят; (— 1 )т+1 "г + 2лга ).
115. (гон; яA+2га)/4), (яA+2т)/4; яга).
116. (лт; яга), [ят; ± -" +я (т + 2га + 1) ].
117. [ + ~+2лт; ±-д-+2яга).
я
118. (лт; arctg2 + nra), ^ _(_!)» п-+лт\ (_i)»iL + ^
х) Если в записи решений *, у системы встречаются двойные знаки, то,
если не г специального указания, следует брать и для х и Для у одновременно
либо верхние; либо нижние знаки.
. 585
119.
120. (nm; 2лга), ( + arccos -^ + 2ntn\ ±
121. ( |) ^| |)
122. (лт; яга; яBр —m —га)), (±-^ + я Bm — га — р); ±х
я
-4
123. (*+ят; nBra + m); EL + nBp + m)j, ^_-^ + ят; ^-. (- я Bn +
1 /' , т
+fl^2p+
124. |-5- + ят; у + яп; —-?+яBр —т —n)J, |— у + ят; — -Я
?-+nB/j —/я —rt+
125. — -J +яп <*<-"¦ +яп. 126. -"
о о 4
127. 2агсс^2 + 2лн<А:<2
128. -?+2лп<х<~ +
129. х = — -2+2яп, 2nnsS
130. arctg/2 + K/iscx<-2+nn, — arctg К2 + яп sgx < ял.
131. л—J- <*«?« —-д-, л— < а:==с л, л + -.- < и^ л+
132 _^ + 2яп<ж<4 + 2яп, ^ + 2яп<ж<~
133. 2пл<д:<4 + 2ял, ^ + 2лл <ж< "- +2лга, "+2ял
2ял, ^ + 2ял<а:<л+2лп, ^ + 2яя< х < ^ + 2яя, -^-
134. ^- + ял <х <-^
135. - -д- +2яй е^ з + 2дл, g +2ям ^ж^ -2Я + 2лл.
136. - + ял =S a: s? arttg 3 + лл.
58G
137. \-2лп^х^ arcsin—^ + 2я», --arcsin—7тт (-
6 8 2 2 |А2 2 2 V2 8
яп ^)(sS-v + 2яп.
138. 2я/г г? ж < arcsin (Vb — V'2) — ?" + 2я"> ^J ~ arcsin (^5-4 '2") +
+ 2ял < х г- ^ -j- 2пп.
140. sin2(a + P). 144. а) а3; б) 225/128. 145. (а-(-й).
146. а) 4/5; б) —1/8; в) 2/^5; г) —2/^5; д) 9/25. 148. я.
149. а = 4, а>5. 150. п ±-^-. 151. яA+2,ч)/2, ± arctg A/2) + ял.
152. 6; -=-; -4-; dt -„ -\-2лп, п>-2; ±~-\~2лп, п^О.
.5 3 о А
2 11 2
153. — ; -Д-; ± „ +2п, л =з 1; t + 2л, лкс—I.
154. —2л/3; —Л/3; 4л/3; 5л/3. 156. 35.
157. —15/2; —3/10; 3/2.
(Д- \~^/2 Я
2ял —-" - , ха = 2.ТТ.Л — -' , л Зз 1.
^ / ^
159. 12л—1. 160. — " +2лл; arctg 0 + 2яя.
161. (—I)1 arcsin У 5~~ -)-ял. 162. /2"я, (V\ +8зГ— l)/2.
2
163.1/2. 164. —1. 165. —arctg A/2), —arctg A/3).
я3 я3 7л3
166. а= , - -<а^т.
JX
167. а) х—любое число, г,'=2лн; б) х—лт, 1/ = ян; в) дс= _t---(-2л/н,
о
Я Л , Я ., , .
у=± -^+2ял; г) i=± ,-|-я«, (/ = ;!: q +fi Bn-|-;n), комбинация знаков
произвольна.
/ я „ \ / 1 5л
168. 0; -о- + 2лн , -„-; -^- + 2з
\ 2 / \2 4
tg'2 1 -L 2
170. При а = _ .-!—р- три решения: х = 0, ж= <-2я; при а^=—1/2
z (z tg 1 — 1)
четыре решения: х = Jt |/ Зл2 +: 2л arccos (arecos л J , комбинация зна-
нов произвольна.
ГЛАВА X
1. 0,6. 2. 1,5. 3. 2; log8 0,1. 4. 2. 5. 3.
°h~\h ... 7. яBл+1)/2. 8. я B«+1), 4.
9. лBл+1)/4. 10.1/2. П. —2 —1^10. 12.2. 13. — 2— J/T6.
587
14. —1. 15. 1. 16. (— 1)»х+яя, 17.7; 14. 18.9; 1/9.
19.3. 20.3. 21.6. 22. ±-?- + 2яп.
23. (— 1)" -"-+я/1. 24.-5. 25. 5я/4. 26. я/4.
27. a) log, 11; б) /б. 28. ш; (—1 )»¦"- +ян. 29. -?- + яп.
30. 5. 31. —0,5. 32. (_l)»-?-
~
33. -Л-- + 2яи. 34. 3; /3/2. 35. /2- 36. 2". 37. 2-/2.
38. 0,25. 39. 9; 1/9. 40. —3; —8. 41. 15; 1.
42. Если аф\, пфО, то х=\, х = а'2~п)/1"-11; если о^1, п = (
1; если а=1, то решений нет.
44. Кб"; /2. 45. 20. 46. 3; /2. 47. 2. 48. 4.
49. 1/9. 50. 8. 51. 5/12. 52. ~ + пп. 53. 2яй. 54. 2; —5.
55. а = —7/4, а<—2. 56. Два решения. 57. 2. 58. 9.
59. (9; 7), G; 9). 60. A0; 0,1). 61. D; 1), A; 9). 62. C; 2).
63. E;— 1). 64. C; loga2). 65. A; 1), (l/jM; '{'Щ.
66. ((— 1)«-Я- + яд; ±-П-+2лт). 67. A/2; 1/4), A/8; 64).
68. (|/2; 1//2), B;1). 69. (9; 27), A/9; 1/3).
70. C; 2). 71. A; 2). 72. E,5; 2,5). 73. A6; 4)
7w
. 1/ —2 I- 75- B; 3)- (с= •). где 1<с<
76. B5; 13). 77. A0 1; Ю-»), A04; 10 i).
78. A,5; 0,5), @,5; 1,5). 79. (—0,5; —0,5).
80. @; 0), D; 4), B+ /7; 3), B-±Vv, l)-
81. @; 1; 2), A; 0; 2), @; 2; 1), B; 0; 1), B; 1; 0), A; 2; 0)
82. (±3; ±2; ±1).
83. (9; 3; /3), (9; 1/3; 1/|/), A/9; 1/3; /з), A/9; 3; 1/К i).
/О О О \
84,
3,
88. а)
L-; -т2—.; -^=V 85. A; —1). 86. а>—1. 87. а = = —1,
21 К35 Kl5,i
4Гз20,5>0; 6)log32>-8-. 89. ]0; 0,5[U]4; +co[.
90. ]—со; —1[ U ]2; + со[. 91. ]—со; — 2[ U ]5/8; + оо[.
92. 1—1; —0,5[U]l; 2[. 93. ]1; + оо[. 94. J6/5; 4/3[.
<j5. ]2 — /2; 3/4]U[13/4; 2 + /2[. 96. ]—19/4; —3[U]4; 23/- [.
97. Если а>1, то | дс | > /а или 0 < ! х | < 1//а; если п < а < 1
; I л-! < у а или [ х I >
88. ]—оо; [U]l; +оо[. 99. [0; 1]. 100. ]— оо; —1[.
101. [0,5; 2]. 102. ]0; 10] U [10е; +оо[.
103. ]0; log328-3[U]log34; +oo[.
'588
104. ]—oo; log3 log3 2[ U ]0; +oo[. Неверно.
105. ]3; +oo[. 106. [l-V; —1/3[ u[l + V; +co[.
107. ^ + 2лп<х<^ + 2я/1. 108. ]— 2; 4[.
109. ]1; l + VU]. 110. ]1; 2[U[3; 4[.
111. ]-oo; -2[U]1; 2[. 112. [log, 0,9; 2[.
113. ]-oo; 0[U]2; +oo[. 114. ]0; 1 /^6]U [1; +oo{.
115. ]—1; _0,5[U]0; 1[. 116. ]l; 2^2"[ul2-^5; 0,5[.
117. Если 0<а<1, то a2<x<l, a3<zx; если a > 1, то 1 < к <а2,
0 < x < <r3.
118. ]2; 3[UJ/T6; + oo[. 119. [0,2; 5]. 120. [0; 1[.
121. Если 0<а<1, то 0<х<а, а~2<ж; если 1 < а, то о~2 <; х < а.
122. ]—1; 0[U]1.5; 4[. 123. ]—0,5; -0,25] U ]0; 0,5].
124. ]3; E + /7)/2] U И; 4,5]. 125. ]1; 2[U[4; +co[.
126. ]l; /(^69-3)/2[. 127. ]l; |^2[UJ2; +oo[.
128. [7; +сс[. 129. ]1; 2] U [16; +оо[.
130. ~- arcsin -i (|АЗ- 1) + 2гш <х< ~ - ~ arcsin -*-
131. Если 0<а< 1, то а"а*'2~ <x!jo; если 1<а, то решений нет.
132. Если а<0, то 1 < а: < (l -\-Vl — 4а)/2; если а = 0, то реше! ий нет;
если 0<а*й1/4, то а <ж < (l —Kl —4а)/2, A + Кп^4а)/2 < х < 1; если
1/4<а<1, то а<л:<1; если 1«?а, то решений нет. Указан ie, По-
Построить для наглядности графики функции х2 и х — а.
133. ]1; 1,5[. 134. а<— 2. 135. | а | > 2.
137. a) log3 30 > log4 60; б) log3 75 > log2 11. 139. {—2; —1; 0; 1}
144. ж1 = я, i/i = 0; x2 = arccos A/3); у2 = (я —arccos (l/З)J; .'3 = я —
— arccos A/3), 1/3= (arccos A/3)J.
145. B; 2). 146. ]1; 2[.
147. а) Открытым луч с началом в точке (8/7; 9/7), проходящим черзз точку
E; 0). б) Внутренние точки четырехугольника ABCD с вершинами А [—2; 3),
В @; 1), СО; 2), D{1; 3) и точки интервала ВС,
148. @; 1), 149. 5.
ГЛАВА XI
1. а) 1/15; б) k(k+\), если
2. а) 27; б) 2; в) 3; 14; г) 10, если *s=10; д) 3; е) [(; 1; 2};
ж) {0; 1; 2; ...; 27}.
3. а) {1; 2; 3}; б) {1; 9; 14; 15; 35}. 4. а) 870; б) 435.
5. 12. 6, 16. 7. 210. 8. 576. 9. 18; 10. 10. 18. 11. 4060.
12. 72. 13. а) 120; б) 60; в) 420; г) 83 160. 14. -уру.
15. 5040 16, 15625. 17. 12. 18. 16. 19. (n+l)I/nl.
20, 945, 21. 330. 22. Может не хватить,
589
23. Если п<7, то чисел с цифрой 9 меньше; если п5г7, то чисел с циф-
po'i 9 больше.
24. a)
а
б) (Л[
\ Г О /
+ 5a-3/2ft3/2_a-5/2ft5/2_
25. а) 89^3—109^2; б) 16.
26. а) 1716a3 Va ft2; б) 5005; в) 153 /2 х8; г) С*™,,*"'80.
27. а) 60; б) 625; 7000; 7000; 1120; 16. 28. 32.
29. а) 27/64; б) УТб 50»С\„. 30. а) 378; б) 245.
31. а) —1; б) 1/16. 33. а) 1/4; б) 1/3; в) 0; г) 5/12. 34. 5/33.
35. 93/168 36. 120/343. 37. 29/52. 38. 164/1081,
39. а) 9/17; б) 8/17.
ГЛАВА XII
,. а) 1-1^
+ С; в) |-ln.2* + 5| + 4ctg * + 3 3
2, а) 2^*— yCosBA;+l)+ - созЗ — 1; б) 1п х —3 , + ^(*«+i + 2—
_1п2-1л
3. F (х) =-| sin Здс + ^ cos х+ ^-. 4. / (ж) = ^здг + ^.
2 7
5. В промежутке |— 3; 1[ имеем F (х) = —=- xJ + .-, ^!-6.v-{ С; в проие-
жутке ]1; 3[ имеем F(x) = — ф(х) + С при х<? и /= (к) = ц. (х) ¦-¦- + <- при
О
где ф(х)= ^жя_
6. 2. 7. Не всегда
8. Не всегда, например, /(х) = создг, /r(x) = sin х + 3. 9. Да.
10. а) ~ х' - | cos За + ? «2Л' + С; б) - I соз7/ - I cos 5/ + С;
в) у x'/2 + 2.v+ J-* + С; г) _L_3" + ^tg^+C; д) ^ И 2и -1 ,+
+ д-D«+1J/3 + С; е) ^-х + С, если ж>1, и -*г+*-! + С, если xsS
^ 1; ж) — 1п | I +cos х 1 + С.
П. а) — xcosx + sin х + С; б) х2 sin x + 2xcosx — 2 sin л + С;
590
12. a) 3,5; б) 1; в) J^L-± (sin 4-sin2); r) i In | ; д)-^ (84/5-24/8);
~2<fi~l— е~*У> ж) sinl+cosl —1; з) 1/B In 2); и) 1.
n I ,4 A- X R-7 7 15 V?k -
13.1. 14. Л- —, B-j-щ^. 15. |/2л, ^
16. a) (x+\)ex\ 6) — 2'*2Mn A+/1); в) — sin и ¦ ecos" ¦ sin3 B cos и -(-5) —
— cosu-esin" • sin3 B sin u + 5).
17. a) 1; 6) 5/12; в) e + J—2; r) ~- + 2; д) 8/3; e) 3-—т; ж) 71n3}
18. In 2- 1-. 19. 0<a<l/6. 20. 200/243.
О
21. 1/8. 23. -" C7—15). 24. ^ n2.
/ о
л , 2л За +1
25 а) ; °» ; B) " (a+l)Ba+l); Г)
Зяа 1^2
ГЛАВА XIII
2.-7=^==. 3. 2а*. 4. 3-Р„. 5. Л аЬ. 6. 1 :4.
0. B„^3)а; ?l^La, 8.^6. 9.3:1; 1:3.
10.7:1. II. ^/Г+2. 12.20 см2. 13.2:1.
П. -J J/^ 7^
20. т(р-Н)+р(п+1)-Ь«(т + 1)+1. 21. ? S. 22.
23. 5:8; 4:1. 24. \ а. 25. g-; g. 26. 1р Я».
27. Указание. Через точки D и А провести прямую до пересечения
с прямой ВМ. Показать, что DM — медиана образовавшегося треугольника.
4а
32.
33. а/2; а2/2й. 34. |/1?±1/?. 35. 6 см2. 36. ^3/2. 37. 3/2.
38. (« — m)/2m. 39. arctg(l//2). 40. 144 см3.
3|
41. W + mn; ^я2 + т/г. 42. 3| E ^2 + 4 ^3). 43.13/20.
44. Использовать векторную алгебру. 45. Использовать результат за-
задачи 44.
46. a V(R + r)IR- 47. 2. 48. 20/17. 49. 8 см. 50. 12 см.
51. /7/2'см. 52.3/2. 53.8:7. 54. Bл+1): 1.
55. л/2; я/3; л/6. 56.
о — п
57. л/4. 58. 3. 59. ]/4/3 — 3. 60. л/3; л/12; 7л/12.
"• 8A -cos а)" «-Я"* 63- Ш5Ф'
64. 2arctgF/7). 65. 2slnJa. 66. 2ctg2a. 67. 2 sin2 a.
1 + 4 cos2 a 4 3
_rt л л 3jx , ,,- Tv
72. —• -g-j -g- (см. решение задачи 15 раздела I),
ГЛАВА XIV
1. Окружность с диаметром АО, где Л—данная точка, 0— i.einp данной
окружности.
2. Окружность с центром в середине отрезка АО (А—данна? точка, 0 —
центр данной окружности) и с радиусом вдвое меньшим радиуса дгшгой окруж-
окружности.
3. Окружность с диаметром ЛВ.
4. Окружность с радиусом | АВ \ и с центром в точке В.
5. Треугольник OAfjAfg, где Мх и М2 — точки, расположенные на сторонах
данного угла на расстоянии I от вершины 0.
6. Отрезок.
о ^ У2s— |ЛВ|2
8. Окружность с радиусом ^ !— и с центром в сере(ине отрезка
2
АВ, если 2s>\ АВ'?; точка (середина отрезка АВ), если 2s=|.lB|2; пустое
множество, если 2s < | АВ |2.
9. Окружность с диаметром АВ, за исключением точек Л и В.
10. Отрезок, соединяющий середину осиования с серединой выситы, опущен-
опущенной на основание.
П. Четыре точки: центр окружности, вписанной в треугольник, образо-
образованный данными прямыми, и три точки, являющиеся центрами < кружностек,
каждая из которых касается одной стороны указанного треугчш пика и про-
продолжений двух других сторон этого треугольника.
12. Окружность с центром в точке Сие радиусом ,' АС \, за исключением
точки А¦
13. Прямая, содержащая гипотенузу.
14. Восьмиугольник, четыре стороны которого конгруэнтны и 1араллельны
3
сторонпм квадрата и удалены от центра квадрата на расстояние равное -=¦ а,
15. Прямая пересечения плоскостей, перпендикулярных сторонам трапеции
и проходящих через их середины.
,592
16. Четыре прямые, перпендикулярные плоскости а и проходящие соответ-
соответственно через те четыре точки этой плоскости, которые указаны в ответе
к задаче 11.
17. Если А ф1, то прямая, лежащая в плоскости, проходящей 1ерез / и
А, параллельная /, не проходящая через А и удаленная от / на ра:стояние
равное расстоянию от А до /2. Если А е /, то прямая /.
18. Прямая, перпендикулярная / и проходящая через А.
19. Если Аф1, то окружность с диаметром ААъ гДе ^i — точкг симмет-
симметричная точке А относительно прямой /. Если /jel, то точка А.
20. Сфера с центром в точке Вис радиусом \ АВ\.
21. Сфера с центром в точке Вис радиусом \АВ\.
22. Дуга окружности с диаметром О А @ —центр шара, А — то'ка пере-
пересечения данной прямой / с плоскостью а, перпендикулярной / и преходящей
через 0), лежа дая в плоскости а и заключенная внутри шара.
23. Сфера радиуса
¦ R, центр которой совпадает с центром данной сферы.
24. Пусть h — расстояние между lt и /2. Если Л = 0, то окружность с цент-
центром в точке пересечения прямых \t и /2 и с радиусом а/2 (задача 2, § 2). Если
0<Лг?а, то окружность, лежащая в плоскости, равноотстоящей от п; раллель-
ных плоскостей, содержащих /s и /2, с центром в середине общего перпенди-
перпендикуляра прямых 1Х и It и с радиусом VcP — Л2/2 (при
вырождается в точку). Если А>а, то пус-
пустое множество.
40. Точка касания окружности, прохо-
проходяще;! через А и В, со стороной угла.
42. Указание. Рассмотрите точки,
симметрич1гые точке М относительно сторон
угла.
44. Пешеход может оказаться в любой
точке фигуры, ограниченной двумя дугами
окружность
J
рис 430
К\КгК КлКц (рис. 430) и четырьмя отрезками А К
ны"! момент пешеход находился в точке 0; | 0А \
Ау, АуКз, KiA. i началь-
началькм, | OKi |=3 км.
ГЛАВА XV
2. Не следует.
6. Если а || E, то у следует провести так, что у(\афф; если orj|,p, то v
следует провести параллельно линии пересечения плоскостей аир.
7. Если данные прямые не параллельны.
9. Пусть а=>а, а\\Ь; Рэб, р || а. Задача не имеет решения, если М е а,
но М ф а, или если М е р, ио М <? Ь.
10. Не единственна. 11. а) Могут; б) не могут.
12. а) Может; б) может; в) не может.
13. а) Не может; б) не может; в) может. 19. аг.
о
20. 1 : 2. 21. т — п + р. 22. 2: 1, считая от точки М,
593
23. 1:5. 24. 2 ; 3; 1 ; 1. 25. 2 : 9. 26. 3 : 1, считая от точки >(.
27. 2:3, считая от вершины S. 28. 2: 1, считая от вершины У.
29. 3 : 7, считая от вершины AL. 30. 5 : 1, считая от вершины В,
31 • -П7Г-а*- 32- а 6 •
16 4
33. Сечение, проходящее через середину ребра АВ. 34. тр\п.
35. ^Ц-^-. 36. 1. Д^-а; 2. -==-. 37. 3:4. 38. 1:3. 39. ^ а.
О д у § 3
3 та —• 1
40. —а. 41. ^г-. 45. AP = a + 2b + c, AQ=-^
4 3 У
46. Ш = A-Х) AB + kCD. 49.1:1; 3:1.
50. ^-~—. 51. 2:3. 54. arccos B/3); arccos A/3).
55. a) arccos (l//T0); б) arccos (l//l"d); в) arccos /275. 56. arcccs A/2/3).
57. a/2; (л —a)/2. 58. a) arccos A/6); 6) arccos E/6).
59. C — /з) : 2. 60. a/2(|-lj. 61. He существует,
1
\:
68. Vb2 —2a2(l ±cosa); b > /2 a. 69. 0//2.
70. 1/V2. 71. X*a. 72. ^a. 73. а) ^а; б,
3 3 4
74. n2: 1, считая от вершин А и D.
75. 3:2, считая от вершим D и В. 76. t/У 10.
64. arccos f-+cos2 а). 65. arccos E/C/б)). 67. л/3.
77. —^—а. 78. а; За. 79. а; -^ 81.
6 „У 2.
82. arccos (cos Р —cos а). 83. arccos —-„-. 84. —За*.
\ ^ /
86. Пусть М и W—середины отрезков ЛС и BD, р = -- (| AC ,!— j BD ;2).
Если M — N, то искомое множество: а) при </0 = Р —все пространство; б) при
) — пустое множество. Если МфЫ, то искомое множество— плоскость,
перпендикулярная прямой МЫ.
88. Середина отрезка PQ, где Р и Q — середины отрезков АВ i CD (если
отрезок вырождается в точку, то его серединой считается эта точка).
ГЛАВА XVI
- 1 ± 2 /3 7 + 2 \ГЪ 7 ± V?, \
3~~~'' ' 3i ' 3 )•
./-3+2/3 21 ± 2/3 21jr/3\
С \ 9 ; 9 ; 9 )'
6. я — 2 arc sin —^=-. 7. a/l — 2 cos a.
/3
Vs — — — —
8. ~-a. 9. SH = SA—SB+SC. 10. a.
13. a) -L-S ctg (a/2); 6) K3Stg|-. 14. -Ц^ a. 15. | a
'
17. -'a2' 18- K^1^, Кб2 — За*. 19. | a.
20. а) д-|/0а; 6) -J VlOa. 21 j/" ^ a.
25. =-a3 sin3 a. 26. 1 : 2, (читая от вершины S. 27. a:i/6,
b
2 K2 a. 30. 2ol/ I — cosJ a cos2 ^. 31. л/6.
28.
32. a) ax = a!/ = az = arccos(l/K3); 6) arcsin
33. a^,si"a. 34. с/У К a/2 Кб.
4 sin p
35. a) 2:1; 6) 14: l; 2:3, считая от вершины А.
36. arcsin A/3). 38. 7. 39. 37/30; 0. 40. @; 0; 3), @; 0; —2,5).
41. О A; 4; 1), /^A; 3; 3), Вг C; 4; 2), D^l; 6; 3); КЗ. 42. -—-.
\ V 2
43. ?/Зй-а« > 44_ 2 ^ ^ _4_ ^ 4g_ ?/j/^ 47_ ^
46 К 5 9
4S. 0,3a. 49. V10/6 см. 50. 1,5 а.
51. Если 0</sSoV3, то р=[/ -^as + i^a? + ?», если (>i}A3, то
52. arcsin ( sin ф -cos-^-J. 53. arcsin ( sin ф]. 54, arccos V-— cos a.
55. a) arctg V%\ 6) — ; в) arccos —; r) arccos y=--
1 9
56. arctg 1^5- 57. a) arccos -„-; 6) arccos-^.
3 о
f) l/ 4a2 {,2
58. a) — г—; 6) 6 см3. 59. arccos (± сtg ф • ctg \|з).
69. aresm(-i=- sin ф • sin A 61. За. 63. .^2A + cosa)/' fl,
\ КЗ j A+2 cos ар
64. —. 65. 5a3, 66. arccos „-. 07. 2 arccos ; •--<а «с Jt.
6 ^ 2 i J 3 . ;
i,S95
2 Sin J
69. З/За. 70. о]/1 23C°Stp- 71. 2 arcsin
/2
cos
72. ^n во всех случаях 73. v. a3 sin2 .- /cos a. 74. —x-r- a3.
75. -^ sin 2a. 76. ~ sin" | tg Ф. 77. -^ S /S~iufa tg p\
79. 3 : 1. 80. ~. 81. map : 1. 82. a) 13 : 23; 6) 5 : 19; в) 19 : 41.
85. 9 : 5. 86. <?2 C + 9) : A +3q). 87. ~- V(c* — b*) (b* — a*).
88.Е.ш»;Щ1си>. m^V. 90. ^3.
91. ~.(l + /3ctgVKtgT; ep = arctgC-l/3).
92. 4V. 93. -^-. 94. -\ V. 95. 3^~2 V.
96.A+ » +')-,- также /I + ' _ 1 \~ ' , если 1
\a 6 И2сУ \a ., V2c) a
97. B0-14 /2): 1. 98. ~V. 99. 27/'^ a».
1J 4
. 102. 1
ГЛАВА XVII
100. а) 2а; б) -Д=а. 101. D + 3(^6): 19. 102. 1B/2 —/j) CM.
V 15 5
I. r = /i = -j/'F7ib 2. 2aV/3- 3. iv. 4. 0//3.
5. ла2 /23/9. 6. 7д/8 /3. 8. 20л/9 КЗ. 9. V И /?/3, /3 /?.
10. Один цилиндр радиуса я,'C/2) и три цилиндра радиуса a
II. 2arctgB//3). 12. J
13. Если 2а=$л/2, то наибольшую площадь, равную -^ /2 sin 2a, имеет
осевое сечение; если 2а > л/2, то наибольшую площадь, равную у /2, имеет
сечение плоскостью, составляющеТ с осью угол, равны arccos (у 2 rosa).
14. SE/2; 5/2; 1), Steq=5n/18. 15. 22,5л. 16. |яп'.
О
17. -г^Д3. 18. arccos (— 1/71). 19. 2arctg |^sin (a/2). 20. 25 К5/3"ясма.
21. 7л/б/3. 22. 2(/2— 1)/?. 23. 16/3 г3. 24. 1:2.
27. -^гЯ3- 28. ^ ^. 29. л/5 ^3. 30. —
01 Л
596
л D/2-5) 18/2-20 i^41_- 35 4 8in«a:os«
36. a. 37. 5^7~а. 38. aV3sina . 39.-^-. 40. |
4 4 (sin a + sin E) 4/2
41. 4см. 42. 4-см. 43. a) r : R = 2/3 — 3; б) 30э. 47. 15
2/2
48. /ГГ5а. 49.1=^ а*. 50. ±?И Л 51. -А-аР. 52. -'
16 16 375
^ а*. 50. ±?И Л 51. -А-аР. 52. ^а.
16 16 375 4/2
,„ а 40 104 сг 4л .„ 2/2 а
53. —: 2а. 64. —см: см. 55. ——. 56. -—;—.
2' 7 7 /3 5j: F 11
57. arccos|-. 58. Верно. 59. Д^-. 60. nRr . 61. а) 8а-; б) 2 г2; в) 8а2.
в2. R-. 63. ?ЦЙ.,. 64. А.
2/3 16
65. » ла2. Указание. Рассмотреть тетраэдр, гомот'.тический
данному, с центром А и коэффициентом 2. 67. 4,5 па3.
1 3
68. Длина основания равна -т-Р, длина боковой стороны -• Р,
4 8
.-^к. 72.2S. 73. ,«„» :/5-2).
j
5. arcsin 1/ ф-- 76.
75. arcsin 1/ ф-- 76. arccos (— --). 77. 1 : 9.
3/2+1 ±1Ло + б/1 з/2-1-|1/1(Г^71
78. ! -г !•—-—R (внешнее касание), — -~ —R
У У
(внутреннее касание).
79. ab/2c, bc/2a, ca/2b.
80. dA = dD = r cosaV 1+siiAf, | AB |=2r cosa. 81. 0,5 V' п (п -\ 2) а.
82. 1: B/2 + 2) :1; 17: (б У'2 + 2) : 17. 83. 0,5г; 1,5г.
84. л(/Г5 ±1). 85.1:2:1. 86.-. 87. -|^ г.
88. F + 3/2) V. 89. 2arctgsina. 90. 2 arclg (/3/2).
ПРИЛОЖЕНИЕ
<-1.
1.-10. 2. {/2-я, J^M + Ll!}. 3.9/2. 4. а
4'гт
5. 3. 6. {— 1 > U [2; +оо|. 7. —\-2nk, ke^Z-
9. {6, 10, 14, 30, 42, 70, 105, 210}. 10. C—|х5)/4.
И. ±^+л/г, teZ. 12. 114 -'- • 13. .^ = — 63/4, х
о о
14. л/4, л/4, Зл/4; Зл/4. 15. 11//Ш. 16. ]— оо; — 2[(J]2; +<Ь[.
697
17. /7 м. 18. Точка минимума е; промежутки убывания ]0; .[ и ]1; е\\
промежуток возрастания [е; +оо[.
19. 60 км/ч. 20. — + 2nk, — ^ + 2л/ (k, IeZ).
21. Точка х = 0 — точка минимума, промежутки убывания: ]-со; 0] и
]lj + оо[, промежуток возрастания [0; 1[.
22. 310 — л. 23.
24. ]-оо; _14/3[U]4;
25. {1/16, 1}. 26. 40 коп., 60 коп., 80 коп. и 1 руб. 27. —б:1.
28. —1. 29. — ~ + лк, avctg7 + nl(k /Z) 30 13
31. 164850. 32. При а е= ]0; л/2],
V V
sin
eZ). 30. ^
= ]0; л/2], a =jfc р двг решения:
; при а е ]0; л/2], р е ]0; л/2], а = р, одю решение:
.. 4а3 . , . . „
; здесь V — ¦ snis(p • cos ф • an а • sin p.
/О
33. {A5; —12)}; 34. j— 6л, —-^-, ol. 35. 100.
36. -Т+-ТГ, — П(Г + пк< 'eZ. 37. ]0; 8/5[U]5/2; +oo[.
38. 2 = 3. 39. —27/8. 40. ]—oo; — 4[Щ—3; 3[ U [6; — oo[.
41. 24; 0. 42. 64/3. 43. 3nR3. 44. 100 столов и 400 стульев.
45. {0, 4/3}. 46. [0; 1]U[4; 16]. 47. -,+kn, arctg2 + fai, k
48. —24. 49. л/3. 50. ±^ + nk, k e= Z-
51. у4' = F;3), M' = M, С = G; 9). 52. С}, <С-], +С},, {6, 7, 8, 9, 10, 11}.
53. e+A + 4, 10~J'. 54. 6) [10/3; +co[.
55.
56. {10}. 57. 9. 58. 2a.
59. 0. 60. 12 —5 In 5.
61. Указание. При гомотетии с центром [ЛС|П[й?>] и коэффициентом
— \CD\I\ АВ\ квадрат, построенный па [ЛВ], перейдет в квадрат, пзстроеннык
на [CD].
62. ]—3; —
63. ~ arctg
, ~ arctg2- у
(k,
64. Отношение объемов «верхнего» и «нижнего» многогранников равно 3/5.
66. ]—1; +оо[. 66. {A/2; 1/4), A/8; 64)}.
67. 5л/12, 5л/12, 7л/12, 7л/12. 68. ~, 2nk — ~, k e Z-
о 2.
69. Если VJV2 = 2, то /^2 = 2/3. 70. arcsin 2 (К'2 —1).
7i. — —. 72. {(Кз; 1), (j/'з; — 1)}.
73. /3-1. 74.
598
75. Если основание равнобедренного треугольника, полученного в течения,
ит на плоскости ABCD, то S = —^—
CDD.C, (или на плоскости BCC,Bi), то S =
лежит на плоскости ABCD, то S = —^—~; если оно лежит па п.юскости
2 k-cos 2a
76. 6>0, а е |-j/-^-6; -{^ U |/б; }/^p&[ или 6 < 0, а -
любое число. 77. 2^4840.
78. При а е [0; 4[, x = nk, при а ф [0; 4[, x = nk и
9.^ ;^
У 2 cos (а/2) A +У —cos а)
80. в = B;_2;-2). 81.0.
82. 2лй, Y + 2nk' feeZ. 83. [1; 3]. 85. 6 + 6.
86. 3 сына и 2 дочери. 87. ~+ ^-, k e Z- 88. {20}.
89. 2, -10. 90. "р^+1). 91. -^ м/с, ± м/с.
^i it
92. ли, у+^, fee Z. 93. ^-см.-Ц^-см. 94. {1/2} U ] -оо; 0[
95. }f. о», ±±а- аа. 96. ^- + " *. * e Z. 97. ]0; + oo[.
98. 6 = 2a/3, V=~a?H. 99. 13. 100. V = y
101. 32. 102. ]0; 1/2] U ]8; 16[. 103. 576. 105.
106. ~7~g U ; ~1+l — • 107. ]—1/6; n/3]U[5i,/3;
108. -1*.
109. 720. 110. ]l; У2[и]2; + оз[. 111. л-
список формул
ФОРМУЛЫ ТРИГОНОМЕТРИИ
1°. Формулы для решений уравнений:
smx = a, * = (—1)я arcsin
cos л: = а, х= + arccosa + 2nn,
tg* = a, x = arctga + nrc,
ctgx = a, x = arcctga + лп,
(a
sin * = 0,
sin x = 1,
x=
где
sin jc = — 1, * = —
cos x = 0, x = 2
cos*=l, д: = 21
2°. Некоторые значения обратных тригонометрических функций
a
Уъ
2
~т
]
т
1
Кг"
—г
Кз\
2
arcsin a
л
3
л
т
л
"
л
"¦ 6"
я
~т
л
3
arccosa
л
6
л
т
л
т
2л
Т
Зл
~г
5л
6
а
Кз
1
1
Уз
1
J
-Уз
arctga
л
л
т
л
"
л
~?
л
— 4
л
arcctg а
л
6"
л
т
л
3
2л
~з"
Зл
4
5л
6
600
3е. Формулы приведения:
sin (— а) = — sin а;
. / л \ . / л , \
sin I -х а I = sin I -j- + а J = cos а;
sin (л — а) = sin а; sin (л + а) = — sin а;
cos(—а) = cos а;
л \ /л
/л \ /л , \
cos I -^— а I = sin а; cos I -„-- + а I = — sin а,
cos (л — а) = cos (л + а) = — cos а;
tg(_a) = — tga;
lg ^-aj = ctga; tg (•? +a)=-ctga;
ctg(—a) = —ctga;
ctgf"-- a) = tga; ctg(~ + a) = —tga;
sin (а + яп) = (—1)" sin a; cos (а + лл)=(— 1)" cos a,
где »gZ.
4°. Формулы, являющиеся верными равенствами для всех знамений
переменных:
sin2 a + cos2 a = 1;
sin 2a = 2 sin a cos a;
cos 2a = cos2 a — sin2 a = 2 cos2 a — 1 = 1 — 2 sin2 a;
sin2 (a/2) = A - cos a)/2; cos2 (a/2) = A + cos a)/2;
sin (a + P) = sin a cos f> + cos a sin |J;
sin (a — P) = sin a cos P — cos a sin P;
cos (a -\- P) = cos a cos P — sin a sin P;
cos (a — P) = cos a cos P + sin a sin P;
sin 3a = sin a B cos 2a + 1) = sin a C — 4 sin2 a);
cos 3a = cos a B cos 2a — 1) = cos a D cos2 a — 3);
sin a cos P = -g- (sin (a + p) + sin (a — P));
cos a cos P = -„- (cos (a + P) + cos (a — P));
sin a sin P = -„- (cos (a — P) — cos (a -\-. P));
601
JlA-
sin a + sin p = 2 sin —jpE cos _ p ;
sin a — sin P =2 sin cos T j
cos a + cos p = 2 cos T" cos —jp- j
cos a — cos P = 2 sin J—=— sin -S—t—)
для всех a e R и feR.
5°. Формулы, являющиеся верными равенствами не для вй'Х з
переменных:
для а ф -у-, n e Z;
1 - tg2 а
для а Ф — + -2- и a =/= -2 + лп, га
для а + р ф a -+nk, а ф -~ +nl, р Ф „ +лт, k, I, me Z;
Z Z Z
для а — Р =/= y + л/г, а =/= у + я/, Р ф „ + ят, fe, I, m e Z;
tff2 а 1
sin" а = , °, " ; cos2a = •
.о 2tga o I —tg2a
s n 2а = , , ° .,—; cos 2а = , , . -,—
1 + tg2 а ' '-4 ~
ДЛЯ
для
аф
аф
- + я
л, п е;
tg a =
п, п е
1;
sin 2a •
l+cos2<xP ,
z.
, 1 — cos 2a
g a 1+cos 2a
602
ФОРМУЛЫ ДЛЯ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ
(в указанных формулах, кроме последней, а>0, аф1):
а"8" —Ь для й > 0;
loga <э^ = Ь для b e R;
loga bc = с loga b для й>0, ceR;
loga *2п = 2" 1о§а (—b) Для 6 < 0, neZl
1°§я Ьс= loga 6 +loga с Л71" Ь > О, С>0;
loga be = loga (—&) + 1°§а (—c) Для ^ < О, С < 0)
b
loga — = logab — lOgaC ДЛЯ ft > 0, C>0;
loga — = loga (—*) — loga (—c) Для * < 0, С < 0j
l°ga "Г = — logo й ДЛЯ Ь > 0;
о
для Ь > 0, с>0, c^t 1}
loga<; b = — lOga b для с ^= 0, b >- 0;
1«ёа2я6=-2—log,_a, Ь ДЛЯ "е^, "?=0, a<0,
ФОРМУЛЫ ДЛЯ ОБЪЕМА ФИГУР
Объем прямоугольного параллелепипеда с измерениями а, Ъ, а
V=abc;
объем призмы:
где Н — высота, S — площадь основания призмы;
где / — длина бокового ребра, S L — площадь перпендикулярного сечеши призмы;
объем пирамиды:
где Н — высота, 6' — площадь основания пирамиды;
603
объем усеченной пирамиды:
где Н—высота, St и S2—площади оснований усеченной пирамиды;
объем цилиндра:
где R—радиус основания, Я—высота цилиндра;
объем конуса:
где R— радиус основания, Я—высота конуса;
объем усеченного конуса
где Я — высота, R и г—радиусы оснований усеченного конуса;
объем шара:
где R — радиус шара;
объем шарового сегмента:
(«- ¦")¦
где Я—высота сегмента, R—радиус шара;
объем шарового сектора;
где R—радиус шара, Я—высота сегментной части сектора;
объем фигуры вращения: пусть криволинейная трапеция ограничена графи-
графиком непрерывной неотрицательной функции j (х), х е [а; Ь\, прямыми х=а,
х = Ь и осью абсцисс, тогда объем фигуры полученной при в[ ащении этой
трапеции вокруг оси абсцисс, вычисляется по формуле
Й04
ФОРМУЛЫ ДЛЯ ПЛОЩАДИ ПОВЕРХНОСТИ
Площадь ортогональной проекции многоугольника:
Snp = S cos <р,
где S —площадь многоугольника, Snp —площадь проекции, ф —угол между
плоскостью многоугольника и плоскостью проекций;
площадь боковой поверхности призмы:
S=PL-l,
где Рх —периметр перпендикулярного сечения, / — Длина бокового реб( а (для
прямой призмы Р±— периметр основания);
площадь боковой поверхности правильной пирамиды:
где Р — периметр основания, А — апофема;
площадь боковой поверхности правильной усеченной пирамиды:
S = I О
где Рх и Р2 —периметры оснований, А — апофема;
площадь боковой поверхности цилиндра:
S = 2nRH,
где R — радиус основания, Я —высота цилиндра;
площадь боковой поверхности конуса:
где R—радиус основания, I — длина образующей;
площадь боковой поверхности усеченного конуса:
где /?!, R? — радиусы оснований, / — длина образующей;
площадь сферы:
где R — радиус;
площадь сферического сегмента:
S=2nRH,
где R — радиус сферы, И — высота сегмента.
605
§
й
n
ста"
Р
8
1
1
ел
Vi
~j
1,000
000
0,707
&
CJi СО У
с? со'с
оэ to -
о — о
л сп"сп
г с-, со
0,839
869
— ел CD
0,766
755
743
- 731
719
СП -J0CCCO
сосососоысососососо
СП СП СП СЛ*СЛ СЛ СЛ СЛ СЛ*СЛ
о
— 00 СЛ ЬО О -J Л
О — *• ~J ОСЛ CJ
СС ОО tO ~J tO СО .
СЛ О -J С". 00 СО t
р
ЛОО.О
0,577
601
625
ЭС-fr'tO
о
слслслслслслслслслст^
— tocoj^oi5;~JoecDO
totototototototototo
¦^ ^ ^ ^ t^ «^ со со о» "^о
СЛ CD 4^ 00 СО "-J ^^ Ц1 OO tO
о ^о
ел ел ел ¦t*-'**- 4^. **¦ j^. со со
ел Со ^^™ оо t^^ ь^^ t*^^ ^^^ оо ^^
747
605
475
356
246
145
050
983
881
804
р р
00 00 00 0о~.р CD CD CD CD CD
--J 00 CD X! О — "ts5 IvOi -i-
СЛСО — OOi4i. — ^J-^-O
OSOSOSOSOSOSOSOiOi^J
— юсо4^ел01-^оосоо
со со to to "to to to to — ~-~
оюоыасомслоо — *.
0,176
194
213
231
249
0,268
287
306
325
344
to со со >^ >^ >^ ui ui
O^J^JOOCO — WO*--J
4-00 — ^jto—*—СЛСЛ
о
cd^cdcd'cdcdcdcdcdcd
CD_CC,.CO
О
^7i CD H"^ ¦f'- ^^j cD t^
о
— — u u-"o О О
CO ^~ СЛ CD >*^
fc- — —
CO ^ ^~ СЛ J^ CO ^—
о
CD CD CO СоЪ CD CO
CO CD CO CO CD CD CD
ОС О CO СЛ &> 00 CD
^^ 00 00 '^^' 00 00 00
to — о
p
0,0000
0175
0349
tooi
OS CO |
1,000
1,000
0,999
...
8
f
r>
COS OS
и
s
f
s
о
m
s
X
m
n
t;
s
X
a°
0
5,73
11,5
17,2
22,9
28,7
34,4
40,1
45,0
45,8
51,6
57,3
63,0
68,8
74,5
80,2
86,0
90,0
а радианов
0
0,1
0,2
0,3
0,4
0,5
0,6
0.7
л
~
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
л
~2
ein a
0,000
0,100
0,199
0,296
0,389
0,479
0,565
0,644
0,707
0,717
0,783
0,841
0,891
0,932
0,964
0,985
0,997
1,000
tga
0,000
+0,100
+0,203
+0,309
+0,423
+0,546
+0,684
+ 0,842
+ 1,000
+ 1,030
4 1,260
+ 1,557
+ 1,965
+ 2,572
+3,602
+5,798
+ 14,10
—
a°
91,7
97,4
103,1
108,9
114,6
120,3
126,1
131,8
135,0
137,5
14^,2
149,0
154,7
160,4
166,2
171,9
177,6
180,0
а радианов
i,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
Зл
~4~
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
л
sin a
1,000
0,992
0,974
0,9-16
0,909
0,863
0,808
0,746
0,707
0,675
0,598
0,516
0,427
0,335
0,239
0,141
0,042
0,000
Iga
—24,23
— 7,697
— 4,286
— 2,927
-2,185
-1,710
-1,374
-1,119
-1,000
-0,916
- 0,747
- O,(iO2
- 0,473
- 0,356
- 0,246
-0,143
- 0,042
0,000
Александр Дмитриевич Кутасов,
Татьяна Сергеевна Пиголкина,
Валерий Иванович Чехлов,
Тамара Харитоновна Яковлева
ПОСОБИЕ ПО МАТЕМАТИКЕ
для поступающих t вузы
M., 1981 г., 608 стр. с илл.
Редактор А. Ф. Лапко
Технический редактор В, Н. Кондакова
Корректоры! С. Н. Макарова, Н. Б, Румянцева
ИБ М> 11556
Сдано в набор 21.05.80. Подписано к печати 29.09.80. Бумага
60??90Vie, тип. № 2. Литературная гарнитура. Высокая пе-
печать. Услобн. печ. л. 38. Уч.-изд. л. 41,Ob. Тираж 200 00С
A-й завод 1—100 000) экз. Заказ Ка 1345. Цена книги 1 р. 60 к.
Издательство «Наука»
Главная редакция физико-математической .литературы
ПТ071, Москва, В¦ 71, Ленинский проспект, 1о
С матриц ордена Октябрьской Революции, ордена Трудового
Красного Знамени Ленинградского производственно-техниче-
производственно-технического объединения «Печатный Двор» имени А. М. Горького
Союзполиграфпрома при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли.
197136, Ленинград, П-136, Чкаловский пр., 15
отпечатано в Ленинградской типографии .V*j 6 ордена Тру-
Трудового Красного Знамени Ленинградского объединения «Тех-
«Техническая книга» им. Евгении Соколовой Союаполиграфпрома
при Государственном комитете СССР по делам издательств.
полиграфии и книжной торговли, 193144, г. Ленинград,
ул. Монсеенко, 10. Заказ 426.