GRAPHICAL
ENUMERATION
Frank Harary
UNIVERSITY OF MICHIGAN ANN ARBOR
Edgar M. Palmer щ
MICHIGAN STATE UNIVERSITY BAST LAN8INO
Academic *m$ Nm York emd Londm Ш»

Ф. Харари, Э. Палмер
ПЕРЕЧИСЛЕНИЕ
ГРАФОВ
Ивре»*д с «нгя|1е«ого Г. П.
■ ■..■■.-■•il ч* i . i •-,
.*)-'H* ; ?!«);.•. Bjfti'j..,11
«МИР* Москва (977

ЦС 519.15
Мвнография по современному, бурно развивающемуся раз-
разделу дискретной математики — теории перечисления графи-
графических объектов. Имя первого автора хорошо известно по
переводам его статей и книги «Теория графов» («Мир», 1973),
В предлагаемой работе наряду с классическими результатами
Редфилда, Пойа и де Брёйна представлевы сравнительно
новые факты, уставовленные Робиисоном, Байнеке и авто-
авторами. Последняя глава содержит интересный обзор решен-
решенных и нерешенных задач перечислевия графов. Изложение
систематичное и достаточно подробвое.
Книга заинтересует математиков, физиков, экономистов
и специалистов, работающих в тех областях звания, где ис-
используются идеи и методы комбинаторного анализа.
Редакция литературы, по математическим наукам
20203-030 v
041@1)—77 *"^" @ Перевод ва русский язык, «Map»,

ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКА
Известно немало задач в физике, химии, биологии, экономике,
статистике и лингвистике, сводящихся к подсчету числа графи-
графических объектов, обладающих заданными свойствами. Некоторые
из таких задач были решены около ста лет назад, другие не ре-
решены до настоящего времени. Найти в явной форме число соот-
соответствующих объектов, как правило, не удается. Однако, исполь-
используя перечислительные теоремы Пойа, де Брёйна и Робинсона,
можно получить ряд тонких соотношений между различными
числовыми характеристиками изучаемых объектов, оценить по-
порядок роста этих характеристик.
На русском языке очень мало литературы по перечислению
графических объектов. Советский читатель имел возможность
познакомиться с методами и задачами перечисления графов по
двум статьям Харари [12, 15], по главе 15 его книги [1], а также
по статье де Брёйна [21. Однако составить четкое представление
о разнообразных подходах, схемах, идеях теории перечисления
графических объектов по этим работам невозможно.
Предлагаемая книга известных американских математиков
Ф. Харари и Э. Палмера является первой в мировой литературе
монографией, содержащей достаточно последовательное и по-
подробное изложение наиболее важных разделов теории перечисле-
перечисления графов. Наряду с классическими результатами Редфилда,
Пойа и де Брёйна в книге представлены сравнительно новые
факты, установленные Робинсоном, Байнеке и самими авторами.

6 ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКА
В конце книги дан интересный обзор решенных и нерешенных
задач перечисления графов.
Первые шесть глав книги являются хорошим введением в те-
теорию перечисления графов. Книга послужит не только матема-
математикам — много ценных примеров и сведений найдут в ней также
физики, экономисты и вообще все специалисты, работающие
в тех областях знания, которые переплетаются с комбинаторным
анализом.
Работы советских авторов в списке литературы не приводятся.
Мы сочли необходимым дать дополнительный список, в который
включили наиболее примечательные работы по перечислительной
тематике теории графов, принадлежащие нашим соотечествен-
соотечественникам. . V .
Г. П. Таврило*
■ L<
' . •..
«.(!•,»/'<■:
Г «e ,
.Ф

Enumerate, count, number, call over,
run over, take an account of, call the roll,
muster, poll, sum up, cast up, tell off,
cipher, reckon, reckon up, estimate,
compute, calculate,
Roget, «Thesaurus»1
ПРЕДИСЛОВИЕ
«Сколько существует графов?» — таков первый вопрос, задавае-
задаваемый многими студентами, слушающими курс теории графов.
Это также первая задача, которую мы пытаемся решить. Упомянем
об одном обстоятельстве: мы узнали окольным путем, что Джордж
Пойа уже подсчитал число графов с заданными числами вершин
и ребер. Отправляясь от его формул, сравнительно просто удалось
перечислить корневые графы, связные графы и ориентированные
графы. Впоследствии мы решили задачи перечисления для других
разнообразных типов графов. А когда были временно исчерпаны
все легкие перечислительные задачи, мы опубликовали статью,
содержавшую 27 нерешенных задач перечисления. К настоящему
времени почти половина этих задач решена, а последовательные
пересмотры первоначального списка 27 нерешенных задач пере-
перечисления регулярно публиковались. Современное состояние дел
в этой области отражено в заключительной главе данной книги.
Хотя Эйлер и решил ряд задач перечисления для некоторых
типов триангулированных многоугольников, расположенных на
плоскости, все же существенные шаги в теории перечисления гра-
графов были сделаны лишь в девятнадцатом столетии. Кэли решил
перечислительные задачи для трех типов деревьев: помеченных,
корневых и обычных. Несколько раньше всемирно известный
инженер-электрик Кирхгоф нашел в неявной форме число остовов
произвольного заданного связного графа, а значит, в частности, —
число помеченных деревьев. Далее следует указать обширный
трактат майора П. А. Мак-Магона, в котором немного затронуты
задачи перечисления графов, — это один из наиболее ранних при-
примеров поддержки военными исследований в области комбинато-
комбинаторики (если не считать работ Архимеда). До Пойа был еще один
кудесник, в совершенстве владеющий искусством комбинаторных
1 Приведены всевозможные синонимы слов «перечислять», «считать»,
«подсчитывать», «пересчитывать» и т. д. — Прим. перев,

8 Предисловие
вычислений. Это — невоспетый герой Дж. Говард Редфилд, кото-
который написал всего лишь одну статью на тему о перечислении графи-
графических объектов, однако в ней он предвосхитил многие более
поздние методы и результаты. Его статья долгое время была
почти совсем неизвестна. И только после появления знаменитой
работы Пойа, послужившей толчком для многочисленных совре-
современных научных исследований в теории перечисления графов,
были по достоинству оценены заслуги Редфилда.
Хотя мы ограничиваемся рассмотрением задач перечисления
различных видов графов, существует много других типов конфи-
конфигураций, которые можно перечислить описываемыми методами.
Автоматы, конечные топологии, булевы функции, ожерелья
и химические изомеры — все эти структуры при беглом взгляде
нельзя отнести к теоретико-графовым. Однако с помощью искус-
искусных превращений все они преобразуются в графы и подграфы,
и это позволяет решить для них соответствующие задачи пере-
перечисления.
На тему каждой из десяти глав нашей книги можно написать
отдельную книгу; более того, уже издана целая книга по тематике
одного из параграфов первой главы — это хотя и формально
написанная, но обстоятельная монография Джона Муна под на-
названием «Перечисление помеченных деревьев». Ясно, что выбор
материала для каждой главы определялся личными вкусами.
План книги таков. Мы рассматриваем сначала (в гл. 1) поме-
помеченные графы, так как они лежат в стороне от наших главных
интересов и, кроме того, их значительно проще перечислять.
Затем в гл. 2 мы устанавливаем основную теорему перечисления
Пойа. С ее помощью мы перечисляем в главе 3 очень много разно-
разнообразных совокупностей деревьев, а потом — в гл. 4 и 5 — раз-
различные виды графов и орграфов. Глава 6 содержит доказательство
мощной теоремы, перечисления степенной группы; там же пока-
показано, как применять эту теорему. Глава 7, названная «Супер-
«Суперпозиция», посвящена задачам перечисления таких конфигураций,
которые могут быть построены путем «наложения одних объектов
на другие». Затем в гл. 8 решается задача перечисления неразло-
неразложимых графов, называемых также блоками; здесь широко исполь-
используются остроумные методы, разработанные покорителем нере-
нерешенных перечислительных задач Р. В. Робинсоном.
Некоторые математики полагают, что знание порядка вели-
величины, представляющей собой число конфигураций определенного
типа, является более важным, чем абсолютно точное представление
числа таких конфигураций в форме, непригодной для вычислений.
Мы считаем, что лучше не приводить нижние и верхние оценки,
а дать асимптотику числа конфигураций для нескольких различ-
различных графических структур. Глава 9 как раз и содержит ряд ре-
результатов по асимптотике теоретико-графовых объектов. Эти

ПРЕДИСЛОВИЕ 9
результаты по необходимости носят иллюстративный характер,
так как и по теоретико-графовой асимптотике можно написать
целую книгу. Наконец, еще одна отличительная особенность
книги: мы даем в заключительной главе новый обширный список
нерешенных задач перечисления графов.
Степень трудности упражнений меняется в широких пределах —
от весьма простых задач до очень сложных и тонких проблем.
Поэтому не все упражнения предназначены для того, чтобы
читатель дал детальные решения их. Довольно часто перечисли-
перечислительные формулы приводятся в упражнениях лишь с целью вклю-
включения соответствующей информации в книгу. Чрезвычайно много
упражнений, не помеченных как таковые, содержится и в основ-
основном тексте книги; они представлены в виде результатов, доказа-
доказательства которых опущены. Мы нумеруем формулы упорядочен-
упорядоченными тройками. Например, формула C.1.7) представляет собой
соотношение 7 в § 1 гл. 3. Полагаем, что читатель простит нам
использование таких сложных обозначений. Конец доказательства
отмечается символом ц.
Мы надеемся и верим, что настоящая книга сделает пере-
перечислительную технику более доступной и более унифицированной.
Это в свою очередь послужит стимулом для исследования откры-
открытых вопросов теории перечисления графов.
БЛАГОДАРНОСТИ
Мы весьма признательны следующим машинисткам отделения
математики Университета штата Мичиган, которые были чрезвы-
чрезвычайно любезны, деловиты, точны и быстры при подготовке не-
нескольких вариантов рукописи этой книги: Фриде Мартин, Глен-
доре Миллиган, Дарлен Робел, Терри Шаулл, Нэнси Супер,
Кэти Требилкотт, Мэри Троянович и в особенности Мэри Рэйнолдс.
Мы благодарны ряду организаций за финансовую поддержку,
оказанную нам в то время, когда мы занимались исследованиями,
связанными с перечислениями различных объектов. Хотя мы упо-
упомянем об этом вскользь, но очень приятно отметить, что один
из нас пользовался субсидией Ведомства военно-морских исследо-
исследований, когда мы в 1966/67 г. приступили к работе над книгой
в Лондонском университетском колледже, где нас радушно при-
принимал К. А. Роджерс. В самое последнее время мы получали
в летние периоды финансовую помощь от Ведомства научных
исследований при ВВС и Национального научного фонда.
Мы благодарны всем тем, о ком упоминается в ссылках. Полез-
Полезные критические замечания были в разное время сделаны Б. Ман-
велом, Р. К. Ридом, П. К. Стокмейером, Р. В. Робинсоном и
А. Дж. Швенком. Особую благодарность мы выражаем Джону
Риордану, уделившему самое пристальное внимание всей книге

10 ПРЕДИСЛОВИЕ
и давшему много полезных советов. Отметим специально, что
каждый из нас благодарит другого.
Наконец, мы признательны издательству Academic Press
за его энтузиазм и эффективную поддержку, оказываемую им тео-
теории графов и комбинаторной теории. Реальное выражение этой
поддержки можно обнаружить в выходных данных тех книг,
которые помещены в списке литературы, а также в существовании
первого журнала, посвященного этому пленительному направле-
направлению в математике, Journal of Combinatorial Theory, выходящему
под редакцией Ф. Харари и Дж.-К. Рота.
Мы готовы заплатить десять центов за всякую опечатку1
(по курсу американского доллара) каждому, кто первый сообщит
о ней любому из нас. Не в пример Гилберту и Сулливану после
этого не перестанем разговаривать друг с другом, а в отличие
от Аллендорфера и Оукли не будем сваливать вину за опечатки
один на другого, а просто объединим усилия, чтобы свалить все
на издателя.
Анн Арбор_ Мичиган ; м„:)у>;н o?v Л"! ' Фрэнк Харари
Западный "" -- —
Мичиган
Западйый Лансинг, ^%;^ •■';, jv^jj^7'-fvv^ f\. -'■ ■■'■••;■ Эдгар М, Палмер
АяглиДсиого
, -• Прим,
S" <■
\\
и -
">> ' О )«, i
4
" ',■:! ''"О! о*

•■■ '--.I '■'■■■(>№''■'' !■-•'*»<• HU\ ivrJl'J i LfU
я тебя люблю?
Дозволь мне перечесть.
Элизабет Баррет Браунинг
Посвящается Джейн и Джепи
IS4-
Яе полагайся без сомнений
Ты на любые ярлыки:
Они от истинных суждений
Порою очень далеки.
Ч. X. Спурджон
Глава 1
ПЕРЕЧИСЛЕНИЕ t u,. -'-'
ПОМЕЧЕННЫХ ОБЪЕКТОВ
Мы рассматриваем в первую очередь задачи перечисления поме-
помеченных объектов; эти задачи всегда решаются значительно легче,
чем соответствующие задачи для непомеченных объектов. Напри-
Например, число помеченных графов немедленно находится с помощью
элементарных соображений, тогда как определение числа непоме-
непомеченных графов требует использования мощных средств из комби-
комбинаторной теории, включая теорему Пойа.
Мы представим в этой главе избранные образцы некоторых
выдающихся и интересных решений ряда задач перечисления
помеченных объектов в теории графов, включая нахождение
числа помеченных графов, связных графов, блоков, эйлеровых
графов, /с-раскрашенных графов, ациклических орграфов, деревьев
и эйлеровых котгуров в эйлеровом орграфе. Часто будут даваться
несколько различных решений одной и той же задачи, так что чи-
читатель сможет познакомиться с большим разнообразием полезных
приемов, методов, подходов и схем. Например, мы увидим, что
когда имеешь дело с задачами перечисления помеченных объектов,
то экспоненциальные производящие функции оказываются есте-
естественным средством для запоминания информации, достаточной
Для решения. С другой стороны, исследуя незначительное коли-
количество данных, можно часто найти очень быстро требуемую фор-
формулу, истинность которой можно затем установить по индукции.

12 ГЛ. 1. ПЕРЕЧИСЛЕНИЕ ПОМЕЧЕННЫХ ОБЪЕКТОВ
1.1. ЧИСЛО СПОСОБОВ, КОТОРЫМИ МОЖНО ПОМЕТИТЬ ГРАФ
Граф G порядка р состоит из конечного непустого множества
V = V (G), содержащего р вершин, и множества X из q неупоря-
неупорядоченных пар различных вершин; при таком определении авто-
автоматически исключаются петли (ребра, соединяющие вершину
с ней самой) и кратные (параллельные) ребра. Пара х = {и, v}
вершин, принадлежащая множеству X, называется ребром графа
G и говорят, что ребро х соединяет вершины и и v. Вершины и ъ v
называются при этом смежными; вершина и и ребро х, так же
как вершина v и ребро х, называются инцидентными друг другу.
Граф с р вершинами и q ребрами называется (р, q)-epa(f)OM. Наша
терминология согласуется с той, которая принята в книге Харари
[1]. Однако мы предполагаем дать большую часть определений.
"i* Pli
г* К»
Рис. 1.1.1 Граф с четырьмя вершинами и пятью ребрами.
Значительно удобнее и нагляднее представлять графы диаграм-
диаграммами. Рассмотрим граф G, выбранный случайным образом, с мно-
множеством вершин V = {vv vit v3, y4} и множеством ребер
= {{vi, v2}, {v2, vs}, {v3, vA), {v^ vt}, {vu vs}}.
r n q a
A—4 о ii
U:r
Рис. 1.1.2 Ц графов четвертого порядка» ' f ' '
Его изображение диаграммой дано на рис. 1.1.1. На этой диаграм-
диаграмме буквами обозначены только вершины. Пять ребер графа G
представлены отрезками прямых, которые соединяют на рисунке
соответствующие пары вершин. Диаграммы всех графов четвертого
порядка, расположенные в соответствии с числом ребер в них,
приведены на рис. 1.1.2. В дальнейшем, допуская некоторое
злоупотребление языком, мы будем называть такие диаграммы
графами, и это не приведет к путанице.

1.1. ЧИСЛО СПОСОБОВ, КОТОРЫМИ МОЖНО ПОМЕТИТЬ ГРАФ 13
В помеченном графе порядка р вершинам приписываются
целые числа от 1 дор. Например, граф, изображенный на рис. 1.1.1,
может быть помечен шестью различными способами, которые
указаны на рис. 1.1.3.
Таким образом, два помеченных графа Gx и G2 считаются
одинаковыми и называются изоморфными тогда и только тогда,
когда существует взаимно однозначное отображение множества
V (Gt) на множество V (G2), сохраняющее не только смежность,
но и распределение пометок. Легко убедиться в том, что на
рис. 1.1.3 представлены все различные распределения пометок
у графа, изображенного на рис. 1.1.1.
Возникают два естественных вопроса. Первый: «Сколько су-
существует помеченных графов порядка рЪ Второй: «Сколько су-
существует графов порядка р?» Первый вопрос настолько легок,
14 14 13 24 23 52
52 23 24 13 14 14
Рис. 1.1.3 Шесть различных распределений пометок в графе. -; •'?'■' ■■
что мы его обсудим сейчас же. Второй вопрос значительно труднее
и будет исследоваться в гл. 4.
Мы ответим на легкий вопрос, незначительно обобщив задачу
следующим образом: найти число помеченных графов с данным
числом вершин и ребер. Пусть Gp (x) — многочлен, у которого
коэффициент при xk равен числу помеченных графов порядка р,
имеющих ровно к ребер. Такой многочлен обычно называется
производящей функцией для помеченных графов с данным числом
вершин и ребер. Если V — множество из р вершин, то суще-
(
(Р\ „
ствует I „ I различных неупорядоченных пар этих вершин. Ь каж-
каждом помеченном графе с множеством вершин V любая пара вер-
вершин является либо смежной, либо нет. Следовательно, число
помеченных графов с к ребрами равно ( \2/ J.
к
Теорема. Производящая функция Gp (x) для помеченных графов
Порядка р задается соотношением
/»л
A.1.1)

14 ГЛ. 1. ПЕРЕЧИСЛЕНИЕ ПОМЕЧЕННЫХ ОБЪЕМОВ
Так как Gp(x) = (l -f x)m и число Gp помеченных графов по-
порядка р равно Gp(l), то
Gp = 2v2/. A.1.2)
Для р = 3 эта формула ярко иллюстрируется рис. 1.1.4.
Таким образом, существуют восемь помеченных графов порядка 3
и только четыре (непомеченных) графа порядка 3. Существуют
64 помеченных графа порядка 4, но только 11 графов порядка 4.
Тогда возникает вопрос: «Сколькими способами можно пометить
данный граф?» Чтобы ответить на этот вопрос, мы должны рассмот-
рассмотреть симметрии, или автоморфизмы, графа. Взаимно однозначное
отображение а множества V (G) на множество V (G1), сохраня-
сохраняющее смежность, обычно называется изоморфизмом. Если G1 = G,
Рис. 1.1.4 Восемь помеченных графов третьего порядка. s „, .<j
то ос является автоморфизмом графа G. Совокупность всех авто-
автоморфизмов графа G, обозначаемая Г (G), образует группу, назы-
называемую группой графа G. Таким образом, элементы группы Г (G)
являются подстановками, действующими на множестве V. Напри-
Например, граф G, изображенный на рис. 1.1.1, имеет в точности четыре
автоморфизма, так что Г (G) содержит следующие подстановки,
записанные здесь с использованием обычного представления
в виде произведения циклов:
Пусть s (G) — | Г (G) | — порядок группы Г (G), обозначающий
число симметрии графа G. Тогда ответ на задачу распределения
пометок, поставленную выше, содержится в следующей теореме.
Теорема. Число способов распределения пометок в данном
графе G порядка р равно
l(G)=p\/s(G). A.1.3)
Доказательство этого утверждения наиболее легко получается,
если использовать теоретико-групповые результаты из гл. 2 и 4
(см. Харари, Палмер, "Рид [1]). Для иллюстрации теоремы мы
просто заметим, что граф G на рис. 1.1.1 имеет p\/s (G) = 4!/4 =
= 6 распределений пометок и шесть различных помеченных гра-

щ
1,1, ЧИШ10 0ПО0ОБОВ; КОТОРЫМИ МОЖНО ПОМЕТИТЬ ГРАФ 15
фов, показанных на рис. 1.1.3, полностью подтверждают формулу
A.1.3) для этого графа G.
Хотя эта теорема сформулирована только для графов, подоб-
подобные ей утверждения справедливы для любых конечных структур
с заданными группами автоморфизмов, таких, как графы с корнями,
орграфы, другие отношения различных типов, симплициальные
комплексы, функции и т. д.
Ориентированный граф, или орграф, D порядка р состоит
из конечного непустого множества V различных объектов, назы-
называемых вершинами, вместе с заданным множеством X, содержащим
Kt О
Л. Л А
<:\ Л/:;Л
< Н
.„ .•■'ч'% -'"■"■ <^> ••'-,
Рис. 1.1.5 16 орграфов третьего порядка. -,'<
q упорядоченных пар различных вершин из множества V. Пара
х = {и, v) точек из множества X называется дугой орграфа D,
и говорят, что вершина и смежна к вершине у; вершина и и дуга х
являются инцидентными друг другу, так же как вершина v
и дуга х. Полу степенью исхода вершины и называется число дуг,
для которых вершина и является первой вершиной; полустепенъю
вахода вершины и называется число дуг, для которых вершина м
является второй вершиной. Диаграммы всех орграфов порядка 3
показаны на рис. 1.1.5. Как и в случае графов, мы обращаемся
с диаграммами орграфов, как с самими орграфами.
В помеченных орграфах порядка р вершинам приписываются
целые числа от 1 до р, и группа орграфа D, обозначаемая Г (D),
состоит из всех подстановок множества вершин V (D) орграфа D,
сохраняющих смежность. Так как число помеченных орграфов
(р(р — 1)\
I , I,
порядка р, имеющих в точности к ребер, равно I , 1, то по-
получаем следующие результаты, которые соответствуют формулам
A.1.1) и A.1.2).

16 ГЛ. 1. ПЕРЕЧИСЛЕНИЕ ПОМЕЧЕННЫХ ОБЪЕКТОВ
Теорема. Производящая функция Dp (х) для полеченных оргра~
фов порядка р задается соотношением
'I (Р (Р1}) A.1.4)
Очевидно, что Dp(x) = Gl(x), так что
DpA) = 2p(p-i> = G*A). '" ' A.1.5)
В круговом турнире заданное множество игроков ведут игру,
правилами которой запрещен ничейный исход. Любые два игрока
встречаются между собой только один раз, и лишь один из них
одерживает победу. Следовательно, турнир представляет собой
орграф, в котором каждая пара вершин соединяется только одной
232323232J2323
Рис. 1.1.6 Восемь помеченных турниров третьего порядка.
дугой. Мы завершим этот параграф замечанием, что число поме-
П
ченных турниров порядка р равно в точности 2V , т. е. такое же,
как и число помеченных графов порядка р, определяемое по фор-
формуле A.1.2). Это наблюдение подтверждается для р = 3 рисун-
рисунками 1.1.4 и 1.1.6. Более того, естественное соответствие между
этими двумя классами графов указывается тем порядком, в ко-
котором графы размещены на этих двух рисунках. Каждый поме-
помеченный турнир соответствует тому помеченному графу, в котором
вершины с пометками i и j смежны тогда и только тогда, когда
i <C j и дуга (i, /) имеется в турнире.
1.2. СВЯЗНЫЕ ГРАФЫ
Пусть G — граф и v0, vv v2, . . ., vn — последовательность
вершин графа G, такая, что вершина vt смежна с вершиной vi+1
при t = 0, 1, ..., п — 1. Такая последовательность вместе с п
ребрами {vt, vi+1}, 0 ^ i ^п — 1, называется маршрутом
длины п. Если ребра в маршруте различные, то он называется
цепью. Если в маршруте различны все вершины (а следовательно,
п ребра), то он называется простой цепью. Связным графом назы-
называется граф, в которомлюбые две различные вершины соединены
простой цепью (рис. 1.2.1). Число помеченных связных графов
порядка 4 может быть вычислено тривиальным образом, если
мы применим формулу A.1.3) к каждому из шести графов, изо-

1.2. СВЯЗНЫЕ ГРАФЫ 17
браженных на рис 1.2.1 Порядки групп этих графов, если идти
сл^ва направо, равны соответственно 2, 6, 2, 8. 4. 24 Поэтому
из формулы A.1.3) следует, что число помеченных связных гра ов
четвертого порядка равно 38. Этот результат не дал никакого
указания, которое помогло бы найти формулу для Ср — числа
связных помеченных графов порядка р. Чтобы достичь этой цели,
нам потребуется несколько определений.
Подграф Н графа G имеет V (Я) с V (G) и Х(Я)с1 (G).
Компонента графа представляет собой максимальный связный
подграф. Граф с корнем (или корневой граф) имеет одну выделен-
выделенную вершину, называемую корнем. Два корневых графа назы-
называются изоморфными, если существует взаимно однозначная
функция, отображающая множество вершин одного графа на
множество вершин другого графа, которая сохраняет не только
смежность, но и корни 1. Аналогичное требование накладывается
и при описании корневых помеченных графов. Эти понятия можно
Рис. 1.2.1 Шесть связных графов четвертого порядка.
сейчас использовать для получения следующей рекурсивной
формулы.
Теорема. Число Ср связных помеченных графов удовлетворяет
соотношению
2 Ck- " A'21)
Чтобы доказать A.2.1), заметим, что если в помеченном графе
делать корнями разные вершины, то получатся разные корневые
помеченные графы. Следовательно, число корневых помеченных
графов порядка р равно pGp. Число корневых помеченных графов,
в которых корень находится в компоненте, содержащей в точности
к вершин, равно kCk I , I Gp.k. Суммируя эти произведения по к
от 1 до р, мы опять получаем выражение для числа корневых
помеченных графов, а именно
х То есть переводит корень одного графа в корень другого графа, —
Прим, перев,^ * .. .»

18 РЛ. 1. ПЕРЕЧИСЛЕНИИ ПОМЕЧЕННЫХ ОБЪЕКТОВ
Значения Ср, приведенные в табл. 1.2.1, помещены в книге
Слоуэна [1].
р
Ср
i
1
2
1
3
4
4
38
5
728
6
26 704
1
7
866 256
251
8
548 592
Таблица 1.2.1
9
66 296 291 072
Важно иметь наготове понятие экспоненциальной производящей
функции и несколько свойств такой функции. Мы поэтому введем
сейчас эти функции и воспользуемся ими, чтобы получить другой
вид формулы A.2.1).
Для всякого к = 1, 2, 3,. . . обозначим через а* число способов,
которыми можно пометить все графы порядка к, обладающие
некоторым свойством Р (а). Тогда формальный степенной ряд
■ < 'i ос 'Ч Ц' ' '
■■'.-• I•• -• вA) = 2(ц#1 ».J& t. ..„ A.2.2)
k-i •"■ ■
называется экспоненциальной производящей функцией для класса
всех графов, рассматриваемых нами в данном случае. Предпо-
Предположим также, что
bkzk/k\ • A.2.3)
другая экспоненциальная производящая функция для класса
графов, удовлетворяющих свойству Р (Ь).
Следующая -лемма дает полезную интерпретацию коэффициен-
коэффициентов произведения а (х) Ь (х) этих двух производящих функций.
Лемма пересчета помеченных графов. Коэффициент при хЧМ
в а (х)Ъ (х) равен числу упорядоченных пар {Gu G2) двух непересе-
непересекающихся графов, где Gx обладает свойством Р (a), Gt обладает
свойством Р (Ь), к — число вершин в Gx U Ga и пометки от 1
до к распределены на графе Gx (J Ga.
Для иллюстрации этой леммы положим, что С (х) — экспонен-
экспоненциальная производящая функция для помеченных связных графов:
С (х) - S Скз*[к |. A.2.4)
k-i
Тогда С {х)С (х) является производящей функцией для упорядо-
упорядоченных пар помеченных связных графов. Разделив этот ряд на 2,
получаем производящую функцию для помеченных графов, име-

щ
1.3. БЛОКИ 19
ющих в точности две компоненты. Аналогично, Сп (хIп\ имеет
при хк/к\ коэффициент, равный числу помеченных графов порядка
к, содержащих в точности п компонент. Если через G (х) обозначим
экспоненциальную производящую функцию для помеченных гра-
графов, то тогда
G(*) = 2 O(x)/nl A.2.5)
п-1
Таким образом, мы имеем следующее экспоненциальное соотно-
соотношение между G (х) и С (х), найденное Ридделом [1].
Теорема. Экспоненциальные производящие функции G (х) и
С (х) для помеченных графов и помеченных связных графов удовлет-
удовлетворяют соотношению
1+G (*)-««*). A.2.6)
Заметим, что A.2.6) остается справедливым и для мультигра-
фов (Гилберт [11). Риордан обратил внимание на замечательное
равенство: Ср = Jp B), где Jр (х) — функция, перечисляющая
деревья с помощью числа инверсий (см. Моллоус и Риордан [1 ]),
и, таким образом, получил следующее рекуррентное соотношение
для Ср:
р-Чр-2\
Кроме того, очевидно, что если известна экспоненциальная
производящая функция для некоторого класса графов, то экс-
экспоненциальная производящая функция для соответствующих
связных графов получается формальным логарифмированием
первого ряда, точно так же как в A.2.6) для всех графов.
Поэтому мы можем сформулировать следующий общий резуль-
результат.
Если 2 4ma:m = exp( 2 атхт\, то для т$* 1
m-o W-i /
т-1
ат = Ат - -А- ^ kakAm.k. A.2.8)
t.3 БЛОКИ
Удаление вершины v из графа G приводит к подграфу G — v
графа G, состоящему из всех вершин графа G, за исключением
вершины v, и всех ребер графа G, не инцидентных вершине v.
Точкой сочленения графа называется такая его вершина, удаление

20 Ml. 1. ПЕРЕЧИСЛЕНИЕ ЙОМЕЧЕЙНЫХ ОБЪЕКТОВ
которой повышает число компонент. Блоксм, или неразложимым
графом, называется связный нетр] вирльный граф, не имеющий
точек сочленения. Мы будем следовать методике Риддела [1]
и Форда и Уленбека [1] при установлении взаимосвязи межлу
производящими функциями для помеченных блоков и помеченных
связных графов. Применяемый здесь подход успешен тольы)
в случае помеченных объектов. В гл. 8 мы увидим, что для пере-
перечисления непомеченных блоков требуется гораздо более сложный
метод.
Так как мы занимаемся задачей перечисления помеченных
объектов, то будем использовать экспоненциальные производя-
2 6 8 М ^^ ~
Рис. 1.3.1 Наименьшие блоки и их числа симметрии. '■• ■ •'• ■ * ~' ">'■■>
щие функции. Пусть В {х) обозначает ряд для пометанных блоков,
так что
A.3.1)
р=2
где Вр — число блоков с р вершинами. Как следует из формулы
A.1.3), приведенной в теореме о числе способов распределения
пометок в графе, коэффициент при хр в В (х) равен сумме величин,
обратных к порядкам групп (непомеченных) блоков с р вершинами.
Следовательно, используя рис. 1.3.1, на котором изображены
наименьшие блоки вместе с порядками их групп, мы получаем
несколько первых членов ряда В (х):
Наша цель состоит в том, чтобы доказать следующую теорему,
где С (х) и В' (х) обозначают обычные формальные производные.
Теорема. Экспоненциальные производящие функции В (х) и
С (х) для помеченных блоков и связных графов удовлетворяют соот-
соотношению
Jn С (х) = В1 (хС (х)). A.3.3)
Чтобы проверить это тождество, обозначим через R (х) экспо-
экспоненциальную производящую функцию для корневых связных поме-

щ
1.8. БЛОКИ 21
ценных графов, так что коэффициент при хр в R (х) есть Rplp\.
Так как Лр == рСр для всех р, то мы имеем равенство
R(x) = xdC(x)/dx. A.3.4)
Обозначим через Rn (x) экспоненциальный ряд для корневых
связных помеченных графов, в которых точно п блоков содержат
корень. Таким образом, Ro (х) = хи
ед = £ Rn(x). и"'., " A.3.5)
п-о
Кроме того, i?! (x) перечисляет корневые связные помеченные
графы, у которых только один блок инцидентен корню. Пред-
Предположим, что S (х) — соответствующий ряд для того случая,
когда корень не помечен, т. е. коэффициент при хр\ равен числу
корневых связных графов с р + 1 вершинами, у которых корень
не помечен. Тогда из леммы пересчета помеченных графов следует,
что i?! (х) — xS (х) и, следовательно, S (х) = i?x (x)/x.
По этой же лемме ряд (Rt (x)lx)nln\ перечисляет п-множества
таких графов, причем каждый корень не помечен. Если эти п
корней отождествить и ввести для них одну пометку, то будем
иметь перечисление корневых помеченных связных графов, у ко-
которых точно п блоков примыкают к корню. Восстановление по-
помеченного корня завершается просто умножением на х:
Rn{x)^x(R1(x)/x)n/nl A.3.6)
Комбинируя две последние формулы, получаем соотношение
1(x)/x). A.3.7)
Теперь мы попытаемся выразить Rt (x) через В (х) и R (х).
Замечаем, что ряд (R (хIх)к~1 перечисляет наборы из к — 1
корневых помеченных связных графов, причем в этих наборах
к — 1 корней не помечаются и не включаются в число подсчиты-
подсчитываемых вершин. Другими словами, коэффициент при хР/р\ в этом
ряду представляет собой число наборов, каждый из которых
состоит из А; — 1 корневых графов; корни графов не помечены,
и общее число вершин в наборе, включая и корни, равно р + к — 1.
Умножая этот ряд на kBk, получаем ряд, перечисляющий корне-
корневые связные графы, у которых к корню примыкает один блок и для
пометки этого блока используются только числа от 1 до к. Нако-
Наконец, чтобы учесть распределение всех пометок, нам нужно только
умножить все на хЧк\. Следовательно, ряд xBk (R(x))k-ll(k — 1)!
перечисляет корневые помеченные связные графы, у которых

22 ГЛ. 1. ПЕРЕЧИСЛЕНИЕ ПОМЕЧЕННЫХ ОБЪЕКТОВ
к корню примыкает точно один блок порядка к. Суммируя по к,
получаем соотношение
у
/?i (*) = *! Bk(R(x))"-i/(k-i)l A.3.8)
Комбинируя две последние формулы, каждая из которых содержит
R1 (x), получаем следующий результат:
\n(R{x)lx) = f1Bk(R(x)f-^l{k-\)\. A.3.9)
Для завершения доказательства надо подставить R (х) =
= х-С (х) из A.3.4) в A.3.9).и
Сравнивая коэффициенты при хр в выражениях, стоящих в ле-
левой и правой частях формулы A.3.3), мы можем прийти к рекур-
рекурсивной формуле для Вр. Коэффициент при хр в левой части фор-
формулы A.3.3) может быть выражен через коэффициенты функции
С (х), если использовать соотношение A.2.8). Для удобства обо-
обозначим через h (p, к) коэффициент при хр{ в (хС {х))к, так что ко-
коэффициент при хр в правой части формулы A.3.3) есть
ЕВ»А(Р, к-1)/(к-1)\. A.3.10)
Следовательно, число Вр помеченных блоков может быть вы-
выражено через числа Ср помеченных связных графов, если исполь-
использовать соотношение A.3.3). Описанный здесь метод можно без
особых затруднений расширить так, чтобы включить в качестве
второго параметра число ребер.
1Л. ЭЙЛЕРОВЫ ГРАФЫ
В этом параграфе мы выведем, следуя довольно точно методике
Рида [5], производящую функцию для помеченных эйлеровых
графов. Степенью вершины v (обозначается через deg v) в графе G
называется число ребер графа G, инцидентных вершине v. Если
каждая вершина графа G имеет четную степень, то граф называ-
называется четным. Эйлеров граф — это связный четный граф.
Пусть Wp — число помеченных четных графов порядка р.
Тогда имеет место следующий несколько неожиданный результат.
Теорема. Число помеченных четных графов порядка р равно
числу помеченных графов порядка р — 1:
(р-1\
Wp = 2K*>. ' A.4,1)

j.4. ЭЙЛЕРОВЫ ГРАФЫ 2В
Чтобы доказать этот результат, мы сейчас установим взаимно
однозначное соответствие между этими двумя классами графов.
Рассмотрим произвольный помеченный граф G порядка р — 1.
Граф G должен иметь четное число вершин нечетной степени.
Добавим к нему вершину v, которой припишем пометку р. Наконец,
из графа G и вершины v строим граф G', соединяя вершину v с каж-
каждой вершиной графа G, имеющей нечетную степень. Этот граф G'
является помеченным четным графом порядка р. Легко видеть,
что описанное соответствие является взаимно однозначным и что
каждый помеченный четный граф порядка р может быть получен
таким способом из некоторого помеченного графа порядка р — 1 .щ
Чтобы получить формулу для числа помеченных эйлеровых
графов, мы будем использовать производящие функции. Итак,
пусть W (х) — экспоненциальная производящая функция для
помеченных четных графов, так что
W(x)-=f, 2^^xPjpl. A.4.2)
p-i
Далее, пусть Up — число помеченных эйлеровых графов
порядка р, так что
' ' fp\ ;'*-iv4 A.4.3)
является соответствующей экспоненциальной производящей функ-
функцией.
Теорема. Экспоненциальная производящая функция U (я) для
помеченных эйлеровых графов удовлетворяет соотношениям
U(x) = ln(W(x)+l) A.4.4)
и)
т2*и
*1
2 2 Uk- AA5)
Формула A.4.4) следует из того факта, упомянутого после ра-
равенства A.2.6), что если известна производящая функция для
произвольного класса графов, то производящая функция для соот-
соответствующих связных графов получается с помощью формального
логарифмирования первого ряда. Рекуррентное соотношение
A.4.5) для Up является следствием формул A.4.4) и A.2.8).и
Для нескольких первых членов ряда U (х) имеем равенство
+.... AА6)

24 ГЛ. t. ПЕРЕЧИСЛЕНИЕ ПОМЕЧЕННЫХ ОБЪЕКТОВ
Четыре эйлеровых графа порядка 5 показаны на рис. 1.4.1
вместе с порядками их групп. Согласно формуле A.1.3), величины,
- 38
обратные к этим числам, должны дать в сумме число -т-т, которое
о 1
представляет собой коэффициент при х5 в ряде U (х). И они в самом
деле дают это число.
Далее мы рассмотрим более трудную задачу — определение
числа помеченных эйлеровых графов с заданным числом вершин
и ребер. Попытаемся установить следующий результат Рида [5].
Ю 8 12 120
Рис. 1.4.1 Четыре эйлеровых графа пятого порядка.
Теорема. Многочлен wp (x), у которого коэффициент при х9
равен числу помеченных графов, имеющих р вершин четной степени
и q ребер, задается формулой
D^)A.4.7,
Для малых значений р находим, что
w1(x) = w2(x)~l, w3(x) = i + xs и wt (x) =
Доказательство. Пусть L — множество всех помеченных гра-
графов порядка р, имеющих в точности q ребер. Рассмотрим какой-
либо граф G из множества L и произвольным образом умножим
каждую из пометок 1, . . ., р на +1 или —1. Так как пометки бу-
будут положительными и отрицательными, то каждую вершину
можно рассматривать как «положительную» или «отрицательную»
в зависимости от знака ее пометки. Каждому ребру приписывается
тогда число +1 или —1, равное произведению знаков вершин,
инцидентных этому ребру. Знак графа G (обозначается через a (G))
тогда определяется как произведение знаков его ребер. Очевидно,
что существует 2Р способов, которыми могут быть приписаны
знаки пометкам данного графа. С другой стороны, предположим,
что знаки уже распределены по р целым числам, которые служат
пометками; тогда существует I £ I разных графов с q ребрами и с
такими р вершинами, знаки которых определены в соответствии
с данным распределением знаков в множестве пометок. Эти по-
понятия проиллюстрированы на рис. 1.4-3-

1.4.
ГРАФЫ
25
Так как о (G) есть знак произведения положительных и отри-
отрицательных чисел, отвечающих смежным вершинам, то положи-
положительные вершины в этом произведении можно опустить. Таким
образом,
о(С) = (-1)°, A.4.8)
где а — сумма степеней отрицательных вершин. С другой стороны,
очевидно, что t
o(G) = (-l)»f A.4.9)
где Ъ — число отрицательных ребер графа G, каждое из которых
соединяет отрицательную вершину с положительной вершиной.
в,- *1
♦,
-з
62: -1
-I
+ 2 -1 -3 -4-1
Рис. 1.4.2 Два графа, имеющие один и тот же знак.
+2
Далее рассмотрим сумму 2° (£)» гДе суммирование ведется
по всем помеченным графам из множества £ м по множеству S,
состоящему из 2? возможных распределений чисел +1 и —1 по
пометкам, сопоставленным вершинам. Как следует из выражений
A.4.8) и A.4.9), эту сумму можно записать двумя различными
способами:
"; A.4.10)
12
G&L (S
Сначала рассмотрим левую часть соотношения A.4.10). Если
G — четный граф, то а — четное число при любых распределениях
из множества S. Следовательно, 2 (—1)" — 2р и граф G вносит 2р
в левую часть соотношения A.4.10). Если граф Сне является чет-
четным, то хотя бы одна его вершина v имеет нечетную степень. Под-
Подмножество распределений из S, для которых пометка вершины v
является положительной, и подмножество распределений из S,
для которых она отрицательна, равномощны и вносят в сумму
2j (—1)" разные по знаку и одинаковые по величине количества.
Следовательно, граф G ничего не вносит в левую часть равенства
A-4.10). Таким образом, левая часть соотношения A.4.10)
равна 2", взятому столько раз, сколько четных графов в множе-
множестве L. .
Далее мы сосредоточим внимание на правой части равенства
A.4.10) и рассмотрим такое распределение из множества S, для

26 ГЛ. 1. ПЕРЕЧИСЛЕНИЕ ПОМЕЧЕННЫХ ОБЪЕКТОВ
которого п вершин положительны и т = р — п отрицательны.
Существует! ) таких распределений. Если выбираются к ребер,
соединяющих положительные вершины с отрицательными, то
(пт\
, I различными способами. Удаление q — к
ребер можно осуществить
^ \2П : • ; > ,. ^ A.4.И)
разнша способами. Суммируя по А; от 0 до q, получаем выражение
k-o
которое вносится в правую часть соотношения A.4.10) каждым
распределением (из множества S) с данными вит. Это выражение
представляет собой коэффициент при & в многочлене
A_д;)птA _|_^n(n-l)/2+m(m-l)/2# „ A.4.13)
Поэтому правая часть равенства A.4.10) является коэффи-
коэффициентом нри ocfl в сумме и
2 1A— x)nm(l+x)"("-i)/2+m(»n-i)/a • • A.4.14)
n-о \Н/
и этот коэффициент равен 2р, взятому столько раз, сколько чет-
четных графов в. L. Замечая, что
мы получаем окончательный результат: искомое число четных
графов равно коэффициенту при зУ в выражении, стоящем в пра-
правой части формулы A.4.7).и
Заметим, кстати, что общее число помеченных четных графов
равно числу wp A), которое получается из A.4.7), если положить
х = 1 и принять соглашение, что у0 = 1, даже когда у = 0:
^ U,p(l) = 2^1)i . A.4.16)
Которое подтверждается формулой A.4.1). ,

(.5, ЧИСЛО А-РАСКРАШЕННЫХ ГРАФОВ • ' 27
Можно воспользоваться формулой A.4.7), чтобы получить
многочлен
Wb (#) = 1 -f- 10а^4- 15а;4 + 12а;5-)- 15а;6 -f- 10a;7 -f- a;10, A.4.17)
а 64 помеченных четных графа, перечисляемых многочленом
ц>5 (а;), можно построить, исходя из семи четных графов, изобра-
изображенных на рис. 1.4.3.
Экспоненциальная производящая функция w (а;, у), пере-
перечисляющая все помеченные четные графы, задается соотношением
оо
и>(х, у) = 2 wР(Х)УР/Р*- ■ A.4.18)
V-1
10 8 12 120
Рис. 1.4.3 Четные графы пятого порядка и их числа симметрии.
Чтобы получить производящую функцию и (х, у) для помеченных
эйлеровых графов, имеющих данное число вершин и ребер, нам
нужно только прологарифмировать ряд 1 + w (x, у):
и(х, y) = ln(l + w(x, у)). J A.4.19)
Это замечание следует из варианта леммы пересчета домеченных
графов для случая двух переменных. ; ": ..
X ■■ г-- <f ■.• .•■■ ::«!
1.5. ЧИСЛО /i-РАСКРАШЕННЫХ ГРАФОВ ,„: '...,.',',,
Раскрашенный граф состоит из графа G с множеством вершин V
и такого отношения эквивалентности на множестве V, что любые
смежные вершины не эквивалентны, к классов эквивалентности
рассматриваются как различные цвета и граф G называется
^-раскрашенным. Два ^-раскрашенных графа изоморфны, если
существует взаимно однозначное соответствие между их множе-
множествами вершин, которое сохраняет не только смежность, но и цвета.
Заметим, что цвета не закреплены постоянно, а являются взаимо-
взаимозаменяемыми. Данный граф может быть /е-раскрашен многими
способами. Например, все 3-раскраски некоторого помеченного
графа порядка 6 показаны на рис. 1.5.1, где буквы а, Ь и с обо-
обозначают цвета, а натуральные числа обозначают пометки.
Следуя Риду [2], и обобщая результат Гилберта [1], мы найдем
формулу для числа домеченных А;-раскрашенных графов порядка р.

28
ГЛ. 1. ПЕРЕЧИСЛЕНИЕ ПОМЕЧЕННЫХ ОБЪЕКТОВ
Пусть рх, . . ., Pk — целые положительные числа, образующие
упорядоченное разбиение числа р, так что
2
A.5.1)
Если через {р} обозначить произвольное решение уравнения
A.5.1), то теорему (и формулу) Рида можно записать в следующей
форме.
Теорема. Число Ср (к) к-раскрашенных помеченных графов
порядка р равно
6 4 а с
Рис. 1.5.1 Все 3-раскраски графа.
Доказательство. Заметим, что число ^-раскрашенных поме-
помеченных графов порядка р, в которых цвета фиксированы,
равно к\Ср (к). Поэтому мы сейчас рассмотрим к фиксированных
цветов. Каждое решение {р} уравнения A.5.1) определяет упоря-
упорядоченное разбиение числа р на к частей, и поэтому мы ищем число
помеченных графов, у которых р{ вершин имеют г-й цвет. Число
способов, которыми могут быть выбраны пометки для вершин,
дается полиномиальным коэффициентом ,,
KPl, Pi, • . м Pk
Очевидно* что существуют
пар вершин, имеющих различные цвета. Так как каждая такая
пара может быть либр смежной, либо нет, то, возводя 2 в степень,
равную выражению A.5.3), и используя равенство A.5.1), мы по-
получаем для общего числа графов с pt вершинами цвета i в точности
то выражение, которое стоит под знаком суммы в формуле A.5.2).

1,5 ЧИСЛО ft-РАСКРАШЕННЫХ ГРАФОВ 29
Суммируя по всем решениям {р} уравнения A.5.1), получаем
произведение к\ Ср (к). Тем самым формула A.5.2) доказана.^
Заметим, что коэффициент при & в многочлене
р
равен числу А;-раскрашенных помеченных (р, д)-графов. Приме-
Применяя, например, это утверждение в случае р = 4, q = 5 и к —■ В,
получим число шесть — число 3-раскрашенных помеченных
D, 5)-графов. В справедливости этого результата легко убедиться
непосредственно, ибо существует лишь один непомеченный D, 5)-
граф и он может быть помечен шестью способами, как это показано
на рис. 1.1.3.
Рекурсивную формулу для Ср (к) нетрудно получить как
следствие:
Р-1 I v
СР (к) = 4" 2 („) 2«>-*)Ся (к-1). A.5.4)
Проверку формулы A.5.4) можно осуществить, выразив произ-
производящую функцию для Ср (к) через производящую функцию Ср (к —
— 1). Значения произведения к\Ср (к) для р ^ 7 приводятся у Рида
12] и были использованы нами при составлении табл. 1.5.1.
Таблица 1.5.1
X
1
2
3
4
5
6
7
1
1
1
1
1
1
1
1
>ч> 2
0
2
12
80
720
9152
165 312
3
0
0
8
192
5120
192 000
10 938 368
4
0
0
0
64
5120
450 560
56 197 120
5
0
0
0
0
1024
24 576
64 225 280
6
0
0
0
ч о
0
32 768
22 020 096
7
.:.■! ■ Q
0
1 .- 0
■■'•■ о
0
0
2 097 152
Заметим, что формула A.2.8) не позволяет * выразить произво-
производящую функцию для связных А;-раскрашенных графов в терминах
производящей функции для А;-раскрашенных графов.
1 Рид сообщил Райту, что и он (см. Рид [2]), и Райт [1] допустили ошибку,
•затем Рид и Райт, чтобы исправить положение вещей, указали в совместной
работе (см. Рид и Райт [1]) на допущенную ранее ошибку. Возможно, что все
РшгуШГЛЯдело несколько иначе, ибо Райт утверждает, что он первый написал

30 ГЛ. 1. ПЕРЕЧИСЛЕНИЕ ПОМЕЧЕННЫХ ОБЪЕКТОВ
1.6. АЦИКЛИЧЕСКИЕ ОРГРАФЫ
Маршрут J длины п в орграфе D внределяется последователь-
последовательностью своих вершин v0, иг, . . ., vn, в которой вершина vt смежна
к вершине vi+1 при / <; п. В замкнутом маршруте начальная
и конечная вершины совпадают. Контур 2 представляет собой
нетривиальный замкнутый маршрут, все вершины которого, исклю-
исключая первую и последнюю, различны. Ациклический орграф не имеет
контуров. Перечисление помеченных ациклических орграфов
довольно легко сейчас осуществить, следуя работе Робинсона [4].
В то же время случай непомеченных ациклических орграфов
требует более мощной техники, которая развивается в гл. 8.
Орграф Е называется расширением орграфа D, если D яв-
является ориентированным подграфом орграфа Е, порожденным под-
подмножеством тех вершин орграфа Е, которые имеют положительные
Рис. 1.6.1 Расширение ациклического орграфа.-
полустепени захода. Каждый ациклический орграф должен содер-
содержать по крайней мере одну вершину с нулевой полустепенью
захода (см. Харари, Норман, Картрайт[1], стр. 64). Следовательно,
всякий ациклический орграф, имеющий хотя бы одну дугу, яв-
является расширением единственного собственного ориентированного
подграфа. Кроме того, каждый ациклический орграф имеет много
расширений, но все они должны быть ациклическими орграфами.
Предположим, что D — ациклический орграф, имеющий в
точности п ^ 1 вершин м(-, полустепень захода которых равна
нулю, и s остальных вершин vt. Мы можем построить расширение
Е орграфа D, содержащее ровно к вершин с нулевой полустепенью
захода: добавляем к новых вершин wt и новые дуги, такие, что
каждая из п вершин и{ является смежной из некоторой новой
вершины wt (однако каждая вершина wt может быть смежной к
1 Точнее, ориентированный маршрут. Однако всюду, где из контекста
ясно, что речь идет об ориентированных объектах, слово «ориентированный»
мы будем опускать. — Прим. перев.
а В оригинале ■=- cycles — Прим. перев*

ч
1.6. АЦИКЛИЧЕСКИЕ ОРГРАФЫ 31
любой вершине v орграфа D). На рис. 1.6.1 новые (добавленные)
вершины обозначены через w,, w2 и юъ\ каждая старая вершина
Ul и и2 с нулевой полустепенью захода является смежной из не-
некоторой вершины wt.
Таким образом, все ациклические орграфы порядка р могут
быть получены с помощью расширения ациклических орграфов,
порядок которых меньше р. Детальнее, пусть ар — число поме-
помеченных ациклических орграфов порядка р и aPik — число таких
же орграфов, у которых ровно к вершин имеют нулевую полу-
полустепень захода. Если к = р, то, конечно, ар, р = 1, так как в этом
случае подходит только вполне несвязный орграф. Очевидно,
что для всех р
Сейчас мы покажем, как может быть выражено apk через ap-k,n
при п ^ р — к. Сначала мы докажем, что всевозможные расшире-
расширения всех ap_k, п орграфов с р — к вершинами, из которых в точ-
точности п вершин имеют нулевую полустепень захода, вносят в зна-
значение aPik число, равное
... V.{;; B*-l)»2*(P—*> (£) ap.k,n. A.6.2)
Мы ищем число помеченных расширений Е всех ap.k n по-
(р\
меченных ациклических орграфов D. Для каждого из I Icno-
\к I
собов расставить пометки у к новых вершин wt в расширении Е
существуют ap_k n распределений пометок в орграфах D, подле-
(р\
жащих расширению. Это объясняет множитель I a k n в выра-
\к I
жении A.6.2). Каждая из п вершин с нулевой полустепенью захода
в орграфе D должна быть смежна по крайней мере из одной новой
вершины wt A г^ i ^к). Следовательно, существуют 2* — 1 воз-
возможностей направить дуги в каждую из этих п вершин, что дает
B* — 1)" для всех вершин. Каждая новая вершина может либо
быть, либо не быть смежной ко всякой из р — п — к вершин,
имеющих в орграфе D положительную полустепень захода. Зна-
Значит, существуют 2Р~п~к возможных комбинаций для каждой
из новых вершин и, следовательно, Bp~n-k)k комбинаций для
T°X таких веРшин- Перемножая все эти выражения, получаем
.2). Суммируя A.6.2) по всеми, имеем соотношение для aptt.

32 ГЛ. 1. ПЕРЕЧИСЛЕНИЕ ПОМЕЧЕННЫХ ОБЪЕКТОВ
Теорема. Число ар, k помеченных ациклических орграфов порядка р,
имеющих ровно к вершин с нулевой полустепенъю захода, удовлет-
удовлетворяет соотношению ,,,*
«р. * = \ B* - l)n 2«*—*) (£) ap.kt „. "" A.6.3)
Таким образом, для нахождения ар можно использовать фор-
формулы A.6.1) и A.6.3). Эти результаты можно также выразить в тер-
терминах производящих функций. Пусть в ряде а (х, у) коэффициент
при xkyp-k равен числу помеченных ациклических орграфов
с р вершинами, из которых в точности к вершин имеют нулевую
/,,, у
Рае» 1.6.2 Два ациклических орграфа третьего порядка, у которых по две
вершины имеют нулевую полустепень захода.
полустепень захода. Тогда несколько первых членов ряда а (х, у)
даются выражением
а (х, у) = х+х* + 2ху
Например, существуют шесть способов расставить пометки
в ациклическом орграфе Dx и три способа расставить пометки
в ациклическом орграфе D2, изображенных на рис. 1.6.2. Всего —
девять способов, что соответствует члену $х2у в ряде а(х, у).
1.7. ДЕРЕВЬЯ
Деревом называется связный граф, не имеющий циклов (см.
Харари [1], гл. 4). Хорошо известно, что всякое нетривиальное
дерево имеет не менее двух висячих вершин (вершин степени 1),
Это следует из того, что если Т — дерево с р вершинами и q реб-
ребрами, то
g = p-i. A.7.1)
Все деревья С не более чем пятью вершинами показаны на рис.
1.7.1 (вместе с числам способов, которыми они могут быть поме-
помечены). Отсюда вытекает, что число tp помеченных деревьев с р
вершинами имеет следующие наименьшие значения: 1, 1, 3, 16(

1.7. ДЕРЕВЬЯ 33
125. Многие авторы справедливо предполагали, исходя из этой
последовательности значений, что формула Для подсчета поме-
помеченных деревьев дается следующей теоремой.
Теорема (Кэли). Число tp помеченных деревьев порядка р равно
tp = pr-*. A.7.2)
Мы дадим наброски только четырех доказательств, принадле-
принадлежащих Кэли, Прюферу, Пойа и Кирхгофу, хотя существует много
других не менее интересных, чем эти, доказательств. Собрание
таких доказательств может быть найдено в статье Муна [1], для
которой как бы продолжением является целая книга Муна [4],
посвященная подсчету различных типов помеченных деревьев.
1 1 3 12 4 60
Рис. 1.7.1 Деревья, порядки которых не выше 5, и число способов распреде- .
ления пометок у каждого из этих деревьев,
Кэли [1] высказал мысль, что существует соответствие между
помеченными деревьями и функциями, отображающими мно-
множество из р — 2 объектов в множество из р объектов. Например,
если р == 5, то существует 53 функций из {а, Ь, с) в {v^ v2, v3,
У4> иъ}- Эти функции перечисляются многочленом
^г+и2+и3 + и1 + иъу. A.7.3)
Слагаемые этого многочлена сопоставляются функциям естествен-
естественным образом. Например, v\ соответствует постоянной функции
/ (х) ~ у4, слагаемое Зг^Уд отвечает трем функциям, которые
отображают только один элемент в vu а два других — в у3, и
®v2v3vb дает шесть функций, отображающих по одному элементу
в v2, у3 и иь. Теперь, умножая многочлен A.7.3) на и^гьги^ь
и получая
v3+ v 4 + vbf v-iV^v^, A.7.4)
устанавливаем тем самым соответствие между слагаемыми из этого
произведения и помеченными деревьями порядка 5. Это соответ-
соответствие с использованием слагаемого \3 l
2 Заказ 443

34 ГЛ. 1. ПЕРЕЧИСЛЕНИЕ ПОМЕЧЕННЫХ ОБЪЕКТОВ
демонстрируется на рис. 1.7.2. Заметим, что в деревьях, соот-
соответствующих слагаемому и\и^и\и^ь, степень вершины, поме- -\
ченной числом к, равна показателю степени у v^. Справедливость
этого высказывания может быть установлена и в общем случае.
Следовательно, число помеченных деревьев, у которых вершины,
помеченные числом к, имеют степень d^, равно полиномиальному
коэффициенту
р-2
2 5 2 4
Рис. 1.7.2 Помеченные деревья, перечисляемые членом v
что доказательство, данное для этого частного случая, применимо
при любом значении р».
Прюфер [1] получил соответствие между помеченными деревь-
деревьями порядка р и наборами из р — 2 элементов (а1, а2, . . ., ар_2),
где каждое а* является целым числом от 1 до р, причем в наборах
допускаются повторения. Таким образом, имеется рР~2 таких
наборов. В заданном помеченном дереве Т возьмем висячую вер-
вершину v, имеющую наименьшую пометку, и выберем пометку аг
вершины, смежной с и. Далее, проделав такой же шаг для дерева
Т — v, находим пометку а2 (дерево Т — v получено из дерева Т
удалением вершины v и ребра, инцидентного вершине и). Этот
процесс оборвется, когда останутся только две смежные вершины.
Заметим, что дерево, изображенное на рис. 1.7.3, соответствует
последовательности B, 4, 1, 2, 4, 4).
Так как каждое помеченное дерево порядка р дает единствен-
единственный набор длины р — 2, то tp ^ рР~*.
Чтобы показать, что tp ^ рР~2, опишем некоторую проце-
процедуру, позволяющую однозначным образом строить по каждому
набору (ох, а2, . . ., ар_2) помеченное дерево. Следуя Муну [4,
стр. 5], обозначим через Ь1 наименьшее целое положительное
число, не встречающееся в наборе (ах, а2, . • ., йр-г)» и пусть
(с2, . . ., ср_2) обозначает набор длины р — 3, получающийся
ЛЯИ [1] щюиллюстрировал это соответствие для р = (
и не стал рассматривать другие случаи, заметив: «Сразу видно,

1.7. ДЕРЕВЬЯ
35
из набора (а2, . . ., ар_2) уменьшением всех его координат, боль-
больших, чем Ь1, на 1. Тогда набор (с2, . . ., ср_2) состоит из чисел,
принадлежащих множеству {1, . . ., р — 1 }, и мы можем пред-
предположить, что существует соответствующее дерево Т порядка
р — 1. Изменим распределение пометок у вершин дерева Т,
3 8
Рис. 1.7.3 Помеченное дерево восьмого порядка.
прибавляя 1 к каждой пометке, превосходящей Ъг — 1. Затем введем
р-ю вершину с пометкой Ъг и соединим ее с вершиной, помеченной
числом ttj в дереве Т. Таким образом, получили единственное
помеченное дерево, соответствующее данному набору длины р — 2.
Далее рассмотрим метод Пойа [1] для нахождения числа по-
помеченных деревьев. Так как число корневых помеченных деревьев
об
42 4
Рне. 1.7.4 3-множество корневых деревьев и соответствующее ему дерево,
корень которого имеет степень 3.
порядка р равно р ■ tp, то экспоненциальная производящая функ-
функция для этих деревьев дается выражением
У = 2 Р*рхр/Р !•
p-i
A.7.6)
Пойа нашел функциональное уравнение для у и затем для нахо-
нахождения tp применил формулу обращения Лагранжа.
Это функциональное уравнение для у будет сейчас выведено.
Из леммы пересчета помеченных графов следует, что уп/п\ явля-
является экспоненциальной производящей функцией для га-множеств
корневых помеченных деревьев. Эти га-множества соответствуют
в точности тем корневым помеченным деревьям, в которых корень
имеет степень га и не помечен. Более точно, это соответствие полу-
получается так: сначала добавляем к каждому га-множеству новую
вершину, не помечая ее, а затем соединяем эту новую вершину
2*

3ft ГЛ. 1. ПЕРЕЧИСЛЕНИЕ ПОМЕЧЕННЫХ ОБЪЕКТОВ
с каждым из старых корней. Описанная идея иллюстрируется
рис. 1.7.4. Умножение выражения уп1п\ на х отвечает приписы-
приписыванию пометки новому корню и включению его в число пересчиты-
пересчитываемых вершин. Таким образом, хуп/п\ перечисляет корневые
помеченные деревья, в которых корень имеет степень п. Сумми-
Суммируя по п, получаем
оо
У = 2 Щп1п\, , A.7.7)
и, следовательно, мы приходим к функциональному уравнению
у = хеУ. A.7.8)
Чтобы найти решение уравнения A.7.8), выразив у как функцию
от х, мы применим весьма полезный частный случай формулы
Лагранжа, приведенный в работе Муна [4, стр. 26] (см. также
Пойа [1]).
Формула обращения Лагранжа. Если функция ф (у) анали-
тична в некоторой окрестности точки у = 0 и ф @) =£ 0, то урав-
уравнение
A.7.9)
имеет единственное решение, задаваемое производящей функцией
A.7.10)
\ ■
коэффициенты которой определяются по формуле';
Применяя эту формулу обращения к уравнению A.7.8), где
Ф iy) ~ еУ, находим
оо
у =2 №-ixklk\ A.7.12)
и, сравнивая это выражение с A.7.6), снова получаем формулу
A.7.2) для tp.
При решении некоторых задач перечисления помеченных объек-
объектов (см. упражнения 1.13а, b и 1.14) удобно использовать обобще-
обобщение формулы A.7.11), принадлежащее Лагранжу. В дополнение
к условиям, наложенным на функцию ф, предположим, что дана
еще одна функция / (у), аналитическая в некоторой окрестности
точки у = 0. Обобщенная формула Лагранжа утверждает, что

1.7. ДЕРЕВЬЯ 37
функция / (у) может быть выражена степенным рядом по х следу-
следующим образом:
k=l
При f (у) = У эта формула приводит к выражениям A.7.10) и
A.7.11). Доказательство формулы A.7.13) можно найти у Гурса
и Хедрика [1].
Более интересный и полезный результат, обычно называемый
«Матричная теорема о деревьях», содержится в работе Кирхгофа
[1]. Число помеченных деревьев может быть быстро получено
как простое следствие этого результата. Матрицей смежности
А = A (G) = [%] помеченного графа G порядка р называется
(р X р)-матрица, в которой ац = 1, если вершины i и / смежны,
и ati = 0 в противном случае. Следовательно, существует взаимно
однозначное соответствие между помеченными графами порядка р
и симметрическими двоичными (р X р)-матрицами с нулевыми диа-
диагональными элементами. Пусть М (G) обозначает матрицу, которая
получается из матрицы —А с помощью подстановки на место i-ro
диагонального элемента в ней числа deg vt. Подграф Н графа G
покрывает граф G, если каждая вершина графа G является вер-
вершиной подграфа1 Н (рис. 1.7.5). ' >: - ; '
Ы
' « Ы i-i -ы
Рис. 1.7.5 Граф и три его остова.
Матричная теорема о деревьях для графов. Для всякого
связного помеченного графа G все кофакторы а матрицы М (G)
равны друг другу и их общее значение представляет собой число
остовных деревьев 3 графа G.
Доказательство этой теоремы можно найти у Харари [1,стр. 181].
Для иллюстрации сформулированного утверждения рассмотрим
1 Такой подграф называют остовнам. — Прим. перев.
2 В другой терминологии — алгебраическое дополнение. — Прим. перев.
3 Остовное дерево называют также остовом или каркасом. — Прим.
перев.

38
ГЛ. 1. ПЕРЕЧИСЛЕНИЕ ПОМЕЧЕННЫХ ОБЪЕКТОВ
граф G, изображенный на рис. 1.7.5. Он имеет три остова, так
как, например, кофактор, соответствующий элементу аи матрицы
г 2-1-1
-1 2-1
_ 0 0-1
o-
0
л
, равен —
-1
-1
0
2
-1
0
-1
3
1
= 3.
Полный граф Кр, в котором любые две вершины смежны, может
быть помечен только одним способом, и каждый его остов соответ-
соответствует своему помеченному дереву. Следовательно, число поме-
помеченных деревьев порядка р получается в результате применения
матричной теоремы о деревьях к графу Кр. Каждый главный
кофактор 1 матрицы М (Кр) есть определитель порядка р — 1:
р-1 -1 ... -1
-1 р-1 ... -1
_1 _1 ...р-1
Вычитая первую строку из каждой другой и прибавляя по-
последние р — 2 столбцов к первому, получаем верхнюю треуголь-
треугольную матрицу, определитель которой равен рР~*.
1.8. ЭЙЛЕРОВЫ КОНТУРЫ В ОРГРАФАХ
В параграфе 1.7 мы показали, что матричная теорема о деревьях
для графов дает один из нескольких методов подсчета помеченных
деревьев, основанный на определении числа остовов помеченного
графа Кр. Сейчас мы приведем только формулировку утверждения,
распространяющего эту теорему на орграфы и дающего число
остовов данного оргафа D, каждый из которых ориентирован по
направлению к некоторой своей вершине.
Предметом данного параграфа является применение этой мат-
матричной теоремы о деревьях для орграфов к помеченному эйлерову
орграфу D с целью получения точной формулы для числа эйлеро-
эйлеровых контуров в орграфе D.
Входящее дерево получается из корневого дерева Т с корнем v
ориентированием всех его ребер по направлению к вершине и.
Выходящее дерево является ориентированно-двойственным к выхо-
выходящему. Ясно, что оба эти множества ориентированных деревьев
1 То есть кофактор, соответствующий диагональному элементу мат-
матрицы. — Прим. перев.

1.8. ЭЙЛЕРОВЫ КОНТУРЫ В ОРГРАФАХ
39
находятся во взаимно однозначном соответствии с множеством
корневых деревьев.
Рассмотрим орграф D, который изображен на рис. 1.8.1
и вершины которого помечены числами 1, 2, 3, 4, 5. Существуют
ровно четыре остовных дерева, выходящих из вершины 1, и два
остовных дерева, входящих в вершину 1 (как показано на рис. 1.8.1,
б и в).
Пусть D — орграф с матрицей смежности А. Определим
диагональную матрицу Mout, у которой (г,г)-элемент равен od vt —
С-
Рис. 1.8.1 Остовы орграфа D, выходящие и входящие в вершину, помечен-
помеченную цифрой 1.
полустепени исхода вершины vt. Затем положим Cout = Mout —A.
Таким образом, сумма всех элементов матрицы Сои±, стоящих
в одной и той же строке, равна нулю, но необязательно это будет
выполняться для столбцов. В действительности, как мы увидим
вскоре, сумма элементов матрицы Cout, стоящих в одном и том жа
столбце, равна также нулю тогда и только тогда, когда D —
эйлеров орграф. Аналогично определяется матрица С]п = Min —
— А. Следующий важный результат был найден Боттом и Мей-
берри [1] и доказан Таттом [1].
A.8.1). Матричная теорема о деревьях для орграфов. Все
кофакторы i-й строки матрицы Cout равны друг другу, и их общее
значение есть число остовов орграфа D, входящих в вершину vt.
Двойственным образом, общее значение кофакторов i-го столбца
матрицы Cin равно числу остовов, выходящих из вершины vr

40
ГЛ. 1. ПЕРЕЧИСЛЕНИЕ ПОМЕЧЕННЫХ ОБЪЕКТОВ
Мы опускаем доказательство, но эту теорему легко проил- *
люстрировать на примере орграфа D, изображенного на рис. 1.8.1, ■
для которого две матрицы, упомянутые в теореме, имеют вид
2-100-1
0
0
0
-1
1
0
0
0
-1
2
0
1
0
-1
2
0
-1
0
-1
1
0
0
0
-1
1
0
0
-1
-1
2
0
0
-1
-1
2
0
0
0
-1
1
-1
0
0
1
2
Используя их, убеждаемся сразу, исходя из первой строки К
рыцы COut ж ив первого столбца матрицы €\п, что орграф D шеег
Рис. 1.8.2 Эйлеров орграф. „
в точности четыре остова, выходящих из вершины 1, и два остова,
входящих в эту вершину (как показано на рис. 1.8.1).
Орграф называется эйлеровым, если существует замкнутый
остовный ориентированный маршрут, проходящий через каждую
дугу точно один раз. Такой маршрут называется эйлеровым кон-
контуром. Один критерий эйлеровости орграфа состоит в следующем
(см. Харари [1], стр. 240): орграф должен быть связным, и для
всякой его вершины, полустепень исхода равна полустепени за-
захода. Например, орграф, показанный на рис. 1.8.1, не является
эйлеровым, а орграф D, изображенный на рис. 1.8.2, эйле-
эйлеров.

1.8. ЭЙЛЕРОВЫ КОНТУРЫ В ОРГРАФАХ
41
Из определения эйлерова орграфа следует, что матрицы Cout
и С1п имеют одинаковые диагонали и поэтому равны. Для ор-
орграфа D, данного на рис. 1.8.2, эта матрица имеет вид
2-1 0 0-1 0"
0 2-1-1 0 0
0 0 1-10 0
0-1 0 2-1 0
-1 0 0 0 2-1
-10 0 0 0 1
Первый шаг в доказательстве матричной теоремы о деревьях
для графов состоит в замечании, что если в матрице сумма элементов
Рис. 1.8.3 Остовы, входящие в вершину vv у орграфа, изображенного
на рис. 1.8.2.
любой строки, так же как и сумма элементов любого столбца,
равна нулю, то всякий кофактор матрицы имеет одно и то же
значение. Следовательно, в силу теоремы 1.8.1, каждый эйлеров
орграф имеет одно и то же число остовов, входящих в каждую вер-
вершину и выходящих из каждой вершины. Например, в приведен-
приведенной выше матрице все кофакторы равны 4, так что существует по
четыре остовных входящих дерева для каждой вершины орграфа
(как показано на рис. 1.8.3).
Теперь мы подготовлены к тому, чтобы применить матричную
теорему о деревьях для орграфов к выводу формулы для числа
эйлеровых контуров в данном орграфе. При доказательстве мы
будем придерживаться изящного изложения Кастелейна [1].
Этот результат впервые был получен де Брёйном и ван Ардене-
Эренфест [1], хотя частный случай был рассмотрен еще раньше
в работе Смита и Татта [1]. Так как для каждой вершины vt эйле-
эйлерова орграфа D выполняется равенство od vt — id vt, то мы можем
обозначить это число через dt.

42 ГЛ.1. ПЕРЕЧИСЛЕНИЕ ПОМЕЧЕННЫХ ОБЪЕКТОВ
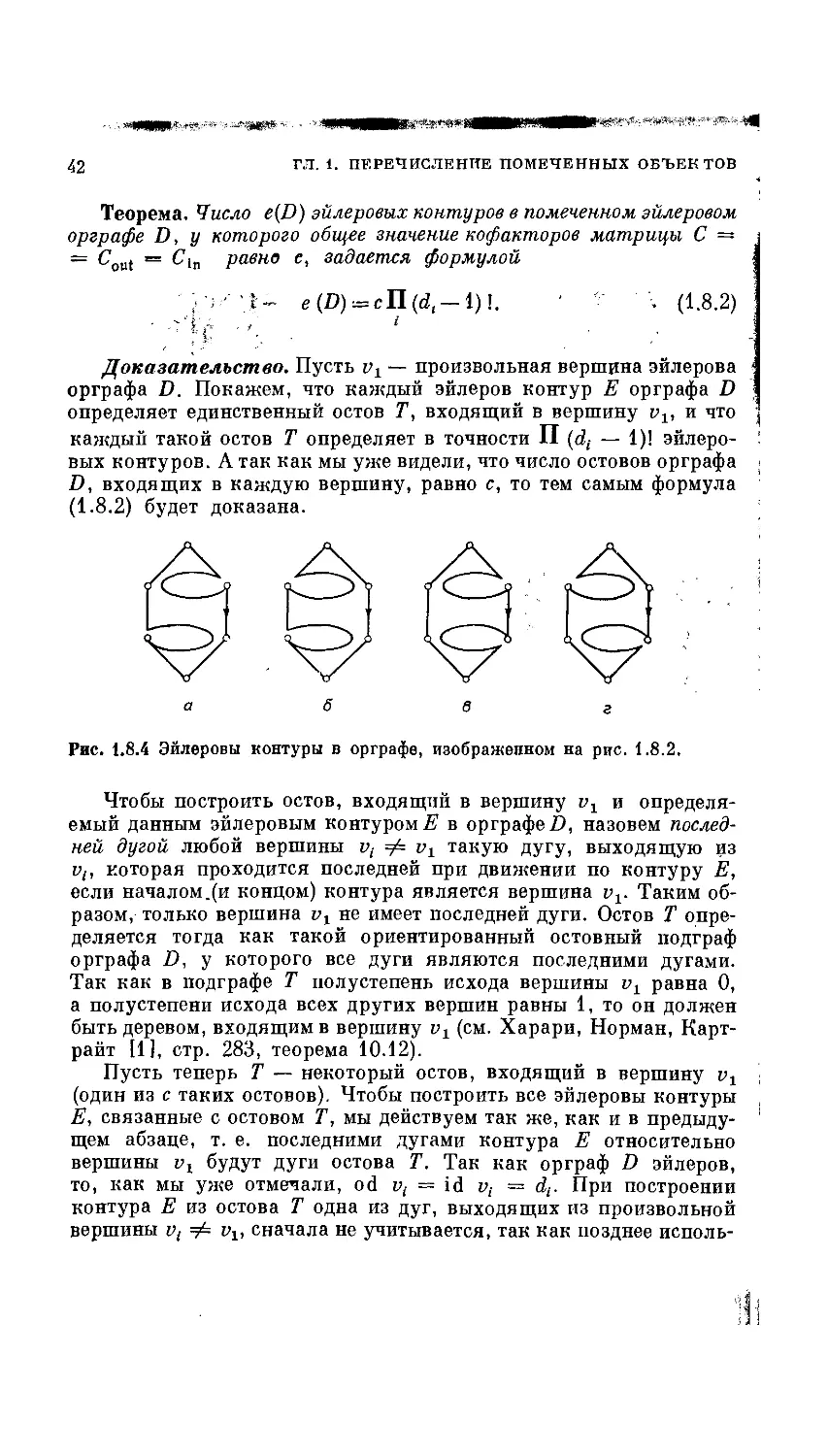
Теорема. Число e(D) эйлеровых контуров в помеченном эйлеровом
орграфе D, у которого общее значение кофакторов матрицы С =
= CoUt = Cln равно е, задается формулой
■'[г
A.8.2)
Доказательство. Пусть vt — произвольная вершина эйлерова '
орграфа D. Покажем, что каждый эйлеров контур Е орграфа D
определяет единственный остов Т, входящий в вершину vv и что
каждый такой остов Т определяет в точности П (d(. — 1)! эйлеро-
эйлеровых контуров. А так как мы уже видели, что число остовов орграфа
D, входящих в каждую вершину, равно с, то тем самым формула
A.8.2) будет доказана.
а 6 в г
Рис. 1.8.4 Эйлеровы контуры в орграфе, изображенном на рис. 1.8.2.
Чтобы построить остов, входящий в вершину v1 и определя-
определяемый данным эйлеровым контуром Е в орграфе D, назовем послед-
последней дугой любой вершины vt =^= vy такую дугу, выходящую из
vit которая проходится последней при движении по контуру Е,
если началом.(и концом) контура является вершина vv Таким об-
образом, только вершина v% не имеет последней дуги. Остов Т опре-
определяется тогда как такой ориентированный остовный подграф
орграфа D, у которого все дуги являются последними дугами.
Так как в подграфе Т полустепень исхода вершины vx равна О,
а полустепени исхода всех других вершин равны 1, то он должен
быть деревом, входящим в вершину vx (см. Харари, Норман, Карт-
райт [1], стр. 283, теорема 10.12).
Пусть теперь Т — некоторый остов, входящий в вершину vx
(один из с таких остовов). Чтобы построить все эйлеровы контуры
Е, связанные с остовом Т, мы действуем так же, как и в предыду-
предыдущем абзаце, т. е. последними дугами контура Е относительно
вершины vt будут дуги остова Т. Так как орграф D эйлеров,
то, как мы уже отмечали, od v{ = id vt = dt. При построении
контура Е из остова Т одна из дуг, выходящих из произвольной
вершины vt Ф иг, сначала не учитывается, так как позднее исполь-

^^
УПРАЖНЕНИЯ 43
зуется как последняя дуга этой вершины; кроме того, одна дуга,
выходящая из вершины vx, резервируется для использования
в качестве первой дуги контура Е. Итак, для каждой вершины
vt (включая вершину vx) существует ровно (dt — 1)! различных
упорядочений дуг, выходящих из vt, по их появлению в контуре Е.
Так как эти выборки независимы, то, перемножая факториалы,
получаем число эйлеровых контуров, определяемых остовом Т.
Но существует с таких остовов, что и доказывает формулу A.8.2).и
A.8.3). Следствие. Если в эйлеровом орграфе каждое dt равно
либо 1, либо 2, то число эйлеровых контуров равно числу с остовов,
входящих в произвольную вершину.
Утверждение мгновенно следует из того, что каждый (dt— 1)! =
= 1. Проиллюстрируем это следствие на примере орграфа D, ко-
который изображен на рис. 1.8.2 и в котором каждое dt равно либо 1,
либо 2. Из вычисления кофакторов, которое предшествовало
рис. 1.8.3, мы знаем, что орграф D имеет в точности четыре эйле-
эйлеровых контура. Они представлены на рис. 1.8.4 в соответствии
с остовными входящими деревьями, показанными на рис. 1.8.3.
УПРАЖНЕНИЯ 1
1.1. Связные помеченные орграфы.
1.2. Помеченные ориентации данного (р, д)-графа, число
симметрии которого равно s.
1.3. Направленные помеченные графы и знаковые помеченные
графы, в которых каждое ребро либо положительно, либо отри-
отрицательно.
1.4. Помеченные {р, д)-графы, не имеющие изолированных вершин.
(Гилберт [1])
1.5. (а) Помеченные связные (р, д)-графы
(m
2J-JJ—
где и = 2 L и вторая сумма берется по всем разбиениям
Pi+ • • • -hPk = P числа р на к частей, /(
(Ь) Помеченные (р, д)-блоки. (Риддел [1])
1.6. Помеченный граф с множеством вершин {v0, vx ,. . ., i>p-i}
называется звездным многоугольником, если из смежности вершин
v0 и vt следует, что для всех к = 1, . . ., р — 1 вершина vk смежна
1 Всяких"! раз, когда в упражнении упоминается некоторый класс графов,
это надо понимать так: читателю предлагается найти перечислительную
формулу для указанного класса графов,

->.■»>
44 ГЛ. 1. ПЕРЕЧИСЛЕНИЕ ПОМЕЧЕННЫХ ОБЪЕКТОВ
с vk+i, где индексы берутся по модулю р. Существует
звездных многоугольников порядка р. (Тернер [1])
1.7. Помеченные четные общие графы (см. § 7.5). (Рид [5])
1.8. Связные графы, у которых не помечены только висячие
вершины. (Мун [3])
1.9. Помеченные деревья, у которых каждая вершина имеет
степень
Л; ■■:» . , ,, (а) 1 или 3, , з-'
■':!■ (Ь) 1 или п, где ге>3. ,-' .
1.10. Помеченные 2-раскрашенные деревья с т вецршнами одного
цвета и п вершинами — другого:
ram-lmn-l# д (СКОЙНС [1])
1.11. Помеченные гомеоморфно несводимые деретця:
±-wr. (Рид [9])
1.12. Помеченные деревья с непомеченными висячими вершинами.
(Указание. Используйте числа Стирлинга второго рода.)
(Харари, Мовшовиц, Риордан [1])
1.13. (а) Помеченные 2-деревья (см. § 3.5):
р —3)р-«. %п (Байнеке и Мун [1])
(b) Помеченные /с-деревья:
L )(Ap — /с2 + 1)р"*-2. (Байнеке и Пшшерт [1])
(c) Реберно-помеченные 2-деревья: •■-■
2(~Л)\ Bр-3)^. „ (Палмер [1])
1.14. Плоским графом называется такой граф, который уложен
на плоскости так, что никакие два его ребра не пересекаются.
Помеченные плоские 2-деревья:
1.15. (а) Помеченные связные функциональные орграфы (см.
§ 3.4):
р
'( —к)\ РР~к+1< (Рабин и Ситгривс)

УПРАЖНЕНИЯ 45
(b) Помеченные связные унициклические графы. (Мун [4])
1.16. Помеченные графы:
(a) Не имеющие висячих вершин.
(b) С заданным числом висячих вершин. (Рид. [9])
1.17. Помеченные кактусы (см. § 3.4), имеющие с2 ребер, не ле-
лежащих на простых циклах, с3 треугольников, с4 четырехуголь-
четырехугольников, . . ., сп простых циклов, содержащих по п вершин:
Р \РС
, , ■ ■■ р .
: . . . 1 .,, . • П ((k-i)\)kckl л -. , -
fc-2 ■■■• ^ . . ' ,
Р
где с = 2 ck — 2. (Харари и Уленбек [1])
1.18. (а) Число с3 треугольников в помеченном графе равно
— tr (А3), где А — матрица смежности графа; число с4 четырех-
четырехугольников и число сь пятиугольников также выражается в тер-
терминах матрицы А. (Харари и Манвел [1])
(Ь) Число простых цепей, содержащих три, четыре и пять
взршин, может быть выражено в терминах матрицы А.
(Картрайт и Глисон [1], Харари и Росс [1])
1.19. Число способов, которыми можно так расположить 2" дво-
двоичных цифр в круговую таблицу, что все 2" последовательностей,
получающихся с помощью разнообразных выборок п последо-
последовательных цифр в этой таблице, различны:
(Указание', применить теорему A.8.2) к эйлеровым орграфам (ис-
(используемый термин не является точным, так как при этом допу-
допускаются петли), получающимся из универсального отношения
S X S на 2-множестве S = {0, 1} с помощью итерированных
реберных орграфов (определение см. в § 10.3)). (де Брёйн [1])

Глава 2
Умепие решать задачи — практическое
искусство, подобное плаванию, или ката-
катанию на лыжах, или игре па фортепиано:
научиться этому можно, лишь подражая
избранным образцам и постоянно тре-
тренируясь. Не ищите в этой книге чудо-
чудодейственного ключа, который откроет
перед вами все двери — научит решать
все задачи. Однако вы найдете в ней
хорошие образцы для подражания и мно-
множество благоприятных возможностей по-
попрактиковаться. Если хотите научиться
плавать — нужно войти в воду, а если
желаете научиться решать задачи —
решайте их.
Джордж Пойа, Математическое открытие '
ТЕОРЕМА ПОИА
Для подсчета числа непомеченных графов задачу переформулиро-
вывают так, чтобы ответ можно было получить, найдя число орбит
некоторой подходящей группы подстановок. Тогда можно восполь-
воспользоваться леммой Бернсаида и выразить число орбит на языке
числа объектов, неподвижных относительно подстановок из рас-
рассматриваемой группы. Каждой группе подстановок отвечает свой
многочлен, называемый цикловым индексом. Это понятие может
быть прослежено еще у Фробениуса как частный случай соответ-
соответствующей формулировки в терминах групповых характеров.
Рудволис и Снаппер [1 ] указали на связь между этими обобщен-
обобщенными характерами и теоремами де Брёйна [2] и Фоулкса [1].
Редфилд [1], открывший цикловые индексы независимо, изобрел
искусные схемы (гл. 7), которые позволили ему путем составле-
составления специального произведения цикловых индексов найти число
классов некоторых матриц. В доказательстве его теоремы пере-
перечисления содержалась в неявной форме лемма Бернсаида. Методы
Редфилда дали ему возможность решать задачи перечисления
для многочисленных интересных комбинаторных структур при
условии, что задачу перечисления в процессе ее рассмотрения
можно было преобразовать в матричную форму, требуемую его
теоремой, и при условии, что для получающихся цикловых ин-
индексов можно было вывести необходимые формулы. Хотя для ре-
решения одних задач этот метод был приспособлен превосходно,
однако его применение к другим задачам сопряжено с определен-
1 Есть русский перевод этой книги: Дж. Пойа, Математическое открытие,
изд-во «Наука», М., 1970,

2.1. ГРУППЫ И ГРАФЫ
47
ными трудностями, так как структуры, для которых решаются
задачи перечисления, должны быть истолкованы как матрицы.
Напротив, классическая теорема перечисления, принадлежащая
Пойа, может быть рассмотрена как средство для перечисления
функций, и поэтому ее много легче применять к большинству
задач теории графов. В своей наибольшей общности теорема
Пойа включает лемму Бернсайда и часто позволяет выражать
полную производящую функцию для класса графов в терминах
подходящего циклового индекса и многочлена, называемого пере-
перечисляющим рядом для фигур. Таким образом, именно общность,
универсальность и легкость при его использовании делают метод
Пойа наиболее мощным инструментом в перечислительном анализе.
2.1. ГРУППЫ И ГРАФЫ
Изучение групп подстановок лучше вести параллельно с изу-
изучением графов, ибо граф воспроизводит «картину» своей группы
автоморфизмов. Таким образом, теоретико-групповые понятия,
необходимые в этой главе, значительно легче усвоить, используя
их толкование в теории графов.
Рассмотрим множество X = A, 2, . . ., п}, и пусть А — не-
некоторая совокупность подстановок множества X, замкнутая
2 ^=A)B)C)'4)
*4= A3I24)
:,, ■">; (*!•••■
Рис. 2.1.1 Граф и его группа.
относительно операции умножения. Тогда А является группой
подстановок на множестве объектов X. Порядок группы А, обо-
обозначаемый | А |, есть число подстановок в Л, а степень группы А —
это число п элементов в множестве объектов X. Например, рассмот-
рассмотрим граф G, изображенный на рис. 2.1.1 и выбранный, как обычно,
наугад. Его четыре вершины составляют множество X целых
чисел 1, 2, 3, 4. Заметим, что список подстановок, приведенных
на рисунке, включает все подстановки множества X, сохраняющие
отношение смежности в графе G. К примеру, вершины 1 и 4 смежны
в G. Подстановка A3) B) D) преобразует вершины 1 и 4 в вершины
3 и 4, и эти образы, 3 и 4, также являются смежными. Таким об-
образом, подстановка A3) B) D) сохраняет смежность вершин 1 и 4.
Так как совокупность подстановок в этом списке замкнута отно-
относительно умножения, то она образует группу. Как уже отмечалось,

ГЛ. 2. ТЕОРЕМА ПОЙА
совокупность Г (G) всех подстановок на множестве V (G), сохра-
сохраняющих смежность, называется группой графа G, или группой
автоморфизмов графа G, а ее подстановки называются авто-
автоморфизмами. Таким образом, группа графа является группой
подстановок, объектами которых являются вершины графа.
G:
Рис. 2.1.2 Дополнение графа, изображенного на рис. 2.1.1.
Дополнение G графа G имеет то же самое множество вершин(
что и граф G, и две вершины и и v смежны в G тогда и только
тогда, когда они не смежны в G. Дополнение четырехвершинного
графа, показанного на рис. 2.1.1, изображено на рис. 2.1.2. Под-
Подстановки, сохраняющие отношение смежности в графе, приведен-
приведенном на рис. 2.1.2, — те же самые, что и у графа, данного на
рис. 2.1.1. В действительности для всякого графа G подстановки,
во
do
об и,
ос иЛ
Рис. 2.1.3 Три графа с одинаковыми группами.
сохраняющие в нем смежность, сохраняют также несмежность,
а поэтому
' T(G) = T(G). B.1.1)
Чтобы решить, одинаковы ли две группы подстановок, нам
теперь требуется более тонкий критерий, чем групповой изомор-
изоморфизм. Рассмотрим три помеченных графа, представленных на
рис. 2.1.3. Они имеют абсолютно одинаковые группы. Различие
между ними заключается лишь в «дополнительности» и пометках.
Удобно поэтому отождествлять группы подстановок, у которых
подстановки отличаются только «названиями» переставляемых
объектов. Исходя из Ътого, дадим следующие определения. Две
группы подстановок А и В с множествами объектов X и Y соот-
соответственно называются изоморфными (и это записывается в виде

2.2. ЦИКЛОВОЙ ИНДЕКС ГРУППЫ ПОДСТАНОВОК 49
А = В), если существует функция h из А на В, такая, что для
всех подстановок ах и а2 из группы Л выполняется равенство
B.1.2)
Если существует, кроме того, взаимно однозначное отображе-
отображение ф из X на Y, такое, что для каждой подстановки а из Л и ка-
каждого элемента г из X справедливо равенство
ф (оке) = h (а) ф (ж), ' B.1.3)
то группы Л и В называются идентичными и мы пишем: А = В.
Таким образом, отображение ф просто заменяет пометки, или
названия, объектов, на которых действует группа А, пометками,
отвечающими группе В. Теперь легко видеть, что группы всех
трех графов изображенных на рис. 2.1.3, идентичны.
2.2. ЦИКЛОВОЙ ИНДЕКС ГРУППЫ ПОДСТАНОВОК
Пусть А — группа подстановок с множеством объектов X =
= {1, 2, . . ., п}. Хорошо известно, что каждая подстановка а
из А может быть единственным образом представлена в виде
произведения непересекающихся циклов. Для каждого к = 1,
2, . . ., п через ]k (а) обозначим число циклов длины к в разло-
разложении подстановки а в произведение непересекающихся циклов.
Тогда цикловой индекс группы А, обозначаемый Z (А) (буква Z
от слова Zyklenzeiger использовалась Пойа [1]), представляет
собой многочлен от переменных sx, s2, . . ., sn, определяемый
формулой
£ " B.2.1)
Когда необходимо указывать переменные, мы будем вместо
Z (А) писать Z (A; slt s2, . . ., sn). Редфилд [1] называл этот
многочлен «group-reduction function», а Пойа [1], который ввел
это понятие независимо, назвал его «цикловым индексом».
В качестве примера рассмотрим симметрическую группу Sn,
действующую на множестве из п объектов. Для п — 3 замечаем,
что тождественная подстановка A) B) C) имеет три единичных
Цикла, дающих слагаемое s\. Три подстановки A) B3), B) A3)
и C) A2) имеют каждая по одному единичному циклу и по одному
Циклу длины 2, так что получается одно слагаемое 3sxs2. Наконец,
Две подстановки A23) и A32) вносят 2s3- Таким образом, имеем
B.2.2)

50 ГЛ. 2. ТЕОРЕМА ПОЙА
На протяжении всей оставшейся части этой книги очень часто
будут использоваться явные формулы для цикловых индексов
пяти известных групп подстановок: симметрической, знакопере-
знакопеременной, циклической, диэдральной и единичной. И Редфилд [1],
и Пойа [1] выразили Z (Sn) на языке разбиений числа п. Заметим,
что каждая подстановка а на п объектах может быть связана
с определенным разбиением числа п, имеющим для каждого
к = 1, 2, . . ., п точно jk (а) частей, равных числу к. Будем зада-
задавать разбиение числа п посредством вектора (/) = (/х, /2, . . ., ;„),
где jk — число частей разбиения, равных к. Итак,
п
w = 2ft/*- B.2.3)
Пусть h (j) — число подстановок в группе Sn, разложение
которых на непересекающиеся циклы определяется разбиением
(/'), так что для каждого к jk = jk (а)- Тогда легко видеть, что
j) = n\ lllk'k.jbl. B.2.4)
/ *
Таким образом, цикловой индекс Z (Sn) имеет вид, приводимый
в следующей теореме.
Теорема. Цикловой индекс симметрической группы дается фор-
формулой
2(#, B.2.5)
где сумма берется по всем разбиениям (j) числа п и h (j) задается
выражением B.2.4).
Цикловой- индекс знакотременной группы Ап, состоящей
из всех четных подстановок группы Sn, выражается в следующем
виде.
Следствие. Цикловой индекс знакопеременной группы дается
формулой
Z(An) = Z(Sn) + Z(Sn; Sl, -s2) s3, -st, . . .). B.2.6)
Для иллюстрации этого следствия заметим, что из B.2.2)
мы имеем
Z (S3; sb -s2, s3) = A/3 !) (sj - Зад + 2s,), B.2.7)
а учитывая B.2.2) и ^2.2.7), получаем
^ . B.2.8)

2.2. ЦИКЛОВОЙ ИНДЕКС ГРУППЫ ПОДСТАНОВОК 51
Часто бывает удобно выразить Z (Sn) через Z (Sk), к <$п.
Для этой цели полагаем по определению Z (S 0) = 1. Тогда ре-
рекурсивная формула, доказательство которой получается непо-
непосредственно по индукции, может быть сформулирована следу-
следующим образом.
Теорема. Цикловой индекс симметрической группы удовлет-
удовлетворяет рекуррентному соотношению
Z{Sn)^n-^skZ{Sn.k). B.2.9)
Циклическая группа степени п, обозначаемая Сп, порож-
порождается циклом A23 . . . п). Редфилд вывел следующую формулу
для Z (С„), используя ф-функцию Эйлера.
Теорема. Цикловой индекс циклической группы Сп дается фор-
формулой
Z (Q =/г* 2 Ф (*)•$/*. B.2.10)
k\n
Диэдралъная группа степени п, обозначаемая Dn, порождается
циклом A23 . . . п) и отражением (Ire) B (re — 1)) C (re — 2)). . . .
Ее цикловой индекс может быть выражен через Z (Сп).
Следствие. Цикловой индекс диэдралъной группы Dn дается
формулой
4n~1)/2 если п нечетное,
/sn/2_^.s2S(^n-2)/2\ если п четное.
B.2.11)
Для иллюстрации этих утверждений можно использовать
B.2.10) и B.2.11), чтобы получить Z (Cs) и Z (Ds), но заметим,
что С3 = i, и D8 = 58. Поэтому Z (С3) и Z (D3) даются также
формулами B.2.8) и B.2.2) соответственно. Наши обозначения
групп завершаются введением символа Еп для единичной группы,
действующей на множестве из ге объектов, так что
Заметим далее, что цикловой индекс не определяет однозначно
группу подстановок. Именно, две группы подстановок А я В
не обязательно идентичны, если их цикловые индексы одинаковы.
В действительности они могут быть даже не изоморфны и все-таки
иметь один и тот же цикловой индекс, как это демонстрируется

52 ГЛ. 2. ТЕОРЕМА ПОЙА
в следующем довольно точном переводе отрывка из работы Пойа
[1, стр. 176]:
Весьма интересно заметить, что две комбинаторно эквивалент-
эквивалентные группы подстановок (имеющие одинаковые цикловые ин-
индексы) не обязательно идентичны. На самом деле, они даже не обя-
обязаны быть изоморфными. Действительно, пусть р — нечетное
простое число и т ^ 3 — целое положительное число (р = т =
= 3 — простейший пример). Хорошо известно (см. Бернсайд [1,
стр. 143]), что существует некоммутативная группа порядка рт,
в которой каждый элемент, кроме единичного, имеет порядок р.
Пусть В — регулярное представление этой группы, рассматри-
рассматриваемое как группа подстановок. Пусть А — регулярное пред-
представление абелевой группы порядка рт и типа (р, р, ..., р). Тогда
А и В являются группами подстановок, у которых порядок и сте-
степень равны рт = d и один и тот же цикловой индекс
так как каждая подстановка из А и В, отличная от единичной,
содержит в точности рт~х циклов длины р.
Этот параграф мы завершим рассмотрением двуместной операции
на группах подстановок, а также формулы для соответствующего
циклового индекса. Пусть А ж В — группы с непересекающимися
множествами объектов X и Y соответственно. Тогда произведе-
произведением * групп А ж В, обозначаемым А В, называется группа под-
подстановок с множеством объектов X w Y, такая, что каждая
пара подстановок а из А и (} из В определяет подстановку оф
из АВ, действующую по правилу: для каждого z из X w Y
{az, zfX,
Ps, zer. <2-2-13>
Таким образом, группа АВ имеет степень | Х\ + | Y\ и порядок
\А\ • \В\. Обозначим произведение А А. . .А из т копий группы А
через Ат. Пойа [1 ] отметил элементарный, но важный факт, что
цикловой индекс произведения равен произведению цикловых
индексов групп-сомножителей.
Теорема. Цикловой индекс произведения АВ дается формулой
Z{AB) = Z(A) • Z(B). B.2.14)
Группа полного графа Кп с п вершинами равна, естественно, Sn.
Кроме того, граф G, компонентами которого являются графы Кп
1 Раньше (см. Харари [1]) мы называли это произведение суммой и обо-
обозначали А + В.

2.3. ЛЕММА БЕРНСАЙДА 53
и Кт с п Ф т, имеет группу Г (G) — SnSm. Следовательно, из
B.2.14) получаем Z (Г (G)) = Z (Sn) ■ Z (Sm). Когда будет необ-
необходимо говорить о цикловом индексе группы некоторого графа,
мы будем часто упрощать обозначение и писать Z (G) вместо
Z (Г (G)). Например, Z (Кп) дается формулами B.2.4) и B.2.5).
2.3. ЛЕММА БЕРНСАЙДА
Три леммы, обсуждаемые ниже, составляют основу разнообраз-
разнообразных подходов к задачам перечисления непомеченных графов.
Хотя, по-видимому, они были известны еще Фробениусу, Шуру
и другим математикам, мы называем их леммами Бернсайда [1].
Пусть А — группа подстановок с множеством объектов X = {1,
2,. . ., п}. Тогда элементы х и у из X называются А-эквивалентными
или подобными, если существует подстановка а из А, такая, что
ах ~ у. Классическим и немедленно получающимся результатом
является утверждение о том, что введенное нами отношение есть
эквивалентность. Классы эквивалентности называются орбитами,
или системами транзитивности группы А.
Для каждого £ из X положим - . .
А(х)={аеА\ах = х}., , B.3.1)
Так определенное множество А (х) называется стабилизатором
элемента х. Заметим, что всякий раз, когда элементы х я у принад-
принадлежат одной и той же орбите, множества А (х) и А (у) являются
сопряженными подгруппами группы А и, следовательно, \А (х)\ =
= \А (у)\. Сейчас мы покажем, что для любого элемента у
из орбиты Y группы А выполняется соотношение
\A\ = \A(y)\.\Y\, B.3.2)
т. е. число элементов в орбите, содержащей элемент у, равно ин-
индексу стабилизатора элемента у в группе А. Чтобы убедиться
в этом, мы сначала разложим группу А в объединение правых
классов смежности по подгруппе А (у):
т
А=[} atA (у),
i-i
Теперь остается только указать естественное взаимно однозначное
соответствие между этими классами смежности и элементами
орбиты Y. Для каждого i — 1, . . ., т сопоставляем классу смеж-
смежности atA (у) элемент at у из Y. Если i Ф], то aty Ф а;г/, так как
иначе бы подстановка а^а, принадлежала подгруппе А (у)
и, следовательно, подстановка а,- являлась бы элементом мно-
множества а/А (у), что противоречит соотношению щА (у) f) а/А (у) =

54 ГЛ. 2. ТЕОРЕМА ПОЙА
= 0. Значит, указанное соответствие является взаимно одно-
однозначным. Для всякого объекта у' из Y при некоторой подстановке
а из А выполняется равенство ау = у". Из разложения группы А
на классы смежности следует, что а = а(-у, если у £ А (у). Следо-
Следовательно, у" = ад и, таким образом, каждый элемент орбиты Y
соответствует некоторому классу смежности. Значит, т есть
число элементов в орбите Y и формула B.3.2) доказана.
Теперь мы подготовлены к доказательству первой леммы,
в которой дается формула, выражающая число N (А) орбит
группы А как среднее арифметическое числа неподвижных точек
всех подстановок группы А.
Лемма Бернсайда. Число N (А) орбит группы А дается фор-
формулой
(a)- B-3.3)
Доказательство. Пусть Хх, Хг, . . ., Хт — орбиты группы
А, и для каждого i = 1, . . ., т пусть xt — элемент г-й орбиты Х{.
Тогда из формулы B.3.2) имеем
m
N(A).\A\^Z\A(xl)\-\Xi\. B.3.4)
Мы видели, что если х ш xt принадлежат одной и той же орбите,
то |А (х)| = \А {xt)\. Следовательно, соотношение B.3.4) можно
иначе записать так:
N(A)-\A\= % \А(х)\, _ B.3.5)
или, в других обозначениях,
N{A)-\A\=Z S I- B-3.6)
ехел()
Теперь, меняя порядок суммирования в правой части формулы
B.3.6) и изменяя соответствующим образом индексы суммиро-
суммирования, имеем
1=2 S 1. B.3.7)
Но 2 ^ есть в точности ]\ (а). Таким образом, для завершения
3C-GOC
доказательства надо обе части разделить на \А\.щ
Для иллюстрации этой леммы рассмотрим граф G, изображен-
изображенный на рис. 2.3.1. Используя обозначения, относящиеся к про-
произведению групп, можно представить группу графа G в виде:
Г (G) — S\S\. Порядок этой группы равен 4, и каждая ее под-

2.3. ЛЕММА БЕРНСАЙДА 55
становка оставляет неподвижными три точки: 3, 5 и 7. Пусть
подстановки обозначены так:
aj = (l)B)C)D)E)F)G), a, = A2) C) D) E) F) G),
a3 = D6) A) B) C) E) G), a4 = A2) D6) C) E) G). (^-й)
Тогда /j (ax) = 7,]\ (a2) = /\ (a3) = 5 и /\ (a4) = 3. Таким
образом, N (T(G)) = V4 G + 5 + 5 -f- 3) = 5. Ясно, конечно, что
орбитами этой группы являются множества {3}, {5}, {7}, {1,2}
и {4, 6}. Заметим, что число орбит в точности совпадает с числом
способов получения из графа G различных непомеченных корне-
корневых графов. Чтобы получить все такие графы, нужно просто
■ К
6
Рис. 2.3.1 Граф с тремя неподвижными вершинами.
выбирать в качестве корня по одной вершине (точке) из каждой
орбиты.
Изредка нам нужно будет ограничивать действие группы А
на некоторое подмножество Y множества X, где Y — объединение
каких-либо орбит группы А. Поэтому обозначим через .4 | У
множество подстановок, действующих на Y и получающихся
с помощью ограничения на подмножество Y соответствующих
подстановок группы А. Для каждой подстановки а из группы А
число элементов в Y, неподвижных относительно подстановки а,
обозначим через ]г (a | Y). Тогда мы можем сформулировать след-
следствие формулы B.3.3).
Ограниченная форма леммы Бернсайда.
B-3.9)
Далее мы дадим незначительное обобщение формулы B.3.3),
называемое взвешенной формой леммы Бернсайда. Пусть R —
произвольное коммутативное кольцо, содержащее множество всех
рациональных чисел, и w — некоторая функция, называемая
весовой функцией, отображающая множество объектов X группы
А в кольцо R. В практических приложениях весовая функция
является постоянной на каждой орбите группы А. Следовательно,

E6 ГЛ. 2. ТЕОРЕМА ГГОЙА
в этом случае мы можем определить вес любой орбиты Х1 как вес
произвольного ее элемента. Для каждой орбиты Х( обозначим
ее вес через w (Х^ и определим его соотношением w (Х{) =
= w (х) для всякого элемента х из Xt.
Взвешенная форма леммы Бернсайда. Сумма весов орбит
группы А дается формулой
т ч л
1 2 2 «(а). "Л B.3.10)
а 6 А ''; ' ' \
Доказательство этой теоремы аналогично доказательству фор- :
мулы B.3.3), и мы его опускаем.
Чтобы проиллюстрировать сформулированную лемму и пред-
представить сумму цикловых индексов в таком виде, который будет
эффективно использоваться в гл. 8, рассмотрим опять граф G,
изображенный на рис. 2.3.1. Вес w (к) каждой вершины к графа
G определим как цикловой индекс стабилизатора вершины к
в группе Г (G). Итак,
(j ;). '"' ' B.3.12)
Заметим, что
ы>A) = ы>B) = ы>D) = ы>F) и ы> C) = и; E) = ы> G); B.3.13)
таким образом, в частности, функция w на каждой орбите посто-
постоянна.
Для этого примера дадим набросок проверки формулы B.3.10),
заметив, что сумма весов орбит равна w A) + w C) -f- w D) -f
+ w E) + w G) = 2m? A) + 2>w C). В нашем случае правая часть
формулы B.3.10) имеет вид
где две суммы, не выписанные в последних фигурных скобках,
немедленно находятся после внимательного рассмотрения под-

2.4. ТЕОРЕМА ПОЙА 57
становок а3 и а4 из B.3.8). Используя B.3.13), можно эту сумму
переписать так: 2ц? A) -f 3w C), что, как мы видели, есть сумма
весов орбит. Проверка закончена.
Аналогично, сумма цикловых индексов по всем различным
корневым графам, получающимся из некоторого графа G, может
быть выражена через веса неподвижных точек (вершин) группы
r(G).
2,4. ТЕОРЕМА ПОЙА ч '
Поскольку в большинстве приложений основной перечисли-
перечислительной теоремы Пойа требуется только вариант с одной пере-
переменной и поскольку в этом случае теорема Пойа понимается к тому
же значительно легче, мы не будем приводить детали трафа-
трафаретного обобщения ее на п переменных.
Сначала введем понятие степенной группы (см. Харари и
Палмер [4]), с которым мы позднее то и дело будем сталкиваться
в этой книге. Пусть А — группа подстановок с множеством
объектов X = {1, 2, . . ., п}, и пусть В — конечная группа
подстановок со счетным множеством объектов Y, содержащим
не менее двух элементов. Тогда степенная группа, обозначаемая
ВА, имеет в качестве множества объектов совокупность Yx всех
функций, действующих из X в У. Подстановками группы ВА
являются все упорядоченные пары подстановок а из А и р1 из В,
записываемые в виде (а; Р). Образ произвольной функции /
из Yx при действии на нее подстановки (а; р1) дается формулой
((а; {})/)(*) = р7(аа;) B.4.1)
при всех i из X.
Для того чтобы привести классическую формулу перечисления
Пойа, мы возьмем В = Е — единичной группе на множестве У.
Рассмотрим теперь степенную группу ЕА, действующую на множе-
множестве Yx. Пусть w : Y -*• {О, 1, 2, . . .} — функция, область
значений которой является множеством неотрицательных целых
чисел и для которой 1кг1 (к) | <^ °° при всех к1). В частности,
для каждого к = 0,1, 2, ... пусть
B.4.2)
будет число||! «фигур» веса к.
Здесь черев w1 (к) обозначен полный прообраз числа к при отображе-
»i — Поим, пеиев.
аии w, — Прим, перев,

58 ГЛ. 2. ТЕОРЕМА ПОЙА
Тогда об элементе у из Y, для которого w (у) = к, говорят,
что он имеет вес к, а функцию w называют весовой функцией.
Далее, ряд
; ■ c{x)=^ckxk \ v ;; B.4.3)
относительно переменной х, который перечисляет элементы мно-
множества Y в соответствии с их весами, называют г «перечисляющим
рядом для фигур».
Вес функции f из Yx определяется формулой
»(/)= S »(/(*)), B-4.4)
Х
и тогда нетрудно показать, что функции, принадлежащие одной
и той же орбите степенной группы ЕА, имеют одинаковые веса.
Следовательно, весом w (F) орбиты F группы ЕА является вес
любой функции / из орбиты F. Так как | иг1 (к) | < оо для всякого
к = 0, 1, 2, . . ., то существует только конечное число орбит
каждого веса. Поэтому обозначим через Ck число орбит веса к.
Тогда ряд
:':: С(х) = ^СкЯ* *ywr 4- B.4.5)
относительно переменной х назовем «перечисляющим рядом для
функций», или, следуя работе Пойа [1], «перечисляющим рядом
для конфигураций» 2. Теперь мы можем, наконец, сформулиро-
сформулировать основную теорему этой книги, выражающую ряд С(х) в тер-
терминах циклового индекса Z (А) и ряда с (х). В приводимой ниже
формуле Z (А, с (х)) является сокращением для Z (А; с (х), с (х2),
с (х% . . .).
Теорема (теорема перечисления Пойа). Ряд С(х), перечисля-
перечисляющий функции, получается с помощью подстановки в цикловой
индекс Z (А) на место каждой переменной sk ряда c(xk), пере-
перечисляющего фигуры. Символически:
C(x) = Z(A, c(x)). B.4.6)
Этот результат используется настолько часто при перечисле-
перечислении графов, что мы вместо «теорема перечисления Пойа» будем
обычно писать для краткости «теорема Пойа».
1 Или «рядом, перечисляющим фигуры». — Прим. перев.
2 Мы его будем называть также «рядом, перечисляющим функции», —
Прим. перев,

.4. ТЕОРЕМА ПОЙА 59
Доказательство. Пусть е — тождественная подстановка на Y.
Тогда для всякой подстановки а из А и любого к = О, 1, 2, ...
обозначим через ф (а, к) число функций веса к, неподвижных
относительно подстановки (а; г). Ограничивая для каждого к
действие степенной группы ЕА на множество функций веса к
и применяя ограниченную форму леммы Бернсайда B.3.9), имеем
СЛ = |Л| 2 Ф(«. *)• BЛ7)
Следовательно,
со
Г (г\ — V I А 1-1 V т In h\ . г* f? 4 ftt
и, меняя порядок суммирования, получаем ,
со
Г (Т\ МИ Т У mfrt И,т' A 4 Q\
СО
Ряд 2 ф(а» Щ'хк перечисляет все функции, неподвижные отно-
сительно подстановки (а; г), и мы постараемся найти другую
форму для этого ряда.
Предположим, что функция / из Yx неподвижна относительно
подстановки (а; г). Тогда ((а; е) /) (х) = / (х) для всех х из X и,
в силу формулы B.4.1), имеем ((а; г) /) (х) = в/ (ах). Таким обра-
образом, для всех х должно выполняться равенство / {ах) = f (x),
т. е. функция / должна быть постоянной на непересекающихся
циклах подстановки а. Обратно, все функции, постоянные на
циклах подстановки а, неподвижны относительно подстановки
(а; е).
Пусть zr — цикл длины г в подстановке а. Если функция /
отображает элементы цикла zr в один из ck элементов множества У,
имеющих вес к, то цикл zr вносит в вес функции/ значение г-к.
Тогда легко видеть, что для каждого к коэффициент при хгк в ряду
со
"i; c(zr) = 2 ckxrk B.4.10)
л . ■, v *=■(>
равен числу способов, которыми можно определить функцию /
на элементах цикла zr так, чтобы она была неподвижна относи-
относительно подстановки (а; г) и чтобы вклад в вес w (/) составлял
г-к. Отсюда следует, что ряд [с (xr)\r перечисляет в соответ-
соответствии с их весами различные способы определения функций,
постоянных на всех циклах длины г подстановки а.

60 ГЛ. 2. ТЕОРЕМА ПОЙА
Рассматривая все циклы подстановки а, мы можем выразить
ряд для функций, постоянных на циклах, в виде произведения
2 ф(о, k)xk = IL [с(з*)\'к1а\ B.4.11)
Теперь B.4.6) следует из B.4.9), B.4.11) и определения Z (А).и
Для иллюстрации теоремы рассмотрим «проблему ожерелья».
На рис. 2.4.1 показаны два ожерелья, каждое с четырьмя бусин-
бусинками. Каждая из бусинок помечена числом из множества X =
= {1, 2, 3, 4}, и две бусинки ожерелья — белые, а две другие —
черные. Ясно, что число помеченных ожерелий с четырьмя бусин-
бусинками, не содержащих бусинки иного цвета, чем белый и черный*
Рис. 2.4.1 Два помеченных ожерелья. , > \
равно 48. Для того чтобы получить число непомеченных ожерелий,
мы должны отождествлять ожерелья такие, как изображенные
на рис. 2.4.1, когда одно ожерелье получается из другого только
отражением или вращением нитки с бусинками. Если положим
Y = {а, Ь), то каждая функция / из X в Y соответствует неко-
некоторому помеченному ожерелью, в котором бусинка с номером
к£Х имеет «цвет» / (к). Таким образом, ожерелье, представимоб
функцией /, имеет |/~1(а)| бусинок одного цвета и If'1 (Ь)\
бусинок другого цвета. Пусть теперь единичная группа Е2 дей-
действует на множестве У. Два ожерелья будут тождественны после
удаления пометок в том случае, когда соответствующие им функ-
функции содержатся в одной и той же орбите степенной группы Е%'.
Если определим w (а) = 0 и w (b) = 1, то 1 + x будет перечисля-
перечисляющим рядом для Y и функция веса к будет представлять ожерелье
с 4 — к белыми и к черными бусинками. Следовательно, пере-
перечисляющий ряд для функций С (х) в этом случае перечисляет
непомеченные ожерелья и коэффициент при хк равен числу тако-
таковых с к черными бусинками. Тогда, в силу формулы B.4.6) из
теоремы Пойа,
C(x) = Z(Dt, 1+3). ■ t1 B.4.12)
Из B.2.11) имеем
4 ,. B.4.13)

2,4. ТЕОРЕМА ПОЙА
61
Тогда выполнив детали, связанные с подстановкой перечисля-
перечисляющего ряда для фигур 1 -f х в цикловой индекс Z (Dt), получаем
С (х) = 1 + z + 2х2 + х3 + х*.
B.4.14)
Шесть непомеченных ожерелий с четырьмя бусинками двух
цветов показаны на рис. 2.4.2.
Общее число ожерелий равно, конечно, С A), и, значит,
общее число их может быть получено с помощью вычисления
значения ряда 1 -f- х, перечисляющего фигуры, при х = 1 и под-
подстановки 2 вместо каждой переменной s^ в цикловой индекс
Z (Dt). Вообще, когда ряд с (х), перечисляющий фигуры, яв-
является многочленом, то ряд С (х), перечисляющий функции, —
тоже многочлен. В этом случае число орбит функций (без учета
Рис. 2.4.2 Ожерелья с четырьмя бусинками.
их весов), равное С A), получается подстановкой с A) вместо
каждой переменной в соответствующий цикловой индекс.
Следствие. Число орбит, определяемых степенной группой
Ет, получается путем подстановки числа т вместо каждой пере-
менной в Z (А):
B.4.15)
, N(Em)=Z{A, m).
Для п переменных мы дадим только формулировку теоремы
перечисления Пойа. Доказательство этой теоремы проводится
так же, как в случае одной переменной. Пусть N — множество
целых неотрицательных чисел и N" = N X . . . X N — декар-
декартово произведение п копий множества N. Как и раньше, множе-
множеством объектов степенной группы ЕА является множество Yx
и весовая функция w : Y -*■ Nn обладает тем свойством, что для
каждого z£Nn выполняется неравенство | w'1 (z)\ <5oo. Покомпо-
Покомпонентная аддитивность в N", веса функций из Y* и орбиты, инду-
индуцированные группой ЕА, определяются как прежде. Коэффициент
при х^х^' . . . х" у ряда с (хг, х%, . . ., хп), перечисляющего
фигуры, равен по определению Iw'1 (rlt r2, . . ., г„)|. Коэффи-
Коэффициент при х[*Хг' . . .х„ у ряда С (хг, х2, . . ., хп), перечисляющего
функции, равен числу орбит веса (tu t2, . . ., tn). Через
Z(A, с (xv хг, . . ., хп)) обозначаем ряд, который получается
с помощью подстановки вместо каждой переменной Sk в Z (А)

62 ГЛ. 2. ТЕОРЕМА ПОЙ,
ряда с (х\, х\, . . ., хкп). Тогда более общий результат, даваемьи
теоремой перечисления Пойа для п переменных, может бытз
сформулирован так.
Теорема. Если с (хи х2, . . ., хп) — перечисляющий ряд дл,
фигур множества Y, то орбиты функций в Yx, определяемы*
степенной группой ЕА, перечисляются в соответствии со своими
весами рядом С (хг, х2, ■ ■ ., хп)
С(хг, х2, . . ., zn) = Z(A, e(xi, x2, . . ., *„)). B.4.16)
Для илюстрации этой теоремы вернемся к проблеме ожерелья.
На этот раз мы хотим найти перечисляющий ряд для ожерелий
с четырьмя бусинками и тремя допустимыми цветами. Поэтому
мы положим Y = {а, Ь, с) и будем рассматривать произвольную
функцию / из X в Y как представление ожерелья с | f'1 (a) \ крас-
красными, I/ (b) | белыми и J/ (с) | голубыми бусинками. Если мы
положим w (а) = @, 0), w (b) = A, 0) и w (с) = @, 1), то
»"(/)= 2 *(/(*)) BА17)
хвХ
и w (/) является упорядоченной парой, у которой первая коорди-
координата равна числу белых бусинок, а вторая координата — числу
голубых. Число красных бусинок, естественно, равно в точности
разности между | X | и числом белых и голубых бусинок. Теперь
в соответствии с определением перечисляющий ряд для фигур
есть с (х) — 1 + xt -f- х2. Следовательно, на основании теоремы
перечисляющий ряд для ожерелий имеет вид
С(хи xa) = Z(Dt, l+хг + хг). B.4.18)
Выполнив действия, связанные с подстановкой перечисля-
перечисляющего ряда для фигур в цикловой индекс Z ф4), получаем
+ 2х\х2 + х\х2 + гххх\ + ххх\ + 2х\х\. B.4.19)
Заметим, что сумму коэффициентов многочлена С (xv x2)
можно легко вычислить, найдя значение Z (Dit 3), которое равно
21; затем сравните с B.4.19).
2.5. РЯД 1 + х — СПЕЦИАЛЬНЫЙ РЯД ДЛЯ ФИГУР
Существует довольно естественное следствие теоремы Пойа,
которое обусловливает важность коэффициентов многочлена,
получаемого в результате подстановки ряда 1 + х в цикловой
индекс произвольной группы подстановок А. Хотя это утвержде-
утверждение устанавливается совсем легко, оно является исключительно

2.5. РЯД 1 + x — СПЕЦИАЛЬНЫЙ РЯД ДЛЯ ФИГУР 63
важным, так как каждая перечислительная формула, получаемая
из теоремы Пойа с использованием ряда 1 + х в качестве ряда
для фигур, неизбежно представляет собой частный случай этого
следствия. Среди таких результатов будут формулы для под-
подсчета числа ожерелий, графов, орграфов, корневых графов и
бихроматических графов. Мы пока отложим подобные приложения
формулируемого ниже следствия до соответствующих глав книги.
Мы отметим сейчас значение этого результата для пяти спе-
специальных групп, цикловые индексы которых даются формулами
B.2.5), B.2.6), B.2.10) — B.2.12). Подобно отдельным элементам
множества X, два r-подмножества S = {ж1, . . ., хг) и S" —
= {x'i, . . ., х'г) из X называются А-эквивалентными, если при
некоторой подстановке а £ А выполняется равенство aS = S'.
B.5.1). Следствие теоремы перечисления Пойа. Коэффициент
при хг в Z (А, 1 + х) равен числу А-эквивалентных классов г-
подмножеств множества X.
Доказательство. В ряде 1 + х, перечисляющем фигуры,
слагаемое 1 = х° можно толковать как отсутствие объекта из X,
а слагаемое х = х1 — как наличие этого объекта. Поэтому хТ
означает, что г различных объектов, образующих г-подмножество,
присутствуют в нем. Утверждение теперь следует непосредственно
из теоремы Пойа.и
Используя данное следствие, видим, что группа подстановок
А является транзитивной тогда и только тогда, когда коэффи-
коэффициент при х в Z (А, 1 + х) равен 1. Кроме того, коэффициенты
этого многочлена, равноотстоящие от его концов, всегда равны,
так как число классов r-подмножеств совпадает с числом классов
(п — г)-подмножеств. Для симметрической группы, как следует
из определения Sn, существует подстановка, отображающая
данное r-подмножество на произвольное другое г-подмножество.
Для группы Ап это также справедливо, но только необходимо
отметить, что требуемое отображение осуществляет четная под-
подстановка. Следующие две формулы могут быть также получены
с помощью тривиальной подстановки двучлена 1 + х в соответ-
соответствующие цикловые индексы:
Z(Sn, l + x) = l+x + x*+... + xn, B.5.2)
+ ... + a». B.5.3)
Единичная группа, естественно, порождает биномиальные
коэффициенты:
Z(En, 1+*) = S (Л*. B.5.4)

64 ГЛ.2. ТЕОРЕМА ПО1
С циклической и диэдральной группами дело обстоит
сколько сложнее. Обычным образом осуществляя формальщ
подстановку двучлена 1 -j" xk вместо переменной s^ в формул
B.2.10), получим 4-
г : Z (Сп, 1 + х) = /г* S Ф (*) A + **)п/*- -: B-5.5)
Однако подобная подстановка в формулу B.2.11) приводит к со
отношению, менее элегантному по форме. Чем выписывать 3TJ
формулу механически, лучше заметим, что мы уже сталкивались
с ней в случае п = 4 (см. формулу B.4.14), в которой приведе|
многочлен, перечисляющий ожерелья с четырьмя бусинкам!
окрашенными в два цвета). Тогда для произвольного га соответ
ствующий резу:
с га бусинками.
ствующий результат дает число типов двухцветных 1 ожерел;
2.6. ВЗАИМНО ОДНОЗНАЧНЫЕ ФУНКЦИИ « 1
Теперь удобно с логической точки зрения иметь в своем рас-
распоряжении такую теорему Пойа, которая выражала бы число
взвешенных взаимно однозначных функций через цикловые
индексы симметрических и знакопеременных групп и перечисля-
перечисляющие ряды для фигур. Мы будем использовать этот результат
позднее при установлении взаимосвязи между производящими
функциями для деревьев и для корневых деревьев.
Пусть с (х) — ряд, перечисляющий элементы некоторого мно-
множества Y в соответствии с их весами, и пусть единичная группа
Е имеет Y в качестве множества объектов. Рассмотрим ограниче-
ограничение степенной группы ЕА на подмножество всех взаимно одно-
однозначных функций из Yx. Если С (х) — перечисляющий ряд для
орбит, состоящих из взаимно однозначных функций и определя-
определяемых группой ЕА, то наша задача формулируется так: выразить
С (х) «на языке» с (х). Сначала рассмотрим случай А = Sn; после
этого решение общей задачи находится быстро. Заметим, что ор-
орбиты взаимно однозначных функций, определяемые группой Е п,
соответствуют га-сочетаниям, или w-подмножествам, элементов из Y.
Следуя Пойа, мы используем выражение Z (Ап — Sn) в качестве
сокращения для Z (Ап) — Z (Sn) и полагаем Z (Ао — So) = 1.
Теорема. Производящая функция С (х), которая перечисляв^
взаимно однозначные функции, отображающие множество из ni
1 Точнее, 2-раскрашешшх, — Прим. перев. 1

rr
2.6. ВЗАИМНО ОДНОЗНАЧНЫЕ ФУНКЦИЙ 65
взаимозаменяемых элементов в совокупность объектов с перечисля-
перечисляющим рядом для фигур с (х), дается формулой
C(x) = Z(An-Sn, c{x)). B.6.1)
Прежде чем доказывать эту теорему, мы проиллюстрируем ее
использование на одном примере для п = 3. Пусть с (х) — про-
производящая функция для множества Y связных графов, так
что коэффициент при хр в с (х) равен числу связных графов
порядка р. Известно, что несколько первых членов ряда с (х)
имеют вид
с (х) = х + х* + 2х3 + Qxi + 21ж5 + И2а:6 -f- B.6.2)
Далее, пусть С (х) — производящая функция для графов, име-
имеющих в точности три компоненты, причем все компоненты в графе
разные. Рассмотрим степенную группу Es* с множеством объектов
Yx- В этом случае орбиты взаимно однозначных функций, опре-
определяемые группой Es\ соответствуют как раз графам, перечи-
перечисляемым функцией С (х). Более того, вес каждой орбиты равен
порядку того графа, который соответствует этой орбите.
Формула для циклового индекса Z (А3 — 53) уже встречалась
в B.2.7). Поэтому, подставляя с (xk) вместо каждой переменной
sk в эту формулу, находим несколько первых членов ряда С(х):
С (х) = 2хв + 7 а;7 -f Мхв 4-.... B.6.3)
Предлагаем читателю убедиться в правильности некоторых
из этих коэффициентов, построив соответствующие графы.
Доказательство. Для доказательства соотношения B.6.1) на-
напомним, что ряд с (х) перечисляет элементы некоторого множества
Y в соответствии с их весами и что группа ESn имеет множество
Yx в качестве множества объектов. Из теоремы Пойа следует,
что ряд, перечисляющий орбиты всех функций, определяемые
группой ESn, есть просто Z (Sn, с (х)). Поэтому достаточно показать,
что ряд Z (Ап, с (х)) считает дважды те орбиты, которые состоят
из взаимно однозначных функций, а все остальные орбиты —
только по одному разу.
Заметим сначала, что если функции взаимно однозначно
отображают множество X на себя, то число орбит, состоящих
из всех таких функций и определяемых группой Епп, равно 2.
Это немедленно следует из следующего легко доказываемого
факта: две взаимно однозначные функции находятся в одной и той
А
же орбите группы Епп тогда и только тогда, когда они обе либо
четные, либо нечетные 1. Таким образом, ряд Z (Ап, с (х)) считает
1 Понимаемые как подстановки множества X. — Прим, перев&
3 Заказ 143

66 ГЛ. 2. ТЕОРЕМА ПОЙА
дважды те орбиты группы Es", которые состоят из взаимно одно-
однозначных функций.
Далее мы покажем, что орбиты группы ES/l, состоящие из
функций, не являющихся взаимно однозначными, считаются
только один раз. Для этого рассмотрим некоторую такую орбиту
и две функции / и g в ней. Тогда существует подстановка а в Sn,
такая, что для всех х из X выполняется равенство / (х) = g (ax).
Необходимо показать, что / и g принадлежат одной и той же
орбите группы Е п. В случае четной подстановки а это следует
из равенства / (х) = g (ах). Предположим теперь, что а — нечет-
нечетная подстановка. Так как функция / не является взаимно одно-
однозначной, то для некоторых хх и х2 из X, таких, что хг Ф х2,
имеем / (хг) = / (х2). Пусть р — подстановка, переставляющая
между собой хг и х2 и оставляющая неподвижными другие эле-
элементы из X. Так как р — транспозиция, то она является нечетной
подстановкой. Тогда ар — четная подстановка и для всякого х
из X f (х) = g (ap#). Значит / и g принадлежат одной и той же
орбите группы ЕАп и, следовательно, ряд Z (Ап, с (х)) считает
орбиты группы Es", состоящие из функций, не являющихся
взаимно однозначными, только один раз.я
В приведенном ниже следствии рассматривается общий слу-
случай, в котором орбиты взаимно однозначных функций на п объек-
объектах определяются не симметрической группой Sn, а произвольной
группой А степени п.
Следствие. Производящая функция С (х), которая перечисляет
взаимно однозначные функции, определяемые перечисляющим ря-
рядом для фигур с (х) и произвольной группой подстановок А степени
п, дается формулой
-Sn, c(x)). B.6.4)
Доказательство. Напомним, что с (х) перечисляет элементы
множества Y в соответствии с их весами и что Z (Ап — Sn, с (х))
перечисляет в соответствии с их весами подмножества множества
Y, состоящие из п элементов. Как обычно, Е обозначает единич-
единичную группу с множеством объектов Y и А обозначает группу
подстановок степени п с множеством объектов X. Рассмотрим
произвольное га-подмножество Y^ множества Y. Мы намереваемся
установить, что число орбит группы Еп , ограниченной на взаимно
однозначные функции в Ff, равно п\1 \А \. Но это заключение
следует немедленно из 'ограниченной формы леммы Бернсайда,
так как в группе Е„ единственной подстановкой, оставляющей
неподвижной произвольную взаимно однозначную функцию в

УПРАЖНЕНИЯ 67
yf, является тождественная подстановка, которая оставляет
неподвижными все п\ таких функций.в
В наших приложениях этой теоремы часто необходимо будет
суммировать многочлены Z {Ап — Sn). Мы иногда пишел Z {А со —
со
— Sea) вместо ^jZ(An— Sn). РиорданЦ] вывел следующую фор-
формулу, аналогичную формуле C.1.1):
(-1)*+»/(**)/*}. B.6.5)
УПРАЖНЕНИЯ
2.1. Доказать лемму Бернсайда B.3.3), дающую число орбит,
определенных произвольной группой, представленной в виде
группы подстановок. Детальнее, пусть А — произвольная (аб-
(абстрактная) группа, и положим ср : А -> В — гомоморфизм из А
в группу подстановок В. Тогда число N (В) орбит группы В
дается формулой
\\2 Ыф())
авА
2.2. Сколько орбит функций определяются степенной группой
£„"'? Сколько орбит определяются группой Е%, если А — А,п,
Ст или Dm?
2.3. Найти две неизоморфные группы подстановок А и В, имеющие
наименьший порядок и удовлетворяющие условию Z (А) — Z (В).
(Пойа [1])
2.4. Доказать, что множество подстановок степенной группы ВА
замкнуто относительно операции умножения.
2.5. Сколько существует ожерелий с пятью бусинками, если
допускаются бусинки трех цветов?
2.6. Если при раскраске вершин куба используются три раз-
разных цвета, то сколько возможно различных кубов?
2.7. Если при раскраске граней куба используются четыре разных
цвета, то сколько получится различных кубов?
2.8. Если допустимы пять разных цветов и каждое ребро графа,
изображенного на рис. 2.3.1, окрашено одним из этих цветов,
то сколько возможно различных раскрашенных графов?
2.9. Пусть G — произвольный граф. Как можно интерпретировать
коэффициенты ряда Z (Г (G), 1 + хI Проиллюстрируйте это,
используя граф, приведенный на рис. 2.3.1.
3*

68
ГЛ. 2. ТЕОРЕМА ПОЙЛ
2.10. Когда множество объектов степенной группы ВА ограничи-
ограничивается взаимно однозначными функциями, то группу обозначают^
через ВА". Найти формулу для циклового индекса Z (ВА*).
(Харари и Палмер [5])
2.11. Найти две изоморфные, но не идентичные группы подста-
подстановок степени 6 и порядка 4, которые имеют одинаковый цикло-
цикловой индекс. (Редфилд [l])i
2.12. Цикловой индекс знакопеременной группы Ап, даваемый;
формулой B.2.6), может быть выражен в следующей форме: ;
2.13.
fit
П *'*./*!
П
s'A
' }'(<-*>.
*"Ч M v/
., •> 'v,,'

Глава 3
Лесоруб] Это дерево ты пощади,
От ветвей его острый топор отведи.
Находил я под ним и приют и покой,
А теперь за чего готов выдержать бой.
Дж. П. Моррис х
Ч1-,
ДЕРЕВЬЯ
В первой главе мы познакомились с несколькими методами опре-
определения числа помеченных деревьев порядка р, числа, равного
рР. Теперь мы рассмотрим более трудную задачу: нахождение
числа непомеченных деревьев, т. е. нахождение числа изоморфных,,
классов деревьев с данным числом вершин. Техника, которую мы
будем использовать, может быть легко приспособлена не только
к нахождению производящей функции для деревьев, обладающих
различными указанными свойствами, но также к подсчету древо-
древовидных структур.
Например, в этой главе мы найдем производящие функции
для корневых деревьев, деревьев, лесов, ориентированных де-
деревьев, гомеоморфно несводимых деревьев, асимметрических
деревьев, унициклических графов, функциональных орграфов,
кактусов и 2-деревьев. Несколько первых коэффициентов многих
из этих производящих функций можно также найти в книге
Слоуэна [1], посвященной последовательностям.
3.1. КОРНЕВЫЕ ДЕРЕВЬЯ
По-видимому, невозможно перечислить деревья, не пере-
перечислив сначала корневые деревья. Поэтому мы начнем с примене-
применения метода Пойа, описанного в предыдущей главе, к нахождению
производящей функции для корневых деревьев. Затем мы восполь-
воспользуемся данной Оттером 11 ] «теоремой о характеристике неподобия»,
чтобы установить взаимосвязь между этой функцией и рядом,
перечисляющим деревья.
1 Моррис Джордж Поуп A802—1867) — американский поэт и журна-
журналист. — Прим. перев.

70 ГЛ, 3. ДЕРЕВЬЯ
Мы используем хорошо известное тождество, в котором про-
просуммированы цикловые индексы всех симметрических групп:
%Z(Sn, /(*)) = ехр{|/(**)/*). C.1.1)
Доказательство формулы C.1.1) опускается; самое простое
из доказательств этого соотношения состоит в сравнении коэффи;
циентов обеих частей (см. упражнение 2.13).
Y
Рис. 3.1.1 Наименьшие корневые деревья.
Полагаем для удобства Z(S0) = i и используем запись Z(SQO)
со
вместо 2iZ(Sn). Тогда левая часть формулы C.1.1) может быть
обозначена через Z(Stx>, /(х)).
Пусть теперь
оо
Г1~\ V1 т ™п /о А О\
р-1
— производящая функция для корневых деревьев. Таким обра-
образом, Тр представляет собой число корневых деревьев порядка р.
Корневые деревья не выше четвертого порядка показаны на рис.
3.1.1. Поэтому-четыре первых слагаемых производящей функции
Т (х) даются соотношением
г (г\ _ г I г2 4- 2г3 4- 4г4 4- (Л \ 31
Следующий результат Пойа [1] можно использовать для
вычисления коэффициентов функции Т (х).
Теорема. Перечисляющий ряд Т (х) для корневых деревьев
удовлетворяет соотношению
Т{х) = х exp JS T (xk)/k\. C.1.4)
Доказательство. Сначала найдем производящую функцию, s
перечисляющую такие корневые деревья, корень которых имеет |
степень п. Замечаем, что каждое иэ таких деревьев естественным |

ц
j.1. КОРНЕВЫЕ ДЕРЕВЬЯ 71
образом соответствует некоторому «сочетанию с пввторениями»
йз п корневых деревьев. Это соответствие для п — 4 проиллю-
проиллюстрировано на рис. 3.1.2. Более подробно: пусть дана некоторая
совокупность из п корневых деревьев; новое корневое дерево
строится путем добавления одной новой вершины и установления
смежности этой вершины с каждым из корней п первоначальных
корневых деревьев. Ясно, что все деревья, у которых корни
имеют степень п, могут быть построены указанным способом.
Чтобы найти число таких деревьев, рассмотрим степенную группу
ESn с множеством объектов Yx, где Е — единичная группа,
X = {1, . • •, п) и Y — множество всех корневых деревьев.
Тогда каждая функция из Yx соответствует некоторому упоря-
упорядоченному набору, состоящему из п корневых деревьев. Опреде-
Определим вес произвольного корневого дерева из Y как число вершин
Рис, 3.1.2 Четыре корневых дерева и соответствующее им дерево, корень
которого имеет степень 4.
в этом дереве. Тогда Т (х) перечисляет элементы Y в соответствии
с их весами и называется «рядом, перечисляющим фигуры», для
множества Y. Таким образом, вес каждой функции из Yx, опре-
определенной в соответствии с формулой B.4.4), представлят собой
общее число вершин в п корневых деревьях из того набора длины
п, которому соответствует взятая функция.
Так как группа Sn состоит из всех подстановок множества X,
то орбиты степенной группы Es" соответствуют в точности корне-
корневым деревьям, у которых корни имеют степень п. Заметим, что
вес каждой орбиты, который является весом и любой функции,
содержащейся в этой орбите, ровно на единицу меньше общего
числа вершин в корневом дереве, сопоставленном орбите. Поэтому,
взяв в теореме Пойа А = Sn и в качестве ряда, перечисляющего
фигуры, производящую функцию Т (х), получаем ряд, пере-
перечисляющий функции: Z (Sn, Т (х)). Коэффициент при х? в Z (Sn,
Т (х)) представляет собой число корневых деревьев порядка
Р + 1, у которых корень имеет степень п. Умножение ряда
Z (Sn, T (х)) на х «подправляет» веса так, что коэффициент при
& в x-Z (Sn, T (х)) равен числу этих деревьев с р вершинами.

72 ГЛ. 3. ДЕРЕВЬЯ
Затем, суммируя по всем возможным значениям п, получаем
само Т{х): *
2(a T(x)). х , C.1.5)
п=0
Доказательство завершается применением тождества C.1.1) к
сумме цикловых индексов, стоящей в правой части соотношения
C.1.5).н
Из этой теоремы следует, что Т (х) однозначно определяется
функциональным уравнением C.1.4), так как формула A.2.8)
дает способ определения коэффициентов функции Т (х) по индук-
индукции. Чтобы увидеть это, положим
оо со ' • «'
2 ««^" = 2 т(я*)/к. C.1.6)
Следовательно,
"Г am = m-*yd.Td - , C.1.7)
и из формулы A.2.8) следует, как у Оттера (I), что /
TP+1 = p-l4ZikakTp.k+1.-^ C.1.8)
Комбинируя C.1.7) и C.1.8), выражаем Тр+1 через Тх, . . ., Тpi
Iid-Td)Tp.li+l. C.1.9)
d/h I
Значительно раньше Кэли [1 ] нашел следующую формулу для
Т (х), которая легко выводится из соотношения C.1.4):
p=i
A-хр)'тр. C.1.10)
Наоборот, формула C.1.10) позволяет установить соотношение
C.1.4). Чтобы убедиться в этом, достаточно показать, что
In (Т (х)/х) = S т (х")/к- C.1.11)
Это осуществляется в три шага: сначала логарифмируются обе
части формулы C.1.10), затем используется тождество
1пA—*") = - %хР*/к C.1.12)
И, наконец, меняется порядок суммирования. .

3.2. НЕКОРНЕВЫЕ ДЕРЕВЬЯ 73
Числа корневых деревьев порядка р для р ^ 26 найдены
Риорданом (см. Риордан [1], стр. 164) и для р ^ 39 — Швенком
с использованием формулы C.1.4). Здесь представлены несколько
первых членов ряда Т (х):
Т (х) = х + х* + 2х3 + 4ж4 + 9ж5
+ 115а;8+286ze +719z10+ C.1.13)
Коэффициенты ряда Т (х) для рг^26 приведены в приложении I.
3.2. НЕКОРНЕВЫЕ ДЕРЕВЬЯ
Для перечисления некорневых деревьев нам сейчас потре-
потребуется только частный случай (при п = 2) утверждения из пара-
параграфа 2.6 о возможности перечисления всех взаимно однозначных
функций, заданных на множестве из п объектов. Пусть
со
1(х)=^1рхр C.2.1)
p=i
— производящая функция для деревьев, так что tp есть число
деревьев порядка р. Соотношение C.2.4), приводимое в основной
теореме данного параграфа, является наиболее изящной из воз-
возможных формул, выражающих ряд t (x) для деревьев через ряд
Т (х) для корневых деревьев. Доказательство формулы C.2.4)
зависит не только от теоремы перечисления взаимно однозначных
функций, но и от следствия из устанавливаемой ниже теоремы
о характеристике неподобия.
Для произвольного графа G обозначим через р* число непо-
неподобных вершин, т. е. число орбит, состоящих из вершин и опре-
определяемых группой Г (G). Группа графа G определяет также классы
подобных блоков. Пусть р* — число неподобных вершин в £-м
классе блоков среди Ь* неподобных блоков. Тогда р" и р, свя-
связываются формулой C.2.2), приводимой в следующей теореме.
Оттер [1] первым получил это утверждение для деревьев, но,
подобно многим теоремам, оно доказывается проще для более
общего случая (см. Харари и Норман 12]). Поэтому мы рассма-
рассматриваем произвольные блоки (вместо обычных ребер, как это
имеет место в деревьях).
Теорема (о характеристике неподобия для графов). Для всякого
графа G
Для иллюстрации теоремы рассмотрим граф порядка 18,
Изображенный на рис. 3.2.1. Вершины этого графа помечены так,

74
ГЛ. 3. ДЕРЕВЬЯ
что подобные вершины имеют одинаковые пометки. Таким обра-
образом, р* = 4. Существует три класса блоков, поэтому Ъ * = 3;
первый класс состоит из мостов, второй — из 4-цикла, а третий
содержит треугольники. В каждом классе существуют две подоб-
подобные вершины, так что р\ = р2 = р*я = 2. Таким образом,'
и р* - 1 = 3, и р\ - 1 + р\ - 1 + р\ - 1 = 3
4 4
Рис. 3.2.1 Граф с тремя неподобными блоками. <
Доказательство. Доказательство теоремы проведем индукцией
по числу классов блоков. Пусть G — произвольный граф. Если
существует точно один класс блоков, т. е. Ъ * = 1, то р * = Pi
и формула C.2.2), очевидно, справедлива. В ином случае рас-
рассмотрим произвольный блок графа G, имеющий в точности одну
точку сочленения, и предположим, что этот блок принадлежит
Рис. 3.2.2 я) Дерево, не имеющее симметричных ребер, и б) дерево, облада-
обладающее симметричным ребром.
классу, номер которого равен единице. Удалим из графа G вер-
вершины всех блоков, входящих в этот класс, оставив только точки
сочленения. Граф G", полученный в результате такой операции,
имеет Ъ * — 1 классов блоков и р * — (pi — 1) классов вершин.
Применяя индуктивное предположение к графу G, имеем формулу
C.2.2) для графа G.^
Чтобы применить эту теорему к деревьям, обозначим числа
неподобных вершин и ребер произвольного дерева Т соответственно
через р * и д*. Ребро дерева Т называется симметричным, если
его концевые вершины подобны. Пусть s — число симметричных
ребер графа. Дерево, изображенное на рис. 3.2.2, а, не имеет

3.2. НЕКОРНЕВЫЕ ДЕРЕВЬЯ 75
симметричных ребер, в то время как дерево, показанное на рис.
3.2.2, б, содержит одно симметричное ребро. Для первого из этих
деревьев р * = 6 и каждый из его пяти классов блоков имеет
5
две неподобные вершины. Следовательно, 5 = р* — 1 =2 B—
—1) = 5. Для второго дерева р * = 2 и один класс блоков имеет
две неподобные вершины, в то время как другой класс, соответ-
соответствующий симметричному ребру, содержит только одну вершину.
Следовательно, 1 = р* — 1 = B — 1) + A — 1) = 1. Найден-
Найденная Оттером теорема о характеристике неподобия для деревьев
формулируется в виде следствия.
Следствие (теорема о характеристике неподобия для деревьев).
Число s симметричных ребер произвольного дерева равно О или 1 и
P*-(g*-s) = l. C.2.3)
Доказательство. Сначала замечаем, что s = 1 тогда и только
тогда, когда дерево бицентрально и две его центральные вершины
подобны, а иначе s = О (см. Харари [1], стр. 52). Затем обращаем
внимание на то, что q * есть число неподобных блоков, так что
Ъ * = q*. Далее, р* = 2 для каждого класса блоков (ребер),
кроме класса с симметричным ребром. Для последнего класса
р* = 1 в силу определения. Итак, правая часть формулы C.2.2)
равна q * — «и доказательство следствия завершено. в
Теперь мы в состоянии закончить наш вывод элегантной фор-
формулы Оттера для ряда t (x).
Теорема. Ряд t (x), перечисляющий деревья, выражается
через ряд Т (х) для корневых деревьев с помощью формулы
t(x) = T(x)—L{T*(x)-T(a*)). C.2.4)
Доказательство. На первом шаге доказательства просумми-
просуммируем формулу C.2.3) по всем деревьям, имеющим точно р вершин.
Получаем
21 = 2р*-2(з*-«). C.2.5)
2jl = *p и 2р* = ^р- Кроме того, 2(<7*~s) равна числу Lp
деревьев, у которых одно ребро, не являющееся симметричным,
выделено как корневое. Следовательно, tp = TP — Lp; поэтому
если L (х) — ряд, перечисляющий реберно-корневые деревья,
У которых корневое ребро не является симметричным, то
t(x) = T(x)-L(x). C.2.6)

76 ГЛ. 3. ДЕРЕВЬЯ
На данном этапе для выражения L (х) через Т (х) мы можем
применить формулу B.6.1) из нашей теоремы о взаимно однознач-
однозначных функциях. Заметим, что любые два различные корневые
дерева определяют реберно-корневое дерево с несимметричным
корневым ребром и это соответствие, проиллюстрированное на
рис. 3.2.3, может быть специфицировано посредством соединения
двух корней штриховым ребром. Таким образом, деревья, пере-
перечисляемые рядом L (х), могут быть интерпретированы как 2-под-
множества, состоящие из графов, перечисляемых рядом Т (х).
«•Vs f
Рис. 3.2.3 Два корневых дерева и соответствующее им рвберво-корневое
дерево.
Следовательно, мы можем применить формулу B.6.1) При п = 2.
Получаем соотношение ' '
Далее, Z (А»— S2) = -^- (s^ — s\ Hj положив Sx == Т (х), s2 = T (x2),
из формул C.2.7) и C.2.6) выводим формулу Оттера для t(x). a
Кэли предвосхитил и результат Пойа о функции Т (х), и
результат Оттера о функции t (x). В самом деле, несложным
упражнением представляется вывод соотношения C.2.4) из перво-
первоначальной формулы Кэли или из формулы Пойа для tp; и Кэли,
и Пойа нашли степенные выражения для tp в виде суммы чисел
t'p и t'p, представляющих собой числа деревьев с одной и двумя
центральными вершинами соответственно. Проверка завершается
выписыванием суммы ^tpxp и использованием поговорки: «Вся-
«Всякий раз, когда видишь повторное суммирование, поменяй знаки
местами».
Значения tp для р ^ 26 вычислены Риорданом [1, стр. 164]
с использованием формулы C.2.4). Несколько первых коэффи-
коэффициентов ряда t (x) даны ниже, а остальные известные значения
tp приводятся в приложении I:
t (х) = х + х2 + х3 + 2х* + Зхъ + Qxe -f I ix1 +
+ 23z8 + 47яв + 106a;10 -f C.2.8)
Лесом называется граф, компоненты которого являются дере-
деревьями. Теперь, когда перечислены деревья, перечисление лесов

3.2. НЕКОРНЕЁЫЕ ДЕРЕВЬЯ
' .-*
77
осуществляется легко. Пусть перечисляют^ ывотачашом для
лесов с р вершинами будет функция ¥ ■■ ■ - - у
9=0
C.2.9)
где /р, q — число лесов с р вершинами и q ребрЗДЗ'-ТрГДа произво-
производящая функция для лесов имеет вид -;> «j^v...
оо
/(*. у)=2г/р-/Р(*)- ? C.2.Ю)
Чтобы получить формулы для /р (х) и / (я, у), воспользуемся
перечисляющим рядом для деревьев. В статье Харари [4] формула
для / (х, у) получена путем подходящего применения теоремы
перечисления Пойа и обобщения формулы C.1.1) на случай про-
произвольной функции g (x, у), зависящей от двух переменных.
Таким образом, число лесов выражается через число деревьев
с помощью следующей формулы:
(со со
2 2 (hi
Используя логарифмы, легко показать, что эта формула может
быть выражена также в виде ' • ;.,
+ f(x, у) =
.^ , г, <3.2.12)
напоминающем формулу Кэли [1] для числа корневых деревьев.
Сейчас мы дадим более явную формулу (см. Харари и Палмер
[И]) для fp (x), выражающую многочлен fp(x) через числа tk.
Теорема. Перечисляющий многочлен для лесов с р вершинами
имеет вид
Лк-1)
C.2.13)
где сумма берется по всем разбиениям (j) числа р.
Доказательство. Используя хорошо знакомую формулу для
числа сочетаний с повторениями (см. Риордан [1], стр. 15),
находим, что число лесов, состоящих в точности из jk fc-вершинных
деревьев, равно биномиальному коэффициенту
h

78 ГЛ. 3. ДЕРЕВЬЯ
Так как каждое из этих деревьев имеет к — 1 ребер, то для любого
Q = 0, i р — 1
где сумма берется по таким разбиениям (/) == (j1, j2, ■ ■ ■, jp)
числа р, которые удовлетворяют соотношению
£1)/*. C.2.15)
Формула C.2.13) для /р (х) может быть получена теперь путем
суммирования по всем разбиениям числа р.н
Пример: используя ряд t (х) для деревьев и формулу C.2.13)
при р = 6, легко находим
U (х) = 1 + х + 2х* + Ах3 + %xi + 6z5. C.2.16)
Умножая соотношение C.2.13) на ур и суммируя по всем воз-
возможным целым положительным числам р, можно получить после
несложных манипуляций формулы C.2.11) и C.2.12).
3.3. ДЕРЕВЬЯ СО СПЕЦИАЛЬНЫМИ СВОЙСТВАМИ
Многие классы деревьев могут быть перечислены с помощью
той процедуры, которая изложена в предыдущих параграфах
этой главы. Обычно сначала с помощью теоремы перечисления
Пойа находят производящую функцию для корневых многооб-
многообразий. Затем «теорема о характеристике неподобия» обеспечивает
нас средством, позволяющим выразить ряд для некорневых де-
деревьев через ряд для корневых деревьев. В этом параграфе мы
рассмотрим несколько задач, которые могут быть успешно решены
указанным способом.
Первая задача относится к. перечислению ориентированных
деревьев. Ориентированное дерево представляет собой дерево,
в котором каждое ребро ориентировано. Пусть г (х) и R (х) —
перечисляющие ряды для ориентированных деревьев и для корне-
корневых ориентированных деревьев соответственно. Все восемь ориен-
ориентированных деревьев четвертого порядка показаны на рис. 3.3.1
и удостоверяют тот факт, что коэффициент при xi в г (х) равен 8.
Следующий результат из статьи Харари и Принса [1] полезен
при нахождении числа ориентированных деревьев.

S.3. ДЕРЕВЬЯ СО СПЕЦИАЛЬНЫМИ СВОЙСТВАМИ 79
Теорема. Перечисляющие ряды r{x)uR (x) для ориентированных
деревьев и корневых ориентированных деревьев удовлетворяют
соотношениям
■^ " R(x) = x exp S R(xh)/k 1 C.3.1)
\ U=i J /
и
: . г {х) = U (х) — R2 {х). C.3.2)
Ряс. 3.3.1 Ориентированные деревья четвертого порядка.
В частности, мы находим
C.3.3)
Первые 21 коэффициентов рядов г (х) и R (х) найдены Риор-
даном [1, стр. 164].
Доказательство. Определим дерево с висячим корнем как такое
корневое дерево, у которого корень имеет степень 1. Пусть R (х) —
перечисляющий ряд для ориентированных деревьев с висячими
Рис. 3.3.2 Три ориентированных дерева с висячими корнями и соответству-
соответствующее им дерево.
корнями. Всякое n-подмножество таких деревьев соответствует
корневому ориентированному дереву, в котором ровно тгдуг инци-
инцидентны корню (см. рис. 3.3.2). Применяя теорему Пойа к симме-
симметрической группе Snc использованием ряда R (хIх в качестве
перечисляющего ряда для фигур, получаем ряд Z (Sn, R (х)/х),
перечисляющий функции и такой, что коэффициент при х?'1
в нем равен числу корневых ориентированных деревьев порядка
р, причем корни в этих деревьях инцидентны п дугам. Использо-
Использование здесь ряда R (х)/х в качестве перечисляющего ряда для
фигур осуществляет назначение нулевых весов корням деревьев

80 гл. з. деревья
с висячими корнями, а следовательно, и корням корневых де-
деревьев. Необходимая корректировка поэтому достигается умно-
умножением ряда Z (Sn, R (х)/х) на х. Затем, суммируя по всем неотри-
неотрицательным целым числам п, выражаем ряд R (х) через R (х)
в следующем виде:
R(x) = xZ(Soa, R(x)lx). C.3.4)
Но для каждого корневого дерева порядка р мы можем построить
два различных дерева порядка р -f- 1 с висячими корнями, до-
добавляя новую дугу, входящую в корень или исходящую из корня.
Так как все деревья с висячими корнями можно получить ука-
указанным способом однозначно, то
R(x) = 2xR(x). - .:': C.3.5)
Подставляя это выражение для R (х) в соотношение C.3.4) и
применяя тождество C.1.1), убеждаемся в справедливости фор-
формулы C.3.1).
Чтобы выразить г (х) через R (х), заметим, что у ориентиро-
ориентированных деревьев, не имеющих симметричных ребер, s = 0. Сле-
Следовательно, уравнение характеристики неподобия для таких
деревьев есть просто,
l=p*-q*. C.3.6)
Как и в случае обычных деревьев, из C.3.6) вытекает, что
г (*) = Я (*)-£(*), C.3.7)
где L (х) является перечисляющим рядом * для таких ориентиро-
ориентированных деревьев, у которых одна из дуг выделена (и названа
корневой дугой): Эти деревья (с корневыми дугами) соответствуют
в точности функциям, отображающим множество {1, 2} в множе-
множество корневых ориентированных деревьев. Если задана такая
функция /, то соответствующее дерево с корневой дугой полу-
получается путем добавления корневой дуги, ориентированной из
корня дерева / A) к корню дерева / B). В этом случае перечисля-
перечисляющий ряд для функций равен просто R2 (х), ибо ряд, перечисля-
перечисляющий фигуры, есть R (х). Заметим, что тот же самый результат
получается и с помощью теоремы перечисления Пойа, именно
Z (E2, R (х)). Таким образом, L (х) = R2 (х) и доказательство
1 Мы уже использовали L (х) в предыдущем параграфе для реберпо-
корневых деревьев, не имеющих симметричных ребер. В параграфе 3.5 то же
самое обозначение L (х) будет использовано в аналогичной ситуации для
2-деревьев. Мы надеемся, что конкретный смысл обозначения будет всегда
ясен из контекста,

3 3. ДЕРЕВЬЯ СО СПЕЦИАЛЬНЫМИ СВОЙСТВАМИ
завершается после подстановки выражения для L (х) в формулу
C.3.7).н
Следующими будут рассмотрены гомеоморфно несводимые дере-
деревья, т. е. деревья, не имеющие вершин степени 2. Все такие деревья
не выше восьмого порядка показаны на рис. 3.3.3. Пусть h (х), Н(х) и
Jf (x) обозначают перечисляющие ряды для следующих трех клас-
классов гомеоморфно несводимых деревьев: а) «обычных» деревьев,
б) корневых деревьев и в) деревьев с висячими корнями. Коэф-
Коэффициенты этих рядов могут быть вычислены с использованием
Рис. 3.3.3 Наименьшие гомеоморфно несводимые деревья.
соотношений, приводимых в следующей теореме (см. статью
Харари и Принса [1]).
Теорема. Перечисляющие ряды Н (х), Н (х) и h (x) для гоме-
гомеоморфно несводимых деревьев удовлетворяют соотношениям
#(*) =
1 + х
=1
(х) =
Я (я)--JL (Я* (х) + Н(*«
C.3.8)
C.3.9)
C.3.10)
C.3.11)
Доказательство. Мы начнем с замечания о том, что /г-под-
множества деревьев с висячими корнями соответствуют таким
В более явной форме
h (х) =
2хв

82
гл. з. дерев!
де ревьям с висячими корнями, у которых вершина, смежная с кор-
корнем, имеет степень п. Это соответствие демонстрируется на рис.
3.3.4, где корни трех деревьев с висячими корнями отождеств-
отождествляются, а новая вершина вводится как висячий корень у нового
дерева. Беря Н (хIх в качестве перечисляющего ряда для фигур,
получаем ряд Z (Sn, H (х)/х), который перечисляет «новые»
Рис. 3.3.4 Три дерева с висячими корнями и соответствующее им дерев)
порядка 11, также имеющее висячий корень.
деревья с висячими корнями. Однако в этом перечислении не учи-
учитываются ни новые корни, ни отождествленные вершины. Надле-
Надлежащая корректировка осуществляется умножением на хг. Затем,
суммируя по всем п i> 2, снова получаем Н (х), но при этом нужно
добавить х2, чтобы учесть дерево порядка 2, имеющее висячий
корень:
П-Z
(Sn, Н
C.3.12)
Рис. 3.3.5 Два дерева с висячими корнями и соответствующее им реберно-
корневое дерево.
Теперь, чтобы получить формулу C.3.8), можно применить тояс-|
дество C.1.1) к соотношению C.3.12). С помощью формулы C.3.8)»|
очевидно, могут быть вычислены коэффициенты ряда Н (х). '!
Далее мы проверим соотношение C.3.9), выражающее корне-
корневые деревья через деревья с висячими корнями. Имеем: ряд
Z (S2, H (х)) перечисляет такие деревья с висячими корнями,
в которых вершина, смежная с корнем, имеет степень 3; ряд
х (Н (х) — Н (х)) перечисляет деревья с висячими корнями»
у которых вершина, смежная с корнем, имеет степень, либо рав-

3.8. ДЕРЕВЬЯ СО СПЕЦИАЛЬНЫМИ СВОЙСТВАМИ
83
иую 1> либо большую 3. Следовательно, ряд Н (х) удовлетворяет
соотношению
Н(х) = х (Я (х) - Я (х)) + Z E„ Я (х)).
C.3.13)
Осуществив подстановку ряда Я (х) в цикловой индекс Z {S а)
и разрешая полученное уравнение относительно Я (х), приходим
к формуле C.3.9).
Наконец, нам необходим перечисляющий ряд L (х) для гоме-
оморфно несводимых реберно-корневых деревьев, у которых
корневое ребро не является симметричным. Имея такой ряд,
мы сможем применить теорему о характеристике неподобия и
Рис. 3.3.6 Асимметрические деревья с небольшим числом вершив.
выразить h (x) через Я {х) и Я (х). Чтобы осуществить этот план,
заметим, что каждая пара различных деревьев с висячими кор-
корнями, содержащая к вершин, соответствует реберно-корневому
дереву, у которого к — 2 вершины и корневое ребро — несимме-
несимметричное. Указанное взаимно однозначное соответствие реали-
реализуется путем соединения вершин, смежных с корнями, корневым
ребром и отбрасыванием корней у исходных деревьев с висячими
корнями (см. рис. 3.3.5). Снова используя формулу B.6.1) из
теоремы о взаимно однозначных функциях, получаем ряд Z (А2 —
— iS2, Я (х)), перечисляющий пары различных деревьев с вися-
висячими корнями. Разделив на х*, подправляем надлежащим обра-
образом веса и, применяя уравнение C.2.3) характеристики неподо-
неподобия, выводим соотношение
h(x)=,H(x)-x-2Z(A2~S2,
C.3.14)
Осуществив подстановку ряда Я (х) в цикловой индекс Z (А2 —
— S2), получаем формулу C.3.10).и
Далее рассмотрим асимметрические деревья, т. е. такие де-
деревья, группы автоморфизмов которых являются единичными
группами. Асимметрические деревья порядков 7, 8 и 9 показаны

84
ГЛ. 3. ДЕРЕЫ
на рис. 3.3.6. Единственным асимметрическим деревом, иоряд<
которого меньше 7, является тривиальное дерево х.
Абсолютом корневого или реберно-корневого дерева Т (об
значение: \Т \) называется некорневое дерево с теми же самын
вершинами и ребрами, что и у дерева Т. Ясно, что если Г (| Т \)
единичная группа, то такой же будет и группа Г (Т). Обратщ
не верно. Наименьшие корневые асимметрические деревья пок,
заны на рис. 3.3.7. Заметим, что группы их абсолютов, вообп
говоря, не являются единичными.
Следующая теорема из работы Харари и Принса [1 ] устана
вливает взаимосвязь между рядами для корневых и некорневыЗ
асимметрических деревьев.
Рис. 3.3.7 Асимметрические корневые деревья с небольшим числом вершин.
Теорема. Пусть и (х) и U (х) — перечисляющие ряды для
деревьев и корневых деревьев с единичными группами автоморфизмов.
Тогда
и (х) = U (х) - 4- (U2 (х) + U (х%
C.3.15)
C.3.16)
Доказательство. Проверка соотношения C.3.15) осуществ-
осуществляется прямым методом. Применяя формулу B.6.1) из теоремы
Пойа о взаимно однозначных функциях, видим, что ряд xZ (An —
— Sn, U (х)) перечисляет корневые деревья с тривиальной груп-
группой и с корнем степени п ^ 1. После суммирования этого ряда
по всем п соотношение B.6.5) дает формулу для U (х).
Так как в рассматриваемых нами деревьях симметричных
ребер нет, то уравнение характеристики неподобия есть просто
1 = р * — q* = р — q. Поэтому, чтобы выразить и (х) через
U (х), мы найдем производящие функции, перечисляющие числа
способов, которыми асимметрические деревья могут быть осна-
оснащены либо корнями, либо корневыми ребрами. Подробнее, пусть
1 То есть дерево, имеющее только одну ве ршину, — Прим, мрев.

3.3. ДЕРЕВЬЯ СО СПЕЦИАЛЬНЫМИ СВОЙСТВАМИ 85
иг (х) и V2 (?) — соответствующие перечисляющие ряды для
корневых и реберно-корневых деревьев, абсолюты которых имеют
единичные группы. Тогда
л. u{x) = Ul(x)-Ua(x). C.3.17)
Пытаясь выразить U1 (х) и U2 (х) через и (х), мы введем пер-
первым делом две производящие функции V1 (x) и У2 (%) — соответ-
соответственно для корневых деревьев и для реберно-корневых деревьев,
причем рассматриваются только такие деревья, которые обладают
следующим свойством: группа Г (Г)дерева?1 является единичной,
а группа Г (| Т |) его абсолюта — не единична. Тогда можем
написать
Vl(x) C.3.18)
-Sa, U{x))-Vt{x). C.3.19)
И вот теперь мы замечаем, что так как
u(x) = U(x)-Z(A2~S2, U{x))-[-V2{x)-V1(x), C.3.20)
то нам необходимо найти разность между Vx(x) и V«(x), выразив
ее через U (х). Мы покажем сейчас, что
Vi И - V2 {x) = U {х% C.3.21)
Рассмотрим все деревья Т, у которых группы не являются
единичными. Возможны два случая в зависимости от вклада
этих деревьев в разность Fx (х) — F2 (x).
Случай 1. Дерево Т не имеет симметричных ребер. Выясним,
сколько корневых деревьев 7" и реберно-корневых деревьев Т",
обладающих единичной группой автоморфизмов, имеют своим
абсолютом дерево Т. Если существуют некоторые такие деревья
Т" или Т", то группа Г (Т) имеет в точности одну нетождественную
подстановку и эта подстановка должна переставлять две ветви,
исходящие из одной и той же вершины vx дерева Т. Каждая из
двух таких ветвей, исходящих из вершины v1, рассматриваемая
как корневое дерево, имеет единичную группу. Если в каждой
из этих ветвей содержится п -\- 1 вершин, то существуют точно п
корневых деревьев Т", абсолют которых совпадает с Т. Кроме
того, реберно-корневые деревья Т", получаемые путем выделения
в качестве корневого ребра любого из п ребер, принадлежащих

86 ГЛ. 3. ДЕРЕВЬЯ
какой-либо из этих двух ветвей, также имеют своим абсолютом
дерево Т. Отсюда делаем вывод, что для всех таких деревьев Т
число корневых деревьев с единичной группой и абсолютом Т
равно числу реберно-корневых деревьев с единичной группой
и тем же самым абсолютом Т. Следовательно, вклад таких де-
деревьев в разность Fj (х) — F2 (х) равен 0.
Случай 2. В дереве Т есть симметричное ребро. Тогда порядок
группы Г (Т) не меньше 2. Если существуют корневые деревья
Т' или реберно-корневые деревья Т" с единичными группами
и абсолютом Т, то группа Г (Т) имеет порядок 2 и нетождествен-
нетождественная подстановка группы переставляет две центральные вершины
дерева Т. Следовательно, если Т имеет In вершин, то существуют
п корневых деревьев Т', таких, что \Т' \ = Т, и п — 1 реберно-
корневых деревьев Т", у которых | У | = Т. Таким образом,
для каждого дерева Т с симметричным ребром и группой порядка
2 число корневых деревьев с абсолютом Т на единицу больше
числа реберно-корневых деревьев с тем же абсолютом Т. Значит,
каждое такое дерево порядка р вносит 1 в коэффициент при хр
в разности Vx (х) — F2 (x).
Следовательно, мы можем сделать заключение, что Fx (x) —
— F2 (x) является производящей функцией для деревьев, у кото-
которых существует симметричное ребро и группа имеет порядок 2.
Но ряд U (х2) как раз перечисляет такие деревья, что устана-
устанавливает справедливость соотношения C.3.21). Для завершения
доказательства нужно подставить — U (х2) вместо F2 (х) — Vl (x)
в выражение C.3.20).н
Формулы C.3.15) и C.3.16) доказанной теоремы использованы
для получения следующих коэффициентов:
и(х)=:х + х'г + х8 + Зх9 + ()х1О+15хи + 29х13 + C.3.22)
В дополнение к ориентированным, гомеоморфно несводимым
и асимметрическим деревьям в статье Харари и Принса [1] можно
найти формулы для многочисленных других типов деревьев,
включая следующие:
1) деревья с данным разбиением (или с данной степенной
спецификацией);
2) деревья с данным диаметром;
3) смешанные деревья \ т. е. деревья, в которых каждое ребро
либо ориентировано, либо нет 2;
1 В оригинале — «directed trees*. — Прим. перев.
2 В оригинале — «...ориентировано в одном или в двух направлениях».
Прим. перев.

3.3. ДЕРЕВЬЯ СО СПЕЦИАЛЬНЫМИ СВОЙСТВАМИ 87
4) деревья, снабженные знаками, т. е. деревья, в которых
каждому ребру приписан плюс или минус;
5) деревья мощности s, т. е. деревья *, у которых любые
две вершины соединены не более чем s ребрами;
6) деревья с данным весом, т. е. деревья, у которых вершинам
сопоставлены целые положительные веса и вес дерева определяется
как сумма весов всех его вершин.
Все эти задачи перечисления деревьев решались способом,
аналогичным тому, который использовался для решения трех
задач перечисления, рассмотренных выше. Подобным образом
можно перечислить деревья, степени вершин которых равны 1
или п (п ^г 3). Пойа [1] решил эту задачу в случае п = 4, опре-
определив, таким образом, производящую функцию для предельных
углеводородов CnH2n+i.
Так как деревья допускают укладку на плоскости, то возни-
возникает вопрос о числе плоских деревьев а порядка р (см. рис. 3.3.8).
Рис. 3.3.8 Четыре различных плоских дерева седьмого порядка.
Когда корневое дерево уложено на плоскости, все его ребра,
инцидентные корню, циклически упорядочиваются. Как показали
Харари, Принс и Татт [1], производящая функция Р (х) для
плоских корневых деревьев может быть представлена в виде
суммы цикловых индексов циклических групп с использованием
ряда Р (х), перечисляющего плоские деревья с йисячими корнями.
Установлено также, что ряд р (х) для плоских деревьев находится
с помощью рядов Р (х) и Р (х). Более того, коэффициенты ряда
Р (х) можно определить в явной форме из первого соотношения,
приводимого в следующей теореме.
1 Точнее: ...связные- мультиграфы, не имеющие простых циклов длипы
п >> 2. — Прим. мрев.
2 Плоское дерево — это дерево, вложенное в евклидову плоскость. Два
плоских дерева называются изоморфными, если существует гомеоморфное
отображение плоскости на себя, сохраняющее ориентацию, и такое, что
оно отображает одно из этих деревьев на другое. — Прим. перев.

88
ГЛ. 3. ДЕРЕВ!
Теорема. Если Р (х), Р (х) и р (х) — перечисляющие ряды
соответствующих трех типов плоских деревьев: с висячими корня
корневых и просто деревьев, то
C.3.
Р/„л r V 7 (Г1 Р ('А!т\ i
_p(x) = P (x) - (l/2a:2) [P~2 (x) - P"(a
C.3.5
C.3.28
Рис. 3.3.9 Пять плоских деревьев пятого порядка, обладающих висячими
корнями.
Несколько первых членов ряда р (х) имеют вид
р (х) = х + х2 + х3 -f 2х* + Зхъ + 6а:6 + 14а:7 + . . Л C.3.26);
Любопытно, что ряд Р (х) является перечисляющим рядом
также для таких плоских деревьев с висячими корнями, у которых^
каждая вершина имеет степень 1 или 3. Точнее, число плоских;
Рис. 3.3.10 Пять плоских деревьев с висячими корнями, имеющие только
вершины первой и третьей степени.
деревьев порядка р, имеющих висячие корни, совпадает с числом
плоских деревьев с висячими корнями, обладающих р — 2 вер-
вершинами степени 3 и р — 1 вершинами степени 1. Этот факт для ]
случая р = 5 иллюстрируется на рис. 3.3.9 и 3.3.10. Двойствен-
Двойственным утверждением к рассмотренному является такое: ряд Р (х) ;

3,4. ДРЕВОВИДНЫЕ ГРАФЫ 89
перечисляет число способов триангулирования выпуклого «-уголь-
«-угольника, в котором одна из сторон выделена как корень и ориенти-
ориентирована; триангулирование при этом осуществляется путем про-
проведения диагоналей, не имеющих точек пересечения, отличных
от вершин га-угольника. Пять пятиугольников, соответствующих
деревьям, изображенным на рис. 3.3.10, приведены на рис. 3.3.11.
Браун В. [2] указал, что этот результат переоткрывался много-
многократно и встречается еще у Эйлера [1].
Коэффициенты ряда Р (х), называемые обычно числами Ката-
лана, подсчитывают также число неассоциативных произведений
Рис. 3.3.11 Пять триангулированных пятиугольников, каждый из которых
имеет ориентированное граничное ребро.
с п сомножителями. Связь деревьев с такими скобочными схемами
превосходно раскрыта в книге Комте [1, стр. 64].
Список решенных задач перечисления деревьев весьма обшир-
обширный, и поэтому значительная часть их включена в упражнения.
3.4. ДРЕВОВИДНЫЕ ГРАФЫ
Техника этой главы может быть приспособлена и к нахожде-
нахождению производящих функций для многих классов таких графов,
которые либо похожи на деревья, либо содержат деревья, как
порожденные подграфы. Мы рассмотрим достаточно подробно
задачи перечисления унициклических графов, функциональных
орграфов, деревьев блоков и точек сочленения, графов блоков
и кактусов.
Сначала осуществим перечисление унициклических графов,
потому что подход, используемый при их перечислении, может
быть приспособлен к перечислению функциональных орграфов.
Унициклический граф является связным графом, имеющим
только один простой цикл. Если G — унициклический граф и его
простой цикл имеет длину п, то G можно рассматривать как граф,
имеющий корневые деревья, возможно тривиальные, прикреплен-
прикрепленные к каждой из п вершин его цикла. Поэтому обозначим через
Y множество корневых деревьев с перечисляющим рядом Т (х),
задаваемым уравнением C.1.4). Если степенная группа Е п имеет
множество объектов Yx, то орбиты, состоящие из функций мно-
множества Yx, соответствуют в точности унициклическим графам.
Следовательно, теорема перечисления Пойа дает такой результат.

90 ГЛ. 3. ДЕРЕВЬЯ
Теорема. Перечисляющий ряд Un(x) для унициклических графов,
у которых простой цикл имеет длину п, дается соотношением
Un(x) = Z(Da,T(x)). C.4.1)
Значения коэффициентов при xh в Un (х) с п ^ 10 и k ^ 10
можно найти в книге Риордана [1, стр. 178].
Орграф называется функциональным, если полустепень исхода
каждой его вершины равна 1. Понятие функционального орграфа
возникает в психологическом контексте при изучении структуры
такой группировки людей, в которой каждый член проявляет
ровно одну черту в своем отношении к другому члену. Сейчас
нашей целью является нахождение такой производящей функции,
коэффициенты которой дают числа попарно неизоморфных функ-
функциональных орграфов с заданными числами вершин (см. Харари
[10]). Мы увидим, что эти орграфы соответствуют функциям,
не имеющим неподвижных точек. Дэвис [1] нашел явную формулу
для числа типов функций, заданных на конечном множестве
(см. также Палмер [2]). Его методы могут быть легко использо-
использованы для решения и этой разновидности задачи. Однако в про-
процессе вывода производящей функции мы выявим некоторые
структурные свойства функциональных орграфов, представля-
представляющие самостоятельный интерес. В частности, функциональный
орграф можно построить из ориентированных циклов и корневых
деревьев.
Если Z — ориентированный цикл функционального орграфа
D, то через D — Z мы обозначаем орграф, который получается
из D удалением всех дуг, принадлежащих циклу Z. Напомним,
что дерево, входящее в вершину и, получается из корневого
дерева с корнем и путем ориентирования каждого его ребра
по направлению к вершине и. Теперь мы подготовлены к тому,
чтобы охарактеризовать функциональные орграфы; доказатель-
доказательство нижеследующего утверждения можно найти у Харари,
Нормана и Картрайта [1, стр. 325].
Теорема. Орграф D является функциональным тогда и только
тогда, когда каждая его слабая компонента состоит в точности
из одного ориентированного цикла Z и для каждой вершины и
цикла Z слабая компонента R (и) орграфа D — Z, содержащая
вершину и, является деревом, входящим в вершину и.
Из этой теоремы и теоремы перечисления Пойа следует, что
перечисляющий ряд v (x) для функциональных орграфов (с пк
циклами длины к) дается формулой
v (х) = S П Z (Snk, Z{Ck, T (*)>, C.4.2)
Я—2

«f»
3.4. ДРЕВОВИДНЫЙ ГРАФЫ 91
где суммирование ведется по каждому щ от 0 до оо. Меняя местами
знаки суммы и произведения, получаем
оо
v{x) + i = Uz{Soa,Z{Ck,T (х))). C.4.3)
Используя формулу C.1.1) для суммирования цикловых
индексов симметрических групп, приходим к следующему утвер-
утверждению.
Теорема. Перечисляющий ряд v (х) для функциональных оргра-
орграфов дается формулой
v (х) +1 = ехр (S A/п) £ % (Ck, T (*»))}. C.4.4)
Искусными алгебраическими преобразованиями Рид [3] свел
эту формулу к такой:
(ЗЛ5)
fl-1
Единственное различие между функциями и функциональными
орграфами состоит в том, что последние не имеют петель (или,
в другой терминологии, неподвижных точек). Таким образом,
v (х) перечисляет функции (точнее, типы изоморфизмов функций),
не имеющие неподвижных точек. Требуется лишь несложно
модифицировать формулу C.4.3), чтобы перечислить общее число
функций. Имеем
UziSn, Z(Ck,T (x))). C.4.6)
k-i
В этой формуле коэффициент при хп представляет собой формулу
«fen (re)» из статьи Дэвиса [1]. Рид [3] нашел числа функциональ-
функциональных орграфов и функций, представленные в табл. 3.4.1.
Таблица 3.4.1
п
Функцио-
Функциональные
орграфы
Функции
1
0
1
2
1
3
3
2
7
4
С
19
5
13
47
в
40
130
7
100
343
8
291
951
9
797
2 615
10
2 273
7 318
И
6 389
20 491

92 ГЛ. 3. ДЕРЕВЬЯ
Часто можно заметить, что связный граф с достаточно большим
числом точек сочленения похож на дерево. Мы сейчас реализуем
это представление в явной форме, сопоставив каждому связному
графу G дерево be (G), которое отражает указанное сходство (см.
Харари и Принс [3]). Дерево блоков и точек сочленения графа G
(обозначение: be (G)) представляет собой граф, у которого мно-
множество вершин есть объединение множества блоков и множества
точек сочленения графа G и две вершины смежны, если одна из них
соответствует блоку графа G, а другая — точке сочленения графа
G, принадлежащей этому блоку. Легко показать, что если G —
связный граф, то граф be (G) действительно является деревом.
Определим теперь bc-дерево, как 2-раскрашенное дерево,
у которого все висячие вершины окрашены в один цвет, например
в голубой, в то время как другой цвет пусть будет коралловым.
Таким образом, расстояние между любыми двумя висячими вер-
вершинами— четное. Отсюда следует (см. Харари [1, стр. 54]), что
каждое бс-дерево есть дерево блоков и точек сочленения некото-
некоторого связного графа и наоборот. Поэтому, чтобы перечислить
деревья блоков и точек сочленения, нам нужно только перечи-
перечислить бс-деревья. Пусть
оо
'(*,?)= 2 Vn*"r. C.4.7)
m=l
n-o
где tm<n — число бс-деревьев с т голубыми и п коралловыми
вершинами. Аналогично, пусть Т (х, у), Тв (х, у) и Тс (х, у) —
перечисляющие ряды соответственно для корневых 6с-деревье]
для корневых бс-деревьев с голубым корнем и для корневы
бс-деревьев с коралловым корнем.
Теорема. Перечисляющие ряды для bc-деревъев удовлетворяю}
Соотношениям '
, Тв(х,у))-Тв(х,у)-1), :\ C.4.4
Тв(х, y)^xZ(Sm, Тс(х, у)) + уТв(х, у), ' ■■•:■ , (ЗАЛ
Т(х, у) = Тв(х, у) + Тс(х, у), C.4.1С
t(x, y) = T{x, у)-Тв(х, у)(Тс(х, у) + уТв(х, у)). C.4.11
Доказательство этой теоремы можно найти у Харари и Принса
[3]. В явной форме
t(x, у) = х + х2у + хЦу+ у*) + х* (у+ (/-{-2ys)+
C.4.12)
Граф блоков данного графа G, обозначаемый В (G), имеет
своими вершинами блоки графа G и две вершины в нем смежны!

3.4. ДРЕВОВИДНЫЕ ГРАФЫ 93
если соответствующие блоки имеют общую вершину. Норман
[1] получил производящую функцию для связных графов, в кото-
которых каждый блок является полным графом. Такими графами как
раз являются графы блоков (см. Харари [1, стр. 45]). Учитывая
это соответствие, можно воспользоваться формулой из предыду-
предыдущей теоремы и получить ряд, перечисляющий графы блоков
(см. Харари и Принс [3]).
Следствие. Ряды В (х) и В (х), перечисляющие связные корневые
и некорневые графы блоков, удовлетворяют соотношениям
+ . . ., C.4.13)
. ... C.4.14)
Правильность первых четырех коэффициентов в формуле C.4.14)
подтверждается рис. 3.4.1.
I Л V М V UV
Рис. ЪЛЛ Наименьшие графы блоков.
Кактус представляет собой связный граф, в котором нет ребер,
лежащих более чем на одном простом цикле. Эти графы раньше
назывались «деревьями Хусими», и их определение х было дано
Уленбеком (см. Уленбек и Форд [1]) и Ридделом Ц], которые
следовали статье Хусими [1] о групповых интегралах в теории
конденсации в статистической механике. Для перечисления какту-
кактусов нам потребуется подходящий вариант теоремы о характеристике
неподобия (см. Харари и Норман [1]), но здесь мы проиллюстри-
проиллюстрируем его использование только для подсчета треугольных кактусов
(см. Харари и Норман [1]),в которых каждое ребро принадле-
принадлежит треугольнику '-.
Пусть дан кактус Н. Обозначим через р*, q* и г* числа
неподобных вершин, неподобных ребер и неподобных простых
Циклов соответственно. Через s обозначим число симметричных
ребер, не принадлежащих простым циклам. Пусть С — произ-
произвольный простой цикл кактуса Н, содержащий п (п ^ 3) вершин.
Тогда А = Г (#)|с есть ограничение группы кактуса Я на цикл С,
и поэтому А — подгруппа группы Dn. Предположим теперь, что
п — четное и | А | = 2. Тогда для нетождественной подстановки а
1 Этот термин подвергался большой критике, потому что деревья Хусими
не обязательно являются деревьями.
2 То есть простому циклу С3. — Прим. перее.

94 ГЛ. 3.
из А имеются две возможности: либо а оставляет неподвиж-
ными две вершины цикла С, либо она оставляет неподвижными
два ребра цикла С. В первом случае назовем С циклом типа \
во втором — циклом типа 2. Пусть г* — число классов подобия
циклов типа i (i = 1, 2). Теперь нужная нам теорема может
быть сформулирована следующим образом (заметим, что для всех
кактусов имеет место частный случай формулы Эйлера — Пуан-
Пуанкаре: р — q -f r — 1).
Теорема (характеристика неподобия для кактусов). Для произ-
произвольного кактуса числа классов вершин, ребер и простых циклов
удовлетворяют соотношению
-r*1 + r\). C.4.15)
А
Рис. 3.4.2 Треугольные кактусы с небольшим числом вершин.
Детали доказательства можно найти в работе Харари и Нор
мана [1].
Треугольный кактус будем называть для краткости А-какту
сом. Применяя' формулу C.4.15) к А-кактусам, находим
1 =/>* ~ ?* + /-*. C/..16
Следовательно, чтобы перечислить А-кактусы, нужно построит]
производящие функции для следующих трех классов А-какту
сов: кактусов, у которых в качестве корня выделяется либо верши
на, либо ребро, либо треугольник. Для удобства условимся считать
что граф, состоящий из одной вершины, является А-кактусоМ
Пусть/) (х) — производящая функция для корневых А-кактусов
т. е. коэффициент при хп представляет собой число корневых дв
ревьев, составленных из п треугольников. Если корень имев'
степень 2, то перечисляющий ряд совпадает как раз с xZ (S2, D (x)
и, следовательно,
, xZ(S%, D(x))). C.4.17I

S.S. 2-ДЕРЕВЬЯ 95
Далее, перечисляющий ряд для реберно-корневых Л-кактусов
имеет вид xD {х) Z {S2, D (х)), а для А-кактусов, корнями кото-
которых являются треугольники, xZ (S3, D (х)). Суммируя теперь
формулу C.4.16) по всем Л-кактусам, получаем соотношение
C.4.19), выражающее перечисляющий ряд d (ж) для Л-кактусов 1
через ряд D (х) для корневых А-кактусов.
Теорема. Ряды D (х) и d (x) для корневых и некорневых тре-
треугольных кактусов удовлетворяют соотношениям
D (ж) = exp \ 2, Ч5- (D2 (xk) + D {x2h))\, C.4.18)
j /r\ n /~\ x (пз/тл Г)/v3\\ 14 A 1Q\
i* i«/i — /-' 1Л1 q V-*-^ \ ) ~~^ '^ \ //• vt-',^,-i-«-'i
В частности, из C.4.18) находим
+ 111жв-|- 345ж' + 1105ж8 +.... C.4.20)
Из C.4.19) следует, что
d (х) = 1 -|- х -\- х2 -\- 2з? -\- 4ж4 + 8хь -\- 19а;6 ~\- 48а;7 -|- 12бж8 + . . .;
C.4.21)
значения нескольких первых коэффициентов ряда согласуются
с графами, изображенными на рис. 3.4.2. Для подробного озна-
ознакомления со свойствами кактусов, состоящих только из четырех-
четырехугольников, можно обратиться к статье Харари и Уленбека [1].
3.5. 2-ДЕРЕВЬЯ
В этом параграфе изучаются некоторые понятия, относя-
относящиеся к деревьям и связанные со структурами достаточно высо-
высокой размерности. Для того чтобы перечислить специальные
двумерные структуры, называемые 2-деревьями, приходится до-
дополнительно развить теорию характеристики неподобия и при-
применять теоремы перечисления Пойа. Наши методы можно при-
приспособить к перечислению таких 2-деревьев, которые уложены
на плоскости, и, таким образом, предлагается новый подход
к старой задаче о нахождении числа триангуляции многоугольника.
1 Коэффициент при хп в d (x) (соответственно в D (х)) равен числу Д-как-
тусов (соответственно корневых Д-кактусов), имеющих в точности «треуголь-
«треугольников. — Прим, nepeet

ГЛ. 3. ДЕРЕВЬЯ
В статье Харари и Палмера 112] мы определили п-плекс как
тг-мерный симплициальный комплекс, в котором каждый /с-сим-
плекс* (к <^п) содержится в некотором re-симплексе. Мы будем
оперировать только с 2-плексами и для удобства называем 0-сим-
плексы, 1-симплексы и 2-симплексы соответственно вершинами,
ребрами и ячейками. Двумерные деревья, называемые также 2-де~
ревъями, теперь можно определить по индукции. 2-плекс с тремя
вершинами есть 2-дерево, и 2-дерево с р + 1 вершинами полу-
получается из 2-дерева с р вершинами добавлением новой вершины
w, смежной о каждой из каких-либо двух смежных вершин и и v,
Рис. 3.5.1 Графы 2-деревьев с небольшим числом вершин
и добавлением еще «сопутствующей им» ячейки {и, v, w}. Опреде-
Определение Ar-дерева при к >> 2 дается подобным образом. Для пере^
числения 2-деревьев нужно только рассмотреть их 1-скелеты, ил»
что то же самое, соответствующие им графы, которые для случа|
р ^ 6 изображены на рис. 3.5.1.
Как обычно, число р* неподобных вершин 2-дерева означае
число орбит на множестве вершин 2-дерева; аналогичные опре
деления даются для числа q* неподобных ребер и для числа
неподобных ячеек.
Теорема (характеристика неподобия для 2-деревьев).
Если 2-дерево имеет q* неподобных ребер, г* неподобных ячеек, Si
неподобных ячеек с двумя подобными ребрами, s2 неподобных ячеек
с тремя подобными ребрами, причем s = st -f 2s2, то имеет
место соотношение
Теперь мы приступим к построению производящей фун-
функции для 2-деревьев. Пусть tn — число 2 2-деревьев с п
1 То есть А-мерный симплекс. —• Прим. перее.
2 Мы используем здесь тот же символ tn, который раньше применяли для
деревьев, а еще раньше — для помеченных деревьев. Но мы истощили
свой запас букв и уповаем лишь на то, что подобное повторение не вызовет
чрезмерно большой путаницы,

3.5. 2-ДЕРЕВЬЯ 97
ячейками. П^вчисярющий ряд для 2-деревьев ,.*' обозначим
через .< .;
' m ■<М^' ' v " *(*)=2*п*п. C.5.2)
i
Чтобы получить формулу для tn, воспользуемся соответствующими
рядами для различных видов корневых 2-деревьев. Сначала
введем в рассмотрение два ряда: Мх (ж) и Ыг (ж) для реберно-
корневых 2-деревьев, у которых корневое ребро является соот-
соответственно симметричным и несимметричным торцевым 1 ребром.
Далее, пусть М (х) и N (х) — ряды для реберно-корневых 2-де-
2-деревьев соответственно с симметричным и несимметричным корне-
корневым ребром *. Следующие два уравнения выражают ряды М± (ж)
и Nх (х) через ряды М (ж) и N (ж):
)), C.5.3)
— S2, l-{-M{x) + 2N(x)). C.5.4)
Затем ^йражаем ряд М (ж) через ряды Мг (ж) и N1{x):
?■?'■
М (ж) = S Z {Sn, Ml (ж) + ЛГХ (*»)). C.5.5)
1
Используя тождество C.1.1), можно записать уравнение C.5.5)
в следующем виде:
C.5.6)
Теперь заметим, что перечисляющий ряд для реберно-корне-
реберно-корневых 2-деревьев, у которых корневое ребро ориентировано, яв-
является просто суммой рядов: М (ж) -\- 2N (х). Учитывая этот
факт, получаем соотношение
М (ж) + 2N (х) = £ Z (Sn, Ml (ж) + 2Л\ (ж)). C.5.7)
п-1
1 В оригинале — «end-line». Имеется в виду такое ребро, которое при-
принадлежит ровно одному треугольнику. — Прим. перев.
* Все ряды в этом параграфе перечисляют различные 2-деревья в соответ-
соответствии с числом ячеек в них. — Прим. перев.
4 Заказ 443

98 гл. з. деревья
Снова применяя тождество C.1.1), можно уравнение C.5.7)
записать в таком виде:
I со 1
1 + М (х) + 2N (х) = ехр £ A/и) [Мх (хп) + 2NX {xn)\ . C.5.8)
(п=1 )
Соотношения C.5.6) и C.5.8) можно использовать для пред-
представления ряда N (ж) через ряды Мх (х) и Nt (x). Применяя все
четыре формулы C.5.3), C.5.4), C.5.6) и C.5.8), можно вычислить
коэффициенты рядов М (х) и N (х). Для нескольких первых
членов этих рядов имеем следующие представления:
C.5.9)
C.5.10)
Ряд для реберно-корневых 2-деревьев обозначим через L (ж),
и так как L (х) = М (х) -\- N (х), то немедленно получаем
C.5.11)
Обозначим через Д (ж) ряд для корневых 2-деревьев, в каж-
каждом из которых в качестве корня выделена ячейка (треугольник).
Можно показать, что
Д (ж) = xZ (St, I + М (х) + 2N («)) -xN(x)(l + M (ж2) + 2N (я2)).
C.5.12)
Имея это выражение для А (ж), подставим в него соотношения
C.5.9) и C.5.10) и получим несколько первых членов ряда Д (ж):
Д(ж) = я + а:2 + Зж3+Юз;4 + 39ж5 + C.5.13)
Следуя обозначениям формулы C.5.1) из теоремы о характе-
характеристике неподобия для 2-деревьев, положим: sx (x) — перечи-
перечисляющий ряд для корневых 2-деревьев, у которых корнем
является ячейка с двумя подобными ребрами; s2 (ж) — пере-
перечисляющий ряд для корневых 2-деревьев, у которых корне-
корневая ячейка имеет три подобных ребра. Оба эти ряда легко выра-
выражаются через ряды Му (х), М (ж) и N (ж):
)), C.5.14)
C.5.15)
Делая соответствующие подстановки, получаем
s1(x)=;z3+2xs + 2xi + 7x5 + . . . , C.5.16)
s2(x) = х+ х*-J- 2х7 + 6я10 + C.5.17)

3.8. 2-ДЕРЕВЬЯ *99
Чтобы вывести формулу для ряда t (ж), перечисляющего 2-де-
ревья, воспользуемся теоремой о характеристике неподобия для
2-деревьев и формулой C.5.1) абсолютно так же, как поступил
Оттер при перечислении деревьев.
Теорема (теорема перечисления для 2-деревьев). Перечислят
ющий ряд для 2-деревъев дается соотношением
l(x)=L(z) + s1{x) + 2s2(x)-2A(x). C.5.18)
Подставляя в эту формулу выражения C.5.11), C.5.13), C.5.16)
и C.5.17), получаем
t(x) = x + x* + 2z3 + 5x*+l2xs + C.5.19)
Заметим, что эта теорема может быть использована для пере-
перечисления 2-деревьев, обладающих специальными свойствами, при
условии, что найдены выражения для рядов L (x), sx (ж), s2 (z)
и Л (я), перечисляющих соответствующие корневые 2-деревья
(имеющие те же свойства).
Триангуляция многоугольника представляет собой граф, полу-
получающийся из регулярного и-угольника путем добавления непере-
непересекающихся хорд до тех пор, пока каждая внутренняя область
не станет треугольником. Очевидно, что для получения п — 2
треугольников нужно провести п — 3 хорд. Производящая функ-
функция для числа различных триангуляции n-угольника, т. е. для
числа неизоморфных триангуляции, рассматриваемых как графы,
была найдена Брауном В. 11], но нашей целью здесь является
изложение совершенно иного подхода к нахождению такой про-
производящей функции. Мы переформулируем задачу (замечая, что
триангуляции многоугольников соответствуют как раз планар-
ным 2-деревьям) в утверждение, относящееся к двумерным сим-
плициальным комплексам. После этого перейдем к перечислению
пленарных 2-деревьев теми же методами, которые использовались
при перечислении 2-деревьев.
Для иллюстрации конфигураций, подлежащих перечислению,
мы приводим на рис. 3.5.2 единственные триангуляции треуголь-
треугольника, квадрата и правильного пятиугольника, а также три раз-
различные триангуляции правильного шестиугольника. Заметим, что
эти графы не рассматриваются ни как корневые, ни как помечен-
помеченные. Обратим внимание также на соответствие между ними и
пленарными 2-деревьями с одной, двумя, тремя и четырьмя ячей-
ячейками.
Перечисление планарных 2-деревьев может быть выполнено
с помощью почти тех же формул, которые уже использовались
для 2-деревьев. Поэтому мы несущественно изменим обозначения,
которые применялись для 2-деревьев, — будем добавлять черту
4*

100
ГЛ. 3. ДЕРЕВЬЯ
над буквой для указания на то, что рассматривается производя-
производящая функция для пленарных 2-деревьев.
Итак, пусть, Мх (х) и Nx (х) — ряды для пленарных реберно-
корневых 2-деревьев, имеющих в качестве корневого ребра соот-
соответственно симметричное и несимметричное торцевое ребро. Тогда
„I--N
Рис. 3.5.2 Триангуляции re-угольников, п = 3, 4, 5, 6.
следующие две формулы (сравните с формулами C.5.3) и C.5.4.))
устанавливают связь между Мх (х) и Nx (ж):
C.5.20)
x)). C.5.21)
Эти два соотношения можно использовать для получения
коэффициентов рядов Мх (х) и Nx (x). Однако, как отмечалось
при перечислении плоских деревьев, формула Эйлера (см. рис.
3.3.11 и уравнение C.3.23)) показывает, что число триангу-
триангуляции корневого * (п -\- 2)-угольника, корневое ребро которого
снабжено ориентацией и является граничным, дается соотноше-
соотношением
. 2 Bл —1I
'п~ (n — i) 1 (я+1)!
C.5.22)
Следовательно,
(х) + 2NX (х) =
Теперь из формулы C.5.23) и уравнения C.5.20) для Мг(х) имеем
C.5.24)
п-1
(я— i

3,5. 2-ДЕРЕВЬЯ
101
Несколько первых членов рядов Мг{х) и N1(x) приводятся
ниже:
C.5.25)
ж8+ C.5.26)
Ряд для пленарных реберно-корневых 2-деревьев обозна-
обозначается через L (ж) и может быть выражен через ряды М1(х)
и ВД:
L(x) = Z(S2,
* Nx{x))~l. C.5.27)
Подстановка выражений C.5.25) и C.5.26) в соотношение C.5.27)
дает
2Г(ж) = ж + 2ж2 + 4ж3+12;г4 + 34ж5 + 111жв + 360ж7 + 1226а;8 +
C.5.28)
Учитывая тот факт, что уравнения и процедуры, относящиеся
к пленарным 2-деревьям, в сущности совпадают с уравнениями
и процедурами для 2-деревьев, мы просто приведем список фор-
формул для Л (ж), s1(x), ss(a;) и 1(х):
A(x) = xZ(S3, l + M1(x) + 2N1(x))-
. ' -aFx (a) (l + Af^a:»)* 27^ (*»)), C.5.29)
\ (х) = М^х) A + Мх (х)) -х{1 + Мг (х3)), C.5.30)
*,(*) = ai^! (а*)+ *A + Я1(«»)) C.5.31)
и, как прежде,
C.5.32)
которая получается навешиванием черты на производящие функ-
функции в уравнении C.5.18), относящемся к теореме перечисления
для 2-деревьев.
Подставляя выражения C.5.25) и C.5.26) для рядов Мх (х)
и Nt (ж) в эти формулы, получаем ряд t (ж) для пленарных 2-де-
2-деревьев. Р. К. Гай (чтобы скоротать время в Сингапуре) с помощью
карандаша, бумаги и настольной счетной машины получил (не-
(неопубликованная работа) первые 23 коэффициента ряда, приве-
приведенные в табл. 3.5.1.

102
ГЛ. 3. ДЕРЕВЬЯ
Таблица 3.5.1
n
1
2
3
4
5
6
7
8
9
10
11
12
Планарные
; . In
i 1
1
;' -. 1
3
4
■■• ri. 12
■ ■*''•■' 27
82
228
733
2 282
7 528
2-деревь«
n
13
14
15
16
17
18
19
20
21
22
23
In
24 834
83 898
285 357
1046 609
3 412 420
11 944 614
42 080 170
149 197 152
532 883 768
1 905 930 975
6 861 221 666
УПРАЖНЕНИЯ
3.1. Разбиение дерева представляет собой последовательность
целых неотрицательных чисел (av а2, а3,.. .), где ат равно числу
вершин степени т. Деревья с данным разбиением.
(Харари и Принс [1])
3.2. Диаметр дерева есть длина наибольшей простой цепи.
Деревья с данным диаметром. (Харари и Принс [1])
3.3. Взвешенное дерево — это такое дерево, каждой вершине
которого сопоставлено некоторое целое положительное число,
называемое весом вершины. Вес дерева равен сумме весов всех
его вершин. Деревья с р вершинами и весом т.
(Харари и Принс [1])
3.4. Дерево, снабженное знаками, — это такое дерево, в котором
каждому ребру приписан плюс или минус. Деревья, снабженные
знаками. (Харари и Принс [1])
3.5. Дерево имеет мощность s, если по крайней мере одна пара
его вершин соединена s ребрами, но не существует двух вершин
в нем, которые соединены более чем s ребрами. Деревья с мощ-
мощностью, не превосходящей s. (Харари и Принс [1 ])
3.6. (а) Связные, (Ь) односторонние, (с) сильные функциональные
орграфы. (Харари [10])
3.7. Кактусы, в которых каждый блок — четырехугольник.
(Харари и Уленбек [11)
3.8. Триангуляции многоугольника, содержащие п внутренних
вершин. (Браун В. [1])
3.9. Деревья с данным числом висячих вершин-

УПРАЖНЕНИЯ ЮЗ
З.Ю. Производящая функция U (х) для корневых асимметриче-
асимметрических деревьев удовлетворяет соотношению
оо
U(x) = х П A + хп)и>1.
3.11. Деревья, вершины которых имеют степени 1 или 4 (пре-
(предельные углеводороды). (Пойа [1])
3.12.. Корневое дерево имеет высоту к, если расстояние от корня
до наиболее удаленной вершины равно к. Корневые деревья
с заданной высотой. (Риордан [2])
3.13. Плоские корневые деревья
(Уолкап [1])
3.14. Леса с q ребрами, не имеющие изолированных вершин.

е
it:
Глава 4
,.. ', Л
ГРАФЫ
Прекрасна правда и правдиво!
Прекрасное — и этого доволънэШ
Дж, Ките, Ода греческой вазе1
Решение пленительной задачи о нахождении числа графов по-
порядка р было впервые опубликовано, по-видимому, в 1927 году.
Автором замечательной статьи, содержащей этот интригующий
результат, был Дж. Г. Редфилда [1]. Почти, тридцать лет эта
пионерская работа оставалась фактически незамеченной, а тем
1 Перевод О. Чухонцева. — Прим. перев.
а Приводим целиком письмо К, Оукли к Ф. Харари, датированное
19 декабря 1963 года.
Говард Редфилд окончил Хаверфордский колледж в 1899 году. Был он
человеком с разносторонними интересами, в мы не имеем подробного списка
того, что он сделал. Сразу после окончания колледжа он работал инженером.
В колледже изучал несколько языков и математику. (В те дни там даже не
было кафедры математики). Окончив Хаверфорд со степенью бакалавра, он
получил степень бакалавра в МТИ и магистра искусств и доктора философии
(по математике) в Гарварде. В течение 1907—1908 годов он изучал романскую
филологию в Парижском университете. В 1908—1909 годах он был препода-
преподавателем математики .в Вустерском политехническом институте (Вустер, штат
Массачусетс). В 1910—1911 годах он преподавал французский язык в Сворт-
морском колледже, а в течение 1912—f914 годов он был ассистентом профес-
профессора романских языков в Принстонском университете. С 1916 года до самой
своей смерти в 1944 году он работал инженером в Уэйне, штат Пенсильвания.
Я был знаком с ним приблизительно с 1938 по 1944 год. Помню, как
в 1940 году он приехал в Хаверфордский колледж и прочитал там несколько
лекций по электронным вычислительным машинам (это было немного раньше
Экерта и Моучли). Зная его, как я в те последние годы, можно хорошо понять,
почему он не стал знаменитым педагогом. Он всегда витал в облаках, никогда
не смотрел на вас, говорил тихо, уставив глаза в пол; читая лекцию, часто
поворачивался к вам спиной, чтобы написать что-то иа доске. Однако его
записи на доске были безупречны. Их можно было фотографировать и печа-
печатать фотоофсетным способом — настолько они были совершенны.
Он часто наведывался в Хаверфорд, чтобы побеседовать в нашем матема-
математическом клубе, и всегда у него было что-нибудь новое. Он был настолько
скромен, что вы никогда не знали, было ли то, о чем он рассказывал, его
собственным результатом или принадлежало кому-либо другому.
Это почти все, что я знаю о нем, за исключением того, что был у него
очень известный брат (Альфред Редфилд) в Вудсхолле, штат Массачусетс*

4.1. ГРАФЫ {05
временем успешно и независимо друг от друга за решение задачи
брались другие математики, включая Р. Л. Дэвиса [1],
А. М. Глисона, С. Голомба, Д. Слепяна и, конечно, Дж. Пойа.
Уже в 1937 году, когда появилась его теорема перечисления,
Пойа мог применить ее к задаче нахождения производящей функ-
функции, перечисляющей графы в соответствии с числами их вершин
и ребер. В письме Дж. Пойа к Ф. Харари, посланном в 1951 году,
содержится формула D.1.9), приводимая ниже, с подставленным
в нее рядом 1 + х, и она проиллюстрирована для случая р = 4.
Но об этом не было известно до появления статьи Харари [4]
в 1955 году, в которой отражены детали доказательства.
В гл. 3 мы уже видели, как может быть применена теорема
Пойа к задачам перечисления деревьев и древовидных структур.
Настоящая глава содержит дальнейшее подтверждение широкой
применимости его метода. Мы займемся перечислением графов,
корневых графов, связных графов, 2-раскрашенных графов,
локально ограниченных графов, раскрашенных графов, булевых
функций и эйлеровых графов.
4.1. ГРАФЫ
Эффективный метод Пойа для перечисления графов требует
построения группы подстановок, орбиты которой соответствуют
в точности изоморфным классам помеченных графов с р вершинами
и q ребрами. После получения явной формулы для соответству-
соответствующего циклового индекса, применив теорему Пойа с рядом
1 + ж в качестве перечисляющего ряда для фигур, находим перечи-
перечисляющий многочлен, в котором коэффициент при xq равен числу
(р, д)-графов.
Более точно, пусть
где т= (£) и gPiq—число (р, д)-графов. Например, если взгля-
взглянуть на рис. 1.1.2, можно убедиться, что
D.1.2)
Заметим, что коэффициенты в этих многочленах всегда «сим-
«симметричны относительно концов», ибо число (р, д)-графов равно
числу (р, т—д)-графов, дополнительных к первоначальным.
Так как теорема Пойа перечисляет орбиты функций, то мы
сначала установим естественное соответствие между графами
и функциями. Пусть X = {1, . . .,р}, в то время как Х<2) обозна-
обозначает все 2-подмножества множества X. Тогда, если У ■= {0, 1},

106 ГЛ. 4. ГРАФЫ
то функции из Х<2> в Y представляют помеченные графы порядка
р. Каждая функция / соответствует тому графу G (/), у которого
множество вершин есть X и вершины i и / смежны тогда и только
тогда, когда /{£,/} = 1. Таким образом, две функции / и h пред-
представляют один и тот же граф, если существует некоторая подста-
подстановка а на множестве X, такая, что всякий раз, когда i и / —
смежные вершины в G (/), вершины ai и а/ смежны в графе G (К).
Следовательно, графы G (/) и G {К) изоморфны тогда и только
тогда, когда для некоторой подстановки а, действующей на мно-
множестве X,
f{t, /} = A{a/, а)} D.1.3)
для всех пар {г, /} из множества Х<2>. Это уравнение подсказы-
подсказывает следующую унарную операцию на группах подстановок,
которая приводит к группе, требуемой для перечисления графов.
Пусть А — группа подстановок с множеством объектов X =
= {1, 2, . . ., р). Парная группа группы А, обозначаемая А <2>, есть
группа подстановок, индуцируемая группой А и действующая
на множестве Х<2>. Точнее, каждая подстановка а группы А
индуцирует подстановку а' группы А^, такую, что для каждого
элемента {i, /} множества Х<а>
a'ii, ]} = {ai,aj}. (АЛА)
Таким образом, степень группы АB> равна (Л ) и А ё£ ЛB\ если
А отлична от Sv Чтобы пояснить это определение, введем ребер-
реберную группу графа — понятие, которое будет также достаточно
полезным и в дальнейшем. Пусть G — граф с множеством вершин
V (G) и множеством ребер X (G). Каждая подстановка а группы
Г (G) индуцирует подстановку а', действующую на множестве
X (G) следующим образом. Если и и v — смежные в G вершины,
так что {u, v) — ребро графа G, то
а'{и, v} = {au, av). D.15)
Эта совокупность подстановок на множестве X (G) образует
группу, обозначаемую Гх (G) и называемую реберной группой
графа G. Например, реберная группа полного графа порядка р
и парная группа симметрической группы степени р идентичны,
т. е.
r1(Kp) = S<^\ ч D.1.6)
Теперь, учитывая формулы D.1.3) и D.1.4), заключаем, что
две функции / и h представляют один и тот же граф тогда и только
тогда, когда существует-подстановка а на множестве X, такая,
что для всех г из XW
f(z) = h(a'z). D.1.7)

4,1. ГРАФЫ ;
107
Таблица 4.1.1
Слагаемое из Z (Si)
*
«1*3
А
«4
Подстановка из S*
A) B) C) D)
A) B) C4)
A) B34)
A2) C4)
A234)
Диаграмма этой
подстановки
Q Q
1 2
Q О
4 3
о о
1 2
Id
Л 3
Но это условие совпадает в точности с требованием, чтобы /
SB)
и h содержались в одной и той же орбите степенной группы Е2 р .
Следовательно, орбиты этой степенной группы соответствуют
различным непомеченным графам порядка р, т. е. изоморфным
классам помеченных графов. Применение теоремы Пойа к пере-
перечислению этих орбит в соответствии с их весами приводит к сле-
следующей разновидности формулы Пойа для перечисления графов.

108
ГЛ. /.. ГРАФЫ
Теорема. Многочлен gp (x), перечисляющий графы порядка
р в соответствии с числом ребер в них, дается соотношением
',! + *), D.1.8)
где
(/)
п
Доказательство. Определим весовую функцию w на множестве
Y — {0, 1}, положив w @) = 0 и w A) = 1. Тогда вес функции,
действующей из Х^ в Y, и вес орбиты, которой она принадле-
принадлежит, определяются обычным образом, как в соотношении B.4.4).
sB)
Значит, вес орбиты, задаваемой группой Е2 " , есть просто число
ребер в соответствующем графе. Тогда формула D.1.8) следует
из теоремы Пойа.
Теперь получим формулу D.1.9) для Z (Spz)), проиллюстри-
проиллюстрировав ее вначале для случая р = 4. В цикловом индексе
Z (SJ = -gL (,* + Ъз\з2 + 8Sls3 + 3»; + 6s4)
D.1.10)
каждое слагаемое может быть представлено одной из отвечающих
ему подстановок, как это показано в табл. 4.1.1.
Каждый из пяти типов подстановок, принадлежащих группе
S4, индуцирует некоторую подстановку из парной группы S[2\
Таблица 4.1.2 содержит все слагаемые циклового индекса Z (S[2)),
индуцируемые соответствующими слагаемыми из Z (St).
Таблица 4.1.2
Слагаемое из Z (S<)
•I
'2
Индуцируемое слагаемое из Z \S\ )
•?
4
,2,2
S2«4

4.1. ГРАФЫ 109
Одно из этих слагаемых иллюстрируется на рис. 4.1.1, где
2-подмножества обозначены ради краткости следующим образом:
Я, 2} = 12 и т. д. Приводя подобные члены, находим, что
■ Z(s{2)) = ^(s\ + 9s\Sl + 8sl + 6s2Si). D.1.11)
Подставляя 1 -+- х в этот цикловой индекс, имеем, как и в фор-
формуле D.1.2),
Z (Si2), 1 + х) = g, (х) = 1 + х + 2х* + За;3 + 2xi + х* + х*. D.1.12)
99 Q % %
Рис, 4.1.1 Подстановка A) B) C4) и индуцируемая ею подстановка в 5B)*
Мы указываем соответствие между слагаемыми, входящими
в цикловые индексы групп Sp и Sp2\ записывая
и т. д. Чтобы получить выражение для Z(Sp^), мы должны
найти отсутствующий член в соотношении
Пусть а — подстановка из Sp, которой в цикловом индексе
Z (Sp) соответствует слагаемое U.skk. Существуют два различных
вклада, которые делаются подстановкой а' в соответствующее
слагаемое циклового индекса Z {Sp2)). Первый вклад определяется
парами таких элементов множества X = {1, 2, . . ., р}, которые
принадлежат общему циклу подстановки а; второй — парами тех
элементов множества X, которые содержатся в разных циклах
подстановки а.
Сейчас мы определим первый из этих вкладов. Пусть zk =
— A2 ... к) — цикл длины к подстановки а. На рис. 4.1.2
показана подстановка из парной группы, индуцируемая циклом
Zk при к = 2, 3, . . ., 6. Очевидно, что если к — нечетно, то цикл
%k индуцирует (к — 1)/2 циклов одной и той же длины, т. е.

НО РЛ. 4. ГРАФЫ
С другой стороны, когда к — четное, то находим
Таким образом, так как существуют jk циклов длины к в подста-
подстановке а, то пары элементов, лежащих в общих циклах, порождают
соответствие
:■ D.1.14)
* '' D.1.15)
для нечетных к и
для четных к.
Чтобы вычислить второй вклад, рассмотрим два цикла zr
и zt в подстановке а. Пуст*, как обычно, [г, t] и (г, t) обозначают
' О
12
А
2
14
24 Л
36 25
46
Рис. 4.1.2 Циклы в Sp и индуцируемые ими подстановки в S*?K
соответственно наименьшее общее кратное и наибольший общий
делитель чисел г и t. Тогда циклы zr и Zf индуцируют на парах
таких элементов, один из которых принадлежит циклу zr, а дру-
другой — циклу zt, ровно (г, t) циклов длины [г, t]. В частности,

4.1. ГРАФЫ Ш
когда г = t = к, то соответствующий «взнос» состоит из к циклов
длины к. Итак, когда г Ф t, то имеем
а если r = t = k, то
/ * С*)
D.1.17)
Теперь, перемножая правые части соотношений D.1.14) —
D.1.17) по всем подходящим случаям, получаем отсутствующий
член в правой части формулы D.1.13). Таким образом, справедли-
справедливость формулы D.1.9) установлена.щ
У-, ,, ♦•,••,!•*.
Рис. 4.1.3 Шесть мультиграфов четвертого порядка с тремя ребрами.
Формулы D.1.8) и D.1.9) были использованы (см. Риордан
[1], стр. 173) для нахождения многочленов gp (х) при р ^ 9.
Коэффициенты для р ^ 10 приведены в приложении I. Цикловые
индексы Z Eр2)) при р ^ 10 даны в приложении III, и мы увидим,
что они играют важную роль в перечислении некоторых видов
графов.
В мультиграфе две вершины могут быть соединены более чем
одним ребром (см. рис. 4.1.3). Пусть тр {х) — производящая
функция для мультиграфов, так что коэффициент при & есть
число мультиграфов с р вершинами и q ребрами. Следующая
теорема из статьи Харари [4] получена видоизменением перечисля-
перечисляющего ряда для фигур, который использовался при перечислении
графов.
Теорема. Производящая функция тр (х) для мулътигр афов
порядка р дается формулой
mp(x) = Z{Sf, 1/A-*)). D.1.18)
Для р = А находим
те4 (х) = 1 + х + Зж2 + бж3 + Их* + 18Ж5 + 32*в +
+ 48z7 + 75;r8 +Ills9+16Oa;io-f-. . . . D.1.19)
Правильность коэффициента при ж8 подтверждается рис. 4.1.3.

i
112 - ГЛ. 4. ГРАФЫ
Следуя Партасарати [1] и Харари и Палмеру [3], мы можем
описать перечисление локально ограниченных графов. Это по
существу сводится к дальнейшему уточнению циклового индекса
парной группы Sp2). Разбиение графа представляет собой последо-
последовательность степеней его вершин, обычно записываемую в порядке
невозрастания. Локально ограниченный граф — это граф с данным
разбиением. Производящая функция, перечисляющая локально
ограниченные графы с р вершинами, является многочленом
N (хи х2, . . ., хр), таким, что каждое слагаемое а^1 хе2' . . . х'рр
удовлетворяет условию
Коэффициент при таком слагаемом есть число графов с раз-
разбиением elt е2, . . ., ер. К примеру, слагаемое в N (xv . . ., хъ),
'11
Рис. 4.1.4 Граф со степенной последовательностью D, 3, 3, 2, 2).
отвечающее графу, изображенному на рис. 4.1.4, имеет вид:
х\х\х\х\х\, ибо последовательность степеней, соответствующая
этому графу, такова: 4, 3, 3, 2, 2.
Чтобы получить формулу для производящей функции, восполь-
воспользуемся естественным представлением, даваемым подходящей сте-
степенной группой. Полагая, как раньше, У = {0, 1}, рассмотрим
функцию W, которая отображает множество Yx<2> в кольцо много-
многочленов, зависящих от переменных xh и определяется формулой
П (xtx,yw.l»m D.1.20)
B>
Тогда в графе, соответствующем функции /, степень вершины i
дается показателем степени у переменной х{ в выражении для
W (/). Введем для удобства линейный оператор 0, действующий
на W (/) в соответствии с правилом: 0 переупорядочивает показа-
показатели степеней так, чтобы они шли в порядке невозрастания, в то
время как сами переменные располагаются в порядке возрастания
индексов (слева направо). Например,
0 (xsxlxlxt) = xlxlxlxt.
Применяя «взвешенный» вариант леммы Бернсайда и формулу
B.3.10), приходим к следующему результату, который был полу-
получен Партасарати в несколько иной форме.

4.2. СВЯЗНЫЕ ГРАФЫ ИЗ
*
Теорема. Производящая функция, перечисляющая локально ог-
ограниченные графы, имеет вид
*8> .... *„) = -!- 2 8/2 W(f)\, D.1.21)
= пA+п^"п ^/(r' s)vr' s)x
x П
"^/
r-четное
г—нечетное
гвг, )
вдесь первое произведение берется по всем различным парам цик-
циклов zr и zs в подстановке а, а два других произведения — по всем^
циклам такой подстановки из группы Sp, которая соответствует
подстановке у. Далее, применяя эту теорему, имеем
N (а*, хг, х3) = A/3 !) {6 (A + ххх2) A + х2х3) A + х1Хг)) +
; . v + 36 (A + xxx2xl) A + зд.)) + 26 A + x\x\xl)\ =
+3 A
х\
х\х2х3 +
Мы должны ясно представлять себе, что указанный метод дает
только формальное решение и не подходит для получения точных
значений или порядков искомых величин.
4.2. СВЯЗНЫЕ ГРАФЫ
Как и в случае помеченных графов, мы убедимся в том, что
производящие функции для графов и связных графов тесно свя-
связаны некоторым соотношением, содержащим экспоненциальную
функцию. Кроме того, связные графы с указанными свойствами
часто могут быть перечислены аналогичным способом в терминах
общего числа графов с теми же свойствами.
Пусть g (x) — производящая функция для графов, так что

114
ГЛ. 4. ГРАФЫ
гДе ёр — число графов порядка р, и пусть. с (х) — соответству.
ющая производящая функция для связных графов, т. е.
С (X) =
D.2.2)
Теперь можно сформулировать теорему Риддела [1], связывающую
эти два степенных ряда.
Теорема. Производящие функции g (х) и с (х) для графов и связ-
связных графов удовлетворяют соотношению
{2 <?(**)/*)• D.2.3)
u-i J
Доказательство. Из теоремы Пойа вытекает, что ряд2 (Sn,c(x))
перечисляет графы, состоящие ровно из п компонент. Следователь-
Следовательно, суммируя этот ряд по всем п, получаем
1 _|_ & (х\ =Z(S с (х)). D 2 4)
Формула D.2.3) выводится из формулы D.2.4) и тождества C.1.1).в
Кэдоган [1] разработал эффективный метод подсчета числа
связных графов порядка р, неявно содержащийся в формуле
D.2.3). Сначала полагаем
2 вр*" —h (! + *(*))• •'■■' D-2.5)
p-i . ■'•>■-""'* ■'••
Тогда из формулы A.2.8) следует, что , ; f
p-i *■'■
k- D.2.6)
В табл. 4.2.1 представлены значения для рар (р ^ 9), вычислен-
вычисленные с использованием уравнения D.2.6) и значений величин gp.
Таблица 4.2.1
Число связных графов
р
1
2
3
4
5
6
7
8
9
«р
1
2
4
11
34
156
1044
12 346
274 668
раР
1
3
7
27
106
681
5972
88 963
2 349 727
ср
1
1
2
6
21
112
853
11117
261 080

4-2, СВЯЗНЫЕ ГРАФЫ 115
Мы далее увидим, как выражаются значения коэффициентов ср
через величины ар.
Так как
ОО 00
S S D-2-7)
p=l ft-1
то, сравнивая коэффициенты при соответствующих степенях,
имеем
рар = 2 dcd. D.2.8)
<Цр
Обращая это соотношение с использованием функции Мёбиуса
ц (d), выражаем числа ср через ар:
D.2.9)
Эта формула Кэдогана была использована для вычисления зна-
значений коэффициентов ср(р s§ 9), помещенных в табл. 4.2.1. Вся-
Всякий раз, когда две произвольные производящие функции удовлет-
удовлетворяют соотношению D.2.3) из теоремы, их коэффициенты свя-
связаны уравнениями D.2.6) и D.2.9). Это часто случается, когда
производящие функции для графов со специальным свойством
и для связных графов с тем же свойством удовлетворяют соот-
соотношению D.2.3). Следовательно, рассматриваемые связные графы
можно перечислить, используя формулы D.2.6) и D.2.9). Напри-
Например, если w (х) — производящая функция для четных графов,
определенных в гл. 1, и функция и (х) перечисляет связные четные
графы, то
i + w(x)= exp JS и(xk)lk\. D.2.10)
U-i J
Следовательно, коэффициенты функции и (х) можно вычислить,
используя коэффициенты функции w (x) и соотношения, подобные
тем, которые даются формулами D.2.6) и D.2.9). Связные четные
графы — это как раз эйлеровы графы. Подробности, относящиеся
к перечислениям таких графов, мы рассмотрим в последнем пара-
параграфе данной главы.
Кэдоган [1] развил свой метод так, чтобы можно было в ка-
качестве параметра при перечислении включить не только число
вершин, но и число ребер. Сейчас набросаем детали этого про-
процесса. Пусть gPt qn cp q — числа (р, <?)-графов и связных (р, ^-гра-
^-графов соответственно. Положим
c(x, y) = 2cPjqxPy<>. D.2.12)

116
ГЛ. 4. ГРАФЫ
Тогда из теоремы перечисления Пойа для случая двух перемен-
переменных следует, что
2
к=1
*, y»)/A
D.2.13)
Пусть для всякого р ^ 1 многочлен Ьр (i/) от аддюкюнной
определяется формулой
, у)).
D.2.14)
Можно покавать (так же, как для случая соотношёвр! D.2.6)),
что
" )-2kbk(y)gp.k(y). D.2.15)
fti
Коэффициенты многочлена fcp (у) можно вычислить, используя
коэффициенты многочлена gp (у) и выражение D.2.15). Положим
для удобства
ьр(у) = Тьр.чУ' D.2.16)
Имеем также соотношение '|Ф '*■ •'
оо
=2
D.2.17)
Приравнивая коэффициенты при х^уч и используя обращение Мё-
Мёбиуса, получаем формулу
_ bp/r,q/rV(r)/r.
Г I(P. Ч)
Число связных (р, 9)-графов
D.2.18)
Таблица 4.2.2
ч
1
2
3
4
5
6
7
8
0 12 3
1
1
1 1
2
4
2
3
5
1
5
6
в
1
5
13
1
7
4
19
33
23
8
2
22
67
89
9
1
20
107
236
10
1
14
132
486
11
9
138
814
12
5
126
1 169
13
2
95
1454

4,3. 2-РАСКРАШЕННЫЕ ГРАФЫ И7
Значения коэффициентов cpq, приводимые в табл. 4.2.2, вычи-
вычислены Кэдоганом с помощью формулы D.2.18).
Ясно, что этот подход можно также использовать для нахо-
нахождения числа связных (р, д)-графов с указанными свойствами.
4.3. 2-РАСКРАШЕННЫЕ ГРАФЫ
В гл. 1 мы видели, что вершины /с-раскрашенного графа раз-
разбиваются на к множеств так, что смежные вершины всегда нахо-
находятся в разных множествах. Вершины каждого множества рас-
рассматриваются тогда как имеющие одинаковый цвет. В этом пара-
параграфе мы сосредоточим свое внимание на 2-раскрашенных графах,
для которых к — 2.
Подставляя D.1.6) в D.1.8), получаем
gp(x) = Z(T1(Kp), i + x). D.3.1)
Теперь весьма плодотворным оказывается обобщение этого урав-
уравнения путем замены Кр произвольным графом G порядка р (см.
Харари [11]). Из следствия B.5.1) теоремы Пойа, которое интер-
интерпретирует ряд Z (А, 1 + х), вытекает, что ряд Z (I\ (G), i+x)
перечисляет 1\ (С)-эквивалентные классы множеств, состоящих
из ребер графа G. Эти классы эквивалентности в точности соот-
соответствуют таким остовным подграфам графа G, каждые два из
которых содержатся в одном и том же классе лишь тогда, когда
существует автоморфизм графа G, переводящий один из этих
подграфов в другой. Если два подграфа не принадлежат одному
и тому же классу, то они называются неподобными.
Теорема. Число неподобных остовных подграфов графа G, содер-
содержащих q ребер, равно коэффициенту при Xя в
Z(rx(G), i + x). D.3.2)
Для иллюстрации этой теоремы рассмотрим D,5)-граф G,
показанный на рис. 4.3.1. Трафаретные вычисления дают формулу
| D.3.3)
Следовательно,
D.3.4)
Правильность коэффициентов в этом многочлене подтверждается
рис. 4.3.1. На этом рисунке штриховые ребра используются для
указания на отсутствие ребра в подграфе, чтобы подчеркнуть
эквивалентность относительно группы графа G. Заметим, что
многочлен D.3.4) дает также числа 2-раскрасок ребер графа G
(«сплошным» и «штриховым» цветами). Мы обнаружим, что эта

118
ГЛ. 4. ГРАФЦ
интерпретация многочлена Z (Гх (G), 1 + х) весьма полезна,
в частности при перечислении 2-раскрашенных графов, которые
рассматриваются нижз.
Полный двудольный граф Кт> „ имеет т + п вершин, из которых
т окрашены в один цвет, аи — в другой, и две вершины смежны
тогда и только тогда, когда они окрашены в разные цвета. Так как
2-раскрашенные графы с т вершинами одного цвета и п верши-
вершинами другого цвета соответствуют в точности остовным подгра-
подграфам графа Кт: „, то из теоремы D.3.2) немедленно следует, что
a 21 21 И И
Г7?
Рис. 4.3.1 Остовные подграфы некоторого графа*
многочлен &,„„ (х), перечисляющий эти 2-раскрашенные графы,
удовлетворяет' соотношению
Например,
х).
&з, 2 (х) = 1 + х + Зя2 + Зх3 + За:4 -f a* +
D.3.5)
D.3.6)
и рис. 4.3.2 подтверждает правильность этих коэффициентов. За-
Заметим, что коэффициенты этих многочленов всегда симметричны
«относительно концов».
Теперь, следуя Харари [7], найдем цикловой индекс реберной
группы графа Кт< п. Проще всего начать со случая, когда т Ф п.
Предположим, что X — множество из т вершин одного цвета
в графе Кт> „, a Y — множество из п вершин другого цвета. Тогда
упорядоченные пары (ж, у) из декартова произведения X X Y
в точности соответствуют ребрам графа Кт: „. Таким образом,
подстановки из группы Гх (Кт% „) состоят из таких подстановок
на множестве пар (х, у), которые индуцируются подстановками

щ
4.3. 2-РАСКРАШЕННЫЕ ГРАФЫ
119
множеств X ж Y. Это наводит на мысль ввести следующую бинар-
бинарную операцию на группах подстановок. Пусть А и В — группы
подстановок с множествами объектов X и У соответственно. Де-
Декартовым произведением групп А и В, обозначаемым А X В,
называется группа подстановок с множеством объектов X X Y,
состоящая из всех упорядоченных пар (а, Р) подстановок а из Л
.■•■»
' \'О(
о о о о
• • •
<
>
Рис. 4.3.2 2-раскрашенные графы с тремя вершинами одного цвета и двумя
вершинами другого цвета.
и р из В. Образ каждого элемента (х, у) из X X Y, определяемый
подстановкой (а, р), имеет вид
(а, р)(ж, у) = (ах, pi/).
Следовательно, для тфп
D.3.7)
D.3.8)
и, подставляя это выражение в формулу D.3.5), получаем теорему
(см. Харари [7]) о перечислении таких 2-раскрашенных графов.
Теорема. Многочлен Ът<п (х), перечисляющий 2-раскрашенные
графы, при тфп дается формулой
D.3.9)
еде
т, п
1 V1 п (>•• oi
(a, p) r, <-i

120
ГЛ. 4. rPA<t>J
На самом деле мы уже вычисляли цикловой индекс группы Sn
X Sn, когда обосновывали формулу D.1.9) для Z Eр2)). В час|
ности, соотношение D.1.16) дает в точности то выражение, kotoj
стоит под знаками суммы и произведения в формуле D.3.10).
Для иллюстрации теоремы воспользуемся формулами D.3.9)
и D.3.10), чтобы установить вид многочлена Ьзл (х), который уже
приводился раньше в соотношении D.3.6). Сначала с помощью
формулы D.3.10) найдем цикловой индекс декартова произведе-
произведения Ss X S 2. В этой группе содержится двенадцать подстановок,
но цикловая структура любой из них, скажем (а, Р), зависит только
от цикловых структур подстановок аир. Цикловые структуры
этих конкретных подстановок получаются из формулы B.2.5),
которая выражает Z (Sn) через разбиения числа п. Существуют
только три разбиения числа 3 и только два разбиения числа 2;
поэтому нам нужно рассмотреть ровно шесть различных видов
пар подстановок. Например, если подстановка а из S3 соответ-
соответствует произведению s^ в Z (S3), a P из S2 является транспози-
транспозицией, то, как следует из формулы D.3.10), подстановка (а, A)
дает вклад sf в цикловой индекс Z (S3 X S2). Так как существуют
три подстановки с такой же цикловой структурой, как у а, то их
общий вклад в цикловой индекс Z (S3 X S2), когда они находятся
в паре с подстановкой р, составляет 3sl. Таблица 4.3.1 отражает
Таблица 4.3.1
Члены циклового индекса Z (S3XS2) '■■
ф
Подстановка
Член циклово-
циклового индекса
с.
sl S2
«3
Sl
sl S2
«3
»" ,i. -.1 2
«2
'2
•l
2 2
s, s2
«s
все вклады, которые вносят в цикловой индекс Z (Ss X S2) пары
из декартова произведения S3 X S2- Следовательно, формула для
этого циклового индекса имеет вид
+ 4sl + 2se). D.3.11)
Подставляя 1 + xk вместо «s в правую часть выражения
'D.3.11), получаем многочлен Ъзл (х), указанный в формуле D.3.6).

43. 2-РАСКРАШЕННЫЕ ГРАФЫ 121
Займемся теперь перечислением 2-раскрашенных графов для
того более тонкого случая, когда т = п. Соответствующий пере-
перечисляющий многочлен обозначим через Ъп (х), а не через Ъп<п (х).
Нетрудно, например, убедиться в том, что
Ь3 (ж) = 1 + х + 2а;2 + 4а:3 + 5а:4 + 5а:5 + 4а:6 + 2а;7 + х9 + х\ D.3.12)
Рис. 4.3.3 подтверждает, что коэффициент при я4 и, следовательно,
при хь равен 5. Стоит заметить, что мы не получаем дополнитель-
дополнительных изоморфных классов этих графов, если считаем, что цвета
взаимозаменяемы.
Как и прежде, мы должны найти формулу для циклового ин-
индекса реберной группы графа Кп> „. Для этой цели удобно опреде-
определить дополнительные операции на группах подстановок.
Рис. 4.3.3 Пять 2-раскрашенных F,4)-графов с тремя вершинами каждого
цвета.
Пусть А и В — группы подстановок с множествами объектов
X — {xlt . . ., xd} и Y = {уг, . . ., уе} соответственно. Компози-
Композиция группы А относительно группы В обозначается через А [В]
и имеет в качестве множества объектов декартово произведение
X X Y. Это понятие было определено Пойа [1] и другими мате-
математиками и иногда называлось «веночным произведением»
(«wreath product»). Для каждой подстановки а из А и каждой
последовательности р1( . . ., §d из d подстановок, принадлежащих
группе В, существует подстановка из А [В], обозначаемая через
[а; р1; . . ., pj и такая, что для всякой упорядоченной пары (а-,-,
У]) £ X X Y выполняется равенство
[«; Pi, .... ?,](*„ У/) = (а*£, р». D.3.13)
Основанием для того, чтобы назвать эту группу композицией
групп А и В, является то, что ее цикловой индекс есть композиция
цикловых индексов Z (А) я Z (В), как это проиллюстрировано в сле-
следующем примере. Возьмем А — С3 и В = 52. Используя различ-
различные буквы для переменных в Z (А) и Z (В), имеем
±(s\ + 2s3), Z(B) =!(*• +О.

122 ГЛ. 4. ГРАФЬ
Теперь ясно, в каком смысле следует понимать, что циклово!
индекс композиции двух групп представляет собой композиции
их цикловых индексов. Пойа доказал, что Z (А [В]) есть много
член, получающийся из Z (А) заменой каждой переменной щ
цикловым индексом Z (В; sk, s2k, s3k, . . .). Таким образом, Z (В
нужно подставить в цикловой индекс группы А, чтобы получит!
цикловой индекс их композиции. Эту процедуру мы часто обозна-
обозначаем через
Z(AB = Z{A)IZ(B)]. D.3.14
Кроме того, для любых двух групп подстановок Л и В и произволь
ного степенного ряда / (х) мы имеем
Z(A\B], f(x)) = Z(A, Z(B, /(*))). D.3.15;
Наиболее типичный пример композиции двух групп подстано
вок получается при рассмотрении графа, состоящего из т непере-
непересекающихся экземпляров графа Кп. Группа такого графа идентич
на группе Sm[Sn]. Как указывалось в соотношении B.1.1),!
граф G и его дополнение G имеют одну и ту же группу автоморфиз-1
мов. Поэтому для описания группы графа КПшП мы используем
тот факт, что дополнение графа Кп<п состоит из двух экземпляров
графа Кп, и получаем формулу
a) = St\Sa]. D.3.16) |
Так как группа Т1{Кп>п) индуцируется группой Г (Кп_„), ]
то для нахождения циклового индекса Z (Тх (КП:П)) можно те-j
перь воспользоваться соотношением D.3.16). Подстановки из |
группы Г (КП: „), относительно которых два /г-множества разного !
цвета инвариантны, соответствуют тем слагаемым в цикловом '
индексе Z(S2 lSn]), которые получаются с помощью замены пере-
переменной sx в Z (S 2) цикловым индексом Z(Sn). Их вклад в Z(T1(Kntn)) .
составляет в точности Z (Sn X Sn). Те подстановки из Г (Кпп),
которые взаимозаменяют два га-множества, вносят Z (Sn; s2, s4,
s6, . . .) в цикловой индекс Z (Г (Кп „)). Таким образом, они
состоят из циклов четной длины, которые всегда заменяют вер-
вершины одного цвета вершинами другого цвета. Их вклад в
Z (Гх (Knin)), как показано в статье Харари [7], равен
7' * V »» П Л П *
Zn=—т->—-г " s* 1Is2* [, ] ()
п ' ** Y\k k)k I *-нсчетное ft r<t
(/)
Эту формулу можно проверить так: рассматриваем циклы,
составленные из вершин чередующихся цветов; затем выясняем,
как эти циклы перемещают все ребра, соединяющие вершины раз-
разного цвета.

4 3, 2-РАСКРАШЕННЫЕ ГРАФЫ i23
Итак, мы нашли, что
Z A\ (Кп, „)) = 4 (Z E„ X 5„) + Z;), D.3.18)
я можем написать формулу для этого циклового индекса, исполь-
используя выражения D.3.10) и D.3.17). Однако существует еще одна
полезная операция на группах подстановок (см. Харари [9]),
которая в частном случае дает группу, идентичную группе Г1(ЛГ„_ „).
Пусть А а В — группы подстановок с множествами объектов X =
= {^l. ^2. • • м^}и7= {уи уг, . . ., уе}, как и выше, но только
теперь мы считаем, что е j> 1. Экспоненциацией [В]А группы А
относительно группы В называется такая группа подстановок
с множеством объектов Yx, у которой подстановки строятся следу-
следующим образом. Каждая подстановка а из Л и всякая последова-
последовательность рх, . . ., prf подстановок из В определяют ровно одну
подстановку (а; р\, . . ., prf), принадлежащую группе [В]А, и эта
подстановка преобразует функцию / в функцию /*, определяемую
для всех х1 £ X правилом
/•(*,) = ?,/(<**,). D.3.19)
Можно легко показать, что различные наборы подстановок а,
Pd . . ., prf приводят к разным подстановкам на множестве Yx
и что эти подстановки образуют группу. Кроме того, если взять
А = 5 2 и В = Sn, то функции из множества Yx соответствуют
в точности ребрам графа K,hn и
Гх (*„,„) = №. D.3.20)
Поэтому теорема перечисления (см. Харари [7]) может быть дана
в следующей форме.
Теорема. Многочлен Ъп (х), перечисляющий 2-раскрашенные
графы с п вершинами каждого цвета, дается формулой
bn(x) = Z([Sn]8; l + x), D.3.21)
где
Z([Sn]S*) = ±(Z(SnxSn) + Z'n). D.3.22)
Как отмечалось выше, эта теорема перечисляет 2-раскрашенные
графы с п вершинами каждого цвета, в которых цвета взаимозаме-
взаимозаменяемы. Простейший случай, когда цвета вершин неизменны, уже
представлен формулой D.3.9) — нужно положить т = п, даже
хотя в той теореме предполагалось, что т Ф п.
Теперь проиллюстрируем теорему о многочлене Ъп (х), построив
формулы, необходимые для нахождения Ь3 (х). Цикловой индекс

V.'
124 ,.. ГЛ. 4. ГРАФЫ
группы Ss X Ss, получаемый с помощью соогаюшения D.3.10),
имеет вид:
Z (Ss х Sa) = -L (si + 6sl4 + 8s* + 9Sls* -H I2ss$t). D.3.23)
Иэ формулы D.3.17) следует, что :
;' Z3=i(s^+3slSI + 2s3se). г :: D.3.24)
Комбинируя эти два соотношения, имеем:
4 (° * * ' ). D.3.25)
Теперь, подставляя в это выражение 1 + xk вместо sk, получаем
формулу D.3.12), дающую многочлен Ъа (х).
Граф называется 2-раскрашиваемым, если он может быть 2-рас-
крашен. Мы только укажем, как могут быть перечислены такие
графы. В статье Харари и Принса [2] установлено, что число
связных 2-раскрешенных графов порядка р равно числу свя-
связных 2-раскрашиваемых графов порядка р. Имея перечисление
2-раскрашенных графов, мы можем перечислить связные 2-рас-
крашенные графы, используя метод, отражаемый формулой D.2.3),
и, таким образом, определить, кроме того, число связных 2-рас-
2-раскрашиваемых графов.
4.4. КОРНЕВЫЕ ГРАФЫ
Корневые помеченные графы были без особых усилий пересчи-
пересчитаны в процессе доказательства формулы A.2.1). Перечисление
корневых (непомеченных) графов является чуть менее очевидным
(см. Харари [4]). Оно связано с построением парной группы путем
незначительной переделки соответствующей симметрической груп-
группы. Эта модификация легко обобщается на корневые графы, у ко-
которых корень представляет собой произвольный порожденный
подграф (см. Харари и Палмер [1 ]), могущий быть и графом, и орг-
орграфом, и мультиграфом.
В настоящем параграфе доказывается только одна теорема,
а именно, теорема, дающая формулу для перечисления корневых
графов G порядка р, у которых корнем является специальный по-
порожденный подграф Н, и при этом в графе G имеются q ребер,
кроме тех, которые принадлежат подграфу Н. Как проиллюстри-
проиллюстрировано в следствиях из этой теоремы, мы получим формулы для
корневых графов, ребердо-корнетгах графов, корневых графов,
у которых в качестве корней выделены треугольники, корневых
графов, у которых корнем является ориентированное ребро, и кор-
корневых графов с корнем, представляющим собой циклическую

S4. КОРНЕВЫЕ ГРАФЫ 125
тройку. Например, все корневые F,5)-графы, у которых в ка-
качестве корня взят треугольник Н=К3, представлены на рис. 4.4.1;
здесь штриховыми ребрами выделен треугольник, являющийся
корнем. Таким образом, в силу принятого выше соглашения, р =
= 6 и q = 2, ибо существуют два дополнительных ребра.
Пусть S — произвольное множество вершин графа G. Поро-
Порожденный подграф ( S > — это максимальный подграф графа G,
имеющий S своим множеством вершин. Таким образом, подграф
( S > содержит все ребра графа G, соединяющие две любые вершины
множества S. Мы пытаемся найти число корневых графов G по-
порядка р, у которых в качестве корня взят порожденный подграф Я
Рис. 4.4.1 F,5)-графы, корнями которых являются треугольники*
порядка п <3 р. Это означает, что в графе G нет ребер, которые
соединяли бы две несмежные вершины подграфа Н.
Группу подстановок, которая необходима нам для применения
теоремы перечисления Пойа (в форме следствия B.5.1)), будем
обозначать через Г (Н) о Sp.n. Эта группа определяется сле-
следующим образом: положим G = Н (J Кр_п и заметим, что произ-
произведение Г (Н) Sp_n является подгруппой группы Г (G), оставля-
оставляющей подграф Н неподвижным. Нам требуется ограничение пар-
парной группы (Г (Н) 5р-„)B) на такие неупорядоченные пары {u, v)
вершин графа G, в которых обе вершины не принадлежат подграфу
Я. Результирующая группа подстановок как раз и обозначается
через Г (Я) о Sp.n.
Если вклад некоторой подстановки в цикловой индекс Z (Sp)
составляет Ш/*, то соответствующий вклад в цикловой индекс
^ (£р2)) обозначается через (IIsj(*)<2). Теперь, когда все необходи-
необходимые обозначения введены, можно сформулировать общий резуль-
результат (см. Харари и Палмер [1]).
Теорема. Многочлен hp (x), перечисляющий корневые графы
порядка р, у которых корнем является порожденный подграф Н
порядка п <^р, дается формулой
= Z(T(H)oSp.n, 1 + 3), . ., D.4.1)

126 ГЛ. 4. ГРАфц
где
п, р-п
|()|(/) t n scr'']
(a, P) r, (-1
D.4.2)
и суммирование ведется по всем парам подстановок а £ Г (Я) и
Р 6 SP-n.
Доказательство. Подстановки группы Г (Я) о Sp.n инду-
индуцируются парами (а, Р) подстановок а из Г (Я) и Р из Sp_n.
Вклад в цикловой индекс Z (Г (Я) о Sp.n), вносимый произволь-
произвольной парой, можно рассматривать как произведение двух сомножи-
сомножителей. В первом сомножителе мы просто отражаем тот факт, что
подстановка (a, P) индуцирует подстановку на множестве ребер,
соединяющих подграф Н с графом Кр.п, абсолютно так, как это
имело место в декартовом произведении (см. теорему D.3.10)).
Второй сомножитель есть (Ш/*(Р))<2), он описывает структуру
подстановки Р, индуцированной на парах вершин в графе Кр.п.щ
Теперь мы можем извлечь несколько следствий из этой теоремы,
выбирая в качестве подграфа Н подграфы частных типов. В нашем
первом приложении мы рассмотрим корневые графы порядка р.
Таким образом, Н = Къ так что Г (Я) = S± и, очевидно, Г (Я) о
° Sp-n — (^i^p-i)B)- Подставляя это выражение в формулу D.4.1),
получаем производящую функцию Gp (x) для корневых графов:
Gp(x) = Z((S1Sp.1)W, 1 + х), D.4.3)
которая, естественно, совпадает с соответствующим результатом,
приводимым в статье Харари [4].
Рассматривая только три вершины, быстро находим
Gs (х) = Z ((StSJM, 1 + х) = 1 [A + xf + A + х) A + *2)] =
Чтобы проиллюстрировать полученный результат для случая
р = 4, замечаем, что
.S,) = A/3 !) (s$ + 3s\s2 + 2Sls3). D.4.4)
Простое использование табл. 4.1.2 дает
2((ЗДB^) = A/3 I) (s? + Ss\sl + 2s2s). D.4.5)
Подставляя 1 + х в этот цикловой индекс, получаем многочлен
lll D.4.6)

44, КОРНЕВЫЕ ГРАФЫ 127
в правильности которого легко убедиться, просматривая графы
четвертого порядка, изображенные на рис. 1.1.2. В общем случае
для получения циклового индекса Z (EХ5р_ 1)<2>) можно, насколь-
насколько это приемлемо, использовать формулы для цикловых индексов
из приложения III.
В нашей следующей иллюстрации возьмем Я = Кг, так что
hp (х) перечисляет реберно-корневые графы:
hp(x) = Z(S2oSp_2, 1 + *). D.4.7)
Тождество
Z(S2oSp_2) = (д/dsj Z (S(p2)) D.4.8)
можно быстро проверить. Поэтому мы можем воспользоваться
формулами для цикловых индексов, помещенными в приложении
III, чтобы при р = 5 получить соотношение
Z (S2oS3) = -i. (s{ + 4s3s3! + 2s33 + 3slS* + 2s3se). D.4.9)
Подставляя 1 + xi находим
hb (x) = 1 + 2x + 6ж2 + 12ж3 + 16ж4 + 16л5 + 12.re +
D.4.10)
Так же легко получается и многочлен, перечисляющий корне-
корневые графы, у которых корнями являются треугольники. Приведем
детали, относящиеся к перечислению таких графов с шестью вер-
вершинами. Так как Г (Я) = S8, то, используя формулу D.4.2),
получаем
Z (SaoSs) = JL (SJ2 + 44 + 6«J + 3s\sl + 9s\s\ +
+ 6s^e + 2s33s31 + 6s1s2ve). D.4.11)
Из формулы D.4.1) следует, что
he (х) = 1 + 2х+ 6ж2 + 15ж3 + 2Ь4 + 38а^
+ 38а;' + 21ж8 + 15ж9 + бж + 2а;11 + а;12.
Графы, перечисляемые коэффициентом при х2 в этом много-
многочлене, показаны на рис. 4.4.1; здесь для ребер треугольника,
являющегося корнем, использованы штриховые линии.
Наша теорема справедлива также в том случае, когда Н пред-
представляет собой орграф. Например, если Н — ориентированное
ребро, то Г (Я) = Е2, и поэтому
hp(x) = Z(E2oSp_2, l + x). D.4.12)

128 ГЛ, 4. ГРАФЫ
Выражение для этого циклового индекса получается из формулы
D.4.2). Для каждой подстановки р из Sp_2 обозначим через
вклад, вносимый ею в цикловой индекс Z (Sp_2)- Тогда
'')t(n,i')m, D.4.13)
Рис. 4.4.2 F,5)-графы, корнями которых являются циклические тройки.
где сумма берется по всем подстановкам Р из Sp_2- Чтобы проил-
проиллюстрировать использование формулы D.4.13) в случае р = 5,
напомним, что Z (S32)) = Z {Ss). Имеем
Z (E2oSs) = A/3 !) ((siJ s\ + 3 (Sls2)V2 + 2 (s3)%). D.4.14)
Тогда из формулы D.4.12) следует, что
А5 (*) = 1 + За; + 9а;2 + 20а;3 + 27а;* + 27аг> + 20жв + № + За;8 + х\
D.4.15)
Графы, перечисляемые коэффициентами этого многочлена, можно
построить без особого труда.
Наконец, мы найдем перечисляющий многочлен для корне-
корневых графов с шестью вершинами, у которых в качестве корня
берется циклическая тройка. В этом случае
Г (Я) = 1 («; + &,). ; ' D.4.16)
Из формулы D.4.2) получаем ■■■*'■
Z (Г (H)oS3) = ± («Г + 3**4 + 2s8lSs8 + 6»,VA + 6eJ). D.4.17)
а из формулы D.4.1) следует, что
К (ж) = 1 + 2а; + 6а;2 + 18а;3 + 34а;4 + 52а* + 62а;в +
+ 52а;'+ 34а;8 + 18а;9 + 6а;1» + 2*» + а;12. D.4.18)
Соответствующие графы с д = 2 показаны на рис. 4.4.2.

i,5. НАДГРАФЫ И РАСКРАШЕННЫЕ ГРАФЫ {20
Конечно, в качестве корня-подграфа Н может быть выбрано
много других графов. В частности, всякий раз когда граф или ор-
орграф Н имеет единичную группу Еп, формула D.2.2) принимает
вид
к)П (П ^)<2)« DЛ19)
3 (^-„) = г
В
где, подобно тому, как это делалось в формуле D.4.13), суммиро-
суммирование ведется по всем подстановкам р* из группы Sp.n.
4.5. НАДГРАФЫ И РАСКРАШЕННЫЕ ГРАФЫ
Перечислению 2-раскрашенных графов был посвящен § 4.3,
а корневые графы, у которых в качестве корня выделялся некото-
рый порожденный подграф, изучались в предыдущем параграфе-
Предметом данного параграфа является распространение этих
исследований на случай перечисления таких корневых графов,
у которых в качестве корня берется не обязательно порожденный
подграф; затем предполагается применить полученные выводи
к перечислению m-раскрашенных графов. Приводимые ниже ре-
результаты представляют собой искусное сочетание довольно про-
прозаического подхода из работы Харари [5] с изящной методологией
Робинсона [1].
Если Н — подграф графа G, то G называется надграфом
графа Н- Вместо утомительной фразы «корневые графы G, у кото-
которых в качестве корня берется подграф Н, не обязательно являю-
являющийся порожденным подграфом», мы предпочитаем говорить «над-
графы графа Я», что обеспечивает более эффективную мнемониче-
мнемоническую схему.
Мы начнем с вывода формулы для числа неподобных р-вершин-
ных надграфов графа Н, также имеющего порядок р. Мы увидим
в нижеследующем уравнении, что эта формула включает в себя
цикловой индекс реберной группы дополнения графа Н. Из метода,
рассмотренного в предыдущем параграфе при перечислении кор-
корневых графов с корнями, представляющими собой порожденные
подграфы Н порядка п, следует, что группа подстановок, необ*
ходимая для исследования надграфов графа Н, может быть полу-
получена расширением множества объектов группы Г (Н) о Sp.n
путем включения ребер из дополнения Н. В частности, если Н —
граф порядка р, то многочлен гр (х), перечисляющий корневые
надграфы графа Н, дается формулой
rp(x)^Z(T1(H), l + z). D.5.1)
Интересен частный случай (см. Харари [5]) формулы D.5.1),
когда граф Н представляет собой цикл Ср порядка р. В этом
5 Заказ 443

130
ГЛ. 4. ГРАФЫ
случае получаем формулу для подсчета общего числа неподобных
гамильтоновых циклов, встречающихся во всех (гамильтоновых)
графах порядка р. Реберную группу 1\ (Ср) можно выразить
на языке веночных произведений (композиций). Например, если
р — 2п + 1, то имеем соотношение
Ti (С2n+1) =
D.5.2)
исходя из которого можно вычислить, используя формулы
B.2.11) и D.3.14), цикловой индекс Z(l\ (C2n+1)). Если р — чет-
четное, то Z (Г*! (С2„)) можно вычислить, умножая каждое слагае-
слагаемое из Z(D2n[En_z\) на соответствующее слагаемое из Z(Dn).
А
Рис. 4.5.1 Восемь графов пятого порядка, корнями которых являются
остовные циклы.
В случае р = Ь формула D.5.2) дает Tl{Cb) = Db [#i] = Db и,
в силу B.2.11), имеем
D.5.3)
Затем, применяя соотношение D.5.1), получаем
D.5.4)
Правильность этого многочлена подтверждается графами, изобра-
изображенными на рис. 4.5.1; здесь корень Сь представляет собой цикл
со штриховыми ребрами.
Вернемся теперь к общему методу перечисления надграфов.
Пусть Н — произвольный подграф порядка п полного графа Кр.
Тогда произведение Г (H)Sp.n есть группа, состоящая из всех
таких подстановок группы Г (Кр) = Sp, которые оставляют под-
подграф Н неподвижным, т. е. они могут переставлять вершины под-
подграфа Н только между собой. Группа, необходимая для перечисле-
перечисления надграфов графа Н, "является ограничением парной группы
(Г (Я) Sp_n)W на такие пары вершин, которые не смежны в Н.
Обозначим это ограничение через Гх (Я, Кр). Заметим, что если

4.S. НАДГРАФЫ И РАСКРАШЕННЫЕ ГРАФЫ 131
Я имеет р вершин, то Г\ (Я, Кр) — 1\ (Я). Кроме того, если Я —
связный граф, то 1\ (Я, Кр) является в точности реберной груп-
группой дополнения графа Я относительно графа Кр.
Мы пока только имеем теорему (см. Харари [5]), дающую
принципиальную возможность найти число надграфов данного
графа, но у нас нет эффективного метода вычисления необходи-
необходимого циклового индекса. Такой алгоритм был предложен Робин-
Робинсоном [1]. Как только эта процедура будет развита, мы тем самым
докажем соответствующую теорему. Следовательно, при подобном
положении дел чрезвычайно удобно в противоположность мудрому
предостережению Уленбека сначала представить доказательство,
а затем уже сформулировать теорему. Чтобы вычислить цикловой
индекс группы Гх (Я, Кр), мы определяем вершинно-реберную
группу графа G, которая обозначается через Г0>1(С), как группу
подстановок, индуцированную группой Г (G) и переставляющую
и вершины, и ребра графа G. Записывая цикловой индекс этой
группы, мы будем различать циклы, составленные из разных
переставляемых объектов, используя для этого два множества
переменных: sk — для вершин и tk — для ребер. Например, если
G — D,5)-граф Kt — х, то
Z(T0,1(Ki-x))^±(si1tl + 2s\s2t1ti2+slt1tl). D.5.5)
Из формулы B.2.14) следует, что цикловой индекс группы
Г (Я) 5р_„ дается соотношением
Z (Г (Я) Sp.a) = Z (Г (Я)) Z (Sp.n). D.5.6)
Аналогично, Z(Y0:1(H))Z(Sp_n) есть цикловой индекс группы,
которая индуцируется группой T(H)Sp_n, действующей на мно-
множестве вершин графа Кр и множестве ребер графа Я. Каждая
подстановка a£T(H)Sp_n вносит в Z(Tol(H))Z(Sp.n) произве-
произведение (И skk) (П tkk). Соответствующий вклад подстановки а
в Z(«Sp2)) обозначим, как обычно, через (П.^*) . Далее, — и вы-
выделим особо этот тонкий прием, осуществленный Робинсоном,—
подстановка а вносит в цикловой индекс группы 1\ (Я, Кр)
произведение (Ylskk) П sft *, ибо умножение на Tlsk k соответ-
ствует исключению тех членов в выражении Ц1 s^ ) , которые
возникают при рассмотрении пар вершин, являющихся смеж-
смежными в графе Я. Поэтому мы определяем линейный опера-
оператор р (такое обозначение отражает заслуги Робинсона) для
вершинно-реберных цикловых индексов, задавая его для про-
произведений таким образом:
)) IЬГ\ . D.5.7)
5*

132 гл. 4. графы
Теперь утверждение о перечислении надграфо* формулируется
в следующем виде. . ... й
Теорема. Многочлен гр (х), перечисляющий надерафы порядка р
произвольного графа Н порядка п ^ р, дается формулой
■: rp(x) = Z(T1(H, Kp), 1 + х), ■ . D.5.8)
где ......»
. г(Тг(Н, Кр)) =p(Z(TOil(H))Z(Sp_n)). D.5.9)
Заметим, что если Н является графом порядка р, как было
в D.5.1), то формула D.5.9) приобретает такой вид:
D.5.10)
Таким образом, оператор р дает нам возможность получить ре-
реберный цикловой индекс произвольного графа, исходя из вер-
шинно-реберного циклового индекса его дополнения.
Мы проиллюстрируем эту теорему для случая Н = Св, т. е.
взяв простой цикл порядка 6, и положим р = 6. Вершинно-ре-
берный цикловой индекс произвольного циклического графа Ср
легко вычисляется с использованием формулы B.2.11), дающей
выражение для Z (Ср). Если р = 6, то имеем
Z (Го, 1 (С,)) = -^ (s\ t\ + si 4 + 2^ t*a + 2Se«e + 3s2lS221\ + 3sl t\ 4). -
D.
Применяя оператор р к соотношению D.5.11), находим
jT D.5.12)
Из D.5.8) и D.5.12) с помощью простых преобразований получаем
явное выражение для гв (х):
гв (х) = 1 + 2х + бх2 + 12Ж3 + 16а;4 + I6z5 +
D.5.13)
Этот многочлен, естественно, можно также получить, используя
соотношения, подобные D.5.2), D.5.3) и D.5.4). Правильность
коэффициента при х2 подтверждается рис. 4.5.2.
Сосредоточим теперь свое внимание на тп-раскрашенных
графах и на нижеследующем утверждении Робинсона [1]; при

4.5. НАДГРАФЫ И РАСКРАШЕННЫЕ ГРАФЫ
133
этом мы будем использовать теорему, связанную с формулой
D.5.8). Как следует из определения, вершины лг-раскрашенного
графа разбиваются на т множеств так, что смежные вершины
всегда принадлежат разным множествам. Вершины одного и того
Рис. 4.5.2 Все шесть F,8)-графов, корнями которых являются остовные
циклы.
же множества имеют одинаковый цвет. Например, 3-раскрашенные
графы, изображенные на рис. 4.5.3, содержат по две вершины
каждого цвета и вершины, соединенные штриховыми ребрами,
имеют одинаковый цвет.
/Л Л
* \ / \ I /
V—J \—If
Рис. 4.5.3 Все девять 3-раскрашенных F,3)-графов с двумя вершинами
каждого цвета.
Как и в § 4.3 при перечислении 2-раскрашенных графов,
мы ищем число лг-раскрашенных графов для специального раз-
разбиения (j) числа р на т частей:
.'•■' m = 2j /a.
D.5.14)
где, как обычно, 2 ^h = P- Пусть bp((j), х)— многочлен, пере-
перечисляющий лг-раскрашенные графы порядка р, для которых раз-
разбиение (j) является цветным1. Например, если р = 6 и разбиение
1 То есть любое подмножество разбиения множества вершин состоит из
вершин одинакового цвета и разные подмножества разбиения «имеют разный
цвет». — Прим. перев.

134 гл. 4. граф ы
имеет вид 2-f-2 + 2, т. е. /2 = 3, то многочлен b6((j), x) пере-
перечисляет 3-раскрашенные графы порядка 6, имеющие по две вер-
вершины каждого цвета. Мы покажем, что для этого разбиения
числа 6 многочлен Ьв ((/), х) имеет вид
h ((/). х) = 1 + х -f- 4а;2 + 9а:3 + 18а:4 -\- 24r5 -f 3Ore +
+ 24х7 + 18х8 + 9х9 + 4х10 + хп + хп. - D.5.15)
Рис. 4.5.3 подтверждает тот факт, что коэффициент при х3 в соот-
соотношении 4.5.15 равен 9.
Мы определяем полный т-долъный граф К (/) для произволь-
произвольного разбиения (/) числа рнаго частей как дополнение объедине-
объединения т полных графов:
K(j)=l)ikKk. D.5.16)
Как и прежде, лг-раскрашенные графы, которые мы хотим подсчи-
подсчитать, являются остовными подграфами графа К ()). Из формулы
D.3.2) следует, что
Ър ((/), x) = Z (Гх (К (;)), 1 + х), D.5.17)
и поэтому мы должны найти метод для определения циклового
индекса группы Гх (К (/)). Но остовные подграфы полного т-доль-
ного графа К (/) являются как раз надграфами графа К (j). Этот
факт подсказывает идею: выразить цикловой индекс группы
Гх (К (/)) на языке оператора р и циклового индекса Z (Го 1 (K(j))),
взяв в формуле D.5.10) Н = К (j). Таким образом, достаточно
найти способ вычисления циклового индекса группы Го> х (К (/)),
и это мы сейчас сделаем.
Обозначим через nG граф, состоящий из п попарно непересе-
непересекающихся экземпляров связного графа G. Как следует из опре-
определения веночного произведения (см. Харари [11, стр.196),
T{nG) = Sn\Y{G)\. D.5.18)
Поэтому, в силу соотношения D.3.14), цикловой индекс для этой
группы равен
Z{T{nG)) = Z{Sn)[Z{T{G))\. . D.5.19)
Уравнение D.5.19) легко обобщить и получить выражение
Z (Го, 1 (nG)) - Z (Sn) [Z (Го, х (G))). D.5.20)
Рассмотрим тот же самый пример, который привел нас к много-
многочлену D,5.15). Подагая G~= К2 Ц п = 3 и используя формулу
D.5.20), имеем
Z (Ге> 1 C*,)) = Z E,) \Z (Го,, (К,))]. D.5.21)

i 5. ЯАДГРАФЫ И РАСКРАШЕННЫЕ ГРАФЫ 135
Далее, Z(T0, г (К2)) = -^-(s^i + s^i), и если вместо каждого Sk
в цикловом индексе Z(S3) мы подставим выражение A/2) (spk~{-
+ *2fc^*)> получающееся из Z (Го_ х (К2)) умножением каждого ин-
индекса у S; и tj на число к, то найдем
S
+ -6-s^3+-6-sei3- D.5.22)
В общем случае, при рассмотрении графа К (j), компоненты
которого являются полными графами, Группа Г (К (;)) может
быть представлена в виде произведения (см. Харари [1], стр. 196)
I. D.5.23)
Из D.5.20) следует, что
(Kk))\. D.5.24)
Обозначим для удобства группу Гм(#п) через 5^'2) и заметим,
что вершинно-реберный цикловой индекс легко получается из
циклового индекса Z (S^). Как отмечалось выше, К (/) = ЗЛГ2,
если р = 6 и/2 = 3. Таким образом, формула D.5.22) дает цикло-
цикловой индекс вершинно-реберной группы дополнения такого пол-
полного 3-дольного графа шестого порядка, который имеет по две вер-
вершины каждого цвета.
Теперь мы можем резюмировать метод Робинсона [1] для пере-
перечисления тп-раскрашенных графов.
Теорема. Многочлен Ър ((/), х), перечисляющий т-раскрашен-
Ние графы порядка р, отвечающие разбиению (j), имеет вид
p D.5.25)
еде
D.5.26)

136 ГЛ. 4. ГРАФЬ
В том примере, который нами рассматривался, мы уже наивд
выражение для Z (S3)[Z (S^1>2)I (см. формулу D.5.22)). Из опре
деления оператора р в случае /2 = 3 следует, что
D.5.27
» Упрощая это выражение, имеем :( , у;
Наконец, делая подстановку Sk = 1 + a;fc в правую часть соот-
соотношения D.5.28), получаем формулу D.5.15). Используя эту тео-
теорему, Робинсон нашел число 3-раскрашенных графов для зна-
значений р ^9 и для всевозможных разбиений.
Мы должны особо подчеркнуть, что, в то время как перечисле-
перечисление 2-раскрашиваемых графов выполнимо (об этом говорилось
в § 4.3), задача перечисления /n-раскрашиваемых графов при
пг ^ 3 остается -нерешенной (см. гл. 10).
4.6. БУЛЕВЫ ФУНКЦИЙ
Булеву функцию п переменных можно рассматривать как
отображение множества всех ^-последовательностей из нулей
и единиц в множество {0, 1}. Другими словами, булева функция
представляет собой подмножество вершин га-куба Qn. Нашей целью
является подсчет числа типов булевых функций с отношением
эквивалентности, определяемым группой п-куба Qn.
Мы видели, что цикловой индекс реберной группы графа G
позволяет подсчитывать остовные подграфы. В данном параграфе
мы исследуем возможности циклового индекса вершинной группы
графа G и увидим, что он полезен при подсчете неподобных мно-
множеств вершин. Наиболее интересное применение этой техники
будет состоять в перечислении типов булевых функций.

4.6. БУЛЕВЫ ФУНКЦИИ J37
Чтобы подготовиться к подсчету булевых функций, мы проин-
проинтерпретируем утверждение B.5.1) о цикловом индексе Z {А, 1 + х)
в случае, когда А есть группа Г (G) данного графа G.
D.6.1). Теорема. Коэффициент при хг в Z (Г (G), 1 + х) равен
числу неподобных множеств, состоящих в точности из г вершин,
при условии, что эквивалентность определяется группой автомор*
физмов графа G.
>
Рис. 4.6.1 Неподобные 2-множества вершин в некотором графе.
Для иллюстрации теоремы рассмотрим граф G, изображенный
на рис. 4.3.1. Цикловой индекс его группы дается соотношением
[f(; )] x(i!S) Dl6>2)~
так что
Z(T(G), 1 + *) = 1+2* +За8+2*» + **. D.6.3)
Правильность среднего слагаемого этого многочлена подтвер-
подтверждается рис. 4.6.1, на котором пары вершин, образующие непо-
неподобные подмножества, обозначены темными точками. Пойа [2]
обнаружил, что ранние работы Джевонса [1] и Клиффорда [1]
о перечислении типов булевых функций приводят к таким число-
числовым результатам, которые не являются полностью правильными.
Задача состояла в нахождении числа «разных» высказываний,
построенных из п предложений х, таких, что каждое из них имеет
два значения истинности: 0 или 1. Используя широко извест-
известные символы V (или) и Д (и) для дизъюнкции и конъюнкции,
можно из предложений Ри Р2 и Р3 составить высказывание Pi V
V (Р^ А Рз)- Далее, если 1 и 0 — два значения истинности, то
сложные высказывания соответствуют естественным образом буле-
булевым функциям. Например, высказывание Рх V (Р* А Рз) со-
соответствует функции /, отображающей тройки @, 0, 0), @, 0, 1)
и @, 1, 0) в 0, а все остальные тройки — в 1. Однако мы хотим
рассматривать два сложных высказывания как эквивалентные
не только тогда, когда они соответствуют равным булевым функ-
функциям, но и в том случае, когда одно из этих высказываний может
быть получено из другого перестановкой предложений или заме-
заменой нескольких предложений их отрицаниями.. Так, например,
"■-Элементарных высказываний. — Дрим, перев^ '('

138
ГЛ. 4. ГРАФЫ
высказывание Рг V {Рг Л Ps) рассматривается как эквивалент-
эквивалентное высказыванию (Р3 V) (П ^i) Л (Ps V -Рг). что можно обо-
обосновать, используя дистрибутивный закон для дизъюнкции
относительно конъюнкции.
Пойа обнаружил, что рассматриваемая задача состоит в опре-
определении числа способов, которыми можно раскрасить 2п вершин
й-куба Qn двумя разными цветами. Это следует из того, что группа
гг-куба Qn идентична группе, переставляющей произвольным об-
образом п предложений и заменяющей предложения их отрицани-
отрицаниями. Мы можем выразить эту группу через симметрические группы,
воспользовавшись операцией экспоненциации (см. Харари [9]):
Y(Qn) = [Szfn. D.6.4)
В этом соотношении группа Sn указывает на то, что п предложе-
предложений Pt можно переставлять как угодно, а группа ^2 учитывает
rv
ли
7
Рис. 4.6.2 Кубы с четырьмя вершинами каждого цвета.
возможность навешивания отрицания на предложения Pi после
того, как они переставлены. Применяя теорему D.6.1) для этой
группы подстановок, можно получить основной результат данного
параграфа. Цикловой индекс этой группы был впервые найден
Слепяном [11, но представлен он был в довольно сложной форме,
в которой невозможно узнать экспоненциацию как таковую.
D.6.5). Теорема. Число N (п, г) различных булевых функций,
зависящих от п переменных и принимающих г ненулевых значений,
равно коэффициенту при хг в Z (liS'2]s", 1 + х).
Для иллюстрации теоремы мы приводим на рис. 4.6.2 шесть
способов раскраски вершин куба Q.A, отвечающих тому случаю,
когда в кубе имеется по четыре вершины каждого цвета. Этим
самым мы проверяем значение коэффициента при х* в Z ([S2]S:>,
1 + х). Заметим, что ожерелья, изображенные на рис. 2.4.2,
соответствуют в точности булевым функциям от двух переменных,
ибо всякое допустимое преобразование ожерелья с четырьмя бу-
бусинками можно заменить соответствующим преобразованием на
2-кубе.
Используя тот факт, что группа Г (Qn) абстрактно изоморфна
веночному произведению Sn IS2], Пойа вычислил цикловые ин-
индексы Z (Г (Qn)) для п s^ 4. Применяя сформулированную выше
теорему, он нашел значения величины N (п, г), представленные
в табл. 4-64.

4,6. БУЛЕВЫ ФУНКЦИЙ
139
Таблица 4.6.1
\^ г
n N^
1
2
3
4
0
1
1
1
1
l
1
1
1
1
2
1
2
3
4
Число
3
1
3
6
булевых
4
1
6
19
5
3
27
функции
в
3
50
7
1
56
8
1
74
Общее число
функций
3
6
22
402
Тесная связь, существующая между булевыми алгебрами и пере-
переключательными схемами, как раз явилась причиной, побудившей
Слепяна [1] вычислить общее число булевых функций для п = 5
и 6. Довольно сложный метод нахождения циклового индекса
Z ([B\Sn) был предложен Харрисоном и Хаем [1], которые ис-
использовали этот метод для подсчета числа некоторых классов
функций алгебры логики х. Наиболее компактные формулы для
Z ([В]А) были найдены Робинсоном и Палмером, как сообщалось
об этом в работе Палмера [3]. Мы дадим набросок некоторых дета-
деталей их подхода, чтобы снабдить читателя приемлемым средством
вычисления циклового индекса, встречающегося в теореме D.6.5).
Сначала определяем произведение для одночленов, обозначая
его через X (сравните с соотношением D.1.16)):
D.6.6)
Как показано в работе Харари [7], если это произведение
распространить на многочлены по линейному закону, то цикловой
индекс Z (А X В) декартова произведения можно представить
в виде
Z{AxB) = Z{A)xZ{B). D.6.7)
Для жаждого целого положительного числа г определяется но»
вый Оператор /,. Сначала определяем его на одночленах;
D.6.8)
D.6.9)
ш|о \*|о/(/-,о) /
1 В оригинале — «.„функций Поста». — Примк

140 ГЛ. 4. ГРАФЫ
Ясно, что оператор У х является тождественным. Применяя к со-
соотношению D.6.9) формулу обращения Мёбиуса, можем написать
(
w\v \k\w/(r,w)
Затем оператор 'Jr распространяется по линейному закону на
многочлены. Приведенные только что пять формул можно исполь-
использовать для выражения циклового индекса Z (\В\А) через цикловые
индексы Z (А) и Z (В), где А и В — произвольные группы подста-
подстановок. Как это делается, станет ясно из рассмотрения примера,
в котором А = S3 и В = S2, т. е. при вычислении циклового
индекса группы куба Q3. Самой трудной частью является вычисле-
вычисление операторов Jr. Сначала вместо каждой переменной sr в цикло-
цикловом индексе Z (S3) подставим оператор /,. Получим такое выраже-
выражение:
Z (Ss; Л, /2, /3) = ~(А+ ЗАЛ + 2У3). D.6.11)
Далее, слагаемые из D.6.11) действуют на Z(S2) следующим
образом:
/; (Z (S,)) = Л (Z E,)) XЛ (Z E2)) х Л (Z Eа)), ■
J1J,(Z(S2)) = J1(Z(S,))xJ2(Z(S2)). ,• •;„.,.„-, ., D.6.12)
В силу определения операторов Jr, имеем
l{ . ■ , D.6.13)
== y (Л (s\) +Л (в,)) = т (&* + *<), J: D-6-14)
D.6.15)
Из соотношений D.6.12) с учетом формул D.6.7), D.6.13) в
D.6.14) получаем равенства
Л (Z(St)) = -р- (»2 + 7si), JtJ2 (Z(S2)) = ± (sy2 + s$ + 2sl).
D.6.16)
Наконец, подставляя многочлены из D.6.15) и D.6.16) в фор-
формулу D.6.11) на место соответствующих слагаемых, находим вы-
выражение для циклового индекса Z([512lSi1) в форме, напомина-
напоминающей уравнения из работы Пойа [2]:
+2i^l). D.W7,

4,7. ЭЙЛЕРОВЫ ГРАФЫ 141
Таким образом, как показано в работе Палмера [3], цикловой
индекс Z ([В)А) произвольной экспоненциации может быть выра-
выражен как образ циклового индекса Z (В) при воздействии на него
оператора Z (A; J1, /2, ■ • .)• На таком пути могут быть в прин-
принципе решены все задачи перечисления, в которых группа конфигу-
конфигураций может трактоваться как экспоненциация.
4.7. ЭЙЛЕРОВЫ ГРАФЫ
Четные графы (у которых каждая вершина имеет четную сте-
степень) и эйлеровы графы (т. е. четные связные графы) были пере-
перечислены в том случае, когда они представляли собой помеченные
объекты, — в § 1.4. Более тонкая задача — для непомеченных
графов — была решена лишь тогда, когда Робинсон [2] увидел
это препятствие именно с присущей его исследованиям перспекти-
перспективой. Чтобы перечислить эйлеровы графы с р вершинами, он сна-
сначала пересчитывает четные р-вершинные графы, а затем приме-
применяет обычную технику для выражения числа связных конфигу-
конфигураций через общее число конфигураций.
Настоящий параграф содержит главным образом доказатель-
доказательство формулы Робинсона для числа четных графов порядка р.
Эта формула очень похожа на аналогичную формулу для пере-
перечисления графов, в которой использовался цикловой индекс
D.1.9) парной группы, порожденной симметрической группой.
Это сходство не случайное, ибо теорема Робинсона базируется на
упомянутом результате.
Теорема. Число wp четных графов порядка р дается формулой
wp = -
где , '
. *(/)=2 (г, Wr/<+2 ()
t fc>i \* / ... ..■
B V D.7.2)
вдесъ sgnx равно 1 при z>>0 и равно 0 при х = 0.
Доказательство. Следуя Робинсону, мы применим тот вариант
леммы Бернсайда, в котором рассматривается ограничение группы
на подходящее подмножество объектов (см. соотношение B.3.9)).
sB)
Мы видели, что орбиты степенной группы Е2 р соответствуют
графам порядка р. Ограничим эту группу на множество F таких
функций, которые представляют четные графы. Тогда мы сможем

142
ГЛ. 4. ГРАФЫ
применить формулу B.3.9), чтобы выразить wp через функции из
множества F, остающиеся неподвижными при воздействии на них
подстановок из этой степенной группы. Другими словами, для
каждой подстановки о из Sp мы ищем число функций / из множе-
■ства F, таких, что
'> /}=/{°», а/}-
D.7.3)
Таким образом, для доказательства теоремы мы должны показать
что если циклы подстановки а определяют разбиение (/) числа р,
"то число функций в множестве F, удовлетворяющих условию
D.7.3), равно 2е W, где е (/) дается формулой D.7.2).
Рис. 4.7.1 Четный граф, неподвижный относительно подстановки A234) E6)
G89) A0) A1) A2) A3).
Прежде чем погрузиться в детали этого доказательства, мы
постараемся сделать трактовку более прозрачной, рассмотрев
для этого четный граф (см. рис. 4.7.1), который соответствует
функции / из множества F, удовлетворяющей условию D.7.3)
для конкретной подстановки а степени 13, а именно
а = A234) E6) G89) A0) A1) A2) A3).
Допуская лишь незначительную вольность речи, мы говорим, что
данный граф неподвижен относительно а. Сплошные и штриховые
ребра применяются для того, чтобы более ярко отразить действие
подстановки а на ребра графа. Смысл того, почему одни ребра
изображены сплошными, а другие — штриховыми, станет, на-
надеемся, ясным в процессе доказательства.
Сначала находим вклад, который вносит подстановка
а в множитель 2е W в том случае, когда ее циклы рассмат-
рассматриваются индивидуал ьно,. Если z* = A 2 3 ... к) — про-
произвольный нечетный цикл подстановки а, то мы знаем,
что zk индуцирует (к — 1)/2 циклов 2-подмножеств множества
{1,2,3 к}. Любая вершина цикла zk инцидентна ровно

ч
4.7. ЭЙЛЕРОВЫ ГРАФЫ
143
двум ребрам в каждом из этих циклов (см., например,
рис 4.7.2, а). Следовательнв, каждый из этих {к — 1)/2 цик-
циклов может либо входить, либо нет в четный граф, являю-
являющийся неподвижным относительно подстановки а. Поэтому вклад
в е Ц), вносимый всеми нечетными циклами при их индиви-
р
дуальном рассмотрении, равен У, ik{k -~ 1)/2 (ср. с D.1.14)).
р
Аналогично, если к — четное, то вклад в е (/) равен У U {к—2I2
(ср. с D.1.15)). Заметим, что любой цикл С длины к12, состоящий
Рис. 4.7.2 Графы, неподвижные относительно нечетной и четной циклических
подстановок.
из 2-подмножеств, не входит в четный граф, так как каждая вер-
вершина цикла %k инцидентна только одному из 2-подмножеств, со-
содержащихся в цикле С. Например, на рис. 4.7.2, б соответству-
соответствующий цикл показан штриховыми ребрами и он вносит нечетный
вклад (единицу) в степень каждой вершины, изображенной на
рисунке
Так же как при перечислении графов (см. § 4.1), мы рассмот-
рассмотрим далее пары циклов zr и zt из подстановки а и такие 2-подмно-
жества, которые имеют по одной вершине в каждом из этих цик-
циклов. При нахождении циклового индекса парной группы мы виде-
видели, что циклы zr и zt индуцируют (г, t) циклов длины [г, t], дей-
действующих на указанных выше 2-подмножествах (ср. с D.1.16)).
Таким образом, каждая вершина цикла z, принадлежит [г, t]Jr
2-подмножествам, содержащимся в одном из таких циклов длины
[г, t]. Заметим, что если t — четное иг — нечетное, то каждая
вершина цикла zr находится в четном числе таких 2-подмножеств.
Памятуя об этом, мы теперь рассмотрим все пары циклов zr и zt,
у которых либо г, либо t — четное. Пусть U — произвольная со-
совокупность циклов таких 2-подмножеств, в которых содержится
ровно по одной вершине из этих двух различных циклов

144 ГЛ. i. ГРАФЫ
zr и zt. Тогда каждая вершина нечетного цикла принадлежит чет-
четному числу 2-подмножеств, входящих в циклы из U. Каждая вер-
вершина четного цикла Zk может содержаться либо в четном, либо
в нечетном числе этих 2-подмножеств. Итак, мы видим, что циклы
из совокупности U могут определить четный граф — надо только
либо добавлять, либо исключать (смотря по тому, что необходимо)
циклы длин к/2, индуцированные циклами zk.
Различая два случая: г Ф t и г = t, мы видим, что общее число
циклов в совокупностях U равно , -1
2 с, ом,+ 2
где по меньшей мере одно из чисел г и t — четное. Следовательно,
полученное выражение представляет собой вклад в е (/), вносимый
парами, объекты которых принадлежат двум любым циклам под-
подстановки а, причем хотя бы один из циклов является четным.
Заметим, что на рис. 4.7.1 для получения четного графа нужно
включить и штриховые ребра цикла A234), и штриховое ребро
цикла E6).
Мы пока еще не рассматривали 2-подмножеств а, содержащие
по одной вершине в каждом из двух различных нечетных циклов.
Выделим один конкретный нечетный цикл, скажем z, и обозна-
обозначим через W совокупность всех таких циклов 2-подмножеств,
которые получаются посредством выбора для каждого нечетного
цикла ъг Ф z одного какого-либо цикла 2-подмножеств, вершины
которого лежат в г и в г,. Таким образом, совокупность W будет
иметь ( 2 izk+i \— 1 циклов. Для каждой выборки, состоящей из
тех циклов 2-подмножеств, которые не принадлежат совокупности
W, мы можем теперь определить четный граф. Это достигается либо
включением, либо исключением (в зависимости от необходимости)
каждого цикла, принадлежащего W, для того, чтобы всякая вер-
вершина из нечетного цикла, отличного от z, находилась в четном
числе 2-подмножеств. Тогда (так как Эйлер доказал, что число
вершин нечетной степени в любом графе должно быть четным)
вершины цикла z тоже будут лежать в четном числе 2-подмножеств.
Число таких циклов, не принадлежащих совокупности W, при
нечетных rut равно
2 (г, t)j,jt+ S B/c + l)
где т — число нечетных циклов, если таковые существуют, и
т = 1, если нечетных циклов нет. На рис. 4.7.1 мы проиллюстри-
проиллюстрировали это при z = A0); здесь W состоит из циклов, содержащих
штриховые ребра, исходящие из вершины 10. После соединения
вершины 11 с вершинами 7, 8, 9,12 и 13 это необходимо в данном

1
УПРАЖНЕНИЯ
145
случае для того, чтобы включить все ребра из совокупности W,
получаем четный граф.
Объединяя все эти рассмотрения и суммируя различные «вкла-
«вклады», убеждаемся в справедливости формулы D.7.2). Таким обра-
образом, четные графы перечислены.в
Робинсон использовал эти формулы для вычисления числа wp
четных графов при р ^ 8:
w (х) = х + я2 + 2х3 + За;4 + ltf> + 16a;6 -f 54z7 + 283х8
D.7.4)
Семь четных графов пятого порядка, показанных на рис. 1.4.3,
когда перечислялись четные помеченные графы, подтверждают
Рис. 4.7.3 Восемь эйлеровых графов шестого порядка. •, л
правильность коэффициента при ж5. Производящая функция и (х)
для эйлеровых графов может быть получена обычным способом,
если снова применить формулу D.2.3), которая перечисляет связ-
связные графы «на языке» всех графов. Несколько первых членов
функции и (х) имеют вид
D.7.5)
Значение коэффициента при х6 подтверждается рис. 4.7.3.
УПРАЖНЕНИЯ
4.1. Найти многочлен, перечисляющий число способов, кото-
которыми можно раскрасить, используя три цвета, ребра: (а) E,^-гра-
E,^-графа, (Ь) графа K3z 3. (Указание: см. теорему D.3.2).)
4.2. Найти цикловые индексы Z (S2 [C3]), Z (C3 [<S2]) и
z (s3 toj).
4.3. Найти цикловой индекс для графа с четырьмя компонентами,
если: (а) каждая компонента является треугольником, (Ь) две
компоненты являются треугольниками, а две другие — изолиро-
изолированными вершинами.

146 ГЛ. 4. ГРАФЫ
4.4. Чистые двумерные симплициалъные комплексы (каждый такой
комплекс состоит из конечного множества X и некоторой совокуп-
совокупности 3-подмножеств множества X).
(Харари [4])
4.5. Мультиграфы мощности s, т. е. мультиграфы, в которых
любая пара вершин соединяется не более чем s ребрами.
4.6. Графы, снабженные знаками, т. е. графы, в которых ребрам
приписаны знаки плюс и минус.
(Харари [3])
4.7. Сбалансированные графы, т. е. графы, снабженные знаками
и не содержащие циклов с нечетным числом отрицательных ре-
ребер.
(Харари и Палмер [10])
4.8. Бершинно-симметрические графы простого порядка р,
группы которых транзитивны.
(Тернер [1])
ViU; •!■'; ;,' 'At '

Глава 5
Лорд Рональд вскочил на коня
и бешеным галопом помчался во
все стороны.
Ликок С,1
ОРГРАФЫ
В этой главе, состоящей из четырех параграфов, перечисляются
орграфы, турниры, ориентации данного графа и «смешанные гра-
графы» (т. е. графы, в которых могут встречаться и дуги, и неориенти-
неориентированные ребра). Кроме всех орграфов, мы перечисляем в первом
параграфе отношения и связные орграфы. Из решения задачи
перечисления турниров выводится в качестве следствия теорема
о перечислении сильных турниров. Наша формула для числа сме-
смешанных графов включает как частные случаи формулы, подсчиты-
подсчитывающие числа графов, орграфов, направленных графов, полных
орграфов и турниров (эти формулы легко могут быть представлены
в явной форме).
Несколько слов о методах перечисления, используемых ниже.
Подсчет орграфов осуществляется с помощью несложной модифи-
модификации метода Пойа, применявшегося при перечислении графов.
Это достигается путем введения новой унарной операции на груп-
группах подстановок. Результатом операции является группа, назы-
называемая редуцированной упорядоченной парной группой, которая
предназначена для того, чтобы действовать на множестве упоря-
упорядоченных пар различных объектов, тех самых объектов, на мно-
множестве которых действует первоначальная группа подстановок.
Цикловой индекс редуцированной упорядоченной парной груп-
группы, порожденной группой Sp, используется для подсчета оргра-
орграфов. Затем, чтобы дать возможность перечислить турниры, этот
цикловой индекс модифицируется путем введения ограничения
на область действия соответствующей степенной группы. Приме-
Применяя эту идею к редуцированной упорядоченной парной группе
произвольного графа и используя в результирующем цикловом
индексе два множества переменных, мы далее получаем возмож-
возможность подсчитать число ориентации графа. Кульминацией в при-
1 Стивен Ликок A869^1944) — канадский юморист, — Прим.. nepeet

1
148 ГЛ. 5. ОРГРАФЫ
ложении этих методов является общая теорема перечисления сме-
смешанных графов. Она доказывается с использованием того же цикло-
циклового индекса, который применяется для перечисления орграфов,
снова с двумя множествами переменных и со специальным перечи-
перечисляющим рядом для фигур.
5.1. ОРГРАФЫ
В этом параграфе продолжена аналогия между выводом
многочлена gp (x), перечисляющего графы, и выводом соответст-
соответствующего циклового индекса парной группы, порожденной груп-
группой Sp. В то время как существует только 11 графов четвертого
порядка, число всех орграфов четвертого порядка равно 218.
Трудно выполнимая задача, связанная с изображением всех 218
орграфов, все же была решена, и диаграммы этих орграфов можно
найти в приложении II в книге Харари [1], стр. 262—265.
Пусть dp (х) — перечисляющий многочлен для орграфов по-
порядка р, так что, например,
E.1.1),
Значения этих коэффициентов подтверждаются рис. 1.1.5.
Мы сейчас покажем, следуя Харари [И], как можно исполь
зовать теорему перечисления Пойа для нахождения dp (x).
Пусть X = {1, 2, ...,/?}, и пусть Х^1 обозначает все упоря
доченные пары различных элементов из X. Если Y — {0, 1}
то функции из XW в Y представляют помеченные орграфы порядк
р. Каждая функция / соответствует тому орграфу D (/) с множест
вом вершин X, в котором существует дуга, идущая из вершины
в вершину /, тогда и только тогда, когда / (i, /) = 1. Таким об
разом, две функции / и g представляют один и тот же орграф, есл
существует подстановка а множества X, такая, что из смежности
вершины i к вершине ;' в орграфе D (/) следует смежность вершины
о» к вершине а/ в орграфе D (g). Значит, орграфы D (/) и D (g)
изоморфны тогда и только тогда, когда для всех пар (i, j) £ XW
выполняется равенство
f(i, j) = g(ai, aj). E.1.2)
Это соотношение подсказывает мысль о введении следующей
унарной операции на группах подстановок. Если А — группа
подстановок с множеством объектов X, то редуцированная упоря-
упорядоченная парная группа группы А, обозначаемая А^, имеет в ка-
качестве множества объектов множество Xt2] и индуцируется груп-
группой А. То есть для всякой подстановки а из Л найдется подстанов-

f
5,1. ОРГРАФЫ
149
Ka а' из Л'21, такая, что образ любой пары (I, /) £ X'*1 при воз-
воздействии на нее подстановкой а' дается формулой
a'(i, /) = («*. <*/)■ : E.1-3)
Мы теперь можем вывести формулу для числа орграфов.
Теорема. Перечисляющий многочлен dp (х) для орграфов по-
порядка р дается следующим выражением:
где
тг
п.
i+x),
E.1.4)
E.1.5)
r
r<t
Доказательство. Уравнение E.1.4) является вариантом след-
следствия B.5.1) из теоремы перечисления Пойа. Мы покажем, что
редуцированная упорядоченная парная группа, порожденная
группой Sp, как раз и является требуемой группой конфигураций.
Две функции / и g, действующие из Х^ в {0, 1}, представляют
один и тот же орграф тогда и только тогда, когда существует под-
подстановка а в Sp, такая, что
= g(u'z)
E.1.6)
для каждой пары z из
Следовательно, орбиты степенной
sm
группы Е2 р соответствуют разным орграфам.
Перечисляющим рядом для фигур является ряд 1 + ж, ибо,
как и в случае графов, дуга (i, j) либо присутствует в орграфе,
либо нет. Таким образом, используя обычные определения B.4.4)
весов функций и орбит, убеждаемся, что вес орбиты группы £2 р
равен числу дуг в соответствующем орграфе. Это доказывает ра-
равенство E.1.4).
Теперь нашей целью является вывод формулы E.1.5) для цикло-
циклового индекса Z (Sp ), но сначала мы проиллюстрируем соответ-
соответствующий прием для случая р — 4, чтобы сделать ясным вывод
более общего циклового индекса. Каждая из подстановок
группы Si индуцирует некоторую подстановку из редуцированной
упорядоченной парной группы S^21. В табл. 5.1.1 приведены слагае-
слагаемые циклового индекса группы Sli\ индуцированные соответству-
соответствующими слагаемыми из Z E

150
ГЛ. 5. ОРГРАФЫ
Таблица 5.1.1
Слагаемое из Z (S«)
■г--* -} ••
ч
Индуцированное слага-
емое из Z (S.)
» S3
•S
Одно из этих слагаемых будет сейчас проиллюстрировано. На
рис. 5.1.1 упорядоченные пары указываются для краткости
следующим образом: A,2) = 12 и т. д.
Собирая все слагаемые, получаем
J-
E.1.7)
а поэтому
Z (S[2\ 1 + х) = dt (х) = 1 + х + 5а;2 + 13а;» + 27а;4 + 38ж» + 48а;6 +
+ x12. E.1.8)
" О О О
о
21
34
43
Рис. 5.1.1 Подстановка A) B) C4) и индуцируемая ею подстановка i
Мы указываем соответствие между слагаемыми цикловых ин-
индексов групп Sp и S$\ используя следующую запись (для опре-
определенности положили р = 4):
и т. д. Чтобы получить выражение для Z(Sp2]), нам нужно найти
недостающий член в правой части соотношения
*{•*£•..■ *£'->? E.1.9)
Точно так же, как при выводе выражения для Z (Sp2)), в слу-
случае, когда рассматривается более чем один цикл в одной и той же

6l. ОРГРАФЫ 151
подстановке а из Sp, существуют два различных вклада в соот-
соответствующее слагаемое из Z Eр21). Первый вклад вносится такими
парами элементов из X, в которых оба элемента принадлежат одному
и тому же циклу подстановки а; второй вклад дают пары элемен-
элементов, лежащих в двух различных циклах подстановки а (каждый
элемент принадлежит «своему» циклу).
Для нахождения первого из этих вкладов рассмотрим цикл
Zk длины к, содержащийся в подстановке а. В множестве XI2'
существует к (к — 1) пар, составленных из элементов, принадле-
принадлежащих циклу Z/,. Эти пары переставляются подстановкой а"
в циклах, длина которых равна к. Следовательно, подстановка
а" переставляет их в к — 1 циклах и длина каждого из этих
циклов равна к. Таким образом, если существует /* циклов длины
к, то пары элементов, лежащих в «общих» циклах, дают рклад
sik "*■ s(k~1)lk- E.1.Ю)
Далее рассмотрим два произвольных цикла подстановки а,
скажем zr и zt длины rut соответственно. В множестве Xt2l суще-
существует 2rt пар (г, /), в которых i переставляется циклом zr, а / —
циклом zt. Эти пары переставляются подстановкой а" в циклах,
длина которых равна [г, t]. Следовательно, подстановка а* пере-
переставляет их в 2 (г, t) циклах и длина каждого из этих циклов равна
[г, t]. Таким образом, вклад, вносимый парами различных циклов,
длина одного из которых равна г, а другого t фг, описывается
следующим соотношением:
s!/s\t-^ s^y>rU. E.1.11)
Наконец, вклад, вносимый парами циклов, имеющими одина-
одинаковую длину к, будет таким:
(lk\
Теперь правая часть соотношения E.1.9), а следовательно
и правая часть формулы E.1.5), получается путем перемножения
правых частей выражений E.1.10), E.1.11) и E.1.12) по всем
подходящим индексам.в
Формулы из доказанной теоремы были использованы для под-
подсчета числа dp орграфов порядка р ^ 8 (см. приложение I и
табл. 5.1.2). Эти результаты согласуются с теми, которые приве-
приведены в статье Обершельпа [1] и которые были найдены с помощью
тех же самых формул.
Петли в орграфах не допускаются, ибо орграфы определяются
как иррефлексивные отношения. Для подсчета числа р-вершин-
ных отношений, которые могут содержать петли, нам необходимо

152
ГЛ. 5. ОРГРАФЫ
расширить множество объектов группы S^ путем введения всех
упорядоченных пар из множества X X Х- Получаемая при этом
группа подстановок называется упорядоченной парной группой
группы Sp и обозначается через SP. Ее цикловой индекс полу-
получается видоизменением формулы E.1.5) для Z (Sp21): нужно умно-
о
о о
сОо
•О» <Оо
*■*<■
Рис. 5.1.2 Отношения на множестве из двух элементов.
I
жить каждое слагаемое на Ш/А. Тогда многочлен гр (а^,,перечисля-
(а^,,перечисляющий отношения, дается формулой ,■ ~rj ■
Г.';-"'l;\. E.1.13)
Из этого уравнения при р = 2 находим ' ч -
г2(х) = 1+2х + Ах2 + 2х3 + х\ ' " E.1.14)
Правильность коэффициентов многочлена г2 (х) проверяется по
рис. 5.1.2.
Орграф называется связным, если, игнорируя все ориентации
на его дугах, получаем связный мультиграф. В книге Харари,
Нормана и Картрайта [11 такие орграфы названы «слабо связными».
Связные орграфы перечисляются «на языке» всех орграфов с по-
помощью метода, идентичного методу, основанному на формуле
Таблица 5.1.2
Связные орграфы
р
1
2
3
4
5
6
7
8
dP
1
3
16
218
9 608
1540 944"
882 033 440
1 793 359 192 848
Р«Р
1
5
40
801
46 821
9185 102
6 163 297 995
14 339 791 693 249
ср
1
2
13
199
9 364
1 530 843
880 471142
1 792 473 955 306

6.2. ТУРНИРЫ
153
D.2.3) и использованному при перечислении связных графов.
Мы завершим наши рассмотрения замечанием, что если в формуле
D.2.6) заменить gp числом dp орграфов порядка р, то уравнение
D.2.9), включающее параметры ар, можно использовать для под-
подсчета числа связных орграфов. Результаты такого подсчета при
р sg 8 приводятся в табл. 5.1.2.
5.2. ТУРНИРЫ
Число помеченных турниров (см. рис. 1.1.6) равно числу по-
помеченных графов; для непомеченных турниров это совсем не так.
Все турниры с 2, 3 и 4 вершинами показаны на рис. 5.2.1. Первый
на этом рисунке турнир с тремя вершинами называется транзи-
Рис. 5.2.1 Наименьшие турниры.
тивной тройкой, а второй — циклической тройкой. Для конкрет-
конкретного всестороннего ознакомления с тематикой турниров можно
обратиться к превосходной монографии Муна [2].
Перечисление турниров осуществлено Дэвисом [1] (см. также
Мун 12], стр. 84).
Теорема. Число Т (р) турниров порядка р дается формулой
т(р)-7Т
р\
E.2.1)
еде звездочка у знака суммы указывает на то, что суммирование
ведется только по таким разбиениям (j), у которых Jk — O при
всех четных к и где
К п)и« -Z h
т, n-l k-l
E.2.2)
Доказательство. Сначала убедимся в правильности формулы
E.2.1). Как и в доказательстве теоремы, связанной с формулой

154 * . ГЛ. 5. ОРГРАФЫ
s[2]
E.1.4), замечаем, что орбиты степенной группы Е2 р соответст-
соответствуют орграфам порядка р. Ограничивая эту группу на множество
F функций /, представляющих турниры, а именно тех функций /,
для которых / (i, j) ф f (/, i), можем применить вариант B.3.9)
леммы Бернсайда. Тогда Т (р) может быть выражено через число
функций иэ множества F, которые неподвижны относительно
подстановок, принадлежащих той же самой степенной группе.
Таким образом, для каждой подстановки а из группы Sp мы ищем
число функций / из множества F, таких, что
/(*, 7') = /(ai, су) E.2.3)
для всех пар (t, j) £ XI2!. Функции, удовлетворяющие соотно-
соотношению E.2.3), являются как раз теми функциями, которые не-
неподвижны относительно подстановки, принадлежащей степенной
группе и индуцируемой подстановкой а. Допуская незначитель-
незначительную вольность речи, будем говорить, что эти функции являются
«неподвижными относительно а». Следовательно, если циклы под-
подстановки а определяют разбиение (;) числа р, то нам надо пока-
показать, что число функций из F, неподвижных относительно а,
равно 2*(".
Пусть снова а' — подстановка группы S\?], индуцируемая
подстановкой а. Определим обращение произвольного данного
цикла z\ содержащегося в некотором разложении подстановки а"
на непересекающиеся циклы: обращением цикла z" является цикл,
который переставляет все упорядоченные пары (г, ;), такие, что
пары (/, i) переставляются циклом z". Цикл z* подстановки а"
называется самообратным, если пара (г, ;) переставляется циклом
г* всякий раз, когда переставляется пара (/, {)•
Чтобы найти вклад, вносимый в t (j) подстановкой а, когда
циклы подстановки а рассматриваются индивидуально, положим,
что / представляет турнир, неподвижный относительно а, так что
выполняется соотношение E.2.3). Следовательно, функция /
на циклах подстановки а' постоянна.
Теперь мы дадим обоснование «использованию звездочки»
у знака суммы в формуле E.2.1). Если z* = A23 ... к) —
произвольный четный цикл подстановки а, то подстановка а"
имеет самообратный цикл z", а именно цикл, действующий и на
пару A, (к/2) + 1), и на пару ((А/2) + 1Д)- Но если / постоянна
на этом самообратном цикле z", то / не является турниром. Итак,
не существует турниров, неподвижных относительно а, если а
содержит некоторый четный цикл. Формула E.2.1) доказана.
Для завершения доказательства теоремы осталось получить
формулу E.2.2). Если Zk — нечетный цикл, то он индуцирует
А — 1 циклов на множестве пар, содержащихся в XW. Эти к — 1
циклов образуют (к — 1)/2 пар взаимно обратных циклов. Нэпом-

i 2. ТУРНИРЫ
155
что произвольный турнир /, неподвижный относительно а,
является константой на циклах подстановки а'. Следовательно,
в каждой из (А; — 1)/2 пар взаимно обратных циклов должны быть
выбраны только элементы одного цикла, чтобы получился турнир,
неподвижный относительно а. Но это значит, что вклад в t(j), вно-
вносимый всеми нечетными циклами подстановки а, равен 2 7* (^ —
— 1)/2, где суммирование ведется по всем нечетным к.
Теперь рассмотрим два цикла zm и zn подстановки а и такие
пары из множества XI2!, которые имеют по одной вершине в каж-
каждом из этих двух циклов. При вычислении циклового индекса
Z (SP ) мы видели, что два таких цикла индуцируют 2 [т, п)
циклов, состоящих из объектов (упорядоченных пар) множества
Х[21- Эти последние циклы образуют (т, п) пар взаимно обратных
циклов. В турнир, неподвижный относительно а, должны быть
включены только такие объекты из XW, которые порождают
в точности один цикл в каждой из (т, п) пар взаимно обратных
циклов. Значит, вклад в t (j), вносимый всеми парами циклов
zm и zn при т =5"^ п, равен 2 7m7n (m> п)- Вклад, вносимый парами
циклов, имеющих одну и ту же длину, равен
Сумми-
Суммируя эти три вклада, получаем формулу E.2.2) для t ()).щ
Значения для Т (р) при р ^ 12, взятые из книги Муна [2],
стр. 87, приведены в табл. 5.2-1.
Таблица 5.2.1
Число турниров
.р
1
2
. 3
4
5
6
7
8
9
10
И
12
1
1
2
4
12
56
456
6 880
191 536
9 733056
903 753 248
154108 311168
th'
.- Орграф называется сильно связным, или сильны*, если лю-
любая пара его вершин взаимно достижима с использованием орвен»

156
ГЛ. S. ОРГРАФЫ
тированных цепейг. Хорошо известно (см. Харари, Норман а
Картрайт [1 ], стр. 306), что турнир является сильным тогда а
только тогда, когда он гамильтонов, т. е. содержит остовньга
ориентированный цикл. Приведем (см. рис. 5.2.2.) все сильные
турниры с пятью вершинами, используя при их изображенаа
искусный прием, предложенный Муном [2], стр. 92: всякий раз,
Рис. 5.2.2 Сильные турниры пятого порядка.
когда дуга на диаграмме отсутствует, это означает, что дуга ори-
ориентирована в соответствии с направлением силы тяжести — из
верхней вершины в нижнюю.
Число сильных турниров просто выражается через число всех
турниров с помощью производящих функций (см. Мун [2], стр. 88).
Для доказательства этого факта требуется ввести несколько опре-
определений. Сильная компонента орграфа D представляет собой мак-
максимальный сильный подграф. Конденсация D* орграфа D имеет
в качестве своих вершин сильные компоненты орграфа D, а дуги
индуцируются дугами 2 орграфа D. Как отмечено в книге Харари,
Нормана и Картрайта [1], стр. 298, конденсация любого турнира
является транзитивным турниром, т. е. индуцирует на множестве
своих вершин линейный порядок.
Теорема. Пусть Т (х) и S (х) — производящие функции для
турниров и сильных турниров соответственно. Тогда
T(x)
i + T(x) •
E.2.4)
1 Другими словами, всякую вершину орграфа можно соединить выхо-
выходящей из нее ориентированной цепью с любой другой вершиной орграфа. —■
Пр им. перев.
2 Другими словами, дуги, соединяющие сильные компоненты орграфа,
«полностью переносятся» в конденсацию, — Прим. перев.

б з. ОРИЕНТАЦИИ ГРАФА \ 157
Доказательство. Чтобы получить S (х), обозначим через Тп (х)
производящую функцию для турниров, имеющих в точности п
сильных компонент. Тогда, в силу приведенных выше рассмотре-
рассмотрений, Тп{х) — Sn {х) и Т (х) = 2^п (х)> что доказывает соотноше-
соотношение E.2.4).и
5.3. ОРИЕНТАЦИИ ГРАФА
Ориентация графа G представляет собой приписывание стре-
стрелок всем ребрам графа G, т. е. упорядочение всех пар его смеж-
смежных вершин. Направленным графом называется орграф, в котором
никакая пара вершин не соединена симметричной парой, дуг.
Таким образом, всякая ориентация графа порождает направлен-
направленный граф. Каждый граф G обладает инвариантом о (G), предста-
представляющим собой число различных ориентации графа G. Легко
проверить, что о(С3) = 2, о(С^ = о(Съ) = 4 и о(С6) = 9.
О О « II
О О » |
Рис. 5.3.1 Ориентации цикла четвертого порядка.
Нашей целью здесь является развитие перечислительного метода
(см. Харари и Палмер [2]) для определения числа о (G) ориента-
ориентации данного графа G. Чтобы достичь этой цели, нам нужно только
обобщить некоторые рассмотрения из предыдущего параграфа.
Там мы нашли число Т (р) турниров порядка р, которое является
просто о (Кр) — числом ориентации полного графа.
Как и в случае графа Кр, формула для о (G) может быть полу-
получена путем применения леммы Бернсайда. Получающееся при этом
выражение можно упростить, используя специальный цикловой
индекс, зависящий от переменных двух типов. Положим, как
обычно, что группа Г (G) действует на множестве X = {1,2, . . -,р}-
Удобно определить орграф D (G), соответствующий графу G.
Вершины орграфа D (G) совпадают с вершинами графа G, а мно-
множество U дуг орграфа D (G) состоит из всех упорядоченных пар
(f, )), таких, что вершины i и ;' смежны в графе G. Таким образом,
ориентация графа G получается путем выбора в точности одной
дуги из каждой пары симметричных дуг, принадлежащих орграфу
D(G).
Редуцированная упорядоченная парная группа T(G)W дей-
действует на множестве всех упорядоченных пар (t, j), у которых i
и j принадлежат X, i ф j и вершины i и j являются смежными
в графе G. Нам, таким образом, требуется ограничение группы

158 - гл. 5. орграфы
подстановок Г (G)[21, именно группа Г (G)£21| U, которая действует
только на дугах из U. Цикловой индекс этой группы обозначим
через Z (Г (G)t2l\U). Чтобы различать между собой разные виды
встречающихся здесь циклов, удобно использовать переменные tk
для самообратных циклов и переменные s^ для пар взаимно обрат-
обратных циклов. Таким образом, это различие проявляется в самом
определении многочлена Z (Г (G)W\U; sk, tk). Заметим, что, как
и в случае турниров, переменные tk возникают только из четных
циклов длины к, содержащихся в автоморфизмах графа G. При-
Приводимая ниже теорема следует из ограниченной формы леммы
Бернсайда (см. соотношение B.3.9)).
Теорема. Число ориентации графа G дается формулой
o(G) = Z{T{G)W\U\ V2, 0). E.3.1)
Заметим, что радикал |/2 после подстановки исчезает, ибо
взаимно обратные циклы встречаются только попарно. Кроме
того, довольно странный перечисляющий ряд для фигур, целиком
состоящий из 0, служит вполне определенной цели: он указывает
на отсутствие симметричных пар дуг.
Мы можем только в принципе вычислить число о (G) для про-
произвольного графа G, потому что цикловой индекс, указанный
в формуле E.3.1), найти непросто. Однако, если G = Ср — цикл
порядка р, то можно получить точную формулу для соответству-
соответствующего циклового индекса. Так как Г (Ср) = Г\ (Ср) — Dp —
диэдральная группа, то мы можем видоизменить формулу B.2.11)
для Z (Dp), чтобы получить выражение для Z (Г (Cp)nX\U; sk,
tk). Учитывая тот факт, что переменные tk вносятся только обра-
обращениями, имеем
d\p
1 P-lj
~2st *2. если p — нечетное,
4 E.3.2)
-г-(S2 + Sz~2^)' если/? —четное.
Следовательно, мы можем написать
О, если р — нечетное,
Наш подход можно хакже приспособить к перечислению на-
направленных графов (см. Харари [6]), но этот результат будет
представлен как частный случай перечисления смешанных графов,
которое рассматривается в следующем параграфе.

6,4. СМЕШАННЫЕ ГРАФЫ 159
5.4. СМЕШАННЫЕ ГРАФЫ
Смешанный граф может содержать как неориентированные
ребра, так и ориентированные. Например, граф, изображенный
на рис 5.4.1, является смешанным графом с двумя неориентиро-
неориентированными и тремя ориентированными ребрами. Неориентированный
Рис. 5.4.1 Смешанный граф четвертого порядка.
граф можно трактовать как смешанный граф, не имеющий ориен-
ориентированных ребер. Далее орграф можно рассматривать как сме-
смешанный граф, заменяя для этого каждую симметричную пару
ориентированных ребер неориентированным ребром.
Нашей целью является получение формулы, перечисляющей
смешанные графы с р вершинами в соответствии с числом неори-
неориентированных и ориентированных ребер в них (см. Харари и
Палмер [7]).
О О Q
о-—•—о а » о а—»—чз
Рис. 5.4.2 16 смешанных графов третьего порядка.
Пусть mpqr — число смешанных графов с р вершинами, q ориен-
ориентированными ребрами и г неориентированными ребрами. Тогда
многочлен тр (х, у), перечисляющий смешанные графы с р вер-
вершинами в соответствии как с числом неориентированных, так
и числом ориентированных ребер, определяется формулой
Я, г
где (J-f^lol- Из рис. 5.4.2 следует, что при р = 3 эта фор-
формула имеет вид
тз (*, У) = 1 -г-* + За;2 + 2х* + j/ + 2xj/ + 3x2j/ + у2 + жг/2 + г/3. E.4.2)

160 ГЛ. 5. ОРГРАФу
Чтобы вывести формулу для тр (х, у), мы воспользуемся
слабо модифицированной формой теоремы Пойа. В этой модифика-
модификации оба вида перечисляющих рядов для фигур применяются
совместно со специальным цикловым индексом, зависящим от
переменных двух типов и рассмотренным в предыдущем параграфе.
Используя обозначения, введенные в § 5.3, получаем равенство
E.4.3)
Таким образом, Z (Sp2]; Sk, £*) является цикловым индексом
редуцированной упорядоченной парной группы Sp21, в котором
переменные sk используются для пар взаимно обратных циклов,
а переменные tk — для самообратных циклов. Мы увидим, что,
подставляя в это выражение вместо каждой переменной sk функ-
функцию A + 2xk -f ykI/2, а вместо каждой переменной tk функцию
1 + Ук/2, получим многочлен тр (х, у).
Теорема. Перечисляющий многочлен для смешанных графов
порядка р дается соотношением
mp{x, V) = Z{Sp, A + 2ж + уУ>, l + yl/'), E.4.4)
где - .. Ji
■.v и
■ ;"- -:'' W
нечетное
(Ik)
V» / П
2k
S.
k * r<w
, ()
X П (s*-«M/*Ib' V» / П sr2(r-f>/rV E 4S
В качестве примера приведем некоторые детали для случая
3. Сначала получаем формулу для циклового индекса:
; sk, tk) = A/3 !) (s\ + 3sltt + 2s32). E.4.6)
Подставляя перечисляющие ряды для фигур: A-f 2а;+г/)'/1
щ'1-j-y^1, приходим к выражению
Д щ(х, y)=~((i + 2x + yK + 3(l+y)(i+2x2 + y2) +
+ 2(i+2z» + y% E.4.7)
которое полностью согласуется с формулой E.4.2), а соответству-
соответствующие ему смешанные гр^фы показаны на рис. 5.4.2.
Соотношение E.4.5) не требует комментариев, кроме замечания
о том, что оно получается из формулы E.1.5) с помощью ее моди-
модификации в соответствии с той частью доказательства формулы

5,4. СМЕШАННЫЕ ГРАФЫ 1б1
E.2.1), где показывается, что каждый четный цикл подстановки
из Sp индуцирует самообратный цикл.
Здесь представлен краткий набросок доказательства формулы
SI2]
E.4.4). Как обычно, степенная группа Е2 р действует на функциях
из множества Yxl21. Так как каждая такая функция / предста-
представляет орграф, скажем, с q ориентированными ребрами и г сим-
симметричными парами дуг, то / можно также трактовать как сме-
смешанный граф с q ориентированными и г неориентированными реб-
ребрами. Очевидно, что любые две функции из множества Yxnl
принадлежат одной и той же орбите степенной группы тогда и
только тогда, когда соответствующие им смешанные графы изо-
изоморфны. Наконец, функциям обычным образом приписываются
веса и, применяя взвешенный вариант леммы Бернсайда (см.
формулу B.3.10)), получают соотношение E.4.4).
Идея использования выражения 1 -\- 2х + У состоит в сле-
следующем: слагаемое 1 соответствует парам несмежных вершин,
в то время как 2х указывает на две возможные ориентации, а у —
на неориентированное ребро. Радикал в выражении A + 2х +
4- уI/2 исчезает в тр (х, у), потому что каждая переменная sk
встречается только в четной степени, ибо взаимно обратные циклы
обязательно появляются парами. Аналогично двучлен 1 + У
отражает, как обычно, отсутствие ребра и наличие неориентиро-
неориентированного ребра (ориентированные ребра просто запрещены для
самообратных циклов). Радикал в 1 4- У1/2 также исчезает в тр (х, у),
ибо, как показано в формуле E.4.5), в единственном ее произ-
произведении, содержащем tk, индексы к — четные. Это в свою очередь
справедливо потому, что каждый самообратный цикл имеет чет-
четную длину.и
Перечисляющие многочлены gp (x) и dp (x) для графов и оргра-
орграфов были уже выведены раньше. Многочлен ор (х) для направлен-
направленных графов найден Харари [6]. Заметим, что каждый из этих
многочленов легко получается из тр (х, у), который является,
таким образом, одновременным обобщением всех трех указанных
перечислительных формул:
dp(x) = mp(x, х% ор(х) = тр(х,0), gp{y)--=mp @, у). E.4.8)
Для р = 3 находим, используя соотношение E.4.7):
ds(x) = т3(х, а;2) =
* о3(х) = т3(х, 0) =
gз (У) = гп3 @, у) = 1 + у + у* + у\ E.4.9)
Правильность этих выражений легко установить с помощью
рис. 5.4.2.
6 Заказ 443

162
ГЛ. 6. ОРГРАФ!
Полный орграф имеет для каждой пары вершин либо ориенти-
ориентированное ребро, либо симметричную пару ребер, соединяющих
эти вершины. Орграф на рис. 5.4.3 является полным ориентиро-
ориентированным графом с пятью вершинами, тремя парами симметричных
дуг и семью ориентированными ребрами.
■. я-.•/<■
Рис. 5.4.3 Полный орграф пятого порядка.
Пусть cpqr — число полных орграфов с р вершинами, имеющих \
в точности q ориентированных ребер и г симметричных пар. Много-;
член ср (х, у), который перечисляет полные орграфы с р вершинами
Рис. 5.4.4 Полные орграфы третьего порядка.
в соответствии и с числом ориентированных ребер, и с числом
симметричных пар, определяется формулой
E.4.10)
где
Из рис. 5.4.4 следует, что при р = 3 формула имеет вид|
с3 (х, у) = 2х3 + Зх*у + ху2 + у3. f
Перечислительная формула для ср (х, у) легко получается \
путем модификации формулы для смешанных графов. Число 1 I
в каждом из двух перечисляющих рядов для фигур — A + 2х + '1
+ уI12 и 1 + у11г — Отражает возможность отсутствия ребра, j
соединяющего пару вершин. Но в полном орграфе всегда суще- |
ствует либо ориентированное ребро, либо симметричная пара, |

УПРАЖНЕНИЯ
163
соединяющие пару вершин. Поэтому подходящими перечисля-
перечисляющими рядами для фигур являются ряды Bх + г/I/2 и г/1/2.
Следствие. Перечисляющий многочлен для полных орграфов
с р вершинами дается формулой
ср(х, y) = ZE[,21; {2х + у)Ч; у1/'). E.4.11)
Из этого следствия немедленно выводим, что число турниров
с р вершинами равно
Г(р) = ерA, 0). E.4.12)
Используя E.4.12) и E.4.5), с помощью несложных преобразова-
преобразований получаем в явной форме формулы E.2.1) и E.2.2).
Общее число ср полных орграфов, если не фиксировать число
ориентированных ребер и симметричных пар, есть
ср = срA, 1). E.4.13)
Например, рис. 5.4.4 показывает, что с3 = 7.
Используя формулу E.4.5), получаем следующее выражение"
ДЛЯ Ср.
Теорема. Число полных орграфов порядка р есть •
cp-JT
E.4.14)
где
Первые пять значений величины ср таковы:
р
Ср
1
1
2
2
3
7
4
42
5
582
УПРАЖНЕНИЯ
5.1. Число полных орграфов порядка р равно числу направленных
графов порядка р.
5.2. Орграфы, у которых полустепень исхода любой вершины
равна 2.
(К. П. Лоэс)
6*

164
ГЛ. 5. ОРГРАФЫ
5.3. Вершинно-симметрические орграфы порядка р, где р ~
простое число. (Указание: используйте метод Тернера [1] для
графов.)
5.4. Число турниров порядка р ^ 5, в которых допускается точно
по одному гамильтонову циклу, равно
р_Д_4\ /А—1
)(
где m = min(A —1, р — к — 3). (Дуглас [1])
5.5. Написать в явном виде формулу для циклового индекса
Z (S2P) и использовать ее для получения многочлена, перечисля
ющего 4-местные отношения.
■■■ -Л

Глава в
Удачные обозначения обладают
утонченностью и будят мысль, порой
делая это, кажется, почти так же, как
искусный учитель.
Бертран Рассел1
ПЕРЕЧИСЛЕНИЕ СТЕПЕННОЙ
ГРУППЫ
Если с (х) — ряд, перечисляющий элементы множества У, и
А — группа подстановок с множеством объектов X, то, как мы
видели в гл. 2, теорема Пойа дает метод для выражения ряда С (х),
перечисляющего взвешенные орбиты в множестве Yx степенной
группы ЕА, в терминах Z (А) и с (х). Существует обширный класс
задач, для решения которых весьма важно уметь перечислять
орбиты в множестве Yx степенной группы ВА, когда группа В
не является единичной. Метод, позволяющий достичь этого обоб-
обобщения теоремы Пойа, был впервые найден де Брёйном [2]. В на-
настоящей главе мы обсудим другой, более естественный метод
(см. Харари и Палмер [4]), который упрощает вычисление по-
посредством устранения ненужных дифференциальных операторов
и путем явного описания группы подстановок, действующей на
множестве функций (именно, степенной группы). По этой причине
упомянутый результат де Брёйна мы в дальнейшем предпочитаем
называть теоремой перечисления степенной группы. В качестве
приложений этой теоремы приводятся решения задач перечисления
самодополнительных графов и орграфов, графов с раскрашенными
ребрами, конечных автоматов и самообратных орграфов.
6.1. ТЕОРЕМА ПЕРЕЧИСЛЕНИЯ СТЕПЕННОЙ ГРУППЫ
Рассмотрим степенную группу ВА с множеством объектов Yx,
где X = {хг, х2, . . ., хт) и Y = {уъ уг, . . ., уп}- Начнем с на-
нахождения формулы для числа орбит группы ВА. Чтобы получить
желаемый результат, мы, используя только определение цикло-
„вого индекса, напишем сначала следующую формулу:
\в\
Л<7)
F.1.1)
уев
А к
1 Рассел, Бертран A872—1970) — английский философ и математик.

166 ГЛ. 6. ПЕРЕЧИСЛЕНИЕ СТЕПЕННОЙ ГРУППЫ
Для каждой подстановки у = (а; Р) из ВА выражение jk (у)
через числа % (а) и % (Р) дается двумя нижеследующими соотно-
соотношениями. Сперва покажем, что
т !
= П B */,({}))'*(О), | FЛ.2)
где /2 sh Ф)*\ к — 1 всякий раз, когда Д(а) = 0.
\s\k )
Затем, при £>1 мы воспользуемся обращением Мёбиуса и
получим формулу
7, (а; р) = A/0 2 ц (*/s) h («s; Ps). F.1.3)
I'
Для обоснования соотношений F.1.2) и F.1.3) рассмотрим
произвольную подстановку у = (а; Р) из степенной группы ВА.
Пусть Zk— цикл длины к в разложении подстановки а на непере-
непересекающиеся циклы. Пусть. S — подмножество тех к элементов
из X, которые переставляются циклом Z/,. Тогда (г^; Р) есть под-
подстановка, действующая на множестве Ys. Определим с^ (Р) как
число функций из Ys, неподвижных относительно подстановки
(zk; P). Тогда ясно, что
F.1.4)
где (с*(Р)/*(а) = 1 всякий раз, когда /*(а) = 0.
Все значения функции /, неподвижной относительно под-
подстановки (г*,; P)v должны принадлежать множеству таких элемен-
элементов, которые переставляются одним отдельным циклом zs длины s,
содержащимся в разложении подстановки р на непересекающиеся
циклы. Положим для такой функции, что f (х) — у при некотором
х из zk и некотором у из zs. Тогда (z<>; P)s / (х) = Ps/ (z\x) = / (zlx).
Но так как / неподвижна относительно {zk; P), то она неподвижна
и относительно (z*; P)s. Следовательно, (zk; P)s / (х) --= f (x) и, зна-
значит, у = / D^)- Аналогично, для всех i имеем j/ = / (z"a;). Далее,
/ (zkx) = Р-1г/, а поэтому уравнения, связывающие между собой х
и у, справедливы также для ZkX и P~V Теперь мы сосредоточим
свое внимание на цикле zs, содержащем элемент у, и рассмотрим
часть (Zk\ zs) подстановки (z^; P). Дальнейшее использование
функции / предполагает некоторую совместимость длин циклов zk
и zs, что, как легко видеть, сводится к выполнимости соотношения:
s\k. Так как у — произвольный элемент цикла zs, то для каждого
цикла zs существуют в точности s таких функций. Таким образом,

5
8.1. ТЕОРЕМА ПЕРЕЧИСЛЕНИЯ СТЕПЕННОЙ ГРУППЫ 167
Ck (Р) = 2sJ's (Р) п> подставляя это выражение в формулу F.1.4),
и*
получаем F.1.2).
Заметим теперь, что если вклад подстановки а в цикловой
т
индекс Z{A) равен П s/*(a), то вклад подстановки а' есть
ki
Так как (а; р*)* = (а*; Р*), то, используя F.1.5), получаем
равенство
h(a'; p') = 2(*. t)jk(a; p), F.1.6)
где суммирование ведется по всем к, таким, что & = (&, £),
т. е. по всем делителям к числа t. Таким образом,
Ыа<; р') = 2 */*(«; Р) F-1.7)
k\t
и обращение Мёбиуса дает соотношение F.1.3).
Нижеследующая теорема используется так часто, что удобно
называть ее короче: ТПСГ (по начальным буквам слов, входящих
в название теоремы). Эта теорема дает возможность находить
число орбит степенной группы ВА, если даны цикловые индексы
Z (А) и Z (В). Ее доказательство можно получить, либо применяя
лемму Бернсайда в форме B.3.3) к формуле F.1.2), либо, как
у Харари и Палмера [4], используя Z (ВА) совместно с теоремой
Пойа в форме B.4.6). Мы не будем вдаваться здесь в детали, ибо
приводимая сейчас теорема представляет собой константную
форму ТПСГ, а ее обобщение — ТПСГ в форме степенного ряда —
дается в дальнейшем.
Теорема (теорема перечисления степенной группы, констант-
константная форма). Число орбит, состоящих из функций множества Yx
и определяемых степенной группой ВА, дается соотношением
S ад d(P), • • ., cm(P))» F.1.8)
рев
еде
с*(Р) = 2»/.(Р). F-1.9)
si*
Мы хотим подчеркнуть, что константная форма ТПСГ равно-
сильна применению леммы Бернсайда к степенной группе.
Для иллюстрации этой теоремы положим в F.1.8) А = D4 —
диэдральная группа четвертой степени, и В = 5а. Получающийся

168
ГЛ. 6. ПЕРЕЧИСЛЕНИЕ СТЕПЕННОЙ ГРУППЫ
при этом результат можно истолковать разнообразными способами,
но использование ожерелий приведет, по-видимому, к наилуч-
наилучшему пониманию. Итак, указанная подстановка групп D4 и S2
в F.1.8) дает число ожерелий, содержащих точно четыре бусинки
двух взаимозаменяемых цветов. Из B.4.13) имеем
= -i (s* + 3s|
; Если подстановка P из группы S2 является тождественной, то
Из F.1.9) получаем ск (Р) = 2 при всех к. Если Р — транспозиция,
Рис. 6.1.1 Четырехбусинные ожерелья с двумя взаимозаменяемыми цветами,
то Ck (P) есть либо 0, либо 2 в соответствии с тем, нечетно или
четно к. Используя F.1.8), имеем
, N(S?') = ±{Z{D4; 2, 2, 2, 2) + Z(D4; 0, 2, 0, 2)}. F.1.10)
Сразу находим, что Z (Z>4; 2, 2, 2, 2) = 6, a Z (ZL; 0, 2, 0, 2) =
= 2; следовательно, в силу F.1.10), число орбит группы S%'
равно 4. Это действительно так, ибо существует только одно
ожерелье, в котором все четыре бусинки с взаимозаменяемыми
цветами имеют одинаковый цвет; существует лишь одно ожерелье,
в котором в точности три бусинки имеют один и тот же цвет, и
существуют два ожерелья, в которых точно две бусинки имеют
одинаковый цвет (см. рис. 6.1.1). Число таких классов ожерелий
с п бусинками п'т цветами равно просто числу орбит группы Smn.
6.2. САМОДОПОЛНИТЕЛЬНЫЕ ГРАФЫ
Теперь воспользуемся константной формой ТПСГ для нахо-
нахождения числа самодополнительных графов с р вершинами. Допол-
Дополнение графа G, обозначаемое через G, имеет те же самые вершины,
что и граф G, и две вершины смежны в G тогда и только тогда,
когда они не являются смежными в G. Граф G называется само-
дополнителъным, если G и G изоморфны. Напомним (см. Ха-
рари [1], стр. 39), что число вершин р в самодополнительном
графе G сравнимо по mod4 либо с 0, либо с 1, так как число ребер
1 (Р'
в графе G должно быть равно
и является целым неотрица-
неотрицательным числом. Кроме тривиального графа, в число трех наи-

6.2. САМОДОПОЛНИТЕЛЬНЫЕ ГРАФЫ 169
меньших самодополнительных графов включаются 4-вершинная
простая цепь и 5-вершинный простой цикл.
Рид [6] показал, как можно подсчитать число самодополни-
самодополнительных графов, первым применив теорему де Брёйна [2] к под-
подсчету графов с точностью до их взаимной дополнительности. Чтобы
описать метод Рида, будем называть два графа эквивалентными
относительно дополнительности, если они изоморфны или один
из них изоморфен дополнению другого. Выразим теперь эту
эквивалентность на языке степенной группы.
Пусть парная группа 5р2) действует на множестве ХB>, со-
состоящем из всех 2-подмножеств множества X = A, 2, . . ., р),
и пусть Y — {0, 1} будет множеством объектов группы Sг. Каж-
Каждая функция /, отображающая ХB) в Y, представляет граф G,
у которого множеством вершин является множество X и вер-
вершины i и j смежны лишь тогда, когда /({г, /}) = 1. Таким образом,
элементы 0 и 1 из множества Y используются для указания соот-
соответственно на существование или отсутствие ребра в графе. Рас-
Рассмотрим степенную группу ВА, у которой А = 5(р2) и В = S21
Ясно, что графы, представимые двумя функциями, эквивалентны
относительно дополнительности тогда и только тогда, когда эти
две функции принадлежат одной и той же орбите рассматриваемой
степенной группы ВА. Поэтому если подстановка (а; @) A)) из
этой группы преобразует функцию / в функцию g, то / и g пред-
представляют изоморфные графы. А если / преобразуется в g под-
подстановкой (а; @, 1)), то две функции представляют взаимно допол-
дополнительные графы. Следовательно, число ар /?-вершииных графов,
подсчитываемых с точностью до их взаимной дополнительности,
равно числу орбит указанной выше степенной группы. Поэтому
мы можем применить константную форму ТПСГ, полагая А =
= Sp2) и В = S2- Рассмотрим две подстановки @) A) и @1) из S 2.
Если р = @) A), то /i (Р) = 2 и /s (Р) = 0 при s > 1; значит,
ch (Р) = 2 для всех к. Для р = @1) имеем /2 (Р) = 1 и /s (P) = 0
при s Ф 2; следовательно, ck (Р) = 2 для четных к и с* (Р) = 0
для нечетных к. Таким образом, в силу формулы F.1.9), число
р-вершинных графов, подсчитываемых с точностью до их взаимной
дополнительности, равно
ap = ±-\Z{sf- 2, 2, . . .) + ZD2); 0, 2, 0, 2, . . .)}. F.2.1)
Затем Рид заметил, что 1ар есть число р-вершинных графов,
если каждый самодополнительный граф считать дважды, а не-
самодополнительный — только один раз. Отсюда следует, что
число самодополнительных графов удовлетворяет соотношению
gp = 2ap-gp, F.2.2)

170 ГЛ. 6. ПЕРЕЧИСЛЕНИЕ СТЕПЕННОЙ ГРУППЫ:;
где gp, как и в соотношении D.2.1), есть число графов с р верши-s
нами. Из результата Пойа (см. формулу D.1.8)) нам известно,?
что gp = Z Eр2); 2, 2, . . .). Подставляя это выражение в F.2.2),?
находим формулу для gp, которая приводится в следующей тео-']
реме.
Теорема. Число gp самодополнителъных графов с р вершинами\
равно
£, = Z(S<?>; 0, 2, 0, 2, ...)• F.2.3)!
Так как gp j> 0 только при р = 0 (mod4) или р = 1 (mod4), то ■
в табл. 6.2.1, взятой из статьи Рида [6], приводятся значения gp ']
лишь для таких р. '
Таблица 6.2,1 ■
Число самодополнительных графов
р
4
1
5
2
8
10
9
36
12
720
13
5 600
16
703 760
17
11220 000
Формула F.2.3) в указанных двух случаях может быть запи-
записана так:
где сумма берется по всем разбиениям (/) числа п и
е У) = 2 £/*(*/*-!)+ 4 2 (r-9/r/f. F.2.6)
k
-l
Дополнение D орграфа D имеет те же самые вершины, что
и орграф D, и вершина к смежна к v в орграфе Z) тогда и только
тогда, когда и не является смежной к v в орграфе D. Число dp
самодополнительных орграфов можно найти с помощью приема,
аналогичного описанному выше для случая графов.

6.3. ВЗВЕШЕННЫЕ ФУНКЦИЙ i71
Теорема. Число йр самодополнителъных орграфов с р вершинами
дается формулой
dp = Z(S[p2\ О, 2, 0, 2, ...)• F.2.7)
Рассматривая число d2n орграфов четного порядка, получаем,
следуя Риду, любопытный результат:
4, = ^. F.2.8)
Однако еще не найдено пока естественного взаимно однознач-
однозначного соответствия между этими самодополнительными графами
и орграфами. Таким образом, d4, de и ds можно найти, используя
данные для р = 8, 12 и 16, помещенные в табл. 6.2.1. Эти и другие
наименьшие значения величины dp показаны в табл. 6.2.2.
Таблица 6.2.2
p
dp
2 i
1
Число
3
4
само дополнительных орграфов
4
10
5
136
6 7
720 44 224
8
703 760
Формула F.2.7) в случае нечетного индекса имеет вид
F.2.9)
где сумма, как и прежде, берется по всем разбиениям числа п.
6.3. ВЗВЕШЕННЫЕ ФУНКЦИИ
Существует много задач перечисления, в которых функциям
назначаются полные веса так, что все функции одной и той же
орбиты степенной группы имеют одинаковый вес. Мы попытаемся
выразить необходимый результат с помощью производящей
функции
C{x) = C0-\-CiX-\-C^ + . . ., F.3.1)
в которой Ct есть число орбит веса i.
Рассмотрим теперь степенную группу ВА, действующую на
множестве Yx; здесь множества А, X и В — конечные, a Y может
быть счетным (чтобы иметь возможность брать в качестве весов
любые целые неотрицательные числа). Пусть w — функция,
отображающая множество Y в множество {0, 1, 2, . . .}. Как

—...итш1ш. •■■ииюш.и. '- " """"■■ ' **—" "■""■■"" Щ
172 ГЛ, 6. ПЕРЕЧИСЛЕНИЕ СТЕПЕННОЙ ГРУППЫ |
i
обычно, w называется весовой функцией и для каждой функции /
из Yx мы определяем вес функции/, обозначаемый w {/), с помощью
соотношения
Так как по предположению множество X — конечное, то
сумма в формуле F.3.2) определена. Если для каждой орбиты
группы ВА все функции, принадлежащие этой орбите, имеют
одинаковый вес, то мы можем определить вес орбиты, положив его
равным весу произвольной функции этой орбиты. Кроме того,
если для каждого г = 0, 1, 2, ... число элементов множества Y,
имеющих вес i, — конечно, то мы можем поставить вопрос о числе
орбит произвольного фиксированного веса. Итак, мы рассматри-
рассматриваем две функции как «одинаковые» тогда и только тогда, когда
они принадлежат одной и той же орбите. Пусть Си — число раз-
различных функций веса к, определяемых заданной степенной груп-
группой. Тогда нахождение ряда С (х), указанного в F.3.1), обеспе-
обеспечивает получение числа орбит данного веса.
Попытаемся теперь сформулировать условия, которые гаран-
гарантировали бы равенство весов у функций, принадлежащих одной
и той же орбите группы ВА. Для этого обозначим через Yt =
— w'1 (i) множество всех элементов на У, имеющих вес i. Мы
видим, что для того, чтобы число функций произвольного конкрет-
конкретного веса было конечно, необходимо, чтобы каждое множество Yt .
было конечным. Через В (Yt) обозначим то подмножество мно-
множества Y, которое состоит из всех объектов р (у), где р £ В,
у £ Yt. Требуемое условие можно теперь сформулировать следу-
следующим образом.
Лемма. Все функции из одной и той же орбиты степенной
группы ВА имеют равные веса тогда и только тогда, когда В (Y{) —
— Y( для каждого i = 0, 1, 2, ... .
Доказательство. Для доказательства достаточности предполо-
предположим, что / и g принадлежат одной и той же орбите группы ВА.
Тогда для некоторой подстановки (а; |3) из ВА имеем равенство
(а; Р) / = g, так что Р/ (ах) — g (х) для всех х из X. Заметим, что
В (Yt) — Yi влечет соотношение w (|3/ (ах)) = w (/ (ах)). Следо-
Следовательно,
"> (8) = 2 w (р/ (си:)) = 2 w (/ (х)) = w (/).
ех ех
Чтобы установить необходимость, предположим, что суще-
существуют элемент у из Y и'подстановка р* из В, такие, что w (у) Ф
=ф w (р*г/). Пусть fug — функции из Yx, определяемые соотно-
соотношениями / (х) — у и g (х) = р# для всех х из X. Тогда / и g при

6.3. ВЗВЕШЕННЫЕ ФУНКЦИИ 173
надлежат одной и той же орбите группы ВА и в то же время w (/) Ф
ф и> (#)•■
Начиная с этого момента, мы предполагаем, что условие,
фигурирующее в лемме, выполняется, а именно, что В (Yt) = Yt
для всякого i — О, 1, 2, .... В этом случае каждая подстановка Р
из В может быть записана в виде произведения
Р = Прг, F.3.3)
где для каждого у из Y имеем р (у) = f>t (у), если у £ Yt.
Чтобы получить производящую функцию С (х), нам теперь
нужно только видоизменить переменные ck (P), встречающиеся
в соотношении F.1.8) из ТПСГ. Пусть у = (а; Р) — произвольная
подстановка степенной группы ВА. Предположим, что z& — не-
некоторый цикл длины к из разложения подстановки а на непересе-
непересекающиеся циклы. Пусть снова S обозначает множество всех
элементов из X, переставляемых циклом z*. Для каждого i = О,
1,2,... определяем с* (Р) как число функций /из Ys, неподвиж-
неподвижных относительно подстановки (z^; P) и удовлетворяющих соот-
соотношению _
Для удобства введем производящую функцию
*) = 2с*(Р)*Ч F.3.5)
Заметим, что с& (р, 1) = ck (P), определенному формулой
F.1.9). Требуемая производящая функция С (х) дается соотно-
соотношением
С(х) = \В\-ь 2 2(A; Cl(p, *), с2(Р, *), • • ., ст(Р, х)). F.3.6)
рев
Используя прием, аналогичный примененному при выводе
формулы F.1.2) для /х (а; Р), получаем
F.3.7)
2t)(P,))«, F.3.8)
Сз(Р, ^«^^(Р^+З/аф,))»»' F.3.9)
*к в общем случае
' F-3-10)
' Собирад вместе эти замечания, получаем следующий результат;

174 ГЛ. в. ПЕРЕЧИСЛЕНИЕ СТЕПЕННОЙ ГРУГ
Теорема (теорема перечисления степенной группы, форма
степенного ряда.) Ряд С (х), перечисляющий в соответствии с ве-
весами классы эквивалентных функций, причем эквивалентность
определяется степенной группой ВЛ, имеет вид
C(x) = \B\-i 2 Z(A; Cl(P, х), с,(р, х), . . ., стф, *)), F.3.11)
Рев
где
)*'. F-3.12)
Н2 B
i \s|fc
,(
s|fc
По аналогии с замечанием, приведенным после формулировки
константной формы ТПСГ, обратим внимание на то, что форма
степенного ряда ТПСГ включает в себя как существенную часть
приложение теоремы Пойа к цикловому индексу степенной группы.
Теорема Пойа немедленно получается из только что сформу-
сформулированной теоремы, если в качестве В взять единичную группу,
действующую на множестве Y. В этом случае В состоит из одной
тождественной подстановки р\ действующей на Y; поэтому Д (р\) =
= |F,-| для каждого i, a /s(p"i) = 0 при всех s=^l. Таким образом,
2 sis(f>i) — \Yi\ Для любого i и скф, х) = ^\Уг\хн Для каждого
s\k i
к = \, 2, . . ., т. Следовательно, подставляя c(xk) вместо скф, х),
имеем
C(x) = Z(A; c(x), с{х% . . ., с (я™)). F.3.13)
Как показано Харари и Палмером [4], разница между выраже-
выражением для С (х) в ТПСГ (в форме степенного ряда) и выражением,
включающим частные производные и приведенным в утверждении
де Брёйна, относящемся к тому же самому результату, является
чисто формальной. Это можно обосновать естественным изменением
обозначений и несложными алгебраическими преобразованиями
(см. упражнение 6.15).
Для иллюстрации теоремы вернемся к задаче об ожерельях,
рассмотренной уже в §6.1. Пусть ZL действует на X = A,2, 3, 4},
и предположим, что Y = A, 2, 3} и w A) = 0, w B) = w C) = 1.
Группа В будет состоять из подстановок A) B) C) и A) B3).
Тогда для получения ряда С (х) можно применить ТПСГ в форме
степенного ряда; при этом коэффициент, стоящий при хк, можно
толковать как число четырехбусинных ожерелий, в которых
4 — к бусинок имеют цвет 1, а А; бусинок имеют взаимозаменяемые
цвета 2 и 3.
Чтобы иметь возможность применить теорему, рассмотрим
сначала подстановку р1 = A) B) C); тогда ск (Р, х) = 1 + 2xh
для каждого к. Если же р1 = A) B3), то ск (р\ х) — 1 в случае

6,4. ГРАФЫ С РАСКРАШЕННЫМИ РЕБРАМИ
175
нечетного к и ck (р1, х) — 1 + 2хк в случае четного Тс. Использо-
Использование формулы F.3.11) дает
Подстановка соответствующих выражений в Z (D4) дает много-
многочлен
С (х) = 1 + х + 4г2 + Зх3 + 4а;4.
Рассматривая рис. 6.3.1, убеждаемся в том, что коэффициент
при х3 действительно равен 3; числа 2 и 3 поставлены около вер-
г
2
3
Рис. 6.3.1 Ожерелья с одним фиксированным цветом и двумя взаимозаменя-
взаимозаменяемыми цветами.
шин, имеющих взаимозаменяемые цвета, а 1 стоит у вершины
с фиксированным цветом.
Заметим, что коэффициент при xi в приведенном выше много-
многочлену равен числу четырехбусинных ожерелий с двумя взаимо-
взаимозаменяемыми цветами. Мы уже знаем из рис. 6.1.1, что это число
равно 4.
Теорему перечисления степенной группы легко приспособить
к решению таких задач, в которых область значений весовой функ-
функции принадлежит произвольному коммутативному кольцу, содер-
содержащему множество всех рациональных чисел. Однако нельзя
сказать, что интуитивно интересные задачи такого уровня общ-
общности существуют в изобилии.
6/*. ГРАФЫ С РАСКРАШЕННЫМИ РЕБРАМИ
Рид [7] получил производящую функцию, перечисляющую
р-вершинные графы, у которых ребра раскрашиваются с исполь-
использованием т взаимозаменяемых цветов. ТПСГ в форме степенного
ряда обеспечивает нам простой подход к задаче нахождения этой
функции.
Пусть А будет парной группой Sp2) с множеством объектов ХB>.
Пусть Y = @, 1, . . ., т}, и рассмотрим симметрическую группу
£т+ц действующую на Y. В качестве В мы берем подгруппу
группы Sm+1, которая оставляет неподвижным элемент 0 из
множества Y, так что Z (В) = SyZ {Sm). Далее, мы определяем
весовую функцию w, отображающую У в множество @,1}:

176
ГЛ. 6. ПЕРЕЧИСЛЕНИЕ СТЕПЕННОЙ ГРУППЫ
w (г/)= 0 тогда и только тогда, когда у = 0. В этом случае каждая
функция /, отображающая ХB> в Y, представляет граф с f'1 (i)
ребрами «цвета г» при i = 1, . . ., т. Кроме того, вес w (/), опре-
определенный в соответствии с формулой F.3.2), есть число ребер
в графе, представимом функцией /. Отсюда следует, что произво-
производящая функция N™ (х), которую мы ищем, получается с помощью
применения соотношения F.3.11) к нашей степенной группе Вл.
Рис. 6.4.\ Графы с ребрами, окрашенными во взаимозаменяемые цвета.
Для иллюстрации приведем некоторые детали в случае т = 3.
В соответствии с данными выше обозначениями имеем Yo = {0}
и Yx = {1, 2, 3}. Для каждой подстановки |3 из В мы должны
вычислить Ck (P, х), используя формулу F.3.10). Напомним, что
для i = 0, 1 коэффициент при xki в ck ф, х) равен 2S/S (P,)- Суще-
ствуют три случая, по одному для каждого типа подстановки.
Случай 1. р = @) A) B) C).
Имеем Ро = @) и рх = A) B) C). Следовательно, )х ф0) = 1
и h (Pi) — 3. Значит, с* (р, д;) = 1 + За;* для всех /с.
Слг/чай 2. р = @) A2) C).
Так как ро = @) и р, = A2) C), то /г (Ро) = 1, h (Pi) = 1
и /г (Pi) = 1- Поэтому 2s/s (Pi) равна /i (Pj) или U (Px) + 2/3 (Px)
в зависимости от того, нечетно или четно к. Следовательно, с^ (Р, х)
есть 1 + xh или 1 + 2>xk в соответствии с тем, нечетно или четно
число к.
Случай 3. р = @) A23).
Так как ро = @) и ^ = A23), то h (р0) = 1 и /3 "(PJ = 1.
Значит, 2S^ (Pi) равна СГили З/з (Pi) в зависимости от того, З^/с
или 3|А:. Поэтому ск (Р, х) равно 1 или 1 + 2>хк в соответствии с тем,
Ъ^к или Щк.

6_5. КОНЕЧНЫЕ АВТОМАТЫ 177
Если р = @) A3) B) или р = @) B3) A), то, «стеста«йюо,
ck (р\ х) дается случаем 2. Из F.3.11) имеем • ' •■
N*{x) = \{Ъ (S^; 1 + Ъх,
; 1 + х, l
Следовательно, для р = 3 получаем
Это соотношение проиллюстрировано рис. 6.4.1; на нем изобра-
изображены все 3-вершинные графы, ребрам которых приписаны взаимо-
взаимозаменяемые цвета а, Ъ, с.
6.5. КОНЕЧНЫЕ АВТОМАТЫ
Харрисон [1] первым решил задачу о нахождении числа раз-
разных автоматов. Если использовать ТПСГ, то, как показано
в статье Харари и Палмера [9], задача о подсчете числа автоматов
с заданными начальными и конечными состояниями может быть
решена весьма просто.
Чтобы подготовить почву, мы сначала перечисляем упорядо-
упорядоченные пары функций относительно произведения двух степенных
групп. После этого вполне конкретно определяем конечные ав-
автоматы — как специальные упорядоченные пары функций. Осу-
Осуществив перечисление автоматов естественным способом с исполь-
использованием степенной группы, мы затем распространяем этот ре-
результат, чтобы предусмотреть также начальные и заключительные
состояния.
Для получения теоремы перечисления упорядоченных пар
функций рассмотрим две группы подстановок: В1 и В 2. Пусть
2j = Ci xDi и ij = C8 X D2 — два произведения групп,
причем степени групп Ct и Dt равны соответственно с,- и dt (i =
= 1, 2). Воспользовавшись формулой D.3.10), дающей цикловой
индекс декартова произведения двух групп, равенством F.1.2),
позволяющим найти число объектов, неподвижных относительно
данной подстановки из степенной группы, и соотношением B.3.3)
из леммы Бернсайда, можно получить следующую теорему.
Теорема. Число орбит, определяемых произвольной подгруппой F
группы (Bi'xD')x(B2lXD*), дается формулой
S ..yi(P,)Y"(V')/fCe')"(P'i. F.5.1)

178
ГЛ. 6. ПЕРЕЧИСЛЕНИЕ СТЕПЕННОЙ ГРУППЫ
где звездочка у знака суммы указывает на то, что суммирование
ведется по всем подстановкам (((Vi, 6\); Pi), (G2* 62); р2)) из F.
Существует много способов определения конечных автоматов.
Для наших целей наиболее удобно сформулировать это понятие
на языке упорядоченных пар функций. Пусть X, Y и S — три
множества с мощностями к, т и п соответственно. Элементы из S
будем называть состояниями; множества X и Y назовем соответ-
соответственно входным и выходным алфавитами. Автоматом называется
упорядоченная пара функций (/х, /2), где/х: S X X ->5и/2: S Х\
X X -»■ Y. Отображение /х называется функцией переходов, а ото-|
бражение /2 — функцией выходов. В соответствии с традиционной!
Рис. 6.5.1 Два изоморфных автомата.
терминологией можно сказать, что если автомат находится в произ-
произвольном заданном состоянии и на его вход подается некоторый
входной символ, то функция /х указывает следующее состояние,
а функция /2 — выходной символ.
Харрисон [1] описал три типа эквивалентности автоматов, но
мы рассмотрим здесь только один из этих трех типов, а именно
изоморфизм; другие типы эквивалентности могут быть исследованы
аналогичным образом. Пусть Sk, Sm и Sn — симметрические
группы с множествами объектов X, Y и S соответственно. Таким
образом, имеется п состояний, к входных символов и т выходных
символов. Два автомата (/х, /2) и (gu g2) называются изоморф-
изоморфными, если существуют подстановки а из Sn, p* из Sk и у из Sm,
такие, что для всех s £ S и х £ X выполняются равенства
x)=>a-ig1(as,
и
F.5.2)
F.5.3)
Таким образом, равенство F.5.2) соответствует переименова-
переименованию состояний, а F.5.3) — перестановке входных символов. На
рис. 6.5.1 показаны два автомата, которые представляют одну
и ту же функцию переходов, если отношением эквивалентности
является определенный выше изоморфизм. Символы 0 и 1 исполь-
использованы для входного алфавита. Пометки обоих состояний и оба
входных символа предполагаются взаимозаменяемыми.

т
6.5, КОНЕЧНЫЕ АВТОМАТЫ 179
Чтобы дать подходящую трактовку решаемой задачи на языке
теории графов, введем следующее понятие. Сетью назовем ориен-
ориентированный граф, в котором допускаются и петли, и кратные дуги
(см. Харари, Норман и Картрайт [1], стр. 5). Если полустепень
исхода каждой вершины равна к и каждой из к дуг, исходящих
из вершины, сопоставлены разные пометки (символы) из входного
алфавита X, то такая сеть реализует функцию переходов некото-
некоторого автомата. Мы помечаем и вершины сети как состояния рас-
рассматриваемого автомата.
Чтобы сделать более ясным данное выше определение изо-
изоморфных автоматов, рассмотрим равенство F.5.2), устанавлива-
устанавливающее эквивалентность функций переходов /х и gv В помеченной
сети, реализующей функцию /х, существует дуга, помеченная
буквой х, исходящая из произвольного состояния s и входящая
в состояние f1 (s, z). Аналогично, в сети, реализующей функ-
функцию gx, существует дуга, помеченная символом $х, исходящая из
произвольного состояния as и входящая в состояние g1 (as, $х).
Таким образом, подстановка ((а, |3); а) из степенной группы
S^nxSk отображает функцию переходов gx в функцию /х и просто
переименовывает состояния вместе с соответствующим переимено-
переименованием входных символов на дугах сети.
Для перечисления автоматов мы должны взять
Применим затем константную форму ТПСГ, беря в качестве F
такую подгруппу группы (S^nXSk) x(^"xS*), которая состоит из
всех подстановок вида (((a, Р); а), ((а, Р); у)). Так как порядок
подгруппы F равен п \к \т !, то получаем следующее утверждение.
Следствие. Число а(п, к, т) автоматов с п состояниями,
к входными и т выходными символами дается формулой
а (п, к, т) = (\/(п \к \т !)) £ / (а, р, а) / (а, р, у), F.5.4)
еде сумма берется по всем подстановкам из подгруппы F, а
/(а, р, Т) = ПП
l
Очевидно, что соотношение F.5.4) можно видоизменить, ис-
используя для этого формулу, дающую число подстановок симметри-
симметрической группы, обладающих заданным разбиением.
В качестве иллюстрации следствия приведем некоторые детали,
относящиеся к нахождению числа а B, 2, 1) автоматов с двумя
состояниями, двумя входными и одним выходным символами.

180
ГЛ. 6. ПЕРЕЧИСЛЕНИЕ СТЕПЕННОЙ ГРУППЬ
Так как существует только одна функция выходов, то формула
F.5.4) несколько упрощается:
«B, 2, 1)=4
п.( 2
S|[p ,
= -i- B4 + 22 + 22 + 22) = 7.
F.5.С
В автомате обычно выделяют одно из состояний, называя его]
начальным состоянием, или источником. Кроме того, может быть]
выделено несколько других состояний, называемых заключителъЛ
ними состояниями. Таким образом, чтобы перечислить эти ав-|
томаты, мы должны перечислить подходящие корневые сети.]
■ * ■
о
Э-
>. t-
о
о
■■•У
Рис. 6.5.2 Семь автоматов, соответствующих соотношению F.5,6),
Конкретнее, мы перечислим сети с одним начальным и t заключи-
заключительными состояниями. Соответствующий метод состоит в при-
применении степенной группы в первоначальном перечислении корне-
корневых графов, данном Харари [4].
Для полного описания группы подстановок, позволяющей
осуществить требуемое перечисление, воспользуемся теми опера-
операциями на группах подстановок, которые дают степенную группу,

6,5, КОНЕЧНЫЕ АВТОМАТЫ
181
произведение и декартово произведение групп. Пусть Н — группа
подстановок: <>>.
действующая на множестве SsxX xYSxx. . ..
Обозначим через а (п, к, т, t) число автоматов с п состояниями,
включая одно начальное и t заключительных состояний, с к вход-
входными и т выходными символами. Пусть F — подгруппа группы Н,
состоящая из всех подстановок, представленных заранее в форме
(((а, Р); а), ((а, Р); у))- Тогда порядок подгруппы F равен
(п — t — 1)! t\ k\ т\. Как и раньше, число таких автоматов
находится с помощью формулы F.5.1).
Следствие. Число автоматов с одним начальным и t заключи-
заключительными состояниями равно
а(п, к, т, г)^[\/((п-г-\)Н\к\т\)]%1(а, р, а)/(а, р, у),
F.5.7)
где суммирование ведется по всем таким подстановкам из Н,
которые имегбт вид (((а, |3); а), ((а, р); -у))> и I (^ Pi у) дается
формулой F.5.5).
В качестве простого примера рассмотрим случай, когда и число
т выходных символов, и число t заключительных состояний
равно 1, а число входных символов равно 2. Тогда имеем
а(п, 2, 1, 1)-11/((л-2I2)]2П П ( 2 s.js
p-lq-l \ s|[p, q]
F.5.8)
Теперь легко подсчитать, что для п — 2 а B, 2, 1, 1) = 10
(см. таблицу 6.5.1 и рис. 6.5.3). В таблице 6.5.1 приведены значе-
значения величины а (п, 2, 1, t) для малых в и 1 = 1,2, . . ., п — 1.
Равные значения "попадаются потому, что а (п, 2, 1, t) — а (п, 2, 1,
Числа а (п, 2, 1, 0
Таблица 6.5.1
"ч t
п Ч^
2
3
4
5
1
10
378
16 576
819 420
2
198
16 576
1 226 900
3
5 614
819 420
4
206 495
п — t — 1) для t = 1, 2, ...,« — 2. Заметим, что из формулы пере-
перечисления F.5.7) следует, что t рассматриваемых заключительных

182
ГЛ. 6. ПЕРЕЧИСЛЕНИЕ СТЕПЕННОЙ ГРУЙ1Щ
состояний отличны от начального состояния. Чтобы допустить и
такую ситуацию, когда начальное состояние само является одним
из заключительных состояний, надо каждое вхождение t в фор-
Рис. 6.5.3 Десять автоматов,подтверждающих значение величины а B,2,1,1).
муле F.5.7) заменить на t —1. Легко перечисляются автоматы с про-
произвольным числом г начальных состояний и числом t заключитель-
заключительных состояний; точно так же нетрудно учесть и число состояний,
которые являются одновременно начальными и заключительными.
6.6. САМООБРАТНЫЕ ОРГРАФЫ
Нашей целью является вывод формулы для перечисляющего
многочлена d'p (х), в котором коэффициент при %ч равен числу
самообратных орграфов е р вершинами и q дугами (см. Харари
и Палмер [5]). Такой орграф D обладает тем свойством, что обрат-
обратный ему орграф D', получаемый из D изменением ориентации всех

g,6. САМООБРАТНЫЕ ОРГРАФЫ 183
его дуг, изоморфен D. По причинам, указанным ниже, при выводе
требуемой формулы теорема Пойа применяется к такому ограни-
ограничению степенной группы, в котором подстановки действуют на
взаимно однозначные функции. Прямой проверкой убеждаемся
в том, что перечисляющий многочлен d'3 (х) для самообратных
орграфов с тремя вершинами имеет вид (ср. с рис. 6.6.1):
d'3 (х) = 1 +х + 2я2 + 2х3 + 2х* + хъ+ х\ F.6.1)
Напомним, что дополнение D орграфа D имеет то же самое
множество вершин, что и орграф D, и вершина и смежна к вер-
вершине v в орграфе Ъ тогда и только тогда, когда она не является
Рис. 6.6.1 Десять самообратных орграфов с тремя вершинами.
смежной к у в орграфе D. Легко видеть, что (D)' = D', т. е. опе-
операции обращения и взятия дополнения орграфа коммутативны.
Это замечание объясняет «концевую» симметрию коэффициентов
многочлена d'p {x), которая, например, явно выражена в соотно-
соотношение F.6.1) при р — 3.
Два орграфа Dx и Вг с одним и тем же множеством вершин
называются эквивалентными относительно обращения, если либо
D1 ^ D2, либо D'i^D2- (Отметим аналогию с понятием экви-
эквивалентности графов относительно свойства дополнительности.)
Мы теперь хотим получить формулу для многочлена ср {х), пере-
перечисляющего р-вершинные орграфы с точностью до их взаимной
обратимости. Для осуществления этого мы должны найти, как
и в случае графов, подходящую группу подстановок, к которой
можно было бы применить теорему Пойа.
Пусть S2 действует на {1, 2} и рассмотрим степенную группу
Sp', действующую на множестве Х^1- 2> всех функций, отобража-
отображающих множество A, 2} в X. Легко заметить естественное соответ-
соответствие между элементами из X'21 (представляющими упорядочен-
упорядоченные пары различных элементов из X) и взаимно однозначными
функциями из Х*ь 2>. Каждая упорядоченная пара (i, j) из Xi21
соответствует такой взаимно однозначной функции, которая
отображает 1 в £, а 2 в ;. Значит, мы можем рассмотреть ограни-
ограниченную степенную группу Ssl, где ограничение осуществляется

184 ГЛ. в. ПЕРЕЧИСЛЕНИЕ СТЕПЕННОЙ ГРУППЫ
на множество всех взаимно однозначных функций, но которые
как бы действуют на элементах множества Х[21. Более конкретно,
подстановки из S^2 состоят из таких упорядоченных пар (а; Р)
подстановок а £ S2 и Р 6 Sp, что для всякой пары (г, /) из X tai
выполняется соотношение
Г (Рг, р/), если а =
Пусть теперь jE — единичная группа, действующая на множе-
множестве Y — {0, 1 }. Рассмотрим степенную группу 5, которая пред-
представляет собой степенную группу с основанием Е% и показателем
S®* и действует на множестве Yxnl всех функций, отображающих
X'21 в множество Y. Каждая такая функция / представляет ор-
орграф, вершинами которого являются элементы множества X =
= {1, 2, . . ., р}, где i смежна к / только тогда, когда / (i, /) = 1.
Таким образом, элементы 0 и 1 из множества Y указывают на
отсутствие или на принадлежность дуги орграфу.
Пусть /t и /2 — две из этих функций, и пусть представленные
ими орграфы будут соответственно D1 и D2- Имеем D{ s D2
или Dx s ZJ тогда и только тогда, когда существует подстановка
у из В, такая, что v/i = ft- Это вытекает из того факта, что для
подстановки у = ((а; Р); е) орграф, представленный функцией yfv
изоморфен D1 или D[ в соответствии с тем, является а подстанов-
подстановкой A) B) или A2).
Итак, эквивалентность орграфов относительно обращения соот-
соответствует эквивалентности функций из множества У^'21, опре-
определяемой с помощью степенной группы В.
Применяя теперь теорему Пойа (это мы вправе делать, потому
что основанием степенной группы является группа Е^), мы полу-
получаем следующий результат, который требуется для перечисления
самообратных графов.
Теорема. Многочлен ср (х), перечисляющий орграфы с точностью
до взаимной обратимости, дается формулой
х).
F.6.3)
Существуют формулы, которые могут быть использованы для
выражения циклового индекса произвольной ограниченной сте-
степенной группы ВА*, где ограничение осуществляется на множе-
множество тех взаимно однозначных функций, которые рассматриваются
в данной задаче. Однако в частном случае, когда А = 52 и В =
= Sp, может быть дана"более явная формула для циклового
индекса. Какова бы ни была подстановка а из Sp, обозначим,
как и раньше, разбиение числа р, определяемое подстановкой а,

6,6. САМОСБРАТНЫЕ ОРГРАФЫ 185
через (У) = (j'i> Ь. • • • Л>)> гДе 7* равно числу попарно непересека-
непересекающихся циклов длины /с в подстановке а. Тогда вклад в Z\S *),
вносимый подстановкой (A2); а), равен
, x П 8к*-1)/«»*. п 5(*-2)/^да-2/ц1-л(*))-/А) F64)
ft нечетное ft четное
где т] (ft) = 1, если ft/2 — нечетное число, и r\ (ft) = 0 в ином
случае.
Следовательно, цикловой индекс группы Si можно выразить
в виде
Z (Ssp*) = A/2р!)(р \Z (^a]) +eS /(«)\ F.6.5)
Сделаем теперь простое замечание, касающееся самообратных
графов и подобное тому, которое было сделано Ридом относи-
относительно самодополнительных графов. Именно, многочлен 1ср (х)
подсчитывает каждый самообратный орграф дважды, а каждый
несамообратный — только один раз. Следовательно, многочлен
2ср (х) — dp (x) подсчитывает каждый самообратный орграф в точ-
точности один раз. Итак, мы имеем
dp(x) = 2cp(x)-dp(x). F.6.6)
Это соотношение вместе с формулами E.1.4) и F.6.3) дает сле-
следующий результат.
Теорема. Перечисляющий многочлен dp (x) для самообратных
орграфов равен
d'p(x) = 2Z(ssp*, i + x)-Z(S™, 1+4 F.6.7)
Для упрощения записи соотношения F.6.7) положим
/(а).
Хотя это выражение не связано явно с группой подстановок, мы
все же определяем подстановку в него 1 + х, имея в виду по-
построение многочлена, получаемого путем замены каждой перемен-
переменной sk в F {Spi) двучленом 1 + xk. Комбинируя соотношение
F.6.7) и формулу F.6.5) для Z (S^t), приходим к равенству
\ l+x).
F.6.8)

186
ГЛ. в. ПЕРЕЧИСЛЕНИЕ СТЕПЕННОЙ ГРУППЫ
Для иллюстрации построим многочлен й'ъ (х), перечисляющий
самообратные орграфы с тремя вершинами. Цикловой индекс
симметрической группы S3 имеет вид
Z(S3) = ± (*J
F.6.1
Из этого соотношения и формулы F.6.4) для /(а) получаем
Формула F.6.8) дает для р =
= 1 -f- х + 2я2 + 2х3 + 2а;4 + х* + х\
F.6.11
а для р =
= 1 + а: + За;2 + 5х3 + 9х* + Юхъ +
4-10ж7 + 9л:8 + 5а;9 + За;104-а;11+а;12. F.6.12)
Коэффициенты этих многочленов можно обстоятельно про-
проверить с помощью рассмотрения диаграмм четырехвершинных
орграфов; такие диаграммы приводятся в статье Харари и Пал-
мера [6] и в книге Харари [1] (см. приложение II, стр. 262—
265). На рис. 6.6.2 показаны все пять самообратных орграфов
с четырьмя вершинами и тремя дугами.
Рис. 6.6.2 Пять самообратных орграфов.
Несложная модификация формулы F.6.7) приводит к много-
многочлену г'р (х), перечисляющему самообратные орграфы, в которых
допускаются петли. Допуская в орграфах существование петель,
мы получаем, естественно, графы, соответствующие отношениям.
Нетрудно видеть, как можно использовать степенную группу Sp',
чтобы подсчитать число отношений с точностью до их взаимной
обратимости. Напомним, что упорядоченная парная группа S2P
действует на всех упорядоченных парах (где элементы в парах

6,в. САМООБРАТНЫЕ ОРГРАФЫ t 187
необязательно различны), как группа, индуцированная симме-
симметрической группой 5Р. Как показано в E.1.13), многочлен гр (х),
перечисляющий отношения, имеет вид
F.6.13)
Но тогда многочлен г'р(х) дается формулой
) F.6.14)
Для использования соотношения F.6.14) удобно ввести сле-
следующее обозначение для каждой подстановки а из 5р:
/(о) = /(оJ s[K F.6.15)
ft-i
Тогда цикловой индекс степенной группы Sp1 можно записать так:
2№)=^&(рм№)+ 2 '(«))• F-6-16)
Пусть теперь
i^j ^ («)- F-6.17)
Тогда формулу для г'р(х) можно представить в следующем виде:
r'p(x) = H(S*\ \ + x). F.6.18)
Пусть dp — общее число самообратных орграфов с р вершинами.
Тогда, принимая во внимание соотношение F.6.7), видим, что
сГр = dp A). Чтобы выразить формулу для d'p в относительно
приемлемой форме, введем следующие обозначения. Для каждой
подстановки а из 5Р положим
2 B, [г, *])(r, t)jrit. F.6.19)
. '•> Так как замена на 2 каждого вхождения $/, в ^"(^р2) (см. фор-
иуды F.6.8) и F.6.4)) дает dp(i), то имеем
F.6.20)

188 ГЛ. в. ПЕРЕЧИСЛЕНИЕ СТЕПЕННОЙ ГРУППЫ
Аналогичная формула легко получается и для общего числа г*
самообратных отношений с р вершинами. В табл. 6.6.1 приведены
значения dp и г'р для р = 1, 2, . . ., 6.
' О О О о-™
О—О <О . " <ГХ) '" OCX)
Рис. 6.6.3 Самообратные отношения на двух вершинах.
Восемь самообратных отношений с двумя вершинами изобра-
изображены на рис. 6.6.3.
Таблица 6,6.1
Число самообратных орграфов и самообратных отношений с р вершинами
р
dp
г'р
1
1
2
УПРАЖНЕНИЯ
2
3
8
3
10
44
4
70
436
708
7 176 ~
6
15248
222 368
6.1. (а) Рассмотрим множество всех функций, отображающих
множество из т элементов в множество из п элементов. Сколько
существует орбит в этом множестве, определяемых степенными
группами ЕЕпт, Esnm и S%m?
(b) Сколько орбит функций, отображающих множество из т
элементов на множество из п элементов, определяются этими сте-
степенными группами? {Указание; используйте биномиальные коэф-
коэффициенты или числа Стирлинга второго рода.)
(Палмер [21)
6.2. Найти формулы для Z{SC3>), Z{cfa), z(sf) и z[cf).
(Рид [6])
6.3. ip = S(-l>fo,^ (Фрухт и Харари [1])
я
6.4. Найти такой ряд С (х, у), в котором коэффициент при xrys
равен числу шестибусинных ожерелий, имеющих г бусинок двух
взаимозаменяемых цветов, s бусинок двух других взаимозаменя-
взаимозаменяемых цветов и 6 — г — s красных бусинок.
6.5. Найти ряд ./V (х, у), в котором коэффициент при хгу$ равен
числу графов с четырьмя вершинами, г ребрами двух взаимо-

УПРАЖНЕНИЯ » 189
заменяемых цветов и s ребрами трех других взаимозаменяемых
цветов.
6.6. Каким числом способов можно раскрасить грани куба, ис-
цользуя три цвета, два из которых взаимозаменяемые?
6.7. Каким числом способов можно раскрасить грани куба, ис-
цользуя два взаимозаменяемых цвета?
6.8. Найти формулу для Z(S^").
6.9. Самодополнительные эйлеровы графы. (Робинсон [2])
6.10. Самообратные направленные графы и самодополнитель-
самодополнительные направленные графы. (Шридхаран [1])
6.11. Число самодополнительных турниров порядка 2га равно
1 У>* Bга) 1 тт „ft/|/2 -pr „(г, <)/,/,
Bn) I Zi тт Л, , 1А * 1А *
где звездочка у знака суммы указывает на то, что суммирование
ведется по всем разбиениям (/) числа 2тг, таким, что jk Ф 0 только
тогда, когда Учетное и 4{к Самодополнительные турниры не-
нечетного порядка.
6.12. Отношения, не имеющие транзитивных троек, а также ор-
орграфы, не имеющие транзитивных троек. (Шарп [1])
6.13. Орграфы, у которых обращение изоморфно дополнению.
(Палмер [6])
6.14. Рассмотрим граф, ребрам которого сопоставлены плюсы
и минусы. Такой граф называется самонегативным, если он изо-
изоморфен графу, который получается из него путем замены плюсов
на минусы и, наоборот, минусов — на плюсы. Самонегативные
графы. (Рид [7])
6.15. Для формулировки полиномиальной формы ТПСГ, данной
г
де Брёйном [2], удобно положить В = П В{, где В1 действует
на Yt. Во многих приложениях группа В имеет такой вид. Пусть
рев, k
Тогда многочлен С (х), перечисляющий орбиты степенной группы
ВА, имеет вид
; J-, ..., J—\Z{B)~\ ;
' dz, ' dzm ) v 'JzA-o
здесь предполагается, что в Z(B), полученном из Z(Bt), i = 0, I,
«. .j 7*1 осуществлена замена
[m/ft]

Глава 7
Кашу маслом не испортишь/
Пословица'
За вином они обычно обсуждают самые
важные дела. Решение, принятое па
таком совещании, на следующий день
хозяин дома, где они находятся, еще
раз предлагает [на утверждение] го-
гостям уже в трезвом виде. Если они
и трезвыми одобряют это решение, то
выполняют. И наоборот: решение, приня-
принятое трезвыми, они еще раз обсуждают
во хмелю.
Геродот о персах а.
СУПЕРПОЗИЦИЯ
Существует несколько естественных способов определить объе-
объединение совокупности графов. В каждом случае мы будем назы-
называть соответствующее объединение «суперпозицией». Три из таких
суперпозиций проиллюстрированы на рис. 7.0.1. Задача нахожде-
нахождения числа «разных» суперпозиций, которые могут быть получении
ИЛИ
ИЛИ
A)
Рис. 7.0.1 Три различные суперпозиции.
с использованием данного множества графов, решается для многих
интересных частных случаев. Редфилд [1] первым получил такое
решение. Его теорема перечисления, если ее соединить с его же
«теоремой декомпозиции», пригодна также для перечисления графов
и орграфов. Предметом данной главы является изложение перечис-
перечислительных методов Редфилда в современных обозначениях и тер-
минологии (см. Харари и Палмер [8], Палмер [4], Фоулкс [2]).
7.1. ТЕОРЕМА ПЕРЕЧИСЛЕНИЯ РЕДФИЛДА
Операции Л и (J над цикловыми индексами были использо-
использованы Редфилдом для формулировки результатов, заключенных
1 В оригинале: «If it tastes good already, it will ta3te even better witb
paprika on it»; Old Hungarian saying. — Прим. перев. "
2 Геродот, История, Изд-во «Наука», Ленинград, 1972, пер. Г. А. Страто-
вовского. — Прим. перев.

7.1. ТЕОРЕМА ПЕРЕЧИСЛЕНИЯ РЁДФЙЯДА 191
в его «теореме перечисления» и в его «теореме декомпозиции».
Эти операции были применены Ридом [1] для вывода его «супер-
«суперпозиционной теоремы» и были интерпретированы Фоулксом [I]
как скалярные произведения определенной группы характеров.
Обе эти операции можно ввести в весьма общей форме.
Обозначим через R кольцо рациональных многочленов от
переменных s^ s2, . . ., sd. Операция f) сначала определяется
для последовательности s'i's^ . . . s'dd, s^1 . . . sj<* , . . . иэ т ~>* 2
мономов, принадлежащих кольцу В.:
I d \m-l
(s'«s<< . . . s'j) П («'•«'• . . . s>/) П . . . = ^П kl4k ! j , G.1.1)
если ik = jk = • • • для всех к, и равно 0 в ином случае (Ь° = 1
даже тогда, когда Ъ = 0). Затем операцию П можно распростра-
распространить по линейному закону на произвольные многочлены от этих
переменных.
Вторая операция — операция (J , определяется для мономов
«на языке» операции П •
(s'tf . . . s1/) U («fs/. . . . s1/) U . . . =
' = [(ЗД. . . . s'/) П Ц'^ • • • si/) П . . .] «!•*(,' • . . s'/. G.1.2)
Эта операция также распространяется линейным образом на
произвольные многочлены от рассматриваемых переменных.
Итак, результат применения операции П представляет собой
число, в то время как применение операции (J приводит к много-
многочлену. На практике эти операции применяются только к цикловым
индексам т групп подстановок одинаковой степени. Для иллю-
иллюстрации приведем детали вычислений в случае, когда т = 2
и соответствующими группами являются циклическая и ди-
эдральная группы степени 4:
G.1.3)
(i i 2), G.1.4)
Z (С,) П Z (Я4) = ±- [(si П si) + 3 (*; П *|) +
+ 4(s4ns4)]=^-B4 + 24 + 16) = 2, G.1.5)
Z (Q U Z (Z?4) = ^ B4s* + 24»| + 16s4). G.1.6)
Таким образом, Z (C4) П Z (D4) есть в точности сумма всех коэф-
коэффициентов из Z (C4) U Z {D)

192
ГЛ. 7, СУПЕРПОЗИЦИЯ
Пусть W — совокупность всех (т X /г)-матриц, в которых
элементы каждой строки попарно различны и являются объек-
объектами некоторого множества S, содержащего ровно п элементов.
Таким образом, в W входят (п\)т матриц. Две матрицы из W
называются эквивалентными по столбцам (или колонно-эквива-
лентными), если они могут быть получены друг из друга пере-
перестановкой столбцов. Легко видеть, что существует (/г!) соот-
соответствующих классов эквивалентности. Далее определяем еще
одно отношение эквивалентности — уже для упомянутых классов
эквивалентности (для классов эквивалентности по столбцам).
Пусть Сг и С2 — два таких класса, и пусть Въ В2, . . ., Вт —
группы подстановок с множеством объектов S. Тогда Сх и С2
Рис. 7.1.1 Суперпозиции двух циклов.
называются эквивалентными относительно (ВЪВ^, . . ., Вт),
если существуют набор подстановок (р^, р2, • • •> Рт). где р, £ В{,
для каждого i, и матрица [юц] £ Clf такие, что [р,н>,/] £ С2-
Другими словами, подстановка р,- переставляет элементы £-й
строки в некоторой матрице из С%, i = 1, 2, . . ., т, и в результате
этого получается матрица из класса С2. Теорема перечисления
Редфилда выражает число этих классов «на языке» цикловых
индексов групп Bt и операции (].
Теорема (теорема перечисления Редфилда). Число N [Ви
В2, . . ., Вт] классов (т X п)-матриц, эквивалентных относи-
относительно групп подстановок (Bv B2, . . ., Вт), дается формулой
N[Bu В2,
Л Z(Bt) Л ... Л Z(Bm). G.1.7)
Этот результат можно обосновать, построив сначала группу под-
подстановок, орбиты которой представляют собой классы матриц,
подлежащие перечислению. Формула G.1.7) следует затем из
леммы Бернсайда (см. B.3.3)), которую надо применить к по-
построенной группе.
Покажем сейчас, как можно использовать эту теорему для
подсчета числа суперпозиций произвольного множества графов.
Пусть Gv G2, . . ., Gm — т графов, каждый из которых имеет
одно и то же множество вершин, содержащее п элементов. Пусть,
кроме того, для каждого i = 1, 2, . . ., т ребра графа Gi поме-
помечены числом i (или раскрашены цветом i). Суперпозиция этих
графов имеет то же самое множество вершин, и всякие две из них,

1 !. TEOt>EMA ПЕРЕЧИСЛЕНИЯ РЕДФИЛДА 193
например и и v, смежны по ребру i в том случае, если и и v смежны
в графе Gt. Таким образом, ребра суперпозиции помечены, а вер-
дшны — нет. Для иллюстрации мы приводим на рис. 7.1.1 все
суперпозиции, которые могут быть построены из двух циклов
порядка 5. Для указания двух цветов использованы сплошные
и штриховые ребра.
Редфилд [1] и Рид [1] заметили, что число различных супер-
суперпозиций равно просто числу классов (т X я)-матриц, эквива-
эквивалентных относительно (Г (Gx), Г (t?2), • • •. Г (Gm)). Таким обра-
образом, мы можем найти число суперпозиций при условии, что нам
известны цикловые индексы Z (£?;) групп Г (£?,) рассматриваемых
графов. Используемая здесь запись Z (G) вместо Z (Г (G)) хотя
и противоречит принятым обозначениям, однако является удобной.
Следствие. Число различных суперпозиций т графов Gh каждый
из которых имеет одно и то же множество непомеченных вершин,
равно
Z(G)[\Z(Gt)ft ... [)Z(Gm). G.1.8)
Например, чтобы найти число суперпозиций двух циклов по-
порядка я, мы можем вычислить Z (Dn) (] Z (Dn), так как группа
такого цикла есть Dn. Если п = 5, то, используя формулу B.2.11),
имеем
Z(Db) = -jo К + Ч + 5slS|). G.1.9)
Из определения операции П следует, что
Z (Db) n Z (Db) = J- ((*; n sj) +16 (ч П st) +
G.1.10)
что согласуется с числом суперпозиций, изображенных
на рис. 7.1.1. Теорема перечисления Редфилда может быть исполь-
использована для подсчета числа суперпозиций и в тех случаях, когда
«конституэнты» являются орграфами или когда среди конституэнт
имеются и графы, и орграфы. Сам Редфилд проиллюстрировал
свою теорему, строя суперпозиции циклов и ориентированных
циклов, которые он использовал и отдельно друг от друга, и со-
совместно. На рис. 7.1.2 показаны две суперпозиции ориентиро-
ориентированного и неориентированного циклов порядка 4, что подтвер-
подтверждает соотношение G.1.5).
Наконец, предположим, что граф G имеет п вершин и только
одно ребро. Тогда число суперпозиций, построенных с исполь-
7 Заказ 443

194 ' . •-•■ гл. 7. суперпозиций
зованием т экземпляров графа G, равно числу мультиграфов,
у которых по п вершин и каждое ребро раскрашено в свой цвет!
Рис. 7.1.2 Две суперпозиции ориентированного и неориентированного цикло
Так как Z (G) = Z (£2) Z (£„_2), то соответствующее чис
равно П -произведению длины т:
Z(S2)Z(Sn.2)f] ... [)Z(St)Z{Sn_t).
При т =* п = 3 значение этого произведения равно 5. Соотве!
ствующие суперпозиции показаны на рис. 7.1.3, где сплошны|
штриховые и пунктирные ребра относятся к разным экземпляра
графа G.
7.2. ТЕОРЕМА ДЕКОМПОЗИЦИИ РЕДФИЛДА
Теорема декомпозиции U -произведений не используется не
посредственно для целей перечисления, но она может приме
няться при нахождении циклового индекса парной группы ;
и редуцированной упорядоченной парной группы Slp21. Кроме
Рис. 7.1.3 Суперпозиции трех ребер на трех перпшнах.
того, она предлагает способ получения формулы для суммы цикло- •
вых индексов групп всех графов. Последняя формула, как уста-
установлено Робинсоном [3], играет важную роль в перечислении
блоков.
Чтобы сформулировать теорему, мы сначала свяжем естествен- !
ным образом с каждым из N [Ви В2, ■ • ., Вт] классов матриц, ■
перечисляемых в соответствии с формулой G.1.7), группу под-
подстановок. Предположим, что [м>(/] — (т X /г)-матрица из &-го
класса. Тогда группа подстановок Аь, ассоциируемая с этим
классом, состоит из всех подстановок у, таких, что у является
элементом каждой группы Bt и матрицы [wl/] и \yUii\ принадле-
принадлежат одному и тому же классу, т. е. эти матрицы эквивалентны
i

1 2. ТЕОРЕМА ДЕКОМПОЗИЦИИ РЕДФИЛДА
столбцам. При применении теоремы декомпозиции Редфилда
Гют отГшение смежности в каждом «>™л?^б^^
онтном) графе. Например, группами суперпозиции, изображенных
на ри?. 7 1.2, являются циклическая группа С4 и веночное произ-
ведение £2 1£21-
Теорема (теорема декомпозиции Редфилда). Пусть ВгВ,
/ _ m груп/г подстановок степени п, и пусть N будет
чис'ломплассов (тХ п)-матРщ, эквивалентных относительно {В
п В ) Тогда N групп подстановок Ни Н 2, . ■ ■, «л, ас™
циируемыхс'этими классами, удовлетворяют условию
Z(Bi) U Z(B2) U ... U Z(Bm)~iz(Hk). G.2.1)
i
рис. 7.1.2.
"--ааателъство. Для доказательства теоремы *«
поостым теоретико-групповым тождеством, называемым
Т_*„-„„ Лп-пппа 6vnfiT иметь широкую область при-
в виде
чУисел причемэта функция
на классах
из каждой орбиты. Положим для каждого к = 1, Z, . . .,
Тогда имеем следующее обобщение леммы Бернсайда.
Лемма Редфилда. ^
=2И.|-'-2 ф«»>.
2
Пповепка соотношения G.2.3) осуществляется аналогично
азГелГству взвешенной ф^рмы леммы Бернсайда (см. формулу
доказательству взвешенной формы
7*

196 ГЛ. 7. СУПЕРПОЗИЦИЯ
B.3.10)) и поэтому нами опускается. Заметим, что если выбрать i
Ф (а) = 1 для всех а, то соотношение G.2.3) преобразуется в pa-i
венство B.3.3) из леммы Бернсайда. |
Возьмем в качестве элементов группы А все наборы а = (Р1(*
Рг. • м Рш), где р( £ В(, i = 1, 2, . . ., т. Умножение в А опре-1
деляется покомпонентно. Подстановка а' действует следующим*
образом на классы эквивалентности, определяемые отношением'
эквивалентности по столбцам. Класс, содержащий матрицу [н;^], f
преобразуется подстановкой а" в класс, которому принадлежит!
п
матрица [р,-ц;(/-]. Наконец, ф (а) = "-s1^, если каждая компо- >
нента Р; определяет одно и то же разбиение (/) числа п, и ф (а) = 0'
в ином случае. Доказательство равенстваG.2.1) теперь может быть
завершено применением леммы Редфилда (см. соотношение 7.2.3)).щ
Декомпозиция U -произведений необязательно является одно-
однозначной, но существуют несколько случаев, важных для нас,
в которых декомпозиция осуществляется однозначным образом
(см. Редфилд [1] и особенно Фоулкс [1] для полного ознакомления
с затронутым вопросом). Теперь мы займемся цикловыми инде-
индексами циклических групп. Пусть а — подстановка на множестве
из п объектов, имеющая порядок г.Пусть Z (а) обозначает цикло-
цикловой индекс циклической группы, порожденной подстановкой а.
Тогда имеем
а если а состоит только из единственного цикла длины г, то фор-1
мула Редфилда для Z (а) легко проверяется: ]
где ф — эйлерова ф-функция. Следующий результат является
следствием теоремы декомпозиции и приводится в работе Ред-
Редфилда [1], но в совершенно иной форме.
Следствие. Если В является группой подстановок степени п
и а — произвольная подстановка на множестве из п символов,
имеющая порядок г, то
где ik — однозначно определяемые неотрицательные целые числа.
Из теоремы декомпозиции (см. формулу G.2.1)) следует, что
Z (В) [J Z (а) равно сумме цикловых индексов групп, явля-
являющихся подгруппами и группы В, и циклической группы, поро-

7.2. ТЕОРЕМА ДЕКОМПОЗИЦИИ РЕДФИЛДА 197
жденной подстановкой а. Коэффициент ik определяется одно-
однозначно, так как цикловые индексы Z (а*) независимы. Кроме того,
сформулированное следствие можно использовать для вычисления
циклового индекса производной группы двух групп подстановок,
которая вводится следующим образом.
Пусть группы А и В имеют одно и то же множество объектов
X = A, 2, . . ., п}, которое является также множеством объек-
объектов симметрической группы Sn; пусть В — подгруппа группы А.
Производная группа групп А и В обозначается через А/В и имеет
в качестве множества объектов совокупность всех правых смежных
классов группы А по подгруппе В. Для каждой подстановки а
из А существует подстановка а* из А/В, такая, что, каков бы
ни был правый смежный класс рБ из группы А, его образ, опре-
определяемый подстановкой а", равен ар/?, т. е. справедливо соотно-
соотношение
а' (РЯ) = офВ. G.2.7)
Таким образом, подстановками производной группы А/В яв-
являются все те подстановки на множестве смежных классов, кото-
которые индуцируются группой А при левостороннем умножении.
Следовательно, группа А/В является гомоморфным образом
группы Л и ее степень равна \А \l\B\. Цикловой индекс Z (SJB)
можно получить с помощью следующего следствия.
Следствие. Пусть а — подстановка из Sn, имеющая порядок г.
Если SJB — производная группа, то для каждого к\г подста-
подстановка а" из SJB содержит ik циклов длины, к, где ik — коэффициент
при Z (ak) в декомпозиции [] -произведения Z (В) \j Z (а).
Итак, вклад подстановки а" в Z (SJB) равен П s^fe. Для ил-
люстрации мы, следуя Редфилду, найдем с помощью этого след-
следствия цикловой индекс Z (^б/О^^з))-
Из формул B.2.4) и B.2.5) имеем
Z (Sb) = A/5 !) (s\ + 10s3s2+ 20s2s3-f ibs^* + 30sxs4 + 20s2s3 + 24sE),
G.2.8)
| G-2.9)
Теперь предположим, что а является подстановкой из S&
с цикловой структурой s2s3, так что /2 (а) =='/з (а) = 1 и порядок а
равен 6. Так как делителями числа 6 являются числа 1, 2, 3 и 6,
то формула G.2.6) влечет равенство
Z (St) Z E,)UZ (a) = hZ (a) + i2Z (a2) + iaZ (а») + ieZ (ae). G.2.10)
С другой стороны, так как из G.2.4) следует, что
Z (a) = -J-(se + 2S>Sa + 2s;s,+ «»*,), G.2.11)

198 г ' ГЛ. 7. СУПЕРПОЗИЦИЯ
то находим ■'<■-'? .i't. ■#;-:.• ■::-'l'f:- ..^- •■>> ,;>
Объединяя соотношения G.2.10) и G.2.12), получаем ■
) = -f-si + TS2S3 + Tsis3 + Ts3i^ G-2-13)
Член s2s3 B левой части равенства G.2.13) принадлежит только
слагаемому itZ (а). Значит, коэффициент при s2s3 в левой части
G.2.13) есть ^/3. Но этот же коэффициент в правой части соотно-
соотношения G.2.13) равен 1/3; следовательно, гх = 1. Вычитая Z (а)
из обеих частей формулы G.2.13), приходим к равенству
) = |-^ + i-^s2. G.2.14)
Член s\ss в левой части соотношения G.2.14) входит только в сла-
слагаемое i2Z (a2), а так как он не содержится в правой части, то
£2 = 0. Далее, коэффициент при s^s^ в левой части равенства
G.2.14) есть г3/2, в правой — 1/2; поэтому i3 = 1. Вычитая Z (а3)
из обеих частей формулы G.2.14), получаем
и, следовательно, ц = 1. Таким образом, цикловая структура
подстановки а* из Sb/(S2S3) описывается одночленом s^gV Зна-
Значит, все 20 подстановок из Sb, имеющих структуру s2s3, вносят
в Z (Sb/(S2S3)) вклад, равный B0/5!) SjS3se. Далее, замечаем, что
а2 имеет структуру s\s3, и так как (а2)" = (а'J, то все 20 под-
подстановок, обладающих структурой SiS3, вносят в цикловой ин-
индекс производной группы общий вклад B0/5!) s^. Аналогично,
подстановка а3 имеет структуру s\s2 и все подстановки с такой
структурой дают член A0/5!) s\sl. Мы можем продолжать в том же
духе, чтобы найти вклады, вносимые в цикловой индекс произ-
производной группы другими подстановками из Sb (соответствующие
вклады определяются путем выбора таких элементов, которые
порождают максимальные циклические подгруппы). После завер-
завершения всех вычислений имеем
Z (SJ(S2SS)) = A/5 !) (sjo + 10sS + i5s*
-f 20siS8se + 30s2s2 + 24s2). G.2.15)
Редфилд [1], стр. 451—453, использовал эту процедуру, чтобы
найти цикловые индексы Z (SJ(S2Sn_1)) для п sg 7.

7.2. ТЕОРЕМА ДЕКОМПОЗИЦИИ РЕДФИЛДА 199
Далее мы покажем, что леммой Редфилда (см. G.2.3)) можно
воспользоваться для получения формулы Робинсона (см. Робин-
Робинсон [3]), дающей сумму цикловых индексов групп всех графов.
В следующей главе мы увидим, что формула G.2.18), которая
будет выведена сейчас, является существенно важной при пере-
перечислении блоков. Пусть, как обычно, Sp обозначает симметриче-
симметрическую группу, действующую на множестве X = A, 2, . . ., р},
а парная группа S(p2) имеет в качестве множества объектов ХB) —
совокупность всех 2-подмножеств из X Обозначим через Sp1'2>
группу, индуцированную группой Sp и действующую на множе-
множестве X U Х<2>. При р > 2 обе группы Sp2) и Sp1'2) абстрактно
изоморфны группе Sp. В формуле для циклового индекса группы
Sp1>2) мы используем два множества переменных, sk и tk, чтобы
различать между собой циклы 1-подмножеств и 2-подмножеств
(буква s применяется для единичных подмножеств, а буква t —
для двухэлементных подмножеств). Это различие отражено в за-
записи Z (S^p1'2); sk, tk) циклового индекса группы Sp1'2). Итак, если
подстановка а из Sp индуцирует подстановку а" из Sp2\ то вклад„
подстановки а в Z (Sp'2)) можно записать в виде
П s*kk(a)\ (Й t'k^
где r=(j). .-...-..
Пусть Е2 — единичная группа подстановок, действующая на
множестве Y = {0, 1}. Функция класса для группы Sp опреде-
определяется соотношением
m /п\ _ тт Jk '*> in о \ а\
Применяем лемму Редфилда (см. формулу G.2.3.)) к представле-
нию Esp группы SP. Тогда правая часть формулы G.2.3) равна
), где суммирование ведется по всем (неизоморфным) гра-
графам с р вершинами.
B)
Для каждой подстановки из Esp , имеющей вид (а'; @) A)),
выполняется равенство
А (а'; @)A)) = П 2'ь1а'\ G.2.17)
Следовательно, левая часть соотношения G.2.3) равна

200 ГЛ. 7. СУПЕРПОЗИЦИЯ
Но это выражение есть просто Z (£(р'2); «ь 2). И мы пришли
к утверждению, полученному Робинсоном [3].
Теорема. Сумма цикловых индексов всех графов с р вершинами
дается формулой
2Z(G) = Z{S^2\ sk, 2). G.2.18)
Еще один вариант формулы G.2.18) получается в том случае,
когда каждое tk в Z (iSp1' 2)) заменяется на 1 + tk. Мы имеем сумму
цикловых индексов вершинно-реберных групп Гол (G) всех гра-
графов с р вершинами:
г№Л); **. 1 + <*). G.2.19)
7.3. ГРАФЫ И ОРГРАФЫ
В этом параграфе мы покажем, как графы и орграфы можно
рассматривать в виде «суперпозиций» и, следовательно, как их
можно перечислять с помощью теоремы перечисления Редфилда.
Сначала мы заметим, что формулу G.1.7) можно использовать
для подсчета некоторых взаимно однозначных функций. Напомним
(см. параграф 6.6), что ВА* обозначает ограничение степенной
группы ВА на подмножество всех взаимно однозначных функций.
Следствие. Если А и В — группы подстановок степени п, то
число орбит, определяемых ограничением степенной группы ВА*,
равно Z (А) П Z (В).
Доказательство получается с использованием соотношения
G.1.7) для т = 2. В самом деле, каждый класс эквивалентности
B, /г)-матриц, эквивалентных по столбцам, является взаимно
однозначной функцией, отображающей одно множество объектов
(первую строку матрицы) в другое (во вторую строку матрицы).
Такие классы эквивалентности являются эквивалентными отно-
относительно групп А и В тогда и только тогда, когда соответству-
соответствующие им взаимно однозначные функции принадлежат одной
и той же орбите группы ВА*.Я
Найдем тзперь число gPi q графов с р вершинами и q ребрами.
Чтобы достичь этого, обозначим, как обычно, через £р2) парную
группу с множеством объектов ХB\ где X = A, 2, . . ., р).
Пусть также Y = Yt [j Y2 будет множеством, состоящим из
/р\
г = I „ I целых положительных чисел, причем Yx = {1, 2, . . ., q}
и Yz = {q + 1, . . ., г}. Если у группы Sq множеством объектов
является Yу, а у группы Sr_q — множество Y2, то мы можем
образовать произведение S4Sr.Q, имеющее цикловой индекс
Z (Sq) Z (Sr.4). Взяв А = £р2) а В = SgSr.q, можно показать,

7.3. ГРАФЫ И ОРГРАФЫ 201
что орбиты ограниченной степенной группы являются как раз
изоморфными классами графов с р вершинами и q ребрами. Каж-
Каждая взаимно однозначная функция /: Х<2> ->■ Y представляет
граф с множеством вершин X, и в этом графе вершины i и / смежны
только в том случае, когда / {i, /} есть элемент множества Yx.
Ясно, что эти функции принадлежат одной и той же орбите
группы ВА* тогда и только тогда, когда они представляют изо-
изоморфные графы. Следовательно, как заметил Редфилд, графы
могут быть перечислены с помощью П -произведений.
Теорема. Число (р, д)-графов равно
q), G.3.1)
Редфилд, используя формулу, подобную G.3.1), смог вычислить
числа р-вершинных графов (р sg 7), не имеющих изолированных
вершин. Он, если применять терминологию Уайтхеда и Рас-
Рассела [1], рассматривал р-вершинные графы как «симметричные
антирефлексивные двоичные отношения над областями из р эле-
элементов». Точной формулы, такой, как D.1.9), для Z (Sp2)) он не
получил. Но парную группу можно представить в виде производ-
производной группы. Поэтому Редфилд имел возможность воспользо-
воспользоваться следствиями из своей теоремы декомпозиции, чтобы вывести
подходящую формулу для циклового индекса Z (Sp2)). Для парной
группы справедливо соотношение
S^^S^S,.,). G.3.2)
Доказательство зтой формулы мы опускаем, но заметим, что сте-
степень каждой ее части равна (р2) (ср. с формулой G.2.15) для
Ъ (SJ(S2S3))). Таким образом, теорема декомпозиции была основ-
основной частью перечислительной техники Редфилда. Сделаем краткие
замечания, относящиеся к выводу соответствующих формул для
ориентированных графов. Так как
S[P2]=SP/(E2SP_2), G.3.3)
то цикловой индекс Z (S}?1) редуцированной упорядоченной пар-
парной группы можно найти с помощью двух следствий из теоремы
декомпозиции. После этого получается формула для числа dPt я
орграфов с р вершинами и q дугами:
), G.3.4)
г = р (р — 1).

202 ГЛ. 7. СУПЕРПОЗИЦИЯ
7.4. ОБОБЩЕНИЕ ТЕОРЕМЫ ПЕРЕЧИСЛЕНИЯ РЕДФИЛДА
В этом параграфе мы построим более общую группу подстано-
подстановок, чем та, которая требовалась при доказательстве теоремы
перечисления Редфилда, и дадим точную формулу для числа
орбит в этой новой группе. Полученный результат позволит нам
перечислить графы, являющиеся суперпозициями взаимозаменя-
взаимозаменяемых экземпляров одного и того же графа (см. Палмер и Робин-
Робинсон [1, 2]), а также даст новый подход к перечислению мульти-
графов (см. Палмер [4]).
Пусть А ж В — группы подстановок с множествами объектов
X = {1, 2, . . ., то} и Y = {1, 2, . . ., п) соответственно, и пусть
W — совокупность всех (то X и)-матриц, в которых элементы
каждой строки попарно различны и являются объектами множе-
множества Y. Матричная группа [А; В] групп А и В действует на
множестве всех классов эквивалентности, определяемых экви-
эквивалентностью по столбцам, рассматриваемой на совокупности W.
Это действие осуществляется в соответствии со следующим прави-
правилом. Для каждой подстановки а из А и каждого набора plt p2,
. . ., р,„ из то подстановок, принадлежащих группе В, существует
подстановка в [А; В], обозначаемая [а; рх, Р2, • • •, РтЬ такая,
что класс эквивалентности, содержащий матрицу [г%], преобра-
преобразуется этой подстановкой в класс, которому принадлежит матрица
l$iwai,i ]• Другими словами, сначала подстановка а переставляет
строки, а затем каждая подстановка Р,- переставляет элементы
в г-й строке. Например, пусть А = S2 и В = £2 [Е2], так что
матричная группа [S2; S2 [E2]] преобразует B, 4)-матрицы. Если
возьмем а = A2), р\ = A) B) C) D) и Р2 = A2) C4), то под-
подстановка [a; Pi, p2] преобразует класс, содержащий матрицу
1 2 3 4\
3 1 4 2Г
3 14
в класс, которому принадлежит матрица ■ „ . , „
Из определения следует, что если А = Ет — единичная группа
подстановок, то число N [Ет; В] орбит матричной группы равно
П-произведению, примененному к то экземплярам циклового ин-
индекса Z (В). Значит, если В является группой графа G, имеющего
порядок п, то N \Ет\ Г (G)] есть число суперпозиций, составлен-
составленных из то экземпляров графа G. С другой стороны, N [Sm; Г (G)]
есть число суперпозиций, в которых копии графа G взаимозаменя-
взаимозаменяемы. Для иллюстрации рассмотрим простую цепь Р4 порядка 4.
Все восемь графов, являющихся суперпозициями двух экземпля-
экземпляров цепи P4i даны на рис. 7.4.1. Сплошные и штриховые ребра
используются для того, чтобы можно было отличить друг от друга

7.4. ОБОБЩЕНИЕ ТЕОРЕМЫ ПЕРЕЧИСЛЕНИЯ РКД<ЬИЛДА
203
два экземпляра цепи Р4- Если в графах, изображенных на ри-
рисунке, взаимозаменить сплошые и штриховые ребра, то два по-
последних графа на рис. 7.4.1 «поменяются местами», а остальные
«перейдут» в себя. Итак, рис. 7.4.1 подтверждает, что N [Е2;
Г (Pt)] — 8 и N [S2; Г (Р^] = 7; это последнее число вычислено
ниже (см. формулу G.4.13)).
Чтобы сформулировать теорему, дающую формулу для числа
N 1А; В] орбит матричной группы [А; В], нам потребуются
несколько определений. Как обычно, R обозначает кольцо поли-
полиномов, зависящих от переменных su s2, . . ., sn. Для каждого
целого положительного числа г определим функцию Jг: В. -+■ R.
Рис. 7.4.1 Суперпозиции двух простых цепей четзертого порядка.
Удобно сначала определить последовательность функций dlt
d2, . . ., зависящую от целых чисел г и к ^ 1. Для каждого i
положим , :. ,
\ ski/k, если i\r и (r/i,/с) = 1, ;„/
d, — \ п G.4.1)
(О в ином случае. '
Используя, как обычно, St для обозначения симметрической
группы /-Й степени, определим Jr (s'k) с помощью равенства
?/; dlt d2, . . ., dj). G.4.2)
Заметим, что для произвольного простого числа р формула
G.4.2) может быть переписана в следующем виде:
О, если р\к и p<fj,
О ! к/ (р-1)/Р4") кШР) I Р//р), если р| * и р | /,
t//p]
21 {i\^p-1)tstkpslk-tp)l{(i-~tp)\t\pt), если pfft.
G.4.3)
Затем определяем функцию 3г для одночленов s[«s/« . . . s|":
G.4.4)

204 ''ii(l ГЛ. 7. СУПЕРПОЗИЦИЯ
Далее функция Jr распространяется по линейному закону на
все кольцо R. В частности,
^ () G.4.5)
рев \*=i /
A(ZE)) = ZE). G.4.6)
Теперь мы определяем произведение для всей совокупности
функций—{Л}:
4-4°... А< (Z (В)) = A' (Z (В)) и Jli (Z (В)) и... и J1:1 (Z (В)),
G.4.7)
где каждое Jl/ (Z (В)) представляет собой сокращение для (J -про-
-произведения длины i,, т. е. J'f (Z (В)) = Л (Z (В)) [}... U Jr (Z (В))
и «сомножитель» Jr(Z(B)) берется г, раз.
Теорема. Число орбит N [А; В], определяемых матричной
группой [Л; В], равно
N[A; B]-[Z(A; J,, /2l . . ., Jm)Z(B)]Srl. G.4.8)
Применим эту теорему к нахождению числа TV [S2; Г (Р4)]
Графов, являющихся суперпозициями двух взаимозаменяемых
экземпляров цепи Р4-
Цикловые индексы групп Г (Р4) и S2 имеют вид
Z(Г (P4)) = i-(«* + *«), . . ' G.4.9)
Z E2; Л, Л) = ~?(А + Л). ' ' G.4.10)
Из G.4.6) следует, что J1(Z(T(Pi))) = Z(T(Pt)), а из G.4.3)
получаем
/2 (Z (Г (Pt))) =. ± (Sj + 6sje8 + 3s| + 2я4). G.4.11)
Легко видеть, что
= Т {т B4si + 8s2) + Т (si
Полагая в этом выражении s* = 1 для всех А, приходим
к равенству
7V[S2; Г(Р4)] = 7, G.4.13)
которое согласуется с рис. G.4.1).

7.4. ОБОБЩЕНИЕ ТЕОРЕМЫ ПЕРЕЧИСЛЕНИЯ РЕДФИЛДА 205
Таблица 7.4.1
Суперпозиции циклов
л
3
4
5
6
■V [£,; Dn]
1
2
4
12
l
2
4
10
N \E,; Dn]
1
5
24
391
N [Sy, Dn)
1
3
9
89
Числа суперпозиций двух и трех циклов порядков п =s 6
даны в табл. 7.4.1. Заметим, что если составляющие (конститу-
энтные) циклы взаимозаменяемы, то существуют две пары экви-
эквивалентных суперпозиций двух циклов шестого порядка.
Используя матричную группу, можно также подсчитать число
тр ч мультиграфов с р вершинами и q ребрами. Пусть G является
объединением К2 [} Кр_2 двух непересекающихся (по верши-
вершинам) графов. Тогда суперпозиции, построенные с использованием q
взаимозаменяемых экземпляров графа G, соответствуют в точности
указанным выше мультиграфам. Так как Г (G) = S2SP_2, то мы
получаем следующее утверждение из статьи Палмера [4].
Теорема. Число mPi q мулътиграфов с р вершинами и q ребрами
дается формулой
mp,q=[Z(Sq; А, /4) . . ., /,)(Z(S,)Z(Sp_8))l,fc-i. G.4.14)
Сейчас мы набросаем некоторые детали, относящиеся к на-
нахождению числа тъл. Прежде всего формула G.2.9) дает произ-
произведение Z E2) Z E3), a Z (iS4; Jх, /2> ^з> J*) получается из соотно-
соотношения D.1.10). Используя далее равенства G.4.1), . . ., G.4.5),
имеем
/, (Z E2) Z E,)) = \ (s\ + 10sJsf + l5slS| + 2s\sa + 2s2
/, (Z (,S2) Z E,)) = -jg- (*J + 20e|s, + 4s3s2 + 8Sas3 + 3Sls|), G.4.15)
Jt (Z (S2) Z E,)) = -L- (s\ + 10s»sf + 15slS» + 30slS4 + 2s\s3 + 2s2s3).
Применяя формулу G.4.7), определяющую произведения, на-
находим

206 . ! 'Л ч f Л. 7. §|ШЕРЛ03ИЦЙЯ
.1==40, G.4.16)
Следовательно, т5>4 = —j- A07 + 162 + 40 + 69 + 30) = 17.
Существенным преимуществом описанного метода является то,
что, во-первых, при его использовании нужны только формулы
для цикловых индексов симметрических групп, а, во-вторых,
числа mPjq вычисляются непосредственно.
7.5. ОБЩИЕ ГРАФЫ
В общем графе допускаются и кратные ребра, и кратные петли.
По определению каждая петля вносит в степень соответствующей
вершины вклад, равный 2. В данном параграфе мы покажем,
как Рид [1] смог перечислить общие графы со специальной после-
последовательностью степеней вершин (он осуществил это, найдя вза-
взаимно однозначное соответствие между указанными графами и не-
некоторыми суперпозициями).
Сначала нам понадобится формула для числа 2-раскрашенных
мультиграфов, т. е. таких мультиграфов, у которых множество
К",<! '■
Рис. 7.5.1 Два двудольных графа. ■ . . •;
вершин разбито на два подмножества — одно подмножество со-
состоит только из красных вершин, а другое — из синих, причем
каждое ребро графа соединяет некоторую красную вершину
с синей вершиной. На рис 7.5.1 показаны 2-раскрашенные графы
с двумя красными вершинами, имеющими степень 3, и тремя
синими вершинами, имеющими степень 2. Следующая теорема
дает формулу для числа 2-раскрашенных графов со специальными
степенями вершин.
Теорема. Число 2-раскрашенных графов, которые для каждого
целого положительного числа к имеют ровно т> красных вершин
степени к и ровно bk синих вершин степени к, дается формулой
G.5.1)

7.5. ОБЩИЕ ГРАФЫ 207
Например, легко показать, что Z(S3 IS21) f]Z (S2 [S3]) = 2.
Это согласуется с рис. 7.5.1.
Доказательство. Пусть G1 — граф, содержащий для каждого
k ровно rk компонент связности, представляющих собой полные
графы с к вершинами. Аналогично, пусть граф G2 имеет для каж.
дого к ровно bk компонент, являющихся полными графами по,
рядка к. Замечаем, что число ребер в 2-раскрашенных графах
подлежащих перечислению, равно <? = 2 кгь = 2 ^*- Следова-
Следовала к
тельно, графы G1 и G2 имеют одно и то же число вершин, а именно q.
Если компоненты графа Gx интерпретировать как красные вер-
вершины, а компоненты графа Ga —как синие вершины, то каждая
суперпозиция графов G1 и G2 соответствует, очевидно, некоторому
2-раскрашенному графу. Это соответствие является, как легко
видеть, взаимно однозначным, и, следовательно, число 2-раскра-
2-раскрашенных графов равно Z (Gx) П Z (G2). Далее группы Г (Gx) и
Г (G2) могут быть представлены в виде произведения веночных
произведений; это приводит к формуле G.5.1).^
Перейдем к поиску формулы, дающей число таких общих
графов, которые для всякого целого к имеют ровно dk вершин
степени к. Следовательно, число ребер в каждом из этих графов
равно 9 = у2 kdk. Предположим, что все вершины в таком графе
раскрашены в красный цвет, и затем на каждом ребре поставим
новую синюю вершину. Получим 2-раскрашенный граф, в котором
все q синих вершин имеют степень 2. Указанное соответствие
между общими графами и 2-раскрашенными графами является,
очевидно, взаимно однозначным. Поэтому мы приходим к следу-
следующему результату.
Следствие. Число общих графов, которые для каждого к имеют
в точности dk вершин степени к, дается формулой
S2\). G.5.2)
Например, число общих графов с двумя вершинами степени 3
равно Z {S2 [Ss]) П Z (S3 \S 21) = 2. Соответствующие этому
числу два общих графа можно получить путем изъятия вершинх
степени 2 у графов, изображенных на рис. 7.5.1.
Формулы для подсчета общих однородных графов и общих
кубических графов получаются сразу же, как частные случаи
формулы G.5.2).
1 Вершина выбрасывается, а «концы» ребер, инцидентных ей, «склеи-
раются»; из двух ребер получается при этом одно ребро. — Прим. перев.

208 ГЛ. 7. СУПЕРПОЗПЦПя'
Следствие. Число общих п-вершинных графов, являющихся
однородными графами степени к, равно
Z(Sn[Sk])f]Z(Snk/2[S2\). G.5.3)
Следствие. Число общих кубических графов с 2п вершинами
находится по формуле
Z(S2n[S3])f\Z(S3n[S2}). G.5.4)
В формулах, выведенных выше, мы имели дело с перечисле-
перечислением непомеченных графов. Рид [11 с большим успехом применил
суперпозиционную теорию к перечислению различных типов
помеченных графов. Из формулы G.5.4), например, довольно
просто следует, что число общих кубических графов с 2и помечен-
помеченными вершинами равно
Z(E2n[S3]HZ(S3n[S2}). G.5.5)
Нашей следующей целью является получение формул для
перечисления помеченных кубических графов, не имеющих петель
и кратных ребер. Соответствующий результат будет выражен
в форме, удивительно напоминающей соотношение G.5.4). Сна-
Сначала мы докажем более общие результаты; после чего случай
кубических графов получается мгновенно.
Как и в формуле B.6.1), разность Z (Ak) — Z (Sk) будем обозна-
часть через Z (Ak — S/,). Будем также использовать обозначения
из гл. 4, относящиеся к цикловому индексу веночного произ-
произведения. В частности, если Р1 и Р% — многочлены от переменных
sx, s2, . . ., то Рг [Р2] обозначает многочлен, получаемый путем
замены каждой переменной sk, принадлежащей многочлену Рг,
таким многочленом, который строится из Р2 с помощью следующей
процедуры: индексы всех переменных, входящих в Р2, умно-
умножаются на к. Значит, выражения вида Z (Sq) \Z (A2 — S2)]
и Z (S3n) [Z {A 2 — S2)] уже определены.
Три нижеследующих утверждения получаются путем примене-
применения теоремы перечисления Пойа с подходящими группами и пере-
перечисляющими рядами для фигур и, кроме того, путем представления
соответствующих коэффициентов в виде (~| -произведений (подроб-
(подробности см. у Рида [1]). Эти три результата и их следствия поз-
позволяют перечислить три вида помеченных графов с заданным
разбиением и три вида помеченных кубических графов: A) мульти-
графы, B) общие графы, не имеющие кратных ребер, C) графы.
Теорема. Число помеченных мулътиграфов с dk вершинами
степени к и, следовательно, с д = —^ЫА ребрами дается
формулой
(П^ G.5.6)

7.5. ОБЩИЕ ГРАФЫ • 209
Применим теперь эту теорему для кубических графов с In вер-
вершинами. Получаем следующее утверждение.
Следствие. Число помеченных кубических мулътиграфов с 2п
вершинами равно
Z(Е2п [53]) П Z ESn) [Z (A.2-S2)]. G.5.7)
Исключая кратные ребра, но допуская петли, получаем еще
одну теорему.
Теорема. Число помеченных общих графов, которые не имеют
кратных ребер и содержат ровно q ребер и dk вершин степени к,
дается формулой
Z (nEdk[Sk]^nZ(Aq-Sq)[Z(S2)\. G.5.8)
Применив эту формулу к кубическим графам, получаем
Следствие. Число помеченных общих кубических графов с 2п
вершинами и без кратных ребер равно
Z (Е2п [5,1) П Z (А3п - 5а„) [Z E8I. G.5.9)
Наконец, запрещая и петли, и кратные ребра, выводим сле-
следующие утверждения.
Теорема. Число помеченных графов с q ребрами и dk вершинами
степени к равно
TL} G.5.10)
Следствие. Число помеченных кубических графов с 2п вершинами
и, следовательно, с Зп ребрами находится по формуле
-5а)]. G.5.11)
Вычисление выражений G.5.7), G.5.9) и G.5.11) сопряжено
со значительным количеством выкладок. Однако Риду [1] уда-
удалось получить несколько общих результатов, относящихся к пре-
преобразованию этих соотношений и к их оценке. Например, в случае
формулы G.5.11) он доказал следующее утверждение.
Следствие. Число помеченных кубических графов с 2п вершинами
равно
(-I)''/! . /7с19ч
6 Ck-j)\Bk-i)\i\(n-k)\ (j)
/, * '
кроме того, при достаточно больших значениях п это число асимп-
асимптотически равно
F">!е . G.5.13)
288" {Зп) ! \ • 1 >

210 ГЛ. 7. СУПЕРПОЗИЦИЯ
Дальнейшее обсуждение проблемы вычисления [~| -произведе-
-произведений, а также рассмотрение методов, использующих S-функцш
можно найти у Рида [8]. Другие асимптотические результат^
излагаются в гл. 9.
УПРАЖНЕНИЯ
7.1. Сколько суперпозиций можно получить, используя три
ориентированных цикла шестого порядка?
7.2. Найти две группы подстановок А ш В, таких, чтобы декомпо-
декомпозиция U -произведения Z (А) [) Z (В) (в сумму цикловых индексов)
была неоднозначной. (Редфилд [1])
7.3. Выразить Z (A; Jlt . . ., Jm)Z (В) в виде суммы N [А; В]
цикловых индексов. (Палмер и Робинсон [2])
7.4. Сколько орбит, состоящих из взаимно однозначных функций,
определяют ограниченные степенные группы Е ш, Е^т и S^*m ?
7.5. Парная группа Sp2) и производная группа SP/(S2SP_2)
идентичны.
7.6. Используя соотношение G.2.6), вычислить Z (Se/(S2S4)).
7.7. Сколько существует графов, являющихся суперпозициями
трех взаимозаменяемых экземпляров ориентированного цикла
шестого порядка?
7.8. Вычислить число (а) общих кубических графов порядков
4, 6 и 8, (Ь) помеченных кубических графов тех же порядков.
7.9. Нарисовать 12 суперпозиций двух циклов шестого порядка
и 10 суперпозиций с взаимозаменяемыми циклами.
7.10. Коэффициент при хт в Z (Sn/B, 1/A — х)) равен N [Sm;
В]. Следовательно, производящая функция для суперпозиций,
построенных с использованием взаимозаменяемых экземпляров
произвольного графа G порядка р, равна Z (Sp/T (G), 1/A — х)).

Глава 8
Not merely a chip of the old
block, but the old block itself.
Edmund Burke l
БЛОКИ
В 1950 году на заседании Американского Математического обще-
общества физик-теоретик Г. Э. Уленбек прочитал лекцию, посвящен-
посвященную памяти Гиббса. Лекция называлась «Нерешенные задачи
статистической механики», и наряду с другими задачами в ней
была сформулирована задача перечисления блоков. Впоследствии
Риддел [1] и Форд с Уленбеком [1] перечислили помеченные
блоки (см. § 1.3). Однако лишь Робинсону [3] удалось решить
задачу перечисления непомеченных блоков.
Так как в гл. 4 мы уже перечислили связные графы, то для
перечисления блоков достаточно найти число связных графов,
имеющих хотя бы одну точку сочленения. Обычные производящие
функции для этой цели не подходят: они не несут достаточного
количества информации о структуре графов. Подходящая в этом
случае техника включает использование сумм цикловых индексов
групп графов (см. § 7.2). Подобный прием неявно содержался
еще в редфилдовской теореме декомпозиции (см. Редфилд [1]),
но был полностью развит только Робинсоном в его решении задачи
перечисления непомеченных блоков. Метод Робинсона можно
также использовать для перечисления графов с данными блоками,
связных графов без висячих вершин, ациклических орграфов и
других видов графов. Материал данной главы возник по существу
благодаря работам Робинсона.
8.1. ОБОБЩЕНИЕ ЛЕММЫ РЕДФИЛДА
Для доказательства теоремы композиции, содержащейся в § 8.3,
нам нужно несложное обобщение леммы Редфилда (см. формулу
G.2.3)). Пусть А — группа подстановок с множеством объектов
X, и пусть R — коммутативное кольцо, содержащее кольцо
1 Не просто копня отца, а сам живой отец (Эдмунд Бёрк), — Прим,
перев.

212 ГЛ. 8. БЛОКИ
рациональных чисел. Пусть функция ф отображает декартово
произведение А X X в R и удовлетворяет следующему условию:
для любых подстановок а и Р из Л и любого объекта х из X
если ссх = $у = х, то <р (а, х) = <р (РаР, у). (8.1.1)
Орбиту, определяемую группой А и со держащую, объект х,
обозначим через х. Положим А (х) = {а £ А\ах = х}. Тогда
новая лемма может быть сформулирована следующим образом.
Лемма. Для всякой функции <р, удовлетворяющей условию
(8.1.1), справедливо тождество
<р(а, *). (8.1.2)
)
Доказательство этого утверждения проводится так же, как и дока-
доказательство формулы G.2.3): надо поменять порядок суммирования
в левой части соотношения (8.1.2). Условие (8.1.1) позволяет
тогда вместо суммирования по всем элементам из X применить
суммирование по орбитам, определяемым группой А в множе-
множестве Х.н
Заметим, что тождество (8.1.2) справедливо и в том случае,
когда X — бесконечное счетное множество; при этом требуется,
чтобы все участвующие в рассмотрении суммы были определены.
Если г|) — функция класса для группы А, то <р (a, x) = ty (а)
и условие (8.1.1), очевидно, выполняется; соотношение (8.1.2)
переходит тогда в формулу G.2.3) из леммы Редфилда.
8.2. КОМПОЗИЦИЯ ГРУПП
Чтобы сформулировать теорему композиции, приводимую
в § 8.3, необходимо обобщить определение композиции (или веноч-
веночного произведения) групп подстановок. Мы дадим также формулу
для циклового индекса этой новой группы, обобщив формулу Пойа
(см. соотношение D.3.15)).
Как отмечается в книге Харари [1], стр. 196, любой граф G
можно представить в виде: G = nlGl [} n^Gi \J ■■• [} nrGr, где
ni — число компонент графа G, изоморфных графу Gt. В этом
случае группу графа G можно записать как произведение компо-
композиций соответствующих групп:
Г(С) = П5 [Г(У. (8.2.1)
Например, граф 2К1Ъ, [} ЗЛГ2, изображенный на рис. 8.2.1,
имеет следующую группу автоморфизмов:
Г B* х,, U ЗК2) = E, [ЗД) E, [5,]). (8.2.2)

-mm
8,2. КОМПОЗИЦИЯ ГРУПП 213
Пусть Gl = KlinGi—К2- Тогда всякая функция /, отобра-
отображающая множество X = {1, 2, 3, 4, 5} в Y = {1, 2}, соответст-
соответствует естественным образом некоторому графу, компонентами
которого являются графы К1Л и Кг. Например, любая функция
Д отображающая два элемента из X в 1, а остальные три — в 2,
соответствует графу 2GX U 3G2. Положим / A) = / B) = 1 и
f C) = / D) = / E) = 2. Тогда подстановки а, действующие на X
и такие, что
/(*) = /(ах) (8.2.3)
для всех х из X, образуют группу, идентичную произведению
S2i>3. Эта группа обозначается через Sb (/), потому что она со-
Рис. 8.2.1 Граф 1КЪ 2 U ЗКг.
стоит из таких подстановок группы Sb, которые оставляют непод-
неподвижной функцию /. Группа Sb (/) показывает, какие компоненты
графа 2GX |J 3G2 можно переставлять друг с другом. Памятуя
об этом примере, мы сейчас займемся обобщением композиции
групп.
Пусть А — группа подстановок с множеством объектов X =
= A, 2, . . ., в}, и пусть / — функция, действующая из X в
Y = {1, 2, . . ., т}. Подгруппа А (/) группы А определяется
следующим образом:
Л (/) = {а6 Л |Vs6* (/(*) = /<«*))}. (8.2.4)
Если для каждого i из Y положить Xt = f'1 (i), то a (Xt) = Xt
при всяком i £ Y и любой подстановке а £ А (/). Пусть Bit
i = 1, . . ., т, обозначает некоторую группу подстановок с мно-
множеством объектов Yj. Тогда обобщенная композиция групп, обо-
обозначаемая через A (f) [Вх, . . ., Вт\, имеет своим множеством
т
объектов объединение U (X,- X Yt). Для любой подстановки
а £ А (/) и любого набора Xj, . . ., xm функций, таких, что
х,-: Xt ->- Bh i = 1, . . ., т (т. е. т,- (х) является подстановкой
группы Bt), существует подстановка в группе А (/) [Blt . . ., В1П],
обозначаемая (а; хх, . . ., тш) и действующая на упорядоченные
пари (х, у) в соответствии с правилом:
(а; хь . . ., хт)(х, у) = (ссх, %1{х)у), (8.2.5)
всякий раз, когда (х, у) принадлежит X, X Yt. Нетрудно про-
проверить, что так определенные подстановки действительно обра-
образуют группу относительно умножения. Группа A {f)[Bu . . ., Bm\t

214 гл. 8. блока
если говорить образно, переставляет экземпляры множеств Yh
i = l, . . ., т, причем для каждого элемента множества X,
берется по одному экземпляру. Экземпляры множества Yt пере-
переставляются между собой с помощью подстановок из А (/), в то
время как элементы каждого экземпляра переставляются незави-
независимо, с использованием групп Bt.
Так как для каждого i выполняется равенство: a (Xt) = X,,
то при всяком к мы можем определить jk (а, Х(-) — число циклов
длины к, содержащихся в ограничении подстановки а на множе-
множество Хг Обобщение формулы D.3.15) можно тогда дать в следу-
следующей форме.
Теорема. Цикловой индекс обобщенной композиции групп дается
соотношением
Z{A(f)[Bu ..., Вт])~
т
= I Л if) I 2 П П (Z (Bh sk, s2k, s3k, . . .))'* (a' *'>. (8.2.6)
aeA (/) 1=1 k
Заметим, что если т = 1, то Z (А (/) [BJ) = Z (А (/)) [Z EJ]
и формула (8.2.6) преобразуется в формулу D.3.15). Доказатель-
Доказательство соотношения D.3.15) можно приспособить для доказатель-
доказательства равенства (8.2.6).
A.1) 11.3) B.1) B.3) C.1) D,1) E,1)
A,2) B.2) C.2) D.2) E,2) ■
Рис. 8.2.2 Граф 2ffll2 U ЪКг с множеством вершин (Х^ X Ух) U (Х2 X К«).
Для того чтобы проиллюстрировать теорему, вернемся к при-
примеру, рассмотренному выше, в котором А = Sb, f A) = / B) = 1
и / C) = / D) = / E) == 2. В этом случае Хг = {1, 2} и Х2 =
= {3, 4, 5}. Возьмем Вг = Г (Kli2) = 515,иВ! = Г (К2) = S2
с множествами объектов У\ = {1, 2, 3} и У2 = {1,2} соответст-
соответственно. Тогда множеством объектов группы 55 (/) [5152,52]
будет множество (Хх X Yx) [} (Х2 X Y2) и упорядоченные пары
из него сопоставляются вершинам графа 2ATli2 \j 3K2 так, как
указано на рис. 8.2.2.
Каждая функция тг: Хг ->■ Г (Kli2) связывает с каждым
экземпляром графа К1Л некоторую подстановку из Т(К1г);
функция т2: Х2 ->■ Г (К^) делает то же самое с графом К2. Пред-
Предположим, что (а; т1, т2) £ Sb (/) [S^^, 52]. Из равенства (8.2.5)
следует, что тг A) и хх B) переставляют вершины двух экземпля-
экземпляров графа Kh2, а т2 C), х2 D) и т2 E) переставляют вершины трех

g.3. ТЕОРЕМА КОМПОЗИЦИИ 215
экземпляров графа К2. Тогда а переставляет компоненты графа
1К\,г U ЗЛГ2 между собой. Таким образом, мы видим, что
Г BKlt 8 U ЪКг) = Sb (/) [S&, 581 (8.2.7)
Наконец, из формулы (8.2.6) следует, что цикловой индекс
группы этого графа имеет вид
Z E6 (/) [SxSt, St]) = A/2 ! 3 1) {(Z (SiSj? + Z E,58; sa> s4)} X
X {(Z (St)f + 3Z (S8) Z (S2; s2, s4) + 2Z E8; s3, s,)}.
Справедливость приведенного соотношения легко доказать, при-
применив формулы D.3.14), B.2.14) и (8.2.2).
8.3. ТЕОРЕМА КОМПОЗИЦИИ
Для всякого множества Ц6 графов будем обозначать через
Z {Ш) сумму цикловых индексов групп всех графов из множества
Ш (ср. с формулой G.2.18), в которой рассматривалась сумма
цикловых индексов групп всех графов порядка р). В частном
случае каждая из этих групп может быть обобщенной компози-
композицией групп, построенной из подгруппы группы А и последова-
последовательности групп Вг, В2, Bs, .... Мы покажем здесь, как полу-
получается Z (s5#), если известны цикловые индексы Z (А) и Z (Bt),
* = 1, 2, 3, ... .
Рассмотрим важный частный случай. Пусть А — группа под-
подстановок с множеством объектов X = {1,2, . . ., п}. Пусть Y —
непустое подмножество множества целых положительных чисел.
Для каждого i £ Y возьмем группу подстановок Bt с множеством
объектов Yt. Практически это означает, что каждый элемент i
из Y соответствует некоторому графу с группой Bt и множеством
вершин У,-. В наших рассмотрениях мы требуем, чтобы в совокуп-
совокупности {Yt} одна и та же фиксированная мощность была не более
чем у конечного числа множеств Yt, так что сумма ^jZ (B^, взятая
по всем i £ Y, определена.
Для каждой функции /: X -у Y определяем, как и выше,
подгруппу А (/) группы А- Далее, на множестве таких функций
(из X в Y) вводим отношение эквивалентности: две функции / и g
называются эквивалентными относительно группы А, и это запи-
записывается в виде / ~ g, если для некоторой подстановки а из А
и для всех х £ X выполняется равенство
f(x) = g(ax). (8.3.1)
Другими словами, / ■—g означает, что функции / и g принадлежат
одной и той же орбите степенной группы ЕЛ- Обозначим множество
классов эквивалентности (множество орбит) через 5F. Свяжем

1
216 ГЛ. 8. БЛОКИ
теперь с каждой функцией / некоторую обобщенную композицию
групп: если / (X) = {ilt . . ., im}, то соответствующая группа
строится из групп А (/) и В[,, . . ., Bt и может быть обозначена
через А (/) \В,^ . . ., Bt ]. Если / и g эквивалентны, то А (/)
и A (g) являются идентичными группами подстановок. Действи-
Действительно, если / (х) = g (ух) для некоторой подстановки у из А
и при всех х £ X, то у A (f)y'1 = A (g), т. е. группы А (/) и
A (g) — сопряженные. Более того, группы А (/) [В,,, . . ., Bt ]
и A (g) [Btl, . . ., Bt \ — также идентичны. Значит, цикловые
индексы этих групп совпадают и мы можем естественным образом
определить цикловой индекс Z (F) произвольного класса экви-
эквивалентности F, принадлежащего множеству <£": полагаем Z (F)
равным цикловому индексу обобщенной композиции групп, опре-
определяемой произвольной функцией / из F. Введем обозначение:
Z (#")= 2 % (F). Тогда основной результат, содержащийся
в нижеследующей теореме, связывает Z (&~) с Z (А) и Z {Bt).
Напомним, что через Z (А) \У^2 (В,-)] мы обозначаем степенной
ряд, получаемый путем замены каждой переменной s^ в цикловом
индексе Z (А) на
^Z(B sk, sm, s3k, . . .), v.
где сумма берется по всем i £ Y. •
Теорема композиции. Сумма Z (&~) цикловых индексов полу-
получается посредством образования композиции циклового индекса
Z (А) относительно T]Z (Bt):
; ,;;i (8.3.2)
где суммирование ведется по всем i £ Y. •
Доказательство. Рассмотрим представление группы А в виде
степенной группы ЕА с множеством объектов Yx, т. е. А' = Z?4
и для каждой подстановки а из Л существует подстановка а* иа
А", такая, что
(a'f)x = f(ax) (8.3.3)
при любой функции / £ Yx и при всех х £ X.
Пусть R — кольцо степенных рядов, зависящих от перемен-*
ных Si, s2, s3, . . . и рассматриваемых над полем рациональны!
чисел. Определим отображение q>: А' X Yx —>- R с помощью фор-
формулы
<р(а\ /) = П П (Z(Bt; sk, s2k, . . .))>*(«• *<). (8.3.4)
ft 1§ЦХ)

«пашни»» • • эди—ва
8.4. СВЯЗНЫЕ ГРАФЫ "' 217
Можно убедиться в том, что ф удовлетворяет условию (8.1.1).
Но тогда, применяя лемму из § 8.1, имеем
ИГ 2 2 ч>(«',/) = 2И (Z)l-1 2 ф(«',/), (8.з.5)
где первая сумма, стоящая в правой части, берется по всем клас-
классам F па&~, а /есть некоторый элемент из F. Заметим, что, хотя
лемма из § 8.1 сформулирована только для того случая, когда
суммы конечны, она справедлива и в более общем случае: когда
все суммы определены. В соотношении (8.3.5) все суммы опреде-
определены, ибо мы ранее потребовали, чтобы одинаковая степень была
не более чем у конечного числа групп Bt.
Используя формулы (8.3.4) и (8.2.6), легко заметить, что пра-
правая часть равенства (8.3.5) равна Z {&~). Нетрудно также про-
проверить, что для всякой подстановки а из А
2 Ф(«\ /) = П ( 2 ВД; Sk, s2k, . . .)V*(a). (8.3.6)
Этим доказательство теоремы завершается.н
8/i. СВЯЗНЫЕ ГРАФЫ
Целью нашей является представление суммы цикловых индек-
индексов всех связных графов в виде функции от суммы цикловых
индексов всех графов. Этого можно достичь с помощью теоремы
композиции. Если 'З — множество всех графов, то из формулы
G.2.18) следует, что
со
Z(S0=2z(S(nll8); s*. 2). (8.4.1)
Поэтому мы можем считать, что Z (S?) нам известно. Теперь при-
применим еще один подход к нахождению Z (9), а именно такой под-
подход, который был применен при получении производящей функции
для связных графов. Пусть 6 — множество всех связных графов,
а множество §п состоит из всех графов, имеющих ровно п ком-
компонент. Рассмотрим симметрическую группу 5„, действующую
на множестве X, и все функции /: X -> Q. Каждая такая фучк-
ция представляет тот элемент из Зп, который имеет |/~х (G)|
компонент, изоморфных связному графу G из G- Ясно, что функ-
функции, эквивалентные относительно Sn, представляют один и тот же
граф из $п. Каждой функции / : X -»- 6 можно сопоставить
обобщенную композицию групп, являющуюся как раз группой
графа, представляемого функцией /. Для получения суммы Z С§п)
цикловых индексов всех неэквивалентных функций можем приме-
применить теорему композиции; приходим к следующему равенству:
(8.4.2)

218 ''"•"'" '"""'■■" ГЛ. 8. БЛОКИ
Суммируя его повеем п, имеем "'■" "'•' ■■-'■?] *'■'■■€' '
оо .
' Z($)=2Z(Sn)[Z(e% ' *■■■ (8.4.3)
11
2
1=1
Но так как
■• (8.4.4)
U=i ) ■ -■■• ,
см. формулу C.1.1)), то
I со -I ■;.'■-■■ :;
1 + Z (9) = ехр 2 (sk/k) \z (C01 • (8.4.5)
Используя идею Кэдогана [1], мы можем с помощью обращения
Мёбиуса разрешить соотношение (8.4.5) относительно Z (С)
(подробности см. у Робинсона [3]). Получаем следующее утвер-
утверждение.
Теорема. Если 'S и G — соответственно множество всех
графов и множество всех связных графов, то
-1 (8.4.6)
Применяя формулу (8.4.1), можем написать несколько первых
Яленов ряда Z (§}:
. Z (9) = Sl + sl + s2 + ± s» + 2Sls2 + -|- s3 + -| s\ + 4*;S,+
^ Si + .... ^ (8.4.7)
Подставляя это выражение в (8.4.6), имеем
Z (в) = % + -~ s\ + y s2 + \ s\ i i| *
|^ .S4+.... (8.4.8)
Заметим, что, полагая s* = 1 в тех частях рядов Z (9) а
Z (С), которые состоят только из слагаемых с общей «степенью»
сомножителей, не превосходящей 4, получаем числа 18 и 10; это
соответственно число графов и число связных графов с не более
чем 4 вершинами. Стоит также подчеркнуть, что, хотя формула]
(8.4.6) дает точное выражение для Z F), много проще вычислят^
Z (Q) непосредственно, используя равенство (8.4.5). Сделаем|
еще одно замечание. Пусть 6Р — множество всех связных р-вер^
шинпых графов и 'Sip) — множество всех таких графов, каждая»

8,5. СУММЫ ЦИКЛОВЫХ ИНДЕКСОВ КОРНЕВЫХ ГРАФОВ 219
компонента которых содержит не менее р вершин. Тогда ()
= 3? и Z FР) состоит как раз из тех слагаемых, входящих в
Ъ Ф (р)), которые имеют порядок р. Применяя теорему компози-
композиции, имеем
. (8.4.9)
Значит, Z (Ср) можно найти последовательно для каждого р.
8.5. СУММЫ ЦИКЛОВЫХ ИНДЕКСОВ КОРНЕВЫХ ГРАФОВ
Сейчас мы установим взаимосвязь между суммами цикловых
индексов для некоторой совокупности графов и соответствующей
совокупности корневых графов. Граф G можно сделать корневым,
взяв в качестве корня произвольную из его вершин. Поэтому
корневой граф можно рассматривать как упорядоченную пару
(G, и), где и — вершина графа G. Два корневых графа (G, и) и
(G, v) являются одинаковыми (изоморфными) тогда и только тогда,
когда вершины и и v принадлежат одной и той же орбите группы
графа G. Множество автоморфизмов графа (G, и) состоит из всех
автоморфизмов графа G, оставляющих вершину и неподвижной.
Однако для удобства мы не будем включать корень в множество
объектов, на котором действует группа рассматриваемого корне-
корневого графа. Обозначим через Ш произвольное множество графов,
а через Ж" —множество всех различных корневых графов, кото-
которые могут быть получены путем указания корня в графах из Ш-
Несколько злоупотребляя обозначениями, мы снова будем исполь-
использовать запись Z (Ш) и Z (Ш') для сумм цикловых индексов всех
графов из Ш и всех корневых графов из Ж'' ■ Для установления
взаимосвязи между Z (JB€) и Z (Ш1) можно применить лемму Ред-
филда (см. формулу G.2.3)).
Теорема. Сумма Z (£$') цикловых индексов для корневых графов
равна частной производной от Z (Ш) по первой переменной:
(8.5.1)
Доказательство. Легко видеть, что достаточно доказать теоре-
теорему для того случая, когда Ж состоит из одного графа G. Применяем
лемму Редфилда к группе графа G, беря в качестве функции класса
Ф(а) = Ш{*(а\ (8.5.2)
где а — произвольная подстановка из группы графа G. Тогда
левая часть формулы G.2.3) дает s1-dZ (G)/dsv а правая часть
равна stZ ()
Рассмотрим в качестве примера полный граф Кп. Его группа
ость Sn. Этот граф можно сделать корневым только одним спосо-

220 ГЛ. 8. БЛОКИ
бом, и группой соответствующего корневого графа является
»?rt_j. Следовательно, справедливо равенство
dZiS^/ds^ZiS^), (8.5.3)
которое можно также проверить с помощью соотношения B.2.5).
8.6. БЛОКИ
Сначала найдем сумму цикловых индексов всех корневых
блоков. Другими словами, если $ — множество всех блоков, то
мы ищем выражепие для Z {$')■ Этого можно достичь, представив
Z (&) через Z (Ж), а затем обращая полученное соотношение.
Используя теорему композиции, замечаем, что сумма цикловых
индексов всех связных корневых графов, у которых корни не
являются точками сочленения, дается формулой
Z(Я') №(&)].
Применяя еще раз теорему композиции, видим, что сумма цикло-
цикловых индексов всех связпых корневых графов, у которых корень
инцидентен в точности п блокам, равна
z (.<?„) R<f')M (&)]].
Суммируя это выражение по всем п и используя равенство (8.4.4),
получаем
f (Sk/k)[ZC8')[s1Z(e')]\). (8.6.1)
Так как Z (Gr) — dZ F) dsx, то, обращая формулу (8.6.1), можем
найти Z (Ж)- Однако, как и в случае определения Z (G), легче,
пожалуй, для получения Z {Ж) применять экспоненциальное
соотношение (8.6.1) непосредственно, как это продемонстрировано
дальше.
Обозначим через С'(р) множество всех корневых связных
графов, у которых всякий блок, содержащий корень, имеет не
менее р вершин. Так как у одновершинного графа нет блоков, то
Z(C'B)) = Z((?"). (8.6.2)
Если <%р — множество всех р-вершинных блоков, то Z($t'p)
состоит из всех таких слагаемых, входящих в Z (С'(р)), порядок
которых равен р — 1.
Пусть теперь 3£'р будет множеством всех корневых связных
/ьвершинных графов, каждый блок в которых содержит корень.
Действуя таким же способом, как при получении формулы (8.6.1),
находим
Q= exp If («*/*) [Z{Я',) [SiZ(&)]]}. (8.6.3)
U-i I

8.6. БЛОКИ , 221
Ясно, что .
)
Комбинируя соотношения (8.6.3) и (8.6.4), имеем
| — X (sk/k) [Z(&'Р) [SiZ(&)}]). (8.6.5)
Следовательно, если известны Z {Жр) и Z (С'(р)), то формулу
(8.6.5) можно использовать для получения Z F' (р + 1)). Но
Z {9H'pv\) состоит из всех слагаемых, входящих в Z(E'(p + 1))
и имеющих порядок р. Поэтому Z ($'р) можно определять после-
последовательно для всех р 5г 2. Наконец,
(8.6.6)
р-2
и суммирование начинается с р = 2 потому, что одновершинный
граф, в силу нашего соглашения, исключается из множеств $
и $'.
Пусть Z ($?р) |Sl=0 — ряд, который получается из Z($p) заме-
заменой каждого вхождения переменной sx нулем; другими словами,
Z (^p)|s, =o является таким вкладом в Z (J?p), который вносят
все автоморфизмы, не имеющие неподвижных вершин. Применяя
это обозначение, можем записать такое равенство:
(8.6.7)
Следовательно, нам осталось найти Z($P)|S|=O. Нам понадобится
следующее утверждение из работы Робинсона [3].
Теорема. Пусть у связного графа G существует автоморфизм,
не имеющий неподвижных вершин. Тогда граф G содержит един-
единственный блок, вершины которого при любом автоморфизме графа
G переставляются только между собой.
Мы имеем также равенство
o (8.6.8)
и, применяя теорему композиции, заключаем, что сумма цикло-
цикловых индексов всех связных корневых графов, корнями которых
являются блоки, равна Z {Ж) [stZ F')\-
Следовательно, в силу теоремы (8.5.1), вклад, вносимый
в Z (О) всеми автоморфизмами, не имеющими неподвижных

222 ГЛ. 8. БЛОКИ
вершин, равен в точности выражению, получающемуся из
Z C8) \svZ ((?")] в результате подстановки st = 0:
|Sl=0. (8.6.9)
На практике, конечно, можно пользоваться равенством
B(^)|5,=о)М(С'I=2(^I%2(C')]|51,о. (8-6.10)
Для последовательного определения Z(^p)|Sl=,0 при всех
р >г 2 обозначим через $(р) множество всех неразложимых гра-
графов (блоков), имеющих не менее чем р вершин. Заметим, что
j$ B) = .$ и что Z(^p)|Sl.,0 состоит из всех слагаемых порядка р,
входящих в Z{^{p))\s-iZ(e')\\sl^. Так как &{2) = &, то формула
(8.6.9) приводит к соотношению
-o. (8.6.11)
Кроме того, очевидно, что .
-^ (8.6.12)
•' Следующее утверждение вытекает из того факта, что <М (р)
разбивается на два непересекающихся подмножества 9&Р и
(8.6.13)
Его можно доказать индукцией по числу р. В частности, если
Z(^p)|s,=o и Z C8 (р)) [sxZ (С)] |s,-o известны, то из (8.6.13) можно
найти Z(^(p + I)) [stZ ((?")] |Sl-o, в котором слагаемые порядка
р -f-1 являются как раз слагаемыми из Z C§p+i)\st=o-
Наконец, имеем
Z(&)\Sl=0= Sz(^p)|s,=0 (8.6.14)
и георема Робинсона, позволяющая перечислить блоки, может
быть сформулирована в следующей форме.
Теорема. Сумма Z @) цикловых индексов всех блоков дается
формулой
-о,- :■ (8.6.15)
- о
где Z (&) определяется из соотношения (8.6.1), в Z @t)\,,_0 нахо- i
дится с помощью формул (8.6.11) и (8.6.13). I

1. ГРАФЫ С ДАННЫМИ БЛОКАМИ 223
Таблица 8.6.1
Число блоков порядка р
р
Ьр
1
0
9
1
3
1
4
3
5
10
6
56
7
468
8
7123
9
194 066
Для читателя может быть поучительным использование этого
метода для нахождения всех слагаемых в Z (<%), имеющих поря-
порядок не выше четвертого. Приведем эти члены:
Z (<%) - ~- s\ + i- s2 + -i- s\ + \ НЧ + -|" S3 + -J2 s* + 8*s» +
+ Ts» + TSl?3 + т s« + • • • • (8-6-16)
Число р-вершинных блоков равно, естественно, сумме коэффи-
коэффициентов многочлена Z {3$р).
Описанный метод перечисления блоков был запрограммирован
Остервейлом [И, и результаты вычислений для графов с неболь-
небольшим числом вершин приведены в табл. 8.6.1.
8.7. ГРАФЫ С ДАННЫМИ БЛОКАМИ
Часто класс графов можно описать на языке блоков, содержа-
содержащихся в графах из этого класса. Например, деревья являются
такими связными графами, все блоки которых изоморфны графу
К2; у графов блоков все блоки представляют собой полные графы1;
кактусы являются связными графами, у которых блоки — либо
ребра, либо циклы; множество всех связных графов, не имеющих
висячих вершин, совпадает в точности с множеством всех нетри-
нетривиальных связных графов, у которых концевые блоки не изо-
изоморфны графу Кг. Для того чтобы перечислить некоторые из
этих классов графов, мы обобщай ряд результатов из предыду-
предыдущего параграфа. Мы приведем также обобщенную форму метода,
предложенного Норманом [1] для подсчета числа графов с дан-
данными блоками. В своем изложении мы опять будем следовать
работе Робинсона [3]!
Пусть 2D — класс блоков и Ж — множество всех таких связ-
связных графов, у которых блоками являются только графы из класса
ЗЬ. Первый результат, выражающий Z (Ж') через Z {ЗУ), можно
установить способом, аналогичным примененному для проверки
соотношения (8.6.1).
1 См., например, Харарй ,Щ:, ctp. 45. «— Прим, пер ев,

\
224 ГЛ. 8, БЛОКИ
Теорема. Сумма Z (Ж') цикловых индексов связных корневых
графов, блоки которых принадлежат множеству 2D, дается фор-
формулой
(sk/k)\ZBy)[SlZ(X*)]]}. (8.7.1)
Если Z (£>) известно, то Z {ЗУ) = д Z {2>)/ds1 и формулу (8.7.1)
можно использовать для получения Z (Ж')- Следующая теорема
выражает Z (Ж) через Z (Ж').
Теорема. Сумма Z (Ж) цикловых индексов связных графов, блоки
которых принадлежат множеству <Ю, дается формулой
(ZB>)\Sl=0){SlZ(Ж')}. (8.7.2)
Доказательство этого утверждения аналогично доказательству
соотношения (8.6.9). Заметим, что мы могли бы использовать эту
теорему для вывода формулы (8.6.9), ибо при Ж — G и ЗЬ = $
формула (8.7.2) влечет равенство (8.6.9). Для того чтобы проиллю-
проиллюстрировать использование соотношения (8.7.2), мы покажем,
как можно получить сумму цикловых индексов деревьев. Пусть
<F — множество всех деревьев, а класс iZ> состоит только из пол-
полного графа Кг. Таким образом, Z {%£>') = sl7 и в силу (8.7.1), имеем
S (sk/k) [SlZ(T')}). (8.7.3)
Далее, Z (9~") можно определить из этого равенства рекурсивно.
Например, слагаемые в Z {£Г'), имеющие порядок ниже пятого,
выглядят так:
+ 4 s\s2 + A si + A Sls3 -f 4 h + • • •• (8.7.4)
Эти слагаемые соответствуют корневым деревьям, порядки кото-
которых меньше 6. Из (8.7.3) и C.1.1) следует, что
Z {Т1) = 1 + S z (Sk) [»iZ (Г')] + ... (8.7.5)
Поэтому слагаемые пятого порядка в Z@~') могут быть вычис-
вычислены с помощью следующих пяти соотношений:
^ + s'S+т

8.7. ГРАФЫ С ДАННЫМИ БЛОКАМИ 225
Z (S2) [stZ(Г')] =. . . + ^- s[ + -§- sBlS2 + -|-
Z E8) M @" )] = ... + 4 si + «i»2 + -f %4 +. .. , ; (8.7.6)
-f
2E») [«iZ(УI = -go"«' +12"s3lS3 + TSlS^ + T 2
4 ■ s- +—S2S3 + —s6+. . . .
Собирая вместе все эти слагаемые, имеем
2
Далее, Z(£D)\Sl=0 = -^-(si + s2)|Sl=0 = s2/2, и поэтому из (.8.7.2) вы-
вытекает равенство
Z(T) = \Z(T')dSl + (s2/2) [SyZ(Г1)]. (8.7.7)
..,- * о
Используя (8.7.4), можем вычислить несколько первых члено-
у второго слагаемого, стоящего в правой части формулы (8.7.7):
4 s2 [Slz{T')\ = 4 s2+4- s2+т s2+4SiS*+• • • • (8-7-8>
Интегрируя Z@~') и прибавляя к получаемому выражению соот-
соответствующие члены из (8.7.8), находим все слагаемые в Z(ST)
порядка не выше шестого:
■■h+ -|-si + Ts2 + l-si + 4SlS2 + Ts* + T
_1_ 2 J_ I — 54-— 3 4- —
2 3 24 4 8
4" sis
(8.7.9)
Правильность полученного соотношения можно проверить,
просуммировав все коэффициенты в нем и сравнив найденный
8 Заказ 443

226 ГЛ. 8. БЛОКП
результат с числом деревьев, у которых меньше семи вершин
(см. формулу C.2.8)).
Ниже приводится робинсоновское обобщение метода Нор-
Нормана [1], позволяющего найти число графов с данными блоками.
Теорема. Сумма Z (Ж) цикловых индексов графов, блоки которых
принадлежат множеству SD, дается формулой
Z {Ж) = («! + Z {2)) — sxZ (&)) [Sl Z (Ж)]. (8.7.10)
Заметим, что в соотношениях (8.7.1) и (8.7.10) Z (Ж') nZ {Ж)
можно заменить производящими функциями. Однако этого нельзя
делать в равенстве (8.7.2). Кроме того, когда требуются суммы
цикловых индексов, то значительно легче использовать не фор-
формулу (8.7.10), а формулу (8.7.2).
В заключение этого параграфа применим развитую здесь тех-
технику к перечислению связных графов без висячих вершин.
Следующая теорема Робинсона [3] дает возможность получить
соответствующую сумму цикловых индексов (путем обращения
приведенной в ней формулы).
Теорема. Сумма Z (JC) цикловых индексов для множества Ж,
состоящего us всех связных графов без висячих вершин, удовлетво-
удовлетворяет соотношению
Z{e) = Z{T) + Z{JC)[slZ(T')\. • (8.7.11)
Доказательство этого утверждения использует теорему компо-
композиции и тот факт, что связные графы, не являющиеся деревьями,
соответствуют перечисляемым здесь графам с приписанными им
корневыми деревьями. Последнее соответствие годится также
в качестве основы для подсчета числа помеченных графов, полу-
получаемых из графов множества jfc.
Для обращения формулы (8.7.11) заметим, что (р + ^-вер-
^-вершинный граф из класса С либо принадлежит множеству JC, либо
его максимальный подграф, не имеющий висячих вершин, содер-
содержит меньше, чем р -f- 1, вершин. Далее, если JCP — подмножество
из JC, состоящее из всех тех графов, которые имеют не более р
вершин, то слагаемые порядка р +1 в Z {JCP) \sxZ (#"')] соответ-
соответствуют всем связным (р + 1)-вершинным графам, отличным
от деревьев, но все же имеющим висячие вершины. Следовательно,
слагаемые порядка р + 1 в Z (&~) + Z (JCP) \stZ (#"')] вносятся
всеми связными (р -\- 1)-вершинными графами, содержащими
хотя бы одну висячую вершину. Поэтому разность Z (J?p+1) —
— Z (JCP) состоит из слагаемых порядка р + 1, принадлежащих

t
8.8. АЦИКЛИЧЕСКИЕ ОРГРАФЫ 227
Например, чтобы найти Z(JC^ — Z(J[3), мы начинаем с
4s +
(8-7-12)
и, воспользовавшись соотношением (8.7.4), получаем
Z {Жь) [siZ (Щ = 4"s* + Т »is» + т Sa + Т ** + Т »'*» + • • • •
(8.7.13)
Затем из формул (8.4.8), (8.7.4) и (8.7.13) получаем равенство
{s2 + {¥, + {s, (8.7.14)
Сумма всех коэффициентов этой разности равна 3, и, действи-
действительно, существует в точности три связных четырехвершинных
графа, не имеющих висячих вершин.
8.8. АЦИКЛИЧЕСКИЕ ОРГРАФЫ
В § 1.6 мы видели, что всякий ациклический орграф содержит
хотя бы одну вершину с нулевой полустепенью захода и что любое
расширение ациклического орграфа также ациклично. Робинсон
[4] использовал эти факты, чтобы перечислить и помеченные, и
непомеченные ациклические орграфы. Однако он обнаружил, что
для перечисления непомеченных ациклических орграфов необхо-
необходимо объединить всю информацию о симметриях всех ацикличе-
ациклических орграфов. Это объединение было достигнуто путем исполь-
использования таких сумм цикловых индексов, в которых проводится
различие между циклами вершин с нулевыми полустепенями
захода и циклами остальных вершин. Тогда для цикловых индек-
индексов можно определить такую билинейную операцию, что сумма
цикловых индексов, отвечающая всевозможным расширениям
любого ациклического орграфа D, выражается через Z (D) и
Z (Sn). Это приводит к рекурсивной формуле для суммы цикло-
цикловых индексов всех ациклических орграфов порядка р.
Мы довольно часто применяли для записи цикловых индексов
два множества переменных. Так, например, чтобы различать
вершины и ребра, мы в § 4.4 и 7.2 использовали переменные s*
и tk (при перечислении надграфов и при записи суммы цикловых
индексов вершинно-реберных групп р-вершинных графов (см.
формулу G.2.19))). Кроме того, при перечислении смешанных гра-
графов в § 5.4 переменные S/, и t^ появились в цикловом индексе
редуцированной упорядоченной парной группы (см. соотношение
5.4.5)); переменные sk соответствовали парам взаимно обратных
циклов, а переменные tk — самообратным циклам-

228 гл. 8. блоки
Здесь мы выражаем цикловой индекс группы орграфа D,
используя два множества переменных: sk — для циклов вершин
с нулевыми полустепенями захода, а ^ — для циклов других
вершин. В силу этого соглашения, ациклические орграфы D-y
и D 2, изображенные на рис. 1.6.2, имеют следующие цикловые
индексы: Z (Dt) = 4*1 и ^ (D2) = -£-($1^ + Mi)-
Теперь можно воспользоваться леммой Редфилда (см. формулу
G.2.3)), чтобы получить другое представление для суммы цикло-
цикловых индексов всех р-вершинных расширений ациклического
орграфа Do порядка р — п. Пусть А = Sn X Г (Do). Группа А
индуцирует группу А", множество объектов которой состоит из
всех расширений орграфа Do, являющихся ациклическими оргра-
орграфами и имеющих ровно по п вершин с нулевыми полустепенями
захода. Это представление группы А может быть сделано явным,
если использовать ограниченную степенную группу; но так как
подобный подход мы применяли довольно часто, то приведенного
указания вполне достаточно. Для каждой подстановки р из
Г (Do) обозначим через /* число циклов длины А;, содержащих
только вершины с нулевыми полустепенями захода, а через mk
обозначим число циклов длины к, переставляющих другие вер-
вершины орграфа Do. Если а — подстановка из Sn, то пусть ik —
число циклов подстановки а, имеющих длину А;. Такое обилие
переменных может показаться излишним, но их наличие сделает
наши формулы менее беспорядочными. Для каждой подстановки
(а, Р) из А определяем функцию класса:
Ф(а, р) = П4*4*+т*. (8.8.1)
Подстановку в А', индуцируемую подстановкой (а, Р), обозна-
обозначим через (а, Р)\ и пусть jt ((а, р)") — число расширений, непо-
неподвижных относительно (а, Р)'. Применяя формулу G.2.3), можем
заключить, что
где первая сумма берется по всем таким расширениям орграфа Do,
Которые имеют ровно п вершин с нулевыми полустепенями захода.
Число 7\ ((а, р)') зависит только от цикловой структуры подста-
подстановок а и р и может быть представлено в явной форме:
h((a, р)') = 1Ц2* -l) -2й . (8.8.3)
Обратите внимание -на сходство правой части формулы
(8.8.3) с вкладом

8.8. АЦИКЛИЧЕСКИЕ ОРГРАФЫ 229
вносимым подстановкой (а, ($) в цикловой индекс декартова про-
произведения Sn X Г (Do) (см. соотношение D.3.10)). Заменяя в при-
приведенном выражении каждую переменную str> k\ на 2, получаем
почти полностью правую часть формулы (8.8.3), за исключением
слагаемого —1 в каждом сомножителе. Наличие —1 указывает
на то, что в каждом орграфе, неподвижном относительно (ос, {$)',
все вершины, принадлежащие орграфу Do, имеют положительные
полустепени захода.
Для формулировки теоремы перечисления исключительно на
языке цикловых индексов определим билинейную операцию *,
введя ее вначале для одночленов:
Ilsl* * П 4*£* = h ((ее, р)«) ф (ее, р), (8.8.4)
h к
где правая часть определяется с помощью соотношений (8.8.1)
и (8.8.3). Продолжив эту операцию по линейному закону, мы
можем переписать равенство (8.8.2) в следующем виде:
2Z(D) = ZEn)*Z(D0). (8.8.5)
Наконец, суммируя это уравнение, получаем основное утвер-
утверждение данного параграфа.
Теорема. Сумма Z C№р) цикловых индексов множества &вр
всех ациклических орграфов порядка р удовлетворяет соотношению
z{mP)^^z{sn)*z{^ep.n), . J....-- (8.8.6)
где Z (е5#о) = 1 wo определению.
Робинсон предпочел выразить свою перечислительную фор-
формулу на языке суммы цикловых индексов множества Шв всех аци-
ациклических орграфов. Равенство Робинсона получается путем
суммирования соотношения (8.8.6) по всем р:
п-1
(8.8.7)
Однако для вычисления числа ар ациклических орграфов порядка
р удобнее применять равенство (8.8.6). Например, чтобы опреде-
определить а4, нам нужны Z (SWi), Z {&€%) и Z (ей?3). Их легко найти,
если воспользоваться рис. 8.8.1:
(8.8.8)

230
ГЛ. 8. БЛОК
Используя формулы (8.8.1) и (8.8.3), как это предписан
в определении билинейной операции* (см. соотношение (8.8.4)
имеем
Z E,)*
-1 S3! + y
+ -i
(8.8.9)
Складывая эти четыре равенства, получаем Z (offli), сумма
коэффициентов которого равна 31 — числу ациклических оргра-
ЛАД
Рис, 8.8.1. Ациклические орграфы третьего порядка.
фов порядка 4. Робинсон использовал описанный метод, чтобы
вычислить числа, помещенные в табл. 8.8.1.
Таблица 8.8.1
Ациклические орграфы *Ь
р
ар
1
1
2
2
3
6
4
31
5
302
6
5984
УПРАЖНЕНИЯ
8.1. Найти сумму цикловых индексов всех таких графов, которые
состоят из треугольников и четырехвершинных циклов и имеют
ровно четыре компоненты связности.
8.2. Найти сумму Z (<ЙЪ) цикловых индексов всех пятивершинных
блоков (см. соотношение (8.6.16) для Z (<Sk) с А; <5).
8.3. Найти несколько первых членов производящих функций,
перечисляющих такие связные графы, блоки которых являются
полными графами порядка: (а) 2, (Ь) 3, (с) 4 или (d) являются
четырехвершинными циклами.
8.4. Используя методы данной главы, перечислить (а) кактусы
и (Ь) графы блоков.
8.5. Изобразить все 31 ациклических орграфов четвертого по-
порядка (см. табл. 8.8.1). (Указание: используйте приложение II
из книги Харари Ц].)

Глава 9
He дело ботаника вырывать сорняки.
Достаточно, если он может сказать,
как быстро они растут.
С. Норткот Паркинсон 1
АСИМПТОТИКА
Имеются в основном два метода получения асимптотических фор-
формул для графов. И оба они по существу содержатся в опублико-
опубликованных и неопубликованной работах Пойа (последняя — в виде
письма, полученного нами в 1951 году). Выбор метода зависит от
того, «древовидны» или нет те графы или структуры, которые
подлежат перечислению.
Асимптотику числа графов, принадлежащих различным мно-
множествам, изучали и Риддел [1], и Пойа. Некоторые из их резуль-
результатов были улучшены Обершельпом [1] и Райтом [3, 41. В трех
первых параграфах данной главы мы приводим детали методов,
позволяющих найти асимптотику числа графов и числа орграфов.
Эти методы, по-видимому, можно успешно применять к разно-
разнообразным классам графов (см., например, Палмер [5] и Ха-
рари [8]).
В § 9.4 мы рассматриваем асимптотические оценки для связ-
связных графов и блоков. После этого результаты § 9.1 можно
использовать для установления следующих утверждений:
почти все графы — связные и почти все графы являются бло-
блоками.
Пойа [1] нашел асимптотику для числа таких деревьев, кото-
которые представляют предельные углеводороды (в этих деревьях
все вершины имеют только степени, равные 1 или 4). Его подход
был усовершенствован и обобщен Оттером [1] и применен Фордом
и Уленбеком [1] в серии работ, посвященных графам с данными
блоками и, следовательно, кактусам, а также обычным деревьям.
Параграф 9.5 содержит оттеровское решение этой задачи.
1 С. Норткот Паркинсон (р. в 1909 г.) — английский писатель, историк
и социолог, известный русскому читателю по переводам его сатирических
произведений: «Закон Паркинсона или Пути прогресса», «Секрет Питера»,
«Зятья и прочие». «Закон отсрочки» и др. — Прим. перев.

232 ■■'■.<■<■'■ t «n .. - ГЛ.9. АСИМПТОТИКА
9.1. ГРАФЫ
Пойа получил следующую формулу, дающую аешштотику
числа gp графов порядка р:
gp~2&)/p\ ; . (9.1.1)
Из формулы D.1.9) следует, что 2^2'/р\ является наибольшим
членом, вносимым в число gp, представленное в виде Z(Sp, 2).
Доминантность этого члена эвристически можно объяснить так:
деление числа 2^2' (равного числу помеченных графов порядка р)
на величину р\ равносильно «устранению пометок». Формулу
(9.1.1) можно улучшить (см. Обершельп Ш) и получить более
точную аппроксимацию величины gp, вводя члены порядка
I{р\ 2Рк1г) при к = 2, 3, ... . Следующая теорема дает
одно из таких усовершенствований — для случая к = 3.
Теорема. Число gp графов порядка р удовлетворяет соотно-
соотношению
Доказательство. Напомним, что число подстановок в Sp,
соответствующих разбиению (/) числа р, обозначается через h (/)
и дается формулой B.2.4). Число q (/) реберных циклов, опреде-
определяемых каждой из этих подстановок 1, можно найти из формулы
D.1.9) для циклового индекса парной группы Sp2):
k k r<t
Обозначим через gpk\ к —0, 1, . . ., р, вклад в gp, вносимый
всеми такими разбиениями (/), у которых ровно р — к единич-
единичных частей, т. е.
^ = A^1J * W) 2'»>, (9.1.4)
где суммирование ведется по всем разбиениям (/) с /i = p — к.
Тогда, естественно,
8P = ie(Pk) ■ ■" (9-1.5)
1 Реберные циклы — это циклы подстановок соответствующей парной
группы. — Прим. перев.

9.1. ГРАФЫ
и из формул (9.1.3) и (9.1.4) сразу же следует, что г; ' . - •
^0) = 2^) \р\. (9.1.6)
Рассмотрим при А; = 2 разбиение (/) = (р — 2, 1, 0, . . ., 0) с
j\ = p — 2 и 72 = 1. Соотношение (9.1.3) дает
д(р-2, 1, 0, ..., 0) = (р2-Зр + 4)/2. ■- (9.1.7)
Следовательно, используя формулу (9.1.4), можем написать
ЛрО) = 2р(р-1)/2". (9.1.8)
Аналогично, находим, что -
(V0) (9.1.9)
). (9.1.10)
Лемма. Для каждого целого положительного числа п выпол-
выполняется асимптотическое равенство
Доказательство леммы. Сначала установим верхние оценки
для величин g<£\ Для каждого А; рассмотрим все такие разбиения
(/) числа р, у которых ]\ = р — к. Подставляя jx — р — к и
7'2 = к12 в правую часть соотношения (9.1.3), получаем верхнюю
оценку для q (/): ,„,, ,
9(/)*? (J)+y(A-P^ + A:2/2). . (9.1.12)
Далее, число подстановок, действующих на множестве из р объек-
объектов и оставляющих неподвижными в точности р — к объектов,
не превосходит р\/(р — к)\ (см. Риордан [1], стр.72). Следо-
Следовательно, можем написать
Так как отношение р\1(р — А;)! ограничено сверху величиной рк,
то граница для g^ может быть увеличена следующим образом:
gV ^ ^(p0V/B(p-i-*/2)/2)ft. (9.1.14)
В нашем сдучае к ^ р, поэтому .
fflffl * ■. ■ (9.1.15)

234 ГЛ. 9. АСИМПТОТИКА
Суммируя это неравенство по к, п^,кщр, имеем
ZW + WiKpYT/wy. (9.1.16)
к-п k-n
Но сумма, стоящая в правой части последнего соотношения,
является частной суммой геометрической прогрессии, причем
знаменатель этой прогрессии стремится к нулю при возрастании р.
Следовательно,
S № *S ^ (p VT/2>>/*)n, (9.1.17)
к-п
где с превосходит единицу и при больших значениях р сколь
угодно близко к ней.
Далее, так как
2 gV « tf, « S gF+gPO (p»/2p»/«), (9.1.18)
fc-0 *-0
то имеем
1 < gp[j£ ST ^1 + 0 (p"/2"«/*), (9.1.19)
что подтверждает соотношение (9.1.11). Лемма доказана.
Теперь мы можем продолжить доказательство теоремы. Для
обеспечения требуемой оценки погрешности мы воспользуемся
формулой (9.1.14) и положим в ней к = п; получаем
*{ g2V/ (9.1.20)
Следовательно,
in
2^) = ^0)О(р"/2'"'/2). ; (9.1.21)
k-n
Из неравенства (9,1.17) вытекает, что "ru*; ».:o
2 g£) = g(P0)O((PV2l2p/*yn+1). (9.1.22)
к-гп+i
Но _
О ((р ]/2 /2"/*Jn+1) = 0(р»/2р»/*), (9.1.23)
поэтому, объединяя соотношения (9.1.21) и (9.1.22), находим
(9.1.24)
Для завершения доказательства теоремы и формулы (9.1.2) доста-
достаточно положить в (9.1.24) п = 3 и затем к обеим частям приба-
вить № + &\ш

9.2. ОРГРАФЫ
235
Мы закончим этот параграф, приведя такое усовершенствова-
усовершенствование формулы для gp, которое содержит gp3) и £р4). Из соотношений
(9.1.9), (9.1.10) и (9.1.24) имеем
P2—?
2P
8-
Cp-7)Cp-9)
(Р —4I
22"
(9.1.25)
Заметим, что в этом выражении вторая часть от gp4) включена
в остаточный член. Формула (9.1.2) была использована Обершель-
пом [1] для получения значений первого и второго приближения
величины gp, помещенных в табл. 9.1.1; значения третьего при-
приближения были вычислены им с помощью формулы (9.1.25).
Приближения для числа графов
Таблица 9.1.1
V
2
3
4
5
6
7
8
еР
2
4
11
34
156
1044
12 346
Приближение
первое
1
1,333
2,667
8,533
45,51
416,1
6 660
второе
2
3,333
6,667
19,20
88,18
689,12
9 570
третье
2
4
10
29,87
127,3
896.4
11120
9.2. ОРГРАФЫ
Вывод асимптотических формул для числа орграфов аналоги-
аналогичен выводу соответствующих формул для графов. Поэтому мы
приведем только набросок доказательства теоремы, дающей тре-
требуемую формулу и оценку ошибки аппроксимации. Из формулы
E.1.5) для циклового индекса редуцированной упорядоченной
парной группы Sp21 вытекает, что число q (/) реберных циклов \
определяемых каждой подстановкой, соответствующей разбиению
О'), равно
2() 2 Writ- (9.2.D
(
Как и раньше, для каждого & = 0, 1, . . ., р положим
(9.2.2)
1 См. примечание на стр. 232. — Прим. перев,

236 ГЛ. 9. АСИМПТОТИК А
где суммирование ведется по всем разбиениям (;) с ]г = р — к.
Тогда число dp орграфов порядка р равно сумме всех dpfe). Имеем,
в частности,
4°' = 2Р2-р/р!, (9.2.3)
■'■;■ (9.2.4)
(9.2.5)
Положив в правой части формулы (9.2.1) /1 = р—jft и ;2 =
= к/2, получаем верхнюю оценку величины q (/):
(9.2.6)
;2 =
(9.2.7)
всякий раз, когда ]\ = р — к.
Поэтому
«#)^40)(р72<1'-1-*)'1)*. ' '*" (9.2.8)
Как и в случае графов, можно теперь показать, что
р - , ■■ dp~ 2 4А) : (9.2.9)
p
u-n —u-n L/ (p /^iK ). ■ lo.u.lUI
; Итак, имеем следующую теорему для орграфов.
Теорема. Число dp орграфов порядка р удовлетворяем соотно-
[шению
• ' £--Л- , 2P'~r
а„ == г-
Если же учесть величины dp3) и dp4), то получится такое
равенство:
, 4р(р-1) р7 р! (Зр-7)(Зр-9)
(9.2.12)

9.3. ГРАФЫ С ДАННЫМИ ЧИСЛАМИ ВЕРШИН И РЕБЕР 237
9.3. ГРАФЫ С ДАННЫМИ ЧИСЛАМИ ВЕРШИН И РЕБЕР
Мы видели, что член 2w/p!, вносимый в Z{SP2\ 2) тожде-
тождественной подстановкой, асимптотически равен общему числу
графов порядка р. Поэтому вполне возможно, что для получе-
получения аппроксимации числа gPi q (p, д)-графов надо найти вклад,
вносимый тождественной подстановкой в коэффициенты при хк
многочлена Z{S(P\ 1 + х). To, что указанный вклад равен
(pY '
llph можно увидеть, представив перечисляющий многочлен
в следующем виде:
(9.3.1)
f *
где / (х) определяется этим же уравнением. Можно надеяться,
что приведенная выше аппроксимация соответствует действи-
тельности, ибо \ I р\ равно как раз, в силу формулы A.1.1),
числу помеченных (р, д)-графов, поделенному на р\ (последнее
сделано для «устранения пометок»). Однако мы увидим, что
это соображение может быть использовано лишь тогда, когда q
не очень близко к концам своей области изменения. Например,
(Р\
§р,а — ^ Для всех Р> н0 \ О /\Р^~ ^1р' и стремится к нулю при
возрастании р. На самом-то деле и при всяком фиксированном
значении q
q.,p\~0. (9.3.2)
Границы изменения величины q, для которых справедлива ука-
указанная выше оценка числа gp ?, были установлены Пойа (об этом
говорится в работе Форда и Уленбека [1]), а впоследствии эти
границы были улучшены Обершельпом [1], результат которого
отражен в нижеследующей теореме. Райт [5] получил недавно
необходимое и достаточное условие, обеспечивающее выполни-
выполнимость соотношения (9.3.4) (см. упражнение 9.13).
Теорема. Если при некотором е, таком, что 0 ■< е ■< -т-,
Справедливо равенство
(£)|ЛД-е) ' " (9.3.3)

238
гл. а. асимптотика.
то число gPtq (p, q)-zpa(poe удовлетворяет соотношению
Доказательство. Исходя из определения функции/ (х), зада-
задаваемой формулой (9.3.1), имеем для всех р и q следующие нера-
неравенства:
\%^,Д^Д.+,<^>/,. („5)
Следовательно, достаточно показать, что если q удовлетворяет
условию (9.3.3), то
"(Г
I'J-O- (9.3.6)
Но из формулы (9.1.2), дающей асимптотику величины gP, выте-
вытекает равенство
4 (\ \ ГЪ t гЗ< /9D\ /Q Q 7\
Т \^) ^ \Р /" )• [У.О.1)
Поэтому нужно показать, что при соответствующих значениях q
^/~0' (9.3.8)
Для этого установим существование положительных констант с
и б, таких, что 0 < б ^ — и при всех достаточно больших р
неравенство ]* „ р...
влечет за собой соотношение (9.3.8). И тогда можно подобрать е
так, что будет выполняться равенство (9.3.3).
Далее, функция F (p, q), стоящая в левой части соотношения
(9.3.8), достигает своего наибольшего значения для тех q, кото-
которые расположены у границы области изменения этого параметра.
Таким образом, из (9.3.9) вытекает, что
(9.3.10)
(О
г, 1+6
Применяя формулу Стирлинга к факториалам, встречающимся
в знаменателе правой части неравенства (9.3.10), получаем для

9.3. ГРАФЫ С ДАННЫМИ ЧИСЛАМИ ВЕРШИН И РЕБЕР 239
некоторой константы Сх и достаточно больших значений р сле-
следующую оценку:
. Ч) «£ Ct р22(Рр3Г/2 аарРЪьрР (ар6р)»/*, (9.3.11)
)
С)
где'
(9Д13)
Так как (apbpI!2 — О(р2), то мы еще можем упростить оценку
функции F (р, q) и записать
F (Р, Ч) ^ С, ^— (р* -р - 4cpi^)ap (р2 - р +
2P(p2_p)B)tl/2 (9.3.14)
где С2 —некоторая константа.
Производя несложные преобразования и учитывая равенство
аР + ьР= (g )> имеем
= u2
(9.3.15)
Для наших целей полезно представить полученное неравен-
неравенство в следующем виде:

240
Дмее мы используем равенства *s •■, .;
ГЛ. 9. АСИМПТОТИКА
Д+6 \ Л ,„1+6
1+-
1—■
о/-
(9.3.17)
ср
,1+6
1-
ср
,1+6
о 1+6
с*р
! + ■
7(
•@
(9.3.18)
(9.3.19)
(9.3.20)
Применяя неравенства (9.3.19) и (9.3.20) к равенствам
(9.3.17) и (9.3.18), имеем • :
(9.3.21)
Можно показать, что для всех х, у > 0
ехуцу-Х) < A -f- х/у)« < е*
и, кроме того, для у Зг х > 0
у-*) < A — ж/у)* < е-*,
где
(9.3.22)
Если б < 1, то для некоторой константы AT>4tf2 выпол-
ряется неравенство
Kp*b --Ч, (9.3.23)
Цри условии, что р достаточно большое. -'- ' *
\ Таким образом, для больших значений р ■'„ -; ' ■
F(p, q)s^C2p1eKP26/Bp(p2 — p)i'2), (9.3.24)
где К > 4с2 и б < 1. Если же выбрать б *s -д-,"то получим
соотношение

9.4. СВЯЗНЫЕ ГРАФЫ И БЛОКИ 241
Поэтому F(p, g)~0 при условии, что К <1п2. Для существо-
существования такого К нужно потребовать, чтобы
4с2 < In 2. (9.3.26)
Следовательно, если с = 0,416 и б = у, то из формулы (9.3.9)
вытекает соотношение (9.3.8). Доказательство теоремы закончено.в
Заметим, что рассматриваемая в теореме область изменения
параметра q включает большинство р-вершинных графов, т.е.
где сумма берется по всем тем q, которые удовлетворяют усло-
условию (9.3.9).
Соответствующая теорема для орграфов такова:
Теорема. Если для некоторого е, такого, что 0 <е <^>
выполняется соотношение
\{^e) _ ; (9.3.28)
то число dPi q орграфов с р вершинами и q дугами удовлетворяет
равенству
1
q
Доказательство подобно доказательству соотношеаа» (9.3.4), и,
выполнив все необходимые детали, находим, что если
Iр\
<0,832рЗ/2, (9.3.30)
2
то справедливо равенство (9.3.29).
\/,Л*";'"••.//"■" ;'i*'
9.4. СВЯЗНЫЕ ГРАФЫ И БЛОКИ
Следуя Ридделу [1] и Форду с Уленбеком 11], мы сначала
займемся рассмотрением помеченных графов, а потом получим
соответствующие результаты для непомеченных графов, опираясь
на то положение, что «большинство графов можно рассматри-
рассматривать как помеченные».
Теорема. Число Gp помеченных графов порядка р асимптоти-
асимптотически равно числу Ср связных помеченных графов того же порядка:
GP~CP. (9.4.1)
Таким образом, почти все помеченные графы — связные.

242
гл. 9. асимптот
Доказательство. Разделив обе части уравнения A.2.1) на GJ
получаем
p-\
(9.4.2)
Так как С
неравенства
где
Следовательно, чтобы установить соотношение (9.4.1), достаточно
показать, что lim F(р) = 0. Так как к/p^l, то имеем
Р-+-СО
для всех р, то мы можем написать
CP/Gp^l-F(p), (9.4.3)
Pk)k2~kU"k)- (9Л4)
(9Л5)
Слагаемые, стоящие в правой части этого неравенства, симмет-
симметричны относительно концов области изменения параметра к-
Поэтому
[Р/2]
2) (9.4.6)
Но
и Р — к $2 р/2. Следовательно,
[р/2]
2(
(9A7)
Сумма в правой части этой формулы представляет собой частич-
частичную сумму геометрической прогрессии, знаменатель которой
стремится к нулю при возрастании р. Поэтому F (р)= О (р/2р/2).
Но тогда b'm F (р) = 0 и доказательство тем самым завершено.щ
р-*оо
Райт [2] изучал асимптотическое поведение коэффициентов
двух производящих функций а (х) и Ь(х), связанных соотношением
а (х) = ехр Ъ (х). Приведенную выше теорему и ряд других фак-
фактов можно вывести из его результатов.
Наша следующая задача состоит в установлении такого же
результата, как и соотношение (9.4.1), но для непомеченных гра-
графов. Сначала мы покажем, что большинство графов являются
асимметрическими1, т. е. обладают тривиальной группой авто-
1 В оригинале — тождественными (identity), — Прим. перев,

9 .4. СВЯЗНЫЕ ГРАФЫ И БЛОКИ 243
морфизмов. Этот факт, известный Ридделу [1], Форду с Уленбе-
ком И], Эрдёшу и Реньи [1] и другим исследователям, формули-
формулируется так.
Теорема. Число р-вершинных графов асимптотически равно
числу р-вершинных асимметрических графов, т. е. большинство
графов порядка р могут быть помечены точно р\ способами.
Доказательство. Возьмем равенство A.1.3), дающее число
способов распределения пометок для данного графа, и просумми-
просуммируем это равенство по всем р-вершинным графам. Получим соот-
соотношение
2(*). (9.4.8)
Разделив обе части этого выражения на р! и применив формулу
(9.1.2), получаем
2|Г(С)|-1~*Р. (9.4.9)
Так как вклад каждого графа в сумму из (9.4.9) не превосходит
1, то большинство графов должно вносить 1. Теорема доказана.Л
В качестве следствия из этой теоремы сформулируем одно заме-
замечание, обладающее широкой областью применения и позволяющее
получить ряд асимптотических результатов для непомеченных
графов из соответствующих результатов для помеченных графов
и наоборот*.
Метатеорема. Большинство помеченных графов обладает свой-
свойством «Р» тогда и только тогда, когда большинство непомеченных
графов имеет свойство «Р».
Из этой метатеоремы и соотношения (9.4.1) выводится аналог
теоремы, приведенной в начале параграфа.
Следствие. Почти все графы являются связными.
Для установления следующей теоремы мы воспользуемся
некоторыми результатами из § 1.3, относящимися к помеченным
блокам. Напомним, что Вр является числом помеченных блоков
порядка р.
Теорема. Почти все помеченные графы являются блоками, т. е.
Вр ~ Ср.
Доказательство. Как и в § 1.3, R (х) обозначает экспоненци-
экспоненциальную производящую функцию для корневых связных помечен-
помеченных графов. Введем экспоненциальную производящую функцию
!' В приводимой метатеореме речь идет, естественно, о таких свойствах,
которые «отражают структуру» графов, а не «базируются на распределении
пометок» в графах. Например, свойство «быть помеченным» в этой мета-
метатеореме рассматривать нельзя. — Прим. перев.

244 ГЛ. 9. АСИМПТОТ!
Н (х) с коэффициентами #ь определив ее соотношением
ОО 5
Из формулы A.3.8) вытекает, что Н (х) — Rx (хIх. Подстановка
в выражения A.3.7) и A.3.4) приводит к равенству
со "...
In У Ск+1х*/к\=Н(х). : (9.4.11)
Рассуждениями, аналогичными тем, которые использовались при
доказательстве соотношения (9.4.1), можно установить, что
СР+1~НР. (9.4.12)
Из равенства Н (х) = Rx (x)lx вытекает также следующий
результат: (р -\- 1) Нр равно числу таких корневых связных
(р + 1)-вершинных помеченных графов, в каждом из которых
корень принадлежит в точности одному блоку. Поэтому можно
ввести функцию F (р) с помощью уравнения
(9.4.13)
так что F (р) представляет собой число корневых связных (р + 1)-
вершинных помеченных графов, у которых корень принадлежит
только одному блоку, причем порядки блоков, содержащих
корни, не выше р. Легко видеть, что для F (р) справедлива оценка:
-k). (9.4.14]
Для установления асимптотического равенства Вр ~ С^ а следо-
следовательно равенства Вр ~ Gp, достаточно показать, ЧТО
а это легко делается таким же способом, какой использовался
в доказательстве соотношения (9.4.1).^
Применяя метатеорему, получаем следующий результат.
Следствие. Почти все {непомеченные) графы являются блоками.
Мы не колеблясь формулируем следующее утверждение, хотя
формальное доказательство его не известно.
Гипотеза. Для всякого целого положительного числа п почти все
графы являются п-связными.
Используя общие методы и результаты данной главы, можно
найти долю различных классов графов в том или другом множе-

в.Ь. ДЕРЕВЬЯ 245
стве графов. Например, применяя по существу тот же метод, что
й в доказательстве формулы (9.1.2), можно, исходя из формул
F.2.3) и F.2.7) для самодополнительных графов и орграфов, полу-
получить формулируемые ниже асимптотические результаты (см. Пал-
мер 15]). Напомним, что число вершин в самодополнительном
графе сравнимо с 0 или 1 по модулю 4.
Теорема. Числа gin и gin+i самодополнительных графов даются
соотношениями
gin = B2«г- 2n/n 1) A _|_ п (ге— 1) 2»-*1» + О (и3/28")) (9 -4.15)
и
4-<*" +О (re3/2е")). (9.4.16)
Асимптотические результаты для самодополнительных оргра-
орграфов резюмированы в приводимом ниже утверждении.
Теорема. Асимптотика числа самодополнителъных орграфов
может быть установлена с помощью соответствующих выражений
для самодополнителъных графов, ибо
В заключение этого параграфа мы отметим естественно ожи-
ожидаемый результат о том, что самодополнительные графы и орграфы
встречаются относительно редко. Используя соотношение (9.3.4),
находим асимптотику числа gw r графов с 4ге вершинами и с г =
i
1/2 ребрами. Затем, принимая во внимание формулу
(9.4.15), можем показать, что
g*n/g*n.r~0. _ (9.4.17)
Соответствующие результаты справедливы для gin+i и для
орграфов. Имеет место такое утверждение.
Следствие. Не только почти все графы и орграфы не являются
самодополнительными, но это верно даже и для всех {р, р (р — 1)/4)-
графов и соответственно орграфов.
9.5. ДЕРЕВЬЯ
Пойа [1] нашел асимптотические формулы для числа предель-
предельных углеводородов и других химических соединений. Сделал он
это, используя производящие функции и оперируя с ними как
с обычными аналитическими функциями, так что коэффициенты
могли быть подсчитаны с помощью интегральной формулы Коши.
Оттер [1] заметил, что метод Пойа можно применить к обычным
деревьям, а Форд и Уленбек [1] обнаружили, что этот метод
пригоден также для подсчета числа различных древовидных

246 ГЛ. 9. АСИМПТОТИКА
структур. В данном параграфе мы рассмотрим результаты Оттера
для обычных деревьев и приведем достаточно много деталей соот-
соответствующих рассуждений, так что читатель сможет применить
описанный метод и к другим типам деревьев.
Нам потребуется ряд лемм, первая из которых позволит опери-
оперировать с производящими функциями для всех деревьев и всех
корневых деревьев как с аналитическими функциями.
Лемма. Степенной ряд Т (х) для корневых деревьев сходится
в круге радиуса ц ss-j-.
Доказательство. Следующая формула для числа (р + ^-вер-
^-вершинных корневых деревьев легко выводится из соотношения
C.1.9):
Но поскольку
возрастают, то
и
Ь —1
к—1
коэффициенты
имеем
S
Kl h Zl l p+l-fts-
ftsgfes <p
Tt при xl у ряд а Т (х)
-hs^{plk)Tp+1.h V... .;>
■ Л: ""
P :■
5+1 ^ 2j * к* p + l-fc-
(9.5.1)
с ростом I
P. (9.5.2)
(9.5.3)
Теперь определим другой степенной Р>4^ который буде
Т (
мажорировать ряд Г (ж): ''
/И = 2В^, ,. ■ (9.5.4
где Вх — 1 и для /? ^ 1 ;
Op+l = £j OfrOp+i-k. [У.О.О
Из неравенства (9.5.3) с помощью метода математической ин-
индукции можно вывести соотношение: Тр s^ Вр при всех р 5* l.j
Но функция y = f(x) удовлетворяет уравнению j
у*-у + х = 0. (9.5.6)!
Поэтому, разрешая его относительно у, получаем
j/=-|-(l ± A —4жI/2), (9.5.7)
а так как /@) = 0, то получаем
■t /™\ 1 (\ /А Аг\Ч^\ /Q Ч Я\
J \Х) — ~о~ V —^l-^r^t*^ ^» \ОщО»О)

9.5. ДЕРЕВЬЯ 247
Если разложить эту функцию в ряд Маклорена, то получающиеся
коэффициенты в точности совпадают с коэффициентами ряда
C.3.23), перечисляющего плоские корневые деревья с висячими
корнями (с таким же успехом можно привлечь для нашего случая
и любые другие конфигурации, перечисляемые числами Ката-
лана). Для каждого р
(9.5.9)
и, таким образом, установлена оценка для коэффициентов Тр.
Кроме того, из выражения (9.5.8) следует, что радиус сходи-
мости ряда 2 В^ск равен -г-, а поэтому радиус сходимости ряда
Т (х) не меньше, чем—.
На основании формулы C.2.4), выражающей ряд t (х) для
деревьев через ряд Т (х), мы немедленно заключаем, что ряды
Т (х) и t (x) имеют одинаковые радиусы СХОДИМОСТИ1 Вдобавок,
ряды Т (х) и t (x) мажорируют соответствующие ряды, перечисля-
перечисляющие деревья различных типов, а поэтому ряды для таких де-
деревьев тоже сходятся. Эти результаты были впервые установлены
Пойа [li.
Заметим, что так как все коэффициенты производящей функции
Т (х) положительны, то х = т] является особой точкой ряда Т (х),
а значит, и ряда t (x). С другой стороны, оказывается, что в точке
х — т] ряд Т (х) сходится. Для доказательства этого факта нам
понадобится следующее утверждение.
оо
Лемма. Предел Т (х) при х -> г\ — 0 существует и равен 2 Tky\h.
Доказательство, Так как Т (х) удовлетворяет функцио-
функциональному уравнению C.1.4), то для всех ж 6 @, ц) имеем ра-
равенство
оо
In (Т (х)!х) = Т (х) + S T (xh)[k. (9.5.10)
fc-2
Отсюда следует, что
ln(T(x)/x) ** х (У.Й.И)
и, следовательно, функция Т (х) ограничена на интервале @, ц).
Так как функция Т (х) — монотонная, то предел слева в точке г\
существует и мы полагаем
lim Т(х) = Ь0. (9.5.12)

248 ГЛ. 9. АСИМПТОТИКА
А теперь немедленно получаем, что Ьо — Т (у\).щ
Значение величины Ьо находится с помощью следующей
леммы.
Лемма. Перечисляющий ряд Т (х) для корневых деревьев обла-
обладает таким свойством:
Т(г\) = 1. (9.5.13)
Доказательство. Сначала мы определим комплекснозначную
функцию F (х, у), зависящую от комплексных переменных х и у:
F(x, y) = xexv\y+2lT(xk)lk\-y, ■ '- (9.5.14)
и рассмотрим уравнение
F(x, r/) = 0. (9.5.15)
Используя соотношение C.1.4), можно показать, что у = Т (х)
является единственным аналитическим решением уравнения
(9.5.15). В то же время мы знаем, что это решение имеет особен-
особенность при х = т|. В силу предыдущей леммы, F (г\, Ьо) = 0, и,
кроме того, как легко видеть, функция F (х, у) является аналити-
аналитической отдельно по каждой переменной в окрестностях точек
х = г] и у = Ъо.
Дифференцируя равенство (9.5.14) по у, находим
dFldy = F{x, y) + y — l. (9.5.16)
Так как F (ц, b0) = 0, то в точке (г\, Ьо) частная прризводная
равна
~ -Ьп-1- ;^ (9-5.17)
ду (т), Ь„) ° v
Кроме того, эта частная производная должна в точке (tj, Ьо)
обращаться в нуль 1. Значит, Ьо = 1. С другой стороны, как сле-
следует из теоремы о неявной функции, уравнение (9.5.15) может
иметь только одно решение: у = / (х), аналитическое в окрестно-
окрестности точки т] (и в частности, в самой точке г\). Но таким решением
может быть лишь функция у = Т (х), и мы знаем, что она не анали-
тична при х = т). Тем самым соотношение (9.5.13) доказано.■
Заметим, что (как следует немедленно из формулы (9.5.16))
вторая производная от F (х, у) по у в точке (ц, 1) отлична от 0.
Ниже приводится формулировка теоремы, представляющей
собой некую комбинацию теоремы о неявной функции и замеча-
замечаний Пойа, Оттера, Форда и Уленбека. Ради краткости изложения
доказательство этой теоремы мы опускаем.
1 Иначе решение у = Т (х) было бы аналитично в точке х = ц. — Прим.
перев.

9.5. ДЕРЕВЬЯ 249
Теорема. Пусть функция F (х, у) аналитична отдельно по
каждой своей переменной в некоторой окрестности точки (х0, у0).
Предположим, что выполняются следующие условия:
1) F (х0, г/0) = 0;
2) У = / (#) аналитична при \х\ << |жо| и точка х0 является
единственной особенностью на границе круга сходимости ряда
для функции f (x);
оо
3) если f (х) = 2 fnxn есть разложение функции f в окрест-
окрестn=0
ности нуля, то 2/0 = 2 UA, %/ ■, -.'v,- -i'S, r:fe> 1. :
4) F(x, f(x)) = 0 при | а; |< | ж, |; , -.,.
= 0; . '. ..,-.. .
Тогда функция f(x) может быть разложен^ *'Ь ЬщЩтности
точки х0: ' ' 'а "'' '
со
ли/а
ak(x0-xf'\ (9.5.18)
и если агф0} то
!п~-^х;п+±п-^, ' . (9.5.19)
г
а если 0^ = 0, но а3ф0, то
f^WT<n+in'^' (9-5-20)
Чтобы применить эту теорему, заметим, что функция, опреде-
определенная формулой (9.5.14), удовлетворяет всем предположениям
теоремы при (х0, у0) = (т|, 1) и / (х) = Т (х). Следовательно,
функцию Т (х) можно разложить в ряд вида (9.5.18), и если аг Ф 0,
то коэффициенты Тп ведут себя так, как показано в формуле
(9.5.19). Остаётся доказать, что если
T(x) = i-b1(r\-x)l/z + b2D-x) + b3D-xfli+ ..., (9.5.21)
то Ъг Ф 0 или Ь3 Ф 0, и, естественно, нам нужна аппроксимация
с Ъх и т).
Дифференцируя соотношение (9.5.21), получаем
Г(х)=±-Ъ1(у]-хГи2-Ьг+..., (9.5.22)
где не приведены слагаемые, содержащие т) — х в степени не мень-
меньшей, чем 1/2. Умножая обе части равенства (9.5.22) на разность

250 ГЛ. 9. АСИМПТОТИКА
1 — Т (х), которая получается из формулы (9.5.21), имеем
Т' lv\ (\ Т /т\\ _ Ь2 _1_ /Q ^ С)О\
J. \d,)\L I \J-))—-T IT •••» \<J.O.60)
где снова опущены слагаемые, содержащие г\ — а; в степени не
ниже, чем х/2. Следовательно,
lim T'(x)(l — T(x))=-.-^-bl (9.5.24)
Х-+Х) — О
Дифференцируя равенство C.1.4), получаем ,.
то
V / — VXJ/X | 1 \XJ ^^ 1 yX ) ' X у \%jtO,^jOf
а значит, ' -
Г (х) A - Т (х)) = Г (х)/х + Г (ж) 2 ^' («*) ж". (9.5.26)
fc-2
Таким образом, предел из формулы (9.5.24) можно также полу-
получить, применяя равенство (9.5.26), а поэтому
' (if) if-i. (9.5.27)
Оттер установил, используя соотношения C.1.4) и (9.5.13), что
г\ = 0,3383219... . Затем из уравнения, аналогичного (9.5.27),
он выразил b-i и нашел, что
-^^=0,4399237..., ,, (9.5.28)
а Ъ1 = 2,681127... Следовательно, принимая во внимание фор-
формулу (9.5.19), мы можем сформулировать следующее утверждение,
дающее оценку числа корневых деревьев.
Теорема. Число Тр р-вершинных корневых деревьев удовлетво-
удовлетворяет равенству
Тр = 0,4399237 4^+ О (^ЕЛ. (9.5.29)
Теперь рассмотрим ряд t (x) для (некорневых) деревьев. Из
соотношений C.2.4) и (9.5.21) вытекает, что
t(х) = а0-п1 (г\-х)чг +аг(ц-х) + а3(у\-х)'и + . . ., (9.5.30)
а поэтому
t'(x) = ±a1(r\-x)-il2-(h-4-ai(r\-x)il2+ ... . (9.5.31)

9.5. ДЕРЕВЬЯ
251
Дифференцируя C.2.4), находим .,,
V (х) = Г (х) (\-Т (х)) + Т" (х*) ■ х
(9.5.32)
й, учитывая равенство (9.5.24), заключаем, что lim if (х) сущест-
х->1\-0
вует. Следовательно, аг = 0. Далее мы двумя способами предста-
представим вторую производную t" (x). Из (9.5.31) при аг = 0 имеем
Подставляя правую часть соотношения (9.5.26) в равенство
(9.5.32) и дифференцируя получившееся выражение, находим, что
{
(9.5.34)
где опущенные слагаемые ограничены в окрестности точки tj.
Принимая еще во внимание формулы (9.5.22) и (9.5.27), имеем
f(a;) = -Lb»(ti—ж)~1/24- •.., (9.5.35)
а следовательно, а3 — Ь\1Ъ. После этого, используя формулу
(9.5.20), нетрудно найти оценки для числа деревьев. Так как
(&i/4l/n)rK/2 =0,5349485..., то справедливо следующее утвер-
утверждение.
Теорема. Число tp р-вершинных деревьев удовлетворяет равен-
равенству
tp
0,5349485
+ о( 2
(9.5.36)
В заключение приведем таблицу Оттера (см. табл. 9.5.1), в ко-
которой сравниваются значения величин tp и Тр с приближенными
Таблица 9.5.1
р
1
2
3
4
5
10
15
18
Аппроксимация числа
гр
1
1
2
4
9
719
87 811
1 721159
¥Р
1
1
2
4
9
708
86 965
1 708 440
деревьев
*р
1
1
1
2
3
106
7 741
123 867
7р
2
1
1
2
2
86
7 050
114 875

252 гл- 9- асимптотика
значениями tp и Тр этих же величин; последние получены по
формулам (9.5.36) и (9.5.29) соответственно (без учета остаточных
членов).
УПРАЖНЕНИЯ ?■ ■, ^; • , ' ;
9.1. (а) Отношения, асимптотически. (Обершельп [1 ])
(Ь) Турниры, асимптотически. (Мун [2])
9.2. Связные (р, дг)-графы (помеченные и непомеченные), асимпто-
асимптотически. (Эрдёш и Реньи [1], Райт [4])
9.3. Исследуя соотношение
n=l \ n-l
найти, как быстро должны возрастать /„, чтобы lim Fjfn = 1.
» П-* СО
(Указание: см. статьи Райта.) (Райт [2])
9.4 Для всякого положительного к число gp графов удовлетво-
удовлетворяет равенству
2(f)
гДе <ft(p)~P(P—1) ••• (Р—0^(р) и ^О3) — многочлен от пере-
переменной р степени i — 1. (Райт [3])
9.5. Число помеченных р-вершинных графов, не содержащих
треугольников, асимптотически равно 2(рA + ° (!))■
(Клейтман Д.)
9.6. (а) Число lin самодополнительных турниров равно
)( ))
(Ь) Самодополнительные турниры нечетного порядка, асимпто-
асимптотически.
9.7. Почти все
(а) турниры — сильные; .,...',... (Мун и Мозер [1])
!■.h (b) орграфы — сильные; ', (Мун и Мозер [2])
) (с) орграфы — гамильтоновы; ' (Мун [5])
(d) графы — гамильтоновы. (Мун [5])
9.8. Число связных помеченных функциональных орграфов по-
порядка р асимптотически равно (nliyi^pv-1!2. (Реньи [2], Кац[1]).
9.9. Число чистых 2-мерных симплициальных комплексов' по»
11 Двумерный симплициальныи комплекс называется чистым, если каж-
каждый одномерный симплекс в нем является гранью некоторого двумерного
симплекса. — Прим, перев, „. ; „,. . •

УПРАЖНЕНИЯ ; 253
С) ■
рядка р асимптотически равно 2V3'//?1.
9.10. Вероятность того, что выбранная случайным образом вер-
вершина помеченного р-вершинного дерева является висячей, стре-
стремится к 1/е при возрастании р. (Реньи [1])
9.И. Почти все деревья имеют нетривиальные автоморфизмы.
(Форд и Уленбек [1])
9.12. Для справедливости равенства (9.3.4) достаточно, чтобы
min \q, \2) — q)>Zplap. (Райт [5])
9.13. Необходимым и достаточным условием для (9.3.4) является
следующее:
lim
p-»-oo
I 2 min (о, U) — а) , \ /п « .сп
Wl vz/—— — lnp)=oo. (Раит E])
\ P I

Глава 10
Не внаю, каким я предстаю перед чело-
вечеством, но самому себе я кажусь маль-
мальчиком, играющим на берегу моря и развле-
развлекающим сейчас самого себя, а потом —
собирающим отшлифованные морем голыши
или более красивые, чем обычно, раковины.
А великий океан истины лежит предо мной
абсолютно нетронутый!
Исаак Ньютон
НЕРЕШЕННЫЕ ЗАДАЧИ
Хотя разнообразная, усложненная, малопонятная и специализи-
специализированная терминология может затуманить истинное положение
вещей, но факт остается фактом: очень многие модельные (схем-
(схемные, структурные) и конфигурационные задачи становятся графи-
графическими по своей природе, если их соответствующим образом
переформулировать. Более того, представив задачу на языке
графов или родственных им образований, можно значительно
легче выявить ее концептуальные трудности. Мы приводим здесь
обширный набор задач перечисления графов, содержащий доста-
достаточный материал для изысканий специалистов нашего времени
и последующих поколений.
Раньше существовали списки, включающие ровно двадцать
семь нерешенных задач перечисления графов. Теперь мы снимем
ограничение на число задач и представим здесь мириады все еще
открытых вопросов теории перечисления графических объектов.
В каждом параграфе данной главы мы помечаем символами П1.1,
П1.2, . . . совокупности родственных по какому-либо признаку
задач перечисления графов. В некоторых случаях соответству-
соответствующая информация приводится в виде нескольких первых членов
производящей функции.
Мы не выделили явно задачи, относящиеся к перечислениям
различных типов деревьев, ибо, как нам кажется, существующих
методов вполне достаточно для решения этих задач. О перечисле-
перечислении помеченных деревьев см. Мун [4] и гл. 1 данной книги, о пере-
перечислении непомеченных деревьев см. гл. 3.
10.1. ПОМЕЧЕННЫЕ ГРАФЫ
Последующие параграфы включают нерешенные задачи пере-
перечисления как помеченных, так и непомеченных графов. Обычно
«помеченный случай» бывает более податливым, чем «непомечен-

10.2. ОРГРАФЫ 255
ный случай», ибо связан с меньшей симметрией. Однако сущест-
существуют два примечательных исключения, когда непомеченные кон-
конфигурации пересчитаны, а помеченные — нет:
Ш.1. Помеченные самообратные орграфы.
Непомеченные самообратные орграфы были пересчитаны в гл. 6
с использованием теоремы перечисления степенной группы.
П1.2. Помеченные самодополнителъные графы.
Число самодополнительных графов и орграфов было опреде-
определено Ридом [6] (см. гл. 6).
«Помеченные случаи» обеих этих задач остаются нерешенными.
10.2. ОРГРАФЫ
Существует много таких нерешенных задач, относящихся к ор-
орграфам, которые лучше формулировать параллельно с соответст-
соответствующими задачами для графов, что и будет сделано в последу-
последующих параграфах. Однако имеется ряд задач, которые стоит
отдельно упомянуть здесь, ибо они связаны со структурными
свойствами, присущими исключительно орграфам.
П2.1. Сильные орграфы.
Напомним (см. гл. 5), что орграф называется сильным, если
каждая пара его вершин является взаимно достижимой с помощью
ориентированных простых цепей. Нашему большому другу
Рис. 10.2.1. Сильные орграфы третьего порядка.
Р. Робинсону несколько лет назад удалось перечислить как
помеченные, так и непомеченные сильные орграфы, но пока еще
он не нашел времени подробно изложить эти интересные, важные
и трудные результаты. Надеемся, что он осуществит это в течение
текущего десятилетия. Его методы основаны на рассмотрении
конденсации D* произвольного орграфа D (вершинами конден-
конденсации D* являются сильные компоненты орграфа D) и на исполь-
использовании его же техники, базирующейся на суммах цикловых
индексов и изложенной в гл. 8.

256 ГЛ. 10. НЕРЕШЕННЫЕ ЗАДАЧИ
Все орграфы четвертого порядка приведены в книге Харари
[1], стр. 262—265. Как показано в работе Харари и Палмера [6],
существуют 83 сильных орграфа четвертого порядка. Значит,
перечисляющий ряд для сильных орграфов начинается так:
П2.2. Односторонние орграфы.
Орграф называется односторонне связным, или односторонним,
если для любых двух вершин по крайней мере одна достижима
из другой. Хотя односторонние компоненты орграфа не дают,
вообще говоря, его разбиения, но все же метод Робинсона, упомя-
упомянутый выше при рассмотрении задач перечисления сильных оргра-
орграфов, можно приспособить и к односторонним орграфам. Перечис-
Перечисляющий ряд для односторонних орграфов, как подсчитал Р. К. Рид,
начинается такими слагаемыми:
Справедлива теорема (см. Харари, Норман и Картрайт [1],
стр. 66): орграф является односторонним тогда и только тогда,
когда его конденсация содержит единственную простую остов-
ную цепь. Поэтому подходящая модификация метода перечисле-
перечисления сильных орграфов может быть полезной при подсчете одно-
односторонних орграфов. И Робинсон действительно реализовал это
в своем подходе к задаче перечисления односторонних орграфов,
но пока еще полученные им результаты не только не опублико-
опубликованы, но даже и не написаны.
П2.3. Орграфы с источниками.
Вершина орграфа называется источником, если все другие
вершины орграфа достижимы из нее. Двойственным образом
определяется сток. Существует, естественно, одинаковое число
орграфов с источником и орграфов со стоком; эти совокупности
взаимно обратны. Перечисляющий ряд для описанных орграфов
начинается так:
В сильном орграфе каждая вершина является одновременно
источником и стоком. Задача перечисления орграфов, облада-
обладающих и источником, и стоком, также не решена. Робинсон и
здесь заявляет, что он может пересчитывать эти виды орграфов.
П2.4. Транзитивные орграфы.
Орграф называется транзитивным, если из принадлежности
ему дуг uv м vw вытекает принадлежность ему дуги uw. Легко
видеть, что транзитивные орграфы порядка р соответствуют в точ-

@.3. ГРАФЫ С ДАННЫМИ СТРУКТУРНЫМИ СВОЙСТВАМИ 257
ности конечным топологиям, определенным на множестве из р
элементов. Конечные топологии перечислены только для «поме-
«помеченного случая» (см. Эванс, Харари, Линн [1]) с использованием
чисел Стирлинга второго рода.
Первые четыре слагаемых в перечисляющем ряду для непоме-
непомеченных транзитивных орграфов имеют вид
Не известен даже следующий член ряда. Для помеченного
случая подсчитаны первые девять коэффициентов перечисля-
перечисляющего ряда; оказалось, что машинное время, необходимое для
вычисления коэффициентов этого ряда, растет по экспоненте.
Значения восьми первых коэффициентов приведены в табл. П6
приложения I.
П2.5. Орграфы, являющиеся одновременно самодополнительными
и самообратными.
Существует только два орграфа порядка 3, которые одновре-
одновременно и самодополнительные, и самообратные — это циклическая
и транзитивная тройки. Перечисляющий ряд для описанных
орграфов начинается так:
х + х2 + 2а? + 4х*-{- ... .
Задача перечисления указанных орграфов представляет собой
новый интересный тип задачи, которая, по-видимому, требует
для своего решения подходящего обобщения леммы Бернсайда.
П2.6. Эйлеровы орграфы.
Эйлеровы графы были также перечислены Робинсоном [2],
однако та техника, которая использовалась при перечислении
графов, не приспособлена для решения соответствующей задачи,
относящейся к орграфам. Перечисляющий ряд для эйлеровых
орграфов начинается так:
х + х- + 3z3 +12х* + 68z5 + • • . •
Коциг обратил внимание на частный случай этой задачи: перечис-
перечисление эйлеровых турниров; начальные члены соответствующего
ряда таковы:
х + х3 + хъ + Зя' + ....
10.3. ГРАФЫ С ДАННЫМИ СТРУКТУРНЫМИ СВОЙСТВАМИ
Мы в этой книге уже показывали, как можно подсчитывать
разнообразные графы со специальными структурными свойст-
свойствами. Типичными примерами таких графов являются графы,
7г9 заказ 443

258 ГЛ. 10. НЕРЕШЕННЫЕ ЗАДАЧИ
характеризуемые их циклической структурой: деревья, уници-
клические графы и функциональные орграфы. Свойство связности
мы рассматривали при перечислении связных графов, блоков и
графов блоков. В данном параграфе мы коснемся следующих
восьми категорий графов:
a) гамильтоновы графы,
b) эйлеровы (р, д)-графы,
c) графы с локальными подграфами, ■
d) асимметрические графы,
e) симметрические графы, ч*
f) графы, обладающие квадратным корнем,
g) реберные и тотальные графы,
h) графы клик и графы интервалов.
Каждая из этих категорий содержит в свою очередь несколько
отдельных задач перечисления, так что в данном параграфе пред-|
ставлено много разнообразных задач. Кроме того, всякий раз,
когда в литературе по теории графов появляется новое струк-;
турное свойство, можно формулировать задачу о нахождении
числа графов, обладающих этим свойством.
П3.1. Гамилътоновы графы.
Граф (или орграф) называется гамилътоновым, если он содер- 1
жит простой остовный цикл (соответственно остовный контур). |
Такие графы и орграфы не подсчитаны пока ни для помеченного, 1
ни для непомеченного случаев. Перечисляющий ряд для непоме- \
ченных гамильтоновых графов начинается так: ]
а первые слагаемые перечисляющего ряда для непомеченных
гамильтоновых орграфов имеют вид
х2 + 4r3 + 60z4 + ... .
Гамильтоновы графы являются наиболее известным частным
случаем графов, содержащих специальный подграф, а именно
простой остовный цикл. Можно также выделить еще некоторые
классы графов, используя подграфы другого вида, такие, как 1-
фактор, 1-базу, циклы данной длины или полные графы данного
порядка. Мы будем подробно говорить на эту тему в § 10.6.
П3.2. Эйлеровы графы.
Робинсон [2] перечислил эйлеровы р-вершинные графы, не
обращая внимания на число ребер в них (см. § 4.7). Более труд-
трудной является задача перечисления эйлеровых (р,дг)-графов,
когда число ребер также представляет собой перечислительный

@.3. ГРАФЫ С ДАННЫМИ СТРУКТУРНЫМИ СВОЙСТВАМИ 259
параметр. Для эйлеровых графов шестого порядка перечисля-
перечисляющий полином имеет вид ,,
где показатели степеней указывают на число ребер.
Другим интересным параметром для эйлеровых графов явля-
является наименьшее число циклов, объединение которых дает исход-
исходный граф. Этот параметр появился благодаря следующзй теореме
(см. Харари [1]), стр. 83): связный граф является эйлеровым
тогда и только тогда, когда его множество ребер можно разбить
на простые циклы.
ПЗ.З. Локальные подграфы.
Пусть дан граф Н. Требуется найти число таких графов по-
порядка р, у которых каждая вершина принадлежит некоторому
подграфу, изоморфному Н. Например, если Н — треугольник, то
соответствующий ряд начинается так:
Аналогичная задача возникает и для числа графов, в которых
каждое ребро принадлежит треугольнику. Подобные вопросы
встают, естественно, и для орграфов.
П3.4. Асимметрические графы.
Не существует нетривиальных графов, порядок которых
меньше 6 и которые имеют единичную группу автоморфизмов. При
р = 6 существуют восемь асимметрических графов. В § 9.4 мы пока-
показали, что асимптотически большинство графов обладает единич-
единичной группой. Но точной формулы для числа асимметрических
р-вершинных графов не известно. Аналогичная задача стоит и
для асимметрических орграфов. Перечисляющий ряд для асиммет-
асимметрических орграфов начинается так:
Асимметрические деревья были перечислены Харари и Прин-
сом [1]. Стокмейер [1] перечислил асимметрические уницикличе-
ские графы и асимметрические функциональные орграфы. В дей-
действительности Стокмейер получил формулу для числа графов
(и орграфов) с данной группой автоморфизмов. Но ее использо-
использование предполагает знание всей решетки подгрупп симметриче-
симметрической группы Sp. Поэтому, несмотря на то что с теоретической
точки зрения перечисление асимметрических графов и оргра-
орграфов осуществлено, его нельзя, строго говоря, рассматривать как
решение соответствующей задачи (см. табл. П10 в приложении II).

260 ГЛ. 10. НЕРЕШЕННЫЕ ЗАДАЧИ
П3.5. Симметрические графы.
В вершинно-симметрическом графе группа автоморфизмов
транзитивна на множестве вершин. Реберно-симжтрический граф
определяется соответствующим образом. Симметрический граф
является одновременно вершинно-симметрическим и реберно-
симметрическим.
Тернер [1] подсчитал вершинно-симметрические графы по-
порядка р для случая простого числа вершин. Чао [1] доказал, что
однородный симметрический граф степени п и простого порядка р
существует тогда и только тогда, когда п — четное и делит р — 1;
более того, для каждой пары р, п такой граф единствен с точ-
точностью до изоморфизма. Других результатов о числе симметри-
симметрических графов не известно.
П3.6. Графы, обладающие квадратным корнем.
Квадрат G2 графа G имеет то же множество вершин, что и граф
G, и вершипы и и v смежны в G2 лишь тогда, когда расстояние
между ними в графе G равно 1 или 2. Степени (?*, G4, . . . опре-
определяются аналогично. Известна характеризация графов, облада-
обладающих квадратным корнем (см. Харари [1], стр. 38); подобные
результаты для орграфов найдены Геллером [1]. Перечисление
графов и орграфов, обладающих корнем ге-й степени, может не
оказаться нерешаемой задачей.
П3.7. Реберные графы и тотальные графы.
У реберного графа L (G) графа G множеством вершин является
множество всех ребер графа G; вершины в L (G) смежны, если
смежны соответствующие им ребра в G. Граф называется ребер-
реберным, если он есть реберный граф некоторого графа. Это понятие
было введено Уитни [1], который показал, что реберный граф Я
является реберным графом только одного графа, кроме того слу-
случая, когда Н = К3. Таким образом, число связных реберных
графов порядка р > 3 равно в точности числу связных графов,
имеющих р ребер. Используя таблицу из статьи Кэдогана [1],
дающую число связных графов, получаем начальные слагаемые
производящей функции для связных реберных графов с данным
числом вершин:
х + х2 + 2х3 + 5х* + 12хъ + 30z6 + 79z'-f-227z8 + ....
Возникающая здесь задача состоит в следующем: найти более
прямой метод, пригодный также и для подсчета реберных графов
с данными числами вершин и ребер. Такой подход должен, веро-
вероятно, использовать одну из структурных теорем о реберных гра
фах (см. соответствующие утверждения в гл. 8 книги Харари [1])

10.4. ГРАФЫ С ДАННЫМ ПАРАМЕТРОМ 261
Как показано в статье Харари и Нормана 13], число связных
орграфов с q дугами не совпадает с числом связных реберных
орграфов порядка q. Следовательно, мы не имеем даже окольного
подхода к перечислению реберных орграфов.
Тотальный граф Т (G) графа G имеет в качестве множества
вершин все вершины и ребра графа G; смежность определяется
естественным образом (см. Харари [1], стр.103). Известно, что
тотальный граф Т (G) является квадратом графа подразбиений
S (G), получаемого с помощью добавления к каждому ребру графа
G новой вершины1 степени 2. Однако сомнительно, что этот факт
облегчит поиски перечислительной формулы.
П3.8. Графы клик и графы интервалов.
Кликой графа G называется любой максимальный полный
подграф графа G. Граф клик графа G имеет в качестве множества
вершин все клики графа G и смежность определяется через непу-
непустые пересечения соответствующих (двух) клик. Множеством
вершин графа интервалов является некоторая совокупность интер-
интервалов действительной прямой, а смежность снова определяется
через пересечение. В циклически жестком графе не содержится
простых циклов, отличных от треугольников. Известно, что эти
классы графов связаны друг с другом (посредством характериза-
ционных теорем). Например, структурную характеризацию графов
клик дали Роберте и Спенсер [1] (см. об этом в книге Харари [1],
стр. 35).
10.4. ГРАФЫ С ДАННЫМ ПАРАМЕТРОМ
Задачи перечисления проще предлагать, нежели решать.
Например, всякий раз когда в нашем поле зрения появляется
новый параметр, мы немедленно можем сформулировать соответст-
соответствующую задачу перечисления. Задачи перечисления графов с дан-
данными параметрами естественным образом разбиваются на под-
подмножества, соответствующие связанным между собой параметрам.
Мы выделяем следующие десять категорий параметров:.
a) радиус и диаметр,
b) обхват и окружение,
c) наименьшая и наибольшая степени,
d) связность,
e) числа независимости и покрытия,
f) числа, связанные с кликами,
g) число пересечения,
1 То есть граф S (G) получается из графа G путем подразбиения каждого
ребра графа G на два новых ребра, — Прим, перев,
в Заказ 443

262 '' fit. 10. НЕРЕШЁННЫЕ ЗАДАЧ
; h) древесность, " ' ~
i) род, толщина, крупность, число скрещиваний, • I
j) хроматические числа. j
Для каждой из указанных категорий мы определяем соответ^!
ствующие инварианты и описываем частичные успехи, достигну-;
тые в этих направлениях. ;
П4.1. Радиус и диаметр.
Эксцентриситетом е (v) вершины v графа G называется наи'
большее из расстояний от вершины v до других вершин графа.
Радиус г (G) есть наименьший из эксцентриситетов вершин в графе
G, а диаметр d (G) — наибольший из эксцентриситетов.
Таким образом, радиус графа G равен 1 тогда и только тогда,
когда в графе существует вершина v0, смежная со всеми другими
вершинами графа. Легко подсчитывается число р-вершинных
графов радиуса 1, ибо оно в точности совпадает с общим числом
графов порядка р—1. Но уже для графов радиуса 2 не существует
прямых способов подсчета их числа.
Для деревьев диаметр аппроксимируется двойным радиусом.
Деревья с заданным диаметром перечислены Харари и Принсом
[1]. Для графов справедливо тривиальное высказывание: р-вер-
шинный граф с диаметром d = 1 совпадает с Кр.
Соответствующие задачи имеют место и для орграфов. Входной
и выходной радиусы орграфа D определены в книге Харари,
Нормана и Картрайта [1] на стр. 162. Эти инварианты, так же
как и диаметр, существуют всегда в сильно связном орграфе D.
П4.2. Обход и окружение.
Обход графа есть наименьшая из длин его простых циклов;
окружение — наибольшая из таких длин. Пусть сп — число
циклов длины п в графе G. Спрашивается, сколько существует
Графов со следующим набором чисел циклов разной длины: (с3,
с4, ..., ср). Ответ на этот общий вопрос позволил бы со значительно
Меньшими трудностями подсчитать, например, такие структуры:
a) графы с данным обхватом и
тем более
b) графы с данным окружением, '
c) графы, содержащие треугольники,
d) графы, содержащие четырехугольники,
e) гамильтоновы графы,
f) графы с данным числом циклов.
Перечисление унициклических графов, проведенное в § 3.4,
является весьма незначительным шагом в этом направлении.

10.4. ГРАФЫ С ДАННЫМ ПАРАМЕТРОМ 263
П4.3. Наименьшая и наибольшая степени.
Наименьшая степень б и наибольшая степень А являются
естественными параметрами, которые можно рассматривать в за-
задачах перечисления. Хотя и существуют утверждения теоретиче-
теоретического характера, относящиеся к перечислениям графов с данным
разбиением (Партасарати [1 ]) и орграфов с данным разбиением
(Харари и Палмер [31), эти утверждения не имеют прямого отно-
отношения к б и А.
Рассмотрим графы с б ^ п >> 0. При п — 1 получаем все
графы без изолированных вершин. Этот случай исследуется легко.
Случай п = 2 охватывает все графы, не имеющие ни висячих, ни
изолированных вершин. Такие графы перечислены Робинсоном
[31 с использованием метода сумм цикловых индексов, развитого
для перечисления блоков (см. § 8.6). При п = 3 приходим к го-
меоморфно несводимым графам без висячих вершин.
П4.4. Связность.
Связностью и (реберной связностью X) графа G называется
наименьшее число вершин (ребер), после удаления которых
получаем несвязный или тривиальный граф. Граф G называется
п-связным, если и ^ п. Таким образом, число графов со связностью
п равно разности между числом тг-связных графов и числом (тг+1)-
связных графов.
И 0-связные, и 1-связные графы перечислены, ибо указанные
множества представляют собой соответственно все графы и все
связные графы. 2-связные графы с р :=> 3 вершинами образуют
множество всех блоков; они были перечислены Робинсоном (см.
гл. 8). Перечисление n-связных графов при п >> 3, очевидно,
требует более мощных методов, чем те, которые существуют
сейчас.
Встает вопрос и о числе графов с данными и и Я,, а также (част-
(частный случай) о числе графов, у которых х, = К-
П4.5. Числа независимости и покрытия.
Множество вершин (ребер) называется независимым, если ника-
никакие два его элемента не являются смежными. Вершинное число
независимости C0 графа G — это наибольшее число независимых
вершин графа G. Реберное число независимости (Зх определяется
аналогично. Говорят, что вершина v и ребро х покрывают друг
друга, если v инцидентна х. Числом вершинного покрытия а0
графа G называется наименьшее число вершин, покрывающих
все ребра графа; число реберного покрытия ах графа G опреде-
определяется подобным образом.

264 ГЛ. 10. НЕРЕШЕННЫЕ ЗАДАЧИ
Учитывая классическое равенство из теории графов: а0 + Ро =
= р =at + Pi, заключаем, что нужно только упомянуть о зада~
чах перечисления графов с данным вершинным числом независим
мости ро и с данным числом р\. Перечисление графов по этшЛ
параметрам кажется интуитивно более легким, чем перечислений,
графов с данными числами покрытий; однако из приведенного"
выше равенства это не следует.
П4.6. Числа, связанные с кликами.
Существуют несколько инвариантов, связанных с кликами.
Один из них — наибольший порядок клик графа G, который мы
можем записать в виде ро (G), ибо он равен наибольшему числу
независимых вершин в дополнении G графа G. Вот еще некоторые
числа, связанные с кликами:
a) число клик,
b) наименьший порядок клик,
c) наименьшее число клик, покрывающих все вершины графа G,
d) аналогичная характеристика для покрытия ребер графа G,
e) наибольшее число попарно не пересекающихся клик.
Последний инвариант является, очевидно, вершинным числом
независимости графа клик данного графа G. А первый инвариант
представляет собой число вершин в этом же графе клик. Вообще,
всякий инвариант графа клик данного графа G превращается
указанным способом в инвариант самого графа G. Ни одна из этих
задач не вселяет надежду на быстрое ее решение.
П4.7. Число пересечения.
Числом пересечения ш (G) данного графа G порядка р назы-
называется наименьшее число элементов в множестве S, таком, что
существует семейство Slt S2, • ■■fSp различных непустых под-
подмножеств множества 51, объединение которых равно S, и вершины
vt и V/ смежны в графе G тогда и только тогда, когда St {]S,- Ф 0.
Вариацией этого инварианта является число со0, отличающееся
от со только тем, что соответствующие ему подмножества S{ могут
не быть различными; так, например, ш0 (Кр) = 1.
Кажется сомнительным, что существует какой-либо метод для
перечисления графов с данным числом пересечения или с любой
из его возможных вариаций.
П4.8. Древесностъ.
Древесностъ графа G есть наименьшее число попарно реберно-
непересекающихся ациклических подграфов, объединение которых
равно G. Наибольшее число попарно реберно-непересекающихся

10.4. ГРАФЫ С ДАННЫМ ПАРАМЕТРОМ 265
подграфов графа G, которые содержат циклы и дают после объе-
объединения весь граф G, называется недревесностъю графа G. Как
отмечено в статье Харари [13], эти две характеристики составляют
пару инвариантов: инвариант покрытия (древесность) и инвариант
упаковки (недревесность). Другая такая пара состоит, во-первых,
из числа цепного покрытия 1, равного наименьшему числу простых
цепей, объединение которых совпадает с графом G и, во-вторых,
из «упаковочного двойника» числа цепного покрытия *. Такие
инварианты кажутся безнадежными для использования их в ка-
качестве параметров перечисления; то же самое можно сказать
и о числе остовов в графе, которое Брукс, Смит, Стоун и Татт [1]
назвали сложностью графа.
П4.9. Род, толщина, крупность, число скрещиваний.
Эти и другие топологические инварианты вполне могут ока-
оказаться наиболее неподатливыми из всех инвариантов, имеющих
какое-либо отношение к задачам перечисления. Род у графа G
равен наименьшему из родов ориентируемых поверхностей, на
которых граф G можно уложить так, чтобы никакие два его pje6pa
не пересекались 3. Толщина 9 есть наименьшее число пленарных
подграфов, объединение которых совпадает с графом G. Круп-
Крупность | — это наибольшее число реберно-непересекающихся не-
планарных подграфов, объединение которых равно G. Наконец,
число скрещиваний v есть наименьшее число пар пересекающихся
ребер графа G при расположении этого графа на плоскости 4.
Если G — планарный граф, то у (G) = v (G) = 0, 9 (G) = 1
и | (G) не определено. Существует много других топологических
инвариантов, относящихся к графам, но все они настолько же
непригодны для целей перечисления графов, как и приведенные
выше четыре инварианта.
П4.10. Хроматические числа.
Хроматическим числом X графа G называется наименьшее
число красок, необходимое для такого раскрашивания вершин
графа G, при котором никакие две смежные вершины не окрашены
1 В оригинале: the covering path number. — Прим. перев.
2 Этот «упаковочный двойник» можно определить, например, как наиболь-
наибольшее число таких попарно реберно-непересекающихся подграфов графа G,
которые не содержат изолированных вершин, отличны от простых цепей
и после объединения дают весь граф G. — Прим. перев.
3 Точнее, любая точка пересечения каких-либо ребер в укладке графа G
на данной поверхности не является внутренней точкой никакого ребра графа
G. — Прим. перев.
* Ребра в каждой паре пересекаются только в одной точке; точки пере-
пересечения каждой пары ребер отличны друг от друга и не совпадают ни с одной
иа вершин графа. — Прим. перев.

266 ГЛ. 10. НЕРЕШЕННЫЕ ЗАДАЧИ
в один цвет. Реберно-хроматическое число %' (тотально-хромати-
(тотально-хроматическое число %") графа G представляет собой хроматическое число
реберного графа L (G) (соответственно тотального графа Т (G)).
Некоторые авторы называют число %' хроматическим индексом
графа.
Граф G называется п-хроматическим, если % = п, и G назы-
называется п-рискрашиваемым, если % ^ п. Робинсоном [1] были
перечислены тг-раскрашенные графы (см. § 4.5), а 2-раскрашива-
емые графы перечислены Харари и Принсом [2]. В настоящее
время, по-видимому, невозможно перечислить даже 3-раскраши-
ваемые графы.
10.5. ПОДГРАФЫ ДАННОГО ГРАФА
В большинстве задач этого параграфа требуется найти число
неподобных подграфов данного графа G, изоморфных некоторому
графу Н. Таким образом, с помощью группы графа G выясняется,
можно или нет рассматривать два различных вхождения подграфа
Н как эквивалентные. Аналогичные вопросы можно сформулиро-
сформулировать и для орграфов.
П5.1. Гамилътоновы циклы.
Число всех простых остовных циклов в данном помеченном
графе или помеченном орграфе можно выразить в чисто теорети-
теоретическом виде (на языке матрицы смежности), используя метод
Картрайта и Глисона Т. [1]. Но вычисление требуемых при этом
чисел практически не осуществимо, и случается, что задача еще
сильнее усложняется даже тогда, когда число классов подобия
такое, о котором можно только мечтать. Лишь для специальных
графов, таких, как Кр, можно выписать ответ, исходя из элемен-
элементарных комбинаторных принципов.
Наиболее интересный частный случай этой задачи возникает
тогда, когда заданный граф является тг-кубом Qn\ этот случай
находит приложение в теории кодирования. Легко заметить,
что существует только один класс подобия простых остовных
циклов в Q2 и в Q3. Гилберт [1] показал, что соответствующий
перечисляющий ряд начинается так:
Но при п ►> 4 значения коэффициентов не известны. Число поме-
помеченных гамильтоновых циклов в Qn также найдено лишь для
п е^ 4. И не ясно, сколько требуется машинного времени, чтобщ
■гочдо вычислить следующий коэффициент,

10.5. ПОДГРАФЫ ДАННОГО ГРАФА 267
П5.2. Простые циклы данной длины. ' " > : •' '
Задача состоит в нахождении числа неподобных простых цик-
циклов длины к в р-вершинном графе и является обобщением задачи
П5.1. Задача легко решается в частных случаях. Например,
существует ровно один класс подобия простых остовных циклов
длины 2/с в полном двудольном графе Кт „ при т, п ^> к. В «поме-
(т\(п\
ченном случае» ответ на тот же самый вопрос таков: I I I X
\к I \k j
X к\ (к—1)!/2. Решение «помеченной задачи» для простых циклов
длины 3, 4 и 5 в данном графе или орграфе, полученное в терми-
терминах матрицы смежности, можно найти в статье Харари и Ман-
вела [1].
П5.3. Полные графы.
Как упоминалось выше, число треугольников К3 в данном
помеченном графе вычислить можно. Задача определения числа
вхождений графа Кп, п > 3, в данный помеченный граф остается
нерешенной. В «непомеченном» случае для получения числа не-
неподобных треугольников необходимо знать не только общее число
треугольников, но и во что эти треугольники преобразуются под
воздействием группы данного графа.
у--.к-у ■;.№.'•■■- . ■•'.
П5.4. Остовы.
Число помеченных остовов данного помеченного графа може?
быть вычислено с помощью матричной теоремы о деревьях. Но не
известно соответствующего метода для нахождения числа различ-
различных (неизоморфных) остовов данного (непомеченного) графа.
Трудность решения последней задачи демонстрируется примером,
в котором заданный граф является полным графом порядка р.
В этом случае число различных остовов равно числу р-вершинных
деревьев; число таких деревьев впервые было подсчитано Кэли.
Задача о подсчете числа неподобных остовов в данном графе также
не решена.
П5.5. Факторы.
Пусть G — помеченный граф, обладающий 1-фактором, т. е.
остовным подграфом, состоящим из независимых ребер (см. Ха-
Харари [1], стр. 106). Число различных 1-факторов графа G известно
только в очень частных случаях. Например, граф Кш имеет
Bтг)!/2"тг! 1-факторов, а граф Кп<п имеет ровно тг! 1-факторов.
Факторизацией (или l-факторизацией) графа G называется
разбиение множества всех ребер графа G на 1-факторы, если

268 ГЛ. 10. НЕРЕШЕННЫЕ ЗАДАЧИ
такое разбиение существует. Известно, что граф К%п имеет 1-фак-
торизацию, но число их найдено только при малых тг. Недавно
Уоллис установил, что граф Ks имеет ровно шесть 1-факторизаций.
В силу классической теоремы Кёнига (см., например, Харари [11,
стр. 107), каждый регулярный двудольный граф Кп< „ имеет
1-факторизацию, так что здесь тоже возникает вопрос о числе
1-факторов.
П5.6. Эйлеровы циклы в данном эйлеровом графе.
Известна точная формула для числа эйлеровых контуров в дан-
данном орграфе (см. формулу A.8.2)). Однако для графов никакого
прогресса в этом направлении нет. Один из возможных подходов
к решению этой задачи состоит в следующем: нужно рассмотреть
все ориентации данного эйлерова графа G, получается набор
эйлеровых орграфов Dlt D2, ••• Если ei — число эйлеровых
контуров в Dt, то 2е( равна общему числу ориентированных
эйлеровых циклов в графе G. Но сказать-то легко, а как это сде-
сделать? Например, в частном случае, когда G = K2n+i, нужно
иметь в наличии матрицы смежности всех эйлеровых турниров
порядка 2тг + 1!
10.6. НАДГРАФЫ ДАННОГО ГРАФА
В задачах этого параграфа спрашивается о числе графов по-
порядка р, являющихся надграфами данного графа Н. При под-
подсчете таких графов может оказаться полезной экстремальная
теория графов. Например, если Н = К3, то теорема Турана
показывает, что в случае, когда граф G имеет более чем [р2/4]
ребер, то в нем содержится треугольник К3. Следовательно, для
решения соответствующей задачи перечисления достаточно рас-
рассмотреть только графы, у которых не больше чем [р2/4] ребер.
С другой стороны, решение такой задачи перечисления приво-
приводит к решению соответствующей экстремальной задачи. Варианты
всех этих задач существуют также и для орграфов.
П6.1. Простые циклы.
Подсчет надграфов треугольника эквивалентен подсчету гра-
графов, обхват которых равен 3. Однако надграфы простого цикла
Сп порядка п :=> 4 не соответствуют графам обхвата п, ибо послед-
последние не содержат вообще простых циклов меньшей, чем тг, длины.
Перечисляющий ряд надграфов цикла С4 начинается так:

10.7. ГРАФЫ И РАСКРАСКА 269
П6.2. Полные графы. ■
Задача о подсчете числа надграфов графа Кп уже появлялась
в различных оформлениях для случая п = 3. Поэтому наши
интересы здесь сосредоточены на случаях п ^ 4. Решение соот-
соответствующей экстремальной задачи дается общей теоремой Ту-
рана (см., например, Харари [1], стр. 33).
П6.3. Полные двудольные графы.
Задача состоит в подсчете надграфов графа КП1:П. Так как АГ2;2
является простым циклом длины 4, то мы уже сталкивались с этим
трудным частным случаем. Заметим, что надграфы графа Кп<п
представляют собой такие графы, у которых наибольшая степень
равна по крайней мере п (ср. с задачей П4.3).
П6.4. Простые цепи.
Подсчет надграфов простой цепи Рп порядка п осуществляется
легко для малых п. Например, если п = 4, то среди связных
графов порядка ;=>4 только звезды К1 т не являются надграфами
цепи Pt. А чтобы решить задачу подсчета числа надграфов цепи Рп
для каждого п, надо уметь подсчитывать такие связные графы
порядка ^>п, у которых диаметр любого остова меньше п. Эта
задача родственна задаче П5.4.
10.7. ГРАФЫ И РАСКРАСКА
Существует естественный метод обоснования гипотезы четырех
красок D КГ), базирующейся на рзшэнии некоторых задач
перечисления графов:
4КГ: Каждый планарный граф 4-раскрашиваем.
ПЭ4КГ: Число пленарных графов равно числу 4-раскрашиваемых
пленарных графов. (ПЭ4КГ означает перечислительный
эквивалент гипотезы четырех красок).
Известно, что первые 39 коэффициентов в перечисляющих
рядах этих двух классов графов (стоящие при соответствующих
степенях!) одинаковы1 (см. Оре и Стемпл [1]). Существует не-
несколько возможных направлений исследований, определяемых
двумя различными «степенями свободы»:
1. Можно по-разному выбирать параметр перечисления: либо
число вершинр, либо число ребер q, либо яр, и q, либо диаметр d,
либо произвольный другой подходящий параметр.
1 Из результата Донца [1] следует, что таким свойством обладают пер-
первые 41 коэффициентов упомянутых перечисляющих рядов. А совсем не-
недавно появилось сообщение (см. Appei К., Haken W-, Every planar map
is four colorable, Bull, of Amer. Math. Soc, 82, № 5 A976) о том, что
гипотеза четырех красок является истинным утверждением,— Прим. перее.

270 ГЛ. 10. НЕРЕШЕННЫЕ ЗАДАЧИ
2. Можно выбирать тот или иной тип графов, соблюдая при
этом единственное условие: и планарные графы, и 4-раскрашива-
емые планарные графы должны одновременно обладать этими
выбранными (характерными для рассматриваемого типа графов)
свойствами. Вот некоторые из таких свойств:
a) планарные графы (как в ПЭ4КГ),
b) корневые планарные графы,
c) реберно-корневые планарные графы,
d) планарные графы, у которых корнями являются треуголь-
треугольники,
e) помеченные планарные графы,
i—j) предыдущие пять свойств, но с заменой в них планарных
графов на плоские,
к) плоские графы, которые превращаются в корневые в резуль-
результате следующей трехшаговой процедуры:
A) выбираем произвольное ребро х в плоском графе G,
B) ориентируем ребро х произвольным образом,
C) выделяем произвольным образом одну из двух граней,
инцидентных ребру х, и называем эту грань внешней. Для шага
A) имеются q возможностей, так как у графа G всего q ребер;
для шагов B) и C) имеются по две возможности. Перемножая
все эти числа, видим, что общее число описанных ориентации
(ориентации по Татту) плоского графа равно 4д. Указанная
ориентация рассматривалась в статье Харари и Татта [1], посвя-
посвященной группе автоморфизмов пленарного графа. Достаточно
полный обзор разнообразных приемов перечисления ориентиро-
ориентированных по Татту плоских карт дан в работе Татта [3], и мы от-
отсылаем читателя, интересующегося соответствующей проблемати-
проблематикой, к указанной работе.
П7.1. Планарные и плоские графы.
Все деревья являются пленарными, так что число планарных
деревьев равно числу всех деревьев. Плоские унициклические
графы легко перечисляются с помощью теоремы перечисления
Пойа (см. соотношение B.4.6)): в качестве перечисляющего ряда
для фигур нужно взять перечисляющий ряд для плоских корне-
корневых деревьев, а в качестве группы конфигураций надо использо-
использовать диэдральную группу.
Все десять приведенных выше вариаций (см. (a)—(j)) пере-
перечислительного эквивалента гипотезы четырех красок остаются
нерешенными.
П7.2. п-раскрашиваемые графы.
Эта задача решена только для п = 2 и совпадает с задачей
П4.10.

10.8. ВАРИАЦИИ НА ТЕМУ О ГРАФАХ 271
П7.3. Планарные n-раскрашиваемые графы.
Эта задача не решена для всех п > 1. Даже при п — 2 данная
задача является весьма трудной, ибо связана с описанием гомео-
гомеоморфизмов графа К33.
П7.4. Самодвойственные плоские графы.
Граф G*, двойственный к данному плоскому графу G, строится
следующим образом: в каждой области (грани) графа G, включая
и внешнюю область, выбирается по одной точке (вершины графа
G*); если две области имеют общее ребро х, то точки, выбранные
в этих областях, соединяются ребром х*, пересекающим только
ребро х. В результате такого построения всегда получается плос-
плоский общий граф, в котором могут быть и петли, и кратные ребра.
Тетраэдр является самодвойственным графом, тогда как куб
и октаэдр двойственны друг другу; то же самое можно сказать
о додекаэдре и икосаэдре.
Если бы удалось решить задачи П7.1 и П7.3, то, сличая полу-
полученные решения для п — 4, можно было бы обосновать ПЭ4КГ,
а следовательно, и 4КГ. Все это, конечно, можно осуществить
и путем сравнения любой другой пары классов планарных графов,
лишь бы эти графы (из разных классов) получались одним и тем
же способом; например, графы должны иметь корни одного и того
же вида г. Можно с уверенностью утверждать, что 4КГ не будет
обоснована в скором времени с помощью ПЭ4КГ. Кроме того,
распространяющиеся иногда слухи о том, что 4КГ будто бы ре-
решена, в любом случае не дают ответа на приведенные выше весьма
трудные перечислительные вопросы.
10.8. ВАРИАЦИИ НА ТЕМУ О ГРАФАХ
Существует много конфигураций, которые не являются гра-
графами per se 2, но по своей природе — суть графические объекты.
Ограниченные пространственные возможности позволяют нам
указать перечислительные задачи только для некоторых из этих
структур. Мы рассматриваем здесь следующие конфигурации:
симплициальные комплексы, латинские квадраты, узлы, полимино,
а также конфигурации на шахматной доске и замощения.
П8.1. Симплициалъные комплексы.
Симплициалъный комплекс состоит из конечного непустого
множества V точек и некоторой совокупности подмножеств
1 Скажем, все графы в рассматриваемой паре классов являются реберно-
корневыми. — Прим. перев.
2 Здесь: сами по себе {лат,),. — Прим, перец.

272 ГЛ. 10. НЕРЕШЕННЫЕ ЗАДАЧИ
множества V, называемых симплексами, при этом должны выпол-
выполняться следующие условия: каждая точка из V является симплек-
симплексом, каждое непустое подмножество симплекса тоже является
симплексом. Размерность симплекса S равна по определению
\S\ —1; размерность комплекса равна наибольшей из размерностей
принадлежащих ему симплексов.
Несмотря на то что число n-размерных комплексов подсчитано
только при п = 1, когда комплексы представляют собой графы
(более точно, 1-размерные комплексы — это графы, не явля-
являющиеся вполне несвязными), существуют и другие частные случаи,
которые могут быть успешно изучены. В чистом п-комплексе
каждый максимальный симплекс имеет размерность 0 или п.
Таким образом, каждый граф является чистым 1-комплексом.
Указания по поводу того, как подсчитывать чистые га-комплексы,
даны в статье Харари [111. Например, задача перечисления чи-
чистых 2-комплексов с р вершинами решается путем подстановки
1 + х в цикловой индекс триадной группы Sp — эта группа
индуцируется группой Sp и действует на 3-подмножествах мно-
множества объектов. Формула для этого циклового индекса приве-
приведена в работе Обершельпа [1]. Пусть s (у) =2sp2/p — производя-
производящая функция для чистых 3-размерных симплициальных комплек-
комплексов. С помощью прямых вычислений мы обнаружили, что эта
функция начинается так:
» (У) = У + Уг + 2*/3 + 5i/4 + 3V + 2136г/6 + 7013488?/' + ... .
Пусть теперь spqr обозначает общее число комплексов не выше
чем второй размерности, имеющих р точек @-симплексов), q ли-
линий A-симплексов) и г клеток B-симплексов). Пусть sp (x, у) =
~llispqrx9yr — перечисляющий многочлен для таких комплексов
с р точками. Для р = 4 этот многочлен имеет вид
* [2 + у) +
Задача состоит в определении sp (x, у) для произвольного р.
Решение этой задачи позволило бы получить соответствующий
результат и для комплексов большей размерности.
П8.2. Латинские квадраты.
Латинский квадрат представляет собой квадратную матрицу
порядка га, в которой каждая строка и каждый столбец являются
перестановкой целых чисел 1,2, . . ., п. Если Ln — число квад-
квадратов порядка п, в которых и первая строка, и первый столбец
являются естественно упорядоченной перестановкой: 1, 2, ...

10.8. ВАРИАЦИИ НА ТЕМУ О ГРАФАХ 273
..., п, то общее число латинских квадратов порядка п, очевидно,
равно п\ (п—1)!L,,. Нижеследующие значения величины Ln для
re ^ 7 взяты из книги Риордана [1], стр. 248:
х + х2 + х3 + Ах* + 56а:5 + 9408а:6 + 16942080а;7 + ... .
Латинские квадраты можно также толковать как 2-раскрашен-
ные графы Кп>п, в которых раскрашены и ребра. Вершины щ
одного цвета соответствуют строкам латинского квадрата, в то
время как вершины vt другого цвета отвечают столбцам. Каждое
ребро графа Кп<п окрашивается в один из п цветов так, чтобы
каждая вершина графа была инцидентна ровно одному ребру
каждого цвета.
Число различных латинских квадратов уменьшится, если на
множестве квадратов ввести следующем образом эквивалентность:
допускаются перестановки в множзствах строк, столбцов и сдмвэ-
лов. Несколько первых коэффициентов перечисляющего ряда для
латинских квадратов с такой эквивалентностью были получены
Дж. Дж. Зейделем (неопубликованный результат):
Пусть А = [ац] и В = [btj] — два латинских квадрата
порядка п. Они называются ортогональными, если все пг пар
(atj, b,/) являются различными. Задача о подсчете числа пар
ортогональных латинских квадратов не решена, так же как
задача о числе ортогональных т-ок.
П8.3. Узлы и узловые графы.
На рис. 10.8.1 показаны первые семь узлов из числа тех, кото-
которые приведены в книге Райдемайстера [1], стр. 70; эти узлы со-
содержатся также в статье Александера и Бригса [1]. Каждый изо-
изображенный на рисунке узел спроектирован на плоскость с наи-
наименьшим числом пересечений (скрещиваний). Со всякой такой
минимальной плоской проекцией узла можно связать граф,
взяв в качестве вершин графа точки пересечения, а в качестве
ребер — дуги кривых, соединяющие пары последовательных то-
точек пересечения. Так построенные графы (вернее, мультиграфы)
для приведенных выше семи узлов изображены на рис. 10.8.2.
Очевидно, что каждый такой граф является регулярным степени 4.
Узловым графом (или графом узла) называется граф, соответ-
соответствующий минимальной плоской проекции узла. Через GPi n обо-
обозначается граф, сопоставленный узлу рп (см. рис. 10.8.1 и 10.8.2).
Как показал Т. Браун [1], граф узла не является узловым
инвариантом. Этот факт он обосновал, представив «узловое произ-
произведение» узлов 3: и 4, двумя разными способами так, что один
из получившихся узловых графов имеет четыре двойных ребра,

274
ГЛ. 10. НЕРЕШЕННЫЕ ЗАДАЧИ
а другой — три двойных ребра (определение узлового произведе-
произведения дано в статье Харари [2]).
Таким образом, мы скорее должны говорить о некотором]
графе узла, а не об определенном графе узла!
Рис. 10.Р.1. Наименьшие узлы.
Обратно, различные узлы могут иметь одинаковые узловые
графы; наиболее замечательным известным примером такого рода
является граф узлов 817,819, 820 и 82i, изображенный на рис. 10.8.3.
G6.1 . G6.2
Рис. 10.8.2. Наименьшие графы узлов.
1
Т. Браун установил следующий критерий: 1
плоский мультиграф представляет собой узловой граф тогда :|
и только тогда, когда >
а) он является регулярным графом степени 4, <

10.8 ВАРИАЦИИ НА ТЕМУ О ГРАФАХ 275
b) он является блоком,
c) плоская кривая, порождаемая описываемым ниже способом,
является эйлеровым циклом. Процесс построения кривой таков:
выбираем произвольную вершину графа в качестве начальной точки
кривой и двигаемся из этой вершины по произвольному инци-
инцидентному ей ребру; далее, находясь в некоторой вершинэ и,
двигаемся из нее по такому ребру графа, которое ведет в вершину
v, инцидентную ребру, противолежащему вершине и (на каждом
шаге, естественно, перемещаемся по ещэ не пройденному ребру;.
Теперь, после того как мы узнали, какие графы являются
Рис. 10.8.3. Узловой граф четырех различных узлов.
узловыми, естественным образом возникает несколько перечис-
перечислительных вопросов.
1. Сколько существует р-вершшшых узловых графов?
Заметим, что этот вопрос отличен от вопроса о числе узлов,
ибо, как было отмечено выше, граф узла не является узловым
инвариантом.
2. Сколько существует р-вершинных узловых графов, содержа-
содержащих т пар кратных ребер? Из имеющихся данных следует, что,
по-видимому, всегда т ^ 2.
« 3. Заменяя каждую пару двойных ребер одним ребром, полу-
': чаем «подлинный» граф (не являющийся мультиграфом). Спраши-
Спрашивается, сколько существует таких графов.
4. Какие специальные классы узловых графов можно выделить
и перечислить г?
П8.4. Конфигурации на шахматной доске.
Мы сформулируем лишь незначительное число из большого
количества задач, связанных с расположением фигур на шахмат-
шахматной доске, имеющей размеры п X п. Все эти задачи могут быть
проинтерпретированы на теоретико-графовом языке и проиллю-
проиллюстрированы многими способами.
В задаче о ладьях спрашивается, каким числом способов можно
расположить п ладей на (п X ге)-доске так, чтобы никакая ладья
1 То есть решить соответствующую перечислительную задачу для них,
Цри.ч. перев,

276 ГЛ. 10. НЕРЕШЕННЫЕ ЗАДАЧИ
не угрожала другой. Другими словами, нет ни одной пары ладей,
расположенных на одной и той же горизонтали или вертикали.
Решение дается числом га!, если не отождествляются конфигура-
конфигурации, преобразуемые друг в друга путем таких вращений и отра-
отражений доски, которые сохраняют два цвета полей (квадратов)
доски. Число различных конфигураций, получаемых после отож-
отождествления в указанном выше смысле, подсчитано для га ^ 7
(см. Крейчик [1]):
+ 2а:3 + 7z4 + 23а:5 + Ибо:6 + 694а:7 + ... .
Всякое допустимое расположение га ладей, при котором ни-
никакие две из них не угрожают друг другу по диагонали, соответ-
соответствует, очевидно, конфигурации из задачи о ферзях. Последняя
задача не решена ни в помеченном, ни в непомеченном случаях.
Число различных конфигураций для га ^ 12 подсчитано Крейчи-
ком [1] при условии, что не отождествляются конфигурации, пере-
переводящиеся друг в друга с помощью таких вращений и отражений
доски, которые сохраняют 2-раскраску полей:
х + 2xi + 10а:5 + 4r6 + 4(k7 + 92a:8 + 352a:9 +
+ 724a;10 + 2680.Г11 + 14 200a:12 + ... .
Аналогичные задачи можно сформулировать для слонов и ко-
коней. Можно рассмотреть и такие вариации рассмотренных задач,
которые определяются выбором формы доски, например прямо-
прямоугольной, L-образной, треугольной. Более интересной задачей
с точки зрения теории перечисления является задача о нахожде-
нахождении числа различных ладейных многочленов, определенных
в книге Риордана [1], стр. 197.
В задаче другого типа, связанной с шахматной доской, спра-
спрашивается, сколько существует различных способов так обойти
конем все поля доски, имеющей размеры т X п, чтобы каждое
поле, кроме начального, посещалось конем только один раз,
а начальное — два раза (в начале и в конце обхода). Очевидно,
что такие обходы представляют собой помеченные гамильтоновы
циклы в «конеподобном» графе порядка т- га. Многочисленные
частные результаты, относящиеся к этой задаче, можно найти
в книге Крейчика [1].
П8.5. Задачи о росте клеток.
Все «квадратные полимино», имеющие не более четырех кле-
клеток, показаны 1 на рис. 10.8.4. Таким образом, полимино «раз-
1 В оригинале: «square animals» — «квадратные животные». Мы приняли
адесь термин «полимино» вместо «животного» (см. Харари [1], стр. 227).
О полимино см. Харари [12], стр. 205, 209. — Дрил. перев.

10.8. ВАРИАЦИИ НА ТЕМУ О ГРАФАХ
277
растается» (в плоскости) в результате «наращивания» квадратных
клеток одного и того же размера, которые «прикрепляются»
к любой из «свободных» сторон у клеток, образующих полимино.
Мы предполагаем, кроме того, что полимино являются односвяз-
ными, т. е. не имеют дыр (см. рис. 10.8.5).
□ СП [
Mill LI
Рис. 10.8.4. Наименьшие квадратные полимино.
Рид [4] придумал удобную схему, позволившую ему вычислить
число полимино, односвязных и неодносвязных, состоящих не
более чем из десяти клеток. Эти результаты, а также неопублико-
неопубликованные результаты Паркина приведены в табл. 10.8.1. Клэрнер
[1J, использовав изящные аналитические методы, установил
Рис. 10.8.5. Наименьшее полимино, не являющееся односвязным.
нижние оценки для полимино обоих видов. Однако формул, да-
дающих возможность определять число полимино с п клетками,
пока не найдено. Заметим, что наименьшее неодносвязное полимино
(см. рис. 10.8.5) имеет семь клеток и является единственным семи-
клеточным неодносвязным полимино. Таким образом, из 107 семи-
клеточных квадратных полимино только одно неодносвязно.
Та блица 10.8.1
Клетки
Полимино
Неодносвязные полпмино
Квадратные
1
1
0
2
1
0
3
2
0
4
5
0
полимино
5
12
0
6
35
0
7
107
1
8
т
о
9
1248
37
10
4 271
384

278
ГЛ. 10. НЕРЕШЕННЫЕ ЗАДАЧИ
Существуют многочисленные вариации этой задачи (см. Ха-
рари [12]). Если вместо квадратов брать треугольники, то coo«j
ветствующий перечисляющий ряд начинается так:
Если же рассматривать полимино из шестиугольников,
получим
Мы можем сформулировать задачу о числе тороидальных поли--;
мино, т.е. полимино, расположенных на поверхности рода 1' ]
Д /57
ЛЛ7
i
Рис. 10.8.6 Наименьшие треугольные полимино.
(вместо рода 0 — в случае плоскости). Наконец, мы можем ис-
использовать вместо квадратов кубы и интересоваться числом про-
пространственных полимино. Много других вопросов, относящихся
I •■>/> "."?.'.■*'.■
Рис. 10.8.7. Наименьшие шестиугольные полимино.
к задачам замощения, можно найти в книге Голомба [1], в кото-
которой ярко продемонстрировано, как такие конструкции приводят
к танталовым головоломкам-

10.8. ВАРИАЦИИ НА ТЕМУ О ГРАФАХ 279
П8.6. Задача Изинга. '■'■■"■■■.
Изинг [1] поставил задачу, которая носит его ими, и решил
ее для одномерного случая. Онзагер [1] первым нашел решение
в двумерном случае, но нет никакого прогресса в поисках решения
этой задачи для больших размерностей.
В двумерном решетчатом графе ЬШуП вершинами являются
упорядоченные пары (i, j), i = 1, 2, ..., m;j = 1, 2, ..., п. Две вер-
вершины смежны, если евклидово расстояние между ними равно 1.
Таким образом, Ь,П:П есть декартово произведение Рт X Рп двух
простых цепей. Обычно в физических приложениях эти графы
изображаются на торе с отождествлением противолежащих сто-
сторон 1. Решетчатый d-мерный граф определяется аналогично.
Рис. 10.8.8. Решетчатый граф.
Задача состоит в нахождении числа Aq различных помеченных
четных подграфов с q ребрами.
Под площадью четного подграфа двумерной решетки мы пони-
понимаем наименьшую площадь, ограниченную попарно реберно-не-
пересекающимися простыми циклами этого подграфа 2. В «дву-
«двумерной задаче Изинга с магнитным полем» требуется найти произ-
производящую функцию для помеченных четных подграфов, принимая
в качестве параметров перечисления число ребер в подграфе
и площадь подграфа.
Другой вариант задачи Изинга известен в литературе как
«взаимодействие между неближайшими соседями». Рассмотрим
надграф решетчатого графа, получаемый добавлением обеих
диагоналей в каждом квадрате графа. Задача опять состоит в пе-
перечислении четных подграфов такого графа (точнее, надграфа).
Для более детального ознакомления с различными задачами
Изинга можно порекомендовать описательную статью Харари[14].
1 Точнее: сторона, соответствующая i = 1, отождествляется со стороной,
отвечающей i = т, и, аналогично, сторона с / = 1 отождествляется со сторо-
стороной / = п. — Прим. перев.
2 Предполагается, что подграф — связный, а совокупность попарно-
непересекающихся простых циклов удовлетворяет условию: всякое ребро
подграфа принадлежит какому-нибудь из этих циклов, — Прим, перев

Ведь правда — будет правдой до конца,
Как ни считай.
Шекспир В., Мера за меру i
ПРИЛОЖЕНИЕ I
Это приложение содержит девять таблиц, в которых представлены
числа графов разных видов. Хотя большинство из помещенных
здесь данных встречается в основном тексте книги, все же удобно
илеть их собранными вместе. Таблицы и их содержание таковы:
Ш. Графы
П2. Связные графы
ПЗ. Графы, связные графы и блоки
П4. Орграфы, связные орграфы и симметричные отно-
отношения
П5. Самодополнительные орграфы, самообратные орграфы
и самообратные отношения
П6. Помеченные конечные топологии
П7. Деревья, корневые деревья, асимметрические деревья
и гомеоморфно несводимые деревья
П8. Турниры
П9. Асимптотическая аппроксимация для графов и тур-
турниров
В двух первых таблицах параметрами являются число вершин р
и число ребер q, во всех остальных — только число вершин р.
Размеры первой таблицы, содержащей числа (р, д)-графов,
такие же, как и той таблицы, которая помещена в книге Харари
[1] на стр. 249. Главное отличие этих двух таблиц состоит в том,
что приводимая ниже таблица не имеет опечаток. Таблица для
числа (р, <?)-графов была впервые напечатана в книге Риордана [1 ],
стр. 173.
Данные, помещенные во второй таблице, взяты из статьи Кэ-
догана [1]. Несколько большую информацию можно получить из
каталога Слоуэна [1].
1 Комедия в 5 действиях, Пер. Т, Л, Щепкиной-Куперник. «Искусство»,
М.-Л., 1939, с, 155,

ПРИЛОЖЕНИЕ I
281
Таблица П1
N\ p
Я N.
0
1
2
3
4
,5
6
7
8
9
10
11
12
13
14
15
16
17
18
8р
1
1
1
2
1
1
2
1
1
1
1
4
Число
1
1
2
3
2
1
1
11
(р,
5
1
1
2
4
6
6
6
4
2
1
1
34
<7)-графо«
с
1
1
2
5
9
15
21
24
24
21
15
9
5
2
1
1
156
7
1
1
2
5
10
21
41
65
97
131
148
148
131
97
65
41
21
10
5
1044
8
1
1
2
5
И
24
56
115
221
402
663
980
1312
1557
1646
1557
1312
980
663
12 346
9
1
1
2
5
И
25
63
148
345
771
1637
3 252
5 995
10120
15 615
21933
27 987
32 403
34 040
274 668
Таблица Л2
p N^
1
2
3
4
5
6
7
8
0 12 3
1
1
1 1
2
Число
4
2
3
5
1
5
6
связных (p,
6
1
5
13
11
7
4
19
33
23
q)-графов
8
2
22
67
89
9
1
20
107
236
10
1
14
132
486
11
9
138
814
12
5
126
1169
13
2
95
1454
В таблице ПЗ помещены числа г_ Для Р ^ 24, ср — для р ^ 10
и Ър — для р sg 9. Числа gp (p s-g 9) приводятся у Риордана [1],
стр. 173, у Харари [1], стр. 249 \ у Обершельпа [1], Робинсона
1 В таблице Ш книги Харари [i] числа g$ и g, приведены с ошибками.
Прим, перев..

I
Число графов, связных графов и блоков
Таблица ПЗ
1 I
2 2 '"'*-'-■ ,
3 4 . . .. "
4 II ' ' .
. 5 34 г-.' ■-;•■'
Ч>156 • • ' *
7' 1044 , •
8- 12346 . Г:" , ,
9 274668 , "' . » . . ~? , .
10 12005 168 ; ' >;'■• --■ .. ■ Л * .' -,
И 1018 997 864 ,: , ' ,
12 165 091 172 592 - i ;, ■ '
ЛЗ 50 502 031367 952 :. ■''•" ". >.' . ■ . :''
14. 29 054 155 657 235 488 ! * . "
15 31426 485 969 804 308 768 ,; v- ' •*;
16 64001015 704 527 557 894 928 . : ';
17 245935864 153532932683719776 ,": ' "; О. i '5
18 1787 577 725 145 611 700 547 878 190 848 I. '.•;' "
19 24637809253125004 524 383007491432768 ' ■'■;
20 645 490 122 795 799 841856 164 638 490 742 749 440 ' ;,
21 32220272899808983433 502244253755283616097664
22 307О.846483О94 144 3О0637 568 517 187 105 410 586657 814 272
23 559 946 939 699 792080 597 976 380 819 462 179 812 276 348 458 981 632
•24 195 704 906 302078 447 922 174 862 416 726 256 004 122 075 267 063 365 754 368
1
2
«
21
112
853"" ■"
11117
261 080
11 716571
0
\
1
3
10
? S6 X
468
7 123
194 066

ПРИЛОЖЕНИЕ I
283
[3] и других авторов. Числа gp для р ^ 24 были вычислены Кин-
Кингом и Палмером [1] с помощью электронной вычислительной
машины. Число связных графов ср для р ^ 8 подсчитал Кэдоган
11], а число блоков Ър для ,р ^ 9 нашел Робинсон [3].
Числа орграфов (числа dp) и симметричных отношений для
значений р ^8 подсчитаны Обершельпом [1]. Эти результаты
приведены в табл. П4. У Слоуэна [1] помещены значения dp
для р ^ И.
Таблица П4
Число орграфов, связных орграфов и симметричных отношений
р
1
2
3
4
5
6
7
8
Орграфы
1
3
16
218
9 608
1 540 944
882 033 440
1 793 359 192 848
Связные орграфы
1
2
13
199
9 364
1 530 843
880 471142
1 792 473 955 306
Симметричные
отношения
2
6
20
90
544
5096
79 264
2 208 612
В таблице П5 приведены числа самодополнительных орграфов,
самообратных орграфов и самообратных отношений.
Таблица П5
Число самодвойственных отношений
р
1
2
3
4
5
6
7
8
Самодополнительные
орхрафы
1
1
4
10
" ■ . 136
720
44 224
703 760
Самообратные орграфы
<:1 ! '■
' 3
ю
70
708
15 248
543 520
Самообратные отношения
2
8
44
436
7176
222 368
Число помеченных конечных топологий с р вершинами, кото-
которое равно числу помеченных транзитивных орграфов, вычислено
для р ^7 в статье Эванса, Харари и Линна [1]. Б. Стаблфилд
нашел число таких топологий в случае р = 8.
Табл. П7, содержащая числа деревьев, корневых деревьев,
асимметрических деревьев и гомеоморфно несводимых деревьев,
взята из книги Харари [1], стр. 266. Часть данных э ней взята

284
Число помеченных конечных топологий
ПРИЛОЖЕНИЕ I
Таблица Пв
1
2 <
3 '
4
5
6
7
8
Помеченные топологии
1
.•■■..•<;,<j ' 4 -;■,-••< ■'
?!>.-.. 29 '
355
6 942
209 527 ■
• Л~ 9 535 241
642 779 354
из книги Риордана [1], стр. 164. А. Швенк из Мичиганского
университета, используя ЭВМ, нашел значения всех этих величин
для р sg: 39.
Таблица П7
Число деревьев, корневых деревьев, асимметрических деревьев
в гомеоморфно несводимых деревьев
р
1
2
3
4
5
6
7
8
9
10
11
12
<р
1
1
1
2
3
6
11
2,3
47
106
235
551
1
1
2
4
9
20
48
115
286
719
1842
4766
'р
1
0
0
0
0
0
1
1
3
6
15
29
1
1
0
1
1
2
2
4
5
10
14
26
А.
13
14
15
16
17
18
19
20
21
22
23
24
25
26
'р
1301
3159
7741
19 320
. 48 629
' 123 867
317 955
823 065
2 144 505
5 623 756
14 828 074
39 299 897
104 6 6 890
279 793 450
тр
12 486
32 973
'■ 87 811
235 381
634 847
1 721 159
4 688 676
12 826 228
35 221 832
97 055 181
268 282 855
743 724 984
2 067 174 645
5 759 636 510
П. Стейн из Научной лаборатории в Лос-Аламосе составил
программу для подсчета числа турниров на ЭВМ и получил соот-
соответствующие результаты для р ^ 30, помещенные в таблице П8.1
В табл. П9 приводятся значения отношения 2Р (р)/2/р!,
которое, как было установлено в гл. 9, дает асимптотическую
аппроксимацию для числа gp графов и числа Т (р) турниров с р
вершинами. И эти данные были любезно предоставлены нам
Паулом Стейном.
1 В этой таблице в оригинале допущена опечатка: число турниров при
р=24 равно 195 692 027 657 521876 084 316 842 660 833 482 785 J73 437 775 365 039
898 624. — Прим. перев

.4i sck-jk. v\.i. .iU: i'v*u- .:'■,.„ , 4 Таблица П&
Число турниров
1 1
2 .
3 2
4 4
5 12
6 56
7 4J6
8 6 880
9 191 536
10 9 733 056 • • .
11 903 753 248 -■■.:;... . .
12 154 108 311 168 i < • • .
13 48 542 114686912 • *
14 28 4OI423 719I22 3O4
15 31O2IOO2 16O355 166 848
16 63 530 415 842 308 265100 288
17 244912778438520759443245824 . }
Г8 1 783 398 846 284 777 9T5 419 600 287 232 ;
19 2460564117I260376770598O0397828I472
20 645 022 068 557 873 570931850 526 424 042 500 096 *
21 32 207 364 031661175 384 456 332 260 036 660040 346 624 ~' . ■
22 3070 169883 150468336193188889 176239554269865953280
23 559 879 382 429 394075 397 997 876 821117 309 031348 506 639 435 776 ■,'
24 195692027657521876O843 1684266O8334827851734377775365039898624 . ■ 5"
25 131326 696 677 895OO2 13145O257 7O9 457 767 557I7OO27O52 967O27 982 788 816 896
26 169484 335125246268 100514597385576342667 201246238506672327765919863947264
27 421 255 599 848 131 447 082 003 884 098 323 929 861 369544621 589 389 269 735 693 986 231 100612608
28 2 019 284 625 667 208 265 086 928 694 043 799 677 058 780 746 074 756 618 649 807 453 554 008 410 636 526 845 952
29 18 691 296I82 213 7I2 4O7 784 892 577 100643 237 772 159 079 535 345 610 331 272 616 359 410643 727 554 822 061 146 112
30 334 493 774 260 141 796 028 606 267 674 709 437 232 608 940 215 918 926 763 659 414 050 175 507 824 571 200950 884 097 540096000

' - --.-■■■■ .■■*■:: Таблица П9
Асимптотика числа турниров и графов
3 i ■ ' '•■ ■ '-■■" ■ ." • ■ ■■-■--..■. . ■ ,
4 2 - ' " "■"'■ ■ ' > « ' '•■> *:- ■ К=. . • ■ -;■.
5 8 ; ■; -^**: -i.- ■■ -'Л ■ ■ ■.*"••■. v
6 45 "' • '/ ■ '--. ■•■■- " - • -:- ■■•--. •
7 416 ;' •*'" ■•' "' ; "* ' """' * '■•■ '■ ■ ..;, ,.
8 6657 '" •"" • ";" •'"- ■■ •'->
9 189 372 "" -"'■•■
10 9695869 ' ■ ■ ! ' ■ ' ,
11 902 597 327 <-.-... ,. ,
12 154 043 277 297 • .. ■ . ■. ,. ■-♦ •
13 48 535 48183164? ;.. . . . £ ,
14 28400 190 511 772 276 . - ■ . - . ' .-
15 31020581422991798 557 .' - !
16 63 530 150 754 287 203 445 810 , \ ' ' '- - '
17 244 912 468 225 468 597 942 626 507 " ' .у . . ' , ■ - "
18 I783 398 168 624 923 337I96 4412O1196
19 24 605 638 395 579 573 858 211783 276 124 626 . - ■" "
20 645022047 157081180948706971513641417725 ■ V ,* .
21 32207 363719989693 161641493 398 185 145868257 184
22 307016987455OI73863 3328536892268534I0359422313 75O } ,
23 559879381978490975464019 198266910789847 137671 663 161 697
24 195 692 027 612 492 717 696 053 131613 974 749 458 250 743 733 957 146 609 599
25 13! 326 696 669 310 184 928 548 229 462 563 319 608 278 228 391409 823 336 516 656 557
26 169484335 122 115 1956573998624700760559О34707О9678462703895275433435498631 • ••
27 421 255 599 845 942 668 803 919 924 597 149 559 454 904 184 585 016 179 214 085 529 813 478 905 185 546
28 2 019 284 625 664 270 536 611 378 920 477 168 898 079 934 218 310482 029 759 803 193 187 192 943 926 121 612 944
29 18 691 296 182 206 129 806 987 592 941 623 330025 693 264 356 626 820 456 495 804 849 429 663 146 992 789 154 562 961 044
30 334 493 774 260 104 102 715 593 766 508 469 331 712 364 208 913 311 144 737 971 969 122 91О864 452 626 959 027 797 528 575 878 018

Не загромождай свой стол:
пусть на нем будет не более
, j. семи, но не менее трех блюд.
Вильям Кинг, Искусство стряпни 1
ПРИЛОЖЕНИЕ II
В таблице ШО приведены частоты групп четырехвершинных
орграфов и исправлены четыре элемента из таблицы такого же
типа, которая была впервые напечатана в работе Харари и Пал-
мера [6].
Таблица П10
Распределение четырехвершиииых орграфов
в соответствии с их группами автоморфизмов
^■^^ Число
Группа ^^-^
Si
Et
S2&2
So [E2\
EVS3
EXCS
C4
Всего
0
1
0
0
0
0
0
0
0
0
1
I
0
1
0
0
0
0
0
0
0
1
2
0
2
1
1
1
0
0
0
0
5
3
0
3
7
. 0
0
2
1
0
0
13
4
0
6
16
1
2
0
0
1
1
27
5
0
10
28
0
0
. 0
. 0
0
0
38
б
0
6
32
2
4
2
2
0
0
48
1
: 22
. 52
2
3
2
1
1
1
85
Всего
2
50
136
6
10
6
4
2
2
218
Следующая таблица содержит данные, полученные Стокмейе-
ром [1] и относящиеся к орграфам порядка 5. Как упоминалось
в задаче П3.4 в гл. 10, вычисление этих чисел требует знания
элементов решетки подгрупп группы S5.
Кинг, Вильям A663—1712) — английский писатель. — Прим,, перев.

ПРИЛОЖЕНИЕ II
Таблица Пц
Распределение пятивершияиых орграфов в соответствии
с их группамп автоморфизмов
N. Число
^v. дуг
Группа^
Еь
EsS-г
S2 [EzlEx
Е2С3
EiCt
E1S2S2
с!
E2S3
С2С3
EiD4
Db
S2S3
EiSt
Sb
Всего
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
2
0
1
1
0
0
2
0
0
0
0
0
1
0
0
5
3
5
8
0
0
0
0
0
2
1
0
0
0
0
0
16
4
28
13
6
1
1
7
0
2
0
1
0
0
2
0
61
5
107
43
0
0
0
0
1
2
1
0
0
0
0
0
154
G
278
59
22
2
0
13
0
2
0
0
0
3
0
0
379
7
591
105
0
4
0
0
0
7
0
0
0
0
0
0
707
s
962
124
38
2
3
18
0
1
0
3
0
3
1
0
1155
9
1314
168
0
2
0
0
0
4
2
0
0
0
0
0
1490
to
1431
148
49
6
0
26
1
8
0
0
1
0
0
0
1670
> 11
3285
521
67
11
4
40
1
21
4
4
0
7
3
1
3 969
Hccro
8001
1190
183
28
8
106
3
50
8
8
1
14
6
2
9 608
4- i *

Лучше — синица в руках,
4 чем журавль в небе.
Пословица
ПРИЛОЖЕНИЕ III
ФОРМУЛЫ ДЛЯ ЦИКЛОВЫХ ИНДЕКСОВ СИММЕТРИЧЕСКИХ
ГРУПП Sn ПРИ п ^ 10
2 (S4) = ^i-(st + 6s2s24- 8,
Z(Se) = -±T(se1+l5s\s2 +
4-144Sls54-15s32-
2E7) = yr(sl4-21sis24-
4- 504s2!S5 4- 105s,
4-210s2s34-504si
Z(St)*=±-(s\ + 28sls2 +
4-1344s3s64-420
s1s34-3s24-6s4).
20s2s3 4- lSs^-2 4- 30siS4 4- 20s2s3 4- 24s5).
40s3jS3 4- 45s2s^ 4- 90s?s4 4- 12O.v2s3 +
4-90s2S4 + 40s324-120se).
70s4lS3 4- iO5s\s\ 4- 210s3s44- 420sis2s3 +
s2 4- 630s!S2s4 4- 280sis| 4- 840Slse 4-
,ee+420»,»4+720s7).
112s51s34- 210s4s2 4-420sls44- 1120s3s2s3
s\sl 4- 2520e;»,e4 4- 1120s2s2 4- 3360s2se 4
+ 1 eSOs^Sg + 4032sxs2s5 + ЗЗбОв^^ + 5760siS7 + 105s£
4- 1260s2s4 + 1120s2s2 4- 3360s2se + 2688sas5 +
4-1260s2 + 5040s8).

290
4т (s? -1- 36sjs2 + 168^3
У!
+ 3024s4s6 + 1260s*s3 + 7560s* s2s4 + 3360s*s32 +
+ 7560s?s|s3+ 945slS2 + 10080s?se + 18 144s*s2s6
+ 15120s?s3s4 -f 25 920s\sj -f И MOsislst+ 10
+ 30 240s!S2se 4 24 192SXS3S5 + 11 340sxs42 + 45 360s!s8
+ 2520s^s3 + 9072s^s5 + 15 120s2s3s4 + 25 920s2s7
+ 20 160s3se + 18 144s4s5+40 320s9).
щ (»Г + 45s?s2 + 240sIs3 + 630selS22 + 1260s?s4 +
+ 5040sljs2s3 + 6048siS5 + 3150sJs2 +18 900s4!s2s4 +
+ 8400s *sl + 25 200s4! se + 25 200s3iS^s3 + 60 480s?s2s5
+ 50 400s?s3s4 + 86 400s?s7 + 4725s?s| + 56 700sJs|s4
151 200si s2se + 120
ПРИЛОЖЕНИЕ III
+ 2520s?s2s3 +
151 200Sls2s3s4 +259 200slS2s7 +22 400siS3+201
181 440s!S4s3 + 403 200siS9 + 945s'2 +18
25 200s^s.? + 75 600s^se +120 960s2.53s5 +
56 700s2s4 + 226 800s2s8 + 50 400s3S4+ 172
151200s4se+72 )
ФОРМУЛЫ ДЛЯ ЦИКЛОВЫХ ИНДЕКСОВ ПАРНЫХ ГРУПП S%
ПРИ п==с10
\°
= -L- (s\
?>) = jt (si6
4-
+
+ 45s3lS2e + 90slS2s«
« + 90Sls2s43
Ga)) =yj- (si1

lit
291
.
+ 420s21s2s3s
280s7
1120s}»Ss$»,-t-
1120^
5760s*
+ 420s°s2s4
420s41s22 + 2520s2lS324
40328^810+ 3360s,s|sJslt +
2s32s4 + l 120Sls534 +
s3s4 + 2688s3s2s15 + 1260s'oS^ + 5040s4s^).
168sl5s37 + 378sj2s212 + 756sl°s2s« +
+18144s2lS^4sl0 +15 120Sls2s3s3s12 4 25 920slS57 +
-h 24192s2s3s16
45 360s4s48
2 + 20160s2s5e + 18 144s2s4s2s2o + 40 320s49).
-^T D5 + 45»; V. + 240s211S« l74 1
+ 5040s111s52s3ese + 6048sl°s57 + 3150s9lSJ8 + 18 900*1*5»!
+ 8400sels313 + 25 200s?s3s^ + 25 ^
+ 120960Sls3stsl5+ 56 TOOsxsJeJ0 + 226800s
+ 25 200s?s^s^s^ + 90 720s\s\sls\0 +151 200*!*^^* Jses12 +■
+ 259 200s1s2s7s14 + 22 400sJ6 + 201 №Os33st +
+ 181 440s2s2s3s20 + 403 200^ + 945s5!*2,0 +18 900s3s72*I +
+25 200s21s2s^4 + 75 600s2s22s3see+120960s1s3s2ses10s15 +
+ 56 700sis!si° + 226 ^ ^?
+362880s5sio).

Украшать каждое научное сочинение
библиографией—обычай, преследующий цель
доказать компетентность автора путем
демонстрации той кучи мусора, которую
ему пришлось просеять, чтобы добыть
крупицу истины.
Д-р Лоуренс Дж. Петер 1
СПИСОК ЛИТЕРАТУРЫ
Александер, Бриге (Alexander J. W., Briggs G. В.)
[1] On types of knotted curves, Ann. of Math., 28 A938), 562—586.
Байнеке, Мун (Beineke L. W., Moon J. W.)
[1] Several proofs of the number of labeled 2-dimensional trees, В сб.
Proof Techniques in Graph Theory (ed. Harary F.), Acad. Press, New
York, 1969, pp. 11—20.
Байнеке, Пипперт (Beineke L. W., Pippert R. E.)
[1] On the number of k-dimensional trees, /. Combinatorial Theory, 6
A969), 200—205.
Бернсайд (Burnside W.)
[1] Theory of Groups of Finite Order B nd edition), p. 191, Theorem VII.
Cambridge Univ. Press, London, 1911. Reprinted by Dover, New York,
1955.
Ботт, Мейберрв (Bott R., Mayberry J. P.)
[1] Matrices and tress, В сб. Economic Activity Analysis (ed. Morgen-
stern 0.), Wiley, New York, 1954, pp. 391—400.
Браун В. (Brown W. G.)
[1] Enumeration of triangulations of the disk, Proc. London Math. Soc,
14 A964), 746-768.
[2] Historical note on a recurrent combinatorial problem, Amer. Math,
Monthly, 72 A965), 973—977.
Брауе Т. (Brown Т. А.)
[1] A note on some graph related to knots, /. Combinatorial Theory, I
A966), 498—>J.
де Брёйн (de Bruijn N. G.)
[1] Одна комбинаторная задача, Кибернетический сб., № 6 (новая
серия), изд-во «Мир», М., 1969, стр. 33—40.
[2] Теория перечисления Пойа, в сб. «Прикладная комбинаторная
математика» (под ред. Беккеибаха Э.), изд-во «Мир», М., 1968,
стр. 61—106.
де Брёйн, ван Ардене-Эренфест (de Bruijn N. G., van Aardenne-Ebrenfest Т.)
[1] Circuits and trees in oriented graphs, Simon Stevin, 28 A951),
203-217.
1 Возможно, Лоуренс Джеймс A781—1813)—американский военно-мор-
военно-морской деятель, — Прим. мрев.

СПИСОК ЛИТЕРАТУРЫ
293
Брукс, Смит, Стоун, Татт (Brooks R. L., Smith С. А. В., Stone A. H., Tutte
VV. Т.)
[1] The dissection of rectangles into squares, Duke Math. /., 7 A940),
Геллер (Geller D. P.)
[1] The square root of a digraph, /. Combinatorial Theory, 5 A968), 320—
Гилберт (Gilbert E. N.)
[1] Enumeration of labelled graphs, Canad. J. Math., 8 A956), 405—411.
Голомб (Golomb S.)
[1] Полимино, изд-во «Мир», М., 1975.
Гурса, Хедрик (Goursat E., Hedrick E. R.)
[1] Л Course in Mathematical Analysis, vol. 1, pp. 404—405, Ginn, Bos-
Boston, 1904.
Джевонс (Jevons W. S.)
[1] The Principles of Science Bnd edition), pp. 134—146, MacMillan,
London and New Yur^, 1892.
Johcu. Г. A.
[1]* О нижней границе числа вершин плоских критических графов,
Кибернетика, 4 A971), 76—85.
Дуглас (Douglas R. L.)
[1] Tournaments that admit exactly one Hamiltonian cycle, Proc. London
Math. Sac, 21 A970), 716^-730.
Дэвис (Davis R. L.)
[1] The number of structures of finite relations, Proc. Amer. Math. Soc,
4 A053), 486-495.
Изинг (Ising E.)
[1] Beitrag zur Theorie des Ferromagnetismus, Z. Physik, 31 A925),
253-258.
Картрайт, Глисон (Cartwright D., Gleason T.)
[1] The number of paths and cycles in a digraph, Psychometrika, 31 A966),
179-199.
Кастелейн (Kasteleyn P. W.)
[1] Graph theory and crystal physics, в сб. Graph Theory and Theoretical
Physics (под ред. Harary F.), Academic Press., New York, 1937,
pp.44—110.
Кац (Katz L.)
[1] Probability of indecomposability ofarandom mapping function, Ann.
Math. Statist,, 26 A955), 512—">17.
Knur, Шлмер (King С, Ра!тчг Е. М.)
[1] Calculation of the number of graphs of order p ф 1 A) 24 (в печати) _
Кирхгоф (Kirchhoff G.)
[1] Uber die Auflosung der Gleichungen, auf welche man bei der Unter-
suchung der linearen Verteilung galvanischer Strome gefiihrt wird,
Ann. Phys. Chem., 72 A847), 497—508.
Клиффэрд (Clifford VV. K.)
[1] Mathematical Papers, pp. 1—16, London, 1882.
Клэршр (Klarnar D. A.)
[1] Cell growth problems, Canad. J. Math., 19 A967), 851—863.
Комто (Comtet L.)
[1] Analyse Combinatoire, vol. 1, Presses Universitaires de France, Paris,
1970.
Кренчик (Kraitchik M.)
[1] Mathematical Recreations, Norton, New York, 1942.

294 .-...*. СПИСОК ЛИТЕРАТУРЫ
Кэдоган (Cadogan С. С.) ' '
[1] The mobius function and connected graphs, /. Combinatorial Theory,
11B A371), 193—200.
Кэли (Gayley A.)
[1] A theorem on trees, Quart. J. Math. Oxford Ser., 23 A889), 376—378;
Collected Papers, Cambridge, 13 A897), 26—28.
Моллоус, Риордан (Mallows С. L., Riordan J.)
[1] The inversion enumerator for labeled trees, Bull. Amer. Math. Soc,
74 A968), 92-94.
Мув (Moon J.)
[1] Various proofs of Cayley's formula for counting trees, в сб. A Seminar
on Graph Theory (под ред. Harary F.), Holt, New York, 1967,
pp. 70—78.
[2] Topics on Tournaments, Holt, New York, 1968.
[3] Connected graphs with unlabeled end points, /. Combinatorial Theory,
6 A969), 65—66.
[4] Counting Labeled Trees, Canad. Math. Congress, Montreal, 1970,
. [5] Almost all graphs have a spanning cycle, Canad. Math. Bull. 15
A972), 39—41.
Мун, Мозер (Moon J., Moser L.)
[1] Almost all tournaments are irreducible, Canad. Math. Bull., 5A962),
61-65. 1 A966), 153-156.
[2] Almost all @,l)-matrices are primitive, Studia Scl. Math. Hungar.,
1 A966), 153-156.
Норман (Norman R. Z.)
[1] On the number of linear graphs with given blocks, Dissertation, Univ.
of Michigan, Ann Arbor, 1954.
Обершельп (Oberschelp W.)
[1] Kombinatorische Anzahlbestimmungen in Relationen, Math. Ann.,
174 A967), 53—58.
Онзагер (Onsager L.)
[1] Crystal stratistics 1, a two-dimensional model with an order-disorder
transition, Phys. Rev., 65 A944), 117—149.
Ope, Стемпл (Ore 0., Stemple G. J.)
[1] Numerical methods in the four color problem, в сб. Recent Progress in
Combinatorics (под ред. Tutte W. Т.), Academic Press, New York, 1969.
Остервейл (Osterweil L.)
[1] Enumeration of nonseparable graphs on fewer than 10 points (в печати).
Остин (Austin Т. L.)
[1] The enumeration of point labelled chromatic graphs and trees, Canad.
J. Math., 12 A960), 535—545.
Оттер (Otter R.)
[1] The number of trees, Ann. of Math., 49 A948), 583—599.
Палмер (Palmer E. M.)
[1] On the number of labeled 2-trees, /. Combinatorial Theory, 6 A969),
206-207.
: [2] Combinatorial problems in set-theoretic form, Math. Mag., 42 A969),
32—37.
[3] The exponentiation group as the automorphism group of a graph,
в сб. Proof Techniques in Graph Theory (под ред. Harary F.), Acade-
Academic Press, New York, 1969, pp. 125—131.
[4] Methods for the enumeration of multigraphs, в сб. The Many Facets
of Graph Theory (под ред. Chartrand G. and Kapoor S.), Springer
Publ., New York, 1969, pp. 251—261.

СПИСОК ЛИТЕРАТУРЫ 295
[5] Asymptotic formulas for the number of self-complementary graphs
and digraphs, Mathematika, 17 A970), 85—90.
[6] Graphical enumeration methods, в сб. New Directions in the Theory
of Graphs (под ред. Harary F.), Academic Press, New York, 1972.
Палмер, Рид (Palmer E. M., Read R. G.)
[1] On the number of plane 2-trees, /. London Math. Soc. (в печати).
Палмер, Робинсон (Palmer E. M., Robinson R. W.)
[1] The matrix group of two permutation groups, Bull. Amer. Math. Soc.
73 A967), 204—207.
[2] Enumeration under two representations of the wreath product (в печа-
печати).
Партасарати (Parthasarathy К. R.)
[1] Enumeration of ordinary graphs with given partition, Canad. J. Math.,
20 A968), 40—47.
Попа (Polya G.)
[1] Kombinatorische Anzahlbestimmungen fur Gruppen, Graphen und
chemische Verbindungen, Ada Math., 68 A937), 145—254.
[2] Sur les types des propositions composees, /. Symbolic Logic, 5 A940),
98-103.
Прюфер (Priifer H.)
[1] Neuer Beweis eines Satzes iiber Permutationen, Arch. Math. Phys.,
27 A918), 742-744.
Райдемайстер (Reidemeister K.)
[1] Knotentheorie, Springer-Verlag, Berlin, 1932. Reprinted by Chelsea,
New York, 1948.
Райт (Wright E. M.)
[1] Counting coloured graphs, Canad. J. Math., 13 A961), 683—693.
[2] A relationship between two sequences I, II and III, Proc London,
Math. Soc, 17 A967), 296—304, 547—552; /. London Math. Soc,
43 A968), 720-724.
[3] The number of graphs on many unlabelled nodes, Math. Ann., 183,
A969), 250—253.
[4] Asymptotic enumeration of connected graphs, Proc Roy. Soc. Edin-
Edinburgh Sect. A, 68 A970), 298—308.
[5] Graphs on unlabelled nodes with a given number of edges, Acta Math.
168 A971), 1-9.
Редфилд (Redfield I. H.)
[1] The theory of group-reduced distributions, Amer. J. Math., 49 A927),
433—455.
Реньи (Renyi A.)
[1] Some remarks of the theory of trees, Publ. Math. Inst. Hungar.
Acad. Sci., 4 A959), 73—85.
[2] On connected graphs, Publ. Math. Inst. Hungar, Acad. Set., 4, A959),
385-388.
Рид (Read R. C.)
[1] The enumeration of locally restricted graphs, I and II, /. London
Math. Soc, 34 A959), 417—436; 35 A960), 344—351.
[2] The number of k-colored graphs on labelled nodes, Canad. J. Math.)
12 A960), 409—413.
[3] A note on the number of functional digraphs, Math. Ann., 143A961),
109-110.
[4] Contributions to the cell growth problem, Canad. J. Math., 14,
A962), 1-20.
[5] Euler graphs on labelled nodes, Canad. J. Math., 14 A962), 482—486.
[6] On the number of self-complementary graphs and digraphs, /. London
Math._ Soc, 38 A963), 99—104,

296 СПИСОК ЛИТЕРАТУРЫ
[7] Some applications of a theorem of de Bruijn, в сб. Graph Theory and
Theoretical Physics (под ред. Harary F.), Academic Press, New York,
1967, pp. 273-280.
[8] The use of S-functions in combinatorial analysis, Canad. J. Math.,
20 A968), 808—841.
[9] Some unusual enumeration problems, Ann. N. Y. Acad. Set., 175
A970), 314—326.
Рид, Райт (Read R. C, Wright E. M.)
[1] Coloured graphs: A correction and extension, Canad. J. Math, (в печати).
Риддел (Riddell R. J.)
[1] Contributions to the theory of condensation, Dissertation, Univ.
of Michigan, Ann Arbor, 1951.
Риордан (Riordan J.)
[1] Введение в комбинаторный анализ, ИЛ, М., 1963.
[2] The enumeration of trees by height and diameter, IBM J. Res.Develop.
4 A960), 473-478.
Роберте, Спеисер (Roberts F. S., Spencer J. H.)
[1] A characterization of clique graphs, /. Combinatorial Theory, 10B
A971), 102-108.
Робинсон (Robinson R. W.)
[1] Enumeration of colored graphs, /. Combinatorial Theory, 4 A968),
181 — 190.
[2] Enumeration of euler graphs, в сб. Proof Techniques in Graph Theory
(под ред. Harary F.), Academic Press, New York, 1969, pp. 147—
153.
[3] Enumeration of non-separable graphs, /. Combinatorial Theory, 9
A970), 327—356.
[4] Enumeration of acyclic digraphs, в сб. Combinatorial Mathematics
and its Applications (под ред. Bose R. С. и др.), Univ. of North
Carolina, Chapel Hill, 1970, pp. 391—399.
Рудволис, Снаппер (Rudvalis A., Snapper E.)
[1] Numerical polynomials for arbitrary characters, /. Combinatorial The-
Theory, 10A A971), 145—159.
Скойнс (Scoins H. I.)
[1] The number of trees with nodes of alternate parity, Proc. Cambridge
Philos. Soc, 58 A962), 12—16.
Слепян (Slepian D.)
[1] On the number of symmetry types of Boolean functions of n variables,
Canad. J. Math., 5 A953), 185—193.
Слоуэн (Sloane N. J.)
[1] Handbook of Integer Sequences, Academic Press, New York, 1973.
Смит, Татт (Smith С. А. В., Tutte W. T.)
[1] On unicursal paths in a network of degree 4, Amer. Math. Monthly, 48
A941), 233-237.
Стокмейер (Stockmeyer P. K.)
[1] The enumeration of graphs with prescribed automorphism group,
Dissertation, Univ. of Michigan, Ann Arbor, 1971.
Татт (Tutte W. T.)
[1] The dissection of equilateral triangles into equilateral triangles, Proct
Cambridge Philos. Soc, 44 A948), 463—482.
[2] The number of planted trees with a given partition, Amer. Math.
Monthly, 71 A964), 212—2П.
[3] The enumerative theory of planar maps, в сб. A Survey of Combina-
Combinatorial Theory (под ред-. Srivastav J. N. и др.), North-Hoi land, Amster-
Amsterdam, 1973, 437-448.
Тернер (Turner J.)
[1] Point-symmetric graphs with a prime number of points, /, Combina-
Combinatorial Theory, 3 A967), 136-145,

СПИСОК ЛИТЕРАТУРЫ 297
Уайтхед, Рассел (Whitehead A. N., Russell В.)
[1] Principia Mathematica, vol. II, p. 301, Cambridge Univ. Press, Lon-
London and New York, 1912.
Уитни (Whitney H.)
[1] Congruent graphs and the connectivity of graphs, Amer. J. Math.,
54 A932), 150-168.
Уленбек, Форд (Uhlenbeck G. E., Ford G. W.)
[1] Lectures in Statistical Mechanics, Amer. Math. Soc, Providence
Rhode Island, 1963.
Уолкап (Walkup D. W.)
[1] The number of plane trees, Mathematika (в печати).
Форд, Норман, Уленбек (Ford G. W., Norman R. Z., Uhlenbeck G. E.)
[1] Combinatorial problems in the theory of graphs II, Proc. Nat. Acad.
Sci. U.S.A., 42 A956), 203-208.
Форд, Уленбек (Ford G. W., Uhlenbeck G. E.)
[1] Combinatorial problems in the theory of graphs, I, III and IV, Proc.
Nat. Acad. Sci. U. S.A., 42 A956), 122—128, 529—535; 43 A957),
163-167.
Фоулкс (Foulkes H. 0.)
[1] On Redfield's group reduction functions, Canad. J. Math., 15 A963),
272-284.
[2] On Redfield's range-correspondences, Canad. J. Math., 18 A966),
1060-1071.
Фрухт, Харари (Frucht R., Harary F.)
[I] Self-complementary generalized orbits of permutation group, Canad.
Math. Bull, (в печати).
Харари (Harary F.)
[1] Теория графов, изд-во «Мир», М., 1973.
[2] On the algebraic structure of knots, Amer. Math. Monthly, 56 A949),
.. . 466-468.
[3] On tho notion of balance of a signed graph, Michigan Math. J., 2
,r,,:, A953-1954), 143-146.
.' [4] The number of linear, directed, rooted, and connected graphs, Tram.
Amer. Math. Soc, 78 A955), 445—463.
" [5] The number of dissimilar supergraphs of a linear graph, Pacific J.
Math., 7 A957), 903-911.
■ " [6] The number of oriented graphs, Michigan Math. J., 4 A957), 221—224.
[7] On the number of bicolored graphs, Pacific J. Math., 8 A958), 743—
.-*•'." 755.
[8] Note on Carnap's relational asymptotic relative frequencies, /. Symbo-
Symbolic Logic, 23 A958), 257-260.
[9] Exponentiation of permutation groups, Amer. Math. Monthly, 66
'*"• A959), 572-575.
[10] The number of functional digraphs, Math. Ann., 138A959),
203-210.
[II] Applications of Polya's theorem to permutation groups, в сб.
A Seminar on Graph Theory (под ред. Harary F.), Holt, New York,
1967, pp. 25-33.
1 [12] Задачи перечисления графов, УМН, 24, № 5 A9С9), 179—214.
[13] Covering and packing in graphs I, Ann. N. Y. Acad. Sci., 175 A970),
198-205.
[14] A graphical exposition of the Ising problem, /. Austral. Math. Soc,
12 A971), 365—377.
[15] Комбинаторные задачи перечисления графов, в сб. «Прикладная
комбинаторная математика» (под ред. Беккенбаха Э.), изд-во
«Мир», М., 1968, 107—140.
Ю Заказ 443

298 СПИСОК ЛИТЕРАТУРЫ
Харари, Кинг, Мовшовяд, Рид (Нагагу F., King С, Mowshowitz A., Read R. С.)
[1] Cospectral graphs and digraphs, Bull. London Math. Soc, 3 A971),
321—328
Харари, Манвел (Нагагу F., Manvel В.),
[1] On the number of cycles in a graph, Mat. Casopts Sloven. Akad.
Vied., 21, №1 A971), 55-63.
Харари, Мовшовиц, Риордан (Нагагу F., Mowshowitz A., Riaordan J.)
[1] Labeled trees with unlabeled endpoints, /. Combinatorial Theory, 6
A969), 60-64.
Харари, Норман (Нагагу F., Norman R. Z.)
[1] The dissimilarity characteristic of Husimi trees, Ann. of Math.,
58 A953), 134-141.
[2] Dissimilarity characteristic theorems for graphs, Proc. Amer. Math.
Soc, 11 (I960), 332-334.
[3] Some properties of line digraphs, Rend. Circ. Mat. Palermo, 9 A901),
161-168.
Харари, Норман, Картрайт (Нагагу F., Norman R. Z., Cartwright D.)
|l] Structural Models: An Introduction to the Theory of Directed Graphs,
Wiley, New York, 1965.
Харари, Палмер (Нагагу F., Palmer E. M.)
[1] The number of graphs rooted at an oriented line, ICC Bull., 4 A965),
91—98.
[2] On the number of orientations of a given graph, Bull. Acad. Polon,
Scl. Ser. Sci. Math. Astronom. Phys., 14 A966), 125—128.
[3] Enumeration of locally restricted digraphs, Canad. J. Math., 18,
A966), 853—860.
[4] The power group enumeration theorem. /. Combinatorial Theory,
1 A966), 157—173.
[5] Enumeration of self-converse digraphs, Maihematika, 13 A966),
151 — 157.
[6] The groups of the small digraphs, /. Indian Statist. Assoc, 4 A966),
155—169.
[7] Enumeration of mixed graphs, Proc. Amer. Math. Soc, 17 A966),
682—687.
[8] The enumeration methods of Redfield, Amer. J. Math., 89 A967),
373—384.
[9] Enumeration of finite automata, Information and Control, 10 A967),
499-508.
[10] On the number of balanced signed graphs, Bull. Math. Biophys.,
29 A967), 759—765.
[11] Note on the number of forests, Mat. Casopis Sloven. Akad. Vted., 19,
№ 2 A969), 110-112.
[12] On acyclic simplicial complexes, Mathematika, 15 A968), 119—122.
Харари, Палмер, Рид (Нагагу F., Palmer E. M., Read R. C.)
[1] The number of ways to label a structure, Psychometrtka, 32A967),
155-155.
Харари, Принс (Нагагу F., Prins G.)
[1] The number of homeomorphically irreducible trees, and other species,
Ada Math., 101 A959), 141—162.
[2] Enumeration of bicolourable graphs, Canad. J. Math., 15 A963),
237—248.
[3] The Ыоск-cutpoint-tree of a graph, Publ. Math. Debrecen, 13 A966),
103-107.
Харари, Принс, Татт (Нагагу F., Prins G., Tutte W. T.)
[1] The number of plane trees, Indagationes Math., 26 A964), 319 — 329.

СПИСОК ЛИТЕРАТУРЫ 299
Харари, Росс (Нагагу F., Ross I. С.)
[1] On the determination of redundancies in sociometric chains, Psycho-
metrika, 17 A952), 195—208.
Харари, Татт (Harary F., Tutte W. T.)
[1] On the order of the group of a planar map, /. Combinatorial Theory, 1
A966), 394—395.
Харари, Уленбек (Harary F., Uhlenbeck G. E.)
[1] On the number of Husimi trees, Proc. Nat. Acad. Set. U. S. A.,
39 A953), 315—322.
Харрисон (Harrison M. A.)
[1] A census of finite automata, Canad. J. Math., 17, № 1 A965), 100—
113.
Харрисон, Хай (Harrison M. A., High R. G.)
[1] On the cycle index of a product of a permutation groups, J. Combina-
Combinatorial Theory, 4 A968), 277—299.
Хватал, Харари (ChvatalV., Harary F.)
[1] Generalized Ramsey theory for graphs, Bull. Amer. Math. Soc. A972).
Хусими (Husimi K.)
[1] Note on Mayer's theory of cluster integrals, /. Chem. Phys., 18 A950),
682—684.
Чао (Chao С Y.)
[1] On the classification of symmetric graphs with a prime number of-
vertices, Trans. Amer. Math. Soc, 158 A971), 247—256.
Шарп (Sharp Jr. H.)
[1] Enumeration of vacuously transitive relations, Discrete Math, (в печа-
печати).
Шридхарае (Sridharan M. R.)
[1] Self-complementary and self-converse oriented graphs, Indagationes
Math., 32 A970), 441-447.
Эванс. Харари, Линн (Evans J. W., Harary F., Lynn M. S.)
[1] On the computer enumeration of finite topologies, Comm. ASM, 10
A967), 295—298.
Эйлер (Euler L.)
[1] Novi Comment., Acad. Scl. Imperials Petropolitanae, 7A758—1759),
13-14.
Эрдёш, Реньи (Erdos P., Renyi A.)
[1] Asymmetric graphs, Acta Math. Acad. Sci. Hungar, 14 A963), 293—
315.
ДОПОЛНИТЕЛЬНЫЙ СПИСОК ЛИТЕРАТУРЫ
Коганов Л. М.
[1] О приложениях перечислительной схемы Н. Дж. де Брёйна, в сб.
Вопросы кибернетики, вып. 16, часть I, «Советское радио», М.,
1975, 68-73.
Козина А. В., Козырев В. П.
[1] Перечисление кратчайших связывающих сетей с дополнительными
ограничениями, Кибернетика, 6 A974), 109 — 115.
Козырев В. П.
[1] Перечисление транзитивных ориентации графа и вложение транзи-
транзитивных графов, в сб. Вопросы кибернетики, вып. 15, «Советское
радио», М., 1975, 44—60.
10*

300 СПИСОК ЛИТРРАТУРЫ
[2] Перечисление гамильтоновых цепей графа и изучение гамнльтоново
связных графов, Журнал вычислительной математики и математи-
математической физики (в печати).
Козырев В. П., Коршунов А. Д.
[1] О величине разреза в случайном графе, Проблемы кибернетики, 29,
«Наука», М., 1974, 27-62.
Коршунов А. Д.
[1] Об асимптотических оценках числа приведенных конечных автома-
автоматов, Дискретный анализ, 6 A966), Новосибирск, 35—50.
Лисковец В. А.
[1] Число связных инициальных автоматов, Кибернетика, 3 A969),
16—19.
[2] Число сильно связных ориентированных графов, Математические
заметки, 8, № 6 A970), 721—732.
[3] К перечислению сильно связных ориентированных графов, Докл.
АН БССР, 17, № 12 A973), 1077—1080.
[4] Некоторые результаты комбинаторной теории перечисления графов,
I, в сб. Комбинаторный и асимптотический анализ, Красноярск,
1975, 9-36.
Петренюк Л. П., Петренюк А. Я.
[1] Перечень десятивершинных однородных графов степени 4, в сб,
Вопросы кибернетики, вып. 15, «Советское радио», М., 1975, 71—76,
Попов В. А., Скибенко И. Т., Мокляк Н. Г.
[1] О числе типов систем jr-значных логических функций, Кибернетика,
6 A973), 18-27.
Селиванов Б. И.
[1] О цикловом индексе экспоненциации групп, в сб. Комбинаторный
анализ, вып. 1, Изд-во Московского университета, 1971, 79—90.
[2] Перечисление однородных гиперграфов с простой цикловой структу-
структурой, в сб. Комбинаторный анализ, вып. 2, Изд-во Московского уни-
университета, 1972, 60—67.
Страздинь И. Э.
[1 ] О числе типов /-ичных функций, Ученые записки Рижского политех-
политехнического института, 10, вып. 1, 1963.
[2] О числе типов обратимых двоичных многополюсников, Автоматика
и вычислительная техника, 1 A974), 30—34.
[3] Об одном теоретико-групповом способе получения комбинаторных
чисел, в сб. Вопросы кибернетики, вып. 16, часть 1, «Советское
радио», М., 1975, 103—110, ■ , , ,
M'V

Я вошел в комнату и увидел за столом
человека, которого вычислил бесконечно
давно.
А. и Г. Вайнеры «Лекарство против
страха»1
Именной указатель2
Александер (Alexander J. W.) 273,
292
Алендорфер (Allendoerfer) 10
Ардене-Эренфест ван (van Aardenne-
Ehrenfest T.) 41, 292
Архимед (Archimedes) 7
Байнеке (Beineke L. W.) 4,5 44, 292
Беккенбах (Beckenbach E. F.) 292
Бернсайд (Burnside W.) 52, 53, 292
Ботт (Bott R.) 39, 292
Боуз (Bose R. C.) 296
Браун В. (Brown W. G.) 89, 99,102,
292
Браун Т. (Brown Т. А.) 273, 274,
292
Брёйн де (de Bruiin N. G.) 4,5, 41, 45,
46, 165, 169, 175, 189, 292
Бриге (BriggsG. B.) 273, 292
Брукс (Brooks R. L.) 265, 293
Гай (Guy R. K.) 101
Геллер (Geller D. P.) 260, 293
Гилберт (Gilbert E. N.) 10, 19,
43, 266, 293
Глисон A. (Gleason A. M.) 105
Глисон Т. (Gleason Т.) 45, 266,
Голомб (Golomb S.) 105, 278,
Гурса (Goursat E.) 37, 293
27,
293
293
1 Роман напечатан в «Искателе»,
№ 1 и 2 за 1976 г.; фраза из № 2,
стр. 33.
2 В оригинале именной указатель
отсутствует. Мы сочли целесообраз-
целесообразным поместить в русском переводе
именной указатель, снабдив его под-
подходящим эпиграфом. — Прим. пе-
рев.
Джевонс (Jevons W. S.) 137, 293
Донец Г. А. 269, 293
Дуглас (Douglas R. J.) 164, 293
Дэвис (Davis R. L.) 90, 91, 105,
153, 293
Зейдель (Seidel J. J.) 273
Изинг (Ising E.) 279, 293
Капур (Kapoor S. E.) 294
Картрайт (Cartwright D.) 30, 42, 45,
90, 152, 156, 179, 256, 262, 266,
293, 298
Кастелейн (Kasteleyn P. W.) 41, 293
Кац (Katz L.) 252, 293
Кинг (King С.) 283, 293, 297
Кирхгоф (KirchhoffG.O,33, 37, 293
Клейтман (Kleitman D.) 252
Клиффорд (Clifford W. K.) 137, 293
Кларнер (Klarner D. A.) 277, 293
Коганов Л. М. 299
Козина А. В. 299
Козырев В. П. 299, 300
Комте (Comtet L.) 89, 293
Коршунов А. Д. 300
Коциг (Kotzig A.) 257
Крейчик (Kraitchik M.) 276, 294
Кэдоган (CadoganC. С.) 114, 115,
117, 218, 260, 280, 283, 293
Кэли (Cayley A.) 7, 33, 34, 72, 76,
77, 267, 294
Лине (LynnM. S.) 257, 283, 299
Лисковец В. А. 300
Лоэс (Lawes С. Р.) 163

302
Мак-Магон (MacMahon P. A.) 7
Манвел (Manvel В.) 9, 45, 267, 298
Мейберри (Mayberry J. P.) 39, 292
Мовшовиц (Mowshowitz A.) 44, 298
Мозер (MoserL.) 252, 294
Мокляк Н. Г. 300
Моллоус (Mallows С. L.) 19, 293
Моргенштерн (Morgenatern О.) 292
Мун (Moon J. W.) 8, 33, 34, 36, 44,
45, 153, 155, 156, 252, 254, 292,
294
Норман (Norman R. Z.) 30, 42, 73,
90, 93, 94, 152, 156, 179, 223, 226,
256, 261, 262, 294, 297, 298
Обершельп (Oberschelp W.) 151, 231,
232, 235, 237, 252, 272, 281, 283,
294
Онзагер (Onsager L.) 279, 294
Ope (Ore О.) 269, 294
Остервейл (Osterweil L.) 223, 294
Остин (Austin T. L.) 294
Оттер (Otter R.) 69, 72, 73, 75, 76,
99, 231, 245, 246, 248, 251, 294
Оукли (Oakley С.) 10, 104
Палмер (Palmer E. M.) 5,10, 14, 44,
57, 68, 77, 90, 96, 112, 124, 125,
139, 141, 146, 157, 159, 167, 174,
177, 182, 186, 188—190, 205, 210,
231, 245, 256, 263, 283, 287, 293,
294, 295, 298
Паркип (Parkin) 277
Партасарати (Parthasarathy К. Р.)
112, 263, 295
Петренюк А. Я. 300
Петренюк Л. П. 300
Пипперт (Pippert R. Е.) 44, 292
Пойа (Polya G.L,5,7,8, 33, 35, 36,
49, 50, 52, 58, 64, 67, 70, 76, 87,
103, 105, 121, 122, 137, 138, 140,
231, 232, 237, 245, 247, 248, 295
Попов В. А. 300
Принс (PrinsG.) 78, 81, 84, 86, 87,
92, 93, 102, 124, 259, 262, 266, 298
Прюфер (Prufer H.) 33, 34, 295
Рабин (Rubin M.) 44
Райдемайстер (Reidemeister К.-) 273,
295
Райт (Wright E. М.) 29, 231, 237,
242, 252, 253, 295, 296
Рассел (Russell В.) 201, 297
ИМЕННОЙ УКАЗАТЕЛЬ
Редфилд (Redfield I. H.) 4,5,8,46,
49—51, 68, 104, 190, 193, 196—198,
201, 202, 210, 2Н, 295
PeHbH(Renyi А.) 243, 252, 253, 295,
299
Рид (Read R. С.) 9, 14, 22, 24, 27-
29, 44, 45, 91, 169—171, 175, 185,
188, 189, 191, 193, 206, 208—210,
255, 256, 277, 295, 296, 298
Риддел (Riddell R. J.) 19, 20, 43,
93, 114, 211, 231, 241, 243, 296
Риордан (Riordan J.) 9, 19, 44, 67,
73, 76, 77, 79, 90, 103, 111, 233, 273,
276, 280, 281, 284, 294, 296, 298
Роберте (Roberts F. S.) 261, 296
Робинсон (Robinson R. W.L, 5,8,9,
30, 129, 131, 132, 135, 136, 139,
141, 145, 189, 194, 199, 200, 202,
210, 211, 218, 221, 223, 226, 227,
229, 230, 255—258, 263, 266, 281,
283, 294, 296
Роджерс (Rogers C. A.) 9
Росс (Ross I. C.) 45, 298
Рота (Rota G.-C.) 10
Рудволис (Rudvalis A.) 46, 296
Селиванов Б. И. 300
Ситгривс (Sitgreaves) 44
Скибенко И. Т. 300
Скойнс (Scoins H. J.) 44, 296
Слепян (Slepian D.) 105, 138, 139, 296
Слоуэи (Sloane N. J.) 18, 69, 280,
283, 296
Смит (Smith С. А. В.) 41, 265, 293, 296
Снаппер (Snapper E.) 46, 296
Спенсер (Spencer J. H.) 261, 296
Сривастава (Srivastava J. N.) 296
Стаблфилд (Stubblefield В.) 283
Стейн (Stein P.) 284
Стемпл (Stemple G. J.) 269, 294
Стокмейер (Stockmeyer P. K.) 9, 259,
287, 296
Стоун (Stone A. H.) 265, 293
Страздинь И. Э. 300
Сулливан (Sullivan D. D.) 10
Татт (Tutte W. T.) 39, 41, 87, 265,
270, 292, 294, 296, 298
Тернер (Turner J.) 44, 146, 164, 260,
296
Уайтхед (Whitehead A. N.) 201, 297
Уитни (Whitney H.) 260, 297
Уленбек (Uhlenbeck G. E.) 20, 45,
93, 95, 102, 131, 211, 231, 237, 241,
243, 245, 248, 253, 297, 299

ИМЕННОЙ УКАЗАТЕЛЬ
Уолкап (Walkup D. W.) 103, 297
Уоллис (Wallis W.) 268
Форд (Ford G. W.) 20, 93, 211, 231,
237, 241, 243, 245, 248, 253, 296
Фоулкс (Foulkes H. О.) 46, 190, 191,
196, 297
Фробениус (Frobenius G.) 46, 53
Фрухт (Frucht R.) 188, 297
Хай (High R. С.) 139, 299
Харари (Harary F.) 5, 10, 12, 14,
30, 32, 37, 40, 42, 44, 45, 52, 57,
68, 73, 75, 77, 78, 81, 84, 86, 87,
90, 92-96, 102, 104, 105, 111,
112, 117—119, 122-126, 129, 131,
134, 135, 138, 139, 146, 148, 152,
156—159, 161, 165, 167, 168, 174,
177, 179, 180, 182, 186, 188, 190,
212, 223, 230, 231, 256, 257, 259-
263, 265—270, 272, 274, 276, 278—
281, 283, 287, 292-299
303
Харрисон (Harrison M. А.) 139, 177,
178, 299
Хватал (Chvatal V.) 299
Хедрик (Hedrick E. R.) 37, 293
Хусими (Husimi К.) 93, 298, 299
Чао (Chao С. Y.) 260, 299
Чартрэнд (Chartrand G.) 294
Шарп (Sharp Jr. H.) 189, 299
Швенк (Schwenk A. J.) 9, 73, 284
Шридхаран (Sridharan M. R.) 189,
299
Шур (Schur J.) 53
Эванс (Evans J. W.) 257, 283, 299
Эйлер (EulerL.) 7, 89, 100, 144, 299
Эрдёш (Erdos P.) 243, 252, 299
Ci v. •.;

И все же, *
Будучи «Нигде»,
Находишься ты
Где-то. .>', ..' ■ ■<
А. А, Милн, «По метишце»
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Мы приводим в тексте определения почти всех понятий, используемых
в этой книге. Для удобства читателя некоторые понятия определялись не-
несколько раз. Все они помещены в этом указателе. Терминология согласуется
с той, которая принята в книге Харари [1J.
Абсолют корневого дерева (absolute of a rooted tree) 84
— реберно-корневого дерева (of a line rooted tree) 84
Автомат (automaton) 178
Автоматы изоморфные (isomorphic automata) 178
Автоморфизм графа (automorphism of graph) 14, 48 ;
Блок (block) 20 ' ■ ;'"
Булева функция (boolean function) 136
Вершина графа (point of a graph) 12 . . ...'. ,
— инцидентная дуге (incident with a arc) 15 , * '
ребру (with a line) 12 •, " *
— орграфа (of a digraph) 15 ' ' ..,, ^
— покрывает ребро (covers line) 263 . . ' *'" .
— смежная к вершине (adjacent to a point) 15
Вершины смежные (adjacent points) 12
— соединены ребром (join by a line) 12 """*•■ '
Вес вершины дерева (weight of a point of a tree) 102 . . ..
— дерева (of a tree) 102
— орбиты (of a orbit) 56, 58, 172
— функции (of a function) 58 ; .
Весовая функция (weight function) 55, 58, 172
Взвешенная форма леммы Бернсайда (weighted form of Burnside's 1еЩШ4) i
56
Входной алфавит автомата (input alphabet of an automaton) 178
Высота корневого дерева (height of a footed tree) 103
Выходной алфавит автомата (output alphabet of an automation) 178 >,
Гипотеза четырех красок (four color conjecture) 269 <
Граф (graph) 12 .-

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 305
Граф асимметрический (identity) 242 •"' '■'"'■•. ...-■ , ,, , >
— блоков (block) 92 :*v ■ t
— вершинно-симметрический (point-symmetric) 146, 260 ' '„'"■" '-,
— галшльтонов (hamiltonian) 258 . .,'•
— двойственный к плоскому графу (dual of a plane graph) 271 ;,,„.. •
— двумерный решетчатый (two-dimensional lattice) 279 , ,s<< ,'.". :
— знаковый помеченный (signed labeled) 43 ': '."« -
— интервалов (interval) 261
— клик (clique) 261
— корневой (rooted) 17
— локально ограниченный (locally restricted) 112
— направленный (oriented) 157
— — помеченный (labeled) 43
— неразложимый (non-separable) 20
— обладающий квадратным корнем (which has a square root) 260
— общий (general) 206
— ориентированный (directed) 15, 147
— плоский (plane) 44 . . , *
— подразбиений (subdivision) 261
— полный (complete) 38
— — двудольный (bipartite) 118 , ;. v s . . v
— — m-дольный (m-partite) 134 " . .»
— помеченный (labeled) 13 ■ ■ , , ,
— раскрашенный (colored) 27
— реберно-симметрический (line-symmetric) 260
— реберный (line) 260 - , ,
— решетчатый d-мерный (d-dimensional lattice) 279 , ' ■ , ^,
— самодополнительный (self-complementary) 168
— самонегативнып (self-negational signed) 189
— сбалансированный (balanced signed) 146 • *
— связный (connected) 16 ,■
— симметрический (symmetric) 260 . , >• . -*,
— с корнем (rooted) 17 f
— смешанный (mixed) 159 'fit ^1
— снабженный знаками (signed) 146
— тождественный (identity) 242 " " • . . „
— тотальный (total) 261 «. . _. , , • '*
— узла, узловой (knot) 273 * .\, ...,:.".
— унициклический (unicyclic) 89 «,-
— — помеченный связный (labeled connected) 45 . ,.
— циклически жесткий (rigid circuit) 261 ./ , _
— четный (even) 22 ••......
— эйлеров (eulerian) 22, 141 . , ,- . ,
— 2-раскрашенный (bicolored) 117 > '•»..• .-.,.' •':
— 2-раскрашиваемый (bicolorable) 124 > .,
— к -раскрашенный (к -colored) 27, 117 ■ .... • ..
— m-раскрашенный (m-colored) 129, 132, 133 .
— m-раскрашиваемый (m-colorable) 136 . ' . ■
— п-раскрашиваемый (те-colorable) 266
— ге-связный (rc-connected) 263
— гс-хроматический (rc-chromatic) 266
Графы корневые изоморфные (isomorphic rooted graphs) 17
— помеченные изоморфные (isomorphic labeled) 13
— fc-раскрашешше изоморфные (isomorphic fc-colored) 27
— эквивалентные относительно дополнительности (equivalent up to comple-
complementation) 169 , ,
Группа автоморфизмов графа (automorphism group of a graph) 48
— графа (of a graph) 14, 48 ,'.:.,.■

306 ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Группа графа вершинно-реберная (point-liue): 131 "">' '
— — реберная (line) 106 - • . ';-
— диэдральная (dihedral) 51 '■ •"";• ' ■ j'
— единичная (identity) 51 ■ <'<> '->">;' < •
— знакопеременная (alternating) 50 >r :'■ "■' ■ •' •»«' ■ t'
— матричная (matrix) 202 ■;: >! . ■', • > •>,; ■ ^
— орграфа (of a digraph) 15 ' *> ; ^;s
— парная (pair) 106
— подстановок на множестве объектов (permutation group with object set) 47
— производная (derived) 197
— редуцированная упорядоченная парная (reduced ordered pair) 147, 148
— симметрическая (symmetric) 49
— степенная (power) 57
— триадная (triad) 272
— упорядоченная парная (ordered pair) 152
— циклическая (cyclic) 51 ;
Группы подстановок идентичные (identical permutation groups) 49
— — изоморфные (isomorphic) 48
Декартово произведение групп (cartesian product of groups) 119
Дерево (tree) 32
— асимметрическое (identity) 83 .*■■
— блоков и точек сочленения (block-cutpoint) 92 <-гк
— взвешенное (weighted) 102 г,Л.
— входящее (to a point) 38
— выходящее (from a point) 38 > -<;
— гомеоморфно несводимое (homeomorphically irreducible) 81 *,? -t'J
— данного веса (of given weight) 87 4$
— данной мощности (of given strength) 87, 102 • -■■!■
— двумерное (two-dimensional) 96
— корневое данной высоты (rooted, with given height) 103
— непомеченное (unlabeled) 69
— ориентированное (oriented) 78 j
— остовное (spanning) 37 '■'*> •• <Ttb
— плоское (plane) 87 W- f •
— с висячим корнем (planted) 79
данной степенной спецификацией (with a given degree specification)
86, 102
— — данным разбиением (with a given partition) 86, 102
— смешанное (directed) 86
— снабженное знаками (signed) 87, 102
— Хусими (Husimi) 93
Диаметр графа (diameter of a graph) 262
— дерева (of a tree) 102
Дополнение графа (complement of a graph) 48, 168
— орграфа (of a digraph) 170, 183
Древесностъ графа (arboricity of a graph) 264
Дуга инцидентная вершине (incident with a point) 15 j
— орграфа (arc of a digraph) 15 i
— последняя (exit) 42 1
Задача Изинга (Ising problem) 279 '
— о ладьях (roock) 275 •
— — росте клеток (cell growth) 276
— — ферзях (queens) 276 .;
Звездный многоугольник (starred polygon) 43 -■>< ■ I
Злак графа (sign of a graph) 24 1

ГГРЕДМЕ-ГНЫЙ УКАЗ.^ЕЛЬ ЗО7
Изоморфизм графов (isomorphism of graphs) 14 * ••'$'•
Источник автомата (source of an automaton) 180 ,
— орграфа (of a digraph) 256 ... ,] •
Кактус (cactus) 93
— помеченный (labeled) 45
— треугольный (triangular) 93
Каркас (spanning tree) 37
Квадрат графа (square of a graph) 260
Класс подобных блоков (class 01 simmilar blocks) 73
Клика графа (clique of a graph) 261
Комплекс симплициальный (simplicial complex) 271
— — чистый двумерный (pure two-dimensional) 146, 252
Композиция групп (composition of groups) 121
Компонента графа (component of a graph) 17
— орграфа сильная (of a digraph, strong) 156
Конденсация орграфа (condensation of a digraph) 156, 255
Контур (cycle) 30
Корень графа (root of a graph) 17
Крупность графа (coarseness of a graph) 265
Латинский квадрат (Latin square) 272
Лемма Бернсайда (Burnside's lemma) 54
— пересчета помеченных графов (labeled counting lemma) 18
— Редфилда (Redfield's lemma) 195
Лес (forest) 76
Маршрут длины п (walk of length n) 16
— — — ориентированный (directed) 30
— замкнутый (closed) 30
Матрица смежности помеченного графа (adjacency matrix of a labeled graph)
37
Матрицы, эквивалентные по столбцам (column equivalent matrices) 192
Матричная теорема о деревьях для графов (matrix-tree theorem for graphs) 37
— — — — — орграфов (digraphs) 39
Мультиграф (multigraph) 111
— данной мощности (of given strength) 146
— 2-раскрашенный (bicolored) 206
Надграф (supergraph) 129
Недревесность графа (anarboricity of a graph) 265
Независимое множество вершин (independent set of points) 263
— — ребер (of lines) 263
Обобщение теоремы перечисления Редфилда (a generalization of Redfield's
enumeration theorem) 202
Обобщенная композиция групп (generalized composition group) 213
Обращение цикла подстановки (converse of a cycle of a permutation) 154
Обход графа (girth of a graph) 262
Ограниченная форма леммы Бернсайда (restricted form of Burnside's lemma)
55
Окружение графа (circumference of a graph) 262
Орбита (orbit) 53

308 ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Орграф (digraph) 15 ' ,;,'■*,.
— ациклический (acyclic) 30 -■■ .-• -.-.■--
— вершинно-симметрический (point-symmetric) 164 " * -.. :"*';'
— гамильтонов (hamiltonian) 258
— обратный к данному орграфу (converse of given digraph) 182 '
— односторонне связный (unilaterally connected) 256
— односторонний (unilateral) 256 - *■ ■
— полный (complete) 162 - • . -
— самообратный (self-converse) 182 - • "- "
— связный (connected) 152 • - ■ ■
— сильно связный (strongly connected) 155, 255 • . r : ' -t
— сильный (strong) 155, 255 ;
— слабо связный (weakly connected) 152 ■' •-<■'<
— соответствующий графу (of a graph) 157
— транзитивный (transitive) 256 -:\
— функциональный (functional) 90 ' -
— — помеченный связный (labeled connected) 44
— эйлеров (eulerian) 40
Орграфы итерированные реберные (iterated line digraphs) 45
— эквивалентные относительно обращения (equivalent up to conversion) 183
Ориентация графа (orientation of a graph) 157
Ортогональные латинские квадраты (orthogonal Latin squares) 273
Остов (spanning tree) 37
Перечисляющий ряд для конфигураций (configuration counting series) 58
— — — фигур (figure) 58
— — — функций (function) 58
Петля (loop) 12 * <■■
Площадь четного подграфа двумерной решетки (area «f an evee subgraph
of a two-dimensional lattice) 279 < .
Подграф (subgraph) 17 ,/ ^ * ■
— остовный (spanning) 37 I?"\4v,
— покрывает граф (spans the graph) 37 „ '. ''.,,';, ■> '" ,
— порожденный (induced) 125 ' -:!,■•
Подграфы неподобные (dissimilar subgraphs) 117
Полимино квадратное (square animals) 276
— неодносвязное (holey) 277 ' *
— односвязное (simply connected) 277 • ' '' , '
— тороидальное (toroidal) 278
— треугольное (traingular) 278 "' ' ' " '
— шестиугольное (hexagonal) 278
Полиномиальная форма теоремы перечисления степенной грушш (polinomUl
form of the power group enumeration theorem) 189 .
Полустепень захода (indegree) 15 . , ' ■
— исхода (outdegree) 15 ■
Порядок графа (order of a graph) 12 ,, '
— группы (order of a group) 47 *
Проблема ожерелья (necklace problem) 60, 62
Произведение групп (product of a groups) 52 ■
— — веночное (wreath) 121 ,''•*''''. V
Производящая функция (generating function) 13 !'''', *
— — экспоненциальная (exponential) 18 ' " .
Радиус графа (radius of a graph) 262 ;
Разбиение графа (partition of a graph) 12
— дерева (of a tree) 102 • ■■ -*: , »*\ -I'
— цветное (color) 133 ■.., «•• t*'-'* ' •• '■''■•■.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 1 ,..,/ 309
Размерность комплекса (dimension of a complex) 272 '.,..- -■*..-■?, •
— симплекса (of a simplex) 272
Расширение орграфа (extension of a digraph) 30 t..;--
Ребра кратные (multiple lines) 12 ; •
Ребро графа (line of a graph) 12 .
— дерева симметричное (of a tree, symmetry) 74 »
— инцидентное вершине (incident with a point) 12
— покрывает вершину (covers point) 263 с ;. : а
— соединяет вершины (joins points) 12
— торцевое (end-line) 97 .
Род графа (genus of a graph) 265
Ряд, перечисляющий конфигурации (configuration counting series) 58
— — фигуры (figure) 58
— — функции (function) 58
Связность (connectivity) 263 ••"'
— реберная (line-connectivity) 263
Сеть (net) 179
Симплекс (simplex) 272
Система транзитивности группы (transitivity system of a group) 53
Сложность графа (complexity) 265
Состояние автомата (state of an automaton) 178 ^
— — заключительное (terminal) 180
— — начальное (initial) 180
Стабилизатор элемента (stabilizer of an element) 53
Степень вершины (degree of a point) 22
— группы подстановок (of a permutation group) 47
Сток орграфа (sink of a digraph) 256
Сумма цикловых индексов всех графов данного множества (cycle index sum
of the groups of all graphs in given set) 215
Суперпозиция графов (superposition of graphs) 190, 192
Теорема декомпозиции Редфилда (Redfield's decomposition theorem) 195
— композиции (composition) 216
— о характеристике неподобия для графов (dissimilarity characteristic theo-
theorem for graphs) 73
— — — — — деревьев (trees) 75
— — — — — кактусов (cacti) 94
— — — — — 2-деревьев B-trees) 96
— перечисления для 2-деревьев (enumeration theorem for 2-trees) 99
— — Пойа (Polya's enumeration) 58
Редфилда (Redfield's) 192
— — степенной группы, константная форма (power group, constant form) 167'
— — — — форма степенного ряда (power series form) 174
Толщина графа (thickness of a graph) 265
Точка комплекса (point of a complex) 271
— сочленения (cutpoint) 19
Триангуляция многоугольника (triangulation of a polygon) 99
Тройка транзитивная (transitive triple) 153
— циклическая (cyclic) 153
Турнир (tournament) 16, 153
Удаление вершины из графа (removal of a point from a graph) 19
Факторизация графа (factorization of a graph) 267
Формула обращения Лагранжа (Lagrangc's inversion formula) 35, 36 . ■

310 ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Формула Оттера (Otter's) 75
Функции, эквивалентные относительно группы (equivalent functions with
respect to group) 215
Функция выходов (output function) 178
— класса (class function) 195, 199 > ;н
— переходов (input function) 178 ■';■..•• *»..•'■,.''.
Хроматический индекс (chromatic index) 266 •.' 4 .--,,..
Цвет вершины (color of a point) 27
Цепь (trail) 16 . , ,.
— простая (path) 16
Цикл подстановки самообратный (self-converse cycle of a permutation) 154
— типа 1 (type-1) 94
— типа 2 (type-2) 94
Цикловой индекс группы подстановок (cycle index of a permutation group) 49
Число вершинного покрытия (point-covering number) 263
— независимости вершинное (point-independence) 263
— — реберное (line) 263
— пересечения (intersection) 264
— реберного покрытия (line-covering) 263
— реберно-хроматическое (line-chromatic) 266
— скрещиваний (crossing) 265 ;. .„
— тотально-хроматическое (total-chromatic) 266 ,5 "'.'.
— хроматическое (chromatic) 265 '
Эйлеров контур (eulerian trail) 40 ,;
Эквивалентность относительно (Bi, В2, . . ., Вт) (equivalence with respect
to (Bi, B2, . . ., Bm)) 192 ^;';
Экспоненциация групп (exponentiation of groups) 123
Эксцентриситет вершины (eccentricity of a point) 262
Элементы подобные (similar elements) 53 ' * i
Ячейка (cell) 96 \ ' [
1-скелет 2-дерева A-skeleton of a 2-tree) 96 ... ..
1-фактор графа A-factor of a graph) 267
1-факторизация графа A-faktorization of a graph) 267
2-дерево помеченное (labeled 2-tree) 44
— — плоское (plane) 44
— реберно-помеченное (line-labeled) 44
fcc-дерево Fc-tree) 92
fc-дерево помеченное (labeled k-tree) 44
гс-комплекс чистый (pure «-complex) 272
га-куб (n-cube) 136
га-плекс (n-plex) 96
(p, д)-граф ((р, g)-graph) 12
Л-эквивалентные элементы (Л-equivalent elements) 53
— г-подмножества (r-subsets).63
•S-функция E-function) 210
А-кактус (Д-cactus) 94
П -произведение (cap-product) 191
(j-произведение (cup-product) 191 ,

Варкалосъ. Хливкие шорьки
Пырялись по наве,
И хрюкотали зелюки.
Как мюмзики в мове.
Льюис Кэррол, Бармаглот I
УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
A (G) матрица смежности графа G 37
А | Y ограничение группы А на множество У 55
А (/) подгруппа подстановок группы А, индуцированная функцией
/ 213
А (х) стабилизатор элемента х 53, 212
Ад число различных помеченных четных подграфов в решетча-
решетчатом графе, имеющих q ребер 279
Ап знакопеременная группа степени п 50
В (G) граф блоков графа G 92
В (х) экспоненциальная производящая функция для помеченных
блоков 20
В (х) перечисляющий ряд для графов блоков 93
В (х) перечисляющий ряд для корневых графов блоков 93
Вр число помеченных блоков с р вершинами 20, 243
С (х) лкспоненциальная производящая функция для помеченных
связных графов 18
() перечисляющий ряд для конфигураций 58, 171
С (*i, . . ., хп) перечисляющий ряд для конфигураций 61
C число орбит веса i 171
число орбит веса к 58
циклическая группа степени п 51
число связных помеченных графов с р вершинами 17, 241
число ^-раскрашенных помеченных графов порядка р 28
с
Ср
(х)
*п)
с.
Сп
Ср
(к)
1 «Алиса в стране чудес. Сквозь зеркало и что там увидела Алиса», кн. 2.
Издательство литературы на иностранных языках, София, 1967, стр. 135, пере-
перевод Д. Г. Орловской.
2 Здесь собраны символы, буквы и другие знаки в том виде, в каком они
обычно использовались в этой книге. Они разбиты на четыре категории: латин-
латинские буквы, греческие буквы, рукописные буквы и операции на группах и гра-
графах,

12 УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
D ориентированный граф 15 . . •
D дополнение орграфа D 170, 183
D' орграф, обратный к орграфу D 182
D* конденсация орграфа D 156, 255
D (G) орграф, соответствующий графу G 157
D (х) перечисляющий ряд для корневых треугольных кактусов 94
Dp (x) производящая функция для помеченной орграфов порядка р 16
Dn диэдральная группа степени п 51
D — Z орграф, получающийся из D после удаления всех дуг, при-
принадлежащих циклу Z 90
En единичная группа степени n ,51i ■•:-.'.-
G граф 12 •'*•'.
G дополнение графа G 48, 168 у ■
G* граф, двойственный к плоскому графу G 271
G2 квадрат графа G 260
G3 куб графа G 260
G (х) экспоненциальная производящая функция для помеченных гра-
графов 19
Gp число помеченных графов порядка р 14, 241
Gp (х) производящая функция для помеченных графов порядка р 13
Gp (x) производящая функция для корневых графов порядка р 126
Gp, n узловой граф, сопоставленный узлу рп 273
G — v граф, получающийся из графа G после удаления вершины у 19
(G, и) корневой граф G, корнем которого является вершина и 219
Н (х) перечисляющий ряд для гомеоморфно несводимых корневых де-
_ ревьев 81
Н (х) перечисляющий ряд для гомеоморфно несводимых корневых де-
деревьев с висячим корнем 8
К (j) полный m-дольный граф, соответствующий разбиению (J)
на т частей 134
Кт, п полный двудольный граф с т+ п вершинами 118
Кр полный р-вершинный граф 37
L (G) реберный граф графа G 260 "*•
L (х) перечисляющий ряд для реберно-корневых деревьев с несимметрич-
несимметричным корневым ребром 75
L (х) перечисляющий ряд для ориентированных корневых деревьев,
у которых корнем является дуга 80
L (х) перечисляющий ряд для реберно-корневых гомеоморфно несводимых
деревьев с несимметричным корневым ребром 83
L (х) перечисляющий ряд для реберио-корневых 2-деревьев 98
L (х) перечисляющий ряд для пленарных реберно-корневых 2-деревьев
101
£щ. л двумерный решетчатый граф 279

УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ 313
; Ln число латинских квадратов порядка п с естественно
упорядоченными первыми строкой и столбцом 272
* . ■ Lp ,.-• число р-вершинных реберно-корневых деревьев с не-
несимметричным корневым ребром 75
' М (х) перечисляющий ряд для реберно-корневых 2-деревьев
с симметричным корневым ребром 97
М1 (х) перечисляющий ряд для реберно-корневых 2-деревьев,
у которых корневое ребро является торцевым и сим-
_ метричным 97
Мj (ж) перечисляющий ряд для пленарных реберно-корневых
2-деревьев, у которых корневое ребро является
; ■' » торцевым и симметричным 100
N (А) число орбит группы подстановок А 5-4
Ш, [Ви Bt, i . ., Вщ] число классов (т X п)-матриц, эквивалентных отно-
относительно групп подстановок (В1, . . ., Вт) 192
1" " ' N (п, г) число типов n-местных булевых функций, каждая
пз которых имеет ровно г единичных значений 138
N (х) перечисляющий ряд для реберно-корневых 2-де-
2-деревьев с несимметричным корневым ребром 97
ьи. ' '• !- ^i(x) перечисляющий ряд для реберно-корневых 2-деревьев,
у которых корневое ребро является торцевым и не^~
симметричным 97
; N1 (x) перечисляющий ряд для пленарных реберно-корневых
s'. . . 2-деревьев, у которых корневое ребро является
^ ' ■"i* торцевым и несимметричным 100
N™ (х);,. производящая функция для р-вершинных графов,
i >!•. у которых ребра раскрашены в т взаимозаменяемых
цветов 176
//(xv . . ., хр) . производящая функция для локально ограниченных
р-вершинных графов 112
Р (х) перечисляющий ряд для плоских корневых деревьев
_ 87
Р (х) перечисляющий ряд для плоских корневых деревьев
с висячими корнями 87
Р„ простая n-вершинная цепь 269
Qn n-мерный куб (п-куб) 136
R (х) экспоненциальная производящая функция для связ-
ных корневых помеченных графов 20
R (х) перечисляющий ряд для ориентированных корневых
_ деревьев 78
R (х) перечисляющий ряд для ориентированных корневых
деревьев с висячими корнями 79
Яр число р-вершинных связных корневых помеченных
графов 21
Rn (x) экспоненциальная производящая функция для таких
. . связных корневых помеченных графов, у которых
' корень принадлежит ровно п блокам 21

т
Тв
ТС
|
т
т
т
т
(х,
(х
(х
Тп
Т
т\
(G)
(Р)
(х)
(*)
У)
, У)
, У)
Тр
Тр
(*)
314 УКАЗАТЕЛЬ ОБОЗНАЧРНИЙ
( S ) подграф, порожденный подмножеством вершин S 125
S (G) граф подразбиений графа G 261 ~
S (х) производящая функция для сильных турниров 156
Sn симметричная группа степени п 49
5^1>2) вершинно-реберная группа графа Кп 135, 199
дерево 32
абсолют корневого или реберно-корневого дерева 84
тотальный граф графа G 261
число турниров порядка р 153
производящая функция для корневых деревьев 70
производящая функция для турниров 156
производящая функция для корневых бс-деревьев 92
производящая функция для корневых бс-деревьев с голубым кор-
корнем 92
производящая функция для корневых бс-деревьев с коралловым
корнем 92
число корневых деревьев порядка р 70
приближенное число корневых р-вершинных деревьев 252
производящая функция для турниров, имеющих ровно п сильных
компонент 157
U (х) экспоненциальная производящая функция для помеченных эйлеро-
эйлеровых графов 23
U (х) перечисляющий ряд для асимметричных корневых деревьев 84
Ux (х) перечисляющий ряд для корневых деревьев, имеющих асимметри-
асимметрические абсолюты 85'
U% (х) перечисляющий ряд для реберно-корневых деревьев, имеющих
асимметрические абсолюты 85
Up число помеченных эйлеровых графов порядка р 23
Un (х) перечисляющий ряд для унициклических графов, у которых цикл
имеет длину п 90
V{D) множество вершин орграфа D 15
V (G) множество вершин графа G 12
Vl (x) перечисляющий ряд для асимметрических корневых деревьев
с неасимметрическими абсолютами 85
Fa (x) перечисляющий ряд для асимметрических реберно-корневых
деревьев с неасимметрическими абсолютами 85
W (х) экспоненциальная производящая функция для четных помечен-
помеченных графов 23
Wp число четных помеченных графов порядка р 22
X {D) множество дуг орграфа D 15
X (G) множество ребер графа G 12
'^ множество всех 2-подмножеств множества X 105
множество всех упорядоченных пар различных элементов из
X 148

; a
a (n
(n,
, k.
a
k,
m,
(*,
m)
t)
У)
ap
ap
УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ 315
Z (A) цикловой индекс группы подстановок А 49
Z (G) цикловой индекс группы автоморфизмов графа G 53
ZD0O— 5га) разность сумм цикловых индексов всех групп Ап и Sn 67
Z (S<s>) сумма цикловых индексов всех симметрических групп Sn 70
Z (А) X Z (В) произведение цикловых индексов 139
Z (а) цикловой индекс циклической группы, порожденной подста-
подстановкой а 196
число автоматов с п состояниями, к входными и т выходными
символами 179
число автоматов с п состояниями, из которых t — заключи-
заключительные, к входными и т выходными символами 181
производящая функция для помеченных циклических оргра-
орграфов, перечисляемых с учетом числа вершин, имеющих
нулевую полустепень захода 32
число помеченных ациклических р-верщинных орграфов 31
число р-вершинных графов, перечисляемых с учетом экви-
эквивалентности относительно дополнительности 169
ар, k число таких помеченных ациклических р-вершинных оргра-
орграфов, у которых ровно к вершин имеют нулевую полустепень,
захода 31
1 'н ' 6* число неподобных блоков в графе 73
6с (G) дерево блоков и точек сочленения графа G 92
!i Ьт, п (*) многочлен, перечисляющий остовные подграфы полного дву-
двудольного графа Кщ.п при тфп 118
Ьп (х) многочлен, перечисляющий остовные подграфы полного дву-
-,. дольного графа Кп,п 121
Ьп ((/)> х) многочлен, перечисляющий m-раскрашенные р-вершинные
графы, определяемые цветным разбиением (/) числа т
133
* с (х) перечисляющий ряд для фигур 58
с (ж) производящая функция для связных графов (парамет-
(параметром перечисления является число вершин в графе) 114
с (ж, у) производящая функция для связных графов (параметры
перечисления — число вершин и число ребер в графе) 115
с (хи i2, . . ., хп) перечисляющий ряд для фигур 61
Ck число фигур веса к 57
ср число связных р-вершинных графов 114
ср (х) многочлен, перечисляющий р-вершинные орграфы с учетом
эквивалентности относительно обращения 184
ср (х, у) многочлен, перечисляющий полные р-вершинные оргра-
орграфы в соответствии с числом дуг и с числом симметричных
пар дуг в них 162
Cp,q число связных (р, д)-графов 115
срцТ число полных р-вершинных орграфов, имеющих ровно д
«непарных» дуг и ровно г симметричных пар дуг 162

316 УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
d(G) диаметр графа G 262
degv степень вершины v 22
d (x) перечисляющий ряд для треугольных кактусов 95
и ,-, . ... dp число р-вершинных орграфов 151, 236
d'v число самообратных р-вершинных орграфов 187
dp число самодополнительных р-вершинных орграфов
170
dp (x) многочлен, перечисляющий р-вершинные орграфы
148, 161
dp (x) многочлен, перечисляющий самообратные р-вер-
р-вершинные орграфы 182
*' ' * dp,q число орграфов с р вершинами и q дугами 201
v e (D) число эйлеровых контуров в помеченном «йюеройОМ
подграфе D 42 . ,
е (v) эксцентриситет вершины v 262 •
' ' / (х, у) производящая функция для лесов 77
/р (х) многочлен, перечисляющий р-вершинные леса 77
/р, q число лесов с р вершинами и q ребрами 77
g (х) производящая функция для графов ИЗ
g (x, у) производящая функция для графов (параметры
перечисления — число вершин и число ребер
" ■ , •• в графе) 115
-'•', - '' •" ' '■ . gp (x) производящая функция для р-вершинных графов
: ,. ..- 105, 161
■'*!■'■.;. ■.'')•.?'•* . gp число р-вершинных графов 114, 232
, gp число самодополнительных графов с р вершинами
'**■■■■' ■■¥:• ''>■■• 169
: ' ' gp,q число (р, д)-графов 105, 115, 200, 237
*,.-;: *• ..-.; h (/) число подстановок симметрической группы, име-
^. i' ■' ющих цикловую структуру, определенную раз-
: •■ ■■ биением (/') 50
' h (x) перечисляющий ряд для гомеоморфно несводимых
-а* >■•.* ' ixr деревьев 81
t:)' •' ■ , . hp (x) многочлен, перечисляющий графы порядка р с кор-
;«-,'. „, ' .: нем, представляющим собой некоторый порожден-
, г ч , ный подграф Н порядка ге< р 125
(/) = (/х, /2, , . ., /п) вектор, определяющий такое разбиение числа п,
в котором в точности jk частей, равных к 5С
]к (а) число ^-циклов в разложении подстановки а на
непересекающиеся циклы 49
I{G) число различных распределений ООНЮМС ва мно-
.• жестве вершин графа G 14

УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ 317
тр (ж) производящая функция для мультиграфов порядка р 111
тр (ж, у) многочлен, перечисляющий р-вершинные смешанные графы в соот-
соответствии с числом дуг и числом ребер в них 159
тр, q число мультиграфов с р вершинами и q ребрами 205
mPqr число смешанных графов с р вершинами, q дугами и г ребрами 169
nG граф, состоящий из п различных экземпляров связного графа G
134
о (G) число различных ориентации графа G 157
odv полустепень исхода вершины v 39
op (x) многочлен, перечисляющий направленные р-вершинные графы 161
р число вершин в графе и орграфе 12, 15
[р] произвольное упорядоченное разбиение числа р на несколько
положительных частей 28
р* число неподобных вершин в графе 73
р j число неподобных вершин в j-м классе подобия блоков 73
р (х) перечисляющий ряд для плоских деревьев 87 ■■ ]■•„
q число ребер в графе или число дуг в орграфе 12, 15
а* число неподобных ребер в дереве, или в кактусе, или в 2-дереве
74, 93, 96
q (/) число реберных циклов, определяемых подстановкой с цикловой
структурой (/) 232, 235
г (G) радиус графа G 262
г* число неподобных циклов в кактусе 93
г* число неподобных ячеек в 2-дереве 96 « ■•'■ *■
г (х) перечисляющий ряд для ориентированных деревьев 78
г' число самообратных р-верпшнных отношений 188
гр (х) многочлен, перечисляющий корневые надграфы некоторого'
р-вершинного графа 129 ***"
гр (х) многочлен, перечисляющий р-вершинные отношения 152
г' (х) многочлен, перечисляющий самообратные р-вершинные отношения
186
s число симметричных ребер в дереве 74 *.
s (G) число симметрии графа G (порядок группы автоморфизмов графа'С)
14 ■ г. -
s (у) производящая функция для чистых 3-размерных симплициальных
комплексов 272
sj (x) перечисляющий ряд для 2-деревьев, у которых корнем является
ячейка с двумя подобными ребрами 98
sx (x) перечисляющий ряд для пленарных 2-деревьев, у которых .^<ф§ем
является ячейка с двумя подобными ребрами 101 r) I ^
sa (х) перечисляющий ряд для 2-деревьев, у которых корнемЧявляртСя *
ячейка с тремя подобными ребрами 98 <."; " ^Ч "vч*

318 ' указатель обозначений
s2 (x) перечисляющий ряд для пленарных 2-деревьев, у которых корнем
является ячейка с тремя подобными ребрами 101
Sp (x, у) перечисляющий многочлен для комплексов не ниже чем второй
размерности, имеющих р точек (параметры перечисления — число
.« линий и число клеток в комплексе) 272
spqr число комплексов не ниже чем второй размерности, имеющих р
точек, q линий и г клеток 272
t(х) производящая функция для деревьев 73 •-,'-.-
t (ж) перечисляющий ряд для 2-деревьев 97
t (x) перечисляющий ряд для пленарных 2-деревьев 101 '"''.'".
t (ж, у) ряд, перечисляющий деревья блоков и точек сочленения 92
tn число 2-деревьев с п ячейками 96 '
tp число помеченных р-вершинных деревьев 32
tp число деревьев порядка р 73 '•
tp приближенное число р-вершинных деревьев 252 .т.
tm, п число бс-деревьев с т голубыми и п коралловыми вершивши 92
и, v, w вершины графов и орграфов 12, 14 ;lf: ,
(и, и) дуга орграфа 15 *" >
{и, и) ребро графа 12
и (х) перечисляющий ряд для асимметрических деревьев 84
и (х) производящая функция для связных четных графов 115, 145
и (х, у) производящая функция для помеченных эйлеровых графов (пара-
(параметры— число вершин и число ребер в графе) 27
v (х) перечисляющий ряд дня функциональных орграфов 90
w весовая функция 55 > ,,
w (F) вес орбиты 58
w (Х() вес орбиты 56 . :/^
w (/) вес функции 58
w (х) производящая функция для четных графов 115, 145
w (х, у) экспоненциальная производящая функция для помеченных четных
графов 27
wp число четных р-вершинных графов 141
wp (x) многочлен, перечисляющий помеченные р-вершинные четные графы
24
х ребро графа или дуга орграфа 12, 15
х орбита, содержащая элемент х 212
Г (D) группа орграфа D 15
Г (G) группа графа 14, 48
I\ (G) реберная группа графа 106
Го>1 (G) вершинно-реберная группа графа 131

УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ 319
; Д наибольшая степень вершин графа 263
Д (х) перечисляющий ряд для 2-деревьев, у которых корнем является
ячейка (треугольник) 98
Д (х) перечисляющий ряд для планарных 2-деревьев, у которых корнем
является ячейка 101
(а; Р) подстановка из степенной группы 57
а о число вершинного покрытия графа 263
а1 число реберного покрытия графа 263
0 вершинное число независимости графа 263
, реберное число независимости графа 263
7 род графа 265
б наименьшая степень вершин графа 263
е тождественная подстановка 59
радиус круга сходимости производящей функции для деревьев
и производящей функции для корневых деревьев 246
9 толщина графа 265 ["'■■
v. связность графа 263
А, реберная связность графа 263
v число скрещиваний графа 265
\ крупность графа 265
р линейный оператор Робинсона, действующий на вершинно-ребер-
рые цикловые индексы 131

О УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
о (G) знак графа G, ребра которого помечены специальным образом
числами +1 и —1 24
% хроматическое число графа 265
%' реберно-хроматическое число графа 266
у" тотально-хроматическое .число графа 266
ю0 (G) одна из вариаций числа пересечения графа 264
множество всех блоков 220
множество всех корневых блоков 220
множество всех блоков с не менее чем р вершинами
множество всех р-вершинных блоков 220
множество всех корневых р-вершинных блоков 220
С множество всех связных графов 217 '
С множество всех связных корневых графов 220
Ср множество всех связных р-вершинных графов 218
G] j множество всех корневых связных графов, у которых всякий блок,
содержащий корень, имеет не менее чем р вершин 220
множество всех графов 217
множество всех графов, имеющих ровно п компонент 217
множество всех таких графов, каждая компонента которых содер-
содержит не менее чем р вершин 218
множество всех различных корневых графов, которые могут быть
получены путем выделения корня в графах из множества^ 219
множество всех корневых связных р-вершинных графов, каждый
блок в которых содержит корень 220
_; & множество всех деревьев 224 ^ °>k'«v 'Ч ч ••»< -.«- /
Z (Ж) суию циклопа индексов всех графе* й»
лив

1£(АЗАТЕЛЬ ОБОЗНАЧЕНИЙ
А = В идентичность групп А ц В i&
А В произведение групп А ж В 52
ВА степенная группа 57
321
' В
А*
ограниченная степенная группа 68
\ ' ^' . А X В декартово произведение групп А и В 119
А [В] композиция групп (веночное произведение групп) А
и В 121
[В]А экспоненциация групп А я В 123
А /В производная группа групп А и В 197
; [А; В] матричная группа групп А и В 202
А (/) [Blt . . ., Вт] обобщенная композиция групп 213
[а; Рц . , ., рт] подстановка из матричной группы 202
(а; т1, . . ., тт) подстановка из обобщенной композиция групп 213
, парНая
редуцированная упорядоченная парная группа 148
Sp ;•..; упорядоченная парная группа группы Sp 152
5* триадная группа группы Sp 272
■
Г(Я)О5р-„ специальное ограничение парной
' 125
4КГ гипотеза четырех красок 269
ПЭ4КГ перечислительный эквивалент гшютеш четырёх кра-
сок 269

(i ■ , . ;?, .;;•;; ^.-^
ОГЛАВЛЕНИЕ
Королевский Математик был лысый близо-
близорукий человек, носивший на голове ермолку,
а за каждым ухом — по карандашу. Он бил
одет в черный костюм с белыми циф-
цифрами.
«Я не желаю выслушивать длинный пе-
перечень всего того, что вы навычисляли
для меня с 1907 года», — сказал ему король,
— «Я просто хочу, чтобы вы прямо сейчас
постигли, как достать луну для прин-
принцессы Леноры. Когда она получит лупу,
она снова станет здоровой».
«Я счастлив, что вы упомянули обо всем
вычисленном мной для вас с 1907 года,
— сказал Королевский Математик. —
Так случилось, что перечень всего этого
у меня с собой».
Джеймс Сёрбер, «Много лун»
Предисловие переводчика , . 5
Предисловие 7
Глава 1. ПЕРЕЧИСЛЕНИЕ ПОМЕЧЕННЫХ ОБЪЕКТОВ ... 11
1.1 Число способов, которыми можно пометить граф 12
1.2. Связные графы 16
1.3. Блоки 19
' 1.4. Эйлеровы графы 22
1.5. Число /с-раскрашенных графов 27
1.6. Ациклические орграфы 30
1.7. Деревья 32
1.8. Эйлеровы контуры в орграфах 38
■ Упражнения 43
Гаава 2. ТЕОРЕМА ПОЙА 46
2.1. Группы и графы 47
2.2. Цикловой индекс группы подстановок 49
.2.3. Лемма Бернсайда 53
2.4. Теорема Пойа 57
2.5. Ряд 1 + а: — специальный ряд для фигур 62
2.6. Взаимно однозначные функции 64
Упражнения 67
Глава 3. ДЕРЕВЬЯ .' 69
3.1. Корневые деревья 69
3.2, Некорневые деревья 73

J-'к
ОГЛАВЛЕНИЕ 323
'ч' 3.3. Деревья со специальными свойствами ] 78
! 3.4. Древовидные графы 89
3.5. 2-деревья 95
Упражнения 102
Глава 4. ГРАФЫ 104
4.1. Графы 105
4.2. Связные графы ИЗ
• 4.3. 2-раскрапшгаые графы 117
4.4. Корневые графы 124
4.5. Надграфы и раскрашенные графы 129
4.6. Булевы функции 136
4.7. Эйлеровы графы 141
Упражнения 145
Глава 5. ОРГРАФЫ 147
5.1. Орграфы 148
5.2. Турниры 153
5.3. Ориентации граф! 157
5.4. Смешанные графы 159
Упражнения 163
Глава 6. ПЕРЕЧИСЛЕНИЕ СТЕПЕННОЙ ГРУППЫ 165
6.1. Теорема перечисления степенной группы 165
<-' 6.2. Самодополнительныо графы 168
., . 6.3. Взвешенные функции 171
6.4. Графы с раскрашенными ребрами 175
6.5. Конечные автоматы 177
6.6. Самообратные орграфы 182
Упражнения 188
Глава 7. СУПЕРПОЗИЦИЯ 190
7.1. Теорема перечисления Редфилда 190
7.2. Теорема декомпозиции Редфилда 194
7.3. Графы и орграфы 200
7.4. Обобщение теоремы перечисления Редфилда 202
7.5. Общие графы 206
Упражнения 210
Глава 8. БЛОКИ 211
8.1. Обобщение леммы Редфилда 211
8.2. Композиция групп 212
8.3. Теорема композиции 215
8.4. Связные графы 217
8.5. Суммы цикловых индексов корневых графов 219
8.6. Блоки 220
8.7. Графы с данными блоками 223

3241- ОГЛАВЛЕНИЕ
-• 8.8. Ациклические орграфы 227
Упражнения 230
Глава 9. АСИМПТОТИКА 231
9.1. Графы 232
£■"; 9.2. Орграфы 235
' ■ 9.3. Графы с данными числами вершин и ребер , 237
;| 9.4. Связные графы и блоки 241
;•;: 9.5. Деревья 245
Упражнения 252
tлава 10. НЕРЕШЕННЫЕ ЗАДАЧИ 254
;, 10.1. Помеченные графы 254
'*> 10.2. Орграфы 255
. 10.3. Графы с данными структурными свойствами 257
■'• 10.4. Графы с данным параметром 261
р' 10.5. Подграфы данного графа 266
10.6. Надграфы данного графа 268
10.7. Графы и раскраска 269
10.8. Вариации на тему о графах 271
Приложение I 280
Приложение II 287
Приложение III 289
Список литературы 292
Именной указатель 301
Предметный указатель ;■ i . 304
Указатель обозначений 311
■ "'■•', ;;
*■■* ..•: i . . ;■ ■ • -,.•■• • • ■■ .■ .■■••'-? •'•■;■ • ' ■■» ' •
'г5 . ■'■'_■/■ >
£».,-' ■'.,.'■•".

"* . -
<i '-.-■}■
Jt
■•Ь.у *:■»■
Уважаемый читатель/
Ваши замечания о содержании книги, ее оформлении,
качестве перевода и другие просим присылать по адресу:
129820, Москва, И-110, ГСП, 1-й Рижский пер., д. 2,
издательство «Мир».

Ф. Харари, Э. Палмер ' * ч ';! ' -
ПЕРЕЧИСЛЕНИЕ -
ГРАФОВ
Редактор А. А. Бряндинская
Художник В. И. Шаповалов 'tfV <■
Художественный редактор Н.Г.Блинов '
Технический редактор Т. А. Максимова : :
Сдано в набор 17/V 1976 г. '■
Подписано к печати 7/XII 1976 г. ,;
Бумага тип. М« 1 60X90'/n=10,25 бум. л.
Печ. л. 20,50. Уч.-изд. л. 18,38 К
Изд. М« 1/8636. Цена 1 р. 53 к. Зак. 4'»3
ИЗДАТБ'.ЛЬСТВО «МИР», Москва, 1-й Рижский пер., 2
Отпечатано в ордена Трудового Красного Знамени
Ленинградской типографии Ml 2 имени Евгении Соколовой
Союзполиграфпрома при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли,
198052. Ленинград, Л-52, Измайловский проспект, 29
Набсанов Ленинградской типографии № 6 Союзполиграфпрома Государствен-
Государственного комитета Совета Министров СССР по делам издательств, полиграфии
и книжной торговли,
196006, Ленинград, Московский пр., 91

ИМЕЕТСЯ В ПРОДАЖЕ
Математическая экономика. Равновесные модели, оптимальное планирова-
планирование и управление. Сб. перев., «Мир», 1974, 99 коп.
Математическая экономика сложилась как самостоятельная научная дисцип-
дисциплина со своим объектом изучения и аппаратом, основанным на методах
функционального анализа, топологии, теории дифференциальных уравнений
и др. Появилось много работ советских и зарубежных авторов, развивающих
классические исследования фон Неймана, Л. В. Канторовича и Л. С. Пон-
трягина.
Предлагаемый сборник содержит статьи видных зарубежных ученых (Эрроу,
Рокафеллара, Олеха, Лихнеровича и др.). Эти статьи разбиваются на две
группы; в первой предлагается новый алгоритм решения игр и анализа эко-
экономических моделей, рассматривается модель регулирования цен и поведения
покупателей. Во второй группе статей дается экономическая интерпретация
принципа максимума Понтрягина, рассматриваются модели оптимального
контроля внешней среды и защиты ее от загрязнения.
Книга рассчитана на математиков различных специальностей, инженеров,
экономистов и специалистов по АСУ, Она будет полезна аспирантам и студен-
студентам указанных специальностей.
Уважаемый читатель! . '
Заказ на книгу направляйте по адресу:
191040, Ленинград, Пушкинская ул., 2, магазин № 5 «Техническая книга».
Книга будет выслана наложенным платежом,