г Ы
А.И,Герасимович
Н-А-Рысюк
МАТЕМАТИЧЕСКИЙ
АНАЛИЗ

А. И. Герасимович
Н. А. Рысюк
МАТЕМАТИЧЕСКИЙ
АНАЛИЗ
СПРАВОЧНОЕ ПОСОБИЕ
В двух частях
Часть 1
МИНСК
«ВЫШЭЙШАЯ ШКОЛА»
1989

ББК22.161я2
Г37
УДК517@35.5)
Рецензенты:: кафедра высшей математики Белорусского института
инженеров железнодорожного транспорта; кафедра высшей математики
Вильнюсского инженерно-строительного института
Библиотека
-1 мат.- >-;тнкя
я механики Ура.-.ьсю-^о
отделения АН СССР
Герасимович А. И., Рысюк Н. А.
Г37 Математический анализ: Справ, пособие. В 2 ч. Ч. 1.—
Мн.: Выш. шк., 1989.—287 с: ил.
ISBN 5-339-00084-2.
Рассматриваются основные вопросы дифференциального и интегрального
исчисления функций одной переменной, предусмотренные программой курса
«Высшая математика» для технических вузов. Содержатся примеры и задачи,
иллюстрирующие теоретические положения, приводятся алгоритмы некоторых
методов..
Для студентов технических вузов всех форм обучения, инженеров, а также
для тех, кто самостоятельно изучает курс высшей математики.
Г—	¦««•¦•¦-
ISBN 5-339-00084-2 (ч.1)
ISBN 5-339-00269-1	© Издательство «ВЫшэйшая школа», 1989

ПРЕДИСЛОВИЕ
Ускоренное развитие науки и техники предъявляет повышенные
требования к математическому образованию современных инжене-
инженеров. Главное из них — это ориентация обучения студентов на при-
применение математических методов к решению прикладных задач и
широкое использование ЭВМ в учебном процессе. Основой матема-
математической подготовки инженера является общий курс высшей мате-
математики. Опыт показывает, что успешному освоению этого курса спо-
способствует работа не только с учебниками и учебными пособиями,
написанными, как правило, «академическим» языком, но и использо-
использование различного рода вспомогательных изданий — справочников
и методических справочных пособий, отражающих уровень препода-
преподавания общего курса высшей математики в конкретном вузе.
Вниманию читателя предлагается справочное пособие по мате-
математическому анализу, которое разработано на кафедре высшей ма-
математики № 2 Белорусского политехнического института — голов-
головного втуза республики. Оно написано в соответствии с программой
общего курса высшей математики для технических вузов.
В данном пособии сделан упор на применение математического
аппарата по готовым схемам (формулам, теоремам и определениям).
Доказательства ряда теорем и выводы формул,не приведенные здесь,
читатель может найти в учебных изданиях, указанных в списке ли-
литературы.
Пособие имеет следующую структуру. В нем содержатся опреде-
определения основных понятий, формулировки теорем и следствий из них,
приводятся доказательства наиболее важных теорем и выводы мно-
многих формул. Начало доказательств теорем, следствий и свойств
обозначено символом >, а конец — <]. Для наиболее употребитель-
употребительных определений и теорем дается вторая (краткая) их запись с по-
помощью кванторов и логических символов. Кроме того, в пособии
приводятся примеры решения задач, иллюстрирующие теоретиче-
теоретические положения, а также алгоритмы и программы решения некото-
некоторых задач общего курса высшей математики с помощью численных
методов на программируемом микрокалькуляторе «Электроника
БЗ-34» и ЭВМ, что подготавливает читателя к использованию вы-
вычислительной техники.
У предлагаемого справочного пособия довольно широкий адрес.
Оно может быть использовано студентами технических вузов всех
форм обучения для организации самостоятельной работы по изуче-
изучению общего курса высшей математики, преподавателями вузов и
техникумов — при подготовке лекционных курсов, практических и
семинарских занятий. Инженерам и научно-техническим работникам

оно поможет получить необходимую информацию по практическому
применению дифференциального и интегрального исчисления.
Пособие состоит из двух частей. В первой части изложено диф-
дифференциальное и интегральное исчисление функций одной перемен-
переменной: элементы теории множеств, числовые функции, их пределы и
дифференцирование, векторные и комплексные функции действи-
действительного аргумента, неопределенный и определенный интегралы и их
применение. В приложениях содержатся формулы для вычисления
координат центров масс некоторых фигур и таблица основных мето-
методов интегрирования.
Главы 1—7 написали совместно А. И. Герасимович и Н. А. Рысюк,
главы 8—10 и приложения — А. И. Герасимович.
Авторы выражают благодарность рецензентам: коллективу ка-
кафедры высшей математики Белорусского института инженеров же-
железнодорожного транспорта (заведующая кафедрой — кандидат
физико-математических наук Ж. Е. Буховец) и коллективу кафедры
высшей математики Вильнюсского инженерно-строительного инсти-
института (заведующий кафедрой — кандидат физико-математических
наук В. С. Лютикас) — за ценные советы и замечания, способство-
способствовавшие улучшению пособия, а также сотрудникам кафедры высшей
математики № 2 Белорусского политехнического института — за
помощь, оказанную при подготовке рукописи к изданию.
Все отзывы и пожелания просьба присылать по адресу: 220048,
Минск, проспект Машерова, 11, издательство «Вышэйшая школа».
Авторы

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
=*¦ — знак логического следования
-«¦ — знак равносильности (эквивалентности)
€ — знак принадлежности
-*— знак соответствия
1. — равенство по определению
у — квантор общности	А
3 — квантор существования	Е
(а, Ь, с, ...}—множество, состоящее из элементов а, Ь, с, ...
0 — пустое множество
A U В — объединение множеств А и В
А П В — пересечение множеств А и В
А\В — разность множеств А и В
A, U\A — дополнение множества А до универсального множества U
А еВ — множество А является подмножеством множества В.
А с В — множество А является собственным подмножеством мно-
множества В
{х|Я(д:)}—множество элементов х, удовлетворяющих условию Р(х)
sup А — точная верхняя грань множества А
inf А — точная нижняя грань множества А
f: X-*-Y — функция f, отображающая множество X в (на) множество Y
/*"': Y-*-X — функция, обратная к функции f, отображающая множество
Y в (на) множество X
D(f)—область определения функции f
E(f)— множество значений функции f
!а8 —композиция функций f и g, т. е. сложная функция, состав-
составленная из функций f н g
[а; Ь] — замкнутый промежуток (отрезок; сегмент; числовой отрезок)
с началом а и концом Ь, а<Ь
]а; Ь[ — открытый промежуток (интервал; открытый числовой от-
отрезок) с началом а н концом Ь, а > b
[а; Ь[ — полуоткрытый промежуток (полуинтервал; числовой отрезок,
открытый справа) с началом а и концом b, a < Ь
]а; Ь] — полуоткрытый промежуток (полуинтервал; числовой отрезок,
открытый слева) с началом а и концом Ь, а<.Ь
[а; + оо[, ]— оо; а] —бесконечные промежутки (числовые лучи)
]а; оо[, ] — оо; а[ — бесконечные промежутки (открытые числовые лучи)
o(P(jc)) — бесконечно малая функция более высокого порядка, чем p(jc)
О.(а) =
= (х| \х — а\ < е) — е-окрестность точки а

jc — a\ < e) — проколотая е-окрестность точкя а
i — мнимая единица, i2 = — 1
Re z — действительная часть комплексного числа г
Im г — мнимая часть комплексного числа г
z — число, сопряженное комплексному числу г
Arg г — аргумент комплексного числа z
arg г — главное значение аргумента комплексного числа г
(ип) — последовательность с n-м членом ип
N — множество натуральных чисел
Z — множество целых чисел
Q — множество рациональных чисел
R — множество действительных чисел
R+ — множество положительных действительных чисел
Ro — множество неотрицательных действительных чисел
R_ — множество отрицательных действительных чисел
С — множество комплексных чисел

1. МНОЖЕСТВА
1.1. ПОНЯТИЕ МНОЖЕСТВА. ЛОГИЧЕСКИЕ СИМВОЛЫ
Множества. Способы задания. Понятие множества считается
первоначальным, неопределяемым. Под множеством понимают со-
совокупность определенных и отличных друг от друга объектов, объе-
объединенных общим характерным признаком в единое целое. В мате-
математике вместо термина «множество» часто говорят «система»,
«класс», «семейство», «совокупность».
Объекты или предметы, из которых состоит множество, назы-
называют элементами множества.
Множества и их элементы обозначают обычно буквами латин-
латинского алфавита: множества — прописными А, В, С,..., их элементы —
строчными а, 6, с, ... Если элемент а принадлежит множеству А,
то пишут а 6 А; если а не принадлежит множеству А, пишут а<?\.
Множество задается или перечислением его элементов, или ука-
указанием характеристики свойств элементов.
Если множество А состоит из элементов а, Ь, с, d, то пишут
, def , ,	„
А ={а, Ь, с, d)
(читается: «Л по определению есть множество с элементами а, Ь,
с, d»).
Если множество А задается указанием характерного свойства
Р(х) его элементов, это записывают так:
А={х\Р(х)}.
Множество, состоящее из одного элемента, называют одноэле-
одноэлементным и обозначают {а}. Множество, не содержащее ни одного
элемента, называют пустым и обозначают символом 0.
Например, множество действительных корней уравнения х2 + 1 = 0 пусто.
Все множества делятся на конечные и бесконечные.
Множества, состоящие из конечного числа элементов, называются
конечными.
Так, например, множество студентов потока, множество жителей города, мно-
множество решений кубического уравнения, множество вершин или диагоналей какого-
либо многоугольника конечны.
Множество, не являющееся конечным, называется бесконечным.
Например, множество натуральных чисел, множество всех прямых, проходящих
через фиксированную точку плоскости, бесконечны.

Если А — конечное множество, то число его элементов обозна-
обозначают через |Л| и называют мощностью множества А.
Элементами множеств могут быть объекты самой различной при-
природы. В математике чаще рассматриваются множества, состоящие
из чисел, точек, кривых и т. д.
Логические символы. При формулировке теорем и их доказа-
доказательств приходится повторять отдельные слова и выражения. Чтобы
сократить записи, используют приводимые ниже логические символы.
Квантор общности обозначается V, читается: «любой», «всякий»,
«каждый». С помощью квантора общности V выражение «для любого
х из множества М» можно записать короче: Yx?M; выражение «во
всяком треугольнике ABC» записывают в виде V ААВС.
Квантор существования обозначается 3, читается: «существует»,
«найдется». С помощью квантора существования Я выражение
«существует х, принадлежащее множеству М, такое, что ...» записы-
записывают так: 3*6 М:. Двоеточие означает «имеет место», «такое, что».
Если для записи выражения используется несколько кванторов, то все, что отно-
относится к одному из них, иногда заключают в скобки. Например, выражение «для
любого е > 0 существует б > 0, такое, что для всех х, отличных от хо и удовлетво-
удовлетворяющих неравенству \х— *ol <в. выполняется неравенство |/(*) — Ь\ < е> записы-
записывают в виде
\x-xa\ <&=>\f(x) — b\ < e.
Символ логического следованиям означает «следует», «выте-
«вытекает». Например, выражение «из утверждения а следует утвержде-
утверждение Ь» записывают так: а=$-Ь.
Символ эквивалентностиообозначает равносильность утверж-
утверждений, расположенных по разные стороны от него, и читается: «тогда
и только тогда, когда ...», «равносильно...», «необходимо и доста-
достаточно». Например, выражение «в любом треугольнике ABC сторона
АС равна стороне ВС тогда и только тогда, когда угол А равен углу
В» записывают в виде МаАВС: AC = BCo/LA— A.B.
Отношения между множествами. Существуют различные отно-
отношения между множествами. Рассмотрим два из них: равенство и
включение.
Определение 1.1. Множества А и В называются равными,
если каждый элемент множества А является элементом множества
В и, наоборот, каждый элемент множества В является элементом
множества А.
Равенство множеств А и В обозначают А = В. Равные множе-
множества состоят из одних и тех же элементов.
Напрямер, если А — множество корней уравнения (* — 1) (х — 2) (х — 3) = 0, т. е.
А = \х I (х — 1) (х — 2) (* — 3) = 0), и В — множество натуральных чисел, меньших 4,
т. е. В = {х 6 N | х < 4), то А = В.
Равенство множеств обладает следующими свойствами:
1)	А=А (рефлексивность);
2)	А = В, В == С=>-Л = С (транзитивность);
3)	А=В=>В =А (симметричность).
Если множество А не равно множеству В, то пишут А ф В.

Определение 1.2. Множество А (А Ф 0) называется под-
подмножеством множества В {В Ф 0), если каждый элемент множе-
множества А является элементом множества В.
Если А — подмножество множества В, то пишут А ^В (чита-
(читается: «множество А является подмножеством множества В», или
«Л содержится в В», или «Л включено в В», или «множество В со-
содержит множество Л».
Понятие подмножества определяет между двумя множествами
отношение включения. Если Л =В и.Л =^ В, то Л называют собствен-
собственным подмножеством множества В и обозначают Л а В. Введенное
отношение с: называют отношением строгого включения.
Известно, что всякое натуральное число п 6 N является целым,
поэтому N с: Z. Но всякое целое число р ? Z является рациональным,
следовательно, Z с: Q. Всякое же рациональное число q 6 Q является
действительным, поэтому Q с: R. Следовательно, N с: Z с: Q cr R.
Не следует думать, что отношения включения или равенства
определены для всех множеств.
Например, множества рациональных и иррациональных чисел не равны между
собой и ни одно из них не является подмножеством другого.
1.2. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Над множествами определяют операции, во многом сходные с
арифметическими. Введем понятие таких операций только для случая
двух множеств Л и В. Будем рассматривать всевозможные под-
подмножества одного и того же множества, которое называют основным
или универсальным. Обозначим универсальное множество буквой U.
Например, в планиметрии в качестве универсального множества можно рас-
сматрявать множество всех точек плоскости R2. Тогда различные фигуры на плоскости
будут подмножествами R2. Прн изучении функций действительной переменной за
универсальное множество принимают множество действительных чисел R и т. д.
Определение 1.3. Объединением множеств А и В называется
множество A \J В, содержащее те и только те элементы, которые
принадлежат хотя бы одному из множеств А или В (или обоим одно-
одновременно) :
A U В ={х | х 6Л или х 6 В или х ? Л и * ? 5}
Например, если Л = {2, 3, 4, 6), В = {1, 2, 3, 4, 5, 6), то А [} В = {1, 2, 3, 4, 5, 6).
Геометрически объединение множеств интерпретируется с по-
помощью диаграмм Эйлера — Венна. На этих диаграммах множества
изображаются точками кругов, треугольников или геометрических
фигур произвольной формы. Геометрическая интерпретация объеди-
объединения множеств Лив дана на рис. 1.1.
Операция объединения множеств удовлетворяет коммутативному
и ассоциативному законам:

Очевидно, что
А[)А=А, Л
0 =А, A\jU=U.
Рис.
Определение 1.4. Пересечением мно-
множеств А и В называется множество А [)В, со-
состоящее из всех тех и только тех элементов,
каждый из которых принадлежит обоим
множествам одновременно:
А[)В={х\хеА и хеВ].
Например, если Л={1, 3, 7, 8), В = {2, 3, 4, 8), то А(]В = {3, 8).
Геометрическая интерпретация пересечения множеств А и В дана
на рис. 1.2. Так же, как и операция объединения, операция пересече-
пересечения подчиняется коммутативному и ассоциативному законам, т. е.
Очевидно, что
А[)А=А,
= 0, A(]U =
Операции объединения и пересечения подчиняются дистрибутив-
дистрибутивным законам:
Определение 1.5. Разностью двух множеств В и А называется
множество В\А, состоящее из всех тех и только тех элементов, кото-
которые принадлежат В, но не принадлежат А:
В\А = {х | х 6 В, но
Геометрическая интерпретация разности двух множеств дана на
рис. 1.3.
Ж
Ж
m
А
щ
ж
'и;
Ш
Ш
Рис. 1.2
Рис. 1.3
Р не. 1.4
Пусть, например, Z — множество целых чисел р. Примем это множество за
универсальное и рассмотрим два его подмножества:
А = {р | 0 < р < 30}, В = {р I 10 < р < 40}.
Тогда
A U В = {р}0 < р < 40), ЛПб = (р1Ю<р< 30), В\А = {р I 30 < р < 40).
10

Определение 1.6. Разность U\A называется дополнением
множества А до универсального множества U и обозначается А:
Геометрическая интерпретация множества А дана на рис. 1.4.
Очевидно, что
A\JA = U, АПА = 0, А=А,  = (/, G=0.
Введем теперь операцию декартова произведения двух произ-
произвольных множеств А и В. Пара элементов (х; у), х?А, у?В, назы-
называется упорядоченной, если указан порядок записи элементов х и у.
При этом считается, что (хп у\) = (х2; уч) тогда и только тогда, когда
х\ = х2, у\ = уч. Элементы х и у упорядоченной пары (х; у) называются
координатами этой пары (х — первая координата, у — вторая).
Упорядоченные пары принято заключать в круглые скобки, в отличие
от неупорядоченных пар, которые, как и множества элементов, за-
записываются в фигурных скобках.
Определение 1.7. Декартовым произведением двух множеств
А и В называется множество, обозначаемое Л X В, состоящее из
всевозможных упорядоченных пар (х; у):
; y)\e
Например, если Л = {1, 2, 3), й = {3, 4), то:
А X В = {A; 3), {1; 4), B; 3), B; 4), C; 3), C; 4)),
ВХА ={C; 1), C; 2), C; 3), D; 1), D; 2), D; 3)).
Сравнивай А X В и В X А, видим, что в об-
общем случае А X В Ф В X А.
Замечание. Если А = В, то А X А назы-
называют декартовым квадратом и обозначают
А2, т. е. А2 = АхА.
Боковую поверхность прямого кругового
цилиндра радиусом R — 1 и высотой Н можно
задать декартовым произведением множеств
АХ В. где А = {(*; у) 6 R V + у2 = 1); В =
2
В
1
3 *
Если y4={*eRIK*<3}; fl = (i/eR|l<
<: 1/ <: 2), то декартовым произведением АХВ яв-
является прямоугольник, изображенный на рис. 1.5.
1.3. ОТОБРАЖЕНИЕ МНОЖЕСТВ. ЭКВИВАЛЕНТНОСТЬ МНОЖЕСТВ
Пусть Л, В — произвольные множества и / — закон (правило),
по которому каждому элементу а 6 А ставится в соответствие един-
единственный элемент Ь 6 В. Тогда говорят, что задано отображение f
множества А в множество В, или оператор f, переводящий множе-
множество А в множество В. Отображение f множества А в В обозначают
/: Л-vB или А-+В (читается: «/ отображает А в В»).
Элемент b 6 В, в который отображен а 6 Л, называют образом
элемента а при отображении f и обозначают Да). Элемент а в этом
случае называют прообразом элемента Да).
Определение отображения коротко записывают так:
11

f: A+BoVatA ЯЬ^В: b = f(a).
Множество образов всех элементов а ? А при отображении f на-
называют образом множества А при этом отображении и обозначают
f(A):
Задание отображения предполагает задание тройки (А, /, В),
где А — отображаемое множество; В — множество значений отобра-
отображения; f — закон, по которому каждому элементу а?А ставится в
соответствие элемент Ъ 6 В.
Определение 1.8. Отображение f: А->В называют взаимно
однозначным или биективным, если каждый элемент b 6 В является
образом только одного элемента а?А (рис. 1.6):
/ — взаимно однозначное отображением
BZ а б A: b = f(a),
а\ Ф a2=^f{ax) ф f(a2).
Если отображение f: A->B есть взаимно однозначное соответ-
соответствие между элементами множеств Л и В, то можно говорить об об-
обратном отображении.
Определение 1.9. Отображение f~* называют обратным к
отображению f, если a->-6, b->-a, т. е. элементу Ь?В ставится в со-
соответствие тот элемент а?А, образом которого при отображении
f является Ь:
Г1: B^AoYbtB ЯаеА: a = f~l(b).
Если f~' — отображение, обратное к f, то f — отображение,
обратное к f~\ поэтому их называют взаимно обратными отобра-
отображениями.
Например, пусть В — множество всех кругов, f — отображение, ставищее в со-
соответствие каждому кругу его площадь. Тогда f: fi-*-R-|_ взаимно однозначно.
а р Ъ R
Рис. 1.6	Рис. 1.7
Определение 1.10. Два множества А и В называются экви-
эквивалентными (равномощными), если существует хотя бы одно взаимно
однозначное отображение одного множества на другое.
Эквивалентность множеств А а В обозначается так: А ~ В (чи-
(читается: «множество А эквивалентно множеству В»).
12

Например, пусть N — множество натуральных чисел, А — множество четных
натуральных чисел. Установим между ними взаимно однозначное соответствие с
помощью соотношения л-<->-2ге, т. е.
2, ..:, п,
I t
2,
I' i"" i ""
2, 4, .... 2», ...
Таким образом, множество всех натуральных чисел эквивалентно собствен-
собственному подмножеству четных натуральных чисел.
Пример 1.1. Показать, что множества точек любых двух отрезков [а; Ь\ н [с; d]
эквивалентны между собой.
Решение. Взаимно однозначное соответствие между точками этих отрезков
осуществим следующим образом. Расположим данные отрезки на параллельных
прямых и через концы отрезков проведем примые до нх взаимного пересечения в
точке О (рис. 1.7). Из точки О проведем всевозможные лучи, пересекающие оба
отрезка. Тогда любой точке Р€[я; Ь] соответствует единственная точка Q6[c; d],
н наоборот, т. е. между точками отрезков [а; Ь\ и [с; d] существует взаимно однознач-
однозначное соответствие.
Отношение эквивалентности множеств обладает следующими
свойствами:
1)	А ~ А V А (рефлексивность);
2)	если А ~ В, то В ~ А V А, В (симметричность);
3)	если А ~ В, В ~ С, то А ~ CV А, В, С (транзитивность).
Всякое множество, эквивалентное множеству натуральных чисел,
называется счетным.
Примером счетного множества может быть множество четных
натуральных чисел, множество рациональных чисел. Если множе-
множество счетно, то его элементы можно занумеровать.
1.4. ЧИСЛОВЫЕ МНОЖЕСТВА
Множество натуральных чисел. Множество натуральных чисел
обозначают буквой N:
N = {1,2, 3, ...},
а его элементы — п.
Множество N обладает следующими свойствами:
. 1) сумма и произведение двух натуральных чисел являются на-
натуральными числами, т. е. Vrti, л2 6 N:ni + л2 6 N, ni-n26N. Обе
операции подчиняются коммутативному и ассоциативному законам,
а умножение — еще и дистрибутивному закону относительно сложе-
сложения;
2)	операции вычитания и деления в N невыполнимы, так как
V ль п2 6 N П\/п2 не всегда принадлежит N, а П\—«2 6N, если
Л2<«Ь
3)	16N;
4)	n6N=^n+l6N;
Ъ) если AfsN, l?Af и п?М =>(п + 1NМ, то М = N (аксиома
индукции);
6) NcR, счетно и бесконечно.
Множество целых чисел. Объединение натуральных чисел, чисел,
им противоположных и нуля составляет множество целых чисел Z:
Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}.
13

Элементы множества Z, т. е. целые числа, будем обозначать р.
Множество Z обладает следующими свойствами:
1)	NcZcR;
2)	Z счетно и бесконечно;
3)	Z упорядочено, т. е. для любых двух целых чисел р\, рч^Ъ
имеет место одно и только одно из трех соотношений: р\ <Zp2, р\ =
— pi, Р\ > рч\
4)	в Z определены операции сложения, умножения и вычитания,
т. е. Vpi, р2 6 Z:pi +P26Z, р\ -рч^Ъ, рх —p2?Z.
В множестве Z невыполнима операция деления чисел (частное
двух целых чисел не всегда целое). Расширением множества Z яв-
является множество рациональных чисел Q.
Множество рациональных чисел Q. Множество чисел вида р/п,
где р 6 Z; л 6 N, является множеством рациональных чисел Q, его
элементы обозначают q, т. е.
Множество рациональных чисел Q обладает следующими свой-
свойствами:
1)	NcZcQ;
2)	Q с R, счетно и бесконечно;
3)	Q упорядочено;
4)	любое рациональное число q = р/п может быть записано в
виде конечной или бесконечной периодической десятичной дроби;
5)	множество Q плотно, т. е. для любых q\, 92 6Q найдется по
крайней мере одно рациональное число q, такое, что q\ < q < <7г-
Действительно, если взять, например q = (q\ -f- <72)/2, то ясно, что
q\ <<7<<72;
6)	У7ь <72 6 Q: q\ < qi 3 п 6 N : nqx > q2 (аксиома Архимеда*);
7)	в множестве Q выполнимы четыре арифметические операции
(кроме деления на нуль), причем сложение и умножение подчиня-
подчиняются коммутативному и ассоциативному законам, а умножение —
еще и дистрибутивному закону относительно сложения.
Любое рациональное число можно изобразить точкой на числовой
прямой. Однако не каждой точке этой прямой будет соответствовать
рациональное число.
Например, точке, отстоящей от начала координат на расстоянии, равном длине
диагонали квадрата с единичной стороной, не соответствует никакое рациональное
число (не существует такого рационального числа q = р/п, квадрат которого был бы
равен 2).
Следовательно, между множеством рациональных чисел и множе-
множеством точек числовой прямой не существует взаимно однозначного
соответствия.
Числа, которые нельзя представить в виде отношения двух целых
чисел р/п, р 6 Z, «6N, называют иррациональными.
Например, числа -ф, -\/з^ я, lg 2, lg 3, sin 20° являются иррациональными.
* Архимед (ок. 287—212 до н. э.)—древнегреческий механик и математик.
14

Иррациональные числа можно представить в виде бесконечной
непериодической десятичной дроби.
Множество действительных чисел. Объединение рациональных
и иррациональных чисел составляет множество действительных чи-
чисел R. Перечислим основные свойства множества действительных
чисел R, большинство из которых совпадает со свойствами множе-
множества Q: NcZcQcR;R бесконечно, упорядочено, для него имеет
место аксиома Архимеда. Кроме того, в отличие от множества Q,
множество R несчетно и между действительными числами и точками
числовой оси существует взаимно однозначное соответствие, т. е.
каждому действительному числу х соответствует единственная точка
числовой оси и, наоборот, каждой точке числовой оси соответствует
единственное действительное число х6 R.
В множестве R определены операции сложения, вычитания, умно-
умножения, деления На любое действительное число, отличное от нуля,
возведения в степень и др. Все эти операции подчиняются приво-
приводимым ниже аксиомам.
Аксиомы сложения
Al. Yx, y(:R'-x-\-y — y-\-x (коммутативный закон).
А2. Vjc, у, z 6 R: (x -f- у) -f- z = x -f- (у + z) (ассоциативный закон).
A3. H06R:V*€R, х-\-0 = х (существование в R нуля).
А4. V*6R Н( — *NR:* + (—лс) = О (существование в R противо-
противоположного элемента).
Аксиомы умножения
А5. Vjc, t/6R\{0}: x-y = y-x (коммутативный закон).
А6. Ух, у, z ? R\{0}: х-(у • z) = (x-у)-z (ассоциативный закон).
А7. 3 1 6 R: 1 • лс = jc V лс € R (существование нейтрального эле-
элемента).
А8. V*€ R\{0} Hjc~': x-x = 1 (существование обратного эле-
элемента).
А9. VJc, у, z 6 R:(x -f- у) • z = x • z -f-у • z (дистрибутивный закон
относительно сложения).
Аксиомы порядка
АЮ. V х, у 6 R-хФ у=$*х<. у или у <. х.
All. V*, y?R:x^Ly и у^ х=^х = у.
А12. \х, у, z?R:x^y и
Аксиома полноты (непрерывности)
А13. Если непустые множества X, KcR таковы, чтоЧх^Х и
У выполняется неравенство х^у, то Hc?R, такое, что ^
Первые три вида аксиом выполняются на множестве рациональ-
рациональных чисел. Аксиома непрерывности справедлива только в R.
15

При изучении функций одной действительной переменной рас-
рассматривают подмножества множества R, такие, как интервал, полу-
полуинтервал, отрезок (сегмент), полуотрезок; их называют промежут-
промежутками.
Интервал с концами а и Ь:
Отрезок с концами а
[а;
Полуинтервалы:
г , г def , _ ,
la; ol =at Rla =
и b:
def
ь]={хен
^x<b},
1 h\ def /
€RU<
Ь].
Интервалы и полуинтервалы могут быть бесконечными:
[a- +oo[ = {*6Rl*>a},]a; + «>[ = {*€ RU> 4
]_оо; 6[ = {x€RU<H ]-oo; 6]={x€R|x<4
]_оо; +oo[ = {x€RI -оо<л:<оо}.
Промежуток [а; Ь] называют замкнутым, промежутки ]а; Ь[,
]a; -f- оо [, ] — оо; Ь[, ] — оо; -\- оо [ — открытыми, остальные — полу-
полуоткрытыми.
Абсолютная величина (модуль) действительного числа. Дейст-
Действительные числа могут быть положительными и отрицательными.
Иногда приходится рассматривать абсолютную величину действи-
действительного числа, игнорируя его знак.
Определение 1.11. Абсолютной величиной (модулем) дейст-
действительного числа х называется число х, если х ^ 0, и число —х, если
х<0.
Модуль числа х обозначают \х\ и записывают
"Н-
х Vx<0.
Если х изображается точкой М числовой оси, то |дс| =ОМ.
Основные свойства абсолютной величины числа следуют из опре-
определения. Приведем их.
1.	|*| ^0.
2.	|х| = |-х|.
3.	— \х\ <х< UI.
4.	Ve>0: U|<eo — е<л:<е.
5.	\х + у\^\х\ + \у\ Yx, yeR.
>	Действительно, в силу свойства 3, —|jc|^jc^U|, —\у\ ^
<^У<^\у\- Сложив почленно эти неравенства, находим — (\х\ +
+ 1у1)^^ + У^A^1 + \у\)- Согласно свойству 4, полученное двой-
двойное неравенство равносильно неравенству U-f-yl ^ \х\ -(- \у\- О
6.	\x-y\^\x\-\y\Vx, yeR.
>	Справедливо равенство х = у-\-(х — у) V х, y6R- Перейдем
к модулю в обеих частях полученного равенства. Тогда
16

откуда следует, что \х— у\ ^ \х\ — \у\. <
7. Vx,ytR:\xy\ = \x\ \y\ и \j-\ = -М- при */#0.
1.5. ОГРАНИЧЕННЫЕ МНОЖЕСТВА.
ВЕРХНИЕ И НИЖНИЕ ГРАНИ ЧИСЛОВЫХ МНОЖЕСТВ
Рассмотрим произвольное множество A с R. Введем понятие
ограниченности множества сверху (снизу).
Определение 1.12. Множество действительных чисел А назы-
называется ограниченным сверху (снизу), если существует такое дейст-
действительное число М (число пг), что каждый элемент х?А удовлетво-
удовлетворяет неравенству х^М(х^ пг). При этом число М (число пг) на-
называется верхней гранью (нижней гранью) множества А.
Любое ограниченное сверху множество А 6 R имеет бесконечно
много верхних граней. В самом деле, если действительное число М
является одной из верхних граней множества А, то любое действи-
действительное число М' > М также является верхней гранью множества
А (так как *<М=^х< М' VAf' > М).
Например, множество целых неотрицательных чисел Zo ограничено снизу. В ка-
качестве нижней грани этого множества можно взять любое действительное число /п,
удовлетворяющее неравенству m ^ 0.
Определение 1.13. Наименьшая из всех верхних граней огра-
ограниченного сверху множества А с R называется точной верхней
гранью. Другими словами, действительное число М является точной
верхней гранью множества A cz R, если
V* б А: х < М и V М' < М 3 х0 > М', х0 6 А.
Точную верхнюю грань обозначают М = supA, или M = sudjc
(от лат. supremum — наивысшее).
Определение 1.14. Наибольшая из всех нижних граней огра-
ограниченного снизу множества A cz R называется точной нижней гранью.
Другими словами, действительное число пг является точной нижней
гранью множества AcR, если
:x^m и Vпг' > m 3 х0 < пг', хо?А.
Точную нижнюю грань обозначают пг = inf А, или пг = inf x (от
лат. infimum — наинизшее).
Определение 1.15. Множество, ограниченное сверху и снизу,
называется ограниченным.
Примерами ограниченных множеств являются: fa; b], ]a; b[, множество значений
cos х н т. д.
Среди множеств, принадлежащих R, существуют такие, которые
не являются ограниченными. Их называют неограниченными множе-
множествами. J'^^*~i*iiT^rr——""——-.¦•("

Например, ]а; оо [, N являются множествами, которые ограничены только снизу.
Множества Z, О. неограничены как сверху, так и снизу.
Для множеств, неограниченных сверху, принимают дополнитель-
дополнительно sup Л = со, а для неограниченных снизу полагают inf А = — оо.
Замечание. Символы — оо и оо часто используют в приложениях. Их при-
присоединяют к R и считают, что —оо < *<; оо
Множество R, пополненное — со и со, обозначают R и называют
расширенным множеством действительных чисел.
Приведем несколько примеров.
1.	Пусть А = [2; 5], тогда m = inf А = 2, М = sup A = 5.
2.	Пусть Zo—множество всех неотрицательных целых чисел, тогда т =
— inf {plp€Zo) = 0, M = sup{p|pgZ0)= oo.
3.	Пусть R — множество действительных чисел, тогда m = inf R = inf \x | x 6 R} =
= — oo, M = sup R = oo.
4.	Пусть A = (x | x2 < 5, x 6 R), тогда m = inf A = inf{* | —-y5 <х<^/ъ, х 6 R} =
= — -\JE, M = sup {л: | — -\JE< x < Vs". x € R} = V^-
Точные грани множества А могут как принадлежать, так и не
принадлежать ему. Например, пусть Л=]а; Ь], тогда а = inf A ? А,
sup A = b ? А. В случае, если точная верхняя (нижняя) грань при-
принадлежит множеству А, она совпадает с наибольшим (наименьшим)
элементом этого множества, т. е. supA = maxA, inf A = miri/4.
Например, пусть A =[l/n\n?ti]. Тогда sup /1 = 1, inf Л = 0. Точная верхняя
грань достигается и равна наибольшему элементу множества A (sup A = max А = 1),
нижняя грань inf А ?А.
1.6. МНОЖЕСТВО КОМПЛЕКСНЫХ ЧИСЕЛ
Определение. Основные понятия. Существуют задачи, для реше-
решения которых действительных чисел недостаточно. Например, квад-
квадратное уравнение х2 + 1 =0 не имеет решения в множестве действи-
действительных чисел, так как не существует действительного числа, квадрат
которого равнялся бы — 1: х'г + 1 = 0^*2 = — 1.
Обозначим i = ~у — 1. Тогда формальное решение уравнения х2 -f-
-f- a2 = 0 можно записать в следующем виде: *|,2=±ш. Таким
образом, возникла необходимость расширить множество действи-
действительных чисел R до нового числового множества, в котором все
алгебраические уравнения
аохп + аххп-1 + ... + а„ = 0, а0, аи ..., an6R
имели бы решения. Таким множеством является множество комп-
комплексных чисел.
Определение 1.16. Комплексным числом z называется число
вида х + iy, где х, y?R, а i удовлетворяет условию /2 = — 1.
Число х называется действительной частью комплексного числа
z, а число у — мнимой частью комплексного числа z. Для этих чисел
приняты обозначения:
х — Re(x-f iy) = Rez, y = \m(x-\-iy) = lmz
18

(от фр. reel — действительный, imaginaire—мнимый).
Множество комплексных чисел обозначается С. Так как любое
действительное число х можно рассматривать как комплексное число,
т. е. х = х-\-Ы, то множество действительных чисел содержится в
множестве комплексных чисел: Re С или с учетом рассмотренных
ранее числовых множеств NcZcQcRcC.
Два комплексных числа Z\ —xi -\-iy\ и Z2 = A'2-f-н/2 называются
равными тогда и только тогда, когда Х\=х%, ух=у2, т. е.
хх + iyi =
Комплексное число z = 0 -f- Oi называется нулем и обозначается 0.
Оно совпадает с числом 0 множества действительных чисел:
z = x-\-iy — Оох = 0, у = Оох2 + У2 = 0.
Понятие неравенства для комплексных чисел существует лишь в
смысле отрицания равенства, т. е. Z\ Ф z2 означает, что число Z\ не
равно числу z2. Понятия «меньше» и «больше» для комплексных
чисел не определены.
Определение 1.17. Комплексное число z = x — iy называется
сопряженным комплексному числу z = x-\- iy. Вообще, два комплекс-
комплексных числа, отличающихся лишь знаком при мнимой части, назы-
называются комплексно-сопряженными.
Геометрическое изображение комплексных чисел. Модуль и аргу-
аргумент комплексного числа. Каждое комплексное число х -f- iy можно
изображать геометрически точкой с координатами х, у на плоскости
R2 (в декартовой прямоугольной системе координат), либо как вектор
z, проекции которого на оси Ох и Оу соответственно равны хну.
При этом координатную плоскость Оху называют комплексной
плоскостью, ось абсцисс — действительной осью, ось ординат —
мнимой осью комплексной плоскости.
Итак, каждому комплексному числу z = *-f-n/ соответствует
определенная точка М(х; у) комплексной плоскости и, наоборот, каж-
каждой точке М(х; у) этой плоскости соответствует определенное число
z = х-\-iy, т. е. между точками плоскости R и элементами множе-
множества С (комплексными числами) существует взаимно однозначное
соответствие. Таким образом, комплексная плоскость является ге-
геометрической моделью множества С.
Из геометрической интерпретации множеств R и С следует, что
С есть расширение R, так как множеству действительных чисел R
соответствует множество точек прямой Ох (действительная ось),
а множеству комплексных чисел С — вся плоскость R2.
Определение 1.18. Расстояние от точки z(x; у) до начала ко-
координат называется модулем комплексного числа г (обозначается
г\ или г)
\г\ = г =
Определение 1.19. Аргументом комплексного числа назы-
называется угол ф, который образует радиус-вектор точки z(x; у) с поло-
19

жительным направлением оси Ох.
Для г Ф 0 аргумент г определяется равенствами (рис. 1.8):
и	и
Модуль комплексного числа z определяется однозначно, а аргу-
аргумент — с точностью до слагаемого 2&л, k 6 Z.
Значение аргумента, удовлетворяющее условию —л<ф=?^л,
называется главным.. Главное значение аргумента комплексного
числа обозначается arg z, а множество всех значений аргумента —
Argz:
Если комплексные числа равны, то их модули равны, а аргументы
отличаются на 2kn, k ? Z.
Рис. 1.8
Пример 1.2. Определить, какие множества точек плоскости заданы следующими
условиями (а, р, у, б 6 R, г,, г2 ? R (г, > 0, г2 > 0); а ? С): 1) Re г = а; 2) а < Re z < р;
3) Imz<7; 4) (a<Rez<p)n(Y<Imz<6); 5) r, < |z| < r2; 6) a<argz<p;
7) |z — а| < r; 8) ri < |z — а| < r2.
Решение. 1. Условие Re z = а-»-лг = а. задает прямую, параллельную мнимой
оси Оу.
2.	Условие а ^ Re z< р-»-а ^лг<С р определяет бесконечную вертикальную
полосу между прямыми лг = а и лг = р, включая прямую х = а (рнс. 1.9).
3.	Условие Im z ^ уоу ^ у задает полуплоскость, расположенную ниже пря-
прямой у = у (рнс. 1.10).
4.	Условия (а < Re z < р) П G < Im z < 6)-»-(а < к < Р) П G < У < 6) задают
прямоугольник, ограниченный прямыми к = а, к = р, у = у, у = Ь, причем стороны
y = Y нлг = р не включаютси в этот прямоугольник (рис. 1.11).
5.	Условие Г1<|г|^Г2 определяет кольцо между двумя концентрическими
окружностями с центром в начале координат н радиусами г\ и гг, причем внутренняя
окружность исключается из рассматриваемого множества точек (рис. 1.12).
6.	Условие а < arg z <C p задает бесконечный сектор, ограниченный лучами
argz = a и argz = p, причем сами лучи исключаются (рис. 1.13).
7.	Условие \z — а\ < г, где rgR (r>0); а 6 С, определяет точки z, удаленные
от точки а иа расстояние, меньшее г. Такие точки заполняют круг радиусом г с
центром в точке а (рис. 1.14).
8.	Условие г, < \г — а\ < г2 задает кольцо между концентрическими окружно-
окружностями радиусами г, и гг с центрами в точке а, причем внутренняя окружность исклю-
исключается из рассматриваемого множества точек (рис. 1.15).
Алгебраическая форма комплексного числа. Действия над комп-
комплексными числами в алгебраической форме. Запись комплексного
20

/////
Рис. 1.11
0
Рис. 1.14
о	x
Рис. 1.13
Рис. 1.15
числа в виде х + iy называется алгебраической формой комплексного
числа.
Операции над комплексными числами определяются таким обра-
образом, чтобы для их частного случая — действительных чисел — эти
операции совпадали с известными. При выполнении алгебраиче-
алгебраических действий над комплексными числами считают всегда (У—аJ =
= — а. Это предположение служит основой при операциях над
комплексными числами. Формально действия над комплексными
числами производятся по тем же правилам, что и действия над
многочленами (в частности, двучленами) с действительными коэф-
коэффициентами, если заменить в результате i2 =—1, i3 =—i, i4=l
и т. д.
Суммой комплексных чисел называется комплексное число, дейст-
действительная и мнимая части которого равны суммам соответствую-
соответствующих частей слагаемых:
= (Х{ + Х2) + %1 + У2).	A.1)
Разностью комплексных чисел называется комплексное число,
действительная и мнимая части которого равны разностям соответ-
соответственно действительных и мнимых частей этих чисел:
2i — z2 = (х, + iy\) — (х2 + и/2) = (*i — х2) + i{y\ — У2). A.2)
Заметим, что сумма или разность двух комплексных чисел может
оказаться числом действительным (например, сумма комплексно-
сопряженных чисел 2 + 2 = (x -j- iy) + (х — iy) = 2x 6 R.
Из формул A.1) и A.2) следует, что сложение (вычитание)
комплексных чисел производится так же, как сложение и вычитание
векторов: при сложении (вычитании) векторов их соответствующие
21

координаты складываются (вычитаются). При этом модуль разности
двух комплексных чисел
Izi — z2\ = l(*i+u/i) — (x2+,itfz)\ ==;;
= \(Xi— x2) + i(yi— уг)\ = л1{х[—х2J + (у1^у2J
есть расстояние между точками z\ и z2. Для любых zu z2?C имеет
место неравенство треугольника
Умножение комплексных чисел z\ = X\ -f- iy\ и z2 = *2 -f- *У2 опре-
определим формулой
zxz2 = (jci -f- 'УО (*2 + 'Уг) = *i*2 -f- x\y2i + x2y\i + yiy2i2 =
{	) ( 4- )
Заметим, что произведение двух комплексно-сопряженных, не
равных нулю, чисел равно положительному действительному числу.
В самом деле,
zz = (х 4- iy) (х — iy) = х2 4- *{/» — *J/t — У2'2 = -«2 4- У2-
Деление комплексного числа Z\ на г2ф0 вводится как действие,
обратное умножению, т. е. под частным z\/z2y гяФО понимается
комплексное число г: Z2Z = zj. Частное получается путем умножения
числителя и знаменателя дроби Zi/z2 на число г2, комплексно-со-
комплексно-сопряженное знаменателю:
2л _
_
z2 Х2 + 1У2 (хг + iyz) (x? — iy2)
_ x,x2 + У1У2 1 ¦ x2y, —
Возведение комплексного числа z в степень п(п? N) рассматри-
рассматривается как умножение г на себя п раз. Определим натуральные
степени мнимой единицы i для п:
{
4,
-i Vn = 4^4-3,
Теперь легко находить результаты возведения комплексного числа
в степень с натуральным показателем.
Например:
(* + iyf = х2 + 2xyt + /У = (х2 - у2) + 2xyi,
{х + iyf = x3 + Ъх\1у) + 3x(iyf + (iyf = (x3 - 3V
Умножение, деление и возведение в степень комплексных чисел
значительно упрощается, если представить их в тригонометрической
форме.
Тригонометрическая форма комплексного числа. Действия над
комплексными числами в тригонометрической форме. Любому комп-
22

лексному числу г 6 С, заданному в алгебраической форме, соответ-
соответствует точка комплексной плоскости, положение которой однозначно
определяется ее декартовыми координатами х, у. Эту же точку
можно однозначно определить заданием аргумента и модуля комп-
комплексного числа z.
Действительно, пусть на комплексной плоскости выбраны тонка О
и луч Ои с началом в точке О. Совместим точку О с началом декарто-
декартовой системы координат, а луч — с действительной осью. Тогда каждой
точке z(x; у) можно поставить в соответствие два числа: г — по-
полярный радиус, равный длине отрезка ОМ, и ф — полярный угол,
равный углу между полярной осью и лучом ОМ; при этом О ^ г <
< оо, —Жф^я. Числа г, ф называют полярными координатами
точки М (рис. 1.16).
Так как	.	.
x = rcos(p, y = rsm<p,	A.3)
то
z = х -f- iy = г cos ф -f- ir sin ф = r(cos ф -f- i sin ф).
Итак,
z = r(cos ф + i sin ф).
A.4)
Выражение A.4) называется тригонометрической формой комп-
комплексного числа. Для того чтобы перейти от алгебраической формы
комплексного числа к тригонометрической с помощью формул A.3),
связывающих декартовы и полярные координаты, находят модуль
комплексного числа г = \z\ =Л)Хг-\-у2, затем по формулам
cos ф = —
sin
определяют аргумент ф: tg ф = у/х.
л ул
¦X X	ш W
Рис. 1.16	Рис. 1.17
Для главного значения аргумента справедливы соотношения:
(arctg(y/x) Vx>0,
ф = arg z =< arctg(y/x) -fnVx<0, Vy^O,
^arctg(y/x) — яУ*<0, Vy<0.
Действительно, главное значение arctg(y/x) заключено между
— я/2 и л/2, поэтому:
23

1)	если точка z лежит в I или IV четверти, т. е. х>0 (рис. 1.17),
то argz=arctg(y/x);
2)	если точка z лежит во II четверти, т. е. х<0, у^О (рис.
1.18, а), то — я/2 < arctg(y/*X 0 и argz = arctg(y/x) + я;
3)	если точка z расположена в III четверти, т. е. х<0, у<0
(рис. 1.18, б), то 0< arctg(y/x)<я/2, следовательно, argz =
= — я + arctg(y/x).
II У1
in
II
т
Рис. 1.18
IV
Пример 1.3. Представить в тригонометрической форме комплексное число z =
= — 1 — ('-\/3 и изобразить его геометрически.
Решение. Для геометрического изображения комплексного числа z = — 1 —
— -\j3i построим точку М(—1; — ^Jd) и радиус-вектор ОМ. Точка М и вектор ОМ
являются геометрическим изображением комплексного числа г. Вычислим
Найдем аргумент. Так как х < 0, у < 0, то комплексное число z лежит в III чет-
четверти (это видно из рис. 1.19). Следовательно,
q> = arctg(j//x) — л = arctg(—-ф/— 1) — л =
— я = —2л/3
и тогда
z = -1 - -fit =
-1- л^ + / sin ( - у
Тригонометрической формой комплексно-
комплексного числа удобно пользоваться при выполне-
выполнении операций умножения, деления, возведе-
возведения в степень и извлечения корня.
Пусть
Z\ = ri(cos<jpi -|-1 sin <pi),
22 = /(cos фг + i sin фг).
Тогда
rir2(cos ф1 -f-isin(pi) (созфг-Нэшфг) =
= rir2(cos ф1 cos фг — sin ф| sin фг) +
-f- i (sin ф| cos ф2 -f- cos Ф1 s'n Ф2)=
= rir2(cos (ф1 + фг) + i sin (ф1 + фг)),

т. е. ziz2 = Г1Г2(со8(ф| + ф2) +1sin^i +
Таким образом, при умножении комплексных чисел в тригоно-
тригонометрической форме их модули перемножаются, а аргументы скла-
складываются.
Аналогично при zi Ф О
Zi 	 ri(cos ф[ +( sin ф[) 	 г, (cos <pi + i sin <f{) (cos <рг — I sin <рг)
2г	r2(cos ф2 +1 sin ф2)	г2(со5ф2 + 1 sin фг) (cos фг — isin ф2)
= ^ cos((p,_ ) + (sin(q)|-(p2) = ^(СО8( _ г) . sjn( _ }
r2	cos фг + sin-* ф2	rj
Итак,
/	(со8(ф1 — ф2) + i sh%i — ф2)).
Следовательно, при делении комплексных чисел их модули де-
делятся, а аргументы вычитаются.
Число г", где z = r(cos ф -f- i sin ф); z6C; n 6 N, можно рассмат-
рассматривать как умножение z на себя п раз:
z" = (г (cos ф + i sin ф))" = г" (cos пер + i sin «ф)=>-
=*-z" = r"(cos «ф +1 sin «ф), \zn\=rn, arg zn = n arg г. A.5)
Из формулы A.5) следует, что при г = 1
(cos ф + i sin ф)" = cos «ф + i sin «ф.	A.6)
Формулу A.6) называют формулой Муавра*.
Корень -уго степени п 6 N из комплексного числа z0 определяется
как комплексное число г, которое, будучи возведено в степень п,
дает число го, т. е. г" = го. Запишем го, г в тригонометрической форме:
20 = го (cos фо + i sin фо), z = r (cos ф -f- i sin ф). Тогда
zn = r"(cos «ф + i sin Пф) = ro(cos ф0 + i sin фо)=*-
=>r" = ro, иф = фо + 2А;я или ф = *° + 2fe" , fe 6 Z, r=V^
Итак,
^ ^( (p + 2fe" +fsin » + 2to).	A.7)
Из формулы A.7) следует, что среди значений ~уг<> различными
являются только п, все они получаются при /г = 0, п—1.
Исходя из формулы A.7), можно показать, что геометрически
точки, соответствующие различным значениям корня n-й степени из
комплексного числа го = r0(cos <ро + < sin ф0), располагаются в верши-
вершинах правильного га-угольника с центром в точке О, причем одна из
вершин (соответствующая /г = 0) имеет полярные координаты
, Фо/п).
Абрахам де Муавр A667—1754) —английский математик.
25

Пример 1.4. Пусть z\ = 1 — \3 », z% — 1 +». Требуется записать Z\ и z2 в триго-
тригонометрической форме и найти Z|Z2, Z1/Z2, z?, V
Решение. Чтобы записать комплексное число z в тригонометрической форме,
надо найти его модуль и аргумент:
|z,| = "V1 +3 = 2, argz, =arctg( — -\/§/l) = arctg( — л/5)= —я/3.
Тогда Zi = 2(cos(—л/3) + i sin(—л/3)).
Представим г.г в тригонометрической форме:
+ 1 = -тД arg z2 = arctg 1 = л/4, z2 = -fi(cos(n/4) + i sin(n/4)).
( —n/3 + л/4) +» sin(-л/3 + я/4)) =
= 2-\/2(cos(n/12) — j sin(n/12)),
-^- = —y=(cos (— я/3 — л/4) + i sin (— л/3 — л/4)) =
= V2~(cos (— 7л/12) — ( sin Gл/12)),
-J-л)+«sin (--|л)) =-2-
= 0, ,, 2.
В частности, z0 ==-V^(cos(n/12) +j sin(n/12)) при fe = 0, z, ="V^(cosCn/4) +
+ CsinCn/4)) при k={, z2 = -V2(cosA7n/12) + isinA7n/12)) при k = 2, или z0 =
= 1,084 + 0,29W, z, = -0,794 + 0,794», z2 = -0,291 -r 1,084»
Дадим геометрическую интерпретацию полученных значений ~угг = ~у1 + '¦ Мо-
Модули всех Zj, /= 0, 1, 2, равны у2 « 1,122. Следовательно, точки Zo, Zi, z2 лежат на
окружности радиусом г= 1,122 с центром в начале координат. Построив эти точки
в декартовой системе координат Оху, заметим, что они являются вершинами пра-
правильного треугольника, вписанного в окружность (рис. 1.20).
Показательная форма комплексного числа. Наиболее удобной
формой комплексного числа является показательная. Чтобы полу-
получить ее, воспользуемся формулой Эйлера*, устанавливающей связь
между показательной и тригонометрическими функциями:
е>* = cos ф -f i sin ф, ф 6 R	A-8)
(е = 2,7182818...— иррациональное число).
Пусть комплексное число г записано в тригонометрической форме:
z — r(cos ф -f- i sin ф). Используя формулу Эйлера A.8), получаем
z =
A.9)
Это и есть показательная форма комплексного числа, где г =
= \z\; ф =
• Леонард Эйлер A707—1783) — выдающийся математик, механик, физик и
астроном, член Петербургской академии наук, большую часть жизни провел в Рос-
России, по происхождению швейцарец.
26

Функция ещ обладает свойствами показательной функции с дейст-
действительным показателем, поэтому формулы умножения, деления,
возведения в натуральную степень для комплексных чисел в пока-
показательной форме имеют простой вид.
Если zi = riei<f, z2 = ri&*>\ то
г1г2 = г,г2е'('р'+Ч	A.10)
Если z2 Ф 0, то
-Ч	A.11)
z2	r2
Если п g N, z = гещ, то
Z" = (
n
Zk = -^ =
A.12)
A.13)
Пример 1.5. Найти zzx, z/z,, -\jz и z12, если z= 1 — <', Zi = 1 +-\/3i.
Решение. Запишем z и Zi в показательной форме:
|z| =V^ argz = arctg(—1)= —п
Ui | = 2, arg z, = arctgV3 = n
Тогда по формулам A.10) — A13) получим
= йе"/3.
, z/z, = ^L-'7*, ft = л/*= ^/т*"" и), А _ оТГ
Прн ft = 0 zo = 1^/2е-'*/20, при ft = Т^имеем соответственно z, = '^/2 е'7я/20, z2 =
= '^/2 е'3"/4, z3 = '-д/2 e1'23»/2», z4 = ^/2 е'31л/2°. Точки z0, 2,, z2, z3, z, являются вершина-
вершинами праввльного пятиугольника, вписанного в окружность радиусом V^ да 1,072 с цент-
центром в начале координат (рнс. 1.21). Полярный угол точки Zo <ро = —л/20, а поляр-
полярные углы остальных точек получаются последовательным прибавлением угла 2л/5
к <ро: <р* = фо + 2nft/5, ft = 1,4.
Найдем z12 = (-^I2е~3<°. Так как на основании формулы Эйлера A.8) eiip =
= cos ч> +1 sin <р, то е~3ш = cos Зл — ( sin Зл = — 1, и, следовательно, z12 =
= -(V2I2=-64.
Решение уравнений в С. Рассмотрим уравнение
ах2 + Ьх + с = 0, а, Ь, c6R,
27

и воспользуемся правилом решения квадратных уравнений в R.
1.	Запишем коэффициенты уравнения а, Ь, с и найдем его дискри-
дискриминант D = Ь2 — 4ас.
2.	Сравним дискриминант D с нулем. Если D^O, уравнение
имеет действительные корни; если D < О, уравнение имеет комплекс-
комплексные корни.
3.	Определим действительные корни уравнения по формулам
Xl-2	2а
а комплексные корни — по формулам
Xl2 =	_	.
Таким образом, любое квадратное уравнение разрешимо в С.
Пример 1.6. Найти корни уравнения х2 + 2дс + 5 = 0.
Решение. Коэффициенты уравнения а = 1, й = 2, с = 5; D = Ь2 — 4ас =
4 — 20 = —16. Дискриминант отрицательный, уравнение имеет комплексные корни.
Находим корни уравнения:
-Ь±1л[\Р\~ _ -
=	Г
х" =ъГ	2	l±2t-
Если коэффициенты квадратного уравнения az2 + bz + с = 0 —
комплексные числа, то его корни определяются по формулам:
Пример 1.7. Решить квадратное уравнение za + E — 2i)z + 5(l—1) = 0.
Решение. Имеем
_ -E-2t)±VE-2fJ-20(l-0 _ -5 + 2t±l
Z'2	2	2	'
Корни уравнения: z{ = —2 + 1, zz= —3 + «.
Теперь рассмотрим двучленное уравнение
zn — а = 0,
где а Ф 0 — комплексное число; п 6 N.
Пусть argа = ф, тогда а=|а|е*ф и г" = а-Ф*-г"= |а|е*ф.
Корни двучленного уравнения определяются по формулам
Zk =
2л^
Пример 1.8. Решить двучленные уравнения: 1) z3	V . =0; 2) г8 — 8 = 0.
2-1/2
Решение. 1. Находим модуль и аргумент числа
1+1 - A+0A-0
_
28

2т/2
Число . jf . запишем в показательной форме: *' ^* = 2е~й1/4. Тогда z3 =
2лB	_.	з/-
= —.—^-^-»-z=2e ш'4=>-г* = "v2e'( »/4+2*")/3 ft = o, 1, 2, т. е. уравнение имеет три
1+» 0Г-	а Г"	' аг-
корня: zo = -\/2e-"'/l2 при fe = 0, z, =-\/2е7"< при ft= I, z2 = -\/2e5"'/4 при ft = 2.
2. Аргумент действительного числа равен нулю, поэтому arg8 = 0, |8|=8.
Уравнение запишем в виде
z8 = 8em=>zk = М%еш/\ ft
Таким образом, данное уравнение имеет восемь корней: zo= у 8, Zi="v8e"'/4,
z6 = л/ве5^4, z6 = л/ве3", z7 у
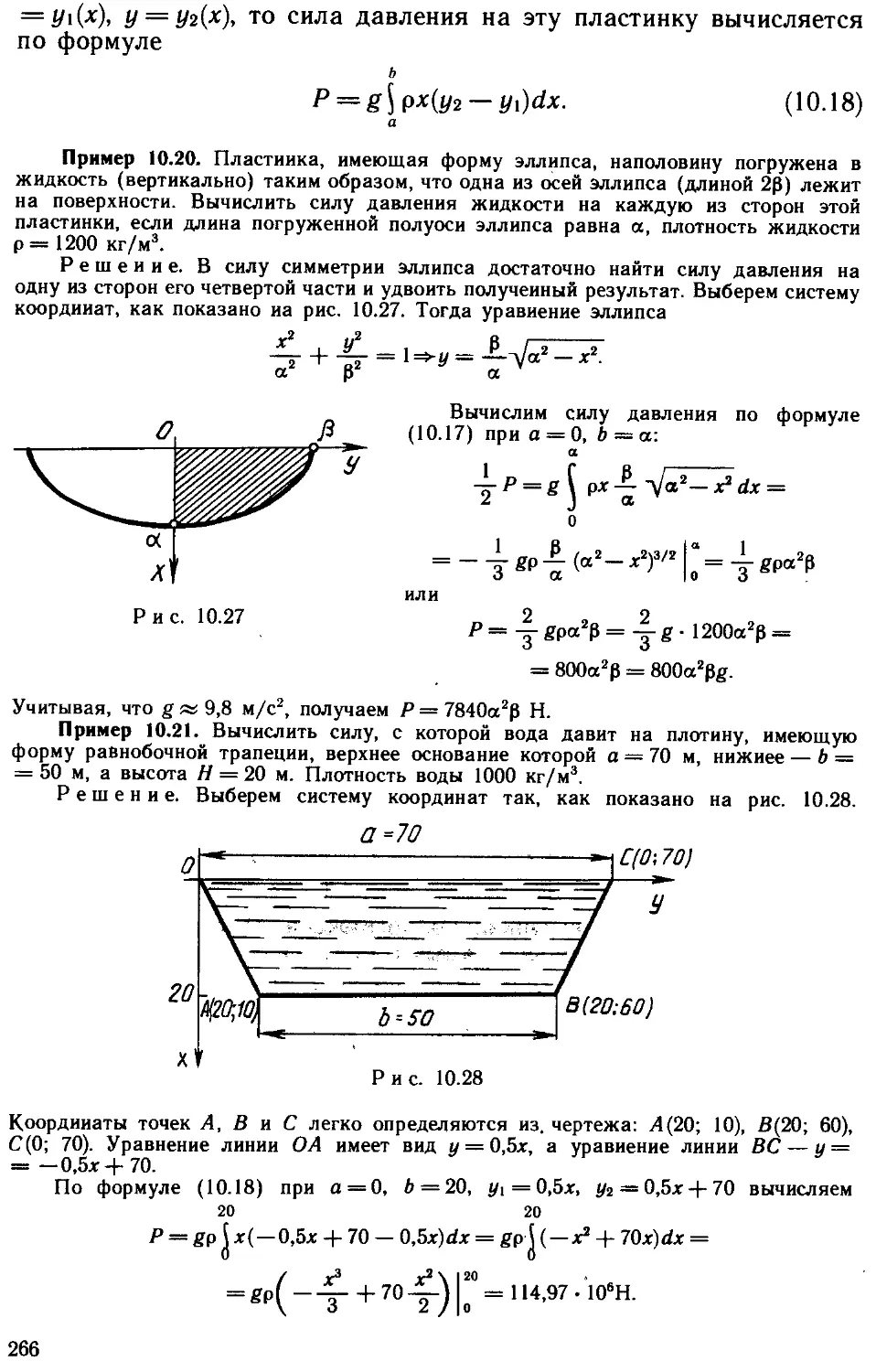
Рассмотрим алгебраическое уравнение степени п с комплексными
коэффициентами, т. е. уравнение вида:
аягя + ап_1г"-' + ... + 0,2 + 00 = 0, апф0, «6N. A.14)
Решение данного уравнения при п > 2 является задачей неизмеримо
более сложной. Вопрос о существовании корней этого уравнения
решается с помощью следующей теоремы.
Теорема 1.1 (Гаусса*). Каждое алгебраическое уравнение имеет
в множестве комплексных чисел хотя бы один корень.
Эту теорему принято называть основной теоремой алгебры. Опи-
Опираясь на нее, можно доказать; что левая часть уравнения A.14)
допускает представление в виде произведения:
ап(z - г,)«¦ (г - z2)"' ¦ ¦ ¦ (z - Zk)a\
где Z|, z% ..., Zk — корни уравнения A.14); аь а2, ..., a*6 N, причем
ai + о&2 + ... + а* = п. Тогда говорят, что число Z\ является корнем
кратности ai, гг — корнем кратности аг и т. д. Если условиться
считать корень уравнения столько раз, какова его кратность, то
можно сформулировать следующую теорему.
Теорема 1.2. Каждое алгебраическое уравнение степени п имеет
в множестве комплексных чисел ровно п корней.
Указанная теорема является теоремой существования,
т. е. отвечает на вопрос о существовании корней у произвольного
алгебраического уравнения, но не дает метода их нахождения.
Решения уравнений второй степени и двучленных уравнений
были показаны на примерах. Существуют формулы для решения
уравнений третьей и четвертой степени, однако они настолько гро-
громоздки, что ими предпочитают не пользоваться. Для уравнений сте-
степени выше четвертой подобных формул в общем случае нет.
* Карл Фридрих Гаусс A777—1855)—выдающийся немецкий ученый.

2. ЧИСЛОВЫЕ ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ
ПЕРЕМЕННОЙ
2.1. ПОНЯТИЕ ФУНКЦИИ. СПОСОБЫ ЗАДАНИЯ
Пусть D — произвольное подмножество действительных чисел
(DsR). Если каждому числу x?D поставлено в соответствие не-
некоторое вполне определенное действительное число y = f(x), то гово-
говорят, что на множестве D определена числовая функция f. Множество
D называется областью определения функции, а множество Е =
= \у 6 RI у = f(x), х ? D) — множеством значений функции.
Так как определение функции совпадает с определением отобра-
отображения множества D->~E, то термины «функция», «отображение»,
«преобразование» в дальнейшем будут употребляться как синони-
синонимы. Для записи функции применяют следующие обозначения: у =
= f(x), f: D-+E, D-+E, где f — некоторый закон соответствия.
Принята следующая терминология: х — независимая переменная
или аргумент, у — зависимая переменная. Иногда, если речь идет о
функции как отображении D-+E, f(x) называют образом элемента
х, а х — прообразом элемента f(x). При этом множество Е называют
образом множества D, множество D — прообразом множества Е.
В данной главе будем рассматривать числовые функции одной
действительной переменной: DsR, ?=R. Чтобы определить функ-
функцию у = f(x), нужно задать множество D и закон (правило, соот-
соответствие) /, переводящий элементы х множества D в элементы у
множества Е.
Наиболее широко применяемыми способами задания функции яв-
являются аналитический, табличный, графический и программный.
Аналитический способ задания функции состоит в том, что с по-
помощью формулы конкретно устанавливается алгоритм вычисления
значений функции f(x) для каждого из значений х 6 D.
и	.	5x4- sin2x
Например, формула у =	р	:	определяет у как функцию х анали-
аналитически, tg * + аг«1П х
Если дана функция y — f(x), то частное значение функции, т. е.
значение функции при некотором значении аргумента х0, записывают
в виде f(xQ) или у | *=*„.
Например, если f(x) = Зх2 + 5х + е*, то f(l) = 8 + е, fB) = 22 + е2.
При аналитическом задании функции область определения D
либо указывают, например у = х2, D(f) = [1; 2], либо понимают под D
множество значений аргумента х, при которых данная формула
имеет смысл, т. е. те значения, которым соответствуют действитель-
30

ные значения зависимой переменной у. В этом случае говорят, что
D является естественной областью определения функции.
Например, для у = х* естественной областью определения функции является
множество D(f) = R.
Условимся в тех случаях, когда функция задана аналитически
и область ее определения не указана, подразумевать под D(f) естест-
естественную область определения.
Пример 2.1. Найти область определення D и множество значений ? функции
Решение. Естественной областью определения функцни является множество
?»(f) = {д: I 4 — д:2 > 0} = {х | |х|<2} = ]-2; 2[,
а множеством значений E(fl — \y\y^ 1/2} = [1/2; оо[.
Аналитически функция может быть задана не одной, а несколь-
несколькими формулами. Такие функции называют составными.
Приведем примеры составных функций.
1. Функция
f(x)
(x+l V*€]-5; 0[,
= < 0 при х = 0,
Kx2 — 6 V*€]0; 31;
область ее определения D(f) = ]—-5; 3[.
2. Единичная функция Хевисайда*
4«-{J J*<°.
(ее график приведен на рис. 2.1).
3. Функция сигнум, или функция знака:
(-Х Ух<0,
sgn х =1 0 при х = О,
(график этой функции изображен на рис. 2.2).
4. Функция Дирихле**
«¦Hi
1, если х — рациональное число,
если х — иррациональное число.
?/ i i
1
о
Рис. 2.1
7
Рис. 2.2
* Олнвер Хевисайд A850—1925) — английский ученый и инженер.
** Петер Густав Лежен Дирихле A805—1859)—немецкий математик.
31

Аналитически функция y = f(x), х?[а; b], может быть неявно
задана уравнением F(x, у) = 0, если V х ?[а; b]F(x, f(x)) = O. В не-
некоторых случаях, разрешив уравнение F(x, у) = 0 относительно у,
удается получить явное задание той же функции.
Например, уравнение Зх — у + 2 = 0 неявно задает функцию у = Ък + 2, D(f) =
= R. Уравнение к — {/2=0 неявно задает две числовые функции: y = -\Jx{D{f) =
= R+) и у2= —0Г(?»(О= R+).
Аналитически функция y = f{x) может быть задана в параметри-
параметрическом виде (более подробно об этом см. в § 2.6). Заметим, что ана-
аналитическое описание функции зависит от выбранной системы ко-
координат. (Аналитическое задание функции в полярной системе ко-
координат будет рассмотрено в § 2.6.)
Табличный способ задания функции осуществляется табличным
перечислением п значений аргумента х\, х^,..., х„ и соответствующих
им значений функции у\, у^,..., уп- Известны таблицы значений лога-
логарифмической функции, тригонометрических функций и др. Этот спо-
способ задания функции широко применяется на практике в тех случаях,
когда значения функции имеют определенный физический смысл и
находятся в результате эксперимента. К достоинствам табличного
способа относят то, что для значений аргумента х\, Х2,..., хп из табли-
таблицы сразу можно получить значения функции у\, у2,.~, уп (т. е. не нуж-
нужны дополнительные вычисления). Его недостатками являются:
отсутствие наглядности (трудно судить о характере изменения
функции); невозможность определения промежуточных значений
функции по таблице; затруднения в непосредственном применении
математического аппарата.
Если функция задана аналитически, то для нее всегда можно по-
построить таблицу (т. е. табулировать функцию). Если функция задана
таблично, то в общем случае найти аналитическое выражение функ-
функции по ее табличным данным невозможно. Однако с помощью интер-
интерполирования функции можно найти формулу (и не одну) для таблич-
таблично заданной функции, которая будет давать точные табличные
значения функции и ее приближенные значения, не входящие в таб-
таблицу. Такие формулы называют интерполяционными. Для состав-
составления таблиц функций в настоящее время используют ЭВМ.
Графический способ задания функции состоит в представлении
функции у = f(x) графиком в некоторой системе координат. Графи-
Графиком Г функции у = f(x) называют множество точек М(х; у) плоскости
R2, координаты которых связаны данной функциональной зависи-
зависимостью, т. е. Г = {М(х; у) ? R21 у = f(x)}. Чаще всего график функции
есть некоторая линия. Если аргумент х принимает отдельные зна-
значения, например *?N, то графиком функции является множество
изолированных точек.
Например, графики функций у = п, у = п), п ? N, представляют собой мно-
множества изолированных точек плоскости R2.
Не всякая линия плоскости R2 является графиком числовой
функции у = f(x). Так, линия, изображенная на рис. 2.3, не является
32

графиком функции, поскольку одному значению x\?D соответству-
соответствует три значения у\, у2, у3.
В технике и медицине применяются различные приборы-самописцы, регистри-
регистрирующие ход и изменения некоторых величин с течением времени. Они графически
задают эти величины как функции времени. Например, в медицине электрокар-
электрокардиограф вычерчивает электрокардиограмму — кривую изменения электрических им-
импульсов сердечной мышцы. В метеорологии вычерчиваются кривые, изображающие
зависимость между давлением и временем (барограммы) и т. д.
Графический способ задания функции нагляден, но не удобен для
применения математического аппарата.
За последние годы в связи с бурным развитием и применением
ЭВМ широко распространился, стал одним из основных программный
способ задания функции, при котором функция задается с помощью
указания программы на одном из машинных языков. Этот способ
задания функции используют при решении различных задач на
ЭВМ. Разработаны стандартные программы, т. е. набор команд, за-
задающих функцию. Они могут быть составлены заранее и храниться в
оперативном запоминающем устройстве или во внешнем запоми-
запоминающем устройстве вычислительной машины.
Отметим, что указанные способы задания функции (аналити-
(аналитический, табличный, графический и программный), являясь наиболее
употребительными, не исчерпывают всех возможных способов.
В частности, можно задать функцию, описав словами закон соот-
соответствия f, позволяющий по данному х ? D определить у 6 Е. Такой
способ задания функции называется описательным или словесным.
Например, функция Е{х) (читается: «антье от *>), обозначаемая также [х], опреде-
определяется как наибольшее целое число, не превосходящее х. Эту же функцию можно
задать аналитически и графически (рис. 2.4):
-2
-1
Рис. 2.3
12 3 4 5 X
-7
¦2
Рис. 2Л
Таким образом, задание функции каким-либо способом не исклю-
исключает возможности ее задания и другими способами.
2 Зак. 1270
33

2.2. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ПОВЕДЕНИЯ ФУНКЦИЙ
Начальный этап исследования функции. Одной из основных
задач математического анализа является анализ функций. Изучить
или проанализировать функцию у = f(x) — значит охарактеризовать
поведение этой функции на области определения D(f) и построить ее
график.
Средствами элементарной математики для функции f(x) с об-
областью определения D(f) в большинстве случаев можно определить
следующие характеристики:
1)	нули и знак функции на множестве x^D(f);
2)	четность или нечетность;
3)	периодичность;
4)	интервалы возрастания, убывания; ограниченность.
Нули функции и знак функции на множестве X ^D(f). Значение
х 6 D(f), при котором функция f обращается в нуль, называется
нулем функции, т. е. нули функции являются корнями уравнения
f(x) = O.
В интервале, на котором функция положительна, график ее рас-
расположен над осью Ох, а в интервале, на котором она отрицатель-
отрицательна,— под осью Ох; в нуле функции график имеет общую точку
с осью Ох.
Четность и нечетность функции. Числовая функция f называется
четной (нечетной), если выполняются следующие условия: 1) область
ее определения симметрична относительно точки О, т. е. для каждой
точки х ? D(f) существует точка — х ? D(f); 2) для любого х из обла-
области определения выполняется равенство f( — x) = f(x)(f(—х) =
= -f(x))-
Итак,
f(x) — четная функцияоЧх ? D(f): (-* € ОД П (/(-*) = /(*)),
f(x) — нечетная функция -*>Vx ?D{f):{—x?D (f))(](f(—x) =
= -Я*))-
Например, функции /(.*) = х2, f(x) = cos 2x, f(x)=\x\—четные; функции
2х
f(x) = х3, f(x) =ns tg x, f(x) = sin 3x, f (x) = -j	jr, f(x) = sgn x — нечетные; функции
x2
f(x) = x -(- ?\ f{x) = —XT' f(x)~ Jc3~ ' не являются ни четными, ни нечетными.
По определению ось Оу является осью симметрии графика любой
четной функции, а начало координат — центром симметрии графика
нечетной функции. Графики функций, не обладающих свойствами
четности или нечетности, не симметричны. При изучении поведения
четной (нечетной) функции достаточно изучить ее при любом х>0
и продолжить это изучение по симметрии на любое х<0.
Периодичность функции. Функция f называется периодической,
если для нее существует такое число Т Ф 0, что выполняются сле-
следующие условия: 1) при любом х из области определения функции
числа х — Т и х + Т также принадлежат области определения;
2) f(x) = f(x-T) = f(x + n
Таким образом,
34

f(x) — периодическая функция^-
о-ЯТ ф 0: Vx ZD(f):(x±T)Z D(f) f| f(x ±T) = f(x).
Число Т Ф О, прибавление которого к аргументу или вычитание
из него не меняет значение функции f(x), называется периодом функ-
функции. Заметим, что если число Т является периодом функции f (x) для
любого п ? N, то число пТ — также период этой функции. Если
существует наименьший положительный период функции, то его
называют основным периодом. Употребляя термин «период» функ-
функции, будем иметь в виду ее основной период. Если Т — период функ-
функции у = f(x), то достаточно построить график на одном из интервалов
длиной Т, а затем произвести параллельный перенос его вдоль оси
Ох на dtTk, k 6 Z. На рис. 2.5 дана геометрическая интерпретация
определения периодической функции.
Рис. 2.5
Если функция f(х) — периодическая и ее период равен Т, то
функция f((ox) — тоже периодическая и ее период равен Т/ш.
Например, функции sin x, cos 2xr sin (jc/3), tg (jc/5), tg 5x, ctg 2x, x — [x] являются
периодическими на своих естественных областях определения, причем их основные
периоды соответственно равны: 2л, л, 6л, 5л, л/5, л/2, 1.
Заметим, что к периодическим функциям также относится функ-
функция f(x) = c(c = const), D(f) = R. Любое число Т 6 R является перио-
периодом этой функции, но наименьшего (основного) периода Т функция
не имеет.
Монотонные функции. Функция у = f(x) называется возрастаю-
возрастающей (убывающей) на множестве X, если большему значению аргу-
аргумента из этого множества соответствует большее (меньшее) значе-
значение функции.
Функция у = f(x) называется неубывающей (невозрастающей)
на множестве X, если большему значению аргумента из этого мно-
множества соответствует не меньшее (не большее) значение функции.
Итак,
lt x2?X:x]<.X2=>f(xi)<.f(x2);
Vх\, хч?Х:х\ <X2=^f(xi)> f(x2);
X : х\ < хч=$~\(х\) ^ f(яг);
f)f()
f(x) возрастает на X
f(x) убывает на X
f(x) не убывает на X
f(x) не возрастает на X
35

Возрастающие и убывающие на множестве х функции называют-
называются монотонными на этом множестве. На рис. 2.6, а — г дана геомет-
геометрическая интерпретация определений монотонных функций.
Очевидно, что любая возрастающая на множестве X функция
f является неубывающей на этом множестве (обратное утверждение
несправедливо). Аналогично любая убывающая на множестве X
функция является невозрастающей на этом множестве.
Иногда возрастающие и убывающие функции называют строго
монотонными, а неубывающие и невозрастающие — монотонными
в широком смысле.
Например, функция у = 2" является строго монотонной (возрастающей); функ-
функция у — [х] (где [х] — целая часть числа х) — монотонная в широком смысле (неубы-
(неубывающая). Функция у = с(с = const) является монотонной в широком смысле. Ее
можно называть как неубывающей, так и иевозрастающей.
f Возрастает
О а	Ъ х
в
f не убывает
f убывает
а
Ъ X
f не Возрастает
Ь а
Рис. 2.6
Ограниченные функции. Функция у = f(x) называется ограни-
ограниченной сверху (снизу) на множестве X^D(f), если существует такое
число М ? R, что при любых х из множества xl=D{f) выполняется
условие f(x) < М {f(x) > М).
Функция y = f(x) называется ограниченной на множестве х =
?D(f), если существует такое положительное число М, что для лю-
любых х из области определения функции (или множества X) выполня-
выполняется условие \f(x)\ ^.M. Таким образом,
f(x) ограничена сверху на Хо ЗМ 6 R: \x?X=>f{x)^M;
f(x) ограничена снизу на ХоЗМ 6 R: V* 6 X=>f(x) $г М; B.1)
/(*) ограничена на ХоЯМ € R: V* € Х=> I /(*) К М.
На рис. 2.7 дана геометрическая интерпретация ограниченных
функций (на рис. 2.7, а функция ограничена снизу на множестве
36

Рис. 2.7
X = [а; Ь], на рис. 2.7, б — ограничена сверху на множестве
Х = [а; Ь], на рис. 2.7, в— ограничена на множестве X = [а; Ь\).
Например, функция f(х) = 2 + х2 является ограниченной снизу в своей естест-
естественной области определения R, так как 2 ^ 2 + к2 V* 6 D(f), т. е. ЗЛ1 = 2: f(jc) ^ М.
Функция sin х ограничена в своей естественной области определения R, поскольку
I sin х\ < 1 V*6 D(f), т. е. ЯМ = 1: | sin х\ < 1. Функция tg * ограничена сверху на от-
отрезке [0; л/3], так как tg х s^-ф Vx 6[0; л/3], т. е. ЯМ=~ф: tgje^V3-
Функция у = f (х) называется неограниченной сверху (снизу) на
множестве X^D(f), если соответствующие условия ограниченности
B.1) для этих функций ие выполняются.
Дадим более строгое определение неогра-
неограниченной сверху функции.
Функция f(x) называется неограниченной
сверху на множестве X ^D(f), если для лю-
любого числа М существует число х ? D(f),
такое, что f(x)^M.
Например, функция f(x)= \/x (рис. 2.8) является
неограниченной сверху на множестве ]0; 1[, так как
для любого М > 0 существует такое число *6]0; 1[
в частности, х= ¦
А, что }(-
Л+М>
> М. Если М ^ 0, то число х можно принять любым
из интервала ]0; 1 [.
2.3. СЛОЖНАЯ ФУНКЦИЯ. ОБРАТНАЯ ФУНКЦИЯ
Сложная функция. Пусть на некотором множестве D определена
числовая функция и = ц>(х) и Е(и) — множество значений функции
37

и. Далее, пусть на множестве Е(и) задана функция y = f()((f)
?= ?(«)). Тогда функция ф переводит (ставит в соответствие, отобра-
отображает) элементы х в элементы и, а функция / переводит элементы
и в элементы у:
Таким образом, в конечном итоге каждому значению x?D(f) ста-
ставится в соответствие (посредством промежуточной переменной и)
одно вполне определенное значение у ? E(f), где E(f) — множество
значений функции у = f(u):
E(f) = \У € R IУ = Ки), и = <р(д), х € Я(Ф».
В этом случае у называют сложной функцией аргумента х или функ-
функцией от функции (записывают у = f(q>(x))). Часто сложную функцию
называют также композицией функций f и ф или суперпозицией
функций и обозначают /оф. При этом функцию и = <р(х) называют
промежуточным аргументом, х — независимой переменной.
Пусть у = f(ф(х)) — сложная функция. Ее можно разбить на от-
отдельные звенья (говорят также «записать в виде цепочки равенств»):
y = f(u), и = ф(лг).
Пусть у = /(ф('ф(^))) — сложная функция двух промежуточных
аргументов /ив:
у =	X^^
Ее можно представить в виде цепочки равенств: y = f(t), < = ф(ы),
Например, функция у = -^Jax -(- 6 является сложной. Ее можно записать в виде
следующей цепочки равенств:
у = "у и, и = ах + 6.
, D(<p) = R, f(*) = -\?
Функция !/•= sin2 B*+1) является сложной функцией двух промежуточных
аргументов < и и. Действительно, у нее можно выделить промежуточные звенья:
у — t2, t — sin u, u = 2* -(- 1.
Таким образом, # = sin2Bx+ 1) является сложным отображением:
где $(*) в 2х + 1; ip(«) = sin u; f (/) = t2; D(f°<f°$) = R\ E(f <><j><>ij>) = (i/1 у = sin2 Bx +
+ 1), *€R} = IO;I].
Сложными являются функции: у = In Bx + 6), у = sin лг, i/ = arcsin ?*, {/ =
= -\/sin (l/jc2i i/ = lg sin * и т. д.
Обратная функция. Функция y = f{x) является отображением
множества D(f)-+E(f), где D(f) — область определения; E(f)— мно-
множество значений функции y = f(x).
Рассмотрим взаимно однозначные (биективные) отображения
f (см. § 1.3), т. е. взаимно однозначные функции.
При взаимно однозначном отображении множества D на мно-
множество Е каждый элемент у множества Е является образом одного
38

и только одного элемента х множества D и наоборот, т. е.
у = I(х) — взаимно однозначная функцияо
D ay?E:y = f(x); \х\, X2^D, Х\Фх
Например, функция у — х3, D(f) = E(f)=R, является взаимно однозначной
(f — биективное отображение множества R на множество R), так как каждому
значению к ? R соответствует единственный элемент j/€R, такой, что у = х3
(х-Ь-х3), причем у является образом только одного элемента * (рис. 2.9) и, наоборот,
каждому элементу у ? R соответствует только одни элемент х ? R, такой, что х =
Так как каждому элементу у ? Е(у) ставится в соответствие единственный эле-
элемент x?D, то соотношение x = njy также является функцией, обратной к функции
у = х3.
Пусть у = f(x) (D-+E) — взаимно однозначное (биективное) ото-
отображение. Так как при биективном отображении каждому элементу
y?E(f) ставится в соответствие единственный элемент x?D(f), то
говорят, что на множестве Е определена функция, обратная к функ-
функции y = f(x), которую обозначают x = f~l(y) или, более кратко, f~l.
Если функция f~l является обратной по отношению к функции
/, то функция f является обратной по отношению к/~', т. е. (/"')"' =
= f. На этом основании функции [и f~' называют взаимно обрат-
обратными.
У А . -
•1
у-х
Рис. 2.9
-Л О	Л
Рис. 2.10
Например, функция у = х2, D{f) = R, E(f) = R+.не является взаимно однозначной.
Действительно, для каждого элемента (образа) g 6 ? существует два прообраза
— х а х (рис. 2.10), т. е. обратное отображение E-*-D функцией не является, так
как любому у ? Е соответствует не один, а два элемента х.
Приведенный пример показывает, что не всякая функция у =
= f(x) имеет обратную. Функция, имеющая обратную, называется
обратимой.
Теорема 2.1. Если числовая функция y = f(x) монотонна, то
существует обратная функция x = f~l(y). При этом, если f — возра-
возрастающая функция, то и f~' — возрастающая, а если f — убываю-
убывающая, то и f ~' — убывающая.
Заметим, что монотонность функции является лишь достаточ-
достаточным условием ее обратимости, т. е. существуют немонотонные обра-
обратимые функции.
39

Рассмотрим методику построения графика обратной функции.
Пусть у = f (*)^монотонна на [a;b], т. е. для нее существует обратная
функция x = f~l(y). По существу эти две функции (рис. 2.11) выра-
выражают одну и ту же зависимость между переменными хну. Только
при функциональной зависимости y = f(x) мы рассматриваем х
как аргумент, у как функцию. При функциональной зависимости
x = f {(У) аргументом служит у, функцией — х, поэтому график
обратной функции х ~ f 1(у) совпадает с графиком функции у = f(x)
(см. рис. 2.11).
Если же у обратной функции, так же как и у данной, аргумент
обозначить через х, а зависимую переменную через у, то обратная
функция запишется в виде y*=f~l(x).
Функции х = f ~' (у) и у = f ~' (х) различаются только обозначением
зависимой и независимой переменных. Поэтому, чтобы из графика
функции x = f~l(y), совпадающего с графиком функции y~f{x), по-
получить график функции y = f-\x), достаточно поменять местами
оси Ох и Оу, т. е. повернуть плоскость чертежа вокруг биссектри-
биссектрисы первого координатного угла.
Таким образом, график обратной функции y = f~l(x) симметри-
симметричен графику данной функции y = f(x) относительно биссектрисы
первого координатного угла.
Рис. 2.12
Приведем примеры обратных функций.
На рис. 2.12 изображены графики функции у — х3 и обратной ей функции
я функции у = г с D(f)=R не существует обратной функции. Однако если
эту функцию рассматривать только в области D(f)=K+, где она монотонна, то
для иее существует обратная функция у = л]к. Аналогично для функции у = х2
с D(f)= R_ существует обратная функция у = —л[х (рис. 2.13).
Сформулируем общее правило нахождения обратной функции
для взаимно однозначной функции у = f(x):
40

1)	решая уравнение y = f(x) относительно х, находим x = f~1(y);
2)	меняя обозначения переменной х на у, а у на х, получаем
функцию y = f-\x), обратную к данной.
-4
У
у
У
У1
4
А
I'2
1 ~4
1
Ри
/ У*Зх+2
7 /1/--*
/ у--(х-2Щ^
-
с. 2.14
Рис. 2.13
Пример 2.2. Показать, что функция у — Зх + 2 имеет обратную, и найти ее ана-
аналитическое выражение.
Решение. Функция y = 3x + 2 V*?R монотонно возрастает и, следова-
следовательно, имеет обратную. Решив уравнение у = Зх + 2 относительно х, получим
х = f~'(y) = (y — 2)/3. Поменяв местами обозначения, найдем обратную функцию
у = (~[(х) = (х — 2)/3. Графики этих функций приведены на рис. 2.14.
2.4. ОСНОВНЫЕ ЧИСЛОВЫЕ ФУНКЦИИ И ИХ ГРАФИКИ
Линейная функция у = ах + b (a,b 6 R). Область определения
этой функции D(f)= R, а множество значений
при а = 0.
Линейная функция возрастает при а > 0, убывает при а < 0.
График функции — прямая линия с угловым коэффициентом
k = a = iga, отсекающая на оси Оу отрезок, равный b (рис. 2.15).
Квадратичная функция у = ах2 + Ьх +
+ с(а, b, c6R, a^O). Рассмотрим два
случая.
1. Пусть а>0. Тогда D(f) = R,
?(/) = ] 4ас~—; ооГ. Функция убывает
на промежутке ]— оо; — Ь/Bа)\ возраста-
возрастает на промежутке [ — Ь/Bа); оо[. График
функции — парабола с осью х = —Ь/Bа),
вершиной в точке Nl( — —\ Aac~b \ и /
ветвями, направленными вверх (рис. 2.16, а).	Рис. 2.15
41

а
• Рис. 2.16
2. Пусть теперь а<0. Тогда D(f)=R, E(f) = ~\ -оо; 4ас47
Функция возрастает на промежутке ]—оо; —Ь/Bа)} и убывает на
промежутке [ — Ь/Bа); + оо[. График функции — парабола с осью
х=—Ь/Bа), вершиной в точке N( — 5-; ас~—) и ветвями, на-
направленными вниз (рис. 2.16, б).
Степенная функция у = ха (а ? R). Рассмотрим наиболее часто
встречающиеся случаи.
1.	Пусть а = 2л, п 6 N, г/ = х2". Тогда Z)(f) = R, ?(f) = [0; 00 [.
Функция четная, убывает на промежутке ] — оо; 01, возрастает на
промежутке ]0; оо[. График — парабола порядка 2п (рис. 2.17).
2.	Пусть а = 2/1+1, п € N, y = x2n+l. Тогда D(f)=R, E(f)=R.
Функция нечетная, возрастает на R. График — парабола порядка
2п+ 1 (рис. 2.18).
3.	Пусть о=-2л, n€N, y=l/x2n. Тогда D(f)=R\jO}, ?(f) =
= ]0; оо[. Функция четная, возрастает на промежутке ] — оо; 0[,
убывает на промежутке ]0; +оо[. Графики функции \/х2п для п =
= 1 и п = 2 изображены на рис. 2.19.
4.	Пусть о= -2/1+1, /i?N, г/=1/л:2п-1. Тогда D(/)=R\{0},
-/ о
Рис. 2.17
Рис. 2.18
42

П'1,2
Рис. 2.20
?(f)=R\{0}. Функция нечетная, убывает на промежутках ] — оо; 0[,
]0; + °°[- Графики функции \/х для п= 1 и п = 2 изображены
на рис. 2.20.
5. Пусть <x?Z, y = xa. Тогда D(f) = }0; oo[, ?@ = 10; оо[. При
некоторых a D(f) и ?(/) могут быть шире. Часто, например, встре-
встречается функция у = х/2 (или у2 = х3). График — ветвь полукуби-
полукубической параболы (рис. 2.21).
Показательная функция у = ах (а > 0, а Ф 1). Область определе-
определения этой функции D(f) = R, а множество значений E(f) = ]0; оо[. При
0 < а < 1 функция убывает, при а > 1 — возрастает. График функ-
функции изображен на рис. 2.22.
Если а = е (е« 2,71828...). то функция у = ех называется экспо-
нентой: у = ех = ехр(х), D{\) = R, E(f) = ]0; oof. График экспоненты
дан на рис. 2.23.
Логарифмическая функция y = logax (a>0, аф\). Эта функ-
функция обратна показательной. Область ее определения D(f) = ]O; oo[,
множество значений ?(/)= R. При 0<а< 1 функция убывает, при
а > 1 — возрастает. Ее график изображен на рис. 2.24.
Рис. 2.21
43

Рис. 2.23
y=lnx
Рис. 2.24
Если а = е, то у = \пх называется
функцией натурального логарифма.
График функции у=^\пх приведен на
рис. 2.25.
Тригонометрические функции у —
— sin х, у = cos х, у = tg х, у = ctg х.
Функция у — sin x; D(f) — R, E(f) —
= [—1; 1]. Она нечетная, периодиче-
периодическая с периодом Т = 2л. Функция
возрастает на промежутках [ — л/2+
+ 2л/г; л/2 -+- 2л/г], убывает на проме-
промежутках [л/2 + 2л/г; Зл/2 -+- 2л/г], k ? Z.
График — синусоида (рис. 2.26).
(f)R ?(f [] О
Рис. 2.25
Функция y = cosx; D(f)=R, ?(/) = [—1; 1]. Она четная, пе-
периодическая. Период Т = 2л. Функция возрастает на промежутках
[{2k — 1)л; 2kn\ убывает на промежутках [2л/г; Bk-\-\)n\ k?Z.
График — косинусоида (см. рис. 2.26).
Функция y = tgx; D(f)=R\{n/2+nk\k?Z\ ?(/)=R. Она
нечетная, периодическая. Период Т = л. Функция возрастает на
D(f), т..е на промежутках ) — n/2-\-nk; л/2 + л/г[, k?Z. График —
тангенсоида (рис. 2.27).
Функция y = ctgx; D(f)=R\[nk\k?Z], ?(ft=R. Она нечет-
нечетная, периодическая с периодом Г = л. Функция убывает на D(f),
т. е. на промежутках }nk; л + л/г[, k ? Z. График — котангенсоида
(рис. 2.28).
К тригонометрическим относят также реже используемые
функции: w = secx =	, w = cosecx = -:—.
^^	V	COS X U	Sin X
Обратные тригонометрические функции у — arcsin х, у = arccos x,
^ = arctgJt, i/ = arcctgx. Они определяются как функции, обратные
соответствующим тригонометрическим функциям.
Функция у = arcsin х (рис. 2.29): у = arcsin хох = sin у;
D(f) = [—\; I], E(f) — [ —л/2; л/2]. Она нечетная, возрастает на D{f);
arcsin 0 = 0, arcsin A/2) = л/6, arcsin (У2/2) = л/4, arcsin (Уз/2) =
= л/3, arcsin 1 = л/2.
44

у-- cosx у-- sinx
37Т/2 /2Ж SX/2 X
Рис. 2.26
WI2 X	-я\-Я/\ О
Рис. 2.27
-Ж/2 -1
Рис. 2.29
Рис. 2.30
Функция i/ = arccosx (рис. 2.30): у = arccos хох = cos у,
D(f) = [—l; 1], E(f) — [O; я]. Она убывает на D(f); arccos(-l) = л,
arccos(—Уз/2)=5л/6, arccos( — -\/2/2) = Зл/4, arccos(—1/2) =
= 2л/3, arccos@) = n/2, arccos(l/2) = n/3, arccos(-\/^/2) = л/4,
arccos(-\/3/2) = л/6, arccos 1 =0.
Функция t/ = arctgх (рис. 2.31): у = arctgxox — tgу; D(f) =
= R, E(f) = ] — л/2; л/2[. Она нечетная, возрастает на D(f); arctg 0 =
= 0, acrtg(l/-\/3) = n/6, arctg 1= л/4, arctg-\/3 = л/3.

J
0
к
¦Л/2
Рис 2.31	Рис. 2.32
Функция у = arcctg х (рис. 2.32): у = arcctg xox = ctg у;
D(f)=R, E(J)=']O; п[. Она убывает на D(f); arcctg(—-\/з) = 5л/6,
arcctg(—1) = Зл/4, arcctg(—1/-\/3) = 2л/3, -^ arcctgO —л/2,
arcctg(l/-y3) = л/3, arcctg 1 =л/4, arcctg Vз = л/6.
Исходя из свойства взаимно обратных функций f(f~l(x)) =
= f~l(f(x)) = x и соотношений между тригонометрическими функ-
функциями, можно вычислить значения тригонометрических функций от
обратных тригонометрических функций.
Например,
cos(arcsin х)
sin(arcsin x)= х,
= V' — sin2(arcsin x) = V' — •«*»
если \х\ < 1 и т. д.
Значения тригонометрических функций от обратных тригоно-
тригонометрических функций приведены в табл. 2.1.
Таблица 2.1
sin
cos
tg
ctg
arcsin x
X
A*1 <1)
V1-*2
(|x|<l)
X
Vi-*2
(I*KI)
X
@<|*|<l)
arccos x
Vl— x1
A*1 <1)
X
(W<l)
X
@<|*|<l)
д;
Vi-*2
(|X|<1)
arctg д:
д:
V1 +^
1
V1 +*2
X
1
д;
(*#0)
arcctg *
1
VT+7"
д:
Vi-ь*2
i
X
(хфО)
X
46

Для сумм обратных тригонометрических функций одного аргу-
аргумента справедливы следующие соотношения:
arcsin х + arccos х = л/2, arctg х + arcctg х = л/2,
arcsin JC + arcsin ( — jc) = 0, arccos x-\- arccos( — х) = л,
arctg x -\- arctg (— х) = 0, arcctg x + arcctg (— х) = л.
Можно рассматривать обратные тригонометрические функции
от тригонометрических функций: у = arcsin (sin х) (рис. 2.33), у =
= arccos (cos х), у = arctg(tg х) (рис. 2.34), у = arcctg(ctgx).
y=arcsLn(sLnx)
Рис. 2.33
>Я/2
-2К/ -1Я/2/-
-Я -П/2
arctg ttgx)
Я ZTiiy2JC
Рис. 2.34
Гиперболические функции у = sh х, у = ch x, у = th x, y = cth x.
Функция y = shx = (e" — е~х)/2 (синус гиперболический); D(f) =
= R, E(f)=R. Она нечетная, возрастает на R (рис. 2.35).
Функция у = ch х =-(е* -{- е~х)/2 (косинус гиперболический);
D(f)=R, E(J) = [l; +oo[. Функция четная, убывает на промежутке
] — оо; 0], возрастает на [0; +°°[ (см. рис. 2.35).
Функция i/ = thx = sh x/ch x (тангенс гиперболический).
Тогда thx = (ex — e-x)/(ex + e-x); D(f) = R, ?(/) = ] —1; 1[. Функция
нечетная, возрастает на D(f) (рис. 2.36).
Функция у = cth х = ch x/sh x (котангенс гиперболический).
Тогда у = cth х = {6х + е~х)/(ех - е~х); D(f) = R\{0}, E(f)= R\[- 1; 1].
Функция нечетная, убывает на промежутках ] — оо; 0[ и ]0; + °° I
(см. рис. 2.36).
Обратные гиперболические функции у = ar§h х, у = arch x, у =
= arthx, i/ = arcthx. Они определяются как функции, обратные со-
соответствующим геперболическим функциям.
Функция «/ = arshjc (ареа-синус); D(f)=R, E(f)=R (рис.
2.37);
47

у = arsh xo-x — sh y=>y = \n(x + У*2 + 1 ).
Действительно, из определения гиперболического синуса
х = sh у = (е" — е-уI2^-еР — е~у — 2х — 0=$-е2у — 2хе" —1=0,
t2 - 2xt - 1 = 0(е» = t)^e" = x + ^/x2+loy = 1п(л: + V^+T).
Функция нечетная, возрастает на D(f).
У-Shx,
Рис. 2.35
Рис. 2.36
у = arch xox = ch y=>y = \п(х + -jx2 — l).
Рис. 2.37
Рис. 2.38
Функция возрастает на D(f).
Функция ?/ = arthx (ареа-тангенс); D(f) = ] — I; 1[, E(f)=R
(рис. 2.39);	'
= arth
= th
x = у In
jT
Функция нечетная, возрастает на D(f).
Функция «/ = arcthx (ареа-котангенс); D(f)=R\[ — 1; 1],
?(f)=R\{0} (рис. 2.40);
t/ = arcth jc-ф»х = cth x=> arcth x = -i- In ¦* + .
48

t/=arcrthx
I
Рис. 2.39
Рис. 2.40
Она нечетная, убывает на промежутках ] — сю; —1[, ]1; 4-°°[-
Кроме перечисленных, существуют кусочно-постоянные функции,
например функция сигнум (у = sgn х), функция Хевисайда, функция
антье от х(у = [х]).
2.5. КЛАССИФИКАЦИЯ ФУНКЦИЙ
Рассмотренные в предыдущем параграфе функции: степенную,
показательную, логарифмическую, тригонометрические, обратные
тригонометрические, называют основными элементарными функ-
функциями.
Все функции, полученные с помощью конечного числа арифме-
арифметических действий над основными элементарными функциями, а
также их композиций, составляют класс элементарных функций.
Примерами элементарных функций являются: f(x) = \x\, f(x) = logo arcsin 3'" +
tg5*, f(x)
3 —
, f(x) =
и т. д.
У
В математическом анализе используются чаще всего элементар-
элементарные функции.
Имеет место следующая классификация элементарных функций.
1.	Функция вида
Рп(х) = aox" + аххп~х + а2ха-2 + ... + ап,
где п ? 1МЩ0}, а0, а\, а2, ..., ал 6 R, называется целой рациональной
функцией или многочленом степени п. Многочлен первой степени
называют также линейной функцией.
2.	Функция, представляющая собой отношение двух целых ра-
рациональных функций:
Pm(x) _
Qn(x)
называется дробно-рациональной.
Совокупность целых рациональных и дробно-рациональных
функций образует класс рациональных функций.
49

3. Функция, полученная с помощью конечного числа суперпози-
суперпозиций и четырех арифметических действий над степенными функциями
как с целыми, так и с дробными показателями, и не являющаяся
рациональной, называется иррациональной.
Например, функции y=
/(*)=
= Vl-j-x — л/l — х являются иррациональными.
/(*)
Рациональные и иррациональные функции образуют класс ал-
алгебраических функций.
4. Всякая функция, не являющаяся алгебраической, называется
трансцендентной. К трансцендентным функциям относятся все основ-
основные элементарные функции, кроме степенной функции с рациональ-
рациональными показателями, а также гиперболические и обратные гипербо-
гиперболические функции.
Рассмотренная классификация элементарных функций представ-
представлена на следующей схеме:
Элементарные функции
I Алгебраические функции	Г Трансцендентные функции
L
Рациональные функции
J L
_L
Иррациональные функции
J
Целые функции
Дробные рациональные функции I
В математике рассматривают и неэлементарные функции, не
относящиеся к элементарным, например составные функции у =
= [х], у = sgn х, функцию Хевисайда и др.
2.6. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ
И В ПОЛЯРНЫХ КООРДИНАТАХ
Параметрическое задание функции. Пусть х = ср(<), у = ^(t) —
две функции одной независимой переменной /? Т. Если x = <p(t) мо-
монотонна на Т, то существует обратная к ней функция t = qi~l(x).
Поэтому функцию i/ = i|)(<), t = (p~l(x) можно рассматривать как
сложную функцию, переводящую элемент х в элемент у посредством
промежуточной переменной t:
Переменную t называют параметром. В этом случае говорят, что
50

сложная функция у = F{x)oy = г|)(?), ? = ф 1(х) задана параметри-
параметрически и пишут:
Р5$}	B.2)
В формуле B.2) функция <p(f) для удобства записи обозначена
x(t), a ty(t) — через y{f). Параметр t может иметь различный смысл,
определяемый характером функциональной зависимости. Так, па-
параметрическое задание функции часто применяют при описании
траектории движения точки. Если точка движется на плоскости, то
ее координаты хну являются функциями времени. Задав эти функции:
х = x(t), у = y(t), t?T, мы полностью определим траекторию движе-
движения точки за промежуток времени Т (здесь t — момент времени).
От параметрического задания функции B.2) иногда можно перейти
к явному заданию функции у = F(x), исключив параметр t.
Всякую функцию, заданную явно (у = f(x)), можно задать пара-
параметрически. Действительно,
Параметрическое задание функций иногда имеет преимущество
перед другими формами их задания. В некоторых случаях непосред-
непосредственная связь между у и х может быть весьма сложной, в то время
как функции x(t) и y(t), определяющие функциональную зависимость
у от х через параметр t, оказываются простыми.
Например, пусть х = 3t + 1> У = I/'2, < 6 ]0; °о [. Эти две функции параметрически
задают в интервале ]0; оо[ функцию F(x) = 9/(x— IJ. Действительно, исключив из
первого уравнения параметр t = — (х— 1) и подставив его во второе уравнение, по-
о
лучим явное (непосредственное) задание функции F(x).
Пусть у= \/х, D(f) = ]O; oo[. Выберем параметр t = х. Тогда
У =
Функцию у= \/х параметрически можно задать и уравнениями:
У = <
т. е. одну и ту же функцию можно параметрически задать различными аналитическими
выражениями.
Параметрическое задание некоторых линий на плоскости. Мно-
Множество точек М(х; у) числовой плоскости R2, координаты которых
удовлетворяют уравнениям x = x(t), y = y(t), t?T, параметрически
задает некоторую линию L ? R2-
Рассмотрим параметрическое задание наиболее часто употребляе-
употребляемых в математическом анализе линий.
1. Прямая
2. Окружность с центром в начале координат и радиусом, рав-
равным а:
51

Здесь параметр t — угол между положительным направлением
оси Ох и радиусом-вектором ОМ текущей точки М(х; у) окружности,
отсчитываемый против хода часовой стрелки (рис. 2.41).
Легко видеть, что для любой точки М(х; у)
х2 + у2 = a2(cos21 + sin2 t)=>x2 + у2 = a2.
3. Эллипс
x2 , «2 . .
Эллипс можно получить сжатием окружности радиусом а в Ь/а
раз вдоль оси Оу (рис. 2.42). При такой деформации окружности
Рис. 2.41
Ч
Рис. 2.42
параметрические уравнения эллипса получаются из параметрических
уравнений окружности умножением ординаты на Ь/а:
х = a cos t, n ^ . ^ с,Л (x — acht,	r\^-t	о„
y = asint,	J^lt/^a—sin t = b sin/,
От параметрических уравнений эллипса можно перейти к кано-
каноническому уравнению. Для этого достаточно решить их относительно
cos t и sin t:
cos t = ±, sin t = ^-) + (У-) = cos21 + sin2
a	b \a/ \b /
4.	Парабола
В частности,
5.	Гипербола
t,2 =
-^ '€[0; оо [.
4 + 4=1-
cr b*
52

Справедливость параметрического задания гиперболы следует из
свойства ch21 — sh21 = 1 гиперболических функций.
6. Декартов лист (рис. 2.43) — кривая третьего порядка, урав-
уравнение которой в декартовой системе координат имеет вид
х =
х3 + У3 — Заху =
1-И3' /_
= tg(OM, Ъх).
У =
1 -И3
Эта кривая симметрична относительно биссектрисы у = х.
Параметрические уравнения декартова листа можно получить,
положив у = tx:
х3 + у3 - Заху = О,
y = tx
=>-х =
, O~x).
Рис. 2.43
Рис. 2.44
7. Астроида (рис. 2.44) — замкнутая линия, являющаяся тра-
траекторией точки, лежащей на окружности круга радиусом г, который
катится по внутренней стороне неподвижного круга радиусом а(а =
= 4г). Ее уравнение имеет вид
+ у^ -
0 < t < 2л.
8. Циклоида (рис. 2.45) — это кривая, описываемая точкой ок-
окружности, катящейся без скольжения по прямой линии. Циклоида
состоит из конгруэнтных дуг, каждая из которых соответствует пол-
полному обороту катящегося круга. Параметрические уравнения ци-
циклоиды:
х = a(t — sin t), tcQ\
y — a{\ —cost), ftK-J
Полярная система координат. Кроме декартовой системы ко-
53

ординат Оху, на плоскости R2 иногда используют полярную систему
координат.
Полярная система координат задается: точкой О, называемой
полюсом, лучом Ои, называемым полярной осью, и выбранной на
полярной оси единицей масштаба (рис. 2.46).
Полярными координатами точки М ? R2 (не совпадающей с по-
полюсом), называют полярный радиус г(М)= \ОМ\ точки М и поляр-
полярный угол ф(М), т. е. угол, на который надо повернуть ось Ох до сов-
совпадения ее с вектором ОМ (ф(М) > 0, если поворот совершается
против хода часовой стрелки, и ф(М) <0 в противном случае).
Запись М(г; ц>) означает, что точка М имеет полярные координаты
г и ф.
Полярный угол ц>(М) принимает бесконечное множество значений,
отличающихся друг от друга на 2kn, k ? Z. Значение полярного угла
О ^ ф •< 2л называют главным. (Иногда в качестве главного значе-
значения принимают —л < <р < л.)
Положение любой точки М на плоскости однозначно определя-
определяется координатами г и ф, причем 0^г<С°о, 0 ^ ф ¦< 2л. Если
точка М совпадает с полюсом О, то ее радиус-вектор равен нулю
(г(М) = 0), а полярный угол ф можно выбирать любым.
Обобщенными полярными координатами точки М называют ее
полярные координаты г и ф, такие, что — оо ¦< г ¦< °°, — оо ¦< ф ¦<
Чтобы указать точку М(г; ф) в обобщенной полярной системе ко-
координат, надо построить луч, образующий с полярной осью и угол ф,
затем отложить г единиц масштаба на нем, если г > 0, и на его
продолжении, если г ¦< 0.
Mtl2-.It/3)
0
а
Рис. 2.46
Рис. 2.47
54

На рис. 2.47 изображены в обобщенной полярной системе координат точки М\ B;
л/3) и М2{—3; л/4).
В дальнейшем, если специально не оговорено, под г и ф понимаем
полярные координаты точки.
Иногда приходится пользоваться одновременно как декартовыми,
так и полярными координатами на плоскости. При этом естественно
поставить две взаимно обратные задачи: 1) зная полярные коорди-
координаты г и ф точки М, найти ее декартовы координаты х и у; 2) зная
декартовы координаты хну точки М, найти ее полярные координаты.
Решение этих задач зависит от взаимного расположения полярной
оси и осей декартовой системы координат. В частном случае, когда
полярная ось Ои совпадает с осью абсцисс и все три оси Ох, Оу и Ои
имеют общую единицу масштаба, зависимость между декартовыми
и полярными координатами находится из определения тригоно-
тригонометрических функций sin ф и cos ф (рис. 2.48): cos ф = дг/г, sin ф =
= у/г, откуда
х = г cos ф, у — г sin ф.	B.3)
Формулы B.3) выражают декартовы координаты точки через
ее полярные координаты. Чтобы выразить полярные координаты
через декартовы, возведем обе части каж-
каждого из равенств B.3) в квадрат, а затем
сложим полученные равенства почленно.
В результате получим:
х2 + у2 = г2 (cos2 ф -f sin2 ф) или х2 + у2 = г2,
откуда
B.4)
Поделив почленно второе из равенств
B.3) на первое, имеем:
У,
0
Л
X
г;ср)
У
X
и
Рис. 2.48
j	J-.	B.5)
Формулы B.4) и B.5) выражают полярные координаты точки
через ее декартовы координаты. Заметим, что если 0 ^ ф < 2л, то
найденному значению tg ф = у/х соответствуют два значения ф. Из
этих двух значений выбирают то, при котором выполняются равен-
равенства B.3), т. е. угол ф выбирается по знакам sin ф и cos ф.
Зная связь между декартовыми и полярными координатами точки,
уравнение линии L на плоскости можно записать в виде F(r, ф) = О
или г = г(ф).
Область определения функции в полярной системе координат
будем обозначать D(r), множество значений — Е(г).
Уравнения некоторых линий в полярной системе координат.
1. Прямая линия. Прямая линия, проходящая через полюс:
у = fex-e^-tg ф = k
(х = г cos ф, у — г sin ф=Ф-г sin ф = kr cos y=>ig ф = k).
Прямая линия, не проходящая через полюс:
55

Ах + By + С = Oor =
cos(q> — a) '
где р — расстояние от прямой до полюса; а — угол наклона нормаль-
нормального вектора прямой п(А, В).
2. Окружность. Окружность с центром в начале координат
и радиусом, равным а (рис. 2.49, а):
х2 + у2 = а2ог = а.
лои
Рис. 2.49
Действительно, воспользовавшись формулами перехода от де-
декартовых координат к полярным (х = г cos ф, у = г sin у=>х2 -j- У2 =
= г2), имеем
г = -\/*2 -f y2
r = а.
Окружность радиусом а с центром, смещенным по оси абсцисс
вправо на а единиц (рис. 2.49, б):
(дс — af -\- у2 = а2ог = 2а cos ф.
Окружность радиусом а с центром, смещенным по оси ординат
вверх на а единиц (рис. 2.49, в):
х2 + (у — аJ = а2-$ь-г = 2а sin ф.
3. Линии второго порядка (эллипс, гипербола, пара-
парабола) . Уравнение эллипса, гиперболы и параболы в полярной системе
координат имеет вид
1 	 и f*r\C m *	*	'
1 — 8 COS ф '
где р — Параметр; е — эксцентриситет.
При е •< 1 уравнение B.6) определяет эллипс (полюс совпадает
с левым фокусом эллипса); при е > 1 — гиперболу (полюс совпадает
с правым фокусом гиперболы); при е= 1 — параболу. (Во всех слу-
случаях полярная ось сонаправлена с горизонтальной осью кривой.)
Отметим, что при е > 1 уравнение B.6) следует рассматривать в
обобщенных полярных координатах, в противном случае оно будет
описывать только правую ветвь гиперболы.
Чтобы перейти к декартовой системе координат, в уравнении
B.6) положим г = -\Jx2 + у2, cos ф = x/^Jx2 + у2. Подставив эти зна-
56

ченияв формулу B.6), получим после упрощения уравнения эллипса,
гиперболы и параболы в декартовой системе координат.
Пример 2.3. Определить, какие линии заданы уравнениями: 1) г =		;
9	3
3) г = —	. Записать в декартовых координатах урав-
4 — 5 cos ф ' "'	1 — cos ф
нения этих линий и построить их.
Решение. 1. Это уравнение вида B.6). Оно определяет одну из кривых второго
порядка: эллипс, гиперболу или параболу. Преобразуем уравнение к виду
9/5
1 - D/5)cos ф '
Так как е = 4/5< 1, то получили уравнение эллипса.
Чтобы записать уравнение кривой в декартовых координатах, воспользуемся
формулами перехода от полярных координат к декартовым. Получим:
9/5
~ 5-*= IT* -2T(*-4) +У
l-D/5)W^ + i/2
81 72
25Н" 25
225
25
(*-4)г
25
¦V-1-
т. е. имеем уравнение эллипса в декартовых координатах (рис. 2.50);
2. Преобразуем уравнение к виду B.6), получим
. _	9/4
1 — E/4) cos
Это уравнение гиперболы.
yl\
Рис. 2.50
Перейдем к декартовым координатам
,/3~П_	9/4
Рис. 2.51
«г/	1С I тс ¦* • Та =^' 1 с % 1 Тс~ % ~~~ У Н Г^~==
16
т. е. получили уравнение гиперболы в декартовых координатах (рис. 2.51).
3. Это уравнение определяет параболу. Найдем ее уравнение в декартовых
координатах:
(рис. 2.52).
57

asinZa
X
—»
и
Рис. 2.52
Рис. 2.53
4.	Р о з ы. Розами называют семейство кривых, уравнение которых
в полярных координатах записывается в виде:
г = a sin &ф или r = acoskq>,	B.7)
где a, k — положительные числа. При любых a, k, ф г ^ а, поэтому
можно сделать вывод, что все кривые располагаются внутри круга
радиусом а. Вследствие периодичности функций sin ky и cos ky розы
состоят из конгруэнтных лепестков, симметричных относительно
наибольших радиусов, каждый из которых равен а.
Количество лепестков розы зависит от значения k. Если k —
целое число, роза состоит из k лепестков при нечетном k и из 2k ле-
лепестков при четном k. Если k = О, то первое из уравнений B.7) опре-
определяет точку, совпадающую с полюсом, второе — окружность ра-
радиусом а с центром в полюсе (см. рис. 2.49, а). Если k = 1, то урав-
уравнение г = асовф определяет окружность радиусом а/2 с центром,
смещенным от полюса на а/2 единиц вправо, а уравнение г =
= asin9 — окружность радиусом а/2 с центром, смещенным от
полюса на а/2 единиц вверх. Если k = 2, уравнения B.7) опреде-
определяют четырехлепестковые розы, отличающиеся друг от друга распо-
расположением на плоскости, причем роза г = a sin 2ф может быть полу-
получена из розы г = асоз2ф поворотом ее на угол я/4 (рис. 2.53). Если
k = 3, уравнения B.7) определяют трехлепестковые розы, причем
роза г = a sin Зф получается из розы г = a cos Зф поворотом ее на
угол я/6 (рис. 2.54).
5.	Спирали. Спираль Архимеда (рис. 2.55) определяется как
58

Рис. 2.55
траектория точки, участвующей одновременно в двух равномерных
движениях, одно из которых совершается вдоль прямой, а другое —
по окружности. Полярное уравнение спирали Архимеда имеет вид
т. е. полярный радиус точки линейно зависит от ее полярного угла с
коэффициентом пропорциональности а, где D(r) = R; E(r) = R
(см. рис. 2.55). Данная кривая состоит из двух ветвей, одна из ко-
которых раскручивается против хода часовой стрелки и соответствует
положительным значениям ф, другая — по ходу часовой стрелки и
соответствует отрицательным значениям ф. Спираль Архимеда сим-
симметрична относительно перпендикуляра к полярной оси, на котором
лежат точки пересечения ее ветвей (двойные точки спирали) (см.
рис. 2.55).
Гиперболическая спираль (рис. 2.56) —г это кривая, полярное
уравнение которой имеет вид
г = а/ф, а>0,
где D(r)= R\{0}; ?(r) = R\{0}. Прямая, параллельная полярной оси
и удаленная от нее на расстояние а, является асимптотой гипербо-
гиперболической спирали.
Логарифмическая спираль (рис. 2.57) — это кривая, полярное
уравнение которой
где а>0, аф\\ D(r) = R; ?(r) = ]0; оо[. Она пересекает все свои
и
Рис. 2.57
Рис. 2.58
59

радиусы-векторы под одним и тем же углом. Это свойство кривой
используют в технике.
Синусоидальными спиралями нызывают семейство кривых, урав-
уравнение которых в полярных координатах имеет вид
гт = ат sin
или гт = ат cos
В зависимости от т уравнение определяет кривые различных
форм. При т=\ уравнение г = асозф или r = as\ny определяет
окружность (см. рис. 2.49). При т=1/2 уравнение г = acos2-|-=>-
=^'¦=y(l-|-со5ф) или r = asin2-|-=^r = -|-(l — cos ф) определяет
кардиоиду (рис. 2.58). При т = 2 уравнение г2 = а2зт2ф или г2 =
= a2 cos 2ф определяет кривую, которую называют лемнискатой
Бернулли* (рис. 2.59)!
г2* a2cas2<jp>
Рис. 2.59
AJ3,4;fi/4)
Рис. 2.60
а
Пример 2.4. Построить кривую г = 2A -+-
+ cos ф).
Решение. Уравнение линии задано в по-
полярных координатах. Область определения функ-
функции /)(/¦)= R, область ее значений Е(г) =
= [0; 4]. Вследствие периодичности функции
cos ф достаточно построить точки для ф ? [0; 2л],
а так как эта функция четиая, можно ограничить-
ограничиться значениями ф ? [0; я]. Остальные точки по-
построим по симметрии относительно полярной оси.
В табл. 2.2 даны координаты наиболее
характерных точек кривой. Для ее построения
найдем точки А,, Аг, Аз, At, Аъ, соединим их
плавной линией, затем достроим кривую, пользу-
пользуясь свойством симметрии. Получим кардиоиду
(рис. 2.60).
Таблица 2.2
ф
г
А,
0
4
А2
я/4
3,4
А3
я/2
2
А,
ЪпЦ
0,6
Аь
я
0
Якоб Бернулли A654—1705) —швейцарский математик.
60

2.7. ПРОСТЕЙШИЕ МЕТОДЫ ПОСТРОЕНИЯ ГРАФИКОВ ФУНКЦИЙ
В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ
При графическом изображении функции у = f{x) можно исполь-
использовать следующие рассуждения.
Если L — график функции у = f(x) в Оху, то:
1)	график функции у== —f(x) получен зеркальным отражением
L относительно оси Ох;
2)	график функции y = f( — х) получен зеркальным отражением
L относительно оси Оу;
3)	график функции y = f(x — а) получен смещением кривой L
вдоль оси Ох на величину а;
4)	график функции у = b -\- f(x) получен смещением кривой L
вдоль оси Оу на величину Ь;
5)	график функции y = f(ax), a>0, аФ 1, получен сжатием в а
раз при а> 1 или растяжением в \/а раз при а< 1 кривой L вдоль
оси Ох;
6)	график функции у = bf(x), b > О, Ь Ф 1, получен растяжением
в Ь раз при Ь > 1 или сжатием при Ь < 1 кривой L вдоль оси Оу.
Для построения графика функции y = Af(k(x-\-a))-\-b следует
построить:
1)	график функции y = f(x) — кривую L;
2)	затем график функции у = f(x,-{- а) — кривую L\ — смещением
кривой L на а единиц влево по оси абсцисс;
3)	график функции у = f(k(x-\-а)) — кривую L% — сжатием
кривой L\ в k раз вдоль оси абсцисс при k > 1 и растяжением ее
при k < 1;
4)	график у = А{ (k(x + а)) — кривую L3 — растяжением в А раз
вдоль оси ординат кривой Li при А > 1 и сжатием ее при А < 1;
5)	график функции у = Af(k(x + а)) + Ь сдвигом криьой L3 вдоль
оси ординат на Ь единиц.
Пример 2.5. Построить график функции у = 3 sinBjc + л/3) преобразованием
графика функции у = sin x.
Решение. Для построения графика функции i/ = 3 sinBjc-)-л/3) запишем ее
в виде у = 3 sin 2(x -\- л/6) и воспользуемся указанными выше правилами.
Сначала построим график функции у = sin x, затем график функции у =
= sin (х + л/6) смещением синусоиды на л/6 единиц влево по оси абсцисс. Зиая график
функции у = sin (х + л/6), строим график функции у = sin 2 (х + л/6) сжатием
в два раза кривой у = sin (jc + л/6) вдоль оси абсцисс. Растяжением в три раза
вдоль оси ординат кривой у = sin 2(x + л/6) строим график искомой функции
у = 3 sin Bх + л/3) (рис. 2.61).
Зная графики функций f\(x) и faM, можно геометрически по-
построить график их линейной комбинации aif\(x) + aifiix), где аь
осгб R. Для этого ординаты точек графика f\(x) умножаются на а.\,
ординаты точек графика /г(*) — на аг и складываются. Их сумма и
определяет ординаты точек графика линейной комбинации функций.
Если известны графики функций fi(x) и /г(дс), то для построения
графика функции у — fi(x)f2{x) надо найти произведения ординат
точек графиков сомножителей. Они и будут ординатами точек гра-
графика произведения функций.
61

Р и с. 2.6!
Для построения графика функции y — U{x)/h{x) ПРИ условии,
что h(x) Ф 0, нужно найти частное ординат точек графиков функций
f\(x) и /г(х), которые определяют ординаты точек искомого графика
функции.

3. ПРЕДЕЛЫ
3.1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ И ЕЕ ПРЕДЕЛ
Числовая последовательность. Если каждому натуральному числу
га G N поставлено в соответствие некоторое вполне определенное
число xn = f(n), хп? R, то говорят, что на множестве N задана числовая
последовательность. Таким образом, числовая последовательность —
это числовая функция f, определенная на множестве натуральных
чисел N (отображающая множество N в R (f: N->-R)).
Числовую последовательность обозначают так:
(Xn) — (Xl, Х2, Х3, ...)•
Число f(n) называется га-м или общим членом последовательности
и обозначается х„, а формула х„ — f(n) называется формулой общего
члена последовательности.
Примеры числовых последовательностей:
((_1)») = (_1, +1, _1, +1, ...), (sin па) = (sin а, sin 2а, ...).
Так как последовательность (хп) является числовой функцией,
то к ней применимо большинство понятий, введенных в § 2.2 для
числовых функций, характеризующих поведение последовательно-
последовательности на D(f) =ti. Существуют последовательности ограниченные
(ограниченные снизу, сверху), последовательности возрастающие,
убывающие, монотонные, неубывающие, невозрастающие и даже
периодические. Однако нельзя говорить о четных и нечетных после-
последовательностях, поскольку на множеств N нет двух взаимно про-
противоположных чисел. Сформулируем эти понятия для числовых
последовательностей, взяв за основу соответствующие определения
для числовых функций:
(х„) — ограничена снизу на	N оЯпг gR:jcn^mVragN;
(хп) — ограничена сверху на No3Af ? R:xn^M Vn 6 N;
(хп) — ограничена на N	оЯМ,гп ? R:m^jcn^M Vra?N;
(xn) — возрастает на N	oVrai, гагб N:rai <га2=>х„, <х„2;
(хп) — убывает на N	oVnt, п2? N:rai <га2=*-х„, > хП1;
(хп) — не убывает на N	оУпи п2? N:rai <ra2=^xn, <х„2;
(х„) — не возрастает на N	oVn\, ra26 N:ni <пч=^хП1 ^хПг.
Возрастающие и убывающие последовательности называются
монотонными.
63

Например, последовательность ( 1-|	\=/2, -^-, -^-, ...V график которой
приведен иа рнс. 3.1, является убывающей, так какУпь Пг€ N
11	1
2
Г
0
. о
1
О
1
2
О
1
3
О
1
4
о
S
О
в
О
1
7
о
8 п
Рис. 3.1
—
числа т = 0 и УИ = 3, такие, что
огРаиичена- Действительно, существуют
0<-
) —6
= 3 —¦
.<,).
п+2	п+2	п+2
Последовательность
(п cos пл) = (cos л, 2 cos 2л, 3 cos Зл, ..., л cos пл, ,..)
является неограниченной, так как |ncosnn|=n может превзойти любое сколь
угодно большое число М 6 R-	^
Предел числовой последовательности. Операция предельного
перехода является одной из основных в математическом анализе.
Впервые понятие предела встречается в элементарной математике,
где с помощью предельных переходов определяется длина окруж-
окружности, объемы цилиндра и конуса и т. д. Оно также используется
при определении суммы бесконечно убывающей прогрессии.
Введем понятие предела числовой последовательности, которое
позволит нам в дальнейшем определить и другие, более сложные,
операции предельного перехода.
Определение 3.1. Число а называется пределом числовой
последовательности (хп), если для любого сколь угодно малого по-
положительного числа е найдется такое натуральное число по(е), что
для всех п > по члены этой последовательности удовлетворяют не-
неравенству \хп — а|<Се.
В этом случае говорят, что последовательность имеет предел и
пишут lim xn = а.
Используя кванторы, определение предела последовательности
можно записать более кратко:
lim jc/^
\х„ — а\
64

Последовательности, имеющие предел Игл хп = а, а? R, называют
П—*-оо
сходящимися (к числу а), а последовательности, не имеющие ко-
конечного предела,— расходящимися.
Так как [\х„ — а\ < е} = Ot(a), то из определения предела следует,
что если число а является пределом последовательности (хп), то в
произвольную сколь угодно малую е-окрестность точки а попадают
все члены этой последовательности, начиная с некоторого га > га0.
На рис. 3.2 дана геометрическая интерпретация определения
предела числовой последовательности: Пггис = а тогда и только
а
а-е
а
i
0
0
///////
W/Л
0
2. J
1
Ч
ш<
Щ
. "о
- г
5
1
6
1 1
7 В
'Л
9
10 П
'	Рис. 3.2
тогда, когда для любого е > 0 существует по(е) (в данном случае
п0 = 5), такое, что при любых п > п0 все точки (га; хп) находятся в за-
заштрихованной на рис. 3.2 полосе, ограниченной прямыми а — ей
а + е. В этой е-окрестности содержатся все члены последователь-
последовательности, за исключением конечного их числа.
Пример 3.1. Пусть (*")=( „ + i ) =(у' Т! Т' " Д°казать- чт0 lim *" = '•
Решение. Если провести прямую х„= 1 (рис. 3.3), то видно, что все точки
последовательности (jcn) приближаются к этой прямой.
а-г
0
О
1
/
2
J
Уг/Л
4
'/7//
5
В
i
7
1
в
1
9
п
Рис. 3.3
Зададим е. Пусть, например, е = 0,01. Найдем такой номер последовательности
по 6 N, чтобы V л > по выполнялось неравенство |jcn — 11 < e:
где
—I — целая часть числа —. Если е = 0,01, для выполнения неравенства
\Хп— 1| <е достаточно взять По = т77п
99. Тогда Уп>99=>\х„— 1| <0,01,
т. е. lim
—г-
п + 1
= ••
3 Зак. 1270
65

Заметим, что для вычисления пределов редко пользуются определением 3.1,
чаще применяют различные приемы преобразования n-го члена, например
,. п	1
||т „ _i_ i ~ 1|т | _|_ | /„ = '•
Здесь мы воспользовались правилами вычисления предела частного последова-
Мпис„	¦
тельиостей lim —— = "г*00— и lim —= 0, известными из курса средней школы.
л-*оо Уп	lim у„	л-юо П
П-*-оо
Постоянная последовательность (хп) = (с, с, ...) сходится к числу с (lim c = c),
Л-+-0О
так как при любом е>0 условие \с — с\ <е выполняется для всех п 6 N.
Последовательность ((—1)") = (—1, 1, —1, ...) является расходящейся, так как
при л->-сю ее общий член не стремится ни к какому числу.
Во всех предыдущих случаях под пределом последовательности
понималось некоторое число. Иногда встречаются неограниченные
последовательности, такие, что с увеличением п общий член после-
последовательности (хп) неограниченно возрастает. Такие последователь-
последовательности называют бесконечно большими.
Примерами бесконечно больших последовательностей являются последователь-
последовательности
1) (и); 2) (-и); 3) ((-1Г+Ч
Члены первой последовательности принимают только положительные значения.
В этом случае говорят, что последовательность имеет бесконечный предел, и пишут
lim х„ = +оо. Члены второй последовательности принимают только отрицательные
rt-*-oo
значения. В этом случае говорят, что последовательность имеет бесконечный предел,
и пишут Птдс„=—сю. Члены третьей последовательности по модулю неограни-
неограниченно возрастают, принимая то положительные, то отрицательные значения. В этом
случае говорит, что хп имеет бесконечный предел, и пишут, не указывая знака беско-
бесконечности, lim xn = сю.
Дадим определения последовательностей, имеющих бесконечный
предел, используя кванторы:
lim хп = + оо о VM e R+ 3 по е N: Vre > по=>хп > М;
lim хп = oooVM g R 3raoG N: Vra > rao=^|jcn| > M.
n~*-oo
Числовую последовательность называют бесконечно малой, если
lim хп = 0:
lim Jtn = OoVe>0 3no? N:Vra > rao=^|jcn| < e.
¦ '	rt-*-op
Например, последовательности (дс„) = t —^-), (xn) = ( sin —l являются бесконечно
малыми.
Признаки сходимости числовых последовательностей. Сформули-
Сформулируем необходимый признак сходимости числовых последователь-
последовательностей.
66

Теорема 3.1. Если последовательность (хп) сходится, то она
ограничена:
limхп = а=>НЛ4 ? R: \хп\ <М.
О Пусть (хп) — сходящаяся последовательность. Так как
limjcn = a, то для любого е>0 существует натуральное число
П—*-оо
по ? N, такое, что для любого п> п0 выполняется неравенство \хп —
— а\ < е. Тогда для любого е>0 имеет место неравенство:
|лс„| = Un-a + a|< \xn-a\ + |a|<|a|+e,
т. е. \х„\ < \а\ +е.
Пусть М = тах{\а\+г; \xt\, \x2\, ..., Un_i|}. Тогда |xn|<AJ
VragN, что и означает ограниченность числовой последователь-
последовательности. <
Заметим, что ограниченность последовательности является не-
необходимым, но не достаточным признаком сходимости последова-
последовательности.
Например, последовательность ((—1)") = (—1, +1, —1, +1, ...) является огра-
ограниченной расходящейся последовательностью.
Теперь сформулируем достаточный признак сходимости число-
числовых последовательностей.
Теорема 3.2. Всякая ограниченная монотонная последователь-
последовательность сходится.
Отметим, что монотонность ограниченной последовательности
является достаточным, но не необходимым условием ее сходимости,
т. е. существуют ограниченные сходящиеся немонотонные последо-
последовательности.
/1 1 1 1 1 1 \
Например, последовательность f —, ——, —, ——, —, ——, ...1 имеет своим
пределом 0, т. е. сходится, хотя и не монотонна.
Теорема 3.3. Если limjtn = a, \\mzn = a и, начиная с некоторого
номера п, выполняется неравенство хп^уп^ гп, то lim yn = а:
cn= limzn = a)=*> 31im yn = a.
О Воспользуемся определением предела:
:>0 Hrai?N:|jtn — а\ < е Vra > п\,
N: \zn — a\ <e Vra > га2.
Пусть га0 = max(rai, п2). Тогда для любого га > га0 будут одновре-
одновременно выполняться неравенства:
(а — е < хп < а + е\ „ , < < z .
/п — а I < е V га > По-
67

Это и означает, что предел последовательности (уп) равен а. <
Число е. Натуральные логарифмы. Рассмотрим последователь-
последовательность (*л) = Ц1 Н—\ V Докажем, что она сходится, и найдем ее
предел.
Применим формулу бинома Ньютона*
_!_ П(П— l)-(rt-ft-H) „n-kgk |	L П(П — 1)(П— 2)-1 „QQn
-Г	_	а р + ...+	-s	ар
для последовательности (*„):
(.+!)"-¦ + ¦ +i('4)+i('-iH-l-)+-+
Тогда
'<1 + 1+ + + + ^<2 + +
Л	1 V ..Л	« \
Н п + 1/ V п + 1/#
Следовательно, jcn<jcn+i.
Последовательность (jcn) возрастает и ограничена, значит, она
A \"
1 -|—) < 3. Предел этой последовательности
называют числом е:
Число е является иррациональным: е = 2,7182818... В математи-
математическом анализе е играет особую роль. Логарифмы по основанию е
называются натуральными, их обозначают
lnad=logea.
Модуль перехода от натуральных логарифмов к десятичным обозна-
обозначают М = lge = 0,4343... Тогда
lg a = M In a = lg e • In a.
* Исаак Ньютон A643—1727) —выдающийся английский физик, механик, астро-
астроном и математик.
68

Вычисление пределов числовых последовательностей. Вычисления
пределов числовых последовательностей основаны на ряде теорем,
которые приводятся ниже.
Определение 3.2. Суммой, разностью, произведением и ча-
частным двух последовательностей (хп), (уп) называются последователь-
последовательности (х„ + Уп), {х„ — Уп), {хпуп), (хп/уп) соответственно (при делении
предполагается, что все члены последовательности уп отличны от
нуля).
Произведение последовательности (хп) и числа- с можно рассмат-
рассматривать как произведение последовательности (хп) и постоянной по-
последовательности {уп) = {с), все члены которой равны с. В резуль-
результате получим последовательность (схп).
Теорема 3.4. Если последовательности (хп) и (уп) сходятся и
limjtn = a, Hm yn = b, то:
1) Mm (хп±Уп)= limxn
2)	lim (схп) = с lim xn = ca;
3)	\\хп(хпуп) — \imxn • \imyn = ab;
lim xn
4)	\\т^ = \Птупф0\ = ^^-=±.
л-»оо уп n-*<x>	lim у„ b
Если limjtn = limi/n = 0, то хп/уп называют неопределенностью
вида -jT-. Аналогично определяются неопределенности вида —, 0 • со,
со — со. Для вычисления таких пределов теорема 3.4 неприменима.
Вычисление пределов для неопределенных выражений вида —, —,
Iе", со — со, 0- оо называют раскрытием соответствующих неопре-
неопределенностей.
Рассмотрим методику раскрытия неопределенностей на конкрет-
конкретных примерах.
Пример 3.2. Вычислить предел частного двух последовательностей:
х^ _ Зп2 — In + 1
~у7 ~ 2 — Ьп — 6п2 '
оо
Решение. Имеем неопределенность вида —. Разделив числитель н знаме-
знаменатель на п2, получим	°°
Хп	,.	П	П1	1
lim — = lim
п-*-оо Уп
Уп	rt-J-oo 2
Пример 3.3. Вычислить предел разности двух последовательностей:
Хп — Уп= У"" +П—П.
Решение. Имеем неопределенность вида оо — оо. Умножив и разделив ее
на выражение -^пг + п + п, получим
69

lim (xn — yn) — lim — _ ¦ > ¦ 	= lim —_		= -^-.
(I v 2/1
1 -?—) ¦
П /
Решение. Имеем неопределенность вида 1°°. Тогда
(|ч 2л	,	1 \1	,	I \п
1+—) = lim(l+ —) lim A+ —) =е2.
Пример 3.5. Вычислить предел произведения двух последовательностей х„ =
= П2 И уп = -г.
п
Ре ш е н и е. Так как lim jcn = oo, lim у„ = 0, то имеем неопределенность вида
О • ею. Раскроем ее:
lim (хпуп)— lim n2— = lim — = 0.
3.2. ПРЕДЕЛ ЧИСЛОВОЙ ФУНКЦИИ
Конечный предел функции при *->-jto. Пусть функция f(x) опре-
определена в проколотой окрестности точки х0, т. е. на множестве бь{хй) =
= {jc|O< |jc — хй\ < б}. В точке jc0 значение f(jco) может быть не
определено.
Приведем определение конечного предела функции при jc->-jc0
на языке последовательностей (по Гейне*).
Определение 3.3. Число уо называется пределом функции
у =*= f(x) в точке х0 (или при х-*-х0), если для любой последо-
последовательности точек хп?Оь(хо), сходящейся к х0, последовательность
соответствующих значений функции f(xn) сходится к у0:
Уо = \imf(x)oW(xn): lim х„ = jc0 => lim f(xn) = уо-
X2 — 1
Например, рассмотрим функцию f(x) =	г-; D(f) = R\(l} (рис. 3.4). Эта функ-
функция не определена в точке хо = 1, но определена для любой Ов(*о). Используя опре-
х2 — 1
деление предела функции по Гейие, докажем, что lim	— = 2.
х->-1 X — 1
Пусть (jc«) — произвольная последовательность с общим членом хпф\, такая,
что lim х„ = 1.
X2,— 1
Образуем последовательность f(xn) = ——-. Так как х„ Ф 1, то f(xn) = х„ + 1=>
Хп — 1
=> lim f(xn) = lim (xn + 1) = 2, т. е. lim **~-] = 2.
Дадим еще одно определение конечного предела функции при
х-*-хо на языке «е — б» (по Коши**).
* Эдуард Гейне A821—1881) — немецкий математик.
** Огюстен Луи Коши A789—1857) —французский математик.
70

7
ШШШШ
Ш/Ш/Ш//Ш///////////////////////А
щ
1 2 J
Рис. 3.4
Рис. 3.5
Определение 3.4. Число t/o называется пределом функции
y~f(x) в точке хо (или при х-+.хо), если для любого е >0 можно
указать такое число б (в) > 0, что при всех х, удовлетворяющих
условию 0< |л: — агоI < б, выполняется неравенство \f(x)-—yo\ < e:
у0 = lim f (
0 36 >
0< |х —хо|<
в.
В определении 3.4 используются понятия г-окрестности и проко-
проколотой 8~окрестности:
Oe(yo) = {y = f{x)\\f(x) — yo\<iti}, Об(хо)=={х|0 < \х — хо\ •< б},
поэтому его и называют определением на языке «е — б» и\кратко
записывают так;	' ^
(/o=limf(x)^Ve>O 36>0:Vx6 0e(xo)=>KxN 08(y0)- \
Геометрическая интерпретация определения конечного предел^
функции по Коши дана на рис. 3.5. Из рисунка видно, что б&(хо)
отображается функцией в Ое(</о), т. е. любому х из проколотой б-окре-
стности точки хо соответствует значение f (x), попадающее в е-окрест-
ность точки i/o-
Определения предела функции в точке х0 по Гейне и по Коши
эквивалентны, т. е. число у<> — предел функции в точке х0 в смысле
определения по Гейне тогда и только тогда, когда i/o является пре-
пределом функции в смысле определения по Коши.
Пример 3.6. Доказать, пользуясь определением предела функции по Коши, что
lim х ~ - = 2.
Решение. Пусть е > 0. Найдем такое 6 = 6(е), чтобы для всех значений ж,
отличных от 1 и удовлетворяющих неравенству I*—1|<8, выполнялось нера-
неравенство | ?^ll _ 2 I < e.
х— 1
Так как
• 0 существует б = 6(е) (а именно: 6 = е), такое, что для всех х, удовлетворяющих
'• то для любого
условию 0 < \х — 11 < 6, будет выполняться неравенство
и следует, что lim
хг— 1
	—
* — 1
х2 — 1
—~j
I
2 < е, откуда
2.
71

Односторонние пределы функции. При рассмотрении конечного
предела функции при х-+хй предполагалось, что точка х, прибли-
приближаясь к хо, могла оставаться как слева, так и справа от нее.
Иногда приходится рассматривать предел функции f(x) при усло-
условии, что точка х, приближаясь к точке х0, остается либо правее, либо
левее ее.
Введем понятие левой и правой окрестностей точки х0.
Левой ^-окрестностью точки х0 (обозначается Ов(х0 — 0)) назы-
называется множество всех х, удовлетворяющих неравенству 0 ^ хо —
— х < б (рис. 3.6): О8(хо — 0) = {х 10 < х0 — х < 6}.
Правой Ь-окрестностью точки хо (обозначается Оь{хо + 0))
называется множество всех х, удовлетворяющих неравенству 0 ^
<х — хо<6 (см. рис. 3.6):Ов(хо + 0) = {д;|0<х —Хо<6).
Проколотые правая и левая б-окрестности получаются «выкалы-
«выкалыванием» из соответствующих б-окрестностей точки Хо, например
68(хо - 0) = {х 10 < хо - х < б).
Приведем определение конечных односторонних пределов функ-
функции в точке Хо на языке «е — б», используя понятие окрестности.
Определение 3.5. Число уо называется левым пределом
(левосторонним пределом или пределом слева) функции у = f(x)
в точке Хо, если для любого е >¦ 0 существует б = б(е) >• 0, такое, что
ИЛИ Uo — ПХп —
def
Обозначают предел слева lim /(*) =
X—*-Xq — О
, Аналогично определяется правый предел функции f(x) в точке х0.
/' Определение 3.6. Число Уо называется правым пределом
(правосторонним пределом или пределом справа) функции у =
= f(x) в точке хо, если для любого в > О существует б = б(е) > О,
такое, что Ух ? 6ь(х0 + 0)=>f(x) ? Ot(y0).
Предел справа функции в точке обозначают lim f(x) — y0
def
ИЛИ Un =
Замечание. Если в точке х0 функция \{х) имеет конечные правый и левый
пределы и они равны между собой, то это число является пределом фуикции в точке Хо:
Kft
2
1
г №)-
о
Рис. 3.6
1 г
Рис. 3.7
72

lim f(x) = lim f(x) = lim f (x).
X-*Xo	ДГ-оДГо — О	ДГ-+ДГО + 0
Пример 3.7. Найти односторонние пределы функции
/4V*6]-°o; 2],
V*6]2; «>[
в точке ха = 2 (рис. 3.7).
Решение. Вычислим:
FB — 0) = lim f(x)= lim (хг/4) = 1, fB + 0) = lim f(x)= lim x = 2.
дг—2-0	x—2-0	jc—2 + 0	*—2 + 0
Так как односторонние пределы существуют, но fB — 0) ф fB + 0), в точке
хо = 2 функция предела не имеет.
Конечный предел функции при х->-оо, х->- + оо и х-*—оо.
Дадим определение конечного предела функции на языке последо-
последовательностей.
Определение 3.7. Число уо называется пределом функции
y = f(x) при х->-оо, если для любой бесконечно большой последова-
последовательности (хп) значений аргумента, соответствующая последователь-
последовательность (f(xn)) значений функции сходится к у0:
X—*¦ оо	П—>¦ оо	П—*¦ оо
Определение 3.8. Число уо называется пределом функции
у = f(x) при х-*- + оо (х-*— оо), если для любой бесконечно большой
последовательности (хп) значений аргумента, элементы которой по-
положительны (отрицательны), соответствующая последовательность
(f(xn)) значений функции сходится к уо-
Пределы функции у = f(x) при х-*- + оо и х-»— оо обозначают
соответственно:
i/o= lim f{x) и t/o= lim f(x).
ДГ-» + оо	дг-». — оо
Например, пусть f(x) = —. Эта функция имеет предел при х-»-±оо, равный
нулю. Действительно, если (хя) — любая бесконечная последовательность значений
аргумента, то соответствующая последовательность значений функции (f(xn)) =
= (—, —, —, ...I является бесконечно малой, т. е. lim — =0.
Можно дать равносильные определения конечного предела функ-
функции при х->- оо, х->- -|- оо или х->— оо на языке «е — б». Например,
сформулируем определение конечного предела функции при х->- + оо.
Определение 3.9. Число уо называется пределом функции
y — f(x) при х->- + оо, если для любого в > 0 существует положи-
положительное число М, такое, что неравенство \f(x) — уо\ <е выполняется
для всех х, при которых х>М:
i/o= lim Дх)о Ve > 0 ЗМ > 0:Vx >М=И^(х) — t/ol < в.
Множество [х\х > М) = Ов(оо) называют Ь-окрестностью беско-
бесконечно удаленной точки.
Геометрически это означает, что график функции y = f(x) будет
73

находиться в полосе, ограниченной прямыми у = Уо — е, у = уо-\-в
при любом х > М (рис. 3.8).
Бесконечные пределы функции при х-+х0. Рассмотрим случай,
когда функция y = f(x) при х-+х0 по абсолютной величине неогра-
неограниченно возрастает. Такая функция не имеет конечного предела,
поэтому необходимо обобщить понятие предела функции.
Определение ЗЛО. Предел
функции y=f(x) при х-+хо назы-
называется бесконечным, если для лю-
любого положительного числа М су-
существует число б > 0, такое, что
для всех значений х, удовлетво-
удовлетворяющих неравенству О < | х —
— х01 < б, будет выполняться не-
неравенство \f(x)\ > М.
Если f(x) стремится к беско-
бесконечности при х-*-хо, то ее назы-
Р и с. 3.8	вают бесконечно большой функци-
функцией и пишут \imf(x)= оо:
limf(x)=
M.
Если f(x) стремится к бесконечности при х-+х0 и при этом прини-
принимает только положительные или только отрицательные значения,
пишут соответственно: \imf(x)= +00 или \imf(x)= —00.
На рис. 3.9 дана геометрическая интерпретация бесконечных
Рис. 3.9
пределов НтДх)=+оо, lim/:(x)= — 00 функции f(x) при х-+хй:
X-*-Xq	Х—*Хо
график функции f(x) расположен в полуплоскости у>М, если
\\mf(x)= +00 (рис. 3.9, а) и в полуплоскости у <. — М, если
limf(je)= —00 (рис. 3.9, б).
74

Определение бесконечного предела функции, приведенное выше,
дано на языке «е — б», т. е. по Коши. Запишем это же определение
на языке последовательностей.
Функция f(x) имеет бесконечный предел \\mf{x)= оо, если для
дг-Kto
любой сходящейся к хо последовательности (хп) значений аргумента
х соответствующая последовательность (f(xn)) значений функции
является бесконечно большой.
Бесконечный предел функции при х->~± оо. Существуют функ-
функции, обладающие следующим свойством: при неограниченном увели-
увеличении \х\ значения \f(x)\ также неограниченно возрастают.
Определение 3.11. Предел функции y = f{x) при х->- + оо
(или х->— оо) называется бесконечным, если для любого сколь
угодно большого числа М ? R найдется такое число N > О, что нера-
неравенство \f(x)\ > М выполняется для любого х, для которого \х\ > N:
N=>\f(x)\ > М.
М
Стремление функции к бесконечности при х-*- оо означает, что
график функции при Vх (\х\ > N) выходит за пределы полосы, огра-
ограниченной прямыми у = М и у = —М.
Геометрическая интерпретация бесконечного
предела функции /(.*) = *э при |х|-»-оо (Iimx3= оо)
даиа на рис. 3.10.	*-*°°
Замечание. Множество {х\х > jV} = Os(oo)
можно формально считать 6-окрестностью бесконечно
удаленной точки, множество \у\у> М}= Ое(оо) —
е-окрестностью бесконечно удаленной точки. Тогда
определение бесконечного предела функции при х-*-
-*¦ оо можно записать на языке «е — 6» (т. е. по
Коши), используя понятие окрестности:
lim f(x) = оо о Ve > 0 Яб > 0; V* € Ов(оо )=»-
,	,..- ¦.	¦ |/
-м
Р и с. 3.10
-N
Пример 3.8. Доказать, что
Решение. Чтобы получить f (х) > М доста-
достаточно принять 6 — х > М2. Тогда х < 6 — М1 и
M]	6М2[
N
3.3. БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ
Определение 3.12. Функция f(x) называется бесконечно малой
функцией (или бесконечно малой) при х~+хъ, если lim/:(jt) = 0.
х-«-дго
Аналогично определяются бесконечно малые функции при х-*- оо,
х->- + оо, х->—оо, х—*-хо — 0, х-*-Хо-\-О.
Определение 3.13. Функция f(x) называется бесконечно боль-
большой функцией (или бесконечно большой) при х-+х0, если lim/(jc) =
ДГ->-ДГо
	 ОО .
Приведем равносильные определения бесконечно малых функций
75

по Коши (на языке «е —б») и по Гейне (на языке последователь-
последовательностей) .
Определение 3.14. Функция f(x) называется бесконечно ма-
малой при х-*-хо, если для любого е > 0 существует б > 0, такое, что
для любого х(Е Oe(*o) \f{x)\ < e.
Определение 3.15. Функция f(x) называется бесконечно малой
при х-*-хо, если для любой сходящейся к хо последовательности
(хп) значений аргумента х, отличных от хо, соответствующая после-
последовательность (f(xn)) значений функции является бесконечно малой.
Бесконечно малые функции принято обозначать строчными бук-
буквами греческого алфавита а, р, у, ...
Например, функция f{x) = sinx при х->-0 является бесконечно малой, так как
lim sin jc = 0. Функция f(x)= l/х2 при х-*- оо является бесконечно малой, поскольку
дг-*О
lim 1/х2 = 0. Функция f(x)=l/x2 при х-*~0 — бесконечно большая, так как
JC-*-OO
lim 1/x2 = оо.
*->-0
Из приведенных примеров следует, что функция, имеющая одно и то же анали-
аналитическое выражение, при разных значениях хо может быть и бесконечно малой,
и бесконечно большой. Поэтому для задания функции необходимо указывать ее
область определения D(f).
Теорема 3.5. Если функция f(x) при х-+х0 — бесконечно большая,
то функция \/f(x) при х-*-х0— бесконечно малая.
Верно и такое утверждение: если функция f(x) при х-*-х0 —
бесконечно малая, то функция l/f(x)npux->-xa—бесконечно большая.
Например, функция f(x) = x* при х->-0 является бесконечно малой, а функция
	= —т- при x-t-О — бесконечно большой.
f(x) х*
3.4. ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ
Вычисление пределов значительно упрощается, если использо-
использовать теоремы о пределах суммы (разности), произведения и частного
сходящихся последовательностей.
Теорема 3.6. Если функции f(x) и g(x) в точке Хо имеют конечные
пределы, т. е. l\mf(x) = a, lim g{x) = b, то:
1)	\im(f(x)±g(x)) = a±b;
2)	lim(f(x)g(x)) = ab;
В теореме 3.6 пп. 1,2 верны для любого конечного числа слагае-
слагаемых и сомножителей, а именно:
1)	Hm(f1{x)±...±fn{x))=\imfl(x)±...±\imfn(x);
X-*Xq	Х-+Хй	Х-*-Хо
2)	Hm(fl(x)-fn(x))=\imfl(x)-\imfn(x).
Х-+Хо	Х-*-Хо	JC-KCO
76

Непосредственно из последнего равенства следуют правила на-
нахождения пределов натуральной степени функции и корня. Если
limf(x)=a", то
\im(f(x))n = an, /16N,
lim"vf(x) = -\/a (a>0, n — четное).
В табл. 3.1 даны соотношения пределов суммы, произведения и
частного двух функций f(x) и g(x), распространенные на случай
бесконечного предела функции.
Таблица 3.1
lim ЦХ)
х-**.
а
а
оо
0
0
оо
+ ОО
— оо
+ ОО
— оо
lim g(x)
Jt-*xo
b
оо
b
0
оо
0
+ OO
— оо
— оо
+ ОО
limCfW + gW)
x-*xt
a + b
оо
ч ОО
0
оо
оо
+ ОО
— оо
Неопределен-
Неопределенность оо — оо
Неопределен-
Неопределенность оо — оо
lim f(x)g(x)
х-~х.
ab
оо (а=И=0)
оо (ЬфО)
0
Неопределен-
Неопределенность 0 • оо
Неопределен-
Неопределенность оо • 0
+ ОО
+ ОО
— оо
— оо
0
оо
Неопределен-
0
НОСТЬ -jr
0
оо
Неопределен-
оо
НОСТЬ
оо
Неопределен-
оо
иость —
оо
Неопределеи-
оо
НОСТЬ
оо
Неопределен-
оо
НОСТЬ
оо
Итак, предел суммы, произведения или частного двух функций
равен соответственно сумме, произведению или частному пределов
этих функций, если функции имеют конечные пределы (в случае
частного предел знаменателя не равен нулю). Во всех остальных
случаях арифметические операции над пределами функций дают О,
77

оо или неопределенность. Если вычисление пределов приводит к не-
неопределенным выражениям вида оо — оо, О- оо,-2-,_°?., необходимо
О оо
провести дополнительные исследования, т. е. «раскрывать неопреде-
неопределенности» (методика раскрытия неопределенностей изложена в § 3.7).
Теорема 3.7. Если функция f(x) при х-+хо имеет конечный пре-
предел уо, то f(x) — t/o — бесконечно малая функция при х-+х0.
\> По условию теоремы существует lim f(x) = y0. Рассмотрим
функцию f(x) — уо. Вычислим
lim (/(*) — уо) = lim f(x) — lim y0 = Уо — Уо — 0.
х-*-Ха	х-+ха	х-*хо
Следовательно, функция f(x) — уо — бесконечно малая при
х-+х0. <\
Следствие. Если при х-+х0 функция f{x) имеет конечный пре-
предел, то в $б(*о) она представима в виде f(x) = yo-\-a(x), где а(х) —
бесконечно малая функция при х-*-хо-
Теорема 3.8 (о сравнении функций). Если в Ов(хо) справедливо
функциональное неравенство f(x) ^ ц>(х) и существуют конечные
пределы lim f(x), lim q>(x), то lim f(x) < lim
X	X
Теорема З.9. Если в Об(х0) справедливы функциональные не-
неравенства г|)(х)^ f(x)^i ф(х) и существует limip(jc)= \imq>(x) = yo,
Х^-Хп	Х^-Хп
г/обК, то существует \imf(x) = yo.
X--X0
\> По условию теоремы ^(х) ^ f(x) ^ <р(х). Согласно теореме 3.8,
lim t(jc) < lim f(x) < lim w(x)
дг-»дг0	x-*Xo	x-*xo
ИЛИ
уо < lim f(x) < yo=> lim f(x) = y0. <\
Теорема 3.10. Если в окрестности точки Хо задана сложная функ-
функция y = f(u(x)) и существуют пределы lim«(x) = «0 (и(х)Ф0 при
Х-+Х0
х Ф х0), lim Дм) = уо, то существует предел сложной функции у =
= f(u(x)) Сточке хо и
lim f(u(x))= lim f (и).
X-*Xo	U-*-Uo	,
Пример 3.9. Найти lim sin (x1 + я/2).
*->-o
Решение. Так как данная функция — сложная, ее можно представить в виде
f (ф М)= s'n ". гДе и —х2 -{- я/2. Тогда
lim и = lim (х2 + я/2) = я/2=>- lim sir^x2 + л/2) = lim sin и = 1.
0	О	/2
дг->-дго
3.5. ПЕРВЫЙ И ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ
Первый замечательный предел. Докажем, что lim 52?_f = i. Так
*->-о *
как f(x) = ^-^ является четной функцией, рассмотрим ее только на
78

интервале ]0; л/2[. Возьмем дугу AM единичного круга, соответст-
соответствующую углу, радианная мера которого равна х (рис. 3.11). Тогда
|ОЛ| = 1, \МР\ = sin х, \ОР\ =cosx. Площадь сектора О AM за-
заключена между площадями треугольников ОМА и ОТ А:
^	±±	)АТ\.
Так как \0A\~
= tg X, ТО
sin x<x<
„ 1
\РМ| = sin x, \АТ\ =
cos*
O-COS X <.
sin х
sin x
1.
sin*
В силу четности функций cos x и
л
последнее двойное неравенство справед-
справедливо и для интервала ]—я/2; 0[.
Таким образом, для любого х ? ] — я/2;
0[ U ]0; я/2[ выполняется неравенство
Sln х <с 1. Другими словами, при
Рнс. 3.11
cos х
х-*-0 предел отношения -
Согласно теореме 3,9,
заключен между 1 и limcosjc=l.
m
.-0 X
Его называют первым замечательным пределом. Этот предел исполь-
используют для раскрытия некоторых неопределенностей вида -j-.
Пример 3.10. Вычислить пределы:
0 X
; 2)
; 3) lim
дг-0
Решение. Применим первый замечательный предел. Имеем:
.... tg х sin х ..
1) hm-S—= lim	lim
0 X
1
О X
sin Ъх
_>о х ,_*о cos л:
sin Ъх 2х
-=1;
2)	lim . -h-
> ^о tg2x
3)	,im tgx-sin^ = |im (tzx_ J^cosx
2x ^\ _ J>_
tg 2x 2 / ~~ 2 '
x3	*-o\ *	*2 / " 2 2
Второй замечательный предел. В § 3.1 было определено число е
\-\—) = е, n?N. В общем
случае это число можно определить как предел функции f(x) =
= ('1+4-^ при х-^оо:
79

lim
X-*-oo
Это и есть второй замечательный предел.
/ 1 \х	1
Если в равенстве lim( 1 -\—) =е положить — = t, то при х->-
ДГ-ЮО\	*/	*
-v оо f->-0. Тогда получим другую форму записи второго замеча-
замечательного предела
Второй замечательный предел применяется для раскрытия не-
неопределенностей вида 1°°.
Пример 3.11. Найти lim А -\	) .
ДГ-» СХ>\	X /
Решение. При х-*- оо получаем неопределенность вида 1°°. Имеем
Пример 3.12. Найти lim ( * ) .
X-+ оо \ X — О /
Решение. Разделив числитель и знаменатель на х, получим
.. /х + 2\' ,. {X+2/xf	е2 .
lim | —¦—1 = lim —i—¦—'—!-	=	г = еь.
х-Ъ) х-» (l+(-3/x)Y е-3
3.6. СВОЙСТВА БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ.
СРАВНЕНИЕ АСИМПТОТИЧЕСКОГО ПОВЕДЕНИЯ ФУНКЦИЙ
Свойства бесконечно малых функций. Приведем ряд теорем, ис-
используемых при сравнении бесконечно малых функций.
Теорема 3.11. Конечная сумма бесконечно малых функций в
6б(хо) есть функция, бесконечно малая в 6{,(х0).
\> Если а,(х), <= 1, п,— бесконечно малые функции в 6б(*о), то
п
limai(x) = 0, t'=l, п. Так как lim 2 a;(jc)= 2 limaj(jc) = 0, то
конечная сумма бесконечно малых функций есть функция беско-
бесконечно малая. <]
Теорема 3.12. Произведение бесконечно малой функции и функ-
функции, ограниченной в Ов(*о), есть бесконечно малая функция.
\> Пусть ц>(х) ограничена в Об(*о), т. е.
ЗМ >0: Ух
а а(х) — бесконечно малая функция в Об(*о)- Тогда
Ve/M>0 Зб,>0:?л;6О8,Ы^|а(л;)|<Е/М.
Возьмем 6 = minF, 61), тогда |a(x)|<e/M и |ф(х)| < М V
g 6б(хо). Рассмотрим произведение а(х)ф(х) в д6(хо):
80

\
±
т. ё. a(x)q>(x) — бесконечно малая функция. <1
Следствие 1. Произведение некоторого числа и бесконечно
малой функции в 6ь(хо) есть бесконечно малая функция.
Следствие 2. Произведение двух бесконечно малых функций
в Оь(хо) есть бесконечно малая функция.
Теорема 3.13. Частное от деления бесконечно малой функции
а(х) в Оь{хо) на функцию ц>(х), такую, что lim ц>(х) Ф О, есть беско-
jc-»-Xo
нечно малая функция.
\> Так как а(х) — бесконечно малая функция, то lim a(x) =
Х-+-Хо
= 0. Рассмотрим a(x)/(f(x), тогда
, .	lim a(x)
цтИ®.= ~»	о	о
х_^0 <р(х)	lim <f(x) lira «p(jc)
x-+-Xq	x-*-Xa
и а(х)/ц>(х) — бесконечно малая функция. <1
Сравнение асимптотического поведения функций. Под асимпто-
асимптотикой, или асимптотическим поведением функции в окрестности
некоторой точки х06 R, понимают описание поведения функции
вблизи точки хо, в которой функция, как правило, не определена.
Асимптотическое поведение функции обычно характеризуют с
помощью другой, более простой или более изученной функции, ко-
которая в окрестности исследуемой точки с малой относительной
погрешностью воспроизводит значения изучаемой функции.
Определение 3.16. Если а(х), $(х) — бесконечно малые функ-
функции и
то они называются бесконечно малыми одного порядка малости.
Для таких функций принято обозначение а(х) = O(fi(x)). Запись
а(х)^0(\) означает, что функция а(х) при х-*-хо ограничена, т. е.
0A) — множество ограниченных функций при х^»хо.
Если а(х), Р(х) — бесконечно большие функции и lim-^^ =
= с Ф 0, то они называются бесконечно большими одного порядка
роста при x-*-xq.
Например, функции а(х) = sin Зх, р(*) = 2х при *->-0 имеют одинаковый порядок
малости, так как
lira Si* ' lim 3si* 	 3 /0
"Го 2x ~ 2 П> З* ~ 2 ^U>
т. e. 2x = O(sin Зх) и sin Зх = О(х) при *->-0.
Определение 3.17. Если функции а(х), $(х)—бесконечно
малые и
81

то они называются эквивалентными при x-vxo.
Функции а(х) и Э(л;), эквивалентные при х^х0, называют также
асимптотически равными при x^-xq. Асимптотическое равенство
(эквивалентность) функций обозначается символом ~ или «:
а{х)~${х) или а(х)ш$(х) при х->хо.
Например, sin x ~ х при х-»-0, так как lim	= 1.
Если функция а(х) такова, что lima(x) = 0, то при х-*-хо спра-
Х-*Хо
ведливы следующие асимптотические равенства:
+
sin
arcsin
a{x)
In
~
T
A
a(x),
a(x),
tg a(x) <-
arctga(
"Y 1 +«(.
- a(x),
n v />
Теорема 3.14. Предел отношения двух бесконечно малых функ-
функций равен пределу отношения эквивалентных им функций, т. е. если
при x-vxo а(х)~ ai(x), Э(х)~ Pi(x), го
I> Запишем
a(x) ^ a(x)
Переходя в этом равенстве к пределу при х->хо и учитывая, что
Hm-^to^l, limi&. = l, находим
Теорема 3.14 используется при вычислении пределов, так как
каждую бесконечно малую (или только одну) можно заменить беско-
бесконечно малой, ей эквивалентной.
Пример 3.13. Найти lim
lim
sin 2x
Решение. Так как sin 2x ~ 2x при x->-0 + 0, то
sin 2x .. 2x .. . /-
	—— = lim —— = lim 2-v/x = (
Пример 3.14. Найти lim
2
	^—.
tgD —JC2)
82

Решение. При х-+2 tgD — х2) ~ 4 — дс2. Тогда
.: х —5* + 6 ,. х2 — 5х + & .. (х — 2)(х — 3)	.. (х — Э)
hm	-г— = lim	j— = lim -	^——- = — lim -
tD 2)	42	42
	-г— = lim	j— = lim -	^——- = — lim -	 = —.
tgD — x2) x+2 4-х2	х-»2 4-х2	*^2B + х) 4
Определение 3.18. Если функции а(х), Р(х)— бесконечно
е
малые и
то говорят, что а(х) является бесконечно малой функцией более вы-
высокого порядка по сравнению с функцией р(х).	^
В этом случае пишут: а(х) = о(Р(дс)). Запись а(х)^оA) при х^х0
означает, что функция а(х) является бесконечно малой при х-*-хо,
т. е. оA) — множество бесконечно малых функций при x-*-xq.
Если функции а(х) и р(х) при х^>~хо— бесконечно малые и а(х) =
= o(P(x)) при х-+х0, то а(х) является бесконечно малой более высо-
высокого порядка, чем р(х).
Например, функция а(х) = х5 при х-»-0 является бесконечно малой более вы-
высокого порядка, чем р(лс) = sin jc3, т. е. х5 = o(sin x3), так как
Х
lira	5" *= l'm
i j
sin
Определение 3.19. Если функции а(х), р(х) — бесконечно
малые и
х-+х, (P(JC))*
то а(х) называется функцией k-го порядка малости по сравнению
с Р(х).
В частности, если а(х), р(х) — эквивалентные бесконечно малые
функции при х-^-хо, то а(х) — функция fe-ro порядка малости по
сравнению с р(х).
Если а(х), р(х) — бесконечно большие функции при х^*~х<> и
lim a^t = с Ф 0, k > 0, то а(х) — функция k-го порядка роста по
*-**а (Р(*))
сравнению с
Пример 3.15. Доказать, что а(х) — р(х) имеет второй порядок малости по срав-
4
нению с х при jc->-0, если a(jc)= -^——, р(дс) = 2 — х.
х2
Решение. Найдем а(х) — р(лт) = -^-т—. Имеем
Z-\- х
lim —w , w = lim
x-0 x2	x-»q
Пример 3.16. Определить порядок роста бесконечно большой функции /(*) =
= х3 + 12х + 3 относительно х при х-»- оо.
Решение. Так кал
.. /, , 12 , 3\ .
= hm ( 1 +_ + _)= 1,
X	X /
83

то порядок роста f(x) по сравнению с х при х-»- оо равен 3.
Соотношения вида
о(х) = 0(Р(х)), о(х) = о(Э(х)), а(х)~Э(х) при х^хо
называют асимптотическими оценками.
3.7. ОСНОВНЫЕ ПРИЕМЫ РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТЕЙ
Раскрытие неопределенности вида — Неопределенное выра-
выражение вида — получаем при нахождении \imf(x), xo?D(f), если f(x)
является дробью, числитель и знаменатель которой содержит мно-
множители (х — хо)а, а 6 R. Основная трудность раскрытия неопреде-
неопределенности в этом случае состоит в выделении множителей вида (х —
— хо)а в числителе и знаменателе дроби. Затем преобразуем дробь
и получаем f(x) = (x — xo)afi(x), a ? R, причем xo^D(fi). Тогда
{О, если а > О,
fi(xo), если а = 0,
оо, если а<0.
Способы выделения множителей числителя и знаменателя дроби
зависят от вида f(x).
1. Пусть f(x) — рациональная дробь. В этом случае числитель и
знаменатель дроби разлагают на множители.
Пример 3.17. Найти пределы:
х* + хз	х* + Зх + 2 „. ,. х*-\
) ira-7—-—-; 2) lim —^	¦—; 3) lim	-.
' ох3 + 2хг	2 2х* + х6	i(xlJ
Решение. 1. lim *(*+') =цтх±±1-=о.
2( + 2) х-*о х + 2
2. lim 1 + Ь±1_= lira _J?+2MfL+ii_ = „га
2^+6	2{ + 2)(Ъ/2)
+ 2)(х-Ъ/2) х-»-2 2{х — 3/2)
. .. лс2 — I	(х-1)(дс+1) ..
3. hm	—- = lim -i—¦—'-±—i—'- = lira ¦
2. Пусть f(x) — дробь, содержащая иррациональные выражения.
В этом случае выделение множителей вида (х — хо)а достигается
переводом иррациональностеи в числитель или знаменатель, а также
заменой переменной на новую переменную.
Пример 3.18. Найти пределы:
X~l
1) lira ХЧ1~Х ¦ 2)
о+о ^
Решение. 1. lim —^-==—= lim sfx^jl —x — Q.
.r-*0+0 -Jx	хЦ) + 0
84

2. „m
= —4. Можно найти этот предел и с помощью замены переменной. Обозна-
Обозначим х + 4 = /2, тогда
lim	—=
**° 2 - У*+ 4
= lira
.. B-0B + 0
= — lira -i	 м , ' = —4.
(_^2 2 — t
L^i_=limM-
3. li
3. Пусть f (x) — дробь, содержащая тригонометрические функции.
Для раскрытия неопределенности в этом случае используют первый
замечательный предел или эквивалентные бесконечно малые функ-
функции.
Пример 3.19. Найти пределы:
.. .. tg2 Зх n ,. sin2 jc + х*	,. 1—cos x
1) lim —	; 2) lira	?	; 3) lim	=	.
(->о 2х	x^o 5xJ	x^o jc
Решение. 1. lim
	^
lim -
2. hm
3. lim
5x2
1 — COS X
\tg23x~Cxf
4 I .. / sin x sin x , Д 1
- = -=- lim (	 +jcz )==-=-.
2*
.. 9x
= hm -^-:
lim
2sin2(x/2)
= lira —-r- = lim — = oo.
Раскрытие неопределенности вида —. Неопределенное выражение
вида — получается при нахождении lim f (х), х0 <? D(f), в основном
в тех случаях, когда предельное значение аргумента является беско-
бесконечным, a f(x) — рациональная дробь или дробь, содержащая ирра-
ирра. /Если хб R то ^ преобразуют в
циональности. /Если хоб R, то ^ преобразуют в -^-Л
Выделением множителей ха, а 6 R, в числителе и хр, р ? R, в зна-
знаменателе и последующим их сокращением приводим функцию к виду
/(x) = x°-p/i(x), причем xoeD{ft). Тогда
НтД*)== limxa-(ifl(x) =
X-*-Xo	JC-t-JCo
1. Пусть f(x) — рациональная дробь вида
!0, если а < P,
fi{x0), если a = p,
оо, если a > p.
Преобразуем эту дробь к виду
85

Находим
), если п<Ст,
1
х-*ао	Li0!.	i От	\°0
limf(x) = Hmxn-m	?	?_={« если п = т, C.1)
. , frl ,	, frm	I fro	Ч	'
froH	Г---+— I oo, если « > m.
Пример 3.20. Найти пределы:
,. .. 2* + 3* + 4 о, ,. 4х + 5* + 3 ,. ,.
1) lim —г—!	!	; 2) lim 	г-!	¦	; 3) hm
Решение. Для нахождения пределов используем формулу C.1). Тогда:
1) п = 3, m = 5, n<m=s- lim * 	i—=-0;
Х5 + 6х + 7
2)	п = т = 3=*- lim 	т-1	!	= —;
;	х-*» 7х3 + &х + 1 7
3)	п = 4, т = 2, п > т =*- lim 	!	!
г + 1
2. Пусть f(x) — дробь, содержащая иррациональности. Тогда,
как и в п. 1, в числителе и знаменателе дроби выделяются множители
ха, х^, где а, Э — максимально возможные показатели степеней
(а, Э 6 Q)- Затем производится сокращение дроби на ху (у = min(a, Э)).
Пример 3.21. Найти предел lim
Решение. Имеем
х	х	,
= •
Раскрытие неопределенности вида 0- оо. Неопределенное выра-
выражение вида 0- оо сводится к неопределенности вида -^ или ^.
Методику раскрытия этой неопределенности покажем на примере.
Пример 3.22. Найти предел lim -5- (tg x + 2х\
Х-+0ХГ
Решение. Непосредствеииая подстановка предельного значения х = 0 пряводит
к неопределенности вида оо • 0. Преобразовав данное выражение, получим неопреде-
0
леииость вида —:
x-+0
86

Раскрытие неопределенности вида <х> — с». Неопределенное вы-
выражение вида оо — оо преобразуется к неопределенности вида -^
оо
ИЛИ — .
оо
Пример 3.23. Вычислить lim (-у^2 — 2х — I — л/х2 — 7х + 3).
X-t-± оо
Решение. Непосредственная подстановка предельного значения аргумента
х = ± ж» приводит к неопределенности вида оо — оо. Выполним следующее пре-
преобразование:
lim (V*2-2x-l - V*2-7x + 3)= lim
oo
Получили неопределенность вида —. Раскроем ее, разделив все члены получен-
полученного выражения на х. Имеем:
*-*+ °°Vl -2А-1
lira	5-4/х,	-A V*<0.
-*-°° — -Jl-2/x-l/x2 — Vl— 7/х	г
Раскрытие неопределенности вида 1°°. Неопределенное выраже-
выражение вида 1°° получаем при вычислении пределов
если Итф(х)= 1, а Нтг|)(х)= оо. В этом случае для раскрытия не-
Jt->-JCo	Х^-Ха
определенности применяют второй замечательный предел, полагая
ф(х)= 1 +a(x) и преобразуя выражение к виду
lim (<р(х))*М = lim ((A + ф)) '/«(«))»(*)¦(*) =
Приходим к неопределенности вида О* оо, о раскрытии которой го-
говорилось выше.
Пример 3.24. Найти пределы:
1) lim(l+sinxI/jr; 2) lim(l+—Y.
-r-О	х-°о\	*/
Решение. 1. Так как lim (I -f- sin x)= I, lira— = оо, имеем неопределен-
неопределенность вида 1". Для ее раскрытия воспользуемся указанной методикой:
sinjc ijm sinx
lim((l+sinxI/sinx) x = e*-° * =e,
.. sin x
так как lim	= 1.
2. Поскольку Hm(lH	) == 1, limjc=oo, имеем неопределенность вида 1".
jr-t- оо \	X /	x-+ оо
87

Следовательно,
В данном параграфе было рассмотрено раскрытие неопределен-
неопределенностей вида -уг, —, 0- с», 1°°, с» — с». Для раскрытия неопределен-
ностей вида 0°, <х>° целесообразнее использовать правило Лопиталя
(см. §5.15).

4. НЕПРЕРЫВНЫЕ ФУНКЦИИ
4.1. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ
И НА МНОЖЕСТВЕ
Интуитивное представление о непрерывной функции обычно свя-
связывают с такой функцией, график которой — непрерывная линия.
Определение 4.1. Функция у = /(х) называется непрерывной
в точке Хо, если выполняются следующие три условия:
1)	функция y = f(x) определена в точке хо, т. е. xo?D(f);
2)	существует lim f(x);
3) \imf(x) = f(x0).
Если в точке хо нарушено хотя бы одно из условий 1—3, то функ-
функция называется разрывной в точке хо, а точка х0 — точкой разрыва.
Если воспользоваться определением предела функции в точке по
Коши, то можно дать эквивалентное определение непрерывной функ-
функции в точке Хо на языке «е — б».
Определение 4.2. Функция f(x) называется непрерывной в
точке Хо, если для любого заданного числа е > 0 можно найти такое
число 6>0 (зависящее от е и х0), что для всех х, для которых
\х — хо\<СЬ, будет выполняться неравенство \f(x) — /(*оI <е, или
в более краткой записи:
f(x) непрерывна в точке
36>0:Vx U-x
Так как х — хо = Ах— приращение аргумента, a f(x) — f(xo) =
= Ay — приращение функции в точке хо, то определение 4.2 можно
сформулировать следующим образом: функция f(x) непрерывна в
точке хо, если V б> О Н б> 0: |Ддс| <6=НАу| <е, т. е. Ду->-0 при
Ax-vO. Таким образом, получаем еще одно определение непрерыв-
непрерывности.
Определение 4.3. Функция f(x) называется непрерывной в
точке хо, если бесконечно малому приращению аргумента Ах со-
соответствует бесконечно малое приращение функции Ду, т. е. lim Ay =
= 0.
В некоторых случаях приходится пользоваться понятием одно-
односторонней непрерывности.
Определение 4.4. Функция f(x), определенная в некоторой
левой (правой) окрестности точки хо, называется непрерывной слева
(справа) в точке хо, если существует предел слева (справа) функ-
функции y = f(x) и он равен f(x0).
Другими словами,
89

f(x) непрерывна справа в точке xqO 3 lim f(x) = f(xo),
х-кго + О
f(x) непрерывна слева в точке хо*&- 3 lim f(x) = f(xo).
Из определения односторонней непрерывности в точке хо следует,
что функция f(x), определенная в некоторой б-окрестности точки хо,
непрерывна в точке хо тогда и только тогда, когда она непрерывна
в этой точке слева и справа.
Определение 4.5. Функция f(x), непрерывная во всех точках
некоторого множества X, называется непрерывной на этом мно-
множестве.
Если X = [а; Ь], то для непрерывности функции на [а; Ь] требуется,
чтобы f(x) была непрерывна во всех внутренних точках отрезка,
непрерывна справа на левом его конце, т. е. в точке а, и непрерывна
слева на правом его конце, т. е. в точке Ь.
4.2. ТОЧКИ РАЗРЫВА ФУНКЦИИ И ИХ КЛАССИФИКАЦИЯ
Если хотя бы одно из условий определения 4.1 не выполнено,
то точка хо является точкой разрыва. Различают следующие случаи:
1)	если условие 2 определения 4.1 выполнено и при этом хо?
? D(f) или lim f(x) Ф f{x0), то точка х0 называется точкой устранимого
Х-+-ХО
разрыва;
2)	если условие 2 определения 4.1 нарушено, т. е. не существует
lim f(x), но при этом существуют два конечных односторонних предела
Х-+Хо
lim f(x) = f(x0 — 0), lim f{x) = f(xo-{-0), не равные друг другу, то точ-
точка хо называется точкой разрыва первого рода, а разность f(xo + 0)—
—	f(xo — 0) — скачком функции f(x) в точке хо\
3)	если хотя бы один из односторонних пределов равен + <х> или
—	оо или вообще не существует, то точка хо называется точкой раз-
разрыва второго рода.
Таким образом, при исследовании функции на непрерывность
необходимо проверить выполнение условий определения 4.1. Если
хо — точка разрыва, то для установления характера разрыва не-
необходимо вычислить односторонние пределы.
Пример 4.1. Исследовать на непрерывность функцию \{х)=	.
Решение. Область определения данной функции D(f)= R\{0). Следовательно,
jco = 0 — точка разрыва. Выясним характер этой точки разрыва. Так как
,. sin х , , sin x ,	„> _,..	.	.
lim 	= 1, lim 	=1 и xo — OtD(f), то точка хо = 0 является точкой
х-*0—о х	х-*0+0 х
устранимого разрыва. График этой функции дан на рис. 4.1.
Функцию f(x) =	можно доопределить в точке хо = 0 таким образом, чтобы
она была непрерывной на R. Другими словами, если положить
/(*) = (
1, х = (
90

Рис. 4.1
то f(x) будет непрерывна в точке х0 = 0 и на множестве R.
Пример 4.2. Исследовать на непрерывность функцию f(x) =
1
х-\
Решение. Область определения данной функции D(f) = {х\ х— 1 Ф 0) =
= R\(l). Следовательно, хо = 1 — точка разрыва. Выясним характер точки разрыва.
Имеем
1
lim
:_l_0 X— 1
= — оо, lim
1
l+o х— 1
Следовательно, хо = 1 — точка разрыва второго рода. График этой функции
изображен на рис. 4.2.
Рис. 4.2
Пример 4.3. Исследовать на непрерывность функцию
( —х V
/	2
Рис. 4.3
= *2 + 1 V
VO1.
1,
Решение. Область определения этой функции D(f) = R. Функция f(x) является
составной. Составляющие ее функции непрерывны на R. Поскольку функция зада-
задается различными выражениями, то проверить на непрерывность надо точки «стыка»,
т. е. х\ =0, хг = 1. Именно в этих точках может нарушаться непрерывность иссле-
исследуемой функции.
Исследуем точку х\ =0. Здесь f@) = 0. Вычислим
lim /
дг-^О — 0
= lim (—*) = 0,
дг-^О—0
lim f(x)= lim (x2+l)=l.
й) + 0	О + 0
Так как lim f(x), lim f(x) существуют, конечны, но lim Нх)Ф lim fix),
ж—0-0	ж—0 + 0	х^- 0-0	х-* 0 + 0
то х\ = 0 — точка разрыва первого рода. В этой точке функция имеет скачок:
lim f{x)- lim f(x)= 1-0=1.
0 + 0	00
91

Исследуем точку х%
1. Имеем f(l)= 1. Кроме того,
о aiim fix
lim f(x)= lim
->1— 0	*->!— О
lim f(je)= lim 2 = 2
->1+0	ж-П+0
}
В точке хг = 1 функция непрерывна.
Итак, f(x) разрывна в точке Х\ = 0 (х\ 6 />(/)). График этой функции приведен на
рнс. 4.3.
Пример 4.4. Исследовать на непрерывность функцию Дл:) = 91/<2~*) в точках
х, =0, х2 = 2.
Решение. Область определения данной функции D(f) = R\B). Исследуем точку
х,=0:
lim F
-*о—о
lim f
-.-O+O
2	Г-	\
)=g'/2=3;U
Значит, в точке xt=0 f(x) непрерывна. Рассмотрим теперь точку х2 = 2? D(f).
Так как функция не определена в этой точке, то хг = 2 — точка разрыва функции.
Исследуем характер разрыва:
lim f(x)= lim 91/B-° = 9+~ = оо,
ж-*2 — 0	*-*2 — 0
lim /(*)= lim д'Л2-*) = д-~ =0.
Поскольку одни нз односторонних пределов равен бесконечности, то х? = 2 — точка
разрыва второго рода. Схематический график поведения функции в окрестности
точки разрыва х% = 2 дан на рнс. 4.4.
Пример 4.5. Исследовать на непрерывность функцию
!sin —
х=0.
Решение. Область определения данной функции D(f)= R. Докажем, исполь-
используя определение предела по Гейне, что в точке «стыка> х = 0 lim f(x) не существует.
ж-«-о
Для этого построим две последовательности значений аргумента:
_2	2_	2	_2_ 2	2
5я ' 9л	 яA +4я) ' " " 7п ' Пл	 пC + 4п) ' "'
Обе последовательности сходятся к числу 0. Запишем последовательностя значений
У*
3
2
1
0
1
А
\
1
¦ к**^	»
1 \Z 3 х
1
1
Рнс. 4.4
92

функции sin(l/j:), соответствующие построенным последовательностям аргумента:
1, 1	 1, ... н —1	 —1, ...
Пределами этих последовательностей будут числа 1 н — 1 соответственно. Таким
образом, построены две последовательности значений аргумента функции f(x) =
= sin (I /jc), такие, что соответствующие последовательности значений дайной функции
имеют различные пределы. Следовательно, функция sinA /jc) при х-*-0 не имеет пре-
предела. Согласно классификации точек разрыва, х = 0 — точка разрыва второго рода.
График функции изображен на рнс. 4.5.
4.3. ДЕЙСТВИЯ НАД НЕПРЕРЫВНЫМИ ФУНКЦИЯМИ.
НЕПРЕРЫВНОСТЬ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Сформулируем теоремы о непрерывности функций, полученных в
результате арифметических действий над непрерывными функциями,
а также их композиции.
Доказательства этих теорем однотипны и основываются на опре-
определении непрерывности функции в точке.
Теорема 4.1. Если функции f(x) и g(x) непрерывны в точке х0, то
и функции f(x) ± g(x), f(x)g(x) непрерывны в точке х0. Если, кроме
того, g(x0) Ф 0, то функция f(x)/g(x) является также непрерывной
в точке х0.
>	Докажем, например, непрерывность функции f(x)g(x) в точке
х0. Из непрерывности функций f(x) и g(x) в точке х0 следует, что
\imf(x) = f(x0), \img(x) = g(x0). Тогда
Х~*-Хо	Х~*-Хо
lim f(x)g{x) = lim f(x) lim g(x) = f(xo)g(xo),
x~*-xo	x~+xo	x~+xo
т. е. функция f(x)g(x) непрерывна в точке х0. Аналогично доказы-
доказываются другие утверждения теоремы. <
Теорему 4.1 можно обобщить на случай конечного числа функ-
функций: алгебраическая сумма и произведение конечного числа функций,
непрерывных в точке хо, непрырывны в точке х0.
Следствиями теоремы 4.1 являются также теоремы 4.2 и 4.3.
Теорема 4.2. Многочлен Рп(х) = а0 + atx +... + апх", ak 6 R,
k = О, п, является функцией, непрерывной для любого x?R.
Теорема 4.3. Всякая рациональная функция P(x)/Q(x) непре-
непрерывна в любой точке л:6 R, для которой Q(x)^0, где Р(х), Q(x) —
многочлены.
Сформулируем теорему о непрырывности сложной функции.
Теорема 4.4. Сложная функция, являющаяся композицией ко-
конечного числа непрерывных в точке хо функций, непрерывна в
точке Хо.
>	Докажем эту теорему для случая, когда сложная функция
является композицией двух непрерывных в точке лг0 функций / и ср.
Пусть у = 1(и), м = ф(л:), тогда по определению сложной функции
у = f°yoy = /(Ф(л;)) = F(x).
Теорема утверждает, что если функция у(х) непрерывна в точке
хо, а функция f(u) непрерывна в точке м0, то сложная функция F(x)
непрерывна в точке х0.
93

Действительно, пусть х-*-х0. Тогда из непрерывности функции
ф(*) следует, что lim ф(лг) = ф(хо) = мо, т. е. что ы->ы0. Поскольку
Х~+Ха
f(u) непрерывна в точке и0, то lim f(u) = f(u0). Но так как и = ц>(х),
то последнее равенство можно записать в виде
ИЛИ
lim F(x) = F(x0). <
Х—-ХВ
Из определения 4.1 непрерывной функции в точке х0 и теоремы
4.4 следует, что
или в частном случае
т. е. символы предела и непрерывной функции перестановочны.
Приведем без доказательства теорему о непрерывности обратной
функции.
Теорема 4.5. Пусть функция y = f(x) определена, непрерывна и
монотонна на некотором множестве X и пусть Y — множество ее
значений. Тогда на множестве Y обратная функция х = f~' (у) моно-
монотонна и непрерывна.
Теорема 4.6. Основные элементарные функции непрерывны во
всех точках, принадлежащих их области определения.
> Приведем доказательство только для тригонометрических
и показательной функций. Будем исходить из определения 4.3 не-
непрерывности функции в точке х0. Для функции у = sin x
lim Ay = lim(sin(je0 + Ах) — sin *0) = 0.
Для функции у = cos х
lim Аи = lim (cos(je0 -4- Ах) — cos лг0) = 0.
д*—о д*-о
Отсюда, на основании теоремы 4.1, следует, что соответствующие
частные функций sin* и cos* являются непрерывными функциями
в своих естественных областях определения: функция tgx непре-
непрерывна на множестве R, за исключением точек Xk = я/2 + kn, &?Z:
функция ctgx непрерывна на множестве R, за исключением точек
xk = kn, k?Z.
Для показательной функции у = а* (а>0, аф\) имеем
lim Ay = lim (ax'+Ax — ах°) = a" lim аЛж — а" = 0.
А0	&X-+0	Длг-И)
Непрерывность логарифмической функции и обратных тригоно-
тригонометрических функций следует из теоремы 4.5 о непрерывности об-
обратной функции. <
Так как основные элементарные функции, согласно теореме 4.6,
94

непрерывны на своих естественных областях определения D(f), то
из теорем 4.1 —4.6 следует, что всякая элементарная функция не-
непрерывна во всех точках, принадлежащих ее естественной области
определения.
4.4. СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ
Приведем несколько теорем, характеризующих свойства непре-
непрерывных на отрезке функций.
Теорема 4.7 (Вейерштрасса*). Если функция f(x) непрерывна на
отрезке [а; Ь], то на этом отрезке она ограничена и достигает своих
нижней и верхней граней, т. е. на нем существуют по крайней мере
две точки d и Сг (рис. 4.6), такие, что
nci)=lnif(x), f(c2) = sup f(x).
[о; Ь]	[а; Ь]
Например, функция f(x) = x* непрерывна на отрезке [ — 2; 3]. Она ограничена
на [ — 2; 3] (|д^| < 9) и существуют такие две точки С\ =0 и сг = 3, принадлежащие
отрезку [—2; 3], что
= o= inf x2, /(c2) = 9= sup х2.
[-2:3]	[-2;3]
Заметим, что непрерывная функция на открытом промежутке
]а; Ь[ может быть неограниченной и, следовательно, не иметь своих
точных нижней и верхней граней. Такой функцией является, на-
например, функция tgx на интервале ] —я/2; л/2[.
Теорема 4.8. Если функция f(x) непрерывна в точке х0 и f(x0) Ф 0,
то существует такая окрестность точки хо, в которой знак функции
совпадает со знаком f(xo).
Геометрическая интерпретация теоремы 4.8 дана на рис. 4.7
(случаю f(x0) > 0 соответствует рис. 4.7, а, случаю f(x0) < 0 —
рис. 4.7, б).
Р н с. 4.6
Рис. 4.7
Например, функция /(*) = sin * непрерывна в точке х0 = л/4, и sin (л/4) =
= л]2/2 > 0. Существует такая окрестность точки хо = л/4, в которой функция
sin х сохраняет знак, т. е. sin x > 0.
Теорема 4.9 (Больцано** — Коши). Если функция f(x) непре-
* Карл Вейерштрасс A815—1897) —немецкий математик.
** Бернгард Больцано A781—1848) —чешский математик.
95

рывна на отрезке [а; Ь) и на его концах принимает значения разных
знаков, то внутри этого отрезка существует по крайней мере одна
точка, в которой значение функции равно нулю:
f(x):f(a)f(b)<O^Zxoe]a; Ь\: /(*„) = 0.
Геометрический смысл теоремы заключается в следующем: если
точки A (a; f(a)) и B(b; f(b)) графика функции f(x), соответствующие
концам отрезка [а; Ь], лежат по разные стороны от оси Ох (рис. 4.8),
то график функции хотя бы в одной точке отрезка пересекает ось Ох.
Функция f(x), график которой представлен на рис. 4.9, имеет три точки: х\, х%, хз,
где f(x) = 0.
Замечание. Если f(x) непрерывна и монотонна на [a; ft],то существует един-
единственная точка х0, такая, что f(x0) = 0.
B(b;f(b))
A(a;f(a))
rA(a-,f(a))
Рис. 4.1
Рис. 4.9
Теорема 4.10 (о промежуточных значениях). Пусть f(x) непре-
непрерывна на отрезке [а; Ь] и f(a) = A, f(b) = В. Тогда для любого числа С,
заключенного между А и В, найдется такая точка с 6 [а; Ь], что
№ = с.
Эта теорема геометрически очевидна. Рассмотрим график функ-
функции f(x) (рис. 4.10). Пусть f(a) = A и f(b) = B. Тогда прямая у = С,
где С — любое число, заключенное между А и В, пересечет график
функции по крайней мере в одной точке. Если же f(x) непрерывна и
монотонна на [а; Ь\, то существует единственная точка с ? [а; Ь\,
такая, что f(c) = С.
Теорему 4.10 можно переформулировать так: непрерывная функ-
функция, переходя от одного значения к другому, обязательно прини-
принимает все промежуточные значения.
В курсе математического анализа
встречаются кусочно-непрерывные на
отрезке [а; Ь] функции.
Определение 4.6. Функция f(x)
называется кусочно-непрерывной на от-
отрезке [а; Ь], если она непрерывна во
всех внутренних точках [а; Ь] за исклю-
исключением, быть может, конечного числа
точек, в которых эта функция имеет
разрыв первого рода или устранимый
разрыв, и, кроме того, она имеет одно-
Р и с 4.Ю	сторонние пределы в точках а и Ь.
У
в
с
А
0
Nlbiflb))
У
t
M(a;f(a))
i i
I
¦ <¦
*> X
96

Функция f(x) называется кусочно-непрерывной на числовой пря-
прямой, если она кусочно-непрерывна на любом отрезке этой прямой.
Например, функция f(x) = [x] (см. рис. 2.4) кусочно-непрерывна на любом от-
отрезке, и, следовательно, иа всей числовой прямой. (Напомним, что запись[х] обозначает
целую часть числа х.) Функция [х] в точках х = п, п ? Z, непрерывна справа н раз-
рывиа слева; во всех остальных точках она непрерывна как справа, так и слева.
4.5. РАВНОМЕРНАЯ НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Из множества функций, непрерывных на числовом промежутке,
полезно выделить равномерно-непрерывные.
Определение 4.7. Функция f(x) называется равномерно-не-
равномерно-непрерывной на множестве D cz R, если для любого е > О найдется
б(е) > 0, такое, что для любых х\, х2 6 D, удовлетворяющих условию
\х\ —х2\ <б, выполняется неравенство \f(xi) — f(x2)\ <e.
Пример 4.6. Доказать, что линейная функция f(x) = 2x-\- l равномерно-непре-
равномерно-непрерывна на R.
Решение. Для доказательства равномерной непрерывности данной функцнн
для е>0 выберем 6 = е/2. Тогда для любых х\, х% б R, таких, что \х\—хг\ <Ь,
выполняется неравенство \](x\\ — \(xi)\ < е, т. е. \2х\ + 1 — 2xi — 1| = 2\xt — х2\ <
< 26 = е.
Следовательно, функция f(x)=2x+ 1 равномерно-непрерывна на R. Это значит,
что малые изменения аргумента влекут за собой малые изменения функции на любом
подмножестве множества R (рис. 4.11).
Если f(x) равномерно-непрерывна на множестве D, то она не-
непрерывна на множестве D. Чтобы в этом убедиться, достаточно
положить х\ = х, х2 = х0. Тогда из определения равномерной непре-
непрерывности функции следует определение непрерывной функции в
точке х0.
Обратное утверждение не всегда справедливо. Условие, при ко-
котором непрерывная функция является и равномерно-непрерывной,
определяется теоремой Кантора* о равномерной непрерывности.
Рис. 4.11
Рис. 4.12
* Георг Кантор A845^—1918) —немецкий математик.
4 Зак. 1270
97

Теорема 4.11 (Кантора). Функция, непрерывная на отрезке,
равномерно-непрерывна на этом отрезке.
Пример 4.7. Исследовать иа равномерную непрерывность следующие функции:
1) f(x) = x/D — x2) на отрезке [—1; 1]; 2) f(x) = 5/x2 на интервале ]0; 3].
Решение. 1. Функция f(x) = х/(9 — х-) непрерывна на отрезке [— 1; 1]. Тогда,
согласно теореме Кантора, она равномерно-непрерывна на [—1; 1].
2. Функция f(x) = 5/x2 непрерывна на интервале ]0; 3], но не является равно-
равномерно-непрерывной на нем, так как для любых х, достаточно близких к нулю, малые
изменения аргумента могут привести к большим изменениям функции, (см. рис. 4.12).
Для любого е ;> 0 невозможно подобрать 6>0, такое, чтобы из неравенства \х\ —
— xz\ <6 следовало \f{x{) — f{xz)\ <е на ]0; 3]. Из рис. 4.12 видно, что при х\, х2,
близких к правому концу промежутка ]0; 3], малым изменениям аргумента соответ-
соответствуют малые изменения функции. При хи хг, близких к левому концу этого проме-
промежутка, малые изменения аргумента приводят к большим изменениям функции.

5. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
5.1. ПОНЯТИЕ ПРОИЗВОДНОЙ.
МЕХАНИЧЕСКИЙ И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Определение производной. Пусть функция y = f(x) определена
в некоторой окрестности точки х0. Если фиксированное значение
аргумента х0 получает приращение Ах (положительное или отрица-
отрицательное), такое, что х0 + Длс? О&(х0), то приращение функции опре-
определяется выражением Af(x0) = f(xo + Дя).— /(¦*<>)•
Определение 5.1. Производной функции y = f(x) в произ-
произвольной фиксированной точке х0 называется предел (если он суще-
существует и конечен) отношения приращения функции к приращению
аргумента при условии, что последнее стремится к нулю.
Наиболее употребительные обозначения производной функции
y = f(x) в точке хо: у'(х0), /'(*„),
Таким образом,
у'(хо)=
l
А*—О /S.X	А*—О	Ах
Производная функции y = f{x) в произвольной точке х обозна-
обозначается так: у', f'(x), |, ±, ±f(x).
При каждом конкретном числовом значении х производная (если
она существует при данном х) функции у = f(x) представляет собой
определенное число. Значениям переменной х ставятся в соответ-
соответствие определенные значения переменной f'(x). Следовательно, про-
производная является функцией аргумента х. Можно сказать, что функ-
функция f(x) «порождает» (или «производит») функцию f'(x) (отсюда
и название «производная»).
Если для некоторого значения х
lim -г?- = + °° ИЛИ Нт М- = — оо,
Ах— О ЬХ	Ах—0 Дх
то говорят, что для этого значения х существует бесконечная про-
производная.
В дальнейшем под выражением «функция имеет производную»
будем понимать существование конечной производной, если не ого-
оговорено противное.
Определение 5.2. Если функция f определена в левосторон-
левосторонней (правосторонней) окрестности точки х0 и существует конечный
или бесконечный предел этой функции:
99

¦)•
Hm	( Hm
д*-о-о	Ax	Чл*-.о+о	Ах
то он называется соответственно конечной или бесконечной произ-
производной слева (справа) функции f в точке х0 и обозначается f'(x0 —
-О)(/'(*о + О)).
Левую и правую производные называют односторонними произ-
производными. Из свойств пределов следует, что если функция /, опреде-
определенная в некоторой окрестности точки х0, имеет конечную «произ-
«производную f'(x0), то существуют производные слева и справа, причем
Операция нахождения производной функции / называется диф-
дифференцированием. Для отыскания производной от данной функции
у = f(x), согласно определению, необходимо выполнить следующие
действия:
1) придав фиксированному аргументу x?D(f) приращение Ах,
вычислить значение функции
2) найти соответствующее приращение функции
3) составить отношение приращения функции к приращению
аргумента
Ay _ f
\х	\х
4) найти предел данного отношения при Дх->-0
Рассмотрим несколько примеров нахождения производной функ-
функции.
Пример 5.1. Найти производную функции у = х.
Решение. Пусть у—х. Даднм аргументу х приращение Ах. Тогда Ау =
= (х + Ах) — х, т. е. Ау = Ах. Следовательно, по определению
Пример 5.2. Найтн производную функции у = х3.
Решение. Дадим фиксированному значению аргумента х приращение Ах.
Тогда:
f
) y + y (	f
2)	Ay = (x + Axf —х? = (З*2 + ЗхДдг + Ддг2) Ах;
3)	-|^- = З*2 + ЪхАх + Ах2;
4)	у'= Urn -^-= lim (З*2 + ZxAx + Ах2) == Зх2.
д*->о Ах а*-й)
Следовательно, (х3)' = Зх2.
Пример 5.3. Найти производную функции y = cosx.
100

Решение. Дадим аргументу х приращение Ах. Тогда:
1)	у + Ay = cos (x + Ах);
2)	Ay = cos (х + Ах) — cos х = —2 sin ( х -\——\ sin —5—;
_	,. sin(Ax/2) .	,	.. . / , Ах\
Так как игл 	; ' =1, то у = — lim sin ( дс -^—тг—1 = —sin дс.
Дх->о Адг/2	A*-*o \	2 /
Следовательно, (cos х)' = —sin x..
Механический смысл производной. Рассмотрим функцию y=f{x),
определенную и непрерывную в некоторой окрестности точки х0.
Если аргумент х0 функции получает приращение Да: (положительное
или отрицательное), такое, что хо + Да: принадлежит той же окрест-
окрестности точки Хо, то соответствующее приращение функции ДДа:о) =
= /(*о + Д*) — f(x), средняя скорость изменения функции
уср = ДДа:0)/Да:,
а мгновенная скорость ее изменения
Их-ьО Ах
В этом состоит механический смысл производной,
т. е. производная — математическая модель мгновенной скорости
процесса, описываемого функцией }(х). В зависимости от содержа-
содержательной сущности функции можио получить широкий круг математи-
математических моделей скорости протекания процессов. Рассмотрим некото-
некоторые из них.
1. Пусть материальная точка М движется неравномерно и у =
= s(t) — функция, устанавливающая зависимость пути от времени t.
Тогда мгновенная скорость движения в момент времени t0 есть произ-
производная от пути s по времени t:
ds
v =
at
Hm
At	&.t-rO	At
2. Пусть y = v(t)—функция, описывающая процесс изменения
скорости неравномерного движения в зависимости от времени t.
Тогда мгновенное ускорение материальной точки в фиксированный
момент времени t0 есть производная от скорости v по времени t:
di
Д(—о
3. Пусть y = Q(T) — функция, описывающая процесс изменения
количества теплоты, сообщаемой телу при нагревании его до темпе-
температуры Т. Тогда теплоемкость тела есть производная от количества
теплоты Q по температуре Т:
dT т**т« ьт-*о AT дг-м)	AT
101

4. Пусть необходимо определить линейную плотность неоднород-
неоднородного тонкого стержня длиной /, где т — масса стержня, концы
которого имеют координаты 0 и х0 (предполагается, что ось Ох на-
направлена по стержню). Ясно, что масса стержня является функци-
функцией х: f(x) — т(х). Тогда линейная плотность неоднородного тонкого
стержня в точке х0 есть производная от массы т по длине /:
•><*»-¦?
= lim
т (хо + Ах) — т (
_
5. Пусть y = <b(t) — функция, описывающая процесс изменения
магнитного потока в зависимости от времени t. Тогда мгновенное
значение электродвижущей силы индукции равно скорости изме-
изменения магнитного потока, т. е. производной от магнитного потока Ф
по времени t:
= lim —
At
6. Пусть y = q(t) — функция, описывающая процесс изменения
заряда в колебательном контуре в зависимости от времени t. Тогда
сила тока в контуре в момент времени to равна производной заряда q
по времени t:
= lim	—¦
t = t0 ¦ д<_*о	At
Геометрический смысл производной. Рассмотрим задачу о прове-
проведении касательной к произвольной плоской кривой. Пусть L — дуга
плоской кривой, Мо — точка этой кривой, МоМ —- секущая (рис. 5.1).
Если точка М движется по кривой к точке Мо, то секущая поворачи-
поворачивается вокруг точки Мо и стремится к некоторому предельному поло-
положению М07\
Определение 5.3. Касательной к кривой L в точке Мо называ-
называется прямая МоТ, которая представляет собой предельное положение
секущей М0М при стремлении по кривой точки М к точке Мо
(см. рис. 5.1).
Если предельного положения секущей не существует, то говорят,
что в точке Мо провести касательную
нельзя. Это бывает в случае, когда точка
Мо является точкой излома, или заостре-
заострения, кривой (см. рис. 5.2, а, б, в).
Пусть кривая L является графиком
функции f(x) и точка М(л:0; f(xo))?L
(рис. 5.3). Предположим, что касательная
к кривой в точке Мо существует. Угловой
коэффициент секущей МоМ k = tg q> =
_ = Af(xo)/Ax. Если Дл:-»-0, то точка М
движется по кривой к точке Мо и секущая
ММо стремится к своему предельному
положению М0Т. Таким образом,
102
У
Рис. 5.1

k = tg a = lim tg ф = lim
MM	Дх0
= f (
E.1)
т. е. если кривая L является графиком функции f(x), то из равенст-
равенства E.1) следует геометрический смысл производной:
производная от функции f(x) при х = х0 равна угловому коэффици-
коэффициенту касательной к графику функции в точке с абсциссой хо.
Р и с. 5.2
Уравнения касательной и нор-	у
мал и. Угол между кривыми. Для
составления уравнений касатель-
касательной и нормали к плоской кривой f(x +4X)
используем геометрическую интер-
интерпретацию производной. Пусть кри- ч
вая задана уравнением у — f(x).
Угловой коэффициент касательной
к ней в точке Мо(хо', у о), где у0 =
= f(x0), k = f'(x0). Уравнение каса-
касательной можно найти, используя
уравнение прямой, проходящей
через данную точку в заданном направлении:
Но k = f'(xo), поэтому
у-уо = Г(хо)(х-хо)
есть уравнение искомой касательной.
Так как угловые коэффициенты касательной и нормали связаны
условием перпендикулярности kmp«= —\/kKac, то уравнение норма-
нормали в точке Мо(хо; у0) имеет вид
Рис. 5.3
у — yo = k(x —
Углом между кривыми называют угол между касательными к
кривым в точке их пересечения. Две линии называют ортогональ-
ортогональными, если они пересекаются под прямым углом.
Пример 5.4. Найти угол, под которым синусоида пересекает ось Ох в начале
координат.
103

Решение. Так как у = sin х, у' — cos х и у'@) = 1, то касательная, а значит,
и синусоида, пересекают ось Ох под таким углом а, для которого tg а = 1, т. е. под
углом а = я/4.
5.2. ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ.
ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Дифференцируемость функции. Пусть функция у = f(x) определе-
определена в некоторой окрестности точки х0.
Определение 5.4. Функция у = f(x) называется дифференци-
дифференцируемой в точке хо, если ее приращение в этой точке f(xo + Ах) — f(x0)
может быть представлено в виде
f(x0 + Ax)-f(x0) = AAx + o(Ax),	E.2)
где А — некоторое действительное число; о(Ах) — бесконечно малая
функция более высокого порядка малости, чем Ах, при Ах->-0.
Таким образом, дифференцируемость функции в точке хо означа-
означает, что с точностью до бесконечно малых более высокого порядка,
чем приращение аргумента Да:, приращение функции представимо
в виде линейной функции от Ах.
Теорема 5.1. Для того чтобы функция у = f (x) была дифферен-
дифференцируема в точке х0, необходимо и достаточно, чтобы в точке Хо су-
существовала конечная производная f'(xo) = A.
Связь между непрерывностью и дифференцируемостью функции
в данной точке устанавливает
Теорема 5.2. Если функция у = f(x) дифференцируема в некото-
некоторой точке, то она и непрерывна в этой точке.
> Действительно, если функция у = f(x) дифференцируема в точ-
точке хо, то в силу условия дифференцируемое™ E.2) ее приращение
в этой точке представимо в виде Ау = ААх-\-о{Ах) при Дх-»-О.
Тогда
lim Ay = A lim Ax + lim o(Ax) = О,
что и означает непрерывность функции f в точке х0. <
Из теорем 5.1 и 5.2 непосредственно вытекает
Следствие. Если функция y = f(x) в некоторой точке имеет
производную, то она непрерывна в этой точке.
Утверждение, обратное теореме 5.2, вообще говоря, неверно,
т. е. из непрерывности функции у = f(x) в точке хо еще не следует ее
дифференцируемость в этой точке. Поясним связь между непрерыв-
непрерывностью и дифференцируемостью на примерах.
Рассмотрим функцию у = |дс|. Очевидно, что эта функция определена н непрерыв-
непрерывна иа R. Покажем, что функция / в точке хо = 0 не имеет производной. Действительно,
при дс^О у=\х\=х, Ду = Дх. Вычислим производную функции справа в точке
хо = О:
f @ + 0) = lim -т- = \.
Аналогично при х<0 имеем у = \х\= —х, Ау = — \х. Следовательно, произ-
производная слева
Av
f'@-0)= lim —2- = —1.
104

Так как /'@ — О)ф /'(О + 0), то не существует f'{0). Функция f(x) неднфферен-
цируема в точке ха = 0 (рис. 5.4).
Теперь рассмотрим функцию f(x) = ^Jx. Функция f определена н непрерывна иа R.
Докажем, что в точке хо = 0 функция ие имеет конечной производной, т. е. недиффе-
ренцируема. Действительно, по определению
f (x)= hm
Д0
+ &x)-f(x)
= hm
Длг
х + Ах — х
= lim
Тогда f'@)—°°, т. е. не существует конечной производной в точке дсо = 0.
На рис. 5.2 изображены графи-
графики функций, для которых в точке
х0 не существует конечной произ-
производной. В этой точке графики
имеют изломы. Функции, графики
которых изображены на рис. 5.2,
имеют различные односторонние
производные. На рис. 5.5 и 5.6
изображены графики, недиффе-
ренцируемые в точке х0 функций,
которые непрерывны в точке х0 и не имеют изломов.
Если функция f дифференцируема в любой точке х 6 [а; Ь], то гово-
говорят, что она дифференцируема на [а; Ь].
Дифференциал функции. При изучении необходимых и достаточ-
достаточных условий дифференцируемости функции f в точке х0 было пока-
У-
X
Рис. 5.4
\
0 х0 л
Рис. 5.5
Рис. 5.6
зано, что если функция f дифференцируема в точке х0, то ее прира-
приращение в этой точке (в силу равенства E.2) и теоремы 5.1) предста-
вимо в виде
Отсюда если 1'(хо)фО, то
105

lim-
= Hm(l +
o(A*)
¦)-•
Следовательно, при Дл:-»-0 приращение функции \f(x0) и выраже-
выражение f'(xo)Ax являются эквивалентными бесконечно малыми функци-
функциями, т. е. при Дл:-»-0 можно приближенно считать, что \f (хо)«
«^'(дсо)Лдс. Величину f'(xo)hx, являющуюся главным (линейным)
членом приращения функции f в точке х0, называют дифференциа-
дифференциалом функции и обозначают df(x<>). Таким образом, по определению
= f'(xo)Ax.
В частности, если у = х, то у' = 1, и, следовательно, dy = dx =
= \х, т. е. дифференциал и приращение независимой переменной
равны между собой. Поэтому дифференциал функции f в точке х0
можно представить в виде df(xo) = f'(x0)dx.
Из определения дифференциала следует
т. е. дифференциал функции в точке х0 отличается от соответствую-
соответствующего приращения функции на бесконечно малую величину более
высокого порядка, чем Ах, при \х->-0.
На рис. 5.7 дана геометрическая интерпретация дифференциала
f() Т	f ()
р	р
функции y = f(x). Так как f (*) =
g а, дифференциал функции изме-
измеряется отрезком ТР, т. е. диффе-
дифференциал dy функции у = f(x) в точ-
точке хо изображается приращением
ординаты точки касательной, про-
веденной в М(х0; f(x0)) к линии у =
Например, дифференциал функции
у = х2 в точке хо для приращения Ддс dy —
= 2х0Ах. Он является линейным слагаемым
приращения функции относительно Ах:
hf (дс0) = (дс0 -|- ДхJ — дсо = 2дсоА* + Дх2-
Дифференциал функции мож-
можно использовать для вычисления
приближенных значений функции. Действительно, заменяя прира-
приращение функции в точке х0 ее дифференциалом, получаем прибли-
приближенную формулу
Рис. 5.7
Пример 5.5. Вычислить Д(/ н dy, если у = х2, хо = 1 ¦ dx = 0,02.
Решение. Имеем: Ду = A,02J - I2 = 0,0404, у' = 2х, у'{\) = 2, dy = 2-0,02 =
0,04. Относительная погрешность (\dy — Ау\/\Ау\ = |0,04 — 0,04041/0,04 = 0,01.
Пример 5.6. Вычислить приближенно "у 10.
Решение. Принимая f(x) = ~\jx, дсо — 9, Ас=1, имеем: f'(xo) =
Г(9)=Т, f(9) = 3. Тогда
т.1~3,16.
106

5.3. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ СЛОЖНОЙ ФУНКЦИИ.
ИНВАРИАНТНОСТЬ ФОРМЫ ДИФФЕРЕНЦИАЛА
Производная сложной функции. Пусть y = f(u(x)) = (fou)(x)
(запись f°u означает, что сложная функция является композицией
функции [им).
Установим правило, позволяющее найти производную сложной
функции у = f(u(x)), если известны производные составляющих ее
функций у = ди) и и = и(х). Придадим фиксированному значению
аргумента х приращение \х. Этому приращению соответствует при-
приращение Аи функции и(х). Приращению Аи, в свою очередь, соответ-
соответствует приращение Ду функции y—f(u) в точке х. Составим отношение
_ К")-/("о) "-"о
Ддс	х — Хв	и — но х — хо
Ду	Af Ди
Ддг	Ди Ддс
При Да:-^0 приращения Дн, Af в силу дифференцируемости
соответствующих функций стремятся к нулю. Так как по определению
Ai-vO Ах	V ' Дц-0
то
Функцию и иногда называют промежуточным аргументом, ах —
основным аргументом. Таким образом, можно сформулировать сле-
следующее.
Правило дифференцирования сложной функции. Производная
сложной функции равна произведению производной этой функции
по промежуточному аргументу и производной промежуточного аргу-
аргумента по основному аргументу.
Полученное правило легко распространяется на сложную функ-
функцию, зависящую от нескольких аргументов, т. е. на композицию
нескольких функций.
Действительно, предположим, что функции y = f(u), u = u(v),
v = v{t), t = t(x) дифференцируемы. Рассмотрим сложную функцию F
переменной х через посредство промежуточных функций f, и, v, t:
F(x) — f(u(v(t(x)))). Придадим фиксированному значению х прираще-
приращение Да:, тогда t получит приращение At, v — приращение Ди, и —
приращение Ди.
Запишем Ay/Ах в следующем виде:
Ду 	 Ду Ди Ди Д<	,г оч
~д* дп~ ~Kv дГ ~Кх'	*• ' '
Так как н, v, t дифференцируемы, а следовательно, и непре-
непрерывны, то в силу непрерывности при Дл:-»-0 приращения Ди-»-0,
Ди-»-0 и Д<->-0. Переходя к пределам в равенстве E.3), имеем
Дифференциал сложной функции. Инвариантность формы диффе-
дифференциала. Пусть дана сложная функция y = f(u), u = u(x). Выше
107

мы определили дифференциал в точке х<> как произведение производ-
производной от функции f в точке хо и дифференциала независимой пере-
E.4)
где dx = Ах.
Если же переменной является и, то у' = f'u(u)u'(x) и, следователь-
следовательно, dy = f'u(u)u'(x)dx. Так как u'(x)dx = du, то в случае сложной
функции имеем
^	dy = f'{u)du.	E.5)
Формулы E.4) и E.5) для дифференциала совпадают по форме
записи, однако они имеют различный смысл: в первой из них dx =
= Ах, а во второй du = н'(ж)йл:.
Таким образом, дифференциал функции всегда равен произве-
произведению производной и дифференциала аргумента и не зависит от
того, является ли величина, по которой взята производная, незави-
независимой переменной или же только промежуточным аргументом. В этом
и заключается свойство инвариантности формы дифференциала.
Из свойства инвариантности следует, что /'(*о)= ~j-, т. е. про-
производная функции в точке численно равна отношению дифферен-
дифференциалов функции dy и переменной dx независимо от того, является ли
функция у = f(x) функцией независимой переменной х либо сложной
функцией.
5.4. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Установим правила, по которым можно находить производные и
дифференциалы алгебраической суммы, произведения и частной*"
функций, зная производные слагаемых, сомножителей, делимого и
делителя. При их выводе будут использованы теоремы о пределах
суммы, произведения и частного.
Пусть функции и = и(х) и v — v(x) дифференцируемы в точке
jco и некоторой ее окрестности. Тогда справедливы следующие пра-
правила дифференцирования.
Правило дифференцирования алгебраической суммы функций.
Производная (дифференциал) алгебраической суммы конечного
числа дифференцируемых функций равна алгебраической сумме
производных (дифференциалов) отдельных слагаемых.
Е> Рассмотрим функцию у = и{х)-\- v(x). Дадим фиксированному
значению аргумента х приращение Ах. Тогда функции и = и(х) и
v = v(x) получат приращения Аи и Аи, а функция у — приращение
Ay = ku-\-Av. Таким образом, по определению
у' = нт AL = iim A1 + &S- = lim *L + lim -?.
Так как по предположению функции и и v дифференцируемы,
то
lim -7— = и', lim —г— = v'.
Даг-»о Аде	Дж-»о Ддг
108

Следовательно,
у = и + v=>yf = и' -\- v'.
Так как дифференциал функции f в точке х равен произведению
производной и дифференциала аргумента, то, умножив обе части
формулы, выражающей правило дифференцирования алгебраиче-
алгебраической суммы, на дифференциал аргумента y'dx = u'dx -f- v'dx, полу-
получим соответствующее правило для дифференциалов:
dy = du-\- dv. <]
Это правило легко обобщается на случай любого конечного
числа слагаемых, а именно: если функции и\(х), иг(х), ..., ип(х)
дифференцируемы, то их сумма также дифференцируема. При этом
п	п	п
у= 2 uk{x)^y'= 2 u'k(x)^dy= S duk(x).
k=\	k=\	k=\
Правило дифференцирования произведения функций. Производ-
Производная (дифференциал) произведения двух дифференцируемых функций
равна сумме произведений производной (дифференциала) первого
сомножителя на второй и производной (дифференциала) второго
сомножителя на первый, т. е.
у = ни=^у' = u'v + v'u=s~dy = vdu + udv.
> Пусть у = u(x)v(x). Когда аргументу х придают приращение
Да:, то функции и, v и у получают соответственно приращения
Дм, Аи и Ду, причем
Ду = (и + Дм) (v + Ди) — uv = иДн + нДи + ДнДи.
Составим отношение
Ддс	Лх	Ддс	Ддс
В последнем равенстве приращения Дм, Ди и Ду зависят от Да:,
а и и и не зависят от Да: (и, v — значения функции, соответствующие
начальному значению аргумента а:).
Используя теоремы о пределах функций, находим
Так как
m$L=v\im-?-+u lim -^- + Hm
ж—О Д*	Дж—0 Дх	Дж—0 Дх	Дж—О
-??-=0', lim 4^="'. Hm4L =
о Ддс	дж-»о Ддс	Дх-»о ах
так как функция v = v(x) непрерывна.
Итак, окончательно имеем:
у = uv=>y' = н'и + v'u=$~dy
(Дифференциал dy функции получается умножением левой и правой
частей равенства у' = u'v + v'u на dx.) <]
Правило дифференцирования произведения двух функций ме-
методом математической индукции легко можно распространить на
109

случай любого конечного числа сомножителей: если Ui(x), t: = 1,я,—
дифференцируемые в некоторой окрестности точки х функции и
п
у = П щ(х), то
1=1
п	п	, п	п
у'= 2 и/(лг) П Uk(x)=>dy= 2 dii/(*) П и*(ж),
i=i *=i	i=i	*=i
г. е. производная (дифференциал) произведения равна сумме произ-
произведений производной (дифференциала) каждого из сомножителей и
остальных сомножителей.
Правило дифференцирования частного функций. Производная
(дифференциал) дроби (частного двух дифференцируемых функций)
равна дроби, у которой знаменатель есть квадрат знаменателя дан-
данной дроби, а числитель представляет собой разность между произве-
произведением знаменателя данной дроби на производную (дифференциал)
ее числителя и произведением числителя на производную (дифферен-
(дифференциал) знаменателя.
> Пусть y = u/v, где и = и(х), v = v(x) — дифференцируемые
функции, у(х)ф{>. Придавая фиксированному аргументу х прираще-
приращение Да:, находим приращение функции у:
д 	 и + Ди 	 и 	 иДи — иДи
У v + Ди	v	v(v + Аи)
Составим отношение
Ди	Ди
Ду 	 Ах	Ах
Д*	v(v + Ди)
Перейдя к пределу при Дл:-»-0 с учетом того, что ПтДи = 0
(из дифференцируемости функции следует, что она непрерывна),
получим
, Ди ,. Ди
v hm -rr	и hm -г—
|. Ду 	 Дх—о Ад: Дх—о А*
д*—о А* - v Hm (v + Аи) -
Дх-0	'
Следовательно,
Постоянную можно рассматривать как функцию, принимающую
одинаковые значения при всех значениях аргумента х: у = с V* 6 R-
Дадим аргументу х приращение Да:, тогда у -f- \y = с, откуда
Ду = с — с = 0. Следовательно, по определению
у = с=>у' = O=^dy = 0.
Из выведенных выше формул дифференцирования суммы и произ-
произведения функций вытекают некоторые следствия.
Следствие 1. Пусть функция и(х) имеет производную в точке х,
НО

тогда функция у = си(х) (с — const) также имеет в этой точке произ-
производную (дифференциал), причем
у = си(х)=*-у' = cu'(x)=^dy = cdu(x).
Следствие 2. Пусть функции и\ (х), и2(х), ..., ип(х) имеют произ-
производные в точке х, тогда линейная комбинация этих функций равна
такой же линейной комбинации соответствующих производных, т. е.
у = С\и\ (х) + с2и2(х) +... + спип(х)=>у' = c\u\{x) + c2u'2(x) +... +
+ С„и'п(х).
5.5. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ОСНОВНЫХ
ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Производная и дифференциал логарифмической функции. Пусть
у = log,,*, где а> 0, аф\. Придадим фиксированному значению
*'€ D(y) приращение Ах. Тогда
АУ = lOga(* + А*) — l0ga* == logo(l + AX/X).
Следовательно, по определению
у' = Пт ^ = lim '°g-('+^A) = J_ loga iim (
х In a
Здесь мы воспользовались вторым замечательным пределом
A + х
Итак,
р	р
lim A + хУ'х = е и непрерывностью логарифмической функции.
у = loga х^у' = JL loga е =
Для сложной функции имеем
у = loga и(х)=>у' = -±- logaе • и'(х) = ~^—^du = f"(,x) .
Э	&a V / Э	ц^ &а	\ /	и(х)\па	и(х) \ti п
В частном случае при а = е
Производная и дифференциал степенной функции. Пусть у =
= (и(х))а, а ? R. Рассмотрим вначале случай, когда и(лс) > 0. Если
ы(д:)>0, то In 1/ = a In м(*). Продифференцируем полученное равен-
равенство почленно по правилу дифференцирования сложной функции,
считая у функцией от х:
(In у)'= (а \пи(х))'^^ = ^1^у'= у ^^^
v *' v	y " у	и(х)	и(х)
=>y' = a(u(x))a-lu'(x).
Пусть теперь и(х)<0. Представим функцию у = (и(х))а в виде
(— \)a(v(x))a, где v{x)>Q. Тогда

Итак,
у = (и(х))а^у' = a(u(x)f-xu'{x)=^dy = au{xf- ldu(x).
Производная и дифференциал показательной функции. Пусть
у = a"w, где 0<аф 1; и(х) — непрерывная функция. Тогда In y =
= и(х) In а. Дифференцируем левую и правую части полученного
равенства по правилу дифференцирования сложной функции, счи-
считая у функцией от х. Имеем
у'/у = In а • и'(х)=>у' = и In а • и'(х)=*-у' = аи(х) In a • и'(х).
Итак,
у = auW=^y' = a"w In a • u'{x)^dy = a"w In a • du(x).
В частном случае,
у = eu(t)^y' = euWu'
Производные и дифференциалы тригонометрических функций.
Пусть у = sin х. Дадим фиксированному значению х приращение Л*.
Тогда
Ду = sin (х + Л*) — sin х = 2 sin -^- cos
Согласно определению,
у' = Пт 4*- = lim si"(A;o/2)cos^+^
(При вычислении предела мы использовали первый замечательный
smx
предел lim smx = 1 и свойство непрерывности функции y = cosx:
lim cos (* + Л*/2) = cos д:.)
О
Итак,
у = sin x=s*y = cos x=s*dy — cos
Для сложной функции имеем
у = sin и(х)=$-у' = и'(х) cos u{x)=$-du = cos u(x)du(x).
Аналогично доказывается, что
y = cos u(x)=*-y' = —M'(*)sin u(x)=*~dy = —sin u(x)du(x).
Пусть y = tgx. Так как tg * = sin дг/cos x, то для нахождения
производной функции у = tg * воспользуемся правилом дифференци-
дифференцирования частного. Если cos*=^0, получим
,	,, у	/sin*\'	 (sin x)' cos x — (cos x)' sin x 	 cos2 x + sin2 x
\ cos х )	cos2 х	cos2 x
Итак,
cos2 x
112

Для сложной функции имеем
Аналогично доказывается, что
у = ctg u(x)^y'	?
y	? ^dy	Щ.
sin2 и(х)	sin2 и(х)
5.6. ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ.
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ОБРАТНЫХ
ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Производная обратной функции. Пусть функция y = f(x) моно-
монотонна на отрезке [а; Ь] и имеет производную у' = ('(х)фО. Пусть,
далее, f(a) = a, f(b) = $. Тогда существует обратная (по отноше-
отношению к функции у = f(x)) функция х = ф(у), которая является не-
непрерывной и монотонной на [а; р]: y = f(x)ox = ф(у).
Дадим фиксированному значению аргумента у обратной функции
приращение Ду. Этому приращению соответствует приращение обрат-
обратной функции, причем в силу ее монотонности Д* Ф 0. Найдем про-
производную обратной функции. По определению
х'у = ф'(у) = lim ~ = lim -5-4л- = ,. ' /А > = -777-Г-
" т vs/ д</—о Ьу Дж—о Ьу/Ьх	hm(A.y/Ax) fix)
Ax->-0
Таким образом доказана следующая
Теорема 5.3. Если функция y = f{x) монотонна на отрезке [а; Ь]
и имеет во всех точках интервала ]а; Ь[ ненулевую производную
у' — f'(x), то обратная функция х = у(у) дифференцируема во всех
точках интервала ]f(a); f(b)[ и для любого у? ]f(a); f(b)[ ее производ-
производная равна \/f'(x).
Производные и дифференциалы обратных тригонометрических
функций. Пусть у = arcsin x. Найдем производную этой функции.
Рассмотрим обратную функцию x = s'my. В интервале ] —л/2; я/2[
она монотонна, ее производная х'у = cos у не обращается в нуль. Сле-
Следовательно, используя соотношения между производными взаимно
обратных функций, имеем
•Vl-sin'i/
(перед квадратным корнем выбран знак « + », так как на интервале
] —л/2; л/2[ cosy>0).
Итак,
у= arcsin x=t*y'x =
Для сложной функции имеем
у = arcsin u(x)^y'x
Л/1 - и2(х)
Аналргично доказывается, что
из

у = ardtos и{
Пусть у = arctg *. Множество возможных значений этой функ-
функции — Е(у) = ]—л/2; л/2[. Для функции у = arctg х существует
обратная функция х = tg у, причем ее производная х'у = —5— не
cos* у
обращается в нуль. Таким образом, используя соотношения между
производными взаимно обратных функций, имеем
Итак,
у = arctg х^у' = -
Для сложной функции имеем
Аналогично доказывается, что
5.7. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ
Найдем производные гиперболических функций. Для функции
у = sh х имеем
Следовательно,
у = sh д:=>-у' = ch x=*-dy = ch xdx.
Поступая аналогично, находим производные и дифференциалы
остальных гиперболических функций:
у = ch х =*-у' = sh х =>dy = sh xdx;
У = cth
sh2
Замечание. Не обязательно выводить и запоминать формулы диффе-
дифференцирования для обратных гиперболических функций, так как каждая из них
выражаетси через натуральный логарифм сложного аргумента. Их всегда можно по-
получить, продифференцировав обратные гиперболические функции по правилу диф-
114

^ференцировання сложной функции. Например, производная функции
у= -д- 1п ( -р^—J, где х g R, имеет вид
, 1 1— х 2	1
= arthjc
5.8. ТАБЛИЦА ПРОИЗВОДНЫХ ОСНОВНЫХ
ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
На практике чаще всего находят производные элементарных
функций f(u), аргумент которых является простой или сложной
функцией независимой переменной х. Для их отыскания использу-
используются правила дифференцирования суммы, произведения и частного
функций, а также формулы для производных основных элементар-
элементарных функций, выведенные в предыдущих параграфах.
Приведем основные правила дифференцирования функций.
I. у = си=>у' = си'.
II. у = и -\- v=$~y' = и' -\- v'.
III.	y — uv=>y' = u'v-\-v'u.
IV.	y=JL^y>= "'"-"'»,
V. y = f(u), и = и(х)=>у' = Ги(и)и'(х).
VI. у = f(	L
В табл. 5.1 даны формулы дифференцирования основных элемен-
элементарных функций.
Приведенные выше правила и формулы дифференцирования
функций составляют основу дифференциального исчисления. Исполь-
Таблица 5.1
Функция
Производная
Функции
Производная
У— С
= и", а 6 R
у = cos и
У = lOgo U
у — \п и
у = $in и
у' = аиа~'и
у' = a" In а- и'
у' = еии'
и'
у' = — sin и- и'
"'
У =
cos2u
и'
У =	г
sm
У' =
и In a
, и
у =v
у' = cos и • и'
у = arcsin и
у = arccos и
у = arctg и
у = arcctg и
у-
</'= —
У' =
У =-
sin' и
и'
1+и2
115

зуя их, можно найти производную и дифференциал любой элементар-
элементарной функции.
5.9. ДИФФЕРЕНЦИРОВАНИЕ НЕЯВНЫХ ФУНКЦИЙ
Пусть функция y = f{x) задана уравнением F(x, y) = 0. В этом
случае говорят, что функция у задана неявно.
Пусть уравнение F(x, </) = О задает у как неявную функцию х,
т. е. у = у{х). Предположим, что функция у дифференцируема.
Если в уравнении F(x, y) = 0 под у подразумевать функцию у(х), то
это уравнение обращается в тождество по аргументу х: F(x, у(х)) = О
Vx ? [а; Ь]. Дифференцируем его по х, считая, что у есть функция х.
Получаем новое уравнение, содержащее х, у и у'. Разрешая его от-
относительно у', находим производную искомой функции у = f(x), за-
заданной в неявном виде.
Пример 5.7. Найти производную функции х2 + Зху + у2 + 1 = 0, заданной
неявно.
Решение. Дифференцируя по х неявную функцию и считая, что у — функция
от х, имеем 2 + З j З' + 2' 0 О
я и е. Дифференцируя по х неявную функцию и
2х + 3у + Зху' + 2уу' = 0. Отсюда
2х + 3у
Отметим, что в этом случае у' = g(x, у).
5.10. ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ.
ПРОИЗВОДНАЯ СТЕПЕННО-ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ
Логарифмическое дифференцирование. Правило дифференциро-
дифференцирования сложной функции позволяет в некоторых" случаях значи-
значительно упростить задачу нахождения ее производной.
Пусть функция f(x) дифференцируема на отрезке [а; Ь] и f(x) > 0
Vx ? [а; b]. Тогда определен \п у = \п f(x). Рассматривая \nf(x) как
сложную функцию аргумента х, можно вычислить производную
этой функции в фиксированной точке х, принимая y = f(x) за про-
промежуточный аргумент. Применяя правило дифференцирования
сложной функции, имеем
(In «,)'=-?-= (In ft*))',
откуда у' = у(\п f(x))'.
Производную от логарифма функции называют логарифмической
производной.
Логарифмическое дифференцирование удобно применять, если
требуется найти производную большого числа сомножителей. Дейст-
Действительно, пусть y = u\Ui---Un, где каждая из функций ы„ i=\, n,
дифференцируема и ы, > 0 V x?D{f). Логарифмируя функцию у,
имеем In t/ = In и\ + In «2 + •. + In un- Отсюда
у	U\ ' U2	'"	Un
Умножая левую и правую части последнего равенства на у, имеем
116

I

Пример 5.8. Продифференцировать функцию у = -
Решение. Найдем 1п у = 2 1п (х + 1) — 3 1п (х + 2) — 4 1п (* + 3). Имеем
у' _ 2	3	4_
у ~ х+\ jc + 2 * + 3'
откуда
2	3	4 \	(х+ иСб^Ч- 14д: + 5)
(х + 2f(x + ЗL \ х
/ 2	3	4 \ =
4 \ х + 1 * + 2 д: + 3/
Производная степенно-показательной функции. Пусть у = m(x)"w,
где и(х)>0, т. е. основание степени и(х) и ее показатель v(x) явля-
являются функциями переменной х. Функции и(х) и и(д:) предполагаем
дифференцируемыми для рассматриваемых значений х. Логариф-
Логарифмируя степенно-показательную функцию, имеем
In у = v(x) In u(x).
Дифференцируем последнее равенство с учетом того, что правая
и левая его части являются сложными функциями аргумента х.
Получаем
откуда
у> = U{x)v{t) In u(x) • v'(x) + v(x) и(хУ(х)~1 • и'(х).
.Таким образом, производная степенно-показательной функции
равна сумме производных этой функции, если ее рассматривать
сначала как показательную, а затем как степенную.
Например, если у = х", то у' = дг"Aп х + 1).
5.11. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ,
ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
Пусть функция у = у(х) задана параметрически:
Предположим, что функции ф(<) и ty(t) дифференцируемы для
любого t ? Т и ф'(<)=^0. Кроме этого, будем считать, что функция
х = ф(<) имеет обратную функцию t = ф~'(*), которая также диффе-
дифференцируема. Тогда функцию у = у(х), заданную уравнениями E.6),
можно рассматривать как сложную функцию y = ty(t), t = (p~i(x),
считая t промежуточным аргументом.
Продифференцировав функцию y = ty(t), t = (f>~l(x), по правилу
дифференцирования сложной функции, получим y'x = ^'(t)t'x. Произ-
Производную t'x найдем по правилу дифференцирования обратной
функции:
117

V — — — '
Итак, применяя для удобства записей обозначения ф'(/),= .
7) = u't, окончательно имеем:
Пример 5.9. Найти производную функции
х =
у
Решение. Согласно формулам E.7), имеем:
(/(' (ft sin <)f'
ф@-	( )
= a cos t,\
= b sin t, J
Следовательно,
J
х = a cos t.
5.12. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
Общие сведения. Производная от функции y = f(x) является
также функцией от х и может быть дифференцируема.
Производная от производной функции у = f(x) называется про-
производной второго порядка или второй производной функции и обо-
обозначается: у", f"(x), d2y/dx2. Таким образом,
Вторая производная имеет простой механический смысл. Пусть
s = s(t) — закон движения материальной точки, тогда первая про-
производная определяет скорость движения v = s'(t). Вторая же про-
производная есть скорость изменения скорости движения, т. е. ускоре-
ускорение а = -g- = s"'(О-
Аналогично вводятся производные третьего, четвертого и более
высоких порядков.
Производная от производной второго порядка функции у = /(*)
называется производной третьего порядка и обозначается: у'",
Аналогично
yivd=lf(y'")' = fIV(A:).
Производной п-го порядка от функции у = f(x) называется про-
производная от производной (п — 1)-го порядка:
118

Рассмотрим примеры нахождения производных высших по-
порядков.
Пример 5.10. Найти производную л-го поридка от функции у = 1п A +*).
Решение. Выполнии последовательное дифференцирование, находим:
1	1	1-2
{'/у\	 ____ f"tr\	 t'"lr\
fix)- l+x, f(x)- {i+xf, f (x)--
1 О *}	I'I \(А*Ь О/1*»
Пример 5.11. Найти производную л-го поридка от функции y = s\nx.
Решение. Выполнии последовательное дифференцирование, получаем:
у"
= — sin x = sin ( х + 2 у V
(/")= S
Производные высших порядков от функции, заданной неявно.
В § 5.9 было дано правило нахождения первой производной от
функции, заданной неявно, и показано на примере, что у'х в общем
случае содержит как аргумент х, так и функцию у.
По определению вторая производная от функции у = f(x) есть
производная от первой производной. Следовательно, для нахождения
второй производной надо продифференцировать найденную первую
производную по аргументу х, продолжая рассматривать у как
функцию от х. В выражение для второй производной войдут х, у и у'.
Подставляя вместо у' его значение, находим у", зависящую только от
хну. Аналогично поступаем при нахождении у'", yiv и производных
более высоких порядков.
Пример 5.12. Найти производную третьего поридка от функции y — f(x), за-
заданной уравнением х2 + у2 = а2.
Решение. Найдем первую производную 2х + 2уу'=0, откуда у' = -~х/у. Диф-
Дифференцируй данное уравнение вторично, получаем у" =(—х/у)' — — (у — у'х)/у*.
Так как у' = —х/у, имеем у" = —(х2 + у2)/у3= —а2/и3. Дифференцируй у" с уче-
учетом полученных выражений дли у" и у" и того, что х + у2 = а , находим
у'" = (-а2/у3)'х = (-а2у-3)'х = За2!/" V = За2у-А(-х/у) = -За2*/!/5.
Производные высших порядков от функции, заданной параметри-
параметрически. Пусть у — функция от х, заданная уравнениями
Поскольку вторая производная от у по х есть первая производ-
производная от у'х по х, то задача нахождения второй производной сводится
к отысканию первой производной от функции, заданной параметри-
параметрически (см. $ 5.11):
119

Следовательно, по определению первой производной для функ-
функции, заданной параметрически, имеем:
у'* =
Аналогично находится третья производная:
* = Ф@
и производные высших порядков.
Пример 5.13. Найти у'", если *^f C?S,
Решение. Выполняя последовательное дифференцирование, получаем:
,	Ь_
у! b cost	b	Ух~ а
Ух = —Г = 	:—Т =	Ctg t,
" x't —asm t	a s
x = a cos t;
xi	— a sin f	a2 sin31 x = acost;
(	Ь у
(у,')'.	\	n2 «in3 t I ,	ЧЛ cne /
У"' = —7
/	* V	^y	3ucos< 1
V a2 sin3 / / , _ 3fc cos f "'	a3 sin5 < ' J
— a sin <	a3 sin51 ' x = acost.
Замечание. Если в формулу для вычисления второй производной у" =
— (y'x)!/x't подставить yx = yi/xl и выполнить дифференцирование по t, можно по-
получить другую формулу для вычисления уЧ, а именно:
У"
Так как в механике производные по t обозначают у, х, последнюю формулу
можно записать в виде
_ ух-ух Л
У"
X —
5.13. ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
Рассмотрим функцию у = f(x). Дифференциал этой функции dy —
= f'(x)dx зависит от х и dx = kx, причем Л* от х не зависит, так
как приращение в данной точке х можно выбирать независимо от
точки х. В этом случае dx в формуле первого дифференциала будет
постоянным. Тогда выражение f'(x)dx зависит только от х и его мож-
можно дифференцировать по х.
Дифференциал от дифференциала функции у = f(x) в данной точ-
120

ке х называется дифференциалом второго порядка или вторым
дифференциалом.
Дифференциал второго порядка обозначается d2y или d2f(x). Та-
Таким образом,
Аналогично дифференциал третьего порядка от функции у = f(x)
d3y=d(d*y).
Вообще дифференциал п-го порядка (или п-й дифференциал)
функции у = f (х) определяется как дифференциал от дифференциала
(п — 1)-го порядка:
Найдем выражение для второго дифференциала функции у =
= f(x), полагая dx в формуле dy = f'(x)dx первого дифференциала
постоянным. Тогда
d2y = d(dy) = d(f'(x)dx) = d(f'(x))dx =
= (f"(x)dx)dx = f"(x)(dxf,
т ё	"*
d2y = f"(x)(dxf.	feS-и
Аналогично
d*y = d(d2y) = d(f"(x) {dxJ) = d(f" (x)) (dxJ =
= (f'"(x)dx) (dxJ =* f'"(x) (dxf.
Можно установить справедливость формулы для дифференциала
га-го порядка
В дальнейших записях скобки при степенях dx будем опускать:
d(n)y = fW
Отсюда следует, что производная п-го порядка есть отношение
ее дифференциала п-го порядка к n-й степени дифференциала не-
независимой переменной:
В частности, при п= 1, 2, 3 получим соответственно:
f'(x) — ^- f"(x) = ^- Г"(х) = -^-
' {Х)~ dx' ' {Х) dx*' I [X) dx'-
При этом предполагаем, что аргумент х функции y = f(x) является
независимой переменной.
Выведем теперь формулы для вычисления дифференциалов
высших порядков в случае, когда аргумент х является дифференци-
дифференцируемой функцией х = ф(/) некоторой переменной /. Как видно из
121

рис. 5.8, для одного и того же А/, но
для разных / (и, следовательно, для
разных х) приращения Ах различны,
т. е. в этом случае dx = А* нельзя счи-
считать независимыми от х, так как dx
является дифференциалом функции:
О t U U t. tr t
Поэтому при вычислении d у по опре-
Р и с. 5.8	, def
делению (d2y=d(dy) = d(f'(x)dx)) бу-
будем считать его дифференциалом от произведения двух функций
f'(x) и dx, т. е.
d2y = d(f'(x)dx) = d(f'(x))dx + f'(x)d2x =
= (f"(x)dx)dx + f'(x)d2x = f"(x)dx2 + f'(x)d2x.
Итак,
Таким образом, в случае, когда аргумент х не является неза-
независимой переменной, второй дифференциал d2y определяется форму-
формулой, состоящей из двух слагаемых.
Покажем, что ранее выведенная формула для второго дифферен-
дифференциала d2y = f"(x)dx2 (в случае, когда х — независимая переменная)
является частным случаем формулы E.8). Действительно, если х —
независимая переменная, то d х = (x")dx2 = 0 • dx2 = О, и второе сла-
слагаемое в формуле E.8) отсутствует.
Приведем формулу для вычисления дифференциала третьего
порядка:
d3y = f'"{x)dxz + 3f"(x)dxd2x + f'(x)d3x.
Из полученных формул для d2y, d3y следует, что при вычислении
дифференциалов более высоких порядков от сложной функции про-
происходит нарушение инвариантности формы. Другими словами, фор-
формулы для дифференциалов порядка выше первого различны. Их вид
зависит от того, является ли аргумент х независимой переменной или
дифференцируемой функцией другой переменной. (Напомним, что
для дифференциала первого порядка его форма записи остается
неизменной.)
5.14. ТЕОРЕМЫ О СРЕДНЕМ ЗНАЧЕНИИ
Теоремы о среднем — одно из свойств дифференцируемых
функций. Одним из важнейших классов (множеств) функций, изуча-
изучаемых в курсе математического анализа и имеющих первостепенное
значение при решении задач практического характера, является
класс непрерывных функций. В предыдущей главе мы показали, что
класс дифференцируемых функций является подмножеством мно-
множества непрерывных функций. Дифференцируемые функции пред-
представляют особый интерес, так как большинство задач техники и
122

естествознания приводят к исследованию функций, имеющих про-
производную. Такие функции обладают некоторыми общими свойствами,
среди которых важную роль играет ряд теорем, объединенных общим
названием теоремы о среднем. В каждой из этих теорем утвержда-
утверждается существование на отрезке [а; Ь] такой точки, в которой иссле-
исследуемая функция y = f{x) обладает тем или иным свойством.
Теорема 5.4 (Ролля*). Пусть функция f(x) удовлетворяет сле-
следующим условиям на отрезке [а; Ь\.
1)	f(x) определена и непрерывна на [а; Ь\,
2)	f(x) дифференцируема на ]а; Ь[;
3)	f(a) = f(b).
Тогда существует по крайней мере одна точка |?]а; Ь[, такая, что
ГF) = о.
> Известно, что если f(x) непрерывна на [а; Ь], то на этом отрезке
она принимает свое наибольшее М и наименьшее m значения
(см. теорему 4.1) Возможны два случая.
1.	M = mof{x) = consi=>f'(x) = 0 V*6[a; b].
2.	М > m. Тогда из условия f (a) = f (b) следует, что хотя бы одно
из двух значений М или m функция принимает в некоторой внутрен-
внутренней точке ? отрезка [а; Ь]. Пусть для определенности f(|) = m
(рис. 5.9). Это означает, что f(x)^f(l-)Yx(i[a; b].
Покажем, что f'(|) = 0. Согласно условию 2 теоремы Ролля,
для функции f(x) существуют конечные производные f (!)У|?]я; Ь[.
Это условие равносильно существованию разных односторонних
пределов:
V66]a; Ь[ ЗГA)=
ч> lim
о—о	Ах	дх-»о+о
Найдем односторонние пределы. Так как М > т, то f (| + Ах) —
(lH V|6]a; b[. Следовательно,
Геометрически теорему Ролля можно пояснить следующим обра-
образом: если непрерывная на отрезке [a; b] и дифференцируемая в интер-
интервале ]а; Ь[ функция f(x) принимает на концах этого отрезка равные
значения, то на графике этой функции найдется хотя бы одна такая
точка С с абсциссой х = |, в которой касательная параллельна оси Ох
(см. рис. 5.9).
Замечание. Условия теоремы Ролля являются достаточными, но не необхо-
необходимыми. Например, функция f(x) = x3 определена и непрерывна на [—1; 1], диффе-
дифференцируема во всех внутренних точках этого отрезка, однако для нее не выпол-
выполняется третье условие теоремы Ролля: /(—1) =^= f(l). Тем не менее, существует точка
| = 0, такая, что f'(l) = 0 (рис, 5,10).
Мишель Ролль A652—1719) — французский математик.
123

/77
В
а
Ь X
Рис. 5.9
Рис. 5.10
На рис. 5 11 изображен график разрывной и недифференцируемой на [а; Ь] функ-
функции, для которой существует точка g ? \а; Ь[, такая, что /'(|) = 0.
Теорема 5.5 (Лагранжа*). Если функция f(x)' непрерывна на от-
отрезке [а; Ь] и дифференцируема на интервале ]а; Ь[, то существует
по крайней мере одна точка |6]а; Ь[, такая, что
\f(b)-f(a) = f'(l)(b-a).\	E.9)
> Составим вспомогательную функцию
cp(x)=*(b-a)f(x)-(f(b)-f(a))x.
Покажем, что функция ср(х) удовлетворяет условиям теоремы
Ролля. Действительно: 1) у(х) непрерывна на [а; Ь], так как явля-
является суммой непрерывных на [а; Ь] функций; 2) <р(*) дифференци-
дифференцируема на ]а; Ь[, так как является суммой дифференцируемых на
]а; Ь[ функций; 3) <p(a) = <p(b) = bf(a) — af(b). Итак, <р(*) удовлетво-
удовлетворяет условиям теоремы Ролля, причем
<p'(x) = (b-a)f'(x)-(f(b)-f(a)).
По теореме Ролля существует точка |6]а; Ь[, такая, что
Ф'(|) = 0, т. е.
(Ь - а)П1) - (f(b) - f(a)) = Oof(b) - f(a) = f'(?) (b - а). О
Теорему Лагранжа иногда называют также теоремой о конеч-
конечных приращениях.
Рис. 5.12
* Жозеф-Луи Лагранж A736—1813) —французский математик.
124

Формулу E.9) называют формулой Лагранжа. Иногда ее записы-
записывают в виде
f(b)-f(a) =m le]Q. bl	EЛ0)
Поясним теорему Лагранжа геометрически. Выражение (f(b) —
— f(a))/{b — a) — k представляет собой угловой коэффициент хорды
АВ, a f'(l) — угловой коэффициент касательной к кривой f(x) в точ-
точке С. Поэтому, согласно соотношению E.10), теорема Лагранжа
утверждает, что между точками Л и В на дуге АВ найдется по
крайней мере одна точка С, в которой касательная параллельна
хорде АВ, при условии, что в каждой точке дуги АВ существует
касательная (рис. 5.12). (Напомним, что в силу условия f(a) =
= f(b) теорема Ролля утверждает, что в точке С касательная
параллельна оси абсцисс.)
Если в формуле Лагранжа E.9) положить f(a) = f(b), получим
теорему Ролля, т. е. теорема Ролля является частным случаем
теоремы Лагранжа.
Положим в формуле Лагранжа E.9) а = х0, b = хо + Ах. Тогда
она примет вид
E.11)
где х0 < | < xQ + Ал:. Формула E.11) связывает приращения аргу-
аргумента и функции, поэтому ее называют формулой конечных при-
приращений.
Формула Лагранжа в виде E.11) дает точное выражение при-
приращения функции через вызвавшее его приращение аргумента в отли-
отличие от дифференциала функции, который определяет приближенное
значение приращения функции: Ay « dy = f (xo)Ax. Заметим, что
в приближенных вычислениях приращение функции заменяют чаще
дифференциалом, т. е. полагают Aymdy. Формула E.11) приме-
применяется реже, так как для ее использования необходимо указать точку
I 6 ]а; Ь[, что, вообще говоря, не всегда удается.
Приведем пример использования формулы конечных приращений
для нахождения приближенного значения функции ^(аг) в фиксиро-
фиксированной точке х0 + Ах.
Пример 5.14. Пользуясь формулой конечных приращений, найти приближенное
значение sin 31°.
Решение. Запишем формулу конечных приращений для функции f(x) =
== sin jc иа [хо; х0 + Ах]: sin(;eo + Ах) — sin х0 = cos |Ддс, S6[*o; xo+Ax\. Отсюда
следует, что sin (дсо + Д*) = sin хо + cos ?Д*.
Для вычисления приближенного значения sin 31° перейдем от градусной к
радианной мере угла:
sin 31° = —^— • 31 = sin 0,541.
180°
Имеем sin 0,541 = sin -?- + cos g • 0,0175, л/6 < g < 0,541. Возьмем cos g ж cos л/6 =
о
= Уз/2, тогда sin 0,541 « -i- + ^L- ¦ 0,0175 = 0,515.
125

Обобщением теоремы Лагранжа является теорема Коши.
Теорема 5.6 (Коши). Пусть функции f(x) и g(x) удовлетворяют
следующим условиям:
1)	непрерывны на отрезке [а; Ь];
2)	дифференцируемы в интервале ]а; Ь[, причем g'(x)=?0
Vx?]a; b[. Тогда существует по крайней мере одна точка |6]а; Ь[,
ЧТ°	ПЬ)-На) _ ГA)	E12)
8(b)-g(a) ~ W
> Составим вспомогательную функцию:
Ф(х) = f(x)- f(a) - ffj^
Заметим, что ё(Ь)Ф g(a). Действительно, если бы g(&) = g(a),
то для функции g(x) на отрезке [а; Ь] были бы выполнены все усло-
условия теоремы Ролля, и по этой теореме внутри отрезка [а; Ь] нашлась
бы по крайней мере одна точка |, для которой ?'(!) = О, что про-
противоречит условию теоремы. Следовательно, g{b) Ф g(a).
Покажем, что вспомогательная функция (р(х) удовлетворяет усло-
условиям теоремы Ролля. Действительно: 1) у(х) непрерывна на [a; b] как
сумма непрерывных на [а; Ь] функций; 2) у(х) дифференцируема на
}а; Ь[ как сумма дифференцируемых на ]а; Ь[ функций; 3) ф(а) = 0,
(
Найдем
По теореме Ролля существует точка 16 ]а; Ь[, такая, что ф'(|) = 0;
Легко видеть, что если положить в формуле E.12) g(x) = x,
то все условия теоремы Коши будут выполнены, и формула Ко-
Коши E.12) «перейдет» в формулу Лагранжа E.9). Таким образом,
теорема Лагранжа является частным случаем теоремы Коши.
Геометрические интерпретации теорем Коши и Лагранжа совпа-
совпадают. Действительно, обозначим независимую переменную через t и
будем считать, что функции y=-f(t), x = g(t) являются параметри-
параметрическими уравнениями некоторой линии. Когда параметр t «про-
«пробегает» отрезок [t\\ U], текущая точка перемещается по какой-то
дуге, начальная точка А которой имеет координаты {g(t\)\ f{t\)),
а конечная В — (?(/2); f(<г))- Угловой коэффициент хорды, стягива-
стягивающей эти точки, k = —~+—Цг/т. Производная от функции, задан-
ной параметрически, dy/dx = f'{t)/g'(t). Из формулы
126

следует, что если дуга задана в параметрической форме: x = g(t),
y = f(t), t\^t^.t2, то на ней найдется такая точка С, в которой
касательная параллельна хорде, стягивающей эту дугу.
5.15. ПРАВИЛО ЛОПИТАЛЯ
При раскрытии неопределенностей (см. § 3.7) полезна следующая
теорема, впервые доказанная И. Бернулли*.
Теорема 5.7 (правило Лопиталя**). Если функции f(x) и g(x)
удовлетворяют следующим условиям:
1)	определены и дифференцируемы на интервале }а; Ь[, за исклю-
исключением, быть может, точки х0, причем g(x) Ф О и g'(x) Ф О Vx 6 ]а; Ь[\
2)	lim f(x) = lim g(x) = 0 (либо lim f(x)= lim g(x) = oo (+oo
X—*-Xt)	X-*-Xq	X-*~Xo	X-+Xq
или —oo));
3)	существует предел (конечный или бесконечный) отношения
производных
Щ
то существует также предел отношения функций \\т-±Щ, причем
лг-*Хо g\X)
iWi?)	E.13)
limi=limi?
х+х« g(x)	x^xo g'(x)
> Приведем доказательство теоремы только для случая раскры-
раскрытия неопределенностей вида -ту-. Доопределим функции / и g в точке
х = *о, положив f(x0) = g(x0) = 0. Доопределенные таким образом
функции будут непрерывны в точке х0. Рассмотрим отрезок \х0; х\
где дг0 < х < Ь. На этом отрезке функции fug непрерывны, а на
интервале ]а; х[ — дифференцируемы. Следовательно, по теореме
Коши существует точка | (а < х0 < | < х) такая, что
f(x)-f(xo) _ ПЕ)
e(x)-g(x0) g'(i)'
С учетом того, что f(х0) = g(x0) = 0, имеем
Ж = Ш	E 14)
g(x) g'<g>-	^Aq>
Если х-+х0, то и Ъ-*-х0, поэтому, согласно условию 3 теоремы,
из равенства E.14) следует, что
lim JW = ,im Ш <
х^х» g(X)	x^x, g'(x) ^
Смысл правила Лопиталя, задаваемого формулой E.13), заклю-
заключается в том, что оно позволяет свести вычисление предела отноше-
* Иоганн Бернулли A667—1748) —швейцарский математик.
** Гильом Франсуа Лопиталь A661 —1704)—французский математик.
127

ния функций в случае неопределенности вида -^ или — к пределу
отношения производных, который очень часто вычисляется проще.
Правило Лопиталя справедливо и в случае х0 = оо. Если произ-
производные f'(x) и g'(x) удовлетворяют тем же требованиям, что и са-
V (х)
ми функции f(x) и g(x), и lim ' „) ' существует, применив дважды
правило Лопиталя, найдем
Ит Ж = нп, Ш. = Пт П±.
х^хс, g(x)	х^хо g (х)	х-х„ g"(x)
Правило Лопиталя можно применять до тех пор, пока не будет
получена дробь, для которой условия, предусмотренные теоремой,
уже не выполняются.
Приведем несколько примеров раскрытия неопределенностей раз-
различного типа с помощью правила Лопиталя.
Пример 5.15. Вычислить lim
х^О
Решение. Непосредственная подстановка предельного значения * = 0 при-
приводит к неопределенности вида -jr-. Для ее раскрытия трижды применим правило
Пппнта па*	"
Лопиталя:
а* 	 л* 	 Оу	а* _1_ л — * 	 О
lim	-3	= lim	3	~ 'lm
Пример 5.16. Вычислить lim
хО +
	6	 = У
—;	.
Ctg X
Решение. Непосредственная подстановка предельного значения приводит к
неопределенности вида — . Применяя правило Лопиталя, имеем:
In Ъх .. \/х .. —sin2*
lim —	= lim ——	, , = lim 	=
CtgAC x-^+Q \/( — S\n2x) дг^О+О	X
,. . .. sin*
= lim sin x lim	 = 0.
0 + 0	0 + 0 X
Пример 5.17. Вычислить lim [	-,	1.
х-»о \ х tg * /
Решение. Непосредственная подстановка предельного значения * = 0 дает
неопределенность вида оо — оо. Приведя дробь к общему знаменателю, получим
неопределенность вида — (см. пример 5.15):
.. / 1	1 \ .. tg* —* .. 1/cos2*—1
lim (	1 = lim —S	= lim —	5— =
x-*o \ * tg * / x-+o x tg * x-*o tg * + */cos'! *
..	sin2*	.. sin 2*	-
= Mm —;—r~.—. . .- = Mm —.—;	^— = U.
*—0 * + (sin 2*)/2 x-o 1 + cos 2*
Пример 5.18. Вычислить lim (* In *).
x—0+0
Решение. Непосредственная подстановка предельного значения приводит к
неопределенности вида 0 • оо. Представляя произведение функций в виде частного,
оо
сводим данную неопределенность к неопределенности вида — (см. пример 5.16):
128

lim (x In x) = lim 	= lim	—s-= lim (—x) = 0.
0 + O	x-.-0 + O \/x	x-H) + 0 — \/x	x-H)+0
Пример 5.19. Вычислить lim Xх.
x*0 + 0
Решение. Непосредственная подстановка предельного значения приводит к не-
неопределенности вида 0и. Раскрытие неопределенности вида 0" предварительным
логарифмированием дает неопределенность вида 0-оо (см. пример 5.18). Обозна-
Обозначим у = Xх, тогда In у = х In x. Имеем:
1-1	¦•	•	•• 'n x
lim In у = Inn x In x = lim —r-.— = 0,
0+0	0 + 0	х-*0 + 0 \/x
lim In у = In lim у = 0=*- lim у = 1.
O + O	xM> + 0	хЮ + О
Пример 5.20. Вычислить lim я'/V*
Решение. После непосредственной подстановки предельного значения по-
получаем неопределенность вида оо°. Предварительным логарифмированием заданной
оо	г~
функции приводим данную неопределенность к виду —. Обозначим у = х'/л1",
тогда 1п у = ——In х. Имеем:
V*	In*	2
lim 1п(/= lim —— = lim —— = 0,
х-*+оо	Х-++ОО Г^	х->- + оо _П
lim In у = In lim (/ = 0=*- lim (/ = e°=l.
X-*- + OO	X-*- + OO	X-*- + OO
Пример 5.21. Вычислить lim (cos x)l/r'.
Решение. После непосредственной подстановки предельного значения по-
получаем неопределенность вида 1°°. Предварительное логарифмирование сводит дан-
данную неопределенность к неопределенности вида -тг-. Обозначим у = (cos xI/г>, тогда
In у = —г- In cos х. Имеем:
х
,. ,	,. In cos x ,. — tg*	1 .. sin* .. 1	1
lim In у = lim	;	= lim	=— =	lim	• lim	= ——,
x-*o	*-*o x	x^-o 2x	2 x-»o x x^-o cos x	2
lim In у = In lim у =	т-=> lim у = е~1/г — ——.
x^0 *	«О*	2 х-*О*	Г
5.16. ФОРМУЛА ТЕЙЛОРА
Формула Тейлора1" с остаточным членом в форме Пеано.** В ма-
математическом анализе формула Тейлора — одна из важнейших; она
имеет много теоретических приложений и является основой прибли-
приближенных вычислений.
Известно, что наиболее простыми функциями в смысле вычисле-
вычисления их значений являются многочлены. Возникает вопрос о возмож-
возможности замены функции f в окрестности точки х0 многочленом некото-
некоторой степени.
Из определения дифференцируемости функции f в точке х0 сле-
следует, что если у = f(х) дифференцируема в точке хо, то ее прираще-
приращение можно представить в виде Af(x0) = f'(x0)Ax + o(Ax), т. е.
* Брук Тейлор A685—1731) —английский математик.
** Джузеппе Пеано A858—1932) — итальянский математик.
5 Зак 1270	129

f(x) = f(x0) + f (xo) (x - xo) + o(x - xo).
Другими словами, существует многочлен первой степени
Pl(x)
такой, что при х^-Хо
E.15)
причем Р\(х) удовлетворяет следующим условиям: Pi(xo) = f(xo),
Pi() bf'()
Поставим более общую задачу. Пусть функция, определенная
в некоторой окрестности точки х0, имеет в этой точке п производных
Р(хо), f"(xQ), f'"{xo), ..., /(л)(*о). Требуется выяснить, существует ли
многочлен Рп{х) степени не выше п, такой, что
f(x) = Pn(x) + o(x — x0)n.	E.16)
Найдем многочлен степени не выше п (запись которого анало-
аналогична E.15)):
Рп(х) = bo + bl(x-xo) + Ь2(х - xof + ... + Ьп(х -хо)п, E.17)
при условии, что значения многочлена Р„(х) и всех его производных
до п-го порядка включительно в точке х0 совпадают со значениями
функции f(x) и ее соответствующих производных в той же точке:
f(Хо) = Рп(Хо), f'(Xo) = Pn(Xo), ..., f"\xo) — Pft\xo).	E.18)
Определим коэффициенты bo, b\, ..., bn многочлена E.17) так,
чтобы они удовлетворяли условиям E.18). Найдем предварительно
производные от Рп(х):
Р'п(х) = Ь\+ 2Ь2(х — Хо) + ЗЬ3(х — Xof +... + nbn(x — Хо)"'1,
р{(х) = 2- \Ь2+2>-2-Ьг{х — Хъ) + ...-\-п{п — \)Ьп{х — Хо)п-2,
Р'У(х) = 3 • 2 • 1Ь3 +... + п(п — 1)(« — 2)Ьп(х — Хо)п-\	E.19)
Pin\x) = п(п - I) (п - 2)-¦ -2 • 1Ьп.
Подставляя в левые и правые части равенств E.17) и E.18)
вместо х значение х0, находим значения всех коэффициентов bi
i = 0, п:
Ьо = f(x0),
Подставляя найденные значения коэффициентов в равенство
E.17), получаем многочлен вида
130

Ра(х) = f(x0) + f (jco) (x - jco) +
2!
- *oJ +... +
(x - xof,
который называется многочленом Тейлора функции f(x).
Докажем, что многочлен Тейлора удовлетворяет условию E.16).
Обозначим через Rn(x) разность значений данной функции и по-
построенного многочлена Тейлора:
Rn(x) = f(x)-Pn(x).
На рис. 5.13 приведены графики функции у = f(x) и ее многочлена
Тейлора в окрестности точки х0- Как видно из рис. 5.13, Rn(x) есть
погрешность, возникающая при замене
функции f (х) многочленом Рп(х) в у j,
окрестности точки xq. Для тех значений
х из окрестности точки х0, для которых
погрешность Rn(x) достаточно мала,
многочлен Рп(х) дает приближенное
представление функции.
Согласно определению многочлена
Р„(х), из условий E.18) следует, что
Rn(x0) = R'n(xo) = ... = Rbn)(xo) = 0.
Докажем, что
RnW
Рис. 5.13
Rn(x) = о((х —
lim
= 0.
ности
lim
Применим п раз правило Лопиталя для раскрытия неопределен-
(х-xof
Rjx)
(x-xof
вида —:
= lim —
= ...= lim
-"
(ж)
П\(Х—Д
п\
= 0,
т. е. Rn(x) = о((х — хо)") при х^>-х0. Таким образом, доказана следую-
следующая важная
Теорема 5.8. Если функция у = f(x) определена и п раз диффе-
дифференцируема в Оь(хо), то при х->-х0 имеет место формула
Нх) = Пхо) + Г(хо)(х-.
+
2!
(x - xof +... +
n\
или в более краткой форме записи
(х-.
k\
о(х — хо)п,
E.20)
где Rn(x) = о((х — хо)п) — остаточный член в форме Пеано.
Формула E.20) называется формулой Тейлора n-го порядка с
остаточным членом в форме Пеано.
Если в формуле Тейлора E.20) положить хо = 0, получим част-
131

ный внд формулы Тейлора, называемый обычно формулой Макло-
рена*:
Ж, +...+ .№
Остаточный член формулы Тейлора в форме Лагранжа. Сущест-
Существуют различные виды запнсн остаточного члена Rn{x) формулы
Тейлора. Получим представление его в форме Лагранжа.
Потребуем, чтобы функция f имела п + 1 производную в окрест-
окрестности точки Хо. Введем новую функцию g(x) = {x— Jto)"+1. Очевид-
Очевидно, что
g(xo) = g'(xo) = ... = gw(xo) = O, g<"+'>(*) = (n+l)!#0.
Применим к функциям Rn{x) = f(x) — Pn(x) и g(x) = (x — xo)n+[
теорему Кошн. Тогда в силу условия Rn(xo) = R'n(xo) =... = #(пл)(*в) = О
получим
Rn(x) _/?„(*)-/?»(*<>) _ Rk{ci) _ R'njc^-R'njxo) _
g(x)	g{x)-g(xo)	g'nid)	g'n(ci)-g'n(xo)
где ci€]xo; x[; c26]^o; ci[; ...; cn?}x0; с„_|[; l€}x0; cn[cz}xo; x[.
Таким образом, мы показали, что
Rn(x) _ /?{,"+ '>(?)
g(x)
где 16 }хо; х[. С учетом того, что g(x) = (x — xo)n+\ g(n+ l\Q = (n + 1)!,
&+l)	+l5). имеем
Щ (х - хоу+[, 16 ]*о; х[.	E.21)
Формулу E.21) называют остаточным членом формулы Тейлора
в форме Лагранжа.
Так как ? ? ]*о; х[, то ? можно представить так: ? = Jto + 6С* — *о).
где 0<с9<С1, т. е. остаточный член в форме Лагранжа можно
записать в виде
Таким образом, формула Тейлора с остаточным членом в форме
Лагранжа имеет внд
где
* Колин Маклореи A698—1746) —шотландский математик.
132

Если в формуле Тейлора положить хо = 0, получим частный вид
формулы Тейлора — формулу Маклорена. Так как ? = хо + 6(х—
— дсо), 0 < 9 < 1, то при хо = О I = 0х. Поэтому остаточный член
формулы Маклорена
а сама формула Маклорена с остаточным членом в форме Лагранжа
имеет вид
, E.22)
где 0<9< 1.
5.17. РАЗЛОЖЕНИЕ ПО ФОРМУЛЕ МАКЛОРЕНА
НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Разложение по формуле Маклорена функции f(x) = ex. Находим
последовательные производные от }(х) = е*:
f'(x) = e\
f'@)= 1,
/W@)= 1,
Подставляя полученные значения f@), f'@), ..., f-n)@), f-n+l)(Qx)
в формулу E.22), имеем
^ .^
1I
E.23)
где 0 < 6 < 1.
Разложение по формуле Маклорена функции f(x) = sin x. На-
Находим последовательные производные от f(x) = sin x:
f(x) = sin x,
, /'(*) = cos x = s\n (x-\- я/2),
f"(x) =	Sin x = sin (jt + 2|
f'"(x) = — cos д: = sin (x + 3 ^),
= Sin
/<"+'>(*) = sin
n+l)-i),
133

Г@)=-1,
Подставляя полученные значения в формулу E.22), имеем
sin (вдс+ (n+l)у),
E.24)
где 0 < 0 < 1.
Разложение по формуле Маклорена функции f(x) = cos x. Вы-
Вычислив значения последовательных производных от функции f(х) =
= cos х при jt = O, имеем (с учетом того, что ^п)(дс) = соз (х-\-п-^-\
+ _?_ cos @*+ („+!)-?),	E-25)
где 0 < 0 < 1.
Разложение по формуле Маклорена функции f(jc) = In A -\-х).
Функция f(x) = In A + х) определена и бесконечно дифференцируема
на интервале ] — 1; оо[. Найдем последовательные производные
от этой функции:
Г{х) {\+хГ\
f"(x)=-(l+x)-2
f'"(x) = 2- 1A +х)-
(«- 1IA
l +х)-(л-"
()
/'@)— 1,
f"@)
Подставляя вычисленные значения в формулу E.22), получаем
разложение In A +дс) по формуле Маклорена с остаточным членом
в форме Лагранжа:
134

E.26)
Разложение по формуле Маклорена функции f(x) = (\+х)т.
Функция f(jt) = (l -\-x)m, m 6 R, определена и бесконечно диффе-
дифференцируема на интервале ] — 1; 1[. Разложим ее по формуле Макло-
Маклорена. Для этого найдем последовательно производные от f(x) =
f(x) (l+x),
f'(x) = m(\+x)m-[,
f" (*) = m(m-1)A+
f'"(x) = m(m - I) (m -
- n)
f@)=l,
f'@) = m,
Г@) (
- n + 1),
)(
=т(т — l)(m-
Подставляя найденные значения функции и ее производных в
точке xq = 0 в формулу E.22), имеем
(l+x)m=l+mx+
rn{rn-\)-(m-n+\)
E.27)
где
Rn(x)=
Полученные разложения функций, задаваемые формулами
E.23) — E.27), называют основными и используют для представ-
представления многих функций по формуле Тейлора.
Приведем несколько примеров:
Пример 5.22. Разложить по формуле Тейлора функцию f(x) — e~x' в окрестности
точки хо = 0.
Решение. Указанное разложение можно найти, вычислив /@), /'@), ...,
/("'@) и применив формулу E.22), но проще использовать разложение функции
f(x) = e", задаваемое формулой E.23). Заменив в формуле E.23) х на —х2, получим
е~' = 1 — •
где
rf
135

Пример 5.23. Разложить по формуле Тейлора функцию /(jc)=ln(jc) в окрест-
окрестности ТОЧКИ Х(, = 1.
Решение. Воспользуемся основным разложением функции f(x) = In (I + х),
задаваемым формулой E.26). Заменяя в нем х иа х— 1, имеем
2 '--_3K		_, (х-\)
3
где
/?„(*) = (-1)"+1 —
есть остаточный член в форме Лагранжа.
5.18. ПРИЛОЖЕНИЯ ФОРМУЛЫ ТЕЙЛОРА
Использование формулы Тейлора для выделения главной части
функции. Если функция f(x) определена в О&(х0), то для выделения
ее главной части удобно использовать формулу Тейлора с остаточ-
остаточным членом в форме Пеано.
Пусть f(x) и g(x) определены в 0&(хо) и при х-+-хо возможно
представление
f(x) = g(x) + o(g(x)).	E.28)
Тогда функция g(x) называется главной частью функции \(х) в окрест-
окрестности точки хй.
Из формулы E.28) следует, что
М _ 1 | °(g(*)) ^ iim /W _1
т. е. при х-+-хо главная часть функции g(x) и сама функция f(x)
являются эквивалентными функциями.
Пример 5.24. Выделить главную часть- функции f(х) = х* + 2х* + 5х в Ов@).
х \ 2х \ Ьх
Решение. Так как Iim 	г	= 1, то функция f>(x) — bx является
главной частью f(x) в Ов@), т. е.
х* + 2х2 + 5х = 5* + оE*).
Пример 5.25. Выделить главную часть функции f(x) = х3 + 2дс + 1 в Ов(оо).
х3 -\- 2х -\- 1
Решение. Так как Iim — 3 — = 1, то функция g(jc) = jc3 является
х-*-оо	X
главной частью f(x) в Ов(оо).
Следует отметить, что если не задан вид функции, ее главная
часть определяется неоднозначно.
Действительно, в примере 5.24 главной частью функции f(x) = х1 + 2х2 + 5х
в Ов@) является также функция gi(х) = 2х2 + Ьх, поскольку
.. f(x) .. *4 + 2* + 5* ,
Iim lv '¦ = Iim 	—z	'	= l=>
()	2' + Ъ
(
* + 2x2 + 5x = 2x2 + 5x + oBx2 + 5x).
Формула Тейлора с остаточным членом в форме Пеано дает об-
общий метод выделения главной части функции f(x) в окрестности рас-
136

сматриваемой точки хо. Из формулы E.20) следует, что главной
частью функции f(x) в окрестности точки хо является ее многочлен
Тейлора. Для выделения главной части функции удобно использо-
использовать основные разложения с остаточными членами в форме Пеано:
е 1 -T-JC-I- 2| -г---!- „, -г-о^дс ),
3! ' С|	7| ' *** ' \	/
г2	г*	г2п
спч.х=\	-	I- —	I- 4-(	\)—	-I-
Bя+1I
(x2n+l),
o(x
A+Jc)=1+aJC+J?^iJC+...+	jc +
Таким образом, используя многочлен Тейлора функции f(x) в
окрестности точки хо, можно записать асимптотические (прибли-
(приближенные) формулы для f(x) в О&(х0): е* ~ 1 -\-х, е* ~ 1 +дс + дс2/2!,
sin х ~ дс, sin дс ~ х — х3/3\. Повышая степень многочлена Тейлора,
можно получить более точные приближения функции. Графики
функций у = е*, у = sin x и их многочленов Тейлора изображены на
рис. 5.14 и 5.15.
/ 2
Рис. 5.14
Рис. 5.15
Использование формулы Тейлора для вычисления приближенных
значений функции. Если известны значения функции и ее производ-
производных в точке дс0, то для вычисления приближенных значений функции
в 0&(хо) удобно использовать формулу Тейлора с остаточным чле-
членом в форме Лагранжа E.23).
Значения f(x) в Оь(хо) вычисляют по формуле
f(x)t
погрешность приближения
I/?„(*)!= ¦"" '
1I
(*--
л!
Хо < 6 < X.
137

Пример 5.26. Вычислить еол с точностью до 0,001.
Решение. Запишем формулу Маклореиа для е":
При х = 0,1 имеем
'--1 | °Л | °'0
Погрешность приближения ие должна превышать 0,001, следовательно,
/?„(*)= v^j^ < 0,001.
Поскольку eole < 2, то——{	< 0,001. Полагая л=1, 2, 3	 иахо-
дим, что последнее неравенство выполняется, начиная с л = 3.
Итак, с точностью до 0,001
В частном случае при п = 1 функция \(х) аппроксимируется
многочленом первой степени
с погрешностью
tfsM = -ф- (* - *оJ. дсо < 6 < дс.	E.29)
Так как по определению х — х0 = Ах, f'(xo)Ax = df(x0),
то
Погрешность, возникающая при применении такой приближен-
приближенной формулы, не превышает модуля остатка /?2(х), задаваемого
формулой E.29).
Пример 5.27. Найти с помощью дифференциала функции площадь 5 круга
радиусом г= 1,01. Оценить погрешность вычисления.
Решение. Площадь круга S = nr2. Полагая го=1, Дг = 0,01 и заменяя
приращение функции S = S(r) ее дифференциалом, имеем:
S(r)« S(r0) + dS(r0) = S(r0) + S'(ro)Ar,
S(l,01) * S(l) + 2л • 0,01 = 1,02я.
При этом погрешность ие превосходит
Л(г) = -^j=i-(г - г„J, го < Е < г.
Так как S"(r) = 2я и не зависит от г, то
R2(r) = -^- 0,012 = 0,0001я.
Пример 5.28. Найтн приближенное значение функции f(x) = е"'~х в точке дс = 0,03
с помощью дифференциала. Оценить погрешность вычислений.
138

Решение. Запишем приближенную формулу для вычислеиия значений f(x) =
= е" с помощью дифференциала в окрестности точки х<>:
¦ f(x)« f(xB) + df(xB) = f(x0) + f'(xo)&x.
Так как х0 = 0, x = 0,03, Д* = 0,03, то
/@,03) «/@) +/'@H,03
с погрешностью
R2 = HJ?L x2 = -Qp- @,03J, 0 < I < 0,03.
Найдем /'@) и /"(?):
/'(*) = Bх-1)е*'-*=>/'@)=-1,
f"(x) = 2ех'-х + Bх — l)V'-*=>/"(g) < 3.
Следовательно, /@,03)» 1 +(—1)- 0,03 = 0,97 с погрешностью R2(x)<	Цр-'- =
= 0,0017.
Формула Тейлора используется также при исследовании функции
на экстремум, в теории рядов, при вычислении интегралов.

6. ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ
ПРОИЗВОДНЫХ
6.1. ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ
С помощью производной функции можно произвести полное ее
исследование (найти промежутки возрастания и убывания, экстре-
экстремумы, точки перегиба, промежутки выпуклости и вогнутости, асимп-
асимптоты графика) и построить график этой функции.
Теорема 6.1. Для того чтобы дифференцируемая на ]а; Ь[ функция
не убывала (не возрастала) на этом интервале, необходимо и до-
достаточно, чтобы f (дс)^О (f (дсХ 0) для всех х?]а; Ь[. Если же для
любого х 6 ]а; b[ f'(x) > 0 (fix) <0), то функция f возрастает (убы-
(убывает) на этом интервале.
Другими словами:
1)	f(x) не убывает на }а\ Ь{ -^V x?]a; b[: f'(x)^O;
2)	f(x) возрастает на ]а; Ь{ оУхе]а; b[: f'(x)>0;
3)	f(x) не возрастает на }а; b[oVx?]a; b[: f'(x)^.O;
4)	f(x) убывает на }а; Ь[ -<=>Yx?]a; b[: f'(x)<0.
> 1. Рассмотрим случай неубывающей функции.
Необходимость: Пусть f(x) не убывает на ]а; Ь[. Тогда Уде ?]а;
Ь[ при Ддс > 0
Ду = f{x + /ix) - f{x) >0^^- ^ 0=> Ит-^ = fix) > 0 V* 6 ]а; Ь[.
Достаточность. Пусть f (х) ^0 Vх?]а; Ь[. Тогда по формуле
Лангранжа имеем f(x2) — f(xi) = f'(%)(x2 — xi). Так как /'(?)^0
(дс|<|<дс2), тоУдс,, х2е]а; 6[:дс|<дс2 f(x2) — f(x\)^sO, т. е. f не
убывает на ]а; Ь[.
2. Докажем теорему для случая возрастающей функции. Пусть
f'(x)>0 на 1а; Ь[. ТогдаУ|6]а; Ь[ f'(l)>0 и поэтому Vx,, x2:x{ <
<x2=>fix2) — f(xi) = f (l)(x2 — xi)>0, т. e. fix) возрастает на
]а; Ь{. <
Подчеркнем, что условия теоремы для возрастающей и убываю-
убывающей функций достаточны, но не необходимы.
Например, функция у = х3 возрастает иа ] —1; 1[, однако производная в точке
х = 0 обращается в нуль.
Геометрический смысл теоремы состоит в следующем: касатель-
касательная к графику возрастающей на ]а; Ь[ функции (]'(х) > 0) составляет
острый угол с осью Ох; касательная к графику убывающей на ]а; Ь[
функции (f'(x)<zO) образует тупой угол с осью Ох. Если функция
140

f(x) на }a\ b[ является постоянной: f(x) = C, С = const, то f'(x) = 0
и касательная к графику функции параллельна оси Ох.
Пример 6.1. Найти интервалы возрастания и убывания функции /(*)= 1/A +
+ Л
Решение. Функция f(x) = 1/A + дг) определена, непрерывна и дифференци-
дифференцируема на R. Для отыскания интервалов монотонности функции найдем f'(x):
f'(x)=-2x/(l+xj.
Из теоремы 6.1 следует, что f(x) возрастает на некотором множестве, если f'(x) > 0.
Решим неравенство —2*/A +*2J > 0. Оно выполняется на ] — оо; Of. Следова-
Следовательно, {(х)= 1/A + х2) возрастает на ] — об; Of. По той же теореме f(x) убывает на
множестве, где f(x)<0. Неравенство — 2х/(\ +х2J < 0 выполняется на ]0; oof.
Итак, функция f(x)=	убывающая на 10; oof. Ее графиком (рис. 6.1)
1 +х2
является кривая, которую называют локоном Аньези*.
6.2. ТОЧКИ ЛОКАЛЬНОГО ЭКСТРЕМУМА ФУНКЦИИ.
НЕОБХОДИМОЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ СУЩЕСТВОВАНИЯ
ЭКСТРЕМУМА ФУНКЦИИ
Экстремум функции. Особую роль в исследовании поведения
функции на множестве играют точки, разделяющие интервалы воз-
возрастания и убывания функции. Для функции y — f(x) на интервале
]а; Ь[ такой точкой является точка х0, отделяющая интервал возра-
возрастания f(x) ]а; хо[ от интервала убывания ]х0; Ь[ функции (рис. 6.2).
Из рисунка видно, что существует Оь(х0) F > 0), такая, что f(x0) >
Определение 6.1. Точка х0 называется точкой локального макси-
максимума (минимума) функции f(x), если существует Ь-окрестность точки
Рис. 6.2
Рис. 6.3
* Мария Гаэтана Аньези A718—1799) —итальянский математик.
141

хо, такая, что для всех х ? Об(*о) выполняется неравенство
Д/(*о) = f(x) - f(x0) < 0 (Af(x0) = /(*)- /Ы > О).
Значение f(x0) называют локальным максимумом (минимумом) функ-
функции и пишут
= f(x0) ( min f(x) = f(x0)).
х[H,(хо)
Точки максимума или минимума функции называют точками
экстремума функции, а максимумы и минимумы функции называ-
называются экстремумами функции.
Из приведенных рассуждений следует, что экстремумы функции
носят локальный характер — это наибольшее или наименьшее зна-
значения функции по сравнению с близлежащими ее значениями.
Если функция f(x) на [а; Ь] имеет несколько максимумов и мини-
минимумов, то возможен случай, когда максимум функции меньше ее
минимума.
Например, на рис. 6.3 точки хи х3 являются точками максимума функции f(x),
а *2, *4 — точками ее минимума, ио f(xi)<f(xt).
Наименьшее и наибольшее значения функции на [а; Ь] в отличие
от локальных ее экстремумов называют абсолютными минимумом
и максимумом функции f(x) и обозначают min f (x), maxf(x).
хе[а; 6]	х?[а; Ь]
Для функции, график которой изображен иа рис. 6.3, абсолютным минимумом
будет /(а), абсолютным максимумом — /(&).
Необходимое условие существования экстремума функции. Спра-
Справедлива следующая
Теорема 63. Если в точке х0 функция f(x) достигает экстремума,
то ее производная в этой точке равна нулю или не существует.
> Пусть f(x) в точке х0 достигает максимума. Тогда существует
б&(х0), такая, что
пРид*<о I^±MnZM>0, при д*>о к*«+^
Если пределы левых частей этих неравенств при Дх-»-0 сущест-
существуют, то:
П + *)П) =f'(xo-O)>O,
= f>{Xo + 0)<0.
Если производные функции f'(x±O) в точке х0 равны нулю, то
существует f'(x0) = f'(x0 — 0) = f'(x0 + 0) = 0.
Если f'(x0 — 0) и /'(jCo + O) отличны от нуля, то f'(x0) не сущест-
существует.
142

Аналогично доказывается случай, когда х0 — точка минимума. <]
Геометрический смысл теоремы 6.2 заключается в следующем:
в точках экстремума функции f(x) касательная к ее графику парал-
параллельна оси абсцисс, если существует f'(xo) = 0 (рис. 6.4, а); парал-
параллельна оси ординат, если f'(x0) бесконечна (рис. 6.4, б); существуют
не совпадающие левая и правая касательные, если f'(x0 — 0)=?^
=jfcf'(xo + 0) (рис. 6.4, в).
в
а О
Рис. 6.4
Точки, в которых производная функции у = f(x) обращается в
нуль или не существует, называют критическими или точками воз-
возможного экстремума. Точки, в которых производная функции у =
= f(x) обращается в нуль, называют стационарными.
Критическая точка х0 называется угловой точкой функции f(x),
если f'(x0 — 0)?=f(хо-\-0) (см. рис. 6.4, в). Критическая точка х0
называется точкой возврата функции, если ее левая f'(x0 — 0) и пра-
правая f'(xo-\-0) производные бесконечны (см. рис. 6.4, б).
Не всякая критическая точка функции f(x) является точкой ее
локального экстремума.
Например, * = 0 — критическая точка функции f(x) = x5, так как \'(х) — Ъх*
при х = 0 обращается в нуль, но х = 0 не является точкой локального экстремума
функции. В этой точке функция возрастает.
Достаточные условия существования экстремума. Выяснить, ка-
какая из критических точек функции будет точкой ее локального экст-
экстремума, можно с помощью трех достаточных признаков существо-
существования экстремума функции.
Теорема 6.3. (первый достаточный признак существования экст-
экстремума функции). Пусть хо — критическая точка непрерывной функ-
функции f(x). Если f'(x) при переходе через точку хо меняет знак с « + » на
« — », то хо — точка локального максимума; если f'(x) при переходе
через точку х0 меняет знак с « — » на « + », то х0 — точка локального
минимума; если f'(x) при переходе через точку х0 не меняет знак,
то' хо не является точкой локального экстремума.
t> Пусть Хо — точка возможного экстремума, причем f'(x) > 0
6 О6(л:о - 0) и f'{x) < 0 Vx e 0&{х0 + 0).
Тогда
при f'(x) > 0 Vx е О6(х0 - 0)=>f(xo) > f(x),
при f{x) < 0 V* 6 О6(хо + 0)=*f(*о) > f(x)
143

т. е. точка хо является точкой локального максимума.
Аналогично доказывается и существование точки локального
минимума.
Если f'(x) сохраняет знак в окрестности точки х0, то в этой окрест-
окрестности функция монотонна, т. е. точка х0 не является точкой локаль-
локального экстремума. <]
На рис. 6.5 дана геометрическая интерпретация точки локаль-
локального максимума.
Пример 6.2. Найти локальные экстремумы функции f(x)=-^-x3—о"*2-
Решение. Данная функции определена и непрерывна на R. Ее производная
f'(x) = x2 — х также непрерывна на R. Найдем стационарные точки функции из
уравнения р(х) — 0: хг — х = 0=>*i =0, х2= 1.
а о
<f'(x)>0
X
Ри
*o)=O
о b ^
:. 6.5
7 J
Рис. 6.6
Исследуем знак производной в окрестностях стационарных точек.
Если х 6 Ое@ — 0), то р(х) = х2 — х > 0; если х 6 Ое@ + 0), то /'(*) < 0. В точке
х = 0 Р(х) меняет знак с «-|-» на «—». Следовательно, стационарная точка * = 0
является точкой локального максимума функции: max f(x) = f(O) = O.
*ео.(о)
Если х?Оь(\ —0), то р(х) = х2 — х<0; если *€Oe(l -f 0), то /'(х)>0. В точке
х= 1 р(х) меняет знак с «—» на « + ». Значит, стационарная точка х= 1 есть точка
локального минимума функции: min f(x) = f(i)=—1/6.
eo(i)
График функции
e()
) = — x3—^-
о	2
приведен на рис. 6.6
Теорема 6.4 (второй достаточный признак существования экст-
экстремума функции). Стационарная точка хо функции f(x), дважды
дифференцируемой в О^(х0), является точкой локального минимума
f(x), если f"(x0) >¦ 0, и точкой локального максимума, если f"{xQ) < 0.
> Пусть выполнены условия теоремы и f"(xo)>0. Тогда f'(x)
в О(,(х0) возрастает, но f'(xo) = 0, следовательно, в О6(х0) f (х)
меняет знак с « —» на « + » (рис. 6.7). Согласно теореме 6.3, точка
хо является точкой локального минимума функции f(x).
Если f"(xo)<Z0, то f'(x) в О(,(х0) убывает, но f'(xo) = 0, следова-
следовательно, в Оь(х0)производная функции f'(x)меняет знаке «-|-» на « — »
(рис. 6.8). Тогда, согласно теореме 6.3, точка хо является точкой
локального максимума функции f(x). <]
Пример 6.3. Используя теорему 6.4, найти локальные экстремумы функции
f(*) = *74*72
144

У\
я-т
а о	х0 ь л
Рис. 6.7
а к0 ь х
Рис. 6.8
Решение. Данная функция определена, непрерывна н дважды дифференци-
дифференцируема на R. Определим стационарные точки f(x):
f'(x) = х3 — х, х3 — х = 0=>*i = 0, х2 = — 1, х3 = 1.
Найдем значения /"@), f"(±l). Учитывая, что f"(x) = 3x2 — 1, получаем f"@) =
= —1 < 0, т. е. *i=0 — точка локального максимума функции: maxf(x) = 0;
€О@)
€()
f"(— 1) = 2>0, следовательно, х2= — 1—точка локального минимума функции:
min f(x) = —1/4; /"A) = 2 > 0, т. е. х3 = 1 — точка локального минимума функ-
функции: min f(x)= —1/4.
График функции у = х*/А — х2/2 приведен на рис. 6.9.
Теорема 6.5 (третий достаточный	у
признак существования экстремума
функции). Пусть функция f(x) —
п раз непрерывно
в точке х0
ывно дифференцируема ,. \
U f \Хо) = f \Xq) = ... = - \ _ л
О, fn(xo) ф- 0. Тогда:	N.
О
1)	если п — четное и fn(xo)<.0,
то х0 — точка локального макси-	MHl~1/4)
мума.	Р н с 6 9
2)	если п — четное и f(xQ)>0,
то хо — точка локального минимума;
3)	если п — нечетное, то х0 не является точкой локального экст-
экстремума.
Пример 6.4. Найти локальные экстремумы функции f(x) = x* — Ах3.
Решение. Данная функция определена, непрерывна н дифференцируема на R.
Найдем стационарные точки f(x):
f'(x) = Ах3 — 12*2, Ах3 - 12*2 = 0=>*,,2 = 0, х3 = 3,
f"(x) = 12х2 — 24*, /"C) = 36 > 0, /"@) = 0.
Стационарная точка х = 3 является точкой локального минямума функции:
^mta f(*) = K3)--27.
Для исследования стационарной точки х = 0 находим {'"(х) = 2Ах — 24,
/'"@)=—24. Согласно теореме 6.5, точка х = 0 не является точкой локального
экстремума f(x).
145

6.3. АБСОЛЮТНЫЕ ЭКСТРЕМУМЫ ФУНКЦИИ НА ОТРЕЗКЕ
Одной из основных характеристик функции f(x) на отрезке [а; Ь]
являются ее абсолютные экстремумы, т. е. наибольшее и наимень-
наименьшее значения f(x) на [а; Ь].
Если функция f(x) непрерывна на [а; Ь], то наибольшее и наимень-
наименьшее значения она принимает на концах этого отрезка или в точках
ее локального экстремума. Следовательно, для отыскания абсолют-
абсолютных экстремумов min f(х), max f(x) надо найти ее значения на кон-
цах отрезка [а; Ь], в точках локального экстремума и выбрать со-
соответственно наименьшее и наибольшее из них.
Если х\, хч, ..., хп — точки локальных экстремумов, то
(x) = minlf(a), f(b), f(xt), ..., f(xn%
Ь]
7(*) = max{f(a), f(b), f(x,)	 f(xn)}.
*?[<•; b]
Пример 6.5. Найти абсолютные экстремумы функции f(x) = x3— б*2 + 9* на
U4].
Решение. Определяем стационарные точки /(*):
f'(x) = 3x2 — 12л:+9, З*2—
= l, х2 = 3.
Вычисляем значения /(*) на концах отрезка и в стационарных точках: /(—1) =
= —16, /D) = 4, Д1) = 4, /C) = 0. Тогда
min f(x) = min{—16, 4, 4, 0)= —16.
e[i4]
max
) = max{— 16, 4, 4, 0} = 4.
Наименьшее значение даииая функция принимает на левом конце отрезка в
точке х= — 1, наибольшее — в стационарной точке х— 1 и на правом конце отрезка
в точке х = 4. График функции у = х3 — бдс2 + 9дг приведен на рис. 6.10.
Пример 6.6. Найти ширину бруска наибольшей прочности, который можно
вырезать из бревна диаметром 25 см (рис. 6.11), считая, что прочность бруска с пря-
прямоугольным сечением пропорциональна ширине и кубу высоты.
Решение. Обозначим через х шири-
ширину бруска, через h — его высоту. Тогда
прочность бруска у = kh3x, где k — коэф-
коэффициент пропорциональности. Из Д ABC
(см. рис. 6.11) находим
h = V252 — х2=>у = kfjjB52 — х2K.
Определим стациоиарные точки функ-
функции у = *WB52 - х2K:
Mf(-1'r16)
Рис. 6.10
146

у' = k VB52 - x2)* -
тогда
252 — 4*2 = 0=>2л: = ±25=>* = ± 12,5.
По условию задачи х € ]0; 25[. Следовательно, наибольшаи прочность бруска
будет при ширине х = 12,5 см. В этой точке функция у = kx~\jBb2 — я2K имеет локаль-
локальный максимум, так как у" = 0.
6.4. ИССЛЕДОВАНИЕ ФУНКЦИИ НА ВЫПУКЛОСТЬ И ВОГНУТОСТЬ.
ТОЧКИ ПЕРЕГИБА ФУНКЦИИ
Определение 6.2. График дифференцируемой функции у =
= f(x) называется выпуклым вниз (или вогнутым) на ]а; Ь[, если
дуга кривой у == f(x) V х 6 }а; Ь[ расположена выше любой касатель-
касательной, проведенной к графику этой функции (рис. 6.12).
Определение 6.3. График дифференцируемой функции у =
= f(x) называется выпуклым вверх (или выпуклым) на ]а; Ь[, если
дуга кривой y = f(x)Yx?]a; b[ расположена ниже любой касатель-
касательной, проведенной к графику этой функции (рис. 6.13).
Ь X
У,
г
ь
т
Рис. 6.12
Рис. 6.13
Определение 6.4. Точка М(х0; f(x0)) графика дифференцируе-
дифференцируемой функции у = f(x), в которой направление выпуклости меняется
на противоположное, называется точкой перегиба (рис. 6.14).
Сформулируем достаточный признак вогнутости (выпуклости)
графика функции.
Теорема 6.6. Если функция y = f(x) на }а; Ь[ дважды дифферен-
дифференцируема и f"(x)>0 Ух?}а; Ь[, то график этой функции на }а\ Ь[
вогнутый (выпуклый вниз). Если функция y = f(x) на ]а; Ь[ дважды
дифференцируема и f"(x) < 0 Vx 6 ]а; b[, то график этой функции на
]а; Ь[ выпуклый.
> Пусть на интервале ]а; b[ f"{x)>Q. Возьмем точку хо(:]а; Ь[
и покажем, что все точки графика функции y = f(x) на ]а; Ь[ лежат
выше касательной к нему в точке хо, т. е. что ординаты этих точек
больше ординат точек касательной с одной и той же абсциссой.
Уравнение касательной к кривой y = f(x) в точке с абсциссой х0:
Y - f(x0) = Г (хо) (х - хо)^ Y = f(x0) + Г (х0) (х - х0),
где Y — ординаты точек касательной. Разность ординат точек кривой
и касательной
у - Y = f(x) - f(x0) - f'(xo) (x - хо).
147

Применяя формулу Лагранжа E.9) к функции f(x) на [х0; х], по-
получаем
y-Y = f'(l)(x- х0) - f'(*„) (х - хо)=>
где ? 6 ]*о; x[cz]a; b[. Применяя формулу Лагранжа к функции
f (l) — f'(x0) на [х0; I], находим
а о
Рис. 6.14
О а
1 6]*0; ?[с]а; &[. В последнем равенстве f"(?i)>0, а I — хо > 0,
если х — х0 > 0, или I — хо<0, если х — х0 < 0. Следовательно,
у >¦ У, т. е. ординаты точек кривой больше ординат точек касатель-
касательной при одной и той же абсциссе. Точки кривой у = f(x) на ]а; Ь[ лежат
выше точек касательной к кривой.
График функции y = f(x) на ]а; Ь[ — вогнутый (рис. 6.15).
Доказательство выпуклости графика функции на ]а; Ь[ проводится
аналогично. <1
Пример 6.7. Найти интервалы выпуклости и вогнутости графика фугкции f(x) =
= 1/A+/).
Решение. Даииая функция определена, непрерывна и дифференцируема иа
R, причем
(i+<
A+*2K'
Для определения интервалов выпуклости и вогнутости графика функции найдем
решения неравенств /"(*)< 0 и \" (*) > 0:
3x1 ~х <o32
]—оо; —
; оо [.
Кривая, изображающая график функции, иа ]—оо; —1/-\/3[—вогиутаи, на
] — 1 /д/З; 1 /д/3[ — выпуклая, иа ] 1 /д/З; оо [ — вогнутая. В точках х = — 1 /-^/з", х =
= 1/-уЗ она меняет направление выпуклости, т. е. по определению это ее точки пере-
перегиба, в которых вторая производная f"(*) = 0, а в их окрестностях {"(х) меняет знак.
График функции изображен иа рис. 6.1.
Сформулируем достаточные условия существования точек пере-
перегиба.
148

МB\-1В)
Теорема 6.7. Если для функции f(x) вто-
вторая производная f"{x) в некоторой точке х0
обращается в нуль или не существует и при
переходе через нее меняет свой знак, то
точка М(х0; f(xo)) является точкой перегиба
графика функции.
> Пусть f"(xo) = 0 или не существует.
Если И*)<0 в O6(xo-0) и И*)>9
в Оь(х0 -\- 0). то точка кривой с абсциссой
х0 отделяет интервал выпуклости от интер-
интервала вогнутости. Если f"(x)>0 в О6(х0—
— 0) и f"(x) < 0 в Оь(х0 + 0), то эта точка от-
отделяет интервал вогнутости от интервала
выпуклости кривой. В обоих случаях точка
(х0; f(x0)) является точкой перегиба графика
функции. <]
Пример 6.8. Найти точки перегиба графика функ-
функции {(х)== х* — Ах3.
Решение. Данная функция определена, непре-
непрерывна и дифференцируема на R, причем
f'(x) = 4л:3 - 12*2, f"(x) = \2х2 — 2Ах;
f»(x) = 0=>jc2 — 2х = 0=>jc, =0, x2 = 2.
Исследуем знак {"(х) в Ов@) и ОвB). В Ое@ — 0) вторая производная ^"(л:) > 0,
а в Ое@ + 0) ["(х) < 0. Следовательно, точка О@; 0) является точкой перегиба кривой
(см. рис. 6.16). В О„B — 0) П*)<0. в ОеB + 0)/"(Jr^ > 0. Значит, точка МB; -16)
является точкой перегиба графика функции f(x) = x* — Ах3 (рис. 6.16).
NC;-27)
Рнс. 6.16
6.5. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
При исследовании поведения функции на бесконечности, т. е.
при х-+ +оо и при х-*- — оо, или вблизи точек разрыва второго
рода часто оказывается, что расстояния между точками графика
функции и точками некоторой прямой с теми же абсциссами сколь
угодно малы. Такую прямую называют асимптотой графика.
Различают асимптоты вертикальные (т. е. параллельные оси орди-
ординат) и наклонные. Частным случаем наклонной асимптоты является
горизонтальная асимптота.
Прямая х = х0 называется вертикальной асимптотой графика
функции у = f(x), если хотя бы один из односторонних пределов в
точке хо равен бесконечности, т. е. lim f(x)= ±«э или lim f(x) =
х-гхо — 0	х~+Хо + О
= ±ОО.
Очевидно, что непрерывные на R функции вертикальных асимптот
не имеют; такие асимптоты существуют только в точках разрыва
второго рода функции у = f(x). Следовательно, для отыскания верти-
вертикальных асимптот графика функции надо определить те значения х,
при которых хотя бы один из односторонних пределов функции
бесконечен.
149

Пример 6.9. Найти вертикальиые асимптоты графика фуикции у
Х2-\
Решение. Данная функция при *=±1 имеет разрыв второго рода, следо-
следовательно, прямые х= —1, х=\ являются вертикальными асимптотами ее графика
(рис. 6.17). Вычисляя односторонние пределы в этих точках, имеем:
lim /(*)= lim —.	- = +оо, lim;
lim
— i+o х2 — 1
1
1+0 X2 — 1
Прямая у = kx + b называется наклонной (если k = 0 — гори-
горизонтальной) асимптотой графика функции y = f(x) при х-»-+оо
(х-*—оо), если функцию f(x) можно представить в виде f(x) =
= kx + b + а(х), где а (я)-*-0 при *-»-+ оо (*-»— оо).
Теорема 6.8. Для того чтобы график функции у = f(x) имел на-
наклонную асимптоту у = kx + b, необходимо и достаточно, чтобы су-
существовали конечные пределы:
Нт Ж = й, lim {f{x)-kx) = b.	F.1)
Х-+ ± ОО *	*->- ± ОО
> Необходимость. Предполагаем, что у = kx-\- b — наклонная
асимптота графика функции у = f(x). Тогда справедливо представ-
представление f(x) = kx + b + &(х), где а(х) — бесконечно малая при х-*- оо.
Следовательно,
lim (f(x) — kx) = lim (b + <*(*)) = fe.
X-*- OO	JC-* OO
Достаточность. Пусть существуют пределы F.1), тогда, согласно
следствию из теоремы 3.7. (см. § 3.4), из второго равенства F.1) по-
получаем f(x) = kx + b + а(х) при х-»- + оо. Последнее представление
функции f(х) означает, что прямая у = kx + b является наклонной
асимптотой графика функции y = f(x).
Итак, теорема доказана для случая х->- оо. Доказательство теоре-
теоремы для случая х-*- — оо производится аналогично. <]
Замечание. При нахождении наклонных асимптот графика функции воз-
возможны следующие случаи: 1) оба предела F.1) существуют и не зависят от знака
бесконечности, тогда прямая у = kx-\- b называется двусторонней асимптотой; 2) оба
предела F.1) существуют, но при х-*- ± оо они различны, тогда имеем две односто-
односторонние наклонные асимптоты; 3) если хотя бы одни из пределов F.1) ие существует,
то наклонных асимптот нет.
Пример 6.10. Найти асимптоты линии U—	г-
1+х2
Решение. Данная функция определена и непрерывна на R. Вертикальных
асимптот иет. Для нахождения невертикальиых асимптот вычисляем пределы F.1):
lim iW-= lim 	L_-=0, lim (f(x)-kx)
х-^±оо X	*->-±oo A-|-*)*	x-^±oo
Оба предела существуют и не зависят от знака оо. Следовательно, прямая у = 0
является двусторонней асимптотой (см. рис. 6.1).
150

n
Рис. 6.17
Рис. 6.18
Пример 6.11. Найти асимптоты гиперболы хг — у2 = 1.
Решение. Запишем фуикцию в явном виде: у = ± д/*2 — 1. Функция опреде-
определена и непрерывна на множестве ] — оо; — 1|Щ1; оо[. Находим пределы F.1):
!=lim(± VElJJ)=±1^=±1,
X—*¦ оо \	"	/
lim
lim
Асимптотами гиперболы являются прямые у— ±х (рис. 6.18).
Пример 6.12. Найти асимптоты кривой у = -\]х.
Решение. Данная функция определена и непрерывна на R+. Вертикальных
асимптот иет. Для определения наклонных
от ет. Для определения на
асимптот находим пределы F.1):
¦-т/х
х_>.оо X
b= lim (/(*) — kx)= lim ~Jx= oo.
Второй предел бесконечен, следова-
следовательно, кривая
(рис. 6.19).
асимптот не имеет
Рис. 6.19
6.6. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
Исследование дважды дифференцируемой функции y = f(x) на
D(f) (за исключением, быть может, конечного множества точек)
и построение ее графика можно выполнять по приводимой ниже
схеме.
1. Находим D(f), определяем точки разрыва, вертикальные асимп-
асимптоты, нули, точки пересечения графика функции с осью Оу, пе-
периодичность, симметрию.
151

2.	Находим невертикальные асимптоты графика функции (если
они существуют).
3.	С помощью первой производной функции определяем ста-
стационарные точки и интервалы монотонности.
4.	С помощью второй производной определяем интервалы вогну-
вогнутости и выпуклости графика функции, точки перегиба.
5.	Находим локальные экстремумы функции на D(f).
По результатам исследований строим график функции, для удоб-
удобства сводя их в таблицу, построение которой покажем на примерах.
X3
Пример 6.13. Исследовать функцию у =	 и построить ее график.
3 — х
Решение. Для построения графика функции проведем ее исследование по
указанной выше схеме.
1.	Находим ?>(/). Данная функция определена для хф ± "уЗ:
D(f) = ]-oo; _^[U]_V? V3[U]V3; oo [.
Функции непрерывна на ?>(/); л: = ± 3 — точки разрыва второго рода, л: = ±3 —
вертикальные асимптоты графика функции. Функция у = 0 при х = 0, т. е. график
функции пересекает координатные оси в начале координат. Функция иепериодичиа.
1-хK —х3
Оиа нечетная, так как D(f) симметрична и f( — x)= —f(x), т. е. -	'—=	- .
3 — xi 3 — xi
Следовательно, график функции симметричен относительно начала координат и до-
достаточно исследовать функцию для х > 0.
2.	Для нахождения иевертикальиых асимптот вычислим пределы F.1):
. ,. f(x) ..	х3
k= lim -i-^- = lim 	5— = — 1,
X	x-»oo C — X)X
b = lim (f(x) - kx) = lim (V-^- +x)= lim ** + 3*-** _ 0>
X-* oo	x-+ oo \ d — X	/ х-* oo	3 — X
т. е. прямаи y= —x явлиетси наклонной асимптотой графика функции.
3. Находим первую производную функции у = f(x):
У
C-д:2J '
Она определена на D(f). В промежутке [0; + оо [ производная обращается в нуль в
точках х\ = 0, Х2 = 3.
Определяем интервалы монотонности из неравенств у' > 0 н у' < 0 Ух > 0.
Имеем
*
C-х2J
на
*2(9-*2)
т.е.функция возрастает иа ]0; V^IU] V^i 3[.
Аналогично
< 0=>-9 — х2 < 0=>х > 3,
C-х2J
т. е. функция убывает на ]3; оо [.
4. Вычислием вторую производную функции y = f{x):
,/= A8л: — 4Х3) C — х2J — (9х2 — *4JC — х2) ( — 2х) 6х (9 + хг)
C-д:2L	C-д:2K '
Оиа определена на D(f). Находим интервалы вогнутости и выпуклости графика
функции из неравенств у" > 0, у" < 0 Ух > 0. Тогда
152

Щ9
х > 0,	( х > 0,
3—*2>0 I — -\/3 < * <-\/3
C-х2K
т. е. кривая вогнута иа ]0; -уЗ[. Аналогично
6*(9 + *г)
(З-*2K
<0=
Г*>0
Ъ-*2
т. е. кривая выпукла иа ]y3; оо [. В точке
* = 0 у" = 0 и T'W<0 в О8@ —0),
a f"(*)>0 в О«@ + 0), т. е. точка кривой с
абсциссой х = 0 отделяет интервал выпук-
выпуклости кривой от ее интервала вогнутости.
Тогда О@; 0) является точкой перегиба
кривой.
5. Определяем с помощью второй про-
производной }"{х) локальные экстремумы. Так
как f"C) = 0, точка А\ с абсциссой х = 3
является точкой локального максимума.
В силу симметрии графика фуикции точка Лг
с абсциссой х = —3 является точкой локаль-
локального минимума. Итак, max fix) = —4,5,
min Дд;) = 4,5.
*ео,(-з)
Результаты исследования фуикции у =
= /(*) иа [0; оо[ заносим в табл. 6.1.
Исходя из результатов, содержащихся
в табл. 6.1, строим график данной фуикции
(рис. 6.20).
Рис. 6.20
Таблица 6.1
X
У'
У"
У
0
0
0
0
точка
перегиба
]0; л&
+
+
Не существует
Не существует
Не существует
+
—
3
0
—
— 4,5
max
]3; «[
—
—
ч
6.7. ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ
Под интерполированием, функции f(x) на отрезке [а; Ь] понимают
восстановление этой функции с заданной степенью точности по
таблице п ее значений на [а; Ь]:
X
К*)
Хо
К*о)
Х\
хг
Хп-1
Хп
153

Точки Хо, хи ..., xn (xo = a, xn = b) называют узлами интерполи-
интерполирования.
Функцию f(x) приближенно заменяют многочленом Рп(х) = аохп +
+ aixn~' + ... + а„, значения которого совпадают со значениями
f(x) в узлах интерполирования:
Pn(Xi) = f(Xi), i = o7~n~.	F.2)
Многочлен Рп{х) называют интерполяционным многочленом степени
п функции f(x) на [а; Ь]. Для определения коэффициентов многочлена
Рп(х) используем условия F.2):
а„ = f (лс0),'
аох1 + щхТ' + ... + а„ = f(xt), [	F.3)
Получим систему п + 1 уравнений с п + 1 неизвестными.
Определитель системы F.3)
1
х'\~х ... 1
„га „га— 1
Хо Хо
¦ П ytl — 1	1
п Хп	-•• I
если Хо, х\, .... хп различны. Можно показать, что он равен
П (xi¦ — Xj). Действительно, определитель второго порядка
= Хо — Xi\
Хо 1 I
*, 1 I
определитель третьего порядка
Хо
Х\
„2
Xi
Хо
Х\
Х2
1
1
1
=
Хо	Хо	1
Х\ — Хо Х\ — Хо О
Xi — Хо Хч — Хо О
= {х\ — х1){х2 — хо) — (*i — xl){xx — Хо) = (xt — хо)(х2 — xo)(xt — х2)
и т. д.
Система F.3) имеет единственное решение. Следовательно, су-
существует единственный интерполяционный многочлен Рп(х), коэф-
коэффициенты которого определяются из системы F.3). Однако опре-
определение коэффициентов интерполяционного многочлена из системы
F.3) связано с громоздкими вычислениями.
Будем искать интерполяционный многочлен Рп{х) в виде
Рп (х) = ао(х — х,) (* — х2) ¦ ¦ ¦ (х — х„) + а, (д: — х0) (х — х2) ¦ ¦ ¦ (х — хп) +
+ а2(х — хо) (х — х^ (х — х3)---(х — хп) + ... + ап(х — хо)-(х — хп-{).
Полагая в последнем равенстве * = **, t = 0, n, и учитывая
условия F.2), находим коэффициенты Рп(х):
— хп)
154

— х0) (х{
i — х„)
1М
Интерполяционный многочлен примет вид
+ ¦
(X — Хр)(х — Х2) ¦¦¦ (X — Х„)
-ХЯ)
[х — хп-{)
Тогда
{Хп — Хо){Хп—Х1)--(Хп—Х„-{IК >'
, Л (х—хо)-(х — х,-1)(х — х,+ 1)
( — */-i) (x, —
xi — xn)
- F-4)
Равенство F.4) называется интерполяционной формулой Лаг-
Лагранжа.
Простейшим и широко используемым при работе с функциями,
заданными таблично, является линейное интерполирование, т. е.
интерполирование многочленом первой степени Pi(x) = aix-\-ao.
Линейное интерполирование удобно использовать, если известно,
что на отрезке [а; Ь] данная функция мало отличается от линейной.
Пример 6.14. Функция y = f(x) задана таблично:
X
/м
1
2
2,5
1
3
2,2
4
3
Построить для этой функции интерполяционный многочлен Лагранжа третьей степени
на отрезке [1; 4].
Решение. Воспользуемся формулой F.4):
" ' B,5—1) B,5 —3) B,5-4)
w IW A-2,5) A-3) A-4)
^'w C - 1) C - 2,5) C - 4) + n > D - 1) D - 2,5) D - 3)
4) —
-2,2(х-\)(х-2,5)(х-4)+^.(х-1)(х-2,5)(х-3)=>Р3(х) =
После построения интерполяционного многочлена Лагранжа для
f(x) на [а; Ь] возникает вопрос об оценке точности приближения
функции f(x) многочленом Рп(х).
Разность между функцией f(x) и ее интерполяционным много-
многочленом Рп(х), т. е.
155

rn(x) = f(x)-Pn(x),
называется остаточным членом интерполирования.
Если известно, что на [а; Ь] функция f(x) n -\- 1 раз дифференци-
дифференцируема, то
b],
F.5)
где
= max\f-n+t\x)\; (а(х) = (х —хо)(х —
Jt? [о; Ь]
xit i —
= 0, n,— узлы интерполирования.
Оценка остаточного члена интерполирования F.5) требует опре-
определенной информации о поведении рассматриваемой функции на
[a; b], которая, как правило, отсутствует.
Иногда, выбрав достаточно большое число узлов интерполиро-
интерполирования, можно получить хорошее приближение интерполируемой
функции. Известны примеры, когда последовательность интерполя-
интерполяционных многочленов Лагранжа функции f(x) с возрастанием числа
узлов интерполирования не стремится к этой функции.
На практике для получения достаточно хорошего приближения
функции вместо построения интерполяционного многочлена высокой
степени используют кусочную интерполяцию многочленами более
низких степеней, т. е. на каждом отрезке [хг, Xi+i] строится свой
многочлен. Часто используется кусочно-линейная интерполяция.
Получающиеся при этом кусочно-многочленные функции с однород-
однородной структурой на каждом промежутке (многочлен одной и той же
степени) называются сплайн-функциями или просто сплайнами (от
англ. spline — рейка). Простейший пример сплайна — ломаная.
В настоящее время в приложениях чаще всего используются
приближения кубическими сплайнами, так как последовательность
интерполяционных кубических сплайнов на равномерной сетке узлов
всегда сходится к интерполируемой непрерывной функции, а если
дифференциальные свойства функции улучшаются, то и сходимость
улучшается. Кроме того, алгоритмы построения сплайнов достаточно
просто реализуются на ЭВМ.
Пример 6.15. Построить линейный сплайн S,(x) н иайти 5,@,5) для функции
у = f(x), заданной таблично:
X
м
0
1
0,2
1,5
0,4
1,7
0,6
1,3
0,8
1,7
1
2
1,2
2,1
1,4
2,5
1,6
3
1,8
3,2
2
3,5
Решение. Линейный сплайн S,(x) задается уравнением прямой, проходящей
через две точки:
yi	Xi+,—Xi
Вводя понятие шага разбиения A
156
*/+1 —Xi
—*,-, имеем

"Г5Ж
/,/7 1,2 1,4 1.6 1,8 2 X
Рис. 6.21
Так как 0,5 е [0,4; 0,6] (х, = 0,4,
— 0,4)
1,3— 1,7
= 0,6), то S1 @,5) = f @,4) + @,5 —
0,2
=1,5 (рис. 6.21).
6.8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
Постановка задачи. Рассмотрим задачу нахождения действи-
действительных корней уравнения
Д*) = о,	F.6)
где f(x) — алгебраическая или трансцендентная функция.
Известные точные методы решения уравнений пригодны только
для узкого класса уравнений (квадратных, биквадратных, дву-
двучленных алгебраических, некоторых тригонометрических, показа-
показательных, логарифмических). Однако в общем случае решения урав-
уравнения F.6) находятся приближенно.
Нахождение приближенных значений действительных корней
уравнения F.6) состоит из двух этапов: 1) отделение корней (опре-
(определение малых отрезков [а; Ь], в которых находится только один
действительный корень уравнения); 2) приближенное вычисление
(уточнение) отделенного корня до заданной точности.
Отделение действительных корней. Под отделением действитель-
действительного корня уравнения f(x) = 0 понимают нахождение отрезка [а; Ь],
в котором лежит только один корень данного уравнения. Этот от-
отрезок называют промежутком изоляции корня.
Известны различные графические и аналитические методы отде-
отделения корней уравнения F.6).
Наиболее наглядный метод отделения корней уравнения f(x) =
= 0 состоит в определении координат точек пересечения графика
функции y = f(x) с осью абсцисс. Абсциссы xf точек пересечения
157

графика y==f(x) с осью Ох являются корнями уравнения F.6). На
рис. 6.22 хорошо видны промежутки изоляции корней уравнения
f(x) = O. Это отрезки [а; а], [с{; с2], [с2; с3], [с3; Ь].
Если f — сложная функция, то построение графика у = f (x) может
вызвать затруднения. В этом случае целесообразно использовать
следующий прием. Уравнение f(x) = q>i(x) — ф2(х) = 0 надо записать
в виде ф1(*) = ф2(л:), подобрав функции q>i, ф2 так, чтобы сравни-
сравнительно просто строились графики функций у = (р{(х), г/ = ф2(х). Аб-
Абсциссы точек пересечения этих графиков и будут корнями уравнения
F.6). На рис. 6.23 показаны два промежутка изоляции корней урав-
уравнения F.6): [а; с] и [с; Ь].
Рис. 6.22
Рис. 6.23
Промежутки изоляции корней уравнения можно получить ана-
аналитически, опираясь на теоремы о свойствах функций, непрерывных
на отрезке.
Если, например, функция f(x) на [а; Ь] непрерывна и f(a)f(b) < О,
то, согласно теореме Больцано — Коши (см. § 4.4), она имеет на
[а; Ь] хотя бы один нуль.
Если функция f(x) на [а; Ь] удовлетворяет условиям теоремы
Больцано — Коши и монотонна на этом отрезке, то на [а; Ь] сущест-
существует только один корень уравнения f(x) = 0.
Таким образом, уравнение f(x) = O имеет на [а; Ь] единственный
корень, если:
1)	функция y = f(x) непрерывна на [а; Ь]\
2)	f(a)f(b)<0;
3)	f'(x) сохраняет знак на [а; Ь].
Пример 6.16. Найти промежутки изоляции действительных корней уравнения
х3 + х — 1 = 0.
Решение. Воспользуемся графическим методом отделения корней. Уравнение
запишем в виде х3 = 1 — х и построим графики функций у = х3 и у = 1 — х.
Абсцисса единственной точки пересечения графиков функций принадлежит от-
отрезку [0; 1] (рис. 6.24). Следовательно, уравнение имеет один действительный корень
х* на [0; 1].
Проверим правильность определения промежутка изоляции корня уравнения
аналитически. Действительно, f(x) = х3 -\-х— 1 иа [0; 1] непрерывна, Д0)=—1,
f(l)=l, т. е. Д0)Д1)<0. Производная f'(x) = 3x1+l иа [0; 1] сохраняет знак
(/'(*)> 0 У*6[О; 1]). Таким образом, уравнение х3 + х — 1 = 0 иа [0; 1] имеет один
действительный корень.
Уточнение корня. Постановка задачи. Допустим, что искомый
корень уравнения F.6) отделен, т. е. найден отрезок [а; Ь], на кото-
158

•-№)
Рис. 6.24
Рис. 6.25
ром имеется один и только один корень уравнения. Любую точку этого
отрезка можно принять за приближенное значение корня. Погреш-
Погрешность такого приближения не превосходит длины отрезка [а; Ь].
Следовательно, задача отыскания приближенного значения корня с
заданной точностью е сводится к нахождению отрезка [а; Ь] (\Ь —
— а\ <С е), содержащего только один корень уравнения F.6). Эту
задачу называют задачей уточнения корня.
Далее будем считать, что корень F.6) отделен, и рассмотрим
основные методы уточнения корней.
Метод половинного деления. Пусть известно, что на [а; Ь] содер-
содержится единственный действительный корень уравнения f(x) = 0 и
f(a) <; @), f(b) > 0 (рис. 6.25). Требуется найти его значение с задан-
заданной точностью е. Отрезок [а; Ь] делим пополам, определяем точку
с = {а-\-Ь)/2 и f(c). Если /(с)<0, f(b)>0 (как показано на рис.
6.25), то корень уравнения х*?[с; Ь] (если /(с)>0, /:(а)<0, то
х* 6 [а; с]), т. е. отрезок [а; Ь] изоляции корня уравнения сузили до
отрезка [с; Ь].
Если \Ь — с\ < е, то искомый корень уравнения х* найден с за-
заданной точностью е, и любое число из [с; Ь] можно рассматривать
как его приближенное значение. В противном случае процесс деле-
деления отрезка пополам продолжается до тех пор, пока длина получен-
полученного отрезка изоляции корня не станет меньше заданной точности е.
Может случиться, что на каком-то шаге деления получим точку
Ci, такую, что f(ci) = O. Тогда с, будет точным значением корня урав-
уравнения.
В методе половинного деления погрешность решения находится в
прямой зависимости от числа деления отрезка пополам. При п деле-
делениях погрешность равна \Ь — а|/2". Следовательно, если взять до-
достаточно большое п, то искомый корень уравнения может быть вы-
вычислен с любой степенью точности. Рассмотренный метод удобен
тем, что в нем используются однотипные вычислительные операции.
Его легко применять при проведении вычислений на ЭВМ.
Метод хорд. Пусть на [а; Ь] находится единственный корень урав-
уравнения f(x) = 0, f(a) < 0, f(b) > 0 и f'(x), f"(x) сохраняют знак на этом
отрезке. Точки A (a; f(aj) и B(b; f(b)) дуги кривой на [а; Ь] соединим
159

хордой АВ, уравнение которой
y — f(a) _ х — а
f(b)-f(fl) Ь-а
F.7)
Абсцисса Х\ точки пересечения хорды с осью Ох является первым
приближением значения корня х* (рис. 6.26). Значение х\ найдем,
решив совместно уравнения хорды F.7) и оси абсцисс:
v-№ _ x-t
№-f(a) b->
	 	 f(a) F — a)
~° №-f(a)'
F.8)
Итак, первое приближение значения корня xt определяется фор-
формулой
х _	№(Ь-а)
Л' " f(b)-f(a) '
т. е. получили суженный промежуток [дсь'б] изоляции корня. Приме-
Применив к нему формулу F.8), найдем второе приближение значения
корня х2:
*2 = *|- f (ft) _/(*,) •
Продолжая этот процесс, получаем л-е приближение значения корня
уравнения:
f(Xn-i)(b — Xn-[)
Xn = Xn-l— f{b)_f{Xni) ¦
При этом замечаем, что в формуле F.9) точка b фиксируется, т. е.
один конец хорды с абсциссой b неподвижен, а другой при каждом
приближении меняется (является подвижным).
Из рис. 6.26 видно, что f(b) >0и кривая вогнута, следовательно,
Неподвижным является тот конец хорды, где знак f (x) совпадает
со знаком f"(x). Если неподвижным является конец хорды с абсцис-
абсциссой а, т. е. f(a) и f"(a) имеют одинаковые знаки, то л-е приближение
значения корня "уравнения определяется по формуле
B{b;f(b)) у <
а
A(a;f(a))
Рис. 6.26
Ь Л
A (a-,f fa))
Рис. 6.27
B(b;f(b))
160

г —г , . /(*—1)(*—i-a)	f6 1Q\
Оба (итерационные) процесса F.9) и F.10) сходятся, причем
U«-x*K-!?Gs?Lf m= min \f'(x)\,
m	6[ft]
= max
Метод касательных (метод Ньютона). Пусть на [а; Ь] имеется
единственный корень уравнения f(x) = 0, f(a) f(b) < 0 и f"(x) на [a; b]
сохраняет знак.
Из рис. 6.27 видно, что если провести касательную к графику
функции у = f(x) в точке с абсциссой а (в этой точке знаки f(x) и
f"(x) совпадают), то абсцисса точки пересечения касательной с
осью Ох будет первым приближением корня уравнения. Касательная,
проведенная к кривой в точке с абсциссой Ь, может пересечь ось
абсцисс в точке, не принадлежащей [а; Ь] (в этой точке знаки f(x) и
f"(x) противоположны).
Запишем уравнение касательной к графику функции y = f(x)
в точке, в которой f(x) и f"(x) имеют одинаковые знаки. В случае,
изображенном на рис. 6.27, такой точкой является точка с 'абсцис-
'абсциссой а. Запишем уравнение касательной к кривой в этой точке:
y-f(a) = f'(a)(x-a).
Найдем точку пересечения касательной с осью Ох:
Полученное значение х и есть первое приближение х\ значения корня
уравнения.
Второе приближение значения корня уравнения найдем, приме-
применив метод касательных к отрезку \х\\ Ь]. Получим
Х<1 — Х\ — -гут—г-.
Повторяя вычисления, находим расчетную формулу
Хя = хп-1--^^,пек	F.П)
причем
(а, если f{a)f(c)<0,
xo = i b, если f(a)f(c)>0,
К если f(c) = O,
(а,
= i b,
Кс,
где с —а	\(ь\ — н\ • Тогда последовательность (хп) сходится к
корню х* при л-»-оо и для любого л 6 N справедливы неравенства:
6 Зак. 1270	161

I Y 	r* I
2m
\Хп Хп—\) ,
где m= min |/'(дс)|; Mi = max \f"(x)\.
xt[a; b]	xt[a; b)
Метод секущих — хорд. Методы хорд и касательных требуют
анализа функции f(x), так как сходимость последовательности (хп)
к х* зависит от свойств функции f(x). На практике удобно использо-
использовать методы, не требующие предварительного исследования функ-
функции f(x). Одним из таких методов является метод секущих — хорд.
В основу этого метода положена формула F.11) метода касатель-
касательных, в которой точное значение производной }'{хп-\) заменяется при-
приД*-1) —f (*«-«) ^ расчетная формула имеет вид
ближенным
„_1 — хп-г

Хп-Хп-1
Xa— I — Xn—2
Метод дает сходимость при любом выборе на отрезке изоляции
[а; Ь] нулевого х0 и первого х\ приближений, что, безусловно, очень
удобно для практики.
Приближенное решение уравнений с помощью программируемых
микрокалькуляторов и ЭВМ. Методы уточнения корней уравнения
(метод хорд, метод касательных, метод секущих — хорд) удобно
реализовать на ЭВМ.
Ниже приводятся две программы 1 и 2 приближенного решения
уравнения методом хорд для программируемого микрокалькулятора
«Электроника БЗ-34».
Расчетная формула для программы 1:
Jf n — Xn—l
._i— a)
f (*„_,)-Да)
Программа 1
Адрес
ко-
команды
00
01
02
03
04
05
06
07
08
09
Нажимае-
Нажимаемые кла-
клавиши
пв
ИПА
ПП
28
ПС
ИПВ
ПП
28
t
ипс
Код
опе-
операции
4L
6—
53
28
4[
6L
53
28
0Е
6[
Адрес
ко-
команды
10
11
12
13
14
15
16
17
18
19
Нажимае-
Нажимаемые кла-
клавиши
ИПВ
ИПА
—
X
ИПВ
ХУ
ПВ
Код
опе-
операции
11
13
6L
6—
11
12
6L
14
11
4L
Адрес
ко-
команды
20
21
22
23
24
25
26
27
Нажимае-
Нажимаемые кла-
клавиши
FBx
Fx*
ипд
Fx<0
05
ИПВ
С/П
Код
опе-
операции
0
22
61
11
5[
05
ЛЬ
50
Ввод данных: а-»РА, е2-»РД, 6->-РХ.
Расчетная формула для программы 2:
К*-,) (ft-«._,)
"	' K6)f(*)
162

Программа 2
Адрес
ко-
команды
00
01
02
03
04
05
06
07
08
09
Нажимае-
Нажимаемые кла-
клавиши
ПА
ИПВ
ПП
28
ПС
ИПА
ПП
28
t
ипс
Код
опе-
операции
4—
6L
53
28
4[
6—
53
28
ОЕ
6[
Адрес
ко-
команды
10
и
12
13
14
15
16
17
18
19
Нажимае-
Нажимаемые кла-
клавиши
ипв
ИПА

X
ИПА
н.
ПА
Код
опе-
операции
11
13
6L
6—
11
12
6—
14,
10
4	1
Адрес
ко-
команды
20
21
22
23
24
25
26
27
Нажимае-
Нажимаемые кла-
аиши
FB*
ипд
Fx<0
05
ИПА
С/П
Код
опе-
операции
0
22
6Г
11
5[
05
6—
50
Ввод данных: 6-»-РВ, е2-»-РД, а-»РХ.
Программу 1 используют, если неподвижен конец а отрезка изоля-
изоляции корня, т. е. если функция f(x) и ее вторая производная в точке
а имеют одинаковые знаки (f(a)f"(a) > 0). Программа 2 применяется,
если неподвижен конец b отрезка изоляции корня [а; Ь], т. е. если
функция f(x) и ее вторая производная в точке b имеют одинаковые
знаки {f{b)f"{b)>0).
Вычисления считаются выполненными с заданной точностью е,
если два последовательных приближения хп-\ и хп удовлетворяют
условию
\хп — хп-\\ <го(хп — xn-iJ<E2.
Пример 6.17. Вычислить методом хорд с точностью до 0,0001 корни уравнения
х — cos х = 0.
Решение. Переписав уравнение в виде х = cos x и построив графики функ-
функций у = cos х и у = х, замечаем, что они пересекаются в одной точке х* 6 [0; 1]. Таким
образом, уравнение х — cosx = 0 имеет только одни корень х*6[0; 1].
Выясним, какой из концов отрезка [0; 1] изоляции корня неподвижен:
f (х) = х — cos х, f@) = — 1, f A) = 1 — cos 1 > 0,
n*) = cosx, f"@)=l, f"(l) = cosl>0.
Так как функция f (x) и ее вторая производная в точке х = 1 имеют одинаковые
знаки, то конец Ь неподвижен и для вычисления корня уравнения х* надо восполь-
воспользоваться программой 2. Для ее применения необходимо составить подпрограмму
вычисления значений функции f(x) = x — cos х:
Адрес команды
28
29
30
31
Нажимаемые клавиши
F COS
в/о
Код операции
0Е
1Г
11
52
Вводим программу (адреса 0—27), подпрограмму (адреса 28—31) и ясход]
данные в память микрокалькулятора; а = 0, 6 = 1, в2= 1 • 10~8 @->-РА, 1 • 10~
-РД. I-PX).
ясходиые
в .
163

Результат счета: х* = 0,73908.
Приведем программу приближенного'решения уравнения методом
секущих — хорд (см. программу 3).
Расчетная формула для программы 3:
Хп = Хп—1 — f(xn— l)
хп-\ — Хп-г
Указание. Значения хо и Х\ (хо < х\) выбираются произвольно из отрезка [а; Ь]
изоляции корня.
Исходные данные: хо, Х\, е2 (вводятся следующим образом;
2
РД).
Программа 3
Адрес
ко-
команды
00
01
02
03
04
05
06
07
08
09
10
11
Нажимае-
Нажимаемые кла-
клавиши
ИПА
ПП
34
ПС
ИПВ
ПП
34
ПД
ИПА
ИПС
t
ипд
Код
опе-
операции
6—
53
34
4[
6L
53
34
4Г
6—
6[
0Е
6Г
Адрес
ко-
команды
12
13
14
15
16
17
18
19
20
21
22
23
Нажимае-
Нажимаемые кла-
клавиши
ПС
ху
—
ИПА
ИПВ
—
X
+
ИПВ
ХУ
пв
Код
опе-
операции
4[
14
11
13
6—
6L
11
12
10
6L
14
4L
Адрес
ко-
команды
24
25
26
27
28
29
30
31
32
33
Нажимае-
Нажимаемые кла-
клавиши
ХУ
ПА
f72
ИПО

F*<0
04
ИПВ
С/П
Код
опера-
операции
14
4—
11
22
60
11
5[
04
6L
50
Пример 6.18. Найти методом секущих—хорд корень уравнения х — cos * = 0
с точностью до в = 0,0001.
Решение. Искомый корень **€[0; 1]. Выберем х0 = 0,5, *i=0,7, в2 =
= 1 • 10~8.
Составим подпрограмму вычисления значений функции f(x) = x — cos x:
Адрес команды
34
35
36
37
Нажимаемые клавиши
Fcos
в/о
Код операции
ОЕ
1Г
11
52
Вводим программу (адреса 00—33), подпрограмму (адреса 34—37) и исходные
данные в память микрокалькулятора БЗ-34 @,5-»-РА, 0,7-»-РВ, 1 • 10~8-»-Р0).
Результат счета: х* = 0,73906. Время счета —около 40 с.
Пример 6.19. Составить ФОРТРАН-программу решения уравнения х3 + 2х —
— 8 = 0 методом хорд с точностью до 0,0001.
Решение. Графически отделяя корни данного уравнения, замечаем, что оно
имеет корень на отрезке [1; 2]. Находим: f'(x) = Зх2 + 2, т= min f'(x) = 5, M =
= max f'(x) = 14. Следовательно, S = (М — т)/т = 1,8.
164

ФОРТРАН-программа решения данного уравнения методом хорд нмеет следую-
следующий вид:
EXTERNAL F
ROOT*CHORD (F,1.,2.,1.8,. 0001)
WRITE C.1) ROOT
1 FORMAT (IX,'X»',F6.4)
STOP
END
FUNCTION CHORD (F,A,B,S,EPS) ¦
FA=F(A)
FB = F(B)
X=A-(B-A) -FA/(FB-FA)
FX = F (X)
IF (FA'FX.GT.O) GOTO 2
1	X=-X-(X-A)-FX/(FX-FA)
FX = F(X)
DX = S-ABS(X-X1)
X1=X
IF (DX.GT.EPS) GOTO 1
CHORD=X
RETURN
2	X = X-(B-X)-FX/(FB-FX)
FX = F(X)
DX = S-ABS (X-X1)
X1-X
IF (DX.GT.EPS) GOTO 2
CHORD-X
RETURN
ENO
FUNCTION F (X)
F = X+2'X-8
RETURN
ENO
Входные параметры: А, В — концы промежутка изоляции (А = 1, В = 2);
S (S=l,8); EPS — предельная абсолютная погрешность (EPS = 0,0001); F—имя
подпрограммы-функции вычисления значений f(x).
Результат счета: х= 1,6702.
Пример 6.20. Составить ФОРТРАН-программу решения уравнения х3 + 2х —
— 30 = 0 методом касательных с точностью до 0,0001.
Решение. Графически отделяя корни данного уравнения, замечаем, что оно
имеет кореиь на отрезке [2; 3]. Находим: f'(x) = Зх2 + 2, f"(x) = 6x, m = min /'(*) =
х6[2; 3]
= 14, Mi = ma3rf"(*)= 18. Следовательно, S = -^~ = -гг-
х6[2;3]	2/П	14
Запишем ФОРТРАН-программу решения данного уравнения 'методом каса-
касательных.
EXTERNAL F,FO
ROOT-TANGEN (F,FD,2.,3, 0.64286,0.0001)
WRITE C,1) ROOT
1 FORMAT AX/X--.F6.4)
STOP
END
FUNCTION TANGEN (F,FD,A,B,S,EPS)
FA=F(A)
C-A- (B-A) -FA/(FB-FA)
P=FA-F(C)
IF (P) 2,1,3
1	TANGEN-C
RETURN
2	X = A
GOTO 4
3	X = B
4	Xl-X
X = X-F (X)/FD(X)
IF (S« (X1-X) .GT.EPSI GOTO4
TANGEN=X
RETURN
END
FUNCTION F(X)
165

F = X--3+2-X-30
RETURN
END
FUNCTION FD(X)
FD=a-(X>+2.
RETURN
END
Входные параметры: А, В — концы промежутка нзоляцнн корня (А = 2, В = 3);
S (S = 9/14); EPS — предельная абсолютная погрешность (EPS = 0,0001); F — нмя
подпрограммы-функции вычнслення f (x); FD — имя подпрограммы-функции вычисле-
вычисления f'(x).
Результат счета: х = 2,8930.
Пакет программ приближенных методов решения нелинейных
уравнений /(*) = 0 описан в литературе (см. [4, с. 88—96]). В этих
программах вычисление функции f(x) оформляется в виде фрагмента
программы, вписываемого в текст основной программы вместо много-
многоточия. В указанной работе содержатся также методы решения
алгебраических уравнений степени не выше пятой (см. [4, с. 97—100]).
Решение алгебраических уравнений более высоких степеней {п ^ 6)
целесообразно проводить на ЭВМ с большим быстродействием по
стандартным программам.

7. ВЕКТОРНЫЕ И КОМПЛЕКСНЫЕ ФУНКЦИИ
ДЕЙСТВИТЕЛЬНОГО АРГУМЕНТА
7.1. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА.
ГОДОГРАФ
В курсе математики и ее многочисленных приложениях часто при-
приходится иметь дело не только с числовыми функциями, но и с функ-
функциями, у которых область определения D или множество значе-
значений Е состоят из элементов другой природы, например D с R,
а ? — подмножество множества свободных векторов У3-
Пусть Т с R, A c= V3-
Определение 7.1. Векторной функцией действительного аргу-
аргумента (вектор-функцией скалярного аргумента) называется отобра-
отображение, которое каждому действительному числу t?T ставит в со-
соответствие один и только один вектор а 6 A с У3-
Вектор-функцию принято обозначать а = a(t), t?T. Различным
значениям t?T будут соответствовать разные значения вектор-
функции, т. е. вектор a = a(tf) имеет определенную длину (модуль)
и определенное направление. Таким образом, вектор a = a(tf) может
изменяться как по величине, так и по направлению. Выберем общую
точку приложения О векторов a = a(f) (рис. 7.1). При непрерывном
изменении аргумента t конец вектора a = a(tf) описывает некоторую
линию L.
Определение 7.2. Линия L, описываемая в пространстве
концом вектора а при непрерывном изменении аргумента t g T c= R,
называется годографом вектор-функции скалярного аргумента a.(t).
Рис. 7.2
Рис. 7.1
Рис. 7.3
167

С физической точки зрения годограф вектор-функции можно рас-
рассматривать как траекторию движущейся в пространстве материаль-
материальной точки, а всякую линию L в пространстве как годограф некоторой
вектор-функции.
Замечание. Если предположить, что вектор а = а(<) изменяется только по
длине, а его направление остается постоянным, то ja(f) | / € Т) есть множество связан-
связанных векторов, расположенных на луче, выходящем из точки О. Годографом такой
вектор-функции является луч L (рис. 7.2), если T=R.
Если предположить, что при изменении t модули векторов а = а(<) не меняются,
а изменяется только направление, то векторы из множества ja(f) 11 6 Т) будут нахо-
находиться в шаре радиусом |а(<)| с центром в точке О. Годографом такой функции
является линия, принадлежащая сфере радиусом |a(f)l (рис. 7.3).
Для удобства изучения и аналитического описания вектор-функ-
вектор-функции а = а@ и ее годографа выберем систему координат {О, i, j, k}.
В качестве начала координат возьмем общую точку О приложения
векторов а = а(/). Если OM = a(t), то а = а@ называют радиусом-
вектором точки М и обозначают г@ (рис. 7.4). Любой радиус-вектор
r{t) = OM пространства R3 задается своими координатами x(t), y(t),
z(t) (координаты вектора совпадают с координатами точки М ? L
(см. рис. 7.4)) и может быть разложен по ортам i, j, k:
Так как каждой упорядоченной тройке чисел х, у, г соответст-
соответствует единственный радиус-вектор г = г@, то задание вектор-функции
эквивалентно заданию трех числовых функций x = x(t), y = y(t).
г@ = x(t)i + y(t)l + z(t)ko\ у = y(t), t 6 T.
Исследование векторной функции скалярного аргумента сводится
к исследованию трех числовых функций x = x(t), y = y(t), z = z(t),
определенных на множестве Т.
Пример 7.1. Найти частные значения вектор-функции r(t) = 4 cos /1 -f- 3 sin t\ -f-
-f 2k, 16 [0; 2л], при t\ = 0, 12 = л/4 и изобразить ее годограф.
Решение. Рассмотрим координаты t(t): x(t) = A cost, y(t) = 3 sin t, z(t) = 2.
При <i = 0 имеем x@) = 4, i/@) = 0, г@) = 2. Следовательно, r@) = 41+ 2k. Анало-
Аналогично находим частное значение вектор-функции при t\ = л/4:
4-J =4 cos-2-1 + 3sin-^-j + 2k =
Годографом L данной вектор-функции является кривая, параметрические урав-
уравнения которой х = 4 cos t, у — 3 sin t, г = 2, 16 [0; 2л]. Исключим из первых двух
уравнений параметр t. Известно, что для любого t sin21 -fcos21 = 1. Из первого
уравнения имеем cos t = х/4, из второго — sin t = y/3. Следовательно, эти уравнения
хг и2
эквивалентны уравнению —-f-^_=l. Итак, уравнения годографа в декартовых
х2 и2
координатах имеют вид: 7ё+7Г='. г = 2- Они определяют эллипс с полуосями
а = 4, b = 3, расположенный в плоскости г = 2 (рис. 7.5).
Пример 7.2. Записать уравнение годографа вектор-функции в декартовых ко-
координатах, если г(/) = B/ — 1I + C< — 5)j + C — /)k, t € R.
168

Zi
О	у
Рис. 7.4
Рис. 7.5
Решение. Рассмотрим функции, задающие годограф L:
* = 2< —1,	\
у = 3< — 5, t б R. )
z=-t + 3. J
Это параметрические уравнения прямой в простраистве. Исключая из последней
системы параметр t, приходим к каноническим уравнениям прямой
х+ 1 _ у + 5 _ г — 3
2	3	—1 '
Таким образом, годограф L — прямая линия, проходящая через точку Л1(—1;
— 5; 3), с направляющим вектором S = B; 3; —1).
7.2. ПРОИЗВОДНАЯ ВЕКТОР-ФУНКЦИИ
ДЕЙСТВИТЕЛЬНОГО АРГУМЕНТА.
ГЕОМЕТРИЧЕСКИЙ И МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Введем понятие предела, непрерывности и производной для век-
вектор-функции г = г(^). Предположим, что вектор-функция г(^) =
= x{t)\ -{-y(t)i + z(t)k определена в некоторой окрестности точки
^о 6 Т. Это означает, что в окрестности точки ^0 определены и число-
числовые функции x(t), y(t), z(t).
Определение 7.3. Вектор г0 = xoi + г/oj + zok называется пре-
пределом вектор-функции r(t) = x(t)\ +y{t)l -{-z(t)k при t^t0, если она
определена в Ob(to) и
lim z(t) = z0.
\imx(t) =
lim y(t) =
t—to
В этом случае пишут: limr(^) = ro или
lim г@ = lim x{t)\ + lim y{t)\ + lim z(t)k = xoi + yQ\ + zok.
t-*-to	t-*-to	t-*-to	t-*-t0
Таким образом, для того чтобы вычислить предел вектор-функ-
вектор-функции, достаточно найти соответствующие пределы координат этой
функции. Если хотя бы один из пределов координат функции г(^) не
существует, то не существует и limr(^).
169

Пример 7.3. Вычислить lim r(t), если г@ = C* + 2I + Bt — l)j +A — t)k.
t—*-2
Решение. Согласно определению 7.3,
lim г(/) = limC* + 2I + limB/ — l)j + lim(l — t)k = 8i + 3j — к.
(—2	(—2	(—2	(—2
Основные правила нахождения пределов справедливы и для
вектор-функции действительного аргумента:
1)	Нт(г,@ + г2@) = Нт г,(t) + lim г2@;
t-*to	<-W0	l—tt,
2)	lim(r,(/)f r2@) = (limri@, Нт r2(f));
t-*-to	t-*-to	t—*-tn
3)	lim[n@, г2</)] = {НтГ|@, lim r2(f)].
Определение 7.4. Вектор-функция r(t) называется непрерыв-
непрерывной в точке to, если она определена в Oe(to) и	_,
Hmr(t) = r(to)o\imr(t) =
= lim x(t)\ + lim y(t)i + lim z(t)k = хо\ + уо) + zok.
t—*-to	t—*-to	t-*-ti)
Введем понятие производной вектор-функции в данной точке ?о-
Для этого дадим аргументу t0 приращение At=?O н рассмотрим
вектоо Ar(tn) = r(tn-\-At) — r(to). Составим отношение
_ r(to + \t)-r(to)
At	At
Определение 7.5. Если существует предел отношения при-
приращения Лг(/о) вектор-функции в точке to к приращению скалярного
аргумента At при Л/->-0, то этот предел называется производной
вектор-функции r(t) в точке to и обозначается г'(to) или r(t0).
Таким образом,
Так как
Лго(*о) = (x(to + At) - *(/0)I + (y(to + At) - y(to))i +
+ (z(t0 + At) - zo(t))k = Ax(to)\ + Ay(to)) + Az(to)K
то по определению
Вычисление производных от векторной функции скалярного
аргумента в точке ?о сводится к вычислению производных ее коорди-
координат.
Выясним геометрический и механический смысл производной
вектор-функции, т. е. вектора г'(?0). Пусть вектор-функция г(/) опре-
определена на множестве Т, непрерывна в точке to?T к кривая L —
годограф функции г(/). Пусть точке Mo?L соответствует значение
г(*о), а точке M\?L — значение г(*0 + At), где А* Ф 0. Тогда прира-
приращение вектор-функции Дг(*о) = г(/о + At) — r(to), представляющее
170

собой разность двух векторов, есть вектор, соединяющий конец
вектора уменьшаемого с концом вектора вычитаемого (рис. 7.6).
Отношение Дг(<0)/Д< представляет собой вектор, коллинеарный
вектору Дг(<о), так как он отличается лишь скалярным множителем.
Таким образом, вектор Ar(to)/At (см. рис. 7.6) совпадает по направле-
Рис. 7.6
нию с секущей МОМХ. При Д<->-0 точка Mi стремится к Мо, переме-
перемещаясь по кривой L, а секущая МцМ\ занимает предельное положение,
определяемое касательной к годографу L в точке Мо. Отсюда сле-
следует, что вектор
совпадает по направлению с касательной к годографу в точке Мо и
направлен в сторону возрастания t. Итак, с геометрической точки
зрения производная вектор-функции в точке to есть вектор г'(to),
направленный по касательной к годографу этой функции в сторону
возрастания параметра t.
Выясним механический смысл производной вектор-функции.
Предположим, что материальная точка движется по траектории,
являющейся годографом вектор-функции r(t), где роль параметра t
играет время движения. За промежуток времени \t точка на кривой
переместится из положения Мо в положение М. Вектор Дг(/0) задает
перемещение материальной точки за время М. Отношение Дг(<0)/Д*
есть средняя скорость перемещения точки за время Д*. Переходя
к пределу при \t-*0, получим мгновенную скорость v точки в момент
времени t0:
v = r'(t0) = li
= x'(to)\ + y'(to)} + z'(to)k.
At-<-0
Таким образом, механический смысл производной от вектор-
функции состоит в том, что г'(to) есть вектор мгновенной скорости
171

перемещения материальной точки по траектории, являющейся го-
годографом функции.
Производная вектор-функции r'(t) является, в свою очередь,
вектор-функцией скалярного аргумента, и ее также можно диффе-
дифференцировать.
Производная функции r'(t) в точке t = t0 называется второй про-
производной вектор-функции r(t) no скалярному аргументу t в точке to
* г(/о) , Лг'Щ , f(t0).
dt	dt |'=<о
и обозначается так: r"(t0),
Мы показали, что с механической точки зрения производная
г'(*о) равна скорости v(^0) движения материальной точки в момент
времени to:
Вектор a(fo). равный производной скорости v(t) по времени t в
момент to, называют ускорением:
Механический смысл второй производной от вектор-функции
состоит в том, что г"(to) есть вектор ускорения движения материаль-
материальной точки в данный момент времени to-
Пример 7.4. Найти скорость и ускорение мате-
материальной точки М, движущейся с постоянной угло-
угловой скоростью ft) по окружности х2 + у2 = R2
(рис. 7.7).
Решение. Пусть М — произвольная точка
окружности. Обозначим через ф угол между радиу-
радиусом-вектором точки М и положительным направле-
направлением оси Ох. По условию ф = ь)<, где / — время
движения. Выразим координаты точки М как функ-
функции времени (см. рис. 7.7):
х = R cos ф = R cos (о/, у = R sin ф = R sin ft)/.
Следовательно, радиус-вектор точки М
г = х\ + у\ = R cos to/I + R sin to/j,
скорость v(/) движения точки М
v = г'@ = (R cos ft)/)'i + (R sin ft>/)'j = — Ra> sin ш/i + Ra> cos ш/j,
модуль скорости
I v I =~v(—Яш s'n <utf -\-(R<o cos ft)<J = (oR.
Найдем скалярное произведение векторов v и г:
(v, г) = — R2a> sin to/ cos ft)/ + R2a> cos to/ sin to/ = 0,
т. е. векторы v и г взаимно перпендикулярны. Отсюда следует, что вектор v направ-
направлен по касательной к окружности, по которой движется точка М.
Найдем ускорение а(/):
— R(i>2 COS ft)/i — R(i>2 Sin ft)/j =
Рис. 7.7
= — ьJ(Л cos ft)/i + # sin (o/j) = — ftJr(/).
Следовательно, векторы г и а имеют противоположные направления. Таким
172

образом, ускорение материальной точки, движущейся с постоянной угловой скоростью
по окружности, в каждый момент времени направлено к центру этой окружности.
7.3. УРАВНЕНИЯ КАСАТЕЛЬНОЙ ПРЯМОЙ
И НОРМАЛЬНОЙ ПЛОСКОСТИ
К ПРОСТРАНСТВЕННОЙ КРИВОЙ
Из курса аналитической геометрии известно, что каждому урав-
уравнению с тремя неизвестными F(x, у, z) = 0 (или в явной форме z =
= f(x, у)) соответствует в декартовой системе координат Oxyz неко-
некоторая поверхность.
Кривая в пространстве рассматривается как линия пересечения
двух поверхностей и определяется системой двух уравнений
Fx(x, у, 2) = 0,1
F2(x, у, z) = 0J
Кривую в пространстве можно задать также параметрически:
x = x(t), y = y(t), z = z(t), teT.	G.1)
Найдем канонические уравнения касательной прямой к прост-
пространственной кривой L, заданной параметрически уравнениями G.1),
в некоторой ее точке М0(х0; уо\ Zo), соответствующей значению па-
параметра ?о ? Т. Искомые уравнения имеют вид
Х — Хд __ У—Уо _ Z — ZQ
т	п	р '
где т, п, р — проекции направляющего вектора прямой s = (т, п, р).
Кривая L ? R3 есть годограф вектор-функции r(t) = x{t)\ -j- y(t)j -j-
-f- z(t)k, а вектор г'(*о) направлен по касательной к кривой L в точке
Мо{хо; t)o\ Zo). Следовательно, можно положить s = r'(t0)om —
= x'(t0), n = y'{t0), p = z'{t0). Тогда искомые уравнения касательной
прямой примут вид
Х — Хд
x'(t0)	y'(to)
Определение 7.6. Нормальной плоскостью к пространствен-
пространственной кривой называется плоскость, перпендикулярная касательной
прямой и проходящая через точку касания.
Пусть М0(х0; уо\ z0) — точка касания (рис. 7.8). Уравнение плоско-
плоскости а, проходящей через эту точку, имеет вид
где п = (Л, В, С) — нормальный вектор плоскости. Из определения
нормальной плоскости следует, что векторы п = (Л, В, С) и г'(to)
коллинеарны, поэтому можно положить A = x'(to), B = y'(to), C =
= z'(to). Тогда искомое уравнение плоскости будет иметь вид:
x'(to)(x - хо) + y'(to)(y-yo) + z'(to)(z - zo) = 0.	G.3)
Пример 7.5. Найти уравнения касательной прямой и нормальной плоскости к
годографу L, заданному параметрически уравнениями:
173

Zi
Рис. 7.8
x = a cos /,
i/ = о sin /, / 6 R, о == const, b = const,
6
(x =
J i/ =
в точке Mo, соответствующей параметру to = я/3. Эта кривая называется винтовой
линией (рис. 7.9). При любом t
х2 + у2 = o2(cos2 / + sin2 /) = о2.
Это означает, что винтовая линия расположена на цилиндрической поверхности
х2 + у2 = о2. Отсюда следует, что если точка М движется по винтовой линии, ее
проекция N на плоскости Оху перемещается по окружности радиусом о с центром в
начале координат, причем t является полярным углом точки N (см. рис. 7.9). При
изменении параметра / от 0 до 2я точка N описывает полную окружность, а аппли-
аппликата г точки М увеличивается на Л = 2пЬ. Эта величина называется шагом винто-
винтовой линии.
Решение. Определим координаты точки касания:
я о	.я л/3	, я
хо = a cos — = —, уо = а sin — = -^— о, го = Ь -^-.
Найдем проекции вектора г'(/о) иа оси координат:
ал/if
x'(to)= — о sin -5- = — ¦ „¦-,
у.
z'(to) = b.
Подставив значения x'(to), y'(to), z'(to) в формулы G.2) и G.3), найдем уравнения
касательной прямой
'—2 а 2-'
и иормальной плоскости
ал/з~
а/2
174

7.4. КРИВИЗНА КРИВОЙ
Дифференциал длины дуги. Пусть кривая L — график непре-
непрерывно дифференцируемой функции у = f(x). Такую кривую называют
гладкой. Возьмем точку А за начало отсчета. Пусть М ? L, тогда
длина дуги AM будет функцией абсциссы х точки М (рис. 7.10).
Обозначим эту функцию 1{х):АМ = 1{х). -Найдем дифференциал
функции 1(х), который называют дифференциалом длины дуги. По
определению дифференциал функции l(x) dl = l'(x)dx. Найдем выра-
выражение для 1'{х). По определению Г(х) есть предел отношения длины
дуги ММ\ к Ах:
¦ 1{Х)	11 А\
Примем без доказательства следующую теорему.
Теорема 7.1. Предел отношения длины дуги гладкой кривой к
длине стягивающей ее хорды при стремлении длины дуги к нулю
равен единице:
lim

|ЛШ,|
^ 1
На основании теоремы 7.1 и свойств эквивалентных бесконечно
малых величин (см. теорему 3.14) при нахождении предела G.4)
заменим дугу ММ] эквивалентной ей хордой |MMi| = ~\jAx2 -\- А у2.
Тогда
Отсюда
G.5)
Д.
о	х
Рис. 7.10
х 0 х x+dx х
Рис. 7.11
75

Внеся dx под знак корня, получим простой, легко запоминаю-
запоминающийся вид формулы для дифференциала дуги:
+ dy2.	G.6)
Из формулы G.6) следует, что с геометрической точки зрения
дифференциал дуги в точке М с абсциссой х равен длине соответ-
соответствующего отрезка касательной к линии L в точке М(х; у). Это отре-
отрезок МТ (рис. 7.11). Таким образом, за приближенное значение дуги
ММ\ при достаточно малом Дд: принимается дифференциал этой
дуги, т. е. отрезок касательной МТ.
Если кривая L задана параметрически уравнениями x = x{t),
у = y(t), t?T, то, используя принятые в механике обозначения х\ =
= х, y't = У, имеем
Подставляя у'х = у/х в формулу G.5), получаем
Кривизна кривой. Основные определения. Одной из важных ха-
характеристик кривой является мера ее изогнутости — кривизна.
Например, о двух плоских кривых АСВ с L\ и ADB с L^ (рис. 7.12) можно ска-
сказать, что кривая /-г более изогнута, чем L\.
Рис. 7.12	Рис. 7.13
Однако для того, чтобы строго оценить степень изогнутости
плоской линии, необходимо ввести количественную характеристику
ее изогнутости (кривизны).
Рассмотрим на кривой точки М и Mi. Проведем в этих точках
касательные к кривой. При переходе по кривой из точки М в точку Mi
касательная поворачивается на угол Дф, который называется углом
смежности (рис. 7.13). Отношение угла смежности дуги к ее длине
называется средней кривизной дуги:
КСр = Дф/Д/.
Средняя кривизна характеризует среднюю изогнутость кривой
на всей дуге. На отдельных участках кривой кривизна может значи-
176

тельно отличаться от средней. Чтобы избежать такой неопределен-
неопределенности, вводится количественная мера изогнутости кривой в точке М.
Эта характеристика основана на том, что чем меньше дуга L (см.
рис. 7.13), тем лучше средняя кривизна характеризует изогнутость
линии вблизи точки М.
Определение 7.7. Кривизной К линии L в точкеМ называется
предел, к которому стремится средняя кривизна /Сср дуги MM i линии
L при стремлении точки Mi к точке М:
К = Hm Kcp =
Д/-*0
Вычисление кривизны кривой. Пусть кривая L является годо-
годографом дважды дифференцируемой векторной функции действи-
действительного аргумента r(t) (рис. 7.14). Кривизна кривой К = lim |Дф/Д/|.
Угол смежности Дф — угол между
r(t) и t(t -f At). Вектор г (/ -f ДО =
= r(t) -\- At(t). Из векторного произ-
произведения векторов t(t) и t(t) -f- Дг(О
находим:
sin Дф
|г|
At]\
Рис. 7.14
так как [f, f] = 0.
При Дг-»-0 Д/-^0 и Дф-^-О,
а также Дф ~ sin \q>( lim sin Аф = Л.
\ Дф-*о Лф	/
Следовательно, кривизна
= Hm
Лф
= lim
sin Лф
Л/
= lim
[г.
\M+t\
= lim-
1*1
Если
3, то r(t + M)-*-t(t) и |Д/| « |Дг|; тогда
K=\[t, f]l/|f|3.
G.7)
Формула G.7) используется для вычисления кривизны плоской
(пространственной) кривой L, если она является годографом дважды
дифференцируемой векторной функции г(?).
Пример 7.6. Вычислить кривизну кривой r(t) = e'i + е~'\ + <-у2к в любой точке
t и при / = 0.
Решение. Кривизна кривой, являющейся годографом вектор-функции, вы-
вычисляется по формуле G.7). Находим:
r@ = e'i — е~Ч + У2к, ?(/) = е'\ + е~'],
177

i j к
[t(t), ?(/)] = ё -e~' л/2
ё е-' О
|[f (/), f (ОН = I -Уге-'i
|f(/)| = |e'i-e-'j
'j + 2к| = -^2e~11 + 2еа' + 4
e1 + e"'),
V*2' + е~2' + 2 = е' + е"'.
Следовательно, в любой точке / кривизна
V2
&(е + е)__ ф
(«• + в-Г (^ + е-'J
так как x(t) = e', y(t) = e~'.
Кривизна кривой в точке / = О К = —=..
Замечание. Часто при задании векторной функции скалярного аргумента
в качестве параметра / используется так называемый натуральный параметр I —
длина дуги L. В этом случае формула для вычнслення кривизны имеет более простой
внд, так как |г(/)| = 1 и вектор г(/) перпендикулярен к вектору г(/): /С=|г(/I.
Вычисление кривизны плоской кривой, заданной параметрически.
Пусть гладкая плоская кривая L задана параметрически уравне-
уравнениями
х = x(t), ,г
Запишем вектор-функцию r(t) = x(t)i-\-y(t)} и воспользуемся
формулой G.7) для определения кривизны этой кривой. Находим
r(t) = x{t)\ + y(t)i, f(t) = x(t)i + y(t)). Тогда
i j k
[r@. f@1 =
x(t) y(t) 0
= {?{t)y{t)-x(t)y(t)k,-
\[t(t).
x(t) y(t) 0
= \x(t)y(t)-x{t)y(t)\,
Получаем формулу для определения кривизны кривой, заданной па-
параметрически:
KQ1I - IP-
|r@l3
(f + y2K'2
G.8)
Вычисление кривизны плоской кривой в декартовых координа-
координатах. Если кривая L задана уравнением у = f (x), то формулу для вы-
вычисления ее кривизны можно получить из формулы G.8), положив
в ней t = х.
Действительно, уравнение линии L можно записать в параметри-
параметрическом виде:
У = f (ОД
х = t. !
Тогда из формулы G.8) имеем К =
уравнению линии в декартовой системе координат,
178
или, переходя к

K_ \d2y/dx2\
{\+(dy/dxff>*
Пример 7.7. Вычислить кривизну кривой у = 1пх в точке х=\.
Решение. Находим у' = \/х, у" = — l/х2. На основании формулы G.9) кри-
кривизна кривой у = In х в любой ее точке М с абсциссой х
I-1A2!	1*1
A +1Д2K'2
Следовательно, при х = 1 имеем
_ _1_
.1 ~ 23/2 — 4
Пример 7.8. Найти кривизну в любой точке циклоиды x = a(t — sin/), y =
= оA — cos /).
Решение. Имеем:
х = оA — cos /), i' = о sin /, jf = о sin /, у = о cos /,
ух — уХ= —о2A — cos /), *2 + jr2 = 2о2A — cos /).
На основании формулы G.9) получаем
„	I —а2A — cos /)|
1
4а sin (//2)
Радиус, круг и центр кривизны. Проведем к кривой L нормаль в
точке М(х; у) и отложим на этой нормали в сторону вогнутости
кривой отрезок MN = R (рис. 7.15), по величине обратный кривизне
K:R= l/K. Отрезок MN называется радиусом кривизны, точка jV —
центром кривизны, а круг с центром в точке N и радиусом R —
кругом кривизны кривой в точке М(х; у).
Если кривая L задана в декартовой системе координат Оху урав-
уравнением у = 1{х), то ее радиус кривизны находится по формуле
к~ ил '
Если кривая L задана параметрически, то ее радиус кривизны
определяется по формуле
о
Рис. 7.15
Рис. 7.16
179

\'y'x — yx\
. Если L — годограф вектор-функции г = r(t), то
R_
Irl3
Эволюта и эвольвента. Из определения центра кривизны следует,
что каждой точке М кривой L соответствует точка N — центр кри-
кривизны кривой L' в точке М.
Определение 7.8. Множество точек L' центров кривизны
линии L называется ее эволютой, а сама линия L по отношению к
своей эволюте называется эвольвентой.
Выведем уравнение эволюты кривой L, заданной уравнением
r(t) = xl-\- у]. Пусть jV(|; т])— центр кривизны линии L в точке М
(рис. 7.16). Тогда для любой точки М(х; </)g L имеем ON = ОМ-\-
-\-MN. Обозначим ON = гь ОМ = г, MN = Rn°, где п° — единич-
единичный вектор нормали кривой L. Тогда
r, = r + /?n0.	G.10)
Уравнение G.10) называется векторным уравнением эволюты
кривой L.
Выведем уравнение эволюты кривой L в координатной форме.
Запишем разложения векторов г, и г по базису B = {i, j}: n =
= |i + Tij, r = #i + i/j. Найдем вектор п°, исходя из следующих со-
соображений. Единичный вектор касательной к кривой L.
^_ r'(Q _ xi + yj ^ i • | 6 {
|r'(/)l V^Tj?2 V^t2+y2 V^+72
Продифференцируем равенство т2 = 1 no t. Имеем
Таким образом, вектор нормали п=—^.
Найдем координаты вектора п:
*	\)=-у *y--E
ху-ух , . п_ -г- У 8_!	*
^ + у2K
j^n°==F—Lii—i^j.
/•г ¦ Л2\3/2
Подставим n , R = -—±?1— в векторное уравнение эволюты
\ух — ух\
*2 + У2	*2 + f
i/	i + x
ху — уХ	ху — ух
ог,@ = г@ + Лп°.
180

Отсюда, приравнивая коэффициенты при i и j в левой и правой
частях выражения, находим:
^±L	^±?	G.П)
ху — ух	ху — ух
Формулы G.11) являются параметрическими уравнениями эво-
эволюты L' кривой L. Сама же кривая L, заданная уравнениями: х =
= x(t), у = y(t), t?T, является эвольвентой по отношению к кри-
кривой V.
Пример 7.9. Найти кривизну, радиус кривизны, координаты центра кривизны
параболы у = х2 в произвольной точке *о. Записать уравнение ее эволюты.
Решение. Вычислим последовательно производные: /'(*о) = 2*о, f"(xo) = 2.
Тогда
A+44K'2'	2
Найдем координаты центра кривизны N(%; r\) по формулам G.11):
t 1 + 4;cg , , 1 + 4x1
S = *o — 2хв	^	, Л = 4 Н	!2	•
Так, например, в точке О@; 0) К = 2, R = 1/2, 5 = 0, л = 1/2-
Считая *о = t, запишем параметрические уравнения эволюты параболы:
Из первого уравнения определяем t ^ —\/*/4, из второго находим t2 =
у-1/2 .
	^	. Следовательно, уравнение эволюты параболы имеет вид
или, после преобразований,
i
27
Итак, центром кривизны является точка N@; 1/2).
Следовательно, эволюта параболы у = х2 — полукубическая парабола. На рис.
7.17 изображены парабола у = хг, эвольвента, ее эволюта и круг кривизны в точке
О@, 0).
Укажем без вывода два важных свойства эволюты и эвольвенты,
устанавливающие связь между ними.
1.	Нормаль к эвольвенте L является касательной к эволюте L'
в соответствующей точке (рис. 7.18).
2.	Если на некотором участке эвольвенты радиус кривизны изме-
изменяется монотонно, то приращение радиуса кривизны на этом участке
равно по абсолютной величине длине дуги соответствующего участка
эволюты. (Так, например, на рис. 7.18 \N\N2\ =/?2 —/?ь IjV2JV3I =
= /?з — /?2 и т. д.)
Указанные свойства позволяют приближенно найти эволюту по эвольвенте или
эвольвенту по эволюте. Натянем гибкую нерастяжимую нить (см. рис. 7.18) вдоль
181

Рис. 7.18
эволюты L', оставив свободный участок M\N\. В точке Л^ поместим карандаш. Будем
развертывать нить, оставляя ее в яатянутом состоянии. Тогда карандаш вычертит
линию, являющуюся эвольвентой для эволюты L' (поэтому эволюту также называют
разверткой). Ясно, что график эвольвенты зависит от длины свободного участка нити,
т. е. данная эволюта V имеет бесконечное множество эвольвент L. В то же время
эвольвента имеет только одну эволюту.
7.5. КОМПЛЕКСНАЯ ФУНКЦИЯ ДЕЙСТВИТЕЛЬНОГО АРГУМЕНТА
И ЕЕ ДИФФЕРЕНЦИРОВАНИЕ
Изучая различные зависимости на множестве действительных
чисел, можно получить числа, не принадлежащие R.
Например, корни уравнения х2 + 1 =0:*i,2 = ± ~у — 1, не являются действи-
действительными числами. Оии принадлежат множеству комплексных чисел С.
Определение 7.9. Если любому t ? Т с: R поставлено в соот-
соответствие комплексное число z = /(/)? С, го f называют комплексной
функцией действительного аргумента и пишут z = f(t) или f: T-*-E,
где Т с: R; Е а С. Множество Т называют областью определения
комплексной функции, а множество E = {z?C\z = f(t), t?T) —
множеством ее значений.
Так как всякое комплексное число z может быть представлено
в виде z = Re z + i Im z ил и ;z = x + iy, то комплексную функцию дей-
действительного аргумента записывают так:
z = x{t) + iy(t).	¦	G.12)
Следовательно, задание комплексной функции действительного
аргумента z = z(t), согласно формуле G.12), равносильно заданию
двух действительных функций x(f) и y(t) действительного аргумента
или заданию вектор-функции r(t) = (x(t)\ -\- y{t)\).
Например, г = (t + 2if=>z = t2 + Ati + 4i2=>z = f — 4 + Ш. Здесь Re г = x(t) =
= f — 4, Im z = y(t) = At.
Задание комплексной функции действительного аргумента г = (t -\- 2tf равно-
равносильно заданию двух функций действительного аргумента x(t) = t2 — 4 и y(t) = At
или заданию векторной функции r(t) = {t2 — 4)l + 4<j.
182

Графиком комплексной функции действительного аргумента,
представленной в виде G.12), является кривая / в комплексной
плоскости, параметрические уравнения которой
Xy=Xy(tj, teTc=]
или годограф вектор-функции скалярного аргумента r(t) = x(t)l +
+ уШ
Пример 7.10. Построить кривую г = 2е", <?f0; я].
Решение. Так как е" = cos t — i sin I, тог = 2 cos t + i2 sin t. Следовательно,
y(t) = 2 sin t, ^ '
откуда y(t) > 0.
Исключив параметр t из системы уравнений, найдем у = -yJA — х2, т. е данная
кривая — верхняя половина окружности радиусом 2 с центром в начале координат
(рис. 7.19).
Определения предела, непрерывности, производной комплексной
функции действительного аргумента существенно не отличаются от
соответствующих определений для действительной функции действи-
действительного аргумента, так как она выражается
через пару действительных функций действи-
действительного аргумента.
Пусть функция z = x(t) + iy(t) определена
в Osito), to? Гс R.
Определение 7.10. Комплексное чис-
число Zo = х0 + н/о называется пределом ком-
комплексной функции действительного аргу-
р и с. 7.19	мента z = x(t) + iy(t) в точке t0, если сущест-
существуют lim x(t) = х0, lim y(t) = у0, и обозна-
чается
lim z(t) = zo = хо + о/о-
(—/о
Если хотя бы один из пределов функций x(t), y(t) в точке to не
существует, то предел функции z(t) в точке to также не существует.
Для нахождения предела комплексной функции действительного
аргумента z(t) используются приемы вычисления пределов действи-
действительной функции действительного аргумента.
Пример 7.11. Найти lim z(t), если z(t) = Bt + if.
Решение. Выделяем действительную и мнимую части функции:
z(t) = 4t2 + АН — l=$-x(t) = At2 — 1, y(t) = At.
Находим: lim x(t) = limDt2—1) = 3, lim y(t) = lim 4< = 4. Следовательно,
lim z@ = limB< + if = limD<2 — 1) + i lim At = 3 + 4/.
/->1	/-.-1	/->!	/-^1
Определение 7.11. Комплексная функция действительного
аргумента z(t) = x(t) + iy(t) называется непрерывной в точке to,
если она определена в Ob(to) и
183

lim z{t) = z(t0).	G.13)
Из равенства G.13) следует выполнение равенств: \imx(t) =
= x(to), lim y(t) = y(to), что означает непрерывность в точке to функ-
функций x(t) и y(t). Если хотя бы одна из этих функций разрывна в точке
t0, то функция z(t) разрывна в точке to-
Исследование комплексной функции действительного аргумента
z(t) = x(t) + iy(t) на непрерывность сводится к исследованию на не-
непрерывность функций x(t) и y(t).
Определение 7.12. Производной комплексной функции z(t) =
= x(t) -\- iy(t) действительного аргумента называется комплексная
функция
z'@=1hti-
\t
Производная комплексной функции z(t) = x(t) -\- iy(t) в точке t
существует, если в этой точке существуют производные x'{t) и y'(t).
Для дифференцирования комплексной функции z(t) = x(t)-\-
-\- iy(t) используются правила дифференцирования функций действи-
действительного аргумента.
Пример 7.12. Найти z'(t), если z(t) = + \ R
Решение. Имеем z(t) = x(t) + iy{t)=>x{t) = t\ y(t) = t*, x'(t) = 2t, y'(t)=4t3.
Следовательно, z'(t) = x'(t) + iy'(t) = 2t + Ш3.
7.6. МНОГОЧЛЕН В КОМПЛЕКСНОЙ ОБЛАСТИ
Теорема Безу*. Основная теорема алгебры. Многочленом п-й сте-
степени в комплексной области называются функции
k	G.14)
где ak, k = 0, п,— коэффициенты многочлена (действительные или
комплексные числа); z — комплексная переменная: z — x-\-iy,
х, y€R.
Если Ok — действительные числа, многочлен G.14) называют
многочленом в комплексной области с действительными коэффи-
коэффициентами. Область определения многочлена G.14) — вся комплекс-
комплексная плоскость, т. е. множество С.
Любому числу zo 6 С соответствует число Pn{zo). Если Pn(zo) = O,
то число Zo называют корнем или нулем многочлена Pn(z).
Два многочлена Pn(z)= 2а*2* и Qn(z)= 2 6*z* называются
k=0	*=0
равными, если выполняются равенства а* = bk, k = 0, п, т. е. если
равны их коэффициенты при одинаковых степенях z.
Теорема 7.2 (Везу). Для того чтобы многочлен Pn(z) имел комп-
* Этьенн Безу A730—1783) —французский математик.
184

лексный корень zo, необходимо и достаточно, чтобы он делился на
двучлен z — 20, т. е. чтобы справедливым было представление
Pn(z) = (z-zo)Pn-i(z),	G.15)
где Pn-i(z) — многочлен степени п — 1.
t> Необходимость. Пусть z0 — корень многочлена Pn(z), тогда
Pn(zo) = O. По формуле Тейлора для многочлена Pn(z) =
п
= 2 bk(z — zof, т. е. многочлен Рп(г) представим в виде G.15).
Достаточность. Если для многочлена Pn(z) справедливо пред-
представление G.15), т. е. Pn(z) = (z — zo)Pn-\(z), то при z = z0 много-
многочлен Pn(zo)=zO, а это означает, что zo — корень многочлена
Pn(z). <
Из теоремы Безу не следует существование корней многочлена
Рп(г). Вопрос о существовании корня многочлена Рп(г) разрешает
Теорема 7.3 (основная теорема алгебры). Всякий многочлен
Pn(z), n€ N, имеет по крайней мере один комплексный корень.
Число Zo называется простым корнем многочлена Pn(z), если
многочлен Рп(г) делится на z — z0, но не делится на (г — z0) . Число
zo называется k-кратным корнем многочлена Рп(г), если Pn(z) де-
делится на (г — zo)* и не делится на (z — Zo)k+l, т. е. представим в виде
Pn(z) = (z — Zo)kPn-k(z), где Pn-k(z) не делится на z — z0.
Пример 7.13. Показать, что Z\ = 0 н z2 =—1 являются корнями многочлена
Рз(г) = г3 + 2гг + z, и определить нх кратность.
Решение. Действительно, Яз@) = 0^-zi =0—корень многочлена Р3(г) =
= z3 + 2z2 + z- Чтобы определить его кратность, разделим Рз(г) на г. Получим Рг{г) =
= z2-j-2z+l- Этот многочлен не делится на г. Следовательно, Z\ = 0 является
простым корнем многочлена Рз(г) = z3 + 2z2 + z.
Аналогично убеждаемся, что гг = — 1 — корень данного многочлена, так как
Р3(—1) = 0. Для определения кратности этого корня воспользуемся представлением
P3(z) = z(z2 + 2z+ 1) или P3(z) = z(z+ If. Как видно, Р3(г) делится на (z+l)\ и,
следовательно, zi =—1 является корнем многочлена Рг{г) кратности 2.
Из основной теоремы вытекает
Следствие. Многочлен Pn(z) имеет п комплексных корней с
учетом их кратности, т. е.
Рп(г) = an(z- z{f (z - z2)"! • • • (z - zs)n\
где zlt z2, ..., zs — различные корни Pn(z); nb n2,..., ns — их кратности,
причем П\ + л2 + ... + ns = п.
Многочлен с действительными коэффициентами. Разложение
его на линейные и квадратные множители. Рассмотрим многочлен п-й
степени	„
Рп(г) = ао + aiz + ... + anzn = 2 anzk,
0

где a* g R; k = 0, n; z 6 С. Для такого многочлена справедливы сле-
следующие две теоремы.
Теорема 7.4. Если Pn(z) — многочлен с действительными коэф-
коэффициентами, то	_
185

т. е. если Pn(z) = A + iB, А, В 6 R, то Рп(г) = А — IB.
t> Для комплексных чисел справедливы следующие равенства:
Z\ ± Z2 — Z\ ± Z2, Z\Z2 = Z\Z2-
_ Действительно, если zx=X\ -\-iy\, Z2 = x2 + iy2, то Zi=jti—а/ь
Z2 = x2 — a/2- Поэтому
Z| ± Z2 = X\ — if/l ± (*2 — il/2) = X\ ± X'2 — i(f/l ± f/2) = Zi ±?2,
Z\Z2 — {X\ — iyi) (*2 — if/2) = ^1^2 + f/lf/2 — i(^lf/2
Для действительных чисел а* = a*. Следовательно,

P»(z) = 2 akzk = 2 ak? = 2 ^? = 2 a*z* = Р„(г),
т. е. если Pn(z) = A+iB, то Pn(?) = A —iB. <
Теорема 7.5. Если многочлен Pn(z) с действительными коэффи-
коэффициентами имеет комплексный корень zo = a-\~ ib, то он имеет и сопря-
сопряженный корень zo = а — ib,
t> Пусть zo = a-\-ib — корень многочлена Рп{г). Тогда Pn(zo) —
= Л + г"В = 0, А, В 6 R.
Комплексное число равно нулю, если равны нулю его действи-
действительная и мнимая части, следовательно, А = О, В = 0.
Вычислим Pn(zo), zo = a — г7>. Согласно теореме 7.4, Pn{za) =
= Л — /В. Учитываем, что Л =0, В =0. Тогда Pn(z0) = 0, т. e. zo —
корень многочлена Pn(z). <
Из теоремы 7.5 следует, что если многочлен Pn{z) с действитель-
действительными коэффициентами имеет комплексные корни, то они входят в его
разложение попарно сопряженными.
Рассмотрим произведение линейных множителей, соответствую-
соответствующих паре комплексно-сопряженных корней: (z — zo) (z — z0), где zo =
= a + «7>:
(z - zo) (z — zo) = (z - a - /6) (z-a + ib) = ((z - a) — ib) ((z — a) +
+ ib) = (z - aJ + b2 = z2 - 2az + a2 + *>2.
Обозначим a2 + 62 = 9, — 2a = p, тогда (z — a — /6) (z — a + ib) =
= z2 + pz + 4, т. е. получили квадратный трехчлен с действитель-
действительными коэффициентами.
Если число zo = а + ib является корнем кратности k многочлена
Рп{г) с действительными коэффициентами, то zo = a — ib является
корнем многочлена той же кратности k.
Из всего сказанного следует, что многочлен с действительными
коэффициентами Pn{z) разложим на множители с действительными
коэффициентами первой и второй степени соответствующей крат-
кратности, т. е.
Pn(z) = an(z - ai)k4z - a2L . .(z - asf(z2 + pxz + qt)m> X ... X
где ki + k2 + ... + ks + 2mi + ... + 2m, = n.
186

Пример 7.14. Разложить на линейные и квадратные множители следующие
многочлены: 1) РзМ = *3 — б*2 + 11* —6; 2) Р4(х) = *4 — 1.
Решение. 1. Найдем кории многочлена Рз(х). Будем искать их среди дели-
делителей свободного члена. Это могут быть числа 1, 2, 3, 6. Находим Р3A) = 0, РзB) = О,
РзC) = 0. Многочлен Рз(х) имеет три различных корни, его можно представить в виде
произведения трех линейиых множителей: х3 — б*2 + 11л: — 6 = (jc — I) (x — 2) (х — 3).
2. Корнями многочлена Р*(х) явлиются числа ±1, так как /М±1) = 0.
Следовательно, многочлен Р*(х) можно представить в виде х* — 1 ==(*—1)(* +
+ \)Р2(х), где Рг(х) = {х* — \)/{х — 1) = х2 -(- 1. Корними многочлена х2 + 1 ивляются
числа ±i. Таким образом, х* — 1 =(х— \)(х + 1)(*2+ 1)- т- е- многочлен Pi{x) раз-
разлагается иа два линейных и один квадратный множители.

8. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
8.1. ПЕРВООБРАЗНАЯ ФУНКЦИИ
И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Основной задачей дифференциального исчисления является на-
нахождение производной /'(*) или дифференциала df = f'(x)dx функции
f(x). В интегральном исчислении решается обратная задача. По
заданной .функции f(x) требуется найти такую функцию F(x), что
F'(x) = f(x) или dF(x) = F'(x)dx = f(x)dx.
Таким образом, основной задачей интегрального исчисления
является восстановление функции F(x) по известной производной
(дифференциалу) этой функции. Интегральное исчисление имеет
многочисленные приложения в геометрии, механике, физике и тех-
технике. Оно дает общий метод нахождения площадей, объемов,
центров тяжести и т. д.
Определение 8.1. Функция F(x), x?Xc=R, называется пер-
первообразной для функции f(x) на множестве X, если она дифференци-
дифференцируема для любого х?Х и F'(x) = f(x) или dF(x) = f(x)dx.
Так, например, первообразной для функции /(*) = sin* на множестве R
является функция F(x)=—cos*, так как F'(x) = ( — cos x)' = sin x или dF(x) =
= d(^-cos x) = sin xdx У х 6 R.
Естественно возникает вопрос: для всякой ли функции f(x) су-
существует первообразная F(x)? Оказывается, не для всякой. Имеет
место следующая
Теорема 8.1. Любая непрерывная на отрезке [а; Ь] функция
f(x) имеет на этом отрезке первообразную F(x).
Будем рассматривать непрерывные на отрезке функции. Даже
при таком ограничении задача восстановления функции F(х) по из-
известной производной (или известному дифференциалу) решается
неоднозначно и не всегда просто.
Если, например, f(x) = e3x, то первообразной для этой функции является ие
только F(x) = — е3*, но также и множество функций — е3* + С, где С — произвольно
о	о
выбранная постоянная.
Теорема 8.2. Если F{(x) и F2(x) — две различные первообразные
одной и той же функции f(x) на множестве х, то они отличаются
друг от друга постоянным слагаемым, т. е. F2(x) = Fl(x)-\-C, где
С — постоянная.
t> Пусть Fi(x) и F2(x) — первообразные функции f(x) на X. Их
разность F(x) = F2(x) — F{(x) является дифференцируемой функцией:
F'(x) = F'2(x) — F'l{x) = f(x) — f(x) = 0. Из теоремы Лагранжа (см.
§ 5.14) следует, что F(*) = C, т. е. F2(x) — F{(x) = С Vx?X. <
Следствие. Если F(x) — некоторая первообразная функции
f(x) на множестве X, то все первообразные этой функции определя-
определясь

ются выражением F(x) + С, где С — произвольная постоянная.
Операция отыскания первообразной F(х) функции f(x) называ-
называется интегрированием.
Определение 8.2. Совокупность F(x)-\- С всех первообразных
функции f(x) на множестве X называется неопределенным интегра-
интегралом и обозначается
\ f(x)dx — Fix) + С.	(8 1)
В формуле (8.1) f(x)dx называется подынтегральным выраже-
выражением, f(x) — подынтегральной функцией, х — переменной интегриро-
интегрирования, а С — постоянной интегрирования.
Термин «интеграл» (от лат. integralis — целостный) был вве-
введен Лейбницем*. Слово «неопределенный» подчеркивает, что в общее
выражение первообразной функции входит постоянное слагаемое,
которое можно выбирать произвольным.
Таким образом, неопределенный интеграл представляет собой
любую функцию, дифференциал которой равен подынтегральному вы-
выражению, а производная — подынтегральной функции.
Например:
1)	\ 2xdx = х2 + С, так как (х2 + С)' = 2х или d(x2 + С) = 2xdx\
2)	\e"dx = е" + С, поскольку (ех + С)' = е" или d(e" + C) = e'dx;
dx
— tgx+C, так как (tgx + C)' =
или d (tg x + С)
С геометрической точки зрения неопределенный интеграл пред-
представляет собой однопараметрическое семейство кривых у = F(x) + С
(С — параметр), обладающих следующим свойством: все касатель-
касательные к кривым в точках с абсциссой х = хо параллельны между собой:
На рис. 8.1 изображен неопределенный интеграл
х2 + С от функции f(x)=2x (\2xdx = х2 + С), т. е.
семейство парабол \у = х2 + С].
Кривые семейства {F(x) + С) называют
интегральными кривыми. Они не пересека-
пересекаются между собой и не касаются друг
друга. Через каждую точку плоскости про-
проходит только одна интегральная кривая.
Все интегральные кривые получаются одна
из другой параллельным переносом вдоль
оси Оу.
Рис. 8.1
* Готфрид Вильгельм Лейбниц A646—1716) —немецкий философ и математик.
189

8.2. ОСНОВНЫЕ СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Рассмотрим свойства неопределенного интеграла, вытекающие из
его определения.
1.	Производная от неопределенного интеграла равна подын-
подынтегральной функции, дифференциал от неопределенного интеграла
равен подынтегральному выражению:
(\f(x)dx)' = f(x) и d(\f(x)dx) = f(x)dx.
t> Пусть \ f(x)dx = F(x) + С. Тогда (\ f(x)dx)' = (F(x) + С)' =
= F'(x) = f(x) и d{\f(x)dx) = {\f(x)dx)'dx = f(x)dx. <
2.	Неопределенный интеграл от дифференциала некоторой функ-
функции равен сумме этой функции и произвольной постоянной:
t> Действительно, так как dF(x) — F'(x)dx, то \F'(x)dx =
= F(x)+C. <
Например, \ 2xe"'dx = \ d(e'') = ex' + С.
3. Постоянный множитель а (о#0) можно выносить за знак
неопределенного интеграла:
t> Действительно, пусть F(x) — первообразная функции f(x):
F'(x) = f(x). Тогда aF(x) — первообразная функции af(x): (aF(x))' =
= aF'(x) = af(x). Отсюда следует, что
' а \ f(x)dx = a(F(x) +C) = aF(x) + С, = \ af(x)dx,
где С\ = аС. <
4. Неопределенный интеграл от алгебраической суммы конечного
числа функций равен алгебраической сумме интегралов от этих
функций:
t> Доказательство проведем для двух функций. Пусть F(х) и
Ф(*) — первообразные функций fi(x) и f2(x): F'(x) = fi(x), Ф'(*) =
= /2(*)- Тогда функции Р(х)±Ф(х) являются первообразными функ-
функций f\(x) ±/г(*). Следовательно,
$ h (x)dx ± \ f2(x)dx = (F(x) + С,) ± (Ф(х) + С2) =
= (F(x) ± Ф(х)) + (С, ±С2) = (F(x) ± Ф(х)) + С =
= J(fi(*)±W*))rf«-<
5. Если F(x) — первообразная функции f(x), то
\f(ax + b)dx=±F(ax + b) + C.
t> Действительно, (i- F(ax + b)\ = -i- F'(ax + b) = f(ax + b). <
190

6 (инвариантность формул интегрирования). Любая формула ин-
интегрирования сохраняет свой вид, если переменную интегрирования
заменить любой дифференцируемой функцией этой переменной:
где и — дифференцируемая функция.
> Воспользуемся свойством инвариантности формы диффе-
дифференциала первого порядка: если dF(x) = F'{x)dx=>dF(u) = F'(u)du,
где и = и(х). Пусть
Докажем, что \f{u)du = F(u)-\- С. Для этого найдем диффе-
дифференциал от левой и правой частей последнего равенства: d($ f(u)du) =
= f(u)du и d(F(u)-\-C) = F'(u)du = f(u)du. Из равенств этих диф-
дифференциалов следует справедливость свойства 6. <]
8.3. ТАБЛИЦА ОСНОВНЫХ ПРАВИЛ
И ФОРМУЛ ИНТЕГРИРОВАНИЯ
Свойства 1—6 неопределенного интеграла, доказанные в § 8.2,
совместно с таблицей неопределенных интегралов образуют основ-
основные правила интегрального исчисления. Так как интегрирование
есть действие, обратное дифференцированию, то большинство из
приводимых формул может быть получено обращением соответст-
соответствующих формул дифференцирования. Другими словами, таблица
основных формул интегрирования получается из таблицы производ-
производных элементарных функций при обратном ее чтении (справа на-
налево) , т. е. если (sin х + С)' = cos jc=^$cos xdx = sin x + С или, в об-
общем случае, (F(x) + С)' = f(x), то \f(x)dx = F(x) + С.
Приведем основные правила интегрирования функций.
I. (\f(u)du)' = f(u).
II. d(\ f (u)du) = f(u)du.
III.	\ dF(u) = F(u) + С
IV.	j af(u)du = a \ f(u)du.
±\fn(u)du.
VI. \ f(au + b)du = -i- F(au + b) + С
Приведем таблицу основных неопределенных интегралов. (Отме-
(Отметим, что здесь, как и в дифференциальном исчислении, буква и
может обозначать как независимую переменную (и = я), так и функ-
функцию от независимой переменной (и = и(х)).)
2. \ audu = -^- + С (а > 0, а Ф 1).
191

3.	\ e"du = eu + С.
4.	$-?=1п|И| + С.
5.	\ sin udu = —cos и 4" С.
6.	J cos «du = sin и 4- С.
7.[-^-=tgu + C.
cos' u
8.
sin
= -ctg и + С.
9.	J sh «du = ch и + С.
10.	^ ch «d« = sh и + С.
11 f_^=th«4-C.
J ch2u
12.
13.
15.
16.
_^L_= > In
и2 — о2 2а
— а
j v«2 ± °2
17.	С *?_ = arcsin ±- 4- С (|и|<|а|).
18.	t л/»2 + a2 du = т л/ + °2 + -y-ln I " + V + a2 \ + С
•19. [ л/а2 - и2 du = 4 л/а2 - «2 + 4" arcsin — 4-С.
Интегралы 1 —17 называются табличными.
Некоторые из приведенных выше формул таблицы интегралов,
не имеющие аналога в таблице производных, проверяются диффе-
дифференцированием их правых частей.
Пример 8.1. Доказать справедливость формулы \	= arcsin — + С.
Решение. Дифференцируем функцию arcsin	\-C:
(arcsin	\-С) =	(—1 = ,	=>-
4	а /* -д/l — и2/а2 \а'х л1аг—иг
/	и \ u'xdx	du
=>d{ arcsin	\-C)=	¦=	.
\	a J ^ai _ u2 ya2 _ U2
Если первообразная F(x) функции f(x) является элементарной
192

функцией, то говорят, что интеграл \ f(x)dx выражается в элемен-
элементарных функциях или f(x) интегрируема в конечном виде. Однако
не всякий интеграл от элементарной функции выражается в эле-
элементарных функциях. (Примеры таких интегралов будут даны в
§ 8.9.)
Используя основные правила интегрирования, можно находить
интегралы от более сложных функций.
Пример 8.2. Найти \ {х2 — 4 cos B* + 1) + e3x)dx.
Решение. Используя правила интегрирования IV — VI и табличные интегралы
1, 3, 6, получаем
\ (х2 — 4 cos Bх + 1) + e3")dx = \ x2dx — 4 \ cos Bх + 1) dx + \ e3xdx =
= у - 2 sin Bх + 1) + -i- е3х + С.
При интегрировании каждого слагаемого появляется своя произвольная по-
постоянная, но в конечном итоге записывают только одну, так как сумма трех постоян-
постоянных есть постоянная. Правильность полученного результата можно проверить диф-
дифференцированием.
В отличие от дифференциального исчисления, где, пользуясь
таблицей производных, можно найти производную или дифференциал
любой заданной функции, в интегральном исчислении нет общих
приемов вычисления неопределенных интегралов, а разработаны
лишь частные методы, позволяющие свести данный интеграл к таб-
табличному.
8.4. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
Непосредственное интегрирование. Вычисление интегралов, осно-
основанное на приведении подынтегрального выражения к табличной
форме и использовании свойств неопределенного интеграла, называ-
называется непосредственным интегрированием.
Например:
2х • 32xdx = [B- 3*Ydx = [ I8"dx = ™' + С;
2) ^	^	[^
3) Usiny,+ cosyj d* = Wsin2y + 2 sin у cos-|-+ cos2 у W =
= \ A + sin x) dx = \ dx + \ sin xdx = x — cos x + С
Интегрирование подстановкой (заменой переменной). Пусть тре-
требуется вычислить интеграл \ f(x)dx, который не является таблич-
табличным. Суть метода подстановки состоит в том, что в интеграле
\ f(x)dx переменную х заменяют переменной / по формуле х = <р(/),
откуда dx = (p'(t)dt.
Теорема 8.3. Пусть функция х = <р(<) определена и дифференци-
дифференцируема на некотором множестве Т и пусть X — множество значений
этой функции, на котором определена функция f(x). Тогда если на
7 Зак. 1270	193

множестве X функция f(x) имеет первообразную, то на множестве
Т справедлива формула
(8.2)
Формула (8.2) называется формулой замены переменной в не-
неопределенном интеграле.
> Формула (8.2) справедлива, если после дифференцирования
обеих ее частей получаются одинаковые выражения. Учитывая, что
f(x) = Дф@) — сложная функция, имеем
Продифференцировав правую часть формулы (8.2), получим
Таким образом, формула (8.2) справедлива. <]
Допустим, что интеграл, стоящий в правой части формулы (8.2),
известен:
Отсюда легко найти искомый интеграл в виде функции от х. Для
этого уравнение х = ф(/) следует разрешить относительно t. Если t —
= ф-'(дс), то
Заметим, что свойство 6 из § 8.2 по существу основано на
методе замены переменной.
Пример 8.3. Вычислить X	¦
Решение. Сделаем подстановку:
е* — 1 = <2=^е* = t2 + 1 =>х = In (t2 + l)=>dx = -^— dt.
Тогда
\ 4* = \ ?dt— = 2 arctg t + C = 2 arctg У** — 1 + С.
J -ilpi— I	J (' + 1)
При интегрировании заменой переменной важно удачно сделать
подстановку. Однако нельзя дать общее правило выбора замены
переменной для интегрирования любой функции. Это можно сделать
только для интегрирования отдельных классов функций (тригономет-
(тригонометрических, иррациональных и т. д.).
Очень часто при вычислении интегралов пользуются приемом
«подведения» подынтегральной функции под знак дифференциала.
По определению дифференциала функции ф'(x)dx = d(q>(x)). Переход
от левой части этого равенства к правой называют «подведением»
множителя (р'(х) под знак дифференциала.
Пусть требуется найти интеграл вида
194

\f(V(x)W(x)dx.
Внесем в этом интеграле множитель <р'(х) под знак дифференциала,
а затем выполним подстановку q>(x) = и (см. § 8.2, свойство 6):
J f(v(x))v'(x)dx = \ f(V(x))d(v(x)) = \ f(u)du.
Если интеграл \ f(u)du — табличный, его вычисляют непосред-
непосредственным интегрированием.
Замечание 1. При интегрировании путем «подведения» под знак диффе-
дифференциала используют свойства дифференциала сложной функции. Напомним, что:
dx=—d(ax + b) =—du, u = ax + b;
x"-'dx= — d(xa)= — du, u = xa;
sin xdx — —d(cos x) = —du, и = cos x;
xex'dx——d(ex')=-^-du, u = e'*;
и т. д.
Пример 8.4. Найти \ -\/l + x? xdx.
Решение. Учитывая, что xdx = -^-d{\ + х2), имеем
Замечание 2. При интегрировании «подведением» под знак дифференциала
промежуточные обозначения ц>(х) = и, как правило, опускают. В более сложных
случаях подстановку делают явно, отделяя необходимые вычисления вертикаль-
вертикальными линиями.
Пример 8.5. Вычислить \ —	—.
J -\/l + 5 cos x
Решение. Заметив, что sin xdx =	— d(\ + 5 cos х),и положив 1 + 5 cos x —
= и, имеем
Г sin xdx _ _i-f (l+5cos*)-1/2rf(l+5cosx) =
J Vl 4- 5 cos x	° J
= — -r--\/l + 5 cos x + С
о
(Здесь использована формула \и l/2du = 2u1/2 + С.)
Легко заметить, что если подынтегр
ф'(дс)/ф(дс), то «подведение» множителя ф'
приводит к табличному интегралу \ —:
Легко заметить, что если подынтегральная функция имеет вид
ф'(дс)/ф(дс), то «подведение» множителя ф'(дс) под знак дифференциала
195

Например,
S. . f sin x , f d(cos x)
tgm* = \	dx= —\ —i	 = \u = cosx =
J cos x J cos x
[ du	. i i , n
= -^-jr = -ln|cosx|+C.
Аналогично
sin x	] sin*
Интегрирование по частям. Метод интегрирования по частям
следует из формулы дифференциала произведения двух функций.
Пусть и(х) и v(x) — две дифференцируемые функции переменной х.
Тогда
d(uv) = udv + vdu.	(8.3)
Интегрируя обе части равенства (8.3), получаем
\ d(uv) = \ udv + \ vdu.
Но так как \ d(uv) = uv + С, то
~	'	(8-4)
\udv = uv — \vdu.
Соотношение (8.4) называется формулой интегрирования по
частям. С помощью этой формулы отыскание интеграла \udv можно
свести к вычислению другого интеграла \vdu. Применять ее целесо-
целесообразно, когда интеграл в правой части формулы (8.4) более прост
для вычисления, нежели исходный.
В формуле (8.4) отсутствует произвольная постоянная С, так как
в правой части этой формулы стоит неопределенный интеграл, со-
содержащий произвольную постоянную.
Пример 8.6. Вычислить \xsinxdx.
Решение. Положим и = х, dv = s'mxdx=—d(cos x). Тогда du = dx, v =
= — $d(cosx)= — cos*. По формуле (8.4) имеем
\ х sin xdx — — х cos x + \ cos xdx — —х cos x + sin x + С.
Если в даииом интеграле положить и — sin x, dv = xdx, то du = cos xdx, v =
= x2/2 и
f	¦	>	*2 •	1 f о
\ x sin xdx = -jj- sin x	o" \ ¦*
т. е. в правой части получился более сложный интеграл, чем в левой. Значит, такое
разбиение подынтегрального выражения на и и dv является неудачным.
Приведем некоторые часто встречающиеся типы интегралов,
вычисляемых методом интегрирования по частям.
1. Интегралы вида$ Pn(x)ekxdx, \ Pn(x)sinkxdx, \ Pn(x)coskxdx
(Рп(х) — многочлен степени п, k — некоторое число). Чтобы найти
эти интегралы, достаточно положить и = Рп(х) и применить формулу
(8.4) п раз.
196

II.	Интегралы вида \ Р„ (х) In xdx, \ Р„(х) arcsin xdx,
\ Рп(х) arccos xdx, \ Pn(x) arctg xdx, \ Рп{х) arcctg xdx (Pn(x) — много-
многочлен степени п относительно х). Их можно найти по частям, принимая
за и функцию, являющуюся множителем при Рп(х).
III.	Интегралы вида \еах cos bxdx, \eaxsin bxdx (a, b —
числа). Они вычисляются двукратным интегрированием по частям.
Пример 8.7. Вычислить Jarcsin xdx.
Решение. Данный интеграл относится к типу II: Ро(*) =
dx
и = arcsin х, du = —==-
¦ 1. Имеем
\ arcsin xdx =
-bf=
dv = dx, v = x
= x arcsin x —
=rarcsin r + i-t(l _ x2)-
2
—x2) = x arcsin x
e " cos — dx.
Решение. Данный интеграл относится к типу III. Возьмем в качестве и
любой из сомножителей при dx и дважды выполним интегрирование по частям. При
повторном интегрировании получим равенство, содержащее исходный интеграл.
Выразив его из этого равенства, имеем
cos—dx —
2
= 2е~' sin -S-
u = e~", du= —e~"dx.
-
x	i x / x \	x
dv = cos — dx, v = 2 \ cos — dl — j = 2 sin —
' sin —- dx =
dv ¦¦
du = — e 'dx.
¦¦ sin — dx, v = —2 cos -=-
х	х Г	х
= 2е~" sin —— 4е~* cos —— 4 \ е~" cos у dx.
Выразив из полученного равенства исходный интеграл, имеем
SX х			X
е~* cos — dx = 2е~" sin —	4е^* cos — + С=>
S. д: . 2 ./ . х	х\
е~х cos у dx = у е-*( sin у — 2 cos yj + С.
8.5. РАЦИОНАЛЬНЫЕ ДРОБИ
Рациональной дробью R(x) называется дробь, числителем и зна-
знаменателем которой являются многочлены, т. е. всякая дробь вида
R(X):
Q-W
Если степень многочлена в числителе больше или равна степе-
степени многочлена в знаменателе (п ^ т), то дробь называется непра-
неправильной. Если степень многочлена в числителе меньше степени
многочлена в знаменателе (п<Спг), то дробь называется пра-
правильной.
197

2х	х + 1
Например, —;	неправильная дробь, —;	правильная дробь.
лг + Зх + 2	х* + х — 2
Всякую неправильную рациональную дробь можно представить
в виде суммы многочлена (целой части) и правильной рациональ-
рациональной дроби (это представление достигается путем деления числителя
на знаменатель по правилу деления многочленов):
где R(x)— многочлен-частное (целая часть) дроби *;; ; Рп(х) —
Чт(Х)
остаток (многочлен степени п<т).
Например,
= х°-2,+ 4*+'
так как
*4-*3	+1 U!
х2 + х + 2'
— ¦*— Целая часть
;; хА + х3 + 2х2	х2 — 2х
= < *Г	— 2х3 — 2х2 + 1
I ~ 2хъ — 2х2 — 4х
4л: + I -«— Остаток
Так как интегрирование многочлена не представляет затрудне-
затруднений, то интегрирование рациональных дробей сводится к интегри-
интегрированию правильных рациональных дробей.
8.6. ИНТЕГРИРОВАНИЕ ПРОСТЕЙШИХ РАЦИОНАЛЬНЫХ ДРОБЕЙ
Простейшей дробью называется правильная рациональная дробь
одного из следующих четырех типов:
1) ——;	2) —-— (м>2);
'х — а	' (x — af x	'
3^ Mx + N .	лл Mx+N ,„-^о\
4
+ px+q'	4) (
Здесь А, а, р, q, M, N — действительные числа, а трехчлен не имеет
действительных корней, т. е. р2/4 — q < 0.
Простейшие дроби первого и второго типов интегрируются не-
непосредственно с помощью основных правил интегрального исчи-
исчисления:
Г Adx =A dx =A[d(x-a) =ьАЫ1х_
) (х — а)	) х — а	) х — а
\ Тх^аТ =
Интеграл от простейшей дроби третьего типа приводится к
198

табличным интегралам путем выделения в числителе дифференциала
знаменателя и приведения знаменателя к сумме квадратов:
М
2
Mp
2
dx
1
Jq-p2/4
Рассмотрим интегрирование простейшей рациональной дроби
четвертого типа \ 2 —~~v- Сделаем замену переменной, поло-
положив х + р/2 = t, откуда dx = dt:
где а2 = q — р2/4. Тогда
Г (Мх + N)dx _ Г М (* + Р/2) + ЛГ-Мр/2 ^ _ м Г
tdt
Интеграл /0 легко вычисляется:
Вычислим интеграл 1п =
d<
3
(<2 + в2)"
— ^ = 4
-. Представим его в виде
dt
--5-
Замечая, что
_r =/„_,, получаем
(8.5)
Для вычисления интеграла \ —г	^ воспользуемся методом ин-
J it -{-а)"
тегрирования по частям:
dv =
tdt
-, v = -
199

t1 Г	dt
2A— n) )
2A — n)(t2 — a2)"-'	2A— n)
1	2A-n) "
Подставляя найденное выражение в формулу (8.5), имеем
/ - ' /2я-з .	t	\
а~ a*\2n-2 ""' 2(l-n)(<2 + e2)"-1A
Формула (8.6) называется рекуррентной. Зная табличный интеграл
^' ~\ г f г = ~~ arctg— + С, по формуле (8.6) можно найти ин-
интеграл h = \ , dt а а и т. д. Действительно,
J (<2 + в2J
Г «и _ ' /' С ^ | <
J (^Ч-в2J в2 V 2 J <2 + a2 T 2(<2 + в
2d\t2 + a2) ' 2e3
Таким образом, получены формулы для интегрирования всех
типов простейших дробей.
8.7. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ
Разложение рациональной дроби на простейшие дроби. Всякую
правильную рациональную дробь Pn(x)/Qm(x) можно представить в
виде суммы конечного числа простейших рациональных дробей
первого — четвертого типов. Для разложения Pn(x)/Qm(x) на простей-
простейшие дроби необходимо разложить знаменатель Qm(x) на линейные
и квадратные множители, для чего надо решить уравнение
Qm(x) = OobQxm + bxxm-'+...+ bm = 0.	(8.7)
Предположим, что уравнение (8.7) решено и найдены его корни.
Согласно основной теореме алгебры, уравнение Qm(x) = 0 имеет
ровно пг корней с учетом их кратности. Корни уравнения (8.7) могут
быть действительными (простыми или кратными) и комплексными
(простыми или кратными). При разложении многочлена Qm{x) на
линейные и квадратные множители следует учитывать, что:
1)	если а является простым корнем многочлена Qm(x) (Qm(a) =
= 0), то Qm(x) делится на х — а без остатка, т. е. Qm(jt) = (jt —
-a)Qm-i(x);
2)	если а является корнем кратности k многочлена Qm(x), то
Qm(x) делится на (* — а)* без остатка, т. е. Qm(x) = (x — a)kQm-k(x);
3)	если комплексное число z = u-\-iv является корнем много-
многочлена Qm(x), то его корнем является также комплексно-сопряжен-
комплексно-сопряженное число г=ы^—iv. В этом случае многочлен делится без остатка
на (* — z)(x — z) = (x — и — iv)(x — и-\-iv) = х2-\-рх-\-q (р==—2ы,
q = u2 + vK p2/4-q<0), т. е. Qm(x) = (x2 + px + q)Qm-2(x);
4)	если комплексно-сопряженные числа и ±iv являются корнями
200

многочлена Qm(x) кратности k, то многочлен Qm(x) представим в
виде произведения Qm(x) = (x2 + рх + q)kQm^2k(x).
Пусть для определенности число а является действительным
корнем многочлена Qm(x) кратности k, число р — действительным
корнем этого многочлена кратности /, комплексно-сопряженные
числа u±iv— s-кратными корнями. Тогда многочлен Qm(x) разло-
разложим на линейные и квадратные множители:
Qm(x) = (х- а?(х - р)'(*2 + рх + q)\
где k -f-1 -f- 2s = m.
Справедлива следующая
Теорема 8.4. Правильную рациональную дробь Pn(x)/Qm(x), где
Qm(x) = (х — а)к{х — р)'(*2 + рх -f- q)s, можно единственным образом
разложить на сумму простейших дробей:
Рп{х) _ А{	. Аг	.	¦ Ak	. В\	. Вг	,
Qm(x)	(х-а) (х-а.J "•" '" (х- а)' "^ (x-f) ' (х-(if "l"
В/ , Mtx + Nx , М2х + JV» , , М.х + Ns
(Л1, A2, ..., Л*, fii, B2, ¦•-, Bi, Mi, Nu M2, M2, .... Ms, Ns — некото-
некоторые действительные числа).
Согласно разложению (8.8), линейным множителям знаменателя
Qm(x) соответствуют простейшие дроби первого и второго типов,
а квадратным множителям — третьего и четвертого типов. При этом
число простейших дробей, соответствующих данному множителю
(линейному или квадратному), равно степени, с которой этот мно-
множитель входит в разложение знаменателя дроби. Формула (8.8)
разложения правильной рациональной дроби на простейшие дроби
остается справедливой для любого конечного числа линейных и
квадратных множителей, входящих в разложение знаменателя
Qm(x).
Проиллюстрируем формулу (8.8) конкретными примерами, не
находя самих коэффициентов разложения.
Например:
п	х*	х*	¦ _ А	Вх + С

(х3-8)(х*+\) (х-2)(х2 + 2х + 4)(х2+\) (х-2)
, Рх Е
*¦+!
2*-3	ABC	P
(дг+ 1)(дг— IK x
x2 + x+\3 = A	Bx+C Px + E E M N
(x — I)(x2 + 4Jx3 x—1 x2 + 4 (x2 + 4J x x2 x3'
Чтобы найти коэффициенты разложения (8.8), чаще всего при-
применяют метод неопределенных коэффициентов и метод частных зна-
значений.
Метод неопределенных коэффициентов. Суть метода неопреде-
неопределенных коэффициентов состоит в следующем. Пусть дано разложе-
разложение правильной рациональной дроби Pn(x)/Qm(x) по формуле (8.8)
201

на простейшие дроби с неопределенными коэффициентами. Приведем
простейшие дроби к общему знаменателю Qm(x) и приравняем мно-
многочлен, получившийся в числителе, многочлену Рп(х).
Для тождественного равенства двух многочленов необходимо и
достаточно, чтобы коэффициенты при одинаковых степенях х этих
многочленов были равны. Учитывая это, приравниваем коэффи-
коэффициенты при одинаковых степенях х в левой и правой частях получен-
полученного тождества. Имеем систему т линейных алгебраических урав-
уравнений для нахождения т неизвестных коэффициентов А\, Лг, ....
Ak, Ви В2, ..., Bk, Ми Nu .-, Ms, Ns.
х2
Пример 8.9. Разложить рациональную дробь —	 на простейшие дроби.
х — 8
Решение. Так как х3 — 8 = (х — 2) (х2 + 2х + 4), то по формуле (8.8) имеем
я2		х2	А	Вх + С
_ Г	о
х3 — 8 (х — 2) (х2 + 2х + 4)
ока неизвестны. Прав
Тогда
х2 ^ А(х2 + 2х + 4) + (Вх + С)(х — 2)
где числа А, В, С пока неизвестны. Правую часть этого разложения приведем к
общему знаменателю. Тогда
х3 — 8 ~~	(х — 2) (х2 + 2х + 4)
Следовательно,
х2 = А (х2 + 2х + 4) + (Вх + С) (х - 2)
или
х2 = (А + В)х2 + BА + С — 2В)х + 4А — 2С.
Приравнивая коэффициенты при одинаковых степенях х, получаем систему урав-
уравнений для нахождения неопределенных коэффициентов А, В к С:
х2
х°
Таким образом,
1=А + В,	Л
0 = 2А + С — 2В, >--
О = 4Л — 2С )
.>. .-fc-f
J
х3 — 8 3(д: —2)
Пример 8.10. Разложить рациональную дробь —	^	 	 на простей-
простейшие дроби.
Решение. Разложим знаменатель на множители:
х" + Их3 + 4*2 - 9 = (х2 + 2хJ - З2 = (х2 + 2х + 3) (х2 + 2х - 3) =
2
Запишем разложение рациональной дроби на простейшие дроби:
7х2 + 26* — 9	_ А	В	Cx + D
х+ 3 ^ х2 + 2х + 3 '
Приведем правую часть разложения к общему знаменателю. Тогда
— 9
(x-l)(x+3)(x* +
_ А(х + 3)(х2 + 2х + 3) + В(х- 1)(^ + 2х + 3) + (Сх + Р)(х - 1)(х + 3)
(х-\)(х
Отбрасывая знаменатель, получаем
202

7х2 + 26х — 9 = А (х + 3) (х2 + 2х + 3) + В(х — 1) (х2 + 2х + 3) +
+ (Cx + D) (х-1)(х + 3)
или	' =
7х2 + 26* - 9 = (А + В + Qx3 + EА + В + 2С + D)x2 +
+ (9А + В — ЗС + 2D)x + 9A—3B — 3D.
Приравнивая коэффициенты прн одинаковых степенях х, имеем:
X3
X2
х1
х°
0 = А + В + С,
26 = 9i4 + В — ЗС + 2i
— 9 = 9Л — ЗВ — 3D,
Следовательно,
7Х2 + 26х — 9
Л
_ ' I ' . 5~2*
+ 3)(х2-' " ' ~
Метод частных значений. При нахождении неопределенных коэф-
коэффициентов вместо того, чтобы сравнивать коэффициенты при одина-
одинаковых степенях х, можно дать переменной х несколько частных зна-
значений (по числу неопределенных коэффициентов) и получить таким
образом систему уравнений относительно неопределенных коэффи-
коэффициентов. Особенно выгодно применять этот метод в случае, когда
корни знаменателя рациональной дроби Pn(x)/Qm{x) просты и дейст-
действительны. Тогда оказывается удобным последовательно полагать х
равным каждому из корней знаменателя.
п	о.. rv	, 4Х2+16Х —8
Пример 8.11. Разложить рациональную дробь 	-j	 на простейшие
дроби.
Решение. По формуле (8.8) получим
4х2+16х —8 4х2+16х — 8 А , В , С
¦ =	1+
х3 —4х	х(х + 2)(х —2) х х + 2 х —2'
Приведя правую часть данного равенства к общему знаменателю и отбросив
последний, имеем
4х2 + 16х — 8 = А(х + 2) (х — 2) + Вх(х — 2) + Сх(х + 2).
Придавая х последовательно частные значения, равные кориим х = 0, х=—2,
х = 2, находим:
— 8= —4
х=—2 —24
х = 2
Таким образом,
1= —4А,~]
[=8В, } =
I = 8С, J
40 = 8С, | | С = 5.
4х2+ 16х —8
—г
х3 — 4х	х х + 2 х — 2 '
Иногда для нахождения неопределенных коэффициентов удобно
применять комбинацию указанных выше методов, т. е. придавать х
ряд частных значений и приравнивать коэффициенты при некоторых
степенях х.
Итак, сформулируем
Правило интегрирования рациональных дробей. Для того чтобы
проинтегрировать рациональную дробь, необходимо выполнить сле-
следующие действия:
203

1) если рассматриваемая рациональная дробь Pk(x)/Qm(x) —
неправильная (k ^ m), представить ее в виде суммы многочлена и
правильной рациональной дроби:
где п<с т; R(x) — многочлен (см. § 8.5);
2)	если рассматриваемая рациональная дробь Pn(x)/Qm(x) —
правильная (п < пг), представить ее в виде суммы простейших ра-
рациональных дробей по формуле (8.8);
3)	интеграл от рациональной дроби представить в виде суммы
интегралов от целой части и от соответствующих простейших дробей
и вычислить эти интегралы.
Пример 8.12. Вычислить
Решение. Подынтегральная дробь — неправильная, поэтому выделим сна-
сначала ее целую часть и проинтегрируем ее, а в полученной правильной дроби разло-
разложим знаменатель на линейные множители:
4х2+16*-8
4л2 + 16* - 8
х(х-2)(х + 2)
х3 , х2
Х-
п , 4д:2 + \Ьх — 8	.	,
Правильную дробь —	—=гг— _. разложим на простейшие дроби и найдем
коэффициенты Л, В, С разложения (см. пример 8.11):
= у + у + 4д: + 2 In UI - 3 1п |д: + 21 + 5 In U - 2| + 1п С =
- 2N
(х + 2K
Пример 8.13. Вычислить
Г хЧх
3 х3 - 8
Решение. Подынтегральная функция представляет собой правильную ра-
циоиальиую дробь, разложение которой на простейшие дроби выполнено в при-
примере 8.11:
-г	dx
х3 — 8
А = 1/3,
В = С = 2/3
-Л
3 (д:-
2)(д:2
-2 ^ х2+ 2х
3 3 х-2 + 3 3
1п |(С(ж — 2) (х2
In -\/С(д:3— 8).
204

Замечание. При вычислении интегралов не всегда нужно прибегать к готовой
схеме. В частности, в примере 8.13 достаточно заметить, что x*dx = -=-d(x? — 8),
О
и сразу получим решение:
= In -^(x3 - 8).
8.8. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
Рациональные функции. Условимся через R(u, v, w, ...) обозна-
обозначать рациональную функцию относительно и, v, ш, ..., т. е. выраже-
выражение, которое получено из любых величин и, v, w, ..., а также действи-
действительных чисел с помощью четырех арифметических действий.
Например, R(u, v)=—f-	;—5—г рациональная функция относительной
и v; R(x, -ух, -ух) —	" 2.	—— рациональная функция относительно х, \х,
х — -ух + ~ух
з/~ „. .	.	sin х — 2 cos2 x	,
-ух; R(s\n xcos х)=	г	рациональная функция относительно
3 sin х + cos x + 1
sin х и cos х.
Выражение ———*-—	 ие является рациональной функцией относительно
переменной х, так как содержит операцию извлечении корня из х, но является рацио-
рациональной функцией относительно -ух и -ух.
/sin .
sin2 x + 3 cos x + 5
тельио sin x, так как содержит операцию извлечении корня из sin x.
r»	vain д -j- ?. tua a	„ ,
Выражение /2—j—	^—^- не ивляетси рациональной функцией относи-
Интегралы вида $/?(sinx, cosx)dx. Универсальная подстановка.
Будем рассматривать интегралы вида
$/?(sin*, cosx)dx	(8.9)
при условии, что они не являются табличными. Вычислить их можно
различными методами, изложенными ранее в § 8.1—8.5. Иногда
бывает достаточно преобразовать подынтегральное выражение, ис-
использовав тригонометрические формулы, применить методы «под-
«подведения» множителя под знак дифференциала, замены переменной
или интегрирования по частям.
Например:
.. Г dx f sin2 х + cos2 х	Г ,	1
1) \	—=\	—<	dx = \tg2x	j— dx +
J cos'jt J cos4*	J	cos2jt
J sin* J sin(A:/2)cos(A:/2) J
sin(x/2)cos(x/2) J tg(x/2)cos2(x/2) J tg(x/2)
= In tg4 +C;
205

3) J cos2 xdx. Для вычисления этого интеграла можно использовать формулу
cos2 х = -д- A + cos 2x) и свести его к табличным:
s2 xdx = -i- ( A + cos 2x)dx = -i-(x + ~ sin 2*) + C.
Заметим, что в интегральном исчислении нет общих правил.
Интегрирование может быть выполнено не единственным способом.
Но даже и тогда, когда имеется теоретическое правило вычисления
интеграла, оно может оказаться далеко не лучшим.
Для вычисления интегралов вида (8.9) существует общая уни-
универсальная схема вычисления, основанная на универсальной триго-
тригонометрической подстановке t = tg(*/2). Этой подстановкой интеграл
(8.9) преобразуется в интеграл от рациональной функции перемен-
переменной t, который, как было показано, всегда выражается в элементар-
элементарных функциях.
Действительно, пусть t = tg(*/2). Выразим sin х, cos х и dx через t:
. = 2sin(*/2)cos(*/2) = 2 tg(*/2) = 2t
sin2(x/2) + cos2(x/2) 1 + tg2(x/2) 1 + t2 '
cos x = cos2(*/2)-s'(*/2) = i-tg2(*/2) = i-<2
sin2(A:/2) + cos2(x/2)	1 + tg2(x/2)	1 + t2 '
x = 2aTdgt, dx = -^T.
Подставляя в подынтегральное выражение (8.9) вместо
sin *,cos х и dx их значения, выраженные через переменную /, имеем
х. cos Мх =
Подынтегральная функция рациональна относительно t.
Заметим, что с помощью универсальной подстановки очень удобно
вычислять интегралы вида
f	dx
Пример 8.14. Вычислить
a cos х + Ь sin x + С
dx
9 + 8 cos x -\- sin x '
Решение. Применим универсальную подстановку tg (x/2) = t:
dxГ2dtГ Ыг
)
t	„.1е	+ С-4-,г.1е^	+С.
^ _|_ 1J+ 16 2 в 4 ^	2 6	4	^
Хотя универсальная подстановка всегда позволяет вычислить
интегралы вида (8.9), однако ее используют сравнительно редко,
так как она часто приводит к интегрированию громоздких рацио-
рациональных дробей. Поэтому в ряде случаев более удобно использовать
частные подстановки.
206

В частности, при вычислении интегралов вида (8.9) можно вос-
воспользоваться следующими рекомендациями.
1.	Если подынтегральная функция нечетна относительно sin x,
т. е. R(— sin x, cosx)=—R(s\n x, cos x), то применяется подста-
подстановка cos x = t.
2.	Если подынтегральная функция нечетна относительно cos x,
т. е. R(s'm х, — cosx)= —У?(sin x, cosjc), to используют подстановку
sin х = t.
3.	Если подынтегральная функция четна относительно sin x и
cos х, т. е. R( — s'mx, —cosx) — R(s'mx, cosjc), to применяется под-
подстановка tg х = t.
Интегралы вида \ sin" x cosm xdx (m, n?Z, m^O, я^О). Если
хотя бы одно из чисел т или п — нечетное, то, отделяя от нечетной
степени один сомножитель и выражая с помощью формулы sin2 x -\-
-f- cos2 х = 1 оставшуюся четную степень через кофункцию, прихо-
приходим к табличному интегралу.
Пример 8.15. Вычислить \sinbxdx.
Решение. Имеем
5 sin5 xdx — \ sin4 x sin xdx = — $ A — cos2 xJd(cos x) = I cos x = t \ =
= -^(l - tjdt = -^(l -2t2+ t*)dt = -t + 1-t3- -t + С =
2	1
= — cos x + — cos3 x	— cos5 x + C.
О	О
Пример 8.16. Вычислить \ sin4 2x cos3 2xdx.
Решение. Имеем
5 sin4 2x cos3 2xdx — \ sin4 2x cos2 2x cos 2xdx =
= \-\ sin4 2x{\ — sin2 2*)d(sin 2x) = |sin 2* = u\ = -M u*(\ — u2)du =
= i- J (и4 - u*)du = -1.и^_-1-и7 + с=_^ sjn6 2x - -i- sin7
Если же тип — четные числа, то степени понижаются по-
посредством перехода к двойному аргументу с помощью тригонометри-
тригонометрических формул:
cos2 х = 1 + c2os2*, sin2 x = '~c2os2*, sin x cos x = -I sin 2x.
Пример 8.17. Вычислить \ cos4 xdx.
Решение. Перейдем к тригонометрическим функциям двойного аргумента:
= -j-^l+2cos2x + ' ' """ )dx=^-x+±-sin2x+-Ls\n4x + C.
Пример 8.18. Вычислить \ sin4 x cos2 xdx.
Решение. Имеем
J sin4 x cos2 xdx = J sin2 jc(sin x cos xf dx =
= \ -~- A — cos 2x)	dx = — V sin2 2xdx	— \ sin2 2x cos 2xdx ==
207

= Т \ ТA ~ cos 4x)dx - IF S si 2*d(sin 2x) =
= 16x - жsin 4x ~ жsi 2x+c-
Интегралы вида \ tg" xdx, \ ctg" xdx (n 6 N, л > 1). Эти интегралы
вычисляются подстановками tg x = < и ctg х = < соответственно.
Если t = tg х, то х = arctg t, dx = —^-. Тогда
Последний интеграл при п ^ 2 является интегралом от непра-
неправильной рациональной дроби, которая вычисляется по правилу
интегрирования рациональных дробей (см. § 8.5, 8.6).
Аналогично если t = ctg х, то х = arcctg t, dx=	х—^, откуда
Пример 8.19. Вычислить \ tg5 xdx.
Решение. Сделав замену переменной, имеем
-J- - L. + -l'n(<2+ 1)+ С = -J-tg4*- -Itg2* + i-ln(tg2*+l) +C
Интегралы вида jj sin mjt cos nxdx, \ cos mx cos nxdx, $sin mxsinnxdx
(m, n ? R). Они вычисляются путем разложения подынтегральной
функции на слагаемые по формулам:
sin mx cos nx = ;j-(sin (m.+ n)* + sin (m — n)x),
cos тл cos nx= у (cos (m +i)* + cos(m — n)x),
sin mx sin nx = -д-( — cos(m+ «)¦* +cos(m — n)x).
Пример 8.20. Вычислить \ sin 5x cos Zxdx.
Решение. Имеем
V sin Ьх cos ЗдсАе = — \ (sin 8дс + sin 2x)dx =
= — T5 cos 8*	r cos 2x + С
ID	4
Аналогично вычисляются два других интеграла.
208

8.9. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
Интегралы вида ) R{x, -\jxmx, -\Jxm\ ...)dx (mt, n\, m2, n2, ...—
целые числа). В этих интегралах подынтегральная функция рацио-
рациональна относительно переменной интегрирования и радикалов от х.
Они вычисляются подстановкой х = ts, где s — общий знаменатель
дробей т\/п\, /лг/яг, ••• При такой замене переменной все отношения
т\/п\ = r\, m.2/ri2 = Г2, ... являются целыми числами, т. е. интеграл
приводится к рациональной функции от переменной t:
J I\\X, ул , ул , ...)UX — j K.\l ,1,1, ...)Sl ill.
Пример 8.21. Вычислить V —p—j—.
^ -\Jx — -\Jx
Решение. Так как общий знаменатель дробей 1/2 и 1/3 равен 6, сделаем
замену * = <6, dx = bthdt. Тогда
= t6 + -jl- tb + -| t* + 2t3 + Z? + Ы + 6 In \t - 11 + С =
= *+-^ +-H/*2 + 2V* + 3S/* + 6^ + 61n li/,-1|+С.
Интегралы вида [ r(x, (^±L\m'/n\ (™ + bd Y'"", ...) dx (m\,^
n\, rn.2, «2, ... — целые числа). Эти интегралы подстановкой
ах + ь 	,s
cx + d ~l '
где s — общий знаменатель дробей т\/п\, т2/п2, ..., сводятся к ра-
рациональной функции от переменной t.
Пример 8.22. Вычислить .
J A *)
Решение. Сделаем замену
1 — х л	\—t2.	Mdt ,	2?
¦¦' • *= ¦ . .-• dx=— r, , ^, , \-x =
l+x '•- ! + ,«¦ -	(l+t'f	l + <2
Тогда
r i	/ i _ v	r n j- /V 4/
Интегралы вида /| = \	x —, h = \—^ x ' —, /3 =
•> -y ax2 + bx + с	^ -y ax2 + Ьх + с
-. Для вычисления интеграла 1\ выделяется пол-
¦ + bx + c
ный квадрат под знаком радикала:
209

du
и применяется подстановка
х + — = и, dx — du.
В результате этот интеграл сводится к табличному: /i=\
В числителе интеграла /2 выделяется дифференциал выражения,
стоящего под знаком радикала, и этот интеграл представляется
в виде суммы двух интегралов:
7 с
dx=
+ bx
_ A f
2°J
где /i — вычисленный выше интеграл.
Вычисление интеграла /3 сводится к вычислению интеграла
подстановкой:
Пример 8.23. Вычислить
' (Зх— \)dx
'У*2+ 2*+ 2
Решение. Имеем интеграл вида
Пример 8.24. Вычислить
д/2 + 2л: — 1
Решение. Имеем интеграл вида /з:
Л
х = —.
и
-$•
+ С.
udu
-\
У1 + 2u - u2
У2-(«-1J
210

= arccos
u — 1
_ l/x — 1 , _
С = arccos ———	1- С
Интегралы вида \R(x, -\[ax2-\-bx + c)dx. Частные случаи вы-
вычисления интегралов данного вида рассмотрены в предыдущем
пункте. Существует несколько различных приемов их вычисления.
Рассмотрим один из таких приемов, основанный на применении
тригонометрических подстановок.
Квадратный трехчлен ах2 -\-bx-\- с путем выделения полного
квадрата и замены переменной может быть представлен в виде
и2± k2. Таким образом, достаточно ограничиться рассмотрением
трех видов интегралов:
h=\R(u, ~Jk2-u2)du, h = \R(u, AJk2 + u2)du,
h = \R(u, V" - k2)du.
Интеграл I\=\R(u, -у/г2 — u2)du подстановкой
u = ksmt (или и = /гсоэО
сводится к интегралу от рациональной функции относительно sin t
и cos t.
Действительно, применим, например, подстановку и = k sin t,
k>0, тогда du — k cos tdt, ~\Jk2 — u2 = k cos t,
$/?(ы,У*г2 - и2) du = \R(k sin t, k cos t)k cos tdt.
Интеграл I2 = \R(u, -\jk2 + u2)du подстановкой
u = ktgt (или u = kctgt)
сводится к интегралу от рациональной функции относительно sin t
и cos t.
Действительно, применим, например, подстановку u = kigt,
k>0, тогда du — k sec2 tdt, -\jk2 + и2 = k sec t,
\R(u, -yJk2 + u2)du = \R(ktgt, k sec t)k sec2 tdt.
Интеграл h = \R(u, -^u2 — k2)du подстановкой
u = k sec t (или и = k cosec t)
сводится к интегралу от рациональной функции относительно sin t
и cos t.
Действительно, применим, например, подстановку и = k sec t,
«2 - k2 = k tg /,
тогда du =
Интегралы от рациональных функций относительно sin t и cos t
вычисляются с помощью методов, изложенных в § 8.8.
211

Пример 8.25. Вычислить [л/а2 — x2dx.	____
Решение. Применим подстановку х = a sin t. Тогда dx = a cos tdt, ~уа2 — дс2 =
= а cos /. Таким образом,
[ л]а2 -~?dx = сД cos2 tdt = -|ЦA +cos 2t)dt = -у-/ +
2	2	2
-^- sin 2/ + С = -^- / + -^- sin / cos / + С.
Выразим f, sin / и cos / через х:
t = arcsin —, sin / = —, cos / = —*	.
a	a	a
Следовательно,
f i		a2	xx /
\ л]a2 — x1dx = ,-5- arcsin	(- -5- -\/a2 — лг2 + С.
Пример 8.26. Вычислить [л]*? + a2dx.
Решение. Применим подстановку х = a tg /. Тогда dx = a sec2 ;
Имеем
!х2 + a2dx =
sec2
cos /
Полученный интеграл можно вычислить с помощью универсальной подстановки
tg(x/2) = z, но она приведет к интегрированию громоздкой рациональной дроби.
Гораздо проще проинтегрировать данную функцию по частям:
и = т/лг + a', du = —=====
/*2 + a2dx =
du = dx, p
-^-^i^I- dx = xV7+"a2-\V^ + a2dx + \
Перенеся \
xVjr' + a2-
a2dx
в левую часть уравнения, получим
Замечание 1. Интегралы J уаа — jA(x, J -улг2 — d*dx также можно вычислять
по частям.
Пример 8.27. Вычислить \
Решение. Применим подстановку х = a tg /. Тогда dx = a sec2 tdt^ja1 ¦+• ^ =
= a sec /:
Г dx	f a sec2 /d/ _ 1 f cos3 / _
J х*л1а2 4-х2 J a< ^6* 'a sec ' a< J s'n<'
1 f A — sin2/)d(sin/) 1 f , . .4_4j/ ... I f, . ..,., . ..
= —p \	—-	 = —j- \ (sin /) 4d(sin /)	j-\ (sin /) zd(sin /) =
a4 J	sin4 /	a4 J	a J
= "" 3a4 sin3 / + a4 sin / +
Выразим sin / через x: x = a tg /=>sin /
dx
. Тогда
3a4x3
212

Замечание 2. Иитегралы вида \R{x, ~уах2 -\- Ьх + c)dx могут быть вычислеиы
также одной из следующих трех подстановок Эйлера:
1)	если а > 0, то используется подстановка -уах2 + Ьх + с = t ± x~\ja\
2)	если а<0, О 0, то применяется подстановка -у ах2 + Ьх + с = tx ± "ус;
3)	если а < 0, а подкоренное выражение раскладывается иа действительные
множители а(х — *i) (х — Хя), то используется подстановка -уах2 -\-bx-\- c = t(x — *о),
где Хо — один из корней трехчлена.
Заметим, что подстановки Эйлера имеют скорее теоретическое, нежели практи-
практическое значение. Их применение часто приводит к громоздким вычислениям.
Интегралы вида \xm(a + bxnjdx (m, n, p6Q, a, b ? R). Рас-
Рассматриваемые интегралы, называемые интегралами от дифферен-
дифференциального бинома xm(a + bxnydx, выражаются через элементарные
функции только в следующих трех случаях:
1) если р ? Z, то применяется подстановка
где s — общий знаменатель дробей тип;
2)	если т g Z, то используется подстановка
а + Ьхл = ts,
где s — знаменатель дроби р = k/s;
3)	если -^t—f-p?Z, то применяется подстановка
где s — знаменатель дроби р = k/s.
Во всех остальных случаях, как было показано П. Л. Чебыше-
вым*, интегралы от дифференциального бинома не выражаются через
элементарные функции
Пример 8.28. Вычислить С \l+jJx dx = [ *~1/2A + х"'*I'Чх.
J sfx	J
Решение. Здесь р = — ? Z, т= —^, "=-j-. —-*— = 2 6 Z, поэтому при-
применим подстановку 1 + xi/A = t3. Тогда x = (t3— IL, dx = 4(t3— If3t2dt,
\ x-x/2(l + xi/A)i/3dx = \(t3 — \)~2t ¦ 4(t3 — lK3t2dt = 12$<3(<3 — \)dt =
= 12 J (<• - Od< = 12D ~ 4) + c = "T^A
Пример 8.29. Вычислить U1/7B* + 3I/3dx
Решение. Здесь p=-^-gZ, m = -^-, я = 1, —^— = -=- ? Z,	(- p =
о	/	л	/	ft
31 . _	¦	A
^ ^r {Z, следовательно, интеграл ие выражается через элементарные функции.
Пример 8.30. Вычислить \	 dX	= \ х~2{\ + x2)-3/2dx.
* Пафиутий Львович Чебышев A821 — 1894) —русский математик и механик.
213

Решение. Здесь р = --| g Z, m = -2, n = 2, m + * = - -i- ? Z, -^-±i +
=—2 ? Z, следовательно, делаем подстановку: х~2 + 1 = t2=$-x = (t2 — 1)~1/2,
i
-	-	-3/2
SC	,	1 4-3/2
*~2(l +*2r3'2d*= -^ (/2 - l)(l + j^-jj (t2 - \)-»Hdt =
' f t2 — 1 .. f,, , 2...
— \-r-"-'\<l-' >a'-'-
8.10. ИНТЕГРАЛЫ, НЕ ВЫРАЖАЮЩИЕСЯ
ЧЕРЕЗ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
В § 8.1—8.9 рассматривались классы элементарных функций,
интегралы от которых выражаются через элементарные функции,
или, что то же, классы интегрируемых в конечном виде функций.
Было отмечено, что всякая непрерывная на [а; Ь] функция f(x)
имеет первообразную, т. е. существует такая функция F(x), что
F'(x) — f(x). Однако не всякую первообразную F(x) можно выразить
через конечное число элементарных функций. Так, при интегриро-
интегрировании дифференциальных биномов \xm{a-\-bxltfdx было отмечено,
что их первообразные выражаются через элементарные функции
(интегрируются в конечном виде) только в трех случаях: 1) p?Z;
2) т ~*~ ? Z; 3) т + р ? Z. Во всех остальных случаях интеграл
от дифференциального бинома не выражается через элементарные
функции.
Приведем примеры интегралов, не выражающихся через эле-
элементарные функции:
\e~x*dx — интеграл Пуассона*
~ sin х
X
COS*
—— dx — интегральный синус,
¦ dx — интегральный косинус,
-г-^	интегральный логарифм,
**
\
\cos(x2)dx, Jsin(^2)d^ — интегралы Френеля*
\ — x — — эллиптический интеграл первого рода,
J -yji — fe2sin2*
\-yl — k2sin2xdx — эллиптический интеграл второго рода.
Каждый из приведенных выше интегралов представляет собой
функцию, не являющуюся элементарной.
* Снмеон Денн Пуассон A781—1840)—французский математик, механик и
физик.
** Огюстен Жан Френель A788—1827) —французский физик.
214

9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
9.1. ИНТЕГРАЛЬНАЯ СУММА.
ПОНЯТИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Пусть функция у = f(x) определена и ограничена на отрезке
[а; Ь], а<Ь. Разобьем [а; Ь] произвольным образом на п частичных
отрезков точками хо, х\, ..., хп и обозначим это разбиение через т„:
тп = {х0, хи ..., хп\а = х0<Х\ <.	Ь)
Пусть kxk = Xk — Xk-\—длина частичного отрезка [xk-й Xk],
k = l, n. На каждом таком отрезке произвольным образом выбе-
выберем точку ?* и составим сумму
п
оп = f{h)&xi + f(h)&X2 + — + f{ln)&xn = 2 / (it)Ax*. (9.1)
Она называется интегральной суммой Римана* для функции f(x) на
отрезке [а; Ь], соответствующей данному разбиению т„ отрезка [а; Ь]
и выбору промежуточных точек ?*, k=\, п.
Пусть к — длина наибольшего частичного отрезка разбиения
т„: А, = max {А**}, называемая диаметром разбиения.
Определение 9.1. Если существует конечный предел инте-
интегральной суммы (9.1) при А,-»-0, не зависящий от способа разбиения
тл отрезка [а; Ь] на частичные отрезки и выбора промежуточных
точек 2-*, то этот предел называют определенным интегралом (или
интегралом Римана) от функции f(x) на отрезке [а; Ь] и обозначают
\ f(x)dx Ш lim
Если указанный предел существует, то функция f(x) называется
интегрируемой на отрезке [а, Ь] (или интегрируемой по Риману).
При этом f(x)dx называется подынтегральным выражением, f(x) —
подынтегральной функцией, х — переменной интегрирования, анЬ —
соответственно нижним и верхним пределами интегрирования.
Заметим, что интегральная сумма не зависит от того, какой буквой обозначен
аргумент данной функции. Следовательно, и ее предел, т. е. определенный интеграл,
не зависит от обозначения переменной интегрирования:
ь	ь	ь
Таким образом, определенный интеграл есть число, равное пре-
* Бернгард Риман A826—1866) —немецкий математик.
215

делу, к которому стремится интегральная сумма, в случае, когда
диаметр разбиения К стремится к нулю.
ь
Обозначение определенного интеграла \ f(x)dx похоже на обозна-
а
чение неопределенного интеграла от той же функции f(x)dx. И это
не случайно. Оказывается, что вычисление определенного интеграла
сводится к вычислению неопределенного интеграла от той же подын-
подынтегральной функции, причем сходство их обозначений облегчает
запись и запоминание формул интегрирования. Однако между опре-
определенным и неопределенным интегралами имеется и существенное
отличие: определенный интеграл от функции f(x) на отрезке [а; Ь]
есть некоторое число, в то время как неопределенный интеграл пред-
представляет собой множество всех первообразных функций F(x) + С для
данной функции f(x) на отрезке [а; Ь]. Таким образом, понятия эти
различны.
9.2. ГЕОМЕТРИЧЕСКИЙ И ФИЗИЧЕСКИЙ СМЫСЛ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Геометрический смысл определенного интеграла. Пусть функция
у ==. f(x) непрерывна на отрезке [а; Ь] и f(x) ^ 0. Фигура, ограни-
ограниченная графиком АВ функции у = f(x), прямыми х = а, х = b и осью
Ох (рис. 9.1), называется криволинейной трапецией.
Интегральная сумма и ее слагаемые имеют простой геометри-
геометрический смысл: произведение f(|*)Д** равно площади прямоуголь-
прямоугольника с основанием Ajc* = jc* — xt,-i и высотой /(?*), а сумма а„ =
л
= 2 f(!*)A** представляет собой площадь заштрихованной ступен-
чатой фигуры, изображенной на рис. 9.1. Очевидно, что эта площадь
зависит от разбиения т„ отрезка [а; Ь] на частичные отрезки и вы-
выбора точек Ik-
В
Рис. 9.1
Чем меньше A**, k=\, n, тем площадь ступенчатой фигуры
ближе к площади криволинейной трапеции. Следовательно, за точ-
точную площадь S криволинейной трапеции принимается предел инте-
интегральной суммы при Л,->-0:
216

к=\	а
Таким образом, с геометрической точки зрения определенный
интеграл от неотрицательной функции численно равен площади
соответствующей криволинейной трапеции.
Физический смысл определенного интеграла. Пусть точка дви-
движется прямолинейно вдоль числовой оси с непрерывно меняющейся
скоростью v(t), to^it^LT. Смещение точки за малый промежуток
времени Af* = f*— tk-\ приближенно можно считать равным
п
у(|*)Д^, где ?*6[f*-i; tki Тогда интегральная сумма 2 и(ЫД^
представляет собой приближенное значение пути, пройденного точ-
точкой от момента времени ^о До Т. В пределе при А, = тах{Д^}->-0
получим точное значение этого пути S, т. е.
п	Т
S=lim 2 и(г-*Ш*= \v(t)dt
9.3. УСЛОВИЯ ИНТЕГРИРУЕМОСТИ ФУНКЦИЙ
Рассмотрим условия интегрируемости функций на отрезке [а; Ь),
т. е. условия существования определенного интеграла. При опреде-
определении его как предела интегральной суммы (см. § 9.1) мы предпо-
предполагали, что функция f(x) ограничена на отрезке [а; Ь]. Условие огра-
ограниченности функций на отрезке [а; Ь] является необходимым усло-
условием интегрируемости функций, т. е. справедлива следующая
ь
Теорема 9.1. Если \ f(x)dx существует, то функция f(x) ограничена
а
на отрезке [а; Ь].
[> Действительно, если функция f(x) неограничена на [а; Ь], то
для любого разбиения т„ отрезка [а; Ь] на частичные отрезки
[*0; х\], [х\\ х^], ..., [х„-и хп] найдется хотя бы один частичный
отрезок [Xk-i; Xk], на котором функция будет неограниченной. В силу
неограниченности функции f(x) на отрезке [jc*_i; **] можно выбрать
на нем точку \k так, чтобы абсолютная величина произведения
/(?*)Д** была больше наперед заданного числа. Таким образом,
при любом разбиении тл отрезка [а; Ь] на частичные отрезки инте-
п
тральная сумма 2 /(?*)Д*а будет бесконечно большой по абсолют-
ной величине, а следовательно, не существует конечного предела ин-
интегральной суммы при стремлении диаметра разбиения А. к нулю,
что противоречит условию теоремы. <
Покажем на примере, что ограниченность является необходимым,
но не достаточным условием интегрируемости функции на отрезке
[а; Ь], т. е. что существуют ограниченные функции, не являющиеся
интегрируемыми.
217

Пример 9.1. Доказать, что функция Дирихле
Пх)={к
если х — рациональное число,
если х — иррациональное число
не интегрируема на отрезке [0; 1].
Решение. Действительно, если при разбиении отрезка [0; 1] на частичные
отрезки выбрать на каждом нз них рациональную точку ?*6[x*_i; **], получим
Если же выбрать иррациональную точку ?*, имеем
п	п
а„= 2 f
Таким образом, при разбиении тп отрезка [0; 1] на частичные отрезки интеграль-
интегральная сумма может принимать как значение, равное 0, так и значение, равное 1.
Следовательно, предел интегральной суммы не существует, т. е. не существует опре-
определенный интеграл, хотя функция Дирихле ограничена на всей числовой оси.
Сформулируем без доказательства достаточное условие интегри-
интегрируемости функции.
Теорема 9.2. Если функция f(x) непрерывна на отрезке [а; Ь], то
ь
она интегрируема на этом отрезке, т. е. существует \f(x)d(x).
а
Отметим, что интеграл Римана существует для значительно более
широкого класса функций, нежели рассматриваемый класс непре-
непрерывных функций. В частности, справедлива следующая теорема,
обобщающая теорему 9.2.
Теорема 9.3. Если функция f(x) ограничена на отрезке [а; Ь] и
непрерывна на нем всюду, кроме конечного числа точек разрыва
первого рода, то она интегрируема на этом отрезке.
а
Пример 9.2. Вычислить \ x2dx.
о
Решение. Так как подынтегральная функция является непрерывной на [0; 1],
то определенный интеграл $ x2dx существует и равен площади S криволинейной
о
трапеции, ограниченной параболой у — х2 и прямыми х — I, у = 0 (рис. 9.2). Разобьем
отрезок [0; 1] на п равных частей точками хо = О,
Х|=Дх, Х2 = 2Дх, ..., хп = 1 = пАх, Ах=\/п.
В качестве ?* возьмем крайние правые точки каждо- у
го из отрезков (|* = X/,). Составим интегральную
сумму:
() +
+ 2Axf Ax +... + (n Axf Ах = (ДхK A + 22 +
• i «a i i 2 «(« + 1)Bя+ 1)
Учитывая, что 1 +22 +...+ п2 = —^—¦—^	¦—'-
о
получаем
1	л
Sx2dx = lim an= liiti ^j f(?*)Ax* =
AX-.-0	AX-.-0
Рис. 9.2
218

„^„о ^	6п3
*=1
Таким образом, площадь криволинейной трапеции, ограниченной параболой
у = х2 и прямыми х= 1, у = 0, равна 1/3.
Как видно из примера, непосредственное (по определению) вы-
вычисление определенных интегралов как пределов интегральных сумм
связано с громоздкими вычислениями.
9.4. ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Рассмотрим свойства определенного интеграла.
1.	Если нижний и верхний пределы интегрирования равны (а = Ь),
то интеграл равен нулю:
\f(x)dx = 0.
а
Это свойство следует из определения интеграла.
2.	Если f(x)= 1, то
ь
\йх = Ь — а.
а
\> Действительно, так как f(x)= 1, то
(dx = lim 2 \-Axk= % Axk = b-a. <1
3.	При перестановке пределов интегрирования определенный
интеграл меняет знак на противоположный:
\f{x)dx=-[f{x)dx.
а	Ь
Ь
Интеграл \f(x)dx был определен для случая a<Cb (см. § 9.1).
а
Если а> Ь, свойство 3 рассматривают как дополнение к определе-
определению (доопределение) определенного интеграла. Свойство 3 можно
интерпретировать следующим образом: определенные интегралы
b	, a
\f(x)dx и \f(x)dx являются пределами интегральных сумм, различаю-
различающихся лишь знаком. Это следует из того, что в случае Ь < а все числа
Axk = Xk — Xk-i в разбиении т„ = {а =х0 > *i > ... > хп = Ь) будут
отрицательными (при а<Ь все Дя* > 0).
4.	Постоянный множитель можно выносить за знак определен-
определенного интеграла:
ь	ь
\cf(x)dx = c\f(x)dx Vc?R.
а	а
\> Действительно,
219

\cf(x)dxdM Hm 2 cf(h)Axk = c\im 2 /(
а	Я—0 k = l	X—U ft = l
5. Определенный интеграл от алгебраической суммы конечного
числа интегрируемых на [а; Ь] функций f\(x), /2С*). •••. fn(x) равен
алгебраической сумме определенных интегралов от слагаемых:
\ (Л(х) ± /я(дс) ± ... ± /»(jc))dJC = \ fi{x)dx ± J /aWdJC ± ... ± J /„(*) Ас.
а	а
а
Доказательство этого свойства аналогично приведенному выше.
Замечание. Совокупность свойств 4 и 5 называют свойством линейности:
если f\(x) и ^С*) интегрируемы на [а; Ь], то любая их линейная комбинация C\f\(x)-\-
+ сф(х), с\, с2€ R, также интегрируема на [а; Ь] и
Ь	Ь	Ь
\ (c,f,(*) + aU{x))dx = с, J.f, (x)dx + с2 \ h(x)dx.
а	аи
6 (аддитивность определенного интеграла). Если существуют
с	Ь	Ь
интегралы \f(x)dx и \f(x)dx, то существует также интеграл \f(x)dx
ас	а
и для любых чисел а, Ь, с
\> Действительно, предел интегральной суммы не зависит от
способа разбиения отрезка [a; b] на частичные отрезки и от выбора
|*. Это позволяет при составлении интегральной суммы включить
точку с в число точек разбиения. Пусть с = хт, т. е. [а; Ь] =
= [а; с]U[с; &] = ([а; *,]U[*u *a]U-U[*m-i; xm])\J([xm; xm+i]\J
U...U[*«-.; b]). Тогда
Переходя к пределу при max {Ах*} = А.-»-0, имеем
S f(дс)^дс = f /(дс)«/дс + S f(Je)rfje. <
а	а	с
Геометрический смысл свойства 6 состоит в том, что площадь
криволинейной трапеции с основанием [а; Ь] равна сумме площадей
криволинейных трапеций с основаниями [а; с] и [с; Ь] (рис. 9.3).
7. Если f(x)> 0 Мхе [а; Ь], то
ь
\f(x)dx^0, a<b.
а
> Действительно, так как /(?*)>0 к Ах* ^ 0, то интегральная
220

Рис. 9.4
Л
сумма 2 f(lk)Axk ^ 0. Переходя к пределу в последнем равенстве,
имеем
к=\
2 f(S
=
0.
8 (монотонность определенного интеграла). Если интегрируемые
функции f(x) и <р(х) удовлетворяют неравенству f(x) ^ <р(х) V х 6
? [а; 6], то
\\dx, а<Ь.
> Действительно, так как f (х) — <р(х) ^ OVAf 6 [а; Н то, согласно
свойствам 5 и 7, имеем
6	Ь	Ь	Ь	Ь
\ (f(x) — ф(х))^х = \ f(x)dx - \ <p(x)dx > 0^ \ f(x)dx > \ <p(x)dx. <
а	а	а	а	а
На рис. 9.4 дана геометрическая интерпретация свойства 8. Так
как f (x) ^ <р(х), то площадь криволинейной трапеции аА^Вф не
меньше площади криволинейной трапеции аА\В\Ь.
3 а меч аи и е. Так как —\f{x)\ </(*)< |/(*)| V*6[a; H то
ft	ft	ft	ft	ft
9 (об оценке определенного интеграла). Если m и М — соот-
соответственно наименьшее и наибольшее значения функции f(x), не-
непрерывной на отрезке [a; b], то
ь
m(b — a)^\f(x)dx^M(b—a), а<Ь.	(9.2)
а
> По условию m <:/(*)<:МУ х?[а; b). Применяя свойство 8
ft	ft	ft
к этим неравенствам, имеем m\ dx ^ \ f(x)dx <I M\ dx. Согласно свой-
а	а	а
b
ству 2, \dx = b — а, следовательно,
221

m(b — a)
M(b — a). <
На рис. 9.5 дана геометрическая интерпретация свойства 9 в
случае, когда f(x)^O \x?[a; b). Площадь прямоугольника аА\ВхЬ
равна т(Ь — а), площадь прямоугольника аА^Вф — М(Ь — а). Из
неравенства (9.2) следует, что площадь криволинейной трапеции
аАВЬ не меньше площади первого прямоугольника и не больше
площади второго.
10 (теорема о среднем). Если функция f(x) непрерывна на от-
отрезке [а; Ь], то существует такая точка \ ? [а; Ь], что
т. е. определенный интеграл от непрерывной функции равен произ-
произведению значения подынтегральной функции в некоторой промежу-
промежуточной точке ? отрезка интегрирования [а; Ь] и длины b — а этого
отрезка.
> Известно, что непрерывная функция f(x) на отрезке [a; b] до-
достигает своего наименьшего m и наибольшего М -значений, т. е.
m <I f(x) <M Vx? [a; b]. Из данного неравенства на основании свой-
свойства 9 имеем
ь
m(b — a)< \ f(x)dx<M(b — a).
a
Разделив все члены двойного неравенства на b — a > 0, получим
ь
\ f(*)d*
Af.
b — a
Другими словами, число Я =
I f(*)dx
2
Ь—а
находится между наимень-
наименьшим и наибольшим значениями функции f(x). Поскольку непрерыв-
Ъ л
Рис. 9.6

ная на отрезке [а; Ь] функция f(x) принимает все промежуточные
значения, лежащие между т и М, в том числе и значение к, то суще-
существует 16 [а; &], такое, что f(Q = Я. Значит,
ь
\ f(x)dx
откуда
Число f(Q, определяемое по формуле (9.3), называется интеграль-
интегральным средним значением функции f(x) на отрезке [а; Ь].
На рис. 9.6 дана геометрическая интерпретация свойства 10 в
случае, когда f(x) > 0 \х в [а; Ь]. Так как значение f(?,) (b — а) числен-
численно равно площади прямоугольника с основанием Ь — аи высотой f(g),
то теорема о среднем утверждает, что существует прямоугольник,
равновеликий криволинейной трапеции аАВЬ.
9.5. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
С ПЕРЕМЕННЫМ ВЕРХНИМ ПРЕДЕЛОМ
До сих пор мы рассматривали определенный интеграл с постоян-
постоянными пределами интегрирования а и Ь. Если оставить постоянным
нижний предел интегрирования а, а верхний х изменять так, чтобы
х 6 [а; Ь], то величина интеграла будет изменяться. Интеграл вида
X
а
называется определенным интегралом с переменным верхним пре-
пределом и является функцией верхнего предела х. Здесь для удобства
переменная интегрирования обозначена буквой /, а верхний предел
интегрирования — буквой х.
С геометрической точки зрения, функция Ф(х) в случае f(t) ^ 0
представляет собой площадь заштрихованной на рис. 9.7 криволи-
криволинейной трапеции.
Найдем производную от Ф(х) по х, т. е. производную определен-
определенного интеграла по верхнему пределу.
Теорема 9.4. Производная опре-
определенного интеграла от непрерыв-
непрерывной функции f(x) no его перемен-
переменному верхнему пределу существует
и равна подынтегральной функ-
функции, в которой вместо переменной
интегрирования подставлено зна-
значение верхнего предела:
В
Рис. 9.7
> Возьмем любую точку х ?
6 [а; Ь] и придадим ей приращение
Ах так, чтобы х + Ах ? [а; Ь].
Тогда
223

х + \х	х
Дф(х) = ф(х + Ах) - Ф(х) = \ f(t)dt — \f(t)dt.
а	а
Используя аддитивность определенного интеграла, имеем
ДФ(х) = \f(t)dt +XX)(t)dt ~ \f(t)dt =T
Применяя теорему о среднем, получаем
Ф(х + Ах) - Ф(х) = ' \ 'f(t)dt = f(Z)Ax,
где g?[x; x + Ax].
Если Ах-кО, то х + Ax-vx, g->-x и в силу непрерывности функ-
функции f(x) на отрезке [a; b] /(g)-Kf(x). По определению производной
Ф'(х)= lin
^	|^	/() /()
^^	Ах-<-0 С^С	4ж-»0
(Е-*)
Из теоремы 9.4 следует, что определенный интеграл с перемен-
V	X
ным верхним пределом \ f(t)dt является первообразной для подын-
а
тегральной функции f(x) на отрезке [а; Ь]. Но, согласно теореме 9.2,
X
интеграл \ f(t)dt существует для любого значения х. Таким образом,
а
теорема 9.4 является одновременно и теоремой о существовании
первообразной Ф у каждой непрерывной функции f. Этой первообраз-
первообразной может быть определенный интеграл с переменным верхним пре-
пределом. Таким образом,
т. е. установлена связь между неопределенным и определенным
интегралами.
9.6. ФОРМУЛА НЬЮТОНА —ЛЕЙБНИЦА
Итак, функция f(x), непрерывная на отрезке [а; Ь], имеет на этом
X
отрезке первообразную, например Q>(x) = \f(t)dt.
а
Поставим теперь обратную задачу: зная одну из первообразных
Ф(х) функции f(x) на отрезке [а; Ь], вычислить определенный интеграл
от функции f(x) на этом отрезке или, что то же, найти определенный
интеграл по известному неопределенному.
Пусть F(x) — любая другая первообразная функция f(x) на том же
отрезке [а; Ь]. Так как первообразные Ф(х) и F(x) отличаются друг
от друга постоянным слагаемым, то имеет место равенство
\f(t)dt = F(x) + C Vxefa; b), C?R.
a
224

Подставляя в это равенство значение х = а, имеем
\f(t)dt = F(a) + C=>O = F(a) + C=>C= — F(a),
а
т. е.
\f(t)dt = F(x)-F(a)Vxe[a; Ь).
а
Полагая х = b и обозначая переменную интегрирования через х,
получаем основную формулу интегрального исчисления:
\f(x)dx=*F(b)-F(a)>
(9.4)
которая называется формулой Ньютона — Лейбница.
Формула Ньютона — Лейбница дает правило вычисления опре-
определенного интеграла: значение определенного интеграла на отрезке
[а; Ь] от непрерывной функции f(x) равно разности значений любой ее
первообразной, вычисленной при х = Ь и х = а.
Разность F(b) — F(a) в правой части формулы (9.4) удобно запи-
записывать так: F{x)\ba. Тогда формула Ньютона — Лейбница принимает
следующий вид:
Формула (9.4) позволяет избавиться от вычисления определен-
определенных интегралов как пределов интегральных сумм, и задача вычисле-
вычисления определенного интеграла сводится к задаче вычисления не-
неопределенного интеграла (см. гл. 8).
9.7. ОСНОВНЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Вычисление простейших интегралов с помощью формулы Ньюто-
Ньютона — Лейбница. Если F(x) — одна из первообразных непрерывной
на [а; Ь] функции f(x), то справедлива формула Ньютона — Лейбница
Эта формула позволяет свести вычисление определенного ин-
интеграла к вычислению неопределенного.
Так, например:
л/2
1) \ sinxdx=—cos x
я/2
2
о
—cos -5- +cos 0=1;
I
2) |Fх2 + 3)dx = {2х3 + Зх) Ц = B • I3 + 3 • 1) - B • 0 + 3 • 0) = 5;
8 Зак. 1270	225

— = in x
:ln2—In 1 =1п2;
4)
5)
'¦ — 1
Замена переменной (подстановка) в определенном интеграле.
Этот метод, как и в случае неопределенного интеграла, позволяет
упростить вычисления, т. е. привести подынтегральное выражение к
соответствующей табличной форме. Применение замены переменной
в определенном интеграле базируется на следующей теореме.
Теорема 9.5. Если функция f(x) непрерывна на отрезке [а; Ь],
а функция х = ср(<) непрерывно дифференцируема на отрезке [tf, t2],
([t ]) [ b] (^)	(^) Ь	д ф
фуц	р() р
причем y([ti; t2]) = [a; b] и
= а,
цру	р [ ]
— Ь, то справедлива формула
(9.5)
> Пусть F(x) — первообразная для функции f(x) на отрезке [а; Ь].
Поскольку ф(Л) = а, ф(^) = Ь, то по формуле Ньютона — Лейбница
имеем
\f(x)dx = F(b)- F(a) =
Формула (9.5) называется формулой замены переменной в опре-
определенном интеграле. Для вычисления определенного интеграла по
этой формуле необходимо сделать замену х = ф(^), вычислить dx =
= y'(t)dt, где ф(<) — некоторая непрерывно дифференцируемая
функция, найти пределы интегрирования по t, решив уравнения
ф(*1) = а и q>(t2) = b.
Отметим, что при вычислении интеграла методом замены Пере-
Переменной одновременно с преобразованием подынтегрального выраже-
выражения изменяются соответственно и пределы интегрирования.
9
Пример 9.3. Вычислить \
Решение. Перейдем к новой переменной интегрирования, положив х = t2.
Тогда dx = 2tdt. При а = 0 имеем t\ = л]а = 0, при Ь — 9 <2 = у9 = 3. По форму-
формуле (9.5)
9	3	3
226

Пример 9.4. Вычислить
я/з
f cos*
J sin3 x
dx.
л/6
Решение. Сделаем подстановку sin х = t. Тогда cos xdx = dt. Значению а =
= л/6 соответствует t\ = sin (л/6) = 1/2, значению Ь = я/3— <2 = sin(n/3) =
=-уЗ/2. Применяя формулу (9.5), имеем
л/3	V3/2 .
л/6
1/2
Интегрирование по частям в определенном интеграле. Пусть
и(х) и v(x) — дифференцируемые на отрезке [а; Ь] функции перемен-
переменной х. Тогда d{uv) = udv + vdu. Проинтегрируем обе части послед-
последнего равенства на отрезке [а; Ь]:
ь	ь	ь
\ d(uv)= \ udv + \ vdu.	(9.6)
а	а	а
С другой стороны, по формуле Ньютона — Лейбница
Следовательно, формула (9.6) принимает вид
ь
\
а
udv =
UV
la
b
~\
а
vdu.
(9.7)
Формула (9.7) называется формулой интегрирования по частям
в определенном интеграле.
я
Пример 9.5. Вычислить \ х sin xdx.
О
Решение. Применим формулу (9.7):
¦ х sin xdx =
0
u = x, du = dx,	I
dv = sin xdx, v = —cos x \
л/4
— X COS*
+ \ cos xdx = я + sin x
» J
о
Пример 9.6. Вычислить
-dx.
о
Решение. Применяй формулу (9.7), имеем
л/4
и = х, du~ dx,
dx
- V tg*d* =
О
»/¦*
= JC tg JC	+ In COS X
*/*
= -т- tg -j- + In cos —	In cos 0 =
227

9.8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Понятие несобственных интегралов. При введении понятия опре-
определенного интеграла как предела интегральной суммы (см. § 9.1)
предполагалось, что выполняются следующие условия: 1) пределы
интегрирования а и Ь являются конечными; 2) подынтегральная
функция f(x) на отрезке [а; Ь] непрерывна или имеет конечное число
точек разрыва первого рода. В этом случае определенные интегралы
называются собственными. Если хотя бы одно из указанных условий
не выполняется, то интегралы называются несобственными. При
этом определение 9.1 теряет смысл. Действительно, в случае беско-
бесконечного отрезка интегрирования его нельзя разбить на п частичных
отрезков конечной длины, а в случае неограниченной функции ин-
интегральная сумма не имеет конечного предела.
Несобственные интегралы являются обобщением определенных
интегралов в случаях бесконечных промежутков интегрирования
и неограниченных функций.
Несобственные интегралы с бесконечными пределами интегри-
интегрирования (первого рода). Пусть функция f(x) непрерывна на проме-
промежутке [а; оо [. Тогда она будет непрерывной на любом конечном от-
отрезке [а; Ь], а<Ь. Для функции f(x), непрерывной на [а; Ь], сущест-
существует определенный интеграл 1(Ь), зависящий от верхнего предела
интегрирования:	ь
= \ f(x)dx.
Этот интеграл определяет некоторую величину, например площадь
криволинейной трапеции, ограниченной графиком функции у =
= f(x) 7^ 0, прямыми х = а, х = b и осью абсцисс. Будем неограни-
неограниченно увеличивать верхний предел интегрирования (?>->-+оо). При
этом возможны два случая: либо 1(Ь) при Ь-*--\-<х> имеет предел,
либо не имеет.
Определение 9.2. Несобственным интегралом с бесконечным
верхним пределом интегрирования от непрерывной функции f(x) на
промежутке [а; оо [ называется предел I(b) при Ь-*--\-оо:
]f(x)dx^ lim \f(x)dx.	(9.8)
Аналогично определяется несобственный интеграл с бесконечным
нижним пределом интегрирования от непрерывной функции f(x) на
промежутке ]— оо; Ь]:
ь	ъ
\ f(x)dx$? lim \f(x)dx.	(9.9)
— оо	а-*— оо а
Если пределы в правых частях формул (9.8), (9.9), существуют
и конечны, то соответствующие несобственные интегралы называются
сходящимися, если пределы не существуют или бесконечны,— то
расходящимися.
Несобственный интеграл с двумя бесконечными пределами интег-
228

рирования от непрерывной функции f(x) на промежутке ] — оо; оо[,
оо
обозначаемый \ f(x)dx, предварительно представляют в виде
— оо
] f(x)dx = \ f(x)dx + ]f(x)dx, с€]-оо; оо[<
— оо	— оо	с
Тогда по определению
\ \{x)dx= lim \f(x)dx + \im\f(x)dx,	(9.10)
а—*— оо а
причем этот несобственный интеграл называется сходящимся, если
оба предела существуют. Если хотя бы один из пределов не сущест-
оо
вует или бесконечен, то несобственный интеграл \ f(x)dx называет-
. — оо
ся расходящимся.
Интегралы (9.8) — (9.10) называются также несобственными
интегралами первого рода.
С геометрической точки зрения сходящийся несобственный ин-
оо
теграл \ f(x)dx означает, что фигура, ограниченная кривой у =
а
= f{x) ^ 0, прямыми х = а, у = 0 и бесконечно вытянутая в направ-
направлении оси Ох, имеет конечную площадь S (рис. 9.8). Аналогичная
геометрическая интерпретация имеет место для сходящихся несобст-
несобственных интегралов (9.9) и (9.10).
Пример 9.7. Исследовать на сходимость интеграл \ —, а 6 R.
1 •*-
Решение. Если а ф 1, то
оо	о
Г 4л: ,.	Г dx ,. ж1 —
\	= lim	\	= lim
J x" d—оо	J x* 6—оо 1 — а
lim
1 6-»<x> 1 — а
Следовательно,
1
В случае а = 1 имеем
*" I оо	Уа<1.
W
lim In x
¦¦ lim In b = оо.
ft-*-oo
Итак, интеграл \ — сходится прн а> 1 и расходится при а< 1.
1
ОО
Пример 9.8. Исследовать на сходимость интеграл \
229

Рис. 9.8
Решение. По формуле (9.10), полагай с = 0, имеем
ОО	0	оо	0
( dx	f dx
dx
dx
dx
oo	— oo ¦	0	a	0
= lim arctgjc|2+ lim arctg'Jt|o= litti (arctg 0 — arctg a)
a-*-—*¦ oo	o-*-oo	a-*—oo
+ lim (arctg b ¦*- arctg O)=^-^-n + -^-n = n,
т. е. данный интеграл сходится и определиет площадь S бесконечной криволинейной
трапеции, изображенной на рис. 9.9.
Несобственные интегралы первого рода, определяемые форму-
формулами (9.8)— (9.10), обладают рядом свойств, присущих определен-
определенным (собственным) интегралам. В частности, основная формула
ь
интегрирования Ньютона — Лейбница \ f(x)dx = F(x) | * = F(b) — F(a)
а
в случае сходящегося интеграла \ f(x)dx имеет вид
'	о
а
где через F(oo) обозначен limF(b).
Применение формулы Ньютона — Лейбница к несобственным
интегралам первого рода позволяет сократить записи.
Например,
\e-*dx=-e-*\S'= -e
+ 1 = 1.
Из формулы (9.11) следует, что несобственный интеграл сходится,
когда существует конечный предел F(b) при Ь-ъоо.
Приведем без доказательства три теоремы, с помощью которых
можно исследовать вопрос о сходимости некоторых несобственных
интегралов первого рода.
Теорема 9.6. (признак сравнения). Если на промежутке [а; оо [
230

определены две неотрицательные функции f(x) и у(х), интегрируемые
на каждом конечном отрезке [а; Ь], причем
О < f(x) < ф) V х > а,
оо
то из сходимости интеграла \ y(x)dx следует сходимость интеграла
а
оо	оо
\ f(x)dx, а из расходимости интеграла $ f(x)dx следует расходимость
а	а
оо
интеграла \ q>(x)dx.
а
Теорема 9.7 (предельный признак сравнения). Если, на проме-
промежутке [а; оо [ определены две положительные функции f(x) и ср(х),
интегрируемые на любом конечном отрезке [а; Ь], и существует конеч-
конечный предел
оо	оо
то несобственные интегралы \ f(x)dx и \ q>(x)dx сходятся или расхо-
а	а
дятся одновременно.
Теорема 9.8. Если на промежутке [а; оо [ функция у = f(x) меняет
оо
знак и несобственный интеграл \ \f(x)\dx сходится, то сходится также
а
и \f(x)dx.
а
оо
Отметим, что несобственный интеграл \ f(x)dx называют абсо-
а
лютно сходящимся, если сходится интеграл \ \f(x)\dx.
а
Г dx
Пример 9.9. Исследовать на сходимость несобственный интеграл
Решение. Воспользуемся теоремой 9.6. Сравним данный интеграл с интегралом
оо
I—, который сходится при а> 1 (см. пример 9.7). Так как
Г dx	С dx
то из сходимости интеграла \ —щ- следует сходимость интеграла \
оо
Вопрос о сходимости данного интеграла можно решить и с помощью лредель-
ного признака сравнения (теорема 9.7). Для этого необходимо подобрать неотри-
неотрицательную функцию ф(*), такую, чтобы lim -ii-i- = A > 0, где f(x)=
<f(x)
Выберем <p(jc) из класса функций \/ха. При а = 3/2
231

lim iW_ = iim "	= 1 > 0.
Следовательно, несобственный интеграл \ ——=- так же, как и интеграл
1
-, сходится.
Пример 9.10. Исследовать на сходимость несобственный интеграл \—— dx.
оо
г.	г.	f |sin jc| ,	„	|sinjc|	1
Решение. Рассмотрим интеграл \ 	5—dx.	Так как 	;— =^ —5" • * и
J лг	хг	хг
1
оо	оо
\ —— сходится, то, согласно теореме	9.6, несобственный интеграл \ 	5— dx аб-
J х2	J х2
1	I
солютно сходится.
Несобственные интегралы от неограниченных функций (второго
рода). Пусть функция f(x) определена на промежутке [а; Ь[ и неог-
раничена в левосторонней окрестности точки Ь (Ь — точка разрыва),
т. е. lim f(x) — оо. Будем считать, что функция f(x) интегрируема
*~* ~	4-е
на отрезке [а; Ь — е] для любого е > 0: существует интеграл \ f(x)dx,
а
зависящий от переменного верхнего предела интегрирования.
Определение 9.3. Несобственным интегралом от функции f(x),
непрерывной на промежутке [а; Ь[ и имеющей бесконечный разрыв
в точке х = Ь, или несобственным интегралом второго рода называ-
называется предел интеграла \ f{x)dx при е-»-0:
а
Ь	4-е
$f(x)dx = lim \ f(x)dx, e>0.	(9.12)
а	в-*° а
Аналогично если функция f(x) имеет бесконечный разрыв в точке
х = а, то полагают
4	4
\f(x)dx= lim \ f(x)dx.	(9.13)
d	e->-0 a-fe
Если же функция f(x) имеет разрыв второго рода в некоторой
внутренней точке с отрезка [а; Ь], то, пользуясь свойством адди-
аддитивности определенного интеграла (см. §9.4), данный интеграл пред-
представляют в виде суммы двух интегралов:
\f(x)dx = \f(x)dx + \f(x)dx = \im]f(x)dx+lim \ f(x)dx. (9.14)
а	а	с	ei-»-0a	е«-»-0 с + ч
232

Если пределы в правых частях формул (9.12) — (9.14) суще-
существуют и конечны, то соответствующие несобственные интегралы от
разрывной функции в точках а, Ь и с называются сходящимися,
в противном случае — расходящимися.
С геометрической точки зрения сходящийся несобственный ин-
интеграл второго рода означает, что фигура, ограниченная кривой
У = f(x)< прямыми х = а, х = Ь и бесконечно вытянутая в направлении
оси Оу при х^>-Ь — О (х-»-а + 0, х->-с ± 0), имеет конечную площадь
S (рис. 9.10, а — в соответственно).
Ь-t Ъ к 0 a a+t
Рис. 9.10
Пример 9.11. Исследовать на сходимость несобственный интеграл \ —.
Решение. При jc = O подынтегральная функция \/х имеет бесконечный раз-
разрыв. С учетом формулы (9.13) имеем
Sdx ,. г dx
х е-»о+ J x
0	e
= lim In U|
= lim (In I — In e) = оо,
т. е. несобственный интеграл расходится. Геометрически это означает, что площадь
криволинейной трапеции еАВЬ
при е-»-0 неограниченно возрастает (рис. 9.11).
Пример 9.12. Исследовать иа сходимость несобственный интеграл
Решение. Рассмотрим два случая.
1. Пусть а Ф 1. Тогда
(b— xf
= lim
dx
{b—xf
ь—е
lim [ (b—x)-*d(b—x):
233

(b-
¦¦— lim
в—О 1 —a I"
2. Если a = 1, то
(
— a e-0
-прирс<1,
при a> 1.
dx
6-e
= lim
6— X	8—0
dx = — limln|6 —j
Ь — X	8-Й)
— ln|6 —a|) = oo.
Итак, несобственный интеграл
f dx
) (b-x
сходится при a < 1 н расходится
при a ^ 1.
Вопрос о сходимости несобственных интегралов второго рода
можно решить с помощью приводимых ниже теорем, в которых сфор-
сформулированы признаки сходимости таких интегралов.
Теорема 9.9 (признак сравнения).
Пусть в левой (правой) окрестности
точки b (точки а) определены две
неотрицательные функции f(x) и у(х),
причем 0 s^ f(x) <I ф(х). Тогда из схо-
сходимости несобственного интеграла
ь
\ y{x)dx следует сходимость интегра-
а ь
ла \ f(x)dx, а из расходимости не-
ь
собственного интеграла \ f(x)dx сле-
а
Ь
дует расходимость интеграла\ q>(x)dx.
а
Теорема 9.10 (предельный признак сравнения). Пусть функции
f(x) и ср(х) положительны на промежутке [a; b[, b — точка бесконечного
разрыва функций f(x) и ф(х). Тогда если существует конечный предел
ь	ъ
lim -^-=Л>0, то несобственные интегралы \f(x)dx и \(p(x)dx
*-»(,-е (f(x)	J	J
a	a
сходятся или расходятся одновременно.
Аналогично формулируется предельный признак сравнения не-
несобственных интегралов, имеющих разрыв в точке с?]а; Ь[.
Пример 9.13. Исследовать на сходимость несобственный интеграл
(
Рис. 9.11
Р е ш е н и е. Подынтегральная функция разрывна на левом конце отрезка ин-
интегрирования, т. е. при х = 0. Сравним ее с функцией Ц>(х)= \/л]х:
-\/x + 2jc2 + 3jc
V*€]0;
234

Так как несобственный интеграл от «большей» функции
1	1
[ -^- = lim [ х- i/2dx = lim 2л/*1' = 2
J _/Г «-о J	.-о U
О V*	е
сходится, то иа основании теоремы 9.9 несобственный интеграл от «меньшей» функции
1
Г	dx
\—_—.	также сходится.
J ф + 2х2 + 3х
3
dx
Пример 9.14. Исследовать на сходимость несобственный интеграл V -^—
Решение. Подынтегральная функция f(x) =
7ж+12
1
х2 — 7jc+12 (jc —3)(jc —4)
имеет бесконечный разрыв в точке jc = 3, принадлежащей отрезку интегрирования.
Воспользуемся теоремой 9.10. Подберем неотрицательную функцию ф(*)
так, чтобы lim ^ =А > 0. При а
х—3-0 (p(jt)
C — х)
х—з—о <р(х) х-»з—о (jc —3)(jc —4)	*—з — о jc —4
з
Так как интеграл \ -г	 расходится, то исходный интеграл тоже расходится
1
(см. пример 9.12).	1
Пример 9.15. Исследовать на сходимость несобствецный интеграл \	¦-.
о *
Решение. Подынтегральная функция имеет разрыв в точке jc=1. Сравним
ь
исходный интеграл с интегралом \	 , сходимость которого исследовалась
J (b — х)"
а
в примере 9.12. Для этого преобразуем подынтегральную функцию f(x) так, чтобы
выделить множитель 1 — jc:
Vl-jc4
Воспользуемся теоремой 9.10. Надо подобрать такую функцию (p(jc), чтобы
lim	; = А > 0. Выберем <p(jc) из класса функций 1/1— jc)°. При а =1/2
х-И —О (p(JC)
.. f(x) ,.	л/1 — *	¦¦	'	'
lim J-JJr= 'lm	. ,„¦.,¦,"¦¦1: .''¦¦¦ , ,=-= lim	, ; „,',:,:,„	*= — > 0.
1
Интеграл \	щ- сходится. Следовательно, исходный интеграл тоже схо-
J A jc)
о
дится (см. пример 6).
235

9.9. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Постановка задачи. Пусть требуется вычислить определенный
интеграл
I=\f(x)dx.
а
Если функция f(x) непрерывна на отрезке [а; Ь] и известна ее
первообразная F(x), то определенный интеграл от этой функции
в пределах от а до Ь может быть вычислен по формуле Ньютона —
Лейбница:
I=\f(x)dx = F(b)-F(a).
а
Однако в некоторых случаях невозможно найти первробразную
F(x) по ряду причин: либо F(x) не выражается через элементарные
функции, либо выражается достаточно сложно. В этих случаях опре-
определенный интеграл вычисляют приближенно.
Известно, что определенный интеграл есть некоторое число. Лю-
Любой приближенный метод интегрирования основан на вычислении
приближенного значения этого числа. Пусть / — искомое число,
7—его приближенное значение. Тогда |/ — /| = Д— абсолютная
погрешность вычисления интеграла /. При вычислении определен-
определенных интегралов приближенными методами можно сформулировать
две задачи: 1) найти приближенное значение числа / и оценить
погрешность вычислений; 2) найти приближенное значение числа / с
заданной погрешностью Д, т. е. подобрать метод вычислений таким
образом, чтобы |/ — /|<СД. Рассмотрим несколько основных мето-
методов решения этих задач.
Метод средних прямоугольников. Пусть требуется вычислить
интеграл
I=\f(x)dx,
а
где f{x) — непрерывная функция. Для простоты рассуждений огра-
ограничимся случаем, когда f(x)~^O. В основе приближенного вычисле-
вычисления определенного интеграла / лежит его геометрический смысл:
/ выражает площадь криволинейной трапеции. Разобьем отрезок
[а; Ь] на п равных частичных отрезков точками xk = а -\	^- k.
Ь — а
k = 1, п — 1. Длину каждого отрезка Axk — Xk — Xk~\ =	назо-
=	назовем шагом разбиения. На каждом частичном отрезке [**; хк-\] вы-
выберем точку |* — (Xk-i -\- Хь)/2 и вычислим /(I*) = ук. Тогда по опреде-
определению 9.1
b	n	b	n
\ f(x)dx = lim 2 f(Е*)Адс*-«- \ f(x)dx ж 2 fF
а	Дж-i-O *=1	а	*=1
236

Следовательно,
yk, (9.15)
т. е. площадь криволинейной трапеции аАВЬ приближенно равна
площади ступенчатой фигуры, заштрихованной на рис. 9.12.
В
Рис. 9.12
Формула (9.15) называется формулой средних прямоугольников.
Предположим, что существует непрерывная вторая производная
f"(x) функции f(x) на отрезке [а; Ь]. Тогда можно показать, что
вычисление интеграла / по формуле средних прямоугольников про-
производится с погрешностью, величина которой оценивается нера-
неравенством	з
А(«ХМ2-^-^-,	(9.16)
где М2= sup 1/"(*)!•
[а; Ь]
Пример 9.16. Вычислить методом средних прямоугольников с погрешностью,
ие превышающей 0,01, интеграл
dx
1+*"
Решение. Сначала определим, на какое число частей п следует разбить
отрезок интегрирования [0; 1], чтобы получить заданную точность вычислений. Най-
Найдем п из соотношения (9.16):
suP)!H*)l
suP
ft—aK
24л2
Так как f(x) ¦¦
1+х
¦, то
A+*Г ' У'~ (l+xf
sup irWI= sup 2 =2.
[0:1]	[0; 1] A+xK
237

b — a
точками Xk — a-\-	k, k—\,n, и с помощью йрямых х = Хк
п
построим п «прямолинейных» трапеций (эти трапеции заштрихованы
на рис. 9.13).
Сумма площадей «прямолинейных» трапеций приближенно равна
площади криволинейной трапеции аАВЬ, т. е.
у„_1
Т	2
^ " — *"-'
где yk = f(xk), k=l, л,—основания «прямолинейных» трапеций;
Хк — Хк- 1 = ~°	ИХ ВЫСОТЫ.
п
Таким образом, получена приближенная формула
(9.17)
а
которая называется формулой трапеций. Правая часть этой формулы
является интегральной суммой 1(п), которая при h = ..~а, ->-0
(п->-оо) стремится к данному интегралу /, т. е. точность формулы
трапеций тем выше, чем больше п. При конечном шаге разбиения
h, т. е. при конечном п, вычисления производятся с некоторой
погрешностью А (и), величина которой оценивается неравенством
WI-^^-.	(9-18)
Если задана погрешность вычислений А(п), то, пользуясь не-
неравенством (9.18), можно подобрать такое число п разбиения
отрезка [а; Ь] на частичные отрезки (или, что то же, шаг h), йри
котором приближенное вычисление определенного интеграла будет
выполнено с погрешностью, не превышающей заданную. Если по-
погрешность вычисления не задана, то при фиксированном п можно
оценить ее по формуле (9.18).
Метод параболических трапеций (метод Симпсоиа*), Данный
метод приближенного вычисления определенного интеграла основан
на замене графика подынтегральной функции дугами парабол, оси
которых параллельны оси Оу.
Разобьем отрезок интегрирования [а; Ь] точками Хо = а, х\, Х2, ¦¦¦,
хъп = Ь на 2п равных частей. Обозначим через у0, у\, ..., учп значения
функции \(х) в точках деления (рис. 9.14), Пусть щаг разбиения.
—ILfL = h, точки разбиения Хк = а-\—~а k, k = 1,2n — 1. В силу
свойства аддитивности определенного интеграла (см. § 9.4)
* Томас Симпсои A710^-1761) —английский математик.
239

Следовательно, 2
.Z4/1
25
0,01, откуда п2 >	, т. е. для вычисления интегра-
Ь — а
ла с заданной погрешностью можно принить п = 3. Шаг разбиения
1 -0 1
= ^— -т-
Вычислим значения yt —-г.—гт-, где ?t = (jc*_i -f- Xk)/2, k = 1, 3, и поместим
1 +s*
их в табл. 9.1.
Имеем
следовательно,
478
231 '
Таблица 9.1
к
1
2
3
1.
1/6
3/6
5/6
6/7
6/9
6/11
693
1
1
A<lS0U?,irW|i^L=2 24-9 108
= 0,0093.
Метод трапеций. Этот метод основан на замене графика подын-
подынтегральной функции y = f(x) ломаной линией AM\M2.4Mn-iE
(рис. 9.13).
Разобьем отрезок интегрирования [а; Ь] на п равных частей
В
238

f(x)dx = Jf(x)dx + ?f(x)dx +... + f f(x)dx.
О	'О	Л	*2«-2
Через каждые три точки Мо, М\ и' М2, М2, М3 и М4), .... М2п-2,
Мгп-1 и М2п проведены параболы, уравнения которых ук (х) = акх2 +
-\-bkX-\-Ck, k=l, п. В результате получим п криволинейных тра-
трапеций, ограниченных сверху параболами. Эти трапеции изображены
на рис. 9.14. Заменим площадь криволинейной трапеции, огра-
2п
Рис. 9.14
ничейной графиком функции y = f(x) на [а; Ь\ суммой площадей
фигур, лежащих под параболами, т. е. положим
2	х,
\ f(x)dx « \ (щх2 + Ь\х + Ci)dx + $ (а2х2 + Ь2х + c2)dx + ... +
а	хо	xi
xin
+ \ (апх2 + bnx + cn)dx.	(9.19)
Х1„-г
Вычислим интеграл:
Ct)dx = -у- (ДС1 - ДС§) + -у- («I -
¦Bа,(х|.
Ь — а
6п
Итак,
Аналогично
— Хо) =
6с) =
, , *2 + Х0 . .	.
46,—	Ь4с, 4-
Ьхх
({/о
(а2х2 + Ъ2х
=
У2).
+ У*),
240

(апх2 + bnx -\- cn)dx —
Просуммировав эти интегралы, согласно формуле (9.19), получим:
(а**2 + bkx
2
или
b
Ь —	"
k ^ 1
(9.20)
Эта формула называется формулой парабол или формулой
Симпсона.
Можно доказать, что абсолютная погрешность вычисления опре-
определенного интеграла по формуле Симпсона не превосходит
g^r.	0.21)
Заметим, что если формула Симпсона применяется для вычисле-
вычисления интегралов вида
\Pn(x)dx,
а
где Р„(х) — многочлен степени п, то при п^З sup |PAv(jc)| == 0,
(а; *]
и, следовательно, вычисления производятся без погрешности.
При приближенном вычислении определенного интеграла на ЭВМ
оценка точности вычислений по формуле (9.21 L как правило, не
применяется ввиду трудности нахождения sup |/ (х)\. В таких слу-
чаях используют правило Рунге*.
Для метода Симпсона правило Рунге основано на соотношении
л	л
|/2"~/J < A,	(9.22)
л л
где /„, /2п — приближенные значения определенного интеграла, вы-
вычисленные при разбиении отрезка интегрирования на п и 2п частей
соответственно; Д — заданная точность. При каждом последующем
приближении число отрезков разбиения удваивается. Если условие
(9.22) выполнено, за приближенное значение интеграла принима-
л	л
ется значение /2п, т. е. / = /2п ± А.
• Карл Давид Рунге A856—1927) —немецкий физик и математик.
241

Пример 9.17. Вычислить методом Симпсона с погрешностью, не превышающей
dx
0,001, интеграл
Решение. Вначале определим, на сколько частей следует разбить отрезок
интегрирования [0; 1], чтобы получить заданную точность вычислений. Так как по
условию погрешность не должна превышать 0,001, то л надо подобрать так, чтобы
выполнять неравенство
Для данного примера
IV (ЧЛ _
24
Т+7— —Tl+;?f(i-io^ + 5A
sup I/IV(*)I = 24 sup |5x4 — 10x2 + 11 = 24 • 4 = 96.
@; l]
@; 11
Итак, приближенное вычисление определенного интеграла будет выполнено с
заданной точностью:
Следовательно, можно принять л = 3, 2л = 6.
Вспомогательные вычисления запишем в табл. 9.2.
На основании формулы Симпсона (9.20) имеем
1
+ 4C6/37 + 4 + 4/5 + 36/61)) = 0,7854.
Таблица 9.2
k
0
1
2
3
0
1/6
1/3
1/2
»»=i/(i+.*i)
1
36/37
9/10
4/5
к
4
5
6
2/3
5/6
1
№-=(V0+*i)
9/13
36/61
1/2
Поскольку при п = 3 Д
2430
< 0,00045, то
\l
dx
= 0,7854 ± 0,00045.
Замечание. Так как
dx
= arctg х
= —, то, применяя метод Снмп-
о 4
сона, можно вычислить значение числа я с любой наперед заданной точностью.
В частности, при разбиении отрезка интегрирования на 2л = 6 частей
л « @,7854 ± 0,0004) • 4 = 3,1416 ± 0,0016.
242

Для сравнения отметим, что я = 3,1415...
Очевидно, что точность приближенных формул вычисления опре-
определенных интегралов возрастает с ростом п, т. е. всегда можно подо-
подобрать такое п, чтобы погрешность А вычислений определенного
интеграла не превосходила заданной.
Приближенное вычисление определенных интегралов с помощью
программируемых микрокалькуляторов и ЭВМ. Каждую из при-
приближенных формул (9.15), (9.17) и (9.20) вычисления определенных
интегралов можно рассматривать как алгоритм их приближенного
вычисления. Поэтому рассмотренные методы широко используются
для вычисления определенных интегралов на ЭВМ.
Ниже приводится программа вычисления определенных интегра-
интегралов по формуле Симпсона (см. программу 1) на программируемом
микрокалькуляторе «Электроника БЗ-34».
Адрес
коман-
команды
00
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
Нажимае-
Нажимаемые кла-
клавиши
ПО
С/П
ПА
С/П
ПВ
пп
46
ПС
ИПА
ИПВ
ПА

ипо
•1-
ПВ
пп
Код
опера-
операции
40
50
4
50
4
53
46
4
6—
6
4—
11
60
13
4L
53
Адрес
коман-
команды
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Нажимае-
Нажимаемые кла-
клавиши
46
1
ПП
32
4
ПП
32
2
БП
18
ипс
3
_^
ИПВ
X
С/П
Код
опера-
операции
46
01
53
32
04
53
32
02
5.1
18
6
03
13
6
12
50
*
Адрес
коман-
команды
32
33
34
35
36
37
38
39
40
41
42
43
44
45
Программа 1
Нажимае-
Нажимаемые кла-
клавиши
X
ипс
+
ПС
FLO
40
БП
26
ИПА
ИПВ
+
ПА
ПП
46
Код
опера-
операции
12
6[
10
4[
5Г
40
51
26
6—
6L .
10
4—
53
46
Для применения программы 1 необходимо составить подпрограм-
подпрограмму вычисления значений подынтегральной функции f (x) при условии,
что значение аргумента х находится в регистре РА.
1
Пример 9.18. Вычислить \e~"'/2dx по формуле Симпсона с погрешностью,
не превосходящей 0,00001, используя программируемый микрокалькулятор БЗ-34.
Решение. Заметим, что данный интеграл не выражается в элементарных
функциях. Для обеспечения заданной точности вычислений необходимо подобрать
такое число п разбиений отрезка [0; 1] на частичные отрезки, чтобы выполнялось
неравенство
Д(я)< sup \flv(x)\ (b~~a\ < 0,00001.
[0; 1]	180BлL
243

Так как f(x) = e ~^2, то / lv(x) = е ~^2(xA — бх2 + 3),
sup \е -(x* - 6х2 + 3)| = sup \xA - б*2 - 3| = 3.
[0;!]	[О;!]
Следовательно,
10000°
180 BлL
0,00001 =*„«
960
Для выполнения данного неравенства достаточно взять п = 4, т. е. 2п = 8.
Составим подпрограмму вычисления значений функции f(x) = e~x'/2. Так как
программа оканчивается на 45-м адресе, подпрограмму начнем с 46-го адреса:
Адрес команды
46
47
48
49
50
* 51
52
Нажимаемые клавиши
ИПА
Fx2
2
-^.
1-1
Ft?
в/о
Код операции
в—
22
2
13
0
16
52
Для вычисления исходного интеграла по приведенной выше программе 1 не-
необходимо:
1)	перевести микрокалькулятор в режим программирования, нажав клавиши
F и ПРГ;
2)	ввести программу (адреса команд 00—45) н подпрограмму (адреса команд
46—52) в память микрокалькулятора;
3)	перевести микрокалькулятор в режим автоматических вычислений, нажав
клавиши F и АВТ;
4)	перевести счетчик адресов на 00 нажатием клавйии В/0;
5)	ввести значения 2л = 8, .6 = 1, а = 0 в регистр РХ, нажав последовательно
клавиши: 8 С/П 1 С/П 0 С/П.
После останова на индикаторе высветится приближенное значение интеграла
1
/=(<Г*'/2 Ас = 0,855626.
Пример 9.19. Составить на ФОРТРАНе программу вычисления методом Симп-
сона интеграла $ лг In (I + x)dx с точностью 0,001.
о
Решение. Запишем ФОРТРАН-программу вычисления определенного инте-
ь
грала \ f(x)dx по формуле Снмпсона и подпрограмму вычисления подынтегральной
а
функции х\п A -\-х) с заданной точностью е (отметим, что оценка точности вычисле-
вычислений в программе выполняется по правилу Рунге):
READ A,1) А. В, EPS. N
1	FORMAT CF5.3.I5)
Т - F (А) + F (В)
10-0
2	DN-N
Н - (В-А) /DN
Т1=0.
Т2-0.
N1 =N-2
Х- А
DO3I-1.N1.2
244

Т1 =Т1 +F(X)
T1=T1+F(X)
S- (Т+4.-Т1 + 2.-Т2) -Н/3.
IF (IO.EQ.O) GO TO 4
IF (ABS((S1-S)/15.1.LT.EPS) GOTO5
4	10 = 1
SI =S
N = N «2
GO TO 2
5	WRITE C,6) S
6	FORMAT BX,' S - ', F6.3)
STOP
END
FUNCTION F(FX)
F-FX. ALOG (FX + 1.)
RETURN
END
Входные параметры: А — нижний предел ннтегрнровання; В — верхний предел
ннтегрнровання; EPS — заданная точность; N — начальное чнсло (четное) точек де-
деления отрезка [а; Ь].
Для данного примера /1=0, В = 1, EPS = 0,001, N = 2.
Результат счета: / = 0,250.

10. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
10.1. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР
В ПРЯМОУГОЛЬНОЙ СИСТЕМЕ КООРДИНАТ
Из геометрического смысла определенного интеграла следует,
что если f(x) > 0 Vx 6 [а; Ь], то площадь криволинейной трапеции,
ограниченной кривой y = f(x), осью Ох и прямыми х = а, х — Ь
(рис. 10.1), может быть вычислена по формуле
A0.1)
причем S>0. Если /(х)<0 V*6{a; b], то и \f(x)dx^0, a<b
]	а
У и
О
Рис. 10.2 ¦
(рис. 10.2). Следовательно, в этом случае
S = | \f(x)dx\ = -\f[x)dx = - \ydx.
A0.2)
Если же криволинейная трапеция ограничена кривой х = ср(у),
осью ординат Оу и прямыми у = с, у = d (рис. 10.3), то ее площадь
определяется формулами:
d	d
если <p(y)>0 Vy6[c; d] (рис. 10.3, а), и
если cp(y)<0 Vy6[c; d] (рис. 10.3, б).
246

Если подынтегральная функция f(x) конечное число раз меняет
знак на отрезке [а; Ь], то интеграл A0.1) равен алгебраической
сумме площадей соответствующих криволинейных трапеций, лежа-
лежащих над осью Ох (со знаком « + ») и под этой осью (со знаком « — »)
У,
о
d
с
к
Рис. 10.3
(рис. 10.4). Для того чтобы получить общую площадь заштрихован-
заштрихованной фигуры (см. рис. 10.4), отрезок интегрирования [а; Ь] надо раз-
разбить на частичные отрезки, на которых функция f(x) сохраняет знак,
и применить формулы A0.1), A0.2). Тогда
S = -\f(x)dx + [f(x)dx- \f(x)dx + \ f(x)dx.
Hi
0
C2 , C3
!
b
Рис. 10.4
Если надо вычислить площадь фигуры, ограниченной линиями
у = f{x), у = g(x), х = а, х = Ь, то эту площадь рассматривают как
разность площадей дв)ус криволинейных трапеций аАгВъЪ и аА\В\Ъ
(рис. 10.5). В этом случае можно воспользоваться одной из формул:
S = \(f(x)-g(x))dx,
а
если f(x)^g{x) V*6[a; b] (рис. 10.5, а), или
S = \(g(x)-f(x))dx,
а
если g(jc)>/(jt) V*e[a; b] (рис. 10.5, б).
В случае, когда разность ^(jc) — g(x) не сохраняет знак на от-
247

Рис. 10.5
резке [а; 6],этот отрезок разбивают на частичные отрезки, на каждом
из которых функция f(x) — g(x) сохраняет знак. Например, для слу-
случая, изображенного на рис. 10.6, площадь заштрихованной фигуры
находится по формуле
S = \ (f(x) - g(x))dx + \(g(x) - f(x))dx + \ (f(x) - g(x))dx.
а	с	d
Пример 10.1. Вычислить площадь фигуры, ограниченной косинусоидой y = cosx
и осью Ох при условии 0<ж<я (рис. 10.7).
Рис. 10.6
--COSX
П X
Рис. 10.7
Решение. Так как cos х :> 0 V х б [0; я/2] и cos х < 0 V х б [я/2; я], то
л/2	л	л
S = Si + S2 = \ cos xdx + I \ cos xdx\ =\ |cos x\ dx.
0	n/2	6
Поскольку
л/2
Si = \ cos xdx = sin x
Л/2
= sin -^	sin 0=1,
¦IS
cos xdx
sin я — sin -рг-
1-11 = 1,
л/2
то S = 1 + 1 = 2.
248

Пример 10.2. Вычислить площадь фигуры, ограниченной линиями х = 0, х = 2,
у = 2х — х\ у = 2* (рис. 10.8).
Решение. Функция у — 2х — х2 достигает своего наибольшего значения на
отрезке [0; 2] при х= 1, функция 2* ^ 1 на отрезке [0; 2], т. е. 2х > 2л; — дг* при
0 ij х ^ 2. Тогда требуемую площадь находим по формуле
2
'-Bх — x2))dx =
2х
In 2
-('-§)
In 2
3 '
0'	1 2 X
Рис. Ю.8
-2;
Пример 10.3. Определить площадь S части круга х2 + У2 < 5(* > 0 Г) у > 0),
ограниченной кривыми i/2 = 4ж, х2 = 4у (рис. 10.9).
Решение. Решив систему уравнений
У2 = 4л;,
найдем точку А(\; 2) пересечения окружности хг + У2 = 5 (л; > 0 П г/ > 0) и параболы
</2 = 4х. Аналогичным образом, из системы
ж2 + и2 = !
определим координаты точки В пересечения окружности х2 + у2
и параболы хг = Ау. Получим точку ВB; 1).
Для вычисления искомой площади применим формулу
2
где fl(x)=—; f2(x) =
Следовательно,
1 5 , . 2
_+_(arcsm__
249

1 \ 8,1 2,5	3
Если криволинейная трапеция ограничена линией, заданной урав-
уравнениями в параметрической форме x = x(t), y = y(t), где <i<<<<2,
осью Ох и прямыми х = а, х = Ь, причем x(ti) — a, x(ti) = b, то ее
площадь S при y(t)^O вычисляется по формуле
S~\y{t)x'(t)dt,
A0.3)
которая получена из формулы A0.1) заменой переменной x = x(t),
y = y(t), dx = x'(t)dt. Пределы tu t2 определяют из уравнений а =
{U\b {h)
Пример 10.4. Найти площадь эллипса (рис. 10.10), используя его параметри-
параметрические уравнения х = a cos t, y = bs\nt, 0 < t < 2я.
Решение. Ввиду симметрии эллипса достаточно вычислить площадь его
четвертой части ОВА, расположенной в первом квадранте:
Сделаем замену переменной, воспользовавшись параметрическими уравнениями
эллипса: у = Ь sin t, х = a cos t. Тогда dx = — a sin tdt. Если Х\ = 0, то f i = я/2, если
Хч = а, то ti = 0. Следовательно,
а	0	л/2
S = 4\ydx= — 4аЬ \ sin2 tdt =+2ab \ (\—cos2t)dt =
О	п/2	0
/1	\ I"/2
= 2ай( t— — sin2n I =яай.
Отсюда при а = b—R получим формулу площади круга: Si =я7?2.
Пример 10.5. Вычислить площадь фигуры (рис. 10.11), ограниченной осью Ох
и одной аркой циклоиды
у = а(\ — cos t),
Решение. По формуле A0.3) имеем
2я
S = \а{\ — cos t)a(\ — cos t)dt = a2 \ A — cos tfdt
2л	2п	2я
= a2{ \ dt — 2 5 cos ta* + \ cos2 *<«) = a2( (t — 2 sin *)
ooo	V
к°2яа Л
Рис. 10.10
Рис. 10.11
250

2л
Ц- y\ 0 + cos 20d<) = а2Bя + y(< + у sin 2Л |2Л = Зяа2.
10.2. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР
В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ
Пусть требуется вычислить площадь фигуры, ограниченной ли-
линией /, заданной в полярной системе координат {О, г, ф} уравнением
г = г(ф), а < ф ^ р. За базовую фигуру в полярной системе коорди-
координат принимается криволинейный сектор — фигура, ограниченная
линией г = г(ф) и радиусами-векторами ф = а, ф = Р (рис. 10.12).
При этом криволинейный сектор будем считать правильной фигурой,
т. е. такой, что любой луч ф = ф*, а < ф* < Р, исходящий из полюса
О, пересекает линию г =<г(ф) не более, чем в одной точке. Будем
также предполагать, что функция г = г(ф) непрерывна на отрезке
[«; Р].
Для вычисления площади криволинейного сектора ОАВ приме-
применим алгоритм составления интегральной суммы с последующим
предельным переходом к определенному интегралу (см. § 10.1).
1.	Разобьем отрезок [а; р] на п частичных отрезков точками
а = фо<ф1 < ... < ф„ = Р. ОбоЗНаЧИМ АфА = ф* — фА-Ь k=\, П.
Проведем лучи ф = ф/*, k = l, п. Тогда криволинейный сектор ОАВ
разобьется на п частичных криволинейных секторов (рис. 10.13).
2.	На каждом частичном отрезке [ер*; q>*_i],. k=l, n, выберем
произвольным образом точку 9* и найдем значения функции г(ф)
в этих точках: rk = r(Qk), k=l, n.
3.	Предположим, что на каждом из частичных отрезков [q>*_i;
Ф*] функция г = г(ф) постоянна и совпадает со значением rk = г(Э*).
Тогда каждый частичный криволинейный сектор можно заменить
круговым сектором с радиусом г* = г(9*) и центральным углом Дф*
(см. рис. 10.13). Площадь такого кругового сектора вычисляется
по формуле
За площадь S криволинейного сектора ОАВ примем площадь
фигуры, состоящей из п частичных круговых секторов:
Рис. 10.12	Рис. 10.13

Xг2
A0.4)
Приближенное равенство A0.4) тем точнее, чем меньше отрезки
[ф*-ь ф*], т. е. чем больше п. Правая часть равенства A0.4) является
интегральной суммой для непрерывной функции -»-г2(ф) на отрезке
[«;
Р]
4. За точное значение площади S криволинейного сектора ОАВ
примем предел интегральной суммы A0.4) при Я = тах{Дф*} -»-0:
S= lim -
(П-КОО)
Таким образом, площадь криволинейного сектора вычисляется
по формуле
A0.5)
Пример 10.6. Вычислить площадь фигуры, ограиичеииой кардиоидой г = а(\ +
+ cos ф) (рис. 10.14).
Решение. Кардиоида симметрична относительно полярной оси, следовательно,
искомая площадь равна удвоенной площади криволинейного сектора АВО. Дуга АВО
описывается концом полярного радиуса г при изменении полярного угла от 0 до-я.
Поэтому, согласно формуле A0.5),
л	л
= 2 • -Ц r2d<f = аД A + cos ц,)Чц, =
= а2(|- Ф + 2 sin Ф + -L sin 2Ф) |"о = -| яа2.
Пример 10.7. Вычислить площадь фигуры, ограиичеииой лемнискатой Бериулли
?J VA
Решение. Так как переменные хну входят в исходное уравнение в четных
степенях, то кривая, ограничивающая фигуру, симметрична относительно осей ко-
координат Ох и Оу. Следовательно, для решения задачи достаточно вычислить площадь
четвертой части фигуры, расположенной, например, в первом квадранте, и получен-
полученный результат увеличить в четыре раза.
Запишем уравнение лемнискаты Бериулли в полярной системе координат. Тогда
х = г cos ф, у = г sin ф и уравнение данной кривой примет вид
(л2 cos2 ф + л2 sin2 фJ = а2(л2 cos2tp — г2 sin2 ф)=*-/'2 = а2 cos 2ф
или
Первому квадранту декартовой системы координат соответствует изменение
полярного угла ф от 0 до я/4 (рис. 10.15). Используя формулу A0.5), получаем
252

= 2а2 -s- sin 2Ф
= а2( sin —	sin 0\ = а2.
Пример 10.8. Вычислить площадь фигуры, ограниченной окружностями л =
= Зд/2а cos ф и г = За sin ф.
Решение. Решив совместно данные уравнения, найдем точку А пересечения
окружностей:
т = 3~\J2a cos a>A	r~	г-	г—
г = За sin Ф ^ ) =^ tg Ф = д/2, Ф = arctg -fa л = ад/б.
Итак, 4(arctg-\/2; ад/б~).
Построив эти окружиости (рис. 10.16), заметим, что искомая площадь S фигуры
равна сумме площадей криволинейных секторов ОСА и ОВА. Дуга ОСА описывается
концом полярного радиуса окружиости г = За sin ф при изменении полярного угла ф
от 0 до arctg-^ дуга ОВА — концом полярного радиуса окружиости г = Зд/га cos ф
при изменении ф от arctg-y2 до я/2. Поэтому
Рис. 10.16
253

1 — COS 2ф
л/2
dq> + 9а2
1 + cos 2ф
2
10.3. ВЫЧИСЛЕНИЕ ДЛИНЫ ДУГИ КРИВОЙ
Длина дуги плоской кривой в прямоугольной системе координат.
Пусть функция у = f(x) определена и непрерывна на отрезке [а; Ь]
и кривая / — график этой функции (рис. 10.17). Требуется найти
длину дуги плоской кривой /, заключенной между вертикальными
прямыми х = а и х = Ь.
У
ч
0
У-№>
'¦¦¦¦-¦ \ь.
7\
О''К )
S
*¦ х
'Я
Рис. 10.17
Определим вначале, что мы будем понимать под длиной дуги АВ
плоской кривой /. Для этого разобьем отрезок [а; Ь] произвольным
образом на п частей точками а = хо <L Х\ < ... <^хп = Ь. Обозначим
= Xk — Xk-\, k=\, п. Через точки л;,-, /= 1, п, проведем верти-
вертикальные прямые, параллельные оси Оу, до пересечения с кривой /.
Тогда дуга АВ разобьется на п частей. Соединив каждые две соседние
точки разбиения кривой / отрезками (хордами), получим ломаную
АМ\М2...Мп-\В, вписанную в дугу АВ. Обозначим длину ломаной
через 1п:
ln = \AMx
\Mn-iB\= 2 A/ft,
*=i
где \lk — длина хорды, стягивающей дугу Mk-\Mk.
Длина ломаной является приближенным значением длины дуги
АВ (I ж 1„). Очевидно, что если увеличивать число п точек разбиения
отрезка [а; Ь] на частичные отрезки так, чтобы длина максимального
из них стремилась к нулю, то длина вписанной ломаной стремится
к длине дуги кривой АВ. Если существует конечный предел /„ при
X = max{Axk}—»-0, то этот предел принимается за длину дуги /, а саму
[а;Ь]
254

дугу называют спрямляемой:
I = lim 2 Alk.
A0.6)
Если конечный предел /„ не существует, то и длина дуги не сущест-
существует, а сама дуга называется неспрямляемой.
Покажем теперь, что если функция f(x) на отрезке [а; Ь] имеет
непрерывную производную f'(x), то кривая / — спрямляемая, и вы-
выведем формулу для вычисления ее длины.
Вычислим длину стягивающей хорды Mk-iMk. Так как.Мк~\(хк-\;
*_0), Mk(xk- f(xk)), то
Mk = I Mk _ iMk I =	f^
По теореме Лагранжа (см. § 5.14) имеем
-.; хк[
Следовательно,
Подставляя полученное выражение в формулу A0.6), получаем
I = lim S л/
В правой части формулы A0.7) стоит интегральная сумма для
функции -\J\ +(f МJ на отрезке [а; Ь]. Предел такой суммы суще-
существует и равен определенному интегралу от.этой функции на от-
отрезке [а; Ь\.
I = lim S s/l+(f'(b)JAxk Ш Nl+(f>(x)fdx.
Итак, если функция f(x) имеет на отрезке [а; Ь] непрерывную
производную, то дуга АВ —• спрямляемая и ее длина / вычисляется
по формуле
A0.8)
Пример 10.9. Вычислить длину окружности х2 + у2 = R2-
Решение. Найдем сначала длину четвертой части окружности, лежащей в
первом квадранте. Уравнение дуги этой окружности, лежащей в первом квадранте,
имеет вид у = ~\JR2 — х2, 0 < х <¦ R. Отсюда
У'= —
Следовател ьно,
R
R2-/'
-dx--
= R arcsin —
255

Итак, длина всей окружности / = 2л/?.
Найдем теперь длину дуги плоской кривой в случае, когда урав-
уравнение кривой задано параметрически x = x(t), y = y(t), t?[t\; <г],
где x(t), y(t) — непрерывные функции с непрерывными производ-
производными, причем x'{t)=t=0 V/?[fi; t2].
Для вычисления длины дуги кривой воспользуемся формулой
A0.8), предварительно выполнив замену переменной:
Имеем
/ =
'x = y't/x't.
или
A0.9)
Пример 10.10. Вычислить длину дуги циклоиды х = a(t — sin t), у = а(\ — cos t),
0</<2л (см. рис. 10.12).
Решение. На основании формулы A0.9) имеем
2я 		2я
/ = \ Va2(l — cos tf + a2 sin2 tdt = a\ фA — cos t)dt =
2я
1Л = 4а + 4а = 8а.
Если пространственная кривая задана параметрическими урав-
уравнениями x = x(t), y = y(t), z = z(t), ti^t^t2, где x{t), y(t), z{t) —
непрерывные функции, имеющие непрерывные производные на от-
отрезке [t\; <г], то длина дуги этой кривой определяется по формуле
(шло)
Пример 10.11. Вычислить длину дуги винтовой линии х = a cos t, y = asint,
г = amt, 0 < t < 2л.
Ре ш е и и е. Из параметрических уравнений находим :xi = —a sin t,yi = a cos t,
z!=am. Подставляя полученные значения в формулу A0.10), имеем
2я 	\		2я
/ = \ Vfl2 sin2 t + a2 cos2 t + а*т2Ш = а\ ф + m2dt = 2na-\Jl + тг.
Длина дуги кривой в полярной системе координат. Пусть кривая
задана в полярной системе координат уравнением г = г(ф) V ф 6 [a; P]-
Предположим, что л(ф) и г'(ц>) непрерывны на отрезке [а; р]. Покажем,
что эту кривую можно задать параметрически. Действительно, между
декартовыми и полярными координатами существует следующая
зависимость:
256

Х = Г COS ф
у = г sin ф.
Принимая во внимание, что г = г(ф), получаем
Х = г(ф)С08ф, у -г
y = r(<p)sinq> TCl '
Эти уравнения можно рассматривать как параметрические урав-
уравнения кривой и для вычисления длины дуги применить формулу
A0.9). Найдем производные от л: и у по параметру ф:
ЛГф = Г COS ф — Г Sin ф,
у'у = г' Sin ф + Г COS ф
Следовательно,
J + WJ = г» + (r'f.
/ =
A0.11)
Пример 10.12. Вычислить длину кардиоиды r = a(l+cos(p) (см. рис. 10.14).
Решение. Изменяя полярный угол ф от 0 до л, получим половину искомой
дуги. На основании формулы A0.11) с учетом того, что г' = — a sin cp и ri + (r'J =
= a2(l + cos фJ + a2 sin2 ф = 2a2(l -j- cos ф) = 4a2 сов2(ф/2), имеем
я
'fd(f = 4a[ cos -|-^ф = 8a sin -|-
Дифференциал длины дуги. Длина дуги кривой определяется
формулой
где y = f(x) V х? [а; Ь]. Предположим, что в этой формуле нижний
предел интегрирования остается постоянным, а верхний изменяется.
Обозначим верхний предел буквой х, а переменную интегрирования
буквой t. Длина дуги будет функцией верхнего предела:
Согласно теореме 9.4, функция 1{х) дифференцируема, а ее про-
производная определяется формулой
Отсюда дифференциал дуги dl = l'(x)dx или
Так как у' = dy/dx, то
9 Зак. 1270
257

т. е.
dl2 = dx2 + dy2
(аналог теоремы Пифагора).
В § 7.4 формулы дифференциала дуги были получены при иных
предположениях. Геометрический смысл дифференциала объяснен
там же.
Воспользовавшись свойством интеграла от дифференциала функ-
b
ции, получим еще одну формулу для вычисления длины дуги l = \dl.
а
10.4. ВЫЧИСЛЕНИЕ ОБЪЕМОВ ПРОСТРАНСТВЕННЫХ ТЕЛ
Вычисление объемов тел по известным поперечным сечениям.
Пусть дано тело Т, ограниченное замкнутой поверхностью, и изве-
известна площадь любого его сечения плоскостью, перпендикулярной
к некоторой прямой, например к оси абсцисс (рис. 10.18, а). Эти
Рис. 10.18
сечения будем называть поперечными. Положение поперечного се-
сечения определяется абсциссой точки его пересечения с осью Ох.
Вообще говоря, с изменением х площадь S поперечного сечения
будет изменяться, т. е. является некоторой функцией от х. Обозна-
Обозначим ее S(x). Функцию S(x) будем считать непрерывной на отрезке
[а; Ь], где а и ft — абсциссы крайних сечений тела Т.
Для вычисления объема V тела Т применим алгоритм составления
интегральной суммы и предельного перехода к определенному ин-
интегралу.
1. Разобьем отрезок [а; Ь] на п частичных отрезков точками
а = х0 <Z Xj <: х2 <.... <хп-\ <Хп = Ь. Обозначим Ахк = хк — хк~\,
X = maxjAxft}, k = \, п. Через точки разбиения Xk, k = 1, п, проведем
[а;*]
плоскости, перпендикулярные к оси Ох. Семейство плоскостей х =
— Xk, k—l, п, разобьет данное тело Т на слои, толщина каждого
из которых равна Ал:*, k = \, п.
258

2.	На каждом из частичных отрезков [xk-й Xk\ k=l, n, выбе-
выберем произвольным образом точку |* и найдем значения S(|*) функ-
функции S(x) в этих точках.
3.	Предположим, что на каждом из частичных отрезков [лг*_ь
Хк] функция S = S(x) постоянна и совпадает со значением S(?*).
Тогда каждый слой тела Т представляет собой прямой цилиндр с
основанием S(|s) и образующими, параллельными оси Ох. Объем
такого частичного прямого цилиндра вычисляется по формуле
где Ал:* — высота частичного цилиндра.
Объем V всего тела Т приближенно равен объему фигуры, со-
состоящей из п ступенчатых частичных цилиндров (см. рис. 10.18. б):
У» Z AV*= Z S(
Очевидно, что последнее приближенное равенство тем точнее,
чем меньше диаметр разбиения отрезка [a; b] X = {A)
4. За точное значение искомого объема примем
V=\im 2
Ji—0 к=\
Заметим, что сумма 2 S(|*)Ajc* является интегральной суммой
для непрерывной функции S(x) на отрезке [а; Ь]. Следовательно,
(
Таким образом, объем тела, заключенного между двумя плоско-
плоскостями х = а и^ = (/, в случае, если площадь сечения, проведенная
перпендикулярно к оси Ох, есть известная функция от х: S = S(x)
V*6[a; b], вычисляется по формуле
= \S(x)dx.
A0.12)
Рис. 10.19
259

U2
Пример 10.13. Найти объем тела, ограниченного эллипсоидом —? + -^ -\	т = 1.
аг Ь* с'
Решение. Пересечем эллипсоид плоскостью х = Л. В сечеиии получим эллипс
II2	~2
й2A-Л2/а2) ' с2A-А2/а2)
с полуосями byl—А2/а2 и c-yl—Л2/а2 (рис. 10.19), площадь поперечного сече-
иия которого равна nab (см. § 10.3, пример 10.12). Следовательно, для данного
случая площадь поперечного сечеиия эллипса
S = S(h) = nbc(\-h2/a2).
Искомый объем тела определим по формуле A0.12), в которой заменим х иа Л:
= J S(h)dh=
nbc(\
= \nabc.
При а = 6 = с — г получим шар радиусом г, объем которого V=-z-n.r3.
3
Пример 10.14. Найти объем клина, отсеченного от кругового цилиидра плоско-
плоскостью, проходящей через диаметр его осиоваиия и наклоненной к основанию под
углом а. Радиус осиоваиия равен R (рис. 10.20).
Решение. Примем за ось Ох диаметр осиоваиия кругового цилиидра, по которому
секущая плоскость пересекает основание, а за ось Оу — перпендикулярный ему диа-
диаметр осиоваиия. Тогда уравнение окружности осиоваиия х +y2 = R2.
Площадь сечеиия ABC, отстоящего иа расстоянии х от начала координат О,
a/?3
Следовательно, искомый объем клина
R	R
V = 2^-1 у2 tg adx = tg Л (R2 - x>)dx = -| tg
Вычисление объемов тел вращения. Рассмотрим тело, образован-
образованное вращением вокруг оси Ох криволинейной трапеции аАВЬ, огра-
ограниченной кривой y = f(x), осью Ох и прямыми х = а, х = Ь .(рис.
10.21). Если пересечь это тело плоскостями, перпендикулярными
У'1
У'
0
у fix
(
X
\
\ ш
ш
V/
-7"
%[
ух\
щ
1
э
л
ь
J
л
Рис. 10.21
260

к оси Ох, получим круги, радиусы которых равны модулю ординат
у = f(x) точек данной кривой. Следовательно, площадь сечения
рассматриваемого тела
Применяя формулу A0.12), получаем формулу для вычисления
объема тела вращения
= n\y2dx = n\(f(x)Lx.
A0.13)
Если тело образовано вращением вокруг оси Оу криволинейной
трапеции cCDd (рис. 10.22), то его объем вычисляется по формуле
4
где х = <р(у),
у2
+ ^
,— уравнение кривой CD.
х2
Пример 10.15. Вычислить объем тела, образованного вращением эллипса —
п
j
= 1 вокруг оси Ох.
Решение. По формуле A0.13) имеем
а	а
1/ of 2j	J Яб! , j	,. ,	2л62 / ,	Х3\ \"
V = 2 \ ny2dx = 2\ —— (а2 — х2) dx = —— [а2х	—) =
J	Jfl	а \	3/1о
о
Пример 10.16. Вычислить объем тела, образованного вращением вокруг оси Ох
фигуры, ограниченной кривой у = е" (дс<0) (рис. 10.23).
Решение. Согласно формуле A0.13), получим
-S
e2xdx=Yl
Рис. 10.23
Рис. 10.24
261

Пример 10.17. Вычислить объем тела, образованного вращением вокруг оси Ох
фигуры, ограниченной одной аркой циклоиды x = a(t — sin t), y = a(\—cos t), 0<
<<<2л, и осью Ох (рис. 10.24).
Решение. Для вычисления объема данного тела воспользуемся формулой
A0.13):
2яа
V = л \ y2dx.
о
Сделаем в этом интеграле замену переменной, положив x = a(t — sin t), y = a(l —
— cos 0- Тогда dx = a(\ — cos t)dt. Если x\ = 0, то t, = 0, при *2 = 2ла <2 = 2л.
С учетом произведенной замены имеем:
2яа	2л
V = л \ y2dx = л \ а2A — cos tfa(\ — cos t)dt =
о	о
2я	2л
= яа3 5 A — cos <K<ft = па3 \ A — 3 cos t + 3 cos2 < — cos3 <)<*< =
о
2л	"	2л
= ла3((< — 3 sin ОI " + 3 [ ' + °°S 2- dt = [ A — sin2 О d (sin 0) =
I о	J	2	J
о	о
10.5. ВЫЧИСЛЕНИЕ РАБОТЫ ПЕРЕМЕННОЙ СИЛЫ
Пусть материальная точка движется по прямой линии под дейст-
действием некоторой переменной силы F. Перемещение этой точки зада-
зададим вектором s и предположим, что направление силы совпадает
с направлением перемещения (F||s). Обозначим через |F| и |s|
длины векторов F и s.
Если на всем пути сила F постоянна, то, как известно из меха-
механики, работа А= |F| |s|.
Рассмотрим случай, когда сила F сохраняет постоянное направ-
направление (F || s), но меняется по модулю (|F| Ф const). Вычислим работу
этой переменной силы. За ось Ох примем прямую, вдоль которой
движется материальная точка. Пусть начальная и конечная точки
пути имеют абсциссы а и b(a<cb) соответственно. В каждой точке
отрезка [а; Ь] модуль силы принимает определенное значение и явля-
является некоторой функцией абсциссы, т. е |F| =F(x). Таким образом,
F=|F|i = F(x)i, s = (b — a)\, |s|=6 —a.
Будем считать функцию F(x) непрерывной. Для нахождения ра-
работы переменной силы вновь используем алгоритм, основанный на
составлении интегральной суммы и предельном переходе к опреде-
определенному интегралу.
1. Разобьем отрезок |s| = \а; Ь\ на п частичных отрезков точками
Хк: a = xo<.xi <Ar2< — <Lxn = b, где Ахк — Хк — хк-\, k=\, /г,—
длина /г-ro частичного отрезка. Как известно, работа на всем пути
равна сумме работ на малых его участках. Обозначив работу на
всем пути через А, а работу на частичном отрезке [x*-i; Xk] через
A получим
262

А = 2 АЛ*.
*=i
Если отрезки [хк-\\ хк] брать достаточно малыми, то на каждом
таком отрезке можно считать |F| «const.
2.	Выберем на каждом частичном отрезке [хк-\\ хк] произвольную
точку Ik и найдем значение функции F(x) в точке gft.
3.	Предположим, что на каждом частичном отрезке модуль силы
имеет постоянное значение, равное значению F(x) в точке ?*: |F*| =
= F(lk)- При этом предположении работа силы на отрезке [хк~й лг*1
Работа переменной силы F, совершаемая на всем пути |s| =
— b — а,	п
Л«Л„=2 F(b)Axk.
Очевидно, что Ап представляет собой интегральную сумму, со-
составленную для непрерывной на отрезке [а; Ь] функции F(x).
4. Предел А„ при X = тах{Лл:*}->-0 в силу предположения о не-
прерывности функции F(x) существует и выражает работу перемен-
переменной силы на прямолинейном пути от точки а до точки Ь:
A0.14)
Л = lim 2 F(lk)Axk Ш \ F(x)dx.
Пример 10.18. Вычислить работу, затраченную на растяжение пружины на
0,1 м, если известно, что для удлинения ее на 0,05 м нужно приложить силу в 2 Н.
Решение. По закону Гуна модуль силы F, растягивающей или сжимающей
пружину, пропорционален этому растяжению или сжатию, т. е. |F| = kx, где х —
величина растяжения или сжатия. Из условия имеем, что 2 = k ¦ 0,05, откуда k = 40.
Следовательно, | F^ = F(x) = 40 х.
Согласно формуле A0.14), получаем
0,1
А = \ Wxdx = 20л2 I8-1 = 0,2 Дж.
10.6. ВЫЧИСЛЕНИЕ РАБОТЫ
ЭЛЕКТРОДВИГАТЕЛЯ ПЕРЕМЕННОЙ МОЩНОСТИ
Рассмотрим теперь другую задачу на отыскание работы. Найдем
работу, совершенную двигателем за промежуток времени Д< =
= [а; Ь], если его мощность в момент времени t равна N(?). Как из-
известно, при постоянной мощности двигателя N его работа А = Nht.
Воспользуемся алгоритмом составления интегральной суммы и
предельного перехода к определенному интегралу.
1.	Разобьем временной отрезок [а; Ь] на п частичных отрезков
[tk-i\ tk], k = l, п. Обозначим Atk = tk — f*_i, k=l, n.
2.	Выберем на каждом частичном отрезке произвольным образом
точку т*: tk~\ ^ т*^ tk.
3.	Будем считать мощность на каждом из частичных отрезков
постоянной и равной N{xk). Тогда
263

6=1
4. Считая функцию N(t) непрерывной и переходя к пределу при
А, = тах{Л^}->*0, получаем
A = \N{t)dt.	A0.15)
а
Пример 10.19. Вычислить работу и среднюю мощность переменного тока за
промежуток времени [0; 2л/ш], если сила тока определяется формулой / = /о sin Ы,
где /о — максимальное значение тока; ш — круговая частота; t — время, а сопротивле-
сопротивление цепи равно R.
Решение. Известно, что мощность постоянного тока выражается формулой
N = PR, поэтому, согласно формуле A0.15), работа переменного тока
2я/щ	2я/ш
л	г2п f ¦ 2 iji >2n f 1—COS2@<	ilRn
A — HR \ sin-1 atdt = I%R \ 	~	dt =
= HR [
@
о	о
Средняя мощность переменного тока
А	№
ср 2л/ш	2 '
10.7. ВЫЧИСЛЕНИЕ СИЛЫ ДАВЛЕНИЯ ЖИДКОСТИ
Пусть пластинка, имеющая вид криволинейной трапеции, погру-
погружена вертикально в жидкость, плотность которой р, таким образом,
что ее боковые стороны параллельны поверхности жидкости и нахо-
находятся ниже ее уровня на расстояниях а и b соответственно (рис.
10.25). Требуется определить силу давления жидкости на пластинку.
Если пластинка находится в горизонтальном положении на глу-
глубине h от поверхности жидкости, то сила давления Р жидкости на
эту пластинку будет равна весу столба жидкости, основанием кото-
которого является данная пластинка, а высотой — глубина h, т. е.
P = gphS,	A0.16)
где g = 9,8 м/с2; S — площадь пластинки.
Если же пластинка погружена в жидкость вертикально, то давле-
давление жидкости — сила давления на единицу площади — изменяется
с глубиной погружения.
При решении задачи будем учитывать, что по закону Паскаля
давление в жидкости передается одинаково по всем направлениям,
в том числе и на вертикальную пластинку.
Выберем систему координат так, как показано на рис. 10.25.
Пусть уравнение кривой АВ имеет вид у = f(x), где функция f(x)
непрерывна на отрезке [а; Ь].
Для нахождения силы давления снова используем алгоритм
составления интегральной суммы и предельного перехода к опреде-
определенному интегралу.
1. Разобьем отрезок [а; Ь] на п частичных отрезков [Xk-i; Xk]
точками а = х0 < х\ < ... <Cxn-i <хп = Ь. Обозначим
264

— Xk-u k = \, п. Проведем через точки х0, Х\, ..., хп прямые, парал-
параллельные оси Оу, которые разобьют пластинку на п малых горизон-
горизонтальных полосок.
2. Выберем на каждом частичном отрезке произвольным образом
точку ?*6[**-i; Xk\ k=\, п. Тогда площадь S* малой горизонталь-
горизонтальной полоски
3. Считая, что все точки каждой элементарной пластинки нахо-
находятся на одной глубине h = ?*, значение силы давления на нее можно
вычислить по формуле A0.16):
Просуммировав найденные значения АР*, k = \, n, получим при-
приближенное значение силы давления жидкости на всю пластинку:
k=\
Точность этого приближенного равенства тем больше, чем меньше
длины частичных отрезков [jc*	¦; **].
4. За точное значение Р силы давления жидкости на пластинку
принимается предел Р„ при Я, = та{А}0
: ,	I";
Так как Р„ представляет собой интегральную сумму для непре-
непрерывной функции pxf(x) на отрезке [а; Ь], то указанный предел суще-
существует и выражается определенным интегралом
= g\Pxf(x)dx.
A0.17)
Если в жидкость вертикально погружена пластинка А1В1В2А2
(рис. 10.26), ограниченная прямыми х = а, х = Ь и кривыми у =
Рис. 10.25
в.
265

= t/i(jc), у = У2(х), то сила давления на эту пластинку вычисляется
по формуле
*
P = g\px(y2 — y\)dx.	A0.18)
а
Пример 10.20. Пластинка, имеющая форму эллипса, наполовину погружена в
жидкость (вертикально) таким образом, что одна из осей эллипса (длиной 20) лежит
на поверхности. Вычислить силу давления жидкости на каждую из сторон этой
пластинки, если длина погруженной полуоси эллипса равна о, плотность жидкости
р= 1200 кг/м3.
Решение. В силу симметрии эллипса достаточно найти силу давления на
одну из сторон его четвертой части и удвоить получеиный результат. Выберем систему
координат, как показано иа рис. 10.27. Тогда уравнение эллипса
х2 . о2 .
Вычислим силу давления по формуле
A0.17) при а = 0, й = а:
Р = -j gpo2p = -=- g • 1200о2р =
= 800о2р = 800o2pg.
Учитывая, что gas 9,8 м/с2, получаем Я = 7840о2р Н.
Пример 10.21. Вычислить силу, с которой вода давит на плотину, имеющую
форму равнобочной трапеции, верхнее основание которой а — 70 м, нижнее — Ь =
= 50 м, а высота Я = 20 м. Плотность воды 1000 кг/м3.
Решение. Выберем систему координат так, как показано на рис. 10.28.
п-70
20
~\ С (О; 70}
ВB0;60)
Рис. 10.28
Координаты точек А, В и С легко определяются из. чертежа: АB0; 10), ВB0; 60),
С@; 70). Уравнение линии О А имеет вид о = 0,5*, а уравнение линии ВС — о =
= -0,5*+70.
По формуле A0.18) при а = 0, й = 20, yl=0,5x, «/2 = 0,5* + 70 вычисляем
20	20
P = gp\x(—0,5x + 70 — 0,5*)d* = gp \ (—х2 + 70*)d* =
(JC3	Z2\ I2"
— 4-+70 4-) = 114,97 • 106H.
a	2 / |o
266

10.8. ВЫЧИСЛЕНИЕ СТАТИЧЕСКИХ МОМЕНТОВ,
МОМЕНТОВ ИНЕРЦИИ И КООРДИНАТ ЦЕНТРА МАСС
Общие сведения. Пусть на плоскости задана прямоугольная
система координат Оху.
Определение 10.1. Статическим моментом материальной
точки А(х; у), в которой сосредоточена масса т, относительно оси
Ох (оси Оу) называется величина, численно равная произведению
массы этой точки и расстояния до оси Ох (оси Оу):
Мх = ту (Му = тх).
Определение 10.2. Моментом инерции материальной точки
А(х; у), в которой сосредоточена масса т, относительно оси Ох
(оси Оу, точки О) называется величина, численно равная произве-
произведению массы этой точки и квадрата расстояния до оси Ох (оси Оу,
точки О):
2 I	2 I I I	B + 2)
Если дана система материальных точек А\(х\\ у{), А2(х2-, у2), ...,
А„(х„; уп), в которых сосредоточены массы гп\, /п2, ..., т„, то стати-
статические моменты находятся по формулам:
Мх= 2 mkyk, My= 2 яа,	A0.19)
а моменты инерции — по формулам:
/*= 2 mkyl Iy=i mkxl /о = /, + /,= 2 {xl + yl)mk. A0.20)
Определение 10.3. Центром масс системы материальных
точек называется точка, обладающая тем свойством, что если в ней
п
сосредоточить всю массу М = 2 rnk системы, то статический момент
этой точки относительно любой ее оси равен статическому моменту
данной системы материальных точек относительно той же оси.
Поэтому, обозначая центр масс системы С(хс; ус), получаем:
п	п
Мх = 2 ткук = Мус, My = 2 mkXk = Мхс.
к	к
Таким образом, координаты центра масс системы материальных
точек вычисляются по следующим формулам:
л	л	•
хс = Му/М = ( 2 ткХк)/ 2 гпк,
*Г'	*Г'	A0.21)
t/c = Af,/Af = (^2 mkyk)/^x rtik.
Пусть требуется вычислить статические моменты, моменты инер-
инерции и координаты центра масс однородной плоской материальной
линии или плоской материальной фигуры с известной плотностью р
267